Margin of error статистика - Исправление ошибок и поиск оптимальных решений проблем

What is a Margin of Error?

A margin of error is a statistical measurement that accounts for the difference between actual and projected results in a random survey sample. In simpler terms, the margin of error allows you to gauge the level of unpredictability in data and research outcomes.

For example, let’s say a researcher gives the mean estimate for a survey as 50 with a margin of error of ±5. This means that the actual mean, when calculated, could be any value from 45–55.

The margin of error of a data set directly influences the confidence level of the investigator in the research outcomes. Typically, if your research outcome or survey results have a higher margin of error, it means that the data sets might be unreliable. On the other hand, a lower margin of error indicates that the results truly represent the research population.

Importance of Margin of Error in Surveys, Research, and Polls

1. Margin of Error Helps You Achieve Reliable Outcomes in Research

Margin of error accounts for any disparities between results from the research sample and the target population. Typically, the higher the margin of error, the greater the difference between actual and estimated outcomes, further suggesting that the survey results are less likely to be true for the entire population.

2. It Helps the Researcher Determine How Representative the Sample Is

A low margin of error shows that the sample population closely represents the population of interest in a systematic investigation.

When dealing with a large population of interest, it is impossible to collect data from every variable. So, the researcher has to select a sample population that represents all the subgroups in the original population of interest.

If the sample population excludes some of the groups, then the final results of the poll, survey, or research will not reflect the actual outcome of the original population.

3. Margin of Error Helps You Determine the Confidence Level and Confidence Interval of Your Data Sets

When you know the margin of error of your survey and the value of your observed score, you can easily determine your data set’s confidence interval. Confidence interval is a statistical range of the possible values of a parameter. In contrast, confidence level measures the accuracy rate of your research outcomes of survey results based on the available data.

How to Calculate the Margin of Error

To determine the margin of error of your data sets, you need to ensure that the selected research sample truly represents your population of interest. This starts from identifying the right population of interest to applying the appropriate sampling technique.

Once you have a well-representative sample, you can go ahead to calculate the margin of error using the following formula:

Where;

P-hat = Sample Proportion

n = Sample Size

z = Z-Score

Here’s an example of how to apply this formula to your data.

Let’s say you conducted a poll on how many people use Snapchat for business. Out of 1,000 respondents, 450 chose “yes.” You also have a confidence level of 90%.

Step 1: Determine P-hat

P-hat = Numbers of respondents who chose yes ÷ Total number of respondents

P-hat = 450 ÷ 1000 = 0.45 or 45%

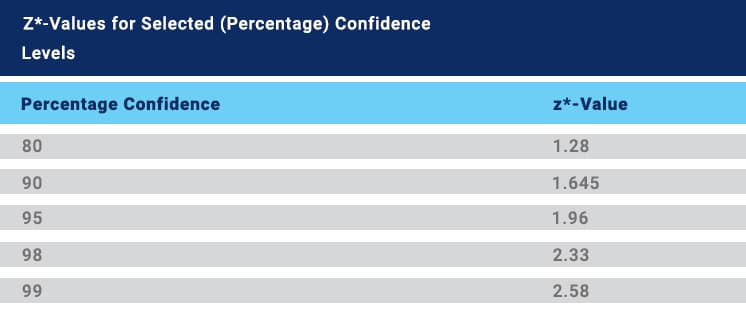
Step 2: Find the Z-Score of the corresponding confidence level. Using this Z-Score table, the Z-score of 90 is 1.645.

Step 3: Apply the Margin of Error formula.

Margin of Error = Z-score × [√P-hat (1–P-hat)] ÷ n]

1.645 × [√(0.45 × 0.55) ÷ 1000]

Margin of Error = 2.6%

Alternatively, you can calculate the margin of error using the standard deviation of your data. This means:

Margin of Error = Z-Score × (S ÷ √n)

If you’d rather not bother with manual calculations, you can use this margin of error calculator to determine the value for your data set.

How to Interpret Margin of Error

What does it mean when your data has a margin of error to a certain percentage? More importantly, how do you interpret this in layman terms to an audience that isn’t “statistics savvy?”

The first thing you should communicate is that margin of error accounts for the maximum difference between outcomes from your sample size and that of the population of interest. So, if you have a margin of error of ±3%, it means the actual results from your target population could be 3% more or less than the estimated value.

For example, suppose your survey shows that 62% of your sample size smoke cigarettes. When you extrapolate this data to the actual population, you would have to add and subtract the margin of error, which means the actual data would fall between 59% and 65%.

Related Statistical Variables in Margin of Error

1. Arithmetic Mean

Arithmetic mean is a statistical measure of distribution that accounts for the average of all the variables in a data set. In other words, arithmetic mean allows you to find the central value of a finite set of variables.

Often, you’d need the mean of your day sets for calculating the measure of error, especially if you need to determine the standard deviation of your data first.

Arithmetic Mean Formula

Arithmetic Mean = Sum of all Variables ÷ Number of Variables

Suppose you have a date set with the following values: 13, 5, 19, 7, 12.

Arithmetic Mean = (13+5+19+7+12) ÷ 5 = 11.2

Importance of Arithmetic Mean

It helps to reduce the margin of error of your data sets, leading to more reliable results.
It allows you to determine the central frequency of a distribution of data.

2. Confidence Intervals vs. Confidence Levels

Confidence interval and confidence level are often used interchangeably, but they do not mean the same thing. Let’s look at some key differences.

Definition

A confidence interval is a range of results from a poll, experiment, or survey that the researcher expects to contain the population parameter of interest. Typically, researchers use the confidence interval of observation to determine whether a parameter will fall between a pair of values around the mean.

On the other hand, the confidence level is the degree of certainty or probability that a survey will produce the same results repeatedly. Theoretically, a confidence level is a measure of accuracy for research outcomes and survey results.

Measurement

Confidence levels are measured in percentages, while confidence intervals are measured in ranges. This means that the confidence level of a data set can be 90% while the confidence interval is 45±50.

Formula

Confidence Interval (C.I) = X ± Z × (S÷√n)

Where;

X = Arithmetic Mean

Z = Confidence Level Value

S = Sample Standard Deviation

n = Sample Size

Since you cannot calculate the confidence level of any observation, most researchers choose an estimated value based on the type of research, sampling technique, and the like. Many times, this ends up as 95%.

Advantages of Confidence of Interval

Confidence interval attaches a measure of accuracy to your sample data. It also helps you to evaluate the reliability of the different variables in an observation.

Advantages of Confidence Level

Like confidence intervals, confidence level allows you to measure the level of accuracy of your data. In addition, it helps you to know if the sample mean is a good or poor representation of the population mean.

3. Standard Deviation

The standard deviation of observation is the amount of variation or dispersion of values around its mean. In other words, it tells you how far apart each value or variable lies from the mean of the same data set. Typically, the higher the standard deviation, the more dispersed the data is.

Understanding standard deviation is an essential part of calculating the margin of error for your data. If you do not have the value for your sample data proportion, you can use standard deviation to determine the margin of error.

Standard Deviation Formula

Where;

s = sample standard deviation

∑ = sum of…

X = each value

x̅ = sample mean

n = number of values in the sample

Importance of Standard of Deviation

It gives you a clear idea of the distribution of data in your observation.
Standard Deviation measures the spread of individual data points.

4. Population Size vs. Sample Size

Also referred to as population of interest, population size is the entire group with the measurable quality or parameter your research is based on. For example, if you’re researching birds of prey in Africa, your population size would be all kinds of birds of prey on the continent.

The sample size is the subset of your population of interest who become direct participants in the research. For example, out of all the birds of prey, you could narrow your research to the African Hawk Eagle in Angola.

5. Critical Value

A critical value is the split point in hypothesis testing that determines whether the researcher accepts or rejects the null hypothesis. When plotted on a graph, the critical value separates the variables into several sections, including the rejection regions. When calculating the margin of error, researchers use the critical value to determine the applicable ranges within the data sets.

Importance of Critical Value

It maps out the range of a confidence interval of observation.
Critical value plays a vital role in significant testing.

6. Z-score

Z-score or standard score accounts for the difference between a given data point and the mean in an observation. It accounts for the standardization of the different data points in the distribution, allowing you to compare scores on other variables.

Importance of Z-Score

It allows you to compare variables from different distributions.
Z-score allows the researcher to calculate the probability of a score occurring within a typical data set.

Margin of Error vs. Standard Error

Because of their similarities, it’s pretty easy for students and researchers to mistake the margin of error for standard error and vice versa. In this section, we’ll look at some key differences between standard error and margin of error. Let’s start with their definitions.

Definition

A margin of error is a statistical measure that accounts for the degree of error received from the outcome of your research sample. On the other hand, standard error measures the accuracy of the representation of the population sample to the mean using the standard deviation of the data set.

Purpose

The purpose of the standard error is to measure the spread of random variables within your data set, while the goal of the margin of error is to estimate how much allowable difference can exist between the research population and sample size.

Formula

Margin of Error = Z-score × [√P-hat (1–P-hat)] ÷ n]

Margin of Error = Z-Score × (S ÷ √n)

Where;

P-hat = Sample Proportion

n = Sample Size

z = Z-Score

S = Standard Deviation

Standard Error = Sample Standard Deviation ÷ √number of samples

Factors That Affect Margin of Error

From all we’ve discussed so far, you should already have a fair idea of the factors that primarily affect the margin of error. These factors are confidence level, sample size, and standard deviation.

It follows that increasing or decreasing any of them will have a dominant effect on the value of margin of error for your data. For example, if your sample size goes from 1,000 to 10,000, your margin of error might increase or reduce to a similar magnitude.

How to Reduce Margin of Error

Since a lower margin means a higher level of accuracy in your research results and sample, it follows that many researchers strive to reduce the margin of error in their systematic investigation. But how do you do this? Here are some ideas you can test out.

Choose a larger sample that allows you to make more observations within your data set. This way, you can have a more exact estimate for the population parameter you’re measuring.
Lower your confidence interval to have a more precise margin of error.
Adopt a one-sided confidence interval which has a smaller margin of error than a two-sided confidence interval.
Reduce the variability within your data sets, so you have more homogeneous values.

Real-Life Applications of Margin of Error

Whether in polling, market research, or simple data collection, a margin of error works in the same way—helping you determine the accuracy of your sample in relation to the actual population of interest. Let’s consider specific applications.

Polling

In polling, a margin of error allows you to accurately extrapolate results for one option to a broader population, with minimal inaccuracy. Here’s what we mean.

Let’s say you conduct a popularity poll for two candidates. Based on the data, you peg the margin of error for Candidate A at 3%. It means there’s a close approximation between the results and the actual popularity of the candidate in the population of interest. So, you can accurately predict future variables using present polling results.

Market Research

In market research, the margin of error shows the level of confidence an organization should have in the data collected from surveys. As mentioned earlier, the higher the margin of error, the less confident you should be in the research samples and, ultimately, the results obtained.

Conclusion

In this article, we’ve discussed the margin of error and its influence on the outcomes of any systematic investigation. Since research is based on collecting samples from a population of interest, you must account for variations between your sample data and the target audience. Calculating the margin of error of your observation is the most effective way to achieve this.

Источник

From Wikipedia, the free encyclopedia

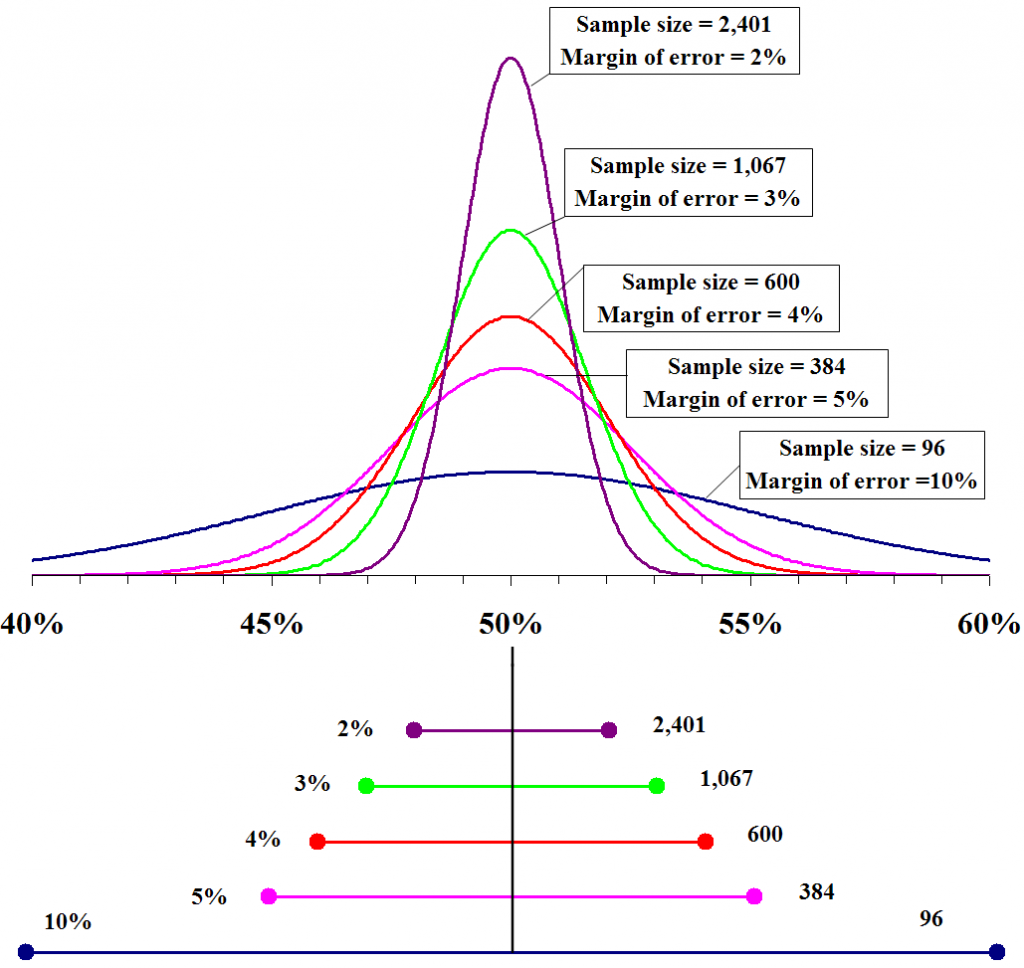
Probability densities of polls of different sizes, each color-coded to its 95% confidence interval (below), margin of error (left), and sample size (right). Each interval reflects the range within which one may have 95% confidence that the true percentage may be found, given a reported percentage of 50%. The margin of error is half the confidence interval (also, the radius of the interval). The larger the sample, the smaller the margin of error. Also, the further from 50% the reported percentage, the smaller the margin of error.

The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, the measure varies.

The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.

Concept[edit]

Consider a simple yes/no poll as a sample of respondents drawn from a population reporting the percentage of yes responses. We would like to know how close is to the true result of a survey of the entire population , without having to conduct one. If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), we would expect those subsequent results ${displaystyle p_{1},p_{2},ldots }$ to be normally distributed about . The margin of error describes the distance within which a specified percentage of these results is expected to vary from .

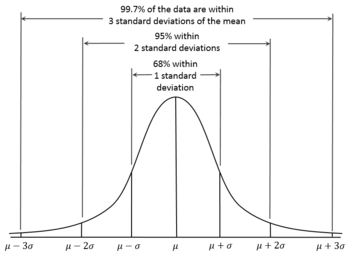
According to the 68-95-99.7 rule, we would expect that 95% of the results ${displaystyle p_{1},p_{2},ldots }$ will fall within about two standard deviations ( ${displaystyle pm 2sigma _{P}}$ ) either side of the true mean . This interval is called the confidence interval, and the radius (half the interval) is called the margin of error, corresponding to a 95% confidence level.

Generally, at a confidence level gamma , a sample sized of a population having expected standard deviation sigma has a margin of error

${displaystyle MOE_{gamma }=z_{gamma }times {sqrt {frac {sigma ^{2}}{n}}}}$

where ${displaystyle z_{gamma }}$ denotes the quantile (also, commonly, a z-score), and ${displaystyle {sqrt {frac {sigma ^{2}}{n}}}}$ is the standard error.

Standard deviation and standard error[edit]

We would expect the normally distributed values ${displaystyle p_{1},p_{2},ldots }$ to have a standard deviation which somehow varies with . The smaller , the wider the margin. This is called the standard error ${displaystyle sigma _{overline {p}}}$ .

For the single result from our survey, we assume that , and that all subsequent results ${displaystyle p_{1},p_{2},ldots }$ together would have a variance ${displaystyle sigma _{P}^{2}=P(1-P)}$ .

${displaystyle {text{Standard error}}=sigma _{overline {p}}approx {sqrt {frac {sigma _{P}^{2}}{n}}}approx {sqrt {frac {p(1-p)}{n}}}}$

Note that corresponds to the variance of a Bernoulli distribution.

Maximum margin of error at different confidence levels[edit]

For a confidence level gamma , there is a corresponding confidence interval about the mean ${displaystyle mu pm z_{gamma }sigma }$ , that is, the interval ${displaystyle [mu -z_{gamma }sigma ,mu +z_{gamma }sigma ]}$ within which values of should fall with probability gamma . Precise values of ${displaystyle z_{gamma }}$ are given by the quantile function of the normal distribution (which the 68-95-99.7 rule approximates).

Note that ${displaystyle z_{gamma }}$ is undefined for , that is, ${displaystyle z_{1.00}}$ is undefined, as is ${displaystyle z_{1.10}}$ .

	${displaystyle z_{gamma }}$			${displaystyle z_{gamma }}$
0.68	0.994457883210	0.999	3.290526731492
0.90	1.644853626951	0.9999	3.890591886413
0.95	1.959963984540	0.99999	4.417173413469
0.98	2.326347874041	0.999999	4.891638475699
0.99	2.575829303549	0.9999999	5.326723886384
0.995	2.807033768344	0.99999999	5.730728868236
0.997	2.967737925342	0.999999999	6.109410204869

Since ${displaystyle max sigma _{P}^{2}=max P(1-P)=0.25}$ at p=0.5 , we can arbitrarily set , calculate ${displaystyle sigma _{P}}$ , ${displaystyle sigma _{overline {p}}}$ , and ${displaystyle z_{gamma }sigma _{overline {p}}}$ to obtain the maximum margin of error for at a given confidence level gamma and sample size , even before having actual results. With

${displaystyle MOE_{95}(0.5)=z_{0.95}sigma _{overline {p}}approx z_{0.95}{sqrt {frac {sigma _{P}^{2}}{n}}}=1.96{sqrt {frac {.25}{n}}}=0.98/{sqrt {n}}=pm 3.1%}$

${displaystyle MOE_{99}(0.5)=z_{0.99}sigma _{overline {p}}approx z_{0.99}{sqrt {frac {sigma _{P}^{2}}{n}}}=2.58{sqrt {frac {.25}{n}}}=1.29/{sqrt {n}}=pm 4.1%}$

Also, usefully, for any reported ${displaystyle MOE_{95}}$

${displaystyle MOE_{99}={frac {z_{0.99}}{z_{0.95}}}MOE_{95}approx 1.3times MOE_{95}}$

Specific margins of error[edit]

If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll reports ${displaystyle p_{a},p_{b},p_{c}}$ as

${displaystyle MOE_{95}(P_{a})=z_{0.95}sigma _{overline {p_{a}}}approx 1.96{sqrt {frac {p_{a}(1-p_{a})}{n}}}=0.89/{sqrt {n}}=pm 2.8%}$

(as in the figure above)

${displaystyle MOE_{95}(P_{b})=z_{0.95}sigma _{overline {p_{b}}}approx 1.96{sqrt {frac {p_{b}(1-p_{b})}{n}}}=0.87/{sqrt {n}}=pm 2.7%}$

${displaystyle MOE_{95}(P_{c})=z_{0.95}sigma _{overline {p_{c}}}approx 1.96{sqrt {frac {p_{c}(1-p_{c})}{n}}}=0.27/{sqrt {n}}=pm 0.8%}$

As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.

Comparing percentages[edit]

Imagine multiple-choice poll reports ${displaystyle p_{a},p_{b},p_{c}}$ as . As described above, the margin of error reported for the poll would typically be ${displaystyle MOE_{95}(P_{a})}$ , as ${displaystyle p_{a}}$ is closest to 50%. The popular notion of statistical tie or statistical dead heat, however, concerns itself not with the accuracy of the individual results, but with that of the ranking of the results. Which is in first?

If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), and report result ${displaystyle p_{w}=p_{a}-p_{b}}$ , we could use the standard error of difference to understand how ${displaystyle p_{w_{1}},p_{w_{2}},p_{w_{3}},ldots }$ is expected to fall about ${displaystyle {overline {p_{w}}}}$ . For this, we need to apply the sum of variances to obtain a new variance, ${displaystyle sigma _{P_{w}}^{2}}$ ,

${displaystyle sigma _{P_{w}}^{2}=sigma _{P_{a}-P_{b}}^{2}=sigma _{P_{a}}^{2}+sigma _{P_{b}}^{2}-2sigma _{P_{a},P_{b}}=p_{a}(1-p_{a})+p_{b}(1-p_{b})+2p_{a}p_{b}}$

where ${displaystyle sigma _{P_{a},P_{b}}=-P_{a}P_{b}}$ is the covariance of ${displaystyle P_{a}}$ and ${displaystyle P_{b}}$ .

Thus (after simplifying),

${displaystyle {text{Standard error of difference}}=sigma _{overline {w}}approx {sqrt {frac {sigma _{P_{w}}^{2}}{n}}}={sqrt {frac {p_{a}+p_{b}-(p_{a}-p_{b})^{2}}{n}}}=0.029,P_{w}=P_{a}-P_{b}}$

${displaystyle MOE_{95}(P_{a})=z_{0.95}sigma _{overline {p_{a}}}approx pm {3.1%}}$

${displaystyle MOE_{95}(P_{w})=z_{0.95}sigma _{overline {w}}approx pm {5.8%}}$

Note that this assumes that $P_{{c}}$ is close to constant, that is, respondents choosing either A or B would almost never chose C (making ${displaystyle P_{a}}$ and ${displaystyle P_{b}}$ close to perfectly negatively correlated). With three or more choices in closer contention, choosing a correct formula for ${displaystyle sigma _{P_{w}}^{2}}$ becomes more complicated.

Effect of finite population size[edit]

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population , but only on the sample size . According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is small.

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula^[1]

${displaystyle operatorname {FPC} ={sqrt {frac {N-n}{N-1}}}}$

…and so, if poll were conducted over 24% of, say, an electorate of 300,000 voters,

${displaystyle MOE_{95}(0.5)=z_{0.95}sigma _{overline {p}}approx {frac {0.98}{sqrt {72,000}}}=pm 0.4%}$

${displaystyle MOE_{95_{FPC}}(0.5)=z_{0.95}sigma _{overline {p}}{sqrt {frac {N-n}{N-1}}}approx {frac {0.98}{sqrt {72,000}}}{sqrt {frac {300,000-72,000}{300,000-1}}}=pm 0.3%}$

Intuitively, for appropriately large ,

${displaystyle lim _{nto 0}{sqrt {frac {N-n}{N-1}}}approx 1}$

${displaystyle lim _{nto N}{sqrt {frac {N-n}{N-1}}}=0}$

In the former case, is so small as to require no correction. In the latter case, the poll effectively becomes a census and sampling error becomes moot.

References[edit]

^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)

Sources[edit]

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.

External links[edit]

«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. «Margin of Error». MathWorld.

Источник

Introduction

While you are learning statistics, you will often have to focus on a sample rather than the entire population. This is because it is extremely costly, difficult and time-consuming to study the entire population. The best you can do is to take a random sample from the population – a sample that is a ‘true’ representative of it. You then carry out some analysis using the sample and make inferences about the population.

Since the inferences are made about the population by studying the sample taken, the results cannot be entirely accurate. The degree of accuracy depends on the sample taken – how the sample was selected, what the sample size is, and other concerns. Common sense would say that if you increase the sample size, the chances of error will be less because you are taking a greater proportion of the population. A larger sample is likely to be a closer representative of the population than a smaller one.

Let’s consider an example. Suppose you want to study the scores obtained in an examination by students in your college. It may be time-consuming for you to study the entire population, i.e. all students in your college. Hence, you take out a sample of, say, 100 students and find out the average scores of those 100 students. This is the sample mean. Now, when you use this sample mean to infer about the population mean, you won’t be able to get the exact population means. There will be some “margin of error”.

You will now learn the answers to some important questions: What is margin of error, what are the method of calculating margins of error, how do you find the critical value, and how to decide on t-score vs z-scores. Thereafter, you’ll be given some margin of error practice problems to make the concepts clearer.

What is Margin of Error?

The margin of error can best be described as the range of values on both sides (above and below) the sample statistic. For example, if the sample average scores of students are 80 and you make a statement that the average scores of students are 80 ± 5, then here 5 is the margin of error.

Calculating Margins of Error

For calculating margins of error, you need to know the critical value and sample standard error. This is because it’s calculated using those two pieces of information.

The formula goes like this:

margin of error = critical value * sample standard error.

How do you find the critical value, and how to calculate the sample standard error? Below, we’ll discuss how to get these two important values.

How do You find the Critical Value?

For finding critical value, you need to know the distribution and the confidence level. For example, suppose you are looking at the sampling distribution of the means. Here are some guidelines.

If the population standard deviation is known, use z distribution.
If the population standard deviation is not known, use t distribution where degrees of freedom = n-1 (n is the sample size). Note that for other sampling distributions, degrees of freedom can be different and should be calculated differently using appropriate formula.
If the sample size is large, then use z distribution (following the logic of Central Limit Theorem).

It is important to know the distribution to decide what to use – t-scores vs z-scores.

Caution – when your sample size is large and it is not given that the distribution is normal, then by Central Limit Theorem, you can say that the distribution is normal and use z-score. However, when the sample size is small and it is not given that the distribution is normal, then you cannot conclude anything about the normality of the distribution and neither z-score nor t-score can be used.

When finding the critical value, confidence level will be given to you. If you are creating a 90% confidence interval, then confidence level is 90%, for 95% confidence interval, the confidence level is 95%, and so on.

Here are the steps for finding critical value:

Step 1: First, find alpha (the level of significance). alpha =1 – Confidence level.

For 95% confidence level, alpha =0.05

For 99% confidence level, alpha =0.01

Step 2: Find the critical probability p*. Critical probability will depend on whether we are creating a one-sided confidence interval or a two-sided confidence interval.

For two-sided confidence interval, p*=1-dfrac { alpha }{ 2 }

For one-sided confidence interval, p*=1-alpha

Then you need to decide on using t-scores vs z-scores. Find a z-score having a cumulative probability of p*. For a t-statistic, find a t-score having a cumulative probability of p* and the calculated degrees of freedom. This will be the critical value. To find these critical values, you should use a calculator or respective statistical tables.

Sample Standard Error

Sample standard error can be calculated using population standard deviation or sample standard deviation (if population standard deviation is not known). For sampling distribution of means:

Let sample standard deviation be denoted by s, population standard deviation is denoted by sigma and sample size be denoted by n.

text {Sample standard error}=dfrac { sigma }{ sqrt { n } }, if sigma is known

text {Sample standard error}=dfrac { s }{ sqrt { n } }, if sigma is not known

Depending on the sampling distributions, the sample standard error can be different.

Having looked at everything that is required to create the margin of error, you can now directly calculate a margin of error using the formula we showed you earlier:

Margin of error = critical value * sample standard error.

Some Relationships

1. Confidence level and marginal of error

As the confidence level increases, the critical value increases and hence the margin of error increases. This is intuitive; the price paid for higher confidence level is that the margin of errors increases. If this was not so, and if higher confidence level meant lower margin of errors, nobody would choose a lower confidence level. There are always trade-offs!

2. Sample standard deviation and margin of error

Sample standard deviation talks about the variability in the sample. The more variability in the sample, the higher the chances of error, the greater the sample standard error and margin of error.

3. Sample size and margin of error

This was discussed in the Introduction section. It is intuitive that a greater sample size will be a closer representative of the population than a smaller sample size. Hence, the larger the sample size, the smaller the sample standard error and therefore the smaller the margin of error.

Image Source: Wikimedia Commons

Margin of Error Practice Problems

Example 1

25 students in their final year were selected at random from a high school for a survey. Among the survey participants, it was found that the average GPA (Grade Point Average) was 2.9 and the standard deviation of GPA was 0.5. What is the margin of error, assuming 95% confidence level? Give correct interpretation.

Step 1: Identify the sample statistic.

Since you need to find the confidence interval for the population mean, the sample statistic is the sample mean which is the average GPA = 2.9.

Step 2: Identify the distribution – t, z, etc. – and find the critical value based on whether you need a one-sided confidence interval or a two-sided confidence interval.

Since population standard deviation is not known and the sample size is small, use a t distribution.

text {Degrees of freedom}=n-1=25-1=24.

alpha=1-text {Confidence level}=1-0.95=0.05

Let the critical probability be p*.

For two-sided confidence interval,

p*=1-dfrac { alpha }{ 2 } =1-dfrac { 0.05 }{ 2 } =0.975.

The critical t value for cumulative probability of 0.975 and 24 degrees of freedom is 2.064.

Step 3: Find the sample standard error.

text{Sample standard error}=dfrac { s }{ sqrt { n } } =dfrac { 0.5 }{ sqrt { 25 } } =0.1

Step 4: Find margin of error using the formula:

Margin of error = critical value * sample standard error

= 2.064 * 0.1 = 0.2064

Interpretation: For a 95% confidence level, the average GPA is going to be 0.2064 points above and below the sample average GPA of 2.9.

Example 2

400 students in Princeton University are randomly selected for a survey which is aimed at finding out the average time students spend in the library in a day. Among the survey participants, it was found that the average time spent in the university library was 45 minutes and the standard deviation was 10 minutes. Assuming 99% confidence level, find the margin of error and give the correct interpretation of it.

Step 1: Identify the sample statistic.

Since you need to find the confidence interval for the population mean, the sample statistic is the sample mean which is the mean time spent in the university library = 45 minutes.

Step 2: Identify the distribution – t, z, etc. and find the critical value based on whether the need is a one-sided confidence interval or a two-sided confidence interval.

The population standard deviation is not known, but the sample size is large. Therefore, use a z (standard normal) distribution.

alpha=1-text{Confidence level}=1-0.99=0.01

Let the critical probability be p*.

For two-sided confidence interval,

p*=1-dfrac { alpha }{ 2 } =1-dfrac { 0.01 }{ 2 } =0.995.

The critical z value for cumulative probability of 0.995 (as found from the z tables) is 2.576.

Step 3: Find the sample standard error.

text{Sample standard error}=dfrac { s }{ sqrt { n } } =dfrac { 10 }{ sqrt { 400 } } =0.5

Step 4: Find margin of error using the formula:

Margin of error = critical value * sample standard error

= 2.576 * 0.5 = 1.288

Interpretation: For a 99% confidence level, the mean time spent in the library is going to be 1.288 minutes above and below the sample mean time spent in the library of 45 minutes.

Example 3

Consider a similar set up in Example 1 with slight changes. You randomly select X students in their final year from a high school for a survey. Among the survey participants, it was found that the average GPA (Grade Point Average) was 3.1 and the standard deviation of GPA was 0.7. What should be the value of X (in other words, how many students you should select for the survey) if you want the margin of error to be at most 0.1? Assume 95% confidence level and normal distribution.

Step 1: Find the critical value.

alpha=1-text{Confidence level}=1-0.95=0.05

Let the critical probability be p*.

For two-sided confidence interval,

p*=1-dfrac { alpha }{ 2 } =1-dfrac { 0.05 }{ 2 } =0.975.

The critical z value for cumulative probability of 0.975 is 1.96.

Step 3: Find the sample standard error in terms of X.

text{Sample standard error}=dfrac { s }{ sqrt { X } }=dfrac { 0.7 }{ sqrt { X } }

Step 4: Find X using margin of error formula:

Margin of error = critical value * sample standard error

0.1=1.96*dfrac { 0.7 }{ sqrt { X } }

This gives X=188.24.

Thus, a sample of 189 students should be taken so that the margin of error is at most 0.1.

Conclusion

The margin of error is an extremely important concept in statistics. This is because it is difficult to study the entire population and the sampling is not free from sampling errors. The margin of error is used to create confidence intervals, and most of the time the results are reported in the form of a confidence interval for a population parameter rather than just a single value. In this article, you made a beginning by learning answering questions like what is margin of error, what is the method of calculating margins of errors, and how to interpret these calculations. You also learned to decide whether to use t-scores vs z-scores and gained information about finding critical values. Now you know how to use margin of error for constructing confidence intervals, which are widely used in statistics and econometrics.

Let’s put everything into practice. Try this Statistics practice question:

Looking for more Statistics practice?

You can find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery in Statistics.

Start practicing here.

Are you a teacher or administrator interested in boosting Statistics student outcomes?

Learn more about our school licenses here.

Источник

In this article we will give you all the vital information on the “margin of error in statistics” This is very vast to compile in just one small article but still we will give you all the essential information just give complete reading to this piece of compilation.

We will be covering all these questions like what is the margin of error in statistics, How to Calculate Margin of Error, How to Calculate Margin of Error: Steps, Some Relationships, Margin of Error Calculation and some more related information/formulas.

What is a margin Error?

The range of values below and above the sample statistic in a confidence interval is called the margin of error. We can also define confidence interval as the way to show the uncertainty with a certain static. for Example from a poll result we get that 98% of confidence interval of 4.88 and 5.26. And if the poll is repeat again using the same parameter and technique. Then we will definitely get results in the interval 4.88 to 5.26 98% of the times.

What is Margin of Error Percentage ?

Margin of error is defined as the difference between true population. And the estimated population from poll result is called “Error percentage of margin”. We can calculate margin of error using these formulas given below :

Margin of error = Product of Critical value and Standard deviation or Margin of error = Product of Critical value and Standard error of the statistic.

How to calculate the margin of error: Steps

Step 1

Calculate the critical value.

Step 2

Calculate the standard deviation or the standard Error.

Step 3

Calculate the Product of critical value with standard deviation or the standard Error. For example critical value= 1.5 and Standard deviation=0.06 then the margin of error calculation will be ‭0.09‬.

calculate using t-distribution calculator on this site find the t-score and the variance and standard deviation calculator will calculator will find the standard deviation from sample.

Margin of Error for a Proportion

To calculator proportion we need sample proportion, sample size and z-score

Where Z is the Z-score.

is the Sample proportion.

n is sample space.

For Example.

A group of people did a survey on 1000 scientists and 380 of thought that climate change was not caused by human pollution. Find the MoE for a 90% confidence interval

Calculate P-hat

Calculate P-hat(sample proportion) by dividing the no. of people who agreed climate change was not caused by human pollution. It means that they answered according to the statement in this example 38% scientist responded positively.

Calculate Z-Score

Calculate the z-score that goes with confidence interval. you’ll need to reference this critical values. A 90% confidence interval has a z-score of 1.64.

Use Margin of Error Formula

Using the formula of the margin of error find the value.

=1.64√[{0.38(0.62)}1000]

=1.64*0.0153=0.0252

Get the Result

Calculate the percentage of the step 3 and then we get thee value of the margin of error is 2.52%.

Statistics aren’t accurate Use of margin of Error

It is a very useful method for estimating any value in this method like Calculations assuming random sampling, Different confidence levels plays an important role and also effect of sample size matters a lot. And as the heading the static are never accurate use of margin of error provide better resolution to the estimated result from any polls or survey.
Also this process is easy to estimate as we don’t have to cover the entire size of the things rather we just have to focus on the small sample part of the entire thing and this small sample represents the entire thing. Besides, this way the cost of surveying the entire population.

Conclusion

Now you might be quite confident about the margin of error in statistics. Next time don’t get into trouble while talking about the margin of error in statistics.

Furthermore, get the best math assignment help from the most reliable math assignment helpers in the world.

Concept

Running example

A running example from the 2004 U.S. presidential campaign will be used to illustrate concepts throughout this article. According to an October 2, 2004 survey by Newsweek, 47% of registered voters would vote for John Kerry/John Edwards if the election were held on that day, 45% would vote for George W. Bush/Dick Cheney, and 2% would vote for Ralph Nader/Peter Camejo. The size of the sample was 1,013.^[1] Unless otherwise stated, the remainder of this article uses a 95% level of confidence.

Basic concept

Polls typically involve taking a sample from a certain population. In the case of the Newsweek poll, the population of interest is the population of people who will vote. Because it is impractical to poll everyone who will vote, pollsters take smaller samples that are intended to be representative; that is, a random sample of the population.^[2] It is possible that pollsters sample 1,013 voters who happen to vote for Bush when in fact the population is split, but this is extremely unlikely given that the sample is random.

Sampling theory provides methods for calculating the probability that the poll results differ from reality by more than a certain amount, simply due to chance; for instance, that the poll reports 47% for Kerry but his support is actually as high as 50%, or is really less than 44%. This theory and some Bayesian assumptions suggest that the «true» percentage will probably be fairly close to 47%. The more people that are sampled, the more confident pollsters can be that the «true» percentage is close to the observed percentage. The margin of error is a measure of how close the results are likely to be.

However, the margin of error only accounts for random sampling error, so it is blind to systematic errors that may be introduced by non-response or by interactions between the survey and subjects’ memory, motivation, communication and knowledge.^[3]

Calculations assuming random sampling

This section will briefly discuss the standard error of a percentage, the corresponding confidence interval, and connect these two concepts to the margin of error. For simplicity, the calculations here assume the poll was based on a simple random sample from a large population.

The standard error of a reported proportion or percentage p measures its accuracy, and is the estimated standard deviation of that percentage. It can be estimated from just p and the sample size, n, if n is small relative to the population size, using the following formula:^[4]

Standard error = ${displaystyle {sqrt {frac {p(1-p)}{n}}}}$

When the sample is not a simple random sample from a large population, the standard error must be estimated through more advanced calculations.

In the Newsweek poll, Kerry’s level of support p = 0.47 and n = 1,013. The standard error (.016 or 1.6%) helps to give a sense of the accuracy of Kerry’s estimated percentage (47%). A Bayesian interpretation of the standard error is that although we do not know the «true» percentage, it is highly likely to be located within two standard errors of the estimated percentage (47%). The standard error can be used to create a confidence interval within which the «true» percentage should be to a certain level of confidence.

The estimated percentage plus or minus its margin of error is a confidence interval for the percentage. In other words, the margin of error is half the width of the confidence interval. It can be calculated as a multiple of the standard error, with the factor depending of the level of confidence desired; a margin of one standard error gives a 68% confidence interval, while the estimate plus or minus 1.96 standard errors is a 95% confidence interval, and a 99% confidence interval runs 2.58 standard errors on either side of the estimate.

Definition

The margin of error for a particular statistic of interest is usually defined as the radius (or half the width) of the confidence interval for that statistic.^[5]^[6] The term can also be used to mean sampling error in general. In media reports of poll results, the term usually refers to the maximum margin of error for any percentage from that poll.

Maximum margin of error

The maximum margin of error for any percentage is the radius of the confidence interval when p = 50%. As such, it can be calculated directly from the number of poll respondents. For 95% confidence, assuming a simple random sample from a large population:

(Maximum) margin of error (95%) = 1.96 × ${displaystyle {sqrt {frac {0.5(1-0.5)}{n}}}={frac {0.98}{sqrt {n}}}}$

This calculation gives a margin of error of 3% for the Newsweek poll, which reported a margin of error of 4%. The difference was probably due to weighting or complex features of the sampling design that required alternative calculations for the standard error.

Different confidence levels

For a simple random sample from a large population, the maximum margin of error is a simple re-expression of the sample size n. The numerators of these equations are rounded to two decimal places.

Margin of error at 99% confidence

Margin of error at 95% confidence

Margin of error at 90% confidence

If an article about a poll does not report the margin of error, but does state that a simple random sample of a certain size was used, the margin of error can be calculated for a desired degree of confidence using one of the above formulae. Also, if the 95% margin of error is given, one can find the 99% margin of error by increasing the reported margin of error by about 30%.

Maximum and specific margins of error

While the margin of error typically reported in the media is a poll-wide figure that reflects the maximum sampling variation of any percentage based on all respondents from that poll, the term margin of error also refers to the radius of the confidence interval for a particular statistic.

The margin of error for a particular individual percentage will usually be smaller than the maximum margin of error quoted for the survey. This maximum only applies when the observed percentage is 50%, and the margin of error shrinks as the percentage approaches the extremes of 0% or 100%.

In other words, the maximum margin of error is the radius of a 95% confidence interval for a reported percentage of 50%. If p moves away from 50%, the confidence interval for p will be shorter. Thus, the maximum margin of error represents an upper bound to the uncertainty; one is at least 95% certain that the «true» percentage is within the maximum margin of error of a reported percentage for any reported percentage.

Effect of population size

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of the population of interest. According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is less than 10%.

Other statistics

Confidence intervals can be calculated, and so can margins of error, for a range of statistics including individual percentages, differences between percentages, averages, medians^[7] and totals.

The margin of error for the difference between two percentages is larger than the margins of error for each of these percentages, and may even be larger than the maximum margin of error for any individual percentage from the survey.

Comparing percentages

In a plurality voting system, it is important to know who is ahead. The terms «statistical tie» and «statistical dead heat» are sometimes used to describe reported percentages that differ by less than a margin of error, but these terms can be misleading.^[8]^[9] For one thing, the margin of error as generally calculated is applicable to an individual percentage and not the difference between percentages, so the difference between two percentage estimates may not be statistically significant even when they differ by more than the reported margin of error. The survey results also often provide strong information even when there is not a statistically significant difference.

When comparing percentages, it can accordingly be useful to consider the probability that one percentage is higher than another.^[10] In simple situations, this probability can be derived with 1) the standard error calculation introduced earlier, 2) the formula for the variance of the difference of two random variables, and 3) an assumption that if anyone does not choose Kerry they will choose Bush, and vice versa; they are perfectly negatively correlated. This may not be a tenable assumption when there are more than two possible poll responses. For more complex survey designs, different formulas for calculating the standard error of difference must be used.

The standard error of the difference of percentages p for Kerry and q for Bush, assuming that they are perfectly negatively correlated, follows:

Standard error of difference = ${displaystyle {sqrt {frac {p(1-p)+q(1-q)+2pq}{n}}}.}$

Given the observed percentage difference p − q (2% or 0.02) and the standard error of the difference calculated above (.03), any statistical calculator may be used to calculate the probability that a sample from a normal distribution with mean 0.02 and standard deviation 0.03 is greater than 0.

Applying these calculations to the Newsweek example results in a 75% probability that Kerry was «truly» leading.

Notes

↑ Newsweek (2004-10-02). NEWSWEEK POLL: First Presidential Debate. Press release. Retrieved on 2006-05-31.
↑ Wonnacott and Wonnacott (1990), pp. 4–8.
↑ Sudman, S.L. and Bradburn N.M. (1982) Asking Questions. Jossey-Bass: pp. 17-19
↑ Sample Sizes, Margin of Error, Quantitative Analysis
↑ Lohr, Sharon L. (1999). Sampling: Design and Analysis, 49, Pacific Grove, California: Duxbury Press. «The margin of error of an estimate is the half-width of the confidence interval …»
↑ Stokes, Lynne, Tom Belin (2004). What is a Margin of Error?. (PDF) What is a Survey?. Survey Research Methods Section, American Statistical Association. URL accessed on 2006-05-31.
↑ Income — Median Family Income in the Past 12 Months by Family Size, U.S. Census Bureau. Retrieved February 15, 2007.
↑ Braiker, Brian. «The Race is On: With voters widely viewing Kerry as the debate’s winner, Bush’s lead in the NEWSWEEK poll has evaporated». MSNBC, October 2, 2004. Retrieved on 2007-02-02.
↑ Rogosa, D.R. (2005). A school accountability case study: California API awards and the Orange County Register margin of error folly. In R.P. Phelps (Ed.), Defending
standardized testing (pp. 205–226). Mahwah, NJ: Lawrence Erlbaum Associates.
↑ Drum, Kevin. Political Animal, Washington Monthly, August 19, 2004. Retrieved on 2007-02-15.

References

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0875895468
Wonnacott, T.H. and R.J. Wonnacott (1990). Introductory Statistics, 5th ed., Wiley. ISBN 0471615188.

External links

Eric W. Weisstein, Margin of Error at MathWorld.
Stokes, Lynne, Tom Belin (2004). What is a Margin of Error?. (PDF) What is a Survey?. Survey Research Methods Section, American Statistical Association. URL accessed on 2006-05-31.

fr:Marge d’erreur

zh:误差范围

Источник

Statistics:
Scientific method ·
Research methods ·
Experimental design ·
Undergraduate statistics courses ·
Statistical tests ·
Game theory ·
Decision theory

Concept

Running example

Basic concept

Calculations assuming random sampling

Standard error = ${displaystyle {sqrt {frac {p(1-p)}{n}}}}$

When the sample is not a simple random sample from a large population, the standard error must be estimated through more advanced calculations.

Definition

Maximum margin of error

(Maximum) margin of error (95%) = 1.96 × ${displaystyle {sqrt {frac {0.5(1-0.5)}{n}}}={frac {0.98}{sqrt {n}}}}$

Different confidence levels

For a simple random sample from a large population, the maximum margin of error is a simple re-expression of the sample size n. The numerators of these equations are rounded to two decimal places.

Margin of error at 99% confidence

Margin of error at 95% confidence

Margin of error at 90% confidence

Maximum and specific margins of error

Effect of population size

Other statistics

Confidence intervals can be calculated, and so can margins of error, for a range of statistics including individual percentages, differences between percentages, averages, medians^[7] and totals.

Comparing percentages

The standard error of the difference of percentages p for Kerry and q for Bush, assuming that they are perfectly negatively correlated, follows:

Standard error of difference = ${displaystyle {sqrt {frac {p(1-p)+q(1-q)+2pq}{n}}}.}$

Applying these calculations to the Newsweek example results in a 75% probability that Kerry was «truly» leading.

Notes

↑ Newsweek (2004-10-02). NEWSWEEK POLL: First Presidential Debate. Press release. Retrieved on 2006-05-31.
↑ Wonnacott and Wonnacott (1990), pp. 4–8.
↑ Sudman, S.L. and Bradburn N.M. (1982) Asking Questions. Jossey-Bass: pp. 17-19
↑ Sample Sizes, Margin of Error, Quantitative Analysis
↑ Lohr, Sharon L. (1999). Sampling: Design and Analysis, 49, Pacific Grove, California: Duxbury Press. «The margin of error of an estimate is the half-width of the confidence interval …»
↑ Stokes, Lynne, Tom Belin (2004). What is a Margin of Error?. (PDF) What is a Survey?. Survey Research Methods Section, American Statistical Association. URL accessed on 2006-05-31.
↑ Income — Median Family Income in the Past 12 Months by Family Size, U.S. Census Bureau. Retrieved February 15, 2007.
↑ Braiker, Brian. «The Race is On: With voters widely viewing Kerry as the debate’s winner, Bush’s lead in the NEWSWEEK poll has evaporated». MSNBC, October 2, 2004. Retrieved on 2007-02-02.
↑ Rogosa, D.R. (2005). A school accountability case study: California API awards and the Orange County Register margin of error folly. In R.P. Phelps (Ed.), Defending
standardized testing (pp. 205–226). Mahwah, NJ: Lawrence Erlbaum Associates.
↑ Drum, Kevin. Political Animal, Washington Monthly, August 19, 2004. Retrieved on 2007-02-15.

References

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0875895468
Wonnacott, T.H. and R.J. Wonnacott (1990). Introductory Statistics, 5th ed., Wiley. ISBN 0471615188.

External links

Eric W. Weisstein, Margin of Error at MathWorld.
Stokes, Lynne, Tom Belin (2004). What is a Margin of Error?. (PDF) What is a Survey?. Survey Research Methods Section, American Statistical Association. URL accessed on 2006-05-31.

fr:Marge d’erreur

zh:误差范围

Источник

Погрешность является важным показателем в статистике. Степень погрешности в обследованиях методом случайной выборки известна как предел погрешности. Он выражает случайную ошибку выборки в результатах опроса. Он отражает уверенность, которую исследователи должны иметь в данных, полученных в результате опроса. Он говорит об отклонении от фактической численности населения в процентных пунктах. Например, 95-процентный доверительный интервал с 4-процентной погрешностью указывает на то, что ваша статистика в 95 % случаев будет находиться в пределах 4 % от истинного числа населения. Более широкий предел погрешности в статистике означает меньшую вероятность полагаться на результаты опроса или опроса, а это означает, что будет меньше доверия к способности результатов точно отражать сообщество.

Что такое предел погрешности?

Погрешность говорит вам, на сколько процентов наши результаты отличаются от реального значения. Погрешность определяется как диапазон значений ниже и выше выборочной статистики в доверительном интервале. Доверительный интервал — это способ показать, какова неопределенность с определенной статистикой.

Важность допустимой погрешности

Важность Magin of Error обсуждается ниже в этой статье:

Погрешность показывает, насколько близкими были бы результаты, если бы обследовалась вся совокупность, а не выборочная совокупность.
Чем выше погрешность, тем меньше шансов полагаться на результаты опроса.
Если предел погрешности низкий, это означает, что результаты, полученные по выборке, высоконадежны и будут очень близки к результатам, полученным при обследовании всей совокупности.
Погрешность является очень важным показателем с точки зрения рынка.
Это важный инструмент для исследования рынка, поскольку он показывает степень уверенности, которую исследователи должны придавать данным опроса.
Он используется, чтобы показать, насколько уверен статистик в определении того, являются ли результаты онлайн-опроса или онлайн-опроса репрезентативными для всего населения.

Расчет допустимой погрешности

Каждый человек в популяции имеет шанс быть выбранным для включения в выборку при использовании вероятностной выборки. Используя этот метод, статистики и исследователи могут выбирать участников, которые имеют опыт в своей конкретной области исследований, обеспечивая минимально возможную погрешность данных, полученных из этих выборок. Невероятностная выборка исключает некоторые сегменты населения из-за метода отбора, используемого для создания выборок, который основан на удобстве или рентабельности, а не на применимости. Только при разделении респондентов на группы на основе их интересов и актуальности для данного опроса опросы будут эффективными.

С точки зрения размера выборки формула определяется следующим образом:

M.O.E. = 1 / √(n)

where,
M.O.E. denotes the margin of error
n is the sample size

Эта формула широко не используется, так как она не дает точных результатов, она учитывает только размер выборки, а не какие-либо другие параметры. Но с точки зрения z-индекса и размера выборки формула выглядит так:

M.O.E.= z × σ / √(n)

where,
z denotes the z-index
n is the sample size
σ is the population standard deviation

Таким образом, предел погрешности представляет собой произведение критического значения и стандартного отклонения. В приведенной выше формуле оценка z рассчитывается с использованием уровня достоверности, указанного в вопросе. Некоторые широко используемые z-показатели и уровни достоверности показаны ниже:

Уровень достоверности	Z-оценка
90%	1,645
95%	1,96
99%	2,575

Как рассчитать погрешность?

Выполните шаги, описанные ниже, чтобы рассчитать Magin of Error.

Шаг 1: Найдите критическое значение, т.е. либо t-оценку, либо z-оценку. Как правило, для небольших размеров выборки (менее 30) используйте t-показатель, в противном случае используйте z-показатель.

Шаг 2: Найдите стандартное отклонение или стандартную ошибку.

Шаг 3: Умножьте критическое значение из шага 1 на стандартное отклонение или стандартную ошибку из шага 2.

Пример: если ваше критическое значение равно 1,645, а стандартная ошибка равна 0,26, то:

Margin of Error = 1.645 × 0.26
= 0.4277

Решенные примеры по погрешности

Пример 1. Случайная выборка из 50 студентов имеет средние карманные деньги 2500 и стандартное отклонение 567. Найдите погрешность, если c = 0,95.

Решение:

Given, n = 50

σ = 567

For c = 0.95 i.e. 95% confidence level, z = 1.96

M.O.E = 1.96 × 567 / √(50)

M.O.E. = 157.16

Пример 2: Было опрошено 600 студентов, и было обнаружено, что средний CGPA учащихся составил 8,7 при стандартном отклонении населения 0,2. Рассчитайте погрешность для уровня достоверности 90%.

Решение:

Given, n = 600

σ = 0.2

For confidence level of 90%, z = 1.645

M.O.E = 1.645 × 0.2 / √(600)

M.O.E. = 0.013

Пример 3: В ходе опроса было обнаружено, что средняя заработная плата 5000 сотрудников составляет 350000 со стандартным отклонением населения 0,3. Какова погрешность при доверительном уровне 99%?

Решение:

Given, n = 5000

σ = 0.3

For 99% confidence level, z = 2.575

M.O.E = 2.575 × 0.3 / √(5000)

M.O.E. = 0.0109

Пример 4: Найдите погрешность при опросе населения в 400 человек.

Решение:

Given, sample size = 400

∴M.O.E. = 1 / √(400)

= 1/20

= 0.05

Часто задаваемые вопросы о допустимой погрешности

Вопрос 1: Что вы подразумеваете под погрешностью?

Решение:

The margin of error shows how similar the findings would be if the entire population had been polled as opposed to just a sample.

Вопрос 2: Как определяется z-значение в статистике?

Решение:

Z-score is a metric that quantifies how closely a value relates to the mean of a set of values. Standard deviations of data from their mean are used to calculate Z-score.

Вопрос 3: Может ли погрешность иметь отрицательное значение?

Решение:

The level of accuracy needed in a survey is called the margin of error. For example, a 8% margin of error indicates that the actual results’ variation might be either negative or positive eight points.

Вопрос 4: Как мы можем определить погрешность с уровнем достоверности 85%?

Решение:

It is known that the error value is 0.0219 or z-value, is 1.96 for a 95% confidence level. As a result, the method above may be used to calculate the margin of error at a 85% confidence level.

Связанные ресурсы

Statistics Formulas

Variance and Standard Deviation

Frequency Distributions

Источник

The margin of error is an essential concept for understanding the accuracy and reliability of survey data. In this article, we’ll take a closer look at its definition and its calculation while providing examples of how it’s used in research. We’ll also discuss the importance of considering the margin of error when interpreting survey results and how it can affect the conclusions drawn from the data. So, whether you’re experienced or just starting your journey, this article is a must-read for anyone looking to master the art of margin of error and ensure the accuracy and reliability of their research. Let’s get started!

What is a Margin of Error?

Definition:

The margin of error in statistics is the degree of error in results received from random sampling surveys. A higher margin of error in statistics indicates less likelihood of relying on the results of a survey or poll, i.e. the confidence on the results will be lower to represent a population. It is a very vital tool in market research as it depicts the confidence level the researchers should have in the data obtained from surveys.

A confidence interval is the level of unpredictability with a specific statistic. Usually, it is used in association with the margin of errors to reveal the confidence a statistician has in judging whether the results of an online survey or online poll are worthy to represent the entire population.

A lower margin of error indicates higher confidence levels in the produced results.

When we select a representative sample to estimate full population, it will have some element of uncertainty. We need to infer the real statistic from the sample statistic. This means our estimate will be close to the actual figure. Considering margin of error further improves this estimate.

A well-defined population is a prerequisite for calculating the margin of error. In statistics, a “population” comprises of all the elements of a particular group that a researcher intends to study and collect data. This error can be significantly high if the population is not defined or in cases where the sample selection process is not carried out properly.

Every time a researcher conducts a statistical survey, a margin of error calculation is required. The universal formula for a sample is the following:

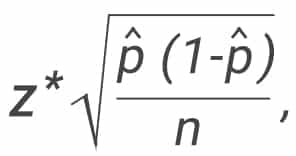
where:

p̂ = sample proportion (“P-hat”).

n = sample size

z = z-score corresponds to your desired confidence levels.

Are you feeling a bit confused? Don’t worry! you can use our margin of error calculator.

Example for margin of error calculation

For example, wine-tasting sessions conducted in vineyards depend on the quality and taste of the wines presented during the session. These wines represent the entire production and depending on how well the visitors receive them, the feedback from them is generalized to the entire production.

The wine tasting will be effective only when visitors do not have a pattern, i.e. they’re chosen randomly. Wine goes through a process to be palatable and similarly, the visitors also must go through a process to provide effective results.

The measurement components prove whether the wine bottles are worthy to represent the entire winery’s production or not. If a statistician states that the conducted survey will have a margin of error of plus or minus 5% at a 93% confidence interval. This means that if a survey was conducted 100 times with vineyard visitors, feedback received will be within a percentage division either higher or lower than the percentage that’s accounted 93 out of 100 times.

In this case, if 60 visitors report that the wines were extremely good. As the margin of error is plus or minus 5% in a confidence interval is 93%, in 100 visitors, it’s safe to conclude that the visitors who comment that the wines were “extremely good” will be 55 or 65 (93%) of the time.

To explain this further, let’s take an example of a survey on volunteering was sent to 1000 respondents out of which 500 agreed to the statement in the survey saying that volunteering makes life better. Calculate margin of error for 95% confidence level.

Step 1: Calculate P-hat by dividing the number of respondents who agreed with the statement in the survey to the total number of respondents. In this case, = 500/1000 = 50%

Step 2: Find z-score corresponding to 95% confidence level. In this case, z score is 1.96

Step 3: Calculate by putting these values in the formula

Step 4: Convert to a percentage

Margin of error in sample sizes:

In probability sampling, each member of a population has a probability of being selected to be a part of the sample. In this method, researchers and statisticians can select members from their area of research so that the margin of error in data received from these samples is as minimum as possible.

In non-probability sampling, samples are formed based on cost-effectiveness or convenience and not on the basis of application and because of this selection process, some sections of the population may get excluded. Surveys will be effective only on filtering members according to interests and application to the survey being conducted.

The industrial standard for confidence level is 95% and these are the margin of error percentages for certain survey sample sizes:

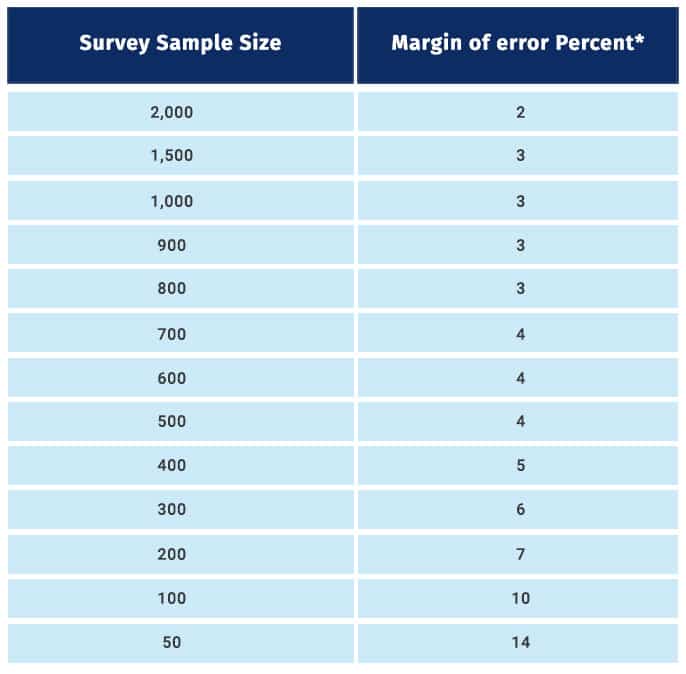
As indicated in this table, to reduce the margin of error to half, for instance, from 4 to 2, the sample size has been increased considerably, from 500 to 2000. As you must have observed, the sample size is inversely proportional to it. Till sample sizes of 1500, there is a significant decrease in it, but beyond that, this decrease reduces.

Ready to take your research game to the next level? Join QuestionPro and elevate your surveys from ho-hum to oh-wow! With our user-friendly platform, you’ll be able to create professional-grade surveys in no time. Plus, with features like customizable templates, advanced analytics, and real-time data collection, you’ll have everything you need to gather accurate, reliable data. So, don’t miss out on the fun. Join QuestionPro today for free and start discovering what your customers, employees, and communities really think. No credit card is needed.

Источник

Margin of error is a statistic that states the number of errors in random sampling in a survey. Margin of error can also be defined as a distance in a certain confidence interval (statistical) from the survey, this distance represents a statistic. Margin of error measures how close the results of the sample are to the results in reality.

In statistic, we calculate the confidence interval to see where the value of the data of sample statistic will fall. The range of values which are below and above the sample statistic in a confidence interval is known as Margin of Error. In other words, it is basically the degree of error in the sample statistic.

Higher the margin of error, lesser will the confidence in the results because the degree of deviation in these results is very high. As its name suggests, the margin of error is a range of values above and below the actual results. For example, if we get a response in a survey wherein 70% people have responded “good” and margin of error is 5%, this means that in general, 65% to 75% of the population think that the answer is “good”.

Calculating Margin of Error

In calculating the error margin, the factors that influence are:

Sample size
The importance of problems in the sample
Statistics or estimators themselves

The larger the sample will increasingly represent the population. But we know in taking samples and the sample itself is always biased. For that we use margin error to reduce the bias that occurs. Bias that can be known from the margin error is the bias arising from the sampling error.

Standard error of proportion and confidence interval.

To find out the margin error calculation, it must first be known about the standard error of proportion and confidence interval.

Confidence interval (CI) is a percentage that describes how close the original value is to the statistics (estimator) measured +/- margin error.

Standard error of proportions measures the accuracy of the estimator of proportions and estimates the standard deviation of percentages.

It can be predicted from p and the size of sample n, if n is small enough then use the formula:

Standard error = √p(1-p)/n

To estimate the proportions of plus and minus, the margin error is the confidence interval for the proportion or percentage. In other words, the error margin is part of the confidence interval. The error margin is calculated by multiplying the standard error with the confidence factor of a certain level of confidence. Example:

The margin (plus – minus estimator) of 1 standard error is 68% confidence interval,
The margin (plus – minus estimator) of 1.96 standard error is 95% confidence interval
The margin (plus – minus estimator) of 2.58 standard error is 99% confidence interval

Maximum margin error

The maximum margin of error for proportions is the distance from the confidence interval when p = 50%. For 95% confidence, the formula is
(maximum) error margin (95%) = 1.96 x √0.5 (1-0.5) / n = 0.98 / √n

Different confidence intervals

The margin error depends on the probability of a confidence interval, like this:

Error margin (99%) confidence = 1.29 / √n
Error margin (95%) confidence = 0.98 / √n
Error margin (90%) confidence = 0.82 / √n

Some mistakes people make in understanding the use of margin errors:

Do not use or do not involve confidence intervals. You will not know what your error margin is if the confidence interval is unknown
Many people believe that the error margin represents the entirety of the error. Even though this is not true, what is included in the margin error is the sampling error and the non sampling error cannot be seen from the margin error.
People sometimes believe that the margin error indicates the quality of the survey, meaning that the smaller the margin error the better the quality of the survey, even though this is not true. Many factors affect the quality of the survey, such as the method used, sampling, etc.

If you like the article we can follow it through the Random Creative Blog Feed or subscribe to get information from us.

Источник

What is a Margin of Error?

Importance of Margin of Error in Surveys, Research, and Polls

1. Margin of Error Helps You Achieve Reliable Outcomes in Research

2. It Helps the Researcher Determine How Representative the Sample Is

3. Margin of Error Helps You Determine the Confidence Level and Confidence Interval of Your Data Sets

How to Calculate the Margin of Error

How to Interpret Margin of Error

Related Statistical Variables in Margin of Error

1. Arithmetic Mean

Arithmetic Mean Formula

Importance of Arithmetic Mean

2. Confidence Intervals vs. Confidence Levels

Definition

Measurement

Formula

Advantages of Confidence of Interval

Advantages of Confidence Level

3. Standard Deviation

Standard Deviation Formula

Importance of Standard of Deviation

4. Population Size vs. Sample Size

5. Critical Value

Importance of Critical Value

Importance of Z-Score

Margin of Error vs. Standard Error

Factors That Affect Margin of Error

How to Reduce Margin of Error

Real-Life Applications of Margin of Error

Concept[edit]

Standard deviation and standard error[edit]

Maximum margin of error at different confidence levels[edit]

Specific margins of error[edit]

Comparing percentages[edit]

Effect of finite population size[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

Introduction

What is Margin of Error?

Calculating Margins of Error

How do You find the Critical Value?

Sample Standard Error

Some Relationships

1. Confidence level and marginal of error

2. Sample standard deviation and margin of error

3. Sample size and margin of error

Margin of Error Practice Problems

Conclusion

Let’s put everything into practice. Try this Statistics practice question:

Looking for more Statistics practice?

What is a margin Error?

What is Margin of Error Percentage ?

How to calculate the margin of error: Steps

Step 1

Step 2

Step 3

Margin of Error for a Proportion

Calculate P-hat

Calculate Z-Score

Use Margin of Error Formula

Get the Result

Statistics aren’t accurate Use of margin of Error

Conclusion

More Question on Margin of Error in Statistics

What is a margin Error?

What is Margin of Error Percentage ?

Concept

Running example

Basic concept

Calculations assuming random sampling

Definition

Maximum margin of error

Different confidence levels

Maximum and specific margins of error

Effect of population size

Other statistics

Comparing percentages

Notes

References