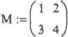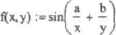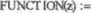Эта глава посвящена основам вычислений в Mathcad. Она содержит все необходимые сведения о применении переменных и функций, операторов Присваивания, численного вывода и символьного вывода (см. разд. 3.1), а также других операторов (см. разд. 3.2). В заключение описываются основные средства управления процессом вычислений в Mathcad (см. разд. 3.3) и уверится несколько слов о том, каким образом происходит выдача сообщений об ошибках при вычислениях (см. разд. 3.4).
3.1. Переменные и функции
Основные инструменты математика — это операции с переменными величинами и функциями. В Mathcad переменные, операторы и функции реализованы в интуитивной форме, т. е. выражения в редакторе вводятся и вычисляются так, как они были бы написаны на листе бумаги. Порядок вычислений в документе Mathcad также очевиден: математические выражения и действия воспринимаются процессором слева направо и сверху вниз.
Перечислим основные действия, которые пользователь может совершать для определения и вывода переменных и функций.
3.1.1. Определение переменных
Чтобы определить переменную, достаточно ввести ее имя и присвоить ей неко-topoe значение, для чего служит оператор присваивания (см. следующий раздел).
3.1.2. Присваивание переменным значений
Чтобы присвоить переменной новое значение, например переменную х сделать равной 10:
Рис. 3.1. Результат ввода оператора присваивания
Результат перечисленных действий показан в листинге 3.1.
Кнопка оператора присваивания для удобства помещена сразу на две панели Calculator (Калькулятор) и Evaluation (Выражения).
Листинг 3.1. Присваивание переменной численного значения
Ввести новое значение переменной возможно как в виде числа, так и в виде математического выражения, содержащего другие переменные (листинг 3.2) и функции (см. следующие разделы), а также в виде строкового выражения (листинг 3.3.). В последнем случае будет создана переменная s не численного, а строкового типа.
Листинг 3.2. Присваивание переменной вычисленного значения выражения
Листинг 3.3. Присваивание переменной строкового значения
Если переменная с некоторым именем создается в данном документе впервые, то для ввода оператора присваивания, вместо двоеточия, допускается использовать символ равенства » :=» на символ равенства. Это делается для конкретного оператора присваивания с помощью пункта View Definition As контекстного меню (рис. 3.2) либо для всего документа с помощью команды Tools / Worksheet Options / Display)(Сервис / Опции документа / Отображение) (см. разд. «Управление отображением некоторых операторов»гл. 2).
Рис. 3.2. Различное отображение оператора присваивания
Помимо разобранного оператора присваивания (а он применяется наиболее часто), существует также возможность глобального присваивания.
- f — имя функции;
- х. — список переменных.
Легче всего ввести написание функции в документ при помощи клавиатуры.
В Mathcad формально можно разделить функции на два типа:
- встроенные функции;
- функции, определенные пользователем.
Применение функций обоих типов в расчетах совершенно одинаково, с тем исключением, что любую встроенную функцию можно сразу использовать в любом месте документа (о вставке встроенных функций в документ читайте в разд. «Знакомство с Mathcad» гл. 1), а пользовательскую функцию необходимо предварительно определить в документе до момента вычисления ее значения.
3.1.4. Определение функции пользователя
Для того чтобы определить функцию пользователя, например f(x,y) = x2-cos (x+y):
- Введите в желаемом месте документа имя функции (f).
- Введите левую скобку «(«, имена переменных через запятую х, у и правую скобку «)». При вводе левой скобки и запятой автоматически будут появляться соответствующие местозаполнители.
- Введите оператор присваивания с панели инструментов или нажатием клавиши .
- Введите в появившийся местозаполнитель выражение, определяющее функцию x 2 -cos(x+y), пользуясь клавиатурой или панелями инструментов.
Результат ввода иллюстрируется листингом 3.4.
Листинг 3.4. Определение функции пользователя
Все переменные, присутствующие справа в выражении определения функции, либо должны входить в список аргументов функции (в скобках, слева после имени функции), либо должны быть определены ранее. В противном случае будет выведено сообщение об ошибке, причем имя неопределенной переменной будет выделено красным цветом (рис. 3.3).
Рис. 3.3. Сообщение об ошибке («Эта переменная или функция ранее не определена»)
3.1.5. Вывод значений переменных и функций
Чтобы вычислить в документе некоторое математическое выражение, которое может состоять из переменных, операторов и функций (встроенных и определенных пользователем):
- Введите это выражение, например х у.
- Нажмите клавишу .
В результате справа от введенного знака равенства появится вычисленное значение выражения (листинг 3.5, предпоследняя строка). Нельзя изменять содержимое выражения справа от знака равенства, поскольку оно есть результат работы вычислительного процессора Mathcad, совершенно скрытой от глаз пользователя. Подчас (когда выражение содержит функции, реализующие разные численные методы, часто в сложных комбинациях) алгоритмы расчета бывают очень затейливыми и занимают существенное время. О том, что некоторое выражение документа находится в стадии вычисления, свидетельствует обрамляющая его зеленая рамка и невозможность предпринять какое-либо действие с программой Mathcad.
Листинг 3.5. Вычисление выражения.
Заметьте, что, перед тем как вычислить значение математического выражения, Вы обязаны определить значение каждой входящей в него переменной (две первых строки листинга 3.5). Вычисляемое выражение может содержать любое количество переменных, операторов и функций. Вывод текущего значения той или иной переменной приведен в последней строке листинга 3.5, а значения функции — в листингах 3.6 и 3.7.
Листинг 3.6. Вывод значения функции.
Листинг 3.7. Вывод значения функции (продолжение листинга 3.6)
При определении функций пользователя через различные переменные важную роль играет присутствие имен этих переменных в списке аргументов или определение их выше в тексте документа. Например, результаты вывода значения функции f (х,у) в листинге 3.6 остались бы точно такими же, если до или после определения функции присвоить переменным х и у некоторые значения. Так происходит потому, что значения аргумента заданы непосредственно в строке вычисления функции. Если же определить функцию f (х) так, как это сделано в листинге 3 8, то она будет зависеть от значения переменной у в момент определения f (х) (т. е. у=5), поскольку у не входит в список аргументов f (х). Фактически f (x) =x 2 -cos (х+5). Даже если где-нибудь ниже в программе пользователь переопределит значение у, Mathcad все равно будет помнить функцию f (х) как выражение x2-cos (х+5) (листинг 3.9).
Листинг 3.8. К определению функций пользователя
Листинг 3.9. К определению функций пользователя (продолжение листинга 3.8)
Внимательнее относитесь к обязательному требованию совпадения количества аргументов при определении и выводе значения функций. Сравните, например, листинги 3.6 и 3.8, в которых, несмотря на одинаковое выражение в правой части определения функции f, создаются две существенно разные функции f (х, у) и f (х), соответственно
Вводя знак равенства для вычисления математических выражений в Math-cad, Вы фактически применяете оператор вычисления или численного вывода (numerical evaluation). Его можно ввести также нажатием кнопки со знаком равенства на одной из панелей инструментов: Calculator (Калькулятор) или Evaluation (Выражения) (см. рис. 3.1). Оператор численного вывода означает, что все вычисления проводятся с числами, а различные встроенные алгоритмы реализуются соответствующими численными методами.
3.1.6. Символьный вывод
Наряду с численным выводом, в Mathcad имеется возможность символьного, или аналитического, вычисления значения выражения. Для символьных вычислений имеется ряд специальных средств, которые будут детально рассмотрены позднее (см. гл. 5), самое простое из них — это оператор символьного вывода (symbolic evaluation). Он обозначается символом -» и в большинстве случаев применяется точно так же, как оператор численного вывода, однако внутреннее различие между действием этих двух операторов огромно. Если численный вывод — это в обычном смысле этого слова «запрограммированный» расчет по формулам и численным методам, скрытый от глаза пользователя, то символьный вывод — результат работы системы искусственного интеллекта, встроенной в Mathcad и называемой символьным процессором. Работа символьного процессора также невидима (и, чаще всего, даже трудно представима) пользователю и заключается в анализе самого текста математических выражений. Конечно, гораздо более узкий круг формул можно рассчитать символьно, хотя бы потому, что, вообще говоря, относительно не такая большая часть математических задач допускает аналитическое решение.
Чтобы попытаться вычислить символьно математическое выражение, например В sin(arcsin(С Х)), где В,С,Х — некоторые переменные:
- Введите это выражение: В sin(asin(С Х)).
- Введите оператор символьного вывода сочетанием клавиш +, либо нажатием соответствующей кнопки (рис. 3.4) на панели Symbolic (Символика) или Evaluation (Выражения).
Рис. 3.4. Кнопка вставки оператора символьного вывода
После этого справа от символа оператора символьного вывода появится определенное аналитически значение выражения (листинг. 3.10) либо сообщение об ошибке «No answer found» (Ответ не найден). Если символьному процессору Mathcad не удается аналитически упростить выражение, то оно будет выдано справа от знака -» в том же виде, что и слева.
Листинг 3.10. Символьный вывод выражения
Листинг 3.11. Символьный вывод выражений, которое не удалось упростить
Присмотритесь внимательнее к листингам 3.10 и 3.11: для символьного вывода не требуется предварительно определять переменные, входящие в левую часть выражения! Если же переменным были все-таки присвоены ранее некоторые значения, символьный процессор просто подставит их в упрощенную формулу и выдаст результат с учетом этих значений (см. в качестве примера два следующих листинга — 3.12 и 3.13).
Точно так же, как рассчитываются численно значения функций, можно вычислять их и с помощью символьного процессора. Сравните соответствующие результаты, которые представлены в листинге 3.12 (конечно, символьный и численный ответы равны: 9 cos(8)=-1.31). Аналогично можно «символьно выводить значения переменных. Например, присвоить некоторой переменной значение функции или сложного выражения (листинг 3.13, вторая строка) и затем вывести значение переменной в символьном виде.
Листинг 3.12. Численный и символьный вывод значения функции
Листинг 3.13. ЧислвйныЙ и символьный вывод
Как показывают приведенные примеры, преимущество символьных вычислений заключается в выдаче аналитического результата, который для математика часто является более ценным. Поэтому, исходя из специфики конкретных задач, решайте, стоит ли наряду с численными расчетами попытаться получить и символьное решение.
3.1.7. Допустимые имена переменных и функций
В заключение перечислим, какие символы можно, а какие нельзя применять в именах, которые пользователь дает переменным и функциям, и перечислим ряд ограничений на присваивание имен. Допустимые символы:
- большие и маленькие буквы — Mathcad различает регистр: так, имена х и х определяют разные переменные. Кроме того, Mathcad различает и шрифт, например имена х и х воспринимаются как разные;
- числа от 0 до 9;
- символ бесконечности (клавиши + + );
- штрих (клавиши + );
- греческие буквы — они вставляются с помощью панели Greek (Греческие символы);
- символ подчеркивания;
- символ процента;
- нижний индекс.
С осторожностью используйте нижний индекс в определении имен переменных и функций, не путая его с индексом векторной переменной. Чтобы ввести имя с нижним индексом, например, K max: введите букву «K», затем точку «.», после чего линии ввода опустятся чуть ниже, и только затем сам нижний индекс max.
Теперь рассмотрим ограничения на имена переменных и функций:
- имя не может начинаться с цифры, символа подчеркивания, штриха или процента;
- символ бесконечности должен быть только первым в имени;
- все буквы в имени должны иметь один стиль и шрифт;
- имена не могут совпадать с именами встроенных функций, констант и размерностей, например sin или TOL. Тем не менее, допускается их переопределение, но тогда одноименная встроенная функция больше не будет использоваться по первоначальному назначению;
- Mathcad не различает имен переменных и функций: если сначала определить функцию f (х), а потом переменную f, то в оставшейся части документа будет утеря* доступ к функции f (x).
В некоторых случаях желательно использовать имена переменных и функций, содержащие символы операторов Mathcad или другие символы, которые нельзя вставлять в имена непосредственно. Для этого существуют две возможности.
Во-первых, имя, составленное из любых символов и заключенное в квадратные скобки, Mathcad будет воспринимать корректно (рис. 3.5, сверху). Например, чтобы ввести имя :
- Нажмите клавиши + + — появится пара квадратных скобок с местозаполнигелем внутри.
- Введите в местозаполяитель последовательность любых символов, например a+b.
Рис. 3.5. Специальные символы в именах переменных
Во-вторых, если Вас не устраивает наличие квадратных скобок в имени, то вставить в него специальные символы можно чуть более сложным способом. Например, для ввода имени a+b:
- Введите первый символ (а), который должен быть допустимым для имен Mathcad.
- Нажмите клавиши + + для перехода в специальный «текстовый» режим редактирования.
- Введите последовательность любых символов (+).
- Еще раз нажмите клавиши + + , чтобы вернуться в обычный режим редактирования. Теперь можно продолжать ввод допустимых символов в имя (b).
Результат этих действий показан в нижней строке рис. 3.5. Если требуется, чтобы имя начиналось со специального символа (средняя строка рис. 3.5), то необходимо выполнить все пункты 1-4, вводя в начале имени произвольный допустимый символ, а по завершении ввода просто стирая его.
Каждый оператор в Mathcad обозначает некоторое математическое действие в виде символа. В полном согласии с терминологией, принятой в математике, ряд действий (например, сложение, деление, транспонирование матрицы и т. п.) реализован в Mathcad в виде встроенных операторов, а другие действия (например, sin, erf и т. п.) — в виде встроенных функций. Каждый оператор действует на одно или два числа (переменную или функцию), которые называют операндами. Если в момент вставки оператора одного или обоих операндов не хватает, то недостающие операнды будут отображены в виде местозаполнителей. Символ любого оператора в нужное место документа вводится одним из двух основных способов:
- нажатием соответствующей клавиши (или сочетания клавиш) на клавиатуре;
- нажатием указателем мыши соответствующей кнопки на одной из математических панелей инструментов.
Напомним, что большинство математических панелей содержат сгруппированные по смыслу математические операторы, а вызвать эти панели на экран можно нажатием соответствующей кнопки на панели Math (Математика).
Везде в этом разделе будем рассматривать только второй способ вставки оператора Те же, кто предпочитает использовать клавиатуру, найдут перечень горячих клавиш в приложении 2.
Выше мы рассмотрели особенности применения трех операторов: присваивания (см. разд. 3.1.2), численного (см. разд. 3.1.5) и символьного вывода (см. разд. 3.1.6). Разберем в данном разделе действие прочих операторов Mathcad и возможности определения операторов пользователя.
3.2.1. Арифметические операторы
Операторы, обозначающие основные арифметические действия, вводятся с панели Calculator (Калькулятор), показанной на рис. 3.6:
- сложение и вычитание: + — (листинг 3.14);
- умножение и деление: / + (листинг 3.15);
- факториал: ! (листинг 3.16);
- модуль числа: |х| (листинг 3.16);
- квадратный корень: (листинг 3.17); степени: (листинг 3.17);
- возведение х в степень у: х y (листинг 3.17);
- изменение приоритета: скобки (листинг 3.18);
- численный вывод: = (все листинги).
Рис. 3.6. Панель Calculator
Листинг 3.14. Операторы сложения, вычитания и отрицания
Листинг 3.15. Операторы деления и умножения
Листинг 3.16. 0ператор факториала и модуля
Листинг 3.17. Операторы извлечения корня и возведения в степень
Листинг 3.18. Оператор изменения приоритета ()
Как видно, с помощью этой панели можно ввести не только перечисленные операторы, но и их часто используемые комбинации, например, возведение экспоненты в степень, смешанное произведение и деление, а также мнимую единицу и число я. Заметим, что допускается запись оператора деления как в одну, так и в две строки, что обеспечивается наличием двух соответствующих кнопок на панели Calculator.
Напомним, что в редакторе Mathcad можно выбирать отображение оператора умножения (см. разд. «Управление отображением некоторых операторов» гл. 2). Для того чтобы поменять его:
- Щелкните правой кнопкой мыши на выражении, содержащем оператор умножения.
- Выберите первый пункт появившегося контекстного меню View Multiplication As (Представление умножения).
- В подменю выберите пункт, соответствующий стилю представления умножения: в виде обычной точки (Dot), точки с уменьшенным расстоянием от него до сомножителей (Narrow Dot), толстой точки (Large Dot), крестика (X), без символа с небольшим расстоянием между сомножителями (Thin Space), вообще вместе (No Space). Чтобы просмотреть, как будет выглядеть выражение в двух последних представлениях, нужно снять с него выделение. Чтобы вернуть представление по умолчанию, выберите в подменю контекстного меню пункт Default.
Некоторых операторов, например таких, как оператор комплексного сопряжения, на панелях инструментов нет (листинг 3.19). Его приходится вводить исключительно с клавиатуры нажатием клавиши в пределах математической области.
Листинг 3.19. Оператор комплексного сопряжения
3.2.2. Вычислительные операторы
Вычислительные операторы вставляются в документы при помощи панели инструментов Calculus (Вычисления). При нажатии любой из кнопок в документе появляется символ соответствующего математического действия, снабженный несколькими местозаполнителями. Количество и расположение местозаполнителей определяется типом оператора и в точности соответствует их общепринятой математической записи. Например, при вставке оператора суммы (рис. 3.7) необходимо задать четыре величины: переменную, по которой надо произвести суммирование, нижний и верхний пределы, а также само выражение, которое будет стоять под знаком суммы (пример заполненного оператора суммы см. ниже в листинге 3.22).
Для того чтобы вычислить неопределенный интеграл, следует заполнить два местозаполнителя: подынтегрального выражения и переменной интегрирования.
Рис. 3.7. Вставка оператора суммирования
После ввода какого-либо вычислительного оператора имеется возможность вычислить его значение либо численно, нажатием клавиши , либо символьно, с помощью оператора символьного вывода.
Перечислим основные вычислительные операторы и приведем простейшие примеры их применения:
- дифференцирование и интегрирование;
- производная (листинг 3.20);
- N-Я производная (листинг 3.20);
- определенный интеграл (листинг 3.21);
- неопределенный интеграл (листинг 3.21).
- сумма (листинг 3.22);
- произведение (листинг 3.22);
- сумма ранжированной переменной (листинг 3.23);
- произведение ранжированной переменной (листинг 3.23).
- двусторонний;
- левый;
- правый.
Листинг 3.20. Операторы вычисления производных
Листинг 3.21. Операторы интегрирования
Листинг 3.22. Операторы суммирования и вычисления произведения
Листинг 3.23. Операторы суммировани и вычисления произведения
О назначении и особенностях использования ранжированных переменных будет рассказано в следующей главе (см. разд. «Ранжированные переменные» гл. 4).
Листинг З.24. Операторы символьного вычисления пределов
В отличие от других, операторы поиска предела могут быть вычислены только символьно (см. гл. 5).
Операторы суммирования и вычисления произведения фактически являются более удобной записью операторов + и х с большим количеством операндов. А вот вычислительные операторы поиска производных и интегралов существенно отличаются от операторов умножения и сложения тем, что реализованы на основе определенных численных методов, которые в скрытой (невидимой для пользователя) форме запускаются вычислительным процессором Mathcad. При численном расчете интегралов и производных необходимо, хотя бы в общих чертах, представлять принцип работы соответствующих алгоритмов, чтобы избежать ошибок и неожиданностей при получении результатов (численным методам интегрирования и дифференцирования посвящена гл. 7).
Рис. 3.8. Поиск бесконечного ряда
Важно отметить, что имеется возможность вычислять интегралы с одним или обоими бесконечными пределами, а также в символьной форме искать значения бесконечных пределов, сумм (рядов) и произведений. Для удобства ввода кнопка с символом бесконечности помещена на ту же панель инструментов Calculus (Вычисления). Пример вставки символа бесконечности в задаче поиска бесконечного ряда приведен на рис. 3.8.
3.2.3. Логические операторы
Результатом действия логических, или булевых, операторов являются только числа 0 (если логическое выражение, записанное с их помощью, истинно) или 1 (если логическое выражение ложно). Чтобы вычислить значение логического выражения, например 1=1 (рис. 3.9):
- Вставьте с панели Boolean (Булевы операторы) соответствующий оператор =.
- В появившиеся местозаполнители вставьте операнды (две единицы).
- Нажмите клавишу , чтобы получить ответ.
Рис. 3.9. Вставка логического оператора
Получается абсурдное на первый взгляд выражение i«i=i. Однако на самом деле все правильно. Справа от оператора вывода записано логическое выражение 1*1 (обратите внимание, что логический знак равенства выглядит по-другому, нежели обычный), которое является истинным. Поэтому значение данного выражения равно 1, что и показано справа от знака равенства.
Перечислим логические операторы:
- больше (Greater Than);
- меньше (Less Than);
- больше или равно (Greater Than or Equal);
- меньше или равно (Less Than or Equal);
- равно (Equal);
- не равно (Not Equal to);
- и (And);
- или (Or);
- исключающее или (Exclusive or);
- отрицание (Not).
Операнды в логических выражениях могут быть любыми числами. Однако если оператор по смыслу применим только к 0 и 1, то любое неравное нулю число по умолчанию принимается равным 1. Но в результате все равно может получиться либо 0, либо 1. Например, ¬ (-0.33)=0.
Примеры действия логических операторов приведены в листингах 3.25 и 3.26.
Листинг 3.25. Операторы сравнения.
Листинг 3.26. Булевы операторы.
Логические операторы чрезвычайно важны при записи подлежащих решению алгебраических уравнений и неравенств в приемлемой для Mathcad форме.
3.2.4. Матричные операторы
Матричные операторы предназначены для совершения различных действий над векторами и матрицами. Поскольку большинство из них реализует численные алгоритмы, о них будет подробно рассказано в части III (см. гл. 9).
3.2.5. Операторы выражения
Почти все вычислительные операторы были рассмотрены выше (см. разд. 3.1). Они сгруппированы на панели Evaluation (Выражения).
- Оценить численно (Evaluate Numerically) (см. разд. 3.1.5)
- Вычислить символьно (Evaluate Symbolically) (см. разд. 3.1.6)
- Присваивание (Definition) (см. разд. 3.1.2)
- Глобальное присваивание (Global Definition)
Рассмотрим различие между операторами обычного присваивания и глобального присваивания (процесс его вставки в документ показан на рис. 3.10). Для того чтобы вычислить выражение, содержащее некоторую переменную или функцию, необходимо, чтобы этой переменной ранее в документе было присвоено какое-либо значение. Иначе будет выдаваться сообщение об ошибке (рис. 3.11). Однако если в любой части документа (например в самом низу) вставить оператор глобального присваивания, то переменная будет определена в любой части документа (листинг 3.27).
Листинг 3.27. Действие операторов присваивания и глобального присваивания
Рис. 3.10. Кнопка глобального присваивания на панели Evaluation
Рис. 3.11. Обычное присваивание сказывается только на нижеследующей части документа
Как видно из листинга 3.27, обычное, или локальное, присваивание переменной х действует от момента х:=10 до момента глобального присваивания х = 5. Вообще говоря, Mathcad анализирует документы на предмет присваивания переменных в два прохода: сначала распознаются все операторы глобального присваивания, и все выражения в документе сверху вниз и слева направо вычисляются в соответствии с ними, а при втором проходе в том же порядке анализируются операторы локального присваивания, и все выражения вычисляются с поправкой на них. Приведем важный пример взаимодействия глобального и локального присваивания (листинг 3.28).
Листинг 3.28. Взаимодействие глобального и локального присваивания
Обратите внимание, что, несмотря на локальное присваивание переменной x:=10 в третьей строке листинга, значение переменной у вычисляется все-таки в соответствии с глобальным значением х = 5, поскольку сама переменная y глобальным образом определена через переменную х.
Аккуратнее относитесь к определению глобальных переменных и, во избежание путаницы, старайтесь не переопределять их локально. Применяйте глобальное присваивание только для определения констант и, по возможности, избегайте случаев, когда оператор вывода предшествует оператору глобального присваивания для улучшения читаемости документов.
Точно так же как Вы глобально присваиваете значение переменной, допускается глобально определять функции (листинг 3.29).
Листинг 3.29. Глобальное определение функции пользователя
Оператор глобального присваивания можно отображать не только в виде тождественного равенства, но и как обычный знак равенства. Для этого вызовите на операторе контекстное меню и в подменю пункта View Definition As выберите пункт Equal (Равенство).
3.2.6. Создание оператора пользователя
Запросы взыскательного пользователя могут отнюдь не исчерпываться набором встроенных операторов Mathcad. Для вставки в документы заранее созданных операторов пользователя применяется панель Evaluation (Выражения).
Выбор имени оператора
Оператор пользователя может иметь абсолютно любое имя (см. ранее раздел «Имена, содержащие операторы и специальные символы» этой главы). Однако, исходя из смысла операторов, логично давать им имена в виде символов. Это удобно делать с помощью коллекции символов, находящейся в справочной информации Mathcad. Выберите в верхнем меню Help / QuickSheets (Справка / Быстрые шпаргалки) и войдите затем в самый последний раздел Extra Math Symbols (Дополнительные символы) открывшегося содержания Шпаргалок. Там Вы увидите целую коллекцию символов, любой из которых можно просто перетащить указателем мыши в нужное место документа.
Присваивать оператору некоторое действие следует точно так же, как функции пользователя.
Создание бинарного оператора
Чтобы создать бинарный оператор, например реализующий действие х у 2:
- Введите имя оператора, например, bin.
- Наберите знак скобки , затем список из двух операндов через запятую, , , , затем закрывающую скобку .
- Введите оператор присваивания .
- Введите выражение, зависящее от операндов, действие которого необходимо присвоить оператору (х-у 2).
Создание унарного оператора
Унарный оператор создается точно так же, только вместо двух операндов, отделенных запятой, Вам следует ввести лишь один операнд. Например, чтобы создать оператор с именем %, реализующий перевод доли числа в проценты и сводящийся к умножению его на 100 (листинг 3.30):
- Введите имя оператора. Для этого нажмите клавиши , + + + , , затем снова + + , потом сотрите в имени букву «а».
- После знака % наберите скобку «(«, далее «х11, затем еще одну скобку «)».
- .
- Введите выражение х100.
Листинг 3.30. Создание унарного оператора пользователя
Использование бинарного оператора
Возможны два вида вставки пользовательского бинарного оператора в документ, отличающиеся только отображением в документе. Чтобы вставить оператор в форме графа (или дерева):
- Нажмите кнопку Tree Operator (Оператор дерево) на панели Evaluation (Выражения) (рис. 3.12, справа).
- В появившиеся местозаполнители введите имя оператора (на вершине графа) и значения операндов (в ответвления дерева).
- Введите оператор присваивания, нажав клавишу .
Результат действия оператора показан на рис. 3.12, внизу слева.
Кроме древовидной формы оператора, допускается использование его в виде последовательности «операнд- имя оператора- другой операнд» (рис. 3.12, вторая строка слева). Чтобы ввести такую форму оператора, следует нажать соседнюю кнопку Infix Operator (Оператор внутри) с изображением xfy.
Рис. 3.12. Применение пользовательского бинарного оператора
Использование унарного оператора
Вставка унарного оператора совершенно аналогична, только вместо двух операндов требуется ввести один (рис. 3.13). Унарный оператор вставляется нажатием кнопки Prefix Operator (Оператор перед) на панели Evaluation (Выражения) либо кнопки Postfix Operator (Оператор после). Первый путь проиллюстрирован правой частью рис. 3.13 (в момент вставки) и результатом действия оператора (слева), а результат вставки оператора по второму пути — левой нижней строкой того же рисунка
Рис. 3.13. Применение пользовательского унарного оператора
3.3. Управление вычислениями
Документ Mathcad — это в полном смысле этого слова компьютерная программа, а сама система Mathcad — настоящая система программирования, правда ориентированная на математика, а не на профессионального программиста. Большинство других сред программирования (знакомых читателю по реализации таких языков, как Си, Фортран, Бейсик и т. п.) разделяют редактирование кода программ и их выполнение, которое можно вызвать предназначенными для этого командами. В Mathcad и код программы, и результат их выполнения объединены в одном документе. Тем не менее, функции редактирования формул и их расчеты выполняются раздельно, и пользователь имеет возможность управлять всеми важнейшими опциями вычислений.
3.3.1. Режимы вычислений
Все примеры, которые мы рассматриваем в этой книге, неявно предполагают, что включен автоматический режим вычислений. Он включается по умолчанию при создании пустого документа, поэтому если вводятся выражения, содержащие операторы вывода, они вычисляются немедленно. Вообще говоря, имеется два режима вычислений:
- автоматический режим (automatic mode) — все вычисления проводятся автоматически по мере ввода формул;
- ручной режим (manual mode) — начало вычислений каждой формулы или всего документа производится пользователем.
Режим вычислений можно выбрать с помощью команды Tools / Calculate / Automatic Calculation (Сервис / Пересчитать / Считать автоматически), как показано на рис. 3.14. Если в этой строке меню установлен флажок проверки, значит, включен автоматический режим, если флажка нет, то редактируется документ в ручном режиме вычислений. Чтобы сменить режим, просто выберите этот пункт меню (например, нажав кнопку мыши в ситуации, показанной на рис 3.14, включите ручной режим).
Режим вычислений устанавливается независимо для каждого документа Одновременно могут быть открыты несколько документов, вычисляемых в различных режимах
Преимущества и недостатки каждого режима очевидны. С одной стороны, автоматические вычисления упрощают работу с документом, поскольку результаты расчетов появляются в реальном времени, и пользователь имеет возможность анализировать их сразу. С другой стороны, если вычисления сложные, то они могут отнимать много времени (что особенно заметно на компьютерах с не слишком мощным процессором и небольшим объемом оперативной памяти). Поэтому зачастую, чтобы продолжить редактирование документа, требуется довольно длительное ожидание завершения расчетов В частности, если поменять какое-либо выражение в начале большого документа, которое влияет на последующие вычисления, то все они пересчитываются заново. В таких случаях часто удобнее редактировать текст в ручном режиме, а вычисления включать по мере необходимости.
Рис. 3.14. Выбор режима вычислений
3.3.2. Прерывание вычислений
Mathcad осуществляет вычисления документа, как это принято в большинстве сред программирования: сверху вниз и слева направо. Пока очередное выражение находится в процессе расчета (вычислительным или символьным процессором), оно выделяется рамкой зеленого цвета (рис. 3.15), а любые действия пользователя по дальнейшему редактированию документа блокируются. Если у вас не слишком быстрый компьютер, а формулы достаточно сложные, то можно наблюдать, как зеленая рамка перескакивает с одного выражения на другое
Чтобы прервать затянувшийся процесс вычислений, нажмите клавишу Появится диалоговое окно, показанное на рис. 3.16, в котором нужно подтвердить прерывание вычислений (ОК). В этом случае выражения, которые Mathcad не успел вычислить, будут помечены в документы красным цветом. Прерванные вычисления возобновляются нажатием клавиши или командой Tools / Calculate / Calculate Now (Математика / Пересчитать / Пересчитать)
Рис. 3.15. Процесс вычисления выражения
Рис. 3.16. Диалоговое окно прерывания вычислений
3.3.3. Вычисления в ручном режиме
Если флажок в строке команды Tools / Calculate / Automatic Calculation (Сервис / Пересчитать / Считать автоматически) снят, пользователь должен запускать вычисления самостоятельно
- Для того чтобы вычислить все формулы во всем документе, выполните команду Tools / Calculate / Calculate Worksheet (Математика / Пересчитать / Пересчитать все).
- Для вычисления всех формул в видимой части документа выберите пункт Tools / Calculate / Calculate Now (Сервис / Пересчитать / Пересчитать) либо нажмите клавишу , либо щелкните на кнопке с изображением знака равенства (Calculate) на стандартной панели инструментов
- Прервать вычисления можно обычным образом, нажав клавишу .
Управлять размером видимой части документа можно при помощи изменения масштаба отображения документа
При редактировании текста в ручном режиме не выполняются ни вычисления, ни построение графиков, а соответствующие места в выражениях формально отмечаются местозаполнителями (рис. 3.17.)
Рис. 3.17. Чтобы запустить вычисления в ручном режиме, нажмите кнопку Calculate
3.3.4. Отключение вычисления отдельных формул
Mathcad позволяет отключить вычисление какой-либо формулы. При этом она не будет влиять на последующие вычисления. Чтобы не вычислять определенную формулу в документе:
- Щелкните правой кнопкой мыши на формуле.
- Выберите в контекстном меню пункт Disable Evaluations (Выключить вычисления), как показано на рис. 3.18.
Эквивалентный способ выключения вычисления отдельной формулы заключается в вызове диалогового окна Properties (Свойства) через одноименный пункт контекстного меню (см. рис. 3.18) или главного меню Format (Формат). В диалоге Properties следует перейти на вкладку Calculation (Вычисления) и установить там флажок Disable Evaluations (Выключить вычисления).
Результат выключения формулы из процесса вычислений проиллюстрирован листингом 3.31. На нем выключен второй из операторов присваивания, о чем можно судить по наличию черного квадрата сразу за формулой. Соответственно, в последней строке выведенное значение переменной х «не чувствует» выключенного присваивания и остается равным 3.
Листинг 3.31. Вычисление второго оператора присваивания выключено
Рис. 3.18. Отключение вычисления формулы с помощью контекстного меню
3.3.5. Оптимизация вычислений
Отличительная черта новых версий Mathcad — улучшенные возможности ускорения численных вычислений за счет применения элементов символьной математики. Непосредственно перед численным расчетом Mathcad автематически пытается упростить выражение, используя символьный процессор. Это называется оптимизацией. За счет того что от версии к версии качество работы символьного процессора улучшается, символьное преобразование зачастую существенно ускоряет расчеты. Режим оптимизации включается либо в документе целиком, либо для отдельных формул.
Чтобы включить или отключить режим оптимизации всех выражений в активном документе, выберите команду Tools / Optimize / Worksheet (Сервис / Оптимизация / Документ), как показано на рис. 3.19. Содержание документа, изображенного на этом же рисунке, помогает понять математический смысл режима оптимизации: для ускорения вычисления нижнего (определенного) интеграла выгодно использовать его аналитическое решение, определенное символьным процессором.
Чтобы изменить режим оптимизации для отдельной формулы, не меняя выбранного режима для остальных выражений документа, выделите эту формулу линиями ввода и выберите в верхнем меню Tools / Optimize / Equation (Сервис / Оптимизация / Уравнение).
Рис. 3.19. Режим оптимизации вычислений
3.3.6. Диалоговое окно Worksheet Options
Наравне с изложенными способами установки режимов вычислений, их также удобно устанавливать для всего документа на вкладке Calculations (Вычисления) диалогового окна Worksheet Options (Опции документа), вызываемого с помощью команды Tools / Worksheet Options (Сервис / Опции документа). Три флажка задают включение соответствующего режима вычислений (рис. 3.20).
- Recalculate automatically (Пересчитать автоматически) — включение режима автоматических вычислений.
- Use strict singularity checking for matrices (Использовать проверку матриц на сингулярность) — опция, появившаяся в версии Mathcad 2001, которая важна при некоторых операциях с матрицами. Она означает проведение дополнительной проверки на сингулярность матрицы перед использованием численных алгоритмов, что позволяет, во избежание неправильного применения численного метода, выдать заранее сообщение об ошибке, если матрица сингулярная.
- Optimize expressions before calculating (Оптимизировать выражения перед вычислением) — включение режима оптимизации.
- Use exact equality for Boolean comparisons (Использовать точное равенство для логического сравнения) — когда флажок выбран, применяется жесткий критерий точного равенства чисел (точнее, числа при сравнении считаются равными, если отличаются по модулю менее чем на 10 -307). Если флажок снят, используется более мягкий критерий (относительное различие чисел по модулю менее чем на 10 -12).
Рис. 3.20. Управление режимом вычислений в диалоговом окне Worksheet Options
Помимо флажков проверки, имеется также пара переключателей, которая позволяет реализовать новый режим ускоренных вычислений (higher speed calculation). Он включается выбором переключателя Higher speed calculation (Ускоренные вычисления), изображенного на рис. 3.20. Чтобы отключить режим ускоренных вычислений, выберите переключатель Backward compatibility (Обратная совместимость). В этом случае вычисления будут проводиться без дополнительной оптимизации по скорости, в точности так же, как в предыдущих версиях (Matvcsd 2000 и ниже) Необходимость таких расчетов может возникнуть, если вдруг Вы столкнулись с сообщениями об ошибках в документах, созданных в предыдущих версиях Mathcad и корректно в них работающих.
3.4. Сообщения об ошибках
Когда процессор Mathcad по тем или иным причинам не может вычислить выражение, он вместо ответа выдает сообщение об ошибке (рис. 3.21). Если курсор находится вне формулы с ошибкой, то в ней имя функции или переменной, которая вызвала ошибку, отмечается красным цветом (сверху на рис. 3.21). При щелчке на такой формуле под ней появляется текстовое сообщение о типе ошибки, обрамленное черным прямоугольником (рис. 3.21, снизу).
Рис. 3.21. Сообщение об ошибке
Если некоторые выражения вызывают ошибку, они просто игнорируются, а следующие выражения в документе по-прежнему вычисляются. Конечно, если формулы, вызвавшие ошибку, влияют на значения нижеследующих формул, то они будут также интерпретированы как ошибочные. Поэтому, встречая в документе сообщения об ошибках, найдите сначала самое первое из них. Часто ее устранение позволяет избавиться и от последующих ошибок.
Как бы хорошо вы ни овладели системой Mathcad, сообщения об ошибках все равно будут появляться в документах. Они могут быть связаны как с орфографическими ошибками, так и с более серьезными внутренними причинами, требующими знания численных алгоритмов расчетов. Искусство математика во многом состоит в умении анализировать ошибочные ситуации и находить правильный выход из них.
Возможности Mathcad можно в полной мере оценить только при использовании переменных и функций.
Два знака равенства
В выражениях Вам необходимо использовать числа (константы), переменные, операторы и знаки равенства. В повседневной жизни мы используем знак равенства = для различных операций. Mathcad, однако, различает эти операции. Наиболее важные из них:
- определение (присвоить значение) – вводится через двоеточие [:]
- вычисление – вводится через знак равенства [=]
Оператор определения не менее важен, чем оператор вычисления. Значение выражения y можно отобразить только после присвоения ему какого-либо значения. x и y здесь являются переменными .
Введите следующие выражения:
Эти два знака равенства принципиально различны, поэтому их не следует путать.
Поместите курсор перед числом 4 в первом выражении:
Удалите число 4 с помощью клавиши и введите 5. Щелкните по пустой области и убедитесь, что результат третьего выражения изменился на 25:
Попробуйте удалить число 25. Вы увидите, что при первом нажатии число станет красным, а при повторном нажатии удалится 25 и знак равенства:
Использование переменных
Введите следующие выражения:
Попробуйте изменить значение x на 100, 0.5, -4 и 0:
Первые два случая дадут в результате число. При -4 получится мнимое число. Да, Mathcadможет работать и с такими числами. При нуле программа выдаст ошибку, а результат будет обведен красным. Если Вы щелкните по неправильному выражению, то получите описание, что может быть не так:
Теперь о том, какие имена можно и нельзя использовать для переменных. Есть несколько правил: имя переменной не может начинаться с цифры и в имени переменной нельзя использовать пробелы и знаки операторов. Имена переменных могут начинаться:
- с любой строчной или прописной буквы
- другие символы, если они не являются операторами
- символы с вкладки Математика –> Операторы и символы –> Символы
- символы из Таблицы символов Windows
Вот несколько примеров:
Переменные можно использовать, только если они были определены ранее. «Ранее» означает, что объявление переменной должно располагать выше или левее выражения, где она используется. Если переменная не объявлена, появится сообщение об ошибке:
Подстрочные индексы
В Mathcad есть два различных вида подстрочных индекса для переменных:
- Описательный подстрочный индекс.
- Индекс массива (матрицы).
Чтобы набрать описательный подстрочный индекс, введите имя переменной, нажмите и наберите подстрочный индекс:
Переменная с описательным подстрочным индексом – это обычная переменная, со своим именем. Индекс массива существенно отличается от него. Этот индекс можно ввести, нажав открывающую квадратную скобку [ после имени переменной. У переменной может быть один или два индекса массива:
Индекс массива должен быть числом. При этом не следует путать виды подстрочных индексов, т.к. они выглядят практически идентично:
Разница видна при щелчке мышью по выражению:
У переменной может быть сразу описательный индекс и индекс массива. Сначала всегда идет описательный индекс:
Функции
Переменные можно использовать, только если они были определены ранее. Однако есть одно важное исключение – определение функции. Можно определить собственную функцию, как на примере ниже:
Переменная a является локальной для функции. Она не определена за пределами функции:
Если Вы определили a до определения функции, значение a не будет изменено в процессе вычисления значения функции.
Внимание: если Вы дали переменной такое же имя, как и функции, Вы больше не сможете использовать эту функцию. У переменной и функции должны быть разные имена:
Этой проблемы можно избежать, задав для переменной и функции разные обозначения. Об этом мы поговорим в уроке 10 «Обозначения и единицы измерения».
Функции могут содержать две и более переменной:
Здесь значения переменных x и y также не изменяются при вычислении функции.
Встроенные функции
В Mathcad есть большое число встроенных функций. Зайдите на вкладку Функции:
Список всех функций можно увидеть, щелкнув по кнопке Все функции.
Заметьте, что тригонометрические функции принимаю в качестве аргумента угол в радианах, а не в градусах. Для использования градусов используйте символ с вкладки Математика –> Операторы и символы –> Символы:
Математика в тексте
В текст можно вставить математическую область. Таким образом, можно использовать над- и подстрочные символы в тексте. Для этого при редактировании текстовой области нажмите кнопку Математика с вкладки Математика –> Области:
Резюме
- В Mathcadесть два различных знака равенства: определить:= и вычислить =.
- Имя переменной обычно начинается с буквы; цифры нельзя использовать в начале переменной. Также можно использовать символы с клавиатуры, с панели Математика –> Операторы и символы –> Символы, с Таблицы символов Windows.
- Чтобы определить переменную и задать ей значение:
- щелкните мышью на пустую область;
- введите имя переменной;
- нажмите [:] для ввода оператора определения;
- введите значение, которое Вы хотите присвоить.
- Чтобы дать переменной описательный подстрочный индекс:
- нажмите ;
- введите подстрочный индекс.
- Чтобы дать переменной индекс массива:
- щелкните мышью в конце имени переменной;
- нажмите открывающую квадратную скобку [;
- введите число – подстрочный индекс.
- Переменную можно использовать ниже или правее места, где она определена.
- Имя функции следует набирать по тем же правилам, что и имя переменной, но ввод имени функции заканчивается вводом [(]. В скобках содержатся аргументы функции.
- Переменные в функциях – локальные, т.е. они определены только при использовании функции.
- Математическую область можно встроить в текст. Эту возможность следует использовать, если необходимо вставить над- и подстрочные символы в текст.
MathCad является мощной системой для работы с формулами, числами, текстами и графиками и предоставляет пользователю возможности электронной таблицы и интерфейс WYSIWYG текстового процессора. Ввод уравнений в MathCad полностью совпадает с привычной типографской математической записью.
Как и в электронных таблицах, любое изменение содержимого рабочего документа вызывает обновление всех зависимых результатов и перерисовку графиков. MathCad позволяет легко читать данные из файлов и подвергать их любой математической обработке: от сложения до вычисления интегралов и производных, обращения матриц и т.д.
С помощью формул MathCad можно решить почти любую математическую задачу аналитически (символьно) либо численно. Объединяя в одном документе текст, графику и математические выкладки, MathCad облегчает понимание самых сложных вычислений.
Ниже приведен краткий список основных характеристик MathCad.
Свободная форма записи, подобная классной доске;
Возможность комбинирования текста, математических выкладок, графиков и рисунков в любом месте документа;
Вырезка и вставка уравнений, текста, графики;
Контекстная интерактивная система справок.
Точность представления чисел — 15 верных десятичных цифр;
Двоичные, восьмеричные, десятичные, шестнадцатеричные числа;
Основные встроенные алгоритмы:
решения систем уравнений и неравенств;
работы с комплексными числами, переменными, функциями;
вычисления сумм, произведений, производных, интегралов;
интерполяции и аппроксимации (линейная, кубическими сплайнами);
быстрых преобразований Фурье;
решения дифференциальных уравнений;
работы с матрицами.
Основные встроенные функции:
теории чисел и комбинаторика;
регрессии и сглаживания;
Символьное дифференцирование и интегрирование;
Обращение, транспонирование матриц;
Разложение выражений на множители;
Многообразие типов графиков (декартовы, полярные координаты; построение поверхностей, линий уровня; картины векторных полей; гистограммы; точечные графики);
Оси графиков могут иметь линейный или логарифмический масштаб;
Возможность выбора типа, толщины и цвета линии, используемой для построения графика;
Построение графиков поверхностей в трех измерениях с различными ракурсами просмотра и в разных масштабах.
ХАРАКТЕРИСТИКА ТЕКСТА И РАБОЧЕГО ДОКУМЕНТА
Размещение текста в любом месте рабочего документа;
Возможность использования шрифтов различных стилей в любой текстовой области;
1.2 Отличия MathCad 2000 от предыдущих версий
Кардинально переработанный и приближенный к интерфейсу MS Office пользовательский интерфейс;
Возможность выделения частей математических выражений буксировкой мышью;
Быстрое построение (QvickPlot) двумерных и трехмерных графиков;
Новая палитра символьной математики с расширенными операторами;
Более удобный и наглядный синтаксис символьных операций;
Новые операторы программирования on error, continue, return;
Возможность применения в программах операторов символьных операций;
Новый тип данных – строковые;
Появление оперативного центра ресурсов (Resource Center) вместо быстрых “шпаргалок” QuiekSheet;
Около 50 новых математических функций, из которых следует особо отметить функции нахождения максимумов и минимумов maximize, minimize, а также функцию odesolve решения дифференциальных уравнений;
улучшенный блок решения систем нелинейных уравнений (теперь их число может достигать 200);
Возможность выбора численного метода решения некоторых задач (например, численного интегрирования);
Улучшенные средства форматирования текста;
Функции редактирования Find и Replace (найти и заменить);
Возможность записи документов в формате HTML;
Существенно улучшенные средства для работы с трехмерными графиками.
Все это дает пользователю новые возможности и новые удобства в работе с системой MathCad, подтверждая её репутацию как одной из самых массовых и удобных в работе математических систем.
Определение переменных в Mathcad
Чтобы определить переменную, достаточно ввести её имя и присвоить ей некоторое значение, для чего служит оператор присваивания.
1. Введите в желаемом месте документа имя переменной.
2. Введите оператор присваивания с помощью клавиши или нажатием соответствующей кнопки Definition (Присваивание) на панели инструментов Calculator (Арифметика) или Evaluation (Выражения).
3. Введите в появившийся фрейм требуемое значение переменной.
Кнопка оператора присваивания для удобства помещена сразу на две панели Calculator и Evaluation .
Ввести новое значение переменной возможно как в виде числа, так и в виде математического выражения, содержащего другие переменные и функции, а также в виде строкового выражения (листинг 3.1). В последнем случае будет создана переменная s не численного, а строкового типа.
Функции в Mathcad записываются в обычной для математика форме, например,
f (x )=sin (x ),
где f (х ) — функция;
f — имя функции;
х — список переменных.
Легче всего ввести написание функции в документ при помощи клавиатуры.
В Mathcad формально можно разделить функции на два типа˸
- встроенные функции;
- функции, определенные пользователем.
Применение функций обоих типов в расчетах совершенно одинаково, с тем исключением, что любую встроенную функцию можно сразу использовать в любом месте документа, а пользовательскую функцию необходимо предварительно определить в документе до момента вычисления её значения.
Определение переменных в Mathcad — понятие и виды. Классификация и особенности категории «Определение переменных в Mathcad» 2015, 2017-2018.
Текстовую область можно разместить в любом незанятом месте документа Mathcad. Чтобы до начала ввода указать программе, что требуется создать не формульный, а текстовый регион, достаточно, перед тем как ввести первый символ, нажать клавишу » (двойная кавычка). В результате на. .
Для выполнения программы-функции необходимо обратиться к имени программы-функции с указанием списка фактических параметров (если в описании программы присутствует список формальных параметров), т. е. (список фактических параметров) Фактические. .
Для набора выражения используются клавиатура и панели инструментов, которые доступны с помощью меню ПросмотрПанели. Например, для расчёта выражения необходимо набрать 1/, затем найти знак корня в панели «Калькулятор». В знаменателе выражения появится шаблон который. .
Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику (например, возвращение различных значений в зависимости от условий), в одну строку не удается. Назначение. .
Для проведения измерений осциллограф нужно настроить, для чего следует задать: расположение осей, по которым откладывается сигнал; нужный масштаб развертки по осям; смещение начала координат по осям, режим работы по входу: закрытый или открытый; режим. .
Для написания программ в среде MathCad существует специальная панель Programmіng (Программирование) (рис.16, а), она относится к панели Math (Математические) (рис.16, б). Язык программирования MathCad имеет предельно малое количество операторов (рис. 16, а). Чтобы написать программу. [читать подробнее] .
Известно, что экспериментальные данные, как правило, задаются дискретно в виде массива данных из двух пар чисел (хі, уі). В связи с этим возникает задача аппроксимации дискретных данных непрерывной функцией f(x). В MathCad для обработки экспериментальных данных существуют. .
MathCad 7.0 Professional – универсальный инструмент для работы с формулами, графиками и текстами. Он обладает мощными вычислительными функциями и возможностью аналитических преобразований.
1. Не создавайте несколько одинаковых тем, ибо модератор может расценить их, как спам и удалить все.
2. Для решения задач по GPSS есть отдельная тема. Все задачи по GPSS опубликовывать в этой теме! Перед опубликовыванием вашей задачи просмотрите всю тему, возможно вы сразу найдете решение.
3. Давайте вашим темам ОСМЫСЛЕННЫЕ названия, а также указывайте язык программирования. Пример: [Pascal]:Работа с файлами и записями.
4. Использования тега CODE обязательно при публикации текста программы.Темы, оформленные с явным игнорированием правил и отсутствием смысла, будут закрыты/удалены!
Вам помогли? Напишите об этом здесь (в портфолио фрилансера)Фрилансерам:
5. Демпинг цен запрещен (даже если Вы готовы работать бесплатно). Цены обсуждаются в приватном общении. Если вы готовы рещить задачу бесплатно, просто решите ее быстрее, чем возникнет предложение сделать это за деньги.
6. Пользователям, входящим в группу Newbie, запрещается предлагать свои услуги (завуалированно в т.ч.)
7. В посте с предложением выполнить работу, обязательно указывать ссылку на свое портфолио в Отзывы, Благодарности, Портфолио Это правило работает и в том случае, если вы выполняете работу бесплатно.
8. Реклама (даже завуалированная) своих фриланских сайтов запрещенаThis variable is undefined mathcad что делать
Пример 2.2. Определение переменной через значение функции
Чтобы присвоить переменной значение матрицы или вектора, последние должны быть просто введены в правый маркер оператора «:-*. О том, как это сделать, мы поговорим в гл. 3. К определениям переменной данного типа можно также отнести и задание вектора значений с помощью оператора ранжированной переменной
Пример 2.3. Присваивание переменной матричного значения
И, Наконец, переменная может быть определена как строка. При этом ее значение обязательно должно быть взято в кавычки.
Пример 2.4. Определение переменной как строки
Значение переменной в Mathcad можно и переопределить: для этого операцию нового присваивания нужно провести правее или ниже старого присваивания.
Человека, впервые столкнувшегося с выполнением расчетов с помощью компьютера, вид оператора Гфисваквания может несколько смутить. Это связано с тем, что в традиционном математическом синтаксисе функции, которые он выполняет, возложены на обычный знак «—*. Ситуация эта, вообще говоря, не совсем характерна для системы Macbcad, разработчики которой стремились максимально близко следовать общепринятым традициям оформлений «бумажной» математики, и связана она с попыткой найти компромисс между этими традициями и нормами программирования. Почему же нельзя использовать один оператор и для присваивания, и для вывода значения, и для указания равенства двух объектив данных или выражений? Дело в том, что программа лишена лотки — поэтому понять из контекста, какие функции в каждом конкретном случае выполнял бы оператор «=», она не смогла бы. По причине этого для каждой операции, которая на бумаге обозначается обычным *—*, в Mathcad имеется индивидуальный оператор. Знак же довольно традицнонен: он является оператором присваивания, например, в языке программирования Pascal. Однако в том случае, если вам нужно подготовить отчет или традиционный вид оператора присваивания для вас более удобен, тип его отображения можно изменить. Сделать это можно двумя способами.
Если вы хотите изменить вид оператора в конкретной формуле, то выполните по нему щелчок правой кнопкой мыши. При этом откроется контекстное меню формулы, в котором следует выбрать всплывающее меню View Definition As
В том случае, если все присваивания В документе должны быть отображены с помощью простого равенства, выполните команду Tools ► Worksheet Options ► Display (Инструменты ► Параметры документа ► Отображение). Здесь в списке Definition (Определение) выберите строку Equal (Равенство). При этом вы измените принятые поумолча-
нию установки документа, и все вводимые в дальнейшем определения будут отображаться как
Кстати, при выделении формулы, оператор присваивания в которой представлен в виде простого равенства, отобразится именно определенная по умолчанию его стандартная форма. Эта особенность необходима для того, чтобы существовала возможность отличить оператор присваивания от оператора мобильного определения, логического равенства или численного вывода, которые могут принимать ту же форму.
Присвоить переменной значение в виде какого-то буквенного выражения можно только в том случае, если все символы или их сочетания, которые в нем используются, определены выше как конкретные числа, матрицы или строки (или же являются системными переменными). Иначе неопределенный символ будет выделен красным цветом и система выдаст сообщение об ошибке: This variable is undefined (Эта переменная не определена).
Функции в Mathcad делятся на две группы:
Техника использования функций обоих типов абсолютно идентична, а вот задание отличается принципиально.
Задание функций пользователя
Счгобенности определения функций пользователя (проще говоря,функций произвольного вила) в Mathcad полностью совпадают с принятыми в математике правилами. Для этого необходимо выполнить следующую последовательность действий.
1.Введите имя функции. В общем случае оно может быть совершенно произвольным, хотя определенные ограничения все-таки имеются. О них мы поговорим немного позже.
2.После имени функции следует ввести пару круглых скобок, в которых через запятую нужно прописать все переменные, от которых зависит функция. Задать функцию с параметром можно только в том случае, если ему выше присвоено конкретное числовое значение. Иначе система выдаст уже знакомое нам сообщение об ошибке: This variable is undefined.
3.Введите оператор присваивания «:-►,
4.На месте черного маркера справа от введенного оператора присваивания задайте вид вашей функции. В выражение определяемой функции могут входить как непосредственно переменные, так и другие встроенные и пользовательские функции.
Пример 2.5. Задание функции пользователя
<я,у, у- + a-f(x, у) + b-cos (FUNCTION (z))
Встроенные функции — это функции, заданные в Mathcad изначально. Поэтому, чтобы их и си ольэовать. достаточно просто корректно набрать имена функций с клавиатуры. Впрочем, существуют и другие способы вставки нужной встроенной функции. Наиболее распространенные из них можно ввести с панели Calculator (Калькулятор), К таким функциям относятся синус, косинус, тангенс, натуральный и десятичный логарифмы, экспонента. Для того же, чтобы задать вес остальные встроенные функции Mathcad, нужно открыть специальное окно Insert Function (Вставить функцию). Проще всего это можно сделать нажатием одноименной кнопки панели Standard (Стандартные) с изображением стилизованного знака функции (рис. 2.1).
Рио. 2,1. Кнопка Insert Function (Вставить функцию> меню Standard (Стандартные)
Также, для того чтобы вызвать дан нос окно (рис. 2.2), можно использовать сочетание клавиш Ctrt+Shtft+F или Ctrt+E. И. наконец, ссылка на нею имеется в меню Insert (Вставка).
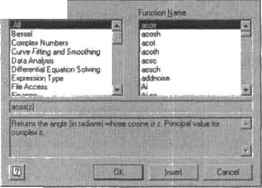
Рис. 2.2. Окно Insert Function (Вставить функцию)
Так как число встроенных функций Mathcad весьма значительно (несколько сотен), для удобства они распределены по тематическим группам. Их список, организованный в алфавитном порядке, расположен в окне Function Category (Категория функций). Всего в Mathcad 32 тематические группы функций.
При выборе определенной категории функций ее содержание отоб1азится в окне Function Name (Имя Функции). Чтобы ввести нужную функцию, выделите ее в списке с помощью мыши или клавиш управления курсором н нажмите ОК (или лучше дважды щелкните на ней мышью).
По умолчанию в окне Function Name (Имя функции) отображается полный список всех встроенных функций, что соответствует категории АИ(Всс). Производить поиск в полном списке несколько быстрее н удобнее, если вы приблизительно знаете написание имени нужной вам функции
На окне Insert Function (Вставить функцию) имеется специальная зона, в которой отображается текст описания выбранной функции. Так, для первой функции списка
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
1 |
|
Ошибка — эта переменная не определена. Как исправить08.01.2017, 20:05. Показов 59390. Ответов 16
Добрый день.
__________________
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
08.01.2017, 20:05 |
|
16 |
|
Модератор 5032 / 3863 / 1327 Регистрация: 30.07.2012 Сообщений: 11,437 |
|
|
08.01.2017, 20:11 |
2 |
|
Nikon19, везде вместо = (символа эквивалентности) поставьте := (символ присваивания). И будет Вам счастье…
1 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:17 [ТС] |
3 |
|
Менял на символ присваивания, после чего такая ошибка возникает внутри самой формулы(сначала пишет, что не определена M,например).
0 |
|
Модератор 5032 / 3863 / 1327 Регистрация: 30.07.2012 Сообщений: 11,437 |
|
|
08.01.2017, 20:18 |
4 |
|
Nikon19, файл в архив и сюда… (НЕ КАРТИНКУ)
0 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:21 [ТС] |
5 |
|
Здесь уже поменял обратно на символ присваивания.
0 |
|
Модератор 5032 / 3863 / 1327 Регистрация: 30.07.2012 Сообщений: 11,437 |
|
|
08.01.2017, 20:36 |
6 |
|
РешениеNikon19, Вам надо объявить еще одну функцию, имя которой Вы используете в последней функции… (желтый фон). Как-то так…
1 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:47 [ТС] |
7 |
|
Большое спасибо! Миниатюры
0 |
|
Модератор 5032 / 3863 / 1327 Регистрация: 30.07.2012 Сообщений: 11,437 |
|
|
08.01.2017, 20:56 |
8 |
|
Nikon19, так Вам надо просто построить график ОПРЕДЕЛЕННОГО вида ИЛИ решить какую-то конкретную задачу и посмотреть, какой график получится? Уточните, пожалуйста.
0 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 21:08 [ТС] |
9 |
|
Есть пример, в рамках которого получено значение вероятности безотказной работы программы. Формула расчета в маткаде представлена. Необходимо построить график (вида как экспоненциальный) в зависимости от времени, но проблема в том, что t=20 в этом примере.
0 |
|
44 / 1 / 0 Регистрация: 14.06.2014 Сообщений: 150 |
|
|
12.09.2017, 15:43 |
10 |
|
Привет всем!
0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,037 |
|
|
12.09.2017, 16:02 |
11 |
|
Nikon19, экспонента так получается,аргумент надо поменять Миниатюры
0 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 19:47 |
12 |
|
ошибка при построении графика (эта переменная не определена)
0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,037 |
|
|
16.10.2021, 20:01 |
13 |
|
wern, график ниже опустите.
1 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 20:11 |
14 |
|
т.е проблема только в положении графика относительно матриц? я передвинул и все получилось, спасибо большое
0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,037 |
|
|
16.10.2021, 20:19 |
15 |
|
т.е проблема только в положении графика относительно матриц? да,так и есть.
1 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 20:34 |
16 |
|
прошу прощения, а что делать когда появляется ошибка «формы этих значений должны совпадать. Это значение имеет форму Unitless а другие имеют форму: [] Unitless»
0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,037 |
|
|
16.10.2021, 20:40 |
17 |
|
wern, десятичная точка в маткаде применяется,а не запятая. Изображения
0 |
Ошибка — эта переменная не определена. Как исправить

Не могу найти ошибку, делал тоже самое на компе в универе, когда начал вбивать дома выдает вот это
Ошибка — эта переменная не определена
Народ, помогите! Делаю все "по инструкции", только вот вычисление не работает. Говорит, что.

Друзья, всем привет, подскажите пожалуйста в чем проблема (см.Скрин или задачу), в Given пишу X1.
Ошибка — эта переменная не определена
Помогите пожалуйста решить задачу или помогите найти ошибку. Уже неделю сижу и ничего не могу найти.
Эта переменная не определена mathcad ошибка
Тип бесконечности вводится нажатием сочетания клавиш + + .
Для изменения алгоритма, использующего бесконечный предел, или для вычисления какого-либо другого интеграла щелкните на интеграле правой кнопкой мыши и измените алгоритм с помощью контекстного меню
Can only evaluate an n-th order derivative when n=0,1..5.
Можно вычислить n-й порядок производной, только когда п=0,1..5
Порядок производной должен быть одним из следующих чисел: 0, 1, 2,. ..5.
Если Вы хотите посчитать производную более высокого порядка, то делайте это с помощью символьного дифференци-
рования
Can’t evaluate this function when its argument less than or equal to zero
Невозможно вычислить эту функцию, когда ее аргумент меньше или равен нулю
Такое сообщение может касаться XY- или полярных графиков, имеющих логарифмические оси, на которых или пределы, или некоторые из значений, не положительны
Отрицательные числа и ноль не могут быть расположены нигде на логарифмических осях. Смените тип осей графика или постройте его для других значений
Can’t converge to a solution
Не сходится к решению
Численный метод расходится (не может найти решения)
Убедитесь, что операция не применяется к функции в области непосредственной близости точки ее сингулярности (деления на ноль). Попробуйте поменять параметры численного метода (например начальное приближение).
Попробуйте увеличить константу TOL, т. е. осуществить поиск решения с худшей погрешностью.
Попробуйте поменять численный алгоритм, если это возможно (вызвав контекстное меню нажатием на месте ошибки правой кнопки мыши)
Can’t define the same variable more than once in the same expression
Невозможно определить ту же самую переменную более одного раза в одном и том же выражении
Вы пытаетесь вычислить одну и ту же переменную дважды в одном выражении
Пример подобной ошибки: если Вы создаете вектор с левой стороной а := и используете это же имя справа, то получите ошибку
Can’t determine what units the result of this operation should have
Невозможно определить, в каких единицах следует быть результату этой операции
Вы возвели выражение, содержащее единицы измерения, в степень, являющуюся переменной в неких пределах или вектором. В результате невозможно определить размерность результата
Если выражение включает в себя единицы измерений, то можно возводить его только в действительную фиксированную степень
Cant divide by zero
Деление на ноль невозможно
Где-то в программе или внутри численного метода возникло деление на ноль
Найдите место деления на ноль и устраните его
Попробуйте поменять параметры численного метода, константы точности или сам численный алгоритм
Could not find a solution
Невозможно найти решение
Численный метод расходится (не может найти решения)
См. «Can’t converge to a solution»
Can’t find the data file you’re trying to use
Невозможно найти файл, который Вы пытаетесь использовать
Невозможно найти файл данных или другой тип файла, к которому Вы обращаетесь
Удостоверьтесь, что такой файл существует в указанном месте
Can’t have anything with units or dimensions here
Здесь нет ничего в единицах измерений или в размерностях
Это выражение использует единицы измерений где-то, где они не разрешены
Единицы измерений не разрешены:
— в аргументах большинства функций;
— в экспонентах; — в верхних и нижних индексах.
Для того чтобы использовать выражения с единицами измерений, вначале переведите это выражение в UnitsOf (выражение)
Can’t have more than one array in a contour plot
Нельзя иметь более одного массива в контурном графике
Вы вводите более одного массива в местозаполнитель контурного или поверхностного графика
Можно иметь только один массив в данном местозаполнителе, т. к. графики могут выдавать лишь одну поверхность в один момент времени
Can’t perform this operation on the entire array at once. Try using «vectorize» to perform it element by element
Невозможно представить эту операцию в целом массиве сразу. Попытайтесь использовать векторизацию, чтобы представить элемент за элементом
Например, можно увидеть это сообщение при попытке разделить один вектор на другой
Для того чтобы применять функцию или оператор к каждому элементу вектора или матрицы, используйте оператор векторизации
Can’t plot this many points
Невозможно начертить график с таким большим количеством точек
Попытка построения графика с числом точек, превосходящим возможное
Попробуйте сделать число точек меньше, чем 150 000
Can’t put a «:=» inside a solve block
Нельзя помещать «:=» внутрь вычислительного блока
Внутри вычислительного блока не должно быть формулировки присваивания. Он должен содержать только булевы выражения
Используйте панель с булевыми операторами
Can’t raise an expression having units to a complex power
Нельзя возводить в комплексную степень ыражение, имеющее единицы измерений
Это выражение содержит единицы измерений, а Вы возводите его в комплексную степень
Выражение с единицами измерений можно возводить только в действительную степень. Для того чтобы возводить в комплексную степень выражение с единицами измерений, вначале переведите это выражение в UnitsOf (выражение) — единицы измерений будут отменены
Can’t solve a system having this many equations
Невозможно решить систему, имеющую так много уравнений
Mathcad не способен решить систему
См. определение термина «вычислительный блок » (гл. 
Can’t understand something in this data file
Невозможно что-то понять в файле данных
Файл, к которому Вы пытаетесь получить доступ при помощи READ или READ*, имеет дефект
Файл должен быть ASCII-текстом
Все строки файла должны иметь тот же номер значений, что используется в READ*
Если файл имеет требуемый формат, а это сообщение продолжает появляться, попробуйте удалить любую часть текста из файла
Can’t understand the name of this function
Невозможно понять имя этой функции
Такое сообщение может появиться, если в качестве имени функции используется, например, число 6(х)
Выражение должно соответствовать требованиям, предъявляемым в Mathcad к написанию имен функций
Can’t understand the way this range variable is defined
Невозможно понять определение ранжированной переменной
Определение ранжированной переменной неверно
Вводя область определения ранжированной переменной, необходимо использовать один из следующих видов:
Rvar := nl . .n2 Rvar := nl,n2 . .пЗ
Cant understand this number
Невозможно понять это число
Это выражение содержит символ или десятичную точку там, где это непозволительно
Вы увидите эту ошибку, например, если случайно запишете число так: .452.
Cant use a range variable in a solve block
Невозможно использовать ранжированную переменную в вычислительном блоке
Эта ошибка появится, если использовать область определения переменной в неподходящем месте
Придумайте алгоритм, не допускающий применения ранжированной переменной в вычислительном блоке
Cannot evaluate this accurately at one or more of the values you specified
Невозможно точно вычислить одно или более значений
Эта ошибка появляется, если попытаться вычислить функцию для аргумента, находящегося за пределами точной области определения функции
Проверьте область определения функции
Cross product is defined only for vectors having exactly three elements
Векторное произведение определяется только для векторов, имеющих точно три элемента
Векторное произведение определяется только для векторов, имеющих точно три элемента
См. определение векторного произведения (гл. 9)
Can’t evaluate this expression. It may have resulted in an overflow or an infinite loop
Невозможно вычислить это выражение. Это может быть результатом переполнения или бесконечных циклов
Это функциональное определение может содержать слишком много вложенных функций. Или функция может быть константой в бесконечных циклах
Проверьте несколько итераций цикла
Degree of the polynomial must be between 1 and 99.
Степень полинома должна находиться в пределах между 1 и 99
Вектор, пропущенный через функцию поиска корней полинома, должен содержать по крайней мере 2 и не более 99 элементов
Dimensions must be >4
Размерность должна быть >4
Эта матрица должна иметь по крайней мере 4 ряда и 4 столбца
Исправление ошибок
Определив выражение, вызвавшее ошибку, нужно его отредактировать с целью устранения ошибки или исправить определение переменной, приведшей к ошибке. После щелчка по выражению и начала редактирования MathCAD удаляет сообщение об ошибке. После щелчка вне уравнения (или нажатия клавиши [F9]), MathCAD повторно вычисляет выражение. Если ошибка устранена, то MathCAD затем повторно вычисляет другие выражения, зависящие от измененного.
Выражение, отмеченное сообщением об ошибке, не обязательно содержит ее причину. Причиной ошибки могут быть функции или переменные, определенные в рабочем документе значительно ранее. Для устранения ошибки придется отредактировать именно ее.
Рассмотрим допустимые в MathCAD имена переменных и функций. Имена в MathCAD могут содержать любые из следующих символов:
· прописные и строчные латинские буквы;
· цифры от 0 до 9
· знак подчеркивания _
· штрих ` Это не апостроф. Находится на одной клавише с тильдой
· греческие буквы. Есть два способа набрать греческую букву: напечатать римский эквивалент и нажать [Ctrl]+Gили щелкнуть по соответствующему символу на палитре греческих символов
· символ бесконечности, который можно задать как комбинацию клавиш[Ctrl]+[Shift]+Z.
· Имена переменных и функций не могут включать пробелы или любые другие символы, не перечисленные выше.
MathCAD не делает различий между именами переменных и именами функций. Если определить вначале f(x), а затем переменную f, окажется невозможным использовать f(x) где-либо ниже определения f некоторые имена уже используются MathCAD для встроенных констант, единиц измерения и функций. Хотя эти имена можно переопределить, этот уничтожит их встроенные значения.
MathCAD различает в именах символы верхнего и нижнего регистра, а также различные шрифты.
Кроме того, среда MathCAD включает так называемые предопределенные переменные. MathCAD содержит 8 переменных, значения которых определены сразу после запуска программы. Они называются встроенными или предопределенными. Эти переменные имеют или общепринятое значение (например, пи или е), или используются как внутренние переменные, управляющие работой MathCAD. Эти переменные можно переопределять, например, определим е:= 2. Ниже этого определения переменная е примет в рабочем документе новое значение.
Приведем примеры некоторых встроенных переменных:
е=2.71828 – основание натурального логарифма;
Е=10^307 – машинная бесконечность;
MathCAD интерпретирует все, начинающееся цифрой, как число. Цифра может сопровождаться:
· цифрами после десятичной точки;
· символами h или o для шеснадцатеричных и восьмеричных чисел; символами i или j для комплексных чисел. Комплексные числа MathCAD воспринимает в форме a+bi (или a+bj). Специальные функции и операторы для работы с комплексными числами:
· Re(z) – вещественная часть числа z;
· Im(z) – мнимая часть числа z;
· Arg(z) – аргумент числа z (угол в комплексной плоскости между вещественной осью и радиус-вектором, определяемым числом z);
· |z| – модуль числа z.
Одиночное число в MathCAD называют скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел — матрицей. Способы создания массива:
· заполнить массив пустых полей
· использовать дискретный аргумент
Можно различать имена векторов, матриц и скаляров, используя различный шрифт для их описания.
Эта переменная не определена mathcad ошибка
MathCAD — это просто! Часть 27. Программирование и ошибки: вместе веселее!
Что ж, хотя мы уже немало всего успели обсудить насчет программирования в такой замечательной математической среде, как MathCAD, еще немало весьма существенных тем осталось за кадром. И, пожалуй, самая существенная из них — это взаимодействие начинающего программиста, пишущего программы в MathCAD’е, и ошибок в его программах. Именно на ней мы с вами сейчас и остановимся.
В общем-то, если сказать, что ошибки никто не любит, это будет не так уж далеко от истины. Точнее, никто не любит собственные ошибки. Чужие любят все, а не только экзаменаторы и разнообразные инспекторы. Однако, к сожалению, при программировании (а написание небольших вспомогательных программок в MathCAD’е, как я уже когда-то давно тому назад говорил, это тоже программирование) ошибки попросту неизбежны. Даже самые лучшие программисты совершают ежедневно множество ошибок, и никто, в общем-то, за это не применяет к ним особых санкций. Существует даже такое мнение, что программа без ошибок совершенно бесполезна — если в ней нет ошибок, значит, в ней нет и никакой полезной функциональности, потому что не ошибается только тот, кто ничего не делает. Так что ошибки в программах — это вполне естественные спутники каждого, кто пишет даже самые маленькие программки, а потому и бояться их не следует. Тем не менее, с ошибками в программах можно и нужно бороться. И для этого существуют специальные средства, некоторые из которых доступны и тем, кто пишет программы в MathCAD’е. Однако, прежде чем рассказывать о том, что это за средства, и как ими нужно пользоваться, нужно, как мне лично кажется, поговорить еще немного о том, вокруг чего будет сосредоточена наша борьба — то есть о самих ошибках.
Поскольку, как я уже говорил, ошибки довольно многочисленны, их имеет смысл классифицировать. Сделать это стоит, в общем-то, уже хотя бы попросту потому, что разные виды ошибок требуют различных к себе подходов, и их устранение требует вложения различного количества труда того, кто писал программу.
Самые простые ошибки — синтаксические. Как вы уже имели возможность воочию убедиться, при программировании очень важно придерживаться определенных правил в записи конструкций. Например, если вы вместо имени функции rkfixed напишете в программе tkfixed, ошибившись при вводе на одну букву и нажав на соседнюю с r клавишу t, то как раз и получите в свое распоряжение самую что ни на есть классическую синтаксическую ошибку. Ни к каким особенно страшным последствиям она (как, впрочем, и все другие ошибки аналогичного класса) не приведет: программа просто не сможет быть выполнена по той причине, что MathCAD не сможет найти функцию, которую вы ему указали. Искать такие ошибки тоже совсем не сложно — они всегда хорошо видны, поскольку даже сама среда подсвечивает их, чтобы можно было найти особенно быстро. Исправлять, соответственно, тоже очень просто: достаточно записать идентификатор правильно, и все в программе станет на положенные места. MathCAD, кстати, избавляет пользователя от множества таких ошибок благодаря необходимости вводить все операторы, управляющие ходом программы, с помощью специальных горячих клавиш или соответствующих кнопок на панели инструментов Программирование. Если бы их нужно было, напротив, набирать вручную с клавиатуры, то и возможности сделать синтаксическую ошибку были бы несравнимо шире.
Второй тип ошибок — ошибки алгоритмические. Это такие ошибки, которые, в принципе, не мешают выполнению программы, но делают результаты такого выполнения полностью лишенными всякого смысла. Многие из таких ошибок — банальные опечатки: там, где нужно было поставить плюс, вы, например, поставили в спешке минус или же сделали что-нибудь другое примерно в таком же духе. Конечно, сказать, что алгоритмические ошибки — это сплошь и рядом одни только опечатки, было бы, мягко говоря, не до конца верно. Потому что очень многие из них являются следствием недостаточности знаний писавшего программу — то есть если ошибочно составлена сама последовательность действий, которые должен сделать MathCAD для того, чтобы вы могли получить интересующий вас результат. Еще великое множество алгоритмических ошибок — результат банальной невнимательности: например, присвоение значения не той переменной, ее необнуление либо, например, вывод не той переменной в качестве результата выполнения вашей программы. В общем-то, именно об алгоритмических ошибках мы с вами сейчас и будем говорить более подробно. Однако есть еще один, особенно неприятный, тип ошибок.
Третий тип — это ошибки мистические. Да-да, именно мистические, я не оговорился. Какие именно это ошибки? Это ошибки, имеющие совершенно непонятную природу и столь же непонятный способ лечения — как правило, это проявления ошибок не в вашей программе, а в каком-то из внутренних компонентов MathCAD’а. К сожалению, эти ошибки, в «большом» программировании встречающиеся не так уж, в общем-то, и часто, в MathCAD’е не такие уж редкие гости. Отчасти это объясняется тем, что MathCAD — это все-таки средство расчетов, а не программирования, которое играет в этой среде второстепенную и вспомогательную роль, но, конечно, когда реально сталкиваешься с такими вот мистическими ошибками, это все не слишком успокаивает. Хотя поначалу почти все ошибки в программах кажутся мистическими, на самом деле большая их часть все-таки имеет рациональную природу. Если же природа появившейся ошибки вам совершенно непонятна, то вам следует коренным образом перестроить структуру программы или хотя бы тот ее фрагмент, в котором локализовалось проявление этой ошибки. Практически во всех случаях этот не слишком хитрый прием позволяет полностью избавить программу от досадной непонятной ошибки.
Что ж, о самих ошибках мы с вами, можно считать, побеседовали. Теперь давайте, пожалуй, перейдем к тому, какими именно способами можно бороться с самыми распространенными из них — то есть алгоритмическими. Об остальных, в общем-то, я уже довольно подробно все рассказал, а вот что касается алгоритмических ошибок, то здесь нужно будет в большинстве случаев прибегнуть к помощи специализированных встроенных в MathCAD инструментов.
Отладка в MathCAD’е
Процесс поиска и устранения алгоритмических ошибок называется по-русски отладкой. По-английски этот же самый процесс называется debugging, то есть, если дословно, «избавление от жучков». В общем-то, и по-русски довольно часто можно услышать термины «дебагинг» или «баг», однако во избежание путаницы мы будем использовать слово «отладка» (если, конечно, не возражаете). Кстати, история возникновения английского термина весьма любопытна, и, вполне возможно, вы ее слышали. Первые компьютеры были машинами весьма громоздкими и дорогостоящими, а потому и всевозможные поломки для них были делом далеко не просто устранимым. Когда выяснилось, что причиной очередной поломки стал жучок, забравшийся внутрь компьютера и вызвавший замыкание, в счете за ремонт записали: «debugging». Рука шутника оказалась легкой — термин, как видите, прижился и используется на протяжении уже многих десятилетий.
В чем же заключается процесс отладки? На самом деле ничего особенно таинственного и трудного для понимания здесь нет. Просто во время отладки у вас есть возможность выполнять программу не сразу «залпом», как это происходит обычно, а пошагово, то есть выполнять последовательно друг за другом каждую строчку программы, делая, когда нужно, паузы для осмысления работы программы и просмотра промежуточных значений каждой из переменных. Отладка используется при разработке любых программ, а потому и создатели MathCAD включили поддержку этого удобного и, в общем-то, достаточно универсального средства выявления ошибок в свой программный продукт. Доступ к инструментам, используемым при отладке программ в MathCAD’е, осуществляется через подпункт Debug меню Tools в главном рабочем окне MathCAD’а (см. соответствующий скриншот).
Стоит отметить, что, поскольку MathCAD — это среда, ориентированная не на программирование, а на различные вычислительные действия, то отладка в ней имеет более широкое применение, чем только отладка программ, которые пишет пользователь. Отлаживать можно и все вычисления даже в том случае, если они выполняются без применения какого-либо программирования с вашей стороны. В общем-то, поскольку такая возможность будет весьма полезной для большинства читателей не столько при программировании в MathCAD’е, сколько при обычных вычислениях, то именно с такой позиции мы с вами и станем рассматривать отладку в этой мощной математической среде. Нам также понадобится панель отладки. Ее включают так же, как все остальные панели инструментов, в меню View -> Toolbars. Конечно, эта панель, как вы могли уже заметить, дублирует отладочное меню в Tools -> Debug, однако, думаю, нажать на кнопку, расположенную на этой панели, будет все-таки проще и быстрее, чем искать соответствующий пункт в надежно спрятанном от пользователя меню.
При переходе в отладочный режим (кнопка либо пункт меню Toggle Debug Mode) внешний вид главного окна MathCAD’а меняется (см. скриншот): внизу появляется специальное окно, используемое для просмотра промежуточной отладочной информации. Оно называется Trace Window.
Однако о том, что именно отображается в этом самом окне, а также о том, что от нас требуется сделать с документом перед тем, как его можно будет уже полноценно отлаживать, мы с вами поговорим, пожалуй, в следующий раз, чтобы не перегружать вас разнообразной полезной информацией. Сейчас же подведем итоги разговора про ошибки, возникающие в процессе написания программ в математической среде MathCAD.
Как видите, ошибок в программах действительно бояться не следует. Это вполне нормальная составляющая процесса программирования, неизбежно проявляющаяся в каждом из результатов этого процесса. Тем не менее, с ошибками можно и нужно бороться, и с большинством из них это можно производить с весьма высокой вероятностью достижения успеха. Хотя, конечно же, встречаются и такие ошибки, с которыми трудно будет разобраться даже тому, кто на программировании, что называется, собаку съел. Но все-таки они встречаются не так уж часто. Так что в программировании, если вы хотите избежать мучений, связанных с поиском ошибок, очень важна ваша внимательность. Если вы будете достаточно внимательны при написании программы, то риск допустить ошибку будет сравнительно невелик. Впрочем, это правило применимо не только к программированию.
Эта переменная не определена mathcad ошибка
Mathcad раскрывается в полной мере при использовании переменных и функций.
Два знака равенства
В математических вычислениях мы используем множество различных констант, переменных, операторов и знаков равенства. Обычно в жизни мы используем знак равенства для многих разных операций, но Mathcad отличает их. Наиболее важными операциями являются:
- определение (присвоение значения) — используется двоеточие;
- вычисление — используется знак равенства.
Важность оператора определения не меньше, чем важность оператора вычисления. В приведенном ниже примере значение y можно вычислить лишь после присвоения ему определенного значения. х и у здесь являются переменными.
Два знака равенства, которые изображены выше, имеют совершенно разные значения, поэтому нужно очень внимательно относится к ним.
Поставьте курсор перед числом 4 в примере выше.
Удалите число 4 клавишей [Delete], и введите 5. Нажмите на пустой области, чтобы выйти из области вычисления и увидите, что результат вычислений поменялся на 25:
Теперь попробуйте провести операцию удаления с числом 25. Вы увидите, что при попытке удаления число подсвечивается красным, а при следующем нажатии удалиться и знак равно.
Использование переменных
Введите такие выражения в область вычисления
Проведите операции замены значения х на такие: 100, 0.5, -4 и 0.
В первых двух случаях вы получите число в качестве результата. В третьем случае у вас будет мнимое число. При значении х ноль программа выведет ошибку и обведет результат красным. Если вы нажмете на красное выделение, то увидите описание проблемы:
Дальше мы поговорим о том, какие имена можно использовать для переменных, а какие нельзя. Существуют такие правила: имя переменной не может начинаться с цифры и в ней нельзя использовать пробелы или знаки операторов. Имена могут начинаться:
- с любой буквы как большой, так и маленькой;
- с других символов, которые не являются операторами;
- с символов из вкладки Математика -> Операторы и символы -> Символы;
- с символов из таблицы символов ОС Windows.
Использование переменных доступно, только если вы определите их заранее. Термин «заранее» обозначает, что присвоение значения переменной должно производиться выше или левее выражения, где эта переменная используется. Если вы не объявили переменную заранее, то появится сообщение об ошибке:
Подстрочные индексы
Mathcad существует два типа подстрочных индексов:
- Описательный подстрочный индекс.
- Индекс массива (матрицы).
Для ввода описательного индекса сначала введите желаемое имя переменной, а потом нажмите комбинацию [Ctrl+-], далее вводите подстрочный индекс.
Переменная, которая имеет описательный индекс — это простая переменная, которой присвоено имя. Индекс массива сильно отличается от него. Такой индекс можно присвоить, если ввести квадратную скобку [ после имени переменной. Переменная может иметь один или два индекса массива:
Индекс массива может иметь только числовое значение. При этом не путайте разные типы индексов, так как они довольно схожи визуально.
Более четко разницу видно, если нажать мышкой на выражение
Любая переменная может иметь оба индекса одновременно: описательный и индекс массива. Сначала всегда будет прописан описательный.
Функции
Использование переменных возможно только при определении их заранее. Но есть исключение из этого правила — определение функции. Можно произвести определение своей функции. Пример ниже.
Переменная а имеет для функции локальное значение. Она не несет определения за пределами этой функции.
Если вы присвоили значение переменной а до определения функции, то значение этой переменной не будет меняться в процессе вычисления функции. Внимание: Если вы присвоили переменной такое же имя, как и функции, вы не сможете использовать эту функцию. Переменная и функции должны иметь разные имена.
Вы не будете сталкиваться с такой проблемой, если будете задавать переменной и функции различные имена. Об обозначениях мы поговорим в уроке 10.
Функции могут иметь более одной переменной.
Значения переменных х и у не изменяются и в этой функции.
Встроенные функции
Mathcad имеет очень много встроенных функций. Перейдите во вкладку Функции.
Все функции вы можете увидеть, если нажмете на кнопку Все функции.
Обратите внимание, что все тригонометрические функции в качестве аргумента получают угол не в градусах, а в радианах. Чтобы использовать градусы нужно выбрать их во вкладке Математика -> Операторы и символы -> Символы.
Математика в тексте
В текстовую область можно поместить область вычислений. Так вы сможете использовать в тексте подстрочные и надстрочные символы. Чтобы сделать это, при редактировании текстовой области нужно нажать на кнопку Математика во вкладке Математика -> Области.
Резюме
1. Mathcad использует два знака равенства отдельно для определения := и для вычисления =.
2. Имя переменной нельзя начинать с цифры. Можно использовать для этого только буквы или символы, отличные от символов операторов. Символы можно вводить с панели Математика -> Операторы и символы -> Символы, а также брать из панели символов Windows.
3. Для определения значения переменной нужно:
- щелкнуть на пустую область;
- ввести имя переменной;
- ввести оператор определения [:=];
- ввести значение переменной.
4. Для присвоения переменной подстрочного описательного индекса нужно:
- нажать мышкой в конце имени переменной;
- нажать [Ctrl+-];
- ввести подстрочный индекс.
5. Для присвоения переменной индекса массива:
- нажмите мышкой в конце имени переменной;
- нажмите на клавиатуре на открывающуюся квадратную скобку [;
- ввести нужный подстрочный индекс.
6. Определять переменную нужно только выше или левее места использования ее в вычислениях.
7. Имя функции вводится с теме же правилами, что и имя переменной, с той лишь разницей, что заканчивать имя функции нужно вводом открывающейся скобки [(]. В них будут размещаться аргументы функции.
8. Переменные в функциях имеют определение только в рамках этой функции.
9. В тексте можно размещать математическую область. Это можно применять при интеграции в текст надстрочных или подстрочных символов.
Глобальное определение в PTC Mathcad 15 и PTC Mathcad Prime 3.0
Оператор глобального определения позволяет определить выражение (переменную, функцию) в любом месте документа.
a)
Рис. 1. Оператор глобального определения в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
Если выражение определено глобально, то его можно использовать в других операциях независимо от того, выше или ниже эти операции находятся в документе:
Рис. 2. Выполнение вычислений с глобальным и локальным определением в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
При необходимости, в Mathcad 15 внешний вид оператора глобального определения можно поменять на символ обычный символ равенства «=». Для это щелкните правой кнопкой мыши по оператору, в контекстном меню выберите View Definition As -> Equal.
Рис. 3. Изменение внешнего вида оператора глобального определения.
В Mathcad 15 возможно переопределение переменных, заданных глобально. В Mathcad Prime 3.0 подобное переопределение выдаст ошибку.
б)
Рис. 4. Переопределение переменной, заданной глобально, в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
Чтобы учесть все определения, Mathcad работает по следующему алгоритму:
1. Первый проход документа сверху вниз – распознавание только операторов глобального определения и вычисление выражений.
2. Второй проход документа – распознавание операторов локального определения и вычисление выражений с поправкой на выражения, которые определенны локально.
Это важно учитывать, если Вы переопределяете выражения, заданные глобально. Демонстрация этого алгоритма приведена на рисунке 5.
Рис. 5. Документ с переопределенными выражениями.
Однако в Mathcad Prime 3.0 выражения, определенные глобально, переопределить уже нельзя (ни локально, ни глобально) – Mathcad выдаст ошибку (рис. 6).
Рис. 6. Попытка переопределить переменную, заданную глобально в Mathcad Prime 3.0.
Другой важный момент при использовании глобального определения: если Вы используете переменные для определения выражений, заданных глобально (т.е. используете переменную справа от символа ?), то эта переменная также должна быть определена глобально, причем выше того выражения, в котором она используется. Иначе переменная не будет определена (рис. 7).
б)
Рис. 7. Неправильное использование переменных в выражениях, заданных глобально, в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
Что значит переменная не определена в маткаде. Сообщения об ошибках
Эта глава посвящена основам вычислений в Mathcad. Она содержит все необходимые сведения о применении переменных и функций, операторов Присваивания, численного вывода и символьного вывода (см. разд. 3.1), а также других операторов (см. разд. 3.2). В заключение описываются основные средства управления процессом вычислений в Mathcad (см. разд. 3.3) и уверится несколько слов о том, каким образом происходит выдача сообщений об ошибках при вычислениях (см. разд. 3.4).
3.1. Переменные и функции
Основные инструменты математика — это операции с переменными величинами и функциями. В Mathcad переменные, операторы и функции реализованы в интуитивной форме, т. е. выражения в редакторе вводятся и вычисляются так, как они были бы написаны на листе бумаги. Порядок вычислений в документе Mathcad также очевиден: математические выражения и действия воспринимаются процессором слева направо и сверху вниз.
Перечислим основные действия, которые пользователь может совершать для определения и вывода переменных и функций.
3.1.1. Определение переменных
Чтобы определить переменную, достаточно ввести ее имя и присвоить ей неко-topoe значение, для чего служит оператор присваивания (см. следующий раздел).
3.1.2. Присваивание переменным значений
Чтобы присвоить переменной новое значение, например переменную х сделать равной 10:
- Введите в желаемом месте документа имя переменной, например х.
- Введите оператор присваивания с помощью клавиши или нажатием соответствующей кнопки Definition (Присваивание) на панели инструментов Calculator или Evaluation (Выражения), как показано на рис. 3.1.
- Введите в появившийся местозаполнитель новое значение переменной (10).
Рис. 3.1. Результат ввода оператора присваивания
Результат перечисленных действий показан в листинге 3.1.
Кнопка оператора присваивания для удобства помещена сразу на две панели Calculator (Калькулятор) и Evaluation (Выражения).
Листинг 3.1. Присваивание переменной численного значения
Ввести новое значение переменной возможно как в виде числа, так и в виде математического выражения, содержащего другие переменные (листинг 3.2) и функции (см. следующие разделы), а также в виде строкового выражения (листинг 3.3.). В последнем случае будет создана переменная s не численного, а строкового типа.
Листинг 3.2. Присваивание переменной вычисленного значения выражения
Листинг 3.3. Присваивание переменной строкового значения
Если переменная с некоторым именем создается в данном документе впервые, то для ввода оператора присваивания, вместо двоеточия, допускается использовать символ равенства » :=» на символ равенства. Это делается для конкретного оператора присваивания с помощью пункта View Definition As контекстного меню (рис. 3.2) либо для всего документа с помощью команды Tools / Worksheet Options / Display)(Сервис / Опции документа / Отображение) (см. разд. «Управление отображением некоторых операторов»гл. 2).
Рис. 3.2. Различное отображение оператора присваивания
Помимо разобранного оператора присваивания (а он применяется наиболее часто), существует также возможность глобального присваивания.
Функции в Mathcad записываются в обычной для математика форме:
- f (х, . ) — функция;
- f — имя функции;
- х. — список переменных.
Легче всего ввести написание функции в документ при помощи клавиатуры.
В Mathcad формально можно разделить функции на два типа:
- встроенные функции;
- функции, определенные пользователем.
Применение функций обоих типов в расчетах совершенно одинаково, с тем исключением, что любую встроенную функцию можно сразу использовать в любом месте документа (о вставке встроенных функций в документ читайте в разд. «Знакомство с Mathcad» гл. 1), а пользовательскую функцию необходимо предварительно определить в документе до момента вычисления ее значения.
3.1.4. Определение функции пользователя
Для того чтобы определить функцию пользователя, например f(x,y) = x2-cos (x+y):
- Введите в желаемом месте документа имя функции (f).
- Введите левую скобку «(«, имена переменных через запятую х, у и правую скобку «)». При вводе левой скобки и запятой автоматически будут появляться соответствующие местозаполнители.
- Введите оператор присваивания с панели инструментов или нажатием клавиши .
- Введите в появившийся местозаполнитель выражение, определяющее функцию x 2 -cos(x+y), пользуясь клавиатурой или панелями инструментов.
Результат ввода иллюстрируется листингом 3.4.
Листинг 3.4. Определение функции пользователя
Все переменные, присутствующие справа в выражении определения функции, либо должны входить в список аргументов функции (в скобках, слева после имени функции), либо должны быть определены ранее. В противном случае будет выведено сообщение об ошибке, причем имя неопределенной переменной будет выделено красным цветом (рис. 3.3).
Рис. 3.3. Сообщение об ошибке («Эта переменная или функция ранее не определена»)
3.1.5. Вывод значений переменных и функций
Чтобы вычислить в документе некоторое математическое выражение, которое может состоять из переменных, операторов и функций (встроенных и определенных пользователем):
- Введите это выражение, например х у.
- Нажмите клавишу .
В результате справа от введенного знака равенства появится вычисленное значение выражения (листинг 3.5, предпоследняя строка). Нельзя изменять содержимое выражения справа от знака равенства, поскольку оно есть результат работы вычислительного процессора Mathcad, совершенно скрытой от глаз пользователя. Подчас (когда выражение содержит функции, реализующие разные численные методы, часто в сложных комбинациях) алгоритмы расчета бывают очень затейливыми и занимают существенное время. О том, что некоторое выражение документа находится в стадии вычисления, свидетельствует обрамляющая его зеленая рамка и невозможность предпринять какое-либо действие с программой Mathcad.
Листинг 3.5. Вычисление выражения.
Заметьте, что, перед тем как вычислить значение математического выражения, Вы обязаны определить значение каждой входящей в него переменной (две первых строки листинга 3.5). Вычисляемое выражение может содержать любое количество переменных, операторов и функций. Вывод текущего значения той или иной переменной приведен в последней строке листинга 3.5, а значения функции — в листингах 3.6 и 3.7.
Листинг 3.6. Вывод значения функции.
Листинг 3.7. Вывод значения функции (продолжение листинга 3.6)
При определении функций пользователя через различные переменные важную роль играет присутствие имен этих переменных в списке аргументов или определение их выше в тексте документа. Например, результаты вывода значения функции f (х,у) в листинге 3.6 остались бы точно такими же, если до или после определения функции присвоить переменным х и у некоторые значения. Так происходит потому, что значения аргумента заданы непосредственно в строке вычисления функции. Если же определить функцию f (х) так, как это сделано в листинге 3 8, то она будет зависеть от значения переменной у в момент определения f (х) (т. е. у=5), поскольку у не входит в список аргументов f (х). Фактически f (x) =x 2 -cos (х+5). Даже если где-нибудь ниже в программе пользователь переопределит значение у, Mathcad все равно будет помнить функцию f (х) как выражение x2-cos (х+5) (листинг 3.9).
Листинг 3.8. К определению функций пользователя
Листинг 3.9. К определению функций пользователя (продолжение листинга 3.8)
Внимательнее относитесь к обязательному требованию совпадения количества аргументов при определении и выводе значения функций. Сравните, например, листинги 3.6 и 3.8, в которых, несмотря на одинаковое выражение в правой части определения функции f, создаются две существенно разные функции f (х, у) и f (х), соответственно
Вводя знак равенства для вычисления математических выражений в Math-cad, Вы фактически применяете оператор вычисления или численного вывода (numerical evaluation). Его можно ввести также нажатием кнопки со знаком равенства на одной из панелей инструментов: Calculator (Калькулятор) или Evaluation (Выражения) (см. рис. 3.1). Оператор численного вывода означает, что все вычисления проводятся с числами, а различные встроенные алгоритмы реализуются соответствующими численными методами.
3.1.6. Символьный вывод
Наряду с численным выводом, в Mathcad имеется возможность символьного, или аналитического, вычисления значения выражения. Для символьных вычислений имеется ряд специальных средств, которые будут детально рассмотрены позднее (см. гл. 5), самое простое из них — это оператор символьного вывода (symbolic evaluation). Он обозначается символом -» и в большинстве случаев применяется точно так же, как оператор численного вывода, однако внутреннее различие между действием этих двух операторов огромно. Если численный вывод — это в обычном смысле этого слова «запрограммированный» расчет по формулам и численным методам, скрытый от глаза пользователя, то символьный вывод — результат работы системы искусственного интеллекта, встроенной в Mathcad и называемой символьным процессором. Работа символьного процессора также невидима (и, чаще всего, даже трудно представима) пользователю и заключается в анализе самого текста математических выражений. Конечно, гораздо более узкий круг формул можно рассчитать символьно, хотя бы потому, что, вообще говоря, относительно не такая большая часть математических задач допускает аналитическое решение.
Чтобы попытаться вычислить символьно математическое выражение, например В sin(arcsin(С Х)), где В,С,Х — некоторые переменные:
- Введите это выражение: В sin(asin(С Х)).
- Введите оператор символьного вывода сочетанием клавиш +, либо нажатием соответствующей кнопки (рис. 3.4) на панели Symbolic (Символика) или Evaluation (Выражения).
Рис. 3.4. Кнопка вставки оператора символьного вывода
После этого справа от символа оператора символьного вывода появится определенное аналитически значение выражения (листинг. 3.10) либо сообщение об ошибке «No answer found» (Ответ не найден). Если символьному процессору Mathcad не удается аналитически упростить выражение, то оно будет выдано справа от знака -» в том же виде, что и слева.
Листинг 3.10. Символьный вывод выражения
Листинг 3.11. Символьный вывод выражений, которое не удалось упростить
Присмотритесь внимательнее к листингам 3.10 и 3.11: для символьного вывода не требуется предварительно определять переменные, входящие в левую часть выражения! Если же переменным были все-таки присвоены ранее некоторые значения, символьный процессор просто подставит их в упрощенную формулу и выдаст результат с учетом этих значений (см. в качестве примера два следующих листинга — 3.12 и 3.13).
Точно так же, как рассчитываются численно значения функций, можно вычислять их и с помощью символьного процессора. Сравните соответствующие результаты, которые представлены в листинге 3.12 (конечно, символьный и численный ответы равны: 9 cos(8)=-1.31). Аналогично можно «символьно выводить значения переменных. Например, присвоить некоторой переменной значение функции или сложного выражения (листинг 3.13, вторая строка) и затем вывести значение переменной в символьном виде.
Листинг 3.12. Численный и символьный вывод значения функции
Листинг 3.13. ЧислвйныЙ и символьный вывод
Как показывают приведенные примеры, преимущество символьных вычислений заключается в выдаче аналитического результата, который для математика часто является более ценным. Поэтому, исходя из специфики конкретных задач, решайте, стоит ли наряду с численными расчетами попытаться получить и символьное решение.
3.1.7. Допустимые имена переменных и функций
В заключение перечислим, какие символы можно, а какие нельзя применять в именах, которые пользователь дает переменным и функциям, и перечислим ряд ограничений на присваивание имен. Допустимые символы:
- большие и маленькие буквы — Mathcad различает регистр: так, имена х и х определяют разные переменные. Кроме того, Mathcad различает и шрифт, например имена х и х воспринимаются как разные;
- числа от 0 до 9;
- символ бесконечности (клавиши + + );
- штрих (клавиши + );
- греческие буквы — они вставляются с помощью панели Greek (Греческие символы);
- символ подчеркивания;
- символ процента;
- нижний индекс.
С осторожностью используйте нижний индекс в определении имен переменных и функций, не путая его с индексом векторной переменной. Чтобы ввести имя с нижним индексом, например, K max: введите букву «K», затем точку «.», после чего линии ввода опустятся чуть ниже, и только затем сам нижний индекс max.
Теперь рассмотрим ограничения на имена переменных и функций:
- имя не может начинаться с цифры, символа подчеркивания, штриха или процента;
- символ бесконечности должен быть только первым в имени;
- все буквы в имени должны иметь один стиль и шрифт;
- имена не могут совпадать с именами встроенных функций, констант и размерностей, например sin или TOL. Тем не менее, допускается их переопределение, но тогда одноименная встроенная функция больше не будет использоваться по первоначальному назначению;
- Mathcad не различает имен переменных и функций: если сначала определить функцию f (х), а потом переменную f, то в оставшейся части документа будет утеря* доступ к функции f (x).
В некоторых случаях желательно использовать имена переменных и функций, содержащие символы операторов Mathcad или другие символы, которые нельзя вставлять в имена непосредственно. Для этого существуют две возможности.
Во-первых, имя, составленное из любых символов и заключенное в квадратные скобки, Mathcad будет воспринимать корректно (рис. 3.5, сверху). Например, чтобы ввести имя :
- Нажмите клавиши + + — появится пара квадратных скобок с местозаполнигелем внутри.
- Введите в местозаполяитель последовательность любых символов, например a+b.
Рис. 3.5. Специальные символы в именах переменных
Во-вторых, если Вас не устраивает наличие квадратных скобок в имени, то вставить в него специальные символы можно чуть более сложным способом. Например, для ввода имени a+b:
- Введите первый символ (а), который должен быть допустимым для имен Mathcad.
- Нажмите клавиши + + для перехода в специальный «текстовый» режим редактирования.
- Введите последовательность любых символов (+).
- Еще раз нажмите клавиши + + , чтобы вернуться в обычный режим редактирования. Теперь можно продолжать ввод допустимых символов в имя (b).
Результат этих действий показан в нижней строке рис. 3.5. Если требуется, чтобы имя начиналось со специального символа (средняя строка рис. 3.5), то необходимо выполнить все пункты 1-4, вводя в начале имени произвольный допустимый символ, а по завершении ввода просто стирая его.
Каждый оператор в Mathcad обозначает некоторое математическое действие в виде символа. В полном согласии с терминологией, принятой в математике, ряд действий (например, сложение, деление, транспонирование матрицы и т. п.) реализован в Mathcad в виде встроенных операторов, а другие действия (например, sin, erf и т. п.) — в виде встроенных функций. Каждый оператор действует на одно или два числа (переменную или функцию), которые называют операндами. Если в момент вставки оператора одного или обоих операндов не хватает, то недостающие операнды будут отображены в виде местозаполнителей. Символ любого оператора в нужное место документа вводится одним из двух основных способов:
- нажатием соответствующей клавиши (или сочетания клавиш) на клавиатуре;
- нажатием указателем мыши соответствующей кнопки на одной из математических панелей инструментов.
Напомним, что большинство математических панелей содержат сгруппированные по смыслу математические операторы, а вызвать эти панели на экран можно нажатием соответствующей кнопки на панели Math (Математика).
Везде в этом разделе будем рассматривать только второй способ вставки оператора Те же, кто предпочитает использовать клавиатуру, найдут перечень горячих клавиш в приложении 2.
Выше мы рассмотрели особенности применения трех операторов: присваивания (см. разд. 3.1.2), численного (см. разд. 3.1.5) и символьного вывода (см. разд. 3.1.6). Разберем в данном разделе действие прочих операторов Mathcad и возможности определения операторов пользователя.
3.2.1. Арифметические операторы
Операторы, обозначающие основные арифметические действия, вводятся с панели Calculator (Калькулятор), показанной на рис. 3.6:
- сложение и вычитание: + — (листинг 3.14);
- умножение и деление: / + (листинг 3.15);
- факториал: ! (листинг 3.16);
- модуль числа: |х| (листинг 3.16);
- квадратный корень: (листинг 3.17); степени: (листинг 3.17);
- возведение х в степень у: х y (листинг 3.17);
- изменение приоритета: скобки (листинг 3.18);
- численный вывод: = (все листинги).
Рис. 3.6. Панель Calculator
Листинг 3.14. Операторы сложения, вычитания и отрицания
Листинг 3.15. Операторы деления и умножения
Листинг 3.16. 0ператор факториала и модуля
Листинг 3.17. Операторы извлечения корня и возведения в степень
Листинг 3.18. Оператор изменения приоритета ()
Как видно, с помощью этой панели можно ввести не только перечисленные операторы, но и их часто используемые комбинации, например, возведение экспоненты в степень, смешанное произведение и деление, а также мнимую единицу и число я. Заметим, что допускается запись оператора деления как в одну, так и в две строки, что обеспечивается наличием двух соответствующих кнопок на панели Calculator.
Напомним, что в редакторе Mathcad можно выбирать отображение оператора умножения (см. разд. «Управление отображением некоторых операторов» гл. 2). Для того чтобы поменять его:
- Щелкните правой кнопкой мыши на выражении, содержащем оператор умножения.
- Выберите первый пункт появившегося контекстного меню View Multiplication As (Представление умножения).
- В подменю выберите пункт, соответствующий стилю представления умножения: в виде обычной точки (Dot), точки с уменьшенным расстоянием от него до сомножителей (Narrow Dot), толстой точки (Large Dot), крестика (X), без символа с небольшим расстоянием между сомножителями (Thin Space), вообще вместе (No Space). Чтобы просмотреть, как будет выглядеть выражение в двух последних представлениях, нужно снять с него выделение. Чтобы вернуть представление по умолчанию, выберите в подменю контекстного меню пункт Default.
Некоторых операторов, например таких, как оператор комплексного сопряжения, на панелях инструментов нет (листинг 3.19). Его приходится вводить исключительно с клавиатуры нажатием клавиши в пределах математической области.
Листинг 3.19. Оператор комплексного сопряжения
3.2.2. Вычислительные операторы
Вычислительные операторы вставляются в документы при помощи панели инструментов Calculus (Вычисления). При нажатии любой из кнопок в документе появляется символ соответствующего математического действия, снабженный несколькими местозаполнителями. Количество и расположение местозаполнителей определяется типом оператора и в точности соответствует их общепринятой математической записи. Например, при вставке оператора суммы (рис. 3.7) необходимо задать четыре величины: переменную, по которой надо произвести суммирование, нижний и верхний пределы, а также само выражение, которое будет стоять под знаком суммы (пример заполненного оператора суммы см. ниже в листинге 3.22).
Для того чтобы вычислить неопределенный интеграл, следует заполнить два местозаполнителя: подынтегрального выражения и переменной интегрирования.
Рис. 3.7. Вставка оператора суммирования
После ввода какого-либо вычислительного оператора имеется возможность вычислить его значение либо численно, нажатием клавиши , либо символьно, с помощью оператора символьного вывода.
Перечислим основные вычислительные операторы и приведем простейшие примеры их применения:
- дифференцирование и интегрирование;
- производная (листинг 3.20);
- N-Я производная (листинг 3.20);
- определенный интеграл (листинг 3.21);
- неопределенный интеграл (листинг 3.21).
- сумма (листинг 3.22);
- произведение (листинг 3.22);
- сумма ранжированной переменной (листинг 3.23);
- произведение ранжированной переменной (листинг 3.23).
- двусторонний;
- левый;
- правый.
Листинг 3.20. Операторы вычисления производных
Листинг 3.21. Операторы интегрирования
Листинг 3.22. Операторы суммирования и вычисления произведения
Листинг 3.23. Операторы суммировани и вычисления произведения
О назначении и особенностях использования ранжированных переменных будет рассказано в следующей главе (см. разд. «Ранжированные переменные» гл. 4).
Листинг З.24. Операторы символьного вычисления пределов
В отличие от других, операторы поиска предела могут быть вычислены только символьно (см. гл. 5).
Операторы суммирования и вычисления произведения фактически являются более удобной записью операторов + и х с большим количеством операндов. А вот вычислительные операторы поиска производных и интегралов существенно отличаются от операторов умножения и сложения тем, что реализованы на основе определенных численных методов, которые в скрытой (невидимой для пользователя) форме запускаются вычислительным процессором Mathcad. При численном расчете интегралов и производных необходимо, хотя бы в общих чертах, представлять принцип работы соответствующих алгоритмов, чтобы избежать ошибок и неожиданностей при получении результатов (численным методам интегрирования и дифференцирования посвящена гл. 7).
Рис. 3.8. Поиск бесконечного ряда
Важно отметить, что имеется возможность вычислять интегралы с одним или обоими бесконечными пределами, а также в символьной форме искать значения бесконечных пределов, сумм (рядов) и произведений. Для удобства ввода кнопка с символом бесконечности помещена на ту же панель инструментов Calculus (Вычисления). Пример вставки символа бесконечности в задаче поиска бесконечного ряда приведен на рис. 3.8.
3.2.3. Логические операторы
Результатом действия логических, или булевых, операторов являются только числа 0 (если логическое выражение, записанное с их помощью, истинно) или 1 (если логическое выражение ложно). Чтобы вычислить значение логического выражения, например 1=1 (рис. 3.9):
- Вставьте с панели Boolean (Булевы операторы) соответствующий оператор =.
- В появившиеся местозаполнители вставьте операнды (две единицы).
- Нажмите клавишу , чтобы получить ответ.
Рис. 3.9. Вставка логического оператора
Получается абсурдное на первый взгляд выражение i«i=i. Однако на самом деле все правильно. Справа от оператора вывода записано логическое выражение 1*1 (обратите внимание, что логический знак равенства выглядит по-другому, нежели обычный), которое является истинным. Поэтому значение данного выражения равно 1, что и показано справа от знака равенства.
Перечислим логические операторы:
- больше (Greater Than);
- меньше (Less Than);
- больше или равно (Greater Than or Equal);
- меньше или равно (Less Than or Equal);
- равно (Equal);
- не равно (Not Equal to);
- и (And);
- или (Or);
- исключающее или (Exclusive or);
- отрицание (Not).
Операнды в логических выражениях могут быть любыми числами. Однако если оператор по смыслу применим только к 0 и 1, то любое неравное нулю число по умолчанию принимается равным 1. Но в результате все равно может получиться либо 0, либо 1. Например, ¬ (-0.33)=0.
Примеры действия логических операторов приведены в листингах 3.25 и 3.26.
Листинг 3.25. Операторы сравнения.
Листинг 3.26. Булевы операторы.
Логические операторы чрезвычайно важны при записи подлежащих решению алгебраических уравнений и неравенств в приемлемой для Mathcad форме.
3.2.4. Матричные операторы
Матричные операторы предназначены для совершения различных действий над векторами и матрицами. Поскольку большинство из них реализует численные алгоритмы, о них будет подробно рассказано в части III (см. гл. 9).
3.2.5. Операторы выражения
Почти все вычислительные операторы были рассмотрены выше (см. разд. 3.1). Они сгруппированы на панели Evaluation (Выражения).
- Оценить численно (Evaluate Numerically) (см. разд. 3.1.5)
- Вычислить символьно (Evaluate Symbolically) (см. разд. 3.1.6)
- Присваивание (Definition) (см. разд. 3.1.2)
- Глобальное присваивание (Global Definition)
Рассмотрим различие между операторами обычного присваивания и глобального присваивания (процесс его вставки в документ показан на рис. 3.10). Для того чтобы вычислить выражение, содержащее некоторую переменную или функцию, необходимо, чтобы этой переменной ранее в документе было присвоено какое-либо значение. Иначе будет выдаваться сообщение об ошибке (рис. 3.11). Однако если в любой части документа (например в самом низу) вставить оператор глобального присваивания, то переменная будет определена в любой части документа (листинг 3.27).
Листинг 3.27. Действие операторов присваивания и глобального присваивания
Рис. 3.10. Кнопка глобального присваивания на панели Evaluation
Рис. 3.11. Обычное присваивание сказывается только на нижеследующей части документа
Как видно из листинга 3.27, обычное, или локальное, присваивание переменной х действует от момента х:=10 до момента глобального присваивания х = 5. Вообще говоря, Mathcad анализирует документы на предмет присваивания переменных в два прохода: сначала распознаются все операторы глобального присваивания, и все выражения в документе сверху вниз и слева направо вычисляются в соответствии с ними, а при втором проходе в том же порядке анализируются операторы локального присваивания, и все выражения вычисляются с поправкой на них. Приведем важный пример взаимодействия глобального и локального присваивания (листинг 3.28).
Листинг 3.28. Взаимодействие глобального и локального присваивания
Обратите внимание, что, несмотря на локальное присваивание переменной x:=10 в третьей строке листинга, значение переменной у вычисляется все-таки в соответствии с глобальным значением х = 5, поскольку сама переменная y глобальным образом определена через переменную х.
Аккуратнее относитесь к определению глобальных переменных и, во избежание путаницы, старайтесь не переопределять их локально. Применяйте глобальное присваивание только для определения констант и, по возможности, избегайте случаев, когда оператор вывода предшествует оператору глобального присваивания для улучшения читаемости документов.
Точно так же как Вы глобально присваиваете значение переменной, допускается глобально определять функции (листинг 3.29).
Листинг 3.29. Глобальное определение функции пользователя
Оператор глобального присваивания можно отображать не только в виде тождественного равенства, но и как обычный знак равенства. Для этого вызовите на операторе контекстное меню и в подменю пункта View Definition As выберите пункт Equal (Равенство).
3.2.6. Создание оператора пользователя
Запросы взыскательного пользователя могут отнюдь не исчерпываться набором встроенных операторов Mathcad. Для вставки в документы заранее созданных операторов пользователя применяется панель Evaluation (Выражения).
Выбор имени оператора
Оператор пользователя может иметь абсолютно любое имя (см. ранее раздел «Имена, содержащие операторы и специальные символы» этой главы). Однако, исходя из смысла операторов, логично давать им имена в виде символов. Это удобно делать с помощью коллекции символов, находящейся в справочной информации Mathcad. Выберите в верхнем меню Help / QuickSheets (Справка / Быстрые шпаргалки) и войдите затем в самый последний раздел Extra Math Symbols (Дополнительные символы) открывшегося содержания Шпаргалок. Там Вы увидите целую коллекцию символов, любой из которых можно просто перетащить указателем мыши в нужное место документа.
Присваивать оператору некоторое действие следует точно так же, как функции пользователя.
Создание бинарного оператора
Чтобы создать бинарный оператор, например реализующий действие х у 2:
- Введите имя оператора, например, bin.
- Наберите знак скобки , затем список из двух операндов через запятую, , , , затем закрывающую скобку .
- Введите оператор присваивания .
- Введите выражение, зависящее от операндов, действие которого необходимо присвоить оператору (х-у 2).
Создание унарного оператора
Унарный оператор создается точно так же, только вместо двух операндов, отделенных запятой, Вам следует ввести лишь один операнд. Например, чтобы создать оператор с именем %, реализующий перевод доли числа в проценты и сводящийся к умножению его на 100 (листинг 3.30):
- Введите имя оператора. Для этого нажмите клавиши , + + + , , затем снова + + , потом сотрите в имени букву «а».
- После знака % наберите скобку «(«, далее «х11, затем еще одну скобку «)».
- .
- Введите выражение х100.
Листинг 3.30. Создание унарного оператора пользователя
Использование бинарного оператора
Возможны два вида вставки пользовательского бинарного оператора в документ, отличающиеся только отображением в документе. Чтобы вставить оператор в форме графа (или дерева):
- Нажмите кнопку Tree Operator (Оператор дерево) на панели Evaluation (Выражения) (рис. 3.12, справа).
- В появившиеся местозаполнители введите имя оператора (на вершине графа) и значения операндов (в ответвления дерева).
- Введите оператор присваивания, нажав клавишу .
Результат действия оператора показан на рис. 3.12, внизу слева.
Кроме древовидной формы оператора, допускается использование его в виде последовательности «операнд- имя оператора- другой операнд» (рис. 3.12, вторая строка слева). Чтобы ввести такую форму оператора, следует нажать соседнюю кнопку Infix Operator (Оператор внутри) с изображением xfy.
Рис. 3.12. Применение пользовательского бинарного оператора
Использование унарного оператора
Вставка унарного оператора совершенно аналогична, только вместо двух операндов требуется ввести один (рис. 3.13). Унарный оператор вставляется нажатием кнопки Prefix Operator (Оператор перед) на панели Evaluation (Выражения) либо кнопки Postfix Operator (Оператор после). Первый путь проиллюстрирован правой частью рис. 3.13 (в момент вставки) и результатом действия оператора (слева), а результат вставки оператора по второму пути — левой нижней строкой того же рисунка
Рис. 3.13. Применение пользовательского унарного оператора
3.3. Управление вычислениями
Документ Mathcad — это в полном смысле этого слова компьютерная программа, а сама система Mathcad — настоящая система программирования, правда ориентированная на математика, а не на профессионального программиста. Большинство других сред программирования (знакомых читателю по реализации таких языков, как Си, Фортран, Бейсик и т. п.) разделяют редактирование кода программ и их выполнение, которое можно вызвать предназначенными для этого командами. В Mathcad и код программы, и результат их выполнения объединены в одном документе. Тем не менее, функции редактирования формул и их расчеты выполняются раздельно, и пользователь имеет возможность управлять всеми важнейшими опциями вычислений.
3.3.1. Режимы вычислений
Все примеры, которые мы рассматриваем в этой книге, неявно предполагают, что включен автоматический режим вычислений. Он включается по умолчанию при создании пустого документа, поэтому если вводятся выражения, содержащие операторы вывода, они вычисляются немедленно. Вообще говоря, имеется два режима вычислений:
- автоматический режим (automatic mode) — все вычисления проводятся автоматически по мере ввода формул;
- ручной режим (manual mode) — начало вычислений каждой формулы или всего документа производится пользователем.
Режим вычислений можно выбрать с помощью команды Tools / Calculate / Automatic Calculation (Сервис / Пересчитать / Считать автоматически), как показано на рис. 3.14. Если в этой строке меню установлен флажок проверки, значит, включен автоматический режим, если флажка нет, то редактируется документ в ручном режиме вычислений. Чтобы сменить режим, просто выберите этот пункт меню (например, нажав кнопку мыши в ситуации, показанной на рис 3.14, включите ручной режим).
Режим вычислений устанавливается независимо для каждого документа Одновременно могут быть открыты несколько документов, вычисляемых в различных режимах
Преимущества и недостатки каждого режима очевидны. С одной стороны, автоматические вычисления упрощают работу с документом, поскольку результаты расчетов появляются в реальном времени, и пользователь имеет возможность анализировать их сразу. С другой стороны, если вычисления сложные, то они могут отнимать много времени (что особенно заметно на компьютерах с не слишком мощным процессором и небольшим объемом оперативной памяти). Поэтому зачастую, чтобы продолжить редактирование документа, требуется довольно длительное ожидание завершения расчетов В частности, если поменять какое-либо выражение в начале большого документа, которое влияет на последующие вычисления, то все они пересчитываются заново. В таких случаях часто удобнее редактировать текст в ручном режиме, а вычисления включать по мере необходимости.
Рис. 3.14. Выбор режима вычислений
3.3.2. Прерывание вычислений
Mathcad осуществляет вычисления документа, как это принято в большинстве сред программирования: сверху вниз и слева направо. Пока очередное выражение находится в процессе расчета (вычислительным или символьным процессором), оно выделяется рамкой зеленого цвета (рис. 3.15), а любые действия пользователя по дальнейшему редактированию документа блокируются. Если у вас не слишком быстрый компьютер, а формулы достаточно сложные, то можно наблюдать, как зеленая рамка перескакивает с одного выражения на другое
Чтобы прервать затянувшийся процесс вычислений, нажмите клавишу Появится диалоговое окно, показанное на рис. 3.16, в котором нужно подтвердить прерывание вычислений (ОК). В этом случае выражения, которые Mathcad не успел вычислить, будут помечены в документы красным цветом. Прерванные вычисления возобновляются нажатием клавиши или командой Tools / Calculate / Calculate Now (Математика / Пересчитать / Пересчитать)
Рис. 3.15. Процесс вычисления выражения
Рис. 3.16. Диалоговое окно прерывания вычислений
3.3.3. Вычисления в ручном режиме
Если флажок в строке команды Tools / Calculate / Automatic Calculation (Сервис / Пересчитать / Считать автоматически) снят, пользователь должен запускать вычисления самостоятельно
- Для того чтобы вычислить все формулы во всем документе, выполните команду Tools / Calculate / Calculate Worksheet (Математика / Пересчитать / Пересчитать все).
- Для вычисления всех формул в видимой части документа выберите пункт Tools / Calculate / Calculate Now (Сервис / Пересчитать / Пересчитать) либо нажмите клавишу , либо щелкните на кнопке с изображением знака равенства (Calculate) на стандартной панели инструментов
- Прервать вычисления можно обычным образом, нажав клавишу .
Управлять размером видимой части документа можно при помощи изменения масштаба отображения документа
При редактировании текста в ручном режиме не выполняются ни вычисления, ни построение графиков, а соответствующие места в выражениях формально отмечаются местозаполнителями (рис. 3.17.)
Рис. 3.17. Чтобы запустить вычисления в ручном режиме, нажмите кнопку Calculate
3.3.4. Отключение вычисления отдельных формул
Mathcad позволяет отключить вычисление какой-либо формулы. При этом она не будет влиять на последующие вычисления. Чтобы не вычислять определенную формулу в документе:
- Щелкните правой кнопкой мыши на формуле.
- Выберите в контекстном меню пункт Disable Evaluations (Выключить вычисления), как показано на рис. 3.18.
Эквивалентный способ выключения вычисления отдельной формулы заключается в вызове диалогового окна Properties (Свойства) через одноименный пункт контекстного меню (см. рис. 3.18) или главного меню Format (Формат). В диалоге Properties следует перейти на вкладку Calculation (Вычисления) и установить там флажок Disable Evaluations (Выключить вычисления).
Результат выключения формулы из процесса вычислений проиллюстрирован листингом 3.31. На нем выключен второй из операторов присваивания, о чем можно судить по наличию черного квадрата сразу за формулой. Соответственно, в последней строке выведенное значение переменной х «не чувствует» выключенного присваивания и остается равным 3.
Листинг 3.31. Вычисление второго оператора присваивания выключено
Рис. 3.18. Отключение вычисления формулы с помощью контекстного меню
3.3.5. Оптимизация вычислений
Отличительная черта новых версий Mathcad — улучшенные возможности ускорения численных вычислений за счет применения элементов символьной математики. Непосредственно перед численным расчетом Mathcad автематически пытается упростить выражение, используя символьный процессор. Это называется оптимизацией. За счет того что от версии к версии качество работы символьного процессора улучшается, символьное преобразование зачастую существенно ускоряет расчеты. Режим оптимизации включается либо в документе целиком, либо для отдельных формул.
Чтобы включить или отключить режим оптимизации всех выражений в активном документе, выберите команду Tools / Optimize / Worksheet (Сервис / Оптимизация / Документ), как показано на рис. 3.19. Содержание документа, изображенного на этом же рисунке, помогает понять математический смысл режима оптимизации: для ускорения вычисления нижнего (определенного) интеграла выгодно использовать его аналитическое решение, определенное символьным процессором.
Чтобы изменить режим оптимизации для отдельной формулы, не меняя выбранного режима для остальных выражений документа, выделите эту формулу линиями ввода и выберите в верхнем меню Tools / Optimize / Equation (Сервис / Оптимизация / Уравнение).
Рис. 3.19. Режим оптимизации вычислений
3.3.6. Диалоговое окно Worksheet Options
Наравне с изложенными способами установки режимов вычислений, их также удобно устанавливать для всего документа на вкладке Calculations (Вычисления) диалогового окна Worksheet Options (Опции документа), вызываемого с помощью команды Tools / Worksheet Options (Сервис / Опции документа). Три флажка задают включение соответствующего режима вычислений (рис. 3.20).
- Recalculate automatically (Пересчитать автоматически) — включение режима автоматических вычислений.
- Use strict singularity checking for matrices (Использовать проверку матриц на сингулярность) — опция, появившаяся в версии Mathcad 2001, которая важна при некоторых операциях с матрицами. Она означает проведение дополнительной проверки на сингулярность матрицы перед использованием численных алгоритмов, что позволяет, во избежание неправильного применения численного метода, выдать заранее сообщение об ошибке, если матрица сингулярная.
- Optimize expressions before calculating (Оптимизировать выражения перед вычислением) — включение режима оптимизации.
- Use exact equality for Boolean comparisons (Использовать точное равенство для логического сравнения) — когда флажок выбран, применяется жесткий критерий точного равенства чисел (точнее, числа при сравнении считаются равными, если отличаются по модулю менее чем на 10 -307). Если флажок снят, используется более мягкий критерий (относительное различие чисел по модулю менее чем на 10 -12).
Рис. 3.20. Управление режимом вычислений в диалоговом окне Worksheet Options
Помимо флажков проверки, имеется также пара переключателей, которая позволяет реализовать новый режим ускоренных вычислений (higher speed calculation). Он включается выбором переключателя Higher speed calculation (Ускоренные вычисления), изображенного на рис. 3.20. Чтобы отключить режим ускоренных вычислений, выберите переключатель Backward compatibility (Обратная совместимость). В этом случае вычисления будут проводиться без дополнительной оптимизации по скорости, в точности так же, как в предыдущих версиях (Matvcsd 2000 и ниже) Необходимость таких расчетов может возникнуть, если вдруг Вы столкнулись с сообщениями об ошибках в документах, созданных в предыдущих версиях Mathcad и корректно в них работающих.
3.4. Сообщения об ошибках
Когда процессор Mathcad по тем или иным причинам не может вычислить выражение, он вместо ответа выдает сообщение об ошибке (рис. 3.21). Если курсор находится вне формулы с ошибкой, то в ней имя функции или переменной, которая вызвала ошибку, отмечается красным цветом (сверху на рис. 3.21). При щелчке на такой формуле под ней появляется текстовое сообщение о типе ошибки, обрамленное черным прямоугольником (рис. 3.21, снизу).
Рис. 3.21. Сообщение об ошибке
Если некоторые выражения вызывают ошибку, они просто игнорируются, а следующие выражения в документе по-прежнему вычисляются. Конечно, если формулы, вызвавшие ошибку, влияют на значения нижеследующих формул, то они будут также интерпретированы как ошибочные. Поэтому, встречая в документе сообщения об ошибках, найдите сначала самое первое из них. Часто ее устранение позволяет избавиться и от последующих ошибок.
Как бы хорошо вы ни овладели системой Mathcad, сообщения об ошибках все равно будут появляться в документах. Они могут быть связаны как с орфографическими ошибками, так и с более серьезными внутренними причинами, требующими знания численных алгоритмов расчетов. Искусство математика во многом состоит в умении анализировать ошибочные ситуации и находить правильный выход из них.
Возможности Mathcad можно в полной мере оценить только при использовании переменных и функций.
Два знака равенства
В выражениях Вам необходимо использовать числа (константы), переменные, операторы и знаки равенства. В повседневной жизни мы используем знак равенства = для различных операций. Mathcad, однако, различает эти операции. Наиболее важные из них:
- определение (присвоить значение) – вводится через двоеточие [:]
- вычисление – вводится через знак равенства [=]
Оператор определения не менее важен, чем оператор вычисления. Значение выражения y можно отобразить только после присвоения ему какого-либо значения. x и y здесь являются переменными .
Введите следующие выражения:
Эти два знака равенства принципиально различны, поэтому их не следует путать.
Поместите курсор перед числом 4 в первом выражении:
Удалите число 4 с помощью клавиши и введите 5. Щелкните по пустой области и убедитесь, что результат третьего выражения изменился на 25:
Попробуйте удалить число 25. Вы увидите, что при первом нажатии число станет красным, а при повторном нажатии удалится 25 и знак равенства:
Использование переменных
Введите следующие выражения:
Попробуйте изменить значение x на 100, 0.5, -4 и 0:
Первые два случая дадут в результате число. При -4 получится мнимое число. Да, Mathcadможет работать и с такими числами. При нуле программа выдаст ошибку, а результат будет обведен красным. Если Вы щелкните по неправильному выражению, то получите описание, что может быть не так:
Теперь о том, какие имена можно и нельзя использовать для переменных. Есть несколько правил: имя переменной не может начинаться с цифры и в имени переменной нельзя использовать пробелы и знаки операторов. Имена переменных могут начинаться:
- с любой строчной или прописной буквы
- другие символы, если они не являются операторами
- символы с вкладки Математика –> Операторы и символы –> Символы
- символы из Таблицы символов Windows
Вот несколько примеров:
Переменные можно использовать, только если они были определены ранее. «Ранее» означает, что объявление переменной должно располагать выше или левее выражения, где она используется. Если переменная не объявлена, появится сообщение об ошибке:
Подстрочные индексы
В Mathcad есть два различных вида подстрочных индекса для переменных:
- Описательный подстрочный индекс.
- Индекс массива (матрицы).
Чтобы набрать описательный подстрочный индекс, введите имя переменной, нажмите и наберите подстрочный индекс:
Переменная с описательным подстрочным индексом – это обычная переменная, со своим именем. Индекс массива существенно отличается от него. Этот индекс можно ввести, нажав открывающую квадратную скобку [ после имени переменной. У переменной может быть один или два индекса массива:
Индекс массива должен быть числом. При этом не следует путать виды подстрочных индексов, т.к. они выглядят практически идентично:
Разница видна при щелчке мышью по выражению:
У переменной может быть сразу описательный индекс и индекс массива. Сначала всегда идет описательный индекс:
Функции
Переменные можно использовать, только если они были определены ранее. Однако есть одно важное исключение – определение функции. Можно определить собственную функцию, как на примере ниже:
Переменная a является локальной для функции. Она не определена за пределами функции:
Если Вы определили a до определения функции, значение a не будет изменено в процессе вычисления значения функции.
Внимание: если Вы дали переменной такое же имя, как и функции, Вы больше не сможете использовать эту функцию. У переменной и функции должны быть разные имена:
Этой проблемы можно избежать, задав для переменной и функции разные обозначения. Об этом мы поговорим в уроке 10 «Обозначения и единицы измерения».
Функции могут содержать две и более переменной:
Здесь значения переменных x и y также не изменяются при вычислении функции.
Встроенные функции
В Mathcad есть большое число встроенных функций. Зайдите на вкладку Функции:
Список всех функций можно увидеть, щелкнув по кнопке Все функции.
Заметьте, что тригонометрические функции принимаю в качестве аргумента угол в радианах, а не в градусах. Для использования градусов используйте символ с вкладки Математика –> Операторы и символы –> Символы:
Математика в тексте
В текст можно вставить математическую область. Таким образом, можно использовать над- и подстрочные символы в тексте. Для этого при редактировании текстовой области нажмите кнопку Математика с вкладки Математика –> Области:
Резюме
- В Mathcadесть два различных знака равенства: определить:= и вычислить =.
- Имя переменной обычно начинается с буквы; цифры нельзя использовать в начале переменной. Также можно использовать символы с клавиатуры, с панели Математика –> Операторы и символы –> Символы, с Таблицы символов Windows.
- Чтобы определить переменную и задать ей значение:
- щелкните мышью на пустую область;
- введите имя переменной;
- нажмите [:] для ввода оператора определения;
- введите значение, которое Вы хотите присвоить.
- Чтобы дать переменной описательный подстрочный индекс:
- нажмите ;
- введите подстрочный индекс.
- Чтобы дать переменной индекс массива:
- щелкните мышью в конце имени переменной;
- нажмите открывающую квадратную скобку [;
- введите число – подстрочный индекс.
- Переменную можно использовать ниже или правее места, где она определена.
- Имя функции следует набирать по тем же правилам, что и имя переменной, но ввод имени функции заканчивается вводом [(]. В скобках содержатся аргументы функции.
- Переменные в функциях – локальные, т.е. они определены только при использовании функции.
- Математическую область можно встроить в текст. Эту возможность следует использовать, если необходимо вставить над- и подстрочные символы в текст.
MathCad является мощной системой для работы с формулами, числами, текстами и графиками и предоставляет пользователю возможности электронной таблицы и интерфейс WYSIWYG текстового процессора. Ввод уравнений в MathCad полностью совпадает с привычной типографской математической записью.
Как и в электронных таблицах, любое изменение содержимого рабочего документа вызывает обновление всех зависимых результатов и перерисовку графиков. MathCad позволяет легко читать данные из файлов и подвергать их любой математической обработке: от сложения до вычисления интегралов и производных, обращения матриц и т.д.
С помощью формул MathCad можно решить почти любую математическую задачу аналитически (символьно) либо численно. Объединяя в одном документе текст, графику и математические выкладки, MathCad облегчает понимание самых сложных вычислений.
Ниже приведен краткий список основных характеристик MathCad.
Свободная форма записи, подобная классной доске;
Возможность комбинирования текста, математических выкладок, графиков и рисунков в любом месте документа;
Вырезка и вставка уравнений, текста, графики;
Контекстная интерактивная система справок.
Точность представления чисел — 15 верных десятичных цифр;
Двоичные, восьмеричные, десятичные, шестнадцатеричные числа;
Основные встроенные алгоритмы:
решения систем уравнений и неравенств;
работы с комплексными числами, переменными, функциями;
вычисления сумм, произведений, производных, интегралов;
интерполяции и аппроксимации (линейная, кубическими сплайнами);
быстрых преобразований Фурье;
решения дифференциальных уравнений;
работы с матрицами.
Основные встроенные функции:
теории чисел и комбинаторика;
регрессии и сглаживания;
Символьное дифференцирование и интегрирование;
Обращение, транспонирование матриц;
Разложение выражений на множители;
Многообразие типов графиков (декартовы, полярные координаты; построение поверхностей, линий уровня; картины векторных полей; гистограммы; точечные графики);
Оси графиков могут иметь линейный или логарифмический масштаб;
Возможность выбора типа, толщины и цвета линии, используемой для построения графика;
Построение графиков поверхностей в трех измерениях с различными ракурсами просмотра и в разных масштабах.
ХАРАКТЕРИСТИКА ТЕКСТА И РАБОЧЕГО ДОКУМЕНТА
Размещение текста в любом месте рабочего документа;
Возможность использования шрифтов различных стилей в любой текстовой области;
1.2 Отличия MathCad 2000 от предыдущих версий
Кардинально переработанный и приближенный к интерфейсу MS Office пользовательский интерфейс;
Возможность выделения частей математических выражений буксировкой мышью;
Быстрое построение (QvickPlot) двумерных и трехмерных графиков;
Новая палитра символьной математики с расширенными операторами;
Более удобный и наглядный синтаксис символьных операций;
Новые операторы программирования on error, continue, return;
Возможность применения в программах операторов символьных операций;
Новый тип данных – строковые;
Появление оперативного центра ресурсов (Resource Center) вместо быстрых “шпаргалок” QuiekSheet;
Около 50 новых математических функций, из которых следует особо отметить функции нахождения максимумов и минимумов maximize, minimize, а также функцию odesolve решения дифференциальных уравнений;
улучшенный блок решения систем нелинейных уравнений (теперь их число может достигать 200);
Возможность выбора численного метода решения некоторых задач (например, численного интегрирования);
Улучшенные средства форматирования текста;
Функции редактирования Find и Replace (найти и заменить);
Возможность записи документов в формате HTML;
Существенно улучшенные средства для работы с трехмерными графиками.
Все это дает пользователю новые возможности и новые удобства в работе с системой MathCad, подтверждая её репутацию как одной из самых массовых и удобных в работе математических систем.
Определение переменных в Mathcad
Чтобы определить переменную, достаточно ввести её имя и присвоить ей некоторое значение, для чего служит оператор присваивания.
1. Введите в желаемом месте документа имя переменной.
2. Введите оператор присваивания с помощью клавиши или нажатием соответствующей кнопки Definition (Присваивание) на панели инструментов Calculator (Арифметика) или Evaluation (Выражения).
3. Введите в появившийся фрейм требуемое значение переменной.
Кнопка оператора присваивания для удобства помещена сразу на две панели Calculator и Evaluation .
Ввести новое значение переменной возможно как в виде числа, так и в виде математического выражения, содержащего другие переменные и функции, а также в виде строкового выражения (листинг 3.1). В последнем случае будет создана переменная s не численного, а строкового типа.
Функции в Mathcad записываются в обычной для математика форме, например,
f (x )=sin (x ),
где f (х ) — функция;
f — имя функции;
х — список переменных.
Легче всего ввести написание функции в документ при помощи клавиатуры.
В Mathcad формально можно разделить функции на два типа˸
- встроенные функции;
- функции, определенные пользователем.
Применение функций обоих типов в расчетах совершенно одинаково, с тем исключением, что любую встроенную функцию можно сразу использовать в любом месте документа, а пользовательскую функцию необходимо предварительно определить в документе до момента вычисления её значения.
Определение переменных в Mathcad — понятие и виды. Классификация и особенности категории «Определение переменных в Mathcad» 2015, 2017-2018.
Текстовую область можно разместить в любом незанятом месте документа Mathcad. Чтобы до начала ввода указать программе, что требуется создать не формульный, а текстовый регион, достаточно, перед тем как ввести первый символ, нажать клавишу » (двойная кавычка). В результате на. .
Для выполнения программы-функции необходимо обратиться к имени программы-функции с указанием списка фактических параметров (если в описании программы присутствует список формальных параметров), т. е. (список фактических параметров) Фактические. .
Для набора выражения используются клавиатура и панели инструментов, которые доступны с помощью меню ПросмотрПанели. Например, для расчёта выражения необходимо набрать 1/, затем найти знак корня в панели «Калькулятор». В знаменателе выражения появится шаблон который. .
Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику (например, возвращение различных значений в зависимости от условий), в одну строку не удается. Назначение. .
Для проведения измерений осциллограф нужно настроить, для чего следует задать: расположение осей, по которым откладывается сигнал; нужный масштаб развертки по осям; смещение начала координат по осям, режим работы по входу: закрытый или открытый; режим. .
Для написания программ в среде MathCad существует специальная панель Programmіng (Программирование) (рис.16, а), она относится к панели Math (Математические) (рис.16, б). Язык программирования MathCad имеет предельно малое количество операторов (рис. 16, а). Чтобы написать программу. [читать подробнее] .
Известно, что экспериментальные данные, как правило, задаются дискретно в виде массива данных из двух пар чисел (хі, уі). В связи с этим возникает задача аппроксимации дискретных данных непрерывной функцией f(x). В MathCad для обработки экспериментальных данных существуют. .
MathCad 7.0 Professional – универсальный инструмент для работы с формулами, графиками и текстами. Он обладает мощными вычислительными функциями и возможностью аналитических преобразований.
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Find эта переменная не определена
Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
Когда ввожу find, оператор выделяется красным с примечанием переменная не определена. Все переменные вроде как задал. Подскажите пожалуйста в чем проблема?
Заранее спасибо за помощь!
-
Korobov V I
- Сообщения: 1609
- Зарегистрирован: Вт янв 21, 2003 5:12 pm
Re: Find эта переменная не определена
Сообщение Korobov V I » Сб ноя 23, 2013 2:09 pm
nikanto писал(а):Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
Когда ввожу find, оператор выделяется красным с примечанием переменная не определена. Все переменные вроде как задал. Подскажите пожалуйста в чем проблема?
Заранее спасибо за помощь!
1. В девятом уравнении переменная «c» набрана в русской раскладке клавиатуры.
2. Вместо функции Find примените функцию Minerr.
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Re: Find эта переменная не определена
Сообщение nikanto » Сб ноя 23, 2013 7:11 pm
Korobov V I писал(а):1. В девятом уравнении переменная «c» набрана в русской раскладке клавиатуры.
2. Вместо функции Find примените функцию Minerr.
спасибо букву исправил, но minerr не помог. Ничего не происходит =( просто равно появляется и все…
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вс ноя 24, 2013 1:34 am
а у меня после равно прямоугольничек черный. как место для цифры. Ладно, спасибо и на этом
-
Vladimir__
- Сообщения: 1660
- Зарегистрирован: Вс дек 21, 2003 8:52 am
Сообщение Vladimir__ » Вс ноя 24, 2013 2:36 pm
nikanto писал(а):а у меня после равно прямоугольничек черный. как место для цифры. Ладно, спасибо и на этом
А какую версию Mathcad вы используете?
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вс ноя 24, 2013 2:49 pm
Mathcad 14. Еще я попробовал подставить полученные значения в систему и равенство не выполняется. Наверное, я не до конца понимаю способ работы этих операторов. Количество неизвестных равно количеству уравнений. Зачем я задаю в начале приближенные значения? Разве здесь нужны итерации? Хотел избежать решения на листочках и трехэтажных подстановок, но, видимо не удастся =(
-
Vladimir__
- Сообщения: 1660
- Зарегистрирован: Вс дек 21, 2003 8:52 am
Сообщение Vladimir__ » Пн ноя 25, 2013 8:59 am
nikanto писал(а):Mathcad 14. Еще я попробовал подставить полученные значения в систему и равенство не выполняется. Наверное, я не до конца понимаю способ работы этих операторов. Количество неизвестных равно количеству уравнений. Зачем я задаю в начале приближенные значения? Разве здесь нужны итерации? Хотел избежать решения на листочках и трехэтажных подстановок, но, видимо не удастся =(
1. Обновите версию до последнего сервис релиза Mathcad 15 M020.
2. Подробнее про работу функцию «Minerr«:
http://www.exponenta.ru/soft/mathcad/us … 5/15_3.asp
http://www.sistemair.ru/dok/mathcad/text/index5-10.html
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вт ноя 26, 2013 2:12 am
Обновил. Minerr заработал. Только я так и не понял, как получить решение этой системы. То, что в табличке — это не корни.
-
VFO
- Сообщения: 4227
- Зарегистрирован: Ср фев 27, 2002 8:03 pm
Re: Find эта переменная не определена
Сообщение VFO » Вт ноя 26, 2013 8:11 am
[quote=»nikanto»]Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
quote]
А почему вы не используете функцию lsolve
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Re: Find эта переменная не определена
Сообщение nikanto » Ср ноя 27, 2013 11:03 am
VFO писал(а):quote]
А почему вы не используете функцию lsolve
Я до этого не пользовался Mathcad и на поисковый запрос «решение системы уравнений Mathcad» мне попалась функция Find. Хотел заставить комп решить мне уравнения, в итоге сижу решаю на листах, ибо так быстрее =)
Сообщения об ошибках в Mathcad
Таблица П4.1. Сообщения об ошибках
Возможные пути устранения
Сообщения об ошибках в численных вычислениях
A «Find» or «Minerr» must be preceded by a matching «Given»
Find или Minerr должны предваряться ключевым словом Given
Эта ошибка выделяет функцию Find или Minerr при их несогласо-
ванности с Given
Каждый вычислите-
льный блок,
который заканчивается функцией Find или Minerr, должен начинаться с ключевого слова Given
All evaluations resulted in either an error or a complex result
Вычисления приводят к ошибке или комплексно-
му результату
Mathcad не может начертить некоторые точки, потому что не существует действительных значений для их нанесения на график
Это сообщение может появиться, если имеется ошибка или все значения комплексные
Arguments in function definitions must be names
Аргументы в определениях функции должны быть именами
Выделенное определение функции содержит неправильный перечень аргументов
В списке аргументов должны быть правильно поименованы переменные, или список имен необходимо отделить запятыми
At least one limit must be infinity
По крайней мере один предел должен быть бесконечным
Когда для интегриро-
вания выбран алгоритм бесконечного предела, то по крайней мере один из пределов интеграла должен быть бесконечным
Тип бесконечности вводится нажатием сочетания клавиш + + .
Для изменения алгоритма, использующего бесконечный предел, или для вычисления какого-либо другого интеграла щелкните на интеграле правой кнопкой мыши и измените алгоритм с помощью контекстного меню
Can only evaluate an n-th order derivative when n=0,1..5.
Можно вычислить n-й порядок производной, только когда п=0,1..5
Порядок производной должен быть одним из следующих чисел: 0, 1, 2,. ..5.
Если Вы хотите посчитать производную более высокого порядка, то делайте это с помощью символьного дифференци-
рования
Can’t evaluate this function when its argument less than or equal to zero
Невозможно вычислить эту функцию, когда ее аргумент меньше или равен нулю
Такое сообщение может касаться XY- или полярных графиков, имеющих логарифмические оси, на которых или пределы, или некоторые из значений, не положительны
Отрицательные числа и ноль не могут быть расположены нигде на логарифмических осях. Смените тип осей графика или постройте его для других значений
Can’t converge to a solution
Не сходится к решению
Численный метод расходится (не может найти решения)
Убедитесь, что операция не применяется к функции в области непосредственной близости точки ее сингулярности (деления на ноль). Попробуйте поменять параметры численного метода (например начальное приближение).
Попробуйте увеличить константу TOL, т. е. осуществить поиск решения с худшей погрешностью.
Попробуйте поменять численный алгоритм, если это возможно (вызвав контекстное меню нажатием на месте ошибки правой кнопки мыши)
Can’t define the same variable more than once in the same expression
Невозможно определить ту же самую переменную более одного раза в одном и том же выражении
Вы пытаетесь вычислить одну и ту же переменную дважды в одном выражении
Пример подобной ошибки: если Вы создаете вектор с левой стороной а := и используете это же имя справа, то получите ошибку
Can’t determine what units the result of this operation should have
Невозможно определить, в каких единицах следует быть результату этой операции
Вы возвели выражение, содержащее единицы измерения, в степень, являющуюся переменной в неких пределах или вектором. В результате невозможно определить размерность результата
Если выражение включает в себя единицы измерений, то можно возводить его только в действительную фиксированную степень
Cant divide by zero
Деление на ноль невозможно
Где-то в программе или внутри численного метода возникло деление на ноль
Найдите место деления на ноль и устраните его
Попробуйте поменять параметры численного метода, константы точности или сам численный алгоритм
Could not find a solution
Невозможно найти решение
Численный метод расходится (не может найти решения)
См. «Can’t converge to a solution»
Can’t find the data file you’re trying to use
Невозможно найти файл, который Вы пытаетесь использовать
Невозможно найти файл данных или другой тип файла, к которому Вы обращаетесь
Удостоверьтесь, что такой файл существует в указанном месте
Can’t have anything with units or dimensions here
Здесь нет ничего в единицах измерений или в размерностях
Это выражение использует единицы измерений где-то, где они не разрешены
Единицы измерений не разрешены:
— в аргументах большинства функций;
— в экспонентах; — в верхних и нижних индексах.
Для того чтобы использовать выражения с единицами измерений, вначале переведите это выражение в UnitsOf (выражение)
Can’t have more than one array in a contour plot
Нельзя иметь более одного массива в контурном графике
Вы вводите более одного массива в местозаполнитель контурного или поверхностного графика
Можно иметь только один массив в данном местозаполнителе, т. к. графики могут выдавать лишь одну поверхность в один момент времени
Can’t perform this operation on the entire array at once. Try using «vectorize» to perform it element by element
Невозможно представить эту операцию в целом массиве сразу. Попытайтесь использовать векторизацию, чтобы представить элемент за элементом
Например, можно увидеть это сообщение при попытке разделить один вектор на другой
Для того чтобы применять функцию или оператор к каждому элементу вектора или матрицы, используйте оператор векторизации
Can’t plot this many points
Невозможно начертить график с таким большим количеством точек
Попытка построения графика с числом точек, превосходящим возможное
Попробуйте сделать число точек меньше, чем 150 000
Can’t put a «:=» inside a solve block
Нельзя помещать «:=» внутрь вычислительного блока
Внутри вычислительного блока не должно быть формулировки присваивания. Он должен содержать только булевы выражения
Используйте панель с булевыми операторами
Can’t raise an expression having units to a complex power
Нельзя возводить в комплексную степень ыражение, имеющее единицы измерений
Это выражение содержит единицы измерений, а Вы возводите его в комплексную степень
Выражение с единицами измерений можно возводить только в действительную степень. Для того чтобы возводить в комплексную степень выражение с единицами измерений, вначале переведите это выражение в UnitsOf (выражение) — единицы измерений будут отменены
Can’t solve a system having this many equations
Невозможно решить систему, имеющую так много уравнений
Mathcad не способен решить систему
См. определение термина «вычислительный блок » (гл. 
Can’t understand something in this data file
Невозможно что-то понять в файле данных
Файл, к которому Вы пытаетесь получить доступ при помощи READ или READ*, имеет дефект
Файл должен быть ASCII-текстом
Все строки файла должны иметь тот же номер значений, что используется в READ*
Если файл имеет требуемый формат, а это сообщение продолжает появляться, попробуйте удалить любую часть текста из файла
Can’t understand the name of this function
Невозможно понять имя этой функции
Такое сообщение может появиться, если в качестве имени функции используется, например, число 6(х)
Выражение должно соответствовать требованиям, предъявляемым в Mathcad к написанию имен функций
Can’t understand the way this range variable is defined
Невозможно понять определение ранжированной переменной
Определение ранжированной переменной неверно
Вводя область определения ранжированной переменной, необходимо использовать один из следующих видов:
Rvar := nl . .n2 Rvar := nl,n2 . .пЗ
Cant understand this number
Невозможно понять это число
Это выражение содержит символ или десятичную точку там, где это непозволительно
Вы увидите эту ошибку, например, если случайно запишете число так: .452.
Cant use a range variable in a solve block
Невозможно использовать ранжированную переменную в вычислительном блоке
Эта ошибка появится, если использовать область определения переменной в неподходящем месте
Придумайте алгоритм, не допускающий применения ранжированной переменной в вычислительном блоке
Cannot evaluate this accurately at one or more of the values you specified
Невозможно точно вычислить одно или более значений
Эта ошибка появляется, если попытаться вычислить функцию для аргумента, находящегося за пределами точной области определения функции
Проверьте область определения функции
Cross product is defined only for vectors having exactly three elements
Векторное произведение определяется только для векторов, имеющих точно три элемента
Векторное произведение определяется только для векторов, имеющих точно три элемента
См. определение векторного произведения (гл. 9)
Can’t evaluate this expression. It may have resulted in an overflow or an infinite loop
Невозможно вычислить это выражение. Это может быть результатом переполнения или бесконечных циклов
Это функциональное определение может содержать слишком много вложенных функций. Или функция может быть константой в бесконечных циклах
Проверьте несколько итераций цикла
Degree of the polynomial must be between 1 and 99.
Степень полинома должна находиться в пределах между 1 и 99
Вектор, пропущенный через функцию поиска корней полинома, должен содержать по крайней мере 2 и не более 99 элементов
Dimensions must be >4
Размерность должна быть >4
Эта матрица должна иметь по крайней мере 4 ряда и 4 столбца
Исправление ошибок
Определив выражение, вызвавшее ошибку, нужно его отредактировать с целью устранения ошибки или исправить определение переменной, приведшей к ошибке. После щелчка по выражению и начала редактирования MathCAD удаляет сообщение об ошибке. После щелчка вне уравнения (или нажатия клавиши [F9]), MathCAD повторно вычисляет выражение. Если ошибка устранена, то MathCAD затем повторно вычисляет другие выражения, зависящие от измененного.
Выражение, отмеченное сообщением об ошибке, не обязательно содержит ее причину. Причиной ошибки могут быть функции или переменные, определенные в рабочем документе значительно ранее. Для устранения ошибки придется отредактировать именно ее.
Рассмотрим допустимые в MathCAD имена переменных и функций. Имена в MathCAD могут содержать любые из следующих символов:
· прописные и строчные латинские буквы;
· цифры от 0 до 9
· знак подчеркивания _
· штрих ` Это не апостроф. Находится на одной клавише с тильдой
· греческие буквы. Есть два способа набрать греческую букву: напечатать римский эквивалент и нажать [Ctrl]+Gили щелкнуть по соответствующему символу на палитре греческих символов
· символ бесконечности, который можно задать как комбинацию клавиш[Ctrl]+[Shift]+Z.
· Имена переменных и функций не могут включать пробелы или любые другие символы, не перечисленные выше.
MathCAD не делает различий между именами переменных и именами функций. Если определить вначале f(x), а затем переменную f, окажется невозможным использовать f(x) где-либо ниже определения f некоторые имена уже используются MathCAD для встроенных констант, единиц измерения и функций. Хотя эти имена можно переопределить, этот уничтожит их встроенные значения.
MathCAD различает в именах символы верхнего и нижнего регистра, а также различные шрифты.
Кроме того, среда MathCAD включает так называемые предопределенные переменные. MathCAD содержит 8 переменных, значения которых определены сразу после запуска программы. Они называются встроенными или предопределенными. Эти переменные имеют или общепринятое значение (например, пи или е), или используются как внутренние переменные, управляющие работой MathCAD. Эти переменные можно переопределять, например, определим е:= 2. Ниже этого определения переменная е примет в рабочем документе новое значение.
Приведем примеры некоторых встроенных переменных:
е=2.71828 – основание натурального логарифма;
Е=10^307 – машинная бесконечность;
MathCAD интерпретирует все, начинающееся цифрой, как число. Цифра может сопровождаться:
· цифрами после десятичной точки;
· символами h или o для шеснадцатеричных и восьмеричных чисел; символами i или j для комплексных чисел. Комплексные числа MathCAD воспринимает в форме a+bi (или a+bj). Специальные функции и операторы для работы с комплексными числами:
· Re(z) – вещественная часть числа z;
· Im(z) – мнимая часть числа z;
· Arg(z) – аргумент числа z (угол в комплексной плоскости между вещественной осью и радиус-вектором, определяемым числом z);
· |z| – модуль числа z.
Одиночное число в MathCAD называют скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел — матрицей. Способы создания массива:
· заполнить массив пустых полей
· использовать дискретный аргумент
Можно различать имена векторов, матриц и скаляров, используя различный шрифт для их описания.
Эта переменная не определена mathcad ошибка
MathCAD — это просто! Часть 27. Программирование и ошибки: вместе веселее!
Что ж, хотя мы уже немало всего успели обсудить насчет программирования в такой замечательной математической среде, как MathCAD, еще немало весьма существенных тем осталось за кадром. И, пожалуй, самая существенная из них — это взаимодействие начинающего программиста, пишущего программы в MathCAD’е, и ошибок в его программах. Именно на ней мы с вами сейчас и остановимся.
В общем-то, если сказать, что ошибки никто не любит, это будет не так уж далеко от истины. Точнее, никто не любит собственные ошибки. Чужие любят все, а не только экзаменаторы и разнообразные инспекторы. Однако, к сожалению, при программировании (а написание небольших вспомогательных программок в MathCAD’е, как я уже когда-то давно тому назад говорил, это тоже программирование) ошибки попросту неизбежны. Даже самые лучшие программисты совершают ежедневно множество ошибок, и никто, в общем-то, за это не применяет к ним особых санкций. Существует даже такое мнение, что программа без ошибок совершенно бесполезна — если в ней нет ошибок, значит, в ней нет и никакой полезной функциональности, потому что не ошибается только тот, кто ничего не делает. Так что ошибки в программах — это вполне естественные спутники каждого, кто пишет даже самые маленькие программки, а потому и бояться их не следует. Тем не менее, с ошибками в программах можно и нужно бороться. И для этого существуют специальные средства, некоторые из которых доступны и тем, кто пишет программы в MathCAD’е. Однако, прежде чем рассказывать о том, что это за средства, и как ими нужно пользоваться, нужно, как мне лично кажется, поговорить еще немного о том, вокруг чего будет сосредоточена наша борьба — то есть о самих ошибках.
Поскольку, как я уже говорил, ошибки довольно многочисленны, их имеет смысл классифицировать. Сделать это стоит, в общем-то, уже хотя бы попросту потому, что разные виды ошибок требуют различных к себе подходов, и их устранение требует вложения различного количества труда того, кто писал программу.
Самые простые ошибки — синтаксические. Как вы уже имели возможность воочию убедиться, при программировании очень важно придерживаться определенных правил в записи конструкций. Например, если вы вместо имени функции rkfixed напишете в программе tkfixed, ошибившись при вводе на одну букву и нажав на соседнюю с r клавишу t, то как раз и получите в свое распоряжение самую что ни на есть классическую синтаксическую ошибку. Ни к каким особенно страшным последствиям она (как, впрочем, и все другие ошибки аналогичного класса) не приведет: программа просто не сможет быть выполнена по той причине, что MathCAD не сможет найти функцию, которую вы ему указали. Искать такие ошибки тоже совсем не сложно — они всегда хорошо видны, поскольку даже сама среда подсвечивает их, чтобы можно было найти особенно быстро. Исправлять, соответственно, тоже очень просто: достаточно записать идентификатор правильно, и все в программе станет на положенные места. MathCAD, кстати, избавляет пользователя от множества таких ошибок благодаря необходимости вводить все операторы, управляющие ходом программы, с помощью специальных горячих клавиш или соответствующих кнопок на панели инструментов Программирование. Если бы их нужно было, напротив, набирать вручную с клавиатуры, то и возможности сделать синтаксическую ошибку были бы несравнимо шире.
Второй тип ошибок — ошибки алгоритмические. Это такие ошибки, которые, в принципе, не мешают выполнению программы, но делают результаты такого выполнения полностью лишенными всякого смысла. Многие из таких ошибок — банальные опечатки: там, где нужно было поставить плюс, вы, например, поставили в спешке минус или же сделали что-нибудь другое примерно в таком же духе. Конечно, сказать, что алгоритмические ошибки — это сплошь и рядом одни только опечатки, было бы, мягко говоря, не до конца верно. Потому что очень многие из них являются следствием недостаточности знаний писавшего программу — то есть если ошибочно составлена сама последовательность действий, которые должен сделать MathCAD для того, чтобы вы могли получить интересующий вас результат. Еще великое множество алгоритмических ошибок — результат банальной невнимательности: например, присвоение значения не той переменной, ее необнуление либо, например, вывод не той переменной в качестве результата выполнения вашей программы. В общем-то, именно об алгоритмических ошибках мы с вами сейчас и будем говорить более подробно. Однако есть еще один, особенно неприятный, тип ошибок.
Третий тип — это ошибки мистические. Да-да, именно мистические, я не оговорился. Какие именно это ошибки? Это ошибки, имеющие совершенно непонятную природу и столь же непонятный способ лечения — как правило, это проявления ошибок не в вашей программе, а в каком-то из внутренних компонентов MathCAD’а. К сожалению, эти ошибки, в «большом» программировании встречающиеся не так уж, в общем-то, и часто, в MathCAD’е не такие уж редкие гости. Отчасти это объясняется тем, что MathCAD — это все-таки средство расчетов, а не программирования, которое играет в этой среде второстепенную и вспомогательную роль, но, конечно, когда реально сталкиваешься с такими вот мистическими ошибками, это все не слишком успокаивает. Хотя поначалу почти все ошибки в программах кажутся мистическими, на самом деле большая их часть все-таки имеет рациональную природу. Если же природа появившейся ошибки вам совершенно непонятна, то вам следует коренным образом перестроить структуру программы или хотя бы тот ее фрагмент, в котором локализовалось проявление этой ошибки. Практически во всех случаях этот не слишком хитрый прием позволяет полностью избавить программу от досадной непонятной ошибки.
Что ж, о самих ошибках мы с вами, можно считать, побеседовали. Теперь давайте, пожалуй, перейдем к тому, какими именно способами можно бороться с самыми распространенными из них — то есть алгоритмическими. Об остальных, в общем-то, я уже довольно подробно все рассказал, а вот что касается алгоритмических ошибок, то здесь нужно будет в большинстве случаев прибегнуть к помощи специализированных встроенных в MathCAD инструментов.
Отладка в MathCAD’е
Процесс поиска и устранения алгоритмических ошибок называется по-русски отладкой. По-английски этот же самый процесс называется debugging, то есть, если дословно, «избавление от жучков». В общем-то, и по-русски довольно часто можно услышать термины «дебагинг» или «баг», однако во избежание путаницы мы будем использовать слово «отладка» (если, конечно, не возражаете). Кстати, история возникновения английского термина весьма любопытна, и, вполне возможно, вы ее слышали. Первые компьютеры были машинами весьма громоздкими и дорогостоящими, а потому и всевозможные поломки для них были делом далеко не просто устранимым. Когда выяснилось, что причиной очередной поломки стал жучок, забравшийся внутрь компьютера и вызвавший замыкание, в счете за ремонт записали: «debugging». Рука шутника оказалась легкой — термин, как видите, прижился и используется на протяжении уже многих десятилетий.
В чем же заключается процесс отладки? На самом деле ничего особенно таинственного и трудного для понимания здесь нет. Просто во время отладки у вас есть возможность выполнять программу не сразу «залпом», как это происходит обычно, а пошагово, то есть выполнять последовательно друг за другом каждую строчку программы, делая, когда нужно, паузы для осмысления работы программы и просмотра промежуточных значений каждой из переменных. Отладка используется при разработке любых программ, а потому и создатели MathCAD включили поддержку этого удобного и, в общем-то, достаточно универсального средства выявления ошибок в свой программный продукт. Доступ к инструментам, используемым при отладке программ в MathCAD’е, осуществляется через подпункт Debug меню Tools в главном рабочем окне MathCAD’а (см. соответствующий скриншот).
Стоит отметить, что, поскольку MathCAD — это среда, ориентированная не на программирование, а на различные вычислительные действия, то отладка в ней имеет более широкое применение, чем только отладка программ, которые пишет пользователь. Отлаживать можно и все вычисления даже в том случае, если они выполняются без применения какого-либо программирования с вашей стороны. В общем-то, поскольку такая возможность будет весьма полезной для большинства читателей не столько при программировании в MathCAD’е, сколько при обычных вычислениях, то именно с такой позиции мы с вами и станем рассматривать отладку в этой мощной математической среде. Нам также понадобится панель отладки. Ее включают так же, как все остальные панели инструментов, в меню View -> Toolbars. Конечно, эта панель, как вы могли уже заметить, дублирует отладочное меню в Tools -> Debug, однако, думаю, нажать на кнопку, расположенную на этой панели, будет все-таки проще и быстрее, чем искать соответствующий пункт в надежно спрятанном от пользователя меню.
При переходе в отладочный режим (кнопка либо пункт меню Toggle Debug Mode) внешний вид главного окна MathCAD’а меняется (см. скриншот): внизу появляется специальное окно, используемое для просмотра промежуточной отладочной информации. Оно называется Trace Window.
Однако о том, что именно отображается в этом самом окне, а также о том, что от нас требуется сделать с документом перед тем, как его можно будет уже полноценно отлаживать, мы с вами поговорим, пожалуй, в следующий раз, чтобы не перегружать вас разнообразной полезной информацией. Сейчас же подведем итоги разговора про ошибки, возникающие в процессе написания программ в математической среде MathCAD.
Как видите, ошибок в программах действительно бояться не следует. Это вполне нормальная составляющая процесса программирования, неизбежно проявляющаяся в каждом из результатов этого процесса. Тем не менее, с ошибками можно и нужно бороться, и с большинством из них это можно производить с весьма высокой вероятностью достижения успеха. Хотя, конечно же, встречаются и такие ошибки, с которыми трудно будет разобраться даже тому, кто на программировании, что называется, собаку съел. Но все-таки они встречаются не так уж часто. Так что в программировании, если вы хотите избежать мучений, связанных с поиском ошибок, очень важна ваша внимательность. Если вы будете достаточно внимательны при написании программы, то риск допустить ошибку будет сравнительно невелик. Впрочем, это правило применимо не только к программированию.
Эта переменная не определена mathcad ошибка
Mathcad раскрывается в полной мере при использовании переменных и функций.
Два знака равенства
В математических вычислениях мы используем множество различных констант, переменных, операторов и знаков равенства. Обычно в жизни мы используем знак равенства для многих разных операций, но Mathcad отличает их. Наиболее важными операциями являются:
- определение (присвоение значения) — используется двоеточие;
- вычисление — используется знак равенства.
Важность оператора определения не меньше, чем важность оператора вычисления. В приведенном ниже примере значение y можно вычислить лишь после присвоения ему определенного значения. х и у здесь являются переменными.
Два знака равенства, которые изображены выше, имеют совершенно разные значения, поэтому нужно очень внимательно относится к ним.
Поставьте курсор перед числом 4 в примере выше.
Удалите число 4 клавишей [Delete], и введите 5. Нажмите на пустой области, чтобы выйти из области вычисления и увидите, что результат вычислений поменялся на 25:
Теперь попробуйте провести операцию удаления с числом 25. Вы увидите, что при попытке удаления число подсвечивается красным, а при следующем нажатии удалиться и знак равно.
Использование переменных
Введите такие выражения в область вычисления
Проведите операции замены значения х на такие: 100, 0.5, -4 и 0.
В первых двух случаях вы получите число в качестве результата. В третьем случае у вас будет мнимое число. При значении х ноль программа выведет ошибку и обведет результат красным. Если вы нажмете на красное выделение, то увидите описание проблемы:
Дальше мы поговорим о том, какие имена можно использовать для переменных, а какие нельзя. Существуют такие правила: имя переменной не может начинаться с цифры и в ней нельзя использовать пробелы или знаки операторов. Имена могут начинаться:
- с любой буквы как большой, так и маленькой;
- с других символов, которые не являются операторами;
- с символов из вкладки Математика -> Операторы и символы -> Символы;
- с символов из таблицы символов ОС Windows.
Использование переменных доступно, только если вы определите их заранее. Термин «заранее» обозначает, что присвоение значения переменной должно производиться выше или левее выражения, где эта переменная используется. Если вы не объявили переменную заранее, то появится сообщение об ошибке:
Подстрочные индексы
Mathcad существует два типа подстрочных индексов:
- Описательный подстрочный индекс.
- Индекс массива (матрицы).
Для ввода описательного индекса сначала введите желаемое имя переменной, а потом нажмите комбинацию [Ctrl+-], далее вводите подстрочный индекс.
Переменная, которая имеет описательный индекс — это простая переменная, которой присвоено имя. Индекс массива сильно отличается от него. Такой индекс можно присвоить, если ввести квадратную скобку [ после имени переменной. Переменная может иметь один или два индекса массива:
Индекс массива может иметь только числовое значение. При этом не путайте разные типы индексов, так как они довольно схожи визуально.
Более четко разницу видно, если нажать мышкой на выражение
Любая переменная может иметь оба индекса одновременно: описательный и индекс массива. Сначала всегда будет прописан описательный.
Функции
Использование переменных возможно только при определении их заранее. Но есть исключение из этого правила — определение функции. Можно произвести определение своей функции. Пример ниже.
Переменная а имеет для функции локальное значение. Она не несет определения за пределами этой функции.
Если вы присвоили значение переменной а до определения функции, то значение этой переменной не будет меняться в процессе вычисления функции. Внимание: Если вы присвоили переменной такое же имя, как и функции, вы не сможете использовать эту функцию. Переменная и функции должны иметь разные имена.
Вы не будете сталкиваться с такой проблемой, если будете задавать переменной и функции различные имена. Об обозначениях мы поговорим в уроке 10.
Функции могут иметь более одной переменной.
Значения переменных х и у не изменяются и в этой функции.
Встроенные функции
Mathcad имеет очень много встроенных функций. Перейдите во вкладку Функции.
Все функции вы можете увидеть, если нажмете на кнопку Все функции.
Обратите внимание, что все тригонометрические функции в качестве аргумента получают угол не в градусах, а в радианах. Чтобы использовать градусы нужно выбрать их во вкладке Математика -> Операторы и символы -> Символы.
Математика в тексте
В текстовую область можно поместить область вычислений. Так вы сможете использовать в тексте подстрочные и надстрочные символы. Чтобы сделать это, при редактировании текстовой области нужно нажать на кнопку Математика во вкладке Математика -> Области.
Резюме
1. Mathcad использует два знака равенства отдельно для определения := и для вычисления =.
2. Имя переменной нельзя начинать с цифры. Можно использовать для этого только буквы или символы, отличные от символов операторов. Символы можно вводить с панели Математика -> Операторы и символы -> Символы, а также брать из панели символов Windows.
3. Для определения значения переменной нужно:
- щелкнуть на пустую область;
- ввести имя переменной;
- ввести оператор определения [:=];
- ввести значение переменной.
4. Для присвоения переменной подстрочного описательного индекса нужно:
- нажать мышкой в конце имени переменной;
- нажать [Ctrl+-];
- ввести подстрочный индекс.
5. Для присвоения переменной индекса массива:
- нажмите мышкой в конце имени переменной;
- нажмите на клавиатуре на открывающуюся квадратную скобку [;
- ввести нужный подстрочный индекс.
6. Определять переменную нужно только выше или левее места использования ее в вычислениях.
7. Имя функции вводится с теме же правилами, что и имя переменной, с той лишь разницей, что заканчивать имя функции нужно вводом открывающейся скобки [(]. В них будут размещаться аргументы функции.
8. Переменные в функциях имеют определение только в рамках этой функции.
9. В тексте можно размещать математическую область. Это можно применять при интеграции в текст надстрочных или подстрочных символов.
Глобальное определение в PTC Mathcad 15 и PTC Mathcad Prime 3.0
Оператор глобального определения позволяет определить выражение (переменную, функцию) в любом месте документа. 
a)
Рис. 1. Оператор глобального определения в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
Если выражение определено глобально, то его можно использовать в других операциях независимо от того, выше или ниже эти операции находятся в документе:
Рис. 2. Выполнение вычислений с глобальным и локальным определением в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
При необходимости, в Mathcad 15 внешний вид оператора глобального определения можно поменять на символ обычный символ равенства «=». Для это щелкните правой кнопкой мыши по оператору, в контекстном меню выберите View Definition As -> Equal.

Рис. 3. Изменение внешнего вида оператора глобального определения.
В Mathcad 15 возможно переопределение переменных, заданных глобально. В Mathcad Prime 3.0 подобное переопределение выдаст ошибку.
б)
Рис. 4. Переопределение переменной, заданной глобально, в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
Чтобы учесть все определения, Mathcad работает по следующему алгоритму:
1. Первый проход документа сверху вниз – распознавание только операторов глобального определения и вычисление выражений.
2. Второй проход документа – распознавание операторов локального определения и вычисление выражений с поправкой на выражения, которые определенны локально.
Это важно учитывать, если Вы переопределяете выражения, заданные глобально. Демонстрация этого алгоритма приведена на рисунке 5.

Рис. 5. Документ с переопределенными выражениями.
Однако в Mathcad Prime 3.0 выражения, определенные глобально, переопределить уже нельзя (ни локально, ни глобально) – Mathcad выдаст ошибку (рис. 6).

Рис. 6. Попытка переопределить переменную, заданную глобально в Mathcad Prime 3.0.
Другой важный момент при использовании глобального определения: если Вы используете переменные для определения выражений, заданных глобально (т.е. используете переменную справа от символа ?), то эта переменная также должна быть определена глобально, причем выше того выражения, в котором она используется. Иначе переменная не будет определена (рис. 7).
б)
Рис. 7. Неправильное использование переменных в выражениях, заданных глобально, в Mathcad 15 (а) и Mathcad Prime 3.0 (б).
































 Эти два знака равенства принципиально различны, поэтому их не следует путать.
Эти два знака равенства принципиально различны, поэтому их не следует путать.