Mean absolute error tensorflow - Исправление ошибок и поиск оптимальных решений проблем

Computes the mean of absolute difference between labels and predictions.

Inherits From: Loss

View aliases

Main aliases

tf.losses.MeanAbsoluteError

Compat aliases for migration

See
Migration guide for
more details.

tf.compat.v1.keras.losses.MeanAbsoluteError

tf.keras.losses.MeanAbsoluteError(
    reduction=losses_utils.ReductionV2.AUTO,
    name='mean_absolute_error'
)

Used in the notebooks

Used in the tutorials
Generate Artificial Faces with CelebA Progressive GAN Model

loss = abs(y_true - y_pred)

Standalone usage:

y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [1., 0.]]
# Using 'auto'/'sum_over_batch_size' reduction type.
mae = tf.keras.losses.MeanAbsoluteError()
mae(y_true, y_pred).numpy()
0.5

# Calling with 'sample_weight'.
mae(y_true, y_pred, sample_weight=[0.7, 0.3]).numpy()
0.25

# Using 'sum' reduction type.
mae = tf.keras.losses.MeanAbsoluteError(
    reduction=tf.keras.losses.Reduction.SUM)
mae(y_true, y_pred).numpy()
1.0

# Using 'none' reduction type.
mae = tf.keras.losses.MeanAbsoluteError(
    reduction=tf.keras.losses.Reduction.NONE)
mae(y_true, y_pred).numpy()
array([0.5, 0.5], dtype=float32)

Usage with the compile() API:

model.compile(optimizer='sgd', loss=tf.keras.losses.MeanAbsoluteError())

Args
`reduction`	Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training tutorial for more details.
`name`	Optional name for the instance. Defaults to ‘mean_absolute_error’.

Args

reduction Type of tf.keras.losses.Reduction to apply to
loss. Default value is AUTO. AUTO indicates that the reduction
option will be determined by the usage context. For almost all cases
this defaults to SUM_OVER_BATCH_SIZE. When used with
tf.distribute.Strategy, outside of built-in training loops such as
tf.keras compile and fit, using AUTO or
SUM_OVER_BATCH_SIZE will raise an error. Please see this custom
training tutorial for
more details.

name Optional name for the instance. Defaults to
‘mean_absolute_error’.

Methods

`from_config`

View source

@classmethod
from_config(
    config
)

Instantiates a Loss from its config (output of get_config()).

Args
`config`	Output of `get_config()`.

Returns
A `keras.losses.Loss` instance.

`get_config`

View source

get_config()

Returns the config dictionary for a Loss instance.

`call`

View source

__call__(
    y_true, y_pred, sample_weight=None
)

Invokes the Loss instance.

Args
`y_true`	Ground truth values. shape = `[batch_size, d0, .. dN]`, except sparse loss functions such as sparse categorical crossentropy where shape = `[batch_size, d0, .. dN-1]`
`y_pred`	The predicted values. shape = `[batch_size, d0, .. dN]`
`sample_weight`	Optional `sample_weight` acts as a coefficient for the loss. If a scalar is provided, then the loss is simply scaled by the given value. If `sample_weight` is a tensor of size `[batch_size]`, then the total loss for each sample of the batch is rescaled by the corresponding element in the `sample_weight` vector. If the shape of `sample_weight` is `[batch_size, d0, .. dN-1]` (or can be broadcasted to this shape), then each loss element of `y_pred` is scaled by the corresponding value of `sample_weight`. (Note on`dN-1`: all loss functions reduce by 1 dimension, usually axis=-1.)

Returns
Weighted loss float `Tensor`. If `reduction` is `NONE`, this has shape `[batch_size, d0, .. dN-1]`; otherwise, it is scalar. (Note `dN-1` because all loss functions reduce by 1 dimension, usually axis=-1.)

Raises
`ValueError`	If the shape of `sample_weight` is invalid.

Источник

Использование функций потерь

Функция потерь (или объективная функция, или функция оценки результатов оптимизации) является одним из двух параметров, необходимых для компиляции модели:

model.compile(loss=’mean_squared_error’, optimizer=’sgd’)
from keras import losses
model.compile(loss=losses.mean_squared_error, optimizer=’sgd’)

Можно либо передать имя существующей функции потерь, либо передать символическую функцию TensorFlow/Theano, которая возвращает скаляр для каждой точки данных и принимает следующие два аргумента:

y_true: истинные метки. Тензор TensorFlow/Theano.

y_pred: Прогнозы. Тензор TensorFlow/Theano той же формы, что и y_true.

Фактически оптимизированная цель — это среднее значение выходного массива по всем точкам данных.

Доступные функции потери

mean_squared_error

keras.losses.mean_squared_error(y_true, y_pred)

mean_absolute_error

keras.losses.mean_absolute_error(y_true, y_pred)

mean_absolute_percentage_error

keras.losses.mean_absolute_percentage_error(y_true, y_pred)

mean_squared_logarithmic_error

keras.losses.mean_squared_logarithmic_error(y_true, y_pred)

squared_hinge

keras.losses.squared_hinge(y_true, y_pred)

hinge

keras.losses.hinge(y_true, y_pred)

categorical_hinge

keras.losses.categorical_hinge(y_true, y_pred)

logcosh

keras.losses.logcosh(y_true, y_pred)

Логарифм гиперболического косинуса ошибки прогнозирования.

log(cosh(x)) приблизительно равен (x ** 2) / 2 для малого x и abs(x) — log(2) для большого x. Это означает, что ‘logcosh’ работает в основном как средняя квадратичная ошибка, но не будет так сильно зависеть от случайного сильно неправильного предсказания.

Аргументы

y_true: тензор истинных целей.
y_pred: тензор прогнозируемых целей.

Возвращает

Тензор с одной записью о скалярной потере на каждый сэмпл.

huber_loss

keras.losses.huber_loss(y_true, y_pred, delta=1.0)

categorical_crossentropy

keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)

sparse_categorical_crossentropy

keras.losses.sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=-1)

binary_crossentropy

keras.losses.binary_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)

kullback_leibler_divergence

keras.losses.kullback_leibler_divergence(y_true, y_pred)

poisson

keras.losses.poisson(y_true, y_pred)

cosine_proximity

keras.losses.cosine_proximity(y_true, y_pred, axis=-1)

is_categorical_crossentropy

keras.losses.is_categorical_crossentropy(loss)

Примечание: при использовании потери categorical_crossentropy ваши данные должны быть в категориальном формате (например, если у вас 10 классов, то целью для каждой выборки должен быть 10-мерный вектор, который является полностью нулевым, за исключением 1 в индексе, соответствующем классу выборки). Для того, чтобы преобразовать целые данные в категорические, можно использовать утилиту Keras to_categorical:

from keras.utils import to_categorical
categorical_labels = to_categorical(int_labels, num_classes=None)

При использовании переменной sparse_categorical_crossentropy loss, ваши данные должны быть целыми. Если у вас есть категориальные данные, следует использовать categoryical_crossentropy.

categoryical_crossentropy — это еще один термин для обозначения потери лога по нескольким классам.

Источник

# Copyright 2015 The TensorFlow Authors. All Rights Reserved. # # Licensed under the Apache License, Version 2.0 (the «License»); # you may not use this file except in compliance with the License. # You may obtain a copy of the License at # # http://www.apache.org/licenses/LICENSE-2.0 # # Unless required by applicable law or agreed to in writing, software # distributed under the License is distributed on an «AS IS» BASIS, # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. # ============================================================================== # pylint: disable=g-classes-have-attributes «»»Built-in loss functions.»»» import abc import functools from tensorflow.python.autograph.core import ag_ctx from tensorflow.python.autograph.impl import api as autograph from tensorflow.python.distribute import distribution_strategy_context from tensorflow.python.eager import context from tensorflow.python.framework import constant_op from tensorflow.python.framework import ops from tensorflow.python.framework import smart_cond from tensorflow.python.framework import tensor_spec from tensorflow.python.framework import tensor_util from tensorflow.python.keras import backend from tensorflow.python.keras.utils import losses_utils from tensorflow.python.keras.utils import tf_utils from tensorflow.python.keras.utils.generic_utils import deserialize_keras_object from tensorflow.python.keras.utils.generic_utils import serialize_keras_object from tensorflow.python.ops import array_ops from tensorflow.python.ops import control_flow_ops from tensorflow.python.ops import math_ops from tensorflow.python.ops import nn from tensorflow.python.ops.losses import losses_impl from tensorflow.python.ops.ragged import ragged_map_ops from tensorflow.python.ops.ragged import ragged_tensor from tensorflow.python.ops.ragged import ragged_util from tensorflow.python.util import dispatch from tensorflow.python.util.tf_export import keras_export from tensorflow.tools.docs import doc_controls @keras_export(‘keras.losses.Loss’) class Loss: «»»Loss base class. To be implemented by subclasses: * `call()`: Contains the logic for loss calculation using `y_true`, `y_pred`. Example subclass implementation: «`python class MeanSquaredError(Loss): def call(self, y_true, y_pred): y_pred = tf.convert_to_tensor_v2(y_pred) y_true = tf.cast(y_true, y_pred.dtype) return tf.reduce_mean(math_ops.square(y_pred — y_true), axis=-1) «` When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, please use ‘SUM’ or ‘NONE’ reduction types, and reduce losses explicitly in your training loop. Using ‘AUTO’ or ‘SUM_OVER_BATCH_SIZE’ will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details on this. You can implement ‘SUM_OVER_BATCH_SIZE’ using global batch size like: «`python with strategy.scope(): loss_obj = tf.keras.losses.CategoricalCrossentropy( reduction=tf.keras.losses.Reduction.NONE) …. loss = (tf.reduce_sum(loss_obj(labels, predictions)) * (1. / global_batch_size)) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=None): «»»Initializes `Loss` class. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. «»» losses_utils.ReductionV2.validate(reduction) self.reduction = reduction self.name = name # SUM_OVER_BATCH is only allowed in losses managed by `fit` or # CannedEstimators. self._allow_sum_over_batch_size = False self._set_name_scope() def _set_name_scope(self): «»»Creates a valid `name_scope` name.»»» if self.name is None: self._name_scope = self.__class__.__name__ elif self.name == ‘<lambda>’: self._name_scope = ‘lambda’ else: # E.g. ‘_my_loss’ => ‘my_loss’ self._name_scope = self.name.strip(‘_’) def __call__(self, y_true, y_pred, sample_weight=None): «»»Invokes the `Loss` instance. Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`, except sparse loss functions such as sparse categorical crossentropy where shape = `[batch_size, d0, .. dN-1]` y_pred: The predicted values. shape = `[batch_size, d0, .. dN]` sample_weight: Optional `sample_weight` acts as a coefficient for the loss. If a scalar is provided, then the loss is simply scaled by the given value. If `sample_weight` is a tensor of size `[batch_size]`, then the total loss for each sample of the batch is rescaled by the corresponding element in the `sample_weight` vector. If the shape of `sample_weight` is `[batch_size, d0, .. dN-1]` (or can be broadcasted to this shape), then each loss element of `y_pred` is scaled by the corresponding value of `sample_weight`. (Note on`dN-1`: all loss functions reduce by 1 dimension, usually axis=-1.) Returns: Weighted loss float `Tensor`. If `reduction` is `NONE`, this has shape `[batch_size, d0, .. dN-1]`; otherwise, it is scalar. (Note `dN-1` because all loss functions reduce by 1 dimension, usually axis=-1.) Raises: ValueError: If the shape of `sample_weight` is invalid. «»» # If we are wrapping a lambda function strip ‘<>’ from the name as it is not # accepted in scope name. graph_ctx = tf_utils.graph_context_for_symbolic_tensors( y_true, y_pred, sample_weight) with backend.name_scope(self._name_scope), graph_ctx: if context.executing_eagerly(): call_fn = self.call else: call_fn = autograph.tf_convert(self.call, ag_ctx.control_status_ctx()) losses = call_fn(y_true, y_pred) return losses_utils.compute_weighted_loss( losses, sample_weight, reduction=self._get_reduction()) @classmethod def from_config(cls, config): «»»Instantiates a `Loss` from its config (output of `get_config()`). Args: config: Output of `get_config()`. Returns: A `Loss` instance. «»» return cls(**config) def get_config(self): «»»Returns the config dictionary for a `Loss` instance.»»» return {‘reduction’: self.reduction, ‘name’: self.name} @abc.abstractmethod @doc_controls.for_subclass_implementers def call(self, y_true, y_pred): «»»Invokes the `Loss` instance. Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`, except sparse loss functions such as sparse categorical crossentropy where shape = `[batch_size, d0, .. dN-1]` y_pred: The predicted values. shape = `[batch_size, d0, .. dN]` Returns: Loss values with the shape `[batch_size, d0, .. dN-1]`. «»» raise NotImplementedError(‘Must be implemented in subclasses.’) def _get_reduction(self): «»»Handles `AUTO` reduction cases and returns the reduction value.»»» if (not self._allow_sum_over_batch_size and distribution_strategy_context.has_strategy() and (self.reduction == losses_utils.ReductionV2.AUTO or self.reduction == losses_utils.ReductionV2.SUM_OVER_BATCH_SIZE)): raise ValueError( ‘Please use `tf.keras.losses.Reduction.SUM` or ‘ ‘`tf.keras.losses.Reduction.NONE` for loss reduction when losses are ‘ ‘used with `tf.distribute.Strategy` outside of the built-in training ‘ ‘loops. You can implement ‘ ‘`tf.keras.losses.Reduction.SUM_OVER_BATCH_SIZE` using global batch ‘ ‘size like:n«`nwith strategy.scope():n‘ ‘ loss_obj = tf.keras.losses.CategoricalCrossentropy(‘ ‘reduction=tf.keras.losses.Reduction.NONE)n….n‘ ‘ loss = tf.reduce_sum(loss_obj(labels, predictions)) * ‘ ‘(1. / global_batch_size)n«`nPlease see ‘ ‘https://www.tensorflow.org/tutorials/distribute/custom_training’ ‘ for more details.’) if self.reduction == losses_utils.ReductionV2.AUTO: return losses_utils.ReductionV2.SUM_OVER_BATCH_SIZE return self.reduction class LossFunctionWrapper(Loss): «»»Wraps a loss function in the `Loss` class.»»» def __init__(self, fn, reduction=losses_utils.ReductionV2.AUTO, name=None, **kwargs): «»»Initializes `LossFunctionWrapper` class. Args: fn: The loss function to wrap, with signature `fn(y_true, y_pred, **kwargs)`. reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. **kwargs: The keyword arguments that are passed on to `fn`. «»» super().__init__(reduction=reduction, name=name) self.fn = fn self._fn_kwargs = kwargs def call(self, y_true, y_pred): «»»Invokes the `LossFunctionWrapper` instance. Args: y_true: Ground truth values. y_pred: The predicted values. Returns: Loss values per sample. «»» if tensor_util.is_tf_type(y_pred) and tensor_util.is_tf_type(y_true): y_pred, y_true = losses_utils.squeeze_or_expand_dimensions(y_pred, y_true) ag_fn = autograph.tf_convert(self.fn, ag_ctx.control_status_ctx()) return ag_fn(y_true, y_pred, **self._fn_kwargs) def get_config(self): config = {} for k, v in self._fn_kwargs.items(): config[k] = backend.eval(v) if tf_utils.is_tensor_or_variable(v) else v base_config = super().get_config() return dict(list(base_config.items()) + list(config.items())) @keras_export(‘keras.losses.MeanSquaredError’) class MeanSquaredError(LossFunctionWrapper): «»»Computes the mean of squares of errors between labels and predictions. `loss = square(y_true — y_pred)` Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[1., 1.], [1., 0.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> mse = tf.keras.losses.MeanSquaredError() >>> mse(y_true, y_pred).numpy() 0.5 >>> # Calling with ‘sample_weight’. >>> mse(y_true, y_pred, sample_weight=[0.7, 0.3]).numpy() 0.25 >>> # Using ‘sum’ reduction type. >>> mse = tf.keras.losses.MeanSquaredError( … reduction=tf.keras.losses.Reduction.SUM) >>> mse(y_true, y_pred).numpy() 1.0 >>> # Using ‘none’ reduction type. >>> mse = tf.keras.losses.MeanSquaredError( … reduction=tf.keras.losses.Reduction.NONE) >>> mse(y_true, y_pred).numpy() array([0.5, 0.5], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.MeanSquaredError()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘mean_squared_error’): «»»Initializes `MeanSquaredError` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘mean_squared_error’. «»» super().__init__(mean_squared_error, name=name, reduction=reduction) @keras_export(‘keras.losses.MeanAbsoluteError’) class MeanAbsoluteError(LossFunctionWrapper): «»»Computes the mean of absolute difference between labels and predictions. `loss = abs(y_true — y_pred)` Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[1., 1.], [1., 0.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> mae = tf.keras.losses.MeanAbsoluteError() >>> mae(y_true, y_pred).numpy() 0.5 >>> # Calling with ‘sample_weight’. >>> mae(y_true, y_pred, sample_weight=[0.7, 0.3]).numpy() 0.25 >>> # Using ‘sum’ reduction type. >>> mae = tf.keras.losses.MeanAbsoluteError( … reduction=tf.keras.losses.Reduction.SUM) >>> mae(y_true, y_pred).numpy() 1.0 >>> # Using ‘none’ reduction type. >>> mae = tf.keras.losses.MeanAbsoluteError( … reduction=tf.keras.losses.Reduction.NONE) >>> mae(y_true, y_pred).numpy() array([0.5, 0.5], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.MeanAbsoluteError()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘mean_absolute_error’): «»»Initializes `MeanAbsoluteError` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘mean_absolute_error’. «»» super().__init__(mean_absolute_error, name=name, reduction=reduction) @keras_export(‘keras.losses.MeanAbsolutePercentageError’) class MeanAbsolutePercentageError(LossFunctionWrapper): «»»Computes the mean absolute percentage error between `y_true` and `y_pred`. `loss = 100 * abs(y_true — y_pred) / y_true` Standalone usage: >>> y_true = [[2., 1.], [2., 3.]] >>> y_pred = [[1., 1.], [1., 0.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> mape = tf.keras.losses.MeanAbsolutePercentageError() >>> mape(y_true, y_pred).numpy() 50. >>> # Calling with ‘sample_weight’. >>> mape(y_true, y_pred, sample_weight=[0.7, 0.3]).numpy() 20. >>> # Using ‘sum’ reduction type. >>> mape = tf.keras.losses.MeanAbsolutePercentageError( … reduction=tf.keras.losses.Reduction.SUM) >>> mape(y_true, y_pred).numpy() 100. >>> # Using ‘none’ reduction type. >>> mape = tf.keras.losses.MeanAbsolutePercentageError( … reduction=tf.keras.losses.Reduction.NONE) >>> mape(y_true, y_pred).numpy() array([25., 75.], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.MeanAbsolutePercentageError()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘mean_absolute_percentage_error’): «»»Initializes `MeanAbsolutePercentageError` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘mean_absolute_percentage_error’. «»» super().__init__( mean_absolute_percentage_error, name=name, reduction=reduction) @keras_export(‘keras.losses.MeanSquaredLogarithmicError’) class MeanSquaredLogarithmicError(LossFunctionWrapper): «»»Computes the mean squared logarithmic error between `y_true` and `y_pred`. `loss = square(log(y_true + 1.) — log(y_pred + 1.))` Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[1., 1.], [1., 0.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> msle = tf.keras.losses.MeanSquaredLogarithmicError() >>> msle(y_true, y_pred).numpy() 0.240 >>> # Calling with ‘sample_weight’. >>> msle(y_true, y_pred, sample_weight=[0.7, 0.3]).numpy() 0.120 >>> # Using ‘sum’ reduction type. >>> msle = tf.keras.losses.MeanSquaredLogarithmicError( … reduction=tf.keras.losses.Reduction.SUM) >>> msle(y_true, y_pred).numpy() 0.480 >>> # Using ‘none’ reduction type. >>> msle = tf.keras.losses.MeanSquaredLogarithmicError( … reduction=tf.keras.losses.Reduction.NONE) >>> msle(y_true, y_pred).numpy() array([0.240, 0.240], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.MeanSquaredLogarithmicError()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘mean_squared_logarithmic_error’): «»»Initializes `MeanSquaredLogarithmicError` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘mean_squared_logarithmic_error’. «»» super().__init__( mean_squared_logarithmic_error, name=name, reduction=reduction) @keras_export(‘keras.losses.BinaryCrossentropy’) class BinaryCrossentropy(LossFunctionWrapper): «»»Computes the cross-entropy loss between true labels and predicted labels. Use this cross-entropy loss for binary (0 or 1) classification applications. The loss function requires the following inputs: — `y_true` (true label): This is either 0 or 1. — `y_pred` (predicted value): This is the model’s prediction, i.e, a single floating-point value which either represents a [logit](https://en.wikipedia.org/wiki/Logit), (i.e, value in [-inf, inf] when `from_logits=True`) or a probability (i.e, value in [0., 1.] when `from_logits=False`). **Recommended Usage:** (set `from_logits=True`) With `tf.keras` API: «`python model.compile( loss=tf.keras.losses.BinaryCrossentropy(from_logits=True), …. ) «` As a standalone function: >>> # Example 1: (batch_size = 1, number of samples = 4) >>> y_true = [0, 1, 0, 0] >>> y_pred = [-18.6, 0.51, 2.94, -12.8] >>> bce = tf.keras.losses.BinaryCrossentropy(from_logits=True) >>> bce(y_true, y_pred).numpy() 0.865 >>> # Example 2: (batch_size = 2, number of samples = 4) >>> y_true = [[0, 1], [0, 0]] >>> y_pred = [[-18.6, 0.51], [2.94, -12.8]] >>> # Using default ‘auto’/’sum_over_batch_size’ reduction type. >>> bce = tf.keras.losses.BinaryCrossentropy(from_logits=True) >>> bce(y_true, y_pred).numpy() 0.865 >>> # Using ‘sample_weight’ attribute >>> bce(y_true, y_pred, sample_weight=[0.8, 0.2]).numpy() 0.243 >>> # Using ‘sum’ reduction` type. >>> bce = tf.keras.losses.BinaryCrossentropy(from_logits=True, … reduction=tf.keras.losses.Reduction.SUM) >>> bce(y_true, y_pred).numpy() 1.730 >>> # Using ‘none’ reduction type. >>> bce = tf.keras.losses.BinaryCrossentropy(from_logits=True, … reduction=tf.keras.losses.Reduction.NONE) >>> bce(y_true, y_pred).numpy() array([0.235, 1.496], dtype=float32) **Default Usage:** (set `from_logits=False`) >>> # Make the following updates to the above «Recommended Usage» section >>> # 1. Set `from_logits=False` >>> tf.keras.losses.BinaryCrossentropy() # OR …(‘from_logits=False’) >>> # 2. Update `y_pred` to use probabilities instead of logits >>> y_pred = [0.6, 0.3, 0.2, 0.8] # OR [[0.6, 0.3], [0.2, 0.8]] «»» def __init__(self, from_logits=False, label_smoothing=0, axis=—1, reduction=losses_utils.ReductionV2.AUTO, name=‘binary_crossentropy’): «»»Initializes `BinaryCrossentropy` instance. Args: from_logits: Whether to interpret `y_pred` as a tensor of [logit](https://en.wikipedia.org/wiki/Logit) values. By default, we assume that `y_pred` contains probabilities (i.e., values in [0, 1]). label_smoothing: Float in [0, 1]. When 0, no smoothing occurs. When > 0, we compute the loss between the predicted labels and a smoothed version of the true labels, where the smoothing squeezes the labels towards 0.5. Larger values of `label_smoothing` correspond to heavier smoothing. axis: The axis along which to compute crossentropy (the features axis). Defaults to -1. reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Name for the op. Defaults to ‘binary_crossentropy’. «»» super().__init__( binary_crossentropy, name=name, reduction=reduction, from_logits=from_logits, label_smoothing=label_smoothing, axis=axis) self.from_logits = from_logits @keras_export(‘keras.losses.CategoricalCrossentropy’) class CategoricalCrossentropy(LossFunctionWrapper): «»»Computes the crossentropy loss between the labels and predictions. Use this crossentropy loss function when there are two or more label classes. We expect labels to be provided in a `one_hot` representation. If you want to provide labels as integers, please use `SparseCategoricalCrossentropy` loss. There should be `# classes` floating point values per feature. In the snippet below, there is `# classes` floating pointing values per example. The shape of both `y_pred` and `y_true` are `[batch_size, num_classes]`. Standalone usage: >>> y_true = [[0, 1, 0], [0, 0, 1]] >>> y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> cce = tf.keras.losses.CategoricalCrossentropy() >>> cce(y_true, y_pred).numpy() 1.177 >>> # Calling with ‘sample_weight’. >>> cce(y_true, y_pred, sample_weight=tf.constant([0.3, 0.7])).numpy() 0.814 >>> # Using ‘sum’ reduction type. >>> cce = tf.keras.losses.CategoricalCrossentropy( … reduction=tf.keras.losses.Reduction.SUM) >>> cce(y_true, y_pred).numpy() 2.354 >>> # Using ‘none’ reduction type. >>> cce = tf.keras.losses.CategoricalCrossentropy( … reduction=tf.keras.losses.Reduction.NONE) >>> cce(y_true, y_pred).numpy() array([0.0513, 2.303], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.CategoricalCrossentropy()) «` «»» def __init__(self, from_logits=False, label_smoothing=0, axis=—1, reduction=losses_utils.ReductionV2.AUTO, name=‘categorical_crossentropy’): «»»Initializes `CategoricalCrossentropy` instance. Args: from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. label_smoothing: Float in [0, 1]. When > 0, label values are smoothed, meaning the confidence on label values are relaxed. For example, if `0.1`, use `0.1 / num_classes` for non-target labels and `0.9 + 0.1 / num_classes` for target labels. axis: The axis along which to compute crossentropy (the features axis). Defaults to -1. reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘categorical_crossentropy’. «»» super().__init__( categorical_crossentropy, name=name, reduction=reduction, from_logits=from_logits, label_smoothing=label_smoothing, axis=axis) @keras_export(‘keras.losses.SparseCategoricalCrossentropy’) class SparseCategoricalCrossentropy(LossFunctionWrapper): «»»Computes the crossentropy loss between the labels and predictions. Use this crossentropy loss function when there are two or more label classes. We expect labels to be provided as integers. If you want to provide labels using `one-hot` representation, please use `CategoricalCrossentropy` loss. There should be `# classes` floating point values per feature for `y_pred` and a single floating point value per feature for `y_true`. In the snippet below, there is a single floating point value per example for `y_true` and `# classes` floating pointing values per example for `y_pred`. The shape of `y_true` is `[batch_size]` and the shape of `y_pred` is `[batch_size, num_classes]`. Standalone usage: >>> y_true = [1, 2] >>> y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> scce = tf.keras.losses.SparseCategoricalCrossentropy() >>> scce(y_true, y_pred).numpy() 1.177 >>> # Calling with ‘sample_weight’. >>> scce(y_true, y_pred, sample_weight=tf.constant([0.3, 0.7])).numpy() 0.814 >>> # Using ‘sum’ reduction type. >>> scce = tf.keras.losses.SparseCategoricalCrossentropy( … reduction=tf.keras.losses.Reduction.SUM) >>> scce(y_true, y_pred).numpy() 2.354 >>> # Using ‘none’ reduction type. >>> scce = tf.keras.losses.SparseCategoricalCrossentropy( … reduction=tf.keras.losses.Reduction.NONE) >>> scce(y_true, y_pred).numpy() array([0.0513, 2.303], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.SparseCategoricalCrossentropy()) «` «»» def __init__(self, from_logits=False, reduction=losses_utils.ReductionV2.AUTO, name=‘sparse_categorical_crossentropy’): «»»Initializes `SparseCategoricalCrossentropy` instance. Args: from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘sparse_categorical_crossentropy’. «»» super().__init__( sparse_categorical_crossentropy, name=name, reduction=reduction, from_logits=from_logits) @keras_export(‘keras.losses.Hinge’) class Hinge(LossFunctionWrapper): «»»Computes the hinge loss between `y_true` and `y_pred`. `loss = maximum(1 — y_true * y_pred, 0)` `y_true` values are expected to be -1 or 1. If binary (0 or 1) labels are provided we will convert them to -1 or 1. Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[0.6, 0.4], [0.4, 0.6]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> h = tf.keras.losses.Hinge() >>> h(y_true, y_pred).numpy() 1.3 >>> # Calling with ‘sample_weight’. >>> h(y_true, y_pred, sample_weight=[1, 0]).numpy() 0.55 >>> # Using ‘sum’ reduction type. >>> h = tf.keras.losses.Hinge( … reduction=tf.keras.losses.Reduction.SUM) >>> h(y_true, y_pred).numpy() 2.6 >>> # Using ‘none’ reduction type. >>> h = tf.keras.losses.Hinge( … reduction=tf.keras.losses.Reduction.NONE) >>> h(y_true, y_pred).numpy() array([1.1, 1.5], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.Hinge()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘hinge’): «»»Initializes `Hinge` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘hinge’. «»» super().__init__(hinge, name=name, reduction=reduction) @keras_export(‘keras.losses.SquaredHinge’) class SquaredHinge(LossFunctionWrapper): «»»Computes the squared hinge loss between `y_true` and `y_pred`. `loss = square(maximum(1 — y_true * y_pred, 0))` `y_true` values are expected to be -1 or 1. If binary (0 or 1) labels are provided we will convert them to -1 or 1. Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[0.6, 0.4], [0.4, 0.6]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> h = tf.keras.losses.SquaredHinge() >>> h(y_true, y_pred).numpy() 1.86 >>> # Calling with ‘sample_weight’. >>> h(y_true, y_pred, sample_weight=[1, 0]).numpy() 0.73 >>> # Using ‘sum’ reduction type. >>> h = tf.keras.losses.SquaredHinge( … reduction=tf.keras.losses.Reduction.SUM) >>> h(y_true, y_pred).numpy() 3.72 >>> # Using ‘none’ reduction type. >>> h = tf.keras.losses.SquaredHinge( … reduction=tf.keras.losses.Reduction.NONE) >>> h(y_true, y_pred).numpy() array([1.46, 2.26], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.SquaredHinge()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘squared_hinge’): «»»Initializes `SquaredHinge` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘squared_hinge’. «»» super().__init__(squared_hinge, name=name, reduction=reduction) @keras_export(‘keras.losses.CategoricalHinge’) class CategoricalHinge(LossFunctionWrapper): «»»Computes the categorical hinge loss between `y_true` and `y_pred`. `loss = maximum(neg — pos + 1, 0)` where `neg=maximum((1-y_true)*y_pred) and pos=sum(y_true*y_pred)` Standalone usage: >>> y_true = [[0, 1], [0, 0]] >>> y_pred = [[0.6, 0.4], [0.4, 0.6]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> h = tf.keras.losses.CategoricalHinge() >>> h(y_true, y_pred).numpy() 1.4 >>> # Calling with ‘sample_weight’. >>> h(y_true, y_pred, sample_weight=[1, 0]).numpy() 0.6 >>> # Using ‘sum’ reduction type. >>> h = tf.keras.losses.CategoricalHinge( … reduction=tf.keras.losses.Reduction.SUM) >>> h(y_true, y_pred).numpy() 2.8 >>> # Using ‘none’ reduction type. >>> h = tf.keras.losses.CategoricalHinge( … reduction=tf.keras.losses.Reduction.NONE) >>> h(y_true, y_pred).numpy() array([1.2, 1.6], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.CategoricalHinge()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘categorical_hinge’): «»»Initializes `CategoricalHinge` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘categorical_hinge’. «»» super().__init__(categorical_hinge, name=name, reduction=reduction) @keras_export(‘keras.losses.Poisson’) class Poisson(LossFunctionWrapper): «»»Computes the Poisson loss between `y_true` and `y_pred`. `loss = y_pred — y_true * log(y_pred)` Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[1., 1.], [0., 0.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> p = tf.keras.losses.Poisson() >>> p(y_true, y_pred).numpy() 0.5 >>> # Calling with ‘sample_weight’. >>> p(y_true, y_pred, sample_weight=[0.8, 0.2]).numpy() 0.4 >>> # Using ‘sum’ reduction type. >>> p = tf.keras.losses.Poisson( … reduction=tf.keras.losses.Reduction.SUM) >>> p(y_true, y_pred).numpy() 0.999 >>> # Using ‘none’ reduction type. >>> p = tf.keras.losses.Poisson( … reduction=tf.keras.losses.Reduction.NONE) >>> p(y_true, y_pred).numpy() array([0.999, 0.], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.Poisson()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘poisson’): «»»Initializes `Poisson` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘poisson’. «»» super().__init__(poisson, name=name, reduction=reduction) @keras_export(‘keras.losses.LogCosh’) class LogCosh(LossFunctionWrapper): «»»Computes the logarithm of the hyperbolic cosine of the prediction error. `logcosh = log((exp(x) + exp(-x))/2)`, where x is the error `y_pred — y_true`. Standalone usage: >>> y_true = [[0., 1.], [0., 0.]] >>> y_pred = [[1., 1.], [0., 0.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> l = tf.keras.losses.LogCosh() >>> l(y_true, y_pred).numpy() 0.108 >>> # Calling with ‘sample_weight’. >>> l(y_true, y_pred, sample_weight=[0.8, 0.2]).numpy() 0.087 >>> # Using ‘sum’ reduction type. >>> l = tf.keras.losses.LogCosh( … reduction=tf.keras.losses.Reduction.SUM) >>> l(y_true, y_pred).numpy() 0.217 >>> # Using ‘none’ reduction type. >>> l = tf.keras.losses.LogCosh( … reduction=tf.keras.losses.Reduction.NONE) >>> l(y_true, y_pred).numpy() array([0.217, 0.], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.LogCosh()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘log_cosh’): «»»Initializes `LogCosh` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘log_cosh’. «»» super().__init__(log_cosh, name=name, reduction=reduction) @keras_export(‘keras.losses.KLDivergence’) class KLDivergence(LossFunctionWrapper): «»»Computes Kullback-Leibler divergence loss between `y_true` and `y_pred`. `loss = y_true * log(y_true / y_pred)` See: https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence Standalone usage: >>> y_true = [[0, 1], [0, 0]] >>> y_pred = [[0.6, 0.4], [0.4, 0.6]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> kl = tf.keras.losses.KLDivergence() >>> kl(y_true, y_pred).numpy() 0.458 >>> # Calling with ‘sample_weight’. >>> kl(y_true, y_pred, sample_weight=[0.8, 0.2]).numpy() 0.366 >>> # Using ‘sum’ reduction type. >>> kl = tf.keras.losses.KLDivergence( … reduction=tf.keras.losses.Reduction.SUM) >>> kl(y_true, y_pred).numpy() 0.916 >>> # Using ‘none’ reduction type. >>> kl = tf.keras.losses.KLDivergence( … reduction=tf.keras.losses.Reduction.NONE) >>> kl(y_true, y_pred).numpy() array([0.916, -3.08e-06], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.KLDivergence()) «` «»» def __init__(self, reduction=losses_utils.ReductionV2.AUTO, name=‘kl_divergence’): «»»Initializes `KLDivergence` instance. Args: reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘kl_divergence’. «»» super().__init__(kl_divergence, name=name, reduction=reduction) @keras_export(‘keras.losses.Huber’) class Huber(LossFunctionWrapper): «»»Computes the Huber loss between `y_true` and `y_pred`. For each value x in `error = y_true — y_pred`: «` loss = 0.5 * x^2 if |x| <= d loss = 0.5 * d^2 + d * (|x| — d) if |x| > d «` where d is `delta`. See: https://en.wikipedia.org/wiki/Huber_loss Standalone usage: >>> y_true = [[0, 1], [0, 0]] >>> y_pred = [[0.6, 0.4], [0.4, 0.6]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> h = tf.keras.losses.Huber() >>> h(y_true, y_pred).numpy() 0.155 >>> # Calling with ‘sample_weight’. >>> h(y_true, y_pred, sample_weight=[1, 0]).numpy() 0.09 >>> # Using ‘sum’ reduction type. >>> h = tf.keras.losses.Huber( … reduction=tf.keras.losses.Reduction.SUM) >>> h(y_true, y_pred).numpy() 0.31 >>> # Using ‘none’ reduction type. >>> h = tf.keras.losses.Huber( … reduction=tf.keras.losses.Reduction.NONE) >>> h(y_true, y_pred).numpy() array([0.18, 0.13], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.Huber()) «` «»» def __init__(self, delta=1.0, reduction=losses_utils.ReductionV2.AUTO, name=‘huber_loss’): «»»Initializes `Huber` instance. Args: delta: A float, the point where the Huber loss function changes from a quadratic to linear. reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial]( https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. Defaults to ‘huber_loss’. «»» super().__init__(huber, name=name, reduction=reduction, delta=delta) @keras_export(‘keras.metrics.mean_squared_error’, ‘keras.metrics.mse’, ‘keras.metrics.MSE’, ‘keras.losses.mean_squared_error’, ‘keras.losses.mse’, ‘keras.losses.MSE’) @dispatch.add_dispatch_support def mean_squared_error(y_true, y_pred): «»»Computes the mean squared error between labels and predictions. After computing the squared distance between the inputs, the mean value over the last dimension is returned. `loss = mean(square(y_true — y_pred), axis=-1)` Standalone usage: >>> y_true = np.random.randint(0, 2, size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.mean_squared_error(y_true, y_pred) >>> assert loss.shape == (2,) >>> assert np.array_equal( … loss.numpy(), np.mean(np.square(y_true — y_pred), axis=-1)) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Mean squared error values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) return backend.mean(math_ops.squared_difference(y_pred, y_true), axis=—1) def _ragged_tensor_apply_loss(loss_fn, y_true, y_pred, y_pred_extra_dim=False): «»»Apply a loss function on a per batch basis. Args: loss_fn: The loss function y_true: truth values (RaggedTensor) y_pred: predicted values (RaggedTensor) y_pred_extra_dim: whether y_pred has an additional dimension compared to y_true Returns: Loss-function result. A dense tensor if the output has a single dimension (per-batch loss value); a ragged tensor otherwise. «»» def rt_is_equiv_dense(rt): «»»Returns true if this RaggedTensor has the same row_lenghts across all ragged dimensions and thus can be converted to a dense tensor without loss of information. Args: rt: RaggedTensor. «»» return math_ops.reduce_all([ math_ops.equal( math_ops.reduce_variance(math_ops.cast(row_lens, backend.floatx())), constant_op.constant([0.])) for row_lens in rt.nested_row_lengths() ]) def _convert_to_dense(inputs): return tuple( rt.to_tensor() if isinstance(rt, ragged_tensor.RaggedTensor) else rt for rt in inputs) def _call_loss(inputs, ragged_output): «»» Adapt the result to ragged or dense tensor according to the expected output type. This is done so that all the return values of the map operation have the same type. «»» r = loss_fn(*inputs) if ragged_output and not isinstance(r, ragged_tensor.RaggedTensor): r = ragged_tensor.RaggedTensor.from_tensor(r) elif not ragged_output and isinstance(r, ragged_tensor.RaggedTensor): r = r.to_tensor() return r def _wrapper(inputs, ragged_output): _, y_pred = inputs if isinstance(y_pred, ragged_tensor.RaggedTensor): return control_flow_ops.cond( rt_is_equiv_dense(y_pred), lambda: _call_loss(_convert_to_dense(inputs), ragged_output), lambda: _call_loss(inputs, ragged_output)) return loss_fn(*inputs) if not isinstance(y_true, ragged_tensor.RaggedTensor): return loss_fn(y_true, y_pred.to_tensor()) lshape = y_pred.shape.as_list()[1:—1] if len(lshape) > 0: spec = ragged_tensor.RaggedTensorSpec(shape=lshape, dtype=y_pred.dtype) else: spec = tensor_spec.TensorSpec(shape=[], dtype=y_pred.dtype) nested_splits_list = [rt.nested_row_splits for rt in (y_true, y_pred)] if y_pred_extra_dim: # The last dimension of a categorical prediction may be ragged or not. rdims = [len(slist) for slist in nested_splits_list] if rdims[0] == rdims[1] — 1: nested_splits_list[1] = nested_splits_list[1][:—1] map_fn = functools.partial(_wrapper, ragged_output=len(lshape) > 1) assertion_list = ragged_util.assert_splits_match(nested_splits_list) with ops.control_dependencies(assertion_list): return ragged_map_ops.map_fn(map_fn, elems=(y_true, y_pred), dtype=spec) @dispatch.dispatch_for_types(mean_squared_error, ragged_tensor.RaggedTensor) def _ragged_tensor_mse(y_true, y_pred): «»»Implements support for handling RaggedTensors. Args: y_true: RaggedTensor truth values. shape = `[batch_size, d0, .. dN]`. y_pred: RaggedTensor predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Mean squared error values. shape = `[batch_size, d0, .. dN-1]`. When the number of dimensions of the batch feature vector [d0, .. dN] is greater than one the return value is a RaggedTensor. Otherwise a Dense tensor with dimensions [batch_size] is returned. «»» return _ragged_tensor_apply_loss(mean_squared_error, y_true, y_pred) @keras_export(‘keras.metrics.mean_absolute_error’, ‘keras.metrics.mae’, ‘keras.metrics.MAE’, ‘keras.losses.mean_absolute_error’, ‘keras.losses.mae’, ‘keras.losses.MAE’) @dispatch.add_dispatch_support def mean_absolute_error(y_true, y_pred): «»»Computes the mean absolute error between labels and predictions. `loss = mean(abs(y_true — y_pred), axis=-1)` Standalone usage: >>> y_true = np.random.randint(0, 2, size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.mean_absolute_error(y_true, y_pred) >>> assert loss.shape == (2,) >>> assert np.array_equal( … loss.numpy(), np.mean(np.abs(y_true — y_pred), axis=-1)) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Mean absolute error values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) return backend.mean(math_ops.abs(y_pred — y_true), axis=—1) @dispatch.dispatch_for_types(mean_absolute_error, ragged_tensor.RaggedTensor) def _ragged_tensor_mae(y_true, y_pred): «»»RaggedTensor adapter for mean_absolute_error.»»» return _ragged_tensor_apply_loss(mean_absolute_error, y_true, y_pred) @keras_export(‘keras.metrics.mean_absolute_percentage_error’, ‘keras.metrics.mape’, ‘keras.metrics.MAPE’, ‘keras.losses.mean_absolute_percentage_error’, ‘keras.losses.mape’, ‘keras.losses.MAPE’) @dispatch.add_dispatch_support def mean_absolute_percentage_error(y_true, y_pred): «»»Computes the mean absolute percentage error between `y_true` and `y_pred`. `loss = 100 * mean(abs((y_true — y_pred) / y_true), axis=-1)` Standalone usage: >>> y_true = np.random.random(size=(2, 3)) >>> y_true = np.maximum(y_true, 1e-7) # Prevent division by zero >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.mean_absolute_percentage_error(y_true, y_pred) >>> assert loss.shape == (2,) >>> assert np.array_equal( … loss.numpy(), … 100. * np.mean(np.abs((y_true — y_pred) / y_true), axis=-1)) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Mean absolute percentage error values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) diff = math_ops.abs( (y_true — y_pred) / backend.maximum(math_ops.abs(y_true), backend.epsilon())) return 100. * backend.mean(diff, axis=—1) @dispatch.dispatch_for_types(mean_absolute_percentage_error, ragged_tensor.RaggedTensor) def _ragged_tensor_mape(y_true, y_pred): «»»Support RaggedTensors.»»» return _ragged_tensor_apply_loss(mean_absolute_percentage_error, y_true, y_pred) @keras_export(‘keras.metrics.mean_squared_logarithmic_error’, ‘keras.metrics.msle’, ‘keras.metrics.MSLE’, ‘keras.losses.mean_squared_logarithmic_error’, ‘keras.losses.msle’, ‘keras.losses.MSLE’) @dispatch.add_dispatch_support def mean_squared_logarithmic_error(y_true, y_pred): «»»Computes the mean squared logarithmic error between `y_true` and `y_pred`. `loss = mean(square(log(y_true + 1) — log(y_pred + 1)), axis=-1)` Standalone usage: >>> y_true = np.random.randint(0, 2, size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.mean_squared_logarithmic_error(y_true, y_pred) >>> assert loss.shape == (2,) >>> y_true = np.maximum(y_true, 1e-7) >>> y_pred = np.maximum(y_pred, 1e-7) >>> assert np.allclose( … loss.numpy(), … np.mean( … np.square(np.log(y_true + 1.) — np.log(y_pred + 1.)), axis=-1)) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Mean squared logarithmic error values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) first_log = math_ops.log(backend.maximum(y_pred, backend.epsilon()) + 1.) second_log = math_ops.log(backend.maximum(y_true, backend.epsilon()) + 1.) return backend.mean( math_ops.squared_difference(first_log, second_log), axis=—1) @dispatch.dispatch_for_types(mean_squared_logarithmic_error, ragged_tensor.RaggedTensor) def _ragged_tensor_msle(y_true, y_pred): «»»Implements support for handling RaggedTensors.»»» return _ragged_tensor_apply_loss(mean_squared_logarithmic_error, y_true, y_pred) def _maybe_convert_labels(y_true): «»»Converts binary labels into -1/1.»»» are_zeros = math_ops.equal(y_true, 0) are_ones = math_ops.equal(y_true, 1) is_binary = math_ops.reduce_all(math_ops.logical_or(are_zeros, are_ones)) def _convert_binary_labels(): # Convert the binary labels to -1 or 1. return 2. * y_true — 1. updated_y_true = smart_cond.smart_cond(is_binary, _convert_binary_labels, lambda: y_true) return updated_y_true @keras_export(‘keras.metrics.squared_hinge’, ‘keras.losses.squared_hinge’) @dispatch.add_dispatch_support def squared_hinge(y_true, y_pred): «»»Computes the squared hinge loss between `y_true` and `y_pred`. `loss = mean(square(maximum(1 — y_true * y_pred, 0)), axis=-1)` Standalone usage: >>> y_true = np.random.choice([-1, 1], size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.squared_hinge(y_true, y_pred) >>> assert loss.shape == (2,) >>> assert np.array_equal( … loss.numpy(), … np.mean(np.square(np.maximum(1. — y_true * y_pred, 0.)), axis=-1)) Args: y_true: The ground truth values. `y_true` values are expected to be -1 or 1. If binary (0 or 1) labels are provided we will convert them to -1 or 1. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Squared hinge loss values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) y_true = _maybe_convert_labels(y_true) return backend.mean( math_ops.square(math_ops.maximum(1. — y_true * y_pred, 0.)), axis=—1) @keras_export(‘keras.metrics.hinge’, ‘keras.losses.hinge’) @dispatch.add_dispatch_support def hinge(y_true, y_pred): «»»Computes the hinge loss between `y_true` and `y_pred`. `loss = mean(maximum(1 — y_true * y_pred, 0), axis=-1)` Standalone usage: >>> y_true = np.random.choice([-1, 1], size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.hinge(y_true, y_pred) >>> assert loss.shape == (2,) >>> assert np.array_equal( … loss.numpy(), … np.mean(np.maximum(1. — y_true * y_pred, 0.), axis=-1)) Args: y_true: The ground truth values. `y_true` values are expected to be -1 or 1. If binary (0 or 1) labels are provided they will be converted to -1 or 1. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Hinge loss values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) y_true = _maybe_convert_labels(y_true) return backend.mean(math_ops.maximum(1. — y_true * y_pred, 0.), axis=—1) @keras_export(‘keras.losses.categorical_hinge’) @dispatch.add_dispatch_support def categorical_hinge(y_true, y_pred): «»»Computes the categorical hinge loss between `y_true` and `y_pred`. `loss = maximum(neg — pos + 1, 0)` where `neg=maximum((1-y_true)*y_pred) and pos=sum(y_true*y_pred)` Standalone usage: >>> y_true = np.random.randint(0, 3, size=(2,)) >>> y_true = tf.keras.utils.to_categorical(y_true, num_classes=3) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.categorical_hinge(y_true, y_pred) >>> assert loss.shape == (2,) >>> pos = np.sum(y_true * y_pred, axis=-1) >>> neg = np.amax((1. — y_true) * y_pred, axis=-1) >>> assert np.array_equal(loss.numpy(), np.maximum(0., neg — pos + 1.)) Args: y_true: The ground truth values. `y_true` values are expected to be either `{-1, +1}` or `{0, 1}` (i.e. a one-hot-encoded tensor). y_pred: The predicted values. Returns: Categorical hinge loss values. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) pos = math_ops.reduce_sum(y_true * y_pred, axis=—1) neg = math_ops.reduce_max((1. — y_true) * y_pred, axis=—1) zero = math_ops.cast(0., y_pred.dtype) return math_ops.maximum(neg — pos + 1., zero) @keras_export(‘keras.losses.huber’, v1=[]) @dispatch.add_dispatch_support def huber(y_true, y_pred, delta=1.0): «»»Computes Huber loss value. For each value x in `error = y_true — y_pred`: «` loss = 0.5 * x^2 if |x| <= d loss = d * |x| — 0.5 * d^2 if |x| > d «` where d is `delta`. See: https://en.wikipedia.org/wiki/Huber_loss Args: y_true: tensor of true targets. y_pred: tensor of predicted targets. delta: A float, the point where the Huber loss function changes from a quadratic to linear. Returns: Tensor with one scalar loss entry per sample. «»» y_pred = math_ops.cast(y_pred, dtype=backend.floatx()) y_true = math_ops.cast(y_true, dtype=backend.floatx()) delta = math_ops.cast(delta, dtype=backend.floatx()) error = math_ops.subtract(y_pred, y_true) abs_error = math_ops.abs(error) half = ops.convert_to_tensor_v2_with_dispatch(0.5, dtype=abs_error.dtype) return backend.mean( array_ops.where_v2(abs_error <= delta, half * math_ops.square(error), delta * abs_error — half * math_ops.square(delta)), axis=—1) @keras_export(‘keras.losses.log_cosh’, ‘keras.losses.logcosh’, ‘keras.metrics.log_cosh’, ‘keras.metrics.logcosh’) @dispatch.add_dispatch_support def log_cosh(y_true, y_pred): «»»Logarithm of the hyperbolic cosine of the prediction error. `log(cosh(x))` is approximately equal to `(x ** 2) / 2` for small `x` and to `abs(x) — log(2)` for large `x`. This means that ‘logcosh’ works mostly like the mean squared error, but will not be so strongly affected by the occasional wildly incorrect prediction. Standalone usage: >>> y_true = np.random.random(size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.logcosh(y_true, y_pred) >>> assert loss.shape == (2,) >>> x = y_pred — y_true >>> assert np.allclose( … loss.numpy(), … np.mean(x + np.log(np.exp(-2. * x) + 1.) — math_ops.log(2.), axis=-1), … atol=1e-5) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Logcosh error values. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) def _logcosh(x): return x + math_ops.softplus(—2. * x) — math_ops.cast( math_ops.log(2.), x.dtype) return backend.mean(_logcosh(y_pred — y_true), axis=—1) @keras_export(‘keras.metrics.categorical_crossentropy’, ‘keras.losses.categorical_crossentropy’) @dispatch.add_dispatch_support def categorical_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0, axis=—1): «»»Computes the categorical crossentropy loss. Standalone usage: >>> y_true = [[0, 1, 0], [0, 0, 1]] >>> y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]] >>> loss = tf.keras.losses.categorical_crossentropy(y_true, y_pred) >>> assert loss.shape == (2,) >>> loss.numpy() array([0.0513, 2.303], dtype=float32) Args: y_true: Tensor of one-hot true targets. y_pred: Tensor of predicted targets. from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. label_smoothing: Float in [0, 1]. If > `0` then smooth the labels. For example, if `0.1`, use `0.1 / num_classes` for non-target labels and `0.9 + 0.1 / num_classes` for target labels. axis: Defaults to -1. The dimension along which the entropy is computed. Returns: Categorical crossentropy loss value. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) label_smoothing = ops.convert_to_tensor_v2_with_dispatch( label_smoothing, dtype=backend.floatx()) def _smooth_labels(): num_classes = math_ops.cast(array_ops.shape(y_true)[—1], y_pred.dtype) return y_true * (1.0 — label_smoothing) + (label_smoothing / num_classes) y_true = smart_cond.smart_cond(label_smoothing, _smooth_labels, lambda: y_true) return backend.categorical_crossentropy( y_true, y_pred, from_logits=from_logits, axis=axis) @dispatch.dispatch_for_types(categorical_crossentropy, ragged_tensor.RaggedTensor) def _ragged_tensor_categorical_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0, axis=—1): «»»Implements support for handling RaggedTensors. Args: y_true: Tensor of one-hot true targets. y_pred: Tensor of predicted targets. from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. label_smoothing: Float in [0, 1]. If > `0` then smooth the labels. For example, if `0.1`, use `0.1 / num_classes` for non-target labels and `0.9 + 0.1 / num_classes` for target labels. axis: The axis along which to compute crossentropy (the features axis). Defaults to -1. Returns: Categorical crossentropy loss value. Expected shape: (batch, sequence_len, n_classes) with sequence_len being variable per batch. Return shape: (batch, sequence_len). When used by CategoricalCrossentropy() with the default reduction (SUM_OVER_BATCH_SIZE), the reduction averages the loss over the number of elements independent of the batch. E.g. if the RaggedTensor has 2 batches with [2, 1] values respectivly the resulting loss is the sum of the individual loss values divided by 3. «»» fn = functools.partial( categorical_crossentropy, from_logits=from_logits, label_smoothing=label_smoothing, axis=axis) return _ragged_tensor_apply_loss(fn, y_true, y_pred) @keras_export(‘keras.metrics.sparse_categorical_crossentropy’, ‘keras.losses.sparse_categorical_crossentropy’) @dispatch.add_dispatch_support def sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=—1): «»»Computes the sparse categorical crossentropy loss. Standalone usage: >>> y_true = [1, 2] >>> y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]] >>> loss = tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred) >>> assert loss.shape == (2,) >>> loss.numpy() array([0.0513, 2.303], dtype=float32) Args: y_true: Ground truth values. y_pred: The predicted values. from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. axis: Defaults to -1. The dimension along which the entropy is computed. Returns: Sparse categorical crossentropy loss value. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) return backend.sparse_categorical_crossentropy( y_true, y_pred, from_logits=from_logits, axis=axis) @dispatch.dispatch_for_types(sparse_categorical_crossentropy, ragged_tensor.RaggedTensor) def _ragged_tensor_sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=—1): «»» Implements support for handling RaggedTensors. Expected y_pred shape: (batch, sequence_len, n_classes) with sequence_len being variable per batch. Return shape: (batch, sequence_len). When used by SparseCategoricalCrossentropy() with the default reduction (SUM_OVER_BATCH_SIZE), the reduction averages the loss over the number of elements independent of the batch. E.g. if the RaggedTensor has 2 batches with [2, 1] values respectively, the resulting loss is the sum of the individual loss values divided by 3. «»» fn = functools.partial( sparse_categorical_crossentropy, from_logits=from_logits, axis=axis) return _ragged_tensor_apply_loss(fn, y_true, y_pred, y_pred_extra_dim=True) @keras_export(‘keras.metrics.binary_crossentropy’, ‘keras.losses.binary_crossentropy’) @dispatch.add_dispatch_support def binary_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0, axis=—1): «»»Computes the binary crossentropy loss. Standalone usage: >>> y_true = [[0, 1], [0, 0]] >>> y_pred = [[0.6, 0.4], [0.4, 0.6]] >>> loss = tf.keras.losses.binary_crossentropy(y_true, y_pred) >>> assert loss.shape == (2,) >>> loss.numpy() array([0.916 , 0.714], dtype=float32) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. label_smoothing: Float in [0, 1]. If > `0` then smooth the labels by squeezing them towards 0.5 That is, using `1. — 0.5 * label_smoothing` for the target class and `0.5 * label_smoothing` for the non-target class. axis: The axis along which the mean is computed. Defaults to -1. Returns: Binary crossentropy loss value. shape = `[batch_size, d0, .. dN-1]`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) label_smoothing = ops.convert_to_tensor_v2_with_dispatch( label_smoothing, dtype=backend.floatx()) def _smooth_labels(): return y_true * (1.0 — label_smoothing) + 0.5 * label_smoothing y_true = smart_cond.smart_cond(label_smoothing, _smooth_labels, lambda: y_true) return backend.mean( backend.binary_crossentropy(y_true, y_pred, from_logits=from_logits), axis=axis) @dispatch.dispatch_for_types(binary_crossentropy, ragged_tensor.RaggedTensor) def _ragged_tensor_binary_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0, axis=—1): «»»Implements support for handling RaggedTensors. Args: y_true: Tensor of one-hot true targets. y_pred: Tensor of predicted targets. from_logits: Whether `y_pred` is expected to be a logits tensor. By default, we assume that `y_pred` encodes a probability distribution. label_smoothing: Float in [0, 1]. If > `0` then smooth the labels. For example, if `0.1`, use `0.1 / num_classes` for non-target labels and `0.9 + 0.1 / num_classes` for target labels. axis: Axis along which to compute crossentropy. Returns: Binary crossentropy loss value. Expected shape: (batch, sequence_len) with sequence_len being variable per batch. Return shape: (batch,); returns the per batch mean of the loss values. When used by BinaryCrossentropy() with the default reduction (SUM_OVER_BATCH_SIZE), the reduction averages the per batch losses over the number of batches. «»» fn = functools.partial( binary_crossentropy, from_logits=from_logits, label_smoothing=label_smoothing, axis=axis) return _ragged_tensor_apply_loss(fn, y_true, y_pred) @keras_export(‘keras.metrics.kl_divergence’, ‘keras.metrics.kullback_leibler_divergence’, ‘keras.metrics.kld’, ‘keras.metrics.KLD’, ‘keras.losses.kl_divergence’, ‘keras.losses.kullback_leibler_divergence’, ‘keras.losses.kld’, ‘keras.losses.KLD’) @dispatch.add_dispatch_support def kl_divergence(y_true, y_pred): «»»Computes Kullback-Leibler divergence loss between `y_true` and `y_pred`. `loss = y_true * log(y_true / y_pred)` See: https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence Standalone usage: >>> y_true = np.random.randint(0, 2, size=(2, 3)).astype(np.float64) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.kullback_leibler_divergence(y_true, y_pred) >>> assert loss.shape == (2,) >>> y_true = tf.keras.backend.clip(y_true, 1e-7, 1) >>> y_pred = tf.keras.backend.clip(y_pred, 1e-7, 1) >>> assert np.array_equal( … loss.numpy(), np.sum(y_true * np.log(y_true / y_pred), axis=-1)) Args: y_true: Tensor of true targets. y_pred: Tensor of predicted targets. Returns: A `Tensor` with loss. Raises: TypeError: If `y_true` cannot be cast to the `y_pred.dtype`. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) y_true = backend.clip(y_true, backend.epsilon(), 1) y_pred = backend.clip(y_pred, backend.epsilon(), 1) return math_ops.reduce_sum(y_true * math_ops.log(y_true / y_pred), axis=—1) @keras_export(‘keras.metrics.poisson’, ‘keras.losses.poisson’) @dispatch.add_dispatch_support def poisson(y_true, y_pred): «»»Computes the Poisson loss between y_true and y_pred. The Poisson loss is the mean of the elements of the `Tensor` `y_pred — y_true * log(y_pred)`. Standalone usage: >>> y_true = np.random.randint(0, 2, size=(2, 3)) >>> y_pred = np.random.random(size=(2, 3)) >>> loss = tf.keras.losses.poisson(y_true, y_pred) >>> assert loss.shape == (2,) >>> y_pred = y_pred + 1e-7 >>> assert np.allclose( … loss.numpy(), np.mean(y_pred — y_true * np.log(y_pred), axis=-1), … atol=1e-5) Args: y_true: Ground truth values. shape = `[batch_size, d0, .. dN]`. y_pred: The predicted values. shape = `[batch_size, d0, .. dN]`. Returns: Poisson loss value. shape = `[batch_size, d0, .. dN-1]`. Raises: InvalidArgumentError: If `y_true` and `y_pred` have incompatible shapes. «»» y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred) y_true = math_ops.cast(y_true, y_pred.dtype) return backend.mean( y_pred — y_true * math_ops.log(y_pred + backend.epsilon()), axis=—1) @keras_export( ‘keras.losses.cosine_similarity’, v1=[ ‘keras.metrics.cosine_proximity’, ‘keras.metrics.cosine’, ‘keras.losses.cosine_proximity’, ‘keras.losses.cosine’, ‘keras.losses.cosine_similarity’, ]) @dispatch.add_dispatch_support def cosine_similarity(y_true, y_pred, axis=—1): «»»Computes the cosine similarity between labels and predictions. Note that it is a number between -1 and 1. When it is a negative number between -1 and 0, 0 indicates orthogonality and values closer to -1 indicate greater similarity. The values closer to 1 indicate greater dissimilarity. This makes it usable as a loss function in a setting where you try to maximize the proximity between predictions and targets. If either `y_true` or `y_pred` is a zero vector, cosine similarity will be 0 regardless of the proximity between predictions and targets. `loss = -sum(l2_norm(y_true) * l2_norm(y_pred))` Standalone usage: >>> y_true = [[0., 1.], [1., 1.], [1., 1.]] >>> y_pred = [[1., 0.], [1., 1.], [-1., -1.]] >>> loss = tf.keras.losses.cosine_similarity(y_true, y_pred, axis=1) >>> loss.numpy() array([-0., -0.999, 0.999], dtype=float32) Args: y_true: Tensor of true targets. y_pred: Tensor of predicted targets. axis: Axis along which to determine similarity. Returns: Cosine similarity tensor. «»» y_true = nn.l2_normalize(y_true, axis=axis) y_pred = nn.l2_normalize(y_pred, axis=axis) return —math_ops.reduce_sum(y_true * y_pred, axis=axis) @keras_export(‘keras.losses.CosineSimilarity’) class CosineSimilarity(LossFunctionWrapper): «»»Computes the cosine similarity between labels and predictions. Note that it is a number between -1 and 1. When it is a negative number between -1 and 0, 0 indicates orthogonality and values closer to -1 indicate greater similarity. The values closer to 1 indicate greater dissimilarity. This makes it usable as a loss function in a setting where you try to maximize the proximity between predictions and targets. If either `y_true` or `y_pred` is a zero vector, cosine similarity will be 0 regardless of the proximity between predictions and targets. `loss = -sum(l2_norm(y_true) * l2_norm(y_pred))` Standalone usage: >>> y_true = [[0., 1.], [1., 1.]] >>> y_pred = [[1., 0.], [1., 1.]] >>> # Using ‘auto’/’sum_over_batch_size’ reduction type. >>> cosine_loss = tf.keras.losses.CosineSimilarity(axis=1) >>> # l2_norm(y_true) = [[0., 1.], [1./1.414, 1./1.414]] >>> # l2_norm(y_pred) = [[1., 0.], [1./1.414, 1./1.414]] >>> # l2_norm(y_true) . l2_norm(y_pred) = [[0., 0.], [0.5, 0.5]] >>> # loss = mean(sum(l2_norm(y_true) . l2_norm(y_pred), axis=1)) >>> # = -((0. + 0.) + (0.5 + 0.5)) / 2 >>> cosine_loss(y_true, y_pred).numpy() -0.5 >>> # Calling with ‘sample_weight’. >>> cosine_loss(y_true, y_pred, sample_weight=[0.8, 0.2]).numpy() -0.0999 >>> # Using ‘sum’ reduction type. >>> cosine_loss = tf.keras.losses.CosineSimilarity(axis=1, … reduction=tf.keras.losses.Reduction.SUM) >>> cosine_loss(y_true, y_pred).numpy() -0.999 >>> # Using ‘none’ reduction type. >>> cosine_loss = tf.keras.losses.CosineSimilarity(axis=1, … reduction=tf.keras.losses.Reduction.NONE) >>> cosine_loss(y_true, y_pred).numpy() array([-0., -0.999], dtype=float32) Usage with the `compile()` API: «`python model.compile(optimizer=’sgd’, loss=tf.keras.losses.CosineSimilarity(axis=1)) «` Args: axis: The axis along which the cosine similarity is computed (the features axis). Defaults to -1. reduction: Type of `tf.keras.losses.Reduction` to apply to loss. Default value is `AUTO`. `AUTO` indicates that the reduction option will be determined by the usage context. For almost all cases this defaults to `SUM_OVER_BATCH_SIZE`. When used with `tf.distribute.Strategy`, outside of built-in training loops such as `tf.keras` `compile` and `fit`, using `AUTO` or `SUM_OVER_BATCH_SIZE` will raise an error. Please see this custom training [tutorial] (https://www.tensorflow.org/tutorials/distribute/custom_training) for more details. name: Optional name for the instance. «»» def __init__(self, axis=—1, reduction=losses_utils.ReductionV2.AUTO, name=‘cosine_similarity’): super().__init__( cosine_similarity, reduction=reduction, name=name, axis=axis) # Aliases. bce = BCE = binary_crossentropy mse = MSE = mean_squared_error mae = MAE = mean_absolute_error mape = MAPE = mean_absolute_percentage_error msle = MSLE = mean_squared_logarithmic_error kld = KLD = kullback_leibler_divergence = kl_divergence logcosh = log_cosh huber_loss = huber def is_categorical_crossentropy(loss): result = ((isinstance(loss, CategoricalCrossentropy) or (isinstance(loss, LossFunctionWrapper) and loss.fn == categorical_crossentropy) or (hasattr(loss, ‘__name__’) and loss.__name__ == ‘categorical_crossentropy’) or (loss == ‘categorical_crossentropy’))) return result @keras_export(‘keras.losses.serialize’) def serialize(loss): «»»Serializes loss function or `Loss` instance. Args: loss: A Keras `Loss` instance or a loss function. Returns: Loss configuration dictionary. «»» return serialize_keras_object(loss) @keras_export(‘keras.losses.deserialize’) def deserialize(name, custom_objects=None): «»»Deserializes a serialized loss class/function instance. Args: name: Loss configuration. custom_objects: Optional dictionary mapping names (strings) to custom objects (classes and functions) to be considered during deserialization. Returns: A Keras `Loss` instance or a loss function. «»» return deserialize_keras_object( name, module_objects=globals(), custom_objects=custom_objects, printable_module_name=‘loss function’) @keras_export(‘keras.losses.get’) def get(identifier): «»»Retrieves a Keras loss as a `function`/`Loss` class instance. The `identifier` may be the string name of a loss function or `Loss` class. >>> loss = tf.keras.losses.get(«categorical_crossentropy») >>> type(loss) <class ‘function’> >>> loss = tf.keras.losses.get(«CategoricalCrossentropy») >>> type(loss) <class ‘…keras.losses.CategoricalCrossentropy’> You can also specify `config` of the loss to this function by passing dict containing `class_name` and `config` as an identifier. Also note that the `class_name` must map to a `Loss` class >>> identifier = {«class_name»: «CategoricalCrossentropy», … «config»: {«from_logits»: True}} >>> loss = tf.keras.losses.get(identifier) >>> type(loss) <class ‘…keras.losses.CategoricalCrossentropy’> Args: identifier: A loss identifier. One of None or string name of a loss function/class or loss configuration dictionary or a loss function or a loss class instance. Returns: A Keras loss as a `function`/ `Loss` class instance. Raises: ValueError: If `identifier` cannot be interpreted. «»» if identifier is None: return None if isinstance(identifier, str): identifier = str(identifier) return deserialize(identifier) if isinstance(identifier, dict): return deserialize(identifier) if callable(identifier): return identifier raise ValueError( f’Could not interpret loss function identifier: {identifier}‘) LABEL_DTYPES_FOR_LOSSES = { losses_impl.sparse_softmax_cross_entropy: ‘int32’, sparse_categorical_crossentropy: ‘int32’ }

Источник

logo

Zero to Mastery TensorFlow for Deep Learning

Home
Fundamentals
Fundamentals
- 00. Getting started with TensorFlow: A guide to the fundamentals
- 01. Neural Network Regression with TensorFlow
  
  01. Neural Network Regression with TensorFlow
  Table of contents
  - What we’re going to cover
  - How you can use this notebook
  - Typical architecture of a regresison neural network
  - Creating data to view and fit
  - Regression input shapes and output shapes
  - Steps in modelling with TensorFlow
  - Improving a model
  - Evaluating a model
    
    Visualize, visualize, visualize
  - Split data into training/test set
  - Visualizing the data
  - Visualizing the model
  - Visualizing the predictions
  - Evaluating predictions
  - Running experiments to improve a model
  - Comparing results
  - Tracking your experiments
  - Saving a model
  - Loading a model
  - Downloading a model (from Google Colab)
  - A larger example
  - Preprocessing data (normalization and standardization)
  - 🛠 Exercises
  - 📖 Extra curriculum
- 02. Neural Network Classification with TensorFlow
Computer Vision
Computer Vision
- 03. Convolutional Neural Networks and Computer Vision with TensorFlow
Transfer Learning
Transfer Learning
- 04. Transfer Learning with TensorFlow Part 1: Feature Extraction
- 05. Transfer Learning with TensorFlow Part 2: Fine-tuning
- 06. Transfer Learning with TensorFlow Part 3: Scaling up (🍔👁 Food Vision mini)
- 07 Milestone Project 1: 🍔👁 Food Vision Big™
Natural Language Processing
Natural Language Processing
- 08. Natural Language Processing with TensorFlow
- 09. Milestone Project 2: SkimLit 📄🔥
Time Series
Time Series
- 10. Milestone Project 3: Time series forecasting in TensorFlow (BitPredict 💰📈)
Preparing for the TensorFlow Developer Certification Exam

There are many definitions for a regression problem but in our case, we’re going to simplify it to be: predicting a number.

For example, you might want to:

Predict the selling price of houses given information about them (such as number of rooms, size, number of bathrooms).
Predict the coordinates of a bounding box of an item in an image.
Predict the cost of medical insurance for an individual given their demographics (age, sex, gender, race).

In this notebook, we’re going to set the foundations for how you can take a sample of inputs (this is your data), build a neural network to discover patterns in those inputs and then make a prediction (in the form of a number) based on those inputs.

What we’re going to cover¶

Specifically, we’re going to go through doing the following with TensorFlow:

Architecture of a regression model
Input shapes and output shapes
- X: features/data (inputs)
- y: labels (outputs)
Creating custom data to view and fit
Steps in modelling
- Creating a model
- Compiling a model
  - Defining a loss function
  - Setting up an optimizer
  - Creating evaluation metrics
- Fitting a model (getting it to find patterns in our data)
Evaluating a model
- Visualizng the model («visualize, visualize, visualize»)
- Looking at training curves
- Compare predictions to ground truth (using our evaluation metrics)
Saving a model (so we can use it later)
Loading a model

Don’t worry if none of these make sense now, we’re going to go through each.

How you can use this notebook¶

You can read through the descriptions and the code (it should all run), but there’s a better option.

Write all of the code yourself.

Yes. I’m serious. Create a new notebook, and rewrite each line by yourself. Investigate it, see if you can break it, why does it break?

You don’t have to write the text descriptions but writing the code yourself is a great way to get hands-on experience.

Don’t worry if you make mistakes, we all do. The way to get better and make less mistakes is to write more code.

Typical architecture of a regresison neural network¶

The word typical is on purpose.

Why?

Because there are many different ways (actually, there’s almost an infinite number of ways) to write neural networks.

But the following is a generic setup for ingesting a collection of numbers, finding patterns in them and then outputing some kind of target number.

Yes, the previous sentence is vague but we’ll see this in action shortly.

Hyperparameter	Typical value
Input layer shape	Same shape as number of features (e.g. 3 for # bedrooms, # bathrooms, # car spaces in housing price prediction)
Hidden layer(s)	Problem specific, minimum = 1, maximum = unlimited
Neurons per hidden layer	Problem specific, generally 10 to 100
Output layer shape	Same shape as desired prediction shape (e.g. 1 for house price)
Hidden activation	Usually ReLU (rectified linear unit)
Output activation	None, ReLU, logistic/tanh
Loss function	MSE (mean square error) or MAE (mean absolute error)/Huber (combination of MAE/MSE) if outliers
Optimizer	SGD (stochastic gradient descent), Adam

Table 1: Typical architecture of a regression network. Source: Adapted from page 293 of Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow Book by Aurélien Géron

Again, if you’re new to neural networks and deep learning in general, much of the above table won’t make sense. But don’t worry, we’ll be getting hands-on with all of it soon.

🔑 Note: A hyperparameter in machine learning is something a data analyst or developer can set themselves, where as a parameter usually describes something a model learns on its own (a value not explicitly set by an analyst).

Okay, enough talk, let’s get started writing code.

To use TensorFlow, we’ll import it as the common alias tf (short for TensorFlow).

In [18]:

import tensorflow as tf
print(tf.__version__) # check the version (should be 2.x+)

import tensorflow as tf
print(tf.__version__) # check the version (should be 2.x+)

Creating data to view and fit¶

Since we’re working on a regression problem (predicting a number) let’s create some linear data (a straight line) to model.

In [19]:

import numpy as np
import matplotlib.pyplot as plt

# Create features
X = np.array([-7.0, -4.0, -1.0, 2.0, 5.0, 8.0, 11.0, 14.0])

# Create labels
y = np.array([3.0, 6.0, 9.0, 12.0, 15.0, 18.0, 21.0, 24.0])

# Visualize it
plt.scatter(X, y);

import numpy as np
import matplotlib.pyplot as plt

# Create features
X = np.array([-7.0, -4.0, -1.0, 2.0, 5.0, 8.0, 11.0, 14.0])

# Create labels
y = np.array([3.0, 6.0, 9.0, 12.0, 15.0, 18.0, 21.0, 24.0])

# Visualize it
plt.scatter(X, y);

Before we do any modelling, can you calculate the pattern between X and y?

For example, say I asked you, based on this data what the y value would be if X was 17.0?

Or how about if X was -10.0?

This kind of pattern discovery is the essence of what we’ll be building neural networks to do for us.

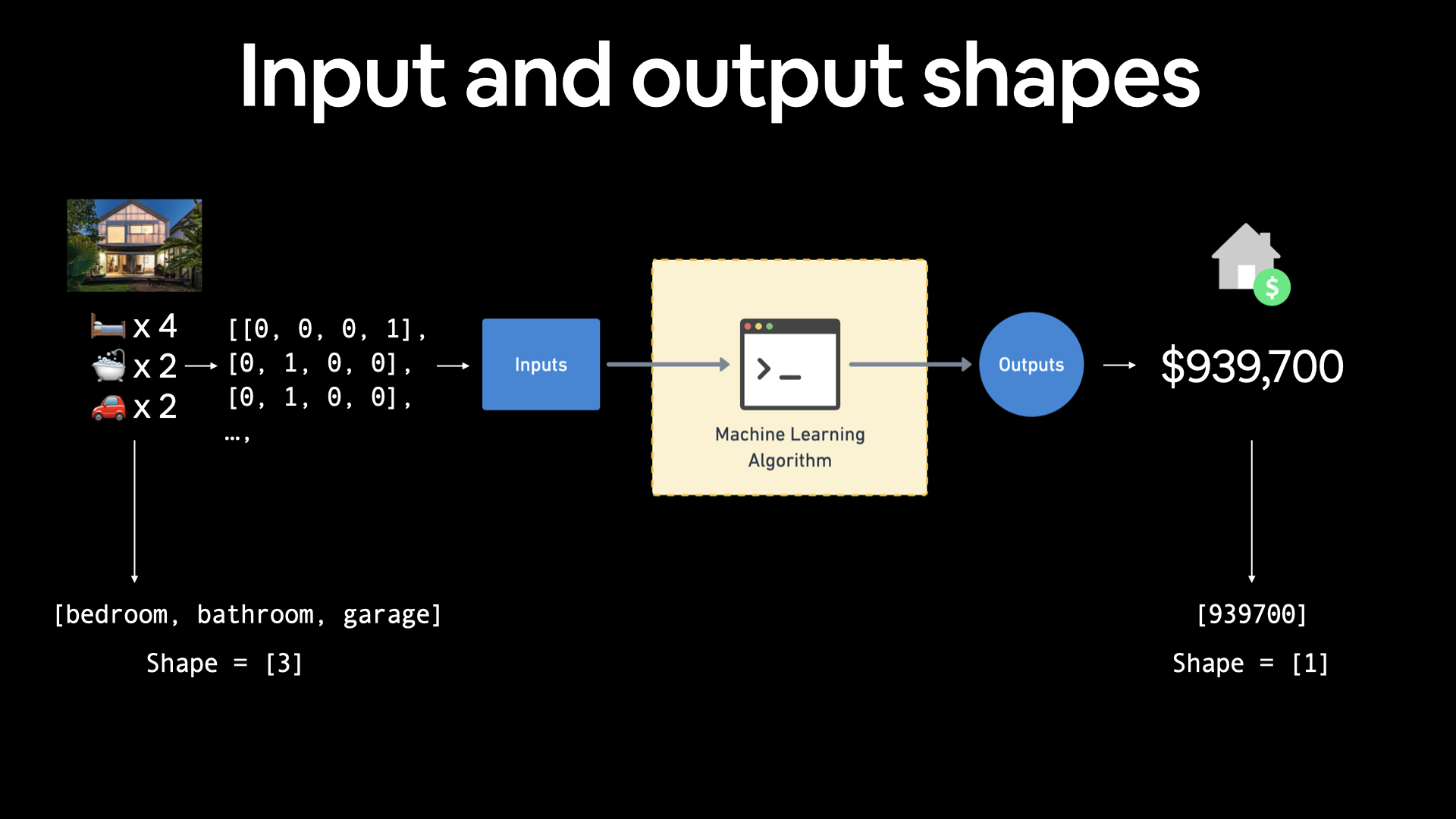
Regression input shapes and output shapes¶

One of the most important concepts when working with neural networks are the input and output shapes.

The input shape is the shape of your data that goes into the model.

The output shape is the shape of your data you want to come out of your model.

These will differ depending on the problem you’re working on.

Neural networks accept numbers and output numbers. These numbers are typically represented as tensors (or arrays).

Before, we created data using NumPy arrays, but we could do the same with tensors.

In [20]:

# Example input and output shapes of a regresson model
house_info = tf.constant(["bedroom", "bathroom", "garage"])
house_price = tf.constant([939700])
house_info, house_price

# Example input and output shapes of a regresson model
house_info = tf.constant([«bedroom», «bathroom», «garage»])
house_price = tf.constant([939700])
house_info, house_price

Out[20]:

(<tf.Tensor: shape=(3,), dtype=string, numpy=array([b'bedroom', b'bathroom', b'garage'], dtype=object)>,
 <tf.Tensor: shape=(1,), dtype=int32, numpy=array([939700], dtype=int32)>)

In [22]:

import numpy as np
import matplotlib.pyplot as plt

# Create features (using tensors)
X = tf.constant([-7.0, -4.0, -1.0, 2.0, 5.0, 8.0, 11.0, 14.0])

# Create labels (using tensors)
y = tf.constant([3.0, 6.0, 9.0, 12.0, 15.0, 18.0, 21.0, 24.0])

# Visualize it
plt.scatter(X, y);

import numpy as np
import matplotlib.pyplot as plt

# Create features (using tensors)
X = tf.constant([-7.0, -4.0, -1.0, 2.0, 5.0, 8.0, 11.0, 14.0])

# Create labels (using tensors)
y = tf.constant([3.0, 6.0, 9.0, 12.0, 15.0, 18.0, 21.0, 24.0])

# Visualize it
plt.scatter(X, y);

Our goal here will be to use X to predict y.

So our input will be X and our output will be y.

Knowing this, what do you think our input and output shapes will be?

Let’s take a look.

In [23]:

# Take a single example of X
input_shape = X[0].shape 

# Take a single example of y
output_shape = y[0].shape

input_shape, output_shape # these are both scalars (no shape)

# Take a single example of X
input_shape = X[0].shape

# Take a single example of y
output_shape = y[0].shape

input_shape, output_shape # these are both scalars (no shape)

Out[23]:

(TensorShape([]), TensorShape([]))

Huh?

From this it seems our inputs and outputs have no shape?

How could that be?

It’s because no matter what kind of data we pass to our model, it’s always going to take as input and return as ouput some kind of tensor.

But in our case because of our dataset (only 2 small lists of numbers), we’re looking at a special kind of tensor, more specifically a rank 0 tensor or a scalar.

In [24]:

# Let's take a look at the single examples invidually
X[0], y[0]

# Let’s take a look at the single examples invidually
X[0], y[0]

Out[24]:

(<tf.Tensor: shape=(), dtype=float32, numpy=-7.0>,
 <tf.Tensor: shape=(), dtype=float32, numpy=3.0>)

In our case, we’re trying to build a model to predict the pattern between X[0] equalling -7.0 and y[0] equalling 3.0.

So now we get our answer, we’re trying to use 1 X value to predict 1 y value.

You might be thinking, «this seems pretty complicated for just predicting a straight line…».

And you’d be right.

But the concepts we’re covering here, the concepts of input and output shapes to a model are fundamental.

In fact, they’re probably two of the things you’ll spend the most time on when you work with neural networks: making sure your input and outputs are in the correct shape.

If it doesn’t make sense now, we’ll see plenty more examples later on (soon you’ll notice the input and output shapes can be almost anything you can imagine).

If you were working on building a machine learning algorithm for predicting housing prices, your inputs may be number of bedrooms, number of bathrooms and number of garages, giving you an input shape of 3 (3 different features). And since you’re trying to predict the price of the house, your output shape would be 1.

Steps in modelling with TensorFlow¶

Now we know what data we have as well as the input and output shapes, let’s see how we’d build a neural network to model it.

In TensorFlow, there are typically 3 fundamental steps to creating and training a model.

Creating a model — piece together the layers of a neural network yourself (using the Functional or Sequential API) or import a previously built model (known as transfer learning).
Compiling a model — defining how a models performance should be measured (loss/metrics) as well as defining how it should improve (optimizer).
Fitting a model — letting the model try to find patterns in the data (how does X get to y).

Let’s see these in action using the Keras Sequential API to build a model for our regression data. And then we’ll step through each.

Note: If you’re using TensorFlow 2.7.0+, the fit() function no longer upscales input data to go from (batch_size, ) to (batch_size, 1). To fix this, you’ll need to expand the dimension of input data using tf.expand_dims(input_data, axis=-1).

In our case, this means instead of using model.fit(X, y, epochs=5), use model.fit(tf.expand_dims(X, axis=-1), y, epochs=5).

In [25]:

# Set random seed
tf.random.set_seed(42)

# Create a model using the Sequential API
model = tf.keras.Sequential([
  tf.keras.layers.Dense(1)
])

# Compile the model
model.compile(loss=tf.keras.losses.mae, # mae is short for mean absolute error
              optimizer=tf.keras.optimizers.SGD(), # SGD is short for stochastic gradient descent
              metrics=["mae"])

# Fit the model
# model.fit(X, y, epochs=5) # this will break with TensorFlow 2.7.0+
model.fit(tf.expand_dims(X, axis=-1), y, epochs=5)

# Set random seed
tf.random.set_seed(42)

# Create a model using the Sequential API
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])

# Compile the model
model.compile(loss=tf.keras.losses.mae, # mae is short for mean absolute error
optimizer=tf.keras.optimizers.SGD(), # SGD is short for stochastic gradient descent
metrics=[«mae»])

# Fit the model
# model.fit(X, y, epochs=5) # this will break with TensorFlow 2.7.0+
model.fit(tf.expand_dims(X, axis=-1), y, epochs=5)

Epoch 1/5
1/1 [==============================] - 0s 313ms/step - loss: 11.5048 - mae: 11.5048
Epoch 2/5
1/1 [==============================] - 0s 7ms/step - loss: 11.3723 - mae: 11.3723
Epoch 3/5
1/1 [==============================] - 0s 5ms/step - loss: 11.2398 - mae: 11.2398
Epoch 4/5
1/1 [==============================] - 0s 8ms/step - loss: 11.1073 - mae: 11.1073
Epoch 5/5
1/1 [==============================] - 0s 7ms/step - loss: 10.9748 - mae: 10.9748

Out[25]:

<keras.callbacks.History at 0x7f8df6701950>

Boom!

We’ve just trained a model to figure out the patterns between X and y.

How do you think it went?

Out[26]:

(<tf.Tensor: shape=(8,), dtype=float32, numpy=array([-7., -4., -1.,  2.,  5.,  8., 11., 14.], dtype=float32)>,
 <tf.Tensor: shape=(8,), dtype=float32, numpy=array([ 3.,  6.,  9., 12., 15., 18., 21., 24.], dtype=float32)>)

What do you think the outcome should be if we passed our model an X value of 17.0?

In [27]:

# Make a prediction with the model
model.predict([17.0])

# Make a prediction with the model
model.predict([17.0])

Out[27]:

array([[12.716021]], dtype=float32)

It doesn’t go very well… it should’ve output something close to 27.0.

🤔 Question: What’s Keras? I thought we were working with TensorFlow but every time we write TensorFlow code, keras comes after tf (e.g. tf.keras.layers.Dense())?

Before TensorFlow 2.0+, Keras was an API designed to be able to build deep learning models with ease. Since TensorFlow 2.0+, its functionality has been tightly integrated within the TensorFlow library.

Improving a model¶

How do you think you’d improve upon our current model?

If you guessed by tweaking some of the things we did above, you’d be correct.

To improve our model, we alter almost every part of the 3 steps we went through before.

Creating a model — here you might want to add more layers, increase the number of hidden units (also called neurons) within each layer, change the activation functions of each layer.
Compiling a model — you might want to choose optimization function or perhaps change the learning rate of the optimization function.
Fitting a model — perhaps you could fit a model for more epochs (leave it training for longer) or on more data (give the model more examples to learn from).

There are many different ways to potentially improve a neural network. Some of the most common include: increasing the number of layers (making the network deeper), increasing the number of hidden units (making the network wider) and changing the learning rate. Because these values are all human-changeable, they’re referred to as hyperparameters) and the practice of trying to find the best hyperparameters is referred to as hyperparameter tuning.

Woah. We just introduced a bunch of possible steps. The important thing to remember is how you alter each of these will depend on the problem you’re working on.

And the good thing is, over the next few problems, we’ll get hands-on with all of them.

For now, let’s keep it simple, all we’ll do is train our model for longer (everything else will stay the same).

In [28]:

# Set random seed
tf.random.set_seed(42)

# Create a model (same as above)
model = tf.keras.Sequential([
  tf.keras.layers.Dense(1)
])

# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
              optimizer=tf.keras.optimizers.SGD(),
              metrics=["mae"])

# Fit model (this time we'll train for longer)
model.fit(tf.expand_dims(X, axis=-1), y, epochs=100) # train for 100 epochs not 10

# Set random seed
tf.random.set_seed(42)

# Create a model (same as above)
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])

# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[«mae»])

# Fit model (this time we’ll train for longer)
model.fit(tf.expand_dims(X, axis=-1), y, epochs=100) # train for 100 epochs not 10

Epoch 1/100
1/1 [==============================] - 0s 319ms/step - loss: 11.5048 - mae: 11.5048
Epoch 2/100
1/1 [==============================] - 0s 6ms/step - loss: 11.3723 - mae: 11.3723
Epoch 3/100
1/1 [==============================] - 0s 5ms/step - loss: 11.2398 - mae: 11.2398
Epoch 4/100
1/1 [==============================] - 0s 4ms/step - loss: 11.1073 - mae: 11.1073
Epoch 5/100
1/1 [==============================] - 0s 6ms/step - loss: 10.9748 - mae: 10.9748
Epoch 6/100
1/1 [==============================] - 0s 6ms/step - loss: 10.8423 - mae: 10.8423
Epoch 7/100
1/1 [==============================] - 0s 6ms/step - loss: 10.7098 - mae: 10.7098
Epoch 8/100
1/1 [==============================] - 0s 9ms/step - loss: 10.5773 - mae: 10.5773
Epoch 9/100
1/1 [==============================] - 0s 7ms/step - loss: 10.4448 - mae: 10.4448
Epoch 10/100
1/1 [==============================] - 0s 6ms/step - loss: 10.3123 - mae: 10.3123
Epoch 11/100
1/1 [==============================] - 0s 14ms/step - loss: 10.1798 - mae: 10.1798
Epoch 12/100
1/1 [==============================] - 0s 9ms/step - loss: 10.0473 - mae: 10.0473
Epoch 13/100
1/1 [==============================] - 0s 7ms/step - loss: 9.9148 - mae: 9.9148
Epoch 14/100
1/1 [==============================] - 0s 8ms/step - loss: 9.7823 - mae: 9.7823
Epoch 15/100
1/1 [==============================] - 0s 9ms/step - loss: 9.6498 - mae: 9.6498
Epoch 16/100
1/1 [==============================] - 0s 5ms/step - loss: 9.5173 - mae: 9.5173
Epoch 17/100
1/1 [==============================] - 0s 6ms/step - loss: 9.3848 - mae: 9.3848
Epoch 18/100
1/1 [==============================] - 0s 6ms/step - loss: 9.2523 - mae: 9.2523
Epoch 19/100
1/1 [==============================] - 0s 5ms/step - loss: 9.1198 - mae: 9.1198
Epoch 20/100
1/1 [==============================] - 0s 5ms/step - loss: 8.9873 - mae: 8.9873
Epoch 21/100
1/1 [==============================] - 0s 6ms/step - loss: 8.8548 - mae: 8.8548
Epoch 22/100
1/1 [==============================] - 0s 6ms/step - loss: 8.7223 - mae: 8.7223
Epoch 23/100
1/1 [==============================] - 0s 7ms/step - loss: 8.5898 - mae: 8.5898
Epoch 24/100
1/1 [==============================] - 0s 4ms/step - loss: 8.4573 - mae: 8.4573
Epoch 25/100
1/1 [==============================] - 0s 6ms/step - loss: 8.3248 - mae: 8.3248
Epoch 26/100
1/1 [==============================] - 0s 7ms/step - loss: 8.1923 - mae: 8.1923
Epoch 27/100
1/1 [==============================] - 0s 5ms/step - loss: 8.0598 - mae: 8.0598
Epoch 28/100
1/1 [==============================] - 0s 5ms/step - loss: 7.9273 - mae: 7.9273
Epoch 29/100
1/1 [==============================] - 0s 5ms/step - loss: 7.7948 - mae: 7.7948
Epoch 30/100
1/1 [==============================] - 0s 5ms/step - loss: 7.6623 - mae: 7.6623
Epoch 31/100
1/1 [==============================] - 0s 7ms/step - loss: 7.5298 - mae: 7.5298
Epoch 32/100
1/1 [==============================] - 0s 4ms/step - loss: 7.3973 - mae: 7.3973
Epoch 33/100
1/1 [==============================] - 0s 5ms/step - loss: 7.2648 - mae: 7.2648
Epoch 34/100
1/1 [==============================] - 0s 6ms/step - loss: 7.2525 - mae: 7.2525
Epoch 35/100
1/1 [==============================] - 0s 7ms/step - loss: 7.2469 - mae: 7.2469
Epoch 36/100
1/1 [==============================] - 0s 5ms/step - loss: 7.2413 - mae: 7.2413
Epoch 37/100
1/1 [==============================] - 0s 5ms/step - loss: 7.2356 - mae: 7.2356
Epoch 38/100
1/1 [==============================] - 0s 6ms/step - loss: 7.2300 - mae: 7.2300
Epoch 39/100
1/1 [==============================] - 0s 6ms/step - loss: 7.2244 - mae: 7.2244
Epoch 40/100
1/1 [==============================] - 0s 5ms/step - loss: 7.2188 - mae: 7.2188
Epoch 41/100
1/1 [==============================] - 0s 7ms/step - loss: 7.2131 - mae: 7.2131
Epoch 42/100
1/1 [==============================] - 0s 5ms/step - loss: 7.2075 - mae: 7.2075
Epoch 43/100
1/1 [==============================] - 0s 7ms/step - loss: 7.2019 - mae: 7.2019
Epoch 44/100
1/1 [==============================] - 0s 5ms/step - loss: 7.1963 - mae: 7.1963
Epoch 45/100
1/1 [==============================] - 0s 6ms/step - loss: 7.1906 - mae: 7.1906
Epoch 46/100
1/1 [==============================] - 0s 5ms/step - loss: 7.1850 - mae: 7.1850
Epoch 47/100
1/1 [==============================] - 0s 7ms/step - loss: 7.1794 - mae: 7.1794
Epoch 48/100
1/1 [==============================] - 0s 5ms/step - loss: 7.1738 - mae: 7.1738
Epoch 49/100
1/1 [==============================] - 0s 5ms/step - loss: 7.1681 - mae: 7.1681
Epoch 50/100
1/1 [==============================] - 0s 5ms/step - loss: 7.1625 - mae: 7.1625
Epoch 51/100
1/1 [==============================] - 0s 6ms/step - loss: 7.1569 - mae: 7.1569
Epoch 52/100
1/1 [==============================] - 0s 6ms/step - loss: 7.1512 - mae: 7.1512
Epoch 53/100
1/1 [==============================] - 0s 6ms/step - loss: 7.1456 - mae: 7.1456
Epoch 54/100
1/1 [==============================] - 0s 31ms/step - loss: 7.1400 - mae: 7.1400
Epoch 55/100
1/1 [==============================] - 0s 7ms/step - loss: 7.1344 - mae: 7.1344
Epoch 56/100
1/1 [==============================] - 0s 6ms/step - loss: 7.1287 - mae: 7.1287
Epoch 57/100
1/1 [==============================] - 0s 7ms/step - loss: 7.1231 - mae: 7.1231
Epoch 58/100
1/1 [==============================] - 0s 8ms/step - loss: 7.1175 - mae: 7.1175
Epoch 59/100
1/1 [==============================] - 0s 11ms/step - loss: 7.1119 - mae: 7.1119
Epoch 60/100
1/1 [==============================] - 0s 7ms/step - loss: 7.1063 - mae: 7.1063
Epoch 61/100
1/1 [==============================] - 0s 7ms/step - loss: 7.1006 - mae: 7.1006
Epoch 62/100
1/1 [==============================] - 0s 7ms/step - loss: 7.0950 - mae: 7.0950
Epoch 63/100
1/1 [==============================] - 0s 7ms/step - loss: 7.0894 - mae: 7.0894
Epoch 64/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0838 - mae: 7.0838
Epoch 65/100
1/1 [==============================] - 0s 6ms/step - loss: 7.0781 - mae: 7.0781
Epoch 66/100
1/1 [==============================] - 0s 7ms/step - loss: 7.0725 - mae: 7.0725
Epoch 67/100
1/1 [==============================] - 0s 6ms/step - loss: 7.0669 - mae: 7.0669
Epoch 68/100
1/1 [==============================] - 0s 5ms/step - loss: 7.0613 - mae: 7.0613
Epoch 69/100
1/1 [==============================] - 0s 7ms/step - loss: 7.0556 - mae: 7.0556
Epoch 70/100
1/1 [==============================] - 0s 26ms/step - loss: 7.0500 - mae: 7.0500
Epoch 71/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0444 - mae: 7.0444
Epoch 72/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0388 - mae: 7.0388
Epoch 73/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0331 - mae: 7.0331
Epoch 74/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0275 - mae: 7.0275
Epoch 75/100
1/1 [==============================] - 0s 5ms/step - loss: 7.0219 - mae: 7.0219
Epoch 76/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0163 - mae: 7.0163
Epoch 77/100
1/1 [==============================] - 0s 8ms/step - loss: 7.0106 - mae: 7.0106
Epoch 78/100
1/1 [==============================] - 0s 7ms/step - loss: 7.0050 - mae: 7.0050
Epoch 79/100
1/1 [==============================] - 0s 6ms/step - loss: 6.9994 - mae: 6.9994
Epoch 80/100
1/1 [==============================] - 0s 10ms/step - loss: 6.9938 - mae: 6.9938
Epoch 81/100
1/1 [==============================] - 0s 10ms/step - loss: 6.9881 - mae: 6.9881
Epoch 82/100
1/1 [==============================] - 0s 6ms/step - loss: 6.9825 - mae: 6.9825
Epoch 83/100
1/1 [==============================] - 0s 8ms/step - loss: 6.9769 - mae: 6.9769
Epoch 84/100
1/1 [==============================] - 0s 8ms/step - loss: 6.9713 - mae: 6.9713
Epoch 85/100
1/1 [==============================] - 0s 12ms/step - loss: 6.9656 - mae: 6.9656
Epoch 86/100
1/1 [==============================] - 0s 6ms/step - loss: 6.9600 - mae: 6.9600
Epoch 87/100
1/1 [==============================] - 0s 16ms/step - loss: 6.9544 - mae: 6.9544
Epoch 88/100
1/1 [==============================] - 0s 9ms/step - loss: 6.9488 - mae: 6.9488
Epoch 89/100
1/1 [==============================] - 0s 11ms/step - loss: 6.9431 - mae: 6.9431
Epoch 90/100
1/1 [==============================] - 0s 6ms/step - loss: 6.9375 - mae: 6.9375
Epoch 91/100
1/1 [==============================] - 0s 5ms/step - loss: 6.9319 - mae: 6.9319
Epoch 92/100
1/1 [==============================] - 0s 7ms/step - loss: 6.9263 - mae: 6.9263
Epoch 93/100
1/1 [==============================] - 0s 7ms/step - loss: 6.9206 - mae: 6.9206
Epoch 94/100
1/1 [==============================] - 0s 5ms/step - loss: 6.9150 - mae: 6.9150
Epoch 95/100
1/1 [==============================] - 0s 8ms/step - loss: 6.9094 - mae: 6.9094
Epoch 96/100
1/1 [==============================] - 0s 6ms/step - loss: 6.9038 - mae: 6.9038
Epoch 97/100
1/1 [==============================] - 0s 7ms/step - loss: 6.8981 - mae: 6.8981
Epoch 98/100
1/1 [==============================] - 0s 10ms/step - loss: 6.8925 - mae: 6.8925
Epoch 99/100
1/1 [==============================] - 0s 5ms/step - loss: 6.8869 - mae: 6.8869
Epoch 100/100
1/1 [==============================] - 0s 13ms/step - loss: 6.8813 - mae: 6.8813

Out[28]:

<keras.callbacks.History at 0x7f8df664db90>

You might’ve noticed the loss value decrease from before (and keep decreasing as the number of epochs gets higher).

What do you think this means for when we make a prediction with our model?

How about we try predict on 17.0 again?

In [29]:

# Remind ourselves of what X and y are
X, y

# Remind ourselves of what X and y are
X, y

Out[29]:

(<tf.Tensor: shape=(8,), dtype=float32, numpy=array([-7., -4., -1.,  2.,  5.,  8., 11., 14.], dtype=float32)>,
 <tf.Tensor: shape=(8,), dtype=float32, numpy=array([ 3.,  6.,  9., 12., 15., 18., 21., 24.], dtype=float32)>)

In [30]:

# Try and predict what y would be if X was 17.0
model.predict([17.0]) # the right answer is 27.0 (y = X + 10)

# Try and predict what y would be if X was 17.0
model.predict([17.0]) # the right answer is 27.0 (y = X + 10)

Out[30]:

array([[30.158512]], dtype=float32)

Much better!

We got closer this time. But we could still be better.

Now we’ve trained a model, how could we evaluate it?

Evaluating a model¶

A typical workflow you’ll go through when building neural networks is:

Build a model -> evaluate it -> build (tweak) a model -> evaulate it -> build (tweak) a model -> evaluate it...

The tweaking comes from maybe not building a model from scratch but adjusting an existing one.

Visualize, visualize, visualize¶

When it comes to evaluation, you’ll want to remember the words: «visualize, visualize, visualize.»

This is because you’re probably better looking at something (doing) than you are thinking about something.

It’s a good idea to visualize:

The data — what data are you working with? What does it look like?
The model itself — what does the architecture look like? What are the different shapes?
The training of a model — how does a model perform while it learns?
The predictions of a model — how do the predictions of a model line up against the ground truth (the original labels)?

Let’s start by visualizing the model.

But first, we’ll create a little bit of a bigger dataset and a new model we can use (it’ll be the same as before, but the more practice the better).

In [31]:

# Make a bigger dataset
X = np.arange(-100, 100, 4)
X

# Make a bigger dataset
X = np.arange(-100, 100, 4)
X

Out[31]:

array([-100,  -96,  -92,  -88,  -84,  -80,  -76,  -72,  -68,  -64,  -60,
        -56,  -52,  -48,  -44,  -40,  -36,  -32,  -28,  -24,  -20,  -16,
        -12,   -8,   -4,    0,    4,    8,   12,   16,   20,   24,   28,
         32,   36,   40,   44,   48,   52,   56,   60,   64,   68,   72,
         76,   80,   84,   88,   92,   96])

In [32]:

# Make labels for the dataset (adhering to the same pattern as before)
y = np.arange(-90, 110, 4)
y

# Make labels for the dataset (adhering to the same pattern as before)
y = np.arange(-90, 110, 4)
y

Out[32]:

array([-90, -86, -82, -78, -74, -70, -66, -62, -58, -54, -50, -46, -42,
       -38, -34, -30, -26, -22, -18, -14, -10,  -6,  -2,   2,   6,  10,
        14,  18,  22,  26,  30,  34,  38,  42,  46,  50,  54,  58,  62,
        66,  70,  74,  78,  82,  86,  90,  94,  98, 102, 106])

Since $y=X+10$, we could make the labels like so:

In [33]:

# Same result as above
y = X + 10
y

# Same result as above
y = X + 10
y

Out[33]:

array([-90, -86, -82, -78, -74, -70, -66, -62, -58, -54, -50, -46, -42,
       -38, -34, -30, -26, -22, -18, -14, -10,  -6,  -2,   2,   6,  10,
        14,  18,  22,  26,  30,  34,  38,  42,  46,  50,  54,  58,  62,
        66,  70,  74,  78,  82,  86,  90,  94,  98, 102, 106])

Split data into training/test set¶

One of the other most common and important steps in a machine learning project is creating a training and test set (and when required, a validation set).

Each set serves a specific purpose:

Training set — the model learns from this data, which is typically 70-80% of the total data available (like the course materials you study during the semester).
Validation set — the model gets tuned on this data, which is typically 10-15% of the total data available (like the practice exam you take before the final exam).
Test set — the model gets evaluated on this data to test what it has learned, it’s typically 10-15% of the total data available (like the final exam you take at the end of the semester).

For now, we’ll just use a training and test set, this means we’ll have a dataset for our model to learn on as well as be evaluated on.

We can create them by splitting our X and y arrays.

🔑 Note: When dealing with real-world data, this step is typically done right at the start of a project (the test set should always be kept separate from all other data). We want our model to learn on training data and then evaluate it on test data to get an indication of how well it generalizes to unseen examples.

In [34]:

# Check how many samples we have
len(X)

# Check how many samples we have
len(X)

In [35]:

# Split data into train and test sets
X_train = X[:40] # first 40 examples (80% of data)
y_train = y[:40]

X_test = X[40:] # last 10 examples (20% of data)
y_test = y[40:]

len(X_train), len(X_test)

# Split data into train and test sets
X_train = X[:40] # first 40 examples (80% of data)
y_train = y[:40]

X_test = X[40:] # last 10 examples (20% of data)
y_test = y[40:]

len(X_train), len(X_test)

Visualizing the data¶

Now we’ve got our training and test data, it’s a good idea to visualize it.

Let’s plot it with some nice colours to differentiate what’s what.

In [36]:

plt.figure(figsize=(10, 7))
# Plot training data in blue
plt.scatter(X_train, y_train, c='b', label='Training data')
# Plot test data in green
plt.scatter(X_test, y_test, c='g', label='Testing data')
# Show the legend
plt.legend();

plt.figure(figsize=(10, 7))
# Plot training data in blue
plt.scatter(X_train, y_train, c=’b’, label=’Training data’)
# Plot test data in green
plt.scatter(X_test, y_test, c=’g’, label=’Testing data’)
# Show the legend
plt.legend();

Beautiful! Any time you can visualize your data, your model, your anything, it’s a good idea.

With this graph in mind, what we’ll be trying to do is build a model which learns the pattern in the blue dots (X_train) to draw the green dots (X_test).

Time to build a model. We’ll make the exact same one from before (the one we trained for longer).

In [37]:

# Set random seed
tf.random.set_seed(42)

# Create a model (same as above)
model = tf.keras.Sequential([
  tf.keras.layers.Dense(1)
])

# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
              optimizer=tf.keras.optimizers.SGD(),
              metrics=["mae"])

# Fit model (same as above)
#model.fit(X_train, y_train, epochs=100) # commented out on purpose (not fitting it just yet)

# Set random seed
tf.random.set_seed(42)

# Create a model (same as above)
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])

# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[«mae»])

# Fit model (same as above)
#model.fit(X_train, y_train, epochs=100) # commented out on purpose (not fitting it just yet)

Visualizing the model¶

After you’ve built a model, you might want to take a look at it (especially if you haven’t built many before).

You can take a look at the layers and shapes of your model by calling summary() on it.

🔑 Note: Visualizing a model is particularly helpful when you run into input and output shape mismatches.

In [38]:

# Doesn't work (model not fit/built)
model.summary()

# Doesn’t work (model not fit/built)
model.summary()

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-38-7d09d31d4e66> in <module>()
      1 # Doesn't work (model not fit/built)
----> 2 model.summary()

/usr/local/lib/python3.7/dist-packages/keras/engine/training.py in summary(self, line_length, positions, print_fn, expand_nested)
   2578     if not self.built:
   2579       raise ValueError(
-> 2580           'This model has not yet been built. '
   2581           'Build the model first by calling `build()` or by calling '
   2582           'the model on a batch of data.')

ValueError: This model has not yet been built. Build the model first by calling `build()` or by calling the model on a batch of data.

Ahh, the cell above errors because we haven’t fit our built our model.

We also haven’t told it what input shape it should be expecting.

Remember above, how we discussed the input shape was just one number?

We can let our model know the input shape of our data using the input_shape parameter to the first layer (usually if input_shape isn’t defined, Keras tries to figure it out automatically).

In [39]:

# Set random seed
tf.random.set_seed(42)

# Create a model (same as above)
model = tf.keras.Sequential([
  tf.keras.layers.Dense(1, input_shape=[1]) # define the input_shape to our model
])

# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
              optimizer=tf.keras.optimizers.SGD(),
              metrics=["mae"])

# Set random seed
tf.random.set_seed(42)

# Create a model (same as above)
model = tf.keras.Sequential([
tf.keras.layers.Dense(1, input_shape=[1]) # define the input_shape to our model
])

# Compile model (same as above)
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[«mae»])

In [40]:

# This will work after specifying the input shape
model.summary()

# This will work after specifying the input shape
model.summary()

Model: "sequential_8"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_8 (Dense)             (None, 1)                 2         
                                                                 
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________

Calling summary() on our model shows us the layers it contains, the output shape and the number of parameters.

Total params — total number of parameters in the model.
Trainable parameters — these are the parameters (patterns) the model can update as it trains.
Non-trainable parameters — these parameters aren’t updated during training (this is typical when you bring in the already learned patterns from other models during transfer learning).

📖 Resource: For a more in-depth overview of the trainable parameters within a layer, check out MIT’s introduction to deep learning video.

🛠 Exercise: Try playing around with the number of hidden units in the Dense layer (e.g. Dense(2), Dense(3)). How does this change the Total/Trainable params? Investigate what’s causing the change.

For now, all you need to think about these parameters is that their learnable patterns in the data.

Let’s fit our model to the training data.

In [41]:

# Fit the model to the training data
model.fit(X_train, y_train, epochs=100, verbose=0) # verbose controls how much gets output

# Fit the model to the training data
model.fit(X_train, y_train, epochs=100, verbose=0) # verbose controls how much gets output

Out[41]:

<keras.callbacks.History at 0x7f8df64e8250>

In [42]:

# Check the model summary
model.summary()

# Check the model summary
model.summary()

Model: "sequential_8"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_8 (Dense)             (None, 1)                 2         
                                                                 
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________

Alongside summary, you can also view a 2D plot of the model using plot_model().

In [43]:

from tensorflow.keras.utils import plot_model

plot_model(model, show_shapes=True)

from tensorflow.keras.utils import plot_model

plot_model(model, show_shapes=True)

Out[43]:

In our case, the model we used only has an input and an output but visualizing more complicated models can be very helpful for debugging.

Visualizing the predictions¶

Now we’ve got a trained model, let’s visualize some predictions.

To visualize predictions, it’s always a good idea to plot them against the ground truth labels.

Often you’ll see this in the form of y_test vs. y_pred (ground truth vs. predictions).

First, we’ll make some predictions on the test data (X_test), remember the model has never seen the test data.

In [44]:

# Make predictions
y_preds = model.predict(X_test)

# Make predictions
y_preds = model.predict(X_test)

WARNING:tensorflow:5 out of the last 5 calls to <function Model.make_predict_function.<locals>.predict_function at 0x7f8df63c6290> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.

In [45]:

# View the predictions
y_preds

# View the predictions
y_preds

Out[45]:

array([[53.57109 ],
       [57.05633 ],
       [60.541573],
       [64.02681 ],
       [67.512054],
       [70.99729 ],
       [74.48254 ],
       [77.96777 ],
       [81.45301 ],
       [84.938255]], dtype=float32)

Okay, we get a list of numbers but how do these compare to the ground truth labels?

Let’s build a plotting function to find out.

🔑 Note: If you think you’re going to be visualizing something a lot, it’s a good idea to functionize it so you can use it later.

In [46]:

def plot_predictions(train_data=X_train, 
                     train_labels=y_train, 
                     test_data=X_test, 
                     test_labels=y_test, 
                     predictions=y_preds):
  """
  Plots training data, test data and compares predictions.
  """
  plt.figure(figsize=(10, 7))
  # Plot training data in blue
  plt.scatter(train_data, train_labels, c="b", label="Training data")
  # Plot test data in green
  plt.scatter(test_data, test_labels, c="g", label="Testing data")
  # Plot the predictions in red (predictions were made on the test data)
  plt.scatter(test_data, predictions, c="r", label="Predictions")
  # Show the legend
  plt.legend();

def plot_predictions(train_data=X_train,
train_labels=y_train,
test_data=X_test,
test_labels=y_test,
predictions=y_preds):
«»»
Plots training data, test data and compares predictions.
«»»
plt.figure(figsize=(10, 7))
# Plot training data in blue
plt.scatter(train_data, train_labels, c=»b», label=»Training data»)
# Plot test data in green
plt.scatter(test_data, test_labels, c=»g», label=»Testing data»)
# Plot the predictions in red (predictions were made on the test data)
plt.scatter(test_data, predictions, c=»r», label=»Predictions»)
# Show the legend
plt.legend();

In [47]:

plot_predictions(train_data=X_train,
                 train_labels=y_train,
                 test_data=X_test,
                 test_labels=y_test,
                 predictions=y_preds)

plot_predictions(train_data=X_train,
train_labels=y_train,
test_data=X_test,
test_labels=y_test,
predictions=y_preds)

From the plot we can see our predictions aren’t totally outlandish but they definitely aren’t anything special either.

Evaluating predictions¶

Alongisde visualizations, evaulation metrics are your alternative best option for evaluating your model.

Depending on the problem you’re working on, different models have different evaluation metrics.

Two of the main metrics used for regression problems are:

Mean absolute error (MAE) — the mean difference between each of the predictions.
Mean squared error (MSE) — the squared mean difference between of the predictions (use if larger errors are more detrimental than smaller errors).

The lower each of these values, the better.

You can also use model.evaluate() which will return the loss of the model as well as any metrics setup during the compile step.

In [48]:

# Evaluate the model on the test set
model.evaluate(X_test, y_test)

# Evaluate the model on the test set
model.evaluate(X_test, y_test)

1/1 [==============================] - 0s 137ms/step - loss: 18.7453 - mae: 18.7453

Out[48]:

[18.74532699584961, 18.74532699584961]

In our case, since we used MAE for the loss function as well as MAE for the metrics, model.evaulate() returns them both.

TensorFlow also has built in functions for MSE and MAE.

For many evaluation functions, the premise is the same: compare predictions to the ground truth labels.

In [49]:

# Calculate the mean absolute error
mae = tf.metrics.mean_absolute_error(y_true=y_test, 
                                     y_pred=y_preds)
mae

# Calculate the mean absolute error
mae = tf.metrics.mean_absolute_error(y_true=y_test,
y_pred=y_preds)
mae

Out[49]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=
array([34.42891 , 30.943668, 27.45843 , 23.97319 , 20.487946, 17.202168,
       14.510478, 12.419336, 11.018796, 10.212349], dtype=float32)>

Huh? That’s strange, MAE should be a single output.

Instead, we get 10 values.

This is because our y_test and y_preds tensors are different shapes.

In [50]:

# Check the test label tensor values
y_test

# Check the test label tensor values
y_test

Out[50]:

array([ 70,  74,  78,  82,  86,  90,  94,  98, 102, 106])

In [51]:

# Check the predictions tensor values (notice the extra square brackets)
y_preds

# Check the predictions tensor values (notice the extra square brackets)
y_preds

Out[51]:

array([[53.57109 ],
       [57.05633 ],
       [60.541573],
       [64.02681 ],
       [67.512054],
       [70.99729 ],
       [74.48254 ],
       [77.96777 ],
       [81.45301 ],
       [84.938255]], dtype=float32)

In [52]:

# Check the tensor shapes
y_test.shape, y_preds.shape

# Check the tensor shapes
y_test.shape, y_preds.shape

Remember how we discussed dealing with different input and output shapes is one the most common issues you’ll come across, this is one of those times.

But not to worry.

We can fix it using squeeze(), it’ll remove the the 1 dimension from our y_preds tensor, making it the same shape as y_test.

🔑 Note: If you’re comparing two tensors, it’s important to make sure they’re the right shape(s) (you won’t always have to manipulate the shapes, but always be on the look out, many errors are the result of mismatched tensors, especially mismatched input and output shapes).

In [53]:

# Shape before squeeze()
y_preds.shape

# Shape before squeeze()
y_preds.shape

In [54]:

# Shape after squeeze()
y_preds.squeeze().shape

# Shape after squeeze()
y_preds.squeeze().shape

In [55]:

# What do they look like?
y_test, y_preds.squeeze()

# What do they look like?
y_test, y_preds.squeeze()

Out[55]:

(array([ 70,  74,  78,  82,  86,  90,  94,  98, 102, 106]),
 array([53.57109 , 57.05633 , 60.541573, 64.02681 , 67.512054, 70.99729 ,
        74.48254 , 77.96777 , 81.45301 , 84.938255], dtype=float32))

Okay, now we know how to make our y_test and y_preds tenors the same shape, let’s use our evaluation metrics.

In [56]:

# Calcuate the MAE
mae = tf.metrics.mean_absolute_error(y_true=y_test, 
                                     y_pred=y_preds.squeeze()) # use squeeze() to make same shape
mae

# Calcuate the MAE
mae = tf.metrics.mean_absolute_error(y_true=y_test,
y_pred=y_preds.squeeze()) # use squeeze() to make same shape
mae

Out[56]:

<tf.Tensor: shape=(), dtype=float32, numpy=18.745327>

In [57]:

# Calculate the MSE
mse = tf.metrics.mean_squared_error(y_true=y_test,
                                    y_pred=y_preds.squeeze())
mse

# Calculate the MSE
mse = tf.metrics.mean_squared_error(y_true=y_test,
y_pred=y_preds.squeeze())
mse

Out[57]:

<tf.Tensor: shape=(), dtype=float32, numpy=353.57336>

We can also calculate the MAE using pure TensorFlow functions.

In [58]:

# Returns the same as tf.metrics.mean_absolute_error()
tf.reduce_mean(tf.abs(y_test-y_preds.squeeze()))

# Returns the same as tf.metrics.mean_absolute_error()
tf.reduce_mean(tf.abs(y_test-y_preds.squeeze()))

Out[58]:

<tf.Tensor: shape=(), dtype=float64, numpy=18.745327377319335>

Again, it’s a good idea to functionize anything you think you might use over again (or find yourself using over and over again).

Let’s make functions for our evaluation metrics.

In [59]:

def mae(y_test, y_pred):
  """
  Calculuates mean absolute error between y_test and y_preds.
  """
  return tf.metrics.mean_absolute_error(y_test,
                                        y_pred)
  
def mse(y_test, y_pred):
  """
  Calculates mean squared error between y_test and y_preds.
  """
  return tf.metrics.mean_squared_error(y_test,
                                       y_pred)

def mae(y_test, y_pred):
«»»
Calculuates mean absolute error between y_test and y_preds.
«»»
return tf.metrics.mean_absolute_error(y_test,
y_pred)

def mse(y_test, y_pred):
«»»
Calculates mean squared error between y_test and y_preds.
«»»
return tf.metrics.mean_squared_error(y_test,
y_pred)

Running experiments to improve a model¶

After seeing the evaluation metrics and the predictions your model makes, it’s likely you’ll want to improve it.

Again, there are many different ways you can do this, but 3 of the main ones are:

Get more data — get more examples for your model to train on (more opportunities to learn patterns).
Make your model larger (use a more complex model) — this might come in the form of more layers or more hidden units in each layer.
Train for longer — give your model more of a chance to find the patterns in the data.

Since we created our dataset, we could easily make more data but this isn’t always the case when you’re working with real-world datasets.

So let’s take a look at how we can improve our model using 2 and 3.

To do so, we’ll build 3 models and compare their results:

model_1 — same as original model, 1 layer, trained for 100 epochs.
model_2 — 2 layers, trained for 100 epochs.
model_3 — 2 layers, trained for 500 epochs.

Build model_1

In [63]:

# Set random seed
tf.random.set_seed(42)

# Replicate original model
model_1 = tf.keras.Sequential([
  tf.keras.layers.Dense(1)
])

# Compile the model
model_1.compile(loss=tf.keras.losses.mae,
                optimizer=tf.keras.optimizers.SGD(),
                metrics=['mae'])

# Fit the model
model_1.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=100)

# Set random seed
tf.random.set_seed(42)

# Replicate original model
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])

# Compile the model
model_1.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[‘mae’])

# Fit the model
model_1.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=100)

Epoch 1/100
2/2 [==============================] - 0s 9ms/step - loss: 15.9024 - mae: 15.9024
Epoch 2/100
2/2 [==============================] - 0s 5ms/step - loss: 11.2837 - mae: 11.2837
Epoch 3/100
2/2 [==============================] - 0s 5ms/step - loss: 11.1074 - mae: 11.1074
Epoch 4/100
2/2 [==============================] - 0s 7ms/step - loss: 9.2991 - mae: 9.2991
Epoch 5/100
2/2 [==============================] - 0s 5ms/step - loss: 10.1677 - mae: 10.1677
Epoch 6/100
2/2 [==============================] - 0s 5ms/step - loss: 9.4303 - mae: 9.4303
Epoch 7/100
2/2 [==============================] - 0s 8ms/step - loss: 8.5704 - mae: 8.5704
Epoch 8/100
2/2 [==============================] - 0s 4ms/step - loss: 9.0442 - mae: 9.0442
Epoch 9/100
2/2 [==============================] - 0s 6ms/step - loss: 18.7517 - mae: 18.7517
Epoch 10/100
2/2 [==============================] - 0s 4ms/step - loss: 10.1142 - mae: 10.1142
Epoch 11/100
2/2 [==============================] - 0s 8ms/step - loss: 8.3980 - mae: 8.3980
Epoch 12/100
2/2 [==============================] - 0s 5ms/step - loss: 10.6639 - mae: 10.6639
Epoch 13/100
2/2 [==============================] - 0s 5ms/step - loss: 9.7977 - mae: 9.7977
Epoch 14/100
2/2 [==============================] - 0s 16ms/step - loss: 16.0103 - mae: 16.0103
Epoch 15/100
2/2 [==============================] - 0s 9ms/step - loss: 11.4068 - mae: 11.4068
Epoch 16/100
2/2 [==============================] - 0s 4ms/step - loss: 8.5393 - mae: 8.5393
Epoch 17/100
2/2 [==============================] - 0s 7ms/step - loss: 13.6348 - mae: 13.6348
Epoch 18/100
2/2 [==============================] - 0s 7ms/step - loss: 11.4629 - mae: 11.4629
Epoch 19/100
2/2 [==============================] - 0s 10ms/step - loss: 17.9148 - mae: 17.9148
Epoch 20/100
2/2 [==============================] - 0s 6ms/step - loss: 15.0494 - mae: 15.0494
Epoch 21/100
2/2 [==============================] - 0s 6ms/step - loss: 11.0216 - mae: 11.0216
Epoch 22/100
2/2 [==============================] - 0s 7ms/step - loss: 8.1558 - mae: 8.1558
Epoch 23/100
2/2 [==============================] - 0s 9ms/step - loss: 9.5138 - mae: 9.5138
Epoch 24/100
2/2 [==============================] - 0s 18ms/step - loss: 7.6617 - mae: 7.6617
Epoch 25/100
2/2 [==============================] - 0s 10ms/step - loss: 13.1859 - mae: 13.1859
Epoch 26/100
2/2 [==============================] - 0s 6ms/step - loss: 16.4211 - mae: 16.4211
Epoch 27/100
2/2 [==============================] - 0s 6ms/step - loss: 13.1660 - mae: 13.1660
Epoch 28/100
2/2 [==============================] - 0s 5ms/step - loss: 14.2559 - mae: 14.2559
Epoch 29/100
2/2 [==============================] - 0s 6ms/step - loss: 10.0670 - mae: 10.0670
Epoch 30/100
2/2 [==============================] - 0s 9ms/step - loss: 16.3409 - mae: 16.3409
Epoch 31/100
2/2 [==============================] - 0s 4ms/step - loss: 23.6444 - mae: 23.6444
Epoch 32/100
2/2 [==============================] - 0s 4ms/step - loss: 7.6215 - mae: 7.6215
Epoch 33/100
2/2 [==============================] - 0s 11ms/step - loss: 9.3221 - mae: 9.3221
Epoch 34/100
2/2 [==============================] - 0s 6ms/step - loss: 13.7313 - mae: 13.7313
Epoch 35/100
2/2 [==============================] - 0s 5ms/step - loss: 11.1276 - mae: 11.1276
Epoch 36/100
2/2 [==============================] - 0s 4ms/step - loss: 13.3222 - mae: 13.3222
Epoch 37/100
2/2 [==============================] - 0s 5ms/step - loss: 9.4763 - mae: 9.4763
Epoch 38/100
2/2 [==============================] - 0s 5ms/step - loss: 10.1381 - mae: 10.1381
Epoch 39/100
2/2 [==============================] - 0s 5ms/step - loss: 10.1793 - mae: 10.1793
Epoch 40/100
2/2 [==============================] - 0s 4ms/step - loss: 10.9137 - mae: 10.9137
Epoch 41/100
2/2 [==============================] - 0s 5ms/step - loss: 7.9063 - mae: 7.9063
Epoch 42/100
2/2 [==============================] - 0s 4ms/step - loss: 10.0914 - mae: 10.0914
Epoch 43/100
2/2 [==============================] - 0s 5ms/step - loss: 8.7006 - mae: 8.7006
Epoch 44/100
2/2 [==============================] - 0s 3ms/step - loss: 12.2047 - mae: 12.2047
Epoch 45/100
2/2 [==============================] - 0s 4ms/step - loss: 13.7970 - mae: 13.7970
Epoch 46/100
2/2 [==============================] - 0s 4ms/step - loss: 8.4687 - mae: 8.4687
Epoch 47/100
2/2 [==============================] - 0s 5ms/step - loss: 9.1330 - mae: 9.1330
Epoch 48/100
2/2 [==============================] - 0s 4ms/step - loss: 10.6190 - mae: 10.6190
Epoch 49/100
2/2 [==============================] - 0s 4ms/step - loss: 7.7503 - mae: 7.7503
Epoch 50/100
2/2 [==============================] - 0s 4ms/step - loss: 9.5407 - mae: 9.5407
Epoch 51/100
2/2 [==============================] - 0s 4ms/step - loss: 9.1584 - mae: 9.1584
Epoch 52/100
2/2 [==============================] - 0s 4ms/step - loss: 16.3630 - mae: 16.3630
Epoch 53/100
2/2 [==============================] - 0s 4ms/step - loss: 14.1299 - mae: 14.1299
Epoch 54/100
2/2 [==============================] - 0s 4ms/step - loss: 21.1247 - mae: 21.1247
Epoch 55/100
2/2 [==============================] - 0s 5ms/step - loss: 16.3961 - mae: 16.3961
Epoch 56/100
2/2 [==============================] - 0s 5ms/step - loss: 9.9806 - mae: 9.9806
Epoch 57/100
2/2 [==============================] - 0s 4ms/step - loss: 9.9606 - mae: 9.9606
Epoch 58/100
2/2 [==============================] - 0s 4ms/step - loss: 9.2209 - mae: 9.2209
Epoch 59/100
2/2 [==============================] - 0s 5ms/step - loss: 8.4239 - mae: 8.4239
Epoch 60/100
2/2 [==============================] - 0s 7ms/step - loss: 9.4869 - mae: 9.4869
Epoch 61/100
2/2 [==============================] - 0s 4ms/step - loss: 11.4355 - mae: 11.4355
Epoch 62/100
2/2 [==============================] - 0s 4ms/step - loss: 11.6887 - mae: 11.6887
Epoch 63/100
2/2 [==============================] - 0s 3ms/step - loss: 7.0838 - mae: 7.0838
Epoch 64/100
2/2 [==============================] - 0s 4ms/step - loss: 16.9675 - mae: 16.9675
Epoch 65/100
2/2 [==============================] - 0s 4ms/step - loss: 12.4599 - mae: 12.4599
Epoch 66/100
2/2 [==============================] - 0s 4ms/step - loss: 13.0184 - mae: 13.0184
Epoch 67/100
2/2 [==============================] - 0s 5ms/step - loss: 8.0600 - mae: 8.0600
Epoch 68/100
2/2 [==============================] - 0s 5ms/step - loss: 10.1888 - mae: 10.1888
Epoch 69/100
2/2 [==============================] - 0s 5ms/step - loss: 12.3633 - mae: 12.3633
Epoch 70/100
2/2 [==============================] - 0s 10ms/step - loss: 9.0516 - mae: 9.0516
Epoch 71/100
2/2 [==============================] - 0s 11ms/step - loss: 10.0378 - mae: 10.0378
Epoch 72/100
2/2 [==============================] - 0s 9ms/step - loss: 10.0516 - mae: 10.0516
Epoch 73/100
2/2 [==============================] - 0s 5ms/step - loss: 12.6151 - mae: 12.6151
Epoch 74/100
2/2 [==============================] - 0s 4ms/step - loss: 10.3819 - mae: 10.3819
Epoch 75/100
2/2 [==============================] - 0s 4ms/step - loss: 9.7229 - mae: 9.7229
Epoch 76/100
2/2 [==============================] - 0s 5ms/step - loss: 11.2252 - mae: 11.2252
Epoch 77/100
2/2 [==============================] - 0s 4ms/step - loss: 8.3642 - mae: 8.3642
Epoch 78/100
2/2 [==============================] - 0s 4ms/step - loss: 9.1274 - mae: 9.1274
Epoch 79/100
2/2 [==============================] - 0s 4ms/step - loss: 19.5039 - mae: 19.5039
Epoch 80/100
2/2 [==============================] - 0s 4ms/step - loss: 14.8945 - mae: 14.8945
Epoch 81/100
2/2 [==============================] - 0s 4ms/step - loss: 9.0034 - mae: 9.0034
Epoch 82/100
2/2 [==============================] - 0s 7ms/step - loss: 13.0206 - mae: 13.0206
Epoch 83/100
2/2 [==============================] - 0s 5ms/step - loss: 7.9299 - mae: 7.9299
Epoch 84/100
2/2 [==============================] - 0s 3ms/step - loss: 7.6872 - mae: 7.6872
Epoch 85/100
2/2 [==============================] - 0s 6ms/step - loss: 10.0328 - mae: 10.0328
Epoch 86/100
2/2 [==============================] - 0s 13ms/step - loss: 9.2433 - mae: 9.2433
Epoch 87/100
2/2 [==============================] - 0s 6ms/step - loss: 12.0209 - mae: 12.0209
Epoch 88/100
2/2 [==============================] - 0s 25ms/step - loss: 10.6389 - mae: 10.6389
Epoch 89/100
2/2 [==============================] - 0s 13ms/step - loss: 7.2667 - mae: 7.2667
Epoch 90/100
2/2 [==============================] - 0s 7ms/step - loss: 12.7786 - mae: 12.7786
Epoch 91/100
2/2 [==============================] - 0s 7ms/step - loss: 7.3481 - mae: 7.3481
Epoch 92/100
2/2 [==============================] - 0s 6ms/step - loss: 7.7175 - mae: 7.7175
Epoch 93/100
2/2 [==============================] - 0s 8ms/step - loss: 7.1263 - mae: 7.1263
Epoch 94/100
2/2 [==============================] - 0s 10ms/step - loss: 12.6190 - mae: 12.6190
Epoch 95/100
2/2 [==============================] - 0s 9ms/step - loss: 10.0912 - mae: 10.0912
Epoch 96/100
2/2 [==============================] - 0s 5ms/step - loss: 9.3558 - mae: 9.3558
Epoch 97/100
2/2 [==============================] - 0s 18ms/step - loss: 12.6834 - mae: 12.6834
Epoch 98/100
2/2 [==============================] - 0s 4ms/step - loss: 8.6762 - mae: 8.6762
Epoch 99/100
2/2 [==============================] - 0s 9ms/step - loss: 9.4693 - mae: 9.4693
Epoch 100/100
2/2 [==============================] - 0s 4ms/step - loss: 8.7067 - mae: 8.7067

Out[63]:

<keras.callbacks.History at 0x7f8e751f5a10>

In [64]:

# Make and plot predictions for model_1
y_preds_1 = model_1.predict(X_test)
plot_predictions(predictions=y_preds_1)

# Make and plot predictions for model_1
y_preds_1 = model_1.predict(X_test)
plot_predictions(predictions=y_preds_1)

WARNING:tensorflow:6 out of the last 6 calls to <function Model.make_predict_function.<locals>.predict_function at 0x7f8df63b8f80> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.

In [65]:

# Calculate model_1 metrics
mae_1 = mae(y_test, y_preds_1.squeeze()).numpy()
mse_1 = mse(y_test, y_preds_1.squeeze()).numpy()
mae_1, mse_1

# Calculate model_1 metrics
mae_1 = mae(y_test, y_preds_1.squeeze()).numpy()
mse_1 = mse(y_test, y_preds_1.squeeze()).numpy()
mae_1, mse_1

Build model_2

This time we’ll add an extra dense layer (so now our model will have 2 layers) whilst keeping everything else the same.

In [67]:

# Set random seed
tf.random.set_seed(42)

# Replicate model_1 and add an extra layer
model_2 = tf.keras.Sequential([
  tf.keras.layers.Dense(1),
  tf.keras.layers.Dense(1) # add a second layer
])

# Compile the model
model_2.compile(loss=tf.keras.losses.mae,
                optimizer=tf.keras.optimizers.SGD(),
                metrics=['mae'])

# Fit the model
model_2.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=100, verbose=0) # set verbose to 0 for less output

# Set random seed
tf.random.set_seed(42)

# Replicate model_1 and add an extra layer
model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tf.keras.layers.Dense(1) # add a second layer
])

# Compile the model
model_2.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[‘mae’])

# Fit the model
model_2.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=100, verbose=0) # set verbose to 0 for less output

Out[67]:

<keras.callbacks.History at 0x7f8df6923cd0>

In [68]:

# Make and plot predictions for model_2
y_preds_2 = model_2.predict(X_test)
plot_predictions(predictions=y_preds_2)

# Make and plot predictions for model_2
y_preds_2 = model_2.predict(X_test)
plot_predictions(predictions=y_preds_2)

Woah, that’s looking better already! And all it took was an extra layer.

In [69]:

# Calculate model_2 metrics
mae_2 = mae(y_test, y_preds_2.squeeze()).numpy()
mse_2 = mse(y_test, y_preds_2.squeeze()).numpy()
mae_2, mse_2

# Calculate model_2 metrics
mae_2 = mae(y_test, y_preds_2.squeeze()).numpy()
mse_2 = mse(y_test, y_preds_2.squeeze()).numpy()
mae_2, mse_2

Build model_3

For our 3rd model, we’ll keep everything the same as model_2 except this time we’ll train for longer (500 epochs instead of 100).

This will give our model more of a chance to learn the patterns in the data.

In [71]:

# Set random seed
tf.random.set_seed(42)

# Replicate model_2
model_3 = tf.keras.Sequential([
  tf.keras.layers.Dense(1),
  tf.keras.layers.Dense(1)
])

# Compile the model
model_3.compile(loss=tf.keras.losses.mae,
                optimizer=tf.keras.optimizers.SGD(),
                metrics=['mae'])

# Fit the model (this time for 500 epochs, not 100)
model_3.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=500, verbose=0) # set verbose to 0 for less output

# Set random seed
tf.random.set_seed(42)

# Replicate model_2
model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tf.keras.layers.Dense(1)
])

# Compile the model
model_3.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[‘mae’])

# Fit the model (this time for 500 epochs, not 100)
model_3.fit(tf.expand_dims(X_train, axis=-1), y_train, epochs=500, verbose=0) # set verbose to 0 for less output

Out[71]:

<keras.callbacks.History at 0x7f8df67b6d90>

In [72]:

# Make and plot predictions for model_3
y_preds_3 = model_3.predict(X_test)
plot_predictions(predictions=y_preds_3)

# Make and plot predictions for model_3
y_preds_3 = model_3.predict(X_test)
plot_predictions(predictions=y_preds_3)

Strange, we trained for longer but our model performed worse?

As it turns out, our model might’ve trained too long and has thus resulted in worse results (we’ll see ways to prevent training for too long later on).

In [73]:

# Calculate model_3 metrics
mae_3 = mae(y_test, y_preds_3.squeeze()).numpy()
mse_3 = mse(y_test, y_preds_3.squeeze()).numpy()
mae_3, mse_3

# Calculate model_3 metrics
mae_3 = mae(y_test, y_preds_3.squeeze()).numpy()
mse_3 = mse(y_test, y_preds_3.squeeze()).numpy()
mae_3, mse_3

Comparing results¶

Now we’ve got results for 3 similar but slightly different results, let’s compare them.

In [74]:

model_results = [["model_1", mae_1, mse_1],
                 ["model_2", mae_2, mse_2],
                 ["model_3", mae_3, mae_3]]

model_results = [[«model_1», mae_1, mse_1],
[«model_2», mae_2, mse_2],
[«model_3», mae_3, mae_3]]

In [75]:

import pandas as pd
all_results = pd.DataFrame(model_results, columns=["model", "mae", "mse"])
all_results

import pandas as pd
all_results = pd.DataFrame(model_results, columns=[«model», «mae», «mse»])
all_results

Out[75]:

	model	mae	mse
0	model_1	18.745327	353.573364
1	model_2	1.909811	5.459232
2	model_3	68.687859	68.687859

From our experiments, it looks like model_2 performed the best.

And now, you might be thinking, «wow, comparing models is tedious…» and it definitely can be, we’ve only compared 3 models here.

But this is part of what machine learning modelling is about, trying many different combinations of models and seeing which performs best.

Each model you build is a small experiment.

🔑 Note: One of your main goals should be to minimize the time between your experiments. The more experiments you do, the more things you’ll figure out which don’t work and in turn, get closer to figuring out what does work. Remember the machine learning practitioner’s motto: «experiment, experiment, experiment».

Another thing you’ll also find is what you thought may work (such as training a model for longer) may not always work and the exact opposite is also often the case.

Tracking your experiments¶

One really good habit to get into is tracking your modelling experiments to see which perform better than others.

We’ve done a simple version of this above (keeping the results in different variables).

📖 Resource: But as you build more models, you’ll want to look into using tools such as:

TensorBoard — a component of the TensorFlow library to help track modelling experiments (we’ll see this later).

Weights & Biases — a tool for tracking all kinds of machine learning experiments (the good news for Weights & Biases is it plugs into TensorBoard).

Saving a model¶

Once you’ve trained a model and found one which performs to your liking, you’ll probably want to save it for use elsewhere (like a web application or mobile device).

You can save a TensorFlow/Keras model using model.save().

There are two ways to save a model in TensorFlow:

The SavedModel format (default).
The HDF5 format.

The main difference between the two is the SavedModel is automatically able to save custom objects (such as special layers) without additional modifications when loading the model back in.

Which one should you use?

It depends on your situation but the SavedModel format will suffice most of the time.

Both methods use the same method call.

In [76]:

# Save a model using the SavedModel format
model_2.save('best_model_SavedModel_format')

# Save a model using the SavedModel format
model_2.save(‘best_model_SavedModel_format’)

INFO:tensorflow:Assets written to: best_model_SavedModel_format/assets

In [77]:

# Check it out - outputs a protobuf binary file (.pb) as well as other files
!ls best_model_SavedModel_format

# Check it out — outputs a protobuf binary file (.pb) as well as other files
!ls best_model_SavedModel_format

assets	keras_metadata.pb  saved_model.pb  variables

Now let’s save the model in the HDF5 format, we’ll use the same method but with a different filename.

In [78]:

# Save a model using the HDF5 format
model_2.save("best_model_HDF5_format.h5") # note the addition of '.h5' on the end

# Save a model using the HDF5 format
model_2.save(«best_model_HDF5_format.h5») # note the addition of ‘.h5’ on the end

In [79]:

# Check it out
!ls best_model_HDF5_format.h5

# Check it out
!ls best_model_HDF5_format.h5

best_model_HDF5_format.h5

Loading a model¶

We can load a saved model using the load_model() method.

Loading a model for the different formats (SavedModel and HDF5) is the same (as long as the pathnames to the particular formats are correct).

In [80]:

# Load a model from the SavedModel format
loaded_saved_model = tf.keras.models.load_model("best_model_SavedModel_format")
loaded_saved_model.summary()

# Load a model from the SavedModel format
loaded_saved_model = tf.keras.models.load_model(«best_model_SavedModel_format»)
loaded_saved_model.summary()

Model: "sequential_12"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_13 (Dense)            (None, 1)                 2         
                                                                 
 dense_14 (Dense)            (None, 1)                 2         
                                                                 
=================================================================
Total params: 4
Trainable params: 4
Non-trainable params: 0
_________________________________________________________________

In [81]:

# Compare model_2 with the SavedModel version (should return True)
model_2_preds = model_2.predict(X_test)
saved_model_preds = loaded_saved_model.predict(X_test)
mae(y_test, saved_model_preds.squeeze()).numpy() == mae(y_test, model_2_preds.squeeze()).numpy()

# Compare model_2 with the SavedModel version (should return True)
model_2_preds = model_2.predict(X_test)
saved_model_preds = loaded_saved_model.predict(X_test)
mae(y_test, saved_model_preds.squeeze()).numpy() == mae(y_test, model_2_preds.squeeze()).numpy()

Loading in from the HDF5 is much the same.

In [82]:

# Load a model from the HDF5 format
loaded_h5_model = tf.keras.models.load_model("best_model_HDF5_format.h5")
loaded_h5_model.summary()

# Load a model from the HDF5 format
loaded_h5_model = tf.keras.models.load_model(«best_model_HDF5_format.h5»)
loaded_h5_model.summary()

Model: "sequential_12"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_13 (Dense)            (None, 1)                 2         
                                                                 
 dense_14 (Dense)            (None, 1)                 2         
                                                                 
=================================================================
Total params: 4
Trainable params: 4
Non-trainable params: 0
_________________________________________________________________

In [83]:

# Compare model_2 with the loaded HDF5 version (should return True)
h5_model_preds = loaded_h5_model.predict(X_test)
mae(y_test, h5_model_preds.squeeze()).numpy() == mae(y_test, model_2_preds.squeeze()).numpy()

# Compare model_2 with the loaded HDF5 version (should return True)
h5_model_preds = loaded_h5_model.predict(X_test)
mae(y_test, h5_model_preds.squeeze()).numpy() == mae(y_test, model_2_preds.squeeze()).numpy()

Downloading a model (from Google Colab)¶

Say you wanted to get your model from Google Colab to your local machine, you can do one of the following things:

Right click on the file in the files pane and click ‘download’.
Use the code below.

In [84]:

# Download the model (or any file) from Google Colab
from google.colab import files
files.download("best_model_HDF5_format.h5")

# Download the model (or any file) from Google Colab
from google.colab import files
files.download(«best_model_HDF5_format.h5»)

A larger example¶

Alright, we’ve seen the fundamentals of building neural network regression models in TensorFlow.

Let’s step it up a notch and build a model for a more feature rich dataset.

More specifically we’re going to try predict the cost of medical insurance for individuals based on a number of different parameters such as, age, sex, bmi, children, smoking_status and residential_region.

To do, we’ll leverage the pubically available Medical Cost dataset available from Kaggle and hosted on GitHub.

🔑 Note: When learning machine learning paradigms, you’ll often go through a series of foundational techniques and then practice them by working with open-source datasets and examples. Just as we’re doing now, learn foundations, put them to work with different problems. Every time you work on something new, it’s a good idea to search for something like «problem X example with Python/TensorFlow» where you substitute X for your problem.

In [85]:

# Import required libraries
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt

# Import required libraries
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt

In [86]:

# Read in the insurance dataset
insurance = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv")

# Read in the insurance dataset
insurance = pd.read_csv(«https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv»)

In [87]:

# Check out the insurance dataset
insurance.head()

# Check out the insurance dataset
insurance.head()

Out[87]:

	age	sex	bmi	children	smoker	region	charges
0	19	female	27.900	0	yes	southwest	16884.92400
1	18	male	33.770	1	no	southeast	1725.55230
2	28	male	33.000	3	no	southeast	4449.46200
3	33	male	22.705	0	no	northwest	21984.47061
4	32	male	28.880	0	no	northwest	3866.85520

We’re going to have to turn the non-numerical columns into numbers (because a neural network can’t handle non-numerical inputs).

To do so, we’ll use the get_dummies() method in pandas.

It converts categorical variables (like the sex, smoker and region columns) into numerical variables using one-hot encoding.

In [88]:

# Turn all categories into numbers
insurance_one_hot = pd.get_dummies(insurance)
insurance_one_hot.head() # view the converted columns

# Turn all categories into numbers
insurance_one_hot = pd.get_dummies(insurance)
insurance_one_hot.head() # view the converted columns

Out[88]:

	age	bmi	children	charges	sex_female	sex_male	smoker_no	smoker_yes	region_northwest	region_southeast	region_southwest
0	19	27.900	0	16884.92400	1	0	0	1	0	0	1
1	18	33.770	1	1725.55230	0	1	1	0	0	1	0
2	28	33.000	3	4449.46200	0	1	1	0	0	1	0
3	33	22.705	0	21984.47061	0	1	1	0	1	0	0
4	32	28.880	0	3866.85520	0	1	1	0	1	0	0

Now we’ll split data into features (X) and labels (y).

In [89]:

# Create X & y values
X = insurance_one_hot.drop("charges", axis=1)
y = insurance_one_hot["charges"]

# Create X & y values
X = insurance_one_hot.drop(«charges», axis=1)
y = insurance_one_hot[«charges»]

Out[90]:

	age	bmi	children	sex_female	sex_male	smoker_no	smoker_yes	region_northwest	region_southeast	region_southwest
0	19	27.900	0	1	0	0	1	0	0	1
1	18	33.770	1	0	1	1	0	0	1	0
2	28	33.000	3	0	1	1	0	0	1	0
3	33	22.705	0	0	1	1	0	1	0	0
4	32	28.880	0	0	1	1	0	1	0	0

And create training and test sets. We could do this manually, but to make it easier, we’ll leverage the already available train_test_split function available from Scikit-Learn.

In [91]:

# Create training and test sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, 
                                                    y, 
                                                    test_size=0.2, 
                                                    random_state=42) # set random state for reproducible splits

# Create training and test sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.2,
random_state=42) # set random state for reproducible splits

Now we can build and fit a model (we’ll make it the same as model_2).

In [92]:

# Set random seed
tf.random.set_seed(42)

# Create a new model (same as model_2)
insurance_model = tf.keras.Sequential([
  tf.keras.layers.Dense(1),
  tf.keras.layers.Dense(1)
])

# Compile the model
insurance_model.compile(loss=tf.keras.losses.mae,
                        optimizer=tf.keras.optimizers.SGD(),
                        metrics=['mae'])

# Fit the model
insurance_model.fit(X_train, y_train, epochs=100)

# Set random seed
tf.random.set_seed(42)

# Create a new model (same as model_2)
insurance_model = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tf.keras.layers.Dense(1)
])

# Compile the model
insurance_model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=[‘mae’])

# Fit the model
insurance_model.fit(X_train, y_train, epochs=100)

Epoch 1/100
34/34 [==============================] - 0s 1ms/step - loss: 8868.5918 - mae: 8868.5918
Epoch 2/100
34/34 [==============================] - 0s 1ms/step - loss: 7887.1606 - mae: 7887.1606
Epoch 3/100
34/34 [==============================] - 0s 1ms/step - loss: 7537.0947 - mae: 7537.0947
Epoch 4/100
34/34 [==============================] - 0s 1ms/step - loss: 7859.4346 - mae: 7859.4346
Epoch 5/100
34/34 [==============================] - 0s 1ms/step - loss: 7639.6699 - mae: 7639.6699
Epoch 6/100
34/34 [==============================] - 0s 2ms/step - loss: 7578.0850 - mae: 7578.0850
Epoch 7/100
34/34 [==============================] - 0s 2ms/step - loss: 7514.6177 - mae: 7514.6177
Epoch 8/100
34/34 [==============================] - 0s 1ms/step - loss: 7694.1338 - mae: 7694.1338
Epoch 9/100
34/34 [==============================] - 0s 1ms/step - loss: 7595.9136 - mae: 7595.9136
Epoch 10/100
34/34 [==============================] - 0s 2ms/step - loss: 7735.9116 - mae: 7735.9116
Epoch 11/100
34/34 [==============================] - 0s 2ms/step - loss: 7444.4189 - mae: 7444.4189
Epoch 12/100
34/34 [==============================] - 0s 2ms/step - loss: 7678.0337 - mae: 7678.0337
Epoch 13/100
34/34 [==============================] - 0s 2ms/step - loss: 7681.5840 - mae: 7681.5840
Epoch 14/100
34/34 [==============================] - 0s 1ms/step - loss: 7702.2842 - mae: 7702.2842
Epoch 15/100
34/34 [==============================] - 0s 1ms/step - loss: 7585.8921 - mae: 7585.8921
Epoch 16/100
34/34 [==============================] - 0s 1ms/step - loss: 7689.5356 - mae: 7689.5356
Epoch 17/100
34/34 [==============================] - 0s 1ms/step - loss: 7509.2036 - mae: 7509.2036
Epoch 18/100
34/34 [==============================] - 0s 1ms/step - loss: 7695.0083 - mae: 7695.0083
Epoch 19/100
34/34 [==============================] - 0s 2ms/step - loss: 7669.3740 - mae: 7669.3740
Epoch 20/100
34/34 [==============================] - 0s 1ms/step - loss: 7901.1362 - mae: 7901.1362
Epoch 21/100
34/34 [==============================] - 0s 2ms/step - loss: 7552.4814 - mae: 7552.4814
Epoch 22/100
34/34 [==============================] - 0s 1ms/step - loss: 7844.9961 - mae: 7844.9961
Epoch 23/100
34/34 [==============================] - 0s 2ms/step - loss: 7642.2485 - mae: 7642.2485
Epoch 24/100
34/34 [==============================] - 0s 2ms/step - loss: 7515.3081 - mae: 7515.3081
Epoch 25/100
34/34 [==============================] - 0s 2ms/step - loss: 7678.3506 - mae: 7678.3506
Epoch 26/100
34/34 [==============================] - 0s 2ms/step - loss: 7653.0269 - mae: 7653.0269
Epoch 27/100
34/34 [==============================] - 0s 2ms/step - loss: 7559.5449 - mae: 7559.5449
Epoch 28/100
34/34 [==============================] - 0s 2ms/step - loss: 7459.9404 - mae: 7459.9404
Epoch 29/100
34/34 [==============================] - 0s 2ms/step - loss: 7618.6177 - mae: 7618.6177
Epoch 30/100
34/34 [==============================] - 0s 1ms/step - loss: 7628.6255 - mae: 7628.6255
Epoch 31/100
34/34 [==============================] - 0s 1ms/step - loss: 7540.4893 - mae: 7540.4893
Epoch 32/100
34/34 [==============================] - 0s 1ms/step - loss: 7486.0186 - mae: 7486.0186
Epoch 33/100
34/34 [==============================] - 0s 2ms/step - loss: 7418.6646 - mae: 7418.6646
Epoch 34/100
34/34 [==============================] - 0s 2ms/step - loss: 7480.7319 - mae: 7480.7319
Epoch 35/100
34/34 [==============================] - 0s 2ms/step - loss: 7615.3115 - mae: 7615.3115
Epoch 36/100
34/34 [==============================] - 0s 1ms/step - loss: 7566.7896 - mae: 7566.7896
Epoch 37/100
34/34 [==============================] - 0s 2ms/step - loss: 7661.0879 - mae: 7661.0879
Epoch 38/100
34/34 [==============================] - 0s 2ms/step - loss: 7522.6816 - mae: 7522.6816
Epoch 39/100
34/34 [==============================] - 0s 2ms/step - loss: 7556.0718 - mae: 7556.0718
Epoch 40/100
34/34 [==============================] - 0s 2ms/step - loss: 7433.5669 - mae: 7433.5669
Epoch 41/100
34/34 [==============================] - 0s 1ms/step - loss: 7722.4312 - mae: 7722.4312
Epoch 42/100
34/34 [==============================] - 0s 2ms/step - loss: 7344.2700 - mae: 7344.2700
Epoch 43/100
34/34 [==============================] - 0s 2ms/step - loss: 7597.4331 - mae: 7597.4331
Epoch 44/100
34/34 [==============================] - 0s 2ms/step - loss: 7338.0132 - mae: 7338.0132
Epoch 45/100
34/34 [==============================] - 0s 2ms/step - loss: 7510.3467 - mae: 7510.3467
Epoch 46/100
34/34 [==============================] - 0s 2ms/step - loss: 7413.5801 - mae: 7413.5801
Epoch 47/100
34/34 [==============================] - 0s 2ms/step - loss: 7451.0391 - mae: 7451.0391
Epoch 48/100
34/34 [==============================] - 0s 2ms/step - loss: 7340.5381 - mae: 7340.5381
Epoch 49/100
34/34 [==============================] - 0s 2ms/step - loss: 7481.9976 - mae: 7481.9976
Epoch 50/100
34/34 [==============================] - 0s 1ms/step - loss: 7468.2842 - mae: 7468.2842
Epoch 51/100
34/34 [==============================] - 0s 1ms/step - loss: 7411.3408 - mae: 7411.3408
Epoch 52/100
34/34 [==============================] - 0s 1ms/step - loss: 7460.0796 - mae: 7460.0796
Epoch 53/100
34/34 [==============================] - 0s 1ms/step - loss: 7601.6606 - mae: 7601.6606
Epoch 54/100
34/34 [==============================] - 0s 2ms/step - loss: 7241.2549 - mae: 7241.2549
Epoch 55/100
34/34 [==============================] - 0s 1ms/step - loss: 7539.6953 - mae: 7539.6953
Epoch 56/100
34/34 [==============================] - 0s 2ms/step - loss: 7293.2012 - mae: 7293.2012
Epoch 57/100
34/34 [==============================] - 0s 2ms/step - loss: 7417.9731 - mae: 7417.9731
Epoch 58/100
34/34 [==============================] - 0s 1ms/step - loss: 7353.0625 - mae: 7353.0625
Epoch 59/100
34/34 [==============================] - 0s 1ms/step - loss: 7643.8247 - mae: 7643.8247
Epoch 60/100
34/34 [==============================] - 0s 2ms/step - loss: 7410.4004 - mae: 7410.4004
Epoch 61/100
34/34 [==============================] - 0s 2ms/step - loss: 7612.8330 - mae: 7612.8330
Epoch 62/100
34/34 [==============================] - 0s 2ms/step - loss: 7387.9087 - mae: 7387.9087
Epoch 63/100
34/34 [==============================] - 0s 2ms/step - loss: 7359.5605 - mae: 7359.5605
Epoch 64/100
34/34 [==============================] - 0s 2ms/step - loss: 7109.0884 - mae: 7109.0884
Epoch 65/100
34/34 [==============================] - 0s 2ms/step - loss: 7396.3223 - mae: 7396.3223
Epoch 66/100
34/34 [==============================] - 0s 2ms/step - loss: 7179.8613 - mae: 7179.8613
Epoch 67/100
34/34 [==============================] - 0s 1ms/step - loss: 7289.7710 - mae: 7289.7710
Epoch 68/100
34/34 [==============================] - 0s 1ms/step - loss: 7523.6973 - mae: 7523.6973
Epoch 69/100
34/34 [==============================] - 0s 1ms/step - loss: 7442.6157 - mae: 7442.6157
Epoch 70/100
34/34 [==============================] - 0s 1ms/step - loss: 7673.4834 - mae: 7673.4834
Epoch 71/100
34/34 [==============================] - 0s 2ms/step - loss: 7276.0337 - mae: 7276.0337
Epoch 72/100
34/34 [==============================] - 0s 2ms/step - loss: 7246.3721 - mae: 7246.3721
Epoch 73/100
34/34 [==============================] - 0s 1ms/step - loss: 7372.0713 - mae: 7372.0713
Epoch 74/100
34/34 [==============================] - 0s 1ms/step - loss: 7512.0762 - mae: 7512.0762
Epoch 75/100
34/34 [==============================] - 0s 2ms/step - loss: 7269.7437 - mae: 7269.7437
Epoch 76/100
34/34 [==============================] - 0s 2ms/step - loss: 7199.5039 - mae: 7199.5039
Epoch 77/100
34/34 [==============================] - 0s 2ms/step - loss: 7261.2920 - mae: 7261.2920
Epoch 78/100
34/34 [==============================] - 0s 2ms/step - loss: 7185.7627 - mae: 7185.7627
Epoch 79/100
34/34 [==============================] - 0s 1ms/step - loss: 7301.7495 - mae: 7301.7495
Epoch 80/100
34/34 [==============================] - 0s 2ms/step - loss: 7002.6309 - mae: 7002.6309
Epoch 81/100
34/34 [==============================] - 0s 1ms/step - loss: 7289.1357 - mae: 7289.1357
Epoch 82/100
34/34 [==============================] - 0s 1ms/step - loss: 7155.3945 - mae: 7155.3945
Epoch 83/100
34/34 [==============================] - 0s 1ms/step - loss: 7475.1709 - mae: 7475.1709
Epoch 84/100
34/34 [==============================] - 0s 1ms/step - loss: 7387.3672 - mae: 7387.3672
Epoch 85/100
34/34 [==============================] - 0s 2ms/step - loss: 7289.9458 - mae: 7289.9458
Epoch 86/100
34/34 [==============================] - 0s 1ms/step - loss: 7268.0942 - mae: 7268.0942
Epoch 87/100
34/34 [==============================] - 0s 2ms/step - loss: 7238.5869 - mae: 7238.5869
Epoch 88/100
34/34 [==============================] - 0s 2ms/step - loss: 7201.7354 - mae: 7201.7349
Epoch 89/100
34/34 [==============================] - 0s 2ms/step - loss: 7538.0757 - mae: 7538.0757
Epoch 90/100
34/34 [==============================] - 0s 2ms/step - loss: 6967.1187 - mae: 6967.1187
Epoch 91/100
34/34 [==============================] - 0s 2ms/step - loss: 7314.1299 - mae: 7314.1299
Epoch 92/100
34/34 [==============================] - 0s 1ms/step - loss: 7192.3115 - mae: 7192.3115
Epoch 93/100
34/34 [==============================] - 0s 1ms/step - loss: 7530.8770 - mae: 7530.8770
Epoch 94/100
34/34 [==============================] - 0s 1ms/step - loss: 7187.3579 - mae: 7187.3579
Epoch 95/100
34/34 [==============================] - 0s 1ms/step - loss: 7561.5635 - mae: 7561.5635
Epoch 96/100
34/34 [==============================] - 0s 1ms/step - loss: 7263.4648 - mae: 7263.4648
Epoch 97/100
34/34 [==============================] - 0s 1ms/step - loss: 7146.2896 - mae: 7146.2896
Epoch 98/100
34/34 [==============================] - 0s 2ms/step - loss: 7247.9238 - mae: 7247.9238
Epoch 99/100
34/34 [==============================] - 0s 2ms/step - loss: 7200.6694 - mae: 7200.6694
Epoch 100/100
34/34 [==============================] - 0s 1ms/step - loss: 7301.6870 - mae: 7301.6870

Out[92]:

<keras.callbacks.History at 0x7f8dedf0cad0>

In [93]:

# Check the results of the insurance model
insurance_model.evaluate(X_test, y_test)

# Check the results of the insurance model
insurance_model.evaluate(X_test, y_test)

9/9 [==============================] - 0s 2ms/step - loss: 8628.2393 - mae: 8628.2393

Out[93]:

[8628.2392578125, 8628.2392578125]

Our model didn’t perform very well, let’s try a bigger model.

We’ll try 3 things:

Increasing the number of layers (2 -> 3).
Increasing the number of units in each layer (except for the output layer).
Changing the optimizer (from SGD to Adam).

Everything else will stay the same.

In [94]:

# Set random seed
tf.random.set_seed(42)

# Add an extra layer and increase number of units
insurance_model_2 = tf.keras.Sequential([
  tf.keras.layers.Dense(100), # 100 units
  tf.keras.layers.Dense(10), # 10 units
  tf.keras.layers.Dense(1) # 1 unit (important for output layer)
])

# Compile the model
insurance_model_2.compile(loss=tf.keras.losses.mae,
                          optimizer=tf.keras.optimizers.Adam(), # Adam works but SGD doesn't 
                          metrics=['mae'])

# Fit the model and save the history (we can plot this)
history = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)

# Set random seed
tf.random.set_seed(42)

# Add an extra layer and increase number of units
insurance_model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(100), # 100 units
tf.keras.layers.Dense(10), # 10 units
tf.keras.layers.Dense(1) # 1 unit (important for output layer)
])

# Compile the model
insurance_model_2.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(), # Adam works but SGD doesn’t
metrics=[‘mae’])

# Fit the model and save the history (we can plot this)
history = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)

In [95]:

# Evaluate our larger model
insurance_model_2.evaluate(X_test, y_test)

# Evaluate our larger model
insurance_model_2.evaluate(X_test, y_test)

9/9 [==============================] - 0s 2ms/step - loss: 4924.3477 - mae: 4924.3477

Out[95]:

[4924.34765625, 4924.34765625]

Much better! Using a larger model and the Adam optimizer results in almost half the error as the previous model.

🔑 Note: For many problems, the Adam optimizer is a great starting choice. See Andrei Karpathy’s «Adam is safe» point from A Recipe for Training Neural Networks for more.

Let’s check out the loss curves of our model, we should see a downward trend.

In [96]:

# Plot history (also known as a loss curve)
pd.DataFrame(history.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs");

# Plot history (also known as a loss curve)
pd.DataFrame(history.history).plot()
plt.ylabel(«loss»)
plt.xlabel(«epochs»);

From this, it looks like our model’s loss (and MAE) were both still decreasing (in our case, MAE and loss are the same, hence the lines in the plot overlap eachother).

What this tells us is the loss might go down if we try training it for longer.

🤔 Question: How long should you train for?

It depends on what problem you’re working on. Sometimes training won’t take very long, other times it’ll take longer than you expect. A common method is to set your model training for a very long time (e.g. 1000’s of epochs) but set it up with an EarlyStopping callback so it stops automatically when it stops improving. We’ll see this in another module.

Let’s train the same model as above for a little longer. We can do this but calling fit on it again.

In [97]:

# Try training for a little longer (100 more epochs)
history_2 = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)

# Try training for a little longer (100 more epochs)
history_2 = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)

How did the extra training go?

In [98]:

# Evaluate the model trained for 200 total epochs
insurance_model_2_loss, insurance_model_2_mae = insurance_model_2.evaluate(X_test, y_test)
insurance_model_2_loss, insurance_model_2_mae

# Evaluate the model trained for 200 total epochs
insurance_model_2_loss, insurance_model_2_mae = insurance_model_2.evaluate(X_test, y_test)
insurance_model_2_loss, insurance_model_2_mae

9/9 [==============================] - 0s 2ms/step - loss: 3494.7285 - mae: 3494.7285

Out[98]:

(3494.728515625, 3494.728515625)

Boom! Training for an extra 100 epochs we see about a 10% decrease in error.

How does the visual look?

In [99]:

# Plot the model trained for 200 total epochs loss curves
pd.DataFrame(history_2.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs"); # note: epochs will only show 100 since we overrid the history variable

# Plot the model trained for 200 total epochs loss curves
pd.DataFrame(history_2.history).plot()
plt.ylabel(«loss»)
plt.xlabel(«epochs»); # note: epochs will only show 100 since we overrid the history variable

Preprocessing data (normalization and standardization)¶

A common practice when working with neural networks is to make sure all of the data you pass to them is in the range 0 to 1.

This practice is called normalization (scaling all values from their original range to, e.g. between 0 and 100,000 to be between 0 and 1).

There is another process call standardization which converts all of your data to unit variance and 0 mean.

These two practices are often part of a preprocessing pipeline (a series of functions to prepare your data for use with neural networks).

Knowing this, some of the major steps you’ll take to preprocess your data for a neural network include:

Turning all of your data to numbers (a neural network can’t handle strings).
Making sure your data is in the right shape (verifying input and output shapes).
Feature scaling:
- Normalizing data (making sure all values are between 0 and 1). This is done by subtracting the minimum value then dividing by the maximum value minus the minmum. This is also referred to as min-max scaling.
- Standardization (making sure all values have a mean of 0 and a variance of 1). This is done by substracting the mean value from the target feature and then dividing it by the standard deviation.
- Which one should you use?
  - With neural networks you’ll tend to favour normalization as they tend to prefer values between 0 and 1 (you’ll see this espcially with image processing), however, you’ll often find a neural network can perform pretty well with minimal feature scaling.

📖 Resource: For more on preprocessing data, I’d recommend reading the following resources:

Scikit-Learn’s documentation on preprocessing data.

Scale, Standardize or Normalize with Scikit-Learn by Jeff Hale.

We’ve already turned our data into numbers using get_dummies(), let’s see how we’d normalize it as well.

In [100]:

import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf

# Read in the insurance dataset
insurance = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv")

import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf

# Read in the insurance dataset
insurance = pd.read_csv(«https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv»)

In [101]:

# Check out the data
insurance.head()

# Check out the data
insurance.head()

Out[101]:

	age	sex	bmi	children	smoker	region	charges
0	19	female	27.900	0	yes	southwest	16884.92400
1	18	male	33.770	1	no	southeast	1725.55230
2	28	male	33.000	3	no	southeast	4449.46200
3	33	male	22.705	0	no	northwest	21984.47061
4	32	male	28.880	0	no	northwest	3866.85520

Now, just as before, we need to transform the non-numerical columns into numbers and this time we’ll also be normalizing the numerical columns with different ranges (to make sure they’re all between 0 and 1).

To do this, we’re going to use a few classes from Scikit-Learn:

make_column_transformer — build a multi-step data preprocessing function for the folllowing transformations:
- MinMaxScaler — make sure all numerical columns are normalized (between 0 and 1).
- OneHotEncoder — one hot encode the non-numerical columns.

Let’s see them in action.

In [102]:

from sklearn.compose import make_column_transformer
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder

# Create column transformer (this will help us normalize/preprocess our data)
ct = make_column_transformer(
    (MinMaxScaler(), ["age", "bmi", "children"]), # get all values between 0 and 1
    (OneHotEncoder(handle_unknown="ignore"), ["sex", "smoker", "region"])
)

# Create X & y
X = insurance.drop("charges", axis=1)
y = insurance["charges"]

# Build our train and test sets (use random state to ensure same split as before)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit column transformer on the training data only (doing so on test data would result in data leakage)
ct.fit(X_train)

# Transform training and test data with normalization (MinMaxScalar) and one hot encoding (OneHotEncoder)
X_train_normal = ct.transform(X_train)
X_test_normal = ct.transform(X_test)

from sklearn.compose import make_column_transformer
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder

# Create column transformer (this will help us normalize/preprocess our data)
ct = make_column_transformer(
(MinMaxScaler(), [«age», «bmi», «children»]), # get all values between 0 and 1
(OneHotEncoder(handle_unknown=»ignore»), [«sex», «smoker», «region»])
)

# Create X & y
X = insurance.drop(«charges», axis=1)
y = insurance[«charges»]

# Build our train and test sets (use random state to ensure same split as before)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit column transformer on the training data only (doing so on test data would result in data leakage)
ct.fit(X_train)

# Transform training and test data with normalization (MinMaxScalar) and one hot encoding (OneHotEncoder)
X_train_normal = ct.transform(X_train)
X_test_normal = ct.transform(X_test)

Now we’ve normalized it and one-hot encoding it, what does our data look like now?

In [103]:

# Non-normalized and non-one-hot encoded data example
X_train.loc[0]

# Non-normalized and non-one-hot encoded data example
X_train.loc[0]

Out[103]:

age                19
sex            female
bmi              27.9
children            0
smoker            yes
region      southwest
Name: 0, dtype: object

In [104]:

# Normalized and one-hot encoded example
X_train_normal[0]

# Normalized and one-hot encoded example
X_train_normal[0]

Out[104]:

array([0.60869565, 0.10734463, 0.4       , 1.        , 0.        ,
       1.        , 0.        , 0.        , 1.        , 0.        ,
       0.        ])

In [105]:

# Notice the normalized/one-hot encoded shape is larger because of the extra columns
X_train_normal.shape, X_train.shape

# Notice the normalized/one-hot encoded shape is larger because of the extra columns
X_train_normal.shape, X_train.shape

Our data is normalized and numerical, let’s model it.

We’ll use the same model as insurance_model_2.

In [106]:

# Set random seed
tf.random.set_seed(42)

# Build the model (3 layers, 100, 10, 1 units)
insurance_model_3 = tf.keras.Sequential([
  tf.keras.layers.Dense(100),
  tf.keras.layers.Dense(10),
  tf.keras.layers.Dense(1)
])

# Compile the model
insurance_model_3.compile(loss=tf.keras.losses.mae,
                          optimizer=tf.keras.optimizers.Adam(),
                          metrics=['mae'])

# Fit the model for 200 epochs (same as insurance_model_2)
insurance_model_3.fit(X_train_normal, y_train, epochs=200, verbose=0)

# Set random seed
tf.random.set_seed(42)

# Build the model (3 layers, 100, 10, 1 units)
insurance_model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(100),
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])

# Compile the model
insurance_model_3.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(),
metrics=[‘mae’])

# Fit the model for 200 epochs (same as insurance_model_2)
insurance_model_3.fit(X_train_normal, y_train, epochs=200, verbose=0)

Out[106]:

<keras.callbacks.History at 0x7f8df4a6da50>

Let’s evaluate the model on normalized test set.

In [107]:

# Evaulate 3rd model
insurance_model_3_loss, insurance_model_3_mae = insurance_model_3.evaluate(X_test_normal, y_test)

# Evaulate 3rd model
insurance_model_3_loss, insurance_model_3_mae = insurance_model_3.evaluate(X_test_normal, y_test)

9/9 [==============================] - 0s 2ms/step - loss: 3171.5774 - mae: 3171.5774

And finally, let’s compare the results from insurance_model_2 (trained on non-normalized data) and insurance_model_3 (trained on normalized data).

In [108]:

# Compare modelling results from non-normalized data and normalized data
insurance_model_2_mae, insurance_model_3_mae

# Compare modelling results from non-normalized data and normalized data
insurance_model_2_mae, insurance_model_3_mae

Out[108]:

(3494.728515625, 3171.577392578125)

From this we can see normalizing the data results in 10% less error using the same model than not normalizing the data.

This is one of the main benefits of normalization: faster convergence time (a fancy way of saying, your model gets to better results faster).

insurance_model_2 may have eventually achieved the same results as insurance_model_3 if we left it training for longer.

Also, the results may change if we were to alter the architectures of the models, e.g. more hidden units per layer or more layers.

But since our main goal as neural network practitioners is to decrease the time between experiments, anything that helps us get better results sooner is a plus.

🛠 Exercises¶

We’ve a covered a whole lot pretty quickly.

So now it’s time to have a play around with a few things and start to build up your intuition.

I emphasise the words play around because that’s very important. Try a few things out, run the code and see what happens.

Create your own regression dataset (or make the one we created in «Create data to view and fit» bigger) and build fit a model to it.
Try building a neural network with 4 Dense layers and fitting it to your own regression dataset, how does it perform?
Try and improve the results we got on the insurance dataset, some things you might want to try include:
- Building a larger model (how does one with 4 dense layers go?).
- Increasing the number of units in each layer.
- Lookup the documentation of Adam and find out what the first parameter is, what happens if you increase it by 10x?
- What happens if you train for longer (say 300 epochs instead of 200)?
Import the Boston pricing dataset from TensorFlow tf.keras.datasets and model it.

Источник