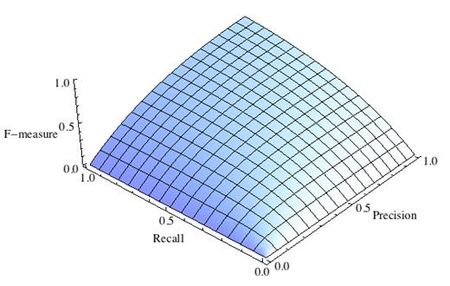
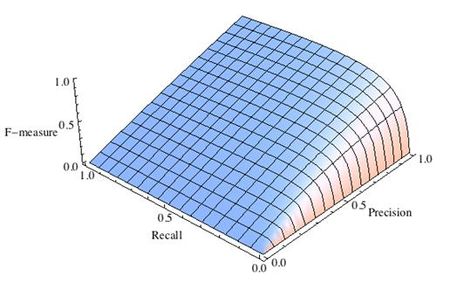
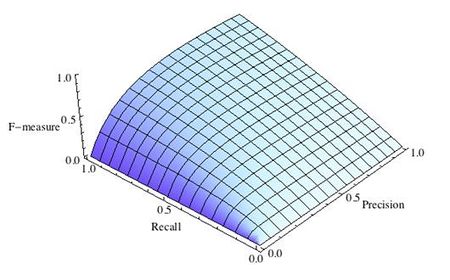
Есть 3 различных API для оценки качества прогнозов модели:
- Метод оценки оценщика : у оценщиков есть
scoreметод, обеспечивающий критерий оценки по умолчанию для проблемы, для решения которой они предназначены. Это обсуждается не на этой странице, а в документации каждого оценщика. - Параметр оценки: инструменты оценки модели с использованием перекрестной проверки (например,
model_selection.cross_val_scoreиmodel_selection.GridSearchCV) полагаются на внутреннюю стратегию оценки . Это обсуждается в разделе Параметр оценки: определение правил оценки модели . - Метрические функции : В
sklearn.metricsмодуле реализованы функции оценки ошибки прогноза для конкретных целей. Эти показатели подробно описаны в разделах по метрикам классификации , MultiLabel ранжирования показателей , показателей регрессии и показателей кластеризации .
Наконец, фиктивные оценки полезны для получения базового значения этих показателей для случайных прогнозов.
3.3.1. В scoring параметрах: определение правил оценки моделей
Выбор и оценка модели с использованием таких инструментов, как model_selection.GridSearchCV и model_selection.cross_val_score, принимают scoring параметр, который контролирует, какую метрику они применяют к оцениваемым оценщикам.
3.3.1.1. Общие случаи: предопределенные значения
Для наиболее распространенных случаев использования вы можете назначить объект подсчета с помощью scoring параметра; в таблице ниже показаны все возможные значения. Все объекты счетчика следуют соглашению о том, что более высокие возвращаемые значения лучше, чем более низкие возвращаемые значения . Таким образом, метрики, которые измеряют расстояние между моделью и данными, например metrics.mean_squared_error, доступны как neg_mean_squared_error, которые возвращают инвертированное значение метрики.
| Подсчет очков | Функция | Комментарий |
| Классификация | ||
| ‘accuracy’ | metrics.accuracy_score |
|
| ‘balanced_accuracy’ | metrics.balanced_accuracy_score |
|
| ‘top_k_accuracy’ | metrics.top_k_accuracy_score |
|
| ‘average_precision’ | metrics.average_precision_score |
|
| ‘neg_brier_score’ | metrics.brier_score_loss |
|
| ‘f1’ | metrics.f1_score |
для двоичных целей |
| ‘f1_micro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_macro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_weighted’ | metrics.f1_score |
средневзвешенное |
| ‘f1_samples’ | metrics.f1_score |
по многопозиционному образцу |
| ‘neg_log_loss’ | metrics.log_loss |
требуетсяpredict_probaподдержка |
| ‘precision’ etc. | metrics.precision_score |
суффиксы применяются как с ‘f1’ |
| ‘recall’ etc. | metrics.recall_score |
суффиксы применяются как с ‘f1’ |
| ‘jaccard’ etc. | metrics.jaccard_score |
суффиксы применяются как с ‘f1’ |
| ‘roc_auc’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr_weighted’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo_weighted’ | metrics.roc_auc_score |
|
| Кластеризация | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score |
|
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score |
|
| ‘completeness_score’ | metrics.completeness_score |
|
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score |
|
| ‘homogeneity_score’ | metrics.homogeneity_score |
|
| ‘mutual_info_score’ | metrics.mutual_info_score |
|
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score |
|
| ‘rand_score’ | metrics.rand_score |
|
| ‘v_measure_score’ | metrics.v_measure_score |
|
| Регрессия | ||
| ‘explained_variance’ | metrics.explained_variance_score |
|
| ‘max_error’ | metrics.max_error |
|
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error |
|
| ‘neg_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_root_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error |
|
| ‘neg_median_absolute_error’ | metrics.median_absolute_error |
|
| ‘r2’ | metrics.r2_score |
|
| ‘neg_mean_poisson_deviance’ | metrics.mean_poisson_deviance |
|
| ‘neg_mean_gamma_deviance’ | metrics.mean_gamma_deviance |
|
| ‘neg_mean_absolute_percentage_error’ | metrics.mean_absolute_percentage_error |
Примеры использования:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sorted(sklearn.metrics.SCORERS.keys()) to get valid options.
Примечание
Значения, перечисленные в виде ValueError исключения, соответствуют функциям измерения точности прогнозирования, описанным в следующих разделах. Объекты счетчика для этих функций хранятся в словаре sklearn.metrics.SCORERS.
3.3.1.2. Определение стратегии выигрыша от метрических функций
Модуль sklearn.metrics также предоставляет набор простых функций, измеряющих ошибку предсказания с учетом истинности и предсказания:
- функции, заканчивающиеся на,
_scoreвозвращают значение для максимизации, чем выше, тем лучше. - функции, заканчивающиеся на
_errorили_lossвозвращающие значение, которое нужно минимизировать, чем ниже, тем лучше. При преобразовании в объект счетчика с использованиемmake_scorerустановите дляgreater_is_betterпараметра значениеFalse(Trueпо умолчанию; см. Описание параметра ниже).
Метрики, доступные для различных задач машинного обучения, подробно описаны в разделах ниже.
Многим метрикам не даются имена для использования в качестве scoring значений, иногда потому, что они требуют дополнительных параметров, например fbeta_score. В таких случаях вам необходимо создать соответствующий объект оценки. Самый простой способ создать вызываемый объект для оценки — использовать make_scorer. Эта функция преобразует метрики в вызываемые объекты, которые можно использовать для оценки модели.
Один из типичных вариантов использования — обернуть существующую метрическую функцию из библиотеки значениями, отличными от значений по умолчанию для ее параметров, такими как beta параметр для fbeta_score функции:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
Второй вариант использования — создание полностью настраиваемого объекта скоринга из простой функции Python с использованием make_scorer, которая может принимать несколько параметров:
- функция Python, которую вы хотите использовать (
my_custom_loss_funcв примере ниже) - возвращает ли функция Python оценку (
greater_is_better=True, по умолчанию) или потерю (greater_is_better=False). В случае потери результат функции python аннулируется объектом скоринга в соответствии с соглашением о перекрестной проверке, согласно которому скоринтеры возвращают более высокие значения для лучших моделей. - только для показателей классификации: требуется ли для предоставленной вами функции Python постоянная уверенность в принятии решений (
needs_threshold=True). Значение по умолчанию неверно. - любые дополнительные параметры, такие как
betaилиlabelsвf1_score.
Вот пример создания пользовательских счетчиков очков и использования greater_is_better параметра:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
3.3.1.3. Реализация собственного скорингового объекта
Вы можете сгенерировать еще более гибкие модели скоринга, создав свой собственный скоринговый объект с нуля, без использования make_scorer фабрики. Чтобы вызываемый может быть бомбардиром, он должен соответствовать протоколу, указанному в следующих двух правилах:
- Его можно вызвать с параметрами (estimator, X, y), где estimator это модель, которая должна быть оценена, X это данные проверки и y основная истинная цель для (в контролируемом случае) или None (в неконтролируемом случае).
- Он возвращает число с плавающей запятой, которое количественно определяет
estimatorкачество прогнозированияXсо ссылкой наy. Опять же, по соглашению более высокие числа лучше, поэтому, если ваш секретарь сообщает о проигрыше, это значение следует отменить.
Примечание Использование пользовательских счетчиков в функциях, где n_jobs> 1
Хотя определение пользовательской функции оценки вместе с вызывающей функцией должно работать из коробки с бэкэндом joblib по умолчанию (loky), его импорт из другого модуля будет более надежным подходом и будет работать независимо от бэкэнда joblib.
Например, чтобы использовать n_jobsбольше 1 в примере ниже, custom_scoring_function функция сохраняется в созданном пользователем модуле ( custom_scorer_module.py) и импортируется:
>>> from custom_scorer_module import custom_scoring_function >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1)
3.3.1.4. Использование множественной метрической оценки
Scikit-learn также позволяет оценивать несколько показателей в GridSearchCV, RandomizedSearchCV и cross_validate.
Есть три способа указать несколько показателей оценки для scoring параметра:
- Как итерация строковых показателей:
>>> scoring = ['accuracy', 'precision']
- В качестве
dictсопоставления имени секретаря с функцией подсчета очков:
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
Обратите внимание, что значения dict могут быть либо функциями счетчика, либо одной из предварительно определенных строк показателей.
- Как вызываемый объект, возвращающий словарь оценок:
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
... y_pred = clf.predict(X)
... cm = confusion_matrix(y, y_pred)
... return {'tn': cm[0, 0], 'fp': cm[0, 1],
... 'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
... scoring=confusion_matrix_scorer)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
3.3.2. Метрики классификации
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности классификации. Некоторые метрики могут потребовать оценок вероятности положительного класса, значений достоверности или значений двоичных решений. Большинство реализаций позволяют каждой выборке вносить взвешенный вклад в общую оценку с помощью sample_weight параметра.
Некоторые из них ограничены случаем двоичной классификации:
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
roc_curve(y_true, y_score, *[, pos_label, …]) |
Вычислить рабочую характеристику приемника (ROC). |
det_curve(y_true, y_score[, pos_label, …]) |
Вычислите частоту ошибок для различных пороговых значений вероятности. |
Другие также работают в случае мультикласса:
balanced_accuracy_score(y_true, y_pred, *[, …]) |
Вычислите сбалансированную точность. |
cohen_kappa_score(y1, y2, *[, labels, …]) |
Каппа Коэна: статистика, измеряющая согласованность аннотаторов. |
confusion_matrix(y_true, y_pred, *[, …]) |
Вычислите матрицу неточностей, чтобы оценить точность классификации. |
hinge_loss(y_true, pred_decision, *[, …]) |
Средняя потеря петель (нерегулируемая). |
matthews_corrcoef(y_true, y_pred, *[, …]) |
Вычислите коэффициент корреляции Мэтьюза (MCC). |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
top_k_accuracy_score(y_true, y_score, *[, …]) |
Top-k Рейтинг по классификации точности. |
Некоторые также работают в многоярусном регистре:
accuracy_score(y_true, y_pred, *[, …]) |
Классификационная оценка точности. |
classification_report(y_true, y_pred, *[, …]) |
Создайте текстовый отчет, показывающий основные показатели классификации. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
hamming_loss(y_true, y_pred, *[, sample_weight]) |
Вычислите среднюю потерю Хэмминга. |
jaccard_score(y_true, y_pred, *[, labels, …]) |
Оценка коэффициента сходства Жаккара. |
log_loss(y_true, y_pred, *[, eps, …]) |
Потеря журнала, также известная как потеря логистики или потеря кросс-энтропии. |
multilabel_confusion_matrix(y_true, y_pred, *) |
Вычислите матрицу неточностей для каждого класса или образца. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите отзыв. |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
zero_one_loss(y_true, y_pred, *[, …]) |
Потеря классификации нулевая единица. |
А некоторые работают с двоичными и многозначными (но не мультиклассовыми) проблемами:
В следующих подразделах мы опишем каждую из этих функций, которым будут предшествовать некоторые примечания по общему API и определению показателей.
3.3.2.1. От бинарного до мультиклассового и многозначного
Некоторые метрики по существу определены для задач двоичной классификации (например f1_score, roc_auc_score). В этих случаях по умолчанию оценивается только положительная метка, предполагая по умолчанию, что положительный класс помечен 1 (хотя это можно настроить с помощью pos_label параметра).
При расширении двоичной метрики на задачи с несколькими классами или метками данные обрабатываются как набор двоичных задач, по одной для каждого класса. Затем есть несколько способов усреднить вычисления двоичных показателей по набору классов, каждый из которых может быть полезен в некотором сценарии. Если возможно, вы должны выбрать одно из них с помощью average параметра.
"macro"просто вычисляет среднее значение двоичных показателей, придавая каждому классу одинаковый вес. В задачах, где редкие занятия тем не менее важны, макро-усреднение может быть средством выделения их производительности. С другой стороны, предположение, что все классы одинаково важны, часто неверно, так что макро-усреднение будет чрезмерно подчеркивать обычно низкую производительность для нечастого класса."weighted"учитывает дисбаланс классов, вычисляя среднее значение двоичных показателей, в которых оценка каждого класса взвешивается по его присутствию в истинной выборке данных."micro"дает каждой паре выборка-класс равный вклад в общую метрику (за исключением результата взвешивания выборки). Вместо того, чтобы суммировать метрику для каждого класса, это суммирует дивиденды и делители, составляющие метрики для каждого класса, для расчета общего частного. Микро-усреднение может быть предпочтительным в настройках с несколькими ярлыками, включая многоклассовую классификацию, когда класс большинства следует игнорировать."samples"применяется только к задачам с несколькими ярлыками. Он не вычисляет меру для каждого класса, вместо этого вычисляет метрику по истинным и прогнозируемым классам для каждой выборки в данных оценки и возвращает их (sample_weight— взвешенное) среднее значение.- Выбор
average=Noneвернет массив с оценкой для каждого класса.
В то время как данные мультикласса предоставляются метрике, как двоичные цели, в виде массива меток классов, данные с несколькими метками указываются как индикаторная матрица, в которой ячейка [i, j] имеет значение 1, если у образца i есть метка j, и значение 0 в противном случае.
3.3.2.2. Оценка точности
Функция accuracy_score вычисляет точность , либо фракции ( по умолчанию) или количество (нормализует = False) правильных предсказаний.
В классификации с несколькими ярлыками функция возвращает точность подмножества. Если весь набор предсказанных меток для выборки строго соответствует истинному набору меток, то точность подмножества равна 1,0; в противном случае — 0, 0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)$$
где $1(x)$- индикаторная функция .
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
В многопозиционном корпусе с бинарными индикаторами меток:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
Пример:
- См. В разделе Проверка с перестановками значимости классификационной оценки пример использования показателя точности с использованием перестановок набора данных.
3.3.2.3. Рейтинг точности Top-k
Функция top_k_accuracy_score представляет собой обобщение accuracy_score. Разница в том, что прогноз считается правильным, если истинная метка связана с одним из kнаивысших прогнозируемых баллов. accuracy_score является частным случаем k = 1.
Функция охватывает случаи двоичной и многоклассовой классификации, но не случай многозначной классификации.
Если $hat{f}_{i,j}$ прогнозируемый класс для $i$-й образец, соответствующий $j$-й по величине прогнозируемый результат и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)$$
где k допустимое количество предположений и 1(x)- индикаторная функция.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
3.3.2.4. Сбалансированный показатель точности
Функция balanced_accuracy_score вычисляет взвешенную точность , что позволяет избежать завышенных оценок производительности на несбалансированных данных. Это макросреднее количество оценок отзыва по классу или, что то же самое, грубая точность, где каждая выборка взвешивается в соответствии с обратной распространенностью ее истинного класса. Таким образом, для сбалансированных наборов данных оценка равна точности.
В двоичном случае сбалансированная точность равна среднему арифметическому чувствительности (истинно положительный показатель) и специфичности (истинно отрицательный показатель) или площади под кривой ROC с двоичными прогнозами, а не баллами:
$$texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )$$
Если классификатор одинаково хорошо работает в любом классе, этот термин сокращается до обычной точности (т. е. Количества правильных прогнозов, деленного на общее количество прогнозов).
Напротив, если обычная точность выше вероятности только потому, что классификатор использует несбалансированный набор тестов, тогда сбалансированная точность, при необходимости, упадет до $frac{1}{n_classes}$.
Оценка варьируется от 0 до 1 или, когда adjusted=True используется, масштабируется до диапазона $frac{1}{1 — n_classes}$ до 1 включительно, с произвольной оценкой 0.
Если yi истинная ценность $i$-й образец, и $w_i$ — соответствующий вес образца, затем мы настраиваем вес образца на:
$$hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}$$
где $1(x)$- индикаторная функция . Учитывая предсказанный $hat{y}_i$ для образца $i$, сбалансированная точность определяется как:
$$texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i$$
С adjusted=True сбалансированной точностью сообщает об относительном увеличении от $texttt{balanced-accuracy}(y, mathbf{0}, w) =frac{1}{n_classes}$. В двоичном случае это также известно как * статистика Юдена * , или информированность .
Примечание
Определение мультикласса здесь кажется наиболее разумным расширением метрики, используемой в бинарной классификации, хотя в литературе нет определенного консенсуса:
- Наше определение: [Mosley2013] , [Kelleher2015] и [Guyon2015] , где [Guyon2015] принимает скорректированную версию, чтобы гарантировать, что случайные предсказания имеют оценку 0 а точные предсказания имеют оценку 1..
- Точность балансировки классов, как описано в [Mosley2013] : вычисляется минимум между точностью и отзывом для каждого класса. Затем эти значения усредняются по общему количеству классов для получения сбалансированной точности.
- Сбалансированная точность, как описано в [Urbanowicz2015] : среднее значение чувствительности и специфичности вычисляется для каждого класса, а затем усредняется по общему количеству классов.
Рекомендации:
- Гийон 2015 ( 1 , 2 ) И. Гайон, К. Беннет, Г. Коули, Х. Дж. Эскаланте, С. Эскалера, Т. К. Хо, Н. Масиа, Б. Рэй, М. Саид, А. Р. Статников, Э. Вьегас, Дизайн конкурса ChaLearn AutoML Challenge 2015 , IJCNN 2015 г.
- Мосли 2013 ( 1 , 2 ) Л. Мосли, Сбалансированный подход к проблеме мультиклассового дисбаланса , IJCV 2010.
- Kelleher2015 Джон. Д. Келлехер, Брайан Мак Нейме, Аойф Д’Арси, Основы машинного обучения для прогнозной аналитики данных: алгоритмы, рабочие примеры и тематические исследования , 2015.
- Урбанович2015 Urbanowicz RJ, Moore, JH ExSTraCS 2.0: описание и оценка масштабируемой системы классификаторов обучения , Evol. Intel. (2015) 8:89.
3.3.2.5. Каппа Коэна
Функция cohen_kappa_score вычисляет каппа-Коэна статистику. Эта мера предназначена для сравнения меток, сделанных разными людьми-аннотаторами, а не классификатором с достоверной информацией.
Показатель каппа (см. Строку документации) представляет собой число от -1 до 1. Баллы выше 0,8 обычно считаются хорошим совпадением; ноль или ниже означает отсутствие согласия (практически случайные метки).
Оценка Каппа может быть вычислена для двоичных или многоклассовых задач, но не для задач с несколькими метками (за исключением ручного вычисления оценки для каждой метки) и не более чем для двух аннотаторов.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
3.3.2.6. Матрица неточностей ¶
Точность функции confusion_matrix вычисляет классификацию пути вычисления матрицы путаницы с каждой строкой , соответствующей истинный классом (Википедия и другие ссылки могут использовать различные конвенции для осей).
По определению запись i,j в матрице неточностей — количество наблюдений в группе i, но предполагается, что он будет в группе j. Вот пример:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
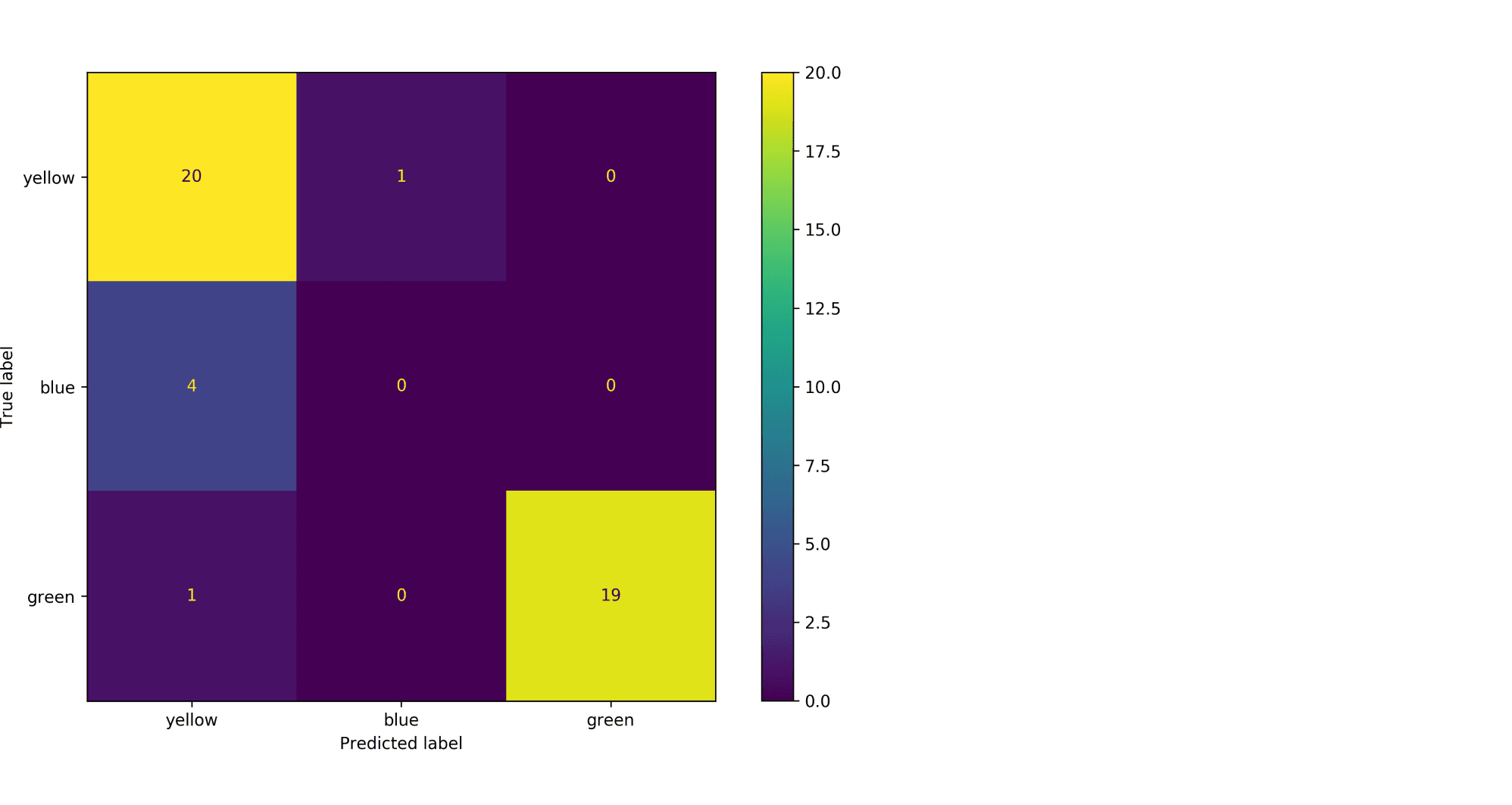
plot_confusion_matrix может использоваться для визуального представления матрицы неточностей, как показано в примере матрицы неточностей, который создает следующий рисунок:
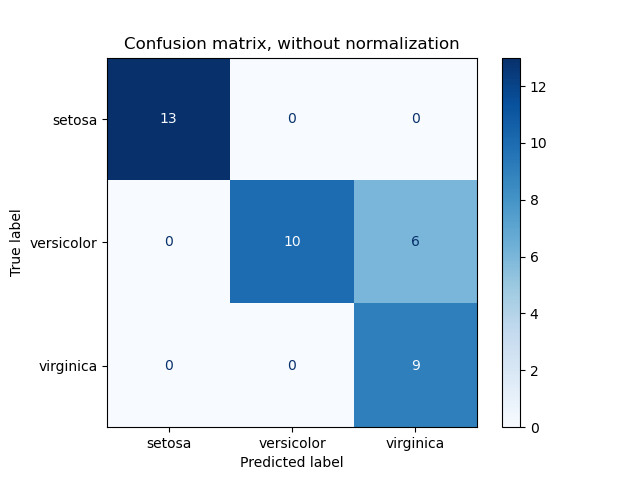
Параметр normalize позволяет сообщать коэффициенты вместо подсчетов. Матрица путаница может быть нормализована в 3 различными способами: 'pred', 'true'и 'all' которые будут делить счетчики на сумму каждого столбца, строки или всей матрицы, соответственно.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
Для двоичных задач мы можем получить подсчет истинно отрицательных, ложноположительных, ложноотрицательных и истинно положительных результатов следующим образом:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
Пример:
- См. В разделе Матрица неточностей пример использования матрицы неточностей для оценки качества выходных данных классификатора.
- См. В разделе Распознавание рукописных цифр пример использования матрицы неточностей для классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования матрицы неточностей для классификации текстовых документов.
3.3.2.7. Отчет о классификации
Функция classification_report создает текстовый отчет , показывающий основные показатели классификации. Вот небольшой пример с настраиваемыми target_names и предполагаемыми ярлыками:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Пример:
- См. В разделе Распознавание рукописных цифр пример использования отчета о классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций, где приведен пример использования отчета о классификации для текстовых документов.
- См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример использования отчета о классификации для поиска по сетке с вложенной перекрестной проверкой.
3.3.2.8. Потеря Хэмминга
hamming_loss вычисляет среднюю потерю Хэмминга или расстояние Хемминга между двумя наборами образцов.
Если $hat{y}_j$ прогнозируемое значение для $j$-я этикетка данного образца, $y_j$ — соответствующее истинное значение, а $n_{labels}$ — количество классов или меток, то потеря Хэмминга $L_{Hamming}$ между двумя образцами определяется как:
$$L_{Hamming}(y, hat{y}) = frac{1}{n_text{labels}} sum_{j=0}^{n_text{labels} — 1} 1(hat{y}_j not= y_j)$$
где $1(x)$- индикаторная функция .
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
В многопозиционном корпусе с бинарными индикаторами меток:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Примечание
В мультиклассовой классификации потери Хэмминга соответствуют расстоянию Хэмминга между y_true и, y_pred что аналогично функции потерь нуля или единицы . Однако, в то время как потеря нуля или единицы наказывает наборы предсказаний, которые не строго соответствуют истинным наборам, потеря Хэмминга наказывает отдельные метки. Таким образом, потеря Хэмминга, ограниченная сверху потерей нуля или единицы, всегда находится между нулем и единицей включительно; и прогнозирование надлежащего подмножества или надмножества истинных меток даст исключительную потерю Хэмминга от нуля до единицы.
3.3.2.9. Точность, отзыв и F-меры
Интуитивно, точность — это способность классификатора не маркировать как положительный образец, который является отрицательным, а отзыв — это способность классификатора находить все положительные образцы.
F-мера ($F_beta$ а также $F_1$ меры) можно интерпретировать как взвешенное гармоническое среднее значение точности и полноты. А $F_beta$ мера достигает своего лучшего значения на уровне 1 и худшего результата на уровне 0. С $beta = 1$, $F_beta$ а также $F_1$ эквивалентны, а отзыв и точность одинаково важны.
precision_recall_curve вычисляет кривую точности-отзыва на основе наземной метки истинности и оценки, полученной классификатором путем изменения порога принятия решения.
Функция average_precision_score вычисляет среднюю точность (AP) от оценки прогнозирования. Значение от 0 до 1 и выше — лучше. AP определяется как
$$text{AP} = sum_n (R_n — R_{n-1}) P_n$$
где $P_n$ а также $R_n$- точность и отзыв на n-м пороге. При случайных прогнозах AP — это доля положительных образцов.
Ссылки [Manning2008] и [Everingham2010] представляют альтернативные варианты AP, которые интерполируют кривую точности-отзыва. В настоящее время average_precision_score не реализован какой-либо вариант с интерполяцией. Ссылки [Davis2006] и [Flach2015] описывают, почему линейная интерполяция точек на кривой точности-отзыва обеспечивает чрезмерно оптимистичный показатель эффективности классификатора. Эта линейная интерполяция используется при вычислении площади под кривой с помощью правила трапеции в auc.
Несколько функций позволяют анализировать точность, отзыв и оценку F-мер:
average_precision_score(y_true, y_score, *) |
Вычислить среднюю точность (AP) из оценок прогнозов. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите рекол. |
Обратите внимание, что функция precision_recall_curve ограничена двоичным регистром. Функция average_precision_score работает только в двоичном формате классификации и MultiLabel индикатора. В функции plot_precision_recall_curve графики точности вспомнить следующим образом .
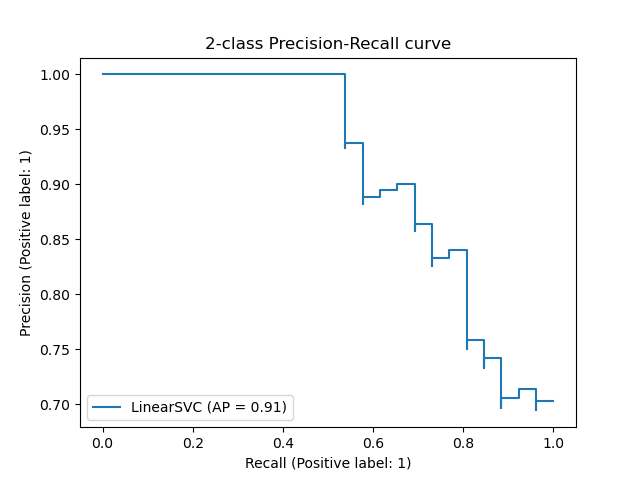
Примеры:
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования
f1_scoreдля классификации текстовых документов. - См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример
precision_scoreиrecall_scoreиспользование для оценки параметров с помощью поиска по сетке с вложенной перекрестной проверкой. - См. В разделе Precision-Recall пример использования
precision_recall_curveдля оценки качества вывода классификатора.
Рекомендации:
- [Manning2008] г. CD Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval , 2008.
- [Everingham2010] М. Эверингем, Л. Ван Гул, CKI Уильямс, Дж. Винн, А. Зиссерман, Задача классов визуальных объектов Pascal (VOC) , IJCV 2010.
- [Davis2006] Дж. Дэвис, М. Гоадрич, Взаимосвязь между точным воспроизведением и кривыми ROC , ICML 2006.
- [Flach2015] П.А. Флэч, М. Кулл, Кривые точности-отзыва-выигрыша: PR-анализ выполнен правильно , NIPS 2015.
3.3.2.9.1. Бинарная классификация
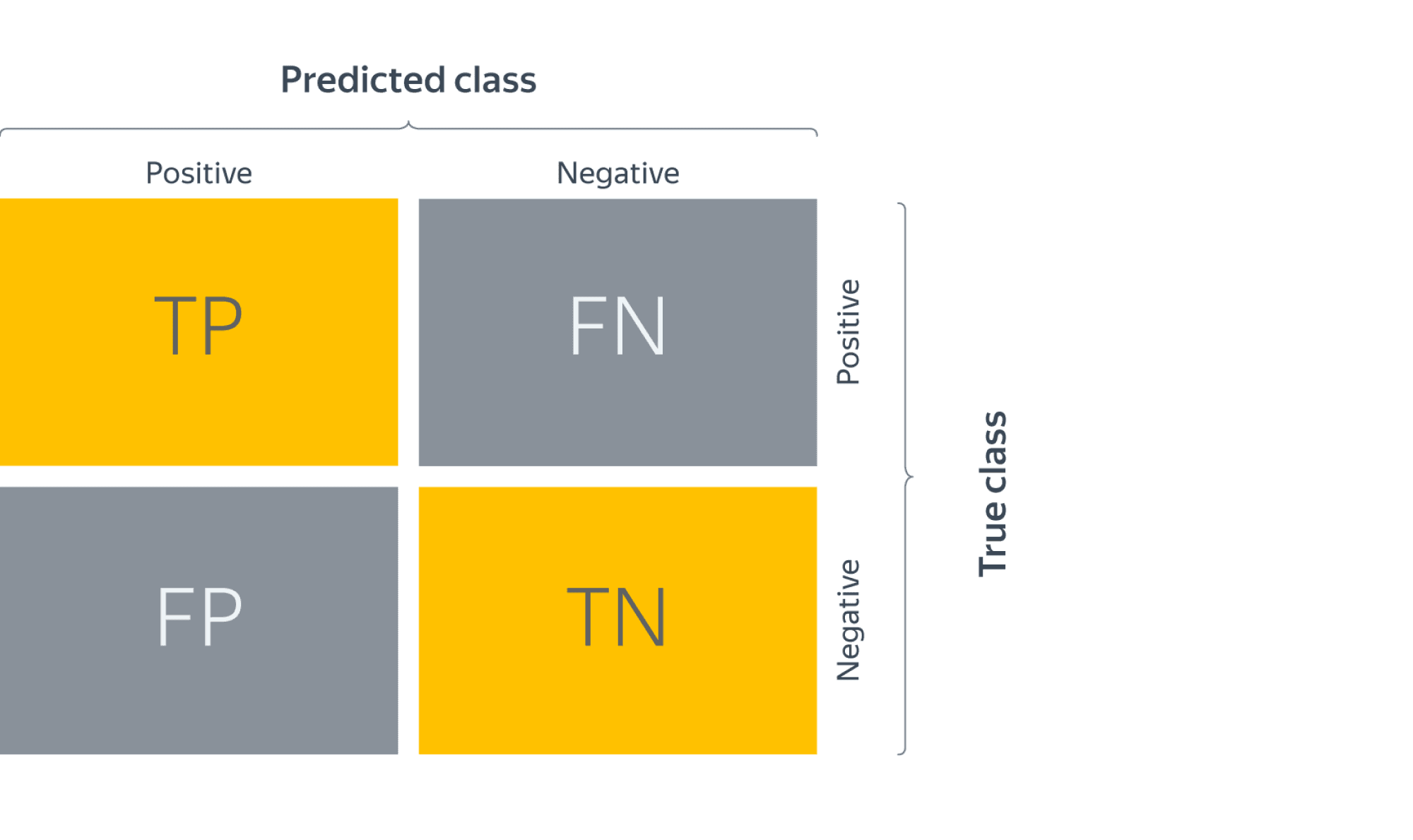
В задаче бинарной классификации термины «положительный» и «отрицательный» относятся к предсказанию классификатора, а термины «истинный» и «ложный» относятся к тому, соответствует ли этот прогноз внешнему суждению ( иногда известное как «наблюдение»). Учитывая эти определения, мы можем сформулировать следующую таблицу:
| Фактический класс (наблюдение) | ||
| Прогнозируемый класс (ожидание) | tp (истинно положительный результат) Правильный результат | fp (ложное срабатывание) Неожиданный результат |
| Прогнозируемый класс (ожидание) | fn (ложноотрицательный) Отсутствует результат | tn (истинно отрицательное) Правильное отсутствие результата |
В этом контексте мы можем определить понятия точности, отзыва и F-меры:
$$text{precision} = frac{tp}{tp + fp},$$
$$text{recall} = frac{tp}{tp + fn},$$
$$F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.$$
Вот несколько небольших примеров бинарной классификации:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 0.5, 0.5, 0. ]) >>> threshold array([0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
3.3.2.9.2. Мультиклассовая и многозначная классификация
В задаче классификации по нескольким классам и меткам понятия точности, отзыва и F-меры могут применяться к каждой метке независимо. Есть несколько способов , чтобы объединить результаты по этикеткам, указанных в average аргументе к average_precision_score (MultiLabel только) f1_score, fbeta_score, precision_recall_fscore_support, precision_score и recall_score функция, как описано выше . Обратите внимание, что если включены все метки, «микро» -усреднение в настройке мультикласса обеспечит точность, отзыв и $F$ все они идентичны по точности. Также обратите внимание, что «взвешенное» усреднение может дать оценку F, которая не находится между точностью и отзывом.
Чтобы сделать это более явным, рассмотрим следующие обозначения:
- $y$ набор предсказанных ($sample$, $label$) пары
- $hat{y}$ набор истинных ($sample$, $label$) пары
- $L$ набор лейблов
- $S$ набор образцов
- $y_s$ подмножество $y$ с образцом $s$, т.е $y_s := left{(s’, l) in y | s’ = sright}$.
- $y_l$ подмножество $y$ с этикеткой $l$
- по аналогии, $hat{y}_s$ а также $hat{y}_l$ являются подмножествами $hat{y}$
- $P(A, B) := frac{left| A cap B right|}{left|Aright|}$ для некоторых наборов $A$ и $B$
- $R(A, B) := frac{left| A cap B right|}{left|Bright|}$ (Условные обозначения различаются в зависимости от обращения $B = emptyset$; эта реализация использует $R(A, B):=0$, и аналогичные для $P$.)
- $$F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)}$$
Тогда показатели определяются как:
| average | Точность | Отзывать | F_beta |
| «micro» | $P(y, hat{y})$ | $R(y, hat{y})$ | $F_beta(y, hat{y})$ |
| «samples» | $frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s)$ |
| «macro» | $frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l)$ |
| «weighted» | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| P(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| R(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}lright| Fbeta(y_l, hat{y}_l)$ |
| None | $langle P(y_l, hat{y}_l) | l in L rangle$ | $langle R(y_l, hat{y}_l) | l in L rangle$ | $langle F_beta(y_l, hat{y}_l) | l in L rangle$ |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
Для мультиклассовой классификации с «отрицательным классом» можно исключить некоторые метки:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Точно так же метки, отсутствующие в выборке данных, могут учитываться при макро-усреднении.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
3.3.2.10. Оценка коэффициента сходства Жаккара
Функция jaccard_score вычисляет среднее значение коэффициентов сходства Jaccard , также называемый индексом Jaccard, между парами множеств меток.
Коэффициент подобия Жаккара i-ые образцы, с набором меток наземной достоверности yi и прогнозируемый набор меток y^i, определяется как
$$J(y_i, hat{y}_i) = frac{|y_i cap hat{y}_i|}{|y_i cup hat{y}_i|}.$$
jaccard_score работает как precision_recall_fscore_support наивно установленная мера, применяемая изначально к бинарным целям, и расширена для применения к множественным меткам и мультиклассам за счет использования average(см. выше ).
В двоичном случае:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
В многопозиционном корпусе с бинарными индикаторами меток:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Задачи с несколькими классами преобразуются в двоичную форму и обрабатываются как соответствующая задача с несколькими метками:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
3.3.2.11. Петля лосс
Функция hinge_loss вычисляет среднее расстояние между моделью и данными с использованием петля лосс, односторонний показателем , который учитывает только ошибки прогнозирования. (Потери на шарнирах используются в классификаторах максимальной маржи, таких как опорные векторные машины.)
Если метки закодированы с помощью +1 и -1, $y$: истинное значение, а $w$ — прогнозируемые решения на выходе decision_function, тогда потери на шарнирах определяются как:
$$L_text{Hinge}(y, w) = maxleft{1 — wy, 0right} = left|1 — wyright|_+$$
Если имеется более двух ярлыков, hinge_loss используется мультиклассовый вариант, разработанный Crammer & Singer. Вот статья, описывающая это.
Если $y_w$ прогнозируемое решение для истинного лейбла и $y_t$ — это максимум предсказанных решений для всех других меток, где предсказанные решения выводятся функцией принятия решений, тогда потеря шарнира в нескольких классах определяется следующим образом:
$$L_text{Hinge}(y_w, y_t) = maxleft{1 + y_t — y_w, 0right}$$
Вот небольшой пример, демонстрирующий использование hinge_loss функции с классификатором svm в задаче двоичного класса:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Вот пример, демонстрирующий использование hinge_loss функции с классификатором svm в мультиклассовой задаче:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels) 0.56...
3.3.2.12. Лог лосс
Лог лосс, также называемые потерями логистической регрессии или кросс-энтропийными потерями, определяются на основе оценок вероятности. Он обычно используется в (полиномиальной) логистической регрессии и нейронных сетях, а также в некоторых вариантах максимизации ожидания и может использоваться для оценки выходов вероятности ( predict_proba) классификатора вместо его дискретных прогнозов.
Для двоичной классификации с истинной меткой $y in {0,1}$ и оценка вероятности $p = operatorname{Pr}(y = 1)$, логарифмическая потеря на выборку представляет собой отрицательную логарифмическую вероятность классификатора с истинной меткой:
$$L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 — y) log (1 — p))$$
Это распространяется на случай мультикласса следующим образом. Пусть истинные метки для набора выборок будут закодированы размером 1 из K как двоичная индикаторная матрица $Y$, т.е. $y_{i,k}=1$ если образец $i$ есть ярлык $k$ взят из набора $K$ этикетки. Пусть $P$ — матрица оценок вероятностей, с $p_{i,k} = operatorname{Pr}(y_{i,k} = 1)$. Тогда потеря журнала всего набора равна
$$L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = — frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}$$
Чтобы увидеть, как это обобщает приведенную выше потерю двоичного журнала, обратите внимание, что в двоичном случае $p_{i,0} = 1 — p_{i,1}$ и $y_{i,0} = 1 — y_{i,1}$, поэтому разложив внутреннюю сумму на $y_{i,k} in {0,1}$ дает двоичную потерю журнала.
В log_loss функции вычисляет журнал потеря дана список меток приземной истины и матриц вероятностей, возвращенный оценщик predict_proba методом.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
Первое [.9, .1] в y_pred означает 90% вероятность того, что первая выборка будет иметь метку 0. Лог лос неотрицательны.
3.3.2.13. Коэффициент корреляции Мэтьюза
Функция matthews_corrcoef вычисляет коэффициент корреляции Матфея (MCC) для двоичных классов. Цитата из Википедии:
«Коэффициент корреляции Мэтьюза используется в машинном обучении как мера качества двоичных (двухклассных) классификаций. Он учитывает истинные и ложные положительные и отрицательные результаты и обычно рассматривается как сбалансированная мера, которую можно использовать, даже если классы очень разных размеров. MCC — это, по сути, значение коэффициента корреляции между -1 и +1. Коэффициент +1 представляет собой идеальное предсказание, 0 — среднее случайное предсказание и -1 — обратное предсказание. Статистика также известна как коэффициент фи ».
В бинарном (двухклассовом) случае $tp$, $tn$, $fp$ а также $fn$ являются соответственно количеством истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных результатов, MCC определяется как
$$MCC = frac{tp times tn — fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.$$
В случае мультикласса коэффициент корреляции Мэтьюза может быть определен в терминах confusion_matrix C для Kклассы. Чтобы упростить определение, рассмотрим следующие промежуточные переменные:
- $t_k=sum_{i}^{K} C_{ik}$ количество занятий k действительно произошло,
- $p_k=sum_{i}^{K} C_{ki}$ количество занятий k был предсказан,
- $c=sum_{k}^{K} C_{kk}$ общее количество правильно спрогнозированных образцов,
- $s=sum_{i}^{K} sum_{j}^{K} C_{ij}$ общее количество образцов.
Тогда мультиклассовый MCC определяется как:
$$MCC = frac{ c times s — sum_{k}^{K} p_k times t_k }{sqrt{ (s^2 — sum_{k}^{K} p_k^2) times (s^2 — sum_{k}^{K} t_k^2) }}$$
Когда имеется более двух меток, значение MCC больше не будет находиться в диапазоне от -1 до +1. Вместо этого минимальное значение будет где-то между -1 и 0 в зависимости от количества и распределения наземных истинных меток. Максимальное значение всегда +1.
Вот небольшой пример, иллюстрирующий использование matthews_corrcoef функции:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
3.3.2.14. Матрица путаницы с несколькими метками
Функция multilabel_confusion_matrix вычисляет класс-накрест ( по умолчанию) или samplewise (samplewise = True) MultiLabel матрицы спутанности для оценки точности классификации. Multilabel_confusion_matrix также обрабатывает данные мультикласса, как если бы они были многоклассовыми, поскольку это преобразование, обычно применяемое для оценки проблем мультикласса с метриками двоичной классификации (такими как точность, отзыв и т. д.).
При вычислении классовой матрицы путаницы с несколькими метками $C$, количество истинных негативов для класса i является $C_{i,0,0}$, ложноотрицательные $C_{i,1,0}$, истинные положительные стороны $C_{i,1,1}$ а ложные срабатывания $C_{i,0,1}$.
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с вводом многозначной индикаторной матрицы:
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
Или можно построить матрицу неточностей для каждой метки образца:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
[1, 1]],
[[1, 1],
[0, 1]]])
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с многоклассовым вводом:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
Вот несколько примеров, демонстрирующих использование multilabel_confusion_matrix функции для расчета отзыва (или чувствительности), специфичности, количества выпадений и пропусков для каждого класса в задаче с вводом многозначной индикаторной матрицы.
Расчет отзыва (также называемого истинно положительным коэффициентом или чувствительностью) для каждого класса:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Расчет специфичности (также называемой истинно отрицательной ставкой) для каждого класса:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Расчет количества выпадений (также называемый частотой ложных срабатываний) для каждого класса:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Расчет процента промахов (также называемого ложноотрицательным показателем) для каждого класса:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
3.3.2.15. Рабочая характеристика приемника (ROC)
Функция roc_curve вычисляет рабочую характеристическую кривую приемника или кривую ROC . Цитата из Википедии:
«Рабочая характеристика приемника (ROC), или просто кривая ROC, представляет собой графический график, который иллюстрирует работу системы двоичного классификатора при изменении ее порога дискриминации. Он создается путем построения графика доли истинных положительных результатов из положительных (TPR = частота истинных положительных результатов) по сравнению с долей ложных положительных результатов из отрицательных (FPR = частота ложных положительных результатов) при различных настройках пороговых значений. TPR также известен как чувствительность, а FPR — это единица минус специфичность или истинно отрицательный показатель ».
Для этой функции требуется истинное двоичное значение и целевые баллы, которые могут быть либо оценками вероятности положительного класса, либо значениями достоверности, либо двоичными решениями. Вот небольшой пример использования roc_curve функции:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
На этом рисунке показан пример такой кривой ROC:
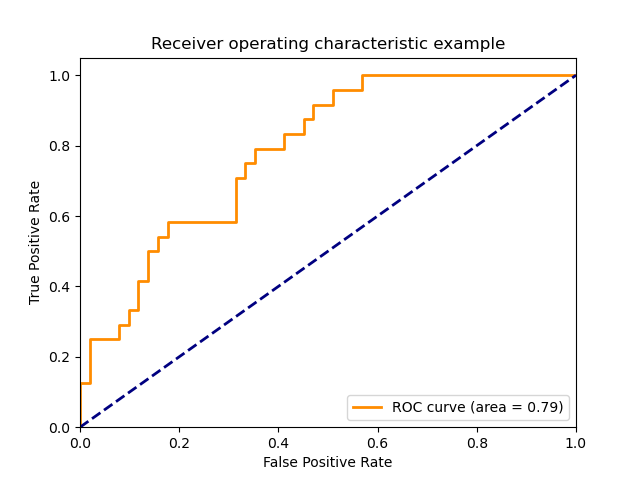
Функция roc_auc_score вычисляет площадь под операционной приемника характеристика (ROC) кривой, которая также обозначается через ППК или AUROC. При вычислении площади под кривой roc информация о кривой суммируется в одном номере. Для получения дополнительной информации см. Статью в Википедии о AUC.
По сравнению с такими показателями, как точность подмножества, потеря Хэмминга или оценка F1, ROC не требует оптимизации порога для каждой метки.
3.3.2.15.1. Двоичный регистр
В двоичном случае вы можете либо предоставить оценки вероятности, используя classifier.predict_proba() метод, либо значения решения без пороговых значений, заданные classifier.decision_function() методом. В случае предоставления оценок вероятности следует указать вероятность класса с «большей меткой». «Большая метка» соответствует classifier.classes_[1] и, следовательно classifier.predict_proba(X) [:, 1]. Следовательно, параметр y_score имеет размер (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
Мы можем использовать оценки вероятностей, соответствующие clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
В противном случае мы можем использовать значения решения без порога.
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
3.3.2.15.2. Мультиклассовый кейс
Функция roc_auc_score также может быть использована в нескольких классах классификации . В настоящее время поддерживаются две стратегии усреднения: алгоритм «один против одного» вычисляет среднее попарных оценок AUC ROC, а алгоритм «один против остальных» вычисляет среднее значение оценок ROC AUC для каждого класса по сравнению со всеми другими классами. В обоих случаях предсказанные метки предоставляются в виде массива со значениями от 0 до n_classes, а оценки соответствуют оценкам вероятности того, что выборка принадлежит определенному классу. Алгоритмы OvO и OvR поддерживают равномерное взвешивание ( average='macro') и по распространенности ( average='weighted').
Алгоритм «один против одного» : вычисляет средний AUC всех возможных попарных комбинаций классов. [HT2001] определяет метрику AUC мультикласса, взвешенную равномерно:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) + text{AUC}(k | j))$$
где $c$ количество классов и $text{AUC}(j | k)$ AUC с классом $j$ как положительный класс и класс $k$ как отрицательный класс. В общем, $text{AUC}(j | k) neq text{AUC}(k | j))$ в случае мультикласса. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'macro'.
[HT2001] мультиклассируют AUC метрика может быть расширена , чтобы быть взвешены по распространенности:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)( text{AUC}(j | k) + text{AUC}(k | j))$$
где cколичество классов. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'weighted'. В 'weighted' опции возвращает распространенность усредненные , как описано в [FC2009] .
Алгоритм «один против остальных» : вычисляет AUC каждого класса относительно остальных [PD2000] . Алгоритм функционально такой же, как и в случае с несколькими этикетками. Чтобы включить этот алгоритм, установите для аргумента ключевого слова multiclass значение 'ovr'. Как и OvO, OvR поддерживает два типа усреднения: 'macro' [F2006] и 'weighted' [F2001] .
В приложениях , где высокий процент ложных срабатываний не терпимый параметр max_fpr из roc_auc_score может быть использовано , чтобы суммировать кривую ROC до заданного предела.
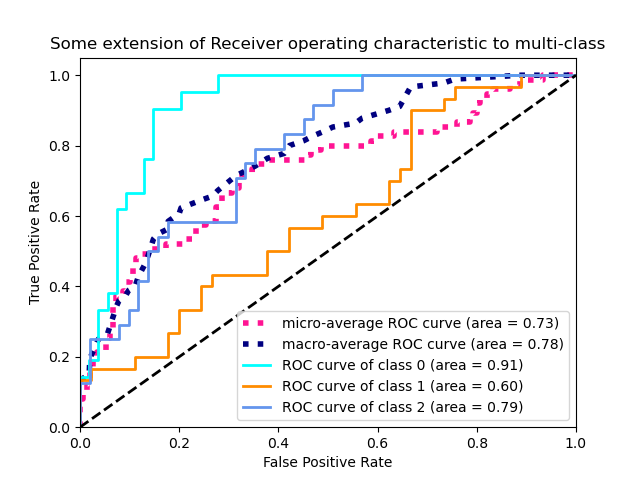
3.3.2.15.3. Кейс с несколькими метками
В классификации несколько меток, функция roc_auc_score распространяются путем усреднения меток , как выше . В этом случае вы должны указать y_score форму . Таким образом, при использовании оценок вероятности необходимо выбрать вероятность класса с большей меткой для каждого выхода.(n_samples, n_classes)
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
И значения решений не требуют такой обработки.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
Примеры:
- См. В разделе « Рабочие характеристики приемника» (ROC) пример использования ROC для оценки качества выходных данных классификатора.
- См. В разделе « Рабочие характеристики приемника» (ROC) с перекрестной проверкой пример использования ROC для оценки качества выходных данных классификатора с помощью перекрестной проверки.
- См. В разделе Моделирование распределения видов пример использования ROC для моделирования распределения видов.
- HT2001 ( 1 , 2 ) Рука, DJ и Тилль, RJ, (2001). Простое обобщение области под кривой ROC для задач классификации нескольких классов. Машинное обучение, 45 (2), стр. 171-186.
- FC2009 Ферри, Сезар и Эрнандес-Оралло, Хосе и Модройу, Р. (2009). Экспериментальное сравнение показателей эффективности для классификации. Письма о распознавании образов. 30. 27-38.
- PD2000 Провост Ф., Домингос П. (2000). Хорошо обученные ПЭТ: Улучшение деревьев оценки вероятностей (Раздел 6.2), Рабочий документ CeDER № IS-00-04, Школа бизнеса Стерна, Нью-Йоркский университет.
- F2006 Фосетт, Т., 2006. Введение в анализ ROC. Письма о распознавании образов, 27 (8), стр. 861-874.
- F2001Фосетт, Т., 2001. Использование наборов правил для максимизации производительности ROC в интеллектуальном анализе данных, 2001. Труды Международной конференции IEEE, стр. 131-138.
3.3.2.16. Компромисс при обнаружении ошибок (DET)
Функция det_curve вычисляет кривую компенсации ошибок обнаружения (DET) [WikipediaDET2017] . Цитата из Википедии:
«График компромисса ошибок обнаружения (DET) — это графическая диаграмма частоты ошибок для систем двоичной классификации, отображающая частоту ложных отклонений по сравнению с частотой ложных приемов. Оси x и y масштабируются нелинейно по их стандартным нормальным отклонениям (или просто с помощью логарифмического преобразования), в результате получаются более линейные кривые компромисса, чем кривые ROC, и большая часть области изображения используется для выделения важных различий в критический рабочий регион ».
Кривые DET представляют собой вариацию кривых рабочих характеристик приемника (ROC), где ложная отрицательная скорость нанесена на ось y вместо истинной положительной скорости. Кривые DET обычно строятся в масштабе нормального отклонения путем преобразования $phi^{-1}$ (с участием $phi$ — кумулятивная функция распределения). Полученные кривые производительности явно визуализируют компромисс типов ошибок для заданных алгоритмов классификации. См. [Martin1997], где приведены примеры и мотивация.
На этом рисунке сравниваются кривые ROC и DET двух примеров классификаторов для одной и той же задачи классификации:
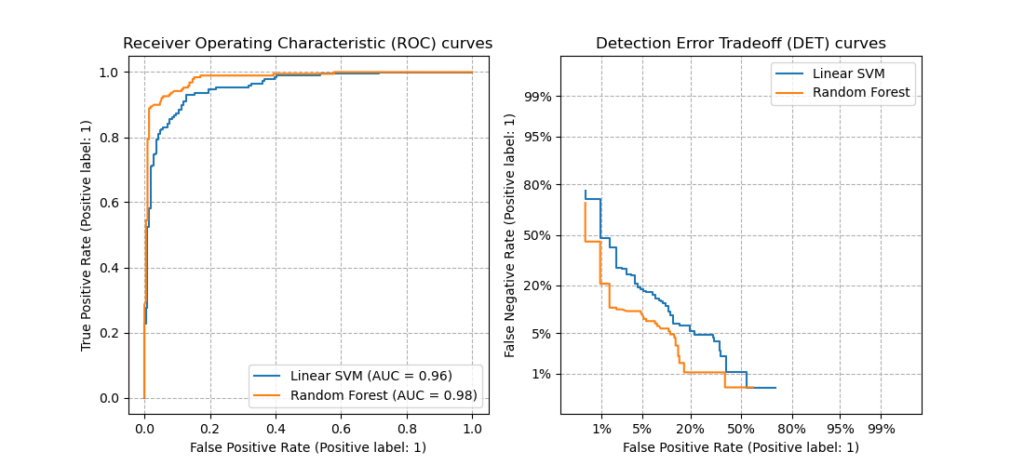
Характеристики:
- Кривые DET образуют линейную кривую по шкале нормального отклонения, если оценки обнаружения нормально (или близки к нормальному) распределены. В [Navratil2007] было показано, что обратное не обязательно верно, и даже более общие распределения могут давать линейные кривые DET.
- При обычном преобразовании масштаба с отклонением точки распределяются таким образом, что занимает сравнительно большее пространство графика. Следовательно, кривые с аналогичными характеристиками классификации легче различить на графике DET.
- С ложноотрицательной скоростью, «обратной» истинной положительной скорости, точкой совершенства для кривых DET является начало координат (в отличие от верхнего левого угла для кривых ROC).
Приложения и ограничения:
Кривые DET интуитивно понятны для чтения и, следовательно, позволяют быстро визуально оценить работу классификатора. Кроме того, кривые DET можно использовать для анализа пороговых значений и выбора рабочей точки. Это особенно полезно, если требуется сравнение типов ошибок.
С другой стороны, кривые DET не представляют свою метрику в виде единого числа. Поэтому для автоматической оценки или сравнения с другими задачами классификации лучше подходят такие показатели, как производная площадь под кривой ROC.
Примеры:
- См. Кривую компенсации ошибок обнаружения (DET) для примера сравнения кривых рабочих характеристик приемника (ROC) и кривых компенсации ошибок обнаружения (DET).
Рекомендации:
- ВикипедияDET2017 Авторы Википедии. Компромисс ошибки обнаружения. Википедия, свободная энциклопедия. 4 сентября 2017 г., 23:33 UTC. Доступно по адресу: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054 . По состоянию на 19 февраля 2018 г.
- Мартин 1997 А. Мартин, Дж. Доддингтон, Т. Камм, М. Ордовски и М. Пшибоцки, Кривая DET в оценке эффективности задач обнаружения , NIST 1997.
- Навратил2007 Дж. Наврактил и Д. Клусачек, « О линейных DET », 2007 г. Международная конференция IEEE по акустике, обработке речи и сигналов — ICASSP ’07, Гонолулу, Гавайи, 2007 г., стр. IV-229-IV-232.
3.3.2.17. Нулевой проигрыш
Функция zero_one_loss вычисляет сумму или среднее значение потери 0-1 классификации ($L_{0−1}$) над $n_{samples}$. По умолчанию функция нормализуется по выборке. Чтобы получить сумму $L_{0−1}$, установите normalize значение False.
В классификации по zero_one_loss нескольким меткам подмножество оценивается как единое целое, если его метки строго соответствуют прогнозам, и как ноль, если есть какие-либо ошибки. По умолчанию функция возвращает процент неправильно спрогнозированных подмножеств. Чтобы вместо этого получить количество таких подмножеств, установите normalize значение False
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда потеря 0-1 $L_{0−1}$ определяется как:
$$L_{0-1}(y_i, hat{y}_i) = 1(hat{y}_i not= y_i)$$
где $1(x)$- индикаторная функция.
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
В случае с несколькими метками с двоичными индикаторами меток, где первый набор меток [0,1] содержит ошибку:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
Пример:
- См. В разделе « Рекурсивное исключение функции с перекрестной проверкой» пример использования нулевой потери для выполнения рекурсивного исключения функции с перекрестной проверкой.
3.3.2.18. Потеря очков по Брайеру
Функция brier_score_loss вычисляет оценку Шиповник для бинарных классов [Brier1950] . Цитата из Википедии:
«Оценка Бриера — это правильная функция оценки, которая измеряет точность вероятностных прогнозов. Это применимо к задачам, в которых прогнозы должны назначать вероятности набору взаимоисключающих дискретных результатов ».
Эта функция возвращает среднеквадратичную ошибку фактического результата. y∈{0,1} и прогнозируемая оценка вероятности $p=Pr(y=1)$ ( pred_proba ) как выведено :
$$BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1}(y_i — p_i)^2$$
Потеря по шкале Бриера также составляет от 0 до 1, и чем ниже значение (средняя квадратичная разница меньше), тем точнее прогноз.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
Балл Бриера можно использовать для оценки того, насколько хорошо откалиброван классификатор. Однако меньшая потеря по шкале Бриера не всегда означает лучшую калибровку. Это связано с тем, что по аналогии с разложением среднеквадратичной ошибки на дисперсию смещения потеря оценки по Бриеру может быть разложена как сумма потерь калибровки и потерь при уточнении [Bella2012]. Потеря калибровки определяется как среднеквадратическое отклонение от эмпирических вероятностей, полученных из наклона ROC-сегментов. Потери при переработке можно определить как ожидаемые оптимальные потери, измеренные по площади под кривой оптимальных затрат. Потери при уточнении могут изменяться независимо от потерь при калибровке, таким образом, более низкие потери по шкале Бриера не обязательно означают более качественную калибровку модели. «Только когда потеря точности остается неизменной, более низкая потеря по шкале Бриера всегда означает лучшую калибровку» [Bella2012] , [Flach2008] .
Пример:
- См. Раздел « Калибровка вероятности классификаторов», где приведен пример использования потерь по шкале Бриера для выполнения калибровки вероятности классификаторов.
Рекомендации:
- Brier1950 Дж. Брайер, Проверка прогнозов, выраженных в терминах вероятности , Ежемесячный обзор погоды 78.1 (1950)
- Bella2012 ( 1 , 2 ) Белла, Ферри, Эрнандес-Оралло и Рамирес-Кинтана «Калибровка моделей машинного обучения» в Хосров-Пур, М. «Машинное обучение: концепции, методологии, инструменты и приложения». Херши, Пенсильвания: Справочник по информационным наукам (2012).
- Flach2008 Флак, Питер и Эдсон Мацубара. «О классификации, ранжировании и оценке вероятности». Дагштульский семинар. Schloss Dagstuhl-Leibniz-Zentrum от Informatik (2008).
3.3.3. Метрики ранжирования с несколькими ярлыками
В многоэлементном обучении с каждой выборкой может быть связано любое количество меток истинности. Цель состоит в том, чтобы дать высокие оценки и более высокий рейтинг наземным лейблам.
3.3.3.1. Ошибка покрытия
Функция coverage_error вычисляет среднее число меток , которые должны быть включены в окончательном предсказании таким образом, что все истинные метки предсказанные. Это полезно, если вы хотите знать, сколько меток с наивысшими баллами вам нужно предсказать в среднем, не пропуская ни одной истинной. Таким образом, наилучшее значение этого показателя — среднее количество истинных ярлыков.
Примечание
Оценка нашей реализации на 1 больше, чем оценка, приведенная в Tsoumakas et al., 2010. Это расширяет ее для обработки вырожденного случая, когда экземпляр имеет 0 истинных меток.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ покрытие определяется как
$$coverage(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} max_{j:y_{ij} = 1} text{rank}_{ij}$$
с участием $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$. Учитывая определение ранга, связи y_scores разрываются путем присвоения максимального ранга, который был бы присвоен всем связанным значениям.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
3.3.3.2. Средняя точность ранжирования метки
В label_ranking_average_precision_score функции реализует маркировать ранжирование средней точности (LRAP). Этот показатель связан с average_precision_score функцией, но основан на понятии ранжирования меток, а не на точности и отзыве.
Средняя точность ранжирования меток (LRAP) усредняет по выборкам ответ на следующий вопрос: для каждой основной метки истинности какая доля меток с более высоким рейтингом была истинной? Этот показатель эффективности будет выше, если вы сможете лучше ранжировать метки, связанные с каждым образцом. Полученная оценка всегда строго больше 0, а наилучшее значение равно 1. Если имеется ровно одна релевантная метка для каждой выборки, средняя точность ранжирования меток эквивалентна среднему обратному рангу .
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$, средняя точность определяется как
$$LRAP(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0} sum{j:y_{ij} = 1} frac{|mathcal{L}{ij}|}{text{rank}{ij}}$$
где $mathcal{L}{ij} = left{k: y{ik} = 1, hat{f}{ik} geq hat{f}{ij} right}$, $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$, |cdot| вычисляет мощность набора (т. е. количество элементов в наборе), и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
3.3.3.3. Потеря рейтинга
Функция label_ranking_loss вычисляет ранжирование потери , которые в среднем более образцы числа пар меток, которые неправильно упорядочены, т.е. истинные метки имеют более низкую оценку , чем ложные метки, взвешенную по обратной величине числа упорядоченных пар ложных и истинных меток. Наименьшая возможная потеря рейтинга равна нулю.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ потеря ранжирования определяется как
$$ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0(ntext{labels} — ||y_i||0)} left|left{(k, l): hat{f}{ik} leq hat{f}{il}, y{ik} = 1, y_{il} = 0 right}right|$$
где $|cdot|$ вычисляет мощность набора (т. е. количество элементов в наборе) и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
Рекомендации:
- Цумакас, Г., Катакис, И., и Влахавас, И. (2010). Майнинг данных с несколькими метками. В справочнике по интеллектуальному анализу данных и открытию знаний (стр. 667-685). Springer США.
3.3.3.4. Нормализованная дисконтированная совокупная прибыль
Дисконтированный совокупный выигрыш (DCG) и Нормализованный дисконтированный совокупный выигрыш (NDCG) — это показатели ранжирования, реализованные в dcg_score и ndcg_score; они сравнивают предсказанный порядок с оценками достоверности, такими как релевантность ответов на запрос.
Со страницы Википедии о дисконтированной совокупной прибыли:
«Дисконтированная совокупная прибыль (DCG) — это показатель качества ранжирования. При поиске информации он часто используется для измерения эффективности алгоритмов поисковой системы или связанных приложений. Используя шкалу градуированной релевантности документов в наборе результатов поисковой системы, DCG измеряет полезность или выгоду документа на основе его позиции в списке результатов. Прирост накапливается сверху вниз в списке результатов, причем прирост каждого результата дисконтируется на более низких уровнях »
DCG упорядочивает истинные цели (например, релевантность ответов на запросы) в предсказанном порядке, затем умножает их на логарифмическое убывание и суммирует результат. Сумма может быть усечена после первогоKрезультатов, и в этом случае мы называем это DCG @ K. NDCG или NDCG @ $K$ — это DCG, деленная на DCG, полученную с помощью точного прогноза, так что оно всегда находится между 0 и 1. Обычно NDCG предпочтительнее DCG.
По сравнению с потерей ранжирования, NDCG может принимать во внимание оценки релевантности, а не ранжирование на основе фактов. Таким образом, если основополагающая информация состоит только из упорядочивания, предпочтение следует отдавать потере ранжирования; если основополагающая информация состоит из фактических оценок полезности (например, 0 для нерелевантного, 1 для релевантного, 2 для очень актуального), можно использовать NDCG.
Для одного образца, учитывая вектор непрерывных значений истинности для каждой цели $y in R^M$, где $M$ это количество выходов, а прогноз $hat{y}$, что индуцирует функцию ранжирования $f$, оценка DCG составляет
$$sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}$$
а оценка NDCG — это оценка DCG, деленная на оценку DCG, полученную для $y$.
Рекомендации:
- Запись в Википедии о дисконтированной совокупной прибыли
- Джарвелин, К., и Кекалайнен, Дж. (2002). Оценка IR методов на основе накопленного коэффициента усиления. Транзакции ACM в информационных системах (TOIS), 20 (4), 422-446.
- Ван, Ю., Ван, Л., Ли, Ю., Хе, Д., Чен, В., и Лю, Т. Ю. (2013, май). Теоретический анализ показателей рейтинга NDCG. В материалах 26-й ежегодной конференции по теории обучения (COLT 2013)
- МакШерри Ф. и Наджорк М. (2008, март). Эффективность вычислений при поиске информации измеряется эффективно при наличии связанных оценок. В Европейской конференции по поиску информации (стр. 414-421). Шпрингер, Берлин, Гейдельберг.
3.3.4. Метрики регрессии
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности регрессии. Некоторые из них были расширены , чтобы обработать случай multioutput: mean_squared_error, mean_absolute_error, explained_variance_score и r2_score.
У этих функций есть multioutput аргумент ключевого слова, который определяет способ усреднения результатов или проигрышей для каждой отдельной цели. По умолчанию используется значение 'uniform_average', которое определяет равномерно взвешенное среднее значение по выходным данным. Если передается ndarrayформа shape (n_outputs,), то ее записи интерпретируются как веса, и возвращается соответствующее средневзвешенное значение. Если multioutputесть 'raw_values'указан, то все неизменные индивидуальные баллы или потери будут возвращены в массиве формы (n_outputs,).
r2_score и explained_variance_score принять дополнительное значение 'variance_weighted' для multioutput параметра. Эта опция приводит к взвешиванию каждой индивидуальной оценки по дисперсии соответствующей целевой переменной. Этот параметр определяет количественно зафиксированную немасштабированную дисперсию на глобальном уровне. Если целевые переменные имеют разную шкалу, то этот балл придает большее значение хорошему объяснению переменных с более высокой дисперсией. multioutput='variance_weighted' — значение по умолчанию r2_score для обратной совместимости. В будущем это будет изменено на uniform_average.
3.3.4.1. Оценка объясненной дисперсии
explained_variance_score вычисляет объясненной дисперсии регрессии балл.
Если $hat{y}$ — расчетный целевой объем производства, y соответствующий (правильный) целевой результат, и $Var$- Дисперсия , квадрат стандартного отклонения, то объясненная дисперсия оценивается следующим образом:
$$explained_{}variance(y, hat{y}) = 1 — frac{Var{ y — hat{y}}}{Var{y}}$$
Наилучшая возможная оценка — 1.0, более низкие значения — хуже.
Вот небольшой пример использования explained_variance_score функции:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990...
3.3.4.2. Максимальная ошибка
Функция max_error вычисляет максимальную остаточную ошибку , показатель , который фиксирует худшую ошибку случае между предсказанным значением и истинным значением. В идеально подобранной модели регрессии с одним выходом он max_error будет находиться 0 в обучающем наборе, и хотя это маловероятно в реальном мире, этот показатель показывает степень ошибки, которую имела модель при подборе.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда максимальная ошибка определяется как
$$text{Max Error}(y, hat{y}) = max(| y_i — hat{y}_i |)$$
Вот небольшой пример использования функции max_error:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
max_error не поддерживает multioutput.
3.3.4.3. Средняя абсолютная ошибка
Функция mean_absolute_error вычисляет среднюю абсолютную погрешность , риск метрики , соответствующей ожидаемого значение абсолютной потери или ошибок $l1$-нормальная потеря.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MAE), оцененная за $n_{samples}$ определяется как
$$text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i — hat{y}_i right|.$$
Вот небольшой пример использования функции mean_absolute_error:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
3.3.4.4. Среднеквадратичная ошибка
Функция mean_squared_error вычисляет среднюю квадратическую ошибку , риск метрики , соответствующую ожидаемое значение квадрата (квадратичной) ошибки или потерю.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная ошибка (MSE), оцененная на $n_{samples}$ определяется как
$$text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (y_i — hat{y}_i)^2.$$
Вот небольшой пример использования функции mean_squared_error:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
Примеры:
- См. В разделе Регрессия повышения градиента пример использования среднеквадратичной ошибки для оценки регрессии повышения градиента.
3.3.4.5. Среднеквадратичная логарифмическая ошибка
Функция mean_squared_log_error вычисляет риск метрики , соответствующий ожидаемому значению квадрата логарифмической (квадратичной) ошибки или потери.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная логарифмическая ошибка (MSLE), оцененная на $n_{samples}$ определяется как
$$text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (log_e (1 + y_i) — log_e (1 + hat{y}_i) )^2.$$
Где $log_e (x)$ означает натуральный логарифм $x$. Эту метрику лучше всего использовать, когда цели имеют экспоненциальный рост, например, численность населения, средние продажи товара в течение нескольких лет и т. Д. Обратите внимание, что эта метрика штрафует за заниженную оценку больше, чем за завышенную оценку.
Вот небольшой пример использования функции mean_squared_log_error:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
3.3.4.6. Средняя абсолютная ошибка в процентах
mean_absolute_percentage_error (MAPE), также известный как среднее абсолютное отклонение в процентах (МАПД), является метрикой для оценки проблем регрессии. Идея этой метрики — быть чувствительной к относительным ошибкам. Например, он не изменяется глобальным масштабированием целевой переменной.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная процентная ошибка (MAPE), оцененная за $n_{samples}$ определяется как
$$text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i — hat{y}_i right|}{max(epsilon, left| y_i right|)}$$
где $epsilon$ — произвольное маленькое, но строго положительное число, чтобы избежать неопределенных результатов, когда y равно нулю.
В функции mean_absolute_percentage_error опоры multioutput.
Вот небольшой пример использования функции mean_absolute_percentage_error:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
В приведенном выше примере, если бы мы использовали mean_absolute_error, он бы проигнорировал небольшие значения магнитуды и только отразил бы ошибку в предсказании максимального значения магнитуды. Но эта проблема решена в случае MAPE, потому что он вычисляет относительную процентную ошибку по отношению к фактическому выходу.
3.3.4.7. Средняя абсолютная ошибка
Это median_absolute_error особенно интересно, потому что оно устойчиво к выбросам. Убыток рассчитывается путем взятия медианы всех абсолютных различий между целью и прогнозом.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MedAE), оцененная на $n_{samples}$ определяется как
$$text{MedAE}(y, hat{y}) = text{median}(mid y_1 — hat{y}_1 mid, ldots, mid y_n — hat{y}_n mid).$$
median_absolute_error Не поддерживает multioutput.
Вот небольшой пример использования функции median_absolute_error:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
3.3.4.8. R² балл, коэффициент детерминации
Функция r2_score вычисляет коэффициент детерминации , как правило , обозначенный как R².
Он представляет собой долю дисперсии (y), которая была объяснена независимыми переменными в модели. Он обеспечивает показатель степени соответствия и, следовательно, меру того, насколько хорошо невидимые выборки могут быть предсказаны моделью через долю объясненной дисперсии.
Поскольку такая дисперсия зависит от набора данных, R² не может быть значимо сопоставимым для разных наборов данных. Наилучшая возможная оценка — 1,0, и она может быть отрицательной (потому что модель может быть произвольно хуже). Постоянная модель, которая всегда предсказывает ожидаемое значение y, игнорируя входные характеристики, получит оценку R² 0,0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ соответствующее истинное значение для общего n образцов, расчетный R² определяется как:
$$R^2(y, hat{y}) = 1 — frac{sum_{i=1}^{n} (y_i — hat{y}i)^2}{sum{i=1}^{n} (y_i — bar{y})^2}$$
где $bar{y} = frac{1}{n} sum_{i=1}^{n} y_i$ и $sum_{i=1}^{n} (y_i — hat{y}i)^2 = sum{i=1}^{n} epsilon_i^2$.
Обратите внимание, что r2_score вычисляется нескорректированное R² без поправки на смещение выборочной дисперсии y.
Вот небольшой пример использования функции r2_score:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925...
Пример:
- См. В разделе « Лассо и эластичная сеть для разреженных сигналов» приведен пример использования показателя R² для оценки лассо и эластичной сети для разреженных сигналов.
3.3.4.9. Средние отклонения Пуассона, Гаммы и Твиди
Функция mean_tweedie_deviance вычисляет среднюю ошибку Deviance Tweedie с powerпараметром ($p$). Это показатель, который выявляет прогнозируемые ожидаемые значения целей регрессии.
Существуют следующие особые случаи:
- когда
power=0это эквивалентноmean_squared_error. - когда
power=1это эквивалентноmean_poisson_deviance. - когда
power=2это эквивалентноmean_gamma_deviance.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя ошибка отклонения Твиди (D) для мощности $p$, оценивается более $n_{samples}$ определяется как
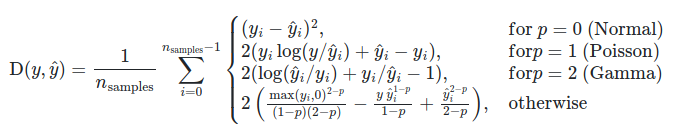
Отклонение от твиди — однородная функция степени 2-power. Таким образом, гамма-распределение power=2 означает, что одновременно масштабируется y_true и y_pred не влияет на отклонение. Для распределения Пуассона power=1 отклонение масштабируется линейно, а для нормального распределения ( power=0) — квадратично. В общем, чем выше, powerтем меньше веса придается крайним отклонениям между истинными и прогнозируемыми целевыми значениями.
Например, давайте сравним два прогноза 1.0 и 100, которые оба составляют 50% от их соответствующего истинного значения.
Среднеквадратичная ошибка ( power=0) очень чувствительна к разнице прогнозов второй точки:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
Если увеличить powerдо 1:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
разница в ошибках уменьшается. Наконец, установив power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
мы получим идентичные ошибки. Таким образом, отклонение when power=2чувствительно только к относительным ошибкам.
3.3.5. Метрики кластеризации
В модуле sklearn.metrics реализованы несколько функций потерь, оценки и полезности. Для получения дополнительной информации см. Раздел « Оценка производительности кластеризации » для кластеризации экземпляров и « Оценка бикластеризации» для бикластеризации.
3.3.6. Фиктивные оценки
При обучении с учителем простая проверка работоспособности состоит из сравнения своей оценки с простыми практическими правилами. DummyClassifier реализует несколько таких простых стратегий классификации:
stratifiedгенерирует случайные прогнозы, соблюдая распределение классов обучающего набора.most_frequentвсегда предсказывает наиболее частую метку в обучающем наборе.priorвсегда предсказывает класс, который максимизирует предыдущий класс (какmost_frequent) иpredict_probaвозвращает предыдущий класс.uniformгенерирует предсказания равномерно в случайном порядке.constantвсегда предсказывает постоянную метку, предоставленную пользователем. Основная мотивация этого метода — оценка F1, когда положительный класс находится в меньшинстве.
Обратите внимание, что со всеми этими стратегиями predict метод полностью игнорирует входные данные!
Для иллюстрации DummyClassifier сначала создадим несбалансированный набор данных:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Далее сравним точность SVC и most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
Мы видим, что SVC это не намного лучше, чем фиктивный классификатор. Теперь давайте изменим ядро:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
Мы видим, что точность увеличена почти до 100%. Для лучшей оценки точности рекомендуется стратегия перекрестной проверки, если она не требует слишком больших затрат на ЦП. Для получения дополнительной информации см. Раздел « Перекрестная проверка: оценка производительности оценщика ». Более того, если вы хотите оптимизировать пространство параметров, настоятельно рекомендуется использовать соответствующую методологию; подробности см. в разделе « Настройка гиперпараметров оценщика ».
В более общем плане, когда точность классификатора слишком близка к случайной, это, вероятно, означает, что что-то пошло не так: функции бесполезны, гиперпараметр настроен неправильно, классификатор страдает от дисбаланса классов и т. Д.
DummyRegressor также реализует четыре простых правила регрессии:
meanвсегда предсказывает среднее значение тренировочных целей.medianвсегда предсказывает медианное значение тренировочных целей.quantileвсегда предсказывает предоставленный пользователем квантиль учебных целей.constantвсегда предсказывает постоянное значение, предоставляемое пользователем.
Во всех этих стратегиях predict метод полностью игнорирует входные данные.
From Wikipedia, the free encyclopedia
The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio defined by the formula:
where At is the actual value and Ft is the forecast value. Their difference is divided by the actual value At. The absolute value of this ratio is summed for every forecasted point in time and divided by the number of fitted points n.
MAPE in regression problems[edit]
Mean absolute percentage error is commonly used as a loss function for regression problems and in model evaluation, because of its very intuitive interpretation in terms of relative error.
Definition[edit]
Consider a standard regression setting in which the data are fully described by a random pair 






In the classical regression setting, the closeness of 


where 
In practice
In practice 
From a practical point of view, the use of the MAPE as a quality function for regression model is equivalent to doing weighted mean absolute error (MAE) regression, also known as quantile regression. This property is trivial since
As a consequence, the use of the MAPE is very easy in practice, for example using existing libraries for quantile regression allowing weights.
Consistency[edit]
The use of the MAPE as a loss function for regression analysis is feasible both on a practical point of view and on a theoretical one, since the existence of an optimal model and the consistency of the empirical risk minimization can be proved.[1]
WMAPE[edit]
WMAPE (sometimes spelled wMAPE) stands for weighted mean absolute percentage error.[2] It is a measure used to evaluate the performance of regression or forecasting models. It is a variant of MAPE in which the mean absolute percent errors is treated as a weighted arithmetic mean. Most commonly the absolute percent errors are weighted by the actuals (e.g. in case of sales forecasting, errors are weighted by sales volume).[3]. Effectively, this overcomes the ‘infinite error’ issue.[4]
Its formula is:[4]
Where 


However, this effectively simplifies to a much simpler formula:
Confusingly, sometimes when people refer to wMAPE they are talking about a different model in which the numerator and denominator of the wMAPE formula above are weighted again by another set of custom weights 
Issues[edit]
Although the concept of MAPE sounds very simple and convincing, it has major drawbacks in practical application,[5] and there are many studies on shortcomings and misleading results from MAPE.[6][7]
To overcome these issues with MAPE, there are some other measures proposed in literature:
- Mean Absolute Scaled Error (MASE)
- Symmetric Mean Absolute Percentage Error (sMAPE)
- Mean Directional Accuracy (MDA)
- Mean Arctangent Absolute Percentage Error (MAAPE): MAAPE can be considered a slope as an angle, while MAPE is a slope as a ratio.[7]
See also[edit]
- Least absolute deviations
- Mean absolute error
- Mean percentage error
- Symmetric mean absolute percentage error
External links[edit]
- Mean Absolute Percentage Error for Regression Models
- Mean Absolute Percentage Error (MAPE)
- Errors on percentage errors — variants of MAPE
- Mean Arctangent Absolute Percentage Error (MAAPE)
References[edit]
- ^ a b de Myttenaere, B Golden, B Le Grand, F Rossi (2015). «Mean absolute percentage error for regression models», Neurocomputing 2016 arXiv:1605.02541
- ^ Forecast Accuracy: MAPE, WAPE, WMAPE https://www.baeldung.com/cs/mape-vs-wape-vs-wmape%7Ctitle=Understanding Forecast Accuracy: MAPE, WAPE, WMAPE. ;
- ^ Weighted Mean Absolute Percentage Error https://ibf.org/knowledge/glossary/weighted-mean-absolute-percentage-error-wmape-299%7Ctitle=WMAPE: Weighted Mean Absolute Percentage Error. ;
- ^ a b «Statistical Forecast Errors».
- ^ a b Tofallis (2015). «A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation», Journal of the Operational Research Society, 66(8):1352-1362. archived preprint
- ^ Hyndman, Rob J., and Anne B. Koehler (2006). «Another look at measures of forecast accuracy.» International Journal of Forecasting, 22(4):679-688 doi:10.1016/j.ijforecast.2006.03.001.
- ^ a b Kim, Sungil and Heeyoung Kim (2016). «A new metric of absolute percentage error for intermittent demand forecasts.» International Journal of Forecasting, 32(3):669-679 doi:10.1016/j.ijforecast.2015.12.003.
- ^ Kim, Sungil; Kim, Heeyoung (1 July 2016). «A new metric of absolute percentage error for intermittent demand forecasts». International Journal of Forecasting. 32 (3): 669–679. doi:10.1016/j.ijforecast.2015.12.003.
- ^ Makridakis, Spyros (1993) «Accuracy measures: theoretical and practical concerns.» International Journal of Forecasting, 9(4):527-529 doi:10.1016/0169-2070(93)90079-3
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
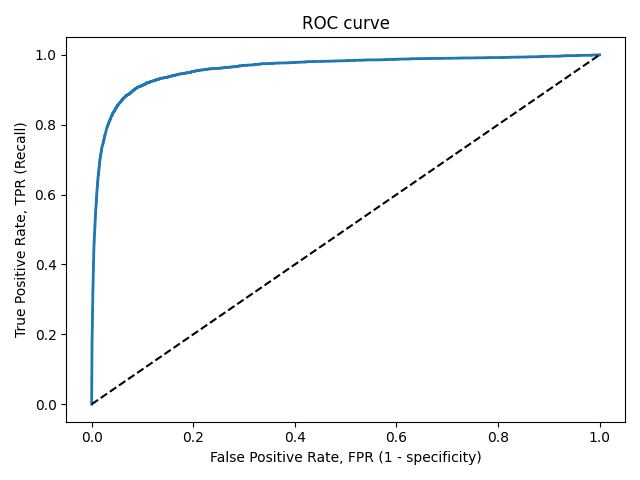
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
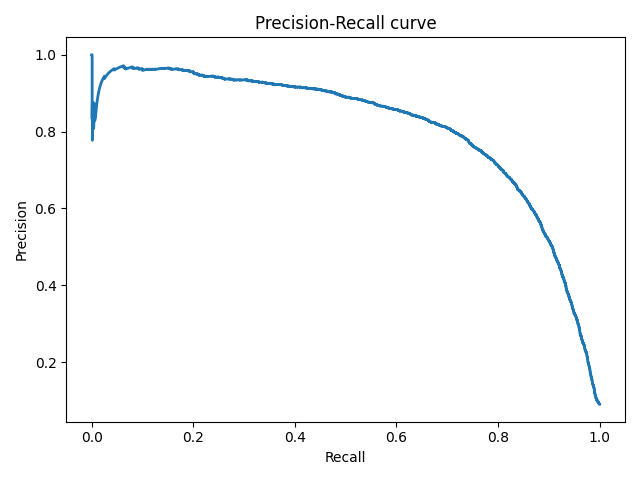
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
From Wikipedia, the free encyclopedia
The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio defined by the formula:
where At is the actual value and Ft is the forecast value. Their difference is divided by the actual value At. The absolute value of this ratio is summed for every forecasted point in time and divided by the number of fitted points n.
MAPE in regression problems[edit]
Mean absolute percentage error is commonly used as a loss function for regression problems and in model evaluation, because of its very intuitive interpretation in terms of relative error.
Definition[edit]
Consider a standard regression setting in which the data are fully described by a random pair 






In the classical regression setting, the closeness of 


where 
In practice
In practice 
From a practical point of view, the use of the MAPE as a quality function for regression model is equivalent to doing weighted mean absolute error (MAE) regression, also known as quantile regression. This property is trivial since
As a consequence, the use of the MAPE is very easy in practice, for example using existing libraries for quantile regression allowing weights.
Consistency[edit]
The use of the MAPE as a loss function for regression analysis is feasible both on a practical point of view and on a theoretical one, since the existence of an optimal model and the consistency of the empirical risk minimization can be proved.[1]
WMAPE[edit]
WMAPE (sometimes spelled wMAPE) stands for weighted mean absolute percentage error.[2] It is a measure used to evaluate the performance of regression or forecasting models. It is a variant of MAPE in which the mean absolute percent errors is treated as a weighted arithmetic mean. Most commonly the absolute percent errors are weighted by the actuals (e.g. in case of sales forecasting, errors are weighted by sales volume).[3]. Effectively, this overcomes the ‘infinite error’ issue.[4]
Its formula is:[4]
Where 


However, this effectively simplifies to a much simpler formula:
Confusingly, sometimes when people refer to wMAPE they are talking about a different model in which the numerator and denominator of the wMAPE formula above are weighted again by another set of custom weights 
Issues[edit]
Although the concept of MAPE sounds very simple and convincing, it has major drawbacks in practical application,[5] and there are many studies on shortcomings and misleading results from MAPE.[6][7]
To overcome these issues with MAPE, there are some other measures proposed in literature:
- Mean Absolute Scaled Error (MASE)
- Symmetric Mean Absolute Percentage Error (sMAPE)
- Mean Directional Accuracy (MDA)
- Mean Arctangent Absolute Percentage Error (MAAPE): MAAPE can be considered a slope as an angle, while MAPE is a slope as a ratio.[7]
See also[edit]
- Least absolute deviations
- Mean absolute error
- Mean percentage error
- Symmetric mean absolute percentage error
External links[edit]
- Mean Absolute Percentage Error for Regression Models
- Mean Absolute Percentage Error (MAPE)
- Errors on percentage errors — variants of MAPE
- Mean Arctangent Absolute Percentage Error (MAAPE)
References[edit]
- ^ a b de Myttenaere, B Golden, B Le Grand, F Rossi (2015). «Mean absolute percentage error for regression models», Neurocomputing 2016 arXiv:1605.02541
- ^ Forecast Accuracy: MAPE, WAPE, WMAPE https://www.baeldung.com/cs/mape-vs-wape-vs-wmape%7Ctitle=Understanding Forecast Accuracy: MAPE, WAPE, WMAPE. ;
- ^ Weighted Mean Absolute Percentage Error https://ibf.org/knowledge/glossary/weighted-mean-absolute-percentage-error-wmape-299%7Ctitle=WMAPE: Weighted Mean Absolute Percentage Error. ;
- ^ a b «Statistical Forecast Errors».
- ^ a b Tofallis (2015). «A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation», Journal of the Operational Research Society, 66(8):1352-1362. archived preprint
- ^ Hyndman, Rob J., and Anne B. Koehler (2006). «Another look at measures of forecast accuracy.» International Journal of Forecasting, 22(4):679-688 doi:10.1016/j.ijforecast.2006.03.001.
- ^ a b Kim, Sungil and Heeyoung Kim (2016). «A new metric of absolute percentage error for intermittent demand forecasts.» International Journal of Forecasting, 32(3):669-679 doi:10.1016/j.ijforecast.2015.12.003.
- ^ Kim, Sungil; Kim, Heeyoung (1 July 2016). «A new metric of absolute percentage error for intermittent demand forecasts». International Journal of Forecasting. 32 (3): 669–679. doi:10.1016/j.ijforecast.2015.12.003.
- ^ Makridakis, Spyros (1993) «Accuracy measures: theoretical and practical concerns.» International Journal of Forecasting, 9(4):527-529 doi:10.1016/0169-2070(93)90079-3
From Wikipedia, the free encyclopedia
The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio defined by the formula:
where At is the actual value and Ft is the forecast value. Their difference is divided by the actual value At. The absolute value of this ratio is summed for every forecasted point in time and divided by the number of fitted points n.
MAPE in regression problems[edit]
Mean absolute percentage error is commonly used as a loss function for regression problems and in model evaluation, because of its very intuitive interpretation in terms of relative error.
Definition[edit]
Consider a standard regression setting in which the data are fully described by a random pair 






In the classical regression setting, the closeness of 


where 
In practice
In practice 
From a practical point of view, the use of the MAPE as a quality function for regression model is equivalent to doing weighted mean absolute error (MAE) regression, also known as quantile regression. This property is trivial since
As a consequence, the use of the MAPE is very easy in practice, for example using existing libraries for quantile regression allowing weights.
Consistency[edit]
The use of the MAPE as a loss function for regression analysis is feasible both on a practical point of view and on a theoretical one, since the existence of an optimal model and the consistency of the empirical risk minimization can be proved.[1]
WMAPE[edit]
WMAPE (sometimes spelled wMAPE) stands for weighted mean absolute percentage error.[2] It is a measure used to evaluate the performance of regression or forecasting models. It is a variant of MAPE in which the mean absolute percent errors is treated as a weighted arithmetic mean. Most commonly the absolute percent errors are weighted by the actuals (e.g. in case of sales forecasting, errors are weighted by sales volume).[3]. Effectively, this overcomes the ‘infinite error’ issue.[4]
Its formula is:[4]
Where 


However, this effectively simplifies to a much simpler formula:
Confusingly, sometimes when people refer to wMAPE they are talking about a different model in which the numerator and denominator of the wMAPE formula above are weighted again by another set of custom weights 
Issues[edit]
Although the concept of MAPE sounds very simple and convincing, it has major drawbacks in practical application,[5] and there are many studies on shortcomings and misleading results from MAPE.[6][7]
To overcome these issues with MAPE, there are some other measures proposed in literature:
- Mean Absolute Scaled Error (MASE)
- Symmetric Mean Absolute Percentage Error (sMAPE)
- Mean Directional Accuracy (MDA)
- Mean Arctangent Absolute Percentage Error (MAAPE): MAAPE can be considered a slope as an angle, while MAPE is a slope as a ratio.[7]
See also[edit]
- Least absolute deviations
- Mean absolute error
- Mean percentage error
- Symmetric mean absolute percentage error
External links[edit]
- Mean Absolute Percentage Error for Regression Models
- Mean Absolute Percentage Error (MAPE)
- Errors on percentage errors — variants of MAPE
- Mean Arctangent Absolute Percentage Error (MAAPE)
References[edit]
- ^ a b de Myttenaere, B Golden, B Le Grand, F Rossi (2015). «Mean absolute percentage error for regression models», Neurocomputing 2016 arXiv:1605.02541
- ^ Forecast Accuracy: MAPE, WAPE, WMAPE https://www.baeldung.com/cs/mape-vs-wape-vs-wmape%7Ctitle=Understanding Forecast Accuracy: MAPE, WAPE, WMAPE. ;
- ^ Weighted Mean Absolute Percentage Error https://ibf.org/knowledge/glossary/weighted-mean-absolute-percentage-error-wmape-299%7Ctitle=WMAPE: Weighted Mean Absolute Percentage Error. ;
- ^ a b «Statistical Forecast Errors».
- ^ a b Tofallis (2015). «A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation», Journal of the Operational Research Society, 66(8):1352-1362. archived preprint
- ^ Hyndman, Rob J., and Anne B. Koehler (2006). «Another look at measures of forecast accuracy.» International Journal of Forecasting, 22(4):679-688 doi:10.1016/j.ijforecast.2006.03.001.
- ^ a b Kim, Sungil and Heeyoung Kim (2016). «A new metric of absolute percentage error for intermittent demand forecasts.» International Journal of Forecasting, 32(3):669-679 doi:10.1016/j.ijforecast.2015.12.003.
- ^ Kim, Sungil; Kim, Heeyoung (1 July 2016). «A new metric of absolute percentage error for intermittent demand forecasts». International Journal of Forecasting. 32 (3): 669–679. doi:10.1016/j.ijforecast.2015.12.003.
- ^ Makridakis, Spyros (1993) «Accuracy measures: theoretical and practical concerns.» International Journal of Forecasting, 9(4):527-529 doi:10.1016/0169-2070(93)90079-3
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
- Среднеквадратичная ошибка (Mean Squared Error)
- Корень из среднеквадратичной ошибки (Root Mean Squared Error)
- Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
- Cредняя абсолютная ошибка (Mean Absolute Error)
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
- Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
- Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
- Средняя относительная ошибка (Mean Relative Error)
- Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
- R-квадрат
- Скорректированный R-квадрат
- Сравнение метрик
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Гораздо легче что-то измерить, чем понять, что именно вы измеряете
Джон Уильям Салливан
Задачи машинного обучения с учителем как правило состоят в восстановлении зависимости между парами (признаковое описание, целевая переменная) по данным, доступным нам для анализа. Алгоритмы машинного обучения (learning algorithm), со многими из которых вы уже успели познакомиться, позволяют построить модель, аппроксимирующую эту зависимость. Но как понять, насколько качественной получилась аппроксимация?
Почти наверняка наша модель будет ошибаться на некоторых объектах: будь она даже идеальной, шум или выбросы в тестовых данных всё испортят. При этом разные модели будут ошибаться на разных объектах и в разной степени. Задача специалиста по машинному обучению – подобрать подходящий критерий, который позволит сравнивать различные модели.
Перед чтением этой главы мы хотели бы ещё раз напомнить, что качество модели нельзя оценивать на обучающей выборке. Как минимум, это стоит делать на отложенной (тестовой) выборке, но, если вам это позволяют время и вычислительные ресурсы, стоит прибегнуть и к более надёжным способам проверки – например, кросс-валидации (о ней вы узнаете в отдельной главе).
Выбор метрик в реальных задачах
Возможно, вы уже участвовали в соревнованиях по анализу данных. На таких соревнованиях метрику (критерий качества модели) организатор выбирает за вас, и она, как правило, довольно понятным образом связана с результатами предсказаний. Но на практике всё бывает намного сложнее.
Например, мы хотим:
- решить, сколько коробок с бананами нужно завтра привезти в конкретный магазин, чтобы минимизировать количество товара, который не будет выкуплен и минимизировать ситуацию, когда покупатель к концу дня не находит желаемый продукт на полке;
- увеличить счастье пользователя от работы с нашим сервисом, чтобы он стал лояльным и обеспечивал тем самым стабильный прогнозируемый доход;
- решить, нужно ли направить человека на дополнительное обследование.
В каждом конкретном случае может возникать целая иерархия метрик. Представим, например, что речь идёт о стриминговом музыкальном сервисе, пользователей которого мы решили порадовать сгенерированными самодельной нейросетью треками – не защищёнными авторским правом, а потому совершенно бесплатными. Иерархия метрик могла бы иметь такой вид:
- Самый верхний уровень: будущий доход сервиса – невозможно измерить в моменте, сложным образом зависит от совокупности всех наших усилий;
- Медианная длина сессии, возможно, служащая оценкой радости пользователей, которая, как мы надеемся, повлияет на их желание продолжать платить за подписку – её нам придётся измерять в продакшене, ведь нас интересует реакция настоящих пользователей на новшество;
- Доля удовлетворённых качеством сгенерированной музыки асессоров, на которых мы потестируем её до того, как выставить на суд пользователей;
- Функция потерь, на которую мы будем обучать генеративную сеть.
На этом примере мы можем заметить сразу несколько общих закономерностей. Во-первых, метрики бывают offline и online (оффлайновыми и онлайновыми). Online метрики вычисляются по данным, собираемым с работающей системы (например, медианная длина сессии). Offline метрики могут быть измерены до введения модели в эксплуатацию, например, по историческим данным или с привлечением специальных людей, асессоров. Последнее часто применяется, когда метрикой является реакция живого человека: скажем, так поступают поисковые компании, которые предлагают людям оценить качество ранжирования экспериментальной системы еще до того, как рядовые пользователи увидят эти результаты в обычном порядке. На самом же нижнем этаже иерархии лежат оптимизируемые в ходе обучения функции потерь.
В данном разделе нас будут интересовать offline метрики, которые могут быть измерены без привлечения людей.
Функция потерь $neq$ метрика качества
Как мы узнали ранее, методы обучения реализуют разные подходы к обучению:
- обучение на основе прироста информации (как в деревьях решений)
- обучение на основе сходства (как в методах ближайших соседей)
- обучение на основе вероятностной модели данных (например, максимизацией правдоподобия)
- обучение на основе ошибок (минимизация эмпирического риска)
И в рамках обучения на основе минимизации ошибок мы уже отвечали на вопрос: как можно штрафовать модель за предсказание на обучающем объекте.
Во время сведения задачи о построении решающего правила к задаче численной оптимизации, мы вводили понятие функции потерь и, обычно, объявляли целевой функцией сумму потерь от предсказаний на всех объектах обучающей выборке.
Важно понимать разницу между функцией потерь и метрикой качества. Её можно сформулировать следующим образом:
-
Функция потерь возникает в тот момент, когда мы сводим задачу построения модели к задаче оптимизации. Обычно требуется, чтобы она обладала хорошими свойствами (например, дифференцируемостью).
-
Метрика – внешний, объективный критерий качества, обычно зависящий не от параметров модели, а только от предсказанных меток.
В некоторых случаях метрика может совпадать с функцией потерь. Например, в задаче регрессии MSE играет роль как функции потерь, так и метрики. Но, скажем, в задаче бинарной классификации они почти всегда различаются: в качестве функции потерь может выступать кросс-энтропия, а в качестве метрики – число верно угаданных меток (accuracy). Отметим, что в последнем примере у них различные аргументы: на вход кросс-энтропии нужно подавать логиты, а на вход accuracy – предсказанные метки (то есть по сути argmax логитов).
Бинарная классификация: метки классов
Перейдём к обзору метрик и начнём с самой простой разновидности классификации – бинарной, а затем постепенно будем наращивать сложность.
Напомним постановку задачи бинарной классификации: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_iin{0, 1}$ построить модель, которая по объекту $x$ предсказывает метку класса $f(x)in{0, 1}$.
Первым критерием качества, который приходит в голову, является accuracy – доля объектов, для которых мы правильно предсказали класс:
$$ color{#348FEA}{text{Accuracy}(y, y^{pred}) = frac{1}{N} sum_{i=1}^N mathbb{I}[y_i = f(x_i)]} $$
Или же сопряженная ей метрика – доля ошибочных классификаций (error rate):
$$text{Error rate} = 1 — text{Accuracy}$$
Познакомившись чуть внимательнее с этой метрикой, можно заметить, что у неё есть несколько недостатков:
- она не учитывает дисбаланс классов. Например, в задаче диагностики редких заболеваний классификатор, предсказывающий всем пациентам отсутствие болезни будет иметь достаточно высокую accuracy просто потому, что больных людей в выборке намного меньше;
- она также не учитывает цену ошибки на объектах разных классов. Для примера снова можно привести задачу медицинской диагностики: если ошибочный положительный диагноз для здорового больного обернётся лишь ещё одним обследованием, то ошибочно отрицательный вердикт может повлечь роковые последствия.
Confusion matrix (матрица ошибок)
Исторически задача бинарной классификации – это задача об обнаружении чего-то редкого в большом потоке объектов, например, поиск человека, больного туберкулёзом, по флюорографии. Или задача признания пятна на экране приёмника радиолокационной станции бомбардировщиком, представляющем угрозу охраняемому объекту (в противовес стае гусей).
Поэтому класс, который представляет для нас интерес, называется «положительным», а оставшийся – «отрицательным».
Заметим, что для каждого объекта в выборке возможно 4 ситуации:
- мы предсказали положительную метку и угадали. Будет относить такие объекты к true positive (TP) группе (true – потому что предсказали мы правильно, а positive – потому что предсказали положительную метку);
- мы предсказали положительную метку, но ошиблись в своём предсказании – false positive (FP) (false, потому что предсказание было неправильным);
- мы предсказали отрицательную метку и угадали – true negative (TN);
- и наконец, мы предсказали отрицательную метку, но ошиблись – false negative (FN). Для удобства все эти 4 числа изображают в виде таблицы, которую называют confusion matrix (матрицей ошибок):
Не волнуйтесь, если первое время эти обозначения будут сводить вас с ума (будем откровенны, даже профи со стажем в них порой путаются), однако логика за ними достаточно простая: первая часть названия группы показывает угадали ли мы с классом, а вторая – какой класс мы предсказали.
Пример
Попробуем воспользоваться введёнными метриками в боевом примере: сравним работу нескольких моделей классификации на Breast cancer wisconsin (diagnostic) dataset.
Объектами выборки являются фотографии биопсии грудных опухолей. С их помощью было сформировано признаковое описание, которое заключается в характеристиках ядер клеток (таких как радиус ядра, его текстура, симметричность). Положительным классом в такой постановке будут злокачественные опухоли, а отрицательным – доброкачественные.
Модель 1. Константное предсказание.
Решение задачи начнём с самого простого классификатора, который выдаёт на каждом объекте константное предсказание – самый часто встречающийся класс.
Зачем вообще замерять качество на такой модели?При разработке модели машинного обучения для проекта всегда желательно иметь некоторую baseline модель. Так нам будет легче проконтролировать, что наша более сложная модель действительно дает нам прирост качества.
from sklearn.datasets
import load_breast_cancer
the_data = load_breast_cancer()
# 0 – "доброкачественный"
# 1 – "злокачественный"
relabeled_target = 1 - the_data["target"]
from sklearn.model_selection import train_test_split
X = the_data["data"]
y = relabeled_target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.dummy import DummyClassifier
dc_mf = DummyClassifier(strategy="most_frequent")
dc_mf.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix
y_true = y_test y_pred = dc_mf.predict(X_test)
dc_mf_tn, dc_mf_fp, dc_mf_fn, dc_mf_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 0 | FN = 53 |
| Истинный класс — | FP = 0 | TN = 90 |
Обучающие данные таковы, что наш dummy-классификатор все объекты записывает в отрицательный класс, то есть признаёт все опухоли доброкачественными. Такой наивный подход позволяет нам получить минимальный штраф за FP (действительно, нельзя ошибиться в предсказании, если положительный класс вообще не предсказывается), но и максимальный штраф за FN (в эту группу попадут все злокачественные опухоли).
Модель 2. Случайный лес.
Настало время воспользоваться всем арсеналом моделей машинного обучения, и начнём мы со случайного леса.
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc.fit(X_train, y_train)
y_true = y_test
y_pred = rfc.predict(X_test)
rfc_tn, rfc_fp, rfc_fn, rfc_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 52 | FN = 1 |
| Истинный класс — | FP = 4 | TN = 86 |
Можно сказать, что этот классификатор чему-то научился, т.к. главная диагональ матрицы стала содержать все объекты из отложенной выборки, за исключением 4 + 1 = 5 объектов (сравните с 0 + 53 объектами dummy-классификатора, все опухоли объявляющего доброкачественными).
Отметим, что вычисляя долю недиагональных элементов, мы приходим к метрике error rate, о которой мы говорили в самом начале:
$$text{Error rate} = frac{FP + FN}{ TP + TN + FP + FN}$$
тогда как доля объектов, попавших на главную диагональ – это как раз таки accuracy:
$$text{Accuracy} = frac{TP + TN}{ TP + TN + FP + FN}$$
Модель 3. Метод опорных векторов.
Давайте построим еще один классификатор на основе линейного метода опорных векторов.
Не забудьте привести признаки к единому масштабу, иначе численный алгоритм не сойдется к решению и мы получим гораздо более плохо работающее решающее правило. Попробуйте проделать это упражнение.
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
ss = StandardScaler() ss.fit(X_train)
scaled_linsvc = LinearSVC(C=0.01,random_state=42)
scaled_linsvc.fit(ss.transform(X_train), y_train)
y_true = y_test
y_pred = scaled_linsvc.predict(ss.transform(X_test))
tn, fp, fn, tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 50 | FN = 3 |
| Истинный класс — | FP = 1 | TN = 89 |
Сравним результаты
Легко заметить, что каждая из двух моделей лучше классификатора-пустышки, однако давайте попробуем сравнить их между собой. С точки зрения error rate модели практически одинаковы: 5/143 для леса против 4/143 для SVM.
Посмотрим на структуру ошибок чуть более внимательно: лес – (FP = 4, FN = 1), SVM – (FP = 1, FN = 3). Какая из моделей предпочтительнее?
Замечание: Мы сравниваем несколько классификаторов на основании их предсказаний на отложенной выборке. Насколько ошибки данных классификаторов зависят от разбиения исходного набора данных? Иногда в процессе оценки качества мы будем получать модели, чьи показатели эффективности будут статистически неразличимыми.
Пусть мы учли предыдущее замечание и эти модели действительно статистически значимо ошибаются в разную сторону. Мы встретились с очевидной вещью: на матрицах нет отношения порядка. Когда мы сравнивали dummy-классификатор и случайный лес с помощью Accuracy, мы всю сложную структуру ошибок свели к одному числу, т.к. на вещественных числах отношение порядка есть. Сводить оценку модели к одному числу очень удобно, однако не стоит забывать, что у вашей модели есть много аспектов качества.
Что же всё-таки важнее уменьшить: FP или FN? Вернёмся к задаче: FP – доля доброкачественных опухолей, которым ошибочно присваивается метка злокачественной, а FN – доля злокачественных опухолей, которые классификатор пропускает. В такой постановке становится понятно, что при сравнении выиграет модель с меньшим FN (то есть лес в нашем примере), ведь каждая не обнаруженная опухоль может стоить человеческой жизни.
Рассмотрим теперь другую задачу: по данным о погоде предсказать, будет ли успешным запуск спутника. FN в такой постановке – это ошибочное предсказание неуспеха, то есть не более, чем упущенный шанс (если вас, конечно не уволят за срыв сроков). С FP всё серьёзней: если вы предскажете удачный запуск спутника, а на деле он потерпит крушение из-за погодных условий, то ваши потери будут в разы существеннее.
Итак, из примеров мы видим, что в текущем виде введенная нами доля ошибочных классификаций не даст нам возможности учесть неравную важность FP и FN. Поэтому введем две новые метрики: точность и полноту.
Точность и полнота
Accuracy — это метрика, которая характеризует качество модели, агрегированное по всем классам. Это полезно, когда классы для нас имеют одинаковое значение. В случае, если это не так, accuracy может быть обманчивой.
Рассмотрим ситуацию, когда положительный класс это событие редкое. Возьмем в качестве примера поисковую систему — в нашем хранилище хранятся миллиарды документов, а релевантных к конкретному поисковому запросу на несколько порядков меньше.
Пусть мы хотим решить задачу бинарной классификации «документ d релевантен по запросу q». Благодаря большому дисбалансу, Accuracy dummy-классификатора, объявляющего все документы нерелевантными, будет близка к единице. Напомним, что $text{Accuracy} = frac{TP + TN}{TP + TN + FP + FN}$, и в нашем случае высокое значение метрики будет обеспечено членом TN, в то время для пользователей более важен высокий TP.
Поэтому в случае ассиметрии классов, можно использовать метрики, которые не учитывают TN и ориентируются на TP.
Если мы рассмотрим долю правильно предсказанных положительных объектов среди всех объектов, предсказанных положительным классом, то мы получим метрику, которая называется точностью (precision)
$$color{#348FEA}{text{Precision} = frac{TP}{TP + FP}}$$
Интуитивно метрика показывает долю релевантных документов среди всех найденных классификатором. Чем меньше ложноположительных срабатываний будет допускать модель, тем больше будет её Precision.
Если же мы рассмотрим долю правильно найденных положительных объектов среди всех объектов положительного класса, то мы получим метрику, которая называется полнотой (recall)
$$color{#348FEA}{text{Recall} = frac{TP}{TP + FN}}$$
Интуитивно метрика показывает долю найденных документов из всех релевантных. Чем меньше ложно отрицательных срабатываний, тем выше recall модели.
Например, в задаче предсказания злокачественности опухоли точность показывает, сколько из определённых нами как злокачественные опухолей действительно являются злокачественными, а полнота – какую долю злокачественных опухолей нам удалось выявить.
Хорошее понимание происходящего даёт следующая картинка: 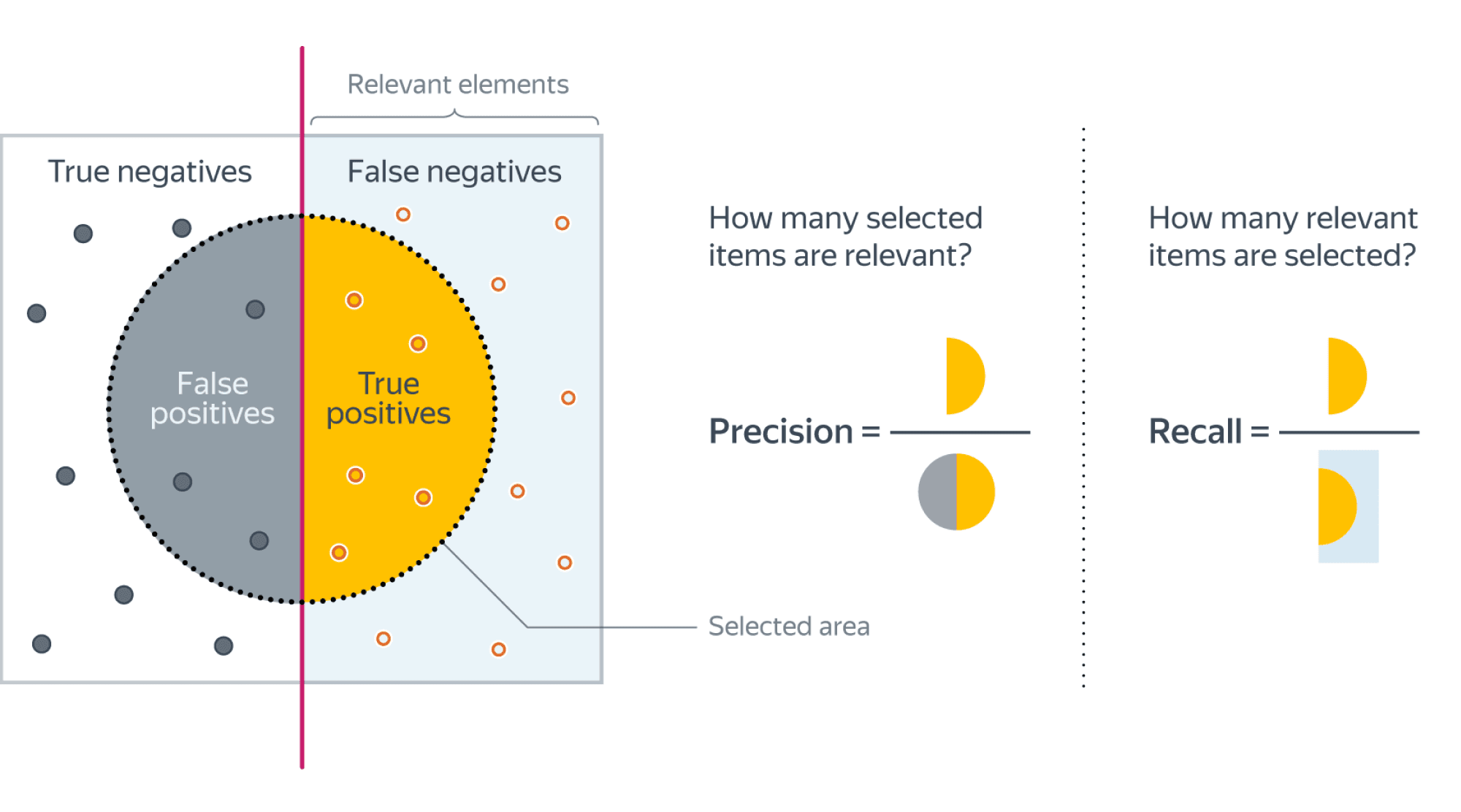
Recall@k, Precision@k
Метрики Recall и Precision хорошо подходят для задачи поиска «документ d релевантен запросу q», когда из списка рекомендованных алгоритмом документов нас интересует только первый. Но не всегда алгоритм машинного обучения вынужден работать в таких жестких условиях. Может быть такое, что вполне достаточно, что релевантный документ попал в первые k рекомендованных. Например, в интерфейсе выдачи первые три подсказки видны всегда одновременно и вообще не очень понятно, какой у них порядок. Тогда более честной оценкой качества алгоритма будет «в выдаче D размера k по запросу q нашлись релевантные документы». Для расчёта метрики по всей выборке объединим все выдачи и рассчитаем precision, recall как обычно подокументно.
F1-мера
Как мы уже отмечали ранее, модели очень удобно сравнивать, когда их качество выражено одним числом. В случае пары Precision-Recall существует популярный способ скомпоновать их в одну метрику — взять их среднее гармоническое. Данный показатель эффективности исторически носит название F1-меры (F1-measure).
$$
color{#348FEA}{F_1 = frac{2}{frac{1}{Recall} + frac{1}{Precision}}} = $$
$$ = 2 frac{Recall cdot Precision }{Recall + Precision} = frac
{TP} {TP + frac{FP + FN}{2}}
$$
Стоит иметь в виду, что F1-мера предполагает одинаковую важность Precision и Recall, если одна из этих метрик для вас приоритетнее, то можно воспользоваться $F_{beta}$ мерой:
$$
F_{beta} = (beta^2 + 1) frac{Recall cdot Precision }{Recall + beta^2Precision}
$$
Бинарная классификация: вероятности классов
Многие модели бинарной классификации устроены так, что класс объекта получается бинаризацией выхода классификатора по некоторому фиксированному порогу:
$$fleft(x ; w, w_{0}right)=mathbb{I}left[g(x, w) > w_{0}right].$$
Например, модель логистической регрессии возвращает оценку вероятности принадлежности примера к положительному классу. Другие модели бинарной классификации обычно возвращают произвольные вещественные значения, но существуют техники, называемые калибровкой классификатора, которые позволяют преобразовать предсказания в более или менее корректную оценку вероятности принадлежности к положительному классу.
Как оценить качество предсказываемых вероятностей, если именно они являются нашей конечной целью? Общепринятой мерой является логистическая функция потерь, которую мы изучали раньше, когда говорили об устройстве некоторых методов классификации (например уже упоминавшейся логистической регрессии).
Если же нашей целью является построение прогноза в терминах метки класса, то нам нужно учесть, что в зависимости от порога мы будем получать разные предсказания и разное качество на отложенной выборке. Так, чем ниже порог отсечения, тем больше объектов модель будет относить к положительному классу. Как в этом случае оценить качество модели?
AUC
Пусть мы хотим учитывать ошибки на объектах обоих классов. При уменьшении порога отсечения мы будем находить (правильно предсказывать) всё большее число положительных объектов, но также и неправильно предсказывать положительную метку на всё большем числе отрицательных объектов. Естественным кажется ввести две метрики TPR и FPR:
TPR (true positive rate) – это полнота, доля положительных объектов, правильно предсказанных положительными:
$$ TPR = frac{TP}{P} = frac{TP}{TP + FN} $$
FPR (false positive rate) – это доля отрицательных объектов, неправильно предсказанных положительными:
$$FPR = frac{FP}{N} = frac{FP}{FP + TN}$$
Обе эти величины растут при уменьшении порога. Кривая в осях TPR/FPR, которая получается при варьировании порога, исторически называется ROC-кривой (receiver operating characteristics curve, сокращённо ROC curve). Следующий график поможет вам понять поведение ROC-кривой.
Желтая и синяя кривые показывают распределение предсказаний классификатора на объектах положительного и отрицательного классов соответственно. То есть значения на оси X (на графике с двумя гауссианами) мы получаем из классификатора. Если классификатор идеальный (две кривые разделимы по оси X), то на правом графике мы получаем ROC-кривую (0,0)->(0,1)->(1,1) (убедитесь сами!), площадь под которой равна 1. Если классификатор случайный (предсказывает одинаковые метки положительным и отрицательным объектам), то мы получаем ROC-кривую (0,0)->(1,1), площадь под которой равна 0.5. Поэкспериментируйте с разными вариантами распределения предсказаний по классам и посмотрите, как меняется ROC-кривая.
Чем лучше классификатор разделяет два класса, тем больше площадь (area under curve) под ROC-кривой – и мы можем использовать её в качестве метрики. Эта метрика называется AUC и она работает благодаря следующему свойству ROC-кривой:
AUC равен доле пар объектов вида (объект класса 1, объект класса 0), которые алгоритм верно упорядочил, т.е. предсказание классификатора на первом объекте больше:
$$
color{#348FEA}{operatorname{AUC} = frac{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j] I^{prime}[f(x_{i}) < f(x_{j})]}{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j]}}
$$
$$
I^{prime}left[f(x_{i}) < f(x_{j})right]=
left{
begin{array}{ll}
0, & f(x_{i}) > f(x_{j}) \
0.5 & f(x_{i}) = f(x_{j}) \
1, & f(x_{i}) < f(x_{j})
end{array}
right.
$$
$$
Ileft[y_{i}< y_{j}right]=
left{
begin{array}{ll}
0, & y_{i} geq y_{j} \
1, & y_{i} < y_{j}
end{array}
right.
$$
Чтобы детальнее разобраться, почему это так, советуем вам обратиться к материалам А.Г.Дьяконова.
В каких случаях лучше отдать предпочтение этой метрике? Рассмотрим следующую задачу: некоторый сотовый оператор хочет научиться предсказывать, будет ли клиент пользоваться его услугами через месяц. На первый взгляд кажется, что задача сводится к бинарной классификации с метками 1, если клиент останется с компанией и $0$ – иначе.
Однако если копнуть глубже в процессы компании, то окажется, что такие метки практически бесполезны. Компании скорее интересно упорядочить клиентов по вероятности прекращения обслуживания и в зависимости от этого применять разные варианты удержания: кому-то прислать скидочный купон от партнёра, кому-то предложить скидку на следующий месяц, а кому-то и новый тариф на особых условиях.
Таким образом, в любой задаче, где нам важна не метка сама по себе, а правильный порядок на объектах, имеет смысл применять AUC.
Утверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.
ПодробнееУтверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.» details=»Продемонстрируем это на следующем примере: пусть наша выборка состоит из $9100$ объектов класса $0$ и $10$ объектов класса $1$, и модель расположила их следующим образом:
$$underbrace{0 dots 0}_{9000} ~ underbrace{1 dots 1}_{10} ~ underbrace{0 dots 0}_{100}$$
Тогда AUC будет близка к единице: количество пар правильно расположенных объектов будет порядка $90000$, в то время как общее количество пар порядка $91000$.
Однако самыми высокими по вероятности положительного класса будут совсем не те объекты, которые мы ожидаем.
Average Precision
Будем постепенно уменьшать порог бинаризации. При этом полнота будет расти от $0$ до $1$, так как будет увеличиваться количество объектов, которым мы приписываем положительный класс (а количество объектов, на самом деле относящихся к положительному классу, очевидно, меняться не будет). Про точность же нельзя сказать ничего определённого, но мы понимаем, что скорее всего она будет выше при более высоком пороге отсечения (мы оставим только объекты, в которых модель «уверена» больше всего). Варьируя порог и пересчитывая значения Precision и Recall на каждом пороге, мы получим некоторую кривую примерно следующего вида:
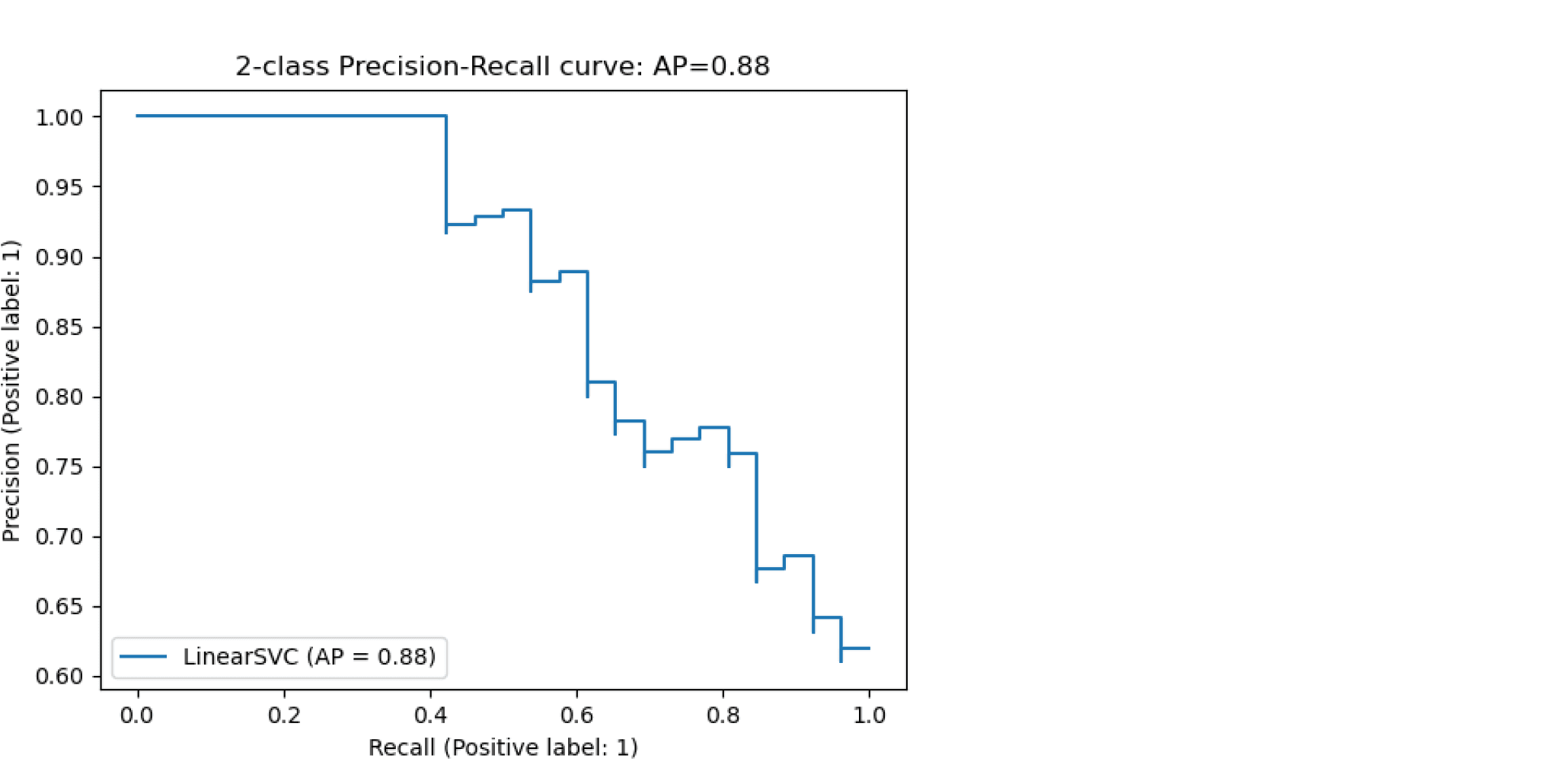
Рассмотрим среднее значение точности (оно равно площади под кривой точность-полнота):
$$ text { AP }=int_{0}^{1} p(r) d r$$
Получим показатель эффективности, который называется average precision. Как в случае матрицы ошибок мы переходили к скалярным показателям эффективности, так и в случае с кривой точность-полнота мы охарактеризовали ее в виде числа.
Многоклассовая классификация
Если классов становится больше двух, расчёт метрик усложняется. Если задача классификации на $K$ классов ставится как $K$ задач об отделении класса $i$ от остальных ($i=1,ldots,K$), то для каждой из них можно посчитать свою матрицу ошибок. Затем есть два варианта получения итогового значения метрики из $K$ матриц ошибок:
- Усредняем элементы матрицы ошибок (TP, FP, TN, FN) между бинарными классификаторами, например $TP = frac{1}{K}sum_{i=1}^{K}TP_i$. Затем по одной усреднённой матрице ошибок считаем Precision, Recall, F-меру. Это называют микроусреднением.
- Считаем Precision, Recall для каждого классификатора отдельно, а потом усредняем. Это называют макроусреднением.
Порядок усреднения влияет на результат в случае дисбаланса классов. Показатели TP, FP, FN — это счётчики объектов. Пусть некоторый класс обладает маленькой мощностью (обозначим её $M$). Тогда значения TP и FN при классификации этого класса против остальных будут не больше $M$, то есть тоже маленькие. Про FP мы ничего уверенно сказать не можем, но скорее всего при дисбалансе классов классификатор не будет предсказывать редкий класс слишком часто, потому что есть большая вероятность ошибиться. Так что FP тоже мало. Поэтому усреднение первым способом сделает вклад маленького класса в общую метрику незаметным. А при усреднении вторым способом среднее считается уже для нормированных величин, так что вклад каждого класса будет одинаковым.
Рассмотрим пример. Пусть есть датасет из объектов трёх цветов: желтого, зелёного и синего. Желтого и зелёного цветов почти поровну — 21 и 20 объектов соответственно, а синих объектов всего 4.
Модель по очереди для каждого цвета пытается отделить объекты этого цвета от объектов оставшихся двух цветов. Результаты классификации проиллюстрированы матрицей ошибок. Модель «покрасила» в жёлтый 25 объектов, 20 из которых были действительно жёлтыми (левый столбец матрицы). В синий был «покрашен» только один объект, который на самом деле жёлтый (средний столбец матрицы). В зелёный — 19 объектов, все на самом деле зелёные (правый столбец матрицы).
Посчитаем Precision классификации двумя способами:
- С помощью микроусреднения получаем $$
text{Precision} = frac{dfrac{1}{3}left(20 + 0 + 19right)}{dfrac{1}{3}left(20 + 0 + 19right) + dfrac{1}{3}left(5 + 1 + 0right)} = 0.87
$$ - С помощью макроусреднения получаем $$
text{Precision} = dfrac{1}{3}left( frac{20}{20 + 5} + frac{0}{0 + 1} + frac{19}{19 + 0}right) = 0.6
$$
Видим, что макроусреднение лучше отражает тот факт, что синий цвет, которого в датасете было совсем мало, модель практически игнорирует.
Как оптимизировать метрики классификации?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы $F$ на валидационной выборке была минимальная/максимальная. Лучший способ добиться минимизации метрики $F$ — оптимизировать её напрямую, то есть выбрать в качестве функции потерь ту же $F(a(X), Y)$. К сожалению, это не всегда возможно. Рассмотрим, как оптимизировать метрики иначе.
Метрики precision и recall невозможно оптимизировать напрямую, потому что эти метрики нельзя рассчитать на одном объекте, а затем усреднить. Они зависят от того, какими были правильная метка класса и ответ алгоритма на всех объектах. Чтобы понять, как оптимизировать precision, recall, рассмотрим, как расчитать эти метрики на отложенной выборке. Пусть модель обучена на стандартную для классификации функцию потерь (LogLoss). Для получения меток класса специалист по машинному обучению сначала применяет на объектах модель и получает вещественные предсказания модели ($p_i in left(0, 1right)$). Затем предсказания бинаризуются по порогу, выбранному специалистом: если предсказание на объекте больше порога, то метка класса 1 (или «положительная»), если меньше — 0 (или «отрицательная»). Рассмотрим, что будет с метриками precision, recall в крайних положениях порога.
- Пусть порог равен нулю. Тогда всем объектам будет присвоена положительная метка. Следовательно, все объекты будут либо TP, либо FP, потому что отрицательных предсказаний нет, $TP + FP = N$, где $N$ — размер выборки. Также все объекты, у которых метка на самом деле 1, попадут в TP. По формуле точность $text{Precision} = frac{TP}{TP + FP} = frac1N sum_{i = 1}^N mathbb{I} left[ y_i = 1 right]$ равна среднему таргету в выборке. А полнота $text{Recall} = frac{TP}{TP + FN} = frac{TP}{TP + 0} = 1$ равна единице.
- Пусть теперь порог равен единице. Тогда ни один объект не будет назван положительным, $TP = FP = 0$. Все объекты с меткой класса 1 попадут в FN. Если есть хотя бы один такой объект, то есть $FN ne 0$, будет верна формула $text{Recall} = frac{TP}{TP + FN} = frac{0}{0+ FN} = 0$. То есть при пороге единица, полнота равна нулю. Теперь посмотрим на точность. Формула для Precision состоит только из счётчиков положительных ответов модели (TP, FP). При единичном пороге они оба равны нулю, $text{Precision} = frac{TP}{TP + FP} = frac{0}{0 + 0}$то есть при единичном пороге точность неопределена. Пусть мы отступили чуть-чуть назад по порогу, чтобы хотя бы несколько объектов были названы моделью положительными. Скорее всего это будут самые «простые» объекты, которые модель распознает хорошо, потому что её предсказание близко к единице. В этом предположении $FP approx 0$. Тогда точность $text{Precision} = frac{TP}{TP + FP} approx frac{TP}{TP + 0} approx 1$ будет близка к единице.
Изменяя порог, между крайними положениями, получим графики Precision и Recall, которые выглядят как-то так:
Recall меняется от единицы до нуля, а Precision от среднего тагрета до какого-то другого значения (нет гарантий, что график монотонный).
Итого оптимизация precision и recall происходит так:
- Модель обучается на стандартную функцию потерь (например, LogLoss).
- Используя вещественные предсказания на валидационной выборке, перебирая разные пороги от 0 до 1, получаем графики метрик в зависимости от порога.
- Выбираем нужное сочетание точности и полноты.
Пусть теперь мы хотим максимизировать метрику AUC. Стандартный метод оптимизации, градиентный спуск, предполагает, что функция потерь дифференцируема. AUC этим качеством не обладает, то есть мы не можем оптимизировать её напрямую. Поэтому для метрики AUC приходится изменять оптимизационную задачу. Метрика AUC считает долю верно упорядоченных пар. Значит от исходной выборки можно перейти к выборке упорядоченных пар объектов. На этой выборке ставится задача классификации: метка класса 1 соответствует правильно упорядоченной паре, 0 — неправильно. Новой метрикой становится accuracy — доля правильно классифицированных объектов, то есть доля правильно упорядоченных пар. Оптимизировать accuracy можно по той же схеме, что и precision, recall: обучаем модель на LogLoss и предсказываем вероятности положительной метки у объекта выборки, считаем accuracy для разных порогов по вероятности и выбираем понравившийся.
Регрессия
В задачах регрессии целевая метка у нас имеет потенциально бесконечное число значений. И природа этих значений, обычно, связана с каким-то процессом измерений:
- величина температуры в определенный момент времени на метеостанции
- количество прочтений статьи на сайте
- количество проданных бананов в конкретном магазине, сети магазинов или стране
- дебит добывающей скважины на нефтегазовом месторождении за месяц и т.п.
Мы видим, что иногда метка это целое число, а иногда произвольное вещественное число. Обычно случаи целочисленных меток моделируют так, словно это просто обычное вещественное число. При таком подходе может оказаться так, что модель A лучше модели B по некоторой метрике, но при этом предсказания у модели A могут быть не целыми. Если в бизнес-задаче ожидается именно целочисленный ответ, то и оценивать нужно огрубление.
Общая рекомендация такова: оценивайте весь каскад решающих правил: и те «внутренние», которые вы получаете в результате обучения, и те «итоговые», которые вы отдаёте бизнес-заказчику.
Например, вы можете быть удовлетворены, что стали ошибаться не во втором, а только в третьем знаке после запятой при предсказании погоды. Но сами погодные данные измеряются с точностью до десятых долей градуса, а пользователь и вовсе может интересоваться лишь целым числом градусов.
Итак, напомним постановку задачи регрессии: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_i in mathbb{R}$ построить модель f(x).
Величину $ e_i = f(x_i) — y_i $ называют ошибкой на объекте i или регрессионным остатком.
Весь набор ошибок на отложенной выборке может служить аналогом матрицы ошибок из задачи классификации. А именно, когда мы рассматриваем две разные модели, то, глядя на то, как и на каких объектах они ошиблись, мы можем прийти к выводу, что для решения бизнес-задачи нам выгоднее взять ту или иную модель. И, аналогично со случаем бинарной классификации, мы можем начать строить агрегаты от вектора ошибок, получая тем самым разные метрики.
MSE, RMSE, $R^2$
MSE – одна из самых популярных метрик в задаче регрессии. Она уже знакома вам, т.к. применяется в качестве функции потерь (или входит в ее состав) во многих ранее рассмотренных методах.
$$ MSE(y^{true}, y^{pred}) = frac1Nsum_{i=1}^{N} (y_i — f(x_i))^2 $$
Иногда для того, чтобы показатель эффективности MSE имел размерность исходных данных, из него извлекают квадратный корень и получают показатель эффективности RMSE.
MSE неограничен сверху, и может быть нелегко понять, насколько «хорошим» или «плохим» является то или иное его значение. Чтобы появились какие-то ориентиры, делают следующее:
-
Берут наилучшее константное предсказание с точки зрения MSE — среднее арифметическое меток $bar{y}$. При этом чтобы не было подглядывания в test, среднее нужно вычислять по обучающей выборке
-
Рассматривают в качестве показателя ошибки:
$$ R^2 = 1 — frac{sum_{i=1}^{N} (y_i — f(x_i))^2}{sum_{i=1}^{N} (y_i — bar{y})^2}.$$
У идеального решающего правила $R^2$ равен $1$, у наилучшего константного предсказания он равен $0$ на обучающей выборке. Можно заметить, что $R^2$ показывает, какая доля дисперсии таргетов (знаменатель) объяснена моделью.
MSE квадратично штрафует за большие ошибки на объектах. Мы уже видели проявление этого при обучении моделей методом минимизации квадратичных ошибок – там это проявлялось в том, что модель старалась хорошо подстроиться под выбросы.
Пусть теперь мы хотим использовать MSE для оценки наших регрессионных моделей. Если большие ошибки для нас действительно неприемлемы, то квадратичный штраф за них — очень полезное свойство (и его даже можно усиливать, повышая степень, в которую мы возводим ошибку на объекте). Однако если в наших тестовых данных присутствуют выбросы, то нам будет сложно объективно сравнить модели между собой: ошибки на выбросах будет маскировать различия в ошибках на основном множестве объектов.
Таким образом, если мы будем сравнивать две модели при помощи MSE, у нас будет выигрывать та модель, у которой меньше ошибка на объектах-выбросах, а это, скорее всего, не то, чего требует от нас наша бизнес-задача.
История из жизни про бананы и квадратичный штраф за ошибкуИз-за неверно введенных данных метка одного из объектов оказалась в 100 раз больше реального значения. Моделировалась величина при помощи градиентного бустинга над деревьями решений. Функция потерь была MSE.
Однажды уже во время эксплуатации случилось ч.п.: у нас появились предсказания, в 100 раз превышающие допустимые из соображений физического смысла значения. Представьте себе, например, что вместо обычных 4 ящиков бананов система предлагала поставить в магазин 400. Были распечатаны все деревья из ансамбля, и мы увидели, что постепенно число ящиков действительно увеличивалось до прогнозных 400.
Было решено проверить гипотезу, что был выброс в данных для обучения. Так оно и оказалось: всего одна точка давала такую потерю на объекте, что алгоритм обучения решил, что лучше переобучиться под этот выброс, чем смириться с большим штрафом на этом объекте. А в эксплуатации у нас возникли точки, которые плюс-минус попадали в такие же листья ансамбля, что и объект-выброс.
Избежать такого рода проблем можно двумя способами: внимательнее контролируя качество данных или адаптировав функцию потерь.
Аналогично, можно поступать и в случае, когда мы разрабатываем метрику качества: менее жёстко штрафовать за большие отклонения от истинного таргета.
MAE
Использовать RMSE для сравнения моделей на выборках с большим количеством выбросов может быть неудобно. В таких случаях прибегают к также знакомой вам в качестве функции потери метрике MAE (mean absolute error):
$$ MAE(y^{true}, y^{pred}) = frac{1}{N}sum_{i=1}^{N} left|y_i — f(x_i)right| $$
Метрики, учитывающие относительные ошибки
И MSE и MAE считаются как сумма абсолютных ошибок на объектах.
Рассмотрим следующую задачу: мы хотим спрогнозировать спрос товаров на следующий месяц. Пусть у нас есть два продукта: продукт A продаётся в количестве 100 штук, а продукт В в количестве 10 штук. И пусть базовая модель предсказывает количество продаж продукта A как 98 штук, а продукта B как 8 штук. Ошибки на этих объектах добавляют 4 штрафных единицы в MAE.
И есть 2 модели-кандидата на улучшение. Первая предсказывает товар А 99 штук, а товар B 8 штук. Вторая предсказывает товар А 98 штук, а товар B 9 штук.
Обе модели улучшают MAE базовой модели на 1 единицу. Однако, с точки зрения бизнес-заказчика вторая модель может оказаться предпочтительнее, т.к. предсказание продажи редких товаров может быть приоритетнее. Один из способов учесть такое требование – рассматривать не абсолютную, а относительную ошибку на объектах.
MAPE, SMAPE
Когда речь заходит об относительных ошибках, сразу возникает вопрос: что мы будем ставить в знаменатель?
В метрике MAPE (mean absolute percentage error) в знаменатель помещают целевое значение:
$$ MAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ left|y_i — f(x_i)right|}{left|y_iright|} $$
С особым случаем, когда в знаменателе оказывается $0$, обычно поступают «инженерным» способом: или выдают за непредсказание $0$ на таком объекте большой, но фиксированный штраф, или пытаются застраховаться от подобного на уровне формулы и переходят к метрике SMAPE (symmetric mean absolute percentage error):
$$ SMAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ 2 left|y_i — f(x_i)right|}{y_i + f(x_i)} $$
Если же предсказывается ноль, штраф считаем нулевым.
Таким переходом от абсолютных ошибок на объекте к относительным мы сделали объекты в тестовой выборке равнозначными: даже если мы делаем абсурдно большое предсказание, на фоне которого истинная метка теряется, мы получаем штраф за этот объект порядка 1 в случае MAPE и 2 в случае SMAPE.
WAPE
Как и любая другая метрика, MAPE имеет свои границы применимости: например, она плохо справляется с прогнозом спроса на товары с прерывистыми продажами. Рассмотрим такой пример:
| Понедельник | Вторник | Среда | |
|---|---|---|---|
| Прогноз | 55 | 2 | 50 |
| Продажи | 50 | 1 | 50 |
| MAPE | 10% | 100% | 0% |
Среднее MAPE – 36.7%, что не очень отражает реальную ситуацию, ведь два дня мы предсказывали с хорошей точностью. В таких ситуациях помогает WAPE (weighted average percentage error):
$$ WAPE(y^{true}, y^{pred}) = frac{sum_{i=1}^{N} left|y_i — f(x_i)right|}{sum_{i=1}^{N} left|y_iright|} $$
Если мы предсказываем идеально, то WAPE = 0, если все предсказания отдаём нулевыми, то WAPE = 1.
В нашем примере получим WAPE = 5.9%
RMSLE
Альтернативный способ уйти от абсолютных ошибок к относительным предлагает метрика RMSLE (root mean squared logarithmic error):
$$ RMSLE(y^{true}, y^{pred}| c) = sqrt{ frac{1}{N} sum_{i=1}^N left(vphantom{frac12}log{left(y_i + c right)} — log{left(f(x_i) + c right)}right)^2 } $$
где нормировочная константа $c$ вводится искусственно, чтобы не брать логарифм от нуля. Также по построению видно, что метрика пригодна лишь для неотрицательных меток.
Веса в метриках
Все вышеописанные метрики легко допускают введение весов для объектов. Если мы из каких-то соображений можем определить стоимость ошибки на объекте, можно брать эту величину в качестве веса. Например, в задаче предсказания спроса в качестве веса можно использовать стоимость объекта.
Доля предсказаний с абсолютными ошибками больше, чем d
Еще одним способом охарактеризовать качество модели в задаче регрессии является доля предсказаний с абсолютными ошибками больше заданного порога $d$:
$$frac{1}{N} sum_{i=1}^{N} mathbb{I}left[ left| y_i — f(x_i) right| > d right] $$
Например, можно считать, что прогноз погоды сбылся, если ошибка предсказания составила меньше 1/2/3 градусов. Тогда рассматриваемая метрика покажет, в какой доле случаев прогноз не сбылся.
Как оптимизировать метрики регрессии?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы F на валидационной выборке была минимальная/максимальная. Аналогично задачам классификации лучший способ добиться минимизации метрики $F$ — выбрать в качестве функции потерь ту же $F(a(X), Y)$. К счастью, основные метрики для регрессии: MSE, RMSE, MAE можно оптимизировать напрямую. С формальной точки зрения MAE не дифференцируема, так как там присутствует модуль, чья производная не определена в нуле. На практике для этого выколотого случая в коде можно возвращать ноль.
Для оптимизации MAPE придётся изменять оптимизационную задачу. Оптимизацию MAPE можно представить как оптимизацию MAE, где объектам выборки присвоен вес $frac{1}{vert y_ivert}$.
- sklearn.metrics.mean_absolute_percentage_error(y_true, y_pred, *, sample_weight=None, multioutput=‘uniform_average’)[source]¶
-
Mean absolute percentage error (MAPE) regression loss.
Note here that the output is not a percentage in the range [0, 100]
and a value of 100 does not mean 100% but 1e2. Furthermore, the output
can be arbitrarily high wheny_trueis small (which is specific to the
metric) or whenabs(y_true - y_pred)is large (which is common for most
regression metrics). Read more in the
User Guide.New in version 0.24.
- Parameters:
-
- y_truearray-like of shape (n_samples,) or (n_samples, n_outputs)
-
Ground truth (correct) target values.
- y_predarray-like of shape (n_samples,) or (n_samples, n_outputs)
-
Estimated target values.
- sample_weightarray-like of shape (n_samples,), default=None
-
Sample weights.
- multioutput{‘raw_values’, ‘uniform_average’} or array-like
-
Defines aggregating of multiple output values.
Array-like value defines weights used to average errors.
If input is list then the shape must be (n_outputs,).- ‘raw_values’ :
-
Returns a full set of errors in case of multioutput input.
- ‘uniform_average’ :
-
Errors of all outputs are averaged with uniform weight.
- Returns:
-
- lossfloat or ndarray of floats
-
If multioutput is ‘raw_values’, then mean absolute percentage error
is returned for each output separately.
If multioutput is ‘uniform_average’ or an ndarray of weights, then the
weighted average of all output errors is returned.MAPE output is non-negative floating point. The best value is 0.0.
But note that bad predictions can lead to arbitrarily large
MAPE values, especially if somey_truevalues are very close to zero.
Note that we return a large value instead ofinfwheny_trueis zero.
Examples
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_percentage_error(y_true, y_pred) 0.3273... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_percentage_error(y_true, y_pred) 0.5515... >>> mean_absolute_percentage_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.6198... >>> # the value when some element of the y_true is zero is arbitrarily high because >>> # of the division by epsilon >>> y_true = [1., 0., 2.4, 7.] >>> y_pred = [1.2, 0.1, 2.4, 8.] >>> mean_absolute_percentage_error(y_true, y_pred) 112589990684262.48
Все курсы > Оптимизация > Занятие 4 (часть 2)
Во второй части занятия перейдем к практике.
Продолжим работать в том же ноутбуке⧉
Сквозной пример
Данные и постановка задачи
Обратимся к хорошо знакомому нам датасету недвижимости в Бостоне.
|
boston = pd.read_csv(‘/content/boston.csv’) |
При этом нам нужно будет решить две основные задачи:
Задача 1. Научиться оценивать качество модели не только с точки зрения метрики, но и исходя из рассмотренных ранее допущений модели. Эту задачу мы решим в три этапа.
- Этап 1. Построим базовую (baseline) модель линейной регрессии с помощью класса LinearRegression библиотеки sklearn и оценим, насколько выполняются рассмотренные выше допущения.
- Этап 2. Попробуем изменить данные таким образом, чтобы модель в большей степени соответствовала этим критериям.
- Этап 3. Обучим еще одну модель и посмотрим, как изменится результат.
Задача 2. С нуля построить модель множественной линейной регрессии и сравнить прогноз с результатом, полученным при решении первой задачи. При этом обучение модели мы реализуем двумя способами, а именно, через:
- Метод наименьших квадратов
- Метод градиентного спуска
Разделение выборки
Мы уже не раз говорили про важность разделения выборки на обучаущую и тестовую части. Сегодня же, с учетом того, что нам предстоит изучить много нового материала, мы опустим этот этап и будем обучать и тестировать модель на одних и тех же данных.
Исследовательский анализ данных
Теперь давайте более внимательно посмотрим на имеющиеся у нас данные. Как вы вероятно заметили, все признаки в этом датасете количественные, за исключением переменной CHAS.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 506 entries, 0 to 505 Data columns (total 14 columns): # Column Non-Null Count Dtype — —— ————— —— 0 CRIM 506 non-null float64 1 ZN 506 non-null float64 2 INDUS 506 non-null float64 3 CHAS 506 non-null float64 4 NOX 506 non-null float64 5 RM 506 non-null float64 6 AGE 506 non-null float64 7 DIS 506 non-null float64 8 RAD 506 non-null float64 9 TAX 506 non-null float64 10 PTRATIO 506 non-null float64 11 B 506 non-null float64 12 LSTAT 506 non-null float64 13 MEDV 506 non-null float64 dtypes: float64(14) memory usage: 55.5 KB |
|
# мы видим, что переменная CHAS категориальная boston.CHAS.value_counts() |
|
0.0 471 1.0 35 Name: CHAS, dtype: int64 |
Посмотрим на распределение признаков с помощью boxplots.
|
plt.figure(figsize = (10, 8)) sns.boxplot(data = boston.drop(columns = [‘CHAS’, ‘MEDV’])) plt.show() |
Посмотрим на распределение целевой переменной.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def box_density(x): # создадим два подграфика f, (ax_box, ax_kde) = plt.subplots(nrows = 2, # из двух строк ncols = 1, # и одного столбца sharex = True, # оставим только нижние подписи к оси x gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк figsize = (10,8)) # зададим размер графика # в первом подграфике построим boxplot sns.boxplot(x = x, ax = ax_box) ax_box.set(xlabel = None) # во втором — график плотности распределения sns.kdeplot(x, fill = True) # зададим заголовок и подписи к осям ax_box.set_title(‘Распределение переменной’, fontsize = 17) ax_kde.set_xlabel(‘Переменная’, fontsize = 15) ax_kde.set_ylabel(‘Плотность распределения’, fontsize = 15) plt.show() |
|
box_density(boston.iloc[:, —1]) |
Посмотрим на корреляцию количественных признаков с целевой переменной.
|
boston.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient() |
Используем точечно-бисериальную корреляцию для оценки взамосвязи переменной CHAS и целевой переменной.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def pbc(continuous, binary): # преобразуем количественную переменную в массив Numpy continuous_values = np.array(continuous) # классы качественной переменной превратим в нули и единицы binary_values = np.unique(binary, return_inverse = True)[1] # создадим две подгруппы количественных наблюдений # в зависимости от класса дихотомической переменной group0 = continuous_values[np.argwhere(binary_values == 0).flatten()] group1 = continuous_values[np.argwhere(binary_values == 1).flatten()] # найдем средние групп, mean0, mean1 = np.mean(group0), np.mean(group1) # а также длины групп и всего датасета n0, n1, n = len(group0), len(group1), len(continuous_values) # рассчитаем СКО количественной переменной std = continuous_values.std() # подставим значения в формулу return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) ) |
|
pbc(boston.MEDV, boston.CHAS) |
Обработка данных
Пропущенные значения
Посмотрим, есть ли пропущенные значения.
|
CRIM 0 ZN 0 INDUS 0 CHAS 0 NOX 0 RM 0 AGE 0 DIS 0 RAD 0 TAX 0 PTRATIO 0 B 0 LSTAT 0 MEDV 0 dtype: int64 |
Выбросы
Удалим выбросы.
|
from sklearn.ensemble import IsolationForest clf = IsolationForest(max_samples = 100, random_state = 42) clf.fit(boston) boston[‘anomaly’] = clf.predict(boston) boston = boston[boston.anomaly == 1] boston = boston.drop(columns = ‘anomaly’) boston.shape |
При удалении выбросов важно помнить, что полное отсутствие вариантивности в данных не позволит выявить взаимосвязи.
Масштабирование признаков
Приведем признаки к одному масштабу (целевую переменную трогать не будем).
|
boston.iloc[:, :—1] = (boston.iloc[:, :—1] — boston.iloc[:, :—1].mean()) / boston.iloc[:, :—1].std() |
Замечу, что метод наименьших квадратов не требует масштабирования признаков, градиентному спуску же напротив необходимо, чтобы все значения находились в одном диапазоне (подробнее в дополнительных материалах).
Кодирование категориальных переменных
После стандартизации переменная CHAS также сохранила только два значения.
|
boston.CHAS.value_counts() |
|
-0.182581 389 5.463391 13 Name: CHAS, dtype: int64 |
Ее можно не трогать.
Построение модели
Создадим первую пробную (baseline) модель с помощью библиотеки sklearn.
baseline-модель
|
X = boston.drop(‘MEDV’, axis = 1) y = boston[‘MEDV’] from sklearn.linear_model import LinearRegression model = LinearRegression() y_pred = model.fit(X, y).predict(X) |
Оценка качества
Диагностика модели, метрики качества и функции потерь
Вероятно, вы заметили, что мы использовали MSE и для обучения модели, и для оценки ее качества. Возникает вопрос, есть ли отличие между функцией потерь и метрикой качества модели.
Функция потерь и метрика качества могут совпадать, а могут и не совпадать. Важно понимать, что у них разное назначение.
- Функция потерь — это часть алгоритма, нам важно, чтобы эта функция была дифференцируема (у нее была производная)
- Производная метрики качества нас не интересует. Метрика качества должна быть адекватна решаемой задаче.
MSE, RMSE, MAE, MAPE
MSE и RMSE
Для оценки качества RMSE предпочтительнее, чем MSE, потому что показывает насколько ошибается модель в тех же единицах измерения, что и целевая переменная. Например, если диапазон целевой переменной от 80 до 100, а RMSE 20, то в среднем модель ошибается на 20-25 процентов.
В качестве практики напишем собственную функцию.
|
# параметр squared = True возвращает MSE # параметр squared = False возвращает RMSE def mse(y, y_pred, squared = True): mse = ((y — y_pred) ** 2).sum() / len(y) if squared == True: return mse else: return np.sqrt(mse) |
|
mse(y, y_pred), mse(y, y_pred, squared = False) |
|
(9.980044349414223, 3.1591208190593507) |
Сравним с sklearn.
|
from sklearn.metrics import mean_squared_error # squared = False дает RMSE mean_squared_error(y, y_pred, squared = False) |
MAE
Приведем формулу.
$$ MAE = frac{sum |y-hat{y}|}{n} $$
Средняя абсолютная ошибка представляет собой среднее арифметическое абсолютной ошибки $varepsilon = |y-hat{y}| $ и использует те же единицы измерения, что и целевая переменная.
|
def mae(y, y_pred): return np.abs(y — y_pred).sum() / len(y) |
|
from sklearn.metrics import mean_absolute_error mean_absolute_error(y, y_pred) |
MAE часто используется при оценке качества моделей временных рядов.
MAPE
Средняя абсолютная ошибка в процентах (mean absolute percentage error) по сути выражает MAE в процентах, а не в абсолютных величинах, представляя отклонение как долю от истинных ответов.
$$ MAPE = frac{1}{n} sum vert frac{y-hat{y}}{y} vert $$
Это позволяет сравнивать модели с разными единицами измерения между собой.
|
def mape(y, y_pred): return 1/len(y) * np.abs((y — y_pred) / y).sum() |
|
from sklearn.metrics import mean_absolute_percentage_error mean_absolute_percentage_error(y, y_pred) |
Коэффициент детерминации
В рамках вводного курса в ответах на вопросы к занятию по регрессии мы подробно рассмотрели коэффициент детерминации ($R^2$), его связь с RMSE, а также зачем нужен скорректированный $R^2$. Как мы знаем, если использовать, например, класс LinearRegression, то эта метрика содержится в методе .score().
Также можно использовать функцию r2_score() модуля metrics.
|
from sklearn.metrics import r2_score r2_score(y, y_pred) |
Для скорректированного $R^2$ напишем собственную функцию.
|
def r_squared(x, y, y_pred): r2 = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum() n, k = x.shape r2_adj = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum() return r2, r2_adj |
|
(0.7965234359550825, 0.7965234359550825) |
Диагностика модели
Теперь проведем диагностику модели в соответствии со сделанными ранее допущениями.
Анализ остатков и прогнозных значений
Напишем диагностическую функцию, которая сразу выведет несколько интересующих нас графиков и метрик, касающихся остатков и прогнозных значений.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
from scipy.stats import probplot from statsmodels.graphics.tsaplots import plot_acf from statsmodels.stats.stattools import durbin_watson def diagnostics(y, y_pred): residuals = y — y_pred residuals_mean = np.round(np.mean(y — y_pred), 3) f, ((ax_rkde, ax_prob), (ax_ry, ax_auto), (ax_yy, ax_ykde)) = plt.subplots(nrows = 3, ncols = 2, figsize = (12, 18)) # в первом подграфике построим график плотности остатков sns.kdeplot(residuals, fill = True, ax = ax_rkde) ax_rkde.set_title(‘Residuals distribution’, fontsize = 14) ax_rkde.set(xlabel = f‘Residuals, mean: {residuals_mean}’) ax_rkde.set(ylabel = ‘Density’) # во втором — график нормальной вероятности остатков probplot(residuals, dist = ‘norm’, plot = ax_prob) ax_prob.set_title(‘Residuals probability plot’, fontsize = 14) # в третьем — график остатков относительно прогноза ax_ry.scatter(y_pred, residuals) ax_ry.set_title(‘Predicted vs. Residuals’, fontsize = 14) ax_ry.set(xlabel = ‘y_pred’) ax_ry.set(ylabel = ‘Residuals’) # в четвертом — автокорреляцию остатков plot_acf(residuals, lags = 30, ax = ax_auto) ax_auto.set_title(‘Residuals Autocorrelation’, fontsize = 14) ax_auto.set(xlabel = f‘Lags ndurbin_watson: {durbin_watson(residuals).round(2)}’) ax_auto.set(ylabel = ‘Autocorrelation’) # в пятом — сравним прогнозные и фактические значения ax_yy.scatter(y, y_pred) ax_yy.plot([y.min(), y.max()], [y.min(), y.max()], «k—«, lw = 1) ax_yy.set_title(‘Actual vs. Predicted’, fontsize = 14) ax_yy.set(xlabel = ‘y_true’) ax_yy.set(ylabel = ‘y_pred’) # в шестом — сравним распределение истинной и прогнозной целевой переменных sns.kdeplot(y, fill = True, ax = ax_ykde, label = ‘y_true’) sns.kdeplot(y_pred, fill = True, ax = ax_ykde, label = ‘y_pred’) ax_ykde.set_title(‘Actual vs. Predicted Distribution’, fontsize = 14) ax_ykde.set(xlabel = ‘y_true and y_pred’) ax_ykde.set(ylabel = ‘Density’) ax_ykde.legend(loc = ‘upper right’, prop = {‘size’: 12}) plt.tight_layout() plt.show() |
Разберем полученную информацию.
- В целом остатки модели распределены нормально с нулевым средним значением
- Явной гетероскедастичности нет, хотя мы видим, что дисперсия не всегда равномерна
- Присутствует умеренная отрицательная корреляция
- График y_true vs. y_pred показывает насколько сильно прогнозные значения отклоняются от фактических. В идеальной модели (без шума, т.е. без случайных колебаний) точки должны были би стремиться находиться на диагонали, в более реалистичной модели нам бы хотелось видеть, что точки плотно сосредоточены вокруг диагонали.
- Распределение прогнозных значений в целом повторяет распределение фактических.
Мультиколлинеарность
Отдельно проведем анализ на мультиколлинеарность. Напишем соответствующую функцию.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def vif(df, features): vif, tolerance = {}, {} # пройдемся по интересующим нас признакам for feature in features: # составим список остальных признаков, которые будем использовать # для построения регрессии X = [f for f in features if f != feature] # поместим текущие признаки и таргет в X и y X, y = df[X], df[feature] # найдем коэффициент детерминации r2 = LinearRegression().fit(X, y).score(X, y) # посчитаем tolerance tolerance[feature] = 1 — r2 # найдем VIF vif[feature] = 1 / (tolerance[feature]) # выведем результат в виде датафрейма return pd.DataFrame({‘VIF’: vif, ‘Tolerance’: tolerance}) |
|
vif(df = X.drop(‘CHAS’, axis = 1), features = X.drop(‘CHAS’, axis = 1).columns) |
Дополнительная обработка данных
Попробуем дополнительно улучшить некоторые из диагностических показателей.
VIF
Уберем признак с наибольшим VIF (RAD) и посмотрим, что получится.
|
vif(df = X, features = [‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’, ‘DIS’, ‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’]) |
Показатели пришли в норму. Окончательно удалим RAD.
|
boston.drop(columns = ‘RAD’, inplace = True) |
Преобразование данных
Применим преобразование Йео-Джонсона.
|
from sklearn.preprocessing import PowerTransformer pt = PowerTransformer() boston = pd.DataFrame(pt.fit_transform(boston), columns = boston.columns) |
Отбор признаков
Посмотрим на линейную корреляцию Пирсона количественных признаков и целевой переменной.
|
boston_t.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient() |
Также рассчитаем точечно-бисериальную корреляцию.
|
pbc(boston_t.MEDV, boston_t.CHAS) |
Удалим признаки с наименьшей корреляцией, а именно ZN, CHAS, DIS и B.
|
boston.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’], inplace = True) |
Повторное моделирование и диагностика
Повторное моделирование
Выполним повторное моделирование.
|
X = boston_t.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’, ‘MEDV’]) y = boston_t.MEDV from sklearn.linear_model import LinearRegression model = LinearRegression() y_pred = model.fit(X, y).predict(X) |
Оценка качества и диагностика
Оценим качество. Так как мы преобразовали целевую переменную, показатель RMSE не будет репрезентативен. Воспользуемся MAPE и $R^2$.
|
(0.7546883769637166, 0.7546883769637166) |
Отклонение прогнозного значения от истинного снизилось. $R^2$ немного уменьшился, чтобы бывает, когда мы пытаемся привести модель к соответствию допущениям. Проведем диагностику.
Распределение остатков немного улучшилось, при этом незначительно усилилась их отрицательная автокорреляция. Распределение целевой переменной стало менее островершинным.
Данные можно было бы продолжить анализировать и улучшать, однако в рамках текущего занятия перейдем к механике обучения модели.
Коэффициенты
Выведем коэффициенты для того, чтобы сравнивать их с результатами построенных с нуля моделей.
|
model.intercept_, model.coef_ |
|
(9.574055157844797e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274])) |
Обучение модели
Теперь когда мы поближе познакомились с понятием регрессии, разобрали функции потерь и изучили допущения, при которых модель может быть удачной аппроксимацией данных, пора перейти к непосредственному созданию алгоритмов.
Векторизация уравнения
Для удобства векторизуем приведенное выше уравнение множественной линейной регрессии
$$ y = begin{bmatrix} y_1 \ y_2 \ vdots \ y_n end{bmatrix} X = begin{bmatrix} x_0 & x_1 & ldots & x_j \ x_0 & x_1 & ldots & x_j \ vdots & vdots & vdots & vdots \ x_{0} & x_{1} & ldots & x_{n,j} end{bmatrix}, theta = begin{bmatrix} theta_0 \ theta_1 \ vdots \ theta_n end{bmatrix}, varepsilon = begin{bmatrix} varepsilon_1 \ varepsilon_2 \ vdots \ varepsilon_n end{bmatrix} $$
где n — количество наблюдений, а j — количество признаков.
Обратите внимание, что мы создали еще один столбец данных $ x_0 $, который будем умножать на сдвиг $ theta_0 $. Его мы заполним единицами.
В результате такого несложного преобразования значение сдвига не изменится, но мы сможем записать уравнение через умножение матрицы на вектор.
$$ y = Xtheta + varepsilon $$
Кроме того, как мы увидим ниже, так нам не придется искать отдельную производную для коэффициента $ theta_0 $.
Схематично для модели с четырьмя наблюдениями (n = 4) и двумя признаками (j = 2) получаются вот такие матрицы.
Функция потерь
Как мы уже говорили, чтобы подобрать оптимальные коэффициенты $theta$, нам нужен критерий или функция потерь. Логично измерять отклонение прогнозного значения от истинного.
$$ varepsilon = Xtheta-y $$
При этом опять же просто складывать отклонения или ошибки мы не можем. Положительные и отрицательные значения будут взаимоудаляться. Для решения этой проблемы можно, например, использовать модуль и это приводит нас к абсолютной ошибке или L1 loss.
Абсолютная ошибка, L1 loss
При усреднении на количество наблюдений мы получаем среднюю абсолютную ошибку (mean absolute error, MAE).
$$ MAE = frac{sum{|y-Xtheta|}}{n} = frac{sum{|varepsilon|}}{n} $$
Приведем пример такой функции на Питоне.
|
def L1(y_true, y_pred): return np.sum(np.abs(y_true — y_pred)) / y_true.size |
Помимо модуля ошибку можно возводить в квадрат.
Квадрат ошибки, L2 loss
В этом случай говорят про сумму квадратов ошибок (sum of squared errors, SSE) или сумму квадратов остатков (sum of squared residuals, SSR или residual sum of squares, RSS).
$$ SSE = sum (y-Xtheta)^2 $$
Как мы уже знаем, на практике вместо SSE часто используется MSE, или вернее half MSE для удобства нахождения производной.
$$ MSE = frac{1}{2n} sum (y-theta X)^2 $$
Ниже код на Питоне.
|
def L2(y_true, y_pred): return np.sum((y_true — y_pred) ** 2) / y_true.size |
На практике у обеих функций есть сильные и слабые стороны. Рассмотрим L1 loss (MAE) и L2 loss (MSE) на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# для построения графиков мы используем x вместо y_true, y_pred # в качестве входящего значения def mse(x): return x ** 2 def mae(x): return np.abs(x) plt.figure(figsize = (10, 8)) x_vals = np.arange(—3, 3, 0.01) plt.plot(x_vals, mae(x_vals), label = ‘MAE’) plt.plot(x_vals, mse(x_vals), label = ‘MSE’) plt.legend(loc = ‘upper center’, prop = {‘size’: 14}) plt.grid() plt.show() |

Очевидно, при отклонении от точки минимума из-за возведения в квадрат L2 значительно быстрее увеличивает ошибку, поэтому если в данных есть выбросы при суммированнии они очень сильно влияют на этот показатель, хотя де-факто большая часть значений такого уровня потерь не дали бы.
Функция L1 не дает такой большой ошибки на выбросах, однако ее сложно дифференцировать, в точке минимума ее производная не определена.
Функция Хьюбера
Рассмотрим функцию Хьюбера (Huber loss), которая объединяет сильные стороны вышеупомянутых функций и при этом лишена их недостатков. Посмотрим на формулу.
$$ L_{delta}= left{begin{matrix} frac{1}{2}(y-hat{y})^{2} & if | y-hat{y} | < delta\ delta (|y-hat{y}|-frac1 2 delta) & otherwise end{matrix}right. $$
Представим ее на графике.
|
plt.figure(figsize = (10, 8)) def huber(x, delta = 1.): huber_mse = 0.5 * np.square(x) huber_mae = delta * (np.abs(x) — 0.5 * delta) return np.where(np.abs(x) <= delta, huber_mse, huber_mae) x_vals = np.arange(—3, 3, 0.01) plt.plot(x_vals, mae(x_vals), label = ‘MAE’) plt.plot(x_vals, mse(x_vals), label = ‘MSE’) plt.plot(x_vals, huber(x_vals, delta = 2), label = ‘Huber’) plt.legend(loc = ‘upper center’, prop = {‘size’: 14}) plt.grid() plt.show() |

Также приведем код этой функции.
|
def huber(y_pred, y_true, delta = 1.0): # пропишем обе части функции потерь huber_mse = 0.5 * (y_true — y_pred) ** 2 huber_mae = delta * (np.abs(y_true — y_pred) — 0.5 * delta) # выберем одну из них в зависимости от дельта return np.where(np.abs(y_true — y_pred) <= delta, huber_mse, huber_mae) |
На сегодняшнем занятии мы, как и раньше, в качестве функции потерь используем MSE.
Метод наименьших квадратов
Нормальные уравнения
Для множественной линейной регрессии коэффициенты находятся по следующей формуле
$$ theta = (X^TX)^{-1}X^Ty $$
Разберем эту формулу подробнее. Сумму квадратов остатков (SSE) можно переписать как произведение вектора $ hat{varepsilon} $ на самого себя, то есть $ SSE = varepsilon^{T} varepsilon$. Помня, что $varepsilon = y-Xtheta $ получаем (не забывая транспонировать)
$$ (y-Xtheta)^T(y-Xtheta) $$
Раскрываем скобки
$$ y^Ty-y^T(Xtheta)-(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$
Заметим, что $A^TB = B^TA$, тогда
$$ y^Ty-(Xtheta)^Ty-(Xtheta)^Ty+(Xtheta)^T(Xtheta)$$
$$ y^Ty-2(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$
Вспомним, что $(AB)^T = A^TB^T$, тогда
$$ y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$
Теперь нужно найти частные производные этих функций
$$ nabla_{theta} J(theta) = y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$
После дифференцирования мы получаем следующую производную
$$ -2X^Ty+2X^TXtheta $$
Как мы помним, оптимум функции находится там, где производная равна нулю.
$$ -2X^Ty+2X^TXtheta = 0 $$
$$ -X^Ty+X^TXtheta = 0 $$
$$ X^TXtheta = X^Ty $$
Выражение выше называется нормальным уравнением (normal equation). Решив его для $theta$ мы найдем аналитическое решение минимизации суммы квадратов отклонений.
$$ theta = (X^TX)^{-1}X^Ty $$
По теореме Гаусса-Маркова, оценка через МНК является наиболее оптимальной (обладающей наименьшей дисперсией) среди всех методов построения модели.
Код на Питоне
Перейдем к созданию класса линейной регрессии наподобие LinearRegression библиотеки sklearn. Вначале напишем функцию гипотезы (т.е. функцию самой модели), снабдив ее еще одной функцией, которая добавляет столбец из единиц к признакам.
$$ h_{theta}(x) = theta X $$
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
def h(x, theta): x = x.copy() add_ones(x) return np.dot(x, theta) |
Перейдем к функции, отвечающей за обучение модели.
$$ theta = (X^TX)^{-1}X^Ty $$
|
# строчную `x` используем внутри функций и методов класса # заглавную `X` вне функций и методов def fit(x, y): x = x.copy() add_ones(x) xT = x.transpose() inversed = np.linalg.inv(np.dot(xT, x)) thetas = inversed.dot(xT).dot(y) return thetas |
Обучим модель и выведем коэффициенты.
|
thetas = fit(X, y) thetas[0], thetas[1:] |
|
(9.3718435789647e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274])) |
Примечание. Замечу, что не все матрицы обратимы. В этом случае можно найти псевдообратную матрицу (pseudoinverse). Для этого в Numpy есть функция np.linalg.pinv().
Сделаем прогноз.
|
y_pred = h(X, thetas) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Создание класса
Объединим код в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
class ols(): def __init__(self): self.thetas = None def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def fit(self, x, y): x = x.copy() self.add_ones(x) xT = x.T inversed = np.linalg.inv(np.dot(xT, x)) self.thetas = inversed.dot(xT).dot(y) def predict(self, x): x = x.copy() self.add_ones(x) return np.dot(x, self.thetas) |
Создадим объект класса и обучим модель.
|
model = ols() model.fit(X, y) |
Выведем коэффициенты.
|
model.thetas[0], model.thetas[1:] |
|
(9.3718435789647e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274])) |
Сделаем прогноз.
|
y_pred = model.predict(X) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Оценка качества
Оценим качество через MAPE и $R^2$.
|
(0.7546883769637167, 0.7546883769637167) |
Мы видим, что результаты аналогичны.
Метод градиентного спуска
В целом с этим методом мы уже хорошо знакомы. В качестве упражнения давайте реализуем этот алгоритм на Питоне для многомерных данных.
Нахождение градиента
Покажем расчет градиента на схеме.
В данном случае мы берем датасет из четырех наблюдений и двух признаков ($x_1$ и $x_2$) и соответственно используем три коэффициента ($theta_0, theta_1, theta_2$).
Пошаговое построение модели
Начнем с функции гипотезы.
$$ h_{theta}(x) = theta X $$
|
def h(x, thetas): return np.dot(x, thetas) |
Объявим функцию потерь.
$$ J({theta_j}) = frac{1}{2n} sum (y-theta X)^2 $$
|
def objective(x, y, thetas, n): return np.sum((y — h(x, thetas)) ** 2) / (2 * n) |
Объявим функцию для расчета градиента.
$$ frac{partial}{partial theta_j} J(theta) = -x_j(y — Xtheta) times frac{1}{n} $$
где j — индекс признака.
|
def gradient(x, y, thetas, n): return np.dot(—x.T, (y — h(x, thetas))) / n |
Напишем функцию для обучения модели.
$$ theta_j := theta_j-alpha frac{partial}{partial theta_j} J(theta) $$
Символ := означает, что левая часть равенства определяется правой. По сути, с каждой итерацией мы обновляем веса, умножая коэффициент скорости обучения на градиент.
|
def fit(x, y, iter = 20000, learning_rate = 0.05): x, y = x.copy(), y.copy() # функцию add_ones() мы объявили выше add_ones(x) thetas, n = np.zeros(x.shape[1]), x.shape[0] loss_history = [] for i in range(iter): loss_history.append(objective(x, y, thetas, n)) grad = gradient(x, y, thetas, n) thetas -= learning_rate * grad return thetas, loss_history |
Обучим модель, выведем коэффициенты и достигнутый (минимальный) уровень ошибки.
|
thetas, loss_history = fit(X, y, iter = 50000, learning_rate = 0.05) |
|
thetas[0], thetas[1:], loss_history[—1] |
|
(9.493787734953824e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274]), 0.1226558115181417) |
Полученный результат очень близок к тому, что было найдено методом наименьших квадратов.
Прогноз
Сделаем прогноз.
|
def predict(x, thetas): x = x.copy() add_ones(x) return np.dot(x, thetas) |
|
y_pred = predict(X, thetas) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Создание класса
Объединим написанные функции в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
class gd(): def __init__(self): self.thetas = None self.loss_history = [] def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def objective(self, x, y, thetas, n): return np.sum((y — self.h(x, thetas)) ** 2) / (2 * n) def h(self, x, thetas): return np.dot(x, thetas) def gradient(self, x, y, thetas, n): return np.dot(—x.T, (y — self.h(x, thetas))) / n def fit(self, x, y, iter = 20000, learning_rate = 0.05): x, y = x.copy(), y.copy() self.add_ones(x) thetas, n = np.zeros(x.shape[1]), x.shape[0] # объявляем переменную loss_history (отличается от self.loss_history) loss_history = [] for i in range(iter): loss_history.append(self.objective(x, y, thetas, n)) grad = self.gradient(x, y, thetas, n) thetas -= learning_rate * grad # записываем обратно во внутренние атрибуты, чтобы передать методу .predict() self.thetas = thetas self.loss_history = loss_history def predict(self, x): x = x.copy() self.add_ones(x) return np.dot(x, self.thetas) |
Создадим объект класса, обучим модель, выведем коэффициенты и сделаем прогноз.
|
model = gd() model.fit(X, y, iter = 50000, learning_rate = 0.05) model.thetas[0], model.thetas[1:], model.loss_history[—1] |
|
(9.493787734953824e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274]), 0.1226558115181417) |
|
y_pred = model.predict(X) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Оценка качества
|
(0.7546883769637167, 0.7546883769637167) |
Теперь рассмотрим несколько дополнительных соображений, касающихся построения модели линейной регрессии.
Диагностика алгоритма
Работу алгоритма можно проверить с помощью кривой обучения (learning curve).
- Ошибка постоянно снижается
- Алгоритм остановится, после истечения заданного количества итераций
- Можно задать пороговое значение, после которого он остановится (например, $10^{-1}$)
Построим кривую обучения.
|
plt.plot(loss_history) plt.show() |
|
plt.plot(loss_history[:100]) plt.show() |
Она также позволяет выбрать адекватный коэффициент скорости обучения.
Подведем итог
Сегодня мы подробно рассмотрели модель множественной линейной регрессиии. В частности, мы поговорили про построение гипотезы, основные функции потерь, допущения модели линейной регрессии, метрики качества и диагностику модели.
Кроме того, мы узнали как изнутри устроены метод наименьших квадратов и метод градиентного спуска и построили соответствующие модели на Питоне.
Отдельно замечу, что, изучив скорректированный коэффициент детерминации, мы начали постепенно обсуждать способы усовершенствования базовых алгоритмов и метрик. На последующих занятиях мы продолжим этот путь в двух направлениях: познакомимся со способами регуляризации функции потерь и начнем создавать более сложные алгоритмы оптимизации.
Но прежде предлагаю в деталях изучить уже знакомый нам алгоритм логистической регрессии.
Дополнительные материалы к занятию.


![{displaystyle g_{text{MAPE}}(x)=arg min _{gin {mathcal {G}}}mathbb {E} left[left|{frac {g(X)-Y}{Y}}right||X=xright]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd980e3610438e202798e285c882e02dfe21d37)