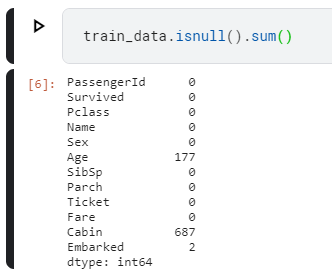
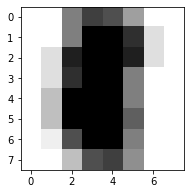There are 3 different APIs for evaluating the quality of a model’s
predictions:
-
Estimator score method: Estimators have a
scoremethod providing a
default evaluation criterion for the problem they are designed to solve.
This is not discussed on this page, but in each estimator’s documentation. -
Scoring parameter: Model-evaluation tools using
cross-validation (such as
model_selection.cross_val_scoreand
model_selection.GridSearchCV) rely on an internal scoring strategy.
This is discussed in the section The scoring parameter: defining model evaluation rules. -
Metric functions: The
sklearn.metricsmodule implements functions
assessing prediction error for specific purposes. These metrics are detailed
in sections on Classification metrics,
Multilabel ranking metrics, Regression metrics and
Clustering metrics.
Finally, Dummy estimators are useful to get a baseline
value of those metrics for random predictions.
3.3.1. The scoring parameter: defining model evaluation rules¶
Model selection and evaluation using tools, such as
model_selection.GridSearchCV and
model_selection.cross_val_score, take a scoring parameter that
controls what metric they apply to the estimators evaluated.
3.3.1.1. Common cases: predefined values¶
For the most common use cases, you can designate a scorer object with the
scoring parameter; the table below shows all possible values.
All scorer objects follow the convention that higher return values are better
than lower return values. Thus metrics which measure the distance between
the model and the data, like metrics.mean_squared_error, are
available as neg_mean_squared_error which return the negated value
of the metric.
|
Scoring |
Function |
Comment |
|---|---|---|
|
Classification |
||
|
‘accuracy’ |
|
|
|
‘balanced_accuracy’ |
|
|
|
‘top_k_accuracy’ |
|
|
|
‘average_precision’ |
|
|
|
‘neg_brier_score’ |
|
|
|
‘f1’ |
|
for binary targets |
|
‘f1_micro’ |
|
micro-averaged |
|
‘f1_macro’ |
|
macro-averaged |
|
‘f1_weighted’ |
|
weighted average |
|
‘f1_samples’ |
|
by multilabel sample |
|
‘neg_log_loss’ |
|
requires |
|
‘precision’ etc. |
|
suffixes apply as with ‘f1’ |
|
‘recall’ etc. |
|
suffixes apply as with ‘f1’ |
|
‘jaccard’ etc. |
|
suffixes apply as with ‘f1’ |
|
‘roc_auc’ |
|
|
|
‘roc_auc_ovr’ |
|
|
|
‘roc_auc_ovo’ |
|
|
|
‘roc_auc_ovr_weighted’ |
|
|
|
‘roc_auc_ovo_weighted’ |
|
|
|
Clustering |
||
|
‘adjusted_mutual_info_score’ |
|
|
|
‘adjusted_rand_score’ |
|
|
|
‘completeness_score’ |
|
|
|
‘fowlkes_mallows_score’ |
|
|
|
‘homogeneity_score’ |
|
|
|
‘mutual_info_score’ |
|
|
|
‘normalized_mutual_info_score’ |
|
|
|
‘rand_score’ |
|
|
|
‘v_measure_score’ |
|
|
|
Regression |
||
|
‘explained_variance’ |
|
|
|
‘max_error’ |
|
|
|
‘neg_mean_absolute_error’ |
|
|
|
‘neg_mean_squared_error’ |
|
|
|
‘neg_root_mean_squared_error’ |
|
|
|
‘neg_mean_squared_log_error’ |
|
|
|
‘neg_median_absolute_error’ |
|
|
|
‘r2’ |
|
|
|
‘neg_mean_poisson_deviance’ |
|
|
|
‘neg_mean_gamma_deviance’ |
|
|
|
‘neg_mean_absolute_percentage_error’ |
|
|
|
‘d2_absolute_error_score’ |
|
|
|
‘d2_pinball_score’ |
|
|
|
‘d2_tweedie_score’ |
|
Usage examples:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sklearn.metrics.get_scorer_names() to get valid options.
Note
The values listed by the ValueError exception correspond to the
functions measuring prediction accuracy described in the following
sections. You can retrieve the names of all available scorers by calling
get_scorer_names.
3.3.1.2. Defining your scoring strategy from metric functions¶
The module sklearn.metrics also exposes a set of simple functions
measuring a prediction error given ground truth and prediction:
-
functions ending with
_scorereturn a value to
maximize, the higher the better. -
functions ending with
_erroror_lossreturn a
value to minimize, the lower the better. When converting
into a scorer object usingmake_scorer, set
thegreater_is_betterparameter toFalse(Trueby default; see the
parameter description below).
Metrics available for various machine learning tasks are detailed in sections
below.
Many metrics are not given names to be used as scoring values,
sometimes because they require additional parameters, such as
fbeta_score. In such cases, you need to generate an appropriate
scoring object. The simplest way to generate a callable object for scoring
is by using make_scorer. That function converts metrics
into callables that can be used for model evaluation.
One typical use case is to wrap an existing metric function from the library
with non-default values for its parameters, such as the beta parameter for
the fbeta_score function:
>>> from sklearn.metrics import fbeta_score, make_scorer >>> ftwo_scorer = make_scorer(fbeta_score, beta=2) >>> from sklearn.model_selection import GridSearchCV >>> from sklearn.svm import LinearSVC >>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]}, ... scoring=ftwo_scorer, cv=5)
The second use case is to build a completely custom scorer object
from a simple python function using make_scorer, which can
take several parameters:
-
the python function you want to use (
my_custom_loss_func
in the example below) -
whether the python function returns a score (
greater_is_better=True,
the default) or a loss (greater_is_better=False). If a loss, the output
of the python function is negated by the scorer object, conforming to
the cross validation convention that scorers return higher values for better models. -
for classification metrics only: whether the python function you provided requires continuous decision
certainties (needs_threshold=True). The default value is
False. -
any additional parameters, such as
betaorlabelsinf1_score.
Here is an example of building custom scorers, and of using the
greater_is_better parameter:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
3.3.1.3. Implementing your own scoring object¶
You can generate even more flexible model scorers by constructing your own
scoring object from scratch, without using the make_scorer factory.
For a callable to be a scorer, it needs to meet the protocol specified by
the following two rules:
-
It can be called with parameters
(estimator, X, y), whereestimator
is the model that should be evaluated,Xis validation data, andyis
the ground truth target forX(in the supervised case) orNone(in the
unsupervised case). -
It returns a floating point number that quantifies the
estimatorprediction quality onX, with reference toy.
Again, by convention higher numbers are better, so if your scorer
returns loss, that value should be negated.
Note
Using custom scorers in functions where n_jobs > 1
While defining the custom scoring function alongside the calling function
should work out of the box with the default joblib backend (loky),
importing it from another module will be a more robust approach and work
independently of the joblib backend.
For example, to use n_jobs greater than 1 in the example below,
custom_scoring_function function is saved in a user-created module
(custom_scorer_module.py) and imported:
>>> from custom_scorer_module import custom_scoring_function >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1)
3.3.1.4. Using multiple metric evaluation¶
Scikit-learn also permits evaluation of multiple metrics in GridSearchCV,
RandomizedSearchCV and cross_validate.
There are three ways to specify multiple scoring metrics for the scoring
parameter:
-
- As an iterable of string metrics::
-
>>> scoring = ['accuracy', 'precision']
-
- As a
dictmapping the scorer name to the scoring function:: -
>>> from sklearn.metrics import accuracy_score >>> from sklearn.metrics import make_scorer >>> scoring = {'accuracy': make_scorer(accuracy_score), ... 'prec': 'precision'}
Note that the dict values can either be scorer functions or one of the
predefined metric strings. - As a
-
As a callable that returns a dictionary of scores:
>>> from sklearn.model_selection import cross_validate >>> from sklearn.metrics import confusion_matrix >>> # A sample toy binary classification dataset >>> X, y = datasets.make_classification(n_classes=2, random_state=0) >>> svm = LinearSVC(random_state=0) >>> def confusion_matrix_scorer(clf, X, y): ... y_pred = clf.predict(X) ... cm = confusion_matrix(y, y_pred) ... return {'tn': cm[0, 0], 'fp': cm[0, 1], ... 'fn': cm[1, 0], 'tp': cm[1, 1]} >>> cv_results = cross_validate(svm, X, y, cv=5, ... scoring=confusion_matrix_scorer) >>> # Getting the test set true positive scores >>> print(cv_results['test_tp']) [10 9 8 7 8] >>> # Getting the test set false negative scores >>> print(cv_results['test_fn']) [0 1 2 3 2]
3.3.2. Classification metrics¶
The sklearn.metrics module implements several loss, score, and utility
functions to measure classification performance.
Some metrics might require probability estimates of the positive class,
confidence values, or binary decisions values.
Most implementations allow each sample to provide a weighted contribution
to the overall score, through the sample_weight parameter.
Some of these are restricted to the binary classification case:
|
|
Compute precision-recall pairs for different probability thresholds. |
|
|
Compute Receiver operating characteristic (ROC). |
|
|
Compute binary classification positive and negative likelihood ratios. |
|
|
Compute error rates for different probability thresholds. |
Others also work in the multiclass case:
|
|
Compute the balanced accuracy. |
|
|
Compute Cohen’s kappa: a statistic that measures inter-annotator agreement. |
|
|
Compute confusion matrix to evaluate the accuracy of a classification. |
|
|
Average hinge loss (non-regularized). |
|
|
Compute the Matthews correlation coefficient (MCC). |
|
|
Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores. |
|
|
Top-k Accuracy classification score. |
Some also work in the multilabel case:
|
|
Accuracy classification score. |
|
|
Build a text report showing the main classification metrics. |
|
|
Compute the F1 score, also known as balanced F-score or F-measure. |
|
|
Compute the F-beta score. |
|
|
Compute the average Hamming loss. |
|
|
Jaccard similarity coefficient score. |
|
|
Log loss, aka logistic loss or cross-entropy loss. |
|
|
Compute a confusion matrix for each class or sample. |
|
|
Compute precision, recall, F-measure and support for each class. |
|
|
Compute the precision. |
|
|
Compute the recall. |
|
|
Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores. |
|
|
Zero-one classification loss. |
And some work with binary and multilabel (but not multiclass) problems:
In the following sub-sections, we will describe each of those functions,
preceded by some notes on common API and metric definition.
3.3.2.1. From binary to multiclass and multilabel¶
Some metrics are essentially defined for binary classification tasks (e.g.
f1_score, roc_auc_score). In these cases, by default
only the positive label is evaluated, assuming by default that the positive
class is labelled 1 (though this may be configurable through the
pos_label parameter).
In extending a binary metric to multiclass or multilabel problems, the data
is treated as a collection of binary problems, one for each class.
There are then a number of ways to average binary metric calculations across
the set of classes, each of which may be useful in some scenario.
Where available, you should select among these using the average parameter.
-
"macro"simply calculates the mean of the binary metrics,
giving equal weight to each class. In problems where infrequent classes
are nonetheless important, macro-averaging may be a means of highlighting
their performance. On the other hand, the assumption that all classes are
equally important is often untrue, such that macro-averaging will
over-emphasize the typically low performance on an infrequent class. -
"weighted"accounts for class imbalance by computing the average of
binary metrics in which each class’s score is weighted by its presence in the
true data sample. -
"micro"gives each sample-class pair an equal contribution to the overall
metric (except as a result of sample-weight). Rather than summing the
metric per class, this sums the dividends and divisors that make up the
per-class metrics to calculate an overall quotient.
Micro-averaging may be preferred in multilabel settings, including
multiclass classification where a majority class is to be ignored. -
"samples"applies only to multilabel problems. It does not calculate a
per-class measure, instead calculating the metric over the true and predicted
classes for each sample in the evaluation data, and returning their
(sample_weight-weighted) average. -
Selecting
average=Nonewill return an array with the score for each
class.
While multiclass data is provided to the metric, like binary targets, as an
array of class labels, multilabel data is specified as an indicator matrix,
in which cell [i, j] has value 1 if sample i has label j and value
0 otherwise.
3.3.2.2. Accuracy score¶
The accuracy_score function computes the
accuracy, either the fraction
(default) or the count (normalize=False) of correct predictions.
In multilabel classification, the function returns the subset accuracy. If
the entire set of predicted labels for a sample strictly match with the true
set of labels, then the subset accuracy is 1.0; otherwise it is 0.0.
If (hat{y}_i) is the predicted value of
the (i)-th sample and (y_i) is the corresponding true value,
then the fraction of correct predictions over (n_text{samples}) is
defined as
[texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)]
where (1(x)) is the indicator function.
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
In the multilabel case with binary label indicators:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
3.3.2.3. Top-k accuracy score¶
The top_k_accuracy_score function is a generalization of
accuracy_score. The difference is that a prediction is considered
correct as long as the true label is associated with one of the k highest
predicted scores. accuracy_score is the special case of k = 1.
The function covers the binary and multiclass classification cases but not the
multilabel case.
If (hat{f}_{i,j}) is the predicted class for the (i)-th sample
corresponding to the (j)-th largest predicted score and (y_i) is the
corresponding true value, then the fraction of correct predictions over
(n_text{samples}) is defined as
[texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)]
where (k) is the number of guesses allowed and (1(x)) is the
indicator function.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
3.3.2.4. Balanced accuracy score¶
The balanced_accuracy_score function computes the balanced accuracy, which avoids inflated
performance estimates on imbalanced datasets. It is the macro-average of recall
scores per class or, equivalently, raw accuracy where each sample is weighted
according to the inverse prevalence of its true class.
Thus for balanced datasets, the score is equal to accuracy.
In the binary case, balanced accuracy is equal to the arithmetic mean of
sensitivity
(true positive rate) and specificity (true negative
rate), or the area under the ROC curve with binary predictions rather than
scores:
[texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )]
If the classifier performs equally well on either class, this term reduces to
the conventional accuracy (i.e., the number of correct predictions divided by
the total number of predictions).
In contrast, if the conventional accuracy is above chance only because the
classifier takes advantage of an imbalanced test set, then the balanced
accuracy, as appropriate, will drop to (frac{1}{n_classes}).
The score ranges from 0 to 1, or when adjusted=True is used, it rescaled to
the range (frac{1}{1 — n_classes}) to 1, inclusive, with
performance at random scoring 0.
If (y_i) is the true value of the (i)-th sample, and (w_i)
is the corresponding sample weight, then we adjust the sample weight to:
[hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}]
where (1(x)) is the indicator function.
Given predicted (hat{y}_i) for sample (i), balanced accuracy is
defined as:
[texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i]
With adjusted=True, balanced accuracy reports the relative increase from
(texttt{balanced-accuracy}(y, mathbf{0}, w) =
frac{1}{n_classes}). In the binary case, this is also known as
*Youden’s J statistic*,
or informedness.
Note
The multiclass definition here seems the most reasonable extension of the
metric used in binary classification, though there is no certain consensus
in the literature:
-
Our definition: [Mosley2013], [Kelleher2015] and [Guyon2015], where
[Guyon2015] adopt the adjusted version to ensure that random predictions
have a score of (0) and perfect predictions have a score of (1).. -
Class balanced accuracy as described in [Mosley2013]: the minimum between the precision
and the recall for each class is computed. Those values are then averaged over the total
number of classes to get the balanced accuracy. -
Balanced Accuracy as described in [Urbanowicz2015]: the average of sensitivity and specificity
is computed for each class and then averaged over total number of classes.
3.3.2.5. Cohen’s kappa¶
The function cohen_kappa_score computes Cohen’s kappa statistic.
This measure is intended to compare labelings by different human annotators,
not a classifier versus a ground truth.
The kappa score (see docstring) is a number between -1 and 1.
Scores above .8 are generally considered good agreement;
zero or lower means no agreement (practically random labels).
Kappa scores can be computed for binary or multiclass problems,
but not for multilabel problems (except by manually computing a per-label score)
and not for more than two annotators.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
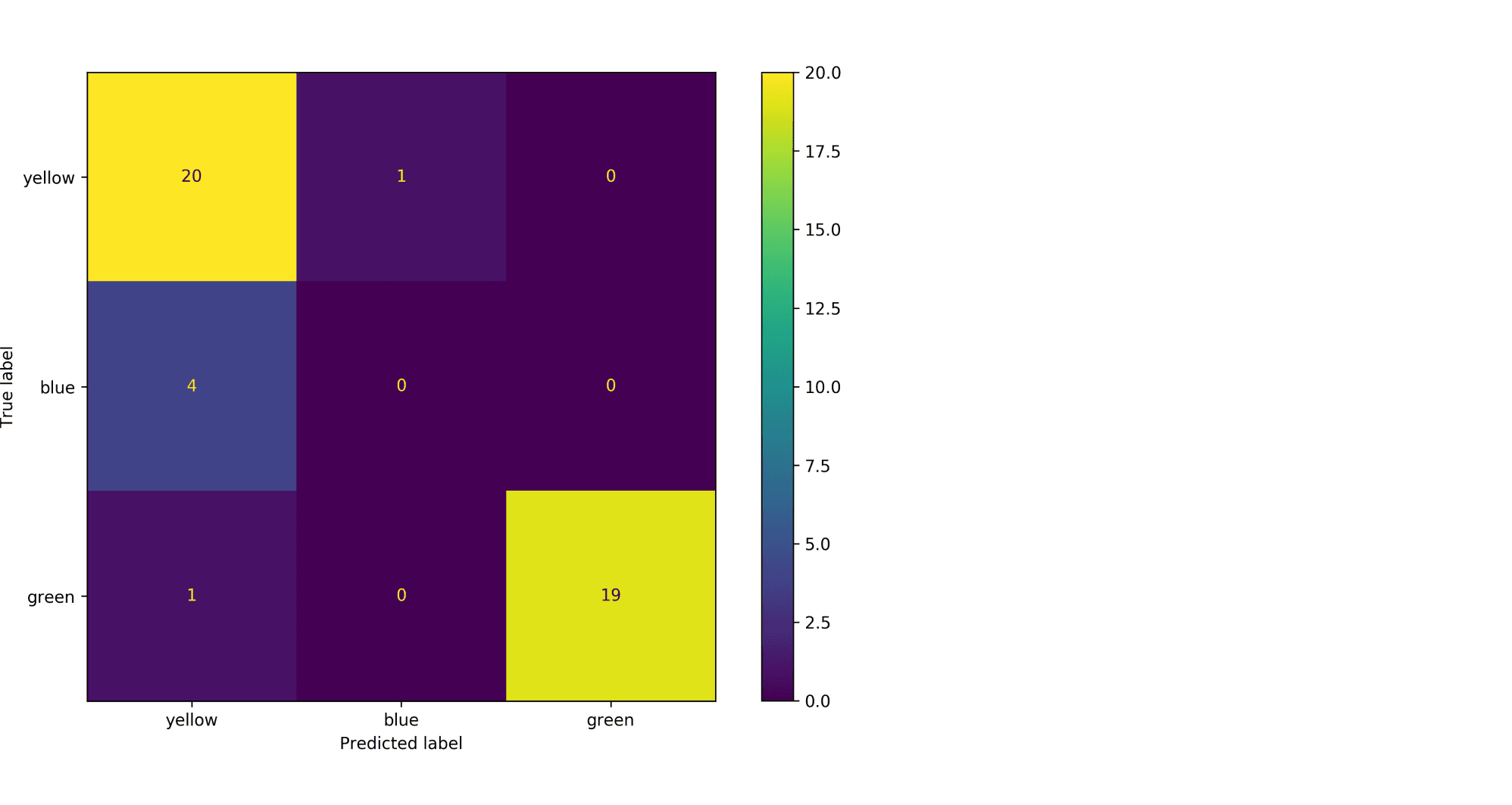
3.3.2.6. Confusion matrix¶
The confusion_matrix function evaluates
classification accuracy by computing the confusion matrix with each row corresponding
to the true class (Wikipedia and other references may use different convention
for axes).
By definition, entry (i, j) in a confusion matrix is
the number of observations actually in group (i), but
predicted to be in group (j). Here is an example:
>>> from sklearn.metrics import confusion_matrix >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> confusion_matrix(y_true, y_pred) array([[2, 0, 0], [0, 0, 1], [1, 0, 2]])
ConfusionMatrixDisplay can be used to visually represent a confusion
matrix as shown in the
Confusion matrix
example, which creates the following figure:
The parameter normalize allows to report ratios instead of counts. The
confusion matrix can be normalized in 3 different ways: 'pred', 'true',
and 'all' which will divide the counts by the sum of each columns, rows, or
the entire matrix, respectively.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> confusion_matrix(y_true, y_pred, normalize='all') array([[0.25 , 0.125], [0.25 , 0.375]])
For binary problems, we can get counts of true negatives, false positives,
false negatives and true positives as follows:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
3.3.2.7. Classification report¶
The classification_report function builds a text report showing the
main classification metrics. Here is a small example with custom target_names
and inferred labels:
>>> from sklearn.metrics import classification_report >>> y_true = [0, 1, 2, 2, 0] >>> y_pred = [0, 0, 2, 1, 0] >>> target_names = ['class 0', 'class 1', 'class 2'] >>> print(classification_report(y_true, y_pred, target_names=target_names)) precision recall f1-score support class 0 0.67 1.00 0.80 2 class 1 0.00 0.00 0.00 1 class 2 1.00 0.50 0.67 2 accuracy 0.60 5 macro avg 0.56 0.50 0.49 5 weighted avg 0.67 0.60 0.59 5
3.3.2.8. Hamming loss¶
The hamming_loss computes the average Hamming loss or Hamming
distance between two sets
of samples.
If (hat{y}_{i,j}) is the predicted value for the (j)-th label of a
given sample (i), (y_{i,j}) is the corresponding true value,
(n_text{samples}) is the number of samples and (n_text{labels})
is the number of labels, then the Hamming loss (L_{Hamming}) is defined
as:
[L_{Hamming}(y, hat{y}) = frac{1}{n_text{samples} * n_text{labels}} sum_{i=0}^{n_text{samples}-1} sum_{j=0}^{n_text{labels} — 1} 1(hat{y}_{i,j} not= y_{i,j})]
where (1(x)) is the indicator function.
The equation above does not hold true in the case of multiclass classification.
Please refer to the note below for more information.
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
In the multilabel case with binary label indicators:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Note
In multiclass classification, the Hamming loss corresponds to the Hamming
distance between y_true and y_pred which is similar to the
Zero one loss function. However, while zero-one loss penalizes
prediction sets that do not strictly match true sets, the Hamming loss
penalizes individual labels. Thus the Hamming loss, upper bounded by the zero-one
loss, is always between zero and one, inclusive; and predicting a proper subset
or superset of the true labels will give a Hamming loss between
zero and one, exclusive.
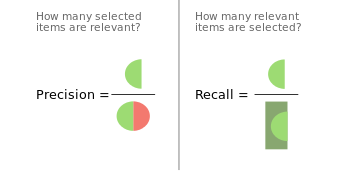
3.3.2.9. Precision, recall and F-measures¶
Intuitively, precision is the ability
of the classifier not to label as positive a sample that is negative, and
recall is the
ability of the classifier to find all the positive samples.
The F-measure
((F_beta) and (F_1) measures) can be interpreted as a weighted
harmonic mean of the precision and recall. A
(F_beta) measure reaches its best value at 1 and its worst score at 0.
With (beta = 1), (F_beta) and
(F_1) are equivalent, and the recall and the precision are equally important.
The precision_recall_curve computes a precision-recall curve
from the ground truth label and a score given by the classifier
by varying a decision threshold.
The average_precision_score function computes the
average precision
(AP) from prediction scores. The value is between 0 and 1 and higher is better.
AP is defined as
[text{AP} = sum_n (R_n — R_{n-1}) P_n]
where (P_n) and (R_n) are the precision and recall at the
nth threshold. With random predictions, the AP is the fraction of positive
samples.
References [Manning2008] and [Everingham2010] present alternative variants of
AP that interpolate the precision-recall curve. Currently,
average_precision_score does not implement any interpolated variant.
References [Davis2006] and [Flach2015] describe why a linear interpolation of
points on the precision-recall curve provides an overly-optimistic measure of
classifier performance. This linear interpolation is used when computing area
under the curve with the trapezoidal rule in auc.
Several functions allow you to analyze the precision, recall and F-measures
score:
|
|
Compute average precision (AP) from prediction scores. |
|
|
Compute the F1 score, also known as balanced F-score or F-measure. |
|
|
Compute the F-beta score. |
|
|
Compute precision-recall pairs for different probability thresholds. |
|
|
Compute precision, recall, F-measure and support for each class. |
|
|
Compute the precision. |
|
|
Compute the recall. |
Note that the precision_recall_curve function is restricted to the
binary case. The average_precision_score function works only in
binary classification and multilabel indicator format.
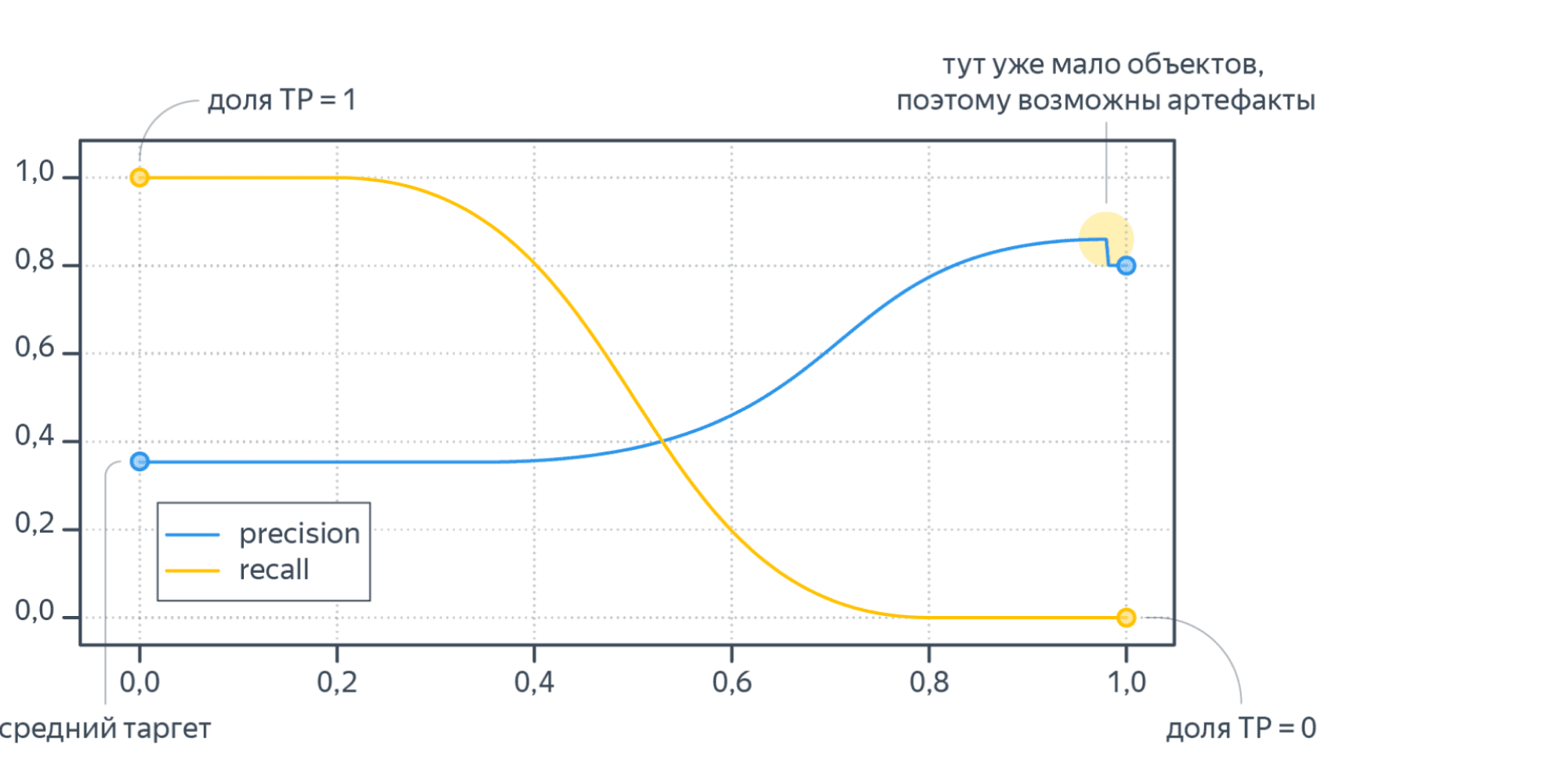
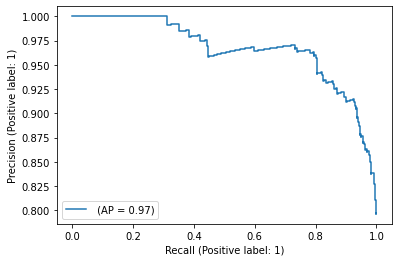
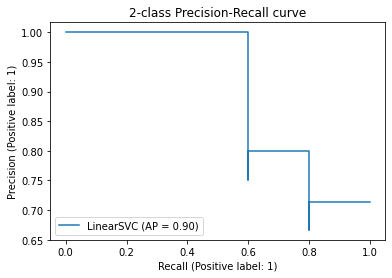
The PredictionRecallDisplay.from_estimator and
PredictionRecallDisplay.from_predictions functions will plot the
precision-recall curve as follows.
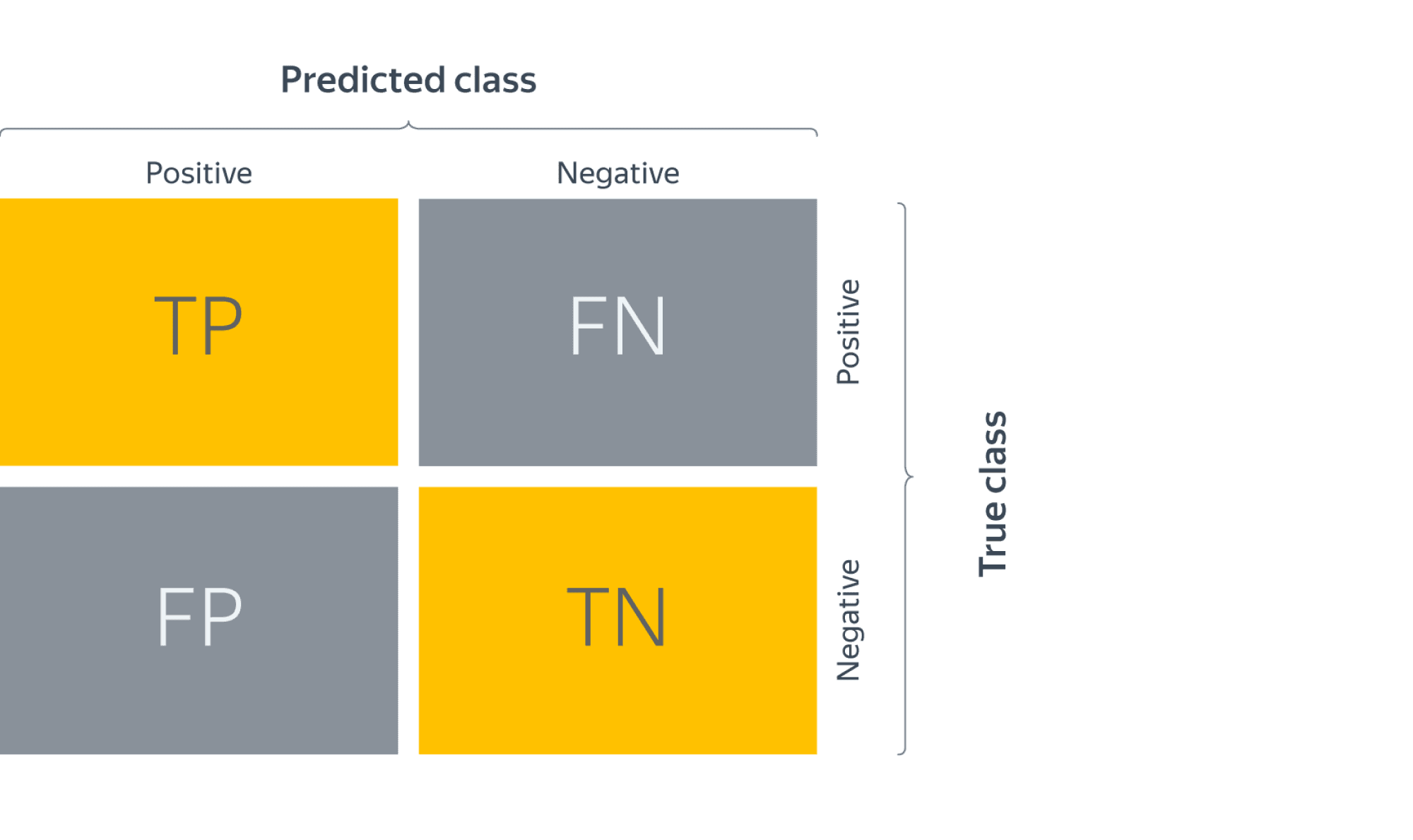
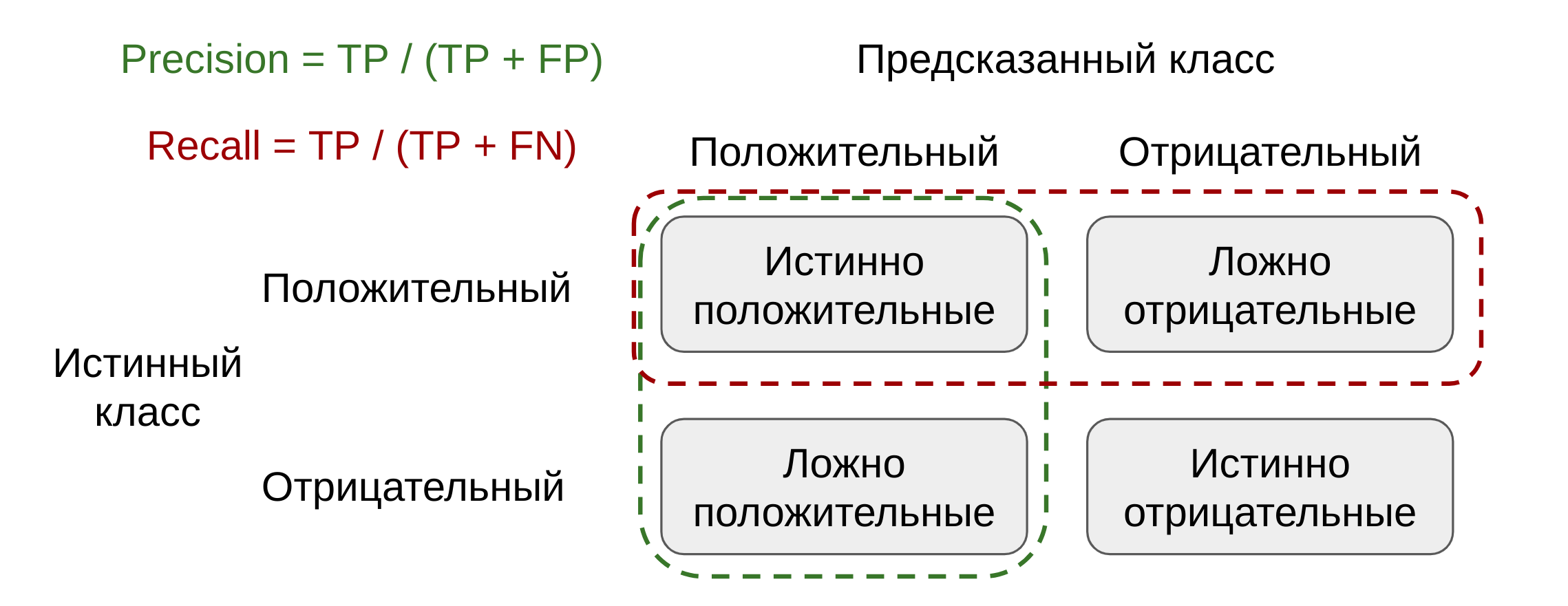
3.3.2.9.1. Binary classification¶
In a binary classification task, the terms ‘’positive’’ and ‘’negative’’ refer
to the classifier’s prediction, and the terms ‘’true’’ and ‘’false’’ refer to
whether that prediction corresponds to the external judgment (sometimes known
as the ‘’observation’’). Given these definitions, we can formulate the
following table:
|
Actual class (observation) |
||
|
Predicted class |
tp (true positive) |
fp (false positive) |
|
fn (false negative) |
tn (true negative) |
In this context, we can define the notions of precision, recall and F-measure:
[text{precision} = frac{tp}{tp + fp},]
[text{recall} = frac{tp}{tp + fn},]
[F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.]
Sometimes recall is also called ‘’sensitivity’’.
Here are some small examples in binary classification:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.5 , 0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 1. , 0.5, 0.5, 0. ]) >>> threshold array([0.1 , 0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
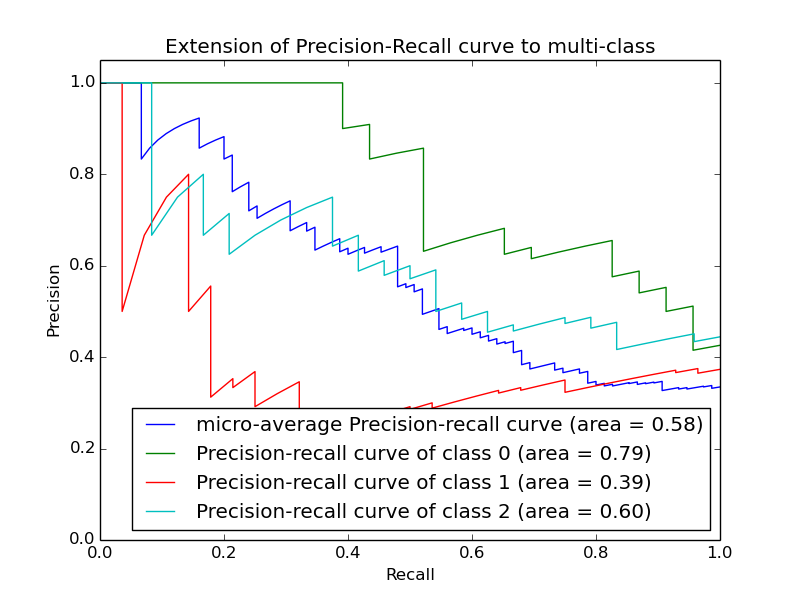
3.3.2.9.2. Multiclass and multilabel classification¶
In a multiclass and multilabel classification task, the notions of precision,
recall, and F-measures can be applied to each label independently.
There are a few ways to combine results across labels,
specified by the average argument to the
average_precision_score (multilabel only), f1_score,
fbeta_score, precision_recall_fscore_support,
precision_score and recall_score functions, as described
above. Note that if all labels are included, “micro”-averaging
in a multiclass setting will produce precision, recall and (F)
that are all identical to accuracy. Also note that “weighted” averaging may
produce an F-score that is not between precision and recall.
To make this more explicit, consider the following notation:
-
(y) the set of true ((sample, label)) pairs
-
(hat{y}) the set of predicted ((sample, label)) pairs
-
(L) the set of labels
-
(S) the set of samples
-
(y_s) the subset of (y) with sample (s),
i.e. (y_s := left{(s’, l) in y | s’ = sright}) -
(y_l) the subset of (y) with label (l)
-
similarly, (hat{y}_s) and (hat{y}_l) are subsets of
(hat{y}) -
(P(A, B) := frac{left| A cap B right|}{left|Bright|}) for some
sets (A) and (B) -
(R(A, B) := frac{left| A cap B right|}{left|Aright|})
(Conventions vary on handling (A = emptyset); this implementation uses
(R(A, B):=0), and similar for (P).) -
(F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)})
Then the metrics are defined as:
|
|
Precision |
Recall |
F_beta |
|---|---|---|---|
|
|
(P(y, hat{y})) |
(R(y, hat{y})) |
(F_beta(y, hat{y})) |
|
|
(frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s)) |
(frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s)) |
(frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s)) |
|
|
(frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l)) |
(frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l)) |
(frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l)) |
|
|
(frac{1}{sum_{l in L} left|y_lright|} sum_{l in L} left|y_lright| P(y_l, hat{y}_l)) |
(frac{1}{sum_{l in L} left|y_lright|} sum_{l in L} left|y_lright| R(y_l, hat{y}_l)) |
(frac{1}{sum_{l in L} left|y_lright|} sum_{l in L} left|y_lright| F_beta(y_l, hat{y}_l)) |
|
|
(langle P(y_l, hat{y}_l) | l in L rangle) |
(langle R(y_l, hat{y}_l) | l in L rangle) |
(langle F_beta(y_l, hat{y}_l) | l in L rangle) |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
For multiclass classification with a “negative class”, it is possible to exclude some labels:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Similarly, labels not present in the data sample may be accounted for in macro-averaging.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
3.3.2.10. Jaccard similarity coefficient score¶
The jaccard_score function computes the average of Jaccard similarity
coefficients, also called the
Jaccard index, between pairs of label sets.
The Jaccard similarity coefficient with a ground truth label set (y) and
predicted label set (hat{y}), is defined as
[J(y, hat{y}) = frac{|y cap hat{y}|}{|y cup hat{y}|}.]
The jaccard_score (like precision_recall_fscore_support) applies
natively to binary targets. By computing it set-wise it can be extended to apply
to multilabel and multiclass through the use of average (see
above).
In the binary case:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
In the 2D comparison case (e.g. image similarity):
>>> jaccard_score(y_true, y_pred, average="micro") 0.6
In the multilabel case with binary label indicators:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Multiclass problems are binarized and treated like the corresponding
multilabel problem:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
3.3.2.11. Hinge loss¶
The hinge_loss function computes the average distance between
the model and the data using
hinge loss, a one-sided metric
that considers only prediction errors. (Hinge
loss is used in maximal margin classifiers such as support vector machines.)
If the true label (y_i) of a binary classification task is encoded as
(y_i=left{-1, +1right}) for every sample (i); and (w_i)
is the corresponding predicted decision (an array of shape (n_samples,) as
output by the decision_function method), then the hinge loss is defined as:
[L_text{Hinge}(y, w) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} maxleft{1 — w_i y_i, 0right}]
If there are more than two labels, hinge_loss uses a multiclass variant
due to Crammer & Singer.
Here is
the paper describing it.
In this case the predicted decision is an array of shape (n_samples,
n_labels). If (w_{i, y_i}) is the predicted decision for the true label
(y_i) of the (i)-th sample; and
(hat{w}_{i, y_i} = maxleft{w_{i, y_j}~|~y_j ne y_i right})
is the maximum of the
predicted decisions for all the other labels, then the multi-class hinge loss
is defined by:
[L_text{Hinge}(y, w) = frac{1}{n_text{samples}}
sum_{i=0}^{n_text{samples}-1} maxleft{1 + hat{w}_{i, y_i}
— w_{i, y_i}, 0right}]
Here is a small example demonstrating the use of the hinge_loss function
with a svm classifier in a binary class problem:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Here is an example demonstrating the use of the hinge_loss function
with a svm classifier in a multiclass problem:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels=labels) 0.56...
3.3.2.12. Log loss¶
Log loss, also called logistic regression loss or
cross-entropy loss, is defined on probability estimates. It is
commonly used in (multinomial) logistic regression and neural networks, as well
as in some variants of expectation-maximization, and can be used to evaluate the
probability outputs (predict_proba) of a classifier instead of its
discrete predictions.
For binary classification with a true label (y in {0,1})
and a probability estimate (p = operatorname{Pr}(y = 1)),
the log loss per sample is the negative log-likelihood
of the classifier given the true label:
[L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 — y) log (1 — p))]
This extends to the multiclass case as follows.
Let the true labels for a set of samples
be encoded as a 1-of-K binary indicator matrix (Y),
i.e., (y_{i,k} = 1) if sample (i) has label (k)
taken from a set of (K) labels.
Let (P) be a matrix of probability estimates,
with (p_{i,k} = operatorname{Pr}(y_{i,k} = 1)).
Then the log loss of the whole set is
[L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = — frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}]
To see how this generalizes the binary log loss given above,
note that in the binary case,
(p_{i,0} = 1 — p_{i,1}) and (y_{i,0} = 1 — y_{i,1}),
so expanding the inner sum over (y_{i,k} in {0,1})
gives the binary log loss.
The log_loss function computes log loss given a list of ground-truth
labels and a probability matrix, as returned by an estimator’s predict_proba
method.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
The first [.9, .1] in y_pred denotes 90% probability that the first
sample has label 0. The log loss is non-negative.
3.3.2.13. Matthews correlation coefficient¶
The matthews_corrcoef function computes the
Matthew’s correlation coefficient (MCC)
for binary classes. Quoting Wikipedia:
“The Matthews correlation coefficient is used in machine learning as a
measure of the quality of binary (two-class) classifications. It takes
into account true and false positives and negatives and is generally
regarded as a balanced measure which can be used even if the classes are
of very different sizes. The MCC is in essence a correlation coefficient
value between -1 and +1. A coefficient of +1 represents a perfect
prediction, 0 an average random prediction and -1 an inverse prediction.
The statistic is also known as the phi coefficient.”
In the binary (two-class) case, (tp), (tn), (fp) and
(fn) are respectively the number of true positives, true negatives, false
positives and false negatives, the MCC is defined as
[MCC = frac{tp times tn — fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.]
In the multiclass case, the Matthews correlation coefficient can be defined in terms of a
confusion_matrix (C) for (K) classes. To simplify the
definition consider the following intermediate variables:
-
(t_k=sum_{i}^{K} C_{ik}) the number of times class (k) truly occurred,
-
(p_k=sum_{i}^{K} C_{ki}) the number of times class (k) was predicted,
-
(c=sum_{k}^{K} C_{kk}) the total number of samples correctly predicted,
-
(s=sum_{i}^{K} sum_{j}^{K} C_{ij}) the total number of samples.
Then the multiclass MCC is defined as:
[MCC = frac{
c times s — sum_{k}^{K} p_k times t_k
}{sqrt{
(s^2 — sum_{k}^{K} p_k^2) times
(s^2 — sum_{k}^{K} t_k^2)
}}]
When there are more than two labels, the value of the MCC will no longer range
between -1 and +1. Instead the minimum value will be somewhere between -1 and 0
depending on the number and distribution of ground true labels. The maximum
value is always +1.
Here is a small example illustrating the usage of the matthews_corrcoef
function:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
3.3.2.14. Multi-label confusion matrix¶
The multilabel_confusion_matrix function computes class-wise (default)
or sample-wise (samplewise=True) multilabel confusion matrix to evaluate
the accuracy of a classification. multilabel_confusion_matrix also treats
multiclass data as if it were multilabel, as this is a transformation commonly
applied to evaluate multiclass problems with binary classification metrics
(such as precision, recall, etc.).
When calculating class-wise multilabel confusion matrix (C), the
count of true negatives for class (i) is (C_{i,0,0}), false
negatives is (C_{i,1,0}), true positives is (C_{i,1,1})
and false positives is (C_{i,0,1}).
Here is an example demonstrating the use of the
multilabel_confusion_matrix function with
multilabel indicator matrix input:
>>> import numpy as np >>> from sklearn.metrics import multilabel_confusion_matrix >>> y_true = np.array([[1, 0, 1], ... [0, 1, 0]]) >>> y_pred = np.array([[1, 0, 0], ... [0, 1, 1]]) >>> multilabel_confusion_matrix(y_true, y_pred) array([[[1, 0], [0, 1]], [[1, 0], [0, 1]], [[0, 1], [1, 0]]])
Or a confusion matrix can be constructed for each sample’s labels:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True) array([[[1, 0], [1, 1]], [[1, 1], [0, 1]]])
Here is an example demonstrating the use of the
multilabel_confusion_matrix function with
multiclass input:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"] >>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"] >>> multilabel_confusion_matrix(y_true, y_pred, ... labels=["ant", "bird", "cat"]) array([[[3, 1], [0, 2]], [[5, 0], [1, 0]], [[2, 1], [1, 2]]])
Here are some examples demonstrating the use of the
multilabel_confusion_matrix function to calculate recall
(or sensitivity), specificity, fall out and miss rate for each class in a
problem with multilabel indicator matrix input.
Calculating
recall
(also called the true positive rate or the sensitivity) for each class:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Calculating
specificity
(also called the true negative rate) for each class:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Calculating fall out
(also called the false positive rate) for each class:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Calculating miss rate
(also called the false negative rate) for each class:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
3.3.2.15. Receiver operating characteristic (ROC)¶
The function roc_curve computes the
receiver operating characteristic curve, or ROC curve.
Quoting Wikipedia :
“A receiver operating characteristic (ROC), or simply ROC curve, is a
graphical plot which illustrates the performance of a binary classifier
system as its discrimination threshold is varied. It is created by plotting
the fraction of true positives out of the positives (TPR = true positive
rate) vs. the fraction of false positives out of the negatives (FPR = false
positive rate), at various threshold settings. TPR is also known as
sensitivity, and FPR is one minus the specificity or true negative rate.”
This function requires the true binary value and the target scores, which can
either be probability estimates of the positive class, confidence values, or
binary decisions. Here is a small example of how to use the roc_curve
function:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
Compared to metrics such as the subset accuracy, the Hamming loss, or the
F1 score, ROC doesn’t require optimizing a threshold for each label.
The roc_auc_score function, denoted by ROC-AUC or AUROC, computes the
area under the ROC curve. By doing so, the curve information is summarized in
one number.
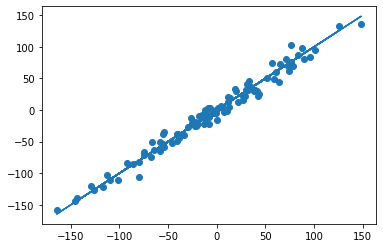
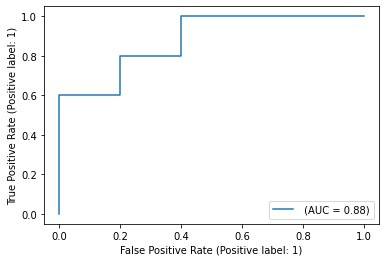
The following figure shows the ROC curve and ROC-AUC score for a classifier
aimed to distinguish the virginica flower from the rest of the species in the
Iris plants dataset:
For more information see the Wikipedia article on AUC.
3.3.2.15.1. Binary case¶
In the binary case, you can either provide the probability estimates, using
the classifier.predict_proba() method, or the non-thresholded decision values
given by the classifier.decision_function() method. In the case of providing
the probability estimates, the probability of the class with the
“greater label” should be provided. The “greater label” corresponds to
classifier.classes_[1] and thus classifier.predict_proba(X)[:, 1].
Therefore, the y_score parameter is of size (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
We can use the probability estimates corresponding to clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
Otherwise, we can use the non-thresholded decision values
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
3.3.2.15.2. Multi-class case¶
The roc_auc_score function can also be used in multi-class
classification. Two averaging strategies are currently supported: the
one-vs-one algorithm computes the average of the pairwise ROC AUC scores, and
the one-vs-rest algorithm computes the average of the ROC AUC scores for each
class against all other classes. In both cases, the predicted labels are
provided in an array with values from 0 to n_classes, and the scores
correspond to the probability estimates that a sample belongs to a particular
class. The OvO and OvR algorithms support weighting uniformly
(average='macro') and by prevalence (average='weighted').
One-vs-one Algorithm: Computes the average AUC of all possible pairwise
combinations of classes. [HT2001] defines a multiclass AUC metric weighted
uniformly:
[frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) +
text{AUC}(k | j))]
where (c) is the number of classes and (text{AUC}(j | k)) is the
AUC with class (j) as the positive class and class (k) as the
negative class. In general,
(text{AUC}(j | k) neq text{AUC}(k | j))) in the multiclass
case. This algorithm is used by setting the keyword argument multiclass
to 'ovo' and average to 'macro'.
The [HT2001] multiclass AUC metric can be extended to be weighted by the
prevalence:
[frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)(
text{AUC}(j | k) + text{AUC}(k | j))]
where (c) is the number of classes. This algorithm is used by setting
the keyword argument multiclass to 'ovo' and average to
'weighted'. The 'weighted' option returns a prevalence-weighted average
as described in [FC2009].
One-vs-rest Algorithm: Computes the AUC of each class against the rest
[PD2000]. The algorithm is functionally the same as the multilabel case. To
enable this algorithm set the keyword argument multiclass to 'ovr'.
Additionally to 'macro' [F2006] and 'weighted' [F2001] averaging, OvR
supports 'micro' averaging.
In applications where a high false positive rate is not tolerable the parameter
max_fpr of roc_auc_score can be used to summarize the ROC curve up
to the given limit.
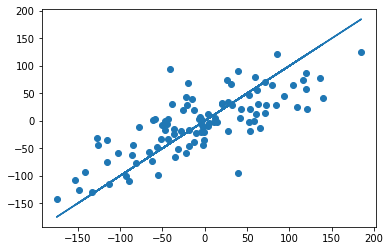
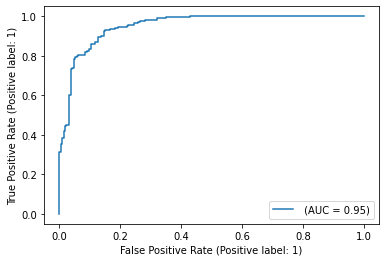
The following figure shows the micro-averaged ROC curve and its corresponding
ROC-AUC score for a classifier aimed to distinguish the the different species in
the Iris plants dataset:
3.3.2.15.3. Multi-label case¶
In multi-label classification, the roc_auc_score function is
extended by averaging over the labels as above. In this case,
you should provide a y_score of shape (n_samples, n_classes). Thus, when
using the probability estimates, one needs to select the probability of the
class with the greater label for each output.
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
And the decision values do not require such processing.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
3.3.2.16. Detection error tradeoff (DET)¶
The function det_curve computes the
detection error tradeoff curve (DET) curve [WikipediaDET2017].
Quoting Wikipedia:
“A detection error tradeoff (DET) graph is a graphical plot of error rates
for binary classification systems, plotting false reject rate vs. false
accept rate. The x- and y-axes are scaled non-linearly by their standard
normal deviates (or just by logarithmic transformation), yielding tradeoff
curves that are more linear than ROC curves, and use most of the image area
to highlight the differences of importance in the critical operating region.”
DET curves are a variation of receiver operating characteristic (ROC) curves
where False Negative Rate is plotted on the y-axis instead of True Positive
Rate.
DET curves are commonly plotted in normal deviate scale by transformation with
(phi^{-1}) (with (phi) being the cumulative distribution
function).
The resulting performance curves explicitly visualize the tradeoff of error
types for given classification algorithms.
See [Martin1997] for examples and further motivation.
This figure compares the ROC and DET curves of two example classifiers on the
same classification task:
Properties:
-
DET curves form a linear curve in normal deviate scale if the detection
scores are normally (or close-to normally) distributed.
It was shown by [Navratil2007] that the reverse is not necessarily true and
even more general distributions are able to produce linear DET curves. -
The normal deviate scale transformation spreads out the points such that a
comparatively larger space of plot is occupied.
Therefore curves with similar classification performance might be easier to
distinguish on a DET plot. -
With False Negative Rate being “inverse” to True Positive Rate the point
of perfection for DET curves is the origin (in contrast to the top left
corner for ROC curves).
Applications and limitations:
DET curves are intuitive to read and hence allow quick visual assessment of a
classifier’s performance.
Additionally DET curves can be consulted for threshold analysis and operating
point selection.
This is particularly helpful if a comparison of error types is required.
On the other hand DET curves do not provide their metric as a single number.
Therefore for either automated evaluation or comparison to other
classification tasks metrics like the derived area under ROC curve might be
better suited.
3.3.2.17. Zero one loss¶
The zero_one_loss function computes the sum or the average of the 0-1
classification loss ((L_{0-1})) over (n_{text{samples}}). By
default, the function normalizes over the sample. To get the sum of the
(L_{0-1}), set normalize to False.
In multilabel classification, the zero_one_loss scores a subset as
one if its labels strictly match the predictions, and as a zero if there
are any errors. By default, the function returns the percentage of imperfectly
predicted subsets. To get the count of such subsets instead, set
normalize to False
If (hat{y}_i) is the predicted value of
the (i)-th sample and (y_i) is the corresponding true value,
then the 0-1 loss (L_{0-1}) is defined as:
[L_{0-1}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i not= y_i)]
where (1(x)) is the indicator function. The zero one
loss can also be computed as (zero-one loss = 1 — accuracy).
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
In the multilabel case with binary label indicators, where the first label
set [0,1] has an error:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
3.3.2.18. Brier score loss¶
The brier_score_loss function computes the
Brier score
for binary classes [Brier1950]. Quoting Wikipedia:
“The Brier score is a proper score function that measures the accuracy of
probabilistic predictions. It is applicable to tasks in which predictions
must assign probabilities to a set of mutually exclusive discrete outcomes.”
This function returns the mean squared error of the actual outcome
(y in {0,1}) and the predicted probability estimate
(p = operatorname{Pr}(y = 1)) (predict_proba) as outputted by:
[BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1}(y_i — p_i)^2]
The Brier score loss is also between 0 to 1 and the lower the value (the mean
square difference is smaller), the more accurate the prediction is.
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
The Brier score can be used to assess how well a classifier is calibrated.
However, a lower Brier score loss does not always mean a better calibration.
This is because, by analogy with the bias-variance decomposition of the mean
squared error, the Brier score loss can be decomposed as the sum of calibration
loss and refinement loss [Bella2012]. Calibration loss is defined as the mean
squared deviation from empirical probabilities derived from the slope of ROC
segments. Refinement loss can be defined as the expected optimal loss as
measured by the area under the optimal cost curve. Refinement loss can change
independently from calibration loss, thus a lower Brier score loss does not
necessarily mean a better calibrated model. “Only when refinement loss remains
the same does a lower Brier score loss always mean better calibration”
[Bella2012], [Flach2008].
3.3.2.19. Class likelihood ratios¶
The class_likelihood_ratios function computes the positive and negative
likelihood ratios
(LR_pm) for binary classes, which can be interpreted as the ratio of
post-test to pre-test odds as explained below. As a consequence, this metric is
invariant w.r.t. the class prevalence (the number of samples in the positive
class divided by the total number of samples) and can be extrapolated between
populations regardless of any possible class imbalance.
The (LR_pm) metrics are therefore very useful in settings where the data
available to learn and evaluate a classifier is a study population with nearly
balanced classes, such as a case-control study, while the target application,
i.e. the general population, has very low prevalence.
The positive likelihood ratio (LR_+) is the probability of a classifier to
correctly predict that a sample belongs to the positive class divided by the
probability of predicting the positive class for a sample belonging to the
negative class:
[LR_+ = frac{text{PR}(P+|T+)}{text{PR}(P+|T-)}.]
The notation here refers to predicted ((P)) or true ((T)) label and
the sign (+) and (-) refer to the positive and negative class,
respectively, e.g. (P+) stands for “predicted positive”.
Analogously, the negative likelihood ratio (LR_-) is the probability of a
sample of the positive class being classified as belonging to the negative class
divided by the probability of a sample of the negative class being correctly
classified:
[LR_- = frac{text{PR}(P-|T+)}{text{PR}(P-|T-)}.]
For classifiers above chance (LR_+) above 1 higher is better, while
(LR_-) ranges from 0 to 1 and lower is better.
Values of (LR_pmapprox 1) correspond to chance level.
Notice that probabilities differ from counts, for instance
(operatorname{PR}(P+|T+)) is not equal to the number of true positive
counts tp (see the wikipedia page for
the actual formulas).
Interpretation across varying prevalence:
Both class likelihood ratios are interpretable in terms of an odds ratio
(pre-test and post-tests):
[text{post-test odds} = text{Likelihood ratio} times text{pre-test odds}.]
Odds are in general related to probabilities via
[text{odds} = frac{text{probability}}{1 — text{probability}},]
or equivalently
[text{probability} = frac{text{odds}}{1 + text{odds}}.]
On a given population, the pre-test probability is given by the prevalence. By
converting odds to probabilities, the likelihood ratios can be translated into a
probability of truly belonging to either class before and after a classifier
prediction:
[text{post-test odds} = text{Likelihood ratio} times
frac{text{pre-test probability}}{1 — text{pre-test probability}},]
[text{post-test probability} = frac{text{post-test odds}}{1 + text{post-test odds}}.]
Mathematical divergences:
The positive likelihood ratio is undefined when (fp = 0), which can be
interpreted as the classifier perfectly identifying positive cases. If (fp
= 0) and additionally (tp = 0), this leads to a zero/zero division. This
happens, for instance, when using a DummyClassifier that always predicts the
negative class and therefore the interpretation as a perfect classifier is lost.
The negative likelihood ratio is undefined when (tn = 0). Such divergence
is invalid, as (LR_- > 1) would indicate an increase in the odds of a
sample belonging to the positive class after being classified as negative, as if
the act of classifying caused the positive condition. This includes the case of
a DummyClassifier that always predicts the positive class (i.e. when
(tn=fn=0)).
Both class likelihood ratios are undefined when (tp=fn=0), which means
that no samples of the positive class were present in the testing set. This can
also happen when cross-validating highly imbalanced data.
In all the previous cases the class_likelihood_ratios function raises by
default an appropriate warning message and returns nan to avoid pollution when
averaging over cross-validation folds.
For a worked-out demonstration of the class_likelihood_ratios function,
see the example below.
3.3.3. Multilabel ranking metrics¶
In multilabel learning, each sample can have any number of ground truth labels
associated with it. The goal is to give high scores and better rank to
the ground truth labels.
3.3.3.1. Coverage error¶
The coverage_error function computes the average number of labels that
have to be included in the final prediction such that all true labels
are predicted. This is useful if you want to know how many top-scored-labels
you have to predict in average without missing any true one. The best value
of this metrics is thus the average number of true labels.
Note
Our implementation’s score is 1 greater than the one given in Tsoumakas
et al., 2010. This extends it to handle the degenerate case in which an
instance has 0 true labels.
Formally, given a binary indicator matrix of the ground truth labels
(y in left{0, 1right}^{n_text{samples} times n_text{labels}}) and the
score associated with each label
(hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}),
the coverage is defined as
[coverage(y, hat{f}) = frac{1}{n_{text{samples}}}
sum_{i=0}^{n_{text{samples}} — 1} max_{j:y_{ij} = 1} text{rank}_{ij}]
with (text{rank}_{ij} = left|left{k: hat{f}_{ik} geq hat{f}_{ij} right}right|).
Given the rank definition, ties in y_scores are broken by giving the
maximal rank that would have been assigned to all tied values.
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
3.3.3.2. Label ranking average precision¶
The label_ranking_average_precision_score function
implements label ranking average precision (LRAP). This metric is linked to
the average_precision_score function, but is based on the notion of
label ranking instead of precision and recall.
Label ranking average precision (LRAP) averages over the samples the answer to
the following question: for each ground truth label, what fraction of
higher-ranked labels were true labels? This performance measure will be higher
if you are able to give better rank to the labels associated with each sample.
The obtained score is always strictly greater than 0, and the best value is 1.
If there is exactly one relevant label per sample, label ranking average
precision is equivalent to the mean
reciprocal rank.
Formally, given a binary indicator matrix of the ground truth labels
(y in left{0, 1right}^{n_text{samples} times n_text{labels}})
and the score associated with each label
(hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}),
the average precision is defined as
[LRAP(y, hat{f}) = frac{1}{n_{text{samples}}}
sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||_0}
sum_{j:y_{ij} = 1} frac{|mathcal{L}_{ij}|}{text{rank}_{ij}}]
where
(mathcal{L}_{ij} = left{k: y_{ik} = 1, hat{f}_{ik} geq hat{f}_{ij} right}),
(text{rank}_{ij} = left|left{k: hat{f}_{ik} geq hat{f}_{ij} right}right|),
(|cdot|) computes the cardinality of the set (i.e., the number of
elements in the set), and (||cdot||_0) is the (ell_0) “norm”
(which computes the number of nonzero elements in a vector).
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
3.3.3.3. Ranking loss¶
The label_ranking_loss function computes the ranking loss which
averages over the samples the number of label pairs that are incorrectly
ordered, i.e. true labels have a lower score than false labels, weighted by
the inverse of the number of ordered pairs of false and true labels.
The lowest achievable ranking loss is zero.
Formally, given a binary indicator matrix of the ground truth labels
(y in left{0, 1right}^{n_text{samples} times n_text{labels}}) and the
score associated with each label
(hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}),
the ranking loss is defined as
[ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}}
sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||_0(n_text{labels} — ||y_i||_0)}
left|left{(k, l): hat{f}_{ik} leq hat{f}_{il}, y_{ik} = 1, y_{il} = 0 right}right|]
where (|cdot|) computes the cardinality of the set (i.e., the number of
elements in the set) and (||cdot||_0) is the (ell_0) “norm”
(which computes the number of nonzero elements in a vector).
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
3.3.3.4. Normalized Discounted Cumulative Gain¶
Discounted Cumulative Gain (DCG) and Normalized Discounted Cumulative Gain
(NDCG) are ranking metrics implemented in dcg_score
and ndcg_score ; they compare a predicted order to
ground-truth scores, such as the relevance of answers to a query.
From the Wikipedia page for Discounted Cumulative Gain:
“Discounted cumulative gain (DCG) is a measure of ranking quality. In
information retrieval, it is often used to measure effectiveness of web search
engine algorithms or related applications. Using a graded relevance scale of
documents in a search-engine result set, DCG measures the usefulness, or gain,
of a document based on its position in the result list. The gain is accumulated
from the top of the result list to the bottom, with the gain of each result
discounted at lower ranks”
DCG orders the true targets (e.g. relevance of query answers) in the predicted
order, then multiplies them by a logarithmic decay and sums the result. The sum
can be truncated after the first (K) results, in which case we call it
DCG@K.
NDCG, or NDCG@K is DCG divided by the DCG obtained by a perfect prediction, so
that it is always between 0 and 1. Usually, NDCG is preferred to DCG.
Compared with the ranking loss, NDCG can take into account relevance scores,
rather than a ground-truth ranking. So if the ground-truth consists only of an
ordering, the ranking loss should be preferred; if the ground-truth consists of
actual usefulness scores (e.g. 0 for irrelevant, 1 for relevant, 2 for very
relevant), NDCG can be used.
For one sample, given the vector of continuous ground-truth values for each
target (y in mathbb{R}^{M}), where (M) is the number of outputs, and
the prediction (hat{y}), which induces the ranking function (f), the
DCG score is
[sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}]
and the NDCG score is the DCG score divided by the DCG score obtained for
(y).
3.3.4. Regression metrics¶
The sklearn.metrics module implements several loss, score, and utility
functions to measure regression performance. Some of those have been enhanced
to handle the multioutput case: mean_squared_error,
mean_absolute_error, r2_score,
explained_variance_score, mean_pinball_loss, d2_pinball_score
and d2_absolute_error_score.
These functions have a multioutput keyword argument which specifies the
way the scores or losses for each individual target should be averaged. The
default is 'uniform_average', which specifies a uniformly weighted mean
over outputs. If an ndarray of shape (n_outputs,) is passed, then its
entries are interpreted as weights and an according weighted average is
returned. If multioutput is 'raw_values', then all unaltered
individual scores or losses will be returned in an array of shape
(n_outputs,).
The r2_score and explained_variance_score accept an additional
value 'variance_weighted' for the multioutput parameter. This option
leads to a weighting of each individual score by the variance of the
corresponding target variable. This setting quantifies the globally captured
unscaled variance. If the target variables are of different scale, then this
score puts more importance on explaining the higher variance variables.
multioutput='variance_weighted' is the default value for r2_score
for backward compatibility. This will be changed to uniform_average in the
future.
3.3.4.1. R² score, the coefficient of determination¶
The r2_score function computes the coefficient of
determination,
usually denoted as (R^2).
It represents the proportion of variance (of y) that has been explained by the
independent variables in the model. It provides an indication of goodness of
fit and therefore a measure of how well unseen samples are likely to be
predicted by the model, through the proportion of explained variance.
As such variance is dataset dependent, (R^2) may not be meaningfully comparable
across different datasets. Best possible score is 1.0 and it can be negative
(because the model can be arbitrarily worse). A constant model that always
predicts the expected (average) value of y, disregarding the input features,
would get an (R^2) score of 0.0.
Note: when the prediction residuals have zero mean, the (R^2) score and
the Explained variance score are identical.
If (hat{y}_i) is the predicted value of the (i)-th sample
and (y_i) is the corresponding true value for total (n) samples,
the estimated (R^2) is defined as:
[R^2(y, hat{y}) = 1 — frac{sum_{i=1}^{n} (y_i — hat{y}_i)^2}{sum_{i=1}^{n} (y_i — bar{y})^2}]
where (bar{y} = frac{1}{n} sum_{i=1}^{n} y_i) and (sum_{i=1}^{n} (y_i — hat{y}_i)^2 = sum_{i=1}^{n} epsilon_i^2).
Note that r2_score calculates unadjusted (R^2) without correcting for
bias in sample variance of y.
In the particular case where the true target is constant, the (R^2) score is
not finite: it is either NaN (perfect predictions) or -Inf (imperfect
predictions). Such non-finite scores may prevent correct model optimization
such as grid-search cross-validation to be performed correctly. For this reason
the default behaviour of r2_score is to replace them with 1.0 (perfect
predictions) or 0.0 (imperfect predictions). If force_finite
is set to False, this score falls back on the original (R^2) definition.
Here is a small example of usage of the r2_score function:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925... >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2] >>> r2_score(y_true, y_pred) 1.0 >>> r2_score(y_true, y_pred, force_finite=False) nan >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2 + 1e-8] >>> r2_score(y_true, y_pred) 0.0 >>> r2_score(y_true, y_pred, force_finite=False) -inf
3.3.4.2. Mean absolute error¶
The mean_absolute_error function computes mean absolute
error, a risk
metric corresponding to the expected value of the absolute error loss or
(l1)-norm loss.
If (hat{y}_i) is the predicted value of the (i)-th sample,
and (y_i) is the corresponding true value, then the mean absolute error
(MAE) estimated over (n_{text{samples}}) is defined as
[text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i — hat{y}_i right|.]
Here is a small example of usage of the mean_absolute_error function:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
3.3.4.3. Mean squared error¶
The mean_squared_error function computes mean square
error, a risk
metric corresponding to the expected value of the squared (quadratic) error or
loss.
If (hat{y}_i) is the predicted value of the (i)-th sample,
and (y_i) is the corresponding true value, then the mean squared error
(MSE) estimated over (n_{text{samples}}) is defined as
[text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (y_i — hat{y}_i)^2.]
Here is a small example of usage of the mean_squared_error
function:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
3.3.4.4. Mean squared logarithmic error¶
The mean_squared_log_error function computes a risk metric
corresponding to the expected value of the squared logarithmic (quadratic)
error or loss.
If (hat{y}_i) is the predicted value of the (i)-th sample,
and (y_i) is the corresponding true value, then the mean squared
logarithmic error (MSLE) estimated over (n_{text{samples}}) is
defined as
[text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (log_e (1 + y_i) — log_e (1 + hat{y}_i) )^2.]
Where (log_e (x)) means the natural logarithm of (x). This metric
is best to use when targets having exponential growth, such as population
counts, average sales of a commodity over a span of years etc. Note that this
metric penalizes an under-predicted estimate greater than an over-predicted
estimate.
Here is a small example of usage of the mean_squared_log_error
function:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
3.3.4.5. Mean absolute percentage error¶
The mean_absolute_percentage_error (MAPE), also known as mean absolute
percentage deviation (MAPD), is an evaluation metric for regression problems.
The idea of this metric is to be sensitive to relative errors. It is for example
not changed by a global scaling of the target variable.
If (hat{y}_i) is the predicted value of the (i)-th sample
and (y_i) is the corresponding true value, then the mean absolute percentage
error (MAPE) estimated over (n_{text{samples}}) is defined as
[text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i — hat{y}_i right|}{max(epsilon, left| y_i right|)}]
where (epsilon) is an arbitrary small yet strictly positive number to
avoid undefined results when y is zero.
The mean_absolute_percentage_error function supports multioutput.
Here is a small example of usage of the mean_absolute_percentage_error
function:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
In above example, if we had used mean_absolute_error, it would have ignored
the small magnitude values and only reflected the error in prediction of highest
magnitude value. But that problem is resolved in case of MAPE because it calculates
relative percentage error with respect to actual output.
3.3.4.6. Median absolute error¶
The median_absolute_error is particularly interesting because it is
robust to outliers. The loss is calculated by taking the median of all absolute
differences between the target and the prediction.
If (hat{y}_i) is the predicted value of the (i)-th sample
and (y_i) is the corresponding true value, then the median absolute error
(MedAE) estimated over (n_{text{samples}}) is defined as
[text{MedAE}(y, hat{y}) = text{median}(mid y_1 — hat{y}_1 mid, ldots, mid y_n — hat{y}_n mid).]
The median_absolute_error does not support multioutput.
Here is a small example of usage of the median_absolute_error
function:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
3.3.4.7. Max error¶
The max_error function computes the maximum residual error , a metric
that captures the worst case error between the predicted value and
the true value. In a perfectly fitted single output regression
model, max_error would be 0 on the training set and though this
would be highly unlikely in the real world, this metric shows the
extent of error that the model had when it was fitted.
If (hat{y}_i) is the predicted value of the (i)-th sample,
and (y_i) is the corresponding true value, then the max error is
defined as
[text{Max Error}(y, hat{y}) = max(| y_i — hat{y}_i |)]
Here is a small example of usage of the max_error function:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
The max_error does not support multioutput.
3.3.4.8. Explained variance score¶
The explained_variance_score computes the explained variance
regression score.
If (hat{y}) is the estimated target output, (y) the corresponding
(correct) target output, and (Var) is Variance, the square of the standard deviation,
then the explained variance is estimated as follow:
[explained_{}variance(y, hat{y}) = 1 — frac{Var{ y — hat{y}}}{Var{y}}]
The best possible score is 1.0, lower values are worse.
In the particular case where the true target is constant, the Explained
Variance score is not finite: it is either NaN (perfect predictions) or
-Inf (imperfect predictions). Such non-finite scores may prevent correct
model optimization such as grid-search cross-validation to be performed
correctly. For this reason the default behaviour of
explained_variance_score is to replace them with 1.0 (perfect
predictions) or 0.0 (imperfect predictions). You can set the force_finite
parameter to False to prevent this fix from happening and fallback on the
original Explained Variance score.
Here is a small example of usage of the explained_variance_score
function:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990... >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2] >>> explained_variance_score(y_true, y_pred) 1.0 >>> explained_variance_score(y_true, y_pred, force_finite=False) nan >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2 + 1e-8] >>> explained_variance_score(y_true, y_pred) 0.0 >>> explained_variance_score(y_true, y_pred, force_finite=False) -inf
3.3.4.9. Mean Poisson, Gamma, and Tweedie deviances¶
The mean_tweedie_deviance function computes the mean Tweedie
deviance error
with a power parameter ((p)). This is a metric that elicits
predicted expectation values of regression targets.
Following special cases exist,
-
when
power=0it is equivalent tomean_squared_error. -
when
power=1it is equivalent tomean_poisson_deviance. -
when
power=2it is equivalent tomean_gamma_deviance.
If (hat{y}_i) is the predicted value of the (i)-th sample,
and (y_i) is the corresponding true value, then the mean Tweedie
deviance error (D) for power (p), estimated over (n_{text{samples}})
is defined as
[begin{split}text{D}(y, hat{y}) = frac{1}{n_text{samples}}
sum_{i=0}^{n_text{samples} — 1}
begin{cases}
(y_i-hat{y}_i)^2, & text{for }p=0text{ (Normal)}\
2(y_i log(y_i/hat{y}_i) + hat{y}_i — y_i), & text{for }p=1text{ (Poisson)}\
2(log(hat{y}_i/y_i) + y_i/hat{y}_i — 1), & text{for }p=2text{ (Gamma)}\
2left(frac{max(y_i,0)^{2-p}}{(1-p)(2-p)}-
frac{y_i,hat{y}_i^{1-p}}{1-p}+frac{hat{y}_i^{2-p}}{2-p}right),
& text{otherwise}
end{cases}end{split}]
Tweedie deviance is a homogeneous function of degree 2-power.
Thus, Gamma distribution with power=2 means that simultaneously scaling
y_true and y_pred has no effect on the deviance. For Poisson
distribution power=1 the deviance scales linearly, and for Normal
distribution (power=0), quadratically. In general, the higher
power the less weight is given to extreme deviations between true
and predicted targets.
For instance, let’s compare the two predictions 1.5 and 150 that are both
50% larger than their corresponding true value.
The mean squared error (power=0) is very sensitive to the
prediction difference of the second point,:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
If we increase power to 1,:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
the difference in errors decreases. Finally, by setting, power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
we would get identical errors. The deviance when power=2 is thus only
sensitive to relative errors.
3.3.4.10. Pinball loss¶
The mean_pinball_loss function is used to evaluate the predictive
performance of quantile regression models.
[text{pinball}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} alpha max(y_i — hat{y}_i, 0) + (1 — alpha) max(hat{y}_i — y_i, 0)]
The value of pinball loss is equivalent to half of mean_absolute_error when the quantile
parameter alpha is set to 0.5.
Here is a small example of usage of the mean_pinball_loss function:
>>> from sklearn.metrics import mean_pinball_loss >>> y_true = [1, 2, 3] >>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.1) 0.03... >>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.1) 0.3... >>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.9) 0.3... >>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.9) 0.03... >>> mean_pinball_loss(y_true, y_true, alpha=0.1) 0.0 >>> mean_pinball_loss(y_true, y_true, alpha=0.9) 0.0
It is possible to build a scorer object with a specific choice of alpha:
>>> from sklearn.metrics import make_scorer >>> mean_pinball_loss_95p = make_scorer(mean_pinball_loss, alpha=0.95)
Such a scorer can be used to evaluate the generalization performance of a
quantile regressor via cross-validation:
>>> from sklearn.datasets import make_regression >>> from sklearn.model_selection import cross_val_score >>> from sklearn.ensemble import GradientBoostingRegressor >>> >>> X, y = make_regression(n_samples=100, random_state=0) >>> estimator = GradientBoostingRegressor( ... loss="quantile", ... alpha=0.95, ... random_state=0, ... ) >>> cross_val_score(estimator, X, y, cv=5, scoring=mean_pinball_loss_95p) array([13.6..., 9.7..., 23.3..., 9.5..., 10.4...])
It is also possible to build scorer objects for hyper-parameter tuning. The
sign of the loss must be switched to ensure that greater means better as
explained in the example linked below.
3.3.4.11. D² score¶
The D² score computes the fraction of deviance explained.
It is a generalization of R², where the squared error is generalized and replaced
by a deviance of choice (text{dev}(y, hat{y}))
(e.g., Tweedie, pinball or mean absolute error). D² is a form of a skill score.
It is calculated as
[D^2(y, hat{y}) = 1 — frac{text{dev}(y, hat{y})}{text{dev}(y, y_{text{null}})} ,.]
Where (y_{text{null}}) is the optimal prediction of an intercept-only model
(e.g., the mean of y_true for the Tweedie case, the median for absolute
error and the alpha-quantile for pinball loss).
Like R², the best possible score is 1.0 and it can be negative (because the
model can be arbitrarily worse). A constant model that always predicts
(y_{text{null}}), disregarding the input features, would get a D² score
of 0.0.
3.3.4.11.1. D² Tweedie score¶
The d2_tweedie_score function implements the special case of D²
where (text{dev}(y, hat{y})) is the Tweedie deviance, see Mean Poisson, Gamma, and Tweedie deviances.
It is also known as D² Tweedie and is related to McFadden’s likelihood ratio index.
The argument power defines the Tweedie power as for
mean_tweedie_deviance. Note that for power=0,
d2_tweedie_score equals r2_score (for single targets).
A scorer object with a specific choice of power can be built by:
>>> from sklearn.metrics import d2_tweedie_score, make_scorer >>> d2_tweedie_score_15 = make_scorer(d2_tweedie_score, power=1.5)
3.3.4.11.2. D² pinball score¶
The d2_pinball_score function implements the special case
of D² with the pinball loss, see Pinball loss, i.e.:
[text{dev}(y, hat{y}) = text{pinball}(y, hat{y}).]
The argument alpha defines the slope of the pinball loss as for
mean_pinball_loss (Pinball loss). It determines the
quantile level alpha for which the pinball loss and also D²
are optimal. Note that for alpha=0.5 (the default) d2_pinball_score
equals d2_absolute_error_score.
A scorer object with a specific choice of alpha can be built by:
>>> from sklearn.metrics import d2_pinball_score, make_scorer >>> d2_pinball_score_08 = make_scorer(d2_pinball_score, alpha=0.8)
3.3.4.11.3. D² absolute error score¶
The d2_absolute_error_score function implements the special case of
the Mean absolute error:
[text{dev}(y, hat{y}) = text{MAE}(y, hat{y}).]
Here are some usage examples of the d2_absolute_error_score function:
>>> from sklearn.metrics import d2_absolute_error_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> d2_absolute_error_score(y_true, y_pred) 0.764... >>> y_true = [1, 2, 3] >>> y_pred = [1, 2, 3] >>> d2_absolute_error_score(y_true, y_pred) 1.0 >>> y_true = [1, 2, 3] >>> y_pred = [2, 2, 2] >>> d2_absolute_error_score(y_true, y_pred) 0.0
3.3.4.12. Visual evaluation of regression models¶
Among methods to assess the quality of regression models, scikit-learn provides
the PredictionErrorDisplay class. It allows to
visually inspect the prediction errors of a model in two different manners.
The plot on the left shows the actual values vs predicted values. For a
noise-free regression task aiming to predict the (conditional) expectation of
y, a perfect regression model would display data points on the diagonal
defined by predicted equal to actual values. The further away from this optimal
line, the larger the error of the model. In a more realistic setting with
irreducible noise, that is, when not all the variations of y can be explained
by features in X, then the best model would lead to a cloud of points densely
arranged around the diagonal.
Note that the above only holds when the predicted values is the expected value
of y given X. This is typically the case for regression models that
minimize the mean squared error objective function or more generally the
mean Tweedie deviance for any value of its
“power” parameter.
When plotting the predictions of an estimator that predicts a quantile
of y given X, e.g. QuantileRegressor
or any other model minimizing the pinball loss, a
fraction of the points are either expected to lie above or below the diagonal
depending on the estimated quantile level.
All in all, while intuitive to read, this plot does not really inform us on
what to do to obtain a better model.
The right-hand side plot shows the residuals (i.e. the difference between the
actual and the predicted values) vs. the predicted values.
This plot makes it easier to visualize if the residuals follow and
homoscedastic or heteroschedastic
distribution.
In particular, if the true distribution of y|X is Poisson or Gamma
distributed, it is expected that the variance of the residuals of the optimal
model would grow with the predicted value of E[y|X] (either linearly for
Poisson or quadratically for Gamma).
When fitting a linear least squares regression model (see
LinearRegression and
Ridge), we can use this plot to check
if some of the model assumptions
are met, in particular that the residuals should be uncorrelated, their
expected value should be null and that their variance should be constant
(homoschedasticity).
If this is not the case, and in particular if the residuals plot show some
banana-shaped structure, this is a hint that the model is likely mis-specified
and that non-linear feature engineering or switching to a non-linear regression
model might be useful.
Refer to the example below to see a model evaluation that makes use of this
display.
3.3.5. Clustering metrics¶
The sklearn.metrics module implements several loss, score, and utility
functions. For more information see the Clustering performance evaluation
section for instance clustering, and Biclustering evaluation for
biclustering.
3.3.6. Dummy estimators¶
When doing supervised learning, a simple sanity check consists of comparing
one’s estimator against simple rules of thumb. DummyClassifier
implements several such simple strategies for classification:
-
stratifiedgenerates random predictions by respecting the training
set class distribution. -
most_frequentalways predicts the most frequent label in the training set. -
prioralways predicts the class that maximizes the class prior
(likemost_frequent) andpredict_probareturns the class prior. -
uniformgenerates predictions uniformly at random. -
constantalways predicts a constant label that is provided by the user.-
A major motivation of this method is F1-scoring, when the positive class
is in the minority.
Note that with all these strategies, the predict method completely ignores
the input data!
To illustrate DummyClassifier, first let’s create an imbalanced
dataset:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Next, let’s compare the accuracy of SVC and most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
We see that SVC doesn’t do much better than a dummy classifier. Now, let’s
change the kernel:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
We see that the accuracy was boosted to almost 100%. A cross validation
strategy is recommended for a better estimate of the accuracy, if it
is not too CPU costly. For more information see the Cross-validation: evaluating estimator performance
section. Moreover if you want to optimize over the parameter space, it is highly
recommended to use an appropriate methodology; see the Tuning the hyper-parameters of an estimator
section for details.
More generally, when the accuracy of a classifier is too close to random, it
probably means that something went wrong: features are not helpful, a
hyperparameter is not correctly tuned, the classifier is suffering from class
imbalance, etc…
DummyRegressor also implements four simple rules of thumb for regression:
-
meanalways predicts the mean of the training targets. -
medianalways predicts the median of the training targets. -
quantilealways predicts a user provided quantile of the training targets. -
constantalways predicts a constant value that is provided by the user.
In all these strategies, the predict method completely ignores
the input data.
From Wikipedia, the free encyclopedia
The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio defined by the formula:
where At is the actual value and Ft is the forecast value. Their difference is divided by the actual value At. The absolute value of this ratio is summed for every forecasted point in time and divided by the number of fitted points n.
MAPE in regression problems[edit]
Mean absolute percentage error is commonly used as a loss function for regression problems and in model evaluation, because of its very intuitive interpretation in terms of relative error.
Definition[edit]
Consider a standard regression setting in which the data are fully described by a random pair 






In the classical regression setting, the closeness of 


where 
In practice
In practice 
From a practical point of view, the use of the MAPE as a quality function for regression model is equivalent to doing weighted mean absolute error (MAE) regression, also known as quantile regression. This property is trivial since
As a consequence, the use of the MAPE is very easy in practice, for example using existing libraries for quantile regression allowing weights.
Consistency[edit]
The use of the MAPE as a loss function for regression analysis is feasible both on a practical point of view and on a theoretical one, since the existence of an optimal model and the consistency of the empirical risk minimization can be proved.[1]
WMAPE[edit]
WMAPE (sometimes spelled wMAPE) stands for weighted mean absolute percentage error.[2] It is a measure used to evaluate the performance of regression or forecasting models. It is a variant of MAPE in which the mean absolute percent errors is treated as a weighted arithmetic mean. Most commonly the absolute percent errors are weighted by the actuals (e.g. in case of sales forecasting, errors are weighted by sales volume).[3]. Effectively, this overcomes the ‘infinite error’ issue.[4]
Its formula is:[4]
Where 


However, this effectively simplifies to a much simpler formula:
Confusingly, sometimes when people refer to wMAPE they are talking about a different model in which the numerator and denominator of the wMAPE formula above are weighted again by another set of custom weights 
Issues[edit]
Although the concept of MAPE sounds very simple and convincing, it has major drawbacks in practical application,[5] and there are many studies on shortcomings and misleading results from MAPE.[6][7]
To overcome these issues with MAPE, there are some other measures proposed in literature:
- Mean Absolute Scaled Error (MASE)
- Symmetric Mean Absolute Percentage Error (sMAPE)
- Mean Directional Accuracy (MDA)
- Mean Arctangent Absolute Percentage Error (MAAPE): MAAPE can be considered a slope as an angle, while MAPE is a slope as a ratio.[7]
See also[edit]
- Least absolute deviations
- Mean absolute error
- Mean percentage error
- Symmetric mean absolute percentage error
External links[edit]
- Mean Absolute Percentage Error for Regression Models
- Mean Absolute Percentage Error (MAPE)
- Errors on percentage errors — variants of MAPE
- Mean Arctangent Absolute Percentage Error (MAAPE)
References[edit]
- ^ a b de Myttenaere, B Golden, B Le Grand, F Rossi (2015). «Mean absolute percentage error for regression models», Neurocomputing 2016 arXiv:1605.02541
- ^ Forecast Accuracy: MAPE, WAPE, WMAPE https://www.baeldung.com/cs/mape-vs-wape-vs-wmape%7Ctitle=Understanding Forecast Accuracy: MAPE, WAPE, WMAPE. ;
- ^ Weighted Mean Absolute Percentage Error https://ibf.org/knowledge/glossary/weighted-mean-absolute-percentage-error-wmape-299%7Ctitle=WMAPE: Weighted Mean Absolute Percentage Error. ;
- ^ a b «Statistical Forecast Errors».
- ^ a b Tofallis (2015). «A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation», Journal of the Operational Research Society, 66(8):1352-1362. archived preprint
- ^ Hyndman, Rob J., and Anne B. Koehler (2006). «Another look at measures of forecast accuracy.» International Journal of Forecasting, 22(4):679-688 doi:10.1016/j.ijforecast.2006.03.001.
- ^ a b Kim, Sungil and Heeyoung Kim (2016). «A new metric of absolute percentage error for intermittent demand forecasts.» International Journal of Forecasting, 32(3):669-679 doi:10.1016/j.ijforecast.2015.12.003.
- ^ Kim, Sungil; Kim, Heeyoung (1 July 2016). «A new metric of absolute percentage error for intermittent demand forecasts». International Journal of Forecasting. 32 (3): 669–679. doi:10.1016/j.ijforecast.2015.12.003.
- ^ Makridakis, Spyros (1993) «Accuracy measures: theoretical and practical concerns.» International Journal of Forecasting, 9(4):527-529 doi:10.1016/0169-2070(93)90079-3
Гораздо легче что-то измерить, чем понять, что именно вы измеряете
Джон Уильям Салливан
Задачи машинного обучения с учителем как правило состоят в восстановлении зависимости между парами (признаковое описание, целевая переменная) по данным, доступным нам для анализа. Алгоритмы машинного обучения (learning algorithm), со многими из которых вы уже успели познакомиться, позволяют построить модель, аппроксимирующую эту зависимость. Но как понять, насколько качественной получилась аппроксимация?
Почти наверняка наша модель будет ошибаться на некоторых объектах: будь она даже идеальной, шум или выбросы в тестовых данных всё испортят. При этом разные модели будут ошибаться на разных объектах и в разной степени. Задача специалиста по машинному обучению – подобрать подходящий критерий, который позволит сравнивать различные модели.
Перед чтением этой главы мы хотели бы ещё раз напомнить, что качество модели нельзя оценивать на обучающей выборке. Как минимум, это стоит делать на отложенной (тестовой) выборке, но, если вам это позволяют время и вычислительные ресурсы, стоит прибегнуть и к более надёжным способам проверки – например, кросс-валидации (о ней вы узнаете в отдельной главе).
Выбор метрик в реальных задачах
Возможно, вы уже участвовали в соревнованиях по анализу данных. На таких соревнованиях метрику (критерий качества модели) организатор выбирает за вас, и она, как правило, довольно понятным образом связана с результатами предсказаний. Но на практике всё бывает намного сложнее.
Например, мы хотим:
- решить, сколько коробок с бананами нужно завтра привезти в конкретный магазин, чтобы минимизировать количество товара, который не будет выкуплен и минимизировать ситуацию, когда покупатель к концу дня не находит желаемый продукт на полке;
- увеличить счастье пользователя от работы с нашим сервисом, чтобы он стал лояльным и обеспечивал тем самым стабильный прогнозируемый доход;
- решить, нужно ли направить человека на дополнительное обследование.
В каждом конкретном случае может возникать целая иерархия метрик. Представим, например, что речь идёт о стриминговом музыкальном сервисе, пользователей которого мы решили порадовать сгенерированными самодельной нейросетью треками – не защищёнными авторским правом, а потому совершенно бесплатными. Иерархия метрик могла бы иметь такой вид:
- Самый верхний уровень: будущий доход сервиса – невозможно измерить в моменте, сложным образом зависит от совокупности всех наших усилий;
- Медианная длина сессии, возможно, служащая оценкой радости пользователей, которая, как мы надеемся, повлияет на их желание продолжать платить за подписку – её нам придётся измерять в продакшене, ведь нас интересует реакция настоящих пользователей на новшество;
- Доля удовлетворённых качеством сгенерированной музыки асессоров, на которых мы потестируем её до того, как выставить на суд пользователей;
- Функция потерь, на которую мы будем обучать генеративную сеть.
На этом примере мы можем заметить сразу несколько общих закономерностей. Во-первых, метрики бывают offline и online (оффлайновыми и онлайновыми). Online метрики вычисляются по данным, собираемым с работающей системы (например, медианная длина сессии). Offline метрики могут быть измерены до введения модели в эксплуатацию, например, по историческим данным или с привлечением специальных людей, асессоров. Последнее часто применяется, когда метрикой является реакция живого человека: скажем, так поступают поисковые компании, которые предлагают людям оценить качество ранжирования экспериментальной системы еще до того, как рядовые пользователи увидят эти результаты в обычном порядке. На самом же нижнем этаже иерархии лежат оптимизируемые в ходе обучения функции потерь.
В данном разделе нас будут интересовать offline метрики, которые могут быть измерены без привлечения людей.
Функция потерь $neq$ метрика качества
Как мы узнали ранее, методы обучения реализуют разные подходы к обучению:
- обучение на основе прироста информации (как в деревьях решений)
- обучение на основе сходства (как в методах ближайших соседей)
- обучение на основе вероятностной модели данных (например, максимизацией правдоподобия)
- обучение на основе ошибок (минимизация эмпирического риска)
И в рамках обучения на основе минимизации ошибок мы уже отвечали на вопрос: как можно штрафовать модель за предсказание на обучающем объекте.
Во время сведения задачи о построении решающего правила к задаче численной оптимизации, мы вводили понятие функции потерь и, обычно, объявляли целевой функцией сумму потерь от предсказаний на всех объектах обучающей выборке.
Важно понимать разницу между функцией потерь и метрикой качества. Её можно сформулировать следующим образом:
-
Функция потерь возникает в тот момент, когда мы сводим задачу построения модели к задаче оптимизации. Обычно требуется, чтобы она обладала хорошими свойствами (например, дифференцируемостью).
-
Метрика – внешний, объективный критерий качества, обычно зависящий не от параметров модели, а только от предсказанных меток.
В некоторых случаях метрика может совпадать с функцией потерь. Например, в задаче регрессии MSE играет роль как функции потерь, так и метрики. Но, скажем, в задаче бинарной классификации они почти всегда различаются: в качестве функции потерь может выступать кросс-энтропия, а в качестве метрики – число верно угаданных меток (accuracy). Отметим, что в последнем примере у них различные аргументы: на вход кросс-энтропии нужно подавать логиты, а на вход accuracy – предсказанные метки (то есть по сути argmax логитов).
Бинарная классификация: метки классов
Перейдём к обзору метрик и начнём с самой простой разновидности классификации – бинарной, а затем постепенно будем наращивать сложность.
Напомним постановку задачи бинарной классификации: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_iin{0, 1}$ построить модель, которая по объекту $x$ предсказывает метку класса $f(x)in{0, 1}$.
Первым критерием качества, который приходит в голову, является accuracy – доля объектов, для которых мы правильно предсказали класс:
$$ color{#348FEA}{text{Accuracy}(y, y^{pred}) = frac{1}{N} sum_{i=1}^N mathbb{I}[y_i = f(x_i)]} $$
Или же сопряженная ей метрика – доля ошибочных классификаций (error rate):
$$text{Error rate} = 1 — text{Accuracy}$$
Познакомившись чуть внимательнее с этой метрикой, можно заметить, что у неё есть несколько недостатков:
- она не учитывает дисбаланс классов. Например, в задаче диагностики редких заболеваний классификатор, предсказывающий всем пациентам отсутствие болезни будет иметь достаточно высокую accuracy просто потому, что больных людей в выборке намного меньше;
- она также не учитывает цену ошибки на объектах разных классов. Для примера снова можно привести задачу медицинской диагностики: если ошибочный положительный диагноз для здорового больного обернётся лишь ещё одним обследованием, то ошибочно отрицательный вердикт может повлечь роковые последствия.
Confusion matrix (матрица ошибок)
Исторически задача бинарной классификации – это задача об обнаружении чего-то редкого в большом потоке объектов, например, поиск человека, больного туберкулёзом, по флюорографии. Или задача признания пятна на экране приёмника радиолокационной станции бомбардировщиком, представляющем угрозу охраняемому объекту (в противовес стае гусей).
Поэтому класс, который представляет для нас интерес, называется «положительным», а оставшийся – «отрицательным».
Заметим, что для каждого объекта в выборке возможно 4 ситуации:
- мы предсказали положительную метку и угадали. Будет относить такие объекты к true positive (TP) группе (true – потому что предсказали мы правильно, а positive – потому что предсказали положительную метку);
- мы предсказали положительную метку, но ошиблись в своём предсказании – false positive (FP) (false, потому что предсказание было неправильным);
- мы предсказали отрицательную метку и угадали – true negative (TN);
- и наконец, мы предсказали отрицательную метку, но ошиблись – false negative (FN). Для удобства все эти 4 числа изображают в виде таблицы, которую называют confusion matrix (матрицей ошибок):
Не волнуйтесь, если первое время эти обозначения будут сводить вас с ума (будем откровенны, даже профи со стажем в них порой путаются), однако логика за ними достаточно простая: первая часть названия группы показывает угадали ли мы с классом, а вторая – какой класс мы предсказали.
Пример
Попробуем воспользоваться введёнными метриками в боевом примере: сравним работу нескольких моделей классификации на Breast cancer wisconsin (diagnostic) dataset.
Объектами выборки являются фотографии биопсии грудных опухолей. С их помощью было сформировано признаковое описание, которое заключается в характеристиках ядер клеток (таких как радиус ядра, его текстура, симметричность). Положительным классом в такой постановке будут злокачественные опухоли, а отрицательным – доброкачественные.
Модель 1. Константное предсказание.
Решение задачи начнём с самого простого классификатора, который выдаёт на каждом объекте константное предсказание – самый часто встречающийся класс.
Зачем вообще замерять качество на такой модели?При разработке модели машинного обучения для проекта всегда желательно иметь некоторую baseline модель. Так нам будет легче проконтролировать, что наша более сложная модель действительно дает нам прирост качества.
from sklearn.datasets
import load_breast_cancer
the_data = load_breast_cancer()
# 0 – "доброкачественный"
# 1 – "злокачественный"
relabeled_target = 1 - the_data["target"]
from sklearn.model_selection import train_test_split
X = the_data["data"]
y = relabeled_target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.dummy import DummyClassifier
dc_mf = DummyClassifier(strategy="most_frequent")
dc_mf.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix
y_true = y_test y_pred = dc_mf.predict(X_test)
dc_mf_tn, dc_mf_fp, dc_mf_fn, dc_mf_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 0 | FN = 53 |
| Истинный класс — | FP = 0 | TN = 90 |
Обучающие данные таковы, что наш dummy-классификатор все объекты записывает в отрицательный класс, то есть признаёт все опухоли доброкачественными. Такой наивный подход позволяет нам получить минимальный штраф за FP (действительно, нельзя ошибиться в предсказании, если положительный класс вообще не предсказывается), но и максимальный штраф за FN (в эту группу попадут все злокачественные опухоли).
Модель 2. Случайный лес.
Настало время воспользоваться всем арсеналом моделей машинного обучения, и начнём мы со случайного леса.
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc.fit(X_train, y_train)
y_true = y_test
y_pred = rfc.predict(X_test)
rfc_tn, rfc_fp, rfc_fn, rfc_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 52 | FN = 1 |
| Истинный класс — | FP = 4 | TN = 86 |
Можно сказать, что этот классификатор чему-то научился, т.к. главная диагональ матрицы стала содержать все объекты из отложенной выборки, за исключением 4 + 1 = 5 объектов (сравните с 0 + 53 объектами dummy-классификатора, все опухоли объявляющего доброкачественными).
Отметим, что вычисляя долю недиагональных элементов, мы приходим к метрике error rate, о которой мы говорили в самом начале:
$$text{Error rate} = frac{FP + FN}{ TP + TN + FP + FN}$$
тогда как доля объектов, попавших на главную диагональ – это как раз таки accuracy:
$$text{Accuracy} = frac{TP + TN}{ TP + TN + FP + FN}$$
Модель 3. Метод опорных векторов.
Давайте построим еще один классификатор на основе линейного метода опорных векторов.
Не забудьте привести признаки к единому масштабу, иначе численный алгоритм не сойдется к решению и мы получим гораздо более плохо работающее решающее правило. Попробуйте проделать это упражнение.
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
ss = StandardScaler() ss.fit(X_train)
scaled_linsvc = LinearSVC(C=0.01,random_state=42)
scaled_linsvc.fit(ss.transform(X_train), y_train)
y_true = y_test
y_pred = scaled_linsvc.predict(ss.transform(X_test))
tn, fp, fn, tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 50 | FN = 3 |
| Истинный класс — | FP = 1 | TN = 89 |
Сравним результаты
Легко заметить, что каждая из двух моделей лучше классификатора-пустышки, однако давайте попробуем сравнить их между собой. С точки зрения error rate модели практически одинаковы: 5/143 для леса против 4/143 для SVM.
Посмотрим на структуру ошибок чуть более внимательно: лес – (FP = 4, FN = 1), SVM – (FP = 1, FN = 3). Какая из моделей предпочтительнее?
Замечание: Мы сравниваем несколько классификаторов на основании их предсказаний на отложенной выборке. Насколько ошибки данных классификаторов зависят от разбиения исходного набора данных? Иногда в процессе оценки качества мы будем получать модели, чьи показатели эффективности будут статистически неразличимыми.
Пусть мы учли предыдущее замечание и эти модели действительно статистически значимо ошибаются в разную сторону. Мы встретились с очевидной вещью: на матрицах нет отношения порядка. Когда мы сравнивали dummy-классификатор и случайный лес с помощью Accuracy, мы всю сложную структуру ошибок свели к одному числу, т.к. на вещественных числах отношение порядка есть. Сводить оценку модели к одному числу очень удобно, однако не стоит забывать, что у вашей модели есть много аспектов качества.
Что же всё-таки важнее уменьшить: FP или FN? Вернёмся к задаче: FP – доля доброкачественных опухолей, которым ошибочно присваивается метка злокачественной, а FN – доля злокачественных опухолей, которые классификатор пропускает. В такой постановке становится понятно, что при сравнении выиграет модель с меньшим FN (то есть лес в нашем примере), ведь каждая не обнаруженная опухоль может стоить человеческой жизни.
Рассмотрим теперь другую задачу: по данным о погоде предсказать, будет ли успешным запуск спутника. FN в такой постановке – это ошибочное предсказание неуспеха, то есть не более, чем упущенный шанс (если вас, конечно не уволят за срыв сроков). С FP всё серьёзней: если вы предскажете удачный запуск спутника, а на деле он потерпит крушение из-за погодных условий, то ваши потери будут в разы существеннее.
Итак, из примеров мы видим, что в текущем виде введенная нами доля ошибочных классификаций не даст нам возможности учесть неравную важность FP и FN. Поэтому введем две новые метрики: точность и полноту.
Точность и полнота
Accuracy — это метрика, которая характеризует качество модели, агрегированное по всем классам. Это полезно, когда классы для нас имеют одинаковое значение. В случае, если это не так, accuracy может быть обманчивой.
Рассмотрим ситуацию, когда положительный класс это событие редкое. Возьмем в качестве примера поисковую систему — в нашем хранилище хранятся миллиарды документов, а релевантных к конкретному поисковому запросу на несколько порядков меньше.
Пусть мы хотим решить задачу бинарной классификации «документ d релевантен по запросу q». Благодаря большому дисбалансу, Accuracy dummy-классификатора, объявляющего все документы нерелевантными, будет близка к единице. Напомним, что $text{Accuracy} = frac{TP + TN}{TP + TN + FP + FN}$, и в нашем случае высокое значение метрики будет обеспечено членом TN, в то время для пользователей более важен высокий TP.
Поэтому в случае ассиметрии классов, можно использовать метрики, которые не учитывают TN и ориентируются на TP.
Если мы рассмотрим долю правильно предсказанных положительных объектов среди всех объектов, предсказанных положительным классом, то мы получим метрику, которая называется точностью (precision)
$$color{#348FEA}{text{Precision} = frac{TP}{TP + FP}}$$
Интуитивно метрика показывает долю релевантных документов среди всех найденных классификатором. Чем меньше ложноположительных срабатываний будет допускать модель, тем больше будет её Precision.
Если же мы рассмотрим долю правильно найденных положительных объектов среди всех объектов положительного класса, то мы получим метрику, которая называется полнотой (recall)
$$color{#348FEA}{text{Recall} = frac{TP}{TP + FN}}$$
Интуитивно метрика показывает долю найденных документов из всех релевантных. Чем меньше ложно отрицательных срабатываний, тем выше recall модели.
Например, в задаче предсказания злокачественности опухоли точность показывает, сколько из определённых нами как злокачественные опухолей действительно являются злокачественными, а полнота – какую долю злокачественных опухолей нам удалось выявить.
Хорошее понимание происходящего даёт следующая картинка: 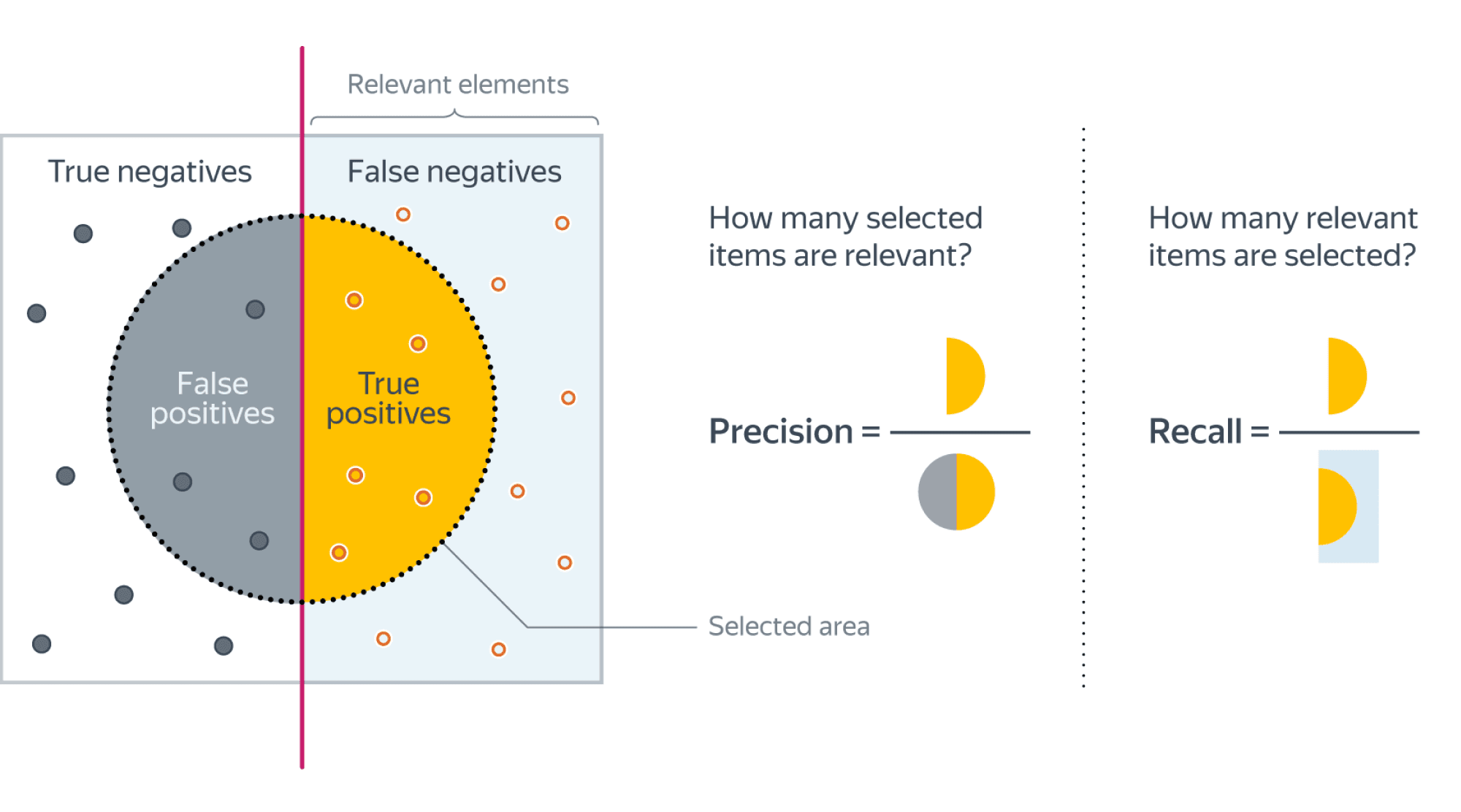
Recall@k, Precision@k
Метрики Recall и Precision хорошо подходят для задачи поиска «документ d релевантен запросу q», когда из списка рекомендованных алгоритмом документов нас интересует только первый. Но не всегда алгоритм машинного обучения вынужден работать в таких жестких условиях. Может быть такое, что вполне достаточно, что релевантный документ попал в первые k рекомендованных. Например, в интерфейсе выдачи первые три подсказки видны всегда одновременно и вообще не очень понятно, какой у них порядок. Тогда более честной оценкой качества алгоритма будет «в выдаче D размера k по запросу q нашлись релевантные документы». Для расчёта метрики по всей выборке объединим все выдачи и рассчитаем precision, recall как обычно подокументно.
F1-мера
Как мы уже отмечали ранее, модели очень удобно сравнивать, когда их качество выражено одним числом. В случае пары Precision-Recall существует популярный способ скомпоновать их в одну метрику — взять их среднее гармоническое. Данный показатель эффективности исторически носит название F1-меры (F1-measure).
$$
color{#348FEA}{F_1 = frac{2}{frac{1}{Recall} + frac{1}{Precision}}} = $$
$$ = 2 frac{Recall cdot Precision }{Recall + Precision} = frac
{TP} {TP + frac{FP + FN}{2}}
$$
Стоит иметь в виду, что F1-мера предполагает одинаковую важность Precision и Recall, если одна из этих метрик для вас приоритетнее, то можно воспользоваться $F_{beta}$ мерой:
$$
F_{beta} = (beta^2 + 1) frac{Recall cdot Precision }{Recall + beta^2Precision}
$$
Бинарная классификация: вероятности классов
Многие модели бинарной классификации устроены так, что класс объекта получается бинаризацией выхода классификатора по некоторому фиксированному порогу:
$$fleft(x ; w, w_{0}right)=mathbb{I}left[g(x, w) > w_{0}right].$$
Например, модель логистической регрессии возвращает оценку вероятности принадлежности примера к положительному классу. Другие модели бинарной классификации обычно возвращают произвольные вещественные значения, но существуют техники, называемые калибровкой классификатора, которые позволяют преобразовать предсказания в более или менее корректную оценку вероятности принадлежности к положительному классу.
Как оценить качество предсказываемых вероятностей, если именно они являются нашей конечной целью? Общепринятой мерой является логистическая функция потерь, которую мы изучали раньше, когда говорили об устройстве некоторых методов классификации (например уже упоминавшейся логистической регрессии).
Если же нашей целью является построение прогноза в терминах метки класса, то нам нужно учесть, что в зависимости от порога мы будем получать разные предсказания и разное качество на отложенной выборке. Так, чем ниже порог отсечения, тем больше объектов модель будет относить к положительному классу. Как в этом случае оценить качество модели?
AUC
Пусть мы хотим учитывать ошибки на объектах обоих классов. При уменьшении порога отсечения мы будем находить (правильно предсказывать) всё большее число положительных объектов, но также и неправильно предсказывать положительную метку на всё большем числе отрицательных объектов. Естественным кажется ввести две метрики TPR и FPR:
TPR (true positive rate) – это полнота, доля положительных объектов, правильно предсказанных положительными:
$$ TPR = frac{TP}{P} = frac{TP}{TP + FN} $$
FPR (false positive rate) – это доля отрицательных объектов, неправильно предсказанных положительными:
$$FPR = frac{FP}{N} = frac{FP}{FP + TN}$$
Обе эти величины растут при уменьшении порога. Кривая в осях TPR/FPR, которая получается при варьировании порога, исторически называется ROC-кривой (receiver operating characteristics curve, сокращённо ROC curve). Следующий график поможет вам понять поведение ROC-кривой.
Желтая и синяя кривые показывают распределение предсказаний классификатора на объектах положительного и отрицательного классов соответственно. То есть значения на оси X (на графике с двумя гауссианами) мы получаем из классификатора. Если классификатор идеальный (две кривые разделимы по оси X), то на правом графике мы получаем ROC-кривую (0,0)->(0,1)->(1,1) (убедитесь сами!), площадь под которой равна 1. Если классификатор случайный (предсказывает одинаковые метки положительным и отрицательным объектам), то мы получаем ROC-кривую (0,0)->(1,1), площадь под которой равна 0.5. Поэкспериментируйте с разными вариантами распределения предсказаний по классам и посмотрите, как меняется ROC-кривая.
Чем лучше классификатор разделяет два класса, тем больше площадь (area under curve) под ROC-кривой – и мы можем использовать её в качестве метрики. Эта метрика называется AUC и она работает благодаря следующему свойству ROC-кривой:
AUC равен доле пар объектов вида (объект класса 1, объект класса 0), которые алгоритм верно упорядочил, т.е. предсказание классификатора на первом объекте больше:
$$
color{#348FEA}{operatorname{AUC} = frac{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j] I^{prime}[f(x_{i}) < f(x_{j})]}{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j]}}
$$
$$
I^{prime}left[f(x_{i}) < f(x_{j})right]=
left{
begin{array}{ll}
0, & f(x_{i}) > f(x_{j}) \
0.5 & f(x_{i}) = f(x_{j}) \
1, & f(x_{i}) < f(x_{j})
end{array}
right.
$$
$$
Ileft[y_{i}< y_{j}right]=
left{
begin{array}{ll}
0, & y_{i} geq y_{j} \
1, & y_{i} < y_{j}
end{array}
right.
$$
Чтобы детальнее разобраться, почему это так, советуем вам обратиться к материалам А.Г.Дьяконова.
В каких случаях лучше отдать предпочтение этой метрике? Рассмотрим следующую задачу: некоторый сотовый оператор хочет научиться предсказывать, будет ли клиент пользоваться его услугами через месяц. На первый взгляд кажется, что задача сводится к бинарной классификации с метками 1, если клиент останется с компанией и $0$ – иначе.
Однако если копнуть глубже в процессы компании, то окажется, что такие метки практически бесполезны. Компании скорее интересно упорядочить клиентов по вероятности прекращения обслуживания и в зависимости от этого применять разные варианты удержания: кому-то прислать скидочный купон от партнёра, кому-то предложить скидку на следующий месяц, а кому-то и новый тариф на особых условиях.
Таким образом, в любой задаче, где нам важна не метка сама по себе, а правильный порядок на объектах, имеет смысл применять AUC.
Утверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.
ПодробнееУтверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.» details=»Продемонстрируем это на следующем примере: пусть наша выборка состоит из $9100$ объектов класса $0$ и $10$ объектов класса $1$, и модель расположила их следующим образом:
$$underbrace{0 dots 0}_{9000} ~ underbrace{1 dots 1}_{10} ~ underbrace{0 dots 0}_{100}$$
Тогда AUC будет близка к единице: количество пар правильно расположенных объектов будет порядка $90000$, в то время как общее количество пар порядка $91000$.
Однако самыми высокими по вероятности положительного класса будут совсем не те объекты, которые мы ожидаем.
Average Precision
Будем постепенно уменьшать порог бинаризации. При этом полнота будет расти от $0$ до $1$, так как будет увеличиваться количество объектов, которым мы приписываем положительный класс (а количество объектов, на самом деле относящихся к положительному классу, очевидно, меняться не будет). Про точность же нельзя сказать ничего определённого, но мы понимаем, что скорее всего она будет выше при более высоком пороге отсечения (мы оставим только объекты, в которых модель «уверена» больше всего). Варьируя порог и пересчитывая значения Precision и Recall на каждом пороге, мы получим некоторую кривую примерно следующего вида:
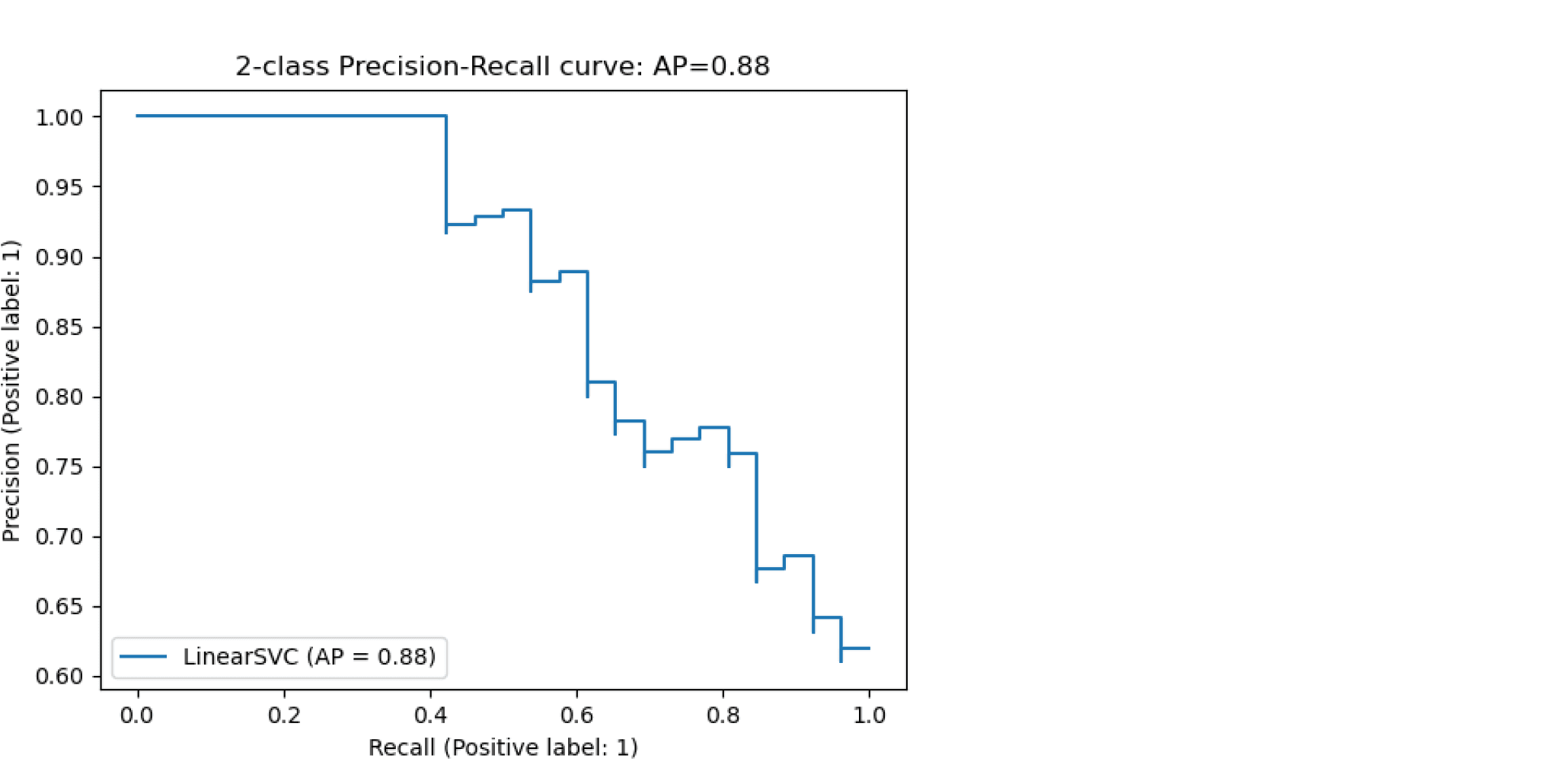
Рассмотрим среднее значение точности (оно равно площади под кривой точность-полнота):
$$ text { AP }=int_{0}^{1} p(r) d r$$
Получим показатель эффективности, который называется average precision. Как в случае матрицы ошибок мы переходили к скалярным показателям эффективности, так и в случае с кривой точность-полнота мы охарактеризовали ее в виде числа.
Многоклассовая классификация
Если классов становится больше двух, расчёт метрик усложняется. Если задача классификации на $K$ классов ставится как $K$ задач об отделении класса $i$ от остальных ($i=1,ldots,K$), то для каждой из них можно посчитать свою матрицу ошибок. Затем есть два варианта получения итогового значения метрики из $K$ матриц ошибок:
- Усредняем элементы матрицы ошибок (TP, FP, TN, FN) между бинарными классификаторами, например $TP = frac{1}{K}sum_{i=1}^{K}TP_i$. Затем по одной усреднённой матрице ошибок считаем Precision, Recall, F-меру. Это называют микроусреднением.
- Считаем Precision, Recall для каждого классификатора отдельно, а потом усредняем. Это называют макроусреднением.
Порядок усреднения влияет на результат в случае дисбаланса классов. Показатели TP, FP, FN — это счётчики объектов. Пусть некоторый класс обладает маленькой мощностью (обозначим её $M$). Тогда значения TP и FN при классификации этого класса против остальных будут не больше $M$, то есть тоже маленькие. Про FP мы ничего уверенно сказать не можем, но скорее всего при дисбалансе классов классификатор не будет предсказывать редкий класс слишком часто, потому что есть большая вероятность ошибиться. Так что FP тоже мало. Поэтому усреднение первым способом сделает вклад маленького класса в общую метрику незаметным. А при усреднении вторым способом среднее считается уже для нормированных величин, так что вклад каждого класса будет одинаковым.
Рассмотрим пример. Пусть есть датасет из объектов трёх цветов: желтого, зелёного и синего. Желтого и зелёного цветов почти поровну — 21 и 20 объектов соответственно, а синих объектов всего 4.
Модель по очереди для каждого цвета пытается отделить объекты этого цвета от объектов оставшихся двух цветов. Результаты классификации проиллюстрированы матрицей ошибок. Модель «покрасила» в жёлтый 25 объектов, 20 из которых были действительно жёлтыми (левый столбец матрицы). В синий был «покрашен» только один объект, который на самом деле жёлтый (средний столбец матрицы). В зелёный — 19 объектов, все на самом деле зелёные (правый столбец матрицы).
Посчитаем Precision классификации двумя способами:
- С помощью микроусреднения получаем $$
text{Precision} = frac{dfrac{1}{3}left(20 + 0 + 19right)}{dfrac{1}{3}left(20 + 0 + 19right) + dfrac{1}{3}left(5 + 1 + 0right)} = 0.87
$$ - С помощью макроусреднения получаем $$
text{Precision} = dfrac{1}{3}left( frac{20}{20 + 5} + frac{0}{0 + 1} + frac{19}{19 + 0}right) = 0.6
$$
Видим, что макроусреднение лучше отражает тот факт, что синий цвет, которого в датасете было совсем мало, модель практически игнорирует.
Как оптимизировать метрики классификации?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы $F$ на валидационной выборке была минимальная/максимальная. Лучший способ добиться минимизации метрики $F$ — оптимизировать её напрямую, то есть выбрать в качестве функции потерь ту же $F(a(X), Y)$. К сожалению, это не всегда возможно. Рассмотрим, как оптимизировать метрики иначе.
Метрики precision и recall невозможно оптимизировать напрямую, потому что эти метрики нельзя рассчитать на одном объекте, а затем усреднить. Они зависят от того, какими были правильная метка класса и ответ алгоритма на всех объектах. Чтобы понять, как оптимизировать precision, recall, рассмотрим, как расчитать эти метрики на отложенной выборке. Пусть модель обучена на стандартную для классификации функцию потерь (LogLoss). Для получения меток класса специалист по машинному обучению сначала применяет на объектах модель и получает вещественные предсказания модели ($p_i in left(0, 1right)$). Затем предсказания бинаризуются по порогу, выбранному специалистом: если предсказание на объекте больше порога, то метка класса 1 (или «положительная»), если меньше — 0 (или «отрицательная»). Рассмотрим, что будет с метриками precision, recall в крайних положениях порога.
- Пусть порог равен нулю. Тогда всем объектам будет присвоена положительная метка. Следовательно, все объекты будут либо TP, либо FP, потому что отрицательных предсказаний нет, $TP + FP = N$, где $N$ — размер выборки. Также все объекты, у которых метка на самом деле 1, попадут в TP. По формуле точность $text{Precision} = frac{TP}{TP + FP} = frac1N sum_{i = 1}^N mathbb{I} left[ y_i = 1 right]$ равна среднему таргету в выборке. А полнота $text{Recall} = frac{TP}{TP + FN} = frac{TP}{TP + 0} = 1$ равна единице.
- Пусть теперь порог равен единице. Тогда ни один объект не будет назван положительным, $TP = FP = 0$. Все объекты с меткой класса 1 попадут в FN. Если есть хотя бы один такой объект, то есть $FN ne 0$, будет верна формула $text{Recall} = frac{TP}{TP + FN} = frac{0}{0+ FN} = 0$. То есть при пороге единица, полнота равна нулю. Теперь посмотрим на точность. Формула для Precision состоит только из счётчиков положительных ответов модели (TP, FP). При единичном пороге они оба равны нулю, $text{Precision} = frac{TP}{TP + FP} = frac{0}{0 + 0}$то есть при единичном пороге точность неопределена. Пусть мы отступили чуть-чуть назад по порогу, чтобы хотя бы несколько объектов были названы моделью положительными. Скорее всего это будут самые «простые» объекты, которые модель распознает хорошо, потому что её предсказание близко к единице. В этом предположении $FP approx 0$. Тогда точность $text{Precision} = frac{TP}{TP + FP} approx frac{TP}{TP + 0} approx 1$ будет близка к единице.
Изменяя порог, между крайними положениями, получим графики Precision и Recall, которые выглядят как-то так:
Recall меняется от единицы до нуля, а Precision от среднего тагрета до какого-то другого значения (нет гарантий, что график монотонный).
Итого оптимизация precision и recall происходит так:
- Модель обучается на стандартную функцию потерь (например, LogLoss).
- Используя вещественные предсказания на валидационной выборке, перебирая разные пороги от 0 до 1, получаем графики метрик в зависимости от порога.
- Выбираем нужное сочетание точности и полноты.
Пусть теперь мы хотим максимизировать метрику AUC. Стандартный метод оптимизации, градиентный спуск, предполагает, что функция потерь дифференцируема. AUC этим качеством не обладает, то есть мы не можем оптимизировать её напрямую. Поэтому для метрики AUC приходится изменять оптимизационную задачу. Метрика AUC считает долю верно упорядоченных пар. Значит от исходной выборки можно перейти к выборке упорядоченных пар объектов. На этой выборке ставится задача классификации: метка класса 1 соответствует правильно упорядоченной паре, 0 — неправильно. Новой метрикой становится accuracy — доля правильно классифицированных объектов, то есть доля правильно упорядоченных пар. Оптимизировать accuracy можно по той же схеме, что и precision, recall: обучаем модель на LogLoss и предсказываем вероятности положительной метки у объекта выборки, считаем accuracy для разных порогов по вероятности и выбираем понравившийся.
Регрессия
В задачах регрессии целевая метка у нас имеет потенциально бесконечное число значений. И природа этих значений, обычно, связана с каким-то процессом измерений:
- величина температуры в определенный момент времени на метеостанции
- количество прочтений статьи на сайте
- количество проданных бананов в конкретном магазине, сети магазинов или стране
- дебит добывающей скважины на нефтегазовом месторождении за месяц и т.п.
Мы видим, что иногда метка это целое число, а иногда произвольное вещественное число. Обычно случаи целочисленных меток моделируют так, словно это просто обычное вещественное число. При таком подходе может оказаться так, что модель A лучше модели B по некоторой метрике, но при этом предсказания у модели A могут быть не целыми. Если в бизнес-задаче ожидается именно целочисленный ответ, то и оценивать нужно огрубление.
Общая рекомендация такова: оценивайте весь каскад решающих правил: и те «внутренние», которые вы получаете в результате обучения, и те «итоговые», которые вы отдаёте бизнес-заказчику.
Например, вы можете быть удовлетворены, что стали ошибаться не во втором, а только в третьем знаке после запятой при предсказании погоды. Но сами погодные данные измеряются с точностью до десятых долей градуса, а пользователь и вовсе может интересоваться лишь целым числом градусов.
Итак, напомним постановку задачи регрессии: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_i in mathbb{R}$ построить модель f(x).
Величину $ e_i = f(x_i) — y_i $ называют ошибкой на объекте i или регрессионным остатком.
Весь набор ошибок на отложенной выборке может служить аналогом матрицы ошибок из задачи классификации. А именно, когда мы рассматриваем две разные модели, то, глядя на то, как и на каких объектах они ошиблись, мы можем прийти к выводу, что для решения бизнес-задачи нам выгоднее взять ту или иную модель. И, аналогично со случаем бинарной классификации, мы можем начать строить агрегаты от вектора ошибок, получая тем самым разные метрики.
MSE, RMSE, $R^2$
MSE – одна из самых популярных метрик в задаче регрессии. Она уже знакома вам, т.к. применяется в качестве функции потерь (или входит в ее состав) во многих ранее рассмотренных методах.
$$ MSE(y^{true}, y^{pred}) = frac1Nsum_{i=1}^{N} (y_i — f(x_i))^2 $$
Иногда для того, чтобы показатель эффективности MSE имел размерность исходных данных, из него извлекают квадратный корень и получают показатель эффективности RMSE.
MSE неограничен сверху, и может быть нелегко понять, насколько «хорошим» или «плохим» является то или иное его значение. Чтобы появились какие-то ориентиры, делают следующее:
-
Берут наилучшее константное предсказание с точки зрения MSE — среднее арифметическое меток $bar{y}$. При этом чтобы не было подглядывания в test, среднее нужно вычислять по обучающей выборке
-
Рассматривают в качестве показателя ошибки:
$$ R^2 = 1 — frac{sum_{i=1}^{N} (y_i — f(x_i))^2}{sum_{i=1}^{N} (y_i — bar{y})^2}.$$
У идеального решающего правила $R^2$ равен $1$, у наилучшего константного предсказания он равен $0$ на обучающей выборке. Можно заметить, что $R^2$ показывает, какая доля дисперсии таргетов (знаменатель) объяснена моделью.
MSE квадратично штрафует за большие ошибки на объектах. Мы уже видели проявление этого при обучении моделей методом минимизации квадратичных ошибок – там это проявлялось в том, что модель старалась хорошо подстроиться под выбросы.
Пусть теперь мы хотим использовать MSE для оценки наших регрессионных моделей. Если большие ошибки для нас действительно неприемлемы, то квадратичный штраф за них — очень полезное свойство (и его даже можно усиливать, повышая степень, в которую мы возводим ошибку на объекте). Однако если в наших тестовых данных присутствуют выбросы, то нам будет сложно объективно сравнить модели между собой: ошибки на выбросах будет маскировать различия в ошибках на основном множестве объектов.
Таким образом, если мы будем сравнивать две модели при помощи MSE, у нас будет выигрывать та модель, у которой меньше ошибка на объектах-выбросах, а это, скорее всего, не то, чего требует от нас наша бизнес-задача.
История из жизни про бананы и квадратичный штраф за ошибкуИз-за неверно введенных данных метка одного из объектов оказалась в 100 раз больше реального значения. Моделировалась величина при помощи градиентного бустинга над деревьями решений. Функция потерь была MSE.
Однажды уже во время эксплуатации случилось ч.п.: у нас появились предсказания, в 100 раз превышающие допустимые из соображений физического смысла значения. Представьте себе, например, что вместо обычных 4 ящиков бананов система предлагала поставить в магазин 400. Были распечатаны все деревья из ансамбля, и мы увидели, что постепенно число ящиков действительно увеличивалось до прогнозных 400.
Было решено проверить гипотезу, что был выброс в данных для обучения. Так оно и оказалось: всего одна точка давала такую потерю на объекте, что алгоритм обучения решил, что лучше переобучиться под этот выброс, чем смириться с большим штрафом на этом объекте. А в эксплуатации у нас возникли точки, которые плюс-минус попадали в такие же листья ансамбля, что и объект-выброс.
Избежать такого рода проблем можно двумя способами: внимательнее контролируя качество данных или адаптировав функцию потерь.
Аналогично, можно поступать и в случае, когда мы разрабатываем метрику качества: менее жёстко штрафовать за большие отклонения от истинного таргета.
MAE
Использовать RMSE для сравнения моделей на выборках с большим количеством выбросов может быть неудобно. В таких случаях прибегают к также знакомой вам в качестве функции потери метрике MAE (mean absolute error):
$$ MAE(y^{true}, y^{pred}) = frac{1}{N}sum_{i=1}^{N} left|y_i — f(x_i)right| $$
Метрики, учитывающие относительные ошибки
И MSE и MAE считаются как сумма абсолютных ошибок на объектах.
Рассмотрим следующую задачу: мы хотим спрогнозировать спрос товаров на следующий месяц. Пусть у нас есть два продукта: продукт A продаётся в количестве 100 штук, а продукт В в количестве 10 штук. И пусть базовая модель предсказывает количество продаж продукта A как 98 штук, а продукта B как 8 штук. Ошибки на этих объектах добавляют 4 штрафных единицы в MAE.
И есть 2 модели-кандидата на улучшение. Первая предсказывает товар А 99 штук, а товар B 8 штук. Вторая предсказывает товар А 98 штук, а товар B 9 штук.
Обе модели улучшают MAE базовой модели на 1 единицу. Однако, с точки зрения бизнес-заказчика вторая модель может оказаться предпочтительнее, т.к. предсказание продажи редких товаров может быть приоритетнее. Один из способов учесть такое требование – рассматривать не абсолютную, а относительную ошибку на объектах.
MAPE, SMAPE
Когда речь заходит об относительных ошибках, сразу возникает вопрос: что мы будем ставить в знаменатель?
В метрике MAPE (mean absolute percentage error) в знаменатель помещают целевое значение:
$$ MAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ left|y_i — f(x_i)right|}{left|y_iright|} $$
С особым случаем, когда в знаменателе оказывается $0$, обычно поступают «инженерным» способом: или выдают за непредсказание $0$ на таком объекте большой, но фиксированный штраф, или пытаются застраховаться от подобного на уровне формулы и переходят к метрике SMAPE (symmetric mean absolute percentage error):
$$ SMAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ 2 left|y_i — f(x_i)right|}{y_i + f(x_i)} $$
Если же предсказывается ноль, штраф считаем нулевым.
Таким переходом от абсолютных ошибок на объекте к относительным мы сделали объекты в тестовой выборке равнозначными: даже если мы делаем абсурдно большое предсказание, на фоне которого истинная метка теряется, мы получаем штраф за этот объект порядка 1 в случае MAPE и 2 в случае SMAPE.
WAPE
Как и любая другая метрика, MAPE имеет свои границы применимости: например, она плохо справляется с прогнозом спроса на товары с прерывистыми продажами. Рассмотрим такой пример:
| Понедельник | Вторник | Среда | |
|---|---|---|---|
| Прогноз | 55 | 2 | 50 |
| Продажи | 50 | 1 | 50 |
| MAPE | 10% | 100% | 0% |
Среднее MAPE – 36.7%, что не очень отражает реальную ситуацию, ведь два дня мы предсказывали с хорошей точностью. В таких ситуациях помогает WAPE (weighted average percentage error):
$$ WAPE(y^{true}, y^{pred}) = frac{sum_{i=1}^{N} left|y_i — f(x_i)right|}{sum_{i=1}^{N} left|y_iright|} $$
Если мы предсказываем идеально, то WAPE = 0, если все предсказания отдаём нулевыми, то WAPE = 1.
В нашем примере получим WAPE = 5.9%
RMSLE
Альтернативный способ уйти от абсолютных ошибок к относительным предлагает метрика RMSLE (root mean squared logarithmic error):
$$ RMSLE(y^{true}, y^{pred}| c) = sqrt{ frac{1}{N} sum_{i=1}^N left(vphantom{frac12}log{left(y_i + c right)} — log{left(f(x_i) + c right)}right)^2 } $$
где нормировочная константа $c$ вводится искусственно, чтобы не брать логарифм от нуля. Также по построению видно, что метрика пригодна лишь для неотрицательных меток.
Веса в метриках
Все вышеописанные метрики легко допускают введение весов для объектов. Если мы из каких-то соображений можем определить стоимость ошибки на объекте, можно брать эту величину в качестве веса. Например, в задаче предсказания спроса в качестве веса можно использовать стоимость объекта.
Доля предсказаний с абсолютными ошибками больше, чем d
Еще одним способом охарактеризовать качество модели в задаче регрессии является доля предсказаний с абсолютными ошибками больше заданного порога $d$:
$$frac{1}{N} sum_{i=1}^{N} mathbb{I}left[ left| y_i — f(x_i) right| > d right] $$
Например, можно считать, что прогноз погоды сбылся, если ошибка предсказания составила меньше 1/2/3 градусов. Тогда рассматриваемая метрика покажет, в какой доле случаев прогноз не сбылся.
Как оптимизировать метрики регрессии?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы F на валидационной выборке была минимальная/максимальная. Аналогично задачам классификации лучший способ добиться минимизации метрики $F$ — выбрать в качестве функции потерь ту же $F(a(X), Y)$. К счастью, основные метрики для регрессии: MSE, RMSE, MAE можно оптимизировать напрямую. С формальной точки зрения MAE не дифференцируема, так как там присутствует модуль, чья производная не определена в нуле. На практике для этого выколотого случая в коде можно возвращать ноль.
Для оптимизации MAPE придётся изменять оптимизационную задачу. Оптимизацию MAPE можно представить как оптимизацию MAE, где объектам выборки присвоен вес $frac{1}{vert y_ivert}$.
Есть 3 различных API для оценки качества прогнозов модели:
- Метод оценки оценщика : у оценщиков есть
scoreметод, обеспечивающий критерий оценки по умолчанию для проблемы, для решения которой они предназначены. Это обсуждается не на этой странице, а в документации каждого оценщика. - Параметр оценки: инструменты оценки модели с использованием перекрестной проверки (например,
model_selection.cross_val_scoreиmodel_selection.GridSearchCV) полагаются на внутреннюю стратегию оценки . Это обсуждается в разделе Параметр оценки: определение правил оценки модели . - Метрические функции : В
sklearn.metricsмодуле реализованы функции оценки ошибки прогноза для конкретных целей. Эти показатели подробно описаны в разделах по метрикам классификации , MultiLabel ранжирования показателей , показателей регрессии и показателей кластеризации .
Наконец, фиктивные оценки полезны для получения базового значения этих показателей для случайных прогнозов.
3.3.1. В scoring параметрах: определение правил оценки моделей
Выбор и оценка модели с использованием таких инструментов, как model_selection.GridSearchCV и model_selection.cross_val_score, принимают scoring параметр, который контролирует, какую метрику они применяют к оцениваемым оценщикам.
3.3.1.1. Общие случаи: предопределенные значения
Для наиболее распространенных случаев использования вы можете назначить объект подсчета с помощью scoring параметра; в таблице ниже показаны все возможные значения. Все объекты счетчика следуют соглашению о том, что более высокие возвращаемые значения лучше, чем более низкие возвращаемые значения . Таким образом, метрики, которые измеряют расстояние между моделью и данными, например metrics.mean_squared_error, доступны как neg_mean_squared_error, которые возвращают инвертированное значение метрики.
| Подсчет очков | Функция | Комментарий |
| Классификация | ||
| ‘accuracy’ | metrics.accuracy_score |
|
| ‘balanced_accuracy’ | metrics.balanced_accuracy_score |
|
| ‘top_k_accuracy’ | metrics.top_k_accuracy_score |
|
| ‘average_precision’ | metrics.average_precision_score |
|
| ‘neg_brier_score’ | metrics.brier_score_loss |
|
| ‘f1’ | metrics.f1_score |
для двоичных целей |
| ‘f1_micro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_macro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_weighted’ | metrics.f1_score |
средневзвешенное |
| ‘f1_samples’ | metrics.f1_score |
по многопозиционному образцу |
| ‘neg_log_loss’ | metrics.log_loss |
требуетсяpredict_probaподдержка |
| ‘precision’ etc. | metrics.precision_score |
суффиксы применяются как с ‘f1’ |
| ‘recall’ etc. | metrics.recall_score |
суффиксы применяются как с ‘f1’ |
| ‘jaccard’ etc. | metrics.jaccard_score |
суффиксы применяются как с ‘f1’ |
| ‘roc_auc’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr_weighted’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo_weighted’ | metrics.roc_auc_score |
|
| Кластеризация | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score |
|
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score |
|
| ‘completeness_score’ | metrics.completeness_score |
|
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score |
|
| ‘homogeneity_score’ | metrics.homogeneity_score |
|
| ‘mutual_info_score’ | metrics.mutual_info_score |
|
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score |
|
| ‘rand_score’ | metrics.rand_score |
|
| ‘v_measure_score’ | metrics.v_measure_score |
|
| Регрессия | ||
| ‘explained_variance’ | metrics.explained_variance_score |
|
| ‘max_error’ | metrics.max_error |
|
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error |
|
| ‘neg_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_root_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error |
|
| ‘neg_median_absolute_error’ | metrics.median_absolute_error |
|
| ‘r2’ | metrics.r2_score |
|
| ‘neg_mean_poisson_deviance’ | metrics.mean_poisson_deviance |
|
| ‘neg_mean_gamma_deviance’ | metrics.mean_gamma_deviance |
|
| ‘neg_mean_absolute_percentage_error’ | metrics.mean_absolute_percentage_error |
Примеры использования:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sorted(sklearn.metrics.SCORERS.keys()) to get valid options.
Примечание
Значения, перечисленные в виде ValueError исключения, соответствуют функциям измерения точности прогнозирования, описанным в следующих разделах. Объекты счетчика для этих функций хранятся в словаре sklearn.metrics.SCORERS.
3.3.1.2. Определение стратегии выигрыша от метрических функций
Модуль sklearn.metrics также предоставляет набор простых функций, измеряющих ошибку предсказания с учетом истинности и предсказания:
- функции, заканчивающиеся на,
_scoreвозвращают значение для максимизации, чем выше, тем лучше. - функции, заканчивающиеся на
_errorили_lossвозвращающие значение, которое нужно минимизировать, чем ниже, тем лучше. При преобразовании в объект счетчика с использованиемmake_scorerустановите дляgreater_is_betterпараметра значениеFalse(Trueпо умолчанию; см. Описание параметра ниже).
Метрики, доступные для различных задач машинного обучения, подробно описаны в разделах ниже.
Многим метрикам не даются имена для использования в качестве scoring значений, иногда потому, что они требуют дополнительных параметров, например fbeta_score. В таких случаях вам необходимо создать соответствующий объект оценки. Самый простой способ создать вызываемый объект для оценки — использовать make_scorer. Эта функция преобразует метрики в вызываемые объекты, которые можно использовать для оценки модели.
Один из типичных вариантов использования — обернуть существующую метрическую функцию из библиотеки значениями, отличными от значений по умолчанию для ее параметров, такими как beta параметр для fbeta_score функции:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
Второй вариант использования — создание полностью настраиваемого объекта скоринга из простой функции Python с использованием make_scorer, которая может принимать несколько параметров:
- функция Python, которую вы хотите использовать (
my_custom_loss_funcв примере ниже) - возвращает ли функция Python оценку (
greater_is_better=True, по умолчанию) или потерю (greater_is_better=False). В случае потери результат функции python аннулируется объектом скоринга в соответствии с соглашением о перекрестной проверке, согласно которому скоринтеры возвращают более высокие значения для лучших моделей. - только для показателей классификации: требуется ли для предоставленной вами функции Python постоянная уверенность в принятии решений (
needs_threshold=True). Значение по умолчанию неверно. - любые дополнительные параметры, такие как
betaилиlabelsвf1_score.
Вот пример создания пользовательских счетчиков очков и использования greater_is_better параметра:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
3.3.1.3. Реализация собственного скорингового объекта
Вы можете сгенерировать еще более гибкие модели скоринга, создав свой собственный скоринговый объект с нуля, без использования make_scorer фабрики. Чтобы вызываемый может быть бомбардиром, он должен соответствовать протоколу, указанному в следующих двух правилах:
- Его можно вызвать с параметрами (estimator, X, y), где estimator это модель, которая должна быть оценена, X это данные проверки и y основная истинная цель для (в контролируемом случае) или None (в неконтролируемом случае).
- Он возвращает число с плавающей запятой, которое количественно определяет
estimatorкачество прогнозированияXсо ссылкой наy. Опять же, по соглашению более высокие числа лучше, поэтому, если ваш секретарь сообщает о проигрыше, это значение следует отменить.
Примечание Использование пользовательских счетчиков в функциях, где n_jobs> 1
Хотя определение пользовательской функции оценки вместе с вызывающей функцией должно работать из коробки с бэкэндом joblib по умолчанию (loky), его импорт из другого модуля будет более надежным подходом и будет работать независимо от бэкэнда joblib.
Например, чтобы использовать n_jobsбольше 1 в примере ниже, custom_scoring_function функция сохраняется в созданном пользователем модуле ( custom_scorer_module.py) и импортируется:
>>> from custom_scorer_module import custom_scoring_function >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1)
3.3.1.4. Использование множественной метрической оценки
Scikit-learn также позволяет оценивать несколько показателей в GridSearchCV, RandomizedSearchCV и cross_validate.
Есть три способа указать несколько показателей оценки для scoring параметра:
- Как итерация строковых показателей:
>>> scoring = ['accuracy', 'precision']
- В качестве
dictсопоставления имени секретаря с функцией подсчета очков:
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
Обратите внимание, что значения dict могут быть либо функциями счетчика, либо одной из предварительно определенных строк показателей.
- Как вызываемый объект, возвращающий словарь оценок:
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
... y_pred = clf.predict(X)
... cm = confusion_matrix(y, y_pred)
... return {'tn': cm[0, 0], 'fp': cm[0, 1],
... 'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
... scoring=confusion_matrix_scorer)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
3.3.2. Метрики классификации
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности классификации. Некоторые метрики могут потребовать оценок вероятности положительного класса, значений достоверности или значений двоичных решений. Большинство реализаций позволяют каждой выборке вносить взвешенный вклад в общую оценку с помощью sample_weight параметра.
Некоторые из них ограничены случаем двоичной классификации:
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
roc_curve(y_true, y_score, *[, pos_label, …]) |
Вычислить рабочую характеристику приемника (ROC). |
det_curve(y_true, y_score[, pos_label, …]) |
Вычислите частоту ошибок для различных пороговых значений вероятности. |
Другие также работают в случае мультикласса:
balanced_accuracy_score(y_true, y_pred, *[, …]) |
Вычислите сбалансированную точность. |
cohen_kappa_score(y1, y2, *[, labels, …]) |
Каппа Коэна: статистика, измеряющая согласованность аннотаторов. |
confusion_matrix(y_true, y_pred, *[, …]) |
Вычислите матрицу неточностей, чтобы оценить точность классификации. |
hinge_loss(y_true, pred_decision, *[, …]) |
Средняя потеря петель (нерегулируемая). |
matthews_corrcoef(y_true, y_pred, *[, …]) |
Вычислите коэффициент корреляции Мэтьюза (MCC). |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
top_k_accuracy_score(y_true, y_score, *[, …]) |
Top-k Рейтинг по классификации точности. |
Некоторые также работают в многоярусном регистре:
accuracy_score(y_true, y_pred, *[, …]) |
Классификационная оценка точности. |
classification_report(y_true, y_pred, *[, …]) |
Создайте текстовый отчет, показывающий основные показатели классификации. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
hamming_loss(y_true, y_pred, *[, sample_weight]) |
Вычислите среднюю потерю Хэмминга. |
jaccard_score(y_true, y_pred, *[, labels, …]) |
Оценка коэффициента сходства Жаккара. |
log_loss(y_true, y_pred, *[, eps, …]) |
Потеря журнала, также известная как потеря логистики или потеря кросс-энтропии. |
multilabel_confusion_matrix(y_true, y_pred, *) |
Вычислите матрицу неточностей для каждого класса или образца. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите отзыв. |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
zero_one_loss(y_true, y_pred, *[, …]) |
Потеря классификации нулевая единица. |
А некоторые работают с двоичными и многозначными (но не мультиклассовыми) проблемами:
В следующих подразделах мы опишем каждую из этих функций, которым будут предшествовать некоторые примечания по общему API и определению показателей.
3.3.2.1. От бинарного до мультиклассового и многозначного
Некоторые метрики по существу определены для задач двоичной классификации (например f1_score, roc_auc_score). В этих случаях по умолчанию оценивается только положительная метка, предполагая по умолчанию, что положительный класс помечен 1 (хотя это можно настроить с помощью pos_label параметра).
При расширении двоичной метрики на задачи с несколькими классами или метками данные обрабатываются как набор двоичных задач, по одной для каждого класса. Затем есть несколько способов усреднить вычисления двоичных показателей по набору классов, каждый из которых может быть полезен в некотором сценарии. Если возможно, вы должны выбрать одно из них с помощью average параметра.
"macro"просто вычисляет среднее значение двоичных показателей, придавая каждому классу одинаковый вес. В задачах, где редкие занятия тем не менее важны, макро-усреднение может быть средством выделения их производительности. С другой стороны, предположение, что все классы одинаково важны, часто неверно, так что макро-усреднение будет чрезмерно подчеркивать обычно низкую производительность для нечастого класса."weighted"учитывает дисбаланс классов, вычисляя среднее значение двоичных показателей, в которых оценка каждого класса взвешивается по его присутствию в истинной выборке данных."micro"дает каждой паре выборка-класс равный вклад в общую метрику (за исключением результата взвешивания выборки). Вместо того, чтобы суммировать метрику для каждого класса, это суммирует дивиденды и делители, составляющие метрики для каждого класса, для расчета общего частного. Микро-усреднение может быть предпочтительным в настройках с несколькими ярлыками, включая многоклассовую классификацию, когда класс большинства следует игнорировать."samples"применяется только к задачам с несколькими ярлыками. Он не вычисляет меру для каждого класса, вместо этого вычисляет метрику по истинным и прогнозируемым классам для каждой выборки в данных оценки и возвращает их (sample_weight— взвешенное) среднее значение.- Выбор
average=Noneвернет массив с оценкой для каждого класса.
В то время как данные мультикласса предоставляются метрике, как двоичные цели, в виде массива меток классов, данные с несколькими метками указываются как индикаторная матрица, в которой ячейка [i, j] имеет значение 1, если у образца i есть метка j, и значение 0 в противном случае.
3.3.2.2. Оценка точности
Функция accuracy_score вычисляет точность , либо фракции ( по умолчанию) или количество (нормализует = False) правильных предсказаний.
В классификации с несколькими ярлыками функция возвращает точность подмножества. Если весь набор предсказанных меток для выборки строго соответствует истинному набору меток, то точность подмножества равна 1,0; в противном случае — 0, 0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)$$
где $1(x)$- индикаторная функция .
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
В многопозиционном корпусе с бинарными индикаторами меток:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
Пример:
- См. В разделе Проверка с перестановками значимости классификационной оценки пример использования показателя точности с использованием перестановок набора данных.
3.3.2.3. Рейтинг точности Top-k
Функция top_k_accuracy_score представляет собой обобщение accuracy_score. Разница в том, что прогноз считается правильным, если истинная метка связана с одним из kнаивысших прогнозируемых баллов. accuracy_score является частным случаем k = 1.
Функция охватывает случаи двоичной и многоклассовой классификации, но не случай многозначной классификации.
Если $hat{f}_{i,j}$ прогнозируемый класс для $i$-й образец, соответствующий $j$-й по величине прогнозируемый результат и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)$$
где k допустимое количество предположений и 1(x)- индикаторная функция.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
3.3.2.4. Сбалансированный показатель точности
Функция balanced_accuracy_score вычисляет взвешенную точность , что позволяет избежать завышенных оценок производительности на несбалансированных данных. Это макросреднее количество оценок отзыва по классу или, что то же самое, грубая точность, где каждая выборка взвешивается в соответствии с обратной распространенностью ее истинного класса. Таким образом, для сбалансированных наборов данных оценка равна точности.
В двоичном случае сбалансированная точность равна среднему арифметическому чувствительности (истинно положительный показатель) и специфичности (истинно отрицательный показатель) или площади под кривой ROC с двоичными прогнозами, а не баллами:
$$texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )$$
Если классификатор одинаково хорошо работает в любом классе, этот термин сокращается до обычной точности (т. е. Количества правильных прогнозов, деленного на общее количество прогнозов).
Напротив, если обычная точность выше вероятности только потому, что классификатор использует несбалансированный набор тестов, тогда сбалансированная точность, при необходимости, упадет до $frac{1}{n_classes}$.
Оценка варьируется от 0 до 1 или, когда adjusted=True используется, масштабируется до диапазона $frac{1}{1 — n_classes}$ до 1 включительно, с произвольной оценкой 0.
Если yi истинная ценность $i$-й образец, и $w_i$ — соответствующий вес образца, затем мы настраиваем вес образца на:
$$hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}$$
где $1(x)$- индикаторная функция . Учитывая предсказанный $hat{y}_i$ для образца $i$, сбалансированная точность определяется как:
$$texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i$$
С adjusted=True сбалансированной точностью сообщает об относительном увеличении от $texttt{balanced-accuracy}(y, mathbf{0}, w) =frac{1}{n_classes}$. В двоичном случае это также известно как * статистика Юдена * , или информированность .
Примечание
Определение мультикласса здесь кажется наиболее разумным расширением метрики, используемой в бинарной классификации, хотя в литературе нет определенного консенсуса:
- Наше определение: [Mosley2013] , [Kelleher2015] и [Guyon2015] , где [Guyon2015] принимает скорректированную версию, чтобы гарантировать, что случайные предсказания имеют оценку 0 а точные предсказания имеют оценку 1..
- Точность балансировки классов, как описано в [Mosley2013] : вычисляется минимум между точностью и отзывом для каждого класса. Затем эти значения усредняются по общему количеству классов для получения сбалансированной точности.
- Сбалансированная точность, как описано в [Urbanowicz2015] : среднее значение чувствительности и специфичности вычисляется для каждого класса, а затем усредняется по общему количеству классов.
Рекомендации:
- Гийон 2015 ( 1 , 2 ) И. Гайон, К. Беннет, Г. Коули, Х. Дж. Эскаланте, С. Эскалера, Т. К. Хо, Н. Масиа, Б. Рэй, М. Саид, А. Р. Статников, Э. Вьегас, Дизайн конкурса ChaLearn AutoML Challenge 2015 , IJCNN 2015 г.
- Мосли 2013 ( 1 , 2 ) Л. Мосли, Сбалансированный подход к проблеме мультиклассового дисбаланса , IJCV 2010.
- Kelleher2015 Джон. Д. Келлехер, Брайан Мак Нейме, Аойф Д’Арси, Основы машинного обучения для прогнозной аналитики данных: алгоритмы, рабочие примеры и тематические исследования , 2015.
- Урбанович2015 Urbanowicz RJ, Moore, JH ExSTraCS 2.0: описание и оценка масштабируемой системы классификаторов обучения , Evol. Intel. (2015) 8:89.
3.3.2.5. Каппа Коэна
Функция cohen_kappa_score вычисляет каппа-Коэна статистику. Эта мера предназначена для сравнения меток, сделанных разными людьми-аннотаторами, а не классификатором с достоверной информацией.
Показатель каппа (см. Строку документации) представляет собой число от -1 до 1. Баллы выше 0,8 обычно считаются хорошим совпадением; ноль или ниже означает отсутствие согласия (практически случайные метки).
Оценка Каппа может быть вычислена для двоичных или многоклассовых задач, но не для задач с несколькими метками (за исключением ручного вычисления оценки для каждой метки) и не более чем для двух аннотаторов.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
3.3.2.6. Матрица неточностей ¶
Точность функции confusion_matrix вычисляет классификацию пути вычисления матрицы путаницы с каждой строкой , соответствующей истинный классом (Википедия и другие ссылки могут использовать различные конвенции для осей).
По определению запись i,j в матрице неточностей — количество наблюдений в группе i, но предполагается, что он будет в группе j. Вот пример:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
plot_confusion_matrix может использоваться для визуального представления матрицы неточностей, как показано в примере матрицы неточностей, который создает следующий рисунок:
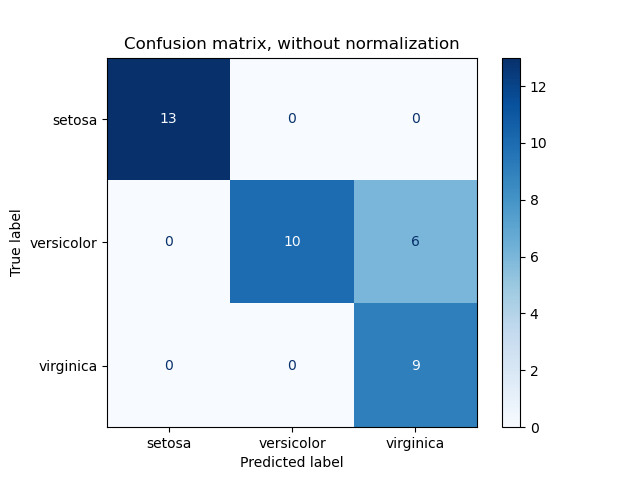
Параметр normalize позволяет сообщать коэффициенты вместо подсчетов. Матрица путаница может быть нормализована в 3 различными способами: 'pred', 'true'и 'all' которые будут делить счетчики на сумму каждого столбца, строки или всей матрицы, соответственно.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
Для двоичных задач мы можем получить подсчет истинно отрицательных, ложноположительных, ложноотрицательных и истинно положительных результатов следующим образом:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
Пример:
- См. В разделе Матрица неточностей пример использования матрицы неточностей для оценки качества выходных данных классификатора.
- См. В разделе Распознавание рукописных цифр пример использования матрицы неточностей для классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования матрицы неточностей для классификации текстовых документов.
3.3.2.7. Отчет о классификации
Функция classification_report создает текстовый отчет , показывающий основные показатели классификации. Вот небольшой пример с настраиваемыми target_names и предполагаемыми ярлыками:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Пример:
- См. В разделе Распознавание рукописных цифр пример использования отчета о классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций, где приведен пример использования отчета о классификации для текстовых документов.
- См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример использования отчета о классификации для поиска по сетке с вложенной перекрестной проверкой.
3.3.2.8. Потеря Хэмминга
hamming_loss вычисляет среднюю потерю Хэмминга или расстояние Хемминга между двумя наборами образцов.
Если $hat{y}_j$ прогнозируемое значение для $j$-я этикетка данного образца, $y_j$ — соответствующее истинное значение, а $n_{labels}$ — количество классов или меток, то потеря Хэмминга $L_{Hamming}$ между двумя образцами определяется как:
$$L_{Hamming}(y, hat{y}) = frac{1}{n_text{labels}} sum_{j=0}^{n_text{labels} — 1} 1(hat{y}_j not= y_j)$$
где $1(x)$- индикаторная функция .
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
В многопозиционном корпусе с бинарными индикаторами меток:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Примечание
В мультиклассовой классификации потери Хэмминга соответствуют расстоянию Хэмминга между y_true и, y_pred что аналогично функции потерь нуля или единицы . Однако, в то время как потеря нуля или единицы наказывает наборы предсказаний, которые не строго соответствуют истинным наборам, потеря Хэмминга наказывает отдельные метки. Таким образом, потеря Хэмминга, ограниченная сверху потерей нуля или единицы, всегда находится между нулем и единицей включительно; и прогнозирование надлежащего подмножества или надмножества истинных меток даст исключительную потерю Хэмминга от нуля до единицы.
3.3.2.9. Точность, отзыв и F-меры
Интуитивно, точность — это способность классификатора не маркировать как положительный образец, который является отрицательным, а отзыв — это способность классификатора находить все положительные образцы.
F-мера ($F_beta$ а также $F_1$ меры) можно интерпретировать как взвешенное гармоническое среднее значение точности и полноты. А $F_beta$ мера достигает своего лучшего значения на уровне 1 и худшего результата на уровне 0. С $beta = 1$, $F_beta$ а также $F_1$ эквивалентны, а отзыв и точность одинаково важны.
precision_recall_curve вычисляет кривую точности-отзыва на основе наземной метки истинности и оценки, полученной классификатором путем изменения порога принятия решения.
Функция average_precision_score вычисляет среднюю точность (AP) от оценки прогнозирования. Значение от 0 до 1 и выше — лучше. AP определяется как
$$text{AP} = sum_n (R_n — R_{n-1}) P_n$$
где $P_n$ а также $R_n$- точность и отзыв на n-м пороге. При случайных прогнозах AP — это доля положительных образцов.
Ссылки [Manning2008] и [Everingham2010] представляют альтернативные варианты AP, которые интерполируют кривую точности-отзыва. В настоящее время average_precision_score не реализован какой-либо вариант с интерполяцией. Ссылки [Davis2006] и [Flach2015] описывают, почему линейная интерполяция точек на кривой точности-отзыва обеспечивает чрезмерно оптимистичный показатель эффективности классификатора. Эта линейная интерполяция используется при вычислении площади под кривой с помощью правила трапеции в auc.
Несколько функций позволяют анализировать точность, отзыв и оценку F-мер:
average_precision_score(y_true, y_score, *) |
Вычислить среднюю точность (AP) из оценок прогнозов. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите рекол. |
Обратите внимание, что функция precision_recall_curve ограничена двоичным регистром. Функция average_precision_score работает только в двоичном формате классификации и MultiLabel индикатора. В функции plot_precision_recall_curve графики точности вспомнить следующим образом .
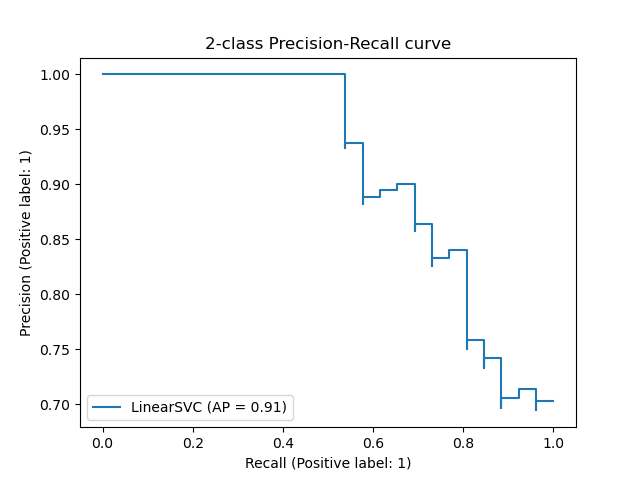
Примеры:
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования
f1_scoreдля классификации текстовых документов. - См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример
precision_scoreиrecall_scoreиспользование для оценки параметров с помощью поиска по сетке с вложенной перекрестной проверкой. - См. В разделе Precision-Recall пример использования
precision_recall_curveдля оценки качества вывода классификатора.
Рекомендации:
- [Manning2008] г. CD Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval , 2008.
- [Everingham2010] М. Эверингем, Л. Ван Гул, CKI Уильямс, Дж. Винн, А. Зиссерман, Задача классов визуальных объектов Pascal (VOC) , IJCV 2010.
- [Davis2006] Дж. Дэвис, М. Гоадрич, Взаимосвязь между точным воспроизведением и кривыми ROC , ICML 2006.
- [Flach2015] П.А. Флэч, М. Кулл, Кривые точности-отзыва-выигрыша: PR-анализ выполнен правильно , NIPS 2015.
3.3.2.9.1. Бинарная классификация
В задаче бинарной классификации термины «положительный» и «отрицательный» относятся к предсказанию классификатора, а термины «истинный» и «ложный» относятся к тому, соответствует ли этот прогноз внешнему суждению ( иногда известное как «наблюдение»). Учитывая эти определения, мы можем сформулировать следующую таблицу:
| Фактический класс (наблюдение) | ||
| Прогнозируемый класс (ожидание) | tp (истинно положительный результат) Правильный результат | fp (ложное срабатывание) Неожиданный результат |
| Прогнозируемый класс (ожидание) | fn (ложноотрицательный) Отсутствует результат | tn (истинно отрицательное) Правильное отсутствие результата |
В этом контексте мы можем определить понятия точности, отзыва и F-меры:
$$text{precision} = frac{tp}{tp + fp},$$
$$text{recall} = frac{tp}{tp + fn},$$
$$F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.$$
Вот несколько небольших примеров бинарной классификации:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 0.5, 0.5, 0. ]) >>> threshold array([0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
3.3.2.9.2. Мультиклассовая и многозначная классификация
В задаче классификации по нескольким классам и меткам понятия точности, отзыва и F-меры могут применяться к каждой метке независимо. Есть несколько способов , чтобы объединить результаты по этикеткам, указанных в average аргументе к average_precision_score (MultiLabel только) f1_score, fbeta_score, precision_recall_fscore_support, precision_score и recall_score функция, как описано выше . Обратите внимание, что если включены все метки, «микро» -усреднение в настройке мультикласса обеспечит точность, отзыв и $F$ все они идентичны по точности. Также обратите внимание, что «взвешенное» усреднение может дать оценку F, которая не находится между точностью и отзывом.
Чтобы сделать это более явным, рассмотрим следующие обозначения:
- $y$ набор предсказанных ($sample$, $label$) пары
- $hat{y}$ набор истинных ($sample$, $label$) пары
- $L$ набор лейблов
- $S$ набор образцов
- $y_s$ подмножество $y$ с образцом $s$, т.е $y_s := left{(s’, l) in y | s’ = sright}$.
- $y_l$ подмножество $y$ с этикеткой $l$
- по аналогии, $hat{y}_s$ а также $hat{y}_l$ являются подмножествами $hat{y}$
- $P(A, B) := frac{left| A cap B right|}{left|Aright|}$ для некоторых наборов $A$ и $B$
- $R(A, B) := frac{left| A cap B right|}{left|Bright|}$ (Условные обозначения различаются в зависимости от обращения $B = emptyset$; эта реализация использует $R(A, B):=0$, и аналогичные для $P$.)
- $$F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)}$$
Тогда показатели определяются как:
| average | Точность | Отзывать | F_beta |
| «micro» | $P(y, hat{y})$ | $R(y, hat{y})$ | $F_beta(y, hat{y})$ |
| «samples» | $frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s)$ |
| «macro» | $frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l)$ |
| «weighted» | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| P(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| R(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}lright| Fbeta(y_l, hat{y}_l)$ |
| None | $langle P(y_l, hat{y}_l) | l in L rangle$ | $langle R(y_l, hat{y}_l) | l in L rangle$ | $langle F_beta(y_l, hat{y}_l) | l in L rangle$ |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
Для мультиклассовой классификации с «отрицательным классом» можно исключить некоторые метки:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Точно так же метки, отсутствующие в выборке данных, могут учитываться при макро-усреднении.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
3.3.2.10. Оценка коэффициента сходства Жаккара
Функция jaccard_score вычисляет среднее значение коэффициентов сходства Jaccard , также называемый индексом Jaccard, между парами множеств меток.
Коэффициент подобия Жаккара i-ые образцы, с набором меток наземной достоверности yi и прогнозируемый набор меток y^i, определяется как
$$J(y_i, hat{y}_i) = frac{|y_i cap hat{y}_i|}{|y_i cup hat{y}_i|}.$$
jaccard_score работает как precision_recall_fscore_support наивно установленная мера, применяемая изначально к бинарным целям, и расширена для применения к множественным меткам и мультиклассам за счет использования average(см. выше ).
В двоичном случае:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
В многопозиционном корпусе с бинарными индикаторами меток:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Задачи с несколькими классами преобразуются в двоичную форму и обрабатываются как соответствующая задача с несколькими метками:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
3.3.2.11. Петля лосс
Функция hinge_loss вычисляет среднее расстояние между моделью и данными с использованием петля лосс, односторонний показателем , который учитывает только ошибки прогнозирования. (Потери на шарнирах используются в классификаторах максимальной маржи, таких как опорные векторные машины.)
Если метки закодированы с помощью +1 и -1, $y$: истинное значение, а $w$ — прогнозируемые решения на выходе decision_function, тогда потери на шарнирах определяются как:
$$L_text{Hinge}(y, w) = maxleft{1 — wy, 0right} = left|1 — wyright|_+$$
Если имеется более двух ярлыков, hinge_loss используется мультиклассовый вариант, разработанный Crammer & Singer. Вот статья, описывающая это.
Если $y_w$ прогнозируемое решение для истинного лейбла и $y_t$ — это максимум предсказанных решений для всех других меток, где предсказанные решения выводятся функцией принятия решений, тогда потеря шарнира в нескольких классах определяется следующим образом:
$$L_text{Hinge}(y_w, y_t) = maxleft{1 + y_t — y_w, 0right}$$
Вот небольшой пример, демонстрирующий использование hinge_loss функции с классификатором svm в задаче двоичного класса:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Вот пример, демонстрирующий использование hinge_loss функции с классификатором svm в мультиклассовой задаче:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels) 0.56...
3.3.2.12. Лог лосс
Лог лосс, также называемые потерями логистической регрессии или кросс-энтропийными потерями, определяются на основе оценок вероятности. Он обычно используется в (полиномиальной) логистической регрессии и нейронных сетях, а также в некоторых вариантах максимизации ожидания и может использоваться для оценки выходов вероятности ( predict_proba) классификатора вместо его дискретных прогнозов.
Для двоичной классификации с истинной меткой $y in {0,1}$ и оценка вероятности $p = operatorname{Pr}(y = 1)$, логарифмическая потеря на выборку представляет собой отрицательную логарифмическую вероятность классификатора с истинной меткой:
$$L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 — y) log (1 — p))$$
Это распространяется на случай мультикласса следующим образом. Пусть истинные метки для набора выборок будут закодированы размером 1 из K как двоичная индикаторная матрица $Y$, т.е. $y_{i,k}=1$ если образец $i$ есть ярлык $k$ взят из набора $K$ этикетки. Пусть $P$ — матрица оценок вероятностей, с $p_{i,k} = operatorname{Pr}(y_{i,k} = 1)$. Тогда потеря журнала всего набора равна
$$L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = — frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}$$
Чтобы увидеть, как это обобщает приведенную выше потерю двоичного журнала, обратите внимание, что в двоичном случае $p_{i,0} = 1 — p_{i,1}$ и $y_{i,0} = 1 — y_{i,1}$, поэтому разложив внутреннюю сумму на $y_{i,k} in {0,1}$ дает двоичную потерю журнала.
В log_loss функции вычисляет журнал потеря дана список меток приземной истины и матриц вероятностей, возвращенный оценщик predict_proba методом.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
Первое [.9, .1] в y_pred означает 90% вероятность того, что первая выборка будет иметь метку 0. Лог лос неотрицательны.
3.3.2.13. Коэффициент корреляции Мэтьюза
Функция matthews_corrcoef вычисляет коэффициент корреляции Матфея (MCC) для двоичных классов. Цитата из Википедии:
«Коэффициент корреляции Мэтьюза используется в машинном обучении как мера качества двоичных (двухклассных) классификаций. Он учитывает истинные и ложные положительные и отрицательные результаты и обычно рассматривается как сбалансированная мера, которую можно использовать, даже если классы очень разных размеров. MCC — это, по сути, значение коэффициента корреляции между -1 и +1. Коэффициент +1 представляет собой идеальное предсказание, 0 — среднее случайное предсказание и -1 — обратное предсказание. Статистика также известна как коэффициент фи ».
В бинарном (двухклассовом) случае $tp$, $tn$, $fp$ а также $fn$ являются соответственно количеством истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных результатов, MCC определяется как
$$MCC = frac{tp times tn — fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.$$
В случае мультикласса коэффициент корреляции Мэтьюза может быть определен в терминах confusion_matrix C для Kклассы. Чтобы упростить определение, рассмотрим следующие промежуточные переменные:
- $t_k=sum_{i}^{K} C_{ik}$ количество занятий k действительно произошло,
- $p_k=sum_{i}^{K} C_{ki}$ количество занятий k был предсказан,
- $c=sum_{k}^{K} C_{kk}$ общее количество правильно спрогнозированных образцов,
- $s=sum_{i}^{K} sum_{j}^{K} C_{ij}$ общее количество образцов.
Тогда мультиклассовый MCC определяется как:
$$MCC = frac{ c times s — sum_{k}^{K} p_k times t_k }{sqrt{ (s^2 — sum_{k}^{K} p_k^2) times (s^2 — sum_{k}^{K} t_k^2) }}$$
Когда имеется более двух меток, значение MCC больше не будет находиться в диапазоне от -1 до +1. Вместо этого минимальное значение будет где-то между -1 и 0 в зависимости от количества и распределения наземных истинных меток. Максимальное значение всегда +1.
Вот небольшой пример, иллюстрирующий использование matthews_corrcoef функции:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
3.3.2.14. Матрица путаницы с несколькими метками
Функция multilabel_confusion_matrix вычисляет класс-накрест ( по умолчанию) или samplewise (samplewise = True) MultiLabel матрицы спутанности для оценки точности классификации. Multilabel_confusion_matrix также обрабатывает данные мультикласса, как если бы они были многоклассовыми, поскольку это преобразование, обычно применяемое для оценки проблем мультикласса с метриками двоичной классификации (такими как точность, отзыв и т. д.).
При вычислении классовой матрицы путаницы с несколькими метками $C$, количество истинных негативов для класса i является $C_{i,0,0}$, ложноотрицательные $C_{i,1,0}$, истинные положительные стороны $C_{i,1,1}$ а ложные срабатывания $C_{i,0,1}$.
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с вводом многозначной индикаторной матрицы:
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
Или можно построить матрицу неточностей для каждой метки образца:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
[1, 1]],
[[1, 1],
[0, 1]]])
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с многоклассовым вводом:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
Вот несколько примеров, демонстрирующих использование multilabel_confusion_matrix функции для расчета отзыва (или чувствительности), специфичности, количества выпадений и пропусков для каждого класса в задаче с вводом многозначной индикаторной матрицы.
Расчет отзыва (также называемого истинно положительным коэффициентом или чувствительностью) для каждого класса:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Расчет специфичности (также называемой истинно отрицательной ставкой) для каждого класса:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Расчет количества выпадений (также называемый частотой ложных срабатываний) для каждого класса:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Расчет процента промахов (также называемого ложноотрицательным показателем) для каждого класса:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
3.3.2.15. Рабочая характеристика приемника (ROC)
Функция roc_curve вычисляет рабочую характеристическую кривую приемника или кривую ROC . Цитата из Википедии:
«Рабочая характеристика приемника (ROC), или просто кривая ROC, представляет собой графический график, который иллюстрирует работу системы двоичного классификатора при изменении ее порога дискриминации. Он создается путем построения графика доли истинных положительных результатов из положительных (TPR = частота истинных положительных результатов) по сравнению с долей ложных положительных результатов из отрицательных (FPR = частота ложных положительных результатов) при различных настройках пороговых значений. TPR также известен как чувствительность, а FPR — это единица минус специфичность или истинно отрицательный показатель ».
Для этой функции требуется истинное двоичное значение и целевые баллы, которые могут быть либо оценками вероятности положительного класса, либо значениями достоверности, либо двоичными решениями. Вот небольшой пример использования roc_curve функции:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
На этом рисунке показан пример такой кривой ROC:
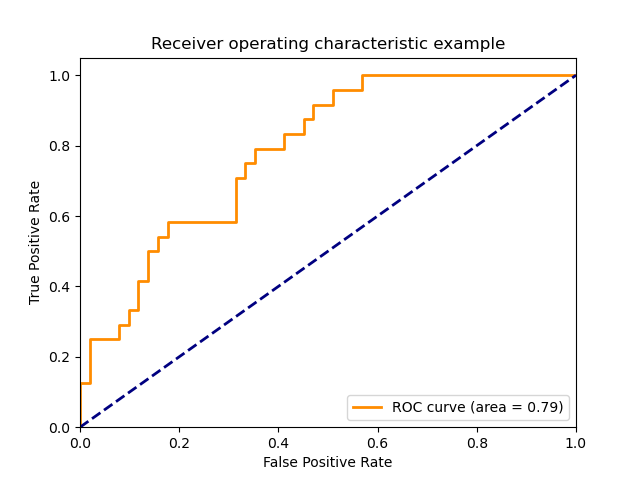
Функция roc_auc_score вычисляет площадь под операционной приемника характеристика (ROC) кривой, которая также обозначается через ППК или AUROC. При вычислении площади под кривой roc информация о кривой суммируется в одном номере. Для получения дополнительной информации см. Статью в Википедии о AUC.
По сравнению с такими показателями, как точность подмножества, потеря Хэмминга или оценка F1, ROC не требует оптимизации порога для каждой метки.
3.3.2.15.1. Двоичный регистр
В двоичном случае вы можете либо предоставить оценки вероятности, используя classifier.predict_proba() метод, либо значения решения без пороговых значений, заданные classifier.decision_function() методом. В случае предоставления оценок вероятности следует указать вероятность класса с «большей меткой». «Большая метка» соответствует classifier.classes_[1] и, следовательно classifier.predict_proba(X) [:, 1]. Следовательно, параметр y_score имеет размер (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
Мы можем использовать оценки вероятностей, соответствующие clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
В противном случае мы можем использовать значения решения без порога.
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
3.3.2.15.2. Мультиклассовый кейс
Функция roc_auc_score также может быть использована в нескольких классах классификации . В настоящее время поддерживаются две стратегии усреднения: алгоритм «один против одного» вычисляет среднее попарных оценок AUC ROC, а алгоритм «один против остальных» вычисляет среднее значение оценок ROC AUC для каждого класса по сравнению со всеми другими классами. В обоих случаях предсказанные метки предоставляются в виде массива со значениями от 0 до n_classes, а оценки соответствуют оценкам вероятности того, что выборка принадлежит определенному классу. Алгоритмы OvO и OvR поддерживают равномерное взвешивание ( average='macro') и по распространенности ( average='weighted').
Алгоритм «один против одного» : вычисляет средний AUC всех возможных попарных комбинаций классов. [HT2001] определяет метрику AUC мультикласса, взвешенную равномерно:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) + text{AUC}(k | j))$$
где $c$ количество классов и $text{AUC}(j | k)$ AUC с классом $j$ как положительный класс и класс $k$ как отрицательный класс. В общем, $text{AUC}(j | k) neq text{AUC}(k | j))$ в случае мультикласса. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'macro'.
[HT2001] мультиклассируют AUC метрика может быть расширена , чтобы быть взвешены по распространенности:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)( text{AUC}(j | k) + text{AUC}(k | j))$$
где cколичество классов. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'weighted'. В 'weighted' опции возвращает распространенность усредненные , как описано в [FC2009] .
Алгоритм «один против остальных» : вычисляет AUC каждого класса относительно остальных [PD2000] . Алгоритм функционально такой же, как и в случае с несколькими этикетками. Чтобы включить этот алгоритм, установите для аргумента ключевого слова multiclass значение 'ovr'. Как и OvO, OvR поддерживает два типа усреднения: 'macro' [F2006] и 'weighted' [F2001] .
В приложениях , где высокий процент ложных срабатываний не терпимый параметр max_fpr из roc_auc_score может быть использовано , чтобы суммировать кривую ROC до заданного предела.
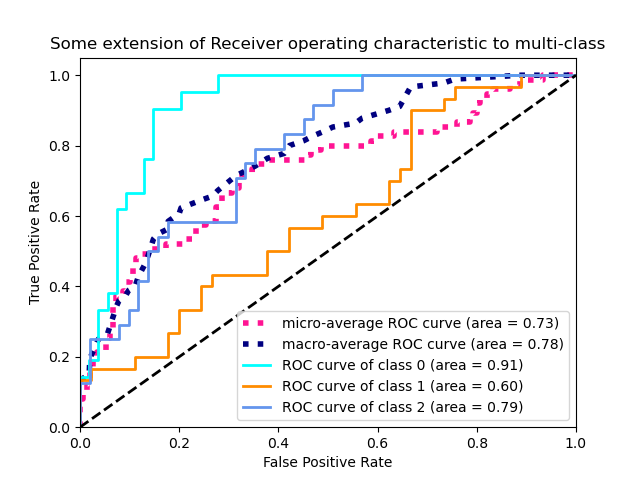
3.3.2.15.3. Кейс с несколькими метками
В классификации несколько меток, функция roc_auc_score распространяются путем усреднения меток , как выше . В этом случае вы должны указать y_score форму . Таким образом, при использовании оценок вероятности необходимо выбрать вероятность класса с большей меткой для каждого выхода.(n_samples, n_classes)
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
И значения решений не требуют такой обработки.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
Примеры:
- См. В разделе « Рабочие характеристики приемника» (ROC) пример использования ROC для оценки качества выходных данных классификатора.
- См. В разделе « Рабочие характеристики приемника» (ROC) с перекрестной проверкой пример использования ROC для оценки качества выходных данных классификатора с помощью перекрестной проверки.
- См. В разделе Моделирование распределения видов пример использования ROC для моделирования распределения видов.
- HT2001 ( 1 , 2 ) Рука, DJ и Тилль, RJ, (2001). Простое обобщение области под кривой ROC для задач классификации нескольких классов. Машинное обучение, 45 (2), стр. 171-186.
- FC2009 Ферри, Сезар и Эрнандес-Оралло, Хосе и Модройу, Р. (2009). Экспериментальное сравнение показателей эффективности для классификации. Письма о распознавании образов. 30. 27-38.
- PD2000 Провост Ф., Домингос П. (2000). Хорошо обученные ПЭТ: Улучшение деревьев оценки вероятностей (Раздел 6.2), Рабочий документ CeDER № IS-00-04, Школа бизнеса Стерна, Нью-Йоркский университет.
- F2006 Фосетт, Т., 2006. Введение в анализ ROC. Письма о распознавании образов, 27 (8), стр. 861-874.
- F2001Фосетт, Т., 2001. Использование наборов правил для максимизации производительности ROC в интеллектуальном анализе данных, 2001. Труды Международной конференции IEEE, стр. 131-138.
3.3.2.16. Компромисс при обнаружении ошибок (DET)
Функция det_curve вычисляет кривую компенсации ошибок обнаружения (DET) [WikipediaDET2017] . Цитата из Википедии:
«График компромисса ошибок обнаружения (DET) — это графическая диаграмма частоты ошибок для систем двоичной классификации, отображающая частоту ложных отклонений по сравнению с частотой ложных приемов. Оси x и y масштабируются нелинейно по их стандартным нормальным отклонениям (или просто с помощью логарифмического преобразования), в результате получаются более линейные кривые компромисса, чем кривые ROC, и большая часть области изображения используется для выделения важных различий в критический рабочий регион ».
Кривые DET представляют собой вариацию кривых рабочих характеристик приемника (ROC), где ложная отрицательная скорость нанесена на ось y вместо истинной положительной скорости. Кривые DET обычно строятся в масштабе нормального отклонения путем преобразования $phi^{-1}$ (с участием $phi$ — кумулятивная функция распределения). Полученные кривые производительности явно визуализируют компромисс типов ошибок для заданных алгоритмов классификации. См. [Martin1997], где приведены примеры и мотивация.
На этом рисунке сравниваются кривые ROC и DET двух примеров классификаторов для одной и той же задачи классификации:
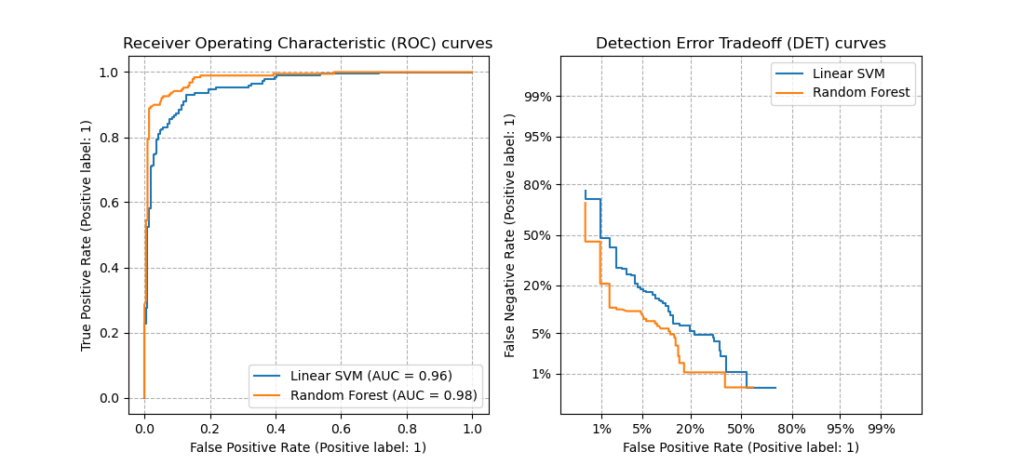
Характеристики:
- Кривые DET образуют линейную кривую по шкале нормального отклонения, если оценки обнаружения нормально (или близки к нормальному) распределены. В [Navratil2007] было показано, что обратное не обязательно верно, и даже более общие распределения могут давать линейные кривые DET.
- При обычном преобразовании масштаба с отклонением точки распределяются таким образом, что занимает сравнительно большее пространство графика. Следовательно, кривые с аналогичными характеристиками классификации легче различить на графике DET.
- С ложноотрицательной скоростью, «обратной» истинной положительной скорости, точкой совершенства для кривых DET является начало координат (в отличие от верхнего левого угла для кривых ROC).
Приложения и ограничения:
Кривые DET интуитивно понятны для чтения и, следовательно, позволяют быстро визуально оценить работу классификатора. Кроме того, кривые DET можно использовать для анализа пороговых значений и выбора рабочей точки. Это особенно полезно, если требуется сравнение типов ошибок.
С другой стороны, кривые DET не представляют свою метрику в виде единого числа. Поэтому для автоматической оценки или сравнения с другими задачами классификации лучше подходят такие показатели, как производная площадь под кривой ROC.
Примеры:
- См. Кривую компенсации ошибок обнаружения (DET) для примера сравнения кривых рабочих характеристик приемника (ROC) и кривых компенсации ошибок обнаружения (DET).
Рекомендации:
- ВикипедияDET2017 Авторы Википедии. Компромисс ошибки обнаружения. Википедия, свободная энциклопедия. 4 сентября 2017 г., 23:33 UTC. Доступно по адресу: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054 . По состоянию на 19 февраля 2018 г.
- Мартин 1997 А. Мартин, Дж. Доддингтон, Т. Камм, М. Ордовски и М. Пшибоцки, Кривая DET в оценке эффективности задач обнаружения , NIST 1997.
- Навратил2007 Дж. Наврактил и Д. Клусачек, « О линейных DET », 2007 г. Международная конференция IEEE по акустике, обработке речи и сигналов — ICASSP ’07, Гонолулу, Гавайи, 2007 г., стр. IV-229-IV-232.
3.3.2.17. Нулевой проигрыш
Функция zero_one_loss вычисляет сумму или среднее значение потери 0-1 классификации ($L_{0−1}$) над $n_{samples}$. По умолчанию функция нормализуется по выборке. Чтобы получить сумму $L_{0−1}$, установите normalize значение False.
В классификации по zero_one_loss нескольким меткам подмножество оценивается как единое целое, если его метки строго соответствуют прогнозам, и как ноль, если есть какие-либо ошибки. По умолчанию функция возвращает процент неправильно спрогнозированных подмножеств. Чтобы вместо этого получить количество таких подмножеств, установите normalize значение False
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда потеря 0-1 $L_{0−1}$ определяется как:
$$L_{0-1}(y_i, hat{y}_i) = 1(hat{y}_i not= y_i)$$
где $1(x)$- индикаторная функция.
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
В случае с несколькими метками с двоичными индикаторами меток, где первый набор меток [0,1] содержит ошибку:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
Пример:
- См. В разделе « Рекурсивное исключение функции с перекрестной проверкой» пример использования нулевой потери для выполнения рекурсивного исключения функции с перекрестной проверкой.
3.3.2.18. Потеря очков по Брайеру
Функция brier_score_loss вычисляет оценку Шиповник для бинарных классов [Brier1950] . Цитата из Википедии:
«Оценка Бриера — это правильная функция оценки, которая измеряет точность вероятностных прогнозов. Это применимо к задачам, в которых прогнозы должны назначать вероятности набору взаимоисключающих дискретных результатов ».
Эта функция возвращает среднеквадратичную ошибку фактического результата. y∈{0,1} и прогнозируемая оценка вероятности $p=Pr(y=1)$ ( pred_proba ) как выведено :
$$BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1}(y_i — p_i)^2$$
Потеря по шкале Бриера также составляет от 0 до 1, и чем ниже значение (средняя квадратичная разница меньше), тем точнее прогноз.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
Балл Бриера можно использовать для оценки того, насколько хорошо откалиброван классификатор. Однако меньшая потеря по шкале Бриера не всегда означает лучшую калибровку. Это связано с тем, что по аналогии с разложением среднеквадратичной ошибки на дисперсию смещения потеря оценки по Бриеру может быть разложена как сумма потерь калибровки и потерь при уточнении [Bella2012]. Потеря калибровки определяется как среднеквадратическое отклонение от эмпирических вероятностей, полученных из наклона ROC-сегментов. Потери при переработке можно определить как ожидаемые оптимальные потери, измеренные по площади под кривой оптимальных затрат. Потери при уточнении могут изменяться независимо от потерь при калибровке, таким образом, более низкие потери по шкале Бриера не обязательно означают более качественную калибровку модели. «Только когда потеря точности остается неизменной, более низкая потеря по шкале Бриера всегда означает лучшую калибровку» [Bella2012] , [Flach2008] .
Пример:
- См. Раздел « Калибровка вероятности классификаторов», где приведен пример использования потерь по шкале Бриера для выполнения калибровки вероятности классификаторов.
Рекомендации:
- Brier1950 Дж. Брайер, Проверка прогнозов, выраженных в терминах вероятности , Ежемесячный обзор погоды 78.1 (1950)
- Bella2012 ( 1 , 2 ) Белла, Ферри, Эрнандес-Оралло и Рамирес-Кинтана «Калибровка моделей машинного обучения» в Хосров-Пур, М. «Машинное обучение: концепции, методологии, инструменты и приложения». Херши, Пенсильвания: Справочник по информационным наукам (2012).
- Flach2008 Флак, Питер и Эдсон Мацубара. «О классификации, ранжировании и оценке вероятности». Дагштульский семинар. Schloss Dagstuhl-Leibniz-Zentrum от Informatik (2008).
3.3.3. Метрики ранжирования с несколькими ярлыками
В многоэлементном обучении с каждой выборкой может быть связано любое количество меток истинности. Цель состоит в том, чтобы дать высокие оценки и более высокий рейтинг наземным лейблам.
3.3.3.1. Ошибка покрытия
Функция coverage_error вычисляет среднее число меток , которые должны быть включены в окончательном предсказании таким образом, что все истинные метки предсказанные. Это полезно, если вы хотите знать, сколько меток с наивысшими баллами вам нужно предсказать в среднем, не пропуская ни одной истинной. Таким образом, наилучшее значение этого показателя — среднее количество истинных ярлыков.
Примечание
Оценка нашей реализации на 1 больше, чем оценка, приведенная в Tsoumakas et al., 2010. Это расширяет ее для обработки вырожденного случая, когда экземпляр имеет 0 истинных меток.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ покрытие определяется как
$$coverage(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} max_{j:y_{ij} = 1} text{rank}_{ij}$$
с участием $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$. Учитывая определение ранга, связи y_scores разрываются путем присвоения максимального ранга, который был бы присвоен всем связанным значениям.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
3.3.3.2. Средняя точность ранжирования метки
В label_ranking_average_precision_score функции реализует маркировать ранжирование средней точности (LRAP). Этот показатель связан с average_precision_score функцией, но основан на понятии ранжирования меток, а не на точности и отзыве.
Средняя точность ранжирования меток (LRAP) усредняет по выборкам ответ на следующий вопрос: для каждой основной метки истинности какая доля меток с более высоким рейтингом была истинной? Этот показатель эффективности будет выше, если вы сможете лучше ранжировать метки, связанные с каждым образцом. Полученная оценка всегда строго больше 0, а наилучшее значение равно 1. Если имеется ровно одна релевантная метка для каждой выборки, средняя точность ранжирования меток эквивалентна среднему обратному рангу .
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$, средняя точность определяется как
$$LRAP(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0} sum{j:y_{ij} = 1} frac{|mathcal{L}{ij}|}{text{rank}{ij}}$$
где $mathcal{L}{ij} = left{k: y{ik} = 1, hat{f}{ik} geq hat{f}{ij} right}$, $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$, |cdot| вычисляет мощность набора (т. е. количество элементов в наборе), и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
3.3.3.3. Потеря рейтинга
Функция label_ranking_loss вычисляет ранжирование потери , которые в среднем более образцы числа пар меток, которые неправильно упорядочены, т.е. истинные метки имеют более низкую оценку , чем ложные метки, взвешенную по обратной величине числа упорядоченных пар ложных и истинных меток. Наименьшая возможная потеря рейтинга равна нулю.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ потеря ранжирования определяется как
$$ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0(ntext{labels} — ||y_i||0)} left|left{(k, l): hat{f}{ik} leq hat{f}{il}, y{ik} = 1, y_{il} = 0 right}right|$$
где $|cdot|$ вычисляет мощность набора (т. е. количество элементов в наборе) и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
Рекомендации:
- Цумакас, Г., Катакис, И., и Влахавас, И. (2010). Майнинг данных с несколькими метками. В справочнике по интеллектуальному анализу данных и открытию знаний (стр. 667-685). Springer США.
3.3.3.4. Нормализованная дисконтированная совокупная прибыль
Дисконтированный совокупный выигрыш (DCG) и Нормализованный дисконтированный совокупный выигрыш (NDCG) — это показатели ранжирования, реализованные в dcg_score и ndcg_score; они сравнивают предсказанный порядок с оценками достоверности, такими как релевантность ответов на запрос.
Со страницы Википедии о дисконтированной совокупной прибыли:
«Дисконтированная совокупная прибыль (DCG) — это показатель качества ранжирования. При поиске информации он часто используется для измерения эффективности алгоритмов поисковой системы или связанных приложений. Используя шкалу градуированной релевантности документов в наборе результатов поисковой системы, DCG измеряет полезность или выгоду документа на основе его позиции в списке результатов. Прирост накапливается сверху вниз в списке результатов, причем прирост каждого результата дисконтируется на более низких уровнях »
DCG упорядочивает истинные цели (например, релевантность ответов на запросы) в предсказанном порядке, затем умножает их на логарифмическое убывание и суммирует результат. Сумма может быть усечена после первогоKрезультатов, и в этом случае мы называем это DCG @ K. NDCG или NDCG @ $K$ — это DCG, деленная на DCG, полученную с помощью точного прогноза, так что оно всегда находится между 0 и 1. Обычно NDCG предпочтительнее DCG.
По сравнению с потерей ранжирования, NDCG может принимать во внимание оценки релевантности, а не ранжирование на основе фактов. Таким образом, если основополагающая информация состоит только из упорядочивания, предпочтение следует отдавать потере ранжирования; если основополагающая информация состоит из фактических оценок полезности (например, 0 для нерелевантного, 1 для релевантного, 2 для очень актуального), можно использовать NDCG.
Для одного образца, учитывая вектор непрерывных значений истинности для каждой цели $y in R^M$, где $M$ это количество выходов, а прогноз $hat{y}$, что индуцирует функцию ранжирования $f$, оценка DCG составляет
$$sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}$$
а оценка NDCG — это оценка DCG, деленная на оценку DCG, полученную для $y$.
Рекомендации:
- Запись в Википедии о дисконтированной совокупной прибыли
- Джарвелин, К., и Кекалайнен, Дж. (2002). Оценка IR методов на основе накопленного коэффициента усиления. Транзакции ACM в информационных системах (TOIS), 20 (4), 422-446.
- Ван, Ю., Ван, Л., Ли, Ю., Хе, Д., Чен, В., и Лю, Т. Ю. (2013, май). Теоретический анализ показателей рейтинга NDCG. В материалах 26-й ежегодной конференции по теории обучения (COLT 2013)
- МакШерри Ф. и Наджорк М. (2008, март). Эффективность вычислений при поиске информации измеряется эффективно при наличии связанных оценок. В Европейской конференции по поиску информации (стр. 414-421). Шпрингер, Берлин, Гейдельберг.
3.3.4. Метрики регрессии
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности регрессии. Некоторые из них были расширены , чтобы обработать случай multioutput: mean_squared_error, mean_absolute_error, explained_variance_score и r2_score.
У этих функций есть multioutput аргумент ключевого слова, который определяет способ усреднения результатов или проигрышей для каждой отдельной цели. По умолчанию используется значение 'uniform_average', которое определяет равномерно взвешенное среднее значение по выходным данным. Если передается ndarrayформа shape (n_outputs,), то ее записи интерпретируются как веса, и возвращается соответствующее средневзвешенное значение. Если multioutputесть 'raw_values'указан, то все неизменные индивидуальные баллы или потери будут возвращены в массиве формы (n_outputs,).
r2_score и explained_variance_score принять дополнительное значение 'variance_weighted' для multioutput параметра. Эта опция приводит к взвешиванию каждой индивидуальной оценки по дисперсии соответствующей целевой переменной. Этот параметр определяет количественно зафиксированную немасштабированную дисперсию на глобальном уровне. Если целевые переменные имеют разную шкалу, то этот балл придает большее значение хорошему объяснению переменных с более высокой дисперсией. multioutput='variance_weighted' — значение по умолчанию r2_score для обратной совместимости. В будущем это будет изменено на uniform_average.
3.3.4.1. Оценка объясненной дисперсии
explained_variance_score вычисляет объясненной дисперсии регрессии балл.
Если $hat{y}$ — расчетный целевой объем производства, y соответствующий (правильный) целевой результат, и $Var$- Дисперсия , квадрат стандартного отклонения, то объясненная дисперсия оценивается следующим образом:
$$explained_{}variance(y, hat{y}) = 1 — frac{Var{ y — hat{y}}}{Var{y}}$$
Наилучшая возможная оценка — 1.0, более низкие значения — хуже.
Вот небольшой пример использования explained_variance_score функции:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990...
3.3.4.2. Максимальная ошибка
Функция max_error вычисляет максимальную остаточную ошибку , показатель , который фиксирует худшую ошибку случае между предсказанным значением и истинным значением. В идеально подобранной модели регрессии с одним выходом он max_error будет находиться 0 в обучающем наборе, и хотя это маловероятно в реальном мире, этот показатель показывает степень ошибки, которую имела модель при подборе.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда максимальная ошибка определяется как
$$text{Max Error}(y, hat{y}) = max(| y_i — hat{y}_i |)$$
Вот небольшой пример использования функции max_error:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
max_error не поддерживает multioutput.
3.3.4.3. Средняя абсолютная ошибка
Функция mean_absolute_error вычисляет среднюю абсолютную погрешность , риск метрики , соответствующей ожидаемого значение абсолютной потери или ошибок $l1$-нормальная потеря.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MAE), оцененная за $n_{samples}$ определяется как
$$text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i — hat{y}_i right|.$$
Вот небольшой пример использования функции mean_absolute_error:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
3.3.4.4. Среднеквадратичная ошибка
Функция mean_squared_error вычисляет среднюю квадратическую ошибку , риск метрики , соответствующую ожидаемое значение квадрата (квадратичной) ошибки или потерю.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная ошибка (MSE), оцененная на $n_{samples}$ определяется как
$$text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (y_i — hat{y}_i)^2.$$
Вот небольшой пример использования функции mean_squared_error:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
Примеры:
- См. В разделе Регрессия повышения градиента пример использования среднеквадратичной ошибки для оценки регрессии повышения градиента.
3.3.4.5. Среднеквадратичная логарифмическая ошибка
Функция mean_squared_log_error вычисляет риск метрики , соответствующий ожидаемому значению квадрата логарифмической (квадратичной) ошибки или потери.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная логарифмическая ошибка (MSLE), оцененная на $n_{samples}$ определяется как
$$text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (log_e (1 + y_i) — log_e (1 + hat{y}_i) )^2.$$
Где $log_e (x)$ означает натуральный логарифм $x$. Эту метрику лучше всего использовать, когда цели имеют экспоненциальный рост, например, численность населения, средние продажи товара в течение нескольких лет и т. Д. Обратите внимание, что эта метрика штрафует за заниженную оценку больше, чем за завышенную оценку.
Вот небольшой пример использования функции mean_squared_log_error:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
3.3.4.6. Средняя абсолютная ошибка в процентах
mean_absolute_percentage_error (MAPE), также известный как среднее абсолютное отклонение в процентах (МАПД), является метрикой для оценки проблем регрессии. Идея этой метрики — быть чувствительной к относительным ошибкам. Например, он не изменяется глобальным масштабированием целевой переменной.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная процентная ошибка (MAPE), оцененная за $n_{samples}$ определяется как
$$text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i — hat{y}_i right|}{max(epsilon, left| y_i right|)}$$
где $epsilon$ — произвольное маленькое, но строго положительное число, чтобы избежать неопределенных результатов, когда y равно нулю.
В функции mean_absolute_percentage_error опоры multioutput.
Вот небольшой пример использования функции mean_absolute_percentage_error:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
В приведенном выше примере, если бы мы использовали mean_absolute_error, он бы проигнорировал небольшие значения магнитуды и только отразил бы ошибку в предсказании максимального значения магнитуды. Но эта проблема решена в случае MAPE, потому что он вычисляет относительную процентную ошибку по отношению к фактическому выходу.
3.3.4.7. Средняя абсолютная ошибка
Это median_absolute_error особенно интересно, потому что оно устойчиво к выбросам. Убыток рассчитывается путем взятия медианы всех абсолютных различий между целью и прогнозом.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MedAE), оцененная на $n_{samples}$ определяется как
$$text{MedAE}(y, hat{y}) = text{median}(mid y_1 — hat{y}_1 mid, ldots, mid y_n — hat{y}_n mid).$$
median_absolute_error Не поддерживает multioutput.
Вот небольшой пример использования функции median_absolute_error:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
3.3.4.8. R² балл, коэффициент детерминации
Функция r2_score вычисляет коэффициент детерминации , как правило , обозначенный как R².
Он представляет собой долю дисперсии (y), которая была объяснена независимыми переменными в модели. Он обеспечивает показатель степени соответствия и, следовательно, меру того, насколько хорошо невидимые выборки могут быть предсказаны моделью через долю объясненной дисперсии.
Поскольку такая дисперсия зависит от набора данных, R² не может быть значимо сопоставимым для разных наборов данных. Наилучшая возможная оценка — 1,0, и она может быть отрицательной (потому что модель может быть произвольно хуже). Постоянная модель, которая всегда предсказывает ожидаемое значение y, игнорируя входные характеристики, получит оценку R² 0,0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ соответствующее истинное значение для общего n образцов, расчетный R² определяется как:
$$R^2(y, hat{y}) = 1 — frac{sum_{i=1}^{n} (y_i — hat{y}i)^2}{sum{i=1}^{n} (y_i — bar{y})^2}$$
где $bar{y} = frac{1}{n} sum_{i=1}^{n} y_i$ и $sum_{i=1}^{n} (y_i — hat{y}i)^2 = sum{i=1}^{n} epsilon_i^2$.
Обратите внимание, что r2_score вычисляется нескорректированное R² без поправки на смещение выборочной дисперсии y.
Вот небольшой пример использования функции r2_score:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925...
Пример:
- См. В разделе « Лассо и эластичная сеть для разреженных сигналов» приведен пример использования показателя R² для оценки лассо и эластичной сети для разреженных сигналов.
3.3.4.9. Средние отклонения Пуассона, Гаммы и Твиди
Функция mean_tweedie_deviance вычисляет среднюю ошибку Deviance Tweedie с powerпараметром ($p$). Это показатель, который выявляет прогнозируемые ожидаемые значения целей регрессии.
Существуют следующие особые случаи:
- когда
power=0это эквивалентноmean_squared_error. - когда
power=1это эквивалентноmean_poisson_deviance. - когда
power=2это эквивалентноmean_gamma_deviance.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя ошибка отклонения Твиди (D) для мощности $p$, оценивается более $n_{samples}$ определяется как
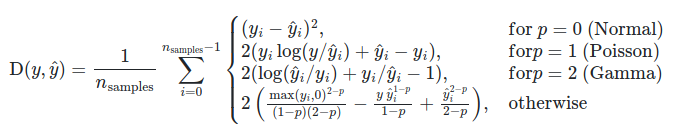
Отклонение от твиди — однородная функция степени 2-power. Таким образом, гамма-распределение power=2 означает, что одновременно масштабируется y_true и y_pred не влияет на отклонение. Для распределения Пуассона power=1 отклонение масштабируется линейно, а для нормального распределения ( power=0) — квадратично. В общем, чем выше, powerтем меньше веса придается крайним отклонениям между истинными и прогнозируемыми целевыми значениями.
Например, давайте сравним два прогноза 1.0 и 100, которые оба составляют 50% от их соответствующего истинного значения.
Среднеквадратичная ошибка ( power=0) очень чувствительна к разнице прогнозов второй точки:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
Если увеличить powerдо 1:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
разница в ошибках уменьшается. Наконец, установив power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
мы получим идентичные ошибки. Таким образом, отклонение when power=2чувствительно только к относительным ошибкам.
3.3.5. Метрики кластеризации
В модуле sklearn.metrics реализованы несколько функций потерь, оценки и полезности. Для получения дополнительной информации см. Раздел « Оценка производительности кластеризации » для кластеризации экземпляров и « Оценка бикластеризации» для бикластеризации.
3.3.6. Фиктивные оценки
При обучении с учителем простая проверка работоспособности состоит из сравнения своей оценки с простыми практическими правилами. DummyClassifier реализует несколько таких простых стратегий классификации:
stratifiedгенерирует случайные прогнозы, соблюдая распределение классов обучающего набора.most_frequentвсегда предсказывает наиболее частую метку в обучающем наборе.priorвсегда предсказывает класс, который максимизирует предыдущий класс (какmost_frequent) иpredict_probaвозвращает предыдущий класс.uniformгенерирует предсказания равномерно в случайном порядке.constantвсегда предсказывает постоянную метку, предоставленную пользователем. Основная мотивация этого метода — оценка F1, когда положительный класс находится в меньшинстве.
Обратите внимание, что со всеми этими стратегиями predict метод полностью игнорирует входные данные!
Для иллюстрации DummyClassifier сначала создадим несбалансированный набор данных:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Далее сравним точность SVC и most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
Мы видим, что SVC это не намного лучше, чем фиктивный классификатор. Теперь давайте изменим ядро:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
Мы видим, что точность увеличена почти до 100%. Для лучшей оценки точности рекомендуется стратегия перекрестной проверки, если она не требует слишком больших затрат на ЦП. Для получения дополнительной информации см. Раздел « Перекрестная проверка: оценка производительности оценщика ». Более того, если вы хотите оптимизировать пространство параметров, настоятельно рекомендуется использовать соответствующую методологию; подробности см. в разделе « Настройка гиперпараметров оценщика ».
В более общем плане, когда точность классификатора слишком близка к случайной, это, вероятно, означает, что что-то пошло не так: функции бесполезны, гиперпараметр настроен неправильно, классификатор страдает от дисбаланса классов и т. Д.
DummyRegressor также реализует четыре простых правила регрессии:
meanвсегда предсказывает среднее значение тренировочных целей.medianвсегда предсказывает медианное значение тренировочных целей.quantileвсегда предсказывает предоставленный пользователем квантиль учебных целей.constantвсегда предсказывает постоянное значение, предоставляемое пользователем.
Во всех этих стратегиях predict метод полностью игнорирует входные данные.
In this tutorial, you’ll learn how to use Python to calculate the MAPE, or the mean absolute percentage error. This error is often used to measure the accuracy of machine learning models.
By the end of this tutorial, you’ll have learned:
- What the Mean Absolute Percentage Error is
- What a good value for the MAPE is
- How to calculate the MAPE in Python
- What some common cautions are with the MAPE
Let’s get started!
What is the Mean Absolute Percentage Error?
The Mean Absolute Percentage Error (MAPE) can be used in machine learning to measure the accuracy of a model. More specifically, the MAPE is a loss function that defines the error of a given model.
The MAPE is calculated by finding the absolute difference between the actual and predicted values, divided by the actual value. These ratios are added for all values and the mean is taken.
More concisely, the formula for the MAPE is:
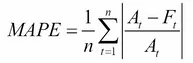
In the formula above:
Σindicates to add all the resulting valuesnis the sample sizeAis the actual valueFis the predicted value
Should the MAPE be High or Low?
The MAPE is a commonly used measure in machine learning because of how easy it is to interpret. The lower the value for MAPE, the better the machine learning model is at predicting values. Inversely, the higher the value for MAPE, the worse the model is at predicting values.
For example, if we calculate a MAPE value of 20% for a given machine learning model, then the average difference between the predicted value and the actual value is 20%.
As a percentage, the error measurement is more intuitive to understand than other measures such as the mean square error. This is because many other error measurements are relative to the range of values. This requires you to jump through some additional mental hurdles to determine the scope of the error.
What is a Good MAPE Score?
The MAPE returns a percentage, which can make it intuitive to understand. Because the percentage reflects the average percentage error, the lower the score the better.
Below, you’ll find some general guidelines on what a good MAPE score is:
| MAPE Score | Interpretation of Score |
|---|---|
| > 50 % | Poor |
| 20% – 50% | Relatively good |
| 10% – 20% | Good |
| < 10% | Great |
A MAPE score, like anything else in machine learning, should not be taken at face value. Keep in mind the range of your data (as lower ranges will amplify the MAPE) and the type of data you’re working with.
As you’ll learn in a later section, the MAPE does have some problems with some data, especially lower volume data. Because of this, make sure you have a good sense of how your data is structured before making decisions using MAPE alone.
Use Python to Calculate the MAPE Score from Scratch
It’s very simple to create a function for the MAPE using the built-in numpy library.
Let’s see how we can do this:
# Creating a Function for MAPE
import numpy as np
def mape(y_test, pred):
y_test, pred = np.array(y_test), np.array(pred)
mape = np.mean(np.abs((y_test - pred) / y_test))
return mapeLet’s break down what we did here:
- We imported numpy to simplify array operations
- We defined a function,
mape, that takes two arrays: the testing array and the predicted array - Both these arrays are converted into numpy arrays
- The MAPE is calculated using the formula above
Let’s run through a very simple machine learning example using a linear regression model in Scikit-Learn:
# A practical example of MAPE in machine learning
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
def mape(y_test, pred):
y_test, pred = np.array(y_test), np.array(pred)
mape = np.mean(np.abs((y_test - pred) / y_test))
return mape
data = load_diabetes()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
lnr = LinearRegression()
lnr.fit(X_train, y_train)
predictions = lnr.predict(X_test)
print(mape(y_test, predictions))
# Returns: 0.339In the example above, we created a simple machine learning model. The model predicted some values – these were stored in the predictions variable.
We tested the accuracy of our model by passing in our predictions and the actual values, y_test into our function, mape(). This returned a value of 0.339, which is equal to 33.9%.
Calculating the MAPE Using Sklearn
Scikit-Learn also comes with a function for the MAPE built-in, the mean_absolute_percentage_error() function from the metrics module.
Like our function above, the function takes the true values and the predicted values as input:
# Using the mean_absolute_percentage_error function
from sklearn.metrics import mean_absolute_percentage_error
error = mean_absolute_percentage_error(y_true, predictions)Let’s recreate our earlier example using this function:
# A practical example of MAPE in sklearn
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_percentage_error
data = load_diabetes()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
lnr = LinearRegression()
lnr.fit(X_train, y_train)
predictions = lnr.predict(X_test)
print(mean_absolute_percentage_error(y_test, predictions))
# Returns: 0.339In the next section, you’ll learn about some common problems with the MAPE score.
Common Problems with the MAPE score
While the MAPE is easy to understand, this simplicity can also lead to some problems. One of the major problems with the MAPE score is how easily it is influenced by values of a low range.
For example, a predicted value of 3 and a true value of 2 indicate an error of 50%. Meanwhile, the data are only 1 off. If the real value was 100 and the predicted value was 101, then the error would only be 1%.
This is where the matter of interpretation comes in. In the example above, a difference between the values of 2 and 3 may be insignificant (in which case the MAPE is a poor metric). However, the difference may actually be incredibly meaningful, in which case the MAPE is a good metric.
Keep in mind the context of your data when interpreting the score.
Conclusion
In this tutorial, you learned how to use Python to calculate the MAPE score. You learned what the MAPE score is and how to interpret it. You also learned how to calculate the score from scratch, as well as how to use a sklearn function to calculate the mean absolute percentage error.
Additional Resources
To learn more about related topics, check out the tutorials below:
- Introduction to Scikit-Learn (sklearn) in Python
- Linear Regression in Scikit-Learn (sklearn): An Introduction
- Calculate Manhattan Distance in Python (City Block Distance)
- Official Documentation: MAPE in Sklearn
Диагностика систем машинного обучения
115 мин на чтение
(169.722 символов)
Что такое метрики эффективности?
Для того, чтобы эффективно проводить обучение моделей необходимо иметь способ оценки, насколько хорошо та или иная модель выполняет свою работу — предсказывает значение целевой переменной. Кажется, мы уже что-то подобное изучали. У каждой модели есть функция ошибки, которая показывает, на сколько модель соответствует эмпирическим значениям. Однако, использование функции ошибки не очень удобно для оценки именно “качества” уже построенных моделей. Ведь эта функция специально создается для единственной цели — организации процесса обучения. Поэтому для оценки уже построенных моделей используется не функция ошибки, а так называемые метрики эффективности — специальные функции, которые показывают, насколько эффективна уже готовая, обученная модель.
Метрики эффективности на первый взгляд очень похожи на функции ошибки, ведь у них одна цель — отличать хорошие модели от плохих. Но делают они это по-разному, по-разному и применяются. К метрикам эффективности предъявляются совершенно другие требования, нежели к функциям ошибки. Поэтому давайте рассмотрим, для чего нужны и те и другие.
Функция ошибки нужна в первую очередь для формализации процесса обучения модели. То есть для того, чтобы подбирать параметры модели именно такими, чтобы модель как можно больше соответствовала реальным данным в обучающей выборке. Да, значение этой функции можно использовать как некоторую оценку качества модели уже после того, как она обучена, но это не удобно.
Функция ошибки нужна, чтобы формализовать отклонения предсказанных моделью значений от реальных. Например, в методе линейной регрессии функция ошибки (среднеквадратическое отклонение) используется для метода градиентного спуска. Поэтому функция ошибки обязательно должна быть везде дифференцируемой, мы это отдельно отмечали, когда говорили про метод градиентного спуска. Это требование — дифференцируемость — нужно исключительно для метода оптимизации, то есть для обучения модели.
Зато функция, которая используется для оценки качества модели совершенно не должна быть аналитической и гладкой. Ведь мы не будем вычислять ее производную, мы только вычислим ее один раз для того, чтобы понять, насколько хорошая модель получилась. Так что не любую метрику эффективности вообще физически возможно использовать как функцию ошибки — метод обучения может просто не сработать.
Кроме того, функция ошибки должна быть вычислительно простой, ведь ее придется считать много раз в процессе обучения — тысячи или миллионы раз. Это еще одно требование, которое совершенно необязательно для метрики эффективности. Она как раз может считаться довольно сложно, ведь вычислять ее приходится всего несколько раз.
Зато метрика эффективности должна быть понятной и интерпретируемой, в отличие от функции ошибки. Раньше мы подчеркивали, что само абсолютное значение функции ошибки ничего не показывает. Важно лишь, снижается ли оно в процессе обучения. И разные значения функции ошибки имеет смысл сравнивать только на одних и тех же данных. Что значит, если значение функции ошибки модели равно 35 000? Да ничего, только то, что эта модель хуже, чем та, у которой ошибка 32 000.
Для того, чтобы значение было более понятно, метрики эффективности зачастую выражаются в каких-то определенных единицах измерения — чеще всего в натуральных или в процентах. Натуральные единицы — это единицы измерения целевой переменной. Допустим, целевая переменная выражается в рублях. То есть, мы предсказываем некоторую стоимость. В таком случае будет вполне понятно, если качество этой модели мы тоже выразим в рублях. Например, так: модель в среднем ошибается на 500 рублей. И сразу становится ясно, насколько эта модель применима на практике.
Еще одно важное отличие. Как мы сказали, требования к функции ошибки определяются алгоритмом оптимизации. Который, в свою очередь зависит от типа модели. У линейной регрессии будет один алгоритм (и одна функция ошибки), а у, например, решающего дерева — другой алгоритм и совершенно другая функция ошибки. Это в частности значит, что функцию ошибки невозможно применять для сравнения нескольких разных моделей, обученных на одной и той же задаче.
И вот для этого как раз и нужны метрики эффективности. Они не зависят от типа модели, а выбираются исходя из задачи и тех вопросов, ответы на которые мы хотим получить. Например, в одной задаче качество модели лучше измерять через среднеквадратическую логарифмическую ошибку, а в другой — через медианную ошибку. Как раз в этом разделе мы посмотрим на примеры разных метрик эффективности, на их особенности и сферы применения.
Кстати, это еще означает, что в каждой конкретной задаче вы можете применять сразу несколько метрик эффективности, для более глубокого понимания работы модели. Зачастую так и поступают, ведь одна метрика не может дать полной информации о сильных и слабых сторонах модели. Тут исследователи ничем не ограничены. А вот функция ошибки обязательно должна быть только одна, ведь нельзя одновременно находить минимум сразу нескольких разных функций (на самом деле можно, но многокритериальная оптимизация — это гораздо сложнее и не используется для обучения моделей).
| Функция ошибки | Метрика эффективности |
|---|---|
| Используется для организации процесса обучения | Используется для оценки качества полученной модели |
| Используется для нахождения оптимума | Используется для сравнения моделей между собой |
| Должна быть быстро вычислимой | Должна быть понятной |
| Должна конструироваться исходя их типа модели | Должна выбираться исходя из задачи |
| Может быть только одна | Может быть несколько |
Еще раз определим, эффективность — это свойство модели машинного обучения давать предсказания значения целевой переменной, как можно ближе к реальным данным. Это самая главная характеристика модели. Но надо помнить, что исходя из задачи и ее условий, к моделям могут предъявляться и другие требования, как сказали бы в программной инженерии — нефункциональные. Типичный пример — скорость работы. Иногда маленький выигрыш в эффективности не стоит того, что модель стала работать в десять раз меньше. Другой пример — интерпретируемость модели. В некоторых областях важно не только сделать точное предсказание, но и иметь возможность обосновать его, провести анализ, выработать рекомендации по улучшению ситуации и так далее. Все эти нефункциональные требования — скорость обучения, скорость предсказания, надежность, робастность, федеративность, интерпретируемость — выходят за рамки данного пособия. Здесь мы сконцентрируемся на измерении именно эффективности модели.
Обратите внимание, что мы старательно избегаем употребления слова “точность” при описании качества работы модели. Хотя казалось бы, оно подходит как нельзя лучше. Дело в том, что “точностью” называют одну из метрик эффективности моделей классификации. Поэтому мы не хотим внести путаницу в термины.
Как мы говорили, метрики эффективности не зависят от самого типа модели. Для их вычисления обычно используется два вектора — вектор эмпирических значений целевой переменной (то есть тех, которые даны в датасете) и вектор теоретических значений (то есть тех, которые выдала модель). Естественно, эти вектора должны быть сопоставимы — на соответствующих местах должны быть значения целевой переменной, соответствующие одном у и тому же объекту. И, конечно, у них должна быть одинаковая длина. То есть метрика зависит от самих предсказаний, но не от модели, которая их выдала. Причем, большинство метрик устроены симметрично — если поменять местами эти два вектора, результат не изменится.
При рассмотрении метрик надо помнить следующее — чем выше эффективность модели, тем лучше. Но некоторые метрики устроены как измерение ошибки модели. В таком случае, конечно, тем ниже, тем лучше. Так что эффективность и ошибка модели — это по сути противоположные понятия. Так сложилось, что метрики регрессии чаще устроены именно как ошибки, а метрики классификации — как метрики именно эффективности. При использовании конкретной метрики на это надо обращать внимание.
Выводы:
- Метрики эффективности — это способ показать, насколько точно модель отражает реальный мир.
- Метрики эффективность должны выбираться исходя из задачи, которую решает модель.
- Функция ошибки и метрика эффективности — это разные вещи, к ним предъявляются разные требования.
- В задаче можно (и, зачастую, нужно) применять несколько метрик эффективности.
- Наряду с метриками эффективности есть и другие характеристики моделей — скорость обучения, скорость работы, надежность, робастность, интерпретируемость.
- Метрики эффективности вычисляются как правило из двух векторов — предсказанных (теоретических) значений целевой переменной и эмпирических (реальных) значений.
- Обычно метрики устроены таким образом, что чем выше значение, тем модель лучше.
Метрики эффективности для регрессии
Как мы говорили в предыдущем пункте, метрики зависят от конкретной задачи. А все задачи обучения с учителем разделяются на регрессию и классификацию. Совершенно естественно, что метрики для регрессии и для классификации будут разными.
Метрики эффективности для регрессии оценивают отклонение (расстояние) между предсказанными значениями и реальными. Кажется, что это очевидно, но метрики эффективности классификации устроены по-другому. Предполагается, что чем меньше каждое конкретное отклонение, тем лучше. Разница между разными метриками в том, как учитывать индивидуальные отклонения в общей метрике и в том, как агрегировать ряд значений в один интегральный показатель.
Все метрики эффективности моделей регрессии покажутся вам знакомыми, если вы изучали математическую статистику, ведь именно статистические методы легли в основу измерения эффективности моделей машинного обучения. Причем, метрики эффективности — это лишь самые простые статистические показатели, которые можно использовать для анализа качества модели. При желании можно и нужно задействовать более мощные статистические методы исследования данных. Например, можно проанализировать вид распределения отклонений, и сделать из этого вывод о необходимость корректировки моделей. Но в 99% случаев можно обойтись простым вычислением одной или двух рассматриваемых ниже метрик.
Так как метрики эффективности позволяют интерпретировать оценку качества модели, они зачастую неявно сравнивают данную модель с некоторой тривиальной. Тривиальна модель — это очень простая, даже примитивная модель, которая выдает предсказания оценки целевой переменной абсолютно без оглядки на эффективность и вообще соответствие реальным данным. Тривиальной моделью может выступать, например, предсказание для любого объекта среднего значения целевой переменной из обучающей выборки. Такие тривиальные модели нужны, чтобы оценить, насколько данная модель лучше или хуже них.
Естественно, мы хотим получить модель, которая лучше тривиальной. Причем, у нас есть некоторый идеал — модель, которая никогда не ошибается, то есть чьи предсказания всегда совпадают с реальными значениями. Поэтому реальная модель может быть лучше тривиальной только до этого предела. У такой идеальной модели, говорят, 100% эффективность или нулевая ошибка.
Но надо помнить, что в задачах регрессии модель предсказывает непрерывное значение. Это значит, что величина отклонения может быть неограниченно большой. Так что не бывает нижнего предела качества модели. Модель регрессии может быть бесконечно далекой от идеала, бесконечно хуже даже тривиальной модели. Поэтому ошибки моделей регрессии не ограничиваются сверху (или, что то же самое, эффективность моделей регрессии не ограничивается снизу).
Поэтому в задачах регрессии
Выводы:
- Метрики эффективности для регрессий обычно анализируют отклонения предсказанных значений от реальных.
- Большинство метрик пришло в машинное обучение из математической статистики.
- Результаты работы модели можно исследовать более продвинутыми статистическими методами.
- Обычно метрики сравнивают данную модель с тривиальной — моделью, которая всегда предсказывает среднее реальное значение целевой переменной.
- Модель могут быть точны на 100%, но плохи они могут быть без ограничений.
Коэффициент детерминации (r-квадрат)
Те, кто раньше хотя бы немного изучал математическую статистику, без труда узнают первую метрику эффективности моделей регрессии. Это так называемый коэффициент детерминации. Это доля дисперсии (вариации) целевой переменной, объясненная данной моделью. Данная метрика вычисляется по такой формуле:
[R^2(y, hat{y}) = 1 — frac
{sum_{i=1}^n (y_i — hat{y_i})^2}
{sum_{i=1}^n (y_i — bar{y_i})^2}]
где
$y$ — вектор эмпирических (истинных) значений целевой переменной,
$hat{y}$ — вектор теоретических (предсказанных) значений целевой переменной,
$y_i$ — эмпирическое значение целевой переменной для $i$-го объекта,
$hat{y_i}$ — теоретическое значение целевой переменной для $i$-го объекта,
$bar{y_i}$ — среднее из эмпирических значений целевой переменной для $i$-го объекта.
Если модель всегда предсказывает идеально (то есть ее предсказания всегда совпадают с реальностью, другими словами, теоретические значения — с эмпирическими), то числитель дроби в формуле будет равен 0, а значит, вся метрика будет равна 1. Если же мы рассмотрим тривиальную модель, которая всегда предсказывает среднее значение, то числитель будет равен знаменателю, дробь будет равна 1, а метрика — 0. Если модель хуже идеальной, но лучше тривиальной, то метрика будет в диапазоне от 0 до 1, причем чем ближе к 1 — тем лучше.
Если же модель предсказывает такие значения, что отклонения их от теоретических получаются больше, чем от среднего значения, то числитель будет больше знаменателя, а значит, что метрика будет принимать отрицательные значения. Запомните, что отрицательные значения коэффициента детерминации означают, что модель хуже, чем тривиальная.
В целом эта метрика показывает силу линейной связи между двумя случайными величинами. В нашем случае этими величинами выступают теоретические и эмпирические значения целевой переменной (то есть предсказанные и реальные). Если модель дает точные предсказания, то будет наблюдаться сильная связь (зависимость) между теоретическим значением и реальным, то есть высокая детерминация, близкая к 1. Если эе модель дает случайные предсказания, никак не связанные с реальными значениями, то связь будет отсутствовать.
Причем так как нас интересует, насколько значения совпадают, нам достаточно использовать именно линейную связь. Ведь когда мы оцениваем связь, например, одного из факторов в целевой переменной, то связь может быть нелинейной, и линейный коэффициент детерминации ее не покажет, то есть пропустит. Но в данному случае это не важно, так как наличие нелинейной связи означает, что предсказанные значения все-таки отклоняются от реальных. Такую линейную связь можно увидеть на графике, если построить диаграмму рассеяния между теоретическими и эмпирическими значениями, вот так:
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, Y)
Y_ = reg.predict(X)
plt.scatter(Y, Y_)
plt.plot(Y, Y)
Здесь мы еще строим прямую $y = y$. Она нужна только для удобства. Вот как может выглядеть этот график:
Здесь мы видим, что точки немного отклоняются от центральной линии, но в целом ей следуют. Такая картина характерна для высокого коэффициента детерминации. А вот как может выглядеть менее точная модель:
И в целом, чем точки ближе к центральной линии, тем лучше модель и тем ближе коэффициент детерминации к 1.
В англоязычной литература эта метрика называется $R^2$, так как в определенных случаях она равна квадрату коэффициента корреляции. Пусть это название не вводит вас в заблуждение. Некоторые думаю, что раз метрика в квадрате, то она не может быть отрицательной. Это лишь условное название.
Пару слов об использовании метрик эффективности в библиотеке sklearn. Именно коэффициент детерминации чаще всего используется как метрика по умолчанию, которую можно посмотреть при помощи метода score() у модели регрессии. Обратите внимание, что этот метод принимает на вход саму обучающую выборку. Это сделано для единообразия с методами наподобие fit().
Но более универсально будет использовать эту метрику независимо от модели. Все метрики эффективности собраны в отдельный пакет metrics. Данная метрика называется r2_score. Обратите внимание, что при использовании этой функции ей надо передавать два вектора целевой переменной — сначала эмпирический, а вторым аргументом — теоретический.
1
2
3
4
5
6
7
8
from sklearn.metrics import r2_score
def r2(y, y_):
return 1 - ((y - y_)**2).sum() / ((y - y.mean())**2).sum()
print(reg.score(X, Y))
print(r2_score(Y, Y_))
print(r2(Y, Y_))
В данном коде мы еще реализовали самостоятельный расчет данной метрики, чтобы пояснить применение формулы выше. Можете самостоятельно убедиться, что три этих вызова напечатают одинаковые значения.
Коэффициент детерминации, или $R^2$ — это одна из немногих метрик эффективности для моделей регрессии, значение которой чем больше, тем лучше. Почти все остальные измеряют именно ошибку, что мы и увидим ниже. Еще это одна из немногих несимметричных метрик. Ведь если в формуле поменять теоретические и эмпирические значения, ее смысл и значение могут поменяться. Поэтому при использовании этой метрики нужно обязательно следить за порядком передачи аргументов.
При использовании этой метрики есть один небольшой подводный камень. Так как в знаменатели у этой формулы стоит вариация реального значения целевой переменной, важно следить, чтобы эта вариация присутствовала. Ведь если реальное значение целевой переменной будет одинаковым для всех объектов выборки, то вариация этой переменной будет равна 0. А значит, метрика будет не определена. Причем это единственная причина, почему эта метрика может быть неопределена. Надо понимать, что отсутствие вариации целевой переменной ставит под сомнение вообще целесообразность машинного обучения и моделирования в целом. Ведь что нам предсказывать если $y$ всегда один и тот же? С другой стороны, такая ситуация может случиться, например, при случайном разбиении выборки на обучающую и тестовую. Но об этом мы поговорим дальше.
Выводы:
- Коэффициент детерминации показывает силу связи между двумя случайными величинами.
- Если модель всегда предсказывает точно, метрика равна 1. Для тривиальной модели — 0.
- Значение метрики может быть отрицательно, если модель предсказывает хуже, чем тривиальная.
- Это одна из немногих несимметричных метрик эффективности.
- Эта метрика не определена, если $y=const$. Надо следить, чтобы в выборке присутствовали разные значения целевой переменной.
Средняя абсолютная ошибка (MAE)
Коэффициент детерминации — не единственная возможная характеристика эффективности моделей регрессии. Иногда полезно оценить отклонения предсказаний от истинных значений более явно. Как раз для этого служат сразу несколько метрик ошибок моделей регрессии. Самая простая из них — средняя абсолютная ошибка (mean absolute error, MAE). Она вычисляется по формуле:
[MAE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} |y_i — hat{y_i}|]
Данная метрика действительно очень проста: это средняя величина разницы между предсказанными и реальными значениями целевой переменной. Причем эта разница берется по модулю, чтобы компенсировать возможные отрицательные отклонения. Мы уже рассматривали похожую функцию, когда говорили о конструировании функции ошибки для градиентного спуска. Но тогда мы отмели использование абсолютного значения, так как эта функция не везде дифференцируема. Но вот для метрики эффективности такого требования нет и MAE вполне можно использовать.
Если модель предсказывает идеально, то, естественно, все отклонения равны 0 и MAE в целом равна нулю. Но эта метрика не учитывает явно сравнение с тривиальной моделью — она просто тем хуже, чем больше. Ниже нуля она быть, конечно, не может.
Данная метрика выражается в натуральных единицах и имеет очень простой и понятный смысл — средняя ошибка модели. Степень применимости модели в таком случае можно очень просто понять исходя из предметной области. Например, наша модель ошибается в среднем на 500 рублей. Хорошо это или плохо? Зависит от размерности исходных данных. Если мы предсказываем цены на недвижимость — то модель прекрасно справляется с задачей. Если же мы моделируем цены на спички — то такая модель скорее всего очень неэффективна.
Использование данной метрики в пакете sklearn очень похоже на любую другую метрику, меняется только название:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
Выводы:
- MAE показывает среднее абсолютное отклонение предсказанных значений от реальных.
- Чем выше значение MAE, тем модель хуже. У идеальной модели $MAE=0$
- MAE очень легко интерпретировать — на сколько в среднем ошибается модель.
Средний квадрат ошибки (MSE)
Средний квадрат ошибки (mean squared error, MSE) очень похож на предыдущую метрику, но вместо абсолютного значения (модуля) используется квадрат:
[MSE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2]
Граничные случаи у этой метрики такие же, как у предыдущей — 0 у идеальной модели, а в остальном — чем больше, тем хуже. MSE у тривиальной модели будет равна дисперсии целевой переменной. Но это не то, чтобы очень полезно на практике.
Эта метрика используется во многих моделях регрессии как функция ошибки. Но вот как метрику эффективности ее применяют довольно редко. Дело в ее интерпретируемости. Ведь она измеряется в квадратах натуральной величины. А какой физический смысл имеют, например, рубли в квадрате? На самом деле никакого. Поэтому несмотря на то, что математически MAE и MSE в общем-то эквивалентны, первая более проста и понятна, и используется гораздо чаще.
Единственное существенное отличие данной метрики от предыдущей состоит в том, что она чуть больший “вес” в общей ошибке придает большим значениям отклонений. То есть чем больше значение отклонения, тем сильнее оно будет вкладываться в значение MSE. Это иногда бывает полезно, когда исходя из задачи стоит штрафовать сильные отклонения предсказанных значений от реальных. Но с другой стороны это свойство делает эту метрику чувствительной к аномалиям.
Пример расчета метрики MSE:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
Выводы:
- MAE показывает средний квадрат отклонений предсказанных значений от реальных.
- Чем выше значение MSE, тем модель хуже. У идеальной модели $MSE=0$
- MSE больше учитывает сильные отклонения, но хуже интерпретируется, чем MAE.
Среднеквадратичная ошибка (RMSE)
Если главная проблема метрики MSE в том, что она измеряется в квадратах натуральных величин, что что будет, если мы возьмем от нее квадратный корень? Тогда мы получим среднеквадратичную ошибку (root mean squared error, RMSE):
[RMSE(y, _hat{y}) = sqrt{frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2}]
Использование данной метрики достаточно привычно при статистическом анализе данных. Однако, для интерпретации результатов машинного обучения она имеет те же недостатки, что и MSE. Главный из них — чувствительность к аномалиям. Поэтому при интерпретации эффективности моделей регрессии чаще рекомендуется применять метрику MAE.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
Выводы:
- RMSE — это по сути корень из MSE. Выражается в тех же единицах, что и целевая переменная.
- Чаще применяется при статистическом анализа данных.
- Данная метрика очень чувствительна к аномалиям и выбросам.
Среднеквадратичная логарифмическая ошибка (MSLE)
Еще одна довольно редкая метрика — среднеквадратическая логарифмическая ошибка (mean squared logarithmic error, MSLE). Она очень похожа на MSE, но квадрат вычисляется не от самих отклонений, а от разницы логарифмов (про то, зачем там +1 поговорим позднее):
[MSLE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (
ln(1 + y_i) — ln(1 + hat{y_i})
)^2]
Данная материка имеет специфическую, но довольно полезную сферу применения. Она применяется в тех случаях, когда значения целевой переменной простираются на несколько порядков величины. Например, если мы анализируем доходы физических лиц, они могут измеряться от тысяч до сотен миллионов. Понятно, что при использовании более привычных метрик, таких как MSE, RMSE и даже MAE, отклонения в больших значениях, даже небольшие относительно, будут полностью доминировать над отклонениями в малых значениях.
Это приведет к тому, что оценка моделей в подобных задачах классическими метриками будет давать преимущество моделям, которые более точны в одной части выборки, но почти не будут учитывать ошибки в других частях выборки. Это может привести к несправедливой оценке моделей. А вот использование логарифма поможет сгладить это противоречие.
Чаще всего, величины с таким больших размахом, что имеет смысл использовать логарифмическую ошибку, возникают в тех задачах, которые моделируют некоторые естественные процессы, характеризующиеся экспоненциальным ростом. Например, моделирование популяций, эпидемий, финансов. Такие процессы часто порождают величины, распределенные по экспоненциальному закону. А они чаще всего имеют область значений от нуля до плюс бесконечности, то есть иногда могут обращаться в ноль.
Проблема в том, что логарифм от нуля не определен. Именно поэтому в формуле данной метрики присутствует +1. Это искусственный способ избежать неопределенности. Конечно, если вы имеете дело с величиной, которая может принимать значение -1, то у вас опять будут проблемы. Но на практике такие особые распределения не встречаются почти никогда.
Использование данной метрике в коде полностью аналогично другим:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
Выводы:
- MSLE это среднее отклонение логарифмов реальных и предсказанных данных.
- Так же, идеальная модель имеет $MSLE = 0$.
- Данная метрика используется, когда целевая переменная простирается на несколько порядков величины.
- Еще эта метрика может быть полезна, если моделируется процесс в экспоненциальным ростом.
Среднее процентное отклонение (MAPE)
Все метрики, которые мы рассматривали до этого рассчитывали абсолютную величину отклонения. Но ведь отклонение в 5 единиц при истинном значении 5 и при значении в 100 — разные вещи. В первом случае мы имеем ошибку в 100%, а во втором — только в 5%. Очевидно, что первый и второй случай должны по-разному учитываться в ошибке. Для этого придумана средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE). В ней каждое отклонение оценивается в процентах от истинного значения целевой переменной:
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, |y_i|)}]
Эта метрика имеет одно критическое преимущество над остальными — с ее помощью можно сравнивать эффективность моделей на разных обучающих выборках. Ведь если мы возьмем классические метрики (например, MAE), то размер отклонений будет очевидно зависеть от самих данных. А в двух разных выборках и средняя величина скорее всего будет разная. Поэтому метрики MAE, MSE, RMSE, MSLE не сопоставимы при сравнении предсказаний, сделанных на разных выборках.
А вот по метрике MAPE можно сравнивать разные модели, которые были обучены на разных данных. Это очень полезно, например, в научных публикациях, где метрика MAPE (и ее вариации) практически обязательны для описания эффективности моделей регрессии.Ведь если одна модель ошибается в среднем на 3,9%, а другая — на 3,5%, очевидно, что вторая более точна. А вот если оперировать той же MAE, так сказать нельзя. Ведь если одна модель ошибается в среднем на 500 рублей, а вторая — на 490, очевидно ли, что вторая лучше? Может, она даже хуже, просто в исходных данных величина целевой переменной во втором случае была чуть меньше.
При этом у метрики MAPE есть пара недостатков. Во-первых, она не определена, если истинное значение целевой переменной равно 0. Именно для преодоления этого в знаменателе формулы этой метрики присутствует $max(epsilon, |y_i|)$. $epsilon$ — это некоторое очень маленькое значение. Оно нужно только для того, чтобы избежать деления на ноль. Это, конечно, настоящий математический костыль, но позволяет без опаски применять эту метрику на практике.
Во-вторых, данная метрика дает преимущество более низким предсказаниям. Ведь если предсказание ниже, чем реальное значение, процентное отклонение может быть от 0% до 100%. В это же время если предсказание выше реального, то верхней границы нет, предсказание может быть больше и на 200%, и на 1000%.
В-третьих, эта метрика несимметрична. Ведь в этой формуле $y$ и $hat{y}$ не взаимозаменяемы. Это не большая проблема и может быть исправлена использованием симметричного варианта этой метрики, который называется SMAPE (symmetric mean absolute percentage error):
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, (|hat{y_i}|, |y_i|) / 2)}]
В русскоязычной литературе данная метрика часто называется относительной ошибкой, так как она учитывает отклонение относительно целевого значения. В английском названии метрики она называется абсолютной. Тут нет никакого противоречия, так как “абсолютный” здесь значит просто взятие по модулю.
С точки зрения использования в коде, все полностью аналогично:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...
Выводы:
- Идея этой метрики — это чувствительность к относительным отклонениям.
- Данная модель выражается в процентах и имеет хорошую интерпретируемость.
- Идеальная модель имеет $MAPE = 0$. Верхний предел — не ограничен.
- Данная метрика отдает предпочтение предсказанию меньших значений.
Абсолютная медианная ошибка
Практически во всех ранее рассмотренных метриках используется среднее арифметическое для агрегации частных отклонений в общую величину ошибки. Иногда это может быть не очень уместно, если в выборке присутствует очень неравномерное распределение по целевой переменной. В таких случаях может быть целесообразно использование медианной ошибки:
[MedAE(y, _hat{y}) = frac{1}{n} median_{i=0}^{n-1}
|y_i — hat{y_i}|]
Эта метрика полностью аналогична MAE за одним исключением: вместо среднего арифметического подсчитывается медианное значение. Медиана — это такое значение в выборке, больше которого и меньше которого примерно половина объектов выборки (с точностью до одного объекта).
Эта метрика чаще всего применяется при анализе демографических и экономических данных. Ее особенность в том, что она не так чувствительна к выбросам и аномальным значениям, ведь они практически не влияют на медианное значение выборки, что делает эту метрику более надежной и робастной, чем абсолютная ошибка.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
Выводы:
- Медианная абсолютная ошибка похожа на среднюю абсолютную, но более устойчива к аномалиям.
- Применяется в задачах, когда известно, что в данных присутствуют выбросы, аномальные , непоказательные значения.
- Эта метрика более робастная, нежели MAE.
Максимальная ошибка
Еще одна достаточно экзотическая, но очень простая метрика эффективности регрессии — максимальная ошибка:
[ME(y, _hat{y}) = max_{i=0}^{n-1}
|y_i — hat{y_i}|]
Как следует из названия, это просто величина максимального абсолютного отклонения предсказанных значений от теоретических. Особенность этой метрики в том, что она вообще не характеризует распределение отклонений в целом. Поэтому она практически никогда не применяется самостоятельно, в качестве единственной метрики.
Эта метрика именно вспомогательная. В сочетании с другими метриками, она может дополнительно охарактеризовать, насколько сильно модель может ошибаться в самом худшем случае. Опять же, в зависимости от задачи, это может быть важно. В некоторых задачах модель, которая в среднем ошибается пусть чуть больше, но при этом не допускает очень больших “промахов”, может быть предпочтительнее, чем более точная модель в среднем, но у которой встречаются сильные отклонения.
Применение этой метрики та же просто, как и других:
1
2
3
4
5
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
Выводы:
- Максимальная ошибка показывает наихудший случай предсказания модели.
- В некоторых задачах важно, чтобы модель не ошибалась сильно, а небольшие отклонения не критичны.
- Зачастую эта метрика используется как вспомогательная совместно с другими.
Метрики эффективности для классификации
Приступим к рассмотрению метрик эффективности, которые применяются для оценки моделей классификации. Для начала ответим на вопрос, почему для них нельзя использовать те метрики, которые мы уже рассмотрели в предыдущей части? Дело в том, что метрики эффективности регрессии так или иначе оценивают расстояние от предсказанного значения до реального. Это подразумевает, что в значениях целевой переменной существует определенный порядок. Формально говоря, предполагается, что целевая переменная измеряется по относительной шкале. Это значит, что разница между значениями имеет какой-то смысл. Например, если мы ошиблись в предполагаемой цене товара на 10 рублей, это лучше, чем ошибка на 20 рублей. Причем, можно сказать, что это в два раза лучше.
Но вот целевые переменные, которые существуют в задачах классификации обычно не обладают таким свойством. Да, метки классов часто обозначают числами (класс 0, класс 1, класс 5 и так далее). И мы используем эти числа в качестве значения переменных в программе. Но это ничего не значит. Представим объект, принадлежащий 0 классу, что бы этот класс не значил. Допустим, мы предсказали 1 класс. Было бы хуже, если бы мы предсказали 2 класс. Можно ли сказать, что во втором случае модель ошиблась в два раза сильнее? В общем случае, нельзя. Что в первом, что во втором случае модель просто ошиблась. Имеет значение только разница между правильным предсказанием и неправильным. Отклонение в задачах классификации не играет роли.
Поэтому метрики эффективности для классификации оценивают количество правильно и неправильно классифицированных (иногда еще говорят, распознанных) объектов. При этом разные метрики, как мы увидим, концентрируются на разных соотношениях этих количеств, особенно в случае, когда классов больше двух, то есть имеет место задача множественной классификации.
Причем метрики эффективности классификации тоже нельзя применять для оценки регрессионных моделей. Дело в том, что в задачах регрессии почти никогда не встречается полное совпадение предсказанного и реального значения. Так как мы работам с непрерывным континуумом значений, вероятность такого совпадения равна, буквально, нулю. Поэтому по метрикам для классификации практически любая регрессионная модель будет иметь нулевую эффективность, даже очень хорошая и точная модель. Именно потому, что для метрик классификации даже самая небольшая ошибка уже считается как промах.
Как мы говорили ранее,для оценки конкретной модели можно использовать несколько метрик одновременно. Это хорошая практика для задач регрессии, но для классификации — это практически необходимость. Дело в том, что метрики классификации гораздо легче “обмануть” с помощью тривиальных моделей, особенно в случае несбалансированных классов (об этом мы поговорим чуть позже). Тривиальной моделью в задачах классификации может выступать модель, которая предсказывает случайный класс (такая используется чаще всего), либо которая предсказывает всегда какой-то определенный класс.
Надо обратить внимание, что по многим метрикам, ожидаемая эффективность моделей классификации сильно зависит от количества классов в задаче. Чем больше классов, тем на меньшую эффективность в среднем можно рассчитывать.Поэтому метрики эффективности классификации не позволяют сопоставить задачи, состоящие из разного количества классов. Это следует помнить при анализе моделей. Если точность бинарной классификации составляет 50%, это значит, что модель работает не лучше случайного угадывания. Но в модели множественной классификации из, допустим, 10 000 классов, точность 50% — это существенно лучше случайного гадания.
Еще обратим внимание, что некоторые метрики учитывают только само предсказание, в то время, как другие — степень уверенности модели в предсказании. Вообще, все модели классификации разделяются на логические и метрические. Логические методы классификации выдают конкретное значение класса, без дополнительной информации. Типичные примеры — дерево решений, метод ближайших соседей. Метрические же методы выдают степень уверенности (принадлежности) объекта к одному или, чаще, ко всем классам. Так, например, работает метод логистической регрессии в сочетании с алгоритмом “один против всех”. Так вот, в зависимости, от того, какую модель классификации вы используете, вам могут быть доступны разные метрики. Те метрики, которые оценивают эффективность классификации в зависимости от выбранной величины порога не могут работать с логическими методами. Поэтому, например, нет смысла строить PR-кривую для метода ближайших соседей. Остальные метрики, которые не используют порог, могут работать с любыми методами классификации.
Выводы:
- Метрики эффективности классификации подсчитывают количество правильно распознанных объектов.
- В задачах классификации почти всегда надо применять несколько метрик одновременно.
- Тривиальной моделью в задачах классификации считается та, которая предсказывает случайный класс, либо самый популярный класс.
- Качество бинарной классификации при прочих равных почти всегда будет сильно выше, чем для множественной.
- Вообще, чем больше в задаче классов, тем ниже ожидаемые значения эффективности.
- Некоторые метрики работают с метрическими методами, другие — со всеми.
Доля правильных ответов (accuracy)
Если попробовать самостоятельно придумать способ оценить качество модели классификации, ничего не зная о существующих метриках, скорее всего получится именно метрика точности (accuracy). Это самая простая и естественная метрика эффективности классификации. Она подсчитывается как количество объектов в выборке, которые были классифицированы правильно (то есть, для которых теоретическое и эмпирическое значение метки класса — целевой переменной — совпадает), разделенное на общее количество объектов выборки. Вот формула для вычисления точности классификации:
[acc(y, hat{y}) = frac{1}{n} sum_{i=0}^{n} 1(hat{y_i} = y_i)]
В этой формуле используется так называемая индикаторная функция $1()$. Эта функция равна 1 тогда, когда ее аргумент — истинное выражение, и 0 — если ложное. В данном случае она равна единице для всех объектов, у которых предсказанное значение равно реальному ($hat{y_i} = y_i$). Суммируя по всем объектам мы получим количество объектов, классифицированных верно. Перед суммой стоит множитель $frac{1}{n}$, где $n$ — количество объектов в выборке. То есть в итоге мы получаем долю правильных ответов исследуемой модели.
Значение данной метрики может быть выражено в долях единицы, либо в процентах, домножив значение на 100%. Чем выше значение accuracy, тем лучше модель классифицирует выборку, то есть тем лучше ответы модели соответствуют значениям целевой переменной, присутствующим в выборке. Если модель всегда дает правильные предсказания, то ее accuracy будет равн 1 (или 100%). Худшая модель, которая всегда предсказывает неверно будет иметь accuracy, равную нулю, причем это нижняя граница, хуже быть не может.
В дальнейшем, для обозначения названий метрик эффективности я буду использовать именно английские названия — accuracy, precision, recall. У каждого из этих слов есть перевод на русский, но так случилось, что в русскоязычных терминах существует путаница. Дело в том, что и accuracy и precision чаще всего переводятся словом “точность”. А это разные метрики, имеющие разный смысл и разные формулы. Accuracy еще называют “правильность”, precision — “прецизионность”. Причем у последнего термина есть несколько другое значение в метрологии. Поэтому, пока будем обозначать эти метрики изначальными названиями.
А вот accuracy тривиальной модели будет как раз зависеть от количества классов. Если мы имеем дело с бинарной классификацией, то модель будет ошибаться примерно в половине случаев. То есть ее accuracy будет 0,5. В общем же случае, если есть $m$ классов, то тривиальная модель, которая предсказывает случайный класс будет иметь accuracy в среднем около $frac{1}{m}$.
Но это в случае, если в выборке объекты разных классов встречаются примерно поровну. В реальности же часто встречаются несбалансированные выборки, в которых распределение объектов по классам очень неравномерно. Например, может быть такое, что объектов одного класса в десять раз больше, чем другого. В таком случае, accuracy тривиальной модели может быть как выше, так и ниже $1/m$. Вообще, метрика accuracy очень чувствительна к соотношению классов в выборке. И именно поэтому мы рассматриваем другие способы оценки качества моделей классификации.
Использование метрики accuracy в библиотеке sklearn ничем принципиальным не отличается от использования других численных метрик эффективности:
1
2
3
4
5
6
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
В данном примере в задаче 4 класса (0, 1, 2, 3) и столько же объектов, по одному на каждый класс. Модель правильно классифицировала первый и третий объект, то есть половину. Поэтому ее accuracy составляет 0,5 или 50%.
Выводы:
- Точность (accuracy) — самая простая метрика качества классификации, доля правильных ответов.
- Может быть выражена в процентах и в долях единицы.
- Идеальная модель дает точность 1.0, тривиальная — 0.5, самая худшая — 0.0.
- Тривиальная модель в множественной сбалансированной задаче классификации дает точность 1/m.
- Метрика точности очень чувствительная к несбалансированности классов.
Метрики классификации для неравных классов (precision, recall, F1)
Как мы говорили ранее, метрика accuracy может быть чувствительна к несбалансированности классов. Рассмотрим типичный пример — диагностика заболевания. Допустим, в случайной выборке людей заболевание встречается один раз на 100 человек. То есть в выборке у нас может быть всего 1% объектов, принадлежащих положительному классу и 99% — отрицательному, то есть почти в 100 раз больше. Какая accuracy будет у абсолютно тривиальной модели, которая всегда предсказывает отрицательный класс? Такая модель будет права в 99% случаев и ошибаться только в 1%. То есть иметь accuracy 0,99. Естественно, ценность такой модели минимальна, несмотря на высокий показатель метрики. Поэтому в случае с сильно несбалансированными классами метрика accuracy не то, чтобы неверна, она непоказательна, то есть не дает хорошего представления о качественных характеристиках модели.
Для более полного описания модели используется ряд других метрик. Для того, чтобы понять, как они устроены и что показывают нужно разобраться с понятием ошибок первого и второго рода. Пока будем рассматривать случай бинарной классификации, а о том, как эти метрики обобщаются на множественные задачи, поговорим позднее. Итак, у нас есть задача бинарной классификации, объекты положительного и отрицательного класса. Идеальным примером для этого будет все та же медицинская диагностика.
По отношению к модели бинарной классификации все объекты выборки можно разделить на четыре непересекающихся множества. Истинноположительные (true positive, TP) — это те объекты, которые отнесены моделью к положительному классу и действительно ему принадлежат. Истинноотрицательные (true negative, TN) — соответственно те, которые правильно распознаны моделью как принадлежащие отрицательному классу. Ложноположительные объекты (FP, false positive) — это те, которые модель распознала как положительные, хотя на самом деле они отрицательные. В математической статистике такая ситуация называется ошибкой первого рода. И, наконец, ложноотрицательные значения (false negative, FN) — это те, которые ошибочно отнесены моделью к отрицательному классу, хотя на самом деле они принадлежат положительному.
В примере с медицинско диагностикой, ложноположительные объекты или ошибки первого рода — это здоровые пациенты, которых при диагностике ошибочно назвали больными. Ложноотрицательные, или ошибки второго рода, — это больные пациенты, которых диагностическая модель “пропустила”, ошибочно приняв за здоровых. Очевидно, что в этой задаче, как и во многих других, ошибки первого и второго рода не равнозначны. В медицинской диагностике, например, гораздо важнее распознать всех здоровых пациентов, то есть не допустить ложноотрицательных объектов или ошибок второго рода. Ошибки же первого рода, или ложноположительные предсказания, тоже нежелательны, но значительно меньше, чем ложноотрицательные.
Так вот, метрика accuracy учитывает и те и другие ошибки одинаково, абсолютно симметрично. В терминах наших четырех классов она может выражаться такой формулой:
[A = frac{TP + TN}{TP + TN + FP + FN}]
Обратите внимание, что если в модели переименовать положительный класс в отрицательный и наоборот, то это никак не повлияет на accuracy. Так вот, в зависимости от решаемой задачи, нам может быть необходимо воспользоваться другими метриками. Вообще, их существует большое количество, но на практике чаще других применяются метрики precision и recall.
Precision (чаще переводится как “точность”, “прецизионность”) — это доля объектов, плавильно распознанных как положительные из всех, распознанных как положительные. Считается этот показатель по следующей формуле: $P = frac{TP}{TP + FP}$. Как можно видеть, precision будет равен 1, если модель не делает ошибок первого рода, то есть не дает ложноположительных предсказаний. Причем ошибки второго рода (ложноотрицательные) вообще не влияют на величину precision, так как эта метрика рассматривает только объекты, отнесенные моделью к положительным.
Precision характеризует способность модели отличать положительный класс от отрицательного, не делать ложноположительных предсказаний. Ведь если мы будем всегда предсказывать отрицательный класс, precision будет не определен. А вот если модель будет всегда предсказывать положительный класс, то precision будет равен доли объектов этого класса в выборке. В нашем примере с медицинской диагностикой, модель, всех пациентов записывающая в больные даст precision всего 0,01.
Метрика recall (обычно переводится как “полнота” или “правильность”) — это доля положительных объектов выборки, распознанных моделью. То есть это отношение все тех же истинноположительных объектов к числу всех положительных объектов выборки: $R = frac{TP}{TP + FN}$. Recall будет равен 1 только в том случае, если модель не делает ошибок второго рода, то есть не дает ложноотрицательных предсказаний. А вот ошибки первого рода (ложноположительные) не влияют на эту метрику, так как она рассматривает только объекты, которые на самом деле принадлежат положительному классу.
Recall характеризует способность модели обнаруживать все объекты положительного класса. Если мы будем всегда предсказывать отрицательный класс, то данная метрика будет равна 0, а если всегда положительный — то 1. Метрика Recall еще называется полнотой, так как она характеризует полноту распознавания положительного класса моделью.
В примере с медицинской диагностикой нам гораздо важнее, как мы говорили, не делать ложноотрицательных предсказаний. Поэтому метрика recall будет для нас важнее, чем precision и даже accuracy. Однако, как видно из примеров, каждый из этих метрик легко можно максимизировать довольно тривиальной моделью. Если мы будет ориентироваться на recall, то наилучшей моделью будет считаться та, которая всегда предсказывает положительный класс. Если только на precision — то “выиграет” модель, которая всегда предсказывает наоборот, положительный. А если брать в расчет только accuracy, то при сильно несбалансированных классах модель, предсказывающая самый популярный класс. Поэтому эти метрики нелья использовать по отдельности, только сразу как минимум две из них.
Так как метрики precision и recall почти всегда используются совместно, часто возникает ситуация, когда есть две модели, у одной из которых выше precision, а у второй — recall. Возникает вопрос, как выбрать лучшую? Для такого случая можно посчитать среднее значение. Но для этих метрик больше подойдет среднее не арифметическое, а гармоническое, ведь оно равно 0, если хотя бы одно число равно 0. Эта метрика называется $F_1$:
[F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN}]
Эта метрика полезна, если нужно одно число, которое в себе объединяет и precision и recall. Но эта формула подразумевает, что нам одинаково важны и то и другое. А как мы заметили раньше, часто одна из этих метрик важнее. Поэтому иногда используют обобщение метрики $F_1$, так называемое семейство F-метрик:
[F_{beta} = (1 + beta^2) frac{P R}{beta^2 P + R}]
Эта метрика имеет параметр $beta > 0$, который определяет, во сколько раз recall важнее precision. Если этот параметр больше единицы, то метрика будет полагать recall более важным. А если меньше — то важнее будет precision. Если же $beta = 1$, то мы получим уже известную нам метрику $F_1$. Все метрики из F-семейства измеряются от 0 до 1, причем чем значение больше, тем модель лучше.
1
2
3
4
5
6
7
8
9
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
Выводы:
- Если классы в задаче не сбалансированы, то метрика точности не дает полного представления о качестве работы моделей.
- Для бинарной классификации подсчитывается количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных объектов.
- Precision — доля истинно положительных объектов во всех, распознанных как положительные.
- Precision характеризует способность модели не помечать положительные объекты как отрицательные (не делать ложно положительных прогнозов).
- Recall — для истинно положительных объектов во всех положительных.
- Recall характеризует способность модели выявлять все положительные объекты (не делать ложно отрицательных прогнозов).
- F1 — среднее гармоническое между этими двумя метриками. F1 — это частный случай. Вообще, семейство F-метрик — это взвешенное среднее гармоническое.
- Часто используют все вместе для более полной характеристики модели.
Матрица классификации
Матрица классификации — это не метрика сама по себе, но очень удобный способ “заглянуть” внутрь модели и посмотреть, насколько хорошо она классифицирует какую-то выборку объектов. Особенно удобна эта матрица в задачах множественной классификации, когда из-за большого количества классов численные метрики не всегда наглядно показывают, какие объекты к каким классам относятся.
С использованием библиотеки sklearn матрица классификации может быть сформирована всего одной строчкой кода:
1
2
3
4
5
6
7
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
В этой матрице по строкам располагаются истинные значения целевой переменной, то есть действительные значения классов. По столбцам же отмечены предсказанные классы. В самой матрице на пересечении строки и столбца отмечается число объектов, которые принадлежат данному действительному классу, но моделью были распознаны как объекты данного предсказанного класса.
Естественно, элементы, располагающиеся на главной диагонали, показывают объекты, которые были правильно распознаны моделью. Элементы же вне этой диагонали — это ошибки классификации. Поэтому чем лучше модель, тем выше должны быть значения по диагонали и тем меньше — вне ее. В идеале все элементы вне главной диагонали должны быть нулевыми.
Но гораздо удобнее представлять ее в графическом виде:
Источник: sklearn.
В таком виде матрица представляется в виде тепловой карты, в которой чем выше значение, тем насыщеннее оттенок цвета. Это позволяет при первом взгляде на матрицу понять, как часто она ошибается и в каких именно классах. В отличие от простых численных метрик, матрица классификации может дать информацию о паттернах распространенных ошибок, которые допускает данная модель.
Практически любое аномальное или тривиальное поведение модели будет иметь отражение в матрице классификации. Например, если модель чаще чем нужно предсказывает один класс, это сразу подсветит отдельный столбец в ней. Если же модель путает два класса, то есть не различает объекты этих классов, то в матрице будут подсвечены четыре элемента, располагающиеся в углах прямоугольника. Еще одно распространенное поведение модель — когда она распознает объекты одного класса, как объекты другого — подсветит один элемент вне главной диагонали.
Эта матрица очень наглядно показывает, как часто и в каких конкретно классах ошибается модель. Поэтому анализ этой матрицы может дать ценную информацию о путях увеличения эффективности моделей. Например, можно провести анализ ошибок на основе показаний данной матрицы — проанализировать объекты, на которых модель чаще всего ошибается. Может, будет выявлена какая-то закономерность, либо общая характеристика. Добавление информации о таких параметрах объектов к матрице атрибутов обычно очень сильно улучшает эффективность моделей.
Выводы:
- Матрица классификации, или матрица ошибок представляет собой количество объектов по двум осям — истинный класс и предсказанный класс.
- Обычно, истинный класс располагается по строкам, а предсказанный — по столбцам.
- Для идеальной модели матрица должна содержать ненулевые элементы только на главной диагонали.
- Матрица позволяет наглядно представить результаты классификации и увидеть, в каких случаях модель делает ошибки.
- Матрица незаменима при анализе ошибок, когда исследуется, какие объекты были неправильно классифицированы.
Метрики множественной классификации
Все метрики, о которых мы говорили выше рассчитываются в случае бинарной классификации, так как определяются через понятия ложноположительных, ложноотрицательных прогнозов. Но на практике чаще встречаются задачи множественной классификации. В них не определяется один положительный и один отрицательный класс, поэтому все рассуждения о precision и recall, казалось бы, не имеют смысла.
На самом деле, все рассмотренные метрики прекрасно обобщаются на случай множественных классов. Рассмотрим простой пример. У нас есть три класса — 0, 1 и 2. Есть пять объектов, каждый их которых принадлежит одному их этих трех классов. Истинные значения целевой переменной такие: $y = lbrace 0, 1, 2, 2, 0 rbrace$. Имеется модель, которая предсказывает классы этих объектов, соответственно так: $hat{y} = lbrace 0, 0, 2, 1, 0 rbrace$. Давайте рассчитаем известные нам метрики качества классификации.
С метрикой accuracy все просто. Модель правильно предсказала класс в трех случаях из пяти — первом, третьем и пятом. А в двух случаях — ошиблась. Поэтому метрика рассчитывается так: $A = 3 / 5 = 0.6$. То есть точность модели — 60%.
А вот precision и recall рассчитываются более сложно. В моделях множественной классификации эти метрики могут быть рассчитаны отдельно по каждому классу. Подход в этом случае очень похож на алгоритм “один против всех” — для каждого класса он предполагается положительным, а все остальные классы — отрицательными. Давайте рассчитаем эти метрики на нашем примере.
Возьмем нулевой класс. Его обозначим за 1, а все остальные — за 0. Тогда вектора эмпирических и теоретических значений целевой пременной станут выглядеть так:
$y = lbrace 1, 0, 0, 0, 1 rbrace$,
$hat{y} = lbrace 1, 1, 0, 0, 1 rbrace$.
Тогда $P = frac{TP}{TP + FP} = frac{2}{3} approx 0.67$, ведь у нас получается 2 истинноположительных предсказания (первый и пятый объекты) и одно ложноположительное (второй). $R = frac{TP}{TP + FN} = frac{2}{2} = 1$, ведь в модели нет ложноотрицательных прогнозов.
$F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN} = frac{2 cdot 2}{2 cdot 2 + 1 + 0} = frac{4}{5} = 0.8$.
Аналогично рассчитываются метрики и по остальным классам. Например, для первого класса вектора целевой переменной будут такими:
$y = lbrace 0, 1, 0, 0, 0 rbrace$,
$hat{y} = lbrace 0, 0, 0, 1, 0 rbrace$. Обратите внимание, что в данном случае получается, что модель ни разу не угадала. Такое тоже бывает, и в таком случае, метрики будут нулевые. Для третьего класса попробуйте рассчитать метрики самостоятельно, а чуть ниже можно увидеть правильный ответ.
Конечно, при использовании библиотечный функций не придется рассчитывать все эти метрики вручную. В библиотеке sklearn для этого есть очень удобная функция — classification_report, отчет о классификации, которая как раз вычисляет все необходимые метрики и представляет результат в виде наглядной таблицы. Вот как будет выглядеть рассмотренный нами пример:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Здесь мы видим несколько строк, соответствующих классам в нашей задаче. По каждому классу рассчитаны метрики precision, recall и $F_1$. Последний столбец называется support — это количество объектов данного класса в используемой выборке. Это тоже важный показатель, так как чем меньше объектов какого-то класса, тем хуже он обычно распознается.
Ниже приведены интегральные, то есть общие метрики эффективности модели. Это три последние строки таблицы. В первую очередь это accuracy — она всегда рассчитывается один раз. Обратите внимание, что в столбце support здесь везде стоит 5 — это общее число объектов выборки. Ниже приведены средние значения по метрикам precision, recall и $F_1$. Почему же строк две? Дело в том, что усреднять эти метрики можно по-разному.
Во-первых, можно взять обычное среднее арифметическое из метрик всех классов. Это называется macro average. Это самый простой способ, но у него есть одна проблема. Почему метрики очень малочисленных классов должны давать тот же вклад в итоговый результат, что и метрики очень многочисленных? Можно усреднить метрики используя в качестве весов долю каждого класса в выборке. Такое усреднение называется weighted average. Обратите внимание, что при усреднении метрика $F_1$ может получиться не между precision и recall.
Отчет о классификации — очень полезная функция, использование которой практически обязательно при анализе эффективности моделей классификации. Особенно для задач множественной классификации. Эта таблица может дать важную информацию о том, какие классы распознаются моделью лучше, какие — хуже, как это связано в численностью классов в выборке. Анализ этой таблицы может навести на необходимость определенных действий по повышению эффективности модели. Например, можно понять, какие данные полезно будет добавить в модель.
Выводы:
- Метрики для каждого класса рассчитываются, полагая данный класс положительным, а все остальные — отрицательными.
- Каждую метрику можно усреднить арифметически или взвешенно по классам. Весами выступают объемы классов.
- В модуле sklearn реализовано несколько алгоритмов усреднения они выбираются исходя их задачи.
- В случае средневзвешенного, F1-метрика может получиться не между P и R.
- Отчет о классификации содержит всю необходимую информацию в стандартной форме.
- Отчет показывает метрики для каждого класса, а так же объем каждого класса.
- Также отчет показывает средние и средневзвешенные метрики для всей модели.
- Отчет о классификации — обязательный элемент представления результатов моделирования.
- По отчету можно понять сбалансированность задачи, какие классы определяются лучше, какие — хуже.
PR-AUC
При рассмотрении разных моделей классификации мы упоминали о том, что они подразделяются на метрические и логические методы. Логические методы (дерево решений, k ближайших соседей) выдают конкретную метку класса,без какой-либо дополнительной информации. Метрические методы (логистическая регрессия, перцептрон, SVM) выдают принадлежность данного объекта к разным классам, присутствующим в задаче. При рассмотрении модели логистической регрессии мы говорили, что предсказывается положительный класс, если значение логистической функции больше 0,5.
Но это пороговое значение можно поменять. Что будет, если мы измени его на 0,6? Тогда мы для некоторых объектовы выборки изменим предсказание с положительного класса на отрицательный. То есть без изменения модели можно менять ее предсказания. Это значит, что изменятся и метрики модели, то есть ее эффективность.
Чем больше мы установим порог, тем чаще будем предсказывать отрицательный класс. Это значит, что в среднем, у модели будет меньше ложноположительных предсказаний, но может стать больше ложноотрицательных. Значит, у модели может увеличится precision, то упадет recall. В крайнем случае, если мы возьмем порог равный 1, мы всегда будем предсказывать отрицательный класс. Тогда у модели будет $P = 1, R = 0$. Если же, наоборот, возьмем в качестве порога 0, то мы всегда будем предсказывать отрицательный класс, а значит у модели будет $P = 0, R = 1$, так как она не будет давать ложноположительных прогнозов, но будут встречаться ложноотрицательные.
Это означает, что эффективность моделей метрической классификации зависит не только от того, как модель соотносится с данными, но и от значения порога. Из этого следует, кстати, что было бы не совсем правильно вообще сравнивать метрики двух разных моделей между собой. Ведь значение этих метрик будет зависеть не только от самих моделей, но и от порогов, которые они используют. Может, первая модель будет лучше, если немного изменить ее пороговое значение? Может, одна из метрик второй модели станет выше, если изменить ее порог.
Это все сильно затрудняет анализ метрических моделей классификации. Для сравнения разных моделей необходим способ “убрать” влияние порога, сравнить модели вне зависимости от его значения. И такой способ есть. Достаточно просто взять все возможные значения порога, посчитать метрики в каждом из них и затем усреднить. Для этого служит PR-кривая или кривая “precision-recall”:
Каждая точка на этом графике представляет собой значение precision и recall для конкретного значения порога. Для построения этого графика выбирают все возможные значение порога и отмечают на графике. Давайте рассмотрим простой пример из 10 точек. Истинные значения классов этих точек равны, соответственно, $y = lbrace 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 rbrace$. Модель (сейчас совершенно неважно, какая) выдает следующие предсказания для этих объектов: $h(x) = lbrace 0.1, 0.2, 0.3, 0.45, 0.6, 0.4, 0.55, 0.7, 0.8, 0.9 rbrace$. Заметим, что модель немного ошибается для средних объектов, то есть она не будет достигать стопроцентной точности. Построим таблицу, в которой переберем некоторые значения порога и вычислим, к какому классу будет относиться объект при каждом значении порога:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,3 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,45 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0,4 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,55 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0,8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0,9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Можно сразу заметить, что чем выше порог, тем чаще предсказывается отрицательный класс. В крайних случаях модель всегда предсказывает либо положительный класс (при малых значениях порога), либо отрицательный (при больших).
Далее, для каждого значения порога рассчитаем количество истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных предсказаний. На основе этих данных легко рассчитать и метрики precision и recall. Запишем это в таблицу:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TP | 5 | 5 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 1 | 0 | |
| TN | 0 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | |
| FP | 5 | 5 | 4 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | |
| FN | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | |
| P | 0,50 | 0,50 | 0,56 | 0,63 | 0,71 | 0,80 | 0,75 | 1,00 | 1,00 | 1,00 | 1,00 | |
| R | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 |
При самом низком значении порога модель всегда предсказывает отрицательный класс, метрика recall равна 1, а метрика precision равна доли отрицательного класса в выборке. Причем ниже этого значения precision уже не опускается. Можно заметить, что в целом при повышении порога precision повышается, а recall понижается. В другом крайнем случае, когда порог равен 1, модель всегда предсказывает отрицательный класс, метрика recall равна 0, а precision — 1 (на самом деле эта метрика не определена, но считается равной именно 1, так как ее значение стремится к этому при повышении порога). За счет чего это происходит?
При повышении порога может произойти один из трех случаев. Первый заключается в том, что данное изменение может не влияет ни на одно предсказание. Так происходит, например, при повышении порога с 0,1 до 0,15. Оценка ни одного объекта не попадает в данный диапазон, поэтому ни одно предсказание не меняется. И, соответственно, не изменится ни одна метрика.
Если же повышение порога все-таки затрагивает один или несколько объектов, то изменение предсказания может произойти только с положительного на отрицательное. Допустим, для простоты, что повышение порога затрагивает только один объект. То есть мы изменяем предсказание по одному объекту с 1 на 0. Второй случай заключается в том, что это изменение правильное. То есть объект в действительности принадлежит отрицательному классу. Так происходит, например, при изменении порога с 0,15 до 0,2. В данном случае первый объект из ложноположительного стал истинно отрицательным. Такое изменение не влияет на recall, но повышает precision.
Третий случай заключается в том, что изменение предсказаные было неверным. То есть объект из истинно положительного стал ложноотрицательным. Это происходит, например, при изменении порога с 0,4 до 0,5 — в данном случае шестой объект становится классифицированным ошибочно. Уменьшение количества истинно положительных объектов снижает обе метрики — и precision и recall.
Таким образом можно заключить, что recall при повышении порога может оставаться неизменным или снижаться, а precision может как повышаться, так и понижаться, но в среднем будет повышаться за счет уменьшения доли ложноположительных предсказаний. Если изобразить рассмотренный пример на графике можно получить такую кривую:
PR-кривая не всегда монотонна, обе метрики могут изменяться как однонаправленно, так и разнонаправленно при изменении порогового значения. Но главный смысл этой кривой не в этом. При таком анализе очень просто обобщить эффективность модели вне зависимости от значения порога. Для этого нужно всего лишь найти площадь под графиком этой кривой. Эта метрика называется PR-AUC (area under the curve) или average precision (AP). Чем она выше, тем качественнее модель.
Давайте порассуждаем, ка будет вести себя идеальная модель. Крайние случаи, когда порога равны 0 и 1, значения метрик будут такими же, как и всегда. Но вот при любом другом значении порога модель будет классифицировать все объекты правильно. И обе метрики у нее будут равны 1. Таким образом, PR-кривая выродится в два отрезка, один из которых проходит из точки (0, 1) в точку (1, 1). и площадь под графиком будет равна 1. У самой худшей же модели метрики будут равны 0, так как она всегда будет предсказывать неверно. И площадь тоже будет равна 0.
У случайной модели, как можно догадаться, площадь под графиком будет равна 0,5. Поэтому метрика PR-AUC может использоваться для сравнения разных моделей метрической классификации вне зависимости от значения порога. Также эта метрика показывает соотношение данной модели и случайной. Если PR-AUC модели меньше 0,5, значит она хуже предсказывает класс, чем простое угадывание.
Выводы:
- Кривая precision-recall используется для методов метрической классификации, которые выдают вероятность принадлежности объекта данному классу.
- Дискретная классификации производится при помощи порогового значения.
- Чем больше порог, тем больше объектов модель будет относить к отрицательному классу.
- Повышение порога в среднем увеличивает precision модели, но понижает recall.
- PR-кривая используется чтобы выбрать оптимальное значение порога.
- PR-кривая нужна для того, чтобы сравнивать и оценивать модели вне зависимости от выбранного уровня порога.
- PR-AUC — площадь под PR-кривой, у лучшей модели — 1.0, у тривиальной — 0.5, у худшей — 0.0.
ROC_AUC
Помимо кривой PR есть еще один довольно популярный метод оценки эффективности метрических моделей классификации. Он использует тот же подход, что и PR-кривая, но немного другие координаты. ROC-кривая (receiver operating characteristic) — это график показывающий соотношение доли истинно положительных предсказаний и ложноположительных предсказаний в модели метрической классификации для разных значений порога.
В этой кривой используются два новых термина — доля истинно положительных и доля ложноположительных предсказаний. Доля истинно положительных предсказаний (TPR, true positive rate), как можно догадаться, это отношение количества объектов выборки, правильно распознанных как положительные, ко всем положительным объектам. Другими словами, это всего лишь иное название метрики recall.
А вот доля ложноположительных предсказаний (FPR, false positive rate) считается как отношение количества отрицательных объектов, неправильно распознанных как положительные, в общем количестве отрицательных объектов выборки:
[TPR = frac{TP}{TP + FN} = R \
FRP = frac{FP}{TN + FP} = 1 — S]
Обратите внимание, что FPR — мера ошибки модели. То есть, чем больше — тем хуже. У идеальной модели $FRP=0$, а у наихудшей — $FPR=1$. Для иллюстрации давайте рассчитаем эти метрики для нашего примера, который мы использовали выше (для дополнительной информации еще приведена метрика accuracy для каждого значения порога):
| y | h(x) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 | |
| FPR | 1,00 | 0,80 | 0,60 | 0,40 | 0,20 | 0,20 | 0,00 | 0,00 | 0,00 | 0,00 | |
| A | 0,50 | 0,60 | 0,70 | 0,80 | 0,80 | 0,70 | 0,80 | 0,70 | 0,60 | 0,50 |
Можно заметить, что при увеличении порога обе эти метрики увеличиваются, начиная со значения 1 до нуля. Причем, движения этих двух показателей всегда однонаправленно. Давайте опять же разберемся, почему так. Если увеличение порога приводит к правильному изменению классификации, то есть изменению ложноположительного значения на истинно отрицательное, то это уменьшит FRP, но не затронет TRP. Если же изменение будет неверным, то есть истинно положительное значение поменялось на ложноотрицательное, это однозначно уменьшит TPR, при этом FRP либо уменьшится так же, либо останется неименным.
В итоге, кривая получается монотонной, причем она всегда проходит через центр координат и через точку (1, 1). В нашем примере кривая будет выглядеть так:
Более сложные данные могут выглядеть с большим количеством деталей, но общая форма и монотонность сохраняются:
Также, как и с кривой PR, важное значение имеет площадь под графиком. Эта метрика называется ROC-AUC и является одной из самых популярных метрик качества метрических моделей классификации. Ее главное преимущество перед другими метриками состоит в том, что она позволяет объективно сопоставить уровень качества разных моделей классификации, решающих одну и ту же задачу, но обученных на разных данных. Это приводит к частому использованию ROC-AUC, например, в научной литературе для представления результатов моделирования.
Существует множество споров, какая диагностическая кривая более адекватно измеряет качество классификации — ROC или PR. Считается, что PR-кривая больше ориентирована на задачи, в которых присутствует дисбаланс классов. Это задачи в которых объектов одного класса значительно больше чем другого, классы имеют разное толкование и, как следствие, ошибки первого и второго рода не равнозначны. Зачастую это модели бинарной классификации. ROC же дает более адекватную картину в задачах, где классов примерно поровну в выборке. Но для полного анализа модели все равно рекомендуется использовать оба метода.
В случае с множественной классификацией построение диагностических кривых происходит отдельно по каждому классу. Так же, как и при расчете метрик precision и recall, каждый класс поочередно полагается положительным, а остальные — отрицательными. Каждая такая частная кривая показывает качество распознавания конкретного класса. Поэтому кривые могут выглядеть примерно так:
Источник: sklearn.
На данном графике мы видим PR-кривую модели множественной классификации из 3 классов. Кроме отдельных значений precision и recall в каждой точке рассчитываются и усредненные значения. Так формируется кривая средних значений. Интегральная метрика качества модели классификации считается как площадь под кривой средних значений. Алгоритм построения ROC-кривой полностью аналогичен.
Выводы:
- ROC-кривая показывает качество бинарной классификации при разных значениях порога.
- В отличие от PR-кривой, ROC-кривая монотонна.
- Площадь под графиком ROC-кривой, ROC_AUC — одна из основных метрик качества классификационных моделей.
- ROC_AUC можно использовать для сравнения качества разных моделей, обученных на разных данных.
- ROC чаще используют для сбалансированных и множественных задач, PR — для несбалансированных.
- Кривые для множественной классификации строятся отдельно для каждого класса.
- Метрика AUC считается по кривой средних значений.
Топ k классов
Все метрики, которые мы обсуждали выше оперируют точным совпадением предсказанного класса с истинным. В некоторых особых задачах может быть полезно немного смягчить это условие. Как мы говорили, метрические методы классификации выдают больше информации — степень принадлежности объекта выборки каждому классу. Обычно, мы выбираем из них тот класс, который имеет наибольшую принадлежность. Но можно выбрать не один класс, а несколько. Таким образом можно рассматривать не единственный вариант класса для конкретного объекта, а 3, 5, 10 и так далее.
Другими словами можно говорить о том, находится ли истинный класс объекта среди 3, 5 или 10 классов, которые выбрала для него модель. Количество классов, которые мы рассматриваем, можно брать любым. В данной метрике оно обозначается k. Таким образом, можно построить метрику, которая оценивает долю объектов выборки, для которых истинный класс находится среди k лучших предсказаний модели:
[tka(y, hat{f}) = frac{1}{n} sum_{i=0}^{n-1}
sum_{j=1}^{k} 1(hat{f_{ij}} = y_i)]
где $hat{f_{ij}}$ — это j-й в порядке убывания уверенности модели класс i-го объекта.
Рассмотрим такой пример. Пусть у нас есть задача классификации из 3 классов. Мы оцениваем 4 объекта, которые имеют на самом деле такие классы:
$y = lbrace 0, 1, 2, 2 rbrace$.
1
2
3
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
Модель предсказывает следующие вероятности для каждого объекта:
1
2
3
4
>>> y_score = np.array([[0.5, 0.2, 0.2],
... [0.4, 0.3, 0.2],
... [0.2, 0.4, 0.3],
... [0.7, 0.2, 0.1]])
То есть для первого объекта она выбирает первый класс, но немного предполагает и второй. А вот, например, последний, четвертый объект она уверенно относит тоже к первому классу. Давайте посчитаем метрику топ-2 для этой модели. Для этого для каждого объекта рассмотрим, какие 2 класса модель называет наиболее вероятными. Для первого — это 0 и 1, для второго — также 0 и 1, причем модель отдает предпочтение 0 классу, хотя на самом деле объект относится к 1 классу. Для третьего — уже 2 и 2 класс, причем класс 1 кажется модели более вероятным, для четвертого — так же наиболее вероятными модели кажутся 0 и 1 класс.
Если бы мы говорили об обычной accuracy, то для такой модели она была бы равна 0,25. Ведь только для первого объекта модель дала правильное предсказание наиболее вероятного класса. Но по метрике топ-2, для целых трех объектов истинный класс находится среди двух наиболее вероятных. Модель полностью ошибается только в последнем случае. Так что эта метрика равна 0,75. Это же подтверждают и автоматические расчеты:
1
2
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
Как мы говорили, количество классов k можно взять любым. В частном случае $k=1$ эта метрика превращается в классическую accuracy. Чем больше возьмем k, тем выше будет значение данной метрики, но слабее условие. Так что брать очень большие k нет никакого смысла. В другом крайнем случае, когда k равно количеству классов, метрика будет равна 1 для любой модели.
Эта метрика имеет не очень много практического смысла. Ведь при прикладном применении моделей машинного обучения важен все-таки итоговый результат классификации. И если модель ошиблась, то модель ошиблась. Но эта метрика может пролить свет на внутреннее устройство модели, показать, насколько сильно она ошибается. Ведь одно дело, если модель иногда называет правильный ответ может и не наиболее вероятным, но в топ, скажем, 3. Совсем другое дело, если модель не находит правильный ответ и среди топ-10. Так что эта метрика может использоваться для диагностики моделей классификации и для поиска путей их совершенствования. Еще она бывает полезна, если две модели имеют равные значения метрики accuracy, но нужно понять, какая их них адекватнее имеющимся данным.
Такие проблемы часто возникают в задачах, где классов очень много. Например, в распознавании объектов на изображениях количество объектов может быть несколько тысяч. А в задачах обработки текста количество классов может определяться количеством слов в языке — сотни тысяч и миллионы (если учитывать разные формы слов). Естественно, что эффективность моделей классификации в таких задачах, измеренная обычными способами будет очень низкой. А данная метрика позволяет эффективно сравнивать и оценивать такие модели.
Выводы:
- Эта метрика — обобщение точности для случая, когда модель выдает вероятности отнесения к каждому классу.
- Вычисляется как доля объектов, для которых правильный класс попадает в список k лучших предсказанных классов.
- Чем больше k, тем выше метрика, но бесполезнее результат.
- Эта метрика часто применяется в задачах с большим количеством классов.
- Применимость этой метрики сильно зависит от характера задачи.
Проблема пере- и недообучения
Проблема Bias/Variance
При решении задачи методами машинного обучения всегда встает задача выбора вида модели. Как мы обсуждали в предыдущих главах, существует большое количество классов модели — достаточно вспомнить линейные модели, метод опорных векторов, перцептрон и другие. Каждая их этих моделей, будучи обученной на одном и том же наборе данных может давать разные результаты. Важно понимать, что мы не говорим о степени подстройки модели к данным. Даже если обучение прошло до конца, найдены оптимальные значения параметров, все равно модели могут и, скорее всего, будут различаться.
Причем многие классы моделей представляют собой не одно, а целое множество семейств функций. Например, та же логарифмическая регрессия — это не одна функция, а бесконечное количество — квадратичные, кубические, четвертой степени и так далее. Множество функций или моделей, имеющих единую форму, но различающуюся значениями параметров составляет так называемое параметрическое семейство функций. Так, все возможные линейные функции — это одно параметрическое семейство, все возможные квадратические — другое, а, например, множество всех возможных однослойных перцептронов с 5 нейронами во входном, 3 нейронами в скрытом и одном нейроне в выходном слое — третье семейство.
Таким образом можно говорить, что перед аналитиком стоит задача выбора параметрического семейства модели, которую он будет обучать на имеющихся данных. Причем разные семейства дадут модели разного уровня качества после обучения. К сожалению, очень сложно заранее предугадать, какое семейство моделей после завершения обучения даст наилучшее качество предсказания по данной выборке.
Что является главным фактором выбора этого семейства? Как показывает практика, самое существенное влияние на эффективность оказывает уровень сложности модели. Любое параметрическое семейство моделей имеет определенное количество степеней свободы, которое определяет то, насколько сложное и изменчивое поведение может демонстрировать получившаяся функция.
Сложность модели можно определять разными способами, но в контексте нашего рассуждения сложность однозначно ассоциируется с количеством параметров в модели. Чем больше параметров, тем больше у модели степеней свободы, возможности изменять свое поведение при разных значениях входных признаков. Конечно, это не означает полной эквивалентности разных типов моделей с одинаковым количеством параметров. Например, никто не говорит, что модель, скажем, регрессии по методу опорных векторов эквивалентна модели нейронной сети с тем же самым количеством весов. Главное, что модели со сходным уровнем сложности демонстрируют сходное поведение по отношению к конкретному набору данных.
Влияние уровня сложности на поведение модели относительно данных наиболее наглядно можно проследить на примере модели полиномиальной модели. Степень полинома — это очень показательная характеристика уровня сложности модели. Давайте рассмотрим три модели регрессии — линейную (которую можно рассматривать как полином первой степени), полином второй и восьмой степени. Мы обучили эти модели на одном и том же датасете и вот что получилось:
Следует отдельно заметить, что в каждом из представленных случаев модель обучалась до конца, то есть до схождения метода численной оптимизации параметров. То есть для каждой модели на графике представлены оптимальные значения параметров. Гладя на эти три графика и то, как эти линии ложатся в имеющиеся точки, можно заметить некоторое противоречие. Естественно предположить, что модель, изображенная на втором графике показывает наилучшее описание точек данных. Но по любой метрике качества третья модель будет показывать более высокий результат.
Человек, глядя на график третьей модели, сразу сделает вывод, что она “слишком” хорошо подстроилась под имеющиеся данные. Сравните это поведение с первым графиком, который демонстрирует самую низкую эффективность на имеющихся данных. Можно проследить, как именно сложность модели влияет на ее применимость. Если модель слишком простая, то она может не выявить имеющиеся сложные зависимости между признаками и целевой переменной. Говорят, что у простых моделей низкая вариативность (variance). Слишком же сложная модель имеет слишком высокую вариативность, что тоже не очень хорошо.
Те же самые рассуждения можно применить и к моделям классификации. Можно взглянуть на форму границы принятия решения для трех моделей разного уровня сложности, обученных на одних и тех же данных:
В данном случае мы видим ту же картину — слишком простая модель не может распознать сложную форму зависимости между факторами и целевой переменной. Такая ситуация называется недообучение. Обратите внимание, что недообучение не говорит о том, что модель не обучилась не до конца. Просто недостаток сложности, вариативности модели не дает ни одной возможной функции их этого параметрического семейства хорошо описывать данные.
Слишком сложные модели избыточно подстраиваются под малейшие выбросы в данных. Это увеличивает значение метрик эффективности, но снижает пригодность модели на практике, так как очевидно, что модель будет делать большие ошибки на новых данных из той же выборки. Такая ситуация называется переобучением. Переобучение — это очень коварная проблема моделей машинного обучения, ведь на “бумаге” все метрики показывают отличный результат.
Конечно, в общем случае не получится так наглядно увидеть то, как модель подстраивается под данные. Ведь в случае, когда данные имеют большую размерность, строить графики в проекции не даст представления об общей картине. Поэтому ситуацию пере- и недообучения довольно сложно обнаружить. Для этого нужно проводить отдельную диагностику.
Это происходит потому, что в практически любой выборке данных конкретное положение точек, их совместное распределение определяется как существенной зависимостью между признаками и целевой переменной, так и случайными отклонениями. Эти случайные отклонения, выбросы, аномалии не позволяют сделать однозначный вывод, что модель, которая лучше описывает имеющиеся данные, является лучшей в глобальном смысле.
Выводы:
- Прежде чем обучать модель, нужно выбрать ее вид (параметрическое семейство функций).
- Разные модели при своих оптимальных параметрах будут давать разный результат.
- Чем сложнее и вариативнее модель, тем больше у нее параметров.
- Простые модели быстрые, но им недостает вариативности, изменчивости, у них высокое смещение (bias).
- Сложные модели могут описывать больше зависимостей, но вычислительно более трудоемкие и имеют большую дисперсию (variance).
- Слишком вариативные (сложные) модели алгоритм может подстраиваться под случайный шум в данных — переобучение.
- Слишком смещенные (простые) модели алгоритм может пропустить связь признака и целевой переменной — недообучение.
- Не всегда модель, которая лучше подстраивается под данные (имеет более высокие метрики эффективности) лучше.
Обобщающая способность модели, тестовый набор
Как было показано выше, не всякая модель, которая показывает высокую эффективность на тех данных, на которых она обучалась, полезна на практике. Нужно всегда помнить, что модели машинного обучения строят не для того, чтобы точно описывать объекты из обучающего набора. На то он и обучающий набор, что мы уже знаем правильные ответы. Цель моделирования — создать модель, которая на примере этих данных формализует некоторые внутренние зависимости в данных для того, чтобы адекватно описывать новые объекты, которые модель не учитывала при обучении.
Полезность модели машинного обучения определяется именно способность описывать новые данные. Это называется обобщающей способностью модели. И как мы показали в предыдущей главе, эффективность модели на тех данных, на которых она обучается, не дает адекватного понимания этой самой обобщающей способности модели. Вместе с тем, обобщающая способность — это главный показатель качества модели машинного обучения и у нас должен быть способ ее измерять.
Конечно, мы не можем измерить эффективность модели на тех данных, которых у нас нет. Поэтому для того, чтобы иметь адекватное представление об уровне качества модели применяется следующий трюк: до начала обучения весь имеющийся датасет разбивают на две части. Первая часть носит название обучающая выборка (training set) и используется для подбора оптимальных параметров модели, то есть для ее обучения. Вторая часть — тестовый набор (test set) — используется только для оценки эффективности модели.
Такая эффективность, измеренная на “новых” данных — объектах, которые модель не видела при своем обучении — дает более объективную оценку обобщающей силы модели, то есть эффективности, которую модель будет показывать на неизвестных данных. В машинном обучении часто действует такое правило — никогда не оценивать эффективность модели на тех данных, на которых она обучалась. Не то, чтобы этого нельзя делать категорически (и в следующих главах мы это часто будем применять), просто нужно осознавать, что эффективность модели на обучающей выборки всегда будет завышенной, ведь модель подстроилась именно к этим данным, включая все их случайные колебания.
Надо помнить, что все рассуждения и выводы в этой и последующих главах носят чисто вероятностный характер. Так что в конкретном случае, тестовая эффективность вполне может оказаться даже выше, чем эффективность на обучающей выборке. Когда мы говорим о наборах данных и случайных процессах, все возможно. Но смысл в том, что распределение оценки эффективности модели, измеренное на обучающих данных имеет значимо более высокое математическое ожидание, чем “истинная” эффективность этой модели.
Для практического применения этого приема надо ответить на два вопроса: как делить выборку и сколько данных оставлять на тестовый датасет. Что касается способа деления, здесь чуть проще — практически всегда делят случайным образом. Случайное разбиение выгодно тем, что у каждого объекта датасета равная вероятность оказаться в обучающей или в тестовой выборке. Причем, эта вероятность независима для всех объектов выборки. Это делает все случайные ошибки выборки нормально распределенными, то есть их математическое ожидание равно нулю. Об этом мы еще поговорим в следующей главе.
Но этот способ не работает в случае со специальными наборами данных. Например с временными рядами. Ведь при разбиении выборки важно, чтобы сами объекты в тестовой выборке были независимы от объектов обучающей. В случае, если мы анализируем какое-то неупорядоченное множество объектов, это почти всегда выполняется. Но для временных рядов это не так. Объекты более позднего времени могут зависеть от предыдущих объектов. Так цена актива за текущий период однозначно зависит от цены актива за предыдущий. Поэтому нельзя допустить, чтобы в обучающей выборке оказались объекты более ранние, чем в обучающей. Поэтому такие временные ряды делят строго хронологически — в тестовую выборку попадает определенное количество последних по времени объектов. Но анализ временных рядов сам по себе довольно специфичен как статистическая дисциплина, и как раздел машинного обучения.
Что касается пропорции деления, то, опять же, как правило, выборку разделяют в соотношении 80/20. То есть если в исходном датасете, например, 1000 объектов, то случайно выбранные 800 из них образуют обучающую выборку, а оставшиеся 200 — тестовую. Но это соотношение “по умолчанию” в общем-то ничем не обосновано. Его можно изменять в любую сторону исходя из обстоятельств. Но для этого надо понимать, как вообще формируется эта пропорция и что на нее влияет.
Что будет, если на тестовую выборку оставить слишком много данных, скажем, 50% всего датасета? Очевидно, у нас останется мало данных для обучения. То есть модель будет обучена на всего лишь небольшой части объектов, которых может не хватить для того, чтобы модель “распознала” зависимости в данных. Вообще, чем больше данных для обучения, тем в целом лучше, так как на маленьком объеме большую роль играют те самые случайные колебания. Поэтому модель может переобучаться. И чем меньше данных, тем переобученнее и “случайнее” будет получившаяся модель. И это не проблема модели, это именно проблема нехватки данных. А чем больше точек данных, тем больше все эти случайные колебания будут усредняться и это сильно повысит качество обученной модели.
А что будет, если наоборот, слишком мало данных оставить на тестовую выборку? Скажем, всего 1% от имеющихся данных. Мы же сказали, что чем больше данных для обучения, тем лучше. Значит, но обучающую выборку надо оставить как можно большую часть датасета? Не совсем так. Да, обучение модели пройдет более полно. Но вот оценка ее эффективности будет не такой надежной. Ведь такие же случайные колебания будут присутствовать и в тестовой выборке. И если мы оценим эффективность модели на слишком маленьком количестве точек, случайные колебания этой оценки будут слишком большими. Другими словами мы получим оценку, в которой будет сильно не уверены. Истинная оценка эффективности может быть как сильно больше, так и сильно меньше получившегося уровня. То есть даже если модель обучается хорошо, мы этого никогда не узнаем с точностью.
То есть пропорция деления выборки на обучающуюся и тестовую является следствием компромисса между полнотой обучения и надежность оценки эффективности. Соотношение 80/20 является хорошим балансом — не сильно много, но и не сильно мало. Но это оптимально для среднего размера датасетов. Если у вас очень мало данных, то его можно немного увеличить в пользу тестовой выборки. Если же данных слишком много — то в пользу обучающей. Кроме того, при использовании кросс-валидации размер тестовой выборки тоже можно уменьшить.Но на практике очень редько используются соотношения больше, чем 70/30 или меньше чем 90/10 — такое значения уже считаются экстремальными.
Выводы:
- Цель разработки моделей машинного обучения — не описывать обучающий набор, а на его примере описывать другие объекты реального мира.
- Главное качество модели — описывать объекты, которых она не видела при обучении — обобщающая способность.
- Для того, чтобы оценить обобщающую способность модели нужно вычислить метрики эффективности на новых данных.
- Для этого исходный датасет разбивают на обучающую и тестовую выборки. Делить можно в любой пропорции, обычно 80-20.
- Чаще всего выборку делят случайным образом, но временные ряды — только в хронологической последовательности.
- Обучающая выборки используется для подбора параметров модели (обучения), а тестовая — для оценки ее эффективности.
- Никогда не оценивайте эффективность модели на тех же данных, на которых она училась — оценка получится слишком оптимистичная.
Кросс-валидация
Как мы говорили ранее, маленькая тестовая выборка проблемна тем, что большое влияние на результат оценки эффективности модели имеют случайные отклонения. Это становится меньше заметно при росте объема выборки, но полностью проблема не исчезает. Эта проблема состоит в том, что каждый раз разбивая датасет на две выборки, мы вносим случайные ошибки выборки. Эта случайная ошибка обоснована тем, что две получившиеся подвыборки наверняка будут демонстрировать немного разное распределение. Даже если взять простой пример. Возьмем группу людей и разделим ее случайным образом на две половины. В каждой половине посчитаем какую-нибудь статистику, например, средний рост. Будут ли в двух группах выборочные средние точно совпадать? Наверняка нет. Обосновано ли чем-то существенным такое различие? Тоже нет, это случайные отклонения, которые возникают при выборке объектов из какого-то множества.
Поэтому разбиение выборки на тестовую и обучающую вносит такие случайные колебания, из-за которых мы не можем быть полностью уверены в получившейся оценке эффективности модели. Допустим, мы получили тестовую эффективность 95% (непример, измеренную по метрике accuracy, но вообще это не важно). Можем ли мы быть уверены, что это абсолютно точный уровень эффективности? Нет, ведь как любая выборочная оценка, то есть статистика, рассчитанная на определенной выборке метрика эффективности представляет собой случайную величину с некоторым распределением. А у этого распределения есть математическое ожидание и дисперсия. Как мы говорили в предыдущей главе, случайное разделение выборки на тестовую и обучающую приводит к тому, что распределение этой величины имеет математическое ожидание, совпадающее с истинным уровнем эффективности модели. Но это именно математическое ожидание. И у этой случайной величины есть какая-то ненулевая дисперсия. Это значит, что при каждом измерении, выборочная оценка может отклоняться от матожидания, то есть быть произвольно больше или меньше.
Есть ли способ уменьшить эту дисперсию, то есть неопределенность при измерении эффективности модели? Да, очень простой. Нужно всего лишь повторить измерение несколько раз, а затем усреднить полученные значения. Так как математическое ожидание случайных отклонений всегда предполагается равным нулю, чем больше независимых оценок эффективности мы получим, тем ближе среднее этих оценок будет к математическом ожиданию распределения, то есть к истинному значению эффективности.
Проблема в том, что эти измерения должны быть независимы, то есть производиться на разных данных. Но кратное увеличение тестовой выборки имеет существенные недостатки — соответствующее уменьшение обучающей выборки. Поэтому так никогда не делают. Гораздо лучше повторить случайное разбиение датасета на обучающую и тестовую выборки еще раз и измерить метрику эффективности на другой тестовой выборки из того же изначального датасета.
К сожалению, это означает, что и обучающая выборка будет другая. То есть нам необходимо будет повторить обучение. Но зато после обучения мы получим новую, независимую оценку эффективности модели. Если мы повторим этот процесс несколько раз, мы сможем усреднить эти значения и получить гораздо более точную оценку эффективности модели.
Имейте в виду, что все, что мы говорим в этой части применимо к любой метрике эффективности или метрике ошибки модели. Чаще всего, на практике измеряют метрики accuracy для моделей классификации и $R^2$ для регрессии. Но вы можете использовать эти методики для оценки любых метрик качества моделей машинного обучения. Напомним, что они должны выбираться исходя из задачи.
Конечно, можно реализовать это случайное разбиение руками и повторить процедуру оценивания несколько раз, но на практике используют готовую схему, которая называется кросс-валидация или перекрестная проверка. Она заключается в том, что датасет заранее делят на несколько равных частей случайным образом. Затем каждая из этих частей выступает как тестовый набор, а остальные вместе взятые — как обучающий:
Источник: Towards Data Science.
На схеме части датасета изображены для наглядности непрерывными блоками, но на самом деле это именно случайные разбиения. Так что они буду в датасете “вперемешку”. Количество блоков, на которые делится выборка задает количество проходов или оценок. Это количество называется k. Обычно его берут равным 5 или трем. Это называется, 5-fold cross-validation. То есть на первом проходе блоки 1,2,3 и 4 в совокупность составляют обучающую выборку. Модель обучается на них, а затем ее эффективность измеряется на блоке 5. Во втором проходе та же модель заново обучается на данных их блоков 1,2,3 и 5, и ее эффективность измеряется на блоке 4. И таким образом мы получаем 5 независимых оценок эффективности модели. Они могут различаться из-за тех самых случайных оценок выборки. Но если посчитать их среднее, оно будет значительно ближе к истинному значению эффективности. Поэтому что статистика.
Количество проходов k еще определяет то, сколько раз будет повторяться обучение модели. Чем больше выбрать k, тем более надежными будут оценки, но вся процедура займет больше машинного времени. Это особенно актуально для моделей, которые сами по себе обучаются долго — например, глубокие нейронные сети. Надо помнить, что использование кросс-валидации сильно замедляет процесс обучения. Если же выбрать k слишком маленьким, то не будет главного эффекта кросс-валидации — усреднения индивидуальных оценок эффективности. Кроме того, чем больше k, тем меньшая часть выборки будет отводиться на тестовый набор. Поэтому k не стоит брать больше, скажем, 10, даже если у вас достаточно вычислительных мощностей.
Кросс-валидация никак не влияет на эффективность модели. Многие думают, что валидированные модели получаются более эффективными. Это не так, просто использование перекрестной проверки позволяет более точно и надежно измерить уже имеющуюся эффективность данной модели. И уж тем более кросс-валидация не может ускорить процесс обучения, совсем наоборот. Но несмотря на это, использование кросс-валидации с k равным 5 или, в крайнем случае, 3, совершенно обязательно в любом серьезном проекте по машинному обучению, ведь оценки, полученные без использования этой методики совершенно ненадежны.
В библиотеке sklearn, естественно, кросс-валидация реализована в виде готовых функций. Поэтому ее применение очень просто. В примере ниже используется кросс-валидация с количеством проходов по умолчанию для получения робастных оценок заранее выбранных метрик (precision и recall):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro','recall_macro']
>>> clf =
svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores =
cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time',
'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
Такой код просто оценивает значение метрик. Но обратите внимание, что он возвращает не просто одно значение метрики, но целый вектор. Это именно те индивидуальные оценки. Из них очень легко получить средние и выборочную дисперсию. Эта выборочная дисперсия как раз и показывает степень уверенности в данной оценке — чем она ниже, тем уверенность больше, как доверенный интервал в статистике. Кроме такого явного использования кросс-валидации для оценки метрик, она зачастую встроена в большое количество функций, которые используют ее неявно. О некоторых таких функциях, осуществляющих оптимизацию гиперпараметров модели, пойдет речь чуть позже.
Выводы:
- Разбиение выборки на обучающую и тестовую может внести случайные ошибки.
- Нужно повторить разбиение несколько раз, посчитать метрики и усреднить.
- Кросс-валидация разбивает выборку на $k$ блоков, каждый из которых используется по очереди как тестовый.
- Сколько задать $k$, столько и будет проходов. Обычно берут 3 или 5.
- Чем больше $k$ тем надежнее оценка, но дольше ее получение, так как модель каждый раз заново обучается.
- Использование кросс-валидации обязательно для получения робастных оценок.
- В библиотеке sklearn кросс-валидация (CV) встроена во многие функции.
Кривые обучения
Как мы говорили раньше, не следует ориентироваться на эффективность модели, измеренную на обучающей выборке, ведь она получается слишком оптимистичной. Но эта обучающая эффективность все равно может дать интересную информацию о работе модели. А именно с ее помощью можно оценить, переобучается модель или недообучается. В этой главе мы расскажем об одном из самых наглядных способов диагностики моделей машинного обучения — кривых обучения.
Построение кривых обучения может быть проведено после разделения датасета на обучающую и тестовую выборки. Происходит это следующим образом. Тестовый набор фиксируется и каждый раз используется один и тот же. Из обучающего набора же сначала берут малую часть, скажем 10% от общего количества точек в нем. Обучают модель на этой малой части, а затем измеряют ее эффективность на этой части и на постоянной тестовой выборке. Первая оценка называется обучающая эффективность (training score), а вторая — тестовая эффективность (test score). Затем повторяют процесс с чуть большей частью обучающей выборки, например, 20%, затем еще с большей и так, пока мы не дойдем до полной обучающей выборки.
На каждом этапе мы измеряем обучающую эффективность (измеренную именно на той части данных, на которых модель училась, не на полной обучающей выборке) и тестовую эффективность. Таким образом мы получаем зависимость эффективности модели от размера обучающей выборки. Эти данные можно построить на графике. Это график и называется кривой обучения (learning curve). Такой график может выглядеть, например, так:
В данном случае, на графике мы видим всего пять точек на каждой кривой. Верхняя кривая показывает обучающую эффективность, нижняя — тестовую. Значит, мы использовали всего пять делений обучающей выборки на подвыборки разного размера. Это размер как раз и отложен на горизонтальной оси. Сколько таких разбиений брать? Если взять слишком мало, то не будет понятна форма графика, а именно она нам важна для диагностики. Если же взять слишком много — то построение кривой обучения займет много времени, так как каждая точка на графике — это заново обученная модель.
Давайте объясним форму этого графика. Слева, когда обучающая выборка мала, обучающая эффективность довольно высока. Это вполне понятно, ведь чем меньше данных, тем проще модели к ним подстроиться. Помните, что через любые две точки можно провести линию (то есть линейную регрессию)? Это, конечно, крайний случай, но в общем, чем меньше обучающая выборка, тем большую эффективность одной и той же модели (параметрического семейства функций) можно на ней ожидать. А вот тестовая эффективность довольно маленькая. Это тоже понятно. Ведь на маленькой выборке модель не смогла обнаружить зависимости в данных так, чтобы эффективно предсказывать значение целевой переменной в новых данных. То есть она подстроилась под конкретные точки без какой-либо обобщающей способности.
Сперва отметим, что обычно кривые обучения демонстрируют некоторые общие тенденции. Например, при малых объемах обучающей выборки, обучающая эффективность модели может быть очень большой. Ведь чем меньше данных, тем проще подобрать параметры любой, пусть даже простой модели, так, чтобы эта модель ошибалась меньше. В самом предельном случае, вспомните, что через любые две точки можно провести прямую. Это значит, что линейная регрессия, обученная на двух точках, всегда будет давать нулевую ошибку или полную, 100%-ю эффективность. То же можно сказать и про квадратичную функцию, обученную на трех точках. Но и в целом, чем меньше данных, тем меньше можно ожидать суммарную ошибку любого рассматриваемого класса моделей на этих данных.
Тестовая же эффективность модели, обученной на малом объеме выборки, скорее всего будет очень невысокой. Это тоже естественно. Ведь модель видела всего малую часть примеров и не может подстроиться под какие-то глобальные зависимости в данных. Поэтому в левой части кривых обучения почти всегда будет большой зазор.
При повышении объема обучающей выборки обучающая же эффективность будет падать. Это связано в тем, что чем больше данных, тем больше пространства для ошибки для конкретной модели. Поэтому чем больше точек описывает модель, тем хуже она это делает в среднем. Это неизбежно и не страшно. Важно то, что тестовая эффективность наоборот, растет. Это происходит потому, что чем больше данных, тем больше вероятность того, что модель подстроится под существенные связи между признаками и целевой переменной, и таким образом, повысит обобщающую способность, свою предсказательную силу.
В итоге, кривая обучения показывает, как изменяется эффективность модели по сравнению к конкретному набору данных. В частности, именно с помощью кривых обучения можно предположить пере- и недообучение модели, что является главной целью диагностики моделей машинного обучения. Например, взглянув на график кривой обучения, приведенный выше, можно ответить на вопрос, хватает ли модели данных для обучения. Для этого можно спросить, улучшится ли тестовая эффективность модели, если добавить в датасет больше точек. Для этого можно мысленно продолжить кривую обучения вправо.
При построении кривых обучения обращайте внимание на деления вертикальной оси. Если вы строите графики с использованием библиотечных инструментов, то они автоматически масштабируются по осям. Имейте в виду, что одна и та же кривая обучения может выглядеть при разном масштабе совершенно по-разному. А навык сопоставления разных кривых очень важен при диагностике моделей. Лучше всего вручную задавать масштаб вертикальной оси и использовать один и тот же для всех графиков в одной задаче.
Обратите внимание, что на графике помимо самих кривых обучения присутствуют еще какие-то полосы. Что они значат? Дело в том, что при построении кривых обучения очень часто применяется кросс-валидация, о которой мы говорили в предыдущей главе. Ведь разбиение выборки на тестовую и обучающую вносит случайные ошибки. Поэтому для построения на кривых обучения более надежных оценок всех измеряемых оценок эффективности процесс повторяют несколько раз и усредняют полученные оценки. Каждая точка на графике — это не просто оценка эффективности, это среднее из всех кросс-валидированных оценок. Именно поэтому, кстати, в легенде нижняя линяя называется не test score, а cross-validation score. А ширина полосы вокруг точки определяется величиной дисперсии этих оценок. Чем шире полоса, тем больше разброс оценки на разных проходах кросс-валидации и тем меньше мы уверены в значении этой оценки. При построении кривых обучения эта неопределенность почти всегда выше при малых объемах обучающей выборки (слева на графике) и меньше — справа.
Выводы:
- Кривая обучения — это зависимость эффективности модели от размера обучающей выборки.
- Для построения кривых обучения модель обучают много раз, каждый раз с другим размером обучающей выборки (от одного элемента до всех, что есть).
- При малых объемах обучающая эффективность будет очень большой, а тестовая — очень маленькой.
- При увеличении объема обучающей выборки они будут сходиться, но обычно тестовая эффективность всегда ниже обучающей.
- Кривые обучения позволяют увидеть, как быстро модель учится, хватает ли ей данных, а также обнаруживать пере- и недообучение.
- Кривые обучения часто используют кросс-валидацию.
Обнаружение пере- и недообучения
Как мы говорили, построение кривых обучения — это исключительно диагностическая процедура. Именно они позволяют нам предполагать, к чему более склонна модель, обученная на конкретном наборе данных — к переобучению или к недообучению. Это важно, так как подходы у повышению эффективности в этих двух случаях будут совершенно противоположными. Давайте предположим, как будут вести себя на кривых обучения переобученные и недообученные модели.
Что будет, если модель слишком проста для имеющихся данных? При увеличении количества объектов в обучающей выборке, эффективность, измеренная на ней же будет вначале заметно падать по причинам, описанным выше. Но постепенно она будет выходить на плато и больше не будет уменьшаться. Это связано с тем, что начиная с какого-то объема выборки в ней будут превалировать нелинейные зависимости, слишком сложные для данной модели. С ростом объема обучающей выборки неизбежно растет тестовая эффективность, но так как модель слишком проста и не может ухватить этих сложных зависимостей в данных, то ее тестовая эффективность не будет повышаться сильно. Причем при достаточном объеме обучающей выборки тестовая и обучающая эффективности будут достаточно близкими. Другими словами, простые модели одинаково работают как на старых, так и на новых данных, но одинаково плохо.
А что будет происходить со слишком сложной моделью для существующих данных? Ее показатели в левой части графика будут аналогичны — высокая обучающая и низкая тестовая эффективности. Причины все те же. Но вот с ростом объема обучающей выборки, разрыв между этими двумя показателями не будет сокращаться так сильно. Модель, обученная на полном датасете покажет высокую эффективность на обучающей выборке, но гораздо более низкую — на тестовой. Это же практически определение переобучения — низкая ошибка, но отсутствие обобщающей способности. Это происходит, как мы уже обсуждали, за счет того, что слишком сложная модель имеет достаточный запас вариативности, чтобы подстроиться под случайные отклонения в данных.
Таким образом, недообученные и переобученные модели демонстрируют совершенно разное поведение на кривых обучения. А значит, недообучение и переобучения можно выявить, проанализировав поведение модели на графике. Типичное переобучение характеризуется большим разрывом между тестовой и обучающей эффективность. Признак типичного недообучения — низкая эффективность как на тестовой, так и на обучающей выборке. Но на практике, конечно, диагностика моделей машинного обучения не такая простая.
На данном графике представлены абстрактные картины, наиболее характерные для недообучения, переобучения, и ситуации, когда сложность модели оптимальна — мы назовем ее качественное обучение. Именно анализируя схожесть кривой обучения исследуемой модели с этими “идеальными” случаями, можно сделать обоснованный вывод о наличии недо- или переобучения модели.
Как вы могли заметить, мы нигде не говорим о четких критериях. Недо- и переобученность моделей — это вообще относительные понятия. И кривые обучения измеряют их только косвенно. Поэтому диагностика не сводится к оценке какой-либо метрики или статистики. Нам нужно оценить общую форму графика кривых обучения, что не является точной наукой. Возникает множество вопросов. Например, мы говорили, что большой зазор между тестовой и обучающей эффективностью — это признак переобучения. Но какой зазор считать большим? Это вопрос интерпретации. Точно так же, что считать низким уровнем эффективности? 50%? Может, 75%? Вообще это очень зависит от самой задачи. В некоторых задачах 80% accuracy — это выдающийся результат, а в других — даже 99% считается недостаточной точностью.
Поэтому рассматривая один график кривой обучения очень сложно понять, особенно без опыта анализа моделей машинного обучения, на что мы смотрим — на слишком простую недообученную модель, или на слишком сложную — переобученную. Вообще, строго говоря, большой зазор между эффективностями модели указывает на присутствующую в модели вариативность (variance), а низкий,не 100%-й уровень обучающей эффективности — на наличие в модели смещения (bias). А любые модели в той или иной степени обладают этими характеристиками. Вопрос в их соотношении друг к другу и к конкретному набору данных.
Чтобы облегчить задачу диагностики модели очень часто эффективность данной модели рассматривают не абстрактно, а сравнивают с аналогами. Практически всегда выбор моделей осуществляется от простого к сложному — сначала строят очень простые модели. Их тестовая эффективность может задать некоторых базовый уровень, планку, по сравнению к которой уже можно готовить об улучшении эффективности у данной, более сложной модели, насколько это улучшение существенно и так далее. Кроме того, строя кривые обучения нескольких моделей можно получить сравнительное представление о том, как эти модели соотносятся между собой, какие из них более недообученные, какие — наоборот.
Ситуация еще очень осложняется тем, что на практике вы никогда не получите таких красивых и однозначных кривых обучения, как в учебнике. Положение точек на кривых обучения зависит, в том числе и от тех самых случайных отклонений в данных, которые так портят нам жизнь. Поэтому в реальности графики могут произвольно искривляться, быть немонотонными. Тестовая эффективность вообще может быть выше обучающей. Что это начит для диагностики? Да в общем-то, ничего, это лишь свидетельствует об особом характере имеющихся данных. И, естественно, чем меньше данных, тем более явно проявляются эти случайности и тем менее показательными будут графики.
Достаточно сильно от этих случайных колебаний помогает применение кросс-валидации. Так как усреднение случайности — это и есть цель перекрестной проверки, она может быть полезна и для “сглаживания” кривых обучения. Еще надо помнить, что во многих библиотеках по умолчанию кривые обучения строятся на основе всего нескольких точек, то есть всего пяти-десяти вариантов размера обучающей выборки. Если такой график не дает достаточной информации, можно попробовать построить кривую по большему количеству точек. Но при этом и случайные колебания тоже могут проявиться сильнее.
Вообще, все факторы, которые улучшают “читаемость” кривых обучения, одновременно сильно замедляют их построение — кросс-валидация, использование большей выборки, построение большего количества точек. Помните, что это приводит к кратному увеличению количества циклов обучения модели.
Как мы говорили, поведение модели в целом не зависит от выбранной метрики, которую вы используете для построения кривых обучения. Поэтому зачастую используют не метрики эффективности, а метрики ошибок. Поэтому графики кривых обучения выглядят “перевернутыми” — тестовая ошибка больше, чем обучающая и так далее. Следует помнить, что все сказанное выше остается справедливым в этом случае, только следует помнить, где у модели высокая эффективность и малая ошибка.
На этом графике вы видите тоже идеальные случаи, но выраженные в терминах величины ошибки, а не эффективности. Можно проследить те же тенденции, но как бы “отраженные” по вертикальной оси.
Как мы говорили, реальные наборы данных, имеющие случайные колебания, ненадежные зависимости, случайные ошибки выборки могут существенно искажать кривые обучения. Рассмотри пример, приближенный к реальности. Возьмем датасет, содержащий рукописные цифры и обучим на нем классификатор по методу опорных векторов с гауссовым ядром. Для примера возьмем значение параметра “гамма”, который задает масштабирование функции расстояния в ядре, равным 0,008. Построив кривые обучения для этой модели мы получаем следующий график:
Данный график, несмотря на свою сложную форму достаточно легко интерпретируется. Мы видим, что обучающая эффективность равна 1 при любых объемах обучающей выборки. То есть модель разделяет классы полностью идеально. Но вот тестовая эффективность всегда остается гораздо ниже. И хотя она растет при увеличении объема обучающей выборки, все равно, даже при использовании полного набора данных, остается большой разрыв между тестовой и обучающей эффективностями модели. Налицо явное и типичное переобучение.
Теперь давайте уменьшим параметр “гамма” в четыре раза. В методе опорных векторов это может ограничить вариативность модели. Получаем следующий график кривых обучения:
Видно, что общее поведение модели значительно улучшилось. Обратите внимание на масштаб вертикальной оси. На первом графике мы говорили о разнице между тестовой и обучающей эффективностью в примерно 0,3. На этом же графике разница сократилась до примерно 0,025 — больше, чем в 10 раз. Это говорит о том, что модель очень сильно увеличила свою обобщающую способность. Давайте теперь уменьшим параметр еще в сто раз и посмотрим на кривую обучения:
Поведение модели явно не улучшилось. Хотя, итоговая эффективность тоже получается достаточно высокой (около 0,9), она все равно значительно меньше, чем в предыдущем случае. Другими словами, дальнейшее сокращение “гаммы” не пошло модели на пользу. Низкая тестовая эффективность и небольшая разница между тестовой и обучающей эффективностью — типичные признаки недообучения.
Обратите внимание, что интерпретация графика кривых обучения и, соответственно, диагностика модели, приобретает гораздо больше смысла к контексте сравнения нескольких моделей. Третья модель дает относительно неплохой результат с тестовой эффективностью в 0,9. Эту модель вполне можно признать валидной и качественно обученной, если бы мы не знали, что мы можем достичь точности в 0,975 (вторая модель).
Для сравнения рассмотрим результаты анализа еще одной модели на тех же самых данных — наивного байесовского классификатора с гауссовым распределением:
Хотя график сильно отличается от любого из трех предыдущих, самое главное, на что следует обратить внимание — низкое значение обучающей эффективности на полном наборе данных. Это показывает, что даже если мы продолжим добавлять данные в обучающую выборку, максимум, на который мы можем рассчитывать — это что тестовая эффективность приблизится к обучающей, которая все равно недостаточная (в данном примере меньше 0,9). Это свидетельствует о недообученности модели.
Как мы говорили, недообучение и переобучение — это условные понятия, которые называют распространенные ситуации при использовании моделей машинного обучения. Недообучение — это когда у модели низкая вариация и высокое смещение. Переобучение — это наоборот, когда низкое смещение и высокая вариация. На самом деле эти свойства в моделях присутствуют всегда. Более тщательный анализ может сделать вывод, что последняя модель имеет как высокую вариацию (что выражается в сильной разнице между эффективностями), так и высокое смещение (об этом говорит низкое значение обучающей эффективности).
Выводы:
- При недообучении тестовая и обучающая эффективности будут достаточно близкими, но недостаточными.
- При переобучении тестовая и обучающая эффективности будут сильно различаться — тестовая будет значительно ниже.
- Пере- и недообучение — это относительные понятия.
- Более простые модели склонны к недообучению, более сложные — к переобучению.
- Диагностика пере- и недообучения очень важна, так как для повышения эффективности предпринимаются противоположные меры.
- Для построения можно использовать функцию ошибки, метрику эффективности или метрику ошибки, важна только динамика этих показателей.
- Диагностика моделей машинного обучения — это не точная наука, здесь нужно принимать в расчет и задачу, и выбор признаков и многие другие факторы.
Методы повышения эффективности моделей
Регуляризация
Как мы говорили, диагностика моделей нужна для поиска путей повышения ее эффективности. И мы выяснили, что пере- и недообучение моделей напрямую связаны с уровнем сложности моделей. Можно рассмотреть гипотетический график, на котором показан уровень ошибок моделей на конкретном наборе данных в зависимости от уровня сложности этой модели. Пока мы не сталкивались с тем, как можно плавно менять уровень сложности модели в рамках одного параметрического класса. Но представим, что речь идет о полиномиальной модели, а по горизонтали отложена степень этого полинома.
Если модель слишком проста, то уровень тестовых и обучающих ошибок будет высок и достаточно близок друг к другу. Мы говорили об этом (правда другими словами, в терминах эффективности) в предыдущей главе. По мере увеличения сложности разрыв между этими уровнями ошибок будет в среднем увеличиваться. Это происходит за счет более глубокой подстройки модели именно к обучающей выборке. Причем уровень ошибок на обучающей выборке будет в среднем падать за счет повышения вариативности модели. Но уровень ошибок не может опуститься ниже нуля. Поэтому либо с какого-то момента он стабилизируется, либо будет асимптотически приближаться к 0. А это значит, что уровень тестовой ошибки неизбежно рано или поздно начнет повышаться с ростом сложности модели. Таким образом, у уровня тестовой ошибки есть некоторое оптимальное значение.
Другими словами, для любого конкретного датасета существует некоторый оптимальный уровень сложности модели, который дает наименьшую ошибку на тестовой выборке. Модели, имеющие более низкую сложность будут недообучаться, а более высокую — переобучаться. Поэтому существует задача нахождения этого оптимального уровня сложности. К сожалению, это не получится сделать методом обучения, или любой другой численной оптимизации, так как изменение уровня сложности модели требует запуска ее обучения заново. Мы не можем непрерывно менять уровень сложности, как какой-то дополнительный параметр модели.
Изучив несколько видов моделей обучения с учителем легко сделать вывод, что сложность модели — это некоторое “встроенное” свойство, которое определяется видом самой модели, то есть параметрическим классом функций, которые аппроксимируются этой моделью. Некоторые модели просто сложнее чем другие. Например, многослойный перцептрон гораздо сложнее линейной регрессии, а глубокое дерево решений сложнее более мелкого.
Выше мы определяли уровень сложности модели через количество ее параметров. Но стоит сказать, что численное значение этих параметров тоже имеет значение. Рассмотрим для примера две модели — линейную ($y = b_0 + b_1 x$) и квадратичную ($y = b_0 + b_1 x + b_2 x^2$). Очевидно, вторая модель сложнее, так как у нее больше параметров. Квадратичная функция имеет больше степеней свободы и демонстрирует нелинейное поведение — рост функции на разных участках может сильно отличаться.
Но что, если параметр $b_2$ у квадратичной модели будет очень маленьким, скажем, $b_2 = 0.0001$. Если у нас есть функция, например, $y = -8 + 15 x + 0.0001 x^2$, то взглянув на ее график мы не отличим ее от линейной. Да, формально она будет относиться к классу квадратичных функций, но на практике она будет почти прямой линией. Рост функции на разных участках будет отличаться, но очень незначительно. Тем более, что нас интересует поведение функции не на всей числовой прямой а в окрестностях имеющихся точек данных. Если на этом участке функция ведет себя как линейная, то для прикладной задачи она и эквивалентна линейной.
То есть чем ближе параметр $b_2$ к нулю, тем эффективно ближе квадратичная модель к линейной. Так можно сказать про любой параметр любой модели обучения с учителем. Только в более сложных моделях связь между конкретным параметром и уровнем сложности не так очевидна, так в случае с полиномиальными функциями. Но в любом случае, чем меньше в модели параметров, существенно отклоняющихся от нуля, тем она проще. Причем, это обычно не распространяется на свободный коэффициент $b_0$, у него особая роль — его значение смещает все предсказания модели (поэтому он часто называется параметром смещения). Его отличие от нуля несущественно. На этом эффекте основан один очень полезный и распространенный на практике математический прием, который позволяет гибко и очень удобно управлять сложностью параметрических моделей машинного обучения. Этот прием называется регуляризация.
Допустим, у нас есть набор данных и мы не знаем, модель какого вида подойдет к нему лучше — линейная или квадратичная. При прочих равных, квадратичная модель всегда даст меньшую величину ошибки и поэтому будет предпочтительнее. Но мы уже видели, что малая ошибка — не всегда показатель качества модели. Если обычная функция ошибки, основанная на суммарном отклонении значений данных от модели (которую мы рассматривали до этого), не дает адекватной оценки качества модели, может стоит ее как-нибудь изменить?
Функция ошибки — это по сути система штрафов. Каждый раз, когда модель ошибается, к значению ошибки прибавляется величина, пропорциональная отклонению. Это — штраф за ошибку модели. Но может быть, мы можем штрафовать что-нибудь еще? Например, уровень сложности модели. Представьте, что мы добавляем к ошибке некоторые штрафы за высокие значения параметров модели. Тогда алгоритм обучения, который минимизирует именно функцию ошибки будет не так сильно отдавать сложным переобученным моделям. Небольшие ошибки модели могут быть скомпенсированы тем, что модель становится более простой.
Причем эти штрафы очень легко выражаются математически. Если штраф за ошибки модели — это некоторое математическое выражение, основанное на отклонениях предсказанных значений от эмпирических, то штрафы за сложность модели — это выражение, основанное на отклонениях параметров самой модели от нуля. Существует несколько конкретных реализаций регуляризации и о них мы поговорим чуть далее. Кстати, регуляризация обычно не затрагивает свободный коэффициент. Причины этого мы только что обсуждали — он не влияет на сложность модели.
В этом и состоит идея регуляризации — модификация функции ошибки таким образом, чтобы штрафовать сложные модели в пользу более простых. Да, достаточно странно складывать отклонения целевой переменной (которые могут быть выражены в натуральных единицах) и безразмерные параметры модели. Это может выглядеть, как сложение метров с красным. Регуляризация — это именно математический трюк. У нее нет физического значения, какой-то внятной интерпретации в терминах предметной области.Это лишь способ отдавать предпочтение моделям с низкими значениями параметров, ведь такие модели ведут себя как более простые и поэтому менее склонны к переобучению.
Можно заметить, что регуляризация — это способ искусственно понизить сложность модели. То есть при использовании регуляризации берут модель более сложную, которая в “чистом” виде будет явно переобучаться на имеющихся данных. Но за счет этих дополнительных штрафов, ее сложность принижают. Причем, самое удобное в регуляризации то, что она параметрическая. То есть соотношением “силы” штрафа за ошибки и штрафа за сложность легко управлять, введя множитель — так называемый параметр регуляризации. Чем он больше, тем сильнее штрафуются сложные модели, то есть даже большие ошибки модели могут быть скомпенсированы небольшим понижением сложности. Таким образом, возвращаясь к графику в начале главы, именно параметр регуляризации может быть отложен на нем по горизонтали.
Регуляризация настолько удобна и универсальна, что большинство библиотечных реализаций тех моделей, которые мы проходили раньше, уже реализуют встроенную регуляризацию. Причем это относится равно как к моделям классификации, так и к моделям регрессии, это прием не зависит от типа задачи обучения с учителем. За счет способности уменьшить сложность любой модели регуляризация является одним их основных способов борьбы с переобучением.
Обратите внимание, что мы в основном говорим именно о борьбе с переобучением. Борьба с недообучением в основном сводится к использованию более сложной модели. В настоящее время разработаны настолько сложные модели, что узким местом современного машинного обучения становятся вычислительные мощности и доступность данных.
Выводы:
- Регуляризация — это способ искусственно ограничить вариативность моделей.
- При использовании регуляризации можно применять более сложные модели и снижать склонность к переобучению.
- Регуляризация модифицирует функцию ошибки модели, добавляя в нее штрафы за повышение сложности.
- Основная идея регуляризации — отдавать предпочтение низким значениям параметров в модели.
- Регуляризация обычно не затрагивает свободный коэффициент $b_0$.
- Регуляризация обычно параметрическая, можно управлять ее степенью.
Ridge
Зачастую переобучение модели, которое является следствием большого количества параметров в модели, появляется потому, что в наборе данных присутствует много “лишних” атрибутов. Количество параметров любой модели обучения с учителем зависит от количества признаков в данных. Для борьбы с этим явлением используется регуляризация. Как мы говорили, регуляризация “штрафует” отклонения параметров модели (за исключением свободного) от нуля. Совершенно естественно формализовать это отклонение так же, как и в самой функции ошибки — как сумму квадратов этих значений. Такая модель называется гребневой регрессией (ridge regression). В ней функция ошибки принимает такой вид:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} b_j^2]
Как мы можем видеть, что функция ошибки аналогична обычной модели регрессии, но имеет одно дополнительное слагаемое — регуляризационный член. Это сумма квадратов значений параметров модели (начиная с первого). Эта сумма умножается на специальный параметр — параметр регуляризации $lambda$. Он как раз отвечает за “силу” регуляризации модели. В передельном случае, когда $lambda = 0$, мы имеем обычную нерегуляризованную регрессию. Чем больше этот параметр, тем сравнительно больший вклад в ошибку дают отклонения параметров модели. То есть, чем больше этот параметр, тем более простые модели мы будем получать после обучения, при достижении минимума этой функции. Естественно, параметр регуляризации не может быть отрицательным, так как в таком случае мы наоборот, будем отдавать предпочтение более сложным моделям. А сложность, как и ошибка могут возрастать неограниченно.
Но если мы модифицируем функцию ошибки, то это влечет изменение и метода градиентного спуска. На самом деле он меняется незначительно. Вспомним, что градиентный спуск основан на вычислении частной производной функции ошибки по параметрам модели. Если взять свободный параметр, то вообще ничего не меняется, так как регуляризационный член от него не зависит:
[frac{partial}{partial b_0} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_0} h_b(x_i)]
Если же рассматривать другие параметры модели, то в выражение производной добавится всего одно небольшое слагаемое:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i) + 2 lambda b_i]
Это слагаемое $2 lambda b_i$ как раз и будет учитывать значения параметров при выполнении шагов градиентного спуска в регуляризованной модели регрессии. В остальном метод обучения никак не меняется. Если мы рассматриваем линейную модель, то получается почти знакомое нам по предыдущим главам выражение:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot x_i + 2 lambda b_i]
Как мы уже говорили, этот прием может быть применен как к задачам классификации, так и к задачам регрессии. Но применяя регуляризованные модели на практике стоит быть внимательнее. Дело в том, что в некоторых моделях (например, в методе опорных векторов) регуляризация задается чуть иначе:
[J(vec{b}) = С frac{1}{m} sum_{i=1}^{m} cost(h_b(x_i) , y^{(i)}) + sum_{j=1}^{n} b_j^2]
Где $C$ — это тоже параметр регуляризации. Обратили внимание, что этот множитель стоит перед другим слагаемым — самой функцией ошибки? Численно, это эквивалентно предыдущей формализации, если полагать, что $C = frac{1}{lambda}$. Но стоит помнить, что в такой форме чем больше $C$, тем меньше регуляризации присутствует в модели.
Гребневую регрессию еще называют регрессией по L2-норме (L2 означает норма Лагранжа второго порядка) или регуляризацией Тихонова. Простыми словами это означает, что мы считаем сумму квадратов параметров.Гребневая регрессия полезна тем, что она может помочь повысить эффективность модели, если в данных присутствует большое количество мультиколлинеарных факторов, то есть атрибутов, которые очень сильно зависят друг от друга. Вообще, мультиколлинеарность в статистике — это в принципе не очень хорошее явление. В машинном обучении она опасна тем, что оптимальные параметры модели становятся гораздо менее устойчивыми, а значит обучение будет не очень надежным. Ну и вдобавок, большое количество признаков, как мы уже говорили, увеличивает количество параметров и порядок сложности модели, что приводит к переобучению. На практике мультиколлинеарные признаки можно обнаруживать и удалять из датасета руками, но гребневая регрессия может это делать автоматически.
Рассмотрим работу гребневой регрессии на примере. Для лучшего понимания того, как регуляризация влияет на получаемую модель, мы возьмем одни и те же данные и построим одну и ту же модель классификации с L2 регуляризацией, но с разными значениями параметра регуляризации. В качестве базовой модели мы используем полином пятой степени. Для начала классификация без регуляризации ($lambda=0$):
Мы видим достаточно сложную границу принятия решения и высокую точность модели — на этих данных эта модель показывает 0,91 accuracy. Давайте возьмем $lambda=2$:
За счет использования регуляризации точность модели немного снизилась и составила 0,89. Граница принятия решения тоже стала более гладкой и простой.
Обратите внимание, что расположение границы принятия решения полностью изменилось по сравнению с первой моделью. Ведь параметр регуляризации — это не то же самое, что и обычный параметр модели, коэффициент в функции. Один и тот же алгоритм, обученный с разными значениями параметра регуляризации даст две совершенно разные модели, не имеющие ничего общего. Поэтому нельзя, например, плавно менять параметр регуляризации и смотреть, как изменится граница принятия решения. И физического смысла параметр регуляризации никакого не несет. Это лишь численная переменная в алгоритме обучения, которая влияет на то, какая модель из определенного параметрического класса будет считаться оптимальной для данной задаче. В дальнейшем такие “сложные” параметры мы будем называть гиперпараметрами.
Увеличим регуляризацию еще больше и получим такую модель:
Точность снизилась еще больше — до 0,85. Очевидно, что точность регуляризованных моделей будет меньше, так как функция ошибки может “променять” точность на упрощение модели. Но в метриках эффективности сложность модели не учитывается, поэтому они падают. Ну и граница принятия решения тоже становится все более плоской.
Рассмотрим влияние регуляризации на модель регрессии. Для этого также возьмем один и тот же набор данных и будем строить на нем разные модели. Также будем использовать полиномиальные признаки пятой степени. Но на этот раз обратим внимание и на сами коэффициенты модели. Для начала посмотрим на модель практически без регуляризации ($lambda=0.1$):
Эта модель имеет точность 0,714 (по метрике r-квадрат) и следующие коэффициенты — 0, -2.84, -4.49, 8.03, -2.92, 0.34. Как видно, все полиномиальные признаки имеют влияние на модель, коэффициенты при них отличаются от нуля существенн. Теперь добавим регуляризацию ($lambda=1$):
Точность модели немного упала — до 0,712. Теперь взглянем на коэффициенты: 0, -2.51, -0.97, 4.48, -1.76, 0.22. Заметно, что все они сильно уменьшились (в абсолютном выражении), особенно третий и четвертый. Это как раз и есть влияние регуляризации — она стремится держать коэффициенты как можно более близкими к нулю, даже за счет понижения точности. А параметр регуляризации — это своего рода “обменный курс” между коэффициентами и точностью. Давайте поднимем его еще сильнее (до $lambda=100$):
Точность модели понизилась более существенно — до 0,698. А вот ее коэффициенты: 0, 0.13, 0.37, 0.49, -0.04, 0.01. По мере увеличения регуляризации ни один из коэффициентов не удалялся от нуля. А некоторые вплотную к нему приблизились. При этом заметим, что ни один коэффициент не стал нулем — гребневая регрессия даже с запредельным уровнем регуляризации стремится оставить в модели все имеющиеся признаки.
Выводы:
- $lambda > 0$ — параметр регуляризации.
- Чем он больше, тем сильнее штрафуются сложные модели.
- Этот прием может применяться как к классификации, так и к регрессии.
- Ridge еще называют регуляризацией по L2-норме. Она же — гребневая регрессия.
- Такая регуляризация делает параметры более робастными к мультиколлинеарности признаков.
Lasso
У гребневой регрессии есть один недостаток, проявляющий себя при работе с данным, в которых есть много “лишних” признаков — она всегда включает в модель все признаки. Но параметры у них могут быть близки к нулю, что затрудняет интерпретацию модели и не сокращает размерность задачи. На практике в данных могут присутствовать не просто мультиколлинеарные атрибуты, но и такие, которые имеют очень маленькое влияние на целевую переменную или не имеют его вообще. Включать их в модель не имеет никакого смысла.
Для решения этой проблемы существует так называемая лассо-регрессия. Она по своей формализации очень похожа на гребневую, но чуть по-другому учитывает значения параметров модели:
[J(vec{b}) = sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} mid b_j mid]
В данном случае говорят о регуляризации по L1-норме. За счет того, что функция абсолютного значения, которая используется здесь не везде дифференцируема, для обучения такой модели используется специальный метод координатного спуска (coordinate descent), а не градиентного. Но рассмотрение всех вариантов алгоритмов обучения выходит за рамки данного пособия. В остальном же использование лассо на практике абсолютно идентично другим моделям обучения с учителем.
Из-за своей специфической формализации, модель лассо стремиться обратить в ноль как можно больше параметров модели. Это значит, что если какой-то признак не оказывает сильного влияния на целевую переменную, то модель с L1-регуляризацией с большой долей вероятности “занулит” этот признак. Это бывает очень полезно в задачах, где в данных присутствует больше количество ненужной информации. Такие задачи еще часто называют разреженными. К ним часто относятся, например, задачи анализа текстов.
В таких задачах регрессия по методу лассо может использоваться для отбора признаков. Часто эта модель потом вообще не используется, а на оставшихся признаках строится какая-то другая модель обучения с учителем. Так лассо-регрессия может играть вспомогательную роль. Регрессию лассо поэтому часто называют методом понижения размерности — после ее применения в модели остаются (ненулевыми) только те признаки, которые действительно влияют на значение целевой переменной. Хотя это не совсем то, что называют понижением размерности в задачах обучения без учителя.
Также как и любая регуляризация, лассо управляет компромиссом между bias и variance модели за счет введения параметра регуляризации. Он имеет точно такой же смысл, как и в гребневой регрессии — чем он больше численно, тем более простые модели будет предпочитать этот алгоритм. Можно построить график зависимость обучающей и тестовой эффективностей модели от значения параметра регуляризации:
Здесь мы видим, что при малых значениях этого параметра наблюдается большая разница между эффективностями. ПО мере увеличения значения параметра регуляризации сложность, а следовательно и обучающая эффективность модели падают, а разница между ними сокращается. Тестовая же эффективность поначалу растет, но начиная в определенного значения параметра регуляризации (в районе $10^{-1}$) снова начинает снижаться. В левой части этого графика мы наблюдаем ситуацию переобучения, а в правой — недообучения. А примерно $10^{-1}$ — это оптимальное значение параметра регуляризации, при котором получается наиболее качественная модель линейной регрессии.
Давайте построим регрессию по методу лассо на тех же данных, на которых строили в предыдущей главе гребневую регрессию. На этот раз ограничимся одной моделью со средним уровнем регуляризации ($lambda=1$):
Обратим внимание на коэффициенты модели: 0, 0, 0, 0.55, 0, 0. Даже при таком небольшом значении параметра регуляризации модель оставила только один признак — признак третьей степени (что мы и видим на графике — это кубическая парабола, только масштабированная по вертикали). В этом и проявляется действие алгоритма лассо — он стремится как можно больше коэффициентов обратить в ноль.
Lasso, кстати, расшифровывается как least absolute shrinkage and selection operator, оператор наименьшего абсолютного сокращения и выбора.
В данном примере можно сделать вывод, что среди полиномиальных признаков только признак третьей степени оказывал сколь-нибудь существенное влияние на целевую переменную. Таким образом, регрессия по методу лассо работает как алгоритм отбора признаков. В дальнейшем можно используя только этот один признак строить и другие модели машинного обучения на данной задаче, или просто ввести его в датасет, таким образом лассо станет основой для инжиниринга признаков.
Выводы:
- Lasso еще называют регуляризацией по L1-норме.
- Lasso заставляет модель использовать меньше ненулевых коэффициентов.
- Фактически, эта регуляризация уменьшает количество признаков, от которых зависит модель.
- Может использоваться для отбора признаков.
- Полезна в задачах с разреженной матрицей признаков.
Elastic net
После прочтения двух предыдущих разделов может появиться вопрос: какой метод регуляризации лучше? Как всегда не существует универсального ответа. Это целиком зависит от данных. С разреженностью признаков лучше справляется лассо, а с мультиколлинеарностью — гребневая модель. Как всегда, когда есть два подхода, каждый со своими преимуществами, есть способ их скомбинировать. Рассмотрим модель, которая обычно называется elastic net или “эластичная сеть”:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 +
lambda_1 sum_{j=1}^{n} | b_j | + lambda_2 sum_{j=1}^{n} b_j^2]
Как мы видим, функция ошибки такой модели комбинирует подходы гребневой и лассо-регрессии. То есть включает в себя регуляризацию и по L1 и по L2 нормам. Поэтому в этой модели присутствует целых два параметра регуляризации, причем они независимы друг от друга и задают не только соотношение регуляризации того или иного типа и классической функции ошибки, но и соотношение силы двух типов регуляризации между собой.
А между тем мы еще не говорили о том, как подбирать оптимальные значение параметров регуляризации. А ведь это достаточно серьезная проблема. Их не подберешь обычным методом обучения — это не просто параметры модели. Чуть позже мы назовем их гиперпараметрами. Но подбирать их можно только непосредственной проверкой, то есть подбором в классическом смысле. И это достаточно трудоемкий процесс, так как надо проверить потенциально бесконечное количество значений, причем еще хорошо бы использовать кросс-валидацию для надежности результатов.
А как быть с двумя гиперпараметрами. Обычно их значения подбираются “наивным” способом, в два прохода. Сначала находится оптимальный параметр $lambda_2$ для гребневой регрессии, а потом он фиксируется и подбирается наилучший параметр $lambda_1$ для лассо. Понятно, что они могут зависеть еще и друг от друга. И чуть позже мы изучим более вычислительно емкий, но правильный способ искать оптимальные значения гиперпараметров.
Давайте построим регрессию методом эластичной сети по уже известным нам данным из двух предыдущих глав. В данном случае используем $lambda_1 = lambda_2 = 10$:
Коэффициенты у модели следующие: 0, 0, 0, 0, 0.202, -0.016. Очень заметно совместное влияние двух регуляризаций. L1 выбирает только самые значимые признаки, оставляя у других коэффициенты равными нулю, а L2 еще приближает к нулю оставшиеся коэффициенты. В результате получается очень компактная модель, которая имеет только очень обоснованные коэффициенты.
Конечно, приведенные в данных главах модели не являются обязательно лучшими или оптимальными для решения данной задачи регрессии. Их цель — проиллюстрировать работу алгоритмов и для этого зачастую приходилось на максимум “выкручивать” регуляризацию. В реальности надо искать оптимальный уровень регуляризации, но об этом речь пойдет в следующих главах.
Выводы:
- По сути, это комбинация регуляризации по L1 и L2 нормам.
- Имеет два параметра, которые определяют соотношение соответствующих норм.
- Комбинирует достоинства предыдущих двух методов.
- Недостаток в необходимости задавать сразу два параметра регуляризации.
Методы борьбы с недообучением
В этой главе мы говорим о диагностике моделей машинного обучения в контексте диагностики недо- и переобучения. И мы много говорили о том, как обнаружить эти состояния модели. Так что же делать, если мы обнаружили, что наша модель недообучается. Сейчас поговорим о типичных путях повышения эффективности моделей. И начнем с более простого случая — недообучения.
В первую очередь напомним себе, что такое недообучение. Это ситуация, когда модель демонстрирует слишком большой bias по отношению к имеющимся данным. Модели не хватает вариативности, чтобы “ухватить” зависимости между признаками и целевой переменной. С точки зрения модели, их вообще нет. Простыми словами можно сказать, что модель слишком проста, примитивна для решения поставленной задачи. При этом может быть такое, что имеющиеся данные действительно не содержат необходимой информации, позволяющей надежно предсказать значение целевой переменной.
Поэтому при недообучении первое о чем нужно подумать: есть ли в датасете информация (признак или комбинация признаков), которые бы определяли значение целевой переменной. Если таких нет, то неважно, сколько точек данных, примеров мы соберем, модель всегда будет недообучаться. Неважно, насколько сложную модель мы будем использовать, она покажет случайных шум. Наиболее эффективный способ борьбы с недообучением — инжиниринг признаков. Необходимо ввести в модель признаки (или атрибуты, неважно, важно чтобы была нужная информация), которые позволят модели предсказать значение целевой переменной.
Помните, как мы решали задачу с полиномиальными признаками, как они превращали нерешаемую задачу классификации в линейно разделимую? Так может произойти в любой задаче. Может, одного свойства объекта нам и не хватает, чтобы превратить случайный перемешанный набор точек в многомерном пространстве в четкую и очевидную зависимость.
К сожалению, нет универсального алгоритма инжиниринга признаков. Это всегда творческая деятельность, которая требует, причем, глубокого знания предметной области. Иногда нужно просто вернуться на этап сбора данных и найти (или сгенерировать) больше информации. Иногда помогает вдумчивое и осмысленное преобразование имеющихся атрибутов. Главный вопрос, который надо себе задать: что в реальности влияет на целевую переменную? Затем собирать как можно больше информации об этом, добавлять ее в модель в виде признаков и надеяться, что это повысит эффективность моделей.
Если такой возможности нет, то очевидно, имеет смысл уменьшить степень регуляризации модели. Конечно, этот способ подходит только, если вы используете регуляризованные модели. Но как мы уже обсуждали выше, очень многие модели используют регуляризацию автоматически. А если она применяется, то можно легко манипулировать ее степенью. Понижение регуляризации приведет к тому, что после обучения мы получим более сложную и вариативную модель, что может исправить ситуацию с недообучением.
Другой очевидный способ — использование более сложных моделей в целом. Имеется в виду смена класса моделей. Если недообучается, например, модель линейной регрессии, стоит попробовать дерево решений. Если недообучилась логистическая — попробуйте многослойный перцептрон. Хотя, регуляризация обычно работает более эффективно, чем использование более сложной модели, она ограничена рамками одного параметрического класса функций.
Возможно стоит попытаться повторить обучение или увеличить количество итераций обучения. Возможна ситуация, когда существующего количества итераций недостаточно для схождения метода обучения к локальному минимуму функции ошибки. Это опять же может происходить вследствие того, что задача слишком сложна. В особо сложных случаях можно использовать предобученные модели. Это так называемое трансферное обучение — когда используют уже обученную модель на каком-то одном наборе данных для решения подобной задачи на другом датасете. Например, существуют так называемые глубокие языковые модели — огромные нейросети с миллиардами параметров, которые обучаются на гигантских корпусах текстов. Они используются для разнообразных задач текстовой аналитики. Конечно, каждый раз нецелесообразно обучать такую огромную модель с нуля — можно воспользоваться уже обученной и дообучить ее (или обучить, например, только последний слой нейронной сети) под собственную задачу. Трансферное обучение — отдельная и очень интересная дисциплина машинного обучения, но ее подробное рассмотрение выходит за рамки этого пособия.
Отдельно стоит сказать, что не поможет при недообучении. Вам вряд ли поможет увеличение объема выборки. Многие думают, что собрать больше данных — это универсальный рецепт эффективности. Это тоже не так. Хотя, большая по объему выборка особенно и не помешает, то есть не уменьшит эффективность модели, она увеличит вычислительную емкость. Другими словами, модель будет обучаться значительно дольше, но без видимого положительного эффекта по эффективности.
Обратите внимание, что мы здесь всегда имеем в виду эффективность, измеренную на тестовой выборке. А еще лучше — с использованием кросс-валидации. Эффективность на обучающей выборке нужна только для диагностики и анализа моделей.
Стоит помнить, что машинное обучение — это всегда итеративный процесс. Построив первую модель нужно ее исследовать и пытаться улучшить, увеличить эффективность. При этом возможно стоит попробовать множество разных видов моделей и способов обработки данных.
Выводы:
- Ввести в модель новые данные об объектах (атрибуты).
- Уменьшение степени регуляризации модели.
- Введение полиномиальных и других суррогатных признаков.
- В целом, инжиниринг признаков.
- Использование более сложных моделей.
- Увеличение количества итераций.
- Трансферное обучение.
Методы борьбы с переобучением
Переобучение на практике более частая и более коварная проблема потому, что несложно взять для решение конкретной задачи более сложную модель. Гораздо труднее заставить ее работать хорошо на новых данных. Проблему переобучения обнаружить сложнее и потому, что при этой ситуации модель работает вроде бы хорошо — дает низкую ошибку на данных. Но на других точках модель почему-то начинает ошибаться гораздо сильнее.
Опять же вспомним, что суть ситуации переобучения состоит в том, что модель оказывается слишком сложной для имеющихся данных и зависимостей в них. Поэтому вместо общих тенденций модель начинает обращать внимание на конкретное расположение точек в обучающей выборке, на случайные флуктуации, которые не несут смысловой нагрузки и не будут повторяться в новых данных.
Чем меньше данных присутствует в обучающей выборке, тем больше в них “шума” по отношению к полезному “сигналу” — информации о случайных колебаниях значений признаков по сравнению с информацией о тенденциях и реальных зависимостях. Поэтому неудивительно, что на малых объемах данных при прочих равных модели склонны к переобучению. Взгляните на график выше — даже человеку неочевидно, что точки выборки образуют линейную тенденцию — их просто слишком мало, чтобы показать эту тенденцию.
Самый действенный способ борьбы с переобучением — собрать больше обучающих примеров.
Если мы добавим больше точек, принадлежащих тому же распределению, мы неизбежно более четко увидим имеющуюся тенденцию. Все дело в том, что основное свойство случайных колебаний — их математическое ожидание равно нулю. То есть значение показателя может под воздействием неизвестных или неучтенных факторов отклоняться от “правильного” значения как в сторону увеличения, так и в сторону уменьшения. Причем вероятность этого примерно равна. И если мы рассматриваем одну точку данных, то сложно сказать, чем обосновано ее конкретное значение — существенными факторами или случайностью. Но если рассмотреть большое множество точек, можно увидеть, что они группируются вокруг некоторого среднего.
Другими словами, при увеличении количества точек обучающей выборки все случайные колебания будут усредняться — на каждое положительное отклонение найдется примерно равное отрицательное. А тенденция же будет, наоборот, усиливаться. В итоге и человеку и модели будет значительно легче эту тенденцию “ухватить”. Посмотрите, например, что будет, если к выборке, изображенной на рисунке выше добавить еще в 10 раз больше точек из того же распределения:
Теперь довольно очевидно, что на лицо линейная тенденция. И даже более сложная полиномиальная функция работает гораздо более эффективно на этих данных. Именно так добавление данных борется с переобучением моделей.
Причем необходимое количество данных зависит от вида тенденции и величины случайных отклонений. Чем более сложная, нелинейная тенденция в данных существует, чем тоньше зависимость целевой переменной от значения атрибутов, тем больше данных нужно для адекватной работы моделей. И чем больше по величине случайные отклонения, чем “сильнее” они размывают эту тенденцию, тем больше данных понадобится. Поэтому не существует какого-то оптимального объема данных, все зависит от конкретной задачи.
Как мы видели на примерах ранее, переобучение зачастую возникает вследствие того, что в модели присутствует большое количество параметров за счет большого количества лишних признаков в датасете. Именно для борьбы с этим используется регуляризация и в целом отбор признаков. Незначимые атрибуты лучше убирать из данных еще на этапе предварительного анализа и очистки данных. Чем меньше в данных будет лишних признаков, тем более четко и ясно будет прослеживаться та самая заветная тенденция.
Однако следует помнить, что регуляризация на практике работает лучше, чем ручное удаление признаков, так как подбор коэффициентов модели происходит автоматически. При этом регуляризация имеет свои недостатки — необходимость подбора параметра регуляризации. Поэтому стоит комбинировать эти способы — если какие-то признаки явно не влияют на целевую переменную — их стоит убрать при обработке данных, а если есть сомнения — то лучше оставить на усмотрение регуляризации.
Кроме того, следует помнить, что в других классах моделей могут применяться и иные способы управления сложностью модели, которые эффективно в чем-то похожи на регуляризацию. Например, в деревьях решений — это ограничение глубины дерева. Мы уже говорили об этом: чем больше слоев в дереве, тем сложнее получается модель. В нейронных сетях для подобного же используются Dropout-слои. Подробно мы не сможем рассказать про все эти способы, тем более что они специфичны для разных классов моделей. Но на практике они применяются примерно также, как и обычная регуляризация.
Как мы видим на втором графике даже после добавления большого количества точек более простая модель все равно описывает выборку лучше, так как полиномиальная модель имеет не очень понятные “хвосты” на концах распределения. Поэтому при обнаружении переобучения стоит задуматься об использовании более простого параметрического класса функций. Этот способ работает лучше в совокупности с увеличением объема выборки. Вообще, комбинация нескольких способов может быть более эффективной, чем применение только одного.
В глубоком обучении есть эмпирическое правило, которое гласит, что количество параметров модели должно быть в 2-3 раза меньше, чем количество примеров в обучающей выборке. Это ни в коем случае не универсальное правило и не гарантия от переобучения. Помните, вся зависит от задачи. Но можно помнить об этом ориентире. Если количество параметров больше, чем рекомендует это правило, вы практически точно получите переобученную модель.
Кроме того, не стоит забывать о ложных корреляциях в данных, которые тоже могут стать причиной переобучения. Хотя, ложные зависимости данных в силу их ограниченности — это явление несколько другой природы, на практике оно проявляет себя точно как переобучение — снижает обобщающую способность модели. Для устранения ложных корреляций необходимо хорошо разбираться в предметной области или привлекать для анализа данных экспертов.
Еще устраняют или сильно снижают переобучение так называемые ансамблевые модели, особенно основанные на методе бустинга. Ансамблевые модели это отдельная большая тема, которую мы не сможем рассмотреть в этой главе, про них можно написать отдельную книгу. Но если вкратце, ансамбль — это набор моделей, обученных на одном и том же наборе данных. Метод бустинга заключается в том, что каждая следующая модель в ансамбле исправляет или компенсирует ошибки предыдущей. В итоге мы получаем такую метамодель, которая может работать более эффективно, чем каждая модель ансамбля по отдельности.
Еще один способ избежать переобучения моделей — ранняя остановка обучения. Раньше мы говорили, что процесс обучения всегда продолжается до полной сходимости, то есть до нахождения оптимальных значений параметров по заданной функции ошибки. Но это не всегда так. В процессе обучения можно контролировать ту самую тестовую эффективность и остановить обучение тогда, когда она начнет падать. Этот способ часто применяется в обучении нейронных сетей, так как оно начинается с малых случайных значений весов (параметров) сети. Поэтому само обучение, то есть подбор весов, немного имеет эффект повышения значения коэффициентов, который противоположен регуляризации, то есть повышение степени сложности модели. Поэтому ранняя остановка обучения эффективно похожа на введение регуляризации в модель. Важно остановить обучение именно в тот момент, когда сложность модели начнет превышать оптимальное значение, после которого начинается переобучение. Это простой, но не очень универсальный способ.
Каждый способ борьбы с переобучением (впрочем как и с недообучением) имеет свои достоинства и недостатки. Не существует универсального алгоритма действий. Поэтому всегда надо исходить из поставленной задачи, а также руководствоваться всеми факторами: характер модели, нефункциональные требования, особенности набора данных, возможность собрать больше точек или атрибутов. При возможности стоит попробовать несколько разных способов увеличения эффективности моделей.
Выводы:
- Ввести в модель данные о новых объектах, использовать выборку большего объема.
- Убрать признаки из модели, использовать отбор признаков, устранить ложные корреляции.
- Увеличить степень регуляризации модели.
- Использовать более простые модели.
- Регуляризация обычно работает лучше уменьшения количества параметров.
- Можно использовать ансамблевые модели.
- Ранняя остановка обучения.
Анализ ошибок
Рассматривая алгоритмические и математические способы повышения эффективности работы моделей машинного обучения не стоит забывать и о самом простом, но в тоже время одном из самых эффективных — ручном анализе ошибок модели. После обучения модели, если она не достигает желаемого уровня эффективности стоит просто обратить внимание на те объекты, на которых она делает ошибки. Этот подход называется анализ ошибок и может дать достаточно неожиданную информацию о модели, данных и самой задаче.
В отдельных случаях анализ ошибок приводит к выводу, что модель работает хорошо. Например, очень известна задача по распознаванию рукописных цифр по картинке. Даже относительно простые модели справляются с ней очень хорошо, но могут не достигать стопроцентной эффективности. Вот пример картинки, которую простая модель может классифицировать неправильно:
Свидетельствует ли эта ошибка о том, что модель обучилась неправильно? Скорее нет, это свидетельствует о низком разрешении картинок и наличии некоторых двусмысленных объектов в обучающей выборке. Такую рукописную цифру и человек бы не распознал.
Кроме того, в данных могут присутствовать просто ошибки. Особенно это касается датасетов, размеченных вручную. Человек мог просто опечататься или ошибиться и в наборе данных появился объект с неправильным значением целевой переменной. На практике все случается и именно ручной анализ ошибок может выявить такую ситуацию.
Ручная проверка индивидуальных объектов, на которых модель работает неправильно часто подсказывает, какие общие характеристики имеют такие объекты или чем они отличаются от остальной выборки. Поняв эти особенности можно найти способы модифицировать признаки таким образом, чтобы лучше учитывать эти особенности. Например, анализируя модель распознавания человека по лицу можно придти к выводу о том, что такая модель значительно чаще ошибается на лицах с растительностью или на людях в очках. Это вполне объяснимо с логической точки зрения. Так что же делать в таком случае? Можно просто собрать больше точек данных, лиц с растительностью или очками. Это не только просто повысит эффективность модели, но и сделает ее более устойчивой к подобным особенностям в принципе.
При проведении анализа ошибок следует ориентироваться на ошибки, которые модель делает именно в тестовой выборке. В задачах классификации в первую очередь следует проанализировать ошибки в тех классах, в которых модель делает больше всего ошибок. Это очень заметно в отчете о классификации и в марице классификации. Обычно бывает, что модель постоянно относит объекты одного класса к какому-то другому. А в задачах регрессии очень логично обратить внимание на объекты, на которых модель ошибается сильнее всего в численном выражении.
Выводы:
- Анализ ошибок — это ручная проверка объектов, на которых модель делает ошибки.
- Анализ характеристик таких объектов может подсказать направление инжиниринга признаков.
- Можно сравнить эти объекты с остальной выборкой. Может, это аномалии.
- В задачах регрессии в первую очередь обращать внимание на объекты с самым высоким отклонением.
Выбор модели
Выводы:
- Задача выбора класса модели для решения определенной задачи.
- Очень сложно сказать априори какой класс модели будет работать лучше на конкретных данных.
- Следует учитывать нефункциональные требования к задаче.
- Обычно начинают с самых простых моделей — они быстро считаются и дают базовый уровень эффективности.
- По результатам диагностики простых моделей принимают решение о дальнейших действиях.
- Можно провести поиск по разным классам моделей для определения самых перспективных.
- Выбор модели — это творческий и исследовательский процесс.
- Есть подходы автоматизации выбора модели (AutoML), но они пока несовершенны.
- В исследовательских задачах модели сравниваются со state-of-the-art.
Гиперпараметры модели
Выводы:
- Гиперпараметр модели — это численное значение, которое влияет на работу модели, но не подбирается в процессе обучения.
- Примеры гиперпараметров — k в kNN, параметр регуляризации, степень полиномиальной регрессии, глубина дерева решения.
- У каждой модели множество гиперпараметров, которые можно посмотреть в документации.
- Гиперпараметры модели нужно задавать до начала обучения.
- Если значение гиперпараметра изменилось, то обучение надо начинать заново.
- Существуют скрытые гиперпараметры модели — степень полинома, количество нейронов и слоев, ядерная функция.
- Оптимизация гиперпараметров и задача выбора модели — одно и то же.
Поиск по сетке
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
tuned_parameters = [
{"kernel": ["rbf"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]},
{"kernel": ["linear"],
"C": [1, 10, 100, 1000]},
]
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
Выводы:
- Поиск по сетке — полный перебор всех комбинаций значений гиперпараметров для поиска оптимальных значений.
- Для его организации надо задать список гиперпараметров и их конкретных значений.
- Непрерывные гиперпараметры надо дискретизировать.
- Поиск по сетке имеет экспоненциальную сложность.
- Чем больше параметров и значений задать, тем лучше модель, но дольше поиск.
- Можно задать критерии поиска — целевые метрики.
Случайный поиск
1
2
3
4
5
6
7
8
9
10
11
12
clf = SGDClassifier(loss="hinge", penalty="elasticnet", fit_intercept=True)
param_dist = {
"average": [True, False],
"l1_ratio": stats.uniform(0, 1),
"alpha": loguniform(1e-2, 1e0),
}
n_iter_search = 15
random_search = RandomizedSearchCV(
clf, param_distributions=param_dist, n_iter=n_iter_search
).fit(X, y)
Выводы:
- Случайный поиск позволяет задать распределение гиперпараметра, в котором будет вестись поиск.
- Случайный поиск семплирует набор значений гиперпараметров из указанных распределений.
- Можно задать количество итераций поиска независимо от количества гиперпараметров.
- Добавление параметров не влияет на продолжительность поиска.
- Результат не гарантируется. Воспроизводимость можно настроить.
Сравнение эффективности моделей (валидационный набор)
Выводы:
- При сравнении нескольких моделей между собой возникает проблема оптимистичной оценки эффективности.
- Поэтому для исследования выбранной модели нужно использовать третью часть выборки — валидационную.
- В терминах существует путаница, главное — три непересекающиеся части выборки.
- Обучающая (train) используется для оптимизации параметров (обучения) модели.
- Валидационная (validation) — для оптимизации гиперпараметров и выбора модели.
- Тестовая (test, holdout) — для итоговой оценки качества, представления результатов.
- Во многих случаях использование кросс-валидации автоматически разбивает выборку. Поэтому тестовая играет роль валидационной.
- Есть проблема глобального переобучения моделей на известных датасетах.

MAPE (Mean Absolute Percentage Error) is a common regression machine learning metric, but it can be confusing to know how to interpret the values. In this post, I explain what MAPE is, how to interpret the values and walk through an example.
What is MAPE?
Mean Absolute Percentage Error (MAPE) is the mean of all absolute percentage errors between the predicted and actual values.
It is a popular metric to use as it returns the error as a percentage, making it both easy for end users to understand and simple to compare model accuracy across use cases and datasets.
Formula for MAPE
The formula for calculating MAPE is as follows:
This formula helps us understand one of the important caveats when using MAPE. In order to calculate this metric, we need to divide the difference by the actual value. This means that if you have actual values close to or at 0 then your MAPE score will either receive a division by 0 error, or be extremely large. Therefore, it is advised to not use MAPE when you have actual values close to 0.
MAPE can be interpreted as the inverse of model accuracy, but more specifically as the average percentage difference between predictions and their intended targets in the dataset. For example, if your MAPE is 10% then your predictions are on average 10% away from the actual values they were aiming for.
MAPE value interpretation
Now that we know how to interpret the definition of MAPE, let’s look at how to interpret the values themselves. It will be dependent upon your use case and dataset, but a general rule I follow is:
| MAPE | Interpretation |
|---|---|
| <10% | Very good |
| 10% — 20% | Good |
| 20% — 50% | OK |
| >50% | Not good |
How to interpret MAPE for time series forecasting
MAPE for time series forecasting can be interpreted as the average percentage error over all time periods in the dataset, specifically the average percentage difference between forecasts and their intended targets. For example, if your dataset is a year period broken down per day and your MAPE is 10%, then the average difference between the daily forecast and the actual over the whole year period is 10%.
Example of interpreting MAPE score
To better understand how to interpret MAPE, let’s look at an example where we are predicting the price of a house.
To start with, we need to calculate the absolute error and then the absolute percentage error for all of our predictions:
| Actual | Prediction | Absolute Difference | Absolute Percentage Difference |
|---|---|---|---|
| 100,000 | 105,000 | 5,000 | 5% |
| 150,000 | 140,000 | 10,000 | 6.7% |
| 250,000 | 270,000 | 20,000 | 8% |
| 120,000 | 121,000 | 1,000 | 0.8% |
From this, we can take the mean of all the values to come to our MAPE value.
MAPE = (5 + 6.7 + 8 + 0.8) / 4 = 5.2%
By using our interpretation table from before, we can say that the interpretation of this value is that on average our predictions are 5.2% away from the targets, which is commonly seen as a very good value.
Related articles
Metric calculators
MAPE calculator
Metric comparisons
RMSE vs MAPE, which is the best regression metric?
MAE vs MAPE, which is best?
Regression metrics
Interpretation of R Squared
Interpretation of RMSE
Interpretation of MSE
Interpretation of MAE
References
scikit-learn MAPE documentation
I’m a Data Scientist currently working for Oda, an online grocery retailer, in Oslo, Norway. These posts are my way of sharing some of the tips and tricks I’ve picked up along the way.
Fit Predict Newsletter
The simple weekly roundup of all the latest news, tools, packages, and use cases from the world of Data Science 📥
Your email address
Please check your inbox and click the link to confirm your subscription.
Please enter a valid email address!
An error occurred, please try again later.
Kaggle – площадка, объединяющая соревновательную систему по исследованию данных, образовательный ресурс по искусственному интеллекту и машинному обучению, а также соцсеть специалистов в указанных областях.
Перед тем, как начать работать, необходимо зарегистрироваться на сайте. Заходим по ссылке, находим кнопку Register и заполняем поля. Уверен, что вы сами с этим отлично справитесь. После регистрации, подтверждения и логина попадаем на главную страницу ресурса.
Слева в столбце мы видим разделы:
- Home – новостная лента, в которую попадают публикации, которые могут вас заинтересовать. Чем выше активность пользователя на сайте, тем точнее рекомендации.
- Competitions – соревнования в области анализа данных. Здесь же находятся учебные соревнования, которые помечены словом Knowledge.
- Datasets – различные наборы данных, с которыми можно поиграться. Также можно выкладывать собственные датасеты.
- Code – раздел, в котором можно создать Jupyter Notebook или посмотреть чужой.
- Discussions – местный аналог форумов.
- Courses – учебные курсы. Довольно приличный объем и приемлемое качество. Раскрыты основные базовые разделы ML.
Отвлечемся пока от Kaggle и поговорим о машинном обучении, а также о решаемых с его помощью задачах.
Теоретический минимум о Machine Learning
Машинное обучение – набор математических, статистических и вычислительных методов, с помощью которых возможно решить задачу путем поиска закономерностей в представленных данных.
Существует огромное количество методов машинного обучения. Здесь я покажу всего несколько самых базовых, а остальные вы сможете найти самостоятельно, пройдя по рекомендованным ссылкам в конце.
Все методы ML можно разделить на несколько крупных групп:
- Обучение с учителем (от англ. Supervised learning) – алгоритмы из этой группы обучаются с помощью заранее подготовленных данных, которые содержат как наборы входных исследуемых признаков, так и “ответы” на эти наборы. “Ответом” является выходное значение, которое должен выдать алгоритм в результате своей работы, т.е. алгоритм “обучается”. К этой группе, например, можно отнести задачи классификации и регрессии.
- Обучение без учителя (от англ. Unsupervised learning) – группа алгоритмов, в которых система спонтанно обучается на входных данных без вмешательства извне. К этой группе можно отнести задачи кластеризации, понижения размерности.
- Обучение с подкреплением (от англ. Reinforcement learning) – группа алгоритмов, в которых система обучается с помощью взаимодействия со средой, в которой она находится. Подробнее можно ознакомиться хотя бы в вики. В моей статье алгоритмы этой группы не рассматриваются.
Задачи машинного обучения
Классификация
Вероятно, это самая популярная задача машинного обучения. Ее суть состоит в присвоении какому-то набору признаков (т.е. свойств объекта) какому-то классу. Например, стоит задача автоматической модерации токсичных комментариев на сайте. Алгоритм получает на вход текст комментария, а на выходе присваивает ему метку: токсичный или нетоксичный. Это пример бинарной классификации. К этому же типу классификации можно отнести задачу выявления сердечно-сосудистых проблем по анализам человека, определение спама в письмах и т.п. Второй тип классификации – множественная (многоклассовая). В ней классов больше двух. Примером может служить классификация жанра книги.
Для демонстрации посмотрим графической решение задачи бинарной классификации. Алгоритм разделяет пространство признаков на две группы.
Для решения задачи обычно используются следующие алгоритмы: логистическая регрессия, KNN, SVM, деревья решений.
Регрессия
Задача регрессии – предсказание (прогнозирование) целевого признака по входным параметрам. Например, предсказание загруженности дороги в зависимости от времени суток, дня недели, погоды, предсказание цены квартиры от количества комнат, этажа, района. Предсказание времени на путь из пункта А в пункт Б в зависимости от пробок и т.п. Т.е. задача регрессии это задача получения неизвестного числа по известным параметрам.
Посмотрим на рисунок. По ряду известных значений y(x) была предсказана кривая – линия регрессии. Ее можно продлить, чтобы предсказывать значения y для неизвестных x.
Для решения задачи применяются следующие алгоритмы и методы: линейная и полиномиальная регрессии, KNN, деревья решений.
Кластеризация
Задача кластеризации состоит в разделении заданной выборки объектов таким образом, чтобы похожие объекты попали в один кластер, а кластеры сильно бы различались между собой. Кластеризацию применяют для анализа и поиска признаков по которым можно объединить объекты, сжатия данных и поиска новизны (что не входит ни в один кластер).
Возникает логичный вопрос: а чем различаются классификация и кластеризация, ведь они решают похожие задачи? При классификации есть набор предопределенных классов, которым обучается алгоритм на наборе примеров. Далее алгоритм предсказывает, к какому классу принадлежит новый объект. При кластеризации используется алгоритм, который пытается сгруппировать набор объектов и определить, существует ли какая-либо взаимосвязь между объектами, т.е. машина учится сама.
Графическим примером кластеризации может быть следующая иллюстрация.
Для решения задачи применяются следующие алгоритмы и методы: K-Means, DBSCAN.
Метрики качества регрессии
Начнем с регрессии. При оценке качества работают с таблицей, содержащей два столбца (помимо индекса): правильные значения и предсказанные. Для простоты рассмотрим четыре строки, и пусть объектами будет количество килограмм картошки для сети ресторанов. Для простоты расчетов возьмем кратные десяти значения.
| Номер | Значение из выборки (сколько в реальности потребовалось кг картошки) | Предсказанное значение (кг) |
| 1 | 200 | 180 |
| 2 | 150 | 190 |
| 3 | 140 | 120 |
| 4 | 160 | 220 |
При таком количестве данных даже визуально можно оценить качество предсказанных данных. Предсказания под номерами 1 и 3 были достаточно точны, номер 2 показал бОльшую ошибку, а в строке номер 4 ошибка оказалась очень большой.
Для тысяч таких строк визуально оценить качество невозможно, необходимы агрегированные показатели.
Mean Absolute Error (MAE) – средняя абсолютная ошибка
Довольно интуитивный способ – сложить ошибки каждого из предсказаний и разделить на количество предсказаний. Посчитаем для нашей таблицы:
В среднем наш алгоритм ошибается на 35 кг картошки. Где-то в плюс, где-то в минус. Такая метрика называется средней абсолютной ошибкой, mean absolute error или MAE.
где yi – предсказанные значения, а xi – реальные известные значения, ei — ошибка i-го предсказания.
Mean Square Error (MSE) – Средняя квадратичная ошибка
Достаточно часто используется похожая метрика, MSE. Она рассчитывается почти так же, только берется не модуль ошибки ei, а ее квадрат.
Для нашего примера:
Но мы получили не ошибку в килограммах, а “кг в квадрате”. Чтобы вернуться к исходной величине, необходимо извлечь из MSE квадратный корень:
По сравнению с RMSE, метрика MAE более интуитивна, т.к. усредняются сами отклонения, но RMSE удобнее использовать при обучении алгоритмов. Хотя для MAE обучение тоже успешно выполняется.
Еще одна особенность метрики MAE — она более устойчива к выбросам, чем RMSE. Это означает, что если для одного объекта ошибка очень большая (объект-выброс), а для остальных объектов – маленькая, то значение MAE подскочит от этого одного объекта меньше, чем RMSE, т.к. в RMSE ошибки возводятся в квадрат. В нашем примере объектом-выбросом является четвертое предсказание.
Quantile loss
Иногда ошибка в меньшую или большую сторону может иметь разное влияние на бизнес. Например, если мы предскажем на одну тысячу единиц товара меньше, чем реально потребуется, то потеряем прибыль: некоторым клиентам не достанется товара. А если мы предскажем на одну тысячу единиц больше товара, чем реально потребуется, то появятся дополнительные издержки на хранение товара.
Предположим, что товар занимает мало места (т.к. площади хранения в ресторанах велики) и расходы на хранение невелики, тогда лучше ошибиться в большую сторону, чем в меньшую. В этом случае отрицательную и положительную разницу домножают на разные коэффициенты, например, возьмем 0.5 и 1.5.
В нашем примере, коэффициент 1.5 будет применен к предсказаниям 1 и 3 (180 < 200 и 120 < 140), а коэффициент 0.5 к остальным. Тогда значение метрики будет равно:
Данная метрика называется квантильной ошибкой.
Само по себе значение метрик MSE или MAE можно сравнивать со средним значением целевой переменной: например, нам нужно предсказывать десятки, при этом допустимы ошибки порядка единиц. Если хочется получать значения ошибки в процентах («алгоритм в среднем ошибается на столько-то процентов»), можно использовать метрики с нормировками.
К примеру, метрика MAPE (mean average percentage error) усредняет значения ошибок, деленных на значение целевой переменной:
В нашем случае, алгоритм в среднем ошибается на 22.1%.
Важно понимать, что идеальных алгоритмов, как и нулевых значений метрик ошибок, в машинном обучении не бывает: такова суть этой области, что она помогает выполнять приблизительные предсказания. Величину метрик обычно определяет заказчик.
Метрики качества классификации
Accuracy – доля правильных ответов
В задаче классификации самой простой метрикой качества является доля правильных ответов (accuracy). Она показывает, в каком проценте случаев алгоритм правильно указал класс объекта.
Для примера будет рассматривать задачу предсказания токсичности комментариев. Т.е. имеем задачу бинарной классификации, где 0 – комментарий нетоксичен, 1 – комментарий токсичен. Возьмем для простоты пять комментариев и сведем все в таблицу.
| ID комментария | Значение в данных (токсичен ли комментарий в действительности) | Предсказанное значение |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 0 | 0 |
| 4 | 0 | 1 |
| 5 | 0 | 0 |
В нашем примере, алгоритм выдал правильные ответы для комментариев 1,2,3,5, т.е. в 80% случаев. Это и есть значение accuracy.
Accuracy – простая и интерпретируемая метрика, но она не отражает полную картину, в частности, в какую сторону алгоритм ошибается чаще. Кроме того, использовать эту метрику может быть неудобно в ситуации с несбалансированными классами, то есть, когда объектов одного класса много больше, чем объектов другого. К примеру, если в данных 95% объектов из класса 0 и 5% из класса 1, а алгоритм всегда предсказывает, что объект относится к классу 0, то его accuracy будет равно 95%, хотя алгоритм совершенно бесполезный! В таких случаях часто используют другие метрики.
Precision and Recall – Точность и полнота
Чтобы понять, что такое точность и полнота, разберемся сначала с возможными типами ошибок. Для этого отлично подходит картинка из википедии.
В нашем примере, если алгоритм пометит нормальный комментарий как токсичный, то ничего особо страшного не произойдет. Этот коммент будет в дальнейшей проверен модератором. Такая ошибка называется ошибкой первого рода (false positive). Если же комментарий будет распознан как нормальный, но он токсичный, то такая ошибка называется ошибкой второго рода (false negative). На мой взгляд, в нашем примере ошибка второго рода страшнее, чем ошибка первого. Но бывает и наоборот.
Для отслеживания двух видов ошибок используют метрики точность (Precision) и полнота (Recall).
- Точность измеряет, какой процент объектов, для которых алгоритм предсказал класс 1, действительно относится к классу 1. В нашем примере, точность – это отношение количества реально токсичных комментариев к количеству помеченных как токсичные. И эта метрика составляет ⅔ = 66%.
- Полнота измеряет, для какого процента объектов класса 1 алгоритм предсказал класс 1. Для нашего примера полнота составляет 100%. Для простоты понимания, в вики формулы расчеты показаны визуально.
Отслеживать обе метрики сразу может быть неудобно, и может понадобиться скомбинировать их в одной. Для этого используют F-меру – среднее гармоническое точности P и полноты R:
Такой способ усреднения был выбран потому, что F-мера принимает высокие значения, только когда обе метрики принимают высокие значения. Иными словами, если хотя бы одна из двух метрик близка к 0, F-мера тоже будет близка к 0. Это свойство не выполняется, например, для среднего арифметического из точности и полноты.
Ансамблевые методы
В этом разделе поговорим про ансамбли – методы, наиболее часто используемые в машинном обучении при работе с табличными данными. Ансамбли обычно применяют в задачах классификации и регрессии, но они годятся и для других задач, которые сводятся к этим двум. Стоит сказать, что это только вершина айсберга и методов машинного обучения очень много. Их обзор можно найти в этой статье.
Вспомним постановку задач регрессии и классификации. В обеих требуется набор табличных данных: по строкам таблицы заданы объекты (например, клиенты), а по столбцам – признаки, то есть некоторые характеристики объектов (возраст, заработная плата, стаж работы клиента и т. д.). Кроме того, нужна разметка данных: для каждого объекта должно быть известно значение целевой переменной (класс в задаче классификации или число в задаче регрессии). Имея набор размеченных данных, мы обучаем алгоритм, который будет предсказывать значение целевой переменной для новых объектов на стадии внедрения.
Ансамблирование чаще всего используют применительно к решающим деревьям, поэтому начнем блок с разбора этого метода.
Решающее дерево – это алгоритм, который делает предсказания на основе серии вопросов об объекте.
Например, покажем решающее дерево, которое определяет возможность проставления оценки по какому-то предмету студенту.
Ансамблирование заключается в том, чтобы обучить несколько алгоритмов и усреднять их предсказания.
Например, строится несколько разных решающих деревьев, и берется среднее результатов их работы. Подробно про ансаблирование в машинном обучении можно почитать тут.
Решаем Titanic на Kaggle
Для начала неплохо было бы ознакомиться с задачей и данными, которые нам предоставляют. Идем на kaggle.com/c/titanic/overview. Изучив описание, узнаем, что нам предстоит решить задачу классификации: по заданным признакам необходимо определить, выживет ли пассажир при крушении Титаника или нет. Предлагаемые данные (раздел Data) состоят из трех файлов .csv: train.csv – обучающая выборка, в которой содержатся метки, выжил ли каждый конкретный пассажир или нет; test.csv – собственно данные для решения, именно в этом файле нам нужно определить выживаемость; gender_submission.csv – пример того, как должен выглядит файл-ответ.
Что нужно делать – понятно. Начинаем смотреть наши данные. Переходим на вкладку Code и нажимаем New notebook.
Таким образом, мы получаем продвинутый jupyter notebook. Чтобы активировать систему, нажмем на значок Play слева от верхней ячейки ноутбука. Система будет запущена и в результате, под ячейкой увидим пути до csv файлов.
Можно приступать. Если вы не знакомы с jupyter notebook и pandas, то рекомендую сначала прочитать данный материал.
Чтение и анализ датасета Titanic
Первым делом, загружаем в датафреймы файлы .csv.
train_data = pd.read_csv('/kaggle/input/titanic/train.csv')
test_data = pd.read_csv('/kaggle/input/titanic/test.csv')
Проверим, что все у нас удачно и взглянем на эти датафреймы. Для примера приведу train_data.
train_data.head()
Первым делом оценим размеры датафрейма. Для этого используем свойство shape.
train_data.shape
В результате получаем (891, 12), т.е. 12 столбцов и 891 строку.
Следующим этапом неплохо было бы оценить количество пустых ячеек в столбцах обучающей выборки. Для этого вызовем:
train_data.isnull().sum()
Получаем, что в столбце Age у нас 177 пропусков, а в Cabin аж 687, что сильно больше половины.
Далее, оценим выживаемость. Для простоты визуализации будем использовать библиотеку seaborn. Для этого подключить ее и matplotlib.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.countplot(x='Survived', data=train_data)
Как видим, выжило людей меньше, чем погибло.
Теперь посмотрим, как с выживаемостью у мужчин и женщин отдельно.
sns.countplot(x='Survived', hue='Sex', data=train_data)
Видим, что мужчин погибло гораздо больше, чем выжило. И большая часть женщин выжила.
Далее взглянем, как зависела выживаемость от класса каюты.
sns.countplot(x='Survived', hue='Pclass', data=train_data)
Видим всплеск среди погибших пассажиров 3 класса.
Не закапываясь глубоко в датасет, видим явную зависимость выживаемости от пола и класса каюты.
В качестве признаков кроме выбранных пола и класса каюты, возьмем количество родителейдетей и количество братьевсестер на борту. Итоговый список признаков будет выглядеть следующим образом:
features = ['Sex', 'Pclass', 'SibSp', 'Parch']
Информацию о выживших и погибших пассажирах поместим в переменную y:
y = train_data['Survived']
Если вы немного отмотаете назад, то увидите, что в столбце Sex находятся не числа, а строки, когда остальные отобранные нами признаки являются числами. Давайте превратим этот столбец в пару фиктивных переменных. Для этого в Pandas есть специальный метод, который называется get_dummies(). Сделаем эту операцию как для обучающей выборки, так и для тестовой.
X = pd.get_dummies(train_data[features])
X_test = pd.get_dummies(test_data[features])
Обратите внимание, что столбец Sex исчез, а вместо него появилось два столбца Sex_female и Sex_male.
Теперь с помощью ансамбля решающих деревьев обучим нашу модель, сделаем предсказание для тестовой выборки и сохраним результат. Ансамбль решающих деревьев называется Random Forest.
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=1)
model.fit(X, y) # обучаем модель
prediction = model.predict(X_test) # делаем предсказание
output = pd.DataFrame({'PassengerId':test_data.PassengerId, 'Survived':prediction})
output.to_csv('my_submission.csv', index=False) # формируем итоговый датафрейм и сохраняем его в csv файл
Вот и все. Осталось отправить результат в соревнование. Для этого в правом верхнем углу наживаем кнопку Save version. После того, как блокнот сохранится, нажимаем на цифру возле этой кнопки.
Откроется окно Version history. В правом списке, нажимаем на многоточие около только что сохраненной версии и нажимаем Submit to competition.
Появляется окошко, в котором нажимаем submit.
Поздравляю! Вы закончили свое первое соревнование на kaggle. Нажмите на view my submission, чтобы взглянуть на результат.
Чем ближе число к 1, тем лучше. Но 0.775, согласитесь, неплохо для первого раза.
Путями улучшения результата могут быть: введение дополнительных признаков, введение своих новых признаков, выбор другого алгоритма, выбор другим параметров алгоритма RandomForestClassifier. Для начала, попробуйте поиграть с числами в этой строке (называются эти числа гиперпараметрами).
model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=1)
Дополнительные материалы для изучения:
- https://github.com/girafe-ai/ml-mipt/tree/master
- https://machinelearning.ru/
При подготовке были использованы материала из Википедии и Летней школы Сбера.

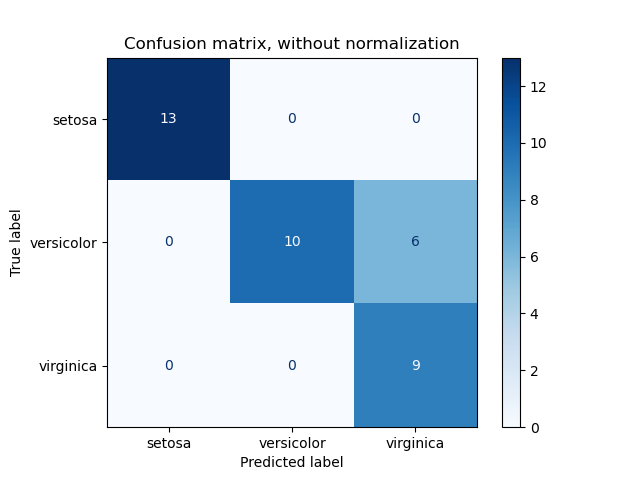
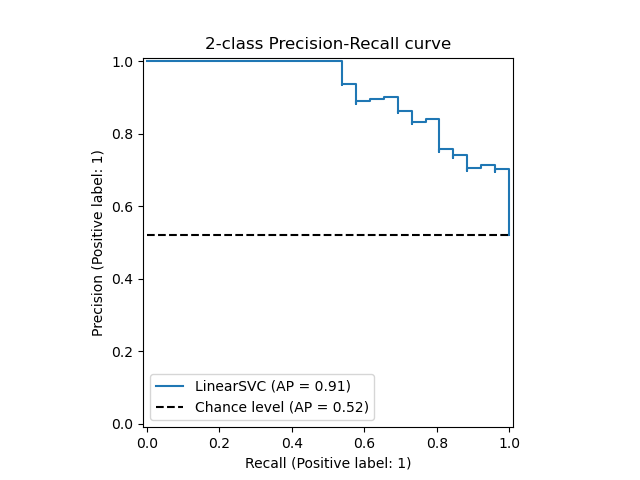
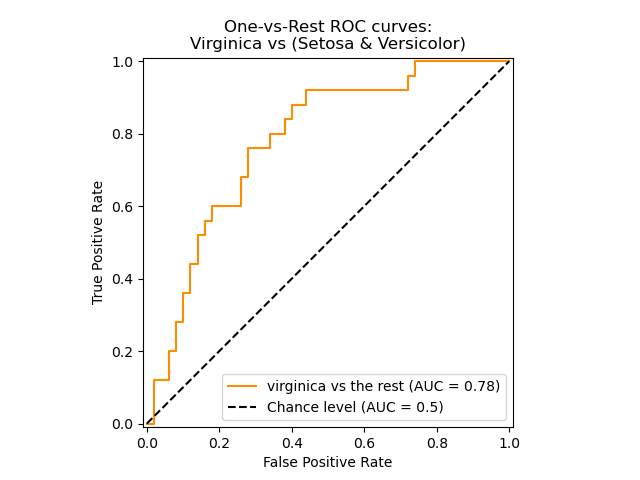
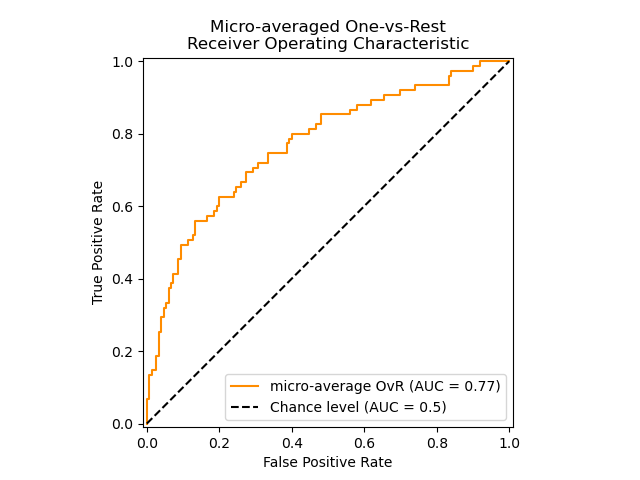
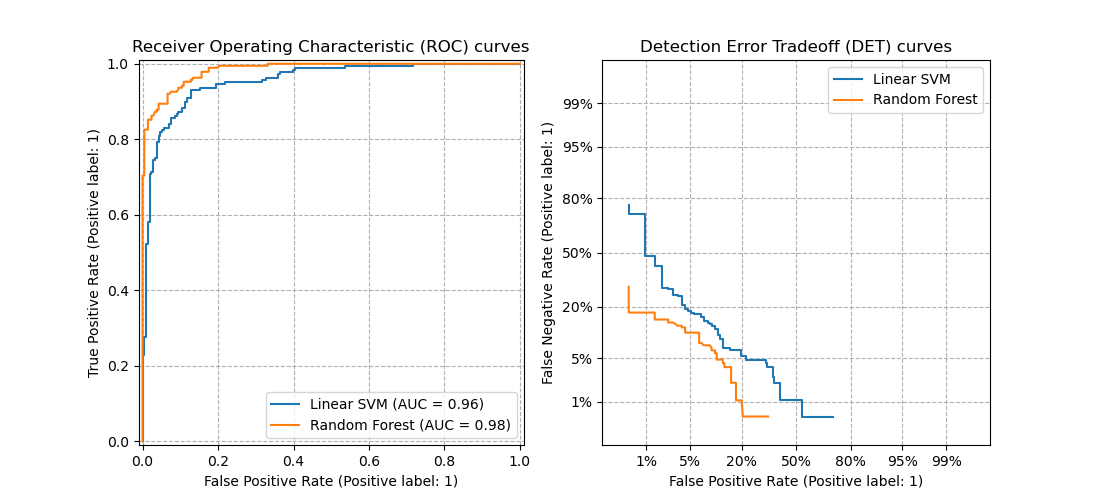
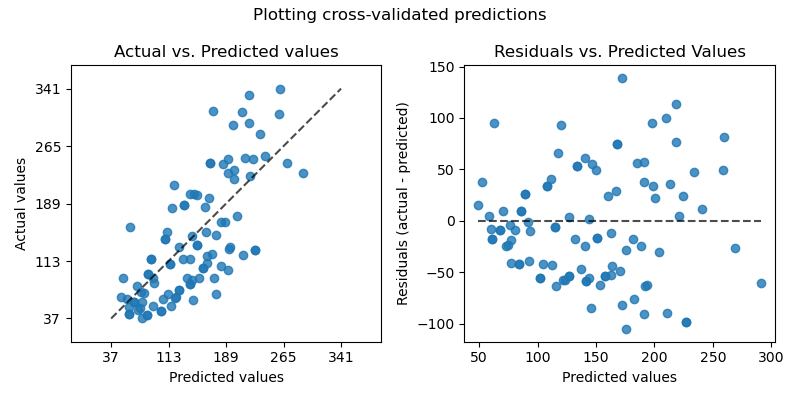

![{displaystyle g_{text{MAPE}}(x)=arg min _{gin {mathcal {G}}}mathbb {E} left[left|{frac {g(X)-Y}{Y}}right||X=xright]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd980e3610438e202798e285c882e02dfe21d37)