From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
- Среднеквадратичная ошибка (Mean Squared Error)
- Корень из среднеквадратичной ошибки (Root Mean Squared Error)
- Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
- Cредняя абсолютная ошибка (Mean Absolute Error)
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
- Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
- Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
- Средняя относительная ошибка (Mean Relative Error)
- Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
- R-квадрат
- Скорректированный R-квадрат
- Сравнение метрик
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
17 авг. 2022 г.
читать 2 мин
Регрессионный анализ — это метод, который мы можем использовать для понимания взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Один из способов оценить, насколько хорошо регрессионная модель соответствует набору данных, — вычислить среднеквадратичную ошибку , которая представляет собой показатель, указывающий нам среднее расстояние между прогнозируемыми значениями из модели и фактическими значениями в наборе данных.
Чем ниже RMSE, тем лучше данная модель может «соответствовать» набору данных.
Формула для нахождения среднеквадратичной ошибки, часто обозначаемая аббревиатурой RMSE , выглядит следующим образом:
СКО = √ Σ(P i – O i ) 2 / n
куда:
- Σ — причудливый символ, означающий «сумма».
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
- n — размер выборки
В следующем примере показано, как интерпретировать RMSE для данной модели регрессии.
Пример: как интерпретировать RMSE для регрессионной модели
Предположим, мы хотим построить регрессионную модель, которая использует «учебные часы» для прогнозирования «экзаменационного балла» студентов на конкретном вступительном экзамене в колледж.
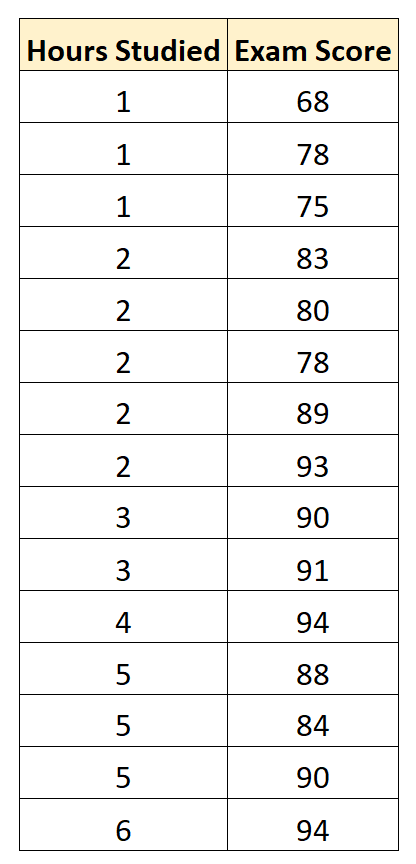
Мы собираем следующие данные для 15 студентов:
Затем мы используем статистическое программное обеспечение (например, Excel, SPSS, R, Python) и т. д., чтобы найти следующую подогнанную модель регрессии:
Экзаменационный балл = 75,95 + 3,08 * (часы обучения)
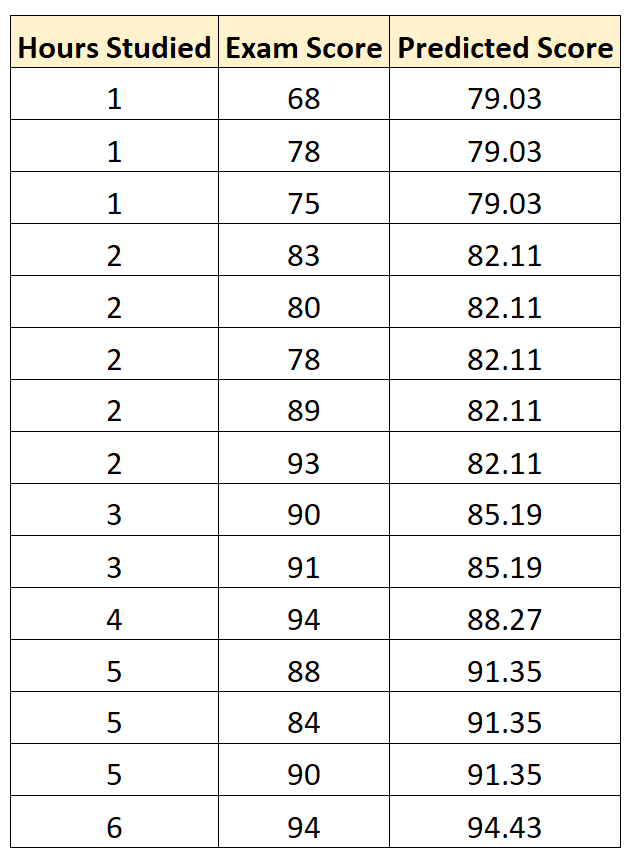
Затем мы можем использовать это уравнение, чтобы предсказать экзаменационную оценку каждого студента, исходя из того, сколько часов они учились:
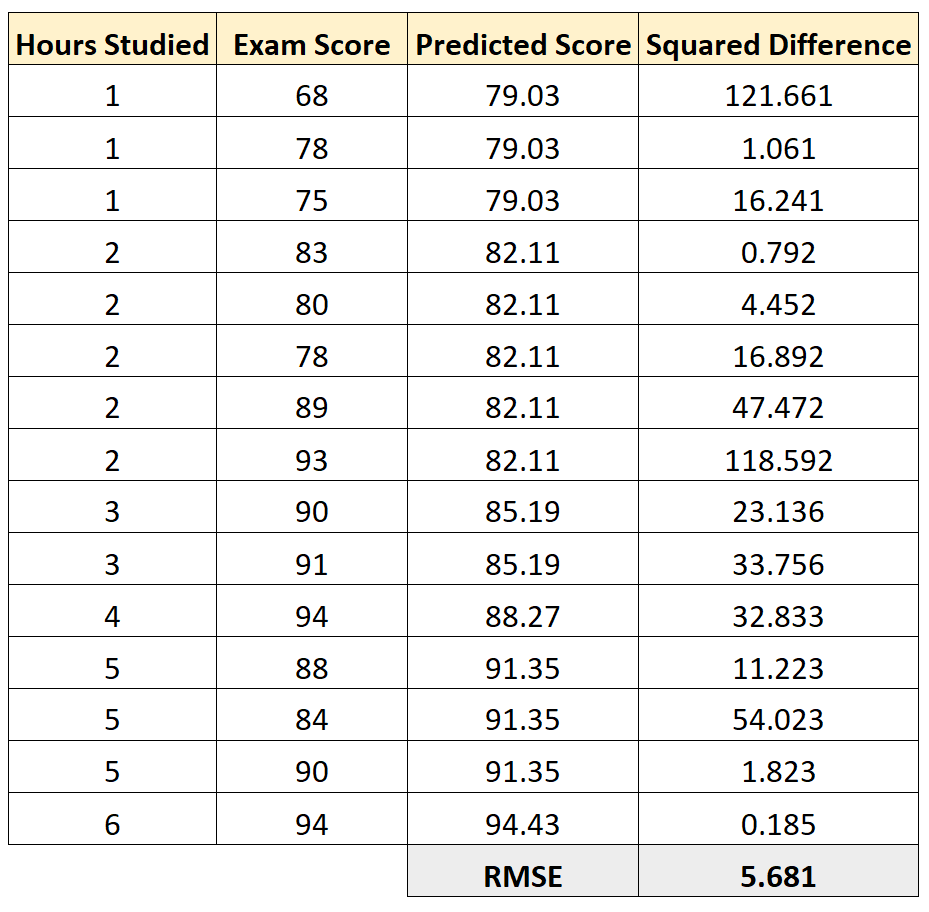
Затем мы можем вычислить квадрат разницы между каждой прогнозируемой оценкой экзамена и фактической оценкой экзамена. Затем мы можем извлечь квадратный корень из среднего значения этих разностей:
RMSE для этой регрессионной модели оказывается равным 5,681 .
Напомним, что остатки регрессионной модели представляют собой разницу между наблюдаемыми значениями данных и значениями, предсказанными моделью.
Остаток = (P i – O i )
куда
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
И помните, что RMSE регрессионной модели рассчитывается как:
СКО = √ Σ(P i – O i ) 2 / n
Это означает, что RMSE представляет собой квадратный корень из дисперсии остатков.
Это значение полезно знать, поскольку оно дает нам представление о среднем расстоянии между наблюдаемыми значениями данных и прогнозируемыми значениями данных.
Это отличается от R-квадрата модели, который сообщает нам долю дисперсии переменной отклика, которая может быть объяснена предикторной переменной (переменными) в модели.
Сравнение значений RMSE из разных моделей
RMSE особенно полезен для сравнения соответствия различных моделей регрессии.
Например, предположим, что мы хотим построить регрессионную модель, чтобы предсказать результаты экзаменов студентов, и мы хотим найти наилучшую возможную модель среди нескольких потенциальных моделей.
Предположим, мы подгоняем три разные модели регрессии и находим соответствующие им значения RMSE:
- RMSE модели 1: 14,5
- RMSE модели 2: 16,7
- RMSE модели 3: 9,8
Модель 3 имеет самый низкий RMSE, что говорит нам о том, что она способна лучше всего соответствовать набору данных из трех потенциальных моделей.
Дополнительные ресурсы
Калькулятор среднеквадратичной ошибки
Как рассчитать RMSE в Excel
Как рассчитать RMSE в R
Как рассчитать RMSE в Python
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
среднеквадратическая ошибка f
среднеквадратичной ошибки
среднеквадратической ошибкой
Предложения
If the hidden layer is linear and the mean squared error is used as the reconstruction criteria, then the Autoencoder will learn the first k principle components of the data.
Если скрытый уровень будет линеен, и среднеквадратическая ошибка используется в качестве критерия реконструкции, то автоассоциатор изучит первые к ключевых компонентов данных.
The mean squared error (MSE) is written as
The evaluation criterion is the root mean squared error (RMSE) between predicted ratings and true ones.
В качестве критерия сходимости брался квадратный корень из среднеквадратичной ошибки (RMSE) между фактическими и прогнозными значениями.
SSIM is designed to improve on traditional methods such as peak signal-to-noise ratio (PSNR) and mean squared error (MSE).
SSIM-индекс является развитием традиционных методов, таких как PSNR (peak signal-to-noise ratio) и метод среднеквадратичной ошибки MSE, которые оказались несовместимы с физиологией человеческого восприятия.
Root of mean squared error (RMSE)
Moreover, the root mean squared error is smaller when using the method of the invention.
Кроме того, среднеквадратичная ошибка меньше при использовании способа, соответствующего изобретению.
This rule changes the connection weights in the way that minimizes the mean squared error of the network.
For example, as stated above, under mean squared error (MSE) the Bayes rule is unique and therefore admissible.
К примеру, как указано выше, под среднеквадратической ошибкой (MSE) Байесовское правило уникально и, следовательно, допустимо.
Use jackknife resampling if the dataset contains a small number of instances, and measure validity with R squared and mean squared error (MSE).
Поможет использование Jackknife-передискретизации, если набор данных содержит небольшое количество экземпляров и проверяет достоверность по квадрату R и среднеквадратичной ошибке (MSE).
For example, knowing that the average forecast is «off» by ±5% is a useful result in and of itself, whereas a mean squared error of 30.8 is not immediately interpretable.
Например, знание того, что точность прогноза ±5%, полезно само по себе, в то время как значение 30.8 для средней квадратической ошибки не может быть так просто проинтерпретировано.
SSIM is designed to improve on traditional methods such as peak signal-to-noise ratio (PSNR) and mean squared error (MSE), which have proven to be inconsistent with human visual perception.
SSIM-индекс является развитием традиционных методов, таких как PSNR (peak signal-to-noise ratio) и метод среднеквадратичной ошибки MSE, которые оказались несовместимы с физиологией человеческого восприятия.
If a Bayes rule is unique then it is admissible. For example, as stated above, under mean squared error (MSE) the Bayes rule is unique and therefore admissible.
Если Байесовское решающее правило уникально, значит оно приемлемо. К примеру, как указано выше, под среднеквадратической ошибкой (MSE) Байесовское правило уникально и, следовательно, допустимо.
To begin the decomposition, we start with the mean squared error
Another important metric is the mean squared error which is defined as
Предложения, которые содержат mean squared error
Результатов: 14. Точных совпадений: 14. Затраченное время: 35 мс
Documents
Корпоративные решения
Спряжение
Синонимы
Корректор
Справка и о нас
Индекс слова: 1-300, 301-600, 601-900
Индекс выражения: 1-400, 401-800, 801-1200
Индекс фразы: 1-400, 401-800, 801-1200
Есть 3 различных API для оценки качества прогнозов модели:
- Метод оценки оценщика : у оценщиков есть
scoreметод, обеспечивающий критерий оценки по умолчанию для проблемы, для решения которой они предназначены. Это обсуждается не на этой странице, а в документации каждого оценщика. - Параметр оценки: инструменты оценки модели с использованием перекрестной проверки (например,
model_selection.cross_val_scoreиmodel_selection.GridSearchCV) полагаются на внутреннюю стратегию оценки . Это обсуждается в разделе Параметр оценки: определение правил оценки модели . - Метрические функции : В
sklearn.metricsмодуле реализованы функции оценки ошибки прогноза для конкретных целей. Эти показатели подробно описаны в разделах по метрикам классификации , MultiLabel ранжирования показателей , показателей регрессии и показателей кластеризации .
Наконец, фиктивные оценки полезны для получения базового значения этих показателей для случайных прогнозов.
3.3.1. В scoring параметрах: определение правил оценки моделей
Выбор и оценка модели с использованием таких инструментов, как model_selection.GridSearchCV и model_selection.cross_val_score, принимают scoring параметр, который контролирует, какую метрику они применяют к оцениваемым оценщикам.
3.3.1.1. Общие случаи: предопределенные значения
Для наиболее распространенных случаев использования вы можете назначить объект подсчета с помощью scoring параметра; в таблице ниже показаны все возможные значения. Все объекты счетчика следуют соглашению о том, что более высокие возвращаемые значения лучше, чем более низкие возвращаемые значения . Таким образом, метрики, которые измеряют расстояние между моделью и данными, например metrics.mean_squared_error, доступны как neg_mean_squared_error, которые возвращают инвертированное значение метрики.
| Подсчет очков | Функция | Комментарий |
| Классификация | ||
| ‘accuracy’ | metrics.accuracy_score |
|
| ‘balanced_accuracy’ | metrics.balanced_accuracy_score |
|
| ‘top_k_accuracy’ | metrics.top_k_accuracy_score |
|
| ‘average_precision’ | metrics.average_precision_score |
|
| ‘neg_brier_score’ | metrics.brier_score_loss |
|
| ‘f1’ | metrics.f1_score |
для двоичных целей |
| ‘f1_micro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_macro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_weighted’ | metrics.f1_score |
средневзвешенное |
| ‘f1_samples’ | metrics.f1_score |
по многопозиционному образцу |
| ‘neg_log_loss’ | metrics.log_loss |
требуетсяpredict_probaподдержка |
| ‘precision’ etc. | metrics.precision_score |
суффиксы применяются как с ‘f1’ |
| ‘recall’ etc. | metrics.recall_score |
суффиксы применяются как с ‘f1’ |
| ‘jaccard’ etc. | metrics.jaccard_score |
суффиксы применяются как с ‘f1’ |
| ‘roc_auc’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr_weighted’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo_weighted’ | metrics.roc_auc_score |
|
| Кластеризация | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score |
|
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score |
|
| ‘completeness_score’ | metrics.completeness_score |
|
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score |
|
| ‘homogeneity_score’ | metrics.homogeneity_score |
|
| ‘mutual_info_score’ | metrics.mutual_info_score |
|
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score |
|
| ‘rand_score’ | metrics.rand_score |
|
| ‘v_measure_score’ | metrics.v_measure_score |
|
| Регрессия | ||
| ‘explained_variance’ | metrics.explained_variance_score |
|
| ‘max_error’ | metrics.max_error |
|
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error |
|
| ‘neg_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_root_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error |
|
| ‘neg_median_absolute_error’ | metrics.median_absolute_error |
|
| ‘r2’ | metrics.r2_score |
|
| ‘neg_mean_poisson_deviance’ | metrics.mean_poisson_deviance |
|
| ‘neg_mean_gamma_deviance’ | metrics.mean_gamma_deviance |
|
| ‘neg_mean_absolute_percentage_error’ | metrics.mean_absolute_percentage_error |
Примеры использования:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sorted(sklearn.metrics.SCORERS.keys()) to get valid options.
Примечание
Значения, перечисленные в виде ValueError исключения, соответствуют функциям измерения точности прогнозирования, описанным в следующих разделах. Объекты счетчика для этих функций хранятся в словаре sklearn.metrics.SCORERS.
3.3.1.2. Определение стратегии выигрыша от метрических функций
Модуль sklearn.metrics также предоставляет набор простых функций, измеряющих ошибку предсказания с учетом истинности и предсказания:
- функции, заканчивающиеся на,
_scoreвозвращают значение для максимизации, чем выше, тем лучше. - функции, заканчивающиеся на
_errorили_lossвозвращающие значение, которое нужно минимизировать, чем ниже, тем лучше. При преобразовании в объект счетчика с использованиемmake_scorerустановите дляgreater_is_betterпараметра значениеFalse(Trueпо умолчанию; см. Описание параметра ниже).
Метрики, доступные для различных задач машинного обучения, подробно описаны в разделах ниже.
Многим метрикам не даются имена для использования в качестве scoring значений, иногда потому, что они требуют дополнительных параметров, например fbeta_score. В таких случаях вам необходимо создать соответствующий объект оценки. Самый простой способ создать вызываемый объект для оценки — использовать make_scorer. Эта функция преобразует метрики в вызываемые объекты, которые можно использовать для оценки модели.
Один из типичных вариантов использования — обернуть существующую метрическую функцию из библиотеки значениями, отличными от значений по умолчанию для ее параметров, такими как beta параметр для fbeta_score функции:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
Второй вариант использования — создание полностью настраиваемого объекта скоринга из простой функции Python с использованием make_scorer, которая может принимать несколько параметров:
- функция Python, которую вы хотите использовать (
my_custom_loss_funcв примере ниже) - возвращает ли функция Python оценку (
greater_is_better=True, по умолчанию) или потерю (greater_is_better=False). В случае потери результат функции python аннулируется объектом скоринга в соответствии с соглашением о перекрестной проверке, согласно которому скоринтеры возвращают более высокие значения для лучших моделей. - только для показателей классификации: требуется ли для предоставленной вами функции Python постоянная уверенность в принятии решений (
needs_threshold=True). Значение по умолчанию неверно. - любые дополнительные параметры, такие как
betaилиlabelsвf1_score.
Вот пример создания пользовательских счетчиков очков и использования greater_is_better параметра:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
3.3.1.3. Реализация собственного скорингового объекта
Вы можете сгенерировать еще более гибкие модели скоринга, создав свой собственный скоринговый объект с нуля, без использования make_scorer фабрики. Чтобы вызываемый может быть бомбардиром, он должен соответствовать протоколу, указанному в следующих двух правилах:
- Его можно вызвать с параметрами (estimator, X, y), где estimator это модель, которая должна быть оценена, X это данные проверки и y основная истинная цель для (в контролируемом случае) или None (в неконтролируемом случае).
- Он возвращает число с плавающей запятой, которое количественно определяет
estimatorкачество прогнозированияXсо ссылкой наy. Опять же, по соглашению более высокие числа лучше, поэтому, если ваш секретарь сообщает о проигрыше, это значение следует отменить.
Примечание Использование пользовательских счетчиков в функциях, где n_jobs> 1
Хотя определение пользовательской функции оценки вместе с вызывающей функцией должно работать из коробки с бэкэндом joblib по умолчанию (loky), его импорт из другого модуля будет более надежным подходом и будет работать независимо от бэкэнда joblib.
Например, чтобы использовать n_jobsбольше 1 в примере ниже, custom_scoring_function функция сохраняется в созданном пользователем модуле ( custom_scorer_module.py) и импортируется:
>>> from custom_scorer_module import custom_scoring_function >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1)
3.3.1.4. Использование множественной метрической оценки
Scikit-learn также позволяет оценивать несколько показателей в GridSearchCV, RandomizedSearchCV и cross_validate.
Есть три способа указать несколько показателей оценки для scoring параметра:
- Как итерация строковых показателей:
>>> scoring = ['accuracy', 'precision']
- В качестве
dictсопоставления имени секретаря с функцией подсчета очков:
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
Обратите внимание, что значения dict могут быть либо функциями счетчика, либо одной из предварительно определенных строк показателей.
- Как вызываемый объект, возвращающий словарь оценок:
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
... y_pred = clf.predict(X)
... cm = confusion_matrix(y, y_pred)
... return {'tn': cm[0, 0], 'fp': cm[0, 1],
... 'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
... scoring=confusion_matrix_scorer)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
3.3.2. Метрики классификации
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности классификации. Некоторые метрики могут потребовать оценок вероятности положительного класса, значений достоверности или значений двоичных решений. Большинство реализаций позволяют каждой выборке вносить взвешенный вклад в общую оценку с помощью sample_weight параметра.
Некоторые из них ограничены случаем двоичной классификации:
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
roc_curve(y_true, y_score, *[, pos_label, …]) |
Вычислить рабочую характеристику приемника (ROC). |
det_curve(y_true, y_score[, pos_label, …]) |
Вычислите частоту ошибок для различных пороговых значений вероятности. |
Другие также работают в случае мультикласса:
balanced_accuracy_score(y_true, y_pred, *[, …]) |
Вычислите сбалансированную точность. |
cohen_kappa_score(y1, y2, *[, labels, …]) |
Каппа Коэна: статистика, измеряющая согласованность аннотаторов. |
confusion_matrix(y_true, y_pred, *[, …]) |
Вычислите матрицу неточностей, чтобы оценить точность классификации. |
hinge_loss(y_true, pred_decision, *[, …]) |
Средняя потеря петель (нерегулируемая). |
matthews_corrcoef(y_true, y_pred, *[, …]) |
Вычислите коэффициент корреляции Мэтьюза (MCC). |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
top_k_accuracy_score(y_true, y_score, *[, …]) |
Top-k Рейтинг по классификации точности. |
Некоторые также работают в многоярусном регистре:
accuracy_score(y_true, y_pred, *[, …]) |
Классификационная оценка точности. |
classification_report(y_true, y_pred, *[, …]) |
Создайте текстовый отчет, показывающий основные показатели классификации. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
hamming_loss(y_true, y_pred, *[, sample_weight]) |
Вычислите среднюю потерю Хэмминга. |
jaccard_score(y_true, y_pred, *[, labels, …]) |
Оценка коэффициента сходства Жаккара. |
log_loss(y_true, y_pred, *[, eps, …]) |
Потеря журнала, также известная как потеря логистики или потеря кросс-энтропии. |
multilabel_confusion_matrix(y_true, y_pred, *) |
Вычислите матрицу неточностей для каждого класса или образца. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите отзыв. |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
zero_one_loss(y_true, y_pred, *[, …]) |
Потеря классификации нулевая единица. |
А некоторые работают с двоичными и многозначными (но не мультиклассовыми) проблемами:
В следующих подразделах мы опишем каждую из этих функций, которым будут предшествовать некоторые примечания по общему API и определению показателей.
3.3.2.1. От бинарного до мультиклассового и многозначного
Некоторые метрики по существу определены для задач двоичной классификации (например f1_score, roc_auc_score). В этих случаях по умолчанию оценивается только положительная метка, предполагая по умолчанию, что положительный класс помечен 1 (хотя это можно настроить с помощью pos_label параметра).
При расширении двоичной метрики на задачи с несколькими классами или метками данные обрабатываются как набор двоичных задач, по одной для каждого класса. Затем есть несколько способов усреднить вычисления двоичных показателей по набору классов, каждый из которых может быть полезен в некотором сценарии. Если возможно, вы должны выбрать одно из них с помощью average параметра.
"macro"просто вычисляет среднее значение двоичных показателей, придавая каждому классу одинаковый вес. В задачах, где редкие занятия тем не менее важны, макро-усреднение может быть средством выделения их производительности. С другой стороны, предположение, что все классы одинаково важны, часто неверно, так что макро-усреднение будет чрезмерно подчеркивать обычно низкую производительность для нечастого класса."weighted"учитывает дисбаланс классов, вычисляя среднее значение двоичных показателей, в которых оценка каждого класса взвешивается по его присутствию в истинной выборке данных."micro"дает каждой паре выборка-класс равный вклад в общую метрику (за исключением результата взвешивания выборки). Вместо того, чтобы суммировать метрику для каждого класса, это суммирует дивиденды и делители, составляющие метрики для каждого класса, для расчета общего частного. Микро-усреднение может быть предпочтительным в настройках с несколькими ярлыками, включая многоклассовую классификацию, когда класс большинства следует игнорировать."samples"применяется только к задачам с несколькими ярлыками. Он не вычисляет меру для каждого класса, вместо этого вычисляет метрику по истинным и прогнозируемым классам для каждой выборки в данных оценки и возвращает их (sample_weight— взвешенное) среднее значение.- Выбор
average=Noneвернет массив с оценкой для каждого класса.
В то время как данные мультикласса предоставляются метрике, как двоичные цели, в виде массива меток классов, данные с несколькими метками указываются как индикаторная матрица, в которой ячейка [i, j] имеет значение 1, если у образца i есть метка j, и значение 0 в противном случае.
3.3.2.2. Оценка точности
Функция accuracy_score вычисляет точность , либо фракции ( по умолчанию) или количество (нормализует = False) правильных предсказаний.
В классификации с несколькими ярлыками функция возвращает точность подмножества. Если весь набор предсказанных меток для выборки строго соответствует истинному набору меток, то точность подмножества равна 1,0; в противном случае — 0, 0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)$$
где $1(x)$- индикаторная функция .
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
В многопозиционном корпусе с бинарными индикаторами меток:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
Пример:
- См. В разделе Проверка с перестановками значимости классификационной оценки пример использования показателя точности с использованием перестановок набора данных.
3.3.2.3. Рейтинг точности Top-k
Функция top_k_accuracy_score представляет собой обобщение accuracy_score. Разница в том, что прогноз считается правильным, если истинная метка связана с одним из kнаивысших прогнозируемых баллов. accuracy_score является частным случаем k = 1.
Функция охватывает случаи двоичной и многоклассовой классификации, но не случай многозначной классификации.
Если $hat{f}_{i,j}$ прогнозируемый класс для $i$-й образец, соответствующий $j$-й по величине прогнозируемый результат и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)$$
где k допустимое количество предположений и 1(x)- индикаторная функция.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
3.3.2.4. Сбалансированный показатель точности
Функция balanced_accuracy_score вычисляет взвешенную точность , что позволяет избежать завышенных оценок производительности на несбалансированных данных. Это макросреднее количество оценок отзыва по классу или, что то же самое, грубая точность, где каждая выборка взвешивается в соответствии с обратной распространенностью ее истинного класса. Таким образом, для сбалансированных наборов данных оценка равна точности.
В двоичном случае сбалансированная точность равна среднему арифметическому чувствительности (истинно положительный показатель) и специфичности (истинно отрицательный показатель) или площади под кривой ROC с двоичными прогнозами, а не баллами:
$$texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )$$
Если классификатор одинаково хорошо работает в любом классе, этот термин сокращается до обычной точности (т. е. Количества правильных прогнозов, деленного на общее количество прогнозов).
Напротив, если обычная точность выше вероятности только потому, что классификатор использует несбалансированный набор тестов, тогда сбалансированная точность, при необходимости, упадет до $frac{1}{n_classes}$.
Оценка варьируется от 0 до 1 или, когда adjusted=True используется, масштабируется до диапазона $frac{1}{1 — n_classes}$ до 1 включительно, с произвольной оценкой 0.
Если yi истинная ценность $i$-й образец, и $w_i$ — соответствующий вес образца, затем мы настраиваем вес образца на:
$$hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}$$
где $1(x)$- индикаторная функция . Учитывая предсказанный $hat{y}_i$ для образца $i$, сбалансированная точность определяется как:
$$texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i$$
С adjusted=True сбалансированной точностью сообщает об относительном увеличении от $texttt{balanced-accuracy}(y, mathbf{0}, w) =frac{1}{n_classes}$. В двоичном случае это также известно как * статистика Юдена * , или информированность .
Примечание
Определение мультикласса здесь кажется наиболее разумным расширением метрики, используемой в бинарной классификации, хотя в литературе нет определенного консенсуса:
- Наше определение: [Mosley2013] , [Kelleher2015] и [Guyon2015] , где [Guyon2015] принимает скорректированную версию, чтобы гарантировать, что случайные предсказания имеют оценку 0 а точные предсказания имеют оценку 1..
- Точность балансировки классов, как описано в [Mosley2013] : вычисляется минимум между точностью и отзывом для каждого класса. Затем эти значения усредняются по общему количеству классов для получения сбалансированной точности.
- Сбалансированная точность, как описано в [Urbanowicz2015] : среднее значение чувствительности и специфичности вычисляется для каждого класса, а затем усредняется по общему количеству классов.
Рекомендации:
- Гийон 2015 ( 1 , 2 ) И. Гайон, К. Беннет, Г. Коули, Х. Дж. Эскаланте, С. Эскалера, Т. К. Хо, Н. Масиа, Б. Рэй, М. Саид, А. Р. Статников, Э. Вьегас, Дизайн конкурса ChaLearn AutoML Challenge 2015 , IJCNN 2015 г.
- Мосли 2013 ( 1 , 2 ) Л. Мосли, Сбалансированный подход к проблеме мультиклассового дисбаланса , IJCV 2010.
- Kelleher2015 Джон. Д. Келлехер, Брайан Мак Нейме, Аойф Д’Арси, Основы машинного обучения для прогнозной аналитики данных: алгоритмы, рабочие примеры и тематические исследования , 2015.
- Урбанович2015 Urbanowicz RJ, Moore, JH ExSTraCS 2.0: описание и оценка масштабируемой системы классификаторов обучения , Evol. Intel. (2015) 8:89.
3.3.2.5. Каппа Коэна
Функция cohen_kappa_score вычисляет каппа-Коэна статистику. Эта мера предназначена для сравнения меток, сделанных разными людьми-аннотаторами, а не классификатором с достоверной информацией.
Показатель каппа (см. Строку документации) представляет собой число от -1 до 1. Баллы выше 0,8 обычно считаются хорошим совпадением; ноль или ниже означает отсутствие согласия (практически случайные метки).
Оценка Каппа может быть вычислена для двоичных или многоклассовых задач, но не для задач с несколькими метками (за исключением ручного вычисления оценки для каждой метки) и не более чем для двух аннотаторов.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
3.3.2.6. Матрица неточностей ¶
Точность функции confusion_matrix вычисляет классификацию пути вычисления матрицы путаницы с каждой строкой , соответствующей истинный классом (Википедия и другие ссылки могут использовать различные конвенции для осей).
По определению запись i,j в матрице неточностей — количество наблюдений в группе i, но предполагается, что он будет в группе j. Вот пример:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
plot_confusion_matrix может использоваться для визуального представления матрицы неточностей, как показано в примере матрицы неточностей, который создает следующий рисунок:
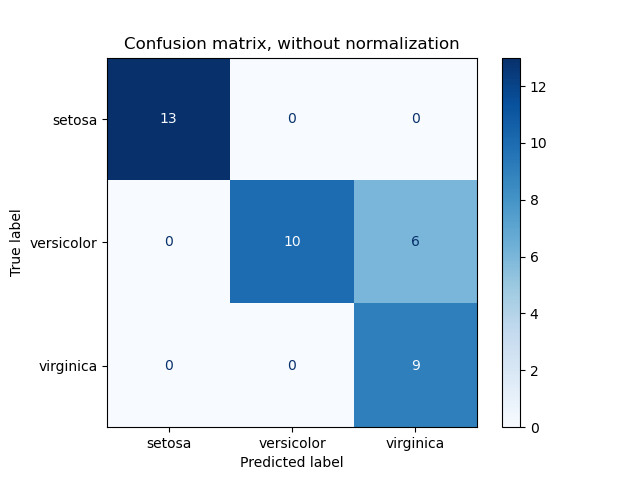
Параметр normalize позволяет сообщать коэффициенты вместо подсчетов. Матрица путаница может быть нормализована в 3 различными способами: 'pred', 'true'и 'all' которые будут делить счетчики на сумму каждого столбца, строки или всей матрицы, соответственно.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
Для двоичных задач мы можем получить подсчет истинно отрицательных, ложноположительных, ложноотрицательных и истинно положительных результатов следующим образом:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
Пример:
- См. В разделе Матрица неточностей пример использования матрицы неточностей для оценки качества выходных данных классификатора.
- См. В разделе Распознавание рукописных цифр пример использования матрицы неточностей для классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования матрицы неточностей для классификации текстовых документов.
3.3.2.7. Отчет о классификации
Функция classification_report создает текстовый отчет , показывающий основные показатели классификации. Вот небольшой пример с настраиваемыми target_names и предполагаемыми ярлыками:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Пример:
- См. В разделе Распознавание рукописных цифр пример использования отчета о классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций, где приведен пример использования отчета о классификации для текстовых документов.
- См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример использования отчета о классификации для поиска по сетке с вложенной перекрестной проверкой.
3.3.2.8. Потеря Хэмминга
hamming_loss вычисляет среднюю потерю Хэмминга или расстояние Хемминга между двумя наборами образцов.
Если $hat{y}_j$ прогнозируемое значение для $j$-я этикетка данного образца, $y_j$ — соответствующее истинное значение, а $n_{labels}$ — количество классов или меток, то потеря Хэмминга $L_{Hamming}$ между двумя образцами определяется как:
$$L_{Hamming}(y, hat{y}) = frac{1}{n_text{labels}} sum_{j=0}^{n_text{labels} — 1} 1(hat{y}_j not= y_j)$$
где $1(x)$- индикаторная функция .
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
В многопозиционном корпусе с бинарными индикаторами меток:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Примечание
В мультиклассовой классификации потери Хэмминга соответствуют расстоянию Хэмминга между y_true и, y_pred что аналогично функции потерь нуля или единицы . Однако, в то время как потеря нуля или единицы наказывает наборы предсказаний, которые не строго соответствуют истинным наборам, потеря Хэмминга наказывает отдельные метки. Таким образом, потеря Хэмминга, ограниченная сверху потерей нуля или единицы, всегда находится между нулем и единицей включительно; и прогнозирование надлежащего подмножества или надмножества истинных меток даст исключительную потерю Хэмминга от нуля до единицы.
3.3.2.9. Точность, отзыв и F-меры
Интуитивно, точность — это способность классификатора не маркировать как положительный образец, который является отрицательным, а отзыв — это способность классификатора находить все положительные образцы.
F-мера ($F_beta$ а также $F_1$ меры) можно интерпретировать как взвешенное гармоническое среднее значение точности и полноты. А $F_beta$ мера достигает своего лучшего значения на уровне 1 и худшего результата на уровне 0. С $beta = 1$, $F_beta$ а также $F_1$ эквивалентны, а отзыв и точность одинаково важны.
precision_recall_curve вычисляет кривую точности-отзыва на основе наземной метки истинности и оценки, полученной классификатором путем изменения порога принятия решения.
Функция average_precision_score вычисляет среднюю точность (AP) от оценки прогнозирования. Значение от 0 до 1 и выше — лучше. AP определяется как
$$text{AP} = sum_n (R_n — R_{n-1}) P_n$$
где $P_n$ а также $R_n$- точность и отзыв на n-м пороге. При случайных прогнозах AP — это доля положительных образцов.
Ссылки [Manning2008] и [Everingham2010] представляют альтернативные варианты AP, которые интерполируют кривую точности-отзыва. В настоящее время average_precision_score не реализован какой-либо вариант с интерполяцией. Ссылки [Davis2006] и [Flach2015] описывают, почему линейная интерполяция точек на кривой точности-отзыва обеспечивает чрезмерно оптимистичный показатель эффективности классификатора. Эта линейная интерполяция используется при вычислении площади под кривой с помощью правила трапеции в auc.
Несколько функций позволяют анализировать точность, отзыв и оценку F-мер:
average_precision_score(y_true, y_score, *) |
Вычислить среднюю точность (AP) из оценок прогнозов. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите рекол. |
Обратите внимание, что функция precision_recall_curve ограничена двоичным регистром. Функция average_precision_score работает только в двоичном формате классификации и MultiLabel индикатора. В функции plot_precision_recall_curve графики точности вспомнить следующим образом .
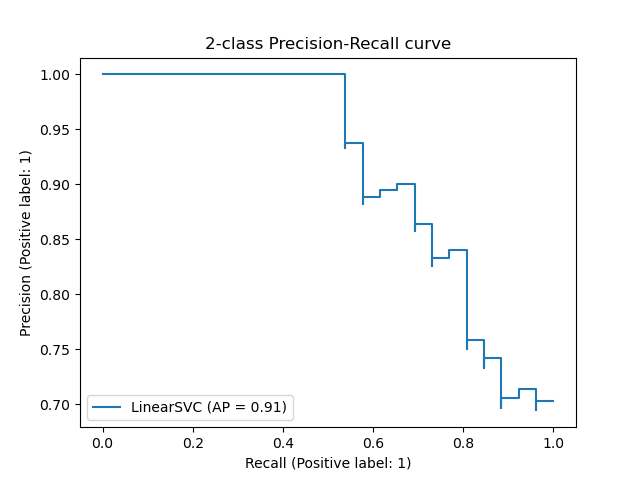
Примеры:
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования
f1_scoreдля классификации текстовых документов. - См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример
precision_scoreиrecall_scoreиспользование для оценки параметров с помощью поиска по сетке с вложенной перекрестной проверкой. - См. В разделе Precision-Recall пример использования
precision_recall_curveдля оценки качества вывода классификатора.
Рекомендации:
- [Manning2008] г. CD Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval , 2008.
- [Everingham2010] М. Эверингем, Л. Ван Гул, CKI Уильямс, Дж. Винн, А. Зиссерман, Задача классов визуальных объектов Pascal (VOC) , IJCV 2010.
- [Davis2006] Дж. Дэвис, М. Гоадрич, Взаимосвязь между точным воспроизведением и кривыми ROC , ICML 2006.
- [Flach2015] П.А. Флэч, М. Кулл, Кривые точности-отзыва-выигрыша: PR-анализ выполнен правильно , NIPS 2015.
3.3.2.9.1. Бинарная классификация
В задаче бинарной классификации термины «положительный» и «отрицательный» относятся к предсказанию классификатора, а термины «истинный» и «ложный» относятся к тому, соответствует ли этот прогноз внешнему суждению ( иногда известное как «наблюдение»). Учитывая эти определения, мы можем сформулировать следующую таблицу:
| Фактический класс (наблюдение) | ||
| Прогнозируемый класс (ожидание) | tp (истинно положительный результат) Правильный результат | fp (ложное срабатывание) Неожиданный результат |
| Прогнозируемый класс (ожидание) | fn (ложноотрицательный) Отсутствует результат | tn (истинно отрицательное) Правильное отсутствие результата |
В этом контексте мы можем определить понятия точности, отзыва и F-меры:
$$text{precision} = frac{tp}{tp + fp},$$
$$text{recall} = frac{tp}{tp + fn},$$
$$F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.$$
Вот несколько небольших примеров бинарной классификации:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 0.5, 0.5, 0. ]) >>> threshold array([0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
3.3.2.9.2. Мультиклассовая и многозначная классификация
В задаче классификации по нескольким классам и меткам понятия точности, отзыва и F-меры могут применяться к каждой метке независимо. Есть несколько способов , чтобы объединить результаты по этикеткам, указанных в average аргументе к average_precision_score (MultiLabel только) f1_score, fbeta_score, precision_recall_fscore_support, precision_score и recall_score функция, как описано выше . Обратите внимание, что если включены все метки, «микро» -усреднение в настройке мультикласса обеспечит точность, отзыв и $F$ все они идентичны по точности. Также обратите внимание, что «взвешенное» усреднение может дать оценку F, которая не находится между точностью и отзывом.
Чтобы сделать это более явным, рассмотрим следующие обозначения:
- $y$ набор предсказанных ($sample$, $label$) пары
- $hat{y}$ набор истинных ($sample$, $label$) пары
- $L$ набор лейблов
- $S$ набор образцов
- $y_s$ подмножество $y$ с образцом $s$, т.е $y_s := left{(s’, l) in y | s’ = sright}$.
- $y_l$ подмножество $y$ с этикеткой $l$
- по аналогии, $hat{y}_s$ а также $hat{y}_l$ являются подмножествами $hat{y}$
- $P(A, B) := frac{left| A cap B right|}{left|Aright|}$ для некоторых наборов $A$ и $B$
- $R(A, B) := frac{left| A cap B right|}{left|Bright|}$ (Условные обозначения различаются в зависимости от обращения $B = emptyset$; эта реализация использует $R(A, B):=0$, и аналогичные для $P$.)
- $$F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)}$$
Тогда показатели определяются как:
| average | Точность | Отзывать | F_beta |
| «micro» | $P(y, hat{y})$ | $R(y, hat{y})$ | $F_beta(y, hat{y})$ |
| «samples» | $frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s)$ |
| «macro» | $frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l)$ |
| «weighted» | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| P(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| R(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}lright| Fbeta(y_l, hat{y}_l)$ |
| None | $langle P(y_l, hat{y}_l) | l in L rangle$ | $langle R(y_l, hat{y}_l) | l in L rangle$ | $langle F_beta(y_l, hat{y}_l) | l in L rangle$ |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
Для мультиклассовой классификации с «отрицательным классом» можно исключить некоторые метки:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Точно так же метки, отсутствующие в выборке данных, могут учитываться при макро-усреднении.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
3.3.2.10. Оценка коэффициента сходства Жаккара
Функция jaccard_score вычисляет среднее значение коэффициентов сходства Jaccard , также называемый индексом Jaccard, между парами множеств меток.
Коэффициент подобия Жаккара i-ые образцы, с набором меток наземной достоверности yi и прогнозируемый набор меток y^i, определяется как
$$J(y_i, hat{y}_i) = frac{|y_i cap hat{y}_i|}{|y_i cup hat{y}_i|}.$$
jaccard_score работает как precision_recall_fscore_support наивно установленная мера, применяемая изначально к бинарным целям, и расширена для применения к множественным меткам и мультиклассам за счет использования average(см. выше ).
В двоичном случае:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
В многопозиционном корпусе с бинарными индикаторами меток:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Задачи с несколькими классами преобразуются в двоичную форму и обрабатываются как соответствующая задача с несколькими метками:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
3.3.2.11. Петля лосс
Функция hinge_loss вычисляет среднее расстояние между моделью и данными с использованием петля лосс, односторонний показателем , который учитывает только ошибки прогнозирования. (Потери на шарнирах используются в классификаторах максимальной маржи, таких как опорные векторные машины.)
Если метки закодированы с помощью +1 и -1, $y$: истинное значение, а $w$ — прогнозируемые решения на выходе decision_function, тогда потери на шарнирах определяются как:
$$L_text{Hinge}(y, w) = maxleft{1 — wy, 0right} = left|1 — wyright|_+$$
Если имеется более двух ярлыков, hinge_loss используется мультиклассовый вариант, разработанный Crammer & Singer. Вот статья, описывающая это.
Если $y_w$ прогнозируемое решение для истинного лейбла и $y_t$ — это максимум предсказанных решений для всех других меток, где предсказанные решения выводятся функцией принятия решений, тогда потеря шарнира в нескольких классах определяется следующим образом:
$$L_text{Hinge}(y_w, y_t) = maxleft{1 + y_t — y_w, 0right}$$
Вот небольшой пример, демонстрирующий использование hinge_loss функции с классификатором svm в задаче двоичного класса:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Вот пример, демонстрирующий использование hinge_loss функции с классификатором svm в мультиклассовой задаче:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels) 0.56...
3.3.2.12. Лог лосс
Лог лосс, также называемые потерями логистической регрессии или кросс-энтропийными потерями, определяются на основе оценок вероятности. Он обычно используется в (полиномиальной) логистической регрессии и нейронных сетях, а также в некоторых вариантах максимизации ожидания и может использоваться для оценки выходов вероятности ( predict_proba) классификатора вместо его дискретных прогнозов.
Для двоичной классификации с истинной меткой $y in {0,1}$ и оценка вероятности $p = operatorname{Pr}(y = 1)$, логарифмическая потеря на выборку представляет собой отрицательную логарифмическую вероятность классификатора с истинной меткой:
$$L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 — y) log (1 — p))$$
Это распространяется на случай мультикласса следующим образом. Пусть истинные метки для набора выборок будут закодированы размером 1 из K как двоичная индикаторная матрица $Y$, т.е. $y_{i,k}=1$ если образец $i$ есть ярлык $k$ взят из набора $K$ этикетки. Пусть $P$ — матрица оценок вероятностей, с $p_{i,k} = operatorname{Pr}(y_{i,k} = 1)$. Тогда потеря журнала всего набора равна
$$L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = — frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}$$
Чтобы увидеть, как это обобщает приведенную выше потерю двоичного журнала, обратите внимание, что в двоичном случае $p_{i,0} = 1 — p_{i,1}$ и $y_{i,0} = 1 — y_{i,1}$, поэтому разложив внутреннюю сумму на $y_{i,k} in {0,1}$ дает двоичную потерю журнала.
В log_loss функции вычисляет журнал потеря дана список меток приземной истины и матриц вероятностей, возвращенный оценщик predict_proba методом.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
Первое [.9, .1] в y_pred означает 90% вероятность того, что первая выборка будет иметь метку 0. Лог лос неотрицательны.
3.3.2.13. Коэффициент корреляции Мэтьюза
Функция matthews_corrcoef вычисляет коэффициент корреляции Матфея (MCC) для двоичных классов. Цитата из Википедии:
«Коэффициент корреляции Мэтьюза используется в машинном обучении как мера качества двоичных (двухклассных) классификаций. Он учитывает истинные и ложные положительные и отрицательные результаты и обычно рассматривается как сбалансированная мера, которую можно использовать, даже если классы очень разных размеров. MCC — это, по сути, значение коэффициента корреляции между -1 и +1. Коэффициент +1 представляет собой идеальное предсказание, 0 — среднее случайное предсказание и -1 — обратное предсказание. Статистика также известна как коэффициент фи ».
В бинарном (двухклассовом) случае $tp$, $tn$, $fp$ а также $fn$ являются соответственно количеством истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных результатов, MCC определяется как
$$MCC = frac{tp times tn — fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.$$
В случае мультикласса коэффициент корреляции Мэтьюза может быть определен в терминах confusion_matrix C для Kклассы. Чтобы упростить определение, рассмотрим следующие промежуточные переменные:
- $t_k=sum_{i}^{K} C_{ik}$ количество занятий k действительно произошло,
- $p_k=sum_{i}^{K} C_{ki}$ количество занятий k был предсказан,
- $c=sum_{k}^{K} C_{kk}$ общее количество правильно спрогнозированных образцов,
- $s=sum_{i}^{K} sum_{j}^{K} C_{ij}$ общее количество образцов.
Тогда мультиклассовый MCC определяется как:
$$MCC = frac{ c times s — sum_{k}^{K} p_k times t_k }{sqrt{ (s^2 — sum_{k}^{K} p_k^2) times (s^2 — sum_{k}^{K} t_k^2) }}$$
Когда имеется более двух меток, значение MCC больше не будет находиться в диапазоне от -1 до +1. Вместо этого минимальное значение будет где-то между -1 и 0 в зависимости от количества и распределения наземных истинных меток. Максимальное значение всегда +1.
Вот небольшой пример, иллюстрирующий использование matthews_corrcoef функции:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
3.3.2.14. Матрица путаницы с несколькими метками
Функция multilabel_confusion_matrix вычисляет класс-накрест ( по умолчанию) или samplewise (samplewise = True) MultiLabel матрицы спутанности для оценки точности классификации. Multilabel_confusion_matrix также обрабатывает данные мультикласса, как если бы они были многоклассовыми, поскольку это преобразование, обычно применяемое для оценки проблем мультикласса с метриками двоичной классификации (такими как точность, отзыв и т. д.).
При вычислении классовой матрицы путаницы с несколькими метками $C$, количество истинных негативов для класса i является $C_{i,0,0}$, ложноотрицательные $C_{i,1,0}$, истинные положительные стороны $C_{i,1,1}$ а ложные срабатывания $C_{i,0,1}$.
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с вводом многозначной индикаторной матрицы:
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
Или можно построить матрицу неточностей для каждой метки образца:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
[1, 1]],
[[1, 1],
[0, 1]]])
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с многоклассовым вводом:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
Вот несколько примеров, демонстрирующих использование multilabel_confusion_matrix функции для расчета отзыва (или чувствительности), специфичности, количества выпадений и пропусков для каждого класса в задаче с вводом многозначной индикаторной матрицы.
Расчет отзыва (также называемого истинно положительным коэффициентом или чувствительностью) для каждого класса:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Расчет специфичности (также называемой истинно отрицательной ставкой) для каждого класса:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Расчет количества выпадений (также называемый частотой ложных срабатываний) для каждого класса:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Расчет процента промахов (также называемого ложноотрицательным показателем) для каждого класса:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
3.3.2.15. Рабочая характеристика приемника (ROC)
Функция roc_curve вычисляет рабочую характеристическую кривую приемника или кривую ROC . Цитата из Википедии:
«Рабочая характеристика приемника (ROC), или просто кривая ROC, представляет собой графический график, который иллюстрирует работу системы двоичного классификатора при изменении ее порога дискриминации. Он создается путем построения графика доли истинных положительных результатов из положительных (TPR = частота истинных положительных результатов) по сравнению с долей ложных положительных результатов из отрицательных (FPR = частота ложных положительных результатов) при различных настройках пороговых значений. TPR также известен как чувствительность, а FPR — это единица минус специфичность или истинно отрицательный показатель ».
Для этой функции требуется истинное двоичное значение и целевые баллы, которые могут быть либо оценками вероятности положительного класса, либо значениями достоверности, либо двоичными решениями. Вот небольшой пример использования roc_curve функции:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
На этом рисунке показан пример такой кривой ROC:
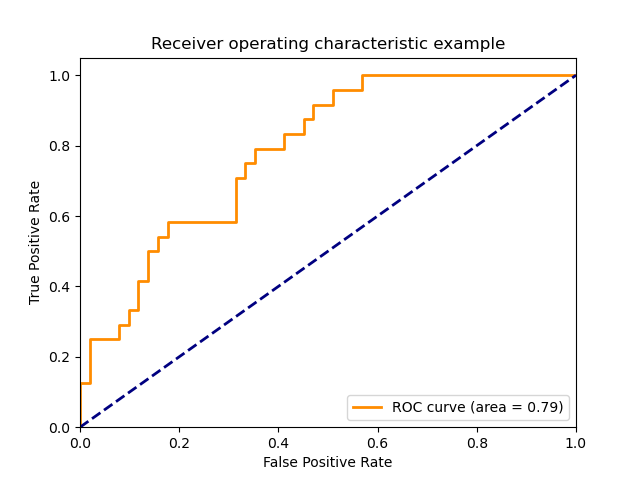
Функция roc_auc_score вычисляет площадь под операционной приемника характеристика (ROC) кривой, которая также обозначается через ППК или AUROC. При вычислении площади под кривой roc информация о кривой суммируется в одном номере. Для получения дополнительной информации см. Статью в Википедии о AUC.
По сравнению с такими показателями, как точность подмножества, потеря Хэмминга или оценка F1, ROC не требует оптимизации порога для каждой метки.
3.3.2.15.1. Двоичный регистр
В двоичном случае вы можете либо предоставить оценки вероятности, используя classifier.predict_proba() метод, либо значения решения без пороговых значений, заданные classifier.decision_function() методом. В случае предоставления оценок вероятности следует указать вероятность класса с «большей меткой». «Большая метка» соответствует classifier.classes_[1] и, следовательно classifier.predict_proba(X) [:, 1]. Следовательно, параметр y_score имеет размер (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
Мы можем использовать оценки вероятностей, соответствующие clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
В противном случае мы можем использовать значения решения без порога.
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
3.3.2.15.2. Мультиклассовый кейс
Функция roc_auc_score также может быть использована в нескольких классах классификации . В настоящее время поддерживаются две стратегии усреднения: алгоритм «один против одного» вычисляет среднее попарных оценок AUC ROC, а алгоритм «один против остальных» вычисляет среднее значение оценок ROC AUC для каждого класса по сравнению со всеми другими классами. В обоих случаях предсказанные метки предоставляются в виде массива со значениями от 0 до n_classes, а оценки соответствуют оценкам вероятности того, что выборка принадлежит определенному классу. Алгоритмы OvO и OvR поддерживают равномерное взвешивание ( average='macro') и по распространенности ( average='weighted').
Алгоритм «один против одного» : вычисляет средний AUC всех возможных попарных комбинаций классов. [HT2001] определяет метрику AUC мультикласса, взвешенную равномерно:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) + text{AUC}(k | j))$$
где $c$ количество классов и $text{AUC}(j | k)$ AUC с классом $j$ как положительный класс и класс $k$ как отрицательный класс. В общем, $text{AUC}(j | k) neq text{AUC}(k | j))$ в случае мультикласса. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'macro'.
[HT2001] мультиклассируют AUC метрика может быть расширена , чтобы быть взвешены по распространенности:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)( text{AUC}(j | k) + text{AUC}(k | j))$$
где cколичество классов. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'weighted'. В 'weighted' опции возвращает распространенность усредненные , как описано в [FC2009] .
Алгоритм «один против остальных» : вычисляет AUC каждого класса относительно остальных [PD2000] . Алгоритм функционально такой же, как и в случае с несколькими этикетками. Чтобы включить этот алгоритм, установите для аргумента ключевого слова multiclass значение 'ovr'. Как и OvO, OvR поддерживает два типа усреднения: 'macro' [F2006] и 'weighted' [F2001] .
В приложениях , где высокий процент ложных срабатываний не терпимый параметр max_fpr из roc_auc_score может быть использовано , чтобы суммировать кривую ROC до заданного предела.
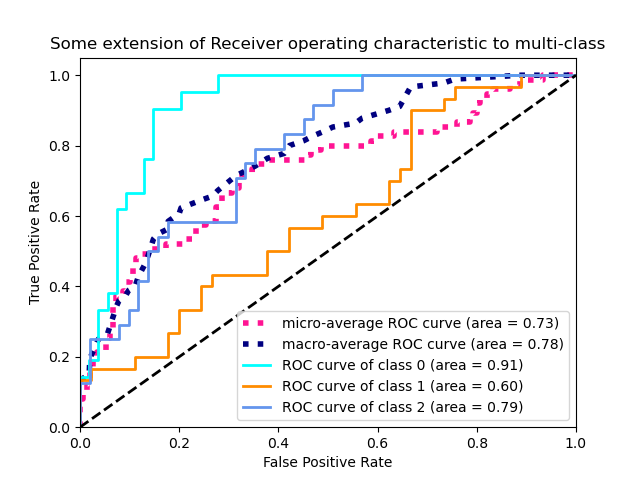
3.3.2.15.3. Кейс с несколькими метками
В классификации несколько меток, функция roc_auc_score распространяются путем усреднения меток , как выше . В этом случае вы должны указать y_score форму . Таким образом, при использовании оценок вероятности необходимо выбрать вероятность класса с большей меткой для каждого выхода.(n_samples, n_classes)
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
И значения решений не требуют такой обработки.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
Примеры:
- См. В разделе « Рабочие характеристики приемника» (ROC) пример использования ROC для оценки качества выходных данных классификатора.
- См. В разделе « Рабочие характеристики приемника» (ROC) с перекрестной проверкой пример использования ROC для оценки качества выходных данных классификатора с помощью перекрестной проверки.
- См. В разделе Моделирование распределения видов пример использования ROC для моделирования распределения видов.
- HT2001 ( 1 , 2 ) Рука, DJ и Тилль, RJ, (2001). Простое обобщение области под кривой ROC для задач классификации нескольких классов. Машинное обучение, 45 (2), стр. 171-186.
- FC2009 Ферри, Сезар и Эрнандес-Оралло, Хосе и Модройу, Р. (2009). Экспериментальное сравнение показателей эффективности для классификации. Письма о распознавании образов. 30. 27-38.
- PD2000 Провост Ф., Домингос П. (2000). Хорошо обученные ПЭТ: Улучшение деревьев оценки вероятностей (Раздел 6.2), Рабочий документ CeDER № IS-00-04, Школа бизнеса Стерна, Нью-Йоркский университет.
- F2006 Фосетт, Т., 2006. Введение в анализ ROC. Письма о распознавании образов, 27 (8), стр. 861-874.
- F2001Фосетт, Т., 2001. Использование наборов правил для максимизации производительности ROC в интеллектуальном анализе данных, 2001. Труды Международной конференции IEEE, стр. 131-138.
3.3.2.16. Компромисс при обнаружении ошибок (DET)
Функция det_curve вычисляет кривую компенсации ошибок обнаружения (DET) [WikipediaDET2017] . Цитата из Википедии:
«График компромисса ошибок обнаружения (DET) — это графическая диаграмма частоты ошибок для систем двоичной классификации, отображающая частоту ложных отклонений по сравнению с частотой ложных приемов. Оси x и y масштабируются нелинейно по их стандартным нормальным отклонениям (или просто с помощью логарифмического преобразования), в результате получаются более линейные кривые компромисса, чем кривые ROC, и большая часть области изображения используется для выделения важных различий в критический рабочий регион ».
Кривые DET представляют собой вариацию кривых рабочих характеристик приемника (ROC), где ложная отрицательная скорость нанесена на ось y вместо истинной положительной скорости. Кривые DET обычно строятся в масштабе нормального отклонения путем преобразования $phi^{-1}$ (с участием $phi$ — кумулятивная функция распределения). Полученные кривые производительности явно визуализируют компромисс типов ошибок для заданных алгоритмов классификации. См. [Martin1997], где приведены примеры и мотивация.
На этом рисунке сравниваются кривые ROC и DET двух примеров классификаторов для одной и той же задачи классификации:
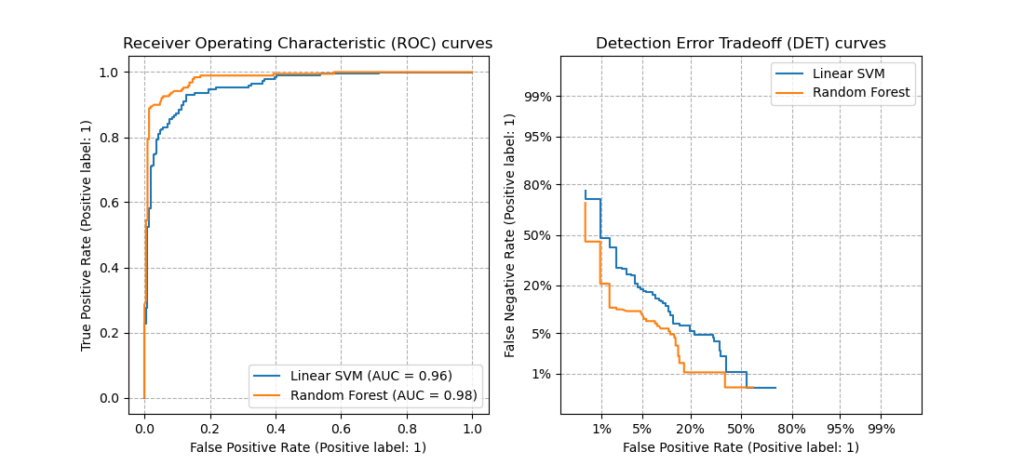
Характеристики:
- Кривые DET образуют линейную кривую по шкале нормального отклонения, если оценки обнаружения нормально (или близки к нормальному) распределены. В [Navratil2007] было показано, что обратное не обязательно верно, и даже более общие распределения могут давать линейные кривые DET.
- При обычном преобразовании масштаба с отклонением точки распределяются таким образом, что занимает сравнительно большее пространство графика. Следовательно, кривые с аналогичными характеристиками классификации легче различить на графике DET.
- С ложноотрицательной скоростью, «обратной» истинной положительной скорости, точкой совершенства для кривых DET является начало координат (в отличие от верхнего левого угла для кривых ROC).
Приложения и ограничения:
Кривые DET интуитивно понятны для чтения и, следовательно, позволяют быстро визуально оценить работу классификатора. Кроме того, кривые DET можно использовать для анализа пороговых значений и выбора рабочей точки. Это особенно полезно, если требуется сравнение типов ошибок.
С другой стороны, кривые DET не представляют свою метрику в виде единого числа. Поэтому для автоматической оценки или сравнения с другими задачами классификации лучше подходят такие показатели, как производная площадь под кривой ROC.
Примеры:
- См. Кривую компенсации ошибок обнаружения (DET) для примера сравнения кривых рабочих характеристик приемника (ROC) и кривых компенсации ошибок обнаружения (DET).
Рекомендации:
- ВикипедияDET2017 Авторы Википедии. Компромисс ошибки обнаружения. Википедия, свободная энциклопедия. 4 сентября 2017 г., 23:33 UTC. Доступно по адресу: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054 . По состоянию на 19 февраля 2018 г.
- Мартин 1997 А. Мартин, Дж. Доддингтон, Т. Камм, М. Ордовски и М. Пшибоцки, Кривая DET в оценке эффективности задач обнаружения , NIST 1997.
- Навратил2007 Дж. Наврактил и Д. Клусачек, « О линейных DET », 2007 г. Международная конференция IEEE по акустике, обработке речи и сигналов — ICASSP ’07, Гонолулу, Гавайи, 2007 г., стр. IV-229-IV-232.
3.3.2.17. Нулевой проигрыш
Функция zero_one_loss вычисляет сумму или среднее значение потери 0-1 классификации ($L_{0−1}$) над $n_{samples}$. По умолчанию функция нормализуется по выборке. Чтобы получить сумму $L_{0−1}$, установите normalize значение False.
В классификации по zero_one_loss нескольким меткам подмножество оценивается как единое целое, если его метки строго соответствуют прогнозам, и как ноль, если есть какие-либо ошибки. По умолчанию функция возвращает процент неправильно спрогнозированных подмножеств. Чтобы вместо этого получить количество таких подмножеств, установите normalize значение False
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда потеря 0-1 $L_{0−1}$ определяется как:
$$L_{0-1}(y_i, hat{y}_i) = 1(hat{y}_i not= y_i)$$
где $1(x)$- индикаторная функция.
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
В случае с несколькими метками с двоичными индикаторами меток, где первый набор меток [0,1] содержит ошибку:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
Пример:
- См. В разделе « Рекурсивное исключение функции с перекрестной проверкой» пример использования нулевой потери для выполнения рекурсивного исключения функции с перекрестной проверкой.
3.3.2.18. Потеря очков по Брайеру
Функция brier_score_loss вычисляет оценку Шиповник для бинарных классов [Brier1950] . Цитата из Википедии:
«Оценка Бриера — это правильная функция оценки, которая измеряет точность вероятностных прогнозов. Это применимо к задачам, в которых прогнозы должны назначать вероятности набору взаимоисключающих дискретных результатов ».
Эта функция возвращает среднеквадратичную ошибку фактического результата. y∈{0,1} и прогнозируемая оценка вероятности $p=Pr(y=1)$ ( pred_proba ) как выведено :
$$BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1}(y_i — p_i)^2$$
Потеря по шкале Бриера также составляет от 0 до 1, и чем ниже значение (средняя квадратичная разница меньше), тем точнее прогноз.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
Балл Бриера можно использовать для оценки того, насколько хорошо откалиброван классификатор. Однако меньшая потеря по шкале Бриера не всегда означает лучшую калибровку. Это связано с тем, что по аналогии с разложением среднеквадратичной ошибки на дисперсию смещения потеря оценки по Бриеру может быть разложена как сумма потерь калибровки и потерь при уточнении [Bella2012]. Потеря калибровки определяется как среднеквадратическое отклонение от эмпирических вероятностей, полученных из наклона ROC-сегментов. Потери при переработке можно определить как ожидаемые оптимальные потери, измеренные по площади под кривой оптимальных затрат. Потери при уточнении могут изменяться независимо от потерь при калибровке, таким образом, более низкие потери по шкале Бриера не обязательно означают более качественную калибровку модели. «Только когда потеря точности остается неизменной, более низкая потеря по шкале Бриера всегда означает лучшую калибровку» [Bella2012] , [Flach2008] .
Пример:
- См. Раздел « Калибровка вероятности классификаторов», где приведен пример использования потерь по шкале Бриера для выполнения калибровки вероятности классификаторов.
Рекомендации:
- Brier1950 Дж. Брайер, Проверка прогнозов, выраженных в терминах вероятности , Ежемесячный обзор погоды 78.1 (1950)
- Bella2012 ( 1 , 2 ) Белла, Ферри, Эрнандес-Оралло и Рамирес-Кинтана «Калибровка моделей машинного обучения» в Хосров-Пур, М. «Машинное обучение: концепции, методологии, инструменты и приложения». Херши, Пенсильвания: Справочник по информационным наукам (2012).
- Flach2008 Флак, Питер и Эдсон Мацубара. «О классификации, ранжировании и оценке вероятности». Дагштульский семинар. Schloss Dagstuhl-Leibniz-Zentrum от Informatik (2008).
3.3.3. Метрики ранжирования с несколькими ярлыками
В многоэлементном обучении с каждой выборкой может быть связано любое количество меток истинности. Цель состоит в том, чтобы дать высокие оценки и более высокий рейтинг наземным лейблам.
3.3.3.1. Ошибка покрытия
Функция coverage_error вычисляет среднее число меток , которые должны быть включены в окончательном предсказании таким образом, что все истинные метки предсказанные. Это полезно, если вы хотите знать, сколько меток с наивысшими баллами вам нужно предсказать в среднем, не пропуская ни одной истинной. Таким образом, наилучшее значение этого показателя — среднее количество истинных ярлыков.
Примечание
Оценка нашей реализации на 1 больше, чем оценка, приведенная в Tsoumakas et al., 2010. Это расширяет ее для обработки вырожденного случая, когда экземпляр имеет 0 истинных меток.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ покрытие определяется как
$$coverage(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} max_{j:y_{ij} = 1} text{rank}_{ij}$$
с участием $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$. Учитывая определение ранга, связи y_scores разрываются путем присвоения максимального ранга, который был бы присвоен всем связанным значениям.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
3.3.3.2. Средняя точность ранжирования метки
В label_ranking_average_precision_score функции реализует маркировать ранжирование средней точности (LRAP). Этот показатель связан с average_precision_score функцией, но основан на понятии ранжирования меток, а не на точности и отзыве.
Средняя точность ранжирования меток (LRAP) усредняет по выборкам ответ на следующий вопрос: для каждой основной метки истинности какая доля меток с более высоким рейтингом была истинной? Этот показатель эффективности будет выше, если вы сможете лучше ранжировать метки, связанные с каждым образцом. Полученная оценка всегда строго больше 0, а наилучшее значение равно 1. Если имеется ровно одна релевантная метка для каждой выборки, средняя точность ранжирования меток эквивалентна среднему обратному рангу .
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$, средняя точность определяется как
$$LRAP(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0} sum{j:y_{ij} = 1} frac{|mathcal{L}{ij}|}{text{rank}{ij}}$$
где $mathcal{L}{ij} = left{k: y{ik} = 1, hat{f}{ik} geq hat{f}{ij} right}$, $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$, |cdot| вычисляет мощность набора (т. е. количество элементов в наборе), и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
3.3.3.3. Потеря рейтинга
Функция label_ranking_loss вычисляет ранжирование потери , которые в среднем более образцы числа пар меток, которые неправильно упорядочены, т.е. истинные метки имеют более низкую оценку , чем ложные метки, взвешенную по обратной величине числа упорядоченных пар ложных и истинных меток. Наименьшая возможная потеря рейтинга равна нулю.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ потеря ранжирования определяется как
$$ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0(ntext{labels} — ||y_i||0)} left|left{(k, l): hat{f}{ik} leq hat{f}{il}, y{ik} = 1, y_{il} = 0 right}right|$$
где $|cdot|$ вычисляет мощность набора (т. е. количество элементов в наборе) и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
Рекомендации:
- Цумакас, Г., Катакис, И., и Влахавас, И. (2010). Майнинг данных с несколькими метками. В справочнике по интеллектуальному анализу данных и открытию знаний (стр. 667-685). Springer США.
3.3.3.4. Нормализованная дисконтированная совокупная прибыль
Дисконтированный совокупный выигрыш (DCG) и Нормализованный дисконтированный совокупный выигрыш (NDCG) — это показатели ранжирования, реализованные в dcg_score и ndcg_score; они сравнивают предсказанный порядок с оценками достоверности, такими как релевантность ответов на запрос.
Со страницы Википедии о дисконтированной совокупной прибыли:
«Дисконтированная совокупная прибыль (DCG) — это показатель качества ранжирования. При поиске информации он часто используется для измерения эффективности алгоритмов поисковой системы или связанных приложений. Используя шкалу градуированной релевантности документов в наборе результатов поисковой системы, DCG измеряет полезность или выгоду документа на основе его позиции в списке результатов. Прирост накапливается сверху вниз в списке результатов, причем прирост каждого результата дисконтируется на более низких уровнях »
DCG упорядочивает истинные цели (например, релевантность ответов на запросы) в предсказанном порядке, затем умножает их на логарифмическое убывание и суммирует результат. Сумма может быть усечена после первогоKрезультатов, и в этом случае мы называем это DCG @ K. NDCG или NDCG @ $K$ — это DCG, деленная на DCG, полученную с помощью точного прогноза, так что оно всегда находится между 0 и 1. Обычно NDCG предпочтительнее DCG.
По сравнению с потерей ранжирования, NDCG может принимать во внимание оценки релевантности, а не ранжирование на основе фактов. Таким образом, если основополагающая информация состоит только из упорядочивания, предпочтение следует отдавать потере ранжирования; если основополагающая информация состоит из фактических оценок полезности (например, 0 для нерелевантного, 1 для релевантного, 2 для очень актуального), можно использовать NDCG.
Для одного образца, учитывая вектор непрерывных значений истинности для каждой цели $y in R^M$, где $M$ это количество выходов, а прогноз $hat{y}$, что индуцирует функцию ранжирования $f$, оценка DCG составляет
$$sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}$$
а оценка NDCG — это оценка DCG, деленная на оценку DCG, полученную для $y$.
Рекомендации:
- Запись в Википедии о дисконтированной совокупной прибыли
- Джарвелин, К., и Кекалайнен, Дж. (2002). Оценка IR методов на основе накопленного коэффициента усиления. Транзакции ACM в информационных системах (TOIS), 20 (4), 422-446.
- Ван, Ю., Ван, Л., Ли, Ю., Хе, Д., Чен, В., и Лю, Т. Ю. (2013, май). Теоретический анализ показателей рейтинга NDCG. В материалах 26-й ежегодной конференции по теории обучения (COLT 2013)
- МакШерри Ф. и Наджорк М. (2008, март). Эффективность вычислений при поиске информации измеряется эффективно при наличии связанных оценок. В Европейской конференции по поиску информации (стр. 414-421). Шпрингер, Берлин, Гейдельберг.
3.3.4. Метрики регрессии
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности регрессии. Некоторые из них были расширены , чтобы обработать случай multioutput: mean_squared_error, mean_absolute_error, explained_variance_score и r2_score.
У этих функций есть multioutput аргумент ключевого слова, который определяет способ усреднения результатов или проигрышей для каждой отдельной цели. По умолчанию используется значение 'uniform_average', которое определяет равномерно взвешенное среднее значение по выходным данным. Если передается ndarrayформа shape (n_outputs,), то ее записи интерпретируются как веса, и возвращается соответствующее средневзвешенное значение. Если multioutputесть 'raw_values'указан, то все неизменные индивидуальные баллы или потери будут возвращены в массиве формы (n_outputs,).
r2_score и explained_variance_score принять дополнительное значение 'variance_weighted' для multioutput параметра. Эта опция приводит к взвешиванию каждой индивидуальной оценки по дисперсии соответствующей целевой переменной. Этот параметр определяет количественно зафиксированную немасштабированную дисперсию на глобальном уровне. Если целевые переменные имеют разную шкалу, то этот балл придает большее значение хорошему объяснению переменных с более высокой дисперсией. multioutput='variance_weighted' — значение по умолчанию r2_score для обратной совместимости. В будущем это будет изменено на uniform_average.
3.3.4.1. Оценка объясненной дисперсии
explained_variance_score вычисляет объясненной дисперсии регрессии балл.
Если $hat{y}$ — расчетный целевой объем производства, y соответствующий (правильный) целевой результат, и $Var$- Дисперсия , квадрат стандартного отклонения, то объясненная дисперсия оценивается следующим образом:
$$explained_{}variance(y, hat{y}) = 1 — frac{Var{ y — hat{y}}}{Var{y}}$$
Наилучшая возможная оценка — 1.0, более низкие значения — хуже.
Вот небольшой пример использования explained_variance_score функции:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990...
3.3.4.2. Максимальная ошибка
Функция max_error вычисляет максимальную остаточную ошибку , показатель , который фиксирует худшую ошибку случае между предсказанным значением и истинным значением. В идеально подобранной модели регрессии с одним выходом он max_error будет находиться 0 в обучающем наборе, и хотя это маловероятно в реальном мире, этот показатель показывает степень ошибки, которую имела модель при подборе.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда максимальная ошибка определяется как
$$text{Max Error}(y, hat{y}) = max(| y_i — hat{y}_i |)$$
Вот небольшой пример использования функции max_error:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
max_error не поддерживает multioutput.
3.3.4.3. Средняя абсолютная ошибка
Функция mean_absolute_error вычисляет среднюю абсолютную погрешность , риск метрики , соответствующей ожидаемого значение абсолютной потери или ошибок $l1$-нормальная потеря.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MAE), оцененная за $n_{samples}$ определяется как
$$text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i — hat{y}_i right|.$$
Вот небольшой пример использования функции mean_absolute_error:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
3.3.4.4. Среднеквадратичная ошибка
Функция mean_squared_error вычисляет среднюю квадратическую ошибку , риск метрики , соответствующую ожидаемое значение квадрата (квадратичной) ошибки или потерю.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная ошибка (MSE), оцененная на $n_{samples}$ определяется как
$$text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (y_i — hat{y}_i)^2.$$
Вот небольшой пример использования функции mean_squared_error:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
Примеры:
- См. В разделе Регрессия повышения градиента пример использования среднеквадратичной ошибки для оценки регрессии повышения градиента.
3.3.4.5. Среднеквадратичная логарифмическая ошибка
Функция mean_squared_log_error вычисляет риск метрики , соответствующий ожидаемому значению квадрата логарифмической (квадратичной) ошибки или потери.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная логарифмическая ошибка (MSLE), оцененная на $n_{samples}$ определяется как
$$text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (log_e (1 + y_i) — log_e (1 + hat{y}_i) )^2.$$
Где $log_e (x)$ означает натуральный логарифм $x$. Эту метрику лучше всего использовать, когда цели имеют экспоненциальный рост, например, численность населения, средние продажи товара в течение нескольких лет и т. Д. Обратите внимание, что эта метрика штрафует за заниженную оценку больше, чем за завышенную оценку.
Вот небольшой пример использования функции mean_squared_log_error:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
3.3.4.6. Средняя абсолютная ошибка в процентах
mean_absolute_percentage_error (MAPE), также известный как среднее абсолютное отклонение в процентах (МАПД), является метрикой для оценки проблем регрессии. Идея этой метрики — быть чувствительной к относительным ошибкам. Например, он не изменяется глобальным масштабированием целевой переменной.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная процентная ошибка (MAPE), оцененная за $n_{samples}$ определяется как
$$text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i — hat{y}_i right|}{max(epsilon, left| y_i right|)}$$
где $epsilon$ — произвольное маленькое, но строго положительное число, чтобы избежать неопределенных результатов, когда y равно нулю.
В функции mean_absolute_percentage_error опоры multioutput.
Вот небольшой пример использования функции mean_absolute_percentage_error:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
В приведенном выше примере, если бы мы использовали mean_absolute_error, он бы проигнорировал небольшие значения магнитуды и только отразил бы ошибку в предсказании максимального значения магнитуды. Но эта проблема решена в случае MAPE, потому что он вычисляет относительную процентную ошибку по отношению к фактическому выходу.
3.3.4.7. Средняя абсолютная ошибка
Это median_absolute_error особенно интересно, потому что оно устойчиво к выбросам. Убыток рассчитывается путем взятия медианы всех абсолютных различий между целью и прогнозом.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MedAE), оцененная на $n_{samples}$ определяется как
$$text{MedAE}(y, hat{y}) = text{median}(mid y_1 — hat{y}_1 mid, ldots, mid y_n — hat{y}_n mid).$$
median_absolute_error Не поддерживает multioutput.
Вот небольшой пример использования функции median_absolute_error:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
3.3.4.8. R² балл, коэффициент детерминации
Функция r2_score вычисляет коэффициент детерминации , как правило , обозначенный как R².
Он представляет собой долю дисперсии (y), которая была объяснена независимыми переменными в модели. Он обеспечивает показатель степени соответствия и, следовательно, меру того, насколько хорошо невидимые выборки могут быть предсказаны моделью через долю объясненной дисперсии.
Поскольку такая дисперсия зависит от набора данных, R² не может быть значимо сопоставимым для разных наборов данных. Наилучшая возможная оценка — 1,0, и она может быть отрицательной (потому что модель может быть произвольно хуже). Постоянная модель, которая всегда предсказывает ожидаемое значение y, игнорируя входные характеристики, получит оценку R² 0,0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ соответствующее истинное значение для общего n образцов, расчетный R² определяется как:
$$R^2(y, hat{y}) = 1 — frac{sum_{i=1}^{n} (y_i — hat{y}i)^2}{sum{i=1}^{n} (y_i — bar{y})^2}$$
где $bar{y} = frac{1}{n} sum_{i=1}^{n} y_i$ и $sum_{i=1}^{n} (y_i — hat{y}i)^2 = sum{i=1}^{n} epsilon_i^2$.
Обратите внимание, что r2_score вычисляется нескорректированное R² без поправки на смещение выборочной дисперсии y.
Вот небольшой пример использования функции r2_score:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925...
Пример:
- См. В разделе « Лассо и эластичная сеть для разреженных сигналов» приведен пример использования показателя R² для оценки лассо и эластичной сети для разреженных сигналов.
3.3.4.9. Средние отклонения Пуассона, Гаммы и Твиди
Функция mean_tweedie_deviance вычисляет среднюю ошибку Deviance Tweedie с powerпараметром ($p$). Это показатель, который выявляет прогнозируемые ожидаемые значения целей регрессии.
Существуют следующие особые случаи:
- когда
power=0это эквивалентноmean_squared_error. - когда
power=1это эквивалентноmean_poisson_deviance. - когда
power=2это эквивалентноmean_gamma_deviance.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя ошибка отклонения Твиди (D) для мощности $p$, оценивается более $n_{samples}$ определяется как
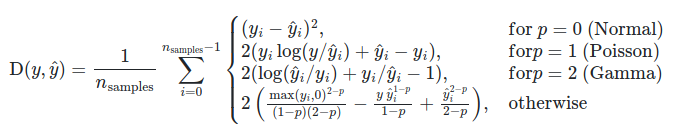
Отклонение от твиди — однородная функция степени 2-power. Таким образом, гамма-распределение power=2 означает, что одновременно масштабируется y_true и y_pred не влияет на отклонение. Для распределения Пуассона power=1 отклонение масштабируется линейно, а для нормального распределения ( power=0) — квадратично. В общем, чем выше, powerтем меньше веса придается крайним отклонениям между истинными и прогнозируемыми целевыми значениями.
Например, давайте сравним два прогноза 1.0 и 100, которые оба составляют 50% от их соответствующего истинного значения.
Среднеквадратичная ошибка ( power=0) очень чувствительна к разнице прогнозов второй точки:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
Если увеличить powerдо 1:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
разница в ошибках уменьшается. Наконец, установив power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
мы получим идентичные ошибки. Таким образом, отклонение when power=2чувствительно только к относительным ошибкам.
3.3.5. Метрики кластеризации
В модуле sklearn.metrics реализованы несколько функций потерь, оценки и полезности. Для получения дополнительной информации см. Раздел « Оценка производительности кластеризации » для кластеризации экземпляров и « Оценка бикластеризации» для бикластеризации.
3.3.6. Фиктивные оценки
При обучении с учителем простая проверка работоспособности состоит из сравнения своей оценки с простыми практическими правилами. DummyClassifier реализует несколько таких простых стратегий классификации:
stratifiedгенерирует случайные прогнозы, соблюдая распределение классов обучающего набора.most_frequentвсегда предсказывает наиболее частую метку в обучающем наборе.priorвсегда предсказывает класс, который максимизирует предыдущий класс (какmost_frequent) иpredict_probaвозвращает предыдущий класс.uniformгенерирует предсказания равномерно в случайном порядке.constantвсегда предсказывает постоянную метку, предоставленную пользователем. Основная мотивация этого метода — оценка F1, когда положительный класс находится в меньшинстве.
Обратите внимание, что со всеми этими стратегиями predict метод полностью игнорирует входные данные!
Для иллюстрации DummyClassifier сначала создадим несбалансированный набор данных:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Далее сравним точность SVC и most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
Мы видим, что SVC это не намного лучше, чем фиктивный классификатор. Теперь давайте изменим ядро:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
Мы видим, что точность увеличена почти до 100%. Для лучшей оценки точности рекомендуется стратегия перекрестной проверки, если она не требует слишком больших затрат на ЦП. Для получения дополнительной информации см. Раздел « Перекрестная проверка: оценка производительности оценщика ». Более того, если вы хотите оптимизировать пространство параметров, настоятельно рекомендуется использовать соответствующую методологию; подробности см. в разделе « Настройка гиперпараметров оценщика ».
В более общем плане, когда точность классификатора слишком близка к случайной, это, вероятно, означает, что что-то пошло не так: функции бесполезны, гиперпараметр настроен неправильно, классификатор страдает от дисбаланса классов и т. Д.
DummyRegressor также реализует четыре простых правила регрессии:
meanвсегда предсказывает среднее значение тренировочных целей.medianвсегда предсказывает медианное значение тренировочных целей.quantileвсегда предсказывает предоставленный пользователем квантиль учебных целей.constantвсегда предсказывает постоянное значение, предоставляемое пользователем.
Во всех этих стратегиях predict метод полностью игнорирует входные данные.
-
1
mean-squared error
English-Russian dictionary of Information technology > mean-squared error
-
2
mean squared error
Универсальный англо-русский словарь > mean squared error
-
3
mean-squared error
Универсальный англо-русский словарь > mean-squared error
-
4
mean-squared error
English-Russian electronics dictionary > mean-squared error
-
5
mean-squared error
The New English-Russian Dictionary of Radio-electronics > mean-squared error
-
6
mean-squared error
English-Russian dictionary of modern telecommunications > mean-squared error
-
7
mean squared error
English-Russian dictionary on experimental design > mean squared error
-
8
frequency-weighted mean-squared error measure
- мера среднеквадратичной ошибки с взвешиванием по частоте
Англо-русский словарь нормативно-технической терминологии > frequency-weighted mean-squared error measure
-
9
block mean-squared error
Большой англо-русский и русско-английский словарь > block mean-squared error
-
10
block mean-squared error
Англо-русский словарь технических терминов > block mean-squared error
-
11
block mean-squared error
Универсальный англо-русский словарь > block mean-squared error
-
12
least mean squared error
Универсальный англо-русский словарь > least mean squared error
-
13
minimum mean squared error
English-Russian dictionary on experimental design > minimum mean squared error
-
14
unconditional mean squared error
English-Russian dictionary on experimental design > unconditional mean squared error
-
15
mean integrated squared error
English-Russian dictionary on experimental design > mean integrated squared error
-
16
error
English-Russian electronics dictionary > error
-
17
error
The New English-Russian Dictionary of Radio-electronics > error
-
18
error
1) ошибка; погрешность
•
to hold measurement errors to… — удерживать погрешности измерений в пределах…;
error of position — 1. погрешность в определении положения или местоположения 2. геод. координатная невязка
Англо-русский словарь технических терминов > error
-
19
error
Английский-русский словарь по теории вероятностей, статистике и комбинаторике > error
-
20
mean
nounсредний, среднее значение
Английский-русский словарь по теории вероятностей, статистике и комбинаторике > mean
Страницы
- Следующая →
- 1
- 2
- 3
См. также в других словарях:
-
Mean squared error — In statistics, the mean squared error (MSE) of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function,… … Wikipedia
-
Mean squared error — Zwei Schätzfunktionen: Die Wahl einer verzerrten Statistik kann hinsichtlich ihrer erwarteten Abweichung vom echten Wert gegenüber einer unverzerrten vorteilhaft sein. Die mittlere quadratische Abweichung oder mittlerer quadratischer Fehler (engl … Deutsch Wikipedia
-
Mean percentage error — In statistics, the mean percentage error (MPE) is the computed average of percentage errors by which estimated forecasts differ from actual values of the quantity being forecast. Formula for mean percentage error calculation is: where at is the… … Wikipedia
-
Mean absolute error — In statistics, the mean absolute error (MAE) is a quantity used to measure how close forecasts or predictions are to the eventual outcomes. The mean absolute error is given by As the name suggests, the mean absolute error is an average of the… … Wikipedia
-
Mean squared prediction error — In statistics the mean squared prediction error of a smoothing procedure is the expected sum of squared deviations of the fitted values from the (unobservable) function g. If the smoothing procedure has operator matrix L, then The MSPE can be… … Wikipedia
-
Mean integrated squared error — In statistics, the mean integrated squared error (MISE) is used in density estimation. The MISE of an estimate of an unknown probability density is given by where ƒ is the unknown density, ƒn is its estimate based on a sample of n iid random… … Wikipedia
-
Minimum mean square error — In statistics and signal processing, a minimum mean square error (MMSE) estimator describes the approach which minimizes the mean square error (MSE), which is a common measure of estimator quality. The term MMSE specifically refers to estimation… … Wikipedia
-
Mean absolute scaled error — In statistics, the mean absolute scaled error (MASE) is a measure of the accuracy of forecasts . It was proposed in 2006 by Australian statistician Rob Hyndman, who described it as a generally applicable measurement of forecast accuracy without… … Wikipedia
-
Root mean square deviation — The root mean square deviation (RMSD) ( also root mean square error (RMSE) ) is a frequently used measure of the differences between values predicted by a model or an estimator and the values actually observed from the thing being modeled or… … Wikipedia
-
Arithmetic mean — In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space. The term arithmetic mean is preferred in mathematics and… … Wikipedia
-
Mean square quantization error — (MSQE) is a figure of merit for the process of analog to digital conversion. As the input is varied, the input s value is recorded when the digital output changes. For each digital output, the input s difference from ideal is normalized to the… … Wikipedia




![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)