Метод минимизации квадратичной ошибки

Прогнозирование временных рядов методом рядов Фурье

Привет, Хабр.

Эта статья посвящена методу долгосрочного прогнозирования временных рядов с помощью рядов Фурье [1-2]. Особенность подхода в том, что в отличие от классических методов прогнозирования и машинного обучения прогнозируется не сама неизвестная функция, а ее коэффициенты разложения в ряд Фурье. Далее по спрогнозированным коэффициентам Фурье восстанавливается неизвестная функция и делается прогноз ее значений на следующий период.

Внимание! Статья содержит множество формул.

Схематично данный метод можно проиллюстрировать следующей анимацией

План статьи

• Временные ряды
• Задача прогнозирования временных рядов
• Ряды Фурье
• Матрица задержек. Прогнозирование временных рядов на один шаг
• Долгосрочное прогнозирование временных рядов с помощью рядов Фурье
• Немного кода

Тем, кто

с мехмата/матфака

хорошо знаком с такими понятиями, как временные ряды и ряды Фурье, можно пропустить первые три раздела данной статьи.

Временной ряд

Временной ряд – значения некоторой величины, измеренные через равные промежутки времени Если принять начальное значение где тогда временной ряд можно записать в виде последовательности

где Примеры временных рядов: стоимость акции, температура воздуха, курс доллара и т.д.

Задача прогнозирования временных рядов

Задача прогнозирования временных рядов заключается в нахождении функции F:

где – отсрочка прогноза, – горизонт прогнозирования.
Т.е. по известным значениям ряда из прошлого необходимо найти его значения в будущем.

Замечание: при прогнозировании временных рядов предполагается, что прошлые значения ряда содержат информацию о его поведении в будущем. В классических же задачах анализа данных считается, что различные наблюдения независимы.

Ряды Фурье

Пусть функция непрерывна на отрезке последовательность функций

является ортонормальной на т.е.

Обозначим

тогда ряд

называется рядом Фурье. Коэффициенты (5) этого ряда называются коэффициентами Фурье функции f(x) по системе (3).
Ряд Фурье – разложение некоторой функции по полной системе ортонормированных функций (по некоторому базису).

Тригонометрические ряды Фурье
Если в качестве системы (3) взять ортонормированную на отрезке систему функций

то разложение произвольной функции f(x) по системе (7) в ряд Фурье на отрезке имеет вид

где коэффициентыи имеют вид

Ряд (8) называется тригонометрическим рядом Фурье. Ряды Фурье по другим системам называют обобщенными рядами Фурье. Далее для краткости под рядом Фурье будем понимать именно тригонометрический ряд Фурье, т.к. в данной статье мы будем иметь дело только с ним.

Теорема Дирихлe: Если функция f(x) задана на отрезке и является на нем кусочно-непрерывной, кусочно-монотонной и ограниченной, то ее тригонометрический ряд Фурье сходится во всех точках отрезка. Если s(x) – сумма тригонометрического ряда Фурье функции f(x), то во всех точках непрерывности этой функции

А во всех точках разрыва

Кроме этого,

Среди всех тригонометрических многочленов

с заданным N частичная сумма ряда Фурье

дает наилучшую (в метрике  пространства функций с интегрируемым квадратом на отрезке ) аппроксимацию функции f(x) [3]. Именно это утверждение является основой для представления функции, значения которой являются исследуемым временным рядом с некоторой периодичностью, в виде частной суммы тригонометрического ряда Фурье.
Пусть f(t) – функция с интегрируемым квадратом на отрезке Замена переводит функцию в

Для этой функции, заданной на отрезке ряд Фурье имеет вид

где

Матрица задержек. Прогнозирование временных рядов на один шаг

Дан временной ряд, содержащий m значений:

Нужно спрогнозировать значение
Одним из методов прогнозирования на один шаг является метод построения матрицы задержек. Суть метода заключается в следующем [4-5]: выбирается некоторое число p – величина задержек, подбирается зависимость значения ряда от p предыдущих значений:

Вид зависимости, как правило, выбирается линейный

Для определения коэффициентов строится матрица задержек:

Если m не кратно p то можно отбросить несколько первых членов ряда. В последней строке выбирается множество S – так называемое множество «ближайших соседей» к значению Количество элементов

Коэффициенты можно найти методом наименьших квадратов или каким-либо другим способом.

где

Из необходимого условия минимума

получаем систему уравнений для нахождения коэффициентов

Величина p выбирается эмпирически.
Можно воспользоваться матричной записью выражения (13)

и вспомнить аналитическое решение данной задачи:

Подставляя полученный вектор в выражение (11), получаем прогноз для значения ряда
Далее метод прогнозирования на один шаг будет использоваться для прогнозирования коэффициентов Фурье на следующий период.

Долгосрочное прогнозирование временных рядов с помощью рядов Фурье

Постоянная длина периода

Пусть дан временной ряд значений некоторого показателя

при этом для значений последовательности (14) наблюдается определенная периодичность. Для исследования временного ряда (14) с постоянной периодичностью (например, продажи какого-либо товара по неделям) предлагается [1-2] использовать тригонометрические ряды Фурье. В этом случае весь набор наблюдений s можно разбить на m периодов длины l+1, а массив измерений (14) можно представить в виде матрицы

размерности  в которой каждая строка является значениями показателя i-го периода (например, i-й недели).
Значения объявляются значениями некоторой функции где аргумент Функцию предлагается заменить частной суммой тригонометрического ряда Фурье по косинусам [6].

Таким образом, получаем для каждого i-го периода частичную сумму ряда Фурье со своими коэффициентами для нахождения которых можно воспользоваться несколькими способами.

1 метод. Минимизация квадратичной ошибки

где Из условия минимума

получаем систему уравнений для нахождения коэффициентов
Количество слагаемых N в этом случае нужно выбирать не более длины периода l.

2 метод. Непосредственно из формулы
Если выбрать N = l, то из формул (16) для определения коэффициентов получаем систему уравнений

3 метод. Численное интегрирование
Вспомним, что

Если длина периода l>20, то для нахождения коэффициентов можно воспользоваться формулами численного интегрирования, при этом достаточно формулы трапеций.

После того, как коэффициенты найдены, строится прогноз для следующего периода по формуле

Переменная длина периода

Пусть теперь длина периода не является постоянной (например, количество дней в месяце). Пусть l – длина i-го периода, i=1, 2, …, m. Для каждого периода i имеем последовательность значений

Пусть вновь Выполним замену переменной

Обозначим

Тогда Заменим на стандартном промежутке частной суммой тригонометрического ряда Фурье

где

Коэффициенты так же, как и для случая постоянных значений длин периодов, можно найти из условия минимизации квадратичной ошибки

где Количество слагаемых N в этом случае нужно выбирать не более половины длины периода l. Также можно посчитать коэффициенты непосредственно из формул (19), либо, при больших длинах периода, можно воспользоваться формулами трапеций.
Таким образом, способ нахождения коэффициентов Фурье для каждого периода зависит от постоянства длин периодов и от их длины. Значения найденных коэффициентов в зависимости от номера периода рассматриваем как временные ряды, которые нужно спрогнозировать на один следующий шаг.

Коэффициенты ряда Фурье

прогнозируются с помощью матрицы задержек (для каждого коэффициента строится своя матрица задержек). Далее, используя полученные значения этих коэффициентов, можно построить прогноз на следующий период по формуле

Резюмируем: для долгосрочного прогнозирования временных рядов

1. Наблюдения каждого периода (каждой недели или каждого месяца) объявляются значениями некоторой функции
2. Функция заменяется частной суммой ряда Фурье
3. Из условия минимума квадратичной ошибки (20) или каким-либо другим способом находятся коэффициенты ряда Фурье для известных периодов
4. Найденные коэффициенты рассматриваются как временные ряды в зависимости от номера периода
5. Для каждого коэффициента строится своя матрица задержек и делается прогноз этого коэффициента на следующий период
6. По спрогнозированным коэффициентам Фурье по формуле (21) находятся значения неизвестной функции (временного ряда) для следующего периода

Немного кода

Попробуем применить данный алгоритм на реальных данных. Возьмем с сайта Росстата среднюю зарплату в России по месяцам за период с 2013-го по 2018-й г.

import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import mean_absolute_error, mean_absolute_percentage_error
sns.set()

data = pd.read_excel('mean_salary.xlsx')
data

Преобразуем данные в удобный формат в виде ряда и построим график

#сюда положим ряд, составленный из средних зп
salary_series = pd.Series()

for _, row in data.drop('year', axis=1).iterrows():
    salary_series = salary_series.append(pd.Series(row.values))

#используем даты в качестве индексов
salary_series.index = pd.date_range('2013-01-01', freq='M', periods=6*12)

#построим график
salary_series.plot(figsize=(12, 6), linewidth=2, fontsize=13)
plt.title('Среднемесячная ЗП в России', fontsize=15)
plt.xlabel('Дата', fontsize=14)
plt.ylabel('Среднемесячная ЗП, руб.', fontsize=14)
plt.show()

Разделим данные на тренировочный (2013 — 2017 гг.) и тестовый (2018 г.) наборы.

train_series = salary_series[salary_series.index.year<2018]
test_series = salary_series[salary_series.index.year==2018]

Перейдем к реализации алгоритма. Наш временной ряд состоит из 5-ти периодов одинаковой длины (12 месяцев), поэтому будем представлять неизвестную функцию в виде формулы (16). Для поиска коэффициентов из формул (17) получаются системы уравнений

def cos(k, t, l):
    """
    Вспомогательная функция косинуса
    """
    return math.cos(math.pi*k*t/l)


def get_matrix_and_vector(period_i: np.ndarray) -> (np.ndarray, np.ndarray):
    
    """
    Возвращает матрицу и вектор свободных членов для нахождения коэффициентов Фурье для i-го периода.
    
    period_i - наблюдения i-го периода
    """
    
    l = len(period_i) - 1
    N = l
        
    y = np.empty((0,))
    matrix = np.empty((0, N+1))
    
    for t in range(0, l+1):
        #первое значение в каждой строке 1/2 -- множитель перед коэффициентом a_0
        row = np.array([.5])
        
        for k in range(1, N+1):
            row = np.append(row, cos(k, t, l))

        row = np.reshape(row, (1, N+1))
        matrix = np.append(matrix, row, axis=0)
        y = np.append(y, period_i[t])
 
    return matrix, y


def solve_system(M: np.ndarray, 
                 b: np.ndarray) -> np.ndarray:
    
    """
    Решает систему линейных уравнений
    M - основная матрица системы
    b - столбец свободных членов
    """
    
    assert np.linalg.det(M) != 0
    return np.linalg.solve(M, b)

Далее реализуем функцию для преобразования входного ряда в матрицу, функции построения матрицы задержек, поиска ближайших соседей и прогнозирования на один шаг.

def get_matrix_from_series(input_series: pd.Series, 
                           m: int, 
                           l: int):
    """
    Преобразует входной ряд в матрицу, 
    где каждая i-я строка -- наблюдения для i-го периода
    
    input_series -- входной ряд
    m -- количество периодов
    l - длина периода
    """
    
    return input_series.values.reshape(m, l)


def get_delay_matrix(input_vector: np.ndarray, 
                     p: int = 1) -> np.ndarray:
    """
    Строит матрицу задержек по входному вектору и величине задержек
    input_vector - входной вектор
    p - величина задержек
    """
    
    input_vector_copy = np.copy(input_vector)
    
    m = input_vector_copy.shape[0] % p
    
    #если длина ряда не кратна p, то удаляем несколько первых значений ряда
    if m != 0:
        input_vector_copy = np.delete(input_vector_copy, range(m))
    
    #определяем размерность матрицы зарежек
    row_dim = input_vector_copy.shape[0] // p
    col_dim = p
    
    #строим матрицу
    delay_matrix = np.resize(input_vector_copy, 
                             new_shape=(row_dim, col_dim)).T    
    
    return delay_matrix


def find_nearest(row: np.ndarray, 
                 p: int) -> set:
    """
    Возвращает индексы ближайших соседей для последнего элемента строки
    row - входная строка
    p - величина задержек
    """
    
    #количество соседей
    neighbors_cnt = 2 * p + 1
    
    last_element = row[-1]
    all_neighbors = row[:-1]

    #находим индексы ближайших соседей
    idx = set(np.argsort(np.abs(all_neighbors-last_element))[:neighbors_cnt])
        
    return idx


def predict_by_one_step(input_vector: np.ndarray, 
                        p: int = 1) -> float :
    """
    Прогнозирование на один шаг с помощью аналитического решения
    input_vector - входной вектор
    p - величина задержек
    """
    
    delay_matrix = get_delay_matrix(input_vector, p)
    last_row = delay_matrix[-1,:]
    nearest_neighbors_indexes = find_nearest(last_row, p)
    
    y = np.empty((0,))
    X = np.empty((0, p+1))
    for index in nearest_neighbors_indexes:
        y = np.append(y, delay_matrix[0, index+1])
        row = np.append(np.array([1]), delay_matrix[:, index])
        row = np.reshape(row, (1, p+1))
        X = np.append(X, row, axis=0)
    
    coef = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
    prediction = sum(np.append(np.array([1]), delay_matrix[:, -1]) * coef)
    
    return prediction

Наконец реализуем функцию поиска коэффициентов для неизвестного периода и функцию прогнозирования временного ряда на следующий период.

def get_new_fourier_coefs(periods: np.ndarray, 
                          p: int = 1) -> list:
    
    """
    Возвращает коэффициенты Фурье для неизвестного периода
    periods - матрица наблюдений для известных периодов, где i-я строчка -- наблюдения i-го периода
    p - величина задержек
    
    """
    
    #список с предсказанными на след. период коэффициентами
    new_coefs = []
    
    #матрица с коэффициентами Фурье за все периоды. Строки -- коэфициенты за период
    coefs_for_all_periods = []
    
    for period in periods:
        
        X, y = get_matrix_and_vector(period)
        
        #находим коэффициенты Фурье, как решение системы линейных уравнений
        fourier_coef_for_period = solve_system(X, y)
        
        coefs_for_all_periods.append(fourier_coef_for_period)
    
    coefs_for_all_periods = np.array(coefs_for_all_periods)
    
    #Прогноз каждого коэффициента Фурье a_k для неизвестного периода
    #Каждый коэф. Фурье рассматривается как временной ряд, который прогнозируется на один шаг
    for i in range(coefs_for_all_periods.shape[1]):
        coef_for_next_period = predict_by_one_step(coefs_for_all_periods[:, i], p=p)
        new_coefs.append(coef_for_next_period)

    return new_coefs


def predict_next_period(new_coefs: list, 
                        l: int):
    """
    Прогнозирует временной ряд на неизвестный период
    
    new_coefs - коэффициенты Фурье для следующего периода
    l - длина периода
    """
    
    new_period = []
    for t in range(0, l):
        s = new_coefs[0] / 2
        for k in range(1, len(new_coefs)):
            s += new_coefs[k]*cos(k, t, l=l-1)

        new_period.append(s)
    
    return new_period

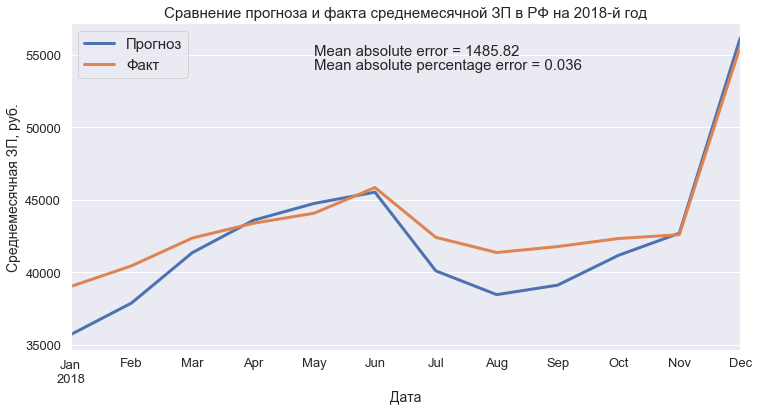
Предскажем тестовый период и сравним с реальными результатами.

m = 5 #количество периодов в train выборке
l = 12 #длина периода
p = 1 #величина задержек

matrix = get_matrix_from_series(train_series, m, l)
new_coefs = get_new_fourier_coefs(matrix, p)
test_pred = predict_next_period(new_coefs, l)
test_pred = pd.Series(test_pred, index=test_series.index)

#ошибка прогноза
mae = round(mean_absolute_error(test_pred, test_series), 2)
mape = round(mean_absolute_percentage_error(test_series, test_pred), 3)


#построим график
test_pred.plot(figsize=(12, 6), linewidth=3, 
               fontsize=13, label='Прогноз')

test_series.plot(figsize=(12, 6), linewidth=3, 
                 fontsize=13, label='Факт')

plt.legend(fontsize=15)
plt.text(test_series.index[4], 55000, f'Mean absolute error = {mae}', fontsize=15)
plt.text(test_series.index[4], 54000, f'Mean absolute percentage error = {mape}', fontsize=15)
plt.title('Сравнение прогноза и факта среднемесячной ЗП в РФ на 2018-й год', fontsize=15)
plt.xlabel('Дата', fontsize=14)
plt.ylabel('Среднемесячная ЗП, руб.', fontsize=14)
plt.show()

Весь код и данные доступны по ссылке на гитхабе.

Благодарю авторов статей [1, 2] за помощь и консультацию при подготовке данной статьи.

Список литературы

1. П.А. Гатин,  В.Н. Семенова, Исследование циклических временных рядов с переменной цикличностью методом рядов Фурье, Вестник ДИТИ, 2018. – № 1(15). – С.91-96
2. П.А. Гатин,  В.Н. Семенова, Об одном подходе к исследованию временных рядов с постоянной цикличностью, ДИТИ НИЯУ МИФИ, 2017. – С. 48-51
3. А.Н. Колмогоров, С.В. Фомин – Элементы теории функций и функционального анализа
4. В.Н. Афанасьев, М.М. Юзбашев, Анализ временных рядов и прогнозирование – М.: Финансы и статистика, Инфра-М, 2010. – 320 c.
5. А.Ю. Лоскутов, О.Л. Котляров, И.А. Истомин, Д.И. Журавлев. Проблемы нелинейной динамики. III. Локальные методы прогнозирования временных рядов. Вестн. Моск. ун-та, сеp. Физ.-астр., 2002, No6, c.3–21.
6. О.С. Амосов, О.С., Муллер Н.В. Исследование временных рядов с применением методов фрактального и вейвлет анализа, Интернет-журнал «НАУКОВЕДЕНИЕ», Выпуск 3

As an alternative explanation, consider the following intuition:

When minimizing an error, we must decide how to penalize these errors. Indeed, the most straightforward approach to penalizing errors would be to use a linearly proportional penalty function. With such a function, each deviation from the mean is given a proportional corresponding error. Twice as far from the mean would therefore result in twice the penalty.

The more common approach is to consider a squared proportional relationship between deviations from the mean and the corresponding penalty. This will make sure that the further you are away from the mean, the proportionally more you will be penalized. Using this penalty function, outliers (far away from the mean) are deemed proportionally more informative than observations near the mean.

To give a visualisation of this, you can simply plot the penalty functions:

Now especially when considering the estimation of regressions (e.g. OLS), different penalty functions will yield different results. Using the linearly proportional penalty function, the regression will assign less weight to outliers than when using the squared proportional penalty function. The Median Absolute Deviation (MAD) is therefore known to be a more robust estimator. In general, it is therefore the case that a robust estimator fits most of the data points well but ‘ignores’ outliers. A least squares fit, in comparison, is pulled more towards the outliers. Here is a visualisation for comparison:

Now even though OLS is pretty much the standard, different penalty functions are most certainly in use as well. As an example, you can take a look at Matlab’s robustfit function which allows you to choose a different penalty (also called ‘weight’) function for your regression. The penalty functions include andrews, bisquare, cauchy, fair, huber, logistic, ols, talwar and welsch. Their corresponding expressions can be found on the website as well.

I hope that helps you in getting a bit more intuition for penalty functions

Update

If you have Matlab, I can recommend playing with Matlab’s robustdemo, which was built specifically for the comparison of ordinary least squares to robust regression:

The demo allows you to drag individual points and immediately see the impact on both ordinary least squares and robust regression (which is perfect for teaching purposes!).

As an alternative explanation, consider the following intuition:

When minimizing an error, we must decide how to penalize these errors. Indeed, the most straightforward approach to penalizing errors would be to use a linearly proportional penalty function. With such a function, each deviation from the mean is given a proportional corresponding error. Twice as far from the mean would therefore result in twice the penalty.

The more common approach is to consider a squared proportional relationship between deviations from the mean and the corresponding penalty. This will make sure that the further you are away from the mean, the proportionally more you will be penalized. Using this penalty function, outliers (far away from the mean) are deemed proportionally more informative than observations near the mean.

To give a visualisation of this, you can simply plot the penalty functions:

Now especially when considering the estimation of regressions (e.g. OLS), different penalty functions will yield different results. Using the linearly proportional penalty function, the regression will assign less weight to outliers than when using the squared proportional penalty function. The Median Absolute Deviation (MAD) is therefore known to be a more robust estimator. In general, it is therefore the case that a robust estimator fits most of the data points well but ‘ignores’ outliers. A least squares fit, in comparison, is pulled more towards the outliers. Here is a visualisation for comparison:

Now even though OLS is pretty much the standard, different penalty functions are most certainly in use as well. As an example, you can take a look at Matlab’s robustfit function which allows you to choose a different penalty (also called ‘weight’) function for your regression. The penalty functions include andrews, bisquare, cauchy, fair, huber, logistic, ols, talwar and welsch. Their corresponding expressions can be found on the website as well.

I hope that helps you in getting a bit more intuition for penalty functions

Update

If you have Matlab, I can recommend playing with Matlab’s robustdemo, which was built specifically for the comparison of ordinary least squares to robust regression:

The demo allows you to drag individual points and immediately see the impact on both ordinary least squares and robust regression (which is perfect for teaching purposes!).