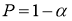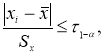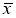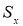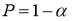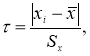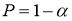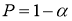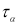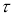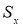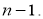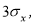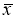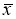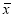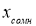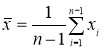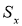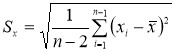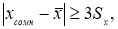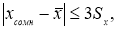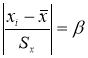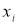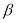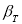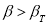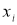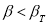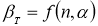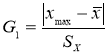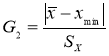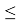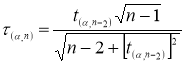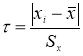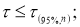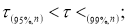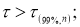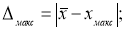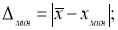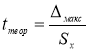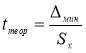Методы отбраковки грубых ошибок - Исправление ошибок и поиск оптимальных решений проблем

Среди результатов выборки иногда
присутствуют наблюдения, сильно
отличающиеся от остальных. Такое
расхождение может возникнуть вследствие
изменения условий бурения, больших
погрешностей при замерах параметров
процесса, свойств пород и т.д. [2].

При обработке статистического материала
необходимо убедиться, что в выборке
отсутствуют грубые ошибки, которые
называются «выскакивающими значениями».
Грубые ошибки необходимо отбраковать.
Для отбраковки используются два метода:
метод Шовене и правило трех сигм.

1.2 Отбраковка по критерию Шовене

При отбраковке по критерию Шовене
значение случайной величины должно
находиться в интервале:

,
(1.4)

где—
критерий Шовене, который находится по
формуле:

,
(1.5)

где
К –
табличный коэффициент. При количестве
измерений
44
он примерно равен 2,55.

Отбраковка непредставительных данных
и проверка на однородность результатов:

Отбраковка производится по критерию
Шовене:

где:
—
критерий Шовене ()

По данным опытного расчета видно, что
грубых ошибок нет, то есть в нашем случае
имеем:

1.3 Отбраковка по правилу «трех сигм»

Второй метод отбраковки грубых ошибок,
использованный в работе, – метод
отбраковки по правилу «трех сигм»,
согласно которому все измерения, не
лежащие в интервале

(1.6)

должны отбрасываться как маловероятные.

При вычислении был получен следующий
интервал:

Также все значения случайных величин
попали в расчетный диапазон.

Коэффициент вариации:

;
(1.7)

При проведении эксперимента коэффициент
вариации не должен превышать 6-7 %.

1.4 Интервальная оценка параметров выборки

Интервальная оценка основана на
определении некоторого интервала,
внутри которого с определенной
вероятностью находится истинное значение
средней величины.

Вероятность того, что
действительное значение измеряемой
величины лежит в пределах
,
представляет собой доверительную
вероятность:

(1.8)

где

— доверительная вероятность,

— уровень значимости.

Доверительный интервал определяет
диапазон, в котором находится истинное
значение средней величины:

(1.9)

где:
—
дисперсия

—
критерий Стьюдента (зависит от принятой
вероятности –

или от уровня значимости —
,
а также кол-во степеней свободы)

В наших расчетах:

или
,
а критерий Стьюдента примем равным:

Таким образом, неравенство

является верным.

1.5 Необходимое и достаточное количество экспериментов

Минимальное необходимое количество
опытов:

(1.10)

где:
—
коэффициент допустимого отклонения

(1.11)

где:
—
допустимое с точки зрения исследователя
отклонение значения случайной величины
от среднего.

В нашем случае допустимое отклонение
примем равным:

Тогда:

Значит, минимальное необходимое
количество опытов будет равно:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

СТРОИТЕЛЬСТВО. Проектирование и строительство дорог, мостов и тоннелей

D0l.org/10.5281/zenodo.1408243 УДК 528.1

М.Д. Герасименко, В.М. Каморный

ГЕРАСИМЕНКО МИХАИЛ ДАНИЛОВИЧ — д.т.н., профессор, главный научный сотрудник, e-mail: mdg@iam.dvo.ru Институт прикладной математики ДВО РАН

(Кафедра геодезии, землеустройства и кадастра Инженерной школы ДВФУ) КАМОРНЫЙ ВАЛЕРИЙ МИХАЙЛОВИЧ — к.т.н., профессор кафедры геодезии, землеустройства и кадастра Инженерной школы, e-mail: kamornyy.vm@dvfu.ru Дальневосточный федеральный университет Суханова ул., 8, Владивосток, 690091

О методах поиска и отбраковки грубых ошибок геодезических измерений

Аннотация: Изложены теоретические основы известной методики выявления и локализации грубых ошибок измерений по поправкам из уравнивания. Обобщены и дополнены достигнутые результаты работы с ее применением. Основы методики заложены еще в 60-х годах прошлого века, но в отечественной геодезической литературе она, к сожалению, до сих пор не нашла должного освещения, хотя при современных способах регистрации измерений и вычислений проблема автоматизированного поиска возможных грубых ошибок является весьма актуальной. Указывается на достоинства и недостатки методики. Эта тема важна при геодезическом обеспечении строительства дорог, тоннелей, других сооружений и объектов. Ключевые слова: уравнивание, поправки измерений, грубые ошибки геодезических измерений.

Введение

В классической теории математической обработки геодезических измерений проблеме поиска грубых ошибок измерений уделялось сравнительно мало внимания. Предполагалось, что такие ошибки должны быть выявлены и исключены до уравнивания применением соответствующей методики измерений и дальнейшим анализом невязок условных уравнений. Этот способ при ручном счете, в зависимости от числа и расположения грубых ошибок в геодезической сети, а также, что особенно важно, от ее сложности, часто оказывается слишком трудоемким и нереализуемым даже для опытного вычислителя.

Между тем практика показала, что в последнее время проблема выявления грубых ошибок измерений обострилась в связи с применением современных методов автоматизированного сбора измерительной информации и ее математической обработки. Эти массивы информации часто вручную детально не анализируются, поэтому в окончательную обработку могут поступать измерения, содержащие грубые ошибки. Причинами их появления могут быть неточность наведения прибора на визирную цель (погрешности идентификации цели),

О статье: поступила: 15.01.2018; финансирование: работа выполнена при частичной поддержке Комплексной программы фундаментальных научных исследований ДВО РАН «Дальний Восток» на 2018 г.

регистрации отсчетов, нумерации пунктов, ошибочное редуцирование, влияние внешней среды и др.

Подобная проблема особенно часто возникает в сложных для наблюдений условиях, при построении геодезических сетей специального назначения, предназначенных для выноса в натуру крупных уникальных инженерных объектов, их геодезического сопровождения в процессе строительства, а также наблюдения за возможными деформациями в процессе эксплуатации.

По указанным причинам при современных способах регистрации измерений и вычислений проблема автоматизированного поиска возможных грубых ошибок является весьма актуальной. Ее решению в последние десятилетия в зарубежной геодезической литературе посвящено множество публикаций [7-12; и др.]. Разрабатываемая методика базируется на анализе результатов уравнивания и выявления грубых ошибок по поправкам из уравнивания. Основы такой методики заложены еще в 60-х годах прошлого столетия голландским профессором В. Баарда, но в отечественной геодезической литературе она, к сожалению, до сих пор не нашла должного освещения. Причем в некоторых публикациях по данной теме по разным причинам, обычно c теоретическими погрешностями и грубыми арифметическими промахами в иллюстративных вычислениях, иногда даже отрицается возможность поиска грубых ошибок по поправкам из уравнивания, на что указывает В.А. Коугия [4, 5].

Поиск и локализация грубых ошибок по результатам уравнивания, к сожалению, не является тривиальной задачей. Проблема состоит в том, что нельзя отождествлять максимальную по модулю недопустимую поправку с грубым результатом измерения, так как в зависимости от геометрии сети максимальное влияние грубой ошибки может проявиться не на соответствующей поправке, а совсем в другом месте геодезической сети [7, 8, 10-12; и др.]. Дело в том, что грубая ошибка при уравнивании «расплывается» и сказывается не только на соответствующей поправке, но и на других поправках измерений. Для решения этой проблемы используются, в частности, средние квадратические ошибки поправок, которые вычисляются с использованием обратной матрицы коэффициентов нормальных уравнений параметрического способа уравнивания.

Цель настоящей статьи — обобщение результатов и дополнение достигнутых успехов в области поиска и локализации грубых ошибок измерений по результатам уравнивания.

Алгоритм поиска грубых ошибок по поправкам из уравнивания

Пусть имеется линеаризованная система уравнений поправок:

V = ЛЗХ + Ь = (Е — Ш-1 ЛТР)Ь, (1)

где V — вектор поправок к результатам измерений, А — матрица коэффициентов уравнений поправок, 5Х — вектор поправок к приближенным значениям параметров, Ь — вектор свободных членов, матрица нормальных уравнений N = ЛТРА, Р — диагональная весовая матрица независимых измерений, Е — единичная матрица.

Из выражения (1) следует, что при нормальности распределения ошибок измерений поправки V также распределены нормально и при отсутствии систематических ошибок измерений имеют нулевое математическое ожидание при дисперсиях . Тогда можно установить [ 1] допустимое значение поправок t — а , которое не может быть превышено с уровнем значимости а , т.е. вероятность

Р(у,| < I-а) = 1 -а. (2)

ВЕСТНИК ИНЖЕНЕРНОЙ ШКОЛЫ ДВФУ. 2018. № 3(36)

Иначе говоря, поправки, удовлетворяющие неравенству | > г • су, можно предполагать недопустимыми. Для недопустимых нормированных поправок, что удобнее, особенно если дальнейший анализ и отбраковка измерений производятся вручную, имеем для заданного числа /, зависящего, согласно (2), от уровня значимости а , выражение

>г . (3)

Критерием (3) проверяются все поправки. Если ему удовлетворяют несколько поправок, грубая ошибка предполагается в измерении с максимальным значением нормированной поправки. Его исключают из обработки и всю процедуру уравнивания и отбраковки повторяют до тех пор, пока все грубые ошибки не будут исключены [5, 7; и др.]. В случае наличия в измеренной информации нескольких грубых ошибок задача их поиска существенно усложняется и не всегда может быть эффективно решена, причем главная опасность состоит в том, что будут отбракованы доброкачественные измерения. Этот недостаток, впрочем, не столь существенен, нежели пропуск грубой ошибки, особенно в ситуации, когда число избыточных измерений велико, как это часто наблюдается в высокоточных инженерно-геодезических сетях специального назначения. Облегчается поиск имеющихся нескольких грубых ошибок тогда, когда они располагаются на удалении в разных частях сети.

Не следует забывать и вопрос о точности собственно измерений, которая предполагается известной. В противном случае вместо принятой для отработки дисперсии единицы веса с0 применяют ее оценку СС0, полученную из уравнивания. Надежность ее вычисления существенным образом зависит от числа избыточных измерений. В случае если при вычислении СС0 были использованы грубые измерения, вместо ¿-критерия для отбраковки грубых измерений применяют т-критерий, предложенный Попом (1975), или же так называемый Датский метод [9].

Дополнительные замечания и рекомендации

Следует отметить, что до анализа отдельных поправок весьма полезным может оказаться их глобальное тестирование, которым проверяется корректность и полнота выбранной модели уравнивания. Для этого вычисляется статистика

Т2 = УТРУ /с02,

которая сравнивается с критическим значением ^-распределения, зависящим от уровня значимости а и числа степеней свободы г, равного числу избыточных измерений в сети. Подобная проверка, насколько нам известно, ранее не предлагалась, по крайней мере в отечественной геодезической литературе.

Если вычисленная величина Т не превосходит критическое значение статистики, то это говорит о том, что нет противоречия между наблюдениями и математической моделью. Но это не гарантирует правильность модели или корректность наблюдений.

В противном случае, когда Т > %, требуются дополнительные исследования на ошибочность модели обработки и собственно наблюдений.

Приведенная методика и другие упомянутые выше методы поиска грубых ошибок измерений по поправкам из уравнивания в настоящее время широко применяются в мировой геодезической практике и доказали свою полезность. Но, как указано в работе [10], такие успехи следует считать чрезвычайно неожиданными и успешными, учитывая те теоретические предположения, по которым эти методы были получены:

1) наблюдения нормально распределены;

2) в измерениях содержится всего одна грубая ошибка;

3) грубая ошибка максимизирует тестируемую статистику соответствующей поправки;

4) одномерные тесты для каждой поправки независимы.

Дополнительную информацию по данной тематике можно найти в работах [2, 5, 8-12; и др.].

При вычислении предельных значений поправок или их нормированных аналогов следует знать диагональные элементы аV = (а^^ ).,. ковариационной матрицы поправок а^у, где а2 — дисперсия единицы веса, а — матрица весовых коэффициентов вектора поправок V . Учитывая, что вектор поправок к измерениям зависит лишь от вектора свободных членов Ь , имеющего матрицу весовых коэффициентов Q = Р -1, с учетом (1) имеем матрицу весовых коэффициентов ^ вектора поправок

а¥ = Q — т-ХЛТ . (4)

Умножая уравнение (4) на дисперсию единицы веса, получаем приведенную в работе В.А. Коугия [5] формулу для ковариационной матрицы поправок

^ = Кь — ЛКХЛТ. (5)

Следует заметить, что формула (5) известна геодезистам более 50 лет, а ее вывод можно найти в книге Ю.В. Линника [6].

Выводы

Изложенная методика реализована нами в программах для ПК и использовалась на практике [2, 3]. Следует заметить, что в работе [2] нами предложена формула, которая позволяет непосредственно вычислять предельные значения поправок измеренных направлений, когда при уравнивании параметрическим способом предварительно исключаются поправки к ориентирующим углам и решается лишь редуцированная система нормальных уравнений. Это позволило уменьшить объем требуемой памяти ЭВМ более чем в два раза и сократить во много раз время вычислений за счет уменьшения числа одновременно решаемых линейных уравнений на треть. Предложенная методика успешно использована при уравнивании производственной сети и поиске грубых ошибок двух циклов измерений в высокоточной линейно-угловой сети, построенной Приморским АГП для обеспечения строительства уникального вантового моста через бухту Золотой Рог в г. Владивостоке, а также низководного моста Де-Фриз-Седанка. В результате математической обработки при уровне значимости 0,05 отбраковывалось от 2 до 6% измерений, т.е. число грубых ошибок может быть чрезвычайно велико. Оно объясняется неблагоприятными условиями измерений: водные преграды, туман, ветер.

Таким образом, рассмотренный алгоритм и его производственное применение убедительно подтвердили правильность метода отбраковки грубых ошибок по поправкам из уравнивания, так как он достаточно уверенно распознает измерения с грубыми ошибками.

СПИСОК ЛИТЕРАТУРЫ

1. Большаков В.Д., Маркузе Ю.И., Практикум по теории математической обработки геодезических измерений. М.: Недра, 1984. 352 с.

2. Герасименко М.Д. К вопросу о выявлении грубых ошибок измерений // Известия вузов. Геодезия и аэрофотосъемка. 2010. № 6. С. 3-6.

3. Герасименко М.Д., Каморный В.М., Кафтан В.И. Обработка плановых и пространственных

геодезических сетей на геодинамических полигонах // Геодезия и картография. 1993. № 2.

С.16-21.

4. Коугия В.А. Замечания о методах отбраковки грубых ошибок измерений. URL: http:// www.-spbogik.ru/images/download/kougiya2011.pdf (дата обращения: 05.01.2018).

5. Коугия В.А. Сравнение двух методов обнаружения и идентификации грубых ошибок измерений // Геодезия и картография. 1998. № 5. С. 23-28.

6. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки измерений. М.: Гос. изд-во физико-математической лит-ры, 1958. 334 с.

7. Ackermann F. Grundlagen und Verfahren zur Erkennung grober Datenfehler. Institut fur Photo-grammretrie der Universitat Stuttgart. Vortrage des Lehrgangs Numerische Photogrammretrie (IV). Schriftenreihe. Heft 7. Stuttgart, 1981, p. 7-23.

8. Bingcai Zhang. A new method of data snooping. Australian J. of Geodesy, Photogrammetry and Surveying. 1987;46-47:103-122.

9. Caspary W.F. Concepts of network and deformation analysis. Monograph 11 School of Surveying, The University of New South Wales, Kensington, 1987, N.S.W., Australia, 183 p.

10. Cen M., Li Z., Ding X., Zhuo J. Gross error diagnostics before least squares adjustment of observations. J. of Geodesy. 2003;77:503-513.

11. Cross P.A., Price D.R. A strategy for the distinction between single and multiple gross errors in geodetic networks. Manuscripta geodaetica. 1985;10:172-178.

12. Ou Z.Q. Sequential tests for outliers in the general linear model. Australian J. of Geodesy, Photogrammetry and Surveying. 1987;50:37-49.

THIS ARTICLE IN ENGLISH SEE NEXT PAGE

Design and Construction of Roads, Bridges, and Tunnels

D0l.org/10.5281/zenodo.1408243

Gerasimenko M., Kamornyy V.

MIKHAIL GERASIMENKO, Doctor of Engineering Sciences, Professor, Chief Researcher, e-mail: mdg@iam.dvo.ru

Institute of Applied Mathematics, FEB RUS (and Department of Geodesy,

Land Management and Cadastre, School of Engineering, FEFU)

VALERIY KAMORNYY, Candidate of Engineering Sciences, Professor, Department

of Geodesy, Land Management and Cadastre, School of Engineering,

e-mail: kamornyy.vm@dvfu.ru

Far Eastern Federal University

8 Sukhanova St., Vladivostok, Russia, 690091

The ways of detection and rejection of gross errors in geodetic measurements

Abstract: The article presents the theoretical basis of the well-known method to detect and localise gross errors of measurements through correction for compensation. The results of the works in which it was applied have been summarised and complemented. The foundation of the technique was laid in the 1960s, yet, unfortunately, it has not been adequately publicised in the national geodetic literature, although today’s ways of the registration of measurements and calculations make the issue of the automated detection of possible gross errors very important. Highlighted are virtues and deficiencies of the method. The issue is significant for the land surveys when building roads, tunnels, and other construction objects.

Key words: adjustment, measurement amendments, geodetic measurements, gross errors. REFERENCES

1. Bolshakov V.D., Markuse Yu.I. Practice on the theory of mathematical processing of geodetic measurements. Moscow, Nedra. 1984, 352 p.

2. Gerasimenko M.D. To the problem of revealing crude measurement errors. Izvestiya Vuzov. Geodesy and aerial photography. 2010;6:3-6.

3. Gerasimenko M.D., Kamorny V.M., Kaftan V.I. Processing of planned and spatial geodetic networks on geodynamic polygons. Geodesy and cartography. 1993;2:16-21.

4. Kougia V.A. Remarks on the methods for rejecting coarse measurement errors. URL: http://www.spbogik.ru/images/download/kougiya2011.pdf — 05.01.2018.

5. Kougiya V.A. Comparison of two methods for detecting and identifying rough measurement errors. Geodesy and Cartography. 1998;5:23-28.

6. Linnik Yu.V. The method of least squares and the foundations of the mathematical-statistical theory of processing dimensions. Moscow, State Publishing House, 1958, 334 p.

8. Bingcai Zhang. A new method of data snooping. Australian J. of Geodesy, Photogrammetry and Surveying. 1987;46-47:103-122.

9. Caspary W.F. Concepts of network and deformation analysis. Monograph 11 School of Surveying, The University of New South Wales, Kensington, 1987, N.S.W., Australia, 183 p.

10. Cen M., Li Z., Ding X., Zhuo J. Gross error diagnostics before least squares adjustment of observations. J. of Geodesy. 2003;77:503-513.

11. Cross P.A., Price D.R. A strategy for the distinction between single and multiple gross errors in geodetic networks. Manuscripta geodaetica. 1985;10:172-178.

12. Ou Z.Q. Sequential tests for outliers in the general linear model. Australian J. of Geodesy, Photogrammetry and Surveying. 1987;50:37-49.

Источник

В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.

Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.

Ключевые слова:

грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.

Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.

Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.

На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.

Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят

,

однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.

Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:

Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).

В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.

В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].

Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.

Задаются вероятностью

Р

или уровнем значимости

α

(

) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».

Проверяемая гипотеза состоит в утверждении, что результат наблюдения

x
_i

не содержит грубой погрешности, т. е. является одним из значений случайной величины

x

с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
_max
или наименьший xmin из результатов наблюдений.

Предложим для практического использования наиболее простые методы отсева грубых погрешностей.

Если в распоряжении экспериментатора имеется выборка небольшого объема

n

≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:

(1)

где

x

_i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения

и среднеквадратичного отклонения

;

τ

_1-
_p
— табличное значение статистики

τ

, вычисленной при доверительной вероятности

Таким образом, для выделения аномального значения вычисляют значение статистики,

(2)

которое затем сравнивают с табличным значением

τ
_1-α

:

τ

≤

τ
_1-α

. Если неравенство

τ

≤

τ

_1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.

Квантили распределения статистики

τ

при уровнях значимости

α

= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности

=

0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости

α

= 0,05 (результат получается с 95 %-й доверительной вероятностью).

Функции распределения статистики

τ

определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности

или уровне значимости

α

можно для чисел измерения п = 3–25 найти те наибольшие значения

которые случайная величина

может еще принять по чисто случайным причинам.

Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения

и среднеквадратичного отклонения

для выборки нового объема

Таблица 1

Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]

n	Уровень значимости α	n	Уровень значимости α
0,10	0,05	0,025	0,01	0,10	0,05	0,025	0,01
3	1,41	1,41	1,41	1,41	15	2,33	2,49	2,64	2,80
4	1,65	1,69	1,71	1,72	16	2,35	2,52	2,67	2,84
5	1,79	1,87	1,92	1,96	17	2,38	2,55	2,70	2,87
6	1,89	2,00	2,07	2,13	18	2,40	2,58	2,73	2,90
7	1,97	2,09	2,18	2,27	19	2,43	2,60	2,75	2,93
8	2,04	2,17	2,27	2,37	20	2,45	2,62	2,78	2,96
9	2,10	2,24	2,35	2,46	21	2,47	2,64	2,80	2,98
10	2,15	2,29	2,41	2,54	22	2,49	2,66	2,82	3,01
11	2,19	2,34	2,47	2,61	23	2,50	2,68	2,84	3,03
12	2,23	2,39	2,52	2,66	24	2,52	2,70	2,86	3,05
13	2,26	2,43	2,56	2,71	25	2,54	2,72	2,88	3,07
14	2,30	2,46	2,60	2,76

В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.

Критерий «трех сигм» применяется для случая, когда измеряемая величина

x

распределена по нормальному закону. По этому критерию считается, что с вероятностью

Р

= 0,9973 и значимостью

α

= 0,0027 появление даже одной случайной погрешности, большей, чем

маловероятное событие и ее можно считать промахом, если

−

x
_i

> 3

S
_x

, где

S
_x

_—

оценка среднеквадратического отклонения (СКО) измерений. Величины

и

S
_x

вычисляют без учета экстремальных значений

x
_i

. Данный критерий надежен при числе измерений

n

≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при

6 <

n

≤100 она равна 4

S
_x

; при 100 <

n

≤1000 − 4,5

S
_x

; при 1000 <

n

≤10000–5

Sx

. Данное правило также используется только при нормальном распределении.

Практические вычисления проводят следующим образом [5, с. 65]:

Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
Вычисляют среднее арифметическое значение выборки

без учета сомнительного значения

измеряемой величины.

(3)

Вычисляют оценку СКО выборки

без учета сомнительного значения

измеряемой величины.

(4)

Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.

Если

то сомнительное значение отбрасывают, как промах.

Если

то сомнительное значение оставляют как равноправное в ряду наблюдений.

Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.

Критерий В. И. Романовского применяется, если число измерений невелико,

n

≤ 20. При этом вычисляется соотношение

(5)

где

— результат, вызывающий сомнение,

— коэффициент, предельное значение которого

определяют по таблице 2. Если

, сомнительное значение

исключают («отбрасывают») как промах. Если

,

сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].

Таблица 2

Значение критерия Романовского

Уровень значимости, α	Число измерений, n
n = 4	n = 6	n = 8	n = 10	n = 12	n = 15	n = 20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.

Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.

(6)

Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев

t

-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.

Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.

Если G1

GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2

GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.

Отсев грубых погрешностей можно производить и для больших выборок (

n

= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].

Известно, что критическое значение

τ

_p
(

p

— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента

t
_{α, n-2}

[6, с. 26]:

(7)

Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (

n

= 100):

1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;

2)

по формуле

вычисляют значение статистики

τ

;

3)

по таблице (или в программе Excel) находят процентные точки

t

-распределения Стьюдента

t

₍

_α,
_n
_-2

₎
:

t

₍₉₅

_{%, 98)}
= 1,6602, и

t
₍

₉₉

_{%, 98)}
= 3,1737;

По предыдущей формуле в программе Excel вычисляют соответствующие точки

t

₍₉₅

_{%, 100)}
= 1,66023и

t

₍₉₉

_{%, 100)}
=3,17374.

Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.

Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)

Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.

Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.

Пример 1.

Имеется выборка из 100 шт. резисторов с номинальным сопротивлением

R

_н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.

Заносим данные измерений в таблицу Excel в ячейки В2:В101
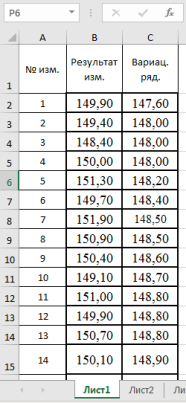
Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)

Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда

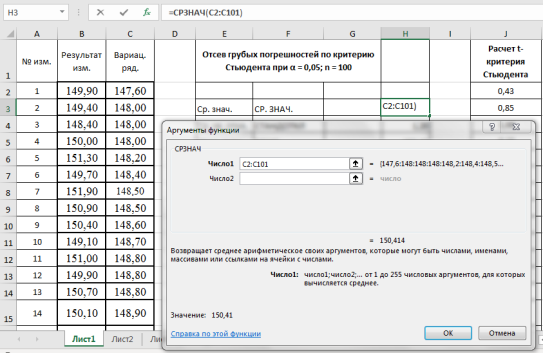
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).

Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки

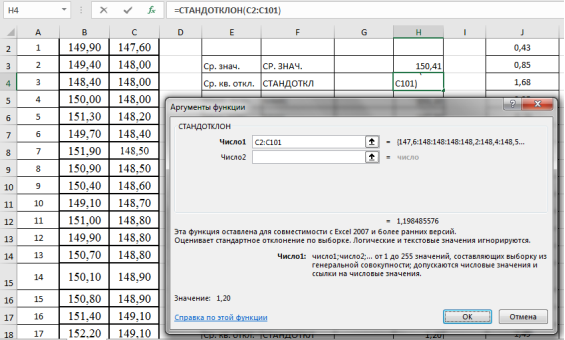
Находим среднеквадратическое отклонение —

S

_x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).

Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения

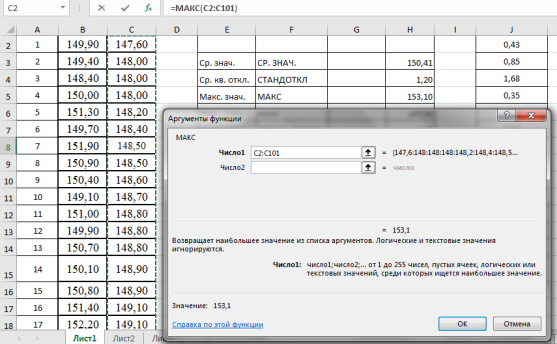
Находим максимальное значение в выборке —

x

_макс
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).

Рис. 4. Фрагмент диалогового окна при нахождении максимального значения

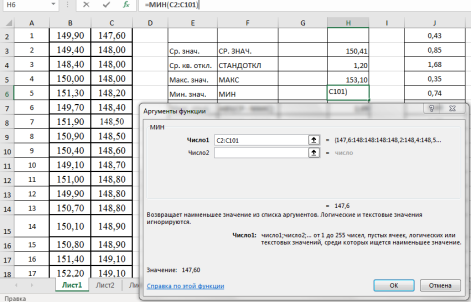
Находим минимальное значение в выборке —

x

_мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).

Рис. 5. Фрагмент диалогового окна при нахождении минимального значения

Находим максимальное и минимальное отклонения — Δ
_макс
и Δ
_мин
. Вводим в ячейки Н7 и Н8 формулы:

Находим теоретическое значение —

t

_теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу

. и

Находим табличное значение

t

_табл.
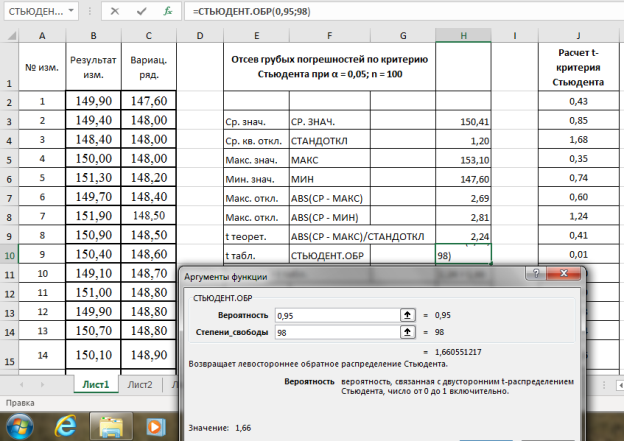
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (

n

-2) — 98, результат в ячейке Н10–1,66 (рис. 6).

Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента

Сравниваем теоретическое значение

t

_теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:

t

_табл
.= 1,6605.
Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).

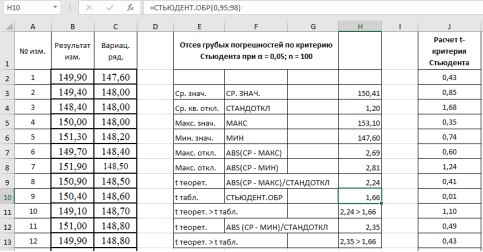
Рис. 7. Фрагмент диалогового окна при окончательном анализе данных

Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.

Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений

n

= 20, β
_табл
= 2,78 (из таблицы 2).

Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского

Выводы

Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.

Литература:

1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.

2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.

3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.

4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.

5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.

6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.

Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.

Источник

1.2 Отбраковка по критерию Шовене

1.3 Отбраковка по правилу «трех сигм»

1.4 Интервальная оценка параметров выборки

1.5 Необходимое и достаточное количество экспериментов