From Wikipedia, the free encyclopedia
The modulation error ratio or MER is a measure used to quantify the performance of a digital radio (or digital TV) transmitter or receiver in a communications system using digital modulation (such as QAM). A signal sent by an ideal transmitter or received by a receiver would have all constellation points precisely at the ideal locations, however various imperfections in the implementation (such as noise, low image rejection ratio, phase noise, carrier suppression, distortion, etc.) or signal path cause the actual constellation points to deviate from the ideal locations.
Transmitter MER can be measured by specialized equipment, which demodulates the received signal in a similar way to how a real radio demodulator does it. Demodulated and detected signal can be used as a reasonably reliable estimate for the ideal transmitted signal in MER calculation.
Definition[edit]
An error vector is a vector in the I-Q plane between the ideal constellation point and the point received by the receiver. The Euclidean distance between the two points is its magnitude.
The modulation error ratio is equal to the ratio of the root mean square (RMS) power (in Watts) of the reference vector to the power (in Watts) of the error. It is defined in dB as:
where Perror is the RMS power of the error vector, and Psignal is the RMS power of ideal transmitted signal.
MER is defined as a percentage in a compatible (but reciprocal) way:
with the same definitions.
MER is closely related to error vector magnitude (EVM), but MER is calculated from the average power of the signal. MER is also closely related to signal-to-noise ratio. MER includes all imperfections including deterministic amplitude imbalance, quadrature error and distortion, while noise is random by nature.
See also[edit]
- Error vector magnitude
- Carrier to Noise Ratio
- Signal-to-noise ratio
References[edit]
- ETSI technical report ETR 290: «Measurement guidelines for DVB systems», Errata 1, May 1997
Как разработчика приборов для измерения параметров телевизионных сигналов меня часто спрашивают, как правильно интерпретировать результаты измерений. В настоящее время для специалистов, обслуживающих системы телеприема, доступно большое количество измерительных приборов, а значит, есть возможность количественно оценить качество телевизионных каналов, в том числе каналов с цифровой модуляцией. Однако при интерпретации измеренных величин до сих пор чувствуются неуверенность и сомнения. В этом материале я изложу свою точку зрения на значимость каждого из параметров, характеризующих качество телевизионного сигнала.
Mой взгляд на этот вопрос в основном формировался в процессе собственных разработок и производства телевизионных измерительных приборов. Но свою лепту внесли и консультации со специалистами всемирно известных компаний, производящих подобные приборы, и общение с операторами кабельных сетей.
Должен оговориться, что все нижеизложенное в первую очередь касается цифрового кабельного телевидения стандарта DVBC. Но в силу родственных связей между форматами DVB-вещания мои рассуждения с некоторыми оговорками можно отнести и к DVB-S, DVB-T, и др.
Содержание
- Пять основных параметров
- BER vs MER
- Самый важный параметр
- Время измерения BER
- Преимущества MER
- Констелляционная диаграмма
- Особенности измерения уровня цифровых сигналов
- Общие рекомендации по оценке качества цифровых каналов
- Использованная литература
Пять основных параметров
Для начала рассмотрим набор измеряемых параметров цифровых каналов, доступных владельцам современных приборов. Как правило, эти приборы позволяют измерять пять параметров.
Первый из них — уровень сигнала в канале. Без сомнения, это один из важнейших параметров, характеризующих качество приема. Несмотря на то, что это самый понятный для специалистов параметр и его с достаточной точностью можно измерить даже приборами, предназначенными для аналоговых сигналов, при анализе результатов измерений иногда встречаются неправильные толкования и недопонимания.
Следующий параметр — MER (Modulation Error Ratio), или Коэффициент ошибок модуляции. По своей сути MER близок параметру SNR (сигнал/шум). В некоторых странах вместо параметра MER применяют EVM (Величина вектора ошибки), но по существу это одно и то же, выражаемое в разных единицах.
Третий параметр — BER (Bit Error Ratio), или Коэффициент битовых ошибок. Он характеризует частоту появления ошибочно восстановленных битов в демодулированном потоке данных и для стандарта DVB-C измеряется в двух точках: до декодера РидаСоломона и после него. Поэтому фактически это два параметра, которым часто присваивают названия preBER и postBER. Параметр postBER — та величина, которую пользователю иногда предъявляют как значение счетчика ошибочных пакетов за интервал наблюдения.
Последний параметр — констелляционная диаграмма, которая представляет собой график расположения символов на амплитуднофазовой плоскости, формируемый с накоплением за определенное время. Как правило, диаграмма рассматривается как некий качественный, а не количественный параметр, позволяющий оценить характер искажений входного радиосигнала.
Теперь можно приступить к более подробному анализу каждого из параметров на предмет их важности в оценке качества принимаемого цифрового сигнала.
BER vs MER
В специализированной литературе, журналах и на интернет-форумах часто разгораются дискуссии о значимости этих параметров; нередко можно встретить мнение, что самым важным и информативным параметром является MER. Сторонники этой точки зрения мотивируют ее тем, что зависимость величины MER от уровня шумов в полосе канала носит более пологий характер по сравнению с кривой BER, поэтому можно точнее оценить запас по устойчивому приему сигнала. В этом высказывании есть, конечно, большая доля истины. В самом деле, диапазон измерения MER, как правило, находится в пределах от 26-27 дБ до 38-42 дБ и выше (для модуляции QAM-256). Это позволяет оценить запас по качеству сигнала от порога синхронизации, когда демодулятор только-только начинает восстанавливать сигнал при значении preBER 1E-2…1E-3 . К тому же значение MER, как правило, более стабильно по сравнению с BER, особенно когда BER ниже 1E-7, что объясняется временем усреднения этих величин. К этому обстоятельству я вернусь немного позже.
Mux: MER-ы бывают пиковые и среднеквадратичные. Среднеквадратичные отражают усредненное значение за период измерения, а пиковые — максимальное. Если измеряется среднеквадратичное, то вполне возможны краткие развалы картинок принормальном MER-е, но переход на измерения пикового значения покажут эти сбои.
Mux: Достижимая точность измерения MER тем выше, чем ниже размерность модуляции измеряемого сигнала. Чем больше точек констелляции должен обрисовать ЦАП, тем меньше у него времени на каждую точку. Karlson2k: MER — хороший показатель, однако не единственный. Для приёмника
скорее важен BER или даже PER (BER после декодера Рида-Соломона). Иногда с одними тем же MER могут быть совсем разные BER.
В «обычных» условиях корреляция между MER и BER достаточно чёткая. Действительно, появление BER свидетельствует о подходе к границе (которая для цифры очень тонкая — здесь ещё есть, ещё чуть-чуть и уже совсем нет). Но как раз граница и важна. Тем не менее, в реальной жизни полно условий, когда чёткость корреляции начинает сбивается. Например — частотный сдвиг, из-за допплеровского эффекта (актуально для DVB-H) или по каким-то другим причинам. Иногда сбой может быть вызван «особенностями» передатчиков. Конечно, на BER сложно ориентироваться при измерениях, особенно «быстрых», и в большинстве случаев достаточно на MER. Но при любых важных измерениях без BER не обойтись.
А на практике для бытовых приёмников важен еще и уровень сигнала. К сожа- лению, разница в минимальном уровне, при котором бытовой приёмник цепляется за сигнал, доходит до 30-35 дБ у разных моделей даже от одного производителя. Штампуется же всё «подешевле». То есть на что ориентироваться при постройке
сети — вопрос ещё тот .
Самый важный параметр
Тем не менее, берусь утверждать, что самый важный параметр из всех измеряемых для цифрового сигнала — BER, а точнее — postBER. Ведь уверенно заявлять, что восстановление потока, полученного за определенный период, было абсолютным, можно только в случае, если postBER за это время оказался равным нулю. В реальности значение для postBER, равное 1E10…1E11, говорит о частоте появления ошибки в восстановленном потоке данных не более 2…20 бит в час. Такой прием можно характеризовать как безошибочный. В соответствии с научной терминологией соответствующий поток данных можно назвать «квазисвободным от ошибок».
У BER есть, правда, один недостаток — невозможность оценить запас сигнала по качеству, за счет которого можно уверенно принимать и восстанавливать цифровой поток в течение длительного времени. В пороговой ситуации уменьшение значения MER для одного канала всего на 1-2 дБ может изменить ситуацию от полного восстановления данных к полной невозможности приема сигнала на этом канале и скачкообразному изменению значения BER.
Но, тем не менее, важность этого параметра весьма высока. Особенно он может быть полезен сторонникам контроля телевизионного изображения. Параметр postBER полностью заменяет контроль картинки за исключением того случая, когда в структуре транспортного потока MPEG присутствуют ошибки, приводящие к артефактам изображения. Но они не всегда приводят к дефектам картинки, заметным на экране монитора, или же искажениям звукового сопровождения, да и вообще появляются достаточно редко.
Зато postBER по сравнению с контролем изображения имеет несколько преимуществ. Во-первых, он показывает общее количество ошибок в транспортном потоке, а не на одной программе, как при контроле картинки.
Во-вторых, вычислению postBER никак не препятствует шифровка потоков системами условного доступа. И для открытых, и для закрытых каналов он вычисляется одинаково.
И, в-третьих, postBER более чувствителен к ошибкам: счетчик невосстановленных пакетов будет неумолимо увеличиваться с каждой следующей ошибкой, хотя «битый» пакет может принадлежать другой программе или вообще не оказывать влияния на картинку или звук и, как результат, будет пропущен при визуальном контроле.
С точки зрения оценки запаса по качеству сигнала более информативен, конечно, preBER. Общеизвестно, что пороговое значение preBER, равное 2E-4, дает возможность восстанавливать данные до требуемых 1E-10…1E-11 значения postBER. Но это как раз тот случай, когда мы находимся на границе между уверенным приемом и отсутствием возможности восстановить сигнал при ухудшении значения MER. Если при измерении параметров мы получаем значение preBER, скажем, 1E-6, это уже указывает на наличие некоего запаса, позволяющего нам быть увереннее в будущем.
Время измерения BER
Большинство приборов для измерения параметров сигналов с цифровой модуляцией имеют нижнюю границу диапазона измерения параметра BER 1E-8 или 1E-9, реже — 1E-10, 1E-11. Совершенно естественно, что пользователи приборов хотят иметь границу как можно ниже, а результат измерения получать как можно быстрее. Давайте посчитаем: если мы используем модуляцию QAM-256 и символьную скорость 6,9 Мбод, то битовая скорость на входе декодера РидаСоломона будет составлять 6,9*8=55,2 Мбит/с. Если вероятность появления ошибки 1E-8, то для измерения этой величины нам надо накопить 108 бит потока данных, из которых один бит будет ошибочным. А накапливать мы их будем в течение 108/55,2×106 = 1,8 с. То есть один неправильно декодированный бит будет появляться, в среднем, раз в две секунды.
Результат, измеренный за этот промежуток времени, будет, конечно, весьма неточным. Для уменьшения случайной погрешности необходимо его усреднить хотя бы за 10 периодов измерения, то есть за 18 секунд. Если мы захотим измерить BER с нижней границей 1E-9, то для этого нам потребуется в 10 раз больше времени: 180 секунд или 3 минуты, а для получения достоверного результата 1E-11 мы должны ждать пять часов! Если использовать модуляцию более низкого порядка или более низкую символьную скорость, время измерения увеличится еще больше
Преимущества MER
MER (Modulation Error Ratio) — это ошибка модуляции, характеризующая отклонение реального символа от местоположения символа идеального на констелляционной диаграмме1.
По сравнению с BER параметр MER предоставляет более оперативную информацию о сигнале. Как я уже упоминал, MER является подобием параметра отношения сигнал/шум, хотя и учитывает большее число факторов, искажающих исходный радиосигнал. Значение параметра так же усредняется по времени, как и все величины, связанные с измерением мощности, но его измерение производится для каждого символа и, учитывая большие символьные скорости, накопление за одну секунду дает достаточно достоверный результат.
Вторым достоинством параметра MER является возможность его измерения с нормированной точностью. Большинство современных микросхем декодеров, на основе которых производятся приборы, позволяют вычислять MER аппаратно или на основе величин амплитуд векторов I и Q.
Под аппаратным вычислением я имею в виду возможность получения среднеквадратичного значения вектора ошибки из одного из внутренних регистров демодулятора. Во всяком случае производители микросхем утверждают, что это именно оно, и измерения, в принципе, это подтверждают. А зная среднеквадратичное значение вектора ошибки, вычислить MER уже несложно.
Использование значений амплитуд векторов квадратур для этих целей часто менее пригодно, потому что от микросхемы можно получить лишь 7 или 8 двоичных разрядов амплитуды QIвекторов. В результате динамический диапазон расчетного значения MER получается весьма низок. А разрядность регистра ошибки, напротив, часто бывает 10-, а то и 16-битная.
Погрешность измерения, связанную с неидеальными параметрами тюнера и демодулятора, можно скорректировать, имея источник сигнала с калиброванным параметром сигнал/шум. Калибровка производится для входного сигнала с добавлением только белого шума, но такой метод, тем не менее, дает весьма хороший результат.
Поэтому погрешность параметра MER для многих приборов является нормированной величиной в отличие от BER. Точность измерения BER зависит от качества приемника и демодулятора прибора, и корректировать ее невозможно. В результате измерение BER разными приборами дает близкие значения при плохом и заметно различающиеся при хорошем (при больших значениях MER).
То есть более качественный прибор показывает более низкие (более близкие к реальным) значения BER. Способность измерять низкие значения BER является хорошим индикатором качества измерительного прибора.
Если это так, возникает вопрос: «А не достаточно ли измерять один только MER для оценки качества принимаемого сигнала, ведь время измерения небольшое. Параметр предоставляет комплексную и точную информацию. С этим можно согласиться, но только в одном случае, когда к исходному сигналу примешивается только белый гауссовский шум. Как показывают практика и тестовое моделирование, при выполнении этого условия MER совпадает с SNR, и поэтому в данном случае для определения значений preBER и postBER можно воспользоваться кривыми зависимости BER от отношения SNR входного сигнала.
Констелляционная диаграмма
К сожалению, в реальной жизни все далеко не так идеально. На пути доставки телевизионного сигнала от источника до конечного пользователя существует великое множество факторов, приводящих к искажению сигнала. В результате для определения качества сигнала все-таки приходится использовать все возможные параметры, в том числе констелляционную диаграмму.
ассмотрим подробнее процесс демодуляции сигнала с цифровой модуляцией. После синхронизации с входным сигналом на выходе блока демодулятора для каждого символа появляются два значения векторов I и Q.2 Пара векторов определяет точку на амплитуднофазовой плоскости, каждая из которых принадлежит одной клетке, определяющей конкретное значение символа. В идеальном случае точки ложатся точно в середины клеток.
В условиях воздействия шума точки получают некоторое смещение от ожидаемого положения, которое носит название вектора выходной ошибки. Если точка остается в пределах своей клетки, демодулятор принимает правильное решение, в противном случае символу присваивается значение соседней клетки, что к появлению ошибки во входном потоке данных. Добавление белого шума к входному сигналу приводит к «размазыванию» точки в пятно круглой формы (рис. 1). Наибольшая частота попадания точки — в центре, а к краю окружности она уменьшается. В этом случае все пятна имеют примерно одинаковый диаметр.
Теперь рассмотрим случай одновременного воздействия белого и фазового шумов на демодуляцию сигнала. На рис. 2 приведена констелляционная диаграмма для сигнала с добавлением паразитной фазовой модуляции (джиттер фазы), из которой видно, что фазовая модуляция приводит к большему отклонению точек от центра клетки с увеличением длины вектора. В результате вероятность возникновения ошибки при декодировании точек в углах констелляционной диаграммы резко увеличивается. При этом значение MER уменьшается не так сильно, потому как смещение для точек ближе к центру диаграммы незначительное.
Ситуация ухудшается еще сильнее в случае, если кроме фазовой модуляции присутствует компрессия сигнала, появившаяся при прохождении им активных устройств в зоне нелинейности их передаточной характеристики. Вершины длинных векторов смещаются к центру констелляционной диаграммы, в результате чего вероятность ошибок для этих векторов увеличивается еще значительнее. На значение MER такие искажения также не оказывают большого влияния.
Ниже приведены результаты моделирования трех перечисленных ситуаций: измерение сигнала QAM-256 в случае воздействия только белого шума, белого шума и фазовой модуляции и белого шума одновременно с компрессией амплитуды сигнала. Три соответствующие констелляционных диаграммы представлены на рис. 3.
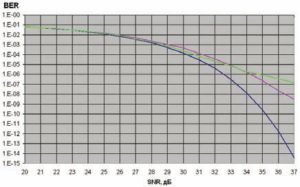
На следующей диаграмме (рис. 4) представлены три кривые зависимости параметра BER при изменении отношения сигнал/шум во входном сигнале. Синяя линия соответствует первому случаю, когда во входном сигнале присутствует только белый шум, фиолетовая — белый шум и фазовая модуляция и, наконец, зеленая — белый шум и компрессия.
Рис. 4. Кривые зависимости параметра BER при изменении отношения сигнал/шум во входном сигнале
Видно, что при низких значениях сигнал/шум линии практически совпадают, но с увеличением параметра они начинают расходиться. Наконец, на последнем графике (рис. 5) приведена зависимость параметра MER при тех же условиях. Из графика видно: при соотношении сигнал/шум 36 дБ при добавления фазовой модуляции к входному сигналу MER уменьшается на 0,5 дБ, при этом значение BER ухудшается сразу на несколько порядков. Еще сильнее влияние компрессии, хотя она и едва различима на констелляционной диаграмме.
Это не единственные случаи искажения в исходном входном сигнале, которые приводят к сильному ухудшению BER при незначительном изменении значения MER. К аналогичным последствиям приводят фазовые искажения квадратур, амплитудный разбаланс векторов квадратур и т.д.
Правда, последние виды искажений возникают реже. Гораздо хуже ситуация с помехой импульсного характера. Такого рода искажения сигнала не редкость, поскольку существует большое количество устройств, излучающих радиосигнал, который может
выступать в роли импульсной помехи для cигнала телевизионного.
При достаточно низкой частоте повторения и короткой длительности такая помеха практически не влияет на значение MER, но при этом может приводить к полной деградации BER. Ситуация осложняется тем, что подобную помеху сложно обнаружить. Часто не помогает и анализатор спектра. К примеру, если мешающий сигнал находится в полосе канала и при этом меньше по мощности на 20-30 дБ, то он маскируется полезным сигналом.
Особенности измерения уровня цифровых сигналов
Пожалуй, самым понятным для цифровых ТВсигналов, как и для аналогового телевидения, является параметр, характеризующий мощность сигнала. Но, тем не менее, довольно часто возникают вопросы, связанные с определением уровня цифровых каналов, поэтому немного внимания уделим и этому параметру.
Для аналогового телевидения измеряется уровень напряжения радиосигнала несущей частоты изображения. Для цифрового ТВ — «мощность радиосигнала в полосе канала» (такое название часто применяется в зарубежной литературе) или «фактический уровень напряжения радиосигналов с цифровой модуляцией в полосе частот распределения радиосигналов», как он называется в российском ГОСТ Р 52023 — «Сети распределительных систем кабельного телевидения». В России параметр принято обычно измерять в дБ относительно 1 микровольта (дБмкВ) как для аналоговых, так и для цифровых каналов.
Мощность3 радиосигнала для цифровых каналов измеряется как уровень напряжения немодулированного сигнала, который на нагрузке 75 Ом рассеивает мощность, эквивалентную мощности сигнала измеряемого канала.
При измерении уровней сигналов с помощью специализированных телевизионных измерителей или универсальных анализаторов спектра следует учитывать, что в аналоговых каналах характер сигнала — узкополосный, то есть основная часть мощности канала сосредоточена в довольно узком частотном диапазоне, а цифровые каналы характеризуются равномерным распределением мощности в полосе канала. В основе работы измерителей уровня лежит принцип селективного вольтметра. То есть в спектре радиосигнала выделяется (отфильтровывается) определенная частотная полоса, а затем измеряется напряжение сигнала, попавшего в эту полосу.
Если при измерении уровня узкополосного сигнала ширина его спектра заведомо меньше полосы измерения4, уровень измеряемого сигнала будет постоянным при изменении полосы измерения в пределах канала. Ситуация меняется при измерении широкополосных сигналов, каковыми являются радиосигналы цифрового телевидения. В этом случае чем шире полоса измерения прибора, тем выше уровень измеряемого напряжения. На рис. 6 представлена спектрограмма частотного диапазона с несколькими телевизионными каналами с аналоговой и цифровой модуляциями.
Спектрограмма была снята с помощью прибора с полосой измерения 230 кГц. На первый взгляд, уровни цифровых каналов ниже аналоговых более чем на 10 дБ. Однако для аналогового канала S20 уровень (Uan) можно определить по спектру как 66 дБмкВ. А для определения мощности сигнала цифрового канала S23 необходимо применить следующую формулу:
Uцк = Uизм + 10lg(Вц/Виз) + К,5
где Uцк — искомая мощность цифрового канала;
Uизм — уровень напряжения измеренный в центре полосы канала; Вц — полоса частот, занимаемая цифровым каналом; Виз — полоса измерения прибора;
К — поправочный коэффициент, компенсирующий погрешности измерения6.
Подставив исходные данные в формулу, получим:
US23 = 53 + 10lg(7,5/0,23) + 1 = 69 дБмкВ.
Таким образом, на самом деле уровень мощности канала S23 на 3 дБ больше, чем S20.
В режиме измерения уровня специализированные телевизионные приборы автоматически производят такой пересчет цифровых каналов с учетом их полосы и отображают их мощность корректно. Но при работе в режиме анализатора спектра и при измерении приборами, не рассчитанными на работу с цифровыми каналами, надо помнить об этой особенности. Такой метод измерения мощности канала в одной частотной точке дает достаточно точный результат только в случае достаточной равномерности АЧХ в полосе канала.
Общие рекомендации по оценке качества цифровых каналов
Кабельные операторы, давно работающие с цифровым телевидением и имеющие большой опыт, советуют классифицировать состояние кабельной сети по трехбалльной шкале. Оценка три балла означает, что параметры каналов в сети соответствуют требованиям качественного приема и обладают достаточным запасом для стабильной, долговременной работы. От оператора при этом требуется только продолжение текущего контроля. Оценка два балла: параметры каналов также соответствуют требованиям качественного приема, но их значения не имеют достаточного запаса для обеспечения долговременной стабильной работы.
Такое состояние сети требует от оператора планового проведения работ для выявления источника проблем и принятия решения о методах восстановления состояния сети до трех баллов. И, наконец, третье состояние сети с оценкой один балл: параметры одного или нескольких каналов не отвечают требованиям качественного приема, что требует от оператора немедленных действий по ремонту или настраиванию сети для поднятия до второго или третьего уровня. Для оценки каждого канала необходимо измерить все параметры на абонентском отводе. Оценка присваивается в соответствии со следующими условиями.
Оценка 3 балла (выполняются все четыре условия): Уровень канала: соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.
MER: не меньше 36 дБ для модуляции QAM-256 и 28 дБ для модуляции QAM-64.
PreBER не превышает 1E7. PostBER: не превышает 1E9.
Оценка 2 балла (выполняются все четыре условия): Уровень канала: соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.
MER: находится в пределах от 34 до 36 дБ для модуляции QAM256 и от 26 до 28 дБ для модуляции QAM64.
PreBER: не превышает 1E6. PostBER: не превышает 1E9.
Оценка 1 балл (выполняется хотя бы одно условие):
Уровень канала: не соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.
MER: значение меньше 34 дБ для модуляции QAM-256 и меньше 26 дБ для модуляции QAM-64.
PreBER: значение выше 1E6. PostBER: значение выше 1E-9.
Если есть возможность контроля констелляционной диаграммы, необходимо добавить еще одно условие. Для оценки «3» форма констелляционной диаграммы не должна содержать ярко выраженных фазовых искажений, дисбаланса квадратур и искажений типа компрессии сигнала. При наличии подобных искажений измеряемому каналу должна быть присвоена оценка не выше двух баллов.
При указании значений параметров я исходил из предположения, что они измерены корректно, в пределах погрешности измерения прибора. Но при определенных условиях измеренные значения могут выпадать за пределы погрешности. В этом случае каналу может быть присвоена оценка, не соответствующая действительности.
Данная методика оценки качества не является, конечно, абсолютной и единственно верной. Каждый оператор может для себя выбрать границы значений параметров для оценки качества сигнала в соответствии с особенностями конкретной сети и отдельных каналов; при этом следует придерживаться общего подхода к методу проверки состояния сети.
——
1 Физический смысл этого параметра и формула для вычисления его среднеквадратичного значения рассмотрены в статьях серии «Цифровое кабельное ТВ. Часть 2. Состав головной станции, расчет ретранслируемого потока», «ТелеСпутник», ноябрь 2007 и «Цифровое кабельное ТВ. Часть 4. Сигнал DVB в распределительной сети. Использование альтернативных стандартов», январь 2008 (прим. ред.).
2 I= A cosφ, а Q = A sinφ где А – амплитуда QAM символа, а φ – фаза символа.
3 Имеется в виду мощностная характеристика, в качестве которой в телевидении принято использовать эквивалентное напряжение немодулированного сигнала, который по мощности равен сигналу телевизионному. Хотя в статье применяется термин «мощность цифрового канала», на самом деле подразумевается как раз напряжение этого эквивалентного сигнала (прим. автора).
4 Полоса измерения определяется полосой пропускания измерительного фильтра (прим. ред.).
5 Так эта формула выглядит в ГОСТ Р 52023 (прим. автора).
6 Коэффициент зависит в основном от параметров детектора (тип детектора и его постоянные времени) и прямоугольности измерительного фильтра. Определяется опытным путем и, как правило, составляет 13 дБ (прим. автора).
Андрей Конорев,
ведущий инженер ООО «Планар»
Использованная литература
- Б.А. Локшин. Цифровое вещание: — от студии к телезрителю.
- ГОСТ Р 52023-2003 «Сети распределительные систем кабельного телевидения».
- ETSI TR 101 290 Measurement guidelines for DVB system.
Коэффициент ошибок модуляции или MER — это мера, используемая для количественной оценки производительности передатчика или приемника цифрового радио (или цифрового телевидения) в системе связи, использующей цифровую модуляцию (например, QAM ). Сигнал, отправленный идеальным передатчиком или принятый приемником, будет иметь все точки совокупности точно в идеальных местах, однако различные недостатки в реализации (например, шум, низкий коэффициент отклонения изображения, фазовый шум, подавление несущей, искажение и т. Д.) или путь прохождения сигнала заставляет фактические точки созвездия отклоняться от идеального местоположения.
MER передатчика можно измерить с помощью специального оборудования, которое демодулирует принятый сигнал аналогично тому, как это делает настоящий радиодемодулятор. Демодулированный и обнаруженный сигнал можно использовать в качестве достаточно надежной оценки идеального переданного сигнала при вычислении MER.
Определение
Вектор ошибки является вектором в плоскости IQ между точкой идеального созвездия и точкой, принимаемой приемником. Евклидово расстояние между двумя точками — это его величина.
Коэффициент ошибок модуляции равен отношению среднего квадратного корня (RMS) мощности (в ваттах) опорного вектора к мощности (в ваттах) ошибки. Он определяется в дБ как:
где P error — это среднеквадратичная мощность вектора ошибок, а P signal — среднеквадратичная мощность идеального переданного сигнала.
MER определяется как процент совместимым (но взаимным) способом:
с такими же определениями.
MER тесно связан с величиной вектора ошибок (EVM), но MER рассчитывается на основе средней мощности сигнала. MER также тесно связан с отношением сигнал / шум . MER включает в себя все недостатки, включая детерминированный дисбаланс амплитуд, квадратурную ошибку и искажение, в то время как шум является случайным по своей природе.
Смотрите также
- Величина вектора ошибки
- Отношение несущей к шуму
- Соотношение сигнал шум
Ссылки
- Технический отчет ETSI ETR 290: «Рекомендации по измерениям для систем DVB», Errata 1, май 1997 г.
This post defines the Modulation Error Ratio (MER) for QAM signals, and shows how to compute it. As we’ll see, in the absence of impairments other than noise, the MER tracks the signal’s Carrier-to-Noise Ratio (over a limited range). A Matlab script at the end of the PDF version of this post computes MER for a simplified QAM-64 system.
Figure 1 is a simplified block diagram of a QAM system. The transmitter includes a source of QAM symbols, a root-Nyquist pulse-shaping filter and a Quadrature modulator. The receiver has a Quadrature downconverter, root-Nyquist filter, and decision block. The wide lines represent complex (I/Q) signals, and the narrow lines represent the real modulated signal. The matched root-Nyquist filters perform the dual tasks of limiting the bandwidth of the transmitted signal while minimizing the interference from other symbols at the sampling instant [1,2]. For our discussion of MER, I have left out the usual key receiver systems of AGC, carrier recovery, clock recovery, and adaptive equalization.
This article is available in PDF format for easy printing.

Figure 1. Simplified QAM system block diagram.
For our purposes, we can model the channel at complex baseband [3], so we can eliminate the Quadrature up and down conversions. Also, we will model the entire system as discrete-time, so the D/A and A/D converters can be left out. We then have the block diagram of Figure 2a, where the channel includes Gaussian noise (AWGN) added to I and Q, plus a block labeled “other impairments”. These could include linear impairments such as multipath, phase noise, and interference. In this article, our focus is on noise, so we’ll leave out the other impairments.
Figure 3 plots some of the labeled signals from Figure 2 for a QAM-16 system with noise. Figure 3a shows the random QAM symbols as a Qmap vs Imap constellation plot. Figure 3b is an eyeplot of the output of the receiver’s root-Nyquist filter, Irx. At this point, the signal has 4 samples per symbol, so the valid sampling instants are spaced 4 samples apart. For our simplified model, the eye opening aligns exactly with every fourth sample (A real-world receiver must compute the correct sample value using a variable interpolator). The eyes are partially closed due to the noise added to the signal. Downsampling Irx and Qrx by 4 at the correct sample alignment gives Idown and Qdown, who’s constellation plot is shown in Figure 3c. The noise is visible as “fuzz” around the nominal constellation points. The final outputs Idec and Qdec are computed in the decision block by rounding (slicing) Idown and Qdown to the nearest allowed symbol value, reproducing the original transmitter constellation (Figure 3d).

Figure 2. Simplified QAM system at complex baseband.
a. Overall block diagram. AWGN: additive white Gaussian noise.
b. Decision block. dI= Idown – Idec; dQ= Qdown – Qdec

Figure 3. Signals from Figure 2 for QAM-16 modulation with added noise.
a. Imap/Qmap constellation b. Irx eyeplot c. Idown/Qdown constellation d. Idec/Qdec constellation
MER Formula
The Modulation Error Ratio is a way to quantify the constellation noise seen in Figure 3c. Figure 4 shows the QAM-16 symbols Qdec vs Idec at the output of the decision block. Also shown is a single received symbol of Idown/Qdown at the input of the decision block. The modulation error ratio of this single symbol is defined as:
$$ MER; (one ,symbol) = frac{I_{dec}^2+Q_{dec}^2}{dI^2+dQ^2}$$
Where dI and dQ are the errors with respect to the target symbol Idec/Qdec. In words, MER is the ratio of the target symbol power to the error power. dI and dQ are computed as shown in the block diagram of the decision block (Figure 2b): dI = Idown – Idec; dQ = Qdown – Qdec.
If N symbols are received, the MER is defined as the average:
$$MER= frac1{N}sum_{i=1}^Nfrac{I_{dec}(i)^2+Q_{dec}(i)^2}{dI(i)^2+dQ(i)^2}$$
If N is large and all symbols are equally likely, we can calculate MER as the ratio of average target symbol power to average error power [4]:
$$MER= frac{avg. target,symbol,power}{avg. error,power} qquad $$
$$=frac{frac1{N}sum_{i=1}^NI_{dec}(i)^2 +Q_{dec}(i)^2}{frac1{N}sum_{i=1}^NdI(i)^2+dQ(i)^2} qquad(1)$$
For a given constellation order, the numerator is a constant – call it Pav:
$$MER=frac{P_{av}}{frac1{N}sum_{i=1}^NdI(i)^2+dQ(i)^2} qquad(2)$$
Since Pav is a constant, we don’t have to evaluate it over all of the received symbols. Instead, we can find Pav by evaluating the numerator of Equation 1 over N = 4 constellation points in the first quadrant of QAM-16. For a square constellation, we’ll use I and Q from the set +/- k/M1/2, where k is odd and M is constellation order. For M= 16, the set is +/- {1/4, 3/4}, and the constellation points in the first quadrant are
$(frac14,frac14) ;(frac14,frac34);(frac34,frac14);(frac34,frac34).$ The average constellation power of QAM-16 is thus:
$$P_{av};(QAM16)= frac14*( (frac14)^2 + (frac14)^2 + (frac14)^2 + (frac34)^2$$
$$+ (frac34)^2 + (frac14)^2 + (frac34)^2 + (frac34)^2 ) = frac58 $$
We can write the MER in dB as:
$$ MER ;(dB)=10log_{10}P_{av} — 10log_{10}left(frac1Nsum_{i=1}^N dI(i)^2+dQ(i)^2right) qquad(3)$$
If noise is the only signal impairment, and if matched (root-Nyquist) filters are used in transmitter and receiver, the MER can equal the signal’s carrier-to-noise ratio (C/N). In reality, accurate estimation of C/N is only possible over a limited range. The maximum MER is limited by impairments of the transmitter and receiver themselves. The low end is also limited: when C/N is low enough to cause symbol errors, the calculated MER loses accuracy. This occurs because each decision error causes the error power calculation for that symbol to be too low. When there are many errors, the calculated MER will be too high.

Figure 4. QAM-16 constellation points (symbols), with target signal vector and error vector.
Example
This example computes MER of a QAM-64 signal with added noise. Matlab code that implements the simplified QAM system is listed in the PDF version of this post. As shown in Figure 2a, Gaussian noise is added to the I and Q channels. Figure 5a shows the spectrum of Ichan + jQchan, which has a C/N of about 30 dB. An eyeplot of the receiver signal Irx is shown in Figure 5b. The receiver constellation is shown in Figure 5c, along with the value of MER calculated by Equation 3. As expected, the calculated MER matches the C/N.
In calculating MER for QAM-64, we used Pav = 21/32 = -1.83 dB. The I and Q values of QAM-64 come from the set +/- {1/8 3/8 5/8 7/8}. The root-Nyquist filters used have excess bandwidth α = 0.25. This gives an occupied signal bandwidth of 1.25*fsymbol = 1.25*fs/4 = .3125 fs (Figure 5a).
A convenient way to calculate the average error power is to filter dI2 + dQ2 using a one-pole IIR filter. The output of the filter can be used to compute a running estimate of MER, as shown in Figure 5d.
Finally, Figure 6 shows the receive constellation with no noise added to the transmitted signal. The MER of 41 dB is a measure of the Inter-symbol interference (ISI) [1,2] of the cascaded transmit and receive root-Nyquist filters in our simplified model.

Figure 5. QAM-64 Model Outputs
a. Spectrum at RX input, showing added noise. b. Eyeplot of Irx
c. Receiver constellation plot. d. MER calculated by filtering dI2 + dQ2 using a one-pole IIR filter.

Figure 6. Receive Constellation with no noise added to the transmitted signal.
References
1. Rice, Michael, Digital Communications, Pearson, 2009, Section A.2.
2. Course Notes EE4061, “Intersymbol Interference/Nyquist Pulse Shaping”, Georgia Institute of Technology, 2011. http://wireless-systems.ece.gatech.edu/4601/lectures-2011/week10.pdf
3. William H. Tranter, et. al., Communication Systems Simulation, Prentice Hall, 2004, section 4.1.1.
4. Cisco Systems, “Digital Transmission: Carrier-to-Noise Ratio, Signal-to-Noise Ratio, and Modulation Error Ratio”, 2006.
http://www.mdmit.pl/apps/mdmit/download/Mibs%20for%20cable%20modems/Hi_res_CNR-SNR_WP_1115b.pdf
Neil Robertson November, 2019 revised 4/17/20
The modulation error ratio or MER is a measure used to quantify the performance of a digital radio (or digital TV) transmitter or receiver in a communications system using digital modulation (such as QAM). A signal sent by an ideal transmitter or received by a receiver would have all constellation points precisely at the ideal locations, however various imperfections in the implementation (such as noise, low image rejection ratio, phase noise, carrier suppression, distortion, etc.) or signal path cause the actual constellation points to deviate from the ideal locations.
Transmitter MER can be measured by specialized equipment, which demodulates the received signal in a similar way to how a real radio demodulator does it. Demodulated and detected signal can be used as a reasonably reliable estimate for the ideal transmitted signal in MER calculation.
Definition
An error vector is a vector in the I-Q plane between the ideal constellation point and the point received by the receiver. The Euclidean distance between the two points is its magnitude.
The modulation error ratio is equal to the ratio of the root mean square (RMS) power (in Watts) of the reference vector to the power (in Watts) of the error. It is defined in dB as:
where Perror is the RMS power of the error vector, and Psignal is the RMS power of ideal transmitted signal.
MER is defined as a percentage in a compatible (but reciprocal) way:
with the same definitions.
MER is closely related to error vector magnitude (EVM), but MER is calculated from the average power of the signal. MER is also closely related to signal-to-noise ratio. MER includes all imperfections including deterministic amplitude imbalance, quadrature error and distortion, while noise is random by nature.
See also
- Error vector magnitude
- Carrier to Noise Ratio
- Signal-to-noise ratio
References
- ETSI technical report ETR 290: «Measurement guidelines for DVB systems», Errata 1, May 1997
This page was last edited on 29 April 2022, at 20:15
Коэффициент ошибок модуляции
Из Википедии, свободной энциклопедии
Перейти к навигации
Перейти к поиску
Коэффициент ошибок модуляции или MER — это мера, используемая для количественной оценки производительности передатчика или приемника цифрового радио (или цифрового телевидения) в системе связи, использующей цифровую модуляцию (например, QAM ). Сигнал, отправленный идеальным передатчиком или принятый приемником, будет иметь все точки совокупности точно в идеальных местах, однако различные недостатки в реализации (например, шум , низкий коэффициент отклонения изображения , фазовый шум , подавление несущей , искажениеи т. д.) или путь прохождения сигнала приводят к тому, что фактические точки созвездия отклоняются от идеального местоположения.
MER передатчика можно измерить с помощью специального оборудования, которое демодулирует принятый сигнал аналогично тому, как это делает настоящий радиодемодулятор. Демодулированный и обнаруженный сигнал можно использовать в качестве достаточно надежной оценки идеального переданного сигнала при вычислении MER.
Определение
Вектор ошибки является вектором в плоскости IQ между точкой идеального созвездия и точкой , принимаемой приемником. Евклидово расстояние между двумя точками — это его величина.
Коэффициент ошибок модуляции равен отношению среднего квадратного корня (RMS) мощности (в ваттах) опорного вектора к мощности (в ваттах) ошибки. Он определяется в дБ как:
где P error — это среднеквадратичная мощность вектора ошибки, а P signal — среднеквадратичная мощность идеального переданного сигнала.
MER определяется как процент совместимым (но взаимным) способом:
с такими же определениями.
MER тесно связан с величиной вектора ошибок (EVM), но MER рассчитывается на основе средней мощности сигнала. MER также тесно связан с отношением сигнал / шум . MER включает в себя все недостатки, включая детерминированный дисбаланс амплитуд , квадратурную ошибку и искажение , в то время как шум является случайным по своей природе.
См. Также
- Величина вектора ошибки
- Отношение несущей к шуму
- Сигнал-шум
Ссылки
- Технический отчет ETSI ETR 290: «Рекомендации по измерениям для систем DVB» , Опечатка 1, май 1997 г.