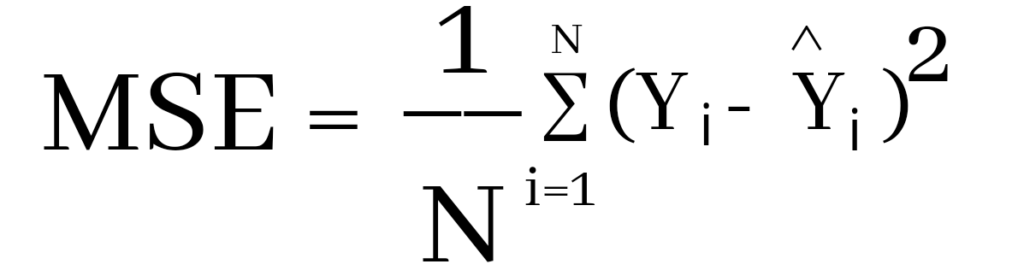The mean squared error is a common way to measure the prediction accuracy of a model. In this tutorial, you’ll learn how to calculate the mean squared error in Python. You’ll start off by learning what the mean squared error represents. Then you’ll learn how to do this using Scikit-Learn (sklean), Numpy, as well as from scratch.
What is the Mean Squared Error
The mean squared error measures the average of the squares of the errors. What this means, is that it returns the average of the sums of the square of each difference between the estimated value and the true value.
The MSE is always positive, though it can be 0 if the predictions are completely accurate. It incorporates the variance of the estimator (how widely spread the estimates are) and its bias (how different the estimated values are from their true values).
The formula looks like below:

Now that you have an understanding of how to calculate the MSE, let’s take a look at how it can be calculated using Python.
Interpreting the Mean Squared Error
The mean squared error is always 0 or positive. When a MSE is larger, this is an indication that the linear regression model doesn’t accurately predict the model.
An important piece to note is that the MSE is sensitive to outliers. This is because it calculates the average of every data point’s error. Because of this, a larger error on outliers will amplify the MSE.
There is no “target” value for the MSE. The MSE can, however, be a good indicator of how well a model fits your data. It can also give you an indicator of choosing one model over another.
Loading a Sample Pandas DataFrame
Let’s start off by loading a sample Pandas DataFrame. If you want to follow along with this tutorial line-by-line, simply copy the code below and paste it into your favorite code editor.
# Importing a sample Pandas DataFrame
import pandas as pd
df = pd.DataFrame.from_dict({
'x': [1,2,3,4,5,6,7,8,9,10],
'y': [1,2,2,4,4,5,6,7,9,10]})
print(df.head())
# x y
# 0 1 1
# 1 2 2
# 2 3 2
# 3 4 4
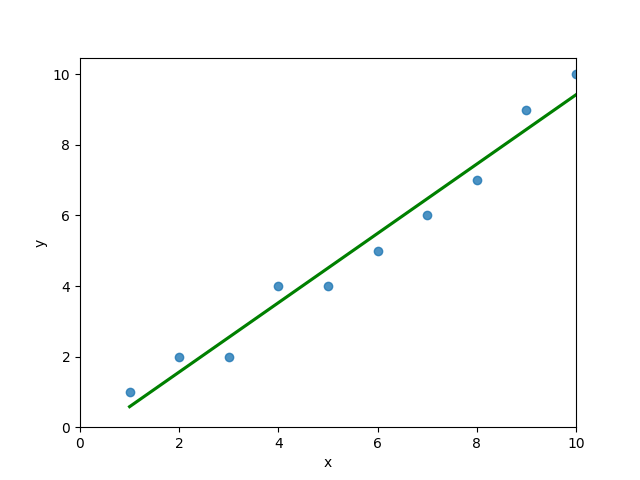
# 4 5 4You can see that the editor has loaded a DataFrame containing values for variables x and y. We can plot this data out, including the line of best fit using Seaborn’s .regplot() function:
# Plotting a line of best fit
import seaborn as sns
import matplotlib.pyplot as plt
sns.regplot(data=df, x='x', y='y', ci=None)
plt.ylim(bottom=0)
plt.xlim(left=0)
plt.show()This returns the following visualization:
The mean squared error calculates the average of the sum of the squared differences between a data point and the line of best fit. By virtue of this, the lower a mean sqared error, the more better the line represents the relationship.
We can calculate this line of best using Scikit-Learn. You can learn about this in this in-depth tutorial on linear regression in sklearn. The code below predicts values for each x value using the linear model:
# Calculating prediction y values in sklearn
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(df[['x']], df['y'])
y_2 = model.predict(df[['x']])
df['y_predicted'] = y_2
print(df.head())
# Returns:
# x y y_predicted
# 0 1 1 0.581818
# 1 2 2 1.563636
# 2 3 2 2.545455
# 3 4 4 3.527273
# 4 5 4 4.509091Calculating the Mean Squared Error with Scikit-Learn
The simplest way to calculate a mean squared error is to use Scikit-Learn (sklearn). The metrics module comes with a function, mean_squared_error() which allows you to pass in true and predicted values.
Let’s see how to calculate the MSE with sklearn:
# Calculating the MSE with sklearn
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(df['y'], df['y_predicted'])
print(mse)
# Returns: 0.24727272727272714This approach works very well when you’re already importing Scikit-Learn. That said, the function works easily on a Pandas DataFrame, as shown above.
In the next section, you’ll learn how to calculate the MSE with Numpy using a custom function.
Calculating the Mean Squared Error from Scratch using Numpy
Numpy itself doesn’t come with a function to calculate the mean squared error, but you can easily define a custom function to do this. We can make use of the subtract() function to subtract arrays element-wise.
# Definiting a custom function to calculate the MSE
import numpy as np
def mse(actual, predicted):
actual = np.array(actual)
predicted = np.array(predicted)
differences = np.subtract(actual, predicted)
squared_differences = np.square(differences)
return squared_differences.mean()
print(mse(df['y'], df['y_predicted']))
# Returns: 0.24727272727272714The code above is a bit verbose, but it shows how the function operates. We can cut down the code significantly, as shown below:
# A shorter version of the code above
import numpy as np
def mse(actual, predicted):
return np.square(np.subtract(np.array(actual), np.array(predicted))).mean()
print(mse(df['y'], df['y_predicted']))
# Returns: 0.24727272727272714Conclusion
In this tutorial, you learned what the mean squared error is and how it can be calculated using Python. First, you learned how to use Scikit-Learn’s mean_squared_error() function and then you built a custom function using Numpy.
The MSE is an important metric to use in evaluating the performance of your machine learning models. While Scikit-Learn abstracts the way in which the metric is calculated, understanding how it can be implemented from scratch can be a helpful tool.
Additional Resources
To learn more about related topics, check out the tutorials below:
- Pandas Variance: Calculating Variance of a Pandas Dataframe Column
- Calculate the Pearson Correlation Coefficient in Python
- How to Calculate a Z-Score in Python (4 Ways)
- Official Documentation from Scikit-Learn
In this article, we are going to learn how to calculate the mean squared error in python? We are using two python libraries to calculate the mean squared error. NumPy and sklearn are the libraries we are going to use here. Also, we will learn how to calculate without using any module.
MSE is also useful for regression problems that are normally distributed. It is the mean squared error. So the squared error between the predicted values and the actual values. The summation of all the data points of the square difference between the predicted and actual values is divided by the no. of data points.
Where Yi and Ŷi represent the actual values and the predicted values, the difference between them is squared.
Derivation of Mean Squared Error
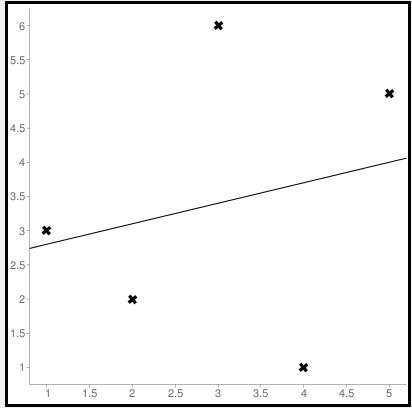
First to find the regression line for the values (1,3), (2,2), (3,6), (4,1), (5,5). The regression value for the value is y=1.6+0.4x. Next to find the new Y values. The new values for y are tabulated below.
| Given x value | Calculating y value | New y value |
|---|---|---|
| 1 | 1.6+0.4(1) | 2 |
| 2 | 1.6+0.4(2) | 2.4 |
| 3 | 1.6+0.4(3) | 2.8 |
| 4 | 1.6+0.4(4) | 3.2 |
| 5 | 1.6+0.4(5) | 3.6 |
Now to find the error ( Yi – Ŷi )
We have to square all the errors
By adding all the errors we will get the MSE
Line regression graph
Let us consider the values (1,3), (2,2), (3,6), (4,1), (5,5) to plot the graph.
The straight line represents the predicted value in this graph, and the points represent the actual data. The difference between this line and the points is squared, known as mean squared error.
Also, Read | How to Calculate Square Root in Python
To get the Mean Squared Error in Python using NumPy
import numpy as np true_value_of_y= [3,2,6,1,5] predicted_value_of_y= [2.0,2.4,2.8,3.2,3.6] MSE = np.square(np.subtract(true_value_of_y,predicted_value_of_y)).mean() print(MSE)
Importing numpy library as np. Creating two variables. true_value_of_y holds an original value. predicted_value_of_y holds a calculated value. Next, giving the formula to calculate the mean squared error.
Output
3.6400000000000006
To get the MSE using sklearn
sklearn is a library that is used for many mathematical calculations in python. Here we are going to use this library to calculate the MSE
Syntax
sklearn.metrices.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average', squared=True)
Parameters
- y_true – true value of y
- y_pred – predicted value of y
- sample_weight
- multioutput
- raw_values
- uniform_average
- squared
Returns
Mean squared error.
Code
from sklearn.metrics import mean_squared_error true_value_of_y= [3,2,6,1,5] predicted_value_of_y= [2.0,2.4,2.8,3.2,3.6] mean_squared_error(true_value_of_y,predicted_value_of_y) print(mean_squared_error(true_value_of_y,predicted_value_of_y))
From sklearn.metrices library importing mean_squared_error. Creating two variables. true_value_of_y holds an original value. predicted_value_of_y holds a calculated value. Next, giving the formula to calculate the mean squared error.
Output
3.6400000000000006
Calculating Mean Squared Error Without Using any Modules
true_value_of_y = [3,2,6,1,5]
predicted_value_of_y = [2.0,2.4,2.8,3.2,3.6]
summation_of_value = 0
n = len(true_value_of_y)
for i in range (0,n):
difference_of_value = true_value_of_y[i] - predicted_value_of_y[i]
squared_difference = difference_of_value**2
summation_of_value = summation_of_value + squared_difference
MSE = summation_of_value/n
print ("The Mean Squared Error is: " , MSE)
Declaring the true values and the predicted values to two different variables. Initializing the variable summation_of_value is zero to store the values. len() function is useful to check the number of values in true_value_of_y. Creating for loop to iterate. Calculating the difference between true_value and the predicted_value. Next getting the square of the difference. Adding all the squared differences, we will get the MSE.
Output
The Mean Squared Error is: 3.6400000000000006
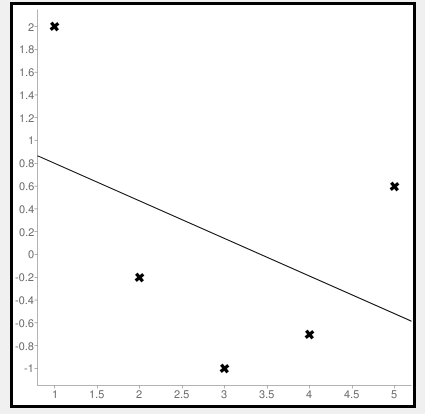
Calculate Mean Squared Error Using Negative Values
Now let us consider some negative values to calculate MSE. The values are (1,2), (3,-1), (5,0.6), (4,-0.7), (2,-0.2). The regression line equation is y=1.13-0.33x
The line regression graph for this value is:
New y values for this will be:
| Given x value | Calculating y value | New y value |
|---|---|---|
| 1 | 1.13-033(1) | 0.9 |
| 3 | 1.13-033(3) | 0.1 |
| 5 | 1.13-033(5) | -0.4 |
| 4 | 1.13-033(4) | -0.1 |
| 2 | 1.13-033(2) | 0.6 |
Code
>>> from sklearn.metrics import mean_squared_error >>> y_true = [2,-1,0.6,-0.7,-0.2] >>> y_pred = [0.9,0.1,-0.4,-0.1,0.6] >>> mean_squared_error(y_true, y_pred)
First, importing a module. Declaring values to the variables. Here we are using negative value to calculate. Using the mean_squared_error module, we are calculating the MSE.
Output
0.884
Bonus: Gradient Descent
Gradient Descent is used to find the local minimum of the functions. In this case, the functions need to be differentiable. The basic idea is to move in the direction opposite from the derivate at any point.
The following code works on a set of values that are available on the Github repository.
Code:
#!/usr/bin/python
# -*- coding: utf-8 -*-
from numpy import *
def compute_error(b, m, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (m * x + b)) ** 2
return totalError / float(len(points))
def gradient_step(
b_current,
m_current,
points,
learningRate,
):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2 / N) * (y - (m_current * x + b_current))
m_gradient += -(2 / N) * x * (y - (m_current * x + b_current))
new_b = b_current - learningRate * b_gradient
new_m = m_current - learningRate * m_gradient
return [new_b, new_m]
def gradient_descent_runner(
points,
starting_b,
starting_m,
learning_rate,
iterations,
):
b = starting_b
m = starting_m
for i in range(iterations):
(b, m) = gradient_step(b, m, array(points), learning_rate)
return [b, m]
def main():
points = genfromtxt('data.csv', delimiter=',')
learning_rate = 0.00001
initial_b = 0
initial_m = 0
iterations = 10000
print('Starting gradient descent at b = {0}, m = {1}, error = {2}'.format(initial_b,
initial_m, compute_error(initial_b, initial_m, points)))
print('Running...')
[b, m] = gradient_descent_runner(points, initial_b, initial_m,
learning_rate, iterations)
print('After {0} iterations b = {1}, m = {2}, error = {3}'.format(iterations,
b, m, compute_error(b, m, points)))
if __name__ == '__main__':
main()
Output:
Starting gradient descent at b = 0, m = 0, error = 5671.844671124282
Running...
After 10000 iterations b = 0.11558415090685024, m = 1.3769012288001614, error = 212.262203123587941. What is the pip command to install numpy?
pip install numpy
2. What is the pip command to install sklearn.metrices library?
pip install sklearn
3. What is the expansion of MSE?
The expansion of MSE is Mean Squared Error.
Conclusion
In this article, we have learned about the mean squared error. It is effortless to calculate. This is useful for loss function for least squares regression. The formula for the MSE is easy to memorize. We hope this article is handy and easy to understand.
Introduction
In this post we’ll cover the Mean Squared Error (MSE), arguably one of the most popular error metrics for regression analysis. The MSE is expressed as:
MSE = frac{1}{N}sum_i^N(hat{y}_i-y_i)^2 (1)
where hat{y}_i are the model output and y_i are the true values. The summation is performed over N individual data points available in our sample.
The advantage of the MSE is that it is easily differentiated, making it ideal for optimisation analysis. In addition, we can interpret the MSE in terms of the bias and variance in the model. We can see this is the case by expressing (1) in terms of expected values, and then expanding the squared difference:
MSE = E[(hat{y}-y)^2]
= E[hat{y}^2 + y^2 – 2hat{y}y]
We can now add positive and negative E(hat{y})^2 terms, and make use of our definitions of bias and variance:
= E(hat{y}^2) – E(hat{y})^2 + E(hat{y})^2 + y^2 – 2yE(hat{y})
= Var(hat{y}) + E(hat{y})^2 – 2yE(hat{y}) + y^2
= Var(hat{y}) + E[hat{y} – y]^2
= Var(hat{y}) + Bias^2(hat{y})
One complication of using the MSE is the fact that this error metric is expressed in termed of squared units. To express the error in terms of the units of y and hat{y}, we can compute the Root Mean Squared Error (RMSE):
RMSE = sqrt{MSE} (2)
In addition, the MSE tends to be much more sensitive the outliers when compared to other metrics, such as the mean absolute error or making use of the median.
Python Coding Example
Here I will make use of the same example used when demonstrating the mean absolute error. First let’s import the required packages:
## imports ##
import numpy as np
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as pltNotice that scikit-learn provides a function for computing the MSE. Like before, let’s create the toy data set and plot the results:
## define two arrays: x & y ##
x_true = np.linspace(0,4*np.pi,50)
y_true = np.sin(x_true) + np.random.rand(x_true.shape[0])
## plot the data ##
plt.plot(x_true,y_true)
plt.title('Sinusoidal Data with Noise')
plt.xlabel('x')
plt.ylabel('y')
plt.show()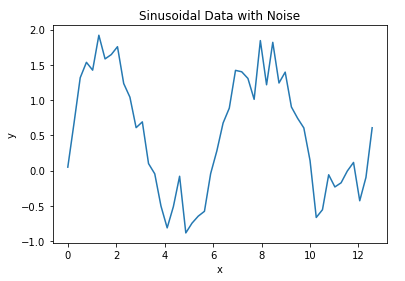
Let’s now assume we have a model that is fitted to these data. We can make a plot of this model together with the raw data:
## plot the data & predictions ##
plt.plot(x_true,y_true)
plt.plot(x_true,y_pred)
plt.title('Sinusoidal Data with Noise + Predictions')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['y_true','y_pred'])
plt.show()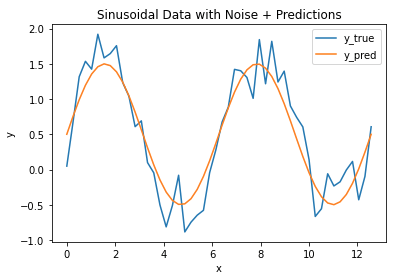
We can see that the model follows the general pattern in the data, however there are differences between the two. We can measure the magnitude of these differences by computing the MSE (and RMSE):
## compute the mse ##
mse = mean_squared_error(y_true,y_pred)
print("The mean sqaured error is: {:.2f}".format(mse))
print("The root mean squared error is: {:.2f}".format(np.sqrt(mse)))The mean sqaured error is: 0.09
The root mean squared error is: 0.30
Remember that the RMSE is in the same units as the data themselves. We can directly compare the RMSE with the MAE computed in an earlier post. The RMSE here (0.30) is slightly larger than the MAE (0.27), which is expected as the squared error is more sensitive to large differences between the model and data.
Finally, we can plot the RMSE as vertical error bars on top of our model output:
## plot the data & predictions with the rmse ##
plt.plot(x_true,y_true)
plt.errorbar(x_true,y_pred,np.sqrt(mse))
plt.title('Sinusoidal Data with Noise + Predictions')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['y_true','y_pred'])
plt.show()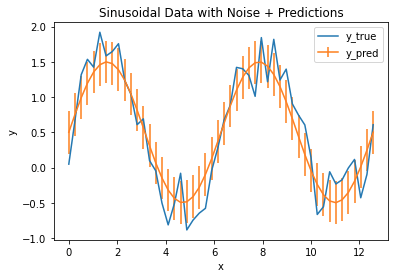
The error bars define the region of uncertainty for our model, and we can see that it covers the bulk of the fluctuations in the data. As such, we can conclude that the MSE/RMSE does a good job at quantifying the error in our model output.
Mean squared error (MSE) of an estimator measures the average of the squared errors, it means averages squared difference between the actual and estimated value.
MSE is almost positive because MSE of an estimator does not account for information that could produce more accurate estimate.
In statistical modelling, MSE is defined as the difference between actual values and predicted values by the model and used to determine prediction accuracy of a model.
In this tutorial, we will discuss about how to calculate mean squared error (MSE) in python.
Mean Squared Error Formula
The mean squared error (MSE) formula is defined as follows:
Where,
n = sample data points
y – actual sizey^ – predictive values
MSE is the means of squares of the errors ( yi – yi^)2.
We will be using numpy library to generate actual and predication values.
As there is no in built function available in python to calculate mean squared error (MSE), we will write simple function for calculation as per mean squared error formula.
pip install numpy
If you don’t have numpy package installed on your system, use below command in command prompt
pip install numpy
Lets understand with examples about how to calculate mean squared error (MSE) in python with given below python code
import numpy as np
def mse(actual,prediction):
return np.square(np.subtract(actual,prediction)).mean()
#define Actual and Prediction data array
actual = np.array([10,11,12,12,14,18,20])
pred = np.array([9,10,13,14,17,16,18])
#Calculate MSE
result = mse(actual,pred)
#print the result
print("Mean squared error (MSE) :", result)
In the above example, we have created actual and prediction array with the help of numpy package array function.
We have written simple function mse() as per mean squared error formula which takes two parameters actual and prediction data array. It calculates mean of the squares of (actual – prediction) using numpy packages square and mean function.
Above code returns mean squared error (MSE) value for given actual and prediction model is 3.42857
Lets check out Mean squared Error (MSE) calculation with few other examples
Info Tip: How to calculate SMAPE in Python!
Example 1 – Mean Squared Error Calculation
Lets assume we have actual and forecast dataset as below
actual = [4,7,3,9,12,8,14,10,12,12]
prediction = [5,7,3,8,10,8,12,11,11,13]
Calculate MSE for given model.
Here, again we will be using numpy package to create actual and prediction array and simple mse() function for mean squared error calculation in python code as below
import numpy as np
def mse(actual,pred):
return np.square(np.subtract(actual,pred)).mean()
#define Actual and Prediction data array
actual = np.array([4,7,3,9,12,8,14,10,12,12])
pred = np.array([5,7,3,8,10,8,12,11,11,13])
#Calculate MSE
result = mse(actual,pred)
#print the result
print("Mean squared error (MSE) :", result)
Above code returns mean squared error (MSE) for given actual and prediction dataset is 1.3
Info Tip: How to calculate rolling correlation in Python!
Example 2 – Mean Squared Error Calculation
Lets take another example with below actual and prediction data values
actual = [-2,-1,1,4]
prediction = [-3,-1,2,3]
Calcualte MSE for above model.
Using below python code, lets calculate MSE
import numpy as np
def mse(actual,pred):
return np.square(np.subtract(actual,pred)).mean()
#define Actual and Prediction data array
actual = np.array([-2,-1,1,4])
pred = np.array([-3,-1,2,3])
#Calculate MSE
result = mse(actual,pred)
#print the result
print("Mean squared error (MSE) :", result)
Above code returns mean squared error (MSE) for given actual and prediction dataset is 0.75. It means it has less squared error and hence this model predicts more accuracy.
Info Tip: How to calculate z score in Python!
Conclusion
I hope, you may find how to calculate MSE in python tutorial with step by step illustration of examples educational and helpful.
Mean squared error (MSE) measures the prediction accuracy of model. Minimizing MSE is key criterion in selecting estimators.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
In machine learning, the mean squared error (MSE) is used to evaluate the performance of a regression model. In regression models, the RMSE is used as a metric to measure model performance and the MSE score is used to evaluate the performance. In this article, I will introduce you to the mean squared error in machine learning and its implementation using Python.
What is Mean Squared Error?
In classification problems, the accuracy score is used as a measure to calculate the performance of a model and the confusion matrix is used to evaluate the model. Just like classification, in regression problems, the RMSE score is used as a metric to measure performance and the mean squared error (MSE) is used to evaluate the performance of a regression model.
Also, Read – Machine Learning Projects Solved and Explained.
The mean squared error (MSE) determines the distance between the set of points and the regression line by taking the distances from the set of points to the regression line and then swapping them. Distances are nothing but errors. Squaring is only done to remove negative values and to give more weight to larger differences.
If the MSE score value is smaller it means you are very close to determining the best fit line which also depends on the data you are working on, so sometimes it may not be possible to get a small MSE score value.
Mean Squared Error using Python
I hope you now have understood what is mean squared error in machine learning. Now let’s have a quick look at how to implement it using the Python programming language. I will start by importing the necessary Python libraries and the dataset to get started with the task of calculating the MSE score using Python:
So here, I am using the diabetes dataset provided by Scikit-learn, let’s simply split the data and train a linear regression model:
So below is how to calculate the MSE score using Python by using the ‘mean_squared_error’ method provided by Scikit-learn:
y_predict = linreg.predict(x_test) print(mean_squared_error(y_test, y_predict))
2548.0723987259703
Summary
The MSE score is used to evaluate the performance of a machine learning model while working on regression problems. When the distance is higher it represents a high error rate and when the distance is lower then you are near to the best fit line. I hope you liked this article on Mean Squared Error in machine learning and its implementation using Python. Feel free to ask your valuable questions in the comments section below.
.. currentmodule:: sklearn
Metrics and scoring: quantifying the quality of predictions
There are 3 different APIs for evaluating the quality of a model’s
predictions:
- Estimator score method: Estimators have a
scoremethod providing a
default evaluation criterion for the problem they are designed to solve.
This is not discussed on this page, but in each estimator’s documentation. - Scoring parameter: Model-evaluation tools using
:ref:`cross-validation <cross_validation>` (such as
:func:`model_selection.cross_val_score` and
:class:`model_selection.GridSearchCV`) rely on an internal scoring strategy.
This is discussed in the section :ref:`scoring_parameter`. - Metric functions: The :mod:`sklearn.metrics` module implements functions
assessing prediction error for specific purposes. These metrics are detailed
in sections on :ref:`classification_metrics`,
:ref:`multilabel_ranking_metrics`, :ref:`regression_metrics` and
:ref:`clustering_metrics`.
Finally, :ref:`dummy_estimators` are useful to get a baseline
value of those metrics for random predictions.
.. seealso:: For "pairwise" metrics, between *samples* and not estimators or predictions, see the :ref:`metrics` section.
The scoring parameter: defining model evaluation rules
Model selection and evaluation using tools, such as
:class:`model_selection.GridSearchCV` and
:func:`model_selection.cross_val_score`, take a scoring parameter that
controls what metric they apply to the estimators evaluated.
Common cases: predefined values
For the most common use cases, you can designate a scorer object with the
scoring parameter; the table below shows all possible values.
All scorer objects follow the convention that higher return values are better
than lower return values. Thus metrics which measure the distance between
the model and the data, like :func:`metrics.mean_squared_error`, are
available as neg_mean_squared_error which return the negated value
of the metric.
| Scoring | Function | Comment |
|---|---|---|
| Classification | ||
| ‘accuracy’ | :func:`metrics.accuracy_score` | |
| ‘balanced_accuracy’ | :func:`metrics.balanced_accuracy_score` | |
| ‘top_k_accuracy’ | :func:`metrics.top_k_accuracy_score` | |
| ‘average_precision’ | :func:`metrics.average_precision_score` | |
| ‘neg_brier_score’ | :func:`metrics.brier_score_loss` | |
| ‘f1’ | :func:`metrics.f1_score` | for binary targets |
| ‘f1_micro’ | :func:`metrics.f1_score` | micro-averaged |
| ‘f1_macro’ | :func:`metrics.f1_score` | macro-averaged |
| ‘f1_weighted’ | :func:`metrics.f1_score` | weighted average |
| ‘f1_samples’ | :func:`metrics.f1_score` | by multilabel sample |
| ‘neg_log_loss’ | :func:`metrics.log_loss` | requires predict_proba support |
| ‘precision’ etc. | :func:`metrics.precision_score` | suffixes apply as with ‘f1’ |
| ‘recall’ etc. | :func:`metrics.recall_score` | suffixes apply as with ‘f1’ |
| ‘jaccard’ etc. | :func:`metrics.jaccard_score` | suffixes apply as with ‘f1’ |
| ‘roc_auc’ | :func:`metrics.roc_auc_score` | |
| ‘roc_auc_ovr’ | :func:`metrics.roc_auc_score` | |
| ‘roc_auc_ovo’ | :func:`metrics.roc_auc_score` | |
| ‘roc_auc_ovr_weighted’ | :func:`metrics.roc_auc_score` | |
| ‘roc_auc_ovo_weighted’ | :func:`metrics.roc_auc_score` | |
| Clustering | ||
| ‘adjusted_mutual_info_score’ | :func:`metrics.adjusted_mutual_info_score` | |
| ‘adjusted_rand_score’ | :func:`metrics.adjusted_rand_score` | |
| ‘completeness_score’ | :func:`metrics.completeness_score` | |
| ‘fowlkes_mallows_score’ | :func:`metrics.fowlkes_mallows_score` | |
| ‘homogeneity_score’ | :func:`metrics.homogeneity_score` | |
| ‘mutual_info_score’ | :func:`metrics.mutual_info_score` | |
| ‘normalized_mutual_info_score’ | :func:`metrics.normalized_mutual_info_score` | |
| ‘rand_score’ | :func:`metrics.rand_score` | |
| ‘v_measure_score’ | :func:`metrics.v_measure_score` | |
| Regression | ||
| ‘explained_variance’ | :func:`metrics.explained_variance_score` | |
| ‘max_error’ | :func:`metrics.max_error` | |
| ‘neg_mean_absolute_error’ | :func:`metrics.mean_absolute_error` | |
| ‘neg_mean_squared_error’ | :func:`metrics.mean_squared_error` | |
| ‘neg_root_mean_squared_error’ | :func:`metrics.mean_squared_error` | |
| ‘neg_mean_squared_log_error’ | :func:`metrics.mean_squared_log_error` | |
| ‘neg_median_absolute_error’ | :func:`metrics.median_absolute_error` | |
| ‘r2’ | :func:`metrics.r2_score` | |
| ‘neg_mean_poisson_deviance’ | :func:`metrics.mean_poisson_deviance` | |
| ‘neg_mean_gamma_deviance’ | :func:`metrics.mean_gamma_deviance` | |
| ‘neg_mean_absolute_percentage_error’ | :func:`metrics.mean_absolute_percentage_error` | |
| ‘d2_absolute_error_score’ | :func:`metrics.d2_absolute_error_score` | |
| ‘d2_pinball_score’ | :func:`metrics.d2_pinball_score` | |
| ‘d2_tweedie_score’ | :func:`metrics.d2_tweedie_score` |
Usage examples:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sklearn.metrics.get_scorer_names() to get valid options.
Note
The values listed by the ValueError exception correspond to the
functions measuring prediction accuracy described in the following
sections. You can retrieve the names of all available scorers by calling
:func:`~sklearn.metrics.get_scorer_names`.
.. currentmodule:: sklearn.metrics
Defining your scoring strategy from metric functions
The module :mod:`sklearn.metrics` also exposes a set of simple functions
measuring a prediction error given ground truth and prediction:
- functions ending with
_scorereturn a value to
maximize, the higher the better. - functions ending with
_erroror_lossreturn a
value to minimize, the lower the better. When converting
into a scorer object using :func:`make_scorer`, set
thegreater_is_betterparameter toFalse(Trueby default; see the
parameter description below).
Metrics available for various machine learning tasks are detailed in sections
below.
Many metrics are not given names to be used as scoring values,
sometimes because they require additional parameters, such as
:func:`fbeta_score`. In such cases, you need to generate an appropriate
scoring object. The simplest way to generate a callable object for scoring
is by using :func:`make_scorer`. That function converts metrics
into callables that can be used for model evaluation.
One typical use case is to wrap an existing metric function from the library
with non-default values for its parameters, such as the beta parameter for
the :func:`fbeta_score` function:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
The second use case is to build a completely custom scorer object
from a simple python function using :func:`make_scorer`, which can
take several parameters:
- the python function you want to use (
my_custom_loss_func
in the example below) - whether the python function returns a score (
greater_is_better=True,
the default) or a loss (greater_is_better=False). If a loss, the output
of the python function is negated by the scorer object, conforming to
the cross validation convention that scorers return higher values for better models. - for classification metrics only: whether the python function you provided requires continuous decision
certainties (needs_threshold=True). The default value is
False. - any additional parameters, such as
betaorlabelsin :func:`f1_score`.
Here is an example of building custom scorers, and of using the
greater_is_better parameter:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
Implementing your own scoring object
You can generate even more flexible model scorers by constructing your own
scoring object from scratch, without using the :func:`make_scorer` factory.
For a callable to be a scorer, it needs to meet the protocol specified by
the following two rules:
- It can be called with parameters
(estimator, X, y), whereestimator
is the model that should be evaluated,Xis validation data, andyis
the ground truth target forX(in the supervised case) orNone(in the
unsupervised case). - It returns a floating point number that quantifies the
estimatorprediction quality onX, with reference toy.
Again, by convention higher numbers are better, so if your scorer
returns loss, that value should be negated.
Note
Using custom scorers in functions where n_jobs > 1
While defining the custom scoring function alongside the calling function
should work out of the box with the default joblib backend (loky),
importing it from another module will be a more robust approach and work
independently of the joblib backend.
For example, to use n_jobs greater than 1 in the example below,
custom_scoring_function function is saved in a user-created module
(custom_scorer_module.py) and imported:
>>> from custom_scorer_module import custom_scoring_function # doctest: +SKIP >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1) # doctest: +SKIP
Using multiple metric evaluation
Scikit-learn also permits evaluation of multiple metrics in GridSearchCV,
RandomizedSearchCV and cross_validate.
There are three ways to specify multiple scoring metrics for the scoring
parameter:
-
- As an iterable of string metrics::
-
>>> scoring = ['accuracy', 'precision']
-
- As a
dictmapping the scorer name to the scoring function:: -
>>> from sklearn.metrics import accuracy_score >>> from sklearn.metrics import make_scorer >>> scoring = {'accuracy': make_scorer(accuracy_score), ... 'prec': 'precision'}
Note that the dict values can either be scorer functions or one of the
predefined metric strings. - As a
-
As a callable that returns a dictionary of scores:
>>> from sklearn.model_selection import cross_validate >>> from sklearn.metrics import confusion_matrix >>> # A sample toy binary classification dataset >>> X, y = datasets.make_classification(n_classes=2, random_state=0) >>> svm = LinearSVC(random_state=0) >>> def confusion_matrix_scorer(clf, X, y): ... y_pred = clf.predict(X) ... cm = confusion_matrix(y, y_pred) ... return {'tn': cm[0, 0], 'fp': cm[0, 1], ... 'fn': cm[1, 0], 'tp': cm[1, 1]} >>> cv_results = cross_validate(svm, X, y, cv=5, ... scoring=confusion_matrix_scorer) >>> # Getting the test set true positive scores >>> print(cv_results['test_tp']) [10 9 8 7 8] >>> # Getting the test set false negative scores >>> print(cv_results['test_fn']) [0 1 2 3 2]
Classification metrics
.. currentmodule:: sklearn.metrics
The :mod:`sklearn.metrics` module implements several loss, score, and utility
functions to measure classification performance.
Some metrics might require probability estimates of the positive class,
confidence values, or binary decisions values.
Most implementations allow each sample to provide a weighted contribution
to the overall score, through the sample_weight parameter.
Some of these are restricted to the binary classification case:
.. autosummary:: precision_recall_curve roc_curve class_likelihood_ratios det_curve
Others also work in the multiclass case:
.. autosummary:: balanced_accuracy_score cohen_kappa_score confusion_matrix hinge_loss matthews_corrcoef roc_auc_score top_k_accuracy_score
Some also work in the multilabel case:
.. autosummary:: accuracy_score classification_report f1_score fbeta_score hamming_loss jaccard_score log_loss multilabel_confusion_matrix precision_recall_fscore_support precision_score recall_score roc_auc_score zero_one_loss
And some work with binary and multilabel (but not multiclass) problems:
.. autosummary:: average_precision_score
In the following sub-sections, we will describe each of those functions,
preceded by some notes on common API and metric definition.
From binary to multiclass and multilabel
Some metrics are essentially defined for binary classification tasks (e.g.
:func:`f1_score`, :func:`roc_auc_score`). In these cases, by default
only the positive label is evaluated, assuming by default that the positive
class is labelled 1 (though this may be configurable through the
pos_label parameter).
In extending a binary metric to multiclass or multilabel problems, the data
is treated as a collection of binary problems, one for each class.
There are then a number of ways to average binary metric calculations across
the set of classes, each of which may be useful in some scenario.
Where available, you should select among these using the average parameter.
"macro"simply calculates the mean of the binary metrics,
giving equal weight to each class. In problems where infrequent classes
are nonetheless important, macro-averaging may be a means of highlighting
their performance. On the other hand, the assumption that all classes are
equally important is often untrue, such that macro-averaging will
over-emphasize the typically low performance on an infrequent class."weighted"accounts for class imbalance by computing the average of
binary metrics in which each class’s score is weighted by its presence in the
true data sample."micro"gives each sample-class pair an equal contribution to the overall
metric (except as a result of sample-weight). Rather than summing the
metric per class, this sums the dividends and divisors that make up the
per-class metrics to calculate an overall quotient.
Micro-averaging may be preferred in multilabel settings, including
multiclass classification where a majority class is to be ignored."samples"applies only to multilabel problems. It does not calculate a
per-class measure, instead calculating the metric over the true and predicted
classes for each sample in the evaluation data, and returning their
(sample_weight-weighted) average.- Selecting
average=Nonewill return an array with the score for each
class.
While multiclass data is provided to the metric, like binary targets, as an
array of class labels, multilabel data is specified as an indicator matrix,
in which cell [i, j] has value 1 if sample i has label j and value
0 otherwise.
Accuracy score
The :func:`accuracy_score` function computes the
accuracy, either the fraction
(default) or the count (normalize=False) of correct predictions.
In multilabel classification, the function returns the subset accuracy. If
the entire set of predicted labels for a sample strictly match with the true
set of labels, then the subset accuracy is 1.0; otherwise it is 0.0.
If hat{y}_i is the predicted value of
the i-th sample and y_i is the corresponding true value,
then the fraction of correct predictions over n_text{samples} is
defined as
texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)
where 1(x) is the indicator function.
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
In the multilabel case with binary label indicators:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
Example:
- See :ref:`sphx_glr_auto_examples_model_selection_plot_permutation_tests_for_classification.py`
for an example of accuracy score usage using permutations of
the dataset.
Top-k accuracy score
The :func:`top_k_accuracy_score` function is a generalization of
:func:`accuracy_score`. The difference is that a prediction is considered
correct as long as the true label is associated with one of the k highest
predicted scores. :func:`accuracy_score` is the special case of k = 1.
The function covers the binary and multiclass classification cases but not the
multilabel case.
If hat{f}_{i,j} is the predicted class for the i-th sample
corresponding to the j-th largest predicted score and y_i is the
corresponding true value, then the fraction of correct predictions over
n_text{samples} is defined as
texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)
where k is the number of guesses allowed and 1(x) is the
indicator function.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
Balanced accuracy score
The :func:`balanced_accuracy_score` function computes the balanced accuracy, which avoids inflated
performance estimates on imbalanced datasets. It is the macro-average of recall
scores per class or, equivalently, raw accuracy where each sample is weighted
according to the inverse prevalence of its true class.
Thus for balanced datasets, the score is equal to accuracy.
In the binary case, balanced accuracy is equal to the arithmetic mean of
sensitivity
(true positive rate) and specificity (true negative
rate), or the area under the ROC curve with binary predictions rather than
scores:
texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )
If the classifier performs equally well on either class, this term reduces to
the conventional accuracy (i.e., the number of correct predictions divided by
the total number of predictions).
In contrast, if the conventional accuracy is above chance only because the
classifier takes advantage of an imbalanced test set, then the balanced
accuracy, as appropriate, will drop to frac{1}{n_classes}.
The score ranges from 0 to 1, or when adjusted=True is used, it rescaled to
the range frac{1}{1 — n_classes} to 1, inclusive, with
performance at random scoring 0.
If y_i is the true value of the i-th sample, and w_i
is the corresponding sample weight, then we adjust the sample weight to:
hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}
where 1(x) is the indicator function.
Given predicted hat{y}_i for sample i, balanced accuracy is
defined as:
texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i
With adjusted=True, balanced accuracy reports the relative increase from
texttt{balanced-accuracy}(y, mathbf{0}, w) =
frac{1}{n_classes}. In the binary case, this is also known as
*Youden’s J statistic*,
or informedness.
Note
The multiclass definition here seems the most reasonable extension of the
metric used in binary classification, though there is no certain consensus
in the literature:
- Our definition: [Mosley2013], [Kelleher2015] and [Guyon2015], where
[Guyon2015] adopt the adjusted version to ensure that random predictions
have a score of 0 and perfect predictions have a score of 1.. - Class balanced accuracy as described in [Mosley2013]: the minimum between the precision
and the recall for each class is computed. Those values are then averaged over the total
number of classes to get the balanced accuracy. - Balanced Accuracy as described in [Urbanowicz2015]: the average of sensitivity and specificity
is computed for each class and then averaged over total number of classes.
References:
| [Guyon2015] | (1, 2) I. Guyon, K. Bennett, G. Cawley, H.J. Escalante, S. Escalera, T.K. Ho, N. Macià, B. Ray, M. Saeed, A.R. Statnikov, E. Viegas, Design of the 2015 ChaLearn AutoML Challenge, IJCNN 2015. |
| [Urbanowicz2015] | Urbanowicz R.J., Moore, J.H. :doi:`ExSTraCS 2.0: description and evaluation of a scalable learning classifier system <10.1007/s12065-015-0128-8>`, Evol. Intel. (2015) 8: 89. |
Cohen’s kappa
The function :func:`cohen_kappa_score` computes Cohen’s kappa statistic.
This measure is intended to compare labelings by different human annotators,
not a classifier versus a ground truth.
The kappa score (see docstring) is a number between -1 and 1.
Scores above .8 are generally considered good agreement;
zero or lower means no agreement (practically random labels).
Kappa scores can be computed for binary or multiclass problems,
but not for multilabel problems (except by manually computing a per-label score)
and not for more than two annotators.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
Confusion matrix
The :func:`confusion_matrix` function evaluates
classification accuracy by computing the confusion matrix with each row corresponding
to the true class (Wikipedia and other references may use different convention
for axes).
By definition, entry i, j in a confusion matrix is
the number of observations actually in group i, but
predicted to be in group j. Here is an example:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
:class:`ConfusionMatrixDisplay` can be used to visually represent a confusion
matrix as shown in the
:ref:`sphx_glr_auto_examples_model_selection_plot_confusion_matrix.py`
example, which creates the following figure:
The parameter normalize allows to report ratios instead of counts. The
confusion matrix can be normalized in 3 different ways: 'pred', 'true',
and 'all' which will divide the counts by the sum of each columns, rows, or
the entire matrix, respectively.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> confusion_matrix(y_true, y_pred, normalize='all') array([[0.25 , 0.125], [0.25 , 0.375]])
For binary problems, we can get counts of true negatives, false positives,
false negatives and true positives as follows:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
Example:
- See :ref:`sphx_glr_auto_examples_model_selection_plot_confusion_matrix.py`
for an example of using a confusion matrix to evaluate classifier output
quality. - See :ref:`sphx_glr_auto_examples_classification_plot_digits_classification.py`
for an example of using a confusion matrix to classify
hand-written digits. - See :ref:`sphx_glr_auto_examples_text_plot_document_classification_20newsgroups.py`
for an example of using a confusion matrix to classify text
documents.
Classification report
The :func:`classification_report` function builds a text report showing the
main classification metrics. Here is a small example with custom target_names
and inferred labels:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
<BLANKLINE>
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
<BLANKLINE>
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
<BLANKLINE>
Example:
- See :ref:`sphx_glr_auto_examples_classification_plot_digits_classification.py`
for an example of classification report usage for
hand-written digits. - See :ref:`sphx_glr_auto_examples_model_selection_plot_grid_search_digits.py`
for an example of classification report usage for
grid search with nested cross-validation.
Hamming loss
The :func:`hamming_loss` computes the average Hamming loss or Hamming
distance between two sets
of samples.
If hat{y}_{i,j} is the predicted value for the j-th label of a
given sample i, y_{i,j} is the corresponding true value,
n_text{samples} is the number of samples and n_text{labels}
is the number of labels, then the Hamming loss L_{Hamming} is defined
as:
L_{Hamming}(y, hat{y}) = frac{1}{n_text{samples} * n_text{labels}} sum_{i=0}^{n_text{samples}-1} sum_{j=0}^{n_text{labels} - 1} 1(hat{y}_{i,j} not= y_{i,j})
where 1(x) is the indicator function.
The equation above does not hold true in the case of multiclass classification.
Please refer to the note below for more information.
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
In the multilabel case with binary label indicators:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Note
In multiclass classification, the Hamming loss corresponds to the Hamming
distance between y_true and y_pred which is similar to the
:ref:`zero_one_loss` function. However, while zero-one loss penalizes
prediction sets that do not strictly match true sets, the Hamming loss
penalizes individual labels. Thus the Hamming loss, upper bounded by the zero-one
loss, is always between zero and one, inclusive; and predicting a proper subset
or superset of the true labels will give a Hamming loss between
zero and one, exclusive.
Precision, recall and F-measures
Intuitively, precision is the ability
of the classifier not to label as positive a sample that is negative, and
recall is the
ability of the classifier to find all the positive samples.
The F-measure
(F_beta and F_1 measures) can be interpreted as a weighted
harmonic mean of the precision and recall. A
F_beta measure reaches its best value at 1 and its worst score at 0.
With beta = 1, F_beta and
F_1 are equivalent, and the recall and the precision are equally important.
The :func:`precision_recall_curve` computes a precision-recall curve
from the ground truth label and a score given by the classifier
by varying a decision threshold.
The :func:`average_precision_score` function computes the
average precision
(AP) from prediction scores. The value is between 0 and 1 and higher is better.
AP is defined as
text{AP} = sum_n (R_n - R_{n-1}) P_n
where P_n and R_n are the precision and recall at the
nth threshold. With random predictions, the AP is the fraction of positive
samples.
References [Manning2008] and [Everingham2010] present alternative variants of
AP that interpolate the precision-recall curve. Currently,
:func:`average_precision_score` does not implement any interpolated variant.
References [Davis2006] and [Flach2015] describe why a linear interpolation of
points on the precision-recall curve provides an overly-optimistic measure of
classifier performance. This linear interpolation is used when computing area
under the curve with the trapezoidal rule in :func:`auc`.
Several functions allow you to analyze the precision, recall and F-measures
score:
.. autosummary:: average_precision_score f1_score fbeta_score precision_recall_curve precision_recall_fscore_support precision_score recall_score
Note that the :func:`precision_recall_curve` function is restricted to the
binary case. The :func:`average_precision_score` function works only in
binary classification and multilabel indicator format.
The :func:`PredictionRecallDisplay.from_estimator` and
:func:`PredictionRecallDisplay.from_predictions` functions will plot the
precision-recall curve as follows.
Examples:
- See :ref:`sphx_glr_auto_examples_model_selection_plot_grid_search_digits.py`
for an example of :func:`precision_score` and :func:`recall_score` usage
to estimate parameters using grid search with nested cross-validation. - See :ref:`sphx_glr_auto_examples_model_selection_plot_precision_recall.py`
for an example of :func:`precision_recall_curve` usage to evaluate
classifier output quality.
References:
| [Manning2008] | C.D. Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval, 2008. |
| [Everingham2010] | M. Everingham, L. Van Gool, C.K.I. Williams, J. Winn, A. Zisserman, The Pascal Visual Object Classes (VOC) Challenge, IJCV 2010. |
Binary classification
In a binary classification task, the terms »positive» and »negative» refer
to the classifier’s prediction, and the terms »true» and »false» refer to
whether that prediction corresponds to the external judgment (sometimes known
as the »observation»). Given these definitions, we can formulate the
following table:
| Actual class (observation) | ||
| Predicted class (expectation) |
tp (true positive) Correct result |
fp (false positive) Unexpected result |
| fn (false negative) Missing result |
tn (true negative) Correct absence of result |
In this context, we can define the notions of precision, recall and F-measure:
text{precision} = frac{tp}{tp + fp},
text{recall} = frac{tp}{tp + fn},
F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.
Sometimes recall is also called »sensitivity».
Here are some small examples in binary classification:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.5 , 0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 1. , 0.5, 0.5, 0. ]) >>> threshold array([0.1 , 0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
Multiclass and multilabel classification
In a multiclass and multilabel classification task, the notions of precision,
recall, and F-measures can be applied to each label independently.
There are a few ways to combine results across labels,
specified by the average argument to the
:func:`average_precision_score` (multilabel only), :func:`f1_score`,
:func:`fbeta_score`, :func:`precision_recall_fscore_support`,
:func:`precision_score` and :func:`recall_score` functions, as described
:ref:`above <average>`. Note that if all labels are included, «micro»-averaging
in a multiclass setting will produce precision, recall and F
that are all identical to accuracy. Also note that «weighted» averaging may
produce an F-score that is not between precision and recall.
To make this more explicit, consider the following notation:
- y the set of true (sample, label) pairs
- hat{y} the set of predicted (sample, label) pairs
- L the set of labels
- S the set of samples
- y_s the subset of y with sample s,
i.e. y_s := left{(s’, l) in y | s’ = sright} - y_l the subset of y with label l
- similarly, hat{y}_s and hat{y}_l are subsets of
hat{y} - P(A, B) := frac{left| A cap B right|}{left|Bright|} for some
sets A and B - R(A, B) := frac{left| A cap B right|}{left|Aright|}
(Conventions vary on handling A = emptyset; this implementation uses
R(A, B):=0, and similar for P.) - F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)}
Then the metrics are defined as:
average |
Precision | Recall | F_beta |
|---|---|---|---|
"micro" |
P(y, hat{y}) | R(y, hat{y}) | F_beta(y, hat{y}) |
"samples" |
frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s) | frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s) | frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s) |
"macro" |
frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l) | frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l) | frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l) |
"weighted" |
frac{1}{sum_{l in L} left|y_lright|} sum_{l in L} left|y_lright| P(y_l, hat{y}_l) | frac{1}{sum_{l in L} left|y_lright|} sum_{l in L} left|y_lright| R(y_l, hat{y}_l) | frac{1}{sum_{l in L} left|y_lright|} sum_{l in L} left|y_lright| F_beta(y_l, hat{y}_l) |
None |
langle P(y_l, hat{y}_l) | l in L rangle | langle R(y_l, hat{y}_l) | l in L rangle | langle F_beta(y_l, hat{y}_l) | l in L rangle |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
For multiclass classification with a «negative class», it is possible to exclude some labels:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Similarly, labels not present in the data sample may be accounted for in macro-averaging.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
Jaccard similarity coefficient score
The :func:`jaccard_score` function computes the average of Jaccard similarity
coefficients, also called the
Jaccard index, between pairs of label sets.
The Jaccard similarity coefficient with a ground truth label set y and
predicted label set hat{y}, is defined as
J(y, hat{y}) = frac{|y cap hat{y}|}{|y cup hat{y}|}.
The :func:`jaccard_score` (like :func:`precision_recall_fscore_support`) applies
natively to binary targets. By computing it set-wise it can be extended to apply
to multilabel and multiclass through the use of average (see
:ref:`above <average>`).
In the binary case:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
In the 2D comparison case (e.g. image similarity):
>>> jaccard_score(y_true, y_pred, average="micro") 0.6
In the multilabel case with binary label indicators:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Multiclass problems are binarized and treated like the corresponding
multilabel problem:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
Hinge loss
The :func:`hinge_loss` function computes the average distance between
the model and the data using
hinge loss, a one-sided metric
that considers only prediction errors. (Hinge
loss is used in maximal margin classifiers such as support vector machines.)
If the true label y_i of a binary classification task is encoded as
y_i=left{-1, +1right} for every sample i; and w_i
is the corresponding predicted decision (an array of shape (n_samples,) as
output by the decision_function method), then the hinge loss is defined as:
L_text{Hinge}(y, w) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} maxleft{1 - w_i y_i, 0right}
If there are more than two labels, :func:`hinge_loss` uses a multiclass variant
due to Crammer & Singer.
Here is
the paper describing it.
In this case the predicted decision is an array of shape (n_samples,
n_labels). If w_{i, y_i} is the predicted decision for the true label
y_i of the i-th sample; and
hat{w}_{i, y_i} = maxleft{w_{i, y_j}~|~y_j ne y_i right}
is the maximum of the
predicted decisions for all the other labels, then the multi-class hinge loss
is defined by:
L_text{Hinge}(y, w) = frac{1}{n_text{samples}}
sum_{i=0}^{n_text{samples}-1} maxleft{1 + hat{w}_{i, y_i}
- w_{i, y_i}, 0right}
Here is a small example demonstrating the use of the :func:`hinge_loss` function
with a svm classifier in a binary class problem:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Here is an example demonstrating the use of the :func:`hinge_loss` function
with a svm classifier in a multiclass problem:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels=labels) 0.56...
Log loss
Log loss, also called logistic regression loss or
cross-entropy loss, is defined on probability estimates. It is
commonly used in (multinomial) logistic regression and neural networks, as well
as in some variants of expectation-maximization, and can be used to evaluate the
probability outputs (predict_proba) of a classifier instead of its
discrete predictions.
For binary classification with a true label y in {0,1}
and a probability estimate p = operatorname{Pr}(y = 1),
the log loss per sample is the negative log-likelihood
of the classifier given the true label:
L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 - y) log (1 - p))
This extends to the multiclass case as follows.
Let the true labels for a set of samples
be encoded as a 1-of-K binary indicator matrix Y,
i.e., y_{i,k} = 1 if sample i has label k
taken from a set of K labels.
Let P be a matrix of probability estimates,
with p_{i,k} = operatorname{Pr}(y_{i,k} = 1).
Then the log loss of the whole set is
L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = - frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}
To see how this generalizes the binary log loss given above,
note that in the binary case,
p_{i,0} = 1 — p_{i,1} and y_{i,0} = 1 — y_{i,1},
so expanding the inner sum over y_{i,k} in {0,1}
gives the binary log loss.
The :func:`log_loss` function computes log loss given a list of ground-truth
labels and a probability matrix, as returned by an estimator’s predict_proba
method.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
The first [.9, .1] in y_pred denotes 90% probability that the first
sample has label 0. The log loss is non-negative.
Matthews correlation coefficient
The :func:`matthews_corrcoef` function computes the
Matthew’s correlation coefficient (MCC)
for binary classes. Quoting Wikipedia:
«The Matthews correlation coefficient is used in machine learning as a
measure of the quality of binary (two-class) classifications. It takes
into account true and false positives and negatives and is generally
regarded as a balanced measure which can be used even if the classes are
of very different sizes. The MCC is in essence a correlation coefficient
value between -1 and +1. A coefficient of +1 represents a perfect
prediction, 0 an average random prediction and -1 an inverse prediction.
The statistic is also known as the phi coefficient.»
In the binary (two-class) case, tp, tn, fp and
fn are respectively the number of true positives, true negatives, false
positives and false negatives, the MCC is defined as
MCC = frac{tp times tn - fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.
In the multiclass case, the Matthews correlation coefficient can be defined in terms of a
:func:`confusion_matrix` C for K classes. To simplify the
definition consider the following intermediate variables:
- t_k=sum_{i}^{K} C_{ik} the number of times class k truly occurred,
- p_k=sum_{i}^{K} C_{ki} the number of times class k was predicted,
- c=sum_{k}^{K} C_{kk} the total number of samples correctly predicted,
- s=sum_{i}^{K} sum_{j}^{K} C_{ij} the total number of samples.
Then the multiclass MCC is defined as:
MCC = frac{
c times s - sum_{k}^{K} p_k times t_k
}{sqrt{
(s^2 - sum_{k}^{K} p_k^2) times
(s^2 - sum_{k}^{K} t_k^2)
}}
When there are more than two labels, the value of the MCC will no longer range
between -1 and +1. Instead the minimum value will be somewhere between -1 and 0
depending on the number and distribution of ground true labels. The maximum
value is always +1.
Here is a small example illustrating the usage of the :func:`matthews_corrcoef`
function:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
Multi-label confusion matrix
The :func:`multilabel_confusion_matrix` function computes class-wise (default)
or sample-wise (samplewise=True) multilabel confusion matrix to evaluate
the accuracy of a classification. multilabel_confusion_matrix also treats
multiclass data as if it were multilabel, as this is a transformation commonly
applied to evaluate multiclass problems with binary classification metrics
(such as precision, recall, etc.).
When calculating class-wise multilabel confusion matrix C, the
count of true negatives for class i is C_{i,0,0}, false
negatives is C_{i,1,0}, true positives is C_{i,1,1}
and false positives is C_{i,0,1}.
Here is an example demonstrating the use of the
:func:`multilabel_confusion_matrix` function with
:term:`multilabel indicator matrix` input:
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
<BLANKLINE>
[[1, 0],
[0, 1]],
<BLANKLINE>
[[0, 1],
[1, 0]]])
Or a confusion matrix can be constructed for each sample’s labels:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True) array([[[1, 0], [1, 1]], <BLANKLINE> [[1, 1], [0, 1]]])
Here is an example demonstrating the use of the
:func:`multilabel_confusion_matrix` function with
:term:`multiclass` input:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
<BLANKLINE>
[[5, 0],
[1, 0]],
<BLANKLINE>
[[2, 1],
[1, 2]]])
Here are some examples demonstrating the use of the
:func:`multilabel_confusion_matrix` function to calculate recall
(or sensitivity), specificity, fall out and miss rate for each class in a
problem with multilabel indicator matrix input.
Calculating
recall
(also called the true positive rate or the sensitivity) for each class:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Calculating
specificity
(also called the true negative rate) for each class:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Calculating fall out
(also called the false positive rate) for each class:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Calculating miss rate
(also called the false negative rate) for each class:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
Receiver operating characteristic (ROC)
The function :func:`roc_curve` computes the
receiver operating characteristic curve, or ROC curve.
Quoting Wikipedia :
«A receiver operating characteristic (ROC), or simply ROC curve, is a
graphical plot which illustrates the performance of a binary classifier
system as its discrimination threshold is varied. It is created by plotting
the fraction of true positives out of the positives (TPR = true positive
rate) vs. the fraction of false positives out of the negatives (FPR = false
positive rate), at various threshold settings. TPR is also known as
sensitivity, and FPR is one minus the specificity or true negative rate.»
This function requires the true binary value and the target scores, which can
either be probability estimates of the positive class, confidence values, or
binary decisions. Here is a small example of how to use the :func:`roc_curve`
function:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
Compared to metrics such as the subset accuracy, the Hamming loss, or the
F1 score, ROC doesn’t require optimizing a threshold for each label.
The :func:`roc_auc_score` function, denoted by ROC-AUC or AUROC, computes the
area under the ROC curve. By doing so, the curve information is summarized in
one number.
The following figure shows the ROC curve and ROC-AUC score for a classifier
aimed to distinguish the virginica flower from the rest of the species in the
:ref:`iris_dataset`:
For more information see the Wikipedia article on AUC.
Binary case
In the binary case, you can either provide the probability estimates, using
the classifier.predict_proba() method, or the non-thresholded decision values
given by the classifier.decision_function() method. In the case of providing
the probability estimates, the probability of the class with the
«greater label» should be provided. The «greater label» corresponds to
classifier.classes_[1] and thus classifier.predict_proba(X)[:, 1].
Therefore, the y_score parameter is of size (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
We can use the probability estimates corresponding to clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
Otherwise, we can use the non-thresholded decision values
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
Multi-class case
The :func:`roc_auc_score` function can also be used in multi-class
classification. Two averaging strategies are currently supported: the
one-vs-one algorithm computes the average of the pairwise ROC AUC scores, and
the one-vs-rest algorithm computes the average of the ROC AUC scores for each
class against all other classes. In both cases, the predicted labels are
provided in an array with values from 0 to n_classes, and the scores
correspond to the probability estimates that a sample belongs to a particular
class. The OvO and OvR algorithms support weighting uniformly
(average='macro') and by prevalence (average='weighted').
One-vs-one Algorithm: Computes the average AUC of all possible pairwise
combinations of classes. [HT2001] defines a multiclass AUC metric weighted
uniformly:
frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) +
text{AUC}(k | j))
where c is the number of classes and text{AUC}(j | k) is the
AUC with class j as the positive class and class k as the
negative class. In general,
text{AUC}(j | k) neq text{AUC}(k | j)) in the multiclass
case. This algorithm is used by setting the keyword argument multiclass
to 'ovo' and average to 'macro'.
The [HT2001] multiclass AUC metric can be extended to be weighted by the
prevalence:
frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)(
text{AUC}(j | k) + text{AUC}(k | j))
where c is the number of classes. This algorithm is used by setting
the keyword argument multiclass to 'ovo' and average to
'weighted'. The 'weighted' option returns a prevalence-weighted average
as described in [FC2009].
One-vs-rest Algorithm: Computes the AUC of each class against the rest
[PD2000]. The algorithm is functionally the same as the multilabel case. To
enable this algorithm set the keyword argument multiclass to 'ovr'.
Additionally to 'macro' [F2006] and 'weighted' [F2001] averaging, OvR
supports 'micro' averaging.
In applications where a high false positive rate is not tolerable the parameter
max_fpr of :func:`roc_auc_score` can be used to summarize the ROC curve up
to the given limit.
The following figure shows the micro-averaged ROC curve and its corresponding
ROC-AUC score for a classifier aimed to distinguish the the different species in
the :ref:`iris_dataset`:
Multi-label case
In multi-label classification, the :func:`roc_auc_score` function is
extended by averaging over the labels as :ref:`above <average>`. In this case,
you should provide a y_score of shape (n_samples, n_classes). Thus, when
using the probability estimates, one needs to select the probability of the
class with the greater label for each output.
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
And the decision values do not require such processing.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
Examples:
- See :ref:`sphx_glr_auto_examples_model_selection_plot_roc.py`
for an example of using ROC to
evaluate the quality of the output of a classifier. - See :ref:`sphx_glr_auto_examples_model_selection_plot_roc_crossval.py`
for an example of using ROC to
evaluate classifier output quality, using cross-validation. - See :ref:`sphx_glr_auto_examples_applications_plot_species_distribution_modeling.py`
for an example of using ROC to
model species distribution.
References:
| [FC2009] | Ferri, Cèsar & Hernandez-Orallo, Jose & Modroiu, R. (2009). An Experimental Comparison of Performance Measures for Classification. Pattern Recognition Letters. 30. 27-38. |
| [PD2000] | Provost, F., Domingos, P. (2000). Well-trained PETs: Improving probability estimation trees (Section 6.2), CeDER Working Paper #IS-00-04, Stern School of Business, New York University. |
| [F2006] | Fawcett, T., 2006. An introduction to ROC analysis. Pattern Recognition Letters, 27(8), pp. 861-874. |
| [F2001] | Fawcett, T., 2001. Using rule sets to maximize ROC performance In Data Mining, 2001. Proceedings IEEE International Conference, pp. 131-138. |
Detection error tradeoff (DET)
The function :func:`det_curve` computes the
detection error tradeoff curve (DET) curve [WikipediaDET2017].
Quoting Wikipedia:
«A detection error tradeoff (DET) graph is a graphical plot of error rates
for binary classification systems, plotting false reject rate vs. false
accept rate. The x- and y-axes are scaled non-linearly by their standard
normal deviates (or just by logarithmic transformation), yielding tradeoff
curves that are more linear than ROC curves, and use most of the image area
to highlight the differences of importance in the critical operating region.»
DET curves are a variation of receiver operating characteristic (ROC) curves
where False Negative Rate is plotted on the y-axis instead of True Positive
Rate.
DET curves are commonly plotted in normal deviate scale by transformation with
phi^{-1} (with phi being the cumulative distribution
function).
The resulting performance curves explicitly visualize the tradeoff of error
types for given classification algorithms.
See [Martin1997] for examples and further motivation.
This figure compares the ROC and DET curves of two example classifiers on the
same classification task:
Properties:
- DET curves form a linear curve in normal deviate scale if the detection
scores are normally (or close-to normally) distributed.
It was shown by [Navratil2007] that the reverse is not necessarily true and
even more general distributions are able to produce linear DET curves. - The normal deviate scale transformation spreads out the points such that a
comparatively larger space of plot is occupied.
Therefore curves with similar classification performance might be easier to
distinguish on a DET plot. - With False Negative Rate being «inverse» to True Positive Rate the point
of perfection for DET curves is the origin (in contrast to the top left
corner for ROC curves).
Applications and limitations:
DET curves are intuitive to read and hence allow quick visual assessment of a
classifier’s performance.
Additionally DET curves can be consulted for threshold analysis and operating
point selection.
This is particularly helpful if a comparison of error types is required.
On the other hand DET curves do not provide their metric as a single number.
Therefore for either automated evaluation or comparison to other
classification tasks metrics like the derived area under ROC curve might be
better suited.
Examples:
- See :ref:`sphx_glr_auto_examples_model_selection_plot_det.py`
for an example comparison between receiver operating characteristic (ROC)
curves and Detection error tradeoff (DET) curves.
References:
| [WikipediaDET2017] | Wikipedia contributors. Detection error tradeoff. Wikipedia, The Free Encyclopedia. September 4, 2017, 23:33 UTC. Available at: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054. Accessed February 19, 2018. |
| [Martin1997] | A. Martin, G. Doddington, T. Kamm, M. Ordowski, and M. Przybocki, The DET Curve in Assessment of Detection Task Performance, NIST 1997. |
| [Navratil2007] | J. Navractil and D. Klusacek, «On Linear DETs,» 2007 IEEE International Conference on Acoustics, Speech and Signal Processing — ICASSP ’07, Honolulu, HI, 2007, pp. IV-229-IV-232. |
Zero one loss
The :func:`zero_one_loss` function computes the sum or the average of the 0-1
classification loss (L_{0-1}) over n_{text{samples}}. By
default, the function normalizes over the sample. To get the sum of the
L_{0-1}, set normalize to False.
In multilabel classification, the :func:`zero_one_loss` scores a subset as
one if its labels strictly match the predictions, and as a zero if there
are any errors. By default, the function returns the percentage of imperfectly
predicted subsets. To get the count of such subsets instead, set
normalize to False
If hat{y}_i is the predicted value of
the i-th sample and y_i is the corresponding true value,
then the 0-1 loss L_{0-1} is defined as:
L_{0-1}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i not= y_i)
where 1(x) is the indicator function. The zero one
loss can also be computed as zero-one loss = 1 — accuracy.
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
In the multilabel case with binary label indicators, where the first label
set [0,1] has an error:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
Example:
- See :ref:`sphx_glr_auto_examples_feature_selection_plot_rfe_with_cross_validation.py`
for an example of zero one loss usage to perform recursive feature
elimination with cross-validation.
Brier score loss
The :func:`brier_score_loss` function computes the
Brier score
for binary classes [Brier1950]. Quoting Wikipedia:
«The Brier score is a proper score function that measures the accuracy of
probabilistic predictions. It is applicable to tasks in which predictions
must assign probabilities to a set of mutually exclusive discrete outcomes.»
This function returns the mean squared error of the actual outcome
y in {0,1} and the predicted probability estimate
p = operatorname{Pr}(y = 1) (:term:`predict_proba`) as outputted by:
BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} - 1}(y_i - p_i)^2
The Brier score loss is also between 0 to 1 and the lower the value (the mean
square difference is smaller), the more accurate the prediction is.
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
The Brier score can be used to assess how well a classifier is calibrated.
However, a lower Brier score loss does not always mean a better calibration.
This is because, by analogy with the bias-variance decomposition of the mean
squared error, the Brier score loss can be decomposed as the sum of calibration
loss and refinement loss [Bella2012]. Calibration loss is defined as the mean
squared deviation from empirical probabilities derived from the slope of ROC
segments. Refinement loss can be defined as the expected optimal loss as
measured by the area under the optimal cost curve. Refinement loss can change
independently from calibration loss, thus a lower Brier score loss does not
necessarily mean a better calibrated model. «Only when refinement loss remains
the same does a lower Brier score loss always mean better calibration»
[Bella2012], [Flach2008].
Example:
- See :ref:`sphx_glr_auto_examples_calibration_plot_calibration.py`
for an example of Brier score loss usage to perform probability
calibration of classifiers.
References:
| [Brier1950] | G. Brier, Verification of forecasts expressed in terms of probability, Monthly weather review 78.1 (1950) |
| [Bella2012] | (1, 2) Bella, Ferri, Hernández-Orallo, and Ramírez-Quintana «Calibration of Machine Learning Models» in Khosrow-Pour, M. «Machine learning: concepts, methodologies, tools and applications.» Hershey, PA: Information Science Reference (2012). |
| [Flach2008] | Flach, Peter, and Edson Matsubara. «On classification, ranking, and probability estimation.» Dagstuhl Seminar Proceedings. Schloss Dagstuhl-Leibniz-Zentrum fr Informatik (2008). |
Class likelihood ratios
The :func:`class_likelihood_ratios` function computes the positive and negative
likelihood ratios
LR_pm for binary classes, which can be interpreted as the ratio of
post-test to pre-test odds as explained below. As a consequence, this metric is
invariant w.r.t. the class prevalence (the number of samples in the positive
class divided by the total number of samples) and can be extrapolated between
populations regardless of any possible class imbalance.
The LR_pm metrics are therefore very useful in settings where the data
available to learn and evaluate a classifier is a study population with nearly
balanced classes, such as a case-control study, while the target application,
i.e. the general population, has very low prevalence.
The positive likelihood ratio LR_+ is the probability of a classifier to
correctly predict that a sample belongs to the positive class divided by the
probability of predicting the positive class for a sample belonging to the
negative class:
LR_+ = frac{text{PR}(P+|T+)}{text{PR}(P+|T-)}.
The notation here refers to predicted (P) or true (T) label and
the sign + and — refer to the positive and negative class,
respectively, e.g. P+ stands for «predicted positive».
Analogously, the negative likelihood ratio LR_- is the probability of a
sample of the positive class being classified as belonging to the negative class
divided by the probability of a sample of the negative class being correctly
classified:
LR_- = frac{text{PR}(P-|T+)}{text{PR}(P-|T-)}.
For classifiers above chance LR_+ above 1 higher is better, while
LR_- ranges from 0 to 1 and lower is better.
Values of LR_pmapprox 1 correspond to chance level.
Notice that probabilities differ from counts, for instance
operatorname{PR}(P+|T+) is not equal to the number of true positive
counts tp (see the wikipedia page for
the actual formulas).
Interpretation across varying prevalence:
Both class likelihood ratios are interpretable in terms of an odds ratio
(pre-test and post-tests):
text{post-test odds} = text{Likelihood ratio} times text{pre-test odds}.
Odds are in general related to probabilities via
text{odds} = frac{text{probability}}{1 - text{probability}},
or equivalently
text{probability} = frac{text{odds}}{1 + text{odds}}.
On a given population, the pre-test probability is given by the prevalence. By
converting odds to probabilities, the likelihood ratios can be translated into a
probability of truly belonging to either class before and after a classifier
prediction:
text{post-test odds} = text{Likelihood ratio} times
frac{text{pre-test probability}}{1 - text{pre-test probability}},
text{post-test probability} = frac{text{post-test odds}}{1 + text{post-test odds}}.
Mathematical divergences:
The positive likelihood ratio is undefined when fp = 0, which can be
interpreted as the classifier perfectly identifying positive cases. If fp
= 0 and additionally tp = 0, this leads to a zero/zero division. This
happens, for instance, when using a DummyClassifier that always predicts the
negative class and therefore the interpretation as a perfect classifier is lost.
The negative likelihood ratio is undefined when tn = 0. Such divergence
is invalid, as LR_- > 1 would indicate an increase in the odds of a
sample belonging to the positive class after being classified as negative, as if
the act of classifying caused the positive condition. This includes the case of
a DummyClassifier that always predicts the positive class (i.e. when
tn=fn=0).
Both class likelihood ratios are undefined when tp=fn=0, which means
that no samples of the positive class were present in the testing set. This can
also happen when cross-validating highly imbalanced data.
In all the previous cases the :func:`class_likelihood_ratios` function raises by
default an appropriate warning message and returns nan to avoid pollution when
averaging over cross-validation folds.
For a worked-out demonstration of the :func:`class_likelihood_ratios` function,
see the example below.
References:
- Wikipedia entry for Likelihood ratios in diagnostic testing
- Brenner, H., & Gefeller, O. (1997).
Variation of sensitivity, specificity, likelihood ratios and predictive
values with disease prevalence.
Statistics in medicine, 16(9), 981-991.
Multilabel ranking metrics
.. currentmodule:: sklearn.metrics
In multilabel learning, each sample can have any number of ground truth labels
associated with it. The goal is to give high scores and better rank to
the ground truth labels.
Coverage error
The :func:`coverage_error` function computes the average number of labels that
have to be included in the final prediction such that all true labels
are predicted. This is useful if you want to know how many top-scored-labels
you have to predict in average without missing any true one. The best value
of this metrics is thus the average number of true labels.
Note
Our implementation’s score is 1 greater than the one given in Tsoumakas
et al., 2010. This extends it to handle the degenerate case in which an
instance has 0 true labels.
Formally, given a binary indicator matrix of the ground truth labels
y in left{0, 1right}^{n_text{samples} times n_text{labels}} and the
score associated with each label
hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}},
the coverage is defined as
coverage(y, hat{f}) = frac{1}{n_{text{samples}}}
sum_{i=0}^{n_{text{samples}} - 1} max_{j:y_{ij} = 1} text{rank}_{ij}
with text{rank}_{ij} = left|left{k: hat{f}_{ik} geq hat{f}_{ij} right}right|.
Given the rank definition, ties in y_scores are broken by giving the
maximal rank that would have been assigned to all tied values.
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
Label ranking average precision
The :func:`label_ranking_average_precision_score` function
implements label ranking average precision (LRAP). This metric is linked to
the :func:`average_precision_score` function, but is based on the notion of
label ranking instead of precision and recall.
Label ranking average precision (LRAP) averages over the samples the answer to
the following question: for each ground truth label, what fraction of
higher-ranked labels were true labels? This performance measure will be higher
if you are able to give better rank to the labels associated with each sample.
The obtained score is always strictly greater than 0, and the best value is 1.
If there is exactly one relevant label per sample, label ranking average
precision is equivalent to the mean
reciprocal rank.
Formally, given a binary indicator matrix of the ground truth labels
y in left{0, 1right}^{n_text{samples} times n_text{labels}}
and the score associated with each label
hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}},
the average precision is defined as
LRAP(y, hat{f}) = frac{1}{n_{text{samples}}}
sum_{i=0}^{n_{text{samples}} - 1} frac{1}{||y_i||_0}
sum_{j:y_{ij} = 1} frac{|mathcal{L}_{ij}|}{text{rank}_{ij}}
where
mathcal{L}_{ij} = left{k: y_{ik} = 1, hat{f}_{ik} geq hat{f}_{ij} right},
text{rank}_{ij} = left|left{k: hat{f}_{ik} geq hat{f}_{ij} right}right|,
|cdot| computes the cardinality of the set (i.e., the number of
elements in the set), and ||cdot||_0 is the ell_0 «norm»
(which computes the number of nonzero elements in a vector).
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
Ranking loss
The :func:`label_ranking_loss` function computes the ranking loss which
averages over the samples the number of label pairs that are incorrectly
ordered, i.e. true labels have a lower score than false labels, weighted by
the inverse of the number of ordered pairs of false and true labels.
The lowest achievable ranking loss is zero.
Formally, given a binary indicator matrix of the ground truth labels
y in left{0, 1right}^{n_text{samples} times n_text{labels}} and the
score associated with each label
hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}},
the ranking loss is defined as
ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}}
sum_{i=0}^{n_{text{samples}} - 1} frac{1}{||y_i||_0(n_text{labels} - ||y_i||_0)}
left|left{(k, l): hat{f}_{ik} leq hat{f}_{il}, y_{ik} = 1, y_{il} = 0~right}right|
where |cdot| computes the cardinality of the set (i.e., the number of
elements in the set) and ||cdot||_0 is the ell_0 «norm»
(which computes the number of nonzero elements in a vector).
Here is a small example of usage of this function:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
References:
- Tsoumakas, G., Katakis, I., & Vlahavas, I. (2010). Mining multi-label data. In
Data mining and knowledge discovery handbook (pp. 667-685). Springer US.
Normalized Discounted Cumulative Gain
Discounted Cumulative Gain (DCG) and Normalized Discounted Cumulative Gain
(NDCG) are ranking metrics implemented in :func:`~sklearn.metrics.dcg_score`
and :func:`~sklearn.metrics.ndcg_score` ; they compare a predicted order to
ground-truth scores, such as the relevance of answers to a query.
From the Wikipedia page for Discounted Cumulative Gain:
«Discounted cumulative gain (DCG) is a measure of ranking quality. In
information retrieval, it is often used to measure effectiveness of web search
engine algorithms or related applications. Using a graded relevance scale of
documents in a search-engine result set, DCG measures the usefulness, or gain,
of a document based on its position in the result list. The gain is accumulated
from the top of the result list to the bottom, with the gain of each result
discounted at lower ranks»
DCG orders the true targets (e.g. relevance of query answers) in the predicted
order, then multiplies them by a logarithmic decay and sums the result. The sum
can be truncated after the first K results, in which case we call it
DCG@K.
NDCG, or NDCG@K is DCG divided by the DCG obtained by a perfect prediction, so
that it is always between 0 and 1. Usually, NDCG is preferred to DCG.
Compared with the ranking loss, NDCG can take into account relevance scores,
rather than a ground-truth ranking. So if the ground-truth consists only of an
ordering, the ranking loss should be preferred; if the ground-truth consists of
actual usefulness scores (e.g. 0 for irrelevant, 1 for relevant, 2 for very
relevant), NDCG can be used.
For one sample, given the vector of continuous ground-truth values for each
target y in mathbb{R}^{M}, where M is the number of outputs, and
the prediction hat{y}, which induces the ranking function f, the
DCG score is
sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}
and the NDCG score is the DCG score divided by the DCG score obtained for
y.
References:
- Wikipedia entry for Discounted Cumulative Gain
- Jarvelin, K., & Kekalainen, J. (2002).
Cumulated gain-based evaluation of IR techniques. ACM Transactions on
Information Systems (TOIS), 20(4), 422-446. - Wang, Y., Wang, L., Li, Y., He, D., Chen, W., & Liu, T. Y. (2013, May).
A theoretical analysis of NDCG ranking measures. In Proceedings of the 26th
Annual Conference on Learning Theory (COLT 2013) - McSherry, F., & Najork, M. (2008, March). Computing information retrieval
performance measures efficiently in the presence of tied scores. In
European conference on information retrieval (pp. 414-421). Springer,
Berlin, Heidelberg.
Regression metrics
.. currentmodule:: sklearn.metrics
The :mod:`sklearn.metrics` module implements several loss, score, and utility
functions to measure regression performance. Some of those have been enhanced
to handle the multioutput case: :func:`mean_squared_error`,
:func:`mean_absolute_error`, :func:`r2_score`,
:func:`explained_variance_score`, :func:`mean_pinball_loss`, :func:`d2_pinball_score`
and :func:`d2_absolute_error_score`.
These functions have a multioutput keyword argument which specifies the
way the scores or losses for each individual target should be averaged. The
default is 'uniform_average', which specifies a uniformly weighted mean
over outputs. If an ndarray of shape (n_outputs,) is passed, then its
entries are interpreted as weights and an according weighted average is
returned. If multioutput is 'raw_values', then all unaltered
individual scores or losses will be returned in an array of shape
(n_outputs,).
The :func:`r2_score` and :func:`explained_variance_score` accept an additional
value 'variance_weighted' for the multioutput parameter. This option
leads to a weighting of each individual score by the variance of the
corresponding target variable. This setting quantifies the globally captured
unscaled variance. If the target variables are of different scale, then this
score puts more importance on explaining the higher variance variables.
multioutput='variance_weighted' is the default value for :func:`r2_score`
for backward compatibility. This will be changed to uniform_average in the
future.
R² score, the coefficient of determination
The :func:`r2_score` function computes the coefficient of
determination,
usually denoted as R^2.
It represents the proportion of variance (of y) that has been explained by the
independent variables in the model. It provides an indication of goodness of
fit and therefore a measure of how well unseen samples are likely to be
predicted by the model, through the proportion of explained variance.
As such variance is dataset dependent, R^2 may not be meaningfully comparable
across different datasets. Best possible score is 1.0 and it can be negative
(because the model can be arbitrarily worse). A constant model that always
predicts the expected (average) value of y, disregarding the input features,
would get an R^2 score of 0.0.
Note: when the prediction residuals have zero mean, the R^2 score and
the :ref:`explained_variance_score` are identical.
If hat{y}_i is the predicted value of the i-th sample
and y_i is the corresponding true value for total n samples,
the estimated R^2 is defined as:
R^2(y, hat{y}) = 1 - frac{sum_{i=1}^{n} (y_i - hat{y}_i)^2}{sum_{i=1}^{n} (y_i - bar{y})^2}
where bar{y} = frac{1}{n} sum_{i=1}^{n} y_i and sum_{i=1}^{n} (y_i — hat{y}_i)^2 = sum_{i=1}^{n} epsilon_i^2.
Note that :func:`r2_score` calculates unadjusted R^2 without correcting for
bias in sample variance of y.
In the particular case where the true target is constant, the R^2 score is
not finite: it is either NaN (perfect predictions) or -Inf (imperfect
predictions). Such non-finite scores may prevent correct model optimization
such as grid-search cross-validation to be performed correctly. For this reason
the default behaviour of :func:`r2_score` is to replace them with 1.0 (perfect
predictions) or 0.0 (imperfect predictions). If force_finite
is set to False, this score falls back on the original R^2 definition.
Here is a small example of usage of the :func:`r2_score` function:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925... >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2] >>> r2_score(y_true, y_pred) 1.0 >>> r2_score(y_true, y_pred, force_finite=False) nan >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2 + 1e-8] >>> r2_score(y_true, y_pred) 0.0 >>> r2_score(y_true, y_pred, force_finite=False) -inf
Example:
- See :ref:`sphx_glr_auto_examples_linear_model_plot_lasso_and_elasticnet.py`
for an example of R² score usage to
evaluate Lasso and Elastic Net on sparse signals.
Mean absolute error
The :func:`mean_absolute_error` function computes mean absolute
error, a risk
metric corresponding to the expected value of the absolute error loss or
l1-norm loss.
If hat{y}_i is the predicted value of the i-th sample,
and y_i is the corresponding true value, then the mean absolute error
(MAE) estimated over n_{text{samples}} is defined as
text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i - hat{y}_i right|.
Here is a small example of usage of the :func:`mean_absolute_error` function:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
Mean squared error
The :func:`mean_squared_error` function computes mean square
error, a risk
metric corresponding to the expected value of the squared (quadratic) error or
loss.
If hat{y}_i is the predicted value of the i-th sample,
and y_i is the corresponding true value, then the mean squared error
(MSE) estimated over n_{text{samples}} is defined as
text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} - 1} (y_i - hat{y}_i)^2.
Here is a small example of usage of the :func:`mean_squared_error`
function:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
Examples:
- See :ref:`sphx_glr_auto_examples_ensemble_plot_gradient_boosting_regression.py`
for an example of mean squared error usage to
evaluate gradient boosting regression.
Mean squared logarithmic error
The :func:`mean_squared_log_error` function computes a risk metric
corresponding to the expected value of the squared logarithmic (quadratic)
error or loss.
If hat{y}_i is the predicted value of the i-th sample,
and y_i is the corresponding true value, then the mean squared
logarithmic error (MSLE) estimated over n_{text{samples}} is
defined as
text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} - 1} (log_e (1 + y_i) - log_e (1 + hat{y}_i) )^2.
Where log_e (x) means the natural logarithm of x. This metric
is best to use when targets having exponential growth, such as population
counts, average sales of a commodity over a span of years etc. Note that this
metric penalizes an under-predicted estimate greater than an over-predicted
estimate.
Here is a small example of usage of the :func:`mean_squared_log_error`
function:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
Mean absolute percentage error
The :func:`mean_absolute_percentage_error` (MAPE), also known as mean absolute
percentage deviation (MAPD), is an evaluation metric for regression problems.
The idea of this metric is to be sensitive to relative errors. It is for example
not changed by a global scaling of the target variable.
If hat{y}_i is the predicted value of the i-th sample
and y_i is the corresponding true value, then the mean absolute percentage
error (MAPE) estimated over n_{text{samples}} is defined as
text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i - hat{y}_i right|}{max(epsilon, left| y_i right|)}
where epsilon is an arbitrary small yet strictly positive number to
avoid undefined results when y is zero.
The :func:`mean_absolute_percentage_error` function supports multioutput.
Here is a small example of usage of the :func:`mean_absolute_percentage_error`
function:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
In above example, if we had used mean_absolute_error, it would have ignored
the small magnitude values and only reflected the error in prediction of highest
magnitude value. But that problem is resolved in case of MAPE because it calculates
relative percentage error with respect to actual output.
Median absolute error
The :func:`median_absolute_error` is particularly interesting because it is
robust to outliers. The loss is calculated by taking the median of all absolute
differences between the target and the prediction.
If hat{y}_i is the predicted value of the i-th sample
and y_i is the corresponding true value, then the median absolute error
(MedAE) estimated over n_{text{samples}} is defined as
text{MedAE}(y, hat{y}) = text{median}(mid y_1 - hat{y}_1 mid, ldots, mid y_n - hat{y}_n mid).
The :func:`median_absolute_error` does not support multioutput.
Here is a small example of usage of the :func:`median_absolute_error`
function:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
Max error
The :func:`max_error` function computes the maximum residual error , a metric
that captures the worst case error between the predicted value and
the true value. In a perfectly fitted single output regression
model, max_error would be 0 on the training set and though this
would be highly unlikely in the real world, this metric shows the
extent of error that the model had when it was fitted.
If hat{y}_i is the predicted value of the i-th sample,
and y_i is the corresponding true value, then the max error is
defined as
text{Max Error}(y, hat{y}) = max(| y_i - hat{y}_i |)
Here is a small example of usage of the :func:`max_error` function:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
The :func:`max_error` does not support multioutput.
Explained variance score
The :func:`explained_variance_score` computes the explained variance
regression score.
If hat{y} is the estimated target output, y the corresponding
(correct) target output, and Var is Variance, the square of the standard deviation,
then the explained variance is estimated as follow:
explained_{}variance(y, hat{y}) = 1 - frac{Var{ y - hat{y}}}{Var{y}}
The best possible score is 1.0, lower values are worse.
Link to :ref:`r2_score`
The difference between the explained variance score and the :ref:`r2_score`
is that when the explained variance score does not account for
systematic offset in the prediction. For this reason, the
:ref:`r2_score` should be preferred in general.
In the particular case where the true target is constant, the Explained
Variance score is not finite: it is either NaN (perfect predictions) or
-Inf (imperfect predictions). Such non-finite scores may prevent correct
model optimization such as grid-search cross-validation to be performed
correctly. For this reason the default behaviour of
:func:`explained_variance_score` is to replace them with 1.0 (perfect
predictions) or 0.0 (imperfect predictions). You can set the force_finite
parameter to False to prevent this fix from happening and fallback on the
original Explained Variance score.
Here is a small example of usage of the :func:`explained_variance_score`
function:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990... >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2] >>> explained_variance_score(y_true, y_pred) 1.0 >>> explained_variance_score(y_true, y_pred, force_finite=False) nan >>> y_true = [-2, -2, -2] >>> y_pred = [-2, -2, -2 + 1e-8] >>> explained_variance_score(y_true, y_pred) 0.0 >>> explained_variance_score(y_true, y_pred, force_finite=False) -inf
Mean Poisson, Gamma, and Tweedie deviances
The :func:`mean_tweedie_deviance` function computes the mean Tweedie
deviance error
with a power parameter (p). This is a metric that elicits
predicted expectation values of regression targets.
Following special cases exist,
- when
power=0it is equivalent to :func:`mean_squared_error`. - when
power=1it is equivalent to :func:`mean_poisson_deviance`. - when
power=2it is equivalent to :func:`mean_gamma_deviance`.
If hat{y}_i is the predicted value of the i-th sample,
and y_i is the corresponding true value, then the mean Tweedie
deviance error (D) for power p, estimated over n_{text{samples}}
is defined as
text{D}(y, hat{y}) = frac{1}{n_text{samples}}
sum_{i=0}^{n_text{samples} - 1}
begin{cases}
(y_i-hat{y}_i)^2, & text{for }p=0text{ (Normal)}\
2(y_i log(y_i/hat{y}_i) + hat{y}_i - y_i), & text{for }p=1text{ (Poisson)}\
2(log(hat{y}_i/y_i) + y_i/hat{y}_i - 1), & text{for }p=2text{ (Gamma)}\
2left(frac{max(y_i,0)^{2-p}}{(1-p)(2-p)}-
frac{y_i,hat{y}_i^{1-p}}{1-p}+frac{hat{y}_i^{2-p}}{2-p}right),
& text{otherwise}
end{cases}
Tweedie deviance is a homogeneous function of degree 2-power.
Thus, Gamma distribution with power=2 means that simultaneously scaling
y_true and y_pred has no effect on the deviance. For Poisson
distribution power=1 the deviance scales linearly, and for Normal
distribution (power=0), quadratically. In general, the higher
power the less weight is given to extreme deviations between true
and predicted targets.
For instance, let’s compare the two predictions 1.5 and 150 that are both
50% larger than their corresponding true value.
The mean squared error (power=0) is very sensitive to the
prediction difference of the second point,:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
If we increase power to 1,:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
the difference in errors decreases. Finally, by setting, power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
we would get identical errors. The deviance when power=2 is thus only
sensitive to relative errors.
Pinball loss
The :func:`mean_pinball_loss` function is used to evaluate the predictive
performance of quantile regression models.
text{pinball}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} alpha max(y_i - hat{y}_i, 0) + (1 - alpha) max(hat{y}_i - y_i, 0)
The value of pinball loss is equivalent to half of :func:`mean_absolute_error` when the quantile
parameter alpha is set to 0.5.
Here is a small example of usage of the :func:`mean_pinball_loss` function:
>>> from sklearn.metrics import mean_pinball_loss >>> y_true = [1, 2, 3] >>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.1) 0.03... >>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.1) 0.3... >>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.9) 0.3... >>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.9) 0.03... >>> mean_pinball_loss(y_true, y_true, alpha=0.1) 0.0 >>> mean_pinball_loss(y_true, y_true, alpha=0.9) 0.0
It is possible to build a scorer object with a specific choice of alpha:
>>> from sklearn.metrics import make_scorer >>> mean_pinball_loss_95p = make_scorer(mean_pinball_loss, alpha=0.95)
Such a scorer can be used to evaluate the generalization performance of a
quantile regressor via cross-validation:
>>> from sklearn.datasets import make_regression >>> from sklearn.model_selection import cross_val_score >>> from sklearn.ensemble import GradientBoostingRegressor >>> >>> X, y = make_regression(n_samples=100, random_state=0) >>> estimator = GradientBoostingRegressor( ... loss="quantile", ... alpha=0.95, ... random_state=0, ... ) >>> cross_val_score(estimator, X, y, cv=5, scoring=mean_pinball_loss_95p) array([13.6..., 9.7..., 23.3..., 9.5..., 10.4...])
It is also possible to build scorer objects for hyper-parameter tuning. The
sign of the loss must be switched to ensure that greater means better as
explained in the example linked below.
Example:
- See :ref:`sphx_glr_auto_examples_ensemble_plot_gradient_boosting_quantile.py`
for an example of using the pinball loss to evaluate and tune the
hyper-parameters of quantile regression models on data with non-symmetric
noise and outliers.
D² score
The D² score computes the fraction of deviance explained.
It is a generalization of R², where the squared error is generalized and replaced
by a deviance of choice text{dev}(y, hat{y})
(e.g., Tweedie, pinball or mean absolute error). D² is a form of a skill score.
It is calculated as
D^2(y, hat{y}) = 1 - frac{text{dev}(y, hat{y})}{text{dev}(y, y_{text{null}})} ,.
Where y_{text{null}} is the optimal prediction of an intercept-only model
(e.g., the mean of y_true for the Tweedie case, the median for absolute
error and the alpha-quantile for pinball loss).
Like R², the best possible score is 1.0 and it can be negative (because the
model can be arbitrarily worse). A constant model that always predicts
y_{text{null}}, disregarding the input features, would get a D² score
of 0.0.
D² Tweedie score
The :func:`d2_tweedie_score` function implements the special case of D²
where text{dev}(y, hat{y}) is the Tweedie deviance, see :ref:`mean_tweedie_deviance`.
It is also known as D² Tweedie and is related to McFadden’s likelihood ratio index.
The argument power defines the Tweedie power as for
:func:`mean_tweedie_deviance`. Note that for power=0,
:func:`d2_tweedie_score` equals :func:`r2_score` (for single targets).
A scorer object with a specific choice of power can be built by:
>>> from sklearn.metrics import d2_tweedie_score, make_scorer >>> d2_tweedie_score_15 = make_scorer(d2_tweedie_score, power=1.5)
D² pinball score
The :func:`d2_pinball_score` function implements the special case
of D² with the pinball loss, see :ref:`pinball_loss`, i.e.:
text{dev}(y, hat{y}) = text{pinball}(y, hat{y}).
The argument alpha defines the slope of the pinball loss as for
:func:`mean_pinball_loss` (:ref:`pinball_loss`). It determines the
quantile level alpha for which the pinball loss and also D²
are optimal. Note that for alpha=0.5 (the default) :func:`d2_pinball_score`
equals :func:`d2_absolute_error_score`.
A scorer object with a specific choice of alpha can be built by:
>>> from sklearn.metrics import d2_pinball_score, make_scorer >>> d2_pinball_score_08 = make_scorer(d2_pinball_score, alpha=0.8)
D² absolute error score
The :func:`d2_absolute_error_score` function implements the special case of
the :ref:`mean_absolute_error`:
text{dev}(y, hat{y}) = text{MAE}(y, hat{y}).
Here are some usage examples of the :func:`d2_absolute_error_score` function:
>>> from sklearn.metrics import d2_absolute_error_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> d2_absolute_error_score(y_true, y_pred) 0.764... >>> y_true = [1, 2, 3] >>> y_pred = [1, 2, 3] >>> d2_absolute_error_score(y_true, y_pred) 1.0 >>> y_true = [1, 2, 3] >>> y_pred = [2, 2, 2] >>> d2_absolute_error_score(y_true, y_pred) 0.0
Visual evaluation of regression models
Among methods to assess the quality of regression models, scikit-learn provides
the :class:`~sklearn.metrics.PredictionErrorDisplay` class. It allows to
visually inspect the prediction errors of a model in two different manners.
The plot on the left shows the actual values vs predicted values. For a
noise-free regression task aiming to predict the (conditional) expectation of
y, a perfect regression model would display data points on the diagonal
defined by predicted equal to actual values. The further away from this optimal
line, the larger the error of the model. In a more realistic setting with
irreducible noise, that is, when not all the variations of y can be explained
by features in X, then the best model would lead to a cloud of points densely
arranged around the diagonal.
Note that the above only holds when the predicted values is the expected value
of y given X. This is typically the case for regression models that
minimize the mean squared error objective function or more generally the
:ref:`mean Tweedie deviance <mean_tweedie_deviance>` for any value of its
«power» parameter.
When plotting the predictions of an estimator that predicts a quantile
of y given X, e.g. :class:`~sklearn.linear_model.QuantileRegressor`
or any other model minimizing the :ref:`pinball loss <pinball_loss>`, a
fraction of the points are either expected to lie above or below the diagonal
depending on the estimated quantile level.
All in all, while intuitive to read, this plot does not really inform us on
what to do to obtain a better model.
The right-hand side plot shows the residuals (i.e. the difference between the
actual and the predicted values) vs. the predicted values.
This plot makes it easier to visualize if the residuals follow and
homoscedastic or heteroschedastic
distribution.
In particular, if the true distribution of y|X is Poisson or Gamma
distributed, it is expected that the variance of the residuals of the optimal
model would grow with the predicted value of E[y|X] (either linearly for
Poisson or quadratically for Gamma).
When fitting a linear least squares regression model (see
:class:`~sklearn.linear_mnodel.LinearRegression` and
:class:`~sklearn.linear_mnodel.Ridge`), we can use this plot to check
if some of the model assumptions
are met, in particular that the residuals should be uncorrelated, their
expected value should be null and that their variance should be constant
(homoschedasticity).
If this is not the case, and in particular if the residuals plot show some
banana-shaped structure, this is a hint that the model is likely mis-specified
and that non-linear feature engineering or switching to a non-linear regression
model might be useful.
Refer to the example below to see a model evaluation that makes use of this
display.
Example:
- See :ref:`sphx_glr_auto_examples_compose_plot_transformed_target.py` for
an example on how to use :class:`~sklearn.metrics.PredictionErrorDisplay`
to visualize the prediction quality improvement of a regression model
obtained by transforming the target before learning.
Clustering metrics
.. currentmodule:: sklearn.metrics
The :mod:`sklearn.metrics` module implements several loss, score, and utility
functions. For more information see the :ref:`clustering_evaluation`
section for instance clustering, and :ref:`biclustering_evaluation` for
biclustering.
Dummy estimators
.. currentmodule:: sklearn.dummy
When doing supervised learning, a simple sanity check consists of comparing
one’s estimator against simple rules of thumb. :class:`DummyClassifier`
implements several such simple strategies for classification:
stratifiedgenerates random predictions by respecting the training
set class distribution.most_frequentalways predicts the most frequent label in the training set.prioralways predicts the class that maximizes the class prior
(likemost_frequent) andpredict_probareturns the class prior.uniformgenerates predictions uniformly at random.-
constantalways predicts a constant label that is provided by the user.- A major motivation of this method is F1-scoring, when the positive class
is in the minority.
Note that with all these strategies, the predict method completely ignores
the input data!
To illustrate :class:`DummyClassifier`, first let’s create an imbalanced
dataset:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Next, let’s compare the accuracy of SVC and most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
We see that SVC doesn’t do much better than a dummy classifier. Now, let’s
change the kernel:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
We see that the accuracy was boosted to almost 100%. A cross validation
strategy is recommended for a better estimate of the accuracy, if it
is not too CPU costly. For more information see the :ref:`cross_validation`
section. Moreover if you want to optimize over the parameter space, it is highly
recommended to use an appropriate methodology; see the :ref:`grid_search`
section for details.
More generally, when the accuracy of a classifier is too close to random, it
probably means that something went wrong: features are not helpful, a
hyperparameter is not correctly tuned, the classifier is suffering from class
imbalance, etc…
:class:`DummyRegressor` also implements four simple rules of thumb for regression:
meanalways predicts the mean of the training targets.medianalways predicts the median of the training targets.quantilealways predicts a user provided quantile of the training targets.constantalways predicts a constant value that is provided by the user.
In all these strategies, the predict method completely ignores
the input data.