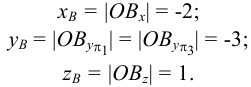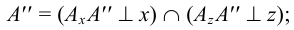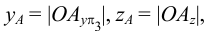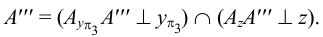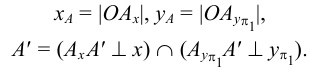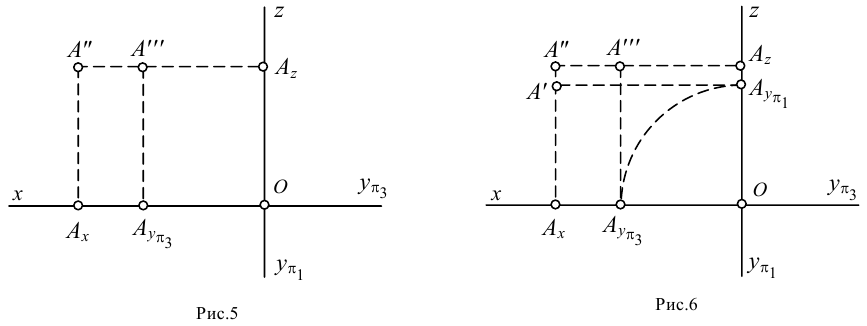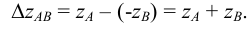Содержание:
Проецирование прямой линии:
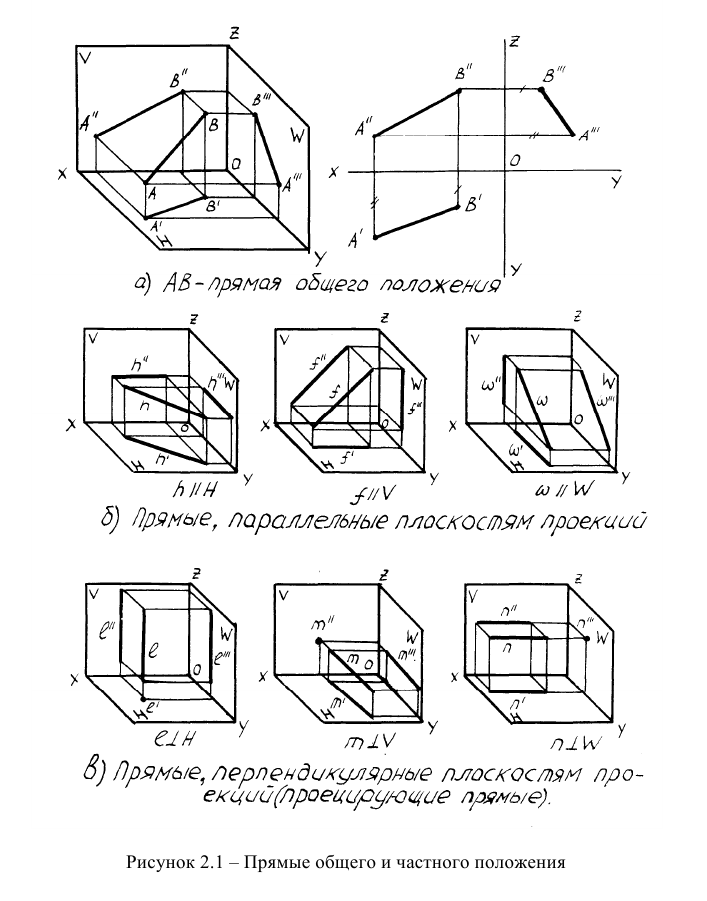
Отрезок прямой линии определяется двумя точками. Следовательно, проекции двух точек определяют проекции отрезка прямой (рисунок 2.1). Проекции отрезка прямой в общем случае всегда будут меньше самого отрезка прямой. В общем случае по проекциям отрезка прямой нельзя определить углы наклона отрезка прямой к плоскостям проекций.
Прямые общего и частного положения
Прямые подразделяются на прямые общего и частного положения. Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения (рисунок 2.1а).
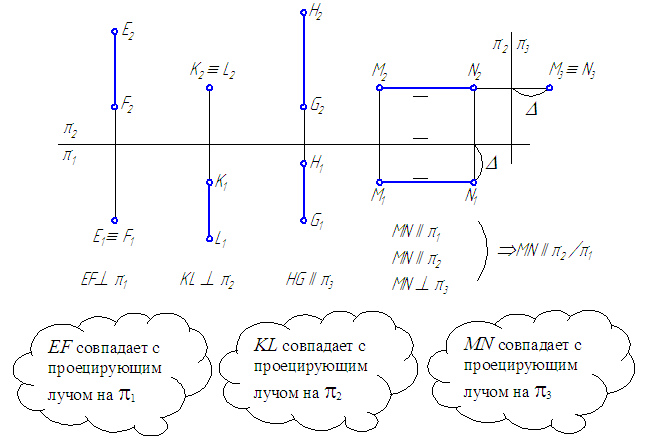
Прямые, параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения (рисунок 2.16, в). Прямые, параллельные плоскостям проекций, называются по имени плоскости, которой они параллельны: горизонталь h, фронталь f и профильная прямая w.
Прямые, перпендикулярные плоскостям проекций, называются проецирующими: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая, в зависимости от плоскости, к которой они перпендикулярны.
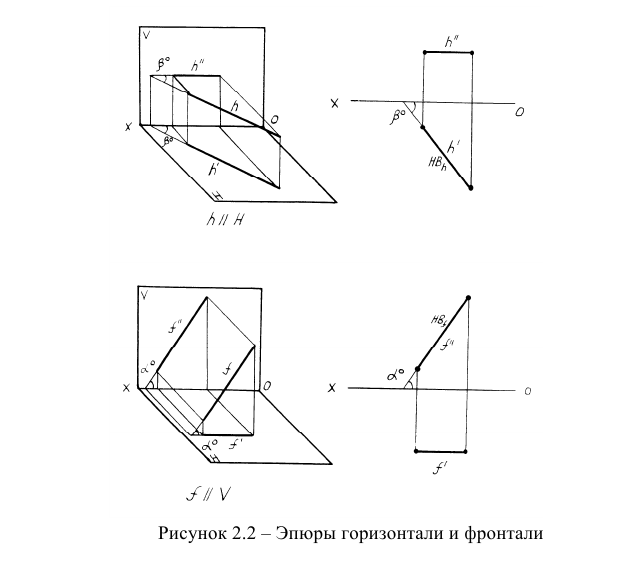
Прямые, параллельные плоскостям проекций
Особенностью эпюра прямых, параллельных плоскостям проекций, является то, что две проекции прямой параллельны осям, а третья проекция наклонена к осям и является натуральной величиной прямой.
Кроме того, по этой проекции прямой можно определить угол наклона прямой к той или иной плоскости проекций.
Среди упомянутых прямых особое место занимают горизонталь h и фронталь f (рисунок 2.2), которые обладают замечательными свойствами и поэтому часто применяются при решении различных задач.
Важнейшими свойствами горизонтали являются: фронтальная
проекция горизонтали
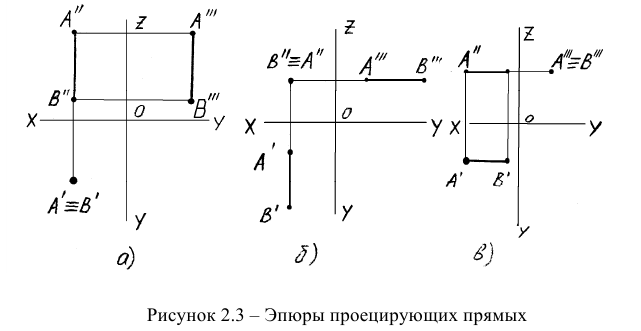
Прямые, перпендикулярные плоскостям проекций
Особенностью эпюра прямых, перпендикулярных плоскостям проекций, является то, что две проекции этих прямых параллельны осям, а третья проекция «вырождается» в точку на той плоскости проекций, которой эта прямая перпендикулярна. Первые две проекции проецирующих прямых являются их натуральной величиной. На рисунке 2.3 представлены эпюры горизонтально- (а), фронтально- (б) и профильно-проецирующих прямых (в).
Определение натуральной величины прямой
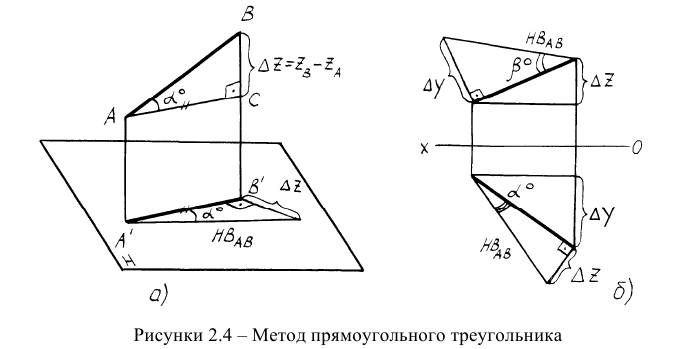
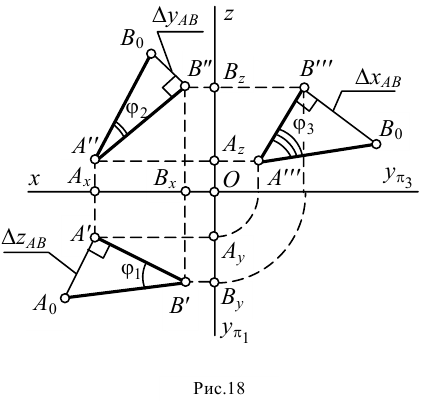
Так как прямая общего положения проецируется на плоскости проекций с искажением, то задача определения натуральной величины (НВ) прямой по её проекциям является важной. С целью определения НВ прямой разработан метод прямоугольного треугольника, сущность которого понятна из пространственного чертежа (рисунок 2.4а).
Для того, чтобы определить натуральную величину прямой по её проекциям, необходимо на одной из её проекций (на любой) построить прямоугольный треугольник, одним катетом которого является сама проекция, а другим катетом — разность недостающих координат концов отрезка прямой. Тогда гипотенуза треугольника будет являться НВ прямой (рисунок 2.46). Недостающей координатой здесь названа та координата, которая не участвует в построении той или иной проекции прямой. Так, например, горизонтальная проекция прямой строится по координатам X и Y её концов.
Координата Z в построениях не участвует и называется недостающей координатой. Таким образом, при построении прямоугольного треугольника на горизонтальной проекции прямой на катете откладывают разность аппликат, а при построении на фронтальной проекции — разность ординат.
При определении НВ прямой методом прямоугольного треугольника одновременно можно определить углы наклона прямой к плоскостям проекций (углы а° и 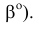
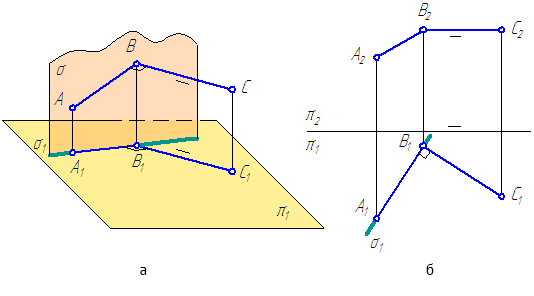
Следы прямой
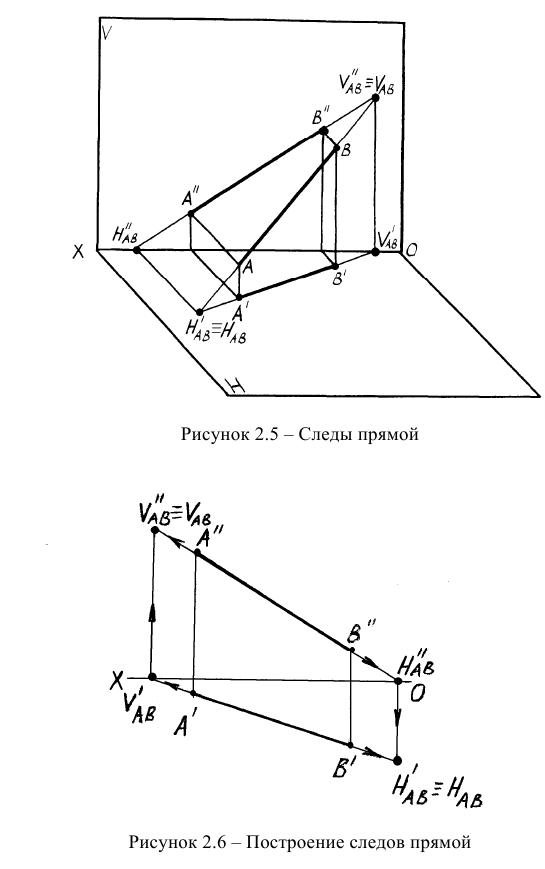
Точки пересечения прямой с плоскостями проекций называются следами прямой. В точках следов прямая переходит из одного октанта в другой. Различают горизонтальный, фронтальный и профильный следы прямой и их соответствующие проекции. На рисунке 2.5 показаны пространственные чертежи прямых общего и частного положения и образование их следов. Прямые, параллельные плоскостям проекций, имеют только два следа, а прямые, перпендикулярные плоскостям проекций, — один след, совпадающий с той проекцией прямой, на которой она проецируется в точку.
Из пространственных чертежей следует методика построения проекций следов прямой на эпюре (рисунок 2.6).
Взаимное положение прямых
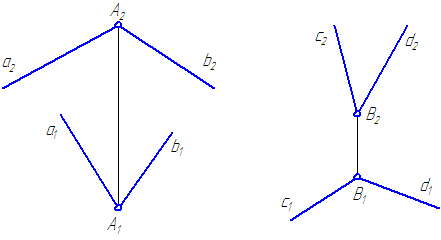
Прямые в пространстве могут быть параллельными, пересекающимися, скрещивающимися и перпендикулярными.
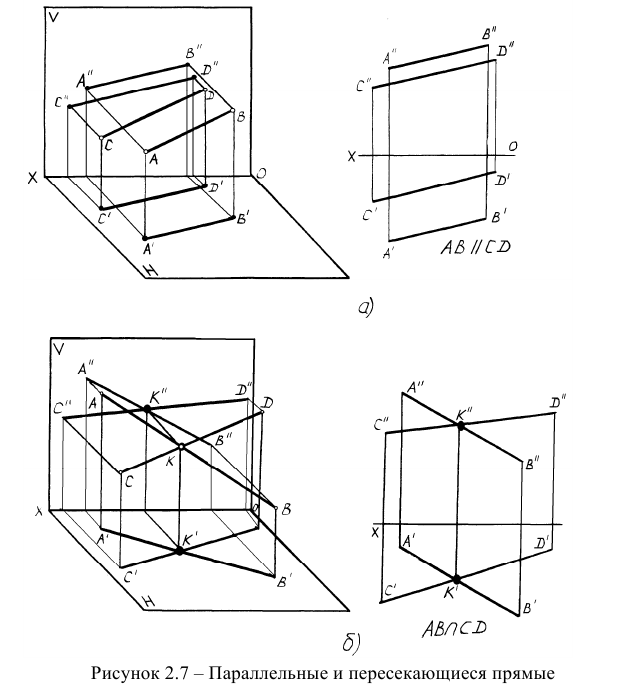
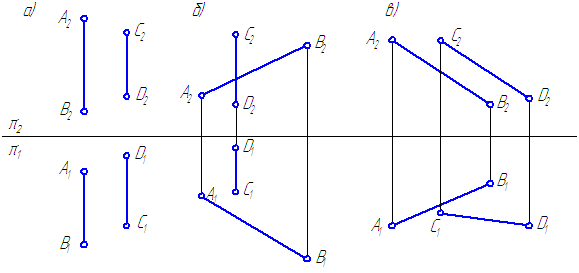
Пространственные чертежи и эпюры параллельных и пересекающихся прямых представлены на рисунке 2.7а, б.
Признаком параллельных прямых на эпюре является параллельность их одноименных проекций.
Пересекающимися прямыми называются прямые, которые имеют общую точку — точку пересечения. Признаком пересекающихся прямых на эпюре является то, что проекции точки пересечения находятся на одной линии связи.
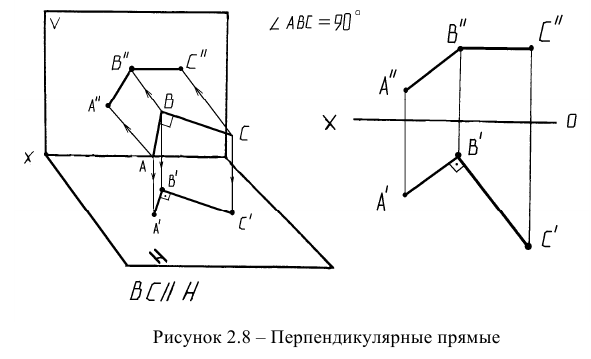
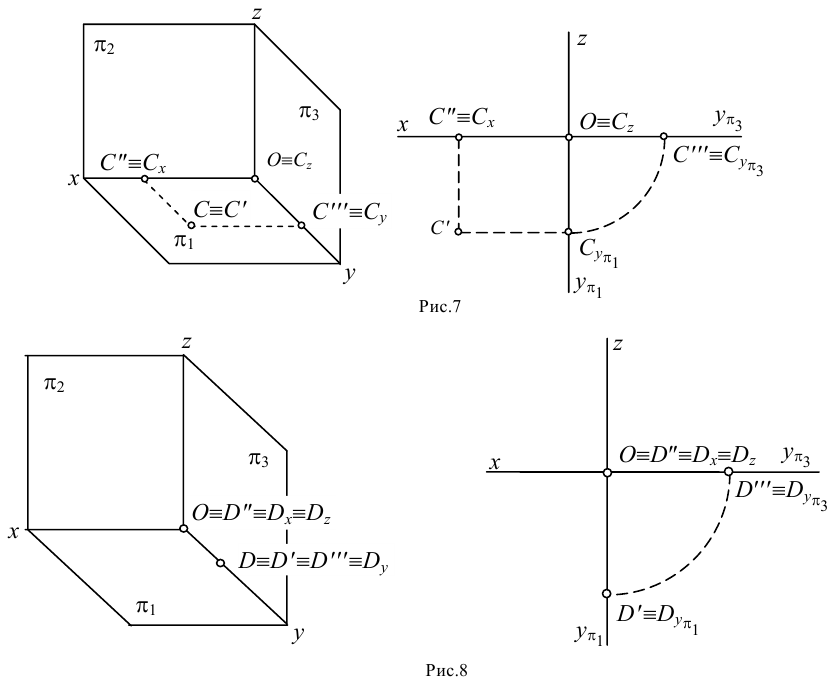
Частным случаем пересекающихся прямых являются перпендикулярные прямые. В соответствии с теоремой о проецировании прямого угла, прямой угол будет проецироваться на плоскость проекций в натуральную величину в том случае, когда одна из его сторон будет параллельна этой плоскости проекций (Рисунок 2.8).
Cкрещивающимися прямыми называются непараллельные прямые, не имеющие общей точки. Скрещивающиеся прямые в пространстве не пересекаются, но на эпюре их одноименные проекции накладываются друг на друга, что создает впечатление пересечения. Признаком скрещивающихся прямых на проекциях является то, что проекции их мнимых точек пересечения не находятся на одной линии связи (рисунок 2.9а). В мнимых точках пересечения конкурируют две точки, принадлежащие разным прямым, или, другими словами, в мнимых точках конкурируют две прямые. Назовем эту область конкурирующим местом.
При рассмотрении скрещивающихся прямых возникает вопрос о видимости проекций прямых в конкурирующих местах. Этот вопрос может быть решен методом конкурирующих точек (конкурирующих прямых).
Сущность метода заключается в следующем:
- Отметить конкурирующее место на рассматриваемой проекции;
- Обозначить конкурирующие точки или записать, какие прямые конкурируют;
- Провести через конкурирующее место линию связи;
- Вдоль линии связи сравнить недостающие координаты конкурирующих точек или конкурирующих прямых;
- На рассматриваемой проекции будет видна та точка или прямая, которая имеет наибольшую недостающую координату.
Так на рисунке 2.96 на горизонтальной проекции будет видна точка 1, принадлежащая прямой AВ, или, проще говоря, прямая АВ, так как аппликата прямой АВ вдоль линии связи наибольшая. На фронтальной проекции также будет видна прямая AВ. так как у неё в конкурирующем месте наибольшая ордината.
Метод конкурирующих точек (прямых) используется и при определении видимости проекций прямой и плоскости, двух плоскостей, прямой и поверхности, ребер многогранников и т.д. При этом считается, что плоскости и поверхности геометрически непрозрачны, а видимость прямой в точке встречи с плоскостью или в точках встречи с поверхностью меняется.
На рисунке 2.10 представлена пространственная схема определения видимости проекций прямой MN и плоскости ABCD, пересекающихся друг с другом в точке К. На горизонтальной проекции в конкурирующем месте будет видна прямая ВС, так как её аппликата больше, чем у прямой MN. На фронтальной проекции в конкурирующем месте будет видна прямая MN, так как ордината у неё больше, чем у прямой АВ.
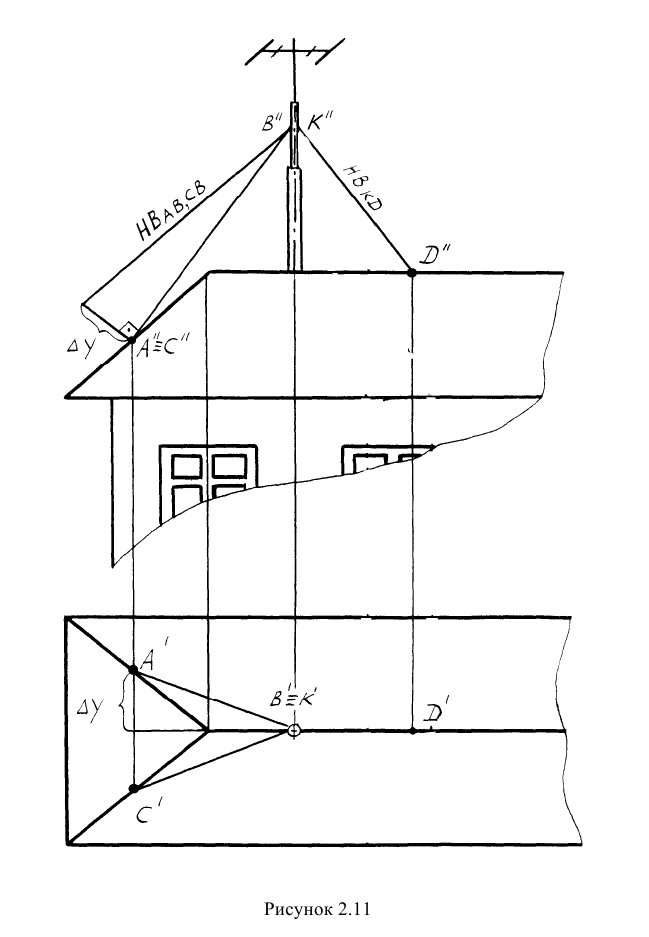
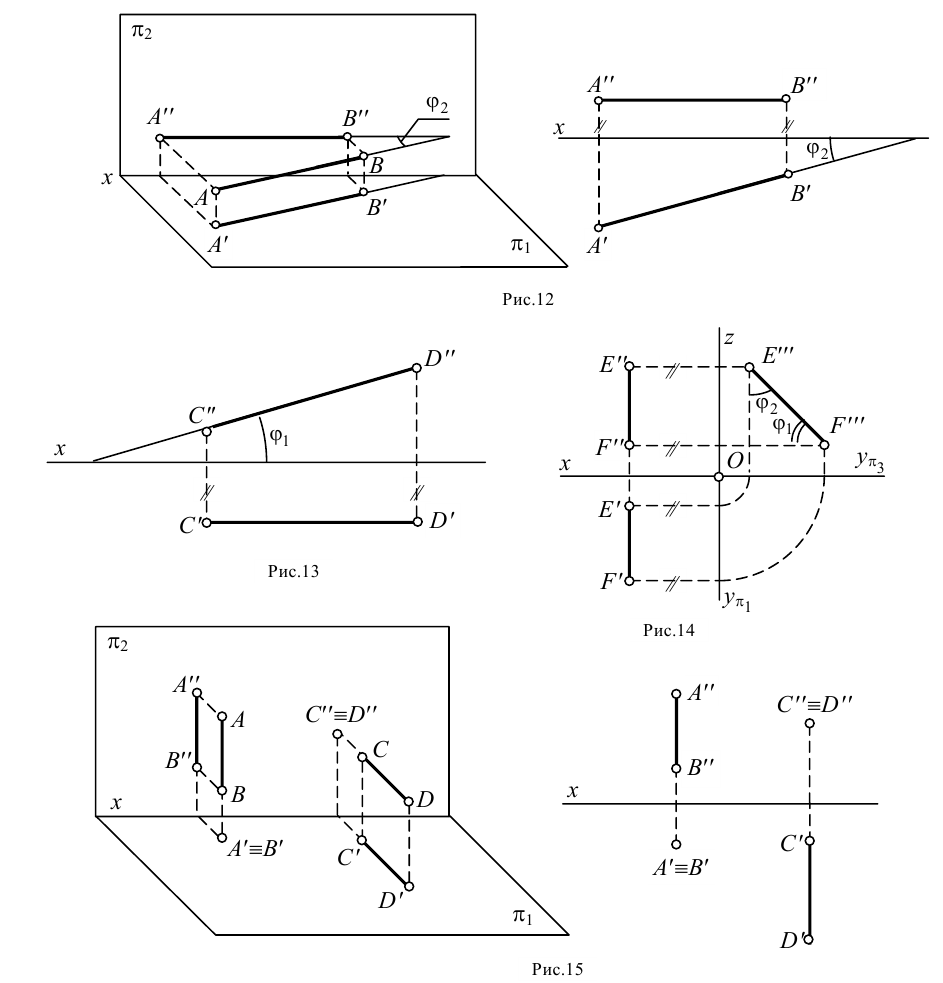
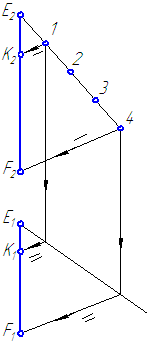
Пример: Определить длину растяжек для крепления антенны к крыше здания (рисунок 2.11).
Решение: Длина растяжек АВ и ВС определена методом прямоугольного треугольника на фронтальной проекции. Длину растяжки KD определять не следует, так как прямая KD является фронталью и её фронтальная проекция 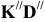
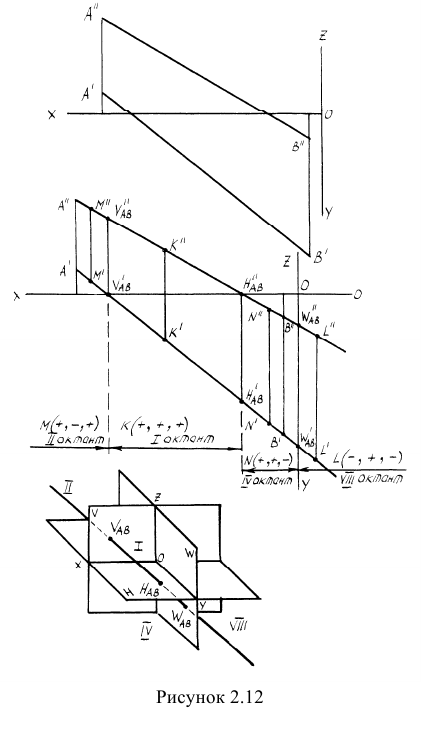
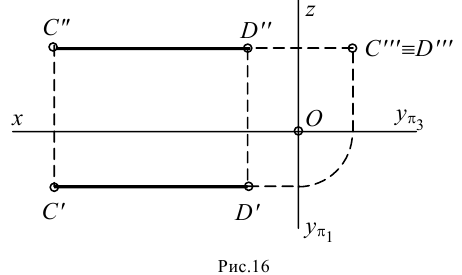
Пример: Построить следы прямой АВ и определить октанты, через которые проходит прямая (рисунок 2.12).
Решение: Задача решена в пространстве и на эпюре. Так как проекции прямой пересекают оси ОХ и 0Y, то в точках пересечения и будут находится проекции горизонтального, фронтального и профильного следов прямой. Далее по знакам координат точек М, К, N, L определяем, что прямая проходит через октанты ll, I, IV и VIII.
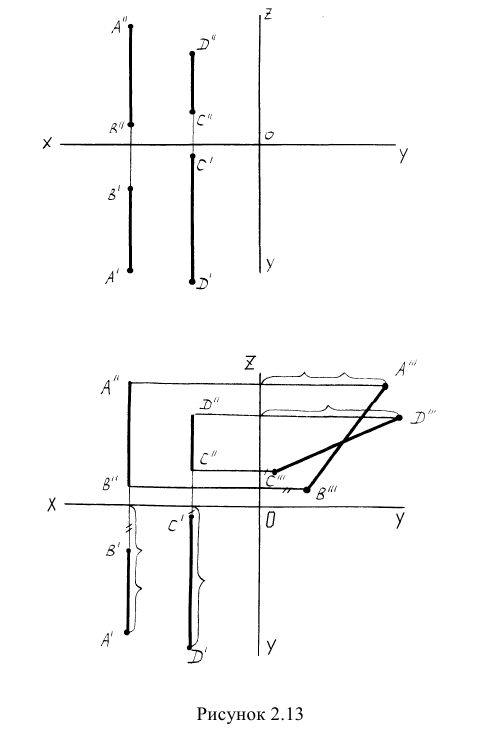
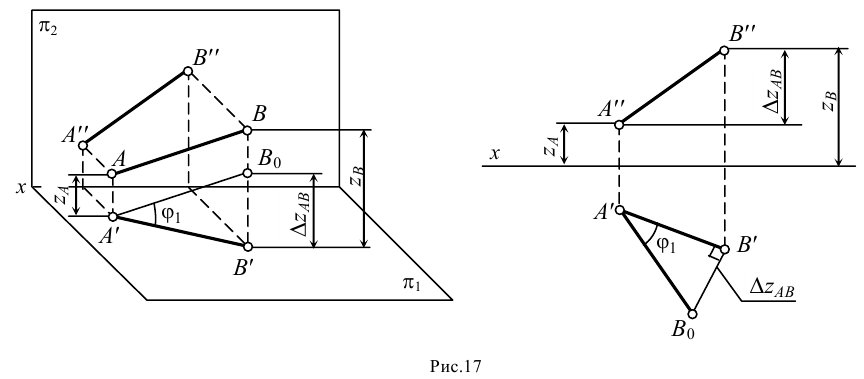
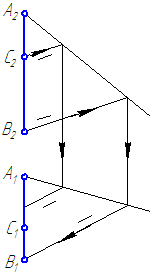
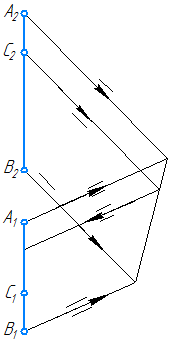
Пример: Определить взаимное положение прямых АВ и CD (рисунок 2.13).
Решение: Анализ проекций двух заданных прямых приводит к выводу, что они являются профильными прямыми, так как обе их проекции параллельны осям 0Y и 0Z. Анализ взаимной параллельности одноименных проекций позволяет сделать предварительный вывод о том, что прямые АВ и CD параллельны друг другу. Однако такой вывод неправомерен, так как для профильных прямых следует проверить параллельность на профильной проекции. Построив профильные проекции 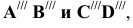
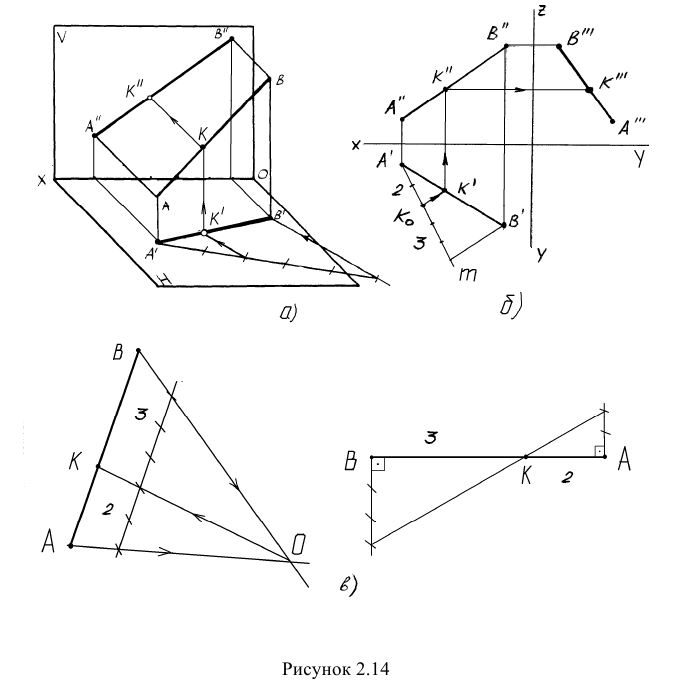
Пример: Разделить отрезок прямой АВ в отношении 2:3 (рисунок 2.14а).
Решение: Так как отношение отрезков прямой линии равно отношению их проекций, то разделить в данном отношении отрезок прямой на эпюре — значит разделить в том же отношении любую его проекцию.
Задача решается исключительно графическим методом. Представленное решение задачи основано на теореме Фалеса: если на одной стороне угла отложить равные или пропорциональные отрезки и провести через засечки любые параллельные прямые, то другая сторона разделится на равные или пропорциональные отрезки. На рисунке 2.14а дано решение задачи в пространственной форме, а на рисунке 2.146 представлен эпюр решения задачи. На горизонтальной проекции вспомогательная прямая m проводится под произвольно углом, и на ней откладывается пять произвольных отрезков равной длины.
На рисунке 2.14в представлены ещё два способа деления отрезка прямой в заданном отношении.
Изготовление любой детали, строительство сооружений, разработка месторождений полезных ископаемых начинается с составления чертежей, планов и схем. Никакие словесные описания не могут заменить чертеж, который позволяет не только определить форму и размеры всех частей предмета, но и получить наглядное представление о нем.
Начертательная геометрия — один из разделов геометрии, в котором свойства пространственных фигур изучают по их изображениям на той или иной поверхности. Чаще всего за такую поверхность принимают плоскость.
Как и любая научная дисциплина, начертательная геометрия имеет терминологию, которую следует хорошо усвоить, чтобы понимать излагаемый материал.
В геометрии вообще и в начертательной геометрии в частности каждое последующее изложение основывается на предыдущем материале. Такая особенность изучаемого предмета требует систематической, последовательной работы над ним.
Потребность в отображении действительности появилась у человека давно. Об этом свидетельствуют многочисленные изображения первобытного человека на стенах пещер и камнях, на предметах и орудиях труда. С развитием человечества совершенствовалась и техника передачи различных символов (письменность, схемы, чертежи). В Древнем Китае, например, была разработана всеобъемлющая знаковая система, где каждому предмету или явлению соответствовал особый знак (иероглиф). В Древнем Египте при возведении сооружений архитекторы использовали чертежи в виде планов и фасадов.
Основные правила и методы построения изображений (планов зданий, земельных угодий, крепостных укреплений) по законам геометрии были разработаны в эпоху античности. В Древней Греции, за 300 лет до нашей эры, сделаны первые шаги к научному обоснованию метода центрального проецирования. В «Оптике» Евклида содержатся 12 аксиом и 61 теорема об условиях «видения» предметов.
Расцвет классической культуры сменился застоем, и только в эпоху Возрождения, благодаря усилиям школ живописи и архитектуры Италии, Нидерландов и Германии, в истории начертательной геометрии начинается новый период развития. К этому времени относится введение целого ряда основных понятий метода проецирования.
С развитием архитектуры, машинного производства, горной промышленности к изображениям предметов стали предъявлять все более высокие требования, что и привело к необходимости обобщения и систематизации знаний по «теории изображений». Работа знаменитого французского геометра и инженера периода Великой французской революции Гаспара Монжа (1746-1818) «Geometrie Descriptive» (1798 г.) представляет собой первое систематическое изложение общего метода изображения пространственных фигур на плоскости, поднявшее начертательную геометрию на уровень самостоятельной научной дисциплины.
Преподавание начертательной геометрии в России началось уже в первые годы XIX в. в Корпусе инженеров путей сообщения и чуть позже в Горном кадетском корпусе. Первый русский профессор начертательной геометрии Я.И. Севастьянов (1796-1849) в 1821 г. составил курс «Основания начертательной геометрии», ставший классическим учебным пособием по этому предмету.
Среди ученых, внесших наиболее значительный вклад в развитие начертательной геометрии, следует отметить академика Е.С. Федорова (1853-1919), преподававшего в Горном институте. На примере решения задач минералогии и кристаллографии он показал применимость методов начертательной геометрии к исследованиям закономерностей материального мира.
В настоящее время начертательная геометрия является базовой общетехнической дисциплиной, составляющей основу инженерного образования. Было бы, однако, большой ошибкой ограничивать значение начертательной геометрии лишь рамками теоретической основы черчения. Ее методы дают возможность решать самые сложные проблемы в различных областях: горно-геологических науках, химии, физике и др.
Образование проекций. Методы проецирования
В начертательной геометрии чертеж — основной инструмент решения различных пространственных задач. К выполняемому чертежу предъявляется ряд особых требований, четыре из которых являются наиболее существенными. Чертеж должен быть: 1) наглядным; 2) обратимым; 3) достаточно простым; 4) точным.
Остановимся более подробно на обратимости чертежа. Под этим свойством понимается возможность точного воспроизведения формы и размеров предмета по его изображению. Действительно, для всех видов технических и горно-геологических чертежей это требование является особенно важным, так как по чертежу в машиностроении изготавливается та или иная деталь, в горном деле осуществляется проходка горных выработок, в геологии — оценка запасов полезного ископаемого и т.д.
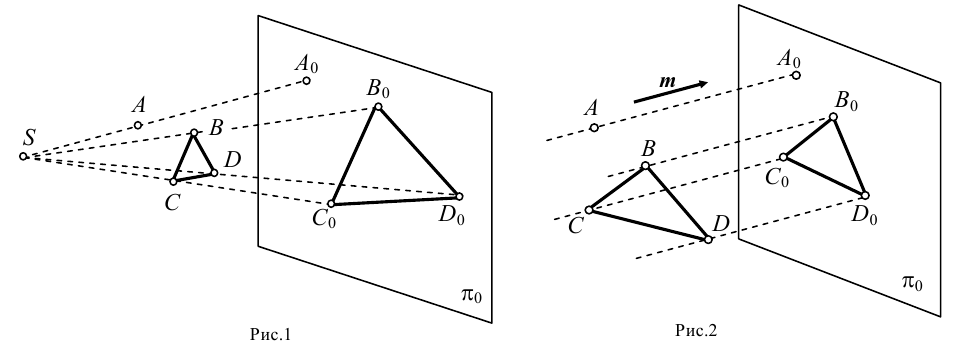
Основным методом получения изображений в начертательной геометрии является проецирование. Чтобы понять сущность проецирования, обратимся к рис.1.
Выбираем центр проецирования — произвольную точку 
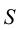
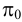
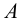
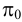
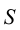
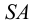
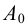
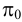
При этом точка 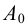
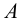
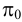
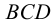
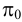
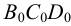
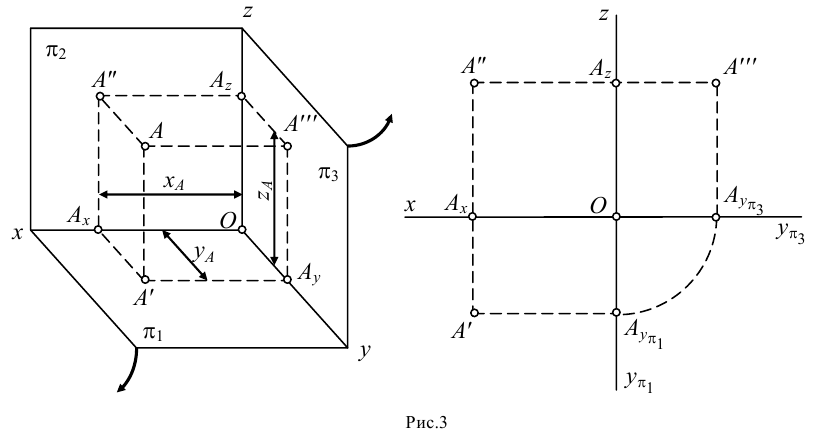
Если проецирование осуществляется из бесконечно удаленной точки пространства (рис.2), то все проецирующие прямые окажутся взаимно параллельными. Этот метод проецирования называется параллельным, а направление 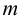
Если направление параллельного проецирования перпендикулярно плоскости проекций, то проецирование называется прямоугольным или ортогональным. Во всех остальных случаях параллельное проецирование называется косоугольным.
Изображения, полученные при помощи центрального проецирования, отличаются хорошей наглядностью, что объясняется устройством зрительного аппарата человеческого глаза. Однако этот метод имеет существенные недостатки. Во-первых, сложно построить изображение предмета. Во-вторых, построенные проекции имеют низкие метрические свойства, поэтому вследствие значительных искажений, возникающих при данном методе проецирования, определить истинные размеры предмета весьма сложно. По этим причинам способ центрального проецирования имеет ограниченное применение в практике и используется, когда от чертежа требуется прежде всего наглядность.
Несмотря на то, что параллельное проецирование, по сравнению с центральным, имеет меньшую наглядность, параллельные проекции, особенно ортогональные, обладают лучшей измеримостью и простотой построения.
Задачи, решаемые методами начертательной геометрии, принято делить на метрические и позиционные.
Метрические задачи имеют целью определение размеров различных предметов по их изображению. К таким задачам относится определение натуральной величины геометрических фигур, расстояний и углов между ними; в горно-геологической практике — это задачи на определение глубины и угла наклона буровых скважин, угла падения пласта полезного ископаемого, углов между осями горных выработок и т.п.
Позиционные задачи позволяют определить взаимное расположение различных объектов: точек, прямых линий, плоскостей, пространственных фигур. К этой категории задач относятся, например, установление точки встречи буровой скважины с плоскостью залежи, построение линии пересечения кровли и подошвы пласта полезного ископаемого с горной выработкой и многие другие.
Для быстрого и удобного решения пространственных задач в начертательной геометрии используют несколько систем изображений, особенности которых приведены в табл.1.
Таблица 1
Основные системы изображения, используемые при проецировании
Область применения той или иной системы изображений зависит, прежде всего, от целей, которые ставятся при построении чертежа. Из представленных в табл.1 систем наиболее широкое применение в техническом проектировании имеет эпюр (ортогональный чертеж). На его основе выполняются рабочие и сборочные чертежи, эскизы деталей, схемы и т.д. Поэтому в дальнейшем изложении курса основное внимание будет уделено именно этому методу построения.
Однако и другие методы проецирования находят применение в горно-геологических работах, поэтому в заключительных разделах будут рассмотрены основные правила изображения предметов при помощи векторных проекций, перспективы, аксонометрической проекции и, более подробно, — проекций с числовыми отметками.
- Заказать чертежи
Ортогональный чертеж. Проецирование точки
Любой предмет пространства можно рассматривать как определенную совокупность отдельных точек этого пространства, поэтому для изображения различных предметов необходимо научиться строить изображения отдельной точки пространства.
Представим в пространстве три взаимно перпендикулярные плоскости (рис.3):
Для наглядного изображения плоскостей проекций взята кабинетная проекция
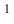
Плоскости проекций пересекаются по прямым, которые называются осями проекций и обозначаются 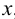
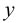
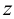
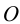
Представим себе также в пространстве некоторую точку 
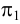
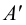
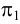
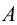
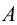
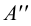
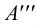
Длины отрезков, измеряемые некоторой установленной единицей длины и равные расстояниям от точки 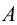
Три координаты точки однозначно определяют ее положение в пространстве.
Взаимно перпендикулярные плоскости, изображенные на рис.3, дают нам пространственный чертеж. Для получения трех проекций точки в плоскости чертежа плоскости проекций 
Фронтальная плоскость проекций 
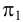
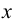
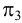
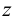
При совмещении плоскости 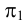
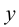
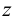
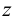
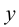
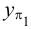
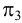
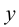
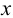
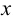
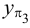
В результате образуется ортогональный чертеж, или эпюр (от франц. epure — чертеж, проект). На эпюре изображают только проекции геометрических объектов, а не сами объекты.
Любые две проекции точки, изображенные на эпюре, связаны между собой линией проекционной связи, перпендикулярной оси проекций (на чертеже ее обозначают штриховой линией):
Вследствие того, что отрезки 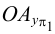
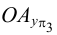
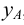
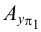
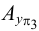
Каждая проекция точки 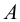
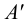
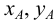
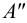
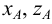
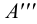
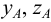
Положение точки 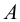
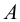
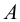
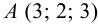
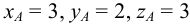
От аналитической формы задания точки легко перейти к графическому изображению этой точки на ортогональном чертеже.
Пример 1. Построить проекции точки 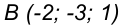
1. Выбираем единичный отрезок (рис.4).
2. С учетом знака откладываем на осях проекций координатные отрезки:
3. Отмечаем точки 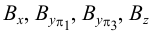
4. Из построенных точек 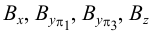
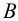
Две проекции точки, построенные на эпюре, однозначно определяют ее положение в пространстве. По двум проекциям заданной точки можно построить третью, и притом только одну.
Пример 2. Построить третью проекцию точки 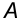
1. Даны фронтальная и профильная проекции точки 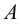
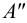
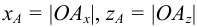
профильная проекция 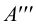
2. Из имеющихся проекций проводим линии проекционной связи, перпендикулярные осям проекций, и определяем координатные отрезки 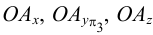
3. На пересечении линий проекционной связи с осями проекций отмечаем точки 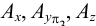
4. Строим третью, горизонтальную проекцию точки 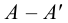
При определении точки 
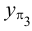
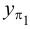
В зависимости от расположения точки относительно плоскостей проекций различают:
1) точки общего положения, не принадлежащие плоскостям проекций (к ним относится, например, точка А на рис.3);
2) точки частного положения, лежащие в плоскостях проекций 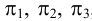
У точки общего положения все три координаты отличны от нуля.
Если точка лежит в плоскости проекций, то ее координата по оси, перпендикулярной этой плоскости проекций, равна нулю. Если точка лежит на оси проекций, то две другие ее координаты равны нулю. Если все три координаты точки равны нулю, то точка лежит в начале координат.
Рассмотрим некоторые частные случаи положения точки: когда точка лежит в какой-нибудь плоскости проекций или на какой-нибудь оси проекций.
Точка 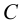
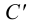
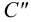
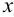
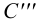
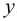
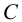
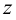
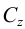
Точка 
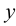
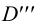
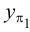
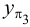
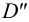
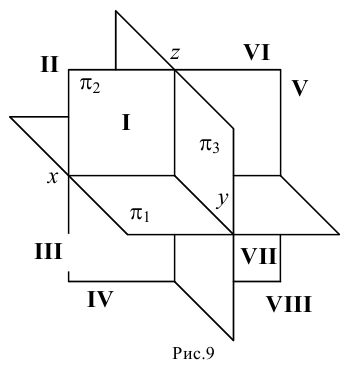
Октанты
Плоскости проекций 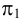
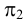
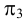
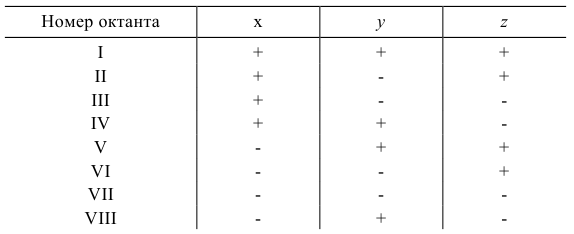
Нумерация октантов в полупространствах приведена на рис.9. Знаки координат в каждом из октантов указаны в табл.2.
Таблица 2
Знаки прямоугольных координат в различных октантах
Проекции отрезка прямой линии. Точка на прямой
Прямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и притом только одну.
Пусть нам даны на эпюре точки 
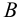
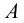
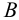
Таким образом, прямая линия на эпюре может быть задана двумя проекциями отрезка, принадлежащего этой прямой. По двум проекциям отрезка всегда можно построить его третью проекцию и притом только одну.
Если прямая не параллельна ни одной из плоскостей проекций, то она пересекает все плоскости проекций и не проецируется ни на одну из них в натуральную величину. Такую прямую называют прямой общего положения. Ни одна из ее проекций не параллельна осям. Прямая 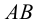
Точка принадлежит прямой линии, если ее проекции лежат на одноименных проекциях этой линии.
Если на прямой 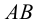
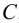
Таким образом, если точка принадлежит заданной прямой, то для построения проекций этой точки на эпюре необходимо и достаточно знать положение хотя бы одной проекции точки, поскольку недостающие проекции легко найти в пересечении линий проекционной связи с соответствующими проекциями прямой.
Прямые частного положения
Прямая, параллельная одной или двум плоскостям проекций, называется прямой частного положения.
Рассмотрим пример, когда прямая параллельна одной плоскости проекций. В этом случае прямая проецируется на эту плоскость в натуральную величину, а две другие проекции -параллельны осям проекций.
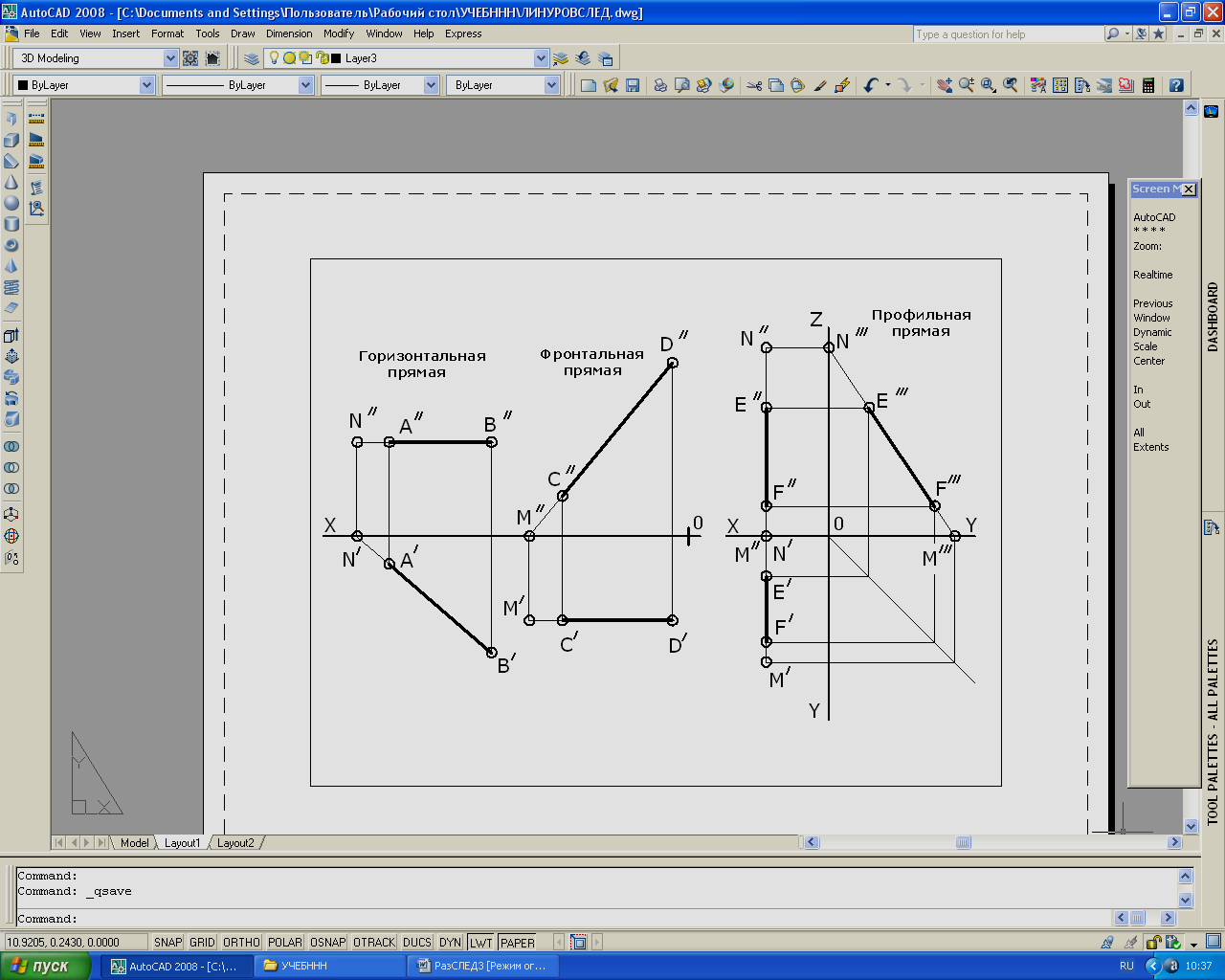
Горизонтальная прямая — прямая, параллельная плоскости 
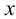
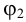
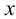
Фронтальная прямая — прямая, параллельная плоскости 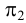
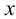
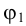
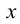
Профильная прямая — прямая, параллельная плоскости 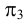
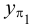
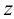
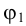
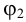
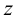
Если прямая параллельна двум плоскостям проекций, т.е. перпендикулярна третьей плоскости проекций, то на эти две плоскости проекции прямая проецируется в натуральную величину, а третья проекция представляет собой точку. Такие прямые называют проецирующими.
Горизонтально-проецирующая прямая — прямая, перпендикулярная плоскости 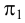
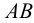
Фронтально-проецирующая прямая -прямая, перпендикулярная плоскости 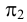
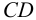
Профильно-проецирующая прямая — прямая, перпендикулярная плоскости 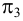
Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
Ортогональная проекция отрезка прямой общего положения на любую плоскость проекций всегда меньше длины самого отрезка. Рассмотрим правила определения натуральной величины отрезка прямой методом прямоугольного треугольника.
Предположим, что точки 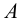
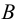
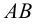
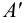
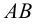

Рассмотрим стороны прямоугольного треугольника 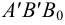
На ортогональном чертеже оказывается достаточно данных для построения треугольника, равного рассмотренному (рис.17). Для этого к горизонтальной проекции 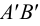
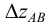
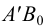
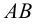
Истинную величину отрезка можно определить, построив прямоугольный треугольник, катетом которого является и фронтальная проекция отрезка (рис.18): при этом второй катет окажется равным разности координат 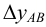
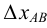
На рис.18 истинная величина отрезка 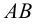
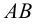
В общем случае, натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка прямой, а вторым — разность «третьих» координат (табл.3).
Под термином «третья координата» подразумевается координата, которая отсутствует в проекции, выбранной в качестве катета прямоугольного треугольника. Так, горизонтальная проекция отрезка строится по координатам 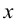
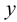
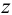
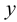
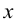
Таблица 3
Геометрические элементы при определении истинной величины отрезка примой 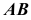
Координаты концов отрезка могут иметь разные знаки. Тогда разность координат определяется с учетом знака. Например, если координата 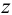
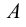
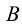
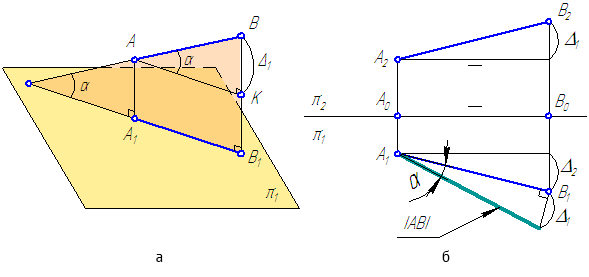
Угол наклона прямой к плоскости проекций — это угол между прямой и ее проекцией. Следовательно, определяя истинную величину отрезка прямой методом прямоугольного треугольника, одновременно можно найти и угол ее наклона к плоскости проекций. Угол между гипотенузой и соответствующей проекцией отрезка равен углу наклона этой прямой к данной плоскости проекций.
Пример 3. Определить истинную величину отрезка 
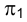
1. По табл.3 определяем, что для нахождения угла наклона к плоскости 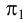
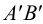
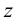
2. Определяем координаты по оси 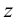
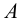
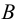
3. Строим прямоугольный треугольник, в котором за катет принимаем горизонтальную проекцию 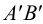
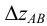
4. Гипотенуза построенного треугольника есть истинная величина отрезка 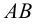
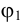
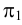
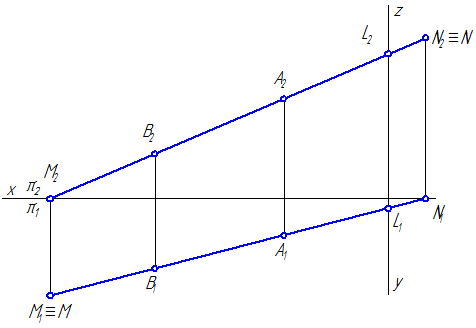
Следы прямой
Следом прямой называется точка пересечения прямой линии с плоскостью проекций. Прямая общего положения пересекает все три плоскости проекций и, следовательно, имеет три следа. Прямая линия частного положения не имеет следа на плоскости проекций, если она параллельна этой плоскости.
Выберем две точки, точку 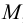
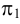
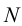
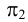
Точка пересечения 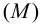
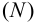
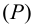
Следы прямой совпадают с проекциями этих следов в той плоскости, где они расположены: 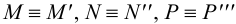
Поскольку точка 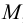
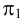
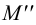
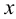
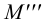
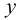
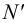
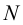
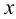
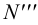
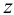
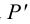
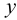
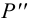
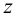
Охарактеризуем особенности построения каждой проекции каждого из трех следов на ортогональном чертеже (рис.20).
Горизонтальный след 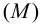
Фронтальный след 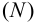
Профильный след 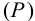
Необходимо отметить, что построение профильных проекций следов 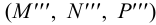
Пример 4. Построить проекции следов прямой 
1. Находим фронтальную проекцию горизонтального следа 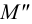
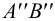
2. Из точки 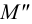
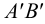
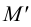
3. По двум проекциям 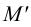
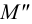
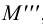
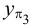
4. Находим горизонтальную проекцию фронтального следа 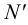
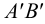
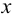
5. Из точки 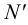
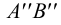
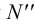
6. По двум проекциям фронтального следа 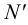
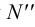
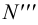
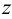
7. В пересечении 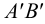
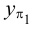
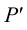
8. В пересечении 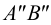
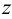
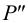
9. По двум проекциям 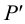
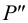
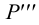
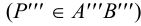
Взаимное положение двух прямых
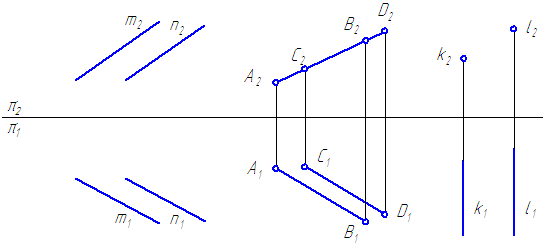
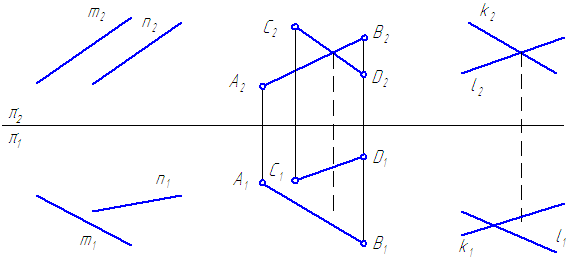
Две прямые могут пересекаться, быть параллельными друг другу и скрещиваться.
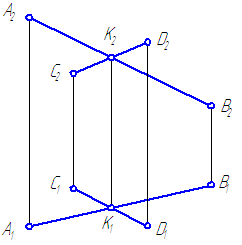
Пересекающиеся прямые имеют одну общую точку. Если прямые линии пересекаются, то одноименные проекции этих прямых тоже пересекаются (рис.22, а), причем проекции точки пересечения лежат на одной линии проекционной связи.
Параллельные прямые лежат в одной плоскости и не имеют общих точек. Одноименные проекции двух параллельных прямых параллельны между собой (рис.22, б).
Скрещивающиеся прямые, в отличие от пересекающихся и параллельных прямых, не лежат в одной плоскости. Хотя одноименные проекции двух скрещивающихся прямых и могут пересекаться, но точки их пересечения не лежат на одной линии проекционной связи (рис.22, в).
Две точки, лежащие на скрещивающихся прямых и на одном перпендикуляре к плоскости проекций, называются конкурирующими. Проекции конкурирующих точек лежат в точке пересечения одноименных проекций скрещивающихся прямых (точки / и 2 на фронтальной плоскости проекций, точки 3 и 4 на горизонтальной плоскости проекций — см. рис.22, в)
Проецирование плоских углов
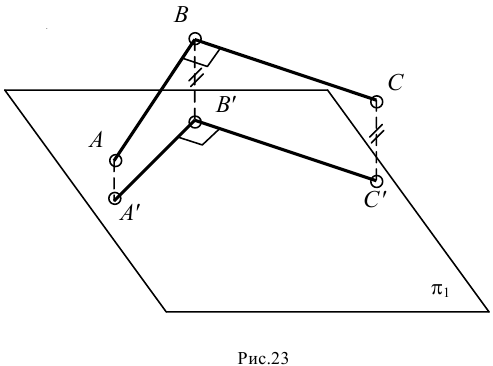
Плоский угол проецируется на плоскость проекций без искажения, если плоскость угла параллельна плоскости проекций. Это справедливо в отношении любого угла — острого или тупого. Исключение составляет только прямой угол, который проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций (рис.23).
- Проецирование плоскости
- Плоскость на эпюре Монжа
- Позиционные задачи
- Методы преобразования эпюра Монжа
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
- Перпендикулярность геометрических объектов
- Метод замены плоскостей проекций
Примечание:
Следы прямых необходимы для построения
следов плоскостей.
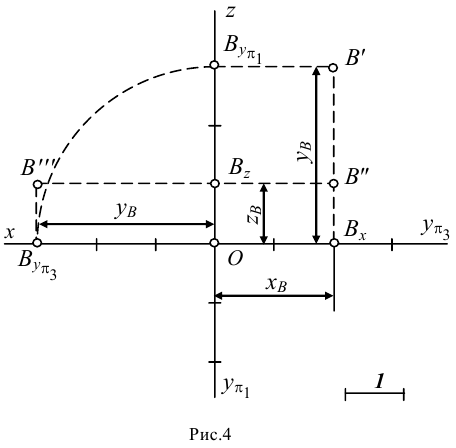
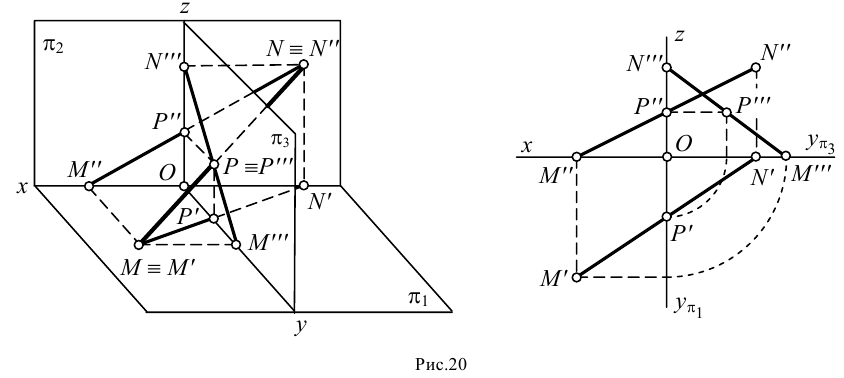
Точки
в которых заданная прямая пересекает
плоскости проекций называют следами
прямой.
При
наличии на чертеже трех плоскостей
проекций (π1
, π2
и
π3)
мы можем иметь три следа заданной прямой:
Точку
пересечения заданной прямой с
горизонтальной плоскостью проекций
называют горизонтальным
следом прямой.
Точку
пересечения заданной прямой с фронтальной
плоскостью проекций называют фронтальным
следом прямой.
Точку
пересечения заданной прямой с профильной
плоскостью проекций называют профильным
следом прямой.
2.5.5.1 Обозначение следов прямых на чертежах
Горизонтальные
следы: M
(M’
M’’
M’’’),
M1
(M1’
M1’’
M1’’’)……
Фронтальные
следы: N
(N’
N’’
N’’’),
N1
(N1’
N1’’
N1’’’)……
Профильные
следы: P
(P’
P’’
P’’’),
P1
(P1’
P1’’
P1’’’)……
2.5.5.2 Построение следов прямых на чертежах
2.5.5.2.1 Модель построения следов прямой общего положения (рис.29)
Рис.
29
Модель
построения следов прямой общего положения
Если
фронтальная
проекция прямой пересекает ось OX
и профильная
проекция прямой пересекает ось OY,
то
мы построим горизонтальный след (M).
Если
фронтальная
проекция прямой пересекает ось OX
и профильная
проекция прямой пересекает ось OY,
то
мы построим горизонтальный след (M).
Если
горизонтальная
проекция прямой пересекает ось OX
и
профильная
проекция прямой пересекает ось OZ,
то
мы построим фронтальный след (N).
Если
фронтальная
проекция прямой пересекает ось OZ
и
горизонтальная
проекция
пересекает ось OY,
то
мы построим профильный след (P).
Очевидно,
что одна из координат
«следа»
равна нулю.
Для
горизонтального следа прямой –
(M)
координата
(Z
=0).
Для
фронтального следа прямой –
(N)
координата
(Y=0).
Для
профильного следа прямой –
(P)
координата
(X=0).
2.5.5.2.2 Построения следов прямой общего на чертеже в трех проекциях (рис.30)
Рис.
30
Чертеж
построения следов прямой общего положения
(AB)
Для
нахождения следа прямой ее нужно
продолжить
до момента, когда хотя бы одна из проекций
прямой пересечет
ось проекций (рис.30).
Задан
чертеж отрезка прямой общего положения
│AB
│.
Алгоритм
решения задачи:
Продолжим
прямую до момента, когда ее фронтальная
проекция пересекает ось OX,
а её
профильная
проекция пересекает ось OY,
тогда
мы построим горизонтальный след (M)
(ZM
=0) (обратите
внимание, координата {-YM}
горизонтального следа (M)
имеет отрицательный
знак
).
Продолжим
прямую до момента, когда ее горизонтальная
проекция
пересекает ось OX
и
профильная
проекция прямой пересекает ось OZ,
тогда
мы построим фронтальный след (N)
(YN
=0).
Продолжим
прямую до момента, когда ее фронтальная
проекция прямой пересекает ось OZ
и
горизонтальная
проекция
пересекает ось OY,
то
мы построим профильный след (P)
(XP
=0).
2.5.5.2.3 Построение следов линий уровня
Линии
уровня не имеют одноименных следов.
Горизонтальная
прямая (AB)
имеет два следа –
фронтальный
след
(N)
(YN
=0)
и профильный
след
(P)
–
не
показан).
Фронтальная
прямая
(CD)
имеет два следа –
горизонтальный
след (M)
(ZM
=0) и
профильный
след
(P)
–
не
показан.
Рис.
31
Построение следов линий уровня
Профильная
прямая (EF)
имеет два следа –
горизонтальный
след (M)
(ZM
=0)
и фронтальный
след
(N)
(YN
=0).
Примечание:
Горизонтальная прямая (AB)
и фронтальная прямая (CD)
построены в системе двух плоскостей
проекций (π1
, π2),
поэтому их профильные следы (PAB
и
PCD)
не показаны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
22.03.201618.32 Mб20Photoshop для профессионалов_Дэн Маргулис_изд.5.pdf
- #
08.02.20154.77 Mб22pilshikov_assembler.djvu
- #
- #
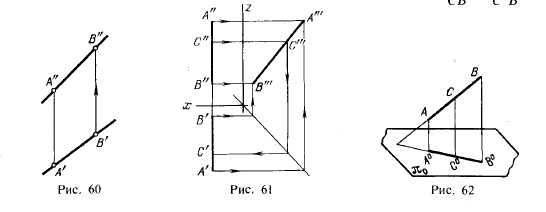
На рис. 60 дан чертеж некоторой прямой общего положения, проходящей через точку А. Если известно, что точка В принадлежит этой прямой и что горизонтальная проекция точки В находится в точке В’, то фронтальная проекция В» определяется так, как показано на рис. 60.
На рис. 61 показано построение точки на профильной прямой. Положим, что задана проекция С» этой точки; надо найти ее горизонтальную проекцию. Построение выполнено при помощи профильной проекции А’”В’” отрезка АВ, взятого на профильной прямой. Ход построения показан стрелками. Сначала определена проекция С'», а по ней — искомая проекция С’.
Одним из свойств параллельного проецирования является то, что отношение
отрезков прямой линии равно отношению их проекций (рис. 62): AC/CB= A°C°/C°B°, так
как прямые АА°, СС° и ВВ° параллельны между собой. Аналогично, отношение отрезков на проекции прямой линии равно отношению отрезков на этой прямой. Если бы точка делила пополам отрезок прямой, то проекция этой точки также делила бы проекцию отрезка пополам, и наоборот.
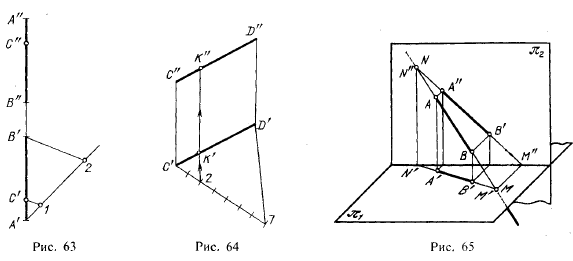
Из сказанного следует, что на рис. 61 деление проекций А»В» и А’В’ точками С» и С’ соответствует делению в пространстве отрезка АВ точкой С в том же отношении. Этим можно воспользоваться для более простого построения точки на профильной прямой. Если (как и на рис. 61) на проекции А»В» (рис. 63) задана проекция С», то, очевидно, надо разделить А’В’ в том же отношении, в каком точка С» делит проекцию А»В». Проведя из точки А’ некоторую вспомогательную прямую, откладываем на ней А’1 = А»С» и 1—2 = ѻ». Проводим прямую В’2 и параллельно ей через точку 1 прямую до пересечения с А’В’ в точке С’. Эта точка представляет собой искомую горизонтальную проекцию точки С, принадлежащей отрезку АВ.
На рис. 64 дан пример деления отрезка прямой линии в некотором заданном отношении.
Отрезок CD разделен в отношении 2:5. Из точки С’ проведена вспомогательная прямая, на которой отложено семь (2 + 5) отрезков произвольной длины, но равных между собой. Проведя отрезок D’7 и параллельно ему через точку 2 прямую, получаем точку К’, причем С’К’: K’D’ = 2: 5; затем находим К». Точка К делит отрезок CD в отношении 2:5.
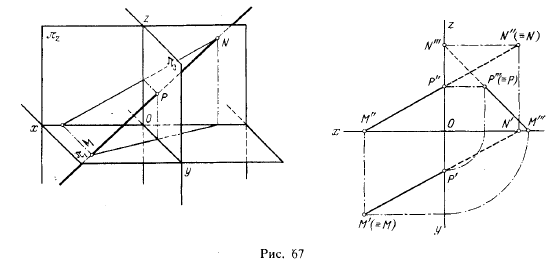
На рис. 65 показаны точки М и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Эти точки называются следами: точка М — горизонтальный след прямой, точка N — ее фронтальный след.
Горизонтальная проекция горизонтального следа (точка М’) совпадает с самим следом, а фронтальная проекция этого следа М» лежит на оси проекций. Фронтальная проекция фронтального следа N» совпадает с точкой N, а горизонтальная проекция N’ лежит на той же оси проекций.
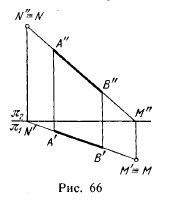
Следовательно, чтобы найти горизонтальный след, надо (рис. 66) продолжить фронтальную проекцию А»В» до пересечения с осью π2/π1 и через точку М» (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси π2/π1 до пересечения с продолжением горизонтальной проекции А’В’. Точка М’ — горизонтальная проекция горизонтального следа; она совпадает с самим следом (≡ знак совпадения).
Для нахождения фронтального следа продолжаем горизонтальную проекцию А’В’ до пересечения с π2/π1 через точку N’ (горизонтальную проекцию фронтального следа) проводим перпендикуляр до пересечения с продолжением фронтальной проекции А»В». Точка N» — фронтальная проекция фронтального следа; она совпадает с самим следом.
По положению точек М и N можно судить, к каким четвертям пространства отнесена данная прямая. На рис. 65 прямая АВ проходит через IV, I и II четверти.
Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.
На рис. 67 прямая пересекает не только пл.π1 и π2, но и пл. π3. Точка Р — профильный след прямой, т. е. след на профильной плоскости проекций. Этот след совпадает с его собственной проекцией на пл. π3, а фронтальная и горизонтальная проекции его лежат соотвегственно на осях z и у.
В данном случае прямая проходит за точкой Р через пятый октант и, встречая далее пл. π2, уходит в шестой октант; прямая из первого октанта выходит в четвертый октант 1).
Соответствующий чертеж дан на рис. 67 справа. Прямая показана в первом октанте — проекции М’Р’. М»Р» п М»‘Р»‘ и в пятом октанте — проекции P’N’, P»N» и P»‘N»‘.
Если плоскости проекций принять за плоскости координат, то у горизонтального следа прямой координата z = 0, у фронтального следа у = 0, у профильного следа х = 0.
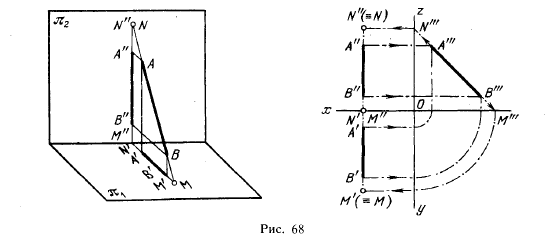
Построение следов профильной прямой (рис. 68) может быть выполнено следующим способом (рис. 68, справа).
1) Условимся показывать на чертежах сплошными линиями те проекции, которые соответствуют положению ^отрезка в первой четверти или в первом октанте.
Строим профильную проекцию (А»‘В»‘), определяем положение профильных проекций горизонтального следа (М'») и фронтального следа (N'») и затем находим положение остальных проекций этих следов (последовательность построения на чертеже показана стрелками).
ВОПРОСЫ К §§ 10-12
- При каком положении относительно плоскостей проекций прямая называется прямой общего положения?
- Как доказывается, что чертеж, содержащий две связанные между собой проекции в виде отрезков прямой линии, выражает именно отрезок прямой линии?
- Как выражается соотношение между проекцией отрезка прямой и самим отрезком?
- Как расположена прямая в системе π1,π2, π3, если все три проекции отрезка этой прямой равны между собой?
- Как построить профильную проекцию отрезка прямой общего положения по данным фронтальной и горизонтальной проекциям?
- Как выполнить построение по вопросу 5 на чертеже без осей проекций?
- Какие положения прямой линии в системе π1,π2, π3 считаются «особыми» (иначе — «частными»)?
- Как располагается фронтальная проекция отрезка прямой линии, если его горизонтальная проекция равна самому отрезку?
- Как располагается горизонтальная проекция отрезка прямой линии, если его фронтальная проекция равна самому отрезку?
- Какое свойство параллельного проецирования касается отношения отрезков прямой линии?
- Как разделить на чертеже отрезок прямой линии в заданном отношении?
- Что называется следом прямой линии на плоскости проекций?
- Какая координата равна нулю: а) для фронтального следа прямой, б) для горизонтального следа прямой?
- Где располагается горизонтальная проекция фронтального следа прямой линии?
- Где располагается фронтальная проекция горизонтального следа прямой линии?
- Может ли быть случай, когда прямая линия в системе π1,π2, π3 имеет следы на каждой к: этих плоскостей, сливающиеся в одну точку?
2.1. Задание прямой на эпюре
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.
а б
Рисунок 2.1 – Проекции прямой
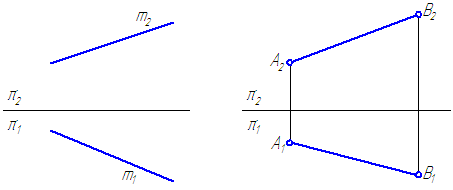
Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.
Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.
2.2. Прямые частного положения
Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения.
Прямые, параллельные плоскостям проекций, называются прямыми уровня.
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).
Рисунок 2.2 – Эпюр горизонтали
Если отрезок параллелен плоскости проекций π1, то его фронтальная проекция А2В2 параллельна оси проекций π1/π2, а горизонтальная проекция отрезка А1В1 определяет истинную величину АВ:
А2А0=В2В0
А2В2 || π2/π1
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).
Рисунок 2.3 – Эпюр фронтали
Если отрезок параллелен плоскости проекций π2, то его горизонтальная проекция параллельна оси проекций π2/π1, а фронтальная проекция отрезка C2D2 определяет истинную величину CD.
С1А0=D1D0
C1D1 || π2/π1
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).
Рисунок 2.4 – Эпюр профильной прямой
Прямые, перпендикулярные плоскостям проекций, называются проецирующими.
Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).
Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).
Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).
Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH
2.3. Метод прямоугольного треугольника
Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.
Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π1 (Рисунок 2.5).
Рисунок 2.5 – Определение истинной величины отрезка общего положения
На рисунке 2.5, а:
АА1 – расстояние от точки А до плоскости проекций π1;
ВВ1 – расстояние от точки В до плоскости проекций π1;
А1В1 – проекция отрезка АВ на π1;
∠(AB; AK)=∠(AB; A1B1)=α – угол наклона прямой АВ к плоскости проекций π1.
ΔАКВ – прямоугольный треугольник, в котором:
АК=А1В1 – катет, равный горизонтальной проекции отрезка АВ;
ВК=ВВ1–АА1=Δ1 – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π1 (то есть, разности координат Z точек А и В);
АВ – гипотенуза ΔАКВ – истинная величина.
При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.
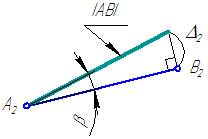
Истинная величина отрезка может быть найдена как гипотенуза прямоугольного треугольника, одним катетом которого является проекция этого отрезка на плоскость проекций (А2В2), а другим – разность координат концов этого отрезка до плоскости (Δ2), в которой ведется построение. Угол между истинной величиной (АВ) и проекцией (А2В2) определяет угол наклона (β) прямой к той плоскости проекций, в которой ведётся построение (Рисунок 2.6).Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π2
2.4. Точка и прямая
Если точка принадлежит прямой, то её проекции:
- Принадлежат одноимённым проекциям данной прямой;
- Лежат на одной линии связи.
Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:
- С1∈А1В1;
- С2∈А2В2;
- С1С2⊥π2/π1;
Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:
{frac{A_2C_2}{C_2B_2}=frac{A_1C_1}{C_1B_1}=frac{AC}{CB}}
Справедливо и обратное утверждение.
Упражнение
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)
Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:
-
- Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е2.
- Отложим на этой прямой от точки Е2 равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
- Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F2.
- Из точки 1 проведём прямую, параллельную прямой (4—F2) до пересечения с проекцией E2F2, таким образом будет найдена фронтальная проекция искомой точки К2.
- Горизонтальную проекцию точки К1 получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.
Упражнение
Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).
Рисунок 2.9а – Решение упражнения 2. Способ 1.
Рисунок 2.9б – Решение упражнения 2. Способ 2.Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.
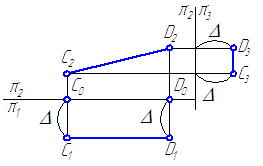
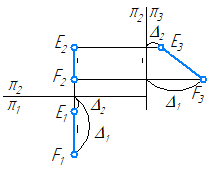
2.5. Следы прямой
След прямой – точка пересечения прямой с плоскостью проекций.
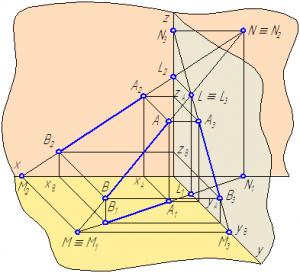
Прямая общего положения в общем случае может быть три следа:
- горизонтальный след M1– точка пересечения прямой с горизонтальной плоскостью проекций π1;
- фронтальный след N2– точка пересечения прямой с фронтальной плоскостью проекций π2;
- профильный след L3 – точка пересечения прямой с профильной плоскостью проекций π3.
След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:
- горизонтальный след совпадает со своей горизонтальной проекцией M≡M1,
- фронтальный – с фронтальной проекцией N≡N2,
- профильный – с профильной проекцией L≡L3 (Рисунок 2.10).
Рисунок 2.10 – Построение следов отрезка прямой АВ
Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).
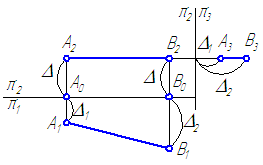
Для построения горизонтального следа прямой АB необходимо:
- Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
- Из точки М2 провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.
Чтобы построить фронтальный след отрезка АB прямой, необходимо:
- Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
- Из точки N1 провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Ниже приводим алгоритм построения следов отрезка прямой АВ:
A1B1 ∩ xO =N1; YN=0; N ∈ xOz (π2) ⇒ AB ∩ xOz=N
A2B2 ∩ xO =M2; ZM=0; M ∈ xOy (π1) ⇒ AB ∩ xOy=M
A1B1 ∩ yO =L1; XL=0; L ∈ yOz (π3) ⇒ AB ∩ yOz=L
A2B2 ∩ zO =L2;
Рисунок 2.11 – Эпюр построения следов отрезка прямой АВПрямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.
2.6. Взаимное расположение прямых
Две прямые в пространстве могут быть:
- параллельными;
- пересекающимися;
- скрещивающимися.
Параллельные прямые – прямые, пересекающиеся в несобственной точке.
Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).
Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).
{{A_2B_2}cap{C_2D_2}=K_2}
{{A_1B_1}cap{C_1D_1}=K_1}
{frac{A_2K_2}{K_2B_2}=frac{A_1K_1}{K_1B_1}}
{frac{C_2K_2}{K_2D_2}=frac{C_1K_1}{K_1D_1}}
Рисунок 2.13 – Пересекающиеся прямыеСкрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).
Рисунок 2.14 — Скрещивающиеся прямые2.7. Проекции плоских углов
Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.
Рисунок 2.15По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.
Теорема о проецировании прямого угла в частном случае
Теорема. Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).
Обратная теорема. Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.
Рисунок 2.16 – Проецирование прямого угла
Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,
причём ВС // π1 (Рисунок 2.16,б).
Доказательство:
- Проведём через отрезок АВ проецирующую плоскость – σ, σ⊥π1;
- Прямые АВ и ВВ1 лежат в плоскости σ;
- ВС⊥ВВ1 так как ВС//π1, а ВВ1⊥π1;
- Следовательно, ВС⊥σ, а значит ВС перпендикулярна и любой прямой, лежащей в плоскости σ, в частности А1В1;
- Следовательно В1С1⊥σ;
- Так как В1С1//ВС, то В1С1⊥А1В1.
2.8. Задачи для самостоятельного решения
1. Построить отрезок прямой АВ // π1, равный 35 мм и наклонённый к π2 под углом 25° (Рисунок 2.17).
Рисунок 2.172. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π2 и π1.
3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π1 и 45° — к плоскости проекций π2.
4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π2/π1 (Рисунок 2.18).
Рисунок 2.18
2.4. Следы прямой линии
Следом прямой линии называется точка пересечения прямой с плоскостью проекций.
В системе двух плоскостей проекций p1 и p2 прямая в общем случае имеет два следа:
- 1. Горизонтальный Н (Н1, Н2);
- 2. Фронтальный F (F1, F2).
Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.11, а).
Установим правило нахождения следов прямой.
Для нахождения горизонтального следа прямой необходимо:
1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку НХ º Н2)
2) восстановить перпендикуляр в точке НХ к оси Х (провести линию связи перпендикулярную к оси Х);
3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром;
4) полученная точка пересечения и будет горизонтальным следом прямой а Н º Н1 (рис. 2.11, б).
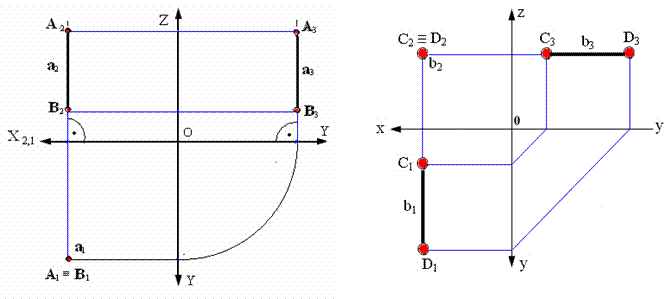
Рис. 2.8. Прямая, перпендикулярная Рис. 2.9. Прямая, перпендикулярная
горизонтальной плоскости проекций фронтальной плоскости проекций
Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций
а б
Рис. 2.11. Изображение следов прямой линии:
а — в пространстве; б — на эпюре
Для нахождения фронтального следа прямой необходимо:
1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка FXº F1);
2) восстановить перпендикуляр в точке FX к оси Х;
3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром;
4) полученная точка пересечения Fº F2 будет фронтальным следом прямой а (рис. 2.11, б).
В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом октанте.
Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.
Начертательная геометрия это наука изучающая методы изображения реальных пространственных объектив – зданий, сооружений, деталей машин – состоящих из совокупности точек, линий, поверхностей и методы решения геометрических задач по данным изображениям.
Содержание:
- Предмет, задачи и метод начертательной геометрии
- Изображение прямой линии в ортогональных проекциях
- Прямые частного положения
- Следы прямой
- Взаимное положение прямых. Понятие конкурирующих точек
- Задание плоскости в ортогональных проекциях. Следы плоскости
- Прямые и точки в плоскости
- Главные линии плоскости
- Плоскости частного положения
- Изображение простейших геометрических поверхностей
- Взаимное положение прямой и плоскости, двух плоскостей. Проекции прямого угла
- Взаимное положение прямой и плоскости, двух плоскостей
- Перпендикулярность прямой и плоскости
- Перпендикулярности двух плоскостей
- Параллельность прямой и плоскости
- Пересечение двух плоскостей
- Пересечение многогранника проецирующей плоскостью
- Решение метрических задач
- Решение метрических задач методами преобразования проекций
- Способ плоско-параллельного перемещения
- Способ замены плоскостей проекций
- Тени в ортогональных проекциях
- Тень прямой общего положения
- Тени прямых частного положения
- Тени плоских фигур
- Тень окружности
- Тени поверхностей. Понятие собственной и падающей тени
- Тени в ортогональных проекциях
- Тени схематизированного здания, состоящего из призматических форм
- Тени фрагментов зданий
- Тень падающая от трубы на крышу
- Тень от барьера на ступенях лестницы
- Аксонометрия
- Стандартные виды аксонометрических проекций
- Построение аксонометрического изображения
- Задача 1.
- Тени в аксонометрии
- Задача 2.
- Задача 3.
- Классификация, образование и изображение кривых поверхностей
- Линейчатые поверхности
- Развертываемые линейчатые поверхности
- Неразвертываемые линейчатые поверхности
- Поверхности вращения
- Линейчатые поверхности вращения
- Нелинейчатые поверхности вращения (криволинейные)
- Поверхности переноса
- Пересечения поверхностей с прямой и плоскостью
- Пересечение кривых поверхностей плоскостью
- Пересечение прямой линии с поверхностью
- Примеры построения пересечение прямой с различными поверхностями
- Пример 1.
- Пример 2.
- Пример 3.
- Взаимное пересечение поверхностей
- Пересечение двух многогранников
- Пересечение гранной и кривой поверхности
- Пересечение двух кривых поверхностей
- Пересечение поверхностей вращения. Метод вспомогательных секущих сфер
- Максимальный радиус сферы
- Теорема Монжа
- Развертка поверхностей
- Развертка поверхностей
- Построение разверток развертываемых поверхностей
- Построение приближенной развертки неразвертываемых поверхностей
- Решение задач с примерами посмотроения по начертательной геометрии
- Задача 1.
- Задача 2.
- Тени основных геометрических форм – цилиндра и конуса
- Тени поверхностей вращения. Способ касательных конусов и цилиндров
- Построение контура собственной тени на торе осуществляется по восьми точкам.
- Построение падающих теней на комбинированных поверхностях вращения
- Метод биссекторного экрана
- Тень от квадратной плиты на колонну
- Построение падающих теней на архитектурных деталях
- Проекции с числовыми отметками. Область применения и сущность способа проецирования
- Проекции точек
- Проекции прямых. Определение натуральной величины и следа отрезка прямой
- Интервал и уклон прямой
- Взаимное положение двух прямых
- Проекции плоскостей. Задание плоскостей. Взаимное положение двух плоскостей
- Взаимное положение двух плоскостей
- Проекции поверхностей. Задание поверхностей. Пересечение поверхности плоскостью
- Пересечение поверхности плоскостью
- Профиль поверхности
- Построение границ земельных работ. Построение сечения вертикальной плоскостью рельефа с планировкой профиля
Начерта́тельная геоме́трия — инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов.
Начерта́тельная геоме́трия — наука, изучающая пространственные фигуры при помощи их проецирования (проложения) перпендикулярами на некоторые три плоскости, которые рассматриваются затем совмещёнными одна с другой. wikipedia.org
Предмет, задачи и метод начертательной геометрии
Вместе с этим решается и очень существенная задача – развитие пространственного воображения. Метод начертательной геометрии – метод проекций. Так как любой предмет можно рассматривать как совокупность множества точек, то сущность метода проецирования рассмотрим на примере точки. Прямоугольные проекции и координаты точек. Эпюр (чертеж) Г.Монжа Изображение проекций точек при различном их положении в пространстве Для построения проекции точки, зададим плоскость П1 – плоскость проекций и точку А – оригинал (любая точка пространства). Проведем через точку А проецирующий луч (АА1) до пересечения с плоскостью П1 в точке А1. Точка А1 и является проекцией точки А на плоскость П1 (рисунок 1.1). Если проецирующий луч АА1 перпендикулярен плоскости проекций П1, то проецирование называется прямоугольным, а точка А1 называется прямоугольной или ортогональной проекцией точки А.

На рисунке 1.1 видно, что одна проекция точки не определяет ее положения в пространстве, так как в точку А1 проецируются все точки проецирующего луча АА1. Для того чтобы положение точки в пространстве было определено, возьмем три взаимно перпендикулярные плоскости П1 , П2 , П3 (рисунок 1.2).

П1 – горизонтальная плоскость проекции; П2 – фронтальная плоскость проекций; П3 – профильная плоскость проекций. Плоскости проекций пересекаясь дают оси проекций – x12; y13; z23. Спроецируем ортогонально точку А на эти плоскости проекций. Получим соответственно: А1 — горизонтальная проекция точки А; А2 — фронтальная проекция точки А; А3 – профильная проекция точки А.
В трехмерном пространстве положение точки определяется тремя (декартовыми) координатами А (xА; yА; zА). Совместив декартовую систему координат с осями проекций, получим начало координат – точку О. Ось ОХ совместим с осью x12, ось ОY – с осью y13, ось ОZ – с осью z23. Горизонтальная плоскость проекции П1 совместится с координатной плоскостью OXY, П2 ≡ XOZ, П3 ≡ YOZ. Тогда точка А и ее проекции определяться координатами:
По чертежу видно, что две проекции точки полностью определяют положение точки в пространстве, так как содержат все три координаты. Для перехода от пространственного чертежа к плоскому, плоскость П1 повернем вокруг оси х12 до совмещения с плоскостью П2. При этом звенья ломаной АХА1 и АХА2 образуют прямую А1А2 перпендикулярную оси x12. Линия А1А2 называется линией связи проекций А1 и А2.
Плоский чертеж состоящий из горизонтальной А1 и фронтальной А2 проекций точки А, расположенных на линии связи А1А2 перпендикулярной оси x12 называется эпюром (ортогональным чертежом) и носит имя основателя начертательной геометрии Г.Монжа (рисунок 1.3).
Иногда возникает необходимость подвум проекциям построить третью. На рисунке 1.4 показано построение профильной проекции А3 по двум заданным горизонтальной А1 и фронтальной А2 с помощью постоянной линии чертежа k123.

Плоскости П1 и П2 делят все пространство на четыре четверти, отмеченные на рисунке 1.5 римскими цифрами I, II, III и IV. Точки могут находиться в любой четверти, лежать на плоскостях проекций или на осях.
Возможно, вас также заинтересует эта ссылка:
Необходимо освоить две задачи:
Первая – по паре проекций точек находящихся на плоскостях проекций определить положение точки в пространстве.
Вторая – по положению точки в пространстве изобразить ее парой проекций.
На рисунке 1.5 точка А находится в I четверти. Все ее координаты имеют положительное значение – фронтальная проекция находится над осью x12, горизонтальная – под осью.
Точка В, находится во II четверти. Ее координата yВ – отрицательна – обе проекции находится над осью. У точки С, находящейся в III четверти отрицательными будут координаты yС и zС.
Фронтальная проекция находится под осью x12, горизонтальная – над осью. У точки D, находящейся в IV четверти, отрицательная координата zD – обе проекции находится под осью x12. У точки Е, находящейся на плоскости П2, координата yЕ = 0, откуда следует, что ее горизонтальная проекция Е1 лежит на оси x12 (если точка лежит на какой-то плоскости проекций, то одна из ее проекций обязательно лежит на оси). Точка К лежит на оси x12, координаты xК и yК равны нулю, а проекции К1 и К2 совпадают (К1 ≡ К2).
Возможно, вас также заинтересует эта ссылка:
Изображение прямой линии в ортогональных проекциях
Положение прямой линии в пространстве определяется двумя ее точками. А из свойств параллельного проецирования известно, что проекции прямых авляются прямыми линиями. Поэтому, для построения прямой (m) достаточно построить проекции двух её точек (А и В) и одноименные проекции точек соединить прямыми (рисунок 1.6). Отсюда можно сделать вывод если точка лежит на прямой, то ее проекции лежат на соответствующих проекциях прямой. Если эта точка делит отрезок АВ в каком либо отношении, то в том же отношении проекции точки делят проекции отрезка.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения. На чертеже ни одна из проекций такой прямой не параллельна оси (рисунок 1.6). Длина ортогональной проекции отрезка прямой общего положения всегда меньше длины самого отрезка.
Возможно, вас также заинтересует эта ссылка:
Прямые частного положения
Прямые параллельные или перпендикулярные плоскостям проекций называются прямыми частного положения.
Различают два вида прямых частного положения:
- — прямые уровня – прямые параллельные плоскостям проекций;
- — проецирующие прямые – прямые перпендикулярные плоскостям проекций.
Прямые уровня (рисунок 1.7).
- а) Горизонтальная прямая – прямая параллельная горизонтальной плоскости П1;
- б) Фронтальная прямая – прямая параллельная фронтальной плоскости П2;
- в) Профильная прямая – прямая параллельная профильной плоскости П3.
На плоскость проекций, которой прямая уровня параллельна, она проецируется в натуральную величину. Проецирующие прямые (рисунок 1.8).
а) горизонтально-проецирующая прямая – прямая перпендикулярная горизонтальной плоскости проекций П1; б) фронтально-проецирующая прямая – прямая перпендикулярная фронтальной плоскости проекций П2;
в) профильно-проецирующая прямая – прямая перпендикулярная профильной плоскости проекций П3.
Возможно, вас также заинтересует эта ссылка:
Следы прямой
Следами прямой АB называются точки пересечения ее с плоскостями проекций (рисунок 1.9). Точка Н – горизонтальный след прямой АВ. Точка F – фронтальный след прямой АВ. Так как следы прямой это точки лежащие на плоскостях проекций, то одна из проекций следа находится на оси x12.
Поэтому для определения на эпюре горизонтального следа прямой (рисунок 1.10) необходимо продолжить фронтальную проекцию прямой до пересечения с осью Х12 и отметить точку Н2 . Из этой точки провести линию проекционной связи до пересечения с горизонтальной проекцией прямой. Получим точку Н1 . Точки Н1 и Н2 определяют горизонтальный след прямой. Аналогично определяется фронтальный след прямой F (F1, F2).
Возможно, вас также заинтересует эта ссылка:
Взаимное положение прямых. Понятие конкурирующих точек
Две прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Их положение в пространстве устанавливается взаимным расположением одноименных проекций.
Если в пространстве две прямые параллельны, то их одноименные проекции также параллельны (рисунок 1.11а).
Параллельность профильных прямых не всегда очевидна. Хотя их горизонтальные и фронтальные проекции параллельны, сами прямые могут быть не параллельны. Для определения их взаимного положения можно построить профильную проекцию. (рисунок 1.11б).
Пересекающиеся прямые – это прямые, имеющие общую точку, следовательно, если прямые в пространстве пересекаются, то точки пересечения их одноименных проекций лежат на одной линии проекционной связи (рисунок 1.12). Скрещивающиеся прямые не имеют общей точки, поэтому точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рисунок 1.13).
Пары точек, у которых какие-либо одноименные проекции совпали, т.е. они лежат на одном проецирующем луче, называются конкурирующими (одна из них «закрывает» другую). Точки M и N – горизонтально-конкурирующие, точки K и L – фронтально-конкурирующие. Из двух конкурирующих точек видна та, у которой больше одна из координат (две другие совпадают).
Например, координата Z у точки М больше, чем у точки N , следовательно, прямая а в этом месте расположена выше прямой в и будет видима при взгляде сверху, т.е. на горизонтальной проекции. Аналогично, у точки L координата Y больше, чем у точки К, следовательно, в этом месте прямая а расположена ближе к зрителю и будет видима на фронтальной проекции. Определение видимости конкурирующих точек позволит нам в дальнейшем определять видимость прямой относительно плоскости.
Возможно, вас также заинтересует эта ссылка:
Задание плоскости в ортогональных проекциях. Следы плоскости
Положение плоскости в пространстве определяется тремя не лежащими на одной прямой точками, прямой и не лежащей на ней точкой, двумя параллельными или пересекающимися прямыми, плоской фигурой. Примеры задания плоскости даны на рисунке 1.14.
Все изображенные на рисунке 1.14 плоскости являются плоскостями общего положения. Плоскостью общего положения называется плоскость не перпендикулярная ни одной из плоскостей проекций. Плоскость также можно задать следами. Следами плоскости называются линии пересечения плоскости с плоскостями проекций (рисунок 1.15).
Т.к. следы плоскости – прямые линии, то для их построения достаточно найти две точки принадлежащие им. Если прямые лежат в плоскости, то их следы лежат на следах плоскости. Следовательно для построения следов плоскости достаточно построить следы двух прямых лежащих в этой плоскости (рисунок Фронтальным следом плоскости ά называется линия ее пересечения с фронтальной плоскостью проекций П2 . Обозначается фронтальный след буквой f 1ά. Фронтальная проекция этого следа f2ά совпадает с самим следом, а горизонтальная f1ά лежит на оси х12 .
Горизонтальный след плоскости – линия пересечения с горизонтальной плоскостью проекций П1 . Аналогично горизонтальный след плоскости hά совпадает со своей горизонтальной проекцией h1ά, а его фронтальная проекция лежит на оси х12 . Они имеют общую точку на оси х – точку схода следов.
Возможно, вас также заинтересует эта ссылка:
Прямые и точки в плоскости
Точка лежит в плоскости, если она лежит на прямой принадлежащей этой плоскости. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
На рисунке 1.17а. фронтальная проекция точки К выбрана произвольно в плоскости ά (∆АВС). Для построения горизонтальной проекции через К2 проведена произвольная прямая проходящая через точки 12 и А2 принадлежащие плоскости ά. Построив горизонтальные проекции точки 11 проведем горизонтальную проекцию прямой принадлежащей плоскости ά и по линии связи найдем на ней горизонтальную проекцию К1. Аналогично построена точка К принадлежащая плоскости 

Главные линии плоскости
Главными линиями плоскости называются ее горизонтали, фронтали и линии наибольшего ската. Горизонтали плоскости – это прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций – h (h1, h2) . Все горизонтали плоскости параллельны между собой и параллельны горизонтальному следу плоскости. Фронтальные проекции горизонталей параллельны оси Х12 (рисунок 1.18).
Фронтали плоскости – это прямые, принадлежащие плоскости и параллельны фронтальной плоскости проекций – f (f1, f2). Все фронтали плоскости параллельны между собой и параллельны фронтальному следу плоскости. Горизонтальные проекции фронталей параллельны оси Х12 (рисунок 1.19).
Плоскости частного положения
Плоскости как и прямые относительно плоскостей проекций могут занимать частное положение. Плоскости, перпендикулярные или параллельные одной из плоскостей проекций, называются плоскостями частного положения.
Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими (рисунок 1.20).
а) горизонтально проецирующая плоскость ά (∆АВС); б) фронтально проецирующая плоскость δ (∆ DEF); в) профильно проецирующая плоскость θ (∆ KLM). Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня (рисунок 1.21).
а) горизонтальная плоскость уровня β, заданная треугольником АВС; б) фронтальная плоскость уровня ε заданная пересекающимися прямыми mn; в) профильная плоскость уровня γ, заданная треугольником KLM.
Изображение простейших геометрических поверхностей
Многогранники представляют собой совокупность отрезков прямых и плоских фигур. На рисунке 1.22 изображены: а) трехгранная прямая призма. б) трехгранная пирамида.
На рисунке 1.23 изображены простейшие кривые поверхности: а) прямой круговой цилиндр. б) прямой круговой конус.
Взаимное положение прямой и плоскости, двух плоскостей. Проекции прямого угла
Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рисунок 2.1).
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рисунок 2.2).
Взаимное положение прямой и плоскости, двух плоскостей
Прямая относительно плоскости может занимать следующие положения: — лежать в плоскости (что рассматривалось ранее); — быть ей параллельна; — пересекать плоскость; — быть перпендикулярной плоскости (т.е. пересекать под прямым углом).
Две плоскости могут быть — взаимно параллельными, — пересекающимися; — взаимно перпендикулярными.
Перпендикулярность прямой и плоскости
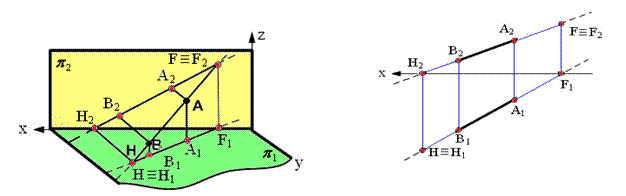
Условие перпендикулярности прямой и плоскости: Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости. Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости. На рисунке 2.3 через точку А(А1;А2) проведена прямая, перпендикулярная плоскости ά(∆ВСD). В плоскости ά проведены горизонталь h (h1,h2) и фронталь f (f1,f2) , затем через А1 проведена горизонтальная проекция перпендикуляра p1 под прямым углом к h1, а через точку А2 фронтальная проекция перпендикуляра p2 под прямым углом к f2. Прямые p1 и p2 есть проекции искомого перпендикуляра р.
Перпендикулярности двух плоскостей
Две плоскости взаимно перпендикулярны, если одна из них содержит перпендикуляр к другой. Пусть через данную прямую m необходимо провести плоскость, перпендикулярную плоскости ά заданной треугольником ∆ВСD (рисунок 2.4). Для решения задачи достаточно на прямой m взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости ά. Пересекающиеся прямые m и р образуют плоскость β, которая содержит прямую р, перпендикулярную плоскости ά, следовательно, плоскости β и ά взаимно перпендикулярны.
Параллельность прямой и плоскости
Условие параллельности прямой и плоскости: Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости. Рассмотрим пример решения задачи на параллельности прямой и плоскости.
Задача: построить фронтальную проекцию прямой n, проходящей через точку А и параллельной плоскости ά (∆KLM). Для решения задачи: Проводим горизонтальную проекцию прямой l1 в плоскости
Строим фронтальную проекцию l2. Через точку А2 проводим n2 параллельную l2. Таким образом получим:
Параллельность двух плоскостей Условие параллельности двух плоскостей: две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Изображенные на рисунке 2.6 плоскости 
Пересечение прямой и плоскости Задача на нахождение точки пересечения прямой линии с плоскостью является первой основной позиционной задачей курса начертатель- ной геометрии.
Алгоритм решения задачи (рисунок 2.7):
- 1. Прямую l заключаем во вспомогательную плоскость σ (удобнее всего в проецирующую);
- 2. Находим линию пересечения (1-2) вспомогательной плоскости с заданной ά;
- 3. Отмечаем точку пересечения К найденной линии пересечения (1-2) с заданной прямой l ;
- 4. Определяем видимость прямой l ;
На основании данного алгоритма определим точку пересечения прямой l с плоскостью ά(∆ВСD) (рисунок 2.8) и с плоскостью 
Пересечение двух плоскостей
Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям. Рассмотрим несколько случаев построения линии пересечения двух плоскостей. 1-й случай – пластины непрозрачные заданы с нахлёстом (рисунок 2.10). Задача сводится к нахождению точек пере-сечения прямых m и n с плоскостью
Соединив точки пересечения К и М получим линию пересечения плоскости 

2-й случай – плоскости заданы на некотором расстоянии, что не дает возможность определить линии пересечения двух плоскостей первым способом. В этом случае используется метод плоскостей-посредников.
Алгоритм решения задачи (рисунок 2.11): 1. Заданные плоскости ά и β рассекаем вспомогательной плоскостью посредником ε; 2. Определяем линию пересечения 1-2 плоскости ά с плоскостью σ и линию пересечения 3-4 плоскости β с плоскостью ε; 3. Определяем точку К – точку пересечения линий 1-2 и 3-4, принадлежащую плоскостям ά и β; 4. Аналогичным образом находим точку L с помощью плоскости посредника σ; 5. Соединив две точки К и М, получим линию пересечения двух плоскостей ά и β. Видимость при этом не определяется.
3-й случай – пересекающиеся плоскости общего положения заданы следами пересекающимися в пределах чертежа (рисунок 2.12). В данном случае в качестве плоскостейпосредников могут быть использованы плоскость проекций П1 и П2.
Пересечение многогранника проецирующей плоскостью
Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью σ (рисунок 2.13)
Решение метрических задач
Метрические задачи К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур. Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольного треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым – разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, на которой ведется построение. На рисунке 3.1 построение натуральной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция А1В1, второй равен разности координат z точек А и В. Угол α между н.в. (натуральной величиной) и катетом проекций равен углу наклона отрезка АВ к плоскости проекций П1. Если необходимо определить угол наклона отрезка АВ к плоскости П2, то построение прямоугольного треугольника ведется на фронтальной проекции.
Решение метрических задач методами преобразования проекций
Положения геометрических образов, при которых расстояния и углы не искажаются на плоскостях проекций Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций. Приведем некоторые из них. 1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2). β– угол наклона к плоскости П2
2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)
Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи. Для такого перехода и служат способы преобразования проекций. Существует несколько способов преобразования проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.
Четыре основных задачи преобразования проекций. Этими способами решаются четыре основные задачи:
- Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
- Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
- Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
- Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)
Решение 1-ой и 2-ой задачи преобразования проекций методом вращения, плоскопараллельного перемещения и замены плоскостей проекций Способ вращения Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая – по прямой параллельной оси проекций. На рисунке 3.10 вокруг оси 



Способ плоско-параллельного перемещения
Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом 





Способ замены плоскостей проекций
Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси. На рисунке 3.12 произведена первая замена – плоскость П2 заменена на новую фронтальную плоскость П4 параллельную прямой АВ. При этом новая ось х14 проводится параллельно проекции А1В1. Линии связи проводятся перпендикулярно оси х14 и на них от х14 откладываются координаты z точек А и В (1 задача).
Далее прямую АВ преобразуем в проецирующую.
Для этого проводим новую ось х54 перпендикулярно проекции А4В4. Т.к. А1В1 параллельна оси х14, расстояние до проекций А5 и В5 будет одинаковое и прямая спроецируется в точку
Решение 3-ой и 4-ой задачи преобразования проекций методом плоскопараллельного перемещения и замены плоскостей проекций Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций. Способ плоскопараллельного перемещения
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь h(h1,h2). Далее h1 располагаем перпендикулярно оси х12. Откладываем на ней отрезок А1L1 и циркулем строим треугольник А1‘В1‘С1‘ равный по величине А1В1С1. На фронтальной проекции треугольник спроецируется в линию (3 задача).
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию А2‘В2‘С2‘ расположить параллельно оси х12, при этом на горизонтальной проекции треугольник спроецируется в натуральную величину (4-я задача) Способ замены плоскостей проекций
При решении задачи методом замены (рисунок 3.14) новую ось х14 проводим перпендикулярно горизонтали h1, тогда на новую фронтальную плоскость П4, треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось х54 провести параллельно плоскости А4В4С4. На новую плоскость П5 треугольник спроецируется в натуральную величину. Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.
Тени в ортогональных проекциях
Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте. Для придания объемности и наглядности ортогональным чертежам зданий и сооружений выполняется построение теней.
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проекции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок 4.1).
Тенью точки на плоскости является точка пересечения светового луча, проведенного через данную точку, с плоскостью. Если тень точки падает на плоскость проекций, то для её построения используется способ следа луча. Т.е. через проекции точки проводим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость – А21.
Кроме этого может быть использован метод выноса. Особенно важен этот метод при построении теней на фасадах зданий. Вынос – это расстояние от точки до фронтальной плоскости или плоскости фасада, если тень строится на фасаде. На рисунке 4.3 y – это вынос.
Тень прямой общего положения
Тенью прямой на плоскость является линия пересечения лучевой плоскости, проведенной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является прямая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек. Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежащую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рисунок 4.4). Для ее нахождения, необходимо строить мнимую тень (В1t), т.е. определить горизонтальный след луча проведенного через точку В.
Тени прямых частного положения
Тени прямых частного положения на плоскостях проекций располагаются всегда определенно и часто служат «опорными» при построении теней различных деталей, включающих такие прямые. Рассмотрим эти случаи. Тень от прямой, на плоскость ей параллельную, располагается параллельно прямой, т.е. параллельно проекции прямой на эту плоскость и равна ей по величине (рисунок 4.5).

Тень от прямой на плоскость, ей перпендикулярную, располагается по проекции луча, т.е. под углом 450 (рисунок 4.6). Если точка лежит на плоскости, то тень совпадает с самой точкой и такая точка называется сама себе тень. В нашем случае это точка В.
Тень на фронтальной плоскости от горизонтальной прямой, расположенной под углом 450 к ней, вертикальна (рисунок 4.7)
Тени плоских фигур
Чтобы построить тень от плоской фигуры, например треугольника, падающую на плоскости проекций достаточно построить тени от вершин (рисунок 4.8). Т.к. тень падает на две плоскости необходимо определять линию излома тени, а, следовательно, построить мнимую тень от вершины В.
Тень от плоской фигуры, на плоскость ей параллельную, изображается фигурой равной ей по величине. Поэтому достаточно построить тень от одной точки и вычертить тень в виде той же фигуры. Так, для построения тени от окружности (рисунок 4.9) достаточно определить тень от центра и вычертить тень в виде такой же окружности.
Тень окружности
Тень окружности обычно строится по восьми точкам. Из них четыре – точки касания окружности к сторонам описанного около окружности квадрата, и четыре – точки пересечения окружности с диагоналями этого квадрата (рисунок 4.10). Тень от квадрата – параллелограмм, диагональ которого BD вертикальна. Точки 1,3,5,7 точки касания к параллелограмму. Точки, лежащие на диагоналях, делят радиус в отношении 0,707. Они могут быть получены без горизонтальной проекции. Для этого на радиусе строим равнобедренный треугольник с углами при основании 450 и дугой окружности определяем положение точек 2,8 и 4,6. Проведем из них лучи до пересечения с диагоналями. Полученные восемь точек соединяем плавной линией, которая будет эллипсом. Практически тень окружности по восьми точкам строят без горизонтальной проекции, которая здесь приведена только для пояснения.
Тени поверхностей. Понятие собственной и падающей тени
Для поверхностей характерны следующие понятия: Собственная тень (ф) – неосвещенная часть поверхности (предмета) рисунок 4.11. Контур собственной тени (m) – граница между освещенной и неосвещенной частью поверхности (предмета). Падающая тень (фt) – тень падающая от одного предмета на другой, или на плоскость. Контур падающей тени (mt) – контур, ограничивающий падающую тень.
Фактически контур падающей тени – это тень от контура собственной тени. Поэтому, обычно, сначала определяют контур собственной тени, а затем уже строят падающую.
Рассмотрим примеры построения теней трехгранной призмы (рисунок 4.12) и прямого кругового конуса (рисунок 4.13). Проведя лучи на горизонтальной проекции касательные к крайним ребрам призмы, определяем контур собственной тени. Она является пространственной ломаной 1,2,3,4,5. Т.к. точки 1 и 5 лежат на плоскости П1 они являются тенями. Поэтому для построения контура падающей тени, достаточно построить тени точек 2,3,4.
Проанализировав построенную тень, мы видим, что тени от ребер 1,2 и 5,4 совпадают с направлением лучей, т.к. они перпендикулярны к плоскости П1. А тени от ребер 2,3 и 3,4 параллельны этим ребрам и равны по величине, т.к. они параллельны плоскости. Учитывая это, построение контуров падающих теней многогранников может быть значительно упрощено.
Для конуса логично сначала построить падающую тень, а затем собственную (рисунок 4.13). Для построения падающей тени, строим тень от вершины конуса (S1t). Из полученной точки проводим касательные к окружности основания. Эти касательные образуют, контур падающей тени (она является тенями от образующих конуса). Поэтому, соединив точки А и В с вершиной конуса S получим границы собственной тени конуса. А затем уже строим фронтальную проекцию контура собственной тени. Аналогично строятся тени пирамидальных поверхностей.
Тени в ортогональных проекциях
Способ лучевых сечений: для построения тени точки М на плоскость α (∆АВС) (рисунок 5.1), проведем через точку М луч и определим точку пересечения луча с плоскостью α. Задача сводится к нахождению точки пересечения прямой (луча) с плоскостью. Через луч проводим горизонтально-проецирующую лучевую плоскость σ. Строим линию пересечения 1-2 плоскости σ и заданной плоскости α. Определяем точку пересечения луча с полученной линией пересечения. Эта точка Mt (M1t, M2t) и будет тенью точки М на плоскости α. Способ обратного луча Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2). Тень от проецирующей прямой SА строится, аналогично предыдущему примеру (рисунок 5.1), методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной – идет по лучевому сечению. Тень от точки S на пластину ESDF не падает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость П1. Для чего строим тень от точки S падающую на П1 и полученную точку S1t, соединяем с точкой В1, т.к. точка В лежит на плоскости П1.
Далее строим тень от пластины ESDF на плоскость П1, для чего строим тени точек С и D и соединяем их с точками Е1 и F1, лежащими на плоскости П1. Полученные тени пересекаются B1S1t и C1tD1t в точке 41t . Из точки пересечения теней проводим обратный луч под углом 450 на прямую C1D1. По вертикальной линии связи находим фронтальную проекцию этой точки. Обратите внимание, что точки 1 и 3, являются точками излома теней падающих на горизонтальную плоскость и на наклонную плоскость α.
Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).
Тени схематизированного здания, состоящего из призматических форм
Здание состоит из двух призматических форм (рисунок 5.4). Обычно сначала строятся тени от двух этих форм падающие на плоскость П1 (т.е. на землю).
Для построения падающих теней определяем контур собственной тени каждой из призм (рисунок 5.4б). Высотная часть здания представляет прямую призму, контур собственной тени которой 1,2,3,4,5, причем точки 1 и 5 лежат на плоскости, поэтому тени строим от трех точек 2,3,4. Контур собственной тени второй призмы – 6,7,8,9. Точка 6 лежит на П1, поэтому строим тени от точек 7,8,9 (рисунок 5.4а). Т.к. две полученные тени пересекаются, определяем общий контур тени. Видим, что точки 2t и 9t являются мнимыми. Поэтому тень от точки 2 очевидно упадет на пристройку, а точка 9 будет в тени и фактически тень не отбросит.
Для построения тени падающей от высотной части здания на пристройку используем метод лучевых сечений. Заключаем луч, проведенный через точку 2 в плоскость δ. Строим сечение призмы – пристройки плоскостью δ. Луч, проведенный из точки 2, пересекает линию сечения в точке 2t(21t, 22t). Т.е. тень падает на наклонную плоскость. Тень от вертикальной прямой 1,2, на горизонтальной проекции совпадает с направлением луча, на фронтальной идет по сечению. Тень от прямой 2,3 на фронтальной проекции совпадает с направлением луча, на горизонтальной идет по сечению.
При построении теней зданий очень важно помнить положение теней прямых частного положения, это значительно упрощает процесс построения.
Тени фрагментов зданий
К фрагментам зданий относятся ниши, козырьки, трубы, лестницы и т.п. Рассмотрим построение теней некоторых из них.
Две изображенные ниши относятся к нишам с плоским днищем, т.е. контур ниши отбрасывает тень на плоскость днища ниши параллельной контуру. Поэтому тени в нишах с плоским днищем повторяют контур ниши. Для построения таких теней достаточно построить тень одной точки, как показано на примере (рисунок 5.5). Если дан лишь фасад здания, необходимо знать глубину ниши и тень построить методом выноса.
В цилиндрической нише (рисунок 5.6) сначала определяем собственную тень. Для чего удобнее провести нормаль (т.е. радиус под углом 450). Получим контурную образующую собственной тени. Падающую тень будет отбрасывать две прямые кромки ниши – вертикальная и продольная. Тень от вертикальной прямой падает на ось ниши. Тень от продольной прямой будет представлять четверть окружности.
Из этого чертежа можно сделать вывод: тень от продольной прямой на фасаде с вертикальными образующими зеркально повторяется план. Этот вывод позволяет построить тень на фасаде от свеса крыши, построив тень одной точки (тень точки 1 на рисунке 5.7). Остальной контур тени зеркально повторяет план.
Тень падающая от трубы на крышу
На рисунке 5.8 дана труба призматической формы. Тень строится методом лучевых сечений. Если отсутствует план здания, то нужно иметь ввиду, что тени от вертикальных прямых на фасаде имеют угол наклона равный углу наклона ската крыши
Тень от барьера на ступенях лестницы
Контур собственной тени барьера (рисунок 5.9), отбрасывающий тень на ступени представляет собой две прямые – горизонтально- проецирующую 1,2 и фронтально-проецирующую 2,3. Из точек 1 и 3 начинается тень. Следовательно, необходимо построить тень точки 2. Для построения падающей тени используется метод лучевых секущих плоскостей.
Аксонометрия
Ортогональные проекции, обладая рядом достоинств, имеют также и определенные недостатки, главным из которых является отсутствие наглядности полученных изображений.
Более наглядными, достаточно простыми по начертанию и позволяющими выполнять измерения, являются аксонометрические проекции. Аксонометрические проекции, также как и ортогональные, строятся по принципу параллельного проецирования, но на одну плоскость. Аксонометрией называется метод отображения пространства на плоскость вместе с системой координат и изображение, полученное этими методом.
На рисунке 6.1, показан принцип получения аксонометрии, точки А. Точка А связана с системой прямоугольных координат OXYZ. На осях отложены единичные отрезки 






Основной теоремой аксонометрии является теорема «Польке-Шварца»: всякий невырождающийся полный четырехугольник можно считать параллельной проекцией тетраэдра наперед заданной формы. С доказательством теоремы можно познакомиться в учебнике (1, 2). Эта теорема позволяет установить зависимость между углом проецирования и коэффициентами искажения. Типы аксонометрических проекций В зависимости от угла проецирования 

По показателям искажения аксонометрия делится на три типа. Если все показатели искажения равны, т.е. 


Однако, при построении аксонометрии натуральные коэффициенты заменяют приведенными, т.е. выраженными целыми числами, что дает увеличение аксонометрического изображения, но на наглядность не влияет.
Стандартные виды аксонометрических проекций
В таблице 6.1 приведены наиболее применяемые стандартные виды аксонометрических проекций.
Построение аксонометрического изображения
Задача 1.
Даны ортогональные проекции схематизированного здания (рисунок 6.2). Построить прямоугольную изометрию.
Прежде всего, выбираем положение ортогональных осей для получения более наглядного изображения (рисунок 6.2). Строим оси аксонометрических проекций под углом 1200 (рисунок 6.3). Построение аксонометрии начинаем с плана, т.е. со вторичной проекции. Так как коэффициенты искажения равны 1, то измеряем, координаты X и Y каждой точки плана и откладываем их на аксонометрических осях. Прямые параллельные в ортогональных проекциях будут оставаться параллельными и в аксонометрии. После построения плана откладываем все высоты параллельно оси Z, т.е. вертикально. Соединив полученные точки с учетом видимости, получим аксонометрию здания.
Тени в аксонометрии
Для придания более наглядного и реалистического изображения архитектурным объектам строят тени. Для построения теней задается положение луча света и его вторичной проекции. В принципе направление лучей выбирается произвольным.
На рисунке 6.4 показано построение тени точки А. Через горизонтальную проекцию А1 проводим луч параллельный вторичной проекции луча ℓ1. Через саму точку А – луч параллельный лучу ℓ. В пересечении лучей получаем At – тень точки А падающую на горизонтальную плоскость. Так как аксонометрия является параллельной проекцией, как и ортогональные проекции, то все закономерности, отмеченные в разделе тени в ортогональных проекциях справедливы и для аксонометрии.
Например: Тень от прямой перпендикулярной плоскости совпадает с направлением проекции луча на эту плоскость. Тень от прямой параллельной плоскости ей параллельна и равна по величине. Тень от прямой на плоскость, которую она пересекает, проходит через эту точку пересечения и т.п.
Задача 2.
Построим тени аксонометрии схематизировано здания (рисунок 6.5). Принимаем направление лучей ℓ и ℓ1 под углом 450. Определяем контур собственной тени при данном освещении. Для высотной части, как и в ортогональных проекциях, контур собственной тени 1,2,3,4,5. Для пристройки – 6,7,8,9. Сначала строим тени падающие на горизонтальную плоскость, т.е. на землю. Затем строим тень, падающую от высотной части на пристройку, используя метод лучевых сечений. Сечение представляет трапецию. Тень от точки 2 падает на наклонную плоскость. По построению мы видим, что тень от ребра 1,2 падает на землю, затем на стену вертикальную и на крышу, т.е. идет по сечению. Далее, чтобы построить тень от прямой 2,3 на наклонной плоскости, находим точку пересечения прямой 2,3 с наклонной плоскостью и соединяет 2t с этой точкой. При оформлении чертежа нужно всегда иметь ввиду, что собственная тень всегда светлее падающей.
Задача 3.
Построить тени козырька на плоскость стены (рисунок 6.6)
Козырек призматический. При заданном направлении лучей определяем контур собственной тени 1,2,3,4,5. Точки 1 и 5 лежит на стене, поэтому строим тени точек 2,3,4. Для построения теней используется метод лучевых секущих плоскостей. Через вторичные проекции точек 21,31,41, проводим лучи параллельны ℓ1, через точки 2,3,4 лучи параллельные ℓ. Находим точки пересечения лучей с плоскостью стены. Соединяем полученные точки отрезками прямых. В принципе можно было определить всего лишь одну точку 2t , т.к. прямые 2,3 и 3,4 параллельны плоскости стены и тени от них им параллельны и равны по величине.
Классификация, образование и изображение кривых поверхностей
В архитектурно-строительной практике широко применяются пространственные криволинейные формы, основу которых представляют различные кривые поверхности в их «чистом» геометрическом виде или составленные из нескольких поверхностей. При выборе исходной поверхности архитектор должен в совершенстве знать геометрию этих поверхностей: их основные характеристики, свойства, принципы образования и изображения и др. Классификация поверхностей на протяжении длительного периода была предметом научных исследований, но пока не удалось установить единую систему, так как за ее основу могут быть взяты разные критерии: характер образующей, признак развертывания и прочее.
В данной лекции приводится один из примеров классификации.
Линейчатые поверхности
Поверхность можно представить образованной перемещением какой-либо линии (образующей) по второй линии (направляющей). Если образующая прямая линия, то поверхность называется линейчатой, в противном случае – нелинейчатой или кривой. Линейчатые поверхности делятся на развертываемые и не развертываемые.
Развертываемые линейчатые поверхности
К развертываемым линейчатым поверхностям относятся: цилиндрическая, коничеcкая и поверхность с ребром возврата Цилиндрическая поверхность образуется параллельным перемещением прямой – образующей по какой-либо криволинейной направляющей (рисунок 7.1).
Если направляющая – замкнутая линия, поверхность называется замкнутой. Линия пересечения плоскостью, перпендикулярной образующим, называется нормальным сечением. Все виды нормального сечения уточняют название поверхности: круговая, эллиптическая, параболическая и др.
Коническая поверхность образуется перемещением прямой (образующей), проходящей через одну неподвижную точку – вершину, по криволинейной направляющей (рисунок 7.2). Неподвижная точка делит образующую на две полупрямые и поэтому поверхность образует две полости. Коническая поверхность, как и цилиндрическая, может быть замкнутой. Если направляющая является окружностью, а вершина расположена на перпендикуляре, восста- новленном в центре окружности, то поверхность называется прямым круговым конусом или поверхностью вращения. В противном случае коническая поверхность называется поверхностью второго порядка.
Поверхность с ребром возврата (торс) образуется при перемещении прямой линии в пространстве, которая все время остается касательной к некоторой пространственной кривой линии, называемой ребром возврата (рисунок 7.3). Эта поверхность двупольная, так как точка касания образует две полупрямые.
Неразвертываемые линейчатые поверхности
К неразвертываемым линейчатым поверхностям относятся поверхности с плоскостью параллелизма: цилиндроиды, коноиды и гиперболические параболы и др. Цилиндроид – поверхность, полученная перемещением прямой образующей, которая все время остается параллельной определенной плоскости, называемой плоскостью параллелизма, по двум кривым направляющим (рисунок 7.4).
- l – образующая;
- m, n – направляющие;
- σ – плоскость параллелизма.
Коноид – поверхность, полученная перемещением прямой образующей, которая все время остается параллельной плоскости параллелизма, по двум направляющим, одна из которых прямая, вторая кривая (рисунок 7.5).
- l – образующая;
- m, n – направляющие;
- σ – плоскость параллелизма.
Гиперболический параболоид – поверхность, полученная перемещением прямолинейной образующей, которая все время остается параллельной плоскости параллелизма по двум прямым направляющим (рисунок 7.6)
- l – образующая;
- m, n – направляющие;
- σ – плоскость параллелизма.
Поверхности вращения
Поверхности вращения образуются вращением какой-либо линии вокруг прямой, называемой осью вращения. Поверхности вращения делятся на линейчатые, когда образующая прямая и нелинейчатые, когда образующая кривая. Точки образующей при вращении дают окружности, называемые параллелями, из которых наибольшая – экватор, наименьшая – горловина. Плоскости, проходящие через ось вращения, пересекают поверхность по меридианам. Меридиан, лежащий в плоскости параллельной плоскости проекций называется главным.
Линейчатые поверхности вращения
В зависимости от положения прямой образующей по отношению к оси вращения, линейчатые поверхности делятся на цилиндрическую, коническую и однополостный гиперболоид вращения. Цилиндрическая поверхность образуется вращением вокруг оси прямой – образующей, параллельной оси вращения (рисунок 7.7).
Коническая поверхность образуется вращением вокруг оси прямой – образующей, которая пересекает ось (рисунок 7.8).
Однополостный гиперболоид вращения образуется вращением прямой – образующей, скрещивающейся с осью вращения. На рисунке 7.9 построен однополостный гиперболоид вращения.
Для построения этой поверхности изображено двенадцать положений образующей. Главным меридианом гиперболоида вращения будет гипербола.
Поэтому если гиперболу вращать вокруг оси, также получим гиперболоид вращения.
Нелинейчатые поверхности вращения (криволинейные)
В зависимости от формы образующей и положения оси вращения получается тот или иной вид поверхности: сфера (рисунок 7.10а), тор (рисунок 7.10б), эллипсоид (рисунок 7.10в) и т.п.
Винтовые поверхности образуются винтовым движением прямой или кривой линии. В первом случае поверхность будет линейчатой, во втором – криволинейной. Рассмотрим построение некоторых из них. Винтовой коноид (прямой геликоид) – образуется перемещением прямой – образующей по двум направляющим – оси и винтовой линии. Плоскостью параллелизма в этом случае является плоскостью проекций П1 (рисунок 7.11). Для построения взято двенадцать положений образующей.
Винтовой коноид является основой для построения винтовой лестницы. Развертывающийся геликоид (эвольвентный геликоид) – относится к поверхностям с ребром возврата. Ребром возврата является винтовая линия. Прямая-образующая перемещается по винтовой линии, оставаясь к ней касательной. Известно,
что если соединить следы касательных к винтовой линии на плоскости перпендикулярной оси, получим эвольвенту окружности. Поэтому, определив фронтальное положение этих следов мы можем построить фронтальные проекции касательных к винтовой линии (рисунок 7.12). Наклонный геликоид – образуется перемещением прямой образующей, которая все время остается параллельной направляющему конусу, по двум направляющим – винтовой линии и оси (рисунок 7.13).
Для построения поверхности наклонного геликоида сначала строим направляющий конус с образующими, а затем уже строим ряд образующих поверхностей, параллельных образующим конуса.
Поверхности переноса
Поверхности переноса образуются поступательным переносом одной кривой линии вдоль другой (рисунок 7.14). Каркасные поверхности, задаются некоторым числом дискретных каркасов. Примером, является обшивка автомобилей, самолетов, кораблей и т.п.
Топографическая поверхность представляется рядом горизонталей поверхности (рисунок 7.15).
Пересечения поверхностей с прямой и плоскостью
В пересечении поверхности плоскостью образуется линия называемая сечением. Сечением многогранника является многоугольник. Для его построения необходимо определить точку пересечения каждого ребра с плоскостью и соединить полученные точки с учетом ви- димости. Фактически решение такой задачи рассматривалось в лекции 2 (рисунок 2.13).
В данной лекции рассмотрим построение линии сечения пирамиды плоскостью Ϭ (рисунок 8.1). Так как плоскость Ϭ фронтальнпроецирующая, фронтальная проекция сечения совпадает с плоскостью Ϭ. Точки 1,2,3 – точки пересечения боковых ребер пирамиды с плоскостью Ϭ. Поэтому достаточно построить горизонтальные проекции этих точек. Точки 11 и 31 находятся по вертикальным линиям связи на ребрах A1S1 и C1S1. Так как ребро SB профильное, для нахождения точки 21 через проекцию 22 проведем прямую 2242, лежащую на грани ASB и параллельную AB. Построив, горизонтальную проекцию определим положение проекции 21. Соединив, полученные точки, получим треугольник. Треугольник видимый, т.к. все грани пирамиды видимые.
Пересечение кривых поверхностей плоскостью
В зависимости от положения секущей плоскости, различают следующие виды конических сечений (рисунок 8.2):
Построение линии сечения конуса по окружности и треугольнику не вызывает затруднений. Для окружности – замеряем радиус, для треугольника – находим точки пересечения с основанием. Построения показаны на рисунок 8. 2. Для построения сечений конуса по эллипсу, параболе, гиперболе, необходимо определить несколько точек, принадлежащих линии сечения. Для нахождения этих точек используется метод плоскостей посредников.
Алгоритм решения задачи состоит в следующем:
- а) проводят плоскости посредники;
- б) строят линии пересечения посредников с данной поверхностью и с плоскостью;
- в) определяют точки пересечения между собой полученных линий;
- г) соединяют полученные точки с учетом видимости.
Для примера рассмотрим построение конуса по эллипсу (рисунок 8.3). Т.к. плоскость Ϭ фронтально-проецирующая, необходимо построить горизонтальную проекцию сечения. В первую очередь строятся опорные точки сечения, в данном случае высшая и низшая точка сечения, лежащая на контурных образующих (1 и 2). 1,2 – большая ось эллипса. Чтобы сечение получилось правильным, необходимо найти положение малой оси 3,4. Для нахождения горизонтальной проекции 31, 41, через фронтальные проекции точек проводим вспомогатель- ную горизонтальную плоскость посредник, которая рассекает конус по окружности. Таким же образом строим промежуточные точки 5,6,7,8. Полученные точки соединяем плавной кривой линией.
Аналогично строятся линии пересечения других поверхностей плоскостями. Гораздо проще строить сечения поверхностей, проецирующими плоскостями, поэтому, если задана плоскость общего положения, имеет смысл выполнить замену плоскостей проекций, перпендикулярно заданной плоскости, а затем уже строить сечение.
Пересечение прямой линии с поверхностью
Для определения точек пересечения прямой линии с поверхностью применяется метод вспомогательных секущих плоскостей (рисунок 8.4) Алгоритм решения задачи следующий:
- 1. Через прямую ℓ проводим вспомогательную секущую плоскость Ϭ.
- 2. Строим линию пересечения m плоскости Ϭ с заданной поверхностью Ф.
- 3. Определяем точки пересечения К и М прямой ℓ с построенной линией пересечения m. Это и будут искомые точки пересечения прямой ℓ с поверхностью.
- 4. Определяем видимость прямой.
Нужно подчеркнуть, что вспомогательная плоскость выбирается такой, чтобы сечение поверхности было простейшим
Рассмотрим несколько примеров на определение точек пересечения прямой с поверхностью.
Примеры построения пересечение прямой с различными поверхностями
Пример 1.
Построить точки пересечения прямой ℓ с поверхностью наклонной трехгранной призмы (рисунок 8.5). Последовательность решения следующая: 1. Через прямую ℓ проводим вспомогательную фронтально-проецирующую плоскость Ϭ. 2. Строим линию пересечения плоскости Ϭ и призмы. Сечением является треугольник 1, 2, 3. 3. Определяем точки пересечения прямой ℓ с треугольником сечения (точки L и М). 4. Определяем видимость прямой ℓ.
Пример 2.
Поострить точки пересечения прямой ℓ с поверхностью наклонного цилиндра (рисунок 8.6). Ход решения:
1. Через прямую ℓ проводим вспомогательную плоскость 
окружностью основания проводим образующие цилиндра. 3. определяем точки пересечения К1 и М1 прямой ℓ1 с линией сечения. Фронтальные проекции точек К2 и М2 определяем по линиям связи. 4. Устанавливаем видимость прямой.
Пример 3.
Построить точки пересечения прямой с поверхностью конуса (рисунок 8.7) Ход решения. 1. Через прямую ℓ проводим плоскость 
4. Определяем видимость прямой ℓ,
Взаимное пересечение поверхностей
Общие положения При пересечении поверхностей образуется линия, которую принято называть линией взаимного пересечения поверхностей. Эта линия пересечения принадлежит одновременно двум поверхностям. Поэтому построение линии пересечения сводится к определению точек одновременно принадлежащих обеим поверхностям. Для нахождения таких точек используется в общем случае метод вспомогательных секущих поверхностей. Сущность способа заключается в следующем: Пусть задано две поверхности 
Общий алгоритм построения линии пересечения поверхностей:
- 1. Введем вспомогательную поверхность Ф.
- 2. Строим линии пересечения поверхности Ф с поверхностями
- 3. Определяем точки пересечения К и М, построенных линий пересечения a и b.
- 4. Многократно повторяя эту операцию, найдем ряд точек, принадлежащих одновременно двум поверхностям.
- 5. Соединяем последовательно точки с учетом видимости.
В качестве посредников могут быть приняты как поверхности, так и плоскости, но целесообразно выбирать такие, которые дают наиболее простые линии пересечения с заданными поверхностями.
Пересечение двух многогранников
Для построения линии пересечения двух многогранников необходимо определить точки пересечения ребер первого многогранника с гранями второго, затем ребер второго с гранями первого. Полученные точки соединить отрезками прямой с учетом видимости. На рисунке 9.2 заданы поверхности трехгранной призмы DEFD‘E‘F‘ и трехгранной пирамиды SABC. Так как призма фронтальнопроецирующая, фронтальная проекция линии пересечения совпадает с гранями призмы, поэтому необходимо построить только горизонтальную проекцию. Для этого определяем точки пересечения ребер пирамиды с гранями призмы. Ребро SС пересекает грани призмы в точках 1 и 2, ребро SB – в точках 3 и 4, ребро SA не пересекает призму. Затем определяем точки пересечения ребер призмы с гранями пирамиды.
По чертежу видим, что только ребро DD‘ пресекает поверхность пирамиды. Для определения точек пересечения 5 и 6 через ребро DD‘ про- водим горизонтальную плоскость, которая пересекает пирамиду по треугольнику. Точки 5 и 6 получаем, как пересечение DD‘ с построенным треугольником. Полученные точки соединяем с учетом видимости. Видимой считается тот отрезок прямой, который принадлежит двум видимым граням поверхностей.
Как видим, линия пересечения двух многогранников представляет собой пространственную ломаную линию. В том случае, когда обе гранные поверхности общего положения, последовательность соединения точек вызывает затруднение. Поэтому для соединения точек используется диаграмма Ананова – условные развертки поверхностей (см. учебник).
Пересечение гранной и кривой поверхности
Линия пересечения гранной и кривой поверхности, представляет собой пространственную кривую линию, с точками излома на ребрах многогранника.
Поэтому сначала определяем точки пересечения ребер многогранника с кривой поверхностью, а затем промежуточные точки и соединяем их с учетом видимости. На рисунке 9.3 заданы поверхности трехгранной призмы и кругового конуса. Так как призма фронтальнопроецирующая, фронтальная проекция линии пересечения совпадает с проекцией боковых граней призмы, поэтому необходимо построить только горизонтальную проекцию линии пересечения. Сначала определяем точки пересечения ребер призмы АА‘, ВВ‘, СС‘ с поверхностью конуса, а затем находим промежуточные точки, принадлежащие линиям пересечения. Для нахождения точек пересечения, используем горизонтальные плоскости посредники, так как они пересекают конус по окружностям, а призму по прямым линиям. Как видим, в данном случае линия пересечения распадается на две отдельные части.
Пересечение двух кривых поверхностей
Линия пересечения двух кривых поверхностей, представляет пространственную кривую линию. Поэтому для ее построения необходимо определить ряд точек принадлежащих этой лини.
На рисунке 9.4 заданы поверхности конуса и сферы. Точки строятся при помощи горизонтальных плоскостей посредников, которые рассекают обе поверхности по окружностям. Обязательно находим опорные точки, к которым относятся высшая и низшая точки линии пересечения и точки границы видимости. Так как оси поверхностей лежат в одной
фронтальной плоскости, контурные образующие поверхностей пересекаются в точках 1 и 2 – это и будет высшая и низшая точки. Точки границы видимости лежат на экваторе сферы, поэтому точки 3 и 3‘ находим с помощью вспомогательной горизонтальной плоскости, проходящей через центр сферы. Она рассекает сферу по экватору, а конус по параллели радиуса R. Взаимно пересекаясь, они и дают точки 3 и 3‘ фронтальную проекцию определяем по вертикальной линии связи на плоскости δ. Затем берем еще две вспомогательные плоскости расположенные выше и ниже плоскости δ и выполняя, аналогичные построения определяем точки 4 и 4‘, 5 и 5‘. Полученные точки соединяем с учетом видимости.
Пересечение поверхностей вращения. Метод вспомогательных секущих сфер
Способ вспомогательных секущих сфер применяется при следующих условиях:
- 1. Пересекающиеся поверхности являются поверхностями вращения.
- 2. Оси этих поверхностей пересекаются.
- 3. Оси поверхностей параллельны одной из плоскостей проекций.
Перед рассмотрением этого способа разберем понятие соосных поверхностей. Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности пересекаются по окружностям перпендикулярным оси вращения. На рисунке 9.5 приведены некоторые из них. Именно то, что поверхности пересекаются по окружностям, которые проецируются в линии и используется в методе сфер.
Рассмотрим пример на рисунок 9.6. Даны поверхности вращения – конус и цилиндр. Так как оси лежат в одной плоскости, можно определить точки пересечения контурных образующих в точках 1 и 2, как в предыдущем примере. Однако, для нахождения промежуточных точек, вспомогательные секущие плоскости не подходят, т.к. горизонтальные плоскости рассекут цилиндр по эллипсам, фронтально-проецирующие – конус по эллипсам. А сам эллипс строить непросто. Поэтому именно в этом случае удобно использовать в качестве посредников – сферы. За центр вспомогательных сфер, принимается точка пересечения осей заданных поверхностей. Далее необходимо определить, размеры радиусов вспомогательных секущих сфер.
Максимальный радиус сферы
Rmax – это расстояние от центра сфер до наиболее удаленной точки пересечения контурных образующих (в данном случае точка 1). Минимальный радиус сферы Rmin – радиус сферы, которая вписана в одну из поверхностей, а другую пересекает. В данном случае минимальная сфера вписана в конус. Минимальная сфера касается поверхности конуса по окружности, а цилиндр пересекает по окружности. Нужно, иметь ввиду, что проекции окружностей пересечения перпендикулярны осям вращения. Эти две окружности пересекаются в точке 32. Фактически таких точек две, они совпадают на фронтальной проекции. Для построения промежуточных точек берем
рем вспомогательные сферы радиусов в пределах от Rmin до Rmax. Они пересекают и поверхность цилиндра, и поверхность конуса по окружностям, которые пересекаясь дают промежуточные точки. Полученные точки соединяются плавной линией. Здесь построена только фронтальная проекция. Для построения горизонтальной проекции, если это необходимо, точки строят как лежащие на окружностях полученных радиусов.
Теорема Монжа
Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения. В этом случае для построения линии пересечения поверхностей используется теорема Г.Монжа, которая формулируется так: Если две поверхности вращения второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечении линий касания. В соответствии с этой теоремой линии пересечения конуса и цилиндра описанного около сферы (рисунок 9.7) будут плоскими кривыми – эллипсами, фронтальные проекции которых изображаются прямыми 1242 и 2232, проходящими через 5252‘ – точки линий пересечения окружностей касания.
Развертка поверхностей
- • Развертка поверхностей. Общие сведения.
- • Построение разверток развертываемых поверхностей: способом триангуляции, способом раскатки, способом нормального сечения.
- • Построение приближенной развертки неразвертываемых поверхностей.
- • Решение задач.
Развертка поверхностей
Общие сведения Разверткой поверхности называется плоская фигура, полученная путем совмещения элементов поверхности с плоскостью. Если для поверхности можно построить её развертку точно без складок и разрывов, то поверхность называется развертываемой, в противном случае – неразвертываемой. К развертываемым поверхностям относятся все гранные, а из линейчатых только – цилиндрические, конические и поверхности с ребром возврата.
Построение разверток развертываемых поверхностей
Существуют следующие способы построения разверток развертываемых поверхностей:
- 1. Способ триангуляции (треугольников);
- 2. Способ раскатки;
- 3. Способ нормального сечения.
Способ триангуляции (треугольников) применяется для построения разверток пирамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо определить натуральные величины всех сторон треугольника. По найденным натуральным величинам сторон вычерчиваются последовательно треугольные грани. Коническая поверхность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде. Рассмотрим пример, построения развертки, конической поверхности (рисунок 10.1) Для построения развертки в конус вписываем двенадцатигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки.
Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие S1 и S7, проецируются в натуральную величину. По полученным натуральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки, состоящую из шести треугольников вписанной в конус пирамиды. Точки основания соединяем плавной кривой линией.
Способ раскатки применяется для построения разверток призматической и цилиндрической поверхности. И если поверхность цилиндрическая, то в нее вписывается призматическая поверхность. Поэтому принцип построения этих разверток одинаков.
Рассмотрим пример построения развертки наклонной треугольной призмы (рисунок 10. 2)
Развертку можно выполнять только в том случае, если боковые ребра призмы параллельны плоскости проекций, как на рисунке 10.2. В противном случае, сначала выполняется преобразование (методом замены строится новая проекция на плоскость параллельную ребрам). При выполнении развертки методом раскатки точки А2 , В2, С2 перемещаются по перпендикулярам к боковым ребрам призмы. А натуральные величины отрезков СВ, ВА, АС берутся из горизонтальной проекции, т.к. основание призмы параллельно плоскости П1. Боковые ребра остаются на развертке параллельными, т.к. каждая грань призмы является параллелограммом.
Способ нормального сечения используется также для построения разверток призматической и цилиндрической поверхностей. Рассмотрим построение развертки призмы изображенной на рисунке 10.3а. Для этого построим нормальное сечение – сечение перпендикулярное боковым ребрам призмы (∆1,2,3).
Определим натуральную величину этого сечения, расположив его параллельно плоскости проекций П1. Для построения развертки боковой поверхности призмы, строим периметр треугольника нормального сечения (рисунок 10.3б). Через точки сечения 1,2,3,1 проводим боковые ребра перпендикулярно сечению и откладываем на них натуральную величину, которая берется из фронтальной проекции рисунка 10.3а.
Соединив построенные точки, получим развертку боковой поверхности данной призмы (рисунок 10.3б).
Построение приближенной развертки неразвертываемых поверхностей
Когда надо развернуть неразвертывающуюся поверхность ее заменяют развертывающейся (цилиндрической, конической, одной или несколькими), имеющей общие линии с данной. Такая замена называется аппроксимацией, а полученная развертка – условной или приближенной. Рассмотрим построение такой развертки на примере полусферы (рисунок 10.4).
Полусферическую поверхность разделим меридиональными плоскостями на дольки (на 12 частей). По высоте сферу делим на несколько частей параллелями. Возьмем одну дольку, ось которой параллельна фронтальной проекции и развернем ее в плоскую фигуру, ось которой будет равна 1/4 длины окружности (рисунок 10.5).
Через точки 1,2,3,4 проводим перпендикуляры к оси дольки и на них откладываем от оси в обе стороны половину ширины каждой дольки измеренную на горизонтальной проекции. Полная развертка составит двенадцать таких долек.
Если развертывающаяся долька начинается с экватора, то на развертке линия экватора изобразится прямой (рисунок 10.5). Если же долька начинается какой-то параллелью, то на развертке эта параллель изобразится окружностью. Например, параллель, проходящая через точку 3. Для нахождения радиуса этой окружности на фронтальной проекции необходимо провести касательную прямую в точке 3, к окружности до пересечения с осью сферы 

Решение задач с примерами посмотроения по начертательной геометрии
Задача 1.
Построить развертку усеченного прямого кругового цилиндра (рисунок 10.7а)
Развертка боковой поверхности цилиндра строится фактически методом нормального сечения, т.к. основание цилиндра перпендикулярно оси. Окружность основания развертывается в прямую линию равную длине окружности (πD). Можно ее построить, отложив размер хорд, соединяющих точки основания. Конечно, длина будет тем точнее, чем на большее число частей разбита окружность. Кривая сечения на развертке изобразится синусоидой (рисунок 10.7б) Для построения полной развертки необходимо к развертке боковой поверхности добавить основание и натуральную величину сечения.
Задача 2.
Построить развертку усеченного прямого кругового конуса (рисунок 10.8а). Так как в прямом круговом конусе все образующие одинаковой длины, развертка представляет собой сектор окружности с радиусом равным длине образующей конуса ℓ, а длина дуги равная длине окружности основания конуса (рисунок 10.8б). Поэтому, разделив окружность основания на 12 частей и затем, отложив на дуге сектора таких же 12 частей, получим развертку.
Угол α также можно определить по формуле:
где d – диаметр основания.
Собственные тени поверхностей вращения • Тени основных геометрических форм цилиндра и конуса. • Тени поверхностей вращения. Способ касательных конусов и цилиндров. • Тени форм, применяемых в архитектурном проектировании: — тени сферы — тора (валика) — тороида (скоции)
Тени основных геометрических форм – цилиндра и конуса
Мы уже рассматривали построение собственных теней простейших геометрических поверхностей – цилиндра и конуса. Для цилиндра теневые образующие определяются двумя лучевыми плоскостями касательными к поверхности цилиндра. Для конуса теневые образующие определяются после построения падающей тени на плоскость основания. В данной лекции рассмотрены рациональные приемы определения границ собственной тени прямого кругового цилиндра (рисунок 11.1) и кругового конуса (рисунок 11.2).
Тень цилиндра может быть построена без плана, т.е. без горизонтальной проекции, что очень удобно в архитектурном проектировании. Теневые образующие проходят через точки А2, В2 отстоящие от оси цилиндра на 0,707 его радиуса (рисунок 11.1) Рациональный прием построения собственной тени кругового конуса приведен на рисунке 11.2. Для прямого конуса выполняются следующие построения (рисунок 11.2а). На основании конуса как на диаметре строится половина окружности. Из нижней точки окружности 1 проводится прямая 1,2 параллельная левой контурной образующей конуса. Из полученной точки 2 проводится прямые под углом 450 к основанию конуса до пересечения с окружностью в точках А и В. Спроецировав точки А и В на основание конуса, определим границы собственной тени А2 S2 , В2 S2.
Для перевернутого конуса, обратного, построения аналогичны предыдущему (рисунок 11.2б). Отличаются тем, что из точки 1 проводится прямая 1,2 параллельная правой образующей конуса.
Следует обратить внимание на величину части поверхности, находящейся в собственной тени: для прямого конуса она меньше половины, для обратного – больше.
Круговые конусы с наклоном образующих под углом 450 и 350 имеют важное значение при построении собственных теней поверхностей вращения.
Построение теней конуса с углом наклона образующей 450 приведено на рисунке
При построении падающей тени на плоскость основания фронтальная проекция луча совпадает на фронтальной проекции с контурной образующей конуса. Для дальнейшего использования необходимо запомнить, что тень занимает: у прямого конуса – четверть поверхности, у обратного – три четверти поверхности.
Построение теней конуса с углом наклона образующей 350 приведено на рисунке 11.5. На рисунке 11.4 показано построение угла 350. ABCD – квадрат. Строим прямоугольник со стороной равной диагонали квадрата. Диагональ этого прямоугольника наклонена к горизонтали под углом 350. Из построения тени конуса с углом наклона образующей 350 видно, что границей тени будет служить одна образующая SA (теоретически), располагающаяся на фронтальной проекции под углом 450. Практически прямой конус будет полностью освещен, а обратный – весь в тени. Образующая SA называется бликовой образующей. Положение образующих – границы тени таких двух конусов надо твердо усвоить, т.к. они будут часто встречаться в последующем, в качестве вспомогательных операций при построении теней.
Тени поверхностей вращения. Способ касательных конусов и цилиндров
Построение контура собственной тени поверхностей вращения осуществляется при помощи способа касательных конусов и цилиндров. Этот способ заключается в следующем: берется конус или цилиндр касательный к поверхности вращения (т.е. описанный или вписанный в данную поверхность); на окружности касания отмечаются точки границы собственных теней касательных поверхностей; эти точки будут принадлежать и границе собственной тени заданной поверхности на той же окружности прикосновения, т.е. на той же параллели. Используя, таким образом, несколько конусов и цилиндров, определяется необходимое количество точек контура собственной тени. Для поверхностей второго порядка достаточно восьми точек, используя один цилиндр (2 точки), прямой и обратный конус с образующей под углом 450 (4 точки), прямой и обратный конус с углом наклона образующей 350 (2 точки)
На рисунке 11.6 построения контура собственной тени выполнены следующим образом. Точки 1 и 2 получены как на цилиндре. Точки 3 и 4 найдены как на касательном конусе с углом наклона образующей 450 Точку касания 3 точно можно определить, проведя нормаль (радиус) из центра дуги очерка поверхности под углом 450. Точка 4 лежит на одной горизонтали с точкой 3. Точка 5 найдена как на касательном конусе с углом наклона образующей 350. Для ее построения из центра дуги очерка поверхности проводим прямую под углом 350 к оси поверхности вращения. Точка пересечения с очерком даст точку А – точку касания конуса с образующей под углом 350. Проводим из точки касания эту образующую перпендикулярно радиусу до пересечения с осью поверхности вращения в точке S. Из точки S проводим прямую под углом 450 до пересечения с основанием конуса (горизонталь проведенная через точку А2).
Промежуточные точки 6 и 7 найдены на линии касания конуса произвольного угла наклона образующей. Построение выполнено аналогично рисунку 11.2а. Тени форм, применяемых в архитектурном проектировании Тени сферы (рисунок 11.7)
Собственная тень проецируется на плоскость П2 и П1 одинаковыми эллипсами. На рисунке 11.7 показано построение эллипса на фронтальной проекции. Точки 1 и 2 находятся как на цилиндре. Точки 3 и 4, 5 и 6 – как на прямом и обратном конусе с углом образующей 450, причем диаметр 5,3 является большой ось эллипса. Точки 7 и 8 определяются на касательном конусе с углом образующей 350. Точки 9 и 10 строятся симметрично 7 и 8 относительно большой оси. Точки 11 и 12 принадлежат малой оси эллипса, которая перпендикулярна большой оси 5,3. Построение точек осуществляется следующим образом. Из точки 5 проводим дугу радиусом сферы до пересечения с контуром. Полученные точки соединяем с точкой 3. Эти прямые пересекут малую ось в точках 11 и 12.
Тени тора (валика) (рисунок 11.8).
Построение контура собственной тени на торе осуществляется по восьми точкам.
Точки 1 и 2 определяются как на цилиндре. Точки 3 и 4, 5 и 6 определяются как на прямом и обратном конусе с углом наклона образующей 450. Точки 7 и 8 получены на касательном прямом и обратном конусе с углом наклона образующей 350. Необходимо помнить, что вершина конуса всегда лежит на оси поверхности вращения.
Построение контура собственной тени скоции осуществляется также по восьми точкам. Только касательные конусы и цилиндр являются вписанными в данную поверхность. Точки 1 и 2 находятся как на цилиндре. Точки 3 и 4, 5 и 6 как на обратном и прямом конусе, соответственно, с углом наклона образующей 450. Высшая и низшая точки 7 и 8 определяются с использованием касательных конусов с углом наклона образующей под углом 350.
Построение падающих теней на комбинированных поверхностях вращения
Рассмотрим построение теней на комбинированной поверхности вращения типа «Ваза» (рисунок 12.1). Комбинированная поверхность состоит из тора, цилиндров, сферы, скоции. Для того, чтобы построить, падающие тени, прежде всего необходимо построить собственные тени, так как контур падающей тени, есть тень от контура собственной тени. Построение собственных теней элементов поверхности вазы были рассмотрены в предыдущей лекции №11: тор (рисунок 11.8), цилиндр (рисунок 11.1), сфера (рисунок 11.7), скоция (рисунок 11.9). Необходимо отметить некоторые закономерности контуров собственных теней: — на линии касания двух разных поверхностей контуры собственных теней этих поверхностей имеют точки перелома (точки 62 и 62‘ на линии касания цилиндра и сферы). Линия падающей тени при этом будет плавной; — когда две соосные поверхности имеют общую линию пересечения, то контуры собственных теней не будут иметь общей точки (точки D2 и 122 на линии пересечения сферы и цилиндра).
Далее приступаем к построению падающих теней. Тень от контура собственной тени тора 12 52 42 32 22 падает на освещенную поверхность цилиндра. Для ее построения используется метод вспомогательного осевого экрана. При этом точки 12 и 22 лежат на осевом экране. Точка 52, лежащая в лучевой плоскости, отбросит тень на ось (5t). Тень 4t и 3t от точек 42 и 32 строится методом выноса. Контур 12 5t 4t 3t 22 – контур тени падающей на фронтальный экран. Пересекая левую образующую цилиндра он дает точку А2t. На одной горизонтали с А2t находим В2t на оси. Высшая точка падающей тени 52t определяется следующим образом.
Находится горизонталь пересечения конуса с углом образующей 350 с цилиндром. Луч проведенный из точки 52 под углом 450 с этой горизонталью и дает точку 52t. Точку С2t – точку исчезновения тени – определяем обратным лучом, построив тень от образующей цилиндра на фронтальный экран. При этом нужно иметь ввиду, что линия контура падающей тени в точке исчезновения (С2t) должна быть касательна к проекции луча.
Далее строим тень, падающую от сферы на цилиндр. Тень начинается из точек E2 и D2. Строим тень от сферы на фронтальный экран. Контур тени, пересекая образующую цилиндра, дает точку N2t. Точку M2t находим на оси на одной горизонтали с N2t. Точку L2t определяем обратным лучом, построив тень образующей цилиндра на фронтальный экран. Нужно обратить внимание на то, что контур падающей тени 

Пересекаясь с контуром скоции, она дает точки K2t и 16t. Точка R2t лежит на одной горизонтали с K2t. Для нахождения высшей точки падающей тени – 132t, точку 152 соединяем с 13t. Эта прямая является образующей конуса с углом 350. Строим горизонталь пересечения этого конуса с поверхностью скоции и находим на ней точку пересечения луча проведенного из точки 132. Соединя- ем полученные точки K2t 132t R2t 16t с таким расчетом, чтобы в точке исчезновения тени F2t, контур тени касался проекции луча.
Метод биссекторного экрана
В некоторых случаях для построения падающих теней на поверхностях вращения удобно использовать вспомогательный биссекторный экран. Эта биссекторная плоскость удобна тем, что тень на нее от горизонтальной окружности проецируется также окружностью радиуса 0,707 данной. Способ биссекторных экранов применяется в сочетании со способом обратных лучей. Для примера рассмотрим построения тени от круглой плиты на круглую колонну (рисунок 12.2). Тень от окружности плиты на биссекторный экран – окружность радиуса R. Тень от левой контурной образующей колонны падает на середину левого радиуса цилиндра
Тень от бликовой образующей колонны 2 падает на ось цилиндра. Тень от средней образующей 3 падает на середину правого радиуса цилиндра. Тень образующей 5 совпадает с тенью образующей 3 при обратном луче. Находим точки пересечения теней образующих, падающих на биссекторный экран, с тенью от плиты и обратными лучами, определяем их положения на соответствующих образующих. На рисунке 12.2 горизонтальная проекция дана только для пояснения построений. Фактически построения могут быть выполнены только по фронтальной проекции.
Тень от квадратной плиты на колонну
Тень от квадратной плиты на цилиндрическую колонну (рисунок 12.3) фактически является тенью от двух прямых 1-2 – фронтально-проецирующей и 2-3 – профильно-проецирующей (по отношению к фасаду – продольной). Нам из предыдущего материала известно, что тень от продольной прямой зеркально повторяется план, т.е. является окружностью того же радиуса, что и колонна. А тень от проецирующей прямой совпадает с направлением луча. Поэтому очевидно, что построение тени можно выполнить по одной фронтальной проекции, т.е. фасаду.
Построение падающих теней на архитектурных деталях
Метод цилиндрических экранов Метод глубинных координат • Тени капители колонны. Способ цилиндрических экранов. Способ глубинных координат. • Тени в цилиндрической нише со сферическим верхом.
Построение тени капители (рисунок 13.1) представляет собой комплексную задачу, объединяющую ранее построенные тени на отдельных частях. Собственные тени на цилиндре и на валике (тор), падающая тень от валика на колонну (цилиндр) выполнена аналогично рисунку 12.1. А построение падающей тени от квадратной плиты на валик строится способом цилиндрических экранов или глубинных координат. Сначала построим тень, от квадратной плиты падающую на колонну.
Построение выполняется аналогично рисунку 12.3. В итоге, контур падающей тени на цилиндрической колонне, складывается из тени падающей от валика и квадратной плиты. Тень от продольной стороны квадрата представляет часть окружности радиуса R. Тень от проецирующей стороны квадрата совпадает с направлением луча, как на колоне, так и на валике. Необходимо построить тень от продольной стороны квадрата на валик. Точки 12t и 22t – точки исчезновения тени находим обратным лучом с фронтального осевого экрана.
Высшую точку 32t и низшую – 42t (мнимую) находим на параллелях проведенных из точек пересечения тени от проецирующей стороны квадрата на валике. Для построения промежуточных точек контура тени применяем вспомогательные цилиндрические экраны. Теневые точки 52t и 62t находим на линии пересечения цилиндрического экрана I с валиком, построив тень как на цилиндре радиуса R1. Аналогично строим теневые точки 72t и (82t), применив цилиндрический экран II радиуса R2. Полученные точки соединяем плавной кривой, учитывая, что в точках 12t и 22t лучи будут касательными к полученной кривой.
Промежуточные точки 52t, 62t и 72t, 82t можно также получить способом глубинных координат. Для этого берется ряд горизонтальных сечений. На примере сечение показано совпадающим с основанием цилиндрического экрана I. Для дальнейшего построения окружность сечения совмещается с фронтальной плоскостью. Определяется координата y, которая откладывается на линии сечения в обе стороны от оси для получения точек 52t и 62t. Аналогично строятся другие точки.
Тени в цилиндрической нише со сферическим верхом (рисунок 13.2) Прежде всего определяем контур собственной тени известными способами (рисунки 11.1, 11.7) Для построения падающей тени в данной комбинированной нише применяется метод фронтальных экранов. Суть метода заключается в том, что тень от окружности на плоскость ей параллельную является окружностью. Тень от контурной образующей цилиндра, а, следовательно, и от точки А падает на ось цилиндра. Необходимо определить промежуточные точки между В2 и А2t, принадлежащие контуру падающей тени от кромки сферической ниши – окружности. Для этого проводим ряд фронтальных экранов (I, II, III, IV). Строим линии пересечения фронтальных плоскостей (экранов) с поверхностью ниши. Определяем положение теней от центра окружности кромки ниши О на каждый из экранов. Из теней центров окружности выполняем засечки на соответствующих линиях сечения, радиусом сферы R.
Точка перегиба тени С, на окружности перехода поверхности цилиндра в поверхность сферы, может быть определена следующим образом. Из центра О проводим прямую с уклоном 2:1, которая определит положение точки С2 на кромке сферической ниши. Луч проведенный из точки С2 даст тень С2t.
Полученные точки соединяем плавной кривой линией.
Проекции с числовыми отметками. Область применения и сущность способа проецирования
Архитектор, проектируя здания и сооружения, всегда учитывает условия их расположения на отдельном участке местности. Нередко эти условия в определенной степени влияют на композиционные решения. Кроме чертежей, относящихся к зданию – планов, разрезов, фасадов и др. – проект должен включать все соображения по организации участка связи здания с рельефом местности. Эта часть проекта называется проектом вертикальной планировки. При разработке проекта вертикальной планировки требуется знания особого метода изображения объектов (рельефа), который получил название проекции с числовыми отметками. Сущность этого метода заключается в том, что объект (рельеф) ортогонально проецируется на одну горизонтальную плоскость. У проекций точек и линий ставятся числа, показывающие расстояния этих точек и линий от условно принятой плоскости проекции, которая называется нулевой. Эти числа и называются числовыми отметками.
Проекции точек
На рисунке 14.1 изображена горизонтальная основная плоскость П0. Точка А находится над плоскостью на высоте четырех единиц масштаба. А3 – проекция точки А на плоскость П0, где 3 – числовая отметка.
Точка С лежит на плоскости П0, поэтому ее проекция – С0. Точка В находится под плоскостью, поэтому ее проекция – В-2, где отметка 2 со зна- ком (-). Для перехода к плоскому чертежу, плоскость П0 совмещается с плоскостью чертежа, граница плоскости не указывается. На чертеже обязательно указывается масштаб. Числовая отметка каждой точки, по сути, заменяет фронтальную проекцию, т.е. соответствует коорди- нате Z (рисунок 14.2).
Проекции прямых. Определение натуральной величины и следа отрезка прямой
Прямая линия в проекциях с числовыми отметками задается своей проекцией на основную плоскость и отметками двух ее точек (рисунке 14.3). Эта прямая является прямой общего положения. Для нее можно, как и в ортогональных проекциях, определить натуральную величину, след на плоскости П0 и углом наклона к плоскости. Если прямую АВ совместить с плоскостью П0 вращением вокруг проекции А2В5, получим натуральную величину. При этом высоты точек необходимо в масштабе чертежа отложить на перпендикулярах к проекции прямой. Прямая, соединяющая полученные точки равна истинной величине отрезка. Точка пересечения натуральной величины отрезка с ее проекцией является горизонтальным следом Н0.
Угол между натуральной величиной и проекцией (φ), является истинной величиной угла наклона прямой к плоскости П. Градуирование прямой Градуирование прямой – построение на проекции прямой последовательного ряда точек с разностью отметок равной единице.
Если концы отрезков имеют целые числовые отметки, то градуирование можно произвести делением отрезка на равные части (рисунок 14.4). В противном случае лучше использовать способ “палетки“. Для этого параллельно прямой, проводим ряд прямых, отстоящих друг от друга на равном расстоянии произвольной величины (рисунок 14.5). Принимаем их за линии уровня и на перпендикулярах находим положение концов отрезка, аналогично нахождению натуральной величины. Отрезок АB пересекаясь с горизонталями даст положение точек с целями числовыми отметками, которые перепроицируем на проекцию прямой.
Интервал и уклон прямой
Расстояние между двумя точками горизонтальной проекции называется горизонтальным проложением L. На рисунке 14.6 – А2.5В4.2 . А расстояние измеренное по вертикали между этими точками, т.е. разность высот называется превышением (J). Уклоном прямой называется, отношение превышения и горизонтальному проложению. На рисунке 14.6 


Прямые частного положения (рисунок 14.7) Если прямая параллельна плоскости, то она задается двумя точками с одинаковыми отметками (прямая АВ), вертикальная же прямая, т.е. перпендикулярная к плоскости П0, задается точкой с двумя разными отметками (прямая СD).
Взаимное положение двух прямых
Рассмотрим условия, при которых прямые будут взаимно параллельны, пересекающиеся или скрещивающие. Прямые взаимно параллельны, когда их проекции параллельны, уклоны (интервалы) взаимно равны и отметки возрастают в одну сторону (рисунок 14.8). Если прямые взаимно пересекаются, то их проекции также пересекаются в точке, которая, будучи отнесена к каждой из прямых имеет одинаковую отметку (рисунок 14.9). Если проекции прямых не удовлетворяют ни одному из этих условий, прямые являются скрещивающимися.
Проекции плоскостей. Задание плоскостей. Взаимное положение двух плоскостей
Плоскость в проекциях с числовыми отметками, также как и в ортогональных проекциях, может быть задана проекциями трех точек, не лежащих на одной прямой, проекциями прямой и точки вне ее, проекциями двух параллельных или пересекающихся прямых или проекцией какой-либо плоской фигуры. Кроме этого, плоскость в проекциях с числовыми отметками можно задать масштабом уклонов. Рассмотрим рисунок 14.10.
Плоскость α является плоскостью общего положения. h0 – след плоскости α на плоскости П. Ряд горизонтальных плоскостей проведенных на расстоянии равном единице рассекут плоскость α по горизонталям (h1 , h2, h3 …). Линия наибольшего ската 0-3 перпендикулярна горизонталям. Проградуированная проекция линии наибольшего ската называется масштабом уклонов плоскости α и обозначается αi. Очевидно, что αi перпендикулярна следу плоскости h0 . Расстояние между проекциями смежных точек равно интервалу линии наибольшего ската, а следовательно и интервалу плоскости α. Через каждую из этих точек можно провести горизонталь перпендикулярно масштабу уклонов (рисунок 14.10). Угол φ между линией наибольшего ската и линией масштаба уклонов называется углом падения.
Угол ψ между направлением главного меридиана и следом плоскости (линией простирания), измеренной против часовой стрелки называется углом простирания.
Взаимное положение двух плоскостей
Две плоскости в пространстве могут пересекаться и быть взаимно параллельными. Если плоскости взаимно параллельны, то масштабы их уклонов взаимно параллельны, интервалы одинаковы и возрастают в одном направлении. Если масштабы уклонов не удовлетворяют хотя бы одному из этих условий, плоскости пересекаются.
Построение линии пересечения двух плоскостей в проекциях с числовыми отметками, как и в ортогональных проекциях, основано на методе вспомогательных секущих плоскостей. В качестве вспомогательных плоскостей берутся горизонтальные, которые пересекут заданные плоскости по одноименным горизонталям. Поэтому линию пересечения двух плоскостей находят определением точек пересечения двух пар горизонталей с одинаковыми отметками (рисунок 14.11).
Если углы наклона плоскостей к плоскости проекций одинаковы, то линия пересечения располагается по биссектрисе угла.
Для нахождения точки пересечения прямой с плоскостью α, необходимо через прямую провести любую вспомогательную плоскость. Определить линию пересечения плоскости γ и вспомогательной. И затем определить точку пересечения прямой с построенной линией пересечения (рисунок 14.12).
Проекции поверхностей. Задание поверхностей. Пересечение поверхности плоскостью
В проекциях с числовыми отметками многогранники можно задать проекциями вершин с числовыми отметками. Например, на рисунке 14.13 изображена трехгранная пирамида, основание которой лежит на предметной плоскости. Если проградуировать одно из ребер пирамиды, можно получить горизонтали граней, а, следовательно, решать различные задачи. Кривые поверхности обычно задают проекциями их горизонталей. Например, прямой круговой конус может быть задан проекцией вершины и горизонталью основания (рисунок 14.14) проградиуровав, образующую можно провести ряд горизонталей конуса.
Топографическая поверхность (поверхность земли) может также задаваться горизонталями, только они являются незакономерными кривыми линиями, соединяющими точки с одинаковыми числовыми отметками (рисунок 14.15).
Пересечение поверхности плоскостью
Основной задачей при выполнении проекта вертикальной планировки, является задача на построение линии пересечения поверхности плоскостью и линии пересечения двух поверхностей. Принцип построении основан также на методе вспомогательных секущих плоскостей, которые рассекают и плоскость, и поверхность по одноименным горизонталям. Определив ряд точек пересечения одноименных горизонталей, получаем линию взаимного пересечения. На рисунке 14.16 дан пример построения линии пересечения плоскости β с рельефом земной поверхности.
Профиль поверхности
Пересечение топографической поверхности с проецирующей плоскостью называется профилем поверхности (рисунок 14.17). Секущая плоскость задана своей горизонтальной проекцией Е-Е. Для построения профиля выберем базовую горизонталь с отметкой, равной или немного ниже, минимальной отметки горизонтали местности, которая получается в сечении с плоскостью Е-Е. После проведения перпендикулярно следу плоскости линий связи, отложим на этих линиях отметки соответствующих горизонталей и соединим их плавной кривой. На профиль нанесем сетку горизонталей с учетом масштаба, принятого в плане.
Построение границ земельных работ. Построение сечения вертикальной плоскостью рельефа с планировкой профиля
Построить линию пересечения откосов горизонтальной строительной площадки с поверхностью земли. Отметка площадки +18.00. Уклон откосов выемки 

- Строим линии пересечения откосов между собой. Так как плоские откосы имеют одинаковый уклон, линии пересечения будут биссектрисами углов 900. Линия пересечения конического откоса насыпи и плоского является параболой, поэтому для ее построения определяем точки пересечения одноименных горизонталей.
Откос выемки будет касаться к коническому откосу, линия касания горизонтальная. Далее находим линии пересечения каждого откоса с поверхность рельефа, для чего находим точки пересечения одноименных горизонталей откосов и земной поверхности. Для нахождения промежуточных точек, лежащих на линиях пересечения откосов, необходимо находить по одной мнимой точки за пределами откоса. Полученные линии пересечения, называются «границей земляных работ». Для наглядности изображения линии бровки выделяются так называемыми «бергштрихами», выполняемыми различной длины и толщины. «Бергштрихи» проводятся перпендикулярно горизонталям, а для конического откоса по радиусам, в сторону уклона. Сечение вертикальной плоскостью построено по линии А – А. На горизонтальной линии наносят точки пересечения этой плоскостью горизонталей рельефа и линий планировки и откладывают на вертикалях их отметки (рисунок 15.2). Соединив точки рельефа, получаем сечение рельефа, а соединив точки планировки, получаем сечение планировки.
Примеры и образцы решения задач:
- Решение задач по инженерной графике
- Решение задач по начертательной геометрии
Услуги по выполнению чертежей:
- Заказать чертежи
- Помощь с чертежами
- Заказать чертеж в компасе
- Заказать чертеж в автокаде
- Заказать чертежи по инженерной графике
- Заказать чертежи по начертательной геометрии
- Заказать черчение
Учебные лекции:
- Инженерная графика
- Оформление чертежей
- Чертеж общего вида и сборочный чертеж
- Техническое рисование
- Машиностроительные чертежи
- Геометрические построения
- Деление окружности на равные части
- Сопряжение линий
- Коробовые кривые линии
- Построение уклона и конусности
- Лекальные кривые
- Параллельность и перпендикулярность
- Методы преобразования ортогональных проекций
- Поверхности
- Способы проецирования
- Метрические задачи
- Способы преобразования чертежа
- Кривые линии
- Кривые поверхности
- Трёхгранник Френе
- Проецирование многогранников
- Проецирование тел вращения
- Развёртывание поверхностей
- Проекционное черчение
- Проецирование
- Проецирование точки
- Проецирование отрезка прямой линии
- Проецирование плоских фигур
- Способы преобразования проекций
- Аксонометрическое проецирование
- Проекции геометрических тел
- Сечение геометрических тел плоскостями и развертки их поверхностей
- Взаимное пересечение поверхностей тел
- Сечение полых моделей
- Разрезы
- Требования к чертежам деталей
- Допуски и посадки
- Шероховатость поверхностей и обозначение покрытий
- Разъемные и неразъемные соединения деталей
- Передачи и их элементы