17 авг. 2022 г.
читать 2 мин
Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между несколькими независимыми переменными и переменной отклика.
К сожалению, одна проблема, которая часто возникает при регрессии, известна как гетероскедастичность , при которой происходит систематическое изменение дисперсии остатков в диапазоне измеренных значений.
Это приводит к увеличению дисперсии оценок коэффициента регрессии, но регрессионная модель этого не учитывает. Это повышает вероятность того, что регрессионная модель объявит термин в модели статистически значимым, хотя на самом деле это не так.
Одним из способов решения этой проблемы является использование надежных стандартных ошибок , которые более «устойчивы» к проблеме гетероскедастичности и, как правило, обеспечивают более точное измерение истинной стандартной ошибки коэффициента регрессии.
В этом руководстве объясняется, как использовать надежные стандартные ошибки в регрессионном анализе в Stata.
Пример: Надежные стандартные ошибки в Stata
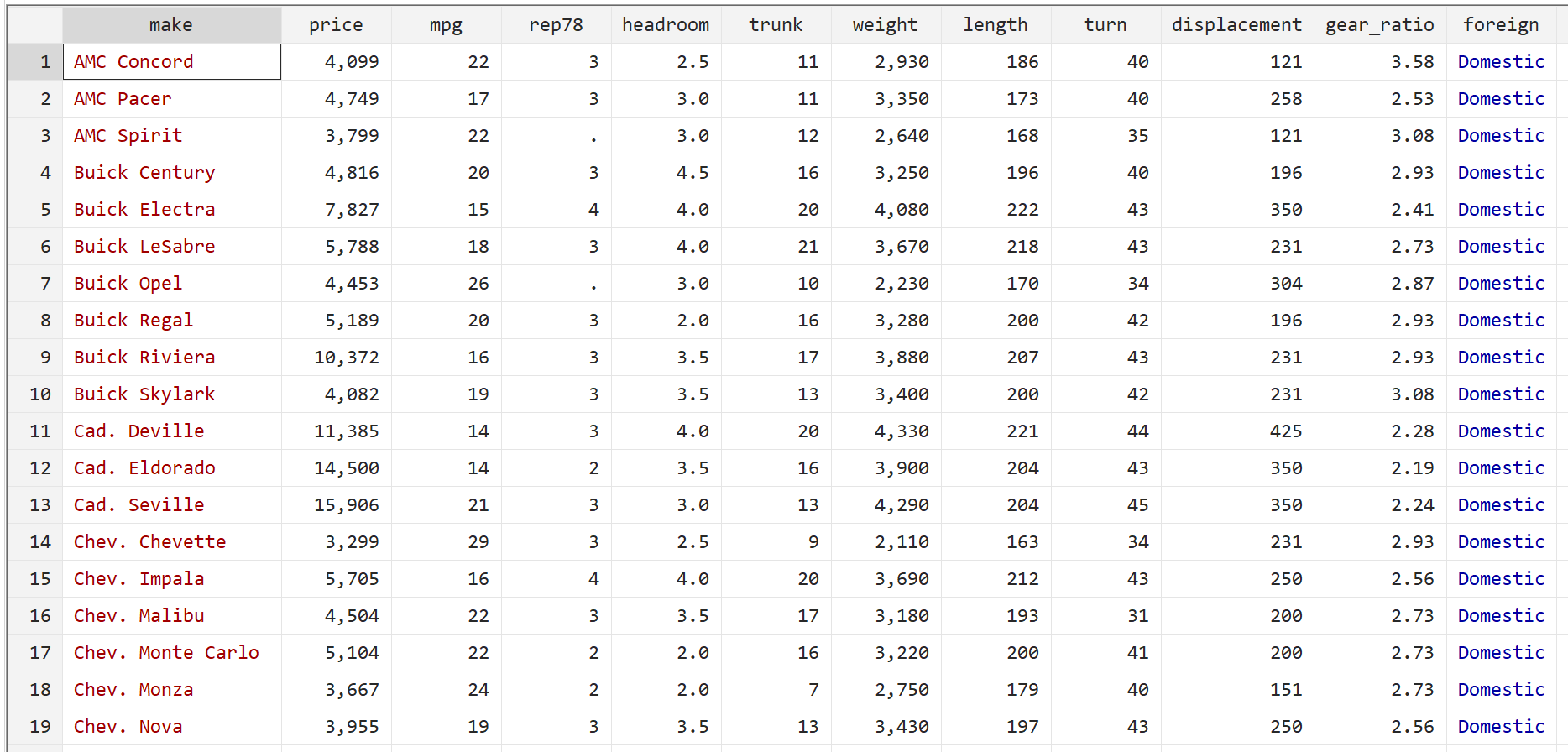
Мы будем использовать встроенный автоматический набор данных Stata, чтобы проиллюстрировать, как использовать надежные стандартные ошибки в регрессии.
Шаг 1: Загрузите и просмотрите данные.
Сначала используйте следующую команду для загрузки данных:
сисус авто
Затем просмотрите необработанные данные с помощью следующей команды:
бр
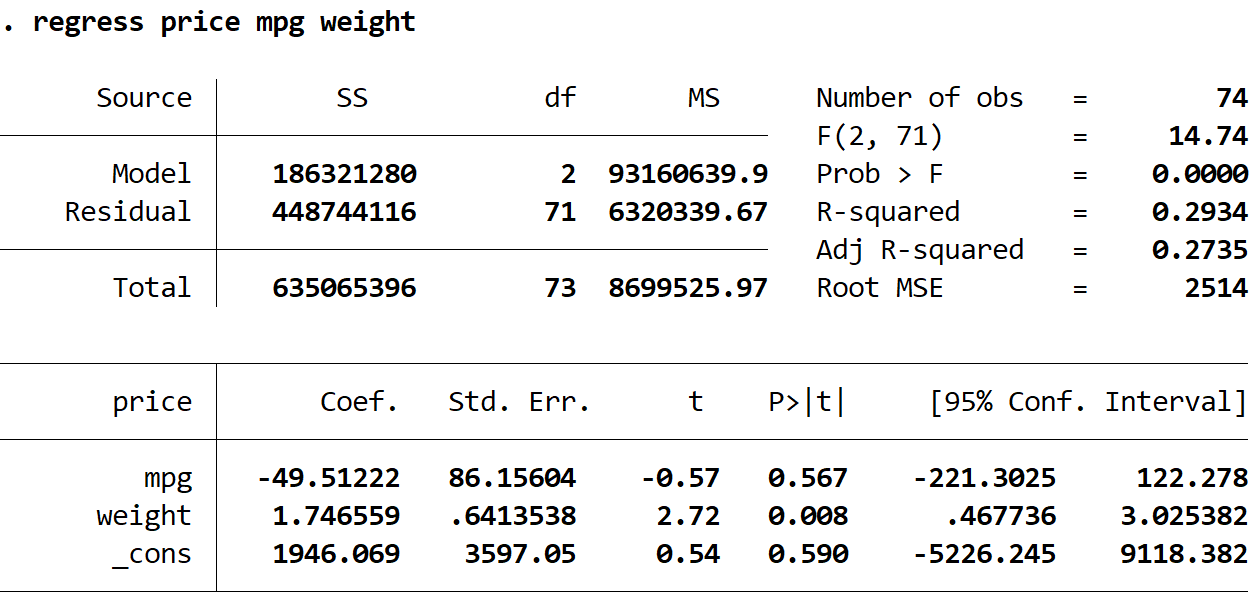
Шаг 2. Выполните множественную линейную регрессию без надежных стандартных ошибок.
Затем мы введем следующую команду, чтобы выполнить множественную линейную регрессию, используя цену в качестве переменной ответа, а мили на галлон и вес в качестве независимых переменных:
регресс цена миль на галлон вес
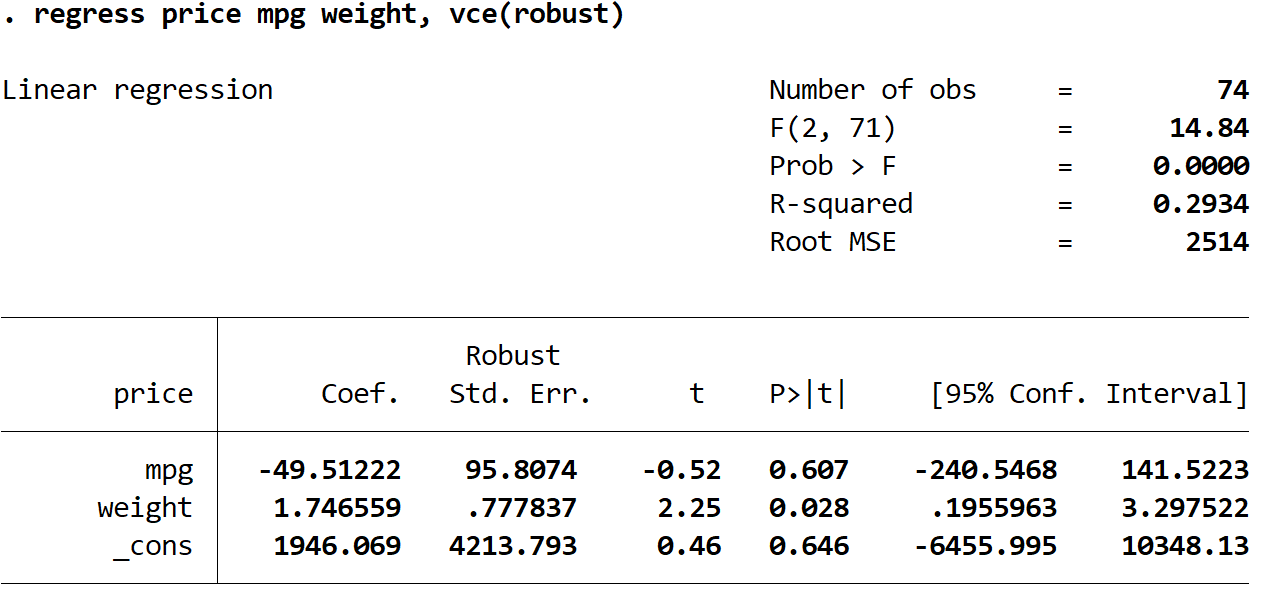
Шаг 3: Выполните множественную линейную регрессию, используя надежные стандартные ошибки.
Теперь мы выполним точно такую же множественную линейную регрессию, но на этот раз мы будем использовать команду vce(робаст) , чтобы Stata знала, что нужно использовать надежные стандартные ошибки:
регресс цена миль на галлон вес, vce(надежный)
Здесь следует отметить несколько интересных вещей:
1. Оценки коэффициентов остались прежними.Когда мы используем надежные стандартные ошибки, оценки коэффициентов вообще не меняются. Обратите внимание, что оценки коэффициентов для миль на галлон, веса и константы для обеих регрессий следующие:
- миль на галлон: -49,51222
- вес: 1.746559
- _cons: 1946.069
2. Изменены стандартные ошибки.Обратите внимание, что когда мы использовали надежные стандартные ошибки, стандартные ошибки для каждой из оценок коэффициентов увеличивались.
Примечание. В большинстве случаев устойчивые стандартные ошибки будут больше, чем обычные стандартные ошибки, но в редких случаях устойчивые стандартные ошибки могут быть меньше.
3. Изменилась тестовая статистика каждого коэффициента. Обратите внимание, что абсолютное значение каждой тестовой статистики t уменьшилось. Это связано с тем, что статистика теста рассчитывается как оценочный коэффициент, деленный на стандартную ошибку. Таким образом, чем больше стандартная ошибка, тем меньше абсолютное значение тестовой статистики.
4. Изменились p-значения.Обратите внимание, что p-значения для каждой переменной также увеличились. Это связано с тем, что меньшая тестовая статистика связана с большими p-значениями.
Хотя p-значения для наших коэффициентов изменились, переменная mpg по-прежнему не является статистически значимой при α = 0,05, а вес переменной по-прежнему статистически значим при α = 0,05.
Надежна ли ваша стандартная ошибка?
Перевод
Ссылка на автора
Практическое руководство по выбору правильной спецификации
Управляющее резюме
- Проблема:Стандартные ошибки по умолчанию (SE), сообщаемые Stata, R и Python, являются правильными только при очень ограниченных обстоятельствах. В частности, эти программы предполагают, что ваша ошибка регрессии распределена независимо и одинаково. На самом деле это не так, что приводит к серьезным ошибкам типа 1 и типа 2 в тестах гипотез.
- Лечение 1:если вы используете OLS, вы должны кластеризовать SE по двум параметрам: индивидуально по годам.
- Лечение 2:если вы используете FE (фиксированный эффект), вы должны кластеризовать SE только на 1 измерение: индивидуальное.
- коды: Вот это ссылка на коды Stata, R и SAS для реализации кластеризации SE.
Если вам интересно об этой проблеме, пожалуйста, продолжайте читать. В противном случае, увидимся в следующий раз 
План на день
В этом посте я собрал бы 69-страничный документ о здравой стандартной ошибке в чит-лист. Эта бумага Опубликованный профессором Митчеллом Петерсеном в 2009 году, на сегодняшний день собрал более 7 879 ссылок. Это остается библией для выбора правильной здравой стандартной ошибки.
Проблема
Обычная практика
В любом классе Stats 101 ваш профессор мог бы научить вас набирать «reg Y X» в Stata или R:
Вы приступаете к проверке своей гипотезы с указанными точечными оценками и стандартной ошибкой. Но в 99% случаев это было бы неправильно.
Ловушка
Чтобы OLS давал объективные и непротиворечивые оценки, нам нужно, чтобы термин ошибки epsilon был распределен независимо и одинаково:
Независимый означает, что никакие серийные или взаимные корреляции не допускаются:
- Последовательные корреляции:для одного и того же человека остатки в разные периоды времени коррелируют;
- Кросс-корреляция:различные индивидуальные остатки коррелируются внутри и / или между периодами.
Одинаковый означает, что все остатки имеют одну и ту же дисперсию (например, гомоскедастичность).
Визуализация проблемы
Давайте визуализируем i.i.d. предположение в дисперсионно-ковариационной матрице.
- Нет последовательной корреляции:все недиагональные записи в красных пузырьках должны быть 0;
- Нет взаимной корреляции:все диагональные записи должны быть одинаковыми — все записи в зеленых прямоугольниках должны быть 0;
- гомоскедастичность:диагональные записи должны быть одинаковыми константами.
Что не так, если вы используете SE по умолчанию без I.I.D. Ошибки?
Вывод выражения SE:
Стандартная ошибка по умолчанию — последняя строка в (3). Но чтобы получить от 1-й до последней строки, нам нужно сделать дополнительные предположения:
- Нам нужно предположение о независимости, чтобы переместить нас с 1-й строки на 2-ю в (3). Визуально все записи в зеленых прямоугольниках И все недиагональные записи в красных пузырьках должны быть 0.
- Нам нужно одинаково распределенное предположение, чтобы переместить нас со 2-й строки на 3-ю. Визуально все диагональные элементы должны быть точно такими же.
По умолчанию SE прав в ОЧЕНЬ ограниченных обстоятельствах!
Цена неправильного
Мы не знаем, будет ли заявленная SE переоценена или недооценена истинная SE. Таким образом, мы можем получить:
- Статистически значимый результат, когда эффекта нет в реальности. В результате команде разработчиков программного обеспечения и продукта может потребоваться несколько часов работы над каким-либо прототипом, который никак не повлияет на итоговую прибыль компании.
- Статистически незначимый результат, когда в действительности наблюдается значительный эффект. Это могло быть для тебя перерывом. Упущенная возможность Очень плохо
На самом деле ложный позитив более вероятен.Там нет недостатка в новичках машинного обучения студентов, заявляющих, что они нашли какой-то шаблон / сигнал, чтобы побить рынок. Однако после развертывания их модели работают катастрофически. Частично причина в том, что они никогда не думали о последовательной или взаимной корреляции остатков.
Когда это происходит, стандартная ошибка по умолчанию может быть в 11 раз меньше, чем истинная стандартная ошибка, что приводит к серьезной переоценке статистической значимости их сигнала.
Надежная стандартная ошибка на помощь!
Правильно заданная надежная стандартная ошибка избавит от смещения или, по крайней мере, улучшит его. Вооружившись серьезной стандартной ошибкой, вы можете безопасно перейти к этапу вывода.
Есть много надежных стандартных ошибок. Выбор неправильного средства может усугубить проблему!
Какую робастную стандартную ошибку я должен использовать?
Это зависит от дисперсионно-ковариантной структуры. Спросите себя, страдает ли ваш остаток от взаимной корреляции, последовательной корреляции или от того и другого? Напомним, что:
- Кросс-корреляция:в течение одного и того же периода времени разные индивидуальные остатки могут быть коррелированы;
- Последовательная корреляция:для одного и того же лица остатки за разные периоды времени могут быть коррелированы
Случай 1: Термин ошибки имеет отдельный конкретный компонент
Предположим, что это истинное состояние мира:
При условии независимости от отдельных лиц, правильная стандартная ошибка будет:
Сравните это с (3), у нас есть дополнительный член, который обведен красным. Превышение или недооценка сообщаемой стандартной ошибки OLS истинной стандартной ошибки зависит от знака коэффициентов корреляции, который затем увеличивается на число периодов времени T.
Где практическое руководство?
Основываясь на большем количестве теории и результатов моделирования, Петерсен показывает, что:
Вы не должны использовать:
- Стандартные ошибки Fama-MacBeth:он предназначен для работы с последовательной корреляцией, а не с перекрестной корреляцией между отдельными фирмами.
- Стандартные ошибки Ньюи-Уэста:он предназначен для учета последовательной корреляции неизвестной формы в остатках одного временного ряда.
Вы должны использовать:
- Стандартные кластерные ошибки:в частности, вы должны объединить вашу стандартную ошибку по фирмам. Обратитесь к концу поста для кодов.
Случай 2: Термин ошибки имеет компонент, зависящий от времени
Предположим, что это истинное состояние мира:
Правильная стандартная ошибка по существу такая же, как (7), если вы поменяете N и T.
Вы должны использовать:
- Стандартные ошибки Fama-MacBeth:так как это то, что он создан для Обратитесь к концу поста для кода Stata.
Случай 3: Термин «ошибка» имеет как твердое, так и временное влияние
Предположим, что это истинное состояние мира:
Вы должны использовать:
- Кластерная стандартная ошибка:кластеризацию следует проводить по двум параметрам — по годам. Обратите внимание, что это не настоящие стандартные ошибки, они просто создают менее предвзятую стандартную ошибку. Смещение становится более выраженным, когда в одном измерении всего несколько кластеров.
коды
Подробные инструкции и тестовые данные Stata, R и SAS от Petersen можно найти Вот, Для моей собственной записи я собираю список кода Stata здесь:
Случай 1: кластеризация по 1 измерению
Регресс зависимая_вариантная независимая_вариабельная, надежный кластер (cluster_variable)
Случай 2: Фама-Макбет
tsset firm_identifier time_identifier
fm independent_variable independent_variables, byfm (by_variable)
Случай 3: кластеризация по двум измерениям
cluster2 зависимая_ переменная independent_variables, fcluster (cluster_variable_one) tcluster (cluster_variable_two)
Случай 4: фиксированный эффект + кластеризация
xtreg variable_variable independent_variables, надежный кластер (cluster_variable_one)
Наслаждайтесь своим недавно найденным крепким миром!
До следующего раза 
From Wikipedia, the free encyclopedia
The topic of heteroskedasticity-consistent (HC) standard errors arises in statistics and econometrics in the context of linear regression and time series analysis. These are also known as heteroskedasticity-robust standard errors (or simply robust standard errors), Eicker–Huber–White standard errors (also Huber–White standard errors or White standard errors),[1] to recognize the contributions of Friedhelm Eicker,[2] Peter J. Huber,[3] and Halbert White.[4]
In regression and time-series modelling, basic forms of models make use of the assumption that the errors or disturbances ui have the same variance across all observation points. When this is not the case, the errors are said to be heteroskedastic, or to have heteroskedasticity, and this behaviour will be reflected in the residuals 
Heteroskedasticity-consistent standard errors that differ from classical standard errors may indicate model misspecification. Substituting heteroskedasticity-consistent standard errors does not resolve this misspecification, which may lead to bias in the coefficients. In most situations, the problem should be found and fixed.[5] Other types of standard error adjustments, such as clustered standard errors or HAC standard errors, may be considered as extensions to HC standard errors.
History[edit]
Heteroskedasticity-consistent standard errors are introduced by Friedhelm Eicker,[6][7] and popularized in econometrics by Halbert White.
Problem[edit]
Consider the linear regression model for the scalar Y.
where 


The ordinary least squares (OLS) estimator is
where 



If the sample errors have equal variance 

where 
When the error terms do not have constant variance (i.e., the assumption of ![{displaystyle mathbb {E} [mathbf {u} mathbf {u} ^{top }]=sigma ^{2}mathbf {I} _{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c38bd674a3bee8eb6338750d7cf3d8ca9ea6911)
where ![{displaystyle mathbf {Sigma } =mathbb {V} [mathbf {u} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0f375e230fb618630294094fa481afa28f375a)
While the OLS point estimator remains unbiased, it is not «best» in the sense of having minimum mean square error, and the OLS variance estimator ![{displaystyle {hat {mathbb {V} }}left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc59a54a62987ab2c5d320a2382371a6d6d0f0e4)
For any non-linear model (for instance logit and probit models), however, heteroskedasticity has more severe consequences: the maximum likelihood estimates of the parameters will be biased (in an unknown direction), as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroskedasticity).[8][9] As pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption.”[10]
Solution[edit]
If the regression errors 



where as above 

Also often discussed in the literature (including White’s paper) is the covariance matrix 

where
and
Thus,
and
Precisely which covariance matrix is of concern is a matter of context.
Alternative estimators have been proposed in MacKinnon & White (1985) that correct for unequal variances of regression residuals due to different leverage.[11] Unlike the asymptotic White’s estimator, their estimators are unbiased when the data are homoscedastic.
Of the four widely available different options, often denoted as HC0-HC3, the HC3 specification appears to work best, with tests relying on the HC3 estimator featuring better power and closer proximity to the targetted size, especially in small samples. The larger the sample, the smaller the difference between the different estimators.[12]
An alternative to explicitly modelling the heteroskedasticity is using a resampling method such as the Wild Bootstrap. Given that the studentized Bootstrap, which standardizes the resampled statistic by its standard error, yields an asymptotic refinement,[13] heteroskedasticity-robust standard errors remain nevertheless useful.
Instead of accounting for the heteroskedastic errors, most linear models can be transformed to feature homoskedastic error terms (unless the error term is heteroskedastic by construction, e.g. in a Linear probability model). One way to do this is using Weighted least squares, which also features improved efficiency properties.
See also[edit]
- Delta method
- Generalized least squares
- Generalized estimating equations
- Weighted least squares, an alternative formulation
- White test — a test for whether heteroskedasticity is present.
- Newey–West estimator
- Quasi-maximum likelihood estimate
Software[edit]
- EViews: EViews version 8 offers three different methods for robust least squares: M-estimation (Huber, 1973), S-estimation (Rousseeuw and Yohai, 1984), and MM-estimation (Yohai 1987).[14]
- Julia: the
CovarianceMatricespackage offers several methods for heteroskedastic robust variance covariance matrices.[15] - MATLAB: See the
hacfunction in the Econometrics toolbox.[16] - Python: The Statsmodel package offers various robust standard error estimates, see statsmodels.regression.linear_model.RegressionResults for further descriptions
- R: the
vcovHC()command from the sandwich package.[17][18] - RATS: robusterrors option is available in many of the regression and optimization commands (linreg, nlls, etc.).
- Stata:
robustoption applicable in many pseudo-likelihood based procedures.[19] - Gretl: the option
--robustto several estimation commands (such asols) in the context of a cross-sectional dataset produces robust standard errors.[20]
References[edit]
- ^ Kleiber, C.; Zeileis, A. (2006). «Applied Econometrics with R» (PDF). UseR-2006 conference. Archived from the original (PDF) on April 22, 2007.
- ^ Eicker, Friedhelm (1967). «Limit Theorems for Regression with Unequal and Dependent Errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 59–82. MR 0214223. Zbl 0217.51201.
- ^ Huber, Peter J. (1967). «The behavior of maximum likelihood estimates under nonstandard conditions». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 221–233. MR 0216620. Zbl 0212.21504.
- ^ White, Halbert (1980). «A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity». Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934. MR 0575027.
- ^ King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015. ISSN 1047-1987.
- ^ Eicker, F. (1963). «Asymptotic Normality and Consistency of the Least Squares Estimators for Families of Linear Regressions». The Annals of Mathematical Statistics. 34 (2): 447–456. doi:10.1214/aoms/1177704156.
- ^ Eicker, Friedhelm (January 1967). «Limit theorems for regressions with unequal and dependent errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics. 5 (1): 59–83.
- ^ Giles, Dave (May 8, 2013). «Robust Standard Errors for Nonlinear Models». Econometrics Beat.
- ^ Guggisberg, Michael (2019). «Misspecified Discrete Choice Models and Huber-White Standard Errors». Journal of Econometric Methods. 8 (1). doi:10.1515/jem-2016-0002.
- ^ Greene, William H. (2012). Econometric Analysis (Seventh ed.). Boston: Pearson Education. pp. 692–693. ISBN 978-0-273-75356-8.
- ^ MacKinnon, James G.; White, Halbert (1985). «Some Heteroskedastic-Consistent Covariance Matrix Estimators with Improved Finite Sample Properties». Journal of Econometrics. 29 (3): 305–325. doi:10.1016/0304-4076(85)90158-7. hdl:10419/189084.
- ^ Long, J. Scott; Ervin, Laurie H. (2000). «Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model». The American Statistician. 54 (3): 217–224. doi:10.2307/2685594. ISSN 0003-1305.
- ^ C., Davison, Anthony (2010). Bootstrap methods and their application. Cambridge Univ. Press. ISBN 978-0-521-57391-7. OCLC 740960962.
- ^ «EViews 8 Robust Regression».
- ^ CovarianceMatrices: Robust Covariance Matrix Estimators
- ^ «Heteroskedasticity and autocorrelation consistent covariance estimators». Econometrics Toolbox.
- ^ sandwich: Robust Covariance Matrix Estimators
- ^ Kleiber, Christian; Zeileis, Achim (2008). Applied Econometrics with R. New York: Springer. pp. 106–110. ISBN 978-0-387-77316-2.
- ^ See online help for
_robustoption andregresscommand. - ^ «Robust covariance matrix estimation» (PDF). Gretl User’s Guide, chapter 19.
Further reading[edit]
- Freedman, David A. (2006). «On The So-Called ‘Huber Sandwich Estimator’ and ‘Robust Standard Errors’«. The American Statistician. 60 (4): 299–302. doi:10.1198/000313006X152207. S2CID 6222876.
- Hardin, James W. (2003). «The Sandwich Estimate of Variance». In Fomby, Thomas B.; Hill, R. Carter (eds.). Maximum Likelihood Estimation of Misspecified Models: Twenty Years Later. Amsterdam: Elsevier. pp. 45–74. ISBN 0-7623-1075-8.
- Hayes, Andrew F.; Cai, Li (2007). «Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation». Behavior Research Methods. 39 (4): 709–722. doi:10.3758/BF03192961. PMID 18183883.
- King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015.
- Wooldridge, Jeffrey M. (2009). «Heteroskedasticity-Robust Inference after OLS Estimation». Introductory Econometrics : A Modern Approach (Fourth ed.). Mason: South-Western. pp. 265–271. ISBN 978-0-324-66054-8.
- Buja, Andreas, et al. «Models as approximations-a conspiracy of random regressors and model deviations against classical inference in regression.» Statistical Science (2015): 1. pdf
From Wikipedia, the free encyclopedia
The topic of heteroskedasticity-consistent (HC) standard errors arises in statistics and econometrics in the context of linear regression and time series analysis. These are also known as heteroskedasticity-robust standard errors (or simply robust standard errors), Eicker–Huber–White standard errors (also Huber–White standard errors or White standard errors),[1] to recognize the contributions of Friedhelm Eicker,[2] Peter J. Huber,[3] and Halbert White.[4]
In regression and time-series modelling, basic forms of models make use of the assumption that the errors or disturbances ui have the same variance across all observation points. When this is not the case, the errors are said to be heteroskedastic, or to have heteroskedasticity, and this behaviour will be reflected in the residuals 
Heteroskedasticity-consistent standard errors that differ from classical standard errors may indicate model misspecification. Substituting heteroskedasticity-consistent standard errors does not resolve this misspecification, which may lead to bias in the coefficients. In most situations, the problem should be found and fixed.[5] Other types of standard error adjustments, such as clustered standard errors or HAC standard errors, may be considered as extensions to HC standard errors.
History[edit]
Heteroskedasticity-consistent standard errors are introduced by Friedhelm Eicker,[6][7] and popularized in econometrics by Halbert White.
Problem[edit]
Consider the linear regression model for the scalar Y.
where 


The ordinary least squares (OLS) estimator is
where 



If the sample errors have equal variance 

where 
When the error terms do not have constant variance (i.e., the assumption of ![{displaystyle mathbb {E} [mathbf {u} mathbf {u} ^{top }]=sigma ^{2}mathbf {I} _{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c38bd674a3bee8eb6338750d7cf3d8ca9ea6911)
where ![{displaystyle mathbf {Sigma } =mathbb {V} [mathbf {u} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0f375e230fb618630294094fa481afa28f375a)
While the OLS point estimator remains unbiased, it is not «best» in the sense of having minimum mean square error, and the OLS variance estimator ![{displaystyle {hat {mathbb {V} }}left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc59a54a62987ab2c5d320a2382371a6d6d0f0e4)
For any non-linear model (for instance logit and probit models), however, heteroskedasticity has more severe consequences: the maximum likelihood estimates of the parameters will be biased (in an unknown direction), as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroskedasticity).[8][9] As pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption.”[10]
Solution[edit]
If the regression errors 



where as above 

Also often discussed in the literature (including White’s paper) is the covariance matrix 

where
and
Thus,
and
Precisely which covariance matrix is of concern is a matter of context.
Alternative estimators have been proposed in MacKinnon & White (1985) that correct for unequal variances of regression residuals due to different leverage.[11] Unlike the asymptotic White’s estimator, their estimators are unbiased when the data are homoscedastic.
Of the four widely available different options, often denoted as HC0-HC3, the HC3 specification appears to work best, with tests relying on the HC3 estimator featuring better power and closer proximity to the targetted size, especially in small samples. The larger the sample, the smaller the difference between the different estimators.[12]
An alternative to explicitly modelling the heteroskedasticity is using a resampling method such as the Wild Bootstrap. Given that the studentized Bootstrap, which standardizes the resampled statistic by its standard error, yields an asymptotic refinement,[13] heteroskedasticity-robust standard errors remain nevertheless useful.
Instead of accounting for the heteroskedastic errors, most linear models can be transformed to feature homoskedastic error terms (unless the error term is heteroskedastic by construction, e.g. in a Linear probability model). One way to do this is using Weighted least squares, which also features improved efficiency properties.
See also[edit]
- Delta method
- Generalized least squares
- Generalized estimating equations
- Weighted least squares, an alternative formulation
- White test — a test for whether heteroskedasticity is present.
- Newey–West estimator
- Quasi-maximum likelihood estimate
Software[edit]
- EViews: EViews version 8 offers three different methods for robust least squares: M-estimation (Huber, 1973), S-estimation (Rousseeuw and Yohai, 1984), and MM-estimation (Yohai 1987).[14]
- Julia: the
CovarianceMatricespackage offers several methods for heteroskedastic robust variance covariance matrices.[15] - MATLAB: See the
hacfunction in the Econometrics toolbox.[16] - Python: The Statsmodel package offers various robust standard error estimates, see statsmodels.regression.linear_model.RegressionResults for further descriptions
- R: the
vcovHC()command from the sandwich package.[17][18] - RATS: robusterrors option is available in many of the regression and optimization commands (linreg, nlls, etc.).
- Stata:
robustoption applicable in many pseudo-likelihood based procedures.[19] - Gretl: the option
--robustto several estimation commands (such asols) in the context of a cross-sectional dataset produces robust standard errors.[20]
References[edit]
- ^ Kleiber, C.; Zeileis, A. (2006). «Applied Econometrics with R» (PDF). UseR-2006 conference. Archived from the original (PDF) on April 22, 2007.
- ^ Eicker, Friedhelm (1967). «Limit Theorems for Regression with Unequal and Dependent Errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 59–82. MR 0214223. Zbl 0217.51201.
- ^ Huber, Peter J. (1967). «The behavior of maximum likelihood estimates under nonstandard conditions». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 221–233. MR 0216620. Zbl 0212.21504.
- ^ White, Halbert (1980). «A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity». Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934. MR 0575027.
- ^ King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015. ISSN 1047-1987.
- ^ Eicker, F. (1963). «Asymptotic Normality and Consistency of the Least Squares Estimators for Families of Linear Regressions». The Annals of Mathematical Statistics. 34 (2): 447–456. doi:10.1214/aoms/1177704156.
- ^ Eicker, Friedhelm (January 1967). «Limit theorems for regressions with unequal and dependent errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics. 5 (1): 59–83.
- ^ Giles, Dave (May 8, 2013). «Robust Standard Errors for Nonlinear Models». Econometrics Beat.
- ^ Guggisberg, Michael (2019). «Misspecified Discrete Choice Models and Huber-White Standard Errors». Journal of Econometric Methods. 8 (1). doi:10.1515/jem-2016-0002.
- ^ Greene, William H. (2012). Econometric Analysis (Seventh ed.). Boston: Pearson Education. pp. 692–693. ISBN 978-0-273-75356-8.
- ^ MacKinnon, James G.; White, Halbert (1985). «Some Heteroskedastic-Consistent Covariance Matrix Estimators with Improved Finite Sample Properties». Journal of Econometrics. 29 (3): 305–325. doi:10.1016/0304-4076(85)90158-7. hdl:10419/189084.
- ^ Long, J. Scott; Ervin, Laurie H. (2000). «Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model». The American Statistician. 54 (3): 217–224. doi:10.2307/2685594. ISSN 0003-1305.
- ^ C., Davison, Anthony (2010). Bootstrap methods and their application. Cambridge Univ. Press. ISBN 978-0-521-57391-7. OCLC 740960962.
- ^ «EViews 8 Robust Regression».
- ^ CovarianceMatrices: Robust Covariance Matrix Estimators
- ^ «Heteroskedasticity and autocorrelation consistent covariance estimators». Econometrics Toolbox.
- ^ sandwich: Robust Covariance Matrix Estimators
- ^ Kleiber, Christian; Zeileis, Achim (2008). Applied Econometrics with R. New York: Springer. pp. 106–110. ISBN 978-0-387-77316-2.
- ^ See online help for
_robustoption andregresscommand. - ^ «Robust covariance matrix estimation» (PDF). Gretl User’s Guide, chapter 19.
Further reading[edit]
- Freedman, David A. (2006). «On The So-Called ‘Huber Sandwich Estimator’ and ‘Robust Standard Errors’«. The American Statistician. 60 (4): 299–302. doi:10.1198/000313006X152207. S2CID 6222876.
- Hardin, James W. (2003). «The Sandwich Estimate of Variance». In Fomby, Thomas B.; Hill, R. Carter (eds.). Maximum Likelihood Estimation of Misspecified Models: Twenty Years Later. Amsterdam: Elsevier. pp. 45–74. ISBN 0-7623-1075-8.
- Hayes, Andrew F.; Cai, Li (2007). «Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation». Behavior Research Methods. 39 (4): 709–722. doi:10.3758/BF03192961. PMID 18183883.
- King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015.
- Wooldridge, Jeffrey M. (2009). «Heteroskedasticity-Robust Inference after OLS Estimation». Introductory Econometrics : A Modern Approach (Fourth ed.). Mason: South-Western. pp. 265–271. ISBN 978-0-324-66054-8.
- Buja, Andreas, et al. «Models as approximations-a conspiracy of random regressors and model deviations against classical inference in regression.» Statistical Science (2015): 1. pdf
Всегда сообщать о надежных (белых) стандартных ошибках?
Angrist и Pischke предположили, что устойчивые (то есть устойчивые к гетероскедастичности или неравные отклонения) стандартные ошибки сообщаются как нечто само собой разумеющееся, а не как их проверка. Два вопроса:
- Как это влияет на стандартные ошибки при этом, когда есть гомоскедастичность?
- Кто-нибудь на самом деле делает это в своей работе?
Ответы:
Использование надежных стандартных ошибок стало обычной практикой в экономике. Надежные стандартные ошибки обычно больше, чем нестабильные (стандартные?) Стандартные ошибки, поэтому эту практику можно рассматривать как попытку быть консервативным.
В больших выборках ( например, если вы работаете с данными переписи с миллионами наблюдений или наборами данных с «всего лишь» тысячами наблюдений), тесты гетероскедастичности почти наверняка окажутся положительными, поэтому такой подход уместен.
Другим средством борьбы с гетероскедастичностью являются взвешенные наименьшие квадраты, но на этот подход не обращают внимания, потому что он изменяет оценки параметров, в отличие от использования устойчивых стандартных ошибок. Если ваш вес неверен, ваши оценки смещены. Однако, если ваш вес верен, вы получаете меньшие («более эффективные») стандартные ошибки, чем OLS с устойчивыми стандартными ошибками.
Во Вводной эконометрике (Woolridge, выпуск 2009, стр. 268) этот вопрос рассматривается. Вулридж говорит, что при использовании устойчивых стандартных ошибок полученная t-статистика имеет распределения, которые похожи на точные t-распределения, если размер выборки велик. Если размер выборки невелик, t-статистика, полученная с помощью надежной регрессии, может иметь распределения, не близкие к t-распределению, и это может отбросить вывод.
Надежные стандартные ошибки обеспечивают объективные оценки стандартных ошибок при гетероскедастичности. Существует несколько статистических учебников, в которых содержится обширное и длительное обсуждение надежных стандартных ошибок. На следующем сайте приведено несколько исчерпывающее резюме об основных стандартных ошибках:
Возвращаясь к вашим вопросам. Использование надежных стандартных ошибок не обходится без предостережений. Согласно Вулриджу (издание 2009 г., стр. 268), в котором используются надежные стандартные ошибки, полученная t-статистика имеет распределения, которые похожи на точные t-распределения, только если размер выборки велик. Если размер выборки невелик, t-статистика, полученная с помощью надежной регрессии, может иметь распределения, не близкие к t-распределению. Это может скинуть вывод. Кроме того, в случае гомоскедастичности устойчивые стандартные ошибки все еще несмещены. Однако они не эффективны. То есть обычные стандартные ошибки являются более точными, чем устойчивые стандартные ошибки. Наконец, использование надежных стандартных ошибок является обычной практикой во многих академических областях.
Есть много причин, чтобы избежать использования надежных стандартных ошибок. Технически, что происходит, так это то, что отклонения взвешиваются на весах, которые вы не можете доказать в реальности. Таким образом, грубость — это просто косметический инструмент. В общем, вы должны помнить о смене модели. Есть много последствий, чтобы иметь дело с гетерогенностью лучше, чем просто закрашивать проблему, возникающую из ваших данных. Воспринимайте это как знак переключения модели. Вопрос тесно связан с вопросом, как бороться с выбросами. Если люди просто удаляют их, чтобы получить лучшие результаты, то же самое происходит при использовании надежных стандартных ошибок, просто в другом контексте.
Я думал, что стандартная ошибка Уайта и стандартная ошибка, вычисленные «нормальным» способом (например, Гессианом и / или OPG в случае максимальной вероятности), были асимптотически эквивалентны в случае гомоскедастичности?
Только при наличии гетероскедастичности «нормальная» стандартная ошибка будет неуместна, что означает, что стандартная ошибка Уайта подходит для гетероскедастичности или без нее, то есть даже если ваша модель гомоскедастична.
Я не могу говорить о 2, но я не понимаю, почему никто не хотел бы рассчитывать White SE и включать в результаты.
У меня есть учебник под названием Введение в эконометрику, 3-е изд. Стоком и Уотсоном, который гласит: «если ошибки гетероскедастичны, то t-статистика, вычисленная с использованием стандартной ошибки только для гомоскедастичности, не имеет стандартного нормального распределения даже в больших выборках». Я полагаю, что вы не сможете провести правильное тестирование логических выводов / гипотез, не имея возможности предположить, что ваша t-статистика распределена как стандартная норма. Я очень уважаю Вулдриджа (фактически, мой выпускник также использовал его книгу), поэтому я считаю, что то, что он говорит о t-stats с использованием надежных SE, требует больших выборок, чтобы быть подходящим, определенно правильно, но я думаю, что мы часто приходится иметь дело с требованием крупной выборки, и мы это принимаем. Однако тот факт, что использование нестабильных SE не даст t-stat с надлежащим стандартным нормальным распределениемдаже если у вас есть большая выборка, вам придется преодолеть гораздо большую проблему.
В R, как я могу вычислить надежные стандартные ошибки, используя vcovHC(), когда некоторые коэффициенты отбрасываются из-за особенностей? Стандартная функция lm, по-видимому, делает правильный расчет стандартных стандартных ошибок для всех фактически оцененных коэффициентов, но vcovHC() выдает ошибку: “Ошибка в хлебе.% *% Мяса.: Несоответствующие аргументы”.
(Фактические данные, которые я использую, немного сложнее. Фактически, это модель, использующая два разных фиксированных эффекта, и я сталкиваюсь с локальными особенностями, от которых я не могу просто избавиться. По крайней мере, я не знал бы, как. Для двух фиксированных эффектов, которые я использую, первый фактор имеет 150 уровней, второй имеет 142 уровня и всего 9 особенностей, которые являются результатом того, что данные были собраны в десять блоков.)
Вот мой вывод:
Call:
lm(formula = one ~ two + three + Jan + Feb + Mar + Apr + May +
Jun + Jul + Aug + Sep + Oct + Nov + Dec, data = dat)
Residuals:
Min 1Q Median 3Q Max
-130.12 -60.95 0.08 61.05 137.35
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1169.74313 57.36807 20.390 <2e-16 ***
two -0.07963 0.06720 -1.185 0.237
three -0.04053 0.06686 -0.606 0.545
Jan 8.10336 22.05552 0.367 0.714
Feb 0.44025 22.11275 0.020 0.984
Mar 19.65066 22.02454 0.892 0.373
Apr -13.19779 22.02886 -0.599 0.550
May 15.39534 22.10445 0.696 0.487
Jun -12.50227 22.07013 -0.566 0.572
Jul -20.58648 22.06772 -0.933 0.352
Aug -0.72223 22.36923 -0.032 0.974
Sep 12.42204 22.09296 0.562 0.574
Oct 25.14836 22.04324 1.141 0.255
Nov 18.13337 22.08717 0.821 0.413
Dec NA NA NA NA
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 69.63 on 226 degrees of freedom
Multiple R-squared: 0.04878, Adjusted R-squared: -0.005939
F-statistic: 0.8914 on 13 and 226 DF, p-value: 0.5629
> model$se <- vcovHC(model)
Error in bread. %*% meat. : non-conformable arguments
Ниже приведен минимальный код для копирования ошибки.
library(sandwich)
set.seed(101)
dat<-data.frame(one=c(sample(1000:1239)),
two=c(sample(200:439)),
three=c(sample(600:839)),
Jan=c(rep(1,20),rep(0,220)),
Feb=c(rep(0,20),rep(1,20),rep(0,200)),
Mar=c(rep(0,40),rep(1,20),rep(0,180)),
Apr=c(rep(0,60),rep(1,20),rep(0,160)),
May=c(rep(0,80),rep(1,20),rep(0,140)),
Jun=c(rep(0,100),rep(1,20),rep(0,120)),
Jul=c(rep(0,120),rep(1,20),rep(0,100)),
Aug=c(rep(0,140),rep(1,20),rep(0,80)),
Sep=c(rep(0,160),rep(1,20),rep(0,60)),
Oct=c(rep(0,180),rep(1,20),rep(0,40)),
Nov=c(rep(0,200),rep(1,20),rep(0,20)),
Dec=c(rep(0,220),rep(1,20)))
model <- lm(one ~ two + three + Jan + Feb + Mar + Apr + May + Jun + Jul + Aug + Sep + Oct + Nov + Dec, data=dat)
summary(model)
model$se <- vcovHC(model)
Модели с особенностями никогда не бывают хорошими, и они должны быть исправлены. В вашем случае у вас есть 12 коэффициентов за 12 месяцев, а также глобальный перехват! Таким образом, у вас есть 13 коэффициентов для оценки только 12 реальных параметров. На самом деле вы хотите отключить глобальный перехват – так что у вас будет что-то большее, чем месячный перехват:
> model <- lm(one ~ 0 + two + three + Jan + Feb + Mar + Apr + May + Jun + Jul + Aug + Sep + Oct + Nov + Dec, data=dat)
> summary(model)
Call:
lm(formula = one ~ 0 + two + three + Jan + Feb + Mar + Apr +
May + Jun + Jul + Aug + Sep + Oct + Nov + Dec, data = dat)
Residuals:
Min 1Q Median 3Q Max
-133.817 -55.636 3.329 56.768 126.772
Coefficients:
Estimate Std. Error t value Pr(>|t|)
two -0.09670 0.06621 -1.460 0.146
three 0.02446 0.06666 0.367 0.714
Jan 1130.05812 52.79625 21.404 <2e-16 ***
Feb 1121.32904 55.18864 20.318 <2e-16 ***
Mar 1143.50310 53.59603 21.336 <2e-16 ***
Apr 1143.95365 54.99724 20.800 <2e-16 ***
May 1136.36429 53.38218 21.287 <2e-16 ***
Jun 1129.86010 53.85865 20.978 <2e-16 ***
Jul 1105.10045 54.94940 20.111 <2e-16 ***
Aug 1147.47152 54.57201 21.027 <2e-16 ***
Sep 1139.42205 53.58611 21.263 <2e-16 ***
Oct 1117.75075 55.35703 20.192 <2e-16 ***
Nov 1129.20208 53.54934 21.087 <2e-16 ***
Dec 1149.55556 53.52499 21.477 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 69.81 on 226 degrees of freedom
Multiple R-squared: 0.9964, Adjusted R-squared: 0.9961
F-statistic: 4409 on 14 and 226 DF, p-value: < 2.2e-16
Тогда это нормальная модель, поэтому у вас не должно быть проблем с vcovHC.
















![{displaystyle {hat {mathbb {V} }}left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]=s^{2}(mathbf {X} ^{top }mathbf {X} )^{-1},quad s^{2}={frac {sum _{i}{widehat {varepsilon }}_{i}^{2}}{n-k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd3f9d86ee8777e0132005ee7b87df048a68faf2)
![{displaystyle mathbb {V} left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]=mathbb {V} {big [}(mathbf {X} ^{top }mathbf {X} )^{-1}mathbf {X} ^{top }mathbf {y} {big ]}=(mathbf {X} ^{top }mathbf {X} )^{-1}mathbf {X} ^{top }mathbf {Sigma } mathbf {X} (mathbf {X} ^{top }mathbf {X} )^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb6038998637f73772725897a122b21a316afdc)
![{displaystyle {begin{aligned}{hat {mathbb {V} }}_{text{HCE}}{big [}{widehat {boldsymbol {beta }}}_{text{OLS}}{big ]}&={frac {1}{n}}{bigg (}{frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{bigg )}^{-1}{bigg (}{frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{widehat {varepsilon }}_{i}^{2}{bigg )}{bigg (}{frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{bigg )}^{-1}\&=(mathbf {X} ^{top }mathbf {X} )^{-1}(mathbf {X} ^{top }operatorname {diag} ({widehat {varepsilon }}_{1}^{2},ldots ,{widehat {varepsilon }}_{n}^{2})mathbf {X} )(mathbf {X} ^{top }mathbf {X} )^{-1},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08d4969a485cdb096fa33d08f7ae04e9d737321b)

![{displaystyle mathbf {Omega } =mathbb {E} [mathbf {X} mathbf {X} ^{top }]^{-1}mathbb {V} [mathbf {X} {boldsymbol {varepsilon }}]operatorname {mathbb {E} } [mathbf {X} mathbf {X} ^{top }]^{-1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35f99e141af80fcd8b22b13dc813519750b87466)

![{displaystyle {widehat {mathbf {Omega } }}_{n}=ncdot {hat {mathbb {V} }}_{text{HCE}}[{widehat {boldsymbol {beta }}}_{text{OLS}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff3af664b1167a553ee899c04356bf8a94df127f)
![{displaystyle {widehat {mathbb {V} }}[mathbf {X} {boldsymbol {varepsilon }}]={frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{widehat {varepsilon }}_{i}^{2}={frac {1}{n}}mathbf {X} ^{top }operatorname {diag} ({widehat {varepsilon }}_{1}^{2},ldots ,{widehat {varepsilon }}_{n}^{2})mathbf {X} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1acd9bb6f131b50940af0e03ee47a684d0a76f8)