Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
Из генеральной
совокупности извлечена выборка объема
n=50:
-
Варианта
x
2
5
7
10
Частота
n
16
12
8
14
Найти
несмещенную оценку генеральной средней.
Решение:
Несмещенной оценкой генеральной средней
является выборочная средняя n=16+12+8+14=50
Ответ:
5,76.
Пример 2
Из
генеральной совокупности извлечена
выборка объема n
:
-
x
1
3
6
26
n
8
40
10
2
Найти
несмещенную оценку генеральной средней.
Решение:
Ответ:4.
Пример 3
По выборке объема
n=41
найдена смещенная оценка D
генеральной дисперсии. Найти несмещенную
оценку дисперсии генеральной совокупности
.
Решение: Искомая
несмещенная оценка дисперсии ген.
совокупности равна исправленной
дисперсии: S
Ответ:
3,075.
Задание 1.Найти
выборочную среднюю по данному распределению
выборки объема n=10:
-
x
1250
1270
1280
n
2
5
3
Ответ:
1269
Задание
2. Найти выборочную среднюю по данному
распределению выборки объема n=20:
-
x
2560
2600
2620
2650
2700
n
2
3
10
4
1
Указание:
Перейти к условным вариантам U
Задание 3. По
выборке объема n=51
найдена смещенная оценка D
ген. дисперсии. Найти несмещенную оценку
дисперсии ген. совокупности.
Ответ:
5,1
Задание 4. В итоге пяти измерений длины стержня одним прибором (без систематических ошибок) получены следующие результаты (в мм.): 92;94;103;105;106.
Найти: a)
выборочную среднюю длину стержня; b)
выборочную и исправленную дисперсии
ошибок прибора. Взяли C=92
Ответ:
Задание 5. В
итоге четырех измерений некоторой
физической величины одним прибором
(без систематических ошибок) получены
следующие результаты: 8;9;11;12.
Найти: a)
выборочную среднюю результатов измерений;
b)
выборочную и исправленную дисперсии
ошибок прибора.
Ответ:
Задание 6. Ниже
приведены результаты измерения роста
(в см.) случайно отобранных 100 студентов.
|
Рост |
154-158 |
158-162 |
162-166 |
166-170 |
170-174 |
174-178 |
178-182 |
|
Число студентов |
10 |
14 |
26 |
28 |
12 |
8 |
2 |
Найти
выборочную среднюю и выборочную дисперсию
роста обследованных студентов.
Указание:
Найти середины интервала и принять их
в качестве вариант.
Ответ:
Задание 7. Найти
выборочную дисперсию по данному
распределению выборки объема n=10:
-
x
186
192
194
n
2
5
3
Ответ:
D
Задание 8. Найти
выборочную дисперсию по данному
распределению выборки объема n=100:
-
x
340
360
375
380
n
20
50
18
12
Указание:
Перейти к условным вариантам U
Ответ:
D
Задание 9.Найти
выборочную дисперсию по данному
распределению выборки объема n=100:
-
x
2502
2804
2903
3028
n
8
30
60
2
Указание:
Перейти к условным вариантам U
Задание
10. Найти выборочную дисперсию по данному
распределению выборки объема n=10:
-
x
0,01
0,04
0,08
n
5
3
2
Ответ:
Задание
11.Покажите,
что при наличии n
наблюдений условием того, чтобы обобщенная
формула (λ1х1
+…+λnxn)
давала несмещенную оценку μ, является
λ1
+…+ λn=1.
Контрольные
вопросы
-
Дать
определение точечной, несмещенной,
смещенной оценки. -
По
какой формуле определяется выборочная
дисперсия
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Тренируй мозг с удовольствием
Развивай память, внимание и мышление c помощью онлайн-тренажеров
Выбрать программу
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_г=sqrt{D_г}]
Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
«Дисперсия: генеральная, выборочная, исправленная» 👇
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_в=sqrt{D_в}]
Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
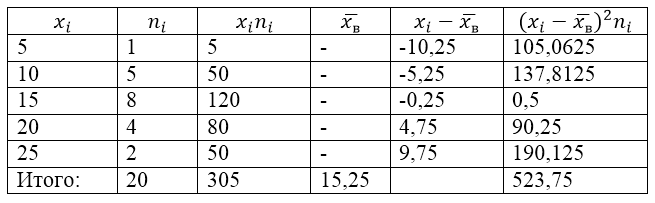
Для решения этой задачи для начала сделаем расчетную таблицу:
Рисунок 2.
Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
То есть
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Найдем выборочную дисперсию по формуле:
[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]
Выборочное среднее квадратическое отклонение:
[{sigma }_в=sqrt{D_в}approx 5,12]
Исправленная дисперсия:
[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]
Исправленное среднее квадратическое отклонение:
[S=sqrt{S^2}approx 5,25]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме