Near shannon limit error correcting coding and decoding turbo codes

From Wikipedia, the free encyclopedia

In information theory, turbo codes (originally in French Turbocodes) are a class of high-performance forward error correction (FEC) codes developed around 1990–91, but first published in 1993. They were the first practical codes to closely approach the maximum channel capacity or Shannon limit, a theoretical maximum for the code rate at which reliable communication is still possible given a specific noise level. Turbo codes are used in 3G/4G mobile communications (e.g., in UMTS and LTE) and in (deep space) satellite communications as well as other applications where designers seek to achieve reliable information transfer over bandwidth- or latency-constrained communication links in the presence of data-corrupting noise. Turbo codes compete with low-density parity-check (LDPC) codes, which provide similar performance.

The name «turbo code» arose from the feedback loop used during normal turbo code decoding, which was analogized to the exhaust feedback used for engine turbocharging. Hagenauer has argued the term turbo code is a misnomer since there is no feedback involved in the encoding process.^[1]

History[edit]

The fundamental patent application for turbo codes was filed on 23 April 1991. The patent application lists Claude Berrou as the sole inventor of turbo codes. The patent filing resulted in several patents including US Patent 5,446,747, which expired 29 August 2013.

The first public paper on turbo codes was «Near Shannon Limit Error-correcting Coding and Decoding: Turbo-codes«.^[2] This paper was published 1993 in the Proceedings of IEEE International Communications Conference. The 1993 paper was formed from three separate submissions that were combined due to space constraints. The merger caused the paper to list three authors: Berrou, Glavieux, and Thitimajshima (from Télécom Bretagne, former ENST Bretagne, France). However, it is clear from the original patent filing that Berrou is the sole inventor of turbo codes and that the other authors of the paper contributed material other than the core concepts.^{[improper synthesis]}

Turbo codes were so revolutionary at the time of their introduction that many experts in the field of coding did not believe the reported results. When the performance was confirmed a small revolution in the world of coding took place that led to the investigation of many other types of iterative signal processing.

The first class of turbo code was the parallel concatenated convolutional code (PCCC). Since the introduction of the original parallel turbo codes in 1993, many other classes of turbo code have been discovered, including serial versions serial concatenated convolutional codes and repeat-accumulate codes. Iterative turbo decoding methods have also been applied to more conventional FEC systems, including Reed–Solomon corrected convolutional codes, although these systems are too complex for practical implementations of iterative decoders. Turbo equalization also flowed from the concept of turbo coding.

In addition to turbo codes, Berrou also invented recursive systematic convolutional (RSC) codes, which are used in the example implementation of turbo codes described in the patent. Turbo codes that use RSC codes seem to perform better than turbo codes that do not use RSC codes.

Prior to turbo codes, the best constructions were serial concatenated codes based on an outer Reed–Solomon error correction code combined with an inner Viterbi-decoded short constraint length convolutional code, also known as RSV codes.

In a later paper, Berrou gave credit to the intuition of «G. Battail, J. Hagenauer and P. Hoeher, who, in the late 80s, highlighted the interest of probabilistic processing.» He adds «R. Gallager and M. Tanner had already imagined coding and decoding techniques whose general principles are closely related,» although the necessary calculations were impractical at that time.^[3]

An example encoder[edit]

There are many different instances of turbo codes, using different component encoders, input/output ratios, interleavers, and puncturing patterns. This example encoder implementation describes a classic turbo encoder, and demonstrates the general design of parallel turbo codes.

This encoder implementation sends three sub-blocks of bits. The first sub-block is the m-bit block of payload data. The second sub-block is n/2 parity bits for the payload data, computed using a recursive systematic convolutional code (RSC code). The third sub-block is n/2 parity bits for a known permutation of the payload data, again computed using an RSC code. Thus, two redundant but different sub-blocks of parity bits are sent with the payload. The complete block has m + n bits of data with a code rate of m/(m + n). The permutation of the payload data is carried out by a device called an interleaver.

Hardware-wise, this turbo code encoder consists of two identical RSC coders, C₁ and C₂, as depicted in the figure, which are connected to each other using a concatenation scheme, called parallel concatenation:

In the figure, M is a memory register. The delay line and interleaver force input bits d_k to appear in different sequences.
At first iteration, the input sequence d_k appears at both outputs of the encoder, x_k and y_1k or y_2k due to the encoder’s systematic nature. If the encoders C₁ and C₂ are used in n₁ and n₂ iterations, their rates are respectively equal to

The decoder[edit]

The decoder is built in a similar way to the above encoder. Two elementary decoders are interconnected to each other, but in series, not in parallel. The decoder operates on lower speed (i.e., ), thus, it is intended for the encoder, and is for correspondingly. yields a soft decision which causes delay. The same delay is caused by the delay line in the encoder. The ‘s operation causes delay.

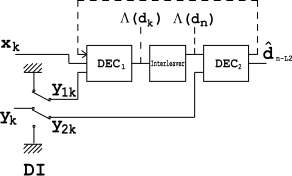
An interleaver installed between the two decoders is used here to scatter error bursts coming from output. DI block is a demultiplexing and insertion module. It works as a switch, redirecting input bits to at one moment and to at another. In OFF state, it feeds both and inputs with padding bits (zeros).

Consider a memoryless AWGN channel, and assume that at k-th iteration, the decoder receives a pair of random variables:

where and are independent noise components having the same variance . is a k-th bit from encoder output.

Redundant information is demultiplexed and sent through DI to (when ) and to (when ).

yields a soft decision; i.e.:

and delivers it to . is called the logarithm of the likelihood ratio (LLR). is the a posteriori probability (APP) of the data bit which shows the probability of interpreting a received bit as . Taking the LLR into account, yields a hard decision; i.e., a decoded bit.

It is known that the Viterbi algorithm is unable to calculate APP, thus it cannot be used in . Instead of that, a modified BCJR algorithm is used. For , the Viterbi algorithm is an appropriate one.

However, the depicted structure is not an optimal one, because uses only a proper fraction of the available redundant information. In order to improve the structure, a feedback loop is used (see the dotted line on the figure).

Soft decision approach[edit]

The decoder front-end produces an integer for each bit in the data stream. This integer is a measure of how likely it is that the bit is a 0 or 1 and is also called soft bit. The integer could be drawn from the range [−127, 127], where:

• −127 means «certainly 0»
• −100 means «very likely 0»
• 0 means «it could be either 0 or 1»
• 100 means «very likely 1»
• 127 means «certainly 1»

This introduces a probabilistic aspect to the data-stream from the front end, but it conveys more information about each bit than just 0 or 1.

For example, for each bit, the front end of a traditional wireless-receiver has to decide if an internal analog voltage is above or below a given threshold voltage level. For a turbo code decoder, the front end would provide an integer measure of how far the internal voltage is from the given threshold.

To decode the m + n-bit block of data, the decoder front-end creates a block of likelihood measures, with one likelihood measure for each bit in the data stream. There are two parallel decoders, one for each of the n⁄2-bit parity sub-blocks. Both decoders use the sub-block of m likelihoods for the payload data. The decoder working on the second parity sub-block knows the permutation that the coder used for this sub-block.

Solving hypotheses to find bits[edit]

The key innovation of turbo codes is how they use the likelihood data to reconcile differences between the two decoders. Each of the two convolutional decoders generates a hypothesis (with derived likelihoods) for the pattern of m bits in the payload sub-block. The hypothesis bit-patterns are compared, and if they differ, the decoders exchange the derived likelihoods they have for each bit in the hypotheses. Each decoder incorporates the derived likelihood estimates from the other decoder to generate a new hypothesis for the bits in the payload. Then they compare these new hypotheses. This iterative process continues until the two decoders come up with the same hypothesis for the m-bit pattern of the payload, typically in 15 to 18 cycles.

An analogy can be drawn between this process and that of solving cross-reference puzzles like crossword or sudoku. Consider a partially completed, possibly garbled crossword puzzle. Two puzzle solvers (decoders) are trying to solve it: one possessing only the «down» clues (parity bits), and the other possessing only the «across» clues. To start, both solvers guess the answers (hypotheses) to their own clues, noting down how confident they are in each letter (payload bit). Then, they compare notes, by exchanging answers and confidence ratings with each other, noticing where and how they differ. Based on this new knowledge, they both come up with updated answers and confidence ratings, repeating the whole process until they converge to the same solution.

Performance[edit]

Turbo codes perform well due to the attractive combination of the code’s random appearance on the channel together with the physically realisable decoding structure. Turbo codes are affected by an error floor.

Practical applications using turbo codes[edit]

Telecommunications:

• Turbo codes are used extensively in 3G and 4G mobile telephony standards; e.g., in HSPA, EV-DO and LTE.
• MediaFLO, terrestrial mobile television system from Qualcomm.
• The interaction channel of satellite communication systems, such as DVB-RCS^[4] and DVB-RCS2.
• Recent NASA missions such as Mars Reconnaissance Orbiter use turbo codes as an alternative to Reed–Solomon error correction-Viterbi decoder codes.
• IEEE 802.16 (WiMAX), a wireless metropolitan network standard, uses block turbo coding and convolutional turbo coding.

Bayesian formulation[edit]

From an artificial intelligence viewpoint, turbo codes can be considered as an instance of loopy belief propagation in Bayesian networks.^[5]

See also[edit]

• Convolutional code
• Viterbi algorithm
• Soft-decision decoding
• Interleaver
• BCJR algorithm
• Low-density parity-check code
• Serial concatenated convolutional codes
• Turbo equalizer
• Forward error correction

References[edit]

Further reading[edit]

Publications[edit]

• Battail, Gérard. «A conceptual framework for understanding turbo codes.» IEEE Journal on Selected Areas in Communications 16.2 (1998): 245–254.
• Brejza, Matthew F., et al. «20 years of turbo coding and energy-aware design guidelines for energy-constrained wireless applications.» IEEE Communications Surveys & Tutorials 18.1 (2016): 8–28.
• Garzón-Bohórquez, Ronald, Charbel Abdel Nour, and Catherine Douillard. «Improving Turbo codes for 5G with parity puncture-constrained interleavers.» Turbo Codes and Iterative Information Processing (ISTC), 2016 9th International Symposium on. IEEE, 2016.

External links[edit]

• «Closing In On The Perfect Code», IEEE Spectrum, March 2004
• «The UMTS Turbo Code and an Efficient Decoder Implementation Suitable for Software-Defined Radios» (International Journal of Wireless Information Networks)
• Dana Mackenzie (2005), «Take it to the limit», New Scientist, 187 (2507): 38–41, ISSN 0262-4079. (preview, copy)
• «Pushing the Limit», a Science News feature about the development and genesis of turbo codes
• International Symposium On Turbo Codes
• Coded Modulation Library, an open source library for simulating turbo codes in matlab
• «Turbo Equalization: Principles and New Results», an IEEE Transactions on Communications article about using convolutional codes jointly with channel equalization.
• IT++ Home Page The IT++ is a powerful C++ library which in particular supports turbo codes
• Turbo codes publications by David MacKay
• AFF3CT Home Page (A Fast Forward Error Correction Toolbox) for high speed turbo codes simulations in software
• Turbo code by Dr. Sylvie Kerouédan and Dr. Claude Berrou (scholarpedia.org).
• 3GPP LTE Turbo Reference Design.
• Estimate Turbo Code BER Performance in AWGN (MatLab).
• Parallel Concatenated Convolutional Coding: Turbo Codes (MatLab Simulink)

Турбо-код состоит из каскада параллельно соединённых систематических кодов. Эти составляющие называются компонентными кодами. В качестве компонентных кодов могут использоваться свёрточные коды, коды Хемминга, Рида — Соломона,  Боуза — Чоудхури — Хоквингема и другие. В зависимости от выбора компонентного кода турбо-коды делятся на свёрточные турбо-коды (англ. Turbo Convolutional Codes, ТСС) и блоковые коды-произведения (англ. Turbo Product Codes, TPC). Согласно последним исследованиям и разработкам, наилучшие практические результаты достигаются при использовании турбокодов на основе кодов Хэмминга или кодов Боуза-Чоудх-ури-Хоквингема.

Энергетический выигрыш, получаемый при использовании турбокодирования в канале с белым гауссовским шумом, составляет от 2 до 4 дБ по сравнению с другими распространенными методами (например, по сравнению с каскадным кодом)

Очевидно, что при энергетическом выигрыше в 3 дБ мощность передатчика может быть уменьшена в 2 раза при прочих равных условиях, либо допустимый коэффициент шума приемника может быть увеличен на 3 дБ

Энергетический выигрыш в 3 дБ позволяет увеличить дальность связи на 40%, либо сократить размеры приемной или передающей антенны на 30%, поскольку коэффициент усиления и эффективная площадь антенны связаны следующим соотношением

Турбо-коды были предложены К. Берроу (C. Berrou), А. Главьё (A. Glavieux) и П. Ситимашимой (P. Thitimajshima) (англ. Ecole Nationale Superieure des Telecommunications de Bretagne (ENST), Высшая национальная школа телекоммуникаций Бретани (Франция)) в 1993 году в статье «Кодирование и декодирование с исправлением ошибок вблизи предела Шеннона: турбо-коды» (англ. «Near Shannon Limit Error-correcting Coding and Decoding: Turbo-code») 

Отмечу преимущества и недостатки  турбо-кодов.  Основное их замечательное свойство состоит в том, что среди всех практически используемых современных методов коррекции ошибок турбо-коды наиболее близко подходят к границе Шеннона теоретическому пределу максимальной пропускной способности зашумленного канала (так же достаточно близко к ней подходят и коды с низкой плотностью проверок на чётность, но их в данной теме рассматривать я не буду).  Другие их преимущества состоят в том, что турбо-коды позволяют увеличить скорость передачи информации, не требуя увеличения мощности передатчика, или они могут быть использованы для уменьшения требуемой мощности при передаче с заданной скоростью. Важным преимуществом турбо-кодов является независимость сложности декодирования от длины информационного блока, что позволяет снизить вероятность ошибки декодирования путём увеличения его длины.

Рис.1.Теоритическая взаимосвязь по Шеннону максимальной пропускной способности канала с ОСШ #

Из недостатков основным является относительно высокая сложность декодирования и большая задержка, которые делают их неудобными для некоторых применений. Но, например, для использования в спутниковых каналах этот недостаток не является определяющим, так как длина канала связи сама по себе вносит задержку, вызванную конечностью скорости света.Ещё один важный недостаток турбо-кодов — сравнительно небольшое кодовое расстояние (то есть минимальное расстояние между двумя кодовыми словами в смысле выбранной метрики). Это приводит к тому, что, хотя при большой входной вероятности ошибки (то есть в плохом канале) эффективность турбо-кода высока, при малой входной вероятности ошибки эффективность турбо-кода крайне ограничена. Поэтому в хороших каналах для дальнейшего уменьшения вероятности ошибки применяют не турбо-коды, а LDPC-коды.

Главный принцип турбо-кодирования – использование двух параллельно работающих элементарных кодеров. При этом информационный блок кодируется дважды, причем второй раз — после предварительного случайного перемежения (перемешивания, перетасовывания и т.п.).

При декодировании кодированный блок можно «расщепить» на два кодовых блока. Это обстоятельство позволяет использовать два декодера, каждый из которых производит декодирование своего кодового блока. Декодированная информация с выхода первого (второго) декодера используется в качестве априорной информации для второго (первого) декодера с целью уточнения результата декодирования. Подобную операцию можно производить многократно. В этом состоит принцип турбо- или итеративного декодирования. 

Турбокоды используют «мягкий вход»-«мягкий выход». Это означает что, чем информационнее последовательность для второго кодирующего устройства, тем более некоррелированный информационный обмен между декодерами. Это позволяет осуществить непрерывное усовершенствование способности кода к исправлению ошибок, процесс декодирования повторяется, чтобы передать больше информации от выхода одного декодера к входу следующего.

Кодер

Рис.2. Кодер #

Один из вариантов построения кодера приведен на рис.2, и, как видно, он представляет собой параллельное соединение двух рекурсивных систематических сверточных кодеров (Recursive Systematic Convolutional Codes — RSC). Оба кодера работают со скоростью равной 1/2. Это означает, что на информационный бит на входе RSC кодер откликается двумя битами на выходе. Значение бита на систематическом выходе верхнего кодера совпадает со значением входного бита, а на втором выходе формируется проверочный бит. На вход второго кодера с выхода перемежителя поступает бит, номер которого j зависит от номера i на входе перемежителя по псевдослучайному закону (i,j=1,..k). (Для этого блок из k информационных символов предварительно перед операцией кодирования должен быть записан в память.) У нижнего кодера систематический выход не используется, а на втором выходе формируется второй проверочный бит. С выхода всего турбо-кодера на модулятор сначала поступает бит с систематического выхода верхнего кодера, а затем два проверочных бита: сначала с верхнего кодера, затем – с нижнего. В результате кодовая скорость r всего турбо-кодера в целом оказывается равной 1/3. В любом случае благодаря использованию систематических сверточных кодеров в кодовом блоке можно явно выделить систематическую и проверочные части. Более того, можно считать, что в канал связи передаются два кодовых блока: первый кодовый блок, состоящий из информационной части и проверочной части верхнего кодера, и второй кодовый блок, состоящий из перемешанной информационной части и проверочной части нижнего кодера. Структура перемежителя сравнительно слабо влияет на его эффективность.

Декодер

Рис. 3. Турбо-декодер. Три итерации (Q=3) #

Рис. 4. Турбо-декодер. Одна итерация #

Из рассмотрения принципа кодирования ясно, что при декодировании блок можно «расщепить» на два кодовых блока, причем информационные части этих двух блоков в силу систематического кодирования и с учетом перемежения идентичны. Значит можно использовать два декодера, каждый из которых производит декодирование своего кодового блока. Информационные части каждого из двух кодовых блоков идентичны, декодированную информацию первого (второго) декодера c учетом перемежения можно использовать в качестве априорной информации для второго (первого) декодера с целью уточнения результата декодирования, тем самым как бы замыкая обратную связь между декодерами двух кодовых блоков. Подобную операцию можно производить многократно. В этом и состоит принцип турбо- или итеративного декодирования. Оптимальный декодер должен быть построен на основе критерия минимума вероятности ошибочного декодирования. Однако построение такого декодера из-за наличия перемежителя встречает трудности. Идея итеративного под-оптимального декодирования оказалась исключительно эффективна.

Вариант построения итеративного декодера представлен на рис. 3 и 4. Декодер для каждой итерации (рис. 4) представляет собой каскадное соединение двух элементарных декодеров: первого и второго. Каждый из этих декодеров выносит решение о переданном символе на основе критерия максимальной апостериорной вероятности (Maximum A Posteriori — MAP), чем обеспечивается минимум вероятности ошибочного декодирования каждым элементарным декодером. На первой итерации от демодулятора на вход первого декодера поступают оценки («мягкие» решения) символов от демодулятора систематической и первой проверочной частей первого кодового блока. На выходе первого декодера формируется оценка («мягкое» решение) информационного символа, которая затем используется в качестве априорной информации о нем для второго декодера. Этот декодер производит оценку символа с выхода перемежителя на основе проверочной части второго кодового слова. На второй и последующих итерациях (рис. 3) декодирования эта оценка обновляется и используется как априорная информация о переданном символе для первого декодера. Таким образом, на вход каждого из двух элементарных декодеров поступают «мягкие» решения, результат декодирования на выходе элементарного декодера – также «мягкое» решение. По этой причине такие схемы получили название декодеров с мягким входом и мягким выходом (Soft Input Soft Output — SISO)4. Окончательное принятие решения о переданном информационном символе выносится нижним декодером. Окончание процесса декодирования происходит либо после выполнения заданного количества Q итерационных циклов, либо после того, как величина поправки результата декодирования достигнет установленного порога.

Вычислительная сложность турбо-декодера в расчете на один информационный бит не зависит от длины информационного блока и сравнима со сложностью декодера Витерби для сверточного кода.

Перемежение в турбо-кодах

 В перемежителях по псевдослучайному закону происходит перемешивание поступающих бит. В турбо-кодах используется перемежение отдельных битов, которое подобно случайным перестановкам. Причём впоследствии, при операциях декодирования этот закон перемежения будет считаться известным. Полученные последовательности поступают на входы кодеров.

Задача перемежителя — преобразовать входную последовательность так, чтобы комбинации бит X₀, соответствующие кодовым словам с низким весом (весом называется число ненулевых бит кодового слова) на выходе первого кодера, были преобразованы в комбинации, дающие кодовые слова с высоким весом на выходах остальных кодеров. Таким образом кодеры получают на выходе кодовые слова с различными весами. При кодировании формируются кодовые слова так, чтобы получалось максимально возможное среднее расстояние между ними (расстоянием между двумя кодовыми словами называется число бит, в которых они различаются). Из-за того что кодовые блоки формируются из почти независимых частей, на выходе турбо-кодера среднее расстояние между кодовыми словами больше, чем минимальное расстояние для каждого компонентного кодера, а следовательно растёт эффективность кодирования.

Перестановка для каждой указанной длины блока k задается определенным переупорядочиванием целых чисел 1,2…,k как предусмотрено следующим алгоритмом (ECSS-E-ST-50-01C). k = 8 * k₀, где k₀ = одному из следующих значений : 223, 223 * 2, 223 * 4, 223 * 5, в зависимости от необходимой глубины перемежителя

Применение

Компаниями France Telecom и Telediffusion de France запатентован широкий класс ТК. Более того, ТК утверждены для помехоустойчивого кодирования несколькими cтандартами космической связи, а также мобильной связи третьего поколения.

Схема кодирования с кодерами на 16 состояний (K=5), максимальной длиной перемежения 16384 и кодовыми скоростями r=1/2,1/3,1/4,1/6 утверждена в 1999 г. американским комитетом CCSDS (Consultative Committee for Space Data Systems) в стандарте передачи телеметрической информации с космических аппаратов. В феврале 2000 г. консорциум DVB утвердил ТК в стандарте DVB-RCS для передачи информации по обратному спутниковому каналу (Return Channel for Satellite — RCS), т.е. в направлении от спутника к абоненту. ТК формируются на основе циклического рекурсивного систематического сверточного кодера (Circular Recursive Systematic Convolutional — CRSC). Использование стандарта совместно с вещательным стандартом DVB-S позволяет проектировать полноценную широкополосную систему спутникового интерактивного цифрового телевидения. Компанией TurboConcept в партнерстве с европейским спутниковым оператором Eutelsat разработан турбо-декодер TC1000 в соответствии со стандартом DVB-RCS. Использование ТК принято также в новом стандарте спутниковой системы связи Inmarsat.

В нарождающихся универсальных мобильных системах (IMT-2000) третьего поколения (3G), предназначенных для передачи и приема мультимедийной информации, ТК также получили широкое применение. В стандарте cdma2000 для высокоскоростного режима передачи информации (больше 14.4 кбит/с) как к абоненту (forward link), так и от абонента (reverse link) используется ТК с 8-ю состояниями (K=4) и кодовыми скоростями r=1/2,1/3,1/4 [15]. В стандарте UMTS для высокоскоростного режима передачи информации (больше 32 кбит/с) и приема с высоким качеством (BER около 10-6) используется ТК с 8-ю состояниями (K=4) и двумя кодовыми скоростями r=1/2 и 1/3 (рис. 5).

Рис. 5. Турбо-кодер, используемый в стандарте UMTS для мобильных систем третьего поколения #

Список источников.

Эта статья является первой моей работой на данную тему. Надеюсь, сведения, представленные в ней помогут вам понять, что же такое турбо-коды и для чего они используются

З.Ы. С удовольствием учту пожелания по поводу статьи, вдруг кто-то захочет получить какую-то более конкретную информацию