Moderators: EViews Gareth, EViews Moderator
-
corbinm
- Posts: 2
- Joined: Wed Feb 05, 2014 4:02 am
Near Singular Matrix Error
Hi,
I am having an issue using e views 8 student version. I am getting the typical near singular matrix error and so far I have been un able to find a solution. The regression I am attempting to run is
excess1 c shortint instiown monthd quarterd yeard shortint*monthd shortint*quarterd shortint*yeard excess0 excess0*monthd excess0*quarterd excess0*yeard excess0*shortint excess0*monthd*shortint excess0*quarterd*shortint excess0*yeard*shortint
This is one of three equations which all include similar variables and has been successfully run on several other country data sets I am testing. However for some reason I run into this problem only on my Indonesia data set and one other data set our of over 60. I’ve tried removing the constant variable and that has done nothing. I need to include all other variables and so I can’t afford to start deleting variables here and there.
Just for reference the dummy variables are monthd quarterd and yeard which indicate different period ends,i.e a month end quarter end or year end date. and there is no over lap, so the last date in jan and feb will have a 1 for month end while the end of march with have a 1 for quarter end but a zero for month end and so on
Any help would be great, Ive attached the .txt file below which im using as my data in e views
- Attachments
-
- Indo Data — Low Vol.txt
- (540.13 KiB) Downloaded 2008 times
-
trubador
- Did you use forum search?
- Posts: 1516
- Joined: Thu Nov 20, 2008 12:04 pm
Re: Near Singular Matrix Error
Postby trubador » Wed Feb 05, 2014 5:33 am
As far as the machine is concerned, you have a perfect (negative) correlation between «excess0*yeard*shortint» and «yeard*shortint» variables. You’ll have to drop one of them…
-
corbinm
- Posts: 2
- Joined: Wed Feb 05, 2014 4:02 am
Re: Near Singular Matrix Error
Postby corbinm » Wed Feb 05, 2014 7:01 am
I see, thank you for your help with that. I am still relatively new to e views and very rusty on my econmetrics. Could you explain the commands for determining this issue as I have a couple other equations which are presenting a similar issue? Further more does this suggest an issue with my data or is it a matter of chance probability that this occurred for the variables in this data set while numerous other identical ones (for other countries) did not run in to this problem?
Thanks again for you quick response and help
-
trubador
- Did you use forum search?
- Posts: 1516
- Joined: Thu Nov 20, 2008 12:04 pm
Re: Near Singular Matrix Error
Postby trubador » Wed Feb 05, 2014 7:52 am
This seems to be a problem with your data. You have generated variables that are nearly identical. You should check your data prior to analysis. For this instance, you can group your variables and look at the correlation matrix.
-
Marcel Visser
- Posts: 5
- Joined: Mon May 18, 2015 3:51 am
Re: Near Singular Matrix Error
Postby Marcel Visser » Mon May 18, 2015 3:59 am
Dear all,
I am receiving the same error code. I attached my original correlation matrix. Even when I do not include the variables for Financial Development and Profitability in the regression I still get the error code.
Does anyone know what I am doing wrong and how i will be able to fix this?
Thanks in advance.
Marcel Visser
- Attachments
-
- tableeviews.csv
- correlation matrix
- (592 Bytes) Downloaded 1196 times
-
EViews Gareth
- Fe ddaethom, fe welon, fe amcangyfrifon
- Posts: 13108
- Joined: Tue Sep 16, 2008 5:38 pm
Re: Near Singular Matrix Error
Postby EViews Gareth » Mon May 18, 2015 7:56 am
What is the equation specification you’re trying to estimate?
-
Marcel Visser
- Posts: 5
- Joined: Mon May 18, 2015 3:51 am
Re: Near Singular Matrix Error
Postby Marcel Visser » Mon May 18, 2015 9:01 am
Dear Gareth,
I found the problem. My variable OPRISK takes the same value for any company year observation in the sample, 2008-2012. So the value only varies when companies change, not when years change. I found somewhere else on this forum that this prevents you from running a cross section fixed effects regression. The regression I try to run is Leverage ratio= c (Financial development) (Inflation) (Marginal tax rate) (OPRISK) (log sales) (profitability) (tangibility). Can I just remove the variable OPRISK and run the regression. Will this accurately remove the year and section effects from the other variables? Because I still need to control for the year and section effects on the other variables. My sample size is very large, 122000 observations per variable. Therefor I cannot upload my file. The thing is i ran a Hausman test which told me to use a fixed effect model. However, the OPRISK variable prevents me from doing this. The book Introductory econometrics for finance also said that you could use a slightly modified version of the Chow test to check if a panel regression was really necessary. It said in some cases you could just pool the data and preform a regular OLS.
If i will not be able to exclude the year and section effects with a fixed effects panel regression, should i then use this approach. And could you please tell me how this is done?
I would like to thank you in advance for your time.
Kind regards,
Marcel Visser
-
said.abouabdo
- Posts: 1
- Joined: Wed Apr 04, 2018 6:06 am
Re: Near Singular Matrix Error
Postby said.abouabdo » Wed Apr 04, 2018 6:58 am
Hello,
Im facing the problem of » Near singular matrix error. Regressors may be perfectly collinear».
The thing is most of my data if not all is formed out of ratings transformed into dummy variables. I do not know what to do in order to generate results? Can anyone suggest any way? In order to decrease the number of variables, ive but all the variables in one group but it does not seem like it is going to work.
- Attachments
-
- all ratings.wf1
- (1.84 MiB) Downloaded 613 times
-
startz
- Non-normality and collinearity are NOT problems!
- Posts: 3750
- Joined: Wed Sep 17, 2008 2:25 pm
Re: Near Singular Matrix Error
Postby startz » Wed Apr 04, 2018 8:57 am
You’re probably going to have to show the equation you are estimating and explain it to get much useful advice.
-
Alina03
- Posts: 16
- Joined: Sat Jul 14, 2018 12:49 am
Re: Near Singular Matrix Error
Postby Alina03 » Sat Jul 14, 2018 5:59 am
Hi, I want to perform White heteroskedasticity test, using a VAR model, but when I click on that test, it appears ”near singular matrix” error. I have 6 variables, annual data from 1995 to 2017. How could I manage this problem? Thank you!
-
startz
- Non-normality and collinearity are NOT problems!
- Posts: 3750
- Joined: Wed Sep 17, 2008 2:25 pm
Re: Near Singular Matrix Error
Postby startz » Sat Jul 14, 2018 6:50 am
You’ll probably have to give more details of exactly what you did. And possibly post your data.
-
Alina03
- Posts: 16
- Joined: Sat Jul 14, 2018 12:49 am
Re: Near Singular Matrix Error
Postby Alina03 » Sat Jul 14, 2018 6:59 am
My variables are dgdp, dge, dgv, dpd, dpr, dh (these variable are already stationary at first or second difference). When I open them as VAR and I want to perform white heteroskedasticity test, it appears the error near singular matrix. But when I exclude one variable, as in capture 1, I can perform that test. Could you help me please. I am so disperate because I have to finish my project.
- Attachments
-
- Eviews — VAR model.wf1
- (20.29 KiB) Downloaded 523 times
-
- Capture2.JPG (81.66 KiB) Viewed 42391 times
-
- Capture1.JPG (85.46 KiB) Viewed 42391 times
-
startz
- Non-normality and collinearity are NOT problems!
- Posts: 3750
- Joined: Wed Sep 17, 2008 2:25 pm
Re: Near Singular Matrix Error
Postby startz » Sat Jul 14, 2018 7:15 am
I believe the White test has more right hand side variables than you have observations, in which case the test can’t be done. It’s not a very informative error message.
By the way, the White test is a large sample test and using it 20 observations probably isn’t valid.
-
Alina03
- Posts: 16
- Joined: Sat Jul 14, 2018 12:49 am
Re: Near Singular Matrix Error
Postby Alina03 » Sat Jul 14, 2018 7:22 am
I don t know if you saw, but I attached the model to take a look at it. What should I do in this case? Is it better to exclude a variable?
-
Alina03
- Posts: 16
- Joined: Sat Jul 14, 2018 12:49 am
Re: Near Singular Matrix Error
Postby Alina03 » Sat Jul 14, 2018 7:26 am
How can I perform a correct VAR model, if I don t test the heteroskedasticity? Finally, I want to present the impulse response functions in my project and I want to assure that the VAR model is correct.
Return to “Estimation”
Who is online
Users browsing this forum: No registered users and 12 guests
Click here follow the steps to fix Near Singular Matrix Error In Eviews and related errors.
|
|
|
|
To Fix (Near Singular Matrix Error In Eviews) error you need to |
|
|
Step 1: |
|
|---|---|
| Download (Near Singular Matrix Error In Eviews) Repair Tool |
|
|
Step 2: |
|
| Click the «Scan» button | |
|
Step 3: |
|
| Click ‘Fix All‘ and you’re done! | |
|
Compatibility:
Limitations: |
Near Singular Matrix Error In Eviews Error Codes are caused in one way or another by misconfigured system files
in your windows operating system.
If you have Near Singular Matrix Error In Eviews errors then we strongly recommend that you
Download (Near Singular Matrix Error In Eviews) Repair Tool.
This article contains information that shows you how to fix
Near Singular Matrix Error In Eviews
both
(manually) and (automatically) , In addition, this article will help you troubleshoot some common error messages related to Near Singular Matrix Error In Eviews error code that you may receive.
Note:
This article was updated on 2023-02-03 and previously published under WIKI_Q210794
Contents
- 1. What is Near Singular Matrix Error In Eviews error?
- 2. What causes Near Singular Matrix Error In Eviews error?
- 3. How to easily fix Near Singular Matrix Error In Eviews errors
What is Near Singular Matrix Error In Eviews error?
The Near Singular Matrix Error In Eviews error is the Hexadecimal format of the error caused. This is common error code format used by windows and other windows compatible software and driver vendors.
This code is used by the vendor to identify the error caused. This Near Singular Matrix Error In Eviews error code has a numeric error number and a technical description. In some cases the error may have more parameters in Near Singular Matrix Error In Eviews format .This additional hexadecimal code are the address of the memory locations where the instruction(s) was loaded at the time of the error.
What causes Near Singular Matrix Error In Eviews error?
The Near Singular Matrix Error In Eviews error may be caused by windows system files damage. The corrupted system files entries can be a real threat to the well being of your computer.
There can be many events which may have resulted in the system files errors. An incomplete installation, an incomplete uninstall, improper deletion of applications or hardware. It can also be caused if your computer is recovered from a virus or adware/spyware
attack or by an improper shutdown of the computer. All the above actives
may result in the deletion or corruption of the entries in the windows
system files. This corrupted system file will lead to the missing and wrongly
linked information and files needed for the proper working of the
application.
How to easily fix Near Singular Matrix Error In Eviews error?
There are two (2) ways to fix Near Singular Matrix Error In Eviews Error:
Advanced Computer User Solution (manual update):
1) Start your computer and log on as an administrator.
2) Click the Start button then select All Programs, Accessories, System Tools, and then click System Restore.
3) In the new window, select «Restore my computer to an earlier time» option and then click Next.
4) Select the most recent system restore point from the «On this list, click a restore point» list, and then click Next.
5) Click Next on the confirmation window.
6) Restarts the computer when the restoration is finished.
Novice Computer User Solution (completely automated):
1) Download (Near Singular Matrix Error In Eviews) repair utility.
2) Install program and click Scan button.
3) Click the Fix Errors button when scan is completed.
4) Restart your computer.
How does it work?
This tool will scan and diagnose, then repairs, your PC with patent
pending technology that fix your windows operating system registry
structure.
basic features: (repairs system freezing and rebooting issues , start-up customization , browser helper object management , program removal management , live updates , windows structure repair.)
Ramsey’s Regression Specification Error Test (RESET) (UE 6.8.1):
Complete Steps 1 — 5 of the section entitled Adding or deleting variables to/from an OLS model in EViews before attempting this section (i.e., EQ02 should be present in the workfile). Follow these steps to carry out the Ramsey’s Regression Specification Error Test (RESET) using the step-by-step approach followed in UE, pp. 193-195:
Step 1. Open the EViews workfile named Chick6.wf1.
Step 2. Open EQ02 by double clicking its icon in the workfile window (see UE, Equation 6.9, p. 194).
Step 3. Select Forecast on the equation menu bar, enter YF in the Forecast name: window, and click OK.3
Step 4. Select Objects/New Object/Equation on the workfile menu bar, enter Y C PC YD YF^2 YF^3 YF^4 in the Equation Specification: window, and click OK (see UE, Equation 6.10, p. 194).
Step 5.Select Name on the equation menu bar, enter EQ03 in the Name to identify object: window, and click OK.
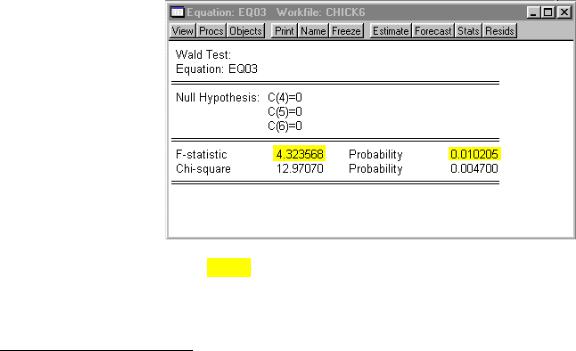
Step 6. Select View/Coefficient Tests/Wald-Coefficient Restrictions on the equation menu bar, enter C(4)=0, C(5)=0, C(6)=0 in the Coefficient restrictions separated by commas: window,4 and click OK
to get the graphic shown on the right.
Step 7. Determine the critical F-statistic from UE, Table B-2 or by entering the formula:
=@qfdist(0.95,3,eq03. @regobseq03.@ncoef) in the command window, pressing Enter, and reading the value on the status line in the lower left of the screen.
Step 8. The F-statistic, highlighted in yellow, is the same as reported in UE, p. 195.5 Since the calculated F-statistic of 4.32 exceeds the critical F-statistic of 2.85, the null hypothesis that the coefficients on the added variables are jointly zero can be rejected at the 5% level. This is in spite of the fact that none of their coefficients are individually significant.
3This creates a new series with forecast values of Y based on the estimated coefficients for EQ02.
4Note that the coefficient restrictions are written as C(i), where i represents the coefficient order number of the variable as it was entered in the Equation Specification: window, following the dependent variable. Thus, C(4),C(5) and C(6) represent the coefficients for YF^2 YF^3 YF^4 in the Equation Specification: Y C PC YD YF^2 YF^3 YF^4.
5The Chi-square statistic is equal to the F-statistic times the number of restrictions under test. In this example, there are three restrictions, so the Chi-square test statistic is three times the size of the F-statistic, but the p-values of both statistics indicate that we can decisively reject the null hypothesis that the three coefficients are zero.

Ramsey’s Regression Specification Error Test (RESET) (EViews):
Complete Steps 1 — 5 of the section entitled Adding or deleting variables to/from an OLS model in EViews before attempting this section (i.e., EQ02 should be present in the workfile). Follow these steps to carry out the Ramsey’s Regression Specification Error Test (RESET) using EViews, built in Ramsey’s RESET Test:
Step 1. Open the EViews workfile named Chick6.wf1.
Step 2. Open EQ02 by double clicking its icon in the workfile window (see UE, Equation 6.9, p. 194).
Step 3. Select View/Stability Tests/Ramsey RESET Test…, enter 3 in the Number of fitted terms: window6, and click OK to get the table below.
Note that the output is very similar to the output achieved with the step-by- step approach in the previous section. In this case, the test results are printed above the regression output table.
Since the calculated F-statistic of 4.32
exceeds the critical F-statistic of 2.85, the null hypothesis that the coefficients on the added variables are jointly zero can be rejected at the 5% level. This
Ramsey RESET Test:
|
F-statistic |
4.323568 |
Probability |
0.010205 |
||||||
|
Log likelihood ratio |
12.92125 |
Probability |
0.004810 |
||||||
|
Test Equation: |
|||||||||
|
Dependent Variable: Y |
|||||||||
|
Method: Least Squares |
|||||||||
|
Date: 07/27/00 Time: 07:26 |
|||||||||
|
Sample: 1951 1994 |
|||||||||
|
Included observations: 44 |
|||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|||||
|
C |
23.80305 |
55.36771 |
0.429908 |
0.6697 |
|||||
|
PC |
-0.591937 |
1.718030 |
-0.344544 |
0.7323 |
|||||
|
YD |
0.360179 |
0.714812 |
0.503880 |
0.6173 |
|||||
|
FITTED^2 |
0.023868 |
0.082475 |
0.289394 |
0.7739 |
|||||
|
FITTED^3 |
-0.000748 |
0.001106 |
-0.676301 |
0.5029 |
|||||
|
FITTED^4 |
5.48E-06 |
5.36E-06 |
1.022646 |
0.3129 |
|||||
|
R-squared |
0.988647 |
Mean dependent var |
43.37500 |
||||||
|
Adjusted R-squared |
0.987154 |
S.D. dependent var |
16.83854 |
||||||
|
S.E. of regression |
1.908510 |
Akaike info criterion |
4.256646 |
||||||
|
Sum squared resid |
138.4116 |
Schwarz criterion |
4.499945 |
||||||
|
Log likelihood |
-87.64622 |
F-statistic |
661.8504 |
||||||
|
Durbin-Watson stat |
0.861509 |
Prob(F-statistic) |
0.000000 |
is in spite of the fact that all of their individual t-statistics are insignificant.
6 The fitted terms are the powers of the fitted values from the original regression, starting with the square or second power. For example, if you specify 3, then the test will add ŷ2, ŷ3, and ŷ4 in the regression. If you specify a large number of fitted terms, EViews may report a near singular matrix error message since the powers of the fitted values are likely to be highly collinear. The Ramsey RESET test is applicable only to an equation estimated by least squares.

Akaike’s Information Criterion (AIC) and the Schwartz Criterion (SC):
Complete Steps 1 — 5 of the section entitled Adding or deleting variables to/from an OLS model in EViews before attempting this section (i.e., EQ01 and EQ02 should be present in the workfile). The Akaike’s Information Criterion (AIC) and Schwartz Criterion (SC) are both printed in the Estimation Output of EViews’ OLS regressions.
Step 1. Open the EViews workfile named Chick6.wf1.
Step 2. Open EQ01 by double clicking its icon in the workfile window (see UE, Equation 6.8, p. 160 or 196) to get the Estimation Output below.
Dependent Variable: Y
Method: Least Squares
Date: 07/26/00 Time: 09:11
Sample: 1951 1994
Included observations: 44
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||
|
C |
31.49604 |
1.312586 |
23.99541 |
0.0000 |
||
|
PC |
-0.729695 |
0.080020 |
-9.118941 |
0.0000 |
||
|
PB |
0.114148 |
0.045686 |
2.498536 |
0.0167 |
||
|
YD |
0.233830 |
0.016447 |
14.21738 |
0.0000 |
||
|
R-squared |
0.986828 |
Mean dependent var |
43.37500 |
|||
|
Adjusted R-squared |
0.985840 |
S.D. dependent var |
16.83854 |
|||
|
S.E. of regression |
2.003702 |
Akaike info criterion |
4.314378 |
|||
|
Sum squared resid |
160.5929 |
Schwarz criterion |
4.476577 |
|||
|
Log likelihood |
-90.91632 |
F-statistic |
998.9207 |
|||
|
Durbin-Watson stat |
0.978759 |
Prob(F-statistic) |
0.000000 |
Step 3. Open EQ02 by double clicking its icon in the workfile window (see UE, Equation 6.9, p. 161) to get the Estimation Output below.
Dependent Variable: Y
Method: Least Squares
Date: 07/26/00 Time: 08:01
Sample: 1951 1994
Included observations: 44
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||
|
C |
32.94193 |
1.251191 |
26.32845 |
0.0000 |
||
|
PC |
-0.700954 |
0.084099 |
-8.334841 |
0.0000 |
||
|
YD |
0.272477 |
0.005936 |
45.90552 |
0.0000 |
||
|
R-squared |
0.984772 |
Mean dependent var |
43.37500 |
|||
|
Adjusted R-squared |
0.984030 |
S.D. dependent var |
16.83854 |
|||
|
S.E. of regression |
2.127957 |
Akaike info criterion |
4.413948 |
|||
|
Sum squared resid |
185.6562 |
Schwarz criterion |
4.535597 |
|||
|
Log likelihood |
-94.10685 |
F-statistic |
1325.737 |
|||
|
Durbin-Watson stat |
0.946570 |
Prob(F-statistic) |
0.000000 |
Note that the AIC & SC information criterion reported in EViews (see numbers highlighted in yellow) are larger when PB is omitted from the OLS regression (i.e., EQ02). Both Akaike’s and the Schwartz Criterion provide evidence that UE, Equation 6.8 (i.e., EViews EQ01) is preferable to UE, Equation 6.9 (i.e., EViews EQ02).
Exercise:
15.Open the EViews workfile named Drugs.wf1. a.
i)Select Objects/New Object/Equation on the workfile menu bar, enter P C GDPN CVN PP DPC IPC CV in the Equation Specification: window, and click OK. Select Name on the equation window menu bar, enter EQ01 in the Name to identify object: window, and click OK.
ii)Select Objects/New Object/Equation on the workfile menu bar, enter P C GDPN CVN PP DPC IPC N in the Equation Specification: window, and click OK. Select Name on the equation window menu bar, enter EQ02 in the Name to identify object: window, and click OK.
b. Open EQ01 and EQ02 at the same time. Use information in these tables, UE 6.8 (Appendix) and the procedures outlined in this guide to determine whether CV and/or N are irrelevant or omitted variables.
c.
d.

Chapter 7: Specification: Choosing A Functional Form
In this chapter:
1.Table with EViews specification for functional forms
2.Calculating «Quasi — R2» in EViews (UE 7.3.1, footnote 5, p. 215)
3.Calculating «Quasi — R2» for a linear versus log-lin model using EViews
4.Coefficient restrictions tests using EViews (UE, Appendix 7.7)
5.The Chow test, alternately termed Chow’s Breakpoint Test (UE, Appendix 7.7)
UE section 7.2 presents alternative functional forms that are useful when specifying econometric models. Linear models are frequently too restrictive to properly fit the functional form suggested by the underlying theory.
The last column of Table 7.1 below shows the correct EViews specification for the alternative functional forms printed in UE, Table 7.1, p. 214. You can use the table as a guide, but you must realize that Y represents the dependent variable while X1 & X2 represent the only independent variables in all of the equations/specifications. Note that a constant (C) should be included in all models even if theory suggests otherwise (see UE, p. 201). You must have a workfile open in order to specify and estimate a regression model. Then, to specify a regression model in EViews, select Objects/New Object/Equation from the workfile menu and enter the appropriate EViews specification (see the last column of the table below), in the Equation Specification: window.1
Table 7.1: EViews Specification of Functional Forms
|
Section |
Equation # |
Fcn. Form |
Equation specification |
EViews |
specification |
||||||||||
|
7.2.1 |
—- |
Linear |
Y = β 0 + β 1X1 + β 2X2 |
Y C X1 |
X2 |
||||||||||
|
7.2.2 |
7.3 |
Double-Log |
lnY = β 0 + β 1lnX1 + β 2lnX2 |
log(Y) C log(X1) log(X2) |
|||||||||||
|
7.2.3 |
7.7 |
Lin-Log |
Y = β 0 + β 1lnX1 |
+ β 2X2 |
Y C log(X1) X2 |
||||||||||
|
7.2.3 |
7.9 |
Log-Lin |
lnY = β 0 + β 1X1 |
+ β 2X2 |
log(Y) C X1 |
X2 |
|||||||||
|
7.2.4 |
7.10 |
Polynomial |
Y = β 0 + β 1X1 + β 2(X12) + β 3X2 |
Y C X1 X1^2 X2 |
|||||||||||
|
7.2.5 |
7.13 |
Inverse |
Y = β 0 + β 1(1/X1) + β 2X2 |
Y C 1/X1 |
X2 |
||||||||||
|
7.5 |
7.20 |
Dummy* |
Y = β 0 + β 1X1 |
+ β 2D1 |
Y C X1 D1 |
||||||||||
|
7.5 |
7.22 |
Dummy** |
Y = β 0 + β 1X1 + β 2D1 + β 3D1X1 |
Y C X1 D1 D1*X1 |
|||||||||||
* Intercept dummy variable. ** Intercept and slope dummy variables.
Calculating «Quasi — R2» in EViews (UE 7.3.1, footnote 5, p. 215):
The dependent variable must be in the same form when using R2 and adjusted R2 to compare the overall goodness of fit between two equations. For example, it would not be appropriate to compare the R2 for a linear model with a double-log or a log-lin model. However, it would be appropriate to compare R2 for a linear model with a lin-log, a
1 Alternately, select Quick/Estimate Equation from the main menu. If this method is used you must name the equation to save it. Select Name on the equation menu bar and enter the desired name in the Name to identify object: window, and click OK.

polynomial, or an inverse functional form model. Likewise, it would be appropriate to compare R2 for double-log and log-lin functional form models. In order to demonstrate the process, the car acceleration data introduced in UE, Exercise 16, p. 234, will be used to demonstrate the process of calculating the quasi-R2. The steps below show how to compare the goodness of fit for models using S (the number of seconds it takes a car to accelerate from 0 to 60 miles per hour) as the dependent variable versus using the natural log of S as the dependent variable. In both models, the independent variables are the same as the original model printed at the top of UE, p. 236.
Calculating «Quasi — R2» for a linear versus a log-lin model using EViews:
Step 1. Open the EViews workfile named Cars7.wk1.
Step 2. Select Objects/New Object/Equation on the workfile menu bar, enter S C T E P H in the Equation Specification: window, and click OK.
Step 3. Select Name on the equation menu bar, write linear in the Name to identify object: window, and click OK. Minimize the equation object named linear.
Step 4. Select Objects/New Object/Equation on the workfile menu bar, enter log(S) C T E P H in the Equation Specification: window (i.e., the log-lin functional form), and click
OK.
Step 5. Select Name on the equation menu bar, write loglin in the Name to identify object: window, and click OK.
Step 6. Select Forecast on the equation menu bar, select S in the Forecast of:2 window, enter SF in the Forecast name: window, uncheck the two boxes in the Output: window (the only objective here is to create a forecast series, not a forecast evaluation), and click OK. A new series named SF appears in the workfile window.
Steps 7, 8 & 9 calculate the quasi-R2 for this regression (UE 7.3.1, footnote 5, p. 215).
Step 7. Minimize the equation window, select Genr on the workfile menu bar, type numerator=(S-SF)^2 in the Enter equation: window, and click OK (this step generates the un-summed variable in the numerator of the quasi-R2 equation).
Step 8. Select Genr on the workfile menu bar, type denominator=(S-@mean(S))^2 in the Enter equation: window, and click OK (this step generates the un-summed variable in the denominator of the quasi-R2 equation).
Step 9. To calculate the quasi-R2, type the following equation in the command window and press Enter: scalar quasir2=1-(@sum(numerator)/@sum(denominator)). A new variable named quasir2 will appear in the workfile window. Double click on it and the value for the quasi-R2 will be displayed in the lower left of the screen (0.783958974). The quasi-R2 calculated in Step 9 (i.e., 0.78) is in-between the R2 from the linear model estimated in Step 2 (i.e., 0.71) and the R2 from the log-lin model estimated in Step 5 (i.e., 0.81).
2 The Forecast procedure in EViews gives you the option of forecasting the transformed dependent variable (i.e., LOG(S) in this case) or the original variable (i.e., S in this case). Select S, since the computation of quasi-R2 requires converting of LOG(S) to S by taking the anti-log of the dependent variable (this can also be done by using the EViews command @exp(LOG(S)).

Coefficient restrictions tests using EViews (UE, Appendix 7.7):
The F-test can be used to test a wide range of hypothesis concerning regression coefficients. For example, suppose that the claim was made that when a car has a manual transmission it increases its acceleration speed (i.e., decreases the number of seconds it takes to accelerate from 0 to 60 miles per hour) just as much as adding 100 horsepower to the car. Translating this into the language of UE, Equation 7.28, p. 235, this means that the absolute value of the coefficient on Ti is 100 times larger than the absolute value of the coefficient on Hi. Just looking at the size of the estimated coefficients, it appears that you can easily reject the hypothesis because the absolute value of the coefficient on Ti is only about 41.5 times larger than the absolute value of the coefficient on Hi (divide the coefficient on Ti by the coefficient on Hi). However, these coefficients are just estimates. Follow these steps to carry out an F-test for the null hypothesis that the absolute value of the coefficient on Ti is 100 times larger than the absolute value of the coefficient on Hi. :
Step 1. Open the EViews workfile named Cars7.wk1.
Step 2. Select Objects/New Object/Equation on the workfile menu bar, enter S C T E P H in the Equation Specification: window, and click OK.
Step 3.Select Name on the equation menu bar, write EQ01 in the Name to identify object: window, and click OK.
Step 4. Select View/Coefficients Tests/Wald-Coefficient Restrictions … on the equation menu bar, enter -C(2)=-100*C(5) in the Coefficients separated by commas: window, and click OK to reveal the following output:3
Wald Test:
Equation: EQ01
|
Null Hypothesis: |
-C(2)=-100*C(5) |
|||||||
|
F-statistic |
2.485049 |
Probability |
0.124472 |
|||||
|
Chi-square |
2.485049 |
Probability |
0.114933 |
|||||
The null hypothesis is -C(2)=-100*C(5), since variable T is the second coefficient and variable H is the fifth coefficient in the EViews Estimation Output from Step 2. The F- statistic compares the residual sum of squares computed with and without the restrictions imposed. If the restrictions are valid, there should be little difference in the two residual sum-of-squares and the F-value should be small. Based on the Wald Test: results table, the null hypothesis cannot be rejected at the 5% level of significance. The calculated F- statistic of 2.49 is less than the critical F-value of 4.14. The critical F-value can be found in UE, Table B-2, p. 609 for 1 degree of freedom in the numerator and 33 (interpolate between the 30 and 40) degrees of freedom in the denominator or EViews can calculate
3 The coefficients should be referred to as C(1), C(2), and so on (do not use series names). Multiple coefficient restrictions must be separated by commas and the restrictions should be expressed as equations involving estimated coefficients and constants. The coefficients should be referred to as C(1), C(2), and so on (do not use series names).

its value.4 The reported probability is the marginal significance level of the F-test. It supports this result in that rejecting the null hypothesis would be wrong less than 12.44% of the time.
The Chi-square statistic is equal to the F-statistic times the number of restrictions under test. In this example, there is only one restriction and so the two test statistics are identical with the p-values of both statistics indicating that we cannot reject the null hypothesis, that the absolute value of the coefficient on Ti is 100 times larger than the absolute value of the coefficient on Hi, at the 10% significance level. The 10% significance critical value for the χ 2 test can be found in UE, Table B-8, p. 619 to be 2.71.
The Chow test, alternately termed Chow’s Breakpoint Test (UE, Appendix 7.7):
Chow’s Breakpoint Test divides the data into two sub-samples.5 It then estimates the same equation for each sub-sample separately, to see whether there are significant differences in the estimated equations. A significant difference indicates a structural change in the relationship.
Follow these steps to apply the Chow breakpoint test, as described in UE, pp. 241-242, to determine whether there was a structural change in the demand for chicken in 1976:
Step 1. Open the EViews workfile named Chick6.wf1.
Step 2. Select Objects/New Object/Equation on the workfile menu bar, enter Y C PC PB YD in the Equation Specification: window, and click OK.
Step 3. Select Name on the equation menu bar, write EQ01 in the Name to identify object: window, and click OK.
Step 4. Select View/Stability Tests/Chow Breakpoint Test… on the equation menu bar, enter
1976 in the Enter one date (observation) for the Forecast Test or one or more dates for the Breakpoint Test: window, and click OK to reveal the following output:
Chow Breakpoint Test: 1976
|
F-statistic |
4.542962 |
Probability |
0.004498 |
|||
|
Log likelihood ratio |
17.98027 |
Probability |
0.001245 |
|||
EViews reports two test statistics for the Chow breakpoint test. The F-statistic is based on the comparison of the restricted and unrestricted sum of squared residuals. EViews calculates the F-statistic using the formula printed in UE, Equation 7.36, p. 242. In this
4 To have EViews calculate the 5% critical F-value for this problem, type the following equation in the command window =@qfdist(0.95,1,eq01.@regobs-eq01.@ncoefs), press Enter and view the following
value on the status bar in the lower left of the screen 
view the following value on the status bar in the lower left of the screen 
5 One major drawback of the breakpoint test is that each sub-sample requires at least as many observations as the number of estimated parameters. This may be a problem if, for example, you want to test for structural change between wartime and peacetime where there are only a few observations in the wartime sample.

case, the calculated F-statistic of 4.54 exceeds the critical F-value of 2.63 for the 5% level of significance so the null hypothesis of no structural change can be rejected. The critical F-value can be found in UE, Table B-2, p. 609 for 4 degrees of freedom in the numerator and 36 (interpolate between the 30 and 40) degrees of freedom in the denominator or EViews can calculate its value.6 The reported probability is the marginal significance level of the F-test. It supports this result in that rejecting the null hypothesis would be wrong less than 0.4498% of the time.
The log likelihood ratio statistic is based on the comparison of the restricted and unrestricted maximum of the log likelihood function. The LR test statistic has an asymptotic χ 2 distribution with degrees of freedom equal to (m-1)*(k+1) under the null hypothesis of no structural change, where m is the number of sub-samples and k is the number of independent variables in the model (i.e., m = 2 in this case because one breakpoint is selected and k = 3). The calculated value for LR test statistic of 17.98 exceeds of 9.49 for the 5% level of significance and 13.28 for the 1% level of significance so the null hypothesis of no structural change can be rejected.7 The reported probability is the marginal significance level of the χ 2 test. It supports this result in that rejecting the null hypothesis would be wrong less than 0.1245% of the time.
6 To have EViews calculate the 5% critical F-value for this problem, type the following equation in the
command window =@qfdist(0.95,eq01.@ncoef,eq01.@regobs-2*eq01.@ncoef), press Enter
and view the following value on the status bar in the lower left of the screen 

Chapter 8: Multicollinearity
In this chapter:
1.Perfect multicollinearity (UE 8.1.1)
2.Detecting multicollinearity with simple correlation coefficients (UE 8.3.1)
3.Calculating Variance Inflation Factors (UE 8.3.2)
4.Transforming multicollinear variables (UE 8.4.3)
5.Exercises
Perfect multicollinearity (UE 8.1.1):
EViews is incapable of generating estimates of regression coefficients when the model specification contains two or more variables that are perfectly collinear. When the equation specification contains two or more perfectly collinear (or even some highly collinear) variables, EViews will put out the error message “Near singular matrix.”
The next two sections explain how EViews can be used to detect severe multicollinearity (UE 8.3). The data for the fish/Pope example found in UE, Table 8.1, p. 267, will be used to demonstrate the two methods discussed in UE.
Detecting multicollinearity with simple correlation coefficients (UE 8.3.1):
High simple correlation coefficients between variables is a sign of multicollinearity. Follow these steps to compute the simple correlation coefficient between variables:
Step 1. Open the EViews workfile named Fish8.wk1.
Step 2. Create a group object for the variables found in UE, Equation 8.24, p. 268 (i.e., F PF PB log(YD) N P). An easy way to create a group object for a set of variables from a regression model is to select Procs/Make Regressor Group on the equation window menu bar (refer to Chapter 3 to review the usual way of creating a group object).
Step 3. Select View/Correlations on the group object menu bar to reveal the simple correlation coefficients between all of the variables in the group.
Step 4. Select Freeze on the group object menu bar to create a table of the simple correlation coefficients. Select Name on the table object menu bar to name the table.
|
F |
PF |
PB |
LOG(YD) |
N |
P |
|
|
F |
1.000000 |
0.847590 |
0.818532 |
0.780012 |
0.736549 |
0.585630 |
|
PF |
0.847590 |
1.000000 |
0.958096 |
0.915320 |
0.883207 |
0.734643 |
|
PB |
0.818532 |
0.958096 |
1.000000 |
0.814890 |
0.781400 |
0.663162 |
|
LOG(YD) |
0.780012 |
0.915320 |
0.814890 |
1.000000 |
0.945766 |
0.744500 |
|
N |
0.736549 |
0.883207 |
0.781400 |
0.945766 |
1.000000 |
0.571129 |
|
P |
0.585630 |
0.734643 |
0.663162 |
0.744500 |
0.571129 |
1.000000 |
To test whether a particular simple correlation coefficient between variables is significant, refer to Performing the t-test of the simple correlation coefficient (UE 5.3.3).
Соседние файлы в папке EViews Guides BITCH
- #
- #
- #
You should upgrade or use an alternative browser.
-
Forums
-
Mathematics
-
MATLAB, Maple, Mathematica, LaTeX
Eviews 3 stage least squares near singular matrix
-
Thread starter
Econrocks -
Start date
Dec 9, 2010
- Dec 9, 2010
- #1
essentially, I control for the fixed effects for the 8 countries in my data set, schooling, and urbanization in 1850. Each equation has a different variable that measure culture (control, obedience, tolerance, and trust). I am using the same instruments of institutions and literacy for each equation. so the only difference with each equation is which culture variable is being used.
System:
gdp_pc_ca9500= C(1)*country1 + C(2)*country15 + C(3)*country2 + C(4)*country3 + C(5)*country4 + C(6)*country5 + C(7)*country7 + C(8)*country8 + C(9)*school + C(10)*urb_1860_1850_30 + C(100)*control
gdp_pc_ca9500= C(12)*country1 + C(12)*country15 + C(14)*country2 + C(15)*country3 + C(16)*country4 + C(17)*country5 + C(18)*country7 + C(19)*country8 + C(20)*school + C(21)*urb_1860_1850_30 + C(101)*obedience
gdp_pc_ca9500= C(23)*country1 + C(24)*country15 + C(25)*country2 + C(26)*country3 + C(27)*country4 + C(28)*country5 + C(29)*country7 + C(30)*country8 + C(31)*school + C(32)*urb_1860_1850_30 + C(102)*tolerance
gdp_pc_ca9500= C(34)*country1 + C(35)*country15 + C(36)*country2 + C(37)*country3 + C(38)*country4 + C(39)*country5 + C(40)*country7 + C(41)*country8 + C(42)*school + C(43)*urb_1860_1850_30 + C(104)*trust
@inst pc_institutions literacy1880
My question is whether or not my problem lies in bad programming (if you can call eviews programming), or in something I’m missing in the theory. If I do it in 3SLS or Multiple equation Generalized method of moments, I get the near singular matrix error (which makes sense, since 3SLS is a special case of GMM).
I would appreciate any help
Answers and Replies
- Dec 9, 2010
- #2
Suggested for: Eviews 3 stage least squares near singular matrix
- Last Post
- Oct 24, 2022
- Last Post
- Mar 2, 2022
- Last Post
- Nov 5, 2019
- Last Post
- Jul 4, 2020
- Last Post
- Jul 6, 2020
- Last Post
- Oct 27, 2021
- Last Post
- Jul 22, 2020
- Last Post
- Jul 27, 2020
- Last Post
- May 18, 2020
- Last Post
- Apr 15, 2021
-
Forums
-
Mathematics
-
MATLAB, Maple, Mathematica, LaTeX


