Near singular matrix error regressors may be perfectly collinear

Соседние файлы в папке EViews Guides BITCH

• #
• #
• #

EViews.com

EViews User Forum

Near Singular Matrix Error

Near Singular Matrix Error

Post by u01uw11 » Tue Mar 10, 2015 7:06 am

First off, I’m not entirely sure if this is the correct subforum to post this; if it isn’t, I apologize.
I’m also a newcomer to both EViews and this forum, so please be gentle .
I use EViews 7.

I’m trying to estimate the effects of women on the board (binarywomen= (0,1)) an interaction term (binarywomen*logii), where logii= log(innovationintensity), where innovationintensity= R&D expenditure/total assets.

I use a few control variables, such as log(innovationintensity), log(size), age, leverage, log(capexintensity), log(agecapitalstock), and board size.

I have unbalanced (incomplete) panel data for all FTSE100 companies over the period 1993-2013.

I can estimate the regression with EITHER cross-section fixed effects (which would translate into firm fixed effects) OR period fixed effects (which would be Year fixed effects), however, when I try to do both together I get the error message «Near Singular Matrix».

I have looked through the forums and apparently this error message pops up when there are issues of multicollinearity, but can’t figure out where this would be the case in my data.

I have also modelled the year dummy variables myself, and used cross-section fixed effects in eviews, but I still get the same error message.

I attached my excel file with the panel data, and the EViews workfile with the final dependent and independent variables.

The model should look like this:

logtobinq c logii logsize age leverage logcei logacs boardsize binarywomen bwlogii yr1 yr2 yr3 yr4 yr5 yr6 yr7 yr8 yr9 yr10 yr11 yr12 yr13 yr14 yr15 yr16 yr17 yr18 yr19 yr20

and using cross-section fixed effects with this regression, I get the error message «Near Singular Matrix».

Any suggestions how I can resolve this?

(PS: If I only use cross-section fixed effects EViews can use 499 observations over 13 periods and 49 cross-sections.)

Источник

EViews User Forum

Near Singular Matrix Error for Impulse response fonctions

Near Singular Matrix Error for Impulse response fonctions

Post by sivakizildag » Fri Nov 18, 2016 10:02 am

In order to analyse the interactions between the following data, I made an SVAR:

— tourist arrivals in France —> A_TOT_SA
— accomodation capacity in number of rooms in hotels (in first difference) —> D(OFF_SA)
— a consumer confidence index for OECD countries —> D(E_OECD)

There is one last dummy variable for the Paris terror attacks (EVENT_ATT_NOV_15).

With these variables, I make the SVAR (SVAR):

1. I estimate the VAR with 4 lags (results in TABLE01)
2. Using matrixes ZA and ZB, I make the VAR and SVAR (results in TABLE02)

When I ask Eviews for the IRF, I get an Error Message: «Near singular matrix».
I aso installed the sirf add-in for scaled IRFs, I also get the same message.

One last things that might help: on the IRF menu, when I switch the Analytic (asymptotic) to None in the Response Standard Errors section, I get the IRFs but without the confidence intervals. Could you please tell me why this is happening?

Thank you very much,

Re: Near Singular Matrix Error for Impulse response fonctions

Post by EViews Matt » Fri Nov 18, 2016 4:12 pm

Let me address your questions in reverse order. First, regarding the missing confidence intervals when you select the «None» option under «Response Standard Errors». The confidence interval presentation make use of the standard errors, so if you choose to omit the standard errors then the confidence intervals are omitted too.

Second, regarding the near singular matrix error when you select the «Analytic (asymptotic)» option under «Response Standard Errors». One of the intermediate calculations performed behind the scenes is the second moment matrix of the VAR regressors, which is then inverted. Unfortunately, for your data that moment matrix is ill-conditioned (the estimated condition number is on the order of 10^18). EViews detects that the moment matrix is near singular and cannot be safely inverted, producing the error you experienced. From a numerical perspective, the problem seems to arise from the large magnitude of your first endogenous variable (a_tot_sa).

Re: Near Singular Matrix Error for Impulse response fonctions

Post by sivakizildag » Mon Nov 21, 2016 9:58 am

Thanks you so much!

Indeed, it works now that I took the first difference with logarithms!

Re: Near Singular Matrix Error for Impulse response fonctions

Post by sivakizildag » Fri Nov 25, 2016 5:00 am

I have another question, about the LR restrictions:

In the SVAR, what are the coefficients estimated in the long-run pattern matrix?

I mean, there is the formula on top: Model: Ae = Bu where E[uu’]=I

Down below we have the estimated A and B matrixes.

So what are the coefficients C(1) to C(5)

Re: Near Singular Matrix Error for Impulse response fonctions

Post by EViews Matt » Mon Nov 28, 2016 11:44 am

It would probably help to review the relevant section of the SVAR documentation, but the short answer is the following relation:

where C is the long-term factorization matrix (the one you specify the pattern for and contains the coefficients), Ψ is the vector moving average matrix, and A and B are the two factorization matrices you’re already familiar with. In order to solve this equation EViews assumes that A = I, so the solution will come in the form of B = Ψ^-1 * C.

Источник

EViews Guides BITCH / EViews_tutorial

Ramsey’s Regression Specification Error Test (RESET) ( UE 6.8.1):

Complete Steps 1 — 5 of the section entitled Adding or deleting variables to/from an OLS model in EViews before attempting this section (i.e., EQ02 should be present in the workfile). Follow these steps to carry out the Ramsey’s Regression Specification Error Test (RESET) using the step-by-step approach followed in UE , pp. 193-195:

Step 1. Open the EViews workfile named Chick6.wf1 .

Step 2. Open EQ02 by double clicking its icon in the workfile window (see UE , Equation 6.9, p. 194).

Step 3. Select Forecast on the equation menu bar, enter YF in the Forecast n ame: window, and click OK . 3

Step 4. Select Objects/New Object/Equation on the workfile menu bar, enter Y C PC YD YF^2 YF^3 YF^4 in the Equation Specification: window, and click OK (see UE , Equation 6.10, p. 194).

Step 5. Select Name on the equation menu bar, enter EQ03 in the N ame to identify object: window, and click OK .

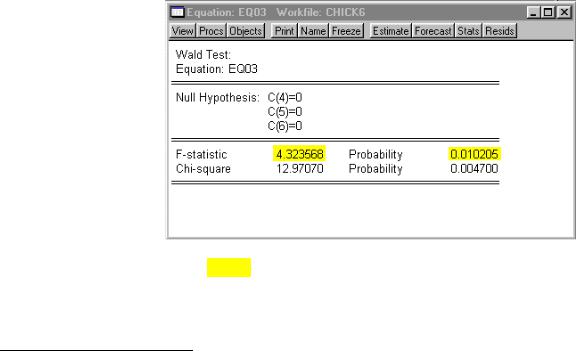
Step 6. Select View/ C oefficient Tests/ W ald-Coefficient Restrictions on the equation menu bar, enter C(4)=0, C(5)=0, C(6)=0 in the Coefficient restrictions separated by commas: window, 4 and click OK

to get the graphic shown on the right.

Step 7. Determine the critical F-statistic from UE , Table B-2 or by entering the formula:

=@qfdist(0.95,3,eq03. @regobseq03.@ncoef) in the command window, pressing Enter , and reading the value on the status line in the lower left of the screen.

Step 8. The F-statistic, highlighted in yellow, is the same as reported in UE , p. 195. 5 Since the calculated F-statistic of 4.32 exceeds the critical F-statistic of 2.85, the null hypothesis that the coefficients on the added variables are jointly zero can be rejected at the 5% level. This is in spite of the fact that none of their coefficients are individually significant.

3 This creates a new series with forecast values of Y based on the estimated coefficients for EQ02 .

4 Note that the coefficient restrictions are written as C(i), where i represents the coefficient order number of the variable as it was entered in the Equation Specification: window, following the dependent variable. Thus, C(4),C(5) and C(6) represent the coefficients for YF^2 YF^3 YF^4 in the Equation Specification: Y C PC YD YF^2 YF^3 YF^4 .

5 The Chi-square statistic is equal to the F-statistic times the number of restrictions under test. In this example, there are three restrictions, so the Chi-square test statistic is three times the size of the F-statistic, but the p-values of both statistics indicate that we can decisively reject the null hypothesis that the three coefficients are zero.

Ramsey’s Regression Specification Error Test (RESET) ( EViews ):

Complete Steps 1 — 5 of the section entitled Adding or deleting variables to/from an OLS model in EViews before attempting this section (i.e., EQ02 should be present in the workfile). Follow these steps to carry out the Ramsey’s Regression Specification Error Test (RESET) using EViews, built in Ramsey’s RESET Test :

Step 1. Open the EViews workfile named Chick6.wf1 .

Step 2. Open EQ02 by double clicking its icon in the workfile window (see UE , Equation 6.9, p. 194).

Step 3. Select View/ S tability Tests/ R amsey RESET Test… , enter 3 in the Number of fitted terms: window 6 , and click OK to get the table below.

Note that the output is very similar to the output achieved with the step-by- step approach in the previous section. In this case, the test results are printed above the regression output table.

Since the calculated F-statistic of 4.32

exceeds the critical F-statistic of 2.85, the null hypothesis that the coefficients on the added variables are jointly zero can be rejected at the 5% level. This

Ramsey RESET Test:

Log likelihood ratio

Dependent Variable: Y

Method: Least Squares

Date: 07/27/00 Time: 07:26

Sample: 1951 1994

Included observations: 44

Mean dependent var

S.D. dependent var

S.E. of regression

Akaike info criterion

Sum squared resid

is in spite of the fact that all of their individual t-statistics are insignificant .

6 The fitted terms are the powers of the fitted values from the original regression, starting with the square or second power. For example, if you specify 3, then the test will add ŷ 2 , ŷ 3 , and ŷ 4 in the regression. If you specify a large number of fitted terms, EViews may report a near singular matrix error message since the powers of the fitted values are likely to be highly collinear. The Ramsey RESET test is applicable only to an equation estimated by least squares.

Akaike’s Information Criterion (AIC) and the Schwartz Criterion (SC):

Complete Steps 1 — 5 of the section entitled Adding or deleting variables to/from an OLS model in EViews before attempting this section (i.e., EQ01 and EQ02 should be present in the workfile). The Akaike’s Information Criterion (AIC) and Schwartz Criterion (SC) are both printed in the E stimation Output of EViews’ OLS regressions.

Step 1. Open the EViews workfile named Chick6.wf1 .

Step 2. Open EQ01 by double clicking its icon in the workfile window (see UE , Equation 6.8, p. 160 or 196) to get the E stimation Output below.

Dependent Variable: Y

Method: Least Squares

Date: 07/26/00 Time: 09:11

Sample: 1951 1994

Included observations: 44

Mean dependent var

S.D. dependent var

S.E. of regression

Akaike info criterion

Sum squared resid

Step 3. Open EQ02 by double clicking its icon in the workfile window (see UE , Equation 6.9, p. 161) to get the E stimation Output below.

Dependent Variable: Y

Method: Least Squares

Date: 07/26/00 Time: 08:01

Sample: 1951 1994

Included observations: 44

Mean dependent var

S.D. dependent var

S.E. of regression

Akaike info criterion

Sum squared resid

Note that the AIC & SC information criterion reported in EViews (see numbers highlighted in yellow) are larger when PB is omitted from the OLS regression (i.e., EQ02 ). Both Akaike’s and the Schwartz Criterion provide evidence that UE , Equation 6.8 (i.e., EViews EQ01 ) is preferable to UE , Equation 6.9 (i.e., EViews EQ02 ).

15. Open the EViews workfile named Drugs.wf1 . a.

i) Select Objects/New Object/Equation on the workfile menu bar, enter P C GDPN CVN PP DPC IPC CV in the Equation Specification: window, and click OK . Select Name on the equation window menu bar, enter EQ01 in the N ame to identify object: window, and click OK .

ii) Select Objects/New Object/Equation on the workfile menu bar, enter P C GDPN CVN PP DPC IPC N in the Equation Specification: window, and click OK . Select Name on the equation window menu bar, enter EQ02 in the N ame to identify object: window, and click OK .

b. Open EQ01 and EQ02 at the same time. Use information in these tables, UE 6.8 (Appendix) and the procedures outlined in this guide to determine whether CV and/or N are irrelevant or omitted variables.

Chapter 7: Specification: Choosing A Functional Form

In this chapter:

1. Table with EViews specification for functional forms

2. Calculating «Quasi — R 2 » in EViews ( UE 7.3.1, footnote 5, p. 215)

3. Calculating «Quasi — R 2 » for a linear versus log-lin model using EViews

4. Coefficient restrictions tests using EViews ( UE , Appendix 7.7)

5. The Chow test , alternately termed Chow’s Breakpoint Test ( UE , Appendix 7.7)

UE section 7.2 presents alternative functional forms that are useful when specifying econometric models. Linear models are frequently too restrictive to properly fit the functional form suggested by the underlying theory.

The last column of Table 7.1 below shows the correct EViews specification for the alternative functional forms printed in UE , Table 7.1, p. 214. You can use the table as a guide, but you must realize that Y represents the dependent variable while X 1 & X 2 represent the only independent variables in all of the equations/specifications. Note that a constant (C) should be included in all models even if theory suggests otherwise (see UE , p. 201). You must have a workfile open in order to specify and estimate a regression model. Then, to specify a regression model in EViews, select Objects/New Object/Equation from the workfile menu and enter the appropriate EViews specification (see the last column of the table below), in the Equation Specification: window. 1

Table 7.1: EViews Specification of Functional Forms

Y = β 0 + β 1 X 1 + β 2 X 2

lnY = β 0 + β 1 lnX 1 + β 2 lnX 2

log(Y) C log(X 1 ) log(X 2 )

Y = β 0 + β 1 lnX 1

Y C log(X 1 ) X 2

lnY = β 0 + β 1 X 1

Y = β 0 + β 1 X 1 + β 2 (X 1 2 ) + β 3 X 2

Y C X 1 X 1 ^2 X 2

Y = β 0 + β 1 (1/X 1 ) + β 2 X 2

Y = β 0 + β 1 X 1

Y = β 0 + β 1 X 1 + β 2 D 1 + β 3 D 1 X 1

Y C X 1 D 1 D1*X1

* Intercept dummy variable. ** Intercept and slope dummy variables.

Calculating «Quasi — R 2 » in EViews ( UE 7.3.1, footnote 5, p. 215):

The dependent variable must be in the same form when using R 2 and adjusted R 2 to compare the overall goodness of fit between two equations. For example, it would not be appropriate to compare the R 2 for a linear model with a double-log or a log-lin model. However, it would be appropriate to compare R 2 for a linear model with a lin-log, a

1 Alternately, select Quick/Estimate Equation from the main menu. If this method is used you must name the equation to save it. Select Name on the equation menu bar and enter the desired name in the N ame to identify object: window, and click OK .

polynomial, or an inverse functional form model. Likewise, it would be appropriate to compare R 2 for double-log and log-lin functional form models. In order to demonstrate the process, the car acceleration data introduced in UE , Exercise 16, p. 234, will be used to demonstrate the process of calculating the quasi-R 2 . The steps below show how to compare the goodness of fit for models using S (the number of seconds it takes a car to accelerate from 0 to 60 miles per hour) as the dependent variable versus using the natural log of S as the dependent variable. In both models, the independent variables are the same as the original model printed at the top of UE , p. 236.

Calculating «Quasi — R 2 » for a linear versus a log-lin model using EViews:

Step 1. Open the EViews workfile named Cars7.wk1 .

Step 2. Select Objects/New Object/Equation on the workfile menu bar, enter S C T E P H in the Equation Specification: window, and click OK .

Step 3. Select Name on the equation menu bar, write linear in the N ame to identify object: window, and click OK . Minimize the equation object named linear .

Step 4. Select Objects/New Object/Equation on the workfile menu bar, enter log(S) C T E P H in the Equation Specification: window (i.e., the log-lin functional form), and click

Step 5. Select Name on the equation menu bar, write loglin in the N ame to identify object: window, and click OK .

Step 6. Select Forecast on the equation menu bar, select S in the F orecast of: 2 window, enter SF in the Forecast n ame: window, uncheck the two boxes in the Output: window (the only objective here is to create a forecast series, not a forecast evaluation), and click OK . A new series named SF appears in the workfile window.

Steps 7, 8 & 9 calculate the quasi-R 2 for this regression ( UE 7.3.1, footnote 5, p. 215).

Step 7. Minimize the equation window, select Genr on the workfile menu bar, type numerator=(S-SF)^2 in the E nter equation: window, and click OK (this step generates the un-summed variable in the numerator of the quasi-R 2 equation).

Step 8. Select Genr on the workfile menu bar, type denominator=(S-@mean(S))^2 in the E nter equation: window, and click OK (this step generates the un-summed variable in the denominator of the quasi-R 2 equation).

Step 9. To calculate the quasi-R 2 , type the following equation in the command window and press Enter : scalar quasir2=1-(@sum(numerator)/@sum(denominator)) . A new variable named quasir2 will appear in the workfile window. Double click on it and the value for the quasi-R 2 will be displayed in the lower left of the screen (0.783958974). The quasi-R 2 calculated in Step 9 (i.e., 0.78) is in-between the R 2 from the linear model estimated in Step 2 (i.e., 0.71) and the R 2 from the log-lin model estimated in Step 5 (i.e., 0.81).

2 The Forecast procedure in EViews gives you the option of forecasting the transformed dependent variable (i.e., LOG(S) in this case) or the original variable (i.e., S in this case). Select S, since the computation of quasi-R 2 requires converting of LOG(S) to S by taking the anti-log of the dependent variable (this can also be done by using the EViews command @exp(LOG(S)) .

Coefficient restrictions tests using EViews ( UE , Appendix 7.7):

The F-test can be used to test a wide range of hypothesis concerning regression coefficients. For example, suppose that the claim was made that when a car has a manual transmission it increases its acceleration speed (i.e., decreases the number of seconds it takes to accelerate from 0 to 60 miles per hour) just as much as adding 100 horsepower to the car. Translating this into the language of UE , Equation 7.28, p. 235, this means that the absolute value of the coefficient on T i is 100 times larger than the absolute value of the coefficient on H i . Just looking at the size of the estimated coefficients, it appears that you can easily reject the hypothesis because the absolute value of the coefficient on T i is only about 41.5 times larger than the absolute value of the coefficient on H i (divide the coefficient on T i by the coefficient on H i ). However, these coefficients are just estimates. Follow these steps to carry out an F-test for the null hypothesis that the absolute value of the coefficient on T i is 100 times larger than the absolute value of the coefficient on H i . :

Step 1. Open the EViews workfile named Cars7.wk1 .

Step 2. Select Objects/New Object/Equation on the workfile menu bar, enter S C T E P H in the Equation Specification: window, and click OK .

Step 3. Select Name on the equation menu bar, write EQ01 in the N ame to identify object: window, and click OK .

Step 4. Select View/ C oefficients Tests/ W ald-Coefficient Restrictions … on the equation menu bar, enter -C(2)=-100*C(5) in the Coefficients separated by commas: window, and click OK to reveal the following output: 3

Источник

Click here follow the steps to fix Near Singular Matrix Error In Eviews and related errors.

Instructions

To Fix (Near Singular Matrix Error In Eviews) error you need to follow the steps below:
Step 1:
Download (Near Singular Matrix Error In Eviews) Repair Tool
Step 2:
Click the «Scan» button
Step 3:
Click ‘Fix All‘ and you’re done!
Compatibility: Windows 7, 8, Vista, XP Download Size: 6MB Requirements: 300 MHz Processor, 256 MB Ram, 22 MB HDD Limitations: This download is a free evaluation version. To unlock all features and tools, a purchase is required.

Note:
This article was updated on 2023-02-03 and previously published under WIKI_Q210794

What is Near Singular Matrix Error In Eviews error?

The Near Singular Matrix Error In Eviews error is the Hexadecimal format of the error caused. This is common error code format used by windows and other windows compatible software and driver vendors.

This code is used by the vendor to identify the error caused. This Near Singular Matrix Error In Eviews error code has a numeric error number and a technical description. In some cases the error may have more parameters in Near Singular Matrix Error In Eviews format .This additional hexadecimal code are the address of the memory locations where the instruction(s) was loaded at the time of the error.

What causes Near Singular Matrix Error In Eviews error?

The Near Singular Matrix Error In Eviews error may be caused by windows system files damage. The corrupted system files entries can be a real threat to the well being of your computer.

There can be many events which may have resulted in the system files errors. An incomplete installation, an incomplete uninstall, improper deletion of applications or hardware. It can also be caused if your computer is recovered from a virus or adware/spyware
attack or by an improper shutdown of the computer. All the above actives
may result in the deletion or corruption of the entries in the windows
system files. This corrupted system file will lead to the missing and wrongly
linked information and files needed for the proper working of the
application.

How to easily fix Near Singular Matrix Error In Eviews error?

There are two (2) ways to fix Near Singular Matrix Error In Eviews Error:

Advanced Computer User Solution (manual update):

1) Start your computer and log on as an administrator.

2) Click the Start button then select All Programs, Accessories, System Tools, and then click System Restore.

3) In the new window, select «Restore my computer to an earlier time» option and then click Next.

4) Select the most recent system restore point from the «On this list, click a restore point» list, and then click Next.

5) Click Next on the confirmation window.

6) Restarts the computer when the restoration is finished.

Novice Computer User Solution (completely automated):

1) Download (Near Singular Matrix Error In Eviews) repair utility.

2) Install program and click Scan button.

3) Click the Fix Errors button when scan is completed.

4) Restart your computer.

How does it work?

This tool will scan and diagnose, then repairs, your PC with patent
pending technology that fix your windows operating system registry
structure.
basic features: (repairs system freezing and rebooting issues , start-up customization , browser helper object management , program removal management , live updates , windows structure repair.)

About Noman Arshed!

Hi! I am Noman Arshed, PhD fellow Islamic Banking and Finance University of Management and Technology Lahore Pakistan & MSc Economics from University of Edinburgh UK. Currently learning Applied Economics and Islamic Finance, its application.

CV : noman arshed cv

Placement:

Lecturer at University of Management and Technology Lahore (Link)

Currently Teaching

• Microeconomics
• Macroeconomics
• Development Economics
• Econometrics
• Research Methodology
• Applied Econometrics (Ms Economics)

I have recently  taught

• Statistics for Economists (Msc Economics University of the Punjab Lahore)

Profiles: Google Scholar

Instructor at The Economics and Social Development Organization

Contact:

• @: noumanarshed55@hotmail.com

Conference Proceedings:

Sulaiman, I., & Arshed, N. (2015). Can Stock Market Development Put Chains on Inflation? A Panel Cointegration Analysis on SAARC Countries. Proceedings of 12th Asian Business Research Conference 8-9 October 2015, Novotel Hotel Bangkok on Siam Square, Bangkok, Thailand

Arshed, N. & Hassan, M.S. (2015). Does Income Inequality Lead to Education Inequality. 13th International Conference on Statistical Sciences Peshawar, Islamic Countries Society of Statistical Sciences.

Publications:

Sulaiman, I., Arshed, N., & Hassan, M. S. (2016). Stock Market Development, Can it Help Reduce Inflation in SAARC Countries? Journal of Accounting, Finance and Economics, 6(1), 101-110.

Arshed, N., Hassan, M. S., & Mushtaq, A. (2016). Smoking Advertisements and Its Impact on Human Behavior. International Journal of Scientific Research and Management. 4(3), 4030-4047.

Arshed, N., & Zahid, A. (2016). Panel Monetary Model and Determination of Multilateral Exchange Rate with Major Trading Partners. International Journal of Recent Scientific Research, 7(4), 10551-10560

Hanif, N., & Arshed, N. (2016). Relationship between School Education and Economic Growth: SAARC Countries. International Journal of Economics and Financial Issues, 6(1), 294-300.

Mamoon, D., Raza, S., & Arshed, N. (2015). Impact of Health Capital and Education on Infant Mortality rate on Districts of Punjab. Journal of Management and Research, 1(2), 9-17

Hassan, M. S., Wajid, A., Irfan, Q. M., Tahir, M. N., & Arshed, N. (2014). Some Price and Non-Price Factors Affecting Imports in Pakistan. Pakistan Journal of Applied Economics, 24(2), 159-177.

Bhatti, M. A., Arshed, N., & Haseeb, M. (2013). Performance of CHEERs Based Equilibrium Exchange Rate of Pakistan. Business and Management Horizons, 1(1), 17.

Projects:

Shopoholic;. Crazy about shopping

A new trend in online shopping

Econistics. Place for research material and lectures on economics. (Under Development)

Built on the motive to provide services on questionnaire making and data collection.

RSPW. Research and Statistical Packages Workshop

Providing specialist services of statistical packages skill training workshops

Food Street. Its all about food.

Founded the website idea and gradually developing it to make it a prime destination for food lovers.

EViews.com

EViews User Forum

Near Singular Matrix Error

Near Singular Matrix Error

Post by corbinm » Wed Feb 05, 2014 4:11 am

I am having an issue using e views 8 student version. I am getting the typical near singular matrix error and so far I have been un able to find a solution. The regression I am attempting to run is

excess1 c shortint instiown monthd quarterd yeard shortint*monthd shortint*quarterd shortint*yeard excess0 excess0*monthd excess0*quarterd excess0*yeard excess0*shortint excess0*monthd*shortint excess0*quarterd*shortint excess0*yeard*shortint

This is one of three equations which all include similar variables and has been successfully run on several other country data sets I am testing. However for some reason I run into this problem only on my Indonesia data set and one other data set our of over 60. I’ve tried removing the constant variable and that has done nothing. I need to include all other variables and so I can’t afford to start deleting variables here and there.

Just for reference the dummy variables are monthd quarterd and yeard which indicate different period ends,i.e a month end quarter end or year end date. and there is no over lap, so the last date in jan and feb will have a 1 for month end while the end of march with have a 1 for quarter end but a zero for month end and so on

Any help would be great, Ive attached the .txt file below which im using as my data in e views

Re: Near Singular Matrix Error

Post by trubador » Wed Feb 05, 2014 5:33 am

Re: Near Singular Matrix Error

Post by corbinm » Wed Feb 05, 2014 7:01 am

I see, thank you for your help with that. I am still relatively new to e views and very rusty on my econmetrics. Could you explain the commands for determining this issue as I have a couple other equations which are presenting a similar issue? Further more does this suggest an issue with my data or is it a matter of chance probability that this occurred for the variables in this data set while numerous other identical ones (for other countries) did not run in to this problem?

Thanks again for you quick response and help

Re: Near Singular Matrix Error

Post by trubador » Wed Feb 05, 2014 7:52 am

Re: Near Singular Matrix Error

Post by Marcel Visser » Mon May 18, 2015 3:59 am

I am receiving the same error code. I attached my original correlation matrix. Even when I do not include the variables for Financial Development and Profitability in the regression I still get the error code.
Does anyone know what I am doing wrong and how i will be able to fix this?

Thanks in advance.

Re: Near Singular Matrix Error

Post by EViews Gareth » Mon May 18, 2015 7:56 am

Re: Near Singular Matrix Error

Post by Marcel Visser » Mon May 18, 2015 9:01 am

I found the problem. My variable OPRISK takes the same value for any company year observation in the sample, 2008-2012. So the value only varies when companies change, not when years change. I found somewhere else on this forum that this prevents you from running a cross section fixed effects regression. The regression I try to run is Leverage ratio= c (Financial development) (Inflation) (Marginal tax rate) (OPRISK) (log sales) (profitability) (tangibility). Can I just remove the variable OPRISK and run the regression. Will this accurately remove the year and section effects from the other variables? Because I still need to control for the year and section effects on the other variables. My sample size is very large, 122000 observations per variable. Therefor I cannot upload my file. The thing is i ran a Hausman test which told me to use a fixed effect model. However, the OPRISK variable prevents me from doing this. The book Introductory econometrics for finance also said that you could use a slightly modified version of the Chow test to check if a panel regression was really necessary. It said in some cases you could just pool the data and preform a regular OLS.

If i will not be able to exclude the year and section effects with a fixed effects panel regression, should i then use this approach. And could you please tell me how this is done?

I would like to thank you in advance for your time.

Kind regards,
Marcel Visser

Re: Near Singular Matrix Error

Post by said.abouabdo » Wed Apr 04, 2018 6:58 am

Re: Near Singular Matrix Error

Post by startz » Wed Apr 04, 2018 8:57 am

Re: Near Singular Matrix Error

Post by Alina03 » Sat Jul 14, 2018 5:59 am

Re: Near Singular Matrix Error

Post by startz » Sat Jul 14, 2018 6:50 am

Источник

EViews.com

EViews User Forum

Ramsey reset specification

Ramsey reset specification

Post by bparksb » Fri Feb 24, 2012 2:29 pm

The Ramsey Reset test uses predicteds in a auxiliary test equation.

The problem is numerical — if the dependent variable is large or small, Y_hat^2, Y_hat^3, Y_hat^4, Y_hat^5 can be very large or very small and will cause a ‘near singular matrix’ message when Eviews attempts to calculate the auxiliary equation.

One ‘fix’ is to use the standardized predicteds rather than the raw predicteds, i.e., (Y_hat-@mean(Y_hat))/@stdev(Y_hat). The standardized variables will be numerically better behaved and the log likelihood is identical (as it must be).

An example follows in which hours of labor is regressed on wages and a Ramsey 3 term test will not compute.
eq01.reset(3) produces
Near singular matrix error. Regressors may be perfectly collinear in «DO_ EQ01.RESET(3)».
while
equation eq02.ls hrs c wage hrsf^2 hrsf^3 hrsf^4 produces
Near singular matrix error. Regressors may be perfectly collinear in «EQUATION EQ02.LS HRS C WAGE HRSF^2 HRSF^3 HRSF^4».

I hope that you implement better numerical in the Ramsey test.

wfcreate(wf=testramsey) u 39
series hrs
series wage
HRS.fill 2157,2174,2062,2111,2134,2185,2210,2105,2267,2205,2121,2109,2108,2047,2174,2067,2159,2257,1985,2184,2084,2051,2127,2102,2098,2042,2181,2186,2108,2188,2203,2077,2196,2093,2173,2179,2200,2052,2197
WAGE.fill 2.905,2.97,2.3,2.511,2.791,3.04,3.222,2.493,2.8,2.356,2.922,2.499,2.796,2.453,3.582,2.909,2.511,2.516,1.423,3.636,2.983,2.573,3.262,3.234,2.28,2.304,2.912,3.015,2.786,3.01,3.273,1.901,3.009,1.899,2.959,2.971,2.98,2.63,3.413

equation eq01.ls hrs c wage
eq01.fit hrsf
eq01.reset(3)
genr hrsfstd = (hrsf-@mean(hrsf))/@stdev(hrsf)
equation eq02.ls hrs c wage hrsf^2 hrsf^3 hrsf^4
equation eq03.ls hrs c wage hrsfstd^2 hrsfstd^3 hrsfstd^4
equation eq04.ls hrs c wage hrsfstd^2 hrsfstd^3 hrsfstd^4 hrsfstd^5
equation eq05.ls hrs c wage hrsfstd^2 hrsfstd^3 hrsfstd^4 hrsfstd^5 hrsfstd^6

Источник

EViews.com

EViews User Forum

Near singular matrix

Near singular matrix

Post by Ydwolf » Fri Oct 07, 2011 3:56 am

For my thesis, I am researching the influence of terrorism on financial markets. Thereby, I study 68 different countries, for which I have written a simple program to generate the same regression for all of these countries. But for some reason, I get the error «Near singular matrix» only for country60(which is Switzerland), although I don’t see any difference in the data or the dummies used. In attachement you can find the workfile and program, just for country60. Can someone please tell me what the problem could be? If it would help, I can also upload the data for all 68 countries. Thank you very much,

Re: Near singular matrix

Post by EViews Glenn » Fri Oct 07, 2011 9:29 am

Re: Near singular matrix

Post by Ydwolf » Sat Oct 08, 2011 1:29 am

And what can I do to solve this? I’m not a real expert in EViews, you see.

Re: Near singular matrix

Post by EViews Gareth » Sat Oct 08, 2011 11:27 am

Re: Near singular matrix

Post by lnp3 » Sat Oct 08, 2011 3:33 pm

well, isn’t the solution «exclude variables that are multi-collinear and re-estimate with different variables»?

Re: Near singular matrix

Post by startz » Sat Oct 08, 2011 8:12 pm

Re: Near singular matrix

Post by lnp3 » Sun Oct 09, 2011 8:51 am

Dear Eviews expert,

Thank you so much for your answer on near singular matrix. I am currently using Eviews 5.1 but will install 7 soon. Can you also help me with this warning? When I run hausman test to determine fixed or random effects estimator, I get this warning.

What should I do to filter the problem? Since Hausman test probability (0.68) is larger than critical value (0.05), it is appropriate estimate with random effect (as I was told, if test value

Re: Near singular matrix

Post by vtodorov » Thu Nov 08, 2012 5:13 am

lnp3 wrote: Dear Eviews expert,

Thank you so much for your answer on near singular matrix. I am currently using Eviews 5.1 but will install 7 soon. Can you also help me with this warning? When I run hausman test to determine fixed or random effects estimator, I get this warning.

What should I do to filter the problem? Since Hausman test probability (0.68) is larger than critical value (0.05), it is appropriate estimate with random effect (as I was told, if test value

Re: Near singular matrix

Post by Rosa.hh » Tue Nov 27, 2012 9:43 am

Dear eviews experts,

Thanks fo the usefull information provided previously. I still have some questions.

I am running an egarch model to determinate the volatility of an interest rate and I would like to include specific events dummies (I am using daily data and eviews 7). However, I am having a multicolinearity problem.

I am not very used to eviews and would like to learn more. I have checked the correlogram matrix and vif in stata and they dont show a problem with my event variables(see results below). However when using eviews and regressing my dependent variables on the events, a problem of multicollinearity appears to exist (message «near singular matrix»). I also tried dropping the constant or one of the dummies, but the problem continues.

I also have calculated the correlation matrix of my event variables in eviews and a problem is pointed out as I get NA as result.

I enclose my workfile.

Would anyone help me understand:

1) Is the multicollinearity problem also related related to the fact that my event dummies are almost always zero, and only 1 for a few observations (7, 5 & 168 obs out of a total of 3425) ?

2) why I do I get NA when calculating the correlation matrix?

Thanks a lot for your help!

Here are results on VIF correlogram matrix (from stata):

. correlate ev_1 ev_3 ev_0510
(obs=3425)

| ev_1 ev_3 ev_0510
————-+—————————
ev_1 | 1.0000
ev_3 | -0.0017 1.0000
ev_0510 | -0.0103 0.1684 1.0000

Источник

Estimation Problems

If the regressors are very highly collinear, EViews may encounter difficulty in computing the regression estimates. In such cases, EViews will issue an error message “Near singular matrix.” When you get this error message, you should check to see whether the regressors are exactly collinear. The regressors are exactly collinear if one regressor can be written as a

22 —Chapter 18. Basic Regression Analysis

linear combination of the other regressors. Under exact collinearity, the regressor matrix X does not have full column rank and the OLS estimator cannot be computed.

You should watch out for exact collinearity when you are using dummy variables in your regression. A set of mutually exclusive dummy variables and the constant term are exactly collinear. For example, suppose you have quarterly data and you try to run a regression with the specification:

y c x @seas(1) @seas(2) @seas(3) @seas(4)

EViews will return a “Near singular matrix” error message since the constant and the four quarterly dummy variables are exactly collinear through the relation:

c = @seas(1) + @seas(2) + @seas(3) + @seas(4)

In this case, simply drop either the constant term or one of the dummy variables.

The textbooks listed above provide extensive discussion of the issue of collinearity.

References

Davidson, Russell and James G. MacKinnon (1993). Estimation and Inference in Econometrics , Oxford: Oxford University Press.

Greene, William H. (2008). Econometric Analysis , 6th Edition, Upper Saddle River, NJ: Prentice-Hall.

Johnston, Jack and John Enrico DiNardo (1997). Econometric Methods , 4th Edition, New York: McGrawHill.

Pindyck, Robert S. and Daniel L. Rubinfeld (1998). Econometric Models and Economic Forecasts , 4th edition, New York: McGraw-Hill.

Wooldridge, Jeffrey M. (2000). Introductory Econometrics: A Modern Approach . Cincinnati, OH: SouthWestern College Publishing.

Источник

EViews.com

EViews User Forum

(New to Eviews) Error with OLS

(New to Eviews) Error with OLS

Post by froppelina » Wed May 17, 2017 5:26 am

I am trying to run a regression of some data, which primarily constitutes of dummy variables.

However, Eviews is rendering an error box upon estimating the equation, and I believe it regards the dummy variables for my years. To clarify: I have observations in my dataset, for which I have created dummy variables for the relevant year, i.e. 2005 (1/0), 2006 (1/0) etc.
(Note: converting to a panel data analysis is not relevant since it actually regards additional variables other than the years)

I am aware that I must leave one of them out, to avoid collinearity. However, even when I do so, I get the error message («Near singular matrix error. Regressors may be perfectly collinear»).

Does anyone perhaps know how to solve this issue so that I can still check for the various years?

Re: (New to Eviews) Error with OLS

Post by startz » Wed May 17, 2017 5:46 am

Re: (New to Eviews) Error with OLS

Post by froppelina » Wed May 17, 2017 5:49 am

Re: (New to Eviews) Error with OLS

Post by startz » Wed May 17, 2017 5:56 am

Look at all the variables you put on the right.

If that doesn’t help find the bug. and it doesn’t always. post exact details about your data and the equation you’re running.

Re: (New to Eviews) Error with OLS

Post by froppelina » Wed May 17, 2017 6:41 am

Thank you. To be honest — I am not quite sure what right hand side variables you are referring to.

I have simplified my dataset if you would like to look at it. To clarify I have made the columns in different colors:
Black: dependent variable
Dark blue (hidden): Indep. variables that are functioning fine
Red: One category for which several dummy variables have been made (rendering error in Eviews). Refers to geography
Green: One category for which several dummy variables have been made (rendering error in Eviews). Refers to year of observation

I have also attached the eviews file (which is the result of the import of the excel file).
Thanks a ton for your help

Note: if you run a regression with dependent: «budpremie» and then just the years or the geographies, you will get the error.

Источник