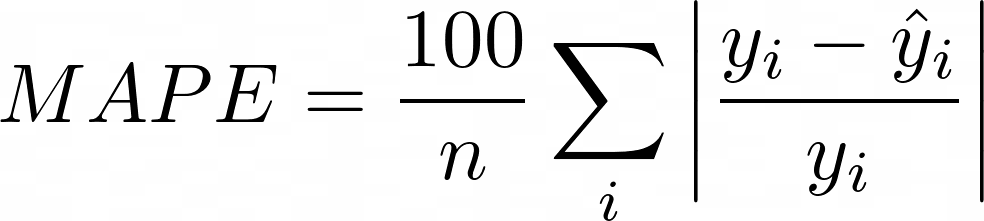Нормализованная среднеквадратичная ошибка

From Wikipedia, the free encyclopedia

The root-mean-square deviation (RMSD) or root-mean-square error (RMSE) is a frequently used measure of the differences between values (sample or population values) predicted by a model or an estimator and the values observed. The RMSD represents the square root of the second sample moment of the differences between predicted values and observed values or the quadratic mean of these differences. These deviations are called residuals when the calculations are performed over the data sample that was used for estimation and are called errors (or prediction errors) when computed out-of-sample. The RMSD serves to aggregate the magnitudes of the errors in predictions for various data points into a single measure of predictive power. RMSD is a measure of accuracy, to compare forecasting errors of different models for a particular dataset and not between datasets, as it is scale-dependent.^[1]

RMSD is always non-negative, and a value of 0 (almost never achieved in practice) would indicate a perfect fit to the data. In general, a lower RMSD is better than a higher one. However, comparisons across different types of data would be invalid because the measure is dependent on the scale of the numbers used.

RMSD is the square root of the average of squared errors. The effect of each error on RMSD is proportional to the size of the squared error; thus larger errors have a disproportionately large effect on RMSD. Consequently, RMSD is sensitive to outliers.^[2][3]

Formula[edit]

The RMSD of an estimator with respect to an estimated parameter is defined as the square root of the mean squared error:

For an unbiased estimator, the RMSD is the square root of the variance, known as the standard deviation.

The RMSD of predicted values for times t of a regression’s dependent variable with variables observed over T times, is computed for T different predictions as the square root of the mean of the squares of the deviations:

(For regressions on cross-sectional data, the subscript t is replaced by i and T is replaced by n.)

In some disciplines, the RMSD is used to compare differences between two things that may vary, neither of which is accepted as the «standard». For example, when measuring the average difference between two time series and ,
the formula becomes

Normalization[edit]

Normalizing the RMSD facilitates the comparison between datasets or models with different scales. Though there is no consistent means of normalization in the literature, common choices are the mean or the range (defined as the maximum value minus the minimum value) of the measured data:^[4]

or .

This value is commonly referred to as the normalized root-mean-square deviation or error (NRMSD or NRMSE), and often expressed as a percentage, where lower values indicate less residual variance. In many cases, especially for smaller samples, the sample range is likely to be affected by the size of sample which would hamper comparisons.

Another possible method to make the RMSD a more useful comparison measure is to divide the RMSD by the interquartile range. When dividing the RMSD with the IQR the normalized value gets less sensitive for extreme values in the target variable.

where

with and where CDF⁻¹ is the quantile function.

When normalizing by the mean value of the measurements, the term coefficient of variation of the RMSD, CV(RMSD) may be used to avoid ambiguity.^[5] This is analogous to the coefficient of variation with the RMSD taking the place of the standard deviation.

Mean absolute error[edit]

Some researchers have recommended the use of the Mean Absolute Error (MAE) instead of the Root Mean Square Deviation. MAE possesses advantages in interpretability over RMSD. MAE is the average of the absolute values of the errors. MAE is fundamentally easier to understand than the square root of the average of squared errors. Furthermore, each error influences MAE in direct proportion to the absolute value of the error, which is not the case for RMSD.^[2] However, MAE is not a substitute, as it accounts only for the systematic errors, while RMSD accounts for both systematic and random errors^{[according to whom?]}.

Applications[edit]

• In meteorology, to see how effectively a mathematical model predicts the behavior of the atmosphere.
• In bioinformatics, the root-mean-square deviation of atomic positions is the measure of the average distance between the atoms of superimposed proteins.
• In structure based drug design, the RMSD is a measure of the difference between a crystal conformation of the ligand conformation and a docking prediction.
• In economics, the RMSD is used to determine whether an economic model fits economic indicators. Some experts have argued that RMSD is less reliable than Relative Absolute Error.^[6]
• In experimental psychology, the RMSD is used to assess how well mathematical or computational models of behavior explain the empirically observed behavior.
• In GIS, the RMSD is one measure used to assess the accuracy of spatial analysis and remote sensing.
• In hydrogeology, RMSD and NRMSD are used to evaluate the calibration of a groundwater model.^[7]
• In imaging science, the RMSD is part of the peak signal-to-noise ratio, a measure used to assess how well a method to reconstruct an image performs relative to the original image.
• In computational neuroscience, the RMSD is used to assess how well a system learns a given model.^[8]
• In protein nuclear magnetic resonance spectroscopy, the RMSD is used as a measure to estimate the quality of the obtained bundle of structures.
• Submissions for the Netflix Prize were judged using the RMSD from the test dataset’s undisclosed «true» values.
• In the simulation of energy consumption of buildings, the RMSE and CV(RMSE) are used to calibrate models to measured building performance.^[9]
• In X-ray crystallography, RMSD (and RMSZ) is used to measure the deviation of the molecular internal coordinates deviate from the restraints library values.
• In control theory, the RMSE is used as a quality measure to evaluate the performance of a State observer.^[10]

See also[edit]

• Root mean square
• Mean absolute error
• Average absolute deviation
• Mean signed deviation
• Mean squared deviation
• Squared deviations
• Errors and residuals in statistics

References[edit]

From Wikipedia, the free encyclopedia

The root-mean-square deviation (RMSD) or root-mean-square error (RMSE) is a frequently used measure of the differences between values (sample or population values) predicted by a model or an estimator and the values observed. The RMSD represents the square root of the second sample moment of the differences between predicted values and observed values or the quadratic mean of these differences. These deviations are called residuals when the calculations are performed over the data sample that was used for estimation and are called errors (or prediction errors) when computed out-of-sample. The RMSD serves to aggregate the magnitudes of the errors in predictions for various data points into a single measure of predictive power. RMSD is a measure of accuracy, to compare forecasting errors of different models for a particular dataset and not between datasets, as it is scale-dependent.^[1]

RMSD is always non-negative, and a value of 0 (almost never achieved in practice) would indicate a perfect fit to the data. In general, a lower RMSD is better than a higher one. However, comparisons across different types of data would be invalid because the measure is dependent on the scale of the numbers used.

RMSD is the square root of the average of squared errors. The effect of each error on RMSD is proportional to the size of the squared error; thus larger errors have a disproportionately large effect on RMSD. Consequently, RMSD is sensitive to outliers.^[2][3]

Formula[edit]

The RMSD of an estimator with respect to an estimated parameter is defined as the square root of the mean squared error:

For an unbiased estimator, the RMSD is the square root of the variance, known as the standard deviation.

The RMSD of predicted values for times t of a regression’s dependent variable with variables observed over T times, is computed for T different predictions as the square root of the mean of the squares of the deviations:

(For regressions on cross-sectional data, the subscript t is replaced by i and T is replaced by n.)

In some disciplines, the RMSD is used to compare differences between two things that may vary, neither of which is accepted as the «standard». For example, when measuring the average difference between two time series and ,
the formula becomes

Normalization[edit]

Normalizing the RMSD facilitates the comparison between datasets or models with different scales. Though there is no consistent means of normalization in the literature, common choices are the mean or the range (defined as the maximum value minus the minimum value) of the measured data:^[4]

or .

This value is commonly referred to as the normalized root-mean-square deviation or error (NRMSD or NRMSE), and often expressed as a percentage, where lower values indicate less residual variance. In many cases, especially for smaller samples, the sample range is likely to be affected by the size of sample which would hamper comparisons.

Another possible method to make the RMSD a more useful comparison measure is to divide the RMSD by the interquartile range. When dividing the RMSD with the IQR the normalized value gets less sensitive for extreme values in the target variable.

where

with and where CDF⁻¹ is the quantile function.

When normalizing by the mean value of the measurements, the term coefficient of variation of the RMSD, CV(RMSD) may be used to avoid ambiguity.^[5] This is analogous to the coefficient of variation with the RMSD taking the place of the standard deviation.

Mean absolute error[edit]

Some researchers have recommended the use of the Mean Absolute Error (MAE) instead of the Root Mean Square Deviation. MAE possesses advantages in interpretability over RMSD. MAE is the average of the absolute values of the errors. MAE is fundamentally easier to understand than the square root of the average of squared errors. Furthermore, each error influences MAE in direct proportion to the absolute value of the error, which is not the case for RMSD.^[2] However, MAE is not a substitute, as it accounts only for the systematic errors, while RMSD accounts for both systematic and random errors^{[according to whom?]}.

Applications[edit]

• In meteorology, to see how effectively a mathematical model predicts the behavior of the atmosphere.
• In bioinformatics, the root-mean-square deviation of atomic positions is the measure of the average distance between the atoms of superimposed proteins.
• In structure based drug design, the RMSD is a measure of the difference between a crystal conformation of the ligand conformation and a docking prediction.
• In economics, the RMSD is used to determine whether an economic model fits economic indicators. Some experts have argued that RMSD is less reliable than Relative Absolute Error.^[6]
• In experimental psychology, the RMSD is used to assess how well mathematical or computational models of behavior explain the empirically observed behavior.
• In GIS, the RMSD is one measure used to assess the accuracy of spatial analysis and remote sensing.
• In hydrogeology, RMSD and NRMSD are used to evaluate the calibration of a groundwater model.^[7]
• In imaging science, the RMSD is part of the peak signal-to-noise ratio, a measure used to assess how well a method to reconstruct an image performs relative to the original image.
• In computational neuroscience, the RMSD is used to assess how well a system learns a given model.^[8]
• In protein nuclear magnetic resonance spectroscopy, the RMSD is used as a measure to estimate the quality of the obtained bundle of structures.
• Submissions for the Netflix Prize were judged using the RMSD from the test dataset’s undisclosed «true» values.
• In the simulation of energy consumption of buildings, the RMSE and CV(RMSE) are used to calibrate models to measured building performance.^[9]
• In X-ray crystallography, RMSD (and RMSZ) is used to measure the deviation of the molecular internal coordinates deviate from the restraints library values.
• In control theory, the RMSE is used as a quality measure to evaluate the performance of a State observer.^[10]

See also[edit]

• Root mean square
• Mean absolute error
• Average absolute deviation
• Mean signed deviation
• Mean squared deviation
• Squared deviations
• Errors and residuals in statistics

References[edit]

Преимущества, недостатки и основные подводные камни

Итак, вы обучили модель, что теперь? Или вы обучили несколько моделей; как решить, какой из них лучше? Хорошо, давай спросим у Google. Хм, Google предлагает множество показателей, которые можно использовать для оценки вашей модели (моделей). Но теперь это становится мета-проблемой: какую метрику следует использовать, чтобы определить, какую модель использовать? Итак, вот список некоторых распространенных показателей с указанием их преимуществ, недостатков и нюансов для начала:

• Средняя абсолютная погрешность (MAE)
• Среднеквадратичная ошибка (MSE)
• Среднеквадратичная ошибка (RMSE)
• Нормализованная среднеквадратичная ошибка (NRMSE)
• Среднеквадратичная ошибка журнала (RMSLE)
• Средняя абсолютная процентная погрешность (MAPE)

Для следующих разделов y — истинное значение, y-hat — прогнозируемое значение, n — количество тестовых экземпляров, а i изменяется от 1 до n. Кроме того, все метрики оцениваются на невидимом тестовом наборе.

Средняя абсолютная ошибка

Средняя абсолютная ошибка — очень интуитивный и поэтому популярный показатель. Это просто среднее расстояние между предсказанными и истинными значениями. Чтобы избежать взаимоисключающих ошибок, мы берем абсолютное значение для каждой вычисляемой ошибки. Лучшей моделью обычно является модель с самым низким значением MAE. Однако есть несколько особенностей, которые следует учитывать при выборе MAE в качестве метрики.

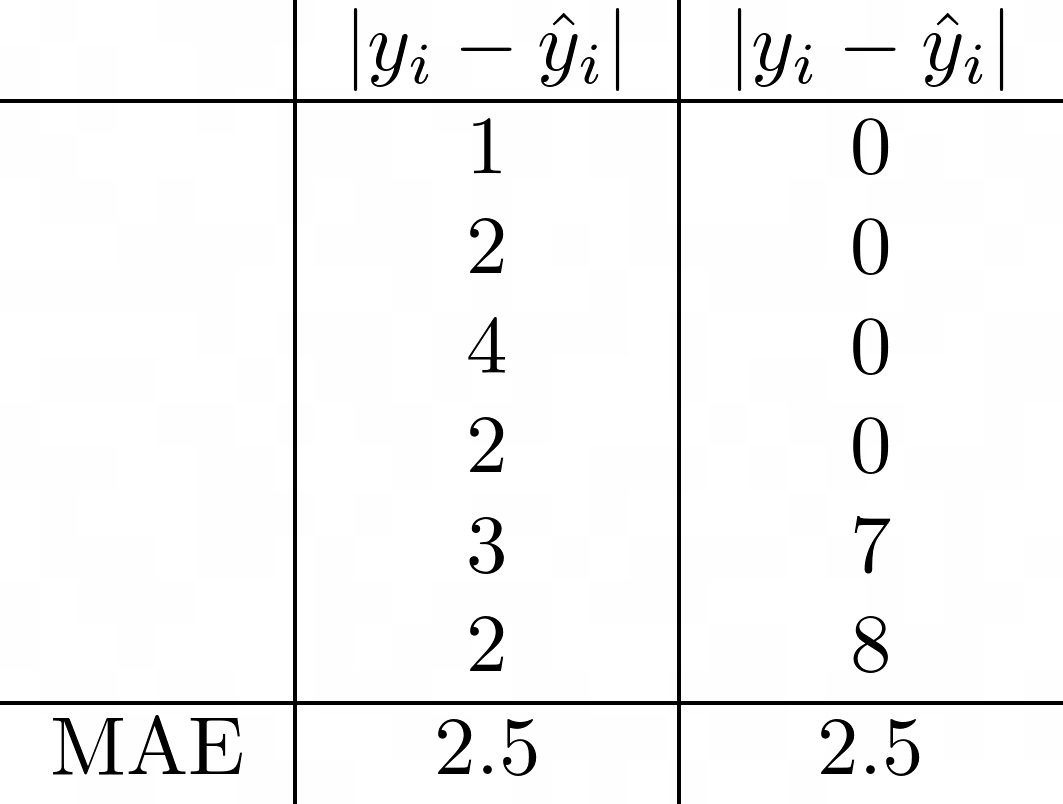
Несмотря на простоту интерпретации, MAE имеет несколько недостатков. Например, он не сообщает вам, имеет ли ваша модель тенденцию к завышению или занижению оценки, поскольку любая информация о направлении уничтожается при взятии абсолютного значения. Кроме того, показатель может быть нечувствительным к большим выбросам. Взгляните на пример ниже.

Слева модель немного не там и там. Однако справа модель пропускает отметки в хвостовой части с гораздо большим отрывом, будучи идеальной в начале и в середине. Тем не менее, MAE для обоих одинаковы. Если вы решили использовать эту метрику, неплохо было бы построить график ошибок, чтобы увидеть любые выбросы, такие как случай 2. В общем, если вы хотите метрику, которая штрафует большие ошибки, вам повезет больше в другом месте.

Среднеквадратичная ошибка

Это подводит меня к среднеквадратическим ошибкам. Как и MAE, мы уничтожаем информацию о направлении, когда исправляем каждую вычисленную ошибку. MSE также всегда больше или равно 0. Однако теперь мы можем различать две модели, указанные выше.

Интересно, что MSE связана с печально известным компромиссом смещения и дисперсии. Можно показать, что ожидаемая тестовая MSE для данной тестовой точки может быть записана как [1]:

где нижний индекс 0 — это индекс точки тестовых данных, а ϵ — это неснижаемый шум или шум в данных.

Дисперсия — это величина, на которую изменяется y-шляпа, когда мы меняем обучающий набор. Обычно более гибкие методы имеют более высокую степень вариативности. Дисперсия также зависит от того, сколько данных у нас есть. Чем больше набор обучающих данных, тем меньше дисперсия. Следовательно, мы можем интерпретировать MSE для данной точки тестовых данных с точки зрения смещения модели и случайного шума в пределах огромных данных.

Смещение возникает, когда мы пытаемся оценить сложные отношения между предикторами и целями с помощью чего-то более простого. Например, мы часто предполагаем, что x и y имеют линейные или полиномиальные отношения, потому что мы знаем форму этих уравнений, что сводит проблему к нескольким параметрам, которые мы можем оценить. На самом деле, у x и y может не быть такой связи.

Наконец, одним из основных недостатков MSE является то, что единицы y возведены в квадрат, что означает, что конечные результаты легко интерпретировать неверно.

Среднеквадратичная ошибка Рура

Как насчет того, чтобы извлечь квадратный корень? RMSE и MSE очень похожи, за исключением того, что RMSE более удобен, потому что он имеет ту же единицу, что и любой y.

Тем не менее, пробовали ли вы когда-нибудь изменить свои цели, чтобы посмотреть, подходите ли вы лучше? Как, например, взять журнал y. Затем вы вычисляете RMSE обоих подходов и видите, что один выше другого. Это несправедливое сравнение, потому что два значения имеют разные единицы измерения. Способ обойти это — разделить на некоторое свойство y, чтобы получить безразмерную метрику, называемую нормализованной среднеквадратичной ошибкой.

Нормализованная среднеквадратическая ошибка

У меня нет здесь уравнений, потому что есть много вещей, на которые можно разделить среднеквадратичное значение. Некоторые распространенные варианты — это среднее значение y, разница между максимальным и минимальным значением y, стандартное отклонение и межквартильный диапазон. Когда выбирать тонкий бизнес, и [2] может предоставить более подробное объяснение, если вам интересно.

Среднеквадратичная ошибка журнала

Я думаю, что эта метрика была введена Kaggle несколько лет назад [3]. Этот показатель следует использовать, если вы хотите указать, как наказываются ошибки. В этом случае мы говорим метрике, чтобы она наказывала недооценку больше, чем переоценку. Например, предположим, что y = 1. Если наша модель дает y-hat = 0, то ошибка составляет [log (1/2)] ² = 0,09. Однако, если модель дает y-hat = 2, тогда ошибка составляет [log (3/2)] ² = 0,03. Если бы мы использовали MSE, то наша ошибка была бы 1 в любом случае.

Также метрика принимает относительную шкалу истинных и прогнозируемых значений. Например, если y = 9 и y-hat = 99, тогда ошибка равна 1. Если, с другой стороны, y = 99 и y-hat = 999, то ошибка все равно 1. Таким образом, эта метрика удобна. когда диапазон ваших целевых значений велик, и вы не хотите штрафовать за большие ошибки, когда и предсказанные, и истинные значения велики.

Однако мне не удалось найти обсуждение некоторых подводных камней, о которых следует помнить здесь. Если вы посмотрите на график log (x), вы увидите, что x не может быть меньше или равным 0. Это означает, что аргумент внутри нашего логарифма (y-hat + 1 / y + 1) не может быть равен до или меньше 0. Затем добавляется ограничение, что y не может быть -1. В противном случае все это взорвется.

Средняя абсолютная ошибка в процентах

MAPE выглядит как двоюродный брат MAE с дополнительным преимуществом, заключающимся в том, что он не имеет единиц измерения. Однако введение разделения также имеет ряд серьезных недостатков. Например, при очень маленьком y_i или y_i = 0 MAPE может взорваться или вообще не быть вычислимым. Он также наследует проблему от MAE, а именно: нет ли верхней границы того, насколько большой может быть каждая ошибка (даже если в названии написано «процент»).

Заворачивать

Надеюсь, вам понравился список и вы узнали что-то новое. Что дальше, это только мое мнение. Я часто вижу упоминание об «интерпретируемости», когда читаю об этих показателях. Я не совсем уверен, что означает «интерпретируемость» и есть ли вообще консенсус по этому поводу. Мои объяснения и то, как я понимаю эти показатели, часто основаны на их поведении в определенных ситуациях. В целом, насколько мы должны подчеркивать «интерпретируемость» метрики, когда есть другие метрики, которые ведут себя больше так, как мы хотим, но их труднее интерпретировать?

Оставайся на связи

Мне нравится писать о науке о данных и науке. Если вам нравится этот пост, подпишитесь на меня в Medium, присоединитесь к моему списку рассылки или станьте членом Medium (я буду получать ~ 50% от ваших членских взносов, если вы воспользуетесь этой ссылкой), если вы не т уже. Увидимся в следующем посте! 😄

Источники

[1] Гарет Джеймс, Даниэла Виттен, Тревор Хасти, Роберт Тибширани. Введение в статистическое обучение: с приложениями в R (2013)

[2] Отто, С.А. (7 января 2019 г.). Как нормализовать RMSE [сообщение в блоге]. Https://www.marinedatascience.co/blog/2019/01/07/normalizing-the-rmse/

[3] https://www.kaggle.com/carlolepelaars/understanding-the-metric-rmsle

[4] https://en.wikipedia.org/wiki/Mean_absolute_percentage_error

• 

Обзор метрик обнаружения аномалий (плюс много дополнительной информации)

Привет, Хабр! На связи снова Юрий Кацер, эксперт по ML и анализу данных в промышленности, а также руководитель направления предиктивной аналитики в компании «Цифрум» Госкорпорации “Росатом”. До сих пор рамках рабочих обязанностей решаю задачи поиска аномалий, прогнозирования, определения остаточного ресурса и другие задачи машинного обучения в промышленности. В рамках рабочих задач мне приходится часто сталкиваться с проблемой правильной оценки качества решения задачи, и, в частности, выбора правильной data science метрики в задачах обнаружения аномалий.

Поскольку речь пойдет о метриках обнаружения аномалий, давайте сначала определимся, что такое аномалия и обнаружение аномалий. В широком смысле аномалия означает отклонение от ожидаемого поведения. Обнаружение аномалий, в свою очередь, представляет собой задачу (или методику) выявления необычных паттернов, не соответствующих ожидаемому поведению. Обнаружение аномалий необходимо в различных областях знаний и прикладных решениях, например, чтобы отслеживать проникновения в компьютерные сети, детектировать аварийные ситуации на электростанциях, выявлять мошенничества при операциях с кредитными картами в банках, определять климатические изменения, создавать системы контроля состояния здоровья и для многого другого. 

Важно заметить, что этой статье мы будем говорить об обнаружении аномалий в данных типа временные ряды. Давайте разберемся, что это такое!

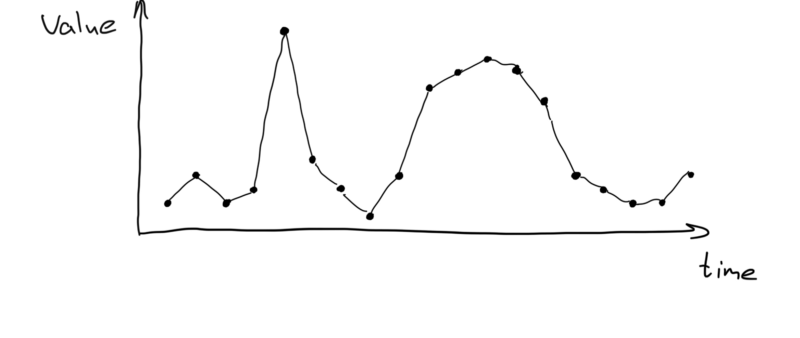
Временной ряд — это последовательность точек или векторов, проиндексированных в хронологическом порядке и представляющих характеристику процесса.

Оценить алгоритмы обнаружения аномалий совсем не просто, поскольку существует множество математических задач и различных метрик, подходящих для конкретных проблем и условий. Часто исследователи и data scientist’ы берут общепринятую метрику, такую как F1, только потому, что ее настоятельно рекомендуют для задач классификации в общем случае. Чтобы помочь избежать неправильного выбора метрик, я решил сделать обзор метрик, используемых для оценки качества решения задач обнаружения аномалий.

Дисклеймер: Информация в статье изложена упрощенно, а сама статья не претендует на всеобъемлющий анализ рассматриваемого вопроса.

Пример и объяснение разницы между функциями потерь, критериями, метриками

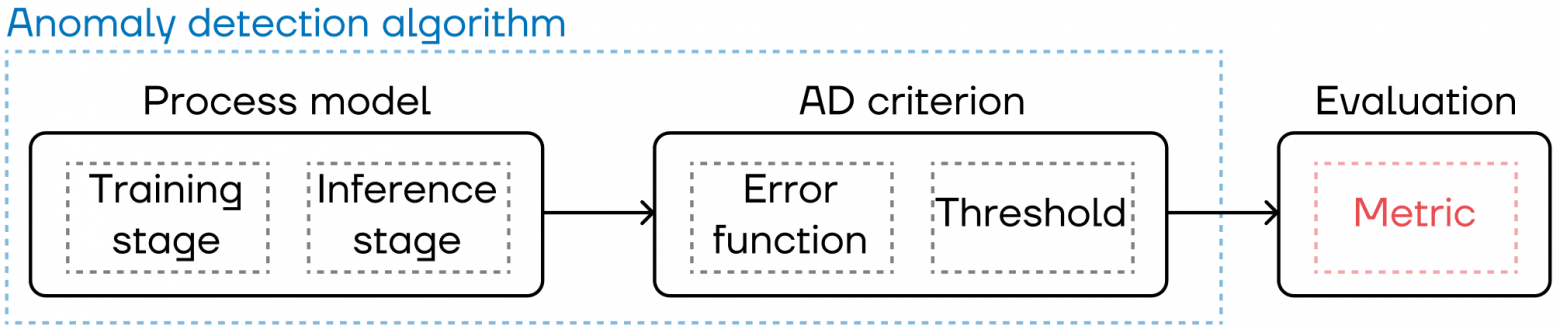
Для лучшего понимания мы на примере объясним, о какой конкретно части алгоритма обнаружения аномалий идет речь в статье. В качестве примера алгоритма возьмем следующий:

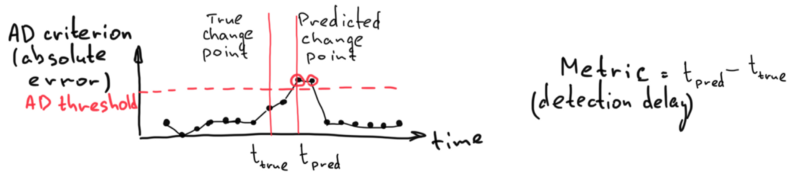
Шаг 1. Прогнозирование (модель процесса): возьмем обученную (на данных нормального режима) модель машинного обучения для прогнозирования некоего существующего сигнала на одну точку вперед в каждый момент времени. Когда модель не совпадает с реальным сигналом, можно говорить, что процесс отклоняется от нормального состояния.

Шаг 2. Критерий обнаружения аномалий: наш алгоритм обнаружения аномалий основан на критерии сравнения функции ошибки (абсолютной ошибки) с заранее рассчитанным (на этапе обучения) порогом. Абсолютная ошибка растет, когда данные отклоняются от нормальных значений, использованных на этапе обучения модели. Превышение порога указывает на обнаружение аномалии.

Шаг 3. Оценка алгоритмов обнаружения аномалий: именно этому шагу и необходимым для него метрикам посвящена эта статья.

Таким образом:

• в статье не рассматриваются функции потерь (cost functions, loss functions), оптимизируемые на этапе обучения алгоритмов машинного обучения в Шаге 1. Однако в качестве функции потерь (loss function) могут быть выбраны функции (критерий, метрика) из Шагов 2 или 3, чтобы максимально повысить качество работы модели;

• в статье не рассматриваются критерии обнаружения аномалий из Шага 2, хотя они похожи на метрики машинного обучения;

• статья посвящена Шагу 3  — оценке алгоритма обнаружения аномалий.

Матрица несоответствий

Прежде чем перейти к метрикам, нужно понять суть матрицы несоответствий (confusion matrix). Вот как она выглядит:

Как читать таблицу:

• tp (истинно положительный): спрогнозировано аномальное значение, и это верно;

• tn (истинно отрицательный): спрогнозировано нормальное значение, и это верно;

• fp (ложноположительный): спрогнозировано аномальное значение, и это неверно;

• fn (ложноотрицательный): спрогнозировано нормальное значение, и это неверно.

Задачи обнаружения аномалий

Для удобства дальнейшей систематизации метрик давайте определим задачи, которые чаще всего выделяют в проблеме обнаружения аномалий, но сначала скажем о различных типах аномалий. По количеству точек аномалии обычно делят на точечные (point) и коллективные (collective). Существуют также контекстуальные (contextual) аномалии, но коллективный и контекстуальный типы иногда объединяют в так называемый range-based тип. Но для простоты мы будем использовать термин коллективная аномалия для range-based, то есть для коллективных и контекстуальных вместе, а определение возьмем отсюда:

Коллективная аномалия — это аномалия, возникающая в виде последовательности временных точек, когда между началом и концом аномалии не существует неаномальных (нормальных) данных.

Подробнее о задаче обнаружения аномалий можно прочитать в другой моей статье.

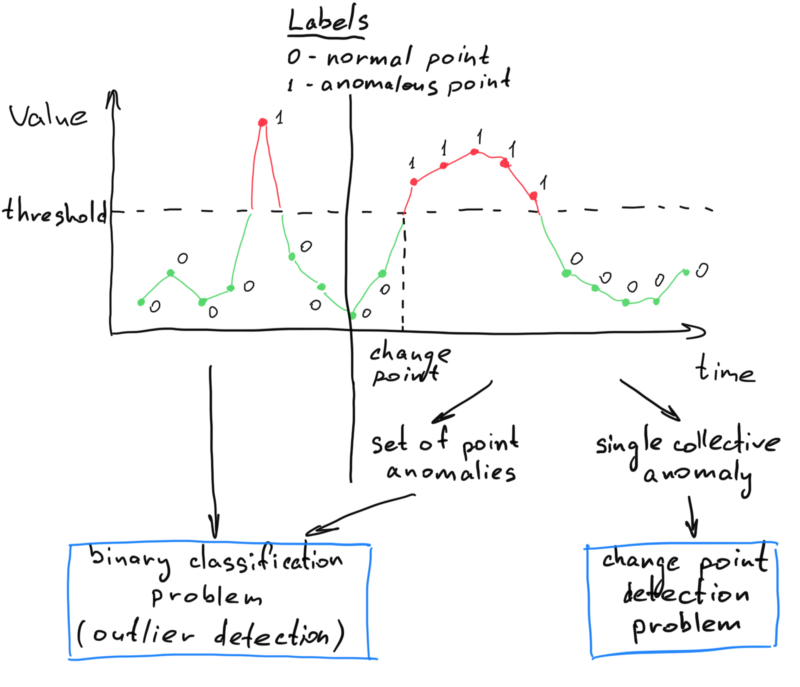
Задача обнаружения аномалий часто трансформируется в задачу бинарной классификации (также часто называемую задачей обнаружения выбросов) и задачу обнаружения точки изменения состояния. Связь между задачами и типами аномалий показана на схеме.

Что это означает? При решении задачи детекции точечных аномалий мы будем использовать и оценивать алгоритмы бинарной классификации. Для коллективных аномалий мы можем использовать и оценивать как алгоритмы бинарной классификации, так и алгоритмы обнаружения точки изменения состояния (в зависимости от прочих условий или постановки бизнес-задачи). Другими словами, алгоритмы обнаружения точки изменения состояния применимы только для коллективных аномалий, потому что необходимо найти конкретную точку изменения состояния, где начинается коллективная аномалия. Однако можно интерпретировать коллективную аномалию как набор точечных аномалий, поэтому алгоритмы бинарной классификации применимы для обоих типов аномалий.

Классы метрик

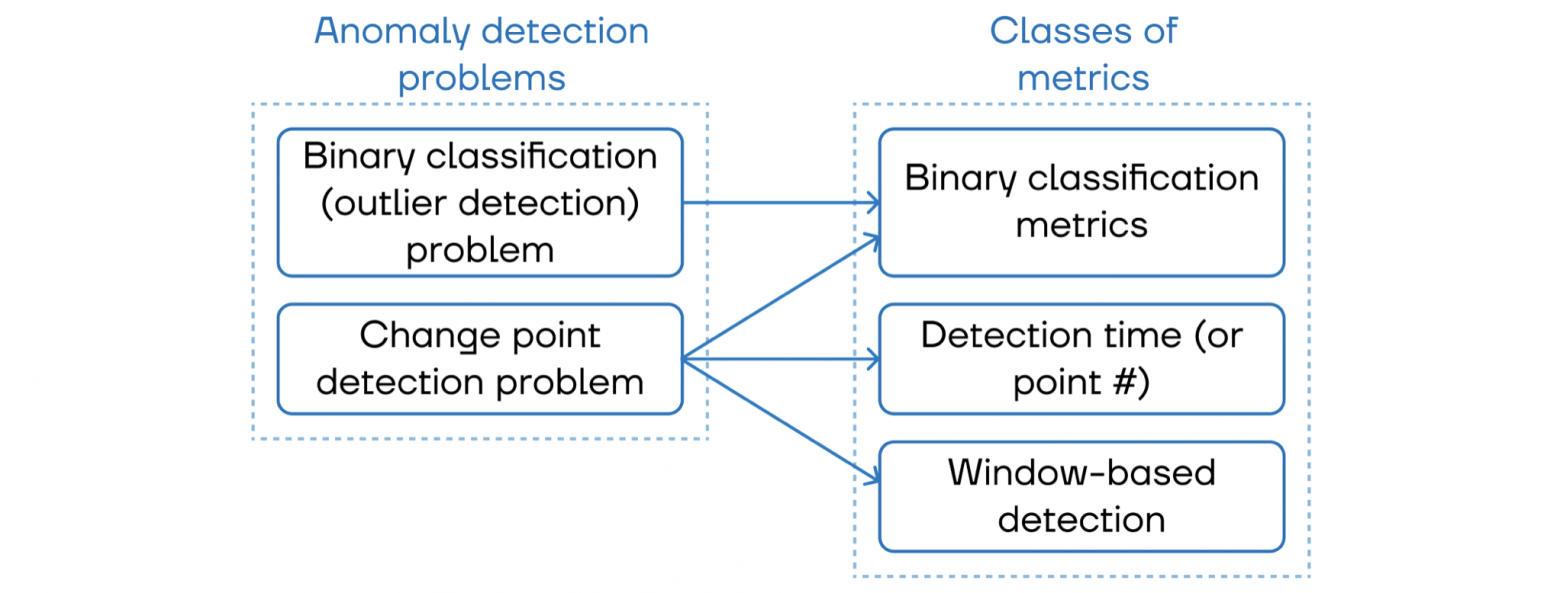
Определив существующие задачи обнаружения аномалий, мы можем связать эти задачи с классами метрик, которые используются для оценки алгоритмов. О классах и метриках, относящихся к каждому классу, поговорим сразу после того, как посмотрим на рисунок ниже, где показана связь между задачами и классами метрик.

Итак, какие бывают классы метрик:

• Метрики бинарной классификации: отнесение результата классификации объекта к одному из двух классов (нормальный, аномальный) с истинной (верной) меткой объекта.

Для задач обнаружения точки изменения состояния метрики бинарной классификации применяются на основе окна: проверяем, находится ли прогнозируемая точка изменения состояния в окне обнаружения, или сравниваем наложение прогнозируемого и истинного окон (положение, размер и т.д.).

Для задачи бинарной классификации метрики бинарной классификации применяются, учитывая каждую точку: проверяем правильность предсказанной метки для каждой точки.

• Обнаружение на основе окна (вне бинарной классификации): сопоставление прогнозируемой точки изменения с окном вокруг фактической точки изменения способом, отличным от бинарной классификации.

• Время (или номер точки) обнаружения: оценка разницы во времени (или номере точки / индексе) между прогнозируемой и фактической точками изменения состояния.

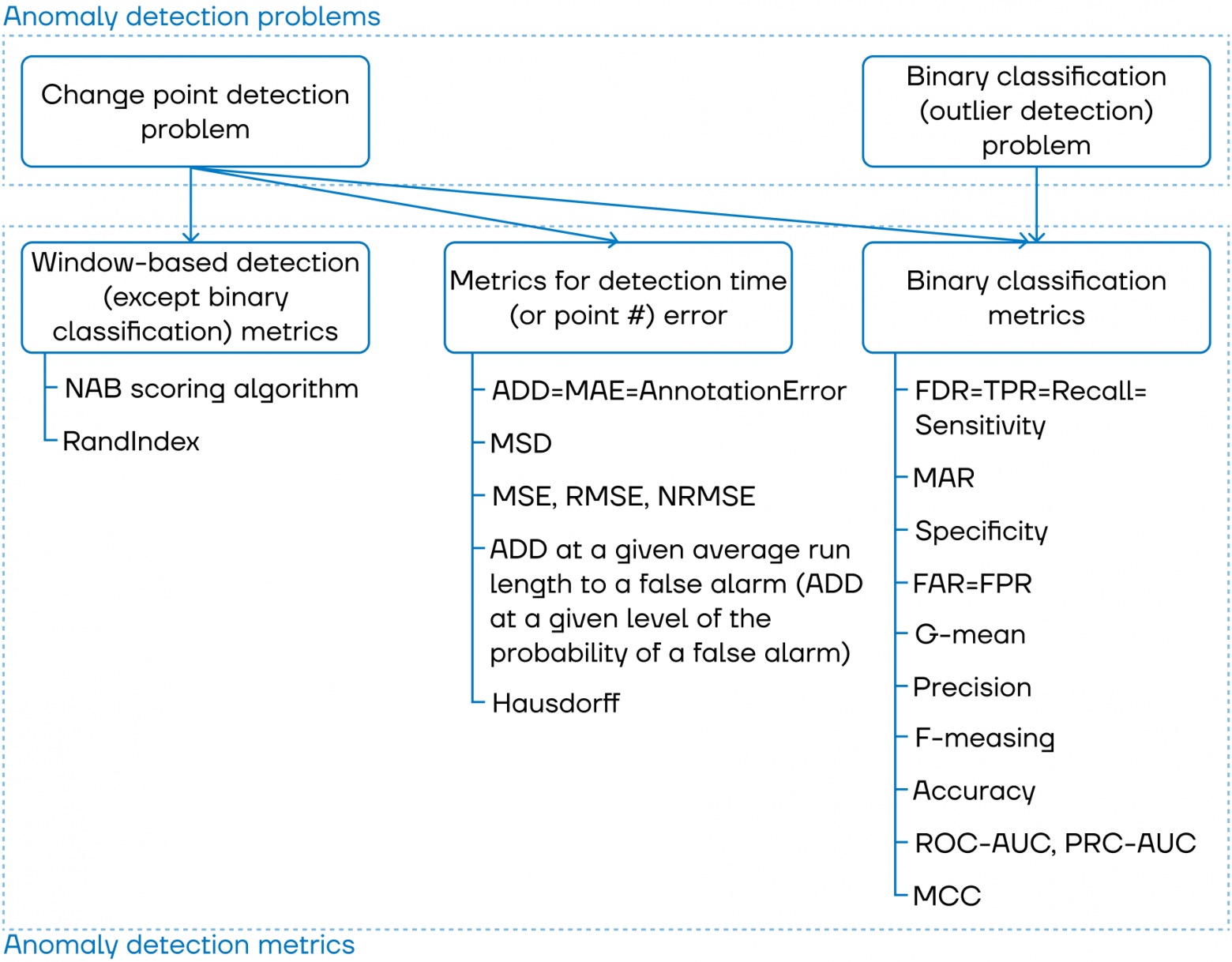
Классификация метрик обнаружения аномалий

В этом разделе покажем классификацию метрик и дадим краткую информацию о каждой из них.

Метрики обнаружения на основе окна (вне бинарной классификации)

• NAB scoring algorithm (Скоринговый алгоритм NAB): основными особенностями этого алгоритма являются вознаграждение за раннее обнаружение и штрафование за ложноположительные и ложноотрицательные результаты. Это делается с помощью специальной функции оценки, которая применяется к окнам аномалий. Каждое окно представляет собой диапазон точек данных, сосредоточенных вокруг эталонной аномалии. Более подробная информация представлена в этой статье.

• Rand Index (Индекс Рэнда): интуитивно индекс равен количеству совпадений между двумя сегментациями (прогнозируемой и эталонной). Более подробная информация представлена в этой статье.

Метрики оценки ошибки времени (или номера точки) обнаружения

• ADD (average detection delay; средняя задержка обнаружения) = MAE (mean absolute error; средняя абсолютная ошибка) = AnnotationError (ошибка разметки): разница между прогнозируемой точкой изменения и истинной точкой изменения (можно измерять во времени, по количеству точек и т. д.). Абсолютное значение разницы между прогнозируемым и фактическим временем точки изменения суммируется и нормализуется на количество точек изменения. Более подробная информация представлена в этой статье.

• MSD (mean signed difference; средняя ошибка со знаком): данная метрика в дополнение к средней абсолютной ошибке (MAE) учитывает направление ошибки (прогнозирует, что аномалия случится до либо после фактического времени точки изменения). Более подробная информация представлена в этой статье.

• MSE (mean squared error; средняя квадратическая ошибка), RMSE (root mean squared error; среднеквадратическая ошибка), NRMSE (normalized root mean squared error; нормализованная среднеквадратическая ошибка): данные метрики служат альтернативами средней абсолютной ошибке (MAE). В этом случае ошибки возводятся в квадрат, и итоговая мера получается очень большой, если в классифицированных данных существуют несколько значительных выбросов. Более подробная информация представлена в этой статье.

• ADD при заданной средней длине серии до ложного срабатывания (или при заданном уровне вероятности ложного срабатывания): служит критерием эффективности для количественной оценки склонности алгоритма обнаружения к ложным срабатываниям. Более подробная информация представлена в этой статье.

• Hausdorff (Метрика Хаусдорфа): равняется наибольшему временному расстоянию между точкой изменения и ее прогнозом. Более подробная информация представлена в этой статье.

Существует еще много подобных метрик, которые подходят для особых областей применения и процедур обнаружения точки изменения состояния (например, средняя задержка обнаружения в наихудшем случае, интегральная средняя задержка обнаружения, максимальная условная средняя задержка обнаружения, среднее время между ложными срабатываниями и другие). О них можно прочитать в монографии Sequential Analysis: Hypothesis Testing and Changepoint Detection. Эта книга посвящена таким метрикам, которые в том числе служат критериями для алгоритмов обнаружения точек изменения состояния. Кроме того, в ней также содержатся рекомендации по выбору критериев или метрик для определения точки изменения в различных случаях, например, для контроля качества:

…Наилучшее решение — максимально быстро обнаруживать нарушения нормальной работы при минимальном количестве ложных срабатываний. … Таким образом, оптимальное решение основывается на компромиссе между скоростью обнаружения или задержкой обнаружения и частотой ложных срабатываний за счет сравнения потерь, на которые указывают истинные и ложные обнаружения.

Метрики бинарной классификации

• FDR (fault detection rate; доля обнаруженных аномалий) = TPR (true positive rate; доля истинно положительных результатов) = Recall (Полнота) = Sensitivity (Чувствительность): отношение количества истинно положительных точек данных (точек изменения) к общему количеству истинно аномальных точек (или точек изменения) (TP+FN). Более подробная информация представлена в этой статье и в этой статье.

• MAR (missed alarm rate; доля пропущенных срабатываний) = 1 — FDR: отношение количества ложноотрицательных точек данных (точек изменения) к общему количеству истинно аномальных точек (или точек изменения) (TP+FN).

• Specificity (Специфичность): отношение количества истинно отрицательных точек данных (точек изменения) к общему количеству нормальных точек (TN+FP). Более подробная информация представлена в этой статье.

• FAR (false alarm rate; доля ложных срабатываний) = FPR (false positive rate; доля ложноположительных результатов) = 1 — Специфичность: отношение количества ложноположительных точек данных (точек изменения) к общему количеству нормальных точек (TN+FP). Служит мерой того, как часто возникает ложное срабатывание.

• G-mean (среднее геометрическое): комбинация Чувствительности и Специфичности. Более подробная информация представлена в этой статье.

• Precision (Точность): отношение количества истинно положительных точек данных (точек изменения) к общему количеству точек, классифицированных как аномальные или точки изменения (TP+FP). Более подробная информация представлена в этой статье.

• F-measure (F-мера): комбинация взвешенной Точности и Полноты (F1-мера представляет собой гармоническое среднее значение точности и полноты). Более подробная информация представлена в этой статье.

• Accuracy (Точность): отношение количества правильно классифицированных точек данных (или точек изменения) к общему количеству точек данных (точек изменения). Более подробная информация представлена в этой статье.

• ROC-AUC ROC-AUC (Receiver Operating Characteristic, area under the curve), PRC-AUC (Precision—Recall curve, area under the curve): полезные инструменты для прогнозирования вероятности бинарного результата. Более подробная информация представлена в этой статье и в этой статье.

• MCC (Matthews correlation coefficient; Коэффициент корреляции Мэтьюса): мера, используемая для определения качества бинарной классификации, которая учитывает все истинно положительные, истинно отрицательные, ложноположительные и ложноотрицательные результаты. Более подробная информация представлена в этой статье.

Различие метрик бинарной классификации для задач обнаружения аномалий

Для задач обнаружения точки изменения состояния:

• tp: количество правильно обнаруженных точек изменения (# of tp).

• fp: количество точек, неправильно определенных как точки изменения (# of fp).

• tn: количество нормальных точек, правильно определенных как нормальные (# of tn).

• fn: количество пропущенных точек изменения (# of fn).

Для задач обнаружения выбросов:

• tp: количество точек данных, правильно определенных как аномальные (# of tp).

• fp: количество нормальных точек данных, неправильно определенных как аномальные (# of fp).

• tn: количество нормальных точек данных, правильно определенных как нормальные (# of tn).

• fn: количество точек данных, неправильно определенных как нормальные (# of fn).

Основное различие между определением результатов tp, fp, tn, fn для обнаружения выбросов и обнаружения точек изменения состояния состоит в том, что в первом случае каждой точке присваивают аномальный или нормальный индекс, а во втором случае каждую точку изменения состояния (или каждую истинную и ложную аномалию) определяют как обнаруженную либо как пропущенную.

Больше о метриках бинарной классификации для обнаружения аномалий во временных рядах можно прочитать в этой статье.

Заключение

Целью статьи было показать, как много метрик существует и практически все из них достаточно популярны используются в работе дата сайентистов при решении задач поиска аномалий. Также для всех метрик даны краткие описания и ссылки на статьи с их подробным описанием, примерами, реализациями и дополнениями.

Практические реализации некоторых метрик вы можете найти в различных библиотеках, как в классических типа sklearn, так и в специализированных, например, в TSAD (метрики для поиска точек изменения) или в PyOD (метрики для точечных аномалий).

Библиография

1. Ahmed, Mohiuddin, et al. “An investigation of performance analysis of anomaly detection techniques for big data in scada systems.” EAI Endorsed Trans. Ind. Networks Intell. Syst. 2.3 (2015): e5.

2. Aminikhanghahi, Samaneh, and Diane J. Cook. “A survey of methods for time series change point detection.” Knowledge and information systems 51.2 (2017): 339–367.

3. Truong, Charles, Laurent Oudre, and Nicolas Vayatis. “Selective review of offline change point detection methods.” Signal Processing 167 (2020): 107299.

4. Artemov, Alexey, and Evgeny Burnaev. “Ensembles of detectors for online detection of transient changes.” Eighth International Conference on Machine Vision (ICMV 2015). Vol. 9875. International Society for Optics and Photonics, 2015.

5. Tatbul, Nesime, et al. “Precision and recall for time series.” arXiv preprint arXiv:1803.03639 (2018).

Среднеквадратичное отклонение

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

---

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

1. Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
2. Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
3. Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

---

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
2. Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
3. Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

---

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
2. Находится сумма всех фактов по всем позициям  (общий фактический объем)
3. Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

---

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

1. Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
2. Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
3. Извлекаем корень из полученного результат — RMSE
4. Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
   1. Разделить на разницу между максимальным и минимальным значением показателей
   2. Разделить на разницу между третьим и первым квартилем значений показателей
   3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

---

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

---

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

Статистика
Контур Статистиков Глоссарий Обозначение Журналы Списки тем Статьи Категория  Математический портал

В среднеквадратичное отклонение (RMSD) или же Средняя квадратическая ошибка (RMSE) является часто используемой мерой различий между значениями (значениями выборки или генеральной совокупности), прогнозируемыми моделью или оценщик и наблюдаемые значения. RMSD представляет собой квадратный корень из второго образец момент различий между прогнозируемыми значениями и наблюдаемыми значениями или среднее квадратичное этих различий. Эти отклонения называются остатки когда вычисления выполняются над выборкой данных, которая использовалась для оценки и называется ошибки (или ошибки предсказания) при вычислении вне выборки. RMSD служит для агрегирования величин ошибок в прогнозах за разное время в единую меру предсказательной силы. RMSD — это мера точность, чтобы сравнивать ошибки прогнозирования разных моделей для определенного набора данных, а не между наборами данных, так как это зависит от масштаба.^[1]

Среднеквадратичное отклонение всегда неотрицательно, и значение 0 (почти никогда не достигается на практике) указывает на точное соответствие данным. В общем, более низкое RMSD лучше, чем более высокое. Однако сравнения между разными типами данных будут недопустимыми, поскольку мера зависит от масштаба используемых чисел.

RMSD — это квадратный корень из среднего квадрата ошибок. Влияние каждой ошибки на RMSD пропорционально величине квадратичной ошибки; таким образом, большие ошибки имеют непропорционально большое влияние на RMSD. Следовательно, RMSD чувствителен к выбросам.^[2][3]

Формула

RMSD оценщик относительно оцениваемого параметра определяется как квадратный корень из среднеквадратичная ошибка:

Для объективный оценщик, RMSD — это квадратный корень из дисперсии, известный как стандартное отклонение.

RMSD прогнозируемых значений на время т из регресс зависимая переменная с переменными, наблюдаемыми за Т раз, вычисляется для Т различные прогнозы как квадратный корень из среднего квадратов отклонений:

(Для регрессий на данные поперечного сечения, нижний индекс т заменяется на я и Т заменяется на п.)

В некоторых дисциплинах RMSD используется для сравнения различий между двумя вещами, которые могут различаться, ни одна из которых не принимается в качестве «стандарта». Например, при измерении средней разницы между двумя временными рядами и , формула принимает вид

Нормализация

Нормализация RMSD облегчает сравнение наборов данных или моделей с разными масштабами. Хотя в литературе нет согласованных средств нормализации, обычно выбирают среднее значение или диапазон (определяемый как максимальное значение минус минимальное значение) измеренных данных:^[4]

или же .

Это значение обычно называют нормированное среднеквадратичное отклонение или же ошибка (NRMSD или NRMSE) и часто выражается в процентах, где более низкие значения указывают на меньшую остаточную дисперсию. Во многих случаях, особенно для небольших выборок, на диапазон выборки, вероятно, влияет размер выборки, что затрудняет сравнения.

Другой возможный способ сделать RMSD более полезным средством сравнения — разделить RMSD на межквартильный размах. При делении RMSD на IQR нормализованное значение становится менее чувствительным к экстремальным значениям целевой переменной.

куда

с и где CDF⁻¹ это квантильная функция.

При нормировании на среднее значение измерений член коэффициент вариации RMSD, CV (RMSD) может использоваться, чтобы избежать двусмысленности.^[5] Это аналогично коэффициент вариации с RMSD вместо стандартное отклонение.

Некоторые исследователи рекомендовали использовать Средняя абсолютная ошибка (MAE) вместо среднеквадратичного отклонения. MAE обладает преимуществами в интерпретируемости перед RMSD. MAE — это среднее абсолютных значений ошибок. MAE принципиально легче понять, чем квадратный корень из среднего квадрата ошибок. Более того, каждая ошибка влияет на MAE прямо пропорционально абсолютному значению ошибки, что не относится к RMSD.^[2]

Приложения

• В метеорология, чтобы увидеть, насколько эффективно математический модель предсказывает поведение атмосфера.
• В биоинформатика, то среднеквадратичное отклонение позиций атомов — мера среднего расстояния между атомами наложенный белки.
• В дизайн лекарств на основе структуры, RMSD является мерой разницы между кристаллической конформацией лиганда конформация и стыковка прогноз.
• В экономика, RMSD используется, чтобы определить, подходит ли экономическая модель экономические показатели. Некоторые эксперты утверждают, что RMSD менее надежен, чем относительная абсолютная ошибка.^[6]
• В экспериментальная психология, RMSD используется для оценки того, насколько хорошо математические или вычислительные модели поведения объясняют эмпирически наблюдаемое поведение.
• В ГИС, RMSD является одним из показателей, используемых для оценки точности пространственного анализа и дистанционного зондирования.
• В гидрогеология, RMSD и NRMSD используются для оценки калибровки модели подземных вод.^[7]
• В визуализация науки, RMSD является частью пиковое отношение сигнал / шум, показатель, используемый для оценки того, насколько хорошо метод восстановления изображения работает по сравнению с исходным изображением.
• В вычислительная нейробиология, RMSD используется для оценки того, насколько хорошо система изучает данную модель.^[8]
• В спектроскопия ядерного магнитного резонанса белков, RMSD используется как мера для оценки качества полученного пучка конструкций.
• Материалы для Приз Netflix были оценены с использованием RMSD на основе нераскрытых «истинных» значений тестового набора данных.
• При моделировании энергопотребления зданий RMSE и CV (RMSE) используются для калибровки моделей по измеренным характеристикам здания.^[9]
• В Рентгеновская кристаллография, RMSD (и RMSZ) используется для измерения отклонения внутренних координат молекулы от значений библиотеки ограничений.

Смотрите также

• Среднеквадратичное значение
• Средняя абсолютная ошибка
• Среднее абсолютное отклонение
• Среднее знаковое отклонение
• Среднеквадратичное отклонение
• Квадратные отклонения
• Ошибки и неточности в статистике

Рекомендации

• Среднеквадратичная ошибка (Mean Squared Error)
• Корень из среднеквадратичной ошибки (Root Mean Squared Error)
• Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
• Cредняя абсолютная ошибка (Mean Absolute Error)
• Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
• Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
• Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
• Средняя относительная ошибка (Mean Relative Error)
• Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
• R-квадрат
• Скорректированный R-квадрат
• Сравнение метрик

«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.

Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.

Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:

• Среднеквадратичная ошибка (MSE).
• Корень из среднеквадратичной ошибки (RMSE).
• Среднеквадратичная ошибка в процентах (MSPE).
• Средняя абсолютная ошибка (MAE).
• Средняя абсолютная ошибка в процентах (MAPE).
• Cимметричная средняя абсолютная процентная ошибка (SMAPE).
• Средняя абсолютная масштабированная ошибка (MASE)
• Средняя относительная ошибка (MRE).
• Среднеквадратичная логарифмическая ошибка (RMSLE).
• Коэффициент детерминации R-квадрат.
• Скорректированный коэффициент детеминации.

Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.

Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.

Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.

В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».

MSE

Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.

Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.

MSE рассчитывается по формуле:

MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},

где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.

Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.

Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.

RMSE

Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:

RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}

MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).

Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:

frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}

Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.

Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.

MSPE

Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:

MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}

Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.

MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.

MAE

Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:

MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |

Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.

Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.

MAPE

Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:

MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}

Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.

SMAPE

Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:

SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}

Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.

Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.

Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).

MASE

Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:

MASE=frac{MAE_{i}}{MAE_{j}}

MASE симметрична и устойчива к выбросам.

MRE

Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:

MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}

Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.

Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.

Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.

RMSLE

Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:

RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}

Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.

Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.

R-квадрат

Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.

В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.

Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:

R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}

Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.

Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.

Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.

Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).

На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.

Скорректированный R-квадрат

Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.

В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).

Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:

R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}

где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.

Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.

Сравнение метрик

Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:

Мера	Сильные стороны	Слабые стороны
MSE	Позволяет подчеркнуть большие отклонения, простота вычисления.	Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости.
RMSE	Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная.	Имеет тенденцию занижать качество модели, чувствительна к выбросам.
MSPE	Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер.	Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки.
MAPE	Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области.	Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.
SMAPE	Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше.	Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения.
MASE	Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели.	Сложность интерпретации.
MRE	Позволяет оценить величину ошибки относительно значения целевой переменной.	Неприменима для наблюдений с нулевым значением выходной переменной.
RMSLE	Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше	Может быть затруднена интерпретация из-за нелинейности.
R-квадрат	Универсальность, простота интерпретации.	Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы.
R-квадрат скорр.	Корректно отражает вклад каждой переменной в модель.	Плохо работает, когда входные переменные зависимы.

В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.

Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.

Другие материалы по теме:

Отбор переменных в моделях линейной регрессии

Репрезентативность выборочных данных

Логистическая регрессия и ROC-анализ — математический аппарат

Нормализация характеристик, стандартизованное понимание

Если набор данных стандартизирован, он будет иметь хороший эффект оптимизации для многих алгоритмов машинного обучения (включая градиентный спуск). Если данные не стандартизированы (например, когда функции набора данных различаются на порядок), многие алгоритмы работают плохо.

Сначала поймите разницу между дисперсией, стандартным отклонением и среднеквадратичной ошибкой.

Дисперсия (дисперсия)

Измерьте степень дисперсии (отклонения) случайной величины или набора данных

В теории вероятностей дисперсия используется для измерения степени отклонения между случайной величиной и ее математическим ожиданием (средним).

В статистике сумма квадратов разницы между каждыми данными и их средним значением.

Предположим, что используется математическое ожидание (среднее значение) набора случайных величин или статистических данных.

E

(

x

)

E(x)

, Тогда его дисперсия выражается как данные и

E

(

x

)

E(x)

Сумма квадратов разностей

∑

[

x

−

E

(

x

)

]

2

sum[x-E(x)]^2

, А затем найти его ожидание (среднее), чтобы получить

D

(

x

)

=

∑

[

x

−

E

(

x

)

]

2

D(x)=sum[x-E(x)]^2

Зачем использовать стандартное отклонение

Согласно вышеизложенному, мы знаем, что дисперсия используется для измерения степени дисперсии (отклонения) случайной величины или набора данных. Формула для стандартного отклонения (также называемая среднеквадратической ошибкой):

σ

=

D

(

x

)

sigma = sqrt {D(x)}

, Дисперсия и стандартное отклонение имеют общее свойство: чем больше значение, тем более пологая кривая распределения, то есть более разбросанная.
Поскольку данные являются случайными, предполагая, что такое же распределение основано на центральной предельной теореме, данные подчиняются распределению Гаусса (нормальному) (типичным примером является ошибка). Давайте посмотрим на область распределения.

При использовании стандартного отклонения мы можем четко увидеть вероятность того, что данные принадлежат определенному значению. (Когда мы обрабатываем функции, мы можем отфильтровать выбросы на основе этого)

Интервал горизонтальной оси

（

μ

−

σ

,

μ

+

σ

）

（mu -sigma,mu +sigma）

Площадь внутри 68,268949%

Интервал горизонтальной оси

（

μ

−

2

σ

,

μ

+

2

σ

）

（mu -2sigma,mu +2sigma）

Площадь внутри 95,449974%

Интервал горизонтальной оси

（

μ

−

3

σ

,

μ

+

3

σ

）

（mu -3sigma,mu +3sigma）

Площадь внутри 99,730020%

Согласно неравенству Чебышева,

x

x

Отклонение

n

n

Вероятность стандартного отклонения расстояния меньше, чем

1

n

2

frac{1}{n^2}

Разница между стандартным отклонением (среднеквадратичной ошибкой) и среднеквадратичной ошибкой

Стандартное отклонение также называется среднеквадратичной ошибкой, а MSE (среднеквадратичная ошибка), среднеквадратическая ошибка, представляет собой сумму квадратов всех ошибок выборки (разность между истинным значением и предсказанным значением), после чего берется среднее значение. MSE — это стандарт для измерения качества модели в регрессионном анализе. Существуют также RMSE, MAE и

R

2

R^2

. Среднеквадратичная ошибка — это отношение между серией данных и средним значением, а среднеквадратичная ошибка — это отношение между серией данных и истинным значением.

M

S

E

=

1

m

∑

i

=

1

m

(

y

(

i

)

−

y

^

(

i

)

)

2

MSE = frac{1}{m}sum_{i=1}^{m}(y ^ {(i)} — hat{y} ^ {(i)}) ^ {2}

Стандартизация и нормализация данных

Стандартизация данных заключается в пропорциональном масштабировании данных для снятия ограничений между данными и преобразовании их в безразмерные данные для облегчения взвешивания и сравнения различных индексных данных. Нормализацию можно назвать своего рода стандартизацией (стандартизация и нормализация данных). Обычно используемые для непрерывных значений, дискретные значения обычно используют labelencoding и onehot для преобразования данных).
Текущие методы стандартизации данных в основном делятся на следующие три типа:

Линейный метод (пороговый метод: метод экстремальных значений и т. Д., Стандартизация, метод удельного веса)
Ломаная линия
Тип кривой

Различные методы стандартизации по-разному влияют на результаты оценки системы, и вы можете попробовать несколько раз во время обучения машинному обучению.

Цель нормализации

• Повышение скорости сходимости модели
• Повысьте точность модели
• Предотвратить взрыв градиента модели

Повышена скорость сходимости модели

В практических приложениях модели, решаемые методом градиентного спуска, обычно необходимо нормализовать, например линейная регрессия, логистическая регрессия, KNN, SVM, нейронная сеть и другие модели.
Если разница в размерах между элементами большая, контур модели эллиптический, а при выполнении градиентного спуска направление градиента — это направление, перпендикулярное контуру, поэтому Модель будет следовать зигзагообразному маршруту, и если скорость обучения слишком велика или слишком мала, градиент будет расходиться или не сходиться.
Если разница в размерах между элементами велика, контур модели является круглым, а скорость итерации будет увеличена. На данный момент вам нужно только настроить скорость обучения. Как показано ниже:

Повысьте точность модели

Когда дело доходит до модели расчета расстояния, если значение объекта сильно отличается, оно будет доминировать в процессе расчета, а объект с небольшим значением может привести к недостатку информации (изменение значения почти не влияет на окончательный результат расчета. влияний). Следовательно, чтобы модель могла полностью изучить информацию о каждой функции, мы должны стандартизировать данные во время анализа модели. Численная стандартизация в основном включает гомотактическую обработку данных и обработку размерностей данных.

Кохемотаксис данных в основном решает проблемы различной природы. Поскольку индикаторы разной природы не могут быть напрямую добавлены для обработки, они преобразуются в одно и то же состояние распределения (стандартное нормальное распределение), так что все индикаторы имеют одинаковое влияние на план оценки. Правильный результат можно получить, сложив.

Безразмерные данные в основном предназначены для решения проблемы сопоставимости данных. Своевременные данные находятся в одном и том же состоянии распределения. Если операция нормализации данных не выполняется между различными характеристиками, всегда будут преобладать более крупные характеристики.

Следовательно, нормализация предназначена для того, чтобы функции между различными измерениями имели определенную степень численного сравнения, что может значительно повысить точность классификатора.

Нормализация данных в глубоком обучении может предотвратить взрыв градиента

Часто используемые методы и характеристики нормализации данных

(1) Мин-макс нормализация

1. Также известный как стандартизация дисперсии, результат отображается в [0,1]

   x

   ∗

   =

   x

   −

   m

   i

   n

   (

   x

   )

   m

   a

   x

   (

   x

   )

   −

   m

   i

   n

   (

   x

   )

   x^* = frac{x-min(x)}{max(x)-min(x)}

2. Использование: этот метод нормализации подходит для ситуаций, когда значения данных относительно сконцентрированы. Когда измерение расстояния, расчет ковариации и данные не соответствуют нормальному распределению, первый метод или другие методы нормализации (не включая Метод Z-оценки). Например, при обработке изображения изображение RGB преобразуется в изображение в градациях серого, и его значение ограничено диапазоном [0 255]
3. Дефекты: на этот метод легко влияют максимальные и минимальные значения, что делает нормализованный результат нестабильным и делает нестабильным последующий эффект использования. На практике вместо max и min можно использовать эмпирические константы.

(2) Метод стандартизации Z-баллов (нормализация с нулевым средним)

1. Данные, обработанные методом стандартизации Z-оценки, будут подчиняться стандартному нормальному распределению, а интервал значений после обработки не [0,1], поэтому его нельзя назвать нормализацией. Его функция преобразования

   x

   ∗

   =

   x

   −

   μ

   σ

   x^* = frac{x-mu}{sigma}

2. Метод стандартизации Z-оценки подходит для ситуаций, когда максимальное и минимальное значения атрибутов неизвестны.Кроме того, метод Z-оценки может использоваться для фильтрации выбросов. В алгоритмах классификации и кластеризации, когда расстояние необходимо для измерения сходства или когда технология PCA используется для уменьшения размерности, стандартизация Z-показателя работает лучше.
3. Дефект: необходимо, чтобы распределение исходных данных было приблизительно гауссовым, иначе эффект будет плохим.

（3）

l

o

g

log

Преобразование функций

1. Также может быть реализован метод преобразования функции журнала в базу 10. Конкретный метод выглядит следующим образом:
   

   x

   ∗

   =

   l

   o

   g

   1

   0

   (

   x

   )

   l

   o

   g

   1

   0

   (

   m

   a

   x

   (

   x

   )

   )

   x^* = frac{log_10(x)}{log_10(max(x))}

метод стандартизации и нормализации sklearn

Мы можем использовать связанные классы, предоставленные в sklearn, для стандартизации набора данных, которые могут преобразовывать функции в один и тот же порядок величины, тем самым устраняя влияние различных порядков величины на алгоритм. Два часто используемых метода:

• StandardScaler
• MinMaxScaler。

StandardScaler преобразует характеристики в форму стандартного нормального распределения. (Среднее значение равно 0, а стандартное отклонение — 1.)
MinMaxScaler преобразует (масштабирует) объект в распределение указанного интервала. По умолчанию (и обычно) мы масштабируем функцию до [0, 1], а также нормализуем этот метод масштабирования.

# Попытайся
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.model_selection import train_test_split

X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
lr = LinearRegression()
lr.fit(X_train, y_train)
# Нестандартизированный набор данных мало влияет на линейную регрессию.
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))

# Нестандартизованный набор данных имеет большое влияние на алгоритм градиентного спуска.
sgd = SGDRegressor(eta0=0.01, max_iter=100)
sgd.fit(X_train, y_train)
print(sgd.score(X_train, y_train))
print(sgd.score(X_test, y_test))