Введение
- В последнее время, с ростом популярности этих двух методов появилось много библиотек на Matlab, R, Python, C ++ и т.д., которые получают на вход обучающий набор и автоматически создают соответствующую нейронную сеть для вашей задачи.
- Однако при использовании готовых библиотек бывает сложно понять, что именно происходит и как мы получаем оптимизированную сеть. А ведь знание основ решения важно для дальнейшего развития этих методов. Итак, в данной статье мы создадим очень простую структуру для алгоритма нейронной сети.
- Мы постараемся понять, как работает базовый тип нейронной сети — перцептрон с одним нейроном и многослойный перцептрон — замечательный алгоритм, который отвечает за обучение сети (градиентный спуск и обратное распространение). Эти сетевые модели будут основой для более сложных моделей, существующих на сегодняшний день.
Краткий обзор истории
- Первая нейронная сеть была задумана Уорренном Маккалоком и Уолтером Питтсом в 1943 году. Они написали великолепную статью о том, как должны работать нейроны, а затем построили модель на основе своих идей — создали простую нейронную сеть с электрическими цепями.
- Исследования в области искусственного интеллекта быстро развивались, и в 1980 году Кунихико Фукусима разработал первую настоящую многослойную нейронную сеть.
- Первоначальной целью нейронной сети было создание компьютерной системы, способной решать проблемы подобно тому, как это делает человеческий мозг. Однако, со временем исследователи сменили фокус и начали использовать нейронные сети для решения особенных задач. С тех пор нейронные сети выполняют самые разнообразные задачи, включая компьютерное зрение, распознавание голоса, машинный перевод, фильтрацию социальных сетей, настольные игры или видеоигры, медицинскую диагностику, прогноз погоды, прогнозирование временных рядов, распознавание (изображения, текста, голоса) и др.
Компьютерная модель нейрона: перцептрон
Перцептрон
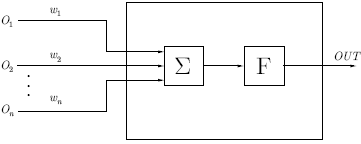
Перцептрон вдохновлен идеей обработки информации единственной нервной клетки, называемой нейроном. Нейрон принимает на вход сигналы через свои дендриты, которые передают электрический сигнал телу клетки. Точно так же перцептрон получает входные сигналы из примеров обучающих данных, которые предварительно взвесили и объединили в линейное уравнение, называемое активацией.
- z = sum(weight_i * x_i) + bias
Где weight — это вес сети, X — это входное значение, i — индекс веса или входные данные, а смещение — это специальный вес, который не имеет множитель в виде входного значения (можем считать, что входные данные всегда равны 1.0).
Затем активация преобразуется в выходное (прогнозируемое) значение с помощью передаточной функции (функция активации).
- y = 1.0 если z >= 0.0, иначе 0.0
Таким образом, перцептрон представляет собой алгоритм классификации проблем с двумя классами (двоичный классификатор), где для разделения двух классов может использоваться линейное уравнение.
Это тесно связано с линейной регрессией и логистической регрессией, которые осуществляют прогнозы аналогичным образом (например, взвешенная сумма входов).
Алгоритм перцептрона — простейший вид искусственной нейронной сети. Это модель одного нейрона, которая может использоваться в задачах классификации двух классов и обеспечивает основу для дальнейшего развития гораздо более крупных сетей.
Входы нейронов представлены вектором x = [x1, x2, x3,…, xN], который может соответствовать, к примеру, ряду торговых цен актива, значениям технических индикаторов, числовой последовательности в пикселях изображения. Когда они попадают к нейрону, они умножаются на соответствующие синаптические веса, которые являются элементами вектора w = [w1, w2, w3, …, wN], и таким образом генерируют значение z, обычно называемое потенциалом активации, согласно выражению:
b обеспечивает более высокую степень свободы и не зависит от входа в это выражение, что обычно соответствует нейрону смещения (склонности). Затем z-значение проходит через функцию активации σ, которая отвечает за ограничение этого значения определенным интервалом (например, 0 — 1), что дает окончательное выходное значение и значение нейрона. Некоторые используемые триггерные функции: шаг, сигмоид, гиперболический тангенс, softmax и ReLU («rectified linear unit»).
Чтобы проиллюстрировать процесс, направленный на достижение предела разделимости классов, ниже мы показываем две ситуации, которые демонстрируют их сближение к стабилизации с учетом только двух входов {x1 и x2}
Веса алгоритма перцептрона следует оценивать на основе данных обучения с использованием стохастического градиентного спуска.
Стохастический градиент
Градиентный спуск — это процесс минимизации функции в направлении градиента функции стоимости.
Это подразумевает знание формулы стоимости, а также производной, чтобы с определенной точки мы могли узнать наклон и могли двигаться в этом направлении, например, вниз по направлению к минимальному значению.
В машинном обучении мы можем использовать метод, который оценивает и обновляет веса для каждой итерации, называемый стохастическим градиентным спуском, чтобы минимизировать ошибку модели в наших обучающих данных.
Принцип работы этого алгоритма оптимизации заключается в том, что каждый обучающий экземпляр показывается модели по одному. Модель делает прогноз для обучающего экземпляра, вычисляет ошибку и обновляет модель, чтобы уменьшить ошибку для следующего прогноза.
Эту процедуру можно использовать для поиска набора весов в модели, который дает наименьшую ошибку для модели в обучающих данных.
Для алгоритма перцептрона на каждой итерации веса w обновляются с использованием уравнения:
- w = w + learning_rate * (expected — predicted) * x
Где w оптимизируется, learning_rate — это скорость обучения, которую мы должны установить (например, 0.1), (expected — predicted) — ошибка прогнозирования для модели в обучающих данных, относящихся к весу, а x — входное значение.
Для стохастического градиентного спуска требуются два параметра:
- Коэффициент обучения: используется для ограничения размера корректировки веса при каждом его обновлении.
- Эпохи — сколько раз обучающие данные должны выполняться при обновлении веса.
Они вместе с обучающими данными будут аргументами для функции.
Нам нужно выполнить 3 цикла в функции:
1. Цикл для каждой эпохи.
2. Цикл для каждой строки в обучающих данных для эпохи.
3. Цикл для каждого веса, который обновляется для одной строке в одной эпохи.
Веса обновляются в зависимости от ошибки, допущенной моделью. Ошибка рассчитывается как разница между фактическим значением и прогнозом, сделанным с помощью весов.
Для каждого входного атрибута есть свой вес, и они постоянно обновляются, например:
- w(t+1)= w(t) + learning_rate * (expected(t) — predicted(t)) * x(t)
Смещение обновляется аналогичным образом, только без входа, поскольку оно не связано с конкретным входным значением:
- bias(t+1) = bias(t) + learning_rate * (expected(t) — predicted(t)).
Применение модели нейрона:
Теперь перейдем к практическому применению.
Этот урок разделен на 2 части:
1. Делаем прогнозы
2. Оптимизация веса сети
Эти шаги обеспечат основу для реализации и применения алгоритма перцептрона к другим задачам классификации.
Нам нужно определить количество столбцов в нашем наборе X, для этого мы определяем константу
#define nINPUT 3
В MQL5 многомерный массив может быть статическим или динамическим только для первого измерения, а поскольку все остальные измерения будут статическими, при объявлении массива необходимо указать размер.
1. Делаем прогнозы
Первый шаг — разработать функцию, которая может делать прогнозы.
Это будет необходимо как при оценке значений весов кандидатов при стохастическом градиентном спуске, так и после завершения модели. Прогнозы надо делать и на тестовых данных, и на новых.
Ниже приведена функция predict, которая прогнозирует выходное значение для строки исходя от определенного набора весов.
Первый вес всегда является смещением, поскольку он автономен и не работает с конкретным входным значением.
template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); }
Перенос нейронов:
Как только нейрон активирован, нам нужно передать активацию, чтобы увидеть, каковы на самом деле выходные данные нейрона.
double activation(const double activation) { return activation>=0.0?1.0:0.0; }
Мы получаем в качестве аргумента в функции прогнозирования входной набор X, массив с весами (W) и строку, для которой прогнозируется входной набор X.
Мы можем придумать небольшой набор данных, чтобы проверить нашу функцию прогнозирования.
Мы также можем использовать заранее подготовленные веса, чтобы делать прогнозы для этого набора данных.
double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
После того, как мы собрали все это вместе, мы можем протестировать нашу функцию прогнозирования ниже.
#define nINPUT 3 void OnStart() { random.seed(42); double dataset[][nINPUT] = { {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003}; for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } double activation(const double activation) { return activation>=0.0?1.0:0.0; }
Есть два входных значения (X1 и X2) и три коэффициента веса (bias, w1 и w2). Уравнение активации, которое мы моделируем для данной проблемы, выглядит так:
activation = (w1 * X1) + (w2 * X2) + b
Или с конкретными значениями веса, мы вручную выбираем как:
activation = (0.206 * X1) + (-0.234 * X2) + -0.1
После завершения работы функции мы получаем прогнозы, которые соответствуют ожидаемым выходным значениям y.
Теперь можем реализовать стохастический градиентный спуск для оптимизации значений веса.
2. Оптимизируем веса сети
Веса для наших обучающих данных можно оценить, используя стохастический градиентный спуск, как было сказано ранее.
Ниже приведена функция train_weights(), которая вычисляет значения веса для набора обучающих данных с использованием стохастического градиентного спуска.
В MQL5 мы не можем получить возврат из этого массива с данными обученных весов, потому что, в отличие от переменных, массивы могут быть переданы в функцию только по ссылке. Это означает, что функция не создает собственный экземпляр массива, а вместо этого работает напрямую с переданным ей массивом. Таким образом, все изменения, осуществляемые в этом массиве внутри функции влияют на исходный массив.
template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); for(int i=0; i<ArrayRange(X, 1); i++) { weights[i]=random.random(); } for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
На каждой эпохе мы отслеживаем сумму квадратичной ошибки (положительное значение), чтобы отслеживать уменьшение ошибки. Это позволяет наблюдать как алгоритм минимизирует ошибку на каждой эпохе.
Давайте протестируем нашу функцию с одним и тем же набором данных, представленным выше.
#define nINPUT 3 void OnStart() { random.seed(42); double dataset[][nINPUT] = { {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[]; train_weights(weights, dataset); ArrayPrint(weights, 20); for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } double activation(const double activation) { return activation>=0.0?1.0:0.0; } template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); ArrayInitialize(weights, 0); for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
Мы используем скорость обучения 0,1 и обучаем модель только для 5 эпох или 5 показов весов для всего набора обучающих данных.
При выполнении примера для каждой эпохи печатается сообщение с суммой квадратичной ошибки для этой эпохи и окончательным набором весов.
Мы видим, как быстро алгоритм выучивает проблему.
Этот тест можно найти в файле PerceptronScript.mq5.
Многослойный перцептрон
- Объединеняем нейроны в слои
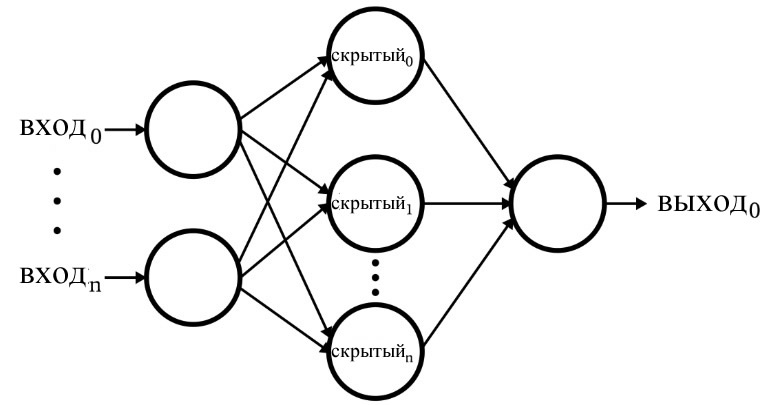
С одним нейроном мало что можно сделать, но мы можем объединить их в многоуровневую структуру, каждый с разным количеством нейронов, и сформировать нейронную сеть, называемую многослойным перцептроном («multi layer perceptron, MLP»). Вектор входных значений X проходит через начальный слой, выходные значения которого связаны со входами следующего уровня, и так далее, пока сеть не предоставит выходные значения последнего слоя в качестве результата. Сеть может быть организована в несколько слоев, что делает ее глубокой и способной выучить все более сложные отношения.
Обучение MLP
Для того, чтобы такая сеть работала, ее нужно обучать. Это как учить ребенка читать. Обучение MLP происходит в контексте машинного обучения с учителем, но как это работает?
Обучение с учителем:
- Нам дается набор отмеченных данных, для которых мы уже знаем какой именно является нашим правильным выходом, и он должен быть аналогичен набору, имея представление о том, что существует связь между входом и выходом.
- Задачи обучения с учителем подразделяются на задачи «регрессии» и «классификации». В задачах регрессии мы пытаемся предсказать результаты на непрерывном выходе, что означает, что мы пытаемся сопоставить входные переменные с некоторой непрерывной функцией. В задачах классификации мы стараемся предсказать результаты на дискретном выходе. Другими словами, мы пытаемся сопоставить входные переменные по разным категориям.
Пример 1:
- Учитывая набор данных о размерах домов на рынке недвижимости, попробуйте спрогнозировать их цену. Цена в зависимости от размера — это непрерывный результат, так что это проблема регрессии.
- Мы могли бы также превратить этот пример в задачу классификации, чтобы прогнозировать о том, «продастся ли дом дороже или дешевле, чем запрашиваемая цена». Здесь мы рассортируем дома по цене на две разные категории.
Обратное распространение
Обратное распространение, без сомнений, является самым важным алгоритмом в истории нейронных сетей — без (эффективного) обратного распространения, было бы невозможно обучить сети глубокого обучения так, как мы это делаем сегодня. Обратное распространение можно считать краеугольным камнем современных нейронных сетей и глубокого обучения.
Разве мы не учимся на ошибках?
Идея алгоритма обратного распространения ошибки состоит в том, чтобы на основе расчетной ошибки, полученной на выходном слое нейронной сети, пересчитать значение весов вектора W последнего слоя нейронов. Затем мы переходим к предыдущему слою и так далее, от конца к началу, то есть, он состоит из обновления всех весов W слоев, от последнего до достижения входного слоя сети путем обратного распространения ошибки, полученной сетью. Другими словами, ошибка вычисляется между тем, что предсказала сеть, и тем, что она была на самом деле (фактический 1, предсказанный 0; у нас есть ошибка!), поэтому мы пересчитываем значения всех весов, начиная с последнего слоя и переходя к первому, всегда обращая внимание на уменьшение этой ошибки.
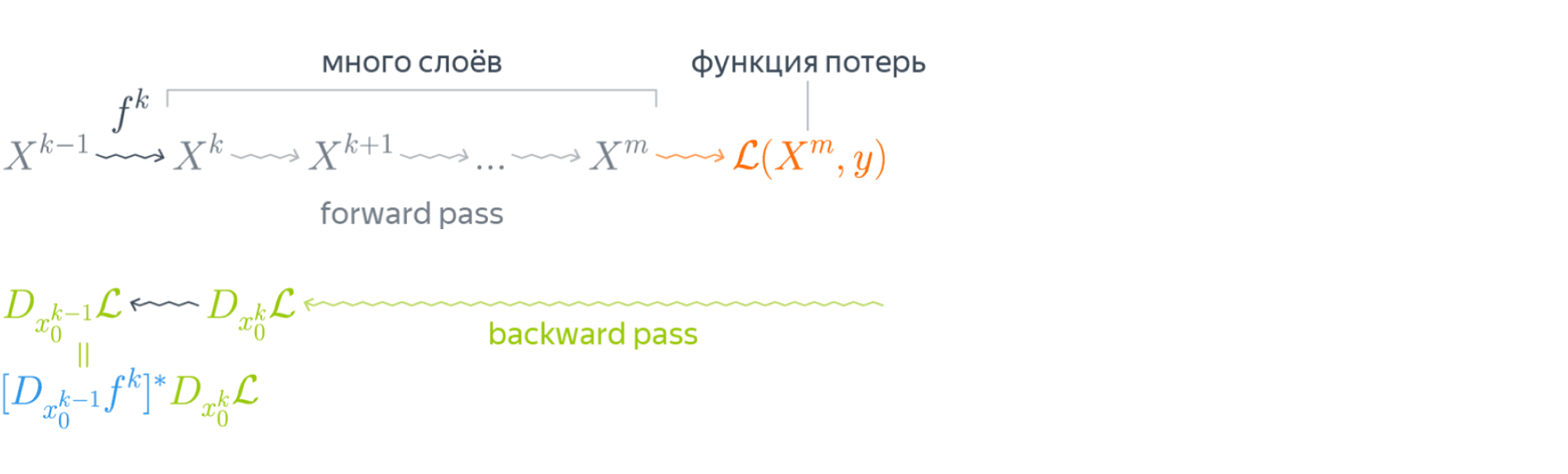
Алгоритм обратного распространения ошибки состоит из двух этапов:
1. Прямой проход («forward pass»), при котором наши входы проходят через сеть и получают прогнозы выхода (этот шаг также известен как фаза распространения).
2. Обратный проход («backward pass»), при котором мы вычисляем градиент функции потерь на последнем слое (то есть слое прогнозирования) сети и используем этот градиент для рекурсивного применения цепного правила («chain rule») для обновления весов в нашей сети (также известного как стадия обновления веса или обратное распространение)
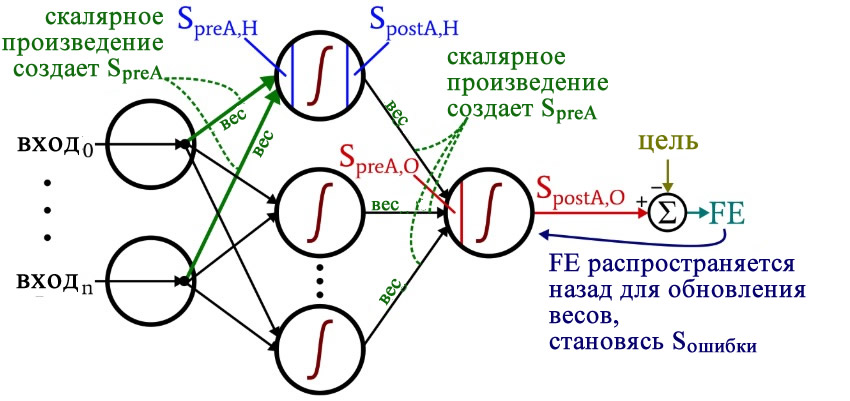
Рассмотрим сеть выше со слоем скрытых нейронов и выходным нейроном. Когда входной вектор распространяется по сети, для текущего набора весов существует выходной Pred(y). Цель обучения с учителем — настроить веса так, чтобы уменьшить разницу между Pred(y) сети и требуемым выходным Req(y). Для этого требуется алгоритм, который уменьшает абсолютную ошибку, что аналогично уменьшению квадратичной ошибки, где:
(1)
Сетевая ошибка = Pred — Req
= E
Алгоритм должен регулировать веса, чтобы минимизировать E². Обратное распространение — это алгоритм, который выполняет минимизацию градиентного спуска E². Чтобы минимизировать E², необходимо рассчитать его чувствительность к каждому весу. Другими словами, нам нужно знать, какое влияние будет иметь изменение каждого веса на E². Если нам будет известно, веса можно будет отрегулировать в направлении, уменьшающем абсолютную ошибку. Последующее описание правила обратного распространения основано на такой диаграмме:
Пунктирная линия представляет нейрон B, который может быть скрытым или выходным нейроном. Выходы n нейронов (O 1 … O n) на предыдущем слое являются взодами для нейрона B. Если нейрон B находится в скрытом слое, он просто является входным вектором. Эти выходы умножаются на соответствующие веса (W1B … WnB), где WnB — вес, соединяющий нейрон n и нейрону B. Функция суммы складывает все эти произведения для получения входных данных, IB, который обрабатывается функцией триггера f(.) нейрона B. f (IB) это выход OB нейрона B. Рассмотрим пример. Назовем нейрон 1 нейроном A и рассмотрим вес WAB между двумя нейронами. Подход, используемый для изменения веса, определяется правилом дельты:
(2)
где — параметр скорости обучения, который определяет скорость обучения, а
является чувствительностью ошибки E² к весу WAB и определяет направление поиска в пространстве весов для нового веса WAB (новый), как изображено на рисунке ниже.
Чтобы минимизировать E², правило дельты обеспечивает необходимое направление изменения веса.
Ключевой концепцией приведенного выше уравнения является вычисление выражения ∂E² /∂WAB, которое состоит в вычислении частных производных функции ошибок E² по отношению к каждому весу вектора W.
Дифференцирование сложной функции:
(3)
и
(4)
поскольку остальные входы нейрона B не зависят от веса WAB. Таким образом, исходя из уравнений (3) и (4), уравнение (2) становится
(5)
и изменение веса WAB зависит от чувствительности квадрата ошибки E² на входе IB, единицы B и входного сигнала OА.
Возможны две ситуации:
1. B — выходной нейрон;
2. B — скрытый нейрон.
Рассмотриваем первый случай:
Поскольку B является выходным нейроном, изменение квадрата ошибки из-за настроки WAB просто является изменением квадрата ошибки выходного сигнала B.
(6)
объединяя уравнение (5) и уравнение (6), получаем
(7)
Правило изменения весов, когда нейрон B является выходным нейроном, если выходная функция активации, f (.), является логистической функцией:
(8)
Дифференцируем уравнение (8) по аргументу x:
(9)
Но,
(10)
при вставке (10) в (9) получаем:
(11)
таким же образом для функции tanh
или для линейной функции (identity)
Так мы получаем:
Рассматривая второй случай:
B это скрытый нейрон
(12)
где O представляет выходной нейрон
(13)
где p это индекс, который охватывает все нейроны, включая нейрон B, который обеспечивает входные сигналы для выходного нейрона. Расширяем правую часть уравнения (13),
(14)
поскольку веса других нейронов WpO (p! = B) не имеют зависимости от OB.
При вставке (13) и (13) в (12):
(15)
Следовательно, теперь это выражается как функция от
, вычисляемая, как описано в уравнении (6).
Полное правило изменения веса WAB между нейроном A, который посылает сигнал нейрону B, является таким:
(16)
где
где fo (.) и fh (.) это скрытые функции активации и выхода соответственно.
Пример
Выход из сети = [tanh(I T .WI)] . WO
HID = [Tanh(I T.WI)] T— выходы скрытых нейронов
ERROR = (выход из сети — нужный выход)
LR = коеффициент обучения
Обновления веса становятся
нейроном с линейным выходом
(17)
WO = WO — ( LR x ERROR x HID )
скрытым нейроном
(18)
WI = WI — { LR x [ERROR x WO x (1- HID 2)] . I T } T
Уравнения 17 и 18 показывают, что изменение веса — это входной сигнал, умноженный на локальный градиент. Это обеспечивает направление, величина которого также зависит от величины ошибки. Если берем направление без величины, все изменения будут одинакового размера, и это будет зависеть от темпа обучения. Вышеуказанный алгоритм является упрощенной версией, так как имеется только один выходной нейрон. В исходном алгоритме допускается более одного выхода, а уменьшение градиента минимизирует общую квадратную ошибку всех выходов. Есть много алгоритмов, которые произошли от исходного алгоритма для увеличения скорости обучения. Они кратко изложены в:
« Back Propagation family album» — Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia».
Обратное распространение — это элегантный и умелый алгоритм. Современные модели глубокого обучения, такие как сверточные нейронные сети, хотя и более совершенные, чем MLP, показали себя намного лучше в таких задачах, как классификация изображений и используют обратное распространение в качестве метода обучения, а также так называемые рекуррентные нейронные сети в условиях естественной языковой обработки, которые также используют этот алгоритм. Самое невероятное, что таким моделям удается находить ненаблюдаемые и непонятные закономерности для нас, людей, что удивляет и позволяет нам считать, что скоро мы получим помощь глубокого обучения для решения многих основных проблем, с которыми сталкивается человечество.
Применение модели MLP
Этот урок разделен на 5 частей:
1. Инициализация сети.
2. Прямое распространение (FeedForward).
3. Обратное распространение.
4. Обучение сети.
5. Прогноз.
Для нашей разработки мы реализуем применение на чистом MQL. Нам уже известно, что существуют библиотеки на других языках, которые уже являются гораздо более сложными, и настоятельно рекомендуется использовать их из практических соображений и соображений производительности, но, как уже было сказано в начале, важно понимать внутреннее устройство таких библиотек, чтобы иметь больший контроль над всем процессом. Мы также не использовали ООП в нашем тесте, поскольку это всего лишь алгоритм для иллюстрации предыдущих уравнений, в нем нет необходимости. Однако в реальных случаях гораздо практичнее использовать ООП, поскольку оно обеспечивает масштабируемость проекта.
1. Инициализация сети
У каждого нейрона есть набор весов, которые необходимо поддерживать. Вес для каждого входного соединения и дополнительный вес для смещения.
Рекомендуем инициализировать веса сети для небольших случайных чисел. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1. Для этого мы создали функцию для генерации случайных чисел.
double random(void) { return ((double)rand())/(double)SHORT_MAX; }
Ниже представлена функция под названием initialize_network(), которая создает веса нашей нейронной сети.
void forward_propagate(void) { int i = 0; for(i = 0; i<numHidden; i++) { hiddenVal[i] = 0.0; for(int j = 0; j<numInputs; j++) { hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]); } hiddenVal[i] = tanh(hiddenVal[i]); } outPred = 0.0; for(i = 0; i<numHidden; i++) { outPred += hiddenVal[i] * weightsHO[i]; } errThisPat = outPred - y[patNum]; }
3. Обратное распространение
Алгоритм обратного распространения назван в честь способа обучения весов
Ошибка вычисляется между ожидаемыми выходами и выходными сигналами сети прямого распространения. Затем эти ошибки передаются обратно по сети от выходного слоя к скрытому слою, перекладывая ответственность за ошибку и обновляя веса по мере их поступления.
Математика ошибки обратного распространения была объяснена выше.
void backward_propagate_error(void) { for(int k = 0; k<numHidden; k++) { double weightChange = LR_HO * errThisPat * hiddenVal[k]; weightsHO[k] -= weightChange; regularisationWeights(weightsHO[k]); } for(int i = 0; i<numHidden; i++) { for(int k = 0; k<numInputs; k++) { double x = 1 - pow(hiddenVal[i],2); x = x * weightsHO[i] * errThisPat * LR_IH; x = x * X[patNum][k]; double weightChange = x; weightsIH[k][i] -= weightChange; } } }
метод regularizationWeights был создан только для регуляризации весов в диапазоне от -5 до 5.
void regularisationWeights(double &weight) { weight<-5?weight=-5:weight>5?weight=5:weight=weight; }
4. Обучение сети
Сеть обучается методом стохастического градиентного спуска.
Это включает в себя несколько итераций, раскрывающих набор обучающих данных в сети, и для каждой строки данных прямое распространение входных данных, обратное распространение ошибки и обновление весов сети.
//# Train a network for a fixed number of epochs void train(void) { for(int j = 0; j <= numEpochs; j++) { for(int i = 0; i<numPatterns; i++) { patNum = rand()%numPatterns; forward_propagate(); backward_propagate_error(); } calcOverallError(); printf("epoch = %d RMS Error = %f",j,RMSerror); } }
5. Прогноз
Делать прогнозы с помощью обученной нейронной сети довольно просто.
Мы уже видели, как распространить паттерн входа для получения выходных данных. Это все, что нам нужно сделать, чтобы осуществить прогноз. Мы можем использовать выходные значения напрямую как вероятность принадлежности паттерна к каждому выходному классу.
void predict(void) { for(int i = 0; i<numPatterns; i++) { patNum = i; forward_propagate(); printf("real = %d predict = %f",y[patNum],outPred); } }
Полный пример можно найти в файле MLP_Script.mq5.
Заключение
Мы занимались вычислениями, задействованными в процессе развития нейрона перцептрона, а также сети нейронов перцептрона, называемой «multi layer perceptron, MLP». В данном процессе мы поняли, как осуществляется обучение этого типа сетей с использованием обратного распространения ошибки и градиентного спуска.
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
Метод обратного распространения ошибки — метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. Полем Дж. Вербосом[1], а также независимо и одновременно А. И. Галушкиным[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)[4]. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.[5]
Для возможноcти применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема.
Cигмоидальные функции активации[]
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):

Рациональная сигмоида:
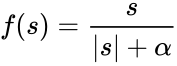
Гиперболический тангенс:
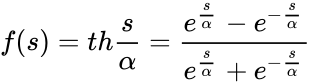
где s — выход сумматора нейрона, 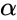
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активациями, то сигмоиды расчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации — нужно расчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции расчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленее пороговой функции активации как 1:4.
Функция оценки работы сети[]
В тех случаях, когда удается оценить работу сети обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:

где 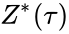
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок поысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе[6].
Описание алгоритма[]
Файл:Neuro.PNG Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть входы 
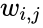
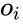
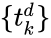
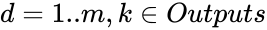

Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого тестового примера. Нам нужно двигаться в сторону, противоположную градиенту, то есть добавлять к каждому весу 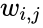
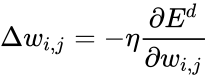
где
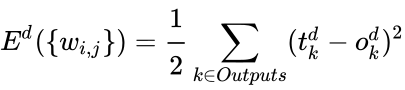
Производная считается следующим образом. Пусть сначала 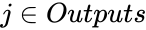
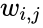
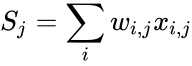

Аналогично, 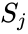
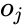
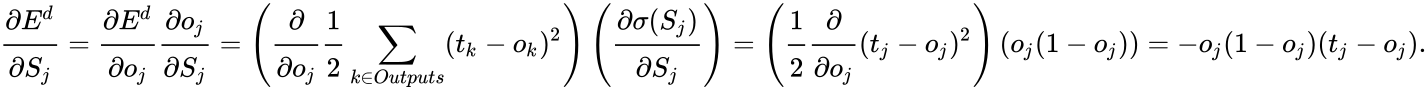
Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае

и

Ну а 
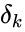
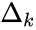
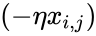
поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:
- для узла последнего уровня

- для внутреннего узла сети

- для всех узлов
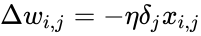
Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм[]
Алгоритм:
BackPropagation 
- Инициализировать
маленькими случайными значениями.
- Повторить NUMBER_OF_STEPS раз:
- Для всех d от 1 до m:
- Подать
на вход сети и подсчитать выходы
каждого узла.
- Для всех
.
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
.
- Для каждого ребра сети {i, j}
.
- Выдать значения
.
Математическая интерпретация обучения нейронной сети[]
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющих обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Недостатки алгоритма[]
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Паралич сети[]
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы[]
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны.
Размер шага[]
Внимательный разбор доказательства сходимости[3] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. П. Д. Вассерман[7] описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня[8] предложена разветвлённая технология оптимизации обучения.
См. также[]
- Сигмоид
- Многослойный перцептрон
Литература[]
- Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.
- Хайкин С. Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.
Внешние ссылки[]
- Копосов А.И., Щербаков И.Б., Кисленко Н.А., Кисленко О.П., Варивода Ю.В. и др. Отчет по научно-исследовательской работе «Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии». — Москва: ВНИИГАЗ, 1995.
- Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ. Красноярск: ИПЦ КГТУ, 2002, 347 с. Рис. 58, табл. 59, библиогр. 379 наименований. ISBN 5-7636-0477-6
Примечания[]
- ↑ Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.
- ↑ Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
- ↑ 3,0 3,1 Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
- ↑ Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
- ↑ Барцев С. И., Гилев С. Е., Охонин В. А., Принцип двойственности в организации адаптивных сетей обработки информации, В кн.: Динамика химических и биологических систем. — Новосибирск: Наука, 1989. — С. 6-55.
- ↑ Миркес Е. М., — Новосибирск: Наука, Сибирская издательская фирма РАН, 1999. — 337 с. ISBN 5-02-031409-9 Другие копии онлайн: [1]
- ↑ Wasserman P. D. Experiments in translating Chinese characters using backpropagation. Proceedings of the Thirty-Third IEEE Computer Society International Conference.. — Washington: D. C.: Computer Society Press of the IEEE, 1988.
- ↑ Горбань А. Н. Обучение нейронных сетей.. — Москва: СП ПараГраф, 1990.
Опр:
Многослойный
персептрон (МП)
– в самой простой версии это сеть с
одним входным (сенсорным)
слоем, одним выходным (моторным)
слоем и одним или несколькими внутренними
(скрытыми)
слоями нейрона. Характерная черта такого
персептрона – прямонаправленность.
Это значит, что информация, преобразуясь,
передается через К скрытых слоев от
входного слоя к выходному, при этом, в
стандартной топологии, узел i
в слое k
= 1,2, … , К+1 соединяется посредством
синаптических весов i
j
k
со всеми узлами j
предыдущего, (k-1)-го
слоя, где k=0
– сенсорный слой, k=К+1
– моторный слой.

*
Нейроны сенсорного и моторного слоев
не имеют активационных функций, т.к. их
задачи – принять и ретранслировать
сигналы на первый скрытый слой (для
сенсорного) и, суммировав сигналы, подать
их на выход (для моторного).
Модифицированные
версии
многослойного персептрона могут иметь:
—
нерегулярные связи между слоями
(неполный граф соединений);
—
прямые связи между несмежными слоями;
—
межнейронные связи внутри одного слоя;
—
обратных связей БЫТЬ НЕ МОЖЕТ.
-
Входной
слой многослойного
персептрона выполняет функции приема
и ретрансляции входных сигналов х1,
х2,
… , хN
на нейроны первого скрытого слоя; -
Основное
нелинейное преобразование сигналов
происходит в скрытых
слоях; -
Выходной
слой
осуществляет суперпозицию взвешенных
сигналов последнего скрытого слоя.
Обучение
многослойного персептрона
Обучение
многослойного персептрона – это задача
оптимизации (подбор оптимальных ij
и порогов АФН так, чтобы ошибка стремилась
к нулю или была равна нулю). Для обучения
МП был предложен алгоритм
«Обратного распространения ошибки»
(Back
Propagation
Error).
В основу этого алгоритма положен метод
градиентного спуска, направленный на
уменьшение ошибки:
Q
M
e
= ½
(yiq
– Yiq)2
q=1
i=1
согласно
которому на каждой итерации поиска
изменяются значения синаптических
весов и порогов АФН. Приращение
синаптических весов и порогов АФН
определяется как:
jik
= –
e
/ jik
, j
= 1..Hk-1,
i
= 1..Hk
(k
= 1..K);
0ik
= –
e
/ 0ik
, j = 1..Hk-1,
I = 1..Hk
(k = 1..K),
где
jik
– синаптический вес связи j-го
нейрона k–1-го
слоя с i-м
нейроном k-го
слоя;
0ik
– порог АФН i-го
нейрона k-го
слоя;
Нk
– число нейронов в k-м
слое;
– настроечный
параметр обучения (0,1];
К
– число слоев персептрона.
Согласно
правилам дифференцирования сложной
функции, производная от функции ошибки
по jik
может быть записана как:
e
/ jik
= (e
/ yik)*(yik
/ sik)*(sik
/ jik)
= (обозн.) = ik
*
yjk-1
(1)
yik
– сигнал на выходе i-го
нейрона k-го
слоя;
Нk-1
sik
=
j
i
k
yjk-1
– 0
ik
– сдвинутая на величину порога взвешенная
сумма входных
j=1
сигналов i-го
нейрона k-го
слоя;
ik
= (e
/ yik)*(yik
/ sik)
*
Выражение (1) и все последующие выкладки
приведены для случая оценки ЛОКАЛЬНОЙ
ОШИБКИ e
= eq,
т.е. для одного шаблона. Поэтому индекс
шаблона опущен и нет
по q.
Представление
производной e
/ yik
через выходы k+1-го
слоя имеет вид:
Нk+1
Нk+1
e
/ yik
=
(e
/ yjk+1)*(yjk+1
/ sjk+1)*(sjk+1
/ yik)
=
(e
/ yjk+1)*(yjk+1
/ sjk+1)*ijk+1
(2)
На
основании этого (*(yik
/ sik))
можно получить рекуррентную формулу:
Нk+1
ik
= [
ik+1ijk+1]
*(yik
/ sik)
(3)
j=1
Эта
формула может быть использована для
пересчета величин ik
со слоя k+1
на слой k
(т.е. в обратную сторону – обратное
распространение ошибки).
Для
слоя К+1 (выходной, последний), с которого
начинается BPE
(ОРО) величина:
iК+1
= (yjК+1
– Yj)*(yjK+1
/ sjK+1)
(4)
Т.о.
итерационная формула для коррекции
значений синаптических весов имеет
вид:
jik+1
= –
ik+1
yjk
(k = K, K-1, … , 1, 0) (5)
Аналогично
получается итерационная формула для
коррекции порогов АФН:
0ik+1
=
ik+1
(k
= K,
K-1,
… , 1, 0) (6)
Выбор
той или иной АФН определяется многими
факторами, среди которых в первую очередь
выделяется существование производной
на всей оси абсцисс и удобство организации
вычислений. С этой точки зрения, в
алгоритме BPE
(ОРО) чаще всего используют сигмаидальную
АФН. Для нее, согласно (4):
iК+1
= a(yj
– Yj)
yj(1
– yj)
– непрерывная функция
(yj
= yjК+1
– сигнал на выходе j-го
нейрона выходного слоя).
Общее
описание алгоритма обратного
распространения ошибки
1.
Инициализация синаптических весов jik
и порогов АФН 0ik
во всех слоях персептрона (j
= 1..Hk-1,
i
= 1..Hk)
как маленьких
величин, например [-1,1].
2.
Выбор очередного шаблона < X
, Y
>
S
из набора тренировочных шаблонов
случайным
образом
или согласно определенному правилу.
3.
Прямой ход:
вычисление фактических выходов
персептрона по формулам:
Нk-1
yjk
= f
(
j
i k
yjk-1
– 0
ik)
, j = 1..Hk-1,
i = 1..Hk,
k = 1..K+1;
j=1
yj0
= xj
– j-я
компонента левой части шаблона.
Вычисление
ошибки и проверка критерия выхода из
алгоритма (достаточная малость ошибки).
4.
Обратный ход:
коррекция значений синаптических весов
и порогов АФН с использованием формул
(3) – (7). Причем коррекция порогов АФН
осуществляется после каждого шаблона
(по распределенной, но не по суммарной
ошибке).
5.
Переход к 2.
-)
Для повышения эффективности алгоритма,
априорный задаваемый параметр
можно заменить на поиск величины шага
вдоль антиградиента с помощью метода
одномерной минимизации. Это может
привести к увеличению времени продолжения
одной итерации алгоритма, но в целом
уменьшит число итераций.
23.
RBF-сеть.
Опр:
RBF-сеть
(Radial
Basis
Function)
– однослойная ИНС, способная
аппроксимировать произвольную непрерывную
функцию в базисе радиально-симметричных
активационных функций нейронов (с любой
заданной точностью).

Алгоритм
обучения RBF-сети
– простой, не требующий рекурсий
алгоритм; аппроксимируемая функция*
задается набором шаблонов:
P
= {< X
, Y
>q,
q
= 1..Q},
где
X
= (X1,
X2,
… , XN)
– вектор переменных (аргументов)
аппроксимируемой функции, определяющий
N-мерное
пространство входных сигналов RBF-сети;
Y
= (Y1,
Y2,
… , YM)
– вектор соответствующих значений
аппроксимируемой функции.
*
Имеется в виду НАБОР аппроксимируемых
функций, число которых (М) определяет
количество выходов RBF-сети.
RBF
– сеть имеет единственный скрытый слой
из Н нейронов, только эти нейроны обладают
радиально-симметричной АФН и осуществляют
нелинейное преобразование поступающих
на их вход сигналов. Синаптические веса
всех связей между нейронами входного
и скрытого слоев принимаются равными
1 (невзвешенная сумма сигналов).
В
АФН i-го
нейрона скрытого слоя:
– X-Ci2*(1/2i)
– [ (Xj
–
Cji)2]*(1/2i)
f
(X, Ci)
= e = e i=1..N
—
вектор
Ci
= (C1i,
C2i,
… , CNi)
– центр
АФН
i-го
нейрона;
—
скаляр i
– ширина
окна АФН i-го
нейрона.
Матричные
выражения для вычисления синаптических
весов
связей между нейронами скрытого и
выходного слоев j
i
(j
= 1..H,
i
= 1..M)
получаются следующим образом:
-
Сигнал
выхода i-го
нейрона выходного слоя, получаемый под
воздействием вектора аргументов q-го
шаблона (Xq)
приравнивается i-му
элементу выходного вектора q-го
шаблона (Yiq):
yi
= 1
i
f(Xq,
C1)
+ 2
i
f(Xq,
C2)
+ … + H
i
f(Xq,
CH)
= yiq
(8)
-
Если
положить H=Q,
Ci
= Xi
(i=1..H),
то уравнение (8) можно представить в
виде:
1
i
fq1
+ 2
i
fq2
+ … + H
i
fqH
= Yqi
,
где
fqi
= f(Xq,Ci)
yqi
= Yqi
– желаемый отклик i-го
выходного нейрона на q-й
шаблон.
-
Записав
аналогичные уравнения для всех выходов
сети и всех шаблонов, получим матричное
уравнение вида:
F
* W
= Y,
где
(9)

-
Синаптические
веса из (9) получаются:
W
= F-1
*
Y
(10)
Алгоритм
синтеза RBF-сети
-
Оопределяется
размер Н скрытого слоя RBF-сети,
равный количеству тренировочных
шаблонов (Н=Q). -
В
качестве центров АФН скрытого слоя
берутся точки пространства входных
сигналов, заданные в наборе тренировочных
шаблонов P:
Ci
= Xi
(i=1..H). -
Задается
ширина окон АФН скрытого слоя i
(i=1..H).
Причем, окна должны покрывать пространство
входных сигналов сети, не накладываясь
друг на друга (эвристические параметры).
-
Формируются
матрицы F
и Y. -
Вычисляется
матрица F-1. -
По
формуле (10) определяется матрица
синаптических весов W,
эти значения должны обеспечить совпадение
точек интерполяционной поверхности с
тренировочными шаблонами в пространстве
выходных сигналов RBF-сети.
*
Наиболее ответственные моменты реализации
алгоритма это:
—
выбор размера скрытого слоя;
—
задание ширины окон АФН,
т.к.
от этого существенно зависит ошибка
аппроксимации в точках входного
пространства, не фигурирующих в наборе
тренировочных шаблонов Р.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
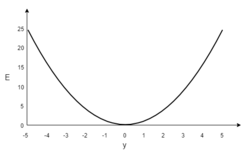
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Многослойные перцептроны
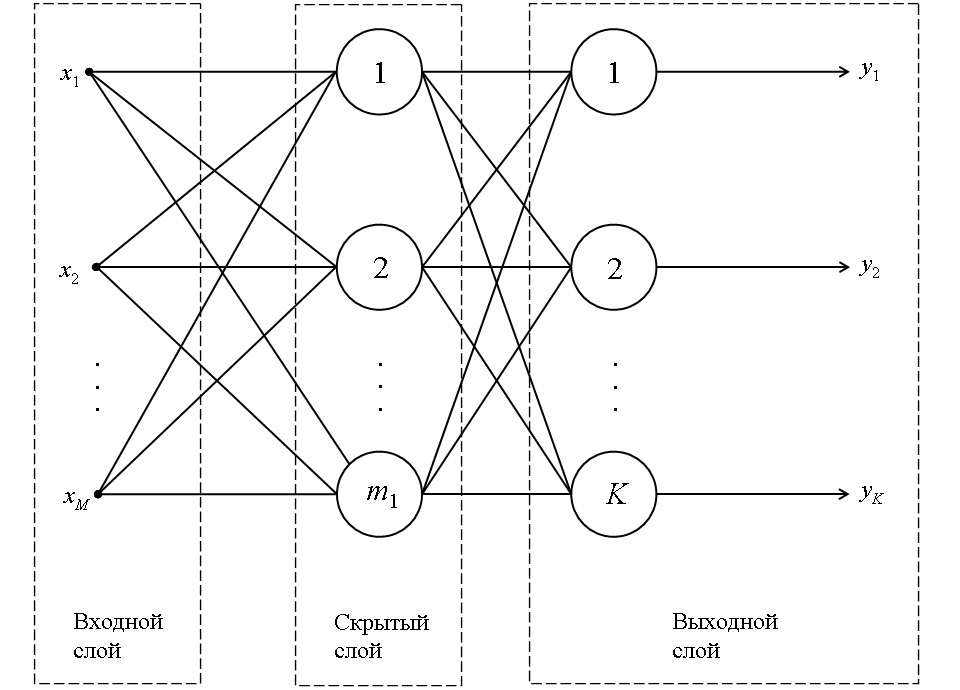
Многослойные перцептроны эффективны при решении тех же самых задач, что и однослойные перцептроны, но обладают значительно большей вычислительной способностью в сравнении с однослойными перцептронами. Благодаря этой своей способности они могут гораздо точнее описывать многомерные зависимости с большой степенью нелинейности и высоким уровнем перекрестного и группового влияния входных переменных на выходные.
Пример двухслойного перцептрона с M входами и K выходами был ранее приведен на рис. 1. При необходимости использования сетей более сложной структуры добавляются новые скрытые слои или наращивается количество нейронов в скрытых слоях.
Рис. 1. Схема двухслойной искусственной нейронной сети
Количество весовых коэффициентов, настраиваемых в процессе обучения многослойного перцептрона с L скрытыми слоями по ml нейронов в каждом, рассчитывается следующим образом:

Для каждого нейрона сети помимо синаптических связей с элементами входного вектора настраивается связь с фиктивным единичным входом (коэффициент смещения).
Для большинства задач, решаемых с помощью многослойных перцептронов, выбор структуры нейронной сети должен осуществляться на основе следующего правила («Правила 2–5»): количество настраиваемых в процессе обучения весовых коэффициентов должно быть в 2–5 раз меньше, чем количество примеров обучающей выборки. Если это соотношение меньше 2, сеть теряет способность к обобщению обучающей информации, а при достижении 1 и меньше просто запоминает ответы для каждого обучающего примера. Если же количество обучающих примеров слишком велико для выбранной структуры сети, нейросетевая модель во многих случаях просто усредняет выходные значения для различных комбинаций входных векторов, теряя способность к корректному отклику в отдельных частных случаях и повышая величину максимальной выборочной ошибки.
Кроме того, при выборе структуры многослойного перцептрона следует задавать количество нейронов в скрытом слое, предшествующем выходному слою, не меньшим, чем количество самих выходов.
Метод Уидроу–Хоффа, рассмотренный в предыдущей главе, не может быть использован для настройки весовых коэффициентов многослойных перцептронов, поскольку он позволяет сделать прямую коррекцию по величине ошибки только для нейронов выходного слоя, тогда как синаптические коэффициенты скрытых нейронов также требуют изменения.
Задача обучения многослойных перцептронов может быть сформулирована как оптимизационная, в которой целевой функцией (критерием оптимизации) является общая ошибка, рассчитанная по обучающей выборке. Соответственно, и решать данную задачу можно как любую задачу многомерной оптимизации с использованием методов детерминированного, градиентного или стохастического поиска.
Наиболее распространенный метод обучения многослойного перцептрона – метод обратного распространения ошибки. Суть данного метода заключается в том, что сигнал ошибки каждого выходного значения, рассчитанный на текущем такте обучения, распространяется по слоям в обратном направлении (от выходного к первому) с учетом тех же весовых коэффициентов, которые использовались при прямом прохождении входных сигналов по нейронной сети и расчете выходных значений.
Алгоритм метода обратного распространения ошибки включает следующие этапы.
1. Весовые коэффициенты многослойного перцептрона выбранной структуры инициализируются небольшими по абсолютной величине (не более M–1(L + 1)–1) случайными значениями, где L – количество скрытых слоев.
2. На входы нейронной сети подается входной вектор одного из примеров обучающей выборки. Производится прямое распространение сигналов по сети с расчетом значений выходных переменных
3. Для каждого рассчитанного значения выходной переменной по соотношению 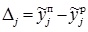

4. По полученным погрешностям рассчитываются невязки нейронов выходного слоя с учетом производных соответствующих активационных функций:

Если активационная функция имеет вид сигмоиды или функции Гаусса, следует воспользоваться соотношениями для аналитического расчета ее производной.
5. В обратной последовательности (от последнего скрытого слоя к первому) рассчитываются невязки нейронов остальных слоев с учетом связывающих слои синаптических связей:

6. Для всех слоев нейронов, кроме первого, пересчитываются значения весовых коэффициентов по следующим соотношениям:


где ν – коэффициент скорости обучения.
Для первого скрытого слоя нейронов коррекция весовых коэффициентов происходит не по выходам предыдущего слоя, а по нормализованным значениям входных переменных нейронной сети:

Для расчета коэффициентов смещения нейронов первого скрытого слоя, как и для всех других слоев, используется соотношение (3).
7. Цикл повторяется с шага 2 до выполнения одного или нескольких условий окончания:
– исчерпано заданное предельное количество эпох обучения;
– достигнут удовлетворительный уровень ошибки по всей обучающей выборке;
– не происходит уменьшения ошибки обучающей выборки на протяжении заданного предельного количества эпох обучения;
– исчерпано заданное предельное физическое время обучения.
На протяжении одной эпохи обучения последовательно или в случайном порядке предъявляются все примеры обучающей выборки, причем каждый пример должен быть предъявлен однократно.
Коэффициент скорости обучения задается положительной константой или переменной величиной (0 < v <= 1), постепенно уменьшающейся в процессе обучения нейронной сети.
Одна из особенностей метода обратного распространения ошибки заключается в том, что средние абсолютные значения невязок уменьшаются от последнего слоя нейронов к первому на порядки. Следствием этого становится практически незначительная величина изменения весовых коэффициентов первых скрытых слоев и, соответственно, требуется очень большое количество эпох обучения для значимой коррекции весов. Для устранения данного недостатка в многослойных перцептронах с более чем одним скрытым слоем можно использовать коэффициент скорости обучения, увеличивающийся от последнего скрытого слоя к первому в пределах одной эпохи обучения, в том числе, значения vl > 1./p>
Ошибки работы всей нейронной сети по обучающей и тестовой выборкам могут быть рассчитаны по соотношениям из предыдущей статьи.
Метод обратного распространения ошибки базовый для обучения многослойных перцептронов, но не единственно возможный. С одной стороны, поскольку задача обучения любых перцептронов, по сути своей, оптимизационная, с этой целью могут использоваться практически любые методы оптимизации многомерных функций. С другой стороны, оптимизируемая функция ошибки (соотношение 3) не просто многомерная, а в большинстве случаев имеет очень высокую размерность в несколько десятков или даже сотен переменных – синаптических коэффициентов, и, к тому же, может обладать очень сложным рельефом поверхности, что делает невозможным использование на практике большинства традиционных методов. В этой связи реальной заменой методов градиентного поиска, адаптированных для обучения нейронных сетей (например, метода обратного распространения ошибки или метода Левенберга–Марквардта), могут быть лишь эволюционные или многоагентные методы (генетические алгоритмы, искусственные иммунные системы и другие), относящиеся к группе методов стохастического поиска. Зачастую такие методы могут быть даже более полезны, поскольку позволяют на любой эпохе обучения оперировать значениями переменных из всей области их определения, а не останавливаются в локальных оптимумах функции ошибки как методы градиентного поиска.
Если сравнивать архитектуры многослойных и однослойных перцептронов, можно выделить несколько ее отличительных особенностей:
– для одного и того же состава входных и выходных переменных в качестве нейросетевой модели могут быть использованы многослойные перцептроны различной структуры (с различным количеством скрытых слоев и нейронов в них), тогда как при использовании однослойных перцептронов возможен лишь один вариант структуры сети;
– многослойные перцептроны позволяют получить более корректное математическое описание многосвязных функциональных зависимостей с ярко выраженной нелинейностью;
– для обучения многослойных перцептронов требуется выбор более сложного алгоритма, чем для обучения однослойных перцептронов;
– обучение многослойных перцептронов занимает большее время и требует больший объем вычислительных ресурсов компьютера.
Рассмотрим пример решения задачи классификации образов с использованием двухслойного перцептрона. Пусть дана выборка данных (табл. 1), включающая 48 примеров. Используем первые 40 примеров для обучения перцептрона, а остальные 8 (выделены курсивом) – для тестирования обученной нейронной сети.
Таблица 1
Исходная выборка данных для обучения и практического
использования двухслойного перцептрона
|
№ |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y3 |
y4 |
|---|---|---|---|---|---|---|---|---|
|
1 |
–0,12 |
0,42 |
0,52 |
0,17 |
–0,64 |
–1,89 |
0 |
1 |
|
2 |
0,97 |
0,66 |
0,47 |
0,37 |
0,39 |
0,51 |
1 |
0 |
|
3 |
–2,60 |
–1,08 |
–0,24 |
–0,10 |
–0,65 |
–1,90 |
0 |
1 |
|
4 |
–1,45 |
–0,61 |
–0,41 |
–0,86 |
–1,96 |
–3,70 |
0 |
1 |
|
5 |
0,55 |
0,97 |
1,11 |
0,97 |
0,55 |
–0,15 |
0 |
1 |
|
6 |
0,54 |
0,53 |
0,57 |
0,64 |
0,75 |
0,90 |
1 |
0 |
|
7 |
0,93 |
0,93 |
1,11 |
1,47 |
2,00 |
2,72 |
1 |
0 |
|
8 |
–4,07 |
–2,36 |
–1,46 |
–1,36 |
–2,06 |
–3,56 |
0 |
1 |
|
9 |
3,66 |
2,25 |
1,73 |
2,08 |
3,31 |
5,42 |
1 |
0 |
|
10 |
4,87 |
2,25 |
0,29 |
–1,02 |
–1,67 |
–1,67 |
1 |
0 |
|
11 |
0,82 |
0,79 |
0,76 |
0,75 |
0,74 |
0,75 |
1 |
0 |
|
12 |
4,29 |
2,19 |
0,62 |
–0,41 |
–0,91 |
–0,88 |
1 |
0 |
|
13 |
–1,06 |
0,91 |
1,89 |
1,86 |
0,83 |
–1,20 |
0 |
1 |
|
14 |
–1,11 |
–0,49 |
–0,46 |
–1,03 |
–2,20 |
–3,97 |
0 |
1 |
|
15 |
0,71 |
–0,31 |
–0,85 |
–0,92 |
–0,51 |
0,37 |
1 |
0 |
|
16 |
–0,93 |
–0,63 |
–0,43 |
–0,35 |
–0,36 |
–0,48 |
0 |
1 |
|
17 |
–4,78 |
–2,71 |
–1,26 |
–0,46 |
–0,29 |
–0,75 |
0 |
1 |
|
18 |
–0,42 |
–0,41 |
–1,16 |
–2,67 |
–4,94 |
–7,97 |
0 |
1 |
|
№ |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y3 |
y4 |
|---|---|---|---|---|---|---|---|---|
|
19 |
3,25 |
2,21 |
1,60 |
1,42 |
1,67 |
2,35 |
1 |
0 |
|
20 |
–2,07 |
–1,40 |
–0,95 |
–0,72 |
–0,71 |
–0,92 |
0 |
1 |
|
21 |
4,35 |
1,59 |
–0,26 |
–1,20 |
–1,22 |
–0,32 |
1 |
0 |
|
22 |
0,68 |
0,13 |
0,04 |
0,42 |
1,27 |
2,58 |
1 |
0 |
|
23 |
–1,63 |
–1,58 |
–2,42 |
–4,16 |
–6,79 |
–10,31 |
0 |
1 |
|
24 |
0,97 |
0,42 |
0,07 |
–0,09 |
–0,05 |
0,18 |
1 |
0 |
|
25 |
–0,38 |
–0,47 |
–0,12 |
0,65 |
1,85 |
3,48 |
1 |
0 |
|
26 |
–2,19 |
–1,51 |
–1,44 |
–2,00 |
–3,16 |
–4,95 |
0 |
1 |
|
27 |
–1,16 |
–1,12 |
–1,16 |
–1,29 |
–1,49 |
–1,77 |
0 |
1 |
|
28 |
–0,80 |
–0,31 |
0,02 |
0,19 |
0,20 |
0,05 |
0 |
1 |
|
29 |
–1,97 |
–0,74 |
–0,04 |
0,13 |
–0,22 |
–1,10 |
0 |
1 |
|
30 |
1,67 |
1,86 |
1,74 |
1,31 |
0,58 |
–0,46 |
0 |
1 |
|
31 |
7,55 |
4,56 |
2,35 |
0,93 |
0,30 |
0,46 |
1 |
0 |
|
32 |
–0,79 |
–0,70 |
–0,69 |
–0,77 |
–0,93 |
–1,17 |
0 |
1 |
|
33 |
4,14 |
1,60 |
–0,24 |
–1,38 |
–1,83 |
–1,58 |
1 |
0 |
|
34 |
–0,91 |
–1,69 |
–1,64 |
–0,75 |
0,97 |
3,52 |
1 |
0 |
|
35 |
–4,79 |
–2,04 |
–0,08 |
1,09 |
1,48 |
1,07 |
0 |
1 |
|
36 |
–3,02 |
–2,26 |
–1,75 |
–1,51 |
–1,51 |
–1,77 |
0 |
1 |
|
37 |
4,36 |
2,67 |
1,82 |
1,82 |
2,66 |
4,35 |
1 |
0 |
|
38 |
2,23 |
1,91 |
2,14 |
2,92 |
4,25 |
6,13 |
1 |
0 |
|
39 |
2,47 |
0,50 |
–0,56 |
–0,70 |
0,06 |
1,73 |
1 |
0 |
|
40 |
0,36 |
–0,39 |
–0,59 |
–0,25 |
0,63 |
2,05 |
1 |
0 |
|
41 |
–2,04 |
–0,29 |
0,53 |
0,42 |
–0,61 |
–2,57 |
0 |
1 |
|
42 |
0,00 |
0,16 |
–0,13 |
–0,88 |
–2,09 |
–3,76 |
0 |
1 |
|
43 |
–2,75 |
–1,95 |
–1,40 |
–1,08 |
–0,99 |
–1,15 |
0 |
1 |
|
44 |
0,64 |
0,17 |
–0,03 |
0,04 |
0,37 |
0,97 |
1 |
0 |
|
45 |
–0,78 |
–1,06 |
–0,87 |
–0,22 |
0,89 |
2,48 |
1 |
0 |
|
46 |
–0,90 |
–1,00 |
–0,98 |
–0,82 |
–0,54 |
–0,13 |
1 |
0 |
|
47 |
0,33 |
1,14 |
1,60 |
1,71 |
1,46 |
0,86 |
0 |
1 |
|
48 |
2,20 |
1,84 |
1,98 |
2,62 |
3,75 |
5,37 |
1 |
0 |
|
Мин. зн. |
–4,79 |
–2,71 |
–2,42 |
–4,16 |
–6,79 |
–10,31 |
0 |
0 |
|
Макс. зн. |
7,55 |
4,56 |
2,35 |
2,92 |
4,25 |
6,13 |
1 |
1 |
Требуется разработать нейросетевую модель на основе двухслойного перцептрона, позволяющую классифицировать тип оптимума некоторой функции (минимум или максимум) по последовательно взятым 6 значениям этой функции на произвольном интервале в произвольных точках.
Соответственно, рассматриваемая нейронная сеть должна иметь 6 входных переменных, кодирующих входную последовательность значений функции, и 2 выходные переменные, позволяющие идентифицировать класс оптимума (y3 – минимум, y4 – максимум): единица указывает на принадлежность классу, 0 – на ее отсутствие. При использовании «Правила 2–5» двухслойный перцептрон с указанным количеством входов и выходов, обучающийся на 40 примерах, может содержать один или два скрытых нейрона. Рассмотрим процедуру обучения нейронной сети с двумя нейронами в скрытом слое (рис. 2).
Рис. 2. Структура двухслойного перцептрона для решения задачи
классификации типа оптимального значения
Выполним линейную нормализацию входных и выходных данных исходной выборки в пределах [0, 1] с использованием соотношения 3 статьи «Способы нормализации переменных». Нормализованные значения, используемые далее для обучения и тестирования двухслойного перцептрона, представлены в табл. 2. Курсивом, как и раньше, выделены тестовые примеры.
Рис. 3. Примеры функций активации типа гистерезиса
Выходные значения в обучающей выборке имеют бинарную форму, поэтому в качестве активационной функции выходных нейронов может выступать как функция единичного скачка (рис. 3, а, б), так и сигмоидная логистическая функция (рис. 3, д) с достаточно большой величиной параметра α, приближающей ее к скачкообразной форме, как показано на рисунке из статьи «Способы нормализации переменных».
Таблица 2
Нормализованная исходная выборка данных для обучения
и практического использования двухслойного перцептрона
|
№ |
||||||||
|---|---|---|---|---|---|---|---|---|
|
1 |
0,378 |
0,431 |
0,616 |
0,612 |
0,557 |
0,512 |
0 |
1 |
|
2 |
0,467 |
0,464 |
0,606 |
0,640 |
0,650 |
0,658 |
1 |
0 |
|
3 |
0,177 |
0,224 |
0,457 |
0,573 |
0,556 |
0,512 |
0 |
1 |
|
4 |
0,271 |
0,289 |
0,421 |
0,466 |
0,438 |
0,402 |
0 |
1 |
|
5 |
0,433 |
0,506 |
0,740 |
0,725 |
0,665 |
0,618 |
0 |
1 |
|
6 |
0,432 |
0,446 |
0,627 |
0,678 |
0,683 |
0,682 |
1 |
0 |
|
7 |
0,464 |
0,501 |
0,740 |
0,795 |
0,796 |
0,793 |
1 |
0 |
|
8 |
0,058 |
0,048 |
0,201 |
0,395 |
0,428 |
0,411 |
0 |
1 |
|
9 |
0,685 |
0,682 |
0,870 |
0,881 |
0,915 |
0,957 |
1 |
0 |
|
10 |
0,783 |
0,682 |
0,568 |
0,444 |
0,464 |
0,526 |
1 |
0 |
|
11 |
0,455 |
0,481 |
0,667 |
0,694 |
0,682 |
0,673 |
1 |
0 |
|
12 |
0,736 |
0,674 |
0,637 |
0,530 |
0,533 |
0,574 |
1 |
0 |
|
13 |
0,302 |
0,498 |
0,904 |
0,850 |
0,690 |
0,554 |
0 |
1 |
|
14 |
0,298 |
0,305 |
0,411 |
0,442 |
0,416 |
0,386 |
0 |
1 |
|
15 |
0,446 |
0,330 |
0,329 |
0,458 |
0,569 |
0,650 |
1 |
0 |
|
16 |
0,313 |
0,286 |
0,417 |
0,538 |
0,582 |
0,598 |
0 |
1 |
|
17 |
0,001 |
0,000 |
0,243 |
0,523 |
0,589 |
0,582 |
0 |
1 |
|
18 |
0,354 |
0,316 |
0,264 |
0,210 |
0,168 |
0,142 |
0 |
1 |
|
19 |
0,652 |
0,677 |
0,843 |
0,788 |
0,766 |
0,770 |
1 |
0 |
|
20 |
0,220 |
0,180 |
0,308 |
0,486 |
0,551 |
0,571 |
0 |
1 |
|
21 |
0,741 |
0,591 |
0,453 |
0,418 |
0,505 |
0,608 |
1 |
0 |
|
22 |
0,443 |
0,391 |
0,516 |
0,647 |
0,730 |
0,784 |
1 |
0 |
|
23 |
0,256 |
0,155 |
0,000 |
0,000 |
0,000 |
0,000 |
0 |
1 |
|
24 |
0,467 |
0,431 |
0,522 |
0,575 |
0,611 |
0,638 |
1 |
0 |
|
25 |
0,357 |
0,308 |
0,482 |
0,679 |
0,783 |
0,839 |
1 |
0 |
|
26 |
0,211 |
0,165 |
0,205 |
0,305 |
0,329 |
0,326 |
0 |
1 |
|
27 |
0,294 |
0,219 |
0,264 |
0,405 |
0,480 |
0,519 |
0 |
1 |
|
28 |
0,323 |
0,330 |
0,512 |
0,614 |
0,633 |
0,630 |
0 |
1 |
|
29 |
0,229 |
0,271 |
0,499 |
0,606 |
0,595 |
0,560 |
0 |
1 |
|
30 |
0,524 |
0,629 |
0,872 |
0,773 |
0,668 |
0,599 |
0 |
1 |
|
31 |
1,000 |
1,000 |
1,000 |
0,719 |
0,642 |
0,655 |
1 |
0 |
|
32 |
0,324 |
0,276 |
0,363 |
0,479 |
0,531 |
0,556 |
0 |
1 |
|
33 |
0,724 |
0,593 |
0,457 |
0,393 |
0,449 |
0,531 |
1 |
0 |
|
34 |
0,314 |
0,140 |
0,164 |
0,482 |
0,703 |
0,841 |
1 |
0 |
|
35 |
0,000 |
0,092 |
0,491 |
0,742 |
0,749 |
0,692 |
0 |
1 |
|
36 |
0,143 |
0,062 |
0,140 |
0,374 |
0,478 |
0,519 |
0 |
1 |
|
37 |
0,741 |
0,740 |
0,889 |
0,845 |
0,856 |
0,892 |
1 |
0 |
|
38 |
0,569 |
0,635 |
0,956 |
1,000 |
1,000 |
1,000 |
1 |
0 |
|
39 |
0,588 |
0,442 |
0,390 |
0,489 |
0,620 |
0,732 |
1 |
0 |
|
40 |
0,417 |
0,319 |
0,384 |
0,552 |
0,672 |
0,752 |
1 |
0 |
|
41 |
0,223 |
0,333 |
0,618 |
0,647 |
0,560 |
0,471 |
0 |
1 |
|
42 |
0,388 |
0,395 |
0,480 |
0,463 |
0,426 |
0,398 |
0 |
1 |
|
43 |
0,165 |
0,105 |
0,214 |
0,435 |
0,525 |
0,557 |
0 |
1 |
|
44 |
0,440 |
0,396 |
0,501 |
0,593 |
0,649 |
0,686 |
1 |
0 |
|
45 |
0,325 |
0,227 |
0,325 |
0,556 |
0,696 |
0,778 |
1 |
0 |
|
46 |
0,315 |
0,235 |
0,302 |
0,472 |
0,566 |
0,619 |
1 |
0 |
|
47 |
0,415 |
0,530 |
0,843 |
0,829 |
0,747 |
0,679 |
0 |
1 |
|
48 |
0,566 |
0,626 |
0,922 |
0,958 |
0,955 |
0,954 |
1 |
0 |
Для обучения двухслойного перцептрона выберем метод обратного распространения ошибки, требующий дифференцируемость активационных функций для всей области определения. Следовательно, остановим выбор активационной функции для всех нейронов, включая скрытый, на сигмоидной логистической функции с α = 2,0, а получаемый аналоговый результат расчета по нейронной сети будем округлять для корректного решения задачи классификации. Коэффициент скорости обучения примем равным 0,5.
В соответствии с алгоритмом метода обратного распространения ошибки зададимся следующими начальными значениями весовых коэффициентов:w01 = 0,03, w11 = –0,08, w21 = –0,06 w31 = 0,02, w41 = 0,02, w51 = –0,08, w61 = –0,07, w02 = 0,02, w12 = –0,05, w22 = –0,01, w32 = 0,05, w42 = –0,04, w52 = –0,01, w62 = 0,01, w03 = 0,04, w13 = 0,01, w23 = 0,04, w04 = 0,07, w14 = 0,02, w24 = 0,01.
Предъявим сети элементы нормализованного входного вектора первого обучающего примера из табл. 2. Расчет состояний и выходных значений нейронов производится с использованием выражений 

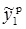
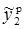


С использованием выражения (8.1) получим погрешности выходных значений: Δ3 = –0,532, Δ4 = 0,458.
Зная выходы всех нейронов, вычислим производные активационной функции в точках, соответствующих состояниям каждого нейрона по соотношению 
Таблица 3
Изменение весовых коэффициентов двухслойного перцептрона
|
№ |
w01 |
w11 |
w21 |
w31 |
w41 |
w51 |
w61 |
w02 |
w12 |
w22 |
w32 |
w42 |
w52 |
w62 |
w03 |
w13 |
w23 |
w04 |
w14 |
w24 |
|
1 |
0,030 |
-0,080 |
-0,060 |
0,020 |
0,020 |
-0,080 |
-0,070 |
0,018 |
-0,051 |
-0,011 |
0,049 |
-0,041 |
-0,011 |
0,009 |
-0,093 |
-0,056 |
-0,026 |
0,184 |
0,076 |
0,067 |
|
2 |
0,021 |
-0,084 |
-0,064 |
0,015 |
0,014 |
-0,086 |
-0,076 |
0,011 |
-0,054 |
-0,014 |
0,045 |
-0,046 |
-0,016 |
0,005 |
0,046 |
0,013 |
0,043 |
0,037 |
0,004 |
-0,006 |
|
3 |
0,021 |
-0,084 |
-0,064 |
0,014 |
0,014 |
-0,086 |
-0,076 |
0,008 |
-0,054 |
-0,015 |
0,043 |
-0,047 |
-0,017 |
0,003 |
-0,087 |
-0,053 |
-0,024 |
0,158 |
0,064 |
0,054 |
|
4 |
0,026 |
-0,083 |
-0,063 |
0,017 |
0,017 |
-0,084 |
-0,074 |
0,012 |
-0,053 |
-0,014 |
0,045 |
-0,046 |
-0,016 |
0,004 |
-0,195 |
-0,107 |
-0,078 |
0,252 |
0,111 |
0,101 |
|
5 |
0,035 |
-0,079 |
-0,058 |
0,023 |
0,023 |
-0,078 |
-0,069 |
0,019 |
-0,050 |
-0,010 |
0,050 |
-0,041 |
-0,011 |
0,009 |
-0,279 |
-0,149 |
-0,120 |
0,326 |
0,147 |
0,138 |
|
6 |
0,013 |
-0,088 |
-0,068 |
0,010 |
0,008 |
-0,093 |
-0,083 |
0,000 |
-0,059 |
-0,019 |
0,038 |
-0,053 |
-0,024 |
-0,004 |
-0,132 |
-0,076 |
-0,046 |
0,180 |
0,075 |
0,065 |
|
7 |
0,003 |
-0,093 |
-0,073 |
0,002 |
0,000 |
-0,101 |
-0,092 |
-0,008 |
-0,062 |
-0,022 |
0,032 |
-0,060 |
-0,030 |
-0,010 |
0,011 |
-0,007 |
0,025 |
0,034 |
0,004 |
-0,008 |
|
8 |
0,004 |
-0,093 |
-0,073 |
0,002 |
0,000 |
-0,101 |
-0,091 |
-0,010 |
-0,062 |
-0,023 |
0,032 |
-0,061 |
-0,031 |
-0,011 |
-0,116 |
-0,070 |
-0,038 |
0,155 |
0,064 |
0,053 |
|
9 |
-0,005 |
-0,099 |
-0,079 |
-0,006 |
-0,008 |
-0,109 |
-0,100 |
-0,017 |
-0,067 |
-0,027 |
0,026 |
-0,066 |
-0,037 |
-0,017 |
0,025 |
-0,005 |
0,031 |
0,011 |
-0,002 |
-0,018 |
|
10 |
-0,005 |
-0,099 |
-0,079 |
-0,006 |
-0,008 |
-0,109 |
-0,100 |
-0,014 |
-0,064 |
-0,025 |
0,028 |
-0,065 |
-0,036 |
-0,016 |
0,145 |
0,052 |
0,090 |
-0,114 |
-0,061 |
-0,080 |
|
11 |
0,000 |
-0,097 |
-0,077 |
-0,002 |
-0,004 |
-0,105 |
-0,096 |
-0,005 |
-0,061 |
-0,021 |
0,033 |
-0,059 |
-0,030 |
-0,010 |
0,241 |
0,097 |
0,137 |
-0,215 |
-0,108 |
-0,129 |
|
12 |
0,007 |
-0,091 |
-0,072 |
0,002 |
0,000 |
-0,101 |
-0,092 |
0,005 |
-0,053 |
-0,014 |
0,040 |
-0,054 |
-0,025 |
-0,005 |
0,316 |
0,132 |
0,174 |
-0,294 |
-0,146 |
-0,168 |
|
13 |
-0,012 |
-0,097 |
-0,081 |
-0,015 |
-0,017 |
-0,115 |
-0,103 |
-0,020 |
-0,061 |
-0,027 |
0,017 |
-0,075 |
-0,042 |
-0,018 |
0,170 |
0,062 |
0,102 |
-0,147 |
-0,075 |
-0,095 |
|
14 |
-0,022 |
-0,100 |
-0,084 |
-0,019 |
-0,021 |
-0,119 |
-0,107 |
-0,034 |
-0,065 |
-0,031 |
0,011 |
-0,081 |
-0,048 |
-0,024 |
0,024 |
-0,009 |
0,029 |
-0,002 |
-0,004 |
-0,023 |
|
15 |
-0,022 |
-0,100 |
-0,085 |
-0,019 |
-0,021 |
-0,119 |
-0,107 |
-0,031 |
-0,064 |
-0,030 |
0,012 |
-0,080 |
-0,046 |
-0,022 |
0,145 |
0,048 |
0,088 |
-0,125 |
-0,062 |
-0,084 |
|
16 |
-0,030 |
-0,103 |
-0,087 |
-0,023 |
-0,025 |
-0,123 |
-0,111 |
-0,043 |
-0,067 |
-0,033 |
0,007 |
-0,086 |
-0,053 |
-0,029 |
0,001 |
-0,021 |
0,018 |
0,018 |
0,006 |
-0,013 |
|
17 |
-0,028 |
-0,103 |
-0,087 |
-0,022 |
-0,024 |
-0,122 |
-0,110 |
-0,045 |
-0,067 |
-0,033 |
0,007 |
-0,087 |
-0,054 |
-0,030 |
-0,124 |
-0,081 |
-0,044 |
0,141 |
0,065 |
0,047 |
|
18 |
-0,021 |
-0,100 |
-0,084 |
-0,020 |
-0,023 |
-0,121 |
-0,109 |
-0,041 |
-0,066 |
-0,032 |
0,008 |
-0,086 |
-0,053 |
-0,030 |
-0,224 |
-0,130 |
-0,093 |
0,239 |
0,113 |
0,095 |
|
19 |
-0,037 |
-0,111 |
-0,095 |
-0,034 |
-0,035 |
-0,133 |
-0,122 |
-0,054 |
-0,074 |
-0,041 |
-0,003 |
-0,097 |
-0,064 |
-0,040 |
-0,076 |
-0,065 |
-0,023 |
0,091 |
0,048 |
0,025 |
|
20 |
-0,031 |
-0,109 |
-0,094 |
-0,032 |
-0,033 |
-0,130 |
-0,118 |
-0,052 |
-0,074 |
-0,040 |
-0,002 |
-0,096 |
-0,062 |
-0,038 |
-0,186 |
-0,116 |
-0,076 |
0,199 |
0,099 |
0,078 |
|
21 |
-0,045 |
-0,120 |
-0,102 |
-0,038 |
-0,039 |
-0,137 |
-0,127 |
-0,062 |
-0,082 |
-0,047 |
-0,007 |
-0,100 |
-0,068 |
-0,045 |
-0,040 |
-0,051 |
-0,006 |
0,053 |
0,033 |
0,008 |
|
22 |
-0,050 |
-0,122 |
-0,104 |
-0,041 |
-0,042 |
-0,141 |
-0,131 |
-0,063 |
-0,082 |
-0,047 |
-0,008 |
-0,101 |
-0,068 |
-0,045 |
0,092 |
0,006 |
0,055 |
-0,080 |
-0,024 |
-0,054 |
|
23 |
-0,052 |
-0,122 |
-0,105 |
-0,041 |
-0,042 |
-0,141 |
-0,131 |
-0,071 |
-0,084 |
-0,048 |
-0,008 |
-0,101 |
-0,068 |
-0,045 |
-0,046 |
-0,062 |
-0,013 |
0,058 |
0,044 |
0,014 |
|
24 |
-0,058 |
-0,125 |
-0,107 |
-0,044 |
-0,045 |
-0,145 |
-0,135 |
-0,072 |
-0,085 |
-0,049 |
-0,008 |
-0,102 |
-0,069 |
-0,047 |
0,087 |
-0,004 |
0,049 |
-0,076 |
-0,015 |
-0,048 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
Итог |
5,133 |
-6,131 |
-1,962 |
3,254 |
2,118 |
-2,005 |
-5,730 |
4,251 |
-5,088 |
-1,598 |
2,685 |
1,606 |
-1,733 |
-4,832 |
1,886 |
-2,721 |
-2,494 |
-1,886 |
2,712 |
2,506 |
По погрешностям и производным активационной функции нейронов выходного слоя рассчитаем их невязки по соотношению (1): δ3 = –0,265, δ4 = 0,227, а с учетом этих значений по соотношению (2) – невязки скрытых нейронов: δ1 = 0,0009, δ2 = –0,0042.
Зная все невязки, выполним коррекцию весовых коэффициентов выходных нейронов по соотношениям (3) и (4) и скрытых нейронов по соотношениям (3) и (5). Новые значения весов записаны в первой строке данных в табл. 3.
В целом, в табл. 3 показано изменение весовых коэффициентов в ходе их коррекции при последовательном предъявлении 24 обучающих примеров первой эпохи обучения. В последней строке показаны значения весовых коэффициентов по окончании 100-й эпохи обучения.
Для обученной нейронной сети проведено тестирование на обучающей и тестовой выборках. Из 40 примеров обучающей выборки правильно оказались распознаны 38 примеров, что соответствует 95 % случаев верной классификации. Ошибки классификации выявлены для примеров №№ 6 и 11. Анализ входных векторов этих примеров показывает, что оптимальное значение в них выражено крайне слабо (отличается на 0,01 от одной из соседних точек) и находится близко к левой или правой границам. Учитывая эти особенности примеров с ошибками, а также ограниченный объем использованной выборки и простоту структуры двухслойного перцептрона, следует признать полученный результат тестирования очень хорошим.
Для тестовой выборки получены правильные результаты классификации в 7 случаях из 8 (табл. 4), что составляет 87,5 %.
Таблица 4
Результаты классификации тестовых примеров
|
№ |
Корректность |
||||
|
41 |
0 |
1 |
0 |
1 |
+ |
|
42 |
0 |
1 |
0 |
1 |
+ |
|
43 |
0 |
1 |
0 |
1 |
+ |
|
44 |
1 |
0 |
1 |
0 |
+ |
|
45 |
1 |
0 |
1 |
0 |
+ |
|
46 |
1 |
0 |
0 |
1 |
– |
|
47 |
0 |
1 |
0 |
1 |
+ |
|
48 |
1 |
0 |
1 |
0 |
+ |
Единственная ошибка для примера № 46 не может объясняться теми же причинами, что для ошибок обучающей выборки. В данном случае очевидная причина – отсутствие примеров с близким характером и диапазоном изменения значений входных переменных в обучающей выборке. Будь обучающая выборка более объемной, этой ошибки, скорее всего, удалось бы избежать.
Если у вас есть статья, заметка или обзор, которыми вы хотите поделиться с аудиторией нашего сайта, присылайте информацию на: neuronus.com@yandex.ru.
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1
vdots
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)
vdots
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$begin{multline*}
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\[0.1cm]
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
end{multline*},$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$begin{multline*}
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
end{multline*}$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$ begin{multline*}
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
end{multline*} $$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
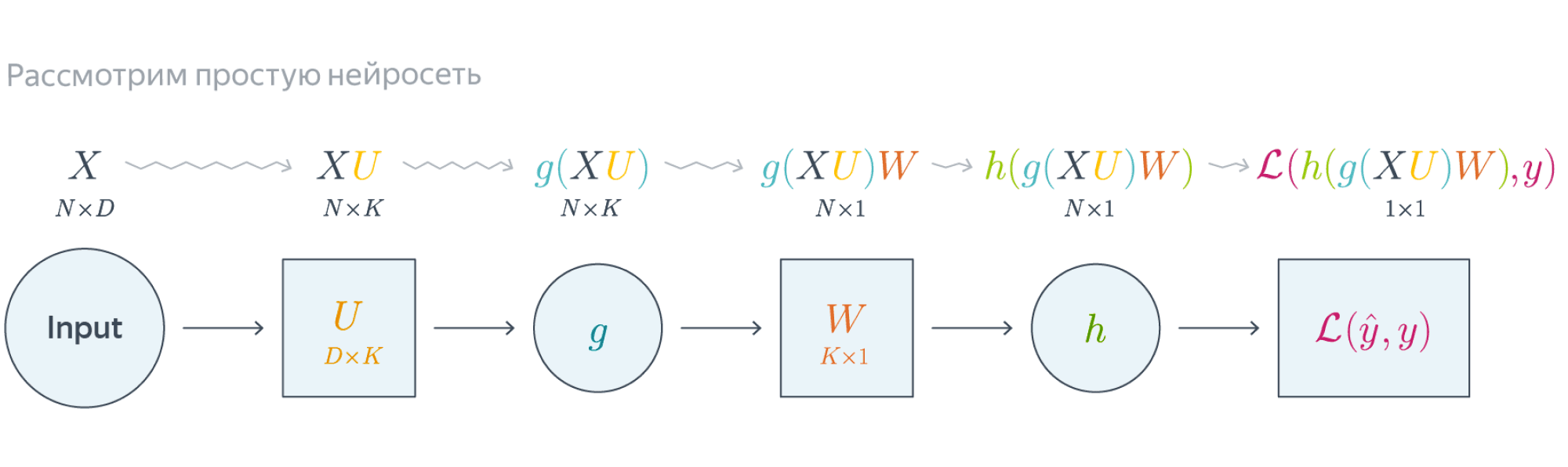
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Формулы обучения и обратное распространение для многослойных перцептронов
Добавлено 8 января 2020 в 18:22
В данной статье представлены формулы, которые мы используем при выполнении вычислений для обновления весовых коэффициентов, а также мы обсудим концепцию обратного распространения.
Добро пожаловать в серию статей по машинному обучению. С остальными статьями серии вы можете ознакомиться в меню с содержанием в начале статьи.
Мы достигли того момента, когда нам нужно тщательно рассмотреть фундаментальную тему теории нейронных сетей: вычислительную процедуру, которая позволяет нам точно настроить веса многослойного перцептрона (MLP, multilayer perceptron), чтобы он мог точно классифицировать входные выборки. Это приведет нас к концепции «обратного распространения», которая также является важным аспектом проектирования нейронных сетей.
Обновление весов
Информационная среда обучения для MLP сложна. Что еще хуже, онлайн-ресурсы используют различную терминологию и обозначения, и, похоже, они даже дают разные результаты. Однако я не уверен, что результаты действительно разные или просто представляют одну и ту же информацию по-разному.
Формулы, содержащиеся в этой статье, основаны на выводах и объяснениях, предоставленных доктором Дастином Стэнсбери в этом посте в блоге. Его объяснение – лучшее, что я нашел, и это отличное место для начала, если вы хотите углубиться в математические и базовые детали градиентного спуска и обратного распространения.
Следующая диаграмма представляет архитектуру, которую мы реализуем в программном обеспечении, и приведенные ниже формулы соответствуют этой архитектуре, которая более подробно обсуждается в следующей статье.
Терминология
Эта тема быстро станет неуправляемой, если мы не будем придерживаться четкой терминологии. Я буду использовать следующие термины:
- Преактивация (сокращенно (S_{preA})): Это относится к сигналу (на самом деле это просто число в контексте одной обучающей итерации), который служит входным для функции активации узла. Он рассчитывается путем выполнения скалярного произведения массива, содержащего веса, и массива, содержащего значения, исходящие из узлов в предыдущем слое. Скалярное произведение эквивалентно выполнению поэлементного умножения двух массивов и затем суммированию элементов массив, полученного в результате этого умножения.
- Постактивация (сокращенно (S_{postA})): Это относится к сигналу (опять же, просто число в контексте отдельной итерации), который выходит из узла. Он создается путем применения функции активации к сигналу преактивации. Я предпочитаю обозначение функции активации (f_{A}()), это логистическая сигмоидная функция.
- В коде на Python вы увидите весовые матрицы, помеченные как ItoH и HtoO. Я использую эти идентификаторы, потому что фраза «веса скрытого слоя» будет неоднозначной – это будут веса, которые применяются до или после скрытого слоя? В моей схеме ItoH указывает веса, которые применяются к значениям, передаваемым из входных узлов в скрытые узлы (ItoH – Input toHidden), а HtoO определяет веса, которые применяются к значениям, передаваемым из скрытых узлов в выходной узел (HtoO – Hidden toOutput).
- Правильное выходное значение для обучающей выборки называется целью и обозначается буквой T (Target).
- Скорость обучения сокращенно обозначается как LR (Learning Rate).
- Конечная ошибка (FE – Final Error) – это разница между сигналом постактивации от выходного узла ((S_{postA,O})) и целью, рассчитывается как (FE = S_{postA,O}-T).
- Сигнал ошибки ((S_{ошибки})) – это последняя ошибка, распространяемая обратно к скрытому слою через функцию активации выходного узла.
- Градиент представляет вклад заданного веса в сигнал ошибки. Мы изменяем веса, вычитая этот вклад (умноженный на скорость обучения, если необходимо).
Некоторые из этих терминов показаны на следующей диаграмме конфигурации нейросети. Я знаю, это выглядит как разноцветный бардак. Приношу извинения. Это насыщенная информацией диаграмма, и, если вы внимательно ее изучите, я думаю, что вы найдете ее очень полезной.
Формулы обновления весовых коэффициентов получаются путем взятия частной производной функции ошибки (мы используем среднюю квадратичную ошибку) относительно веса, который необходимо изменить. Если вы хотите посмотреть математику, обратитесь к посту доктора Стэнсбери; в данной статье мы перейдем непосредственно к результатам. Для весов от скрытых узлов к выходным узлам (HtoO) мы имеем следующее:
[S_{ошибки} = FE times {f_A}'(S_{preA,O})]
[градиент_{HtoO}= S_{ошибки}times S_{postA,H}]
[вес_{HtoO} = вес_{HtoO}- (LR times градиент_{HtoO})]
Мы рассчитываем сигнал ошибки путем умножения конечной ошибки на значение, которое получается, когда мы берем производную функции активации по сигналу преактивации, доставляемому на выходной узел (обратите внимание на штрих, который означает первую производную, в ({f_A}'(S_{preA,O}))). Затем вычисляется градиент путем умножения сигнала ошибки на сигнал постактивации из скрытого слоя. Наконец, мы обновляем вес, вычитая этот градиент из текущего значения веса, и, если мы хотим изменить размер шага, то можем умножить градиент на скорость обучения.
Для весов от входных узлов к скрытым узлам (ItoH) мы имеем следующее:
[градиент_{ItoH} = FE times {f_A}'(S_{preA,O})times вес_{HtoO} times {f_A}'(S_{preA,H}) times вход]
[Rightarrow градиент_{ItoH} = S_{ошибки} times вес_{HtoO} times {f_A}'(S_{preA,H})times вход]
[вес_{ItoH} = вес_{ItoH} — (LR times градиент_{ItoH})]
Для весов от входных узлов к скрытым узлам ошибка должна распространяться обратно через дополнительный слой, и мы делаем это путем умножения сигнала ошибки на вес между скрытым и выходным узлами, соединенный с интересующим скрытым узлом. Таким образом, если мы обновляем вес между входным и скрытым узлами, который ведет к первому скрытому узлу, мы умножаем сигнал ошибки на вес, который соединяет первый скрытый узел с выходным узлом. Затем мы завершаем вычисление, выполняя умножения, аналогичные умножениям обновления весов между скрытыми и выходными узлами: мы берем производную функции активации по сигналу преактивации скрытого узла, а «входное» значение можно рассматривать как сигнал постактивации от входного узла.
Обратное распространение
Приведенное выше объяснение уже коснулось концепции обратного распространения. Я просто хочу кратко подкрепить эту концепцию, а также убедиться, что вы точно познакомились с этим термином, часто появляющимся в обсуждениях нейронных сетей.
Обратное распространение позволяет нам преодолеть дилемму скрытого узла, упоминаемую в восьмой статье. Нам необходимо обновить веса между входными и скрытыми узлами на основе разницы между сгенерированным выходным сигналом нейросети и целевыми выходными значениями, предоставленными обучающими данными, но эти веса влияют на сгенерированное выходное значение косвенно.
Обратное распространение относится к способу, с помощью которого мы отправляем сигнал ошибки обратно к одному или нескольким скрытым слоям и масштабируем этот сигнал ошибки, используя как веса, идущие из скрытого узла, так и производную функции активации скрытого узла. Итоговая процедура служит способом обновления веса на основе вклада этого веса в выходную ошибку, даже если этот вклад скрыт косвенной связью между весом между входным и скрытым узлами и сгенерированным выходным значением.
Заключение
Мы рассмотрели много важных материалов. Я думаю, что в этой статье у нас есть действительно ценная информация об обучении нейронным сетям, и надеюсь, что вы согласны. Серия станет еще более интересной, поэтому следите за обновлениями.
Теги
MLP, Multilayer Perceptron / Многослойный перцептронИскусственный интеллект, ИИ / Artificial Intelligence, AIМашинное обучение / Machine LearningНейросеть / Нейронная сетьПерцептрон / PerceptronСкорость обучения
Аннотация: В лекции рассматривается архитектура многослойного обобщенного персептрона, описывается процедура обратного распространения — алгоритм обучения многослойного персептрона с учителем.
Введение в процедуру обратного распространения
Среди различных структур нейронных сетей (НС) одной из наиболее
известных является многослойная структура, в которой каждый нейрон
произвольного
слоя связан со всеми аксонами нейронов предыдущего слоя или,
в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными.
Когда в сети только один слой, алгоритм ее обучения с учителем
довольно очевиден, так как правильные выходные состояния нейронов единственного
слоя заведомо известны и подстройка синаптических связей идет в
направлении, минимизирующем ошибку на выходе сети. По этому принципу
строится, например, алгоритм обучения однослойного персептрона. В многослойных
же сетях оптимальные выходные значения нейронов всех слоев,
кроме последнего, как правило, не известны, и двух- или более слойный
персептрон
уже невозможно обучить, руководствуясь только величинами ошибок на выходах
НС.
Один из вариантов решения этой проблемы — разработка наборов выходных
сигналов, соответствующих входным, для каждого слоя НС, что, конечно,
является очень трудоемкой операцией и не всегда осуществимо. Второй
вариант — динамическая подстройка весовых коэффициентов синапсов,
в ходе которой выбираются, как правило, наиболее слабые связи и изменяются
на малую величину в ту или иную сторону, а сохраняются только те изменения,
которые повлекли уменьшение ошибки на выходе всей сети. Очевидно,
что данный «метод тыка», несмотря на свою кажущуюся простоту,
требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый
вариант — распространение сигналов ошибки от выходов НС к ее
входам, в направлении, обратном прямому распространению сигналов в
обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения.
Разработка алгоритма обратного распространения сыграла
важную роль в возрождении интереса к искусственным нейронным сетям.
Обратное распространение — это систематический метод для обучения
многослойных искусственных нейронных сетей. Он имеет солидное математическое
обоснование. Несмотря на некоторые ограничения, процедура обратного
распространения сильно расширила область проблем, в которых
могут быть использованы искусственные нейронные сети, и убедительно
продемонстрировала богатые возможности этой методики.
Обучающий алгоритм обратного распространения
Сетевые конфигурации:
Нейрон. На рис. 4.1 показан нейрон, используемый в качестве основного
строительного блока в сетях обратного распространения. Подается множество
входов, идущих либо извне, либо от предшествующего
слоя. Каждый из них умножается на вес, и произведения суммируются:
Рис.
4.1.
Эта сумма, обозначаемая 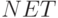
нейрона сети. После того, как величина 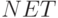
модифицируется с помощью активационной функции, и получается сигнал OUT. Для алгоритмов
обратного распространения обычно используется функция
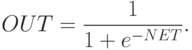 |
( 1) |
Как показывает уравнение (1), эта функция, называемая сигмоидом, весьма удобна, так как имеет
простую производную, что используется
при реализации алгоритма обратного распространения:
 |
( 2) |
Сигмоид, который иногда называется также логистической или сжимающей функцией,
сужает диапазон изменения 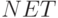
лежит между нулем и единицей. Как указывалось выше, многослойные нейронные
сети обладают большей представляющей мощностью,
чем однослойные, лишь в случае присутствия нелинейности. Сжимающая
функция обеспечивает требуемую нелинейность.

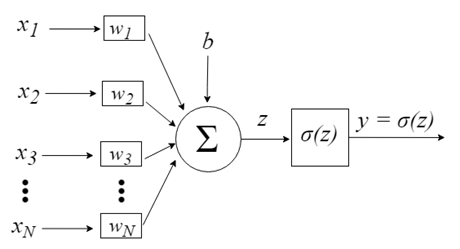
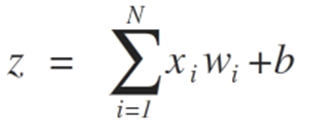
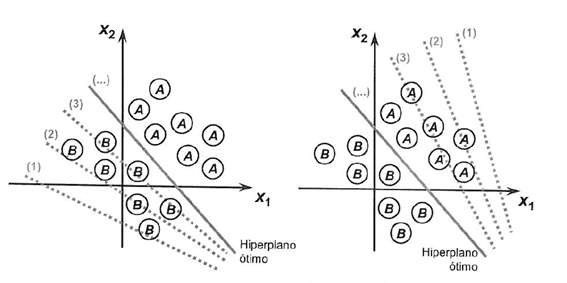
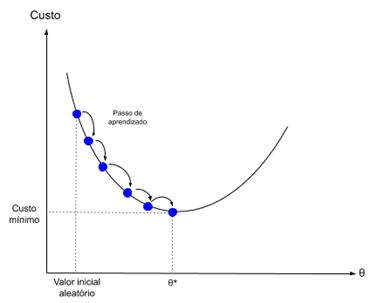
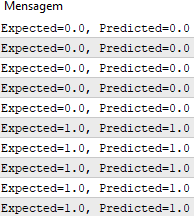
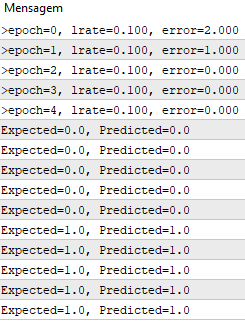
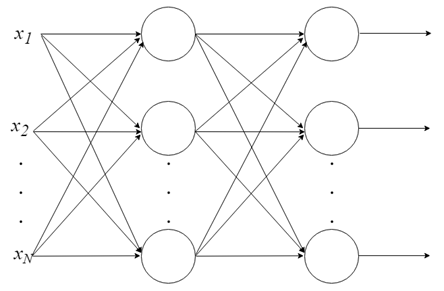
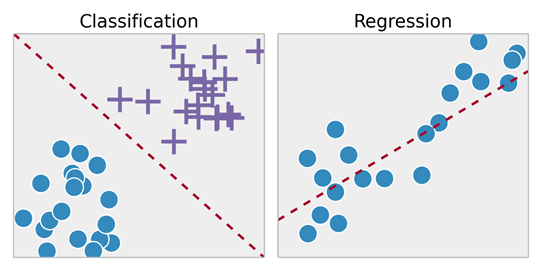
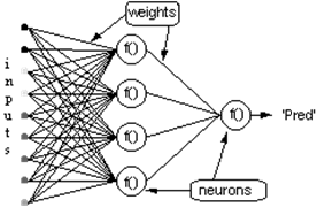
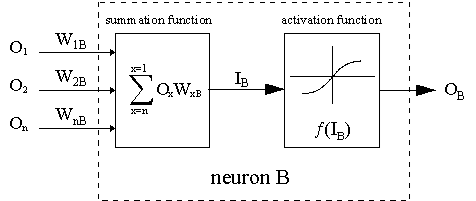
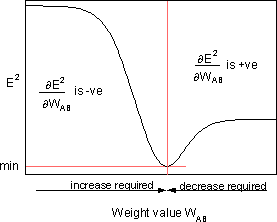
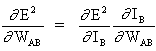
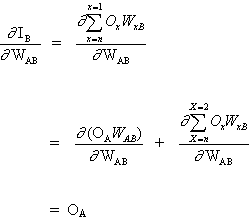
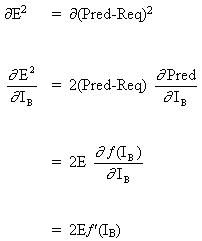
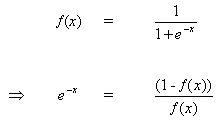
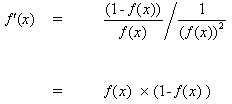
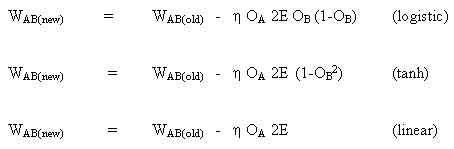
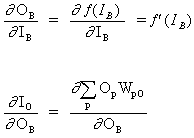
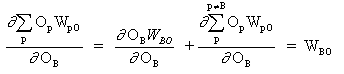
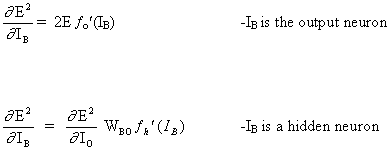
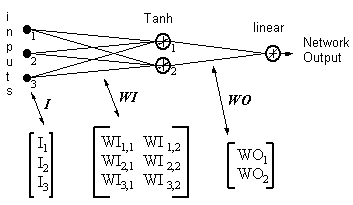
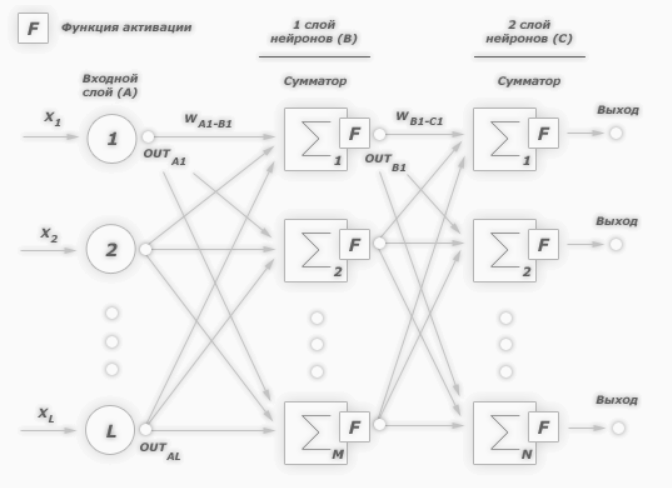

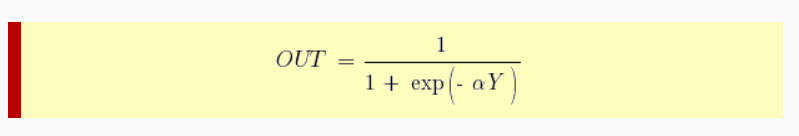
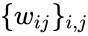 маленькими случайными значениями.
маленькими случайными значениями.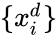 на вход сети и подсчитать выходы
на вход сети и подсчитать выходы 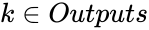
 .
. .
. .
. .
.