Основной
причиной преобразования аналоговой
информации в дискретную форму стало
невозможность улучшения качества
передачи данных в аналоговой форме.
Поэтому на смену аналоговой техники
передачи пришла цифровая техника. В
этой технике используется дискретная
модуляция исходных, непрерывных во
времени аналоговых процессов.
Рассматриваемый принцип импульсно
кодовой модуляции применяют в телефонии.
В этом случае дискретизация происходит
как по времени, так и по амплитуде.
Амплитуда исходной непрерывной функции
измеряется через заданный период
времени, за счёт этого происходит
дискретизация по времени, затем каждый
замер представляется в виде двоичного
числа, определённой разрядности, что
означает дискретизацию по значению.
Устройство, которое выполняет эту
функцию, называется АЦП. После чего
замеры передаются по линиям связи в
виде 0 и 1. При этом применяется те же
методы кодирования, что и при изначально
дискретной информации. На принимающей
стороне коды преобразуются в исходный
последовательности, а ЦАП производит
декодирование в аналоговый сигнал.
Дискретная
модуляция основана на теории отображения
Найквиста. В соответствии с этой теорией
аналоговая непрерывная функция,
переданная в виде последовательности
ей дискретных значений, может быть точно
восстановлена, если частота её
дискретизации была в 2 и более раз выше
частоты самой высокой гармоники спектра
её функции. В том случае, если это условие
не выполняется, то восстановленная
функция будет существенно отличаться
от исходной.
Ошибка
интерполяции равна разности исходного
задержанного процесса и восстановленного
процесса, причем задержка выбирается
такой, чтобы ошибка была минимальной.
∆инт(t)
= x(t — tопт)
— xв(t).
В
системах с обратной связью задержка
восстановленного сигнала нежелательна.
Она может привести не только к увеличению
ошибок моделирования, но и к потере
устойчивости модели. В этом случае
ошибка определяется как:
∆полн(t)
= x(t) — xв(t)
и
называется полной ошибкой.
Так
как ошибки зависят от времени, то для
их числовой оценки используется
среднеквадратическая ошибка, усредненная
за время Т, в течение которого измеряется
ошибка.
5. Эффективное кодирование, назначения, способы реализации, основные ограничения.
Этот
вид кодирования используется для
уменьшения объемов информации на
носителе — сигнале.
Для
кодирования символов исходного алфавита
используют двоичные коды переменной
длины: чем больше частота символа, тем
короче его код. Эффективность кода
определяется средним числом двоичных
разрядов для кодирования одного символа
– lср
по формуле

где
k – число символов исходного алфавита;
ns
– число двоичных разрядов для кодирования
символа s;
fs
– частота символа s; причем

При
эффективном кодировании существует
предел сжатия, ниже которого не
«спускается» ни один метод эффективного
кодирования — иначе будет потеряна
информация. Этот параметр определяется
предельным значением двоичных разрядов
возможного эффективного кода – lпр:
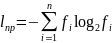
где
n – мощность кодируемого алфавита,
fi
– частота i-го символа кодируемого
алфавита.
Существуют
два классических метода эффективного
кодирования: метод Шеннона-Фано и метод
Хаффмена. Входными данными для обоих
методов является заданное множество
исходных символов для кодирования с их
частотами; результат — эффективные коды.
Метод
Хаффмена построения эффективного кода
реализуется в два этапа: сворачивание
кода и разворачивание кода.
1.
Сворачивание кода.
Формируют
начальную последовательность символов
источника информации путём упорядочивания
по неубыванию вероятностей их появления
на выходе источника. Последние два
символа последовательности объединяют
в один с вероятностью появления на
выходе источника информации, равной
сумме вероятностей появления каждого
из этих символов. Эту операцию повторяют
итеративно до тех пор, пока в
последовательности не останется только
лишь два символа.
2.
Разворачивание кода.
Одному
символу приписываем код 0, а другому 1.
Каждый символ разбивается на две
последовательности в порядке, обратном
порядку сворачивания кода. Эту операцию
повторяют итеративно для каждой из
полученных двух последовательностей
до тех пор, пока имеется последовательность,
состоящая более чем из одного символа.
При этом кодовая комбинация каждой
дочерней последовательности получается
путём приписывания к кодовой комбинации
родительской последовательности символа
0 или 1 справа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Permalink
Cannot retrieve contributors at this time
Лекция 6
Аналогово-Цифровой преобразовтель
Устройство, преобразующее входной аналоговый сигнал в дискретный код.
Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.
— Wikipedia
Статья для общего представления есть на habre:
АЦП бывают линейными и нелинейными, мы будем работать только с линейными АЦП
Основные харатеристика АЦП
-
Разрешение
-
Разрядность
-
Эффективная разрядность
-
-
Передаточная характеристика АЦП
-
Точность
-
Нелинейность
-
Ошибки квантования
-
Частота дискретизации
Разрешение
Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП.
В случае единичного измерения без учёта шумов разрешение напрямую определяется разрядностью АЦП.
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе.
В двоичных АЦП измеряется в битах.
Например, двоичный 8-разрядный АЦП способен выдать 256 дискретных значений (0…255), 2^8=256.Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений.
— Wikipedia
Пример :
-
Диапазон входных значений = от 0 до 3 вольт
-
Разрядность двоичного АЦП 12 бит: 2^12 = 4096 уровней квантования
-
Разрешение двоичного АЦП по напряжению: (3-0)/4096 = 0,0007324 вольт = 0,7324 мВ
Эффективная разрядность
На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным.
При этом реально достижимое разрешение описывается эффективной разрядностью (англ. effective number of bits, ENOB), которая меньше, чем реальная разрядность АЦП.
При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум.
Для достижения заявленной разрядности отношение сигнал/шум входного сигнала должно быть примерно 6 дБ на каждый бит разрядности (6 дБ соответствует двукратному изменению уровня сигнала).
— Wikipedia
Передаточная характеристика АЦП
Передаточная характеристика АЦП — зависимость числового эквивалента выходного двоичного кода от величины входного аналогового сигнала.
Для линейных АЦП всегда возможно провести такую прямую линию, чтобы все точки передаточной характеристики, соответствующие входным значениям delta*2^k где delta — шаг дискретизации, k лежит в диапазоне 0..N, где N — разрядность АЦП, были от неё равноудалены.

Точность
Имеется несколько источников погрешности АЦП.
Ошибки квантования и нелинейности присущи любому аналого-цифровому преобразованию.
Апертурные ошибки, которые являются следствием джиттера (англ. jitter) тактового генератора, они проявляются при преобразовании сигнала в целом (а не одного отсчёта).
Эти ошибки измеряются в единицах, называемых МЗР — младший значащий разряд (LSB англ.).
— Wikipedia
Для 12-битного двоичного АЦП ошибка в 1 МЗР составляет 1/4096 от полного диапазона сигнала, то есть 0,0244 %.
Ошибка квантования
Ошибки квантования являются следствием ограниченного разрешения АЦП. Этот недостаток не может быть устранён ни при каком типе аналого-цифрового преобразования.
Абсолютная величина ошибки квантования при каждом отсчёте находится в пределах от нуля до половины МЗР. В общем случае можно считать, что ошибка квантования равна половине МЗР.
— Wikipedia
Нелинейность
Всем АЦП присущи ошибки, связанные с нелинейностью, которые являются следствием физического несовершенства АЦП.
Это приводит к тому, что передаточная характеристика (в указанном выше смысле) отличается от линейной (точнее от желаемой функции, так как она не обязательно линейна).
Такие ошибки могут быть уменьшены путём калибровки.
— Wikipedia
Частота дискретизации
Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений.
Следовательно, необходимо определить частоту выборки цифровых значений из аналогового сигнала.
Частота, с которой производятся цифровые значения, получила название частота дискретизации АЦП.
Непрерывно меняющийся сигнал с ограниченной спектральной полосой подвергается оцифровке (то есть значения сигнала измеряются через интервал времени T — период дискретизации), и исходный сигнал может быть точно восстановлен из дискретных во времени значений путём интерполяции.
Точность восстановления ограничена ошибкой квантования. Однако в соответствии с теоремой Котельникова — Шеннона точное восстановление амплитуды возможно, только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала.
Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным от начала до конца процесса преобразования (этот интервал времени называют время преобразования).
Эта задача решается путём использования специальной схемы на входе АЦП — устройства выборки-хранения (УВХ).
УВХ, как правило, хранит входное напряжение на конденсаторе, который соединён со входом через аналоговый ключ:
при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании — хранение.
Типы АЦП
-
АЦП прямого(параллельные АЦП) преобразования
-
АЦП последовательного приближения
-
Сигма-дельта АЦП
-
АЦП дифференциального кодирования
-
АЦП сравнения с пилообразным сигналом
-
АЦП с уравновешиванием заряда
-
Оптические АЦП
АЦП последовательного преобразования
Ацп последовательного приближения работает методу половинного деления.
Пример для 8 битного двоичного АПЦ:
-
На компаратор подается значение вначале равное половине опорного напряжения(Uоп/2) (соответствующее установленном старшем бите 1000 0000b)
-
Если компаратор сработал старший бит скидывается, выставляется 1/4 опорного напряжения (Uоп/4) ( 0100 0000b)
-
Если компаратор не сработал старший бит остается, и выставляется 3/4 опорного напряжения (Uоп/4) ( 1100 0000b)
-
И так далее до самого младшего бита.

Сигма Дельта АЦП
Дома, подготовить доклад
АЦП прямого действия
Дома, подготовить доклад
АПП микроконтроллера STM32F411
АЦП(макс 12 разрядов) микроконтроллера STM32F411 работает по принципу последовательного приближения.
-
Основные элементы АЦП:
-
Наличие регулярных и инжектированных каналов – отличие только в том, что инжектированные каналы могут писать данные в 4 регистра с 4 каналов сразу, а регулярный только в один регистр
-
19 аналоговых каналов, 16 из которых которые могут сконфигурированы на работу от внешних источников или 3 внутренних.
-
Внешние каналы поступают на мультиплексор, где выбирается только один из них. Т.е. в один момент времени может быть измерено напряжение только с одного канала.
-
Результат преобразования сохраняется в регистрах данных. Для регулярных каналов это только один 16 битный регистр. Для инжектированных – 4.
-
Запуск преобразования может быть как программным, так и внешним. Внешний запуск может происходить от таймеров или с двух внешних входов.
-
Схема АЦП микроконтроллера STM32F411

Особенности АЦП микроконтроллера STM32F411
-
Разрядность АЦП можно изменять
-
6, 8, 10, или 12 разрядов.
-
-
Для одного канала можно задать разные режимы:
-
однократно измерить аналоговую величину
-
запустить канал в режиме непрерывного измерения.
-
-
Режим сканирования
-
Можно задать группу каналов и порядок следования каналов в группе. Тогда измерения будут идти последовательно друг за другом, входной мультиплексор будет подключать внешние каналы к АЦП по очереди, в соответствии с запрограммированным порядком.
-
-
Функция внешнего запуска для регулярных и инжектированных каналов.
-
Режим “прерывистых” преобразований.
-
Время одного преобразования зависит от частоты тактирования АЦП и времени скорости дискретизации , которое можно настроить.
-
Tconv = Sampling time + 12 cycles. При 1 МГц, а время дискритизации 3 циклам, то полное время преобразование будет 15 тактов или 15 мкс.
-
-
Размах входного сигнала не должен выходить за пределы опорного напряжения Vref.
-
Возможность введения временной задержки, автоматически вставляемой между преобразованиями. Длительность задержки программируется.
-
Генерация запроса для прямого доступа к памяти (режим DMA) во время преобразования в регулярном канале.
Режим одиночного преобразования
В этом режиме АЦП находится сразу после сброса. Бит CONT регистра ADC_CR2 равен 0.
-
Для начала работы с АЦП в этом режиме нужно
-
Настроить нужный порт, подключенный к нужному каналу АЦП на аналоговый вход
-
Подать тактирование на АЦП
-
Выбрать нужный канал для измерения
-
Настроить канал АЦП на нужную частоту преобразования
-
Включить АЦП
-
Начать преобразование
-
Дождаться флага готовности преобразования
-
Считать преобразованное значение
-
Режим сканирования
В этом режиме опрашивается группа каналов.
-
Режим выбирается установкой бита SCAN в регистре ADC_CR1.
-
АЦП опрашивает все каналы, выбранные в регистрах ADC_SQRx (регулярные каналы)
-
Для каждого канала группы выполняется одиночное преобразование. После окончания каждого преобразования следующий канал в группе опрашивается автоматически.
-
Если установлен режим непрерывного преобразования (CONT = 1), то после последнего преобразования в группе, преобразования не прекращаются, а заново начинаются от первого выбранного канала в группе.
-
Если установлен бит DMA, то данные из регистра ADC_DR пересылаются в память после каждого преобразования.
-
В регулярных каналах флаг окончания преобразования EOC может устанавливаться либо в конце каждого преобразования, либо только по окончании всей последовательности. Для этого в регистре ADC_CR2 предусмотрен управляющий бит EOCS
-
EOCS = 0 – бит окончания преобразования EOC устанавливается после завершения всей последовательности регулярных преобразований.
-
EOCS = 1 – бит окончания преобразования EOC устанавливается после завершения каждого регулярного преобразования
-
-
Регистр статуса SR (ADC status register)

- Bit5: OVR
-
Переполнение. Бит указывает, что данные преобразования регулярного канала были потеряны, т.е. программа не успела считать регистр данных регулярного канала, до следующего преобразования.
-
0: было переполнение
-
1: переполнения не было
-
- Bit4: STRT
-
Флаг начала преобразования регулярного канала
-
0: преобразование начато
-
1: преобразование не начато
-
- Bit1: EOC
-
Преобразование регулярных каналов закончено. Можно считывать регистр данных.
-
0: преобразование не закончено
-
1: преобразование закончено
-
Регистр управления CR1 (ADC control register 1)

- Bits25..24: RES[1:0]
-
разрядность АЦП
-
00: разрядность 12 бит (время преобразования 12 + 4 = 16 тактов)
-
01: разрядность 10 бит (время преобразования 11 + 4 = 15 тактов)
-
10: разрядность 8 бит (время преобразования 9 + 4 = 13 тактов)
-
11: разрядность 6 бит (время преобразования 7 + 4 =11 тактов)
-
- Bit8: SCAN
-
Включение режима сканирования. В этом режиме опрашивается группа каналов. АЦП опрашивает все каналы, выбранные в регистрах ADC_SQRx (регулярные каналы)
Для каждого канала группы выполняется одиночное преобразование. После окончания каждого преобразования следующий канал в группе опрашивается автоматически.
Если установлен режим непрерывного преобразования (CONT = 1), то после последнего преобразования в группе, преобразования не прекращаются, а заново начинаются от первого выбранного канала в группе.-
0: режим сканирования выключен
-
1: режим сканирования включен
-
- Bit5: EOCIE
-
Разрешает прерывание по установке флага окончание преобразования EOC
-
0: прерывание запрещено
-
1: прерывание разрешено
-
Регистр управления CR2 (ADC control register 2)

|
|
Регистр настройки времени дискретизации АЦП SMPRx(ADC sample time register)


- Bits0..26 SMPx[2:0]
-
Выбор времени дискретизации для канала от x.
-
000: 3 cycles
-
001: 15 cycles
-
010: 28 cycles
-
011: 56 cycles
-
100: 84 cycles
-
101: 112 cycles
-
110: 144 cycles
-
111: 480 cycles
-
Регистр настройки последовательности преобразований SQR (ADC regular sequence register 1 )

- Bits20..23: L[3:0]
-
Длина последовательности преобразований
-
0000: 1 преобразование
-
0001: 2 преобразований
-
…………
-
1111: 16 преобразований
-

- SQx
-
Номер канала для х преобразования
Регистр данных DR (ADC data register)

- Bits0..15: DATA[15:0]
-
Данные преобразования регулярного канала
Общий регистр управления ССR (ADC common control register ADC_Common)

- Bits23: TSVREFE
-
Подключить сенсор температуры и Vref
-
0: Отключить сенсора температуры и Vref
-
1: Включить сенсор температуры и Vref
-
- Bits16:17: ADCPRE
-
установить частоту работы АЦП
-
00: частота равна PCLK2/2
-
01: частота равна PCLK2/4
-
10: частота равна PCLK2/6
-
11: частота равна PCLK2/8
-
Порядок запуска одиночного АЦ преобразования
-
Подключить АЦП к источнику тактирования – устанавливаем бит ADC1EN в регистре RCC::APB2ENR (АЦП тактируется от шины APB2).
-
Сконфигурировать порты. Определиться по каким каналам будут проводиться измерения, затем соответствующие выводы портов настроить для работы в аналоговом режиме.
-
Сконфигурировать АЦП.
-
Установить разрядность в регистре ADC::CR1
-
Установить режим одиночного преобразование в регистре ADC::CR1 (биты CONT и EOCS установить в нужное значение)
-
Установить количество измерений 1 в регистре ADC1::SQR1 бит L
-
Выбрать канал для первого преобразования в регистре ADC1::SQR3 биты SQ1
-
Установить скорость дискретизации в регистре SMPRx для нужного канала
-
-
Включить АЦП. Это делается установкой бита ADON в регистре ADC::CR2.
-
Запустить АЦП на преобразование установкой бита SWSTART в регистре ADC::CR2 для регулярных каналов
-
Дождаться готовности бита EOC в регистре ADC::SR
-
Считать данные из регистра ADC::DR
Задание
Измерить температуру микроконтроллера с помощью встроенного датчика темпертуры.
-
Прочитать все АЦП в библии все про встроенный датчик температуры на странице 225
-
Включить измерение датчика температуры
-
Сконфигурировать АЦП
-
12 бит
-
Одиночное преобразование
-
Регулярные каналы
-
Время дискретизации 84 цикла
-
Установка EOC после каждого измерения регулярного канала
-
Установить первое измерение с канала куда подключен датчик температуры
-
Раскладываем по полочкам параметры АЦП
Время прочтения
10 мин
Просмотры 47K
Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.
Введение
Начать бы хотелось с интересного философского вопроса: если аналоговый сигнал — это бесконечность, теряем ли мы при оцифровке сигнала бесконечное количество информации? Если это так, тогда какой смысл существования такого неэффективного преобразования?
Для того, чтобы ответить на этот вопрос, разберемся с тем, что такое аналого-цифровое преобразование сигнала. Основной график, который отражает работу АЦП – передаточная характеристика преобразования. В идеальном мире это была бы прямая линия, то есть у каждого аналогового уровня сигнала имелся бы единственный цифровой эквивалент.
Рис. 1: Идеальная характеристика АЦП
Однако из-за наличия различных видов шума, мы не можем увеличивать разрядность АЦП до бесконечности. То есть существует предел, который ограничивает минимальную цену деления шкалы. Другими словами, уменьшая деление шкалы мы рано или поздно «упремся» в шум. Да, конечно, можно сделать хоть 100-битный АЦП, однако большинство бит данного АЦП не будут нести полезную информацию. Именно поэтому характеристика АЦП имеет ступенчатую форму, что равносильно наличию конечной разрядности АЦП.
Проектируя систему необходимо выбирать АЦП, который бы обеспечил отсутствие потери информации при оцифровке. Для того, чтобы выбрать преобразователь, необходимо понять, какие параметры его характеризуют.
Параметры АЦП можно разделить на 2 группы:
- Статические — характеризуют АЦП при постоянном или очень медленно изменяющемся входном сигнале. К данным параметрам можно отнести: максимальное и минимальное допустимое значение входного сигнала, разрядность, интегральную и дифференциальную нелинейности, температурную нестабильность параметров преобразования и др.
- Динамические — определяют максимальную скорость преобразования, предельную частоту входного сигнала, шумы и нелинейности.
Статические параметры
- Максимальный (Vref) и минимальный (обычно 0) уровни входного сигнала — устанавливают диапазон шкалы преобразования, относительно которой будет оцениваться входной сигнал (рис. 1). Также этот параметр может обозначаться как FS — full scale. Для дифференциального АЦП шкала определяется от -Vref до +Vref, однако для упрощения далее будем рассматривать только single-ended шкалы.
- Разрядность (N) — разрядность выходного кода, характеризующая количество дискретных значений (
), которые преобразователь может выдать на выходе (рис. 1).
- Ток потребления (Idd) — сильно зависит от частоты преобразования, поэтому информацию об этом параметре лучше искать на соответствующем графике.
- МЗР (LSB) – младший значащий разряд (Least Significant Bit) — минимальное входное напряжение, разрешаемое АЦП (по сути единичный шаг в шкале преобразования). Определяется формулой:
(рис. 1).
- Ошибка смещения (offset error) – определяется как отклонение фактической передаточной характеристики АЦП от передаточной характеристики идеального АЦП в начальной точке шкалы. Измеряется в долях LSB. При ошибке смещения переход выходного кода от 0 в 1 происходит при входном напряжении отличном от 0.5LSB (рис. 2).
Рис. 2: Ошибка смещения
Существует и другой вариант квантователя, когда переход осуществляется при целых значения LSB (характеристика у него будет смещена относительно первого варианта, который представлен на рисунке 2). Оба этих квантователя равноправны, и для простоты далее будем рассматривать только первый вариант. - Ошибка усиления (gain error) – определяется как отклонение средней точки последнего шага преобразования (которому соответствует входное напряжение Vref) реального АЦП от средней точки последнего шага преобразования идеального АЦП после компенсации ошибки смещения (рис. 3).
Рис. 3: Ошибка усиления
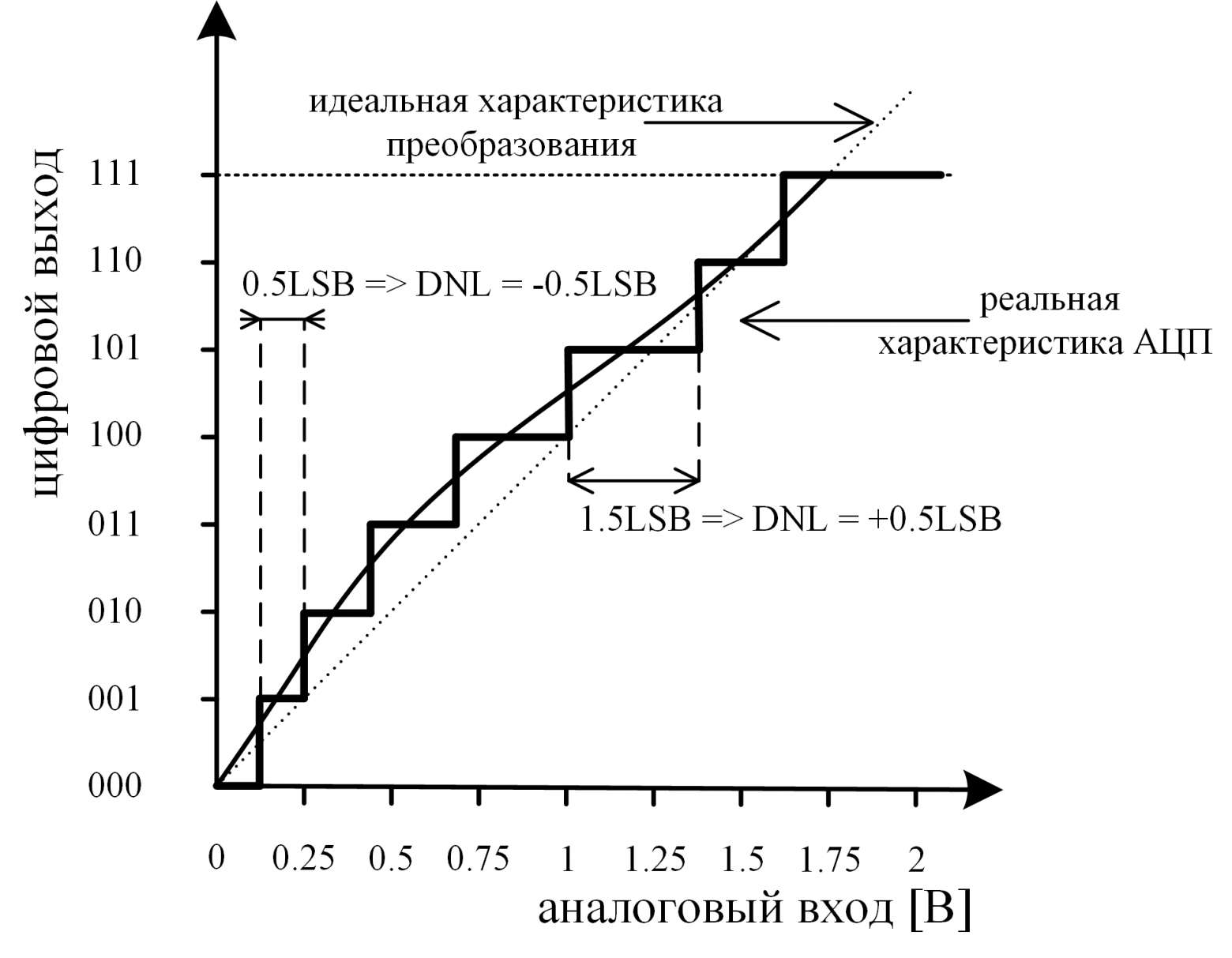
- Дифференциальная нелинейность (DNL — Differential nonlinearity) – отклонение ширины ступеньки на передаточной характеристике реального АЦП от номинальной ширины ступеньки у идеального преобразователя. Из-за дифференциальной нелинейности шаги квантования имеют различную ширину (рис. 4).
Рис. 4: Дифференциальная нелинейность
Для 3-х битного АЦП с рисунка 4:
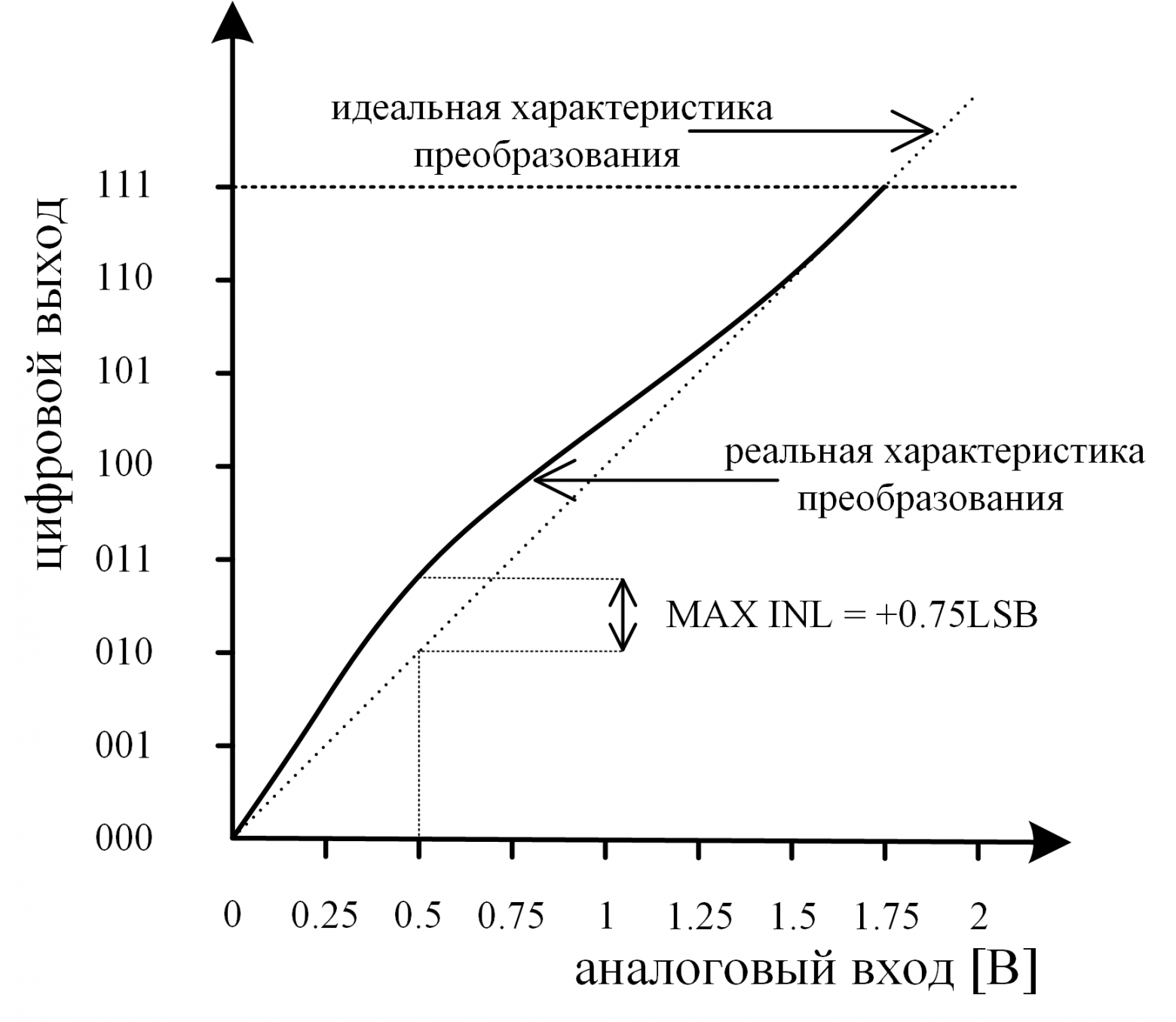
- Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
Рис. 5: Интегральная нелинейность
- Общая нескорректированная ошибка ( TUE — Total Unadjusted Error) – абсолютная ошибка, включающая в себя следующие ошибки: квантования, смещения, усиления и нелинейности. Другими словами, это максимальное отклонение между реальной и идеальной характеристикой преобразования. Для идеального АЦП TUE = 0.5LSB, обусловлена ошибкой квантования (или шум квантования — возникает из-за округления значения аналогового сигнала, которое соответствует цифровому коду). Ошибки усиления и смещения обычно вносят наиболее весомый вклад в абсолютную ошибку. Однако с точки зрения динамических параметров (см. ниже) ошибки смещения и усиления ничтожны, так как они не порождают нелинейных искажений.
Динамические параметры
- Частота дискретизации (fs — sampling frequency) — частота, при которой происходит преобразование в АЦП (ну или 1/Ts, где Ts — период выборки). Измеряется числом выборок в секунду. Обычно под данным обозначением подразумевают максимальную частоту дискретизации, при которой специфицированы параметры преобразователя (рис. 6).
Рис. 6: Процесс преобразования АЦП
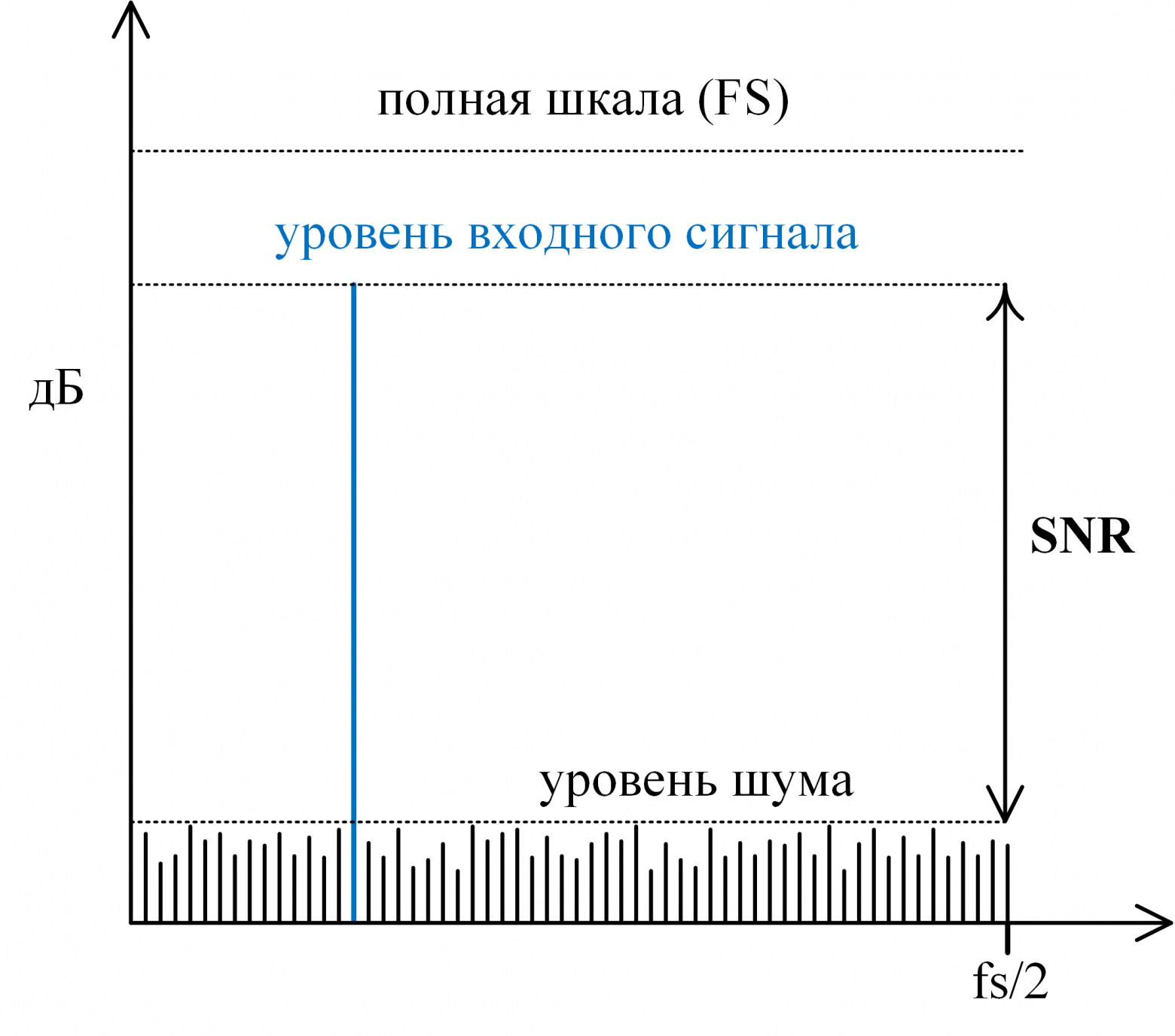
- Отношение сигнал/шум (SNR — Signal-to-Noise Ratio) — определяется как отношение мощности обрабатываемого сигнала к мощности шума, добавляемого в процессе преобразования. SNR обычно выражается в децибелах (дБ) и рассчитывается по следующей формуле:
Наглядно данное выражение продемонстрированно на рисунке 7.
Рис. 7: Отношение сигнал/шум
Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:
Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать, что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW < fs/2), то, применив цифровой фильтр низких частот (либо полосовой, тут зависит все от полосы и несущей) к результату преобразования, можно вырезать часть шума АЦП, а оставшаяся часть будет распределена от 0 до BW (рис. 8). Если шум АЦП равномерно распределен по всем частотам (т.н. «белый» шум) интегральный шум после фильтрации уменьшится в fs/2 / BW раз, что и отражает третий член формулы.
Рис. 8: Увеличение SNR за счет передискретизации
- Общие нелинейные искажения (THD — total harmonic distortion). Прежде, чем сигнал преобразовывается в цифровой код, он проходит через нелинейные блоки, которые искажают сигнал. К примеру, пусть есть сигнал с частотой f. Пройдя через нелинейный блок к нему добавятся компоненты с частотами 2f, 3f, 4f … — 2-я, 3-я, 4-я и т.д. гармоники входного сигнала. Если дискретизированный сигнал разложить в спектр с помощью ДПФ (Дискретного Преобразования Фурье), мы увидим, что все эти гармоники «перенеслись» в первую зону Найквиста (от 0 до fs/2) (рис. 9).
Рис. 9: Нелинейные искажения
Побочные гармоники искажают обрабатываемый сигнал, что ухудшает производительность системы. Этот эффект можно измерить, используя характеристику общие нелинейные искажения. THD определяется как отношение суммарной мощности гармонических частотных составляющих к мощности основной (исходной) частотной составляющей (в некоторых документациях выражается в дБ):
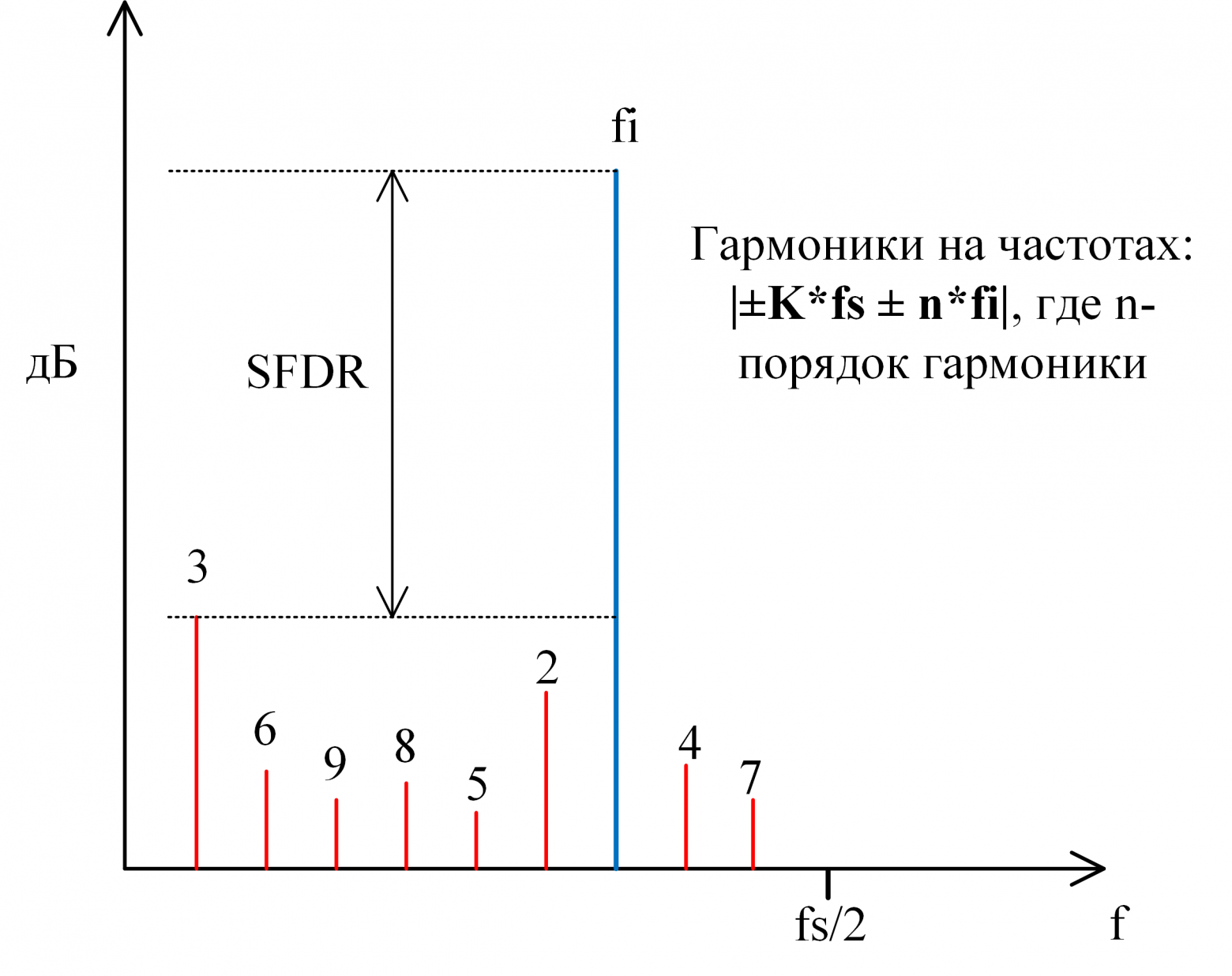
- Динамический диапазон, свободный от гармоник (SFDR — Spurious-Free Dynamic Range). Является отношением мощности полезного сигнала к мощности наибольшего «спура» (любая паразитная составляющая в спектре, не обязательно гармонического происхождения), присутствующего в спектре (рис. 9).
- Отношение сигнал / шум и нелинейные искажения (SINAD — signal-to-noise and distortion ratio). Аналогичен SNR, но помимо шума учитывает все виды помех и искажений, возникающих при аналого-цифровом преобразовании. SINAD является одним из ключевых параметром, характеризующим АЦП (в некоторых источниках обозначается как SNDR):
- Эффективное число бит (ENOB — effective number of bits) – некая абстрактная характеристика, показывающая сколько на самом деле бит в выходном коде АЦП несет в себе полезную информацию. Может принимать дробные значения.
- Интермодуляционные искажения (IMD — intermodulation distortion). Рассмотренные прежде динамические параметры измеряются, когда на вход подается однотональный гармонический сигнал. Такие однотональные тесты хороши, когда АЦП обрабатывает широкополосные сигналы. В этом случае гармоники, располагающиеся выше fs/2 отражаются в первую зону Найквиста и, следовательно, всегда учитываются в расчете параметров. Однако, имея дело с узкополосными сигналами или АЦП с передискретизацией, даже гармоники низкого порядка (2-я, 3-я) могут иметь достаточно высокую частоту, чтобы выйти из рассматриваемого частотного диапазона (или не отразиться в этот диапазон в случае выхода за fs/2). В этом случае эти гармоники не будут учтены, что приведёт к ошибочному завышению динамических параметров.
Для решения этой проблемы используются бигармонические тесты. На вход подают две спектрально чистых синусоиды одинаковой мощности с частотамии
, которые находятся на близком расстоянии друг от друга. Нелинейность преобразователя порождает дополнительные тоны в спектре (их называют интермодуляционными искажениями) на частотах
, где
– произвольные целые числа.
Полезность бигармонического теста в том, что некоторые из интермодуляционных продуктов располагаются в спектре очень близко к исходному сигналу и, следовательно, дают полную информацию о нелинейности АЦП. В частности, интермодуляционные искажения 3-го порядка находятся на частотахи
(рис. 10).
Рис. 10: интермодуляционные искажения
При построении РЧ систем могут быть интересны так же продукты 2-го и более высокого порядка. Параметр АЦП, характеризующий его интермодуляционные искажения n-го порядка, определяется формулой:
[dBc], где
– мощность идентичных синусоид на входе,
– мощность одного из продуктов. Например
– отношение мощности на
к мощности на
Полоса пропускания АЦП и субдискретизация (undersamling/sub-sampling)
Полоса пропускания преобразователя (FPBW — Full Power (Analog) Bandwidth). Обычно ширина полосы преобразователя составляет несколько зон Найквиста. Этот параметр должен быть в спецификации, но, если его нет, можно попробовать самостоятельно оценить минимально возможное значение полосы пропускания для данного АЦП. За период выборки емкость УВХ должна зарядиться с точностью 1 LSB. Если период выборки равен , то ошибка выборки сигнала полной шкалы равна:
Решив относительно t, получаем:
Положив, что , определим минимальную полосу АЦП (для
):
Например, для 16 битного АЦП с частотой дискретизации 80 Мвыб/c и шкалой 2 В ограничение снизу для полосы пропускания, рассчитанное по этой формуле, составит FPBW = 282 МГц.
Analog Bandwidth является очень важным параметром при построении систем, которые работают в режиме субдискретизации (“undersampling”). Объясним это подробнее.
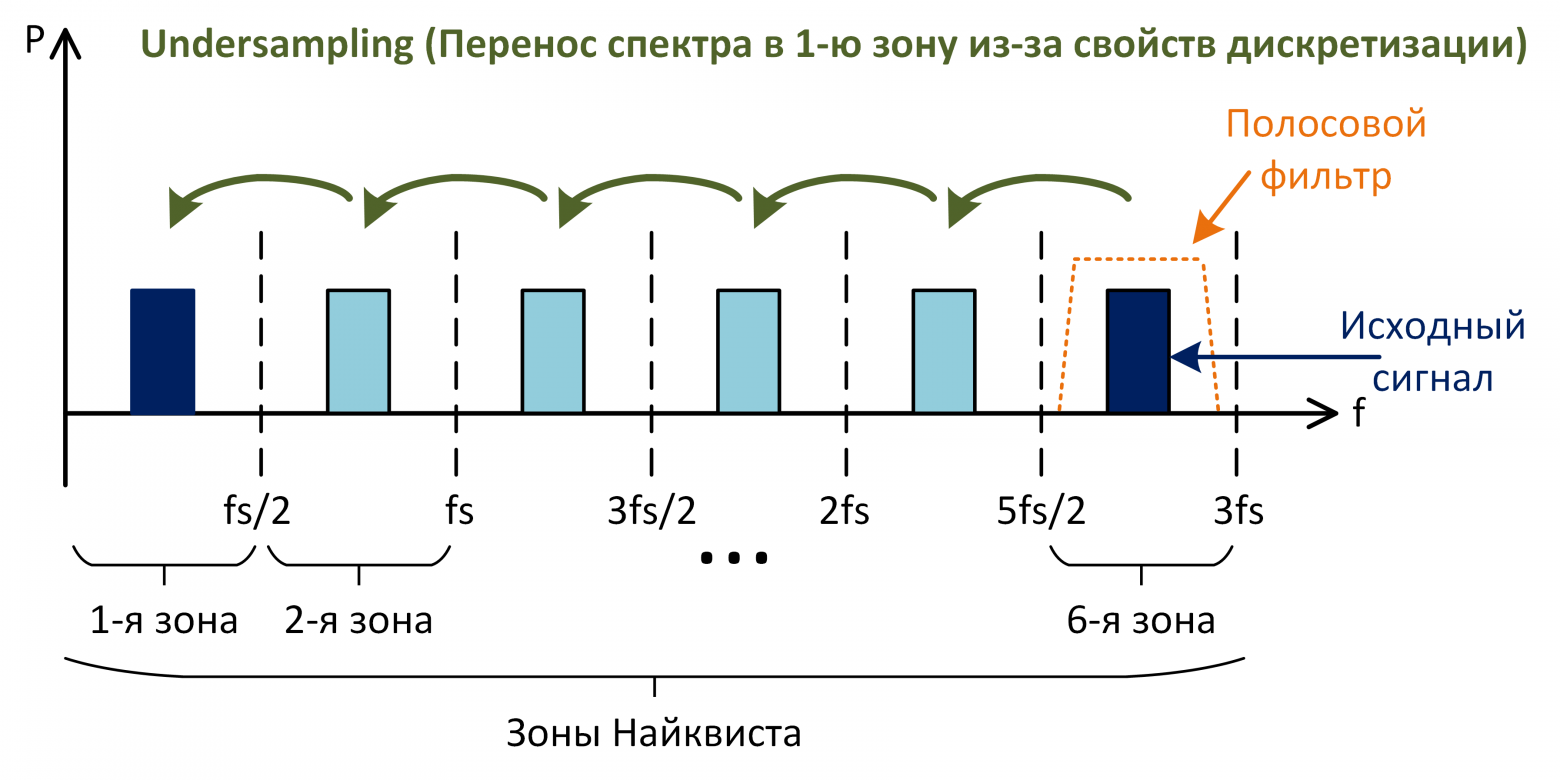
Согласно критерию Найквиста, ширина спектра обрабатываемого сигнала должна быть как минимум в 2 раза меньше частоты дискретизации, чтобы избежать элайзинга. Здесь важно, что именно ширина полосы, а не просто максимальная частота сигнала. Например, сигнал, спектр которого расположен целиком в 6-й зоне Найквиста может быть теоретически дискретизован без потери информации (рис. 11). Ограничив спектр этого сигнала антиэлайзинговым фильтром, его можно подавать на дискретизатор с частотой fs. В результате сигнал отразится в каждой зоне.
Рис. 11: undersampling
Свойство переноса спектра при дискретизации
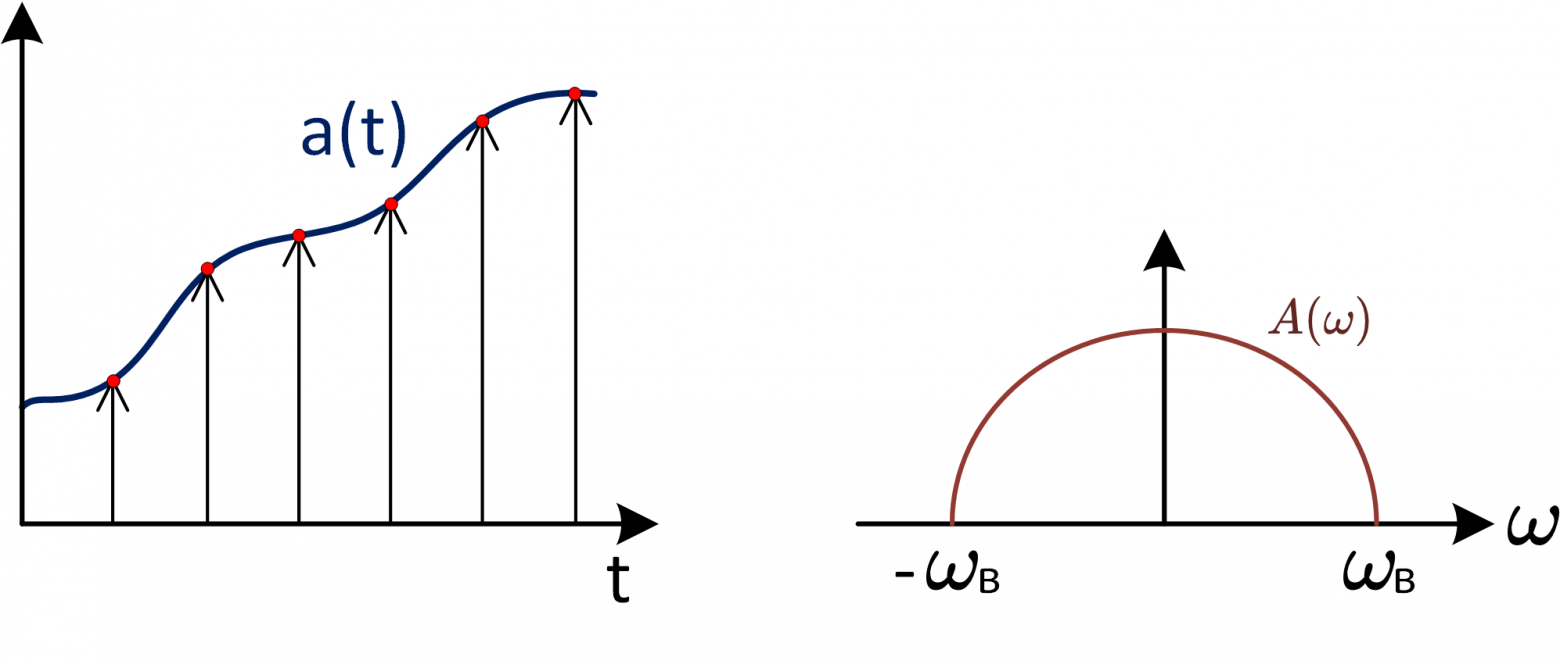
Undersampling или sub-sampling имеет место быть из-за свойств дискретизации. Рассмотрим на примере, пусть имеется сигнал a(t) и его спектральная плотность (рис. 12). Необходимо найти спектральную плотность
сигнала после дискретизации сигнала
.
Рис 12: дискретизация непрерывного сигнала
По фильтрующему свойству дельта-функции:
После дискретизации :
где
С помощью формулы Релея вычислим спектр:
Из этого выражения следует что спектр сигнала будет повторяться во всех зонах Найквиста.
Итак, если есть хороший антиэлайзинговый фильтр, то соблюдая критерий Найквиста, можно оцифровывать сигнал с частотой дискретизации намного ниже полосы АЦП. Но использовать субдискретизацию нужно осторожно. Следует учитывать, что динамические параметры АЦП деградируют (иногда очень сильно) с ростом частоты входного сигнала, поэтому оцифровать сигнал из 6-й зоны так же «чисто», как из 1-й не получится.
Несмотря на это субдискритезация активно используется. Например, для обработки узкополосных сигналов, когда не хочется тратиться на дорогой широкополосный быстродействующий АЦП, который вдобавок имеет высокое потребление. Другой пример – выборка ПЧ (IF-sampling) в РЧ системах. Там благодаря undersampling можно исключить из радиоприемного тракта лишнее аналоговое звено — смеситель (который переносит сигнал на более низкую несущую или на 0).
Сравним архитектуры
На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).
Таблица сравнения архитектур
Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.
Заключение
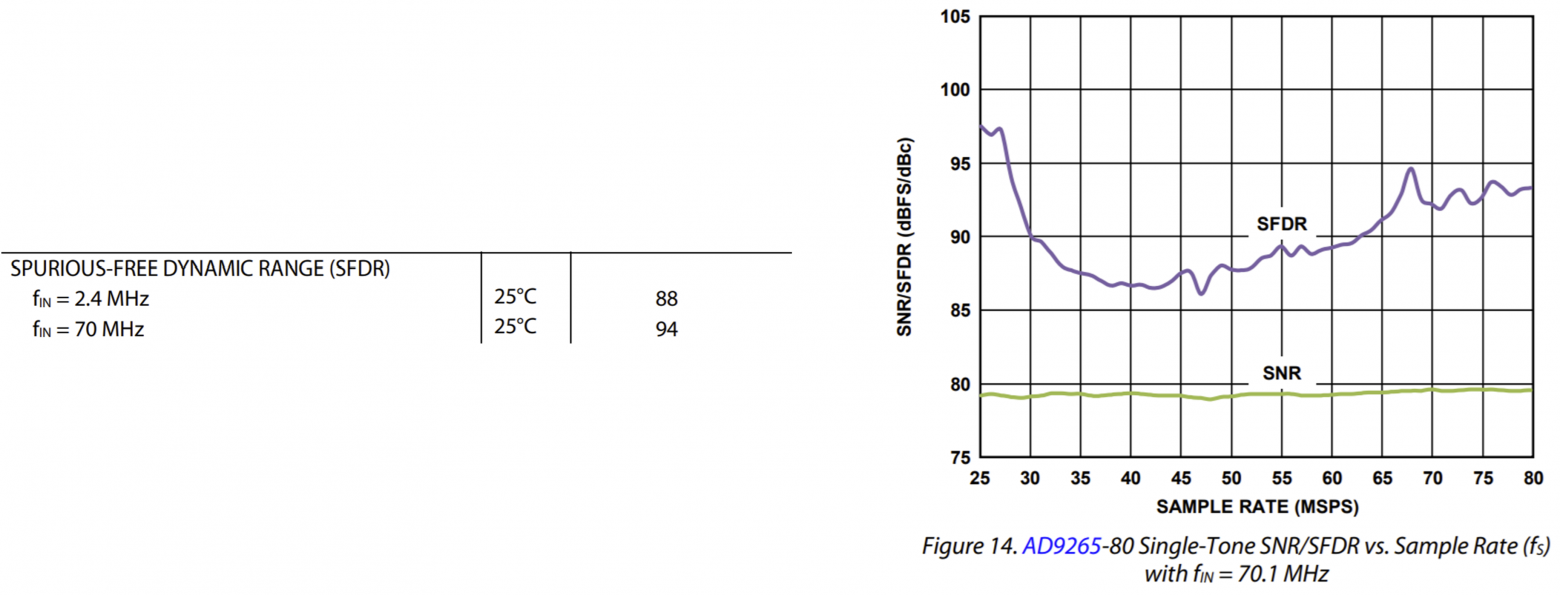
Описав параметры разрабатываемой вами системы, можно понять, какие характеристики АЦП для вас являются критичными. Однако не стоит забывать, что динамические параметры преобразователей сильно зависят от многих факторов (частота дискретизации, частота входного сигнала, амплитуда входного сигнала и тд.) Зачастую в таблицах параметров в документации указывают только «красивые» (с точки зрения маркетинга) цифры. Приведу пример, возьмем АЦП ad9265 и рассмотрим его параметр SFDR при частоте входного сигнала 70 МГц:
Таблица показывает значение SFDR при максимальных значениях частоты дискретизации, однако если вы будете использовать частоту ниже (к примеру 40 МГц), вы не получите этих «хороших» значений. Поэтому советую анализировать характеристики АЦП по графикам, чтобы примерно понимать, сможет ли данная микросхема обеспечить нужную вам точность преобразования.


 Рис. 2: Ошибка смещения
Рис. 2: Ошибка смещения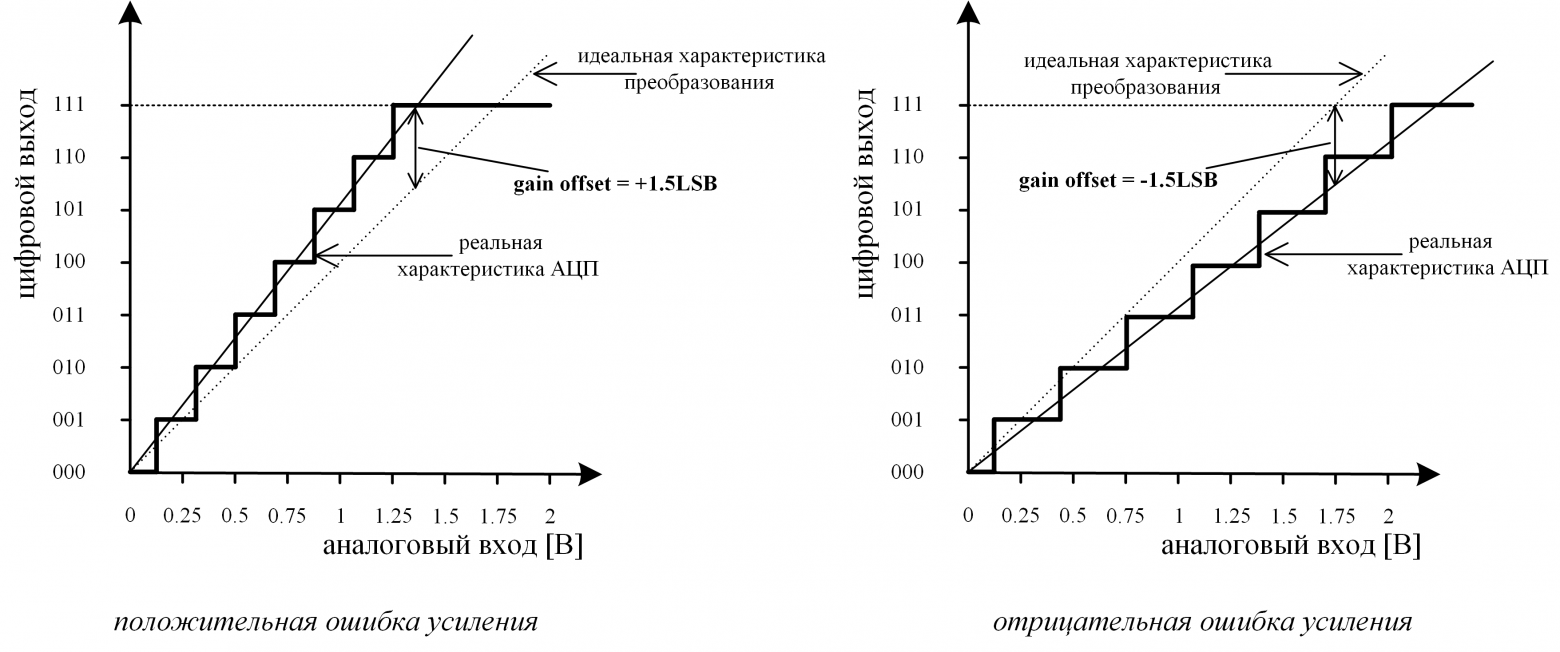 Рис. 3: Ошибка усиления
Рис. 3: Ошибка усиления