Этот пост продолжает серию про функции ошибки и функционалы качества в машинном обучении. Сейчас разберёмся с самой простой подтемой — как измерять качество чёткого ответа в задачах бинарной классификации. Уровень для чтения — начальный;)
Предыдущие посты в блоге на эту тему:
- AUC ROC
- Джини
- Логистическая функция ошибки
- Функции ошибок в задачах регрессии
Рассматриваем задачу классификации на два класса (с метками 0 и 1), на рис. 1 показано её графическое представление.
Пусть классификатор выдаёт метку класса. Используем принятые в этом блоге обозначения: yi – метка i-го объекта, ai – ответ на этом объекте нашего алгоритма, m – число объектов в выборке.
Естественным, простым и распространённым функционалом качества является точность (Accuracy или Mean Consequential Error):
т.е. просто доля (процент) объектов, на которых алгоритм выдал правильные ответы. Недостаток такого функционала очевиден: он плох в случае дисбаланса классов, когда представителей одного из класса существенно больше, чем другого. В этом случае, с точки зрения точности, выгодно почти всегда выдавать метку самого популярного класса. Это может не согласовываться с логикой использования решения задачи. Например, в задаче детектирования очень редкой болезни алгоритм, который всех относит к классу «здоровые», на практике не нужен.
Рассмотрим т.н. матрицу несоответствий / ошибок (confusion matrix) – матрицу размера 2×2, ij-я позиция которой равна числу объектов i-го класса, которым алгоритм присвоил метку j-го класса.
На рис. 2 показана такая матрица для решения рис. 1, также показаны названия элементов матрицы. Два класса делятся на положительный (обычно метка 1) и отрицательный (обычно метка 0 или –1). Объекты, которые алгоритм относит к положительному классу, называются положительными (Positive), те из них, которые на самом деле принадлежат к этому классу – истинно положительными (True Positive), остальные – ложно положительными (False Positive). Аналогичная терминология есть для отрицательного (Negative) класса. Дальше используем естественные сокращения:
- TP = True Positive,
- TN = True Negative,
- FP = False Positive,
- FN = False Negative.
Замечание. Иногда матрицу ошибок изображают по-другому: в транспонированном виде (ответы алгоритма соответствуют строкам, а правильные метки – столбцам).
Замечание. Стандартная терминология немного нелогична: естественно называть положительными объектами объекты положительного класса, но здесь – объекты, отнесённые алгоритмом к положительному классу (т.е. это даже не свойство объектов, а алгоритма). Но в контексте употребления терминов «истинно положительный» и «ложно положительный» это уже кажется логичным.
Для точности (Accuracy) справедлива формула:
Ошибки классификатора делятся на две группы: первого и второго рода. В идеале (когда точность равна 100%) матрица несоответствий диагональная, ошибки вызывают отличие от нуля двух недиагональных элементов:
ошибка 1 рода (Type I Error) случается, когда объект ошибочно относится к положительному классу (= FP/m).
ошибка 2 рода (Type II Error) случается, когда объект ошибочно относится к отрицательному классу (= FN/m).
На заглавном рис. поста показаны известные шуточные иллюстрации ошибок 1 и 2 рода: ошибка 1 рода (слева) и ошибка 2 рода (справа). Когда я объясняю студентам, всегда привожу такой пример, который позволяет запомнить отличие ошибок 1 и 2 рода. Пусть студент приходит на экзамен. Если он учил и знает, то принадлежит классу с меткой 1, иначе — имеет метку 0 (вполне логично называть знающего студента «положительным»). Пусть экзаменатор выполняет роль классификатора: ставит зачёт (т.е. метку 1) или отправляет на пересдачу (метку 0). Самое желаемое для студента «не учил, но сдал» соответствует ошибке 1 рода, вторая возможная ошибка «учил, но не сдал» – 2 рода.
Через введённые выше обозначения выражаются следующие функции:
Полнота (Sensitivity, True Positive Rate, Recall, Hit Rate) отражает какой процент объектов положительного класса мы правильно классифицировали:
Здесь и далее показан числитель формулы (тёмно синим) и знаменатель (тёмно и светло синим). Слева это сделано для матрицы несоответствий, справа – для множеств: круглое – объекты положительного класса, квадратное – положительные объекты по мнению классификатора.
Точность (Precision, Positive Predictive Value) отражает какой процент положительных объектов (т.е. тех, что мы считаем положительными) правильно классифицирован:
Точность и полноту можно неформально называть «ортогональными критериями качества». Легко построить алгоритм со 100%-й полнотой: он все объекты относит к классу 1, но при этом точность может быть очень низкой. Нетрудно построить алгоритм с близкой к 100% точностью: он относит к классу 1 только те объекты, в которых уверен, при этом полнота может быть низкая.
Замечание. Отличайте «Accuracy» и «Precision». К сожалению, по-русски их называют одинаково «точность».
F1-мера (F1 score) является средним гармоническим точности и полноты, максимизация этого функционала приводит к одновременной максимизации этих двух «ортогональных критериев»:
Также рассматривают весовое среднее гармоническое точности (P) и полноты (R) – Fβ-меру (Fβ score):
Обратите внимание, что β здесь не вес в среднем гармоническом:
Почему используется среднее гармоническое понятно из рис. 4, на которых показаны линии уровня различных функций усреднения.
Видно, что линии уровня среднего гармонического сильно похожи на «уголки», т.е. на линии функции min, что вынуждает при максимизации функционала сильнее «тянуть вверх» меньшее значение. Если, например, точность очень мала, то увеличение полноты, пусть и в два раза, не сильно меняет значение функционала. Нагляднее это показано на рис. 5: при точности 10% F1-мера не может быть больше 20%.
При использовании Fβ-меры линии уровня «перекашиваются», один из критериев (точность или полнота) становится важнее при оптимизации, см. рис. 6.
Из функционалов качества, которые получаются из матрицы несоответствий, можно также отметить специфичность (Specificity) или TNR – True Negative Rate:
т.е. процент правильно классифицированных объектов негативного класса. Полноту иногда называют чувствительностью (Sensitivity) и используют в паре со специфичностью для оценки качества, также часто их усредняют (об этом поговорим дальше). Оба функционала имеют смысл «процент правильно классифицируемых объектов одного из класса». Можно ввести понятие полноты Rk для k-го класса: это полнота, если считать класс k положительным, тогда
Также запомним False Positive Rate (FPR, fall-out, false alarm rate):
– доля объектов негативного класса, которых мы ошибочно отнесли к положительному (это нужно для понимания функционала AUC ROC).
Коэффициент Мэттьюса (MCC – Matthews correlation coefficient) равен
его рекомендуют применять для несбалансированных выборок. Давайте разберёмся, что означает эта «сложная формула». Рассмотрим среднее геометрическое точности и полноты:
Теперь возьмём среднее геометрическое точности и полноты класса 0 (т.е. считая это класс положительным), перемножив эти средние геометрические, получим
Логично полученное выражение максимизировать, по аналогии можно выписать выражение для минимизации. Если теперь внимательно посмотреть на формулу MCC, то становится понятным, что она означает и почему её значение лежит на отрезке [–1, +1] (оставляем это как задание читателю).
Каппа Коэна (Cohen’s Kappa)
В задачах классификации часто используют функционал качества Каппа Коэна (Cohen’s Kappa). Его идея довольно простая: поскольку использование точности (Accuracy) вызывает сомнение в задачах с сильном дисбалансом классов, надо её значения немного перенормировать. Делается это с помощью статистики chance adjusted index: мы точность нашего решения (Accuracy) пронормируем с помощью точности, которую можно было получить случайно (Accuracychance). Под случайной здесь понимаем точность решения, которое получено из нашего случайной перестановкой ответов.
здесь красным выделена вероятность угадать класс 0, а синим – класс 1. Действительно, класс k угадывается, если алгоритм выдаёт метку k и объект действительно принадлежит этому классу. Предполагаем, что это независимые события (мы же хотим вычислить случайную точность). Вероятность принадлежности к классу k можно оценить по матрице несоответствий как долю объектов класса k. Аналогично, вероятность выдать метку оцениваем как долю таких меток в ответах построенного алгоритма.
Сбалансированная точность (Balanced Accuracy)
В случае дисбаланса классов есть специальный аналог точности – сбалансированная точность:
Для простоты запоминания – это среднее полноты всех классов (мы ещё вернёмся к этому определению), ну или в других терминах: среднее чувствительности (Sensitivity) и специфичности (Specificity). Отметим, что чувствительность и специфичность тоже, неформально говоря, «ортогональные критерии». Легко сделать специфичность 100%-й, отнеся все объекты к классу 0, при этом будет 0%-я чувствительность, и наоборот, если отнести все объекты к классу 1, то будет 0%-я специфичность и 100%-я чувствительность.
Если в бинарной задаче классификации представителей двух классов примерно поровну, то TP + FN ≈ TN + FP ≈ m/2 и сбалансированная точность примерно равна точности обычной (Accuracy).
Все указанные функционалы реализованы в библиотеке scikit-learn:
Сравнение функционалов
Рассмотрим модельную задачу, в которой плотности распределения классов на оценках, порождённых алгоритмом, линейные, см. рис. 7 (алгоритм выдаёт оценки принадлежности к классу 1 из отрезка [0, 1], именно на этом отрезке они линейные). На рис. 7 показана конечная небольшая выборка, которая соответствует изображённым плотностям, мы же будем считать, что выборка бесконечная, поскольку плотности простые и позволяют в явном виде вычислить функционалы качества даже в случае такой бесконечной выборки. Будем считать, что классы равновероятны, т.е. наша бесконечная выборка сбалансирована. Выбранная задача очень удобна для исследования и уже использовалась при анализе функционала AUC ROC.
Заметим, что подобные распределения возникают в задаче, показанной на рис. 8 (объекты лежат внутри квадрата [0, 1]×[0, 1], два класса разделяются диагональю квадрата), если алгоритм в качестве оценки выдаст значения первого признака.
Изобразив плотности немного по-другому, мы в явном виде можем вычислить элементы матрицы несоответствий при конкретном пороге бинаризации, см. рис. 9. Все они пропорциональны площадям выделенных зон (обратите внимание на масштаб осей):
Теперь можно вывести формулы для рассмотренных функционалов качества как функции от порога бинаризации:
Попробуйте вывести эти формулы сами, кроме того, попробуйте определить пороги бинаризации при которых указанные функционалы максимальны (здесь будет один сюрприз).
Возникает естественный вопрос: на практике у нас нет бесконечных выборок, что изменится, если мы вычислим значения функционалов на конечной, объекты которой сгенерированы в соответствии с указанными распределениями? Частично ответ на этот вопрос показан на рис. 10. Как видно, кривые довольно близки к теоретическим при m=300, при увеличении выборки в 10 раз практически совпадают.
Рассмотрим теперь графики наших функционалов качества как функций от порога бинаризации, см. рис. 11. Заметим, что кроме F1-меры все они симметричны относительно порога 0.5, но это вполне логично. Теперь рассмотрим ситуацию неравновероятных классов, т.е. когда выборка несбалансированна. На рис. 12 показаны графики функционалов в случае, когда класс 1 в два раза чаще встречается в выборке, чем класс 0. Обратите внимание, что все графики стали несимметричными, кроме графика сбалансированной точности – эта функция не зависит от пропорций классов!
Вопросы для самопроверки
В конце серия вопросов с подвохом… если Вы хотите кого-нибудь «завалить» по простой теме «оценка качества в задачах бинарной классификации», то непременно задайте их:
- у какого функционала качества самый маленький оптимальный порог бинаризации в общем случае, почему? Для справки: ответ «у F1-меры» в общем случае неверный (можно даже простой пример привести).
- какой функционал качества действительно имеет смысл использовать в задачах с сильным дисбалансом классов (заметим, что стандартные советы: BA, MCC, κ, F1 обладают совершенно разными свойствами)?
- какой «самый неустойчивый» из перечисленных функционалов (его значения на небольших выборках сильнее отличаются от вычисленных на достаточно больших)?
- что изменится в примерах выше, если от линейных плотностей перейти к нормальным? Как это сделать корректно (и в чём некорректность описанной модельной задачи)?
- верно ли, что максимальное значение точности (т.е. значение точности при оптимальном выборе порога) всегда не меньше максимального значения сбалансированной точности?
Что дальше…
По задачам классификации осталось рассказать про все скоринговые функции оценки качества в задачах бинарной классификации, про AUC ROC и LogLoss уже было. А потом — как все рассмотренные функционалы обобщаются на случай многих классов. Соответствующие посты скоро будут.
Традиционное в последнее время видео к материалу поста я залью чуть позже.
На правах рекламы
С сентября чему-то научиться у автора блога можно в этом замечательном проекте: Ozon Masters. Кроме курса по машинному обучению, будет много других с потрясающими преподавателями: Андрей Соболевский, Иван Оселедец, Павел Клеменков, Юрий Дорн, Александр Дайняк.
From Wikipedia, the free encyclopedia
Sources: Fawcett (2006),[1] Piryonesi and El-Diraby (2020),[2] |
The evaluation of binary classifiers compares two methods of assigning a binary attribute, one of which is usually a standard method and the other is being investigated. There are many metrics that can be used to measure the performance of a classifier or predictor; different fields have different preferences for specific metrics due to different goals. For example, in medicine sensitivity and specificity are often used, while in computer science precision and recall are preferred. An important distinction is between metrics that are independent on the prevalence (how often each category occurs in the population), and metrics that depend on the prevalence – both types are useful, but they have very different properties.
Contingency table[edit]
Given a data set, a classification (the output of a classifier on that set) gives two numbers: the number of positives and the number of negatives, which add up to the total size of the set. To evaluate a classifier, one compares its output to another reference classification – ideally a perfect classification, but in practice the output of another gold standard test – and cross tabulates the data into a 2×2 contingency table, comparing the two classifications. One then evaluates the classifier relative to the gold standard by computing summary statistics of these 4 numbers. Generally these statistics will be scale invariant (scaling all the numbers by the same factor does not change the output), to make them independent of population size, which is achieved by using ratios of homogeneous functions, most simply homogeneous linear or homogeneous quadratic functions.
Say we test some people for the presence of a disease. Some of these people have the disease, and our test correctly says they are positive. They are called true positives (TP). Some have the disease, but the test incorrectly claims they don’t. They are called false negatives (FN). Some don’t have the disease, and the test says they don’t – true negatives (TN). Finally, there might be healthy people who have a positive test result – false positives (FP). These can be arranged into a 2×2 contingency table (confusion matrix), conventionally with the test result on the vertical axis and the actual condition on the horizontal axis.
These numbers can then be totaled, yielding both a grand total and marginal totals. Totaling the entire table, the number of true positives, false negatives, true negatives, and false positives add up to 100% of the set. Totaling the columns (adding vertically) the number of true positives and false positives add up to 100% of the test positives, and likewise for negatives. Totaling the rows (adding horizontally), the number of true positives and false negatives add up to 100% of the condition positives (conversely for negatives). The basic marginal ratio statistics are obtained by dividing the 2×2=4 values in the table by the marginal totals (either rows or columns), yielding 2 auxiliary 2×2 tables, for a total of 8 ratios. These ratios come in 4 complementary pairs, each pair summing to 1, and so each of these derived 2×2 tables can be summarized as a pair of 2 numbers, together with their complements. Further statistics can be obtained by taking ratios of these ratios, ratios of ratios, or more complicated functions.
The contingency table and the most common derived ratios are summarized below; see sequel for details.
| Predicted condition | Sources: [10][11][12][13][14][15][16][17][18]
|
||||
| Total population = P + N |
Positive (PP) | Negative (PN) | Informedness, bookmaker informedness (BM) = TPR + TNR − 1 |
Prevalence threshold (PT) = 
|
|
|
Actual condition |
Positive (P) | True positive (TP), hit |
False negative (FN), type II error, miss, underestimation |
True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = TP/P = 1 − FNR |
False negative rate (FNR), miss rate = FN/P = 1 − TPR |
| Negative (N) | False positive (FP), type I error, false alarm, overestimation |
True negative (TN), correct rejection |
False positive rate (FPR), probability of false alarm, fall-out = FP/N = 1 − TNR |
True negative rate (TNR), specificity (SPC), selectivity = TN/N = 1 − FPR |
|
| Prevalence = P/P + N |
Positive predictive value (PPV), precision = TP/PP = 1 − FDR |
False omission rate (FOR) = FN/PN = 1 − NPV |
Positive likelihood ratio (LR+) = TPR/FPR |
Negative likelihood ratio (LR−) = FNR/TNR |
|
| Accuracy (ACC) = TP + TN/P + N | False discovery rate (FDR) = FP/PP = 1 − PPV |
Negative predictive value (NPV) = TN/PN = 1 − FOR | Markedness (MK), deltaP (Δp) = PPV + NPV − 1 |
Diagnostic odds ratio (DOR) = LR+/LR− | |
| Balanced accuracy (BA) = TPR + TNR/2 | F1 score = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN |
Fowlkes–Mallows index (FM) = 
|
Matthews correlation coefficient (MCC) =  
|
Threat score (TS), critical success index (CSI), Jaccard index = TP/TP + FN + FP |
Note that the rows correspond to the condition actually being positive or negative (or classified as such by the gold standard), as indicated by the color-coding, and the associated statistics are prevalence-independent, while the columns correspond to the test being positive or negative, and the associated statistics are prevalence-dependent. There are analogous likelihood ratios for prediction values, but these are less commonly used, and not depicted above.
Sensitivity and specificity[edit]
The fundamental prevalence-independent statistics are sensitivity and specificity.
Sensitivity or True Positive Rate (TPR), also known as recall, is the proportion of people that tested positive and are positive (True Positive, TP) of all the people that actually are positive (Condition Positive, CP = TP + FN). It can be seen as the probability that the test is positive given that the patient is sick. With higher sensitivity, fewer actual cases of disease go undetected (or, in the case of the factory quality control, fewer faulty products go to the market).
Specificity (SPC) or True Negative Rate (TNR) is the proportion of people that tested negative and are negative (True Negative, TN) of all the people that actually are negative (Condition Negative, CN = TN + FP). As with sensitivity, it can be looked at as the probability that the test result is negative given that the patient is not sick. With higher specificity, fewer healthy people are labeled as sick (or, in the factory case, fewer good products are discarded).
The relationship between sensitivity and specificity, as well as the performance of the classifier, can be visualized and studied using the Receiver Operating Characteristic (ROC) curve.
In theory, sensitivity and specificity are independent in the sense that it is possible to achieve 100% in both (such as in the red/blue ball example given above). In more practical, less contrived instances, however, there is usually a trade-off, such that they are inversely proportional to one another to some extent. This is because we rarely measure the actual thing we would like to classify; rather, we generally measure an indicator of the thing we would like to classify, referred to as a surrogate marker. The reason why 100% is achievable in the ball example is because redness and blueness is determined by directly detecting redness and blueness. However, indicators are sometimes compromised, such as when non-indicators mimic indicators or when indicators are time-dependent, only becoming evident after a certain lag time. The following example of a pregnancy test will make use of such an indicator.
Modern pregnancy tests do not use the pregnancy itself to determine pregnancy status; rather, human chorionic gonadotropin is used, or hCG, present in the urine of gravid females, as a surrogate marker to indicate that a woman is pregnant. Because hCG can also be produced by a tumor, the specificity of modern pregnancy tests cannot be 100% (because false positives are possible). Also, because hCG is present in the urine in such small concentrations after fertilization and early embryogenesis, the sensitivity of modern pregnancy tests cannot be 100% (because false negatives are possible).
Likelihood ratios[edit]
|
This section is empty. You can help by adding to it. (July 2014) |
Positive and negative predictive values[edit]
In addition to sensitivity and specificity, the performance of a binary classification test can be measured with positive predictive value (PPV), also known as precision, and negative predictive value (NPV). The positive prediction value answers the question «If the test result is positive, how well does that predict an actual presence of disease?». It is calculated as TP/(TP + FP); that is, it is the proportion of true positives out of all positive results. The negative prediction value is the same, but for negatives, naturally.
Impact of prevalence on prediction values[edit]
Prevalence has a significant impact on prediction values. As an example, suppose there is a test for a disease with 99% sensitivity and 99% specificity. If 2000 people are tested and the prevalence (in the sample) is 50%, 1000 of them are sick and 1000 of them are healthy. Thus about 990 true positives and 990 true negatives are likely, with 10 false positives and 10 false negatives. The positive and negative prediction values would be 99%, so there can be high confidence in the result.
However, if the prevalence is only 5%, so of the 2000 people only 100 are really sick, then the prediction values change significantly. The likely result is 99 true positives, 1 false negative, 1881 true negatives and 19 false positives. Of the 19+99 people tested positive, only 99 really have the disease – that means, intuitively, that given that a patient’s test result is positive, there is only 84% chance that they really have the disease. On the other hand, given that the patient’s test result is negative, there is only 1 chance in 1882, or 0.05% probability, that the patient has the disease despite the test result.
Likelihood ratios[edit]
|
This section is empty. You can help by adding to it. (July 2014) |
Precision and recall[edit]
|
This section is empty. You can help by adding to it. (July 2014) |
Precision and recall can be interpreted as (estimated) conditional probabilities:
Precision is given by 



Both quantities are therefore connected by Bayes’ theorem.
Relationships[edit]
There are various relationships between these ratios.
If the prevalence, sensitivity, and specificity are known, the positive predictive value can be obtained from the following identity:
If the prevalence, sensitivity, and specificity are known, the negative predictive value can be obtained from the following identity:
Single metrics[edit]
In addition to the paired metrics, there are also single metrics that give a single number to evaluate the test.
Perhaps the simplest statistic is accuracy or fraction correct (FC), which measures the fraction of all instances that are correctly categorized; it is the ratio of the number of correct classifications to the total number of correct or incorrect classifications: (TP + TN)/total population = (TP + TN)/(TP + TN + FP + FN). As such, it compares estimates of pre- and post-test probability. This measure is prevalence-dependent. If 90% of people with COVID symptoms don’t have COVID, the prior probability P(-) is 0.9, and the simple rule «Classify all such patients as COVID-free.» would be 90% accurate. Diagnosis should be better than that. One can construct a «One-proportion z-test» with p0 as max(priors) = max(P(-),P(+)) for a diagnostic method hoping to beat a simple rule using the most likely outcome. Here, the hypotheses are «Ho: p ≤ 0.9 vs. Ha: p > 0.9», rejecting Ho for large values of z. One diagnostic rule could be compared to another if the other’s accuracy is known and substituted for p0 in calculating the z statistic. If not known and calculated from data, an accuracy comparison test could be made using «Two-proportion z-test, pooled for Ho: p1 = p2». Not used very much is the complementary statistic, the fraction incorrect (FiC): FC + FiC = 1, or (FP + FN)/(TP + TN + FP + FN) – this is the sum of the antidiagonal, divided by the total population. Cost-weighted fractions incorrect could compare expected costs of misclassification for different methods.
The diagnostic odds ratio (DOR) can be a more useful overall metric, which can be defined directly as (TP×TN)/(FP×FN) = (TP/FN)/(FP/TN), or indirectly as a ratio of ratio of ratios (ratio of likelihood ratios, which are themselves ratios of true rates or prediction values). This has a useful interpretation – as an odds ratio – and is prevalence-independent. Likelihood ratio is generally considered to be prevalence-independent and is easily interpreted as the multiplier to turn prior probabilities into posterior probabilities. Another useful single measure is «area under the ROC curve», AUC.
Alternative metrics[edit]
An F-score is a combination of the precision and the recall, providing a single score. There is a one-parameter family of statistics, with parameter β, which determines the relative weights of precision and recall. The traditional or balanced F-score (F1 score) is the harmonic mean of precision and recall:
.
F-scores do not take the true negative rate into account and, therefore, are more suited to information retrieval and information extraction evaluation where the true negatives are innumerable. Instead, measures such as the phi coefficient, Matthews correlation coefficient, informedness or Cohen’s kappa may be preferable to assess the performance of a binary classifier.[20][21] As a correlation coefficient, the Matthews correlation coefficient is the geometric mean of the regression coefficients of the problem and its dual. The component regression coefficients of the Matthews correlation coefficient are markedness (deltap) and informedness (Youden’s J statistic or deltap’).[22]
See also[edit]
- Population impact measures
- Attributable risk
- Attributable risk percent
- Scoring rule (for probability predictions)
References[edit]
- ^ Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512.
- ^ Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
- ^ Chicco D.; Jurman G. (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^ Chicco D.; Toetsch N.; Jurman G. (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
- ^ Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
- ^ Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215.
- ^
Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215. - ^
Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. - ^
Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512. - ^
Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. - ^
Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8. - ^
Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17. - ^
Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477. - ^
Chicco D, Toetsch N, Jurman G (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410. - ^
Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003. - ^ Information Retrieval Models, Thomas Roelleke, ISBN 9783031023286, page 76, https://www.google.de/books/edition/Information_Retrieval_Models/YX9yEAAAQBAJ?hl=de&gbpv=1&pg=PA76&printsec=frontcover
- ^ Powers, David M W (2011). «Evaluation: From Precision, Recall and F-Score to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. hdl:2328/27165.
- ^ Powers, David M. W. (2012). «The Problem with Kappa» (PDF). Conference of the European Chapter of the Association for Computational Linguistics (EACL2012) Joint ROBUS-UNSUP Workshop. Archived from the original (PDF) on 2016-05-18. Retrieved 2012-07-20.
- ^ Perruchet, P.; Peereman, R. (2004). «The exploitation of distributional information in syllable processing». J. Neurolinguistics. 17 (2–3): 97–119. doi:10.1016/S0911-6044(03)00059-9. S2CID 17104364.
From Wikipedia, the free encyclopedia
Sources: Fawcett (2006),[1] Piryonesi and El-Diraby (2020),[2] |
The evaluation of binary classifiers compares two methods of assigning a binary attribute, one of which is usually a standard method and the other is being investigated. There are many metrics that can be used to measure the performance of a classifier or predictor; different fields have different preferences for specific metrics due to different goals. For example, in medicine sensitivity and specificity are often used, while in computer science precision and recall are preferred. An important distinction is between metrics that are independent on the prevalence (how often each category occurs in the population), and metrics that depend on the prevalence – both types are useful, but they have very different properties.
Contingency table[edit]
Given a data set, a classification (the output of a classifier on that set) gives two numbers: the number of positives and the number of negatives, which add up to the total size of the set. To evaluate a classifier, one compares its output to another reference classification – ideally a perfect classification, but in practice the output of another gold standard test – and cross tabulates the data into a 2×2 contingency table, comparing the two classifications. One then evaluates the classifier relative to the gold standard by computing summary statistics of these 4 numbers. Generally these statistics will be scale invariant (scaling all the numbers by the same factor does not change the output), to make them independent of population size, which is achieved by using ratios of homogeneous functions, most simply homogeneous linear or homogeneous quadratic functions.
Say we test some people for the presence of a disease. Some of these people have the disease, and our test correctly says they are positive. They are called true positives (TP). Some have the disease, but the test incorrectly claims they don’t. They are called false negatives (FN). Some don’t have the disease, and the test says they don’t – true negatives (TN). Finally, there might be healthy people who have a positive test result – false positives (FP). These can be arranged into a 2×2 contingency table (confusion matrix), conventionally with the test result on the vertical axis and the actual condition on the horizontal axis.
These numbers can then be totaled, yielding both a grand total and marginal totals. Totaling the entire table, the number of true positives, false negatives, true negatives, and false positives add up to 100% of the set. Totaling the columns (adding vertically) the number of true positives and false positives add up to 100% of the test positives, and likewise for negatives. Totaling the rows (adding horizontally), the number of true positives and false negatives add up to 100% of the condition positives (conversely for negatives). The basic marginal ratio statistics are obtained by dividing the 2×2=4 values in the table by the marginal totals (either rows or columns), yielding 2 auxiliary 2×2 tables, for a total of 8 ratios. These ratios come in 4 complementary pairs, each pair summing to 1, and so each of these derived 2×2 tables can be summarized as a pair of 2 numbers, together with their complements. Further statistics can be obtained by taking ratios of these ratios, ratios of ratios, or more complicated functions.
The contingency table and the most common derived ratios are summarized below; see sequel for details.
| Predicted condition | Sources: [10][11][12][13][14][15][16][17][18]
|
||||
| Total population = P + N |
Positive (PP) | Negative (PN) | Informedness, bookmaker informedness (BM) = TPR + TNR − 1 |
Prevalence threshold (PT) = 
|
|
|
Actual condition |
Positive (P) | True positive (TP), hit |
False negative (FN), type II error, miss, underestimation |
True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = TP/P = 1 − FNR |
False negative rate (FNR), miss rate = FN/P = 1 − TPR |
| Negative (N) | False positive (FP), type I error, false alarm, overestimation |
True negative (TN), correct rejection |
False positive rate (FPR), probability of false alarm, fall-out = FP/N = 1 − TNR |
True negative rate (TNR), specificity (SPC), selectivity = TN/N = 1 − FPR |
|
| Prevalence = P/P + N |
Positive predictive value (PPV), precision = TP/PP = 1 − FDR |
False omission rate (FOR) = FN/PN = 1 − NPV |
Positive likelihood ratio (LR+) = TPR/FPR |
Negative likelihood ratio (LR−) = FNR/TNR |
|
| Accuracy (ACC) = TP + TN/P + N | False discovery rate (FDR) = FP/PP = 1 − PPV |
Negative predictive value (NPV) = TN/PN = 1 − FOR | Markedness (MK), deltaP (Δp) = PPV + NPV − 1 |
Diagnostic odds ratio (DOR) = LR+/LR− | |
| Balanced accuracy (BA) = TPR + TNR/2 | F1 score = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN |
Fowlkes–Mallows index (FM) = 
|
Matthews correlation coefficient (MCC) =  
|
Threat score (TS), critical success index (CSI), Jaccard index = TP/TP + FN + FP |
Note that the rows correspond to the condition actually being positive or negative (or classified as such by the gold standard), as indicated by the color-coding, and the associated statistics are prevalence-independent, while the columns correspond to the test being positive or negative, and the associated statistics are prevalence-dependent. There are analogous likelihood ratios for prediction values, but these are less commonly used, and not depicted above.
Sensitivity and specificity[edit]
The fundamental prevalence-independent statistics are sensitivity and specificity.
Sensitivity or True Positive Rate (TPR), also known as recall, is the proportion of people that tested positive and are positive (True Positive, TP) of all the people that actually are positive (Condition Positive, CP = TP + FN). It can be seen as the probability that the test is positive given that the patient is sick. With higher sensitivity, fewer actual cases of disease go undetected (or, in the case of the factory quality control, fewer faulty products go to the market).
Specificity (SPC) or True Negative Rate (TNR) is the proportion of people that tested negative and are negative (True Negative, TN) of all the people that actually are negative (Condition Negative, CN = TN + FP). As with sensitivity, it can be looked at as the probability that the test result is negative given that the patient is not sick. With higher specificity, fewer healthy people are labeled as sick (or, in the factory case, fewer good products are discarded).
The relationship between sensitivity and specificity, as well as the performance of the classifier, can be visualized and studied using the Receiver Operating Characteristic (ROC) curve.
In theory, sensitivity and specificity are independent in the sense that it is possible to achieve 100% in both (such as in the red/blue ball example given above). In more practical, less contrived instances, however, there is usually a trade-off, such that they are inversely proportional to one another to some extent. This is because we rarely measure the actual thing we would like to classify; rather, we generally measure an indicator of the thing we would like to classify, referred to as a surrogate marker. The reason why 100% is achievable in the ball example is because redness and blueness is determined by directly detecting redness and blueness. However, indicators are sometimes compromised, such as when non-indicators mimic indicators or when indicators are time-dependent, only becoming evident after a certain lag time. The following example of a pregnancy test will make use of such an indicator.
Modern pregnancy tests do not use the pregnancy itself to determine pregnancy status; rather, human chorionic gonadotropin is used, or hCG, present in the urine of gravid females, as a surrogate marker to indicate that a woman is pregnant. Because hCG can also be produced by a tumor, the specificity of modern pregnancy tests cannot be 100% (because false positives are possible). Also, because hCG is present in the urine in such small concentrations after fertilization and early embryogenesis, the sensitivity of modern pregnancy tests cannot be 100% (because false negatives are possible).
Likelihood ratios[edit]
|
This section is empty. You can help by adding to it. (July 2014) |
Positive and negative predictive values[edit]
In addition to sensitivity and specificity, the performance of a binary classification test can be measured with positive predictive value (PPV), also known as precision, and negative predictive value (NPV). The positive prediction value answers the question «If the test result is positive, how well does that predict an actual presence of disease?». It is calculated as TP/(TP + FP); that is, it is the proportion of true positives out of all positive results. The negative prediction value is the same, but for negatives, naturally.
Impact of prevalence on prediction values[edit]
Prevalence has a significant impact on prediction values. As an example, suppose there is a test for a disease with 99% sensitivity and 99% specificity. If 2000 people are tested and the prevalence (in the sample) is 50%, 1000 of them are sick and 1000 of them are healthy. Thus about 990 true positives and 990 true negatives are likely, with 10 false positives and 10 false negatives. The positive and negative prediction values would be 99%, so there can be high confidence in the result.
However, if the prevalence is only 5%, so of the 2000 people only 100 are really sick, then the prediction values change significantly. The likely result is 99 true positives, 1 false negative, 1881 true negatives and 19 false positives. Of the 19+99 people tested positive, only 99 really have the disease – that means, intuitively, that given that a patient’s test result is positive, there is only 84% chance that they really have the disease. On the other hand, given that the patient’s test result is negative, there is only 1 chance in 1882, or 0.05% probability, that the patient has the disease despite the test result.
Likelihood ratios[edit]
|
This section is empty. You can help by adding to it. (July 2014) |
Precision and recall[edit]
|
This section is empty. You can help by adding to it. (July 2014) |
Precision and recall can be interpreted as (estimated) conditional probabilities:
Precision is given by 



Both quantities are therefore connected by Bayes’ theorem.
Relationships[edit]
There are various relationships between these ratios.
If the prevalence, sensitivity, and specificity are known, the positive predictive value can be obtained from the following identity:
If the prevalence, sensitivity, and specificity are known, the negative predictive value can be obtained from the following identity:
Single metrics[edit]
In addition to the paired metrics, there are also single metrics that give a single number to evaluate the test.
Perhaps the simplest statistic is accuracy or fraction correct (FC), which measures the fraction of all instances that are correctly categorized; it is the ratio of the number of correct classifications to the total number of correct or incorrect classifications: (TP + TN)/total population = (TP + TN)/(TP + TN + FP + FN). As such, it compares estimates of pre- and post-test probability. This measure is prevalence-dependent. If 90% of people with COVID symptoms don’t have COVID, the prior probability P(-) is 0.9, and the simple rule «Classify all such patients as COVID-free.» would be 90% accurate. Diagnosis should be better than that. One can construct a «One-proportion z-test» with p0 as max(priors) = max(P(-),P(+)) for a diagnostic method hoping to beat a simple rule using the most likely outcome. Here, the hypotheses are «Ho: p ≤ 0.9 vs. Ha: p > 0.9», rejecting Ho for large values of z. One diagnostic rule could be compared to another if the other’s accuracy is known and substituted for p0 in calculating the z statistic. If not known and calculated from data, an accuracy comparison test could be made using «Two-proportion z-test, pooled for Ho: p1 = p2». Not used very much is the complementary statistic, the fraction incorrect (FiC): FC + FiC = 1, or (FP + FN)/(TP + TN + FP + FN) – this is the sum of the antidiagonal, divided by the total population. Cost-weighted fractions incorrect could compare expected costs of misclassification for different methods.
The diagnostic odds ratio (DOR) can be a more useful overall metric, which can be defined directly as (TP×TN)/(FP×FN) = (TP/FN)/(FP/TN), or indirectly as a ratio of ratio of ratios (ratio of likelihood ratios, which are themselves ratios of true rates or prediction values). This has a useful interpretation – as an odds ratio – and is prevalence-independent. Likelihood ratio is generally considered to be prevalence-independent and is easily interpreted as the multiplier to turn prior probabilities into posterior probabilities. Another useful single measure is «area under the ROC curve», AUC.
Alternative metrics[edit]
An F-score is a combination of the precision and the recall, providing a single score. There is a one-parameter family of statistics, with parameter β, which determines the relative weights of precision and recall. The traditional or balanced F-score (F1 score) is the harmonic mean of precision and recall:
.
F-scores do not take the true negative rate into account and, therefore, are more suited to information retrieval and information extraction evaluation where the true negatives are innumerable. Instead, measures such as the phi coefficient, Matthews correlation coefficient, informedness or Cohen’s kappa may be preferable to assess the performance of a binary classifier.[20][21] As a correlation coefficient, the Matthews correlation coefficient is the geometric mean of the regression coefficients of the problem and its dual. The component regression coefficients of the Matthews correlation coefficient are markedness (deltap) and informedness (Youden’s J statistic or deltap’).[22]
See also[edit]
- Population impact measures
- Attributable risk
- Attributable risk percent
- Scoring rule (for probability predictions)
References[edit]
- ^ Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512.
- ^ Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
- ^ Chicco D.; Jurman G. (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^ Chicco D.; Toetsch N.; Jurman G. (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
- ^ Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
- ^ Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215.
- ^
Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215. - ^
Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. - ^
Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512. - ^
Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. - ^
Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8. - ^
Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17. - ^
Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477. - ^
Chicco D, Toetsch N, Jurman G (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410. - ^
Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003. - ^ Information Retrieval Models, Thomas Roelleke, ISBN 9783031023286, page 76, https://www.google.de/books/edition/Information_Retrieval_Models/YX9yEAAAQBAJ?hl=de&gbpv=1&pg=PA76&printsec=frontcover
- ^ Powers, David M W (2011). «Evaluation: From Precision, Recall and F-Score to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. hdl:2328/27165.
- ^ Powers, David M. W. (2012). «The Problem with Kappa» (PDF). Conference of the European Chapter of the Association for Computational Linguistics (EACL2012) Joint ROBUS-UNSUP Workshop. Archived from the original (PDF) on 2016-05-18. Retrieved 2012-07-20.
- ^ Perruchet, P.; Peereman, R. (2004). «The exploitation of distributional information in syllable processing». J. Neurolinguistics. 17 (2–3): 97–119. doi:10.1016/S0911-6044(03)00059-9. S2CID 17104364.
Источники: Fawcett (2006), [1] Piryonesi and El-Diraby (2020), [2] |
Из матрицы неточностей можно вывести четыре основных показателя
Оценка бинарных классификаторов сравнивает два методы присвоения двоичного атрибута, один из которых, как правило , стандартный метод , а другие расследуются. Есть много показателей, которые можно использовать для измерения производительности классификатора или предиктора; разные поля имеют разные предпочтения для конкретных показателей из-за разных целей. Например, в медицине часто используются чувствительность и специфичность , а в информатике предпочтительны точность и отзыв . Важное различие между метриками, которые не зависят от распространенности (как часто каждая категория встречается в популяции), и метриками, которые зависят от распространенности — оба типа полезны, но имеют очень разные свойства.
Таблица непредвиденных обстоятельств
Для данного набора данных классификация (результат работы классификатора этого набора) дает два числа: количество положительных результатов и количество отрицательных результатов, которые в сумме составляют общий размер набора. Чтобы оценить классификатор, один сравнивает его выходные данные с другой эталонной классификацией — в идеале — идеальной классификацией, но на практике — с результатами другого теста золотого стандарта — и перекрестно табулирует данные в таблицу непредвиденных обстоятельств 2 × 2 , сравнивая две классификации. Затем оценивают классификатор относительно золотого стандарта, вычисляя сводную статистику этих 4 чисел. Как правило, эта статистика не зависит от масштаба.(масштабирование всех чисел одним и тем же коэффициентом не влияет на результат), чтобы сделать их независимыми от размера популяции, что достигается за счет использования соотношений однородных функций , наиболее просто однородных линейных или однородных квадратичных функций.
Допустим, мы проверяем некоторых людей на наличие болезни. Некоторые из этих людей болеют болезнью, и наш тест правильно говорит, что они положительные. Их называют истинно положительными (TP). У некоторых есть болезнь, но тест ошибочно утверждает, что это не так. Их называют ложноотрицательными (ЛО). У некоторых нет болезни, и тест говорит, что нет — истинно отрицательные (TN). Наконец, могут быть здоровые люди с положительным результатом теста — ложноположительными (ЛП). Их можно упорядочить в таблицу непредвиденных обстоятельств 2 × 2 ( матрица неточностей ), условно с результатом теста по вертикальной оси и фактическим состоянием по горизонтальной оси.
Затем эти числа можно суммировать, получая как общий итог, так и предельные итоги.. Суммируя всю таблицу, количество истинных положительных, ложно отрицательных, истинных отрицательных и ложных срабатываний составляет в сумме 100% от набора. Суммируя столбцы (складывая по вертикали), количество истинных положительных и ложных положительных результатов составляет 100% от положительных результатов теста, а также для отрицательных результатов. Суммируя строки (складывая по горизонтали), количество истинных положительных и ложных отрицательных результатов составляет в сумме 100% положительных результатов условия (и наоборот для отрицательных результатов). Базовая статистика предельного отношения получается путем деления значений 2 × 2 = 4 в таблице на предельные итоги (строки или столбцы), что дает 2 вспомогательные таблицы 2 × 2, всего 8 соотношений. Эти отношения представлены в 4 дополнительных парах, каждая пара в сумме равна 1, и поэтому каждую из этих производных таблиц 2 × 2 можно суммировать как пару из 2 чисел вместе с их дополнениями.Дополнительную статистику можно получить, взяв отношения этих отношений, отношения отношений или более сложные функции.
Таблица непредвиденных обстоятельств и наиболее распространенные производные коэффициенты приведены ниже; подробности см. в продолжении.
| Прогнозируемое состояние | Источники: [9] [10] [11] [12] [13] [14] [15] [16] »
|
||||
| Общая численность населения = P + N |
Положительный (PP) | Отрицательный (PN) | Информированность, информированность букмекеров (BM) = TPR + TNR — 1 |
Порог распространенности (PT) =√ TPR × FPR — FPR/TPR — FPR |
|
|
Фактическое состояние |
Положительный (P) | Истинно положительный (TP), хит |
Ложноотрицательный (FN), ошибка типа II , промах, недооценка |
Уровень истинных положительных результатов (TPR), отзыв , чувствительность (SEN), вероятность обнаружения, частота совпадений, мощность =TP/п = 1 — FNR |
Частота ложноотрицательных результатов (FNR), частота промахов =FN/п = 1 — TPR |
| Отрицательный (N) | Ложное срабатывание (FP), ошибка типа I , ложная тревога, завышение |
Истинно отрицательный (TN), правильный отказ |
Частота ложных срабатываний (FPR), вероятность ложной тревоги, выпадение =FP/N = 1 — TNR |
Истинно отрицательная скорость (TNR), специфичность (SPC), селективность =TN/N = 1 — FPR |
|
| Распространенность =п/P + N |
Положительная прогностическая ценность (PPV), точность =TP/ПП = 1 — FDR |
Коэффициент ложных пропусков (FOR) =FN/PN = 1 — ЧПС |
Отношение положительного правдоподобия (LR +) =TPR/FPR |
Отрицательное отношение правдоподобия (LR−) =FNR/TNR |
|
| Точность (ACC) =TP + TN/P + N | Коэффициент ложного обнаружения (FDR) =FP/ПП = 1 — PPV |
Отрицательная прогностическая ценность (NPV) =TN/PN = 1 — ДЛЯ | Маркированность (МК), deltaP (Δp) = PPV + NPV — 1 |
Отношение диагностических шансов (DOR) =LR +/LR− | |
| Сбалансированная точность (BA) =TPR + TNR/2 | F 1 балл =2 PPV × TPR/PPV + TPR знак равно 2 TP/2 TP + FP + FN |
Индекс Фаулкса – Маллоуса (FM) = √ PPV × TPR | Коэффициент корреляции Мэтьюза (MCC) = √ TPR × TNR × PPV × NPV — √ FNR × FPR × FOR × FDR |
Оценка угрозы (TS), индекс критического успеха (CSI), индекс Жаккара =TP/TP + FN + FP |
Обратите внимание , что строки соответствуют условию на самом деле быть положительным или отрицательным (или классифицирован как таковой золотого стандарта), как указано цветокодирующей, и связанные с ними статистические данные распространенности независимые, а столбцы соответствуют тест быть положительным или отрицательный, и соответствующая статистика зависит от распространенности. Существуют аналогичные отношения правдоподобия для значений прогноза, но они используются реже и не показаны выше.
Чувствительность и специфичность
Основными статистическими данными, не зависящими от распространенности, являются чувствительность и специфичность .
Чувствительность или истинно положительный показатель (TPR), также известный как отзыв , — это доля людей, которые дали положительный результат и были положительными (True Positive, TP), от всех людей, которые действительно положительны (положительное состояние, CP = TP + FN). Его можно рассматривать как вероятность того, что тест будет положительным, учитывая, что пациент болен . Чем выше чувствительность, тем меньше фактических случаев заболевания остается незамеченным (или, в случае заводского контроля качества, на рынок поступает меньше бракованной продукции).
Специфичность (SPC) или истинно отрицательный показатель (TNR) — это доля людей, у которых тесты были отрицательными и были отрицательными (True Negative, TN), среди всех людей, которые на самом деле были отрицательными (Condition Negative, CN = TN + FP). Как и в случае с чувствительностью, это можно рассматривать как вероятность того, что результат теста будет отрицательным, при условии, что пациент не болен . Чем выше специфичность, тем меньше здоровых людей маркируются как больные (или, в случае фабрики, меньше хороших продуктов выбрасывается).
Взаимосвязь между чувствительностью и специфичностью, а также производительность классификатора можно визуализировать и изучить с помощью кривой рабочих характеристик приемника (ROC).
Теоретически чувствительность и специфичность независимы в том смысле, что можно достичь 100% в обоих случаях (например, в примере с красным / синим шаром, приведенном выше). Однако в более практичных, менее надуманных случаях обычно приходится идти на компромисс, так что они в некоторой степени обратно пропорциональны друг другу. Это потому, что мы редко измеряем то, что хотим классифицировать; скорее, мы обычно измеряем показатель того, что мы хотели бы классифицировать, называемый суррогатным маркером.. Причина, по которой в примере с мячом достижимо 100%, заключается в том, что покраснение и голубизна определяются путем непосредственного определения покраснения и синевы. Однако индикаторы иногда подвергаются риску, например, когда индикаторы имитируют индикаторы или индикаторы зависят от времени и становятся очевидными только после определенного времени задержки. В следующем примере теста на беременность будет использоваться такой индикатор.
Современные тесты на беременность не используют саму беременность для определения статуса беременности; скорее, используется хорионический гонадотропин человека или ХГЧ, присутствующий в моче беременных женщин, в качестве суррогатного маркера, указывающего на то, что женщина беременна. Поскольку ХГЧ также может вырабатываться опухолью , специфичность современных тестов на беременность не может быть 100% (поскольку возможны ложноположительные результаты). Кроме того, поскольку ХГЧ присутствует в моче в таких небольших концентрациях после оплодотворения и раннего эмбриогенеза , чувствительность современных тестов на беременность не может быть 100% (поскольку возможны ложноотрицательные результаты).
Коэффициенты правдоподобия
Положительные и отрицательные прогнозные значения
Помимо чувствительности и специфичности, эффективность теста бинарной классификации может быть измерена с помощью положительной прогностической ценности (PPV), также известной как точность , и отрицательной прогностической ценности (NPV). Положительное значение прогноза отвечает на вопрос: «Если результат теста положительный , насколько хорошо это предсказывает фактическое наличие болезни?». Рассчитывается как TP / (TP + FP); то есть это доля истинных положительных результатов от всех положительных результатов. Значение отрицательного прогноза такое же, но, естественно, для отрицательных.
Влияние распространенности на значения прогнозов
Распространенность оказывает значительное влияние на значения прогнозов. В качестве примера предположим, что существует тест на заболевание с чувствительностью 99% и специфичностью 99%. Если обследовано 2000 человек и распространенность (в выборке) составляет 50%, то 1000 из них больны и 1000 здоровы. Таким образом, вероятны около 990 истинных положительных результатов и 990 истинно отрицательных результатов, из которых 10 ложноположительных и 10 ложноотрицательных. Положительные и отрицательные значения прогноза будут составлять 99%, поэтому результат может быть высоким.
Однако, если распространенность составляет всего 5%, то есть из 2000 человек действительно болеют только 100, то значения прогнозов значительно изменятся. Вероятный результат — 99 истинных положительных результатов, 1 ложный отрицательный результат, 1881 истинно отрицательный результат и 19 ложных положительных результатов. Из 19 + 99 человек с положительным результатом теста только 99 действительно болеют — это интуитивно означает, что, учитывая положительный результат теста пациента, вероятность того, что он действительно болен, составляет всего 84%. С другой стороны, учитывая, что результат теста пациента отрицательный, существует только 1 шанс из 1882 или 0,05% вероятности, что у пациента есть болезнь, несмотря на результат теста.
Коэффициенты правдоподобия
Точность и отзыв
Отношения
Между этими соотношениями существуют различные отношения.
Если распространенность, чувствительность и специфичность известны, положительная прогностическая ценность может быть получена из следующих данных:
Если распространенность, чувствительность и специфичность известны, отрицательная прогностическая ценность может быть получена из следующих данных:
Единые показатели
Помимо парных показателей, существуют также отдельные показатели, которые дают единое число для оценки теста.
Возможно, самая простая статистика — это точность или правильная доля (FC), которая измеряет долю всех экземпляров, которые правильно классифицированы; это отношение количества правильных классификаций к общему количеству правильных или неправильных классификаций: (TP + TN) / общая популяция = (TP + TN) / (TP + TN + FP + FN). Таким образом, он сравнивает оценки вероятности до и после тестирования . Этот показатель зависит от распространенности . Если 90% людей с симптомами COVID не болеют COVID, априорная вероятность P (-) равна 0,9 и простое правило «Классифицируйте всех таких пациентов как больных без COVID». будет на 90% точным. Диагноз должен быть лучше. Можно построить «однопропорциональный z-тест»с p0 как max (priors) = max (P (-), P (+)) для диагностического метода, который надеется превзойти простое правило, используя наиболее вероятный результат. Здесь гипотезы: «Ho: p ≤ 0,9 против Ha: p> 0,9», отвергая Ho при больших значениях z. Одно диагностическое правило можно сравнить с другим, если точность другого известна и вместо p0 при вычислении статистики z. Если это неизвестно и не рассчитано на основе данных, можно провести сравнительный тест точности с использованием «двухпропорционального z-критерия, объединенного для Ho: p1 = p2» . Не очень часто используется дополнительная статистика, неправильная дробь (FiC): FC + FiC = 1 или (FP + FN) / (TP + TN + FP + FN) — это сумма антидиагонали , деленная на всего населения.Неверные дроби, взвешенные по стоимости, можно сравнить с ожидаемыми затраты на неправильную классификацию для разных методов.
Отношение шансов диагностики (DOR) может быть более полезным общим показателем, который может быть определен непосредственно как (TP × TN) / (FP × FN) = (TP / FN) / (FP / TN) или косвенно как отношение отношения отношений (отношения отношений правдоподобия, которые сами по себе являются отношениями истинных показателей или значений прогноза). Это имеет полезную интерпретацию — как отношение шансов — и не зависит от распространенности. Обычно считается, что отношение правдоподобия не зависит от распространенности и легко интерпретируется как множитель, превращающий априорные вероятности в апостериорные . Еще одна полезная единичная мера — это «площадь под кривой ROC», AUC .
Альтернативные показатели
Оценка F — это комбинация точности и отзывчивости , дающая единую оценку. Существует однопараметрическое семейство статистических данных с параметром β, который определяет относительный вес точности и отзыва. Традиционная или сбалансированная оценка F (оценка F1 ) — это гармоническое среднее значение точности и запоминания:
- .
F-баллы не принимают во внимание истинную отрицательную норму и, следовательно, больше подходят для поиска информации и оценки извлечения информации, где истинные отрицательные значения бесчисленны. Вместо этого, такие меры, как фи коэффициента , коэффициента корреляции Matthews , информированности или каппа Коэна может быть предпочтительным , чтобы оценить производительность бинарного классификатора. [17] [18] В качестве коэффициента корреляции , коэффициент корреляции Мэттьюз является геометрическое среднее из коэффициентов регрессии задачи и ее двойного. Составные коэффициенты регрессии коэффициента корреляции Matthews являются отмеченность (deltap) и информированность ( Youden в J статистики или deltap ‘). [19]
См. Также
- Меры воздействия на население
- Приписываемый риск
- Приписываемый риск в процентах
- Правило подсчета очков (для вероятностных прогнозов)
Ссылки
- ^ Фосетт, Том (2006). «Введение в анализ ROC» (PDF) . Письма о распознавании образов . 27 (8): 861–874. DOI : 10.1016 / j.patrec.2005.10.010 .
- ^ Пирьонеси С. Мадех; Эль-Дираби Тамер Э. (01.03.2020). «Аналитика данных в управлении активами: рентабельное прогнозирование индекса состояния дорожного покрытия». Журнал инфраструктурных систем . 26 (1): 04019036. doi : 10.1061 / (ASCE) IS.1943-555X.0000512 .
- ^ Пауэрс, Дэвид МВ (2011). «Оценка: от точности, отзыва и F-меры к ROC, информированности, значимости и корреляции» . Журнал технологий машинного обучения . 2 (1): 37–63.
- Перейти ↑ Ting, Kai Ming (2011). Саммут, Клод; Уэбб, Джеффри И. (ред.). Энциклопедия машинного обучения . Springer. DOI : 10.1007 / 978-0-387-30164-8 . ISBN 978-0-387-30164-8.
- ^ Брукс, Гарольд; Браун, Барб; Эберт, Бет; Ферро, Крис; Джоллифф, Ян; Ко, Тие-Йонг; Роббер, Пол; Стивенсон, Дэвид (26 января 2015 г.). «Совместная рабочая группа ВПМИ / РГЧЭ по исследованиям для проверки прогнозов» . Сотрудничество в области исследований погоды и климата Австралии . Всемирная метеорологическая организация . Проверено 17 июля 2019 .
- ^ Chicco D .; Юрман Г. (январь 2020 г.). «Преимущества коэффициента корреляции Мэтьюза (MCC) над оценкой F1 и точность оценки бинарной классификации» . BMC Genomics . 21 (1): 6-1–6-13. DOI : 10,1186 / s12864-019-6413-7 . PMC 6941312 . PMID 31898477 .
- ^ Chicco D .; Toetsch N .; Юрман Г. (февраль 2021 г.). «Коэффициент корреляции Мэтьюза (MCC) более надежен, чем сбалансированная точность, информированность букмекеров и заметность при оценке двухклассовой матрицы путаницы» . BioData Mining . 14 (13): 1-22. DOI : 10.1186 / s13040-021-00244-Z . PMC 7863449 . PMID 33541410 .
- ^ Tharwat А. (август 2018). «Классификационные методы оценки» . Прикладные вычисления и информатика . DOI : 10.1016 / j.aci.2018.08.003 .
- ^ Фосетт, Том (2006). «Введение в анализ ROC» (PDF) . Письма о распознавании образов . 27 (8): 861–874. DOI : 10.1016 / j.patrec.2005.10.010 .
- ^ Пирьонеси С. Мадех; Эль-Дираби Тамер Э. (01.03.2020). «Аналитика данных в управлении активами: рентабельное прогнозирование индекса состояния дорожного покрытия». Журнал инфраструктурных систем . 26 (1): 04019036. doi : 10.1061 / (ASCE) IS.1943-555X.0000512 .
- ^ Пауэрс, Дэвид МВ (2011). «Оценка: от точности, отзыва и F-меры к ROC, информированности, значимости и корреляции» . Журнал технологий машинного обучения . 2 (1): 37–63.
- Перейти ↑ Ting, Kai Ming (2011). Саммут, Клод; Уэбб, Джеффри И. (ред.). Энциклопедия машинного обучения . Springer. DOI : 10.1007 / 978-0-387-30164-8 . ISBN
978-0-387-30164-8. - ^ Брукс, Гарольд; Браун, Барб; Эберт, Бет; Ферро, Крис; Джоллифф, Ян; Ко, Тие-Йонг; Роббер, Пол; Стивенсон, Дэвид (26 января 2015 г.). «Совместная рабочая группа ВПМИ / РГЧЭ по исследованиям для проверки прогнозов» . Сотрудничество в области исследований погоды и климата Австралии . Всемирная метеорологическая организация . Проверено 17 июля 2019 .
- ^ Chicco D, Jurman G (январь 2020). «Преимущества коэффициента корреляции Мэтьюза (MCC) над оценкой F1 и точность оценки бинарной классификации» . BMC Genomics . 21 (1): 6-1–6-13. DOI : 10,1186 / s12864-019-6413-7 . PMC 6941312 . PMID 31898477 .
- ^ Chicco D, Toetsch N, Jurman G (февраль 2021 г.). «Коэффициент корреляции Мэтьюза (MCC) более надежен, чем сбалансированная точность, информированность букмекеров и заметность при оценке двухклассовой матрицы путаницы» . BioData Mining . 14 (13): 1-22. DOI : 10.1186 / s13040-021-00244-Z . PMC 7863449 . PMID 33541410 .
- ^ Tharwat А. (август 2018). «Классификационные методы оценки» . Прикладные вычисления и информатика . DOI : 10.1016 / j.aci.2018.08.003 .
- ^ Пауэрс, Дэвид МВ (2011). «Оценка: от точности, запоминания и оценки F до ROC, информированности, значимости и корреляции». Журнал технологий машинного обучения . 2 (1): 37–63. hdl : 2328/27165 .
- ^ Пауэрс, Дэвид МВ (2012). «Проблема с каппой» (PDF) . Конференция Европейского отделения Ассоциации компьютерной лингвистики (EACL2012) Совместный семинар ROBUS-UNSUP . Архивировано из оригинального (PDF) 18 мая 2016 года . Проверено 20 июля 2012 .
- ^ Perruchet, P .; Переман, Р. (2004). «Использование распределительной информации при обработке слогов». J. Нейролингвистика . 17 (2–3): 97–119. DOI : 10.1016 / S0911-6044 (03) 00059-9 . S2CID 17104364 .
Учитывая совокупность, члены которой принадлежат к одному из нескольких различных наборов или классов, a Правило классификации или классификатор — это процедура, с помощью которой каждый элемент совокупности предсказывается как принадлежащий к одному из классов. Совершенная классификация — это такая, при которой каждый элемент в генеральной совокупности отнесен к классу, к которому он действительно принадлежит. Несовершенная классификация — это класс, в котором появляются некоторые ошибки, и затем для анализа классификации должен применяться статистический анализ.
Особый вид правил классификации — это двоичная классификация, для задач, в которых есть только два класса.
Содержание
- 1 Правила классификации тестирования
- 2 Бинарная и мультиклассовая классификация
- 3 Таблица ошибок
- 3.1 Ложные срабатывания
- 3.2 Ложноотрицательные результаты
- 3.3 Рабочий пример
- 4 Измерение a классификатор с чувствительностью и специфичностью
- 5 См. также
- 6 Примечания
- 7 Ссылки
Правила классификации тестирования
Дан набор данных, состоящий из пар x и y, где x обозначает элемент совокупность и y класс, к которому он принадлежит, правило классификации h (x) — это функция, которая присваивает каждому элементу x предсказанный класс y ^ = h (x). { displaystyle { hat {y}} = h (x).}
Истинные метки y i могут быть известны, но не обязательно будут соответствовать их приближениям yi ^ = h (xi) { displaystyle { hat {y_ {i}}} = h (x_ {i})}
Некоторые правила классификации являются статическими функциями. Другие могут быть компьютерными программами. Компьютерный классификатор может изучать или реализовывать правила статической классификации. Для обучающего набора данных истинные метки y j неизвестны, но основной целью для процедуры классификации является то, что приближение yj ^ = h (xj) ≈ yj { displaystyle { hat {y_ {j}}} = h (x_ {j}) приблизительно y_ {j}}
Учитывая правило классификации, тест классификации является результатом применения правила к конечной выборке начального набора данных.
Бинарная и мультиклассовая классификация
Классификация может рассматриваться как две отдельные проблемы — двоичная классификация и мультиклассовая классификация. В бинарной классификации, более понятной задаче, задействованы только два класса, тогда как мультиклассовая классификация включает отнесение объекта к одному из нескольких классов. Поскольку многие методы классификации были разработаны специально для двоичной классификации, многоклассовая классификация часто требует комбинированного использования нескольких двоичных классификаторов. Важным моментом является то, что во многих практических задачах бинарной классификации эти две группы не являются симметричными — интерес представляет не общая точность, а относительная доля различных типов ошибок. Например, при медицинском тестировании ложноположительный результат (обнаружение болезни, когда ее нет) рассматривается иначе, чем ложноотрицательный (не обнаружение болезни, когда она присутствует). В мультиклассовых классификациях классы могут рассматриваться симметрично (все ошибки эквивалентны) или асимметрично, что значительно сложнее.
Методы двоичной классификации включают пробит-регрессию и логистическую регрессию. Методы многоклассовой классификации включают полиномиальный пробит и полиномиальный логит.
Таблица смешения

Если функция классификации не идеальна, будут отображаться ложные результаты. В приведенном ниже примере матрицы путаницы для 8 настоящих кошек функция предсказала, что три были собаками, а из шести собак она предсказала, что одна была кроликом, а две — кошками. Из матрицы видно, что рассматриваемая система не умеет различать кошек и собак, но может довольно хорошо различать кроликов и других видов животных.
| Прогноз | ||||
|---|---|---|---|---|
| Кот | Собака | Кролик | ||
| Фактический | Кот | 5 | 3 | 0 |
| Собака | 2 | 3 | 1 | |
| Кролик | 0 | 2 | 11 |
Ложные срабатывания
Ложные срабатывания результат, когда тест ложно (неверно) сообщает о положительном результате. Например, медицинский тест на заболевание может дать положительный результат, указывающий на то, что у пациента есть болезнь, даже если у пациента нет болезни. Мы можем использовать теорему Байеса, чтобы определить вероятность того, что положительный результат на самом деле является ложноположительным. Мы обнаружили, что если заболевание встречается редко, то большинство положительных результатов могут быть ложноположительными, даже если тест относительно точен.
Предположим, что тест на болезнь дает следующие результаты:
- Если тестируемый пациент болен, тест дает положительный результат в 99% случаев или с вероятностью 0,99
- Если у протестированного пациента нет заболевания, тест дает положительный результат в 5% случаев или с вероятностью 0,05.
Наивно можно подумать, что только 5% положительных результатов теста являются ложными, но это не так. совершенно неверно, как мы увидим.
Предположим, что только 0,1% населения страдает этим заболеванием, так что случайным образом выбранный пациент имеет априорную вероятность заболевания 0,001.
Мы можем использовать теорему Байеса, чтобы вычислить вероятность того, что положительный результат теста является ложноположительным.
Пусть A представляет состояние, при котором пациент болен, а B представляет свидетельство положительного результата теста. Тогда вероятность того, что у пациента действительно есть заболевание при положительном результате теста, равна
- P (A | B) = P (B | A) P (A) P (B | A) P (A) + P ( B | ¬ A) P (¬ A) = 0,99 × 0,001 0,99 × 0,001 + 0,05 × 0,999 ≈ 0,019. { Displaystyle { begin {align} P (A | B) = { frac {P (B | A) P (A)} {P (B | A) P (A) + P (B | neg A) P ( neg A)}} \\ = { frac {0.99 times 0,001} {0,99 times 0,001 + 0,05 times 0,999}} \ ~ \ приблизительно 0,019. End { выровнено}}}
и, следовательно, вероятность того, что положительный результат будет ложноположительным, составляет примерно 1 — 0,019 = 0,98, или 98%.
Несмотря на кажущуюся высокую точность теста, заболеваемость настолько мала, что подавляющее большинство пациентов с положительным результатом теста не болеют. Тем не менее, доля пациентов с положительным результатом теста, у которых действительно есть заболевание (0,019), в 19 раз превышает долю людей, которые еще не прошли тест и у которых есть болезнь (0,001). Таким образом, тест не бесполезен, а повторное тестирование может повысить надежность результата.
Чтобы уменьшить проблему ложных срабатываний, тест должен очень точно сообщать об отрицательном результате, когда у пациента нет заболевания. Если тест показал отрицательный результат у пациентов без заболевания с вероятностью 0,999, то
- P (A | B) = 0,99 × 0,001 0,99 × 0,001 + 0,001 × 0,999 ≈ 0,5, { displaystyle P (A | B) = { frac {0.99 times 0.001} {0.99 times 0.001 + 0.001 times 0.999}} приблизительно 0,5,}
, так что теперь 1 — 0,5 = 0,5 — это вероятность ложного срабатывания.
Ложноотрицательные
С другой стороны, ложноотрицательные возникают, когда тест ложно или неправильно сообщает об отрицательном результате. Например, медицинский тест на заболевание может дать отрицательный результат, указывающий на то, что у пациента нет болезни, даже если у пациента действительно есть болезнь. Мы также можем использовать теорему Байеса для вычисления вероятности ложноотрицательного результата. В первом примере выше
- P (A | ¬ B) = P (¬ B | A) P (A) P (¬ B | A) P (A) + P (¬ B | ¬ A) P ( ¬ A) = 0,01 × 0,001 0,01 × 0,001 + 0,95 × 0,999 ≈ 0,0000105. { Displaystyle { begin {выровнен} P (A | neg B) = { frac {P ( neg B | A) P (A)} {P ( neg B | A) P (A) + P ( neg B | neg A) P ( neg A)}} \\ = { frac {0,01 times 0,001} {0,01 times 0,001 + 0,95 times 0,999}} \ ~ \ приблизительно 0,0000105. end {align}}}
Вероятность того, что отрицательный результат будет ложноотрицательным, составляет около 0,0000105 или 0,00105%. Если заболевание встречается редко, ложноотрицательные результаты не будут большой проблемой.
Но если бы 60% населения болело, то вероятность ложноотрицательного результата была бы выше. С помощью вышеуказанного теста вероятность ложноотрицательного результата будет
- P (A | ¬ B) = P (¬ B | A) P (A) P (¬ B | A) P (A) + P (¬ B | ¬ A) P (¬ A) = 0,01 × 0,6 0,01 × 0,6 + 0,95 × 0,4 ≈ 0,0155. { Displaystyle { begin {выровнен} P (A | neg B) = { frac {P ( neg B | A) P (A)} {P ( neg B | A) P (A) + P ( neg B | neg A) P ( neg A)}} \\ = { frac {0,01 times 0,6} {0,01 times 0,6 + 0,95 times 0,4}} \ ~ \ приблизительно 0,0155. end {align}}}
Вероятность того, что отрицательный результат является ложноотрицательным, возрастает до 0,0155 или 1,55%.
Рабочий пример
- view
- talk
- Рабочий пример
- Диагностический тест с чувствительностью 67% и специфичностью 91% применяется к 2030 людям для поиска расстройства распространенность в популяции 1,48%
| Пациенты с раком кишечника. (подтверждено эндоскопией ) | |||||
| Положительное состояние | Отрицательное состояние | Распространенность = (TP + FN) / Total_Population. = (20 + 10) / 2030. ≈ 1,48% | Точность (ACC) = (TP + TN) / Total_Population. = (20 + 1820) / 2030. ≈ 90,64% | ||
| Кал. скрытая. кровь. экран. тест. результат | Тест. результат. положительный | Истинно положительный . (TP) = 20. (2030 x 1,48% x 67%) | ложноположительный . (FP) = 180. (2030 x (100 — 1,48%) x (100 — 91%)) | Прогнозное положительное значение (PPV), Точность = TP / (TP + FP). = 20 / (20 + 180). = 10% | Уровень ложного обнаружения (FDR) = FP / (TP + FP). = 180 / (20 + 180). = 90,0% |
| Тест. результат. отрицательный Активный | Ложноотрицательный . (FN) = 10. (2030 x 1,48% x (100-67%)) | Истинно отрицательный . (TN) = 1820. (2030 x (100 -1,48%) x 91%) | Коэффициент ложных пропусков (FOR) = FN / (FN + TN). = 10 / (10 + 1820). ≈ 0,55% | Прогнозируемое отрицательное значение (NPV) = TN / (FN + TN). = 1820 / (10 + 1820). ≈ 99,45 % | |
| TPR, Вызов, Чувствительность = TP / (TP + FN). = 20 / (20 + 10). ≈ 66,7% | Частота ложных срабатываний (FPR), выпадение, вероятность ложной тревоги = FP / (FP + TN). = 180 / ( 180 + 1820). = 9,0% | Отношение положительного правдоподобия (LR +) = TPR / FPR. = (20/30) / (180/2000). ≈ 7,41 | Отношение шансов диагностики (DOR) = LR + / LR−. ≈ 20,2 | F1оценка = 2 · Точность · Отзыв / Точность + Отзыв. ≈ 0,174 | |
| Частота ложных отрицательных результатов (FNR), Частота промахов. = FN / (TP + FN). = 10 / (20 + 10). ≈ 33,3% | Специфичность, Избирательность, Истинно отрицательная скорость (TNR) = TN / ( FP + TN). = 1820 / (180 + 1820). = 91% | Отрицательное отношение правдоподобия (LR-) = FNR / TNR. = (10 /30)/(1820/2000). ≈0.366 |
Связанные вычисления
- Частота ложных срабатываний (α) = ошибка I типа = 1 — специфичность = FP / (FP + TN) = 180 / (180 + 1820) = 9%
- Уровень ложных отрицательных результатов (β) = ошибка типа II = 1 — чувствительность = FN / (TP + FN) = 10 / (20 + 10) = 33%
- Мощность = чувствительность = 1 — β
- Отношение правдоподобия положительное = чувствительность / (1 — специфичность) = 0,67 / (1 — 0,91) = 7,4
- Отрицательное отношение правдоподобия = (1 — чувствительность) / специфичность = (1 — 0,67) / 0,91 = 0,37
- Порог распространенности = PT = TPR (- TNR + 1) + TNR — 1 (TPR + TNR — 1) { displaystyle PT = { frac {{ sqrt {TPR (-TNR + 1)}} + TNR-1} {(TPR + TNR-1)}}}
= 0,19 =>19,1%
Этот гипотетический скрининговый тест (анализ кала на скрытую кровь) правильно идентифицировал две трети (66,7%) пациентов с колоректальным раком. К сожалению, учет показателей распространенности показывает, что этот гипотетический тест имеет высокий уровень ложноположительных результатов и не позволяет надежно идентифицировать рак прямой кишки в общей популяции бессимптомных людей (PPV = 10%).
С другой стороны, этот гипотетический тест демонстрирует очень точное определение людей, свободных от рака (NPV = 99,5%). Таким образом, при использовании для рутинного скрининга колоректального рака у бессимптомных взрослых отрицательный результат дает важные данные для пациента и врача, такие как исключение рака как причины желудочно-кишечных симптомов или успокаивание пациентов, обеспокоенных развитием колоректального рака.
Измерение чувствительности и специфичности классификатора
При обучении классификатора можно захотеть измерить его производительность, используя общепринятые показатели чувствительности и специфичности. Может быть поучительно сравнить классификатор со случайным классификатором, который подбрасывает монетку в зависимости от распространенности заболевания. Предположим, что вероятность того, что человек болен, равна p { displaystyle p}



Вероятность истинно положительного результата — это вероятность того, что у пациента есть заболевание, умноженная на вероятность того, что случайный классификатор угадает это правильно, или p 2 { displaystyle p ^ {2}}



Итак, хотя сам показатель не зависит от распространенности заболевания, эффективность этого случайного классификатора зависит от распространенности заболевания. Классификатор может иметь производительность, аналогичную этому случайному классификатору, но с более взвешенной монетой (более высокая чувствительность и специфичность). Таким образом, на эти показатели может влиять распространенность заболевания. Альтернативным показателем эффективности является коэффициент корреляции Мэтьюза, для которого любой случайный классификатор получит средний балл 0.
Распространение этой концепции на небинарные классификации дает матрица путаницы.
См. также
- Байесовский классификатор
- Байесовский вывод
- Двоичная классификация
- Правило принятия решения
- Диагностический тест
- Золотой стандарт (тест)
- Функции потерь для классификации
- Медицинский тест
- Чувствительность и специфичность
- Статистическая классификация

























































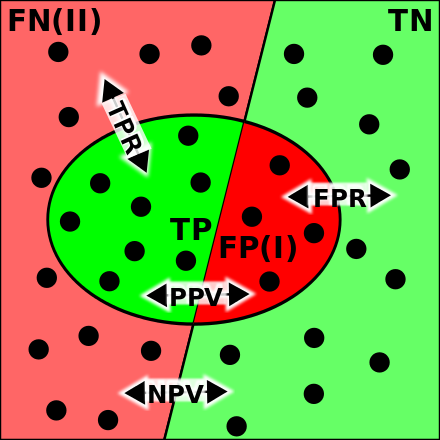




 = 0,19 =>19,1%
= 0,19 =>19,1%