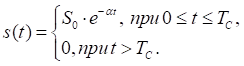Ошибка квантования теорема котельникова

1. Схема системы передачи
   информации

Каналом
передачи информации является совокупность
средств, используемых для этой цели.

Радиотехническим
каналом связи называется канал передачи
информации с помощью электромагнитных
колебаний.

Устройство,
преобразующее информацию в электромагнитное
высокочастотное колебание (радиосигнал),
называется радиопередатчиком, а
устройство, преобразующее принятый
радиосигнал в информацию – радиоприемником.
При прохождении радиосигнала от
передатчика к приемнику по среде
распространения (провод, волновод,
свободное пространство) его параметры
могут изменяться, в том числе и под
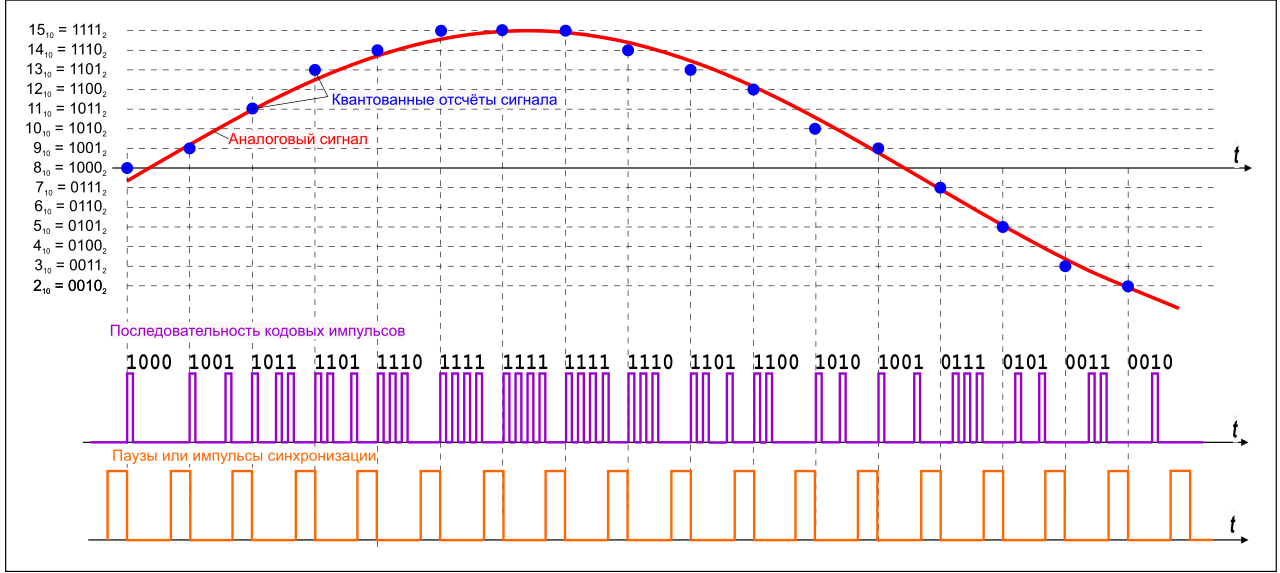
влиянием различного рода помех. На рис.1
показана обобщенная блок-схема система
передачи информации, из которой видно,
что помехи могут оказывать влияние не
только на сигнал, сформированный
передатчиком, но и на сигнал, обрабатываемый
приемником.

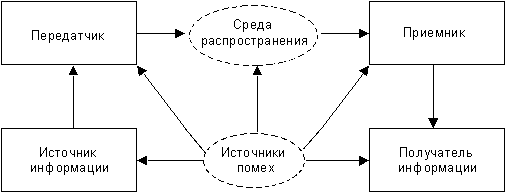
Рис.
1

В
радиотехнической системе сигналы
подвергаются различным преобразованиям.
Некоторые из них являются обязательными
для всех систем, независимо от назначения
и характера передаваемой информации.

Передаваемый
по каналу связи сигнал подвергается
воздействию помех. Источниками внешних
помех являются атмосферные явления,
шумы космического пространства,
индустриальные помехи, помехи других
каналов связи и пр.

Внутренние
помехи возникают вследствие дискретной
природы заряженных частиц, а также из-за
несовершенства аппаратуры.

Под
действием помех сигнал, проходя через
канал связи, искажается. Поэтому одной
из задач при организации канала связи
является повышение помехоустойчивости
канала.

Для
увеличения потока информации, передаваемого
одним каналом связи, применяют частотное
или временнОе разделение каналов в
одной линии связи. При частотном
разделении каналов одно несущее колебание
используется для передачи нескольких
заранее промодулированных разными
частотами сообщений. Эти частоты
называются поднесущими. В приемнике
радиосигнал детектируется, разделяется
фильтрами, и каждый канал затем еще раз
детектируется, выделяя свое низкочастотное
сообщение.

При
временном разделении каналов сообщения
поочередно модулируют несущее колебание
независимо от назначения и характера
передаваемой информации.

1. Теорема Котельникова

Теоре́ма
Коте́льникова (в
англоязычной литературе — теорема
Найквиста — Шеннона или
теорема отсчётов) гласит, что,
если аналоговый
сигнал 
 имеет
финитный (ограниченный по ширине) спектр,
то он может быть восстановлен однозначно
и без потерь по своим дискретным отсчётам,
взятым с частотой строго большей’
удвоенной верхней частоты 
:

Такая
трактовка рассматривает идеальный
случай, когда сигнал начался бесконечно
давно и никогда не закончится, а также
не имеет во временно́й характеристике точек
разрыва.
Именно это подразумевает понятие
«спектр, ограниченный частотой 
».

Разумеется,
реальные сигналы (например, звук на
цифровом носителе) не обладают такими
свойствами, так как они конечны по
времени и, обычно, имеют во временно́й
характеристике разрывы. Соответственно,
их спектр бесконечен. В таком случае
полное восстановление сигнала невозможно
и из теоремы Котельникова вытекают 2
следствия:

• Любой
  аналоговый сигнал может быть восстановлен
  с какой угодно точностью по своим
  дискретным отсчётам, взятым с частотой 
  ,
  где 
   —
  максимальная частота, которой ограничен
  спектр реального сигнала.

• Если
  максимальная частота в сигнале превышает
  половину частоты
  дискретизации,
  то способа восстановить сигнал из
  дискретного в аналоговый без искажений
  не существует.

Говоря
шире, теорема Котельникова утверждает,
что непрерывный сигнал 
 можно
представить в виде интерполяционного
ряда

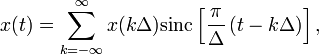
где 
 —
функция sinc.
Интервал дискретизации удовлетворяет
ограничениям 
 Мгновенные
значения данного ряда есть дискретные
отсчёты сигнала 
.

1. Дискретизация и квантование

В
последнее время в технике идет переход
на цифровые методы обработки информации.
Это связано с тем, что цифровую информацию
легче хранить (появились дешевые и
удобные устройства для хранения
информации, такие как жесткие диски
компьютеров или лазерные диски), а также
с тем, что цифровую информацию легко
передавать по современным линиям связи
практически без потерь.

Аналоговый
сигнал — это в простейшем случае число 
,
зависящее от времени 
.
При записи на носитель информации или
воспроизведении с него сигнал неизбежно
искажается различного рода шумами.
Восстановить искаженный сигнал (убрать
шумы) нельзя. Можно, конечно, пытаться
подавлять шумы, используя некоторую
дополнительную информацию (например,
можно подавлять частоты, в которых
сосредоточены шумы), но при этом мы
теряем также и информацию о самом
сигнале, т.е. опять же вносим искажения.

При
оцифровке сигнала 
 производятся
две операции — дискретизация и квантование.
Дискретизация — это замена сигнала x(t)
с непрерывным временем 
 на
дискретизованный сигнал — последовательность
чисел 
 для
дискретного набора моментов времени 
, 
,
…, 
,
…(чаще всего интервалы между моментами
времени 
 берутся
одинаковыми). При дискретизации, конечно,
часть информации о сигнале теряется.
Но если сигнал 
 за
время 
 не
сильно изменяется, числа 
 и 
 близки
друг к другу, то поведение 
 между
временами 
 и 
 нетрудно
восстановить (сигнал практически линейно
изменяется во времени от 
 до 
).
При дискретизации мы теряем частотные
составляющие сигнала с частотами
порядка 
 и
выше.

При
дискретизации время из аналогового как
бы становится цифровым — моменты
времени 
 можно
нумеровать, кодировать. Производится
замена непрерывного времени t на нечто,
которое может принимать не все значения,
а только некоторые, а именно 
, 
,
…, 
,
… Квантование сигнала — это нечто
похожее, только данная процедура
производится не со временем, а со
значением сигнала x. Выбирается некий
набор возможных значение сигнала 
, 
,
…, 
,
… и каждому 
 сопоставляется
ближайшее число из этого набора.

Приведем
конкретный пример дискретизации и
квантования:

Пусть
сигнал 
 такой,
что 
,
шаг дискретизации 
 (т.е.
набор моментов времени 
),
значение сигнала 
 мы
будем записывать с точностью до одной
сотой (т.е. набор значений сигнала 
).
После дискретизации сигнала получим

	=	0.	0.3162…	0.4472…	0.5477…	0.6324…	…
	=	0	0.1	0.2	0.3	0.4	…

Учитывая
точность хранения значений x, после
квантования получаем

	=	0.	0.32…	0.45…	0.55…	0.63…	…
	=	0	0.1	0.2	0.3	0.4	…

При
дискретизации мы теряем высокие ( 
)
частоты сигнала, при квантовании мы
теряем маленькие (меньше 
)
изменения сигнала. Кроме того, получившийся
после квантования сигнал 
 отличается
от реального (но уже дискретизованного)
сигнала 
 на
величину порядка шага квантования (или
кванта) 
.
Это различие носит название шума
квантования, и оно принципиально
неустранимо.

Для
примера, описанного выше, имеем

	=	0.	0.3162…	0.4472…	0.5477…	0.6324…	…
	=	0.	0.32…	0.45…	0.55…	0.63…	…
	=	0	0.1	0.2	0.3	0.4	…
шум квантования		0.	0.00377	0.00279	0.00228	0.00246	…

Иногда,
чтобы внести в сигнал минимальные
искажения, квантование делают так, что
интервалы 
 делают
неравными (нелинейное квантование).
Например, часто делают 
 маленьким
при малом значении сигнала, чтобы
относительная погрешность (шум
квантования/сигнал) не становилась
очень большой при малых 
.
Например, принимают 
,
где 
 —
маленькое число (так называемое
логарифмическое квантование). Нелинейное
квантование позволяет получить при
приемлемой точности хранения сигнала
большой динамический диапазон (отношение
максимального значения сигнала к
минимальному или к величине кванта).

Перевод
аналогового сигнала в цифровой выполняется
специальными устройствами —
аналогово-цифровыми преобразователями
(АЦП). Основными параметрами АЦП являются
частота дискретизации 
 ( 
)
и разрядность АЦП (количество двоичных
разрядов, в которых хранится значение
сигнала 
,
число возможных значений квантованного
сигнала равно 
,
где 
 —
число разрядов). Чем выше разрядность
АЦП, с тем большей точностью можно
хранить сигнал (
 мало),
но тем медленнее он работает (больше 
).

Устройство,
производящее обратную операцию (чтобы
передать оцифрованный сигнал на
какое-нибудь воспроизводящее устройство
(динамик, телевизор, приводной мотор и
т.д.)) называется цифро-аналоговым
преобразователем (ЦАП). Принципиальные
схемы АЦП и ЦАП следует искать в книжках
по радиоэлектронике (о принципах работы
некоторых схем смотри в [1]).

Приведем
для справки параметры известного
стандарта CD: частота дискретизации 
,
линейное квантование, 16 двоичных
разрядов.

Цифровую
информацию можно передать по линии
связи практически без потерь. При
передаче сигнал сначала превращается
в аналоговый, пересылается, после чего
опять оцифровывается. Если линия связи
вносит искажения в сигнал меньше чем
шаг квантования, то после передачи и
оцифровки полученный оцифрованный
сигнал не будет отличаться от начального.
Обычно же информация передается с
помощью двоичных импульсов, т.е. для
восстановления сигнала необходимо лишь
решать, передали 1 или 0. При передаче
двоичной информации по линии связи
естественно слегка смещается время
прибытия импульса, но если смещение
меньше расстояния между импульсами, то
место импульса в общей последовательности
легко восстанавливается. Дополнительную
защиту дает применение кодов с устранением
ошибок (коды Хэмминга, Рида-Соломона и
др.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

3.1. Теорема Котельникова

3.2. Спектр дискретного сигнала

3.3. Аналого-цифровое и цифро-аналоговое преобразование сигналов

3.1. Теорема Котельникова

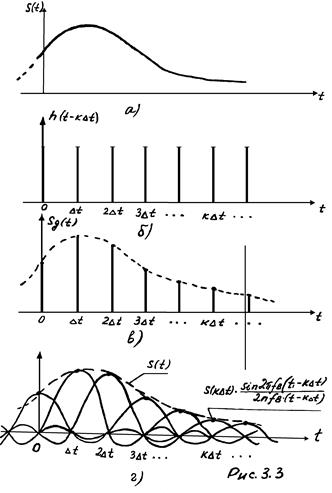
Передача непрерывных (аналоговых) сигналов по линии связи предполагает передачу бесконечного множества их мгновенных значений на протяжении конечного промежутка времени. При этом спектр финитного, т.е. ограниченного во времени, непрерывного сигнала бесконечен. Однако, на практике различные радиотехнические устройства (фильтры, усилители и другие) имеют ограниченную полосу пропускания, что приводит к ограничению спектра сигнала некоторой граничной частотой  (или ), которая определяется свойствами получателя сообщений. Так например, общепринятой нормой в системах передачи речевых сигналов является ограничение спектра сигнала в пределах , в системах телевидения – . Как преодолеть противоречие между ограничением спектра сигнала и конечным временем его существования? Ответ на этот вопрос даёт теорема, сформулированная и доказанная академиком В.А. Котельниковым и получившая название теоремы Котельникова или теоремы отсчётов.

Теорема Котельникова формулируется следующим образом. Непрерывный сигнал , ограниченный по спектру частотой  (или), полностью определяется совокупностью мгновенных значений (отсчётов)  в моменты времени , отстоящие друг от друга на интервал времени  .

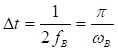
Математически теорема Котельникова определяется выражением

,         (3.1)

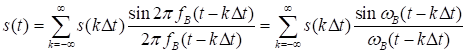
или с учётом (2.12)

,     (3.2)

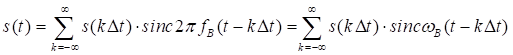
которое представляет собой разложение сигнала  в особого рода ряд по системе базисных функций

,

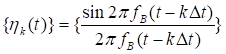
являющихся ортогональными на интервале времени  (сравните с разложением сигнала в ряд Фурье).

Доказательство теоремы Котельникова приведено в литературе  [1]. Мы же остановимся на вопросах физического толкования и практического применения результатов теоремы.

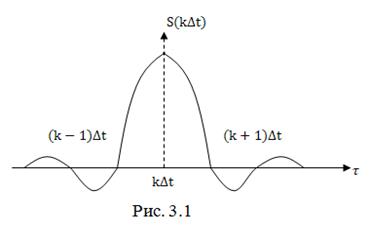
Выделим одно из слагаемых ряда (3.1)

.                            3.3)

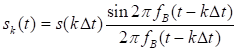
Это слагаемое представляет собой отклик идеального фильтра нижних частот (ФНЧ), т.е. фильтра с постоянным коэффициентом передачи в пределах полосы частот от нуля до , на очень короткий импульс с амплитудой . (рис. 3.1).

Отметим, что в моменты времени ,  и т.д. значения отклика равны нулю. Это определяет механизм восстановления непрерывного сигнала по его отсчётам.

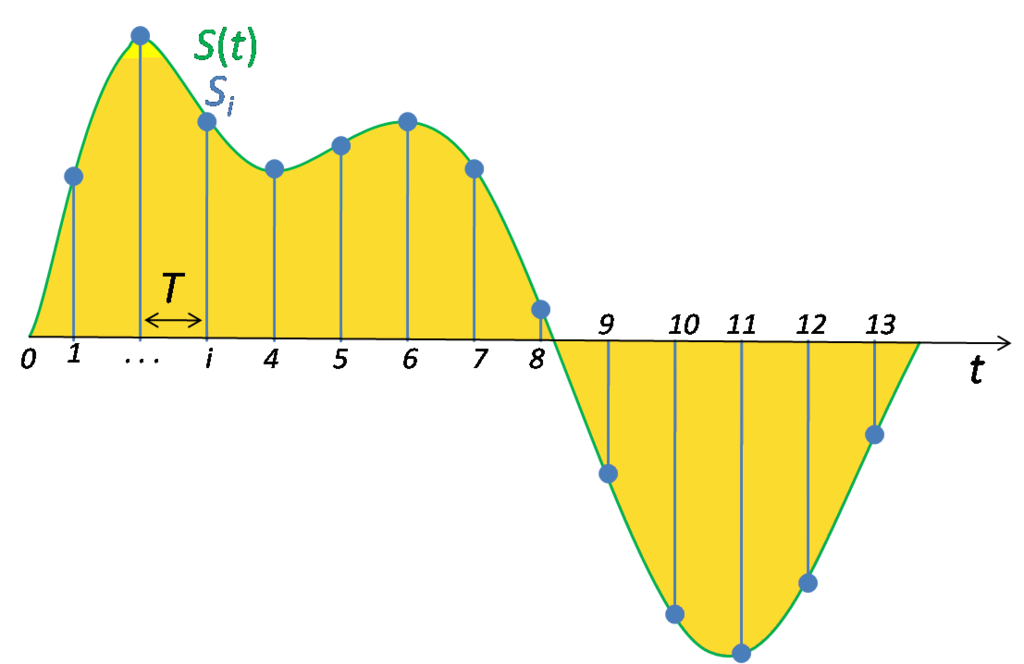
Формирование последовательности отсчётов непрерывного сигнала, которая представляет собой дискретный сигнал, т.к. значение любого отсчёта  сохраняется неизменным в течение интервала времени  (см. классификацию сигналов), осуществляется при помощи импульсного модулятора.

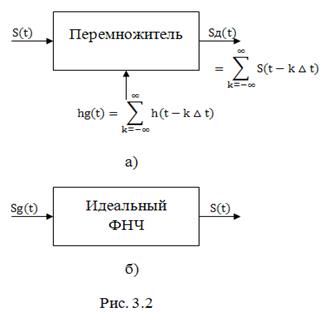
Простейший вариант импульсного модулятора представляет со­бой перемножитель (рис. 3.2), на один вход которого подаётся непре­рывный сигнал , а на второй – последовательность

коротких единичных импульсов вида (1.13), следующих друг за другом с периодом  (рис. 3.2, а). Тогда на выходе перемножителя будет иметь место последовательность коротких импульсов

,

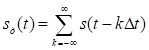
амплитуды которых равны , т.е. соответствуют мгновенным значениям сигнала , отсчитанным в момент времени . (рис 3.3, в).

Процесс формирований последовательности отсчётов называется дискретизацией непрерывного сигнала.

Восстановление непрерывного сигнала осуществляется путём подачи дискретного сигнала  на идеальный фильтр нижних частот. Отклик фильтра на каждый отсчёт определяется выражением (3.2). При этом, в момент времени , значение отклика определяется только k -тым отсчётом дискретного сигнала; отклик на остальные отсчёты равны нулю (Рис. 3.3, г). Суммируясь, эти отклики дают на выходе ФНЧ исходный сигнал .

Отметим два важных обстоятельства.

Во-первых, точное восстановление сигнала имеет место только при 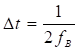. Введя в рассмотрение частоту дискретизации , получим так называемую частоту Найквиста, т.е. минимальное значение частоты дискретизации, при котором возможно точное восстановление непрерывного сигнала. Обычно, на практике частоту дискретизации выбирают выше предела Найквиста. Так, например, частота Найквиста для речевого сигнала при  составляет . В реальных РТИС эта частота составляет .

Во-вторых, точное восстановление сигнала возможно при суммировании бесконечного числа откликов, что соответствует сигналу , неограниченному во времени. Но в действительности, сигналы являются ограниченными и по спектру и по времени. Однако, при определённых допущениях теорема Котельникова справедлива и для этого случая.

Если сигнал, длительностью  ограничивается радиотехническим устройством с граничной частотой , то для его представления в дискретной форме требуется конечное число  отсчетов, где

.                               (3.4)

Таким образом для восстановления сигнала длительностью , ограниченного по спектру частотой  достаточно передать  независимых отсчетов, однозначно связанных с его формой.

Но теоретически сигнал, ограниченный по времени имеет бесконечный спектр. А это означает, что при восстановлении сигнала по  отсчетам будет иметь место ошибка, т.е. восстановленный сигнал ŝ(t) будет отличаться от исходного . Казалось бы, теорема Котельникова неприменима к реальным сигналам. Тем не менее, если к точности восстановления сигнала  по  отсчетам предъявить определенные требования, например, допустить его восстановление с заданным уровнем ошибки, то утверждения теоремы Котельникова можно с успехом распространить на реальные сигналы, несколько изменив частоту дискретизации по сравнению с пределом Найквиста.

Теперь с учетом того, что реальный сигнал длительностью  представляется  отсчетами мгновенных значений, выражение (3.1) принимает вид:

.    (3.5)

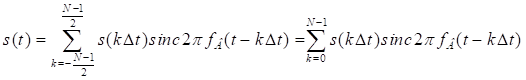
Величина  называется базой сигнала . Понятие базы играет важную роль при представлении непрерывного сигнала конечным числом отсчетов. Соответствующим образом выбранная база определяет информационные показатели сигналов, способность противостоять помехам при передаче по каналам связи, энергетическую скрытность и другие.

Рассмотрим теперь вопрос оценки точности восстановления непрерывного сигнала по совокупности  отсчетов его мгновенных значений. Как уже неоднократно подчеркивалось выше, ограниченный во времени сигнал имеет бесконечный спектр. Согласно равенству Парсеваля (2.50) энергия такого сигнала равна

,    3.6)

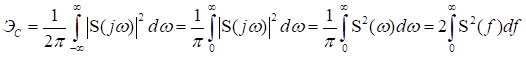
где         или  – энергетический спектр, представленный как функция либо круговой , либо циклической  частоты.

Энергия за пределами частоты (или ) составляет величину

.                        (3.7)

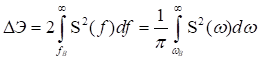
На рис. 3.4 изображен энергетический спектр сигнала, ограниченного во времени и граничная частота .

Площадь под всей кривой характеризует полную энергию сигнала , а площадь заштрихованного участка — ту часть энергии , которая сосредоточена за пределами .

Тогда отношение

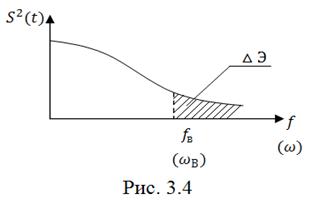
               (3.8)

может  служить  оценкой точности восстановления сигнала. Задаваясь величиной  можно определить частоту , а следовательно и частоту дискретизации .

Рассмотрим следующий пример. Пусть сигнал  на интервале времени  описывается экспоненциальной функцией

Воспользовавшись преобразованием Фурье, найдем спектральную функцию сигнала

.

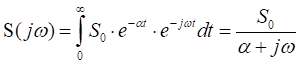
Модуль спектральной функции

,

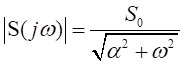
а энергетический спектр

.

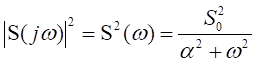
Воспользовавшись выражением (3.5), найдем энергию сигнала

.

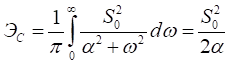
В соответствии с (3.6), вычислим :

.

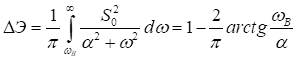
При расчете  и  использован табличный интеграл

.

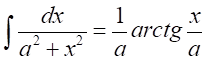
Найдем величину среднеквадратичной ошибки восстановления

.

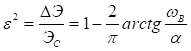
Представим

.

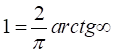
Тогда

,

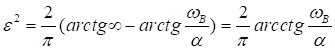
откуда следует

.

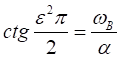
Полагая, что для малых значений

,

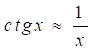
получим

.

Теперь можно найти

,

или переходя к циклическим частотам

.

Частота дискретизации

.

Таким образом, задаваясь величиной  можно определить частоту дискретизации непрерывного сигнала. Очевидно, число отсчетов при дискретизации рассматриваемого сигнала будет равно

.

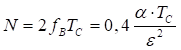
Из приведенного примера следует, что чем меньшую ошибку восстановления требуется обеспечить, тем выше должна быть частота дискретизации.

Теорема Котельникова устанавливает однозначное соответствие между аналоговым сигналом и отсчетами его мгновенных значений во временной области. Оказывается, можно сформулировать теорему отсчетов и в частотной области. При этом примем во внимание, что комплексный спектр одиночного сигнала длительностью  является сплошным. Тогда имеет место следующее утверждение. Спектральная функция  сигнала , ограниченного во времени величиной  полностью определяется совокупностью отсчетов , отстоящих друг от друга на частотный интервал , т.е.

.                     (3.9)

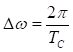
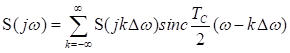
Теорема отсчетов в частотной области основывается на свойстве симметрий преобразований Фурье относительно переменных (или ) и . Суть этого свойства состоит в том, что преобразование Фурье периодического сигнала с периодом  приводит к линейчатой (дискретной) спектральной функции, где отдельные спектральные составляющие (см. подраздел 2.1) отстоят друг от друга по оси частот на величину  (или ), и наоборот, преобразование Фурье периодической спектральной функции с периодом  приводит к дискретной временной функции с периодом .

Исходя из этого свойства, если в (3.2) заменить  на ;  на , а  на , то в результате получим выражение (3.9). Как и в случае разложения сигнала  в ряд Котельникова, разложение его спектра ограничивается  отсчетами. Тогда выражение (3.5) в частотной области принимает вид

.             (3.10)

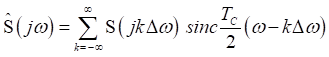
Казалось бы, для восстановления спектральной функции  по совокупности отсчетов , необходимо знать  отсчетов модуля и  отсчетов аргумента комплексных величин . Однако, если учесть, что модуль спектра , т.е. амплитудный спектр является четной функцией, а аргумент , т.е. фазовый спектр – нечетной функцией, то число независимых отсчетов сокращается вдвое и составляет , т.е. равно базе сигнала.

Подводя итог вышеизложенному, отметим, что теорема Котельникова устанавливает принципиальную возможность представления непрерывного сигнала последовательностью его мгновенных значений. Такую операцию иногда называют импульсным преобразованием непрерывного сигнала. Такое преобразование лежит в основе импульсных методов передачи сообщений в радиотехнических системах. Более того, дискретизация непрерывных сигналов в соответствии с теоремой Котельникова является промежуточной операцией при формировании цифровых сигналов, которые в настоящее время нашли самое широкое распространение как в радиотехнических системах передачи сообщений, так и радиоэлектронных системах обработки, отображения и регистрации информации, и во многих других областях.

3.2. Спектр дискретного сигнала

Перейдем теперь к рассмотрению спектра дискретного сигнала. Очевидно, в соответствии с изложенным выше свойством симметрии преобразования Фурье следует ожидать периодического характера спектральной функции дискретного сигнала.

Итак, дискретный сигнал , как уже подчеркивалось выше, формируется на выходе перемножителя, на один вход которого, подается непрерывный сигнал , а на второй – периодическая последовательность коротких импульсов длительностью

,

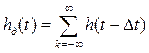
с периодом .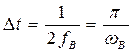

Здесь – функция, определяющая форму импульсов периодической последовательности. Обычно в качестве периодической последовательности импульсов дискретизации выбирают импульсы прямоугольной формы вида (1.13). Периодическую последовательность импульсов дискретизации можно описать выражением

.

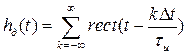
Тогда дискретный сигнал запишется в виде

. (3.11)

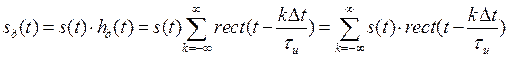
С другой стороны, последовательность прямоугольных импульсов может быть представлена комплексным рядом Фурье

. (3.12)

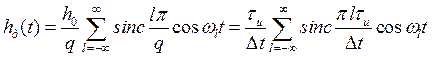
Здесь учтено, что период последовательности равен , амплитуда единичного импульса , а также .

Теперь можно представить с учетом (3.12) в виде ряда

. (3.13)

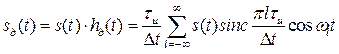
Применим к (3.13) прямое преобразование Фурье

.

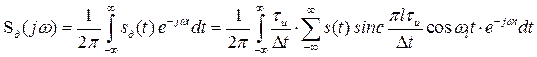
Изменив порядок суммирования и интегрирования, запишем

. (3.14)

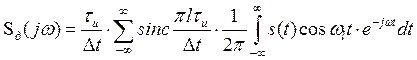
Так как

,

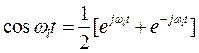
то

.

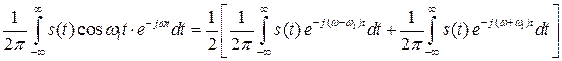
В свою очередь

,

.

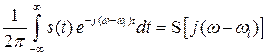
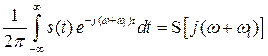
Тогда окончательно выражение (3.14) принимает вид

. (3.15)

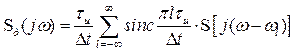
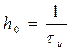
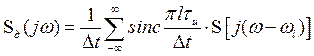
Спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса и выражение (3.15) запишется следующим образом

.

Если устремить к нулю при сохранении единичной площади импульса и перейти к последовательности бесконечно коротких импульсов ( -импульсов), т.е.

, (3.16)

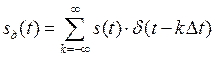
то

,

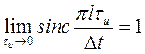
а спектральная функция дискретного сигнала примет вид

. (3.17)

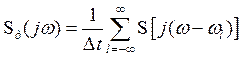
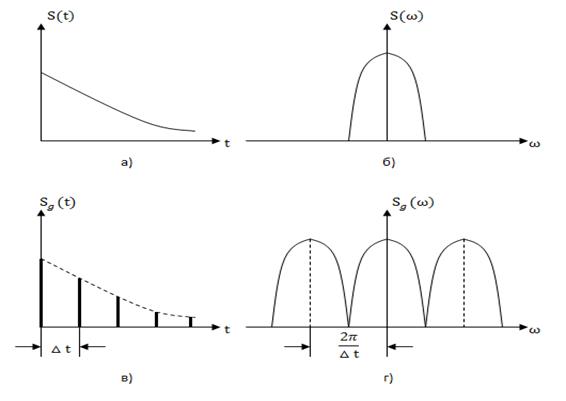
На рис. 3.5, а представлен непрерывный сигнал , а на рис. 3.5, б – условное изображения модуля его спектральной функции .

Как известно, спектр непрерывного одиночного сигнала является сплошным.

Спектр же дискретного сигнала, как это следует из (3.16), представляет собой периодическую по частоте последовательность копий спектров исходного сигнала, сдвинутых относительно друг друга на величину (или ), что составляет период последовательности. Очевидно, периодическим по частоте с тем же периодом является и модуль спектра и его аргумент, т.е. фазовый спектр.

Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации. На рис. 3.5. в, г изображены графики дискретного сигнала и модуля его спектра.

Рис. 3.5

Расположение отдельных составляющих периодической функции спектра дискретного сигнала на оси частот зависит от значения частоты дискретизации . На рис. 3.5,г и на рис. 3.6, а, б изображены соответственно функции дискретного сигнала при частотах дискретизации (или ), (или ) и (или ). Из этих рисунков следует, что при частоте дискретизации, меньшей чем частота, определяемая пределом Найквиста, копии спектра исходного непрерывного сигнала перекрываются, т.е. имеет место явление наложения спектров. Это приводит к искажению исходного сигнала при его восстановлении. Таким образом, и спектральный анализ дискретного сигнала согласуется с выводами теоремы Котельникова.

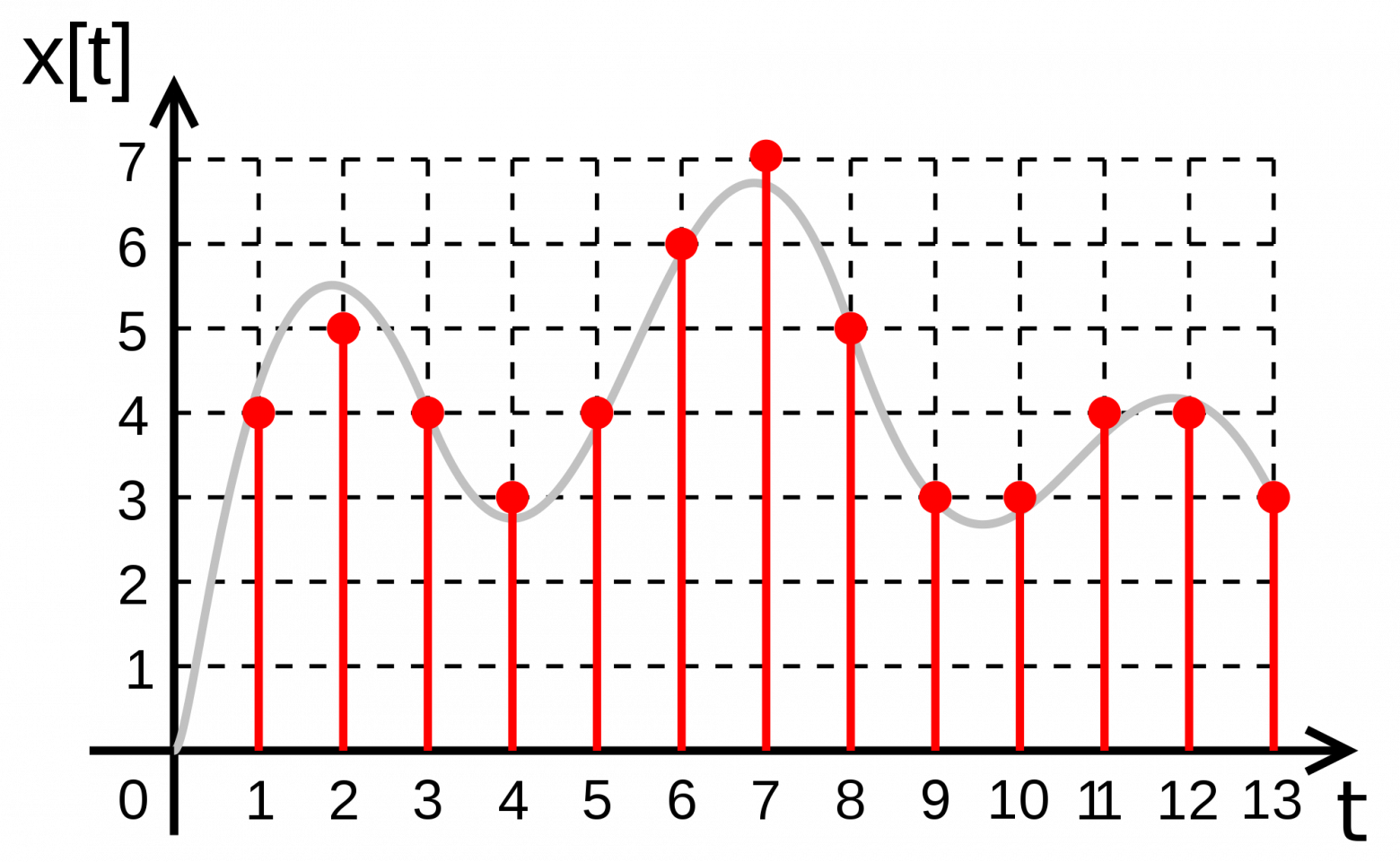
Представление непрерывного сигнала в виде последовательности дискретных отсчётов предполагает, что любой отсчёт может принимать любое значение из непрерывного множества значений . Вместе с тем, цифровые технологии в радиотехнике требуют преобразований совокупности значений отсчётов в цифровую последовательность, т.е. в последовательность чисел. Процесс преобразования аналогового (непрерывного) сигнала в такую последовательность называется аналогово-цифровым преобразованием (АЦП).

Итак, на первом этапе аналогово-цифрового преобразования осуществляется дискретизация непрерывного сигнала, т.е. преобразование в в соответствии с теоремой Котельникова, которая была рассмотрена выше. В результате дискретизации непрерывный (аналоговый) сигнал преобразуется в последовательность отсчётов .

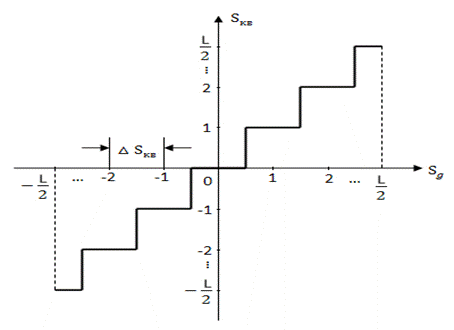
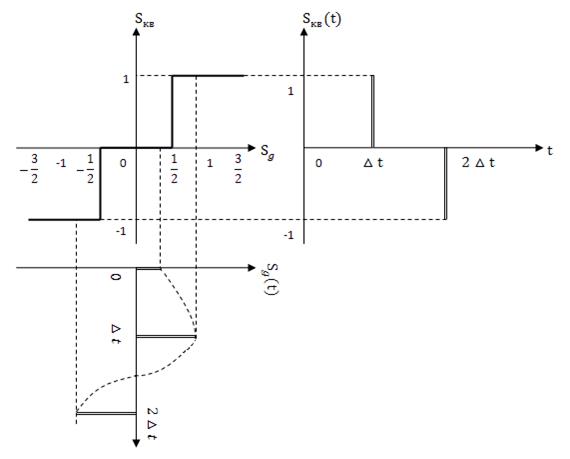
На втором этапе последовательность отсчётов подвергается процедуре квантования по уровню. Квантование по уровню значений отсчётов в простейшем случае представляет собой округление этих значений до ближайшего целого числа. Процедуру квантования осуществляет устройство с амплитудной характеристикой ступенчатого вида, которое называется квантователем. Амплитудная характеристика квантователя изображена на рис. 3.7.

При реализации квантователя диапазон изменения уровня дискретного сигнала разбивается на уровней (включая нулевой), каждый из которых отличается от соседних на величину , называемую шагом квантования.

Рис. 3.7

Таким образом, максимальное и минимальное значения квантованного сигнала соответственно равны

, .

В процессе квантования значение в момент времени сравнивается со значением , где . Квантованный сигнал принимает значение

, (3.18)

если

. (3.19)

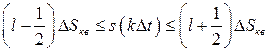
Отметим, что значение запоминается до момента следующего отсчёта дискретного сигнала.

Процедура квантования показана на рис. 3.8.

Рис. 3.8

На этом рисунке изображены фрагмент амплитудной характеристики квантователя, дискретный сигнал , временная диаграмма которого повёрнута на для удобства пояснения процедуры квантования, и квантованный сигнал .

Поясним процедуру квантования. Рассмотрим отсчёт . Поскольку значение этого отсчёта находится в интервале , в соответствии с (3.18) значение квантованного сигнала будет равно , т.к. условие (3.19) выполняется при . Значение отсчёта , как это следует из рисунка, находится в пределах , т.е. условие (3.19) выполняется при , поэтому значение квантованного сигнала . И, наконец, значение отсчёта находится в интервале , а значение квантованного сигнала .

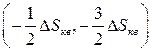
Ввиду того, что при квантовании осуществляется фактически округление значений , квантованный сигнал будет отличаться от дискретного. При этом искажения, вносимые квантователем

, (3.20)

принципиально неустранимы. Поэтому, при преобразовании непрерывного сигнала в цифровой необходимо оценивать степень искажений, вносимых квантователем.

Искажения, вносимые квантователем, целесообразно оценивать величиной среднеквадратичной ошибки. При исследовании процедур квантования было установлено, что величина среднеквадратичной ошибки

.

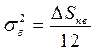
Таким образом, ошибка квантования тем меньше, чем меньше шаг квантования .

Физически при преобразовании реальных сигналов проявляется в виде шума. Поэтому искажения получили название шума квантования.

Сигнал на выходе квантователя уже представляет собой цифровой сигнал, однако, представленный в -ичной системе счисления. Напомним, что любое число может быть представлено в системе счисления с основанием следующим образом:

,

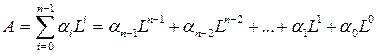
где принимает значение из совокупности значений от до ;

– значность числа (количество разрядов, которым представлено число).

Так, например, число в десятичной системе счисления, т.е. при , записывается следующим образом

.

Нетрудно убедится в том, что любое значение на промежутке времени от момента до момента (вспомним замечание о том, что значение запоминается) равно

.

Иными словами, квантованный сигнал представлен одноразрядным числом в -ичной системе счисления. Так как — число уровней квантования, которое выбирается довольно большим, осуществлять передачу и обработку такого сигнала средствами вычислительной техники, которые оперируют в подавляющем большинстве случаев с числами в двоичной системе счисления, неудобно. Поэтому квантованный сигнал, как число, необходимо перевести из — ичной системы в некоторую другую, более удобную с точки зрения дальнейшей передачи и обработки, систему счисления. Эта операция называется кодированием.

Перевод числа из одной системы счисления в другую сопровождается изменением разрядности числа. Соотношение разрядности числа, представленного в системах с основаниями и определяются формулой

.

Поэтому, при переводе числа из системы с основанием в систему с основанием число разрядов будет равно

, (3.21)

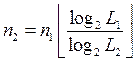
где знак означает округление до ближайшего верхнего целого числа.

Практикой установлено, что для передачи речевого сигнала в цифровой форме необходимо 256 уровней квантования. Эта величина принята в качестве международного стандарта. Значит, при квантовании речевого сигнала значение будет представлено одним разрядом в 256-ричной системе счисления. Для дальнейшей передачи и обработки эти числа обычно переводят в двоичную систему счисления. При этом количество разрядов числа , в соответствии с (3.21), составит

,

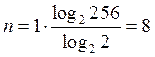
а значение каждого разряда может быть или нулем, или единицей.

Таким образом, в результате кодирования квантованный сигнал принимает форму двоичной последовательности, называемой кодовой комбинацией или кодовым словом.

На рис. 3.9 в качестве примера представлен квантованный сигнал при числе уровней квантования и кодовые слова для значений и . Очевидно при в соответствии с (3.21) число разрядов кодового слова составит

.

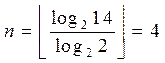
Тогда при кодировании значения образуется кодовое слово 1101, а при кодировании кодовое слово 0101.

Отметим, что минимальное значение квантованного сигнала в рассмотренном случае кодируется кодовым словом 0000 .

Если физически разряд кодового слова представлен в виде прямоугольного импульса амплитудой , то двоичный цифровой сигнал будет иметь вид представленный на рис. 3.9, б.

Длительность кодовой комбинации цифрового двоичного сигнала, очевидно должна быть равна т.е. интервалу дискретизации. Отсюда длительность элемента (разряда) кодовой комбинации

.

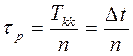
Выше было отмечено, что для уменьшения ошибки квантования необходимо уменьшать величину шага квантования . Однако при этом увеличивается число уровней, что в свою очередь приводит к увеличению разрядности кодовой комбинации цифрового сигнала, уменьшению длительности разряда и, следовательно, расширению спектра цифрового сигнала. Это обстоятельство необходимо учитывать при проектировании систем передачи цифровых сигналов по каналам связи.

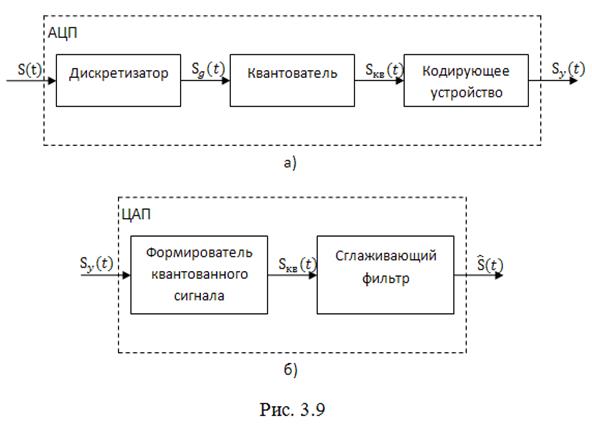
На практике операции дискретизации, квантования и кодирования осуществляются в одном устройстве называемом аналого-цифровым преобразователем (АЦП). Структурная схема АЦП представлена на рис. 3.9, а. На схеме показаны основные элементы АЦП и сигналы на их входах.

Операция обратного преобразования цифрового сигнала в аналоговый выполняется цифро-аналоговым преобразователем (ЦАП), схема которого представлена на рис. 3.9, б, и предусматривает ряд этапов.

В первую очередь цифровой двоичный сигнал подвергается поразрядному взвешенному (с «весом» ) суммированию, в результате чего в моменты времени формируется квантованный сигнал . После этого последовательность значений квантованного сигнала поступает на сглаживающий фильтр с амплитудно-частной характеристикой

в пределах полосы пропускания или . Как известно из предыдущего материала, при поступлении на вход фильтра сигнала в виде короткого импульса амплитудой , сигнал на выходе будет иметь вид

.

Сложение откликов фильтра дает сигнал ŝ(t). Следует подчеркнуть, что восстановленный сигнал ŝ(t) будет отличатся от исходного ввиду наличия ошибки квантования.

Попробуем нестандартно в сравнении с книгами по радиоэлектронике и цифровым системам связи, простыми житейскими примерами объяснить суть теоремы Котельникова. Если читатель еще не знаком с теоремой отсчётов, то рекомендуется сначала изучить ее формулировку в деловом официальном стиле. Смотрите, например, прошлую статью. 

Аналоговые и дискретные процессы в природе

Абсолютное большинство процессов в природе протекают непрерывно, (изменение температуры воздуха на улице, давления, влажности, изменение скорости ветра, колебание электрического тока в проводнике, сияние Солнца). Почему все эти процессы непрерывны? Нам кажется, что время течет непрерывно, а значит в каждый момент времени должно существовать какое-то значение температуры воздуха или значение силы тока в проводнике, или значение интенсивности света Солнца. Непрерывные процессы, функции или сигналы называют аналоговыми (от слова аналог – нечто сходное, подобное чему-то, т.е. функция как модель является аналогом какому-то физическому процессу). Можно наблюдать множество непрерывных процессов в природе, например, непрерывный поток воды в источнике. Струя воды при падении вниз сужается как раз в силу поддержания непрерывности потока.

Аналоговый сигнал даже на конечном временном промежутке подразумевает набор бесконечного числа значений. Однако регистрирующие устройства, как правило фиксируют конечное число значений, поэтому мы получаем дискретные сигналы (дискретный от лат. discretus означает раздельный, состоящий из отдельных частей).

Представление непрерывного и дискретного сигналов.

Дискретные процессы также многочисленны в природе, как и аналоговые состояния. Дискретные процессы не могут находиться в каком-то промежуточном состоянии между определенными значениями. Придумаем несколько примеров из жизни:

1. Из квантовой физики 1-й постулат Бора: электрон в атоме может двигаться только по определенным (можно сказать по дискретным)  орбитам, находясь на которых, он не излучает и не поглощает энергию. Электроны в атоме, находясь на определенных стационарных (т.е. дискретных) орбитах, имеет вполне определённые дискретные значения энергии Е1, Е2, Е3 и т.д.
2. Если вы играете на пианино, то звучащая музыка во времени представляет собой перескоки с одной дискретной ноты на другую, то есть ноты – это отдельно выбранные дискретные звуки.
3. Когда мы поднимаемся по лестнице, ступня в пространстве оси высот находится только на определенной дискретной координате (ступеньке)

Поскольку человек не может оперировать с бесконечными числами и величинами, обычно все округляем до ближайших целых чисел – в результате получаем цифровые сигналы. Например, мы наносим цифровую шкалу на столбик термометра и фиксируем округленное значение температуры. Непрерывное время мы разбиваем на секунды минуты, часы – наносим цифры на циферблат часов. Все символьные и знаковые системы, созданные человечеством для обмена информацией, использует конечное число возможных элементов.

Поскольку все вычислительные информационные устройства могут работать лишь с дискретными символьными системами и с цифровыми сигналами, постоянно возникает необходимость в переходе от существующих в природе непрерывных процессов, к дискретным и цифровым. С развитием цифровой связи и цифровых устройств (микроконтроллеров, компьютеров) постоянно и повсеместно на каждом шагу выполняется аналого-цифровое преобразование сигналов, неотъемлемой частью которого является дискретизация сигналов. Но здесь важно следующее: перейти от непрерывного сигнала к дискретному дело нехитрое – здесь удачно подходит выражение «ломать не строить». По аналогии можно сказать «ломать аналоговый сигнал – не восстанавливать его», здесь все просто реализовать, но главное при этом выполнить дискретизацию правильно. Одно дело просто произвести выборку отдельных значений сигнала, но есть еще другое дело – потом надо будет по этим значениям снова восстановить исходный непрерывный сигнал. Как правильно дискретизировать сигналы говорится в теореме о дискретизации сигналов, или ее можно называть в честь автора – теоремой Котельникова.

Если не знать теорему Котельникова

Итак, мы выяснили, что как и множество процессов в природе, электрические сигналы, используемые во всей электронике и системах связи бывают аналоговые и дискретные. В цифровых системах необходимо переходить от аналоговых сигналов к дискретным, при этом переход должен быть корректным.

Наглядный пример номер раз. Давайте посмотрим на примере двух музыкальных фрагментов, что будет, если осуществлять дискретизацию сигнала некорректно.

Вот что будет при неправильной оцифровке музыки

Исходная музыкальная запись

После неправильной дискретизации

Вот что будет при неправильной оцифровке речи

Исходная запись

После неправильной дискретизации

Наглядный пример № 2. На рисунке ниже представлены 7 сигналов, каждый из которых соответствует своей музыкальной ноте – До, Ре, Ми, Фа, Соль, Ля, Си. Все они оцифрованы с частотой дискретизации 1700 Гц.

Давайте послушаем, что из этого получилось.

Надеюсь, с музыкальным слухом все в порядке и вы услышали, что с последними двумя прозвучавшими нотами что-то не так. Если не знать теорему Котельникова, то будет непонятно, почему звук при дискретизации исказился. Поэтому давайте разбираться в этой теореме.

Наглядное, но нестандартное объяснение теоремы о дискретизации

Представим себе, что мы работники Animal Planet и хотим изучить траекторию движения в джунглях какой-нибудь редкой змейки из красной книги. Назовем, например, изучаемую змею Зигзагусс.

С целью исследования мест обитания змеи и ее повадок цепляем к ее хвосту GPS-датчик, который будет регистрировать ее местоположение в отдельные моменты времени.

Вопрос: как надо запрограммировать датчик, чтобы мы получили точную траекторию движения змейки, т.е. получили самый подробный график траектории движения юркой змейки со всеми ее виляниями и изгибами? Через сколько миллисекунд или секунд датчику необходимо будет записывать и посылать нам очередную координату положения в пространстве?

Допустим, наша змея Зигзагусс ползет гармонично – ее хвост совершает гармонические колебания и ее движения можно описать синусоидальными функциями.

Фото настоящего следа от змеи на песке.

Траектория движения представляет собой колебания с различными частотами. Так вот, по правилам теоремы о дискретизации, чтобы восстановить всю траекторию движения змейки, необходимо найти составляющую колебаний самой высокой частоты.

Если по дискретным точкам мы сможем восстановить составляющую колебаний самой высокой частоты, то мы сможем восстановить всю траекторию змейки. Определим периоды всех колебаний (см. рисунок ниже).

Как видно из рисунка, наименьшим периодом колебаний является период . Следовательно, необходимо подобрать частоту выборки дискретных точек именно для колебания с периодом , тогда и все остальные колебания мы сможем потом восстановить. Другими словами, в соответствии с теоремой о дискретизации (см. формулировку здесь) можно полностью восстановить данную синусоидальную функцию, если брать дискретные точки через интервал времени вдвое меньший длительности периода . Это означает, что необходимо брать точки с таким интервалом, чтобы на период колебания самой высокой частоты приходилось не менее 2-х точек.

В этом случае можно будет с высокой точностью восстановить всю непрерывную траекторию движения исследуемой змеи.

Предположим теперь, что Зигзагусс опьянилась запахом одурманивающего цветка и стала ползти негармонично, несуразно.

В этом случае для определения периода дискретизации нам необходимо самим отыскать гармонию в данной кривой функции, а она есть внутри любого сигнала всегда, что пытался в свое время доказать всем людям французский математик Жан-Батист Фурье. Также как любое тело можно разложить на множество атомов, также и полученную сложную функцию (от траектории змеи), можно разложить на множество гармонических функций. Физические тела разные, потому что они отличаются друг от друга структурой молекул. Например, мы говорим H2O – это вода, что означает: молекула воды состоит из двух атомов водорода H и одного атома кислорода O. Точно также можно сказать, что разные сигналы отличаются разным составом. Например, такой вот сигнал

состоит из двух гармонических функций (синус и косинус) с частотой 1000 Гц и одного синуса с частотой 2000 Гц (2000 Гц означает, что гармоника совершает 2 тысячи колебаний в секунду). В соответствии с условием теоремы Котельникова, о котором мы уже ранее говорили, для такого сигнала временной интервал между дискретными точками необходимо брать таким, чтобы он был меньше половины периода самой высокой частоты. В нашем случае имеется гармоника с максимальной частотой 2 тысячи колебаний в секунду (2000 Гц), значит период сигнала равен 1/2000 = 0.005 секунд и значит период между дискретными точками должен быть менее, чем 0.005/2 = 0.0025 секунды.

Чтобы определить требуемый период между дискретными точками для траектории нашей змейки, необходимо определить из каких гармонических функций она состоит, а точнее нас интересует значение частоты наивысшей гармонической функции (т.е. фиолетовой на рисунке).

Делим период фиолетовой гармоники пополам, и получаем граничное значение для периода дискретизации функции траектории одурманенной змеи. Все, задача решена, можно произвести дискретизацию данного сложного сигнала.

Знаем и соблюдаем условия теоремы Котельникова

Теперь, когда мы знаем теорему Котельникова, давайте еще раз рассмотрим задачу правильного перехода от аналоговых 7 сигналов- музыкальных нот к дискретным. Итак, у нас есть семь гармонических колебаний, с частотами

Для правильной дискретизации, чтобы не было искажений, необходимо взять частоту дискретизации не менее в два раза больше максимальной частоты сигнала. Ранее мы брали частоту 1700 Гц, но как можно посчитать, такая частота подходит для сигналов нот До – Соль (для ноты Соль требуется частота дискретизации 784*2=1568 Гц), а вот для сигналов нот Ля и Си значение 1700 Гц уже не годится.

Еще раз рассмотрим дискретизацию наших сигналов

Как видно из рисунка из-за несоблюдения условий теоремы Котельникова для сигналов Ля и Си с частотами 880 Гц и 988 Гц, через получившиеся дискретные отсчёты можно провести другие гармонические сигналы (красные функции), частоты которых меньше 1700 Гц / 2 = 850 Гц. Произошел эффект, который называют наложение спектров (в англоязычной литературе – aliasing). В рамках данной статьи «для чайников» мы не будем подробно рассматривать этот эффект, поскольку здесь уже требуются знания спектрального анализа сигналов. Этот эффект интересен тем, что объясняет условия теоремы Котельникова с позиций представления сигналов в частотной области (см. рисунок ниже). Если разобраться в этом, то теорема Котельникова и принципы восстановления сигналов станут более понятными. Описание этого эффекта можно найти почти в каждой книге по цифровой обработке сигналов.

Но сейчас новичкам в этой области главное запомнить результат несоблюдения теоремы отсчётов – восстановление сигналов по имеющимся дискретным отсчётам будет неоднозначно. Чтобы такого не происходило, необходимо чтить теорему Котельникова.

Максимальная частота среди наших 7 сигналов 988 Гц (нота Си), следовательно частота дискретизации должна быть больше, чем 2*988=1976 Гц. Важно здесь неуместно отметить, что в 1976 году был создан первый персональный компьютер – начался кустарный выпуск Apple I.

Значит надо выбрать частоту дискретизации больше значения 1976.

Вот как будут звучать семь наших сигналов при частоте дискретизации 2000 Гц.

Задачка для разминки мозгов

Нельзя сказать, что эта задачка очень простая для начинающих и ее решит любой. Новички в этой области не унывайте, если не получится (здесь нужны знания теории сигналов), ну а тот, кто решит, может собой гордиться.

С двух датчиков регистрируются сигналы 

Какой должна быть минимальная частота дискретизации в АЦП по условию теоремы о дискретизации, если К – операция сложения и если К – операция умножения?

Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.

Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.

Чем отличается цифровой аудиосигнал от аналогового?

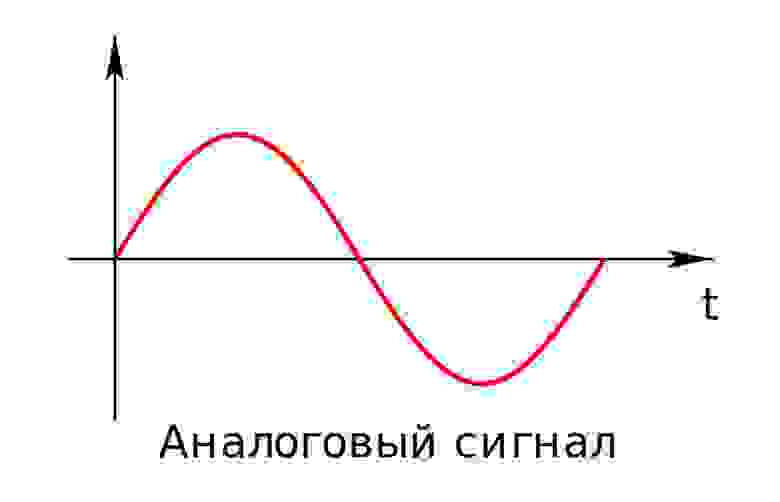
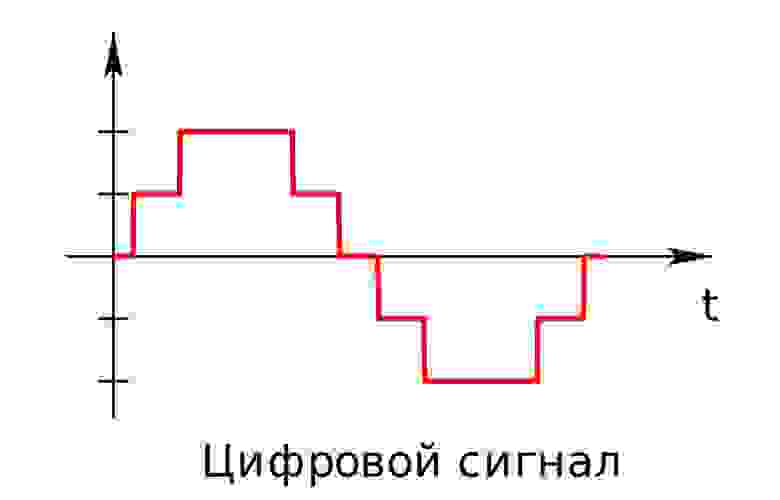
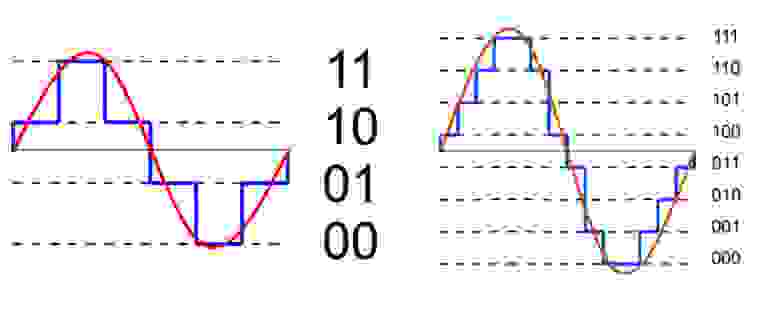
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).

Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).

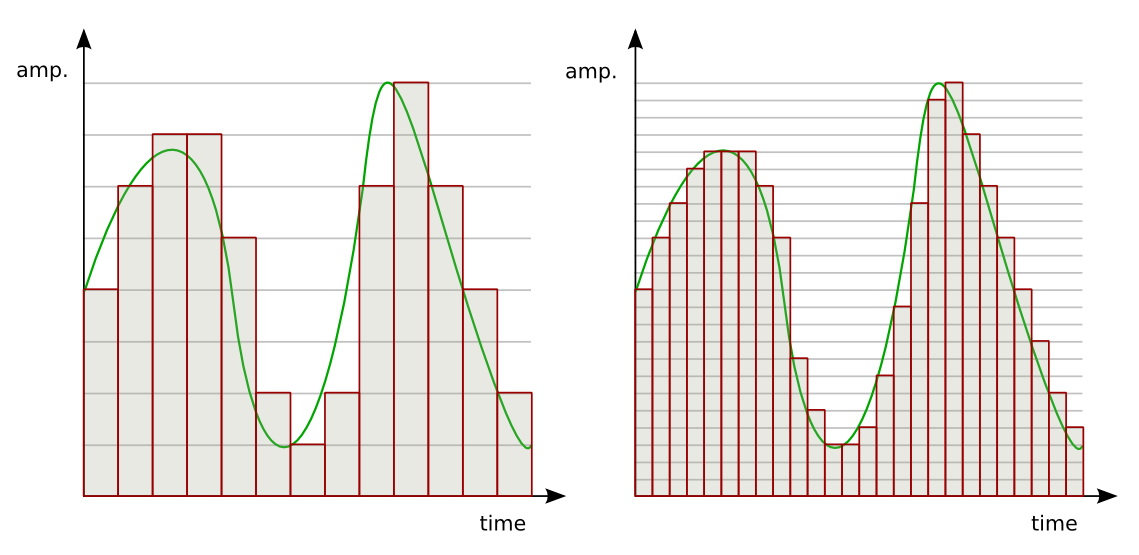
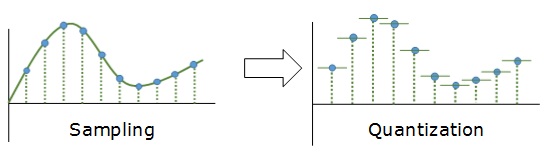
Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.

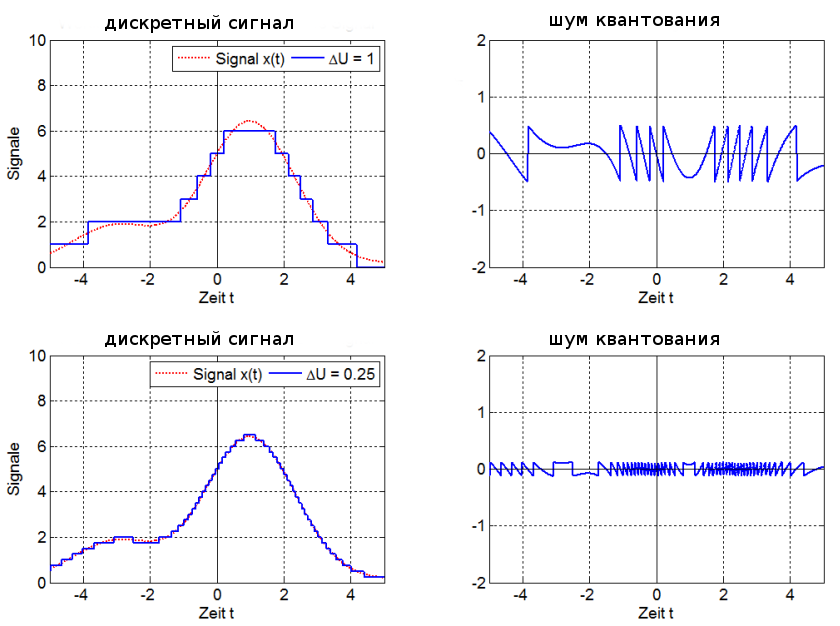
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).

Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).

Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).

Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).

Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)

Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).

Данная формула позволяет вычислить количество уровней квантования:

Если N — количество уровней квантования,
n — разрядность, то

Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.

При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.

Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением ()

Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).

Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).

Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).

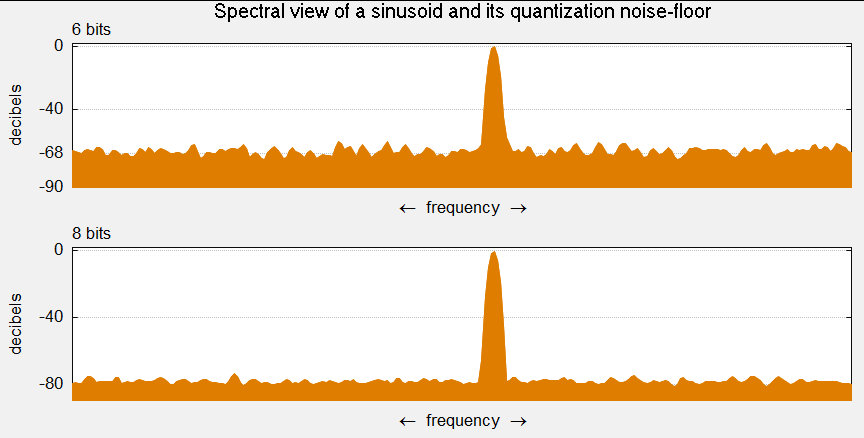
Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.

Аудиопример 1: 8bit/44.1kHz, ~50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.

Аудиопример 2: 4bit/48kHz, ~25dB SNR

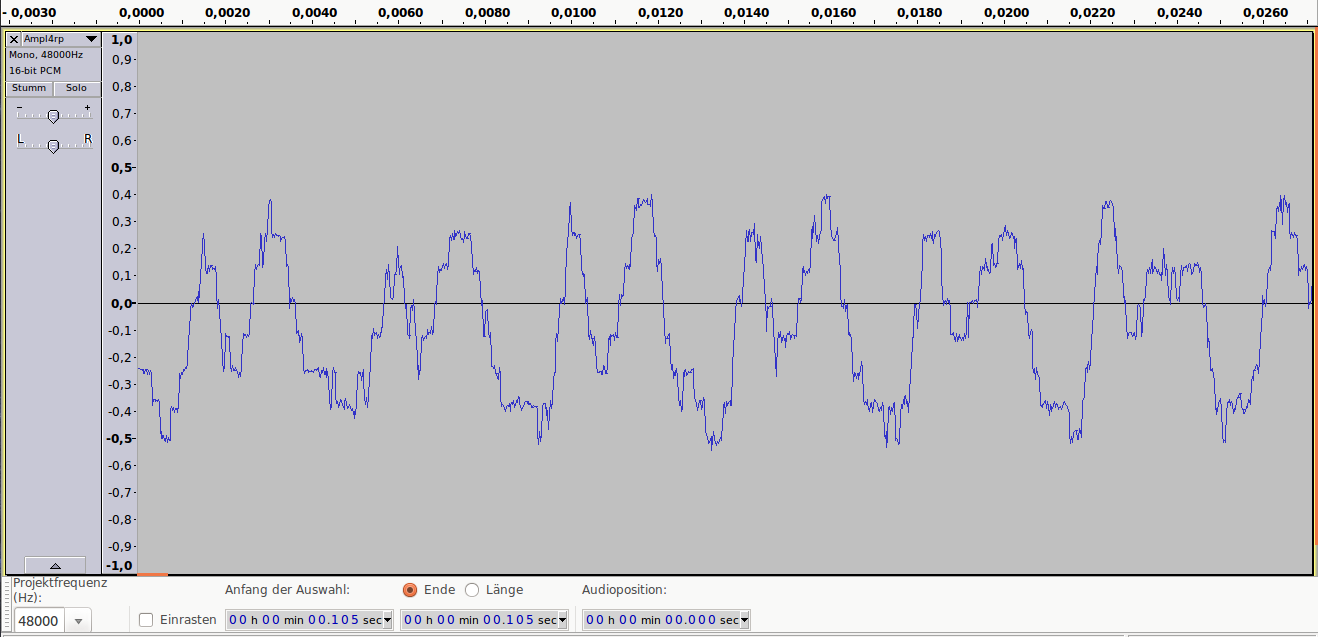
Аудиопример 3: 1bit/48kHz, ~8dB SNR

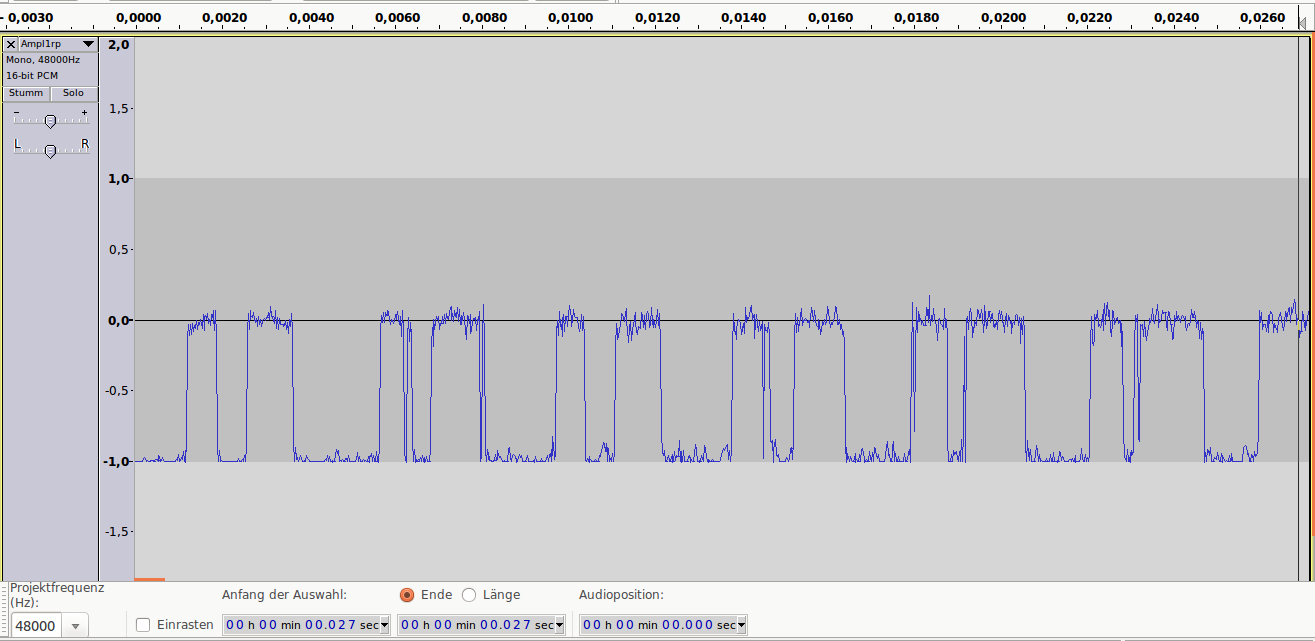
Теперь о дискретизации.

Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то

Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).

Теорема Котельникова гласит:

Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.

Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.

Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?

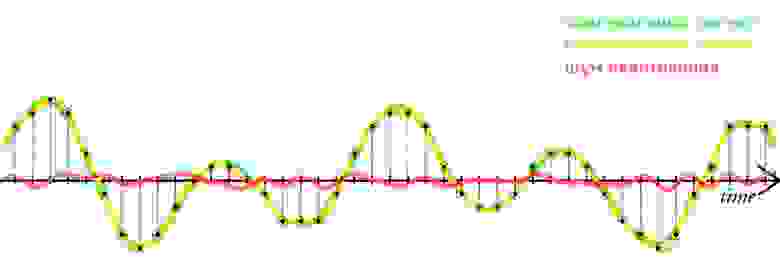
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.

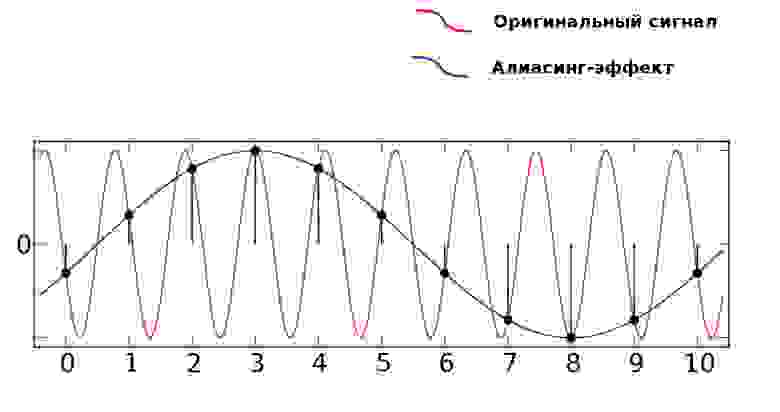
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.

Аудиопример 4: Линейно возрастающая частота от ~100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.

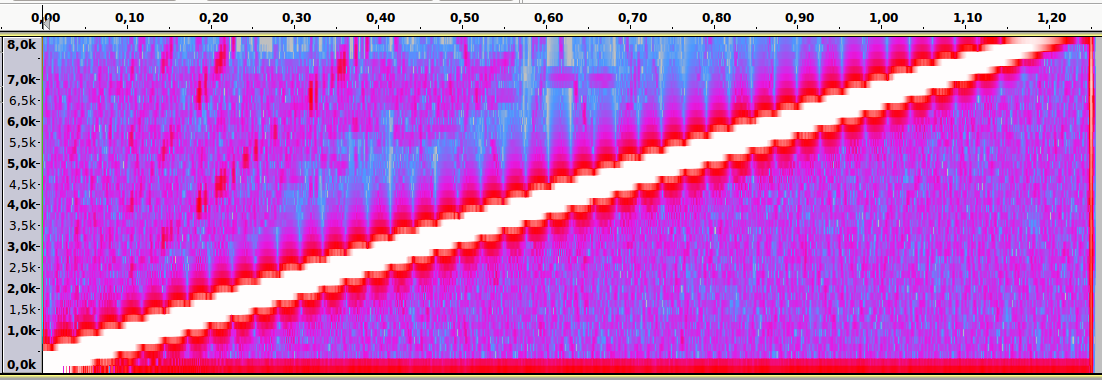
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг

Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.

Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.

Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):

Битрейт = Частота дискретизации * Разрядность * Количество каналов

Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s

При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.

При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.

Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину. 

При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.

ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.

Существуют 3 метода хранения цифрового аудиоматериала:

• Несжатые («сырые») данные
• Данные, сжатые без потерь
• Данные, сжатые с потерями

Несжатый (RAW) формат данных

содержит просто последовательность бинарных значений.
Именно в таком формате хранится аудиоматериал в Аудио-CD. Несжатый аудиофайл можно открыть, например, в программе Audacity. Они имеют расширение .raw, .pcm, .sam, или же вообще не имеют расширения. RAW не содержит заголовка файла (метаданных).

Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.

Аудиоформаты с сжатием без потерь

Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.

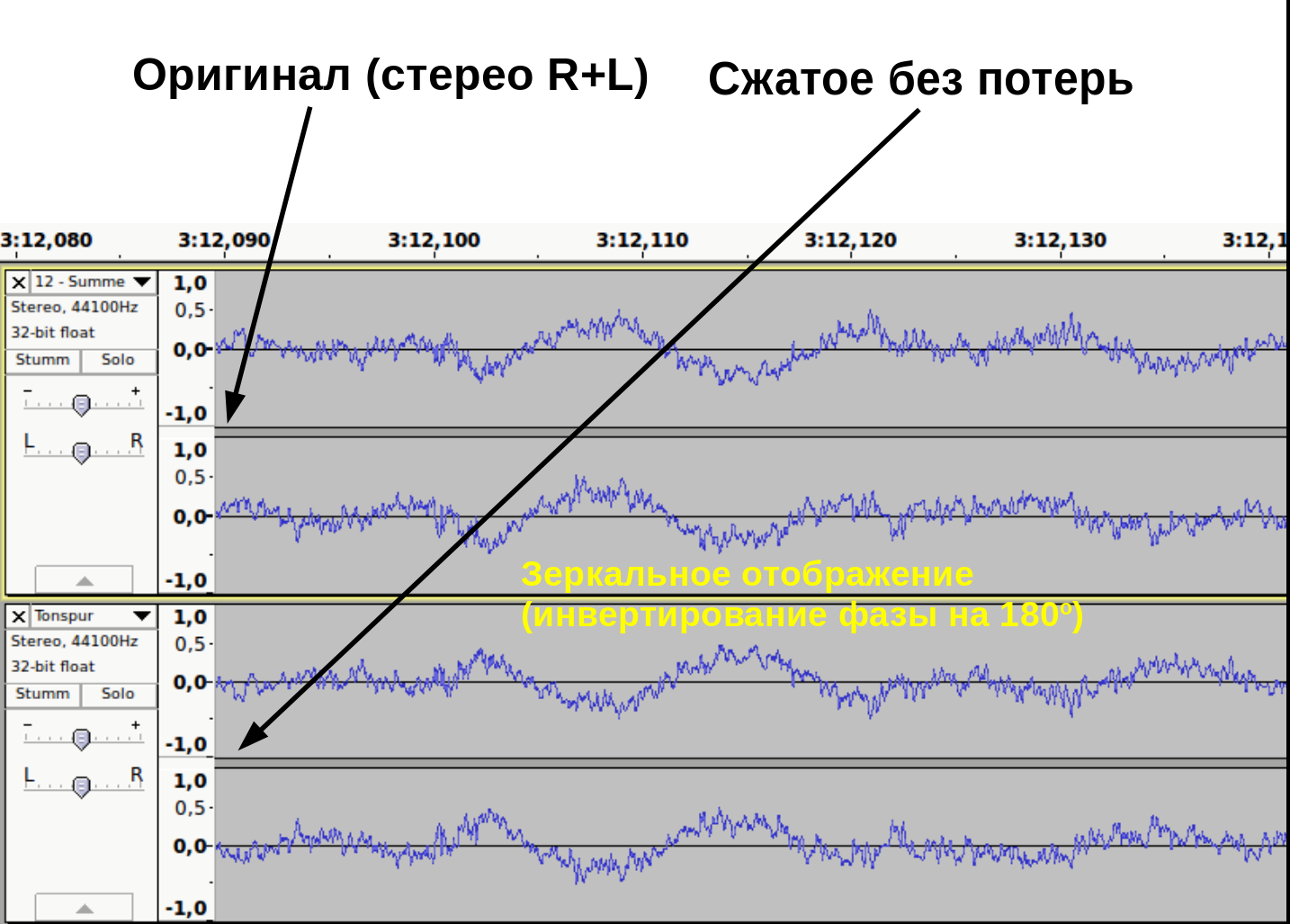
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.

Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).

Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…

При сжатии с потерями

акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».

Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.

Этим и пользуется кодек: 2kHz-звук можно убрать.

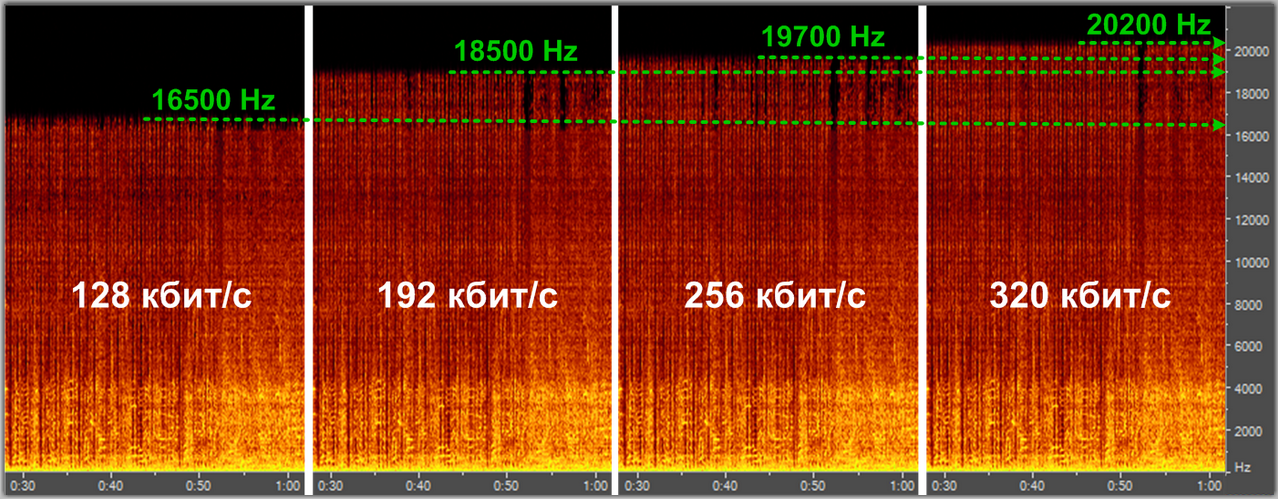
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…

Спасибо за внимание.

UPD:
Если по каким-либо причинам аудиофайлы не загружаются, можете их скачать здесь: cloud.mail.ru/public/HbzU/YEsT34i4c