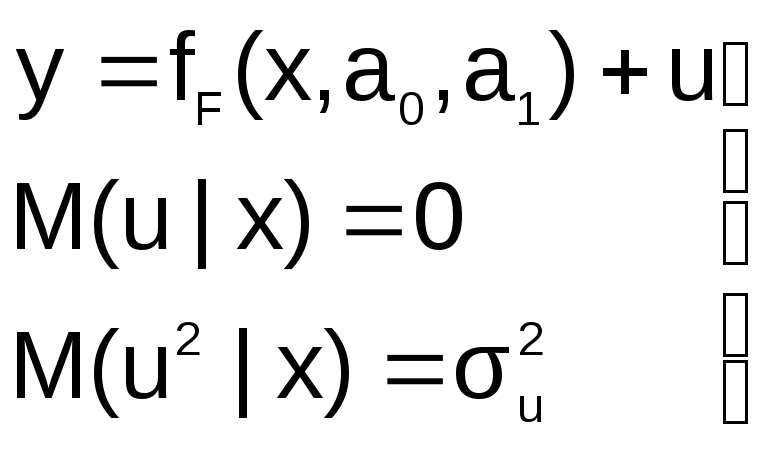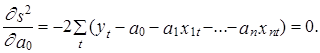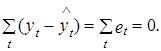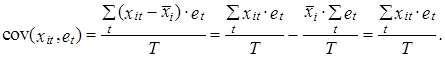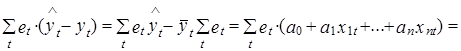Ошибка модели эконометрика

Возможные ошибки спецификации модели:

1. Неправильный выбор вида уравнения
регрессии

2. В уравнение регрессии включена лишняя
(незначимая) переменная

3. В уравнении регрессии пропущена
значимая переменная

1. Неправильный выбор вида функции в
   уравнении

Пусть на первом этапе была сделана
спецификация модели в виде:

в
которой функция f_F(x,a₀,a₁)
выбрана не верно. Предположим, что
y_T=f_T(x,a₀,a₁)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:

И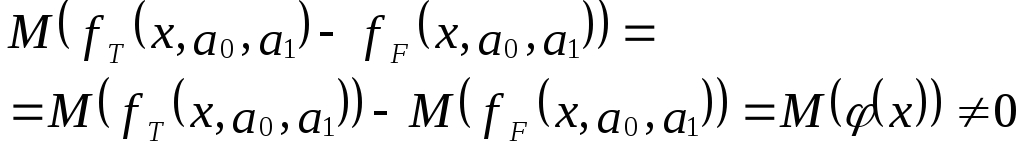з
выражения следует:

Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций f_T
и f_F
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется

Следовательно, в результате оценивания
такой модели параметры а₀ и а₁
будут смещенными

Симптомы наличия ошибки спецификации
первого типа:

1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации

2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений

Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!

В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.

Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.

2. В уравнение регрессии включена
лишняя переменная

П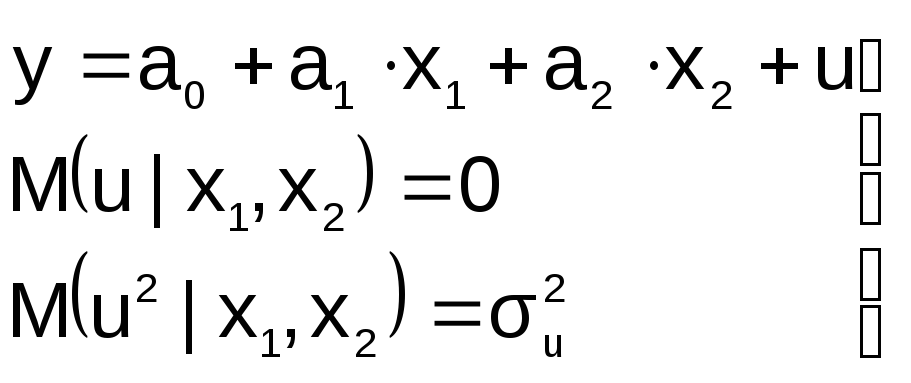усть
на этапе спецификации в модель включена
«лишняя» переменная, например, X₂

«Правильная»
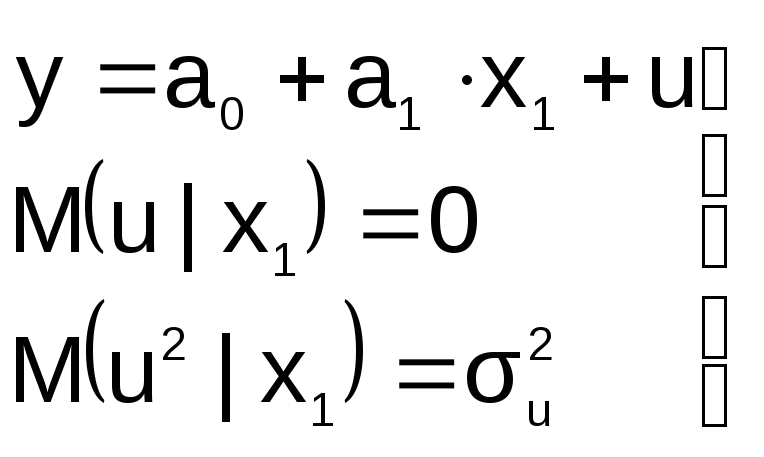
спецификация должна иметь вид:

Последствия:

1.
Оценки параметров а₀, а₁, а₂
останутся несмещенными, но потеряют
свою эффективность (точность)

2. Увеличивается ошибка прогноза по
модели

как за счет ошибок оценок коэффициентов
и σ_u,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора

Диагностика:

В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H₀: a_i=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n₂ = n – (k+1)

3.
В модели не достает важной переменной

Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели

Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель

29. Фиктивные переменные и особенности их использования в моделях.

На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.

Примеры.

Моделирование влияния пола специалистов
на уровень зарплаты.

Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)

Модель инфляции с учетом различных
видов регулирования со стороны государства

Возможны два подхода к решению задачи:

— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной

— учесть влияние качественного фактора
в одной модели

Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели

Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N

Предположим:

1. Зависимость затрат на обучение от
   количества учащихся N в
   обоих типах школ одинакова

2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам

Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:

Y^o
= a₀ +
a₁N +u

Y^s
= b₀ +
a₁N +
v

Обе
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:

Спецификация такой модели имеет вид:

Y = a₀
+ a₁N
+ δd + u

Тогда при d=0 получим Y^o
= a₀ + a₁N
+ u

при d=1 получим Y^s
= (a₀+δ)
+a₁N +
v

d – фиктивная переменная
сдвига

Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор

Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)

Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные

Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена

Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной

В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора

Например:

Однако, если взять спецификацию модели
в виде:

Y=a₀
+ a₁d₁+a₂d₂+a₃d₃+a₄d₄+a₅N+u

при этом всегда верно тождество
d₁+d₂+d₃+d₄=1

Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.

Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает

Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»

Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;

d=1 – профессиональная
школа

Спецификацию модели следует записать
в виде:

Y = a₀
+ a₁N
+ a₂*d
+ a₃dN
+U

50

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В данном разделе рассматриваются некоторые подходы к проверке наличия стандартных свойств (2.20)–(2.23) у “истинной” ошибки эконометрической модели et  на основе анализа соответствующих свойств фактической ошибки еt.

В этой связи сразу следует отметить, что наличие у ошибки еt  каждого из этих свойств не всегда является доказательством присутствия соответствующего свойства и у ошибки et. Иными словами, наличие определенных свойств у ошибки еt  не является необходимым условием существования этих свойств и у истинной ошибки et. Дело в том, что некоторые свойства фактической ошибки еt  являются своего рода ограничениями на ее значения, которые вытекают из критерия МНК как метода оценки параметров модели, т. е. выполняются практически всегда. В то же время   свойства “истинной” ошибки определены теоретическими предпосылками, положенными в основу этой модели. Поэтому вывод о правомочности использования МНК на основе существования таких “априорных” свойств фактической ошибки модели не может считаться обоснованным.

Вместе с тем, если фактическая ошибка et  не обладает некоторым  свойством, то можно говорить о том, что теоретические предпосылки эконометрической модели не подтверждены полученными эмпирическими данными и “качество” ее уравнения не достаточно высоко.

 В этой связи отметим, что к “априорным” свойствам фактической ошибки еt, которые выполняются при использовании МНК всегда, относятся свойства (2.20) и (2.23). Приведем доказательства этого утверждения.

1.   Сумма значений фактической ошибки равна нулю

Условие (2.43) является аналогом свойства (2.20), поскольку  рассматривается как оценка математического ожидания фактической ошибки.

Использование МНК обеспечивает выполнение условия (2.43) автоматически. В самом деле, дифференцируя сумму квадратов ошибки еt   s2  (см. выражение (2.31)) по параметру a0 , получим

Из этого выражения автоматически вытекает, что

2.   Произведение транспонированной матрицы Х¢ на вектор фактической   ошибки е равно нулевому вектору.

Х¢е=0.                                      (2.44)

Условие (2.44) является аналогом условия (2.23), поскольку произведение каждой строки матрицы Х¢  на вектор e представляет собой скалярное произведение вектора значений соответствующих факторов хit   на вектор ошибки.

Тогда векторно-матричное выражение (2.44) можно представить в виде следующей системы скалярных произведений:

где х0t º1 для t=1, 2,…, Т.

Для доказательства справедливости выражения (2.44) представим вектор ошибки е в виде разности фактических и расчетных значений независимой переменной yt

е=у –=у–Х×a.

Получим

Х¢×e=Х¢×(у–Х×a)=Х¢×у–Х¢×Х×a=(Х¢×Х)–1×Х¢×у–(Х¢×Х)–1 ×(Х¢×Х)×a=0.

Из (2.44) и (2.45) автоматически следует, что

Еще раз отметим, что выполнение условий (2.45) и (2.46) не может считаться доказательством отсутствия корреляционных взаимосвязей между значениями независимых переменных хit  и “истинной” ошибкой et. В данном случае эти условия сами являются следствием результатов применения МНК для оценки коэффициентов эконометрической модели, т. е. они как бы выполняются автоматически. Для некоторых классов эконометрических моделей, как это будет показано в главах V и VIII, уже априорно, т. е. до построения модели, можно доказать существование ковариационной связи между некоторыми независимыми переменными и истинной ошибкой модели et. Выполнение условия (2.45) в таком случае не является свидетельством корректности применения “классического” МНК для оценки ее параметров.

3.   Из условий (2.43) и (2.45) также вытекает, что сумма произведений отклонений расчетных значений независимых переменных от ее среднего значения и расчетных значений ошибки равна нулю.

Раскрывая скобки в выражении (2.47), непосредственно получим

Выражение (2.47) включает в себя также и следующее условие:

означающее, что сумма произведений расчетных значений зависимой переменной и ошибки еt   равна нулю.

Здесь еще раз подчеркнем, что условия (2.43)–(2.48) для фактической ошибки еt  эконометрической модели автоматически вытекают из метода оценки ее параметров – МНК, и поэтому их непосредственно нельзя переносить на условия (2.20)–(2.23), характеризующие свойства истинной ошибки e t.

Вместе с тем, условия (2.21) и (2.22) для фактической ошибки еt   не являются “априорными”. Они выполняются лишь в том случае, если исходные предпосылки МНК оказались справедливыми для данной модели, что является свидетельством обоснованного выбора формы ее уравнения, состава учтенных факторов и т. п.

В этой главе мы сконцентрируемся на том, как при помощи эконометрики получать корректные ответы на вопросы о причинно-следственных связях. Чтобы это сделать, нужно верно специфицировать вашу модель. Под верной спецификацией будем понимать такую, которая позволяет получить состоятельные оценки коэффициентов при интересующих вас переменных. А также получить состоятельные стандартные ошибки для тестирования гипотез.

Глава будет устроена так: мы будем перечислять типичные ловушки, которые приводят к неверной спецификации. Далее для каждой такой ловушки мы будем указывать возможные способы избежать её и устранить проблему.

В каких-то случаях мы будем опираться на уже знакомые вам концепции и понятия. В некоторых же ситуациях мы будем, наоборот, ссылаться на более продвинутые методы и модели, с которыми нам ещё предстоит разобраться в следующих главах учебника (надеемся, это станет для вас дополнительной мотивацией все-таки дочитать его до конца).

Напомним, что в предыдущей главе мы сформулировали два важных определения:

• Эндогенный регрессор — регрессор, который коррелирован со случайными ошибками модели.
• Экзогенный регрессор — регрессор, который не коррелирован со случайными ошибками модели.

Кроме того, в той же главе мы выяснили, что для состоятельности оценки коэффициента при переменной необходимо, чтобы эта переменная была экзогенной (точнее, необходимо выполнение предпосылки №4 линейной регрессионной модели со стохастическими регрессорами из главы 6). Если же регрессор эндогенный, результаты вашего моделирования нельзя интерпретировать в терминах причинно-следственных связей. Нарушение предпосылки №4 об экзогенности регрессора — это самая частая проблема при проведении прикладных исследований на пространственных и панельных данных. Поэтому важно понимать, в каких случаях вам следует опасаться её возникновения. Есть следующие типичные ситуации:

1. Эндогенность регрессора из-за пропуска существенной переменной. В качестве важного частного случая тут также следует указать проблему эндогенности из-за самоотбора.
2. Эндогенность регрессора из-за выбора неверной функциональной формы связи.
3. Эндогенность регрессора из-за двусторонней причинно-следственной связи.
4. Эндогенность регрессора из-за ошибок измерения.

В последующих четырех параграфах главы мы подробно обсудим каждый из этих пунктов. В пятом параграфе мы поговорим о других (помимо эндогенности) проблемах, которые могут делать выводы эконометрических исследований необоснованными. В каждом случае мы также укажем основные возможные пути преодоления перечисленных трудностей.