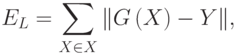Ошибка обучения это ошибка допущенная моделью на учебной множества

Ответы:

1	А
2	Б
3	Б
4	В
5	Г
6	А
7	А
8	Б
9	А
10	б
11	В
12	Б
13	А
14	Б
15	В
16	а
17	а
18	Б
19	Г
20	А
21	В
22	Г
23	А
24	Б
25	в
26	Г
27	А
28	Б
29	А
30	Б

1. Аналитик это …

а)специалист в области анализа имоделирование

б) специалист в предметной области;

в)человек, решающий определенные задачи;

г) человек, который имеет опыт в программировании.

2 Эксперт это …

а) специалист в области анализа и моделирование;

б) специалист в предметной области;

в) человек, решать определенные задачи;

г) человек, который имеет опыт в программировании.

3 Задача классификации сводится к …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

4 Задача регрессии сводится к …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

5 Задача кластеризации заключается в …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

6 Целью поиска ассоциативных правил является …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

7 До предполагаемых моделей относятся такие модели данных:

а) модели классификации и последовательностей;

б) регрессивные, кластеризации, исключений, итоговые и ассоциации;

в) классификации, кластеризации, исключений, итоговые и ассоциации; 

г) модели классификации, последовательностей и исключений.

8 В описательных моделей относятся следующие модели данных:

а) модели классификации и последовательностей;

б) регрессивные, кластеризации, исключений, итоговые и ассоциации;

в) классификации, кластеризации, исключений, итоговые и ассоциации;

г) модели классификации, последовательностей и исключений.

9 Модели классификации описывают …

а) правила или набор правил в соответствии с которыми можно отнести описание любого нового объекта к одному из классов;

б) функции, которые позволяют прогнозировать изменения непрерывных числовых параметров;

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

10Модели последовательностей описывают …

а) правила или набор правил в соответствии с которыми можно

отнести описание любого нового объекта к одному из классов;

б) функции, которые позволяют прогнозировать изменения непрерывных

числовых параметров;

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

11 Регрессивные модели описывают …

а)правила или набор правил в соответствии с которыми можно отнести описание любого нового объекта к одному из классов;

б) функции, которые позволяют прогнозировать изменения непрерывных

числовых параметров;

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

12. Виды лингвистической неопределенности:

а) неточность измерений значений определенной величины, выполняемых

физическими приборами;

б) неопределенность значений слов (Многозначность, размытость,

непонятность, нечеткость); неоднозначность смысла фраз (Синтаксическая и семантическая);

в) случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может стать действительностью); неопределенность значений слов (многозначность, размытость, неясность,

нечеткость)

г) неоднозначность смысла фраз (Синтаксическая и семантическая).

13. Модели исключений описывают …

а) исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

б) ограничения на данные анализируемого массива;

в) закономерности между связанными событиями;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

14 Итоговые модели обнаружат …

а) исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

б) ограничения на данные анализируемого массива;

в) закономерности между связанными событиями;

г) группы, на которые можно разделитьобъекты, данные о которых подвергаются анализа.

15Модели ассоциации проявляют …

а)исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

б) ограничения на данные анализируемого массива;

в) закономерности между связанными событиями;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

16 Виды физической неопределенности данных:

а) неточность измерений значений определенной величины, выполняемых

физическими приборами; случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может

стать действительностью)

б)неопределенность значений слов (Многозначность, размытость, непонятность, нечеткость); неоднозначность смысла фраз (Синтаксическая и семантическая);

в) случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может стать действительностью); неопределенность значений слов (многозначность, размытость, неясность, нечеткость);

г) неоднозначность смысла фраз (Синтаксическая и семантическая).

17 Очистка данных — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков,

дубликатов, противоречий, шумов и т.д.

б) процесс дополнения данных некоторой информацией, позволяющей повысить эффективность развязку аналитических задач

в) объект, содержащий структурированные данные, которые могут оказаться полезными для развязку аналитического задачи

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в котором они могут быть загружены в хранилище данных или аналитическую систему

18 Обогащение — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков, дубликатов, противоречий, шумов и т.д.

б) процесс дополнения данных некоторой информацией, позволяющей

повысить эффективность развязку аналитических задач

в) объект, содержащий структурированные данные, которые могут оказаться

полезными для развязку аналитического задачи

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в

котором они могут быть загружены в хранилище данных или аналитическую систему.

19 Консолидация — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков, дубликатов, противоречий, шумов и т.д.

б) процесс дополнения данных некоторой информацией, позволяющей

повысить эффективность развязку аналитических задач

в) объект, содержащий структурированные данные, которые могут оказаться

полезными для развязку аналитического задачи

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в

котором они могут быть загружены в хранилище данных или

аналитическую систему

20 Транзакция — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

б) разновидность систем хранения, ориентирована на поддержку процесса

анализа данных целостность, обеспечивает, непротиворечивость и

хронологию данных, а также высокую скорость выполнения аналитических

запросов

в) высокоуровневые средства отражения информационной модели и описания структуры данных

г) это установление зависимости дискретной выходной переменной от входных переменных

21 Метаданные — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

б) разновидность систем хранения, ориентирована на поддержку процесса

анализа данных целостность, обеспечивает, непротиворечивость и

хронологию данных, а также высокую скорость выполнения аналитических

запросов

в) высокоуровневые средства отражения информационной модели и описания структуры данных

г) это установление зависимости дискретной выходной переменной от входных переменных

22 Классификация — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

б) разновидность систем хранения, ориентирована на поддержку процесса

анализа данных целостность, обеспечивает, непротиворечивость и хронологию данных, а также высокую скорость выполнения аналитических

запросов

в) высокоуровневые средства отражения информационной модели и описания структуры данных

г) это установление зависимости дискретной выходной переменной от

входных переменных

23 Регрессия — …

а) это установление зависимости непрерывной выходной переменной от

входных переменных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) выявление закономерностей между связанными событиями

г) это установление зависимости дискретной выходной переменной от входных переменных

24 Кластеризация — …

а) это установление зависимости непрерывной выходной переменной от входных переменных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) выявление закономерностей между связанными событиями

г) это установление зависимости дискретной выходной переменной от

входных переменных.

25 Ассоциация — …

а)это установление зависимости непрерывной выходной переменной от

входных переменных

б) эта группировка объектов (наблюдений, событий) на основе данных, описывающих свойства объектов

в) выявление закономерностей между связанными событиями

г) это установление зависимости дискретной выходной переменной от

входных переменных

26 Машинное обучение — …

а) специализированный программный решение (или набор решений), который включает в себя все инструменты для извлечения

закономерностей из сырых данных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, что и отвечает ему

правильный выходной результат.

г) подразделение искусственного интеллекта изучающий методы построения

алгоритмов, способных обучаться на данных

27 Аналитическая платформа — …

а) специализированный программный решение (или набор решений),

который включает в себя все инструменты для извлечения закономерностей из сырых данных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, что и отвечает ему

правильный выходной результат.

г) подразделение искусственного интеллекта изучающий методы построения алгоритмов, способных обучаться на данных

28 Обучающая выборка — …

а) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

б) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

в) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, что и отвечает ему

правильный выходной результат.

г) выявление в сырых данных ранее неизвестных, нетривиальных,

практически полезных и доступных интерпретации знаний, необходимых

для принятия решений в различных сферах человеческой деятельности

29 Ошибка обучения — …

а) это ошибка, допущенная моделью на учебной множества.

б) это ошибка, полученная на тестовых примерах, то есть, что

вычисляется по тем же формулам, но для тестовой множества

в) имена, типы, метки и назначения полей исходной выборки данных

г) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

30 Ошибка обобщения — …

а) это ошибка, допущенная моделью на учебной множества.

б) это ошибка, полученная на тестовых примерах, то есть, что

вычисляется по тем же формулам, но для тестовой множества

в) имена, типы, метки и назначения полей исходной выборки данных

г) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

Ответы:

1	А
2	Б
3	Б
4	В
5	Г
6	А
7	А
8	Б
9	А
10	б
11	В
12	Б
13	А
14	Б
15	В
16	а
17	а
18	Б
19	Г
20	А
21	В
22	Г
23	А
24	Б
25	в
26	Г
27	А
28	Б
29	А
30	Б

1. Аналитик это …

а)специалист в области анализа имоделирование

б) специалист в предметной области;

в)человек, решающий определенные задачи;

г) человек, который имеет опыт в программировании.

2 Эксперт это …

а) специалист в области анализа и моделирование;

б) специалист в предметной области;

в) человек, решать определенные задачи;

г) человек, который имеет опыт в программировании.

3 Задача классификации сводится к …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

4 Задача регрессии сводится к …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

5 Задача кластеризации заключается в …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

6 Целью поиска ассоциативных правил является …

а) нахождения частых зависимостей между объектами или событиями;

б) определения класса объекта по его характеристиками;

в) определение по известным характеристиками объекта значение некоторого его параметра;

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

7 До предполагаемых моделей относятся такие модели данных:

а) модели классификации и последовательностей;

б) регрессивные, кластеризации, исключений, итоговые и ассоциации;

в) классификации, кластеризации, исключений, итоговые и ассоциации; 

г) модели классификации, последовательностей и исключений.

8 В описательных моделей относятся следующие модели данных:

а) модели классификации и последовательностей;

б) регрессивные, кластеризации, исключений, итоговые и ассоциации;

в) классификации, кластеризации, исключений, итоговые и ассоциации;

г) модели классификации, последовательностей и исключений.

9 Модели классификации описывают …

а) правила или набор правил в соответствии с которыми можно отнести описание любого нового объекта к одному из классов;

б) функции, которые позволяют прогнозировать изменения непрерывных числовых параметров;

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

10Модели последовательностей описывают …

а) правила или набор правил в соответствии с которыми можно

отнести описание любого нового объекта к одному из классов;

б) функции, которые позволяют прогнозировать изменения непрерывных

числовых параметров;

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

11 Регрессивные модели описывают …

а)правила или набор правил в соответствии с которыми можно отнести описание любого нового объекта к одному из классов;

б) функции, которые позволяют прогнозировать изменения непрерывных

числовых параметров;

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

12. Виды лингвистической неопределенности:

а) неточность измерений значений определенной величины, выполняемых

физическими приборами;

б) неопределенность значений слов (Многозначность, размытость,

непонятность, нечеткость); неоднозначность смысла фраз (Синтаксическая и семантическая);

в) случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может стать действительностью); неопределенность значений слов (многозначность, размытость, неясность,

нечеткость)

г) неоднозначность смысла фраз (Синтаксическая и семантическая).

13. Модели исключений описывают …

а) исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

б) ограничения на данные анализируемого массива;

в) закономерности между связанными событиями;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

14 Итоговые модели обнаружат …

а) исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

б) ограничения на данные анализируемого массива;

в) закономерности между связанными событиями;

г) группы, на которые можно разделитьобъекты, данные о которых подвергаются анализа.

15Модели ассоциации проявляют …

а)исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

б) ограничения на данные анализируемого массива;

в) закономерности между связанными событиями;

г) группы, на которые можно разделить объекты, данные о которых подвергаются анализа.

16 Виды физической неопределенности данных:

а) неточность измерений значений определенной величины, выполняемых

физическими приборами; случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может

стать действительностью)

б)неопределенность значений слов (Многозначность, размытость, непонятность, нечеткость); неоднозначность смысла фраз (Синтаксическая и семантическая);

в) случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может стать действительностью); неопределенность значений слов (многозначность, размытость, неясность, нечеткость);

г) неоднозначность смысла фраз (Синтаксическая и семантическая).

17 Очистка данных — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков,

дубликатов, противоречий, шумов и т.д.

б) процесс дополнения данных некоторой информацией, позволяющей повысить эффективность развязку аналитических задач

в) объект, содержащий структурированные данные, которые могут оказаться полезными для развязку аналитического задачи

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в котором они могут быть загружены в хранилище данных или аналитическую систему

18 Обогащение — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков, дубликатов, противоречий, шумов и т.д.

б) процесс дополнения данных некоторой информацией, позволяющей

повысить эффективность развязку аналитических задач

в) объект, содержащий структурированные данные, которые могут оказаться

полезными для развязку аналитического задачи

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в

котором они могут быть загружены в хранилище данных или аналитическую систему.

19 Консолидация — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков, дубликатов, противоречий, шумов и т.д.

б) процесс дополнения данных некоторой информацией, позволяющей

повысить эффективность развязку аналитических задач

в) объект, содержащий структурированные данные, которые могут оказаться

полезными для развязку аналитического задачи

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в

котором они могут быть загружены в хранилище данных или

аналитическую систему

20 Транзакция — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

б) разновидность систем хранения, ориентирована на поддержку процесса

анализа данных целостность, обеспечивает, непротиворечивость и

хронологию данных, а также высокую скорость выполнения аналитических

запросов

в) высокоуровневые средства отражения информационной модели и описания структуры данных

г) это установление зависимости дискретной выходной переменной от входных переменных

21 Метаданные — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

б) разновидность систем хранения, ориентирована на поддержку процесса

анализа данных целостность, обеспечивает, непротиворечивость и

хронологию данных, а также высокую скорость выполнения аналитических

запросов

в) высокоуровневые средства отражения информационной модели и описания структуры данных

г) это установление зависимости дискретной выходной переменной от входных переменных

22 Классификация — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

б) разновидность систем хранения, ориентирована на поддержку процесса

анализа данных целостность, обеспечивает, непротиворечивость и хронологию данных, а также высокую скорость выполнения аналитических

запросов

в) высокоуровневые средства отражения информационной модели и описания структуры данных

г) это установление зависимости дискретной выходной переменной от

входных переменных

23 Регрессия — …

а) это установление зависимости непрерывной выходной переменной от

входных переменных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) выявление закономерностей между связанными событиями

г) это установление зависимости дискретной выходной переменной от входных переменных

24 Кластеризация — …

а) это установление зависимости непрерывной выходной переменной от входных переменных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) выявление закономерностей между связанными событиями

г) это установление зависимости дискретной выходной переменной от

входных переменных.

25 Ассоциация — …

а)это установление зависимости непрерывной выходной переменной от

входных переменных

б) эта группировка объектов (наблюдений, событий) на основе данных, описывающих свойства объектов

в) выявление закономерностей между связанными событиями

г) это установление зависимости дискретной выходной переменной от

входных переменных

26 Машинное обучение — …

а) специализированный программный решение (или набор решений), который включает в себя все инструменты для извлечения

закономерностей из сырых данных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, что и отвечает ему

правильный выходной результат.

г) подразделение искусственного интеллекта изучающий методы построения

алгоритмов, способных обучаться на данных

27 Аналитическая платформа — …

а) специализированный программный решение (или набор решений),

который включает в себя все инструменты для извлечения закономерностей из сырых данных

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

в) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, что и отвечает ему

правильный выходной результат.

г) подразделение искусственного интеллекта изучающий методы построения алгоритмов, способных обучаться на данных

28 Обучающая выборка — …

а) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

б) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

в) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, что и отвечает ему

правильный выходной результат.

г) выявление в сырых данных ранее неизвестных, нетривиальных,

практически полезных и доступных интерпретации знаний, необходимых

для принятия решений в различных сферах человеческой деятельности

29 Ошибка обучения — …

а) это ошибка, допущенная моделью на учебной множества.

б) это ошибка, полученная на тестовых примерах, то есть, что

вычисляется по тем же формулам, но для тестовой множества

в) имена, типы, метки и назначения полей исходной выборки данных

г) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

30 Ошибка обобщения — …

а) это ошибка, допущенная моделью на учебной множества.

б) это ошибка, полученная на тестовых примерах, то есть, что

вычисляется по тем же формулам, но для тестовой множества

в) имена, типы, метки и назначения полей исходной выборки данных

г) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

Выбор модели, переоснащение и недооборудование

Ошибка обучения и ошибка обобщения

Ошибка обучения (ошибка обучения) относится к ошибке, которую модель показывает в наборе данных обучения.
Ошибка обобщения — это ожидаемая ошибка модели для любой выборки тестовых данных, которая часто приближается к ошибке в наборе тестовых данных.
Чтобы вычислить ошибку обучения и ошибку обобщения, вы можете использовать функции потерь, представленные ранее, такие как функция потерь квадрата, используемая в линейной регрессии, и функция потерь кросс-энтропии, используемая в регрессии softmax.
Следовательно, ожидаемая ошибка обучения меньше или равна ошибке обобщения. То есть, как правило, параметры модели, полученные из набора обучающих данных, сделают производительность модели на наборе обучающих данных лучше или равной производительности на наборе тестовых данных. Поскольку ошибку обобщения невозможно оценить по ошибке обучения, слепое уменьшение ошибки обучения не означает, что ошибка обобщения будет уменьшена.

Модели машинного обучения должны быть направлены на уменьшение ошибок обобщения.

Выбор модели

Набор для проверки

Набор тестов можно использовать только один раз после выбора всех гиперпараметров и параметров модели. Вы не можете использовать тестовые данные для выбора моделей, таких как параметры настройки.
Зарезервируйте часть данных вне набора обучающих данных и набора тестовых данных для выбора модели. Эта часть данных называется набором данных проверки, или для краткости набором данных проверки.

K-кратная перекрестная проверка

Поскольку набор данных проверки не участвует в обучении модели, слишком расточительно резервировать большой объем данных проверки, когда данных обучения недостаточно. Один из способов улучшить

K

K

Сложите перекрестную проверку (

K

K

-кратная перекрестная проверка). в

K

K

При перекрестной проверке сверток мы разбиваем исходный набор обучающих данных на

K

K

Наборы субданных, которые не пересекаются, мы делаем

K

K

Вторичное обучение и проверка модели. Каждый раз мы используем набор дополнительных данных для проверки модели и других

K

−

1

K-1

Наборы вспомогательных данных для обучения модели. На это

K

K

При обучении и проверке набор дополнительных данных, используемых для проверки модели, каждый раз отличается. Наконец, мы

K

K

Ошибка суб-обучения и ошибка проверки усредняются отдельно.

Недостаточное и переобучение

• Первый тип заключается в том, что модель не может получить более низкую ошибку обучения.Мы называем это явление недостаточным соответствием;
• Другой тип заключается в том, что ошибка обучения модели намного меньше, чем ее ошибка на наборе тестовых данных.Мы называем это явление переобучением. На практике нам приходится иметь дело с недооборудованием и переоборудованием одновременно, насколько это возможно. Хотя существует множество факторов, которые могут вызвать эти две проблемы подгонки, здесь мы сосредоточимся на двух факторах: сложности модели и размере обучающего набора данных.

Сложность модели

Рисунок 3.4 Влияние сложности модели на недостаточное и переобучение

Еще один важный фактор, влияющий на недостаточную и избыточную подгонку, — это размер набора обучающих данных. Вообще говоря, если количество выборок в наборе обучающих данных слишком мало, особенно когда количество параметров модели (по элементам) меньше, вероятность переобучения выше. Кроме того, ошибка обобщения не увеличивается по мере увеличения количества выборок в наборе обучающих данных. Поэтому в пределах допустимого диапазона вычислительных ресурсов мы обычно надеемся, что набор обучающих данных будет больше, особенно когда сложность модели высока, например, модель глубокого обучения с большим количеством слоев.

Подгонка полинома

Нормальная посадка

Недостаточное оснащение

Переоснащение

Снижение веса

В предыдущем разделе мы наблюдали явление переобучения, то есть ошибка обучения модели намного меньше, чем ее ошибка на тестовом наборе. Хотя увеличение набора обучающих данных может уменьшить переобучение, получение дополнительных обучающих данных часто обходится дорого. В этом разделе представлен общий метод решения проблем с переобучением: снижение веса.

L2 регуляризация

Снижение веса эквивалентно

L

2

L_2

Регуляризация нормы (регуляризация). Регуляризация добавляет штрафной член к функции потерь модели, чтобы уменьшить значения изученных параметров модели, что является распространенным методом борьбы с переобучением. Сначала опишем

L

2

L_2

Нормализация регуляризации, а затем объясните, почему это также называется снижением веса.

L

2

L_2

Добавлена ​​регуляризация нормы на основе исходной функции потерь модели.

L

2

L_2

Нормальный штрафной срок для получения функции, которую необходимо минимизировать для обучения.

L

2

L_2

Штраф за норму относится к произведению суммы квадратов каждого элемента весового параметра модели и положительной константы. Возьмите функцию потерь линейной регрессии из раздела 3.1 (линейная регрессия)

ℓ

(

w

1

,

w

2

,

b

)

=

1

n

∑

i

=

1

n

1

2

(

x

1

(

i

)

w

1

+

x

2

(

i

)

w

2

+

b

−

y

(

i

)

)

2

ell(w_1, w_2, b) = frac{1}{n} sum_{i=1}^n frac{1}{2}left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right)^2

Например, где

w

1

,

w

2

w_1, w_2

Весовой параметр,

b

b

Параметр отклонения, образец

i

i

Вход

x

1

(

i

)

,

x

2

(

i

)

x_1^{(i)}, x_2^{(i)}

С этикеткой

y

(

i

)

y^{(i)}

, Количество образцов

n

n

. Использовать векторные весовые параметры

w

=

[

w

1

,

w

2

]

boldsymbol{w} = [w_1, w_2]

Средства с

L

2

L_2

Новая функция потерь нормального штрафного члена имеет вид

ℓ

(

w

1

,

w

2

,

b

)

+

λ

2

n

∥

w

∥

2

,

ell(w_1, w_2, b) + frac{lambda}{2n} |boldsymbol{w}|^2,

Где гиперпараметры

λ

>

0

lambda > 0

. Когда все весовые параметры равны 0, срок штрафа самый маленький. когда

λ

lambda

Когда он больше, штрафной член имеет большую долю в функции потерь, что обычно приближает элемент изученного весового параметра к 0. когда

λ

lambda

Если установлено значение 0, штраф не действует. В приведенной выше формуле

L

2

L_2

Норма в квадрате

∥

w

∥

2

|boldsymbol{w}|^2

После раскладывания

w

1

2

+

w

2

2

w_1^2 + w_2^2

. С

L

2

L_2

После штрафного члена нормы в небольшом пакетном стохастическом градиентном спуске мы будем использовать веса в разделе линейной регрессии.

w

1

w_1

с

w

2

w_2

Метод итерации изменен на

w

1

←

(

1

−

η

λ

∣

B

∣

)

w

1

−

η

∣

B

∣

∑

i

∈

B

x

1

(

i

)

(

x

1

(

i

)

w

1

+

x

2

(

i

)

w

2

+

b

−

y

(

i

)

)

,

w

2

←

(

1

−

η

λ

∣

B

∣

)

w

2

−

η

∣

B

∣

∑

i

∈

B

x

2

(

i

)

(

x

1

(

i

)

w

1

+

x

2

(

i

)

w

2

+

b

−

y

(

i

)

)

.

begin{aligned} w_1 &leftarrow left(1- frac{etalambda}{|mathcal{B}|} right)w_1 — frac{eta}{|mathcal{B}|} sum_{i in mathcal{B}}x_1^{(i)} left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right), w_2 &leftarrow left(1- frac{etalambda}{|mathcal{B}|} right)w_2 — frac{eta}{|mathcal{B}|} sum_{i in mathcal{B}}x_2^{(i)} left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right). end{aligned}

видимый,

L

2

L_2

Вес заказа регуляризации нормы

w

1

w_1

с

w

2

w_2

Умножьте число меньше 1, а затем вычтите градиент без штрафа. следовательно,

L

2

L_2

Регуляризация нормы также называется снижением веса. Ослабление веса увеличивает ограничение модели, которое необходимо изучить, штрафуя параметры модели большими абсолютными значениями, что может быть эффективным при переобучении. В реальных сценариях мы иногда добавляем сумму квадратов элементов отклонения к сроку штрафа.

Pytorch реализация снижения веса

%matplotlib inline
import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append(".")
import d2lzh_pytorch as d2l

print(torch.__version__)

1.3.1

def fit_and_plot_pytorch(wd):
    # Ослабьте весовые параметры. Названия веса обычно заканчиваются на вес
    net = nn.Linear(num_inputs, 1)
    nn.init.normal_(net.weight, mean=0, std=1)
    nn.init.normal_(net.bias, mean=0, std=1)
    optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # Затухание весовых параметров
    optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr)  # Неправильное затухание параметра отклонения
    
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            l = loss(net(X), y).mean()
            optimizer_w.zero_grad()
            optimizer_b.zero_grad()
            
            l.backward()
            
            # Вызвать пошаговую функцию в двух экземплярах оптимизатора, чтобы обновить вес и смещение соответственно
            optimizer_w.step()
            optimizer_b.step()
        train_ls.append(loss(net(train_features), train_labels).mean().item())
        test_ls.append(loss(net(test_features), test_labels).mean().item())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net.weight.data.norm().item())

dropout

Расчетное выражение многослойного персептрона имеет вид

h

i

=

ϕ

(

x

1

w

1

i

+

x

2

w

2

i

+

x

3

w

3

i

+

x

4

w

4

i

+

b

i

)

h_i = phileft(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_iright)

Вот

ϕ

phi

Есть функция активации,

x

1

,

…

,

x

4

x_1, ldots, x_4

Вход, скрытый блок

i

i

Весовой параметр

w

1

i

,

…

,

w

4

i

w_{1i}, ldots, w_{4i}

, Параметр отклонения

b

i

b_i

. Когда для этого скрытого слоя используется метод отбрасывания, скрытые блоки этого уровня будут отброшены с определенной вероятностью. Пусть вероятность отбрасывания равна

p

p

, То есть

p

p

Вероятность

h

i

h_i

Будет очищено, есть

1

−

p

1-p

Вероятность

h

i

h_i

Разделит на

1

−

p

1-p

Сделайте растяжку. Вероятность отбрасывания — это гиперпараметр метода отбрасывания. В частности, пусть случайная величина

ξ

i

xi_i

Вероятности быть 0 и 1 равны

p

p

с

1

−

p

1-p

. При использовании метода отбрасывания мы вычисляем новый скрытый блок

h

i

′

h_i’

h

i

′

=

ξ

i

1

−

p

h

i

h_i’ = frac{xi_i}{1-p} h_i

из-за

E

(

ξ

i

)

=

1

−

p

E(xi_i) = 1-p

,следовательно

E

(

h

i

′

)

=

E

(

ξ

i

)

1

−

p

h

i

=

h

i

E(h_i’) = frac{E(xi_i)}{1-p}h_i = h_i

которыйМетод discard не меняет ожидаемое значение входных данных.。

Многослойный перцептрон с использованием метода отбрасывания для скрытого слоя

Реализация отсева в Pytorch

net = nn.Sequential(
        d2l.FlattenLayer(),
        nn.Linear(num_inputs, num_hiddens1),
        nn.ReLU(),
        nn.Dropout(drop_prob1),
        nn.Linear(num_hiddens1, num_hiddens2), 
        nn.ReLU(),
        nn.Dropout(drop_prob2),
        nn.Linear(num_hiddens2, 10)
        )

for param in net.parameters():
    nn.init.normal_(param, mean=0, std=0.01)

Исчезающий градиент и взрывной градиент

Когда нейронная сеть имеет большое количество слоев, численная стабильность модели имеет тенденцию к ухудшению. Предположим, что слой

L

L

Многослойного перцептрона

l

l

Этаж

H

(

l

)

boldsymbol{H}^{(l)}

Весовой параметр

W

(

l

)

boldsymbol{W}^{(l)}

, Выходной слой

H

(

L

)

boldsymbol{H}^{(L)}

Весовой параметр

W

(

L

)

boldsymbol{W}^{(L)}

. Для удобства обсуждения параметр отклонения не рассматривается, а функции активации всех скрытых слоев устанавливаются как отображение идентичности.

ϕ

(

x

)

=

x

phi(x) = x

. Данный ввод

X

boldsymbol{X}

, Первый из многослойных персептронов

l

l

Вывод слоя

H

(

l

)

=

X

W

(

1

)

W

(

2

)

…

W

(

l

)

boldsymbol{H}^{(l)} = boldsymbol{X} boldsymbol{W}^{(1)} boldsymbol{W}^{(2)} ldots boldsymbol{W}^{(l)}

. В это время, если количество слоев

l

l

Больше,

H

(

l

)

boldsymbol{H}^{(l)}

Расчет может ослабнуть или взорваться. Например, предположим, что входные и весовые параметры всех слоев являются скалярными. Например, весовые параметры равны 0,2 и 5, а выход 30-го слоя многослойного персептрона является входом.

X

boldsymbol{X}

Соответственно и

0.

2

30

≈

1

×

1

0

−

21

0.2^{30} approx 1 times 10^{-21}

(Затухание) и

5

30

≈

9

×

1

0

20

5^{30} approx 9 times 10^{20}

Продукт (взрыв). Точно так же, когда слоев больше, расчет градиента более подвержен затуханию или взрыву.

Произвольно инициализировать параметры модели

Случайная инициализация PyTorch по умолчанию

Есть много способов случайной инициализации параметров модели. использоватьtorch.nn.init.normal_()Сделайте модельnetВесовые параметры использования метода случайной инициализации нормального распределения. Однако в PyTorchnn.ModuleВ параметрах модуля принята более разумная стратегия инициализации (для конкретного метода выборки различных типов слоев см.Исходный код), поэтому нам вообще не нужно рассматривать.

Ксавье случайная инициализация

Существует также более часто используемый метод случайной инициализации, называемый случайной инициализацией Xavier [1].
Предположим, что количество входов полностью связанного слоя равно

a

a

, Количество выходов

b

b

, Случайная инициализация Xavier сделает каждый элемент весового параметра в этом слое случайным образом выборкой с равномерным распределением

U

(

−

6

a

+

b

,

6

a

+

b

)

.

Uleft(-sqrt{frac{6}{a+b}}, sqrt{frac{6}{a+b}}right).

Его конструкция в основном учитывает, что после инициализации параметров модели на дисперсию выходных данных каждого слоя не должно влиять количество входов уровня, а на дисперсию градиента каждого слоя не должно влиять количество выходных данных уровня.

резюме

• Регуляризация добавляет штрафной член к функции потерь модели, чтобы уменьшить значения изученных параметров модели, что является распространенным методом борьбы с переобучением.
• Снижение веса эквивалентно

  L

  2

  L_2

  Регуляризация нормы обычно приближает изученные весовые параметры к 0.

• Снижение веса можно пропустить через оптимизаторweight_decayУкажите гиперпараметры.
• Вы можете определить несколько экземпляров оптимизатора, чтобы использовать разные итерационные методы для разных параметров модели.
• Мы можем справиться с переобучением, используя метод discard.
• Метод отбрасывания используется только при обучении модели.
• Типичными проблемами, связанными с численной стабильностью глубинных моделей, являются затухание и взрыв. Когда нейронная сеть имеет большое количество слоев, численная стабильность модели имеет тенденцию к ухудшению.
• Обычно нам нужно случайным образом инициализировать параметры модели нейронной сети, например весовые параметры.

---

С этим файлом связано 1 файл(ов). Среди них: бух.фин.учёт.rtf.
Показать все связанные файлы

---

Подборка по базе: экономическая теория тест раздел 1.docx, Актуальные вопросы регулирования трудовых отношений.pdf@test_syn, Философия вопросы.docx, экзаменационные вопросы по истории.docx, Перечень вопросов на экзамен по охране труда-1.doc, Примерный перечень вопросов для экзамена Информатика.docx, ПМ 5 практика вопросы.docx, Социология управления вопросы к экзамену.pdf, Актуальные вопросы инфекционной безопасности в работе медицинско, Хим. анализ почв. Вопросы и ответы.pdf

---

Вопрос №1. Теория вероятностей – раздел математики, посвященный:

Изучению закономерностей случайных явлений

Вопрос №2. Значение вероятности события заключено между: 0 и 1

Вопрос №3. Аналитик это …специалист в области анализа и моделирования

Вопрос №4. Эксперт это …специалист в предметной области

Вопрос №5. Задача классификации сводится к …

определению класса объекта по его характеристикам

Вопрос №1. База данных –

предметно-ориентированный, интегрированный, неизменчивый, поддерживающий хронологию набор данных, организованный для целей поддержки принятия решений и единого места сбора и хранения данных организации

Вопрос №2. Случайная величина называется дискретной, если она может принимать только конечное или счетное число значений

Вопрос №3. Иерархические процедуры кластеризации состоят в

1. пошаговом осуществлении: на каждом шаге объединяются 2 или несколько единиц или кластера
2. выборе произвольных кластеров и их объединении
3. том, что на каждом шаге обрабатывается небольшая часть единиц, и полученная картина сопоставляется с предыдущим результатом
4. том, что оперируют сразу со всеми единицами

Вопрос №4. Коэффициент корреляции может принимать значение: от -1 до +1

Вопрос №5. Случайная величина X называется непрерывной, если ее функция распределения

непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек

Вопрос №1. Банк данных – предметно-ориентированный, интегрированный, неизменчивый, поддерживающий хронологию набор данных, организованный для целей поддержки принятия решений и единого места сбора и хранения данных организации

Вопрос №2. К описательным относятся следующие модели данных:

Варианты ответов:

1. модели классификации и последовательностей
2. регрессионные, кластеризации, исключений, итоговые и ассоциации
3. классификации, кластеризации, исключений, итоговые и ассоциации
4. модели классификации, последовательностей и исключений

Вопрос №3.Упорядочить этапы статистического исследования

Тип ответа: Упорядочивание
Варианты ответов:

1. Определение проблемы
2. Разработка подхода к решению проблемы
3. Разработка плана исследования
4. Полевые работы или сбор данных
5. Подготовка данных и их анализ
6. Подготовка отчета и его презентация

Вопрос №4. Data Mining –

Варианты ответов:

1. предметно-ориентированный, интегрированный, неизменчивый, поддерживающий хронологию набор данных, организованный для целей поддержки принятия решений и единого места сбора и хранения данных организации
2. процесс обнаружения в исходных данных ранее неизвестных, нетривиальных, практически полезных и доступных для интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности
3. система программных, языковых, организационных и технических средств, предназначенных для централизованного накопления и коллективного использования данных
4. организованная в соответствии с определенными правилами и поддерживаемая в памяти компьютера именованная совокупность данных, отображающая состояние объектов и их отношений в рассматриваемой предметной области и используемая для удовлетворения информационных потребностей пользователей

Вопрос №5. Корреляционный анализ определяет:

Варианты ответов:

1. интеграл(xdx)+интеграл(ydy)
2. форму связи между X и Y
3. тесноту связи между X и Y
4. производную Y’x

Вопрос №1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если все цифры в числе различны? 60

Вопрос №2. Бросают два кубика. Какие из следующих событий случайные?

Тип ответа: Многие из многих
Варианты ответов:

1. А={на кубиках выпало одинаковое число очков}
2. В={сумма очков на кубиках не превосходит 12}
3. С={сумма очков на кубиках равна 11}
4. D={произведение очков на кубиках равно 11}

Вопрос №3. В коробке 3 красных, 3 желтых, 3 зеленых шара. Вытащили наугад 4 шара. Какие из следующих событий невозможные?

Тип ответа: Многие из многих
Варианты ответов:

1. Все вынутые шары одного цвета.
2. Все вынутые шары разных цветов.
3. Среди вынутых шаров есть шары разных цветов.
4. Среди вынутых есть шары всех трех цветов.

Вопрос №4. В партии из 10 деталей имеются 4 бракованных. Какова вероятность того, что среди наудачу отобранных 5 деталей окажутся 2 бракованные?

Варианты ответов:

1. 0,25
2. 0,476
3. 0,5
4. 0,235

Вопрос №5. Стрелок попадает в десятку с вероятностью 0,05, в девятку – с вероятностью 0,2, в восьмерку – с вероятностью 0,5. Сделан один выстрел. Какова вероятность того, что будет выбито менее 8 очков?

Варианты ответов:

1. 0,1
2. 0,75
3. 0,25
4. 0,9

1. Аналитик это …

а)специалист в области анализа имоделирование

2 Эксперт это …

б) специалист в предметной области;.

3 Задача классификации сводится к …

б) определения класса объекта по его характеристиками;

4 Задача регрессии сводится к …

в) определение по известным характеристиками объекта значение некоторого его параметра;

5 Задача кластеризации заключается в …

г) поиска независимых групп и их характеристик в всем множестве анализируемых данных.

6 Целью поиска ассоциативных правил является …

а) нахождения частых зависимостей между объектами или событиями;

7 До предполагаемых моделей относятся такие модели данных:

а) модели классификации и последовательностей;

8 В описательных моделей относятся следующие модели данных:

б) регрессивные, кластеризации, исключений, итоговые и ассоциации;

9 Модели классификации описывают …

а) правила или набор правил в соответствии с которыми можно отнести описание любого нового объекта к одному из классов;

10Модели последовательностей описывают …

б) функции, которые позволяют прогнозировать изменения непрерывных

числовых параметров;

11 Регрессивные модели описывают …

в) функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме;

12. Виды лингвистической неопределенности:

б) неопределенность значений слов (Многозначность, размытость,

непонятность, нечеткость); неоднозначность смысла фраз (Синтаксическая и семантическая);

13. Модели исключений описывают …

а) исключительные ситуации в записях, которые резко отличаются произвольной признаку от основной множества записей;

14 Итоговые модели обнаружат …

б) ограничения на данные анализируемого массива;

15 Модели ассоциации проявляют …

в) закономерности между связанными событиями;

16 Виды физической неопределенности данных:

а) неточность измерений значений определенной величины, выполняемых

физическими приборами; случайность (или наличие в внешней среде нескольких возможностей, каждая из которых случайным образом может

стать действительностью)

17 Очистка данных — …

а) комплекс методов и процедур, направленных на устранение

причин, мешающих корректной обработке: аномалий, пропусков,

дубликатов, противоречий, шумов и т.д.

18 Обогащение — …

б) процесс дополнения данных некоторой информацией, позволяющей

повысить эффективность развязку аналитических задач

19 Консолидация — …

г) комплекс методов и процедур, направленных на извлечение данных из

различных источников, обеспечение необходимого уровня их

информативности и качества, преобразования в единый формат, в

котором они могут быть загружены в хранилище данных или

аналитическую систему

20 Транзакция — …

а) некоторый набор операций над базой данных, который рассматривается как единственное завершено, с точки зрения пользователя, действие над некоторой информацией, обычно связано с обращением к базе данных

21 Метаданные — …

в) высокоуровневые средства отражения информационной модели и описания структуры данных

22 Классификация — …

г) это установление зависимости дискретной выходной переменной от

входных переменных

23 Регрессия — …

а) это установление зависимости непрерывной выходной переменной от

входных переменных

24 Кластеризация — …

б) эта группировка объектов (Наблюдений, событий) на основе

данных, описывающих свойства объектов

25 Ассоциация — …

в) выявление закономерностей между связанными событиями

26 Машинное обучение — …

г) подразделение искусственного интеллекта изучающий методы построения

алгоритмов, способных обучаться на данных

27 Аналитическая платформа — …

а) специализированный программный решение (или набор решений),

который включает в себя все инструменты для извлечения закономерностей из сырых данных

28 Обучающая выборка — …

б) набор данных, каждая запись которого представляет собой учебный пример, содержащего заданный входной влияние, и соответствующий ему правильный выходной результат

29 Ошибка обучения — …

а) это ошибка, допущенная моделью на учебной множества.

30 Ошибка обобщения — …

б) это ошибка, полученная на тестовых примерах, то есть, что

вычисляется по тем же формулам, но для тестовой множества

1. Алгоритм построения нейронных сетей

   1. Оценка адекватности нейросетевых моделей

При построении
нейросетевых моделей очень важным
являются вопросы оценки их качества.
Для качественной модели нужное минимальное
значение ошибки модели.

Как мера ошибки в
моделях регрессии может рассматриваться
стандартная среднеквадратичная ошибка,
коэффициент множественной корреляции,
судьба естественной дисперсии
прогнозируемого признака, который не
достал объяснения в рамках модели.

В моделях
классификации как мера ошибки может
быть избрана судьба случаев правильно
классифицированных моделью.

В связи с высокими
потенциальными возможностями обучения
нейросетевых моделей важную роль при
оценке адекватности модели играет
вопрос «переобучение» модели. В связи
с этим рассмотрим процесс построения
модели подробнее.

Итак, нужно, чтобы
на основании конечного набора параметров
X, названных учебным множеством, была
построена модель Mod некоторого объекта
Obj. Процесс получения Mod из имеющихся
отрывистых экспериментальных сведений
о системе Obj может рассматриваться, как
обучение модели поведению Obj согласно
заданному критерию, настолько близко,
насколько это возможно. Алгоритмически,
обучение означает подстраивание
внутренних параметров модели (весов
синаптических связей в случае нейронной
сети) с целью минимизации ошибки модели,
которая описывает некоторым образом
отклонения поведения модели от системы
— E = |Obj — Mod |.

Прямое измерение
указанной ошибки модели на практике
невозможно, поскольку функция Obj при
произвольных значениях аргумента
неизвестная. Однако возможное получение
ее оценки:

,

где суммирование
проводится по учебному множеству X. При
использовании базы данных наблюдений
за системой, для обучения может отводиться
некоторая ее часть, названная в этом
случае учебной выборкой. Для учебных
примеров X отклики системы Obj известные.
Таким образом, EX — ошибка обучения для
модели.

В приложениях
пользователя обычно интересуют
предвиденные свойства модели. При этом
главным является вопрос, каким будет
отклик системы на новое влияние, пример
которого отсутствует в базе данных
наблюдений — N. Неизвестная ошибка,
которая допускается моделью Mod на данных,
которые не использовались при обучении,
называется ошибкой обобщения модели
EN.

Основной целью
при построении информационной модели
является уменьшение именно ошибки
обобщения, поскольку минимальная ошибка
обучения гарантирует адекватность
модели лишь в заранее избранных точках
(а в них значение отклика системы известно
и без всякой модели). Проводя аналогии
с обучением в биологии, можно сказать,
что минимальная ошибка обучения отвечает
прямому запоминанию учебной информации,
а минимальная ошибка обобщения —
формированию понятий и привычек, которые
разрешают распространить полученный
из обучения опыт на новые условия.
Последнее значительно более ценное при
проектировании нейросетевых систем,
так как для непосредственного запоминания
информации лучше приспособлены другие,
не нейронные устройства компьютерной
памяти.

Важно отметить,
что минимальная ошибка обучения не
гарантирует минимальную ошибку обобщения.
Классическим примером является построение
модели функции (аппроксимация функции)
по нескольким заданным точкам полиномом
высокого порядка. Значения полинома
(модели) при довольно высокой его степени
являются точными в учебных точках, т.е.
ошибка обучения равняется нулю. Однако
значение в промежуточных точках могут
значительно отличаться от аппроксимирующей
функции, ведь ошибка обобщения такой
модели может быть неприемлемо большой.

Поскольку истинное
значение ошибки обобщения не доступно,
на практике используется ее оценка. Для
ее получения анализируется часть
примеров из имеющейся базы данных, для
которых известны отклики системы, но
которые не использовались при обучении.
Эта выборка примеров называется тестовой
выборкой. Ошибка обобщения оценивается,
как отклонение модели на множестве
примеров из тестовой выборки.

Оценка ошибки
обобщения является принципиальным
моментом при построении модели. На
первый взгляд может показаться, что
сознательный отказ от использования
части примеров при обучении может только
ухудшить итоговую модель. Однако без
этапа тестирования единой оценкой
качества модели будет лишь ошибка
обучения, которая, как уже отмечалось,
мало связана с предвиденными способностями
модели. В профессиональных исследованиях
могут использоваться несколько
независимых тестовых выборок, этапы
обучения и тестирования повторяются
многократно с вариацией начального
распределения весов нейросети, ее
топологии и параметров обучения.
Окончательный выбор «наилучшей»
нейросети делается с учетом имеющегося
объема и качества данных, специфики
задачи, с целью минимизации риска большой
ошибки обобщения при эксплуатации
модели.

Построение нейронной
сети (после выбора входных переменных)
состоит из следующих шагов:

• Выбор
  начальной конфигурации сети.

Проведение
экспериментов с разными конфигурациями
сетей. Для каждой конфигурации проводиться
несколько экспериментов, чтобы не
получить ошибочный результат из-за
того, что процесс обучения попал в
локальный минимум. Если в очередном
эксперименте наблюдается недообучение
(сеть не выдает результат приемлемого
качества), необходимо прибавить
дополнительные нейроны в промежуточный
пласт. Если это не помогает, попробовать
прибавить новый промежуточный пласт.
Если имеет место переобучение (контрольная
ошибка постоянно возрастает), необходимо
удалить несколько скрытых элементов.

• Отбор
  данных

Для получения
качественных результатов учебное,
контрольное и тестовое множества должны
быть репрезентативными (представительными)
с точки зрения сути задачи (больше того,
эти множества должны быть репрезентативными
каждая отдельно). Если учебные данные
не репрезентативны, то модель, как
минимум, будет не очень красивой, а в
худшем случае — непригодной.

• Обучение
  сети

Обучение сети
лучше рассмотреть на примере многослойного
персептрона. Уровнем активации элемента
называется взвешенная сумма его входов
с добавленным к ней предельным значением.
Таким образом, уровень активации
представляет собой простую линейную
функцию входов. Эта активация потом
превратится с помощью сигмавидной (что
имеет S-Образную форму) кривой.

Комбинация линейной
функции нескольких сменных и скалярной
сигмавидной функции приводит к
характерному профилю «сигмавидного
склона», который выдает элемент
первого промежуточного пласта сети.
При изменении весов и порогов изменяется
и поверхность отклика. При этом может
изменяться как ориентация всей
поверхности, так и крутизна склона.
Большим значением весов отвечает более
крутой склон. Если увеличить все веса
в два раза, то ориентация не изменится,
а наклон будет более крутым.

В многослойной
сети подобные функции отклика комбинируются
одна из одной с помощью построения их
линейных комбинаций и применения
нелинейных функций активации. Перед
началом обучения сети весам и порогам
случайным образом присваиваются
небольшие по величине начальные значения.
Тем самым отклики отдельных элементов
сети имеют малый наклон и ориентированы
хаотически — фактически они не связаны
друг с другом. По мере того, как происходит
обучение, поверхности отклика элементов
сети поворачиваются и смещаются в нужное
положение, а значение весов увеличиваются,
поскольку они должны моделировать
отдельные участки целевой поверхности
отклика.

В задачах
классификации исходный элемент должен
выдавать сильный сигнал в случае, если
данное наблюдение принадлежит к классу,
который нас интересует, и слабый — в
противоположном случае. Иначе говоря,
этот элемент должен стремиться
смоделировать функцию, равную единице
в той области пространства объектов,
где располагаются объекты из нужного
класса, и равную нулю вне этой области.
Такая конструкция известная как
дискриминантная функция в задачах
распознавания. «Идеальная»
дискриминантная функция должна иметь
плоскую структуру, так чтобы точки
соответствующей поверхности располагались
или на нулевом уровне.

Если сеть не
содержит скрытых элементов, то на выходе
она может моделировать только одинарный
«сигмавидный склон»: точки, которые
находятся по одну его сторону, располагаются
низко, по другую — высоко. При этом всегда
будет существовать область между ними
(на склоне), где высота принимает
промежуточные значения, но по мере
увеличения веса эта область будет
суживаться.

Теоретически, для
моделирования любой задачи довольно
многослойного персептрона с двумя
промежуточными пластами (этот результат
известный как теорема Колмогорова). При
этом может оказаться и так, что для
решения некоторой конкретной задачи
более простой и удобной будет сеть с
еще большим числом пластов. Однако, для
решения большинства практических задач
достаточно всего одного промежуточного
пласта, два пласта применяются как
резерв в особых случаях, а сети с тремя
пластами практически не применяются.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  16.02.2016603.14 Кб121.doc

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Характер приближений в информационных моделях

Специфичность информационных моделей проявляется не только в способах их синтеза, но и характере делаемых приближений (и связанных с ними ошибок). Отличия в поведении системы и ее информационной модели возникают вследствие свойств экспериментальных данных.

• Информационные модели ab initio являются неполными. Пространства входных и выходных переменных не могут, в общем случае, содержать все параметры, существенные для описания поведения системы. Это связано как с техническими ограничениями, так и с ограниченностью наших представлений о моделируемой системе. Кроме того, при увеличении числа переменных ужесточаются требования на объем необходимых экспериментальных данных для построения модели (об этом см. ниже). Эффект опущенных (скрытых) входных параметров может нарушать однозначность моделируемой системной функции F.
• База экспериментальных данных, на которых основывается модель G рассматривается, как внешняя данность. При этом, в данных всегда присутствуют ошибки разной природы, шум, а также противоречия отдельных измерений друг другу. За исключением простых случаев, искажения в данных не могут быть устранены полностью.
• Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных задачи. Как следствие, получаемые модели будут обладать неодинаковой достоверностью и точностью в различных областях изменения параметров.
• Экспериментальные данные могут содержать пропущенные значения (например, вследствие потери информации, отказа измеряющих датчиков, невозможности проведения полного набора анализов и т.п.). Произвольность в интерпретации этих значений, опять-таки, ухудшает свойства модели.

Такие особенности в данных и в постановке задач требуют особого отношения к ошибкам информационных моделей.

Ошибка обучения и ошибка обобщения

Итак, при информационном подходе требуемая модель G системы F не может быть полностью основана на явных правилах и формальных законах. Процесс получения G из имеющихся отрывочных экспериментальных сведений о системе F может рассматриваться, как обучение модели G поведению F в соответствии с заданным критерием, настолько близко, насколько возможно. Алгоритмически, обучение означает подстройку внутренних параметров модели (весов синаптических связей в случае нейронной сети) с целью минимизации ошибки модели .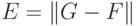

Прямое измерение указанной ошибки модели на практике не достижимо, поскольку системная функция F при произвольных значениях аргумента не известна. Однако возможно получение ее оценки:

где суммирование по X проводится по некоторому конечному набору параметров X, называемому обучающим множеством. При использовании базы данных наблюдений за системой, для обучения может отводиться некоторая ее часть, называемая в этом случае обучающей выборкой. Для обучающих примеров X отклики системы Y известны^{7С учетом описанных выше особенностей экспериментальных данных.}
. Норма невязки модельной функции G и системной функции Y на множестве X играет важную роль в информационном моделировании и называется ошибкой обучения модели.

Для случая точных измерений (например, в некоторых задачах классификации, когда отношение образца к классу не вызывает сомнений) однозначность системной функции для достаточно широкого класса G моделей гарантирует возможность достижения произвольно малого значения ошибки обучения E_L. Нарушение однозначности системной функции в присутствии экспериментальных ошибок и неполноты признаковых пространств приводит в общем случае к ненулевым ошибкам обучения. В этом случае предельная достижимая ошибка обучения может служить мерой корректности постановки задачи и качества класса моделей G.

В приложениях пользователя обычно интересуют предсказательные свойства модели. При этом главным является вопрос, каковым будет отклик системы на новое воздействие, пример которого отсутствует в базе данных наблюдений. Наиболее общий ответ на этот вопрос дает (по-прежнему недоступная) ошибка модели E. Неизвестная ошибка, допускаемая моделью G на данных, не использовавшихся при обучении, называется ошибкой обобщения модели E_G.

Основной целью при построении информационной модели является уменьшение именно ошибки обобщения, поскольку малая ошибка обучения гарантирует адекватность модели лишь в заранее выбранных точках (а в них значения отклика системы известны и без всякой модели!). Проводя аналогии с обучением в биологии, можно сказать, что малая ошибка обучения соответствует прямому запоминанию обучающей информации, а малая ошибка обобщения — формированию понятий и навыков, позволяющих распространить ограниченный опыт обучения на новые условия. Последнее значительно более ценно при проектировании нейросетевых систем, так как для непосредственного запоминания информации лучше приспособлены не нейронные устройства компьютерной памяти.

Важно отметить, что малость ошибки обучения не гарантирует малость ошибки обобщения. Классическим примером является построение модели функции (аппроксимация функции) по нескольким заданным точкам полиномом высокого порядка. Значения полинома (модели) при достаточно высокой его степени являются точными в обучающих точках, т.е. ошибка обучения равна нулю. Однако значения в промежуточных точках могут значительно отличаться от аппроксимируемой функции, следовательно ошибка обобщения такой модели может быть неприемлемо большой.

Поскольку истинное значение ошибки обобщения не доступно, в практике используется ее оценка. Для ее получения анализируется часть примеров из имеющейся базы данных, для которых известны отклики системы, но которые не использовались при обучении. Эта выборка примеров называется тестовой выборкой. Ошибка обобщения оценивается, как норма уклонения модели на множестве примеров из тестовой выборки.

Оценка ошибки обобщения является принципиальным моментом при построении информационной модели. На первый взгляд может показаться, что сознательное не использование части примеров при обучении может только ухудшить итоговую модель. Однако без этапа тестирования единственной оценкой качества модели будет лишь ошибка обучения, которая, как уже отмечалось, мало связана с предсказательными способностями модели. В профессиональных исследованиях могут использоваться несколько независимых тестовых выборок, этапы обучения и тестирования повторяются многократно с вариацией начального распределения весов нейросети, ее топологии и параметров обучения. Окончательный выбор «наилучшей» нейросети выполняется с учетом имеющегося объема и качества данных, специфики задачи, с целью минимизации риска большой ошибки обобщения при эксплуатации модели.

Выбор модели, переоснащение и недооборудование

Ошибка обучения и ошибка обобщения

Ошибка обучения (ошибка обучения) относится к ошибке, которую модель показывает в наборе данных обучения.
Ошибка обобщения — это ожидаемая ошибка модели для любой выборки тестовых данных, которая часто приближается к ошибке в наборе тестовых данных.
Чтобы вычислить ошибку обучения и ошибку обобщения, вы можете использовать функции потерь, представленные ранее, такие как функция потерь квадрата, используемая в линейной регрессии, и функция потерь кросс-энтропии, используемая в регрессии softmax.
Следовательно, ожидаемая ошибка обучения меньше или равна ошибке обобщения. То есть, как правило, параметры модели, полученные из набора обучающих данных, сделают производительность модели на наборе обучающих данных лучше или равной производительности на наборе тестовых данных. Поскольку ошибку обобщения невозможно оценить по ошибке обучения, слепое уменьшение ошибки обучения не означает, что ошибка обобщения будет уменьшена.

Модели машинного обучения должны быть направлены на уменьшение ошибок обобщения.

Выбор модели

Набор для проверки

Набор тестов можно использовать только один раз после выбора всех гиперпараметров и параметров модели. Вы не можете использовать тестовые данные для выбора моделей, таких как параметры настройки.
Зарезервируйте часть данных вне набора обучающих данных и набора тестовых данных для выбора модели. Эта часть данных называется набором данных проверки, или для краткости набором данных проверки.

K-кратная перекрестная проверка

Поскольку набор данных проверки не участвует в обучении модели, слишком расточительно резервировать большой объем данных проверки, когда данных обучения недостаточно. Один из способов улучшить

K

K

Сложите перекрестную проверку (

K

K

-кратная перекрестная проверка). в

K

K

При перекрестной проверке сверток мы разбиваем исходный набор обучающих данных на

K

K

Наборы субданных, которые не пересекаются, мы делаем

K

K

Вторичное обучение и проверка модели. Каждый раз мы используем набор дополнительных данных для проверки модели и других

K

−

1

K-1

Наборы вспомогательных данных для обучения модели. На это

K

K

При обучении и проверке набор дополнительных данных, используемых для проверки модели, каждый раз отличается. Наконец, мы

K

K

Ошибка суб-обучения и ошибка проверки усредняются отдельно.

Недостаточное и переобучение

• Первый тип заключается в том, что модель не может получить более низкую ошибку обучения.Мы называем это явление недостаточным соответствием;
• Другой тип заключается в том, что ошибка обучения модели намного меньше, чем ее ошибка на наборе тестовых данных.Мы называем это явление переобучением. На практике нам приходится иметь дело с недооборудованием и переоборудованием одновременно, насколько это возможно. Хотя существует множество факторов, которые могут вызвать эти две проблемы подгонки, здесь мы сосредоточимся на двух факторах: сложности модели и размере обучающего набора данных.

Сложность модели

Рисунок 3.4 Влияние сложности модели на недостаточное и переобучение

Еще один важный фактор, влияющий на недостаточную и избыточную подгонку, — это размер набора обучающих данных. Вообще говоря, если количество выборок в наборе обучающих данных слишком мало, особенно когда количество параметров модели (по элементам) меньше, вероятность переобучения выше. Кроме того, ошибка обобщения не увеличивается по мере увеличения количества выборок в наборе обучающих данных. Поэтому в пределах допустимого диапазона вычислительных ресурсов мы обычно надеемся, что набор обучающих данных будет больше, особенно когда сложность модели высока, например, модель глубокого обучения с большим количеством слоев.

Подгонка полинома

Нормальная посадка

Недостаточное оснащение

Переоснащение

Снижение веса

В предыдущем разделе мы наблюдали явление переобучения, то есть ошибка обучения модели намного меньше, чем ее ошибка на тестовом наборе. Хотя увеличение набора обучающих данных может уменьшить переобучение, получение дополнительных обучающих данных часто обходится дорого. В этом разделе представлен общий метод решения проблем с переобучением: снижение веса.

L2 регуляризация

Снижение веса эквивалентно

L

2

L_2

Регуляризация нормы (регуляризация). Регуляризация добавляет штрафной член к функции потерь модели, чтобы уменьшить значения изученных параметров модели, что является распространенным методом борьбы с переобучением. Сначала опишем

L

2

L_2

Нормализация регуляризации, а затем объясните, почему это также называется снижением веса.

L

2

L_2

Добавлена ​​регуляризация нормы на основе исходной функции потерь модели.

L

2

L_2

Нормальный штрафной срок для получения функции, которую необходимо минимизировать для обучения.

L

2

L_2

Штраф за норму относится к произведению суммы квадратов каждого элемента весового параметра модели и положительной константы. Возьмите функцию потерь линейной регрессии из раздела 3.1 (линейная регрессия)

ℓ

(

w

1

,

w

2

,

b

)

=

1

n

∑

i

=

1

n

1

2

(

x

1

(

i

)

w

1

+

x

2

(

i

)

w

2

+

b

−

y

(

i

)

)

2

ell(w_1, w_2, b) = frac{1}{n} sum_{i=1}^n frac{1}{2}left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right)^2

Например, где

w

1

,

w

2

w_1, w_2

Весовой параметр,

b

b

Параметр отклонения, образец

i

i

Вход

x

1

(

i

)

,

x

2

(

i

)

x_1^{(i)}, x_2^{(i)}

С этикеткой

y

(

i

)

y^{(i)}

, Количество образцов

n

n

. Использовать векторные весовые параметры

w

=

[

w

1

,

w

2

]

boldsymbol{w} = [w_1, w_2]

Средства с

L

2

L_2

Новая функция потерь нормального штрафного члена имеет вид

ℓ

(

w

1

,

w

2

,

b

)

+

λ

2

n

∥

w

∥

2

,

ell(w_1, w_2, b) + frac{lambda}{2n} |boldsymbol{w}|^2,

Где гиперпараметры

λ

>

0

lambda > 0

. Когда все весовые параметры равны 0, срок штрафа самый маленький. когда

λ

lambda

Когда он больше, штрафной член имеет большую долю в функции потерь, что обычно приближает элемент изученного весового параметра к 0. когда

λ

lambda

Если установлено значение 0, штраф не действует. В приведенной выше формуле

L

2

L_2

Норма в квадрате

∥

w

∥

2

|boldsymbol{w}|^2

После раскладывания

w

1

2

+

w

2

2

w_1^2 + w_2^2

. С

L

2

L_2

После штрафного члена нормы в небольшом пакетном стохастическом градиентном спуске мы будем использовать веса в разделе линейной регрессии.

w

1

w_1

с

w

2

w_2

Метод итерации изменен на

w

1

←

(

1

−

η

λ

∣

B

∣

)

w

1

−

η

∣

B

∣

∑

i

∈

B

x

1

(

i

)

(

x

1

(

i

)

w

1

+

x

2

(

i

)

w

2

+

b

−

y

(

i

)

)

,

w

2

←

(

1

−

η

λ

∣

B

∣

)

w

2

−

η

∣

B

∣

∑

i

∈

B

x

2

(

i

)

(

x

1

(

i

)

w

1

+

x

2

(

i

)

w

2

+

b

−

y

(

i

)

)

.

begin{aligned} w_1 &leftarrow left(1- frac{etalambda}{|mathcal{B}|} right)w_1 — frac{eta}{|mathcal{B}|} sum_{i in mathcal{B}}x_1^{(i)} left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right),\ w_2 &leftarrow left(1- frac{etalambda}{|mathcal{B}|} right)w_2 — frac{eta}{|mathcal{B}|} sum_{i in mathcal{B}}x_2^{(i)} left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right). end{aligned}

видимый,

L

2

L_2

Вес заказа регуляризации нормы

w

1

w_1

с

w

2

w_2

Умножьте число меньше 1, а затем вычтите градиент без штрафа. следовательно,

L

2

L_2

Регуляризация нормы также называется снижением веса. Ослабление веса увеличивает ограничение модели, которое необходимо изучить, штрафуя параметры модели большими абсолютными значениями, что может быть эффективным при переобучении. В реальных сценариях мы иногда добавляем сумму квадратов элементов отклонения к сроку штрафа.

Pytorch реализация снижения веса

%matplotlib inline
import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append(".")
import d2lzh_pytorch as d2l

print(torch.__version__)

1.3.1

def fit_and_plot_pytorch(wd):
    # Ослабьте весовые параметры. Названия веса обычно заканчиваются на вес
    net = nn.Linear(num_inputs, 1)
    nn.init.normal_(net.weight, mean=0, std=1)
    nn.init.normal_(net.bias, mean=0, std=1)
    optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # Затухание весовых параметров
    optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr)  # Неправильное затухание параметра отклонения
    
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            l = loss(net(X), y).mean()
            optimizer_w.zero_grad()
            optimizer_b.zero_grad()
            
            l.backward()
            
            # Вызвать пошаговую функцию в двух экземплярах оптимизатора, чтобы обновить вес и смещение соответственно
            optimizer_w.step()
            optimizer_b.step()
        train_ls.append(loss(net(train_features), train_labels).mean().item())
        test_ls.append(loss(net(test_features), test_labels).mean().item())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net.weight.data.norm().item())

dropout

Расчетное выражение многослойного персептрона имеет вид

h

i

=

ϕ

(

x

1

w

1

i

+

x

2

w

2

i

+

x

3

w

3

i

+

x

4

w

4

i

+

b

i

)

h_i = phileft(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_iright)

Вот

ϕ

phi

Есть функция активации,

x

1

,

…

,

x

4

x_1, ldots, x_4

Вход, скрытый блок

i

i

Весовой параметр

w

1

i

,

…

,

w

4

i

w_{1i}, ldots, w_{4i}

, Параметр отклонения

b

i

b_i

. Когда для этого скрытого слоя используется метод отбрасывания, скрытые блоки этого уровня будут отброшены с определенной вероятностью. Пусть вероятность отбрасывания равна

p

p

, То есть

p

p

Вероятность

h

i

h_i

Будет очищено, есть

1

−

p

1-p

Вероятность

h

i

h_i

Разделит на

1

−

p

1-p

Сделайте растяжку. Вероятность отбрасывания — это гиперпараметр метода отбрасывания. В частности, пусть случайная величина

ξ

i

xi_i

Вероятности быть 0 и 1 равны

p

p

с

1

−

p

1-p

. При использовании метода отбрасывания мы вычисляем новый скрытый блок

h

i

′

h_i’

h

i

′

=

ξ

i

1

−

p

h

i

h_i’ = frac{xi_i}{1-p} h_i

из-за

E

(

ξ

i

)

=

1

−

p

E(xi_i) = 1-p

,следовательно

E

(

h

i

′

)

=

E

(

ξ

i

)

1

−

p

h

i

=

h

i

E(h_i’) = frac{E(xi_i)}{1-p}h_i = h_i

которыйМетод discard не меняет ожидаемое значение входных данных.。

Многослойный перцептрон с использованием метода отбрасывания для скрытого слоя

Реализация отсева в Pytorch

net = nn.Sequential(
        d2l.FlattenLayer(),
        nn.Linear(num_inputs, num_hiddens1),
        nn.ReLU(),
        nn.Dropout(drop_prob1),
        nn.Linear(num_hiddens1, num_hiddens2), 
        nn.ReLU(),
        nn.Dropout(drop_prob2),
        nn.Linear(num_hiddens2, 10)
        )

for param in net.parameters():
    nn.init.normal_(param, mean=0, std=0.01)

Исчезающий градиент и взрывной градиент

Когда нейронная сеть имеет большое количество слоев, численная стабильность модели имеет тенденцию к ухудшению. Предположим, что слой

L

L

Многослойного перцептрона

l

l

Этаж

H

(

l

)

boldsymbol{H}^{(l)}

Весовой параметр

W

(

l

)

boldsymbol{W}^{(l)}

, Выходной слой

H

(

L

)

boldsymbol{H}^{(L)}

Весовой параметр

W

(

L

)

boldsymbol{W}^{(L)}

. Для удобства обсуждения параметр отклонения не рассматривается, а функции активации всех скрытых слоев устанавливаются как отображение идентичности.

ϕ

(

x

)

=

x

phi(x) = x

. Данный ввод

X

boldsymbol{X}

, Первый из многослойных персептронов

l

l

Вывод слоя

H

(

l

)

=

X

W

(

1

)

W

(

2

)

…

W

(

l

)

boldsymbol{H}^{(l)} = boldsymbol{X} boldsymbol{W}^{(1)} boldsymbol{W}^{(2)} ldots boldsymbol{W}^{(l)}

. В это время, если количество слоев

l

l

Больше,

H

(

l

)

boldsymbol{H}^{(l)}

Расчет может ослабнуть или взорваться. Например, предположим, что входные и весовые параметры всех слоев являются скалярными. Например, весовые параметры равны 0,2 и 5, а выход 30-го слоя многослойного персептрона является входом.

X

boldsymbol{X}

Соответственно и

0.

2

30

≈

1

×

1

0

−

21

0.2^{30} approx 1 times 10^{-21}

(Затухание) и

5

30

≈

9

×

1

0

20

5^{30} approx 9 times 10^{20}

Продукт (взрыв). Точно так же, когда слоев больше, расчет градиента более подвержен затуханию или взрыву.

Произвольно инициализировать параметры модели

Случайная инициализация PyTorch по умолчанию

Есть много способов случайной инициализации параметров модели. использоватьtorch.nn.init.normal_()Сделайте модельnetВесовые параметры использования метода случайной инициализации нормального распределения. Однако в PyTorchnn.ModuleВ параметрах модуля принята более разумная стратегия инициализации (для конкретного метода выборки различных типов слоев см.Исходный код), поэтому нам вообще не нужно рассматривать.

Ксавье случайная инициализация

Существует также более часто используемый метод случайной инициализации, называемый случайной инициализацией Xavier [1].
Предположим, что количество входов полностью связанного слоя равно

a

a

, Количество выходов

b

b

, Случайная инициализация Xavier сделает каждый элемент весового параметра в этом слое случайным образом выборкой с равномерным распределением

U

(

−

6

a

+

b

,

6

a

+

b

)

.

Uleft(-sqrt{frac{6}{a+b}}, sqrt{frac{6}{a+b}}right).

Его конструкция в основном учитывает, что после инициализации параметров модели на дисперсию выходных данных каждого слоя не должно влиять количество входов уровня, а на дисперсию градиента каждого слоя не должно влиять количество выходных данных уровня.

резюме

• Регуляризация добавляет штрафной член к функции потерь модели, чтобы уменьшить значения изученных параметров модели, что является распространенным методом борьбы с переобучением.
• Снижение веса эквивалентно

  L

  2

  L_2

  Регуляризация нормы обычно приближает изученные весовые параметры к 0.

• Снижение веса можно пропустить через оптимизаторweight_decayУкажите гиперпараметры.
• Вы можете определить несколько экземпляров оптимизатора, чтобы использовать разные итерационные методы для разных параметров модели.
• Мы можем справиться с переобучением, используя метод discard.
• Метод отбрасывания используется только при обучении модели.
• Типичными проблемами, связанными с численной стабильностью глубинных моделей, являются затухание и взрыв. Когда нейронная сеть имеет большое количество слоев, численная стабильность модели имеет тенденцию к ухудшению.
• Обычно нам нужно случайным образом инициализировать параметры модели нейронной сети, например весовые параметры.