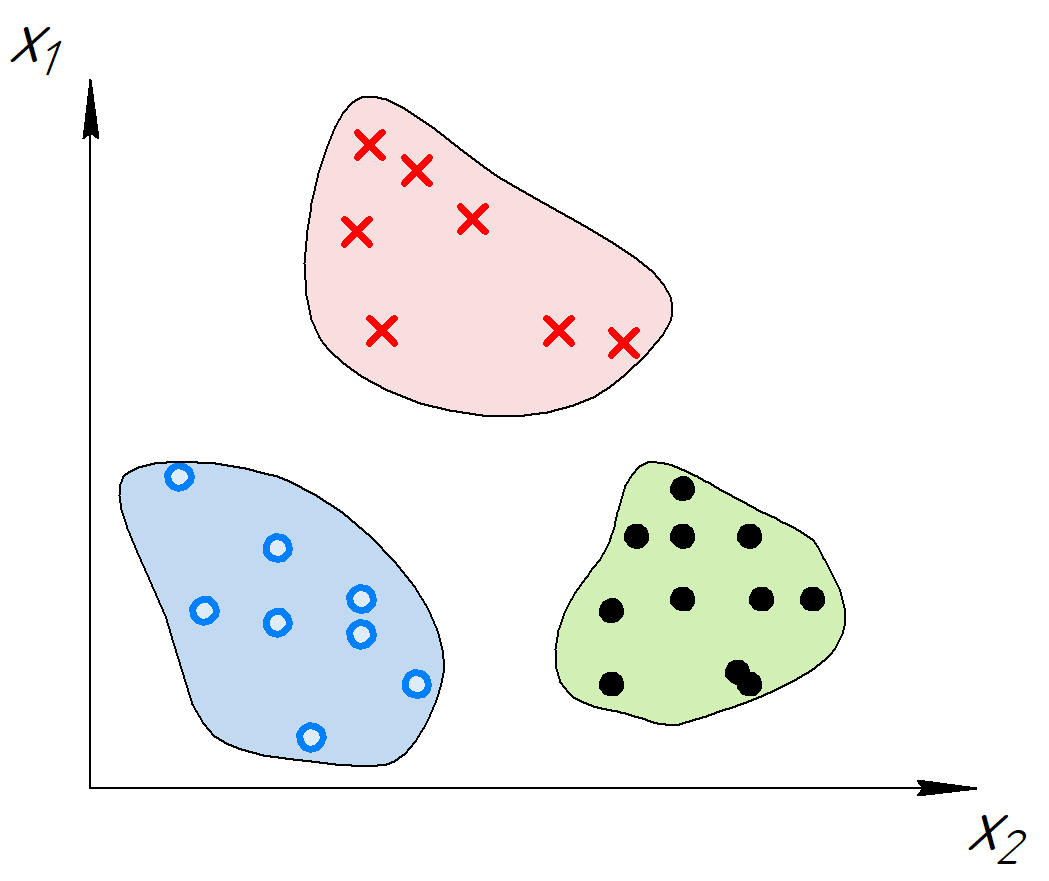
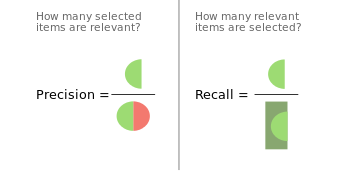
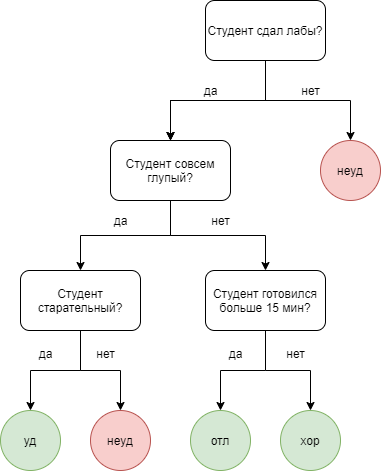
| title | date | categories | tags | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Machine Learning Error: Bias, Variance and Irreducible Error with Python |
2020-11-02 |
|
|
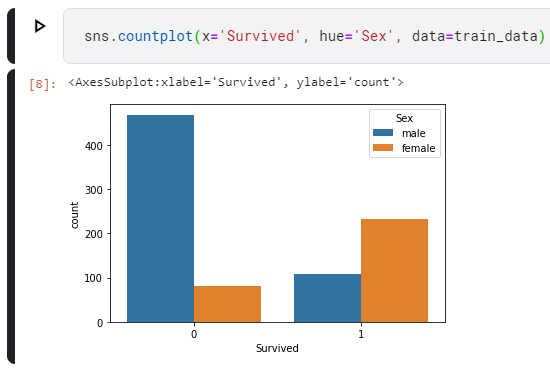
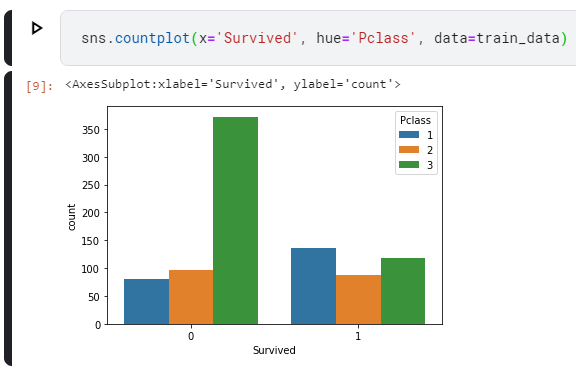
Supervised Machine Learning is one of the most prominent branches of Machine Learning these days. Using a labeled training set and an adequate model, it is possible to create a ML model that demonstrates very impressive results. As we will see, training such a model involves a cycle of feeding forward data through the model, observing how bad it performs, and subsequently optimizing it to make it better.
After some threshold is passed, the training process stops, and the model is trained.
The «observing how bad it performs» part is the focus of today’s article. Because the error, with which the former is expressed, is interesting — because it is composed of multiple error subtypes. This article will focus on these subtypes, which are the bias error, the variance error and the irreducible error. We will find out what error is in general, what those subtypes are, and how we can decompose a TensorFlow ML model into the error subtypes.
Let’s take a look! 
[toc]
Error in supervised machine learning: what is it?
From the article about loss and loss functions, we know about the high-level supervised machine learning process:
- Samples from a labeled dataset are inserted into the model — this is called «feeding the samples forward».
- The machine learning model generates a prediction for each sample.
- All predictions are compared to the labels, called the ground truth, and a loss value is output.
- Based on the loss value, the loss is computed backwards, to find the optimizations for the individual parts of the machine learning model.
- By means of some optimization mechanism (e.g. gradient descent or Adaptive optimization), the model is optimized.
Above, we talked about the «observing how bad it performs» part of training a supervised machine learning model. Note that «how bad» and «loss» have relatively similar meaning — and yes, they are connected.
The «loss value» effectively shows you how bad the model performs — in other words, how much off the model is compared to the ground truth, on average.
Hence, this loss value is also called the model error. Your goal as a machine learning engineer is to create a dataset, find a suitable algorithm, and tweak it accordingly, to generate a model that performs and generalizes well. In other words, it must be accurate in terms of the prediction, and work in a wide range of cases — even with data that the model has never seen before.
And of course, this is quite a challenge.
Error subtypes
Above, we saw that feeding forward the training samples results in a loss or error value. It can be used subsequently for improving your Machine Learning model. Now, we’ll dive into the error concept, and will see that it can be decomposed in a few distinct subtypes: bias error, variance error and irreducible error.
Put simply, the subtypes together compose the notion of ‘error’ in the following manner:
Error = Bias error + Variance error + Irreducible error.
- Bias error: how strict the model generalizes to some designated set of functions.
- Variance error: how much the estimated function will change when the algorithm is trained with differing datasets.
- Irreducible error: error that is neither bias or variance error and is hence relatively random.
Bias error
In Dietterich and Kong (1995), we find that Mitchell (1980) introduces the concept of bias error as follows:
«Any basis for choosing one generalization [hypothesis] over another, other than strict consistency with the observed training instances.»
While this sounds relatively vague — likely on purpose, for generalization purposes — we can relatively easily convert it into a definition that resonates well with ML researchers and engineers:
Bias involves an assumption of the Machine Learning model that the target function to learn is part of a set of target functions. In other words, if a model can only learn — or fit — a few example functions, it is a high-bias model. If the model can learn many functions instead, it is a low-bias model.
Bias, in the context of Machine Learning, is a type of error that occurs due to erroneous assumptions in the learning algorithm.
StackExchange (n.d.)
High bias, by making a lot of assumptions about the target function, simplifies the model and makes the fit less computationally intensive.
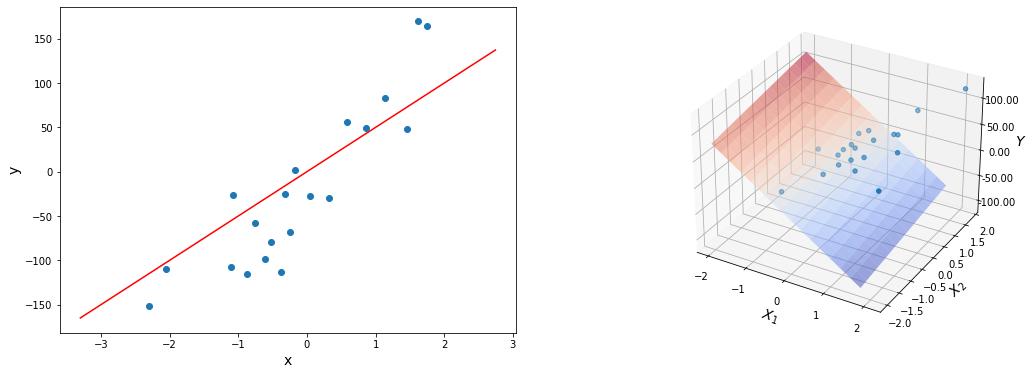
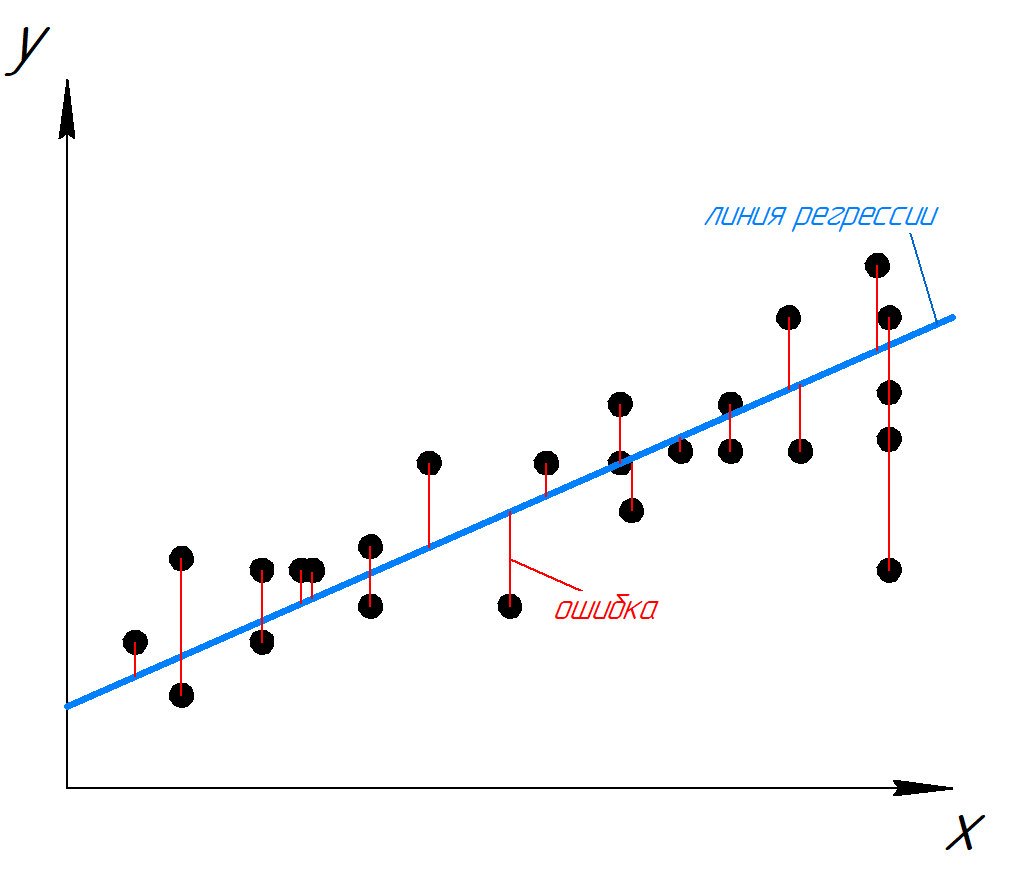
For example, linear regression is a high-bias model, as it attempts to learn fit data to a function of the form [latex]y = a times x + b[/latex], and nothing else:
Bias error quantifies the amount of error that can be attributed to this assumption. In the plot above, we can see that due to the high-bias property of the linear learner, the bias error shall be quite high.
- Models with high bias: linear regression, logistic regression, linear classification, linear neural networks, linear SVMs
- Models with low bias: nonlinear neural networks, nonlinear Support Vector Machines, decision trees.
Your choice for a ML algorithm should never be entirely dependent on the bias assumption of the model. For example, if you have a linear dataset, there is no need to start with neural networks — instead, a linear classifier or linear regression model would likely be able to achieve similar performance at a fraction of the computational cost. Therefore, make sure to think about the characteristics of your dataset, the bias property, but also make sure to consider what we will study next: the variance error.
Variance error
While the bias of a model tells us something about how rigid it is towards fitting a particular function, the variance of our model is related to our datasets:
Variance, in the context of Machine Learning, is a type of error that occurs due to a model’s sensitivity to small fluctuations in the training set.
StackExchange (n.d.)
Say, for example that we are training the same machine learning model with two different datasets. Model-wise, everything is the same — the algorithm is the same, the hyperparameter configuration is the same, and so on. The only thing that differs is the dataset.
Here, it must also be noted that we do not know whether the distributions of the datasets are exactly the same — they could be, but do not necessarily have to be. However, they’re close.
If our model is a high-variance model, it is really sensitive to changes in the dataset, and hence could show highly different performance — even when the changes are small. If it’s low-variance, it’s not so sensitive.
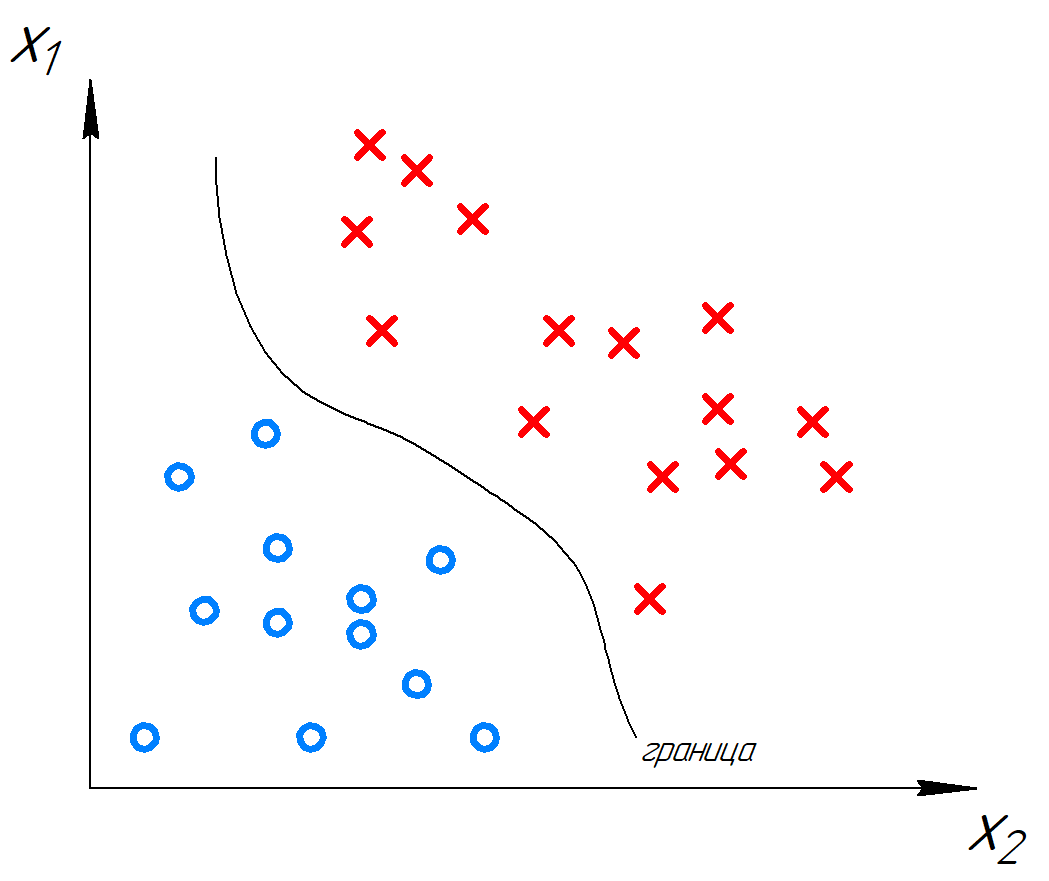
Especially when the model is overfit, the model generally has high variance — and visually, decision boundaries of such models look like this:
- Models with low variance: linear regression, logistic regression, linear classification, linear neural networks, linear SVMs
- Models with high variance: nonlinear neural networks, nonlinear Support Vector Machines, decision trees.
Irreducible error
Some of the model error cannot be ascribed to bias or variance. This irreducible error can for example be random noise, which is always present in a randomly initialized machine learning model.
If we want to reduce the impact of model bias, we can choose a machine learning algorithm that is relatively low-bias — that is, increase model complexity and sensitivity. If we want to reduce model sensitivity to changes in data, we can pick a machine learning algorithm that is more rigid. We cannot remove irreducible error from the machine learning model.
It’s simply something that we have to live with.
The Bias-Variance trade-off
In writing the article, I have dropped some hints that bias and machine learning may be related to each other.
- If you read the article with a critical mind, you perhaps noticed that the list of models with low/high variance is exactly the opposite in the case of bias.
- In the section about irreducible error, reducing the effect of one (say, bias) would be to move into the direction of the other (say, variance).
And the opposite is also true. In fact, bias and variance are related. This is true for statistics and hence also for the field of machine learning. In fact, it is known as the bias-variance trade-off.
The bias–variance trade-off implies that a model should balance underfitting and overfitting: Rich enough to express underlying structure in data and simple enough to avoid fitting spurious patterns
Belkin et al. (2019)
If you compare generating a machine learning model with playing a game of throwing bull’s eye, your optimal end result would be a darts board where all arrows are in the middle of the board:
In Machine Learning terms, this is a model with low bias and low variance.
It is both effective / rich enough «to express structure» (i.e., all near the desired spot, being the center) and simple enough to «[see] spurious patterns» (i.e., darts arrows scattered around the board). In other words, it is a model of which its predictions are «spot on» and «not scattered».
In fact, we can extend the darts board to all four cases between low/high bias and low/high variance.
- If your bias is low and your variance is high, your darts arrows will be near the center but will show some scattering (ML: capable of fitting many patterns, but with some sensitivity to data changes).
- If your bias is high and your variance is low, the darts arrows will be near each other, but not near the center (ML: not so sensitive to data changes, but too biased, and hence predictions that are collectively off).
- If your bias is high and your variance is high, the darts arrows will both be scattered and away from the center (ML: too sensitive and not capable of generating precise predictions).
- If your bias is low and your variance is low, your model is spot on without scattering. This is what you want.
The trade-off in the bias-variance trade-off means that you have to choose between giving up bias and giving up variance in order to generate a model that really works. If you choose a machine learning algorithm with more bias, it will often reduce variance, making it less sensitive to data. This can be good, unless the bias means that the model becomes too rigid. The opposite is also true: if you give up rigidity only to find the model show too much sensitivity, you’ve crossed the balance between bias and variance in the wrong direction.
Your end goal as a ML engineer is to find the sweet spot between bias and variance.
This is no easy task, and it is dependent on your dataset, the computational resources at your disposal (high-bias models are often less resource-intensive compared to low-bias models; the opposite is true for variance), and your ML experience.
Here, the only lesson is that practice makes perfect.
Decomposing your ML error value into error subtypes
If your train a machine learning model, through picking a loss function, you’ll be able to observe loss values throughout the training process and during the model evaluation step.
This loss value can be decomposed into bias and variance error by means of Sebastian Raschka’s Mlxtend Python library, with which one can also plot the decision boundary of a classifier.
More specifically, this can be done by means of the bias_variance_decomp functionality available in the library. Let’s see how it works with the TensorFlow model listed here. It is the MLP classifier that we created with the Chennai Reservoir Level Dataset (click here for the dataset).
- We import a variety of functionality: the bias-variance decomposition functionality from Mlxtend, some TensorFlow things, NumPy and generating a train/test split from Scikit-learn.
- We then load the data from a CSV file and shuffle the dataset.
- We separate features and targets and split the data into a 66/33 train/test split.
- We configure the input shape and subsequently create, configure and fit the model.
- We then evaluate the model and display the loss results.
- Finally, we use Mlxtend to decompose the loss into bias and variance loss: we set the loss function to Mean Squared Error, let it simulate bias and variance for 100 iterations, and initialize it with a random seed
46(this can be any number).
Running the model gives us the components of the bias error and the variance error.
- Note that in November 2020, the Mlxtend package could not yet generate a decomposition for a Keras model. However, this was added quite recently, but was not available in the
piprelease yet. Therefore, make sure to install/upgrade Mlxtend from GitHub (GitHub, n.d.), by means of:
pip install git+git://github.com/rasbt/mlxtend.git
Here is the code.
# Imports
from mlxtend.evaluate import bias_variance_decomp
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import numpy as np
from sklearn.model_selection import train_test_split
# Load data
dataset = np.loadtxt('./chennai_reservoir_levels.csv', delimiter='|', skiprows=1, usecols=(1,2,3,4))
# Shuffle dataset
np.random.shuffle(dataset)
# Separate features and targets
X = dataset[:, 0:3]
y = dataset[:, 3]
# Split
into train/test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Set the input shape
input_shape = (3,)
print(f'Feature shape: {input_shape}')
# Create the model
model = Sequential()
model.add(Dense(16, input_shape=input_shape, activation='relu'))
model.add(Dense(8, activation='relu'))
model.add(Dense(1, activation='linear'))
# Configure the model and start training
model.compile(loss='mean_absolute_error', optimizer='adam', metrics=['mean_squared_error'])
model.fit(X_train, y_train, epochs=25, batch_size=1, verbose=1, validation_split=0.2)
# Test the model after training
test_results = model.evaluate(X_test, y_test, verbose=1)
print(f'Test results - Loss: {test_results[0]} - Accuracy: {test_results[1]*100}%')
# Using Mlxtend to decompose loss
avg_expected_loss, avg_bias, avg_var = bias_variance_decomp(
model, X_train, y_train, X_test, y_test,
loss='mse',
num_rounds=100,
random_seed=46)
print('Average expected loss: %.3f' % avg_expected_loss)
print('Average bias: %.3f' % avg_bias)
print('Average variance: %.3f' % avg_var)
Summary
In this article, we looked at the trade-off between bias error and variance error. We saw that machine learning model error can be decomposed into subtypes, being the bias — or the rigidity of the model in terms of the functions that it can learn — and variance — being the sensitivity to fluctuations in the training data.
Through an example of a darts board, we saw that we want to strike a fair balance between bias and variance — and that we would likely achieve a model with relatively low bias and variance.
Unfortunately, we also saw that this is not always possible. Still, here, it is also important to find a balance between the two. For this reason, we illustrated how the error from a TensorFlow model can be decomposed into bias and variance by means of Mlxtend.
I hope that you have learnt something from today’s article! If you did, please leave a comment in the comments section below — I would definitely appreciate it 😊 Please do the same if you have questions, remarks or other comments. Where possible, I will make sure to answer them!
Thank you for reading MachineCurve today and happy engineering 😎
References
Raschka, S. (n.d.). Mlxtend.evaluate — mlxtend. Site not found · GitHub Pages. https://rasbt.github.io/mlxtend/api_subpackages/mlxtend.evaluate/#bias_variance_decomp
Dietterich, T. G., & Kong, E. B. (1995). Machine learning bias, statistical bias, and statistical variance of decision tree algorithms. Technical report, Department of Computer Science, Oregon State University.
Mitchell, T. M. (1980). The need for biases in learning generalizations. Tech. rep. CBMTR-117, Rutgers University, New Brunswick, NJ.
Belkin, M., Hsu, D., Ma, S., & Mandal, S. (2019). Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences, 116(32), 15849-15854.
StackExchange. (n.d.). What is the meaning of term variance in machine learning model? Data Science Stack Exchange. https://datascience.stackexchange.com/a/37350
Dartboard icon made by Freepik from www.flaticon.com
GitHub. (n.d.). Bias_variance_decomp for keras sequential? · Issue #719 · rasbt/mlxtend. rasbt/mlxtend#719
| title | date | categories | tags | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Machine Learning Error: Bias, Variance and Irreducible Error with Python |
2020-11-02 |
|
|
Supervised Machine Learning is one of the most prominent branches of Machine Learning these days. Using a labeled training set and an adequate model, it is possible to create a ML model that demonstrates very impressive results. As we will see, training such a model involves a cycle of feeding forward data through the model, observing how bad it performs, and subsequently optimizing it to make it better.
After some threshold is passed, the training process stops, and the model is trained.
The «observing how bad it performs» part is the focus of today’s article. Because the error, with which the former is expressed, is interesting — because it is composed of multiple error subtypes. This article will focus on these subtypes, which are the bias error, the variance error and the irreducible error. We will find out what error is in general, what those subtypes are, and how we can decompose a TensorFlow ML model into the error subtypes.
Let’s take a look! 
[toc]
Error in supervised machine learning: what is it?
From the article about loss and loss functions, we know about the high-level supervised machine learning process:
- Samples from a labeled dataset are inserted into the model — this is called «feeding the samples forward».
- The machine learning model generates a prediction for each sample.
- All predictions are compared to the labels, called the ground truth, and a loss value is output.
- Based on the loss value, the loss is computed backwards, to find the optimizations for the individual parts of the machine learning model.
- By means of some optimization mechanism (e.g. gradient descent or Adaptive optimization), the model is optimized.
Above, we talked about the «observing how bad it performs» part of training a supervised machine learning model. Note that «how bad» and «loss» have relatively similar meaning — and yes, they are connected.
The «loss value» effectively shows you how bad the model performs — in other words, how much off the model is compared to the ground truth, on average.
Hence, this loss value is also called the model error. Your goal as a machine learning engineer is to create a dataset, find a suitable algorithm, and tweak it accordingly, to generate a model that performs and generalizes well. In other words, it must be accurate in terms of the prediction, and work in a wide range of cases — even with data that the model has never seen before.
And of course, this is quite a challenge.
Error subtypes
Above, we saw that feeding forward the training samples results in a loss or error value. It can be used subsequently for improving your Machine Learning model. Now, we’ll dive into the error concept, and will see that it can be decomposed in a few distinct subtypes: bias error, variance error and irreducible error.
Put simply, the subtypes together compose the notion of ‘error’ in the following manner:
Error = Bias error + Variance error + Irreducible error.
- Bias error: how strict the model generalizes to some designated set of functions.
- Variance error: how much the estimated function will change when the algorithm is trained with differing datasets.
- Irreducible error: error that is neither bias or variance error and is hence relatively random.
Bias error
In Dietterich and Kong (1995), we find that Mitchell (1980) introduces the concept of bias error as follows:
«Any basis for choosing one generalization [hypothesis] over another, other than strict consistency with the observed training instances.»
While this sounds relatively vague — likely on purpose, for generalization purposes — we can relatively easily convert it into a definition that resonates well with ML researchers and engineers:
Bias involves an assumption of the Machine Learning model that the target function to learn is part of a set of target functions. In other words, if a model can only learn — or fit — a few example functions, it is a high-bias model. If the model can learn many functions instead, it is a low-bias model.
Bias, in the context of Machine Learning, is a type of error that occurs due to erroneous assumptions in the learning algorithm.
StackExchange (n.d.)
High bias, by making a lot of assumptions about the target function, simplifies the model and makes the fit less computationally intensive.
For example, linear regression is a high-bias model, as it attempts to learn fit data to a function of the form [latex]y = a times x + b[/latex], and nothing else:
Bias error quantifies the amount of error that can be attributed to this assumption. In the plot above, we can see that due to the high-bias property of the linear learner, the bias error shall be quite high.
- Models with high bias: linear regression, logistic regression, linear classification, linear neural networks, linear SVMs
- Models with low bias: nonlinear neural networks, nonlinear Support Vector Machines, decision trees.
Your choice for a ML algorithm should never be entirely dependent on the bias assumption of the model. For example, if you have a linear dataset, there is no need to start with neural networks — instead, a linear classifier or linear regression model would likely be able to achieve similar performance at a fraction of the computational cost. Therefore, make sure to think about the characteristics of your dataset, the bias property, but also make sure to consider what we will study next: the variance error.
Variance error
While the bias of a model tells us something about how rigid it is towards fitting a particular function, the variance of our model is related to our datasets:
Variance, in the context of Machine Learning, is a type of error that occurs due to a model’s sensitivity to small fluctuations in the training set.
StackExchange (n.d.)
Say, for example that we are training the same machine learning model with two different datasets. Model-wise, everything is the same — the algorithm is the same, the hyperparameter configuration is the same, and so on. The only thing that differs is the dataset.
Here, it must also be noted that we do not know whether the distributions of the datasets are exactly the same — they could be, but do not necessarily have to be. However, they’re close.
If our model is a high-variance model, it is really sensitive to changes in the dataset, and hence could show highly different performance — even when the changes are small. If it’s low-variance, it’s not so sensitive.
Especially when the model is overfit, the model generally has high variance — and visually, decision boundaries of such models look like this:
- Models with low variance: linear regression, logistic regression, linear classification, linear neural networks, linear SVMs
- Models with high variance: nonlinear neural networks, nonlinear Support Vector Machines, decision trees.
Irreducible error
Some of the model error cannot be ascribed to bias or variance. This irreducible error can for example be random noise, which is always present in a randomly initialized machine learning model.
If we want to reduce the impact of model bias, we can choose a machine learning algorithm that is relatively low-bias — that is, increase model complexity and sensitivity. If we want to reduce model sensitivity to changes in data, we can pick a machine learning algorithm that is more rigid. We cannot remove irreducible error from the machine learning model.
It’s simply something that we have to live with.
The Bias-Variance trade-off
In writing the article, I have dropped some hints that bias and machine learning may be related to each other.
- If you read the article with a critical mind, you perhaps noticed that the list of models with low/high variance is exactly the opposite in the case of bias.
- In the section about irreducible error, reducing the effect of one (say, bias) would be to move into the direction of the other (say, variance).
And the opposite is also true. In fact, bias and variance are related. This is true for statistics and hence also for the field of machine learning. In fact, it is known as the bias-variance trade-off.
The bias–variance trade-off implies that a model should balance underfitting and overfitting: Rich enough to express underlying structure in data and simple enough to avoid fitting spurious patterns
Belkin et al. (2019)
If you compare generating a machine learning model with playing a game of throwing bull’s eye, your optimal end result would be a darts board where all arrows are in the middle of the board:
In Machine Learning terms, this is a model with low bias and low variance.
It is both effective / rich enough «to express structure» (i.e., all near the desired spot, being the center) and simple enough to «[see] spurious patterns» (i.e., darts arrows scattered around the board). In other words, it is a model of which its predictions are «spot on» and «not scattered».
In fact, we can extend the darts board to all four cases between low/high bias and low/high variance.
- If your bias is low and your variance is high, your darts arrows will be near the center but will show some scattering (ML: capable of fitting many patterns, but with some sensitivity to data changes).
- If your bias is high and your variance is low, the darts arrows will be near each other, but not near the center (ML: not so sensitive to data changes, but too biased, and hence predictions that are collectively off).
- If your bias is high and your variance is high, the darts arrows will both be scattered and away from the center (ML: too sensitive and not capable of generating precise predictions).
- If your bias is low and your variance is low, your model is spot on without scattering. This is what you want.
The trade-off in the bias-variance trade-off means that you have to choose between giving up bias and giving up variance in order to generate a model that really works. If you choose a machine learning algorithm with more bias, it will often reduce variance, making it less sensitive to data. This can be good, unless the bias means that the model becomes too rigid. The opposite is also true: if you give up rigidity only to find the model show too much sensitivity, you’ve crossed the balance between bias and variance in the wrong direction.
Your end goal as a ML engineer is to find the sweet spot between bias and variance.
This is no easy task, and it is dependent on your dataset, the computational resources at your disposal (high-bias models are often less resource-intensive compared to low-bias models; the opposite is true for variance), and your ML experience.
Here, the only lesson is that practice makes perfect.
Decomposing your ML error value into error subtypes
If your train a machine learning model, through picking a loss function, you’ll be able to observe loss values throughout the training process and during the model evaluation step.
This loss value can be decomposed into bias and variance error by means of Sebastian Raschka’s Mlxtend Python library, with which one can also plot the decision boundary of a classifier.
More specifically, this can be done by means of the bias_variance_decomp functionality available in the library. Let’s see how it works with the TensorFlow model listed here. It is the MLP classifier that we created with the Chennai Reservoir Level Dataset (click here for the dataset).
- We import a variety of functionality: the bias-variance decomposition functionality from Mlxtend, some TensorFlow things, NumPy and generating a train/test split from Scikit-learn.
- We then load the data from a CSV file and shuffle the dataset.
- We separate features and targets and split the data into a 66/33 train/test split.
- We configure the input shape and subsequently create, configure and fit the model.
- We then evaluate the model and display the loss results.
- Finally, we use Mlxtend to decompose the loss into bias and variance loss: we set the loss function to Mean Squared Error, let it simulate bias and variance for 100 iterations, and initialize it with a random seed
46(this can be any number).
Running the model gives us the components of the bias error and the variance error.
- Note that in November 2020, the Mlxtend package could not yet generate a decomposition for a Keras model. However, this was added quite recently, but was not available in the
piprelease yet. Therefore, make sure to install/upgrade Mlxtend from GitHub (GitHub, n.d.), by means of:
pip install git+git://github.com/rasbt/mlxtend.git
Here is the code.
# Imports
from mlxtend.evaluate import bias_variance_decomp
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import numpy as np
from sklearn.model_selection import train_test_split
# Load data
dataset = np.loadtxt('./chennai_reservoir_levels.csv', delimiter='|', skiprows=1, usecols=(1,2,3,4))
# Shuffle dataset
np.random.shuffle(dataset)
# Separate features and targets
X = dataset[:, 0:3]
y = dataset[:, 3]
# Split
into train/test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Set the input shape
input_shape = (3,)
print(f'Feature shape: {input_shape}')
# Create the model
model = Sequential()
model.add(Dense(16, input_shape=input_shape, activation='relu'))
model.add(Dense(8, activation='relu'))
model.add(Dense(1, activation='linear'))
# Configure the model and start training
model.compile(loss='mean_absolute_error', optimizer='adam', metrics=['mean_squared_error'])
model.fit(X_train, y_train, epochs=25, batch_size=1, verbose=1, validation_split=0.2)
# Test the model after training
test_results = model.evaluate(X_test, y_test, verbose=1)
print(f'Test results - Loss: {test_results[0]} - Accuracy: {test_results[1]*100}%')
# Using Mlxtend to decompose loss
avg_expected_loss, avg_bias, avg_var = bias_variance_decomp(
model, X_train, y_train, X_test, y_test,
loss='mse',
num_rounds=100,
random_seed=46)
print('Average expected loss: %.3f' % avg_expected_loss)
print('Average bias: %.3f' % avg_bias)
print('Average variance: %.3f' % avg_var)
Summary
In this article, we looked at the trade-off between bias error and variance error. We saw that machine learning model error can be decomposed into subtypes, being the bias — or the rigidity of the model in terms of the functions that it can learn — and variance — being the sensitivity to fluctuations in the training data.
Through an example of a darts board, we saw that we want to strike a fair balance between bias and variance — and that we would likely achieve a model with relatively low bias and variance.
Unfortunately, we also saw that this is not always possible. Still, here, it is also important to find a balance between the two. For this reason, we illustrated how the error from a TensorFlow model can be decomposed into bias and variance by means of Mlxtend.
I hope that you have learnt something from today’s article! If you did, please leave a comment in the comments section below — I would definitely appreciate it 😊 Please do the same if you have questions, remarks or other comments. Where possible, I will make sure to answer them!
Thank you for reading MachineCurve today and happy engineering 😎
References
Raschka, S. (n.d.). Mlxtend.evaluate — mlxtend. Site not found · GitHub Pages. https://rasbt.github.io/mlxtend/api_subpackages/mlxtend.evaluate/#bias_variance_decomp
Dietterich, T. G., & Kong, E. B. (1995). Machine learning bias, statistical bias, and statistical variance of decision tree algorithms. Technical report, Department of Computer Science, Oregon State University.
Mitchell, T. M. (1980). The need for biases in learning generalizations. Tech. rep. CBMTR-117, Rutgers University, New Brunswick, NJ.
Belkin, M., Hsu, D., Ma, S., & Mandal, S. (2019). Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences, 116(32), 15849-15854.
StackExchange. (n.d.). What is the meaning of term variance in machine learning model? Data Science Stack Exchange. https://datascience.stackexchange.com/a/37350
Dartboard icon made by Freepik from www.flaticon.com
GitHub. (n.d.). Bias_variance_decomp for keras sequential? · Issue #719 · rasbt/mlxtend. rasbt/mlxtend#719
Регрессия как задача машинного обучения
38 мин на чтение
(55.116 символов)
Постановка задачи регрессии
Источник: Analytics Vidhya.
Задача регрессии — это одна из основных задач машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, наборы данных для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (dependent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Так же надо сказать, что иногда регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия почти не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Линейная регрессия с одной переменной
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
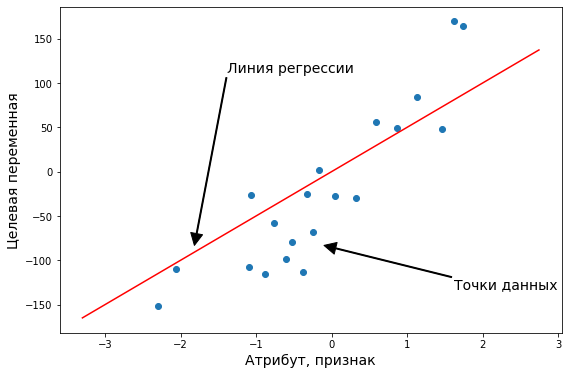
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y.
Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$б которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно, или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
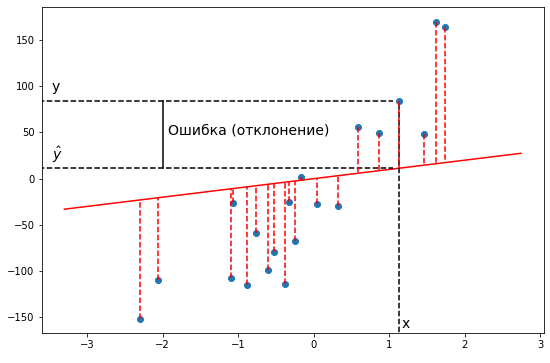
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Возведение в квадрат в этой формуле нужно для того, чтобы положительные отклонения не компенсировали отрицательные. Можно было бы для этого брать, например, абсолютное значение, но эта функция не везде дифференцируема, а это станет нам важно позднее.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
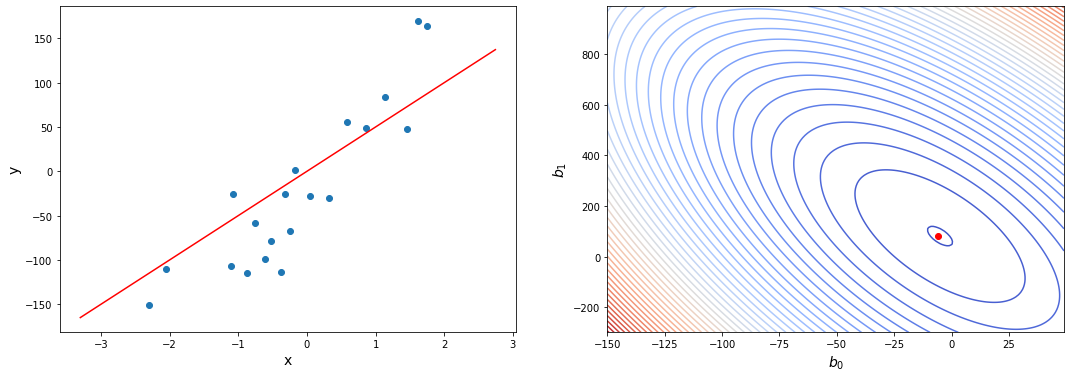
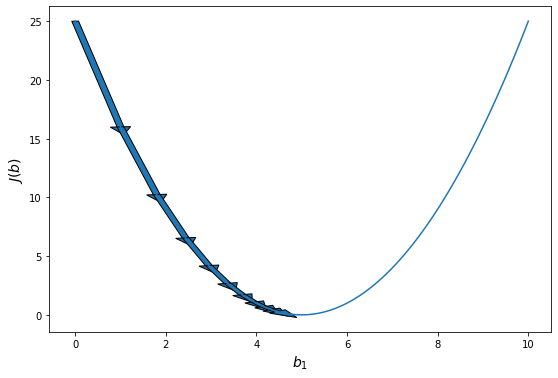
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
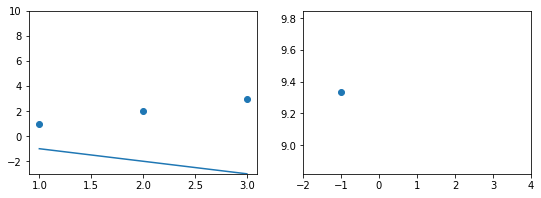
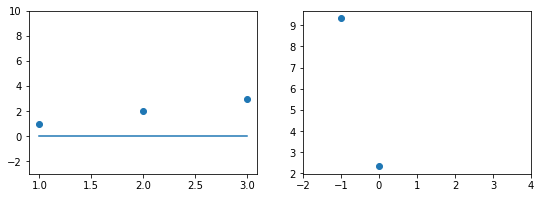
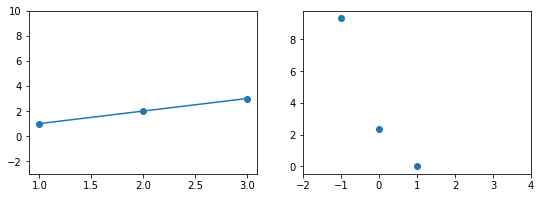
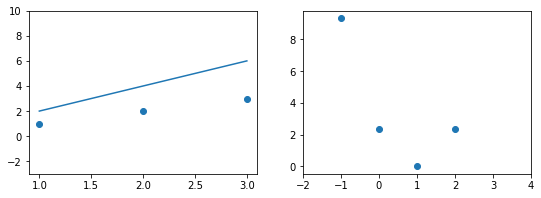
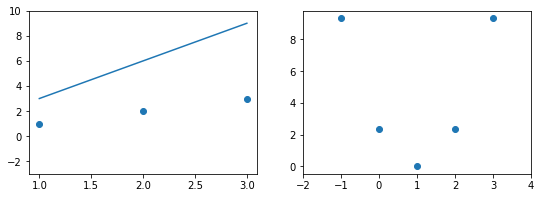
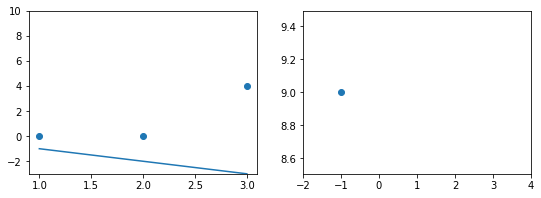
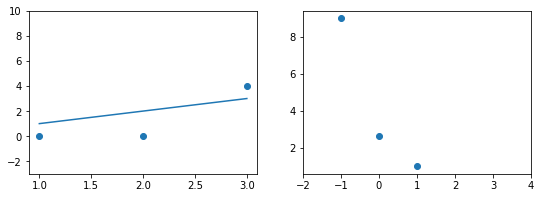
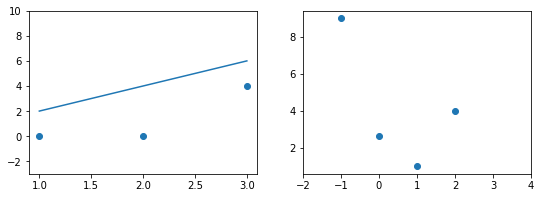
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
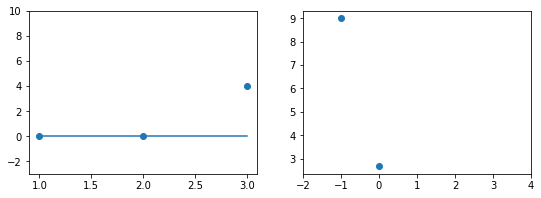
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
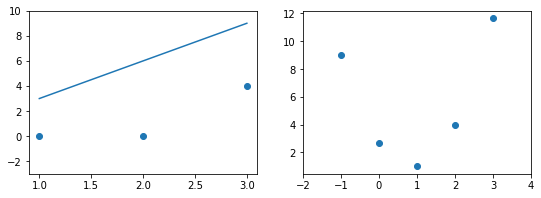
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
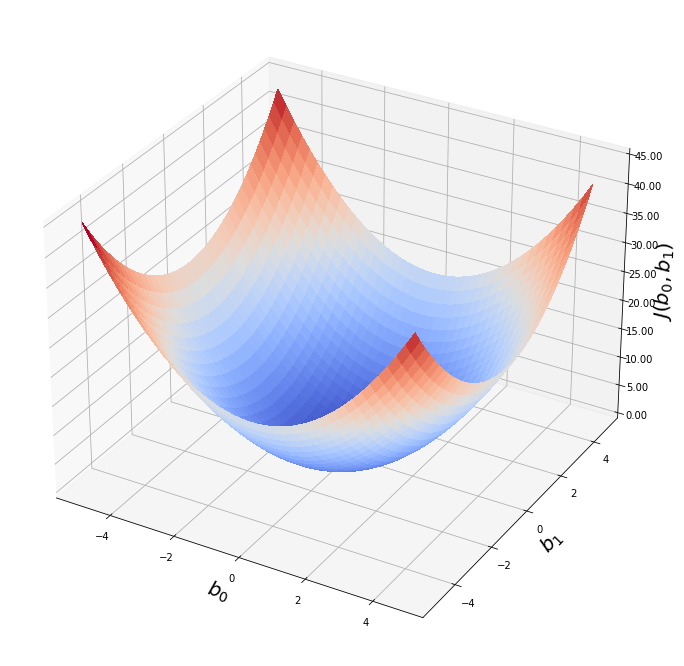
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска.
Это происходит при помощи производной функции ошибки. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит, от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
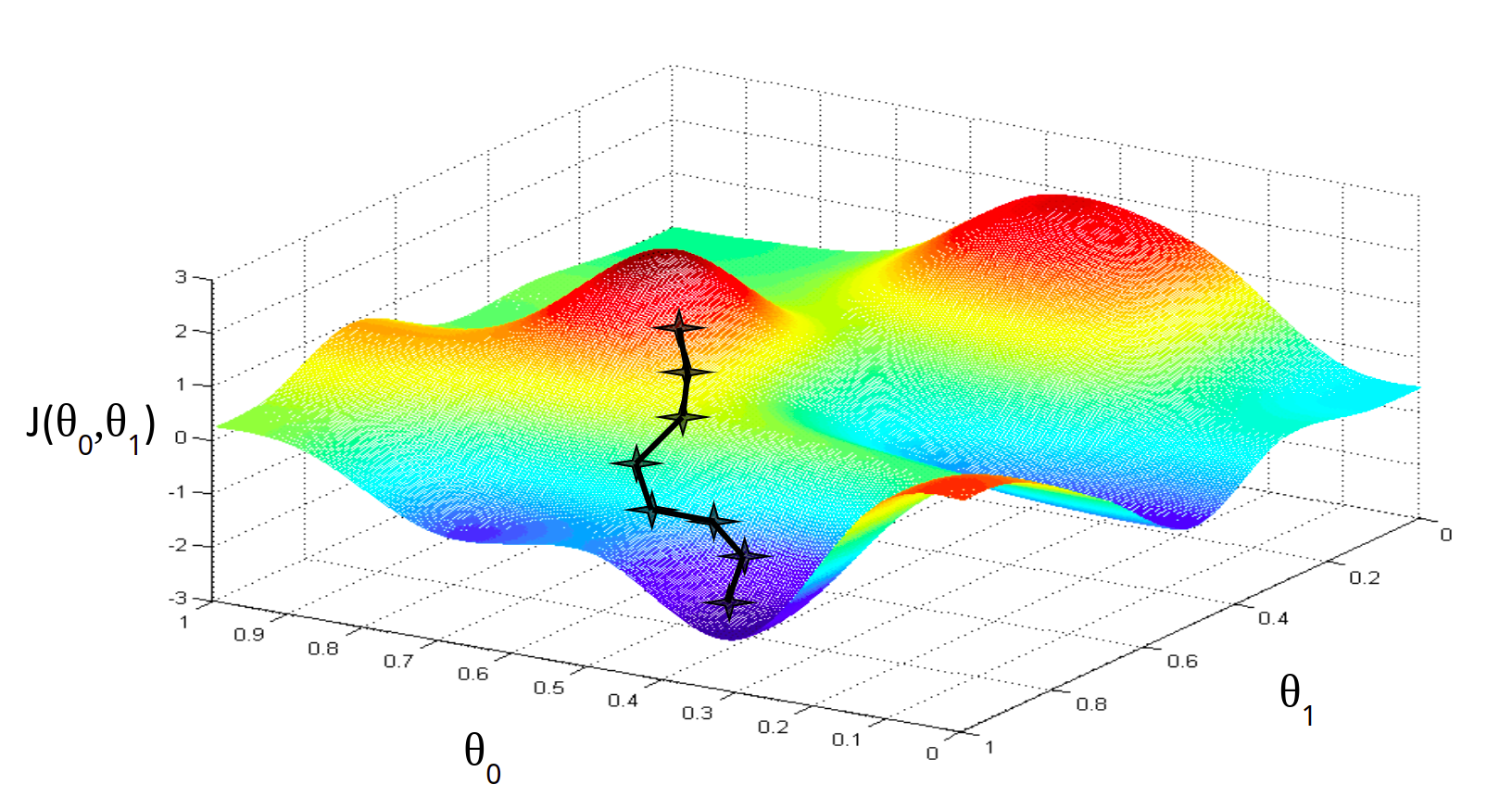
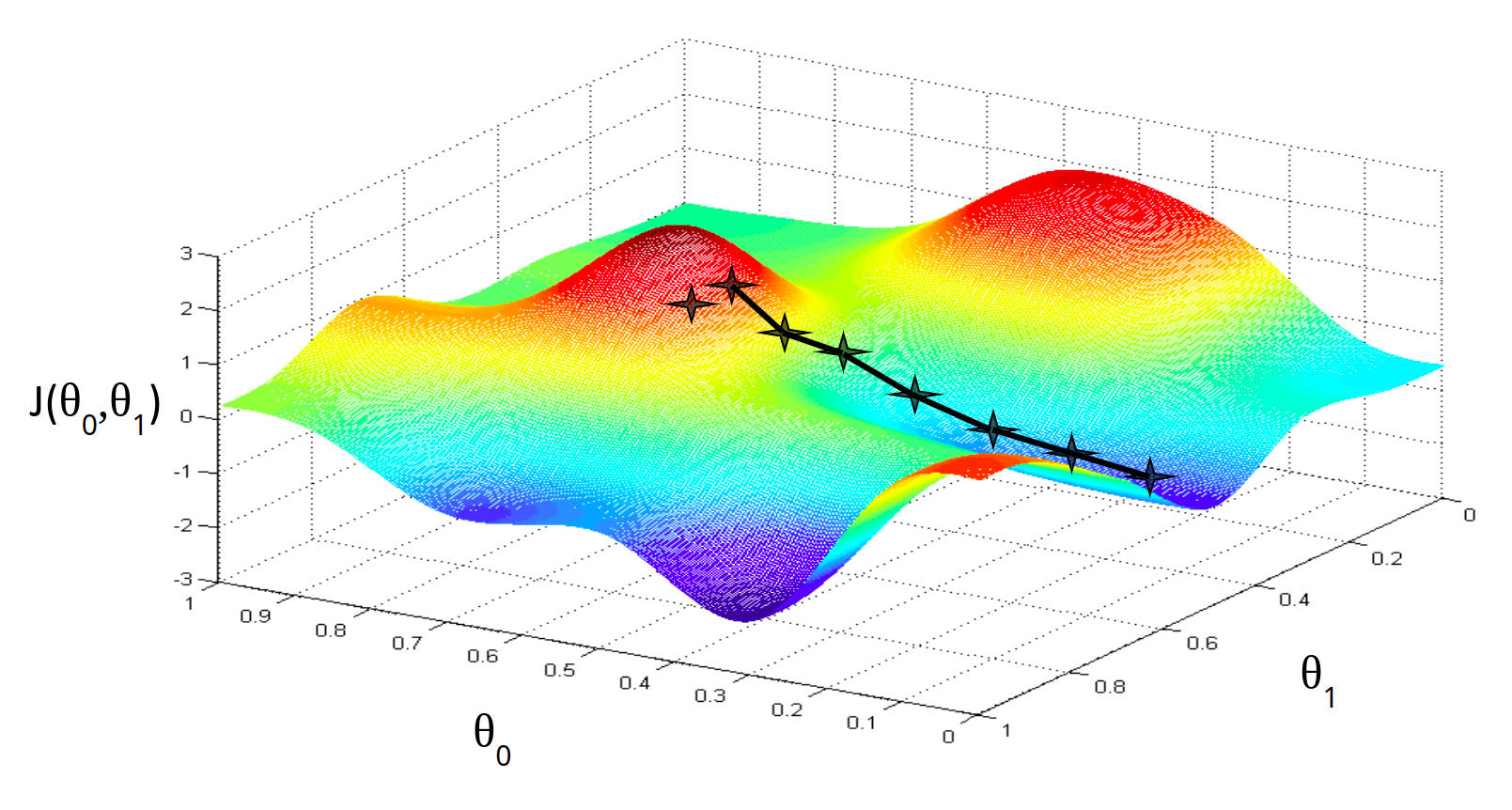
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки:
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Целевая переменная не нормируется.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Источник: Wikimedia.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данном разделе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данного раздела предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
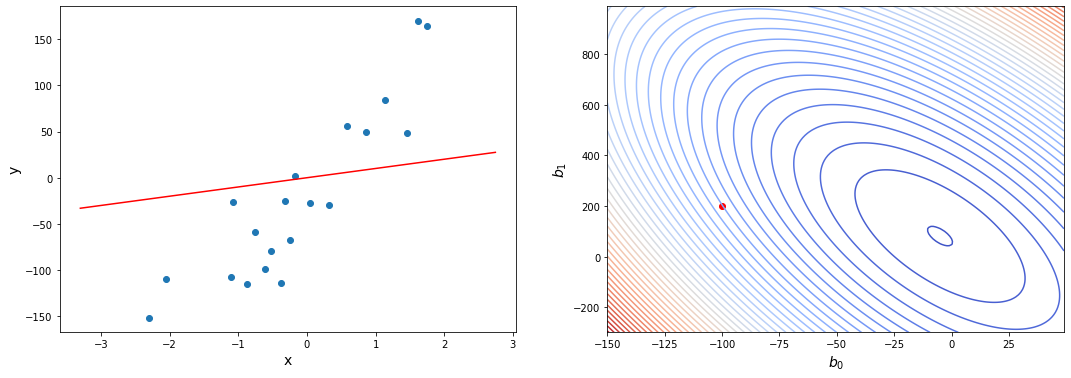
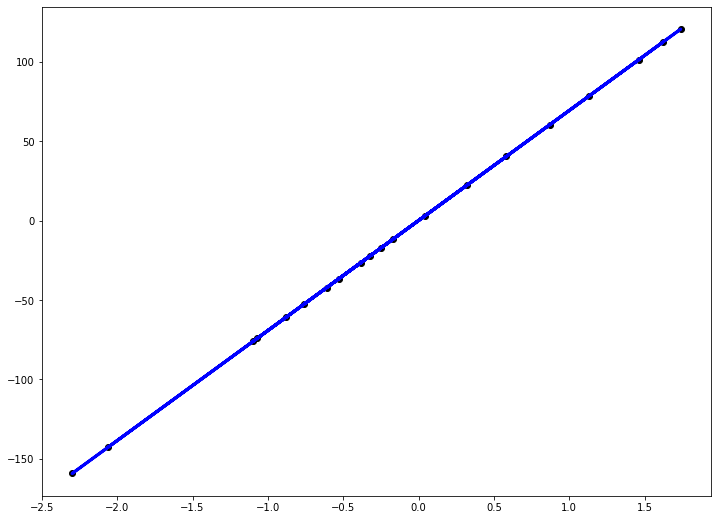
Это код генерирует вот такой вот график:
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()
На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Недочеты в обучении ML-алгоритмов часто приводят к забавным казусам. Например, айфон моего друга определяет его собаку как кошку. Или вот эти два парня, которые не могут воспользоваться лифтом с голосовым управлением, потому что он не понимает их акцент. Или то, как Amazon Alexa пыталась заказать сотни кукольных домиков, потому что приняла выпуск новостей за голос своего владельца. Еще появились шутки про покупку Whole Foods компанией Amazon, которые тоже отлично передают суть дефективных алгоритмов.
Джефф Безос: Алекса, купи мне что-нибудь из Whole Foods.
Alexa: Покупаю Whole Foods.
Безос: ЧТОООО… а, ладно, валяй.
Ключевой принцип науки о данных
Пока я заканчивала работу над обучающей программой Galvanize Data Science, мне пришлось провести немало времени за изучением такого явления, как ошибка алгоритма.
Я сотрудничала с организацией, которая помогает бывшим заключенным вернуться к обучению и таким образом снижает вероятность повторного совершения преступлений. Мне дали задание рассчитать полную стоимость тюремного заключения, то есть прямые и косвенные затраты на содержание одного человека в исправительном учреждении.
При изучении темы я натолкнулась на статью под названием «Машинная ошибка» (Machine Bias), в которой рассказывается о том, что в алгоритмы оценки рисков заложены расовые предрассудки. Оказалось, что из-за алгоритма, который выдает чрезвычайно много ложных положительных результатов для афроамериканцев, людей отправляют за решетку на более долгий срок и не дают права на досрочное освобождение. Деньги налогоплательщиков уходят на содержание в тюрьмах тех, кто на свободе мог бы служить на благо общества, при этом их дети попали в систему государственной опеки.
Из-за необъективного алгоритма люди теряют работу и связи, а после выхода из тюрьмы вынуждены начинать жизнь сначала. В то же время те, кто более способен на преступление, остается на свободе, потому что алгоритм остается слеп к их предрасположенности к криминалу.
Из-за чего появляются эти ложные положительные и отрицательные ответы и так ли это важно? Для начала давайте определим три термина из Матрицы ошибок: точность, полнота и доля правильных ответов.
Точность
Точность – это процент верно классифицированных положительных ответов. При высокой точности алгоритм правильно размечает максимальное количество верных элементов. К примеру, инструменты медицинской диагностики должны быть очень точными, так как болезнь может осложниться, если ее вовремя не обнаружить.
В ситуации, когда время настолько ценно, нужно минимизировать количество ложных негативных откликов. Точно так же, если в системе вашей компании произойдет сбой, лучше иметь точную модель, чтобы:
- устранить проблему,
- найти виновника как можно быстрее, чтобы не отрывать сотрудников от исполнения их обязанностей.
Полнота
В свою очередь, полнота – это доля в процентах возвращенных релевантных элементов. К примеру, если искать в гугле книги из серии про Гарри Поттера, возврат будет равен количеству книг, разделенному на семь.
В идеале полнота равна единице. В этом случае нас ждут проблемы, и пользователям придется вручную копаться в нерелевантных результатах поиска. Вдобавок к этому, если пользователь не получит релевантной выдачи, он вряд ли станет что-то покупать, и это навредит финансовым показателям.
Доля правильных ответов
Рассчитывается как доля верных предсказаний от общего количества элементов в процентах. Этот показатель нельзя считать индикатором качества работы модели, особенно если классы разбалансированы. Чтобы работа с точностью, полнотой, долей правильных ответов и матрицами ошибок имела смысл, обучающие данные должны содержать достоверную информацию о населении, и тогда модель сможет обучиться правильно.
| n=165 | Предсказание: НЕТ | Предсказание: ДА |
| В действительности: НЕТ | 50 | 10 |
| В действительности: ДА | 5 | 100 |
Матрицы ошибок
Матрицы ошибок – это основа матриц эффективности затрат, то есть итоговой стоимости. Для бизнеса этот термин понять легко на примере анализа доходов и расходов. Думаю, в случае с дискриминацией одного класса относительно другого все будет сложнее.
Тем не менее эта работа, пожалуй, даже более срочная и важная. Нашим продуктам уделяют все больше внимания, и ошибки будут все более заметными и значимыми для компаний.
Ошибки машинного обучения, вызванные исходными данными
Крупнейший по объему этап работы в машинном обучении – это сбор и очищение данных, на которых будет учиться модель. Преобразование данных – это не так уж интересно, и постоянно думать о формировании отсчетов, выбросах и распределении генеральной совокупности может быть скучным и утомительным делом. Однако затем из-за таких упущений при обработке данных и появляются ошибки алгоритмов.
Каждый день в мире генерируется 2,5 эксабайт информации, так что данных для обучения наших моделей предостаточно. Есть фотографии лиц с разным цветом кожи, в очках и без них, с широкими или узкими, карими или серыми глазами.
Источник: Giphy
Существуют мужские и женские голоса с самыми разными акцентами. Нежелание принимать во внимание эти культурные особенности данных может привести нас к моделям, которые будут игнорировать, и таким образом маргинализировать, определенную демографическую группу. К примеру, тот случай, когда алгоритм от Google по ошибке принимал лица афроамериканцев за горилл. Или подушки безопасности, которые должны защищать пассажиров, едва не убивали женщин в аварийной ситуации. Эти ложноположительные отклики, то есть заключения алгоритма о том, что все в порядке, когда риск действительно есть, могут стоить кому-то жизни.
Человеческий фактор
Недавно одна моя подруга – инженер ПО – узнавала у консультанта по развитию карьеры, стоит ли ей использовать в резюме и LinkedIn гендерно-нейтральное второе имя, чтобы быстрее найти работу. У ее опасений есть основания: в профессиональном мире сознательные и подсознательные гендерные предрассудки очень сильны. Был случай, когда мужчина и женщина на время обменялись почтовыми адресами и заметили, что отношение к ним в переписке значительно изменилось.
Как бороться с ошибками машинного обучения
Между тем, если нам предстоит обучать машины работе с LinkedIn и резюме, то появляется научный инструмент борьбы с предрассудками, победить которые люди не в состоянии. Некорректные алгоритмы оценки рисков появляются из-за обучения моделей по наборам данных, уже содержащим эти перекосы вследствие исторических причин. Это можно исправить, если работать с историческими предрассудками так, чтобы модель учитывала пол, возраст и расу человека без дискриминации какого-либо меньшинства.
Данные, которые содержатся в моделях обучения с подкреплением, могут привести к резкому улучшению или ухудшению результатов. Экспоненциальный рост или падение качества может привести к более надежным беспилотным автомобилям, которые учатся при каждой своей поездке, или же они могут убедить человека из Северной Каролины в существовании в Вашингтоне банды по торговле людьми, которой на самом деле нет.
Почему машины начинают ошибаться? Мы учим их этому, используя ошибочные тренировочные данные.
Источник
Материалы по теме:
Кто и зачем использует слабый искусственный интеллект
Искусственный интеллект научился определять сексуальную ориентацию по фотографии
Линейная алгебра помогла найти в языке скрытый сексизм
Виртуальные ассистенты часто терпят сексуальные домогательства
Фото на обложке: Франческо Дацци/Shutterstock
Kaggle – площадка, объединяющая соревновательную систему по исследованию данных, образовательный ресурс по искусственному интеллекту и машинному обучению, а также соцсеть специалистов в указанных областях.
Перед тем, как начать работать, необходимо зарегистрироваться на сайте. Заходим по ссылке, находим кнопку Register и заполняем поля. Уверен, что вы сами с этим отлично справитесь. После регистрации, подтверждения и логина попадаем на главную страницу ресурса.
Слева в столбце мы видим разделы:
- Home – новостная лента, в которую попадают публикации, которые могут вас заинтересовать. Чем выше активность пользователя на сайте, тем точнее рекомендации.
- Competitions – соревнования в области анализа данных. Здесь же находятся учебные соревнования, которые помечены словом Knowledge.
- Datasets – различные наборы данных, с которыми можно поиграться. Также можно выкладывать собственные датасеты.
- Code – раздел, в котором можно создать Jupyter Notebook или посмотреть чужой.
- Discussions – местный аналог форумов.
- Courses – учебные курсы. Довольно приличный объем и приемлемое качество. Раскрыты основные базовые разделы ML.
Отвлечемся пока от Kaggle и поговорим о машинном обучении, а также о решаемых с его помощью задачах.
Теоретический минимум о Machine Learning
Машинное обучение – набор математических, статистических и вычислительных методов, с помощью которых возможно решить задачу путем поиска закономерностей в представленных данных.
Существует огромное количество методов машинного обучения. Здесь я покажу всего несколько самых базовых, а остальные вы сможете найти самостоятельно, пройдя по рекомендованным ссылкам в конце.
Все методы ML можно разделить на несколько крупных групп:
- Обучение с учителем (от англ. Supervised learning) – алгоритмы из этой группы обучаются с помощью заранее подготовленных данных, которые содержат как наборы входных исследуемых признаков, так и “ответы” на эти наборы. “Ответом” является выходное значение, которое должен выдать алгоритм в результате своей работы, т.е. алгоритм “обучается”. К этой группе, например, можно отнести задачи классификации и регрессии.
- Обучение без учителя (от англ. Unsupervised learning) – группа алгоритмов, в которых система спонтанно обучается на входных данных без вмешательства извне. К этой группе можно отнести задачи кластеризации, понижения размерности.
- Обучение с подкреплением (от англ. Reinforcement learning) – группа алгоритмов, в которых система обучается с помощью взаимодействия со средой, в которой она находится. Подробнее можно ознакомиться хотя бы в вики. В моей статье алгоритмы этой группы не рассматриваются.
Задачи машинного обучения
Классификация
Вероятно, это самая популярная задача машинного обучения. Ее суть состоит в присвоении какому-то набору признаков (т.е. свойств объекта) какому-то классу. Например, стоит задача автоматической модерации токсичных комментариев на сайте. Алгоритм получает на вход текст комментария, а на выходе присваивает ему метку: токсичный или нетоксичный. Это пример бинарной классификации. К этому же типу классификации можно отнести задачу выявления сердечно-сосудистых проблем по анализам человека, определение спама в письмах и т.п. Второй тип классификации – множественная (многоклассовая). В ней классов больше двух. Примером может служить классификация жанра книги.
Для демонстрации посмотрим графической решение задачи бинарной классификации. Алгоритм разделяет пространство признаков на две группы.
Для решения задачи обычно используются следующие алгоритмы: логистическая регрессия, KNN, SVM, деревья решений.
Регрессия
Задача регрессии – предсказание (прогнозирование) целевого признака по входным параметрам. Например, предсказание загруженности дороги в зависимости от времени суток, дня недели, погоды, предсказание цены квартиры от количества комнат, этажа, района. Предсказание времени на путь из пункта А в пункт Б в зависимости от пробок и т.п. Т.е. задача регрессии это задача получения неизвестного числа по известным параметрам.
Посмотрим на рисунок. По ряду известных значений y(x) была предсказана кривая – линия регрессии. Ее можно продлить, чтобы предсказывать значения y для неизвестных x.
Для решения задачи применяются следующие алгоритмы и методы: линейная и полиномиальная регрессии, KNN, деревья решений.
Кластеризация
Задача кластеризации состоит в разделении заданной выборки объектов таким образом, чтобы похожие объекты попали в один кластер, а кластеры сильно бы различались между собой. Кластеризацию применяют для анализа и поиска признаков по которым можно объединить объекты, сжатия данных и поиска новизны (что не входит ни в один кластер).
Возникает логичный вопрос: а чем различаются классификация и кластеризация, ведь они решают похожие задачи? При классификации есть набор предопределенных классов, которым обучается алгоритм на наборе примеров. Далее алгоритм предсказывает, к какому классу принадлежит новый объект. При кластеризации используется алгоритм, который пытается сгруппировать набор объектов и определить, существует ли какая-либо взаимосвязь между объектами, т.е. машина учится сама.
Графическим примером кластеризации может быть следующая иллюстрация.
Для решения задачи применяются следующие алгоритмы и методы: K-Means, DBSCAN.
Метрики качества регрессии
Начнем с регрессии. При оценке качества работают с таблицей, содержащей два столбца (помимо индекса): правильные значения и предсказанные. Для простоты рассмотрим четыре строки, и пусть объектами будет количество килограмм картошки для сети ресторанов. Для простоты расчетов возьмем кратные десяти значения.
| Номер | Значение из выборки (сколько в реальности потребовалось кг картошки) | Предсказанное значение (кг) |
| 1 | 200 | 180 |
| 2 | 150 | 190 |
| 3 | 140 | 120 |
| 4 | 160 | 220 |
При таком количестве данных даже визуально можно оценить качество предсказанных данных. Предсказания под номерами 1 и 3 были достаточно точны, номер 2 показал бОльшую ошибку, а в строке номер 4 ошибка оказалась очень большой.
Для тысяч таких строк визуально оценить качество невозможно, необходимы агрегированные показатели.
Mean Absolute Error (MAE) – средняя абсолютная ошибка
Довольно интуитивный способ – сложить ошибки каждого из предсказаний и разделить на количество предсказаний. Посчитаем для нашей таблицы:
В среднем наш алгоритм ошибается на 35 кг картошки. Где-то в плюс, где-то в минус. Такая метрика называется средней абсолютной ошибкой, mean absolute error или MAE.
где yi – предсказанные значения, а xi – реальные известные значения, ei — ошибка i-го предсказания.
Mean Square Error (MSE) – Средняя квадратичная ошибка
Достаточно часто используется похожая метрика, MSE. Она рассчитывается почти так же, только берется не модуль ошибки ei, а ее квадрат.
Для нашего примера:
Но мы получили не ошибку в килограммах, а “кг в квадрате”. Чтобы вернуться к исходной величине, необходимо извлечь из MSE квадратный корень:
По сравнению с RMSE, метрика MAE более интуитивна, т.к. усредняются сами отклонения, но RMSE удобнее использовать при обучении алгоритмов. Хотя для MAE обучение тоже успешно выполняется.
Еще одна особенность метрики MAE — она более устойчива к выбросам, чем RMSE. Это означает, что если для одного объекта ошибка очень большая (объект-выброс), а для остальных объектов – маленькая, то значение MAE подскочит от этого одного объекта меньше, чем RMSE, т.к. в RMSE ошибки возводятся в квадрат. В нашем примере объектом-выбросом является четвертое предсказание.
Quantile loss
Иногда ошибка в меньшую или большую сторону может иметь разное влияние на бизнес. Например, если мы предскажем на одну тысячу единиц товара меньше, чем реально потребуется, то потеряем прибыль: некоторым клиентам не достанется товара. А если мы предскажем на одну тысячу единиц больше товара, чем реально потребуется, то появятся дополнительные издержки на хранение товара.
Предположим, что товар занимает мало места (т.к. площади хранения в ресторанах велики) и расходы на хранение невелики, тогда лучше ошибиться в большую сторону, чем в меньшую. В этом случае отрицательную и положительную разницу домножают на разные коэффициенты, например, возьмем 0.5 и 1.5.
В нашем примере, коэффициент 1.5 будет применен к предсказаниям 1 и 3 (180 < 200 и 120 < 140), а коэффициент 0.5 к остальным. Тогда значение метрики будет равно:
Данная метрика называется квантильной ошибкой.
Само по себе значение метрик MSE или MAE можно сравнивать со средним значением целевой переменной: например, нам нужно предсказывать десятки, при этом допустимы ошибки порядка единиц. Если хочется получать значения ошибки в процентах («алгоритм в среднем ошибается на столько-то процентов»), можно использовать метрики с нормировками.
К примеру, метрика MAPE (mean average percentage error) усредняет значения ошибок, деленных на значение целевой переменной:
В нашем случае, алгоритм в среднем ошибается на 22.1%.
Важно понимать, что идеальных алгоритмов, как и нулевых значений метрик ошибок, в машинном обучении не бывает: такова суть этой области, что она помогает выполнять приблизительные предсказания. Величину метрик обычно определяет заказчик.
Метрики качества классификации
Accuracy – доля правильных ответов
В задаче классификации самой простой метрикой качества является доля правильных ответов (accuracy). Она показывает, в каком проценте случаев алгоритм правильно указал класс объекта.
Для примера будет рассматривать задачу предсказания токсичности комментариев. Т.е. имеем задачу бинарной классификации, где 0 – комментарий нетоксичен, 1 – комментарий токсичен. Возьмем для простоты пять комментариев и сведем все в таблицу.
| ID комментария | Значение в данных (токсичен ли комментарий в действительности) | Предсказанное значение |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 0 | 0 |
| 4 | 0 | 1 |
| 5 | 0 | 0 |
В нашем примере, алгоритм выдал правильные ответы для комментариев 1,2,3,5, т.е. в 80% случаев. Это и есть значение accuracy.
Accuracy – простая и интерпретируемая метрика, но она не отражает полную картину, в частности, в какую сторону алгоритм ошибается чаще. Кроме того, использовать эту метрику может быть неудобно в ситуации с несбалансированными классами, то есть, когда объектов одного класса много больше, чем объектов другого. К примеру, если в данных 95% объектов из класса 0 и 5% из класса 1, а алгоритм всегда предсказывает, что объект относится к классу 0, то его accuracy будет равно 95%, хотя алгоритм совершенно бесполезный! В таких случаях часто используют другие метрики.
Precision and Recall – Точность и полнота
Чтобы понять, что такое точность и полнота, разберемся сначала с возможными типами ошибок. Для этого отлично подходит картинка из википедии.
В нашем примере, если алгоритм пометит нормальный комментарий как токсичный, то ничего особо страшного не произойдет. Этот коммент будет в дальнейшей проверен модератором. Такая ошибка называется ошибкой первого рода (false positive). Если же комментарий будет распознан как нормальный, но он токсичный, то такая ошибка называется ошибкой второго рода (false negative). На мой взгляд, в нашем примере ошибка второго рода страшнее, чем ошибка первого. Но бывает и наоборот.
Для отслеживания двух видов ошибок используют метрики точность (Precision) и полнота (Recall).
- Точность измеряет, какой процент объектов, для которых алгоритм предсказал класс 1, действительно относится к классу 1. В нашем примере, точность – это отношение количества реально токсичных комментариев к количеству помеченных как токсичные. И эта метрика составляет ⅔ = 66%.
- Полнота измеряет, для какого процента объектов класса 1 алгоритм предсказал класс 1. Для нашего примера полнота составляет 100%. Для простоты понимания, в вики формулы расчеты показаны визуально.
Отслеживать обе метрики сразу может быть неудобно, и может понадобиться скомбинировать их в одной. Для этого используют F-меру – среднее гармоническое точности P и полноты R:
Такой способ усреднения был выбран потому, что F-мера принимает высокие значения, только когда обе метрики принимают высокие значения. Иными словами, если хотя бы одна из двух метрик близка к 0, F-мера тоже будет близка к 0. Это свойство не выполняется, например, для среднего арифметического из точности и полноты.
Ансамблевые методы
В этом разделе поговорим про ансамбли – методы, наиболее часто используемые в машинном обучении при работе с табличными данными. Ансамбли обычно применяют в задачах классификации и регрессии, но они годятся и для других задач, которые сводятся к этим двум. Стоит сказать, что это только вершина айсберга и методов машинного обучения очень много. Их обзор можно найти в этой статье.
Вспомним постановку задач регрессии и классификации. В обеих требуется набор табличных данных: по строкам таблицы заданы объекты (например, клиенты), а по столбцам – признаки, то есть некоторые характеристики объектов (возраст, заработная плата, стаж работы клиента и т. д.). Кроме того, нужна разметка данных: для каждого объекта должно быть известно значение целевой переменной (класс в задаче классификации или число в задаче регрессии). Имея набор размеченных данных, мы обучаем алгоритм, который будет предсказывать значение целевой переменной для новых объектов на стадии внедрения.
Ансамблирование чаще всего используют применительно к решающим деревьям, поэтому начнем блок с разбора этого метода.
Решающее дерево – это алгоритм, который делает предсказания на основе серии вопросов об объекте.
Например, покажем решающее дерево, которое определяет возможность проставления оценки по какому-то предмету студенту.
Ансамблирование заключается в том, чтобы обучить несколько алгоритмов и усреднять их предсказания.
Например, строится несколько разных решающих деревьев, и берется среднее результатов их работы. Подробно про ансаблирование в машинном обучении можно почитать тут.
Решаем Titanic на Kaggle
Для начала неплохо было бы ознакомиться с задачей и данными, которые нам предоставляют. Идем на kaggle.com/c/titanic/overview. Изучив описание, узнаем, что нам предстоит решить задачу классификации: по заданным признакам необходимо определить, выживет ли пассажир при крушении Титаника или нет. Предлагаемые данные (раздел Data) состоят из трех файлов .csv: train.csv – обучающая выборка, в которой содержатся метки, выжил ли каждый конкретный пассажир или нет; test.csv – собственно данные для решения, именно в этом файле нам нужно определить выживаемость; gender_submission.csv – пример того, как должен выглядит файл-ответ.
Что нужно делать – понятно. Начинаем смотреть наши данные. Переходим на вкладку Code и нажимаем New notebook.
Таким образом, мы получаем продвинутый jupyter notebook. Чтобы активировать систему, нажмем на значок Play слева от верхней ячейки ноутбука. Система будет запущена и в результате, под ячейкой увидим пути до csv файлов.
Можно приступать. Если вы не знакомы с jupyter notebook и pandas, то рекомендую сначала прочитать данный материал.
Чтение и анализ датасета Titanic
Первым делом, загружаем в датафреймы файлы .csv.
train_data = pd.read_csv('/kaggle/input/titanic/train.csv')
test_data = pd.read_csv('/kaggle/input/titanic/test.csv')
Проверим, что все у нас удачно и взглянем на эти датафреймы. Для примера приведу train_data.
train_data.head()
Первым делом оценим размеры датафрейма. Для этого используем свойство shape.
train_data.shape
В результате получаем (891, 12), т.е. 12 столбцов и 891 строку.
Следующим этапом неплохо было бы оценить количество пустых ячеек в столбцах обучающей выборки. Для этого вызовем:
train_data.isnull().sum()
Получаем, что в столбце Age у нас 177 пропусков, а в Cabin аж 687, что сильно больше половины.
Далее, оценим выживаемость. Для простоты визуализации будем использовать библиотеку seaborn. Для этого подключить ее и matplotlib.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.countplot(x='Survived', data=train_data)
Как видим, выжило людей меньше, чем погибло.
Теперь посмотрим, как с выживаемостью у мужчин и женщин отдельно.
sns.countplot(x='Survived', hue='Sex', data=train_data)
Видим, что мужчин погибло гораздо больше, чем выжило. И большая часть женщин выжила.
Далее взглянем, как зависела выживаемость от класса каюты.
sns.countplot(x='Survived', hue='Pclass', data=train_data)
Видим всплеск среди погибших пассажиров 3 класса.
Не закапываясь глубоко в датасет, видим явную зависимость выживаемости от пола и класса каюты.
В качестве признаков кроме выбранных пола и класса каюты, возьмем количество родителейдетей и количество братьевсестер на борту. Итоговый список признаков будет выглядеть следующим образом:
features = ['Sex', 'Pclass', 'SibSp', 'Parch']
Информацию о выживших и погибших пассажирах поместим в переменную y:
y = train_data['Survived']
Если вы немного отмотаете назад, то увидите, что в столбце Sex находятся не числа, а строки, когда остальные отобранные нами признаки являются числами. Давайте превратим этот столбец в пару фиктивных переменных. Для этого в Pandas есть специальный метод, который называется get_dummies(). Сделаем эту операцию как для обучающей выборки, так и для тестовой.
X = pd.get_dummies(train_data[features])
X_test = pd.get_dummies(test_data[features])
Обратите внимание, что столбец Sex исчез, а вместо него появилось два столбца Sex_female и Sex_male.
Теперь с помощью ансамбля решающих деревьев обучим нашу модель, сделаем предсказание для тестовой выборки и сохраним результат. Ансамбль решающих деревьев называется Random Forest.
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=1)
model.fit(X, y) # обучаем модель
prediction = model.predict(X_test) # делаем предсказание
output = pd.DataFrame({'PassengerId':test_data.PassengerId, 'Survived':prediction})
output.to_csv('my_submission.csv', index=False) # формируем итоговый датафрейм и сохраняем его в csv файл
Вот и все. Осталось отправить результат в соревнование. Для этого в правом верхнем углу наживаем кнопку Save version. После того, как блокнот сохранится, нажимаем на цифру возле этой кнопки.
Откроется окно Version history. В правом списке, нажимаем на многоточие около только что сохраненной версии и нажимаем Submit to competition.
Появляется окошко, в котором нажимаем submit.
Поздравляю! Вы закончили свое первое соревнование на kaggle. Нажмите на view my submission, чтобы взглянуть на результат.
Чем ближе число к 1, тем лучше. Но 0.775, согласитесь, неплохо для первого раза.
Путями улучшения результата могут быть: введение дополнительных признаков, введение своих новых признаков, выбор другого алгоритма, выбор другим параметров алгоритма RandomForestClassifier. Для начала, попробуйте поиграть с числами в этой строке (называются эти числа гиперпараметрами).
model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=1)
Дополнительные материалы для изучения:
- https://github.com/girafe-ai/ml-mipt/tree/master
- https://machinelearning.ru/
При подготовке были использованы материала из Википедии и Летней школы Сбера.
В течение последних двух десятилетий технологии искусственного интеллекта — и в первую очередь методы машинного обучения — становятся всё более практичными и доступными: сегодня их могут применять даже разработчики, не владеющие специализированными знаниями в сфере. Всё больше из них применяют прогнозное моделирование, поэтому лидерам и менеджерам необходимо помнить об ошибках, которые могут сделать напрасной всю проделанную командой работу. Издание VentureBeat собрало 9 наиболее распространённых ошибок при обучении моделей и советы о том, как их можно избежать, чтобы корректно построить процесс машинного обучения.
Читать далее
Ошибка 1: смещение выборки
Отправная точка любой программы машинного обучения — формирование обучающей выборки. Обычно организации уже имеют в распоряжении некоторые данные или же знают, где подходящие данные можно получить, например, у государственных учреждений или ассоциаций по своей отрасли. Разработчикам программ машинного обучения, а также их инвесторам, необходимо грамотно сформировать обучающий набор данных. При этом нужно помнить, что выборка должна быть репрезентативной, то есть отражать характеристики совокупности в целом, иначе это может привести к искажению результатов. Например, некорректно проводить опросы исключительно в какой-либо одной точке, где люди с большей вероятность будут обладать теми или иными характеристиками.
Решение: чтобы выборка была репрезентативной, следует выбирать данные в абсолютно случайном порядке, а не использовать некоторый источник лишь потому, что к нему проще получить доступ. Чёткое определение объективного набора данных и логики модели имеют решающее значение при подборе данных. Сотрудничество с предпринимателями, а также помощь сторонних экспертов в оценке критериев отбора на раннем этапе обеспечит разработчикам надёжность выборки
Ошибка 2: отбор нерелевантных признаков
Зачастую разработчики сталкиваются со сложностями при выборе переменных. Отдельные методы машинного обучения требуют более широкого набора признаков. Однако стремясь собрать как можно больше обучающих данных нужно помнить о том, что в них должны присутствовать только подходящие, релевантные признаки.
Решение: чтобы обучаемая модель показывала высокие результаты, нужно провести тщательные исследования и анализ, так как это поможет при выборе и проектировании необходимых признаков. Понимание сферы деятельности и привлечение соответствующих специалистов — два ключевых условия подбора правильных признаков. Помимо этого, такие методы, как рекурсивное исключение признаков, случайный лес, метод главных компонент и автокодировщик помогают проводить обучение на меньшем количестве более информативных признаков.
Ошибка 3: утечка данных
Иногда разработчики машинного обучения непреднамеренно отбирают обучающие данные, отталкиваясь от критериев тех результатов, которые модель пытается предсказать. Как следствие, она покажет неправдоподобно высокие результаты. Например, если команда по ошибке включит переменную, обозначающую лечение заболевания в модель, которая должна предсказывать это заболевание.
Решение: разработчикам нужно быть внимательными при составлении обучающих наборов и использовать только данные, которые на практике будут доступны во время обучения перед тем, как модель будет оценивать результаты.
Ошибка 4: пропущенные данные
В некоторых случаях обучающие массивы могут быть неполными из-за пропущенных в записях значений. Если не сделать на это поправку или предположить, что прощенных значений в выборке нет, это может привести к её сильному смещению. Так, пропущенные значения необязательно будут случайными: например, когда респонденты с меньшей вероятностью будут отвечать на тот или иной вопрос, а подстановка недостающих данных может ввести обучаемую модель в заблуждение.
Решение: если нет возможности построить программу обучения на полных массивах данных, можно применить статистические приёмы, например, исключить пропущенные данные или использовать корректную стратегию подстановки, чтобы рассчитать значения пропущенных данных.
Ошибка 5: неправильное масштабирование и нормализация данных
При составлении обучающего набора для машинного обучения требуется собрать различные типов вводных данных, что может привести к их несбалансированности. Если не привести значения переменных к единой шкале перед тренировкой модели, это может значительно повредить эффективности обучения с использованием таких алгоритмов, как линейная регрессия, метод опорных векторов или метод k-ближайших соседей. Проблемы возникают потому, что широко различающиеся диапазоны значений приведут к большому различию признаков, а это обязательно отразится на результатах. Например, данные по зарплате могут приобрести больший вес, чем возраст, если все эти данные не обработать перед вводом.
Решение: все данные перед тренировкой модели необходимо преобразовать. Это можно сделать с помощью распространённых статистических приёмов, таких как стандартизация или масштабирование признаков в зависимости от типа данных и выбранного командой алгоритма.
Ошибка 6: пренебрежение выбросами
Результаты модели могут серьёзно исказиться, если не принимать во внимание выбросы. Например, алгоритмы вроде AdaBoost увеличивают веса наиболее трудных объектов, которыми часто оказываются выбросы, а деревья решений менее чувствительны к ним. Кроме того, в различных вариантах использования результаты, выделяющиеся из общей выборки, можно учитывать по-разному. Например, при обнаружении мошенничества акцент на выбросах в депозитах будет обязательным условием, в то время как выбросами данных с температурных датчиков можно пренебречь.
Решение: разработчикам стоит либо использовать алгоритмы моделирования, которые корректно учитывают выбросы, либо фильтровать их перед началом обучения. Для начала нужно проверить, содержатся ли в данных выбросы. Наиболее простой способ сделать это — проанализировать массивы данных и вычислить значения, которые значительно отклоняются от среднего.
Ошибка 7: неправильное вычисление признаков
Любые ошибки во вводных данных для обучения модели могут привести к тому, что модель будет выдавать отличные от запланированных, ненадёжные результаты, независимо от того, насколько качественно команда будет проводить обучение. Например, можно понизить эффективность модели для расчёта кредитного рейтинга на основе коэффициента технического использования, если включить данные о неактивных операциях из кредитных отчётов.
Решение: разработчикам нужно тщательно проверить, откуда получены обучающие данные. Критически важно ещё перед началом обучения понять, какие из них — «сырые», а какие — подделаны. Далее перед началом обучения необходимо проверить предположения и подсчёты производных признаков.
Ошибка 8: игнорирование мультиколлинеарных вводных
Применение набора данных без учёта мультиколлинеарных предикторов — ещё одна ошибка при обучении моделей, которая приведёт к неправильным результатам. Мультиколлинеарность означает наличие сильной линейной зависимости между несколькими переменными, что не позволяет оценить влияние какой-либо из них в отдельности. В данном случае незначительные изменения в выбранных признаках могут иметь существенное влияние на результаты.
Решение: Простой способ определить мультиколлинеарность — подсчитать коэффициент корреляции для всех пар переменных. Это даёт ряд возможностей для устранения любой выявленной коллинеарности, таких как построение композиций и отбрасывание избыточных переменных.
Ошибка 9: низкие показатели производительности
Большинство алгоритмов машинного обучения показывают лучшие результаты, когда в обучающих данных различного рода примеры представлены равномерно. Если данные сильно несбалансированы, очень важную роль играют правильные метрики для измерения производительности. Например, при средней штрафной ставке в 1,2 процента доля правильных ответов составит модели достигнет 98,8 процента, и ни в одном из случаев она не предскажет неуплату.
Решение: Если нет возможности создать более сбалансированный набор обучающих данных или же использовать затратный алгоритм обучения, лучшим решением станет подбор бизнес-метрик производительности. Помимо доли правильных ответов есть различные меры производительности модели, например, точность, полнота, F-мера и ROC-кривая (рабочая характеристика приёмника). Определение наиболее подходящей метрики позволит свести к минимуму ошибки при обучении алгоритма.
Важность правильных обучающих данных
Благодаря современным технологиям и инструментам исполнять тренировочные программы для машинного обучения как никогда просто. Однако, чтобы получить надёжные результаты, разработчикам нужно отлично владеть математическим моделированием и статистическими принципами, так как это позволит им подготовить надёжный набор данных, что является важным условием успешного машинного обучения.
«Фонды адмовілі нам 22 разы».