Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
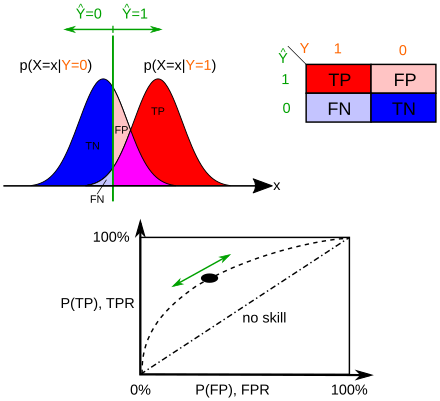
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
При проверке статистических гипотез ошибка I рода — это ошибочное отклонение действительно истинной нулевой гипотезы (также известной как «ложноположительный» результат или вывод; например: «невиновный человек осужден»), а ошибка II рода — это ошибочное принятие фактически ложной нулевой гипотезы (также известное как «ложноотрицательный» вывод или вывод; пример: «виновный не осужден»). [1]Большая часть статистической теории вращается вокруг минимизации одной или обеих этих ошибок, хотя полное устранение любой из них является статистически невозможным, если результат не определяется известным, наблюдаемым причинным процессом. Выбрав низкое пороговое (отсечное) значение и изменив уровень альфа (p), можно повысить качество проверки гипотезы. [2] Информация об ошибках типа I и ошибках типа II широко используется в медицине , биометрии и информатике . [ требуется уточнение ]
Интуитивно, ошибки типа I можно рассматривать как ошибки совершения , т. е. исследователь, к несчастью, приходит к выводу, что что-то является фактом. Например, рассмотрим исследование, в котором ученые сравнивают лекарство с плацебо. Если пациенты, получающие препарат, случайно выздоравливают, чем пациенты, получающие плацебо, может показаться, что препарат эффективен, но на самом деле вывод неверен. И наоборот, ошибки II рода — это ошибки упущения .. В приведенном выше примере, если бы пациенты, получавшие лекарство, не выздоравливали быстрее, чем те, кто получал плацебо, но это была случайная случайность, это была бы ошибка II типа. Последствия ошибки типа II зависят от размера и направления пропущенного определения и обстоятельств. Дорогостоящее лекарство для одного из миллиона пациентов может быть несущественным, даже если оно действительно является лекарством.
Определение
Статистический фон
В статистической теории тестирования понятие статистической ошибки является неотъемлемой частью проверки гипотез . Тест состоит в выборе двух конкурирующих предположений, называемых нулевой гипотезой , обозначаемой H0, и альтернативной гипотезой , обозначаемой H1 . . Это концептуально похоже на приговор в судебном процессе. Нулевая гипотеза соответствует положению подсудимого: точно так же, как предполагается, что он невиновен, пока его вина не доказана, так и нулевая гипотеза считается истинной, пока данные не дают убедительных доказательств против нее. Альтернативная гипотеза соответствует позиции против подсудимого. В частности, нулевая гипотеза также предполагает отсутствие различий или отсутствие связи. Таким образом, нулевая гипотеза никогда не может состоять в том, что существует различие или ассоциация.
Если результат теста соответствует действительности, значит, принято правильное решение. Однако если результат проверки не соответствует действительности, значит, произошла ошибка. Есть две ситуации, в которых решение неверно. Нулевая гипотеза может быть верной, тогда как мы отвергаем H 0 . С другой стороны, альтернативная гипотеза H 1 может быть верной, тогда как мы не отвергаем H 0 . Различают два типа ошибок: ошибку первого рода и ошибку второго рода. [3]
Ошибка I типа
Первый вид ошибок — это ошибочное отклонение нулевой гипотезы в результате процедуры проверки. Такую ошибку называют ошибкой первого рода (ложноположительной) и иногда называют ошибкой первого рода.
С точки зрения примера с залом суда ошибка первого рода соответствует осуждению невиновного подсудимого.
Ошибка второго рода
Второй вид ошибок — ошибочное принятие нулевой гипотезы в результате процедуры проверки. Такая ошибка называется ошибкой второго рода (ложноотрицательная), а также называется ошибкой второго рода.
В примере с залом суда ошибка II рода соответствует оправданию преступника. [4]
Частота ошибок кроссовера
Коэффициент перекрестных ошибок (CER) — это точка, в которой ошибки типа I и ошибки типа II равны, и представляет собой лучший способ измерения эффективности биометрии. Система с более низким значением CER обеспечивает большую точность, чем система с более высоким значением CER.
Ложноположительный и ложноотрицательный
См. дополнительную информацию в разделе: Ложноположительные и ложноотрицательные результаты .
Что касается ложноположительных и ложноотрицательных результатов, положительный результат соответствует отклонению нулевой гипотезы, а отрицательный результат соответствует невозможности отвергнуть нулевую гипотезу; «ложный» означает, что сделанный вывод неверен. Таким образом, ошибка I рода эквивалентна ложноположительному результату, а ошибка II рода эквивалентна ложноотрицательному результату.
Таблица типов ошибок
Табличные соотношения между истинностью/ложностью нулевой гипотезы и результатами проверки: [5]
| Таблица типов ошибок |
Нулевая гипотеза ( H 0 ) |
||
|---|---|---|---|
| Истинный |
Ложь |
||
| Решение о нулевой гипотезе ( H 0 ) |
Не отвергай |
Правильный вывод (истинно отрицательный) (вероятность = 1 − α ) |
Ошибка типа II (ложноотрицательный) (вероятность = β ) |
| Отклонять |
Ошибка типа I (ложноположительный результат) (вероятность = α ) |
Правильный вывод (истинно положительный) (вероятность = 1 − β ) |
Частота ошибок
Результаты, полученные для отрицательного образца (левая кривая), перекрываются с результатами, полученными для положительных образцов (правая кривая). Перемещая пороговое значение результата (вертикальная полоса), можно уменьшить количество ложноположительных результатов (FP) за счет увеличения количества ложноотрицательных результатов (FN) или наоборот (TP = истинно положительные результаты, TPR = истинно положительные результаты). частота, FPR = частота ложных срабатываний, TN = истинные отрицательные значения).
Идеальный тест должен иметь ноль ложноположительных и ноль ложноотрицательных результатов. Однако статистические методы носят вероятностный характер, и нельзя знать наверняка, правильны ли статистические выводы. Всякий раз, когда есть неопределенность, есть вероятность совершить ошибку. Учитывая эту природу статистической науки, все проверки статистических гипотез имеют вероятность совершения ошибок первого и второго рода. [6]
- Частота ошибок первого рода или уровень значимости — это вероятность отклонения нулевой гипотезы при условии, что она верна. Он обозначается греческой буквой α (альфа) и также называется альфа-уровнем. Обычно уровень значимости устанавливается равным 0,05 (5%), подразумевая, что допустимо наличие 5% вероятности ошибочного отклонения истинной нулевой гипотезы. [7]
- Скорость ошибки II рода обозначается греческой буквой β (бета) и связана с мощностью теста , равной 1−β. [8]
Эти два типа коэффициентов ошибок компенсируются друг другом: для любого заданного набора выборок усилия по уменьшению одного типа ошибки обычно приводят к увеличению другого типа ошибки. [9]
Качество проверки гипотез
Та же идея может быть выражена в терминах доли правильных результатов и, следовательно, использована для минимизации частоты ошибок и повышения качества проверки гипотез. Чтобы уменьшить вероятность совершения ошибки типа I, достаточно просто и эффективно сделать значение альфа (p) более строгим. Чтобы уменьшить вероятность совершения ошибки типа II, которая тесно связана с мощностью анализа, либо увеличение размера выборки теста, либо ослабление альфа-уровня могут увеличить мощность анализа. [10] Тестовая статистика является надежной, если частота ошибок типа I находится под контролем.
Также можно использовать различные пороговые значения (отсечки), чтобы сделать тест более специфичным или более чувствительным, что, в свою очередь, повышает качество теста. Например, представьте себе медицинский тест, в котором экспериментатор может измерить концентрацию определенного белка в образце крови. Экспериментатор мог настроить порог (черная вертикальная линия на рисунке), и у людей диагностировали заболевание, если какое-либо число было обнаружено выше этого определенного порога. Согласно изображению, изменение порога приведет к изменению ложноположительных и ложноотрицательных результатов, соответствующих движению по кривой. [11]
Пример
Поскольку в реальном эксперименте невозможно избежать всех ошибок типа I и типа II, важно учитывать степень риска, на который человек готов пойти, чтобы ложно отвергнуть H 0 или принять H 0 . Решением этого вопроса было бы сообщить значение p или уровень значимости α статистики. Например, если p-значение статистического результата теста оценивается как 0,0596, то существует вероятность 5,96%, что мы ошибочно отвергаем H 0 . Или, если мы говорим, что статистика выполняется на уровне α, например 0,05, то мы допускаем ложное отклонение H 0 на уровне 5%. Уровень значимости α, равный 0,05, является относительно распространенным, но не существует общего правила, подходящего для всех сценариев.
Измерение скорости автомобиля
Ограничение скорости на автостраде в США составляет 120 километров в час. Установлено устройство для измерения скорости проезжающих мимо транспортных средств. Предположим, что прибор проведет три измерения скорости проезжающего автомобиля, записывая в виде случайной выборки X 1 , X 2 , X 3 . ГИБДД будет или не будет штрафовать водителей в зависимости от средней скорости. То есть тестовая статистика.
Кроме того, мы предполагаем, что измерения X 1 , X 2 , X 3 моделируются как нормальное распределение N(μ,4). Затем T должно следовать за N (μ, 4/3), а параметр μ представляет собой истинную скорость проезжающего транспортного средства. В этом эксперименте нулевая гипотеза H 0 и альтернативная гипотеза H 1 должны быть
H 0 : µ=120 против H 1 : µ 1 >120.
Если мы выполняем статистический уровень при α = 0,05, то необходимо вычислить
критическое значение c для решения
Согласно правилу замены единиц для нормального распределения. Ссылаясь на Z-таблицу , мы можем получить
Здесь критическая область. То есть, если зафиксированная скорость транспортного средства превышает критическое значение 121,9, водитель будет оштрафован. Тем не менее, еще 5% водителей оштрафованы ложно, так как зарегистрированная средняя скорость превышает 121,9, а реальная скорость не превышает 120, что мы называем ошибкой I рода.
Ошибка II рода соответствует случаю, когда истинная скорость транспортного средства превышает 120 километров в час, но водитель не оштрафован. Например, если истинная скорость автомобиля µ=125, вероятность того, что водитель не будет оштрафован, можно рассчитать как
Это означает, что если истинная скорость транспортного средства равна 125, у водителя есть вероятность 0,36% избежать штрафа, когда статистика выполняется на уровне 125, поскольку зарегистрированная средняя скорость ниже 121,9. Если истинная скорость ближе к 121,9, чем к 125, то вероятность избежать штрафа тоже будет выше.
Следует также учитывать компромиссы между ошибкой первого рода и ошибкой второго рода. То есть в этом случае, если ГАИ не хочет ложно штрафовать невиновных водителей, уровень α можно установить на меньшее значение, например 0,01. Однако, если это так, больше водителей, чья реальная скорость превышает 120 километров в час, например 125, с большей вероятностью избегут штрафа.
этимология
В 1928 году Ежи Нейман (1894–1981) и Эгон Пирсон (1895–1980), оба выдающиеся статистики, обсуждали проблемы, связанные с «решением, можно ли считать конкретную выборку вероятной случайным образом взятой из определенной совокупности». «: [12] и, как заметила Флоренс Найтингейл Дэвид , «необходимо помнить, что прилагательное «случайный» [в термине «случайная выборка»] должно относиться к методу отбора пробы, а не к самой пробе». [13]
Они выявили «два источника ошибок», а именно:
- (а) ошибка отклонения гипотезы, которую не следовало отвергать, и
- (b) ошибка, заключающаяся в том, что не удалось отвергнуть гипотезу, которую следовало отвергнуть.
В 1930 году они подробно остановились на этих двух источниках ошибок, отметив, что:
… при проверке гипотез необходимо учитывать два соображения: мы должны иметь возможность уменьшить вероятность отклонения истинной гипотезы до желаемого низкого значения; тест должен быть разработан таким образом, чтобы он отклонял проверяемую гипотезу, когда она, вероятно, окажется ложной.
В 1933 году они заметили, что эти «проблемы редко представляются в такой форме, чтобы мы могли с уверенностью отличить истинную гипотезу от ложной». Они также отметили, что, решая, не отклонить или отвергнуть конкретную гипотезу среди «набора альтернативных гипотез», H 1 , H 2 …, легко сделать ошибку:
…[и] эти ошибки будут двух видов:
- (I) мы отвергаем H 0 [т.е. гипотезу, которую нужно проверить], когда она верна, [14]
- (II) мы не можем отвергнуть H 0 , когда какая-либо альтернативная гипотеза H A или H 1 верна. (Есть различные обозначения для альтернативы).
Во всех статьях, написанных совместно Нейманом и Пирсоном, выражение H 0 всегда означает «гипотезу, подлежащую проверке».
В той же статье они называют эти два источника ошибок ошибками типа I и ошибками типа II соответственно. [15]
Нулевая гипотеза
Стандартной практикой для статистиков является проведение тестов , чтобы определить, может ли быть подтверждена « спекулятивная гипотеза » относительно наблюдаемых явлений мира (или его обитателей). Результаты такого тестирования определяют, разумно ли конкретный набор результатов согласуется (или не согласуется) с предполагаемой гипотезой.
На том основании, что согласно статистической традиции всегда предполагается, что предполагаемая гипотеза ошибочна, а так называемая « нулевая гипотеза » утверждает, что наблюдаемые явления происходят просто случайно (и что, как следствие, предполагаемый агент не имеет эффект) – тест определит, верна эта гипотеза или нет. Вот почему проверяемую гипотезу часто называют нулевой гипотезой (скорее всего, введенной Фишером (1935, стр. 19)), потому что именно эта гипотеза должна быть либо аннулирована , либо не аннулирована проверкой. Когда нулевая гипотеза аннулируется, можно заключить, что данные подтверждают « альтернативную гипотезу ».«(что является исходным предположением).
Последовательное применение статистиками соглашения Неймана и Пирсона о представлении « гипотезы, подлежащей проверке » (или « гипотезы, подлежащей аннулированию ») выражением H0 , привело к обстоятельствам, при которых многие понимают термин « нулевая гипотеза » как означающий « нулевая гипотеза » — утверждение о том, что рассматриваемые результаты возникли случайно. Это не обязательно так — ключевое ограничение, согласно Фишеру (1966), состоит в том, что « нулевая гипотеза должна быть точной, то есть свободной от неопределенности и двусмысленности, потому что она должна служить основой для «проблемы распределения». из которых критерий значимости является решением. « [16] Как следствие этого, в экспериментальной науке нулевая гипотеза обычно представляет собой утверждение о том, что конкретное лечение не имеет никакого эффекта ; в наблюдательной науке это то, что нет никакой разницы между значением конкретной измеренной переменной и значением экспериментального предсказания.
Статистическая значимость
Если вероятность получения столь же экстремального результата, как и полученный, при условии, что нулевая гипотеза верна, ниже заранее заданной пороговой вероятности (например, 5%), то результат считается статистически значимым . и нулевая гипотеза отвергается.
Британский статистик сэр Рональд Эйлмер Фишер (1890–1962) подчеркивал, что «нулевая гипотеза»:
… никогда не доказывается и не устанавливается, но, возможно, опровергается в ходе экспериментов. Можно сказать, что каждый эксперимент существует только для того, чтобы дать фактам возможность опровергнуть нулевую гипотезу.
- Фишер, 1935, стр. 19.
Домены приложений
Медицина
В медицинской практике различия между применением скрининга и тестирования значительны.
Медицинский осмотр
Скрининг включает в себя относительно дешевые тесты, которые назначаются большим группам населения, ни один из которых не проявляет каких-либо клинических признаков заболевания (например, мазок Папаниколау ).
Тестирование включает гораздо более дорогие, часто инвазивные процедуры, которые назначаются только тем, у кого проявляются некоторые клинические признаки заболевания, и чаще всего применяются для подтверждения предполагаемого диагноза.
Например, в большинстве штатов США новорожденные должны проходить скрининг на фенилкетонурию и гипотиреоз , а также на другие врожденные заболевания .
Гипотеза: «У новорожденных фенилкетонурия и гипотиреоз».
Нулевая гипотеза (H 0 ): «У новорожденных нет фенилкетонурии и гипотиреоза»,
Ошибка I рода (ложноположительный): Верно то, что у новорожденных нет фенилкетонурии и гипотиреоза, но по имеющимся данным мы считаем, что у них есть нарушения.
Ошибка II типа (ложноотрицательный): Истинный факт заключается в том, что у новорожденных есть фенилкетонурия и гипотиреоз, но мы считаем, что, согласно данным, у них нет нарушений.
Хотя они показывают высокий уровень ложноположительных результатов, скрининговые тесты считаются ценными, поскольку они значительно повышают вероятность обнаружения этих расстройств на гораздо более ранней стадии.
Простые анализы крови, используемые для скрининга возможных доноров крови на ВИЧ и гепатит , имеют значительный уровень ложноположительных результатов; однако врачи используют гораздо более дорогие и гораздо более точные тесты, чтобы определить, действительно ли человек заражен одним из этих вирусов.
Возможно, наиболее широко обсуждаемые ложноположительные результаты в медицинском скрининге связаны с процедурой маммографии для скрининга рака молочной железы.. Уровень ложноположительных маммограмм в США составляет до 15%, что является самым высоким показателем в мире. Одним из последствий высокого уровня ложноположительных результатов в США является то, что за любой 10-летний период половина американских женщин, прошедших скрининг, получают ложноположительные маммограммы. Ложноположительные маммограммы обходятся дорого: в США ежегодно тратится более 100 миллионов долларов на последующее тестирование и лечение. Они также вызывают у женщин ненужное беспокойство. В результате высокого уровня ложноположительных результатов в США до 90–95% женщин, получивших положительный результат маммографии, не имеют этого заболевания. Самый низкий показатель в мире в Нидерландах, 1%. Самые низкие показатели, как правило, в Северной Европе, где маммографические снимки считываются дважды и устанавливается высокий порог для дополнительного тестирования (высокий порог снижает мощность теста).
Идеальный скрининговый тест населения должен быть дешевым, простым в применении и по возможности не давать ложноотрицательных результатов. Такие тесты обычно дают больше ложноположительных результатов, которые впоследствии можно устранить с помощью более сложного (и дорогого) тестирования.
Медицинское тестирование
Ложноотрицательные и ложноположительные результаты являются серьезными проблемами в медицинском тестировании .
Гипотеза: «У больных специфическое заболевание».
Нулевая гипотеза (H 0 ): «У пациентов нет специфического заболевания».
Ошибка I типа (ложноположительный результат): «Истинный факт заключается в том, что у пациентов нет определенного заболевания, но врачи судят, что пациент был болен на основании отчетов об испытаниях».
Ложные срабатывания также могут привести к серьезным и нелогичным проблемам, когда искомое состояние встречается редко, как при скрининге. Если тест имеет ложноположительный результат один на десять тысяч, но только один из миллиона образцов (или людей) является истинно положительным, большинство положительных результатов, обнаруженных этим тестом, будут ложными. Вероятность того, что наблюдаемый положительный результат является ложноположительным, можно рассчитать с помощью теоремы Байеса .
Ошибка типа II (ложноотрицательный результат): «Истинный факт заключается в том, что болезнь действительно присутствует, но отчеты об испытаниях дают ложно обнадеживающее сообщение пациентам и врачам об отсутствии болезни».
Ложноотрицательные результаты приводят к серьезным и нелогичным проблемам, особенно когда искомое состояние является распространенным. Если тест с частотой ложноотрицательных результатов всего 10 % используется для проверки популяции с истинной частотой встречаемости 70 %, многие отрицательные результаты, обнаруженные тестом, будут ложными.
Иногда это приводит к неадекватному или неадекватному лечению как больного, так и его заболевания. Типичным примером является использование сердечных нагрузочных тестов для выявления коронарного атеросклероза, хотя известно, что сердечные нагрузочные тесты обнаруживают только ограничения кровотока в коронарных артериях из-за выраженного стеноза .
Биометрия
Биометрическое сопоставление, такое как распознавание отпечатков пальцев , лиц или радужной оболочки глаза , подвержено ошибкам типа I и типа II.
Гипотеза: «Ввод не идентифицирует кого-то в списке искомых людей»
Нулевая гипотеза: «Ввод действительно идентифицирует кого-то в искомом списке людей»
Ошибка I типа (коэффициент ложных отказов): «Истинный факт заключается в том, что человек находится в списке поиска, но система делает вывод, что человек не соответствует данным».
Ошибка II типа (коэффициент ложного совпадения): «Истинный факт заключается в том, что человек не является кем-то из искомого списка, но система делает вывод, что этот человек является тем, кого мы ищем, согласно данным».
Вероятность ошибок типа I называется «коэффициентом ложных отклонений» (FRR) или коэффициентом ложных несоответствий (FNMR), а вероятность ошибок типа II называется «коэффициентом ложного принятия» (FAR) или коэффициентом ложных совпадений ( ФМР).
Если система предназначена для редкого совпадения подозреваемых, то вероятность ошибок типа II можно назвать « коэффициентом ложных тревог ». С другой стороны, если система используется для валидации (а принятие является нормой), то FAR является мерой безопасности системы, а FRR измеряет уровень неудобств для пользователя.
Проверка безопасности
Основные статьи: обнаружение взрывчатых веществ и металлоискатель
Ложные срабатывания регулярно обнаруживаются каждый день при досмотре в аэропортах , которые, в конечном счете, являются системами визуального контроля . Установленная охранная сигнализация предназначена для предотвращения проноса оружия на самолет; тем не менее, они часто настроены на такую высокую чувствительность, что много раз в день реагируют на мелкие предметы, такие как ключи, пряжки ремней, мелочь, мобильные телефоны и кнопки в обуви.
Здесь гипотеза такова: «Предмет — оружие».
Нулевая гипотеза: «Предмет не является оружием».
Ошибка типа I (ложноположительный результат): «Правда в том, что предмет не является оружием, но система все равно подает сигнал тревоги».
Ошибка типа II (ложноотрицательный результат) «Правда в том, что предмет является оружием, но система в это время хранит молчание».
Таким образом, соотношение ложных срабатываний (обнаружение невиновного путешественника как террориста) и истинных срабатываний (обнаружение потенциального террориста) очень велико; и поскольку почти каждый сигнал тревоги является ложноположительным, положительная прогностическая ценность этих скрининговых тестов очень низка.
Относительная стоимость ложных результатов определяет вероятность того, что создатели тестов допустят эти события. Поскольку цена ложноотрицательного результата в этом сценарии чрезвычайно высока (необнаружение бомбы, проносимой в самолет, может привести к сотням смертей), в то время как стоимость ложноположительного результата относительно низка (достаточно простая дальнейшая проверка), наиболее подходящим тест с низкой статистической специфичностью, но высокой статистической чувствительностью (который допускает высокий уровень ложноположительных результатов в обмен на минимальные ложноотрицательные результаты).
Компьютеры
Понятия ложных срабатываний и ложных отрицаний широко распространены в сфере компьютеров и компьютерных приложений, включая компьютерную безопасность , фильтрацию спама , вредоносное ПО , оптическое распознавание символов и многие другие.
Например, в случае фильтрации спама гипотеза состоит в том, что сообщение является спамом.
Таким образом, нулевая гипотеза: «Сообщение не является спамом».
Ошибка типа I (ложное срабатывание): «Методы фильтрации или блокировки спама ошибочно классифицируют законное сообщение электронной почты как спам и, как следствие, мешают его доставке».
Хотя большинство приемов борьбы со спамом могут блокировать или фильтровать большой процент нежелательных сообщений электронной почты, делать это без значительных ложноположительных результатов — гораздо более сложная задача.
Ошибка типа II (ложноотрицательный результат): «Спам-письмо не определяется как спам, но классифицируется как не спам». Низкое количество ложных срабатываний является показателем эффективности фильтрации спама.
Смотрите также
- Бинарная классификация
- Теория обнаружения
- Эгон Пирсон
- Этика в математике
- Ложноположительный парадокс
- Частота ошибок по семейным обстоятельствам
- Показатели эффективности информационного поиска
- Лемма Неймана – Пирсона
- Нулевая гипотеза
- Вероятность гипотезы для байесовского вывода
- Точность и отзыв
- Ошибка прокурора
- Феномен прозоны
- Рабочая характеристика приемника
- Чувствительность и специфичность
- Перекрестные ссылки статистических терминов статистиков и инженеров
- Проверка гипотез, предложенных данными
- Ошибка III типа
Ссылки
- ^ «Ошибка типа I и ошибка типа II» . explorable.com . Проверено 14 декабря 2019 г. .
- ^ Чоу, Ю.В.; Пьетранико, Р .; Мукерджи, А. (27 октября 1975 г.). «Исследования энергии связи кислорода с молекулой гемоглобина». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1424–1431. doi : 10.1016/0006-291x(75)90518-5 . ISSN 0006-291X . ПМИД 6 .
- ^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .
{{cite book}}: CS1 maint: другие ( ссылка ) - ^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .
{{cite book}}: CS1 maint: другие ( ссылка ) - ^ Шескин, Дэвид (2004). Справочник по параметрическим и непараметрическим статистическим процедурам . КПР Пресс. п. 54 . ISBN 1584884401.
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование зонда с ионами галогенидов». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Линденмайер, Дэвид. (2005). Практическая природоохранная биология . Бургман, Марк А. Коллингвуд, Виктория: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357 .
- ^ Чоу, Ю.В.; Пьетранико, Р .; Мукерджи, А. (27 октября 1975 г.). «Исследования энергии связи кислорода с молекулой гемоглобина». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1424–1431. doi : 10.1016/0006-291x(75)90518-5 . ISSN 0006-291X . ПМИД 6 .
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование зонда с ионами галогенидов». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование зонда с ионами галогенидов». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Морой, К .; Сато, Т. (15 августа 1975 г.). «Сравнение метаболизма прокаина и изокарбоксазида in vitro с помощью микросомальной амидазы-эстеразы печени». Биохимическая фармакология . 24 (16): 1517–1521. doi : 10.1016/0006-2952(75)90029-5 . ISSN 1873-2968 . ПМИД 8 .
- ^ НЕЙМАН, Дж.; ПИРСОН, Э.С. (1928). «Об использовании и интерпретации некоторых критериев тестирования для целей статистического вывода, часть I». Биометрика . 20А (1–2): 175–240. doi : 10.1093/биомет/20а.1-2.175 . ISSN 0006-3444 .
- ↑ CIKF (июль 1951 г.). «Теория вероятностей для статистических методов. Ф. Н. Дэвид. [Стр. ix + 230. Издательство Кембриджского университета. 1949. Цена 155.]». Журнал актуарного общества Staple Inn . 10 (3): 243–244. doi : 10.1017/s0020269x00004564 . ISSN 0020-269X .
- ^ Обратите внимание, что нижний индекс в выражении H 0 является нулем (указывающим на ноль ) , а не «О» (указывающим на оригинал ).
- ^ Нейман, Дж.; Пирсон, ES (30 октября 1933 г.). «Проверка статистических гипотез по отношению к априорным вероятностям». Математические труды Кембриджского философского общества . 29 (4): 492–510. Бибкод : 1933PCPS…29..492N . doi : 10.1017/s030500410001152x . ISSN 0305-0041 .
- ^ Фишер, Р.А. (1966). Дизайн экспериментов . 8-е издание. Хафнер: Эдинбург.
Библиография
- Бетц, М.А. и Габриэль, К.Р. , «Ошибки типа IV и анализ простых эффектов», Журнал статистики образования , Том 3, № 2 (лето 1978 г.), стр. 121–144.
- Дэвид, Ф. Н., «Степенная функция для проверки случайности в последовательности альтернатив», Biometrika , Vol.34, Nos.3/4, (декабрь 1947 г.), стр. 335–339.
- Фишер, Р.А., План экспериментов , Оливер и Бойд (Эдинбург), 1935.
- Гэмбрилл, В., «Ложноположительные результаты тестов на заболевания новорожденных беспокоят родителей», День здоровья (5 июня 2006 г.). [1]
- Кайзер, HF, «Направленные статистические решения», Psychological Review , Vol.67, No.3, (май 1960 г.), стр. 160–167.
- Кимбалл, А.В., «Ошибки третьего рода в статистическом консультировании», Журнал Американской статистической ассоциации , том 52, № 278 (июнь 1957 г.), стр. 133–142.
- Любин, А., «Интерпретация значимого взаимодействия», Образовательные и психологические измерения , Том 21, № 4, (зима 1961 г.), стр. 807–817.
- Мараскуило, Л.А. и Левин, Дж.Р., «Подходящие апостериорные сравнения для взаимодействия и вложенных гипотез в анализе дисперсионных планов: устранение ошибок типа IV», Американский журнал исследований в области образования , том 7., № 3, (май 1970 г. ), стр. 397–421.
- Митрофф, И. И. и Фезерингем, Т. Р., «О системном решении проблем и ошибках третьего рода», Behavioral Science , том 19, № 6 (ноябрь 1974 г.), стр. 383–393.
- Мостеллер, Ф., « К -выборочный тест проскальзывания для экстремальной совокупности», Анналы математической статистики , том 19, № 1 (март 1948 г.), стр. 58–65.
- Моултон, RT, «Сетевая безопасность», Datamation , Vol.29, No.7 (июль 1983 г.), стр. 121–127.
- Райффа, Х., Анализ решений: вводные лекции о выборе в условиях неопределенности , Аддисон-Уэсли, (чтение), 1968.
Внешние ссылки
- Предвзятость и смешение – презентация Найджела Панета, Высшая школа общественного здравоохранения Питтсбургского университета