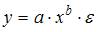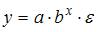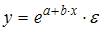Ошибки спецификации эконометрической модели имеют место вследствие - Исправление ошибок и поиск оптимальных решений проблем

к ошибкам спецификации
относятся не неправильный выбор той
или иной математической функции для
,
но и недоучет в уравнении регрессии
какого-то существенного фактора, то
есть использование парной регрессии
вместо множественной.

2. Для регрессионной
модели вида
необходим
минимальный объем наблюдений, содержащий
_____ объектов наблюдения.
«15».

3. Нелинейным по
объясняющим переменным, но линейным по
параметрам уравнением регрессии
является …

4. В модели вида
количество
объясняющих переменных равно …3.

5. При идентификации
модели множественной регрессии
количество
оцениваемых параметров равно …Итого
5 параметров.

1. В модели
множественной регрессии
определитель
матрицы парных коэффициентов корреляции
между факторами,иблизок
к единице. Это означает, что факторы,и…мультиколлинеарны

2. При моделировании
линейного уравнения множественной
регрессии вида
необходимо,
чтобы выполнялось требование отсутствия
взаимосвязи между …

между x₁
и x₂.

3. Дана матрица
парных коэффициентов корреляции.

Коллинеарными
являются факторы …

и
коллинеарны.

4. В модели
множественной регрессии
определитель
матрицы парных коэффициентов корреляции
между факторами,иблизок
к нулю. Это означает, что факторы,и…мультиколлинеарность
факторов.

5. Для эконометрической
модели линейного уравнения множественной
регрессии вида
построена
матрица парных коэффициентов линейной
корреляции (y
– зависимая переменная; х⁽¹⁾,
х⁽²⁾,
х⁽³⁾,
x⁽⁴⁾–
независимые переменные):

Коллинеарными
(тесно связанными) независимыми
(объясняющими) переменными не
являются
…x⁽²⁾
и x⁽³⁾

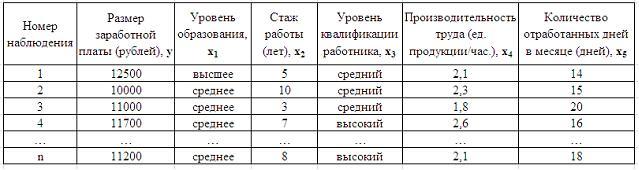
1. Дана таблица
исходных данных для построения
эконометрической регрессионной модели:

Фиктивными
переменными не
являются …

стаж работы

производительность
труда

2. При исследовании
зависимости потребления мяса от уровня
дохода и пола потребителя можно
рекомендовать …

использовать
фиктивную переменную – пол потребителя

разделить
совокупность на две: для потребителей
женского пола и для потребителей мужского
пола

3. Изучается
зависимость цены квартиры (у)
от ее жилой площади (х)
и типа дома. В модель включены фиктивные
переменные, отражающие рассматриваемые
типы домов: монолитный, панельный,
кирпичный. Получено уравнение регрессии:
,
где,Частными
уравнениями регрессии для кирпичного
и монолитного являются …

для типа дома
кирпичный

для типа дома
монолитный

4. При анализе
промышленных предприятий в трех регионах
(Республика Марий Эл, Республика Чувашия,
Республика Татарстан) были построены
три частных уравнения регрессии:

для
Республики Марий Эл;

для
Республики Чувашия;

для
Республики Татарстан.

Укажите вид
фиктивных переменных и уравнение с
фиктивными переменными, обобщающее три
частных уравнения регрессии.

5. В эконометрике
фиктивной переменной принято считать
…

переменную,
принимающую значения 0 и 1

описывающую
количественным образом качественный
признак

1. Для регрессионной
модели зависимости среднедушевого
денежного дохода населения (руб., у)
от объема валового регионального
продукта (тыс. р., х₁)
и уровня безработицы в субъекте (%, х₂)
получено уравнение
.
Величина коэффициента регрессии при
переменнойх₂
свидетельствует о том, что при изменении
уровня безработицы на 1% среднедушевой
денежный доход ______ рубля при неизменной
величине валового регионального
продукта.

изменится на
(-1,67)

2. В уравнении
линейной множественной регрессии:
,
где– стоимость основных фондов (тыс. руб.);–
численность занятых (тыс. чел.);y
– объем промышленного производства
(тыс. руб.) параметр при переменной х₁,
равный 10,8, означает, что при увеличении
объема основных фондов на _____ объем
промышленного производства _____ при
постоянной численности занятых.

на 1 тыс. руб. …
увеличится на 10,8 тыс. руб.

3. Известно, что
доля остаточной дисперсии зависимой
переменной в ее общей дисперсии равна
0,2. Тогда значение коэффициента
детерминации составляет …0,8

4. Построена
эконометрическая модель для зависимости
прибыли от
реализации единицы продукции (руб., у)
от величины оборотных средств предприятия
(тыс. р., х₁):
.
Следовательно, средний размер прибыли
от реализации, не зависящий от объема
оборотных средств предприятия, составляет
_____ рубля. 10,75

5. F-статистика
рассчитывается как отношение ______
дисперсии к ________ дисперсии, рассчитанных
на одну степень свободы.факторной
… остаточной

1. Для эконометрической
модели уравнения регрессии ошибка
модели определяется как ______ между
фактическим значением зависимой
переменной и ее расчетным значением.Разность

2. Величина
называется
…случайной
составляющей

3. В эконометрической
модели уравнения регрессии величина
отклонения фактического значения
зависимой переменной от ее расчетного
значения характеризует …ошибку
модели

4. Известно, что
доля объясненной дисперсии в общей
дисперсии равна 0,2. Тогда значение
коэффициента детерминации составляет
… 0,2

5. При методе
наименьших квадратов параметры уравнения
парной линейной регрессии
определяются
из условия ______ остатков.минимизации
суммы квадратов

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Подборка по базе: инт 01 (Вводная тема. Гигиена как наука).odt, Шаблон модели угроз и нарушителя ИБ.docx, Самоанализ по лепке во второй младшей группе. Тема_ _Конфеты для, Л. Тема № 6.4. Основы трасологии (1).pdf, Лекция. Тема 2. Финансовая модель предприятия и финансовая анали, Практическое занятие. Тема 9. Комплекс стимулирования реализации, Л. Тема № 6.1. Общие положения криминалистики (2).pdf, Бойко В.С._Глоссарий тема 4.docx, Практическое занятие. Тема 2. Маркетинговая информационная систе, Лекция. Тема 5. Планирование маркетинговой деятельности.pdf

Тема 1: Спецификация эконометрической модели

1. Ошибки спецификации эконометрической модели имеют место вследствие …

неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.

3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

4. В модели вида количество объясняющих переменных равно …

5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …

Мультиколлинеарны

2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

x₁ и x₂

3. Дана матрица парных коэффициентов корреляции.

Коллинеарными являются факторы …

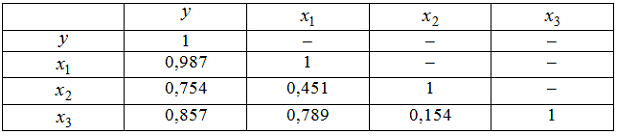
и
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это означает, что факторы , и …

мультиколлинеарны

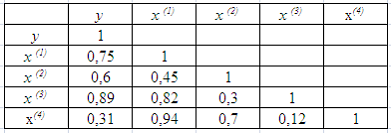
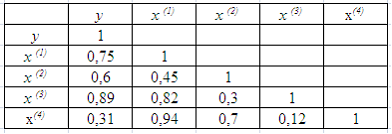
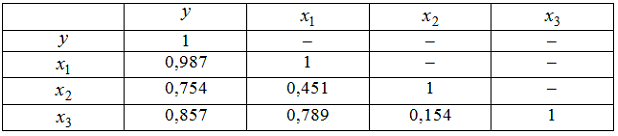
5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х⁽¹⁾, х⁽²⁾, х⁽³⁾, x⁽⁴⁾– независимые переменные):

Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …

x⁽²⁾ и x⁽³⁾

Тема 3: Фиктивные переменные

1. Дана таблица исходных данных для построения эконометрической регрессионной модели:

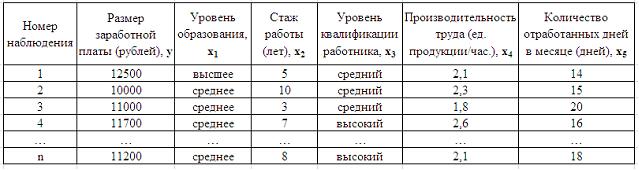
Фиктивными переменными не являются …

стаж работы

производительность труда

2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …

использовать фиктивную переменную – пол потребителя

разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола

3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …

для типа дома кирпичный

для типа дома монолитный

для типа дома кирпичный

для типа дома монолитный

Решение:

Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: или для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид
или для типа дома монолитный.

4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:

для Республики Марий Эл;

для Республики Чувашия;

для Республики Татарстан.

Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.

Итоговое уравнение будет

5. В эконометрике фиктивной переменной принято считать …

переменную, принимающую значения 0 и 1

Тема 4: Линейное уравнение множественной регрессии

1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х₁) и уровня безработицы в субъекте (%, х₂) получено уравнение . Величина коэффициента регрессии при переменной х₂ свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

изменится на (-1,67)

2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х₁, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.

на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …

0,8

4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х₁): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.

10,75

5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.

факторной … остаточной

Тема 5: Оценка параметров линейных уравнений регрессии

1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.

разность
2. Величина называется …

случайной составляющей

3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …

ошибку модели

4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …

0,2
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .

минимизации суммы квадратов

Тема 6: Предпосылки МНК, методы их проверки

1. Для обнаружения автокорреляции в остатках используется …

статистика Дарбина – Уотсона

тест Уайта

критерий Гольдфельда – Квандта

2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …

автокорреляция остатков отсутствует

3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.

положительной

4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.

Гетероскедатичность

5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.

отрицательной

Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК

1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …

несмещенности

2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …

3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю

4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.

нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …

точность оценок выборки увеличивается с увеличением объема выборки
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)

1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.

автокоррелированными и/или гетероскедастичными

2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.

обобщенный

3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников .После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат …

на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда

4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …

средняя величина остатков не равна нулю

5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …

фондоемкости продукции при неизменном уровне трудоемкости продукции
Тема 9: Оценка тесноты связи

1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …

Регрессии

2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …

[–1; 0]

3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …

[0,7; 1]

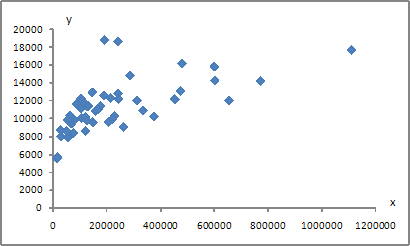
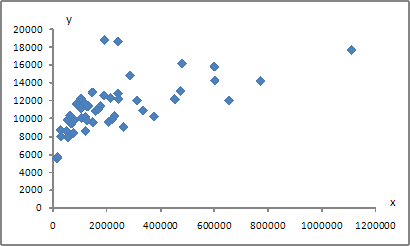
4. Для регрессионной модели вида получена диаграмма

Такое графическое отображение называется …

полем корреляции

Тема 10: Оценка качества подбора уравнения

1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …

0,9
2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений, . Тогда значение коэффициента детерминации равно …

0,8

3. Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина характеризует долю …

остаточной дисперсии
4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …

Источник

1. Ошибки спецификации эконометрической модели имеют место вследствие …

неправильного
выбора математической функции или
недоучета в уравнении регрессии какого-то
существенного фактора

недостоверности
или недостаточности исходной информации

неоднородности
данных в исходной статистической
совокупности

недостаточного
количества данных

Решение:

Спецификацией
модели называется отбор факторов,
включаемых в модель, и выбор математической
функции для
.
Поэтому к ошибкам спецификации относятся
не только неправильный выбор той или
иной математической функции для,
но и недоучет в уравнении регрессии
какого-то существенного фактора, то
есть использование парной регрессии
вместо множественной.

2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.

Решение:

Считается, на
каждый оцениваемый коэффициент регрессии
необходимо не менее 5–7 объектов
статистических наблюдений. Так как
представленная модель содержит 3
независимые переменные, то на каждый
из параметров регрессии при независимой
переменной необходимо по 5–7 наблюдений,
то есть в совокупности не менее 15–21
наблюдения. Берем нижнюю границу
интервала, тогда правильный вариант
ответа – «15».

3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

Решение:

Из приведенных
функций только в функции параметры
имеют степень 1, а объясняющая переменнаях
имеет степень, отличную от 1.

4. В модели вида количество объясняющих переменных равно …

Решение:

Эконометрическая
модель уравнения регрессии может быть
представлена линейным уравнением
множественной регрессии в виде выражения
,
гдеy
– зависимая переменная; x_j
– объясняющая независимая переменная
(j =
1,…, k;
k
– количество независимых переменных);
a,
b_j
– параметры (a
– свободный член уравнения, b_j
– коэффициент регрессии);
–
случайные факторы. Независимые переменныеx_j
называются
также факторами, объясняющими переменными.
На количество объясняющих переменных
в линейном уравнении указывает также
количество коэффициентов регрессии
b_j.
Поэтому количество объясняющих переменных
в модели равно 3.

5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …

Решение:

При оценке модели
множественной регрессии
рассчитываются
следующие параметры: свободный членa
и четыре параметра при независимых
переменных х.
Итого 5 параметров.

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами,иблизок к единице. Это означает, что факторы,и…

независимы

мультиколлинеарны

количественно
измеримы

значимы

Решение:

Для оценки
мультиколлинеарности факторов может
использоваться определитель матрицы
парных коэффициентов корреляции между
факторами. Если факторы не коррелированы
между собой, то матрица парных коэффициентов
корреляции между факторами была бы
единичной. Поскольку все недиагональные
элементы
были
бы равны нулю.,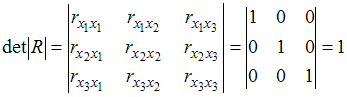
поскольку==и===0.
Если
между факторами существует полная
линейная зависимость и все коэффициенты
парной корреляции равны единице, то
определитель такой матрицы равен
нулю.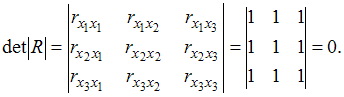Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Подборка по базе: Задание Тема 10.docx, Задание к темам 6-7.docx, 3D моделирование.pdf, Реферат ПСО. Тема 27 Дударева Е.Г. ПСО-19С.docx, Выбор модели информационной системы.pptx, 02 Самостоятельная работа тема 2.docx, 01 Самостоятельная работа тема 1.docx, ОВУ тема1 занятие 1-2.docx, Итоговое задание математическое моделирование.docx, Практическая работа по дисциплине экономическое моделирование.do

Тема 1: Спецификация эконометрической модели

1. Ошибки спецификации эконометрической модели имеют место вследствие …

3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

4. В модели вида количество объясняющих переменных равно …

5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

Мультиколлинеарны

2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

x₁ и x₂

3. Дана матрица парных коэффициентов корреляции.

Коллинеарными являются факторы …

мультиколлинеарны

5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х⁽¹⁾, х⁽²⁾, х⁽³⁾, x⁽⁴⁾– независимые переменные):

Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …

x⁽²⁾ и x⁽³⁾

Тема 3: Фиктивные переменные

1. Дана таблица исходных данных для построения эконометрической регрессионной модели:

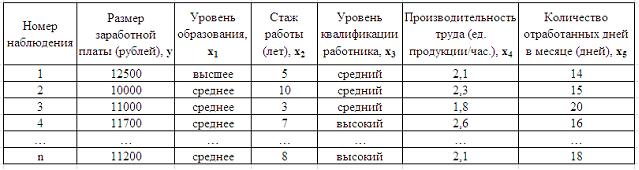
Фиктивными переменными не являются …

стаж работы

производительность труда

использовать фиктивную переменную – пол потребителя

разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола

3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …

для типа дома кирпичный

для типа дома монолитный

для типа дома кирпичный

для типа дома монолитный

Решение:

4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:

для Республики Марий Эл;

для Республики Чувашия;

для Республики Татарстан.

Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.

Итоговое уравнение будет

5. В эконометрике фиктивной переменной принято считать …

переменную, принимающую значения 0 и 1

Тема 4: Линейное уравнение множественной регрессии

1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х₁) и уровня безработицы в субъекте (%, х₂) получено уравнение . Величина коэффициента регрессии при переменной х₂ свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

изменится на (-1,67)

0,8

10,75

факторной … остаточной

Тема 5: Оценка параметров линейных уравнений регрессии

разность
2. Величина называется …

случайной составляющей

ошибку модели

минимизации суммы квадратов

Тема 6: Предпосылки МНК, методы их проверки

1. Для обнаружения автокорреляции в остатках используется …

статистика Дарбина – Уотсона

тест Уайта

критерий Гольдфельда – Квандта

автокорреляция остатков отсутствует

положительной

4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.

Гетероскедатичность

отрицательной

Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК

несмещенности

2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …

нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …

автокоррелированными и/или гетероскедастичными

обобщенный

средняя величина остатков не равна нулю

фондоемкости продукции при неизменном уровне трудоемкости продукции
Тема 9: Оценка тесноты связи

Регрессии

[–1; 0]

[0,7; 1]

4. Для регрессионной модели вида получена диаграмма

Такое графическое отображение называется …

полем корреляции

Тема 10: Оценка качества подбора уравнения

0,8

3. Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина характеризует долю …

Главная / Ответы на новые тесты / Эконометрика / Страница 2

Упражнение 41830:

Номер

Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.

Ответ:

зависимых

эндогенных

экзогенных

независимых

Упражнение 41831:

Номер

Линия регрессии _______ через точку ( , ) :

Ответ:

_ __

x y

1) может пройти

2) всегда проходит

3) несколько раз проходит

4) никогда не проходит

5) может пройти или не пройти

Упражнение 41832:

Номер

МНК автоматически дает ___________ для данной выборки значение коэффициента де-

Ответ:

терминации R2:

1) минимальное

2) максимальное

3) среднее

4) средневзвешенное

5) случайное

Упражнение 41833:

Номер

Множественный регрессионный анализ является ________ парного регрессионного анализа:

Ответ:

1) развитием

2) противоположностью

3) частным случаем

4) подобием

5) эквивалентностью

Упражнение 41834:

Номер

Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется:

Ответ:

1) временной

2) замещающей

3) лаговой

4) лишней

5) сезонной

Упражнение 41835:

Номер

Наиболее частая причина положительной автокорреляции заключается в положительной направленности воздействия ________ переменных:

Ответ:

1) не включенных в уравнение

2) сезонных

3) фиктивных

4) лишних

5) циклических

Упражнение 41836:

Номер

Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия _____________ переменных:

Ответ:

1) не включенных в уравнение

2) лишних

3) сезонных

4) фиктивных

5) циклических

Упражнение 41837:

Номер

Наилучший способ устранения автокорреляции – установление ответственного за нее

Ответ:

фактора и включение соответствующей ___________ переменной в регрессию:

1) фиктивной

2) объясняющей

3) сезонной

4) зависимой

5) циклической

Упражнение 41838:

Номер

Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если ...

Ответ:

средняя величина остатков не равна нулю

остатки гетероскедастичны

остатки автокоррелированны

дисперсия остатков не является постоянной величиной

Упражнение 41839:

Номер

Определение отдельного вклада каждой из независимых переменных в объясненную

Ответ:

дисперсию в случае их коррелированности является ___________ задачей:

1) достаточно простой

2) невыполнимой

3) достаточно сложной

4) первостепенной

5) выполнимой

Упражнение 41840:

Номер

Оценка параметра для модели множественной регрессии в случае двух независимых пе-

Ответ:

ременных вычисляется по формуле: а =

1) 1 1 2 2 b x ? b x

2) 1 1 2 2 y + b x + b x

3) ( ) 1 1 2 2 y + b x ? b x

4) 1 1 2 2 y ? b x ? b x

5) 1 1 2 2 y ?b x + b x

Упражнение 41841:

Номер

Ошибки спецификации эконометрической модели имеют место вследствие ...

Ответ:

неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора

недостоверности или недостаточности исходной информации

неоднородности данных в исходной статистической совокупности

недостаточного количества данных

Упражнение 41842:

Номер

Параметры множественной регрессии ?1 , ?2 ,...?м показывают _________ соответствующих экономических факторов:

Ответ:

1) степень влияния

2) случайность

3) уровень независимости

4) непостоянство

5) цикличность

Упражнение 41843:

Номер

Положительная автокорреляция –ситуация, когда случайный член регрессии в сле-

Ответ:

дующем наблюдении ожидается:

1) противоположного знака по сравнению с настоящим наблюдением

2) того же знака, что и в первом наблюдении

3) того же знака, что и в настоящем наблюдении

4) противоположного знака по сравнению с первым наблюдением

5) равным 0

Упражнение 41844:

Номер

При автокорреляции оценка коэффициентов регрессии становится:

Ответ:

1) смещенной

2) невозможной

3) неэффективной

4) равной 0

5) равной максимальному значению

Упражнение 41845:

Номер

При добавлении еще одной переменной в уравнение регрессии коэффициент детерминации:

Ответ:

1) остается неизменным

2) уменьшается

3) не уменьшается

4) не увеличивается

5) увеличивается

Упражнение 41846:

Номер

При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать ...

Ответ:

использовать фиктивную переменную – пол потребителя

разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола

использовать фиктивную переменную – уровень дохода

исключить из рассмотрения пол потребителя, так как данный фактор нельзя измерить количественным образом

Упражнение 41847:

Номер

При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.

Ответ:

обобщенный

косвенный

двухшаговый

трехшаговый

Упражнение 41848:

Номер

При отрицательной автокорреляции DW:

Ответ:

1) = 0

2) < 2

3) > 2

4) > 1

5) = 1

Упражнение 41849:

Номер

При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу сверхидентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:

Ответ:

для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении

преобразовать структурную форму модели в приведенную форму модели

для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты

на основе коэффициентов приведенной формы модели получить теоретические значения эндогенных переменных, содержащихся в правой части сверхидентифицированных уравнений

применить обычный метод наименьших квадратов, подставив вместо фактических значений эндогенных переменных, стоящих в правой части уравнения, рассчитанные теоретические значения, и получить структурные коэффициенты модели

Упражнение 41850:

Номер

При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу точно идентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:

Ответ:

преобразовать структурную форму модели в приведенную форму модели

коэффициенты приведенной формы модели преобразовать в параметры структурной модели

Упражнение 41851:

Номер

Процесс выбора необходимых переменных для регрессии переменных и отбрасывание

Ответ:

лишних переменных называется:

1) унификацией переменных

2) моделированием

3) спецификацией переменных

4) прогнозированием

5) подгонкой

Упражнение 41852:

Номер

Система независимых эконометрических уравнений может быть идентифицирована с помощью обычного метода наименьших квадратов. Определите последовательность этапов алгоритма оценки параметров для такой модели.

Ответ:

оценка возможности идентификации модели как системы независимых уравнений

разделение системы независимых уравнений на отдельные уравнения регрессии

построение общего вида системы нормальных уравнений для каждого уравнения системы и расчет необходимых значений сумм

решение системы нормальных уравнений для каждого уравнения системы

подстановка найденных значений оценок параметров в уравнения системы

Упражнение 41853:

Номер

Системой эконометрических уравнений не является система линейных _____ уравнений.

Ответ:

нормальных

стандартизованных

рекурсивных

одновременных

Упражнение 41854:

Номер

Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется ...

Ответ:

временным рядом

тенденцией

коррелограммой

автокорреляционной функцией

Упражнение 41855:

Номер

Стандартные отклонения коэффициентов регрессии обратно пропорциональны величи-

Ответ:

не _________, где n – число наблюдений:

1) n

2) n2

3) n3

4) n

5) n4

Упражнение 41856:

Номер

Стандартные ошибки, вычисленные при гетероскедастичности:

Ответ:

1) завышены по сравнению с истинными значениями

2) занижены по сравнению с истинными значениями

3) соответствуют истинным значениям

4) не имеют математического смысла

5) являются случайными

Упражнение 41857:

Номер

Строгая линейная зависимость между переменными – ситуация, когда ________ двух

Ответ:

переменных равна 1 или -1:

1) выборочная корреляция

2) разность

3) сумма

4) теоретическая корреляция

5) произведение

Упражнение 41858:

Номер

Сумма квадратов отклонений величины y от своего выборочного значения ? _____ сумма квадратов отклонений:

Ответ:

1) объясняющая

2) случайная

3) необъясняющая

4) общая

5) результирующая

Упражнение 41859:

Номер

Тест Фишера является:

Ответ:

1) двусторонним

2) односторонним

3) многосторонним

4) многокритериальным

5) трехшаговым

Упражнение 41860:

Номер

Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного ряда y3 будет равно ...

Ответ:

10,65

9,35

1,3

6,51

Упражнение 41861:

Номер

Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для мультипликативной модели временного ряда, содержащего периодические колебания в 4 момента, получены значения сезонных компонент: S1 = 2,087; S2 = 0,632; S3 = 0,931; S4 = 3,256. Известны значения компонент: T5 = 20,6 и E5 = 0,4. Рассчитайте значение уровня временного ряда y5.

Ответ:

17,2

23,1

0,83

Упражнение 41862:

Номер

Условие гетероскедастичности означает, что вероятность того, что случайный член при-

Ответ:

мет какое-либо конкретное значение ________ наблюдений:

1) зависит от числа

2) зависит от времени проведения

3) зависит от номера

4) одинакова для всех

5) не зависит от времени проведения

Упражнение 41863:

Номер

Условие гомоскедастичности означает, что вероятность того, что случайный член при-

Ответ:

мет какое-либо конкретное значение _________ наблюдений:

1) зависит от времени проведения

2) одинакова для всех

3) зависит от номера

4) зависит от числа

5) от характера

Упражнение 41864:

Номер

Фиктивная переменная – переменная, принимающая в каждом наблюдении:

Ответ:

1) ряд значений от 0 до 1

2) только отрицательные значения

3) только два значения 0 или 1

4) только положительные значения

5) случайные

Упражнение 41865:

Номер

Фиктивная переменная взаимодействия – фиктивная переменная, предназначенная для

Ответ:

установления влияния на регрессию __________событий:

1) одновременного наступления нескольких независимых

2) степени взаимосвязи возможных

3) наступления одного из нескольких взаимосвязанных

4) наступления одного из нескольких независимых

5) циклических

Упражнение 41866:

Номер

Фиктивная переменная взаимодействия – это __________ фиктивных переменных:

Ответ:

1) произведение

2) среднее

3) разность

4) сумма

5) отношение

Упражнение 41867:

Номер

Фиктивные переменные включаются в модель множественной регрессии, если необходимо установить влияние каких-либо ___________ факторов:

Ответ:

1) непрерывных

2) дискретных

3) трудноизмеримых

4) случайных

5) циклических

Упражнение 41868:

Номер

Чем больше число наблюдений, тем __________ зона неопределенности для критерия Дарбина-Уотсона:

Ответ:

1) левее расположена

2) уже

3) шире

4) правее расположена

5) неизменна

Упражнение 41869:

Номер

Число степеней свободы для уравнения m-мерной регрессии при достаточном числе

Ответ:

наблюдений n составляет:

1) n/m

2) n-m

3) n-m+1

4) n-m-1

5) m-1

Упражнение 41870:

Номер

Число степеней свободы для уравнения множественной (m-мерной) регрессии при достаточном числе наблюдений n составляет:

Ответ:

1) n-m-1

2) n-m+1

3) n-m

4)m/n

5) n+m+1

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

Тема 1: Спецификация эконометрической модели

1. Ошибки спецификации эконометрической модели имеют место вследствие …

неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора

недостоверности или недостаточности исходной информации

неоднородности данных в исходной статистической совокупности

недостаточного количества данных

Решение:

Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.

2. Для регрессионной модели вида 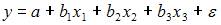необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.

Решение:

Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».

3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

Решение:

Из приведенных функций только в функции параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.

4. В модели вида 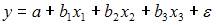количество объясняющих переменных равно …

Решение:

Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения , где y – зависимая переменная; x_j – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, b_j – параметры (a – свободный член уравнения, b_j – коэффициент регрессии); – случайные факторы. Независимые переменные x_j называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии b_j. Поэтому количество объясняющих переменных в модели равно 3.

5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …

Решение:

При оценке модели множественной регрессии рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

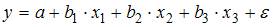
Решение:

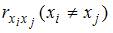
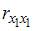
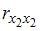
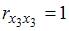
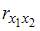
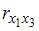
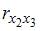
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы были бы равны нулю.
, поскольку = = и = = =0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.

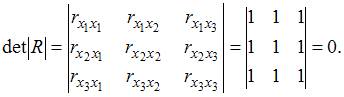
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

Решение:

Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения , где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, b_j – параметры (a – свободный член уравнения, b_j – коэффициент регрессии); – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x₁ и x₂.

Линейная множественная регрессия

Тесты по эконометрике

Введение

1. Эконометрическая модель имеет вид

2. Установите соответствие

а) регрессионная модель	1) x-1=0, x=0x-1, x>0
b) система одновременных уравнений	2) R=a1+b11M+b12Y+ε1,Y=a2+b21R+ε2,
c) модель временного ряда	1. 3) y=a+b1x1+b2x2+ε
4) yt=Tt+St+Et

3. Регрессия – это

a. зависимость значений результативной переменной от значений объясняющих переменных (факторов)

b. правило, согласно которому каждому значению одной переменной ставится в соответствие единственное значение другой переменной

c. правило, согласно которому каждому значению независимой переменной ставится в соответствие значение зависимой переменной

d. зависимость среднего значения результативной переменной от значений объясняющих переменных (факторов)

4. Метод наименьших квадратов …

a. Позволяет получить оценки параметров линейной регрессии, исходя из условия i=1nyi-yi2→min

b. Позволяет получить оценки параметров регрессии, исходя из условия ln⁡(i=1nf(yi,)→max

c. Позволяет проверить статистическую значимость параметров регрессии

d. Позволяет получить оценки параметров нелинейной регрессии, исходя из условия i=1ny-yi2→min

Линейная множественная регрессия

5. Уравнение линейной множественной регрессии

6. Для линейного уравнения множественной регрессии установите соответствие

5. а) Факторные переменные	6. 1) y
7. b) Результативная переменная	8. 2) a
9. c) Параметры	10. 3) a, ε
11. d) Случайная компонента	12. 4) x1, x2
13.	14. 5) ε
15.	16. 6) a, b1, b2

17. Ответ: a-4, b-1, c-6, d-5

7. Проблема спецификации регрессионной модели включает в себя

a. Отбор факторов, включаемых в уравнение регрессии

b. Оценка параметров уравнения регрессии

c. Оценка надежности результатов регрессионного анализа

d. Выбор вида уравнения регрессии

19. Требования к факторам, включаемым в модель линейной множественной регрессии…

a. Число факторов должно быть в 6 раз меньше объема совокупности

b. Факторы должны представлять временные ряды

c. Факторы должны иметь одинаковую размерность

d. Между факторами не должно быть высокой корреляции

21. Верные утверждения относительно мультиколлинеарности факторов

e. В модель линейной множественной регрессии рекомендуется включать мультиколлинеарные факторы

f. Мультиколлинеарность факторов приводит к снижению надежности оценок параметров уравнения регрессии

g. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, большими 0,7

h. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, меньшими 0,3

23. Верные утверждения о включении в уравнение линейной множественной регрессии факторов

i. Включение фактора в модель приводит к заметному возрастанию коэффициента множественной детерминации

j. Коэффициент парной корреляции для фактора и результативной переменной меньше 0,3

k. Значение t-критерия Стьюдента для коэффициента регрессии при факторе меньше табличного значения

l. Фактор должен объяснять поведение изучаемого показателя согласно принятым положениям экономической теории

25. При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается модель с …

m. Одной объясняющей переменной, которая имеет с зависимой переменной наименьший коэффициент корреляции

n. Одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции

o. Несколькими объясняющими переменными, которые имеют с зависимой переменной коэффициенты корреляции по модулю больше 0,5

p. Полным перечнем объясняющих переменных

8. Параметры при факторах в линейной множественной регрессии
y=a+b1x1+b2x2+…+bpxp характеризуют

a. Долю дисперсии результативной переменной, объясненную регрессией в его общей дисперсии

b. Тесноту связи между результативной переменной и соответствующим фактором, при устранении влияния других факторов, включенных в модель

c. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне

d. На сколько процентов в среднем изменяется результативная переменная с изменением соответствующего фактора на 1%

28. Стандартизация переменных проводится по формуле

9. Уравнение множественной регрессии в стандартизованном масштабе имеет вид ty=20+0,9tx1+0,5tx2+ε. На результативный признак оказывает большое влияние:

x. нельзя сделать вывод

10. Уравнение множественной регрессии в естественной форме имеет вид
y=20+0,7×1+0,5×2+ε. На результативный признак оказывает большое влияние:

bb. нельзя сделать вывод

30. К свойствам уравнения регрессии в стандартизированном виде относятся …

cc. Коэффициенты регрессии при объясняющих переменных равны между собой

dd. Постоянный параметр (свободный член уравнения) регрессии отсутствует

ee. Стандартизированные коэффициенты регрессии несравнимы между собой

ff. Входящие в состав уравнения переменные являются безразмерными

32. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии оценивает

gg. Коэффициент парной корреляции

hh. Коэффициент частной корреляции

ii. Коэффициент множественной корреляции

jj. Коэффициент множественной детерминации

34. Установите соответствие

35. а) общая сумма квадратов отклонений TSS	36. 1) y-y2
37. b) регрессионная сумма квадратов отклонений RSS	38. 2) y-x2
39. c) остаточная сумма квадратов отклонений ЕSS	40. 3) y-y2
41.	42. 4) y-y2

43. Коэффициент множественной корреляции для линейной зависимости можно рассчитать по формуле

mm.

45. Верные утверждения относительно коэффициента множественной корреляции

oo. Чем ближе значение к единице Ryx1…xp, тем теснее связь результативного признака со всеми факторами

pp. Чем ближе значение к нулю Ryx1…xp, тем теснее связь результативного признака со всеми факторами

qq. Ryx1…xp принимает значения из промежутка [0, 1]

rr. Ryx1…xp принимает значения из промежутка [– 1, 1]

47. Коэффициент множественной детерминации характеризует

ss. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии

tt. Тесноту связи между результатом и соответствующим фактором, при устранении влияния других факторов, включенных в модель

uu. Долю дисперсии результативного признака, объясненную регрессией в его общей дисперсии

vv. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне

49. Для общей (TSS), регрессионной (RSS) и остаточной (ESS) суммы квадратов отклонений и коэффициента детерминации R2 выполняется равенство …

51. Отношение остаточной дисперсии к общей дисперсии равно 0,05. Это означает …

bbb. Коэффициент детерминации R2=0,95

ccc. Коэффициент детерминации R2=0,05

ddd. Разность (1-R2)=0,95, где R2 – коэффициент детерминации

eee. Разность (1-R2)=0,05, где R2 – коэффициент детерминации

53. Для устранения систематической ошибки остаточной дисперсии для оценки качества модели линейной множественной регрессии используется

fff. Коэффициент множественной детерминации

ggg. Коэффициент множественной корреляции

hhh. Скорректированный коэффициент множественной детерминации

iii. Скорректированный коэффициент частной корреляции

55. Оценка статистической значимости уравнения линейной множественной регрессии в целом осуществляется с помощью

jjj. Критерия Стьюдента

kkk. Критерия Фишера

lll. Критерия Дарбина-Уотсона

56. Оценка статистической значимости коэффициентов линейной множественной регрессии осуществляется с помощью

nnn. Критерия Стьюдента

ooo. Критерия Фишера

ppp. Критерия Дарбина-Уотсона

qqq. Критерия Фостера-Стюарта

57. Если коэффициент регрессии является существенным, то для него выполняются условия

rrr. Фактическое значение t-критерия Стьюдента меньше критического

sss. Фактическое значение t-критерия Стьюдента больше критического

ttt. Доверительный интервал проходит через ноль

uuu. Стандартная ошибка не превышает половины значения параметра

59. Если уравнение регрессии является существенным, то фактическое значение F-критерия …

vvv. больше критического

www. меньше критического

xxx. близко к единице

yyy. близко к нулю

61. Предпосылками МНК являются…

zzz. Дисперсия случайных отклонений постоянна для всех наблюдений

aaaa. Дисперсия случайных отклонений не постоянна для всех наблюдений

bbbb. Случайные отклонения коррелируют друг с другом

cccc. Случайные отклонения являются независимыми друг от друга

63. Укажите выводы, которые соответствуют графику зависимости остатков

dddd. Нарушена предпосылка МНК о независимости остатков друг от друга

eeee. Имеет место автокорреляция остатков

ffff. Отсутствует закономерность в поведении остатков

gggg. Отсутствует автокорреляция остатков

66. При выполнении предпосылок метода наименьших квадратов (МНК) остатки уравнения регрессии, как правило, характеризуются…

hhhh. Нулевой средней величиной

jjjj. Случайным характером

kkkk. Высокой степенью автокорреляции

68. К методам обнаружения гетероскедастичности остатков относятся

llll. Критерий Дарбина-Уотсона

mmmm. Тест Голдфелда-Квандта

nnnn. Графический анализ остатков

oooo. Метод наименьших квадратов

70. Фиктивными переменными в уравнении множественной регрессии являются …

pppp. Качественные переменные, преобразованные в количественные

qqqq. Переменные, представляющие простейшие функции от уже включенных в модель переменных

rrrr. Дополнительные количественные переменные, улучшающие решение

ssss. Комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели

71. Для отражения влияния качественной сопутствующей переменной, имеющей m состояний, обычно включают в модель … фиктивную переменную

Нелинейная регрессия

72. Регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам

73. Регрессии, нелинейные по оцениваемым параметрам

74. Укажите верные утверждения по поводу модели

jjjjj. Относится к типу моделей нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам

kkkkk. Относится к типу моделей, нелинейных по оцениваемым параметрам

lllll. Относится к типу линейных моделей

mmmmm. Нельзя привести к линейному виду

nnnnn. Можно привести к линейному виду

76. Укажите верные утверждения по поводу модели

ooooo. Линеаризуется линейную модель множественной регрессии

ppppp. Линеаризуется линейную модель парной регрессии

qqqqq. Относится к классу нелинейных моделей по объясняющим переменным, но линейных по оцениваемым параметрам

rrrrr. Относится к классу линейных моделей

79. Модель y=a∙bx∙ε относится к классу … эконометрических моделей нелинейной регрессии

81. Модель y=a∙xb∙ε относится к классу … эконометрических моделей нелинейной регрессии

83. Модель y=a+bx+cx2+ε относится к классу … эконометрических моделей нелинейной регрессии

85. Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии…

87. Для получения оценок параметров степенной регрессионной модели y=a∙xb …

iiiiii. Метод наименьших квадратов неприменим

jjjjjj. Требуется подобрать соответствующую подстановку

kkkkkk. Необходимо выполнить логарифмическое преобразование

llllll. Необходимо выполнить тригонометрическое преобразование

89. С помощью метода наименьших квадратов нельзя оценить значения параметров уравнения регрессии …

Уравнение множественной регрессии

Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Отбор факторов обычно осуществляется в два этапа:

теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5	38	71,5
38	318	563,5
71,5	563,5	1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99	0,64	-1,3
0,64	0,1	-0,0988
-1,3	-0,0988	0,14

Получили оценку уравнения регрессии: Y = 34.66 + 1.97X₁-2.45X₂
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 _e/∑(y_i — y_ср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X₁ (%), а также по уровню инфляции X₂ (%).

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X₁	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X₂	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:

Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
Рассчитать частные коэффициенты эластичности. Сделать вывод.
Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.

Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

Матрица Y

7
7
7
7
7
7
8
8
8
10
9
11
9
11
12
12
12
12
14
14

Матрица X T

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619	-0,0262	-0,0183
-0,0262	0,126	-0,0338
-0,0183	-0,0338	0,0102

0,222	-0,00939	-0,00654
-0,00939	0,0452	-0,0121
-0,00654	-0,0121	0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x₁, x₂, x₃ взятых по отдельности. Для каждой объясняющей переменной:

Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации.
Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
Постройте диаграмму остатков.
Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение F_табл определите с помощью функции FРАСПОБР).
Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

источники:

http://megaobuchalka.ru/4/7472.html

http://math.semestr.ru/regress/corel.php

Источник

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

1. Ошибки спецификации эконометрической модели имеют место вследствие …

2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.

3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

4. В модели вида количество объясняющих переменных равно …

5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами,иблизок к единице. Это означает, что факторы,и…

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

Линейная множественная регрессия

Уравнение множественной регрессии

Построение парной регрессионной модели

Читайте также:

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36