From Wikipedia, the free encyclopedia
Out-of-bag (OOB) error, also called out-of-bag estimate, is a method of measuring the prediction error of random forests, boosted decision trees, and other machine learning models utilizing bootstrap aggregating (bagging). Bagging uses subsampling with replacement to create training samples for the model to learn from. OOB error is the mean prediction error on each training sample xi, using only the trees that did not have xi in their bootstrap sample.[1]
Bootstrap aggregating allows one to define an out-of-bag estimate of the prediction performance improvement by evaluating predictions on those observations that were not used in the building of the next base learner.
Out-of-bag dataset[edit]
When bootstrap aggregating is performed, two independent sets are created. One set, the bootstrap sample, is the data chosen to be «in-the-bag» by sampling with replacement. The out-of-bag set is all data not chosen in the sampling process.
When this process is repeated, such as when building a random forest, many bootstrap samples and OOB sets are created. The OOB sets can be aggregated into one dataset, but each sample is only considered out-of-bag for the trees that do not include it in their bootstrap sample. The picture below shows that for each bag sampled, the data is separated into two groups.
Visualizing the bagging process. Sampling 4 patients from the original set with replacement and showing the out-of-bag sets. Only patients in the bootstrap sample would be used to train the model for that bag.
This example shows how bagging could be used in the context of diagnosing disease. A set of patients are the original dataset, but each model is trained only by the patients in its bag. The patients in each out-of-bag set can be used to test their respective models. The test would consider whether the model can accurately determine if the patient has the disease.
Calculating out-of-bag error[edit]
Since each out-of-bag set is not used to train the model, it is a good test for the performance of the model. The specific calculation of OOB error depends on the implementation of the model, but a general calculation is as follows.
- Find all models (or trees, in the case of a random forest) that are not trained by the OOB instance.
- Take the majority vote of these models’ result for the OOB instance, compared to the true value of the OOB instance.
- Compile the OOB error for all instances in the OOB dataset.
An illustration of OOB error
The bagging process can be customized to fit the needs of a model. To ensure an accurate model, the bootstrap training sample size should be close to that of the original set.[2] Also, the number of iterations (trees) of the model (forest) should be considered to find the true OOB error. The OOB error will stabilize over many iterations so starting with a high number of iterations is a good idea.[3]
Shown in the example to the right, the OOB error can be found using the method above once the forest is set up.
Comparison to cross-validation[edit]
Out-of-bag error and cross-validation (CV) are different methods of measuring the error estimate of a machine learning model. Over many iterations, the two methods should produce a very similar error estimate. That is, once the OOB error stabilizes, it will converge to the cross-validation (specifically leave-one-out cross-validation) error.[3] The advantage of the OOB method is that it requires less computation and allows one to test the model as it is being trained.
Accuracy and Consistency[edit]
Out-of-bag error is used frequently for error estimation within random forests but with the conclusion of a study done by Silke Janitza and Roman Hornung, out-of-bag error has shown to overestimate in settings that include an equal number of observations from all response classes (balanced samples), small sample sizes, a large number of predictor variables, small correlation between predictors, and weak effects.[4]
See also[edit]
- Boosting (meta-algorithm)
- Bootstrap aggregating
- Bootstrapping (statistics)
- Cross-validation (statistics)
- Random forest
- Random subspace method (attribute bagging)
References[edit]
- ^ James, Gareth; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert (2013). An Introduction to Statistical Learning. Springer. pp. 316–321.
- ^ Ong, Desmond (2014). A primer to bootstrapping; and an overview of doBootstrap (PDF). pp. 2–4.
- ^ a b Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning (PDF). Springer. pp. 592–593.
- ^ Janitza, Silke; Hornung, Roman (2018-08-06). «On the overestimation of random forest’s out-of-bag error». PLOS ONE. 13 (8): e0201904. doi:10.1371/journal.pone.0201904. ISSN 1932-6203. PMC 6078316. PMID 30080866.
Get this book -> Problems on Array: For Interviews and Competitive Programming
In this article, we have explored Out-of-Bag Error in Random Forest with an numeric example and sample implementation to plot Out-of-Bag Error.
Table of contents:
- Introduction to Random Forest
- Out-of-Bag Error in Random Forest
- Example of Out-of-Bag Error
- Code for Out-of-Bag Error
Introduction to Random Forest
Random Forest is one of the machine learning algorithms that use bootstrap aggregation. Random Forest aggregates the result of several decision trees. Decision Trees are known to work well when they have small depth otherwise they overfit. When they are used ensemble in Random Forests, this weakness of decision trees is mitigated.
Random Forest works by taking a random sample of small subsets of the data and applies a decision tree classification to them. The prediction of the Random Forest is then a combination of the individual prediction of the decision trees either by summing or taking a majority vote or any other suitable means of combining the results.
The sampling of random subsets (with replacement) of the training data is what is referred to as bagging. The idea is that the randomness in choosing the data fed to each decision tree will reduce the variance in the predictions from the random forest model.
The out-of-bag error is the average error for each predicted outcome calculated using predictions from the trees that do not contain that data point in their respective bootstrap sample. This way, the Random Forest model is constantly being validated while being trained. Let us consider the jth decision tree (DT_j) that has been fitted on a subset of the sample data. For every training observation or sample (z_i = (x_i , y_i)) not in the sample subset of (DT_j) where (x_i) is the set of features and (y_i) is the target, we use (DT_j) to predict the outcome (o_i) for (x_i). The error can easily be computed as (|o_i — y_i|).
The out-of-bag error is thus the average value of this error across all decision trees.
Example of Out-of-Bag Error
The following is a simple example of how this works in practice. Consider this toy dataset which records if it rains given the temperature and humidity:
| S/N | Temperature | Humidity | Rained? |
|---|---|---|---|
| 1 | 33 | High | No |
| 2 | 18 | Low | No |
| 3 | 27 | Low | Yes |
| 4 | 20 | High | Yes |
| 5 | 21 | Low | No |
| 6 | 29 | Low | Yes |
| 7 | 19 | High | Yes |
Assume that a random forest ensemble consisting of 5 decision trees (DT_1 … DT_5) is to be trained on the the dataset. Each tree will be trained on a random subset of the dataset. Assuming for (DT_1) that the randomly selected subset contains the first five samples of the dataset. Therefore, the last two samples 6 and 7 will be the out-of-bag samples on which (DT_1) will be validated. Continuing with the assumption, let the following table represent the prediction of each decision tree on each of its out-of-bag samples:
| Tree | Sample S/N | Prediction | Actual | Error (abs) |
|---|---|---|---|---|
| DT1 | 6 | No | Yes | 1 |
| DT1 | 7 | No | Yes | 1 |
| DT2 | 2 | No | No | 0 |
| DT3 | 1 | No | No | 0 |
| DT3 | 2 | Yes | No | 1 |
| DT3 | 4 | Yes | Yes | 0 |
| DT4 | 2 | Yes | No | 1 |
| DT4 | 7 | Yes | Yes | 1 |
| DT5 | 3 | Yes | Yes | 0 |
| DT5 | 5 | No | No | 0 |
From the above, the out-of-bag error is the average error which is 0.5.
We thus see that because only a subset of the decision trees in the ensemble is used in determining each error that is used to compute the out-of-bag score, it cannot be considered as accurate as a validation score on validation data. However, in cases such as this where the dataset is quite small and it is impossible to set aside a validation set, the out-of-bag error can prove to be a useful metric.
Code for Out-of-Bag Error
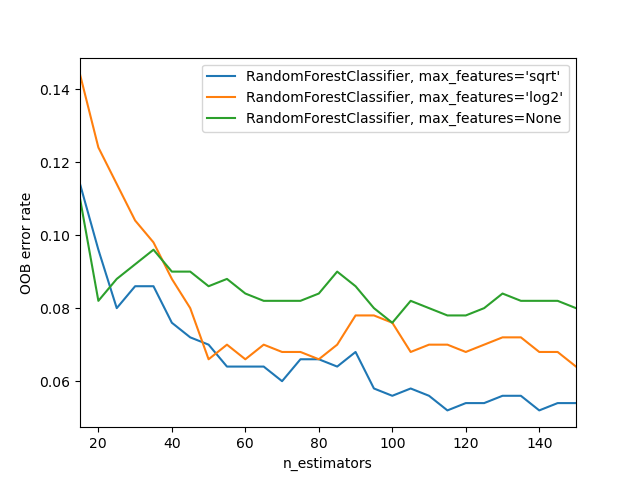
Lastly, we demonstrate the use of out-of-bag error in the estimation of a suitable value for the choice of n_estimators for a random forest model in scikit-learn library. This example is adapted from the documentation. The out-of-bag error is measured at the addition of each new tree during training. The resulting plot shows that the choice of 115 for n_estimators is optimal for the classifier (with ‘sqrt’ max_features) in this example.
import matplotlib.pyplot as plt
from collections import OrderedDict
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
RANDOM_STATE = 123
# Generate a binary classification dataset.
X, y = make_classification(
n_samples=500,
n_features=25,
n_clusters_per_class=1,
n_informative=15,
random_state=RANDOM_STATE,
)
# NOTE: Setting the `warm_start` construction parameter to `True` disables
# support for parallelized ensembles but is necessary for tracking the OOB
# error trajectory during training.
ensemble_clfs = [
(
"RandomForestClassifier, max_features='sqrt'",
RandomForestClassifier(
warm_start=True,
oob_score=True,
max_features="sqrt",
random_state=RANDOM_STATE,
),
),
(
"RandomForestClassifier, max_features='log2'",
RandomForestClassifier(
warm_start=True,
max_features="log2",
oob_score=True,
random_state=RANDOM_STATE,
),
),
(
"RandomForestClassifier, max_features=None",
RandomForestClassifier(
warm_start=True,
max_features=None,
oob_score=True,
random_state=RANDOM_STATE,
),
),
]
# Map a classifier name to a list of (<n_estimators>, <error rate>) pairs.
error_rate = OrderedDict((label, []) for label, _ in ensemble_clfs)
# Range of `n_estimators` values to explore.
min_estimators = 15
max_estimators = 150
for label, clf in ensemble_clfs:
for i in range(min_estimators, max_estimators + 1, 5):
clf.set_params(n_estimators=i)
clf.fit(X, y)
# Record the OOB error for each `n_estimators=i` setting.
oob_error = 1 - clf.oob_score_
error_rate[label].append((i, oob_error))
# Generate the "OOB error rate" vs. "n_estimators" plot.
for label, clf_err in error_rate.items():
xs, ys = zip(*clf_err)
plt.plot(xs, ys, label=label)
plt.xlim(min_estimators, max_estimators)
plt.xlabel("n_estimators")
plt.ylabel("OOB error rate")
plt.legend(loc="upper right")
plt.show()
Пятую статью курса мы посвятим простым методам композиции: бэггингу и случайному лесу. Вы узнаете, как можно получить распределение среднего по генеральной совокупности, если у нас есть информация только о небольшой ее части; посмотрим, как с помощью композиции алгоритмов уменьшить дисперсию и таким образом улучшить точность модели; разберём, что такое случайный лес, какие его параметры нужно «подкручивать» и как найти самый важный признак. Сконцентрируемся на практике, добавив «щепотку» математики.
UPD 01.2022: С февраля 2022 г. ML-курс ODS на русском возрождается под руководством Петра Ермакова couatl. Для русскоязычной аудитории это предпочтительный вариант (c этими статьями на Хабре – в подкрепление), англоговорящим рекомендуется mlcourse.ai в режиме самостоятельного прохождения.
Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).
План этой статьи
- Бэггинг
- Ансамбли
- Бутстрэп
- Бэггинг
- Out-of-bag ошибка
- Случайный лес
- Алгоритм
- Сравнение с деревом решений и бэггингом
- Параметры
- Вариация и декорреляционный эффект
- Смещение
- Сверхслучайные деревья
- Схожесть с алгоритмом k-ближайших соседей
- Преобразование признаков в многомерное пространство
- Оценка важности признаков
- Плюсы и минусы случайного леса
- Домашнее задание №5
- Полезные источники
1. Бэггинг
Из прошлых лекций вы уже узнали про разные алгоритмы классификации, а также научились правильно валидироваться и оценивать качество модели. Но что делать, если вы уже нашли лучшую модель и повысить точность модели больше не можете? В таком случае нужно применить более продвинутые техники машинного обучения, которые можно объединить словом «ансамбли». Ансамбль — это некая совокупность, части которой образуют единое целое. Из повседневной жизни вы знаете музыкальные ансамбли, где объединены несколько музыкальных инструментов, архитектурные ансамбли с разными зданиями и т.д.
Ансамбли
Хорошим примером ансамблей считается теорема Кондорсе «о жюри присяжных» (1784). Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри и стремится к единице. Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных.
— количество присяжных
— вероятность правильного решения присяжного
— вероятность правильного решения всего жюри
— минимальное большинство членов жюри,
— число сочетаний из
по
Если , то
Если , то
Давайте рассмотрим ещё один пример ансамблей — «Мудрость толпы». Фрэнсис Гальтон в 1906 году посетил рынок, где проводилась некая лотерея для крестьян.
Их собралось около 800 человек, и они пытались угадать вес быка, который стоял перед ними. Бык весил 1198 фунтов. Ни один крестьянин не угадал точный вес быка, но если посчитать среднее от их предсказаний, то получим 1197 фунтов.
Эту идею уменьшения ошибки применили и в машинном обучении.
Бутстрэп
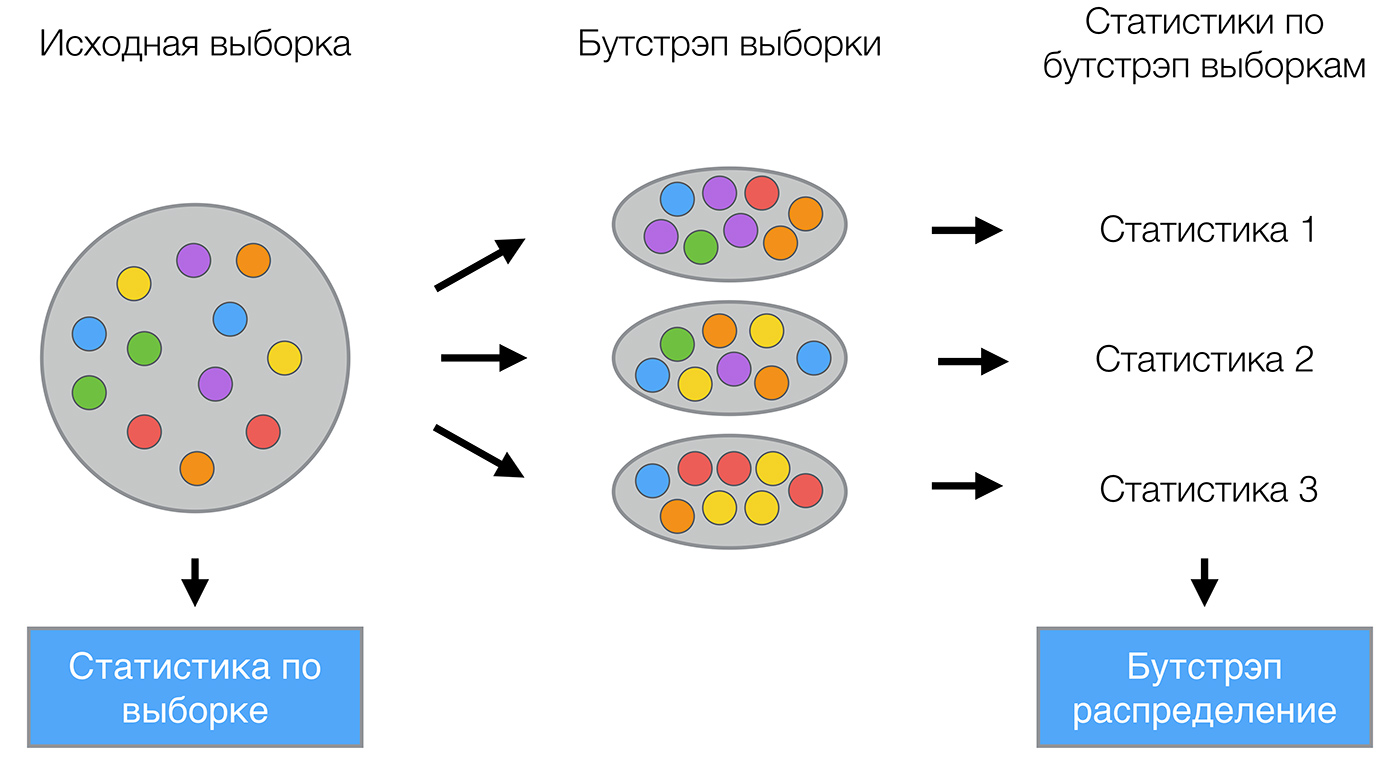
Bagging (от Bootstrap aggregation) — это один из первых и самых простых видов ансамблей. Он был придуман Ле́о Бре́йманом в 1994 году. Бэггинг основан на статистическом методе бутстрэпа, который позволяет оценивать многие статистики сложных распределений.
Метод бутстрэпа заключается в следующем. Пусть имеется выборка размера
. Равномерно возьмем из выборки
объектов с возвращением. Это означает, что мы будем
раз выбирать произвольный объект выборки (считаем, что каждый объект «достается» с одинаковой вероятностью
), причем каждый раз мы выбираем из всех исходных
объектов. Можно представить себе мешок, из которого достают шарики: выбранный на каком-то шаге шарик возвращается обратно в мешок, и следующий выбор опять делается равновероятно из того же числа шариков. Отметим, что из-за возвращения среди них окажутся повторы. Обозначим новую выборку через
. Повторяя процедуру
раз, сгенерируем
подвыборок
. Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.
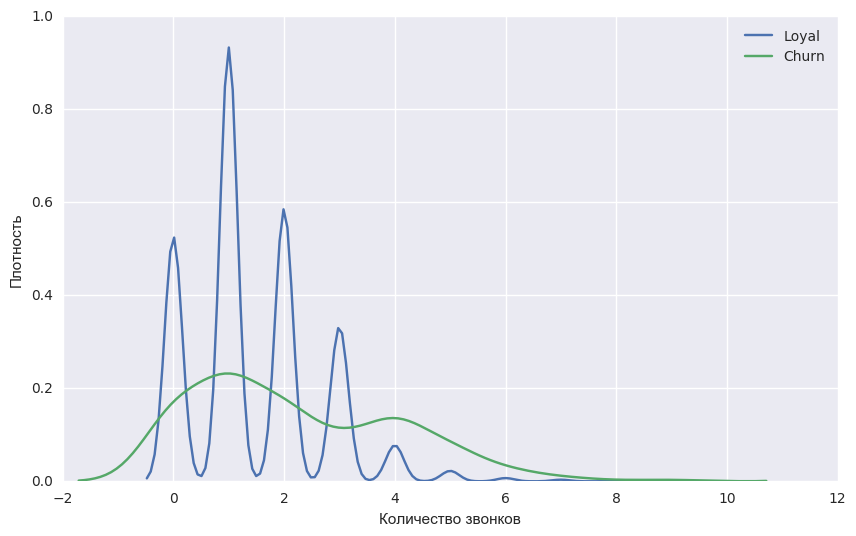
Давайте для примера возьмем уже известный вам набор данных telecom_churn из прошлых уроков нашего курса. Напомним, что это задача бинарной классификации оттока клиентов. Одним из самых важных признаков в этом датасете является количество звонков в сервисный центр, которые были сделаны клиентом. Давайте попробуем визулизировать данные и посмотреть на распределение данного признака.
Код для загрузки данных и построения графика
import pandas as pd
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
import seaborn as sns
%matplotlib inline
telecom_data = pd.read_csv('data/telecom_churn.csv')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == False]['Customer service calls'], label = 'Loyal')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == True]['Customer service calls'], label = 'Churn')
fig.set(xlabel='Количество звонков', ylabel='Плотность')
plt.show()Как вы уже могли заметить, количество звонков в сервисный центр у лояльных клиентов меньше, чем у наших бывших клиентов. Теперь было бы хорошо оценить, сколько в среднем делает звонков каждая из групп. Так как данных в нашем датасете мало, то искать среднее не совсем правильно, лучше применить наши новые знания бутстрэпа. Давайте сгенерируем 1000 новых подвыборок из нашей генеральной совокупности и сделаем интервальную оценку среднего.
Код для построения доверительного интервала с помощью бутстрэпа
import numpy as np
def get_bootstrap_samples(data, n_samples):
# функция для генерации подвыборок с помощью бутстрэпа
indices = np.random.randint(0, len(data), (n_samples, len(data)))
samples = data[indices]
return samples
def stat_intervals(stat, alpha):
# функция для интервальной оценки
boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 - alpha / 2.)])
return boundaries
# сохранение в отдельные numpy массивы данных по лояльным и уже бывшим клиентам
loyal_calls = telecom_data[telecom_data['Churn'] == False]['Customer service calls'].values
churn_calls= telecom_data[telecom_data['Churn'] == True]['Customer service calls'].values
# ставим seed для воспроизводимости результатов
np.random.seed(0)
# генерируем выборки с помощью бутстрэра и сразу считаем по каждой из них среднее
loyal_mean_scores = [np.mean(sample)
for sample in get_bootstrap_samples(loyal_calls, 1000)]
churn_mean_scores = [np.mean(sample)
for sample in get_bootstrap_samples(churn_calls, 1000)]
# выводим интервальную оценку среднего
print("Service calls from loyal: mean interval", stat_intervals(loyal_mean_scores, 0.05))
print("Service calls from churn: mean interval", stat_intervals(churn_mean_scores, 0.05))В итоге мы получили, что с 95% вероятностью среднее число звонков от лояльных клиентов будет лежать в промежутке между 1.40 и 1.50, в то время как наши бывшие клиенты звонили в среднем от 2.06 до 2.40 раз. Также ещё можно обратить внимание, что интервал для лояльных клиентов уже, что довольно логично, так как они звонят редко (в основном 0, 1 или 2 раза), а недовольные клиенты будут звонить намного чаще, но со временем их терпение закончится, и они поменяют оператора.
Бэггинг
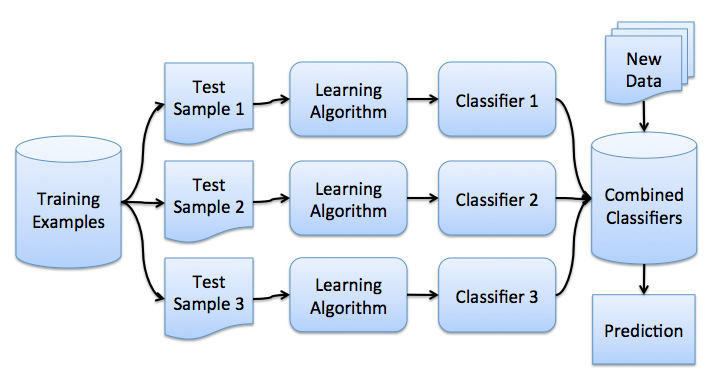
Теперь вы имеете представление о бустрэпе, и мы можем перейти непосредственно к бэггингу. Пусть имеется обучающая выборка . С помощью бутстрэпа сгенерируем из неё выборки
. Теперь на каждой выборке обучим свой классификатор
. Итоговый классификатор будет усреднять ответы всех этих алгоритмов (в случае классификации это соответствует голосованию):
. Эту схему можно представить картинкой ниже.
Рассмотрим задачу регрессии с базовыми алгоритмами . Предположим, что существует истинная функция ответа для всех объектов
, а также задано распределение на объектах
. В этом случае мы можем записать ошибку каждой функции регрессии
и записать матожидание среднеквадратичной ошибки
Средняя ошибка построенных функций регрессии имеет вид
Предположим, что ошибки несмещены и некоррелированы:
Построим теперь новую функцию регрессии, которая будет усреднять ответы построенных нами функций:
Найдем ее среднеквадратичную ошибку:
Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в n раз!
Напомним вам из нашего предыдущего урока, как раскладывается общая ошибка:
Бэггинг позволяет снизить дисперсию (variance) обучаемого классификатора, уменьшая величину, на сколько ошибка будет отличаться, если обучать модель на разных наборах данных, или другими словами, предотвращает переобучение. Эффективность бэггинга достигается благодаря тому, что базовые алгоритмы, обученные по различным подвыборкам, получаются достаточно различными, и их ошибки взаимно компенсируются при голосовании, а также за счёт того, что объекты-выбросы могут не попадать в некоторые обучающие подвыборки.
В библиотеке scikit-learn есть реализации BaggingRegressor и BaggingClassifier, которые позволяют использовать большинство других алгоритмов «внутри». Рассмотрим на практике, как работает бэггинг, и сравним его с деревом решений, пользуясь примером из документации.
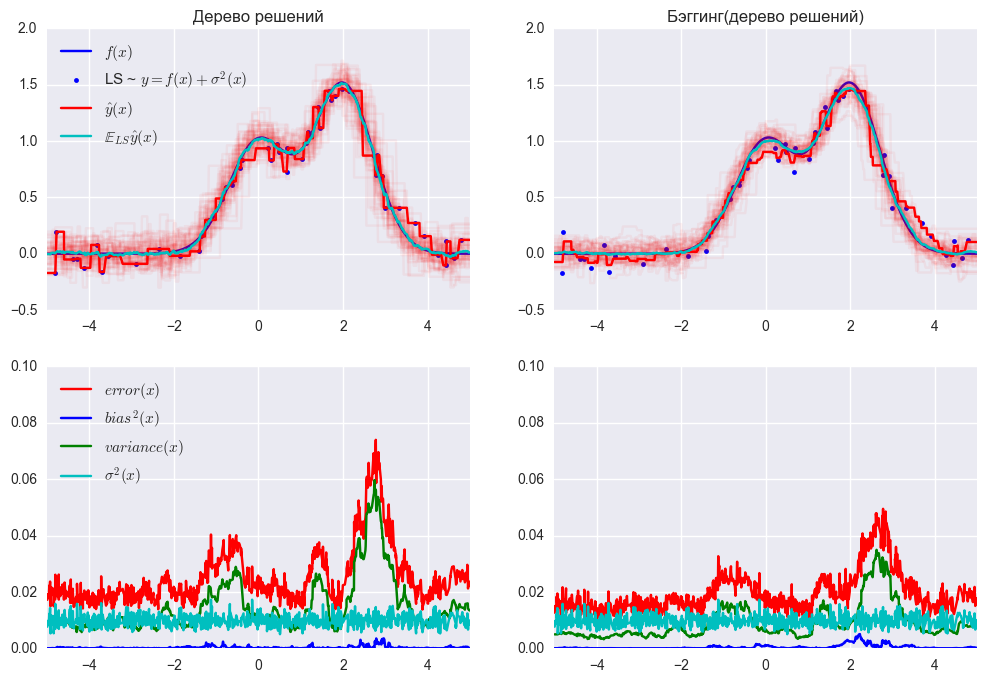
Ошибка дерева решений
Ошибка бэггинга
По графику и результатам выше видно, что ошибка дисперсии намного меньше при бэггинге, как мы и доказали теоретически выше.
Бэггинг эффективен на малых выборках, когда исключение даже малой части обучающих объектов приводит к построению существенно различных базовых классификаторов. В случае больших выборок обычно генерируют подвыборки существенно меньшей длины.
Следует отметить, что рассмотренный нами пример не очень применим на практике, поскольку мы сделали предположение о некоррелированности ошибок, что редко выполняется. Если это предположение неверно, то уменьшение ошибки оказывается не таким значительным. В следующих лекциях мы рассмотрим более сложные методы объединения алгоритмов в композицию, которые позволяют добиться высокого качества в реальных задачах.
Out-of-bag error
Забегая вперед, отметим, что при использовании случайных лесов нет необходимости в кросс-валидации или в отдельном тестовом наборе, чтобы получить несмещенную оценку ошибки набора тестов. Посмотрим, как получается «внутренняя» оценка модели во время ее обучения.
Каждое дерево строится с использованием разных образцов бутстрэпа из исходных данных. Примерно 37% примеров остаются вне выборки бутстрэпа и не используются при построении k-го дерева.
Это можно легко доказать: пусть в выборке объектов. На каждом шаге все объекты попадают в подвыборку с возвращением равновероятно, т.е отдельный объект — с вероятностью
Вероятность того, что объект НЕ попадет в подвыборку (т.е. его не взяли
раз):
. При
получаем один из «замечательных» пределов
. Тогда вероятность попадания конкретного объекта в подвыборку
.
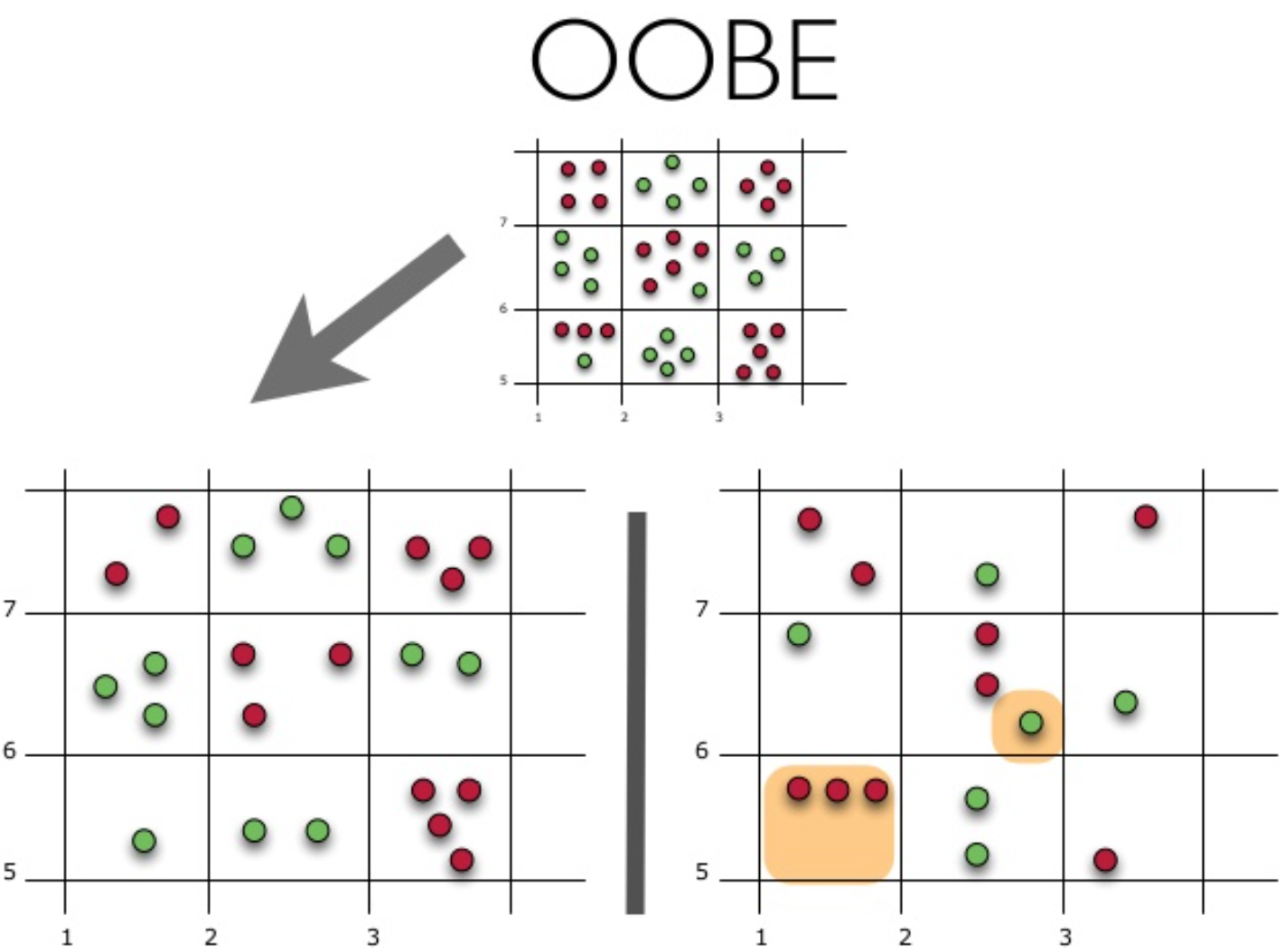
Давайте рассмотрим, как это работает на практике:
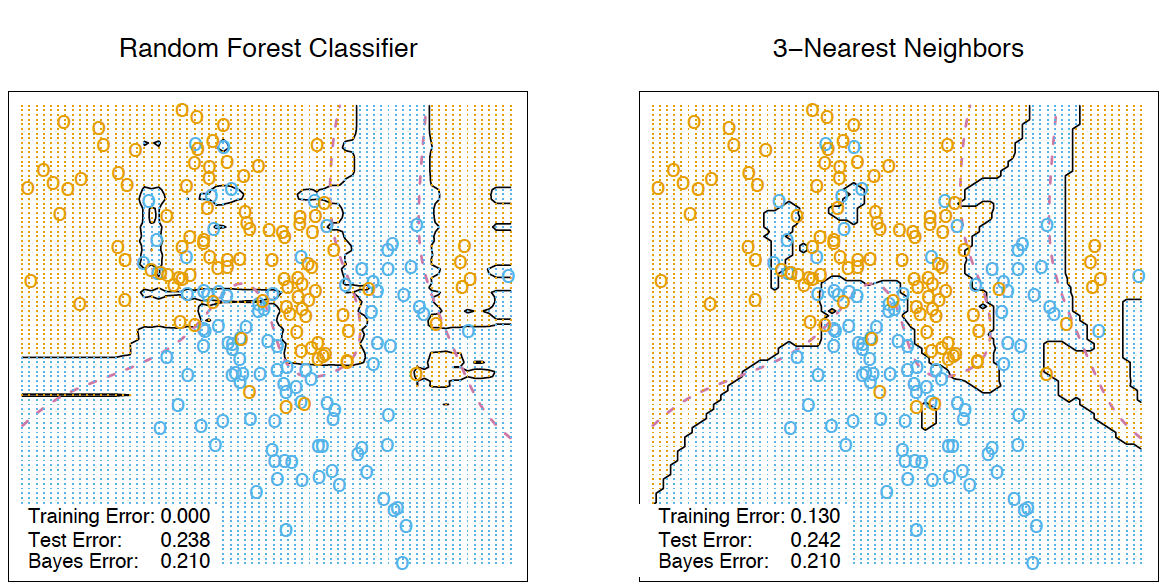
На рисунке изображена оценка oob-ошибки. Верхний рисунок – это наша исходная выборка, ее мы делим на обучающую(слева) и тестовую(справа). На рисунке слева у нас есть сетка из квадратиков, которая идеально разбивает нашу выборку. Теперь нужно оценить долю верных ответов на нашей тестовой выборке. На рисунке видно, что наш классификатор ошибся в 4 наблюдениях, которые мы не использовали для обучения. Значит, доля верных ответов нашего классификатора:
Получается, что каждый базовый алгоритм обучается на ~63% исходных объектов. Значит, на оставшихся ~37% его можно сразу проверять. Out-of-Bag оценка — это усредненная оценка базовых алгоритмов на тех ~37% данных, на которых они не обучались.
2. Случайный лес
Лео Брейман нашел применение бутстрэпу не только в статистике, но и в машинном обучении. Он вместе с Адель Катлер усовершенстовал алгоритм случайного леса, предложенный Хо, добавив к первоначальному варианту построение некоррелируемых деревьев на основе CART, в сочетании с методом случайных подпространств и бэггинга.
Решающие деревья являются хорошим семейством базовых классификаторов для бэггинга, поскольку они достаточно сложны и могут достигать нулевой ошибки на любой выборке. Метод случайных подпространств позволяет снизить коррелированность между деревьями и избежать переобучения. Базовые алгоритмы обучаются на различных подмножествах признакового описания, которые также выделяются случайным образом.
Ансамбль моделей, использующих метод случайного подпространства, можно построить, используя следующий алгоритм:
- Пусть количество объектов для обучения равно
, а количество признаков
.
- Выберите
как число отдельных моделей в ансамбле.
- Для каждой отдельной модели
выберите
как число признаков для
. Обычно для всех моделей используется только одно значение
.
- Для каждой отдельной модели
создайте обучающую выборку, выбрав
признаков из
, и обучите модель.
- Теперь, чтобы применить модель ансамбля к новому объекту, объедините результаты отдельных
моделей мажоритарным голосованием или путем комбинирования апостериорных вероятностей.
Алгоритм
Алгоритм построения случайного леса, состоящего из деревьев, выглядит следующим образом:
- Для каждого
:
Итоговый классификатор , простыми словами — для задачи кассификации мы выбираем решение голосованием по большинству, а в задаче регрессии — средним.
Рекомендуется в задачах классификации брать , а в задачах регрессии —
, где
— число признаков. Также рекомендуется в задачах классификации строить каждое дерево до тех пор, пока в каждом листе не окажется по одному объекту, а в задачах регрессии — пока в каждом листе не окажется по пять объектов.
Таким образом, случайный лес — это бэггинг над решающими деревьями, при обучении которых для каждого разбиения признаки выбираются из некоторого случайного подмножества признаков.
Сравнение с деревом решений и бэггингом
Код для сравнения решающего дерева, бэггинга и случайного леса для задачи регрессии
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
%pylab inline
np.random.seed(42)
figsize(8, 6)
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier, BaggingRegressor
from sklearn.tree import DecisionTreeRegressor, DecisionTreeClassifier
n_train = 150
n_test = 1000
noise = 0.1
# Generate data
def f(x):
x = x.ravel()
return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)
def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 5
X = np.sort(X).ravel()
y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2)
+ np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y
X_train, y_train = generate(n_samples=n_train, noise=noise)
X_test, y_test = generate(n_samples=n_test, noise=noise)
# One decision tree regressor
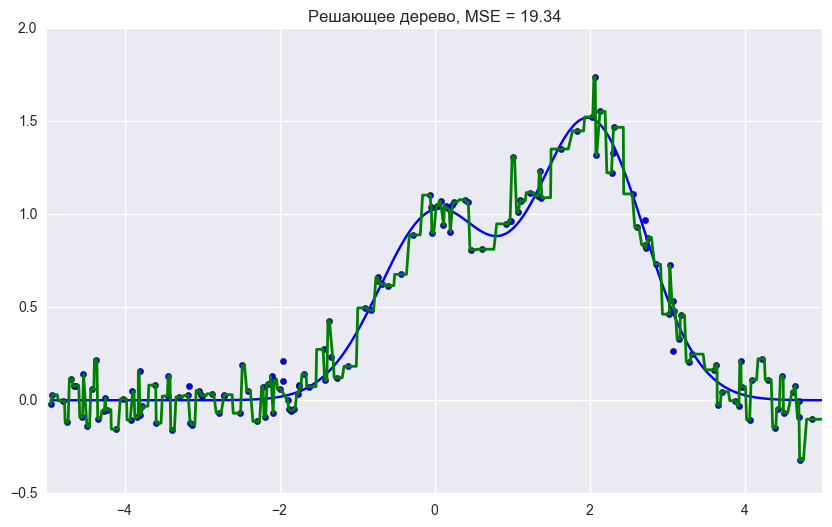
dtree = DecisionTreeRegressor().fit(X_train, y_train)
d_predict = dtree.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, d_predict, "g", lw=2)
plt.xlim([-5, 5])
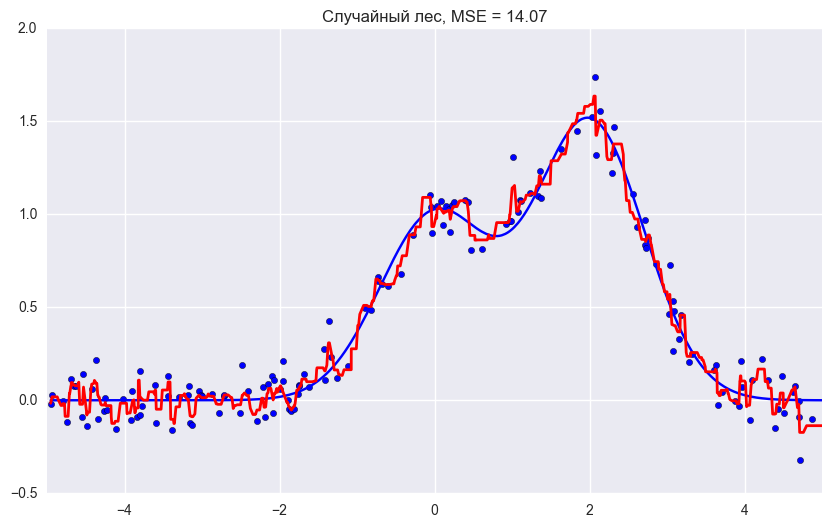
plt.title("Решающее дерево, MSE = %.2f"
% np.sum((y_test - d_predict) ** 2))
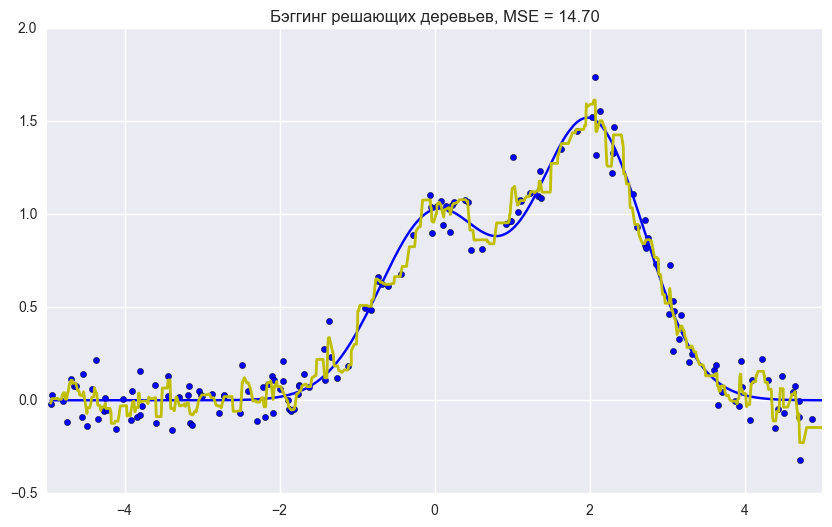
# Bagging decision tree regressor
bdt = BaggingRegressor(DecisionTreeRegressor()).fit(X_train, y_train)
bdt_predict = bdt.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, bdt_predict, "y", lw=2)
plt.xlim([-5, 5])
plt.title("Бэггинг решающих деревьев, MSE = %.2f" % np.sum((y_test - bdt_predict) ** 2));
# Random Forest
rf = RandomForestRegressor(n_estimators=10).fit(X_train, y_train)
rf_predict = rf.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, rf_predict, "r", lw=2)
plt.xlim([-5, 5])
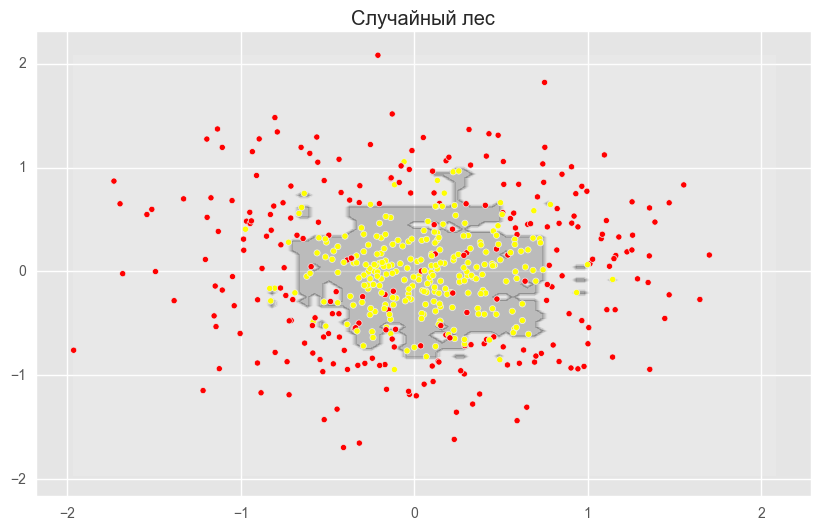
plt.title("Случайный лес, MSE = %.2f" % np.sum((y_test - rf_predict) ** 2));Как мы видим из графиков и значений ошибки MSE, случайный лес из 10 деревьев дает лучший результат, чем одно дерево или бэггинг из 10 деревьев решений. Основное различие случайного леса и бэггинга на деревьях решений заключается в том, что в случайном лесе выбирается случайное подмножество признаков, и лучший признак для разделения узла определяется из подвыборки признаков, в отличие от бэггинга, где все функции рассматриваются для разделения в узле.
Также можно увидеть преимущество случайного леса и бэггинга в задачах классификации.
Код для сравнения решающего дерева, бэггинга и случайного леса для задачи классификации
from sklearn.ensemble import RandomForestClassifier, BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_circles
from sklearn.cross_validation import train_test_split
import numpy as np
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
%matplotlib inline
np.random.seed(42)
X, y = make_circles(n_samples=500, factor=0.1, noise=0.35, random_state=42)
X_train_circles, X_test_circles, y_train_circles, y_test_circles = train_test_split(X, y, test_size=0.2)
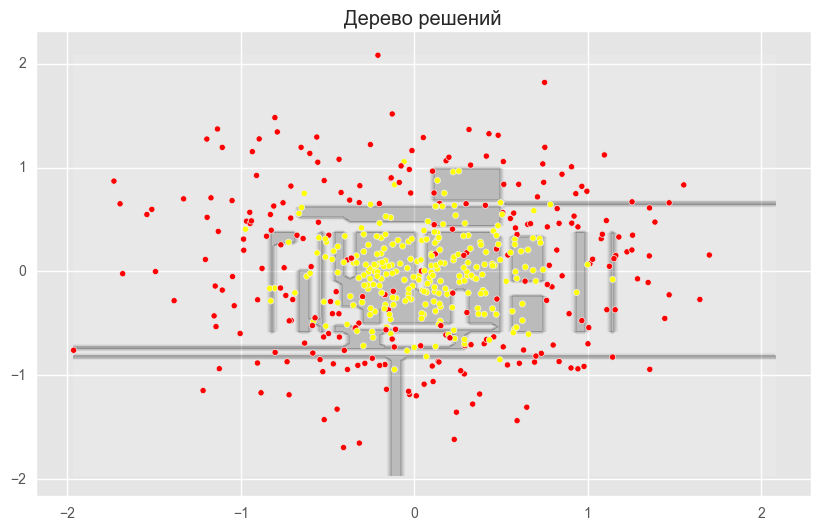
dtree = DecisionTreeClassifier(random_state=42)
dtree.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
plt.title("Дерево решений")
plt.show()
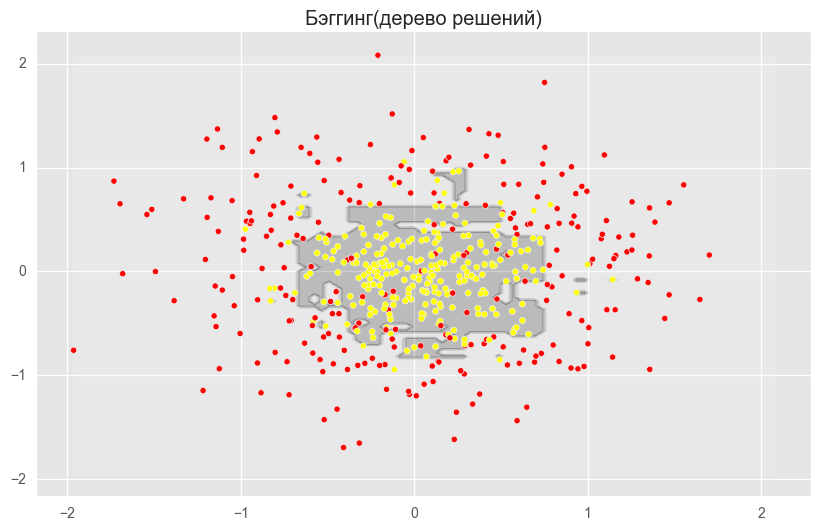
b_dtree = BaggingClassifier(DecisionTreeClassifier(),n_estimators=300, random_state=42)
b_dtree.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = b_dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
plt.title("Бэггинг(дерево решений)")
plt.show()
rf = RandomForestClassifier(n_estimators=300, random_state=42)
rf.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = rf.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
plt.title("Случайный лес")
plt.show()На рисунках выше видно, что разделяющая граница дерева решений очень «рваная» и на ней много острых углов, что говорит о переобучении и слабой обобщающей способности. В то время как у бэггинга и случайного леса граница достаточно сглаженная и практически нет признаков переобучения.
Давайте теперь попробуем разобраться с параметрами, с помощью подбора которых мы cможем увеличить долю правильных ответов.
Параметры
Метод случайного леса реализован в библиотеке машинного обучения scikit-learn двумя классами RandomForestClassifier и RandomForestRegressor.
Полный список параметров случайного леса для задачи регрессии:
class sklearn.ensemble.RandomForestRegressor(
n_estimators — число деревьев в "лесу" (по дефолту – 10)
criterion — функция, которая измеряет качество разбиения ветки дерева (по дефолту — "mse" , так же можно выбрать "mae")
max_features — число признаков, по которым ищется разбиение. Вы можете указать конкретное число или процент признаков, либо выбрать из доступных значений: "auto" (все признаки), "sqrt", "log2". По дефолту стоит "auto".
max_depth — максимальная глубина дерева (по дефолту глубина не ограничена)
min_samples_split — минимальное количество объектов, необходимое для разделения внутреннего узла. Можно задать числом или процентом от общего числа объектов (по дефолту — 2)
min_samples_leaf — минимальное число объектов в листе. Можно задать числом или процентом от общего числа объектов (по дефолту — 1)
min_weight_fraction_leaf — минимальная взвешенная доля от общей суммы весов (всех входных объектов) должна быть в листе (по дефолту имеют одинаковый вес)
max_leaf_nodes — максимальное количество листьев (по дефолту нет ограничения)
min_impurity_split — порог для остановки наращивания дерева (по дефолту 1е-7)
bootstrap — применять ли бустрэп для построения дерева (по дефолту True)
oob_score — использовать ли out-of-bag объекты для оценки R^2 (по дефолту False)
n_jobs — количество ядер для построения модели и предсказаний (по дефолту 1, если поставить -1, то будут использоваться все ядра)
random_state — начальное значение для генерации случайных чисел (по дефолту его нет, если хотите воспроизводимые результаты, то нужно указать любое число типа int
verbose — вывод логов по построению деревьев (по дефолту 0)
warm_start — использует уже натренированую модель и добавляет деревьев в ансамбль (по дефолту False)
)Для задачи классификации все почти то же самое, мы приведем только те параметры, которыми RandomForestClassifier отличается от RandomForestRegressor
class sklearn.ensemble.RandomForestClassifier(
criterion — поскольку у нас теперь задача классификации, то по дефолту выбран критерий "gini" (можно выбрать "entropy")
class_weight — вес каждого класса (по дефолту все веса равны 1, но можно передать словарь с весами, либо явно указать "balanced", тогда веса классов будут равны их исходным частям в генеральной совокупности; также можно указать "balanced_subsample", тогда веса на каждой подвыборке будут меняться в зависимости от распределения классов на этой подвыборке.
)Далее рассмотрим несколько параметров, на которые в первую очередь стоит обратить внимание при построении модели:
- n_estimators — число деревьев в «лесу»
- criterion — критерий для разбиения выборки в вершине
- max_features — число признаков, по которым ищется разбиение
- min_samples_leaf — минимальное число объектов в листе
- max_depth — максимальная глубина дерева
Рассмотрим применение случайного леса в реальной задаче
Для этого будем использовать пример с задачей оттока клиентов. Это задача классификации, поэтому будем использовать метрику accuracy для оценки качества модели. Для начала построим самый простой классификатор, который будет нашим бейслайном. Возьмем только числовые признаки для упрощения.
Код для построения бейслайна для случайного леса
import pandas as pd
from sklearn.model_selection import cross_val_score, StratifiedKFold, GridSearchCV
from sklearn.metrics import accuracy_score
# Загружаем данные
df = pd.read_csv("../../data/telecom_churn.csv")
# Выбираем сначала только колонки с числовым типом данных
cols = []
for i in df.columns:
if (df[i].dtype == "float64") or (df[i].dtype == 'int64'):
cols.append(i)
# Разделяем на признаки и объекты
X, y = df[cols].copy(), np.asarray(df["Churn"],dtype='int8')
# Инициализируем страифицированную разбивку нашего датасета для валидации
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# Инициализируем наш классификатор с дефолтными параметрами
rfc = RandomForestClassifier(random_state=42, n_jobs=-1, oob_score=True)
# Обучаем на тренировочном датасете
results = cross_val_score(rfc, X, y, cv=skf)
# Оцениваем долю верных ответов на тестовом датасете
print("CV accuracy score: {:.2f}%".format(results.mean()*100))Получили долю верных ответов 91.21%, теперь попробуем улучшить этот результат и посмотреть, как ведут себя кривые валидации при изменении основных параметров.
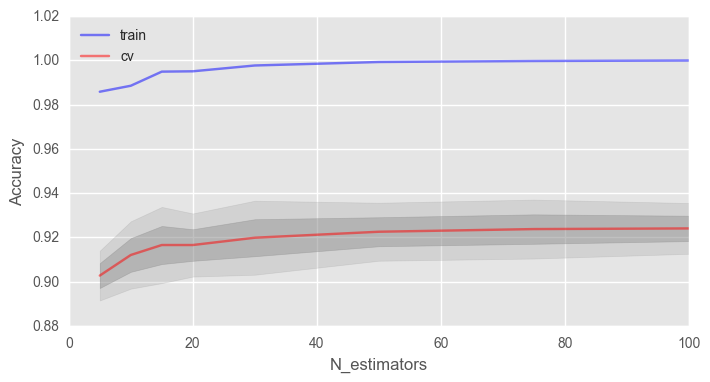
Начнем с количества деревьев:
Код для построения кривых валидации по подбору количества деревьев
# Инициализируем валидацию
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
trees_grid = [5, 10, 15, 20, 30, 50, 75, 100]
# Обучаем на тренировочном датасете
for ntrees in trees_grid:
rfc = RandomForestClassifier(n_estimators=ntrees, random_state=42, n_jobs=-1, oob_score=True)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} trees".format(max(test_acc.mean(axis=1))*100,
trees_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых валидации
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(trees_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(trees_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(trees_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(trees_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("N_estimators")Как видно, при достижении определенного числа деревьев наша доля верных ответов на тесте выходит на асимптоту, и вы можете сами решить, сколько деревьев оптимально для вашей задачи.
На рисунке также видно, что на тренировочной выборке мы смогли достичь 100% точности, это говорит нам о переобучении нашей модели. Чтобы избежать переобучения, мы должны добавить параметры регуляризации в модель.
Начнем с параметра максимальной глубины – max_depth. (зафиксируем к-во деревьев 100)
Код для построения кривых обучения по подбору максимальной глубины дерева
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
max_depth_grid = [3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]
# Обучаем на тренировочном датасете
for max_depth in max_depth_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1, oob_score=True, max_depth=max_depth)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} max_depth".format(max(test_acc.mean(axis=1))*100,
max_depth_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых обучения
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(max_depth_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(max_depth_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Max_depth")Параметр max_depth хорошо справляется с регуляризацией модели, и мы уже не так сильно переобучаемся. Доля верных ответов нашей модели немного возросла.
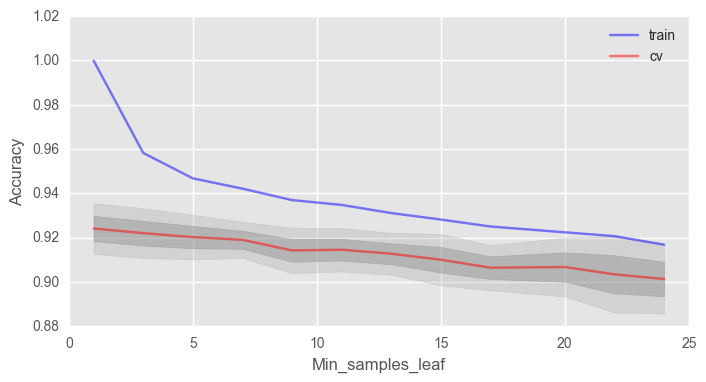
Еще важный параметр min_samples_leaf, он также выполняет функцию регуляризатора.
Код для построения кривых валидации по подбору минимального числа объектов в одном листе дерева
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
min_samples_leaf_grid = [1, 3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]
# Обучаем на тренировочном датасете
for min_samples_leaf in min_samples_leaf_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,
oob_score=True, min_samples_leaf=min_samples_leaf)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} min_samples_leaf".format(max(test_acc.mean(axis=1))*100,
min_samples_leaf_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых валидации
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(min_samples_leaf_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(min_samples_leaf_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Min_samples_leaf")В данном случае мы не выигрываем в точности на валидации, но зато можем сильно уменьшить переобучение до 2% при сохранении точности около 92%.
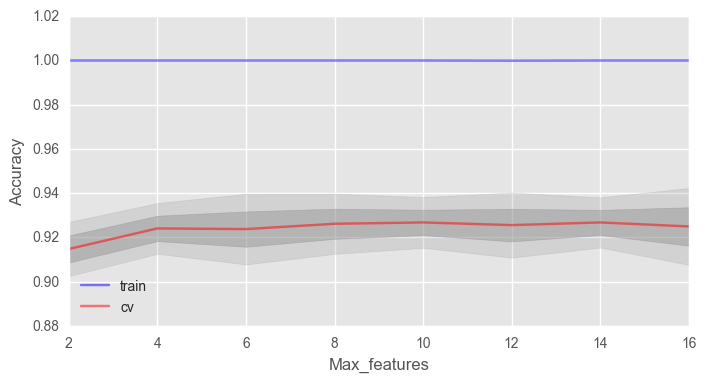
Рассмотрим такой параметр как max_features. Для задач классификации по умолчанию используется , где n — число признаков. Давайте проверим, оптимально ли в нашем случае использовать 4 признака или нет.
Код для построения кривых валидации по подбору максимального количества признаков для одного дерева
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
max_features_grid = [2, 4, 6, 8, 10, 12, 14, 16]
# Обучаем на тренировочном датасете
for max_features in max_features_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,
oob_score=True, max_features=max_features)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} max_features".format(max(test_acc.mean(axis=1))*100,
max_features_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых валидации
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(max_features_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(max_features_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(max_features_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(max_features_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Max_features")В нашем случае оптимальное число признаков — 10, именно с таким значением достигается наилучший результат.
Мы рассмотрели, как ведут себя кривые валидации в зависимости от изменения основных параметров. Давайте теперь с помощью GridSearchCV найдем оптимальные параметры для нашего примера.
Код для подбора оптимальных параметров модели
# Сделаем инициализацию параметров, по которым хотим сделать полный перебор
parameters = {'max_features': [4, 7, 10, 13], 'min_samples_leaf': [1, 3, 5, 7], 'max_depth': [5,10,15,20]}
rfc = RandomForestClassifier(n_estimators=100, random_state=42,
n_jobs=-1, oob_score=True)
gcv = GridSearchCV(rfc, parameters, n_jobs=-1, cv=skf, verbose=1)
gcv.fit(X, y)Лучшая доля верных ответов, который мы смогли достичь с помощью перебора параметров — 92.83% при 'max_depth': 15, 'max_features': 7, 'min_samples_leaf': 3.
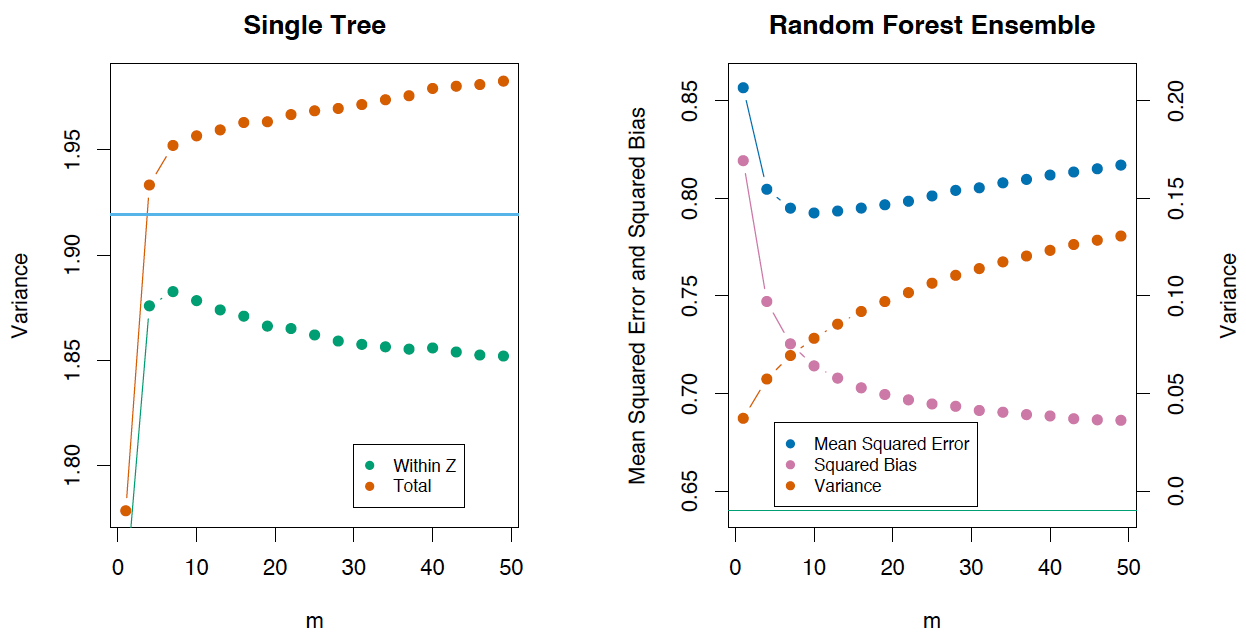
Вариация и декорреляционный эффект
Давайте запишем дисперсию для случайного леса как
Тут
– корреляция выборки между любыми двумя деревьями, используемыми при усреднении
где
и
– случайно выбранная пара деревьев на случайно выбранных объектах выборки
— это выборочная дисперсия любого произвольно выбранного дерева:
Легко спутать
со средней корреляцией между обученными деревьями в данном случайном лесе, рассматривая деревья как N-векторы и вычисляя среднюю парную корреляцию между ними. Это не тот случай. Эта условная корреляция не имеет прямого отношения к процессу усреднения, а зависимость от
в
предупреждает нас об этом различии. Скорее
является теоретической корреляцией между парой случайных деревьев, оцененных в объекте
, которая была вызвана многократным сэмплированием обучающей выборки из генеральной совокупности
, и после этого выбрана данная пара случайных деревьев. На статистическом жаргоне это корреляция, вызванная выборочным распределением
и
.
По факту, условная ковариация пары деревьев равна 0, потому что бустрэп и отбор признаков — независимы и одинаково распределены.
Если рассмотреть дисперсию по одному дереву, то она практически не меняется от переменных для разделения (
), а вот для ансамбля это играет большую роль, и дисперсия для дерева намного выше, чем для ансамбля.
В книге The Elements of Statistical Learning (Trevor Hastie, Robert Tibshirani и Jerome Friedman) есть отличный пример, который это демонстрирует.
Смещение
Как и в бэггинге, смещение в случайном лесе такое же, как и смещение в отдельно взятом дереве
:
Это также обычно больше (в абсолютных величинах), чем смещение «неусеченного» (unprunned) дерева, поскольку рандомизация и сокращение пространства выборки налагают ограничения. Следовательно, улучшения в прогнозировании, полученные с помощью бэггинга или случайных лесов, являются исключительно результатом уменьшения дисперсии.
Сверхслучайные деревья
В сверхслучайных деревьях (Extremely Randomized Trees) больше случайности в том, как вычисляются разделения в узлах. Как и в случайных лесах, используется случайное подмножество возможных признаков, но вместо поиска наиболее оптимальных порогов, пороговые значения произвольно выбираются для каждого возможного признака, и наилучший из этих случайно генерируемых порогов выбирается как лучшее правило для разделения узла. Это обычно позволяет немного уменьшить дисперсию модели за счет несколько большего увеличения смещения.
В библиотеке scikit-learn есть реализация ExtraTreesClassifier и ExtraTreesRegressor. Данный метод стоит использовать, когда вы сильно переобучаетесь на случайном лесе или градиентном бустинге.
Схожесть случайного леса с алгоритмом k-ближайших соседей
Метод случайного леса схож с методом ближайших соседей. Случайные леса, по сути, осуществляют предсказания для объектов на основе меток похожих объектов из обучения. Схожесть объектов при этом тем выше, чем чаще эти объекты оказываются в одном и том же листе дерева. Покажем это формально.
Рассмотрим задачу регрессии с квадратичной функцией потерь. Пусть
— номер листа
-го дерева из случайного леса, в который попадает объект
. Ответ объекта
равен среднему ответу по всем объектам обучающей выборки, которые попали в этот лист
. Это можно записать так
где
Тогда ответ композиции равен
Видно, что ответ случайного леса представляет собой сумму ответов всех объектов обучения с некоторыми весами. Отметим, что номер листа
, в который попал объект, сам по себе является ценным признаком. Достаточно неплохо работает подход, в котором по выборке обучается композиция из небольшого числа деревьев с помощью случайного леса или градиентного бустинга, а потом к ней добавляются категориальные признаки
. Новые признаки являются результатом нелинейного разбиения пространства и несут в себе информацию о сходстве объектов.
Все в той же книге The Elements of Statistical Learning есть хороший наглядный пример сходства случайного леса и k-ближайших соседей.
Преобразование признаков в многомерное пространство
Все привыкли использовать случайный лес для задач обучения с учителем, но также есть возможность проводить обучение и без учителя. С помощью метода RandomTreesEmbedding мы можем сделать трансформацию нашего датасета в многомерное разреженное его представление. Его суть в том, что мы строим абсолютно случайные деревья, и индекс листа, в котором оказалось наблюдение, мы считаем за новый признак. Если в первый лист попал объект, то мы ставим 1, а если не попал, то 0. Так называемое бинарное кодирование. Контролировать количество переменных и также степень разреженности нашего нового представления датасета мы можем увеличивая/уменьшая количество деревьев и их глубины. Поскольку соседние точки данных скорее всего лежат в одном и том же листе дерева, преобразование выполняет неявную, непараметрическую оценку плотности.
3. Оценка важности признаков
Очень часто вы хотите понять свой алгоритм, почему он именно так, а не иначе дал определенный ответ. Или если не понять его полностью, то хотя бы какие переменные больше всего влияют на результат. Из случайного леса можно довольно просто получить данную информацию.
Суть метода
По данной картинке интуитивно понятно, что важность признака «Возраст» в задаче кредитного скоринга выше, чем важность признака «Доход». Формализуется это с помощью понятия прироста информации.
Если построить много деревьев решений (случайный лес), то чем выше в среднем признак в дереве решений, тем он важнее в данной задаче классификации/регрессии. При каждом разбиении в каждом дереве улучшение критерия разделения (в нашем случае неопределенность Джини(Gini impurity)) — это показатель важности, связанный с переменной разделения, и накапливается он по всем деревьям леса отдельно для каждой переменной.
Давайте немного углубимся в детали. Среднее снижение точности, вызываемое переменной, определяется во время фазы вычисления out-of-bag ошибки. Чем больше уменьшается точность предсказаний из-за исключения (или перестановки) одной переменной, тем важнее эта переменная, и поэтому переменные с бо́льшим средним уменьшением точности более важны для классификации данных. Среднее уменьшение неопределенности Джини (или ошибки mse в задачах регрессии) является мерой того, как каждая переменная способствует однородности узлов и листьев в окончательной модели случайного леса. Каждый раз, когда отдельная переменная используется для разбиения узла, неопределенность Джини для дочерних узлов рассчитывается и сравнивается с коэффициентом исходного узла. Неопределенность Джини является мерой однородности от 0 (однородной) до 1 (гетерогенной). Изменения в значении критерия разделения суммируются для каждой переменной и нормируются в конце вычисления. Переменные, которые приводят к узлам с более высокой чистотой, имеют более высокое снижение коэффициента Джини.
А теперь представим все вышеописанное в виде формул.
— предсказание класса перед перестановкой/удалением признака
— предсказание класса после перестановки/удаления признака
Заметим, что, если
не находится в дереве
Расчет важности признаков в ансамбле:
— ненормированные— нормированные
Пример
Рассмотрим результаты анкетирования посетителей хостелов с сайтов Booking.com и TripAdvisor.com. Признаки — средние оценки по разным факторам (перечислены ниже) — персонал, состояние комнат и т.д. Целевой признак — рейтинг хостела на сайте.
Код для оценки важности признаков
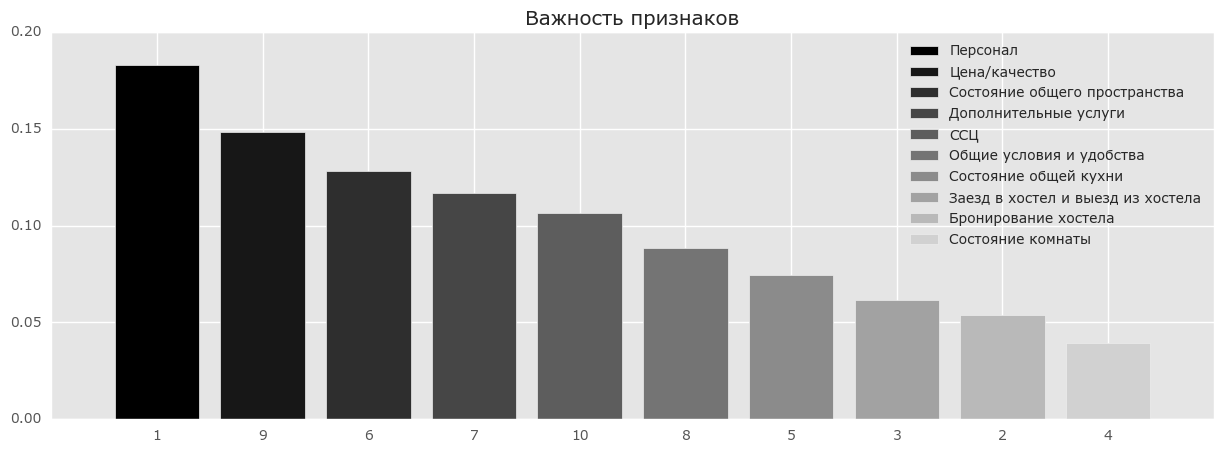
from __future__ import division, print_function # отключим всякие предупреждения Anaconda import warnings warnings.filterwarnings('ignore') %pylab inline import seaborn as sns # russian headres from matplotlib import rc font = {'family': 'Verdana', 'weight': 'normal'} rc('font', **font) import pandas as pd import numpy as np from sklearn.ensemble.forest import RandomForestRegressor hostel_data = pd.read_csv("../../data/hostel_factors.csv") features = {"f1":u"Персонал", "f2":u"Бронирование хостела ", "f3":u"Заезд в хостел и выезд из хостела", "f4":u"Состояние комнаты", "f5":u"Состояние общей кухни", "f6":u"Состояние общего пространства", "f7":u"Дополнительные услуги", "f8":u"Общие условия и удобства", "f9":u"Цена/качество", "f10":u"ССЦ"} forest = RandomForestRegressor(n_estimators=1000, max_features=10, random_state=0) forest.fit(hostel_data.drop(['hostel', 'rating'], axis=1), hostel_data['rating']) importances = forest.feature_importances_ indices = np.argsort(importances)[::-1] # Plot the feature importancies of the forest num_to_plot = 10 feature_indices = [ind+1 for ind in indices[:num_to_plot]] # Print the feature ranking print("Feature ranking:") for f in range(num_to_plot): print("%d. %s %f " % (f + 1, features["f"+str(feature_indices[f])], importances[indices[f]])) plt.figure(figsize=(15,5)) plt.title(u"Важность конструктов") bars = plt.bar(range(num_to_plot), importances[indices[:num_to_plot]], color=([str(i/float(num_to_plot+1)) for i in range(num_to_plot)]), align="center") ticks = plt.xticks(range(num_to_plot), feature_indices) plt.xlim([-1, num_to_plot]) plt.legend(bars, [u''.join(features["f"+str(i)]) for i in feature_indices]);
На рисунке выше видно, что люди больше всего обращают внимание на персонал и соотношение цена/качество и на основе впечатления от данных вещей пишут свои отзывы. Но разница между этими признаками и менее влиятельными признаками не очень значительная, и выкидывание какого-то признака приведет к уменьшению точности нашей модели. Но даже на основе нашего анализа мы можем дать рекомендации отелям в первую очередь лучше готовить персонал и/или улучшить качество до заявленной цены.4. Плюсы и минусы случайного леса
Плюсы:
— имеет высокую точность предсказания, на большинстве задач будет лучше линейных алгоритмов; точность сравнима с точностью бустинга
— практически не чувствителен к выбросам в данных из-за случайного сэмлирования
— не чувствителен к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков, связано с выбором случайных подпространств
— не требует тщательной настройки параметров, хорошо работает «из коробки». С помощью «тюнинга» параметров можно достичь прироста от 0.5 до 3% точности в зависимости от задачи и данных
— способен эффективно обрабатывать данные с большим числом признаков и классов
— одинаково хорошо обрабатывет как непрерывные, так и дискретные признаки
— редко переобучается, на практике добавление деревьев почти всегда только улучшает композицию, но на валидации, после достижения определенного количества деревьев, кривая обучения выходит на асимптоту
— для случайного леса существуют методы оценивания значимости отдельных признаков в модели
— хорошо работает с пропущенными данными; сохраняет хорошую точность, если большая часть данных пропущенна
— предполагает возможность сбалансировать вес каждого класса на всей выборке, либо на подвыборке каждого дерева
— вычисляет близость между парами объектов, которые могут использоваться при кластеризации, обнаружении выбросов или (путем масштабирования) дают интересные представления данных
— возможности, описанные выше, могут быть расширены до неразмеченных данных, что приводит к возможности делать кластеризацию и визуализацию данных, обнаруживать выбросы
— высокая параллелизуемость и масштабируемость.Минусы:
— в отличие от одного дерева, результаты случайного леса сложнее интерпретировать
— нет формальных выводов (p-values), доступных для оценки важности переменных
— алгоритм работает хуже многих линейных методов, когда в выборке очень много разреженных признаков (тексты, Bag of words)
— случайный лес не умеет экстраполировать, в отличие от той же линейной регрессии (но это можно считать и плюсом, так как не будет экстремальных значений в случае попадания выброса)
— алгоритм склонен к переобучению на некоторых задачах, особенно на зашумленных данных
— для данных, включающих категориальные переменные с различным количеством уровней, случайные леса предвзяты в пользу признаков с большим количеством уровней: когда у признака много уровней, дерево будет сильнее подстраиваться именно под эти признаки, так как на них можно получить более высокое значение оптимизируемого функционала (типа прироста информации)
— если данные содержат группы коррелированных признаков, имеющих схожую значимость для меток, то предпочтение отдается небольшим группам перед большими
— больший размер получающихся моделей. Требуетсяпамяти для хранения модели, где
— число деревьев.
5. Домашнее задание
В качестве закрепления материала предлагаем выполнить это задание – разобраться с бэггингом и обучить модели случайного леса и логистической регрессии для решения задачи кредитного скоринга. Проверить себя можно отправив ответы в веб-форме (там же найдете и решение).
Актуальные и обновляемые версии демо-заданий – на английском на сайте курса, вот первое задание. Также по подписке на Patreon («Bonus Assignments» tier) доступны расширенные домашние задания по каждой теме (только на англ.).
6. Полезные источники
– Open Machine Learning Course. Topic 5. Bagging and Random Forest (перевод этой статьи на английский)
– Видеозапись лекции по мотивам этой статьи
– 15 раздел книги “Elements of Statistical Learning” Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
– Блог Александра Дьяконова
– Больше про практические применение случайного леса и других алгоритмов-композиций в официальной документации scikit-learn
– Курс Евгения Соколова по машинному обучению (материалы на GitHub). Есть дополнительные практические задания для углубления ваших знаний
– Обзорная статья «История развития ансамблевых методов классификации в машинном обучении» (Ю. Кашницкий)Статья написана в соавторстве с yorko (Юрием Кашницким). Автор домашнего задания – vradchenko (Виталий Радченко). Благодарю bauchgefuehl (Анастасию Манохину) за редактирование.
A random forest is an ensemble machine-learning model that is composed of multiple decision trees. A decision tree is a model that makes predictions by learning a series of simple decision rules based on the features of the data. A random forest combines the predictions of multiple decision trees to make more accurate and robust predictions.
Random Forests are often used for classification and regression tasks. In classification, the goal is to predict the class label (e.g., “cat” or “dog”) of each sample in the dataset. In regression, the goal is to predict a continuous target variable (e.g., the price of a house) based on the features of the data.
Random forests are popular because they are easy to train, can handle high-dimensional data, and are highly accurate. They also have the ability to handle missing values and can handle imbalanced datasets, where some classes are more prevalent than others.
To train a random forest, you need to specify the number of decision trees to use (the n_estimators parameter) and the maximum depth of each tree (the max_depth parameter). Other hyperparameters, such as the minimum number of samples required to split a node and the minimum number of samples required at a leaf node, can also be specified.
Once the random forest is trained, you can use it to make predictions on new data. To make a prediction, the random forest uses the predictions of the individual decision trees and combines them using a majority vote or an averaging technique.
What is the difference between the OOB Score and the Validation score?
OOB (out-of-bag) score is a performance metric for a machine learning model, specifically for ensemble models such as random forests. It is calculated using the samples that are not used in the training of the model, which is called out-of-bag samples. These samples are used to provide an unbiased estimate of the model’s performance, which is known as the OOB score.
The validation score, on the other hand, is the performance of the model on a validation dataset. This dataset is different from the training dataset and is used to evaluate the model’s performance after it has been trained on the training dataset.
In summary, the OOB score is calculated using out-of-bag samples and is a measure of the model’s performance on unseen data. The validation score, on the other hand, is a measure of the model’s performance on a validation dataset, which is a set of samples that the model has not seen during training.
OOB (out-of-bag) Errors
OOB (out-of-bag) errors are an estimate of the performance of a random forest classifier or regressor on unseen data. In scikit-learn, the OOB error can be obtained using the oob_score_ attribute of the random forest classifier or regressor.
The OOB error is computed using the samples that were not included in the training of the individual trees. This is different from the error computed using the usual training and validation sets, which are used to tune the hyperparameters of the random forest.
The OOB error can be useful for evaluating the performance of the random forest on unseen data. It is not always a reliable estimate of the generalization error of the model, but it can provide a useful indication of how well the model is performing.
Implementation of OOB Errors for Random Forests
To compute the OOB error, the samples that are not used in the training of an individual tree are known as “out-of-bag” samples. These samples are not used in the training of the tree, but they are used to compute the OOB error for that tree. The OOB error for the entire random forest is computed by averaging the OOB errors of the individual trees.
To install NumPy and scikit-learn, you can use the following commands:
pip install numpy pip install scikit-learn
These commands will install the latest versions of NumPy and scikit-learn from the Python Package Index (PyPI). To use the oob_score_ attribute, you must set the oob_score parameter to True when creating the random forest classifier or regressor.
Python3
clf = RandomForestClassifier(n_estimators=100,
oob_score=True,
random_state=0)
Once the random forest classifier or regressor is trained on the data, the oob_score_ attribute will contain the OOB error. For example:
Python3
clf.fit(X, y)
oob_error = 1 - clf.oob_score_
Here is the complete code of how to obtain the OOB error of a random forest classifier in scikit-learn:
Python3
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000,
n_features=10,
n_informative=5,
n_classes=2,
random_state=0)
clf = RandomForestClassifier(n_estimators=100,
oob_score=True,
random_state=0)
clf.fit(X, y)
oob_error = 1 - clf.oob_score_
print(f'OOB error: {oob_error:.3f}')
Output:
OOB error: 0.044
This code will create a random forest classifier, fit it to the data, and obtain the OOB error using the oob_score_ attribute. The oob_score_ attribute will only be available if the oob_score parameter was set to True when creating the classifier.
What are some of the use cases of the OOB error?
One of the main use cases of the OOB error is to evaluate the performance of an ensemble model, such as a random forest. Because the OOB error is calculated using out-of-bag samples, which are samples that are not used in the training of the model, it provides an unbiased estimate of the model’s performance.
Another use case of the OOB error is to tune the hyperparameters of a model. By using the OOB error as a performance metric, the hyperparameters of the model can be adjusted to improve its performance on unseen data.
Additionally, the OOB error can be used to diagnose whether a model is overfitting or underfitting. If the OOB error is significantly higher than the validation score, it may indicate that the model is overfitting and not generalizing well to unseen data. On the other hand, if the OOB error is significantly lower than the validation score, it may indicate that the model is underfitting and not learning the underlying patterns in the data.
Overall, the OOB error is a useful tool for evaluating the performance of an ensemble model and for diagnosing issues such as overfitting and underfitting.
-
Loading metrics
Open Access
Peer-reviewed
Research Article
-
Roman Hornung
On the overestimation of random forest’s out-of-bag error
- Silke Janitza,
- Roman Hornung
x
- Published: August 6, 2018
- https://doi.org/10.1371/journal.pone.0201904
Figures
Abstract
The ensemble method random forests has become a popular classification tool in bioinformatics and related fields. The out-of-bag error is an error estimation technique often used to evaluate the accuracy of a random forest and to select appropriate values for tuning parameters, such as the number of candidate predictors that are randomly drawn for a split, referred to as mtry. However, for binary classification problems with metric predictors it has been shown that the out-of-bag error can overestimate the true prediction error depending on the choices of random forests parameters. Based on simulated and real data this paper aims to identify settings for which this overestimation is likely. It is, moreover, questionable whether the out-of-bag error can be used in classification tasks for selecting tuning parameters like mtry, because the overestimation is seen to depend on the parameter mtry. The simulation-based and real-data based studies with metric predictor variables performed in this paper show that the overestimation is largest in balanced settings and in settings with few observations, a large number of predictor variables, small correlations between predictors and weak effects. There was hardly any impact of the overestimation on tuning parameter selection. However, although the prediction performance of random forests was not substantially affected when using the out-of-bag error for tuning parameter selection in the present studies, one cannot be sure that this applies to all future data. For settings with metric predictor variables it is therefore strongly recommended to use stratified subsampling with sampling fractions that are proportional to the class sizes for both tuning parameter selection and error estimation in random forests. This yielded less biased estimates of the true prediction error. In unbalanced settings, in which there is a strong interest in predicting observations from the smaller classes well, sampling the same number of observations from each class is a promising alternative.
Citation: Janitza S, Hornung R (2018) On the overestimation of random forest’s out-of-bag error. PLoS ONE 13(8):
e0201904.
https://doi.org/10.1371/journal.pone.0201904
Editor: Y-h. Taguchi,
Chuo University, JAPAN
Received: January 15, 2018; Accepted: July 24, 2018; Published: August 6, 2018
Copyright: © 2018 Janitza, Hornung. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Data Availability: All used data are third party data not owned or collected by us. However, all data sets can be accessed by readers using the links provided below in the same manner as we accessed these data. The Colon Cancer data, the Prostate Cancer data and both Breast Cancer data sets were obtained from the website http://ligarto.org/rdiaz/Papers/rfVS/randomForestVarSel.html. The Embryonal Tumor data is available at http://portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi, and the Leukemia data was retrieved from the Bioconductor package golubEsets (URL http://bioconductor.org/packages/release/data/experiment/html/golubEsets.html).
Funding: SJ and RH were both funded by grant BO3139/6-1 from the German Science Foundation (URL http://www.dfg.de). SJ was in addition supported by grant BO3139/2-2 from the German Science Foundation. The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Competing interests: The authors have declared that no competing interests exist.
Introduction
Random forests (RF) [1] have become a popular classification tool in bioinformatics and related fields. They have also shown excellent performance in very complex data settings. Each tree in a RF is constructed based on a random sample of the observations, usually a bootstrap sample or a subsample of the original data. The observations that are not part of the bootstrap sample or subsample, respectively, are referred to as out-of-bag (OOB) observations. The OOB observations can be used for example for estimating the prediction error of RF, yielding the so-called OOB error. The OOB error is often used for assessing the prediction performance of RF. An advantage of the OOB error is that the complete original sample is used both for constructing the RF classifier and for error estimation. By contrast, with cross-validation and related data splitting procedures for error estimation a subset of the samples are left out for RF construction, which is why the resulting RF classifiers are less performant. Another advantage of using the OOB error is its computational speed. In contrast to cross-validation or other data splitting approaches, only one RF has to be constructed, while for k-fold cross-validation k RF have to be constructed [2, 3]. The use of the OOB error saves memory and computation time, especially when dealing with large data dimensions, where constructing a single RF might last several days or even weeks. These reasons might explain the frequent use of the OOB error for error estimation and tuning parameter selection in RF.
The OOB error is often claimed to be an unbiased estimator for the true error rate [1, 3, 4]. However, for two-class classification problems it was reported that the OOB error can overestimate the true prediction error depending on the choices of RF parameters [2, 5]. The bias can be very substantial, as shown in the latter papers, and is also present when using classical cross-validation procedures for error estimation. It was thus recommended by Mitchell [5] to use the OOB error only as an upper bound for the true prediction error. However, Mitchell [5] considered only settings with completely balanced samples, sample sizes below 60 and two response classes, limiting the generality of his results.
Besides the fact that trees in RF are constructed on a random sample of the data, there is a second component which differs between standard classification and regression trees and the trees in RF. In the trees of a RF, not all variables but only a subset of the variables are considered for each split. This subset is randomly drawn from all candidate predictors at each split. The size of this subset is usually referred to as mtry. The purpose of considering random subsets of the predictors instead of all predictors is to reduce the correlation between the trees, that is, to make them more dissimilar. This reduces the variance of the predictions obtained using RF. In practical applications, the most common approach for choosing appropriate values for mtry is to select the value over a grid of plausible values that yields the smallest OOB error [6–8]. In literature on RF methodology, the OOB error has also frequently been used to choose an appropriate value for mtry [9, 10]. In principle, other procedures like (repeated) cross-validation may be applied for selecting an optimal value for mtry, but the OOB error is usually the first choice for parameter tuning. This is due to the fact that, unlike many other approaches such as cross-validation, the whole data can be used to construct the RF and much computational effort is saved since only one RF has to be built for each candidate mtry value. Implementations exist that use the OOB error to select an appropriate value for mtry. In the statistical software R [11], for example, the function tuneRF from the package randomForest [12] automatically searches over a grid of mtry values and selects the value for mtry for which the OOB error is smallest. The latter approach is only valid, if the bias of the OOB error does not depend on the parameter mtry. If, by contrast, the bias of the OOB error does depend on this parameter, the mtry value minimizing the OOB error cannot be expected to minimize the true prediction error and will thus be in general suboptimal, making the OOB error based tuning approaches questionable. To date there are no studies investigating the reliability of the OOB error for tuning parameters like mtry in RF.
The main contribution of this paper is three-fold: (i) the bias and its dependence on mtry in settings with metric predictor variables are quantitatively assessed through studies with different numbers of observations, predictors and response classes which helps to identify so-called “high-risk settings”, (ii) the reasons for this bias and its dependence on mtry are studied in detail, and based on these findings, the use of alternatives, such as stratified sampling (which preserves the response class distribution of the original data in each subsample), is investigated, and (iii) the consequences of the bias for tuning parameter selection are explored.
This paper is structured as follows: In the section “Methods”, simulation-based and real-data based studies are described after briefly introducing the RF method. The description includes an outline of the simulated and real data, the considered settings and several different error estimation techniques that will be used. The results of the studies are subsequently shown in the section “Results”, where also some additional studies are presented, and finally recommendations are given. The results are discussed in the section “Discussion” and the main points are condensed in the section “Conclusions”.
Methods
In this section, the RF method and the simulation-based and real-data based studies are described. Simulated data is used to study the behavior of the OOB error in simple settings, in which all predictors are uncorrelated. This provides insight to the mechanisms which lead to the bias in the OOB error. Based on these results, settings are identified, in which a bias in the OOB error is likely. Subsequently, to assess the extent of the bias in these settings in practice, complex real world data is used.
Random forests and its out-of-bag error
RF is an ensemble of classification or regression trees that was introduced by Breiman [1]. One of the two random components in RF concerns the choice of variables used for splitting. For each split in a tree, the best splitting variable from a random sample of mtry predictors is selected. If the chosen mtry value is too small, it might be that none of the variables contained in the subset is relevant and that irrelevant variables are often selected for a split. The resulting trees have poor predictive ability. If the subset contains a large number of predictors, in contrast, it is likely that the same variables, namely those with the largest effect, are often selected for a split and that variables with smaller effects have hardly any chance of being selected. Therefore, mtry should be considered a tuning parameter.
The other random component in RF concerns the choice of training observations for a tree. Each tree in RF is built from a random sample of the data. This is usually a bootstrap sample or a subsample of size 0.632n. Therefore not all observations are used to construct a specific tree. The observations that are not used to construct a tree are denoted by out-of-bag (OOB) observations. In a RF, each tree is built from a different sample of the original data, so each observation is “out-of-bag” for some of the trees. The prediction for an observation can then be obtained by using only those trees for which the observation was not used for the construction. A classification for each observation is obtained in this way and the error rate can be estimated from these predictions. The resulting error rate is referred to as OOB error. This procedure was originally introduced by Breiman [13] and it has become an established method for error estimation in RF.
Simulation-based studies
The upward bias of the OOB error in different data settings with metric predictor variables was systematically investigated by means of simulation studies.
Settings were considered with
- different associations between the predictors and the response. Either none of the predictors were associated with the response (the corresponding studies termed null case) or some of them were associated (power case);
- different numbers of predictors, p ∈ {10, 100, 1000};
- different numbers of response classes, k ∈ {2, 4}. The studies are termed binary if k = 2 and multiclass if k = 4;
- different response class ratios. An equal number of observations of each response class was used (balanced settings) for k ∈ {2, 4}. For k = 2 two additional settings with unequal response class sizes were simulated (binary unbalanced and binary extremely unbalanced). In the first setting (binary unbalanced), the smaller class comprised 30% of the observations. In the second setting (binary extremely unbalanced), the smaller class comprised approximately 17% (ratio 1:5) of the observations.
- different numbers of observations, n ∈ {nsmall, 100, 1000}, with nsmall = 20 for binary balanced studies, nsmall = 30 for binary unbalanced studies, nsmall = 60 for binary extremely unbalanced studies and nsmall = 40 for multiclass balanced studies.
Since one of the aims was to investigate the bias in dependence on mtry, several RFs with different mtry values were constructed for each setting. The grid of considered mtry values was {1, 2, 3, …, 10} for p = 10, {1, 10, 20, 30, …, 100} for p = 100 and {1, 5, 10, 50, 100, 200, 300, …, 1000} for p = 1000. Note that for mtry = 1 there is no selection of an optimal predictor variable for a split, while for mtry = p the RF method coincides with the bagging procedure which selects the best predictor variable from all available predictors [14]. A large number of trees, referred to as ntree, should be chosen especially if the data are composed of a large number of predictors. It is usually chosen by considering a compromise between accuracy and computational speed. The OOB error stabilized at around 250 trees in convergence studies of Goldstein et al. [15], and they concluded that 1000 trees might be sufficiently large for their genome-wide data set. Also in the studies of Díaz-Uriarte and De Andres [16] the results for RF with 1000 trees were almost the same as those for RF with 40000 trees, and in the high-dimensional settings of Genuer et al. [17] RF with 500 trees and 1000 trees yielded very similar OOB errors. In accordance with these findings the number of trees was set to 1000 in all studies of this paper (including at most ∼ 7000 predictors). Each setting was repeated 500 times to obtain stable results.
Only metric predictor variables were considered in the studies. In the null case study, the predictors X1, …, Xp were independent and identically distributed (i.i.d.), each following a standard normal distribution (see Tables 1 and 2). In the power case study, both, predictors associated with the response and predictors not associated with the response were considered. The predictors not associated with the response followed a standard normal distribution. The distribution of predictors with association was different for each response class. The predictor values for observations from class 1 were always drawn from a standard normal distribution. The predictor values for observations from class 2 (or classes 2, 3, and 4 in settings with k = 4 response classes) were drawn from a normal distribution with variance 1 and a mean different from zero. Tables 1 and 2 give an overview of the distribution of predictors in the response classes for settings with k = 2 and k = 4 response classes, respectively. Let us consider the setting with p = 10 and k = 4 as an example (Table 2). The first two predictors X1 and X2 are associated with the response, while the other predictors X3, …, X10 are not. Accordingly, X3, …, X10 always follow a standard normal distribution, while the distribution of X1 and X2 depends on whether the observation comes from class 1 or from a different class. If the observation comes from class 1 the distribution of X1 and X2 is N(0, 1), and if it comes from class r ∈ {2, 3, 4} the variables Xj, j = 1, 2 follow a normal distribution N(μrj, 1) with μrj drawn independently from N(0.4, 1). Randomly drawing the mean separately for X1 and X2 and for each repetition of the study makes sure that predictors with different effect strengths are considered.
Despite considering metric predictors with different effect strengths, the settings are simplistic because all predictors are uncorrelated. Although assuming no correlations between any of the predictors is not realistic, such settings are important to understand the mechanisms which lead to a bias in the OOB error. The OOB error in more complex settings that include correlated predictors will be explored by means of real data.
Real data-based studies
Based on the results from simulated data, real data sets were considered in which the overestimation of the OOB error is expected to be most pronounced. As will be seen later, a relevant bias of the OOB error is likely to occur in data settings with huge numbers of predictors, p, and small numbers of observations, n. Such settings are typically prevalent with genomic data. Therefore high-dimensional genomic data from the real world are considered for further investigations.
New data for evaluation can easily be generated with simulated data. In contrast to that, in real data applications, the original data has to be split up in order to obtain an independent test data set useable for evaluation. Thus, six genomic data sets were selected that are large enough to randomly split the data into a training and a test set (Table 3). These data sets were often used by various authors for classification purposes [16, 18, 19] and are briefly described in the following. Note that no pre-selection of data sets based on the results obtained for this data was performed, and the results of all six analyzed data sets are reported [20].
Data.
The first considered data is the Colon Cancer data of Alon et al. [21]. The expression levels of 40 tumor and 22 normal colon tissues for 6500 human genes were measured. The considered data set contains the expression of the 2000 genes with highest minimal intensity across the 62 tissues measured using the Affymetrix technology.
Two versions of the Breast Cancer data of van’t Veer et al. [22] were considered. The first version of this data was previously analyzed by Díaz-Uriarte and De Andres [16] and contains k = 3 response classes: 33 patients developed distant metastases within 5 years, 44 remained disease-free for over 5 years and 18 patients had BRCA1 germline mutations. Missing data was imputed by using 5-nearest neighbor imputation. Further details on transformations of the original data are given in the supplement to the paper of Díaz-Uriarte and De Andres [16]. The second version which is considered in this paper is a subset of the data set provided by Díaz-Uriarte and De Andres [16]. This subset does not contain the 18 patients with BRCA1 germline mutations. A differentiation is thus only made between the patients that developed distant metastases within 5 years (n = 33) and patients that remained disease-free for over 5 years (n = 44), meaning the number of response classes is k = 2.
The fourth considered data set is the Prostate Cancer data of Singh et al. [23]. From 1995 to 1997 samples of prostate tumors and adjacent non-tumor prostate tissue were collected from patients undergoing radical prostatectomy at the Brigham and Women’s Hospital. High-quality expression profiles were obtained from 50 non-tumor prostate samples and 52 tumor specimens. The oligonucleotide microarrays contained probes for approximately 12600 genes.
The Embryonal Tumor data of Pomeroy et al. [24] includes 60 patients with embryonal tumors of the central nervous system from whom biopsies were obtained before receiving treatment. The data was used to differentiate between patients who are alive after treatment (n = 21) and those who succumbed to their disease (n = 39) (data set C in [24]). RNA was extracted from frozen specimens and was analyzed with oligonucleotide microarrays containing 7129 probes from 6817 genes.
The Leukemia data [25] consists of 47 patients with acute lymphoblastic leukemia (ALL) and 25 patients with acute myeloid leukemia (AML). The considered data set comprises both, training samples and test samples from Golub et al. [25]. The samples were assayed using Affymetrix Hgu6800 chips and data on the expression of 7129 genes are available.
Settings.
Different settings which were created by modifying the original real data sets were investigated. The aims together with the modifications are outlined in the following:
- Aim 1: To quantitatively assess the overestimation in the OOB error and its consequences for selecting an optimal value for mtry using the OOB error. For this purpose, the original data was used without making any modifications to the data. This study is referred to as “Real data study”.
- Aim 2: To investigate the behavior of the OOB error on data sets with realistic data structures but without any associations between the predictors and the response. To create a data set with realistic data structures, the matrix containing the values of the predictor variables of the real data sets was used and the response values of the original data sets were randomly permuted to break any associations between the predictors and the response. The studies with the permuted response are termed “Real data null case study with correlations”, where the term correlation refers to the correlations between the predictor variables. Note that the data sets obtained in this way only differ to the original data in that none of the predictors are associated with the response, while in the original data some of the predictors are possibly associated.
- Aim 3: To investigate the effect of correlations on the bias in the OOB error in realistic data settings. For this purpose, each predictor variable was permuted separately to create independence between them. This also breaks possible associations between the predictors and the response. This setting is called “Real data null case study without correlations”. Note that, in order to assess the effect of correlations, the results for this study cannot be compared to the results obtained for the real data study (described above) because in the real data study some of the predictors are possibly associated with the response, while in the real data null case study without correlations this is not the case. This makes it impossible to decide whether differences are due to the correlations between predictors or are due to the fact that some of the predictors are associated in one study but not in the other. However, the results of the real data null case study without correlations can be compared to those of the real data null case study with correlations, in which there are correlations between predictors but none of the predictors is associated with the response.
Only a part of the observations was used to construct the RF (training set) while the other part was used for assessing the performance of the RF (test set). The number of trees was always set to 1000. For the data sets with k = 2 response classes, the training set consists of n = 20 observations that were randomly drawn, and for the Breast Cancer data (i.e. the only data set with k = 3), the training set consists of n = 30 observations. In contrast to the simulation studies, the response class ratio in the training set was not fixed. However, a minimum of 8 observations were required from each response class to prevent too few observations from a response class. With only n = 20 observations, this means that the response class distribution is nearly balanced and that only slight class imbalances can occur in the considered settings. Note that we chose to use only 20 and 30 observations, respectively, to train RF since these are settings in which a bias in the OOB error is most likely, as will be shown in the rest of this paper. Although modern studies include far more observations, such small sample sizes are still encountered in practice [26].
For all settings RF with different mtry values were constructed. The grid of mtry values was {1, 10, 100, 500, 1000, 2000, …, p}, with p denoting the total number of predictors. Table 3 shows the grids for the considered data sets. Each setting was repeated 1000 times.
Alternative strategies for error estimation
The following strategies for error estimation were considered as possible alternatives to the OOB error:
- Test error: This error rate was computed using observations that are not part of the set of n observations that were considered for constructing the RF. Since these observations are usually referred to as test observations, the resulting error rate is referred to as test error. In the simulation studies, data for 10000 additional observations (test observations) was generated in order to estimate the prediction error of the RF. The response class distributions were the same in the two samples of size 10000 and n. In the real data studies, the n observations used to construct the RF (n = 20 for k = 2, n = 30 for k = 3) were randomly sampled from all available observations, while making sure that at least 8 observations from each response class were sampled. In order to have the same response class distribution in the two sets, as test set the largest subset of the remaining observations was used in which the response class distribution equals that in the sample of n observations.
- Stratified OOB error: In this paper, the OOB error was also computed for a RF based on a stratified sampling scheme. This strategy was also investigated in the studies of Mitchell [5]. In this stratified sampling scheme, trees were grown on subsamples of size ⌊0.632n⌋, in which the response class distribution of the original data of n observations is preserved in each subsample. The OOB error was computed based on the OOB observations as usual. In this paper, it is referred to as the stratified OOB error. Note that, in contrast to the test error, the (stratified) OOB error uses the n observations for both constructing the RF and estimating its prediction error.
- Cross-validation (CV) error: In contrast to the OOB error, CV is a strategy for estimating the error rate of an arbitrary classification method and is not specific to RF. In all studies 10-fold CV was used. Thus, for each constructed RF, the data was first partitioned into 10 sets of equal size. Each of the 10 sets was then used once for computing the error rate of the RF, while the other 9 sets were used for creating the RF. The CV error was computed as the average of the 10 error rates. While the test and OOB error (stratified and unstratified) estimation strategies use all of the n observations to construct the RF, in l-fold CV the n observations are split into a training and a test set and only the n(l − 1)/l training observations are used to construct a RF. This means that the CV error is computed from l models that are fit based on only a subset of the data. Thus, the CV error slightly overestimates the true prediction error that would be obtained for a model that was fit based on all n observations [27].
- Stratified cross-validation (CV) error: For computing the stratified CV error the data of size n was randomly split into l = 10 sets in a way, that within each set the distribution of response classes is the same as in the original data. The error estimation was then done in exactly the same way as was described for the CV error.
Since the test error is an accurate estimate for the generalization error, it is treated as a “gold standard” in this paper against which the OOB and CV errors (stratified and unstratified) are compared. In simulation studies, one should prefer estimating the error rate by means of an additional large independent test sample. In real data settings, in contrast, the number of observations is limited and is usually not sufficient to enable splitting the data into a training set and a large test set. Moreover, sample sizes are rather small and it is often desired to use all available information for building a model which has high predictive ability. Thus, in real data applications it is rarely the case that there is a large test set available from which the error rate can be computed (prior to externally validating the prediction model), and different approaches to estimating the error rate, such as cross-validation procedures, have to be applied.
Random forest implementation and computational issues
The original RF version of Breiman and its implementation in the R package randomForest [12] was used for all studies. Note that stratified sampling will be investigated in the studies as possible solution to overcome the problem of the bias in the OOB error. In the RF implementation of Liaw and Wiener [12], one can specify a vector which contains the number of observations to be drawn from each class via the argument sampsize in the function randomForest. In the presence of categorical predictors, this RF version is biased with respect to split selection, because predictors with many possible cutpoints are preferentially selected [28–31]. This is, however, not a problem in the studies presented in this paper, because here exclusively metric predictors are considered. Nevertheless, to make sure that the results do not depend on the RF version considered, the RF version of Hothorn et al. [32] was used for some simulation settings in addition. This RF version, while computationally challenging, is unbiased with respect to split selection. Moreover, subsampling (i.e., sampling from the original data without replacement) was used in all studies instead of bootstrapping in order to avoid possible biases induced by the bootstrap [5, 29]. As was suggested, subsamples of size ⌊0.632n⌋ were used, where n denotes the number of observations [29]. Trees were always grown to full size. For this purpose default values for the parameters controlling tree size were not changed in the original RF version. In contrast to that, the parameters controlling tree size in the RF version of Hothorn et al. [32] were set to the most extreme values, such that early stopping was prevented.
Results
Figs 1–5 show the estimated error rates over a grid of mtry values for the five different error estimates (test error, OOB error, stratified OOB error, CV error, stratified CV error). In the following, the bias in the OOB error is quantified based on these results. Further the sources of the bias and the dependence of this bias on RF parameters and data characteristics are investigated, and finally the consequences of using the OOB error for tuning mtry are assessed.
Fig 1. Error rate estimates for the binary null case study (balanced).
Shown are different error rate estimates for the setting with two response classes of equal size and without any predictors with effect. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 500 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g001
Fig 2. Error rate estimates for the binary power case study (balanced).
Shown are different error rate estimates for the setting with two response classes of equal size and with both predictors with effect and without effect. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 500 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g002
Fig 3. Error rate estimates for the binary null case study (unbalanced).
Shown are different error rate estimates for the setting with two response classes of unequal size (smaller class containing 30% of the observations) and without any predictors with effect. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 500 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g003
Fig 4. Error rate estimates for the binary power case study (unbalanced).
Shown are different error rate estimates for the setting with two response classes of unequal size (smaller class containing 30% of the observations) and with both predictors with effect and without effect. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 500 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g004
Fig 5. Error rate estimates for the real data study.
Shown are different error rate estimates for six real data sets with two or three response classes, respectively, of nearly the same size. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 1000 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g005
Quantitative assessment of the bias
For the binary null case study (balanced) the true error rate for new observations is 0.5, given that new observations come from both response classes equally often. Fig 1 shows the estimated error rates for the binary null case study (balanced). The test error approximates 0.5 very well in all balanced settings and for all considered mtry values. For small sample sizes (Fig 1a, 1b and 1c; n = 20), the OOB error is larger than the test error which is considered to be a good estimate of the true prediction error. For larger sample sizes (Fig 1d, 1e and 1f; n = 100), the difference between the test error and the OOB error is smaller but still present. Finally, if the sample size is increased to n = 1000 (Fig 1g, 1h and 1i), the OOB error seems to approximate the test error well. When comparing the results for different parameter settings, it can be seen that the overestimation does not only depend on the number of observations but also on the number of predictors, or rather the ratio of the number of observations and predictors. In settings with both, large predictor numbers and small sample sizes (Fig 1c; n = 20, p = 1000), the overestimation is most extreme. Depending on the chosen value for mtry, the difference between the OOB error and the test error lies between 10% and 30% for this setting. In contrast, there is no overestimation in settings with large sample sizes and small predictor numbers (Fig 1g; n = 1000, p = 10). Exactly the same results are obtained for the CV error. This suggests that CV is not a reasonable alternative to the OOB error and, moreover, that there is a common source of the overestimation. In contrast to the OOB error and the CV error, the stratified OOB error and the stratified CV error approximate the test error very well and are reasonable alternatives to the unstratified sampling procedures in the considered study.
Comparable results were obtained for the binary power case study (balanced) (Fig 2). However, the difference between the OOB error (CV error) and the test error is smaller than in the study without any associations. In particular, there is only a small overestimation for large mtry values. Moreover, in contrast to the binary null case study (balanced), there is no overestimation in settings with a moderate sample size of n = 100 (Fig 2d, 2e and 2f). Similar results were also obtained for balanced settings with four response classes (S1 File: Figs S1 and S2). This shows that the overestimation also occurs in settings with more than two response classes.
The findings of the binary null case study (balanced) and the binary power case study (balanced) do not transfer to the settings with unbalanced response classes. In the binary null case study (unbalanced), the OOB error and the CV error are far closer to the test error (Fig 3). For the study with more extreme class imbalance (ratio 1:5) there are hardly any differences between the error rates estimated by the different strategies (S1 File: Fig S3). Overall, this suggests good performance of these two error estimation techniques in unbalanced data settings. It is not surprising that the prediction error is much lower than 0.5 in the unbalanced data settings. If for example all observations are classified into the larger class, one achieves an error rate which equals the proportion of the smaller class. With 30% observations belonging to the smaller class, the proportion of misclassified observations in a null case study could therefore be expected to be about 30%. These expectations are in line with the test error in Fig 3.
Some differences between the stratified OOB error and the test error can be observed in some of the power case settings (Figs 2c, 2f, 2i and 4c). In some balanced settings, the stratified OOB error is larger than the test error especially for mtry values close to one. However, such small mtry values are not recommended. In the presence of many variables without any effect, small mtry values prevent the selection of relevant variables yielding RF that have poor performance [17, 33].
Additional simulation studies with many predictor variables with effect show that if many predictors are associated with the response, there is a larger difference between the stratified procedures and the test error (Fig 6; see S1 File for details on the design). However, in all considered settings the difference between the stratified procedures and the test error is (substantially) smaller than that between the unstratified procedures and the test error.
Fig 6. Error rate estimates for simulation studies with many predictors with effect and n = 20.
Shown are different error rate estimates for an additional simulation study with two response classes of equal size and many predictor variables with effect. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with sample size n = 20 and different numbers of predictors, p. The mean error rate over 500 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g006
To conclude, based on these results we have identified settings with (i) (nearly) balanced response classes, (ii) large predictor numbers, (iii) small sample sizes and (iv) a high signal-to-noise ratio as “high-risk settings” in which a large overestimation in the OOB error can be expected. By now the bias was quantified for rather simplistic settings which might not be realistic. The results for the real world high-dimensional genomic data sets in which (i)–(iv) apply, are shown in Fig 5. They are in line with the results obtained for the simulation studies: the OOB error and the CV error substantially overestimate the true prediction error for all data sets. The difference between the test error and the error estimated by the OOB procedure or CV is about 5%. CV performs worse than the OOB procedure for the Colon Cancer data, the Prostate Cancer data and the Leukemia data (Fig 5a, 5d and 5f). This might be related to the fact that the CV error is computed from models that are fit based on only a subset of the data, yielding only an upper bound of the prediction error [27]. Both CV and OOB error are very similar for the three remaining data sets. The stratified OOB error and the stratified CV error, in contrast, have a good performance approximating the test error very well. A marginal overestimation can, however, be seen for the stratified CV error and the stratified OOB error for two of the data sets (Colon Cancer data, Prostate Cancer data).
Sources of the bias
The main source of the systematic deviation between the OOB error and the test error has already been described in the literature [5]. In the following, this main source is described before the bias and its dependence on specific parameters are detailed.
In a nutshell, the bias is attributable to the trees’ sensitivity to class imbalance. It is well known that classification trees are greatly affected by class imbalance in the sense that trees that were trained on unbalanced samples preferentially classify new observations into the class from which most training observations come. In the context of RF, where the classification trees are constructed using a subset of the data, this is also relevant to settings in which there is an equal number of observations from both classes. Later it will be shown that the impacts of this problem are even more severe for balanced than for unbalanced settings.
Let us assume in the following that we have a sample with an equal number of observations from both response classes. When constructing trees for a RF we randomly draw subsamples (or bootstrap samples) of observations from the original balanced sample. The subsample may comprise for example, 63.2% of the observations contained in the original sample. In contrast to the original sample, the resulting subsamples generally do not include exactly the same number of observations from each class, that is, the subsamples are often not exactly balanced or may even be extremely unbalanced if much more observations from one class are drawn by chance. The degree of class imbalance in the subsample is directly dependent on the sample size of the original sample, n. If n is large the chance for a stronger class imbalance in the subsample will be rather small, while for small n, the chance will be large. As an example, Fig 7 shows the degrees of class imbalance in subsamples of size 63.2% that are drawn from balanced samples of sizes n = 1000, n = 100 and n = 20. The distributions of the frequencies of class 1 observations in the subsamples were determined based on the hypergeometric distribution. As can be seen, there is a high chance of an extreme class imbalance for small samples. For large samples (n = 1000), in contrast, there is only a small degree of class imbalance. The class imbalance in the subsamples yields trees that preferentially predict the class most often represented in the subsample and the more extreme the class imbalance the more extreme the preferential prediction. Thus, the preferential prediction for a class is more pronounced for smaller samples than for larger samples.
Fig 7. Class imbalance in subsamples drawn from a balanced original sample.
Distribution of the frequency of class 1 observations in subsamples of size ⌊0.632n⌋, randomly drawn from a balanced sample with a total of (a) n = 1000, (b) n = 100, and (c) n = 20, observations from classes 1 and 2.
https://doi.org/10.1371/journal.pone.0201904.g007
If a prediction shall be obtained for a new observation, all trees in the RF are used to derive a prediction. Then we expect approximately the same number of trees preferentially predicting class 1 and trees preferentially predicting class 2. Overall, there is no preferential prediction for a new observation. In contrast to that, for OOB observations not all trees but only those trees for which the observation was not part of the subsample, are used to derive the prediction. If assuming that an observation i comes from class 1, for example, there are more subsamples without i that contain more observations from class 2 than subsamples without i that contain more observations from class 1. Accordingly, there are more trees for which observation i is “out-of-bag” preferentially predicting class 2, which is the wrong class. Again, the sample sizes play an important role. If the sample size is large, there are not substantially more subsamples without i that contain more observations from class 2. Then there is hardly any preferential prediction for the wrong class. In contrast to that, if the sample size is small, say n = 10, there are substantially more subsamples without i that contain more observations from class 2, yielding substantially more trees preferentially predicting the wrong class. The mechanism described above is the reason that the OOB predictions are worse than predictions that are obtained from the RF if the observation was not used for the construction of the RF. This mechanism finally leads to an OOB error that is too pessimistic, that is, it overestimates the error to be expected for new data.
In line with results from the literature, our studies suggest that a large amount of the overestimation can be solved by drawing subsamples in which the class distribution of the original data set is preserved [5]. All trees in the RF will then have the same preference for a class, and this preference will depend on the class distribution of the original sample. Thus, also the subset of the trees that is used to derive a prediction for an OOB observation have exactly the same preference for a class, which leads to OOB errors that are unbiased with respect to the error expected for independent test data. Note that computing the OOB error from an RF based on stratified subsamples with sampling fractions that are proportional to class sizes yields the stratified OOB error introduced in the section “Alternative strategies for error estimation”. The results shown in this paper support the findings of Mitchell [5] who claims that most of the bias can be eliminated by this alternative OOB error estimation.
In the following subsections, the reason for the dependence of the overestimation on data characteristics and RF parameters are investigated.
Role of the number of observations.
The role of the sample size has already been described in detail. It was seen that large class imbalance in subsamples is especially a problem for smaller samples. The class imbalance results in trees that tend to more often predict the class that is more represented in the corresponding in-bag sample, or equivalently, that is less often represented in the corresponding OOB sample, leading to higher OOB errors. The dependence of the overestimation on the sample size is seen in the simulation results shown in the section “Quantitative assessment of the bias”. These show that the bias is almost negligible for n = 1000, while it is large for n = 20.
Role of mtry.
Figs 1 and 2 show that, particularly for balanced data, the difference between the OOB error and the test error may strongly depend on the parameter mtry. While for balanced data the difference is larger for smaller mtry values (Figs 1 and 2), for unbalanced data this difference is, in contrast, smaller for smaller mtry values (Figs 3 and 4). The reasons for this are investigated separately for unbalanced and balanced settings in the following.
Let us first consider the setting with unbalanced data and no associations between the predictors and the response (null case study). Although there is no association between the predictors and the response in truth, some of the predictors may discriminate in-bag observations from different classes well by chance. If a large mtry value is used, these predictors are chosen for a split and the in-bag observations can be separated well. This yields trees that predict both classes and not only one of the classes (e.g. the most frequent class). In contrast to that, the well-discriminating predictors are not frequently selected as splitting variables in a tree if mtry is small. The resulting trees cannot discriminate between in-bag observations from different classes well and tend to predict the larger class more often. Then the RF, which uses the majority vote of the trees, predicts the larger class for almost all observations. This can also be seen by inspecting class predictions that are obtained from RFs with different mtry values in empirical studies. The inspection of class predictions was done using simulation studies and is outlined next.
Class predictions were obtained from RFs constructed using 10 observations from class 1 and 20 observations from class 2. The number of predictors, p, was 100. A null case scenario was simulated in which all predictors X1, …, X100 were drawn from a standard normal distribution. Predictions by the RFs were obtained for n = 10000 test observations, with an equal number of observations from class 1 and class 2. The proportion of class 1 (minority class) predictions for the test observations was finally computed. This process was repeated 500 times. Fig 8 shows the frequency of class 1 predictions over the 500 repetitions for different values of mtry. A clear trend can be seen that the larger class (class 2 in this simulation study) is more often predicted if mtry is small. For mtry values close to one, class 2 is almost always predicted.
Fig 8. The trees’ preference for predicting the larger class in dependence on mtry.
Fraction of class 1 (minority class in training sample) predictions obtained for balanced test samples with 5000 observations, each from class 1 and 2, and p = 100 (null case setting). Predictions were obtained by RFs with specific mtry (x-axis). RFs were trained on n = 30 observations (10 from class 1 and 20 from class 2) with p = 100. Results are shown for 500 repetitions.
https://doi.org/10.1371/journal.pone.0201904.g008
The OOB error and the test error are almost the same if mtry is very small because most of the trees in the RF predict the larger class. In contrast to that, the trees do not always predict the larger class if mtry is large, and the phenomenon that for the OOB observations the trees tend to predict the opposite class becomes relevant again. This explains the finding that for large mtry the OOB error is more upwardly biased than for small mtry. However, in contrast to balanced settings in which the trees tend to predict the opposite class for an OOB observation, in unbalanced settings most of the trees have the preference for the same class, namely the largest class in the original sample. This reduces the risk that the trees tend to predict the opposite class for an OOB observation. Thus, the difference between the test error and the OOB error is far smaller in the unbalanced simulation settings than in the balanced simulation settings and is smallest in settings with very extreme class imbalance (S1 File: Fig S4).
Also note that, if mtry is set to 1 the prediction of only one class may yield low error rates in specific settings. These are settings in which most of the observations, for which the predictions shall be obtained, are from the class that is always predicted by the RF. For example, if the test data includes 30% of observations from class 1, and the RF always predicts class 2, then the test error is 30%. The same applies to the OOB error. In the simulated data, for example, the OOB error is estimated based on observations, in which approx. 70% of the observations come from class 2 and 30% come from class 1. In the case of small mtry values, the RF very frequently predicts class 2 (cf. Fig 8), yielding an OOB error close to 30%. This is also the reason why smaller test and OOB errors were obtained for smaller mtry values than for larger mtry values in the unbalanced null case scenarios, seen in Fig 3 and Fig S3 (S1 File). The other error estimation strategies are similarly affected.
Let us now consider the balanced null case study, in which there is an equal number of observations from all classes. When drawing samples for tree construction, it is usually the case that not exactly the same number of observations is drawn from each class. When drawing subsamples of size 0.632n from n = 20 observations (10 from each response class), for example, there is a 50% chance of obtaining subsamples with a different number of observations from each class (cf. Fig 7). When drawing from n = 100 observations, the chance to obtain an unbalanced subsample is about 84%. The trees grown on unbalanced samples tend to predict the larger class more often, especially if mtry is small. However, in contrast to the settings with an unbalanced original data, in the case of a balanced original sample there are approximately as many trees preferentially predicting class 1 as trees preferentially predicting class 2. In the absence of any associations between the predictors and the response, a new observation would then be classified to class 1 by 50% of the trees, while the other 50% of the trees classify the observation to class 2. This is independent of which value for mtry is chosen. Thus, there is no preferential prediction by the RF for new observations in balanced data settings. The test error computed from new observations is therefore not affected by different values for mtry if the original sample is balanced.
The OOB error, in contrast, is affected by the choice of mtry (cf. Fig 1). When obtaining predictions for an OOB observation i that comes from, say class 2, not all trees of a RF are used but only the trees that are constructed based on samples in which the observation was out-of-bag. Most importantly, even if the original sample is completely balanced, in the samples that do not contain the observation i, the proportion of observations from class 1 is higher on average than the proportion of observations from class 2. Thus, by construction, an OOB observation is out-of-bag for trees that tend to more often predict a class different than the true class the OOB observation belongs to. As explained before, this leads to the high OOB error rates observed in Fig 1. The OOB errors even exceed 0.5, which is the error rate of a random prediction in the absence of any associations between predictors and the response. As was outlined in the previous paragraph, the trees’ preference for the larger class in the subsample (i.e., most often the wrong class for the OOB observation) is stronger when small mtry values are used. This explains the finding that the OOB error is larger for RFs in which a small mtry value is used.
So far we focused on the case in which neither of the predictors are associated with the response. The mechanism described for the null case study may also play a role for the power case study, especially if there are only few predictors with effect and if the effects are small. In settings with only few influential predictors and many noise predictors, very small mtry values lead to trees that frequently select irrelevant variables for a split. Similar to the null case study, the trees then preferentially predict the class from which most training observations come. This explains the finding that in the simulation study (including only few relevant variables with rather small effects) the bias in the OOB error is larger for smaller mtry values in balanced settings, while the opposite is true for unbalanced settings.
Role of the predictors.
The simulation results have shown that the bias in the OOB error also greatly depends on the total number of predictors. This is again attributable to the trees’ preference for the larger class. It can be shown that the presence of more predictors leads to a more extreme preference for the majority class. The null case studies presented in the section “Role of mtry” and in Fig 8 were repeated for settings with p = 10 and p = 1000. Fig 9 shows the fraction of class 1 predictions (average of 500 repetitions) for p = 10, p = 100 and p = 1000. It shows that the preference for predicting class 1 by RF is more pronounced for settings with a larger number of predictors.
Fig 9. Trees’ preference for predicting larger class in dependence on mtry and number of predictors.
Fraction of class 1 (minority class in training sample) predictions obtained for balanced test samples with 5000 observations from class 1 and 2, each (null case setting). Predictions were obtained by RFs with specific mtry from a corresponding grid of mtry values ({1, 2, …, 10} for p = 10, {1, 10, 20, …, 100} for p = 100, {1, 100, 200, …, 1000} for p = 1000). RFs were trained on n = 30 observations (10 from class 1 and 20 from class 2) with p ∈ {10, 100, 1000}. The mean fractions over 500 repetitions are shown. The grey dots indicate the most commonly used default choices for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g009
Again, depending on the class imbalance in the data used to construct the RF, a preference for the larger class can be of advantage or disadvantage for the bias in the OOB error. With unbalanced training data, a preference for the majority class will lead to a smaller bias in the OOB error; see the section “Role of mtry”. A larger bias in the OOB error will be obtained in contrast if the training data is balanced.
Correlations between predictors also play a role, as can be seen when comparing the results of the real data null case studies with and without any correlations, respectively (Figs 10 and 11). We observe that the bias of the OOB error and the CV error is larger if predictors are uncorrelated. Intuitively, if predictors are correlated, they contain more or less the same (or at least similar) information. Thus, there is less information contained in correlated predictors than in uncorrelated predictors. A similar mechanism occurs that has been described for the number of predictors: the less information that is contained in the data (e.g. due to a small number of predictors or high correlations), the less extreme the trees’ preference for one of the classes and the smaller the bias in the OOB error.
Fig 10. Error rate estimates for the real data null case study with correlations.
Shown are different error rate estimates for studies based on six real data sets with correlated predictors and two or three response classes, respectively, of nearly the same size. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 1000 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g010
Fig 11. Error rate estimates for the real data null case study without correlations.
Shown are different error rate estimates for studies based on six real data sets with uncorrelated predictors and two or three response classes, respectively, of nearly the same size. The error rate was estimated through the test error, the OOB error, the stratified OOB error, the CV error, and the stratified CV error for settings with different sample sizes, n, and numbers of predictors, p. The mean error rate over 1000 repetitions was obtained for a range of mtry values. The vertical grey dashed line in each plot indicates the most commonly used default choice for mtry in classification tasks, that is .
https://doi.org/10.1371/journal.pone.0201904.g011
Sampling the same number of observations per class in unbalanced data settings
RF’s preferential prediction of classes from which most training observations come from is a well-known phenomenon. A natural consequence of the preferential prediction is that new observations that in truth belong to the majority class have a high chance of correctly being classified into the larger class by the RF. In contrast to that, new observations from the minority class have only a small chance of correctly being classified into the smaller class. Therefore, it is sometimes of interest to measure the prediction performance of RF separately for observations from either class using the so-called class-specific OOB errors. For a class j, the class-specific OOB error is calculated analogous to the usual, class-unspecific OOB error, with the difference that not all training observations are considered, but only those from class j. The class-specific OOB errors as well as the class-specific test error were computed for the binary extremely unbalanced setting, and are represented by the solid lines in Fig S5 (S1 File; for the larger class) and Fig S6 (S1 File; for the smaller class). The class-specific OOB and test errors of the majority class are much smaller than those of the minority class, indicating a strong imbalance regarding the accuracy of RF for predicting observations from the different classes.
An approach called “balanced random forest” [34] tackles this imbalance by drawing the same numbers of observations with replacement from each class for each tree yielding trees that do not preferentially predict a specific class. This balanced RF approach is investigated in this section. The aim of these additional studies is to investigate the class-specific OOB error (and its bias) of the balanced RF approach and to compare it to the class-specific stratified OOB error with sampling fractions proportional to class sizes. In the original balanced RF approach, for each tree first a bootstrap sample is drawn from the smaller class and subsequently, a number of observations equal to the number of observations in the smaller class is drawn with replacement from the larger class. However, the problems associated with bootstrap in the case of standard RF can also be expected to occur for balanced RF. Therefore, the same numbers of observations from each class were drawn without replacement instead. The setting with the extremely unbalanced class sizes was used for this analysis. A number of n* = 0.75nsmall observations were sampled without replacement from each class, where nsmall denotes the number of observations from the smaller class. The number n* = 0.75nsmall was used because using n* = 0.632nsmall would result in very few training observations for each tree in cases in which the number of observations from the minority class is very small. The constant 0.75 was also recommended by Probst et al. [35], who used many publicly available data sets to find optimal default values for various tuning parameters and found that subsampling approximately 75% of observations for the trees in RF delivers good results in the majority of cases. The dashed lines in Figs S5 and S6 (S1 File) represent the class-specific OOB errors and the class-specific test error for the larger and the smaller class, respectively.
For both approaches (balanced RF and RF using stratified sampling with sampling fractions that are proportional to class sizes), the class-specific OOB errors can rarely be distinguished from the corresponding class-specific test errors. Thus, for both approaches, the class-specific OOB errors seem to be almost unbiased.
With respect to predictive ability we note that observations from the smaller class tend to be much better predicted for the balanced RF, in particular for smaller mtry values, including the commonly used choice . While observations from the larger class have more accurate predictions when performing stratified sampling with sampling fractions proportional to class sizes, the class-specific test errors of the larger class are also small when sampling the same numbers (except for the settings with p = 10). Note also that when sampling the same numbers, the class-specific test errors are almost identical for the two classes for each setting. This illustrates that sampling the same numbers of observations leads to an equal prediction performance for both classes.
For p = 10, the class-specific test errors of the larger class are quite high when sampling the same numbers and almost zero when using sampling fractions that are proportional to the class sizes. The reason for the former is that there is relatively few signal in the data for p = 10 (only two predictors with effect); the reason for the latter is that the larger class is almost always predicted when sampling fractions are proportional to class sizes. The latter preference for the larger class also explains why for p = 10 the overall (class-unspecific) test errors shown in Fig S7 (S1 File) are much lower using sampling fractions that are proportional to class sizes than when sampling the same numbers. As expected, no (relevant) systematic differences between the OOB errors and the corresponding overall test errors can be observed, both when sampling fractions are proportional to class sizes and sampling the same numbers. For p = 100, the overall test errors are similar between the two methods. This is also the case for p = 1000 if large values for mtry are chosen; if smaller mtry values are chosen, the overall OOB error obtained when sampling the same numbers is clearly smaller, in particular in the region of .
For unbalanced data, both when sampling the same numbers of observations (balanced RF) and when using sampling fractions that are proportional to the class sizes, the class-specific OOB errors are (almost) unbiased with respect to the corresponding class-specific test errors. Sampling the same numbers of observations from each class yields a RF that has the same prediction performance independent of the class an observation comes from. For observations from the smaller class prediction performance is considerably higher than that obtained when using sampling fractions that are proportional to the class sizes. Nevertheless, for observations from the larger class, sampling fractions that are proportional to the class sizes performs slightly better than sampling the same numbers from each class. In unbalanced settings, in which there is a strong interest in predicting observations from the smaller classes well, sampling the same number of observations from each class might therefore be the method of choice.
Consequences for tuning mtry
The OOB error is frequently used to tune parameters like mtry. From the studies in the section “Quantitative assessment of the bias”, we have seen that the unstratified OOB error and the unstratified CV error often overestimate the true prediction error. Further, it was seen in some settings that the overestimation depends on mtry. This was not the case for the unstratified procedures, which were almost unbiased. In the following, the performance of RF when the mtry value is chosen based on the OOB error, the stratified OOB error, the CV error and the stratified CV error are compared. The performance was measured by the error rate which was computed based on an independent test data set. A different performance between RFs selected based on the stratified and the unstratified error estimation procedures would suggest that the bias affects tuning parameter selection, or in other words, that a suboptimal model might be chosen when the OOB error (or unstratified CV) is used for parameter tuning.
In the considered simulation studies and in the real data studies, there were no systematic differences between the error rates obtained when choosing mtry using the four methods (not shown). However, for the additional simulation studies with many variables with effect, there are differences in the settings with p = 1000 and n = 20. Fig 6c shows that a small mtry of 10 yields the RF with the best performance since the test error is smallest when using this mtry value. The OOB error, however, steadily decreases with larger values for mtry, suggesting that large values of mtry, such as 1000, should be used instead. Fig 12 shows the performance of the resulting RFs for 500 repetitions of the studies. For the setting with p = 1000 and n = 20 (Fig 12c) the mean difference in performance between the OOB error and the stratified OOB error is 1.5%, and the mean difference between the unstratified CV error and the stratified CV error is 1.9%. The bias in the OOB error thus impacts tuning parameter selection and leads to the selection of suboptimal classifiers in this case. However, the impact of the bias is very small and probably of no relevance in practice. For the two settings with smaller predictor numbers (p = 10, p = 100), there is again no difference between the four methods (Fig 12a and 12b).
Fig 12. The effect of the bias of OOB error on RF’s performance when used for mtry selection.
Performance of RF classifiers when mtry was selected based on the OOB error, the stratified OOB error, the unstratified CV error and the stratified CV error for the additional simulation studies with many variables with effect. The performance of RF was measured using a large independent test data set.
https://doi.org/10.1371/journal.pone.0201904.g012
A different concern arising in the context of using the OOB error for choosing the mtry value is whether using the OOB error both for choosing the mtry value and for error estimation leads to any (additional) bias of the OOB error as an estimate of the generalization error. Because the data is used twice in this scenario, first, for optimizing the mtry value and, second, for error estimation, this additional bias might be expected to lead to overoptimism, that is, too small error estimates. The following two procedures are associated with using the data twice, for choosing an optimal mtry value and for error estimation: (1) Use as error estimate of the RF the smallest OOB error obtained in the optimization, that is, the OOB error obtained for the chosen mtry value; (2) First, choose the mtry value using the OOB error, second, construct a RF using the mtry value chosen in the first step, third, calculate the OOB error of the latter RF and, lastly, use this OOB error as error estimate of the RF. In general, procedure (1) can be expected to be associated with a larger optimistic bias than procedure (2) because the smallest OOB error estimate obtained in the optimization can be expected to be overly small. For prediction methods different than RF, error estimation and tuning parameter optimization is usually performed using CV instead of OOB error estimation. In the latter context, the biases of procedures (1) and (2) have already been investigated in the literature, where it was confirmed that the bias of procedure (2) is much less severe than that of procedure (1) [36–38].
In order to investigate whether the biases of procedures (1) and (2) also apply to OOB error based optimization of the mtry value, a small simulation study was conducted in which only the binary power case setting with many variables with effect, p = 1000 and n = 20, was considered, again using 500 repetitions. This setting was chosen because the variability of the OOB error is largest for settings with small n and large p. In this analysis, procedures (1) and (2) were compared with respect to the test error, both when using stratified and unstratified subsampling. The results are shown in Fig S8 (S1 File). For both, stratified and unstratified subsampling, the errors estimated with procedure (1) are smaller than those estimated with procedure (2), confirming that the overoptimism from procedure (1) is larger than that of procedure (2). For unstratified subsampling, procedure (1) yielded error estimates that were slightly larger than the test error. Thus, in the considered setting the negative bias resulting from choosing the smallest OOB error estimate in procedure (1) was obviously strong enough to nearly neutralize the strong inherent positive bias of the unstratified subsampling described before. For stratified subsampling, for which we had observed no (relevant) bias when using fixed mtry values, there is a large downward bias of the error estimates from procedure (1), while the error estimates from procedure (2) are only slightly smaller than the test error.
Two main conclusions are drawn from these studies: (i) When choosing the mtry value using the OOB error, stratified subsampling can yield downwardly biased error rate estimates if the stratified OOB error that is smallest across all mtry values is used as an estimate of the generalization error; (ii) This bias can be greatly reduced by constructing a new RF using the mtry value that was chosen based on the stratified OOB error, and reporting the stratified OOB error of the new RF as an estimate of the generalization error. The latter point can be justified by the very small downward bias from procedure (2) that is observed for stratified subsampling in the analysis, even so the simulation setting with the highest variability of the OOB error estimates was used. Nevertheless, the gold standard procedure is using stratified CV for error estimation, choosing an optimal mtry value using the stratified OOB error in each iteration of the stratified CV.
Discussion
Although it was shown that the OOB error may overestimate the true prediction error [2, 5], the OOB error is still often used in practice as an estimate of the true prediction error in classification tasks (see e.g. [39–41]).
The overestimation is due to the fact that—particularly in the case of balanced data sets—for a particular observation the in-bag samples used to predict the class of that observation tend to feature more observations from the other class. Given the trees’ preferential prediction of the class overrepresented in the training sample this leads to a tendency to predict the opposite class, which in turn leads to the observed overestimation of the error. Due to random variations, different response class distributions in the in-bag and the OOB samples are more likely when the original sample is small. This is the reason why in all the studies shown in this paper, the overestimation in the OOB error was large in small samples. This was also seen in the studies of Mitchell [5] who considered only a few, very specific settings with small sample sizes limiting the conclusions that could be drawn from those studies. The current studies not only confirm the result of Mitchell [5] that the OOB error is biased in balanced settings with small sample sizes, but they also show that there is hardly any overestimation in large samples, which is why the OOB error can be regarded as a good estimate of the true prediction error in large samples. Nevertheless, it is difficult to foresee in which settings the OOB error will be a good estimate of the true prediction error because there are many factors that affect the bias in the OOB error and there is an interplay between the factors. These factors are related to both the data and the parameters of RF.
Concerning parameters in RF, mtry was identified as parameter that has an influence on the bias of the OOB error. Additional studies were performed (not shown) that suggest that the parameters controlling the size of trees, in contrast, have no influence on the bias of the OOB error. Depending on the response class distribution in the original sample, larger values for mtry might increase (unbalanced settings) or decrease (balanced settings) the bias.
The influence of mtry on the bias in the OOB error might be problematic in the context of parameter tuning if the OOB error is used for selecting an appropriate value for mtry. However, although there was a clear influence of mtry on the bias in some of the studies, in only one of them this has lead to the selection of suboptimal RF classifiers. This can be explained by the fact that in nearly all studies, it seemed as if the specific choice of mtry was not crucial. There was a wide range of mtry values that yielded optimal performance, especially for the high-dimensional genomic data sets with values for mtry larger than 100 yielding very similar performance. However, one cannot be sure that this applies to all future data sets. Among our studies there was one study with a clear performance peak at a specific mtry value. In this setting the tuning parameter selection based on the stratified OOB error yielded slightly more accurate RF models than that based on the classical, that is the unstratified, OOB error.
With respect to data-dependent factors, the present studies identified the response class distribution of the original sample, the predictor number, the correlation between predictors as well as their predictive ability as relevant factors that have an effect on the bias. The studies reported in the literature consider only settings in which there is an equal number of observations from all response classes [5]. The results in this paper show that the effect of mtry on the bias depends on the response class distribution of the original sample. For completely balanced samples, we observed a more extreme overestimation of the true error rate for smaller values of mtry. For unbalanced samples the opposite was true. This again underlines that it is difficult to assess whether there will be any bias in future real data applications and how severe this bias is because it depends on several different factors acting together.
In the context of obtaining powerful RF prediction models in the presence of unbalanced data, it might be worthwhile to consider sampling the same number of observations from each response class—in particular, if there is a strong interest in obtaining valid predictions for observations coming from the smaller class as well. This approach was also investigated in this paper for settings with extreme class imbalance and class-specific and overall error rates were assessed. The results suggest that sampling the same numbers of observations from each class could be a promising alternative to using sampling fractions that are proportional to class sizes, since it yielded unbiased OOB error estimates in the considered settings as well.
Of note, the problem that leads to the overestimation in the error rate is not specific to OOB estimation in RF, but is relevant to any data splitting procedure, such as cross-validation. These procedures can be expected to deliver upwardly biased error estimates for any classification method that is sensitive towards class imbalance, which is why many of the results apply to other methods beyond RF as well. In the present studies 10-fold cross-validation also yielded too pessimistic error rates. Therefore, cross-validation and related procedures are not alternatives for preventing the overestimation. Instead stratified procedures, such as stratified cross-validation, have been recommended to bypass this problem [42]. The use of stratified cross-validation for error estimation in the context of RF has not been systematically investigated so far. In the present studies, stratified cross-validation resulted in good approximations of the true prediction error of RF in the considered settings.
It should also be noted that error estimates based on data splitting procedures, such as (stratified) cross-validation estimates or OOB estimates, are, in general, associated with a high variance [43]. There are, however, no general alternative approaches for estimating the generalization error of a prediction model using a single training data set. A more precise error estimate that is in many cases also more realistic can be obtained using a large external validation data set. Note that before applying a prediction model in practice, external validation should always be performed [44, 45].
In benchmarking studies, cross-validation is often applied to compare the performance of different statistical methods. If it is applied in a non-stratified manner, it might happen that the performance for RF might appear worse than it actually is. If RF (or a different method that is sensitive towards class imbalance) is considered as a competing method in a benchmark study, it is recommended to use stratified cross-validation to avoid misinterpretations on the performance of RF or other methods that are similarly affected. Note that this problem is relevant especially to settings in which the original data contains (almost) exactly the same number of observations from the response classes, that is, it is not a problem that is encountered especially in unbalanced data settings.
In the original RF version of Breiman [1], the trees are constructed based on bootstrap samples. In the studies of Mitchell [5], the use of bootstrap sampling was shown to further increase the bias. Irrespective of this, bootstrap sampling has been shown to induce a preferential selection of certain types of predictors for a split [29]. Therefore, the use of bootstrapping in RF is disapproved to avoid misleading conclusions, and the R package party, for example, draws subsamples by default for this reason. Accordingly, the results in this paper are shown for RF that are always constructed based on subsampling—either unstratified or stratified, the latter leading to the correction addressed above.
The studies shown in this paper are mainly based on the original RF version of Breiman [1]. Some of the simulation settings were also performed with the RF version based on conditional inference trees [32] implemented in the R package party to assess whether there are any differences (results not shown). The results obtained for this RF version were very similar suggesting that the conclusions drawn from the studies are not specific to the RF version used. Moreover, the problem is not specific to the use of the error rate as performance measure. Any different measure is affected in the same manner. The area under the curve (AUC), for example, represents the probability that for an observation from the diseased class the predicted probability of being diseased is higher than for an observation from the class of healthy subjects [46]. It is often used as an alternative to the error rate for assessing the prediction accuracy in unbalanced binary classification settings. However, the AUC computed from OOB observations similarly underestimates the true AUC, and one cannot circumvent the problem of the biased OOB error by using a performance measure different than the error rate.
Both the stratified OOB error and the error rate computed from stratified cross-validation also overestimated the true prediction error in some of our studies with metric predictor variables. The overestimation was larger if many variables were associated with the response and only marginal if only few variables were associated. Overall, the overestimation through the stratified procedures was considerably smaller than that obtained through the unstratified procedures, supporting the use of stratified procedures. Future studies might aim at developing alternative error estimation strategies that are both unbiased and computationally tractable.
Finally note that the example data sets considered in our studies are all from the medical field. RF is, however, used in a large variety of application areas and the results and recommendations given in the paper are not limited to applications in the medical field.
Conclusions
Prior to our work, little had been known about the bias of the OOB error, and the OOB error is still frequently used for error estimation in classification settings. Using simulation-based and real-data based studies with metric predictor variables, it was shown that the overestimation is not restricted to binary classification settings and that it is largest in settings with
- an equal number of observations from all response classes (i.e., balanced samples),
- small sample sizes,
- a large number of predictor variables,
- small correlations between predictors and
- weak effects.
These factors act together making it difficult to foresee in which settings the OOB error will greatly overestimate the true prediction error.
The overestimation encountered in settings with metric predictor variables can depend on the parameter mtry. This might be a problem when the OOB error is used for selecting an appropriate value for mtry, a procedure frequently performed in practice. Overall, however, the prediction performance of RF was not substantially affected when using the OOB error for selecting an appropriate value for mtry in the studies shown in this paper. However, one cannot be sure that this applies to all future data.
In line with results reported in the literature [5], the use of stratified subsampling with sampling fractions that are proportional to response class sizes of the training data yielded almost unbiased error rates in most settings with metric predictors. It therefore presents an easy way of reducing the bias in the OOB error. It does not increase the cost of constructing the RF, since unstratified sampling (bootstrap of subsampling) is simply replaced by stratified subsampling.
For any settings that include only metric predictor variables it is thus strongly recommended to use stratified subsampling with sampling fractions that are proportional to class sizes in place of unstratified sampling that is, by default, used in RF. This reduces the risk for misinterpretations regarding the predictive accuracy of RF, and might avoid choosing a value for mtry that possibly leads to suboptimal performance when using the OOB error for parameter tuning.
Supporting information
Acknowledgments
The authors thank Anne-Laure Boulesteix for fruitful discussions and Sarah Tegenfeldt and Jenny Lee for language corrections.
References
- 1.
Breiman L. Random forests. Mach Learn. 2001;45(1):5–32.- View Article
- Google Scholar
- 2.
Bylander T. Estimating generalization error on two-class datasets using out-of-bag estimates. Mach Learn. 2002;48(1-3):287–297.- View Article
- Google Scholar
- 3.
Zhang GY, Zhang CX, Zhang JS. Out-of-bag estimation of the optimal hyperparameter in SubBag ensemble method. Commun Stat Simul Comput. 2010;39(10):1877–1892.- View Article
- Google Scholar
- 4.
Goldstein BA, Polley EC, Briggs F. Random forests for genetic association studies. Stat Appl Genet Mol Biol. 2011;10(1):1–34.- View Article
- Google Scholar
- 5.
Mitchell MW. Bias of the Random Forest out-of-bag (OOB) error for certain input parameters. Open J Stat. 2011;1(3):205–211.- View Article
- Google Scholar
- 6.
Oliveira S, Oehler F, San-Miguel-Ayanz J, Camia A, Pereira J. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For Ecol Manage. 2012;275:117–129.- View Article
- Google Scholar
- 7.
Hassane DC, Guzman ML, Corbett C, Li X, Abboud R, Young F, et al. Discovery of agents that eradicate leukemia stem cells using an in silico screen of public gene expression data. Blood. 2008;111(12):5654–5662. pmid:18305216- View Article
- PubMed/NCBI
- Google Scholar
- 8.
Nicodemus KK, Callicott JH, Higier RG, Luna A, Nixon DC, Lipska BK, et al. Evidence of statistical epistasis between DISC1, CIT and NDEL1 impacting risk for schizophrenia: biological validation with functional neuroimaging. Hum Genet. 2010;127(4):441–452. pmid:20084519- View Article
- PubMed/NCBI
- Google Scholar
- 9.
Nicodemus KK, Malley JD. Predictor correlation impacts machine learning algorithms: implications for genomic studies. Bioinformatics. 2009;25(15):1884–1890. pmid:19460890- View Article
- PubMed/NCBI
- Google Scholar
- 10.
Kim DS, Lee SM, Park JS. In: Wang J, Yi Z, Zurada JM, Lu BL, Yin H, editors. Building Lightweight Intrusion Detection System Based on Random Forest. Berlin, Heidelberg: Springer; 2006. p. 224–230. - 11.
R Core Team. R: A Language and Environment for Statistical Computing; 2013. Available from: http://www.R-project.org/. - 12.
Liaw A, Wiener M. Classification and Regression by randomForest. R News. 2002;2(3):18–22.- View Article
- Google Scholar
- 13.
Breiman L. Out-of-bag estimation. Citeseer; 1996. - 14.
Breiman L. Bagging predictors. Mach Learn. 1996;24(2):123–140.- View Article
- Google Scholar
- 15.
Goldstein BA, Hubbard AE, Cutler A, Barcellos LF. An application of Random Forests to a genome-wide association dataset: methodological considerations & new findings. BMC Genet. 2010;11:1.- View Article
- Google Scholar
- 16.
Díaz-Uriarte R, De Andres SA. Gene selection and classification of microarray data using random forest. BMC Bioinformatics. 2006;7:3. pmid:16398926- View Article
- PubMed/NCBI
- Google Scholar
- 17.
Genuer R, Poggi JM, Tuleau C. Random Forests: some methodological insights. arXiv preprint arXiv:08113619. 2008;. - 18.
Dettling M, Bühlmann P. Boosting for tumor classification with gene expression data. Bioinformatics. 2003;19(9):1061–1069. pmid:12801866- View Article
- PubMed/NCBI
- Google Scholar
- 19.
Tan AC, Gilbert D. Ensemble machine learning on gene expression data for cancer classification. Appl Bioinformatics. 2003;2(3 Suppl):S75–S83. pmid:15130820- View Article
- PubMed/NCBI
- Google Scholar
- 20.
Boulesteix AL. Ten simple rules for reducing overoptimistic reporting in methodological computational research. PLoS Comput Biol. 2015;11(4):e1004191. pmid:25905639- View Article
- PubMed/NCBI
- Google Scholar
- 21.
Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, et al. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci U S A. 1999;96(12):6745–6750. pmid:10359783- View Article
- PubMed/NCBI
- Google Scholar
- 22.
van’t Veer LJ, Dai H, Van De Vijver MJ, He YD, Hart AA, Mao M, et al. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415(6871):530–536.- View Article
- Google Scholar
- 23.
Singh D, Febbo PG, Ross K, Jackson DG, Manola J, Ladd C, et al. Gene expression correlates of clinical prostate cancer behavior. Cancer Cell. 2002;1(2):203–209. pmid:12086878- View Article
- PubMed/NCBI
- Google Scholar
- 24.
Pomeroy SL, Tamayo P, Gaasenbeek M, Sturla LM, Angelo M, McLaughlin ME, et al. Prediction of central nervous system embryonal tumour outcome based on gene expression. Nature. 2002;415(6870):436–442. pmid:11807556- View Article
- PubMed/NCBI
- Google Scholar
- 25.
Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286(5439):531–537. pmid:10521349- View Article
- PubMed/NCBI
- Google Scholar
- 26.
Floares AG, Calin GA, Manolache FB. In: Tan Y, Shi Y, editors. Bigger Data Is Better for Molecular Diagnosis Tests Based on Decision Trees. Springer, Cham; 2016. p. 288–295. - 27.
Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In: International Joint Conference on Artificial Intelligence. IJCAI’95. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.; 1995. p. 1137–1143. - 28.
Kim H, Loh WY. Classification trees with unbiased multiway splits. J Am Stat Assoc. 2001;96(454):589–604.- View Article
- Google Scholar
- 29.
Strobl C, Boulesteix AL, Zeileis A, Hothorn T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinformatics. 2007;8:25. pmid:17254353- View Article
- PubMed/NCBI
- Google Scholar
- 30.
Nicodemus KK. Letter to the Editor: On the stability and ranking of predictors from random forest variable importance measures. Brief Bioinform. 2011;12(4):369–373. pmid:21498552- View Article
- PubMed/NCBI
- Google Scholar
- 31.
Boulesteix AL, Bender A, Bermejo JL, Strobl C. Random forest Gini importance favours SNPs with large minor allele frequency: assessment, sources and recommendations. Brief Bioinform. 2012a;13:292–304.- View Article
- Google Scholar
- 32.
Hothorn T, Hornik K, Zeileis A. Unbiased recursive partitioning: A conditional inference framework. J Comput Graph Stat. 2006;15(3):651–674.- View Article
- Google Scholar
- 33.
Boulesteix AL, Janitza S, Kruppa J, König IR. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdiscip Rev Data Min Knowl Discov. 2012;2(6):493–507.- View Article
- Google Scholar
- 34.
Chain C, Liaw A, Breiman L. Using random forest to learn imbalanced data. University of California, Berkeley; 2004. 666. - 35.
Probst P, Bischl B, Boulesteix AL. Tunability: Importance of hyperparameters of machine learning algorithms. ArXiv preprint; 2018. arXiv:1802.09596. - 36.
Varma S, Simon R. Bias in error estimation when using cross-validation for model selection. BMC Bioinformatics. 2006;7:91. pmid:16504092- View Article
- PubMed/NCBI
- Google Scholar
- 37.
Bernau C, Augustin T, Boulesteix AL. Correcting the optimal resampling-based error rate by estimating the error rate of wrapper algorithms. Biometrics. 2013;69(3):693–702. pmid:23845182- View Article
- PubMed/NCBI
- Google Scholar
- 38.
Hornung R, Bernau C, Truntzer C, Wilson R, Stadler T, Boulesteix AL. A measure of the impact of CV incompleteness on prediction error estimation with application to PCA and normalization. BMC Medical Research Methodology. 2015;15:95. pmid:26537575- View Article
- PubMed/NCBI
- Google Scholar
- 39.
DeVries B, Pratihast AK, Verbesselt J, Kooistra L, Herold M. Characterizing Forest Change Using Community-Based Monitoring Data and Landsat Time Series. PLoS One. 2016;11(3):e0147121. pmid:27018852- View Article
- PubMed/NCBI
- Google Scholar
- 40.
Kim KY, Zhang X, Cha IH. Combined genomic expressions as a diagnostic factor for oral squamous cell carcinoma. Genomics. 2014;103(5):317–322. pmid:24321173- View Article
- PubMed/NCBI
- Google Scholar
- 41.
Marston CG, Danson FM, Armitage RP, Giraudoux P, Pleydell DR, Wang Q, et al. A random forest approach for predicting the presence of Echinococcus multilocularis intermediate host Ochotona spp. presence in relation to landscape characteristics in western China. Appl Geogr. 2014;55:176–183. pmid:25386042- View Article
- PubMed/NCBI
- Google Scholar
- 42.
Witten IH, Frank E. Data Mining: Practical machine learning tools and techniques. San Francisco: Morgan Kaufmann; 2005. - 43.
Molinaro AM, Simon R, Pfeiffer RM. Prediction error estimation: a comparison of resampling methods. Bioinformatics. 2005;21(15):3301–3307. pmid:15905277- View Article
- PubMed/NCBI
- Google Scholar
- 44.
Simon R. When is a genomic classifier ready for prime time? Nature Clinical Practice. 2004;1:4–5. pmid:16264774- View Article
- PubMed/NCBI
- Google Scholar
- 45.
Collins GS, de Groot JA, Dutton S, Omar O, Shanyinde M, Tajar A, et al. External validation of multivariable prediction models: a systematic review of methodological conduct and reporting. BMC Medical Research Methodology. 2014;40:14.- View Article
- Google Scholar
- 46.
Pepe MS. The statistical evaluation of medical tests for classification and prediction. USA: Oxford University Press; 2004.
- Project originally posted on inertia7
- GitHub Repo
Introduction to Random Forest
A Random Forest (also known as Random Decision Forest) is a popular supervised classification method used for predictive modeling both for classification and regression problems (for this tutorial, we will be going over Random Forest in the classification context). Essentially a Random Forest is an entire forest of random uncorrelated decision trees, classified as an ensemble method.
Ensemble methods is the use of multiple learning models to gain better predictive results. For Random Forest, the model creates multiple Decision Trees.
We will be using a famous data set from the UCI Machine Learning Repository, called the Breast Cancer (Diagnostic) data set which deals with binary classification.
Familiarity with Classification and Regression Tree (or CART) modeling is expected for this tutorial, a great resource for CART modeling can be found in Chapter 8 of this book. I will give a brief overview of different CART methodologies culminating to the relevance and preference towards Random Forest, beginning with Decision Trees.
Decision Trees
Decision trees are simple but intuitive models that utilize a top down approach where the root node then creates binary splits until a certain criteria is met. More information on its implementation can be found here.
The binary splitting of nodes will give an outcome of the predicted value based on the interior nodes leading to the terminal (final) nodes. In the classification context, it will output a predicted target class for each terminal node produced.
Although intuitive, Decision trees do have limitations that prevent it from being a useful model in machine learning applications.
Limitations to Decision trees
Decision trees tend to have high variance when utilizing different training and test sets of the same data, since they tend to over-fit on the training data leading to poorly performance on unseen data. This limits the usage of Decision trees in predictive modeling, but through ensemble methods we can create models that produce powerful results utilzing the underlying Decision Trees as a basis for the methodology behind ensembles.
Bootstrap Aggregating Trees
Through a process known as Bootstrap Aggregating (or Bagging), we create an ensemble (forest) of trees where multiple training sets are generated with replacement (meaning data instances or in our case patients can be repeated). Once the training sets are created a CART model is trained on each subsample.
This approach helps reduce variance by averaging the ensemble’s results, creating a majority votes model. Another important feature of Bagging trees is that the model uses the entire feature space when considering node splits. Bagging trees allow the trees to grow without pruning (reducing the tree depth sizes. See this article for more details) resulting in high variance but lower bias, which can help in improving predictive power.
However, a downside to this process is utliziation of the entire feature space since there is a risk of having correlation between trees increasing bias in our model.
Limitation to Bagging Trees
As stated earlier since each new subsample can include repeated observations we can over-fit our model on the training set.
The main limitation of Bagging Trees is the use of the entire feature space when creating splits in the trees. If some variables within our feature space are indicative of certain predictions we run the risk of having a forest of correlated trees, thereby increasing bias and reducing variance.
A simple tweak of Bagging Trees methodology proves advantageous to our models predictive power.
Random Forest
Random Forest aims to reduce the previously mentioned correlation by choosing only a subsample of the feature space at each split. Essentially aiming to make the trees de-correlated, along with pruning of trees by setting a stopping criteria for node splits (more on this later).
The processes outlined in this project are typical of a machine learning project, so I’ve given an outline of what will be done throughout the tutorial.
After this tutorial you will be familiar with how to implement (in python):
- Basic exploratory analysis
- Training and test set creation
- Model fitting using
sklearn - Hyperparamter optimization
- Out of Bag Error Rate
- Calculating Variable Importance
- Test Set calculations
- Cross Validation
- ROC Curve Estimation
Buisness Uses
Random Forest can be used for a plethora of data circumstances including but not limited to:
- Image Classification
- Detecting Fraudulent cases in banking systems
- Recommendation Engines
- Feature Selection
Load Packages
We load our modules into our python environment. I am employing a Jupyter Notebook while running inside a virtualenv environment (the requirements.txt file associated with this repo contains the module information for reproducibility).
We will be primarily using the SciPy stack focusing on pandas, matplotlib, seaborn and sklearn for this tutorial.
# Import modules %matplotlib inline import time import random import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.metrics import roc_curve, auc from sklearn.metrics import confusion_matrix from sklearn.metrics import classification_report from sklearn.model_selection import KFold, cross_val_score from sklearn.model_selection import train_test_split, GridSearchCV from sklearn.metrics import confusion_matrix from sklearn.ensemble import RandomForestClassifier from sklearn.utils.validation import check_is_fitted from sklearn.exceptions import NotFittedError from urllib.request import urlopen plt.style.use('ggplot') pd.set_option('display.max_columns', 500)
Load Data
For this section, I’ll load the data into a Pandas dataframe using urlopen from the urllib.request module.
Instead of downloading a csv, I started implementing this method (inspired by this Python Tutorials) where I grab the data straight from the UCI Machine Learning Database using an http request.
# Loading data and cleaning dataset UCI_data_URL = 'https://archive.ics.uci.edu/ml/machine-learning-databases /breast-cancer-wisconsin/wdbc.data'
I do recommend on keeping a static file for your dataset as well.
Next, I created a list with the appropriate names and set them as the data frame’s column names, then I load them unto a pandas data frame
names = ['id_number', 'diagnosis', 'radius_mean', 'texture_mean', 'perimeter_mean', 'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean','concave_points_mean', 'symmetry_mean', 'fractal_dimension_mean', 'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se', 'compactness_se', 'concavity_se', 'concave_points_se', 'symmetry_se', 'fractal_dimension_se', 'radius_worst', 'texture_worst', 'perimeter_worst', 'area_worst', 'smoothness_worst', 'compactness_worst', 'concavity_worst', 'concave_points_worst', 'symmetry_worst', 'fractal_dimension_worst'] dx = ['Benign', 'Malignant']
breast_cancer = pd.read_csv(urlopen(UCI_data_URL), names=names)
Cleaning
We do some minor cleanage like setting the id_number to be the data frame index, along with converting the diagnosis to the standard binary 1, 0 representation using the map() function.
# Setting 'id_number' as our index breast_cancer.set_index(['id_number'], inplace = True) # Converted to binary to help later on with models and plots breast_cancer['diagnosis'] = breast_cancer['diagnosis'].map({'M':1, 'B':0})
Missing Values
Given context of the data set, I know that there is no missing data, but I ran a for-loop that checks to see if there was any missing values through each column. Printing the column name and total missing values for that column, iteratively.
breast_cancer.apply(lambda x: x.isnull().values.ravel().sum())
diagnosis 0
radius_mean 0
texture_mean 0
perimeter_mean 0
area_mean 0
smoothness_mean 0
compactness_mean 0
concavity_mean 0
concave_points_mean 0
symmetry_mean 0
fractal_dimension_mean 0
radius_se 0
texture_se 0
perimeter_se 0
area_se 0
smoothness_se 0
compactness_se 0
concavity_se 0
concave_points_se 0
symmetry_se 0
fractal_dimension_se 0
radius_worst 0
texture_worst 0
perimeter_worst 0
area_worst 0
smoothness_worst 0
compactness_worst 0
concavity_worst 0
concave_points_worst 0
symmetry_worst 0
fractal_dimension_worst 0
dtype: int64
This will be used for the random forest model, where the id_number won’t be relevant.
# For later use in CART models names_index = names[2:]
Let’s preview the data set utilizing the head() function which will give the first 5 values of our data frame.
<iframe width=»798″ height=»280″ frameborder=»0″ src=’https://cdn.rawgit.com/raviolli77/7275dd3c9455f052171b22d3da5185b2/raw/fdc8c659fae9288f1ba1da01103265eb9403fc0b/head.html’></iframe>
Next, we’ll give the dimensions of the data set; where the first value is the number of patients and the second value is the number of features.
We print the data types of our data set this is important because this will often be an indicator of missing data, as well as giving us context to anymore data cleanage.
print("Here's the dimensions of our data frame:n", breast_cancer.shape) print("Here's the data types of our columns:n", breast_cancer.dtypes)
Here's the dimensions of our data frame:
(569, 31)
Here's the data types of our columns:
diagnosis int64
radius_mean float64
texture_mean float64
perimeter_mean float64
area_mean float64
smoothness_mean float64
compactness_mean float64
concavity_mean float64
concave_points_mean float64
symmetry_mean float64
fractal_dimension_mean float64
radius_se float64
texture_se float64
perimeter_se float64
area_se float64
smoothness_se float64
compactness_se float64
concavity_se float64
concave_points_se float64
symmetry_se float64
fractal_dimension_se float64
radius_worst float64
texture_worst float64
perimeter_worst float64
area_worst float64
smoothness_worst float64
compactness_worst float64
concavity_worst float64
concave_points_worst float64
symmetry_worst float64
fractal_dimension_worst float64
dtype: object
Class Imbalance
The distribution for diagnosis is important because it brings up the discussion of Class Imbalance within Machine learning and data mining applications.
Class Imbalance refers to when a target class within a data set is outnumbered by the other target class (or classes). This can lead to misleading accuracy metrics, known as accuracy paradox, therefore we have to make sure our target classes aren’t imblanaced.
We do so by creating a function that will output the distribution of the target classes.
NOTE: If your data set suffers from class imbalance I suggest reading documentation on upsampling and downsampling.
def print_dx_perc(data_frame, col): """Function used to print class distribution for our data set""" try: # Stores value counts col_vals = data_frame[col].value_counts() # Resets index to make index a column in data frame col_vals = col_vals.reset_index() # If the number of unique instances in column exceeds 20 print warning if len(col_vals['index']) > 20: print('Warning: values in column are more than 20 nPlease try a column with lower value counts!') # Else it calculates/prints percentage for each unique value in column else: # Create a function to output the percentage f = lambda x, y: 100 * (x / sum(y)) for i in range(0, len(col_vals['index'])): print('{0} accounts for {1:.2f}% of the {2} column' .format(col_vals['index'][i], f(col_vals[col].iloc[i], col_vals[col]), col)) # try-except block goes here if it can't find the column in data frame except KeyError as e: print('{0}: Not found'.format(e)) print('Please choose the right column name!')
print_dx_perc(breast_cancer, 'diagnosis')
0 accounts for 62.74% of the diagnosis column
1 accounts for 37.26% of the diagnosis column
Fortunately, this data set does not suffer from class imbalance.
Next we will use a useful function that gives us standard descriptive statistics for each feature including mean, standard deviation, minimum value, maximum value, and range intervals.
<iframe width=»798″ height=»350″ frameborder=»0″ src=’https://cdn.rawgit.com/raviolli77/f0b743ab560331bf9382d9a6ad0b8ff7/raw/54d0f327ed07b42294da40303380530edd7b9f3d/describe_breast_cancer.html’></iframe>
We can see through the maximum row that our data varies in distribution, this will be important when considering classification models.
Standardization is an important requirement for many classification models that should be considered when implementing pre-processing. Some models (like neural networks) can perform poorly if pre-processing isn’t considered, so the describe() function can be a good indicator for standardization. Fortunately Random Forest does not require any pre-processing (for use of categorical data see sklearn’s Encoding Categorical Data section).
Creating Training and Test Sets
We split the data set into our training and test sets which will be (pseudo) randomly selected having a 80-20% splt. We will use the training set to train our model along with some optimization, and use our test set as the unseen data that will be a useful final metric to let us know how well our model does.
When using this method for machine learning always be weary of utilizing your test set when creating models. The issue of data leakage is a serious issue that is common in practice and can result in over-fitting. More on data leakage can be found in this Kaggle article
feature_space = breast_cancer.iloc[:, breast_cancer.columns != 'diagnosis'] feature_class = breast_cancer.iloc[:, breast_cancer.columns == 'diagnosis'] training_set, test_set, class_set, test_class_set = train_test_split(feature_space, feature_class, test_size = 0.20, random_state = 42)
NOTE: What I mean when I say pseudo-random is that we would want everyone who replicates this project to get the same results. So we use a random seed generator and set it equal to a number of our choosing, this will then make the results the same for anyone who uses this generator, awesome for reproducibility.
# Cleaning test sets to avoid future warning messages class_set = class_set.values.ravel() test_class_set = test_class_set.values.ravel()
Fitting Random Forest
Now we will create the model no parameter tuning aside from the random seed generator.
What I mean when I say parameter tuning is different machine learning models utilize various parameters which have to be tuned by the person implementing the algorithm. Here I’ll give a brief overview of the parameters I will be tuning in this tutorial:
- max_depth: the maximum splits for all trees in the forest.
- bootstrap: indicating whether or not we want to use bootstrap samples when building trees
- max_features: the maximum number of features that will be used in the node splitting (the main difference previously mentioned between Bagging trees and Random Forest). Typically we want a value that is less than p, where p is all features in our dataset.
- criterion: this is the metric used to asses the stopping criteria for the Decision trees, more on this later
Once we’ve instantiated our model we will go ahead and tune our parameters.
# Set the random state for reproducibility fit_rf = RandomForestClassifier(random_state=42)
Hyperparameters Optimization
Utilizing the GridSearchCV functionality, I create a dictionary with parameters I am looking to optimize to create the best model for our data. Setting the n_jobs to 3 tells the grid search to run 3 jobs in parallel reducing the time the function will take to compute the best parameters. I included the timer to help see how long different jobs took, ultimately deciding on using 3 parallel jobs.
This will help set parameters which I will then use to tune one final paramter; the number of trees in my forest.
np.random.seed(42) start = time.time() param_dist = {'max_depth': [2, 3, 4], 'bootstrap': [True, False], 'max_features': ['auto', 'sqrt', 'log2', None], 'criterion': ['gini', 'entropy']} cv_rf = GridSearchCV(fit_rf, cv = 10, param_grid=param_dist, n_jobs = 3) cv_rf.fit(training_set, class_set) print('Best Parameters using grid search: n', cv_rf.best_params_) end = time.time() print('Time taken in grid search: {0: .2f}'.format(end - start))
Best Parameters using grid search:
{'bootstrap': True, 'criterion': 'gini', 'max_depth': 3, 'max_features': 'log2'}
Time taken in grid search: 8.56
Once we are given the best parameter combination, we set the parameters to our model.
Notice how we didn’t utilize the bootstrap: True parameter, this will make sense in the following section.
# Set best parameters given by grid search fit_rf.set_params(criterion = 'gini', max_features = 'log2', max_depth = 3)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=3, max_features='log2', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=10, n_jobs=1, oob_score=False, random_state=42,
verbose=0, warm_start=False)
Out of Bag Error Rate
Another useful feature of Random Forest is the concept of Out of Bag Error Rate or OOB error rate. When creating the forest, typically only 2/3 of the data is used to train each tree, this gives us 1/3 of unseen data that we can then utilize in a way that is advantageos to our accuracy metrics withou being computationally expensive like cross validation.
When calculating OOB, two parameters have to be changed as outlined below. Also utilizing a for-loop across a multitude of forest sizes, we can calculate the OOB Error rate and use this to asses how many trees are appropriate for our model!
NOTE: When calculating the oob score, setting bootstrap=True will produce errors, but is necessary for oob_score calculation as stated on this example
For the original analysis I compared Kth Nearest Neighbor, Random Forest, and Neural Networks, so most of the analysis was done to compare across different models.
fit_rf.set_params(warm_start=True, oob_score=True) min_estimators = 15 max_estimators = 1000 error_rate = {} for i in range(min_estimators, max_estimators + 1): fit_rf.set_params(n_estimators=i) fit_rf.fit(training_set, class_set) oob_error = 1 - fit_rf.oob_score_ error_rate[i] = oob_error
# Convert dictionary to a pandas series for easy plotting oob_series = pd.Series(error_rate)
fig, ax = plt.subplots(figsize=(10, 10)) ax.set_axis_bgcolor('#fafafa') oob_series.plot(kind='line', color = 'red') plt.axhline(0.055, color='#875FDB', linestyle='--') plt.axhline(0.05, color='#875FDB', linestyle='--') plt.xlabel('n_estimators') plt.ylabel('OOB Error Rate') plt.title('OOB Error Rate Across various Forest sizes n(From 15 to 1000 trees)')
<matplotlib.text.Text at 0x1058c3048>
The OOB error rate starts to oscilate at around 400 trees, so I will go ahead and use my judgement to use 400 trees in my forest. Using the pandas series object I can easily find the OOB error rate for the estimator as follows:
print('OOB Error rate for 400 trees is: {0:.5f}'.format(oob_series[400]))
OOB Error rate for 400 trees is: 0.04835
Utilizing the OOB error rate that was created with the model gives us an unbiased error rate. This can be helpful when cross validating and/or hyperparameter optimization prove to be too computationally expensive, since oob can be calculated with the model estimation.
For the sake of this tutorial I will go over the other traditional methods for machine learning including the training and test error route, along with cross validation metrics.
Traditional Training and Test Set Split
In order for this methodology to work we will set the number of trees calculated using the OOB error rate, and removing the warm_start and oob_score parameters. Along with including the bootstrap parameter.
fit_rf.set_params(n_estimators=400, bootstrap = True, warm_start=False, oob_score=False)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=3, max_features='log2', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=400, n_jobs=1, oob_score=False, random_state=42,
verbose=0, warm_start=False)
Training Algorithm
Next we train the algorithm utilizing the training and target class set we had made earlier.
fit_rf.fit(training_set, class_set)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=3, max_features='log2', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=400, n_jobs=1, oob_score=False, random_state=42,
verbose=0, warm_start=False)
Variable Importance
Once we have trained the model, we are able to assess this concept of variable importance. A downside to creating ensemble methods with Decision Trees is we lose the interpretability that a single tree gives. A single tree can outline for us important node splits along with variables that were important at each split.
Forunately ensemble methods utilzing CART models use a metric to evaluate homogeneity of splits. Thus when creating ensembles these metrics can be utilized to give insight to important variables used in the training of the model. Two metrics that are used are gini impurity and entropy.
The two metrics vary and from reading documentation online, many people favor gini impurity due to the computational cost of entropy since it requires calculating the logarithmic function. For more discussion I recommend reading this article.
Here we define each metric:
$$Gini Impurity = 1 — sum_i p_i$$
$$Entropy = sum_i -p_i * log_2 p_i$$
where $p_i$ is defined as the proportion of subsamples that belong to a certain target class.
Since we are utilizing the Gini Impurity, the impurity measure reaches 0 when all target class labels are the same.
We are able to access the feature importance of the model and using a helper function to output the importance of our variables in descending order.
def variable_importance(fit): """ Purpose ---------- Checks if model is fitted CART model then produces variable importance and respective indices in dictionary. Parameters ---------- * fit: Fitted model containing the attribute feature_importances_ Returns ---------- Dictionary containing arrays with importance score and index of columns ordered in descending order of importance. """ try: if not hasattr(fit, 'fit'): return print("'{0}' is not an instantiated model from scikit-learn".format(fit)) # Captures whether the model has been trained if not vars(fit)["estimators_"]: return print("Model does not appear to be trained.") except KeyError: print("Model entered does not contain 'estimators_' attribute.") importances = fit.feature_importances_ indices = np.argsort(importances)[::-1] return {'importance': importances, 'index': indices}
var_imp_rf = variable_importance(fit_rf) importances_rf = var_imp_rf['importance'] indices_rf = var_imp_rf['index']
def print_var_importance(importance, indices, name_index): """ Purpose ---------- Prints dependent variable names ordered from largest to smallest based on information gain for CART model. Parameters ---------- * importance: Array returned from feature_importances_ for CART models organized by dataframe index * indices: Organized index of dataframe from largest to smallest based on feature_importances_ * name_index: Name of columns included in model Returns ---------- Prints feature importance in descending order """ print("Feature ranking:") for f in range(0, indices.shape[0]): i = f print("{0}. The feature '{1}' has a Mean Decrease in Impurity of {2:.5f}" .format(f + 1, names_index[indices[i]], importance[indices[f]]))
print_var_importance(importances_rf, indices_rf, names_index)
Feature ranking:
1. The feature 'area_worst' has a Mean Decrease in Impurity of 0.12986
2. The feature 'perimeter_worst' has a Mean Decrease in Impurity of 0.12095
3. The feature 'concave_points_worst' has a Mean Decrease in Impurity of 0.11555
4. The feature 'concave_points_mean' has a Mean Decrease in Impurity of 0.10014
5. The feature 'radius_worst' has a Mean Decrease in Impurity of 0.07805
6. The feature 'concavity_mean' has a Mean Decrease in Impurity of 0.06214
7. The feature 'area_mean' has a Mean Decrease in Impurity of 0.05656
8. The feature 'radius_mean' has a Mean Decrease in Impurity of 0.05457
9. The feature 'perimeter_mean' has a Mean Decrease in Impurity of 0.05174
10. The feature 'area_se' has a Mean Decrease in Impurity of 0.04326
11. The feature 'concavity_worst' has a Mean Decrease in Impurity of 0.03866
12. The feature 'compactness_worst' has a Mean Decrease in Impurity of 0.02033
13. The feature 'compactness_mean' has a Mean Decrease in Impurity of 0.01616
14. The feature 'texture_worst' has a Mean Decrease in Impurity of 0.01554
15. The feature 'radius_se' has a Mean Decrease in Impurity of 0.01452
16. The feature 'perimeter_se' has a Mean Decrease in Impurity of 0.01308
17. The feature 'texture_mean' has a Mean Decrease in Impurity of 0.01220
18. The feature 'symmetry_worst' has a Mean Decrease in Impurity of 0.01175
19. The feature 'smoothness_worst' has a Mean Decrease in Impurity of 0.00938
20. The feature 'concavity_se' has a Mean Decrease in Impurity of 0.00910
21. The feature 'concave_points_se' has a Mean Decrease in Impurity of 0.00445
22. The feature 'smoothness_mean' has a Mean Decrease in Impurity of 0.00398
23. The feature 'fractal_dimension_se' has a Mean Decrease in Impurity of 0.00395
24. The feature 'fractal_dimension_worst' has a Mean Decrease in Impurity of 0.00267
25. The feature 'fractal_dimension_mean' has a Mean Decrease in Impurity of 0.00221
26. The feature 'smoothness_se' has a Mean Decrease in Impurity of 0.00217
27. The feature 'symmetry_mean' has a Mean Decrease in Impurity of 0.00205
28. The feature 'texture_se' has a Mean Decrease in Impurity of 0.00204
29. The feature 'symmetry_se' has a Mean Decrease in Impurity of 0.00194
30. The feature 'compactness_se' has a Mean Decrease in Impurity of 0.00099
We can see here that our top 5 variables were area_worst, perimeter_worst, concave_points_worst, concave_points_mean, radius_worst.
This can give us great insight for further analysis like feature engineering, although we won’t go into this during this tutorial. This step can help give insight to the practitioner and audience as to what variables played an important part to the predictions generated by the model.
In our test case, this can help people in the medical field focus on the top variables and their relationship with breast cancer.
def variable_importance_plot(importance, indices, name_index): """ Purpose ---------- Prints bar chart detailing variable importance for CART model NOTE: feature_space list was created because the bar chart was transposed and index would be in incorrect order. Parameters ---------- * importance: Array returned from feature_importances_ for CART models organized by dataframe index * indices: Organized index of dataframe from largest to smallest based on feature_importances_ * name_index: Name of columns included in model Returns: ---------- Returns variable importance plot in descending order """ index = np.arange(len(names_index)) importance_desc = sorted(importance) feature_space = [] for i in range(indices.shape[0] - 1, -1, -1): feature_space.append(names_index[indices[i]]) fig, ax = plt.subplots(figsize=(10, 10)) ax.set_axis_bgcolor('#fafafa') plt.title('Feature importances for Random Forest Model nBreast Cancer (Diagnostic)') plt.barh(index, importance_desc, align="center", color = '#875FDB') plt.yticks(index, feature_space) plt.ylim(-1, 30) plt.xlim(0, max(importance_desc) + 0.01) plt.xlabel('Mean Decrease in Impurity') plt.ylabel('Feature') plt.show() plt.close()
variable_importance_plot(importances_rf, indices_rf, names_index)
The visual helps drive the point of variable importance, since you can clearly see the difference in importance of variables for the ensemble method. Certain cutoff points can be made to reduce the inclusion of features and can help in the accuracy of the model, since we’ll be removing what is considered noise within our feature space.
Cross Validation
Cross validation is a powerful tool that is used for estimating the predicitive power of your model, which performs better than the conventional training and test set. What we are doing with Cross Validation is we are essentially creating multiple training and test sets, then averaging the scores to give us a less biased metric.
In our case we are creating 10 sets within our data set that calculates the estimations we have done already, but then averages the prediction error to give us a more accurate representation of our model’s prediction power, since the model’s performance can vary significantly when utilizing different training and test sets.
Suggested Reading: For a more concise explanation of Cross Validation I recommend reading An Introduction to Statistical Learnings with Applications in R, specifically chapter 5.1!
K-Fold Cross Validation
Here we are employing K-Fold Cross Validation, more specifically 10 folds. So therefore we are creating 10 subsets of our data where we will be employing the training and test set methodology then averaging the accuracy for all folds to give us our estimatation.
Within a Random Forest context if your data set is significantly large one can choose to not do cross validation and use the OOB error rate as an unbiased metric for computational costs, but for this tutorial I included it to show different accuracy metrics available.
def cross_val_metrics(fit, training_set, class_set, estimator, print_results = True): """ Purpose ---------- Function helps automate cross validation processes while including option to print metrics or store in variable Parameters ---------- fit: Fitted model training_set: Data_frame containing 80% of original dataframe class_set: data_frame containing the respective target vaues for the training_set print_results: Boolean, if true prints the metrics, else saves metrics as variables Returns ---------- scores.mean(): Float representing cross validation score scores.std() / 2: Float representing the standard error (derived from cross validation score's standard deviation) """ my_estimators = { 'rf': 'estimators_', 'nn': 'out_activation_', 'knn': '_fit_method' } try: # Captures whether first parameter is a model if not hasattr(fit, 'fit'): return print("'{0}' is not an instantiated model from scikit-learn".format(fit)) # Captures whether the model has been trained if not vars(fit)[my_estimators[estimator]]: return print("Model does not appear to be trained.") except KeyError as e: print("'{0}' does not correspond with the appropriate key inside the estimators dictionary. nPlease refer to function to check `my_estimators` dictionary.".format(estimator)) raise n = KFold(n_splits=10) scores = cross_val_score(fit, training_set, class_set, cv = n) if print_results: for i in range(0, len(scores)): print("Cross validation run {0}: {1: 0.3f}".format(i, scores[i])) print("Accuracy: {0: 0.3f} (+/- {1: 0.3f})" .format(scores.mean(), scores.std() / 2)) else: return scores.mean(), scores.std() / 2
cross_val_metrics(fit_rf, training_set, class_set, 'rf', print_results = True)
Cross validation run 0: 1.000
Cross validation run 1: 0.957
Cross validation run 2: 0.935
Cross validation run 3: 0.935
Cross validation run 4: 0.957
Cross validation run 5: 0.978
Cross validation run 6: 0.933
Cross validation run 7: 0.889
Cross validation run 8: 1.000
Cross validation run 9: 0.889
Accuracy: 0.947 (+/- 0.019)
Test Set Metrics
Now we will be utilizing the test set that was created earlier to receive another metric for evaluation of our model. Recall the importance of data leakage and that we didn’t touch the test set until now, after we had done hyperparamter optimization.
We create a confusion matrix showcasing the following metrics:
| n = Sample Size | Predicted Benign | Predicted Malignant |
|---|---|---|
| Actual Benign | True Negative | False Positive |
| Actual Malignant | False Negative | True Positive |
predictions_rf = fit_rf.predict(test_set)
Confusion Matrix
Here we create a confusion matrix visual with seaborn and transposing the matrix when creating the heatmap.
def create_conf_mat(test_class_set, predictions): """Function returns confusion matrix comparing two arrays""" if (len(test_class_set.shape) != len(predictions.shape) == 1): return print('Arrays entered are not 1-D.nPlease enter the correctly sized sets.') elif (test_class_set.shape != predictions.shape): return print('Number of values inside the Arrays are not equal to each other.nPlease make sure the array has the same number of instances.') else: # Set Metrics test_crosstb_comp = pd.crosstab(index = test_class_set, columns = predictions) test_crosstb = test_crosstb_comp.as_matrix() return test_crosstb
conf_mat = create_conf_mat(test_class_set, predictions_rf) sns.heatmap(conf_mat, annot=True, fmt='d', cbar=False) plt.xlabel('Predicted Values') plt.ylabel('Actual Values') plt.title('Actual vs. Predicted Confusion Matrix') plt.show()
accuracy_rf = fit_rf.score(test_set, test_class_set) print("Here is our mean accuracy on the test set:n {0:.3f}" .format(accuracy_rf))
Here is our mean accuracy on the test set:
0.965
# Here we calculate the test error rate! test_error_rate_rf = 1 - accuracy_rf print("The test error rate for our model is:n {0: .4f}" .format(test_error_rate_rf))
The test error rate for our model is:
0.0351
As you can see we got a very similar error rate for our test set that we did for our OOB, which is a good sign for our model.
ROC Curve Metrics
Receiver Operating Characteristc Curve, calculates the False Positive Rates and True Positive Rates across different thresholds .
We will now graph these calculations, and being located the top left corner of the plot indicates a really ideal model, i.e. a False Positive Rate of 0 and True Positive Rate of 1, whereas an ROC curve that is at a 45 degree is indicative of a model that is essentially randomly guessing.
We also calculated the Area under the Curve or AUC, the AUC is used as a metric to differentiate the predicion power for those with the disease and those without it. Typically a value closer to one means that our model was able to differentiate correctly from a random sample of the two target classes of two patients with and without the disease.
# We grab the second array from the output which corresponds to # to the predicted probabilites of positive classes # Ordered wrt fit.classes_ in our case [0, 1] where 1 is our positive class predictions_prob = fit_rf.predict_proba(test_set)[:, 1] fpr2, tpr2, _ = roc_curve(test_class_set, predictions_prob, pos_label = 1)
def plot_roc_curve(fpr, tpr, auc, estimator, xlim=None, ylim=None): """ Purpose ---------- Function creates ROC Curve for respective model given selected parameters. Optional x and y limits to zoom into graph Parameters ---------- * fpr: Array returned from sklearn.metrics.roc_curve for increasing false positive rates * tpr: Array returned from sklearn.metrics.roc_curve for increasing true positive rates * auc: Float returned from sklearn.metrics.auc (Area under Curve) * estimator: String represenation of appropriate model, can only contain the following: ['knn', 'rf', 'nn'] * xlim: Set upper and lower x-limits * ylim: Set upper and lower y-limits """ my_estimators = {'knn': ['Kth Nearest Neighbor', 'deeppink'], 'rf': ['Random Forest', 'red'], 'nn': ['Neural Network', 'purple']} try: plot_title = my_estimators[estimator][0] color_value = my_estimators[estimator][1] except KeyError as e: print("'{0}' does not correspond with the appropriate key inside the estimators dictionary. nPlease refer to function to check `my_estimators` dictionary.".format(estimator)) raise fig, ax = plt.subplots(figsize=(10, 10)) ax.set_axis_bgcolor('#fafafa') plt.plot(fpr, tpr, color=color_value, linewidth=1) plt.title('ROC Curve For {0} (AUC = {1: 0.3f})' .format(plot_title, auc)) plt.plot([0, 1], [0, 1], 'k--', lw=2) # Add Diagonal line plt.plot([0, 0], [1, 0], 'k--', lw=2, color = 'black') plt.plot([1, 0], [1, 1], 'k--', lw=2, color = 'black') if xlim is not None: plt.xlim(*xlim) if ylim is not None: plt.ylim(*ylim) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.show() plt.close()
plot_roc_curve(fpr2, tpr2, auc_rf, 'rf', xlim=(-0.01, 1.05), ylim=(0.001, 1.05))
Our model did exceptional with an AUC over .90, now we do a zoomed in view to showcase the closeness our ROC Curve is relative to the ideal ROC Curve.
plot_roc_curve(fpr2, tpr2, auc_rf, 'rf', xlim=(-0.01, 0.2), ylim=(0.85, 1.01))
Classification Report
The classification report is available through sklearn.metrics, this report gives many important classification metrics including:
-
Precision: also the positive predictive value, is the number of correct predictions divided by the number of correct predictions plus false positives, so $tp / (tp + fp)$ -
Recall: also known as the sensitivity, is the number of correct predictions divided by the total number of instances so $tp / (tp + fn)$ where $fn$ is the number of false negatives -
f1-score: this is defined as the weighted harmonic mean of both the precision and recall, where the f1-score at 1 is the best value and worst value at 0, as defined by the documentation -
support: number of instances that are the correct target values
Across the board we can see that our model provided great insight into classifying patients based on the FNA scans. Important metrics to consider would be optimzing the false positive rate since within this context it would be bad for the model to tell someone that they are cancer free when in reality they have cancer.
def print_class_report(predictions, alg_name): """ Purpose ---------- Function helps automate the report generated by the sklearn package. Useful for multiple model comparison Parameters: ---------- predictions: The predictions made by the algorithm used alg_name: String containing the name of the algorithm used Returns: ---------- Returns classification report generated from sklearn. """ print('Classification Report for {0}:'.format(alg_name)) print(classification_report(predictions, test_class_set, target_names = dx))
class_report = print_class_report(predictions_rf, 'Random Forest')
Classification Report for Random Forest:
precision recall f1-score support
Benign 0.99 0.96 0.97 73
Malignant 0.93 0.98 0.95 41
avg / total 0.97 0.96 0.97 114
Metrics for Random Forest
Here I’ve accumulated the various metrics we used through this tutorial in a simple table! Showcasing the power and effectiveness of Random Forest Modeling.
| Model | OOB Error Rate | Test Error Rate | Cross Validation Score | AUC |
|---|---|---|---|---|
| Random Forest | 0.04835 | 0.0351 | 0.947 (+/- 0.019) | 0.996 |
Conclusions
For this tutorial we went through a number of metrics to assess the capabilites of our Random Forest, but this can be taken further when using background information of the data set. Feature engineering would be a powerful tool to extract and move forward into research regarding the important features. As well defining key metrics to utilize when optimizing model paramters.
There have been advancements with image classification in the past decade that utilize the images intead of extracted features from images, but this data set is a great resource to become with machine learning processes. Especially for those who are just beginning to learn machine learning concepts. If you have any suggestions, recommendations, or corrections please reach out to me.