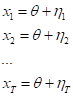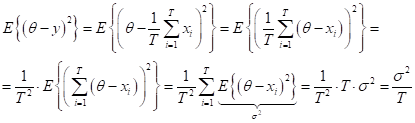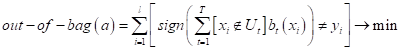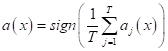From Wikipedia, the free encyclopedia
Out-of-bag (OOB) error, also called out-of-bag estimate, is a method of measuring the prediction error of random forests, boosted decision trees, and other machine learning models utilizing bootstrap aggregating (bagging). Bagging uses subsampling with replacement to create training samples for the model to learn from. OOB error is the mean prediction error on each training sample xi, using only the trees that did not have xi in their bootstrap sample.[1]
Bootstrap aggregating allows one to define an out-of-bag estimate of the prediction performance improvement by evaluating predictions on those observations that were not used in the building of the next base learner.
Out-of-bag dataset[edit]
When bootstrap aggregating is performed, two independent sets are created. One set, the bootstrap sample, is the data chosen to be «in-the-bag» by sampling with replacement. The out-of-bag set is all data not chosen in the sampling process.
When this process is repeated, such as when building a random forest, many bootstrap samples and OOB sets are created. The OOB sets can be aggregated into one dataset, but each sample is only considered out-of-bag for the trees that do not include it in their bootstrap sample. The picture below shows that for each bag sampled, the data is separated into two groups.
Visualizing the bagging process. Sampling 4 patients from the original set with replacement and showing the out-of-bag sets. Only patients in the bootstrap sample would be used to train the model for that bag.
This example shows how bagging could be used in the context of diagnosing disease. A set of patients are the original dataset, but each model is trained only by the patients in its bag. The patients in each out-of-bag set can be used to test their respective models. The test would consider whether the model can accurately determine if the patient has the disease.
Calculating out-of-bag error[edit]
Since each out-of-bag set is not used to train the model, it is a good test for the performance of the model. The specific calculation of OOB error depends on the implementation of the model, but a general calculation is as follows.
- Find all models (or trees, in the case of a random forest) that are not trained by the OOB instance.
- Take the majority vote of these models’ result for the OOB instance, compared to the true value of the OOB instance.
- Compile the OOB error for all instances in the OOB dataset.
An illustration of OOB error
The bagging process can be customized to fit the needs of a model. To ensure an accurate model, the bootstrap training sample size should be close to that of the original set.[2] Also, the number of iterations (trees) of the model (forest) should be considered to find the true OOB error. The OOB error will stabilize over many iterations so starting with a high number of iterations is a good idea.[3]
Shown in the example to the right, the OOB error can be found using the method above once the forest is set up.
Comparison to cross-validation[edit]
Out-of-bag error and cross-validation (CV) are different methods of measuring the error estimate of a machine learning model. Over many iterations, the two methods should produce a very similar error estimate. That is, once the OOB error stabilizes, it will converge to the cross-validation (specifically leave-one-out cross-validation) error.[3] The advantage of the OOB method is that it requires less computation and allows one to test the model as it is being trained.
Accuracy and Consistency[edit]
Out-of-bag error is used frequently for error estimation within random forests but with the conclusion of a study done by Silke Janitza and Roman Hornung, out-of-bag error has shown to overestimate in settings that include an equal number of observations from all response classes (balanced samples), small sample sizes, a large number of predictor variables, small correlation between predictors, and weak effects.[4]
See also[edit]
- Boosting (meta-algorithm)
- Bootstrap aggregating
- Bootstrapping (statistics)
- Cross-validation (statistics)
- Random forest
- Random subspace method (attribute bagging)
References[edit]
- ^ James, Gareth; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert (2013). An Introduction to Statistical Learning. Springer. pp. 316–321.
- ^ Ong, Desmond (2014). A primer to bootstrapping; and an overview of doBootstrap (PDF). pp. 2–4.
- ^ a b Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning (PDF). Springer. pp. 592–593.
- ^ Janitza, Silke; Hornung, Roman (2018-08-06). «On the overestimation of random forest’s out-of-bag error». PLOS ONE. 13 (8): e0201904. doi:10.1371/journal.pone.0201904. ISSN 1932-6203. PMC 6078316. PMID 30080866.
From Wikipedia, the free encyclopedia
Out-of-bag (OOB) error, also called out-of-bag estimate, is a method of measuring the prediction error of random forests, boosted decision trees, and other machine learning models utilizing bootstrap aggregating (bagging). Bagging uses subsampling with replacement to create training samples for the model to learn from. OOB error is the mean prediction error on each training sample xi, using only the trees that did not have xi in their bootstrap sample.[1]
Bootstrap aggregating allows one to define an out-of-bag estimate of the prediction performance improvement by evaluating predictions on those observations that were not used in the building of the next base learner.
Out-of-bag dataset[edit]
When bootstrap aggregating is performed, two independent sets are created. One set, the bootstrap sample, is the data chosen to be «in-the-bag» by sampling with replacement. The out-of-bag set is all data not chosen in the sampling process.
When this process is repeated, such as when building a random forest, many bootstrap samples and OOB sets are created. The OOB sets can be aggregated into one dataset, but each sample is only considered out-of-bag for the trees that do not include it in their bootstrap sample. The picture below shows that for each bag sampled, the data is separated into two groups.
Visualizing the bagging process. Sampling 4 patients from the original set with replacement and showing the out-of-bag sets. Only patients in the bootstrap sample would be used to train the model for that bag.
This example shows how bagging could be used in the context of diagnosing disease. A set of patients are the original dataset, but each model is trained only by the patients in its bag. The patients in each out-of-bag set can be used to test their respective models. The test would consider whether the model can accurately determine if the patient has the disease.
Calculating out-of-bag error[edit]
Since each out-of-bag set is not used to train the model, it is a good test for the performance of the model. The specific calculation of OOB error depends on the implementation of the model, but a general calculation is as follows.
- Find all models (or trees, in the case of a random forest) that are not trained by the OOB instance.
- Take the majority vote of these models’ result for the OOB instance, compared to the true value of the OOB instance.
- Compile the OOB error for all instances in the OOB dataset.
An illustration of OOB error
The bagging process can be customized to fit the needs of a model. To ensure an accurate model, the bootstrap training sample size should be close to that of the original set.[2] Also, the number of iterations (trees) of the model (forest) should be considered to find the true OOB error. The OOB error will stabilize over many iterations so starting with a high number of iterations is a good idea.[3]
Shown in the example to the right, the OOB error can be found using the method above once the forest is set up.
Comparison to cross-validation[edit]
Out-of-bag error and cross-validation (CV) are different methods of measuring the error estimate of a machine learning model. Over many iterations, the two methods should produce a very similar error estimate. That is, once the OOB error stabilizes, it will converge to the cross-validation (specifically leave-one-out cross-validation) error.[3] The advantage of the OOB method is that it requires less computation and allows one to test the model as it is being trained.
Accuracy and Consistency[edit]
Out-of-bag error is used frequently for error estimation within random forests but with the conclusion of a study done by Silke Janitza and Roman Hornung, out-of-bag error has shown to overestimate in settings that include an equal number of observations from all response classes (balanced samples), small sample sizes, a large number of predictor variables, small correlation between predictors, and weak effects.[4]
See also[edit]
- Boosting (meta-algorithm)
- Bootstrap aggregating
- Bootstrapping (statistics)
- Cross-validation (statistics)
- Random forest
- Random subspace method (attribute bagging)
References[edit]
- ^ James, Gareth; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert (2013). An Introduction to Statistical Learning. Springer. pp. 316–321.
- ^ Ong, Desmond (2014). A primer to bootstrapping; and an overview of doBootstrap (PDF). pp. 2–4.
- ^ a b Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning (PDF). Springer. pp. 592–593.
- ^ Janitza, Silke; Hornung, Roman (2018-08-06). «On the overestimation of random forest’s out-of-bag error». PLOS ONE. 13 (8): e0201904. doi:10.1371/journal.pone.0201904. ISSN 1932-6203. PMC 6078316. PMID 30080866.
Пятую статью курса мы посвятим простым методам композиции: бэггингу и случайному лесу. Вы узнаете, как можно получить распределение среднего по генеральной совокупности, если у нас есть информация только о небольшой ее части; посмотрим, как с помощью композиции алгоритмов уменьшить дисперсию и таким образом улучшить точность модели; разберём, что такое случайный лес, какие его параметры нужно «подкручивать» и как найти самый важный признак. Сконцентрируемся на практике, добавив «щепотку» математики.
UPD 01.2022: С февраля 2022 г. ML-курс ODS на русском возрождается под руководством Петра Ермакова couatl. Для русскоязычной аудитории это предпочтительный вариант (c этими статьями на Хабре – в подкрепление), англоговорящим рекомендуется mlcourse.ai в режиме самостоятельного прохождения.
Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).
План этой статьи
- Бэггинг
- Ансамбли
- Бутстрэп
- Бэггинг
- Out-of-bag ошибка
- Случайный лес
- Алгоритм
- Сравнение с деревом решений и бэггингом
- Параметры
- Вариация и декорреляционный эффект
- Смещение
- Сверхслучайные деревья
- Схожесть с алгоритмом k-ближайших соседей
- Преобразование признаков в многомерное пространство
- Оценка важности признаков
- Плюсы и минусы случайного леса
- Домашнее задание №5
- Полезные источники
1. Бэггинг
Из прошлых лекций вы уже узнали про разные алгоритмы классификации, а также научились правильно валидироваться и оценивать качество модели. Но что делать, если вы уже нашли лучшую модель и повысить точность модели больше не можете? В таком случае нужно применить более продвинутые техники машинного обучения, которые можно объединить словом «ансамбли». Ансамбль — это некая совокупность, части которой образуют единое целое. Из повседневной жизни вы знаете музыкальные ансамбли, где объединены несколько музыкальных инструментов, архитектурные ансамбли с разными зданиями и т.д.
Ансамбли
Хорошим примером ансамблей считается теорема Кондорсе «о жюри присяжных» (1784). Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри и стремится к единице. Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных.
— количество присяжных
— вероятность правильного решения присяжного
— вероятность правильного решения всего жюри
— минимальное большинство членов жюри,
— число сочетаний из
по
Если , то
Если , то
Давайте рассмотрим ещё один пример ансамблей — «Мудрость толпы». Фрэнсис Гальтон в 1906 году посетил рынок, где проводилась некая лотерея для крестьян.
Их собралось около 800 человек, и они пытались угадать вес быка, который стоял перед ними. Бык весил 1198 фунтов. Ни один крестьянин не угадал точный вес быка, но если посчитать среднее от их предсказаний, то получим 1197 фунтов.
Эту идею уменьшения ошибки применили и в машинном обучении.
Бутстрэп
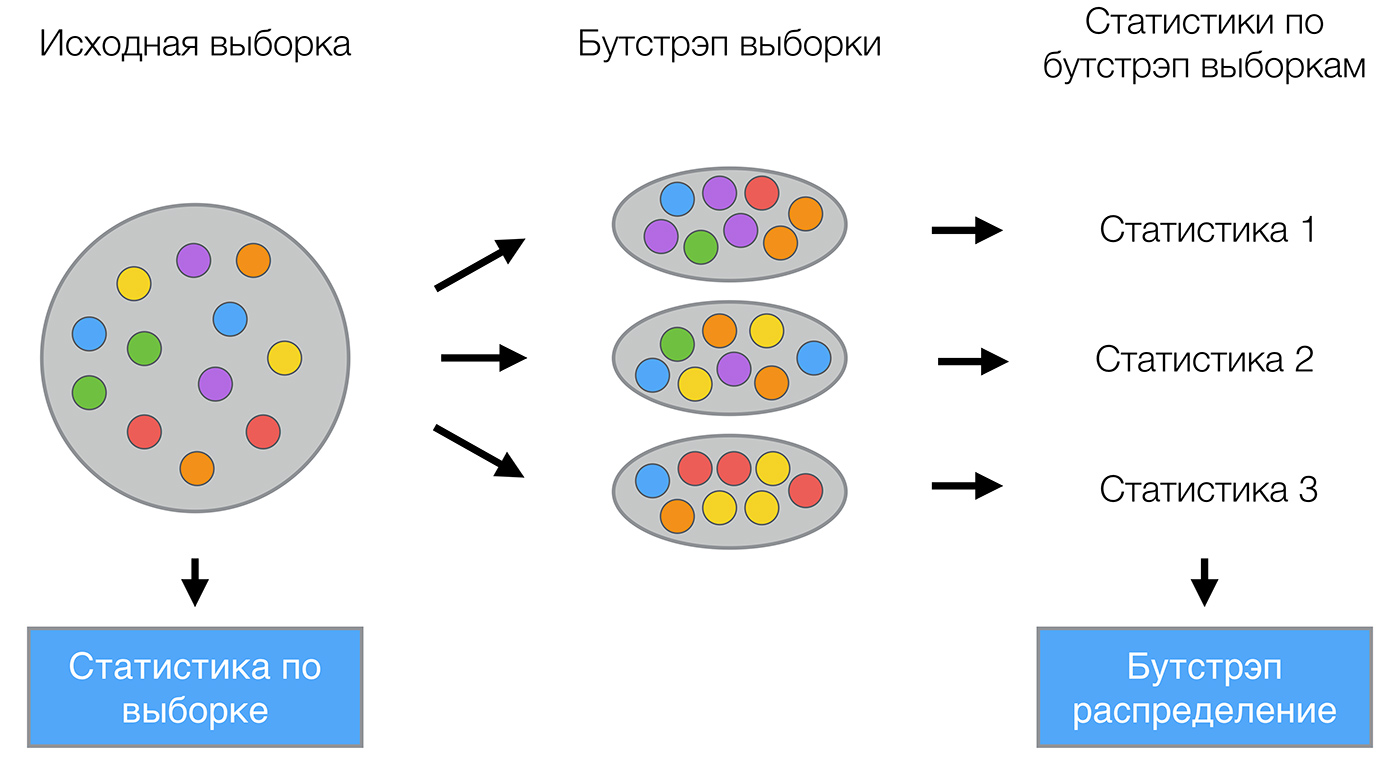
Bagging (от Bootstrap aggregation) — это один из первых и самых простых видов ансамблей. Он был придуман Ле́о Бре́йманом в 1994 году. Бэггинг основан на статистическом методе бутстрэпа, который позволяет оценивать многие статистики сложных распределений.
Метод бутстрэпа заключается в следующем. Пусть имеется выборка размера
. Равномерно возьмем из выборки
объектов с возвращением. Это означает, что мы будем
раз выбирать произвольный объект выборки (считаем, что каждый объект «достается» с одинаковой вероятностью
), причем каждый раз мы выбираем из всех исходных
объектов. Можно представить себе мешок, из которого достают шарики: выбранный на каком-то шаге шарик возвращается обратно в мешок, и следующий выбор опять делается равновероятно из того же числа шариков. Отметим, что из-за возвращения среди них окажутся повторы. Обозначим новую выборку через
. Повторяя процедуру
раз, сгенерируем
подвыборок
. Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.
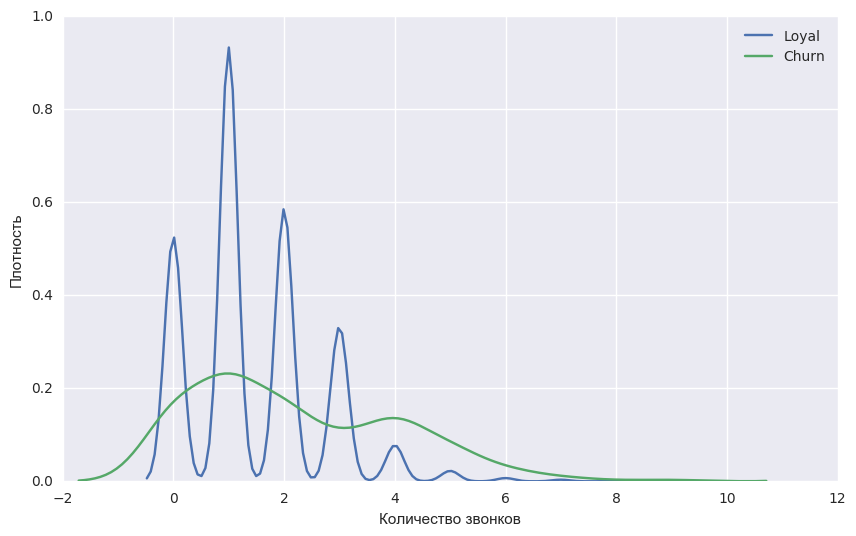
Давайте для примера возьмем уже известный вам набор данных telecom_churn из прошлых уроков нашего курса. Напомним, что это задача бинарной классификации оттока клиентов. Одним из самых важных признаков в этом датасете является количество звонков в сервисный центр, которые были сделаны клиентом. Давайте попробуем визулизировать данные и посмотреть на распределение данного признака.
Код для загрузки данных и построения графика
import pandas as pd
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
import seaborn as sns
%matplotlib inline
telecom_data = pd.read_csv('data/telecom_churn.csv')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == False]['Customer service calls'], label = 'Loyal')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == True]['Customer service calls'], label = 'Churn')
fig.set(xlabel='Количество звонков', ylabel='Плотность')
plt.show()Как вы уже могли заметить, количество звонков в сервисный центр у лояльных клиентов меньше, чем у наших бывших клиентов. Теперь было бы хорошо оценить, сколько в среднем делает звонков каждая из групп. Так как данных в нашем датасете мало, то искать среднее не совсем правильно, лучше применить наши новые знания бутстрэпа. Давайте сгенерируем 1000 новых подвыборок из нашей генеральной совокупности и сделаем интервальную оценку среднего.
Код для построения доверительного интервала с помощью бутстрэпа
import numpy as np
def get_bootstrap_samples(data, n_samples):
# функция для генерации подвыборок с помощью бутстрэпа
indices = np.random.randint(0, len(data), (n_samples, len(data)))
samples = data[indices]
return samples
def stat_intervals(stat, alpha):
# функция для интервальной оценки
boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 - alpha / 2.)])
return boundaries
# сохранение в отдельные numpy массивы данных по лояльным и уже бывшим клиентам
loyal_calls = telecom_data[telecom_data['Churn'] == False]['Customer service calls'].values
churn_calls= telecom_data[telecom_data['Churn'] == True]['Customer service calls'].values
# ставим seed для воспроизводимости результатов
np.random.seed(0)
# генерируем выборки с помощью бутстрэра и сразу считаем по каждой из них среднее
loyal_mean_scores = [np.mean(sample)
for sample in get_bootstrap_samples(loyal_calls, 1000)]
churn_mean_scores = [np.mean(sample)
for sample in get_bootstrap_samples(churn_calls, 1000)]
# выводим интервальную оценку среднего
print("Service calls from loyal: mean interval", stat_intervals(loyal_mean_scores, 0.05))
print("Service calls from churn: mean interval", stat_intervals(churn_mean_scores, 0.05))В итоге мы получили, что с 95% вероятностью среднее число звонков от лояльных клиентов будет лежать в промежутке между 1.40 и 1.50, в то время как наши бывшие клиенты звонили в среднем от 2.06 до 2.40 раз. Также ещё можно обратить внимание, что интервал для лояльных клиентов уже, что довольно логично, так как они звонят редко (в основном 0, 1 или 2 раза), а недовольные клиенты будут звонить намного чаще, но со временем их терпение закончится, и они поменяют оператора.
Бэггинг
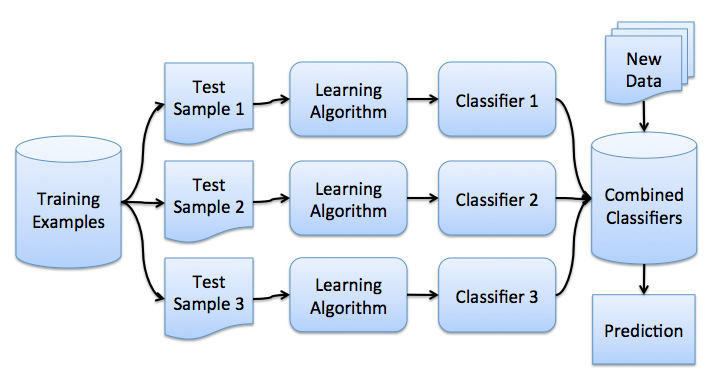
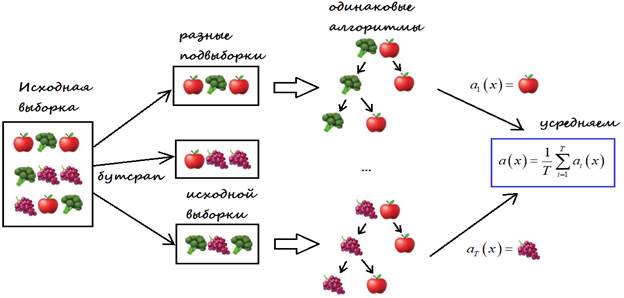
Теперь вы имеете представление о бустрэпе, и мы можем перейти непосредственно к бэггингу. Пусть имеется обучающая выборка . С помощью бутстрэпа сгенерируем из неё выборки
. Теперь на каждой выборке обучим свой классификатор
. Итоговый классификатор будет усреднять ответы всех этих алгоритмов (в случае классификации это соответствует голосованию):
. Эту схему можно представить картинкой ниже.
Рассмотрим задачу регрессии с базовыми алгоритмами . Предположим, что существует истинная функция ответа для всех объектов
, а также задано распределение на объектах
. В этом случае мы можем записать ошибку каждой функции регрессии
и записать матожидание среднеквадратичной ошибки
Средняя ошибка построенных функций регрессии имеет вид
Предположим, что ошибки несмещены и некоррелированы:
Построим теперь новую функцию регрессии, которая будет усреднять ответы построенных нами функций:
Найдем ее среднеквадратичную ошибку:
Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в n раз!
Напомним вам из нашего предыдущего урока, как раскладывается общая ошибка:
Бэггинг позволяет снизить дисперсию (variance) обучаемого классификатора, уменьшая величину, на сколько ошибка будет отличаться, если обучать модель на разных наборах данных, или другими словами, предотвращает переобучение. Эффективность бэггинга достигается благодаря тому, что базовые алгоритмы, обученные по различным подвыборкам, получаются достаточно различными, и их ошибки взаимно компенсируются при голосовании, а также за счёт того, что объекты-выбросы могут не попадать в некоторые обучающие подвыборки.
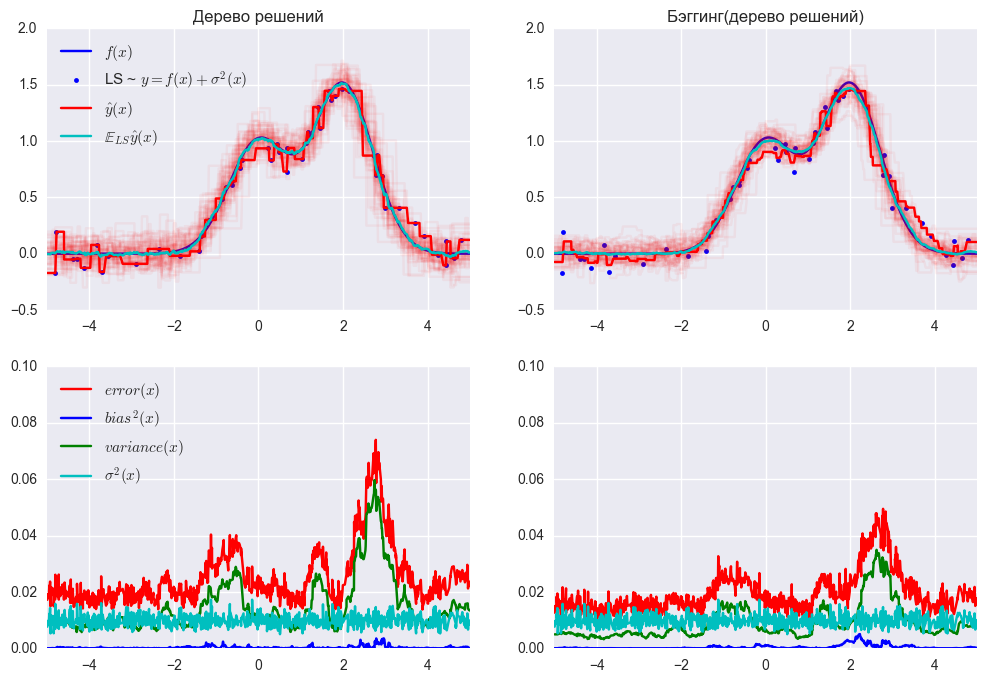
В библиотеке scikit-learn есть реализации BaggingRegressor и BaggingClassifier, которые позволяют использовать большинство других алгоритмов «внутри». Рассмотрим на практике, как работает бэггинг, и сравним его с деревом решений, пользуясь примером из документации.
Ошибка дерева решений
Ошибка бэггинга
По графику и результатам выше видно, что ошибка дисперсии намного меньше при бэггинге, как мы и доказали теоретически выше.
Бэггинг эффективен на малых выборках, когда исключение даже малой части обучающих объектов приводит к построению существенно различных базовых классификаторов. В случае больших выборок обычно генерируют подвыборки существенно меньшей длины.
Следует отметить, что рассмотренный нами пример не очень применим на практике, поскольку мы сделали предположение о некоррелированности ошибок, что редко выполняется. Если это предположение неверно, то уменьшение ошибки оказывается не таким значительным. В следующих лекциях мы рассмотрим более сложные методы объединения алгоритмов в композицию, которые позволяют добиться высокого качества в реальных задачах.
Out-of-bag error
Забегая вперед, отметим, что при использовании случайных лесов нет необходимости в кросс-валидации или в отдельном тестовом наборе, чтобы получить несмещенную оценку ошибки набора тестов. Посмотрим, как получается «внутренняя» оценка модели во время ее обучения.
Каждое дерево строится с использованием разных образцов бутстрэпа из исходных данных. Примерно 37% примеров остаются вне выборки бутстрэпа и не используются при построении k-го дерева.
Это можно легко доказать: пусть в выборке объектов. На каждом шаге все объекты попадают в подвыборку с возвращением равновероятно, т.е отдельный объект — с вероятностью
Вероятность того, что объект НЕ попадет в подвыборку (т.е. его не взяли
раз):
. При
получаем один из «замечательных» пределов
. Тогда вероятность попадания конкретного объекта в подвыборку
.
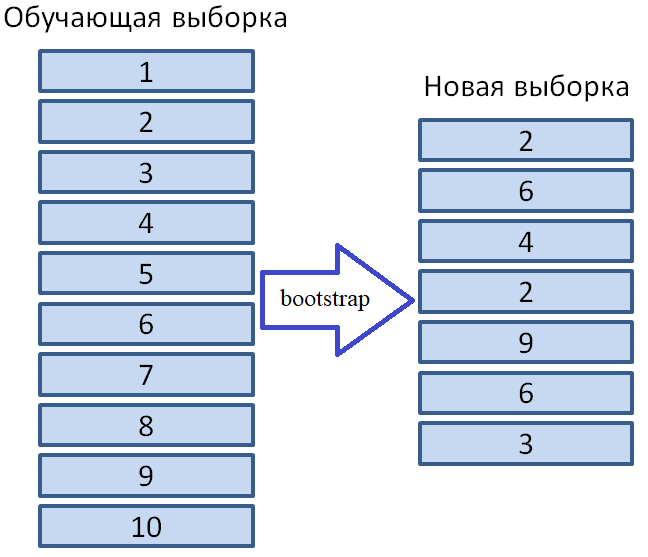
Давайте рассмотрим, как это работает на практике:
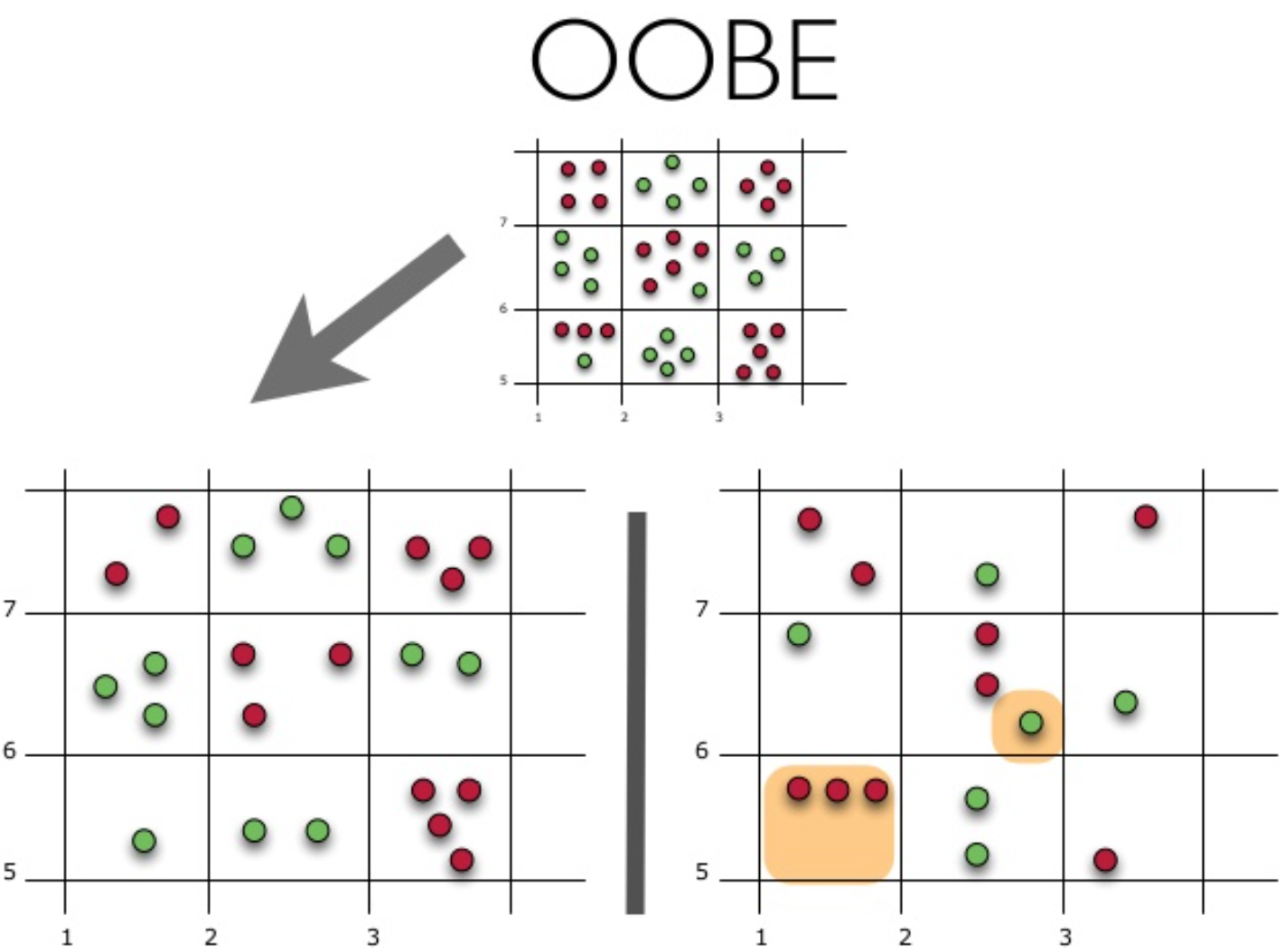
На рисунке изображена оценка oob-ошибки. Верхний рисунок – это наша исходная выборка, ее мы делим на обучающую(слева) и тестовую(справа). На рисунке слева у нас есть сетка из квадратиков, которая идеально разбивает нашу выборку. Теперь нужно оценить долю верных ответов на нашей тестовой выборке. На рисунке видно, что наш классификатор ошибся в 4 наблюдениях, которые мы не использовали для обучения. Значит, доля верных ответов нашего классификатора:
Получается, что каждый базовый алгоритм обучается на ~63% исходных объектов. Значит, на оставшихся ~37% его можно сразу проверять. Out-of-Bag оценка — это усредненная оценка базовых алгоритмов на тех ~37% данных, на которых они не обучались.
2. Случайный лес
Лео Брейман нашел применение бутстрэпу не только в статистике, но и в машинном обучении. Он вместе с Адель Катлер усовершенстовал алгоритм случайного леса, предложенный Хо, добавив к первоначальному варианту построение некоррелируемых деревьев на основе CART, в сочетании с методом случайных подпространств и бэггинга.
Решающие деревья являются хорошим семейством базовых классификаторов для бэггинга, поскольку они достаточно сложны и могут достигать нулевой ошибки на любой выборке. Метод случайных подпространств позволяет снизить коррелированность между деревьями и избежать переобучения. Базовые алгоритмы обучаются на различных подмножествах признакового описания, которые также выделяются случайным образом.
Ансамбль моделей, использующих метод случайного подпространства, можно построить, используя следующий алгоритм:
- Пусть количество объектов для обучения равно
, а количество признаков
.
- Выберите
как число отдельных моделей в ансамбле.
- Для каждой отдельной модели
выберите
как число признаков для
. Обычно для всех моделей используется только одно значение
.
- Для каждой отдельной модели
создайте обучающую выборку, выбрав
признаков из
, и обучите модель.
- Теперь, чтобы применить модель ансамбля к новому объекту, объедините результаты отдельных
моделей мажоритарным голосованием или путем комбинирования апостериорных вероятностей.
Алгоритм
Алгоритм построения случайного леса, состоящего из деревьев, выглядит следующим образом:
- Для каждого
:
Итоговый классификатор , простыми словами — для задачи кассификации мы выбираем решение голосованием по большинству, а в задаче регрессии — средним.
Рекомендуется в задачах классификации брать , а в задачах регрессии —
, где
— число признаков. Также рекомендуется в задачах классификации строить каждое дерево до тех пор, пока в каждом листе не окажется по одному объекту, а в задачах регрессии — пока в каждом листе не окажется по пять объектов.
Таким образом, случайный лес — это бэггинг над решающими деревьями, при обучении которых для каждого разбиения признаки выбираются из некоторого случайного подмножества признаков.
Сравнение с деревом решений и бэггингом
Код для сравнения решающего дерева, бэггинга и случайного леса для задачи регрессии
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
%pylab inline
np.random.seed(42)
figsize(8, 6)
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier, BaggingRegressor
from sklearn.tree import DecisionTreeRegressor, DecisionTreeClassifier
n_train = 150
n_test = 1000
noise = 0.1
# Generate data
def f(x):
x = x.ravel()
return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)
def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 5
X = np.sort(X).ravel()
y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2)
+ np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y
X_train, y_train = generate(n_samples=n_train, noise=noise)
X_test, y_test = generate(n_samples=n_test, noise=noise)
# One decision tree regressor
dtree = DecisionTreeRegressor().fit(X_train, y_train)
d_predict = dtree.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, d_predict, "g", lw=2)
plt.xlim([-5, 5])
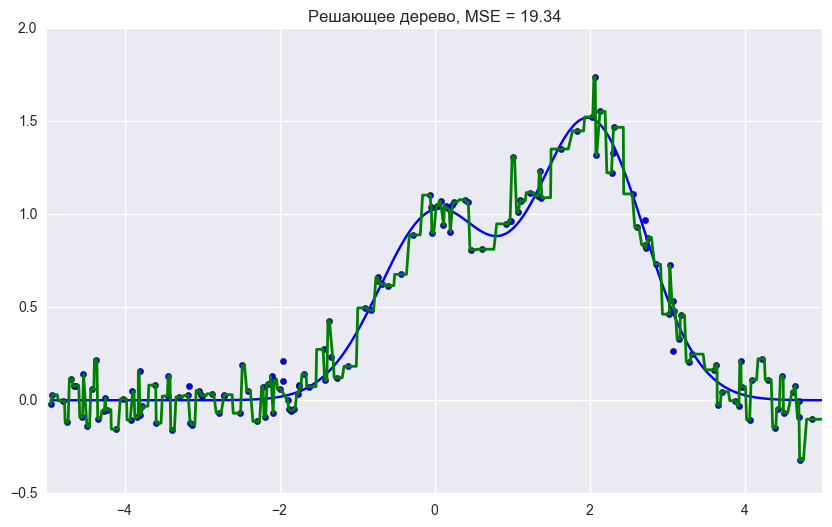
plt.title("Решающее дерево, MSE = %.2f"
% np.sum((y_test - d_predict) ** 2))
# Bagging decision tree regressor
bdt = BaggingRegressor(DecisionTreeRegressor()).fit(X_train, y_train)
bdt_predict = bdt.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, bdt_predict, "y", lw=2)
plt.xlim([-5, 5])
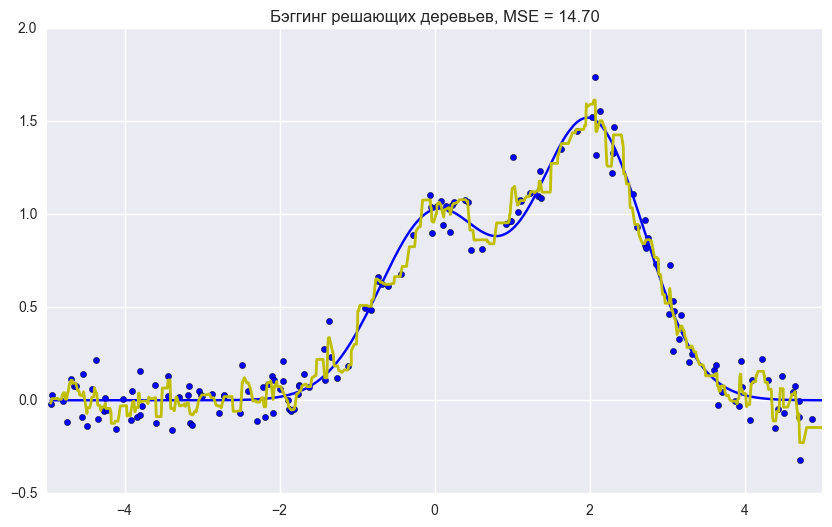
plt.title("Бэггинг решающих деревьев, MSE = %.2f" % np.sum((y_test - bdt_predict) ** 2));
# Random Forest
rf = RandomForestRegressor(n_estimators=10).fit(X_train, y_train)
rf_predict = rf.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, rf_predict, "r", lw=2)
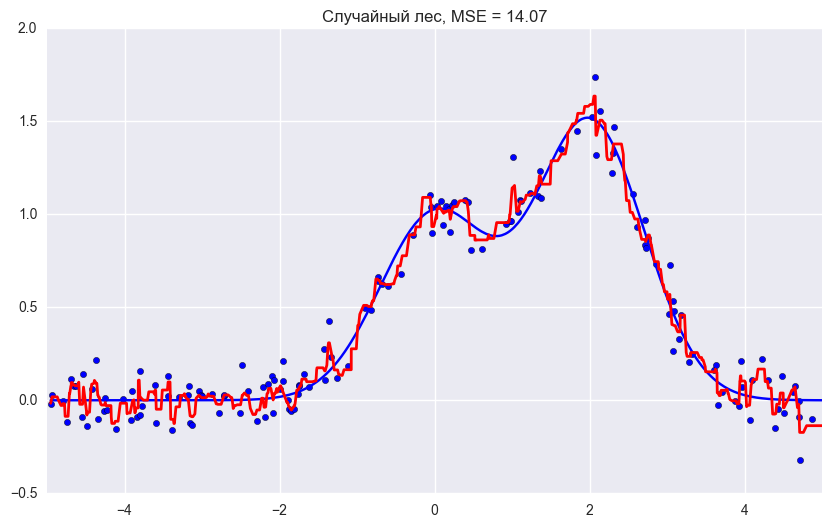
plt.xlim([-5, 5])
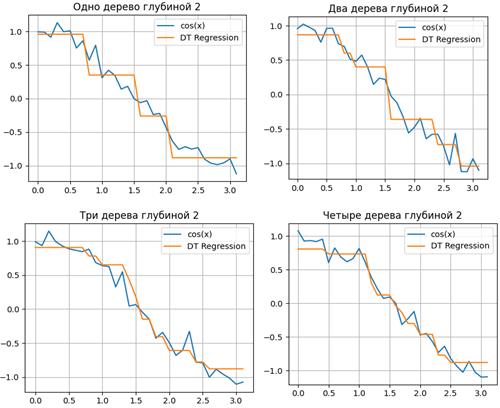
plt.title("Случайный лес, MSE = %.2f" % np.sum((y_test - rf_predict) ** 2));Как мы видим из графиков и значений ошибки MSE, случайный лес из 10 деревьев дает лучший результат, чем одно дерево или бэггинг из 10 деревьев решений. Основное различие случайного леса и бэггинга на деревьях решений заключается в том, что в случайном лесе выбирается случайное подмножество признаков, и лучший признак для разделения узла определяется из подвыборки признаков, в отличие от бэггинга, где все функции рассматриваются для разделения в узле.
Также можно увидеть преимущество случайного леса и бэггинга в задачах классификации.
Код для сравнения решающего дерева, бэггинга и случайного леса для задачи классификации
from sklearn.ensemble import RandomForestClassifier, BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_circles
from sklearn.cross_validation import train_test_split
import numpy as np
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
%matplotlib inline
np.random.seed(42)
X, y = make_circles(n_samples=500, factor=0.1, noise=0.35, random_state=42)
X_train_circles, X_test_circles, y_train_circles, y_test_circles = train_test_split(X, y, test_size=0.2)
dtree = DecisionTreeClassifier(random_state=42)
dtree.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
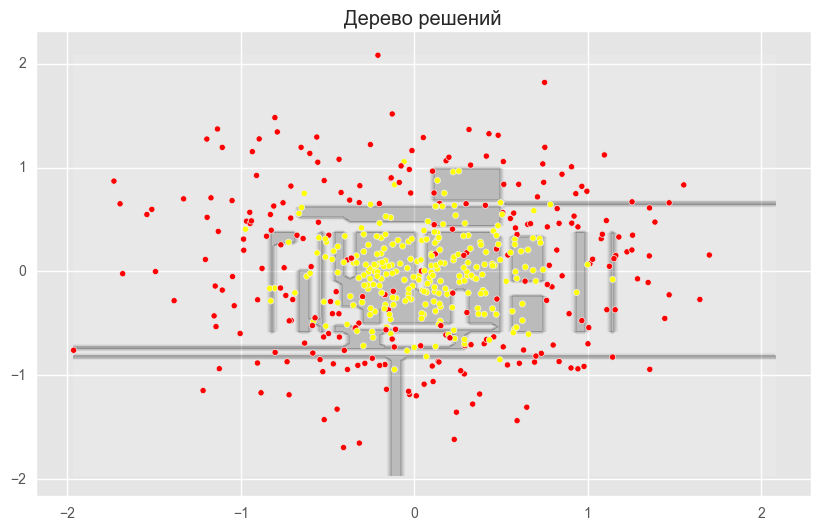
plt.title("Дерево решений")
plt.show()
b_dtree = BaggingClassifier(DecisionTreeClassifier(),n_estimators=300, random_state=42)
b_dtree.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = b_dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
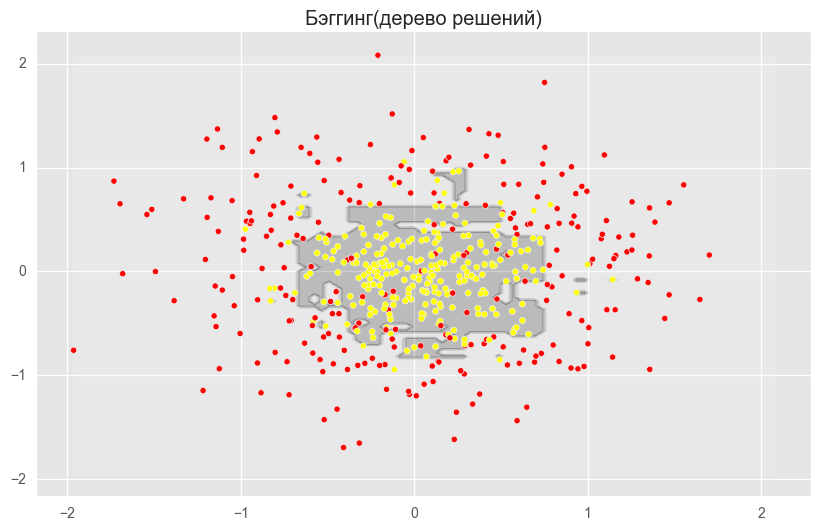
plt.title("Бэггинг(дерево решений)")
plt.show()
rf = RandomForestClassifier(n_estimators=300, random_state=42)
rf.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = rf.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
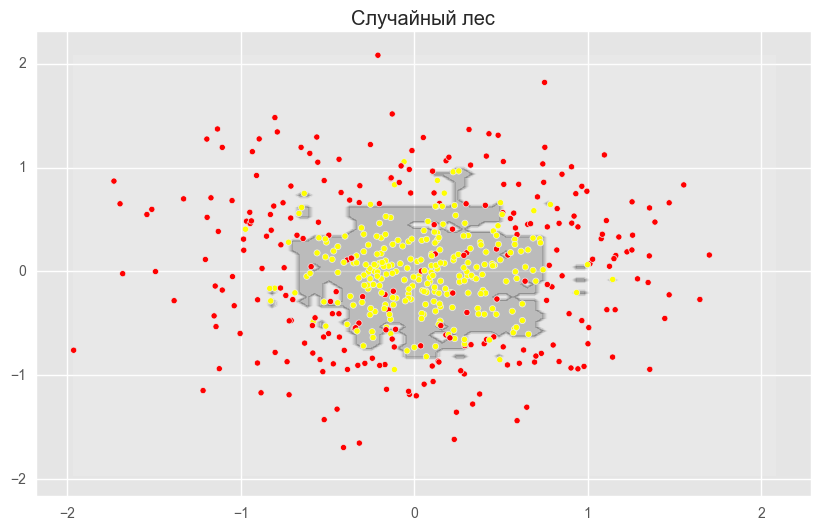
plt.title("Случайный лес")
plt.show()На рисунках выше видно, что разделяющая граница дерева решений очень «рваная» и на ней много острых углов, что говорит о переобучении и слабой обобщающей способности. В то время как у бэггинга и случайного леса граница достаточно сглаженная и практически нет признаков переобучения.
Давайте теперь попробуем разобраться с параметрами, с помощью подбора которых мы cможем увеличить долю правильных ответов.
Параметры
Метод случайного леса реализован в библиотеке машинного обучения scikit-learn двумя классами RandomForestClassifier и RandomForestRegressor.
Полный список параметров случайного леса для задачи регрессии:
class sklearn.ensemble.RandomForestRegressor(
n_estimators — число деревьев в "лесу" (по дефолту – 10)
criterion — функция, которая измеряет качество разбиения ветки дерева (по дефолту — "mse" , так же можно выбрать "mae")
max_features — число признаков, по которым ищется разбиение. Вы можете указать конкретное число или процент признаков, либо выбрать из доступных значений: "auto" (все признаки), "sqrt", "log2". По дефолту стоит "auto".
max_depth — максимальная глубина дерева (по дефолту глубина не ограничена)
min_samples_split — минимальное количество объектов, необходимое для разделения внутреннего узла. Можно задать числом или процентом от общего числа объектов (по дефолту — 2)
min_samples_leaf — минимальное число объектов в листе. Можно задать числом или процентом от общего числа объектов (по дефолту — 1)
min_weight_fraction_leaf — минимальная взвешенная доля от общей суммы весов (всех входных объектов) должна быть в листе (по дефолту имеют одинаковый вес)
max_leaf_nodes — максимальное количество листьев (по дефолту нет ограничения)
min_impurity_split — порог для остановки наращивания дерева (по дефолту 1е-7)
bootstrap — применять ли бустрэп для построения дерева (по дефолту True)
oob_score — использовать ли out-of-bag объекты для оценки R^2 (по дефолту False)
n_jobs — количество ядер для построения модели и предсказаний (по дефолту 1, если поставить -1, то будут использоваться все ядра)
random_state — начальное значение для генерации случайных чисел (по дефолту его нет, если хотите воспроизводимые результаты, то нужно указать любое число типа int
verbose — вывод логов по построению деревьев (по дефолту 0)
warm_start — использует уже натренированую модель и добавляет деревьев в ансамбль (по дефолту False)
)Для задачи классификации все почти то же самое, мы приведем только те параметры, которыми RandomForestClassifier отличается от RandomForestRegressor
class sklearn.ensemble.RandomForestClassifier(
criterion — поскольку у нас теперь задача классификации, то по дефолту выбран критерий "gini" (можно выбрать "entropy")
class_weight — вес каждого класса (по дефолту все веса равны 1, но можно передать словарь с весами, либо явно указать "balanced", тогда веса классов будут равны их исходным частям в генеральной совокупности; также можно указать "balanced_subsample", тогда веса на каждой подвыборке будут меняться в зависимости от распределения классов на этой подвыборке.
)Далее рассмотрим несколько параметров, на которые в первую очередь стоит обратить внимание при построении модели:
- n_estimators — число деревьев в «лесу»
- criterion — критерий для разбиения выборки в вершине
- max_features — число признаков, по которым ищется разбиение
- min_samples_leaf — минимальное число объектов в листе
- max_depth — максимальная глубина дерева
Рассмотрим применение случайного леса в реальной задаче
Для этого будем использовать пример с задачей оттока клиентов. Это задача классификации, поэтому будем использовать метрику accuracy для оценки качества модели. Для начала построим самый простой классификатор, который будет нашим бейслайном. Возьмем только числовые признаки для упрощения.
Код для построения бейслайна для случайного леса
import pandas as pd
from sklearn.model_selection import cross_val_score, StratifiedKFold, GridSearchCV
from sklearn.metrics import accuracy_score
# Загружаем данные
df = pd.read_csv("../../data/telecom_churn.csv")
# Выбираем сначала только колонки с числовым типом данных
cols = []
for i in df.columns:
if (df[i].dtype == "float64") or (df[i].dtype == 'int64'):
cols.append(i)
# Разделяем на признаки и объекты
X, y = df[cols].copy(), np.asarray(df["Churn"],dtype='int8')
# Инициализируем страифицированную разбивку нашего датасета для валидации
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# Инициализируем наш классификатор с дефолтными параметрами
rfc = RandomForestClassifier(random_state=42, n_jobs=-1, oob_score=True)
# Обучаем на тренировочном датасете
results = cross_val_score(rfc, X, y, cv=skf)
# Оцениваем долю верных ответов на тестовом датасете
print("CV accuracy score: {:.2f}%".format(results.mean()*100))Получили долю верных ответов 91.21%, теперь попробуем улучшить этот результат и посмотреть, как ведут себя кривые валидации при изменении основных параметров.
Начнем с количества деревьев:
Код для построения кривых валидации по подбору количества деревьев
# Инициализируем валидацию
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
trees_grid = [5, 10, 15, 20, 30, 50, 75, 100]
# Обучаем на тренировочном датасете
for ntrees in trees_grid:
rfc = RandomForestClassifier(n_estimators=ntrees, random_state=42, n_jobs=-1, oob_score=True)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} trees".format(max(test_acc.mean(axis=1))*100,
trees_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых валидации
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(trees_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(trees_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(trees_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(trees_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
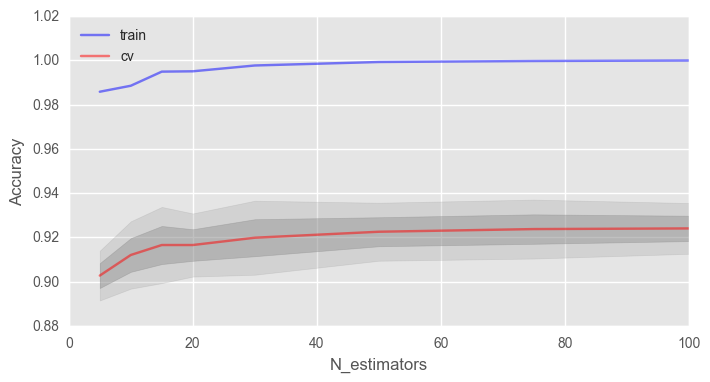
ax.set_xlabel("N_estimators")Как видно, при достижении определенного числа деревьев наша доля верных ответов на тесте выходит на асимптоту, и вы можете сами решить, сколько деревьев оптимально для вашей задачи.
На рисунке также видно, что на тренировочной выборке мы смогли достичь 100% точности, это говорит нам о переобучении нашей модели. Чтобы избежать переобучения, мы должны добавить параметры регуляризации в модель.
Начнем с параметра максимальной глубины – max_depth. (зафиксируем к-во деревьев 100)
Код для построения кривых обучения по подбору максимальной глубины дерева
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
max_depth_grid = [3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]
# Обучаем на тренировочном датасете
for max_depth in max_depth_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1, oob_score=True, max_depth=max_depth)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} max_depth".format(max(test_acc.mean(axis=1))*100,
max_depth_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых обучения
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(max_depth_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(max_depth_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Max_depth")Параметр max_depth хорошо справляется с регуляризацией модели, и мы уже не так сильно переобучаемся. Доля верных ответов нашей модели немного возросла.
Еще важный параметр min_samples_leaf, он также выполняет функцию регуляризатора.
Код для построения кривых валидации по подбору минимального числа объектов в одном листе дерева
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
min_samples_leaf_grid = [1, 3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]
# Обучаем на тренировочном датасете
for min_samples_leaf in min_samples_leaf_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,
oob_score=True, min_samples_leaf=min_samples_leaf)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} min_samples_leaf".format(max(test_acc.mean(axis=1))*100,
min_samples_leaf_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых валидации
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(min_samples_leaf_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(min_samples_leaf_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
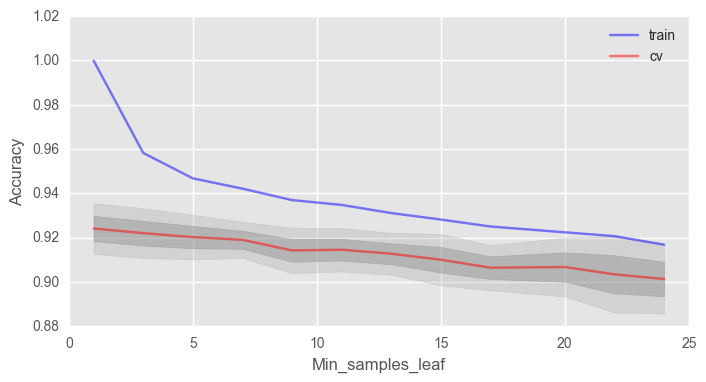
ax.set_xlabel("Min_samples_leaf")В данном случае мы не выигрываем в точности на валидации, но зато можем сильно уменьшить переобучение до 2% при сохранении точности около 92%.
Рассмотрим такой параметр как max_features. Для задач классификации по умолчанию используется , где n — число признаков. Давайте проверим, оптимально ли в нашем случае использовать 4 признака или нет.
Код для построения кривых валидации по подбору максимального количества признаков для одного дерева
# Создаем списки для сохранения точности на тренировочном и тестовом датасете
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
max_features_grid = [2, 4, 6, 8, 10, 12, 14, 16]
# Обучаем на тренировочном датасете
for max_features in max_features_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,
oob_score=True, max_features=max_features)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("Best accuracy on CV is {:.2f}% with {} max_features".format(max(test_acc.mean(axis=1))*100,
max_features_grid[np.argmax(test_acc.mean(axis=1))]))Код для построения графика кривых валидации
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(max_features_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(max_features_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(max_features_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(max_features_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
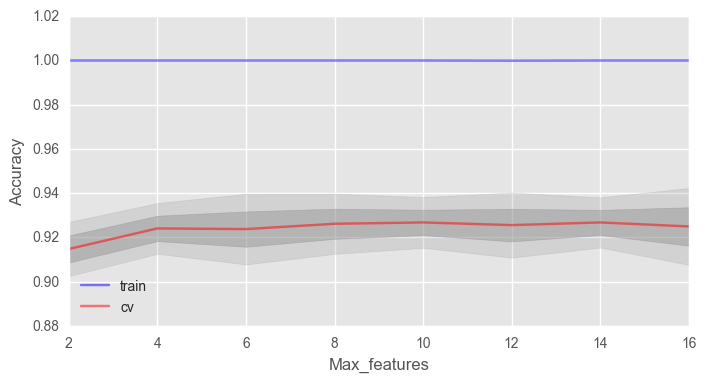
ax.set_xlabel("Max_features")В нашем случае оптимальное число признаков — 10, именно с таким значением достигается наилучший результат.
Мы рассмотрели, как ведут себя кривые валидации в зависимости от изменения основных параметров. Давайте теперь с помощью GridSearchCV найдем оптимальные параметры для нашего примера.
Код для подбора оптимальных параметров модели
# Сделаем инициализацию параметров, по которым хотим сделать полный перебор
parameters = {'max_features': [4, 7, 10, 13], 'min_samples_leaf': [1, 3, 5, 7], 'max_depth': [5,10,15,20]}
rfc = RandomForestClassifier(n_estimators=100, random_state=42,
n_jobs=-1, oob_score=True)
gcv = GridSearchCV(rfc, parameters, n_jobs=-1, cv=skf, verbose=1)
gcv.fit(X, y)Лучшая доля верных ответов, который мы смогли достичь с помощью перебора параметров — 92.83% при 'max_depth': 15, 'max_features': 7, 'min_samples_leaf': 3.
Вариация и декорреляционный эффект
Давайте запишем дисперсию для случайного леса как
Тут
– корреляция выборки между любыми двумя деревьями, используемыми при усреднении
где
и
– случайно выбранная пара деревьев на случайно выбранных объектах выборки
— это выборочная дисперсия любого произвольно выбранного дерева:
Легко спутать
со средней корреляцией между обученными деревьями в данном случайном лесе, рассматривая деревья как N-векторы и вычисляя среднюю парную корреляцию между ними. Это не тот случай. Эта условная корреляция не имеет прямого отношения к процессу усреднения, а зависимость от
в
предупреждает нас об этом различии. Скорее
является теоретической корреляцией между парой случайных деревьев, оцененных в объекте
, которая была вызвана многократным сэмплированием обучающей выборки из генеральной совокупности
, и после этого выбрана данная пара случайных деревьев. На статистическом жаргоне это корреляция, вызванная выборочным распределением
и
.
По факту, условная ковариация пары деревьев равна 0, потому что бустрэп и отбор признаков — независимы и одинаково распределены.
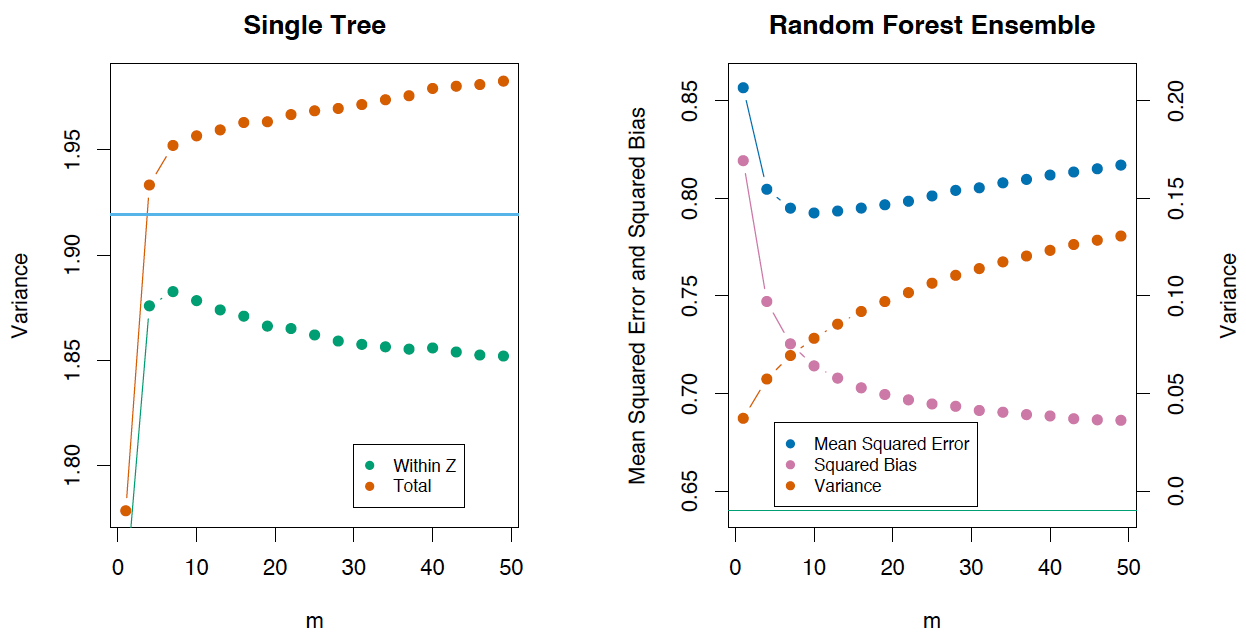
Если рассмотреть дисперсию по одному дереву, то она практически не меняется от переменных для разделения (
), а вот для ансамбля это играет большую роль, и дисперсия для дерева намного выше, чем для ансамбля.
В книге The Elements of Statistical Learning (Trevor Hastie, Robert Tibshirani и Jerome Friedman) есть отличный пример, который это демонстрирует.
Смещение
Как и в бэггинге, смещение в случайном лесе такое же, как и смещение в отдельно взятом дереве
:
Это также обычно больше (в абсолютных величинах), чем смещение «неусеченного» (unprunned) дерева, поскольку рандомизация и сокращение пространства выборки налагают ограничения. Следовательно, улучшения в прогнозировании, полученные с помощью бэггинга или случайных лесов, являются исключительно результатом уменьшения дисперсии.
Сверхслучайные деревья
В сверхслучайных деревьях (Extremely Randomized Trees) больше случайности в том, как вычисляются разделения в узлах. Как и в случайных лесах, используется случайное подмножество возможных признаков, но вместо поиска наиболее оптимальных порогов, пороговые значения произвольно выбираются для каждого возможного признака, и наилучший из этих случайно генерируемых порогов выбирается как лучшее правило для разделения узла. Это обычно позволяет немного уменьшить дисперсию модели за счет несколько большего увеличения смещения.
В библиотеке scikit-learn есть реализация ExtraTreesClassifier и ExtraTreesRegressor. Данный метод стоит использовать, когда вы сильно переобучаетесь на случайном лесе или градиентном бустинге.
Схожесть случайного леса с алгоритмом k-ближайших соседей
Метод случайного леса схож с методом ближайших соседей. Случайные леса, по сути, осуществляют предсказания для объектов на основе меток похожих объектов из обучения. Схожесть объектов при этом тем выше, чем чаще эти объекты оказываются в одном и том же листе дерева. Покажем это формально.
Рассмотрим задачу регрессии с квадратичной функцией потерь. Пусть
— номер листа
-го дерева из случайного леса, в который попадает объект
. Ответ объекта
равен среднему ответу по всем объектам обучающей выборки, которые попали в этот лист
. Это можно записать так
где
Тогда ответ композиции равен
Видно, что ответ случайного леса представляет собой сумму ответов всех объектов обучения с некоторыми весами. Отметим, что номер листа
, в который попал объект, сам по себе является ценным признаком. Достаточно неплохо работает подход, в котором по выборке обучается композиция из небольшого числа деревьев с помощью случайного леса или градиентного бустинга, а потом к ней добавляются категориальные признаки
. Новые признаки являются результатом нелинейного разбиения пространства и несут в себе информацию о сходстве объектов.
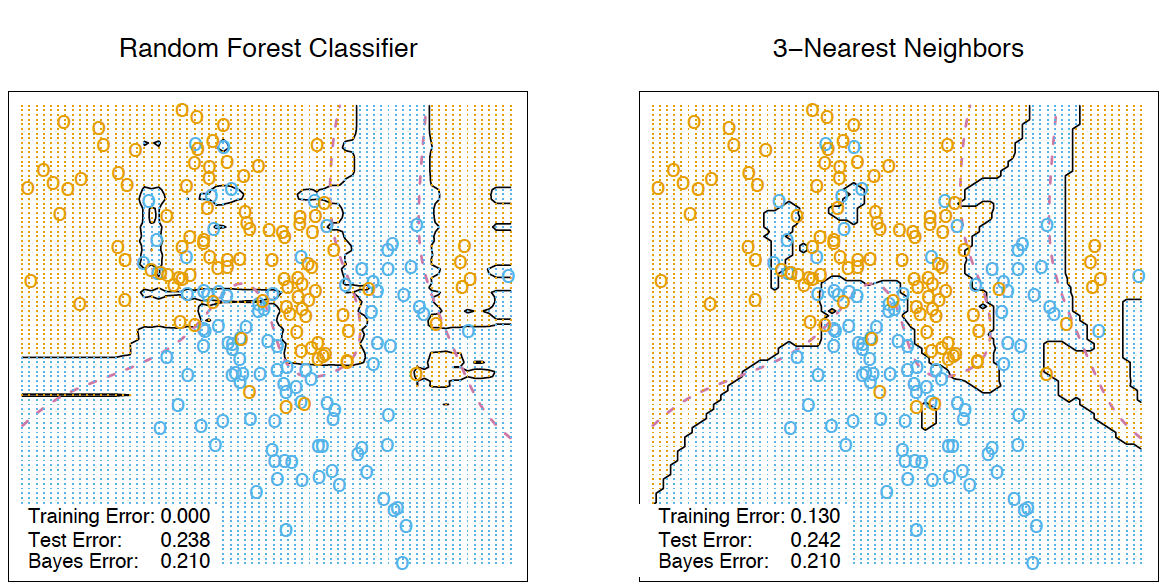
Все в той же книге The Elements of Statistical Learning есть хороший наглядный пример сходства случайного леса и k-ближайших соседей.
Преобразование признаков в многомерное пространство
Все привыкли использовать случайный лес для задач обучения с учителем, но также есть возможность проводить обучение и без учителя. С помощью метода RandomTreesEmbedding мы можем сделать трансформацию нашего датасета в многомерное разреженное его представление. Его суть в том, что мы строим абсолютно случайные деревья, и индекс листа, в котором оказалось наблюдение, мы считаем за новый признак. Если в первый лист попал объект, то мы ставим 1, а если не попал, то 0. Так называемое бинарное кодирование. Контролировать количество переменных и также степень разреженности нашего нового представления датасета мы можем увеличивая/уменьшая количество деревьев и их глубины. Поскольку соседние точки данных скорее всего лежат в одном и том же листе дерева, преобразование выполняет неявную, непараметрическую оценку плотности.
3. Оценка важности признаков
Очень часто вы хотите понять свой алгоритм, почему он именно так, а не иначе дал определенный ответ. Или если не понять его полностью, то хотя бы какие переменные больше всего влияют на результат. Из случайного леса можно довольно просто получить данную информацию.
Суть метода
По данной картинке интуитивно понятно, что важность признака «Возраст» в задаче кредитного скоринга выше, чем важность признака «Доход». Формализуется это с помощью понятия прироста информации.
Если построить много деревьев решений (случайный лес), то чем выше в среднем признак в дереве решений, тем он важнее в данной задаче классификации/регрессии. При каждом разбиении в каждом дереве улучшение критерия разделения (в нашем случае неопределенность Джини(Gini impurity)) — это показатель важности, связанный с переменной разделения, и накапливается он по всем деревьям леса отдельно для каждой переменной.
Давайте немного углубимся в детали. Среднее снижение точности, вызываемое переменной, определяется во время фазы вычисления out-of-bag ошибки. Чем больше уменьшается точность предсказаний из-за исключения (или перестановки) одной переменной, тем важнее эта переменная, и поэтому переменные с бо́льшим средним уменьшением точности более важны для классификации данных. Среднее уменьшение неопределенности Джини (или ошибки mse в задачах регрессии) является мерой того, как каждая переменная способствует однородности узлов и листьев в окончательной модели случайного леса. Каждый раз, когда отдельная переменная используется для разбиения узла, неопределенность Джини для дочерних узлов рассчитывается и сравнивается с коэффициентом исходного узла. Неопределенность Джини является мерой однородности от 0 (однородной) до 1 (гетерогенной). Изменения в значении критерия разделения суммируются для каждой переменной и нормируются в конце вычисления. Переменные, которые приводят к узлам с более высокой чистотой, имеют более высокое снижение коэффициента Джини.
А теперь представим все вышеописанное в виде формул.
— предсказание класса перед перестановкой/удалением признака
— предсказание класса после перестановки/удаления признака
Заметим, что, если
не находится в дереве
Расчет важности признаков в ансамбле:
— ненормированные— нормированные
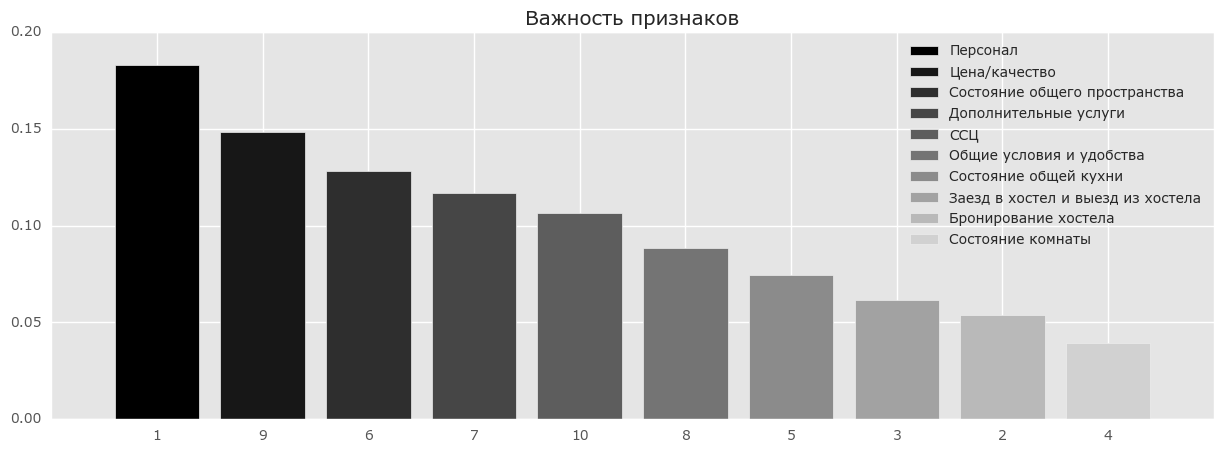
Пример
Рассмотрим результаты анкетирования посетителей хостелов с сайтов Booking.com и TripAdvisor.com. Признаки — средние оценки по разным факторам (перечислены ниже) — персонал, состояние комнат и т.д. Целевой признак — рейтинг хостела на сайте.
Код для оценки важности признаков
from __future__ import division, print_function # отключим всякие предупреждения Anaconda import warnings warnings.filterwarnings('ignore') %pylab inline import seaborn as sns # russian headres from matplotlib import rc font = {'family': 'Verdana', 'weight': 'normal'} rc('font', **font) import pandas as pd import numpy as np from sklearn.ensemble.forest import RandomForestRegressor hostel_data = pd.read_csv("../../data/hostel_factors.csv") features = {"f1":u"Персонал", "f2":u"Бронирование хостела ", "f3":u"Заезд в хостел и выезд из хостела", "f4":u"Состояние комнаты", "f5":u"Состояние общей кухни", "f6":u"Состояние общего пространства", "f7":u"Дополнительные услуги", "f8":u"Общие условия и удобства", "f9":u"Цена/качество", "f10":u"ССЦ"} forest = RandomForestRegressor(n_estimators=1000, max_features=10, random_state=0) forest.fit(hostel_data.drop(['hostel', 'rating'], axis=1), hostel_data['rating']) importances = forest.feature_importances_ indices = np.argsort(importances)[::-1] # Plot the feature importancies of the forest num_to_plot = 10 feature_indices = [ind+1 for ind in indices[:num_to_plot]] # Print the feature ranking print("Feature ranking:") for f in range(num_to_plot): print("%d. %s %f " % (f + 1, features["f"+str(feature_indices[f])], importances[indices[f]])) plt.figure(figsize=(15,5)) plt.title(u"Важность конструктов") bars = plt.bar(range(num_to_plot), importances[indices[:num_to_plot]], color=([str(i/float(num_to_plot+1)) for i in range(num_to_plot)]), align="center") ticks = plt.xticks(range(num_to_plot), feature_indices) plt.xlim([-1, num_to_plot]) plt.legend(bars, [u''.join(features["f"+str(i)]) for i in feature_indices]);
На рисунке выше видно, что люди больше всего обращают внимание на персонал и соотношение цена/качество и на основе впечатления от данных вещей пишут свои отзывы. Но разница между этими признаками и менее влиятельными признаками не очень значительная, и выкидывание какого-то признака приведет к уменьшению точности нашей модели. Но даже на основе нашего анализа мы можем дать рекомендации отелям в первую очередь лучше готовить персонал и/или улучшить качество до заявленной цены.4. Плюсы и минусы случайного леса
Плюсы:
— имеет высокую точность предсказания, на большинстве задач будет лучше линейных алгоритмов; точность сравнима с точностью бустинга
— практически не чувствителен к выбросам в данных из-за случайного сэмлирования
— не чувствителен к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков, связано с выбором случайных подпространств
— не требует тщательной настройки параметров, хорошо работает «из коробки». С помощью «тюнинга» параметров можно достичь прироста от 0.5 до 3% точности в зависимости от задачи и данных
— способен эффективно обрабатывать данные с большим числом признаков и классов
— одинаково хорошо обрабатывет как непрерывные, так и дискретные признаки
— редко переобучается, на практике добавление деревьев почти всегда только улучшает композицию, но на валидации, после достижения определенного количества деревьев, кривая обучения выходит на асимптоту
— для случайного леса существуют методы оценивания значимости отдельных признаков в модели
— хорошо работает с пропущенными данными; сохраняет хорошую точность, если большая часть данных пропущенна
— предполагает возможность сбалансировать вес каждого класса на всей выборке, либо на подвыборке каждого дерева
— вычисляет близость между парами объектов, которые могут использоваться при кластеризации, обнаружении выбросов или (путем масштабирования) дают интересные представления данных
— возможности, описанные выше, могут быть расширены до неразмеченных данных, что приводит к возможности делать кластеризацию и визуализацию данных, обнаруживать выбросы
— высокая параллелизуемость и масштабируемость.Минусы:
— в отличие от одного дерева, результаты случайного леса сложнее интерпретировать
— нет формальных выводов (p-values), доступных для оценки важности переменных
— алгоритм работает хуже многих линейных методов, когда в выборке очень много разреженных признаков (тексты, Bag of words)
— случайный лес не умеет экстраполировать, в отличие от той же линейной регрессии (но это можно считать и плюсом, так как не будет экстремальных значений в случае попадания выброса)
— алгоритм склонен к переобучению на некоторых задачах, особенно на зашумленных данных
— для данных, включающих категориальные переменные с различным количеством уровней, случайные леса предвзяты в пользу признаков с большим количеством уровней: когда у признака много уровней, дерево будет сильнее подстраиваться именно под эти признаки, так как на них можно получить более высокое значение оптимизируемого функционала (типа прироста информации)
— если данные содержат группы коррелированных признаков, имеющих схожую значимость для меток, то предпочтение отдается небольшим группам перед большими
— больший размер получающихся моделей. Требуетсяпамяти для хранения модели, где
— число деревьев.
5. Домашнее задание
В качестве закрепления материала предлагаем выполнить это задание – разобраться с бэггингом и обучить модели случайного леса и логистической регрессии для решения задачи кредитного скоринга. Проверить себя можно отправив ответы в веб-форме (там же найдете и решение).
Актуальные и обновляемые версии демо-заданий – на английском на сайте курса, вот первое задание. Также по подписке на Patreon («Bonus Assignments» tier) доступны расширенные домашние задания по каждой теме (только на англ.).
6. Полезные источники
– Open Machine Learning Course. Topic 5. Bagging and Random Forest (перевод этой статьи на английский)
– Видеозапись лекции по мотивам этой статьи
– 15 раздел книги “Elements of Statistical Learning” Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
– Блог Александра Дьяконова
– Больше про практические применение случайного леса и других алгоритмов-композиций в официальной документации scikit-learn
– Курс Евгения Соколова по машинному обучению (материалы на GitHub). Есть дополнительные практические задания для углубления ваших знаний
– Обзорная статья «История развития ансамблевых методов классификации в машинном обучении» (Ю. Кашницкий)Статья написана в соавторстве с yorko (Юрием Кашницким). Автор домашнего задания – vradchenko (Виталий Радченко). Благодарю bauchgefuehl (Анастасию Манохину) за редактирование.
Невозможно не восхищаться машинным обучением. Машины невероятно мощны. Даже Стив Балмер считает, что машинное обучение станет новой эрой вычислительной техники. В наши дни этот феномен окружён многочисленными слухами. Ману Дживан (Manu Jeevan) предлагает обзор основных концепций машинного обучения. dev.by публикует перевод его статьи.
Читать далее
Методы ансамблей (коллективные методы)
Классно, когда владеешь этими методами. Дерево принятия решений работает не очень хорошо, но очень быстро.
Методы ансамблей — это алгоритмы обучения, которые строят ряд классификаторов и затем классифицируют новые точки данных, суммируя результаты их предсказаний. В этой статье я буду говорить о некоторых популярных методах, например, бэггинге, бустинге и случайных лесах.
Если бы меня попросили рассказать про методы ансамблей одним предложением, я сформулировал бы это так: «Агрегация предсказаний нескольких классификаторов с целью повышения точности».
Но если вы хотите обучать множественные классификаторы, вам нужно больше данных. Чем больше степеней свободы имеет ваша модель, тем больший объём данных модель старается вместить и тем больше точек данных вам понадобится. Здесь и пригодится бутстрэп.
Бутстрэп
Вы используете имеющиеся данные и пытаетесь их приумножить — в этом суть бутстрэпинга. Возьмите N точек данных и введите N раз с заменой — в результате вы получите несколько наборов одного размера. Поскольку вы используете замену, каждый из этих образцов будет немного отличаться. Вы можете использовать каждый из наборов данных отдельно.
Помните, что вы не можете делать перекрёстную проверку в этом случае, потому что у вас есть бутстрэп образцы х1 и х2 и некоторые точки присутствуют как в х1, так и в х2.
Для лучшего понимания бутстрэпинга читайте эту ветку на Stack Exchange.
Бэггинг
Первый из методов ансамблей, о котором мы поговорим, называется бэггинг (bagging — сокр. от bootstrap aggregation).
Один из недостатков деревьев принятия решений в том, что они выглядят по-разному при наличии небольшой разницы в данных. Ансамбли превращают этот недостаток в преимущество.
Бэггинг состоит из следующих шагов:
- Получение нескольких образцов с помощью замены из вашего набора данных (бутстрэпинг).
- Обучение классификатора для каждого образца.
- Усреднение результатов каждого классификатора.
Когда каждый бутстрэп-образец выглядит немного иначе, вы получаете разные деревья принятия решений. Вы можете усреднить их и получить хорошую классификацию. Бэггинг значительно снижает переобучение.
Основная идея бэггинга — усреднить «шумные» и несмещённые модели для создания модели с низким расхождением в рамках классификации. Посмотрите это видео, чтобы лучше понять, что такое бэггинг.
Случайный лес
Случайный лес использует много деревьев принятия решений для создания классификации. В качестве параметров используется число признаков и число деревьев. Случайный лес — это готовый классификатор, большую часть времени вам не придётся думать об этих параметрах.
Если вы разобрались с концепцией деревьев принятия решений, понять случайные леса вам будет нетрудно. Я бы порекомендовал вам прочесть введение в случайные леса для дилетантов от Эдвина Чена и посмотреть это видео.
Вероятность ошибки случайного леса зависит от корреляции между деревьями и от силы отдельных деревьев.
Но если вы увеличите количество признаков при каждом разделении, увеличится и корреляция между деревьями, и сила отдельных деревьев. Если ваши деревья не очень отличаются, усреднение не даст улучшений, на которые вы рассчитываете. Отдельные деревья должны быть действительно сильными, если вы хотите, чтобы каждое дерево чему-то научилось. Здесь нужен компромисс.
а) Out-Of-Bag-ошибка
OOB-ошибка — это встроенная версия расчёта ошибки теста. Это очень удобно, потому что вам не нужно откладывать набор данных в самом начале. Вы берёте бутстрэп-сэмпл, который покрывает 60% оригинальных точек данных, и у вас есть 30% неиспользованных. Суть в том, что вы можете использовать эти 30% как точки для оценки ошибки теста. Если я делаю бутстрэп-сэмплы и в конце получаю 500 штук — это для каждого отдельного дерева, не для всего леса — у меня есть бутстрэп-сэмпл и оставшиеся точки, которые в него не вошли. Я могу использовать их для оценки результатов теста для каждого отдельного дерева (не всего леса). Суть в том, что вы можете сделать это для каждого дерева, и это даст характеристику случайного леса, потому что вы знаете, насколько сильны отдельные деревья.
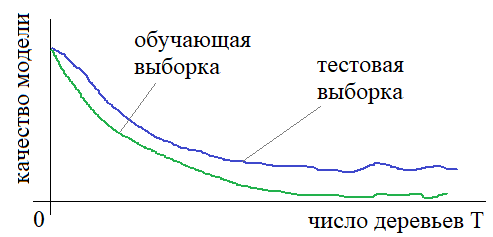
И всё же, я не считал бы OOB-ошибку ошибкой теста. Если вы изобразите их зависимость друг от друга, в большинстве случаев вы увидите возрастание, потому что это ненастоящая ошибка теста.
Можно использовать OOB-ошибку для валидации — таким образом вы можете подбирать оптимальное количество деревьев. Прочтите эту статью, чтобы узнать больше о OOB-ошибке.
b) Значимость переменной
Случайные леса позволяют вычислить эвристику для определения «значимости» параметра в предсказании цели. Она замеряет изменения в точности предсказаний, если вы возьмёте и перемешаете значения данного параметра между точками данных в тестовом наборе. Чем больше при этом снижается точность, тем более значимым считается параметр.
Допустим, есть 1000 мужчин и 1000 женщин. Измерим рост каждого человека и смоделируем предсказание роста по полу. В контексте случайного леса вы можете оценить точность предсказания out-of-bag.
Если пол не влияет на рост, вы должны получить примерно ту же точность предсказания при случайном переставлении значений М/Ж.
Так и работает значимость переменной случайных лесов: перемешайте наблюдаемые значения в рамках одной переменной, пересчитайте точности предсказаний и сравните полученные результаты с изначальными данными. Если перемешанные данные дают такие же предсказания, как и исходные, переменная, очевидно, не так важна для предсказания. Если же с перемешанными значениями точность предсказаний падает, переменная значима.
Несбалансированные классы
Несбалансированные классы означают, что у вас есть 8000 точек класса А и 2000 точек класса В. Ваша задача сделать так, чтобы классификатор понимал важность точек класса В. Один из вариантов — использовать сэмплы (продолжайте делать сэмплы, пока не получите два набора данных одинакового размера). Другой вариант — разбить на сэмплы большой класс. Случайный лес предоставляет хорошее решение для этого: вы можете создавать подсэмплы для каждого дерева. Таким образом, все деревья теперь сбалансированы, в итоге алгоритм получит все значения из большого класса.
Точность и полнота
Точность и полнота — оценочная метрика проблем классификации с асимметричными классами. Во многих приложениях необходимо контролировать соотношение точности и полноты.
Рассмотрим пример прогнозирования рака. Если вы модифицируете свою гипотезу (h(x)) до 0.7, чтобы уверенно прогнозировать рак, вы получите классификатор с высокой точностью и низкой полнотой. Иными словами, у пациента рак, но вы ошиблись, сообщив ему, что рака нет. Если вы установите (h(x)) на 0.3, вы получите высокую полноту и низкую точность. В этом случае классификатор может предсказать, что у большинства из них есть рак. Для большинства классификаторов это будет компромиссом между точностью и полнотой.
Есть ли способ определить порог автоматически? Как решить, какой из них лучше? И тут наступает очередь F-метрик. F-метрика — средство гармонизации точности и полноты.
Чтобы лучше понять, что такое точность и полнота, посмотрите эти видео-лекции (неделя 6) или прочитайте этот текст.
Бустинг
Это один из методов ансамблей, но он делает больше, чем просто усреднение. Вы обучаете один классификатор, смотрите на результаты и вносите коррективы. Вы обучаете второй, смотрите на результаты, вносите коррективы и усредняете их при помощи весов. Классификатору, который показал хороший результат, я хочу присвоить больший вес, второй получает меньший вес.
Для многих приложений бустинг подходит лучше, чем бэггинг. Читайте больше о бустинге здесь.
AdaBoost
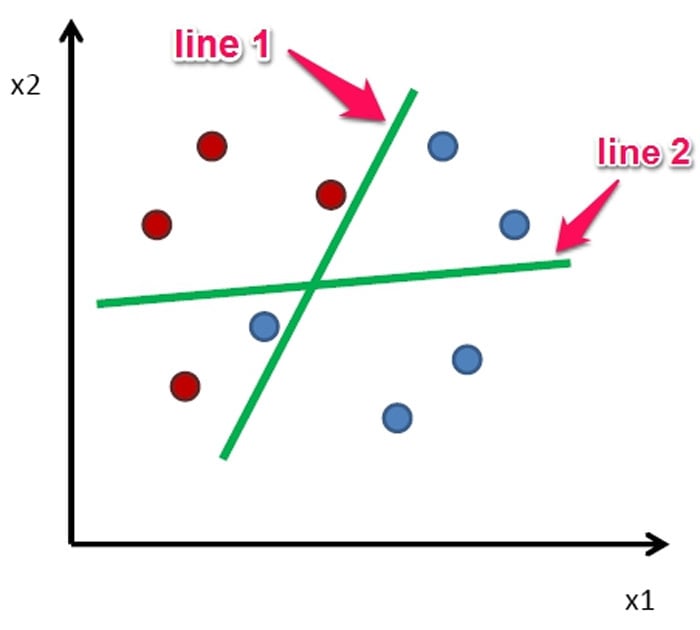
В AdaBoost вы рисуете одну границу решений и смотрите на классификации — несколько точек будут ошибочными. Я присвою этим точкам большой вес (они не классифицированы, линия 1 на рисунке). И следующему классификатору, который буду обучать, я скажу обратить больше внимания на эти точки. В итоге получим другую границу решений (линия 2). Вместо того, чтобы вносить неразбериху, я смотрю на работу предыдущего классификатора и пытаюсь исправить совершенные им ошибки.
В большинстве случаев AdaBoost работает даже с «пнями». Пни решений — одноуровневое дерево принятия решений, с одним разветвлением. На практике, линия AdaBoost будет не прямой, а ломанной.
Заключение
Итак, я рассказал о некоторых наиболее важных концептах машинного обучения. Концепцию ансамблей я бы хотел передать этой цитатой Джеймса Суровецки (James Surowiecki):
«Коллективное знание разнообразной и независимой группы людей обычно превышает знания каждого отдельного индивида и может быть учтено путем голосования».
Кстати, метод ансамблей использовали победители Netflix prize — посмотрите видео.
Не Duolingo единым.

Note
Click here
to download the full example code or to run this example in your browser via Binder
The RandomForestClassifier is trained using bootstrap aggregation, where
each new tree is fit from a bootstrap sample of the training observations
(z_i = (x_i, y_i)). The out-of-bag (OOB) error is the average error for
each (z_i) calculated using predictions from the trees that do not
contain (z_i) in their respective bootstrap sample. This allows the
RandomForestClassifier to be fit and validated whilst being trained [1].
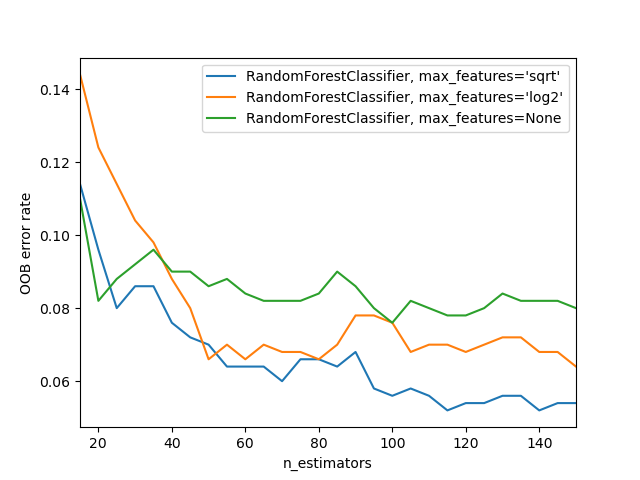
The example below demonstrates how the OOB error can be measured at the
addition of each new tree during training. The resulting plot allows a
practitioner to approximate a suitable value of n_estimators at which the
error stabilizes.
# Author: Kian Ho <hui.kian.ho@gmail.com> # Gilles Louppe <g.louppe@gmail.com> # Andreas Mueller <amueller@ais.uni-bonn.de> # # License: BSD 3 Clause import matplotlib.pyplot as plt from collections import OrderedDict from sklearn.datasets import make_classification from sklearn.ensemble import RandomForestClassifier RANDOM_STATE = 123 # Generate a binary classification dataset. X, y = make_classification( n_samples=500, n_features=25, n_clusters_per_class=1, n_informative=15, random_state=RANDOM_STATE, ) # NOTE: Setting the `warm_start` construction parameter to `True` disables # support for parallelized ensembles but is necessary for tracking the OOB # error trajectory during training. ensemble_clfs = [ ( "RandomForestClassifier, max_features='sqrt'", RandomForestClassifier( warm_start=True, oob_score=True, max_features="sqrt", random_state=RANDOM_STATE, ), ), ( "RandomForestClassifier, max_features='log2'", RandomForestClassifier( warm_start=True, max_features="log2", oob_score=True, random_state=RANDOM_STATE, ), ), ( "RandomForestClassifier, max_features=None", RandomForestClassifier( warm_start=True, max_features=None, oob_score=True, random_state=RANDOM_STATE, ), ), ] # Map a classifier name to a list of (<n_estimators>, <error rate>) pairs. error_rate = OrderedDict((label, []) for label, _ in ensemble_clfs) # Range of `n_estimators` values to explore. min_estimators = 15 max_estimators = 150 for label, clf in ensemble_clfs: for i in range(min_estimators, max_estimators + 1, 5): clf.set_params(n_estimators=i) clf.fit(X, y) # Record the OOB error for each `n_estimators=i` setting. oob_error = 1 - clf.oob_score_ error_rate[label].append((i, oob_error)) # Generate the "OOB error rate" vs. "n_estimators" plot. for label, clf_err in error_rate.items(): xs, ys = zip(*clf_err) plt.plot(xs, ys, label=label) plt.xlim(min_estimators, max_estimators) plt.xlabel("n_estimators") plt.ylabel("OOB error rate") plt.legend(loc="upper right") plt.show()
Total running time of the script: ( 0 minutes 3.850 seconds)
Gallery generated by Sphinx-Gallery
Ошибка вне сумки — Out-of-bag error
| Часть серии по |
| Машинное обучение и сбор данных |
|---|
|
Проблемы
|
|
Контролируемое обучение
|
|
Кластеризация
|
|
Снижение размерности
|
|
Структурированный прогноз
|
|
Обнаружение аномалий
|
|
Искусственная нейронная сеть
|
|
Обучение с подкреплением
|
|
Теория
|
|
Площадки для машинного обучения
|
|
Глоссарий искусственного интеллекта
|
|
Статьи по Теме
|
Вне сумки (OOB) ошибка, также называемый смета вне сумки, это метод измерения ошибки предсказания случайные леса, усиленные деревья решений, и другие машинное обучение модели, использующие начальная агрегация (упаковка). Bagging использует подвыборку с заменой для создания обучающих выборок для модели, на которой можно учиться. Ошибка OOB — это средняя ошибка прогноза для каждой обучающей выборки. xᵢ, используя только деревья, у которых не было xᵢ в их образце начальной загрузки.[1]
Агрегирование бутстрапа позволяет определить готовую оценку улучшения эффективности прогнозирования путем оценки прогнозов по тем наблюдениям, которые не использовались при построении следующего базового обучающегося.
Набор данных вне сумки
Когда начальная агрегация выполняется, создаются два независимых набора. Один набор, образец начальной загрузки, представляет собой данные, выбранные как «готовые к использованию» путем выборки с заменой. Набор вне сумки — это все данные, не выбранные в процессе отбора проб.
Когда этот процесс повторяется, например, при построении случайного леса, создается множество образцов начальной загрузки и наборов OOB. Наборы OOB могут быть объединены в один набор данных, но каждая выборка считается несуществующей только для деревьев, которые не включают ее в свою выборку начальной загрузки. На рисунке ниже показано, что для каждого отобранного пакета данные разделены на две группы.
Визуализация процесса упаковки. Отобрать 4 предмета из оригинального набора с заменой и показать наборы вне сумки.
Вычисление ошибки вне сумки
Поскольку каждый набор вне сумки не используется для обучения модели, это хороший тест на производительность модели. Конкретный расчет ошибки OOB зависит от реализации модели, но общий расчет выглядит следующим образом.
- Найдите все модели (или деревья, в случае случайного леса), которые не обучаются экземпляром OOB.
- Получите большинство голосов за результат этих моделей для экземпляра OOB по сравнению с истинным значением экземпляра OOB.
- Скомпилируйте ошибку OOB для всех экземпляров в наборе данных OOB.
В упаковка процесс можно настроить в соответствии с потребностями модели. Чтобы модель была точной, размер обучающей выборки начальной загрузки должен быть близок к размеру исходного набора.[2]. Кроме того, необходимо учитывать количество итераций (деревьев) модели (леса), чтобы найти истинную ошибку OOB. Ошибка OOB стабилизируется на протяжении многих итераций, поэтому рекомендуется начинать с большого количества итераций.[3].
Сравнение с перекрестной проверкой
Ошибка выдачи багажа и перекрестная проверка (CV) — это разные методы измерения оценки погрешности машинное обучение модель. На протяжении многих итераций оба метода должны давать очень схожую оценку ошибки. То есть, как только ошибка OOB стабилизируется, она сведется к перекрестная проверка (в частности, перекрестная проверка без исключения) ошибка[3]. Преимущество метода OOB в том, что он требует меньше вычислений и позволяет тестировать данные во время их обучения.
Смотрите также
- Повышение (мета-алгоритм)
- Агрегирование бутстрапа
- Самостоятельная загрузка (статистика)
- Перекрестная проверка (статистика)
- Случайный лес
- Метод случайных подпространств (упаковка атрибутов)
Рекомендации
- ^ Джеймс, Гарет; Виттен, Даниэла; Хасти, Тревор; Тибширани, Роберт (2013). Введение в статистическое обучение. Springer. С. 316–321.
- ^ Онг, Десмонд (2014). Праймер для начальной загрузки; и обзор doBootstrap (PDF). С. 2–4.
- ^ а б Хасти, Тревор; Тибширани, Роберт; Фридман, Джером (2008). Элементы статистического обучения (PDF). Springer. С. 592–593.
Out-of-bag (OOB) error, also called out-of-bag estimate, is a method of measuring the prediction error of random forests, boosted decision trees, and other machine learning models utilizing bootstrap aggregating (bagging). Bagging uses subsampling with replacement to create training samples for the model to learn from. OOB error is the mean prediction error on each training sample xi, using only the trees that did not have xi in their bootstrap sample.[1]
Bootstrap aggregating allows one to define an out-of-bag estimate of the prediction performance improvement by evaluating predictions on those observations that were not used in the building of the next base learner.
Out-of-bag datasetEdit
When bootstrap aggregating is performed, two independent sets are created. One set, the bootstrap sample, is the data chosen to be «in-the-bag» by sampling with replacement. The out-of-bag set is all data not chosen in the sampling process.
When this process is repeated, such as when building a random forest, many bootstrap samples and OOB sets are created. The OOB sets can be aggregated into one dataset, but each sample is only considered out-of-bag for the trees that do not include it in their bootstrap sample. The picture below shows that for each bag sampled, the data is separated into two groups.
Visualizing the bagging process. Sampling 4 patients from the original set with replacement and showing the out-of-bag sets. Only patients in the bootstrap sample would be used to train the model for that bag.
This example shows how bagging could be used in the context of diagnosing disease. A set of patients are the original dataset, but each model is trained only by the patients in its bag. The patients in each out-of-bag set can be used to test their respective models. The test would consider whether the model can accurately determine if the patient has the disease.
Calculating out-of-bag errorEdit
Since each out-of-bag set is not used to train the model, it is a good test for the performance of the model. The specific calculation of OOB error depends on the implementation of the model, but a general calculation is as follows.
- Find all models (or trees, in the case of a random forest) that are not trained by the OOB instance.
- Take the majority vote of these models’ result for the OOB instance, compared to the true value of the OOB instance.
- Compile the OOB error for all instances in the OOB dataset.
An illustration of OOB error
The bagging process can be customized to fit the needs of a model. To ensure an accurate model, the bootstrap training sample size should be close to that of the original set.[2] Also, the number of iterations (trees) of the model (forest) should be considered to find the true OOB error. The OOB error will stabilize over many iterations so starting with a high number of iterations is a good idea.[3]
Shown in the example to the right, the OOB error can be found using the method above once the forest is set up.
Comparison to cross-validationEdit
Out-of-bag error and cross-validation (CV) are different methods of measuring the error estimate of a machine learning model. Over many iterations, the two methods should produce a very similar error estimate. That is, once the OOB error stabilizes, it will converge to the cross-validation (specifically leave-one-out cross-validation) error.[3] The advantage of the OOB method is that it requires less computation and allows one to test the model as it is being trained.
Accuracy and ConsistencyEdit
Out-of-bag error is used frequently for error estimation within random forests but with the conclusion of a study done by Silke Janitza and Roman Hornung, out-of-bag error has shown to overestimate in settings that include an equal number of observations from all response classes (balanced samples), small sample sizes, a large number of predictor variables, small correlation between predictors, and weak effects.[4]
See alsoEdit
- Boosting (meta-algorithm)
- Bootstrap aggregating
- Bootstrapping (statistics)
- Cross-validation (statistics)
- Random forest
- Random subspace method (attribute bagging)
ReferencesEdit
- ^ James, Gareth; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert (2013). An Introduction to Statistical Learning. Springer. pp. 316–321.
- ^ Ong, Desmond (2014). A primer to bootstrapping; and an overview of doBootstrap (PDF). pp. 2–4.
- ^ a b Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning (PDF). Springer. pp. 592–593.
- ^ Janitza, Silke; Hornung, Roman (2018-08-06). «On the overestimation of random forest’s out-of-bag error». PLOS ONE. 13 (8): e0201904. doi:10.1371/journal.pone.0201904. ISSN 1932-6203. PMC 6078316. PMID 30080866.
Что из ошибки мешка в случайных лесах?
Является ли это оптимальным параметром для нахождения правильного количества деревьев в случайном лесу?
2 ответов
я попытаюсь объяснить:
предположим, что наш набор данных обучения представлен T и предположим, что набор данных имеет M функций (или атрибутов или переменных).
T = {(X1,y1), (X2,y2), ... (Xn, yn)}
и
Xi is input vector {xi1, xi2, ... xiM}
yi is the label (or output or class).
резюме РФ:
алгоритм случайных лесов-это классификатор, основанный в основном на двух методах —
- мешков
- метод случайных подпространств.
Предположим, мы решим иметь S количество деревьев в нашем лесу, то мы сначала создаем S наборы "same size as original" создано из случайной повторной выборки данных в T с заменой (n раз для каждого набора данных). Это приведет к {T1, T2, ... TS} наборы данных. Каждый из них называется набором данных bootstrap. Из-за «with-replacement» каждый набор данных Ti может иметь повторяющиеся записи данных, и Ti может отсутствовать несколько записей данных из исходных наборов данных. Это называется Bootstrapping. (en.wikipedia.org/wiki/Bootstrapping_(статистика))
Bagging-это процесс взятия бутстрапов , а затем агрегирования моделей, изученных на каждом бутстрапе.
теперь RF создает S деревья и использует m (=sqrt(M) or =floor(lnM+1)) случайные компоненты из M варианты для создания любого дерева. Это называется методом случайного подпространства.
для каждого Ti bootstrap dataset вы создаете дерево Ki. Если вы хотите классифицировать некоторые входные данные D = {x1, x2, ..., xM} вы дайте ему пройти через каждое дерево и произвести S выходы (по одному для каждого дерева), которые могут быть обозначены Y = {y1, y2, ..., ys}. Окончательный прогноз-большинство голосов на этом наборе.
ошибка выхода из мешка:
после создания классификаторов (S деревьев) для каждого (Xi,yi) в оригинальном наборе обучения, т. е. T, выделить все Tk, который не включает в себя (Xi,yi). Это подмножество, обратите внимание, представляет собой набор наборов данных boostrap, который не содержит конкретной записи из исходного набора данных. Этот набор называется out-of-bag образцы. Есть n такие подмножества (по одному для каждой записи данных в исходном наборе данных T). Классификатор OOB-это агрегация голосов только за Tk такой, что не содержит (xi,yi).
Out-of-bag оценка ошибки обобщения-это частота ошибок классификатора out-of-bag на обучающем наборе (сравните его с известным yi ‘ s).
почему это важно?
Исследование оценок погрешностей для мешочных классификаторов в Breiman [1996b], дает эмпирические доказательства того, что оценка «вне мешка» столь же точна, как и использование тестового набора того же размера, что и учебный набор. Таким образом с помощью оценки ошибки из мешка устраняет необходимость в наборе отложенных тестов.
(спасибо @Rudolf за исправления. Его комментарии приводятся ниже.)
в оригинальной реализации алгоритма случайного леса Бреймана каждое дерево обучается примерно на 2/3 от общих данных обучения. По мере построения леса каждое дерево может быть протестировано (аналогично исключению перекрестной проверки) на образцах, не используемых при построении этого дерева. Это оценка ошибки out of bag — внутренняя оценка ошибки случайного леса по мере его построения.
На предыдущих
занятиях мы с вами познакомились с идеей построения решающих бинарных деревьев
для задач классификации и регрессии. Однако на практике в чистом виде их почти
не используют. Но активно применяют в ансамблевых методах, которые
включают в себя два весьма эффективных подхода: бэггинг и бустинг.
Именно о бэггинге с использованием деревьев и пойдет речь на этом занятии.
Идея алгоритма
очень проста и была предложена Лео Брейманом в 1994 году. Этот подход оказался
весьма эффективным и используется до сих пор.
Итак, предположим
изначально у нас имеется некоторая обучающая выборка:
На ее основе мы
хотим сформировать несколько разных и, в общем случае, независимых алгоритмов
обработки входного вектора :
А, затем,
усреднить ответы каждого алгоритма для формирования общего решения.
Наверное, здесь
сразу возникает вопрос, зачем нам искусственно создавать несколько независимых
алгоритмов, а потом усреднять их выходы? На самом деле, этому есть вполне
логичное объяснение. Одна известная история гласит, как в 1906 году математик
Фрэнсис Гальтон посетил рынок и увидел, как продавец быка предложил покупателям
небольшую лотерею: угадать точный вес этого быка, который весил 1198 фунтов. От
крестьян посыпались самые разные предположения. Но ни один не назвал точное
значение. Однако, усреднив все ответы, получилось значение 1197 – очень близкое
к истинному. Вот так «мудрость толпы» решила эту непростую задачу.
Эта же идея
заложена в бэггинге, когда мы формируем множество независимых алгоритмов,
каждый выдает свой вариант ответа, а затем, мы его усредняем, чтобы получить
более точное значение.
Этот эффект
уменьшения ошибки при усреднении ответов легко объяснить с позиции теории
вероятностей. Предположим, что верное значение – вес быка – это величина
θ. Тогда ответы крестьян можно представить в виде следующей аддитивной
модели:
Здесь —
случайная величина. Понятно, что ошибка в ответах каждого, составляет:
с дисперсиями
ошибок:
Для простоты, я
буду считать, что все ошибки имеют единую дисперсию (разброс значений):
Тогда, дисперсия
усредненного ответа:
при условии
независимости каждой СВ:
и несмещенности
ошибки (нулевого среднего):
равна:
То есть,
дисперсия одного
отдельного ответа (алгоритма) после усреднения всех результатов, уменьшается в T раз. Это
означает, что итоговая величина становится точнее T независимых
ответов каждого алгоритма.
Обратите
внимание, я здесь постоянно подчеркиваю – независимых ответов. Если
ответы (предположения о весе быка) будут зависеть друг от друга, то простое
усреднение станет уже не лучшим подходом, а в ряде случаев может даже ухудшить
отдельные результаты. Поэтому независимость работы алгоритмов при бэггинге
является ключевым условием.
Бутстрэп (bootstrap)
Так как же нам
сформировать T независимых
алгоритмов, используя всего одну обучающую выборку? Здесь есть несколько идей,
но в бэггинге используется очень простой подход, который носит название бутстрэп
(bootstrap). Суть бутстрэпа
заключается в формировании T новых обучающих
выборок на основе одной исходной .
Для этого случайным образом выбирается k-й элемент выборки
и копируется в новую (в прежней он остается, не удаляется). Затем, эта операция
повторяется m раз – по
заданному размеру новой выборки. Так формируется новая обучающая выборка,
состоящая из элементов исходной с некоторыми повторениями, так как вполне можно
несколько раз случайно отобрать один и тот же элемент. После формирования одной
выборки, переходят к формированию следующей и так T раз для T выборок, которые,
очевидно, будут несколько отличаться друг от друга. Это идея бутстрэпа.
Можно показать,
что формируя, таким образом, новую обучающую выборку длиной ,
она будет использовать, в среднем, образов
из исходной выборки (остальные будут повторяться). Это значит, что оставшуюся
часть выборки в 36,8% можно использовать в качестве отложенной для проверки
качества алгоритма. И это нашло выражение в критерии под названием out-of bag, когда мы
определяем число ошибок по объектам ,
не участвующих в обучении того или иного дерева:
Здесь —
множества объектов, составляющих обучающую выборку для дерева t. В результате out-of bag – это
несмещенная оценка обобщающей способности итогового алгоритма .
Бэггинг с решающими деревьями. Случайный лес
Собственно, само
слово bagging произошло
от сокращения двух английских слов: bootstrap aggregation. Итак, имея T случайных
выборок длиной m элементов (),
мы можем по ним получить T алгоритмов
(классификации или регрессии). Например, используя линейную модель:
можно
сформировать T наборов весовых
векторов:
каждая для своей
обучающей выборки. В результате получаем T различных
алгоритмов:
А, затем,
усредняя ответы от них, формируем общий результат:
Или, устраивая
голосование, решаем задачу классификации:
Как видите, в
теории все просто. Но здесь есть один важный нюанс: алгоритмы в своей
совокупности должны охватывать как можно больше возможных исходов для каждого
входного вектора и,
кроме того, формировать как можно более независимые ответы. В этом смысле
обычные линейные модели не очень пригодны при композиции (в частности, при усреднении
ответов). Гораздо лучшие результаты дают решающие деревья, построенные
независимо на каждой сформированной обучающей выборке (на этапе бустрэпа).
Как ни странно,
приверженность деревьев к переобучению играет положительную роль. Они,
во-первых, получаются довольно разнообразными и, во-вторых, описывают самые
разные исходы для входных векторов .
Затем, при усреднении результатов, эффект переобучения естественным образом
нивелируется (уменьшается) и итоговое выходное значение оказывается достаточно
точным и устойчивым к отдельным выбросам. В ряде задач точность оказывается
выше всех других подходов машинного обучения. Именно поэтому бутстрэп быстро
завоевал свою популярность.
Чтобы решающие
деревья получались еще более разнообразными и формировали менее зависимые
ответы, предлагается при их обучении в каждой промежуточной вершине случайным
образом отбирать некоторое количество признаков и
уже среди них отбирать лучшие для ветвления. Наборы из таких деревьев называют случайным
лесом (random forest). Причем, было
показано, что в задачах классификации число,
а в задачах регрессии .
Есть теоретические выкладки почему это так (кому интересно, можно найти в
литературе по машинному обучению). Сами же признаки и пороги для ветвления
выбираются, как правило, по критерию Джини (он быстрее вычисляется, чем
энтропийный и приводит к практически тем же результатам). А усечений деревьев
уже не делают, они остаются переобученными. Как я уже отмечал, обобщение и
устойчивость выходного значения будет определяться усреднением независимых ответов
от каждого дерева. Причем, для случайного леса кривые качества на обучающей и
проверочной выборках в среднем уменьшаются при увеличении числа деревьев T:
То есть, с
ростом числа T решающих
деревьев в случайном лесе итоговая модель не переобучается, а лишь достигает
некоторого предельного уровня качества. Это очень хорошее свойство случайного
леса, так как мы, фактически, получаем алгоритм, в котором нет сложно
настраиваемых гиперпараметров. Единственный параметр T можно взять,
например, 100, а затем, 500 и сравнить результаты на тестовой выборке. То есть,
подобрать его очень просто. Остальные гиперпараметры для построения решающих
деревьев можно выбирать с позиции некоего здравого смысла. Главное, чтобы
деревья получались глубокими, гарантируя малые смещения в ответах. Напомню, что
под смещением здесь понимается стремление к нулю (в среднем) ошибки прогноза:
Реализация случайного леса на Python
Вот идея
бэггинга с применением случайного леса. Для ее реализации на языке Python в библиотеке Scikit-Learn имеются два
класса:
-
RandomForestClassifier
– случайный лес для задач классификации; -
RandomForestRegressor
– случайный лес для задач регрессии.
У каждого класса
есть следующий набор основных параметров:
-
n_estimators
– число используемых деревьев; -
criterion
– критерий разбиения выборки в промежуточных вершинах; -
max_features
– число признаков, по которым ищется разбиение; -
min_samples_leaf
– минимальное число объектов в листе; -
max_depth
– максимальная глубина дерева.
Подробнее о них
можно почитать на странице русскоязычной документации:
Ниже
представлены результаты аппроксимации функции косинуса с небольшим гауссовским
шумом случайными деревьями:
Программу можно
скачать по ссылке:
machine_learning_41_regression.py
Как видите, при
увеличении числа деревьев одной и той же глубины, повышается точность описания
исходной функции. Это пример реализации бэггинга на случаных деревьях.
Преимущества и недостатки случайного леса
Как и любой алгоритм,
случайные леса имеют свои преимущества и недостатки. К преимуществам можно
отнести:
-
имеет
высокую точность прогнозов (на большинстве задач работает лучше линейных
алгоритмов); точность сравнима с точностью бустинга; -
практически
не чувствителен к выбросам в данных из-за случайного сэмлирования выборок
методом бутсрэпа; -
не
чувствителен к масштабированию (и вообще к любым монотонным преобразованиям)
значений признаков, связано с выбором случайных подпространств; -
не
требует тщательной настройки параметров, хорошо работает «из коробки»; -
способен
эффективно обрабатывать данные с большим числом признаков и классов; -
редко
переобучается, на практике добавление деревьев почти всегда только улучшает
композицию (до определенного, предельного уровня); -
хорошо
работает с пропущенными данными; сохраняет хорошую точность, если большая часть
данных пропущена; -
могут
быть расширены до неразмеченных данных, что приводит к возможности делать
кластеризацию и визуализацию данных, обнаруживать выбросы; -
легко
распараллеливать и масштабировать (увеличивать число деревьев и их глубину).
Недостатки случайного леса
-
в
отличие от одного дерева, результаты случайного леса сложнее интерпретировать; -
алгоритм
работает хуже многих линейных методов, когда в выборке очень много разреженных
признаков (тексты, Bag of words); -
случайный
лес не умеет экстраполировать, в отличие от той же линейной регрессии; -
алгоритм
склонен к переобучению на некоторых задачах, особенно на сильно зашумленных
данных; -
для
данных, включающих категориальные переменные с различным количеством уровней,
случайные леса предвзяты в пользу признаков с большим количеством уровней:
когда у признака много уровней, дерево будет сильнее подстраиваться именно под
эти признаки, так как на них можно получить более высокое значение
оптимизируемого функционала (информационный выигрыш); -
больший
размер получающихся моделей. Требуется O(N∙K) памяти для хранения модели,
где K – число деревьев.
На этом мы
завершим данное занятие. Надеюсь, вы понял, что из себя представляет идея
бэггинга вообще и как он работает для случайного леса.