Sample Percent Error Calculation
ThoughtCo / Nusha Ashjaee
Updated on November 02, 2020
Percent error or percentage error expresses as a percentage the difference between an approximate or measured value and an exact or known value. It is used in science to report the difference between a measured or experimental value and a true or exact value. Here is how to calculate percent error, with an example calculation.
Key Points: Percent Error
- The purpose of a percent error calculation is to gauge how close a measured value is to a true value.
- Percent error (percentage error) is the difference between an experimental and theoretical value, divided by the theoretical value, multiplied by 100 to give a percent.
- In some fields, percent error is always expressed as a positive number. In others, it is correct to have either a positive or negative value. The sign may be kept to determine whether recorded values consistently fall above or below expected values.
- Percent error is one type of error calculation. Absolute and relative error are two other common calculations. Percent error is part of a comprehensive error analysis.
- The keys to reporting percent error correctly are to know whether or not to drop the sign (positive or negative) on the calculation and to report the value using the correct number of significant figures.
Percent Error Formula
Percent error is the difference between a measured or experiment value and an accepted or known value, divided by the known value, multiplied by 100%.
For many applications, percent error is always expressed as a positive value. The absolute value of the error is divided by an accepted value and given as a percent.
|accepted value — experimental value| accepted value x 100%
For chemistry and other sciences, it is customary to keep a negative value, should one occur. Whether error is positive or negative is important. For example, you would not expect to have positive percent error comparing actual to theoretical yield in a chemical reaction. If a positive value was calculated, this would give clues as to potential problems with the procedure or unaccounted reactions.
When keeping the sign for error, the calculation is the experimental or measured value minus the known or theoretical value, divided by the theoretical value and multiplied by 100%.
percent error = [experimental value — theoretical value] / theoretical value x 100%
Percent Error Calculation Steps
- Subtract one value from another. The order does not matter if you are dropping the sign (taking the absolute value. Subtract the theoretical value from the experimental value if you are keeping negative signs. This value is your «error.»
- Divide the error by the exact or ideal value (not your experimental or measured value). This will yield a decimal number.
- Convert the decimal number into a percentage by multiplying it by 100.
- Add a percent or % symbol to report your percent error value.
Percent Error Example Calculation
In a lab, you are given a block of aluminum. You measure the dimensions of the block and its displacement in a container of a known volume of water. You calculate the density of the block of aluminum to be 2.68 g/cm3. You look up the density of a block of aluminum at room temperature and find it to be 2.70 g/cm3. Calculate the percent error of your measurement.
- Subtract one value from the other:
2.68 — 2.70 = -0.02 - Depending on what you need, you may discard any negative sign (take the absolute value): 0.02
This is the error. - Divide the error by the true value:0.02/2.70 = 0.0074074
- Multiply this value by 100% to obtain the percent error:
0.0074074 x 100% = 0.74% (expressed using 2 significant figures).
Significant figures are important in science. If you report an answer using too many or too few, it may be considered incorrect, even if you set up the problem properly.
Percent Error Versus Absolute and Relative Error
Percent error is related to absolute error and relative error. The difference between an experimental and known value is the absolute error. When you divide that number by the known value you get relative error. Percent error is relative error multiplied by 100%. In all cases, report values using the appropriate number of significant digits.
Sources
- Bennett, Jeffrey; Briggs, William (2005), Using and Understanding Mathematics: A Quantitative Reasoning Approach (3rd ed.), Boston: Pearson.
- Törnqvist, Leo; Vartia, Pentti; Vartia, Yrjö (1985), «How Should Relative Changes Be Measured?», The American Statistician, 39 (1): 43–46.
As the name suggests, per cent error is the difference between the exact or known value of something and its approximate or measured value, in percentage form. In scientific experiments, it is used to report the difference between the experimental value to its true or exact value. It is calculated as the percentage of the exact value. As a real-world example, if you look at a gumball machine and make an estimate of how many gumballs are there and then you actually go ahead and calculate the number of gumballs, then you will be able to measure the per cent error you made in your guess.
Per cent error lets you see how far off you are in estimating the value of something from its exact value. These errors could happen due to the imprecision of equipment, measurement (human error or tool error), or some adjustments done in calculation methods (rounding off, etc.). There is a simple and straightforward formula for calculating this per cent error and is given below:
Per cent error = (Approximate or experimental Value — Exact or known Value/Exact or known Value)∗100
If the per cent error is close to 0, then your approximation is very close to the actual or true value. This formula is very important to determine the precision of your calculations. For most applications, the per cent error is represented as a positive number, but for some sciences like chemistry, it is customary to express it as a negative number since a positive value in chemistry would point to a potential problem with the experiment or reactions which are not accounted for.
How to Calculate Percent?
The following steps need to be taken in order to calculate per cent error in any experiment or observation:
You get the “error” value by subtracting one value from another. If you are not keeping the sign, then the order does not matter, but if you are keeping a negative sign, then you get the “error” value by subtracting the exact value from the measured value.
You then divide this “error” value by the known or exact value (not your measured or experimental value).
This division will give you a decimal number. Multiply this decimal value with 100 to convert it into a percentage value.
Finally, you would add a % notation in front of the calculated value to report your per cent error.
Solved Examples on Percent Error
We have here a few diverse examples on calculating per cent errors to delve into the concept and get more clarity:
1. In a concert, it was estimated by the organizers that 90 people would show up but in fact, 120 people came to the concert. Calculate the per cent error in the guess value of organizers.
The formula for percent error =
[frac{text{Estimated or approximate value — known or exact value}}{text{known or exact value}}ast] 100
Putting the above values we get; % error = [frac{mid 90-120mid }{120}ast 100 = frac{30}{120}ast100] = 25%
2. Ole Rømer was a Danish astronomer who observed that depending on the distance of Jupiter from Earth, the periods of Jupiter’s satellites seemed to fluctuate. The satellites took longer to appear from behind the planet if Jupiter was further away from Earth than otherwise. He related this to the speed of light and gave an approximate value, 220,000 km/s, for the velocity of light. The accepted value of the speed of light currently is 299,800 km/s. What percent error did Rømer’s observation have?
% error = [frac{mid2,20,000-299,800 mid }{299,800}ast ] 100 = 26.62%
Method for Finding Per Cent Error
It is quite simple to find per cent error. Students need to know a few important things for finding a per cent error. They must know the estimated value and original value to find the per cent error.
First, they have to find the difference between the estimated value and the original value. The value could be negative or positive. Students can ignore the negative sign. They have to subtract the original value from the estimated value.
After finding the difference students will divide the difference with the original value and multiply with one hundred to get the per cent value. This is the way to find the per cent error for any experiment.
It is quite useful for students in different fields. Therefore, students must understand the formula and the method of calculating the per cent error. Vedantu provides the best information on per cent error. Students can visit the Vedantu website to get the required definition, formula and examples related to the per cent error. This can help students to prepare well for their exams.
Solved Examples for Percent Error
A few solved examples are given here that can help students to understand the type of questions asked in the exam related to the per cent error and they can also understand the method for finding the per cent error.
1. A man installed a stall and thought that daily 100 people would visit the stall but only 80 turned up every day. Calculate the per cent error.
Solutions: Students have to apply the formula:
Estimated value: 100
Original value: 80
Percent error= Estimated value- original value
Original value
100-80
80
¼ x 100= 100 /4 = 25%
The Benefits of Finding Per Cent Errors
There are numerous benefits of finding the per cent errors. A few benefits of finding per cent errors are given here:
Per cent error is important to know the accuracy. Accuracy means the degree of closeness of a measured value to its original value. The per cent error is calculated by dividing the difference of the estimated value and the original value by the original value and multiplying it with 100.
The most important benefit of finding a per cent error is to know how close you are to the true value. The per cent error could be as low as negligible or could be very high depending on your observations. Thus, if the per cent error is very low you can neglect it but if the per cent error is high you have to calculate or measure the things again to get the absolute value.
Few Worked Examples:
1. It is estimated that the distance to the moon is 235,755 miles on a particular day. But, the actual distance is found to be 250,655 miles. Calculate the per cent error.
Ans. The percent error can be calculated as:
235,755 — 250,655/ 250,655 = 0.059 x100 = 5.9%
2. John was planning a hiking trip with friends. He estimated the height of the hiking trail to be 215 ft/mile. But, when he went with his friends he found the actual height of the trail was 230 ft/mile. What was the per cent error in John’s calculation?
Ans. [frac{215-230}{230} =frac{15}{230}] = 0.065 x 100 = 6.5%
3. A school organized a fest that was open for all. Teachers and students estimated that 1000 people will visit every day. But, the actual number of people visiting the fest was 1050. Calculate the per cent error.
Ans. [frac{1000-1050}{1050} =frac{50}{1050}] = 0.047 x 100 = 4.7%
4. A man wanted to prepare a square lawn in front of his house. He estimated it to cover 450 square meters of area. But, when he started digging for the garden the actual area to be covered was 470 meters square. Calculate the per cent error.
Ans. [frac{450-470}{470} =frac{20}{470}] = 0.042 x 100 = 4.2%
Conclusion
Percent error is the difference between a measured value and the exact value of any quantity under observation. It is calculated as the percentage of the exact or known value. One can calculate its value by the formula:
[frac{text{Estimated or approximate value — known or exact value}}{text{known or exact value}}ast] 100
The sign of the percent error is not considered in most applications except in chemistry and some other sciences where it is customary to keep a negative sign. Percent error is a type of error calculation. Few other types of common error calculations are relative error and absolute error.
When we do the analysis we can make errors. Per cent errors help us to determine our errors when we measure something. If the percent error is small it means that we have calculated close to the exact value. For example, if the percent error is only 2% it means that we are very close to the original value but if the percent error is big that is up to 30% it means we are very far off from the original value. Measurement errors are common due to different reasons. Some of the reasons for percent errors are given here:
Percent errors can occur due to imprecise materials available. Sometimes, people doing an experiment do not have proper materials available with them that can lead to percent error.
Errors can also occur due to improper instruments that are available for calculations as the instrument available may not have the capacity to measure a particular item exactly.
Percentage error is an estimation of the inconsistency between a noticed and a valid or acknowledged esteem. While estimating information, the outcome regularly shifts from genuine worth. The error can emerge because of a wide range of reasons that are regularly connected with human error yet can likewise be because of assessments and limits of gadgets utilized in the estimation. Notwithstanding, in such cases, it becomes essential to ascertain the percentage error. The calculation of percentage error includes the outright error, which is basically the contrast between the noticed and the genuine worth. The absolute error is then partitioned by the exact value, bringing about the general error duplicated by 100 to get the percentage error.
The percentage error value is a lot of significant under test computations. It permits us to perceive how far separated the evaluations and the exact value was, concerning a percentage. Hence we really want to process percentage errors experiencing the same thing.
Percent error
Percent/Percentage error is the distinction between the actual value and the estimated value contrasted with the actual value and is communicated in a percentage design. All in all, you track down the distinction between the actual response and the speculated reply, partition it by the actual response, and express it as a percentage. Percent errors demonstrate how gigantic our errors are at the point at which we measure something. For example, a 3% error demonstrates that we got extremely near the acknowledged value, while 80% implies that we were very a long way from the actual value
In simple words, Percentage error is the contrast between a deliberate and exact value, isolated by the known value, and subsequently increased by 100 percent. For some applications, percentage error is communicated as a positive value. Regularly, the absolute value of the error is partitioned by an accepted value and given as a percent.
Percent error formula
The formula for finding percent error,
Percent Error = (Actual Value – Estimated Value)/(Exact value) × 100
Most of the time, the percentage error is expressed as a positive value.
Actual value can be a few times named as true value or exact value.
Finding the Percent Error
Percentage error can be determined utilizing three straightforward advances,
- Work out the error (Deduct assessed esteem from the real worth) and disregard any negative (-) sign. i.e., take the absolute worth of error.
Absolute Error = Approximate Value – Exact Value
- Partition the error by the real worth (in some cases, we might get a decimal number).
Relative Error = (Approximate Value – Exact Value )/( Exact Value)
- Convert that to a percentage (by increasing by 100 connect “%” sign)
Percent Error = {(Approximate Value – Exact Value )/( Exact Value)} × 100 percent.
The absolute worth of the error is separated by a genuine worth and displayed as a percent.
Sample Questions
Question 1: Mr. Raju measured his height and found 6 feet. But later on, by careful observation, he has found his actual height to be 5.5 ft. Find the percent error Raju made in measuring his height.
Solution:
Before solving the problem, let us identify the information,
Actual value = 5.5 ft and Estimated value = 6 ft.
Now,
Step 1: Subtract one value from others to get the absolute value]e of error.
Error = 6 – 5.5
= 0.5
Step 2: Divide the error by actual value.
0.5/5.5 = 0.0909 (up to 4 decimal places)
Step 3: Multiply that answer by 100 and attach the % symbol to express the answer as a percentage
0.0909 × 100 = 9.09%
Therefore Percentage error measured is 9.09%
Question 2: Lakshmi’s mathematical class had 34 children yesterday. She miscounted the class total and recorded it as 28 children. What is Lakshmi’s percent error?
Solution:
The actual number of students = 34
Recorded number of students = 28
Absolute Error = 34 – 28 = 6
Percent Error = 6/28 = 0.21
= 0.21 × 100 = 21%
Lakshmi’s percent error is 21%
Question 3: A boy measured the area of a rectangle plot to be 450 cm². But the actual area of the plot has been recorded as 455 cm². Calculate the percent error of his measurement.
Solution:
Given,
Measured area value = 450 cm²
Actual area value = 455 cm²
Steps of calculation,
Step 1: Subtract one value from another; 455 – 450 = 5
the difference is 5, which is the error.
Step 2: Divide the error by actual value; 5/455 = 0.0109
Step 3: Multiply this value by 100
0.0109 × 100 = 0.109% (expressing it in two decimal points)
Hence, 0.10% is the percent error.
Question 4: A scale measures wrongly a value as 21 cm due to some marginal errors. Calculate the percentage error if the actual measurement of the value is 17 cm.
Solution:
Given in the problem,
Recorded measurement = 21 cm
Actual measurement = 17 cm
Error = Recorded measurement – Actual measurement
= 21 – 17 = 4
Applying the formula for the computation,
Percentage Error = (Error) / (Actual measurement) × 100
= (4/17) × 100 = 0.235 × 100 = 23.5
Percentage Error calculated as 23.5%
Question 5: John expected 30 people to turn up for a job interview, but only 24 did. What was the percentage error?
Solution:
The actual number of people attended = 24
Number of people expected = 30
Absolute Error = 30 – 24 = 6
Percent Error = 6/30 = 0.20
= 0.20 × 100 = 20%
John’s percent error is 20%
Question 6: Sam thought 90 people would turn up to the concert, but in fact, 100 did. What would be Sam’s percent error?
Solution:
The actual number of people came to concert = 100
Number of people Sam expected = 90
Error = Expected number of people attended – Actual number of people
= 100 – 90 = 10
Applying the formula for the computation,
Percentage Error = (Error) / (Actual measurement) × 100
= (10/90) × 100 = 0.235 × 100 = 23.5
Percentage Error calculated as 23.5%
Question 7: Shreya is attempting the precision of a scale in her science lab. She took a weight that she knew had a mass of 30 kg and weighed it. The scale read that the weight weighed 30.4 kg. What is the absolute error of the mass of the weight that Shreya recorded? And also find percent error?
Solution:
Use the absolute error formula to determine this,
Absolute Error = |Actual Value – Measured Value|
Absolute Error = x
Actual Value = 30
Measured Value = 30.4
= |30 – 30.4| = |−0.4| = 0.4
The absolute error was 0.4 kg.
Percentage Error = (Error) / (Actual value) × 100
= (0.4/30) × 100
=1.3333% (Considering upto 2 decimal points)
Therefore Shreya’s percent error is 1.33%
Download Article
Download Article
The percentage error is, formally, the magnitude of the difference between an exact and an approximate value divided by the magnitude of the exact value per 100 cases (percentage form). Essentially, this allows you to see how far off an approximate value and an exact value are in a percentage of the exact value. The error can be because of measuring errors (tools or human error) or because of approximations used in calculating (rounding errors, for example). Regardless, the formula is straight forward and simple to calculate.
-
1
Write down the formula for percentage error. The formula for calculating percentage error is simple: [(|Approximate Value — Exact Value|) / Exact Value] x 100. You will use this as a reference to plug in the two values you need to know.[1]
- The approximate value is your estimated value, and the exact value is the real value.
- For example, if you guess that there will be 9 oranges in a bag, but there are actually 10, 9 is the approximate value, and 10 is your exact value.
-
2
Subtract the exact value from the approximate one. In the example of oranges, you will subtract 10 (the exact value) from 9 (the estimated value). In this case, the result is 9 — 10 = -1. [2]
- This difference is considered the magnitude of difference in approximate and estimated values. This begins to tell you how far off the results were from what they were expected to be.
Advertisement
-
3
Find the absolute value of the top result. Since the formula uses the absolute value of the difference, you can discard a negative sign. In this example, -1 will become just 1.[3]
- In the oranges example, 9 — 10 = -1. The absolute value of -1, written as |-1|, is 1.
- If your result is positive, leave the number as it is. For example, 12 apples (approximate) — 10 apples (exact) = 2. The absolute value of 2 (|2|) is just 2.
- In statistics, taking the absolute value simply means you don’t care which direction your guess was off (either too high—positive—or too low—negative). You just want to know how far off the estimate was from the exact value.
-
4
Divide that result by the absolute exact value. Either with a calculator or by hand, divide the top number by the absolute value of your exact variable. In this example, the exact value is already positive, so you just need to divide 1 (from the previous step) by 10 (the exact number of oranges).[4]
- For this example, 1/|10| = 1/10.
- In some cases, the exact value might be a negative number to begin with. If this is the case, you want to ignore the negative (i.e. take the absolute value of the exact number).[5]
Advertisement
-
1
Convert the fraction into decimal form. To convert the fraction into a percentage, it is easiest to have a decimal number.[6]
For our example, 1/10 = 0.1. Calculators will be able to convert more difficult numbers quickly for you.- If you cannot use a calculator, it may take using long division to convert the fraction to a decimal. Usually, about 4 or 5 digits past the decimal place will be sufficient to round to.
- You should always be dividing a positive number by a positive number when converting to decimal form.
-
2
Multiply the result times 100. Simply multiply the result, 0.1 in this example, by 100. This will convert the answer into percentage form. Just add the percentage symbol to the answer, and you’re done.[7]
- In this example, 0.1 x 100 = 10. Add the percent sign to get 10%, your percentage error.
-
3
Check your work to make sure the answer is correct. Often swapping signs (positive/negative) and dividing can lead to minor errors in your calculations. It is best to go back to check your answer makes sense.[8]
- In our example, we want to make sure that our approximation of 9 oranges is off by 10% of the actual value of oranges. 10% (10% = 0.1) of 10 oranges is 1 (0.1 x 10 = 1).
- 9 oranges + 1 = 10 oranges. This confirms that the guess of 9 was indeed off by just 1 oranges or 10% of the actual value of 10 oranges.
Advertisement
Add New Question
-
Question
In a resistor, the relationship between the voltage V, the current I and resistance R, is given by Ohm’s law: V=IR. If the voltage is constant, how is the relative change in R related to the relative change in the current?
I and R are inversely proportional. That means that as I increases, R decreases by the same percentage (and vice versa).
-
Question
Do I use significant figures while calculating percentage error?
Yes.
-
Question
How do I calculate the percentage error in the kinetic energy of a particle?
Multiplying the relative errors of measuring the mass and the velocities should do.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
You may see the values called experimental (approximate) and theoretical (exact). Make sure to use the value you are comparing against as the exact value.
-
Oddly enough, since you will take the absolute value of the difference in approximate and exact values, it doesn’t matter which order you subtract the values. For example, |8 — 4| = 4 and |4 — 8| = |-4| = 4. The values turn out to be the same!
Thanks for submitting a tip for review!
Advertisement
About This Article
Article SummaryX
To calculate percentage error, use the formula: [(exact value — approximate value)/exact value] x 100. First, subtract the approximate value from the exact value. Then, divide that number by the exact value. Finally, convert fractions to decimal form and multiply your answer by 100 to find the percentage error. If you want to learn how to check your answers, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 610,398 times.
Did this article help you?
Percent Error Formula (Table of Contents)
- Percent Error Formula
- Examples of Percent Error Formula (With Excel Template)
- Percent Error Formula Calculator
Percent Error Formula
Percentage error formula is being used in many scientific reports and especially chemistry; the formula is used to measure the difference between a measured or experimental value and a true or an exact value. The purpose of the percent error formula is to gauge how different is the measured value is from the exact value. The computation of the percent error formula involves the absolute error, which simply is denoted in a positive value most of the times. Note for chemistry and other sciences, it is customary to keep a negative value. Whether error is positive or negative is important. A percentage error formula which is close to zero or equal to zero signifies that the user is very close to the targeted value, which is a positive sign for the user. But, it is very important for the user to know the reason and the rationale behind the cause of the error, which can occur due to various of reasons such as an error occurred during the experiment or a mistake in its own estimation. The formula is all about comparing a guess or an estimate to an exact value.
The formula for Percent Error –
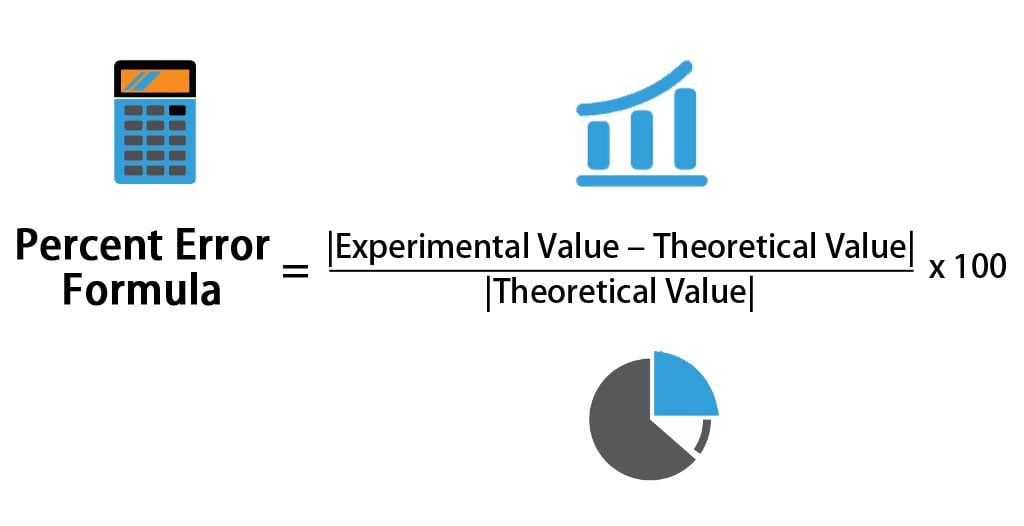
Percent Error = |(Experimental Value – Theoretical Value)| / |Theoretical Value| * 100
Examples of Percent Error Formula (With Excel Template)
Let’s take an example to understand the calculation of Percent Error in a better manner.
You can download this Percent Error Template here – Percent Error Template
Example #1
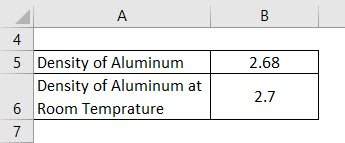
The density of the aluminum block is 2.68 g/cm cube, while the density of the same aluminum block at room temperature is to be 2.70 g/cm cube. Next, calculate the Percent Error of the measurement.
Solution:
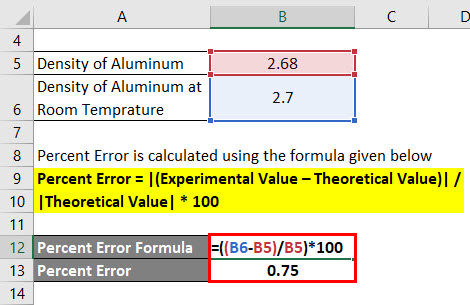
Percent Error is calculated using the formula given below
Percent Error = |(Experimental Value – Theoretical Value)| / |Theoretical Value| * 100
- Percent Error = |(2.7 – 2.68)|/ |2.68| * 100
- Percent Error = 0.75%
Example #2
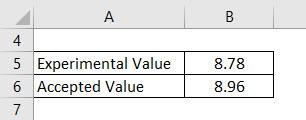
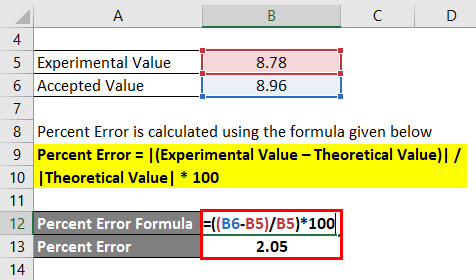
The user needs to find the volume and mass of a paper cube in the experimental lab. When the user is calculating the value of the measurements, it gets the value as 8.78 g/cm cube. Whereas the accepted density of the cube is to be 8.96 g/cm cube. Calculate the percent error.
Solution:
Percent Error is calculated using the formula given below
Percent Error = |(Experimental Value – Theoretical Value)| / |Theoretical Value| * 100
- Percent Error = |(8.96 – 8.78)| / |8.78| * 100
- Percent Error = 2.05%
Example #3
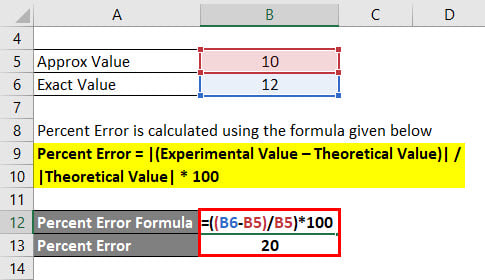
A scale measures wrongly a value of 10 cm due to some marginal error in the computation. The user needs to calculate the percent error of the measurement when the actual value of the scale is to be 12 cm.
Solution:
Percent Error is calculated using the formula given below
Percent Error = |(Experimental Value – Theoretical Value)| / |Theoretical Value| * 100
- Percent Error = |(12 – 10)| / |10| * 100
- Percent Error = 20%
Explanation
The steps to calculate the formula is:-
- Subtract one value from another value as the sign of the formula is not a matter so that any value can be subtracted from any value. The resultant value is your error value which is simply calculated by subtracting one value from another value.
- Divide the error value, which is computed by the exact value or the theoretical value, which will then result in a decimal number.
- After computing, the decimal value simply converts eh decimal number computed into a percentage by multiplying it by 100.
The formula will show a value in percentage form.
Relevance and Uses
- The keys to reporting percent error correctly are to know whether or not to drop the sign (positive or negative) on the calculation and to report the value using the correct number of significant figures.
- It is frequently used in the analysis of scientific research and is used by the physician and in the field of chemistry. Students also when use to do experiments in labs use the percent error formula in order to determine the variance. The acceptable range of error depends on the case to case basis and the quantum of percent error needs to be determined beforehand when experimenting a particular test in the lab always. The use of value with a high percent error in measurement is the judgment of the use.
Percent Error Formula Calculator
You can use the following Calculator
| Experimental Value | |
| Theoretical Value | |
| Percent Error | |
| Percent Error = |
|
||||||||||
|
Recommended Articles
This has been a guide to Percent Error Formula. Here we discuss how to calculate Percent Error along with practical examples. We also provide Percent Error calculator with downloadable excel template. You may also look at the following articles to learn more –
- Guide to Daily Compound Interest Formula
- How To Calculate Salary Using Formula?
- Formula For Market to Book Ratio
- Examples of Maturity Value Formula