|
Horia 0 / 0 / 2 Регистрация: 15.01.2015 Сообщений: 66 |
||||
|
1 |
||||
|
27.04.2015, 22:25. Показов 2574. Ответов 5 Метки нет (Все метки)
выбивает ошибку вот код. помогите пожалуйста. скорее всего проблема с функцией что с рекурсией
__________________
0 |
|
495 / 377 / 136 Регистрация: 27.01.2015 Сообщений: 1,588 |
|
|
27.04.2015, 22:27 |
2 |
|
какая ошибка, что ли?
0 |
|
0 / 0 / 2 Регистрация: 15.01.2015 Сообщений: 66 |
|
|
27.04.2015, 23:27 [ТС] |
3 |
|
в названии темы написано
0 |
|
Супер-модератор 32451 / 20945 / 8105 Регистрация: 22.10.2011 Сообщений: 36,213 Записей в блоге: 7 |
|
|
27.04.2015, 23:31 |
4 |
|
РешениеFunction pow If both base and exponent are zero, it may also cause a domain error on certain implementations. У тебя на первой же итерации цикла (13-14 строки) и показатель и степень равны нулю…
1 |
|
Horia 0 / 0 / 2 Регистрация: 15.01.2015 Сообщений: 66 |
||||
|
28.04.2015, 00:17 [ТС] |
5 |
|||
|
тема закрыта. я еще одну ошибку нашел. вот рабочий код (если кому будет нужен пример).
0 |
|
Fulcrum_013 2057 / 1534 / 167 Регистрация: 14.12.2014 Сообщений: 13,348 |
||||
|
28.04.2015, 05:35 |
6 |
|||
|
помогите пожалуйста. скорее всего проблема с функцией что с рекурсией Скорее с математикой:
при n<=0 будет вылетать
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
28.04.2015, 05:35 |
|
Помогаю со студенческими работами здесь Ошибки вычислений, POW: Domain Error Выдаёт ошибку: acos DOMAIN error,полсе нажатия окей,ещё одну ошибку pow OWERFLAW ERROR Выдаёт ошибку: acos DOMAIN error,полсе… Log domain error Выдает ошибку sqrt: DOMAIN error Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 6 |
Содержание
- pow: DOMAIN error
- FLP32-C. Prevent or detect domain and range errors in math functions
- Domain and Pole Checking
- Range Checking
- Subnormal Numbers
- Noncompliant Code Example ( sqrt() )
- Compliant Solution ( sqrt() )
- Noncompliant Code Example ( sinh() , Range Errors)
- Compliant Solution ( sinh() , Range Errors)
- Noncompliant Code Example ( pow() )
- Compliant Solution ( pow() )
- Noncompliant Code Example ( asin() , Subnormal Number)
- Compliant Solution ( asin() , Subnormal Number)
- Risk Assessment
pow: DOMAIN error
I’m trying to run this short code and when it prints out i get about 20 of these «pow: DOMAIN error» messages, and then my results. Can anyone shed any light on this. I’m not acutally a programer, but got thrust into this in a project for another class, so I’m extremely clueless. I think it might have something to do with the output file. I don’t really know what that is, and I don’t even know if what I have in there is legitimate.
- 2 Contributors 1 Reply 1K Views 11 Hours Discussion Span Latest Post 18 Years Ago Latest Post by Dave Sinkula
>Can anyone shed any light on this.
The pow functions compute x raised to the power y. A domain error occurs if x is finite and negative and y is finite and not an integer value. A domain error may occur if x is zero and y is less than or equal to zero. A range error may occur.
You should really learn how to index arrays properly. The usual idiom is as follows.
That is, an array of size N may be indexed from 0 to N-1.
We’re a friendly, industry-focused community of developers, IT pros, digital marketers, and technology enthusiasts meeting, networking, learning, and sharing knowledge.
Reach out to all the awesome people in our software development community by starting your own topic. We equally welcome both specific questions as well as open-ended discussions.
Источник
FLP32-C. Prevent or detect domain and range errors in math functions
The C Standard, 7.12.1 [ISO/IEC 9899:2011], defines three types of errors that relate specifically to math functions in . Paragraph 2 states
A domain error occurs if an input argument is outside the domain over which the mathematical function is defined.
Paragraph 3 states
A pole error (also known as a singularity or infinitary) occurs if the mathematical function has an exact infinite result as the finite input argument(s) are approached in the limit.
Paragraph 4 states
A range error occurs if the mathematical result of the function cannot be represented in an object of the specified type, due to extreme magnitude.
An example of a domain error is the square root of a negative number, such as sqrt(-1.0) , which has no meaning in real arithmetic. Contrastingly, 10 raised to the 1-millionth power, pow(10., 1e6) , cannot be represented in many floating-point implementations because of the limited range of the type double and consequently constitutes a range error. In both cases, the function will return some value, but the value returned is not the correct result of the computation. An example of a pole error is log(0.0) , which results in negative infinity.
Programmers can prevent domain and pole errors by carefully bounds-checking the arguments before calling mathematical functions and taking alternative action if the bounds are violated.
Range errors usually cannot be prevented because they are dependent on the implementation of floating-point numbers as well as on the function being applied. Instead of preventing range errors, programmers should attempt to detect them and take alternative action if a range error occurs.
The following table lists the double forms of standard mathematical functions, along with checks that should be performed to ensure a proper input domain, and indicates whether they can also result in range or pole errors, as reported by the C Standard. Both float and long double forms of these functions also exist but are omitted from the table for brevity. If a function has a specific domain over which it is defined, the programmer must check its input values. The programmer must also check for range errors where they might occur. The standard math functions not listed in this table, such as fabs() , have no domain restrictions and cannot result in range or pole errors.
No asin(x) -1 Yes No atan(x) None Yes No
exp(x) , exp2(x) , expm1(x)
log(x) , log10(x) , log2(x)
x != 0 && !isinf(x) && !isnan(x)
scalbn(x, n) , scalbln(x, n)
x > 0 || (x == 0 && y > 0) ||
( x is an integer)
x != 0 && ! ( x is an integer)
fmod(x, y) , remainder(x, y) ,
remquo(x, y, quo)
nextafter(x, y) ,
nexttoward(x, y)
Domain and Pole Checking
The most reliable way to handle domain and pole errors is to prevent them by checking arguments beforehand, as in the following exemplar:
Range Checking
Programmers usually cannot prevent range errors, so the most reliable way to handle them is to detect when they have occurred and act accordingly.
The exact treatment of error conditions from math functions is tedious. The C Standard, 7.12.1 [ISO/IEC 9899:2011], defines the following behavior for floating-point overflow:
A floating result overflows if the magnitude of the mathematical result is finite but so large that the mathematical result cannot be represented without extraordinary roundoff error in an object of the specified type. If a floating result overflows and default rounding is in effect, then the function returns the value of the macro HUGE_VAL , HUGE_VALF , or HUGE_VALL according to the return type, with the same sign as the correct value of the function; if the integer expression math_errhandling & MATH_ERRNO is nonzero, the integer expression errno acquires the value ERANGE ; if the integer expression math_errhandling & MATH_ERREXCEPT is nonzero, the «overflow» floating-point exception is raised.
It is preferable not to check for errors by comparing the returned value against HUGE_VAL or 0 for several reasons:
- These are, in general, valid (albeit unlikely) data values.
- Making such tests requires detailed knowledge of the various error returns for each math function.
- Multiple results aside from HUGE_VAL and 0 are possible, and programmers must know which are possible in each case.
- Different versions of the library have varied in their error-return behavior.
It can be unreliable to check for math errors using errno because an implementation might not set errno . For real functions, the programmer determines if the implementation sets errno by checking whether math_errhandling & MATH_ERRNO is nonzero. For complex functions, the C Standard, 7.3.2, paragraph 1, simply states that «an implementation may set errno but is not required to» [ISO/IEC 9899:2011].
The obsolete System V Interface Definition (SVID3) [UNIX 1992] provides more control over the treatment of errors in the math library. The programmer can define a function named matherr() that is invoked if errors occur in a math function. This function can print diagnostics, terminate the execution, or specify the desired return value. The matherr() function has not been adopted by C or POSIX, so it is not generally portable.
The following error-handing template uses C Standard functions for floating-point errors when the C macro math_errhandling is defined and indicates that they should be used; otherwise, it examines errno :
See FLP03-C. Detect and handle floating-point errors for more details on how to detect floating-point errors.
Subnormal Numbers
A subnormal number is a nonzero number that does not use all of its precision bits [ IEEE 754 2006 ]. These numbers can be used to represent values that are closer to 0 than the smallest normal number (one that uses all of its precision bits). However, the asin() , asinh() , atan() , atanh() , and erf() functions may produce range errors, specifically when passed a subnormal number. When evaluated with a subnormal number, these functions can produce an inexact, subnormal value, which is an underflow error. The C Standard, 7.12.1, paragraph 6 [ISO/IEC 9899:2011], defines the following behavior for floating-point underflow:
The result underflows if the magnitude of the mathematical result is so small that the mathematical result cannot be represented, without extraordinary roundoff error, in an object of the specified type. If the result underflows, the function returns an implementation-defined value whose magnitude is no greater than the smallest normalized positive number in the specified type; if the integer expression math_errhandling & MATH_ERRNO is nonzero, whether errno acquires the value ERANGE is implementation-defined; if the integer expression math_errhandling & MATH_ERREXCEPT is nonzero, whether the ‘‘underflow’’ floating-point exception is raised is implementation-defined.
Implementations that support floating-point arithmetic but do not support subnormal numbers, such as IBM S/360 hex floating-point or nonconforming IEEE-754 implementations that skip subnormals (or support them by flushing them to zero), can return a range error when calling one of the following families of functions with the following arguments:
- fmod ((min+subnorm), min)
- remainder ((min+ subnorm ), min)
- remquo ((min+ subnorm ), min, quo)
where min is the minimum value for the corresponding floating point type and subnorm is a subnormal value.
If Annex F is supported and subnormal results are supported, the returned value is exact and a range error cannot occur. The C Standard, F.10.7.1 [ISO/IEC 9899:2011], specifies the following for the fmod() , remainder() , and remquo() functions:
When subnormal results are supported, the returned value is exact and is independent of the current rounding direction mode.
Annex F, subclause F.10.7.2, paragraph 2, and subclause F.10.7.3, paragraph 2, of the C Standard identify when subnormal results are supported.
Noncompliant Code Example ( sqrt() )
This noncompliant code example determines the square root of x :
However, this code may produce a domain error if x is negative.
Compliant Solution ( sqrt() )
Because this function has domain errors but no range errors, bounds checking can be used to prevent domain errors:
Noncompliant Code Example ( sinh() , Range Errors)
This noncompliant code example determines the hyperbolic sine of x :
This code may produce a range error if x has a very large magnitude.
Compliant Solution ( sinh() , Range Errors)
Because this function has no domain errors but may have range errors, the programmer must detect a range error and act accordingly:
Noncompliant Code Example ( pow() )
This noncompliant code example raises x to the power of y :
This code may produce a domain error if x is negative and y is not an integer value or if x is 0 and y is 0. A domain error or pole error may occur if x is 0 and y is negative, and a range error may occur if the result cannot be represented as a double .
Compliant Solution ( pow() )
Because the pow() function can produce domain errors, pole errors, and range errors, the programmer must first check that x and y lie within the proper domain and do not generate a pole error and then detect whether a range error occurs and act accordingly:
Noncompliant Code Example ( asin() , Subnormal Number)
This noncompliant code example determines the inverse sine of x :
Compliant Solution ( asin() , Subnormal Number)
Because this function has no domain errors but may have range errors, the programmer must detect a range error and act accordingly:
Risk Assessment
Failure to prevent or detect domain and range errors in math functions may cause unexpected results.
Источник
На чтение 3 мин Обновлено 18.01.2023
Pow domain error c builder

|
Профиль Репутация: нет Как ловить ошибку в C++Builder 5 при возведении отрицательного числа в степень 0,5 например? такой try-блок поймать ее не может:
а функцию Power(double a, double) (которая вроде должна работать) не находит компайлер! такой вариант тоже на проходит:
Как быть? |
||||||||
|
| segmentation_fault |
|
||
Шустрый Профиль Репутация: нет
А ты Math.h подключил? |
|||
|
Эксперт
Профиль
Группа: Экс. модератор
Сообщений: 2124
Регистрация: 25.3.2002
Где: Москва
Репутация: 47
Всего: 59
| Vyacheslav |
|
||
Цитата(Андракула @ 16.1.2007, 15:48  ) ) |
| такой try-блок поймать ее не может: |
| Цитата(C++Builder Help) |
| Return Value |
On success, pow and powl return the value calculated of x to the power of y.
Sometimes the arguments passed to these functions produce results that overflow or are incalculable. When the correct value would overflow, the functions return the value HUGE_VAL (pow) or _LHUGE_VAL (powl). Results of excessively large magnitude can cause the global variable errno to be set to
ERANGE Result out of range
If the argument x passed to pow or powl is real and less than 0, and y is not a whole number, or if x is 0 and y is less than 0, or you call pow(0,0), the global variable errno is set to
EDOM Domain error
Error handling for these functions can be modified through the functions _matherr and _matherrl.
    |
 |
Профиль
Группа: Участник
Сообщений: 13
Регистрация: 29.9.2005
Репутация: нет
Всего: нет
про Хелп я что то не понял, я же пытался ее с _matherr поямать, но не получилось
| Андракула |
|
||
|
| stmamont |
|
||

Опытный Профиль Репутация: 3 Подключать надо Math.hpp для работы с Power по-моему Это сообщение отредактировал(а) stmamont — 16.1.2007, 16:31 |
|||
|
Эксперт
Профиль
Группа: Экс. модератор
Сообщений: 2124
Регистрация: 25.3.2002
Где: Москва
Репутация: 47
Всего: 59
| Vyacheslav |
|
||
| Код |
| #include #include #include |
#pragma argsused
int main(int argc, char* argv[])
<
double f = pow(-100,0.5);
if (errno == EDOM)
std::cout
    |
 |
Профиль
Группа: Участник
Сообщений: 13
Регистрация: 29.9.2005
Репутация: нет
Всего: нет
Да с #include все работает!
| Андракула |
|
||
|
Эксперт
Профиль
Группа: Экс. модератор
Сообщений: 2124
Регистрация: 25.3.2002
Где: Москва
Репутация: 47
Всего: 59
| Vyacheslav |
|
||
Цитата(Андракула @ 16.1.2007, 16:26  ) ) |
| про Хелп я что то не понял, я же пытался ее с _matherr поямать, но не получилось |
| Код |
| #include #include #include #include #include |
int _matherr (struct _exception *a)
<
throw std::domain_error(«pow: DOMEN error»);
return 0;
>
#pragma argsused
int main(int argc, char* argv[])
<
try <
double f = pow(-100,0.5);
>
catch(std::exception& exp)
<
std::cout



















1. Публиковать ссылки на вскрытые компоненты
2. Обсуждать взлом компонентов и делиться вскрытыми компонентами
- Литературу по С++ Builder обсуждаем здесь
- Действия модераторов можно обсудить здесь
- С просьбами о написании курсовой, реферата и т.п. обращаться сюда
- Настоятельно рекомендуем заглянуть в DRKB (Delphi Russian Knowledge Base) — крупнейший в рунете сборник материалов по Дельфи
- FAQ раздела лежит здесь!
Если Вам понравилась атмосфера форума, заходите к нам чаще! С уважением, Rrader.
| 0 Пользователей читают эту тему (0 Гостей и 0 Скрытых Пользователей) |
| 0 Пользователей: |
| « Предыдущая тема | C++ Builder | Следующая тема » |
[ Время генерации скрипта: 0.1173 ] [ Использовано запросов: 21 ] [ GZIP включён ]
Источник
Читайте также: Fatal error call to undefined function main in
Adblock
detector
//—————————————————————————
#include <vcl.h>
#include <math.h>
#pragma hdrstop
#include «Unit1.h»
//—————————————————————————
#pragma package(smart_init)
#pragma link «CSPIN»
#pragma resource «*.dfm»
#define gbp_cad 38
#define approx_point 30
#define prognoz_point 7
#define max_stepen_pol 5
TForm1 *Form1;
double A[gbp_cad][2], *a=NULL, *b=NULL, **sums=NULL, approx[approx_point+1], prognoz[prognoz_point+1];
int pol, N, K, r=0; //pol — степень аппроксимируещего полинома
//—————————————————————————
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//—————————————————————————
void Refresh() //освобождаем массивы
{for(int i=0; i<pol; i++){
delete [] sums[i];
}
delete [] a;
delete [] b;
delete [] sums;
}
//—————————————————————————
void memory_for_massiv() //выделяем память для массивов
{int i,j,k;
a = new double[pol];
b = new double[pol];
sums = new double*[pol];
for(i=0; i<pol; i++)
{sums[i] = new double[pol];
a[i]=0;
b[i]=0;
for(j=0; j<pol; j++)
sums[i][j] = 0;
}
}
//—————————————————————————
void set_koef() //заполняем коэфиценты системы уравнений и столбец свободных членов
{for(int i=0; i<pol; i++)
{for(int j=0; j<pol; j++)
{sums[i][j] = 0;
for(int k=0; k<N; k++)
sums[i][j] += pow(A[k][0], i+j); }
}
for(int i=0; i<pol; i++)
{for(int k=0; k<N; k++)
b[i] += pow(A[k][0], i) * A[k][1];
}
}
//—————————————————————————
void approximation() //аппроксимируем
{for (int i=0;i<N;i++)
{approx[i]=0;
for(int j=0; j<pol; j++)
approx[i]+=a[j]*pow(A[i][0],j);
}
}
//—————————————————————————
void extrapolation() //прогнозируем
{for (int i=0;i<prognoz_point;i++)
{prognoz[i]=0;
for (int j=0;j<pol;j++)
prognoz[i]+=a[j]*pow(A[i+N][0],j);
}
}
//—————————————————————————
void Calculations() //все вычисления
{int i=0,j=0,k=0;
double M,s;
memory_for_massiv();
set_koef();
for(k=0; k<pol; k++) // применяем метод гаусса для приведения к треугольному виду
{for(i=k+1; i<pol; i++)
{if(sums[k][k]==0)
{ShowMessage(«Solution is not exist.»);
return;
}
M = sums[i][k] / sums[k][k];
for(j=k; j<pol; j++)
{sums[i][j] -= M * sums[k][j];
}
b[i] -= M*b[k];
}
}
for(i=K; i>=0; i—)
{s = 0;
for(j = i; j<pol; j++)
s = s + sums[i][j]*a[j];
a[i] = (b[i] — s) / sums[i][i];
}
}
//—————————————————————————
void __fastcall TForm1::FormCreate(TObject *Sender)
{
CSpinEdit1->MinValue=1;
CSpinEdit1->MaxValue=max_stepen_pol;
Button3->Enabled=false;
Memo1->Lines->LoadFromFile(«data.txt»);
if (Memo1->Lines->Count<gbp_cad) {ShowMessage(«Ваш файл содержит меньше 38 точек»); exit(1);}
Memo1->Visible=false;
for (int n=0;n<+37;n++)
{
A[n][0]=n;
A[n][1]=StrToFloat(Memo1->Lines->Strings[n]); //заполняем массив из txt файла
}
for (int i=0;i<=30;i+=2)
Chart1->Series[0]->AddXY(A[i][0],A[i][1]);
N=approx_point+1;
}
//—————————————————————————
void __fastcall TForm1::Button1Click(TObject *Sender) //кнопка аппроксимации
{
Button3->Enabled=true;
{Chart1->Series[1]->Clear();
Chart1->Series[2]->Clear();
Chart1->Series[3]->Clear();
Refresh();
}
K=CSpinEdit1->Value;
pol=K+1;
Calculations();
approximation();
for (int i=0;i<N;i++)
Chart1->Series[1]->AddXY(A[i][0],approx[i]);
r=1;
}
//—————————————————————————
void __fastcall TForm1::Button2Click(TObject *Sender) //скользящая средняя
{
float k=(StrToFloat(Memo1->Lines->Strings[26])+StrToFloat(Memo1->Lines->Strings[28])+StrToFloat(Memo1->Lines->Strings[30]))/3;
float p=(StrToFloat(Memo1->Lines->Strings[28])+StrToFloat(Memo1->Lines->Strings[30])+k)/3;
float o=(StrToFloat(Memo1->Lines->Strings[30])+k+p)/3;
float n=(k+p+o)/3;
float z=(o+n)/2;
Chart1->Series[2]->AddXY(30,StrToFloat(Memo1->Lines->Strings[30]));
Chart1->Series[2]->AddXY(32,k);
Chart1->Series[2]->AddXY(34,p);
Chart1->Series[2]->AddXY(36,o);
Chart1->Series[2]->AddXY(37,z);
}
//—————————————————————————
void __fastcall TForm1::Button3Click(TObject *Sender) //дорисовываем прогноз
{
{extrapolation();
Chart1->Series[3]->AddXY(A[approx_point][0],approx[approx_point]);
for (int i=0;i<prognoz_point;i++)
Chart1->Series[3]->AddXY(A[i+N][0],prognoz[i]);
}
}
//—————————————————————————
The C Standard, 7.12.1 [ISO/IEC 9899:2011], defines three types of errors that relate specifically to math functions in <math.h>. Paragraph 2 states
A domain error occurs if an input argument is outside the domain over which the mathematical function is defined.
Paragraph 3 states
A pole error (also known as a singularity or infinitary) occurs if the mathematical function has an exact infinite result as the finite input argument(s) are approached in the limit.
Paragraph 4 states
A range error occurs if the mathematical result of the function cannot be represented in an object of the specified type, due to extreme magnitude.
An example of a domain error is the square root of a negative number, such as sqrt(-1.0), which has no meaning in real arithmetic. Contrastingly, 10 raised to the 1-millionth power, pow(10., 1e6), cannot be represented in many floating-point implementations because of the limited range of the type double and consequently constitutes a range error. In both cases, the function will return some value, but the value returned is not the correct result of the computation. An example of a pole error is log(0.0), which results in negative infinity.
Programmers can prevent domain and pole errors by carefully bounds-checking the arguments before calling mathematical functions and taking alternative action if the bounds are violated.
Range errors usually cannot be prevented because they are dependent on the implementation of floating-point numbers as well as on the function being applied. Instead of preventing range errors, programmers should attempt to detect them and take alternative action if a range error occurs.
The following table lists the double forms of standard mathematical functions, along with checks that should be performed to ensure a proper input domain, and indicates whether they can also result in range or pole errors, as reported by the C Standard. Both float and long double forms of these functions also exist but are omitted from the table for brevity. If a function has a specific domain over which it is defined, the programmer must check its input values. The programmer must also check for range errors where they might occur. The standard math functions not listed in this table, such as fabs(), have no domain restrictions and cannot result in range or pole errors.
|
Function |
Domain |
Range |
Pole |
|---|---|---|---|
|
|
|
No |
No |
asin(x) |
-1 <= x && x <= 1 |
Yes | No |
atan(x) |
None | Yes | No |
|
|
|
No |
No |
|
|
|
Yes |
No |
asinh(x) |
None | Yes | No |
|
|
|
Yes |
Yes |
|
|
None |
Yes |
No |
|
|
None |
Yes |
No |
|
|
None |
Yes |
No |
|
|
|
No |
Yes |
|
|
|
No |
Yes |
|
|
|
Yes |
No |
logb(x) |
x != 0 |
Yes | Yes |
|
|
None |
Yes |
No |
|
|
None |
Yes |
No |
|
|
|
Yes |
Yes |
|
|
|
No |
No |
erf(x) |
None | Yes | No |
|
|
None |
Yes |
No |
|
|
|
Yes |
Yes |
|
|
None |
Yes |
No |
|
|
|
Yes |
No |
|
|
None |
Yes |
No |
|
|
None |
Yes |
No |
|
|
None |
Yes |
No |
Domain and Pole Checking
The most reliable way to handle domain and pole errors is to prevent them by checking arguments beforehand, as in the following exemplar:
double safe_sqrt(double x) {
if (x < 0) {
fprintf(stderr, "sqrt requires a nonnegative argument");
/* Handle domain / pole error */
}
return sqrt (x);
}
Range Checking
Programmers usually cannot prevent range errors, so the most reliable way to handle them is to detect when they have occurred and act accordingly.
The exact treatment of error conditions from math functions is tedious. The C Standard, 7.12.1 [ISO/IEC 9899:2011], defines the following behavior for floating-point overflow:
A floating result overflows if the magnitude of the mathematical result is finite but so large that the mathematical result cannot be represented without extraordinary roundoff error in an object of the specified type. If a floating result overflows and default rounding is in effect, then the function returns the value of the macro
HUGE_VAL,HUGE_VALF, orHUGE_VALLaccording to the return type, with the same sign as the correct value of the function; if the integer expressionmath_errhandling & MATH_ERRNOis nonzero, the integer expressionerrnoacquires the valueERANGE; if the integer expressionmath_errhandling & MATH_ERREXCEPTis nonzero, the «overflow» floating-point exception is raised.
It is preferable not to check for errors by comparing the returned value against HUGE_VAL or 0 for several reasons:
- These are, in general, valid (albeit unlikely) data values.
- Making such tests requires detailed knowledge of the various error returns for each math function.
- Multiple results aside from
HUGE_VALand0are possible, and programmers must know which are possible in each case. - Different versions of the library have varied in their error-return behavior.
It can be unreliable to check for math errors using errno because an implementation might not set errno. For real functions, the programmer determines if the implementation sets errno by checking whether math_errhandling & MATH_ERRNO is nonzero. For complex functions, the C Standard, 7.3.2, paragraph 1, simply states that «an implementation may set errno but is not required to» [ISO/IEC 9899:2011].
The obsolete System V Interface Definition (SVID3) [UNIX 1992] provides more control over the treatment of errors in the math library. The programmer can define a function named matherr() that is invoked if errors occur in a math function. This function can print diagnostics, terminate the execution, or specify the desired return value. The matherr() function has not been adopted by C or POSIX, so it is not generally portable.
The following error-handing template uses C Standard functions for floating-point errors when the C macro math_errhandling is defined and indicates that they should be used; otherwise, it examines errno:
#include <math.h>
#include <fenv.h>
#include <errno.h>
/* ... */
/* Use to call a math function and check errors */
{
#pragma STDC FENV_ACCESS ON
if (math_errhandling & MATH_ERREXCEPT) {
feclearexcept(FE_ALL_EXCEPT);
}
errno = 0;
/* Call the math function */
if ((math_errhandling & MATH_ERRNO) && errno != 0) {
/* Handle range error */
} else if ((math_errhandling & MATH_ERREXCEPT) &&
fetestexcept(FE_INVALID | FE_DIVBYZERO |
FE_OVERFLOW | FE_UNDERFLOW) != 0) {
/* Handle range error */
}
}
See FLP03-C. Detect and handle floating-point errors for more details on how to detect floating-point errors.
Subnormal Numbers
A subnormal number is a nonzero number that does not use all of its precision bits [IEEE 754 2006]. These numbers can be used to represent values that are closer to 0 than the smallest normal number (one that uses all of its precision bits). However, the asin(), asinh(), atan(), atanh(), and erf() functions may produce range errors, specifically when passed a subnormal number. When evaluated with a subnormal number, these functions can produce an inexact, subnormal value, which is an underflow error. The C Standard, 7.12.1, paragraph 6 [ISO/IEC 9899:2011], defines the following behavior for floating-point underflow:
The result underflows if the magnitude of the mathematical result is so small that the mathematical result cannot be represented, without extraordinary roundoff error, in an object of the specified type. If the result underflows, the function returns an implementation-defined value whose magnitude is no greater than the smallest normalized positive number in the specified type; if the integer expression
math_errhandling & MATH_ERRNOis nonzero, whethererrnoacquires the valueERANGEis implementation-defined; if the integer expressionmath_errhandling & MATH_ERREXCEPTis nonzero, whether the ‘‘underflow’’ floating-point exception is raised is implementation-defined.
Implementations that support floating-point arithmetic but do not support subnormal numbers, such as IBM S/360 hex floating-point or nonconforming IEEE-754 implementations that skip subnormals (or support them by flushing them to zero), can return a range error when calling one of the following families of functions with the following arguments:
fmod((min+subnorm), min)remainder((min+subnormremquo((min+subnorm
where min is the minimum value for the corresponding floating point type and subnorm is a subnormal value.
If Annex F is supported and subnormal results are supported, the returned value is exact and a range error cannot occur. The C Standard, F.10.7.1 [ISO/IEC 9899:2011], specifies the following for the fmod(), remainder(), and remquo() functions:
When subnormal results are supported, the returned value is exact and is independent of the current rounding direction mode.
Annex F, subclause F.10.7.2, paragraph 2, and subclause F.10.7.3, paragraph 2, of the C Standard identify when subnormal results are supported.
Noncompliant Code Example (sqrt())
This noncompliant code example determines the square root of x:
#include <math.h>
void func(double x) {
double result;
result = sqrt(x);
}
However, this code may produce a domain error if x is negative.
Compliant Solution (sqrt())
Because this function has domain errors but no range errors, bounds checking can be used to prevent domain errors:
#include <math.h>
void func(double x) {
double result;
if (isless(x, 0.0)) {
/* Handle domain error */
}
result = sqrt(x);
}
Noncompliant Code Example (sinh(), Range Errors)
This noncompliant code example determines the hyperbolic sine of x:
#include <math.h>
void func(double x) {
double result;
result = sinh(x);
}
This code may produce a range error if x has a very large magnitude.
Compliant Solution (sinh(), Range Errors)
Because this function has no domain errors but may have range errors, the programmer must detect a range error and act accordingly:
#include <math.h>
#include <fenv.h>
#include <errno.h>
void func(double x) {
double result;
{
#pragma STDC FENV_ACCESS ON
if (math_errhandling & MATH_ERREXCEPT) {
feclearexcept(FE_ALL_EXCEPT);
}
errno = 0;
result = sinh(x);
if ((math_errhandling & MATH_ERRNO) && errno != 0) {
/* Handle range error */
} else if ((math_errhandling & MATH_ERREXCEPT) &&
fetestexcept(FE_INVALID | FE_DIVBYZERO |
FE_OVERFLOW | FE_UNDERFLOW) != 0) {
/* Handle range error */
}
}
/* Use result... */
}
Noncompliant Code Example (pow())
This noncompliant code example raises x to the power of y:
#include <math.h>
void func(double x, double y) {
double result;
result = pow(x, y);
}
This code may produce a domain error if x is negative and y is not an integer value or if x is 0 and y is 0. A domain error or pole error may occur if x is 0 and y is negative, and a range error may occur if the result cannot be represented as a double.
Compliant Solution (pow())
Because the pow() function can produce domain errors, pole errors, and range errors, the programmer must first check that x and y lie within the proper domain and do not generate a pole error and then detect whether a range error occurs and act accordingly:
#include <math.h>
#include <fenv.h>
#include <errno.h>
void func(double x, double y) {
double result;
if (((x == 0.0f) && islessequal(y, 0.0)) || isless(x, 0.0)) {
/* Handle domain or pole error */
}
{
#pragma STDC FENV_ACCESS ON
if (math_errhandling & MATH_ERREXCEPT) {
feclearexcept(FE_ALL_EXCEPT);
}
errno = 0;
result = pow(x, y);
if ((math_errhandling & MATH_ERRNO) && errno != 0) {
/* Handle range error */
} else if ((math_errhandling & MATH_ERREXCEPT) &&
fetestexcept(FE_INVALID | FE_DIVBYZERO |
FE_OVERFLOW | FE_UNDERFLOW) != 0) {
/* Handle range error */
}
}
/* Use result... */
}
Noncompliant Code Example (asin(), Subnormal Number)
This noncompliant code example determines the inverse sine of x:
#include <math.h>
void func(float x) {
float result = asin(x);
/* ... */
}
Compliant Solution (asin(), Subnormal Number)
Because this function has no domain errors but may have range errors, the programmer must detect a range error and act accordingly:
#include <math.h>
#include <fenv.h>
#include <errno.h>
void func(float x) {
float result;
{
#pragma STDC FENV_ACCESS ON
if (math_errhandling & MATH_ERREXCEPT) {
feclearexcept(FE_ALL_EXCEPT);
}
errno = 0;
result = asin(x);
if ((math_errhandling & MATH_ERRNO) && errno != 0) {
/* Handle range error */
} else if ((math_errhandling & MATH_ERREXCEPT) &&
fetestexcept(FE_INVALID | FE_DIVBYZERO |
FE_OVERFLOW | FE_UNDERFLOW) != 0) {
/* Handle range error */
}
}
/* Use result... */
}
Risk Assessment
Failure to prevent or detect domain and range errors in math functions may cause unexpected results.
|
Rule |
Severity |
Likelihood |
Remediation Cost |
Priority |
Level |
|---|---|---|---|---|---|
|
FLP32-C |
Medium |
Probable |
Medium |
P8 |
L2 |
Automated Detection
|
Tool |
Version |
Checker |
Description |
|---|---|---|---|
| Astrée |
22.04 |
stdlib-limits |
Partially checked |
| Axivion Bauhaus Suite |
7.2.0 |
CertC-FLP32 | Partially implemented |
| CodeSonar |
7.2p0 |
MATH.DOMAIN.ATAN MATH.DOMAIN.TOOHIGH MATH.DOMAIN.TOOLOW MATH.DOMAIN MATH.RANGE MATH.RANGE.GAMMA MATH.DOMAIN.LOG MATH.RANGE.LOG MATH.DOMAIN.FE_INVALID MATH.DOMAIN.POW MATH.RANGE.COSH.TOOHIGH MATH.RANGE.COSH.TOOLOW MATH.DOMAIN.SQRT |
Arctangent Domain Error Argument Too High Argument Too Low Floating Point Domain Error Floating Point Range Error Gamma on Zero Logarithm on Negative Value Logarithm on Zero Raises FE_INVALID Undefined Power of Zero cosh on High Number cosh on Low Number sqrt on Negative Value |
| Helix QAC |
2022.4 |
C5025 C++5033 |
|
| Parasoft C/C++test |
2022.2 |
CERT_C-FLP32-a |
Validate values passed to library functions |
| PC-lint Plus |
1.4 |
2423 |
Partially supported: reports domain errors for functions with the Semantics *dom_1, *dom_lt0, or *dom_lt1, including standard library math functions |
| Polyspace Bug Finder |
R2022b |
CERT-C: Rule FLP32-C | Checks for invalid use of standard library floating point routine (rule fully covered) |
| PRQA QA-C |
9.7 |
5025 | |
| PRQA QA-C++ |
4.4 |
5033 | |
| RuleChecker |
22.04 |
stdlib-limits |
Partially checked |
| TrustInSoft Analyzer |
1.38 |
out-of-range argument | Partially verified. |
Related Vulnerabilities
Search for vulnerabilities resulting from the violation of this rule on the CERT website.
Related Guidelines
Key here (explains table format and definitions)
CERT-CWE Mapping Notes
Key here for mapping notes
CWE-391 and FLP32-C
Intersection( CWE-391, FLP32-C) =
- Failure to detect range errors in floating-point calculations
CWE-391 — FLP32-C
- Failure to detect errors in functions besides floating-point calculations
FLP32-C – CWE-391 =
- Failure to detect domain errors in floating-point calculations
CWE-682 and FLP32-C
Independent( INT34-C, FLP32-C, INT33-C) CWE-682 = Union( FLP32-C, list) where list =
- Incorrect calculations that do not involve floating-point range errors
Bibliography


18 Years Ago
Hi,
I’m trying to run this short code and when it prints out i get about 20 of these «pow: DOMAIN error» messages, and then my results. Can anyone shed any light on this. I’m not acutally a programer, but got thrust into this in a project for another class, so I’m extremely clueless. I think it might have something to do with the output file. I don’t really know what that is, and I don’t even know if what I have in there is legitimate.
Thanks!
#include <iostream.h>
#include <math.h>
#include <stdlib.h>
#include <fstream.h>
//Global Variables
const int nvar =3;
const int nmom =3;
double delta;
double A[nvar+1][nvar+1];
double B[nvar+1][nvar+1];
double C[nvar+1][nvar+1];
double beni[nvar+1];
double benij[nvar+1][nvar+1];
double v[nvar+1][nmom+1]; //in delme norberg
double dydx[nvar+1][nmom+1];
double mu[nvar+1][nvar+1];
//Program Headers
void derivs(double t, double yt[nvar+1][nmom+1], double dyt[nvar+1][nmom+1]);
double fact (int n);
double comb (int i,int j);
double power (double i,double j);
//Specify Output File
ofstream outfile
("h:/bcppexe/derivs/output/test.txt", ios::out); //how do you direct an output file?
main()
{
double delta = 0.05;
A[1][2] = 0.0004;
A[1][3] = 0.0005;
A[2][3] = 0.0005;
A[2][1] = 0;
A[3][1] = 0;
A[3][2] = 0;
B[1][2] = 0.0000034674;
B[1][3] = 0.000075858;
B[2][3] = 0.000075858;
B[2][1] = 0;
B[3][1] = 0;
B[3][2] = 0;
C[1][2] = 0.06;
C[1][3] = 0.038;
C[2][3] = 0.038;
C[2][1] = 0;
C[3][1] = 0;
C[3][2] = 0;
A[1][1] = 0;
B[1][1] = 0;
C[1][1] = 0;
A[2][2] = 0;
B[2][2] = 0;
C[2][2] = 0;
A[3][3] = 0;
B[3][3] = 0;
C[3][3] = 0;
beni[1] = 0;
beni[2] = 0;
beni[3] = 0;
benij[1][3] = 1;
benij[2][3] = 1;
benij[1][2] = 0;
benij[2][1] = 0;
benij[3][1] = 0;
benij[3][2] = 0;
benij[1][1] = 0;
benij[2][2] = 0;
benij[3][3] = 0;
for(int i=0; i <= nvar; i++)
{
for(int j=0; j <= nmom; j++)
{
v[i][j] = 0; //Initializing the matrix of yt values to zero, and setting the boundary condition
dydx[i][j] = 0; //Initializing the matrix of the ODE to zero
v[i][0] = 1; //Setting the boundary condition for the 0th moment
}
}
derivs(60, v, dydx);
return 0;
}
void derivs(double t, double yt[nvar+1][nmom+1], double dyt[nvar+1][nmom+1])
{
int i;
int j;
int r;
int q;
double summation[nvar +1][nmom +1];
double mu_start[nvar+1];
double sum_part[nvar+1][nmom+1];
double mu[nvar+1][nvar+1];
for(i=1; i <= nvar; i++)
{
for(j=1; j <= nvar; j++)
{
mu[i][j] = A[i][j] + B[i][j] * pow(10, (C[i][j]*t));
}
}
for(i=1; i <= nvar; i++)
{
mu_start[i] = 0;
for(j=1; j <= nvar; j++)
{
mu_start[i] += mu[i][j];
}
}
for(i=1; i <= nvar; i++) //sums up the second part of the summation in Norberg's equation
{
for(q=1; q <= nmom; q++)
{
sum_part[i][q] = 0;
for(j=1; j <= nvar; j++)
{
for(r=0; r <= q; r++)
{
sum_part[i][q] += comb(q,r) * pow(benij[i][j], r) * yt[j][q-r];
}
}
}
}
for(i=1; i <= nvar; i++) //multiplies and stores the total summation in Norberg's equation
{
for(q=1; q <= nmom; q++)
{
summation[i][q] = mu_start[i] * sum_part[i][q];
}
}
for(i=1; i <= nvar; i++)
{
for(q=1; q <= nmom; q++)
{
yt[i][q] = 0;
yt[i][0] = 1;
dyt[i][q] = ((((q * delta) + mu_start[i]) * yt[i][q]) - (q * beni[i] * yt[i][q-1]) - (summation[i][q]));
}
}
for(i=1; i <= nvar; i++)
{
for(q=1; q <= nmom; q++)
{
cout << dyt[i][q] << endl;
}
}
char w;
cin>>w;
}
double fact (int n)
{
if (n < 0) return 0;
double f = 1;
while (n > 1) f *= n--;
return f;
}
double comb (int i,int j)
{
double c = 1;
if (j==0) return c;
else c = (fact (i)) / (fact (j) * fact (i-j));
return c;
}
double power (double i,double j)
{
double p=1;
if (j == 0) return 1;
else if (i==0) return 0;
else p = pow(i,j);
return p;
}
Edited
10 Years Ago
by Dani because:
Formatting fixed
Table of Contents
- Introduction
- ⚠️What Is a Math Domain Error in Python?
- ➥ Fixing “ValueError: math domain error”-sqrt
- 💡 Solution 1: Using “cmath” Module
- 💡 Solution 2: Use Exception Handling
- ➥ “ValueError: math domain error” Examples
- ✰ Scenario 1: Math Domain Error While Using pow()
- ✰ Scenario 2: Python Math Domain Error While Using log()
- ✰ Scenario 3: Math Domain Error While Using asin()
- 📖 Exercise: Fixing Math Domain Error While Using Acos()
- Conclusion
Introduction
So, you sit down, grab a cup of coffee and start programming in Python. Then out of nowhere, this stupid python error shows up: ValueError: math domain error. 😞
Sometimes it may seem annoying, but once you take time to understand what Math domain error actually is, you will solve the problem without any hassle.
To fix this error, you must understand – what is meant by the domain of a function?
Let’s use an example to understand “the domain of a function.”
Given equation: y= √(x+4)
- y = dependent variable
- x = independent variable
The domain of the function above is x≥−4. Here x can’t be less than −4 because other values won’t yield a real output.
❖ Thus, the domain of a function is a set of all possible values of the independent variable (‘x’) that yield a real/valid output for the dependent variable (‘y’).
If you have done something that is mathematically undefined (not possible mathematically), then Python throws ValueError: math domain error.
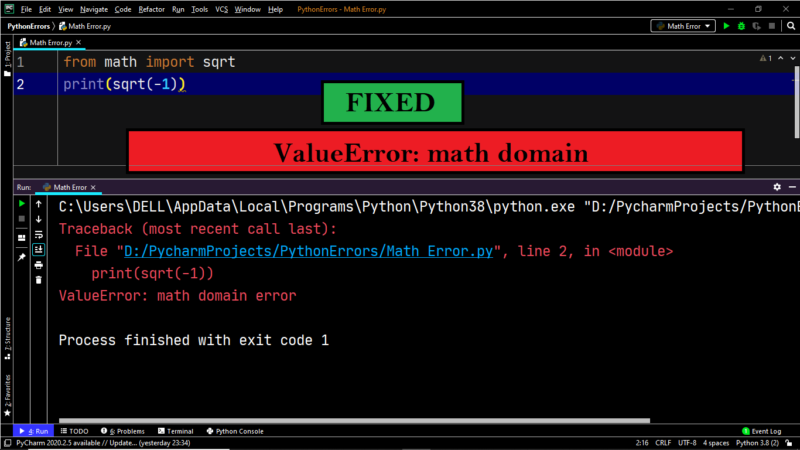
➥ Fixing “ValueError: math domain error”-sqrt
Example:
|
from math import * print(sqrt(—5)) |
Output:
|
Traceback (most recent call last): File «D:/PycharmProjects/PythonErrors/Math Error.py», line 2, in <module> print(sqrt(—5)) ValueError: math domain error |
Explanation:
Calculating the square root of a negative number is outside the scope of Python, and it throws a ValueError.
Now, let’s dive into the solutions to fix our problem!
💡 Solution 1: Using “cmath” Module
When you calculate the square root of a negative number in mathematics, you get an imaginary number. The module that allows Python to compute the square root of negative numbers and generate imaginary numbers as output is known as cmath.
Solution:
|
from cmath import sqrt print(sqrt(—5)) |
Output:
2.23606797749979j
💡 Solution 2: Use Exception Handling
If you want to eliminate the error and you are not bothered about imaginary outputs, then you can use try-except blocks. Thus, whenever Python comes across the ValueError: math domain error it is handled by the except block.
Solution:
|
from math import * x = int(input(‘Enter an integer: ‘)) try: print(sqrt(x)) except ValueError: print(«Cannot Compute Negative Square roots!») |
Output:
Enter an integer: -5
Cannot Compute Negative Square roots!
Let us have a look at some other scenarios that lead to the occurrence of the math domain error and the procedure to avoid this error.
➥ “ValueError: math domain error” Examples
✰ Scenario 1: Math Domain Error While Using pow()
Cause of Error: If you try to calculate a negative base value raised to a fractional power, it will lead to the occurrence of ValueError: math domain error.
Example:
|
import math e = —1.7 print(math.pow(—3, e)) |
Output:
Traceback (most recent call last):
File “D:/PycharmProjects/PythonErrors/Math Error.py”, line 3, in
print(math.pow(-3, e))
ValueError: math domain error
Solution: Use the cmath module to solve this problem.
- Note:
- Xy = ey ln x
Using the above property, the error can be avoided as follows:
|
from cmath import exp,log e = —1.7 print(exp(e * log(—3))) |
Output:
(0.0908055832509843+0.12498316306449488j)
✰ Scenario 2: Python Math Domain Error While Using log()
Consider the following example if you are working on Python 2.x:
|
import math print(2/3*math.log(2/3,2)) |
Output:
Traceback (most recent call last):
File “main.py”, line 2, in
print(2/3*math.log(2/3,2))
ValueError: math domain error
Explanation: In Python 2.x, 2/3 evaluates to 0 since division floors by default. Therefore you’re attempting a log 0, hence the error. Python 3, on the other hand, does floating-point division by default.
Solution:
To Avoid the error try this instead:
from __future__ import division, which gives you Python 3 division behaviour in Python 2.7.
|
from __future__ import division import math print(2/3*math.log(2/3,2)) # Output: -0.389975000481 |
✰ Scenario 3: Math Domain Error While Using asin()
Example:
|
import math k = 5 print(«asin(«,k,«) is = «, math.asin(k)) |
Output:
Traceback (most recent call last):
File “D:/PycharmProjects/PythonErrors/rough.py”, line 4, in
print(“asin(“,k,”) is = “, math.asin(k))
ValueError: math domain error
Explanation: math.asin() method only accepts numbers between the range of -1 to 1. If you provide a number beyond of this range, it returns a ValueError – “ValueError: math domain error“, and if you provide anything else other than a number, it returns error TypeError – “TypeError: a float is required“.
Solution: You can avoid this error by passing a valid input number to the function that lies within the range of -1 and 1.
|
import math k = 0.25 print(«asin(«,k,«) is = «, math.asin(k)) #OUTPUT: asin( 0.25 ) is = 0.25268025514207865 |
📖 Exercise: Fixing Math Domain Error While Using Acos()
Note: When you pass a value to math.acos() which does not lie within the range of -1 and 1, it raises a math domain error.
Fix the following code:
|
import math print(math.acos(10)) |
Answer:
Conclusion
I hope this article helped you. Please subscribe and stay tuned for more exciting articles in the future. Happy learning! 📚

 Сообщение было отмечено Horia как решение
Сообщение было отмечено Horia как решение



 » title=»>» width=»8″ height=»8″/> возведение числа в дробную степень
» title=»>» width=»8″ height=»8″/> возведение числа в дробную степень 

 Загрузка .
Загрузка .