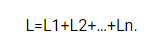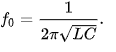Индуктивность характеризует свойства элементов электрической цепи накапливать энергию магнитного поля. Также это мера связи между током и магнитным полем. Ещё её сравнивают с инерцией электричества – также, как массу с мерой инерции механических тел.
Содержание
- 1 Явление самоиндукции
- 2 Последовательное и параллельное соединение индуктивностей
- 2.1 Параллельное соединение
- 2.2 Последовательное соединение
- 3 Некоторые практические вопросы и конструкции катушек индуктивности
- 3.1 Добротность катушки индуктивности
- 3.2 Экранный эффект
- 3.3 Подстроечная индуктивность
- 3.4 Переменная индуктивность (вариометр)
- 3.5 Индуктивность в виде печатной спирали
- 3.6 Катушка с секционной намоткой
- 3.7 Катушка индуктивности на тороидальном сердечнике
Явление самоиндукции
Если ток, идущий через проводящий контур, изменяется по величине, то возникает явление самоиндукции. В этом случае изменяется магнитный поток через контур, и на выводах рамки с током возникает ЭДС, называемая ЭДС самоиндукции. Эта ЭДС противоположна направлению тока и равна:
ε=-∆Ф/∆t=-L*(∆I/∆t)
Очевидно, что ЭДС самоиндукции равна скорости изменения магнитного потока, вызванного изменением протекающего по контуру тока, а также пропорциональна скорости изменения тока. Коэффициент пропорциональности между ЭДС самоиндукции и скоростью изменения тока называется индуктивностью и обозначается L. Эта величина всегда положительна, и имеет единицу измерения в СИ 1 Генри (1 Гн). Также используются дробные доли – миллигенри и микрогенри. Об индуктивности в 1 Генри можно говорить, если изменение тока на 1 ампер вызывает ЭДС самоиндукции в 1 Вольт. Индуктивностью обладает не только контур, но и отдельный проводник, а также катушка, которую можно представить как множество последовательно включенных контуров.
В индуктивности запасается энергия, которую можно вычислить, как W=L*I2/2, где:
- W – энергия, Дж;
- L – индуктивность, Гн;
- I – ток в катушке, А.
И здесь энергия прямо пропорциональна индуктивности катушки.
Важно! В технике индуктивностью также называется устройство, в котором происходит запасание электрического поля. Реальный элемент, наиболее близкий к такому определению – катушка индуктивности.
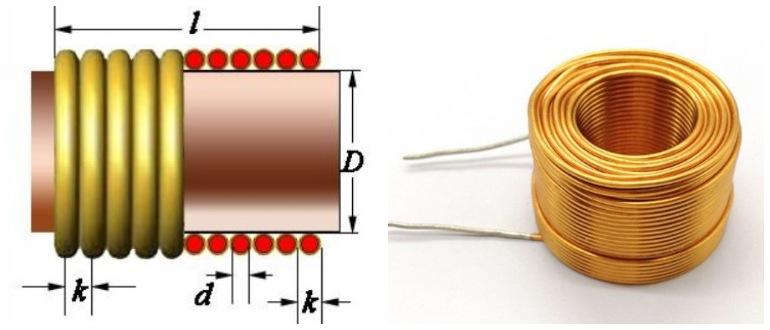
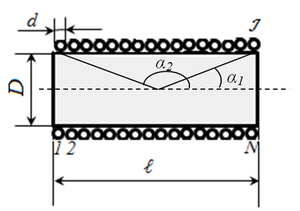
Общая формула для расчета индуктивности физической катушки имеет сложный вид и для практических вычислений неудобна. Полезно запомнить, что индуктивность пропорциональна количеству витков, диаметру катушки и зависит от геометрической формы. Также на индуктивность влияет магнитная проницаемость сердечника, на котором расположена обмотка, но не влияет ток, протекающий по виткам. Для вычисления индуктивности каждый раз надо обращаться к приведенным формулам для конкретной конструкции. Так, для цилиндрической катушки её основная характеристика вычисляется по формуле:
L=μ*μ*(N2*S/l),
где:
- μ – относительная магнитная проницаемость сердечника катушки;
- μ – магнитная постоянная, 1,26*10-6 Гн/м;
- N – количество витков;
- S – площадь витка;
- l – геометрическая длина катушки.
Для вычисления индуктивности для цилиндрической катушки и катушек других форм лучше воспользоваться программами-калькуляторами, в том числе онлайн-калькуляторами.
Последовательное и параллельное соединение индуктивностей
Индуктивности можно соединять последовательно или параллельно, получая набор с новыми характеристиками.
Параллельное соединение
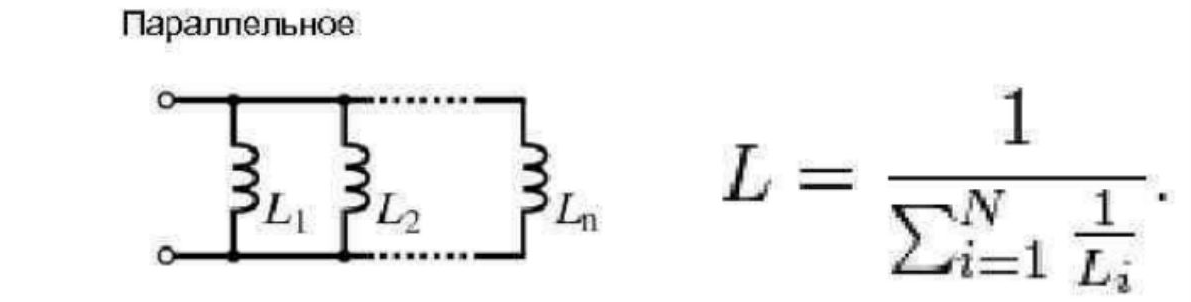
При параллельном соединении катушек напряжение на всех элементах равны, а токи (переменные) распределяются обратно пропорционально индуктивностям элементов.
- U=U1=U2=U3;
- I=I1+I2+I3.
Общая индуктивность цепи определяется, как 1/L=1/L1+1/L2+1/L3. Формула справедлива для любого количества элементов, а для двух катушек упрощается до вида L=L1*L2/(L1+L2). Очевидно, что итоговая индуктивность меньше индуктивности элемента с наименьшим значен
Последовательное соединение
При таком виде соединения через цепь, составленную из катушек, течёт один и тот же ток, а напряжение (переменное!) на каждом компоненте цепи распределяется пропорционально индуктивности каждого элемента:
- U=U1+U2+U3;
- I=I1=I2=I3.
Суммарная индуктивность равна сумме всех индуктивностей, и будет больше индуктивности элемента с наибольшим значением. Поэтому такое соединение используют при необходимости получить увеличение индуктивности.
Важно! При соединении катушек в последовательную или параллельную батарею формулы расчёта верны только для случаев, когда исключено взаимное влияние магнитных полей элементов друг на друга (экранировкой, большим расстоянием и т.д.). Если влияние существует, то общее значение индуктивности будет зависеть от взаимного расположения катушек.
Некоторые практические вопросы и конструкции катушек индуктивности
На практике применяют различные конструкции катушек индуктивности. В зависимости от назначения и области применения устройства можно выполнить различным способом, но надо учитывать эффекты, возникающие в реальных катушках.
Добротность катушки индуктивности
У реальной катушки, кроме индуктивности, есть ещё несколько параметров, и один из самых важных – добротность. Эта величина определяет потери в катушке и зависит от:
- омических потерь в проводе обмотки (чем больше сопротивление, тем ниже добротность);
- диэлектрических потерь в изоляции провода и каркасе обмотки;
- потерь в экране;
- потерь в сердечнике.
Все эти величины определяют сопротивление потерь, а добротностью называют безразмерную величину, равную Q=ωL/Rпотерь, где:
- ω = 2*π*F – круговая частота;
- L – индуктивность;
- ωL – реактивное сопротивление катушки.
Можно приближённо говорить о том, что добротность равна отношению реактивного (индуктивного) сопротивления к активному. С одной стороны, с ростом частоты растёт числитель, но в то же время за счет скин-эффекта растёт и сопротивление потерь за счет уменьшения полезного сечения провода.
Экранный эффект
Для уменьшения влияния посторонних предметов, а также электрических и магнитных полей и взаимного влияния элементов посредством этих полей, катушки (особенно высокочастотные) часто помещают в экран. Кроме полезного эффекта, экранирование вызывает снижение добротности катушки, снижение её индуктивности и повышение паразитной ёмкости. Причём чем ближе стенки экрана к виткам катушки, тем выше вредное влияние. Поэтому экранированные катушки практически всегда выполняют с возможностью подстройки параметров.
Подстроечная индуктивность
В некоторых случаях требуется точно установить значение индуктивности на месте после подключения катушки к другим элементам цепи, компенсируя отклонение параметров при настройке. Для этого применяются разные способы (переключения отводов витков и т.п.), но наиболее точный и плавный метод – подстройка с помощью сердечника. Он выполняется в виде стержня с резьбой, который можно вворачивать и выворачивать внутри каркаса, настраивая индуктивность катушки.
Переменная индуктивность (вариометр)
Там, где требуется оперативная регулировка индуктивности или индуктивной связи, применяются катушки другой конструкции. Они содержат две обмотки – подвижную и неподвижную. Общая индуктивность равна сумме индуктивностей двух катушек и взаимной индуктивности между ними.
Изменением относительного положения одной катушки к другой, регулируется общее значение индуктивности. Такое устройство называется вариометром и часто применяется в связной аппаратуре для настройки резонансных контуров в тех случаях, когда применение конденсаторов переменной ёмкости по каким-то причинам невозможно. Конструкция вариометра довольно громоздкая, что ограничивает область его применения.
Шаровой вариометр
Индуктивность в виде печатной спирали
Катушки с небольшой индуктивностью можно выполнять в виде спирали из печатных проводников. Достоинством такой конструкции являются:
- технологичность производства;
- высокая повторяемость параметров.
К недостаткам относят невозможность точной подстройки при регулировке и сложность получения больших значений индуктивности – чем выше индуктивность, тем больше катушка занимает места на плате.
Катушка с секционной намоткой
Индуктивность без ёмкости бывает только на бумаге. При любой физической реализации катушки сразу же возникает паразитная межвитковая ёмкость. Это во многих случаях вредное явление. Паразитная ёмкость складывается с ёмкостью LC-контура, снижая резонансную частоту и добротность колебательной системы. Также у катушки возникает собственная резонансная частота, которая провоцирует нежелательные явления.
Для снижения паразитной ёмкости применяют различные способы, самый простой из которых – намотка индуктивности в виде нескольких последовательно включенных секций. При таком включении индуктивности складываются, а суммарная ёмкость снижается.
Катушка индуктивности на тороидальном сердечнике
Линии магнитного поля цилиндрической катушки
Линии магнитного поля цилиндрической катушки индуктивности проводят через внутреннюю часть обмотки (если там сердечник – то через него) и замыкаются снаружи через воздух. Этот факт влечёт за собой несколько недостатков:
- снижается индуктивность;
- характеристики катушки меньше поддаются расчёту;
- любой предмет, внесенный во внешнее магнитное поле, меняет параметры катушки (индуктивность, паразитная ёмкость, потери и т.п.), поэтому во многих случаях требуется экранировка.
От этих недостатков во многом свободны катушки, намотанные на тороидальных сердечниках (в виде кольца или «бублика»). Магнитные линии проходят внутри сердечника в виде замкнутых петель. Это означает, что внешние предметы практически не оказывают влияние на параметры намотанной на таком сердечнике катушки, и экранировка для такой конструкции не нужна. Также увеличивается индуктивность при прочих равных параметрах, а характеристики проще рассчитать.
Линии магнитного поля тороидальной катушки
К недостаткам катушек, намотанных на торах, относят невозможность плавной подстройки индуктивности на месте. Другая проблема – высокая трудоёмкость и низкая технологичность намотки. Впрочем, это относится ко всем индуктивным элементам в целом, в большей или меньшей степени.
Также общим недостатком физической реализации индуктивности являются высокие массогабаритные показатели, относительно невысокая надежность и низкая ремонтопригодность.
Поэтому в технике от индуктивных компонентов стараются избавляться. Но это возможно далеко не всегда, поэтому намоточные компоненты будут использоваться как в обозримом будущем, так и в среднесрочной перспективе.
При самоиндукции, как и при всяком процессе индукции, индуцированная в катушке э. д. с. пропорциональна скорости изменения магнитного потока через витки катушки (§ 141). Магнитный же поток пропорционален силе тока в цепи.
Если в некоторый момент
сила тока в цепи равна
, то магнитный поток
будет пропорционален
, т. е.
, (157.1)
где
– коэффициент пропорциональности, зависящий от числа витков, размеров и формы катушки и, следовательно, имеющий различные значения для различных катушек. Пусть через небольшой промежуток времени, к моменту
, сила тока в цепи стала равной
и, следовательно, в этот момент магнитный поток
.
Таким образом, за время
магнитный поток изменился на
. Обозначив, как и прежде, небольшие разности
,
,
соответственно через
, найдем (§ 141) э. д. с. индукции с помощью соотношения
. (157.2)
Характеризующий катушку множитель
называется индуктивностью катушки. Если катушка такова, что при изменении тока на
А в течение времени
с в цепи возникает э. д. с.
В, то индуктивность подобной катушки принимают за единицу для измерения индуктивности. Эта единица получила название генри (Гн) в честь американского физика Джозефа Генри (1797- 1878). Таким образом, если измерять индуктивность катушки в генри, ток в амперах, а время в секундах, то э. д. с. самоиндукции выразится с помощью формулы (157.2) в вольтах. Если, например, индуктивность катушки равна 5 Гн и ток в ней изменяется на 1 А за 0,02 с, то средняя индуцированная э. д. с.
.
Расчеты и эксперимент дают, что индуктивность очень длинной катушки (соленоида) определяется формулой
, (157.3)
где
– число витков,
– площадь сечения,
– длина катушки,
– относительная магнитная проницаемость среды, заполняющей катушку. Таким образом, индуктивность катушки тем больше, чем больше площадь ее сечения, ибо это условие увеличивает магнитный поток через катушку при одном и том же токе в ней. Если вставить в катушку железный сердечник (§ 144), индуктивность ее сильно возрастает, так как относительная магнитная проницаемость железа очень велика.
В соответствии с формулой (157.3)
,
откуда следует, что
может быть выражена в генри на метр (Гн/м) (§ 126). Напомним, что
и
– безразмерные величины.
Явление индукции, а следовательно, и самоиндукции происходит не только в катушках, но и в проводниках любой формы, в том числе и в прямолинейных проводниках. Поэтому любой проводник характеризуется определенным значением индуктивности. Однако для большинства проводников, не имеющих формы катушки, индуктивность настолько мала, что обычно на самоиндукцию в таких проводниках можно не обращать внимания. Только при очень быстрых изменениях тока, когда отношение
становится очень большим, приходится считаться с э. д. с. самоиндукции, возникающей даже в таких линейных проводниках.
157.1.
Какова индуктивность катушки, в которой индуцируется э. д. с., равная 50 В, при изменении тока на 0,02 А за 0,01 с?
157.2.
Как уменьшить индуктивность катушки при условии, что ее длина и поперечное сечение останутся неизменными?
157.3.
Зависит ли индуктивность катушки с железным сердечником от силы тока в ней?
Индуктивность катушки
Способность
катушки индуктировать на себе э. д. с.
самоиндукции называется индуктивностью
катушки.
Единицей
измерения индуктивности является Генри
(Гн)
Индуктивностью
в 1 Гн обладает такая катушка, изменения
тока в которой на 1 А в секунду создает
э. д. с. самоиндукции равной 1 В.
10-3 Гн
миллигенри мГн
10-6 Гн
микрогенри мкГн
Величина
индуктивности прямо пропорциональна
размерам катушки и числу витков. Кроме
того, индуктивность
зависит
также от материала введенного в
катушку сердечника и наличия
экрана.
Качество работы катушки
индуктивности в цепях переменного
тока характеризуется добротностью.
Добротность Q катушки определяют как
отношение ее индуктивного сопротивления
ХL=
ωL=2пfL к активному R, при рабочей
частоте f:Q=ωL/R=2пfL/R. Активное
сопротивление включает сопротивление
провода обмотки катушки и сопротивление,
обусловленное потерями электрической
энергии в каркасе, сердечнике, экране
и изоляции.
Чем
меньше активное сопротивление, тем выше
добротность катушки и ее качество.
Витки катушки, разделенные слоем
изоляции, образуют элементарный
конденсатор. В многослойных катушках
емкость возникает между отделными
слоями. Таким образом, катушка обладает
не только индуктивными, но и емкостными
свойствами. В большинстве случаев
собственная емкость катушки является
вредной, и ее стремятся уменьшить. Для
этого применяются специальные формы
каркаса катушки и способы намотки
провода.
Назначение сердечников в катушках индуктивности
Сердечник
увеличивает индуктивность катушки.
Действительно катушка с сердечником
обладает большим магнитным полем а
значит на ней будет индуктироваться
большая э. д. с. самоиндукции.
Если
положение сердечника в катушке можно
изменять, значит можно изменять
индуктивность катушки.
Изображение
сердечников на схемах
Взаимоиндукция
Явление
взаимоиндукции наблюдается между близко
расположенными катушками. Сущность
взаимоиндукции заключается в переносе
электрической энергии из одной цепи в
другую посредством общего магнитного
поля: в одном из контуров электрическая
энергия преобразуется в энергию
магнитного поля, в другом контуре
происходит обратный переход энергии
магнитного поля в электрическую энергию.
Из сказанного следует, что магнитное
поле является переносчиком электрической
энергии из одной цепи в другую.
Взаимная
индуктивность между двумя катушками
зависит от их размеров, числа витков,
взаимного расположения и магнитной
проницаемости среды.
N18
Электромагнитные
колебания —
это периодические изменения со временем
электрических и магнитных величин
(заряда, силы тока, напряжения,
напряженности, магнитной индукции и
др.) в электрической цепи.
Для
возбуждения и поддержания электромагнитных
колебаний требуются определенные
системы, простейшей из которых
является колебательный
контур — цепь,
состоящая из включенных последовательно
катушки индуктивностью L,
конденсатора емкостью С и
резистора сопротивлением R (это
может быть сопротивление провода катушки
и проводов, соединяющих катушку с
конденсатором) (рис. 1). Идеальный
контур Томсона —
колебательный контур без активного
сопротивления (R =
0).
Рис.
1
Рассмотрим свободные
электромагнитные колебания —
колебания, происходящие в идеальном
колебательном контуре за счет расходования
сообщенной этому контуру энергии,
которая в дальнейшем не пополняется.
Рисунок 2 иллюстрирует характерные
стадии колебаний в контуре за один
период.
Отсчет
времени t мы
начинаем с момента подключения к контуру
заряженного конденсатора. В этот момент
(рис. 2, а) напряженность электрического
поля E⃗ в
конденсаторе (направленная сверху
вниз), а также напряжение U на
обкладках конденсатора максимальны, а
тока в контуре еще нет, следовательно,
отсутствует и магнитное поле.
При
этом вся энергия W колебательного
контура заключена в электрическом поле
конденсатора, т.е.
W=We0=CU202=q202C.
В
промежутке времени от 0 до T4 (рис.
2, б) конденсатор, разряжаясь, создает
через контур ток I,
идущий по часовой стрелке. При этом
согласно правилу Ленца в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию этого тока. При разряде
конденсатора уменьшаются напряженность
электрического поля E⃗ (сохраняя
прежнее направление) и напряжение U между
его обкладками, следовательно, уменьшается
энергия электрического поля в конденсаторе.
Сила тока I и
индукция B⃗ магнитного
поля, создаваемого этим током,
увеличиваются, т.е. возрастает энергия
магнитного поля в катушке индуктивности.
Следовательно, энергия электростатического
поля конденсатора превращается в энергию
магнитного поля катушки.
К
моменту времени t=T4 (рис.
2, в) конденсатор полностью разряжается,
напряжение U между
его обкладками становится равным нулю,
и электрическое поле в нем
отсутствует E⃗ =0. К
этому времени ток 1 в контуре и
индукция B⃗ магнитного
поля этого тока достигают максимальных
значений. Следовательно, вся энергия
контура заключена в этот момент в его
магнитном поле, т.е.
W=WM0=LI202.
При
этом вся энергия W колебательного контура
заключена в электрическом поле
конденсатора, т.е.
W=We0=CU202=q202C.
В
промежутке времени от 0 до T4 (рис. 2, б)
конденсатор, разряжаясь, создает через
контур ток I, идущий по часовой стрелке.
При этом согласно правилу Ленца в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию этого тока. При разряде
конденсатора уменьшаются напряженность
электрического поля E⃗
(сохраняя прежнее направление) и
напряжение U между его обкладками,
следовательно, уменьшается энергия
электрического поля в конденсаторе.
Сила тока I и индукция B⃗
магнитного поля, создаваемого этим
током, увеличиваются, т.е. возрастает
энергия магнитного поля в катушке
индуктивности. Следовательно, энергия
электростатического поля конденсатора
превращается в энергию магнитного поля
катушки.
К
моменту времени t=T4 (рис. 2, в) конденсатор
полностью разряжается, напряжение U
между его обкладками становится равным
нулю, и электрическое поле в нем
отсутствует E⃗
=0. К этому времени ток 1 в контуре и
индукция B⃗
магнитного поля этого тока достигают
максимальных значений. Следовательно,
вся энергия контура заключена в этот
момент в его магнитном поле, т.е.
W=WM0=LI202.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Inductance | |
|---|---|
|
Common symbols |
L |
| SI unit | henry (H) |
| In SI base units | kg⋅m2⋅s−2⋅A−2 |
|
Derivations from |
|
| Dimension | M1·L2·T−2·I−2 |
Inductance is the tendency of an electrical conductor to oppose a change in the electric current flowing through it. The flow of electric current creates a magnetic field around the conductor. The field strength depends on the magnitude of the current, and follows any changes in current. From Faraday’s law of induction, any change in magnetic field through a circuit induces an electromotive force (EMF) (voltage) in the conductors, a process known as electromagnetic induction. This induced voltage created by the changing current has the effect of opposing the change in current. This is stated by Lenz’s law, and the voltage is called back EMF.
Inductance is defined as the ratio of the induced voltage to the rate of change of current causing it. It is a proportionality factor that depends on the geometry of circuit conductors and the magnetic permeability of nearby materials.[1] An electronic component designed to add inductance to a circuit is called an inductor. It typically consists of a coil or helix of wire.
The term inductance was coined by Oliver Heaviside in May 1884.[2][3] It is customary to use the symbol 
History[edit]
The history of electromagnetic induction, a facet of electromagnetism, began with observations of the ancients: electric charge or static electricity (rubbing silk on amber), electric current (lightning), and magnetic attraction (lodestone). Understanding the unity of these forces of nature, and the scientific theory of electromagnetism began in the late 18th century.
Electromagnetic induction was first described by Michael Faraday in 1831.[7][8] In Faraday’s experiment, he wrapped two wires around opposite sides of an iron ring. He expected that, when current started to flow in one wire, a sort of wave would travel through the ring and cause some electrical effect on the opposite side. Using a galvanometer, he observed a transient current flow in the second coil of wire each time that a battery was connected or disconnected from the first coil.[9] This current was induced by the change in magnetic flux that occurred when the battery was connected and disconnected.[10] Faraday found several other manifestations of electromagnetic induction. For example, he saw transient currents when he quickly slid a bar magnet in and out of a coil of wires, and he generated a steady (DC) current by rotating a copper disk near the bar magnet with a sliding electrical lead («Faraday’s disk»).[11]
Source of inductance[edit]
A current 



The negative sign in the equation indicates that the induced voltage is in a direction which opposes the change in current that created it; this is called Lenz’s law. The potential is therefore called a back EMF. If the current is increasing, the voltage is positive at the end of the conductor through which the current enters and negative at the end through which it leaves, tending to reduce the current. If the current is decreasing, the voltage is positive at the end through which the current leaves the conductor, tending to maintain the current. Self-inductance, usually just called inductance, 
Thus, inductance is a property of a conductor or circuit, due to its magnetic field, which tends to oppose changes in current through the circuit. The unit of inductance in the SI system is the henry (H), named after Joseph Henry, which is the amount of inductance which generates a voltage of one volt when the current is changing at a rate of one ampere per second.
All conductors have some inductance, which may have either desirable or detrimental effects in practical electrical devices. The inductance of a circuit depends on the geometry of the current path, and on the magnetic permeability of nearby materials; ferromagnetic materials with a higher permeability like iron near a conductor tend to increase the magnetic field and inductance. Any alteration to a circuit which increases the flux (total magnetic field) through the circuit produced by a given current increases the inductance, because inductance is also equal to the ratio of magnetic flux to current[12][13][14][15]
An inductor is an electrical component consisting of a conductor shaped to increase the magnetic flux, to add inductance to a circuit. Typically it consists of a wire wound into a coil or helix. A coiled wire has a higher inductance than a straight wire of the same length, because the magnetic field lines pass through the circuit multiple times, it has multiple flux linkages. The inductance is proportional to the square of the number of turns in the coil, assuming full flux linkage.
The inductance of a coil can be increased by placing a magnetic core of ferromagnetic material in the hole in the center. The magnetic field of the coil magnetizes the material of the core, aligning its magnetic domains, and the magnetic field of the core adds to that of the coil, increasing the flux through the coil. This is called a ferromagnetic core inductor. A magnetic core can increase the inductance of a coil by thousands of times.
If multiple electric circuits are located close to each other, the magnetic field of one can pass through the other; in this case the circuits are said to be inductively coupled. Due to Faraday’s law of induction, a change in current in one circuit can cause a change in magnetic flux in another circuit and thus induce a voltage in another circuit. The concept of inductance can be generalized in this case by defining the mutual inductance 




Self-inductance and magnetic energy[edit]
If the current through a conductor with inductance is increasing, a voltage 





From (1) above
When there is no current, there is no magnetic field and the stored energy is zero. Neglecting resistive losses, the energy 

If the inductance 
Inductance is therefore also proportional to the energy stored in the magnetic field for a given current. This energy is stored as long as the current remains constant. If the current decreases, the magnetic field decreases, inducing a voltage in the conductor in the opposite direction, negative at the end through which current enters and positive at the end through which it leaves. This returns stored magnetic energy to the external circuit.
If ferromagnetic materials are located near the conductor, such as in an inductor with a magnetic core, the constant inductance equation above is only valid for linear regions of the magnetic flux, at currents below the level at which the ferromagnetic material saturates, where the inductance is approximately constant. If the magnetic field in the inductor approaches the level at which the core saturates, the inductance begins to change with current, and the integral equation must be used.
Inductive reactance[edit]
The voltage (

When a sinusoidal alternating current (AC) is passing through a linear inductance, the induced back-EMF is also sinusoidal. If the current through the inductance is 
where 



Thus the amplitude (peak value) of the voltage across the inductance is
Inductive reactance is the opposition of an inductor to an alternating current.[20] It is defined analogously to electrical resistance in a resistor, as the ratio of the amplitude (peak value) of the alternating voltage to current in the component
Reactance has units of ohms. It can be seen that inductive reactance of an inductor increases proportionally with frequency 

Calculating inductance[edit]
In the most general case, inductance can be calculated from Maxwell’s equations. Many important cases can be solved using simplifications. Where high frequency currents are considered, with skin effect, the surface current densities and magnetic field may be obtained by solving the Laplace equation. Where the conductors are thin wires, self-inductance still depends on the wire radius and the distribution of the current in the wire. This current distribution is approximately constant (on the surface or in the volume of the wire) for a wire radius much smaller than other length scales.
Inductance of a straight single wire[edit]
As a practical matter, longer wires have more inductance, and thicker wires have less, analogous to their electrical resistance (although the relationships aren’t linear, and are different in kind from the relationships that length and diameter bear to resistance).
Separating the wire from the other parts of the circuit introduces some unavoidable error in any formulas’ results. These inductances are often referred to as “partial inductances”, in part to encourage consideration of the other contributions to whole-circuit inductance which are omitted.
Practical formulas[edit]
For derivation of the formulas below, see Rosa (1908).[21]
The total low frequency inductance (interior plus exterior) of a straight wire is:
where
The constant 0.75 is just one parameter value among several; different frequency ranges, different shapes, or extremely long wire lengths require a slightly different constant (see below). This result is based on the assumption that the radius 

For sufficiently high frequencies skin effects cause the interior currents to vanish, leaving only the currents on the surface of the conductor; the inductance for alternating current, 
where the variables 

In an example from everyday experience, just one of the conductors of a lamp cord 10 m long, made of 18 AWG wire, would only have an inductance of about 19 μH if stretched out straight.
Mutual inductance of two parallel straight wires[edit]
There are two cases to consider:
- Current travels in the same direction in each wire, and
- current travels in opposing directions in the wires.
Currents in the wires need not be equal, though they often are, as in the case of a complete circuit, where one wire is the source and the other the return.
Mutual inductance of two wire loops[edit]
This is the generalized case of the paradigmatic two-loop cylindrical coil carrying a uniform low frequency current; the loops are independent closed circuits that can have different lengths, any orientation in space, and carry different currents. Nonetheless, the error terms, which are not included in the integral are only small if the geometries of the loops are mostly smooth and convex: they do not have too many kinks, sharp corners, coils, crossovers, parallel segments, concave cavities or other topological «close» deformations. A necessary predicate for the reduction of the 3-dimensional manifold integration formula to a double curve integral is that the current paths be filamentary circuits, i.e. thin wires where the radius of the wire is negligible compared to its length.
The mutual inductance by a filamentary circuit 

where
Derivation[edit]
where
where
Stokes’ theorem has been used for the 3rd equality step. For the last equality step, we used the retarded potential expression for 
Self-inductance of a wire loop[edit]
Formally, the self-inductance of a wire loop would be given by the above equation with 


where
Inductance of a solenoid[edit]
A solenoid is a long, thin coil; i.e., a coil whose length is much greater than its diameter. Under these conditions, and without any magnetic material used, the magnetic flux density 
where 





When this is combined with the definition of inductance 
Therefore, for air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current.
Inductance of a coaxial cable[edit]
Let the inner conductor have radius 





Inductance of multilayer coils[edit]
Most practical air-core inductors are multilayer cylindrical coils with square cross-sections to minimize average distance between turns (circular cross -sections would be better but harder to form).
Magnetic cores[edit]
Many inductors include a magnetic core at the center of or partly surrounding the winding. Over a large enough range these exhibit a nonlinear permeability with effects such as magnetic saturation. Saturation makes the resulting inductance a function of the applied current.
The secant or large-signal inductance is used in flux calculations. It is defined as:
The differential or small-signal inductance, on the other hand, is used in calculating voltage. It is defined as:
The circuit voltage for a nonlinear inductor is obtained via the differential inductance as shown by Faraday’s Law and the chain rule of calculus.
Similar definitions may be derived for nonlinear mutual inductance.
Mutual inductance[edit]
Mutual inductance is defined as the ratio between the EMF induced in one loop or coil by the rate of change of current in another loop or coil. Mutual inductance is given the symbol M.
Derivation of mutual inductance[edit]
The inductance equations above are a consequence of Maxwell’s equations. For the important case of electrical circuits consisting of thin wires, the derivation is straightforward.
In a system of 


Here 




where 






Mutual inductance and magnetic field energy[edit]
Multiplying the equation for vm above with imdt and summing over m gives the energy transferred to the system in the time interval dt,
This must agree with the change of the magnetic field energy, W, caused by the currents.[25] The integrability condition
requires Lm,n = Ln,m. The inductance matrix, Lm,n, thus is symmetric. The integral of the energy transfer is the magnetic field energy as a function of the currents,
This equation also is a direct consequence of the linearity of Maxwell’s equations. It is helpful to associate changing electric currents with a build-up or decrease of magnetic field energy. The corresponding energy transfer requires or generates a voltage. A mechanical analogy in the K = 1 case with magnetic field energy (1/2)Li2 is a body with mass M, velocity u and kinetic energy (1/2)Mu2. The rate of change of velocity (current) multiplied with mass (inductance) requires or generates a force (an electrical voltage).
Circuit diagram of two mutually coupled inductors. The two vertical lines between the windings indicate that the transformer has a ferromagnetic core . «n:m» shows the ratio between the number of windings of the left inductor to windings of the right inductor. This picture also shows the dot convention.
Mutual inductance occurs when the change in current in one inductor induces a voltage in another nearby inductor. It is important as the mechanism by which transformers work, but it can also cause unwanted coupling between conductors in a circuit.
The mutual inductance, 


The mutual inductance also has the relationship:
where
Once the mutual inductance, 
where
The minus sign arises because of the sense the current 

Coupling coefficient[edit]
The coupling coefficient is the ratio of the open-circuit actual voltage ratio to the ratio that would be obtained if all the flux coupled from one magnetic circuit to the other. The coupling coefficient is related to mutual inductance and self inductances in the following way. From the two simultaneous equations expressed in the two-port matrix the open-circuit voltage ratio is found to be:
where
while the ratio if all the flux is coupled is the ratio of the turns, hence the ratio of the square root of the inductances
thus,
where
The coupling coefficient is a convenient way to specify the relationship between a certain orientation of inductors with arbitrary inductance. Most authors define the range as 


Matrix representation[edit]
Mutually coupled inductors can be described by any of the two-port network parameter matrix representations. The most direct are the z parameters, which are given by
where 



Equivalent circuits[edit]
T-circuit[edit]
T equivalent circuit of mutually coupled inductors
Mutually coupled inductors can equivalently be represented by a T-circuit of inductors as shown. If the coupling is strong and the inductors are of unequal values then the series inductor on the step-down side may take on a negative value.
This can be analyzed as a two port network. With the output terminated with some arbitrary impedance, 

where 

For tightly coupled inductors where 
which is independent of the load impedance. If the inductors are wound on the same core and with the same geometry, then this expression is equal to the turns ratio of the two inductors because inductance is proportional to the square of turns ratio.
The input impedance of the network is given by,
For 
Thus, current gain, 
is met, in which case,
and
π-circuit[edit]
π equivalent circuit of coupled inductors
Alternatively, two coupled inductors can be modelled using a π equivalent circuit with optional ideal transformers at each port. While the circuit is more complicated than a T-circuit, it can be generalized[29] to circuits consisting of more than two coupled inductors. Equivalent circuit elements 

Equivalent circuit element values can be calculated from coupling coefficients with
where coupling coefficient matrix and its cofactors are defined as
and
For two coupled inductors, these formulas simplify to
and
and for three coupled inductors (for brevity shown only for 

and
Resonant transformer[edit]
When a capacitor is connected across one winding of a transformer, making the winding a tuned circuit (resonant circuit) it is called a single-tuned transformer. When a capacitor is connected across each winding, it is called a double tuned transformer. These resonant transformers can store oscillating electrical energy similar to a resonant circuit and thus function as a bandpass filter, allowing frequencies near their resonant frequency to pass from the primary to secondary winding, but blocking other frequencies. The amount of mutual inductance between the two windings, together with the Q factor of the circuit, determine the shape of the frequency response curve. The advantage of the double tuned transformer is that it can have a wider bandwidth than a simple tuned circuit. The coupling of double-tuned circuits is described as loose-, critical-, or over-coupled depending on the value of the coupling coefficient 
Stongly-coupled self-resonant coils can be used for wireless power transfer between devices in the mid range distances (up to two metres).[30] Strong coupling is required for a high percentage of power transferred, which results in peak splitting of the frequency response.[31] [32]
Ideal transformers[edit]
When 
where
Conversely the current:
where
The power through one inductor is the same as the power through the other. These equations neglect any forcing by current sources or voltage sources.
Self-inductance of thin wire shapes[edit]
The table below lists formulas for the self-inductance of various simple shapes made of thin cylindrical conductors (wires). In general these are only accurate if the wire radius 
| Type | Inductance | Comment |
|---|---|---|
| Single layer solenoid |
The well-known Wheeler’s approximation formula for current-sheet model air-core coil:[33][34]
This formula gives an error no more than 1% when |
|
| Coaxial cable (HF) |

|
|
| Circular loop[35] | ![{displaystyle {mathcal {L}}=mu _{0} r left[ln left({frac {8r}{a}}right)-2+{tfrac {1}{4}}Y+{mathcal {O}}left({frac {a^{2}}{r^{2}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275873f317db17a666dc61f9d7890f7822266d6d)
|
|
| Rectangle from round wire[36] |
|
|
| Pair of parallel wires |
![{displaystyle {mathcal {L}}={frac { mu _{0}}{pi }} ell left[ln left({frac {s}{a}}right)+{tfrac {1}{4}}Yright]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89810637f022906cff6123b58e8ed787ec045386)
|
|
| Pair of parallel wires (HF) |
|
|



where



See also[edit]
- Electromagnetic induction
- Gyrator
- Hydraulic analogy
- Leakage inductance
- LC circuit, RLC circuit, RL circuit
- Kinetic inductance
Footnotes[edit]
References[edit]
- ^ Serway, A. Raymond; Jewett, John W.; Wilson, Jane; Wilson, Anna; Rowlands, Wayne (1 October 2016). «32». Physics for global scientists and engineers (2 ed.). p. 901. ISBN 9780170355520.
- ^ Baker, Edward Cecil (1976). Sir William Preece, F.R.S.: Victorian Engineer Extraordinary. Hutchinson. p. 204. ISBN 9780091266103..
- ^ Heaviside, Oliver (1894). Electrical Papers, Vol. 1. Macmillan and Company. p. 354.
- ^ Elert, Glenn. «The Physics Hypertextbook: Inductance». Retrieved 30 July 2016.
- ^ Davidson, Michael W. (1995–2008). «Molecular Expressions: Electricity and Magnetism Introduction: Inductance».
- ^ «A Brief History of Electromagnetism» (PDF).
- ^ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson / Prentice Hall. p. 255. ISBN 978-0-13-241326-8.
- ^ «Joseph Henry». Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2013-12-13. Retrieved 2006-11-30.
- ^ Pearce Williams, L. (1971). Michael Faraday: A Biography. pp. 182–183. ISBN 9780671209292.
- ^ Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624.
- ^ Pearce Williams, L. (1971). Michael Faraday: A Biography. pp. 191–195. ISBN 9780671209292.
- ^ Singh, Yaduvir (2011). Electro Magnetic Field Theory. Pearson Education India. p. 65. ISBN 978-8131760611.
- ^ Wadhwa, C.L. (2005). Electrical Power Systems. New Age International. p. 18. ISBN 8122417221.
- ^ Pelcovits, Robert A.; Farkas, Josh (2007). Barron’s AP Physics C. Barron’s Educational Series. p. 646. ISBN 978-0764137105.
- ^ Purcell, Edward M.; Morin, David J. (2013). Electricity and Magnetism. Cambridge Univ. Press. p. 364. ISBN 978-1107014022.
- ^ Sears and Zemansky 1964:743
- ^ a b Serway, Raymond A.; Jewett, John W. (2012). Principles of Physics: A Calculus-Based Text, 5th Ed. Cengage Learning. pp. 801–802. ISBN 978-1133104261.
- ^ a b Ida, Nathan (2007). Engineering Electromagnetics, 2nd Ed. Springer Science and Business Media. p. 572. ISBN 978-0387201566.
- ^ a b Purcell, Edward (2011). Electricity and Magnetism, 2nd Ed. Cambridge University Press. p. 285. ISBN 978-1139503556.
- ^ Gates, Earl D. (2001). Introduction to Electronics. Cengage Learning. p. 153. ISBN 0766816982.
- ^ a b Rosa, E.B. (1908). «The self and mutual inductances of linear conductors». Bulletin of the Bureau of Standards. U.S. Bureau of Standards. 4 (2): 301 ff. doi:10.6028/bulletin.088.
- ^ Neumann, F. E. (1846). «Allgemeine Gesetze der inducirten elektrischen Ströme». Annalen der Physik und Chemie (in German). Wiley. 143 (1): 31–44. Bibcode:1846AnP…143…31N. doi:10.1002/andp.18461430103. ISSN 0003-3804.
- ^ Jackson, J. D. (1975). Classical Electrodynamics. Wiley. pp. 176, 263. ISBN 9780471431329.
- ^ Dengler, R. (2016). «Self inductance of a wire loop as a curve integral». Advanced Electromagnetics. 5 (1): 1–8. arXiv:1204.1486. Bibcode:2016AdEl….5….1D. doi:10.7716/aem.v5i1.331. S2CID 53583557.
- ^ The kinetic energy of the drifting electrons is many orders of magnitude smaller than W, except for nanowires.
- ^ Nahvi, Mahmood; Edminister, Joseph (2002). Schaum’s outline of theory and problems of electric circuits. McGraw-Hill Professional. p. 338. ISBN 0-07-139307-2.
- ^ Thierauf, Stephen C. (2004). High-speed Circuit Board Signal Integrity. Artech House. p. 56. ISBN 1580538460.
- ^ Kim, Seok; Kim, Shin-Ae; Jung, Goeun; Kwon, Kee-Won; Chun, Jung-Hoon (2009). «Design of a Reliable Broadband I/O Employing T-coil». JSTS:journal of Semiconductor Technology and Science. 9 (4): 198–204. doi:10.5573/JSTS.2009.9.4.198. S2CID 56413251.
- ^ Radecki, Andrzej; Yuan, Yuxiang; Miura, Noriyuki; Aikawa, Iori; Take, Yasuhiro; Ishikuro, Hiroki; Kuroda, Tadahiro (2012). «Simultaneous 6-Gb/s Data and 10-mW Power Transmission Using Nested Clover Coils for Noncontact Memory Card». IEEE Journal of Solid-State Circuits. 47 (10): 2484–2495. Bibcode:2012IJSSC..47.2484R. doi:10.1109/JSSC.2012.2204545. S2CID 29266328.
- ^ Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J. D.; Fisher, P.; Soljacic, M. (6 July 2007). «Wireless Power Transfer via Strongly Coupled Magnetic Resonances». Science. 317 (5834): 83–86. Bibcode:2007Sci…317…83K. CiteSeerX 10.1.1.418.9645. doi:10.1126/science.1143254. PMID 17556549. S2CID 17105396.
- ^ Sample, Alanson P.; Meyer, D. A.; Smith, J. R. (2011). «Analysis, Experimental Results, and Range Adaptation of Magnetically Coupled Resonators for Wireless Power Transfer». IEEE Transactions on Industrial Electronics. 58 (2): 544–554. doi:10.1109/TIE.2010.2046002. S2CID 14721.
- ^ Rendon-Hernandez, Adrian A.; Halim, Miah A.; Smith, Spencer E.; Arnold, David P. (2022). «Magnetically Coupled Microelectromechanical Resonators for Low-Frequency Wireless Power Transfer». 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS). pp. 648–651. doi:10.1109/MEMS51670.2022.9699458. ISBN 978-1-6654-0911-7. S2CID 246753151.
- ^ Wheeler, H.A. (1942). «Formulas for the Skin Effect». Proceedings of the IRE. 30 (9): 412–424. doi:10.1109/JRPROC.1942.232015. S2CID 51630416.
- ^ Wheeler, H.A. (1928). «Simple Inductance Formulas for Radio Coils». Proceedings of the IRE. 16 (10): 1398–1400. doi:10.1109/JRPROC.1928.221309. S2CID 51638679.
- ^ Elliott, R.S. (1993). Electromagnetics. New York: IEEE Press. Note: The published constant −3⁄2 in the result for a uniform current distribution is wrong.
- ^ Grover, Frederick W. (1946). Inductance Calculations: Working formulas and tables. New York: Dover Publications, Inc.
General references[edit]
- Frederick W. Grover (1952). Inductance Calculations. Dover Publications, New York.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Wangsness, Roald K. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 0-471-81186-6.
- Hughes, Edward. (2002). Electrical & Electronic Technology (8th ed.). Prentice Hall. ISBN 0-582-40519-X.
- Küpfmüller K., Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959.
- Heaviside O., Electrical Papers. Vol.1. – L.; N.Y.: Macmillan, 1892, p. 429-560.
- Fritz Langford-Smith, editor (1953). Radiotron Designer’s Handbook, 4th Edition, Amalgamated Wireless Valve Company Pty., Ltd. Chapter 10, «Calculation of Inductance» (pp. 429–448), includes a wealth of formulas and nomographs for coils, solenoids, and mutual inductance.
- F. W. Sears and M. W. Zemansky 1964 University Physics: Third Edition (Complete Volume), Addison-Wesley Publishing Company, Inc. Reading MA, LCCC 63-15265 (no ISBN).
External links[edit]
- Clemson Vehicular Electronics Laboratory: Inductance Calculator
| Inductance | |
|---|---|
|
Common symbols |
L |
| SI unit | henry (H) |
| In SI base units | kg⋅m2⋅s−2⋅A−2 |
|
Derivations from |
|
| Dimension | M1·L2·T−2·I−2 |
Inductance is the tendency of an electrical conductor to oppose a change in the electric current flowing through it. The flow of electric current creates a magnetic field around the conductor. The field strength depends on the magnitude of the current, and follows any changes in current. From Faraday’s law of induction, any change in magnetic field through a circuit induces an electromotive force (EMF) (voltage) in the conductors, a process known as electromagnetic induction. This induced voltage created by the changing current has the effect of opposing the change in current. This is stated by Lenz’s law, and the voltage is called back EMF.
Inductance is defined as the ratio of the induced voltage to the rate of change of current causing it. It is a proportionality factor that depends on the geometry of circuit conductors and the magnetic permeability of nearby materials.[1] An electronic component designed to add inductance to a circuit is called an inductor. It typically consists of a coil or helix of wire.
The term inductance was coined by Oliver Heaviside in May 1884.[2][3] It is customary to use the symbol 
History[edit]
The history of electromagnetic induction, a facet of electromagnetism, began with observations of the ancients: electric charge or static electricity (rubbing silk on amber), electric current (lightning), and magnetic attraction (lodestone). Understanding the unity of these forces of nature, and the scientific theory of electromagnetism began in the late 18th century.
Electromagnetic induction was first described by Michael Faraday in 1831.[7][8] In Faraday’s experiment, he wrapped two wires around opposite sides of an iron ring. He expected that, when current started to flow in one wire, a sort of wave would travel through the ring and cause some electrical effect on the opposite side. Using a galvanometer, he observed a transient current flow in the second coil of wire each time that a battery was connected or disconnected from the first coil.[9] This current was induced by the change in magnetic flux that occurred when the battery was connected and disconnected.[10] Faraday found several other manifestations of electromagnetic induction. For example, he saw transient currents when he quickly slid a bar magnet in and out of a coil of wires, and he generated a steady (DC) current by rotating a copper disk near the bar magnet with a sliding electrical lead («Faraday’s disk»).[11]
Source of inductance[edit]
A current 



The negative sign in the equation indicates that the induced voltage is in a direction which opposes the change in current that created it; this is called Lenz’s law. The potential is therefore called a back EMF. If the current is increasing, the voltage is positive at the end of the conductor through which the current enters and negative at the end through which it leaves, tending to reduce the current. If the current is decreasing, the voltage is positive at the end through which the current leaves the conductor, tending to maintain the current. Self-inductance, usually just called inductance, 
Thus, inductance is a property of a conductor or circuit, due to its magnetic field, which tends to oppose changes in current through the circuit. The unit of inductance in the SI system is the henry (H), named after Joseph Henry, which is the amount of inductance which generates a voltage of one volt when the current is changing at a rate of one ampere per second.
All conductors have some inductance, which may have either desirable or detrimental effects in practical electrical devices. The inductance of a circuit depends on the geometry of the current path, and on the magnetic permeability of nearby materials; ferromagnetic materials with a higher permeability like iron near a conductor tend to increase the magnetic field and inductance. Any alteration to a circuit which increases the flux (total magnetic field) through the circuit produced by a given current increases the inductance, because inductance is also equal to the ratio of magnetic flux to current[12][13][14][15]
An inductor is an electrical component consisting of a conductor shaped to increase the magnetic flux, to add inductance to a circuit. Typically it consists of a wire wound into a coil or helix. A coiled wire has a higher inductance than a straight wire of the same length, because the magnetic field lines pass through the circuit multiple times, it has multiple flux linkages. The inductance is proportional to the square of the number of turns in the coil, assuming full flux linkage.
The inductance of a coil can be increased by placing a magnetic core of ferromagnetic material in the hole in the center. The magnetic field of the coil magnetizes the material of the core, aligning its magnetic domains, and the magnetic field of the core adds to that of the coil, increasing the flux through the coil. This is called a ferromagnetic core inductor. A magnetic core can increase the inductance of a coil by thousands of times.
If multiple electric circuits are located close to each other, the magnetic field of one can pass through the other; in this case the circuits are said to be inductively coupled. Due to Faraday’s law of induction, a change in current in one circuit can cause a change in magnetic flux in another circuit and thus induce a voltage in another circuit. The concept of inductance can be generalized in this case by defining the mutual inductance 




Self-inductance and magnetic energy[edit]
If the current through a conductor with inductance is increasing, a voltage 





From (1) above
When there is no current, there is no magnetic field and the stored energy is zero. Neglecting resistive losses, the energy 

If the inductance 
Inductance is therefore also proportional to the energy stored in the magnetic field for a given current. This energy is stored as long as the current remains constant. If the current decreases, the magnetic field decreases, inducing a voltage in the conductor in the opposite direction, negative at the end through which current enters and positive at the end through which it leaves. This returns stored magnetic energy to the external circuit.
If ferromagnetic materials are located near the conductor, such as in an inductor with a magnetic core, the constant inductance equation above is only valid for linear regions of the magnetic flux, at currents below the level at which the ferromagnetic material saturates, where the inductance is approximately constant. If the magnetic field in the inductor approaches the level at which the core saturates, the inductance begins to change with current, and the integral equation must be used.
Inductive reactance[edit]
The voltage (

When a sinusoidal alternating current (AC) is passing through a linear inductance, the induced back-EMF is also sinusoidal. If the current through the inductance is 
where 



Thus the amplitude (peak value) of the voltage across the inductance is
Inductive reactance is the opposition of an inductor to an alternating current.[20] It is defined analogously to electrical resistance in a resistor, as the ratio of the amplitude (peak value) of the alternating voltage to current in the component
Reactance has units of ohms. It can be seen that inductive reactance of an inductor increases proportionally with frequency 

Calculating inductance[edit]
In the most general case, inductance can be calculated from Maxwell’s equations. Many important cases can be solved using simplifications. Where high frequency currents are considered, with skin effect, the surface current densities and magnetic field may be obtained by solving the Laplace equation. Where the conductors are thin wires, self-inductance still depends on the wire radius and the distribution of the current in the wire. This current distribution is approximately constant (on the surface or in the volume of the wire) for a wire radius much smaller than other length scales.
Inductance of a straight single wire[edit]
As a practical matter, longer wires have more inductance, and thicker wires have less, analogous to their electrical resistance (although the relationships aren’t linear, and are different in kind from the relationships that length and diameter bear to resistance).
Separating the wire from the other parts of the circuit introduces some unavoidable error in any formulas’ results. These inductances are often referred to as “partial inductances”, in part to encourage consideration of the other contributions to whole-circuit inductance which are omitted.
Practical formulas[edit]
For derivation of the formulas below, see Rosa (1908).[21]
The total low frequency inductance (interior plus exterior) of a straight wire is:
where
The constant 0.75 is just one parameter value among several; different frequency ranges, different shapes, or extremely long wire lengths require a slightly different constant (see below). This result is based on the assumption that the radius 

For sufficiently high frequencies skin effects cause the interior currents to vanish, leaving only the currents on the surface of the conductor; the inductance for alternating current, 
where the variables 

In an example from everyday experience, just one of the conductors of a lamp cord 10 m long, made of 18 AWG wire, would only have an inductance of about 19 μH if stretched out straight.
Mutual inductance of two parallel straight wires[edit]
There are two cases to consider:
- Current travels in the same direction in each wire, and
- current travels in opposing directions in the wires.
Currents in the wires need not be equal, though they often are, as in the case of a complete circuit, where one wire is the source and the other the return.
Mutual inductance of two wire loops[edit]
This is the generalized case of the paradigmatic two-loop cylindrical coil carrying a uniform low frequency current; the loops are independent closed circuits that can have different lengths, any orientation in space, and carry different currents. Nonetheless, the error terms, which are not included in the integral are only small if the geometries of the loops are mostly smooth and convex: they do not have too many kinks, sharp corners, coils, crossovers, parallel segments, concave cavities or other topological «close» deformations. A necessary predicate for the reduction of the 3-dimensional manifold integration formula to a double curve integral is that the current paths be filamentary circuits, i.e. thin wires where the radius of the wire is negligible compared to its length.
The mutual inductance by a filamentary circuit 

where
Derivation[edit]
where
where
Stokes’ theorem has been used for the 3rd equality step. For the last equality step, we used the retarded potential expression for 
Self-inductance of a wire loop[edit]
Formally, the self-inductance of a wire loop would be given by the above equation with 


where
Inductance of a solenoid[edit]
A solenoid is a long, thin coil; i.e., a coil whose length is much greater than its diameter. Under these conditions, and without any magnetic material used, the magnetic flux density 
where 





When this is combined with the definition of inductance 
Therefore, for air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current.
Inductance of a coaxial cable[edit]
Let the inner conductor have radius 





Inductance of multilayer coils[edit]
Most practical air-core inductors are multilayer cylindrical coils with square cross-sections to minimize average distance between turns (circular cross -sections would be better but harder to form).
Magnetic cores[edit]
Many inductors include a magnetic core at the center of or partly surrounding the winding. Over a large enough range these exhibit a nonlinear permeability with effects such as magnetic saturation. Saturation makes the resulting inductance a function of the applied current.
The secant or large-signal inductance is used in flux calculations. It is defined as:
The differential or small-signal inductance, on the other hand, is used in calculating voltage. It is defined as:
The circuit voltage for a nonlinear inductor is obtained via the differential inductance as shown by Faraday’s Law and the chain rule of calculus.
Similar definitions may be derived for nonlinear mutual inductance.
Mutual inductance[edit]
Mutual inductance is defined as the ratio between the EMF induced in one loop or coil by the rate of change of current in another loop or coil. Mutual inductance is given the symbol M.
Derivation of mutual inductance[edit]
The inductance equations above are a consequence of Maxwell’s equations. For the important case of electrical circuits consisting of thin wires, the derivation is straightforward.
In a system of 


Here 




where 






Mutual inductance and magnetic field energy[edit]
Multiplying the equation for vm above with imdt and summing over m gives the energy transferred to the system in the time interval dt,
This must agree with the change of the magnetic field energy, W, caused by the currents.[25] The integrability condition
requires Lm,n = Ln,m. The inductance matrix, Lm,n, thus is symmetric. The integral of the energy transfer is the magnetic field energy as a function of the currents,
This equation also is a direct consequence of the linearity of Maxwell’s equations. It is helpful to associate changing electric currents with a build-up or decrease of magnetic field energy. The corresponding energy transfer requires or generates a voltage. A mechanical analogy in the K = 1 case with magnetic field energy (1/2)Li2 is a body with mass M, velocity u and kinetic energy (1/2)Mu2. The rate of change of velocity (current) multiplied with mass (inductance) requires or generates a force (an electrical voltage).
Circuit diagram of two mutually coupled inductors. The two vertical lines between the windings indicate that the transformer has a ferromagnetic core . «n:m» shows the ratio between the number of windings of the left inductor to windings of the right inductor. This picture also shows the dot convention.
Mutual inductance occurs when the change in current in one inductor induces a voltage in another nearby inductor. It is important as the mechanism by which transformers work, but it can also cause unwanted coupling between conductors in a circuit.
The mutual inductance, 


The mutual inductance also has the relationship:
where
Once the mutual inductance, 
where
The minus sign arises because of the sense the current 

Coupling coefficient[edit]
The coupling coefficient is the ratio of the open-circuit actual voltage ratio to the ratio that would be obtained if all the flux coupled from one magnetic circuit to the other. The coupling coefficient is related to mutual inductance and self inductances in the following way. From the two simultaneous equations expressed in the two-port matrix the open-circuit voltage ratio is found to be:
where
while the ratio if all the flux is coupled is the ratio of the turns, hence the ratio of the square root of the inductances
thus,
where
The coupling coefficient is a convenient way to specify the relationship between a certain orientation of inductors with arbitrary inductance. Most authors define the range as 


Matrix representation[edit]
Mutually coupled inductors can be described by any of the two-port network parameter matrix representations. The most direct are the z parameters, which are given by
where 



Equivalent circuits[edit]
T-circuit[edit]
T equivalent circuit of mutually coupled inductors
Mutually coupled inductors can equivalently be represented by a T-circuit of inductors as shown. If the coupling is strong and the inductors are of unequal values then the series inductor on the step-down side may take on a negative value.
This can be analyzed as a two port network. With the output terminated with some arbitrary impedance, 

where 

For tightly coupled inductors where 
which is independent of the load impedance. If the inductors are wound on the same core and with the same geometry, then this expression is equal to the turns ratio of the two inductors because inductance is proportional to the square of turns ratio.
The input impedance of the network is given by,
For 
Thus, current gain, 
is met, in which case,
and
π-circuit[edit]
π equivalent circuit of coupled inductors
Alternatively, two coupled inductors can be modelled using a π equivalent circuit with optional ideal transformers at each port. While the circuit is more complicated than a T-circuit, it can be generalized[29] to circuits consisting of more than two coupled inductors. Equivalent circuit elements 

Equivalent circuit element values can be calculated from coupling coefficients with
where coupling coefficient matrix and its cofactors are defined as
and
For two coupled inductors, these formulas simplify to
and
and for three coupled inductors (for brevity shown only for 

and
Resonant transformer[edit]
When a capacitor is connected across one winding of a transformer, making the winding a tuned circuit (resonant circuit) it is called a single-tuned transformer. When a capacitor is connected across each winding, it is called a double tuned transformer. These resonant transformers can store oscillating electrical energy similar to a resonant circuit and thus function as a bandpass filter, allowing frequencies near their resonant frequency to pass from the primary to secondary winding, but blocking other frequencies. The amount of mutual inductance between the two windings, together with the Q factor of the circuit, determine the shape of the frequency response curve. The advantage of the double tuned transformer is that it can have a wider bandwidth than a simple tuned circuit. The coupling of double-tuned circuits is described as loose-, critical-, or over-coupled depending on the value of the coupling coefficient 
Stongly-coupled self-resonant coils can be used for wireless power transfer between devices in the mid range distances (up to two metres).[30] Strong coupling is required for a high percentage of power transferred, which results in peak splitting of the frequency response.[31] [32]
Ideal transformers[edit]
When 
where
Conversely the current:
where
The power through one inductor is the same as the power through the other. These equations neglect any forcing by current sources or voltage sources.
Self-inductance of thin wire shapes[edit]
The table below lists formulas for the self-inductance of various simple shapes made of thin cylindrical conductors (wires). In general these are only accurate if the wire radius 
| Type | Inductance | Comment |
|---|---|---|
| Single layer solenoid |
The well-known Wheeler’s approximation formula for current-sheet model air-core coil:[33][34]
This formula gives an error no more than 1% when |
|
| Coaxial cable (HF) |

|
|
| Circular loop[35] | ![{displaystyle {mathcal {L}}=mu _{0} r left[ln left({frac {8r}{a}}right)-2+{tfrac {1}{4}}Y+{mathcal {O}}left({frac {a^{2}}{r^{2}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275873f317db17a666dc61f9d7890f7822266d6d)
|
|
| Rectangle from round wire[36] |
|
|
| Pair of parallel wires |
![{displaystyle {mathcal {L}}={frac { mu _{0}}{pi }} ell left[ln left({frac {s}{a}}right)+{tfrac {1}{4}}Yright]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89810637f022906cff6123b58e8ed787ec045386)
|
|
| Pair of parallel wires (HF) |
|
|



where



See also[edit]
- Electromagnetic induction
- Gyrator
- Hydraulic analogy
- Leakage inductance
- LC circuit, RLC circuit, RL circuit
- Kinetic inductance
Footnotes[edit]
References[edit]
- ^ Serway, A. Raymond; Jewett, John W.; Wilson, Jane; Wilson, Anna; Rowlands, Wayne (1 October 2016). «32». Physics for global scientists and engineers (2 ed.). p. 901. ISBN 9780170355520.
- ^ Baker, Edward Cecil (1976). Sir William Preece, F.R.S.: Victorian Engineer Extraordinary. Hutchinson. p. 204. ISBN 9780091266103..
- ^ Heaviside, Oliver (1894). Electrical Papers, Vol. 1. Macmillan and Company. p. 354.
- ^ Elert, Glenn. «The Physics Hypertextbook: Inductance». Retrieved 30 July 2016.
- ^ Davidson, Michael W. (1995–2008). «Molecular Expressions: Electricity and Magnetism Introduction: Inductance».
- ^ «A Brief History of Electromagnetism» (PDF).
- ^ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson / Prentice Hall. p. 255. ISBN 978-0-13-241326-8.
- ^ «Joseph Henry». Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2013-12-13. Retrieved 2006-11-30.
- ^ Pearce Williams, L. (1971). Michael Faraday: A Biography. pp. 182–183. ISBN 9780671209292.
- ^ Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624.
- ^ Pearce Williams, L. (1971). Michael Faraday: A Biography. pp. 191–195. ISBN 9780671209292.
- ^ Singh, Yaduvir (2011). Electro Magnetic Field Theory. Pearson Education India. p. 65. ISBN 978-8131760611.
- ^ Wadhwa, C.L. (2005). Electrical Power Systems. New Age International. p. 18. ISBN 8122417221.
- ^ Pelcovits, Robert A.; Farkas, Josh (2007). Barron’s AP Physics C. Barron’s Educational Series. p. 646. ISBN 978-0764137105.
- ^ Purcell, Edward M.; Morin, David J. (2013). Electricity and Magnetism. Cambridge Univ. Press. p. 364. ISBN 978-1107014022.
- ^ Sears and Zemansky 1964:743
- ^ a b Serway, Raymond A.; Jewett, John W. (2012). Principles of Physics: A Calculus-Based Text, 5th Ed. Cengage Learning. pp. 801–802. ISBN 978-1133104261.
- ^ a b Ida, Nathan (2007). Engineering Electromagnetics, 2nd Ed. Springer Science and Business Media. p. 572. ISBN 978-0387201566.
- ^ a b Purcell, Edward (2011). Electricity and Magnetism, 2nd Ed. Cambridge University Press. p. 285. ISBN 978-1139503556.
- ^ Gates, Earl D. (2001). Introduction to Electronics. Cengage Learning. p. 153. ISBN 0766816982.
- ^ a b Rosa, E.B. (1908). «The self and mutual inductances of linear conductors». Bulletin of the Bureau of Standards. U.S. Bureau of Standards. 4 (2): 301 ff. doi:10.6028/bulletin.088.
- ^ Neumann, F. E. (1846). «Allgemeine Gesetze der inducirten elektrischen Ströme». Annalen der Physik und Chemie (in German). Wiley. 143 (1): 31–44. Bibcode:1846AnP…143…31N. doi:10.1002/andp.18461430103. ISSN 0003-3804.
- ^ Jackson, J. D. (1975). Classical Electrodynamics. Wiley. pp. 176, 263. ISBN 9780471431329.
- ^ Dengler, R. (2016). «Self inductance of a wire loop as a curve integral». Advanced Electromagnetics. 5 (1): 1–8. arXiv:1204.1486. Bibcode:2016AdEl….5….1D. doi:10.7716/aem.v5i1.331. S2CID 53583557.
- ^ The kinetic energy of the drifting electrons is many orders of magnitude smaller than W, except for nanowires.
- ^ Nahvi, Mahmood; Edminister, Joseph (2002). Schaum’s outline of theory and problems of electric circuits. McGraw-Hill Professional. p. 338. ISBN 0-07-139307-2.
- ^ Thierauf, Stephen C. (2004). High-speed Circuit Board Signal Integrity. Artech House. p. 56. ISBN 1580538460.
- ^ Kim, Seok; Kim, Shin-Ae; Jung, Goeun; Kwon, Kee-Won; Chun, Jung-Hoon (2009). «Design of a Reliable Broadband I/O Employing T-coil». JSTS:journal of Semiconductor Technology and Science. 9 (4): 198–204. doi:10.5573/JSTS.2009.9.4.198. S2CID 56413251.
- ^ Radecki, Andrzej; Yuan, Yuxiang; Miura, Noriyuki; Aikawa, Iori; Take, Yasuhiro; Ishikuro, Hiroki; Kuroda, Tadahiro (2012). «Simultaneous 6-Gb/s Data and 10-mW Power Transmission Using Nested Clover Coils for Noncontact Memory Card». IEEE Journal of Solid-State Circuits. 47 (10): 2484–2495. Bibcode:2012IJSSC..47.2484R. doi:10.1109/JSSC.2012.2204545. S2CID 29266328.
- ^ Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J. D.; Fisher, P.; Soljacic, M. (6 July 2007). «Wireless Power Transfer via Strongly Coupled Magnetic Resonances». Science. 317 (5834): 83–86. Bibcode:2007Sci…317…83K. CiteSeerX 10.1.1.418.9645. doi:10.1126/science.1143254. PMID 17556549. S2CID 17105396.
- ^ Sample, Alanson P.; Meyer, D. A.; Smith, J. R. (2011). «Analysis, Experimental Results, and Range Adaptation of Magnetically Coupled Resonators for Wireless Power Transfer». IEEE Transactions on Industrial Electronics. 58 (2): 544–554. doi:10.1109/TIE.2010.2046002. S2CID 14721.
- ^ Rendon-Hernandez, Adrian A.; Halim, Miah A.; Smith, Spencer E.; Arnold, David P. (2022). «Magnetically Coupled Microelectromechanical Resonators for Low-Frequency Wireless Power Transfer». 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS). pp. 648–651. doi:10.1109/MEMS51670.2022.9699458. ISBN 978-1-6654-0911-7. S2CID 246753151.
- ^ Wheeler, H.A. (1942). «Formulas for the Skin Effect». Proceedings of the IRE. 30 (9): 412–424. doi:10.1109/JRPROC.1942.232015. S2CID 51630416.
- ^ Wheeler, H.A. (1928). «Simple Inductance Formulas for Radio Coils». Proceedings of the IRE. 16 (10): 1398–1400. doi:10.1109/JRPROC.1928.221309. S2CID 51638679.
- ^ Elliott, R.S. (1993). Electromagnetics. New York: IEEE Press. Note: The published constant −3⁄2 in the result for a uniform current distribution is wrong.
- ^ Grover, Frederick W. (1946). Inductance Calculations: Working formulas and tables. New York: Dover Publications, Inc.
General references[edit]
- Frederick W. Grover (1952). Inductance Calculations. Dover Publications, New York.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Wangsness, Roald K. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 0-471-81186-6.
- Hughes, Edward. (2002). Electrical & Electronic Technology (8th ed.). Prentice Hall. ISBN 0-582-40519-X.
- Küpfmüller K., Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959.
- Heaviside O., Electrical Papers. Vol.1. – L.; N.Y.: Macmillan, 1892, p. 429-560.
- Fritz Langford-Smith, editor (1953). Radiotron Designer’s Handbook, 4th Edition, Amalgamated Wireless Valve Company Pty., Ltd. Chapter 10, «Calculation of Inductance» (pp. 429–448), includes a wealth of formulas and nomographs for coils, solenoids, and mutual inductance.
- F. W. Sears and M. W. Zemansky 1964 University Physics: Third Edition (Complete Volume), Addison-Wesley Publishing Company, Inc. Reading MA, LCCC 63-15265 (no ISBN).
External links[edit]
- Clemson Vehicular Electronics Laboratory: Inductance Calculator
Начинающие электрики и радиотехники часто задаются вопросом: «Что называют индуктивностью проводника?». Индуктивность – коэф. пропорциональности между током, проходящем в замкнутом контуре, и магнитным полем. Простыми словами — некий элемент (чаще всего катушка) может накапливать это самое магнитное поле.
Электрическая цепь и индуктивность
В физике индуктивность показывает реальные электромагнитные характеристики цепи. У узком смысле, определяется единый элемент, который обладает высокой самоиндукцией. Обычно – это катушка индуктивности. Ей может считаться любой элемент с сердечником, имеющий более 1 витка проволоки.
Измерительная система
В чем измеряется индуктивность? Международная система стандарта обозначает единицу измерения индуктивности как Гн (сокращение от физика из США — Генри). Катушка имеет 1 Гн, если при изменении значения тока на 1 А в 1 сек., напряжение на выходе составит 1В.
А вот расчет отличается, в зависимости от системы стандартизирования. В гауссовской системе и СГС в измерения происходят в сантиметрах из пропорции: 1Гн = 109 см.
Вместо сантиметровой системы иногда используется термин «адгенри».
В СГСЭ единица указывается не всегда. А как измерить индуктивность, если необходимы точные показания? В редких случаях вводятся «статгенри» (1 статгенри ≈ 8,987552⋅1011).
Способы соединения
Как и в случае с другими компонентами, элементы самоиндукции могут соединяться разными способами. Индуктивность катушек зависит от типа подключения.
В расчетах используется буквенное обозначение L, т.е. Ленц. Понимать их нужно, как энергию магнитного поля конкретной катушки.
Параллельное соединение
Для множества элементов формула индуктивности выглядит так:
Для двух она значительно упрощается:
При параллельном соединений плюс соединяется с плюсом, а минус с минусом. При этом:
Напряжение у всех элементов одинаковое. Сила тока равна в месте контакта равна силе тока отдельных элементов.
Последовательное соединение
Суть последовательного соединения – подключение плюса к минусу. Формула расчета намного проще: достаточно сложить показатели все элементов цепи:
Показатель добротности
Добротность – это отношение между реактивным и индуктивным (активным) сопротивлением.
Активное – это показатель естественного сопротивления материала. Реактивное возникает, если изменения действующего значения напряжения, тока или емкости.
Для измерения используется следующее уравнение:
Q=2∙π∙f∙L/R,
Где:
- π– число Пи, равное 3,14;
- F – частотность;
- R – сопротивление.
Проблема может возникать с понятием «частота», т.к. многие не знают, что представляет собой колебательный контур. Это некоторая цепь, в которой присутствует катушка.
Как правило, колебательный контур состоит из источника питания, индукционного элемента и конденсатора. Определяется частота по формуле Томсона (она же формула резонансной частоты).
Чем выше показатель частотности, тем «добротнее» считается катушка.
Многовитковые и одновитковые катушки
От чего зависит индуктивность катушки? Во многом она связана с кол-вом витков вокруг сердечника.
В одновитковом контуре используется формула, которая определяет характеристику через ампераж и электромагнитный поток.
Выглядит она так:
Ф/I
В многовитковых катушках этот же параметр равен квадрату каждого витка, т.к. увеличивается потокосцепление:
L1 х N2.
Для правильного расчета многовитковых катушек учитывается так же геометрические параметры и намоточный тип.
Соленоидные катушки
В соленоиде кол-во витков увеличено, а сечение намоточного провода меньше. Узнать характеристики соленоида можно из следующего уравнения:
Здесь:
0 – магнитная константа, которая равна 1.25663706 × 10-6 м кг с-2 А-2; N – число витков провода, вокруг сердечника; S – площадь сечения обмотки; I – длина.
Кольцевая
Формула тора схода соленоидом с одним исключением – предполагается, что он бесконечный. Поэтому используется такая формула:
Где R – радиус кольца.
Продолговатые катушки
Разновидность катушки, при котором проволока накручивается на шест. Для ее измерения применяют следующее уравнение:
Где:
- µe – показатель магнитной проницаемости среды;
- µi – показатель магнитной проницаемости материала;
- i – длина проводника;
- r – радиус.
Показатели проницаемости вы можете найти в таблице ниже:
Сферы применения
Что такое индуктивность – ясно, но где ее можно использовать? Вообще, найти их можно практически в каждом электроприборе. Например, они повсеместно встречаются в блоках питания.
В источниках тока в процессе работы происходит понижение/повышение напряжения, за что отвечает трансформатор – по сути, 2 или более катушки, которые объединённые последовательно. Причем с увеличением циклической частоты повышается эффективность.
Например, в самолетах используются 400-герцовые трансформаторы, вместо бытовых и промышленных 60 Гц.
Также их можно встретить в:
- электрические фильтры;
- зарядные устройства;
- нагреватели;
- электрические магниты;
- крупная бытовая техника.

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Блок питания 0…30 В / 3A
Набор для сборки регулируемого блока питания…
Подробнее
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Введение
Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.
При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.
Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio
— наведение, побуждение — и обозначают совершенно разные понятия.
Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.
Определение индуктивности
В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:
или
Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.
При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:
Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:
То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.
Проведём исследование поведения тока в индуктивности:
Рис. 2. Физическая реализация эксперимента
Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.
Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.
Проведём исследование напряжения на катушке индуктивности:
Рис. 6. Осциллограмма напряжения на индуктивности (голубая)
В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.
Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.
Индуктивность кругового кольца круглого сечения
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид
При этом его индуктивность можно вычислить по следующему выражению
для постоянного тока
где R – радиус витка, м, R = D/2;
r – радиус провода, м, r = d/2;
μ – магнитная постоянная, μ = 4π•10-7 Гн/м.
Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.
Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).
Для постоянного тока индуктивность составит
На частоте 50 кГц
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
В каких единицах измеряется
Впервые индуктивность была вычислена американским ученым-физиком Джоном Генри и была названа в его честь – Генри, сокращенно Гн. Диапазон индуктивности очень широк, в приведенной ниже таблице видно, какие производные существуют:
| Кратные | Дольные | ||||||
| Величина | Название | Обозначение | Величина | Название | Обозначение | ||
| 101 | декагенри | даГн | daH | 10-1 | децигенри | дГн | dГн |
| 102 | гектогенри | гГн | hH | 10-2 | сантигенри | сГн | cГн |
| 103 | килогенри | кГн | kH | 10-3 | миллигенри | мГн | mГн |
| 106 | мегагенри | МГн | MH | 10-6 | микрогенри | мкГн | µГн |
| 109 | гигагенри | ГГн | GH | 10-9 | наногенри | нГн | nГн |
| 1012 | терагенри | ТГн | TH | 10-12 | пикогенри | пГн | pГн |
| 1015 | петагенри | ПГн | PH | 10-15 | фемтогенри | фГн | fГн |
| 1018 | эксагенри | ЭГн | EH | 10-18 | аттогенри | аГн | aГн |
| 1021 | зеттагенри | ЗГн | ZH | 10-21 | зептогенри | зГн | zГн |
| 1024 | иоттагенри | ИГн | YH | 10-24 | иоктогенри | иГн | yГн |
Первые две строчки производных в каждой части таблицы применять не рекомендуют, указывают либо в десятых или сотых долях генри, либо десятках и сотнях. В СИ используется указанное обозначение в других системах, таких как СГМС обозначение может отсутствовать, либо применяется статгенри ≈ 8,987552⋅1011 или абгенри.
Индуктивность, L — измеряется в Генри (Гн). Индуктивное сопротивление XL — измеряется в Омах (Ом)
Индуктивность соленоида
Катушка в форме соленоида (конечной длины).
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) B{displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки является фактически постоянной и (приближённо) равна
B=μNil{displaystyle displaystyle B=mu _{0}Ni/l}
или
B=μni,{displaystyle displaystyle B=mu _{0}ni,}
где μ{displaystyle mu _{0}} − магнитная постоянная, N{displaystyle N} − число витков, i{displaystyle i} − ток, записанный в амперах , l{displaystyle l} − длина катушки в метрах и n{displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{displaystyle B} , умноженному на площадь поперечного сечения S{displaystyle S} и число витков N{displaystyle N}:
Ψ=μN2iSl=μn2iV,{displaystyle displaystyle Psi =mu _{0}N^{2}iS/l=mu _{0}n^{2}iV,}
где V=Sl{displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):
L=μN2Sl=μn2V.{displaystyle displaystyle L=mu _{0}N^{2}S/l=mu _{0}n^{2}V.}
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель μ{displaystyle mu } — относительную магнитную проницаемость сердечника:
L=μμN2Sl=μμn2V.{displaystyle displaystyle L=mu _{0}mu N^{2}S/l=mu _{0}mu n^{2}V.}
В случае, когда μ>>1{displaystyle mu >>1}, можно (следует) под S
понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Одновитковой контур и катушка
Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.
Где применяется катушка (дроссель, индуктивность)
Активное сопротивление
Дроссели имеют примитивную конструкцию: просто намотанный витками на каком-либо сердечнике проводник. В то же время в таком приборе нечему ломаться. Также у дросселей широчайший функционал и десятки применений. Из всего этого следует, что в какой бы точке города ни находился человек, в радиусе 1 км от него всегда будут тысячи катушек индуктивности, настолько они распространены.
Катушка как электромагнит
Самое простое применение катушки – это электромагнит. С подобным применением каждый сталкивается, заходя в подъезд. Сила, удерживающая дверь на месте и препятствующая несанкционированному доступу чужака, берётся из электромагнита. Он находится сверху.
Электрический ток, проходя по виткам катушки, создаёт вокруг неё переменное электромагнитное поле. Оно возбуждает в металлическом «бруске», расположенном на двери, вихревые токи, которые так же создают магнитное поле. В результате получаются два управляемых магнита. Они притягиваются друг к другу. Тем самым дверь надёжно удерживается на месте.
Другое применение электромагнитов в быту – индукционные плиты. Катушка наводит в металлической посуде переменный высокочастотный ток. Он, в свою очередь, своим тепловым действием разогревает кастрюлю. В промышленности нечто подобное используется для разогрева и плавки металлов. Только в таком случае применяются на порядки более высокие мощности и другие частоты тока.
Индуктивность как фильтр
Импульсные блоки питания, электрические двигатели и диммеры для регулировки яркости ламп накаливания выбрасывают в сеть большое количество искажений и помех. Вызвано это неравномерностью потребляемого тока. Для борьбы с подобными сетевыми шумами применяются специальные фильтры на основе конденсаторов и дросселей.
Данный узел представляет собой небольшую катушку из медного эмалированного провода диаметром 0,2-2 мм. Обмотка наматывается на ферритовый сердечник. Чаще всего он изготовлен в форме кольца, немного реже встречаются так называемые «гантельки».
Подобные фильтры имеются в компьютерных блоках питания, компактных люминесцентных лампах (иногда не ставят, экономят), на выходах сварочных инверторов.
Также фильтр может быть звуковым. Его задача – срезать определённый диапазон частот. Индуктивные свойства этого прибора таковы, что он хорошо проводит низкие частоты, а высокие – приглушает. Поэтому дроссели используют для того, чтобы до динамиков дошёл только бас. По факту ослаблено будут слышны и другие частоты. Для более эффективной работы фильтра нужны дополнительные детали: конденсаторы и операционные усилители.
Катушка как источник ЭДС
Китайская промышленность удивила школьников 2000-х новой игрушкой – вечным фонариком. Его не нужно было заряжать. Фонарик работал от катушки индуктивности, около которой под действием движения рук перемещался магнит. Он наводил в обмотке переменную ЭДС, которая питала осветительный прибор.
Подобное явление объясняется законом электромагнитной индукции. Если проводник (рамка) находится в переменном электромагнитном поле, то в нём начинает наводиться электродвижущая сила. Иными словами, появляется напряжение.
Закон этот совсем неигрушечный, ведь он используется в работе генераторов на подавляющем большинстве электростанций, в том числе любые ТЭЦ, ГЭС, АЭС и ветряки. По подобному принципу работают динамомашины, питающие фары велотранспорта.
Две катушки – трансформатор
Ещё одно распространённое применение – это электрический трансформатор. Конструктивно он состоит из двух и более катушек, расположенных на одном железном или ферритовом сердечнике. Подобный агрегат работает только с переменным напряжением. Если на первичную обмотку подать ток, то он создаст в сердечнике магнитный поток. Он, в свою очередь, наведёт ЭДС во вторичной обмотке. Напряжения во входной и выходной катушках прямо зависят от количества их витков.
Таким образом, можно трансформировать 220 В из розетки в 12 В, необходимых для питания небольшой стереосистемы, или преобразовать 10 000 вольт в 220 для передачи от подстанции к жилым домам. Подобным методом можно добиться и повышения напряжения, т.е. превратить 12 В обратно в 220.
Катушка индуктивности — элемент колебательного контура
Сейчас это уже редкость, но раньше для подстройки нужной радиостанции использовали колебательный контур. Он состоит из двух элементов, включенных параллельно: катушки индуктивности и переменного конденсатора. Работая в паре, они способны выделить из множества окружающих сигналов именно тот, который требуется. При попадании на антенну приёмника нужной частоты электромагнитных волн колебательный контур входит в резонанс. Процесс сопровождается лавинообразным увеличением ЭДС. Частота, на которой это происходит, зависит от индуктивности катушки и ёмкости конденсатора.
Катушка индуктивности – дроссель ДРЛ ламп
Несмотря на то, что освещение улиц и промышленных предприятий стремительно переходит на LED светильники, по СНГ всё ещё осталось огромное количество мест, где используются устаревшие дуговые ртутные люминесцентные лампы типа ДРЛ. Более всего они распространены в мелких городах и на второстепенных улицах. Их можно узнать по характерному холодно-белому свету и долгому розжигу.
ДРЛ лампы не способны работать без пускорегулирующего дросселя. Он обладает высоким индуктивным сопротивлением и призван ограничить пусковой ток осветительного прибора. Дроссели для ламп подбираются, исходя из их мощности. Наиболее распространённые номиналы – 250, 400 и 1000 Вт. Информация о мощности указывается на самом дросселе. Там же можно найти схемы включения.
Из вышесказанного можно подчеркнуть, что катушка индуктивности является консервативным и давно освоенным на практике электронным компонентом. Однако спрос на его применение по-прежнему не спадает. Поэтому знания, необходимые для расчета катушек и их правильного включения, необходимы каждому специалисту, имеющему дело с электроникой.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
Ce = C : (1 — 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Зачем нужен расчёт индуктивности
Индуктивность: формула
Расчет индуктивности нужен, потому что конструктивно это могут быть по-разному выполненные катушки. Применение дросселей в разных отраслях электрики и электроники, их работа под влиянием постоянного и переменного тока требуют тщательного подбора индуктивности, добротности и стабильности работы. При выполнении своими руками дросселей заданного параметра L нужно выполнить расчёт. Для каждого типа индуктивного двухполюсника используется своя формула.
Индуктивность соленоида
Катушка в форме соленоида (конечной длины).
Соленоид — катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного сердечника плотность магнитного потока (или магнитная индукция) B{displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки вдали от её концов (приближённо) равна
B=μNil{displaystyle displaystyle B=mu _{0}Ni/l}
или
B=μni,{displaystyle displaystyle B=mu _{0}ni,}
где μ{displaystyle mu _{0}} − магнитная постоянная, N{displaystyle N} − число витков, i{displaystyle i} − ток в амперах , l{displaystyle l} − длина катушки в метрах и n{displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{displaystyle B} , умноженному на площадь поперечного сечения S{displaystyle S} и число витков N{displaystyle N}:
Ψ=μN2iSl=μn2iV,{displaystyle displaystyle Psi =mu _{0}N^{2}iS/l=mu _{0}n^{2}iV,}
где V=Sl{displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):
L=μN2Sl=μn2V.{displaystyle displaystyle L=mu _{0}N^{2}S/l=mu _{0}n^{2}V.}
Если катушка внутри полностью заполнена магнитным сердечником, то индуктивность отличается на множитель μ{displaystyle mu } — относительную магнитную проницаемость сердечника:
L=μμN2Sl=μμn2V.{displaystyle displaystyle L=mu _{0}mu N^{2}S/l=mu _{0}mu n^{2}V.}
В случае, когда μ>>1{displaystyle mu >>1}, под S
можно понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.
Изготовление
Катушки индуктивности могут быть приобретены или изготовлены самостоятельно. Обычно приобретаются большие изделия. Наверное, никто не захочет самостоятельно наматывать дроссель для люминесцентной лампы. Небольшие обмотки для радиоэлектроники легко и с удовольствием изготавливаются своими руками. Навыки самостоятельного изготовления будут полезны при ремонте катушек или при изменении их рабочих параметров. Для увеличения их индуктивности используются специальные магнитные сердечники. Их изготавливают из смеси оксида железа с оксидами других металлов.
Воспользуйтесь другими онлайн калькуляторами:
Изолированная магнитная проволока наматывается непосредственно на магнитный сердечник, покрытый тонким слоем изолирующей бумаги. Перед изготовлением необходимо определить параметры с помощью специальных расчётных формул или программ. С их помощью будет определен размер и тип сердечника, число витков и диаметр проволоки.
Воспользуйтесь другими онлайн калькуляторами:
- Расчет веса электрического кабеля
- Онлайн расчет силы тока в цепи
- Перевод Ватт в Амперы
- Расчет потерь напряжения
- Онлайн расчет сечения кабеля
Применение катушек в технике
Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:
- сглаживание пульсаций и помех, накопление энергии;
- создание магнитных полей в различных устройствах;
- фильтры цепей обратной связи;
- создание колебательных контуров;
- трансформаторы (устройство из двух катушек, связанных индуктивно);
- силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
- ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
- применение катушек в качестве электромагнитов различных исполнительных механизмов;
- обмотки электромагнитных реле;
- индукционные печи;
- установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
L = N х F : I.
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Особенности применения дросселей в схемах
Дроссели можно соединять последовательно и параллельно.
[Индуктивность последовательно соединенных дросселей
] = [
Индуктивность первого дросселя
] + [
Индуктивность второго дросселя
]
[Индуктивность параллельно соединенных дросселей
] = 1 / (1 / [
Индуктивность первого дросселя
] + 1 / [
Индуктивность второго дросселя
])
На рисунке приведены типовые схемы на катушках индуктивности. (А) — Индуктивный делитель переменного напряжения. [Напряжение на нижнем дросселе
] = [
Входное напряжение
] * [
индуктивность нижнего дросселя
] / ([
индуктивность нижнего дросселя
] + [
индуктивность верхнего дросселя
]) (Б) — Фильтр высших частот. (В) — Фильтр низших частот.
(читать дальше…) :: (в начало статьи)
:: ПоискТехника безопасности :: Помощь
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.
Вот одна формула = * * / / , по которой получается, что чем больше ток через дроссель, тем больше получается число витков — что в корне противоречит теории — чем нужен больший ток, тем должно быть меньше число витков (ЭТО Читать ответ…
А что такое E в первой формуле, прямо таки получается огромная величина индуктивности. В первой формуле правдоподобно, если индуктивность в микрогенри Если я правильно понял, то, например, E-3 означает 0.001? Читать ответ…
Как рассчитать и изготовить самому дроссель ВЧ, индуктивностью 5мкГн, на ток 3-4А ? Читать ответ…
Еще статьи
Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить… Приемы намотки импульсного дросселя / трансформатора….
Инвертор, преобразователь, чистая синусоида, синус… Как получить чистую синусоиду 220 вольт от автомобильного аккумулятора, чтобы за…
Преобразователь однофазного в трехфазное. Конвертер одной фазы в три. … Схема преобразователя однофазного напряжения в трехфазное….
Резонансный инвертор, преобразователь напряжения повышающий. Схема, ко… Инвертор 12/24 в 300. Резонансная схема….
Диодные схемы. Схемные решения. Схемотехника. Частота, мощность, шумы…. Классификация, типы полупроводниковых диодов. Схемы, схемные решения на диодах. …
Простой импульсный прямоходовый преобразователь напряжения. 5 — 12 вол… Схема простого преобразователя напряжения для питания операционного усилителя….
Понижающий импульсный источник питания. Онлайн расчет. Форма. Подавлен… Как рассчитать понижающий импульсный преобразователь напряжения. Как подавить пу…
Диод универсальный маломощный КД510, 2Д510. Справочник, справочные дан… Характеристики и применение маломощных кремниевых диодов КД510А (2Д510А)…
Индуктивное сопротивление – как его найти
Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:
XL=2*П*v*L
Здесь употреблены следующие обозначения:
- XL – рассматриваемая величина.
- Символом «П» обозначено число Пи.
- V представляет собой частоту.
- L — это обозначение величины индуктивности.
Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».
Катушки с различными сердечниками
Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:
I = U / XL
I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.
Конфигурация магнитного поля катушки
Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.
При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.
Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.
Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.
Магнитное поле провода
К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.
Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.
При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Индуктивность, ее единица си. Индуктивность длинного соленоида.
Индукти́вность
(или
коэффициент самоиндукции
) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность , краем которой является этот контур. .
—магнитный поток, — ток в контуре, — индуктивность.
Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока :
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током :
.
Конвертер величин
Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
Здесь
X
L — реактивное сопротивление катушки в омах (Ом),
Z
L — импеданс катушки в омах (Ом),
ω = 2πf
— угловая частота в рад/с,
f
— частота в герцах (Гц),
L
— индуктивность в генри (Гн),
j
— мнимая единица.
Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.
Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике
В отличие от конденсаторов, которые препятствуют изменению напряжения
, приложенного к их обкладкам, катушки индуктивности препятствуют изменению
текущего в них тока
. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока
. На них создается падение напряжения, прямо пропорциональное
скорости изменения тока
. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие
реактивного сопротивления
. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
L индуктивности и текущего через нее тока
I
от частоты
f
для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока
Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Если реальная катушка индуктивности подключена к источнику постоянного напряжения
, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.
Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.
/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму
Если к катушке индуктивности приложено переменное синусоидальное напряжение
, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. В точке (
ωt
=
π
/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке
скорость изменения тока
максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или
π
/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте
. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности
X
L велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.
Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.
Автор статьи: Анатолий Золотков
Колебательный контур
Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.
Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.
Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.
Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)
Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.
Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.
Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.
Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.
Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:
где:
- n — повое число витков катушки;
- n1 — число витков катушки, указанное в описании;
- d— диаметр имеющеюся провода;
- d1 — диаметр провода, указанный в описании.
В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:
(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).
Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:
При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.
Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.
Рис. 2. Катушки индуктивности. Пример.
Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.
Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.
Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:
Новая катушка на каркасе с увеличенным диаметром:
Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.
Программа позволяет производить расчет следующих типов катушек индуктивности:
- Одиночный круглый виток
- Однослойная виток к виткуВ качестве начальных параметров при расчете катушки можно выбрать два варианта:
- Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
- Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
- Однослойная катушка с шагом
- Катушка с не круглой формой витков
- Многослойная катушка В качестве начальных параметров при расчете катушки можно выбрать два варианта:
- Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
- Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода и приблизительная длина провода для намотки.
- Тороидальная однослойная катушка
- Катушка на ферритовом кольце
- Катушка в броневом сердечнике(Ферритовом и карбонильном)
- Тонкопленочная катушка(Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)
Подробнее о Coil32 …
Довольно часто перед радиолюбителем встает вопрос: » Как рассчитать индуктивность катушки?». Катушки используются и в высокочастотной связной аппаратуре, и при конструировании акустических систем, и даже взглянув на материнскую плату компьютера, Вы и там обнаружите индуктивные элементы. С помощью программы Coil32 можно быстро рассчитать индуктивность катушки. В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки можно «не отходя от кассы» рассчитать емкость конденсатора в колебательном контуре.
В чем преимущества программы перед аналогами?
- Программа рассчитывает индуктивность многих типов катушек. Можно подобрать оптимальный вариант, либо пересчитать катушку под имеющийся каркас.
- Результаты всех расчетов выводятся в текстовое поле, откуда их можно сохранить в файл. В дальнейшем Вы можете их просмотреть, чтобы не пересчитывать заново. Можно открыть этот файл в «MS Word» и распечатать.
- Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
- Рассчитываются основные параметры колебательного контура для однослойной катушки
- Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце
- Для катушек в броневых сердечниках есть возможность выбрать один из нескольких стандартных, что позволяет рассчитать катушку несколькими щелчками мыши.
- Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
- В Сети часто встречаются программы для расчета индуктивности, работающие под DOS, о преимуществах Windows-интерфейса, думаю, говорить не приходится.
- Программа имеет возможность расширения функционала с помощью дополнительных плагинов для расчета индуктивностей
- Программа имеет мультиязычный интерфейс и скины, дополнительные наборы скинов можно найти на .
Программа распространяется в стиле «Portable» и не имеет установщика. Для установки программы распакуйте архив программы в любой каталог и запустите на выполнение файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
- µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
- l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
В чем измеряется индуктивность катушки
Понятие индуктивности. Единицы измерения. Катушки индуктивности. (10+)
Индуктивность. Понятие. Единицы измерения
Материал является пояснением и дополнением к статье:
Единицы измерения физических величин в радиоэлектронике Единицы измерения и соотношения физических величин, применяемых в радиотехника.
В самом начале изучения электричества исследователи заметили, что мотки провода при подаче на них напряжения ведут себя странно. Сила тока через них не подчиняется классическому закону Ома. Электрический ток не возникает сразу после подачи напряжения, а нарастает постепенно со временем. Прекратить этот ток тоже непросто. При разрыве цепи возникает искра в месте разрыва. Создается впечатление, что электрический ток в мотке провода обладает инерцией. Теоретические изыскания подтвердили это наблюдение. В катушках индуктивности после подачи на них напряжения происходит накопление энергии в магнитном поле и постепенный рост электрического тока. Если внешний источник отключить, то катушка продолжает поддерживать на своих вывода напряжение достаточное для постепенного убывания силы тока по мере исчерпания накопленной энергии. Если в цепи разрыв, то скачек напряжения может быть очень большим. Теоретические он должен быть бесконечным, но на практике либо происходит пробой места разрыва или изоляции самой катушки, либо вся энергия поглощается паразитными емкостями между витками.
Если подключить катушку индуктивности к батарейке, а потом разорвать цепь, держа одной рукой за один контакт места разрыва, а другой рукой — за другой, то Вы получите ощутимый удар тока. Если катушка обладает большой индуктивности и хорошими параметрами, то Вас может даже убить, хотя вроде бы в Ваших руках обычная батарейка. Кстати на этом эффекте основана работа электрошокера.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Добротность катушки
Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.
Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:
где:
- π – число пи, ≈3,14,
- f – частота,
- R – сопротивление.
Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает
Изготовление дросселя
Сначала определимся с материалом магнитопровода (сердечника). Если частота больше 10 кГц, то используем ферриты, если меньше 3 кГц, то железо, если между этими значениями, то решаем, исходя из конкретных условий.
Дросселя изготавливаются с зазором в сердечнике. Правильная толщина зазора в сочетании с нужным числом витков обеспечивает нужные параметры дросселя.
П
рактика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность авторам
При проектировании дросселя как минимум необходимо обеспечить:
- Нужную индуктивность,
- Допустимую магнитную индукцию, исключающую насыщение,
- Нужный диаметр обмоточного провода, подходящий под предполагаемую силу тока (обмотка с расчетным числом витков должна поместиться в окно магнитопровода).
Одним из подходов к расчету является итерационный: исходя из нужной максимальной силы тока и индуктивности, рассчитываем зазор и число витков. Исходя из числа витков, площади окна магнитопровода и плотности заполнения окна (около 0.6), определяем максимальную толщину провода, которым может быть выполнена обмотка. Проверяем, подходит ли такой провод под нужный ток. Если да, расчет окончен. Если нет, то выбираем больший магнитопровод и рассчитываем для него. В случае, если расчет дает слишком толстый провод (больше 1 кв. мм), то обмотку лучше выполнять жгутом более мелких проводов.
Формулы для расчетов:
[индуктивность дросселя, Гн
] = [
1.257E-9
] * [
площадь сечения магнитопровода, кв. мм
] * [
количество витков
]^2 / [
зазор в сердечнике, мм
]
[максимальное значение индукции, Тл
] = [
1.257E-3
] * [
максимально возможная сила тока, А
] * [
количество витков
] / [
зазор в сердечнике, мм
]
Для железа максимальная индукция выбирается в районе 1 Тл. Для ферритов: при частоте до 100 кГц — 0.3 Тл, при частоте выше 100 кГц — 0.1 Тл. Если необходимо снизить потери на перемагничивание магнитопровода, то максимальная индукция выбирается еще меньше.
[число витков
] = [
1E6
] * [
индуктивность, Гн
] * [
максимально возможная сила тока, А
] / [
площадь сечения магнитопровода, кв. мм
] / [
максимальное значение индукции, Тл
]
[зазор в сердечнике, мм
] = [
1.257E-3
] * [
максимально возможная сила тока, А
] * [
число витков
] / [
максимальное значение индукции, Тл
]
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
B= µ0nI,
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
E = LI2 :2,
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Расчет катушек на кольцах Amidon из порошкового железа:
Ферритовые кольца фирмы Amidon не имеют цветовой маркировки (блестящие черные либо тускло-серые), Здесь калькулятор для их расчета. Изделия из порошкового железа (карбонильного) маркируются цветом в зависимости от материала кольца. – здесь полный набор характеристик. Расчет ведется по формуле:
ВЫБЕРИТЕ КОЛЬЦО:
| Тип материала кольца – | 123678101215171826304052 |
| Типоразмер кольца – | T-5T-10T-12T-16T-20T-25T-30T-37T-44T-50T-68T-80T-94T-106T-130 |
Доступная информация о кольце:
Цветовой код: Материал: Рабочие частоты LC цепей Начальная магнитная проницаемость (μ): Размеры (OD x ID x H): дюймммAL фактор: мкГн/(N/100)2ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:
| L | = мГнмкГннГн | – Требуемая индуктивность |
Рассчитать
Результат:
МАТЕРИАЛ №0
: В основном используется на частотах выше 100 МГц. Индуктивность (или число витков), полученная из расчетов, исходя из заданного параметра AL, не может быть достаточно точной и сильно зависит от техники намотки.
МАТЕРИАЛ №1
: Очень похож на материал №3 за исключением более высокого объемного сопротивления и повышенной стабильности.
МАТЕРИАЛ №2
: Carbonyl ‘E’ порошковый материал с высоким объемным сопротивлением. Для изготовления высокодобротных катушек на частотах от 2 МГц до 20 МГц.
МАТЕРИАЛ №3
: Carbonyl ‘HP’ материал с прекрасной стабильностью и добротностью для низких частот от 50 КГц до 500 КГц.
МАТЕРИАЛ №6
: Carbonyl ‘SF’ материал. Предназначен для катушек с высокой добротностью и температурной стабильностью для частот 20 МГц — 50 МГц.
МАТЕРИАЛ №7
: Carbonyl ‘TH’ материал. Очень похож на №2 и №6, но имеет более высокую температурную стабильность.
МАТЕРИАЛ №8
: Этот материал имеет низкие потери в сердечнике и хорошую линейность в условиях высокого смещения по кривой намагничивания. Хороший высокочастотный материал. Самый дорогой материал.
МАТЕРИАЛ №10
: Порошковый материал «W». Обеспечивает хорошую добротность и высокую стабильность для частот от 40 МГц до 100 МГц.
МАТЕРИАЛ №12
: Синтетический оксидный материал, который обеспечивает хорошую добротность и умеренную стабильность для частот от 50 МГц до 200 МГц. Если высокое значение Q имеет первостепенное значение, этот материал является хорошим выбором. Если первостепенное значение имеет стабильность, предпочтительным будет материал № 17.
МАТЕРИАЛ №15
: Карбонильный материал «GS6». Обладает отличной стабильностью и хорошей добротностью. Хороший выбор для коммерческих частот вещания, где важны «Q» и стабильность.
МАТЕРИАЛ №17
: Это новый карбонильный материал, который очень похож на материал № 12, но он обладает лучшей температурной стабильностью. Однако по сравнению с материалом № 12 наблюдается небольшая потеря добротности, составляющая около 10% в диапазоне от 50 МГц до 100 МГц. На частотах выше 100 МГц добротность хуже примерно на 20%.
МАТЕРИАЛ №18
: Этот материал имеет низкие потери в сердечнике, аналогично материалу № 8, но с более высокой проницаемостью и более низкой стоимостью. Хорошие характеристики насыщения при постоянном токе.
МАТЕРИАЛ №26
: Материал с пониженным содержанием водорода. Обладает наивысшей проницаемостью из всех порошковых материалов. Используется для фильтров электромагнитных помех и дросселей постоянного тока.
МАТЕРИАЛ №30
: Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.
МАТЕРИАЛ №40
: Недорогой материал. Имеет характеристики, похожие на очень популярный материал № 26. Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.
МАТЕРИАЛ №52
: Этот материал имеет более низкие потери в сердечнике при высокой частоте и такую же проницаемость, что и материал № 26. Популярен для новых конструкций высокочастотных дросселей.
Ссылки по теме:
Факторы, влияющие на индуктивность катушки
На индуктивность катушки оказывают влияние следующие основные факторы:
Число витков провода в катушке: При прочих равных условиях, увеличение числа витков приводит к увеличению индуктивности; уменьшение числа витков приводит к уменьшению индуктивности.
Пояснение: чем больше количество витков, тем больше будет магнитодвижущая сила для заданной величины тока.
Площадь поперечного сечения катушки: При прочих равных условиях, катушка с большей площадью поперечного сечения будет иметь большую индуктивность; а катушка с меньшей площадью поперечного сечения — меньшую индуктивность.
Пояснение: Катушка с большей площадью поперечного сечения оказывает меньшее сопротивление формированию магнитного потока для заданной величины магнитодвижущей силы.
Длина катушки: При прочих равных условиях, чем больше длина катушки, тем меньше ее индуктивность; чем меньше длина катушки, тем больше ее индуктивность.
Пояснение: Чем больше длина катушки, тем большее сопротивление она оказывает формированию магнитного потока для заданной величины магнитодвижущей силы.
Материал сердечника: При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше магнитная проницаемость сердечника — тем меньше индуктивность.
Пояснение: Материал сердечника с большей магнитной проницаемостью способствует формированию большего магнитного потока для заданной величины магнитодвижущей силы.
Приблизительное значение индуктивности любой катушки можно найти по следующей формуле:
Следует понимать, что данная формула дает только приблизительные цифры. Одной из причин такого положения дел является изменение величины магнитной проницаемости при изменении напряженности магнитного поля (вспомните нелинейность кривой В/Н для разных материалов). Очевидно, если проницаемость (µ) в уравнении будет непостоянна, то и индуктивность (L) также будет в некоторой степени непостоянна. Если гистерезис материала сердечника будет существенным, то это непременно отразится на индуктивности катушки. Разработчики катушек индуктивности пытаются минимизировать эти эффекты, проектируя сердечник таким образом, чтобы его намагниченность никогда не приближалась к уровням насыщения, и катушка работала в более линейной части кривой B/H.
Если катушку сделать таким образом, что любой из вышеперечисленных факторов у нее можно механически изменить, то получится катушка с регулируемой величиной индуктивности или вариометр. Наиболее часто встречаются вариометры, индуктивность которых регулируется количеством витков или положением сердечника (который перемещается внутри катушки). Пример вариометра с изменяемым количеством витков можно увидеть на следующей фотографии:
Это устройство использует подвижные медные контакты, которые подключаются к катушке в различных точках ее длины. Подобные катушки, имеющие воздушный сердечник, применялись в разработке самых первых радиоприемных устройств.
Катушка с фиксированными значениями индуктивности, показанная на следующей фотографии, представляет собой еще одно раритетное устройство, использовавшееся в первых радиостанциях. Здесь вы можете увидеть несколько витков относительно толстого провода, а так же соединительные выводы:
А это еще одна катушка индуктивности, так же предназначенная для радиостанций. Для большей жесткости ее провод намотан на керамический каркас:
Многие катушки индуктивности обладают небольшими размерами, что позволяет монтировать их непосредственно на печатные платы. Посмотрев внимательно на следующую фотографию, можно увидеть две расположенные рядом катушки:
Две катушки индуктивности расположены справа в центре этой платы и имеют обозначения L1 и L2. В непосредственной близости от них находятся резистор R3 и конденсатор С16. Показанные на плате катушки называются «торроидальными», так как их провод намотан вокруг сердечника, имеющего форму тора.
Как резисторы и конденсаторы, катушки индуктивности могут выполняться в корпусе для поверхностного монтажа (SMD). На следующей фотографии представлено несколько таких катушек:
Две индуктивности здесь расположены справа в центре платы. Они представляют собой маленькие черные чипы с номером «100», а над одной из них можно увидеть обозначение L5.
Индуктивность контура — теоретические основы
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
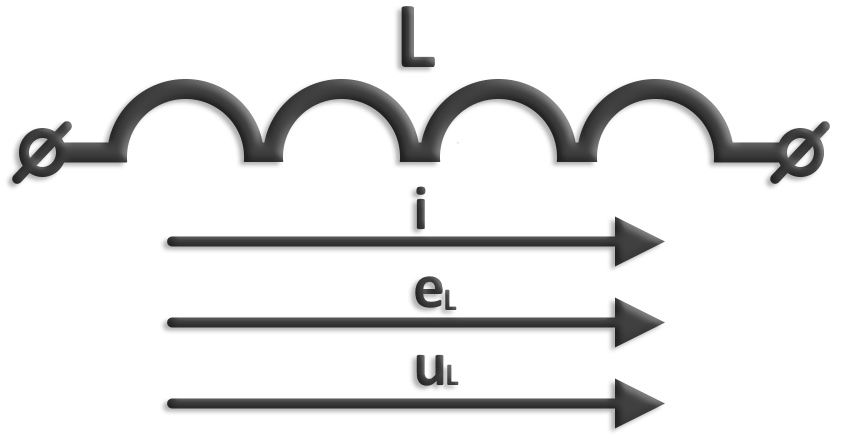
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током
катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
Напряжение на индуктивности уравновешивает ЭДС и может быть записано в
виде uL=-eL=dΨ/dt=L×di/dt.
Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Электрическая цепь и индуктивность контура
Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.
Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
-
- Индукционный ток возникает только при изменении линий магнитной индукции.
-
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Самоиндукция и измерение индуктивности
Индуктивность проводника
При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.
Напряжение ЭДС определяется формулой расчета индукции:
Ꜫ=-L∙di/dt.
То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».
Как найти индуктивность контура
Формула, которая является простейшей для нахождения величины, следующая:
- L = F : I,
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
- Ei = -L х dI : dt.
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
- W = L I2 : 2.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
- L= µ0n2V,
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
- L = µ0N2S : l,
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Обозначение и единицы измерения
Сопротивление тока: формула
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Джозеф Генри
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C : (1 – 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
- Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
“Катушка ниток”
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
- I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от “витков в квадрате”.
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
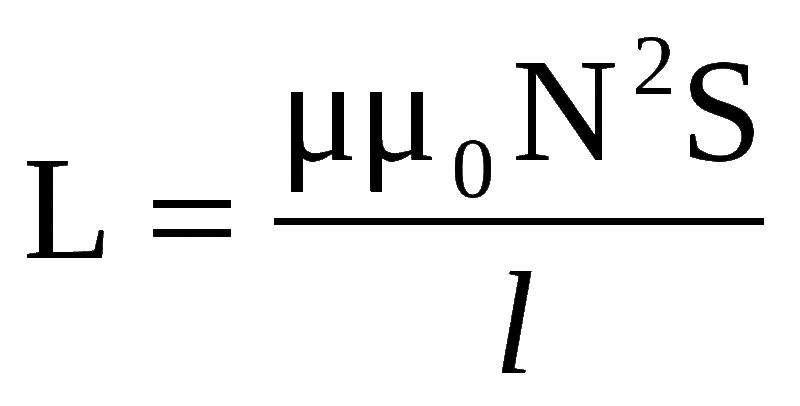
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
-
µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр); - N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.

Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
-
l — длина проводника в метрах; - r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
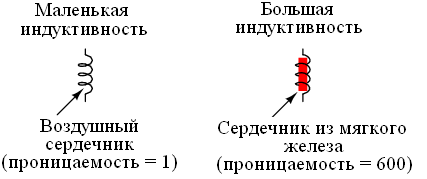
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Польза и вред
Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.
Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.
Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.
Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.
Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними











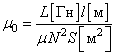


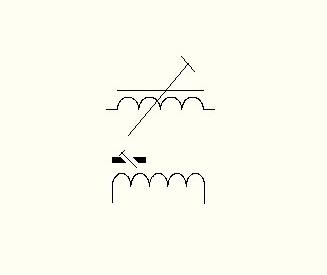





![{displaystyle {begin{aligned}{frac {{text{d}}U}{{text{d}}t}}&=L(i),i,{frac {{text{d}}i}{{text{d}}t}}\[3pt]{text{d}}U&=L(i),i,{text{d}}i,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d65035bcbf7356315ad7c132bef205c2808d2823)

![{displaystyle {begin{aligned}U&=Lint _{0}^{I},i,{text{d}}i\[3pt]&={tfrac {1}{2}}L,I^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f88094cd0bacb95c7052b70ccca2a1fbe5b417a)

![{displaystyle {begin{aligned}v(t)&=L{frac {{text{d}}i}{{text{d}}t}}=L,{frac {text{d}}{{text{d}}t}}left[I_{text{peak}}sin left(omega tright)right]\&=omega L,I_{text{peak}},cos left(omega tright)=omega L,I_{text{peak}},sin left(omega t+{pi over 2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dad77f4c1a6127e7e85ee68ac5bfbfc3fedd456d)


![{displaystyle L_{text{DC}}=200{text{ }}{tfrac {text{nH}}{text{m}}},ell left[ln left({frac {,2,ell ,}{r}}right)-0.75right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39dc33d2f27647bf40a0b2261866624a63f7ecc5)
![{displaystyle L_{text{AC}}=200{text{ }}{tfrac {text{nH}}{text{m}}},ell left[ln left({frac {,2,ell ,}{r}}right)-1right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c01f6774dfc67af4b2f63877692be926882acc2e)



![{displaystyle L={frac {mu _{0}}{4pi }}left[oint _{C}oint _{C'}{frac {dmathbf {x} cdot mathrm {d} mathbf {x} '}{|mathbf {x} -mathbf {x} '|}}right]+{frac {mu _{0}}{4pi }},ell ,Y+Oquad {text{ for }};left|mathbf {s} -mathbf {s} 'right|>{frac {1}{2}}a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fefe884e507eeb3094c00028b474d6a0847574eb)


















![{displaystyle [mathbf {z} ]=s{begin{bmatrix}L_{1} M\M L_{2}end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a52fa6c8463d2d333ae13bfa9d566fc7f936d38d)









![{displaystyle {begin{aligned}L_{S_{ij}}&={frac {det(mathbf {K} )}{-mathbf {C} _{ij}}}\[3pt]L_{P_{i}}&={frac {det(mathbf {K} )}{sum _{j=1}^{N}mathbf {C} _{ij}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4739bf3c70b2d1403383f6f5d774cbda23a101d4)















![{displaystyle {begin{aligned}{mathcal {L}}={frac {mu _{0}}{pi }} {biggl [} &ell _{1}ln left({frac {2ell _{1}}{a}}right)+ell _{2} ln left({frac {2ell _{2}}{a}}right)+2{sqrt {ell _{1}^{2}+ell _{2}^{2} }}\&-ell _{1} sinh ^{-1}left({frac {ell _{1}}{ell _{2}}}right)-ell _{2}sinh ^{-1}left({frac {ell _{2}}{ell _{1}}}right)\&-left(2-{tfrac {1}{4}}Y right)left(ell _{1}+ell _{2}right) {biggr ]}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/657fa5b4fe9cb240b275e22390f6f4d6df4c5f3b)