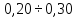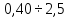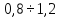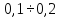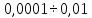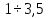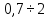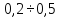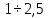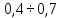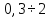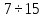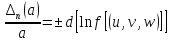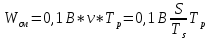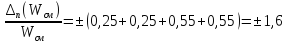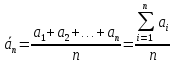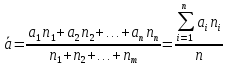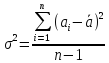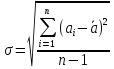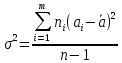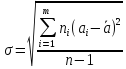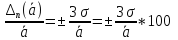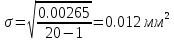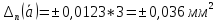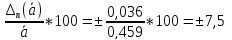Предельная ошибка измерений - Исправление ошибок и поиск оптимальных решений проблем

Предельные ошибки при различных способах измерения

	Способ и прибор	Ошибка %
1	Стальная гом-я лента
2	Угломеры оптические
3	Тахометры центробежные
4	Весы торговые и автомобильные Технические Аналоговые
5	Динамометры тяговые пружинные Гидравлические Электрические
6	Ртутные монометры
7	Секундомеры
8	Ртутные термометры
9	Твердомеры ударного действия

Ошибки опытов

Под
опытом подразумевается совокупность
разовых измерений различных величин в
одних и тех же условиях. Способы измерения
можно разбить на два вида:

—
измерить прямые, когда данную величину
измеряют непосредственно

—
измерения косвенные, когда искомая
величина является функцией измеряемых
величин.

Можно
по-разному ставить опыт и выбирать
способы измерений, так как измерения
косвенные зависят от ряда прямых, то
при прочих равных условиях, выгодней
тот способ, при котором будет меньше
прямых измерений, а значит меньше и
сумма ошибок. Предельную относительную
ошибку опыта определяют на основании
следующих правил:

Ошибка
суммы заложена между наибольшей и
наименьшей из относительных ошибок
слагаемых, практически берут или
наибольшую относительную ошибку или
среднюю арифметическую.
Ошибка
произведения или частного от деления
равна сумме относительных ошибок
сомножителей или соответственно
делимого и частного
Ошибка
n-ой степени какого-то основания (значения
величины) в n раз больше относительной
ошибки основания.

Во
всех случаях установление точности
опыта, точности вычисления результата
должна определяться точностью измерений.
Если рассматривать ошибку измерения
как частное значение переменной величины,
предельную относительную ошибку опыта
можно вычислить по формуле:

А
– является функцией переменных, то есть
предельная относительная ошибка а равна
дифференциалу её натурального логарифма,
причем следует брать сумму абсолютных
значений всех членов такого выражения.
Данное уравнение дает возможность
решить обратную задачу: определить
необходимую точность измерений различными
способами, если задана общая точность
опыта, но проще поступить таким образом:
установить требование заранее к
метрологическим показателям приборов
(цена или интервал деления, пределы
измерения, порог чувствительности,
измерительное усилие, погрешность и
вариация показаний). Вычислить предельную
ошибку и по ней подобрать недостающую
аппаратуру и заменив приборы дающие
слишком большую предельную погрешность.
Используя эту формулу можно найти
измерения, при которых предельная
относительная ошибка функции будет
наименьшей. Условием определенного
решения является наличие минимума
функции. Рассмотрим порядок вычисления
предельной ошибки опыта. Установим
предельную относительную ошибку
вычисления производительности агрегата.

В
– ширина агрегата

v— скорость агрегата

Т_р– время работы агрегата

Учитывая
подобранную в этом примере аппаратуру
и средние данные таблицы, получим
предельную ошибку.

Из
изложенного можно сделать вывод: для
того, чтобы правильно подобрать аппаратуру
необходимо провести сравнительную
оценку точности различных способов
измерения, в данном случае полезно
заранее задаться точностью опыта.
Точность измерений должна быть
целесообразной, указав на три основные
обоснования:

Заключается
в практическом использовании результатов
(при технологическом процессе заточки
лезвия нельзя добиться его затупленности
меньше 10 микрон, тогда не следует
измерять износ с точностью до десятых
долей микрона).
В
некоторых случаях нецелесообразно
измерять с ошибкой меньше некоторых
колебаний значений измеряемой величины.
Экономическая
сторона. Чем точнее измерительная
аппаратура, тем она сложнее и дороже,
тем больше затраты не её ремонт и
калибровку. Может оказаться, что при
таком количестве измерений и той же
надежности, что и при большем количестве
измерений, прибором дающем несколько
большую ошибку, стоимость измерений
дорогим прибором будет выше.

При
определении величины случайных ошибок,
кроме предельной, вычисляют статистическую
ошибку многократных измерений, её
устанавливают после измерений при
помощи методов математической статистики
и теории ошибок. Если, например, диаметр
вала, вязкость масла измерять по одному
разу, случайные ошибки могут исказить
результат, поэтому лучше измерять
какую-либо практически постоянную
величину несколько раз и брать среднюю
арифметическую этих измерений. Среднее
арифметическое измерение является
наиболее вероятным значением измеряемой
величины при данном количестве соединений.

В
теории ошибок доказывается, чем больше
проведено измерений какой-либо величины,
тем меньше суммарная ошибка средней и
при бесконечном числе измерений,
случайная ошибка средней бесконечно
мала.

Лекция
5 – 19.10.11

Чем
больше значений случайных ошибок и
разброс, рассеяние отсчетов, тем больше
число раз необходимо измерять одну и
ту же величину чтобы достигнуть заданной
точности и надежности измерений.
Рассеяние результатов измерений
указывает на большую или меньшую их
изменчивость т оценивается средним
квадратом отклонений наблюдаемых
значений а_iот их средних h’ и
квадратным корнем из среднего квадрата.

Среднее
арифметическое
сумме всех отдельных результатов
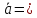
измерений а_i, a_nделение на
количество измерений.

Если
все измерения сгруппированы в m классов
с разными количествами измерений в
каждом классе, то следует вычислять
взвешенную среднюю арифметическую:

а₁,
а₂, а_m– среднее по классу

Отношение
любого отдельного результата измерений
от средней арифметической можно
представить как разность а_iи.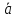

а_i– результат любого измерения.

Дисперсией
случайной величиныназывается среднее
значение величины от её среднего
значения.

Корень
квадратный из дисперсии называется
средним квадратическим отклонением
или стандартом.

При
разделении всех измерений на n классов
с массовыми средними дисперсия будет
равна:

Стандарт:

Стандарт
имеет значение величины, для которой
он вычислен. Дисперсия и стандарт это
меры рассеяния или изменчивости. Чем
больше дисперсия или стандарт, тем
больше рассеяны значения измерений.
Таким образом при измерении неизменной
величины СКО (стандарт) является мерой
точности среднего арифметического
значения неоднократно измеренной
величины. Если же неоднократно измеримая
величина переменна, то вычисленное по
её измерениям значение стандарта
показывает не только меру точности как
случайную ошибку измерений, но и меру
изменчивости переменной.

Абсолютное
значение стандарта зависит и от
совершенства измерительных приборов.
Если одну и ту же величину измерять при
помощи приборов различной точности
абсолютное значение стандарта будет
меньше при измерении более точным
прибором. Например, если d_отвизмерить сначала нутромером со шкалой
в мм, а затем индикатором со шкалой в
микронах значение стандарта при последних
измерениях будет меньше.

Это
обстоятельство имеет важное значение
при выборе числа опытов.

Для
большинства технических измерений
можно считать, что наибольшей ошибкой
средней арифметической многократных
измерений является абсолютная величина
равная трем стандартная или относительная
величина.

Эта
ошибка называется наибольшей возможной
статической в отличие от придельной
ошибки.

В
качестве примера приведем результаты
проверки на точность показаний
пневматического калибратора, которым
измеряли относительную не плотность в
одном из цилиндров дизельного двигателя.

Было
проведено 20 измерений, при которых
двигатель работая на оборотах близким
к номинальным, по 2-3мин. И получен ряд
значений неплотности.

0,465 0,450 0,425

Отсюда
наибольшая возможная статистическая
ошибка:

Если
предельную ошибку устанавливают до
измерений, а наибольшую статистическую
вычисляют по результатам неоднократных
измерений. Наибольшая статистическая
ошибка при измерении неизменной величина
будет меньше предельной, так как
отклонения отдельных измерений от
средней неоднозначны как это принято
для предельной ошибки. Иногда из значения
измеряемой величины отсчитывают с
большей точностью, чем это предположено
для предельной ошибки.

Точность
разовых измерений оценивают только по
предельной ошибке. При неоднократных
измерениях до их начала следует
пользоваться предельной ошибкой (для
прибора аппаратуры и представления о
возможностях измерений). А после измерений
оценивать их точность по наибольшей
возможной статистической ошибке.

Лекция
6 – 21.10.11

Измерения,
дающие дисп или одинаковой величины,
называют равноточными. Равноточность
измерений серий и опытов облегчает
обработку результатов измерений и
уменьшает суммарные ошибки исследования.

Практически
добиться равноточности измерений можно
только в тех случаях, когда измерение
будет проводить опытный человек одним
и тем же прибором в одинаковых условиях.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.

При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,

Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.

Отсчет по шкале прибора указывает непосредственно измеряемое значение.
Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).

Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.

Различают абсолютную (∆ X) и относительную (δ) погрешности измерений.
Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,

Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),

Как вычислить погрешность измерений?

Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).

расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.

Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.

У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).

Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.

В чем измеряется погрешность?

Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.

Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.

Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.

Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Как найти абсолютную погрешность измерительного прибора?

Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.

Что такое погрешность метода измерений?

По источнику возникновения — Инструментальная погрешность Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки, Методическая погрешность Методической называют погрешность, обусловленную несовершенством метода измерений.

Что такое погрешность измерительного прибора?

Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.

Как определить погрешность деления?

Как определить погрешность и объем жидкости — Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл. Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл: V = 40 + 2 × 5 = 50 мл.

Как рассчитывается приведенная погрешность?

Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений.

Общие требования» и им подобных.
Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия.
Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.

Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.

Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).

По характеру проявления:

систематические (могут быть исключены из результатов);
случайные;
грубые или промахи (как правило не включаются в результаты измерений).

В зависимости от эксплуатации приборов:

основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.

Наимено вание погреш ности

Формула

Форма выражения, записи

Обозначение класса точности

В докумен тации

На сред стве изме рений

Абсолют ная

Δ = X д — X изм

Δ = ±50 мг Примеры: Номинальная масса гири 1 кг ±50 мг Диапазон измерения весов среднего III класса точности от 20 г до 15 кг ±10 г

Класс точности: М 1 Класс точности: средний III Примечание: на многие виды измерений есть свои НД по выражению погрешностей, здесь для примера взято для гирь и весов.

М 1

Относи тельная

δ = (Δ ⁄ X д ) · 100

δ = ±0,5 Пример: Измеренное значение изб.

Как вычислить абсолютную погрешность формула?

Поиск: Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).

Чему равна абсолютная погрешность?

При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения.

Для чего нужна погрешность измерений?

Каждое физическое измерение в исследованиях и промышленности сопровождается определенной погрешностью. Даже незначительные колебания в условиях окружающей среды могут влиять на измерение и вызывать отклонения, которые делают результат измерения ненадежным.

Для получения правильных результатов измерений необходимо учитывать связанную с результатами погрешность. Погрешность измерений указывает на недостающую информацию о настоящем значении измеряемой величины. Она определяется параметром, выраженным в процентах и относящимся к результату измерения, который обозначает отклонение значений, которое обоснованно можно присвоить измеряемой величине на основе имеющейся информации.

Другими словами, это диапазон, в пределах которого с определенной вероятностью находится истинное значение измеряемой величины.

Как найти абсолютную погрешность пример?

Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности.
Обозначим точное число буквой А, а буквой а – приближение к точному числу.
Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях.
Тогда формула будет выглядеть следующим образом: Δа=А-а.
Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.

Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения. Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см.

Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Как определить цену деления и погрешность?

Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков.

Что такое максимальная погрешность измерений?

Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Как рассчитывается приведенная погрешность?

Общие требования» и им подобных. Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия. Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.

Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).

По характеру проявления:

систематические (могут быть исключены из результатов);
случайные;
грубые или промахи (как правило не включаются в результаты измерений).

В зависимости от эксплуатации приборов:

основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.

Наимено вание погреш ности

Формула

Форма выражения, записи

Обозначение класса точности

В докумен тации

На сред стве изме рений

Абсолют ная

Δ = X д — X изм

М 1

Относи тельная

δ = (Δ ⁄ X д ) · 100

δ = ±0,5 Пример: Измеренное значение изб.

Как вычислить погрешность функции?

Главная страница УЧЕБНЫЕ МАТЕРИАЛЫ ПРОГРАММА КУРСА КОНСПЕКТЫ ЛЕКЦИЙ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ВОПРОСЫ К ЗАЧЁТУ РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Кафедра физхимии ЮФУ (РГУ) ЧИСЛЕННЫЕ МЕТОДЫ И ПРОГРАММИРОВАНИЕ Материалы к лекционному курсу Лектор – Щербаков И.Н. Пусть X – некоторая величина, истинное значение которой известно или неизвестно и равно x*, Число x, которое можно принять за значение величины X, мы будем называть ее приближенным значением или просто приближенным числом. Число x называют приближенным значением по недостатку, если оно меньше истинного значения ( x < x* ), и по избытку, если оно больше ( x > x* ). Например, число 3,14 является приближенным значением числа π по недостатку, а 2,72 – приближенным значением числа е (основание натурального логарифма) по избытку. Абсолютная погрешность приближенного числа есть абсолютная величина разности между истинным значением величины и данным ее приближенным значением. Δx = | x * – x | Поскольку истинное значение величины обычно остается неизвестным, неизвестной остается также и абсолютная погрешность. Вместо нее приходится рассматривать оценку абсолютной погрешности, так называемою предельную абсолютную погрешность, которая означает число, не меньшее абсолютной погрешности (далее, в том случае, если это не принципиально, будем под абсолютной погрешностью понимать именно предельную абсолютную погрешность). Абсолютная погрешность приближенного числа не в полной мере характеризует его точность. Действительно, погрешность в 0,1 г слишком велика при взвешивании реактивов для проведения микро-синтеза, допустима при взвешивании 100 г колбасы, и не может быть замечена при измерении массы, например, железнодорожного вагона. Более информативным показателем точности приближенного числа является его относительная погрешность, Относительной погрешностью δx приближенного значения величины X называют абсолютную величину отношения его абсолютной погрешности к истинному значению этой величины. Часто эту относительную погрешность выражают в процентах. C учетом положительности абсолютной погрешности можно записать: δx = Δx / | x* | Ввиду того, что фактически вместо абсолютной погрешности приходится рассматривать предельную, относительную погрешность также заменяют предельной относительной погрешностью, которая означает число, не меньшее относительной погрешности. Более того, при отыскании предельной относительной погрешности приходится заменять неизвестное истинное значение величины x* приближенным – x, Последняя замена обычно не отражается на величине относительной погрешности ввиду близости этих значений и малости абсолютной погрешности. δx = Δx / | x | Например, для приближенного значения π = 3,14 предельная абсолютная погрешность составляет 0,0016, а относительная – 0,00051 или 0,051%. Выражение относительной погрешности в процентах иногда называют процентной погрешностью.

Как рассчитать абсолютную погрешность?

Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).

Adblock
detector

Источник

СКАЧАТЬ .pdf

О.А. Цыбульский
АО «ПромСервис», г. Димитровград, Ульяновская обл., Российская Федерация,
e-mail:

multimer@list.ru
Приведены формулы для нормирования предельной относительной погрешности прибора. С использованием критерия совокупного показателя точности и диапазона прибора показано преимущество нормирования по расширенной формуле, содержащей три составляющих предельной погрешности: аддитивную, мультипликативную и гиперболическую. Такое нормирование учитывает гиперболическую нелинейность характеристики преобразования, свойственную приборам с параметрическими преобразователями и многим приборам с широким диапазоном измерения, имеющим дробно-линейное (проективное уравнение измерения. Для приборов с широким диапазоном измерения предложено применять расширенную формулу нормирования предельной относительной погрешности измерения.

Ключевые слова: измерение, широкий диапазон, нормирование, полоса предельной погрешности, критерий, плотность вероятности, дробно-линейное (проективное) уравнение измерения, гиперболическая составляющая.

Formulas are given for normalizing the limiting relative error of the device. Using the criterion of the aggregate indicator of accuracy and range of the device, the advantage of standardization is shown by an extended formula containing three components of the marginal error: additive, multiplicative and hyperbolic. Such rationing takes into account the hyperbolic non-linearity of the conversion characteristic inherent in devices with parametric converters and many devices with a wide measuring range having a linear-fractional (projective) measurement equation. For instruments with a wide measuring range, it is proposed to use the extended formula for normalizing the limiting relative measurement error.

Точность прибора в диапазоне измерений нормируют полосой предельной погрешности. При нормировании широкодиапазонных приборов диапазон измерения разделяют на поддиапазоны. В каждом поддиапазоне предельная погрешность задана либо значением мультипликативной составляющей, либо двухчленной формулой, включающей аддитивную и мультипликативную составляющие погрешности. В руководствах по эксплуатации представлены большие таблицы, нормирующие относительные погрешности в каждом поддиапазоне и для каждой модификации прибора. Значения погрешностей и границы поддиапазонов могут задаваться достаточно произвольно. Это осложняет анализ и сравнение результатов измерений прибороводного типа.

С повышением точности измерения и расширением динамического диапазона приборов требуется учитывать нелинейную составляющую полосы погрешности. В [1] отмечено, что «наиболее общим видом формулы текущей относительной погрешности является трехчленная формула».

Формулы для нормирования предельной относительной погрешности прибора.

В настоящий момент для нормирования предельной относительной погрешности прибора в широком диапазоне измерения применяется формула, содержащая две (аддитивную и мультипликативную) составляющие предельной погрешности:

где X, X_н – текущее значение измеряемой величины и нижняя граница диапазона измерений соответственно;
δ_а=Δ_а/X_н – составляющая аддитивной погрешности измерения Δ_а;
δ_м – мультипликативная составляющая.

Существует целый класс измерительных преобразователей, относящихся к параметрическим преобразователям (например, измерительные мосты), предельная относительная погрешность которых описывается формулой с тремя составляющими – аддитивной, мультипликативной и гиперболической [1]. Это связано с тем,что согласно теореме вариации для измерительных цепей характеристика преобразования параметрических преобразователей, к которым относится большинство датчиков, имеет дробно-линейную функцию преобразования. Дробно-линейная функция описывает равностороннюю гиперболу. Даже после линеаризации характеристики параметрического преобразования (например, при введении обратной связи) остаточная нелинейность сохраняется. Остаточная гиперболическая нелинейность включается в суммарную погрешность в качестве погрешности нелинейности характеристики преобразования. Гиперболическая нелинейность характеристики преобразования имеет одну особенность, важную для измерительных приборов. Осуществляемое дробно-линейной функцией преобразование относится к проективным, образующим группу, т. е. «каждую конечную последовательность преобразований можно заменить одним преобразованием этой же группы» [2].

Структурная схема широкодиапазонного измерительного прибора, как правило, состоит из последовательной цепочки линейных преобразователей. Существование в этой цепочке хотя бы одного преобразователя с дробно-линейной характеристикой делает результирующую характеристику также дробно-линейной.

Соответственно, формула нормирования предельной погрешности этого преобразования должна включать нелинейную гиперболическую составляющую.
В работе [3] на примерах преобразователей расхода и калибратора-вольтметра показано, что не только при параметрических преобразованиях, но и в ряде других широкодиапазонных приборов предельную относительную погрешность измерений можно нормировать во всем диапазоне измерений формулой с тремя составляющими погрешности: аддитивной, мультипликативной и гиперболической:

где X_в –верхняя границы диапазона измерений;
δ_г=Δ_г/X_в–составляющая погрешности нелинейности (гиперболической) Δ_г при X=X_в.

Формула (2) содержит в виде частных случаев двухчленное (1) и одночленное представление предельной погрешности, т.е. позволяет осуществлять нормирование всеми применяемыми в настоящее время способами. Одновременнов формуле (2) учтена специфика параметрических и широкодиапазонных приборов, для которых становится существенной погрешность нелинейности. Третья – гиперболическая составляющая предельной относительной погрешности, в отличие от аддитивной и мультипликативной составляющих, нормирует гиперболическую нелинейность функции преобразования прибора.

В работе [3] показано, что для приборов с широким диапазоном измерения формулу нормирования предельной относительной погрешности (2) можно представить в удобном виде:

где δX_н, δX_в–предельные относительные погрешности соответственно в нижней и верхней границах диапазона измерений.
Применение формул (2), (3) позволяет во многих случаях нормировать предельную погрешность прибора во всём диапазоне измерений без поддиапазонов. Для примера сравним табличное нормирование расходомера Прамер-550-D в диапазоне измерений 1–1000 м3/час с нормированием по формуле (2). В таблице приведены значения нормируемых параметров X_н, δX_н, X_в, δX_в расходомера, где строки 1–3 соответствуют табличному нормированию в поддиапазонах, строка 4–нормированию по трёхчленной формуле (2) во всём диапазоне.

Формула нормирования предельной относительной погрешности расходомера Прамер-550-D (в диапазоне 1–1000м3/час) имеет вид

В диапазоне измерения расхода 0,1–100 м3/час получены составляющие полосы предельной относительной погрешности:
δ_а=4,86%; δ_м=0,57 %; δ_г=0,43 %, т.е. в формуле нормирования (4) в явном виде указаны значения основных метрологических параметров прибора:
диапазон измерения и составляющие полосы предельной относительной погрешности. Формула (4) получена аппроксимацией полосы погрешности, заданной табличным способом, по трём точкам:X_н=0,1; δX_н=5 %; X=1; δX=1 %; X_в=100; δX_в=1 %.

Рис. Нормирование предельной относительной погрешности расходомера Прамер-550-D табличным способом и по формуле (2)

Критерий эффективности совокупного показателя точности и диапазона прибора. На рисунке изображены полосы предельной относительной погрешности, заданные табличным способом и по
формуле (2). Нормирование по формуле (2) позволяет более адекватно задать значение предельной относительной погрешности в любой точке диапазона измерения. Для оценки преимущества нормирования с помощью формулы (2) используем критерий Nэфф совокупного показателя точности и диапазона прибора [1]. Для аддитивно-мультипликативной полосы предельной относительной погрешности (1) этот критерий определим как

где D=X_в/X_н – динамический (относительный) диапазон измерений.
Физический смысл критерия N_эфф– количество эффективных (реальных) квантов (делений), на которые данный прибор может разделить диапазон измерений с заданной полосой предельной погрешности, т. е. сколько непересекающихся интервалов предельной абсолютной погрешности последовательно уложатся в диапазон измерений. Это ресурс, которым обладает прибор для проведения измерения, и чем больше N_эфф, тем точнее прибор. Выражение (5) показывает взаимосвязь параметров измерительного преобразования.

При разделении диапазона измерения прибора на поддиапазоны количество эффективных квантов всего диапазона измерений равно сумме эффективных квантов всех поддиапазонов. В случае
D выражение (5) можно представить в удобном для анализа виде

где δX_в≈δ_м, δX_н=δ_а+δ_м – соответственно, предельные относительные погрешности на верхней и нижней границах диапазона измерений.
Поскольку критерий (6) был предложен для полосы предельной погрешности с двухчленной формулой нормирования, то для расчёта числа эффективных квантов шкалы прибора, предельная погрешность которого нормируется по формуле (2) с тремя составляющими погрешности, в работе [4] получено расширенное выражение критерия:

где δX_н≈δ_а+δ_м, δX_в≈δ_г+δ_м–относительные погрешности соответственно на нижней и верхней границах диапазона измерений при условии
D = X_в/X_н 1.

По критерию (7) можно определить более эффективный способ нормирования. Например, при нормировании относительной предельной погрешности расходомера Прамер-550-D табличным способом (см. таблицу) число эффективных квантов N_эфф=267, при нормировании по формуле (2) Nэфф=366. Следовательно, точность при нормировании табличным способом меньше в 366/267=1,371 раз или на 37,1%. Таким образом, применение монотонной функции (2) вследствие большего количества составляющих позволяет более адекватно (без потерь точности и разделения на поддиапазоны) нормировать полосу предельной погрешности, чем табличный метод.

Дробно-линейное уравнение измерения прибора. Полоса предельной относительной погрешности (2) в логарифмическом масштабе имеет U-образный вид (см. рисунок). Увеличение погрешности в верхней части диапазона U-образной полосы предельной относительной погрешности определяется нелинейной (гиперболической) составляющей погрешности. При описании
характеристики преобразования прибора с помощью линейной функции гиперболическую составляющую погрешности по возможности корректируют. Однако если вместо линейного уравнения измерения применять дробно-линейное (проективное) уравнение [4,5], то гиперболическая составляющая будет учтена и её не надо будет корректировать.
В общем случае дробно-линейное (проективное) уравнение измерения имеет вид

где a₀, b₀, b₁ – постоянные масштабные коэффициенты;
Х, Х_оп – измеряемая и опорная величины;
К – выходной код аналого-цифрового преобразователя (АЦП).

Для перехода от линейного к дробно-линейному уравнению необходимо, чтобы измерительный прибор осуществлял сравнение измеряемого сигнала не с фиксированным опорным сигналом,
формируемым мерой, а с линейной комбинацией опорного и измеряемого сигналов [5]. В этом случае характеристика преобразования вместо линейной функции станет равносторонней гиперболой, а полоса предельной относительной погрешности прибора описываться формулой (2).

Способ преобразования шкалы измерений с целью задания требуемой полосы предельной погрешности с помощью дробно-линейного (проективного) преобразования линейной шкалы измерения
предложен в [5,6]. Способ позволяет более рационально распределить эффективные кванты по шкале измеряемой величины АЦП с линейной шкалой квантования. Увеличение относительной погрешности квантования в нижней части линейной измерительной шкалы является существенным фактором, ограничивающим диапазон измерения.

Применение дробно-линейного (проективного) преобразования позволяет с помощью преобразования линейной измерительной шкалы получить «квазилогарифмическую» шкалу, существенно расширяющую диапазон измерения. При этом полоса предельной погрешности соответствует трёхчлену (2).
Если оставить уравнение измерений линейным, то в зависимости от алгоритма аппроксимации градуировочной кривой, например, минимизации по диапазону абсолютной или относительной погрешности аппроксимации, можно получить полосу погрешности, описываемую одно-, двух- или трёхчленной формулой нормирования. Посчитав количество эффективных квантов, можно убедиться,что наибольшее значение критерия, а значит, и наибольшую точность обеспечивает трёхчленная формула нормирования.

Подтверждение целесообразности применения трёхчленной формулы. Существуют (помимо критерия эффективности) факторы, подтверждающие целесообразность нормирования по трёхчленной
формуле. Количество эффективных квантов ограничено, и это только ресурс, заложенный в прибор. Ресурс надо эффективно применить: распределить кванты по шкале измерений, чтобы оптимизировать информационные, финансовые потери (далее – потери) вследствие погрешности измерений. Для этого требуется дополнительная информация об измеряемой величине: о частоте появления различных значений измеряемой величины, а также о законе изменения плотности вероятности измеряемой величины. Потери при измерении определяются не только погрешностью измерения δХ_i, но и частотой появления значения Х_i. Если вероятность появления значения Х_i близка к нулю, то потери из-за большой погрешности измерения малы и ими можно пренебречь (за исключением особых случаев, когда важно само экстремальное значение). Но если вероятность появления значения Х_i максимальна, то погрешность измерения должна быть минимальна.

Влияние плотности вероятности измеряемой величины на закон изменения предельной погрешности по диапазону измерения подробно исследовано П.В. Новицким в информационной теории измерений [1]. В результате он сделал вывод, что при измерениях в широком диапазоне необходимо применять закон априорного логарифмически-равномерного распределения измеряемой величины:

Согласно выражению (9) оптимальной с информационной точки зрения является шкала с постоянной относительной погрешностью.
Впервые этот закон сформулирован в работе К. Шеннона [7]: в результате общего анализа больших множеств (в общем случае) наиболее характерным законом изменения плотности распределения для больших множеств является логарифмически-равномерный закон распределения.

Гипотезу К. Шеннона о логарифмически-равномерном законе априорного распределения плотности вероятностей экспериментально проверил П. В. Новицкий и подтвердил, что в центральной части широкого диапазона измерений закон можно трактовать, как логарифмически-равномерный. При этом на краях диапазона измерений наблюдалось снижение плотности P(lnX), т. е. закон распределения приближался к логарифмически-нормальному. Именно такой характер распределения с физической точки зрения Шеннон считал наиболее вероятным. Тем не менее, в дальнейшем для упрощения анализа было принято простое логарифмически-равномерное распределение, соответствующее применению шкалы измерения с постоянной относительной погрешностью.Но априори понятно, что предельная относительная погрешность должна возрастать на концах диапазона измерения. Полоса погрешности, нормируемая трёхчленной формулой для предельной относительной погрешности, этой закономерности соответствует.

В настоящее время во многих приборах (например, расходомерах) предельная относительная погрешность так и нормируется постоянной относительной погрешностью. Однако если погрешность на краях диапазона будет выше, чем в центральной части, то количество эффективных квантов станет больше. Вблизи нижней границы диапазона приборов это утверждение выполняется, а вблизи верхней границы, как правило, нет. Конечно, можно игнорировать эту закономерность и нормировать предельную относительную погрешность во всём диапазоне постоянным значением. Это целесообразно для измерительной шкалы с бесконечным количеством эффективных квантов. Но в реальном приборе количество эффективных квантов ограничено, и требование уменьшения погрешности противоречит требованию расширения диапазона измерения. Ресурса прибора не хватает для обеспечения наивысшей точности в наибольшем диапазоне.

Современные приборы обеспечивают большие динамические диапазоны измерений. Например, при выборе расходомера максимальный расход задают ориентировочно в 3–10 раз больше
ожидаемого среднесуточного расхода [8,9]. Учитывают не только возможное превышение максимального расхода над среднесуточным в 2–5 раз, но и увеличение верхней границы дополнительно в 1,5-2 раза с учётом запаса расхода «на вырост». Естественно, вероятность появления больших расходов меньше вероятности среднесуточного расхода. Таким образом, верхняя половина диапазона измерения имеет в среднем малую вероятность использования, а значит в ней допустима погрешность большая по сравнению с погрешностью при среднем расходе. Однако в действительности, все выпускаемые расходомеры имеют наивысшую точность и, соответственно, наибольшие затраты эффективных квантов именно вблизи верхней границы диапазона.

Если предельная относительная погрешность прибора с увеличением верхней границы измерения имеет тенденцию к росту, то ее целесообразно нормировать по формуле (2) с гиперболической
составляющей, поскольку она обеспечивает требуемую форму полосы погрешности. Чтобы формула нормирования (2) задавала наивысшую точность измерения в точке, соответствующей расчётному среднему значению, необходимо соблюдение равенства

Например, при нормировании расходомера Прамер-550-D (см.рисунок) минимальная погрешность измерения согласно (10) соответствует точке .

Ещё один фактор в пользу применения трёхчленной формулы нормирования связан с использованием именно гиперболической составляющей. Как отмечено выше, U-образный вид полосы предельной относительной погрешности достаточно распространён в измерительных приборах:во всех параметрических измерительных преобразователях [1], а также во многих широкодиапазонных приборах [3]. В работах [4,5] показано, что если полоса предельной относительной погрешности измерительного аналого-цифрового преобразования описывается функцией вида (2), то характеристика этого преобразования дробно-линейная функция. Преобразование, описываемое дробно-линейной функцией, изучается в рамках проективной (наиболее фундаментальной) геометрии. Применению в технических дисциплинах геометрических моделей посвящено много работ, например [10–14].

В работе [15] рассмотрена закономерность проявления проективных свойств в характеристике преобразования измерительных приборов при большом динамическом диапазоне преобразования.

Показано, что с увеличением динамического диапазона и изменением полосы предельной относительной погрешности от чисто аддитивной до U-образной изменяется уравнение измерения от линейного к дробно-линейному. Аналогичная закономерность характерна, например, для изобразительного искусства и фотографии при проецировании отображаемого объекта на плоскость картины или фотоплёнки. Согласно теории перспективы с увеличением размера объекта в глубину пространства закономерности евклидовой геометрии при изображении объекта меняются на закономерности проективной геометрии. В алгебраической записи это соответствует переходу от линейного уравнения к дробно-линейному. Это же происходит и с уравнением линейного измерения (аналого-цифрового преобразования) при переходе от узкого к широкому динамическому диапазону измерения. При измерениях также осуществляется проецирование объекта измерения на измерительную шкалу.

В работе [16] показано, что линейное аналого-цифровое преобразование является частным случаем такого дробно-линейного преобразования. Выполнено сравнение характеристик линейного и
дробно-линейного (проективного), построенного на той же линейной элементной базе, аналого-цифровых преобразований. Показано, что дробно-линейное аналого-цифровое преобразование эффективнее линейного и решает задачи оптимизации погрешности квантования, расширения диапазона измерений, снижения разрядности преобразователя. При этом все выражения, критерии, инварианты, справедливые для линейного преобразования, являются частным случаем соответствующих выражений, критериев и инвариантов дробно-линейного преобразования. Это же относится и к формуле нормирования предельной погрешности измерений. Таким образом, формула (2) нормирует полосу предельной погрешности приборов с дробно-линейным (проективным) уравнением измерения и, в частном случае –без гиперболической составляющей, нормирует полосу предельной погрешности приборов с линейным уравнением измерения.

Заключение. Расширенная формула представления предельной относительной погрешности (2) позволяет более качественно (без потерь точности) нормировать полосу предельной погрешности в широком диапазоне измерений. Формула (2) в общем случае соответствует полосе предельной погрешности дробно-линейного (проективного) уравнения измерения. В то время, как формула представления предельной относительной погрешности (1) в общем случае соответствует полосе предельной погрешности линейного уравнения измерения. Линейное уравнение измерения является частным случаем дробно-линейного (проективного) уравнения измерения. Таким образом, чтобы учесть нелинейность характеристики преобразования в полосе погрешности линейного измерительного прибора целесообразно при нормировании предельной относительной погрешности применять расширенную формулу нормирования (2) с тремя составляющими погрешности и использовать дробно-линейное уравнение измерения (8).

Список литературы:

1. Новицкий П.В. Основы информационной теории измерительных устройств. Л.:Энергия, 1968. 248с.
2. Ефимов Н. В. Высшая геометрия. Москва: Физматлит, 2004.
3. Цыбульский О.А. Погрешность широкодиапазонных измерений//Законодательная и прикладная метрология. 2010.№ 4. С.5–10.
4. Цыбульский О. А. Критерий для обобщенной оценки широкодиапазонного прибора по точности и диапазону измерений // Измерительная техника. 2014. № 5. С. 5–7.
5.Цыбульский О.А. Дробно-линейное уравнение измерений //Измерительная техника. 2017. №5. С. 25–30.
6. Пат. №2618903 РФ / Цыбульский О.А. //Изобретения. Полезные модели. 2017. Бюл.№ 14.
7. Шеннон К. Работы по теории информации и кибернетике. М.:Иностранная литература,1963.
8. Николадзе Г.И., Сомов М. А. Водоснабжение. М. Стройиздат,1995.
9. Ионин А. А. Газоснабжение. М.:изд. Лань, 2012.
10. Мазин В.Д. Обобщенная геометрическая модель измерительного преобразования//Междунар. науч.-практ.конф. «175 лет ВНИИМ им. Д.И. Менделеева и национальной системе обеспечения единства измерений», Санкт-Петербург, 14–15 июня 2017. СПб.: Издательство: Издательско-полиграфическая ассоциация высших учебных заведений 2017. С. 253.
11. Мазин В.Д. Векторное выражение единицы физической величины//Измерительная техника 2019. № 3. С. 26–29. DOI:
10.32446/0368-1025it.2019-3-26-29
12. Penin A. Analysis of electrical circuits with variable load regime parameters: projective geometry method. 2nd edition. Cham, Springer International Publishing Switzerland, 2016. 417p. DOI https://doi.org/10.1007/978-3-319-28451-4
13. Пенин А .А. Инварианты параметров источников неизменной мощности// Электричество.2018.№ 12.С. 52–63.
14. Пенин А. А., Сидоренко А. Проективная геометрия в электронике, технике и живой природе//Россия и Германия. 2014. Т. 2. № 6. С. 44–49.
15. Цыбульский О.А. Проективные свойства широкодиапазонных измерений // Измерительная техника. 2013. № 1. С. 27–29.
16. Цыбульский О.А. Сравнение характеристик линейного и дробно-линейного (проективного) аналого- цифровых преобразований.// Международный форум «Микроэлектроника-2017». 3-я международная научная конференция «Электронная компонентная база и электронные модули» Сборник докладов. Республика Крым г. Алушта, 02-07 октября 2017 г.// НАНОИНДУСТРИЯ. Спецвыпуск 2018 (82) ТЕХНОСФЕРА, С.344-350

Refe rences

1. Novitskii P. V. Osnovy informacionnoj teorii izmeritel’nyh ustrojstv [Fundamentals of information theory of measuring devices]. Leningrad, Energiy Publ., 1968, 248 p. [In Russ.].
2. Efimov N. V. Higher geometry. Moscow: Fizmatlit, 2004. [In Russ.].
3. Tsybul’skii O.A. Pogreshnost’ shirokodiapazonnykh izmereniI// Zakonodatel’naya i prikladnaya metrologiYA. 2010.№ 4. S.5–10. [In Russ.].
4. Tcybulskii O. A. Measurement Techniques, 2014, vol. 57, no. 5, рр. 479–483. DOI: 10,1007 / s11018-014-0484-2
5. Tsybul’skiy O.A. Measurement Techniques, 2017, vol. 60, no. 5, рр. 443–450. DOI 10.1007/s11018-017-1215-2
6. Pat. No. 2618903 of the Russian Federation / Tcybulskii O. A.//Inventions. 2017. Bull. №14 [In Russ.].
7. Shennon K. Raboty po teorii informatsii i kibernetike.M.:Inostrannaya literatura,1963. [In Russ.].
8. Nikoladze G.I., Somov M. A. Vodosnabzheniye. M. Stroyizdat, 1995.[In Russ.].
9. Ionin A. A. Gazosnabzheniye. M.:izd. Lan’, 2012 [In Russ.].
10. Mazin V.D. Obobshchennaya geometricheskaya model’izmeritel’nogo preobrazovaniya//Mezhdunar. nauch.-prakt.konf. «175 let VNIIM im. D.I. Mendeleyeva i natsional’noy sisteme obespecheniya yedinstva izmereniy», Sankt-Peterburg, 14–15 iyunya 2017. SPb.: Izdatel’stvo: Izdatel’sko-poligraficheskaya assotsiatsiya vysshikh uchebnykh zavedeniy 2017. S. 253. [In Russ.].
11. Mazin V.D. Vektornoye vyrazheniye yedinitsy fizicheskoy velichiny//Izmeritel’naya tekhnika 2019. № 3. S. 26–29. DOI: 10.32446/0368-1025it.2019-3-26-29
12. Penin A. Analysis of electrical circuits with variable load regime parameters: projective geometry method. 2nd edition. Cham, Springer International Publishing Switzerland, 2016. 417 p.
13. Penin A .A. Invarianty parametrov istochnikov neizmennoy moshchnosti// Elektrichestvo.2018.№ 12.S. 52–63. [In Russ.].
14. Penin A. A., Sidorenko A. Proyektivnaya geometriya v elektronike, tekhnike i zhivoy prirode//Rossiya i Germaniya. 2014. T. 2. № 6. S. 44–49. [In Russ.].
15. Tcybulskii O. A. Measurement Techniques, 2013, vol. 56, no. 1, pp 37–40. DOI https://doi.org/10.1007/s11018-013-0155-8
16. Tsybul’skii O.A. Sravneniye kharakteristik lineynogo i drobnolineynogo (proyektivnogo) analogo- tsifrovykh preobrazovaniy.//Mezhdunarodnyy forum «Mikroelektronika-2017». 3-ya Mezhdunarodnaya nauchnaya konferentsiya «Elektronnaya komponentnaya baza i elektronnyye moduli» Sbornik dokladov. Respublika Krym g. Alushta, 02-07 oktyabrya 2017 g.// NANOINDUSTRIYA. petsvypusk 2018 (82) TEKHNOSFERA, S.344-350 [In Russ.].

Источник