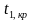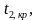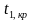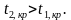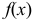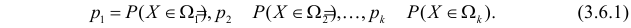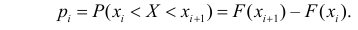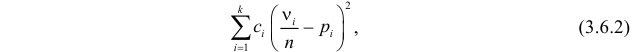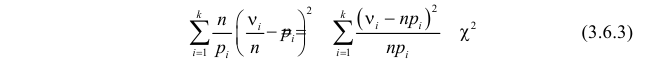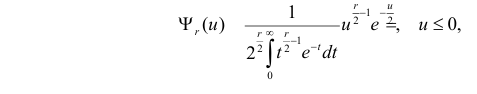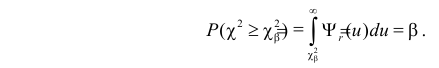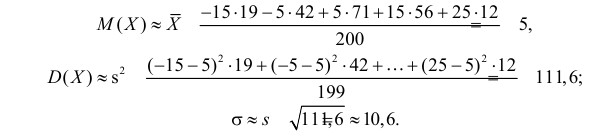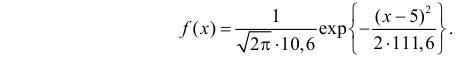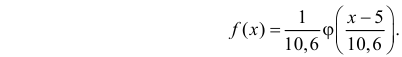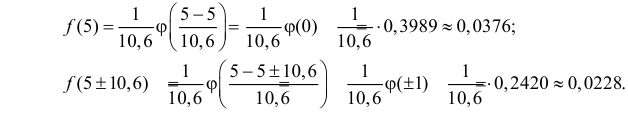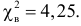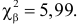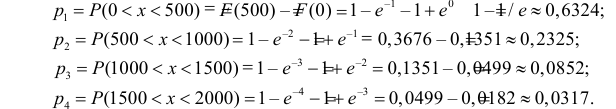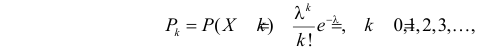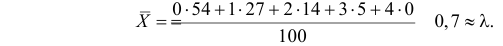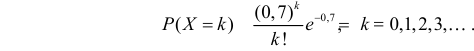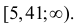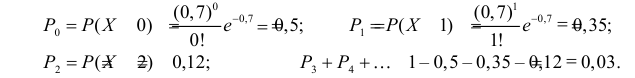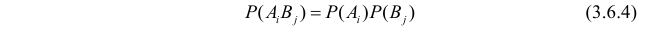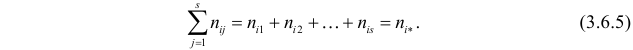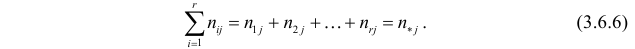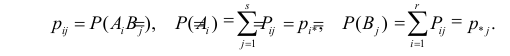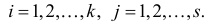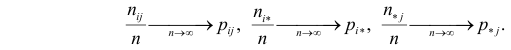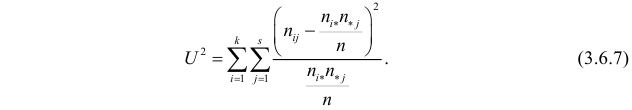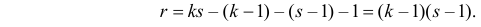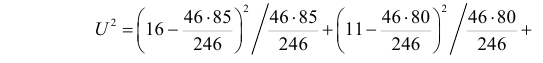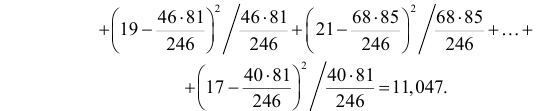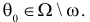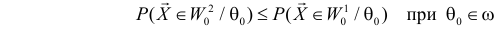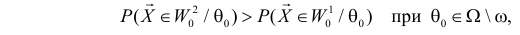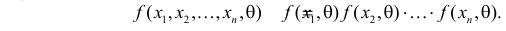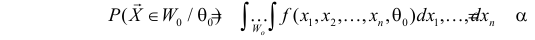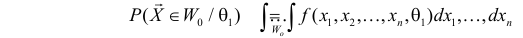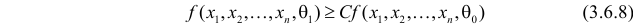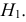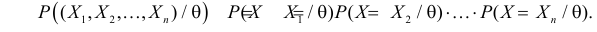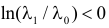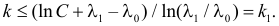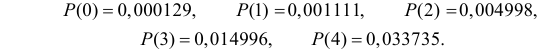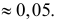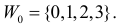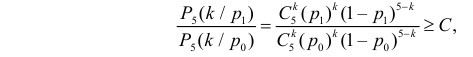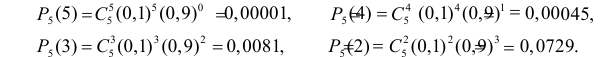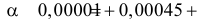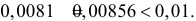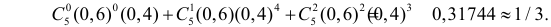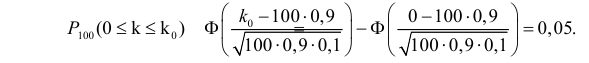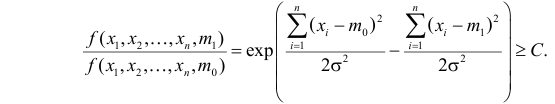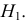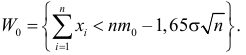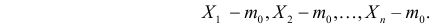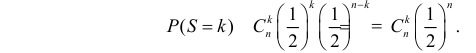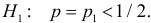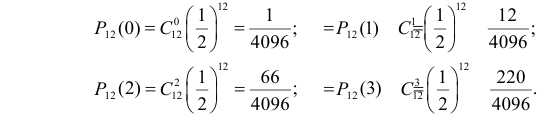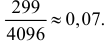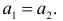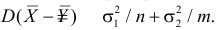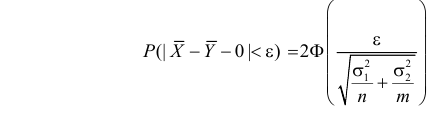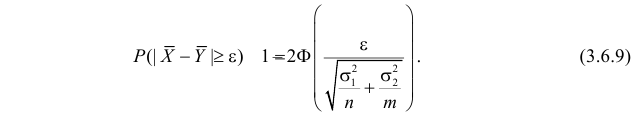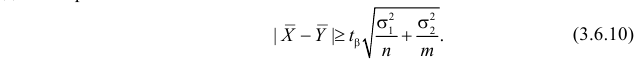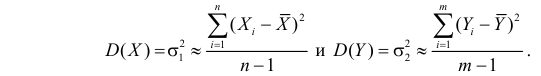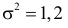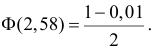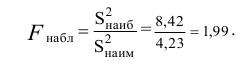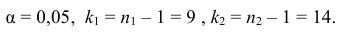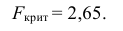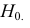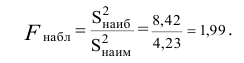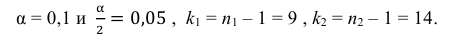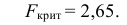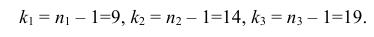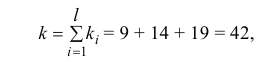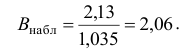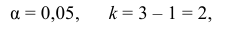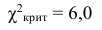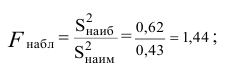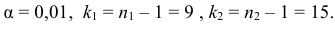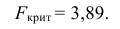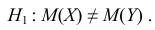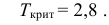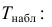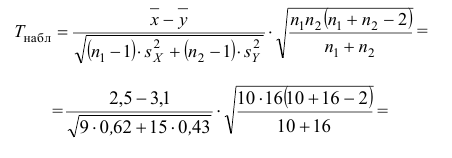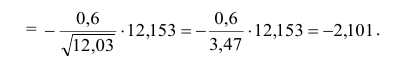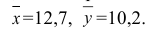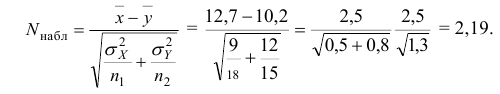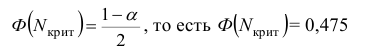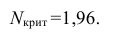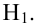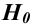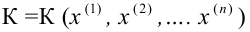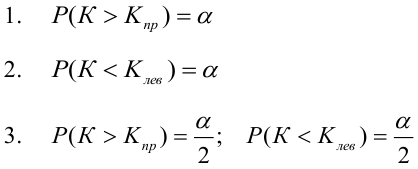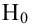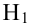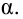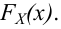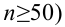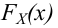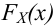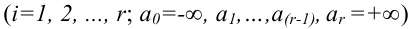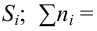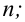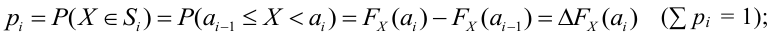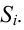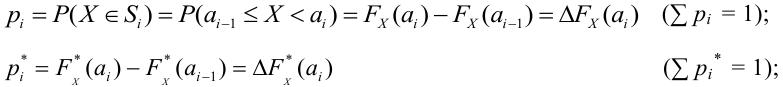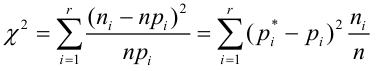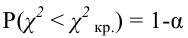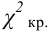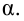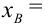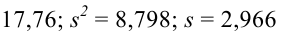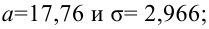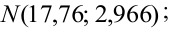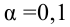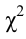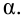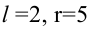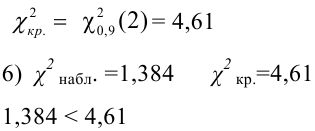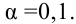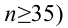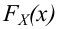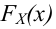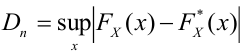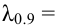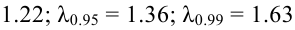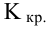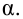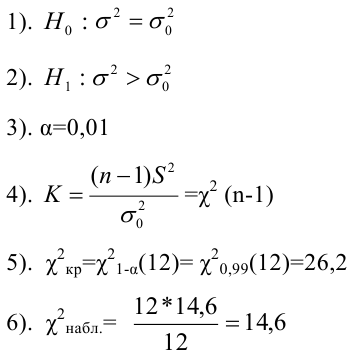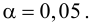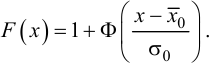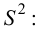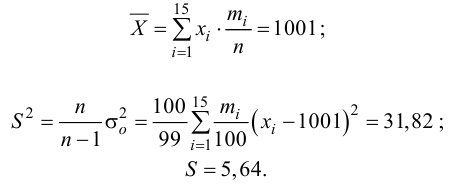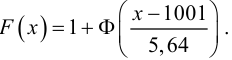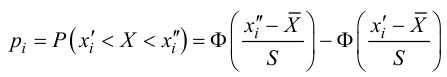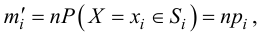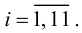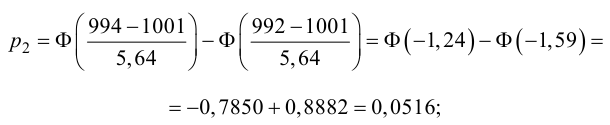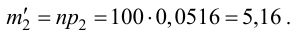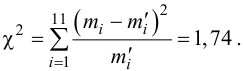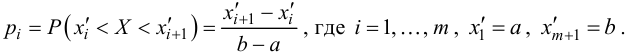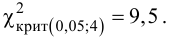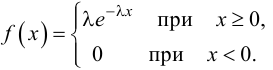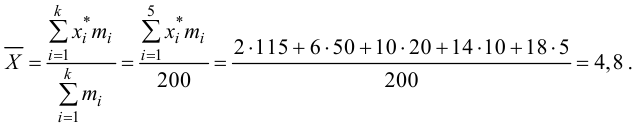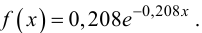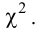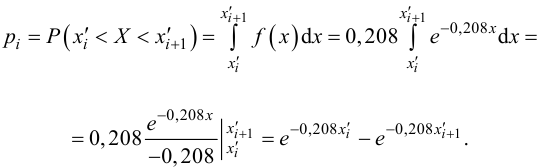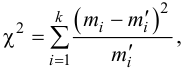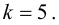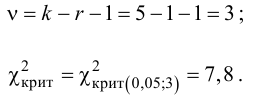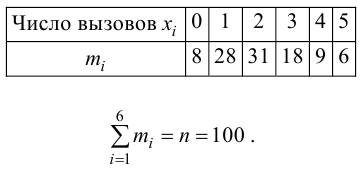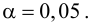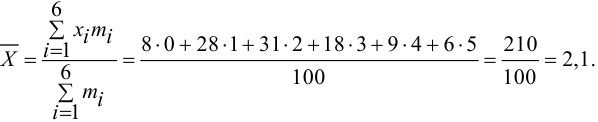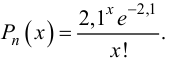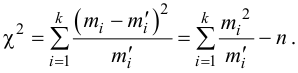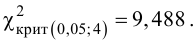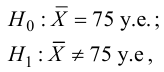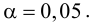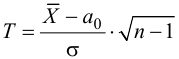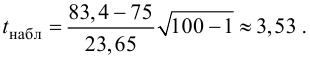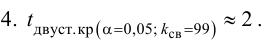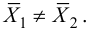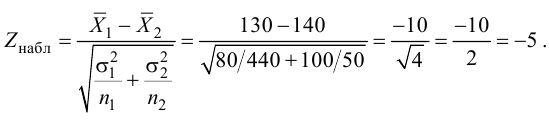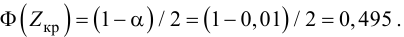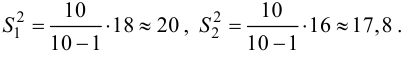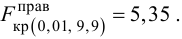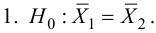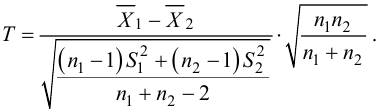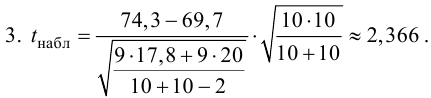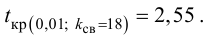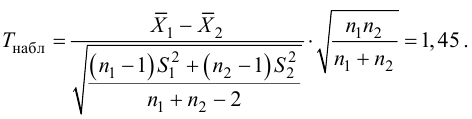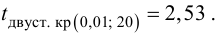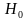Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки, встроенные в систему: их роль в статистике
Время прочтения
6 мин
Просмотры 11K
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:
До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
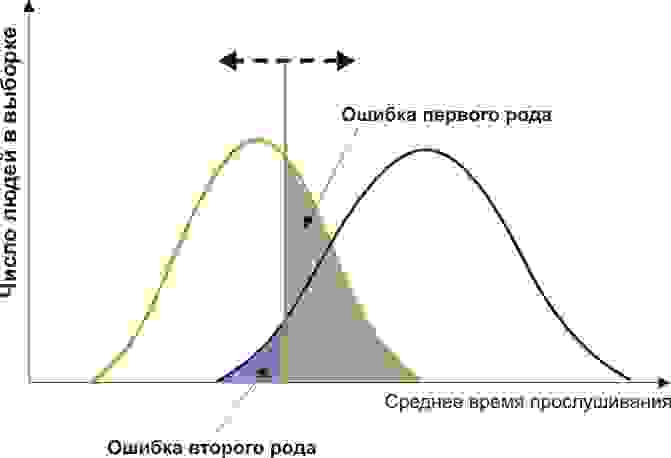
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):
Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
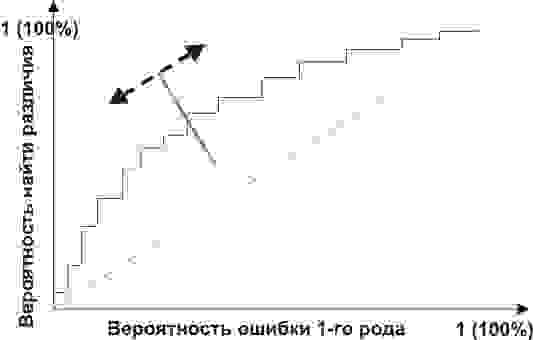
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
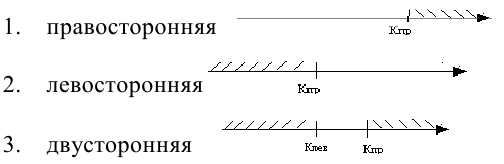
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
5.3. Ошибки первого и второго рода
Ошибка первого рода состоит в том, что гипотеза будет отвергнута, хотя на самом деле она правильная. Вероятность
допустить такую ошибку называют уровнем значимости и обозначают буквой («альфа»).
Ошибка второго рода состоит в том, что гипотеза будет принята, но на самом деле она неправильная. Вероятность
совершить эту ошибку обозначают буквой («бета»). Значение
называют мощностью критерия – это вероятность отвержения неправильной
гипотезы.
В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения .
И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении
вероятности —
отвергнуть правильную гипотезу растёт вероятность — принять неверную гипотезу (при прочих равных условиях).
Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей и
, при этом учитывается тяжесть последствий, которые
повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару
нестатистических примеров.
Петя зарегистрировался в почтовике. По умолчанию, – он считается добропорядочным пользователем. Так считает антиспам
фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до
адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может
совершить ошибку двух типов:
1) с вероятностью ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
за спам и Петю за спаммера) или
2) с вероятностью ошибочно принять нулевую гипотезу (хотя Петя редиска).
Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра
целесообразно уменьшить уровень значимости , «пожертвовав» вероятностью
(увеличив её). В результате в основной ящик будут попадать все
«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью 
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность следует увеличить (в пользу уменьшения
вероятности ). Не хотел я
приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой
дилеммой. Видимо, таки, надо рассказать:
У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение
достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному
увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.
Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные
решения (упаси вас).
Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается
на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,
достаточно, возвращаемся к теме:


| Оглавление |
Содержание:
Проверка статистических гипотез:
Статистической гипотезой называется гипотеза, которая относится к виду функции распределения, к параметрам функции распределения, к числовым характеристикам случайной величины и т.д., и которую можно проверить на основе опытных данных. Например, предположение о том, что отклонение истинного размера детали от расчетного имеет нормальный закон распределения, является статистической гипотезой. Предположение о наличии жизни на Марсе статистической гипотезой не является, так как оно не выражает какого-либо утверждения о законе распределения или иных характеристиках случайной величины.
Пример статистической гипотезы
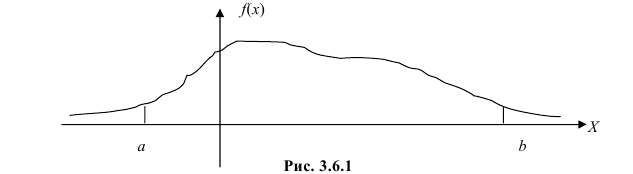
Рассмотрим упрощенный пример. Пусть выдвинута гипотеза о том, что плотность вероятности
Есть возможность произвести только одно наблюдение. В этом случае выборочным пространством служит числовая ось. Из рис. 3.6.1 видно, что значения случайной величины из отрезка 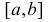
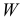
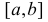
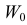
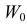
В случае выборки объема 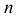
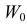
Статистическим критерием называют правило, указывающее, когда статистическую гипотезу следует принять, а когда отвергнуть. Построение статистического критерия сводится к выбору в выборочном пространстве критической области 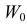
Даже при верной гипотезе наблюдения могут сложиться неблагоприятно, в итоге выборка может попасть в критическую область и гипотеза будет отвергнута. Вероятность такого исхода 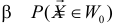
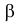
Статистический критерий в описанном виде может быть сложным, и трудно будет установить, принадлежит ли выборка критической области или нет. Поэтому предпочитают на выборочном пространстве задать некоторую функцию, которая каждой выборке ставит в соответствие определенное число. Значения функции, которые соответствуют критической области, естественно считать критическими значениями. Проверка гипотезы тогда сводится к вычислению по выборке значения этой функции и проверке, является ли оно критическим. Есть функции, не зависящие от вида проверяемой гипотезы. Одна из таких функций дает знаменитый критерий «хи-квадрат».
Критерий согласия «хи-квадрат»
Пусть выдвинута гипотеза о законе распределения случайной величины X. Требуется проверить, насколько эта гипотеза правдоподобна. Для этого разобьем множество возможных значений случайной величины на 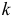
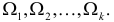
Например, если выдвинута гипотеза, что случайная величина X имеет функцию распределения 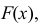
Нужно проверить, согласуется ли наша гипотеза с опытными данными.
Идея проверки гипотезы состоит в сравнении теоретических вероятностей разрядов (3.6.1) с фактически наблюдаемыми частотами попадания в эти разряды. Для этого производится 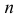
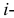

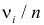
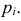
где 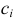
Если же гипотеза ложная, то при больших 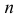
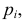
Английский статистик К. Пирсон (1900 г.) показал, что при выборе коэффициентов 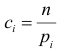
имеет распределение, которое не зависит от выдвинутой гипотезы и определяется функцией плотности вероятности
где 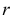
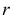


При данной гипотезе и фиксированном числе наблюдений величина 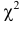
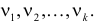



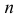
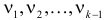
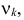


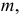

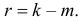


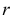
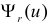
Составлены специальные таблицы (см. прил., табл. П4), в которых для любого 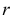

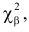
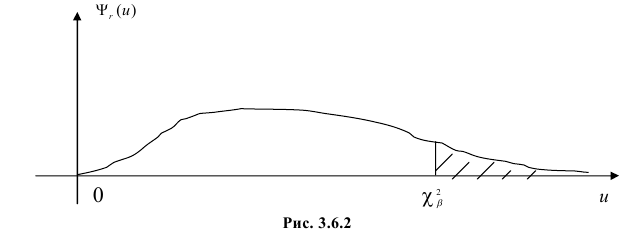
На рис. 3.6.2 заштрихованная площадь равна 
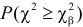
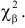
Предположим, что гипотеза верна. Выберем вероятность 

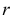
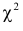
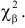
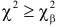
Итак, построена критическая область: 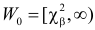

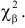
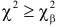
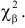
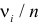
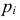
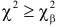
Если же окажется, что 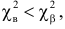
Замечание 1. Хотя и маловероятно, чтобы 
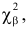


Замечание 2. Каждый разряд вносит в величину 
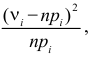
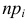
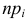
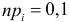

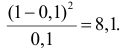
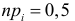
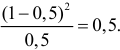
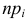
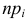
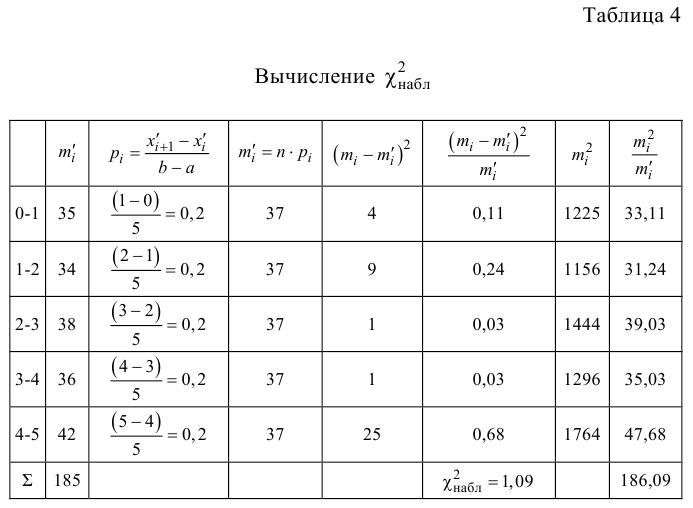
Пример №1
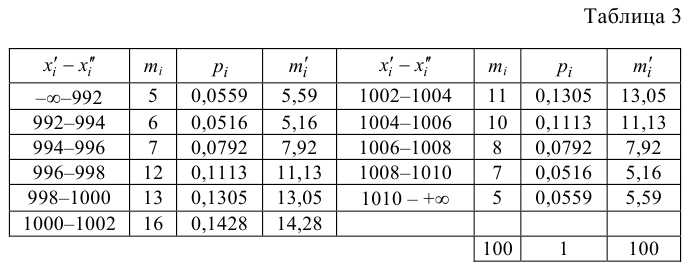
Были исследованы 200 изготовленных деталей на отклонение истинного размера от расчетного. Сгруппированные данные исследований приведены в виде статистического ряда:
Требуется по данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о типе закона распределения отклонений. Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). Построить на том же графике функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить согласуется ли выдвинутая гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.
Решение. Для того чтобы получить представление о виде закона распределения изучаемой величины, построим гистограмму. Для этого над каждым интервалом построим прямоугольник, площадь которого численно равна частоте попадания в интервал (рис. 3.6.3).
По виду гистограммы можно выдвинуть предположение о том, что исследуемая случайная величина имеет нормальный закон распределения. Параметры нормального закона (математическое ожидание и дисперсию) оценим на основе опытных данных, считая в качестве представителя каждого интервала его середину:
Итак, выдвинем гипотезу, что исследуемая случайная величина имеет нормальный закон распределения 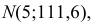
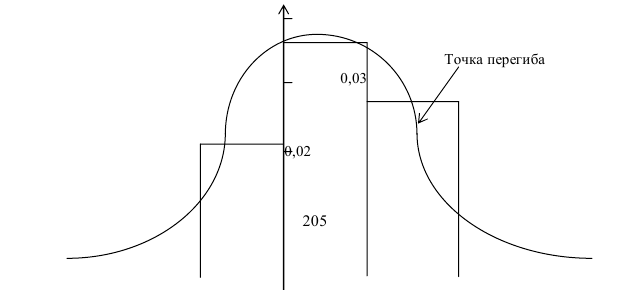
График 
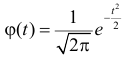
Например, точка максимума и точки перегиба имеют ординаты соответственно
График функции 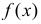
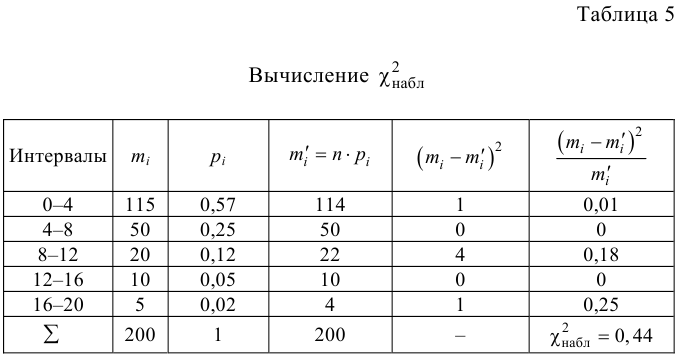
Вычислим меру расхождения между выдвинутой гипотезой и опытными данными, т.е. величину 
Аналогично:
Вычисление 
Итак, мера расхождения между гипотезой и опытными данными равна
Построим критическую область для уровня значимости 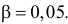


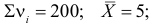
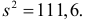
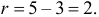

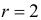

Критическая область для проверки гипотезы имеет вид 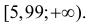
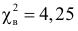
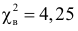
Ответ. Гипотеза опытным данным не противоречит.
Пример №2
В виде статистического ряда приведены сгруппированные данные о времени безотказной работы 400 приборов.
Согласуются ли эти данные с предположением, что время безотказной работы прибора имеет функцию распределения 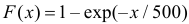
Решение. Вычислим вероятности, приходящиеся в соответствии с гипотезой на интервалы:
Вычислим 
Число степеней свободы равно трем, так как на четыре величины 
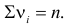
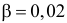
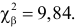
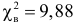
Ответ. Гипотеза опытным данным противоречит.
Пример №3
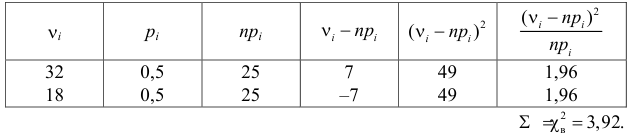
Монету подбросили 50 раз. Герб выпал 32 раза. С помощью критерия «хи-квадрат» проверить, согласуются ли эти результаты с предположением, что подбрасывали симметричную монету.
Решение. Выдвинем гипотезу, что монета была симметричной. Это означает, что вероятность выпадения герба при каждом броске равна 1/2. В описанном опыте герб выпал 32 раза и 18 раз выпала цифра. Вычисляем
Число степеней свободы для 
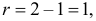

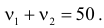
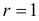
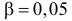
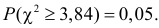
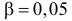

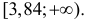
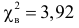
Ответ. Предположение о симметричности монеты не согласуется с опытными данными.
Пример №4
Для каждого из 100 телевизоров регистрировалось число выходов из строя в течение гарантийного срока. Результаты представлены в виде статистического ряда:
Согласуются ли эти данные с предположением о том, что число выходов из строя имеет пуассоновский закон распределения?
Решение. Если случайная величина Х – число выходов из строя телевизора, имеет пуассоновский закон распределения, то
где параметр 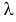
Оценим параметр из опытных данных. В законе распределения Пуассона параметр 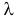
Итак, выдвигаем гипотезу, что изучаемая случайная величина имеет закон распределения
Для проверки выдвинутой гипотезы зададим уровень значимости, например, равный 0,02. Последние три разряда, содержащие мало наблюдений, можно объединить. В итоге имеем три разряда и число степеней свободы равно 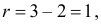

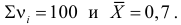
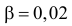
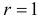
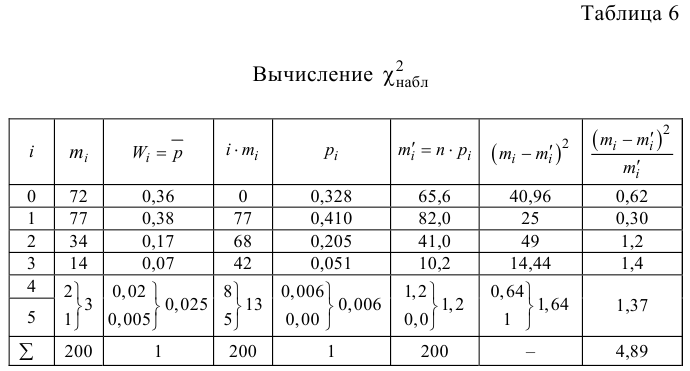
Вычислим теперь 
Вычисление 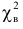
Вычисленное значение в критическую область не входит. Вывод: гипотеза о пуассоновском законе распределения изучаемой случайной величины опытным данным не противоречит.
Ответ. Гипотеза не противоречит опытным данным.
Пример №5
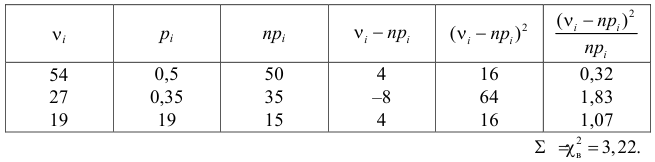
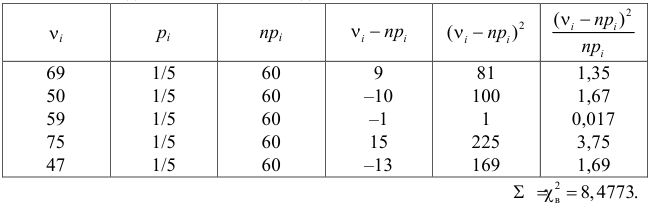
В течение пяти рабочих дней недели на контактный телефон фирмы поступило соответственно 69, 50, 59, 75, 47 звонков. Можно ли считать при уровне значимости 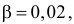
Решение. Сначала построим критическую область. Общее количество звонков равно 300. Число степеней свободы равно 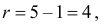
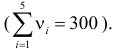
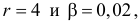
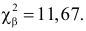
Выдвинем гипотезу, что интенсивность звонков не зависит от дня недели, т.е. с вероятностью 1/5 каждый вызов может поступить в любой рабочий день недели.
В предположении, что гипотеза верна, вычислим значение 
Сумма элементов последнего столбца дает 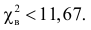
Ответ. Гипотеза опытным данным не противоречит.
Проверка гипотезы о независимости двух случайных величин
Постановка задачи. Можно ли по результатам наблюдений двух случайных величин сделать вывод об их зависимости или независимости. В приложениях эта задача имеет следующую постановку. Пусть каждый элемент генеральной совокупности обладает двумя признаками A и B, признак A имеет градации (или уровни) 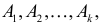
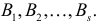
Естественно считать, что A и B независимы, если при выборе любого элемента генеральной совокупности независимы события «признак A принимает значение 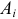
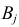
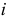
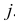
для всех 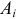
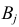
Пусть у взятых наугад 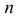
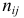
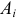
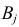
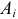
Аналогично, число наблюдений признака 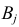
Обычно результаты наблюдений оформляют в виде таблицы, которую называют таблицей сопряженности признаков.
Таблица сопряженности признаков:
Введем обозначения для вероятностей. Положим
Необходимо проверить гипотезу 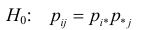
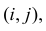
Если наблюдений много (хотя бы несколько десятков), то по теореме Бернулли
Критерий основан на сравнении наблюдаемых чисел появления комбинаций признаков с числами появлений, которые должны были бы быть, если бы признаки были независимы и не подвергались различным случайностям.
Поскольку вероятность наступления двух независимых событий равна произведению вероятностей этих событий, то за оценку вероятности совместного появления событий 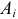
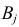
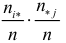
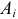
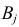
Эту величину можно назвать теоретическим числом появлений пары 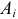
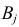
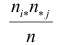
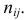
Если гипотеза 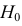
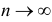
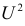
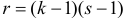
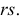
Определяя 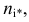
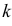
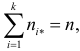
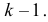
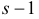
В таблице распределения 
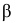
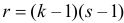
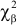
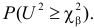
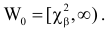
Пример №6
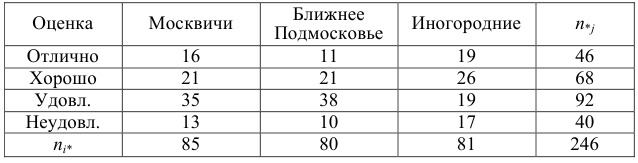
Данные о сдаче экзамена 246 студентами сгруппированы в зависимости от места окончания студентом средней школы.
Можно ли по этим данным заключить, что успеваемость студентов практически не зависит от места получения ими среднего образования? (Уровень значимости взять, например, равным 0,05.)
Решение. Предположим, что успеваемость студентов не зависит от места получения среднего образования (это гипотеза, которую предстоит проверить). Число степеней свободы равно 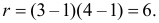
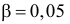
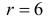
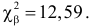
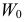
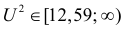
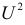
Вычисленное значение 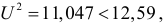
Ответ. Предположение о независимости успеваемости студентов от места получения ими среднего образования не противоречит опытным данным.
Проверка параметрических гипотез
Критерий для проверки гипотезы формируют за счет отнесения к критической области выборок, которые при данной гипотезе наименее вероятны. Но может оказаться, что одинаково маловероятных выборок при данной гипотезе больше, чем это необходимо для формирования критерия данного уровня значимости. Тогда трудно решить какие именно выборки следует включать в критическую область. Этих трудностей можно избежать, если вместе с проверяемой гипотезой рассматривать и альтернативные гипотезы.
Пусть случайная величина Х имеет функцию распределения 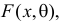
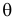
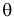
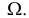
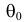
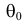
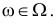
Определение. Параметрической статистической гипотезой 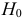
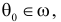
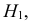
Гипотезу 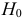
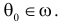
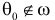
Гипотеза, однозначно определяющая вероятностное распределение, называется простой. В противном случае гипотезу называют сложной. Например, гипотеза о симметричности и однородности игрального кубика проста, так как однозначно определяет вероятности всех исходов при подбрасывании кубика. Гипотеза о том, что ошибка измерений имеет нормальный закон распределения, является сложной, так как при разных значениях параметров получаются разные нормальные законы распределения.
Простая параметрическая гипотеза против простой альтернативы может быть описана указанием одной точки 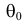
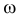
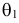
Параметрическую гипотезу проверяют по обычной схеме. Производят 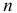
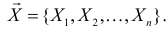
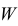
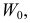
При любом критерии проверки статистической гипотезы по результатам наблюдений возможны ошибки двух типов: ошибка первого рода возникает при отклонении гипотезы 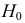
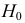
Обозначим через 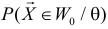
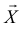
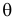
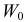
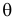
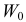
Заметим, что 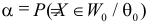
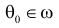
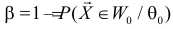
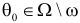
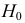
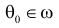
Разным критериям для проверки гипотезы 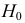
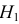
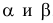
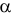
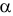
Учет ошибок первого и второго рода позволяет сравнивать между собой критерии. Пусть 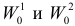
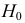
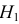
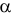
и
то критерий 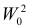
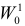
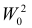
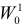
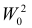
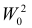
Пусть необходимо проверить гипотезу 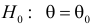
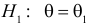
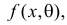
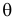
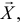
Согласно сформулированным требованиям относительно ошибок первого и второго рода, критическую область следует выбрать так, чтобы при заданном 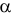
и при этом вероятность
была наибольшей.
Такую задачу впервые решили в начале тридцатых годов прошлого века Ю. Нейман и Э. Пирсон, и полученный ими результат носит их имя. Для формулировки этого результата понадобится понятие взаимной абсолютной непрерывности функций, которое состоит в том, что в каждой точке функции или обе равны нулю, или обе нулю не равны.
Лемма Неймана–Пирсона
Если 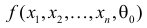
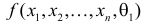
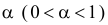
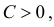
образуют критическую область 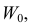
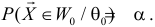
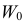
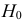
Замечание. Для дискретных величин в неравенстве (3.6.8) роль 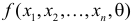
Пример №7
Известно, что при тщательном перемешивании теста изюмины распределяются в нем примерно по закону Пуассона, т.е. вероятность наличия в булочке 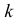
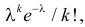
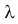
Построить критерий для проверки гипотезы о том, что 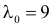
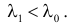
Решение. Для проверки гипотезы 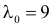
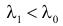
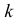
где С – некоторая постоянная.
Тогда 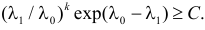
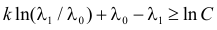
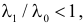
Итак, в критическую область следует включить значения 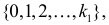
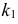
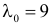
Отсюда следует, что если включить в критическую область значения для числа изюмин 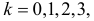
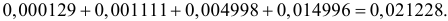
Заметим, что при добавлении в критическую область значения 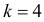
Ответ.
Пример №8
Изготовитель утверждает, что в данной большой партии изделий только 10% изделий низкого сорта. Было отобрано наугад пять изделий и среди них оказалось три изделия низкого сорта. С помощью леммы Неймана–Пирсона построить критерий и проверить гипотезу о том, что процент изделий низкого сорта действительно равен 10 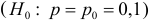
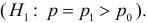
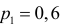
Решение. Согласно проверяемой гипотезе 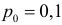
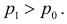
где С – некоторая постоянная.
После сокращения на 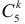
Прологарифмируем обе части неравенства
или
Так как 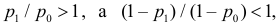
Значит, в критическую область следует включить те из значений 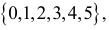
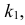
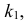
Если к критической области отнести значения 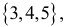
В условиях задачи оказалось, что среди пяти проверенных три изделия бракованных. Значение 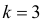
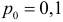
Вероятностью ошибки второго рода называется вероятность принять ложную гипотезу. Гипотеза 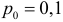
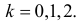
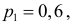
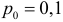
Вероятность ошибки второго рода велика потому, что критерий построен на скудном статистическом материале (всего пять наблюдений!).
Ответ. При уровне значимости 0,01 нулевую гипотезу отвергаем.
Пример №9
Количество первосортных изделий в крупной партии не должно быть менее 90%. Для проверки выбрали наугад 100 изделий. Среди них оказалось только 87 изделий первого сорта. Можно ли считать при вероятности ошибки первого рода, равной 0,05, что в данной партии менее 90 % первосортных изделий?
Решение. Построим критическую область для проверки гипотезы 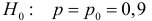
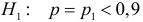
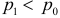
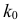
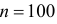
Откуда, с учетом нечетности функции Лапласа, имеем 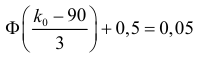
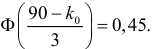
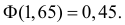
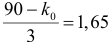
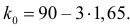
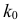
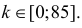
Ответ. Наличие в выборке менее 90% первосортных изделий можно объяснить случайностями выборки.
Пример №10
Случайная величина Х имеет нормальный закон распределения 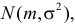
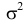
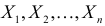
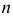
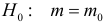
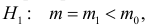
Решение. Так как наблюдения независимы, то 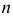
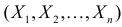
Поэтому по лемме Неймана–Пирсона к критической области должны быть отнесены те выборки, для которых
После логарифмирования неравенства получаем
откуда
Так как по условию 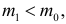
Итак, в критическую область следует включать выборки, для которых 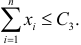
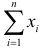
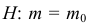
Отсюда 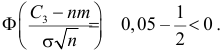
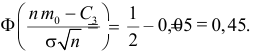
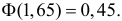
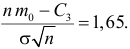
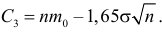
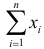
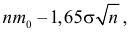
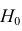
Ответ.
Проверка гипотезы о значении медианы
Пусть Х непрерывная случайная величина, а m – значение ее медианы, т.е. 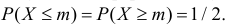
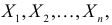
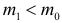
Предположим, что значение m действительно равно m0 (т.е. верна нулевая гипотеза 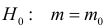
Если гипотеза верна, то 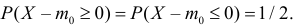
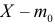
Величину S можно представить в виде 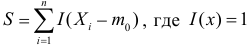
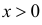
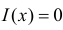
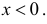
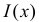
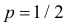
Очевидно, что при медиане равной 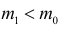
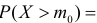
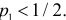
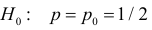
Согласно лемме Неймана–Пирсона для любого 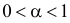
образуют критическую область наиболее мощного критерия. Так же как и в примере 3.19 легко показать, что в критическую область следует относить в первую очередь самые маленькие значения k. Остается только найти наибольшее k, для которого 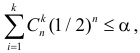
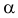
Пример №11
По результатам независимых наблюдений случайной величины 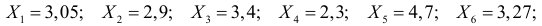
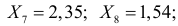
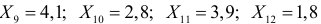
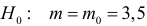
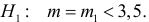
Решение. Ошибка первого рода совершается, когда отвергается верная гипотеза. Предположим, что нулевая гипотеза верна и медиана m действительно равна 3,5. Только в трех наблюдениях результаты превосходят 3,5. Как было показано выше, при альтернативе 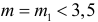
Откуда 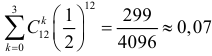
Ответ.
Проверка гипотезы о равенстве математических ожиданий
Пусть над случайной величиной X проделано n независимых наблюдений, в которых получены результаты 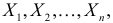
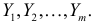
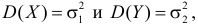
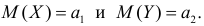
Предположим, что гипотеза верна. Так как серии опытов достаточно велики, то для средних арифметических имеем приближенные равенства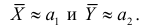
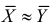
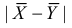
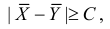
Свяжем эту постоянную C с уровнем значимости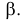
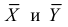
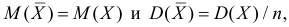
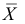
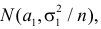
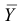
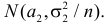
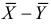
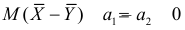
Запишем для нормального закона распределения 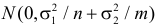
или
По заданному 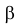
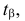
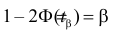
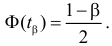
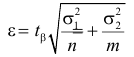
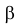
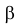
Замечание 1. Если дисперсии неизвестны, то большое число наблюдений в каждой серии позволяет достаточно точно оценить дисперсии по этим же опытным данным:
Пример №12
Среднее арифметическое результатов 25 независимых измерений некоторой постоянной величины равно 90,1. В другой серии из 20 независимых измерений получено среднее арифметическое, равное 89,5. Дисперсия ошибок измерения в обоих случаях одинакова и равна 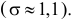
Решение. Выдвигаем гипотезу, что в каждой из серий измерялась одна и та же постоянная величина. Зададимся, например, уровнем значимости 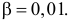
Тогда критическая область для проверки гипотезы определяется неравенством 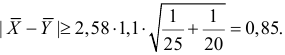
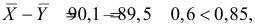
Ответ. Предположение о равенстве математических ожиданий не противоречит опытным данным.
Пример №13
По двум независимым выборкам объемов 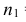
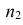
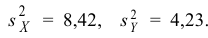
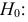
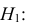
Решение. 1) По данным выборки вычисляем
2) По табл. П 2.7 (см. приложение 2), учитывая значения
находим число:
3) Сравниваем: так как 1,99 < 2,65, т.е. 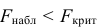
Ответ: гипотеза 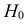
Пример №14
По двум независимым выборкам объемов 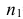
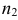
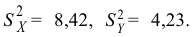
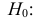
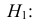
Решение. 1) По данным выборки вычисляем
2) По табл. П 2.7 (см. приложение 1), учитывая значения
находим число:
3) Сравниваем: так как 1,99 < 2,65, т.е. 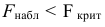
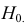
Ответ: гипотеза H0 : D(X)=D(Y) принимается.
Пример №15
По трем независимым выборкам объемов 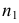
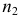
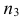
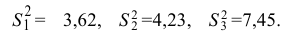
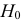
Решение. 1) По данным выборок вычисляем:
2) По табл. П 2.5 (см. приложение 2), учитывая значения
находим число
3) Сравниваем: так как 2,06 < 6,0 , т.е. 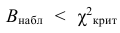
Ответ: гипотезу 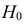
Пример №16
По двум независимым выборкам объемов 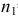
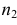
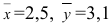
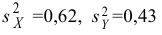
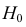
M(X) = M(Y) при конкурирующей гипотезе 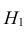
Решение 1) Так как 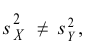
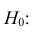
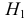
а) По данным выборки вычисляем
б) По табл. П 2.7 (см. приложение 2), учитывая значения
находим число:
в) Сравниваем: так как 1,44 < 3,89, т.е. 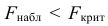
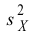
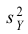
2) Проверим гипотезу 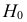
а) Найдем по табл. П 2.6 (см. приложение 2) значение 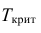
б) Найдем число
в) Сравнить числа 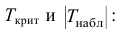
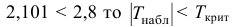
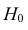
Ответ: гипотеза 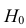
Пример №17
По двум независимым выборкам объемов 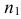
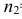
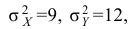
При уровне значимости α = 0,05 проверить гипотезу 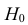
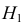
Решение. Воспользуемся замечанием 6. 1) Вычислим:
2) Находим 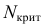
используя табл. П 2.2 (см. приложение 2).
Следовательно,
3) Сравниваем: так как 2,19 > 1,96, т.е. 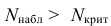
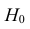
Значит, различие генеральных математических ожиданий значительное.
Ответ: гипотеза 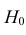
Определение статистической гипотезы
Определение: Статистической гипотезой называется гипотеза о виде неизвестного распределения или о параметрах известного распределения. Выдвинутую гипотезу называется основной (нулевой) и обозначается 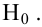
Гипотеза называется простой, если она содержит только одно предположение. Сложная гипотеза состоит из простых.
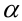
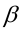
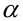
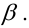
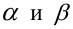
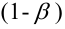
Статистический критерий проверки основной гипотезы Н0
Статистический критерий проверки основной гипотезы
Определение. Для проверки основной гипотезы 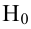
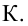
Определение. Областью принятия гипотезы 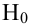
Выбор одного из этих случаев определяется видом конкурирующей гипотезы.
Основные шаги при проверке статистических гипотез:
1) выдвигаем
2) выдвигаем
3) задаем 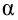
4) строим статистический критерий
5) строим критическую область
6) считаем наблюдаемое значение критерия и сравниваем с критическими точками
7) если наблюдаемое значение попадает в область принятия гипотезы, то нет причины отвергать 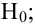
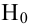
Проверка гипотезы о виде распределения случайной величины. Критерий согласия Пирсона
Пусть 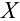
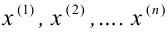
1) 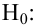
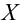
2) 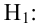
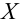
3) задаем 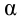
4) строим статистический критерий
Разобьем область, которой принадлежат результаты измерений, на 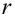
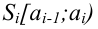
Пусть
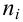
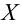
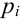
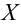
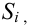
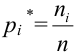
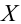
Тогда
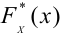
За меру отклонения истинной функции распределения 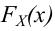
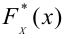
Теорема Пирсона:
Какова бы ни была 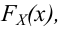
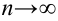
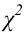
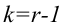
Замечание. Если в процессе проверки гипотезы приходится производить оценку параметров распределения, то количество степеней свободы 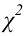
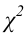
5) строим критическую область
Критическая область — правосторонняя
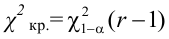
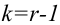
6) считаем наблюдаемое значение критерия 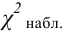
7) Вывод: если 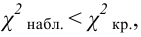
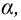
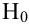
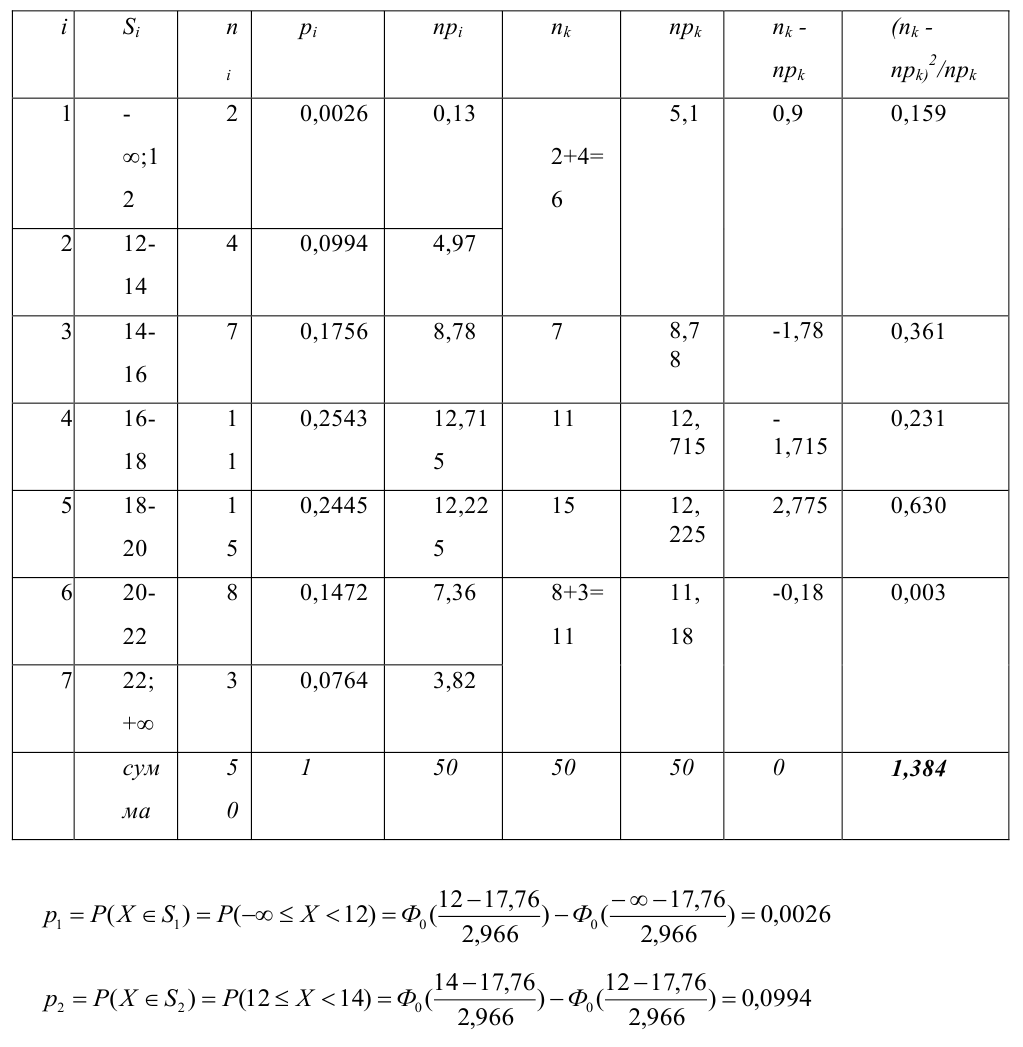
Пример №18
По выборке объема 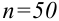
В качестве параметров нормального распределения выберем их точечные оценки:
1) 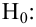
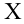
2) 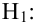
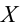
3)
4) строим статистический критерий
Замечание: если для какого-либо интервала не выполняется условие 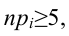
1,384 — наблюдаемое значение статистического критерия
5) строим критическую область
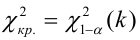
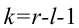
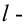
7) Вывод: нет оснований отвергнуть нулевую гипотезу на уровне значимости
Критерий Колмогорова — Смирнова
в классическом виде является более мощным, чем критерий Пирсона; используется для проверки гипотезы о соответствии эмпирического любому теоретическому непрерывному распределению 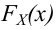
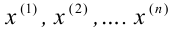
1) 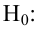
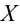
2) 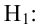
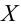
3) 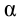
4) строим статистический критерий
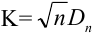
5) строим критическую область
Критическая область — правосторонняя; критические значения 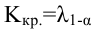
6) сравниваем наблюдаемое значение критерия 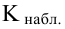
7) Вывод: если 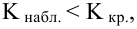
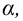
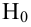
Проверка гипотез о параметрах известного распределения генеральной совокупности
Проверка гипотез о параметрах нормально распределенной генеральной совокупности

Пример №19
На завод поступила партия станков. По результатам исследования 13 станков найдена исправленная выборочная дисперсия размера изготовления станками деталей 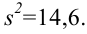
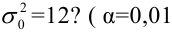
Решение:
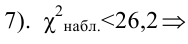
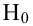
Проверка гипотез о параметре 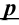
(сравнение относительной частоты с гипотетической вероятностью 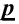
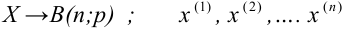
В электронных таблицах Excel для проверки гипотез о параметрах нормально распределенных генеральных совокупностей по результатам экспериментов есть специальные тесты, упрощающие процедуру вычислений.
Двухвыборочный 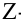
Двухвыборочный 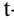
Парный двухвыборочный 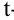
Двухвыборочный 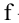
Пример №20
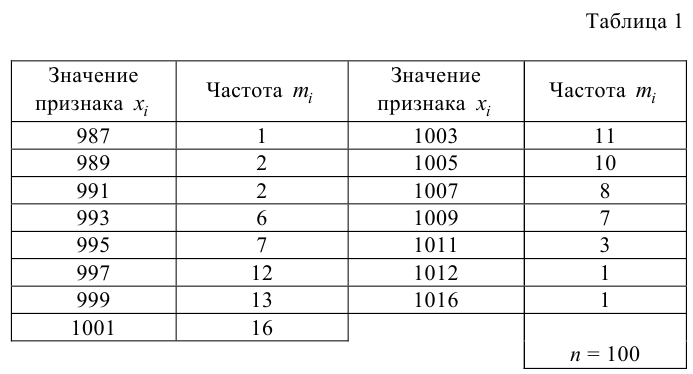
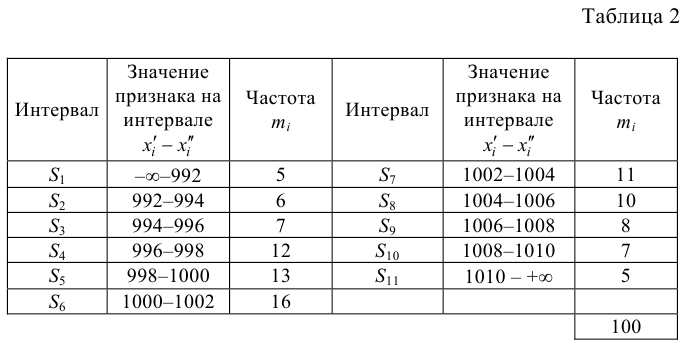
На предприятии провели выборочный опрос работающих об их средней заработной плате за предыдущий год. Данные опроса представлены в табл. 1.
С помощью критерия Пирсона проверить гипотезу о том, что средняя заработная плата по всему предприятию распределена по нормальному закону с уровнем значимости
Решение. Найдем функцию распределения признака 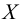
Для этого предварительно вычислим среднюю выборочную и исправленную статическую дисперсию
За функцию распределения признака 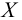
Выполним разбиение области значений случайной величины 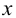
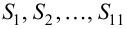
Для расчета теоретического ряда частот необходимо предварительно вычислить значения вероятностей 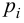
и применить формулу для вычисления теоретических частот:
где —
Например.
Значение функции 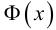
Значения 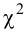
Так как два параметра распределения признака в генеральной совокупности находились на основании выборки, то функцию 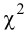
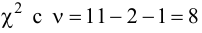
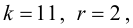
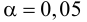
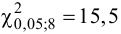
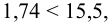
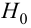
Следует отметить, что на практике все шире начинают применять критерии согласия не столько для проверки согласия экспериментальных данных с некоторой гипотетической функцией, сколько для подбора наилучшей функции распределения, хотя выбор подходящего закона должен основываться прежде всего на понимании механизма изучаемого явления.
Пример №21
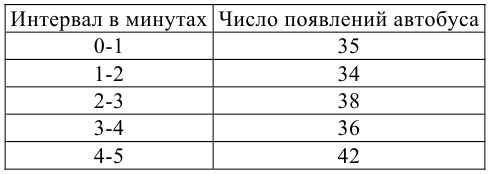
Наблюдалось следующее распределение по минутам числа появлений на остановке автобуса, имеющего пятиминутный интервал движения.
Проверить гипотезу о равномерном законе распределения.
Решение. 1. Вычисляем по данному вариационному ряду вероятности 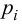
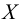
2. Для проверки гипотезы о том, что число появлений автобуса на остановке есть случайная величина, распределенная по равномерному закону, вычисляем критерии 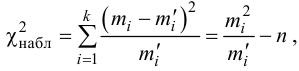
Контроль: 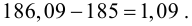
3. Определяем 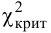
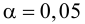
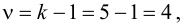
4.Так как 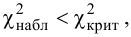
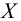
Пример №22
Рассмотрим вариационный ряд.
1. Если построить гистограмму частостей, то ее вид будет напоминать экспоненциальную кривую. Поэтому произведем «выравнивание» статистических данных по показательному закону. Запишем его дифференциальную функцию:
Для нахождения точечной оценки параметра 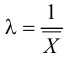
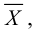
Тогда 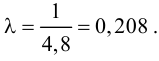
2. Для проверки соответствия эмпирических данных с предполагаемым показательным законом распределения применим критерий согласия
3. Вычислим вероятности попадания случайной величины 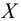
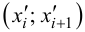
Для нахождения 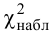
4. Найдем в таблице критических точек 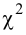
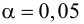
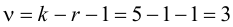
5. Так как 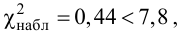
Пример №23
Из продукции цеха случайно отобрано 200 выборок по 5 деталей. Регистрировалось число бракованных деталей. В итоге получен вариационный ряд:
Требуется, используя критерий Пирсона при уровне значимости 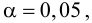
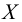
1. Найдем частость 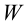
По формуле Бернулли 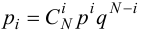
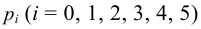
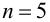
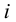
2. Для проверки нулевой гипотезы выдвигаем критерий
где 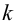
3. Вычисляем 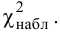
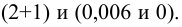
4. Находим 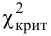
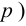
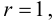
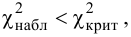
Пример №24
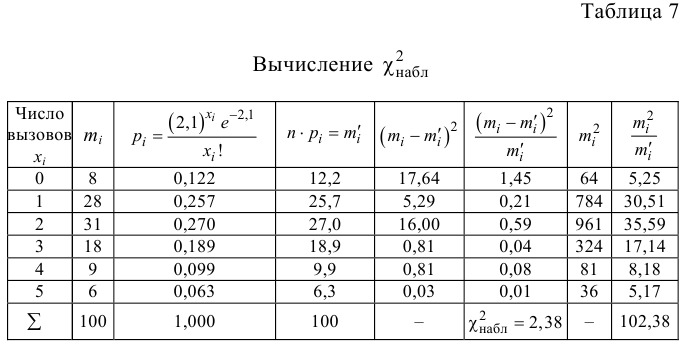
Проведено наблюдение за числом вызовов телефонной станции. С этой целью в течение 100 случайно выбранных 5-секундных интервалов времени регистрировалось число вызовов. Получен следующий вариационный ряд:
Проверить, используя критерий 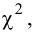
Вероятность ровно 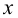
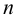
1. Найдем точечную оценку параметра 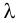
Таким образом, функция вероятностей предполагаемого закона Пуассона имеет вид
2.Применим критерии
3. Находим 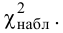
Контроль: 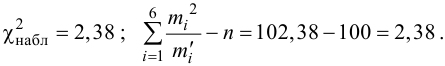
4. По таблице П5 по заданному уровню значимости и числу степеней свободы 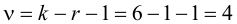
5. Так как 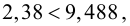
Итак, мы рассмотрели критерий 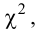
Пример №25
Менеджер кредитного отдела нефтяной компании выясняет, является ли среднемесячный баланс владельцев кредитных карточек, равным 75 у.е. Аудитор случайным образом отобрал 100 счетов и нашел, что среднемесячный баланс владельцев составил 83,4 у.е. с выборочным стандартным отклонением, равным 23,65 у.е. Определить на 5%-м уровне значимости, может ли этот аудитор утверждать, что средний баланс отличен от 75 у.е.
Решение. 1. Исходя из условия задачи, сформулируем гипотезы:
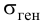
2. Для проверки гипотезы 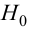
с двусторонней критической областью.
3. Вычислим
5. Так как 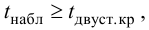
Пример №26
По двум независимым выборкам, объемы которых 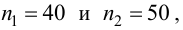
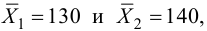
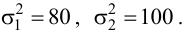
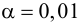
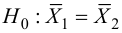
Решение. Найдем наблюдаемое значение критерия:
По условию конкурирующая гипотеза имеет вид 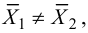
Найдем правую критическую точку из равенства
По таблице П2, часть 1, функции Лапласа находим 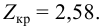
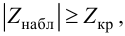
Пример №27
Менеджер предприятия решил выяснить, существует ли разница в производительности труда рабочих дневной и вечерней смены. Случайно организованная выборка 10 рабочих дневной смены показала, что средний выпуск продукции составил 74,3 ед./ч, а выборочная дисперсия оказалась равной 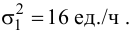
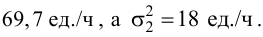
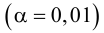
Решение. Так как выборочные дисперсии различны, проверим предварительно нулевую гипотезу 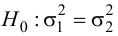
Найдем отношение большей исправленной дисперсии к меньшей: 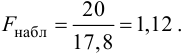
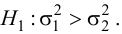
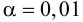
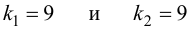
Так как 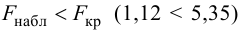
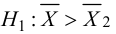
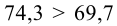
2. В качестве критерия проверки нулевой гипотезы примем случайную величину
4. Находим 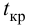
Так как 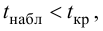
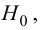
не существует разницы в производительности труда рабочих дневной и вечерней смены, а имеющие место различия случайны, незначимы.
Пример №28
Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены малые выборки, объемы которых 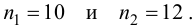
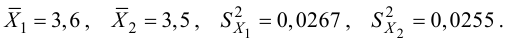
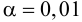
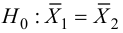
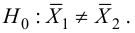
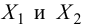
Решение. Рассматриваемый в этом параграфе критерий предполагает, что генеральные дисперсии одинаковы, но исправленные дисперсии различны, поэтому вначале нужно сравнить дисперсии, используя критерий Фишера-Сиедекора. Сделаем это, приняв в качестве альтернативной гипотезы 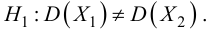
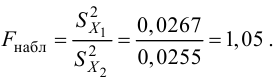
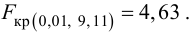
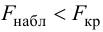
Сравним средние, для чего вычислим наблюдаемое значение критерия Стьюдента:
По условию, альтернативная гипотеза имеет вид 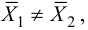
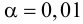
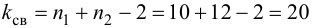
Так как 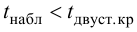
Таким образом, средние размеры изделий существенно не различаются.
- Регрессионный анализ
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
Ошибки первого и второго рода. Понятие о статистических критериях
Проверить статистическую гипотезу – значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. При этом проверяемая гипотеза может подтвердиться, а может и не подтвердиться. Проверка статистических гипотез сопряжена с возможностью допустить ошибку.
Ошибка первого рода состоит в том, что будет отвергнута верная гипотеза.
Ошибка второго рода состоит в том, что будет принята ложная гипотеза.
Вероятность совершения ошибки первого рода обозначается 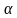
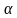
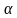
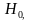
Вероятность не отклонить ложную гипотезу обозначается 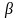
При проверке нулевой гипотезы могут возникнуть следующие ситуации (табл.):
|
|
верная |
ложная |
|
отклоняется |
Ошибка второго рода |
Решение верное |
|
не отклоняется |
Решение верное |
Ошибка второго рода |
Проверка любой статистической гипотезы осуществляется с помощью статистического критерия.
Статистический критерий – это случайная величина [статистика], которая используется с целью проверки нулевой гипотезы.
В дальнейшем статистический критерий непараметрических гипотез будем обозначать, как правило, буквой
Статистические критерии носят название соответственно распределению: 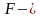
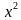
Наблюдаемое значение статистического критерия – это значение критерия, которое рассчитано по выборке с определенным законом распределения.
Множество всех возможных значений выбранного статистического критерия разделяется на два непересекающихся подмножества. Первое из этих подмножеств включает в себя значения критерия, при которых нулевая гипотеза отвергается, а второе – те значения критерия, при которых нулевая гипотеза принимается.
Критическая область – это множество возможных значений статистического критерия, при которых нулевая гипотеза отвергается.
Область принятия гипотезы [область допустимых значений] – это множество возможных значений статистического критерия, при которых нулевая гипотеза принимается.
В том случае, если наблюдаемое значение статистического критерия (рассчитанное по выборочной совокупности) принадлежит критической области, нулевую гипотезу отвергают. Если же наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то нулевая гипотеза принимается.
Критические точки [квантили] – это точки, которые разграничивают критическую область и область принятия гипотезы.
Выделяют одностороннюю и двустороннюю критические области. Дадим определения данных критических областей на примере условного статистического критерия 
Правосторонняя критическая область определяется неравенством 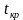
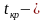
Левосторонняя критическая область определяется неравенством 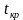
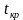
Двусторонняя критическая область определяется неравенствами