| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?'».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 p2 p4 p8 p16
Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| 9 | 511 | 502 | Hamming(511,502) | 502/511 ≈ 0.982 |
| … | ||||
| m | 
|

|
Hamming
|

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]
Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]
The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?'».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 p2 p4 p8 p16
Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| 9 | 511 | 502 | Hamming(511,502) | 502/511 ≈ 0.982 |
| … | ||||
| m | 
|

|
Hamming
|

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]
Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]
The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной 


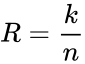
Если исходные 
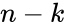
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из 

- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Линейный блоковый код — такой код, что множество его кодовых слов образует 



Это значит, что операция кодирования соответствует умножению исходного 
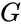
Пусть 

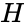

Минимальное расстояние и корректирующая способность
-
Основная статья: Расстояние Хемминга
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 
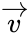


Минимальное расстояние Хемминга 
, округляем «вниз», так чтобы
.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 

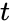
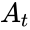


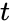

Таким образом получив искажённый код из 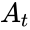

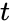
Поясним на примере. Предположим, что есть два кодовых слова 










Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 





Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 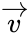
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 


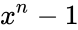
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 
Порождающий (генераторный) полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному 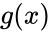
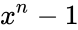
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления 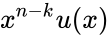
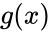
Таким образом, вид полинома 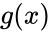
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | 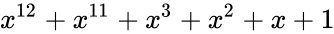
|
| CRC-16 | 16 | 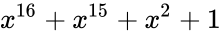
|
| CRC-CCITT | 16 | 
|
| CRC-32 | 32 | 
|
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома 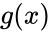
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Свёрточные коды
Файл:ECC NASA standard coder.png Свёрточный кодер (
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
-
Основная статья: Граница Хэмминга
Пусть имеется двоичный блоковый 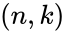
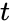
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
- Цифровая связь
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
Литература
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0
Ссылки
Имеется викиучебник по теме:
Обнаружение и исправление ошибок
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Обнаружение и исправление ошибок. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Рассмотрим,
чем определяется способность блочного
кода обнаруживать и исправлять ошибки,
возникшие при передаче.
Пусть
U
= (U0,
U1,
U2,
…Un-1)
— двоичная последовательность длиной
n.
Число
единиц
(ненулевых компонент) в этой
последовательности называется
весом
Хемминга
вектора U
и обозначается w(U).
Например,
вес Хемминга вектора U
=
( 1001011
) равен четырем, для вектора U
=
( 1111111
)
величина w(U)
составит 7 и т.д.
Таким
образом, чем больше единиц в двоичной
последовательности, тем больше ее вес
Хемминга.
Далее, пусть U и V будут
двоичными последовательностями длиной
n.
Число разрядов, в которых эти
последовательности различаются,
называется расстоянием Хемминга между
U и V и обозначается
d( U, V).
Например,
если U
=
( 1001011
), а V
= ( 0100011
), то d(
U, V) = 3.
Задав
линейный код, то есть определив все 2k
его кодовых слов, можно вычислить
расстояние между всеми возможными
парами кодовых слов. Минимальное из них
называется минимальным
кодовым расстоянием кода
и обозначается dmin.
Можно
проверить и убедиться, что минимальное
кодовое расстояние для рассматриваемого
нами в примерах (7,4)-кода
равно трем: dmin(7,4)
=
3.
Для этого нужно записать все кодовые
слова (7,4)-кода
Хемминга (всего 16 слов), вычислить
расстояния между их всеми парами и взять
наименьшее значение. Однако можно
определить dmin
блочного кода и более простым способом.
Доказано,
что расстояние между нулевым кодовым
словом и одним из кодовых слов, входящих
в порождающую матрицу (строки порождающей
матрицы линейного блочного кода сами
являются кодовыми словами, по определению),
равно dmin.
Но расстояние от любого кодового слова
до нулевого равно весу Хемминга этого
слова. Тогда dmin
равно минимальному
весу Хемминга
для
всех строк порождающей матрицы кода .
Если
при передаче кодового слова по каналу
связи в нем произошла одиночная
ошибка,
то расстояние Хемминга между переданным
словом U
и принятым вектором r
будет равно единице. Если при этом одно
кодовое слово не перешло в другое (а при
dmin
>
1 и при одиночной ошибке это невозможно),
то ошибка будет
обнаружена
при декодировании.
В
общем случае если блочный код имеет
минимальное расстояние dmin,
то он
может обнаруживать любые сочетания
ошибок при их числе, меньшем или равном
dmin
—
1,
поскольку никакое сочетание ошибок при
их числе, меньшем, чем dmin
—
1,
не может перевести одно кодовое слово
в другое.
Но
ошибки могут иметь кратность и большую,
чем dmin—
1,
и тогда они останутся
необнаруженными.
При
этом среднюю вероятность необнаруживаемой
ошибки можно определить следующим
образом.
Пусть
вероятность ошибки в канале связи равна
Pош.
Тогда вероятность того, что при передаче
последовательности длины n
в ней произойдет одна ошибка, равна
Р1
= n
Pош
( 1- Рош)n-1,
(1.36)
соответственно,
вероятность l-кратной
ошибки —
Pl
=Cnl
Pошl
( 1- Pош)n-l,
(1.37)
где
Cnl
— число возможных комбинаций из
n
символов кодовой последо-вательности
по l
ошибок.
По
каналу связи передаются кодовые слова
с различными весами Хемминга. Положим,
что ai
— число слов с весом i
в данном коде (всего слов в коде длиной
n
—
).
А
теперь определим, что такое необнаруживаемая
ошибка.
Обнаружение ошибки производится путем
вычисления синдрома принятой
последовательности. Если принятая
последовательность не является кодовым
словом ( тогда синдром не равен нулю),
то считается, что ошибка есть. Если же
синдром равен нулю, то полагаем, что
ошибки нет (принятая последовательность
является кодовым словом). Но
тем ли, которое передавалось? Или же в
результате действия ошибок переданное
кодовое слово перешло в другое кодовое
слово данного кода:
r
= U
+ е = V,
(1.38)
то
есть сумма переданного кодового слова
U
и вектора ошибки е
даст новое
кодовое слово V
? В этом случае, естественно, ошибка
обнаружена быть не может.
Но
из определения двоичного линейного
кода следует, что если
сумма кодового слова и некоторого
вектора е
есть кодовое слово, то вектор е
также представляет собой кодовое слово.
Следовательно,
необнаруживаемые ошибки будут возникать
тогда, когда сочетания ошибок будут
образовывать кодовые слова.
Вероятность
того, что вектор е
совпадает с кодовым словом, имеющим вес
i
,
равна
Pi
=
Pошi
(1- Рош)n-i
. (1.39)
Тогда полная
вероятность возникновения необнаруживаемой
ошибки
.
(1.40)
Пример:
рассматриваемый нами (7,4)-код
содержит по семь кодовых слов с весами
w
= 3 и w
= 4 и одно
кодовое слово с весом w
= 7, тогда
(1.41)
или,
при Рош
= 10
-3,
Р(Е)
7
10
-9.
Другими
словами, если по каналу передается
информация
со скоростью V
=
1кбит/с и в канале в среднем каждую
секунду
будет происходить искажение одного
символа, то в среднем семь принятых слов
на 109
переданных будут проходить через декодер
без обнаружения ошибки (одна необнаруживаемая
ошибка за 270 часов).
Таким
образом, использование даже такого
простого кода позволяет на несколько
порядков снизить вероятность
необнаруживаемых ошибок.
Теперь
предположим, что линейный блочный код
используется для исправления ошибок.
Чем определяются его возможности по
исправлению?
Рассмотрим
пример, приведенный на рис. 1.9. Пусть U
и V
представляют
пару кодовых слов кода с
кодовым расстоянием d
,
равным минимальному — d
min
для
данного
кода.

Рис.
1.9
Предположим,
передано кодовое слово U,
в
канале произошла одиночная
ошибка
и принят вектор а
(не
принадлежащий коду).
Если
декодирование производится оптимальным
способом, то есть по
методу максимального правдоподобия,
то в
качестве оценки U*
нужно
выбрать ближайшее к а
кодовое
слово.
Таковым
в данном случае будет U,
следовательно, ошибка будет устранена.
Представим
теперь, что произошло две ошибки и принят
вектор b.
Тогда
при декодировании по максимуму
правдоподобия в
качестве оценки будет выбрано ближайшее
к b
кодовое слово, и им будет
V.
Произойдет ошибка декодирования.
Продолжив
рассуждения для dmin
=
4, dmin
=
5
и т.д., нетрудно сделать вывод, что ошибки
будут устранены, если их кратность l
не превышает величины
l<
INT (( dmin – 1 )/2) ,
(1.41)
где
INT (X)
— целая часть Х.
Так,
используемый нами в качестве примера
(7,4)-код
имеет dmin
= 3 и,
следовательно, позволяет
исправлять лишь одиночные ошибки:
l
= INT
(( dmin
– 1
)/2)=INT((3-1)/2)=1
.
(1.42)
Таким
образом, возможности
линейных блочных кодов по обнаружению
и исправлению ошибок определяются их
минимальным кодовым расстоянием.
Чем
больше dmin,
тем большее число ошибок в принятой
последовательности можно исправить.
А
теперь определим вероятность того, что
возникшая в процессе передачи ошибка
не будет все же исправлена при
декодировании.
Пусть,
как и ранее, вероятность ошибки в канале
будет равна Рош.
Ошибки, возникающие в различных позициях
кода, считаем независимыми.
Вероятность
того, что принятый вектор r
будет иметь какие-нибудь (одиночные,
двукратные, трехкратные и т.д.) ошибки,
можно определить как
Рош
= P1
+ P2
+ P3
+… + Pn
,
(1.43)
где
Р1
— вероятность того, что в r
присутствует
одиночная ошибка;
Р2
—
вероятность того, что ошибка двойная и
т.д.;
Рn
— вероятность того, что все n
символов
искажены.
Определим вероятность ошибок заданной
кратности:
Р1
=
Вер{ошибка
в 1-й позиции ИЛИ ошибка во 2-й позиции
..ИЛИ в n-й позиции}
= = Рош(1-
Рош)n-1
+ Рош(1-
Рош)n-1
+…Рош(1-
Рош)n-1
= п
Рош(1-
Рош)n-;
(1.44)
Р2
=
Вер{ошибка
в 1-й И во 2-й позиции ИЛИ ошибка во 2-й И
в 3-й позиции…}
=
=
P2ош(1-Рош)n-2
+…Р2ош(1-
Рош)
n-2 =
Р2ош(1-
Рош)
n-2.
(1.45)
Аналогичным
образом
Р3
=
Р3ош(1-
Рош)n-3
и т.д.
(1.46)
Декодер,
как мы показали, исправляет все ошибки,
кратность которых не превышает
,
(1.47)
то
есть все ошибки кратности J
l будут
исправлены.
Тогда
ошибки декодирования — это ошибки с
кратностью, большей кратности исправляемых
ошибок l,
и их вероятность
.
(1.48)
Для
(7,4)-кода
Хемминга минимальное расстояние dmin
=
3,
т.е. l
=
1.
Следовательно, ошибки кратности 2 и
более исправлены не будут и
.
(1.49)
Если
Рош<<
1,
можно считать (1-
Рош)
1
и, кроме того, Р3ош<<
Р2ош.
Тогда
.
(1.50)
Так, например,
при вероятности ошибки в канале Рош
= 10 -3 вероятность
неисправления ошибки Р(N)
2 10
-5, то есть при такой
вероятности ошибок в канале кодирование
(7.4)-кодом позволяет снизить
вероятность оставшихся неисправленными
ошибок примерно в пятьдесят раз.
Если
же вероятность ошибки в канале будет
в сто раз меньше Рош
= 10 -5, то вероятность
ее неисправления составит уже Р(N)
210
-9, или в 5000 раз
меньше!
Таким
образом, выигрыш от помехоустойчивого
кодирования (который можно определить
как отношение числа ошибок в канале к
числу оставшихся неисправленными
ошибок) существенно зависит от свойств
канала связи.
Если
вероятность ошибок в канале велика, то
есть канал не очень хороший, ожидать
большого эффекта от кодирования не
приходится, если же вероятность ошибок
в канале мала, то корректирующее
кодирование уменьшает ее в значительно
большей степени.
Другими
словами, помехоустойчивое кодирование
существенно улучшает свойства хороших
каналов, в плохих же каналах оно большого
эффекта не дает.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
10.06.2015684.82 Кб13P4.pdf
- #
- #
- #
- #
| Обноружение ошибок | ||||
| Исправление ошибок | ||||
| Коррекция ошибок | ||||
| Назад | ||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = 
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.
| Двоичные коды Хэмминга | |
|---|---|
 Код Хэмминга (7,4) (с r = 3) Код Хэмминга (7,4) (с r = 3) |
|
| Назван в честь | Ричард У. Хэмминг |
| Классификация | |
| Тип | Код линейного блока |
| Длина блока | 2 — 1, где r ≥ 2 |
| Длина сообщения | 2 — r — 1 |
| Коэффициент | 1 — r / (2 — 1) |
| Расстояние | 3 |
| Размер алфавита | 2 |
| Обозначение | [2 — 1, 2 — r — 1, 3] 2 — код |
| Свойства | |
| совершенный код | |
|
В информатике и телекоммуникациях, коды Хэмминга являются семейством линейного исправления ошибок коды. Коды Хэмминга могут обнаруживать до двух битовых ошибок или исправлять однобитовые ошибки без обнаружения неисправленных ошибок. Напротив, простой код четности не может исправлять ошибки и может обнаруживать только нечетное количество битов с ошибкой. Коды Хэмминга — это совершенные коды, то есть они достигают наивысшей возможной скорости для кодов с их длиной блока и минимальным расстоянием, равным трем. Ричард В. Хэмминг изобрел коды Хэмминга в 1950 году как способ автоматического исправления ошибок, вносимых считывающими устройствами перфокарт. В своей оригинальной статье Хэмминг развил свою общую идею, но специально сосредоточился на коде Хэмминга (7,4), который добавляет три бита четности к четырем битам данных.
В математические термины, коды Хэмминга — это класс двоичных линейных кодов. Для каждого целого числа r ≥ 2 существует код с длиной блока n = 2 — 1 и длиной сообщения k = 2 — r — 1. Следовательно, скорость кодов Хэмминга равна R = k / n = 1 — r / (2 — 1), что является максимально возможным для кодов с минимальным расстоянием, равным трем (т. е. минимальное количество битовых изменений, необходимых для перехода от любого кодового слова к любому другому кодовому слову, равно трем) и длина блока 2-1. Матрица проверки на четность кода Хэмминга строится путем перечисления всех столбцов длины r, которые не равны нулю, что означает, что двойной код из код Хэмминга — это сокращенный код Адамара. Матрица проверки на четность имеет свойство, состоящее в том, что любые два столбца являются попарно линейно независимыми.
Из-за ограниченной избыточности, которую коды Хэмминга добавляют к данным, они могут обнаруживать и исправлять ошибки только при низком уровне ошибок. Это случай компьютерной памяти (ECC-память ), где битовые ошибки крайне редки, а коды Хэмминга широко используются. В этом контексте часто используется расширенный код Хэмминга, имеющий один дополнительный бит четности. Расширенные коды Хэмминга достигают расстояния Хэмминга, равного четырем, что позволяет декодеру различать, когда возникает не более одной однобитовой ошибки, и когда возникают любые двухбитовые ошибки. В этом смысле расширенные коды Хэмминга предназначены для исправления одиночной ошибки и обнаружения двойной ошибки, сокращенно SECDED .
Содержание
- 1 История
- 1.1 Коды, предшествующие Хэммингу
- 1.1.1 Четность
- 1.1.2 Код два из пяти
- 1.1.3 Повторение
- 1.1 Коды, предшествующие Хэммингу
- 2 кода Хэмминга
- 2.1 Общий алгоритм
- 3 кода Хэмминга с дополнительной четностью (SECDED)
- 4 [7,4 ] Код Хэмминга
- 4.1 Построение G и H
- 4.2 Кодирование
- 4.3 [7,4] Код Хэмминга с дополнительным битом четности
- 5 См. Также
- 6 Примечания
- 7 Ссылки
- 8 Внешние ссылки
История
Ричард Хэмминг, изобретатель кодов Хэмминга, работал в Bell Labs в конце 1940-х годов над компьютером Bell Model V., электромеханическая релейная машина с временем цикла в секундах. Ввод подавался на перфоленту шириной семь восьмых дюйма, которая имела до шести отверстий в ряду. В будние дни при обнаружении ошибок в реле машина останавливалась и мигала, чтобы операторы могли исправить проблему. В нерабочее время и в выходные дни, когда не было операторов, машина просто переходила к следующему заданию.
Хэмминг работал по выходным и все больше разочаровывался в необходимости перезапускать свои программы с нуля из-за обнаруженных ошибок. В записанном на пленку интервью Хэмминг сказал: «И поэтому я сказал:« Черт побери, если машина может обнаружить ошибку, почему она не может определить местоположение ошибки и исправить ее? »». В течение следующих нескольких лет он работал над проблемой исправления ошибок, разрабатывая все более мощный набор алгоритмов. В 1950 году он опубликовал то, что теперь известно как код Хэмминга, который до сих пор используется в таких приложениях, как память ECC.
Коды, предшествующие Хэммингу
Ряд простых кодов обнаружения ошибок использовался и до Коды Хэмминга, но ни один из них не был столь же эффективен, как коды Хэмминга в том же объеме.
Четность
Четность добавляет один бит, который указывает, было ли количество единиц (битовых позиций со значением один) в предыдущих данных четным или нечетное. Если при передаче изменяется нечетное количество битов, сообщение изменит четность, и в этот момент может быть обнаружена ошибка; однако бит, который изменился, мог быть самим битом четности. Наиболее распространенное соглашение состоит в том, что значение четности, равное единице, указывает, что в данных есть нечетное количество единиц, а значение четности, равное нулю, указывает, что существует четное количество единиц. Если количество измененных битов четное, контрольный бит будет действительным и ошибка не будет обнаружена.
Более того, четность не указывает, какой бит содержит ошибку, даже если он может ее обнаружить. Данные должны быть полностью отброшены и повторно переданы с нуля. В шумной среде передачи успешная передача может занять много времени или может никогда не произойти. Однако, хотя качество проверки четности оставляет желать лучшего, поскольку он использует только один бит, этот метод дает наименьшие накладные расходы.
Код два из пяти
Код два из пяти — это схема кодирования, которая использует пять битов, состоящих ровно из трех нулей и двух единиц. Это дает десять возможных комбинаций, достаточных для представления цифр 0–9. Эта схема может обнаруживать все одиночные битовые ошибки, все битовые ошибки с нечетными номерами и некоторые битовые ошибки с четными номерами (например, переворачивание обоих 1-битов). Однако он по-прежнему не может исправить ни одну из этих ошибок.
Повторение
Другой используемый в то время код повторял каждый бит данных несколько раз, чтобы гарантировать, что он был отправлен правильно. Например, если бит данных, который должен быть отправлен, равен 1, код повторения n = 3 отправит 111. Если три полученных бита не идентичны, во время передачи произошла ошибка. Если канал достаточно чистый, большую часть времени в каждой тройке будет изменяться только один бит. Следовательно, 001, 010 и 100 соответствуют 0 биту, а 110, 101 и 011 соответствуют 1 биту, причем большее количество одинаковых цифр (‘0’ или ‘1’) указывает, что бит данных должен быть. Код с этой способностью восстанавливать исходное сообщение при наличии ошибок известен как код исправления ошибок. Этот код с тройным повторением является кодом Хэмминга с m = 2, поскольку имеется два бита четности и 2 — 2 — 1 = 1 бит данных.
Однако такие коды не могут правильно исправить все ошибки. В нашем примере, если канал переворачивает два бита и получатель получает 001, система обнаружит ошибку, но сделает вывод, что исходный бит равен 0, что неверно. Если мы увеличим размер битовой строки до четырех, мы сможем обнаружить все двухбитовые ошибки, но не сможем исправить их (количество битов четности четное); при пяти битах мы можем как обнаруживать, так и исправлять все двухбитовые ошибки, но не все трехбитные ошибки.
Более того, увеличение размера строки битов четности неэффективно, так как в нашем исходном случае пропускная способность снижается в три раза, а эффективность резко падает, когда мы увеличиваем количество дублирований каждого бита для обнаружения и исправьте больше ошибок.
Коды Хэмминга
Если в сообщение включено больше исправляющих ошибок битов, и если эти биты могут быть расположены так, что разные неправильные биты дают разные результаты ошибок, то плохие биты могут быть идентифицированы. В семибитном сообщении существует семь возможных однобитовых ошибок, поэтому три бита контроля ошибок потенциально могут указывать не только на то, что произошла ошибка, но и на то, какой бит вызвал ошибку.
Хэмминг изучил существующие схемы кодирования, включая две из пяти, и обобщил их концепции. Для начала он разработал номенклатуру для описания системы, включая количество битов данных и битов исправления ошибок в блоке. Например, четность включает в себя один бит для любого слова данных, поэтому, предполагая ASCII слова с семью битами, Хэмминг описал это как код (8,7), всего восемь битов, из которых семь являются данными. Пример повторения будет (3,1), следуя той же логике. Кодовая скорость — это второе число, деленное на первое, для нашего примера с повторением 1/3.
Хэмминг также заметил проблемы с переворачиванием двух или более битов и описал это как «расстояние» (теперь оно называется расстоянием Хэмминга, после него). Четность имеет расстояние 2, поэтому одно переключение бита можно обнаружить, но не исправить, и любые два изменения бита будут невидимы. Повторение (3,1) имеет расстояние 3, так как три бита необходимо перевернуть в одной и той же тройке, чтобы получить другое кодовое слово без видимых ошибок. Он может исправлять однобитовые ошибки или обнаруживать, но не исправлять, двухбитовые ошибки. Повторение (4,1) (каждый бит повторяется четыре раза) имеет расстояние 4, поэтому переворот трех битов можно обнаружить, но не исправить. Когда три бита в одной группе меняются местами, могут возникнуть ситуации, когда попытка исправить приведет к неправильному кодовому слову. Как правило, код с расстоянием k может обнаруживать, но не исправлять k — 1 ошибок.
Хэмминга интересовали сразу две проблемы: как можно больше увеличить расстояние и в то же время как можно больше увеличить скорость кода. В 1940-х годах он разработал несколько схем кодирования, которые значительно улучшили существующие коды. Ключом ко всем его системам было перекрытие битов четности, чтобы им удавалось проверять друг друга, а также данные.
Общий алгоритм
Следующий общий алгоритм генерирует код исправления одиночных ошибок (SEC) для любого количества битов. Основная идея состоит в том, чтобы выбрать биты с исправлением ошибок так, чтобы индекс-XOR (XOR всех битовых позиций, содержащих 1) был равен 0. Мы используем позиции 1, 10, 100 и т. Д. ( в двоичном формате) в качестве битов исправления ошибок, что гарантирует возможность установки битов исправления ошибок так, чтобы индекс-исключающее ИЛИ всего сообщения был равен 0. Если получатель получает строку с индексом-исключающее ИЛИ 0, он может заключить повреждений не было, в противном случае индекс-XOR указывает индекс поврежденного бита.
Алгоритм может быть выведен из следующего описания:
- Пронумеруйте биты, начиная с 1: бит 1, 2, 3, 4, 5, 6, 7 и т. Д.
- Запись номера битов в двоичном формате: 1, 10, 11, 100, 101, 110, 111 и т. д.
- Все позиции битов, которые являются степенями двойки (имеют один бит 1 в двоичной форме их позиции) являются битами четности: 1, 2, 4, 8 и т. д. (1, 10, 100, 1000)
- Все остальные битовые позиции, с двумя или более 1 битами в двоичной форме их позиции, являются данными биты.
- Каждый бит данных включен в уникальный набор из 2 или более битов четности, что определяется двоичной формой его битовой позиции.
- Бит четности 1 охватывает все битовые позиции, для которых установлен наименьший значащий бит: бит 1 (сам бит четности), 3, 5, 7, 9 и т. Д.
- Бит четности 2 охватывает все позиции битов, для которых установлен второй младший значащий бит: бит 2 (сам бит четности), 3, 6, 7, 10, 11 и т. Д.
- Бит четности 4 охватывает все позиции битов, для которых установлен третий младший значащий бит: биты 4–7, 12–15, 20–23 и т. Д.
- Бит четности 8 охватывает все биты позиции, в которых установлен четвертый младший значащий бит: биты 8–15, 24–31, 40–47 и т. д.
- Как правило, каждый бит четности охватывает все биты, для которых выполняется побитовое И позиция четности и позиция бита не равны нулю.
Если байт данных, который должен быть закодирован, равен 10011010, то слово данных (с использованием _ для представления битов четности) будет __1_001_1010, а кодовое слово — 011100101010.
Выбор четности, четной или нечетной, не имеет значения, но один и тот же выбор должен использоваться как для кодирования, так и для декодирования.
Это общее правило можно показать визуально:
-
Положение бита 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Биты кодированных данных p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Четность. бит. охват p1 p2 p4 p8 p16
Показаны только 20 закодированных битов (5 четности, 15 данных), но шаблон продолжается бесконечно. Ключевой особенностью кодов Хэмминга, которую можно увидеть при визуальном осмотре, является то, что любой заданный бит включен в уникальный набор битов четности. Чтобы проверить наличие ошибок, проверьте все биты четности. Шаблон ошибок, называемый синдромом ошибки , определяет бит с ошибкой. Если все биты четности верны, ошибки нет. В противном случае сумма позиций ошибочных битов четности идентифицирует ошибочный бит. Например, если биты четности в позициях 1, 2 и 8 указывают на ошибку, то бит 1 + 2 + 8 = 11 является ошибочным. Если только один бит четности указывает на ошибку, сам бит четности ошибочен.
Как видите, если у вас есть m битов четности, он может охватывать биты от 1 до 2 m — 1 { displaystyle 2 ^ {m} -1}

| Биты четности | Всего битов | Биты данных | Имя | Скорость |
|---|---|---|---|---|
| 2 | 3 | 1 | Хэмминга (3,1). (Triple код повторения ) | 1/3 ≈ 0,333 |
| 3 | 7 | 4 | Хэмминга (7,4) | 4/7 ≈ 0,571 |
| 4 | 15 | 11 | Хэмминга(15,11) | 11/15 ≈ 0,733 |
| 5 | 31 | 26 | Хэмминга (31,26) | 26/31 ≈ 0,839 |
| 6 | 63 | 57 | Хэмминга(63,57) | 57/63 ≈ 0,905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0,945 |
| 8 | 255 | 247 | Hamming(255,247) | 247 / 255 ≈ 0,969 |
| … | ||||
| m | n = 2 м — 1 { displaystyle n = 2 ^ {m} -1} |
k = 2 m — m — 1 { displaystyle k = 2 ^ {m} -m-1 } |
Хэмминга (2 м — 1, 2 м — м — 1) { displaystyle (2 ^ {m} -1,2 ^ {m} -m-1)} |
(2 м — m — 1) / (2 m — 1) { displaystyle (2 ^ {m} -m-1) / (2 ^ {m} -1)} |
Коды Хэмминга с дополнительной четностью (SECDED)
Коды Хэмминга имеют минимальное расстояние 3, что означает, что декодер может обнаруживать и исправлять одиночную ошибку, но не может отличить двойную битовую ошибку некоторого кодового слова от одиночной битовой ошибки другого c. одесловие. Таким образом, некоторые двухбитовые ошибки будут неправильно декодированы, как если бы они были одноразрядными ошибками, и, следовательно, останутся необнаруженными, если не будет предпринята попытка исправления.
Чтобы исправить этот недостаток, коды Хэмминга могут быть расширены дополнительным битом четности. Таким образом, можно увеличить минимальное расстояние кода Хэмминга до 4, что позволяет декодеру различать одиночные битовые ошибки и двухбитовые ошибки. Таким образом, декодер может обнаруживать и исправлять одиночную ошибку и в то же время обнаруживать (но не исправлять) двойную ошибку.
Если декодер не пытается исправить ошибки, он может надежно обнаружить тройные битовые ошибки. Если декодер исправляет ошибки, некоторые тройные ошибки будут ошибочно приняты за одиночные и «исправлены» до неправильного значения. Таким образом, исправление ошибок — это компромисс между уверенностью (способностью надежно обнаруживать тройные битовые ошибки) и отказоустойчивостью (способностью продолжать работу перед лицом однобитовых ошибок).
Этот расширенный код Хэмминга популярен в системах памяти компьютеров, где он известен как SECDED (сокращенно от «исправление одиночных ошибок», «обнаружение двойных ошибок»). Особенно популярен код (72,64), усеченный (127,120) код Хэмминга плюс дополнительный бит четности, который имеет такие же объемы служебных данных, как и код четности (9,8).
[7,4] Код Хэмминга

В 1950 году Хэмминг представил [7,4] Код Хэмминга. Он кодирует четыре бита данных в семь битов, добавляя три бита четности. Он может обнаруживать и исправлять однобитовые ошибки. С добавлением общего бита четности он также может обнаруживать (но не исправлять) двухбитовые ошибки.
Построение G и H
Матрица G: = (I k — AT) { displaystyle mathbf {G}: = { begin {pmatrix} { begin {array} {c | c} I_ {k} — A ^ { text {T}} \ end {array}} end {pmatrix}}}
и H: = (AI n — k) { displaystyle mathbf {H}: = { begin {pmatrix} { begin {array} {c | c} A I_ {nk} \ end {array}} end {pmatrix}}}
Это конструкция из G и H в стандартной (или систематической) форме. Независимо от формы, G и H для линейных блочных кодов должны удовлетворять
HGT = 0 { displaystyle mathbf {H} , mathbf {G} ^ { text {T}} = mathbf {0}}
Поскольку [7, 4, 3] = [n, k, d] = [2 — 1, 2−1 − m, 3]. Матрица проверки на четность Hкода Хэмминга строится путем перечисления всех столбцов длины m, которые попарно независимы.
Таким образом, H — это матрица, левая часть которой представляет собой все ненулевые наборы из n элементов, где порядок наборов из n элементов в столбцах матрицы не имеет значения. Правая часть — это просто (n — k) — единичная матрица.
Итак, G может быть получена из H путем транспонирования левой части H с единичной k- единичной матрицей в левой части G.
Код образующей матрицы G { displaystyle mathbf {G }}

G: = (1 0 0 0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 0 0 1 1 1 1) 4, 7 { displaystyle mathbf {G}: = { begin {pmatrix} 1 0 0 0 1 1 0 \ 0 1 0 0 1 0 1 \ 0 0 1 0 0 1 1 \ 0 0 0 1 1 1 1 \ end {pmatrix}} _ {4,7}}
и
H: = (1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 0 0 1) 3, 7. { displaystyle mathbf {H}: = { begin {pmatrix} 1 1 0 1 1 0 0 \ 1 0 1 1 0 1 0 \ 0 1 1 1 1 0 0 1 \ end {pmatrix}} _ {3,7}.}
Наконец, эти матрицы можно преобразовать в эквивалентные несистематические коды с помощью следующих операций:
- Перестановки столбцов (замена столбцов)
- Операции с элементарными строками (замена строки линейной комбинацией строк)
Кодирование
- Пример
Из вышеприведенной матрицы имеем 2 = 2 = 16 кодовых слов. Пусть a → { displaystyle { vec {a}}}
![{ displaystyle { vec {a}} = [a_ {1 }, a_ {2}, a_ {3}, a_ {4}], quad a_ {i} in {0,1 }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



Например, пусть a → = [1, 0, 1, 1] { displaystyle { vec {a}} = [1,0,1,1]}![{ displaystyle { vec {a}} = [1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)

x → = a → G = (1 0 1 1) (1 0 0 0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 0 0 1 1 1 1) = (1 0 1 1 2 3 2) = (1 0 1 1 0 1 0) { displaystyle { vec {x}} = { vec {a}} G = { begin {pmatrix} 1 0 1 1 end {pmatrix}} { begin {pmatrix} 1 0 0 0 1 1 0 \ 0 1 0 0 0 1 0 1 \ 0 0 1 1 0 0 0 0 1 \ 0 0 1 1 0 0 0 0 0 1 \ 0 0 1 1 0 0 0 0 0 0 1 \ end {pmatrix}} = { begin {pmatrix} 1 0 1 1 2 3 2 end {pmatrix}} = { begin {pmatrix} 1 0 1 1 0 1 0 end {pmatrix}}}
[7,4] Код Хэмминга с дополнительным бит четности

Код Хэмминга [7,4] можно легко расширить до кода [8,4], добавив дополнительный бит четности поверх (7, 4) закодированное слово (см. Хэмминга (7,4) ). Это можно суммировать с помощью исправленных матриц:
- G: = (1 1 1 0 0 0 0 1 1 0 0 1 1 0 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 1 0) 4, 8 { displaystyle mathbf {G}: = { begin {pmatrix} 1 1 1 0 0 0 0 1 \ 1 0 0 1 1 1 0 0 1 \ 0 1 0 1 0 1 0 1 \ 1 1 0 1 0 0 0 1 0} end {p : = (1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 1) 4, 8. { displaystyle mathbf {H}: = { begin {pmatrix} 1 0 1 0 1 0 1 0 \ 0 1 1 0 0 1 1 0 \ 0 0 0 1 1 1 1 1 0 \ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 end _ {424>}. форма. Чтобы получить G, можно использовать элементарные операции со строками для получения матрицы, эквивалентной H в систематической форме:
- H = (0 1 1 1 1 0 0 0 1 0 1 1 0 1 0 0 1 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1) 4, 8. { displaystyle mathbf {H} = left ({ begin {array} {cccc | cccc} 0 1 1 1 1 0 0 0 \ 1 0 1 1 0 1 0 0 \ 1 1 0 1 0 0 0 1 0 \ 1 1 1 0 1 end массив) {0} {0}
Например, первая строка в этой матрице представляет собой сумму второй и третьей строк H в несистематической форме. Используя приведенную выше систематическую конструкцию для кодов Хэмминга, матрица A очевидна, а систематическая форма G записывается как
- G = (1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 1 0 0 1 0 1 1 0 1 0 0 0 1 1 1 1 0) 4, 8. { displaystyle mathbf {G} = left ({ begin {array} {cccc | cccc} 1 0 0 0 0 1 1 1 1 \ 0 1 0 0 1 0 1 1 \ 0 0 1 0 1 1 0 0 1 \ 0 0 0 1 1 end array. {} {}
Несистематическая форма G может быть сокращена по строке (с использованием элементарных операций со строкой), чтобы соответствовать этой матрице.
Добавление четвертой строки эффективно вычисляет сумму всех битов кодового слова (данные и четность) как четвертый бит четности.
Например, 1011 кодируется (с использованием несистематической формы G в начале этого раздела) в 01100110, где синие цифры — данные; красные цифры — это биты четности из кода Хэмминга [7,4]; а зеленая цифра — это бит четности, добавленный кодом [8,4]. Зеленая цифра делает четность кодовых слов [7,4] четной.
Наконец, можно показать, что минимальное расстояние увеличилось с 3 в коде [7,4] до 4 в коде [8,4]. Следовательно, код можно определить как [8,4] код Хэмминга.
Чтобы декодировать код Хэмминга [8,4], сначала проверьте бит четности. Если бит четности указывает на ошибку, исправление одиночной ошибки (код Хэмминга [7,4]) укажет местоположение ошибки, а «нет ошибки» указывает бит четности. Если бит четности правильный, то исправление одиночной ошибки укажет (побитовое) исключающее ИЛИ из двух местоположений ошибок. Если местоположения равны («нет ошибки»), то двойная битовая ошибка либо не произошла, либо исчезла сама собой. В противном случае произошла двойная битовая ошибка.
См. Также
- Теория кодирования
- Код Голея
- Код Рида – Мюллера
- Исправление ошибок Рида – Соломона
- Турбокод
- Код проверки четности с низкой плотностью
- Граница Хэмминга
- Расстояние Хэмминга
Примечания
Ссылки
Внешние ссылки
- Визуальное объяснение кодов Хэмминга
- CGI-скрипт для вычисления расстояний Хэмминга (от R. Tervo, UNB, Канада)
- Инструмент для вычисления кода Хэмминга
- H = (0 1 1 1 1 0 0 0 1 0 1 1 0 1 0 0 1 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1) 4, 8. { displaystyle mathbf {H} = left ({ begin {array} {cccc | cccc} 0 1 1 1 1 0 0 0 \ 1 0 1 1 0 1 0 0 \ 1 1 0 1 0 0 0 1 0 \ 1 1 1 0 1 end массив) {0} {0}
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Содержание
Раздел разработан в 2010 г. при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом КОДИРОВАНИЕ
.
Код Хэмминга
Будем рассматривать двоичные коды, т.е. упорядоченные наборы (строки) $ (x_1,dots,x_{n}) $ из $ n_{} $ чисел $ {x_1,dots,x_n}subset {0,1} $. Множество таких наборов, рассматриваемое вместе с операцией умножения на константы $ 0_{} $ или $ 1_{} $ и операцией поразрядного сложения по модулю $ 2_{} $:
$$ (x_1,dots,x_n)oplus (y_1,dots,y_n)=(x_1oplus y_1 ,dots,x_noplus y_n ) =
$$
$$ = (x_1+y_1 pmod{2},dots,x_n+y_n pmod{2}) $$
образует линейное пространство, которое мы будем обозначать $ mathbb V^n $, а собственно составляющие его наборы будем называть векторами; причем, для определенности, именно векторами-строками. Это пространство состоит из конечного числа векторов: $ operatorname{Card} (mathbb V^n)=2^n $.
Расстояние Хэмминга
Расстоянием Хэмминга между двумя векторами $ B=(b_1,dots,b_n) $ и $ C=(c_1,dots,c_n) $ из $ mathbb V^n $ называется число разрядов, в которых эти слова отличаются друг от друга; будем обозначать его $ rho(B,C) $.
?
Доказать, что
$ rho(B,C)= displaystyle sum_{j=1}^n left[ (1-b_j)c_j+ (1-c_j)b_j right] $ .
Весом Хэмминга вектора $ B=(b_1,dots,b_n) $ называется число его отличных от нуля координат, будем обозначать его $ w(B) $. Таким образом1)
$$ w(B)= b_1+dots+b_n, qquad rho(B,C)=|b_1-c_1|+dots+ |b_n-c_n|=w(B-C) . $$
Расстояние Хэмминга является метрикой в пространстве $ mathbb V^n $, т.е. для любых векторов $ {X_1,X_2,X_3} subset mathbb V^n $ выполняются свойства
1.
$ rho(X_1,X_2) ge 0 $, и $ rho(X_1,X_2) = 0 $ тогда и только тогда, когда $ X_1=X_2 $;
2.
$ rho(X_1,X_2) = rho(X_2,X_1) $;
3.
$ rho(X_1,X_3)le rho(X_1,X_2)+ rho(X_2,X_3) $ («неравенство треугольника»).
Пусть теперь во множестве $ mathbb V^n $ выбирается произвольное подмножество $ mathbb U $, содержащее $ s_{} $ векторов: $ mathbb U={ U_1,dots,U_s } $. Будем считать эти векторы кодовыми словами, т.е. на вход канала связи будем подавать исключительно только эти векторы; само множество $ mathbb U $ будем называть кодом. По прохождении канала связи эти векторы могут зашумляться ошибками. Каждый полученный на выходе вектор будем декодировать в ближайшее (в смысле расстояния Хэмминга) кодовое слово множества $ mathbb U $. Таким образом, «хорошим» кодом — в смысле исправления максимального числа ошибок — может считаться код $ mathbb U $, для которого кодовые слова далеко отстоят друг от друга. С другой стороны, количество кодовых слов $ s_{} $ должно быть достаточно велико, чтобы делать использование кода осмысленным; во всяком случае, будем всегда считать $ s>1 $.
Минимальное расстояние между различными кодовыми словами кода $ mathbb U $, т.е.
$$ d=min_{{j,k}subset {1,dots,s } atop jne k} rho (U_j,U_k) $$
называется кодовым расстоянием кода $ mathbb U $; будем иногда также писать $ d(mathbb U) $.
Т
Теорема. Код $ mathbb U $ с кодовым расстоянием $ d_{} $
a) способен обнаружить от $ 1_{} $ до $ d-1 $ (но не более) ошибок;
б) способен исправить от $ 1_{} $ до $ leftlfloor displaystyle frac{d-1}{2} rightrfloor $ (но не более) ошибок. Здесь $ lfloor rfloor $ — целая часть числа.
Доказательство. Если $ U_1 $ — переданное кодовое слово, а $ V_{} $ — полученный на выходе с канала вектор с $ tau_{} $ ошибками, то $ rho(U_1,V)=tau $. Мы не сможем обнаружить ошибку если $ V_{1} $ совпадет с каким-то другим кодовым словом $ U_2 $, т.е. при условии $ rho(U_2,V)=0 $. Оценим
$ rho(U_2,V) $ при условии, что $ tau le d-1 $. По неравенству треугольника
3
получаем
$$ rho(U_2,V) ge rho(U_1,U_2)-rho(U_1,V) ge d-tau ge 1>0 . $$
Для доказательства части б) предположим, что $ 2,tau le d-1 $. Тогда те же рассуждения приведут к заключению
$$ rho(U_2,V) ge d-tau ge (2,tau+1)-t > tau = rho(U_1,V) , $$
т.е. вектор $ V_{} $ ближе к $ U_1 $, чем к любому другому кодовому слову.
♦
П
Пример. Код Адамара строится на основании матрицы Адамара — квадратной матрицы, элементами которой являются только числа $ {+1,-1} $; при этом ее строки (как, впрочем, и столбцы) попарно ортогональны. Так, матрица Адамара порядка $ 8_{} $ —
$$
H=left(
begin{array}{rrrrrrrr}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \
-1 & 1 &-1 & 1 & -1 & 1 &-1 & 1\
1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \
-1 & 1 & 1 & -1 & -1 & 1 & 1 & -1 \
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \
-1 & 1 &-1 & 1 & 1 & -1 &1 & -1\
1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \
-1 & 1 & 1 & -1 & 1 & -1 & -1 & 1
end{array}
right) .
$$
Код строится следующим образом. Берутся строки матрицы $ H_{} $ и умножаются на $ +1 $ и на $ -1 $; в каждой строке множества
$$ H^{[1]},H^{[2]},dots,H^{[8]},-H^{[1]},-H^{[2]},dots,-H^{[8]} $$
производится замена $ +1 to 0, -1 to 1 $. Получаются $ 16 $ векторов
$$
(00000000), (10101010), (00110011), (10011001), (00001111), (10100101), (00111100),
(10010110),
$$
$$
(11111111), (01010101), (11001100), (01100110), (11110000), (01011010), (11000011),
(01101001),
$$
которые обозначим $ U_1,dots,U_8,U_{-1},dots,U_{-8} $.
Поскольку строки $ pm H^{[j]} $ и $ pm H^{[k]} $ ортогональны при $ jne k_{} $ и состоят только из чисел $ pm 1 $, то ровно в половине своих элементов они должны совпадать, а в половине — быть противоположными. Соответствующие им векторы $ U_{} $ будут совпадать в половине своих компонент и различаться в оставшихся. Таким образом
$$ rho( U_{pm j}, U_{pm k}) = 4 quad npu quad jne k, rho( U_{j}, U_{-j}) = 8 , $$
и кодовое расстояние равно $ 4_{} $. В соответствии с теоремой, этот код способен обнаружить до трех ошибок, но исправить только одну. Так, к примеру, если при передаче по каналу связи слова $ U_8=(00111100) $ возникает только одна ошибка и на выходе получаем $ V_8= (00111101) $, то $ rho(U_8,V_8)=1 $, в то время как $ rho(U_j,V_8)ge 3 $ для других кодовых слов. Если же количество ошибок возрастет до двух —
$ tilde V_8= (00111111) $, — то $ rho(U_8,tilde V_8)=2 $, но при этом также $ rho(U_9,tilde V_8)=2 $. Ошибка обнаружена, но однозначное декодирование невозможно.
♦
Т
Теорема. Если существует матрица Адамара порядка $ n_{}>2 $, то
а) $ n_{} $ кратно $ 4_{} $, и
б) существует код $ mathbb U subset mathbb V^n $, состоящий из $ 2,n $ кодовых слов, для которого кодовое расстояние $ d=n/2 $.
Проблема построения кодов Адамара заключается в том, что существование матриц Адамара произвольного порядка $ n_{} $ кратного $ 4_{} $ составляет содержание не доказанной2) гипотезы Адамара. Хотя для многих частных случаев $ n_{} $ (например, для $ n=2^m, m in mathbb N $, см.
☞
ЗДЕСЬ ) матрицы Адамара построены.
Т
Теорема. Если код $ mathbb U subset mathbb V^n $ может исправлять самое большее $ m_{} $ ошибок, то количество $ s_{} $ его слов должно удовлетворять следующему неравенству
$$ s le frac{2^n}{C_n^0+C_n^1+dots+C_n^m} , $$
где $ C_n^{j} $ означает биномиальный коэффициент.
Число в правой части неравенства называется верхней границей Хэмминга для числа кодовых слов.
Доказательство. Для простоты предположим, что одно из кодовых слов кода $ mathbb U $ совпадает с нулевым вектором: $ U_1=mathbb O_{1times n} $. Все векторы пространства $ mathbb V_n $, отстоящие от $ U_1 $ на расстояние $ 1_{} $ заключаются во множестве
$$ (100dots 0), (010 dots 0), dots, (000 dots 1) ; $$
их как раз $ n=C_n^1 $ штук. Векторы из $ mathbb V^n $, отстоящие от $ mathbb O_{} $ на расстояние $ 2_{} $ получаются в ходе расстановки двух цифр $ 1_{} $ в произвольных местах нулевого вектора. Нахождение количества способов такой расстановки относится к задачам комбинаторики, и решение этой задачи можно найти
☞
ЗДЕСЬ. Оно равно как раз $ C_n^{2}=n(n-1)/2 $. Аналогичная задача расстановки $ j_{} $ единиц в $ n_{} $-векторе имеет решением число $ C_n^j $.
Таким образом общее количество векторов, отстоящих от $ mathbb O_{} $ на расстояние $ le m_{} $
равно $ C_n^1+dots+C_n^m $.
Вместе в самим $ mathbb O_{} $-вектором получаем как раз число из знаменателя границы Хэмминга.
Предыдущие рассуждения будут справедливы и для любого другого кодового слова из $ mathbb U $ — каждое из них можно «окружить $ m_{} $-окрестностью» и каждая из этих окрестностей будет содержать
$$ 1+C_n^1+dots+C_n^m $$
векторов из $ mathbb V^n $. По предположению теоремы, эти окрестности не должны пересекаться. Но тогда общее количество векторов $ mathbb V^n $, попавших в эти окрестности (для всех $ s_{} $ кодовых слов) не должно превышать количества векторов в $ mathbb V^n $, т.е. $ 2^{n} $.
♦
?
Доказать, что если $ n_{} $ — нечетно, а $ m=lfloor n/2 rfloor=(n-1)/2 $ то верхняя граница Хэмминга равна в точности $ 2_{} $.
П
Пример. Для $ n=10 $ имеем
| $ m_{} $ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ sle $ | 93 | 18 | 5 | 2 | 1 |
Чем больше ошибок хотим скорректировать (при фиксированном числе $ n_{} $ разрядов кодовых слов) — тем меньше множество кодовых слов.
Коды, для которых верхняя граница Хэмминга достигается, называются совершенными.
Линейные коды
Идея, лежащая в основе этих кодов достаточно проста: это — обобщение понятия контрольной суммы. Если вектор $ (x_1,dots,x_k) in mathbb V^k $ содержит информационные биты, которые требуется передать, то для контроля целостности при передаче их по каналу присоединим к этому вектору еще один «служебный» бит с вычисленным значением
$$ x_{k+1}=x_1+dots+x_k pmod{2} . $$
Очевидно, $ x_{k+1}=1 $ если среди информационных битов содержится нечетное число единиц, и $ x_{k+1}=0 $ в противном случае. Поэтому этот бит называют битом четности. Кодовым словом становится вектор
$$ X=(x_1,dots,x_k,x_{k+1}) in mathbb V^{k+1} . $$
По прохождении его по каналу, для полученного вектора $ Y=(y_1,dots,y_k,y_{k+1}) $ производится проверка условия
$$ y_{k+1} = y_1+dots+y_k pmod{2} . $$
Если оно не выполнено, то при передаче произошла ошибка. Если же сравнение оказывается справедливым, то это еще не значит, что ошибки при передаче нет — поскольку комбинация из двух (или любого четного числа) ошибок не изменит бита четности.
Для более вероятного обнаружения ошибки вычислим несколько контрольных сумм — выбирая различные разряды информационного вектора $ (x_1,dots,x_k) $:
$$
begin{array}{lclcll}
x_{k+1}&=&x_{i_1}+&dots&+x_{i_s} pmod{2}, \
x_{k+2}&=&x_{j_1}+&dots&+x_{j_t} pmod{2}, \
vdots & & vdots \
x_n &=&x_{ell_1}+& dots & +x_{ell_w} pmod{2}.
end{array}
$$
Полученные биты присоединим к информационному блоку. Кодовым словом будет вектор
$$ X=(x_1,dots,x_k,x_{k+1},dots,x_n) in mathbb V^n , $$
который и поступает в канал связи. По прохождении его по каналу, для соответствующих разрядов полученного вектора $ Y_{} $ проверяется выполнимость контрольных сравнений. Если все они выполняются, то ошибка передачи считается невыявленной.
На первый взгляд кажется, что при увеличении количества контрольных сумм увеличивается и вероятность обнаружения ошибки передачи. Однако с увеличением количества разрядов кодового слова увеличивается и вероятность появления этой ошибки.
П
Пример. Если вероятность ошибочной передачи одного бита по каналу равна $ P_1=0.1 $, то вероятность появления хотя бы одной ошибки при передаче $ k_{} $ битов равна $ P_k= 1-(0.9)^k $, т.е.
| $ k $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $ P_k $ | 0.1 | 0.19 | 0.271 | 0.344 | 0.410 | 0.469 | 0.522 | 0.570 | 0.613 | 0.651 |
♦
Обычно, количество проверочных соотношений берется меньшим (и даже много меньшим) количества информационных битов3). Осталось только понять как составлять эти проверочные соотношения так, чтобы они смогли реагировать на ошибки передачи по каналу связи.
Сначала формализуем предложенную выше идею. В пространстве $ mathbb V^n $ выделим некоторое подпространство $ mathbb V^n_{[k]} $, состоящее из векторов
$$ (x_1,dots,x_k,x_{k+1},dots,x_n) , $$
первые $ k_{} $ компонентов которых считаются произвольными, а оставшиеся $ n-k_{} $ полностью определяются первыми посредством заданных линейных соотношений:
$$ begin{array}{lclcll}
x_{k+1}&=&h_{k+1,1}x_1+&dots&+h_{k+1,k}x_k pmod{2} \
vdots & & vdots \
x_n &=&h_{n1}x_1+& dots & +h_{nk}x_k pmod{2}
end{array} qquad npu qquad {h_{jell}} subset {0,1} .
$$
Кодовые слова выбираются именно из подпространства $ mathbb V^n_{[k]} $, их количество равно $ operatorname{Card} (mathbb V^n_{[k]} )=2^k $. При этом начальная часть каждого кодового слова, т.е. вектор $ (x_1,dots,x_k) $, заключает информацию, которую нужно передать — эти разряды называются информационными. Остальные разряды кодового слова, т.е. биты вектора $ (x_{k+1},dots,x_n) $, которые вычисляются с помощью выписанных линейных соотношений, являются служебными — они называются проверочными и предназначены для контроля целостности передачи информационных разрядов по каналу связи (и/или коррекции ошибок). Код такого типа называется линейным (n,k)-кодом.
В дальнейшем будем экономить на обозначениях: знак операции $ +_{} $ будет означать суммирование по модулю $ 2_{} $.
П
Пример. Пусть $ n=5, k=3 $. Пусть проверочные биты связаны с информационными соотношениями
$$ x_4=x_1 + x_2, x_5=x_1 + x_3 . $$
Тогда $ mathbb V^5_{[3]} $ состоит из векторов
$$ (00000), (10011), (01010), (00101), (11001), (10110), (01111), (11100) . $$
♦
Для описания пространства $ mathbb V^n_{[k]} $ привлечем аппарат теории матриц. С одной стороны, в этом подпространстве можно выбрать базис — систему из $ k_{} $ линейно независимых векторов: обозначим их $ {X_1,dots,X_k} $. Матрица, составленная из этих векторов-строк,
$$
mathbf G=left( begin{array}{c} X_1 \ vdots \ X_k end{array} right)_{ktimes n}
$$
называется порождающей матрицей кода. Так, в только что приведенном примере в качестве порождающей матрицы может быть выбрана
$$
mathbf G=
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \
0 & 1 & 0 & 1 & 0 \
0 & 0 & 1 & 0 &1
end{array}
right) qquad mbox{ или } qquad
mathbf G=
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \
1 & 1 & 0 & 0 & 1 \
1 & 1 & 1 & 0 & 0
end{array}
right) .
$$
Любая строка $ X_{} $ кода может быть получена как линейная комбинация строк порождающей матрицы:
$$ X=alpha_1 X_1+alpha_2X_2+dots+alpha_k X_k quad npu quad {alpha_1,dots,alpha_k} subset {0,1} . $$
Можно переписать это равенство с использованием операции матричного умножения:
$$ X=(alpha_1,dots,alpha_k) mathbf G . $$
Так, продолжая рассмотрение предыдущего примера:
$$
(x_1,x_2,x_3,x_4,x_5)=(x_1,x_2,x_3)
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \
0 & 1 & 0 & 1 & 0 \
0 & 0 & 1 & 0 &1
end{array}
right)=
$$
$$
=(x_1+x_2,x_2+x_3,x_3)
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \
1 & 1 & 0 & 0 & 1 \
1 & 1 & 1 & 0 & 0
end{array}
right) pmod{2} .
$$
С другой стороны, для описания $ mathbb V^n_{[k]} $ имеются проверочные соотношения. Объединяя их в систему линейных уравнений, перепишем их с использованием матричного формализма:
$$
(x_1,dots,x_k,x_{k+1},dots,x_n) cdot
left(begin{array}{cccc}
h_{k+1,1} & h_{k+2,1} & dots &h_{n1} \
h_{k+1,2} & h_{k+2,2} & dots & h_{n2} \
vdots & & & vdots \
h_{k+1,k} & h_{k+2,k} & dots & h_{nk} \
-1 & 0 & dots & 0 \
0 & -1 & dots & 0 \
vdots & & ddots & vdots \
0 & 0 & dots & -1
end{array}
right)= (0,0,dots,0)_{1times (n-k)}
$$
или, в альтернативном виде, с использованием транспонирования4):
$$
underbrace{left(begin{array}{llclcccc}
h_{k+1,1} & h_{k+1,2} & dots &h_{k+1,k} & 1 & 0 & dots & 0 \
h_{k+2,1} & h_{k+2,2} & dots & h_{k+2,k}& 0 & 1 & dots & 0 \
vdots & & & vdots & dots & & ddots & vdots \
h_{n1} & h_{n2} & dots & h_{nk} & 0 & 0 & dots & 1 \
end{array}
right)}_{mathbf H}left( begin{array}{c} x_1 \ x_2 \ vdots \ x_n end{array} right)
=left( begin{array}{c} 0 \ 0 \ vdots \ 0 end{array} right)_{(n-k)times 1}
$$
Матрица $ mathbf H_{} $ порядка $ (n-k)times n $ называется проверочной матрицей кода5). Хотя вторая форма записи (когда вектор-столбец неизвестных стоит справа от матрицы) более привычна для линейной алгебры, в теории кодирования чаще используется именно первая — с вектором-строкой $ X_{} $ слева от матрицы:
$$ Xcdot mathbf H^{top} = mathbb O_{1times k} . $$
Для приведенного выше примера проверочные соотношения переписываются в виде
$$ x_1 + x_2 +x_4=0, x_1 + x_3 + x_5=0 $$
и, следовательно, проверочная матрица:
$$ mathbf H=
left( begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \
1 & 0 & 1 & 0 & 1
end{array}
right) .
$$
Т
Теорема 1. Имеет место матричное равенство
$$ mathbf G cdot mathbf H^{top} = mathbb O_{ktimes (n-k)} .$$
Доказательство. Каждая строка матрицы $ mathbf G $ — это кодовое слово $ X_{j} $ , которое, по предположению, должно удовлетворять проверочным соотношениям $ X_j cdot mathbf H^{top} = mathbb O_{1times k} $. Равенство из теоремы — это объединение всех таких соотношений в матричной форме. Фактически, порождающая матрица $ mathbf G $ состоит из строк, составляющих фундаментальную систему решений системы уравнений $ X mathbf H^{top}= mathbb O $.
♦
=>
Если проверочная матрица имеет вид $ mathbf H=left[ P^{top} mid E_{n-k} right] $,
где $ E_{n-k} $ — единичная матрица порядка $ n — k_{} $, $ P_{} $ — некоторая матрица порядка $ k times (n-k) $, а $ mid_{} $ означает операцию конкатенации, то порождающая матрица может быть выбрана в виде $ mathbf G = left[ E_k mid P right] $.
Доказательство следует из предыдущей теоремы, правила умножения блочных матриц —
$$ mathbf G cdot mathbf H^{top} = E_k cdot P + P cdot E_{n-k} = 2P equiv mathbb O_{ktimes (n-k)} pmod{2} , $$
и того факта, что строки матрицы $ mathbf G $ линейно независимы. Последнее обстоятельство обеспечивается структурой этой матрицы: первые $ k_{} $ ее столбцов являются столбцами единичной матрицы. Любая комбинация
$$ alpha_1 mathbf G^{[1]}+dots+alpha_k mathbf G^{[k]} $$
строк матрицы дает строку $ (alpha_1,dots,alpha_k,dots ) $ и для обращения ее в нулевую необходимо, чтобы $ alpha_1=0,dots,alpha_k=0 $.
♦
Видим, что по структуре матрицы $ mathbf G $ и $ mathbf H $ очень похожи друг на друга. Задав одну из них, однозначно определяем другую. В одном из следующих пунктов, мы воспользуемся этим обстоятельством — для целей исправления ошибок оказывается выгоднее сначала задавать $ mathbf H $.
Т
Теорема 2. Кодовое расстояние линейного подпространства $ mathbb V^{n}_{[k]} $ равно минимальному весу его ненулевых кодовых слов:
$$ d( mathbb V^{n}_{[k]})= min_{ U in mathbb V^{n}_{[k]} atop U ne mathbb O } w(U) . $$
Доказательство. Линейное подпространство замкнуто относительно операции сложения (вычитания) векторов. Поэтому если $ {U_1,U_2}subset mathbb V^{n}_{[k]} $, то и $ U_1-U_2 in mathbb V^{n}_{[k]} $, а также $ mathbb O in V^{n}_{[k]} $. Тогда
$$ rho(U_1,U_2)=rho(U_1-U_2, mathbb O)= w(U_1-U_2) . $$
♦
Кодовое расстояние дает третью характеристику линейного кода — теперь он описывается набором чисел $ (n,k,d) $.
Т
Теорема 3. Пусть $ d_{} $ означает кодовое расстояние кода $ mathbb V^{n}_{[k]} $ с проверочной матрицей $ mathbf H $. Тогда любое подмножество из $ ell_{} $ столбцов этой матрицы будет линейно независимо при $ ell < d $. Обратно, если любое подмножество из $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимо, то $ d > ell $.
Доказательство. Если $ d_{} $ — кодовое расстояние, то, в соответствии с теоремой 2, ни одно ненулевое кодовое слово $ Xin mathbb V^{n}_{[k]} $ не должно иметь вес, меньший $ d_{} $. Если предположить,
что столбцы $ {mathbf H_{[i_1]},dots,mathbf H_{[i_{ell}]}} $ линейно зависимы при $ ell< d $, то
существуют числа $ x_{i_1},dots,x_{i_{ell}} $ не все равные нулю, такие что
$$ x_{i_1}mathbf H_{[i_1]}+dots+x_{i_{ell}} H_{[i_{ell}]} = mathbb O . $$
Придавая всем остальным переменным $ {x_1,dots,x_n} setminus { x_{i_1},dots,x_{i_{ell}} } $ нулевые значения, получаем вектор $ X_{} in mathbb V^n $, удовлетворяющий равенству
$$ x_1 mathbf H_{[1]}+dots + x_n mathbf H_{[n]} = mathbb O , $$
и вес этого вектора $ le ell< d $. Но тогда этот вектор принадлежит и $ mathbb V^{n}_{[k]} $ поскольку $ mathbf H X^{top} = mathbb O $.
Это противоречит предположению о весе кодовых слов. Следовательно любые $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимы если $ ell < d $.
Обратно, пусть любые $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимы, но существует кодовое слово $ X_{}=(x_1,dots,x_n) ne mathbb O $ веса $ le ell $. Пусть, для определенности, $ x_{ell+1}=0,dots, x_{n}=0 $. Тогда
$$ x_1 mathbf H_{[1]}+dots + x_{ell} mathbf H_{[ell]}= mathbb O $$
при хотя бы одном из чисел $ {x_j}_{j=1}^{ell} $ равном $ 1_{} $. Но это означает, что столбцы
$ mathbf H_{[1]},dots, mathbf H_{[ell]} $ линейно зависимы, что противоречит предположению.
♦
Испровление ашибок
До сих пор мы не накладывали ни каких дополнительных ограничений ни на порождающую ни на проверочную матрицы кода: любая из них могла быть выбрана почти произвольной.
Теперь обратимся собственно к задаче обнаружения (а также возможной коррекции) ошибок при передаче кодового слова по зашумленному каналу связи.
Если $ Xin mathbb V^{n}_{[k]} $ — кодовое слово, а $ Yin mathbb V^n $ — вектор, получившийся по прохождении этого слова по каналу, то $ Y-X $ называется вектором ошибок. Понятно, что при $ w(Y-X)=0 $ ошибки при передаче нет.
Предположим, что $ w(Y-X)=1 $, т.е. что при передаче произошла ошибка ровно в одном разряде кодового слова $ X_{} $. Попробуем ее обнаружить исходя из предположения, что кодовое слово выбиралось во множестве $ mathbb V^{n}_{[k]} $ линейного $ (n,k) $-кода, определенного в предыдущем пункте при какой-то проверочной матрице $ mathbf H $. Если для полученного вектора $ Y_{} $ выполняются все проверочные условия:
$$ Y cdot mathbf H^{top} = mathbb O_{1times k} , $$
(или, что то же $ Y in mathbb V^{n}_{[k]} $), то ошибка передачи считается не выявленной.
Для произвольного вектора $ Y in mathbb V^{n} $ вектор-строка
$$ S=Y cdot mathbf H^{top} in mathbb V^{k} $$
называется синдромом вектора Y. C точки зрения линейной алгебры его можно интерпретировать как показатель отхода вектора $ Y_{} $ от гиперплоскости, заданной системой однородных уравнений $ Xcdot mathbf H^{top}=mathbb O $.
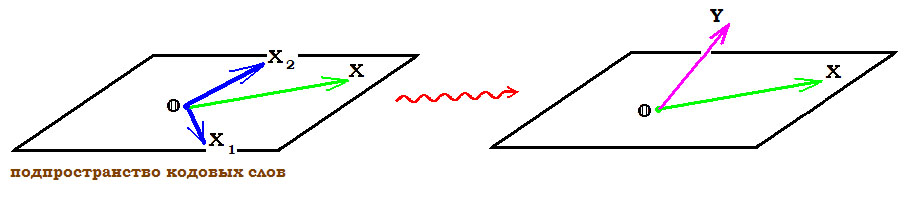
Если синдром $ S_{} $ ненулевой: $ Y cdot mathbf H^{top} ne mathbb O_{1times k} $,
то полученный вектор $ Y_{} $ не принадлежит множеству $ mathbb V^{n}_{[k]} $ допустимых кодовых слов. Факт ошибки подтвержден. Изначально мы предположили, что произошла только одна ошибка, т.е.
$$ Y-X= {mathfrak e}_j = big(underbrace{0,dots,0,1}_{j},0,dots,0big) $$
при некотором $ jin {1,dots n} $. Тогда
$$ S= Y cdot mathbf H^{top} = (X+{mathfrak e}_j) cdot mathbf H^{top}=Xcdot mathbf H^{top}+
{mathfrak e}_j cdot mathbf H^{top}=
$$
$$
=mathbb O_{1times k} + mathbf H_{[j]}^{top} = mathbf H_{[j]}^{top}
$$
при $ mathbf H_{[j]} $ означающем $ j_{} $-й столбец проверочной матрицы $ mathbf H $. Таким образом получили соответствие
$$ {}_{} mathbf{HOMEP} mbox{ поврежденного бита} mathbf{=HOMEP} mbox{ столбца проверочной матрицы.} $$
И, следовательно, мы получили возможность обнаружить место повреждения — по факту совпадения синдрома со столбцом проверочной матрицы. К сожалению, реальность оказывается более сложной…
П
Пример. В примере предыдущего пункта проверочная матрица была выбрана в виде
$$ mathbf H=
left( begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \
1 & 0 & 1 & 0 & 1
end{array}
right) .
$$
Если при передаче кодового слова $ (10011) $ произошла ошибка в первом бите, т.е. $ Y=(00011) $, то синдром
$$ S=Y cdot mathbf H^{top} = (11) $$
однозначно укажет на номер столбца матрицы $ mathbf H $. Если же ошибка произошла в четвертом бите, т.е. $ Y=(10001) $, то
$$ S=(10) , $$
но таких6) столбцов в матрице $ mathbf H $ два!
♦
Вывод. Для однозначного обнаружения места ошибки7) достаточно, чтобы все столбцы матрицы $ mathbf H $ были различными.
Столбцами этой матрицы являются транспонированные строки пространства $ mathbb V^{n-k} $.
Построение кода
Итак, исходя из соображений, завершающих предыдущий пункт, будем строить код, исправляющий одну ошибку, беря за стартовую точку именно матрицу $ mathbf H $. Выбираем ее произвольного порядка $ Mtimes N $ при $ {M,N} in mathbb N, M<N $ и вида
$$ mathbf H_{Mtimes N} = left[ tilde P mid E_M right] , $$
где матрица $ E_M $ — единичная порядка $ M_{} $, а матрица $ tilde P $ имеет порядок $ Mtimes (N-M) $, и столбцы ее должны быть различными, ненулевыми и отличаться от столбцов матрицы $ E_M $. По этой проверочной матрице — в соответствии со следствием к теореме $ 1 $ из
☞
ПУНКТА — строим порождающую матрицу:
$$ mathbf G_{(N-M)times N} = left[ E_{N-M} mid tilde P^{top} right] . $$
Строки матрицы $ mathbf G $ могут быть взяты в качестве базисных векторов подпространства кодовых слов.
П
Пример. Пусть $ M=2 $. Здесь имеем единственный вариант:
$$ mathbf H_{2times 3} = left( begin{array}{c|cc} 1 & 1 & 0 \ 1 & 0 & 1 end{array} right) , $$
поскольку в $ mathbb V^2 $ имеется лишь одна ненулевая строка, отличная от $ (10) $ и $ (01) $. Таким образом $ N=3 $ и
$$ mathbf G_{1times 3}=( 1, 1, 1 ) . $$
Следовательно, подпространство кодовых слов в $ mathbb V^3 $ является одномерным, и имеем всего два возможных кодовых слова: $ (000) $ и $ (111) $.
Пусть $ M=3 $. В $ mathbb V^3 $ имеется уже большой выбор строк, отличных от $ (100), (010), (001) $. Так, можно взять
$$
mathbf H_{3times 4} = left( begin{array}{c|ccc} 1 & 1 & 0 & 0 \ 1 & 0 & 1 & 0 \ 1 & 0 & 0 & 1 end{array} right) quad mbox{ или } quad
mathbf H_{3times 5} = left( begin{array}{cc|ccc} 1 & 0 & 1 & 0 & 0 \ 1 & 1 & 0 & 1 & 0 \ 0 & 1 & 0 & 0 & 1 end{array} right)
$$
$$
mbox{ или } quad
mathbf H_{3times 6} =
left( begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \ 1 & 1 & 0 & 0 & 1 & 0 \ 0 & 1 & 1 & 0 & 0 & 1 end{array} right) quad mbox{ или } quad
mathbf H_{3times 7} =
left( begin{array}{cccc|ccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 & 0 \ 1 & 0 & 1 & 1 & 0 & 0 & 1 end{array} right) .
$$
Соответственно,
$$ mathbf G= (1, 1, 1, 1) quad quad mbox{ или } quad
mathbf G=
left( begin{array}{cc|ccc} 1 & 0 & 1 & 1 & 0 \ 0 & 1 & 0 & 1 & 1 end{array} right)
quad
$$
$$
mbox{ или } quad
mathbf G=
left( begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 1 & 0 \ 0 & 1 & 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 1 & 0 & 1 end{array} right)
quad quad mbox{ или } quad
mathbf G=
left( begin{array}{cccc|ccc} 1 & 0 & 0 & 0 & 1 & 1 & 1 \ 0 & 1 & 0 & 0 & 1 & 1 & 0 \ 0 & 0 & 1 & 0 & 0 & 1 & 1 \ 0 & 0 & 0 & 1 & 1 & 0 & 1
end{array} right) .
$$
Кодовых векторов в соответствующих кодах будет $ 2^1,2^2,2^3,2^4 $. Любой из них способен исправить одну ошибку, полученную в ходе передачи.
♦
Если поставить задачу максимизации числа кодовых слов, то матрицу $ mathbf H $ следует выбирать самой широкой, т.е. делать $ N_{} $ максимально возможным. При фиксированном $ M_{} $ это достигается при выборе $ N=2^M-1 $. Тогда соответствующий линейный $ (n,k) $-код имеет значения параметров $ n=2^M-1,k=2^M-M-1 $, и именно он обычно и выбирается в качестве кода Хэмминга.
Найдем величину его кодового расстояния $ d_{} $. В соответствии с теоремой $ 3 $ из
☞
ПУНКТА, $ d>ell $, если любое подмножество из $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимо. Поскольку столбцы проверочной матрицы кода Хэмминга все различны, то любая пара из них линейно независима (свойство
3
☞
ЗДЕСЬ ). Следовательно, $ d>2 $. По теореме из
☞
ПУНКТА, получаем —
Если при передаче произошла ровно одна ошибка, то код Хэмминга способен ее исправить; если при передаче произошло ровно две ошибки, то код Хэмминга достоверно устанавливает лишь факт наличия ошибки.
Если попробовать исправить заглавие предыдущего пункта, исходя только из информации о структуре набора составляющих текст букв, то этой информации оказывается недостаточно: набор букв в правильном тексте будет таким же
П
Пример. Для проверочной матрицы $ (7,4) $-кода Хэмминга
$$
mathbf H_{3times 7} =
left( begin{array}{ccccccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 & 0 \ 1 & 0 & 1 & 1 & 0 & 0 & 1 end{array} right)
$$
вектор $ X=(0011110) $ является кодовым. Если при передаче произошла лишь одна ошибка и на выходе канала получили вектор $ Y=(1011110) $, то синдром этого вектора $ S=Y mathbf H^{top}=(111) $. Поскольку $ S^{top} $ совпадает с первым столбцом матрицы $ mathbf H $, то заключаем, что ошибка произошла в первом разряде. Тут же исправляем его на противоположный: $ X=Y+mathfrak e_1 $.
Если при передаче произошло две ошибки и на выходе канала получили вектор $ tilde Y=(1011010) $, то синдром этого вектора $ S=tilde Y mathbf H^{top}=(011) $. Поскольку синдром ненулевой, то факт наличия ошибки подтвержден. Однако корректно исправить ее — по аналогии с предыдущим — не удается. $ S^{top} $ совпадает с третьим столбцом матрицы $ mathbf H $, но в третьем разряде полученного вектора ошибки нет.
Наконец, если при передаче произошли три ошибки и на выходе канала получили вектор $ widehat Y=(1011011) $, то синдром этого вектора $ S=widehat Y mathbf H^{top}=(010) $. Наличие ошибки подтверждено, исправление невозможно. Если же — при передаче того же вектора $ X=(0011110) $ — получаем вектор
$ widehat Y_1=(1111111) $ (также с тремя ошибками), то его синдром оказывается нулевым: $ widehat Y_1 mathbf H^{top}=(000) $ и ошибка не обнаруживается.
♦
Проблема сравнения синдрома полученного вектора $ Y_{} $ со столбцами проверочной матрицы $ mathbf H $ с целью определения места ошибки — не такая тривиальная, особенно для больших $ n_{} $. Для упрощения этой процедуры воспользуемся следующим простым соображением. Размещение проверочных разрядов в конце кодового слова обусловлено лишь соображениями удобства изложения учебного материала. С точки зрения практической реализации, $ n-k $ проверочных разрядов можно разместить в любых местах кодового слова $ X_{} $ и даже «вразбивку», т.е. не подряд. Перестановке разрядов в кодовом слове будет соответствовать перестановка столбцов в матрице $ mathbf H $, при этом само множество столбцов остается неизменным — это транспонированные строки пространства $ mathbb V^{n-k} $ (ненулевые и различные). Рассмотрим $ (n,k) $-код Хэмминга при $ n=2^M-1,k=2^M-M-1, M ge 2 $. Тогда каждую ненулевую строку пространства $ mathbb V^{n-k}= mathbb V^M $ можно интерпретировать как двоичное представление числа из множества
$ {1,2,3,dots,2^M-1} $. Пусть
$$ j=underline{{mathfrak b}_1{mathfrak b}_2 dots {mathfrak b}_{M-1} {mathfrak b}_{M}}=
{mathfrak b}_1 times 2^{M-1}+{mathfrak b}_2 times 2^{M-2}+dots+{mathfrak b}_{M-1} times 2+ {mathfrak b}_{M} quad npu quad { {mathfrak b}_j}_{j=1}^Msubset {0,1} quad — $$
— двоичное представление числа $ j_{} $. Переупорядочим столбцы проверочной матрицы $ mathbf H $ так, чтобы
$$ mathbf H_{[j]}=left[ {mathfrak b}_1{mathfrak b}_2 dots {mathfrak b}_{M-1} {mathfrak b}_{M}right]^{top} , $$
т.е. чтобы $ j_{} $-й столбец содержал двоичное представление числа $ j_{} $. При таком упорядочении,
синдром произвольного вектора $ Y_{} $, отличающегося от кодового слова $ X_{} $ в единственном разряде, является двоичным представлением номера этого разряда:
$$ {bf mbox{СИНДРОМ }} (Y)=mathbf{HOMEP} (mbox{ошибочный разряд}) . $$
Осталось теперь выяснить какие разряды кодового слова содержат проверочные биты.
П
Пример. Для $ (7,4) $-кода Хэмминга матрицу $ mathbf H $, построенную в предыдущем примере, переупорядочим по столбцам; будем рассматривать ее в виде
$$
begin{array}{c}
left( begin{array}{ccccccc}
0 & 0 & 0 & 1 & 1 & 1 & 1 \
0 & 1 & 1 & 0 & 0 & 1 & 1 \
1 & 0 & 1 & 0 & 1 & 0 & 1
end{array} right) \
begin{array}{ccccccc}
uparrow & uparrow & uparrow & uparrow & uparrow & uparrow & uparrow \
scriptstyle 1 & scriptstyle 2 & scriptstyle 3 & scriptstyle 4 & scriptstyle 5 & scriptstyle 6 & scriptstyle 7
end{array}
end{array}
$$
Распишем проверочные соотношения $ Xmathbf H^{top}=mathbb O $ покомпонентно:
$$
left{
begin{array}{ccccccc}
& & & x_4&+x_5&+x_6&+x_7=0 \
&x_2&+x_3& & & +x_6&+x_7=0 \
x_1& & +x_3& & +x_5 & & +x_7=0
end{array} right. quad iff
$$
$$
iff quad
left{
begin{array}{ccccccc}
x_1& & +x_3& & +x_5 & & +x_7=0 \
&x_2&+x_3& & & +x_6&+x_7=0 \
& & & x_4&+x_5&+x_6&+x_7=0
end{array} right.
$$
Переписанные в последнем виде, эти уравнения представляют конечный пункт прямого хода метода Гаусса решения системы линейных уравнений, а именно — трапециевидную форму этой системы. Если бы мы поставили задачу поиска общего решения этой (однородной) системы и нахождения фундаментальной системы решений, то в качестве зависимых переменных однозначно бы выбрали $ x_1, x_2, x_4 $. Выпишем это общее решение 
$$
x_1=x_3+x_5+x_7, x_2=x_3+x_6+x_7, x_4=x_5+x_6+x_7 .
$$
Это и есть проверочные соотношения, а проверочными разрядами кодового вектора являются $ 1_{} $-й, $ 2_{} $-й и $ 4_{} $-й.
Проверим правильность этих рассуждений. Придадим оставшимся разрядам произвольные значения, например:
$ x_3=1,x_5=1,x_6=0,x_7=1 $. Тогда $ x_1=1, x_2=0,x_4=0 $ и кодовый вектор $ X=(1010101) $. Пусть на выходе из канала он превратился в $ Y=(1000101) $. Синдром этого вектора $ Ymathbf H^{top}=(011) $ — это двоичное представление числа $ 3_{} $. И ведь действительно: ошибка — в третьем разряде!
♦
Алгоритм построения (n,k)-кода Хэмминга
для $ n=2^M-1,k=2^M-M-1, M ge 2 $.
1.
Строится матрица $ mathbf H $ порядка $ M times (2^M-1) $ из столбцов, представляющих двоичные представления чисел $ {1,2,3,dots,2^M-1} $ (младшие разряды — внизу).
2.
Проверочные разряды имеют номера, равные степеням двойки: $ 1,2,2^2,dots,2^{M-1} $.
3.
Проверочные соотношения получаются из матричного представления $ Xmathbf H^{top}=mathbb O $ выражением проверочных разрядов через информационные.
Можно немного улучшить код Хэмминга, увеличив кодовое расстояние до $ 4_{} $.
?
Является ли $ 8_{} $-мибитный код Адамара из примера
☞
ПУНКТА линейным кодом?
.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
[2]. Марков А.А. Введение в теорию кодирования. М.Наука. 1982
Аннотация[править]
Здесь мы рассмотрим основные принципы и методы надёжной и
эффективной передачи данных между двумя машинами, соединёнными
каналом. Под каналом следует понимать любую физическую среду
передачи данных. Посредством этой физической среды
нужно научиться передавать биты так, чтобы они безошибочно
принимались получателем точно в той последовательности,
в какой они были переданы.
Канальный уровень[править]
На уровне канала данных решается ряд проблем, присущих
только этому уровню:
- реализация сервиса для сетевого уровня,
- разбиение потока бит на кадры,
- управление потоком кадров,
- обработка ошибок передачи.
Основная задача канального уровня — обеспечить сервис сетевому уровню,
а это значит помочь передать данные с сетевого уровня одной машины на
сетевой уровень другой машины.
Разбиение на кадры[править]
Сервис, создаваемый канальным уровнем для сетевого, опирается на
сервис, создаваемый физическим уровнем. На физическом уровне
протекают потоки битов. Значение посланного бита не обязательно
равно принятому, и количество посланных битов не обязательно
равно количеству принятых. Всё это требует специальных усилий на
канальном уровне по обнаружению и исправлению ошибок.
Типовой подход к решению этой проблемы — разбиение потока битов
на кадры и подсчёт контрольной суммы для каждого кадра при
посылке данных.
Контрольная сумма — это, в общем смысле, функция от
содержательной части кадра (слова длины 
значений которой — слова фиксированной длины 
Эти r бит добавляются обычно в конец кадра. При приёме
контрольная сумма вычисляется заново и сравнивается с той, что
хранится в кадре. Если они различаются, то это признак ошибки
передачи. Канальный уровень должен принять меры к исправлению
ошибки, например, сбросить плохой кадр, послать сообщение об
ошибке тому кто прислал этот кадр. Разбиение потока битов на
кадры — задача не простая. Один из способов — делать
временную паузу между битами разных кадров. Однако, в сети, где
нет единого таймера, нет гарантии, что эта пауза сохранится или,
наоборот, не появятся новые. Так как временные методы ненадёжны,
то применяются другие. Здесь мы рассмотрим три основных:
- счетчик символов;
- вставка специальных стартовых и конечных символов или последовательностей бит;
- специальная кодировка на физическом уровне.
Первый метод очевиден. В начале каждого кадра указывается сколько
символов в кадре. При приёме число принятых символов
подсчитывается опять. Однако, этот метод имеет существенный
недостаток — счётчик символов может быть искажён при передаче.
Тогда принимающая сторона не сможет обнаружить границы кадра.
Даже обнаружив несовпадение контрольных сумм, принимающая
сторона не сможет сообщить передающей какой кадр надо переслать,
сколько символов пропало. Этот метод ныне используется редко.
Второй метод построен на вставке специальных символов.
Обычно для этого используют управляющие последовательности:
последовательность 
для конца кадра. 

TeXt, 
потеряна граница текущего кадра, надо просто искать
ближайшую последовательность 



нужно избегать появления этих комбинаций внутри самого тела
кадра. Это осуществляется дублированием комбинаций 
встречающихся внутри тела кадра, и удаление дублей после
получения кадра. Недостатком этого метода является
зависимость от кодировки (кодозависимость).
По мере развития сетей эта связь становилась все более и более
обременительной и был предложен новый очевидный кодонезависимый
метод — управляющие последовательности должны быть
бит-ориентированными. В частности, в протоколе 
начинается и заканчивается со специального флаг-байта: 01111110.
Посылающая сторона, встретив последовательно 5 единиц внутри тела
кадра, обязательно вставит 0. Принимающая сторона, приняв 5
последовательных единиц обязательно удалит следующий за ними 0,
если таковой будет. Это называется bit-stuffing. Если
принято шесть и за ними следует ноль, то это управляющий сигнал:
начало или конец кадра, а в случае, когда подряд идут более шести
единиц, — сигнал ожидания или аварийного завершения.
(а) 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 (б) 0 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1
Bit Stuffing. (a) исходные данные (б) посылаемые данные. Жирным отмечены вставленные нули.
Таким образом, кадр легко может быть распознан по
флаг-байту. Если граница очередного кадра по какой-то
причине была потеряна, то все что надо делать — ловить
ближайший флаг-байт.
И наконец, последний метод используется там, где конкретизирована
физическая среда. Например, в случае проводной связи для передачи
одного бита используется два импульса. 1 кодируется как переход
высокое-низкое, 0 — как низкое-высокое. Сочетания низкое-низкое
или высокое-высокое не используются для передачи данных, и их
используют для границ кадра.
На практике используют, как правило, комбинацию этих методов.
Например, счётчик символов с флаг-байтами. Тогда, если число
символов в кадре соответствует кодировке границы кадра, кадр
считается переданным правильно.
Контроль ошибок[править]
Решив проблему разбиения на кадры, мы приходим к следующей
проблеме: как обеспечить, чтобы кадры, пройдя по физическому
каналу с помехами, попадали на сетевой уровень по назначению, в
надлежащей последовательности и в надлежащем виде?
Частичное решение этой проблемы осуществляется посредством
введения обратной связи между отправителем и получателем в
виде кадра подтверждения, а также специального кодирования,
позволяющего обнаруживать или даже исправлять ошибки
передачи конкретного кадра.
Если кадр-подтверждение несет положительную информацию, то
считается что переданные кадры прошли нормально, если там
сообщение об ошибке, то переданные кадры надо передать
заново.
Однако, возможны случаи когда из-за ошибок в канале
кадр исчезнет целиком. В этом случае получатель не будет
реагировать никак, а отправитель будет сколь угодно долго ждать
подтверждения. Для решения этой проблемы на канальном уровне
вводят таймеры. Когда передаётся очередной кадр, то одновременно
устанавливается таймер на определённое время. Этого времени должно
хватать на то, чтобы получатель получил кадр, а отправитель
получил подтверждение. Если отправитель не получит подтверждение
раньше, чем истечёт время, установленное на таймере то он будет
считать, что кадр потерян и повторит его еще раз.
Однако, если кадр-подтверждение был утерян, то вполне возможно, что один и
тот же кадр получатель получит дважды. Как быть? Для решения
этой проблемы каждому кадру присваивают порядковый номер. С
помощью этого номера получатель может обнаружить дубли.
Итак, таймеры, нумерация кадров, флаг-байты,
кодирование и обратная связь — вот основные средства на канальном уровне,
обеспечивающие надёжную доставку каждого кадра до сетевого
уровня в единственном экземпляре. Но и с помощью этих
средств невозможно достигнуть стопроцентной надёжности
передачи.
Управление потоком[править]
Другая важная проблема, которая решается на канальном уровне
— управление потоком. Вполне может
случиться, что отправитель будет слать кадры столь часто, что
получатель не будет успевать их обрабатывать(например, если
машина-отправитель более мощная или загружена слабее, чем
машина-получатель). Для борьбы с такими ситуациями вводят
управления потоком. Это управление предполагает обратную связь
между отправителем и получателем, которая позволяет им
урегулировать такие ситуации. Есть много схем управления потоком
и все они в основе своей имеют следующий сценарий: прежде, чем
отправитель начнёт передачу, он спрашивает у получателя сколько
кадров тот может принять. Получатель сообщает ему определённое
число кадров. Отправитель после того, как передаст это число
кадров, должен приостановить передачу и снова спросить получателя,
как много кадров тот может принять, и т.д.
Помехоустойчивое кодирование[править]
Характеристики ошибок[править]
Физическая среда, по которой передаются данные, не может быть
абсолютно надёжной. Более того, уровень шума бывает очень
высоким, например в беспроводных системах связи и телефонных
системах. Ошибки при передаче — это реальность, которую
надо обязательно учитывать.
В разных средах характер помех разный. Ошибки могут быть
одиночные, а могут возникать группами, сразу по несколько. В
результате помех могут исчезать биты или наоборот — появляться
лишние.
Основной характеристикой интенсивности помех в канале
является параметр шума — p. Это число от 0 до 1, равное
вероятности инвертирования бита, при условии, что он был
передан по каналу и получен на другом конце.
Следующий параметр — 
события, но при условии, что предыдущий бит также был
инвертирован.
Этими двумя параметрами вполне можно ограничиться при построении
теории. Но, в принципе, можно было бы учитывать аналогичные
вероятности для исчезновения бита, а также использовать полную
информацию о пространственной корреляции ошибок, — то есть
корреляции соседних ошибок, разделённых одним, двумя или более
битами.
У групповых ошибок есть свои плюсы и минусы. Плюсы
заключаются в следующем. Пусть данные передаются блоками по
1000 бит, а уровень ошибки 0,001 на бит. Если ошибки
изолированные и независимые, то 63 % (
возникают группами по 100 сразу, то ошибки будут содержать
1 % (
Зато, если ошибки не группируются, то в каждом кадре они невелики,
и есть возможность их исправить. Групповые ошибки портят
кадр безвозвратно. Требуется его повторная пересылка, но в
некоторых системах это в принципе невозможно, — например,
в телефонных системах, использующие цифровое кодирование,
возникает эффект пропадания слов/слогов.
Для надёжной передачи кодов было предложено два основных метода.
Первый — добавить в передаваемый блок данных нескольких «лишних» бит так, чтобы, анализируя
полученный блок, можно было бы сказать, есть в переданном
блоке ошибки или нет. Это так называемые коды с обнаружением ошибок.
Второй — внести избыточность настолько, чтобы,
анализируя полученные данные, можно не только замечать
ошибки, но и указать, где именно возникли искажения. Это
коды, исправляющие ошибки.
Такое деление условно. Более общий вариант — это коды,
обнаруживающие k ошибок и исправляющие l ошибок, где

* Элементы теории передачи информации[править]
Информационным каналом называется пара зависимых
случайных величин 
называется входом другая выходом канала. Если случайные величины
дискретны и конечны, то есть имеют конечные множества событий:
то канал определяется матрицей условных вероятностей


будет значение 
значение 
Входная случайная величина определяется распределением


выходе вычисляется по формуле
Объединённое распределение на

Информация 
канал, есть взаимная информация входа и выхода:
(eq:inf)
где
Если случайные величины 

есть 


((eq:inf)) можно из следующего соображения: энтропия случайной
величины равна информации, которую мы получаем при одном её
измерении. 

содержится по отдельности во входе и в выходе. Но часть этой
информации общая, её нам и нужно найти.
равна величине объединённой информации. В теории
меры[1] есть выражение
аналогичное ((eq:inf)):
Распределение входной случайной величины 
варьировать и получать различные значения I. Её максимум
называется пропускной способностью канала
(eq:cdef)
Эта функция есть решение задачи
Задача 1.
(task:shanon) Каково максимальное количество информации,
которое можно передать с одним битом по каналу

Конец задачи.
Итак, пропускная способность есть функция на множестве стохастических матриц[2].
Стандартный информационный канал это
(eq:sm)
То есть канал с бинарным алфавитом и вероятностью помехи p
(p — вероятность того, что бит будет случайно
инвертирован). Его пропускная способность равна
Эта функция является решением задачи на максимум ((eq:cdef))
для матрицы ((eq:sm)).
begin{figure}[t!]
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/cideal.eps} caption{ 
Пропускная способность канала как функция вероятности
инвертирования бита.} (fig:cideal)
end{figure}
Эта функция 
помехоустойчивого кодирования — если мы хотим с абсолютной
надёжностью передать по каналу с пропускной способностью C
сообщение длиной m, то минимальное количество бит, которое нам
нужно будет передать 
помехоустойчивое кодирование, обеспечивающее вероятность
незамеченной ошибки в переданном слове меньше, чем 
раздувает данные в 
Кодирование, при котором в этом пределе достигается
равенство, называется эффективным. Отметим, что
абсолютно надёжного способа передачи конечного количества
данных по каналу с помехами не существует: то есть

Задача дуальная (task:shanon) формулируется следующим
образом
Задача 2.
(task:dual)
Мы хотим передавать информацию со скоростью V по каналу с
пропускной способностью C. Какова минимальная вероятность
ошибочной передачи одного бита?
Конец задачи.
Решением будет функция заданная неявно




Оказывается, вероятность ошибки растет не так уж и быстро.
Например, если по каналу передавать данных в два раза
больше, чем его пропускная способность, то лишь 11 бит из
ста будут переданы с ошибкой.
begin{figure}[t!]
psfrag{v}{v} psfrag{p}{ 
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/pv.eps} caption{ 
минимальная вероятность ошибки в одном бите как функция от
отношения скорости передачи и пропускной способности 
(fig:pv)
end{figure}
Построение конкретных способов кодирования, приближающихся
по пропускной способности к теоретической границе —
сложная математическая задача.
Метод «чётности» и общая идея[править]
Простым примером
кода с обнаружением одной ошибки является код с битом чётности.
Конструкция его такова: к исходному слову добавляется бит
чётности. Если в исходном слове число единичек чётно, то значение
этого бита 0, если нечётно — 1. Таким образом допустимые слова
этого кода имеют чётное количество единичек. Если получено слово
с нечётным количеством единичек, то при передаче произошла ошибка.
В случае вероятных групповых ошибок эту технику можно
скорректировать. Разобъём передаваемые данные на n слов по k
бит и расположим их в виде матрицы 
каждого столбца вычислим бит чётности и разместим его в
дополнительной строке. Матрица затем передается по строкам. По
получению матрица восстанавливается, и если обнаруживется
несоответствие, то весь блок передается повторно. Этот метод
позволяет обнаружить групповые ошибки длины 
Задача 3.
Слово длиной n с чётным количеством единиц передано по каналу с
уровнем шума p. Покажите, что вероятность того, что при
передаче произошли ошибки и мы их не заметили равна
Что можно привести к виду
Например, при 


Конец задачи.
Следующая задача повышенной сложности.
Задача 4. (task:errmod) Пусть у нас есть возможность контролировать
сумму единичек по модулю d. Тогда вероятность нефиксируемых
ошибок в слове длиной n при передаче его по каналу с шумом p
равна 
Примечание. Интерес здесь представляет неявно
заданная функция 
содержания полезной информации

бит как функция от величины шума и вероятности незамеченных
ошибок. Чем выше желаемая надёжность передачи, то есть чем меньше
вероятность 
полезной информации.
Конец задачи.
Итак, с помощью одного бита чётности мы повышаем надёжность
передачи, и вероятность незамеченной ошибки равна

При 

дублированию каждого бита. Рассмотрим общую идею того, как с
помощью специального кодирования можно добиться сколь угодно
высокой надёжности передачи.
Общая идея На множестве слов длины n определена
метрика Хемминга: расстояние Хемминга между двумя словами
равно количеству несовпадающих бит. Например,
Задача 5.
Докажите, что 
Конец задачи.
Если два слова находятся на расстоянии r по Хеммингу,
это значит, что надо инвертировать ровно r разрядов, чтобы
преобразовать одно слово в другое. В описанном ниже
кодировании Хемминга любые два различных допустимых слова
находятся на расстоянии 
обнаруживать d ошибок, то надо, чтобы слова отстояли друг
от друга на расстояние 
исправлять ошибки, то надо чтобы кодослова отстояли друг от
друга на 
переданное слово содержит d ошибок, оно, как следует из
неравенства треугольника, все равно ближе к правильному
слову, чем к какому-либо еще, и следовательно можно
определить, исходное слово. Минимальное расстояние Хемминга
между двумя различными допустимыми кодовыми словами
называется расстоянием Хемминга данного кода.
Элементарный пример помехоустойчивого кода — это код, у
которого есть только четыре допустимых кодовых слова:
Расстояние по Хеммингу у этого кода 5, следовательно он может
исправлять двойные ошибки и замечать 4 ошибки. Если получатель
получит слово 0001010111, то ясно, что исходное слово имело
вид 0000011111. Коэффициент раздувания равен 5. То есть
исходное слово длины m будет кодироваться в слово длины 
Отметим что имеет смысл говорить о двух коэффициентах:
Первый есть функция от переменной n, а второй, обратный
ему, — от переменной m.
Здесь мы подошли к довольно трудной задаче —
минимизировать коэффициент раздувания для требуемой
надёжности передачи. Она рассматривается в разделе (theory).
Циклические коды[править]
На практике активно применяются полиномиальные коды
или циклические избыточные коды (Cyclic Redundancy Code
— CRC).
CRC коды построены на рассмотрении битовой строки как
строки коэффициентов полинома. k-битовая строка
соответствует полиному степени 
— коэффициент при старшей степени. Например, строка 110001
представляет полином 
принадлежат полю 
Основная идея заключена в том, чтобы пересылать только такие
сообщения, полиномы которых делятся на некоторый фиксированный
полином 
на 
ошибок, если они один допустимый полином (то есть полином
делящийся на 
Полином 
на парах допустимых полиномов.
Есть два очевидных способа кодирования сообщения в полином,
который делится на 
сообщения на 
количество бит так, чтобы результирующий полином делился на

Отправитель и получатель заранее договариваются
о конкретном полиноме-генераторе 

равна l.
Мы добавляем контрольные l бит в конец передаваемого
блоку так, чтобы получился полином кратный генератору

он проверяет его делимость на G. Если есть остаток 
Алгоритм кодирования CRC:
Дано слово W длины m. Ему соответствует полином 
- Добавить к исходному слову W справа r нулей. Получится слово длины
и полином :
- Разделить полином
на
и вычислить остаток от деления
:
- Вычесть остаток (вычитание в
то же самое, что и сложение) из полинома
:
Слово, которое соответствует полиному
, и есть результат.
Рис. (fig:crc) иллюстрирует этот алгоритм для блока
1101011011 и 
begin{figure}[h!]
psfrag{Remainder}{Остаток}
centeringparbox{0.66textwidth}{
begin{tabular}{lcl}
Слово&:&1101011011 \
Результат&:&11010110111110
end{tabular}}
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/crc2.eps}
caption{CRC — полиномиальное кодирование}
(fig:crc)
end{figure}
Этот метод позволяет отлавливать одиночные ошибки и
групповые ошибки длины не более степени полинома.
Существует три международных стандарта на вид 

Два остальных — для 8 разрядных. 

одиночные, двойные ошибки, групповые ошибки длины не более 16 и
нечётное число изолированных ошибок с вероятностью 0.99997.
* Теоретический предел[править]
(theory) В примечании
к задаче (task:errmod) было указано как можно получить
значение коэффициента содержания полезной информации (КПС) на
один бит, если передавать данные по каналу с шумом p словами
длиной n бит, при условии, чтобы вероятность незамеченной
ошибки была меньше 
Но ясно, что указанная там функция дает лишь оценку снизу
оптимального значения КПС
— возможно, существует другие методы контролирования
ошибок, для которых он выше. Теория информации позволяет нам
найти точное значение этого коэффициента.
Сформулируем задачу о кодировании, обнаруживающем ошибки.
Для начала предположим, что наличие ошибки фиксируется с
абсолютной точностью.
Задача 6.
(task:err)
Мы хотим передавать информацию блоками, которые содержали
бы m бит полезной информации, так, чтобы
вероятность ошибки в одном бите равнялась p, а
правильность передачи «фиксировалось контрольной суммой». Найти
минимальный размер блока 

Конец задачи.
Решение.
Для передачи m бит с вероятностью ошибки в отдельном бите
p требуется передать 
(см. задачу (task:dual)). Кроме того мы хотим сообщать
об ошибке в передаче. Её вероятность равна 
значит информация, заложенная в этом сообщении,


Конец решения.
Заметим, что 
сообщение об ошибке в нём равносильно передаче самого бита.
Если передавать эти сообщения по каналу с уровнем помех p, то
количество бит на одно сообщение равно 
теоретическая оценка для количества лишних бит равна
Понятно, что данная теоретическая оценка занижена.
Коды Хэмминга[править]
Элементарный пример кода исправляющего ошибки был показан на
странице pageref{simplecode}. Его обобщение очевидно. Для
подобного кода, обнаруживающего одну ошибку, КПС равен 
единице с помощью кодов Хемминга. В частности, при кодировании
11 бит получается слово длинной 15 бит, то есть

Оценим минимальное количество контрольных
разрядов, необходимое для исправления одиночных ошибок. Пусть
содержательная часть составляет m бит, и мы добавляем ещё r
контрольных. Каждое из 
его неправильных вариантов с ошибкой в одном бите. Такими
образом, с каждым из 
слов и эти множества не должны пересекаться. Так как общее число
слов 
Этот теоретический предел достижим при использовании
метода, предложенного Хеммингом. Идея его в следующем: все
биты, номера которых есть степень 2, — контрольные,
остальные — биты сообщения. Каждый контрольный бит
отвечает за чётность суммы некоторой группы бит. Один и тот
же бит может относиться к разным группам. Чтобы определить
какие контрольные биты контролируют бит в позиции k надо
разложить k по степеням двойки: если 
бит относится к трём группам — к группе, чья чётность
подсчитывается в 1-ом бите, к группе 2-ого и к группе 8-ого
бита. Другими словами в контрольный бит с номером
заносится сумма (по модулю 2) бит с номерами, которые имеют
в разложении по степеням двойки степень 
(eq:hem)
Код Хемминга оптимален при 

![{displaystyle m=n-[log _{2}(n+1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d24a7d287da182a9c3ab18a6fbd87ef3988a6b9)
![{displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)


n однозначно определяет m).
Пример для 
- Невозможно разобрать выражение (неизвестная функция «fbox»): {displaystyle fbox{10110100111}to fbox{fbox{0}fbox{0}1fbox{1}011fbox{0}0100111} }
- Невозможно разобрать выражение (неизвестная функция «fbox»): {displaystyle hphantom{fbox{10110100111}to};; lefteqn{,b_1}hphantom{fbox{0}} lefteqn{,b_2}hphantom{fbox{0}} lefteqn{b_3}hphantom{1} lefteqn{;b_4}hphantom{fbox{1}011} lefteqn{,b_8}hphantom{fbox{0}} lefteqn{b_9}hphantom{010011} lefteqn{b_{15}}hphantom{1} }
Получив слово,
получатель проверяет каждый контрольный бит на предмет
правильности чётности и складывая номера контрольных бит, в
которых нарушена чётность. Полученное число, есть XOR номеров
бит, где произошла ошибка. Если ошибка одна, то это число есть
просто номер ошибочного бита.
Например, если в контрольных разрядах 1, 2, 8 обнаружено
несовпадение чётности, то ошибка в 11 разряде, так как
только он связан одновременно с этими тремя контрольными
разрядами.
begin{figure}[h!]
psfrag{Check bits}{hspace{-12mm}Контрольные биты}
centeringincludegraphics[clip=true,
width=0.65textwidth]{pictures/hem.eps} caption{Кодирование
Хемминга} (fig:hem)
end{figure}
Задача 7.
Покажите, что 

Конец задачи.
Код Хемминга может исправлять только единичные ошибки. Однако,
есть приём, который позволяет распространить этот код на случай
групповых ошибок. Пусть нам надо передать k кодослов.
Расположим их в виде матрицы одно слово — строка. Обычно,
передают слово за словом. Но мы поступим иначе, передадим слово
длины k, из 1-ых разрядов всех слов, затем — вторых и т. д. По
приёме всех слов матрица восстанавливается. Если мы хотим
обнаруживать групповые ошибки размера k, то в каждой строке
восстановленной матрицы будет не более одной ошибки. А с
одиночными ошибками код Хемминга справится.
Анализ эффективности[править]
Начнём c небольшого примера. Пусть у нас есть канал с уровнем
ошибок 
передаче блоками по 
10 контрольных бит: 1, 2, dots, 
приходится 1013 бит полезной информации. При передаче 1000
таких блоков потребуется 
В тоже время для обнаружения единичной ошибки достаточно одного
бита чётности. И если мы применим технику повторной передачи, то
на передачу 1000 блоков надо будет потратить 1000 бит
дополнительно и примерно 
повторно. То есть на 1000 блоков приходится один попорченый, и
дополнительная нагрузка линии составляет 

Хемминга плох для такого канала. Надо правильно выбрать длину
блока — если 
Рассмотрим этот вопрос подробнее. Пусть нам нужно передать
информацию M бит. Разобьем её на L блоков по 
и будем передавать двумя способами
— с помощью кодов Хемминга и без них. При этом будем
считать, что в обоих случаях осуществлено предварительное
кодирование, позволяющее с вероятностью
определять ошибочность передачи. Это осуществляется путем
добавления «лишней» информации. Обозначим коэффициент
раздувания для этого кодирования 
этого кодирования каждый блок несёт информацию

1) Без кода Хемминга.
Если пересылать информацию
блоками по 
обнаружения ошибки, то получим, что в среднем нам придётся
переслать D бит:
Где 
повторной передачи равная вероятности ошибки умноженной на
вероятность того, что мы её заметим. Коэффициент раздувания
равен
2) С кодом Хемминга.
При кодировании методом Хемминга слова длины 
(eq:hnm)
Для отдельного блока вероятность
безошибочной передачи равна 
одинарной ошибки 
что произошло более чем одна ошибка, и мы это заметили
— в этом случае требуется повторная передача кадра.
Количество передаваемых данных:
И коэффициент раздувания
где 
функция. Удобно записать соответствующие коэффициенты
полезного содержания:
,
(eq:kps)
Легко обнаружить что при 

оказывается эффективнее, то есть 
begin{figure}[h!]
psfrag{knc}{кпс} psfrag{n}{n}
centeringincludegraphics[clip=true,
width=0.48textwidth]{pictures/kps.eps}
centeringincludegraphics[clip=true,
width=0.48textwidth]{pictures/kps2.eps} caption{

в канале с помехами как функция размера элементарного блока.}
parbox{0.85textwidth}{small Светлый график — без кодирования Хемминга;\
Темный график — с кодированием Хемминга;
\Параметры: 

(fig:kps)
end{figure}
begin{figure}[h!]
psfrag{C}{C} psfrag{p}{p}
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/kpseff.eps}
caption{
содержания в канале с помехами как функция уровня помех.}
parbox{0.97textwidth}{ small Светлый график — без кодирования Хемминга;\ Темный график — с кодированием Хемминга;\Тонкий график — теоретический
предел, задаваемый функцией 

end{figure}
Значение 
формулах ((eq:kps)) можно оценить как
Напомним, что 
надёжности передачи
— чем меньше 
По определению 
ошибочной передачи блока при условии, что «контрольная сумма
сошлась» и кадр засчитан правильно переданным.
Такое выражение для
получается из формулы
Но это безусловно лишь оценочная формула. Оптимальное
значение 
зависит от p.
Из графика на рисунке (fig:kps) хорошо видно, что при
больших n код Хемминга начинает работать на пользу.
Но зависимость КПС от n не есть критерий эффективности
кода. Эффективность кода определяется функцией
На рисунке (fig:kpseff) показан график этой функции и из
него ясно, что код Хемминга можно использовать с пользой
всегда — при любых 
возможность выбирать подходящее n.
Коды как линейные операторы[править]
То, что на множестве {0,1} есть структура числового поля,
позволяет осуществлять алгебраические интерпретации кодирования.
Заметим, в частности, что как коды Хемминга, так и циклические
коды линейны:\ 1) отношения ((eq:hem)) на
с. pageref{eq:hem}, связывающие контрольные биты кода Хемминга с
другими линейны,\ 2) остаток от деления суммы многочленов на
третий равен сумме остатков.\ То есть кодирование в этих двух
случаях есть линейное отображение из 

матрица кода Хемминга 
соотношения ((eq:hem))). Исходное слово есть

(слова соответствуют столбцам).
Процесс выявления ошибок тоже линейная операция, она
осуществляется с помощью проверочной матрицы 
Пусть принято слово 

случае правильной передачи должно быть равно 000. Значение

слова 
((eq:hem)) и, таким образом, 
бит в которых произошла ошибка, как векторов в 
Заметим, что столбцы проверочной матрицы представляют собой
последовательно записанные в двоичной форме натуральные
числа от 1 до 7.
Вычиcление рабочей матрицы для циклических кодов
основывается на значениях 
её часть равна единичной, так m бит сообщения помещаются
без изменения в начало слова, а нижние r строчек есть m
столбцов высоты r состоящие из коэффициентов многочленов


dots, 




Рабочая и проверочная матрицы равны
то есть
Кроме рабочей и проверочной матриц есть ещё множество порождающих матриц 

слова образуют линейное подпространство 

которой образуют базис этого подпространства, называется
порождающей. В частности, рабочая матрица является порождающей.
Способность обнаруживать и исправлять ошибки однозначно
определяется подпространством L. Порождающих, рабочих и
проверочных матриц соответствующих L несколько.
Действительно, в порождающей и рабочей матрицах можно осуществлять
элементарные операции со столбцами, а в проверочной — со
строчками. Матрицы 

всегда удовлетворяют отношениям
где


Любая порождающая матрица может использоваться как
рабочая.
Декодирующая матрица 

таким свойством может быть несколько. Множество декодирующих
матриц определяется рабочей матрицей:
где 

подпространстве L все декодирующие матрицы действуют одинаково.
Они отличаются на подпространстве ортогональном L. Приведём
декодирующую матрицу для 

К каждой строчке декодирующей матрицы можно добавить любую
линейную комбинацию строчек из проверочной матрицы. Следует
отметить, что процесс исправления ошибок для кодов Хемминга
нелинеен и его нельзя «внедрить» в декодирующую матрицу.
Сформулируем теперь основные моменты, касающиеся линейных кодов.
- Процесс кодирования и декодирования — линейные операторы. :
- Обнаружение ошибок равносильно проверке принадлежности полученного слова подпространству L допустимых слов. Для этого необходимо найти проекцию
(синдром ошибки) полученного слова на
— тоже линейная операция. Для правильно переданного слова
. :
- В случае, когда векторы подпространства L достаточно удалены друг от друга в смысле метрики Хемминга, есть возможность обнаруживать и исправлять некоторые ошибки. В частности, значение синдрома ошибки в случае кода Хемминга равно векторной сумме номеров бит, где произошла ошибка.
- Комбинация (композиция) линейных кодов есть снова линейный код.
Практические методы помехоустойчивого кодирования все основаны на
линейных кодах. В основном это модифицированные CRC, коды
Хемминга и их композиции. Например 
чётность. Такой код может исправлять уже две ошибки. Построение
эффективных и удобных на практике задача сходная с творчеством
художника. На практике важны не только корректирующая способность
кода, но и вычислительная сложность процессов кодирования и
декодирования, а также спектральная характеристика
результирующего аналогового сигнала. Кроме того, важна
способность исправлять специфические для данного физического
уровня групповые ошибки.
Задача 8.
Для данной проверочной матрицы постройте рабочую и декодирующую
матрицу. Докажите, что кодовое расстояние равно 4.
Подсказка
- Это проверочная матрица
плюс условие на чётность числа единичек в закодированном слове вместе с дополнительным восьмым контрольным битом.
- Кодовое расстояние равно минимальному количеству линейно зависимых столбцов в
.
Конец задачи.
Задача 9.
Посторойте декодирующую и проверочную матрицу для циклического
кода с 

рабочей матрицы использовалась матрица
Конец задачи.
*Коды Рида-Соломона[править]
После перехода на язык линейной алгебры естественно возникает
желание изучить свойства линейных кодов над другими конечными
числовыми полями. С помощью такого обобщения появились коды
Рида-Соломона.
Коды Рида-Соломона являются циклическими кодами над
числовым полем отличным от 
Напомним, что существует бесконечное количество конечных полей, и
количество элементов в конечном поле всегда равно степени
простого числа. Если мы зафиксируем число элементов 
найдётся единственное с точностью до изоморфности конечное поле с
таким числом элементов, которое обозначается как

многочленов по модулю неприводимого[3] многочлена 
полем 
многочленов с действительными коэффициентами неприводимыми
многочленами являются только квадратные многочлены с
отрицательным дискриминантом. Поэтому существует только
квадратичное расширение действительного поля — комплексные
числа. А над конечным полем существуют неприводимые многочлены
любой степени. В частности, над 

модулю 

Примеры протоколов канала данных[править]
HDLC протокол[править]
Здесь мы познакомимся с группой протоколов давно известных, но
по-прежнему широко используемых. Все они имеют одного
предшественника — SDLC (Synchronous Data Link Control) —
протокол управления синхронным каналом, предложенным фирмой IBM
в рамках SNA. ISO модифицировала этот протокол и выпустила
под названием HDLC — High level Data Link Control. MKTT
модифицировала HDLC для X.25 и выпустила под именем LAP —
Link Access Procedure. Позднее он был модифицирован в LAPB.
Все эти протоколы построены на одних и тех же принципах. Все
используют технику вставки специальных последовательностей
битов. Различия между ними незначительные.
begin{figure}[h!]
centeringincludegraphics[clip=true,
width=0.88textwidth]{pictures/frame.eps} caption{Типовая
структура кадра} (fig:frame)
end{figure}
На рис. (fig:frame) показана типовая структура кадра.
Поле адреса используется для адресации терминала, если их
несколько на линии. Для линий точка-точка это поле
используется для различия команды от ответа.
- Поле Control используется для последовательных номеров кадров, подтверждений и других нужд.
- Поле Data может быть сколь угодно большим и используется для передачи данных. Надо только иметь ввиду, что чем оно длиннее тем, больше вероятность повреждения кадра на линии.
- Поле Checksum — это поле используется CRC кодом.
Флаговые последовательности 01111110 используются для
разделения кадров и постоянно передаются по незанятой линии
в ожидании кадра. Существуют три вида кадров: 

Организация поля Control для этих трех видов кадров показана на
рис. (fig:cfield). Как видно из размера поля Seq в окне
отправителя может быть до 7 неподтверждённых кадров. Поле
Next используется для посылки подтверждения вместе с
передаваемым кадром. Подтверждение может быть в форме номера
последнего правильно переданного кадра, а может быть в форме
первого не переданного кадра. Какой вариант будет использован —
это параметр.
begin{figure}[h!]
centeringincludegraphics[clip=true,
width=0.88textwidth]{pictures/cfield.eps} caption{Cтруктура поля
Control}
parbox{0.66textwidth}{small (а) Информационный кадр (
(б) Управляющий кадр (
кадр (Unnumbered) }
(fig:cfield)
end{figure}
Разряд 
Когда компьютер приглашает терминал к передаче он
устанавливает этот разряд в P. Все кадры, посылаемые
терминалами имеют здесь P. Если это последний кадр,
посылаемый терминалом, то здесь стоит F.

- Тип 0 — уведомление в ожидании следующего кадра (RECEIVE READY). Используется когда нет встречного трафика, чтобы передать уведомление в кадре с данными.
- Тип 1 — негативное уведомление (REJECT) — указывает на ошибку при передаче. Поле Next указывает номер кадра, начиная с которого надо перепослать кадры.
- Тип 2 — RECEIVE NOT READY. Подтверждает все кадры, кроме указанного в Next. Используется, чтобы сообщить источнику кадров об необходимости приостановить передачу в силу каких-то проблем у получателя. После устранения этих проблем получатель шлет RECEIVE REDAY, REJECT или другой надлежащий управляющий кадр.
- Тип 3 — SELECTIVE REJECT — указывает на необходимость перепослать только кадр, указанный в Next. LAPB и SDLC не используют этого типа кадров.
Третий класс кадров — Unnubered. Кадры этого класса иногда
используются для целей управления, но чаще для передачи данных
при ненадёжной передаче без соединения.
Все протоколы имеют команду DISConnect для указания о разрыве
соединения, SNRM и SABM — для установки счётчиков кадров в ноль,
сброса соединения в начальное состояние, установки
соподчинённости на линии. Команда FRMR — указывает на
повреждение управляющего кадра.
- ^ Идея рассмотрения информации как меры на множестве ещё не до конца исчерпала себя — такой меры ещё не построено. Однако доказано, что с помощью этой аналогии можно доказывать неравенства, например
.
- ^ Матрица называется стохастической, если все её элементы неотрицательны и сумма элементов в каждом столбце равна единице.
- ^ Многочлен называется неприводимым, если он не разлагается в произведение многочленов меньшей степени.





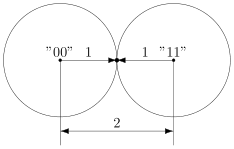

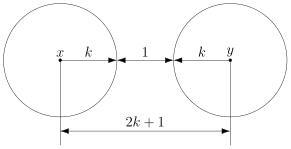

 , округляем «вниз», так чтобы
, округляем «вниз», так чтобы  .
.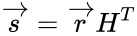 , где
, где 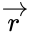 — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.






















































































