Для проверки
гипотезы
используют специально подобранную
случайную величину, точное или приближенное
распределение которой известно.
Случайная величина
Q,
служащая для проверки гипотезы
называетсястатистическим
критерием
или просто критерием.
Наблюдаемым значением
называют значение критерия, вычисленное
по выборке.
После выбора
критерия множество всех его возможных
значений разбивают на 2 непересекающихся
подмножества:
-
Одно из них содержит
значение критерия, при котором
отвергается – оно называетсякритической
областью S. -
Другое содержит
значение критерия, при котором гипотеза
принимается
–оно
называется областью принятия гипотезы.
(допустимая область
).
Критическими
точками
называют
точки, определяющие критическую область
от области принятия гипотезы, различают;
-
односторонние и
двусторонние критические области.
Односторонние
делятся
на:
-
правостороннюю
критическую область; -
левостороннюю
критическую область;
В частности, если
критические точки симметричны относительно
нуля, то двусторонняя область определяется
по модулю
|Q|>.
В общем случае
критерий представляет собой многомерную
случайную величину, однако, в дальнейшем
будем рассматривать простейшие одномерные
критерии.
Критическая и
допустимая область есть одномерные
числовые множества. Вид критической
области зависит от вида основной и
альтернативной гипотезы.
§ 4. Уровень значимости и мощность критерия.
Определение.
-
Вероятность
совершить ошибку
первого рода
называют уровнем
значимости критерия
и обозначают,
.
Вероятность ошибки
второго рода обозначают
.
-
Мощностью
критерия
называют вероятность
попадания критерия в критическую
область при условии, что справедлива
альтернативная гипотеза
,
(т. е мощность критерия — это вероятность
недопустимости ошибки второго рода.)
Обычно для
используют
стандартное значение:α
=
0,05, α = 0,01.
Как бы ни была мала
величина
, попадание
в критическую область есть только
маловероятное, но не абсолютно невозможное
событие.
Чем меньше
,
тем менее вероятно допустить ошибку
первого рода. С уменьшениемуменьшается критическая область.
При
=
0, гипотеза—
будет всегда приниматься независимо
от результатов выборки. Уменьшение,
влечет за собой увеличение вероятности
ошибки второго рода.
Одновременное
уменьшение ошибок первого и второго
рода возможно лишь при увеличении объема
выборки.
Обычно при проверке
гипотеза задаются определенным уровнем
значимости
и объемом выборкиn.
Критерий выбирается так, чтобы мощность
критерия была максимальной.
§ 5. Виды критических областей.
Пусть проверяется
гипотеза о равенстве некоторого параметра
генерального распределения, например
генерального среднего
,
и для проверки гипотезы используется
критерийQ,
распределения которого имеет вид :
1.
Если в
качестве альтернативной гипотезы
выдвигается
,
,
то критическую область естественно
определять,
т.е выбратьлевостороннюю
критическую область
.
Задавшись уровнем
значимостииз
уравнения,
находим левостороннюю область.
2. При
альтернативной гипотезе
.
Критическая область определяется из
уравнения,
называетсяправосторонняя
критическая область.
-
Если альтернативная
гипотеза формулируется в виде
,
то строитсядвусторонняя
критическая область.
Критические точки
находятся из уравнения
.
Чаще всего
двустороннюю критическую область
строят как симметричную:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
План:
1. Статистические гипотезы. Основные понятия.
2. Гипотезы о законе распределения.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
1.
Статистические гипотезы. Основные понятия.
Статистическая гипотеза— это утверждение о виде неизвестного
распределения или параметрах известного распределения. Статистические гипотезы
проверяются по результатам выборки статистическими методами в ходе эксперимента
(эмпирическим путем) с помощью статистических критериев.
В тех случаях, когда
известен закон, но неизвестны значения его параметров (дисперсия или
математическое ожидание) в конкретной ситуации, статистическую гипотезу
называют параметрической.
Например, предположение
об ожидаемом среднем доходе по акциям или разбросе дохода являются
параметрическими гипотезами.
Когда закон
распределения генеральной совокупности не известен, но есть основания
предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его
распределения называются непараметрическими.
Например, можно
выдвинуть гипотезу, что число дневных продаж в магазине или доход населения
подчинены нормальному закону распределения.
По содержанию статистические гипотезы можно классифицировать:
1.
Гипотезы о типе вероятностного закона
распределения случайной величины, характеризующего явление или процесс.
2.
Гипотезы об однородности двух или более
обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных
совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые
выборочные характеристики различаются между собой статистически значимо или
нет.
3.
Гипотезы о свойствах числовых значений
параметров исследуемой генеральной совокупности. Больше ли значения параметров
некоторого заданного номинала или меньше и т.д.
4.
Гипотезы о вероятностной зависимости двух
или более признаков, характеризующих различные свойства рассматриваемого
явления или процесса. При этом определяется характер этой зависимости.
Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).
Выдвинутую гипотезу называют основной или нулевой и обозначают H0
. Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают
H1.
Под статистическим
критерием понимают однозначно определенное правило, устанавливающее
условие, при котором проверяемая гипотеза отвергается либо не отвергается.
Пример:
Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных условиях используются статистические
данные, на основании которых делается вывод о том, является ли данное массовое
заболевание эпидемией. Предполагается, что существует некоторый критерий-
уровень доли заболевших, критический для этого заболевания, который
устанавливается по ранее имевшимся случаям.
Различают три вида критериев:
1.
Параметрические критерии—
критерии значимости, которые служат для проверки гипотез о параметрах
распределения генеральной совокупности при известном виде распределения.
2.
Критерии согласия—
позволяют проверить гипотезы о соответствии распределений генеральной
совокупности известной теоретической модели.
3.
Непараметрические критерии—
используются в гипотезах, когда не требуется знаний о конкретном виде
распределения.
Проверка
параметрических гипотез проводится на основе критериев значимости., а
непараметрических- критериев согласия.
Задача проверки
статистических гипотез сводится к исследованию генеральной совокупности по
выборке. Множество возможных значений элементов выборки может быть разделено на
два непересекающихся подмножества- критическую область и область принятия
гипотезы.
Областью принятия гипотезы или областью допустимых значений Iдоп
называют совокупность значений критерия,
при которых эту гипотезу принимают.
Критической областью
Iкр называют множество значений критерия, при
котором гипотезу отвергают.
Наблюдаемые значения критерия (статистика)
Kнабл
называют такое значение критерия, которое
находится по данным выборки.
Границы критической области, отделяющие ее от
области принятия гипотезы, называют критическими точками и обозначают
Kкр.
Для определения
критической области задается уровень значимости
—
некая малая вероятность попадания критерия в критическую область.
Уровень значимости— вероятность принятия
конкурирующей гипотезы, тогда как справедлива основная.
С помощью уровня
значимости определяются границы критической области.
Основной принцип проверки статистических гипотез
состоит в следующем: если наблюдаемое значение статистики критерия попадает (не
попадает) в критическую область, то гипотеза H0
отвергается (принимается), а гипотеза H1
принимается (отвергается) в качестве одного из
возможных решений с формулировкой «гипотеза
H0 противоречит (не противоречит) выборочным
данным на уровне значимости
».
В зависимости от
содержания альтернативной гипотезы осуществляется выбор критической области:
левосторонней, правосторонней, двусторонней. Если смысл исследования заключается
в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения
или увеличения), то говорят об односторонней критической области. Если смысл
исследования- выявить различия в изучаемых параметрах, но характер их
отклонения от контрольных (или теоретических) не известен, то говорят о
двусторонней критической области.
Однако, принятие той
или иной гипотезы не дает оснований утверждать, что она верна. Результат
проверки статистической гипотезы лишь устанавливают на определенном уровне
значимости ее соответствие (несоответствие) результатам эксперимента.
При проверке
статистических гипотез возможны следующие ошибки:
1.
Отвергнута правильная
H0, а принята неправильная гипотеза
H1 — ошибка
первого рода.
2. Отвергнута правильная альтернативная
гипотеза
H1 и
принята неправильная нулевая гипотеза H0
—
ошибка второго рода.
Заметим, что уровень значимости —
есть вероятность ошибки первого рода. Ошибка первого рода называется
-риском. Обычно они задаются
некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго
рода называются -риском, а вероятность ее
допустить обозначается
(вероятность того, что принята гипотеза
H0
, когда на самом деле справедлива
альтернативная гипотеза H1
.
Можно доказать, что с
уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода
и наоборот. Поэтому, на практике пытаются подбирать значения параметров
и
опытным путем в целях минимизации суммарного
эффекта от возможных ошибок. При принятии управленческих решений для
одновременного уменьшения ошибок первого и второго рода самым действенным
средством является увеличение объема выборки, что согласуется с законом больших
чисел.
На бытовом уровне
ошибки второго рода могут иметь более трагические последствия, чем ошибки
первого рода.
2. Гипотеза о законе распределения. Критерий согласия Пирсона (
X2
-критерий).
Критериями согласия называют критерии, в
которых гипотеза определяет закон распределения либо полностью, либо с
точностью до небольшого числа параметров.
Причины расхождения
результатов эксперимента и теоретических характеристик могут быть вызваны малым
объемом выборки, неудачным способом группировки наблюдений, ошибками в
выборе гипотезы о виде распределения
генеральной совокупности и др.
Рассмотрим
универсальный критерий согласия Пирсона. Проверка гипотезы о том, что
эмпирическая частота мало отличается от соответствующей теоретической частоты,
осуществляется с помощью величины X2
—
меры расхождения между ними.
Для произвольной
выборки, когда распределение непрерывно или число различных вариант велико, все
пространство наблюдаемых вариант делят на конечное число непересекающихся
областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую
вероятность.
Для применения критерия
согласия Пирсона необходимо:
1. Вычислить значение статистики по формуле:
, где
pi –вероятность
принятия значения
xi, ni.
— эмпирическая частота для
соответствующего
xi. n— объем выборки. s— число вариант выборки.
2.
По
соответствующей таблице распределения Пирсона найти критическое значение , где k = s –
r
– 1 – число степеней свободы, s—
число различных вариант или интервалов группировки, r— число неизвестных параметров
предполагаемого теоретического распределения,
— выбранный уровень значимости. Это
значит, что строится правосторонний интервал.
3.
Если
,
то основная гипотеза отвергается, в противном случае- принимается, т.е. чем
больше отклонение, тем меньше согласованы теоретическое и эмпирическое
распределение. Поэтому принято использовать только правостороннюю критическую
область.
Расчетная таблица имеет вид:
|
Интервалы |
Середины |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
Пример:
По таблице
эмпирического распределения изменения в процентах темпа роста акций проверьте
гипотезу о нормальном распределении выборки.
|
Интервалы |
(-2; |
(-1; |
(0; |
(1; |
Итого |
|
ni |
7 |
14 |
18 |
11 |
50 |
|
pi |
0,157 |
0,341 |
0,341 |
0,157 |
1 |
Решение:
Гипотезу о нормальном
распределении проверим по критерию Пирсона.
|
Интервалы |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
|
(-2; |
7 |
0,157 |
7,85 |
0,7225 |
0,092 |
|
(-1; |
14 |
0,341 |
17,05 |
9,3025 |
0,546 |
|
(0; |
18 |
0,341 |
17,05 |
0,9025 |
0,053 |
|
(1; |
11 |
0,157 |
7,85 |
9,925 |
1,264 |
|
Итого |
|
По таблице найдем
при
=0,05
и k = s – r – 1 = 4 – 2 – 1 = 1. s = 4 – число
интервалов. r
= 2- число параметров теоретического (нормального) распределения.
Имеем . Т.к. 1,955 < 3,841, то
, т.е. гипотеза о нормальном
распределении подтверждается.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
Установление двусторонней критической
области на уровне значимости
для
проверки гипотезы соответствует отысканию соответствующего доверительного
интервала с надежностью
.
Рассмотрим условия применения некоторых
статистических гипотез.
|
Тип гипотезы H0 |
Границы критической области на уровне значимости |
Статистика наблюдений |
|
О числовом значении |
|
|
|
О числовом значении |
Распределение |
|
|
О числовом значении |
Распределение Пирсона |
|
Пример:
Результаты исследований в течение 35 лет
показали, что среднее изменение доходности векселей равно 5,5 %. Полагая, что
изменение доходности подчиняется нормальному закону распределения с
среднеквадратическим отклонением равным 2 %, на уровне значимости
, решите: можно ли принять 6 % в качестве нормативного процента
(математического ожидания) изменения доходности.
Решение:
По условию задачи
нулевая гипотеза
. Так как
, то в качестве альтернативной гипотезы
возьмем гипотезу:
, которой соответствует левосторонняя
критическая область с интервалом.
Найдем границы
критической области:
По таблице значений
функции Ф(х) найдем
, т.е. левосторонняя критическая область
лежит в интервале.
Найдем статистику
наблюдений:
.
Имеем:, нет основания отвергать нулевую
гипотезу. Значит, в качестве нормативного процента можно принять 6 %.
Пример:
Точность работы
программы проверяют по дисперсии контролируемого количества символов в коде,
которая не должна превышать 0,1. По выборке из 15 сообщений вычислена
исправленная оценка дисперсии 0,22. При
уровне значимости 0,05 проверьте, обеспечивает ли программа необходимую
точность.
Решение:
Имеем: n = 15, s2 = 0,22
, ,
.
Сформулируем гипотезу о
числовом значении дисперсии:
H0 — программа обеспечивает необходимую точность
;
H1 —
программа не обеспечивает необходимую точность
.
Определим статистику: .
Найдем границы
критической области:
.
Поскольку 30,8 >
23,7;
, принимаем гипотезу H1, т.к.
H0 противоречит опытным данным. Вывод: программа
не обеспечивает необходимую точность.
Проверка гипотез
Общий обзор
Определение нулевой и альтернативной гипотезы, уровня статистической значимости
Получение статистики критерия, определение критической области
Получение значения р (достигнутого уровня значимости)
Применение значения р
Проверка гипотез против доверительных интервалов
Общий обзор
Часто делают выборку, чтобы определить аргументы против гипотезы относительно популяции (генеральной совокупности). Этот процесс известен как проверка гипотез (проверка статистических гипотез или проверка значимости), он представляет количественную меру аргументов против определенной гипотезы.
Установлено 5 стадий при проверке гипотез:
- Определение нулевой (
) и альтернативной гипотезы (
) при исследовании. Определение уровня значимости критерия.
- Отбор необходимых данных из выборки.
- Вычисление значения статистики критерия, отвечающей
.
- Вычисление критической области, проверка статистики критерия на предмет попадания в критическую область.
- Интерпретация достигнутого уровня значимости р и результатов.
Определение нулевой и альтернативной гипотез, уровня статистической значимости
При проверке значимости гипотезу следует формулировать независимо от используемых при ее проверке данных (до проведения проверки). В таком случае можно получить действительно продуктивный результат.
Всегда проверяют нулевую гипотезу (), которая отвергает эффект (например, разница средних равняется нулю) в популяции.
Например, при сравнении показателей курения у мужчин и женщин в популяции нулевая гипотеза означала бы, что показатели курения одинаковые у женщин и мужчин в популяции.
Затем определяют альтернативную гипотезу (), которая принимается, если нулевая гипотеза неверна. Альтернативная гипотеза больше относится к той теории, которую собираются исследовать. Итак, на этом примере альтернативная гипотеза
заключается в утверждении, что показатели курения различны у женщин и мужчин в популяции.
Разницу в показателях курения не уточнили, т.е. не установили, имеют ли в популяции мужчины более высокие или более низкие показатели, чем женщины. Такой подход известен как двусторонний критерий, потому что учитывают любую возможность, он рекомендуется постольку, поскольку редко есть уверенность заранее в направлении какого-либо различия, если таковое существует.
В некоторых случаях можно использовать односторонний критерий для гипотезы , в котором направление эффекта задано. Его можно применить, например, если рассматривать заболевание, от которого умерли все пациенты, не получившие лечения; новый препарат не мог бы ухудшить положение дел.
Уровень значимости. Важным этапом проверки статистических гипотез является определение уровня статистической значимости , т.е. максимально допускаемой исследователем вероятности ошибочного отклонения нулевой гипотезы.
Получение статистики критерия, определение критической области
После того как данные будут собраны, значения из выборки подставляют в формулу для вычисления статистики критерия (примеры различных статистик критериев см. ниже). Эта величина количественно отражает аргументы в наборе данных против нулевой гипотезы.
Критическая область. Для принятия решения об отклонении или не отклонении нулевой гипотезы необходимо также определить критическую область проверки гипотезы.
Выделяют 3 вида критических областей:
- двусторонняя:
Рис. 1 Двусторонняя критическая область
- левосторонняя:
Рис. 2 Левосторонняя критическая область
- правосторонняя:
Рис. 3 Правосторонняя критическая область
— заданный исследователем уровень значимости.
Если наблюдаемое значение критерия (K) принадлежит критической области (Kкр, заштрихованная область на рис.1-3), гипотезу отвергают, если не принадлежит — не отвергают.
Для краткости можно записать и так:
| K | > Kкр — отклоняем H0
| K | < Kкр — не отклоняем H0
Получение значения р (достигнутого уровня значимости)
Все статистики критерия подчиняются известным теоретическим распределениям вероятности. Значение статистики критерия, полученное из выборки, связывают с уже известным распределением, которому она подчиняется, чтобы получить значение р, площадь обоих «хвостов» (или одного «хвоста», в случае односторонней гипотезы) распределения вероятности.
Большинство компьютерных пакетов обеспечивают автоматическое вычисление двустороннего значения р.
Значение р — это вероятность получения нашего вычисленного значения критерия или его еще большего значения, если нулевая гипотеза верна.
Иными словами, p — это вероятность отвергнуть нулевую гипотезу при условии, что она верна.
Нулевая гипотеза всегда относится к популяции, представляющей больший интерес, нежели выборка. В рамках проверки гипотезы мы либо отвергаем нулевую гипотезу и принимаем альтернативу, либо не отвергаем нулевую гипотезу. Подробнее об ошибках при проверке гипотез
Применение значения р
Следует решить, сколько аргументов позволят отвергнуть нулевую гипотезу в пользу альтернативной. Чем меньше значение р, тем сильнее аргументы против нулевой гипотезы.
-
Традиционно полагают, если р < 0,05, (
=0,05) то аргументов достаточно, чтобы отвергнуть нулевую гипотезу, хотя есть небольшой шанс против этого. Тогда можно отвергнуть нулевую гипотезу и сказать, что результаты значимы на 5% уровне.
-
Напротив, если р > 0,05, то аргументов недостаточно, чтобы отвергнуть нулевую гипотезу. Не отвергая нулевую гипотезу, можно заявить, что результаты не значимы на 5% уровне. Данное заключение не означает, что нулевая гипотеза истинна, просто недостаточно аргументов (возможно, маленький объем выборки), чтобы ее отвергнуть.
Уровень значимости (т.е. выбранная «граница отсечки») 5% задается произвольно. На уровне 5% можно отвергнуть нулевую гипотезу, когда она верна. Если это может привести к серьезным последствиям, необходимо потребовать более веских аргументов, прежде чем отвергнуть нулевую гипотезу, например, выбрать значение = 0,01 (или 0,001).
Определение результата только как значимого на определенном уровне граничного значения (например 0, 05) может ввести в заблуждение. Например, если р = 0,04, то нулевую гипотезу отвергаем, но если р = 0,06, то ее не отвергли бы. Действительно ли они различны? Мы рекомендуем всегда указывать точное значение р, обычно получаемое путем компьютерного анализа.
Проверка гипотез против доверительных интервалов
Доверительные интервалы и проверка гипотез тесно связаны. Первоначальная цель проверки гипотезы состоит в том, чтобы принять решение и предоставить точное значение р.
Доверительный интервал (ДИ) количественно определяет изучаемый эффект (например, разницу в средних) и дает возможность оценить значение результатов. ДИ предоставляют интервал вероятных значений для истинного эффекта, поэтому его также можно использовать для принятия решения даже без точных значений р.
Например, если бы гипотетическое значение для данного эффекта (например, значение, равное нулю) находилось вне 95% ДИ, можно было бы счесть гипотетическое значение неправдоподобным и отвергнуть . В этом случае станет известно, что р < 0,05, но не станет известно его точное значение
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид:
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Финансовые аналитики часто сталкиваются с конкурирующими идеями о том, как работают финансовые рынки. Некоторые из этих идей развиваются через личные исследования или опыт работы с рынками; другие появляются благодаря взаимодействию с коллегами; и многие другие появляются в результате публикаций в профессиональной литературе по финансам и инвестициям.
Но как может аналитик определить насколько истинны или ложны те или иные идеи?
Когда мы можем свести идею или предположение к определенному утверждению о значении величины, такому как среднее значение совокупности, идея становится статистически проверяемым утверждением или гипотезой.
Аналитик может захотеть исследовать такие вопросы, как:
- Отличается ли средняя доходность данного взаимного фонда от средней эталонной доходности?
- Изменится ли волатильность доходности акции, после того как эта акция будет добавлена в рыночный индекс акций?
- Влияет ли разница между ценами продажи и покупки акции, связанная с числом дилеров, на рынок этой акции?
- Поддерживают ли данные национального рынка облигаций прогноз, полученный на основе экономической теории о временной структуре процентных ставок (связь между доходностью и сроком погашения)?
Для решения этих вопросов, мы используем концепцию и методы проверки статистических гипотез.
Проверка статистических гипотез (англ. ‘hypothesis testing’) является частью статистического вывода, и представляет собой процесс принятия суждений о более крупной группе (совокупности) на основе небольшой фактически наблюдаемой группе (выборке).
Концепции и методы проверки гипотез обеспечивают объективные средства для оценки того, подтверждают ли имеющиеся доказательства гипотезу. После статистической проверки гипотезы мы должны иметь четкое представление о вероятности того, верна ли гипотеза или нет.
Проверка статистических гипотез была мощным инструментом в научном развитии инвестиций. Как написал Роберт Л. Кан (Robert L. Kahn) из Института социальных исследований (Анн-Арбор, штат Мичиган):
«Мельница науки перемалывает только тогда, когда гипотезы и данные находятся в непрерывном и тесном контакте».
Основные акценты этого чтения сосредоточены на основах проверки гипотез и проверке гипотез, касающихся среднего значения и дисперсии, — двух величин, весьма часто использующихся в инвестициях.
Сначала мы приведем обзор процедуры проверки гипотез. Затем обратимся проверке гипотез о среднем, гипотез о разнице между средними и среднем значении разности. В следующем разделе этого чтения, мы рассмотрим проверку гипотез о дисперсии и различиях между дисперсиями, а также проверку гипотез о значении коэффицента корреляции.
В завершение мы рассмотрим непараметрические методы статистического вывода.
Проверка гипотезы, как мы уже упоминали, является частью области статистики, известной как статистический вывод. Традиционно область статистического вывода имеет два направления: статистическая оценка и проверка гипотез.
Статистическая оценка отвечает вопрос:
«Чему равно значение этого параметра (например, среднего значения по совокупности)?»
Ответ на этот вопрос дается в виде доверительного интервала, построенного вокруг точечной оценки. В случае со средним значением, мы строим доверительный интервал для среднего значения совокупности вокруг выборочного среднего, полученного в результате точечной оценки.
Например, предположим, что выборочное среднее равно 50 и 95-процентный доверительный интервал для среднего населения составляет (50 pm 10) (доверительный интервал составляет от 40 до 60). Если доверительный интервал правильно построен, то есть 95-процентная вероятность того, что интервал от 40 до 60 содержит среднее значение совокупности.
Мы обсуждали построение и интерпретацию доверительных интервалов в чтении о выборочном методе и статистической оценке.
Вторая ветвь статистического вывода, проверка гипотез, имеет несколько иную направленность.
Проверка статистических гипотез отвечает на вопрос:
«Равно ли значение параметра (например, среднего значения по совокупности) 45 (или другому конкретному значению)?»
Утверждение «среднее совокупности равно 45» является гипотезой. Статистическая гипотеза (англ. ‘hypothesis’) определяется как утверждение об одной или нескольких совокупностях.
Этот раздел посвящен концепции проверки гипотез. Процесс проверки гипотезы является частью строгого подхода к получению знаний, известного как научный метод (англ. ‘scientific method’).
Научный метод начинается с наблюдений и формулировки теории организации и объяснения наблюдений. Мы судим о правильности теории по ее способности давать точные прогнозы — например, предсказывать результаты новых наблюдений.
Чтобы быть проверяемой, теория должна быть способна делать предсказания, ошибочность которых можно показать.
Если прогнозы верны, мы продолжаем поддерживать теорию, как возможно правильное объяснение наших наблюдений. Когда в результатах наблюдений важна оценка риска, как в области финансов, мы можем попытаться сделать объективное, основанное на вероятности, суждение о том, поддерживают ли новые данные прогноз.
Проверка статистических гипотез играет ключевую роль, когда важна оценка риска.
В своей ежедневной работе финансовый аналитик может сталкиваться с вопросами, на которые он может дать ответы различного качества.
Когда аналитик правильно формулирует проверяемую гипотезу, проверяет ее и составляет отчет о проверке гипотезы, он следует нормам научного метода.
Конечно, логика аналитика, экономическое обоснование, источники информации, и, возможно, другие факторы также оказывают определенное влияние на качество ответа на заданный вопрос.
См. работу Freeley и Steinberg (2008) для обсуждения влияния критического мышления на мотивированное принятие решений.
Мы начнем изучение проверки гипотез со следующего списка из семи шагов.
Этапы проверки статистических гипотез.
Этапы проверки гипотезы заключаются в следующем:
- Формулировка гипотезы.
- Определение соответствующей тестовой статистики (статистики критерия) и ее распределения вероятностей.
- Определение уровня значимости.
- Формулировка правила принятия решения.
- Сбор данных и расчет тестовой статистики.
- Принятие статистического решения.
- Принятие экономического или инвестиционного решения.
Этот список этапов основан на списке из работы Daniel и Terrell (1995).
Мы расскажем о каждом из этих этапов, используя в качестве иллюстрации проверку гипотезы о премии за риск для американских акций. Описанный процесс представляет собой традиционный подход к проверке гипотез.
В завершении мы рассмотрим часто используемую альтернативу этих шагов — подход, основанный на p-значении.
1 этап. Формулировка гипотезы.
Первым шагом в проверке гипотезы является формулировка гипотезы. Мы всегда формулируем две гипотезы: нулевую гипотезу (или нуль), обозначаемую как (H_0), и альтернативную гипотезу, обозначаемую как (H_a).
Определение нулевой гипотезы.
Нулевая гипотеза — это гипотеза, которую нужно проверить. Например, мы могли бы предположить, что среднее по совокупности премии за риск для американских акций меньше или равно нулю.
Нулевая гипотеза (нуль, англ. ‘null hypothesis’) — это утверждение, которое считается истинным, если только используемая для проверки гипотезы выборка не дает убедительные доказательства того, что нулевая гипотеза неверна. Когда такие доказательства присутствуют, мы переходим к альтернативной гипотезе.
Определение альтернативной гипотезы.
Альтернативная гипотеза (альтернатива или конкурирующая гипотеза, англ. ‘alternative hypothesis’) — это гипотеза, которая принимается, когда нулевая гипотеза отвергается. Наша альтернативная гипотеза заключается в том, что среднее по совокупности премии за риск для американских акций больше нуля.
Предположим, что наш вопрос касается значения параметра совокупности (theta), по отношению к одному возможному значению параметра, (theta_0) (они читаются, соответственно, как «тета» и «тета ноль»).
Греческие буквы, такие как (sigma), зарезервированы для параметров совокупности. Римские курсивные буквы, например, (s), используются для выборочных статистик.
Примерами параметра совокупности являются среднее по совокупности (mu) и дисперсия совокупности (sigma^2). Мы можем сформулировать три различные пары нулевых и альтернативных гипотез и обозначить их согласно утверждению альтернативной гипотезы.
Формулировки гипотез.
Мы можем сформулировать нулевые и альтернативные гипотезы тремя различными способами:
- 1-я формулировка: (H_0: theta = theta_0) (нулевая гипотеза) и (H_a: theta neq theta_0) (альтернативная гипотеза «не равно»).
- 2-я формулировка: (H_0: theta leq theta_0) (нулевая гипотеза) и (H_a: theta > theta_0) (альтернативная гипотеза «больше чем»).
- 3-я формулировка: (H_0: theta geq theta_0) (нулевая гипотеза) и (H_a: theta < theta_0) (альтернативная гипотеза «меньше, чем»).
В нашем примере с американскими акциями, (theta = mu_{RP} ), что представляет собой среднее по совокупности премии за риск для американских акций. Кроме того, (theta_0 = 0 ), и мы используем вторую из указанных выше трех пар гипотез.
1-я формулировка представляет собой двустороннюю проверку гипотезы (англ. ‘ two-sided hypothesis test’ или ‘two-tailed hypothesis test’): Мы отвергаем нуль в пользу альтернативы, если данные свидетельствуют о том, что параметр совокупности либо меньше, либо больше, чем (theta_0 ).
В отличие от этого, 2-я и 3-я формулировки являются односторонней проверкой гипотезы (англ. ‘one-sided hypothesis test’ или ‘one-tailed hypothesis test’).
В формулировках 2 и 3 мы отвергаем нуль только тогда, когда данные свидетельствуют о том, что параметр совокупности соответственно, либо больше, либо меньше, чем (theta_0 ). Альтернативная гипотеза имеет только одну сторону.
Обратите внимание, что в каждом из описанных выше случаев, мы формулируем нулевые и альтернативные гипотезы так, что они учитывают все возможные значения параметра. В формулировке 1, например, параметр или равен гипотетическому значению (theta_0 ) (по нулевой гипотезе) или не равен гипотетическому значению (theta_0 ) (по альтернативной гипотезе).
Эти два утверждения логически исчерпывают все возможные значения параметра.
Несмотря на то, что формулировать гипотезы можно различными способами, мы всегда проводим проверку нулевой гипотезы в точке равенства, (theta = theta_0 ). Если нуль это (H_0: theta = theta_0), (H_0: theta leq theta_0) или (H_0: theta geq theta_0), мы на самом деле проверяем (theta = theta_0 ). Логика проста.
Предположим, что гипотетическое значение параметра равно 5.
Рассмотрим нулевую гипотезу (H_0: theta leq 5), с альтернативной гипотезой «больше чем» (H_a: theta > 5) .
Если у нас есть достаточно доказательств, чтобы отклонить (H_a: theta = 5) в пользу (H_a: theta > 5), то у нас, безусловно, также есть достаточные доказательства, чтобы отвергнуть гипотезу о том, что параметр (theta) равен некоторому меньшему значению, например, 4.5 или 4.
Напомним, что расчет для проверки нулевой гипотезы является одинаковым для всех трех формулировок. Различия в трех формулировках мы увидим в ближайшее время, — они заключаются в определении того, следует ли отклонить нулевую гипотезу.
Как мы выбираем нулевые и альтернативные гипотезы?
Вероятно, наиболее распространенными являются альтернативные гипотезы «не равно». Мы отвергаем нуль, поскольку данные свидетельствуют о том, что параметр больше или меньше, чем (theta_0).
Иногда, однако, у нас могут быть условия, имеющие вид «ожидаем», «подозреваем» или «надеемся на то, что», которые означают, что мы хотим найти благоприятные доказательства.
Часть этого обсуждения выбора гипотез взята из работы Bowerman, O’Connell и Murphree (2016).
В этом случае, мы можем сформулировать альтернативную гипотезу, как утверждение о том, что это условие является истинным. При этом нулевой гипотезой будет утверждение о том, что это условие не истинно. Если данные подтверждают отклонение нуля и принятие альтернативы, то мы статистически подтвердили наши ожидания того, что было истиной.
Например, экономическая теория предполагает, что инвесторы требуют положительную премию за риск по акциям (премия за риск определяется как ожидаемая доходность акций за вычетом безрисковой ставки).
Следуя принципу с формулировки альтернативы в виде условия «надеемся на то, что», сформулируем следующие гипотезы:
- (H_0:) Среднее по совокупности премии за риск для американских акций меньше или равно 0.
- (H_a:) Среднее по совокупности премии за риск для американских акций положительно.
Обратите внимание, что альтернативные гипотезы «больше чем» и «меньше чем» отражают убеждения исследователя сильнее, чем альтернативная гипотеза «не равно».
Для того, чтобы подчеркнуть свое нейтральное отношение к гипотезам, исследователь может иногда выбрать альтернативную гипотезу «не равно», когда выбор односторонней альтернативной гипотезы также разумен.
2 этап. Определение тестовой статистики и ее распределения вероятностей.
Второй этап проверки гипотез заключается в определении соответствующей тестовой статистики и ее распределения вероятностей.
Определение тестовой статистики.
Тестовая статистика, тест-статистика или статистика критерия (т.е. статистика, лежащая в основе критерия, англ. ‘test statistic’) является величиной, рассчитанной на основе выборки, значение которой является основанием для принятия решения о том, следует ли отклонить нулевую гипотезу.
Средоточием нашего статистического решения является значение тестовой статистики. Очень часто (во всех случаях, которые мы рассмотрим в этом чтении) тестовая статистика имеет следующий вид:
( Large stBf{Тестовая}{статистика} = { stRm{Выборочная}{статистика} — stRm{Значение параметра}{совокупности при $H_0$} over text{Стандартная ошибка выборочной статистики}} ) (Формула 1)
Для нашей премии за риск, например, интересующий параметр совокупности — это средняя по совокупности премия за риск (mu_{RP}). Мы обозначаем гипотетическое значение среднего по совокупности населения для (H_0) как (mu_0). Переформулировав гипотезу с использованием символов, мы проверяем нуль (H_0: mu_{RP} leq mu_0 ) и альтернативу (H_a: mu_{RP} > mu_0 ).
Однако, поскольку в соответствии с нулем мы проверяем условие ( mu_0 = 0), то мы пишем (H_0: mu_{RP} leq 0 ) и (H_a: mu_{RP} > 0 ).
Выборочное среднее обеспечивает оценку среднего по совокупности. Таким образом, мы можем использовать выборочное среднее премии за риск ( overline X_{RP}), рассчитанное на основе исторических данных, в качестве выборочной статистики в Формуле 1.
Стандартное отклонение выборочной статистики, известное как «стандартная ошибка» статистики, является знаменателем в Формуле 1.
В этом примере выборочной статистикой является выборочное среднее. Для выборочного среднего ( overline X ), рассчитанного по выборке, отобранной из совокупности со стандартным отклонением ( sigma ), стандартная ошибка определяется по одной из двух формул:
(large dst
sigma_{overline X} = {sigma over sqrt n} ) (Формула 2)
если нам известно стандартное отклонение совокупности (sigma), или
(large dst
s_{overline X} = {s over sqrt n} ) (Формула 3)
когда мы не знаем стандартное отклонение совокупности и нам необходимо использовать стандартное отклонение выборки (s) оценки стандартной ошибки.
В этом примере, поскольку мы не знаем стандартное отклонение совокупности, порождающей доходность, мы используем Формулу 3.
Таким образом, тестовая статистика определяется по формуле:
( large dst
{overline X_{RP} — mu_0 over s_{overline X}} = {overline X_{RP} — 0 over s big / sqrt n } )
Заменяя (mu_0) на 0, мы используем тот уже отмеченный факт, что мы тестируем любую нулевую гипотезу в точке равенства, а также тот факт, что здесь (mu_0 = 0).
Итак, мы определили тестовую статистику, чтобы проверить нулевую гипотезу.
Какому распределению вероятностей она соответствует?
В этом чтении мы будет использовать четыре распределения вероятности для тестовых статистик:
- t-распределение Стьюдента (для t-теста);
- Стандартное нормальное или z-распределение (для z-теста);
- Распределение хи-квадрат (( chi^2 )) (для хи-квадрат теста); а также
- F-распределение (для F-теста).
Мы обсудим детали этих вариантов позже, но предположим, что мы можем провести z-тест, основанный на центральной предельной теореме, потому что наша выборка американских акций имеет много наблюдений.
Центральная предельная теорема говорит о том, что выборочное распределение выборочного среднего будет приблизительно нормальным со средним (mu) и дисперсией (sigma^2 / n), когда выборка имеет большой размер.
Выборка, которую мы будем использовать для этого примера, содержит 118 наблюдений.
В итоге, тестовая статистика для проверки гипотезы о средней премии за риск равна ( overline X_{RP} big / s_{overline X}).
Мы можем выполнить z-тест, поскольку мы можем правдоподобно предположить, что тестовая статистика следует стандартному нормальному распределению.
3 этап. Определение уровня значимости.
Третьим этапом проверки гипотез является определение уровня значимости. Когда тестовая статистика рассчитана, возможны два действия:
- Мы отвергаем нулевую гипотезу или
- Мы не отвергаем нулевую гипотезу.
Выбор действия основан на сравнении вычисленной тестовой статистики с заданным возможным значением или значениями. Значения, которые мы выбираем, основаны на выбранном уровне значимости. Уровень значимости отражает то, какие основанные на выборке доказательства нам необходимы, чтобы отвергнуть нуль.
По аналогии с судом, необходимая доказательная база может меняться в зависимости от характера гипотез и серьезности последствий совершения ошибки.
Возможны четыре результата при проверке нулевой гипотезы:
- Мы отвергаем ложную нулевую гипотезу. Это правильное решение.
- Мы отвергаем истинную нулевую гипотезу. Это называется ошибкой I рода (англ. ‘Type I error’).
- Мы не отвергаем ложную нулевую гипотезу. Это называется ошибкой II рода (англ. ‘Type II error’).
- Мы не отвергаем истинную нулевую гипотезу. Это правильное решение.
Проиллюстрируем эти результаты в Таблице 1.
|
Решение |
Ситуация |
|
|---|---|---|
|
(H_0) Истина |
(H_0) Ложь |
|
|
(H_0) не отвергается |
Правильное решение |
Ошибка II рода |
|
(H_0) отвергается (принимается (H_a)) |
Ошибка I рода |
Правильное решение |
Когда мы принимаем решение при проверке гипотезы, мы рискуем допустить ошибку I или II рода. Это взаимоисключающие ошибки:
- Если мы ошибочно отвергаем нуль, мы можем допустить только ошибку I рода.
- Если мы ошибочно не отвергаем нуль, мы можем допустить только ошибку II рода.
Вероятность ошибки I рода при проверке гипотезы обозначается греческой буквой альфа: (alpha). Эта вероятность также известна как уровень значимости проверки (англ. ‘level of significance’).
Например, уровень значимости 0.05 для проверки означает, что есть 5-процентная вероятность отклонения истинной нулевой гипотезы.
Вероятность ошибки II рода обозначается греческой буквой бета: (beta).
Управление вероятностью ошибок двух типов предполагает компромисс. При прочих равных, если мы уменьшаем вероятность ошибки I рода, задав меньший уровень значимости (скажем, 0.01, а не 0.05), мы увеличиваем вероятность совершить ошибку II рода, потому что мы отвергаем нуль реже, в том числе, когда он является ложным.
Единственным способом уменьшить вероятность ошибок обоих типов одновременно является увеличение размера выборки (n).
Количественный компромисс между двумя типами ошибок на практике, как правило, невозможен, потому что вероятность ошибки II рода очень трудно определить количественно.
Рассмотрим пример с парой гипотез: (H_0: theta leq 5) и (H_a: theta > 5).
Поскольку каждое истинное значение (theta) больше 5 делает нулевую гипотезу ложной, каждое значение (theta) больше 5 имеет различную (beta) (вероятность ошибки II рода).
В отличие от этого, нам достаточно только констатировать вероятность ошибки I рода при (theta = 5). Таким образом, как правило, мы указываем только вероятность ошибки I рода, когда выполняем проверку гипотезы.
В то время как уровень значимости проверки является вероятностью ошибочно отвергнуть нулевую гипотезу, то мощностью критерия или мощностью проверки (англ. ‘power of a test’) является вероятность правильного отклонения нулевой гипотезы — то есть вероятность отвергнуть нуль, если он ложный.
Мощность критерия, на самом деле, равна 1 минус вероятность ошибки II рода.
Когда при проведении проверки имеется более одной статистики критерия, мы должны предпочесть самую мощную из них, при прочих равных условиях.
Тем не менее, у нас не всегда есть информация об относительной мощности критерия для конкурирующих статистик критерия.
В итоге, стандартный подход к проверке гипотез включает только определение уровня значимости (вероятности ошибки I рода). Наиболее целесообразно устанавливать этот уровень значимости до расчета тестовой статистики (статистики критерия). Если мы указываем его после вычисления тестовой статистики, на нас может повлиять результат расчета, что умаляет объективность проверки.
Мы можем использовать три наиболее распространенных уровня значимости для проведения проверки гипотезы: 0.10, 0.05 и 0.01.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.10, то у нас есть доказательства того, что нулевая гипотеза неверна.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.05, то у нас есть убедительные доказательства того, что нулевая гипотеза неверна.
И если мы можем отклонить нулевую гипотезу на уровне значимости 0.01, то у нас есть очень убедительные доказательства того, что нулевая гипотеза неверна.
Для нашего примера с премией за риск, мы установим уровень значимости 0.05.
4 этап. Формулировка правила принятия решения.
Четвертый этап проверки гипотезы заключается в формулировке правила принятия решения (англ. ‘decision rule’).
Общий принцип формулируется просто.
Когда мы проверяем нулевую гипотезу, если мы находим, что рассчитанное значение статистики критерия (тестовой статистики) является экстремальным или более экстремальным, чем заданное значение или значения, определенные установленным уровнем значимости (alpha), то мы отвергаем нулевую гипотезу. Мы говорим, что результат является статистически значимым (англ. ‘statistically significant’).
В противном случае, мы не отвергаем нулевую гипотезу, и говорим, что результат не является статистически значимым. Значение или значения, с которым мы сравниваем вычисленную статистику критерия, чтобы принять наше решение, являются точками отклонения (критическими значениями) для проверки гипотезы.
Термин «точка отклонения» (англ. ‘rejection point’) является описательным синонимом для более традиционного термина «критическое значение» (англ. ‘critical value’).
Определение критического значения для статистики критерия.
Критическое значение или точка отклонения (англ. ‘critical value’) для тестовой статистики (статистики критерия) представляет собой значение, с которой сравнивается вычисленная тестовая статистика, чтобы решить, следует ли отклонять или не отклонять нулевую гипотезу.
Для односторонней проверки, мы указываем критическое значение, используя символ для тестовой статистики с индексом (alpha), обозначающим заданную вероятность ошибки I рода, например, (z_alpha).
Для двусторонней проверки, мы указываем критическое значение (z_{alpha/2}).
Для того, чтобы проиллюстрировать применение критических значений, предположим, что мы используем z-тест и выбрали уровень значимости 0.05.
Для проверки пары гипотез (H_0: theta = theta_0) и (H_a: theta neq theta_0), существуют два критических значения, — одно отрицательное и одно положительное.
Для двухсторонней проверки при уровне значимости 0.05, суммарная вероятность ошибки I рода должна быть равна 0.05. Таким образом, 0.05 / 2 = 0.025 вероятности должно быть в каждом хвосте распределения тестовой статистики при нулевой гипотезе.
Следовательно, двумя критическими значениями будут (z_{0.025} = 1.96) и (-z_{0.025} = -1.96). Пусть (z) является вычисленным значением тестовой статистики. Мы отвергаем нуль, если находим, что (z < -1.96) или (z > 1.96). И мы не отвергаем нуль, если (-1.96 leq z leq 1.96).
Для проверки пары гипотез (H_0: theta leq theta_0) и (H_a: theta > theta_0) при уровне значимости 0.05, критическим значением будет (z_{0.05} = 1.645). Мы отвергаем нулевую гипотезу, если (z > 1.645). Значение стандартного нормального распределения таково, что 5% результатов лежат правее точки (z_{0.05} = 1.645).
Для проверки пары гипотез (H_0: theta geq theta_0) и (H_a: theta < theta_0), критическим значением будет (-z_{0.05} = -1.645). Мы отвергаем нулевую гипотезу, если (z < -1.645).
График 2 иллюстрирует проверку (H_0: mu = mu_0) и (H_a: mu neq mu_0) при уровне значимости 0.05 с использованием z-теста.
Термин «область принятия гипотезы» (англ. ‘acceptance region’) является традиционным названием для множества значений тестовой статистики, при которых мы не отвергаем нулевую гипотезу.
Традиционное название, однако, неточное. Мы должны избегать использования таких фраз, как «принять нулевую гипотезу», потому что такое утверждение подразумевает неоправданно большую степень убежденности в нуле, когда мы не отвергаем его.
Аналогия с некоторыми судами (например, в Соединенных Штатах) заключается в том, что если присяжные не выносят вердикт о виновности (альтернативная гипотеза), наиболее точным будет сказать, что жюри не удалось отклонить нулевую гипотезу о невиновности обвиняемого (что следует из принципа презумпции невиновности).
По обеим сторонам от области принятия решения находятся области отклонения или критические области (англ. ‘rejection region’ или ‘critical region’).
Если нулевая гипотеза заключается в том, что ( mu = mu_0 ) истинно, тестовая статистика имеет 2.5-процентный шанс попадания в левую критическую область и 2.5-процентный шанс попадания в правую критическую область.
Любое вычисленное значение тестовой статистики, которое попадает в любую из этих двух областей, заставляет нас отвергнуть нулевую гипотезу при уровне значимости 0.05. Критические значения 1.96 и -1.96 рассматриваются как разделительные линии между областями принятия и отклонения гипотезы.
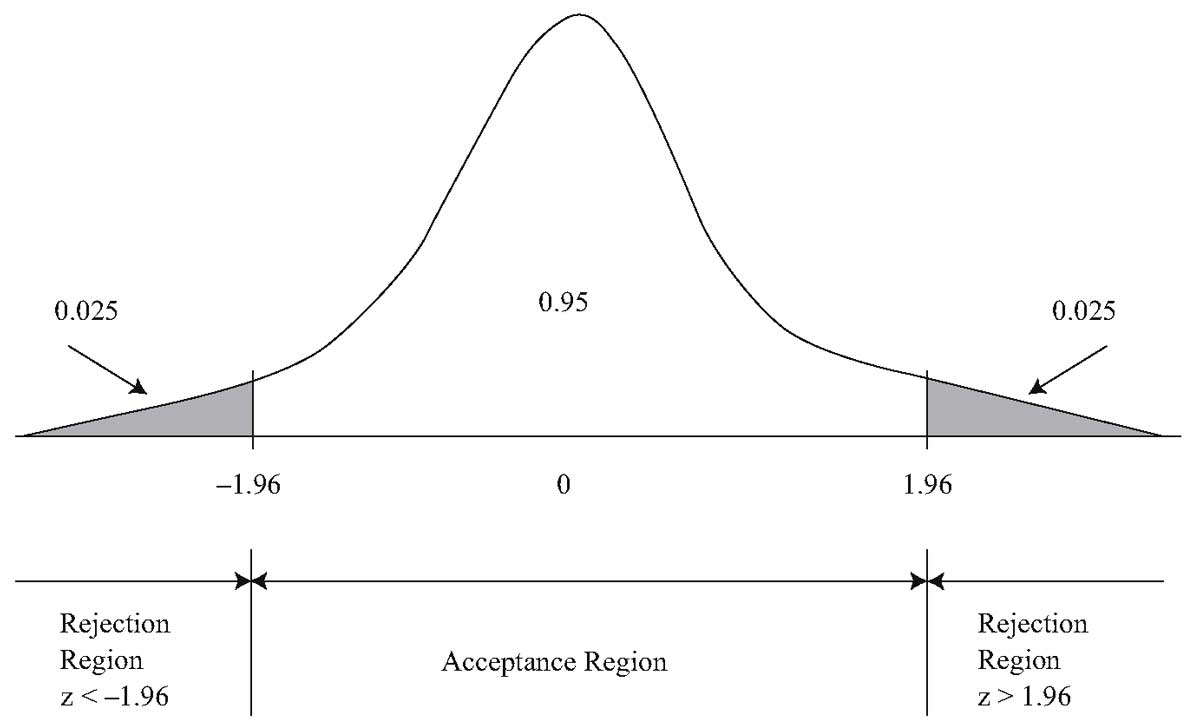
График 2 дает хорошую возможность подчеркнуть взаимосвязь между доверительными интервалами и проверкой гипотез. 95-процентный доверительный интервал для среднего по совокупности (mu), основанного на выборочном среднем (overline X), задается диапазоном от (overline X — 1.96s_{overline X}) до (overline X + 1.96s_{overline X}), где (s_{overline X}) является стандартной ошибкой выборочного среднего (Формула 3).
Так же, как и при проверке гипотезы, мы можем использовать этот доверительный интервал, основанный на стандартном нормальном распределении, когда у нас есть большая выборка.
Альтернативная проверка гипотезы и доверительный интервал используют t-распределение. Мы рассмотрим эти концепции в следующем разделе.
Теперь рассмотрим одно из условий для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} > 1.96)
Здесь (mu_0) является гипотетическим значением среднего по совокупности. Условие гласит, что отклонение гипотезы является оправданным, если тестовая статистика превышает 1.96.
Умножив обе стороны неравенства на (s_{overline X}), мы получим ( overline X — mu_0 > 1.96 s_{overline X}), или после преобразования, ( overline X — 1.96 s_{overline X} > mu_0), что можем также записать в виде ( mu_0 < overline X — 1.96 s_{overline X}).
Это выражение означает, что если гипотетическое среднее по совокупности (mu_0), меньше нижнего предела 95-процентного доверительного интервала, основанного на выборочном среднем, мы должны отвергнуть нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область справа).
Теперь мы можем взять другое условие для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} < -1.96)
и, используя алгебру, как и ранее, мы преобразуем его к виду:
( dst mu_0 > overline X — 1.96 s_{overline X})
Если гипотетическое среднее по совокупности больше, чем верхний предел 95-процентного доверительного интервала, мы отвергаем нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область слева).
Таким образом, уровень значимости в двусторонней проверке гипотезы можно интерпретировать точно так же, как доверительный интервал (1 — alpha).
Таким образом, когда гипотетическое значение параметра совокупности для нулевой гипотезы находится вне соответствующего доверительного интервала, то нулевая гипотеза отвергается. Мы могли бы использовать доверительные интервалы для проверки гипотез, но на практике финансовые аналитики, как правило, этого не делают.
Вычисление тестовой статистики (одно число, по сравнению с двумя числами для обычного доверительного интервала) более эффективно. Также, на практике аналитики редко сталкиваются с односторонними доверительными интервалами.
Кроме того, только вычислив тестовую статистику, мы можем получить p-значение, полезный показатель значимости результатов (мы обсудим p-значение далее).
Вернемся к нашей проверке премии за риск.
Мы сформулировали гипотезы (H_0: mu_{RP} leq 0) и (H_a: mu_{RP} > 0). Мы определили тестовую статистику как ( overline X_{RP} / s_{overline X}) и определили, что она следует стандартному нормальному распределению.
Таким образом, мы выполняем односторонний z-тест.
Мы определили уровень значимости 0.05. Для этого одностороннего z-теста, критическая точка при уровне значимости 0.05 составляет 1.645. Мы отвергаем нуль, если вычисленная z-статистика больше, чем 1.645.
График 3 иллюстрирует эту проверку.
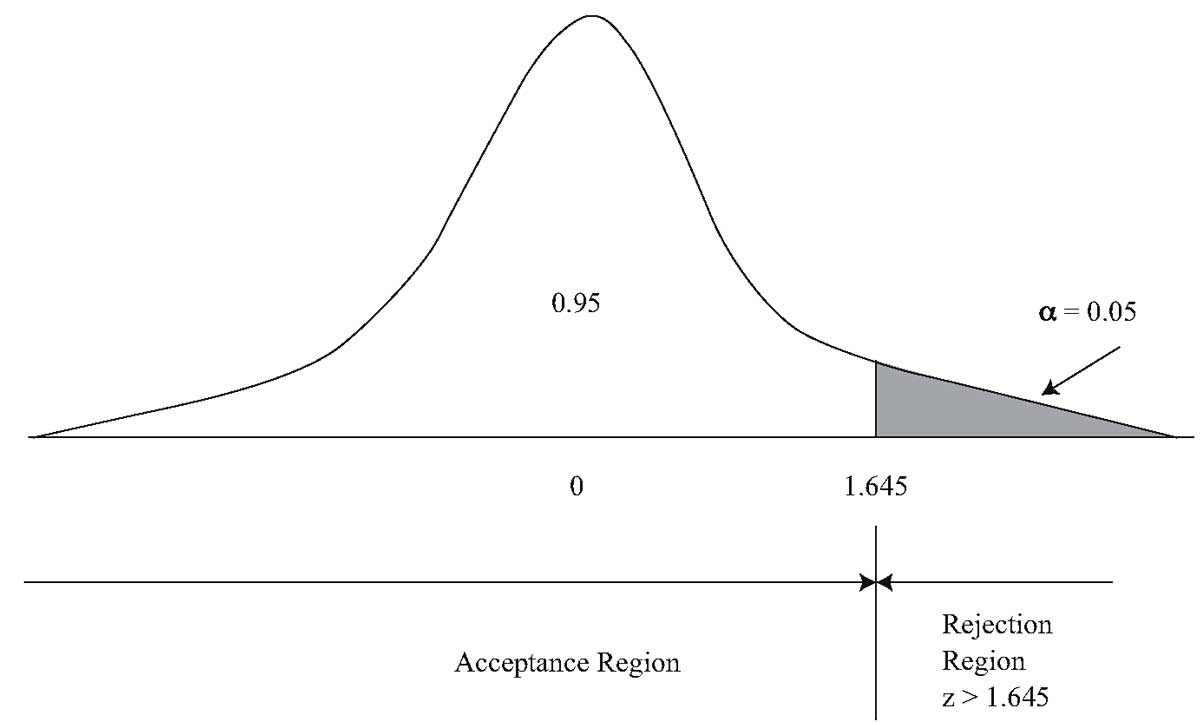
5 этап. Сбор данных и расчет тестовой статистики.
Пятый шаг в проверке гипотез заключается в сборе данные и расчете тестовой статистики. Качество наших выводов зависит не только от уместности статистической модели, но и от качества данных, которые мы используем при проведении проверки.
В первую очередь мы должны проверить данные на наличие ошибок измерений. Нам также необходимо учесть другие проблемы, в том числе систематическую ошибку выборки и систематическую ошибку временного периода.
Систематическая ошибка выборки — это смещение выборки, связанное с систематическим исключением некоторых элементов совокупности в соответствии с определенным признаком.
Одним из типов систематической ошибки выборки является систематическая ошибка выжившего. Например, если мы определим нашу выборку, как облигации взаимных фондов США, которые продолжают деятельность в настоящее время, и мы сделаем выборку доходности только по этим фондам, мы будем систематически исключать фонда, которые не выжили (прекратили деятельность) к настоящему моменту.
Прекратившие деятельность фонды, скорее всего, в среднем хуже оставшихся фондов. В результате, эффективность фондов, рассчитанная на основе этой выборки, может быть смещена вверх.
Систематическая ошибка временного периода связана с вероятностью того, что когда мы используем выборку из временных рядов, наш статистический вывод может быть чувствительным к начальным и конечным датам периода выборки.
В нашей гипотезе о премии за риск мы имеем дело с американскими акциями. Согласно Dimson, Marsh и Staunton (2018) за период с 1900 по 2017 год включительно (118 ежегодных наблюдений), среднеарифметическая премия за риск для американских акций по отношению к доходности облигаций (overline X_{RP}) составила 7.5% в год.
Выборочное стандартное отклонение годовой премии за риск составило 19.5%. Используя Формулу 3, найдем стандартную ошибку выборочного среднего:
( dst s_{overline X} = s big / sqrt n = 19.5% / sqrt {118} ) = 1.795%.
Тестовая статистика равна:
( dst z = overline X_{RP} big / s_{overline X}) = 7.5%/1.795% = 4.18.
6 этап. Принятие статистического решения.
Шестой этап проверки гипотезы означает принятие статистического решения.
В нашем примере, поскольку тестовая статистика (z = 4.18) больше критического значения 1.645, мы отвергаем нулевую гипотезу в пользу альтернативной гипотезы о том, что премия за риск для американских акций является положительной.
Первые шесть шагов являются статистическими шагами. Наше итоговое решение принимается с использованием статистического решения.
7 этап. Принятие экономического или инвестиционного решения.
Седьмой и заключительный шаг в проверке гипотез заключается в принятии экономического или инвестиционного решения. Экономическое или инвестиционное решение принимает во внимание не только статистические решения, но и все соответствующие экономические вопросы.
На шестом этапе, мы нашли убедительные статистические доказательства того, что премия за риск для американских акций является положительной. Величина расчетной премии за риск, 7.5% в год, является также очень значимой экономически.
Исходя из этих соображений, инвестор может принять решение инвестировать часть средств в американские акции. Ряд нестатистических соображений, таких как толерантность инвестора к риску и его финансовое положение, может также повлиять на процесс принятия решений.
Предшествующее обсуждение поднимает проблему, которая часто возникает на этом этапе принятия решений. Мы часто находим, что небольшие различия между переменной величиной и ее гипотетическим значением являются статистически значимыми, но не значимыми экономически.
Например, мы можем проверить инвестиционную стратегию и отклонить нулевую гипотезу о том, что средняя доходность стратегии равна нулю на основе большой выборки.
Формула 1 показывает, что чем меньше стандартная ошибка выборочной статистики (делитель в формуле), тем больше значение тестовой статистики и тем больше шанс на то, что нулевая гипотеза будет отклонена, при прочих равных условиях. Стандартная ошибка уменьшается по мере увеличения размера выборки (n), так что при очень больших выборках, мы можем отклонить нулевую гипотезу.
Мы можем обнаружить, что, хотя стратегия обеспечивает статистически значимую положительную среднюю доходность, результаты не являются экономически значимыми, если учесть транзакционные издержки, налоги и риски.
Даже если мы приходим к выводу, что результаты стратегии являются экономически значимыми, мы должны изучить логику того, почему стратегия могла бы работать в будущем, прежде чем реализовывать ее фактически. Такие соображения нельзя включить в проверку гипотезы.
Перед тем как завершить тему процесса проверки гипотез, мы должны обсудить важный альтернативный подход, называемый подходом проверке гипотез с. Аналитики и исследователи часто включают в отчеты о проверке гипотез p-значение (также называемое предельным уровнем значимости, англ. ‘marginal significance level’).
Определение p-значения.
P-значение (p-уровень значимости или p-критерий, англ. ‘p-value’) является наименьшим уровнем значимости, при котором может быть отвергнута нулевая гипотеза.
Для значения тестовой статистики 4.18 в проверке гипотезы о премии за риск, с помощью функции электронной таблицы для стандартного нормального распределения, мы вычисляем р-значение 0.000015. Мы можем отклонить нулевую гипотезу на этом уровне значимости.
Чем меньше р-значение, тем сильнее доказательства против нулевой гипотезы и в пользу альтернативной гипотезы. P-значение для двухсторонней проверки того, что параметр равен нулю, часто генерируется автоматически с помощью статистических и эконометрических программ.
Мы можем использовать электронные таблицы для расчета p-значения. В Microsoft Excel, например, мы можем использовать функции TTEST, NORMSDIST, CHIDIST и FDIST для расчета р-значений для f-тестов, z-тестов, хи-квадрат тестов, и F-тестов, соответственно.
Мы можем использовать р-значение в рамках процедуры проверки гипотез, представленной выше, в качестве альтернативы критическим значениям.
Если р-значение меньше нашего заданного уровня значимости, мы отвергаем нулевую гипотезу. В противном случае, мы не отвергаем нулевую гипотезу.
Используя p-значение таким образом, мы приходим к такому же выводу, что и при использовании критических значений. Например, поскольку 0.000015 меньше 0.05, мы отвергаем нулевую гипотезу в проверке гипотезы о премии за риск.
P-значение, тем не менее, обеспечивает более точную информацию о силе доказательств, чем подход с использованием критических значений. P-значение 0.000015 указывает на то, что нулевая гипотеза отвергается на гораздо меньшем уровне значимости, чем 0.05.
Если один исследователь рассматривает вопрос, используя уровень значимости 0.05, а другой исследователь использует уровень значимости 0.01, читатель может столкнуться с проблемой, сравнивая полученные результаты.
Эта проблема породила подход к представлению результатов проверки гипотез, при котором указываются p-значения и не указывается спецификация уровня значимости (этап 3). Интерпретация статистических результатов остается на усмотрение пользователя исследования. Этот подход к представлению результатов иногда называют подходом к проверке гипотез с использованием р-значения.
Davidson и MacKinnon (1993) оспорили достоинство этого подхода:
«Подход с использование p-значения по не обязательно заставит нас принять решение о нулевой гипотезе. Если мы получим p-значение равное, скажем, 0.000001, мы почти наверняка захотим отклонить нуль.
Но если мы получим p-значение равное, скажем, 0.04, или даже 0.004, мы не обязаны отклонять его. Мы можем просто отбросить результат прочь, как информацию, которая ставит под сомнение нулевую гипотезу, но сама по себе не убедительна.
Мы считаем, что это несколько агностическое отношение к статистическим проверкам, в которых p-значения рассматриваются просто как части информации, которую мы можем использовать, но можем и не использовать». (Стр. 80)











