Средняя и предельная ошибки выборки
Средняя ошибка выборкивсегда
присутствует в выборочных исследованиях
и появляется вследствие того, что
обследуются не все единицы статистической
совокупности, а лишь ее часть.
Средняя ошибка выборки превращается в
предельную ошибкуΔ
при умножении ее на коэффициент
доверияt, который задается
предварительно, исходя из требуемой
точности наблюдения. Предельная ошибка
позволяет судить об «истинном» размере
параметра в генеральной совокупности
с определенной степенью вероятности
|
|
При типическом и серийном
отборе, при расчете ошибки выборки
вместо общей дисперсии (σ2)
следует использовать
среднюю из внутригрупповых дисперсий
и межгрупповую дисперсию,
где—
частная дисперсия i группы,объем i группы
Формулы предельной ошибки случайной
выборки при определении средней
Для повторного отбора
|
|
где |
Для бесповторного отбора
|
|
Формулы предельной ошибки случайной
выборки при определении доли
Для повторного отбора
|
|
где |
Для бесповторного отбора
|
|
где |
Формулы численности случайной
выборки при определении средней величины
|
Для повторного |
Для |
|
|
|
Формулы численности случайной выборки при определении доли изучаемого признака
|
Для повторного |
Для |
|
|
|
Предельная разница между генеральной
и выборочной средней соответствует
величине предельной ошибки
|
для средней |
для доли: |
|
|
|
Значения вероятности и соответственно
tнаходятся по таблицам
распределения:
-
Лапласа
-
Стьюдента (в случае малой выборки)
Формулы случайной выборки подходят и
для механической выборки.
При необходимости округления, при
случайной выборке – округление в большую
сторону, при механической – в меньшую.
Малая выборка
Если численность выборочной совокупности
не более 30 единиц, то средняя ошибка
малой выборки при определении средней
величины рассчитывается по формуле:
|
при определении доли |
|
|
|
|
Для расчета ошибки малой выборки
применяется уточненная формула дисперсии
|
|
где n-1 — |
Типы задач выборочного наблюдения
-
определение ошибки выборки,
-
определение численности выборочной
совокупности n
, -
определение вероятности того, что
выборочная средняя (или доля) отклонится
от генеральной не более, чем на заданную
величину t=Δ/μ, -
оценка случайности расхождений
показателей выборочных наблюдений, -
перенос выборочных характеристик на
генеральную совокупность.
Проверка гипотез о средней и доле
Оценка случайности расхождений
показателей выборочных наблюдений
|
|
|
-
Если при n>30 коэффициент t<3, то делается
вывод о случайности расхождений. -
Если n≤ 30 , то полученное
значение t сравнивают с табличным,
определяемым по таблице распределения
Стьюдента -
Если
,
расхождение считается существенным. -
Если
,
расхождение считается случайным.
Методы переноса выборочных данных на
генеральную совокупность
-
метод взвешивания;
-
метод перевзвешивания;
-
метод заполнения случайным подбором
в классах замещения.
Повторный и бесповторный отбор.
Ошибка выборки
Краткая теория
На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.
При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.
Выборка может осуществляться по схеме повторного и бесповторного
отбора.
В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.
Выборка может осуществляться отдельными единицами или сериями
(гнездами).
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.
На основании приемов классической выборки решаются следующие
задачи:
а) определяются границы среднего значения показателя по генеральной
совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
;
при
;
при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной
совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным
значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:
где
– доля признака по генеральной совокупности.
Типическая (районированная) выборка
Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.
Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:
где
– средняя из внутригрупповых дисперсий
по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:
где
– численности единиц совокупности групп по выборке.
Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю
из частных выборочных средних
.
Для случая пропорционального отбора это определяется по формуле:
При непропорциональном отборе средняя из внутригрупповых дисперсий вычисляется по
формуле:
где
– численность единиц групп по генеральной
совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:
Средняя дисперсия доли
признака из групповых дисперсий доли
при
типической пропорциональной выборке вычисляется по формуле:
Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:
Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:
а средняя доля признака:
Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель
.
Серийная выборка
Серийная ошибка выборки
может применяться в двух вариантах:
а) объем серий различный
б) все серии имеют
одинаковое число единиц (равновеликие серии).
Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии
и
производится отбор не единиц совокупности, а серий
. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки
при
серийном отборе исчисляются по формулам:
а) при повторном отборе
б) при бесповторном отборе
где
– число
серий в генеральной совокупности;
– число
отобранных серий;
– межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:
где
–
среднее значение признака в каждой из отобранных серий;
– межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:
Определение численности выборочной совокупности
При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.
Примеры решения задач
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Задача 2
В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.
Решение
Численность
выборки можно найти по формуле:
В нашем случае:
Вывод к задаче
Таким образом численность
выборки должна составить 2661 чел.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала |
Средняя месячная заработная плата, руб. |
Среднее квадратическое отклонение, руб. |
Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Выборка. Типы выборок. Расчет ошибки выборки
Калькуляторы
Калькулятор расчета ошибки и размера выборки
Калькулятор расчета статистической значимости различий
Генеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих
определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и
времени. Примеры генеральных совокупностей
- Все жители Москвы (10,6 млн. человек по данным переписи 2002 года)
- Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года)
- Юридические лица России (2,2 млн. на начало 2005 года)
- Розничные торговые точки, осуществляющие продажу продуктов питания (20 тысяч на начало 2008 года) и
т.д.
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей
генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на
всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и
нерепрезентативной для разных генеральных совокупностей.
Пример:
- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население
Москвы. - Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать
москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках
соответственно.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от
ошибки никак не зависит от размера выборки.
Пример:
Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой
всех москвичей.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера
выборки. Чем больше размер выборки, тем она ниже.
Пример:
Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной
вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об
ошибке выборки, подразумевают именно статистическую ошибку.
Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих
результаты исследования в определенную сторону.
Пример:
- Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни.
Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например,
дома). - Проблема респондентов, отказывающихся отвечать на вопросы
анкеты (доля «отказников» в Москве, для разных опросов,
колеблется от 50% до 80%)
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот
или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные
1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов,
наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата
рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер
генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы
(страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются
случайным образом. Объекты внутри групп обследуются сплошняком.
2.Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности,
типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60
лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для
каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны
попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной
совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки
используются в маркетинговых исследованиях достаточно
часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег,
знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за
исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда
необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход,
респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения
и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство
интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром –
активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает
проблема выбора признака и определения его типичного значения.
Курс лекций по теории статистики
Более подробную информацию по выборочным наблюдениям можно получить просмотрев видеокурс по теории статистики:
Выборочное наблюдение Способы формирование выборки
Специальные виды отбора
Калькулятор расчета ошибки и размера выборки (для простой случайной выборки)
Пояснения к полям:
Доверительная вероятность
Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по
выборочным данным. В практике исследований чаще всего используют 95%-ую доверительную вероятность
Ошибка выборки (доверительный интервал)
Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное
истинное значение оцениваемого параметра распределения.
Доля признака
Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют,
необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Калькулятор расчета статистической значимости различий
Калькулятор позволяет проверить есть ли статистически значимая разница между долями признака, полученными из
независимых выборок.
Например, если до начала рекламной кампании марку знали 55% респондентов, а по окончании – 60% — есть ли между этими
долями статистически значимая разница, или же эта разница укладывается в ошибку выборки?
Примечание. Эта процедура может законно использоваться, только если обе выборки удовлетворяют следующему условию:
произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, должны быть не меньше 5.
Оставить свои комментарии по затронутой теме Вы можете на наших страницах в Facebook и Вконтакте.
При перепечатке материалов ссылка на маркетинговое агентство обязательна
FDF Group © 2023
Разработка сайта — Монохром
1.1. Ошибки
выборочного наблюдения
Средняя
ошибка выборки показывает, как генеральная средняя отклоняется в среднем от выборочной средней в ту или другую сторону. Формула
расчета средней ошибки выборки определяется видом исследуемого признака единиц
совокупности (количественный или альтернативный) и
способом отбора (бесповторный или повторный).
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
, где
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный

число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный

доля
·
Если отбор бесповторный, а признак
альтернативный
Предельная ошибка выборки— показывающая с определенной степенью вероятности
отклонения средней от выборочной средней.
Предельная ошибка выборки
, где параметр t зависит
от вероятности
Некоторые значения параметра t приведены
в таблице:
|
Вероятность, p |
0.95 |
0.954 |
0.9876 |
0.9907 |
0.9973 |
0.9999 |
|
Параметр t |
1.96 |
2.0 |
2.5 |
2.6 |
3.0 |
4.0 |
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
, где
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный

число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный

доля
·
Если отбор бесповторный, а признак
альтернативный
Доверительный интервал для генеральной средней
Доверительный интервал для
генеральной доли
Пример расчета доверительного
интервала:
При выборочном обследовании 5% продукции по методу случайного
бесповторного отбора получены данные о содержании сахара в образцах:
|
Сахарность, % |
Число |
|
16-17 17-18 18-19 19-20 20-21 |
10 158 154 50 28 |
|
На основании этих данных вычислите:
1. Средний процент сахаристости.
2. Дисперсию и среднее квадратическое
отклонение.
3. С вероятностью 0.954 возможные пределы среднего значения
сахаристости продукции для всей партии.
4. С вероятностью 0.997 возможный процент продукции высшего
сорта по всей партии, если известно, что из 400 проб, попавших в выборку , 80
ед. отнесены к продукции высшего сорта.
Решение.
1.
Средний процент сахаристости найдем по формуле средней взвешенной
, где xi–
середина i-го интервала
=18,32 %
2.
Дисперсия
=336,49
D(X)=336.49–
18.322=0.8676
Среднее квадратическое отклонение
=0,93%
5. Предельная ошибка для
среднего процента сахаристости
для вероятности 0,954 параметр t=2.0
Доверительный интервал для среднего значения процента
сахаристости
С вероятностью 0,954 можно утверждать, что в генеральной
совокупности средний процент сахаристости лежит в пределах от 18,23% до 18,41%.
5. Доля продукции высшего сорта в выборочной совокупности
Предельная ошибка для
доли продукции высшего сорта
для вероятности 0,997 параметр t=3.0
Доверительный интервал для доли продукции высшего сорта
С вероятностью 0,997 можно утверждать, что в генеральной
совокупности доля продукции высшего сорта лежит в пределах от 14,0% до 26,0%.

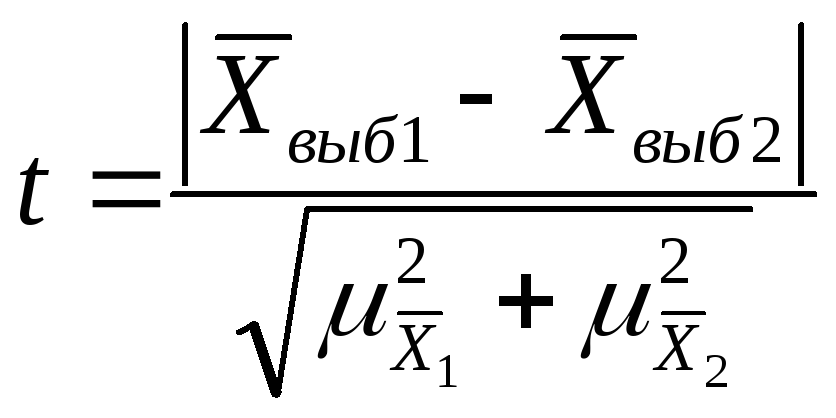
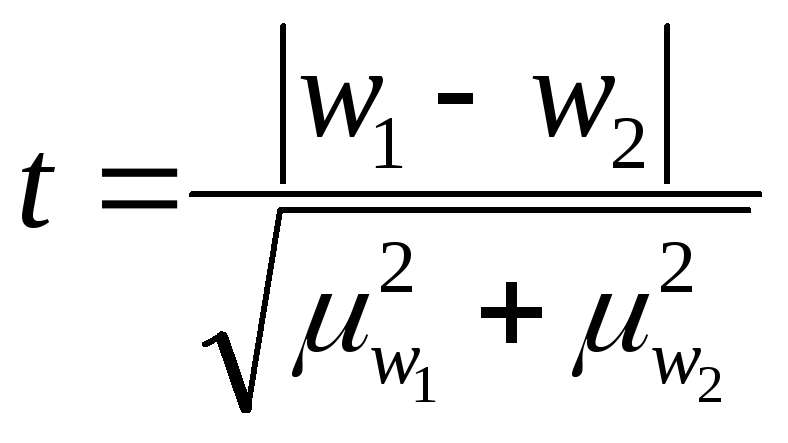













 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп
















