Тест по теории вероятностей с ответами
Нет времени или сил пройти тест онлайн? Поможем сдать тест дистанционно для любого учебного заведения: подробности.
Вопрос 1. Какое из утверждений относительно генеральной и выборочной совокупностей является верным?
- A. выборочная совокупность – часть генеральной
- B. генеральная совокупность – часть выборочной
- C. выборочная и генеральная совокупности равны по численности
- D. правильный ответ отсутствует
Вопрос 2. Сумма частот признака равна:
- A. объему выборки n
- B. среднему арифметическому значений признака
- C. нулю
- D. единице
Вопрос 3. Ломаная, отрезки которой соединяют точки с координатами $(x_i,n_i)$, где $x_i$– значение вариационного ряда, $n_i$ – частота, – это:
- A. гистограмма
- B. эмпирическая функция распределения
- C. полигон
- D. кумулята
Вопрос 4. Какие из следующих утверждений являются верными?
- A. выборочное среднее является интервальной оценкой математического ожидания M(X), а выборочная дисперсия – интервальной оценкой дисперсии D(X)
- B. выборочное среднее является точечной оценкой математического ожидания M(X), а выборочная дисперсия — интервальной оценкой дисперсии D(X)
- C. выборочное среднее является точечной оценкой математического ожидания M(X), а выборочная дисперсия — точечной оценкой дисперсии D(X)
- D. выборочное среднее является интервальной оценкой математического ожидания M(X), а выборочная дисперсия – точечной оценкой дисперсии D(X)
Вопрос 5. Уточненная выборочная дисперсия $S^2$ случайной величины $X$ обладает следующими свойствами:
- A. является смещенной оценкой дисперсии случайной величины X
- B. является несмещенной оценкой дисперсии случайной величины X
- C. является смещенной оценкой среднеквадратического отклонения случайной величины X
- D. является несмещенной оценкой среднеквадратического отклонения случайной величины X
Вопрос 6. По выборке объема $n = 10$ получена выборочная диcперсия $D^* = 90$. Тогда уточненная выборочная дисперсия $S^2$ равна
- A. 100
- B. 80
- C. 90
- D. 81
Вопрос 7. Оценка $a^*$ параметра $a$ называется несмещенной, если:
- A. она не зависит от объема испытаний
- B. она приближается к оцениваемому параметру при увеличении объема испытаний
- C. выполняется условие $M(a^*) = a$
- D. она имеет наименьшую возможную дисперсию
Вопрос 8. При увеличении объема выборки n и одном и том же уровне значимости $a$, ширина доверительного интервала
- A. может как уменьшиться, так и увеличиться
- B. уменьшается
- C. не изменяется
- D. увеличивается
Вопрос 9. Может ли неизвестная дисперсия случайной величины выйти за границы, установленные при построении ее доверительного интервала с доверительной вероятностью $gamma$?
- A. может с вероятностью $1-gamma$
- B. может с вероятностью $gamma$
- C. может только в том случае, если исследователь ошибся в расчетах
- D. не может
Вопрос 10. Статистической гипотезой называют:
- A. предположение относительно статистического критерия
- B. предположение относительно параметров или вида закона распределения генеральной совокупности
- C. предположение относительно объема генеральной совокупности
- D. предположение относительно объема выборочной совокупности
Сдаем тесты по ТВиМС: цены, результаты, отзывы
Вопрос 11. При проверке статистической гипотезы, ошибка первого рода — это:
- A. принятие нулевой гипотезы, которая в действительности является неверной
- B. отклонение альтернативной гипотезы, которая в действительности является верной
- C. принятие альтернативной гипотезы, которая в действительности является неверной
- D. отклонение нулевой гипотезы, которая в действительности является верной
Вопрос 12. Мощность критерия – это:
- A. вероятность не допустить ошибку второго рода
- B. вероятность допустить ошибку второго рода
- C. вероятность отвергнуть нулевую гипотезу, когда она неверна
- D. вероятность отвергнуть нулевую гипотезу, когда она верна
Вопрос 13. Какие из названных распределений используются при проверке гипотезы о числовом значении математического ожидания при неизвестной дисперсии?
- A. распределение Стьюдента
- B. распределение Фишера
- C. нормальное распределение
- D. распределение хи-квадрат
Вопрос 14. Что представляет собой критическая область?
- A. все возможные значения критерия, при которых принимается нулевая гипотеза
- B. все возможные значения критерия, при которых не может быть принята ни нулевая, ни альтернативная гипотеза
- C. все возможные значения критерия, при которых есть основание принять альтернативную гипотезу
- D. нет правильного ответа
Вопрос 15. Для чего при проверке гипотезы о равенстве средних двух совокупностей должна быть проведена вспомогательная процедура?
- A. чтобы установить, равны ли объемы выборок
- B. чтобы установить, равны ли дисперсии в генеральных совокупностях
- C. чтобы установить, равны ли объемы выборок и равны ли дисперсии в генеральных совокупностях
- D. нет правильного ответа
Сдадим ваш тест на хорошо или отлично
ТЕСТЫ
по курсу «Теория вероятностей и
математическая статистика»
-
Вероятность события
это:
-
; 2.
;
3.
-
числовая мера появления события
в
испытаниях;
-
отношение
где
число
появлений событий А в
испытаниях;
-
число элементарных событий в некотором
подмножестве
.
2. Какие способы задания вероятностей
вы знаете:
-
классический, динамический, точечный,
геометрический; -
статистический, геометрический,
биноминальный, классический; -
геометрический, классический,
дискретный, статистический; -
классический, геометрический, точечный,
статистический; -
классический, геометрический,
статистический, комбинаторный.
3. Когда применяется классический
способ задания вероятности:
-
пространство элементарных событий
бесконечно, все события равновозможные
и независимые; -
пространство элементарных событий
замкнуто, все события независимы; -
пространство элементарных событий
конечно, все события равновозможные; -
пространство элементарных событий
конечно, все элементарные события
независимы.
4. Когда применяется геометрический
способ задания вероятности:
-
пространство элементарных событий
бесконечно, все события равновозможные
и независимые; -
пространство элементарных событий
замкнуто, все события независимы; -
пространство элементарных событий
конечно, все события равновозможные; -
пространство элементарных событий
конечно, все элементарные события
независимы.
5. Назовите основные аксиомы вероятностей:
6. Суммой двух событий
и
называют:
-
событие
,
состоящее из элементарных событий,
принадлежащих или событию
или
;
-
событие
,
состоящее из элементарных событий,
принадлежащих или событию
или
;
-
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
-
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
-
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
7.
Произведением двух событий
и
называют:
-
событие
,
состоящее из элементарных событий,
принадлежащих или событию
или
;
-
событие
,
состоящее из элементарных событий,
принадлежащих или событию
или
;
-
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
-
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
-
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
-
Вероятность суммы двух совместных
событий
равна:
-
Вероятность
произведения двух совместных событий
рана:
-
Формула
полной вероятности:
-
Законы
распределения случайной дискретной
величины представляются в виде:
-
функции
распределения
и совокупностью значений
;
-
функции
распределения
и функции плотности распределения
;
-
функции
распределения
и совокупностью значений
;
-
функции
распределения
и рядом распределения
; -
функции
распределения
и
;
-
функции
распределения
и
.
-
Законы распределения непрерывной
случайной величины представляются в
виде:
-
функции
распределения
и совокупностью значений
;
-
функции
распределения
и функции плотности распределения
;
-
функции
распределения
и совокупностью значений
;
-
функции
распределения
и рядом распределения
; -
функции
распределения
и
;
-
функции
распределения
и
.
-
Функция
распределения случайной величины это:
-
Вероятность
того, что
-
Вероятность
того, что
-
Вероятность
того, что -
Вероятность
того, что
-
Вероятность
того, что.
-
Функция
плотности распределения случайной
величины
это:
-
средняя
плотность распределения вероятности
на интервале
,
равная
;
-
предельная
средняя плотность вероятности на
интервале
,
равная;
-
предельная
средняя плотность вероятности на
интервале
,
равная;
-
предельная
средняя плотность вероятности на
интервале
,
равная;
-
средняя
плотность распределения вероятности
на интервале
,
равная
;
-
Основные
числовые характеристики дискретных
случайных величин это:
-
Среднее
арифметическое, дисперсия, квантиль,
моменты
-того
порядка, мода и медиана; -
Дисперсия,
центральные и начальные моменты
-того
порядка, среднее геометрическое, мода
и медиана; -
Математическое
ожидание, мода, медиана, дисперсия,
среднее квадратичное отклонение,
центральные и начальные моменты
-того
порядка. -
Математическое
ожидание, среднее арифметическое,
дисперсия, среднее квадратичное
отклонение, мода, медиана, центральные
и начальные моменты
-того
порядка. -
Математическое
ожидание, мода, медиана, дисперсия,
среднее квадратичное отклонение,
центральные и начальные моменты
-того
порядка, эксцесс, асимметрия.
-
Функция
распределения
и
функция плотности распределения имеют
следующие
свойства:
-
Дисперсия
случайно величины равна:
-
Математическое
ожидание непрерывной случайной величины
равно:
-
-
-
-
-
-
.
-
Нормальный
закон распределения имеет следующую
функцию плотности распределения
:
-
Для
нормального закона распределения
вероятность попадания случайной
величины в интервал
равен:
-
Сущность
предельных теорем и закона больших
чисел заключается:
-
В
определении числовых характеристик
случайных величин при большом числе
наблюдаемых данных; -
В
поведении числовых характеристик и
законов распределения наблюдаемых
значений случайных величин; -
В
определении области применения
нормального закона распределения
случайных величин при сложении большого
количества случайных величин; -
В
поведении числовых характеристик и
законов распределения случайных
величин при увеличении числа наблюдений
и опытов. -
В
определении суммарных значений основных
характеристик законов распределения.
-
Коэффициент
корреляции случайных величин
характеризует:
-
Степень
независимости между случайными
величинами; -
Степень
нелинейной зависимости между случайными
величинами; -
Степень
линейной зависимости между случайными
величинами; -
Степень
регрессии между случайными величинами; -
Степень
разброса двух величин относительно
математического ожидания. -
Степень
отклонения двух величин от их
математических ожиданий.
-
Марковским
случайным процессом называют такие
процессы, у которых:
-
Плотность
совместного распределения произвольных
сечений полностью определяет поведение
процесса; -
Плотность
совместного распределения произвольных
сечений полностью определяет поведение
процесса; -
Плотность
совместного распределения произвольных
сечений полностью определяет поведение
процесса; -
Плотность
совместного распределения произвольных
сечений полностью определяет поведение
процесса; -
Плотность
совместного распределения произвольных
сечений полностью определяет поведение
процесса;
-
Марковскими
цепями называю случайных процесс, у
которого:
-
Сама
функция подчиняется нормальному закону
распределения; -
Сама
функция подчиняется показательному
закону распределения; -
Сама
функция имеет дискретный характер; -
Сама
функция имеет непрерывный характер; -
Сама
функция подчиняется биноминальному
закону распределения;
-
К
оценкам генеральной совокупности
предъявляются следующие требования:
-
Оценка
должна быть стационарной, эргодичной
и эффективной; -
Оценка
должна быть состоятельной, эргодичной
и эффективной; -
Оценка
должна быть состоятельной, стационарной
и эргодичной ; -
Оценка
должна быть состоятельной, эффективной
и несмещенной; -
Оценка
должна быть несмещенной, стационарной
и эффективной;
-
Статистической
гипотезой называют:
-
Предположение
относительно параметров и вида закона
распределения генеральной совокупности; -
Предположение
относительно объема генеральной
совокупности; -
Предположение
относительно параметров и вида закона
распределения выборки; -
Предположение
относительно объема выборочной
совокупности; -
Предположение
относительно статистического критерия
;
-
При
проверки статистической гипотезы
ошибка первого рода это:
-
Принятие
в действительности неверной гипотезы; -
Отвержение
в действительности правильной гипотезы; -
Принятие
в действительности правильной гипотезы; -
Отвержение
в действительности неправильной
гипотезы;
-
В
критерии Колмогорова за меру качества
согласия эмпирического и теоретического
распределения принимается:
-
Относительное
расхождение между теоретической и
эмпирической частотами попадания
случайной величины в интервал; -
Максимальное
расхождение по модулю между теоретической
и эмпирической частотами попадания
случайной величины в интервал; -
Среднее
квадратичное отклонение между
теоретической и эмпирической частотами
попадания случайной величины в интервал; -
Максимальное
расхождение модуля разности между
эмпирической и теоретической функциями
распределения; -
Максимальное
расхождение модуля разности между
эмпирической и теоретической функциями
плотности распределения;
-
Дисперсионный
анализ позволяет:
-
Установить
степень влияния фактора на изменчивость
признака; -
Установить
количество факторов влияния на
изменчивость признака; -
Установить
степень влияния факторов на дисперсию; -
Установить
степень влияния фактора на среднее
значение; -
Установить
степень влияния фактора на числовые
характеристики случайной величины;
-
Задачами
регрессионного анализа являются:
-
Выявление
связи между случайными величинами и
оценка их тесноты; -
Выявление
связи между случайными величинами и
их числовыми характеристиками; -
Выявление
уравнения связи между случайными
величинами; -
Выявление
уравнения связи между случайной
зависимой переменной и неслучайными
независимыми переменными и оценка
неизвестных значений зависимой
переменной; -
Выявление уравнения связи между
неслучайной зависимой переменной и
случайными независимыми переменными
и оценка неизвестных значений независимой
переменной; -
Выявление
уравнения связи между неслучайной
независимой переменной и случайными
независимыми переменными и оценка
неизвестных значений зависимой
переменной;
Задачи
-
В
урне 6 белых и 4 черных шара. Из нее
вынимают подряд 3 шара. Найти вероятность
того, что оба шара черные? -
Продавец
мороженного в солнечный день может
заработать 10 $., а в дождливый – 3. Чему
равна ожидаемая выручка, если вероятность
того, что день окажется дождливым, равна
0,4? -
В
банк подано 5 заявок фирм на получение
кредита. Вероятность получить кредит
для каждой фирмы равна 0,5. Найти
вероятность того, что из пяти фирм
кредит получит ровно 3 фирмы? -
Случайная
величина задана функцией распределения:
Найти плотность распределения
случайной величины и вычислить
вероятность того, что
.
-
Коробки
с шоколадом упаковываются автоматики
чески: средний вес коробки равен 1,06 кГ,
а его среднее квадратичное отклонение
равно 0,25 кГ. Найти практически возможный
максимальный вес одной коробки, если
масса коробок поднимается нормальному
закону распределения.
-
В
урне 2 белых и 7 черных шара. Из нее
вынимают подряд 2 шара. Найти вероятность
того, что оба шара черные? -
Продавец
мороженного в солнечный день может
заработать 5 $., а в дождливый – 2. Чему
равна ожидаемая выручка, если вероятность
того, что день окажется дождливым, равна
0,5? -
В
банк подано 3 заявок фирм на получение
кредита. Вероятность получить кредит
для каждой фирмы равна 0,6. Найти
вероятность того, что из пяти фирм
кредит получит ровно 2 фирмы? -
Случайная
величина задана функцией распределения:
Найти плотность распределения
случайной величины и вычислить
вероятность того, что
.
-
Коробки
с шоколадом упаковываются автоматики
чески: средний вес коробки равен 1,0 кГ,
а его среднее квадратичное отклонение
равно 0,2 кГ. Найти практически возможный
максимальный вес одной коробки, если
масса коробок поднимается нормальному
закону распределения.
-
В
урне 4 белых и 4 черных шара. Из нее
вынимают подряд 2 шара. Найти вероятность
того, что оба шара черные? -
Продавец
мороженного в солнечный день может
заработать 12 $., а в дождливый – 6. Чему
равна ожидаемая выручка, если вероятность
того, что день окажется дождливым, равна
0,8? -
В
банк подано 7 заявок фирм на получение
кредита. Вероятность получить кредит
для каждой фирмы равна 0,8. Найти
вероятность того, что из пяти фирм
кредит получит ровно 4 фирмы? -
Случайная
величина задана функцией распределения:
Найти плотность распределения
случайной величины и вычислить
вероятность того, что
.
-
Коробки
с шоколадом упаковываются автоматики
чески: средний вес коробки равен 0,5 кГ,
а его среднее квадратичное отклонение
равно 0,1 кГ. Найти практически возможный
максимальный вес одной коробки, если
масса коробок поднимается нормальному
закону распределения.
-
Из группы деталей делается случайная
выборка ( с возвратом) 20 штук. Найти
доверительный интервал для генерального
среднего с вероятностью 0,95, если
результаты выборки представлены в
таблице:Вес деталей, кГ
500
510
520
530
Количество (частота)
3
6
10
1
-
Предполагается произвести выборочное
обследование 2000 ламп с целью установления
продолжительности их горения. Каким
должен быть объем повторной выборки,
чтобы можно было гарантировать с
вероятностью 0,9, что генеральное среднее
отличается от выборочного по абсолютной
величине меньше, чем на 20 часов, если
генеральная дисперсия меньше 10000 часов.
-
Распределение признака Х в выборке
дается следующим вариационным рядом:
|
3,0-3,6 |
3,6-4,2 |
4,2-4,8 |
4,8-5,4 |
5,4-6,0 |
6,0-6,6 |
6,6-7,2 |
|
2 |
8 |
35 |
43 |
22 |
15 |
5 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Методика проверки статистических гипотез
- 2 Альтернативная методика на основе достигаемого уровня значимости
- 3 Типы критической области
- 4 Ошибки первого и второго рода
- 5 Свойства статистических критериев
- 6 Типы статистических гипотез
- 7 Типы статистических критериев
- 7.1 Критерии согласия
- 7.2 Критерии сдвига
- 7.3 Критерии нормальности
- 7.4 Критерии однородности
- 7.5 Критерии симметричности
- 7.6 Критерии тренда, стационарности и случайности
- 7.7 Критерии выбросов
- 7.8 Критерии дисперсионного анализа
- 7.9 Критерии корреляционного анализа
- 7.10 Критерии регрессионного анализа
- 8 Литература
- 9 Ссылки
Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.
Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.
Методика проверки статистических гипотез
Пусть задана случайная выборка — последовательность
объектов из множества
.
Предполагается, что на множестве существует некоторая неизвестная вероятностная мера
.
Методика состоит в следующем.
- Формулируется нулевая гипотеза
о распределении вероятностей на множестве
. Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая
и альтернативная
. Иногда альтернатива не формулируется в явном виде; тогда предполагается, что
означает «не
». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.
- Задаётся некоторая статистика (функция выборки)
, для которой в условиях справедливости гипотезы
выводится функция распределения
и/или плотность распределения
. Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика
. Вывод функции распределения
при заданных
и
является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для
; в статистических пакетах имеются готовые вычислительные процедуры.
- Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число
. На практике часто полагают
.
- На множестве допустимых значений статистики
выделяется критическое множество
наименее вероятных значений статистики
, такое, что
. Вычисление границ критического множества как функции от уровня значимости
является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.
- Собственно статистический тест (статистический критерий) заключается в проверке условия:
Итак, статистический критерий определяется статистикой
и критическим множеством , которое зависит от уровня значимости
.
Замечание.
Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна.
Тому есть две причины.
Альтернативная методика на основе достигаемого уровня значимости
Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в докомпьютерную эпоху. Чаще всего использовались таблицы, в которых для некоторых априорных уровней значимости были выписаны критические значения. В настоящее время результаты проверки гипотез чаще представляют с помощью достигаемого уровня значимости.
Достигаемый уровень значимости (пи-величина, англ. p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия
где
— критическая область критерия.
Другая интерпретация:
достигаемый уровень значимости — это вероятность при справедливости нулевой гипотезы получить значение статистики, такое же или ещё более экстремальное, чем
Если достигаемый уровень значимости достаточно мал (близок к нулю), то нулевая гипотеза отвергается.
В частности, его можно сравнивать с фиксированным уровнем значимости;
тогда альтернативная методика будет эквивалентна классической.
Типы критической области
Обозначим через значение, которое находится из уравнения
, где
— функция распределения статистики
.
Если функция распределения непрерывная строго монотонная,
то есть обратная к ней функция:
-
.
Значение называется также
—квантилем распределения
.
На практике, как правило, используются статистики с унимодальной (имеющей форму пика) плотностью распределения.
Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения.
Поэтому чаще всего возникают критические области одного из трёх типов:
- Левосторонняя критическая область:
-
- определяется интервалом
.
- пи-величина:
- определяется интервалом
- Правосторонняя критическая область:
-
- определяется интервалом
.
- пи-величина:
- определяется интервалом
- Двусторонняя критическая область:
-
- определяется двумя интервалами
- пи-величина:
- определяется двумя интервалами
Ошибки первого и второго рода
- Ошибка первого рода или «ложная тревога» (англ. type I error,
error, false positive) — когда нулевая гипотеза отвергается, хотя на самом деле она верна. Вероятность ошибки первого рода:
- Ошибка второго рода или «пропуск цели» (англ. type II error,
error, false negative) — когда нулевая гипотеза принимается, хотя на самом деле она не верна. Вероятность ошибки второго рода:
| Верная гипотеза | |||
|---|---|---|---|
| |
|
||
| Результат применения критерия |
|
|
(Ошибка второго рода) |
| |
(Ошибка первого рода) |
|
Свойства статистических критериев
Мощность критерия:
— вероятность отклонить гипотезу
, если на самом деле верна альтернативная гипотеза
.
Мощность критерия является числовой функцией от альтернативной гипотезы .
Несмещённый критерий:
для всех альтернатив
или, что то же самое,
для всех альтернатив .
Состоятельный критерий:
при
для всех альтернатив
.
Равномерно более мощный критерий.
Говорят, что критерий с мощностью является равномерно более мощным, чем критерий с мощностью
, если выполняются два условия:
;
для всех рассматриваемых альтернатив
, причём хотя бы для одной альтернативы неравенство строгое.
Типы статистических гипотез
- Простая гипотеза однозначно определяет функцию распределения на множестве
. Простые гипотезы имеют узкую область применения, ограниченную критериями согласия (см. ниже). Для простых гипотез известен общий вид равномерно более мощного критерия (Теорема Неймана-Пирсона).
- Сложная гипотеза утверждает принадлежность распределения к некоторому множеству распределений на
. Для сложных гипотез вывести равномерно более мощный критерий удаётся лишь в некоторых специальных случаях.
Типы статистических критериев
В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.
Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.
- Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.
- Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.
Критерии согласия
Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.
- Критерий Колмогорова-Смирнова
- Критерий хи-квадрат (Пирсона)
- Критерий омега-квадрат (фон Мизеса)
Критерии сдвига
Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.
- Критерий Стьюдента
- Критерий Уилкоксона-Манна-Уитни
Критерии нормальности
Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.
- Критерий Шапиро-Уилка
- Критерий асимметрии и эксцесса
Критерии однородности
Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.
Критерии симметричности
Критерии симметричности позволяют проверить симметричность распределения.
- Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
- Критерий знаков
- Коэффициент асимметрии
Критерии тренда, стационарности и случайности
Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.
Критерии выбросов
Критерии дисперсионного анализа
Критерии корреляционного анализа
Критерии регрессионного анализа
Литература
- Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
- Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006. — 816 с.
Ссылки
- Statistical hypothesis testing — статья в англоязычной Википедии.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Введение в проверку гипотез
17 авг. 2022 г.
читать 2 мин
Статистическая гипотеза – это предположение о параметре совокупности .
Например, мы можем предположить, что средний рост мужчины в США составляет 70 дюймов.
Предположение о росте является статистической гипотезой , а истинный средний рост мужчины в США является популяционным параметром .
Проверка гипотезы — это формальный статистический тест, который мы используем, чтобы отвергнуть или не опровергнуть статистическую гипотезу.
Два типа статистических гипотез
Чтобы проверить, верна ли статистическая гипотеза о параметре совокупности, мы получаем случайную выборку из совокупности и выполняем проверку гипотезы на выборочных данных.
Существует два типа статистических гипотез:
Нулевая гипотеза , обозначаемая как H 0 , представляет собой гипотезу о том, что выборка данных происходит чисто случайно.
Альтернативная гипотеза , обозначаемая как H 1 или H a , представляет собой гипотезу о том, что на выборочные данные влияет какая-то неслучайная причина.
Проверка гипотез
Проверка гипотезы состоит из пяти шагов:
1. Сформулируйте гипотезы.
Сформулируйте нулевую и альтернативную гипотезы. Эти две гипотезы должны быть взаимоисключающими, поэтому, если одна верна, другая должна быть ложной.
2. Определите уровень значимости для гипотезы.
Определите уровень значимости. Распространенные варианты: .01, .05 и .1.
3. Найдите тестовую статистику.
Найдите тестовую статистику и соответствующее значение p. Часто мы анализируем среднее значение или долю населения, и общая формула для нахождения тестовой статистики выглядит следующим образом: (выборочная статистика — параметр совокупности) / (стандартное отклонение статистики)
4. Отклонить или не отклонить нулевую гипотезу.
Используя тестовую статистику или p-значение, определите, можете ли вы отклонить или не отклонить нулевую гипотезу на основе уровня значимости.
Значение p говорит нам о силе доказательств в поддержку нулевой гипотезы. Если p-значение меньше уровня значимости, мы отклоняем нулевую гипотезу.
5. Интерпретируйте результаты.
Интерпретируйте результаты проверки гипотезы в контексте заданного вопроса.
Два типа ошибок принятия решений
Есть два типа ошибок принятия решений, которые можно сделать при проверке гипотезы:
Ошибка I типа: вы отвергаете нулевую гипотезу, когда она на самом деле верна. Вероятность совершения ошибки первого рода равна уровню значимости, часто называемому альфа и обозначаемому как α.
Ошибка типа II: вы не можете отвергнуть нулевую гипотезу, когда она на самом деле ложна. Вероятность совершения ошибки типа II называется мощностью теста или бета и обозначается как β.
Односторонний и двусторонний тесты
Статистическая гипотеза может быть односторонней или двусторонней.
Односторонняя гипотеза предполагает утверждение «больше» или «меньше».
Например, предположим, что средний рост мужчины в США больше или равен 70 дюймам. Нулевой гипотезой будет H0: µ ≥ 70 дюймов, а альтернативной гипотезой будет Ha: µ < 70 дюймов.
Двусторонняя гипотеза предполагает утверждение «равно» или «не равно».
Например, предположим, что мы предполагаем, что средний рост мужчины в США равен 70 дюймам. Нулевой гипотезой будет H0: µ = 70 дюймов, а альтернативной гипотезой будет Ha: µ ≠ 70 дюймов.
Примечание. Знак «равно» всегда включается в нулевую гипотезу, будь то =, ≥ или ≤.
По теме: Что такое гипотеза направления?
Типы проверки гипотез
Существует множество различных типов проверки гипотез, которые вы можете выполнять в зависимости от типа данных, с которыми вы работаете, и цели вашего анализа.
Следующие руководства содержат объяснение наиболее распространенных типов проверки гипотез:
Введение в одновыборочный t-критерий
Введение в двухвыборочный t-критерий
Введение в t-критерий парных выборок
Введение в Z-тест одной пропорции
Введение в двухпропорционный Z-тест
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).

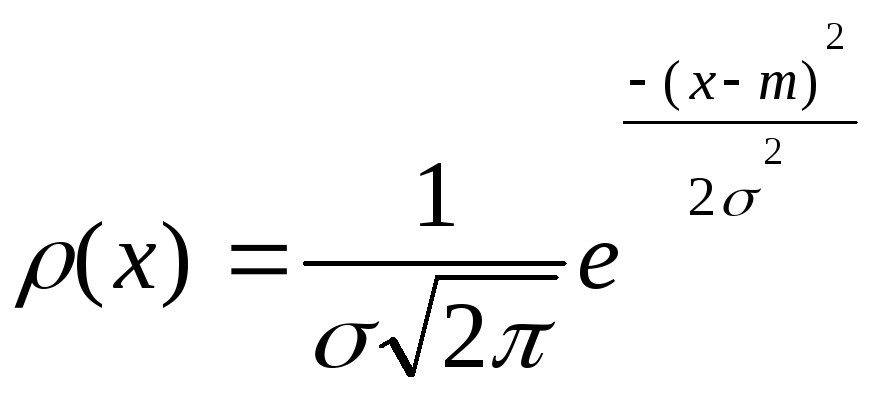





 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.