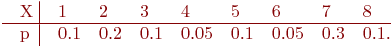Аннотация: Рассказывается методика построения кодов, минимальное расстояние между кодовыми словами которых равно заданному числу. Математическое обосновании кодов Боуза-Чоудхури-Хоккенгема, упражнения для самопроверки. Рассматриваются циклические избыточные коды(CRC) и их применение на практике
Остался открытым вопрос о методике построения кодов, минимальное расстояние
между кодовыми словами которых равно заданному числу. В 1960 году независимо
Боуз (Bose), Чоудхури (Chaudhuri) и Хоккенгем (Hocquengem) открыли способ
построения полиномиальных кодов, удовлетворяющих таким требованиям. Эти коды
получили названия кодов Боуза-Чоудхури-Хоккенгема или БЧХ-кодов (BCH codes).
БЧХ-коды могут быть не только двоичными, например, на практике достаточно
широко используются недвоичные коды Рида-Соломона (Reed, Solomon), но
далее будут рассматриваться только двоичные.
Многочлен 

если 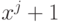

для 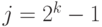

Например, многочлен 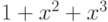
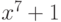
при 

делит 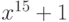
но не делит 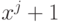
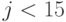
Кодирующий многочлен 
которого 
строится так. Находится примитивный многочлен минимальной степени 

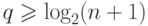

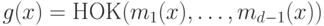
— многочлены минимальной степени, имеющие корнями соответственно 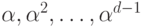
Построенный кодирующий многочлен производит код с минимальным расстоянием
между кодовыми словами, не меньшим 
Пример. Нужно построить БЧХ-код с длиной кодовых слов 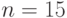
минимальным расстоянием между кодовыми словами 
многочлена равна 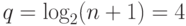

Пусть 
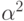
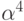
корни. Минимальным многочленом для 
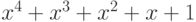
Следовательно,
Степень полученного многочлена равна 8,
следовательно, построенный БЧХ-код будет 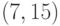
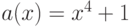
закодировано кодовым словом 
111001100000100.
Можно построить11
двоичный БЧХ-код с кодовыми словами длины
и нечетным минимальным расстоянием 
контрольных символов не больше 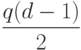
Первый БЧХ-код, примененный на практике, был 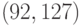
исправляющим ошибки кратности до 5, но наиболее широкое распространение получил 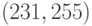
БЧХ-коды умеренной длины не слишком далеки от совершенных или
квазисовершенных кодов. Коды Хэмминга, например, являются БЧХ-кодами, а
БЧХ-коды с минимальным весом кодового слова 5 — квазисовершенны. Но
с ростом длины кодовых слов качество БЧХ-кодов падает. Код Голея,
например, — это не код БЧХ.
Упражнение 45
Найти кодирующий многочлен БЧХ-кода 
и минимальным расстоянием между кодовыми словами 7. Использовать примитивный
многочлен 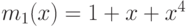

Проверить, будут ли 
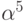
многочленов 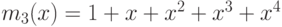
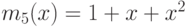
Циклические избыточные коды
Циклический избыточный код (Cyclical Redundancy Check — CRC)
имеет фиксированную длину и используется для обнаружения ошибок.
Наибольшее распространения получили коды CRC-16 и CRC-32, имеющие длину 16
и 32 бита соответственно. Код CRC строится по исходному сообщению
произвольной длины, т.е. этот код не является блочным в строгом смысле этого
слова. Но при каждом конкретном применении этот код — блочный, 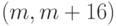
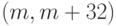
CRC-32.
Вычисление значения кода CRC происходит посредством деления многочлена,
соответствующего исходному сообщению (полином-сообщение), на фиксированный
многочлен (полином-генератор). Остаток от такого деления и есть код CRC,
соответствующий исходному сообщению. Для кода CRC-16 полином-генератор имеет
степень 16, а для CRC-32 — 32. Полиномы-генераторы подбираются специальным
образом и для кодов CRC-16/32 стандартизированы Международным консультативным
комитетом по телеграфной и телефонной связи (CCITT). Для CRC-16, например, стандартным
является полином-генератор 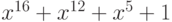
Пример построения CRC-4 кода для сообщения 11010111, используя
полином-генератор 
соответствует полином 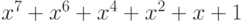
справа.
Полиному 
есть CRC-4 код.
Существуют быстрые алгоритмы для расчета CRC-кодов, использующие
специальные таблицы, а не деление многочленов с остатком.
CRC-коды способны обнаруживать одиночную ошибку в любой позиции и, кроме
того, многочисленные комбинации кратных ошибок, расположенных близко друг от
друга. При реальной передаче или хранении информации ошибки обычно
группируются на некотором участке, а не распределяются равномерно по всей
длине данных. Таким образом, хотя для идеального случая двоичного
симметричного канала CRC-коды не имеют никаких теоретических преимуществ по
сравнению, например, с простыми контрольными суммами, для реальных систем эти
коды являются очень полезными.
Коды CRC используются очень широко: модемами, телекоммуникационными
программами, программами архивации и проверки целостности данных и многими
другими программными и аппаратными компонентами вычислительных систем.
Упражнение 46
Построить CRC-4 код для сообщений 10000000 и 101111001, используя
полином-генератор 
Главная / Безопасность /
Основы теории информации и криптографии / Тест 10
Основы теории информации и криптографии — тест 10
Упражнение 1:
Номер 1
Способ построения полиномиальных кодов, минимальное расстояние между кодовыми словами которых равно заданному числу, был открыт:
Ответ:
(1) Чоудхури
(2) Боузом
(3) Хоккенгемом
Номер 2
Коды Рида-Соломона являются:
Ответ:
(1) двоичными коды
(2) недвоичными кодами
(3) полиномными кодами
Номер 3
Способ построения полиномиальных кодов, минимальное расстояние между кодовыми словами которых равно заданному числу, был открыт:
Ответ:
(1) Боузом
(2) Чоудхури
(3) Хоккенгемом
Упражнение 2:
Номер 1
Многочлен g(x) степени k называется примитивным, если:
Ответ:
(1) xj+1 НЕ делится на g(x) и делится без остатка на j
(2) x2+1 делится на g(x) без остатка для j=3k-1 и не делится ни для какого меньшего значения j
(3) xj+1 делится на g(x) без остатка для j=2k-1 и не делится ни для какого меньшего значения j
Номер 2
Первый БЧХ-код, примененный на практике, был:
Ответ:
(1) (231,255)-код
(2) (92,127)-код
(3) (102,250)-код
Номер 3
Наиболее широкое распространение получил:
Ответ:
(1) (231,255)-код
(2) (92,127)-код
(3) (102,250)-код
Упражнение 3:
Номер 1
Код Голея - это:
Ответ:
(1) невозможно определить принадлежность кода Голея к коду БЧХ
(2) код БЧХ
(3) не код БЧХ
Номер 2
Коды Хэмминга являются:
Ответ:
(1) не код БЧХ
(2) код БЧХ
(3) невозможно определить принадлежность кода Хэмминга к коду БЧХ
Номер 3
Найти кодирующий многочлен БЧХ-кодаg(x)с длиной кодовых слов 15 и минимальным расстоянием между кодовыми словами 7. Использовать примитивный многочленm1(x)=1+x+x4с корнем. Проверить, будут ли
и
корнями соответственно многочленов
m3(x)=1+x+x2+x3+x4иm5(x)=1+x+x2:
Ответ:
(1) g(x) = 1 + x + x2 + x4 + x5 + x8 + x10
(2) g(x) = 1 + x + x3 + x4 + x6 + x9 + x10
(3) g(x) = 1 + x + x3 + x5 + x7 + x9
Упражнение 4:
Номер 1
Циклический избыточный код имеет:
Ответ:
(1) временную длину
(2) переменную длину
(3) фиксированную длину
Номер 2
Для кода CRC-16 полином-генератор имеет степень:
Ответ:
(1) 32
(2) 16
(3) 64
Номер 3
Для кода CRC-32 полином-генератор имеет степень:
Ответ:
(1) 32
(2) 16
(3) 64
Упражнение 5:
Номер 1
Вычисление значения кода CRC происходит посредством:
Ответ:
(1) деления многочлена, соответствующего исходному сообщению, на фиксированный многочлен. Целая часть от такого деления и есть код CRC
(2) деления фиксированного многочлена на многочлен, соответствующего исходному сообщению. Остаток от такого деления и есть код CRC
(3) деления многочлена, соответствующего исходному сообщению, на фиксированный многочлен. Остаток от такого деления и есть код CRC
Номер 2
CRC-коды способны обнаруживать:
Ответ:
(1) только смежные ошибки
(2) одиночную ошибку в любой позиции и, кроме того, многочисленные комбинации кратных ошибок, расположенных близко друг от друга
(3) одиночную ошибку в любой позиции, кроме многочисленных комбинаций кратных ошибок, расположенных близко друг от друга
Номер 3
При реальной передаче или хранении информации ошибки:
Ответ:
(1) обычно группируются на некотором участке
(2) распределяются равномерно по всей длине данных
(3) группируются в нескольких участках, распределенных неравномерно
Упражнение 6:
Номер 1
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
Ответ:
(1) 1111
(2) 1011
(3) 1000
Номер 2
Построить CRC-4 код для сообщения 101111001, используя полином-генератор x4+1:
Ответ:
(1) 1001
(2) 1111
(3) 1100
Номер 3
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
Ответ:
(1) 1000
(2) 1101
(3) 1001
-
Циклические избыточные коды
CRC.
Имеют фиксированную длину и используются
для обнаружения ошибок. Наибольшее
распространение получили коды CRC-16 и
CRC-32, имеющие длину 16 и 32 бита соответственно.
Код CRC строится по исходному сообщению
произвольной длины, т. е. этот код не
является блочным в строгом смысле этого
слова. Но при каждом конкретном применении
этот код — блочный, (m, m + 16)-код для CRC-16
или (m, m + 32)-код для CRC-32. Вычисление
значения кода CRC происходит посредством
деления многочлена, соответствующего
исходному сообщению (полином-сообщение),
на фиксированный многочлен
(полином-генератор). Остаток от такого
деления и есть код CRC, соответствующий
исходному сообщению. Для кода CRC-16
полином-генератор имеет степень 16, а
для CRC-32 — 32. Полиномы-генераторы
подбираются спец. образом и для кодов
CRC-16/32 стандартизированы. Для CRC-16,
например, стандартным является
полином-генератор x16
+ x12
+ x5
+ 1.
Существуют быстрые
алгоритмы для расчета CRC-кодов, использующие
специальные таблицы, а не деление
многочленов с остатком.
CRC-коды способны
обнаруживать одиночную ошибку в любой
позиции и, кроме того, многочисленные
комбинации кратных ошибок, расположенных
близко друг от друга. При реальной
передаче или хранении информации ошибки
обычно группируются на некотором
участке, а не распределяются равномерно
по всей длине данных. Таким образом, для
реальных систем эти коды являются очень
полезными.
Коды CRC используются
очень широко: модемами, телекоммуникационными
программами, программами архивации и
проверки целостности данных и многими
другими программными и аппаратными
компонентами вычислительных систем.
-
Шифрование данных. Примеры простых методов шифрования. Шифр-перестановка и шифр-смещение
Шифрование
— способ преобразования открытой
информации в закрытую и обратно.
Применяется для хранения важной
информации в ненадёжных источниках или
передачи её по незащищённым каналам
связи.
В
зависимости от структуры используемых
ключей методы шифрования подразделяются
на
-
симметричное
шифрование: посторонним лицам может
быть известен алгоритм шифрования, но
неизвестна небольшая порция секретной
информации — ключа, одинакового для
отправителя и получателя сообщения; -
асимметричное
шифрование: посторонним лицам может
быть известен алгоритм шифрования, и,
возможно, открытый ключ, но неизвестен
закрытый ключ, известный только
получателю.
Одним
из простейших методов шифрования
является шифр
простой замены
– класс методов шифрования, которые
сводится к созданию по определённому
алгоритму таблицы шифрования, в которой
для каждой буквы открытого текста
существует единственная сопоставленная
ей буква шифра-текста. Само шифрование
заключается в замене букв согласно
таблице. Для расшифровки достаточно
иметь ту же таблицу, либо знать алгоритм,
по которой она генерируется. Частным
случаем данного метода является шифр
Цезаря
– это вид шифра подстановки, в котором
каждый символ в открытом тексте заменяется
буквой находящейся на некоторое
постоянное число позиций левее или
правее него в алфавите. Например, в шифре
со сдвигом 3, А была бы заменена на Г, Б
станет Д, и так далее.
Шифр-перестановка.
В
шифре перестановки буквы открытого
текста не замещаются на другие, а меняется
сам порядок их следования. Например, в
шифре простой колонной перестановки
исходный открытый текст записывается
построчно (число букв в строке фиксировано),
а шифр-текст получается считыванием
букв по колонкам. Расшифрование
производится аналогично: шифр-текст
записывается поколонно, а открытый
текст можно затем прочесть по горизонтали.
Также возможно использование ключа.
Количество букв в строке есть количество
букв в ключе.Каждой букве ключа ставиться
порядковый номер(порядок следования
определяет алфавит). Если первая буква
(слева направо) имеет порядковый номер,
например,n,
то первым считывается столбец n
(номер слева направо) и т.д.
Шифр-смещение.
Для
данного метода шифрования требуется
построение таблицы кодов (например,
номер следования буквы в алфавите,
т.е.буква А будет иметь код 1, Б – 2, В –
3 и т.д.). В сообщении под каждым символом
исходного сообщения пишется кодовое
слово. Затем код каждого символа исходного
сообщения складывается с кодом находящимся
под ним символа ключа и полученный в
результате код образует символ. Если
сумма кодов превосходит максимальный
код, то из этой суммы вычитается размер
максимального кода.
-
Криптосистемы
без передачи ключей
-
Криптосистемы
с открытым ключом
-
Электронная
подпись
-
Системы передачи
дискретных сообщений. Виды сигналов
Дискретные сообщения как форма
представления информации состоят из
конечного набора возможных значений.
Физический процесс отображения сообщения
называется сигналом. Сигнал характеризуется
своим уровнем и моментами изменения
данного уровня. Виды сигналов:
-
непрерывные
сигналы непрерывного времени (непрерывные
или аналоговые) – уровни сигнала могут
изменяться в любой момент времени и
любым образом (принимать любые значения); -
непрерывные
сигналы дискретного времени – могут
принимать произвольные значения, но
изменяются только в определённые
моменты времени; -
дискретные сигналы
непрерывного времени – могут изменяться
в произвольные моменты, но принимают
только разрешённые дискретные значения; -
дискретные сигналы
дискретного времени (дискретные) –
уровни меняются только в дискретные
моменты и принимают только дискретные
значения.
Сигналы, формируемые
на выходе преобразователя дискретного
сообщения в сигнал, являются по
информационному параметру дискретными.
Это цифровые
сигналы данных (ЦСД).
Элемент ЦСД
– часть цифрового сигнала, отличающаяся
от других частей значением одного из
инф. параметров.
Значащая позиция
– это фиксируемое значение состояния
инф. параметра.
Значащий момент
– это момент, в кот.происходит смена
значений сигнала.
Значащие интервалы
– это интервалы времени между двумя
соседними зн.моментами. Минимальный
интервал 0
наз. единичным.
Сигналы могут
быть:
-
изохронными (любой
ЗИ равен 0
или целому их числу) -
анизохронными
(произвольная длительность, но не менее
чем 0)
Передача сообщений
реализуется посредством информационных
каналов —
совокупности устройств, объединенных
линиями связи и предназначенных для
передачи инф-ии от её источника
(начальногоустр-ва канала) до приемника
(конечного устр-ва канала).В дискретных
каналахсигналы
на входе и выходе представляют собой
последовательность символов некоторых
алфавитов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ответы на курс: Основы теории информации и криптографии
Древовидные коды также называют:
| параллельными кодами | |
| последовательными кодами | |
| управляющими кодами |
Преимущество матричного кодирования заключается в:
| определении объема полученных данных еще до начала кодирования | |
| использовании гораздо меньшего объема памяти по сравнению с другими методами кодирования | |
| использовании большего объема памяти по сравнению с другими методами кодирования |
Коды с исправлением ошибок предназначены для:
| управления ошибками в ходе отправки и получения сообщения | |
| восстановления с вероятностью, близкой к единице, посланного сообщения | |
| выявления вероятности, близкой к единице, наличие ошибок |
Код Хэмминга:
| не групповой код | |
| натуральный код | |
| групповой код |
Для кодирующей матрицы  найти вероятность правильной передачи:
найти вероятность правильной передачи:
| Pправильной передачи = p4+p3q | |
| Pправильной передачи = p2+p2q | |
| Pправильной передачи = p3+p2q |
Блочный код называется групповым, если:
| сообщение кодируется несколькими методами последовательно | |
| он образует группу вместе с другими кодами | |
| его кодовые слова образуют группу |
Для кодирующей матрицы  найти вероятность необнаружения ошибки:
найти вероятность необнаружения ошибки:
| Pнеобнаружения ошибки = 2p3q3 + pq3 | |
| Pнеобнаружения ошибки = 2p2q3 + pq4 | |
| Pнеобнаружения ошибки = 4p4q3 + pq4 |
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
| 1101 | |
| 1001 | |
| 1000 |
Первый БЧХ-код, примененный на практике, был:
| (92,127)-код | |
| (102,250)-код | |
| (231,255)-код |
Код Голея — это:
| код БЧХ | |
| невозможно определить принадлежность кода Голея к коду БЧХ | |
| не код БЧХ |
При реальной передаче или хранении информации ошибки:
| распределяются равномерно по всей длине данных | |
| группируются в нескольких участках, распределенных неравномерно | |
| обычно группируются на некотором участке |
Первая и наиболее известная система с открытым ключом называется:
| DES | |
| PGP | |
| RSA |
Особенностью системы с ключевым словом является:
| три уровня секретности | |
| один уровень секретности | |
| два уровня секретности |
Нужно послать секретные сообщения 25 и 2 для JB и 14 для CIA, используя следующие записи открытой книги паролей криптосистемы RSA — JB: 77,7; CIA: 667,15
| 43, 41; 256 | |
| 53, 31; 295 | |
| 53, 51; 247 |
Системы с ключевым словом характеризуются тем, что:
| широко применяются до сих пор | |
| в настоящее время очень редко применяются | |
| вышли из применения |
Большинство тегов языка HTML:
| самодостаточные | |
| нуждаются в двойном закрытии | |
| парные |
Самым распространенным типом данных в компьютерном мире является:
| графические файлы | |
| динамические библиотеки | |
| текстовые файлы |
Аналоговая информация характеризуется:
| непрерывным процессом изменения некоторой величины | |
| последовательными точными значениями некоторой величины | |
| повторными процессами распределения случайной величины |
Кибернетика — это наука:
| о способах взаимодействиях различных абстрактных объектов | |
| об общих законах управления системами | |
| об общих законах получения, хранения, передачи и переработки информации |
Чем ниже частота дискретизации, тем:
| точнее происходит перевод непрерывной информации в дискретную | |
| эффективнее и быстрее происходит перевод непрерывной информации в дискретную | |
| менее точно происходит перевод непрерывной информации в дискретную |
В таблице кодировки ASCII+ печатные и управляющие символы занимают:
| все 256 символов таблицы | |
| первые 127 позиций таблицы | |
| последние 127 позиций таблицы | |
| последние 128 позиций таблицы | |
| первые 128 позиций таблицы |
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Вычислить HX1.
| HX1 = 1.51 бит/сим | |
| HX1 = 2 бит/сим | |
| HX1 = 2.5 бит/сим |
Определить HZ, если задана дискретная случайная величина Z=(X1+1)2-X2, где независимые дискретные случайные величины X1, X2 могут с равной вероятностью принимать значение либо 0, либо 1:
| HZ = 1 бит/сим | |
| HZ = 2 бит/сим | |
| HZ = 2.5 бит/сим |
Дискретная случайная величина X равна количеству «гербов», выпавших на двух идеальных монетках. Найти энтропию X:
| HX=1.8 бит/сим | |
| HX=2.5 бит/сим | |
| HX=1.5 бит/сим |
По теории Шеннона:
| смысл сообщений НЕ имеет никакого отношения к теории информации | |
| нельзя дать точный ответ насчет зависимости между смыслом сообщений и теории информации | |
| смысл сообщений имеет прямое отношения к теории информации |
Перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью pi, где i — это номер лампочки. Среднее время, необходимое для правильного ответа испытуемого, пропорционально:
Про дискретную случайную величину X известно, что ее значениями являются буквы кириллицы. Произведен ряд последовательных измерений X, результат которых — «ТЕОРИЯИНФОРМАЦИИ». Составить на основании этого результата приблизительный закон распределения вероятностей этой дискретной случайной величины и оценить минимальную среднюю длину кодов для X:
 Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита:
Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита:
| 1.7 бит/сим | |
| 1.3 бит/сим | |
| 1.56 бит/сим |
Метод Шеннона-Фэно состоит в том, что:
| значения дискретной случайной величины располагают в порядке возрастания их вероятностей, а затем последовательно умножают на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1 | |
| значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1 | |
| значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 1, а к коду второй — 0 |
Среднее количество бит, приходящихся на одно кодируемое значение дискретной случайной величины:
| не может быть меньшим, чем энтропия этой дискретной случайной величины | |
| не может быть большей, чем энтропия этой дискретной случайной величины | |
| строго равна энтропии этой дискретной случайной величины |
Суть основной теоремы о кодировании при отсутствии помех заключается в том, что:
| при очень малой длине n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения. Данное правило действует только на короткие сообщения | |
| с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения | |
| с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет очень удалено от энтропии единицы сообщения |
Размер сжатия:
| может быть сколь угодно большим | |
| не может быть больше некоторого теоретические предела | |
| ограничивается лишь потребностями пользователя |
Вычислить HX для кодов Хаффмена и Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей  :
:
Вычислить ML(X) для кода Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей  :
:
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
Преимущество арифметического кодирования позволяет:
| кодировать символы одним байтом | |
| кодировать некоторые символы менее чем одним битом | |
| кодировать некоторые символы только несколькими битами |
Закодировать сообщение «КИБЕРНЕТИКИ», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
| код(КИБЕРНЕТИКИ) = ‘К’0′И’00′Б’100′Е’000′Р’1 100′Н’1111000′Т’100110111 | |
| код(КИБЕРНЕТИКИ) = ‘К’0′И’00′Б’101′Е’010′Р’1 100′Н’1100001′Т’100110001 | |
| код(КИБЕРНЕТИКИ) = ‘К’0′И’00′Б’100′Е’000′Р’1 100′Н’1111000′Т’101010001 |
Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длины кодов Хаффмена, блочного Хаффмена (для блоков длины 2 и 3) для сообщения ABAAAB:
| LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 6 бит, LХаффмена-3(ABAAAB) = 4 бита | |
| LХаффмена-1(ABAAAB) = 6 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 5 бит | |
| LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 6 бит |
Cообщение, полученное путем сжатия адаптивным алгоритмом Хаффмена с упорядоченным деревом имеет вид: ‘A’0′F’00′X’0111110101011011110100101. Определить длину несжатого сообщения в битах:
| 117 бит | |
| 120 бит | |
| 125 бит |
Составить арифметический код для сообщения BAABC, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/3, P(X=B)=7/15, P(X=C)=1/5:
| 01100001 | |
| 01100111 | |
| 01011111 |
Дискретная случайная величина X может принимать три различных значения. Если считать сложность построения кода пропорциональной количеству различных значений кодируемой дискретной случайной величины, то блочный код для X по сравнению с неблочным сложнее строить в:
| в 81 раз | |
| в 25 раз | |
| в 27 раз |
Закодировать сообщение «AABCDAACCCCDBB», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
| код(AABCDAACCCCDBB) = ‘A’10′B’00′C’011′D’00011001111100110011110 | |
| код(AABCDAACCCCDBB) = ‘A’10′B’00′C’000′D’00011001111100110011001 | |
| код(AABCDAACCCCDBB) = ‘A’11′B’11′C’010′D’00011001111100110000101 |
Словарные алгоритмы преимущественно отличаются от статистических тем, что:
| позволяют кодировать последовательности символов одинаковой длины | |
| позволяют быстрее кодировать символы | |
| позволяют кодировать последовательности символов разной длины |
Закодировать сообщения «КИБЕРНЕТИКИ», вычислить длины в битах полученных кодов, используя алгоритм LZSS (словарь — 12 байт, буфер — 4 байта):
Алгоритм LZ77 использует «скользящее» по сообщению окно, разделенное на две части, выполняющие определенные функции:
| первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим еще незакодированные символы входного потока | |
| первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим уже закодированные, но еще не просмотренные символы входного потока | |
| первая включает уже просмотренную часть сообщения. Вторая является буфером, содержащим еще незакодированные символы входного потока. Первая и вторая части равны |
Статистическими методами называют:
Закодировать сообщения «AABCDAACCCCDBB», вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь — 12 байт, буфер — 4 байта):
Алгоритм LZSS отличается от LZ77 следующим:
| возможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря | |
| скоростью работы | |
| длина подстроки, которую можно закодировать, НЕ ограничена размером буфера | |
| производимыми кодами |
Задержка сигнала во времени представляет собой:
| интервал времени от отправки сигнала передатчиком до его приема приемником | |
| интервал времени от создания сигнала до его прочтения приемником и удаления | |
| интервал времени от отправки сигнала передатчиком до его приема приемником и обратной отправки к передатчику |
Видеоинформацию можно сжать:
| очень неплотно, всего на несколько процентов | |
| очень слабо — она практически не сжимаема | |
| очень плотно, до 100 и более раз | |
| до 10000 и более раз |
Устройства канала связи представляют собой:
| совокупность устройств, объединенных линиями связи, предназначенных для передачи информации от источника информации до ее приемника | |
| устройства, просто передающие усиленным принятый сигнал | |
| устройство, определяющее интервал времени от отправки сигнала передатчиком до его приема приемником |
Cжатие с потерями позволяет:
| предоставить более эффективные методы сжатия данных без удаления информации | |
| добавлять некоторую часть к исходной информации | |
| отбрасывать часть исходной информации |
Для сжатия графической информации с потерями в конце 80-х установлен стандарт:
| GIF | |
| ICO | |
| WMF | |
| BMP | |
| JPEG |
Сжатие с потерями используется в основном для видов данных:
Специальные таблицы для перевода неформальных данных в цифровой вид называются:
| символьные преобразователями | |
| таблицами взаимодействия | |
| таблицами шифрования | |
| таблицами кодировки |
Противоположность информации:
| неопределенность | |
| определенность | |
| сущность |
Функция f-инъекция, если:
| она зависит от двух и более аргументов | |
| на разных значениях аргумента она принимает разные значения | |
| на разных значениях аргумента она принимает одинаковые значения | |
| в роли аргумента выступает функция |
Дискретная случайная величина X может принимать три различных значения. При построении блочного кода с длиной блока 4 для X необходимо будет рассмотреть дискретную случайную величину X — выборку четырех значений X. X может иметь:
| 75 различных значений | |
| 81 различное значение | |
| 27 различных значений |
Вычислить длины в битах сообщения «СИНЯЯ СИНЕВА СИНИ» в коде ASCII+ и его полученного кода
| L(СИНЯЯ СИНЕВА СИНИ) = 124 бит, длина исходного сообщения = 148 бит | |
| L(СИНЯЯ СИНЕВА СИНИ) = 114 бит, длина исходного сообщения = 136 бит | |
| L(СИНЯЯ СИНЕВА СИНИ) = 104 бит, длина исходного сообщения = 124 бит |
Атрибут ALT тега IMG используется для:
| указания способа выравнивания картинки | |
| указания URI файла с графикой | |
| указания альтернативного текста, показываемого вместо картинки, в случае, когда файл с графикой недоступен или его тип неизвестен браузеру | |
| определения рамки картинки |
Составить адаптивный арифметический код с маркером конца для сообщения BAABC:
| 01000010111001 | |
| 01000010110100 | |
| 01000011000011 |
Наиболее широкое распространение получил:
| (102,250)-код | |
| (231,255)-код | |
| (92,127)-код |
Правильные ответы выделены зелёным цветом.
Все ответы: В курсе излагаются основные понятия и факты теории информации. Рассмотрены способы измерения, передачи и обработки информации.
Кибернетика — это наука:
(1) об общих законах управления системами
(2) о способах взаимодействиях различных абстрактных объектов
(3) об общих законах получения, хранения, передачи и переработки информации
Способ построения полиномиальных кодов, минимальное расстояние между кодовыми словами которых равно заданному числу, был открыт:
(1) Чоудхури
(2) Боузом
(3) Хоккенгемом
Криптография определяет:
(1) раздел теории информации, в котором изучаются и разрабатываются системы кодирования информации
(2) раздел кибернетики, в котором изучаются и разрабатываются системы изменения письма с целью сделать его более понятным
(3) раздел математики, в котором изучаются и разрабатываются системы изменения письма с целью сделать его непонятным для непосвященных лиц
Самым распространенным типом данных в компьютерном мире является:
(1) динамические библиотеки
(2) графические файлы
(3) текстовые файлы
Информация — это:
(1) объект, несущий в себе определенное значение
(2) материальная сущность, при помощи которой с любой точностью можно описывать любые сущности
(3) нематериальная сущность, при помощи которой с любой точностью можно описывать реальные, виртуальные и понятийные сущности
Энтропия дискретной случайной величины представляет собой:
(1) среднее количество бит, которое нужно передавать по каналу связи о текущем значении данной дискретной случайной величины, чтобы полностью описать ее
(2) максимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной дискретной случайной величины
(3) минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной дискретной случайной величины
Цель сжатия состоит в:
(1) изменении(как в увеличении, так и в сжатии) количества бит, необходимых для хранения или передачи информации
(2) увеличении количества байт, необходимых для хранения или передачи информации
(3) уменьшении количества бит, необходимых для хранения или передачи заданной информации
Бинарное дерево называется упорядоченным, если:
(1) его узлы НЕ могут быть перечислены в порядке убывания веса
(2) его узлы находятся на разных ярусах
(3) его узлы могут быть перечислены в порядке неубывания веса и в этом перечне узлы, имеющие общего родителя, должны находиться рядом, на одном ярусе
Статистическими методами называют:
(1) словарные алгоритмы
(2) арифметическое кодирование
(3) метод Шеннона-Фэно
(4) алгоритм Ферма
(5) метод Хаффмена
Cжатие с потерями позволяет:
(1) предоставить более эффективные методы сжатия данных без удаления информации
(2) добавлять некоторую часть к исходной информации
(3) отбрасывать часть исходной информации
Коды делятся на классы:
(1) коды с обнаружением ошибок
(2) коды с корректированием ошибок
(3) коды с исправлением ошибок
(4) коды с управлением ошибками
(5) коды с изъятием ошибок
Блочный код называется групповым, если:
(1) сообщение кодируется несколькими методами последовательно
(2) он образует группу вместе с другими кодами
(3) его кодовые слова образуют группу
Основной категорией кибернетики является:
(1) энергия
(2) распознавание
(3) управление
(4) взаимодействие
Многочлен g(x) степени k называется примитивным, если:
(1) xj+1 НЕ делится на g(x) и делится без остатка на j
(2) x2+1 делится на g(x) без остатка для j=3k-1 и не делится ни для какого меньшего значения j
(3) xj+1 делится на g(x) без остатка для j=2k-1 и не делится ни для какого меньшего значения j
Системы с ключевым словом характеризуются тем, что:
(1) широко применяются до сих пор
(2) вышли из применения
(3) в настоящее время очень редко применяются
Различают виды разметок текста:
(1) внешняя
(2) управляющая
(3) физическая
(4) арифметическая
(5) логическая
Общая схема передачи информации имеет вид:
(1) исходная информация — сжатие — шумозащитное кодирование — канал связи — декодирование шумозащитных кодов — дешифровка — полученная информация
(2) исходная информация — сжатие — шифрование — шумозащитное кодирование — канал связи(проявляется действие шумов) — декодирование шумозащитных кодов — распаковка — дешифровка — полученная информация
(3) исходная информация — шифровка — сжатие — шумозащитное кодирование — канал связи(проявляется действие шумов) — декодирование шумозащитных кодов — распаковка — дешифровка — полученная информация
(4) исходная информация — шифровка — сжатие — канал связи — распаковка — дешифровка — полученная информация
(5) исходная информация — шифровка — сжатие — шумозащитное кодирование — канал связи — декодирование шумозащитных кодов — дешифровка — распаковка — полученная информация
Перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью pi, где i — это номер лампочки. Среднее время, необходимое для правильного ответа испытуемого, пропорционально:
(1) 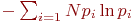
(2) числу лампочек N
(3) величине энтропии 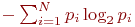
Выбрать верные утверждения:
(1) 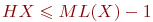
(2) 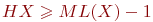
(3) 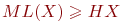
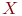
(4) 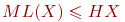
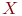
Вычислить длины кодов Хаффмена и арифметического для сообщения AAB, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/3, P(X=B)=2/3:
(1) LХаффмена = 3.5 бита, Lарифметический = 4.4 бита
(2) LХаффмена = 4 бита, Lарифметический = 3 бита
(3) LХаффмена = 3 бита, Lарифметический = 4 бита
Основная идея LZ77 состоит в том, что:
(1) заменяются только четные вхождения некоторой строки символов в сообщении
(2) первое и последующие вхождения некоторой строки символов в сообщении заменяются ссылками на примитив
(3) второе и последующие вхождения некоторой строки символов в сообщении заменяются ссылками на ее первое вхождение
Основная идея сжатия графической информации с потерями заключается в том, что:
(1) каждая точка в картинке характеризуется одним атрибутом: цветом
(2) каждая точка в картинке характеризуется двумя равноважными атрибутами: яркостью и цветом
(3) каждая точка в картинке характеризуется тремя равноважными атрибутами: яркостью, цветом и насыщенностью
Простой код с обнаружением ошибок основан на:
(1) взаимодействии с другим кодом
(2) булевом методе проверки
(3) схеме проверки четности
Свойства совершенного кода могут быть представлены в виде:
(1) для совершенного (m,n)-кода, исправляющего все ошибки веса, не большего k, выполняется соотношение 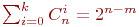
(2) совершенный код, исправляющий все ошибки веса, не большего k, в столбцах таблицы декодирования содержит все слова, отстоящие от кодовых на расстоянии, не большем k. Верно и обратное утверждение
(3) таблица декодирования совершенного кода, исправляющего все ошибки в не более чем k позициях, имеет в качестве лидеров все строки, содержащие не более k единиц. Верно и обратное утверждение
Теория информации представляет собой:
(1) абстрактную категорию, необходимую для изучения кибернетики в целом, определяющую аспекты использования информации
(2) концепцию, согласно которой осуществляется доступ к информации
(3) математическую теорию, посвященную измерению информации, ее потока, «размеров» канала связи и т.п.
Код Голея — это:
(1) невозможно определить принадлежность кода Голея к коду БЧХ
(2) код БЧХ
(3) не код БЧХ
Проблема нераскрываемого шифра является:
(1) стойкость шифра
(2) скорость шифрования
(3) способ передачи ключа
Основными форматами текста с разметкой являются:
(1) XLS
(2) HTML
(3) TeX
(4) DOC
(5) PDF
Клод Шеннон предложил способ изменения количества информации:
(1) средствами визуального определения
(2) путем непосредственного использования символов
(3) содержащейся в одной случайной величине, относительно другой случайной величины
Если задана функция 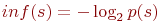
s-это предложение, смысловое содержание которого измеряется, p(s) — вероятность истинности s, то эта функция обладает свойствами:
(1) если s-истинно, то 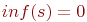
(2) 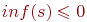
(3) если 

(4) 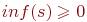
(5) если 

Суть основной теоремы о кодировании при отсутствии помех заключается в том, что:
(1) при очень малой длине n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения. Данное правило действует только на короткие сообщения
(2) с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет очень удалено от энтропии единицы сообщения
(3) с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения
Дискретная случайная величина X может принимать три различных значения. При построении блочного кода с длиной блока 4 для X необходимо будет рассмотреть дискретную случайную величину X — выборку четырех значений X. X может иметь:
(1) 75 различных значений
(2) 27 различных значений
(3) 81 различное значение
Алгоритм LZ77 выдает коды, состоящие из:
(1) двух элементов
(2) пяти элементов
(3) трех элементов
Видеоинформацию можно сжать:
(1) до 10000 и более раз
(2) очень неплотно, всего на несколько процентов
(3) очень плотно, до 100 и более раз
(4) очень слабо — она практически не сжимаема
Последовательные коды характеризуются тем, что:
(1) значение каждого символа зависит от части предшествующего фрагмента сообщения
(2) значение очередного контрольного символа НЕ зависит от всего предшествующего фрагмента сообщения
(3) значение очередного контрольного символа зависит от всего предшествующего фрагмента сообщения
Для кодирующей матрицы 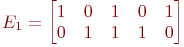
При формальном представлении информации:
(1) ряду однородных объектов ставится в соответствие некий код, позволяющий индентифицировать любой объект из данных однородных объектов по этому коду
(2) совокупности объектов ставится в соответствие формальный код
(3) каждому описываемому объекту или понятию ставится в соответствие некоторый числовой код
Циклический избыточный код имеет:
(1) временную длину
(2) переменную длину
(3) фиксированную длину
Между абонентами A и B установлен секретный канал связи без передачи ключей при заданных p=167 и их первых ключах 15 и 21. Описать процесс передачи сообщения 17 (от B к A):
(1) A отправляет B 115, B возвращает 63, A окончательно отправляет 140
(2) A отправляет B 58, B возвращает 94, A окончательно отправляет 115
(3) B отправляет A 135, A возвращает 15, B окончательно отправляет 143
Большинство тегов языка HTML:
(1) нуждаются в двойном закрытии
(2) самодостаточные
(3) парные
Укажите свойства меры информации и энтропии:
(1) если X константа, то HX = 0
(2) 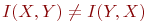
(3) I(X,Y) = HX + HY - H(X,Y), где 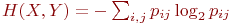
(4) если X, Y независимы, то I(X,Y) = 0
(5) I(X,Y) = 0 только если 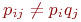
(6) I(X,Y) = I(Y,X)

code1 для дискретной случайной величины X:
(1) ML1(X)=2.2 бит/сим
(2) ML1(X)=3.5 бит/сим
(3) ML1(X)=3 бит/сим
Метод Шеннона-Фэно состоит в том, что:
(1) значения дискретной случайной величины располагают в порядке возрастания их вероятностей, а затем последовательно умножают на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1
(2) значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 1, а к коду второй — 0
(3) значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1
Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длины кодов Хаффмена, блочного Хаффмена (для блоков длины 2 и 3) для сообщения ABAAAB:
(1) LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 6 бит
(2) LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 6 бит, LХаффмена-3(ABAAAB) = 4 бита
(3) LХаффмена-1(ABAAAB) = 6 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 5 бит
Код, выдаваемый LZSS, начинается с:
(1) собственно кода, без префикса
(2) двубитного префикса
(3) однобитного префикса
Устройства канала связи представляют собой:
(1) устройство, определяющее интервал времени от отправки сигнала передатчиком до его приема приемником
(2) совокупность устройств, объединенных линиями связи, предназначенных для передачи информации от источника информации до ее приемника
(3) устройства, просто передающие усиленным принятый сигнал
Следующее утверждение верно:
(1) d(a,b) = w(a-b)
(2) 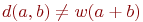
(3) d(a,b) = w(a+b)
Для кодирующей матрицы 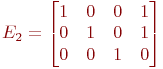
(1) mind = 3
(2) mind = 2
(3) mind = 1
Информация может быть нескольких типов:
(1) непрерывная
(2) устойчивая
(3) дискретная
(4) частотная
(5) повторная
Вычисление значения кода CRC происходит посредством:
(1) деления многочлена, соответствующего исходному сообщению, на фиксированный многочлен. Целая часть от такого деления и есть код CRC
(2) деления фиксированного многочлена на многочлен, соответствующего исходному сообщению. Остаток от такого деления и есть код CRC
(3) деления многочлена, соответствующего исходному сообщению, на фиксированный многочлен. Остаток от такого деления и есть код CRC
Алгоритм DES предназначен для шифровки:
(1) ровно 32 бит исходных данных
(2) более 64 бит исходных данных
(3) ровно 64 бит исходных данных
(4) менее 64 бит исходных данных
Специальные символы можно ввести в документ, используя их имена, заключенные между:
(1) & и !
(2) # и ;
(3) & и ;
(4) @ и ;
(5) % и %
Найти энтропию дискретной случайной величины X, заданной распределением

code4 для дискретной случайной величины X:
(1) ML3(X)=2.8 бит/сим
(2) ML3(X)=3 бит/сим
(3) ML4(X)=2.2 бит/сим
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
(1) Винера
(2) Хаффмена
(3) Шеннона-Фэно
(4) Берга
Закодировать сообщение BBCBBC, используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
(1) 'C'01'B'0100
(2) 'B'11'C'1001
(3) 'B'10'C'1101
При чрезмерном увеличении размера словаря и буфера для алгоритмов LZ77 и LZSS, то это приведет:
(1) к снижению стойкости кода
(2) к увеличению эффективности кодирования
(3) к снижению эффективности кодирования
Простейший код для борьбы с шумом представляет собой:
(1) условное повторение кода в целом
(2) тройное повторение каждого бита
(3) контроль четности
Имеется (8,9)-код с проверкой четности. Вычислить вероятность ошибочной передачи без использования кода, если вероятность ошибки при передаче каждого бита равна 1%:
Для кодирующей матрицы 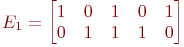
(1) Pправильной передачи = p3 + 4p4q + 3p3q2
(2) Pправильной передачи = p4 + 4p4q + 2p2q2
(3) Pправильной передачи = p5 + 5p4q + 2p3q2
Частота дискретизации определяет:
(1) время, в течении которого затухают колебания исследуемой величины
(2) период между измерениями непрерывной величины, колеблющихся разных разных фазах
(3) период между измерениями значений непрерывной величины
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
(1) 1111
(2) 1011
(3) 1000
Нужно послать секретные сообщения 25 и 2 для JB и 14 для CIA, используя следующие записи открытой книги паролей криптосистемы RSA — JB: 77,7;
CIA: 667,15
(1) 43, 41; 256
(2) 53, 31; 295
(3) 53, 51; 247
Элементы SGML делятся на категории:
(1) ссылки на данные — им соответствуют элементы разметки HTML типа &
(2) описательные конструкции компонент документа в их структурной взаимосвязи — они не входят в HTML, но определяют его
(3) описательные маркеры — определяют структуру документа — им соответствуют элементы разметки HTML типа H1, P, A, IMG и т.п.
(4) инструкции по обработке текста
Определить HZ, если задана дискретная случайная величина Z=(X1+1)2-X2, где независимые дискретные случайные величины X1, X2 могут с равной вероятностью принимать значение либо 0, либо 1:
(1) HZ = 1 бит/сим
(2) HZ = 2.5 бит/сим
(3) HZ = 2 бит/сим
Дискретная случайная величина X задана распределением P(X=2n)=1/2n, n=1,2,..., Найти энтропию X:
(1) HX = 1 бит/сим
(2) HX = 2.2 бит/сим
(3) HX = 2 бит/сим

ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита:
(1) 1.3 бит/сим
(2) 1.7 бит/сим
(3) 1.56 бит/сим
Вычислить длины в битах сообщения «КИБЕРНЕТИКИ» в коде ASCII+ и его полученного кода
(1) L(КИБЕРНЕТИКИ) = 98 бит, длина исходного сообщения = 102 бита
(2) L(КИБЕРНЕТИКИ) = 72 бита, длина исходного сообщения = 75 бит
(3) L(КИБЕРНЕТИКИ) = 85 бит, длина исходного сообщения = 88 бит
Запатентованным является алгоритм:
(1) LZ78
(2) LZSS
(3) LZW
Передатчик задается случайной величиной со следующими законами распределениями вероятностей: P(X1=-1)=1/4, P(X1=0)=1/2, P(X1=1)=1/4. Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу передатчиком, обеспечивающую сколь угодно высокую надежность передачи:
(1) 8000/3.5 ≈ 2285.71 сим/сек
(2) 8000/2 ≈ 4000 сим/сек
(3) 8000/3 ≈ 2666.67 сим/сек
Преимущество матричного кодирования заключается в:
(1) определении объема полученных данных еще до начала кодирования
(2) использовании большего объема памяти по сравнению с другими методами кодирования
(3) использовании гораздо меньшего объема памяти по сравнению с другими методами кодирования
Полиномиальный код с кодирующим многочленом g(x) кодирует слово сообщения a(x) многочленом:
(1) b(x)=a(x)g(x)=b0+b1x+ ... +bn+1xn+1
(2) b(x)=a(x)g(x)=b0+b1x+ ... +bnxn
(3) b(x)=a(x)g(x)=b0+b1x+ ... +bn-1xn-1
Суть теоремы о выборках заключается в том, что:
(1) частота дискретизации должна быть 44.1КГц
(2) для точной дискретизации ее частота должна быть не менее чем в три раза выше наибольшей частоты гармоники, входящей в дискретизируемую величину
(3) для точной дискретизации ее частота должна быть не менее чем в два раза выше наибольшей частоты гармоники, входящей в дискретизируемую величину
Преимущество формата PostScript заключается в том, что:
(1) он зависим от физических устройств воспроизведения
(2) он легко редактируется вручную
(3) он независим от физических устройств воспроизведения
(4) благодаря его универсальности, он может заменять собой табличный и текстовый процессоры
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Дискретная случайная величина Y равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е. Y=X1+X2. Вычислить I(X1,Y):
Распаковать сообщение 'A'0'F'00'X'0111110101011011110100101, полученное по адаптивному алгоритму Хаффмена с упорядоченным деревом
(1) FFXAAAXFXAXFFAA
(2) AFXFFAXFXAXAAAF
(3) AFXAFFXFXAXAFFA
Закодировать сообщения «КИБЕРНЕТИКИ», вычислить длины в битах полученных кодов, используя алгоритм LZW (словарь — ASCII+ и 16 фраз):
(1) 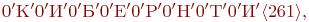
(2)
0’К’0’И’0’Б’0’Е’0’Р’0’Н’
1 langle 9,1 rangle 0’Т’1 langle 5,1 rangle 1 langle 5,2 rangle,
длина 3 * 7 + 7 * 9 = 84 бит
(3) 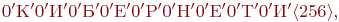
ЦВМ служит для:
(1) определения повторных величин
(2) обработки непрерывной информации
(3) обработки дискретной информации
Разделами кибернетики являются:
(1) дискретная математика
(2) теория информации
(3) теория алгоритмов
(4) теория машин и механизмов
(5) теория распознавания образов
(6) теория вероятностей
Коды Рида-Соломона являются:
(1) двоичными коды
(2) недвоичными кодами
(3) полиномными кодами
Простейшая система шифрования основана на том, что:
(1) выбирается сложный алгоритм кодирования данных
(2) происходит замена каждого знака письма на другой знак по выбранному правилу
(3) происходит замена целого письма одним символом
Компьютерный шрифт представляет собой:
(1) обычный текст
(2) набор именованных кодами рисунков знаков
(3) набор видеофайлов
Противоположность информации:
(1) сущность
(2) неопределенность
(3) определенность
Энтропия определяет:
(1) теорию информации
(2) меру уравновешенности системы
(3) раздел кибернетики
(4) способ кодирования информации
Размер сжатия:
(1) может быть сколь угодно большим
(2) не может быть больше некоторого теоретические предела
(3) ограничивается лишь потребностями пользователя
При кодировании методом Хаффмена и на 0 и на 1 придется тратить:
(1) максимум один бит
(2) не менее одного бита
(3) не менее одного байта
Словарные алгоритмы преимущественно отличаются от статистических тем, что:
(1) позволяют кодировать последовательности символов одинаковой длины
(2) позволяют кодировать последовательности символов разной длины
(3) позволяют быстрее кодировать символы
Сжатие с потерями используется в основном для видов данных:
(1) полноцветная графика
(2) видеоинформация
(3) звук
(4) текстовая информация
Коды с исправлением ошибок предназначены для:
(1) выявления вероятности, близкой к единице, наличие ошибок
(2) восстановления с вероятностью, близкой к единице, посланного сообщения
(3) управления ошибками в ходе отправки и получения сообщения
Если код является групповым, то:
(1) наибольшее расстояние между двумя кодовыми словами меньше либо равно наибольшему весу нулевого слова
(2) наименьшее расстояние между двумя кодовыми словами равно наименьшему весу ненулевого слова
(3) наибольшее расстояние между двумя кодовыми словами равно наименьшему весу ненулевого слова
Сущность принципа управления заключается в том, что:
(1) движение и действие больших масс или передача и преобразование больших количеств энергии направляется и контролируется при помощи еще больших количеств энергии
(2) движение и действие больших масс или передача и преобразование больших количеств энергии направляется и контролируется при помощи небольших количеств энергии, несущих информацию
(3) движение и действие малых масс или передача и преобразование малых количеств энергии направляется и контролируется при помощи больших количеств энергии
Первый БЧХ-код, примененный на практике, был:
(1) (231,255)-код
(2) (92,127)-код
(3) (102,250)-код
Особенностью системы с ключевым словом является:
(1) три уровня секретности
(2) один уровень секретности
(3) два уровня секретности
При логической разметке указывается:
(1) что нужно сделать с выбранным фрагментом текста: показать курсивным, приподнять, центрировать, сжать, подчеркнуть и т.п.
(2) структурный смысл выбранного фрагмента: примечание, начало раздела, конец подраздела, ссылка на другой фрагмент и т.п.
(3) управляющие элементы, необходимые для правильного определения документа
Общая схема передачи информации имеет вид:
(1) исходная информация — шифровка — сжатие — шумозащитное кодирование — канал связи — декодирование шумозащитных кодов — дешифровка — распаковка — полученная информация
(2) исходная информация — сжатие — шифрование — шумозащитное кодирование — канал связи(проявляется действие шумов) — декодирование шумозащитных кодов — распаковка — дешифровка — полученная информация
(3) исходная информация — шифровка — сжатие — канал связи — распаковка — дешифровка — полученная информация
(4) исходная информация — шифровка — сжатие — шумозащитное кодирование — канал связи(проявляется действие шумов) — декодирование шумозащитных кодов — распаковка — дешифровка — полученная информация
(5) исходная информация — сжатие — шумозащитное кодирование — канал связи — декодирование шумозащитных кодов — дешифровка — полученная информация
Выбрать верные утверждения:
(1) 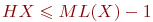
(2) 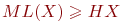
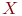
(3) 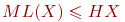
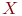
(4) 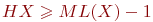
Составить арифметический код для сообщения BAABC, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/4, P(X=B)=1/2, P(X=C)=1/4:
(1) 010001101
(2) 010001011
(3) 010001001
Алгоритм LZ77 использует «скользящее» по сообщению окно, разделенное на две части, выполняющие определенные функции:
(1) первая включает уже просмотренную часть сообщения. Вторая является буфером, содержащим еще незакодированные символы входного потока. Первая и вторая части равны
(2) первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим еще незакодированные символы входного потока
(3) первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим уже закодированные, но еще не просмотренные символы входного потока
Для сжатия графической информации с потерями в конце 80-х установлен стандарт:
(1) GIF
(2) JPEG
(3) BMP
(4) ICO
(5) WMF
Блочный код заменяет:
(1) четный блок из m символов более длинным блоком из n символов
(2) каждый блок из m символов более длинным блоком из n символов
(3) каждый блок из m символов более коротким блоком из n символов
Двоичный блочный (m,n)-код называется оптимальным, если:
(1) он не изменяет вероятность ошибочного декодирования
(2) он минимизирует вероятность ошибочного декодирования
(3) он управляет вероятностью кодирования
Теория информации изучает:
(1) аспекты использования данных
(2) измерение информации, ее потока, «размеров» канала связи и т.п.
(3) абстрактные категории различных математических объектов
Коды Хэмминга являются:
(1) не код БЧХ
(2) код БЧХ
(3) невозможно определить принадлежность кода Хэмминга к коду БЧХ
Зашифровать сообщение «КИБЕРНЕТИКА» ключом «ДИСК»:
(1) ПТКРХЗЩЮНФЫ
(2) ПТУРХЧЧЮНФЫ
(3) ПТУВЛЧДЮНФЯ
World Wide Web базируется на стандартах:
(1) TeX
(2) URI
(3) HTML
(4) HTTP
(5) PDF
Функция f-инъекция, если:
(1) на разных значениях аргумента она принимает одинаковые значения
(2) на разных значениях аргумента она принимает разные значения
(3) она зависит от двух и более аргументов
(4) в роли аргумента выступает функция
Если задана функция 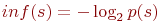
s-это предложение, смысловое содержание которого измеряется, p(s) — вероятность истинности s, то если 
Кодирование, основанное на основной теореме о кодировании при отсутствии помех:
(1) легко реализуемо
(2) практически не реализуемо
(3) невозможно
Дискретная случайная величина X может принимать три различных значения. Если считать сложность построения кода пропорциональной количеству различных значений кодируемой дискретной случайной величины, то блочный код для X по сравнению с неблочным сложнее строить в:
(1) в 81 раз
(2) в 27 раз
(3) в 25 раз
К недостаткам алгоритма LZ77 следует отнести:
(1) невозможность применять алгоритм для больших объемов информации
(2) с ростом размеров словаря скорость работы алгоритма-кодера пропорционально замедляется
(3) неэффективность алгоритма в целом
(4) кодирование одиночных символов очень неэффективно
Стандарт LPC используется для:
(1) сжатия видеоинформации
(2) сжатия речи
(3) сжатия текстовой информации
(4) распаковки графических файлов
Расстоянием (Хэмминга) между двоичными словами длины n называется:
(1) количество четных позиций, в которых эти слова не встречаются
(2) количество позиций, в которых эти слова различаются
(3) количество позиций, в которых эти слова совпадают
Для кодирующей матрицы 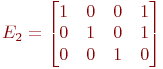
Специальные таблицы для перевода неформальных данных в цифровой вид называются:
(1) символьные преобразователями
(2) таблицами кодировки
(3) таблицами взаимодействия
(4) таблицами шифрования
Для кода CRC-16 полином-генератор имеет степень:
Первая и наиболее известная система с открытым ключом называется:
К парным тегам языка HTML относятся:
(1) BODY
(2) I
(3) BR
(4) CODE
(5) IMG
Известно что 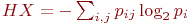
i pij равно либо qj, либо 0 при условии:
(1) 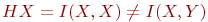
(2) HX = I(X,X) = I(X,Y)
(3) 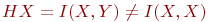

code2 для дискретной случайной величины X:
(1) ML2(X)=3 бит/сим
(2) ML2(X)=2.2 бит/сим
(3) ML2(X)=3.2 бит/сим
По методу Хаффмена код строится:
(1) на основе реляционной теории
(2) при помощи двоичного дерева
(3) посредством линейной структуры
Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длину арифметического кода для сообщения ABAAAB:
(1) Lарифметический(ABAAAB) = 2 бита
(2) Lарифметический(ABAAAB) = 1 бит
(3) Lарифметический(ABAAAB) = 1.5 бит
Собственно код, выдаваемый LZSS, состоит из:
(1) символ
(2) длина
(3) смещение
(4) примитив
Эффективность канала характеризуется:
(1) задержка сигнала во времени
(2) скоростью передачи информации
(3) достоверность передачи информации
(4) надежность работы
Неравенством Варшамова — Гильберта называют выражение:
Для кодирующей матрицы 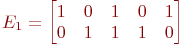
(1) Pнеобнаружения ошибки = 2p3q3 + pq3
(2) Pнеобнаружения ошибки = 2p2q3 + pq4
(3) Pнеобнаружения ошибки = 4p4q3 + pq4
Информация может быть нескольких типов:
(1) непрерывная
(2) частотная
(3) повторная
(4) устойчивая
(5) дискретная
CRC-коды способны обнаруживать:
(1) только смежные ошибки
(2) одиночную ошибку в любой позиции и, кроме того, многочисленные комбинации кратных ошибок, расположенных близко друг от друга
(3) одиночную ошибку в любой позиции, кроме многочисленных комбинаций кратных ошибок, расположенных близко друг от друга
Алгоритм DES предназначен для шифровки:
(1) ровно 64 бит исходных данных
(2) менее 64 бит исходных данных
(3) ровно 32 бит исходных данных
(4) более 64 бит исходных данных
Тег IMG позволяет:
(1) выделить текст жирным шрифтом
(2) вставить графическую картинку в документ
(3) создать нижний индекс текста
(4) создать верхний индекс текста
Значения дискретной случайной величины X1 и X2 определяются подбрасыванием двух идеальных монет, а дискретная случайная величина Y равна сумме количества «гербов», выпавших при подбрасывании этих монет. В Y содержится:
(1) I(Y, X1) = 1.5 бит/сим информации об X1
(2) I(Y, X1) = 0.5 бит/сим информации об X1
(3) I(Y, X1) = 5.0 бит/сим информации об X1

X:
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
(1) Винера
(2) Шеннона-Фэно
(3) Берга
(4) Хаффмена
Закодировать сообщение «AABCDAACCCCDBB», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
(1) код(AABCDAACCCCDBB) = 'A'10'B'00'C'011'D'00011001111100110011110
(2) код(AABCDAACCCCDBB) = 'A'10'B'00'C'000'D'00011001111100110011001
(3) код(AABCDAACCCCDBB) = 'A'11'B'11'C'010'D'00011001111100110000101
«Скользящее» окно НЕ использует алгоритм:
(1) LZ77
(2) LZ78
(3) LZSS
Простейший код, исправляющий ошибки представляет собой:
(1) контроль четности
(2) тройное повторение каждого бита
(3) условное повторение кода в целом
Имеется (8,9)-код с проверкой четности. Вычислить вероятность того, что в случае ошибки этот код ее не обнаружит, если вероятность ошибки при передаче каждого бита равна 0.1%:
Для кодирующей матрицы 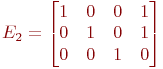
(1) Pправильной передачи = p2+p2q
(2) Pправильной передачи = p4+p3q
(3) Pправильной передачи = p3+p2q
Чем ниже частота дискретизации, тем:
(1) точнее происходит перевод непрерывной информации в дискретную
(2) менее точно происходит перевод непрерывной информации в дискретную
(3) эффективнее и быстрее происходит перевод непрерывной информации в дискретную
Построить CRC-4 код для сообщения 101111001, используя полином-генератор x4+1:
(1) 1001
(2) 1111
(3) 1100
Пользователь системы RSA выбрал p1=11 и p2=47. Некоторые числа из 12, 33, 125, 513 он может выбрать для открытого ключа. Вычислить для них закрытый ключ:
TeX представляет собой:
(1) язык управляющей разметки
(2) особый язык программирования
(3) редактор формул
(4) текстовый процессор
Определить характер зависимости между X1 и Z, если задана дискретная случайная величина Z=(X1+1)2-X2, где независимые дискретные случайные величины X1, X2 могут с равной вероятностью принимать значение либо 0, либо 1:
(1) невозможно определить характер зависимости, т.к. Z — функция от X_1
(2) Z полностью определяет X_1 и, следовательно, X_1 — это функция от Z
(3) X_1 и Z — не зависимы
Про дискретную случайную величину X известно, что ее значениями являются буквы кириллицы. Произведен ряд последовательных измерений X, результат которых — «ТЕОРИЯИНФОРМАЦИИ». Составить на основании этого результата приблизительный закон распределения вероятностей этой дискретной случайной величины и оценить минимальную среднюю длину кодов для X:
Вычислить HX для кодов Хаффмена и Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей 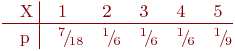
Вычислить длины в битах сообщения «СИНЯЯ СИНЕВА СИНИ» в коде ASCII+ и его полученного кода
(1) L(СИНЯЯ СИНЕВА СИНИ) = 104 бит, длина исходного сообщения = 124 бит
(2) L(СИНЯЯ СИНЕВА СИНИ) = 114 бит, длина исходного сообщения = 136 бит
(3) L(СИНЯЯ СИНЕВА СИНИ) = 124 бит, длина исходного сообщения = 148 бит
Закодировать сообщения «AABCDAACCCCDBB», вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь — 12 байт, буфер — 4 байта):
(1) 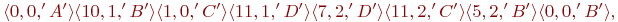
(2) 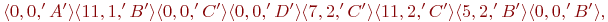
(3) 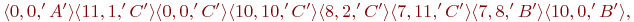
Передатчик задается случайной величиной со следующими законами распределениями вероятностей: P(X2=-1)=1/3, P(X2=0)=1/3, P(X_2=1)=1/3. Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу передатчиком, обеспечивающую сколь угодно высокую надежность передачи:
(1) ≈ 2690 сим/сек
(2) ≈ 2523 сим/сек
(3) ≈ 2400 сим/сек
Вычислить минимальную и максимальную оценки количества дополнительных разрядов r для кодовых слов длины n, если требуется, чтобы минимальное расстояние между ними было d. Рассмотреть случаи n = 32, d = 3 и n = 23, d = 7:
Построить кодовые слова квазисовершенного (9,n)-кода, исправляющего однократные ошибки, для тех сообщений, которые соответствуют числам 55, 200 и декодировать слова 1000001000001, 1100010111100, полученные по каналу связи, использующему этот код:
(1)
55_10 = 001010101 to 0001011010111, 200_10 to 100001111000,
1000001000001 to 000100101, 1100010111100 to 001011101
(2)
55_10 = 001010101 to 0001001010111, 200_10 to 100011001000,
1000001000001 to 000100101, 1100010111100 to 001011101
(3)
55_10 = 001010101 to 0000011010001, 200_10 to 100011001110,
1000001000001 to 011010101, 1100010111100 to 0110111101
Устройства для преобразования непрерывной информации в дискретную называются:
(1) ЦАП
(2) АЦП
(3) универсальный преобразователь
Причины, по которым документы PostScript сравнительно редко используются в WEB-страницах:
(1) они сложны для отображения браузерами
(2) они весьма велики по размерам
(3) они могут содержать в себе шрифты, защищенные авторскими правами
(4) они обладают правами доступа
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Вычислить HX1.
(1) HX1 = 2.5 бит/сим
(2) HX1 = 2 бит/сим
(3) HX1 = 1.51 бит/сим
Cообщение, полученное путем сжатия адаптивным алгоритмом Хаффмена с упорядоченным деревом имеет вид: 'A'0'F'00'X'0111110101011011110100101. Определить длину несжатого сообщения в битах:
(1) 125 бит
(2) 120 бит
(3) 117 бит
Закодировать сообщения «КИБЕРНЕТИКИ», вычислить длины в битах полученных кодов, используя алгоритм LZSS (словарь — 12 байт, буфер — 4 байта):
(1) 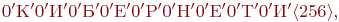
(2)
0’К’0’И’0’Б’0’Е’0’Р’0’Н’
1 langle 9,1 rangle 0’Т’1 langle 5,1 rangle 1 langle 5,2 rangle,
длина 3 * 7 + 7 * 9 = 84 бит
(3)
0’К’0’И’0’Б’0’Е’Р’0’Н’
1 langle 9,1 rangle 0’Т’1 langle 5,2 rangle,
длина 3 * 7 + 7 * 9 = 84 бит
АВМ служит для:
(1) обработки дискретной информации
(2) обработки непрерывной информации
(3) определения повторных величин
Предметом исследования кибернетики являются:
(1) системы, рассматриваемые абстрактно, вне зависимости от их материальной природы
(2) строго материальные системы
(3) только системы автоматизированного производства
Способ построения полиномиальных кодов, минимальное расстояние между кодовыми словами которых равно заданному числу, был открыт:
(1) Боузом
(2) Чоудхури
(3) Хоккенгемом
Шифры простой замены:
(1) легко поддаются расшифровке
(2) не поддаются расшифровке
(3) очень сложны для расшифровки
Разметка текста позволяет:
(1) вносить в простой текст дополнительную информацию об его оформлении или структуре
(2) изменять язык текста
(3) распечатывать документ на принтере или другом устройстве вывода
Канал связи представляет собой:
(1) среду передачи информации
(2) средства для передачи информации
(3) совокупность средств, преобразующих информацию
Префиксным называется кодирование:
(1) при котором каждый код не является префиксом другого кода
(2) при котором каждый код является префиксом другого кода
(3) при котором каждому коду соответствует определенный префикс из таблицы значений
Среднее количество бит, приходящихся на одно кодируемое значение дискретной случайной величины:
(1) не может быть меньшим, чем энтропия этой дискретной случайной величины
(2) не может быть большей, чем энтропия этой дискретной случайной величины
(3) строго равна энтропии этой дискретной случайной величины
Преимущество арифметического кодирования позволяет:
(1) кодировать некоторые символы менее чем одним битом
(2) кодировать некоторые символы только несколькими битами
(3) кодировать символы одним байтом
Популярность алгоритмов LZ обусловлена:
(1) простотой при высокой эффективности сжатия
(2) сложностью в работе, но гибкими настройками
(3) неэффективным сжатием, но высокая скорость работы
Сжатие с потерями обычно проходит в:
(1) два этапа
(2) три этапа
(3) четыре этапа
Коды с обнаружением ошибок предназначены для:
(1) выявления вероятности, близкой к единице, наличие ошибок
(2) восстановления с вероятностью, близкой к единице, посланного сообщения
(3) управления ошибками в ходе отправки и получения сообщения
Совершенным является:
(1) групповой (m,n)-код, исправляющий все ошибки веса, не большего k, и никаких других
(2) (m,n)-код, исправляющий все ошибки веса, не меньшего k, и никаких других
(3) групповой (m,n)-код, исправляющий все ошибки веса
Сущность принципа управления заключается в том, что:
(1) движение и действие малых масс или передача и преобразование малых количеств энергии направляется и контролируется при помощи больших количеств энергии
(2) движение и действие больших масс или передача и преобразование больших количеств энергии направляется и контролируется при помощи небольших количеств энергии, несущих информацию
(3) движение и действие больших масс или передача и преобразование больших количеств энергии направляется и контролируется при помощи еще больших количеств энергии
Наиболее широкое распространение получил:
(1) (231,255)-код
(2) (92,127)-код
(3) (102,250)-код
Нераскрываемый шифр характеризуется тем, что:
(1) в качестве ключа используется строго определенная последовательность
(2) в качестве ключа используется случайная последовательность
(3) в качестве ключа используется любой файл системы
При физической разметке точно указывается:
(1) что нужно сделать с выбранным фрагментом текста: показать курсивным, приподнять, центрировать, сжать, подчеркнуть и т.п.
(2) управляющие элементы, необходимые для правильного определения документа
(3) структурный смысл выбранного фрагмента: примечание, начало раздела, конец подраздела, ссылка на другой фрагмент и т.п.
Общая схема передачи информации имеет вид:
(1) исходная информация — шифровка — сжатие — шумозащитное кодирование — канал связи(проявляется действие шумов) — декодирование шумозащитных кодов — распаковка — дешифровка — полученная информация
(2) исходная информация — шифровка — сжатие — канал связи — распаковка — дешифровка — полученная информация
(3) исходная информация — сжатие — шифрование — шумозащитное кодирование — канал связи(проявляется действие шумов) — декодирование шумозащитных кодов — распаковка — дешифровка — полученная информация
(4) исходная информация — шифровка — сжатие — шумозащитное кодирование — канал связи — декодирование шумозащитных кодов — дешифровка — распаковка — полученная информация
(5) исходная информация — сжатие — шумозащитное кодирование — канал связи — декодирование шумозащитных кодов — дешифровка — полученная информация
Вычислить 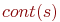
s1, про которое известно, что оно достоверно на 50%, и предложения s2, достоверность которого 25%:
Выбрать верные утверждения:
(1) 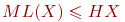
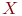
(2) 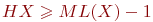
(3) 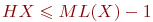
(4) 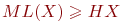
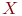
Составить арифметический код для сообщения BAABC, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/3, P(X=B)=7/15, P(X=C)=1/5:
(1) 01011111
(2) 01100001
(3) 01100111
Алгоритм LZ77 выдает коды, состоящие из элементов:
(1) смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера
(2) длина этой подстроки
(3) первый символ буфера, следующий за подстрокой
Сжатие видеоинформации основано на том, что:
(1) при переходе от одного кадра фильма к другому на экране обычно почти ничего не меняется. Таким образом, сжатая видеоинформация представляет собой запись некоторых базовых кадров и последовательности изменений в них
(2) при переходе от одного кадра фильма к другому на экране меняется значительная часть информации. Таким образом, сжатая видеоинформация представляет собой запись всех кадров
(3) при переходе от участка фильма к другому на экране обычно ничего не меняется. Таким образом, сжатая видеоинформация представляет собой запись нескольких параметров видеофайла
Древовидные коды также называют:
(1) последовательными кодами
(2) параллельными кодами
(3) управляющими кодами
Код Хэмминга:
(1) групповой код
(2) не групповой код
(3) натуральный код
Дискретная информация характеризуется:
(1) повторными процессами распределения случайной величины
(2) непрерывным процессом изменения некоторой величины
(3) последовательными точными значениями некоторой величины
Найти кодирующий многочлен БЧХ-кода g(x) с длиной кодовых слов 15 и минимальным расстоянием между кодовыми словами 7. Использовать примитивный многочлен m1(x)=1+x+x4 с корнем 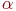
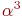
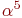
m3(x)=1+x+x2+x3+x4 и m5(x)=1+x+x2:
(1) g(x) = 1 + x + x2 + x4 + x5 + x8 + x10
(2) g(x) = 1 + x + x3 + x4 + x6 + x9 + x10
(3) g(x) = 1 + x + x3 + x5 + x7 + x9
Между абонентами A и B установлен секретный канал связи без передачи ключей при заданных p=167 и их первых ключах 15 и 21. Описать процесс передачи сообщения 22 (от A к B):
(1) A отправляет B 58, B возвращает 94, A окончательно отправляет 115
(2) A отправляет B 58, B возвращает 85, A окончательно отправляет 105
(3) A отправляет B 62, B возвращает 75, A окончательно отправляет 123
HTML представляет собой:
(1) язык логической разметки
(2) язык программирования
(3) управляющий язык определения документа
Если дискретные случайные величины X и Y заданы законами распределения P(X=Xi)=pi, P(Y=Yj)=qj и совместным распределением P(X=Xi,Y=Yj)=pij, то количество информации, содержащейся в X относительно Y равно:
Если задана функция 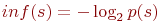
s-это предложение, смысловое содержание которого измеряется, p(s) — вероятность истинности s, то:
(1) 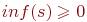
(2) 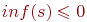
(3) 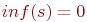
s — истинно
Недостатками кодирования, основанного на основной теореме о кодировании при отсутствии помех, являются:
(1) такое кодирование делает невозможным отправку сообщения по частям
(2) отправка сообщения по частям происходит очень медленно
(3) исходная длина кода не должна передаваться вместе с сообщением
(4) необходимость отправки или хранения собственно полученного кода вместе с его исходной длиной
Вычислить длины в битах сообщения «AABCDAACCCCDBB» в коде ASCII+ и его полученного кода
(1) L(AABCDAACCCCDBB) = 62 бит, длина исходного сообщения = 112 бит
(2) L(AABCDAACCCCDBB) = 52 бит, длина исходного сообщения = 94 бит
(3) L(AABCDAACCCCDBB) = 76 бит, длина исходного сообщения = 137 бит
Алгоритм LZSS отличается от LZ77 следующим:
(1) производимыми кодами
(2) скоростью работы
(3) длина подстроки, которую можно закодировать, НЕ ограничена размером буфера
(4) возможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря
Канал информационный представляет собой:
(1) совокупность устройств, объединенных линиями связи, предназначенных для передачи информации от источника информации до ее приемника
(2) устройства, просто передающие усиленным принятый сигнал
(3) устройство, определяющее интервал времени от отправки сигнала передатчиком до его приема приемником
Весом двоичного слова a=a1 ... a_n называется:
(1) количество единиц в нем
(2) количество нулей в нем
(3) общее количество цифр в нем
Для кодирующей матрицы 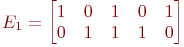
(1) mind = 3
(2) mind = 4
(3) mind = 2
В таблице кодировки ASCII+ печатные и управляющие символы занимают:
(1) первые 128 позиций таблицы
(2) первые 127 позиций таблицы
(3) все 256 символов таблицы
(4) последние 128 позиций таблицы
(5) последние 127 позиций таблицы
Для кода CRC-32 полином-генератор имеет степень:
Основными достоинствами DES являются:
(1) используется только один ключ фиксированной длины 56 бит (в системах с открытым ключом длина ключа должна быть более 300 бит)
(2) сложность алгоритма, но большая гибкость
(3) зашифровав сообщение с помощью одной программы, для расшифровки можно использовать другую
(4) относительная простота алгоритма обеспечивает высокую скорость работы (как минимум, на порядок выше скорости работы алгоритма для криптосистемы с открытым ключом)
(5) достаточно высокая стойкость алгоритма (стойкость конкретного зашифрованного сообщения зависит от выбора ключа)
К самодостаточным тегам языка HTML относятся:
(1) BR
(2) BODY
(3) IMG
(4) U
(5) EM

code3 для дискретной случайной величины X:
(1) ML3(X)=2.2 бит/сим
(2) ML3(X)=2.8 бит/сим
(3) ML3(X)=3 бит/сим
Максимально плотно сжимает метод:
(1) Хаффмена
(2) Шеннона-Фэно
(3) Винера
Закодировать сообщение «СИНЯЯ СИНЕВА СИНИ», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
(1) код(СИНЯЯ СИНЕВА СИНИ) = 'С'0'И'
00'Н'100'Я'001100' '101001011100'Е'11000'В'10100'А'1010101101101111
(2) код(СИНЯЯ СИНЕВА СИНИ) = 'С'0'И'
00'Я'101'Я'001101' '101001011100'С'11110'И'10100'И'1010111101101011
(3) код(СИНЯЯ СИНЕВА СИНИ) = 'С'0'И'
01'Я'100'Я'111100' '101001011100'Е'11010'В'11100'А'1010111100101010
LZ77 и LZSS обладают следующими очевидными недостатками:
(1) невозможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря
(2) длина подстроки, которую можно закодировать, ограничена размером оперативной памяти компьютера
(3) длина подстроки, которую можно закодировать, ограничена размером буфера
Задержка сигнала во времени представляет собой:
(1) интервал времени от отправки сигнала передатчиком до его приема приемником
(2) интервал времени от отправки сигнала передатчиком до его приема приемником и обратной отправки к передатчику
(3) интервал времени от создания сигнала до его прочтения приемником и удаления
Имеется (8,9)-код с проверкой четности. Вычислить вероятность того, что в случае ошибки этот код ее не обнаружит, если вероятность ошибки при передаче каждого бита равна 1%:
Для кодирующей матрицы 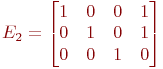
(1) Pнеобнаружения ошибки = p3q + 3p2q2 + 3pq3
(2) Pнеобнаружения ошибки = p4q + 3p2q3 + 3pq3
(3) Pнеобнаружения ошибки = p3q2 + 4p2q2 + 3pq3
Информация может быть нескольких типов:
(1) непрерывная
(2) частотная
(3) дискретная
(4) повторная
(5) устойчивая
При реальной передаче или хранении информации ошибки:
(1) обычно группируются на некотором участке
(2) распределяются равномерно по всей длине данных
(3) группируются в нескольких участках, распределенных неравномерно
Алгоритм DES предназначен для шифровки:
(1) более 64 бит исходных данных
(2) менее 64 бит исходных данных
(3) ровно 64 бит исходных данных
(4) ровно 32 бит исходных данных
Атрибут ALT тега IMG используется для:
(1) указания альтернативного текста, показываемого вместо картинки, в случае, когда файл с графикой недоступен или его тип неизвестен браузеру
(2) указания URI файла с графикой
(3) определения рамки картинки
(4) указания способа выравнивания картинки
Определить HX1, если задана дискретная случайная величина Z=(X1+1)2-X_2, где независимые дискретные случайные величины X1, X_2 могут с равной вероятностью принимать значение либо 0, либо 1:
(1) I(Z,X1) = I(X1,X1) = HX1 = 1 бит/сим
(2) I(Z,X1) = I(X1,X1) = HX1 = 1.5 бит/сим
(3) HX1 = 2 бит/сим
Дискретная случайная величина X равна количеству «гербов», выпавших на двух идеальных монетках. Найти энтропию X:
(1) HX=1.5 бит/сим
(2) HX=2.5 бит/сим
(3) HX=1.8 бит/сим
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
(1) Винера
(2) Берга
(3) Хаффмена
(4) Шеннона-Фэно
Закодировать сообщение «КИБЕРНЕТИКИ», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
(1) код(КИБЕРНЕТИКИ) = 'К'0'И'00'Б'100'Е'000'Р'1
100'Н'1111000'Т'100110111
(2) код(КИБЕРНЕТИКИ) = 'К'0'И'00'Б'101'Е'010'Р'1
100'Н'1100001'Т'100110001
(3) код(КИБЕРНЕТИКИ) = 'К'0'И'00'Б'100'Е'000'Р'1
100'Н'1111000'Т'101010001
Закодировать сообщения «СИНЯЯ СИНЕВА СИНИ», вычислить длины в битах полученных кодов, используя алгоритм LZW (словарь — ASCII+ и 16 фраз):
(1) 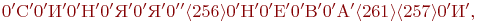
(2) 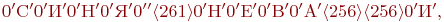
(3) 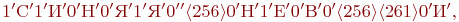
По каналу связи без шума могут передаваться четыре сигнала длительностью 1 мс каждый. Вычислить емкость такого канала:
(1) 2000 бод
(2) 1000 бод
(3) 2500 бод
Имеется (8,9)-код с проверкой четности. Вычислить вероятность ошибочной передачи без использования кода, если вероятность ошибки при передаче каждого бита равна 0.1%:
При полиномиальном кодировании каждое сообщение:
(1) отождествляется с многочленом
(2) отождествляется с множеством
(3) представляется в виде числа
Чем выше частота дискретизации, тем:
(1) точнее происходит перевод непрерывной информации в дискретную
(2) менее точно происходит перевод непрерывной информации в дискретную
(3) эффективнее и быстрее происходит перевод непрерывной информации в дискретную
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
(1) 1000
(2) 1101
(3) 1001
Пользователь системы RSA, выбравший p1=17, p2=11 и a = 61, получил шифрованное сообщение m1=3. Дешифровать m1:
PostScript представляет собой:
(1) универсальный язык программирования, предоставляющий большой набор команд для работы с графикой и шрифтами
(2) управляющий язык разметки
(3) текстовый процессор
(4) программа для просмотра файлов PDF
По теории Шеннона:
(1) смысл сообщений НЕ имеет никакого отношения к теории информации
(2) смысл сообщений имеет прямое отношения к теории информации
(3) нельзя дать точный ответ насчет зависимости между смыслом сообщений и теории информации
Вычислить ML(X) для кода Хаффмена для X. Дискретная случайная величина X задается следующим распределением вероятностей 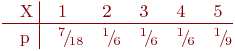
Составить адаптивный арифметический код с маркером конца для сообщения BAABC:
(1) 01000010111001
(2) 01000011000011
(3) 01000010110100
Закодировать сообщения «AABCDAACCCCDBB», вычислить длины в битах полученных кодов, используя алгоритм LZ78 (словарь — 16 фраз):
(1)
langle 0,’A’rangle langle 1,’B’ rangle langle 0,’C’ rangle langle 0,’D’ rangle langle 1,’A’ rangle langle 3,’C’ rangle
langle 6,’D’ rangle langle 0,’B’ rangle langle 0,’B’ rangle,
длина 9 * 12 = 108 бит
(2)
langle 4,’A’rangle langle 1,’B’ rangle langle 1,’C’ rangle langle 1,’D’ rangle langle 0’A’ rangle langle 2,’C’ rangle
langle 5,’D’ rangle langle 7,’B’ rangle,
длина 9 * 10 = 90 бит
(3)
langle 0,’A’rangle langle 0,’C’ rangle langle 0,’D’ rangle langle 3,’C’ rangle
langle 6,’D’ rangle langle 0,’B’ rangle langle 0,’B’ rangle,
длина 9 * 14 = 126 бит
Передатчик задается случайной величиной со следующими законами распределениями вероятностей: P(X3=n)=2-n,, n=1,2,... . Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу передатчиком, обеспечивающую сколь угодно высокую надежность передачи:
(1) ≈ 2000 сим/сек
(2) ≈ 1900 сим/сек
(3) ≈ 2256.78 сим/сек
Вычислить минимальную оценку по Плоткину количества дополнительных разрядов r для кодовых слов матричного кода, если требуется, чтобы минимальное расстояние между ними было d. Рассмотреть случаи n = 32, d = 3 и n = 23, d = 7:
Принадлежат ли коду Голея кодовое слово 10000101011111010011111:
(1) нет
(2) да
(3) невозможно дать точного ответа
Устройства для преобразования дискретной информации в аналоговую называются:
(1) ЦАП
(2) АЦП
(3) универсальный преобразователь
TeX популярен:
(1) в академических кругах
(2) среди обычных пользователей
(3) среди программистов
(4) в среде мультимедиа
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Дискретная случайная величина Y равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е. Y=X1+X2. Вычислить HY:
Cообщение, полученное путем сжатия адаптивным алгоритмом Хаффмена с упорядоченным деревом имеет вид: 'A'0'F'00'X'0111110101011011110100101. Определить длину сжатого кода в битах:
(1) 52 бит
(2) 62 бит
(3) 58 бит
Закодировать сообщения «СИНЯЯ СИНЕВА СИНИ», вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь — 12 байт, буфер — 4 байта):
(1)
langle 0,0,’С’ rangle langle 0,0,’И’ rangle langle 0,0,’Н’ rangle
langle 0,0,’Я’ rangle langle 11,1′ ‘ rangle langle 6,3,’Е’ rangle langle 0,0,’В’ rangle langle 0,0,’А’ rangle langle 5,4,’И’ rangle,
длина 9 * 15 = 135 бит
(2) 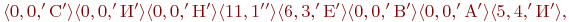
(3) 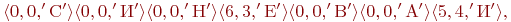
Программа для АВМ представляет собой:
(1) электрическую схему из заданного набора электронных компонент, которую нужно физически собрать
(2) программу, написанную на языках высокого уровня
Основной категорией кибернетики является:
(1) энергия
(2) управление
(3) распознавание
(4) взаимодействие
Для печати документа на принтере или показе на экране используется:
(1) логическая разметка
(2) физическая разметка
(3) управляющая разметка
Аналоговая информация характеризуется:
(1) последовательными точными значениями некоторой величины
(2) непрерывным процессом изменения некоторой величины
(3) повторными процессами распределения случайной величины
Если непрерывные случайные величины X, Y заданы плотностями распределения вероятностей pX(t1), pY(t2) и pXY(t1,t2), то количество информации, содержащейся в X относительно Y равно:
Бит определяет информацию:
(1) которая может быть представлена любым целым числом
(2) содержащуюся в 8 байтах
(3) в ответе на вопрос «да» или «нет»
Кодирование представляет собой:
(1) преобразование дискретной информации
(2) преобразование аналоговой информации
(3) искусственное создание помех в канале связи при передаче информации
Вычислить ML(X) для кода Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей 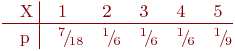
Принадлежат ли коду Голея кодовое слово 11000111011110010011111:
(1) да
(2) не
(3) невозможно дать точного ответа
Байт состоит из:
(1) трех 2-битных полубайт
(2) двух 4-битных полубайт или тетрад
(3) двух 3-битных полубайт или триад
Обновлено: 12.02.2023
В учебном пособии излагаются основные понятия и факты теории информации. Рассмотрены способы измерения, передачи и обработки информации. Значительное внимание уделено свойствам меры информации, характеристикам канала связи, помехозащитному, уплотняющему и криптографическому кодированию. Кроме того, рассмотрены вопросы формализации информации, в частности, в документах Internet. Изложение сопровождается большим количеством примеров и упражнений. Учебное пособие написано на основе односеместрового 108 часового курса лекций и материалов для практических занятий, используемых автором в учебной работе со студентами-третьекурсниками в течении 5 лет на кафедре «Моделирование систем и информационные технологии» МАТИ — Российского государственного технологического университета им. К.Э. Циолковского. Для студентов втузов соответствующих специальностей и всех интересующихся вопросами точной работы с информацией и методами построения кодов с полезными свойствами.
Приведенный ниже текст получен путем автоматического извлечения из оригинального PDF-документа и предназначен для предварительного просмотра.
Изображения (картинки, формулы, графики) отсутствуют.
Аннотация: В лекции дается понятие криптографии, использование ее на практике, различные методы криптографии, их свойства и методы шифрования. Вводится понятие нераскрываемый шифр. Подробно описываются две системы шифрования: криптосистема без передачи ключей и криптосистема с открытым ключом. Хорошее математическое обоснование систем. Суть электронной подписи. Рассказывается о стандарте шифрования данных DES
Криптография (тайнопись) — это раздел математики, в котором изучаются и разрабатываются системы изменения письма с целью сделать его непонятным для непосвященных лиц. Известно, что еще в V веке до нашей эры тайнопись использовалась в Греции. В современном мире, где все больше и больше услуг предоставляется через использование информационных технологий, проблема защиты информации методами криптографии имеет первостепенное значение . Сегодня большая часть обмена информацией проходит по компьютерным сетям и часто (в бизнесе, военным и прочее) нужно обеспечивать конфиденциальность такого обмена. Теоретические основы классической криптографии впервые были изложены Клодом Шенноном в конце 1940-х годов.
Простейшая система шифрования — это замена каждого знака письма на другой знак по выбранному правилу. Юлий Цезарь, например, заменял в своих секретных письмах первую букву алфавита на четвертую, вторую — на пятую, последнюю — на третью и т.п., т.е. A на D, B на E, Z на C и т.п. Октавиан Август заменял каждую непоследнюю букву алфавита на следующую, а последнюю на первую. Подобные шифры, называемые простой заменой или подстановкой, описаны в рассказах «Пляшущие человечки» А. К. Дойла, «Золотой жук» Э. По и других.
| Т | Е | О | Р | И | Я | И | Н | Ф | О | Р | М | А | Ц | И | И |
| 20 | 6 | 16 | 18 | 10 | 33 | 10 | 15 | 22 | 16 | 18 | 14 | 1 | 24 | 10 | 10 |
| К | И | Б | Е | Р | Н | Е | Т | И | К | А | К | И | Б | Е | Р |
| 12 | 10 | 2 | 6 | 18 | 15 | 6 | 20 | 10 | 12 | 1 | 12 | 10 | 2 | 6 | 18 |
| 32 | 16 | 18 | 24 | 28 | 15 | 16 | 2 | 32 | 28 | 19 | 26 | 11 | 26 | 16 | 28 |
| Ю | О | Р | Ц | Ъ | Н | О | Б | Ю | Ъ | С | Ш | Й | Ш | О | Ъ |
Если в качестве ключа использовать случайную последовательность, то получится нераскрываемый шифр. Проблема этого шифра — это способ передачи ключа.
Полиному соответствуют биты 0101 — это и есть CRC-4 код.
Существуют быстрые алгоритмы для расчета CRC-кодов, использующие специальные таблицы, а не деление многочленов с остатком.
CRC-коды способны обнаруживать одиночную ошибку в любой позиции и, кроме того, многочисленные комбинации кратных ошибок, расположенных близко друг от друга. При реальной передаче или хранении информации ошибки обычно группируются на некотором участке, а не распределяются равномерно по всей длине данных. Таким образом, хотя для идеального случая двоичного симметричного канала CRC-коды не имеют никаких теоретических преимуществ по сравнению, например, с простыми контрольными суммами, для реальных систем эти коды являются очень полезными.
Коды CRC используются очень широко: модемами, телекоммуникационными программами, программами архивации и проверки целостности данных и многими другими программными и аппаратными компонентами вычислительных систем.
11. Лекция: Основы теории защиты информации
лекции дается понятие криптографии, использование ее на практике, различные методы криптографии, их свойства и методы шифрования. Вводится понятие нераскрываемый шифр. Подробно описываются две системы шифрования: криптосистема без передачи ключей и криптосистема с открытым ключом. Хорошее математическое обоснование систем. Суть электронной подписи. Рассказывается о стандарте шифрования данных DES
Криптография (тайнопись) — это раздел математики, в котором изучаются и разрабатываются системы изменения письма с целью сделать его непонятным для непосвященных лиц. Известно, что еще в V веке до нашей эры тайнопись использовалась в Греции. В современном мире, где все больше и больше услуг предоставляется через использование информационных технологий, проблема защиты информации методами криптографии имеет первостепенное значение. Сегодня большая часть обмена информацией проходит по компьютерным сетям и часто (в бизнесе, военным и прочее) нужно обеспечивать конфиденциальность такого обмена. Теоретические основы классической криптографии впервые были изложены Клодом Шенноном в конце 1940-х годов.
Простейшая система шифрования — это замена каждого знака письма на другой знак по выбранному правилу. Юлий Цезарь, например, заменял в своих секретных письмах первую букву алфавита на четвертую, вторую — на пятую, последнюю — на третью и т.п., т.е. A на D, B на E, Z на C и т.п. Октавиан Август заменял каждую непоследнюю букву алфавита на следующую, а последнюю на первую. Подобные шифры, называемые простой заменой или подстановкой, описаны в рассказах «Пляшущие человечки» А. К. Дойла, «Золотой жук» Э. По и других.
Прежде всего, разберемся в терминологии.
Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.
Шифр Атбаша
Например, есть у нас алфавит, который полностью соответствует обычной латинице.
И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра
Шифр Цезаря
Опять же, для наглядности, возьмем латиницу
И теперь сместим вправо или влево каждую букву на ключевое число значений.
Например, ключ у нас будет 4 и смещение вправо.
Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v
Шифруем его и получаем следующий несвязный текст:
Шифр Вернама (XOR-шифр)
Исходный алфавит — все та же латиница.
XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.
Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.
Переведем их в бинарный код и выполним XOR:
В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:
С виду — совершенно несвязный набор чисел, но мы-то знаем.
Шифр кодового слова
Например, возьмем для разнообразия, кириллический алфавит.
Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.
Получим в итоге следующий нечитаемый бред:
Шифр Плейфера
Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.
Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.
Шифрование выполняется по нескольким несложным правилам:
1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.
Например, EH становится LE.
2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.
Например, если бы у нас была биграмма LX, то она стала бы DL.
3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.
Например, биграмма RA.
Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.
Читайте также:
- Сообщение про год тигра в начальных классах
- Сообщение про город михайловка
- Сообщение кусп что это
- Сообщение о посвящение в рыцари
- Сообщение о пропаже кота
Теоретическое преимущество
Cтраница 2
Необходимо подчеркнуть, что из стратегических преимуществ иерархического подхода, которые на настоящем этапе развития АСУ становятся особенно наглядными, не следует требование сразу же отказаться от хорошо зарекомендовавших себя одноуровневых оптимизационных процедур. Теоретические преимущества должны подкрепляться эффективностью конкретных разработок, создание которых сопряжено с преодолением значительных трудностей. Одноуровневые оптимизационные процедуры в перспективе могут с успехом использоваться для моделирования некоторых важных этапов иерархической схемы расчетов.
[16]
Объем вычислений здесь примерно такой же, как и в случае криволинейных интегралов. Теоретическое преимущество второго метода состоит в том, что не нужно налагать никаких ограничений на гладкость границы области, хотя на практике это не играет роли.
[17]
Главным отличием крупносерийного и мелкосерийного процессов является использование поточной сборочной линии. Расчеты показывают небольшое теоретическое преимущество применения такой линии, даже с учетом потерь на балансировку времени.
[18]
Для противоточной конденсации требуется меньше затрат холода, чем при прямоточной, так как количество отводимого конденсата меньше, и уходит он из конденсатора при более высокой температуре. Однако практическая реализация теоретических преимуществ противоточной конденсации встречает ряд трудностей. При схеме противотока увеличение скорости газа вызывает унос капель конденсата, а снижение скорости сказывается на значениях коэффициентов теплоотдачи. Изменения расходов газа и тепловых нагрузок конденсаторов, неизбежные при работе системы газоразделения, также вызывают нарушение режима работы противоточного конденсатора.
[19]
Баулина относились к частному случаю свободного доступа ( без сопротивлений рх 0) эжектируемого воздуха к соплу эжектора. В случае сопротивлений на линии всасывания теоретические преимущества ввода сопла в трубу не столь велики; однако и при этих условиях возможный рост коэффициента эжекции не настолько мал, чтобы не мог быть надежно выявлен при экспериментальном исследовании.
[20]
Лаплас, Бертран и Пуанкаре, всегда подчеркивали условность постулата среднего арифметического, указывая, что постулат медианы имеет не меньше теоретических прав на практическое использование. Соответственно этому связанный с первым постулатом принцип наименьшей суммы квадратов не имеет никаких теоретических преимуществ перед принципом наименьшей суммы модулей, связанным с медианой.
[21]
При реальной передаче или хранении информации ошибки обычно группируются на некотором участке, а не распределяются равномерно по всей длине данных. Таким образом, хотя для идеального случая двоичного симметричного канала CRC-коды не имеют никаких теоретических преимуществ по сравнению, например, с простыми контрольными суммами, для реальных систем эти коды являются очень полезными.
[22]
Эти законы не выполнялись бы, если бы в системе с плавающей точкой для дробных частей операндов вместо прямого кода использовался дополнительный код; см. упр. С этой точки зрения прямой код для представления чисел с плавающей точкой имеет некоторое теоретическое преимущество.
[23]
Проектирование, расчет и исследование оптимальной системы управления электроприводом, как существенно нелинейной и не приводящейся к линейной, являются более сложными и менее точными. Следовательно, приближенно рассчитанная и менее качественно налаженная оптимальная система может при ее эксплуатации полностью потерять н те незначительные теоретические преимущества по быстродействию, которые заложены в ее принципе.
[25]
С приближает регенеративный конденсационный цикл по термодинамическому совершенству к бинарным ртутно-водя-ным циклам. Величина сравнительной экономии эрт 4 % при регенеративном процессе в верхнем и нижнем циклах является величиной, достаточной лишь только для того, чтобы признать для паротурбинных станций большой мощности теоретическое преимущество бинарного цикла перед конденсационным регенеративным циклом водяного пара.
[26]
По их данным, при использовании этого параметра наблюдается очень хорошая линейность связи параметра пика с количеством вещества в разных частях хромато-граммы. Теоретические преимущества этого параметра пика не ясны.
[27]
Использование критерия ожидаемой полезности для оценки экономической эффективности инвестиционных проектов предполагает построение функции полезности субъекта. Это достаточно сложная задача, особенно если речь идет о функции полезности предприятия. По этой причине, хотя теоретические преимущества данного подхода очевидны, практического применения он пока не нашел.
[28]
Внутренняя норма прибыли обладает тем преимуществом, что при ее определении не делается никаких предположений относительно будущих прибылей, хотя, с другой стороны, мы, конечно, не можем допускать определенности, связанной с необоснованной оценкой будущих входов, выходов и масштабных коэффициентов. Внутренняя норма прибыли обеспечивает простой способ сравнения проектов различных размеров, поскольку мера эффективности в данном случае не зависит от размера проекта. Как бы ни были велики теоретические преимущества внутренней нормы прибыли, мы тем не менее оказываемся перед фактом, что подобная мера используется пока чрезвычайно редко при оценке проектов и особенно в тех случаях, когда дело касается общественных работ.
[29]
Вид спектральной кривой несколько изменяется при такой замене. На кривых lge f ( v) полосы поглощения имеют более симметричный контур и располагаются более или менее равномерно вдоль оси абсцисс. Спектр с линейной шкалой v имеет и чисто теоретические преимущества перед спектром с линейной разверткой по А. Поскольку именно v ( а не К) линейно связано с энергией излучения ( E — hcv), то в спектре lge / ( v) одинаковым интервалам на оси абсцисс соответствуют одинаковые разности энергий. Наоборот, в спектре ge, f ( K) одинаковым интервалам на оси абсцисс соответствуют различные энергетические эквиваленты. Это обстоятельство, в частности, делает очевидной предпочтительность записи УФ-спектра-в шкале v при изображении полос, проявляющих колебательную тонкую структуру: только при такой форме записи спектра расстояния между компонентами тонкой структуры полосы одинаковы и прямо соответствуют частоте колебания группы.
[30]
Страницы:
1
2
3

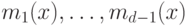

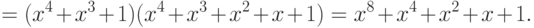
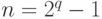
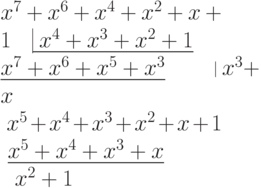

 . Проверить, будут ли
. Проверить, будут ли  и
и  корнями соответственно многочленов
корнями соответственно многочленов 







 найти вероятность правильной передачи:
найти вероятность правильной передачи: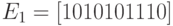 найти вероятность необнаружения ошибки:
найти вероятность необнаружения ошибки: Вычислить
Вычислить  :
: