192 Часть II. Алгоритмические методы скалярной оптимизации
Из выражения (9.7) видно, что ввиду наличия быстро затухающей и мед ленно затухающей экспонент отчетливо выделяются два участка с суще ственно различным поведением решения. Первый, сравнительно непро должительный, характеризуется большими значениями производных dXi{i)ldx и означает спуск на дно оврага. На дне выполняются условия типа (9.2) и норма вектора градиента, а с ней и производные dXi(z)ldx становятся относительно малыми. Поэтому для второго участка харак терно относительно плавное изменение переменных х,. Таким образом, прослеживается полная аналогия с поведением решений так называемых жестких систем обыкновенных дифференциальных уравнений. В связи с этим в [32] было предложено следующее общее определение.
Определение 9.1
Функционал J(x) называется овраэюным, если отвечающая ему система дифференциальных уравнений (9.6) — жесткая.
Однако при решении задач оптимизации более конструктивным может оказаться приведенное ниже непосредственное определение овражного функционала. Это определение не содержит, в частности, таких неестест венных для задач оптимизации требований, как необходимость задания промежутка интегрирования уравнения (9.6), что предполагается в тео рии жестких систем.
|
Определение 9.2 |
|||
|
Функционал |
J(x)eC^(D),D(zR» называется овражным |
(жестким) во |
|
|
множ:естве Qd D, если найдутся такие числа 5 > О, а » |
1, что |
||
|
1) |
УхеО,:Х,[Г(х)]>сХ„[Гх)]; |
||
|
2) |
fxsQ:Axg |
min J{x’)<zXAx)nQ |
(9.8) |
3)lxeQ:L[X^{x)nQ<a-‘L[X^{x)l
где CD) — множество дважды непрерывно дифференцируемых на D функционалов;
|
X,(.x) = {x’eR»\x’-x<b};Q, |
= jX,(,x); |
|
X&Q |
Х,{А) — собственные числа матрицы вторых производных А = J’Xx), упо рядоченные по убыванию: Х(А) >Х2(А) > … >ХХАу, L(S) — минимальная константа Липшица в соотношении
\jx)- Jx)\<L(S)\х —х\;/xxeSczR
|
Глава 9. Проблема плохой обусловленности |
193 |
Основным в определении 9.2 является первое условие, констатирующее резко несимметричное расположение спектра матрицы J’Xx) относитель но начала координат: G [-m, Л/], М » w > 0. Второе и третье условия необходимы для описания свойства устойчивости множества Q: можно показать, что все ТСН, начинающиеся в любой точке х G Qg, быстро по падают в достаточно малую окрестность Q^ (е « 6) множества Q и ос таются там до выхода из множества б§.
Как правило, оказывается достаточной более грубая модель явления овражности (жесткости), когда предполагается, что собственные числа матрицы вторых производных можно отчетливо разделить на две груп пы, в одну из которых входят собственные числа, по модулю намного превосходящие элементы второй группы. Будет использоваться следую щее определение.
Пусть в D czR» задана г-мерная поверхность (конфигурационное про странство)
Q = [xGDg,(x) = 0, / = 1,А7-г)}, g,eCD).
Определение 9.3
Функционал J(x)e CD)y DczR» называется овражным (жестким) в мно
|
жестве б, если найдутся такие числа 5 > О, а » |
1, что |
|
|
1) |
/xeQ,:[Г(х)]>…>Х„_,.[Г(х)] > аХ„_^^Г{х)] >…> a|Xj7″(;c)]|; |
|
|
2) |
fxEQ:Argmin J(x) с X.(x)nQ |
(9.9) |
|
3) |
VxG(2:L[X5(jc)ne]<CT-^L[X5(jc)]. |
Число r называется размерностью (дна) оврага Q. Пример 9.1. Рассмотрим квадратичный функционал
|
f(x) = /2{АХ,Х) — {Ь,х) -^с; с = const. |
(9.10) |
Пусть собственные числа Л, матрицы А =/»(х) удовлетворяют неравенст вам (9.9), а Ui означают соответствующие собственные векторы. Предпо ложим, что det ^ ^ О и обозначим через х* решение уравнения Ах = Ь.
|
194 |
Часть II. Алгоритмические методы скалярной оптимизации |
|
|
Примем |
||
|
Q = [xeR»{x-xu.) |
= 0, / = 1,^-г}; |
IVrfll
Можно доказать, что все три условия будут выполнены.
Таким образом, для квадратичных функционалов при сдвинутом в точку X* начале координат дно оврага Q совпадает с линейной оболочкой (9.11) собственных векторов, отвечающих малым собственным числам. Это согласуется с интуитивными представлениями, развитыми в
разд. 9.1.
На этом примере можно проиллюстрировать значение отдельных усло вий в определениях 9.2 и 9.3. Действительно, для квадратичного функ ционала (9.10) первое и второе условия могут выполняться для всего пространства Q = R» и любого 5 > 0. Необходимая линейная оболочка собственных векторов может быть выделена только при дополнительном требовании, эквивалентном третьему условию. В то же время требования 1, 3 также оказываются недостаточными. В этом случае сдвиг линейной оболочки Q, являющейся дном оврага, вдоль любого из не вошедших в оболочку собственных векторов не приведет к нарушению условий 1 и 3, а условие 2 при этом нарушится.
Рассмотренные выше модели явления овражности не являются исчерпы вающими. Однако они описывают наиболее существенные стороны большинства практических ситуаций, связанных с задачами оптимиза ции реальных и проектируемых систем.
Определение 9.4
Пусть Vx G Q, det J»(x) Ф 0. Наименьшее из чисел а, удовлетворяющих оп ределению 9.2, называется степенью овралсносты J(x) в Q и обозначается г|(0. Отношение
r|(jc) = Aj (х) / min X. (х), xeQ
называется локальной степенью овражности J{x) в точке х. Для вырож денных матриц J»{x) величина г)(х) принимается равной бесконечности.
Если J»(x) > О, то
г|(;с) = cond[y»(x)] = maxX.(x)/min А.,(х).
|
Глава 9. Проблема плохой обусловленности |
195 |
В общем случае справедливо неравенство 1 < л < cond{J’). При наличии больших по модулю отрицательных собственных чисел к{х) (т. е. при отсутствии овражной ситуации) возможно неравенство ц(х) « cond[/»(x)]. Из высокой степени овражности Дх) в точке х следу ет плохая обусловленность матрицы J’Xx) обратное неверно. Дейст
|
вительно, пусть спектр |
матрицы J’Xx) |
расположен в множестве |
|
[-М, т] и [т, М], М»т> |
О, включая |
граничные значения. Тогда |
г(х) = 1, а cond[/»(^)] = М/т» 1. Данный функционал не будет отно ситься к классу овражных, что естественно, ибо трудностей при его ми нимизации, например методом наискорейшего спуска, не возникает. От личие между двумя характеристиками г](х) и cond[/»(x)] функционала J(x) часто игнорируется и овражными называют функционалы с боль шим числом cond(/»), что не оправдывается с позиций основных вы числительных трудностей, возникающих при решении задач оптимиза ции. Однако, учитывая указанную выше связь между г(х) и cond(y»)? овражные задачи, т. е. задачи минимизации овражных или жестких функционалов, далее будут называться плохо обусловленными задача ми оптимизации.
В каждом конкретном случае различные значения г|(х) следует считать большими. Здесь существует полная аналогия с понятием плохой обу словленности матрицы. В большинстве случаев все определяется точно стью вычислений и типом применяемого алгоритма оптимизации. Тра диционно принято классифицировать задачу как плохо обусловленную, если
где / — длина применяемой разрядной сетки компьютера. Однако и при меньших значениях г для многих алгоритмов могут возникать значи тельные вычислительные трудности, особенно если овражная структура сопровождается отсутствием выпуклости J(x).
Дополнительным фактором, характеризующим степень сложности оп тимизационной задачи и затрудняющим применение традиционных ал горитмов минимизации, является наличие многомерных оврагов с г> I. В указанной ситуации целый ряд методов, специально ориентированных на решение плохо обусловленных задач, становится неэффективным.
Рассмотрим практические методы распознавания овражной ситуации, играющие роль критериев овражности. Наиболее существенной характе ристикой оказывается значение показателя г в допустимой области из менения управляемых параметров.
|
196 |
Часть II. Алгоритмические методы скалярной оптимизации |
|
|
Своеобразным индикатором может служить метод простого градиентно |
||
|
го спуска (ПГС), реализуемый по схеме |
||
|
х’^’=д:’-ЛДх’) |
(9.13) |
|
|
с постоянным шагом hs |
R |
Принадлежность J(x) к классу овражных в этом случае проявляется в не обходимости применения относительно малых значений h. Попытки уве личения h вызывают потерю свойства релаксационности (монотонного убывания) последовательности {/(х^)} и значения /(х^) начинают резко возрастать. Если для некоторого фиксированного h (наибольшего из возможных) удалось заставить процесс (9.13) протекать без полной оста новки, то можно количественно оценить величину ц. Для этого процесс
(9.13) продолжается до тех пор, пока отношение IUT-^^»*»^)!! /1|/Х-^^)!! не установится около некоторого значения х. Тогда справедливо равенство
Соотношение (9.14) является основным для грубой практической оценки степени овражности минимизируемого функционала в окрестности те кущей точки. Доказательство соотношения (9.14) дано в главе 11, посвя щенной градиентным схемам оптимизации.
В силу изложенного можно рекомендовать процесс оптимизации начи нать с помощью метода ПГС. Если задача простая и степень овражности функционала невелика, то уже этот стартовый метод достаточно быстро приведет в малую окрестность оптимума. В противном случае будет по лучено значение г|, что позволит правильно оценить ситуацию и выбрать наиболее рациональный алгоритм.
Другой метод оценки Г| сводится к вычислению матрицы Гессе функцио нала и решению для нее полной проблемы собственных значений. Тогда на основе непосредственной проверки выполнения неравенства (9.9) для вычисленных собственных чисел делается вывод о значении Г|. При этом определяется также размерность дна оврага г. Главный недостаток тако го подхода заключается в существенных вычислительных трудностях принципиального характера, возникающих при определении малых соб ственных значений. Известно, что абсолютная погрешность dk пред ставления любого собственного значения матрицы А за счет относитель ного искажения 5 ее элементов удовлетворяет неравенству
сГк<пЪкх1
|
Глава 9. Проблема плохой обусловленности |
197 |
где |X,| = max|Xj. Принимая 5 = Ем = 2″‘, где Ем— относительная машин ная точность (машинное эпсилон), а t — длина разрядной сетки мантис сы числа, получим оценку для абсолютных искажений собственных чисел из-за ошибок округления:
Параметр е„ известен для каждого компьютера. Из последнего неравен ства можно сделать следующее заключение. Если все вычисленные собст венные числа матрицы А = J»(x) достаточно велики, т. е. |Х,| > WEMIXII, ТО параметр г| может быть вычислен непосредственно. Если же некоторые из
вычисленных собственных чисел удовлетворяют неравенству |Л,| <«ем|Х1|, то все они должны быть отнесены к блоку малых собственных чисел, а для г имеем границу снизу:
Качественным признаком плохой обусловленности оптимизационной задачи может служить существенное различие в результатах оптимиза ции, например, методом ПГС при спуске из различных начальных точек. Получаемые результирующие точки обычно расположены достаточно далеко друг от друга и не могут рассматриваться как приближения к единственному решению или конечной совокупности решений (при на личии локальных минимумов). Описанная ситуация, как правило, озна чает наличие оврага, а точки остановки применяемой поисковой про цедуры трактуются как элементы дна оврага Q.
9.3. Основные причины возникновения овражных целевых функционалов
Несмотря на то, что типичность овражной ситуаций может считаться установленным экспериментальным фактом, определенный интерес пред ставляет выяснение основных причин появления оврагов в задачах моде лирования и численной оптимизации.
Естественная причина появления овражной ситуации может быть связа на с наличием некоторых неучтенных устойчивых связей между управ ляемыми параметрами, определяемых внутренними законами функцио нирования моделируемой системы. Если уравнения связей известны, то часть управляемых параметров может быть исключена из рассмотрения. В этом случае наличие овражной ситуации целесообразно трактовать как
|
198 |
Часть IL Алгоритмические методы скалярной оптимизации |
следствие некоторой избыточности в математическом описании объекта. С позиций приведенных в предыдущем разделе определений эти неиз вестные соотношения между управляемыми параметрами можно тракто вать как уравнения дна оврага.
Таким образом, поверхности уровня отдельных критериальных характе ристик системы могут иметь овражный характер в силу естественных, в известном смысле не зависящих от исследователя причин.
Фактор агрегированности аргументов минимизируемого функционала.
Выбор множества управляемых параметров (аргументов функционала) обычно производится по результатам анализа их влияния на основные характеристики оптимизируемой системы, а также исходя из реальных возможностей изменения этих параметров в нужных пределах. Результа том такого вполне естественного подхода является ситуация, когда век тор выходных характеристик у оптимизируемой системы в действитель ности зависит от S агрегатов:
|
;; = 0(ZbZ2,…,z,), |
(9.16) |
где
Zi =фДл:); i = ls;s<n.
Подтверждением сказанному служит широко применяемый на практи ке метод декомпозиции, связанный с выделением этапов аппроксимации и реализации в процессе оптимального выбора параметров х, (см. разд. 8.4). Прямое решение задачи /(х)-^ min в пространстве парамет ров X в данном случае связано с наличием овражной ситуации. Действи тельно, значение J{x) мало меняется на множестве, определяемом равен ствами
Поэтому последние уравнения фактически являются уравнениями дна оврага. Следовательно, фактор агрегированности естественным образом указывает на овражную ситуацию.
Во многих случаях соотношения (9.16) неизвестны, хотя агрегированные переменные z„ полностью определяющие выходные параметры объекта оптимизации, по-прежнему существуют. Поэтому применение изложент ного в главе 8 метода декомпозиции, в определенной степени исключаю щего проблему овражности, невозможно.
Отметим также возможную причину появления овражной ситуации в ре зультате возникновения агрегатов при оптимизации динамических сис тем, описываемых жесткими системами обыкновенных дифференциаль ных уравнений.
|
Глава 9. Проблема плохой обусловленности |
199 |
Рассмотрим пример.
Пусть функционирование системы описывается вектор-функцией u{t) = [t/i(/), U2(t)], являющейся решением жесткой дифференциальной сис темы, где
|
ЩО) = [xiexp(-.4/) + (xi + X2)Qxp(-at)]t (А » |
а) |
|
|
«2(0 = [x2exp(-50 + (xi + X2)exp(-fe0]^ (5 » |
b). |
(9.17) |
Требуется получить оптимальные значения параметров Xi, Xi из условия наилучшего совпадения u{t) с заданной вектор-функцией u{t) для t €
|
Е |
[/о, 7]- Если предположить, что ^о ^’^п.с, где Тп.с— длина погранично |
|
го |
слоя, определяющего почти полное затухание экспонент tx^{-Ai), |
Qxp(-Bt), то из соотношений (9.17) видно, что поведение решения u(t) для
^ ^ Uo, Т] будет определяться агрегатом z = Xi + Xi. Если продолжать счи тать Хх и Xi независимыми параметрами, то для оптимизационной задачи
У (Х) = [Wj (f1) — Й; (г, ) f + [^2 (^1) — «2 (^1 )]^ -«^ ^*^’
X
где /i = 1 G [^05 7]^ степень овражности равна г| = 1,8 х 10^ Мы здесь пред полагали, что заданная вектор-функция м(0 определяется соотноше ниями (9.17) при а = 1; Z? = 1,5; ^ = 20; 5 = 15. Степень овражности рас считывалась по формуле:
exp(-min(a, 6))
ехр(-тах(Л, 5))
Таким образом, до тех пор, пока не разработаны регулярные методы вы деления агрегатов для последующей декомпозиции исходной задачи оп тимизации, необходимо работать в пространстве переменных х, в усло виях отчетливо выраженной овражной ситуации.
Методы учета ограничений. Овражная ситуация может быть внесена в задачу оптимизации при учете ограничений с помощью построения обобщенного критерия оптимальности. Рассмотрим эффект овражности, возникающий при использовании методов штрафных функций и моди фицированных функций Лагранжа. На почти обязательное наличие ов ражной ситуации в подобных случаях указывается во многих работах.
Рассмотрим в качестве примера ограничения в виде равенств
5Д^) = 0, ;=1,р.
200 Часть II. Алгоритмические методы скалярной оптимизации
Тогда, согласно методу штрафных функций, задача сводится к миними зации вспомогательных функционалов
р
JQ (Л:, а) = / (х) + а ^ g] {х) -> min
7=1
С достаточно большим положительным коэффициентом а. При этом структура расширенного критерия 7о, содержащего большой параметр а, как правило, оказывается овражной, даже если исходный функционал J{x) этим свойством не обладает.
Пример 9.2. Пусть требуется найти х^ и ^2, минимизирующие квадратич ный функционал/(х) = х^^ + Xi при условии Xi = 2. Задача имеет очевид ное решение л:* =2, jc* = 0. Поступим формально и составим вспомога тельный функционал согласно общей рецептуре метода штрафных функций:
/о {х) = х,2 + Х2^ + а (х, — If = [(Х| — b^f /а,^]-^ [(х2 — Ьг? I aj^] + d,
где а, = ^1 + а; ^2 = U *i = 2 а / ( а + 1); ^2 = 0; Й? = 4а/(а + 1).
Уравнение линии уровня Jo(x) = const является уравнением эллипса с центром в точке (fei, 62) и длинами полуосей, относящихся как а2/а, =
= Vl + cj. При больших значениях а, обеспечивающих относительно точ ное выполнение ограничения Х] = 2, линии уровня оказываются сильно вытянутыми (рис. 9.3).
Чем точнее выполняются ограничения, тем ярче выражен эффект овражности. В данном случае степень овражности равна г| = 1 + а. Заметим, что линии уровня исходного функционала являются сферами и явление овражности отсутствует.
На практике метод штрафных функций широко используется на началь ных этапах оптимизации, при этом применяются такие возможно боль шие значения а, для которых удается достигнуть относительно быстрого убывания Jo(x) при достаточно точном выполнении ограничений. Для последующего уточнения решения привлекаются более тонкие стратегии, которые, как правило, оказываются и существенно более трудоемкими. Кроме того, метод штрафных функций до сих пор не имеет разумных альтернатив в некоторых критических ситуациях, характерных для ре альных задач оптимизации.
Например, при наличии вырожденного минимума оптимизационной за дачи, когда нарушается условие линейной независимости градиентов
|
Глава 9. Проблема плохой обусловленности |
201 |
gj{x), могут потерять работоспособность все методы учета ограниче ний, основанные на обычной и модифицированной функциях Лагранжа, а также на линеаризации ограничений. Метод же штрафных функций в указанной ситуации применим. Он оказывается наименее чувствитель ным ко всем формам вырождения.
Рис. 9.3. Метод штрафных функций
Второй критической ситуацией, возникающей в практике оптимизации, является неоправданное завышение функциональных требований к объ екту оптимизации, которое приводит к пустому множеству D допусти мых значений управляемых параметров. В подобном случае наиболее целесообразно применять метод штрафных функций, позволяющий по лучить такое решение задачи ||gW|| -^min, для которого значение J(x)
минимально. Другие методы либо теряют смысл, либо заведомо не будут сходящимися.
В силу изложенного наличие алгоритмов оптимизации, сохраняющих работоспособность при достаточно высокой степени овражности мини мизируемых функционалов, оказывается чрезвычайно желательным. Этот вывод подтверждается также тем фактом, что и при использовании
Соседние файлы в папке books
- #
- #
- #
- #
— численные методы отыскания минимумов функций многих переменных. Пусть задана ограниченная снизу дважды непрерывно дифференцируемая по своим аргументам функция
для к-рой известно, что при нек-ром векторе 

Существует много методов, позволяющих получить указанную последовательность векторов. Однако общим недостатком большинства алгоритмов является резкое ухудшение их свойств в случаях, когда поверхности уровня минимизируемой функции 


Функции овражного типа локально характеризуются плохой обусловленностью матриц двух производных (матриц Гессе)
что приводит к сильному изменению функции 
Дважды непрерывно дифференцируемая по своим аргументам функция J(х)наз. овражной функцией (см. [1]), если существует нек-рая область 


Степень овражности характеризуется числом
Если собственные значения 
то число r наз. размерностью оврага функции 

Системы дифференциальных уравнений, описывающие траекторию спуска овражной функции 
являются жесткими дифференциальными системами. В частности, когда функция J(х)сильно выпуклая и матрица Гессе положительно определена (все ее собственные значения строго больше нуля), неравенства (1) совпадают с известным требованием плохой обусловленности матрицы Гессе
В этом случае спектральное число обусловленности совпадает со степенью овражности.
Метод покоординатного спуска (см. [2])
несмотря на простоту и универсальность, в овражной ситуации эффективен лишь в редких случаях ориентации оврагов вдоль координатных осей.
Предложена (см. [2]) модернизация метода (4), состоящая в использовании процедуры вращения осей координат так, чтобы одна из осей была направлена вдоль 
Схема метода наискорейшего спуска задается разностным уравнением
где 
Для сильно выпуклой овражной функции, в частности квадратичной
последовательность 

где С=const,
Так как для овражной функции 
Аналогичная картина наблюдается и для простой градиентной схемы (см. [4])
Ускорение ее сходимости основано на использовании результатов предыдущих итераций для уточнения дна оврага. Может быть использован (см. [4] [5]) градиентный метод (7) с вычислением на каждой итерации отношения 

Далее из точки xk+1 продолжается спуск градиентным методом до следующего ускоряющего шага.
Различные версии метода параллельных касательных (см. [4] — [6]) основаны на выполнении ускоряющего шага вдоль направления 

Вметоде оврагов (см. [7]) предлагается провести локальные спуски градиентным методом (7) из двух случайно выбранных исходных точек, а затем выполнить ускоряющий шаг по направлению, задаваемому двумя полученными на дне оврага точками.
Все эти методы немногим сложнее градиентного метода (7) и построены на его основе. Ускорение сходимости получается для одномерных оврагов. В более общих случаях многомерных оврагов, где сходимость этих схем резко замедляется, приходится обращаться к более мощным методам квадратичной аппроксимации, в основе к-рых лежит метод Ньютона
Точка минимума функции (6) удовлетворяет системе линейных уравнений
и при условии абсолютной точности всех вычислений для квадратичной функции метод Ньютона независимо от степени овражности (2) и размерности оврагов приводит к минимуму за один шаг. На самом деле, при больших числах обусловленности k(D)при ограниченной разрядности вычислений задача получения решения (9) может быть некорректной, и небольшие деформации элементов матрицы Dи вектора 
При умеренных степенях овражности в выпуклой ситуации метод Ньютона часто оказывается более предпочтительным по скорости сходимости, чем другие, напр, градиентные, методы.
Большой класс квадратичных (квазиньютоновских) методов основан на использовании сопряженных направлений (см. [2], [3], [8]). Эти алгоритмы для случая минимизации выпуклой функции оказываются весьма эффективными, ибо, имея квадратичное окончание, они не требуют вычисления матрицы двух производных.
Иногда (см. [8]) итерации строятся по схеме
где Е- единичная матрица. Скаляр 

Существует ряд аналогичных подходов (см. [8]), основанных на получении строго положительно определенных аппроксимаций матрицы Гессе. При минимизации овражных функций такие алгоритмы оказываются малоэффективными из-за трудностей в подборе параметров 
Более целесообразно обобщение метода Ньютона на случай минимизации овражных функций проводится на базе непрерывного принципа оптимизации. Функции J(х)ставится в соответствие дифференциальная система (3), интегрируемая системным методом (см. Жесткая дифференциальная система). Алгоритм минимизации принимает вид
Предложен [1] алгоритм минимизации овражной функции, основанный на использовании свойств жестких систем. Пусть функция 


где 
Вместе с тем система дифференциальных уравнений спуска для овражной функции (6)
имеет решение, в к-ром в силу условия (1) слагаемые с сомножителями 
Другими словами, компоненты вектора х(t)удовлетворяют равенству
быстро переходящему в стационарную связь
где 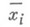

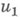


По функции (13) с помощью конечноразностной аппроксимации находится новая матрица 



Если степень овражности не понижается или понижается незначительно, то процесс исключения координат вектора хпродолжается рекурсивно до необходимого ее уменьшения.
Лит.:[1] Ракитский Ю. В., Устинов С. М., Черноруцкий И. Г., Численные методы решения жестких систем, М., 1979; [2] Сеа Ж., Оптимизация. Теория и алгоритмы, пер. с франц., М., 1973; [3] Пшеничный Б. Н., Данилин Ю. М., Численные методы в экстремальных задачах, М., 1975; [4] Поляк Б. Т., «Экономика и математич. методы», 1967, т. 3, № 6, с. 881-902; [5] Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М., 1963; [6] Уайлд Д.- Д ж., Методы поиска экстремума, пер. с англ., М., 1967; [7] Гельфанд И. М., Цетлин М. Л., «Докл. АН СССР», 1961, т. 137, № 2, с. 295-98; [8] Численные методы условной оптимизации, пер. С англ., М., 1977.
Ю. В. Ракитский.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Овражность
Cтраница 1
Овражность такого типа частично устраняется переходом к параметрам In A i и Et, которые применялись в примерах предыдущей главы ( см. с. Появление оврагов у функций отклонений может быть связано с формой кинетического уравнения и с недостаточной информативностью результатов экспериментов по отношению к параметрам постулируемой модели. Математически овражность выражается в том, что матрица вторых производных функции отклонений имеет большой разброс собственных значений. При этом поверхность второго порядка, локально аппроксимирующая функцию отклонений, сильно вытянута вдоль одних направлений и сжата в других. Наличие оврагов сильно затрудняет поиск минимума функции отклонений.
[1]
Ввиду сильной овражности функционала Vs минимизация может быть сопряжена со значительными вычислительными трудностями.
[2]
Конечно, овражность критерия связана не только с неединственностью решения. Возможна ситуация, когда, строго говоря, задача определения констант имеет единственное решение, но столбцы матрицы Якоби почти зависимы, определитель информационной матрицы Фишера ( 16) близок к нулю.
[3]
Если степень овражности не понижается или понижается незначительно, то процесс исключения координат вектора х продолжается рекурсивно до необходимого ее уменьшения.
[4]
При умеренных степенях овражности в выпуклой ситуации метод Ньютона часто оказывается более предпочтительным по скорости сходимости, чем другие, напр, градиентные, методы.
[5]
С аналитической точки зрения овражность означает, что матрица квадратичной формы ( матрица Гесса или гессиан) в (3.160) имеет большой разброс собственных значений. Известно, что интегрирование таких жестких систем вызывает значительные вычислительные трудности, поэтому остановимся на классе методов минимизации, в основе которых лежат численные методы интегрирования градиентных систем дифференциальных уравнений. Эти методы наиболее часто применяются для решения задач химической кинетики и теоретически наиболее обоснованы.
[6]
Ньютона независимо от степени овражности ( 2) и размерности оврагов приводит к минимуму за один шаг.
[7]
Отмеченный эффект — увеличение овражности линий уровня функции Ф ( ж, С) с ростом параметра штрафа С, — как правило, имеет место и в общем случае.
[8]
Рассмотрим другую стратегию измерений, при которой овражности не будет.
[9]
В этом случае спектральное число обусловленности совпадает со степенью овражности.
[10]
Бели же взять rk слишком большим, вспомогательная задача может иметь плохое решение из-за овражности.
[11]
Однако, как отмечалось выше, целевые функции в задачах акустической оптимизации являются сложными функциями параметров и, помимо ярко выраженной овражности, обладают обычно многими экстремумами, а области допустимых значений параметров в общем случае невыпуклы и многосвязны.
[12]
Оптимальное проектирование электрических машин сводится к задаче нелинейного программирования, имеющей общий характер, причем ее особенностями1 являются пологость целевой функции многопараметричность, многоэкстремальность, овражность гиперпространства допустимых решений. Если в большинстве экстремальных задач овраг обращается сильной вытянутостью ( в топологическом представлении) линий уровня целевой функции, то в задачах электромеханики овражные ситуации чаще образуются из-за малости угла, образованного линиями уровня целевой функции и границей допустимой области.
[13]
Оптимальное проектирование электрических машин сводится к задаче нелинейного программирования, имеющей общий характер, причем ее особенностями являются пологость целевой функции, многопарамет-ричность, многоэкстремальность, овражность гиперпространства допустимых решений.
[14]
Приведенные здесь дифференцируемые точные штрафные функции могут рассматриваться как модифицированные функции Лагранжа ( см. разд. Проблема овражности при решении вспомогательных задач является здесь не такой острой, как при применении обычных штрафных функций ( см. разд.
[15]
Страницы:
1
2