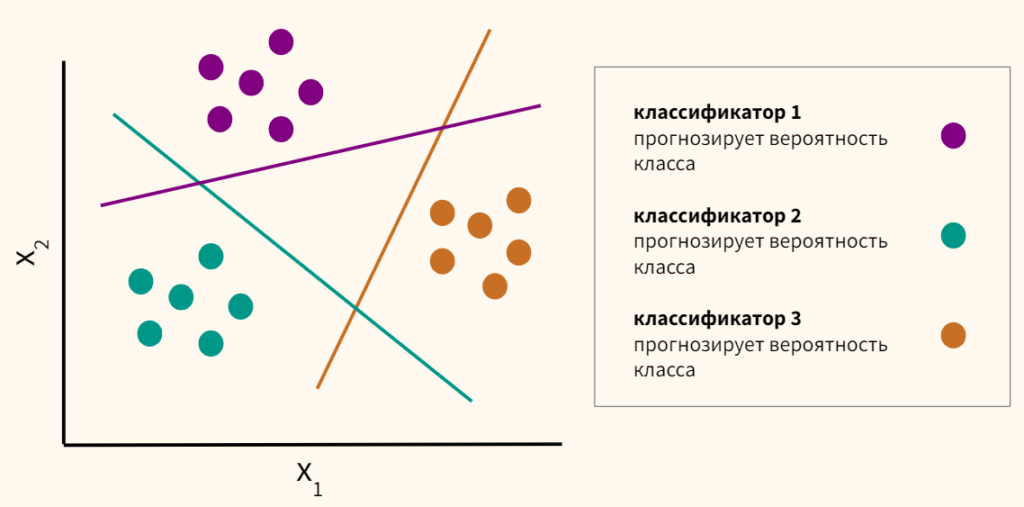
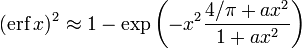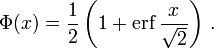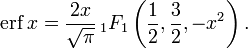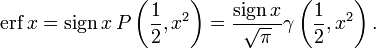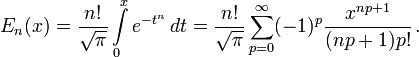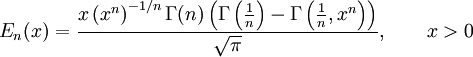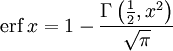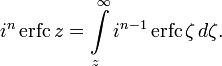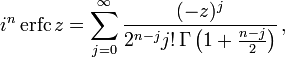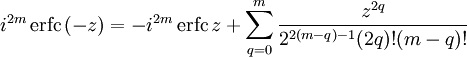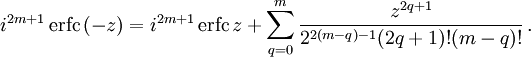| Error function | |
|---|---|

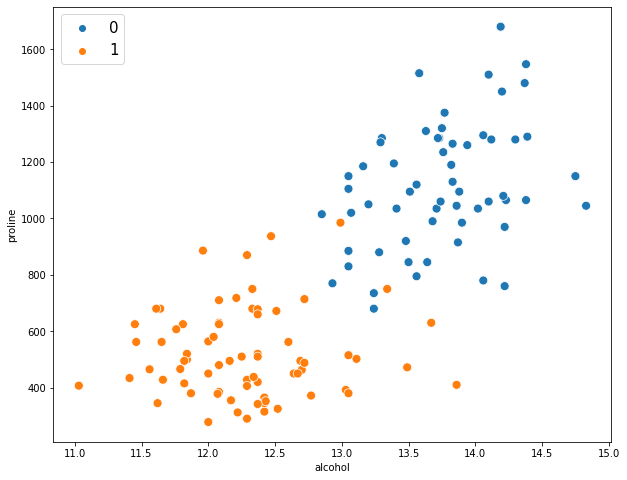
Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
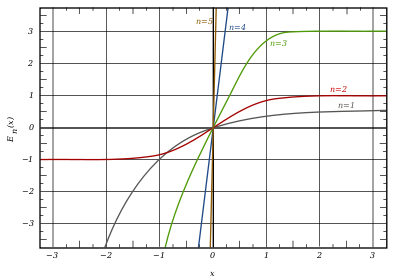
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции
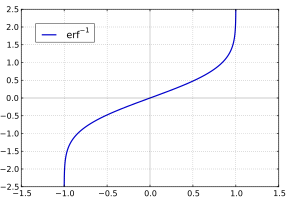
Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0\tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. \ left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) \ [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) \ [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 \ operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок

π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
Функция ошибок (также называемая функция ошибок Гаусса) — не элементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
- [math]displaystyle{ operatorname{erf},x = frac{2}{sqrt{pi}}intlimits_0^x e^{-t^2},mathrm dt }[/math].
Дополнительная функция ошибок, обозначаемая [math]displaystyle{ operatorname{erfc},x }[/math] (иногда применяется обозначение [math]displaystyle{ operatorname{Erf},x }[/math]), определяется через функцию ошибок:
- [math]displaystyle{ operatorname{erfc},x = 1-operatorname{erf},x = frac{2}{sqrt{pi}} intlimits_x^{infty} e^{-t^2},mathrm dt }[/math].
Комплексная функция ошибок, обозначаемая [math]displaystyle{ w(x) }[/math], также определяется через функцию ошибок:
- [math]displaystyle{ w(x) = e^{-x^2}operatorname{erfc},(-ix) }[/math].
Свойства
- Функция ошибок нечётна:
-
- [math]displaystyle{ operatorname{erf},(-x) = -operatorname{erf},x. }[/math]
- Для любого комплексного [math]displaystyle{ x }[/math] выполняется
-
- [math]displaystyle{ operatorname{erf},bar{x} = overline{operatorname{erf},x} }[/math]
- где черта обозначает комплексное сопряжение числа [math]displaystyle{ x }[/math].
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
-
- [math]displaystyle{ operatorname{erf},x= frac{2}{sqrt{pi}}sum_{n=0}^infinfrac{(-1)^n x^{2n+1}}{n! (2n+1)} =frac{2}{sqrt{pi}} left(x-frac{x^3}{3}+frac{x^5}{10}-frac{x^7}{42}+frac{x^9}{216}- cdotsright) }[/math]
- Это равенство выполняется (и ряд сходится) как для любого вещественного [math]displaystyle{ x }[/math], так и на всей комплексной плоскости, согласно признаку Д’Аламбера. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
-
- [math]displaystyle{ operatorname{erf},x= frac{2}{sqrt{pi}}sum_{n=0}^infinleft(x prod_{i=1}^n{frac{-(2i-1) x^2}{i (2i+1)}}right) = frac{2}{sqrt{pi}} sum_{n=0}^infin frac{x}{2n+1} prod_{i=1}^n frac{-x^2}{i} }[/math]
- поскольку [math]displaystyle{ frac{-(2i-1) x^2}{i (2i+1)} }[/math] — сомножитель, превращающий [math]displaystyle{ i }[/math]-й член ряда в [math]displaystyle{ (i+1) }[/math]-й, считая первым членом [math]displaystyle{ x }[/math].
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка [math]displaystyle{ z=infty }[/math] будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
-
- [math]displaystyle{ frac{d}{dx},operatorname{erf},x=frac{2}{sqrt{pi}},e^{-x^2}. }[/math]
- Первообразная функции ошибок, получаемая способом интегрирования по частям:
-
- [math]displaystyle{ F(x)=xoperatorname{erf}(x) + frac{e^{-x^2}}{sqrt{pi}}. }[/math]
- Обратная функция ошибок представляет собой ряд
-
- [math]displaystyle{ operatorname{erf}^{-1},x=sum_{k=0}^infinfrac{c_k}{2k+1}left (frac{sqrt{pi}}{2}xright )^{2k+1}, }[/math]
- где c0 = 1 и
- [math]displaystyle{ c_k=sum_{m=0}^{k-1}frac{c_m c_{k-1-m}}{(m+1)(2m+1)} = left{1,1,frac{7}{6},frac{127}{90},ldotsright}. }[/math]
- Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
- [math]displaystyle{ operatorname{erf}^{-1},x=frac{1}{2}sqrt{pi}left (x+frac{pi x^3}{12}+frac{7pi^2 x^5}{480}+frac{127pi^3 x^7}{40320}+frac{4369pi^4 x^9}{5806080}+frac{34807pi^5 x^{11}}{182476800}+dotsright ). }[/math][1]
- Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных величин подчиняется нормальному распределению со стандартным отклонением [math]displaystyle{ sigma }[/math], то вероятность, что величина отклонится от среднего не более чем на [math]displaystyle{ a }[/math], равна [math]displaystyle{ operatorname{erf},frac{a}{sigma sqrt{2}} }[/math].
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с начальными условиями, описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших [math]displaystyle{ x }[/math] полезно асимптотическое разложение для дополнительной функции ошибок:
- [math]displaystyle{ operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}. }[/math]
Хотя для любого конечного [math]displaystyle{ x }[/math] этот ряд расходится, на практике первых нескольких членов достаточно для вычисления [math]displaystyle{ operatorname{erfc},x }[/math] с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
Другое приближение даётся формулой
- [math]displaystyle{ (operatorname{erf},x)^2approx 1-expleft(-x^2frac{4/pi+ax^2}{1+ax^2}right) }[/math]
где
- [math]displaystyle{ a = frac{8}{3pi}frac{pi — 3}{4 — pi}. }[/math]
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым [math]displaystyle{ Phi(x) }[/math]
- [math]displaystyle{ Phi(x) = frac{1}{2}biggl(1+operatorname{erf},frac{x}{sqrt{2}}biggl). }[/math]
Обратная функция к [math]displaystyle{ Phi }[/math], известная как нормальная квантильная функция, иногда обозначается [math]displaystyle{ operatorname{probit} }[/math] и выражается через нормальную функцию ошибок как
- [math]displaystyle{
operatorname{probit},p = Phi^{-1}(p) = sqrt{2},operatorname{erf}^{-1}(2p-1).
}[/math]
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
- [math]displaystyle{ operatorname{erf},x=
frac{2x}{sqrt{pi}},_1F_1left(frac{1}{2},frac{3}{2},-x^2right). }[/math]
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
- [math]displaystyle{ operatorname{erf},x=operatorname{sign},x,Pleft(frac{1}{2}, x^2right)={operatorname{sign},x over sqrt{pi}}gammaleft(frac{1}{2}, x^2right). }[/math]
Обобщённые функции ошибок
График обобщённых функций ошибок [math]displaystyle{ E_n(x) }[/math]:
серая линия: [math]displaystyle{ E_1(x)=(1-e^{-x})/sqrt{pi} }[/math]
красная линия: [math]displaystyle{ E_2(x)=operatorname{erf},x }[/math]
зелёная линия: [math]displaystyle{ E_3(x) }[/math]
синяя линия: [math]displaystyle{ E_4(x) }[/math]
жёлтая линия: [math]displaystyle{ E_5(x) }[/math].
Некоторые авторы обсуждают более общие функции
- [math]displaystyle{ E_n(x) = frac{n!}{sqrt{pi}} intlimits_0^x e^{-t^n},mathrm dt
=frac{n!}{sqrt{pi}}sum_{p=0}^infin(-1)^pfrac{x^{np+1}}{(np+1)p!},. }[/math]
Примечательными частными случаями являются:
- [math]displaystyle{ E_0(x) }[/math] — прямая линия, проходящая через начало координат: [math]displaystyle{ E_0(x)=frac{x}{e sqrt{pi}} }[/math]
- [math]displaystyle{ E_2(x) }[/math] — функция ошибок [math]displaystyle{ operatorname{erf},x }[/math].
После деления на [math]displaystyle{ n! }[/math] все [math]displaystyle{ E_n }[/math] с нечётными [math]displaystyle{ n }[/math] выглядят похоже (но не идентично), это же можно сказать про [math]displaystyle{ E_n }[/math] с чётными [math]displaystyle{ n }[/math]. Все обобщённые функции ошибок с [math]displaystyle{ ngt 0 }[/math] выглядят похоже на полуоси [math]displaystyle{ xgt 0 }[/math].
На полуоси [math]displaystyle{ xgt 0 }[/math] все обобщённые функции могут быть выражены через гамма-функцию:
- [math]displaystyle{ E_n(x) = frac{Gamma(n)left(Gammaleft(frac{1}{n}right)-Gammaleft(frac{1}{n},x^nright)right)}{sqrtpi},
quad quad
xgt 0 }[/math]
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
- [math]displaystyle{ operatorname{erf},x = 1 — frac{Gammaleft(frac{1}{2},x^2right)}{sqrtpi} }[/math]
Повторные интегралы дополнительной функции ошибок
Повторные интегралы [math]displaystyle{ operatorname{I^n erfc} }[/math] дополнительной функции ошибок определяются как[1]
- [math]displaystyle{ operatorname{I^0 erfc},z = operatorname{erfc},z }[/math],
- [math]displaystyle{ operatorname{I^n erfc},z = intlimits_z^infty operatorname{I^{n-1}erfc},zeta,dzeta, }[/math] для [math]displaystyle{ ngt 0 }[/math].
Их можно разложить в ряд:
- [math]displaystyle{
operatorname{I^nerfc},z
=
sum_{j=0}^infty frac{(-z)^j}{2^{n-j}j!,Gamma left( 1 + frac{n-j}{2}right)},,
}[/math]
откуда следуют свойства симметрии
- [math]displaystyle{
operatorname{I^{2m}erfc},(-z)
= -operatorname{I^{2m}erfc},z
+ sum_{q=0}^m frac{z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}
}[/math]
и
- [math]displaystyle{
operatorname{I^{2m+1}erfc},(-z)
=operatorname{I^{2m+1}erfc},z
+ sum_{q=0}^m frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!},.
}[/math]
Реализации
В стандарте языка Си (ISO/IEC 9899:1999, пункт 7.12.8) предусмотрены функция ошибок [math]displaystyle{ operatorname{erf} }[/math] и дополнительная функция ошибок [math]displaystyle{ operatorname{erfc} }[/math]. Функции объявлены в заголовочных файлах math.h (для Си) или cmath (для C++). Там же объявлены пары функций erff(), erfcf() и erfl(), erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта «Boost».
В языке Java стандартная библиотека математических функций java.lang.Math не содержит[2] функцию ошибок. Класс Erf можно найти в пакете org.apache.commons.math.special из не стандартной библиотеки, поставляемой[3] Apache Software Foundation.
Системы компьютерной алгебры Maple[2], Matlab[3], Mathematica и Maxima[4] содержат обычную и дополнительную функции ошибок, а также обратные к ним функции.
В языке Python функция ошибок доступна[4] из стандартной библиотеки math, начиная с версии 2.7. Также функция ошибок, дополнительная функция ошибок и многие другие специальные функции определены в модуле Special проекта SciPy[5].
В языке Erlang функция ошибок и дополнительная функция ошибок доступны из стандартного модуля math[5].
В Excel функция ошибок представлена, как ФОШ и ФОШ.ТОЧН[6]
См. также
- Функция Гаусса
- Функция Доусона
- Гауссов интеграл
Примечания
- ↑ Carslaw, H. S. & Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ↑ Math (Java Platform SE 6). Дата обращения: 28 марта 2008. Архивировано 29 августа 2009 года.
- ↑ Архивированная копия (недоступная ссылка). Дата обращения: 28 марта 2008. Архивировано 9 апреля 2008 года.
- ↑ 9.2. math — Mathematical functions — Python 2.7.10rc0 documentation
- ↑ Язык Erlang. Описание Архивная копия от 20 июня 2012 на Wayback Machine функций стандартного модуля
math. - ↑ Функция ФОШ. support.microsoft.com. Дата обращения: 15 ноября 2021. Архивировано 15 ноября 2021 года.
Литература
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T. & Flannery, Brian P. (2007), Section 6.2. Incomplete Gamma Function and Error Function, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. — Т. 7.
- Nikolai G. Lehtinen. Error functions (April 2010). Дата обращения: 25 мая 2019.
Ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной переменной, определяемой как:
Этот интеграл представляет собой специальную ( неэлементарную ) сигмовидную функцию, которая часто встречается в уравнениях вероятности, статистики и дифференциальных уравнений в частных производных . Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, то значение функции также является действительным.
В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y, которая нормально распределена со средним значением 0 и стандартным отклонением
1/√ 2, erf x — вероятность того, что Y попадает в диапазон [- x, x ] .
Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как
и функция мнимой ошибки ( erfi ), определяемая как
где i — мнимая единица .
Имя
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, тогда erf (а/σ √ 2) — вероятность того, что ошибка единичного измерения находится между — a и + a для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.
Ошибки и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные условия задаются ступенчатой функцией Хевисайда .
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X ~ Norm [ μ, σ ] (нормальное распределение со средним μ и стандартным отклонением σ ) и константа L < μ :
где A и B — некоторые числовые константы. Если L достаточно далеко от среднего, а именно μ — L ≥ σ √ ln k, то:
поэтому вероятность стремится к 0 при k → ∞ .
Вероятность того, что X находится в интервале [ L a, L b ], может быть получена как
Характеристики
Интегрируем exp (- z 2 )
erf z
Свойство erf (- z ) = −erf z означает, что функция ошибок является нечетной функцией . Это напрямую связано с тем, что подынтегральное выражение e — t 2 является четной функцией (интегрирование четной функции дает нечетную функцию и наоборот).
Для любого комплексного числа z :
где г представляет собой комплексно сопряженное из г .
Подынтегральное выражение f = exp (- z 2 ) и f = erf z показано на комплексной плоскости z на рисунках справа с раскраской области .
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf z стремится к единице при z → + ∞ и −1 при z → −∞ . На мнимой оси он стремится к ± i ∞ .
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x > 1 ».
Определяющий интеграл не может быть вычислен в замкнутой форме в терминах элементарных функций, но, раскладывая подынтегральное выражение e — z 2 в его ряд Маклорена и интегрируя член за членом, можно получить ряд Маклорена функции ошибок как:
которое выполняется для любого комплексного числа z . Члены знаменателя — это последовательность (последовательность A007680 в OEIS ) в OEIS .
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
потому что — (2 к — 1) z 2/к (2 к + 1)выражает множитель для превращения k- го члена в ( k + 1) -й член (считая z первым членом).
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
которое выполняется для любого комплексного числа z .
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразная функции ошибки, получаемый путем интегрирования по частям, является
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
где H — полиномы Эрмита физиков .
Серия Bürmann
Разложение, которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана :
где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c 1 =31 год/200и c 2 = —341/8000, полученное приближение показывает свою наибольшую относительную ошибку при x = ± 1,3796, где она меньше 0,0036127:
Обратные функции
Для комплексного числа z не существует уникального комплексного числа w, удовлетворяющего erf w = z, поэтому истинная обратная функция будет многозначной. Однако для −1 < x <1 существует уникальное действительное число, обозначенное erf −1 x, удовлетворяющее
Функция обратной ошибки обычно определяется с помощью области (-1,1), и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | <1 комплексной плоскости, используя ряд Маклорена
где c 0 = 1 и
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
(После отмены дроби числителя / знаменателя представляют собой записи OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ± ∞ равно ± 1 .
Для | z | <1, имеем erf (erf −1 z ) = z .
Обратная дополнительная функция ошибок определяются как
Для действительного x существует уникальное действительное число erfi −1 x, удовлетворяющее erfi (erfi −1 x ) = x . Функция обратной мнимой ошибки определяется как erfi −1 x .
Для любого вещественного х, метод Ньютона может быть использован для вычисления ЕрФИ -1 х, а для -1 ≤ х ≤ 1, следующие сходится ряд Маклорена:
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :
где (2 n — 1) !! — двойной факториал числа (2 n — 1), который является произведением всех нечетных чисел до (2 n — 1) . Этот ряд расходится для любого конечного x, и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 выполняется
где остаток в обозначениях Ландау равен
при x → ∞ .
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Непрерывное расширение фракции
Цепная дробь расширение дополнительной функции ошибок является:
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 с заменой переменных.
Факторный ряд
Обратный факторный ряд :
сходится при Re ( z 2 )> 0 . Здесь
z n обозначает возрастающий факториал, а s ( n, k ) обозначает число Стирлинга первого рода со знаком . Также существует представление бесконечной суммой, содержащее двойной факториал :
Численные приближения
Приближение с элементарными функциями
- Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:
(максимальная ошибка: 5 × 10 −4 )
где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
(максимальная ошибка: 2,5 × 10 −5 )
где p = 0,47047, a 1 = 0,3480242, a 2 = −0,0958798, a 3 = 0,7478556
(максимальная ошибка: 3 × 10 −7 )
где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
(максимальная ошибка: 1,5 × 10 −7 )
где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429.
Все эти приближения верны для x ≥ 0 . Чтобы использовать эти приближения для отрицательного x, используйте тот факт, что erf x — нечетная функция, поэтому erf x = −erf (- x ) .
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даются формулами
- Вышеупомянутое было обобщено до сумм из N экспонент с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимирован или ограничен величиной 2 Q̃ ( √ 2 x ), где
В частности, существует систематическая методология решения числовых коэффициентов {( a n, b n )}N
n = 1которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ), Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a n, b n )}N
n = 1для многих вариаций экспоненциальных приближений и границ до N = 25 были выпущены в открытый доступ в виде исчерпывающего набора данных. - Точная аппроксимация дополнительной функции ошибок для x ∈ [0, ∞) дана Karagiannidis & Lioumpas (2007), которые показали для соответствующего выбора параметров { A, B }, что
Они определили { A, B } = {1.98,1.135}, что дает хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу.
- Одноканальная нижняя граница
где параметр β может быть выбран так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
-
- Другое приближение дает Сергей Виницкий, используя свои «глобальные приближения Паде»:
куда
Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а относительная ошибка меньше 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
- Приближение с максимальной погрешностью 1,2 × 10 −7 для любого действительного аргумента:
с участием
а также
Таблица значений
| Икс | erf x | 1 — эрф х |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 070 | 0,119 794 930 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 120 | 0,047 714 880 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 910 | 0,000 022 090 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Дополнительная функция ошибок
Дополнительная функция ошибок, обозначаемая ERFC, определяется как
который также определяет erfcx, масштабированную дополнительную функцию ошибок (которую можно использовать вместо erfc, чтобы избежать арифметического переполнения ). Другая форма erfc x для x ≥ 0 известна как формула Крейга в честь ее первооткрывателя:
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc x = 2 — erfc (- x ) для получения erfc ( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом:
Функция мнимой ошибки
Функция мнимой ошибки, обозначаемая erfi, определяется как
где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Когда функция ошибок оценивается для произвольных комплексных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
Кумулятивная функция распределения
Функция ошибок по существу идентична стандартной нормальной кумулятивной функции распределения, обозначаемой Φ, также называемой нормой ( x ) в некоторых языках программного обеспечения, поскольку они различаются только масштабированием и преобразованием. Действительно,
или переставил для erf и erfc :
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
Обратное из Ф называется нормальной функции квантиль, или пробит функции и могут быть выражены в терминах функции обратной ошибки как
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Он имеет простое выражение в терминах интеграла Френеля .
С точки зрения регуляризованном гамма — функции P и неполной гамма — функции ,
sgn x — знаковая функция .
Обобщенные функции ошибок
График обобщенных функций ошибок E n ( x ) :
серая кривая: E 1 ( x ) =1 — е — х/√ π
красная кривая: E 2 ( x ) = erf ( x )
зеленая кривая: E 3 ( x )
синяя кривая: E 4 ( x )
золотая кривая: E 5 ( x ) .
Некоторые авторы обсуждают более общие функции:
Известные случаи:
- E 0 ( x ) — прямая линия, проходящая через начало координат: E 0 ( x ) =Икс/е √ π
- E 2 ( x ) — функция ошибок, erf x .
После деления на п ! , все E n для нечетных n похожи (но не идентичны) друг на друга. Точно так же E n для четного n выглядят похожими (но не идентичными) друг на друга после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне графика x .
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
а также
Реализации
Как реальная функция реального аргумента
- В Posix -совместимый операционных систем, заголовок math.h возвестят и математическая библиотека libm должна обеспечивать функции
erfиerfc( двойной точности ), а также их одинарной точности и повышенной точности аналоговerff,erflиerfcf,erfcl. - GNU Scientific Library предоставляет
erf,erfc,log(erf), и масштабируемые функции ошибок.
Как сложная функция сложного аргумента
-
libcerf, цифровая библиотека C для сложных функций ошибок, обеспечивает комплексные функции
cerf,cerfc,cerfcxи реальные функцииerfi,erfcxпримерно с 13-14 точностью цифр, на основе функции Фаддеева, как реализовано в MIT Фаддеевого пакете
Смотрите также
- Гауссовский интеграл по всей действительной прямой
- Функция Гаусса, производная
- Функция Доусона, перенормированная функция мнимой ошибки
- Интеграл Гудвина – Стэтона
По вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функции ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, хвостовая вероятность нормального распределения
использованная литература
дальнейшее чтение
- Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
внешние ссылки
- MathWorld — Эрф
- Таблица интегралов функций ошибок
График функции ошибок
В математике функция ошибок — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
.
Дополнительная функция ошибок, обозначаемая 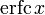
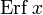
.
Комплексная функция ошибок, обозначаемая w(x), также определяется через функцию ошибок:
.
Содержание
- 1 Свойства
- 2 Применение
- 3 Асимптотическое разложение
- 4 Родственные функции
- 4.1 Обобщённые функции ошибок
- 4.2 Итерированные интегралы дополнительной функции ошибок
- 5 Реализация
- 6 См. также
- 7 Литература
- 8 Внешние ссылки
Свойства
- Функция ошибок нечётна:
- Для любого комплексного x выполняется
где черта обозначает комплексное сопряжение числа x.
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
Это равенство выполняется (и ряд сходится) как для любого вещественного x, так и на всей комплексной плоскости. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
поскольку 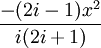
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка
будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Обратная функция ошибок представляет собой ряд
где c0 = 1 и
Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
[1]
Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных чисел подчиняется нормальному распределению со стандартным отклонением σ, то вероятность, что число отклонится от среднего не более чем на a, равна 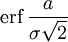
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с граничными условиями описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших x полезно асимптотическое разложение для дополнительной функции ошибок:
Хотя для любого конечного x этот ряд расходится, на практике первых нескольких членов достаточно для вычисления 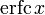
Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым Φ(x)
Обратная функция к Φ, известная как нормальная квантильная функция, иногда обозначается 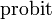
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
Обобщённые функции ошибок
График обобщённых функций ошибок En(x):
серая линия:
красная линия:
зелёная линия: E3(x)
синяя линия: E4(x)
жёлтая линия: E5(x).
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
После деления на n! все En с нечётными n выглядят похоже (но не идентично). Все En с чётными n тоже выглядят похоже, но не идентично, после деления на n!. Все обощённые функции ошибок с n > 0 выглядят похоже на полуоси x > 0.
На полуоси x > 0 все обобщённые функции могут быть выражены через гамма-функцию:
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Итерированные интегралы дополнительной функции ошибок
Итерированные интегралы дополнительной функции ошибок определяются как
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализация
В стандартах языков Си и C++ функция ошибок 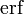
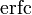
double erf(double x) и double erfc(double x). Функции находятся в заголовочных файлах math.h или cmath. Там же есть пары функций erff(),erfcf() и erfl(),erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта Boost.
В языке [2]. Класс Erf есть в пакете org.apache.commons.math.special от [3]. Однако эта библиотека не является одной из стандартных библиотек Java 6.
Matlab[4] и
В языке Special проекта scipy [5].
См. также
- Функция Гаусса
Литература
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (См. часть 7)
Внешние ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
Wikimedia Foundation.
2010.
Все курсы > Оптимизация > Занятие 5
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.
- Если $ f_w(x) < 0,5 rightarrow hat{y} = 0 $
- Если $ f_w(x) geq 0,5 rightarrow hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможное решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 leq h(x) leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = frac{1}{1+e^{-z}} $$

Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = Xtheta rightarrow h_{theta}(x) = frac{1}{1+e^{-(Xtheta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия» нет. Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(—z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{theta}(x) = P(y = 1 | x; theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $theta$ (probability of y = 1 given x, parameterized by $theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; theta) = 1-P(y = 1 | x; theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{theta}(x) geq 0,5 $$
$$ y = 0, h_{theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z geq 0 $, а так как $ z = Xtheta $, то можно сказать, что
- $h_{theta}(x) geq 0,5$ и $ y = 1$, когда $ Xtheta geq 0 $, и соответственно
- $h_{theta}(x) < 0,5 $ и $ y = 0$, когда $ Xtheta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить это пространство на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.

Возникает вопрос. Как, зная коэффициенты $theta_0$, $theta_1$ и $theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = theta_0 + 0 + theta_2 x_2 rightarrow x_2 = -frac{theta_0}{theta_2} rightarrow c = -frac{theta_0}{theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = theta_1x_1^b + theta_2x_2^b + theta_0-(theta_1x_1^a + theta_2x_2^a + theta_0) $$
$$ -theta_2(x_2^b-x_2^a) = theta_1(x_1^b-x_1^a) $$
А значит,
$$ frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -frac{theta_1}{theta_2} rightarrow m = -frac{theta_1}{theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
# возьмем большое отрицательное значение z = —999 1 / (1 + np.exp(—z)) |
|
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = frac{1}{1+e^{-z}} = frac{1}{1+e^{-z}} times frac{e^z}{e^z} = frac{e^z}{e^z(1+e^{-z})} = frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
z = 999 1 / (1 + np.exp(—z)) |
При этом вторая стабильна при очень больших отрицательных значениях.
|
z = —999 np.exp(z) / (np.exp(z) + 1) |
Объединим обе части с помощью условия.
|
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Можно также использовать функцию expit() библиотеки scipy.
|
from scipy.special import expit expit(999), expit(—999) |
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
Пропишем это на Питоне.
|
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([—3, 1, 1]) # подадим их в модель h(x, thetas) |
|
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.

Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула функции логистической ошибки
Вначале посмотрим на нее на графике.

Разберемся, как она работает. Наша модель $h_{theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; theta)) = -log(h_{theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях, близких к нулю.
$$ -log(1-P(y = 1 | x; theta)) = -log(1-h_{theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(theta) = begin{cases} -log(h_{theta}(x)) | y=1 \ -log(1-h_{theta}(x)) | y=0 end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на $y$, а правую на $1-y$. Тогда, если речь идет о классе 1, первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ ‘y’ :[1, 1, 1, 0, 0, 1, 1, 0], ‘y_pred’ :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |
Найдем вероятность принадлежности к классу 1.
|
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output[‘y=1 prob’] = np.where(output[‘y’] == 0, 1 — output[‘y_pred’], output[‘y_pred’]) output |
Возьмем отрицательный логарифм из каждой вероятности.
|
output[‘-log’] = —np.log(output[‘y=1 prob’]) output |
Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, —np.log(x_vals), label = ‘-log(h(x)) | y = 1’) # выведем каждое из значений отрицательного логарифма plt.scatter(output[‘y=1 prob’], output[‘-log’], color = ‘r’) # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel(‘h(x)’, fontsize = 16) plt.ylabel(‘loss’, fontsize = 16) plt.title(‘Функция логистической ошибки’, fontsize = 18) plt.legend(loc = ‘upper right’, prop = {‘size’: 15}) plt.grid() plt.show() |
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e—9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) # сложим и разделим на количество наблюдений return —np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
objective(output[‘y’], output[‘y_pred’]) |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(theta)$,
$$ G = y cdot log(h) + (1-y) cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(theta)$ — линейная функция $xtheta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ frac{partial G}{partial theta} = frac{partial G}{partial h} cdot frac{partial h}{partial z} cdot frac{partial z}{partial theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ frac{partial}{partial x} ln f(x) = frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ frac{partial G}{partial h} left[ y cdot log(h) + (1-y) cdot log(1-h) right] $$
$$ = y cdot frac{partial G}{partial h} [log(h)] + (1-y) cdot frac{partial G}{partial h} [log(1-h)] $$
$$ = frac{1}{h}y + frac{1}{1-h} cdot frac{partial G}{partial h} [1-h] cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = frac{h}{y} + frac{frac{partial G}{partial h} (1-h) (1-y)}{1-h} = frac{h}{y}+frac{(0-1)(1-y)}{1-h} $$
$$ = frac{y}{h}-frac{1-y}{1-h} = frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ frac{partial h}{partial z} left[ frac{1}{1+e^{-z}} right] = frac{partial h}{partial z} left[ (1+e^{-z})^{-1}) right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) cdot (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = frac{1}{1+e^{-z}} cdot frac{e^{-z}}{1+e^{-z}} = frac{1}{1+e^{-z}} cdot frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = frac{1}{1+e^{-z}} cdot left( frac{1+e^{-z}}{1+e^{-z}}-frac{1}{1+e^{-z}} right) $$
$$ = frac{1}{1+e^{-z}} cdot left( 1-frac{1}{1+e^{-z}} right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ frac{partial z}{partial theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ frac{partial J}{partial theta} = frac{y-h}{h(1-h)} cdot h(1-h) cdot x_j cdot frac{1}{n} = x_j cdot (y-h) cdot frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ nabla_{theta} J = X^T(h(Xtheta)-y) times frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.
Объявим соответствующую функцию.
|
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df[‘target’] = data.target # посмотрим на первые три строки df.head(3) |
Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
df.shape, np.unique(df.target) |
|
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df[‘target’])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |
Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # выведем результат plt.show() |
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X — X.mean()) / X.std() X.head() |
Проверим результат.
|
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |
Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas — 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[—1] |
|
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 — отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность, близкая к нулю, говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками — фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = —thetas[0]/thetas[2], —thetas[1]/thetas[2] c, m |
|
(0.1227046263531282, -0.915731474695505) |
|
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
array([-2.15362589, 2.12194856]) |
|
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, ‘k’, lw = 1, ls = ‘—‘) # дополнительно отобразим наши данные, sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color=’tab:blue’, alpha = 0.2) # plt.fill_between(xd, yd, ymax, color=’tab:orange’, alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel(‘x_1’) # plt.ylabel(‘x_2’) plt.show() |
На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст «правильные» копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст «правильную» копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # приведем признаки к одному масштабу X = (X — X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[—1] |
|
(array([ 0.23234188, —1.73394252, —1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
|
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
# подготовим данные X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствующие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
accuracy_score(y, y_pred) |
И построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, хотя веса модели и предсказанные вероятности немного отличаются, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
# найдем сдвиг и наклон для уравнения решающей границы c, m = —model.intercept_ / model.coef_[0][1], —model.coef_[0][0] / model.coef_[0][1] c, m |
|
(array([0.12536569]), -0.8521526076691505) |
|
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, ‘k’, lw=1, ls=‘—‘) sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |
Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.
Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = theta_{0}x_0 + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим, улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
# посмотрим на первое наблюдение X.head(1) |
|
# должно получиться шесть признаков X_poly[:1] |
|
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
Построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
# сделаем копию исходного датафрейма с нужными признаками predictions = df[[‘alcohol’, ‘proline’]].copy() # и добавим новый столбец с прогнозными значениями predictions[‘y_pred’] = y_pred # посмотрим на результат predictions.head(3) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {‘wspace’ : 0.2}) # на левом подграфике выведем фактические классы sns.scatterplot(data = df, x = ‘alcohol’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) # на правом — прогнозные sns.scatterplot(data = predictions, x = ‘alcohol’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз’, fontsize = 14) # зададим общий заголовок fig.suptitle(‘Бинарная полиномиальная регрессия’, fontsize = 16) plt.show() |
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df — df.mean())/df.std() # добавим целевую переменную df[‘target’] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df[‘target’])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
df = df[[‘flavanoids’, ‘proline’, ‘target’]].copy() df.head(3) |
Посмотрим, насколько легко можно разделить эти классы.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = ‘bright’, s = 100) # добавим легенду plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.show() |
Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_theta^{(i)}(x) = P(y = i | x; theta), i in {0, 1, 2} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 первым классом будет класс 0, а классы 1 и 2 — нулевым ovr_0[‘target’] = np.where(df[‘target’] == target[0], 1, 0) ovr_1[‘target’] = np.where(df[‘target’] == target[1], 1, 0) ovr_2[‘target’] = np.where(df[‘target’] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax1) ax1.set_title(‘Прогнозирование класса 0’, fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax2) ax2.set_title(‘Прогнозирование класса 1’, fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax3) ax3.set_title(‘Прогнозирование класса 2’, fontsize = 14) plt.show() |
Обучение моделей
|
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[[‘flavanoids’, ‘proline’]] y = ova_n[‘target’] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
# вновь перенесем данные из исходного датафрейма X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T all_probs.shape |
|
# каждая из 178 строк — это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу.
|
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз one-vs-rest’, fontsize = 14) plt.show() |
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop(‘target’, axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x[‘target’] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop(‘target’, axis = 1).copy() ovr_df[‘target’] = np.where(x[‘target’] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
Сравнение с sklearn
Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] ovr_model = LogisticRegression(multi_class = ‘ovr’) ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = ‘ovr’) poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
Результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Полиномиальная регрессия’, fontsize = 14) plt.show() |
Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные на несколько датасетов и использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
X = df[[‘flavanoids’, ‘proline’]] add_ones(X) X.head(3) |
Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
y = df[‘target’] y_enc = ohe(df[‘target’]) y_enc[:3] |
|
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
y_lb = lb.transform(y) y_lb[:5] |
|
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $theta_0$) и трех классов.
Инициализируем веса.
|
thetas = np.zeros((3, 3)) thetas |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ text{softmax}(z)_{i} = frac{e^{z_i}}{sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-Xtheta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
z = np.dot(—X, thetas) z.shape |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ text{softmax}(z)_{i} = frac{e^{z_i-max(z)}}{sum_{k=1}^N e^{z_k-max(z)}} $$
|
# axis = -1 — это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = —1, keepdims = True)[:5] |
|
array([[0.], [0.], [0.], [0.], [0.]]) |
|
z = z — np.max(z, axis = —1, keepdims = True) z[:5] |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
arr = np.array([—2, 3, 0, —7, 6]) arr — max(arr) |
|
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
numerator = np.exp(z) numerator[:5] |
|
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
denominator = np.sum(numerator, axis = —1, keepdims = True) denominator[:5] |
|
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
softmax = numerator / denominator softmax[:5] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
def stable_softmax(x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax |
|
probs = stable_softmax(X, thetas) probs[:3] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = frac{e^{z_1}}{e^{z_1}+e^0} = frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмоиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности наблюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде переключателя. Здесь при умножении «срабатывает» только первая вероятность $1 times 0,3 + 0 times 0,4 + 0 times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна).
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Если бы модель в своих вероятностях ошибалась меньше, то и общая ошибка была бы меньше.
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=—np.log(x_arr)) plt.title(‘Plot of -log(x)’) plt.xlabel(‘x’) plt.ylabel(‘-log(x)’); |
Напишем функцию.
|
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
ce = cross_entropy(probs, y_enc) ce |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ nabla_{theta}J = frac{1}{n} times X^T cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc — probs))) |
|
gradient_softmax(X, probs, y_enc) |
|
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e—9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas — 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $theta_0$)) и достигнутый уровень ошибки.
|
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
loss_history[0], loss_history[—1] |
|
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
accuracy_score(y, y_pred) |
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e—9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas — 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc — probs))) def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[—1] |
|
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = ‘multinomial’) # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
y_pred = model.predict(X) accuracy_score(y, y_pred) |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию логистической регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.
Рассмотрим обучение нейронных сетей.






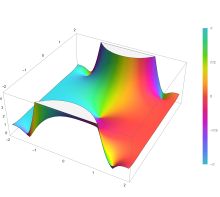
![{displaystyle {begin{aligned}Pr[Xleq L]&={frac {1}{2}}+{frac {1}{2}}operatorname {erf} {frac {L-mu }{{sqrt {2}}sigma }}\&approx Aexp left(-Bleft({frac {L-mu }{sigma }}right)^{2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{displaystyle Pr[Xleq L]leq Aexp(-Bln {k})={frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{displaystyle {begin{aligned}Pr[L_{a}leq Xleq L_{b}]&=int _{L_{a}}^{L_{b}}{frac {1}{{sqrt {2pi }}sigma }}exp left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right),mathrm {d} x\&={frac {1}{2}}left(operatorname {erf} {frac {L_{b}-mu }{{sqrt {2}}sigma }}-operatorname {erf} {frac {L_{a}-mu }{{sqrt {2}}sigma }}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)
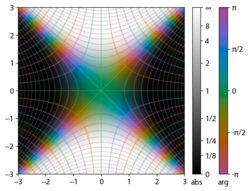


![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z-{frac {z^{3}}{3}}+{frac {z^{5}}{10}}-{frac {z^{7}}{42}}+{frac {z^{9}}{216}}-cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }left(zprod _{k=1}^{n}{frac {-(2k-1)z^{2}}{k(2k+1)}}right)\[6pt]&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z}{2n+1}}prod _{k=1}^{n}{frac {-z^{2}}{k}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{displaystyle {begin{aligned}operatorname {erfi} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z+{frac {z^{3}}{3}}+{frac {z^{5}}{10}}+{frac {z^{7}}{42}}+{frac {z^{9}}{216}}+cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{displaystyle {begin{aligned}operatorname {erf} x&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left(1-{frac {1}{12}}left(1-e^{-x^{2}}right)-{frac {7}{480}}left(1-e^{-x^{2}}right)^{2}-{frac {5}{896}}left(1-e^{-x^{2}}right)^{3}-{frac {787}{276480}}left(1-e^{-x^{2}}right)^{4}-cdots right)\[10pt]&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left({frac {sqrt {pi }}{2}}+sum _{k=1}^{infty }c_{k}e^{-kx^{2}}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)







![{displaystyle {begin{aligned}operatorname {erfc} x&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}left(1+sum _{n=1}^{infty }(-1)^{n}{frac {1cdot 3cdot 5cdots (2n-1)}{left(2x^{2}right)^{n}}}right)\[6pt]&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}sum _{n=0}^{infty }(-1)^{n}{frac {(2n-1)!!}{left(2x^{2}right)^{n}}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)























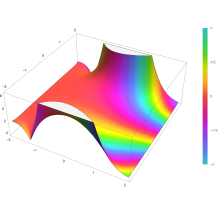
![{displaystyle {begin{aligned}operatorname {erfc} x&=1-operatorname {erf} x\[5pt]&={frac {2}{sqrt {pi }}}int _{x}^{infty }e^{-t^{2}},mathrm {d} t\[5pt]&=e^{-x^{2}}operatorname {erfcx} x,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)



![{displaystyle {begin{aligned}operatorname {erfi} x&=-ioperatorname {erf} ix\[5pt]&={frac {2}{sqrt {pi }}}int _{0}^{x}e^{t^{2}},mathrm {d} t\[5pt]&={frac {2}{sqrt {pi }}}e^{x^{2}}D(x),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

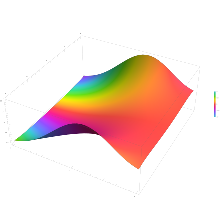
![{displaystyle {begin{aligned}Phi (x)&={frac {1}{sqrt {2pi }}}int _{-infty }^{x}e^{tfrac {-t^{2}}{2}},mathrm {d} t\[6pt]&={frac {1}{2}}left(1+operatorname {erf} {frac {x}{sqrt {2}}}right)\[6pt]&={frac {1}{2}}operatorname {erfc} left(-{frac {x}{sqrt {2}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{displaystyle {begin{aligned}operatorname {erf} (x)&=2Phi left(x{sqrt {2}}right)-1\[6pt]operatorname {erfc} (x)&=2Phi left(-x{sqrt {2}}right)\&=2left(1-Phi left(x{sqrt {2}}right)right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)







![{displaystyle {begin{aligned}operatorname {i} ^{n}!operatorname {erfc} z&=int _{z}^{infty }operatorname {i} ^{n-1}!operatorname {erfc} zeta ,mathrm {d} zeta \[6pt]operatorname {i} ^{0}!operatorname {erfc} z&=operatorname {erfc} z\operatorname {i} ^{1}!operatorname {erfc} z&=operatorname {ierfc} z={frac {1}{sqrt {pi }}}e^{-z^{2}}-zoperatorname {erfc} z\operatorname {i} ^{2}!operatorname {erfc} z&={tfrac {1}{4}}left(operatorname {erfc} z-2zoperatorname {ierfc} zright)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)








![{ displaystyle Pr [X leq L ] = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma }} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72302c46832449e128a4d4e1adb28b514131270)









![{ displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left (1 - { frac {1} {12}} left (1 -e ^ {- x ^ {2}} right) - { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2}} right) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2 }} right) ^ {4} - cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1 -e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ddba05e595a553fee25644a3542188281bd844)







![{ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1+ sum _ {n = 1} ^ { infty} (-1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ { n}}} right] = { frac {e ^ {-x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc8c3aefff3ba787b080c5186dd3aec8ec76ef9)





![{ displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b} { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, му, sigma in mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6adc2c661b24b44dc1e3d7e16be70023daacd8)

 обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)} обозначает знаковое число Стирлинга первого рода.
обозначает знаковое число Стирлинга первого рода.

 (максимальная ошибка: 2,5 × 10)
(максимальная ошибка: 2,5 × 10) (максимальная ошибка: 3 × 10)
(максимальная ошибка: 3 × 10) (максимальная ошибка: 1,5 × 10)
(максимальная ошибка: 1,5 × 10)

 , что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}





![{ displaystyle { begin {align} operatorname {erfc} (x) = 1- operatorname {erf} (x) \ [5pt ] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8808e6f3ad9aab23f14d55db707a39388d256788)


![{ displaystyle { begin {align} operatorname {erfi} (x) = - i operatorname {erf} (ix) \ [5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2 }} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4480a8ec17e274a7ad6b8ef25cc76234d48c0433)
![{ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x } e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x } { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} справа)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19dc7206f8b3b571e81153816c478abd91a679e)








![{ displaystyle { begin {align} operatorname { i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operatorname {ierfc} (z) = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac { 1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b57abb0a01139b31a14f5a8d651e4aa2e5f4f2)






![{ displaystyle { begin {align} Pr [L_ {a} leq X leq L_ {b}] & = int _ {L_ {a}} ^ {L_ {b}} { frac {1} {{ sqrt {2 pi}} sigma}} exp left (- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}} right) , dx \ & = { frac {1} {2}} left ( operatorname {erf} { frac {L_ {b} - mu} {{ sqrt {2}} sigma}} - operatorname {erf} { frac {L_ {a} - mu} {{ sqrt {2}} sigma}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b3e43d593e389ed348ff56374118ab644fcec8)



![{ displaystyle { begin {align} operatorname {erfc} x & = 1- operatorname {erf} x \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] & = e ^ {- x ^ {2}} operatorname {erfcx} x, end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/582ae24086ba008f0466a71991c48c405c8248ad)


![{ displaystyle { begin {align} operatorname {erfi} x & = - i operatorname {erf} ix \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { 0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] & = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (х), конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937f1aaa2801d245f8056cad15f727ccee0ba1a7)
![{ displaystyle { begin {align} Phi (x) & = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac { -t ^ {2}} {2}} , dt \ [6pt] & = { frac {1} {2}} left (1+ operatorname {erf} { frac {x} { sqrt {2}}} right) \ [6pt] & = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right ) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c70647a7aa4dea3272cb7d90888444e1928c401)
![{ displaystyle { begin {align} operatorname {i} ^ {n} ! operatorname {erfc} z & = int _ {z} ^ { infty} operatorname {i} ^ {n-1} ! operatorname {erfc} zeta , d zeta \ [6pt] operatorname {i} ^ {0} ! operatorname {erfc} z & = operatorname {erfc} z \ operatorname {i} ^ {1} ! Operatorname {erfc} z & = operatorname {ierfc} z = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc } z \ operatorname {i} ^ {2} ! operatorname {erfc} z & = { tfrac {1} {4}} left ( operatorname {erfc} z-2z operatorname {ierfc} z вправо) \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d9046debe25c6cb2fa3709a961ac6a9715a37f)
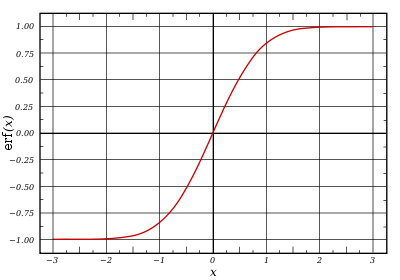
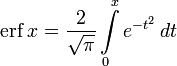 .
.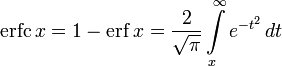 .
.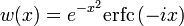 .
.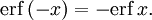

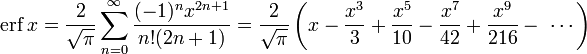
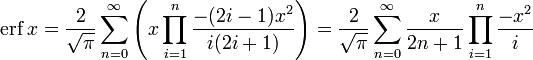
 будет для неё существенно особой.
будет для неё существенно особой.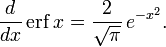
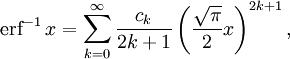

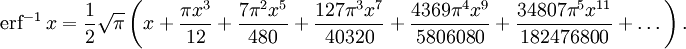 [1]
[1]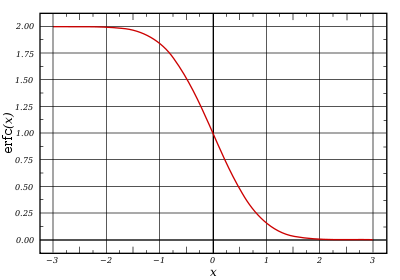
![operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}.,](https://dic.academic.ru/pictures/wiki/files/50/2d5fe0b0f05b66753a4dc4d68612c2e1.png)