From Wikipedia, the free encyclopedia
Verification and validation of computer simulation models is conducted during the development of a simulation model with the ultimate goal of producing an accurate and credible model.[1][2] «Simulation models are increasingly being used to solve problems and to aid in decision-making. The developers and users of these models, the decision makers using information obtained from the results of these models, and the individuals affected by decisions based on such models are all rightly concerned with whether a model and its results are «correct».[3] This concern is addressed through verification and validation of the simulation model.
Simulation models are approximate imitations of real-world systems and they never exactly imitate the real-world system. Due to that, a model should be verified and validated to the degree needed for the model’s intended purpose or application.[3]
The verification and validation of a simulation model starts after functional specifications have been documented and initial model development has been completed.[4] Verification and validation is an iterative process that takes place throughout the development of a model.[1][4]
Verification[edit]
In the context of computer simulation, verification of a model is the process of confirming that it is correctly implemented with respect to the conceptual model (it matches specifications and assumptions deemed acceptable for the given purpose of application).[1][4]
During verification the model is tested to find and fix errors in the implementation of the model.[4]
Various processes and techniques are used to assure the model matches specifications and assumptions with respect to the model concept.
The objective of model verification is to ensure that the implementation of the model is correct.
There are many techniques that can be utilized to verify a model.
These include, but are not limited to, having the model checked by an expert, making logic flow diagrams that include each logically possible action, examining the model output for reasonableness under a variety of settings of the input parameters, and using an interactive debugger.[1]
Many software engineering techniques used for software verification are applicable to simulation model verification.[1]
Validation[edit]
Validation checks the accuracy of the model’s representation of the real system. Model validation is defined to mean «substantiation that a computerized model within its domain of applicability possesses a satisfactory range of accuracy consistent with the intended application of the model».[3] A model should be built for a specific purpose or set of objectives and its validity determined for that purpose.[3]
There are many approaches that can be used to validate a computer model. The approaches range from subjective reviews to objective statistical tests. One approach that is commonly used is to have the model builders determine validity of the model through a series of tests.[3]
Naylor and Finger [1967] formulated a three-step approach to model validation that has been widely followed:[1]
Step 1. Build a model that has high face validity.
Step 2. Validate model assumptions.
Step 3. Compare the model input-output transformations to corresponding input-output transformations for the real system.[5]
Face validity[edit]
A model that has face validity appears to be a reasonable imitation of a real-world system to people who are knowledgeable of the real world system.[4] Face validity is tested by having users and people knowledgeable with the system examine model output for reasonableness and in the process identify deficiencies.[1] An added advantage of having the users involved in validation is that the model’s credibility to the users and the user’s confidence in the model increases.[1][4] Sensitivity to model inputs can also be used to judge face validity.[1] For example, if a simulation of a fast food restaurant drive through was run twice with customer arrival rates of 20 per hour and 40 per hour then model outputs such as average wait time or maximum number of customers waiting would be expected to increase with the arrival rate.
Validation of model assumptions[edit]
Assumptions made about a model generally fall into two categories: structural assumptions about how system works and data assumptions. Also we can consider the simplification assumptions that are those that we use to simplify the reality.[6]
Structural assumptions[edit]
Assumptions made about how the system operates and how it is physically arranged are structural assumptions. For example, the number of servers in a fast food drive through lane and if there is more than one how are they utilized? Do the servers work in parallel where a customer completes a transaction by visiting a single server or does one server take orders and handle payment while the other prepares and serves the order. Many structural problems in the model come from poor or incorrect assumptions.[4] If possible the workings of the actual system should be closely observed to understand how it operates.[4] The systems structure and operation should also be verified with users of the actual system.[1]
Data assumptions[edit]
There must be a sufficient amount of appropriate data available to build a conceptual model and validate a model. Lack of appropriate data is often the reason attempts to validate a model fail.[3] Data should be verified to come from a reliable source. A typical error is assuming an inappropriate statistical distribution for the data.[1] The assumed statistical model should be tested using goodness of fit tests and other techniques.[1][3] Examples of goodness of fit tests are the Kolmogorov–Smirnov test and the chi-square test. Any outliers in the data should be checked.[3]
Simplification assumptions[edit]
Are those assumptions that we know that are not true, but are needed to simplify the problem we want to solve.[6] The use of this assumptions must be restricted to assure that the model is correct enough to serve as an answer for the problem we want to solve.
Validating input-output transformations[edit]
The model is viewed as an input-output transformation for these tests. The validation test consists of comparing outputs from the system under consideration to model outputs for the same set of input conditions. Data recorded while observing the system must be available in order to perform this test.[3] The model output that is of primary interest should be used as the measure of performance.[1] For example, if system under consideration is a fast food drive through where input to model is customer arrival time and the output measure of performance is average customer time in line, then the actual arrival time and time spent in line for customers at the drive through would be recorded. The model would be run with the actual arrival times and the model average time in line would be compared with the actual average time spent in line using one or more tests.
Hypothesis testing[edit]
Statistical hypothesis testing using the t-test can be used as a basis to accept the model as valid or reject it as invalid.
The hypothesis to be tested is
- H0 the model measure of performance = the system measure of performance
versus
- H1 the model measure of performance ≠ the system measure of performance.
The test is conducted for a given sample size and level of significance or α. To perform the test a number n statistically independent runs of the model are conducted and an average or expected value, E(Y), for the variable of interest is produced. Then the test statistic, t0 is computed for the given α, n, E(Y) and the observed value for the system μ0
and the critical value for α and n-1 the degrees of freedom
is calculated.
If
reject H0, the model needs adjustment.
There are two types of error that can occur using hypothesis testing, rejecting a valid model called type I error or «model builders risk» and accepting an invalid model called Type II error, β, or «model user’s risk».[3] The level of significance or α is equal the probability of type I error.[3] If α is small then rejecting the null hypothesis is a strong conclusion.[1] For example, if α = 0.05 and the null hypothesis is rejected there is only a 0.05 probability of rejecting a model that is valid. Decreasing the probability of a type II error is very important.[1][3] The probability of correctly detecting an invalid model is 1 — β. The probability of a type II error is dependent of the sample size and the actual difference between the sample value and the observed value. Increasing the sample size decreases the risk of a type II error.
Model accuracy as a range[edit]
A statistical technique where the amount of model accuracy is specified as a range has recently been developed. The technique uses hypothesis testing to accept a model if the difference between a model’s variable of interest and a system’s variable of interest is within a specified range of accuracy.[7] A requirement is that both the system data and model data be approximately Normally Independent and Identically Distributed (NIID). The t-test statistic is used in this technique. If the mean of the model is μm and the mean of system is μs then the difference between the model and the system is D = μm — μs. The hypothesis to be tested is if D is within the acceptable range of accuracy. Let L = the lower limit for accuracy and U = upper limit for accuracy. Then
- H0 L ≤ D ≤ U
versus
- H1 D < L or D > U
is to be tested.
The operating characteristic (OC) curve is the probability that the null hypothesis is accepted when it is true. The OC curve characterizes the probabilities of both type I and II errors. Risk curves for model builder’s risk and model user’s can be developed from the OC curves. Comparing curves with fixed sample size tradeoffs between model builder’s risk and model user’s risk can be seen easily in the risk curves.[7] If model builder’s risk, model user’s risk, and the upper and lower limits for the range of accuracy are all specified then the sample size needed can be calculated.[7]
Confidence intervals[edit]
Confidence intervals can be used to evaluate if a model is «close enough»[1] to a system for some variable of interest. The difference between the known model value, μ0, and the system value, μ, is checked to see if it is less than a value small enough that the model is valid with respect that variable of interest. The value is denoted by the symbol ε. To perform the test a number, n, statistically independent runs of the model are conducted and a mean or expected value, E(Y) or μ for simulation output variable of interest Y, with a standard deviation S is produced. A confidence level is selected, 100(1-α). An interval, [a,b], is constructed by
,
where
is the critical value from the t-distribution for the given level of significance and n-1 degrees of freedom.
- If |a-μ0| > ε and |b-μ0| > ε then the model needs to be calibrated since in both cases the difference is larger than acceptable.
- If |a-μ0| < ε and |b-μ0| < ε then the model is acceptable as in both cases the error is close enough.
- If |a-μ0| < ε and |b-μ0| > ε or vice versa then additional runs of the model are needed to shrink the interval.
Graphical comparisons[edit]
If statistical assumptions cannot be satisfied or there is insufficient data for the system a graphical comparisons of model outputs to system outputs can be used to make a subjective decisions, however other objective tests are preferable.[3]
ASME Standards[edit]
Documents and standards involving verification and validation of computational modeling and simulation are developed by the American Society of Mechanical Engineers (ASME) Verification and Validation (V&V) Committee. ASME V&V 10 provides guidance in assessing and increasing the credibility of computational solid mechanics models through the processes of verification, validation, and uncertainty quantification.[8] ASME V&V 10.1 provides a detailed example to illustrate the concepts described in ASME V&V 10.[9] ASME V&V 20 provides a detailed methodology for validating computational simulations as applied to fluid dynamics and heat transfer.[10] ASME V&V 40 provides a framework for establishing model credibility requirements for computational modeling, and presents examples specific in the medical device industry. [11]
See also[edit]
- Verification and validation
- Software verification and validation
References[edit]
- ^ a b c d e f g h i j k l m n o p Banks, Jerry; Carson, John S.; Nelson, Barry L.; Nicol, David M. Discrete-Event System Simulation Fifth Edition, Upper Saddle River, Pearson Education, Inc. 2010 ISBN 0136062121
- ^ Schlesinger, S.; et al. (1979). «Terminology for model credibility». Simulation. 32 (3): 103–104. doi:10.1177/003754977903200304.
- ^ a b c d e f g h i j k l m Sargent, Robert G. «VERIFICATION AND VALIDATION OF SIMULATION MODELS». Proceedings of the 2011 Winter Simulation Conference.
- ^ a b c d e f g h Carson, John, «MODEL VERIFICATION AND VALIDATION». Proceedings of the 2002 Winter Simulation Conference.
- ^ NAYLOR, T. H., AND J. M. FINGER [1967], «Verification of Computer Simulation Models», Management Science, Vol. 2, pp. B92– B101., cited in Banks, Jerry; Carson, John S.; Nelson, Barry L.; Nicol, David M. Discrete-Event System Simulation Fifth Edition, Upper Saddle River, Pearson Education, Inc. 2010 p. 396. ISBN 0136062121
- ^ a b 1. Fonseca, P. Simulation hypotheses. In Proceedings of SIMUL 2011; 2011; pp. 114–119. https://www.researchgate.net/publication/262187532_Simulation_hypotheses_A_proposed_taxonomy_for_the_hypotheses_used_in_a_simulation_model
- ^ a b c Sargent, R. G. 2010. «A New Statistical Procedure for Validation of Simulation and Stochastic Models.» Technical Report SYR-EECS-2010-06, Department of Electrical Engineering and Computer Science, Syracuse University, Syracuse, New York.
- ^ “V&V 10 – 2006 Guide for Verification and Validation in Computational Solid Mechanics”. Standards. ASME. Retrieved 2 September 2018.
- ^ “V&V 10.1 – 2012 An Illustration of the Concepts of Verification and Validation in Computational Solid Mechanics”. Standards. ASME. Retrieved 2 September 2018.
- ^ “V&V 20 – 2009 Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer”. Standards. ASME. Retrieved 2 September 2018.
- ^ “V&V 40 Industry Day”. Verification and Validation Symposium. ASME. Retrieved 2 September 2018.
From Wikipedia, the free encyclopedia
Verification and validation of computer simulation models is conducted during the development of a simulation model with the ultimate goal of producing an accurate and credible model.[1][2] «Simulation models are increasingly being used to solve problems and to aid in decision-making. The developers and users of these models, the decision makers using information obtained from the results of these models, and the individuals affected by decisions based on such models are all rightly concerned with whether a model and its results are «correct».[3] This concern is addressed through verification and validation of the simulation model.
Simulation models are approximate imitations of real-world systems and they never exactly imitate the real-world system. Due to that, a model should be verified and validated to the degree needed for the model’s intended purpose or application.[3]
The verification and validation of a simulation model starts after functional specifications have been documented and initial model development has been completed.[4] Verification and validation is an iterative process that takes place throughout the development of a model.[1][4]
Verification[edit]
In the context of computer simulation, verification of a model is the process of confirming that it is correctly implemented with respect to the conceptual model (it matches specifications and assumptions deemed acceptable for the given purpose of application).[1][4]
During verification the model is tested to find and fix errors in the implementation of the model.[4]
Various processes and techniques are used to assure the model matches specifications and assumptions with respect to the model concept.
The objective of model verification is to ensure that the implementation of the model is correct.
There are many techniques that can be utilized to verify a model.
These include, but are not limited to, having the model checked by an expert, making logic flow diagrams that include each logically possible action, examining the model output for reasonableness under a variety of settings of the input parameters, and using an interactive debugger.[1]
Many software engineering techniques used for software verification are applicable to simulation model verification.[1]
Validation[edit]
Validation checks the accuracy of the model’s representation of the real system. Model validation is defined to mean «substantiation that a computerized model within its domain of applicability possesses a satisfactory range of accuracy consistent with the intended application of the model».[3] A model should be built for a specific purpose or set of objectives and its validity determined for that purpose.[3]
There are many approaches that can be used to validate a computer model. The approaches range from subjective reviews to objective statistical tests. One approach that is commonly used is to have the model builders determine validity of the model through a series of tests.[3]
Naylor and Finger [1967] formulated a three-step approach to model validation that has been widely followed:[1]
Step 1. Build a model that has high face validity.
Step 2. Validate model assumptions.
Step 3. Compare the model input-output transformations to corresponding input-output transformations for the real system.[5]
Face validity[edit]
A model that has face validity appears to be a reasonable imitation of a real-world system to people who are knowledgeable of the real world system.[4] Face validity is tested by having users and people knowledgeable with the system examine model output for reasonableness and in the process identify deficiencies.[1] An added advantage of having the users involved in validation is that the model’s credibility to the users and the user’s confidence in the model increases.[1][4] Sensitivity to model inputs can also be used to judge face validity.[1] For example, if a simulation of a fast food restaurant drive through was run twice with customer arrival rates of 20 per hour and 40 per hour then model outputs such as average wait time or maximum number of customers waiting would be expected to increase with the arrival rate.
Validation of model assumptions[edit]
Assumptions made about a model generally fall into two categories: structural assumptions about how system works and data assumptions. Also we can consider the simplification assumptions that are those that we use to simplify the reality.[6]
Structural assumptions[edit]
Assumptions made about how the system operates and how it is physically arranged are structural assumptions. For example, the number of servers in a fast food drive through lane and if there is more than one how are they utilized? Do the servers work in parallel where a customer completes a transaction by visiting a single server or does one server take orders and handle payment while the other prepares and serves the order. Many structural problems in the model come from poor or incorrect assumptions.[4] If possible the workings of the actual system should be closely observed to understand how it operates.[4] The systems structure and operation should also be verified with users of the actual system.[1]
Data assumptions[edit]
There must be a sufficient amount of appropriate data available to build a conceptual model and validate a model. Lack of appropriate data is often the reason attempts to validate a model fail.[3] Data should be verified to come from a reliable source. A typical error is assuming an inappropriate statistical distribution for the data.[1] The assumed statistical model should be tested using goodness of fit tests and other techniques.[1][3] Examples of goodness of fit tests are the Kolmogorov–Smirnov test and the chi-square test. Any outliers in the data should be checked.[3]
Simplification assumptions[edit]
Are those assumptions that we know that are not true, but are needed to simplify the problem we want to solve.[6] The use of this assumptions must be restricted to assure that the model is correct enough to serve as an answer for the problem we want to solve.
Validating input-output transformations[edit]
The model is viewed as an input-output transformation for these tests. The validation test consists of comparing outputs from the system under consideration to model outputs for the same set of input conditions. Data recorded while observing the system must be available in order to perform this test.[3] The model output that is of primary interest should be used as the measure of performance.[1] For example, if system under consideration is a fast food drive through where input to model is customer arrival time and the output measure of performance is average customer time in line, then the actual arrival time and time spent in line for customers at the drive through would be recorded. The model would be run with the actual arrival times and the model average time in line would be compared with the actual average time spent in line using one or more tests.
Hypothesis testing[edit]
Statistical hypothesis testing using the t-test can be used as a basis to accept the model as valid or reject it as invalid.
The hypothesis to be tested is
- H0 the model measure of performance = the system measure of performance
versus
- H1 the model measure of performance ≠ the system measure of performance.
The test is conducted for a given sample size and level of significance or α. To perform the test a number n statistically independent runs of the model are conducted and an average or expected value, E(Y), for the variable of interest is produced. Then the test statistic, t0 is computed for the given α, n, E(Y) and the observed value for the system μ0
and the critical value for α and n-1 the degrees of freedom
is calculated.
If
reject H0, the model needs adjustment.
There are two types of error that can occur using hypothesis testing, rejecting a valid model called type I error or «model builders risk» and accepting an invalid model called Type II error, β, or «model user’s risk».[3] The level of significance or α is equal the probability of type I error.[3] If α is small then rejecting the null hypothesis is a strong conclusion.[1] For example, if α = 0.05 and the null hypothesis is rejected there is only a 0.05 probability of rejecting a model that is valid. Decreasing the probability of a type II error is very important.[1][3] The probability of correctly detecting an invalid model is 1 — β. The probability of a type II error is dependent of the sample size and the actual difference between the sample value and the observed value. Increasing the sample size decreases the risk of a type II error.
Model accuracy as a range[edit]
A statistical technique where the amount of model accuracy is specified as a range has recently been developed. The technique uses hypothesis testing to accept a model if the difference between a model’s variable of interest and a system’s variable of interest is within a specified range of accuracy.[7] A requirement is that both the system data and model data be approximately Normally Independent and Identically Distributed (NIID). The t-test statistic is used in this technique. If the mean of the model is μm and the mean of system is μs then the difference between the model and the system is D = μm — μs. The hypothesis to be tested is if D is within the acceptable range of accuracy. Let L = the lower limit for accuracy and U = upper limit for accuracy. Then
- H0 L ≤ D ≤ U
versus
- H1 D < L or D > U
is to be tested.
The operating characteristic (OC) curve is the probability that the null hypothesis is accepted when it is true. The OC curve characterizes the probabilities of both type I and II errors. Risk curves for model builder’s risk and model user’s can be developed from the OC curves. Comparing curves with fixed sample size tradeoffs between model builder’s risk and model user’s risk can be seen easily in the risk curves.[7] If model builder’s risk, model user’s risk, and the upper and lower limits for the range of accuracy are all specified then the sample size needed can be calculated.[7]
Confidence intervals[edit]
Confidence intervals can be used to evaluate if a model is «close enough»[1] to a system for some variable of interest. The difference between the known model value, μ0, and the system value, μ, is checked to see if it is less than a value small enough that the model is valid with respect that variable of interest. The value is denoted by the symbol ε. To perform the test a number, n, statistically independent runs of the model are conducted and a mean or expected value, E(Y) or μ for simulation output variable of interest Y, with a standard deviation S is produced. A confidence level is selected, 100(1-α). An interval, [a,b], is constructed by
,
where
is the critical value from the t-distribution for the given level of significance and n-1 degrees of freedom.
- If |a-μ0| > ε and |b-μ0| > ε then the model needs to be calibrated since in both cases the difference is larger than acceptable.
- If |a-μ0| < ε and |b-μ0| < ε then the model is acceptable as in both cases the error is close enough.
- If |a-μ0| < ε and |b-μ0| > ε or vice versa then additional runs of the model are needed to shrink the interval.
Graphical comparisons[edit]
If statistical assumptions cannot be satisfied or there is insufficient data for the system a graphical comparisons of model outputs to system outputs can be used to make a subjective decisions, however other objective tests are preferable.[3]
ASME Standards[edit]
Documents and standards involving verification and validation of computational modeling and simulation are developed by the American Society of Mechanical Engineers (ASME) Verification and Validation (V&V) Committee. ASME V&V 10 provides guidance in assessing and increasing the credibility of computational solid mechanics models through the processes of verification, validation, and uncertainty quantification.[8] ASME V&V 10.1 provides a detailed example to illustrate the concepts described in ASME V&V 10.[9] ASME V&V 20 provides a detailed methodology for validating computational simulations as applied to fluid dynamics and heat transfer.[10] ASME V&V 40 provides a framework for establishing model credibility requirements for computational modeling, and presents examples specific in the medical device industry. [11]
See also[edit]
- Verification and validation
- Software verification and validation
References[edit]
- ^ a b c d e f g h i j k l m n o p Banks, Jerry; Carson, John S.; Nelson, Barry L.; Nicol, David M. Discrete-Event System Simulation Fifth Edition, Upper Saddle River, Pearson Education, Inc. 2010 ISBN 0136062121
- ^ Schlesinger, S.; et al. (1979). «Terminology for model credibility». Simulation. 32 (3): 103–104. doi:10.1177/003754977903200304.
- ^ a b c d e f g h i j k l m Sargent, Robert G. «VERIFICATION AND VALIDATION OF SIMULATION MODELS». Proceedings of the 2011 Winter Simulation Conference.
- ^ a b c d e f g h Carson, John, «MODEL VERIFICATION AND VALIDATION». Proceedings of the 2002 Winter Simulation Conference.
- ^ NAYLOR, T. H., AND J. M. FINGER [1967], «Verification of Computer Simulation Models», Management Science, Vol. 2, pp. B92– B101., cited in Banks, Jerry; Carson, John S.; Nelson, Barry L.; Nicol, David M. Discrete-Event System Simulation Fifth Edition, Upper Saddle River, Pearson Education, Inc. 2010 p. 396. ISBN 0136062121
- ^ a b 1. Fonseca, P. Simulation hypotheses. In Proceedings of SIMUL 2011; 2011; pp. 114–119. https://www.researchgate.net/publication/262187532_Simulation_hypotheses_A_proposed_taxonomy_for_the_hypotheses_used_in_a_simulation_model
- ^ a b c Sargent, R. G. 2010. «A New Statistical Procedure for Validation of Simulation and Stochastic Models.» Technical Report SYR-EECS-2010-06, Department of Electrical Engineering and Computer Science, Syracuse University, Syracuse, New York.
- ^ “V&V 10 – 2006 Guide for Verification and Validation in Computational Solid Mechanics”. Standards. ASME. Retrieved 2 September 2018.
- ^ “V&V 10.1 – 2012 An Illustration of the Concepts of Verification and Validation in Computational Solid Mechanics”. Standards. ASME. Retrieved 2 September 2018.
- ^ “V&V 20 – 2009 Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer”. Standards. ASME. Retrieved 2 September 2018.
- ^ “V&V 40 Industry Day”. Verification and Validation Symposium. ASME. Retrieved 2 September 2018.
Проверка и валидация компьютерных имитационных моделей проводится во время разработки имитационной модели с конечной целью создания точной и достоверной модели.[1][2] «Имитационные модели все чаще используются для решения проблем и помощи в принятии решений. Разработчики и пользователи этих моделей, лица, принимающие решения, использующие информацию, полученную на основе результатов этих моделей, и лица, на которых влияют решения, основанные на таких моделях, являются все справедливо озабочены тем, являются ли модель и ее результаты «правильными».[3] Эта проблема решается путем проверки и валидации имитационной модели.[4]
Имитационные модели являются приблизительной имитацией реальных систем, и они никогда не имитируют в точности реальную систему. В связи с этим модель должна быть проверена и утверждена в степени, необходимой для ее предполагаемого назначения или применения.[3]
Проверка и валидация имитационной модели начинается после документирования функциональных спецификаций и завершения первоначальной разработки модели.[5] Верификация и валидация — это итеративный процесс, который происходит на протяжении всей разработки модели.[1][5]
Проверка
В контексте компьютерного моделирования проверка модели — это процесс подтверждения того, что она правильно реализована по отношению к концептуальной модели (соответствует спецификациям и предположениям, которые считаются приемлемыми для данной цели приложения).[1][5]Во время верификации модель тестируется для поиска и исправления ошибок в реализации модели.[5]Для обеспечения соответствия модели спецификациям и предположениям в отношении концепции модели используются различные процессы и методы. Цель проверки модели — убедиться, что реализация модели верна.
Существует множество методов, которые можно использовать для проверки модели, включая, помимо прочего, проверку модели экспертом, создание логических блок-схем, включающих каждое логически возможное действие, проверку выходных данных модели на разумность в различных условиях. настройки входных параметров и с помощью интерактивного отладчика.[1]Многие методы разработки программного обеспечения, используемые для проверка программного обеспечения применимы для верификации имитационной модели.[1]
Проверка
Валидация проверяет точность представления модели реальной системы. Валидация модели определяется как «подтверждение того, что компьютеризированная модель в пределах ее области применимости обладает удовлетворительным диапазоном точности, совместимым с предполагаемым применением модели».[3] Модель должна быть построена для конкретной цели или набора задач, а ее применимость должна определяться для этой цели.[3]
Есть много подходов, которые можно использовать для проверки компьютерной модели. Подходы варьируются от субъективных обзоров до объективных статистических тестов. Один из широко используемых подходов состоит в том, чтобы разработчики моделей определяли достоверность модели с помощью серии тестов.[3]
Нейлор и Фингер [1967] сформулировали трехэтапный подход к проверке достоверности модели, который получил широкое распространение:[1]
Шаг 1. Постройте модель с высокой достоверностью.
Шаг 2. Подтвердите допущения модели.
Шаг 3. Сравните преобразования ввода-вывода модели с соответствующими преобразованиями ввода-вывода для реальной системы.[6]
Действительность лица
Модель, имеющая действительность лица кажется разумной имитацией системы реального мира для людей, знакомых с системой реального мира.[5] Подтверждение подлинности проверяется тем, что пользователи и люди, знакомые с системой, проверяют выходные данные модели на разумность и в процессе выявляют недостатки.[1] Дополнительным преимуществом участия пользователей в проверке является то, что доверие к модели для пользователей и доверие пользователя к модели возрастают.[1][5] Чувствительность к входным данным модели также может использоваться для оценки достоверности лица.[1] Например, если моделирование проезда в ресторан быстрого питания было выполнено дважды с темпами прибытия клиентов 20 в час и 40 в час, тогда ожидается, что выходные данные модели, такие как среднее время ожидания или максимальное количество ожидающих клиентов, увеличатся с прибытием. ставка.
Проверка допущений модели
Предположения, сделанные в отношении модели, обычно делятся на две категории: структурные предположения о том, как работает система, и предположения о данных. Также мы можем рассмотреть допущения упрощения, которые мы используем для упрощения реальности.[7]
Структурные допущения
Предположения о том, как работает система и как она устроена физически, являются структурными предположениями. Например, количество серверов в фаст-фуде проезжает по переулку, и если их больше одного, как они используются? Серверы работают параллельно, когда клиент завершает транзакцию, посещая один сервер, или один сервер принимает заказы и обрабатывает платежи, в то время как другой готовит и обслуживает заказ. Многие структурные проблемы в модели возникают из-за неверных или неверных предположений.[5] Если возможно, необходимо внимательно наблюдать за работой реальной системы, чтобы понять, как она работает.[5] Структура и работа системы также должны быть проверены пользователями реальной системы.[1]
Предположения в отношении данных
Для построения концептуальной модели и проверки модели должен быть достаточный объем соответствующих данных. Отсутствие соответствующих данных часто является причиной неудачных попыток проверки модели.[3] Данные должны быть проверены и получены из надежного источника. Типичная ошибка — это предположение о несоответствующем статистическом распределении данных.[1] Предполагаемая статистическая модель должна быть протестирована с использованием критериев согласия и других методов.[1][3] Примеры критериев согласия: Тест Колмогорова – Смирнова и критерий хи-квадрат. Любые выбросы в данных должны быть проверены.[3]
Допущения упрощения
Являются ли те предположения, которые мы знаем, которые неверны, но необходимы для упрощения проблемы, которую мы хотим решить.[7] Использование этих предположений должно быть ограничено, чтобы гарантировать, что модель достаточно верна, чтобы служить ответом на проблему, которую мы хотим решить.
Проверка преобразований ввода-вывода
Модель рассматривается как преобразование ввода-вывода для этих тестов. Проверочный тест состоит из сравнения выходных данных рассматриваемой системы с выходными данными модели для того же набора входных условий. Данные, записанные во время наблюдения за системой, должны быть доступны для выполнения этого теста.[3] Выходные данные модели, представляющие основной интерес, следует использовать в качестве меры производительности.[1] Например, если рассматриваемая система представляет собой поездку в фастфуд, где входными данными для модели является время прибытия клиента, а выходным показателем эффективности является среднее время ожидания клиента в очереди, тогда фактическое время прибытия и время, проведенное в очереди для клиентов во время проезда. будет записан. Модель будет запускаться с фактическим временем прибытия, и среднее время нахождения в очереди будет сравниваться с фактическим средним временем, проведенным в очереди с использованием одного или нескольких тестов.
Проверка гипотезы
Статистическая проверка гипотез с использованием t-тест может использоваться как основание для принятия модели как действительной или отклонения как недействительной.
Гипотеза, подлежащая проверке:
- ЧАС0 модельная мера эффективности = системная мера эффективности
против
- ЧАС1 модельная мера эффективности ≠ системная мера эффективности.
Тест проводится для заданного размера выборки и уровня значимости или α. Для выполнения теста номер п Выполняются статистически независимые прогоны модели и вычисляется среднее или ожидаемое значение E (Y) для интересующей переменной. Тогда тестовая статистика, т0 вычисляется для данного α, п, E (Y) и наблюдаемое значение для системы μ0
а критическое значение для α и n-1 степеней свободы
рассчитывается.
Если
отклонить H0, модель требует корректировки.
Существует два типа ошибок, которые могут возникнуть при проверке гипотез: отклонение действительной модели, называемое ошибкой типа I или «риск создателей модели», и принятие неверной модели, называемой ошибкой типа II, β или «риском пользователя модели».[3] Уровень значимости или α равен вероятности ошибки типа I.[3] Если α мало, то отказ от нулевой гипотезы является сильным выводом.[1] Например, если α = 0,05 и нулевая гипотеза отклоняется, вероятность отклонения действительной модели составляет всего 0,05. Очень важно снизить вероятность ошибки типа II.[1][3] Вероятность корректного обнаружения неверной модели равна 1 — β. Вероятность ошибки типа II зависит от размера выборки и фактической разницы между значением выборки и наблюдаемым значением. Увеличение размера выборки снижает риск ошибки типа II.
Точность модели как диапазон
Недавно был разработан статистический метод, в котором степень точности модели определяется как диапазон. Этот метод использует проверку гипотез для принятия модели, если разница между интересующей переменной модели и интересующей системной переменной находится в пределах указанного диапазона точности.[8] Требуется, чтобы и системные данные, и данные модели были приблизительно Обычно Независимые и идентично распределенные (NIID). В t-тест статистика используется в этой методике. Если среднее значение модели μм а среднее значение системы равно μs то разница между моделью и системой D = μм — μs. Гипотеза, подлежащая проверке, заключается в том, находится ли D в приемлемом диапазоне точности. Пусть L = нижний предел точности и U = верхний предел точности. потом
- ЧАС0 L ≤ D ≤ U
против
- ЧАС1 D U
подлежит испытанию.
Кривая рабочей характеристики (ОС) — это вероятность того, что нулевая гипотеза будет принята, когда она верна. Кривая OC характеризует вероятность ошибок как I, так и II типа. Кривые риска для риска создателя модели и пользователя модели могут быть построены на основе кривых OC. Сравнение кривых с фиксированным размером выборки между риском разработчика модели и риском пользователя модели можно легко увидеть на кривых риска.[8] Если риск разработчика модели, риск пользователя модели, а также верхний и нижний пределы диапазона точности заданы, то можно рассчитать необходимый размер выборки.[8]
Доверительные интервалы
Доверительные интервалы можно использовать для оценки того, «достаточно ли близка» модель[1] в систему для некоторой интересующей переменной. Разница между известным модельным значением μ0, и системное значение μ проверяется, чтобы увидеть, меньше ли оно значения, достаточно малого для того, чтобы модель действительна в отношении интересующей переменной. Значение обозначается символом ε. Чтобы выполнить тест номер, п, статистически независимые прогоны модели проводятся и среднее или ожидаемое значение E (Y) или μ для представляющей интерес выходной переменной моделирования Y со стандартным отклонением S производится. Выбран уровень достоверности 100 (1-α). Интервал [a, b] строится следующим образом:
,
куда
— критическое значение из t-распределения для данного уровня значимости и n-1 степеней свободы.
- Если | a-μ0| > ε и | b-μ0| > ε, то модель необходимо откалибровать, поскольку в обоих случаях разница больше допустимой.
- Если | a-μ0| <ε и | b-μ0| <ε, то модель приемлема, так как в обоих случаях ошибка достаточно близка.
- Если | a-μ0| <ε и | b-μ0| > ε или наоборот тогда необходимы дополнительные прогоны модели, чтобы сократить интервал.
Графические сравнения
Если статистические допущения не могут быть выполнены или для системы недостаточно данных, для принятия субъективных решений можно использовать графические сравнения выходных данных модели с выходными данными системы, однако предпочтительны другие объективные тесты.[3]
Стандарты ASME
Документы и стандарты, включающие верификацию и валидацию компьютерного моделирования и симуляции, разрабатываются Американское общество инженеров-механиков (ASME) Комитет по проверке и валидации (V&V). ASME V&V 10 предоставляет руководство по оценке и повышению достоверности вычислительных моделей механики твердого тела посредством процессов верификации, валидации и количественной оценки неопределенности.[9] ASME V&V 10.1 предоставляет подробный пример, иллюстрирующий концепции, описанные в ASME V&V 10.[10] ASME V&V 20 предоставляет подробную методологию для проверки компьютерного моделирования применительно к гидродинамике и теплопередаче.[11] ASME V&V 40 обеспечивает основу для установления требований к достоверности модели для компьютерного моделирования и представляет примеры, характерные для индустрии медицинских устройств. [12]
Смотрите также
- Верификация и валидация
- Проверка и проверка программного обеспечения
Рекомендации
- ^ а б c d е ж грамм час я j k л м п о п Бэнкс, Джерри; Карсон, Джон С .; Нельсон, Барри Л .; Николь, Дэвид М. Моделирование дискретных систем Пятое издание, Верхняя Сэдл-Ривер, Pearson Education, Inc., 2010 г. ISBN 0136062121
- ^ Schlesinger, S .; и другие. (1979). «Терминология достоверности модели». Моделирование. 32 (3): 103–104. Дои:10.1177/003754977903200304.
- ^ а б c d е ж грамм час я j k л м Сарджент, Роберт Г. «ПРОВЕРКА И ПРОВЕРКА МОДЕЛИРОВАНИЯ». Материалы Зимней симуляционной конференции 2011 г.
- ^ Hemakumara et al;https://www.researchgate.net/profile/Gpts_Hemakumara/publication/339540267_Field_Verifications_of_the_Arc_GIS_Based_Automation_Landform_Model_Including_the_Recommendations_to_Enhance_the_Automation_System_with_Ground_Reality/links/5e580b9092851cefa1c9dcd3/Field-Verifications-of-the-Arc-GIS-Based-Automation-Landform-Model-Including-the-Recommendations-to- Улучшите-систему-автоматизации-с-наземной-реальностью.pdf
- ^ а б c d е ж грамм час Карсон, Джон, «ПРОВЕРКА И ВАЛИДАЦИЯ МОДЕЛИ». Труды Зимней имитационной конференции 2002 г.
- ^ НЭЙЛОР, Т. Х., И Дж. М. ФИНГЕР [1967], «Верификация компьютерных имитационных моделей», Наука управления, Vol. 2, pp. B92– B101., Цит. По: Бэнкс, Джерри; Карсон, Джон С .; Нельсон, Барри Л .; Николь, Дэвид М. Моделирование дискретных систем Пятое издание, Верхняя Сэдл-Ривер, Pearson Education, Inc., 2010 г., стр. 396. ISBN 0136062121
- ^ а б 1. Фонсека П. Имитационные гипотезы. В материалах SIMUL 2011; 2011; С. 114–119. https://www.researchgate.net/publication/262187532_Simulation_hypotheses_A_proposed_taxonomy_for_the_hypotheses_used_in_a_simulation_model
- ^ а б c Сарджент, Р. Г. 2010. «Новая статистическая процедура для проверки имитационных и стохастических моделей». Технический отчет SYR-EECS-2010-06, Департамент электротехники и компьютерных наук, Сиракузский университет, Сиракузы, Нью-Йорк.
- ^ «V&V 10 — 2006 Руководство по верификации и валидации в вычислительной механике твердого тела». Стандарты. КАК Я. Проверено 2 сентября 2018 года.
- ^ «V&V 10.1 — 2012 Иллюстрация концепций верификации и валидации в вычислительной механике твердого тела». Стандарты. КАК Я. Проверено 2 сентября 2018 года.
- ^ «V&V 20 — Стандарт 2009 для проверки и подтверждения в вычислительной гидродинамике и теплопередаче». Стандарты. КАК Я. Проверено 2 сентября 2018 года.
- ^ «День индустрии V&V 40». Симпозиум по верификации и валидации. КАК Я. Проверено 2 сентября 2018 года.
-
Исследование и проверка модели
Средства
вычислительной техники, которые в
настоящее время широко используются
либо для вычислений при аналитическом
моделировании, либо для реализации
имитационной модели системы, могут лишь
помочь с точки зрения эффективности
реализации сложной модели, но не позволяют
подтвердить правильность той или иной
модели. Проверку на синтаксические
ошибки программа проходит в процессе
компиляции или трансляции. Логические
же ошибки и ошибки формирования самой
математической модели выявляют на
следующем этапе — этапе проверки модели
с использованием готовой (откомпилированной)
моделирующей программы и набора тестовых
данных, полученных на реальной установке.
Проверка
достоверности программы выполняется
в следующей последовательности [161,163]:
а) проверка отдельных частей программы
при решении различных тестовых задач;
б) объединение всех частей программы и
проверка ее в целом;
в) оценка средств моделирования
(затраченных ресурсов).
Для
программы в целом и её отдельных частей
выполняют проверку:
• полноты учета основных факторов и
ограничений, влияющих на работу системы;
• соответствия исходных данных модели
реальным;
• наличия в модели всех данных,
необходимых для накопления ответных
величин;
• правильности преобразования исходных
данных в конечные результаты (например,
при условиях, приводящих к известному
аналитическому решению);
• осмысленности результатов при
нормальных условиях (поступательный
ход модельного времени, отсутствие
переполнения буферов и счетчиков) и в
предельных случаях (пробные прогоны в
условиях перегрузки системы).
Для
программы в целом выполняют проверку
адекватности, устойчивости, чувствительности
и точности модели.
Проверку
адекватности (соответствия)
математической модели исследуемому
процессу необходимо проводить по той
причине, что любая модель является лишь
приближенным отражением реального
процесса вследствие допущений, всегда
принимаемых при составлении математической
модели. На этом этапе устанавливается,
насколько принятые допущения правомерны,
и тем самым определяется, применима ли
полученная модель для исследования
процесса.
Для
проверки адекватности модели осуществляется
воспроизведение, или имитация, объекта
на ЭВМ с помощью программы в соответствии
с задачами исследования. После этого
определяется степень близости машинных
результатов и поведения исследуемого
объекта. При этом существенно не
«абсолютное качество» машинных
результатов, а степень сходства с
объектом исследования. Так, при
моделировании автоколебаний важно не
то, чтобы результаты моделирования в
точности совпадали с реально наблюдаемыми
колебаниями, а чтобы они имели аналогичную
форму и аналогичный характер протекания.
Модель должна обладать только существенными
признаками объекта моделирования.
Если
в ходе моделирования существенное место
занимает реальный физический эксперимент,
то здесь весьма важна и надежность
используемых инструментальных средств,
поскольку сбои и отказы программно-технических
средств могут приводить к искаженным
значениям выходных данных, отображающих
протекание процесса. И в этом смысле
при проведении физических экспериментов
необходимы специальная аппаратура,
специально разработанное математическое
и информационное обеспечение, которые
позволяют реализовать диагностику
средств моделирования, чтобы отсеять
те ошибки в выходной информации, которые
вызваны неисправностями функционирующей
аппаратуры. В ходе машинного эксперимента
могут иметь место и ошибочные действия
самого исследователя. В этих условиях
серьезные задачи стоят в области
эргономического обеспечения процесса
моделирования.
Успешный
результат сравнения (оценки) исследуемого
объекта с моделью свидетельствует о
достаточной степени изученности объекта,
о правильности принципов, положенных
в основу моделирования, и о том, что
алгоритм, моделирующий объект, не
содержит ошибок, т. е. о том, что созданная
модель работоспособна. Такая модель
может быть использована для дальнейших
более глубоких исследований объекта в
различных новых условиях, в которых
реальный объект еще не изучался.
Чаще,
однако, первые результаты моделирования
не удовлетворяют предъявленным
требованиям. Это означает, что, по крайней
мере, в одной из перечисленных выше
позиций (изученность объекта, исходные
принципы, алгоритм) имеются дефекты.
Это требует проведения дополнительных
исследований, корректировки математической
модели. Для этого используются результаты
измерений на самом объекте или на его
физической модели, воспроизводящей в
небольших масштабах основные физические
закономерности объекта моделирования.
После соответствующего изменения
машинной программы снова повторяются
третий и четвертый этапы. Процедура
повторяется до получения надежных
результатов.
При
решении всех задач проектирования с
использованием математического
моделирования важным вопросом также
является получение необходимой точности.
Недостаточная точность моделируемых
данных может привести к ложным выводам
или выбору неправильного варианта
технологического процесса (либо
параметра, что менее опасно). В случае
моделирования на ЭВМ инструментальную
точность ограничивают два существенных
фактора: надежность ЭВМ (или, точнее,
вероятность случайного сбоя в процессе
счета) и вычислительная точность,
связанная с ограниченностью представления
чисел в памяти ЭВМ и неизбежными ошибками
округления. При отсутствии двойного
счета ошибки вследствие случайного
сбоя ЭВМ входят непосредственно в
результаты моделирования и вносят
трудно устранимую дополнительную
погрешность, которая может быть
значительной, особенно при малых
вероятностях исследуемых событий.
Случайные сбои при решении ряда задач
могут быть обнаружены визуальным
контролем с помощью графических дисплеев,
сопряженных с ЭВМ, на которой выполняется
моделирование.
Представление
процессов реальных непрерывных систем
при моделировании в виде временного
ряда сопряжено с дополнительной потерей
точности. Поэтому представление состояний
модели и входных сигналов не может быть
выбрано произвольно, а зависит от
требуемой точности результатов,
характеристик этих сигналов и особенностей
моделируемой системы и должно быть
специально рассчитано.
На
точность и устойчивость результатов
моделирования, а также на его вычислительную
эффективность оказывает значительное
влияние, например, выбранный метод
решения системы обыкновенных
дифференциальных уравнений, описывающих
исследуемый процесс [161,163].
Анализ
чувствительности— это расчет
векторов градиентов выходных параметров.
Наиболее просто анализ чувствительности
реализуется путем численного
дифференцирования. Пусть анализ
проводится в некоторой точкеХномпространства аргументов, в которой
предварительно проведен одновариантный
анализ и найдены значения выходных
параметровYj
ном. ВыделяетсяN параметров-аргументовXi,
влияние которых на выходные параметры
подлежит оценить, поочередно каждый из
них получает приращениеΔXi,
выполняется моделирование, фиксируются
значения выходных параметровYjи подсчитываются значения абсолютных:
и
относительных коэффициентов
чувствительности:
.
Такой
метод численного дифференцирования
называют методом
приращений. Для анализа
чувствительности, согласно методу
приращений, требуется выполнитьN+1 раз одновариантный анализ. Результат
его применения — получение матриц
абсолютной и относительной чувствительности,
элементами которых являются коэффициентыAji
иBji[162].
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Верификация и валидация компьютерных имитационных моделей проводится во время разработки имитационной модели с конечной целью создания точной и достоверной модели. «Имитационные модели все чаще используются для решения проблем и помощи в принятии решений. Разработчики и пользователи этих моделей, лица, принимающие решения, использующие информацию, полученную на основе результатов этих моделей, и лица, на которых влияют решения, основанные на таких моделях, являются все справедливо озабочены тем, являются ли модель и ее результаты «правильными». Эта проблема решается путем проверки и валидации имитационной модели.
Имитационные модели являются приблизительными имитациями реальных систем, и они никогда в точности не имитируют в реальной системе. В связи с этим модель должна быть проверена и подтверждена в степени, необходимой для предполагаемого назначения или применения модели.
Верификация и валидация имитационной модели начинается после того, как функциональные спецификации задокументированы и начальная разработка модели завершена. Верификация и валидация — это итеративный процесс, который происходит на протяжении всей разработки модели.
Содержание
- 1 Ver ification
- 2 Проверка достоверности
- 2.1 Подтверждение достоверности
- 2.2 Проверка допущений модели
- 2.2.1 Структурные допущения
- 2.2.2 Допущения данных
- 2.2.3 Допущения упрощения
- 2.3 Проверка входных данных -выводные преобразования
- 2.3.1 Проверка гипотез
- 2.3.1.1 Точность модели в виде диапазона
- 2.3.2 Доверительные интервалы
- 2.3.3 Графические сравнения
- 2.3.1 Проверка гипотез
- 3 Стандарты ASME
- 4 См. также
- 5 Ссылки
Верификация
В контексте компьютерного моделирования верификация модели — это процесс подтверждения того, что она правильно реализована по отношению к концептуальной модели (это соответствует спецификациям и предположениям, которые считаются приемлемыми для данной цели приложения). Во время верификации модель тестируется для поиска и исправления ошибок в реализации модели. Для обеспечения соответствия модели спецификациям и предположениям в отношении концепции модели используются различные процессы и методы. Цель проверки модели — убедиться, что реализация модели верна.
Есть много методов, которые можно использовать для проверки модели. К ним относятся, помимо прочего, проверка модели экспертом, создание логических блок-схем, включающих каждое логически возможное действие, проверка выходных данных модели на разумность при различных настройках входных параметров и использование интерактивного отладчика. Многие методы разработки программного обеспечения, используемые для верификации программного обеспечения, применимы к верификации имитационной модели.
Валидация
Валидация проверяет точность представления модели реальной системы. Валидация модели определяется как «подтверждение того, что компьютеризированная модель в пределах ее области применимости обладает удовлетворительным диапазоном точности, совместимым с предполагаемым применением модели». Модель должна быть построена для конкретной цели или набора задач, а ее достоверность должна определяться для этой цели.
Существует множество подходов, которые можно использовать для проверки компьютерной модели. Подходы варьируются от субъективных обзоров до объективных статистических тестов. Один из наиболее часто используемых подходов состоит в том, чтобы разработчики моделей определяли достоверность модели с помощью серии тестов.
Нейлор и Фингер [1967] сформулировали трехэтапный подход к валидации модели, который получил широкое распространение:
Шаг 1. Постройте модель с высокой достоверностью.
Шаг 2. Подтвердите допущения модели.
Шаг 3. Сравните преобразования ввода-вывода модели с соответствующими преобразованиями ввода-вывода для реальной системы.
Face validity
Модель, имеющая face validity представляется разумной имитацией системы реального мира для людей, знакомых с системой реального мира. Подтверждение подлинности проверяется тем, что пользователи и люди, знакомые с системой, проверяют выходные данные модели на предмет разумности и в процессе выявляют недостатки. Дополнительным преимуществом вовлечения пользователей в проверку является то, что доверие к модели для пользователей и доверие пользователя к модели возрастают. Чувствительность к входным данным модели также может использоваться для оценки достоверности лица. Например, если моделирование проезда в ресторан быстрого питания было выполнено дважды с темпами прибытия клиентов 20 в час и 40 в час, тогда ожидается, что выходные данные модели, такие как среднее время ожидания или максимальное количество ожидающих клиентов, увеличатся с прибытием. показатель.
Проверка допущений модели
Допущения, сделанные в отношении модели, обычно делятся на две категории: структурные допущения о том, как работает система, и допущения данных. Также мы можем рассмотреть упрощающие предположения, которые мы используем для упрощения реальности.
Структурные предположения
Предположения, сделанные о том, как работает система и как она устроена физически, являются структурными предположениями. Например, количество серверов в фаст-фуде проезжает по переулку, и если их больше одного, как они используются? Работают ли серверы параллельно, когда клиент завершает транзакцию, посещая один сервер, или один сервер принимает заказы и обрабатывает платежи, в то время как другой готовит и обслуживает заказ. Многие структурные проблемы в модели возникают из-за неверных или неверных предположений. Если возможно, необходимо внимательно наблюдать за работой реальной системы, чтобы понять, как она работает. Структура и работа системы также должны быть проверены пользователями реальной системы.
Допущения данных
Должен быть достаточный объем соответствующих данных, доступных для построения концептуальной модели и проверки модели. Отсутствие соответствующих данных часто является причиной неудачных попыток проверки модели. Данные должны быть проверены и получены из надежного источника. Типичная ошибка — это предположение о несоответствующем статистическом распределении данных. Предполагаемая статистическая модель должна быть протестирована с использованием критериев согласия и других методов. Примерами критериев согласия являются тест Колмогорова – Смирнова и критерий хи-квадрат. Следует проверять любые выбросы в данных.
Допущения упрощения
Это те предположения, которые, как мы знаем, не верны, но необходимы для упрощения проблемы, которую мы хотим решить. Использование этих предположений должно быть ограничено, чтобы гарантировать, что модель достаточно верна, чтобы служить ответом на проблему, которую мы хотим решить.
Проверка преобразований ввода-вывода
Модель рассматривается как преобразование ввода-вывода для этих тестов. Проверочный тест состоит из сравнения выходных данных рассматриваемой системы с выходными данными модели для того же набора входных условий. Данные, записанные во время наблюдения за системой, должны быть доступны для выполнения этого теста. Выходные данные модели, представляющие основной интерес, следует использовать в качестве меры производительности. Например, если рассматриваемая система представляет собой поездку в ресторан быстрого питания, где входными данными для модели является время прибытия клиента, а выходным показателем эффективности является среднее время ожидания клиента в очереди, тогда фактическое время прибытия и время, проведенное в очереди для клиентов в проезде. будет записан. Модель будет запускаться с фактическим временем прибытия, и среднее время нахождения в очереди будет сравниваться с фактическим средним временем, проведенным в очереди с использованием одного или нескольких тестов.
Проверка гипотез
Статистическая проверка гипотез с использованием t-критерия может использоваться в качестве основы для признания модели действительной или отклонения ее как недействительной.
Гипотеза, подлежащая проверке:
- H0модельный показатель производительности = системный показатель производительности
по сравнению с
- H1модельным показателем производительности ≠ системный показатель производительности.
Тест проводится для данного размера выборки и уровня значимости или α. Для выполнения теста проводится n статистически независимых прогонов модели и вычисляется среднее или ожидаемое значение E (Y) для интересующей переменной. Затем тестовая статистика t 0 вычисляется для заданных α, n, E (Y) и наблюдаемого значения для системы μ
- t 0 = (E (Y) — u 0) / (S / n) { displaystyle t_ {0} = {(E (Y) -u_ {0})} / {(S / { sqrt {n}})}}
и критическое значения для α и n-1 вычисляются степени свободы
- ta / 2, n — 1 { displaystyle t_ {a / 2, n-1}}
.
Если
- | t 0 |>ta / 2, n — 1 { displaystyle left vert t_ {0} right vert>t_ {a / 2, n-1}}
отклонить H 65>0, модель нуждается в корректировке.
Существует два типа ошибок, которые могут возникнуть при проверке гипотез: отклонение действительной модели, называемое ошибкой типа I, или «риск создателей модели» и принятие неверной модели называется ошибкой типа II, β или «риск пользователя модели». Уровень значимости или α равен вероятности ошибки типа I. Если α мало, то отклонение нулевой гипотезы является сильным выводом. Например, если α = 0,05 а нулевая гипотеза отклоняется, вероятность отклонения действительной модели составляет всего 0,05. Уменьшение вероятности ошибки типа II очень важно. Вероятность правильного обнаружения недействительной модели составляет 1 — β. Вероятность типа Ошибка II зависит от размера выборки и фактическая разница между значением выборки и наблюдаемым значением. Увеличение размера выборки снижает риск ошибки типа II.
Точность модели как диапазон
Недавно был разработан статистический метод, при котором степень точности модели задается как диапазон. Этот метод использует проверку гипотез для принятия модели, если разница между интересующей переменной модели и интересующей системной переменной находится в пределах указанного диапазона точности. Требование состоит в том, чтобы и системные данные, и данные модели были приблизительно Обычно Независимыми и идентично распределенными (NIID). В этом методе используется статистика t-критерия. Если среднее значение модели — μ, а среднее значение системы — μ, то разница между моделью и системой составляет D = μ — μ. Гипотеза, подлежащая проверке, заключается в том, находится ли D в приемлемом диапазоне точности. Пусть L = нижний предел точности и U = верхний предел точности. Затем необходимо проверить
- H0L ≤ D ≤ U
по сравнению с
- H1D < L or D>U
.
Кривая рабочей характеристики (ОС) — это вероятность того, что нулевая гипотеза будет принята, когда она верна. Кривая OC характеризует вероятность ошибок как I, так и II типа. Кривые риска для риска создателя модели и пользователя модели могут быть построены на основе кривых OC. Сравнение кривых с фиксированным размером выборки между риском разработчика модели и риском пользователя модели можно легко увидеть на кривых риска. Если заданы риски разработчика модели, риск пользователя модели, а также верхний и нижний пределы диапазона точности, то можно рассчитать необходимый размер выборки.
Доверительные интервалы
Доверительные интервалы могут быть используется для оценки того, «достаточно ли близка» модель к системе для некоторой интересующей переменной. Проверяется разница между известным модельным значением μ 0 и системным значением μ, чтобы увидеть, меньше ли оно значения, достаточно малого для того, чтобы модель была действительной в отношении этой интересующей переменной. Значение обозначается символом ε. Для выполнения теста проводится ряд n статистически независимых прогонов модели и создается среднее или ожидаемое значение E (Y) или μ для представляющей интерес выходной переменной Y моделирования со стандартным отклонением S. Выбран уровень достоверности 100 (1-α). Интервал [a, b] строится следующим образом:
- a = E (Y) — ta / 2, n — 1 S / nandb = E (Y) + ta / 2, n — 1 S / n { displaystyle a = E (Y) -t_ {a / 2, n-1} S / { sqrt {n}} qquad и qquad b = E (Y) + t_ {a / 2, n-1} S / { sqrt {n}}}
,
где
- ta / 2, n — 1 { displaystyle t_ {a / 2, n-1}}
— критическое значение из t-распределения для заданный уровень значимости и n-1 степеней свободы.
- Если | a-μ 0 |>ε и | b-μ 0 |>ε, то модель необходимо откалибровать, поскольку в обоих случаях разница больше допустимой.
- If | a-μ 0| < ε and |b-μ0| < ε then the model is acceptable as in both cases the error is close enough.
- If | a-μ 0| < ε and |b-μ0|>ε или наоборот, тогда необходимы дополнительные прогоны модели для сокращения интервала.
Графические сравнения
Если статистические допущения не могут быть выполнены или данных для системы недостаточно a графическое сравнение выходных данных модели с выходными данными системы может использоваться для принятия субъективных решений, однако другие объективные тесты предпочтительнее.
Стандарты ASME
Документы и стандарты, включающие проверку и валидацию компьютерного моделирования и моделирования разработаны Комитетом по верификации и валидации (VV) Американского общества инженеров-механиков (ASME). ASME VV 10 предоставляет руководство по оценке и повышению достоверности расчетных моделей механики твердого тела посредством процессов верификации, валидации и количественной оценки неопределенности. ASME VV 10.1 предоставляет подробный пример для иллюстрации концепций, описанных в ASME VV 10. ASME VV 20 предоставляет подробную методологию для проверки компьютерного моделирования применительно к гидродинамике и теплопередаче. ASME VV 40 обеспечивает основу для установления требований к достоверности модели для вычислительного моделирования и представляет примеры, характерные для индустрии медицинских устройств.
См. Также
Ссылки
Как мы можем удостовериться, правильно ли работает средство моделирования? Одним из подходов является метод искусственного решения. Этот процесс включает допущение некого решения, получение исходных условий и других вспомогательных условий согласующихся с первоначальным предположением, решение задачи с этими условиями в качестве входных параметров для пакета моделирования и сравнение полученных результатов с предполагаемым решением. Метод прост в использовании и достаточно универсален. Например, исследователи из Национальной лаборатории Сандия использовали его в некоторых собственных программных разработках.
Проверка и подтверждение
Перед использованием инструмента численного моделирования для прогнозирования результатов предварительно неизвестных ситуаций, мы хотим создать критерий проверки его надежности. Мы можем сделать это либо проверкой того, что пакет для моделирования точно воспроизводит имеющиеся аналитические решения, либо тем, что его результаты согласуются с экспериментальными данными. Это приводит нас к двум тесно взаимосвязанным предметам обсуждения проверке (верификации) и подтверждению (валидации). Давайте проясним, что означают два эти термина в контексте численного моделирования.
Для численного моделирования физической проблемы, мы предпринимаем два шага:
- Построение математической модели физической системы. Это то место, где учитываются все факторы, которые оказывают влияние на наблюдаемое поведение и формулируются основные управляющие уравнения. Результатом зачастую является система неявных связей между входными и выходными величинами. Они часто записываются в виде системы дифференциальных уравнений в частных производных с начальными и граничными условиями, которая в совокупности называется как начально-краевая задача (initial boundary value problem — IBVP).
- Решение математической модели для получения выражений для выходных величин в виде явных функций от входных значений параметров. Однако, такая замкнутая форма решения недоступна для большинства задач, представляющих практический интерес. В таком случае, мы применяем численные методы для получения приближенных решений, часто с помощью вычислительной техники для решения больших систем, в общем случае, нелинейных алгебраических уравнений и неравенств.
Существует две ситуации, при которых могут появиться ошибки. Во-первых, они могут возникнуть в самой математической модели. Потенциальные ошибки вносятся при упущении важного фактора или при допущении нефизичного соотношения между переменными. Подтверждение (валидация) состоит в том, чтобы получить уверенность, что такие ошибки не вносятся при построении математической модели. Проверка (верификация), с другой стороны, заключается в том, чтобы удостовериться, что математическая модель решается достаточно точно. В этом случае, мы должны гарантировать, что численный алгоритм является сходящимся и его компьютерная реализация является корректной, так что численное решение будет точным.
Проще говоря, во время подтверждения, мы спрашиваем, корректно ли мы задали математическую модель для описания физической системы, в то время как при проверке, мы исследуем, получим ли мы точное численное решение математической модели. 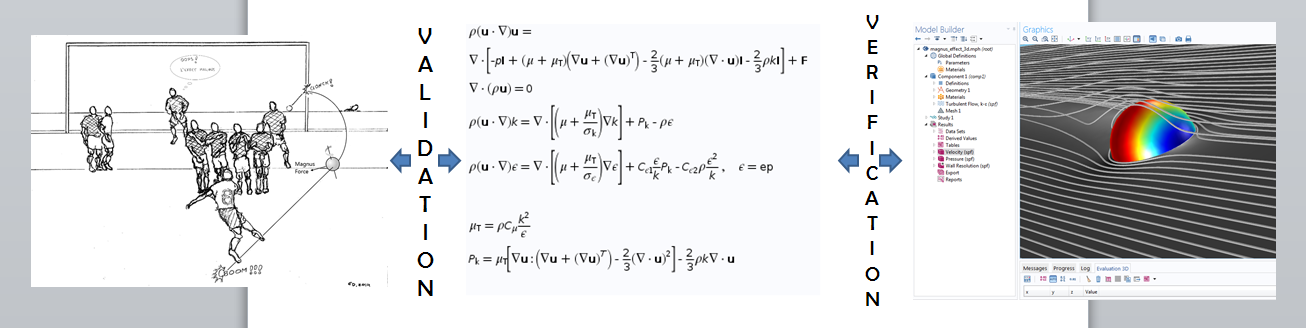
Сравнение между процессами подтверждения и проверки.
Теперь, давайте углубимся в проблему проверки численного решения начально-краевых задач (IBVP-задач).
Различные подходы к процедуре проверки
Как мы можем удостовериться, обеспечивает ли инструмент моделирования достаточно точное решение IBVP-задачи? Одна из возможностей заключается в том, чтобы выбрать задачу, имеющую точное аналитическое решение и использовать точное решение в качестве критерия правильности. Метод разделения переменных, например, можно использовать для получения решения простой IBVP-задачи. Применимость этого подхода ограничивается тем, что большинство задач, представляющих практический интерес, не имеют точного решения, что и является основанием для использования компьютерного моделирования. Тем не менее, этот подход является полезным при проверке работоспособности алгоритмов и программ.
Другим подходом является сравнение результатов моделирования с экспериментальными данными. Вообще, это является сочетанием подтверждения и проверки в одном шаге, который иногда называется пригодность (квалификация). Возможно, но маловероятно, что экспериментальные данные случайно совпадут с неправильным решением в результате комбинации некорректной математической модели и неверного алгоритма или ошибке в программном коде. За исключением таких редких случаев, хорошее соответствие численного решения и экспериментальных результатов подтверждает справедливость математической модели и точность процедуры решения.
Библиотеки Приложений в среде COMSOL Multiphysics содержат множество проверочных моделей (verification models), которые используют один или оба этих подхода. Они сгруппированы по областям физики.
Данные модели доступны в Библиотеках Приложений среды COMSOL Multiphysics.
Что делать, если нам потребуется проверить наши результаты при отсутствии точных математических решений и экспериментальных данных? Мы можем обратиться к методу искусственного решения.
Реализация метода искусственного решения
Целью решения начально-краевой задачи (IBVP-задачи) является нахождения явного выражения для решения в терминах независимых переменных, как правило, пространства и времени, с учетом заданных параметров задачи, таких как свойства материала, а также граничные, начальные и исходные условия. Общая форма исходных условий подразумевает описание всех сил, действующих на тело, таких как гравитация в задачах строительной механики и аэро- и гидродинамики, силы сопротивления в задачах массопереноса и источников тепла в задачах термодинамики.
В методе искусственного решения (Method of Manufactured Solutions — MMS), мы решаем задачу от противного , т.е. начинаем с предполагаемого явного выражения для решения. Затем, мы подставляем решение в дифференциальные уравнения и получаем согласованный набор исходных, начальных и граничных условий. Обычно, это включает в себя оценку ряда производных. Вскоре мы увидим, как макрос на языке символической алгебры среды COMSOL Multiphysics может помочь в этом процессе. Аналогичным образом, мы вычисляем предполагаемое решение в момент времени t = 0 и на границах для получения начальных и граничных условий.
Далее идет этап проверки. С учетом только что полученных исходных и вспомогательных условий, мы применяем инструмент моделирования для получения численного решения IBVP-задачи и сравниваем его с изначально предполагавшимся решением, с которого мы “стартовали”.
Продемонстрируем эти шаги на простом примере.
Проверка одномерной задачи теплопроводности
Рассмотрим 1D задачу теплопроводности в стержне длиной L
A_crho C_p frac{partial T}{partial t} + frac{partial}{partial x}(-A_ckfrac{partial T}{partial x}) = A_cQ, t in (0,t_f), x in (0,L)
с начальным условием
T(x,0) = f(x)
и температурным режимом, поддерживаемым на обоих концах по закону, задаваемым функциями
T(0,t) = g_1(t), quad T(L,t) = g_2(t).
Константами A_c, rho, C_p и k являются площадь поперечного сечения, плотность материала, теплоемкость и коэффициент теплопроводности, соответственно. Источник тепла задается как Q.
Наша цель заключается в проверке решения этой задачи методом искусственного решения. Во-первых, предположим явный вид решения. В качестве такого решения давайте выберем следующее распределение температуры
u(x,t) = 500 K + frac{x}{L}(frac{x}{L}-1)frac{t}{tau} K,
где tau есть характерное время, которое для данного примера выберем равным одному часу. Введем новую переменную u для предполагаемой температуры, чтобы отличить ее от расчетной температуры T.
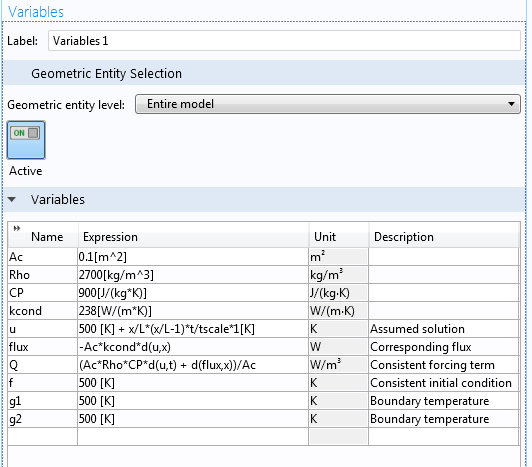
Далее, найдем исходное условие согласующееся с предполагаемым решением. Мы можем вручную вычислить частные производные по координате и времени и подставить их в дифференциальное уравнение для получения Q. Кроме того, поскольку среда COMSOL Multiphysics способна выполнять символические преобразования, то мы будем пользоваться этой встроенной опцией вместо вычисления вручную исходного условия.
В случае однородных материала и свойств поперечного сечения, мы можем объявить A_c, rho, C_p и k как параметры. В общем неоднородном случае для этого потребуются переменные величины, как это проделано для зависящих от времени граничных условий. Обратите внимание на использование оператора d(), одного из встроенных операторов дифференцирования в среду COMSOL Multiphysics, как показано на скриншоте ниже.
Макрос на языке символической алгебры среды COMSOL Multiphysics может автоматизировать оценку частных производных.
Мы выполняем эти символические вычисления с той оговоркой, что мы доверяем символической алгебре. Иначе, любые ошибки наблюдаемые позднее проистекали бы из символических вычислений, а не численного решения. Разумеется, мы можем построить график вычисляемого вручную выражения для Q рядом с результатом символических вычислений, показанных выше, для проверки макроса.
Далее, мы вычисляем начальные и граничные условия. Начальное условие – это предполагаемое решение, вычисленное в момент времени t = 0.
f(x) = u(x,0) = 500 K.
Значения температуры на концах стержня есть g_1(t) = g_2(t) = 500 K.
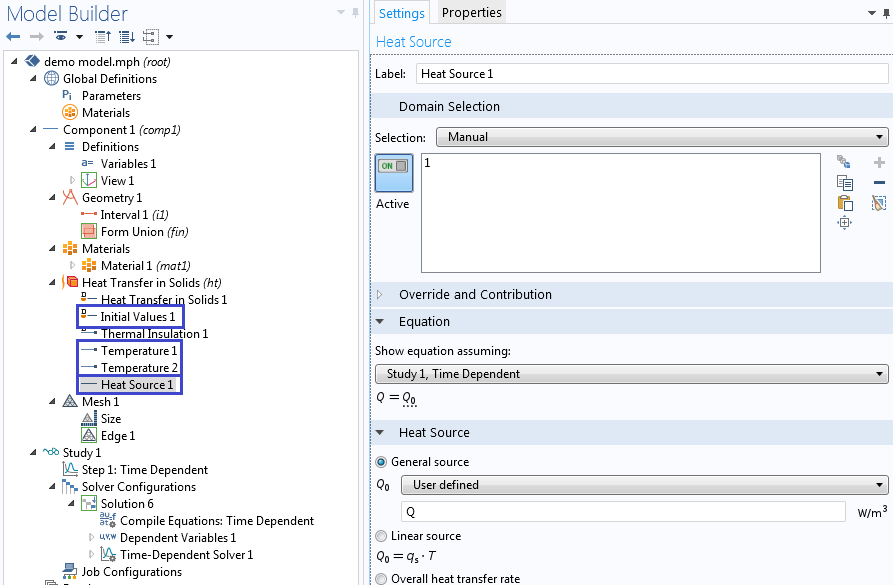
Далее, получим численное решение задачи, используя исходные, а также начальные и граничные условия, которые мы только что вычислили. В этом примере, будем использовать физический интерфейс Теплопередача в твердых телах.
Добавление начальных значений, граничных условий и внешних источников, получаемых исходя из предполагаемого решения.
На завершающем этапе, мы сравним численное решение с предполагаемым решением. Графики ниже показывают температуру по истечении одного дня. Первое решение получено с использованием линейных элементов, в то время как второе решение получается при использовании квадратичных элементов. Для данного типа задач, по умолчанию среда COMSOL Multiphysics выбирает квадратичные элементы.
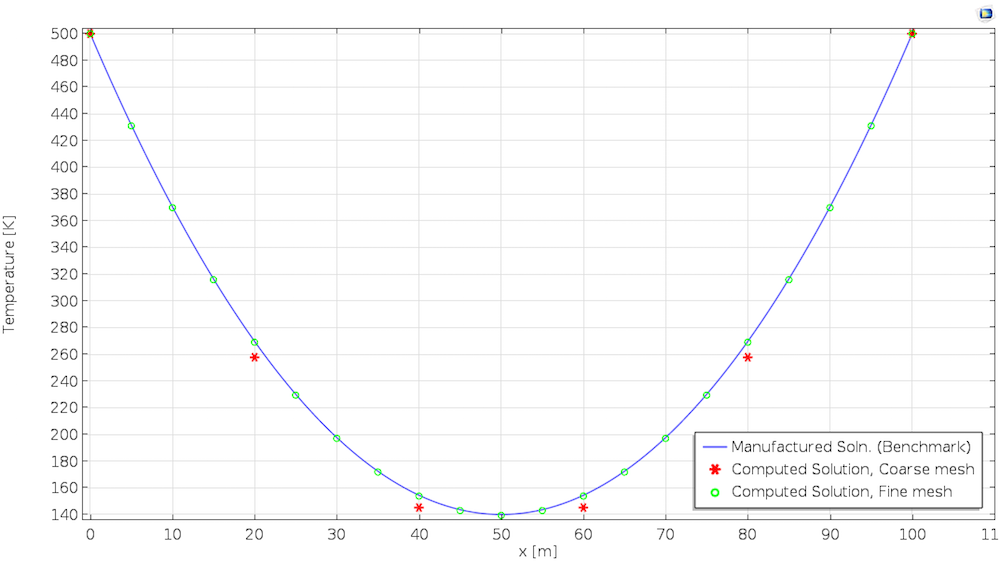
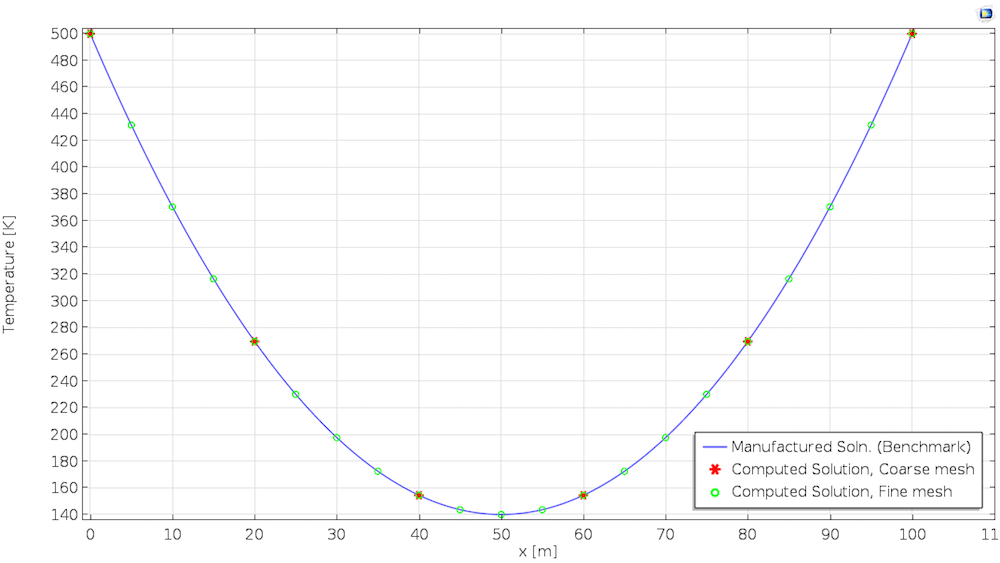
Решение, вычисленное при использовании искусственного решения с линейными элементами (слева) и квадратичными элементами (справа).
Проверка различных частей кода
Метод MMS предоставляет нам необходимую гибкость для проверки различных частей кода. Ради простоты, в приведенном выше примере, мы умышленно оставили многие части IBVP-задачи непроверенными. На практике, каждый элемент в уравнении должен быть проверен в наиболее общем виде. Например, для проверки того, насколько точно программа обрабатывает области с неоднородным поперечным сечением, мы должны определить пространственно-переменную область до получения исходных условий. То же можно сказать и в отношении других коэффициентов уравнения, например для свойств материала.
Аналогичная проверка должна производиться для всех граничных и начальных условий. Если, к примеру, мы хотим на левом конце стержня задать поток тепла взамен температуры, мы сначала оцениваем поток, соответствующий искусственному решению, т. е. -ncdot(-A_ck nabla u) где n есть единичная внешняя нормаль. Для предполагаемого решения в данном примере, направленный внутрь поток на левом конце становится равным frac{A_ck}{L}frac{t}{tau}*1K.
В среде COMSOL Multiphysics для теплопередачи в твердых телах граничными условиями по умолчанию являются условия тепловой изоляции. Что делать, если мы захотим проверить обработку тепловой изоляции на левом краю? Нам нужно будет придумать такое новое искусственное решение, в котором производная обращается в ноль на левом конце. Например, мы можем использовать
u(x,t) = 500 K + (frac{x}{L})^2frac{t}{tau} K.
Обратите внимание, что во время проверки, мы проверяем только, корректно ли решаются уравнения. Мы не затрагиваем вопроса о том, соответствует ли решение физической ситуации.
Важно помнить, что как только мы выдумываем новое искусственное решение, мы должны пересчитать исходные, начальные и граничные условия в соответствии предполагаемым решением. Разумеется, при использовании средств символических вычислений в среде COMSOL Multiphysics, мы освобождены от утомительных вычислений!
Скорость сходимости
Как было показано на графиках выше, решения, получаемые с помощью линейного и квадратичного элемента сходятся по мере уменьшения размера сетки разбиения. Это качественное поведение сходимости придает нам некоторую уверенность в численном решении. Мы можем продолжить тщательное рассмотрение численного метода, изучая его скорость сходимости, которая предоставит нам количественный критерий проверки численной процедуры.
Например, для стационарной модификаци изадачи, стандартная оценка конечного- элементной погрешности для погрешности измеряемой в норме Соболева
m-порядка, есть
||u-u_h||_m leq C h^{p+1-m}||u||_{p+1},
где u и u_h являются точным и конечно-элементным решениями, h является максимальным размером элемента, p -порядок полиномиальной аппроксимации (функция формы). Для m = 0, это дает оценку погрешности
||e|| = ||u-u_h|| = (int_{Omega}(u-u_h)^2dOmega)^{frac{1}{2}} leq C h^{p+1}||u||_{p+1},
где C – константа независимая от сетки разбиения.
Возвращаясь к методу искусственного решения, это означает, что решение с линейным элементом (p = 1) должно показывать сходимость второго порядка при измельчении сетки. Если мы построим график нормы ошибки по отношению к размеру сетки в логарифмическом масштабе, тангенс угла наклона должен асимптотически приближаться к 2. Если этого не происходит, то мы должны будем проверить код или точность и регулярность входных параметров, таких как материальные и геометрические свойства. Как показано на рисунках ниже, численное решение сходится с теоретически ожидаемой скоростью.
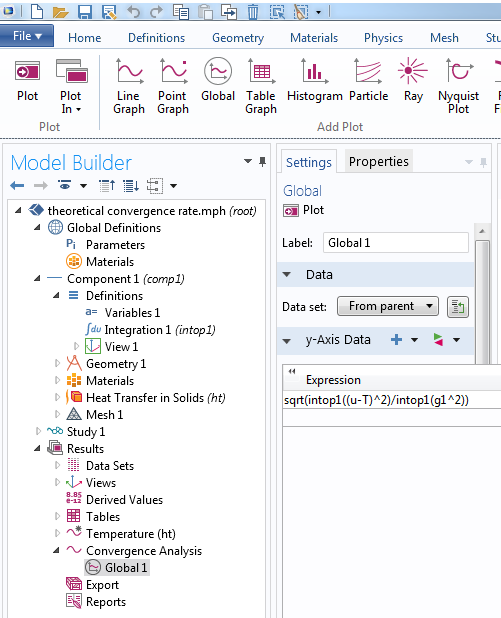
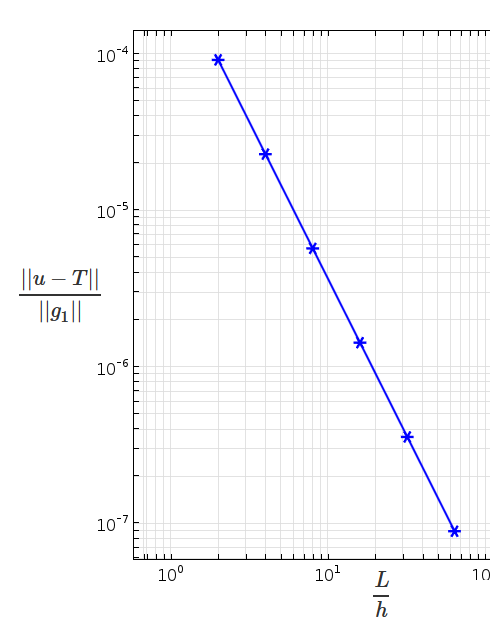
Слева: Использование операторов интегрирования для определения норм. Оператор intop1 определяется для интегрирования по области. Справа: График ошибки в зависимости от размера сетки, построенный в логарифмических осях, показывает второй порядок сходимости в норме L_2 (m = 0) для линейных элементов, что согласуется с теоретической оценкой.
Несмотря на то, что мы всегда должны проверять сходимость, теоретическая скорость сходимости может быть проверена только для тех проблем, для которых, как выше, доступна априорная оценка погрешности. Когда у вас имеются такие задачи, помните, что метод искусственного решения поможет вам удостовериться в том, что ваш код показывает правильное асимптотическое поведение.
Нелинейный задачи и взаимосвязанные междисциплинарные задачи
В случае существенной нелинейности, коэффициенты в уравнении зависят от решения. В задачах теплопроводности, например, коэффициент теплопроводности может зависеть от температуры. В таких случаях коэффициенты должны быть получены из предполагаемого решения.
Взаимосвязанные (мультифизические) задачи имеют несколько управляющих уравнений. Решения предполагаются сразу для всех взаимосвязанных полей, и исходные условия должны быть расчитаны для каждого управляющего уравнения.
Единственность
Обратите внимание, что логика метода искусственного решения сохраняется, только если управляющая система уравнений имеет единственное решение при условиях (исходные, граничные и начальные условия), подразумеваемых предполагаемым решением. Например, в стационарной задаче теплопроводности, доказательство единственности требует положительного значения теплопроводности. В то время, как это довольно просто проверяется в случае изотропной однородной среды, в случае температурной зависимости коэффициента теплопроводности или анизотропии большее внимание должно быть уделено при конструировании решения, чтобы не нарушить такие предположения.
При использовании метода искусственного решения, решение существует по определению. Кроме того, доказательства единственности существуют для гораздо большего класса задач, чем те, для которых у нас имеются точные аналитические решения. Таким образом, метод предоставляет нам большее пространство для маневра, чем поиск точного решения, начиная с исходных, начальных и граничных условий.
Попробуйте Самостоятельно
Встроенная функциональность в виде символических вычислений в среде COMSOL Multiphysics позволяет легко реализовать метод MMS для проверки кода программ, а также для образовательных целей. Несмотря на то, что мы всесторонне тестируем коды наших программ, мы приветствуем любые замечания со стороны наших пользователей. В данном топике был представлен универсальный инструмент, который вы можете использовать для проверки различных физических интерфейсов. Вы также можете проверить свои собственные реализации при использовании моделирования на основе пользовательских уравнений или Построителя интерфейсов для новой физики (Physics Builder) в среде COMSOL Multiphysics. Если у вас есть какие-либо вопросы по данной методике , пожалуйста, не стесняйтесь написать нам!
Информационные ресурсы
- Для всестороннего обсуждения метода искусственного решения, включая его сильные и слабые стороны, посмотрите данный Отчет из Национальной лаборатории Сэндиа (Sandia). В Отчете подробно излагается система “слепых” тестов, в которых один автор заложил ряд ошибок в код программы незаметно от второго автора, который выискивает заложенные “мины” с использованием метода, описанного в этом топике.
- Для расширенной дискуссии по проверке и подтверждению в контексте научных вычислений, ознакомьтесь с
- W. J. Oberkampf and C. J. Roy, Проверка и подтверждение в научных расчетах (Verification and Validation in Scientific Computing), Cambridge University Press, 2010
- Оценка стандартной погрешности в методе конечных элементов имеется в таких книгах, как
- Thomas J. R. Hughes, Метод конечных элементов: Линейный статический и динамический конечно-элементный анализ (The Finite Element Method: Linear Static and Dynamic Finite Element Analysis), Dover Publications, 2000
- B. Daya Reddy, Вводный функциональный анализ: с приложениями к краевым задачам и конечным элементам (Introductory Functional Analysis: With Applications to Boundary Value Problems and Finite Elements), Springer-Verlag, 1997