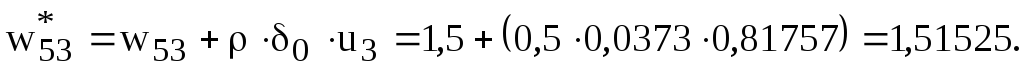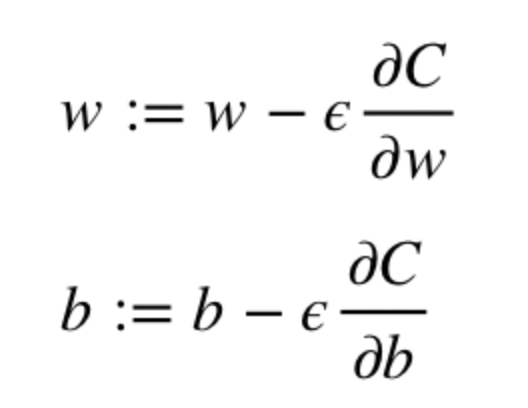Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Введение
- 2 Распространение ошибок
- 2.1 Абсолютная ошибка
- 2.2 Относительная ошибка
- 3 Графы вычислительных процессов
- 3.1 Примеры
- 4 Памятка программисту
- 5 Список литературы
- 6 См. также
Введение
Одним из наиболее важных вопросов в численном анализе является вопрос о том, как ошибка, возникшая в определенном месте в ходе вычислений, распространяется дальше, то есть становится ли ее влияние больше или меньше по мере того, как производятся последующие операции. Крайним случаем является вычитание двух почти равных чисел: даже при очень маленьких ошибках обоих этих чисел относительная ошибка разности может оказаться очень большой. Такая относительная ошибка будет распространяться дальше при выполнении всех последующих арифметических операций.
Одним из источников вычислительных погрешностей (ошибок) является приближенное представление вещественных чисел в ЭВМ, обусловленное конечностью разрядной сетки. Хотя исходные данные представляются в ЭВМ с большой точностью накопление погрешностей округления в процессе счета может привести к значительной результирующей погрешности, а некоторые алгоритмы могут оказаться и вовсе непригодными для реального счета на ЭВМ. Подробнее о представлении вещественных чисел в ЭВМ можно узнать здесь.
Распространение ошибок
В качестве первого шага при рассмотрении такого вопроса, как распространение ошибок, необходимо найти выражения для абсолютной и относительной ошибок результата каждого из четырех арифметических действий как функции величин, участвющих в операции, и их ошибок.
Абсолютная ошибка
Сложение
Имеются два приближения и
к двум величинам
и
, а также соответствующие абсолютные ошибки
и
. Тогда в результате сложения имеем
-
.
Ошибка суммы, которую мы обозначим через , будет равна
-
.
Вычитание
Тем же путем получаем
-
.
Умножение
При умножении мы имеем
-
.
Поскольку ошибки обычно гораздо меньше самих величин, пренебрегаем произведением ошибок:
-
.
Ошибка произведения будет равна
-
.
Деление
Имеем
-
.
Преобразовываем это выражение к виду
-
.
Множитель, стоящий в скобках, при можно разложить в ряд
-
.
Перемножая и пренебрегая всеми членами, которые содержат произведения ошибок или степени ошибок выше первой, имеем
-
.
Следовательно,
-
.
Необходимо четко понимать, что знак ошибки бывает известен только в очень редких случаях. Не факт, например, что ошибка увеличивается при сложении и уменьшается при вычитании потому, что в формуле для сложения стоит плюс, а для вычитания — минус. Если, например, ошибки двух чисел имеют противоположные знаки, то дело будет обстоять как раз наоборот, то есть ошибка уменьшится при сложении и увеличится при вычитании этих чисел.
Относительная ошибка
После того, как мы вывели формулы для распространения абсолютных ошибок при четырех арифметических действиях, довольно просто вывести соответствующие формулы для относительных ошибок. Для сложения и вычитания формулы были преобразованы с тем, чтобы в них входила в явном виде относительная ошибка каждого исходного числа.
Сложение
-
.
Вычитание
-
.
Умножение
-
.
Деление
-
.
Мы начинаем арифметическую операцию, имея в своем распоряжении два приближенных значения и
с соответствующими ошибками
и
. Ошибки эти могут быть любого происхождения. Величины
и
могут быть экспериментальными результатами, содержащими ошибки; они могут быть результатами предварительного вычисления согласно какому-либо бесконечному процессу и поэтому могут содержать ошибки ограничения; они могут быть результатами предшествующих арифметических операций и могут содержать ошибки округления. Естественно, они могут также содержать в различных комбинациях и все три вида ошибок.
Вышеприведенные формулы дают выражение ошибки результата каждого из четырех арифметических действий как функции от ; ошибка округления в данном арифметическом действии при этом не учитывается. Если же в дальнейшем необходимо будет подсчитать, как распространяется в последующих арифметических операциях ошибка этого результата, то необходимо к вычисленной по одной из четырех формул ошибке результата прибавить отдельно ошибку округления.
Графы вычислительных процессов
Теперь рассмотрим удобный способ подсчета распространения ошибки в каком-либо арифметическом вычислении. С этой целью мы будем изображать последовательность операций в вычислении с помощью графа и будем писать около стрелок графа коэффициенты, которые позволят нам сравнительно легко определить общую ошибку окончательного результата. Метод этот удобен еще и тем, что позволяет легко определить вклад любой ошибки, возникшей в процессе вычислений, в общую ошибку.
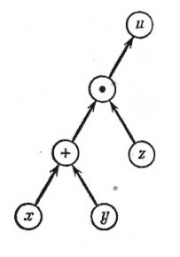
Рис.1. Граф вычислительного процесса
На рис.1 изображен граф вычислительного процесса . Граф следует читать снизу вверх, следуя стрелкам. Сначала выполняются операции, расположенные на каком-либо горизонтальном уровне, после этого — операции, расположенные на более высоком уровне, и т. д. Из рис.1, например, ясно, что x и y сначала складываются, а потом умножаются на z. Граф, изображенный на рис.1, является только изображением самого вычислительного процесса. Для подсчета общей ошибки результата необходимо дополнить этот граф коэффициентами, которые пишутся около стрелок согласно следующим правилам.
Сложение
Пусть две стрелки, которые входят в кружок сложения, выходят из двух кружков с величинами и
. Эти величины могут быть как исходными, так и результатами предыдущих вычислений. Тогда стрелка, ведущая от
к знаку + в кружке, получает коэффициент
, стрелка же, ведущая от
к знаку + в кружке, получает коэффициент
.
Вычитание
Если выполняется операция , то соответствующие стрелки получают коэффициенты
и
.
Умножение
Обе стрелки, входящие в кружок умножения, получают коэффициент +1.
Деление
Если выполняется деление , то стрелка от
к косой черте в кружке получает коэффициент +1, а стрелка от
к косой черте в кружке получает коэффициент −1.
Смысл всех этих коэффициентов следующий: относительная ошибка результата любой операции (кружка) входит в результат следующей операции, умножаясь на коэффициенты у стрелки, соединяющей эти две операции.
Примеры
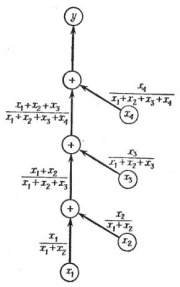
Рис.2. Граф вычислительного процесса для сложения , причем
Применим теперь методику графов к примерам и проиллюстрируем, что означает распространение ошибки в практических вычислениях.
Пример 1
Рассмотрим задачу сложения четырех положительных чисел:
-
,
где
-
.
Граф этого процесса изображен на рис.2. Предположим, что все исходные величины заданы точно и не имеют ошибок, и пусть ,
и
являются относительными ошибками округления после каждой следующей операции сложения. Последовательное применение правила для подсчета полной ошибки окончательного результата приводит к формуле
-
.
Сокращая сумму в первом члене и умножая все выражение на
, получаем
-
.
Учитывая, что ошибка округления равна (в данном случае предполагается, что действительное число в ЭВМ представляется в виде десятичной дроби с t значищими цифрами), окончательно имеем
-
.
Из этой формулы ясно, что максимально возможная ошибка (абсолютная или относительная), обусловленная округлением, становится меньше, если сначала складывать меньшие числа. Результат довольно удивительный, так как вся классическая математика основана на предположении, что при перемене мест слагаемых или их группировке сумма не изменяется. Разница заключается в том, что ЭВМ не может производить вычисления с бесконечно большой точностью, а именно такие вычисления рассматриваются в классической математике.
Пример 2
Вычитание двух почти равных чисел. Предположим, что необходимо вычислить . Тогда из формулы распространения ошибки при вычитании имеем
-
.
Предположим, кроме того, что x и y являются соответствующим образом округленными положительными числами, так что
-
и
.
Если разность x-y мала, то относительная ошибка z может стать большой, даже если абсолютная ошибка мала. Так как в дальнейших вычислениях эта большая относительная ошибка будет распространяться, то она может поставить под сомнение точность окончательного результата вычислений.
Рассмотрим простой пример:
Тогда
Зная x и y, мы можем написать
Как видим, относительные ошибки x и y малы. Однако
Эта относительная ошибка очень велика, и, что важнее всего, она будет распространяться в ходе последующих вычислений.
Памятка программисту
Выводы, полученные выше, можно свести в краткий перечень рекомендаций для практической организации вычислений.
- Если необходимо произвести сложение-вычитание длинной последовательности чисел, работайте сначала с наименьшими числами.
- Если возможно, избегайте вычитания двух почти равных чисел. Формулы, содержащие такое вычитание, часто можно преобразовать так, чтобы избежать подобной операции.
- Выражение вида
можно написать в виде
, а выражение вида
можно написать в виде
. Если числа в разности почти равны друг другу, производите вычитание до умножения или деления. При этом задача не будет осложнена дополнительными ошибками округления.
- В любом случае сводите к минимуму число необходимых арифметических операций.
Список литературы
- Д.Мак-Кракен, У.Дорн. Численные методы и программирование на Фортране. Москва «Мир», 1977
- А. А. Самарский, А. В. Гулин. Численные методы. Москва «Наука», 1989.
См. также
- Практикум ММП ВМК, 4й курс, осень 2008
Распространение — ошибка
Cтраница 2
Для проверки прежде всего по закону распространения ошибок вычисляют среднюю квадратичную ошибку для разности двух средних значений из HI и nz измерений.
[16]
Очень важно четко понимать смысл этих формул распространения ошибок. Мы начинаем арифметическую операцию, имея в своем распоряжении два приближенных значения си. Ошибки эти могут быть любого происхождения. Величины х и у могут быть экспериментальными результатами, содержащими ошибки; они могут быть результатами предварительного вычисления согласно какому-либо бесконечному процессу и поэтому могут содержать ошибки ограничения; они могут быть результатами предшествующих арифметических операций и могут содержать ошибки округления. Естественно, они могут также содержать в различных комбинациях и все три вида ошибок.
[17]
Формулу (3.29) называют законом накопления или законом распространения ошибок.
[18]
Для каждого метода следует оценить по закону распространения ошибки достигаемую точность.
[19]
Сказанное имеет большое значение в вопросе о распространении ошибок при счете по рекуррентным формулам ( ср.
[20]
Таким образом, в арифметике с плавающей запятой распространение ошибок через длинные цепи операций не так сурово, как это предсказывает модель равномерного распределения, так как благоприятное распределение старших разрядов влияет на распространение ошибки через операции умножения и деления.
[22]
При вычислениях следует учитывать такое явление, как распространение ошибок. Ошибка, возникшая на входе вычислительного алгоритма или в определенном месте в ходе вычислений, распространяется дальше. Влияние ошибки на результат по мере выполнения последующих операций может увеличиваться или уменьшаться. Например, при вычитании почти равных чисел даже при достаточно маленьких ошибках представления этих чисел, относительная ошибка их разности может оказаться очень большой.
[23]
Важными инструментами для оценки неопределенности модели служат анализ чувствительности и распространение ошибки.
[24]
Применим теперь методику графов к трем примерам и проиллюстрируем, что означает распространение ошибки в практических вычислениях.
[25]
Чтобы уменьшить потери от сбоев и отказов, порождающих ошибки, надо предотвратить распространение ошибки в вычислительном процессе, так как в противном случае существенно усложнятся и удлинятся процедуры проверки правильности работы программы, определения и устранения искажений в программе, данных и промежуточных результатах.
[26]
Чтобы уменьшить потери от сбоев и отказов, порождающих ошибки, надо предотвратить распространение ошибки в вычислительном процессе, так как в противном случае существенно усложнятся к удлинятся процедуры проверки правильности работы программы, определения и устранения искажений в программе, данных и промежуточных результатах.
[27]
Структура расчетных формул метода прогонки столь проста, что можно пытаться проследить за распространением ошибок в процессе вычислений.
[28]
Также дайте пример сверточного кода со скоростью 1 / 2, К4, который проявляет катастрофические распространения ошибок.
[29]
Исследованы возможности архитектуры вычислительной системы [5.5] для реализации четырех принципов, которые, по мнению автора, не допускают распространения ошибок и тем самым повышают надежность системы. Таким: принципами являются: ограничение области выполнения вычислительного процесса, управление ресурсами, проверка правильности решения и восстановление при сбоях. Применяя эти принципы во время проектирования операционной системы при наличии необходимой аппаратной поддержки, можно, по мнению автора, создать надежные системы.
[30]
Страницы:
1
2
3
4
Содержание
- Лабораторный практикум
- Электронное издание локального распространения
- Формульный компилятор
- 1.1. Содержание работы.
- Лабораторная работа № 4 алгоритм обратного распространения ошибки
- Краткие сведения из теории
Лабораторный практикум
«Теория вычислительных процессов»
для студентов специальности 220400
Электронное издание локального распространения
Все права на размножение и распространение в любой форме остаются за разработчиком
Нелегальное копирование и использование данного продукта запрещено
Составители: Сайкин Александр Иванович, Данилова Татьяна Владимировна
410054, Саратов, ул.Политехническая, 77
Научно-техническая библиотека СГТУ
тел. 52-63-81, 52-56-01
© Саратовский государственный технический университет, 2006
Данный лабораторный практикум предназначен для студентов специальности 220400 «Программное обеспечение вычислительной техники и автоматизированных систем» и рассчитан на 18 аудиторных часов и 20 часов самостоятельной работы студента по изучению литературы, программированию и оформлению отчётов.
Выполнение лабораторных работ составляющих практикум предполагает исследование студентами моделей и характеристик вычислительных процессов. Методика исследований заключается в моделировании вычислительных процессов на ПЭВМ и аналитической обработке полученных результатов.
Лабораторная работа 1
Формульный компилятор
Данная лабораторная работа рассчитана на четыре аудиторных часа. Самостоятельная работа по изучению литературы, оформление отчёта ещё шесть часов.
Объект исследования — формульный транслятор, Цель исследования состоит в изучении проблематики разработки трансляторов с алгоритмических языков. Метод предполагает использование алгоритма рекурсивного спуска и написание программы транслятора. Работа выполняется в дисплейном классе.
1.1. Содержание работы.
Формульный транслятор эта программа, которая переводит исходную программу, написанную на входном языке, в объектный псевдокод, который в последствии, после необходимой оптимизации, может быть заменён машинным кодом с абсолютной адресацией.
Для написания программы на входном языке необходимо создать язык, в который бы входили: заголовок программы, оператор описания типа переменной, оператор ввода переменной, оператор присвоения и оператор вывода результата. Для оператора присвоения необходимо предусмотреть знаки арифметических операций, скобки и элементарные функции, которые выдаются вместе с вариантом задания. А также, разделители и служебные символы. В связи с этим разрабатывается контекстно-свободная грамматика, которая в последствии позволит провести грамматический разбор программы на исходном языке. Грамматическому разбору должен предшествовать лексический анализ, который обычно не вызывает затруднений.
Оператор присвоения имеет общий вид для всех вариантов
Результатом выполнения программы должен быть текст в объектном псевдокоде. Для чего необходимо оговорить его содержание. В работе рекомендуется использовать так называемые четвёрки, имеющие вид
где: КОП — код операции,
А1- адрес первого операнда,
А2 — адрес второго операнда,
А3 — адрес результата.
Хотя возможны и другие варианты, например, по двухадресной и одноадресной схемам.
Используемые данные могут быть как целыми, так и с плавающей точкой.
Источник
Лабораторная работа № 4 алгоритм обратного распространения ошибки
Цель работы. Разработка и исследование алгоритма обратного распространения ошибки для обучения многослойной нейронной сети с помощью изменения весов связей по принципу «победитель получает все».
Что представляет собой многослойная нейронная сеть? Из каких элементов она состоит?
В чем заключается задача обучения многослойной нейронной сети? Охарактеризуйте этапы работы алгоритма обратного распространения, применяемого для ее обучения.
Поясните принцип, положенный в основу обучения многослойной нейронной сети, «победитель получает все».
Краткие сведения из теории
Алгоритм обратного распространения является основным алгоритмом обучения в нейронных сетях, внесший значительный вклад в развитие методов расчета, которые имеют естественное происхождение. Нейронные сети представляют собой упрощенную модель человеческого мозга. Мозг состоит из нейронов, которые соединяются друг с другом с помощью нервных окончаний двух типов: синапсов и аксонов. Через синапсы в ядро нейрона поступают сигналы, а через аксоны нейрон передает сигнал далее. Человеческий мозг состоит примерно из 10 11 нейронов, и каждый нейрон связан с несколькими тысячами других нейронов. Структуру мозга можно рассматривать как многослойную нейронную сеть (рис. 1), состоящую в упрощенном виде из трех слоев: внешний слой передает импульсы от сенсоров из внешней среды, средний слой обрабатывает импульсы, а «выходной» слой выдает результат как действие обратно во внешнюю среду.
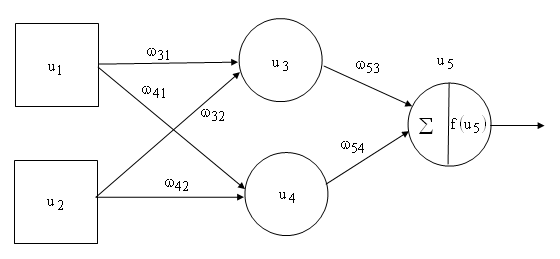
Искусственные нейронные сети имитируют работу мозга. Информация передается между нейронами, а структура и вес нервных окончаний определяют поведение сети. В многослойной нейронной сети входной слой представляет собой ячейки, предназначенные для разделения входных сигналов. Две входные ячейки обозначены идентификаторами (u1, u2), две скрытые ячейки — (u3, u4), выходная ячейка — u5 . Входные ячейки (u1, u2) задают входные значения для сети, а скрытые ячейки через веса ω31, ω32, ω41, ω42 определяют значения функций вида:
где ωb — вход смещения.
Выходная ячейка (u5) получает результат от двух скрытых ячеек (u3, u4)
через веса ω53 и ω54 соответственно. Сумма результатов входов скрытого слоя с весами соединений
позволяет определить значение функции активации f(u5) или передаточной функции нейрона на выходе сети. Среди функций активации наиболее распространенной является сигмойд функция S – образного вида (рис. 2.):
г
Рис.2. Функция сигмойда.
Функция активации должна быть применена и к скрытым ячейкам сети, но в данном примере они опускаются, чтобы показать работу выходного слоя.
Архитектура сети существенно зависит от решаемой задачи, поэтому при ее построении используются следующие эвристические правила:
начальная конфигурация сети содержит один слой с числом скрытых ячеек (нейронов) сети, равным половине общего количества входов и выходов;
если качество обучения недостаточно, то следует увеличить число дополнительных нейронов или количество промежуточных слоев;
если наблюдается процесс переобучения сети, то необходимо проводить корректировку конфигурации сети за счет уменьшения числа нейронов в слое или удаления одного или нескольких слоев.
В процессе обучения нейронной сети ошибка распространяется от выходного слоя к входному слою, то есть в направлении противоположном направлению сигнала при нормальном функционировании сети. Это обстоятельство поясняет происхождение названия алгоритма как алгоритма обратного распространения ошибки, применяемого для обучения сети. Выполнение алгоритма начинается с создания произвольно сгенерированных весов для многослойной сети. Затем процесс, описанный ниже по шагам, повторяется до тех пор, пока средняя ошибка на входе не будет признана достаточно малой.
Шаг 1. Берется пример входного сигнала E с соответствующим правильным значением выхода C.
Шаг 2. Рассчитывается прямое распространение E через сеть, при этом определяются весовые суммы Si и активаторы ui для каждой ячейки.
Шаг 3. Начиная с выходов, выполняется обратное движение через ячейки выходного и промежуточного слоя, при этом программа рассчитывает значения ошибок:

— для всех скрытых ячеек,
где m — обозначает все ячейки, связанные со скрытым узлом, w – заданный вектор веса, u – активация.
Шаг 4. Происходит обновление весов в сети с использованием выражений для весов соединений между скрытым слоем и выходом
для весов соединений между скрытым слоем и входом
Параметр ρ представляет собой коэффициент обучения (или размер шага), указывающий скорость продвижения алгоритма обратного распространения к решению. Тестирование алгоритма лучше начать со значения коэффициента обучения ρ = 0,1 и затем его постепенно повышать.
Рассмотрим работу алгоритма обратного распространения на примере нейронной сети, приведенной на рис. 3. На рисунке смещения выделены подчеркиванием.
Выполним расчет движения входного сигнала по сети, выбрав в качестве функции активации функцию сигмойда вида:
Определение значений функции активации f(u3) и f(u4) указывает на то, что сигнал дошел до скрытого слоя.
Переместим сигнал из скрытого слоя в выходной слой и рассчитаем значение функции активации на выходе из сети:
Правильной реакцией нейронной сети на тестовый входной является сигнал 1,0. Значение, рассчитанное сетью, составляет 0,78139. Это неплохой результат, но можно уменьшить значение ошибки, применив для сети алгоритм обратного распространения.
Д
Применим обратное распространение, начиная с определения ошибки в выходном узле:
Расчет ошибок для двух скрытых узлов связан с определением производной функции сигмойда, которая записывается в виде:
Используя это выражение, рассчитаем ошибки для скрытых узлов
Используем коэффициент ρ = 0,5 для изменения весов. Сначала необходимо обновить веса соединений между выходным и скрытыми слоями:
Теперь необходимо обновить смещение для выходной ячейки:
Изменение весов для скрытого слоя (для входа к скрытым ячейкам) будет:
Последний шаг- это обновление смещений для ячеек:
Обновление весов для выбранного обучающего сигнала завершается. Выполним проверку того, что алгоритм действительно уменьшает ошибку на выходе, введя тот же обучающий сигнал еще раз:
Таким образом, одна итерация алгоритма обратного распространения позволила уменьшить среднеквадратичную ошибку против прежнего значения 0,023895 на 0,001895.
Дать описание исходного кода, реализующего алгоритм обратного распространения для обучения многослойной нейронной сети методу выбора действия (рис. 4). Архитектура такой сети должна иметь выходы, разделенные на классы. При этом выходная ячейка с большей суммой весов является «победителем» группы и допускается к действию. На рисунке четыре входа обозначают: «знания специалиста» (0 – плохие, 1 – поверхностные, 2 – глубокие), «интуиция» (1, если есть интуиция, 0 – в противном случае), «программное обеспечение» (1, если специалист имеет в распоряжении необходимые алгоритмы и программы для работы на компьютере, 0 – в противном случае) и «проблема» (количество проблем в поле зрения). Выходы определяют поведение, которое выберет специалист. Действие «решить проблему» приводит к тому, что специалист решает проблему, которая находится в поле зрения. Действие «переложить решение проблемы на других» вынуждает специалиста признать свое поражение. Действие «отложить решение проблемы на время» связано с тем, что специалист сомневается в успехе дела и ему требуется время на обдумывание своего поступка. Действие «игнорировать существование проблемы» вынуждает специалиста не принимать никаких действий по решению проблемы, чтобы не потерять рабочее место.
Составить полный листинг программы в соответствии с пунктом 1 рабочего задания, включив в него инициализированные данные для обучения сети (табл. 1).
Создать в среде Delphi программу — исполняемый файл, который может загружаться и выполняться под управлением Windows на основе пункта 2 рабочего задания.
П
Выполнить анализ работы программы обучения нейронной сети с помощью алгоритма обратного распространения на демонстрационном примере, приведенном в пункте 4 рабочего задания, путем изменения следующих параметров:
количества итераций на обучение сети в диапазоне от 5000 до 10000 (значение диапазона выбирается произвольно);
числа скрытых ячеек на единицу в большую и меньшую сторону;
Источник
Что такое распространение ошибок? (Определение и пример)
17 авг. 2022 г.
читать 2 мин
Распространение ошибки происходит, когда вы измеряете некоторые величины a , b , c , … с неопределенностями δ a , δ b , δc …, а затем хотите вычислить какую-то другую величину Q , используя измерения a , b , c и т. д.
Получается, что неопределенности δa , δb , δc будут распространяться (т.е. «растягиваться») на неопределенность Q.
Для вычисления неопределенности Q , обозначаемой δ Q , мы можем использовать следующие формулы.
Примечание. Для каждой из приведенных ниже формул предполагается, что величины a , b , c и т. д. имеют случайные и некоррелированные ошибки.
Сложение или вычитание
Если Q = a + b + … + c – (x + y + … + z)
Тогда δ Q = √ (δa) 2 + (δb) 2 + … + (δc) 2 + (δx) 2 + (δy) 2 + … + (δz) 2
Пример. Предположим, вы измеряете длину человека от земли до талии как 40 дюймов ± 0,18 дюйма. Затем вы измеряете длину человека от талии до макушки как 30 дюймов ± 0,06 дюйма.
Предположим, вы затем используете эти два измерения для расчета общего роста человека. Высота будет рассчитана как 40 дюймов + 30 дюймов = 70 дюймов. Неопределенность в этой оценке будет рассчитываться как:
- δ Q = √ (δa) 2 + (δb) 2 + … + (δc) 2 + (δx) 2 + (δy) 2 + … + (δz) 2
- δ Q = √ (.18) 2 + (.06) 2
- δ Q = 0,1897
Это дает нам окончательное измерение 70 ± 0,1897 дюйма.
Умножение или деление
Если Q = (ab…c) / (xy…z)
Тогда δ Q = |Q| * √ (δa/a) 2 + (δb/b) 2 + … + (δc/c) 2 + (δx/x) 2 + (δy/y) 2 + … + (δz/z) 2
Пример: Предположим, вы хотите измерить отношение длины элемента a к элементу b.Вы измеряете длину a как 20 дюймов ± 0,34 дюйма, а длину b как 15 дюймов ± 0,21 дюйма.
Отношение, определенное как Q = a/b , будет рассчитано как 20/15 = 1,333.Неопределенность в этой оценке будет рассчитываться как:
- δQ = | Q | * √ (δa/a) 2 + (δb/b) 2 + … + (δc/c) 2 + (δx/x) 2 + (δy/y) 2 + … + (δz/z) 2
- δ Q = |1,333| * √ (0,34/20) 2 + (0,21/15) 2
- δ Q = 0,0294
Это дает нам окончательное соотношение 1,333 ± 0,0294 дюйма.
Измеренное количество, умноженное на точное число
Если A точно известно и Q = A x
Тогда δ Q = |A|δx
Пример: предположим, что вы измеряете диаметр круга как 5 метров ± 0,3 метра. Затем вы используете это значение для вычисления длины окружности c = πd .
Длина окружности будет рассчитана как c = πd = π*5 = 15,708.Неопределенность в этой оценке будет рассчитываться как:
- δ Q = |A|δx
- δ = | π | * 0,3
- δ Q = 0,942
Таким образом, длина окружности равна 15,708 ± 0,942 метра.
Неуверенность в силе
Если n — точное число и Q = x n
Тогда δ Q = | Вопрос | * | н | * (δ х/х )
Пример: предположим, что вы измеряете сторону куба как s = 2 дюйма ± 0,02 дюйма. Затем вы используете это значение для вычисления объема куба v = s 3 .
Объем будет рассчитан как v = s 3 = 2 3 = 8 дюймов 3.Неопределенность в этой оценке будет рассчитываться как:
- δ = | Вопрос | * | н | * (δ х/х )
- δ Q = |8| * |3| * (.02/2)
- δ Q = 0,24
Таким образом, объем куба равен 8 ± 0,24 дюйма 3 .
Общая формула распространения ошибок
Если Q = Q(x) является любой функцией от x , то общая формула распространения ошибок может быть определена как:
δ Q = |dQ / dX |δx
Обратите внимание, что вам редко придется выводить эти формулы с нуля, но может быть полезно знать общую формулу, используемую для их вывода.
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
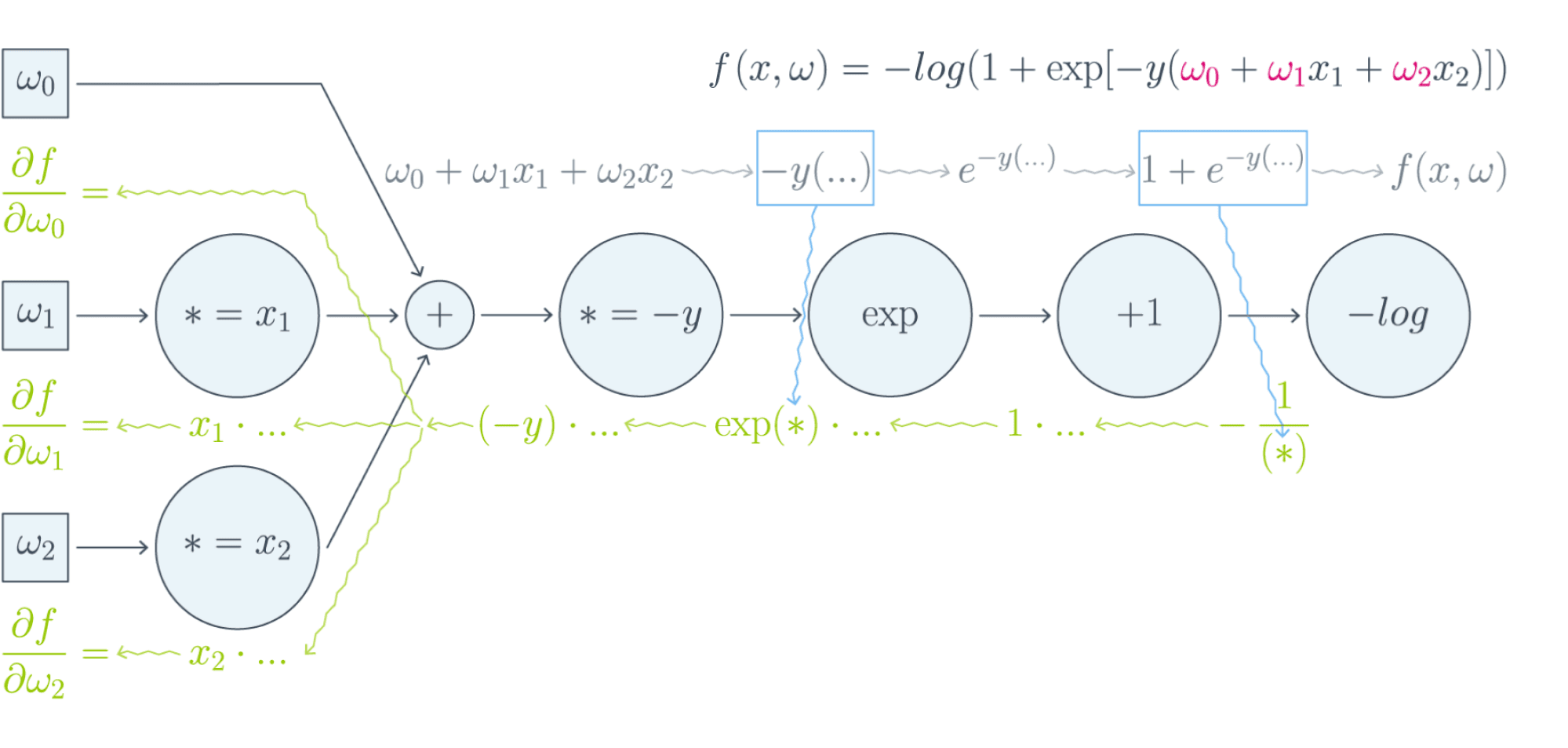
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
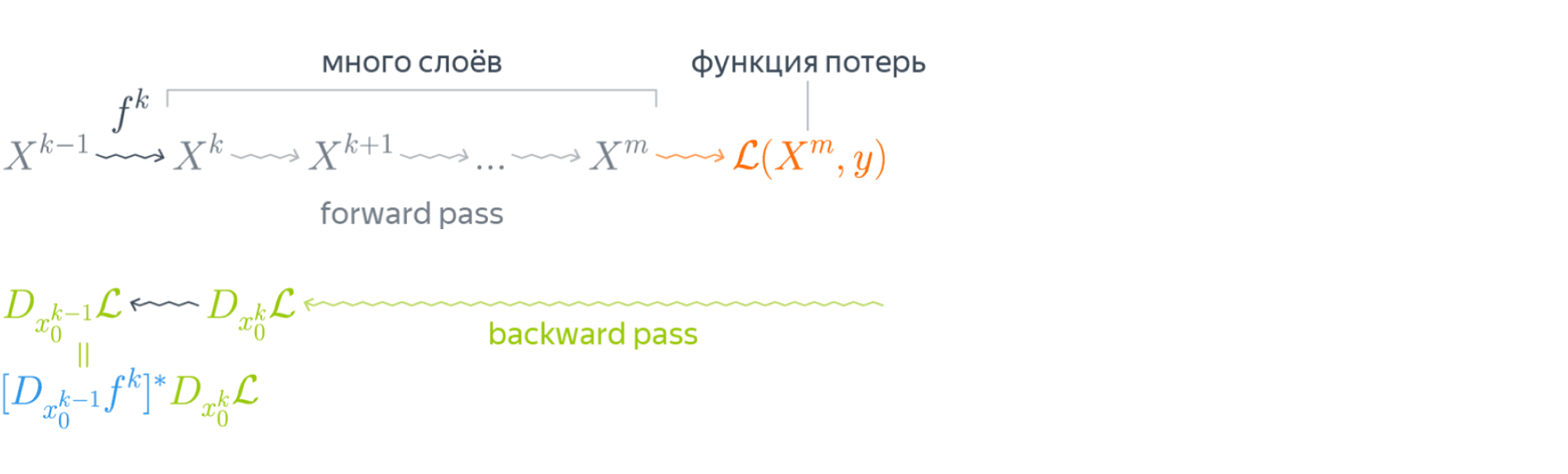
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1
vdots
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)
vdots
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$begin{multline*}
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\[0.1cm]
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
end{multline*},$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$begin{multline*}
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
end{multline*}$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$ begin{multline*}
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
end{multline*} $$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
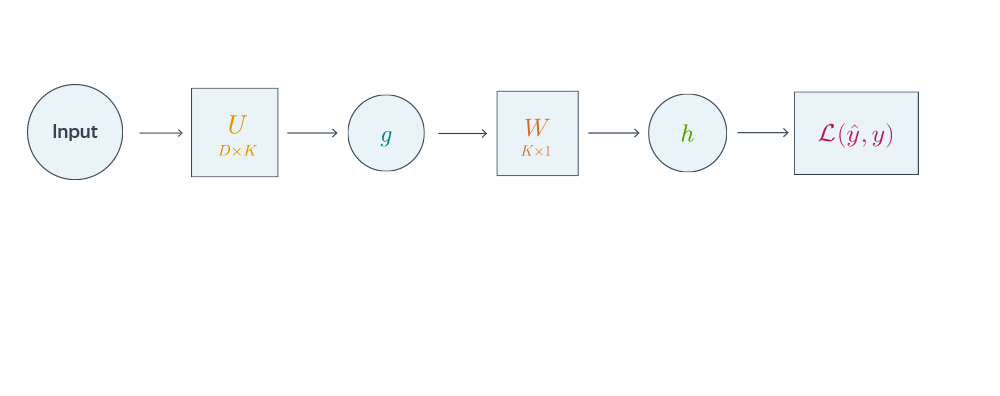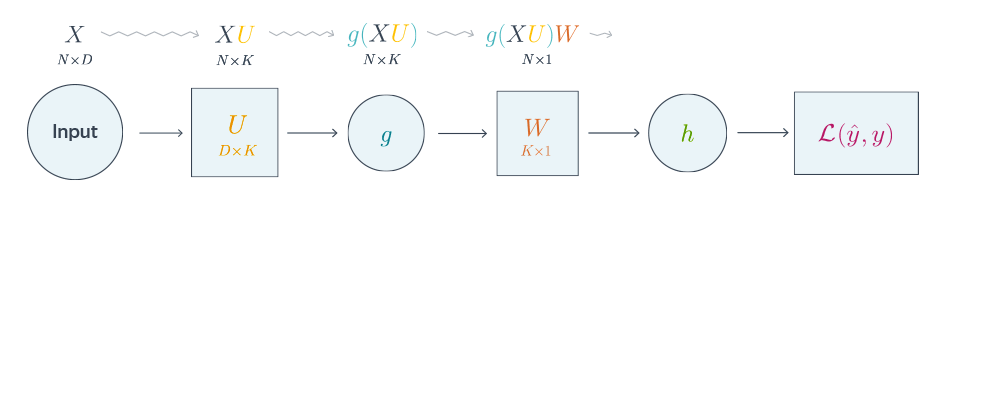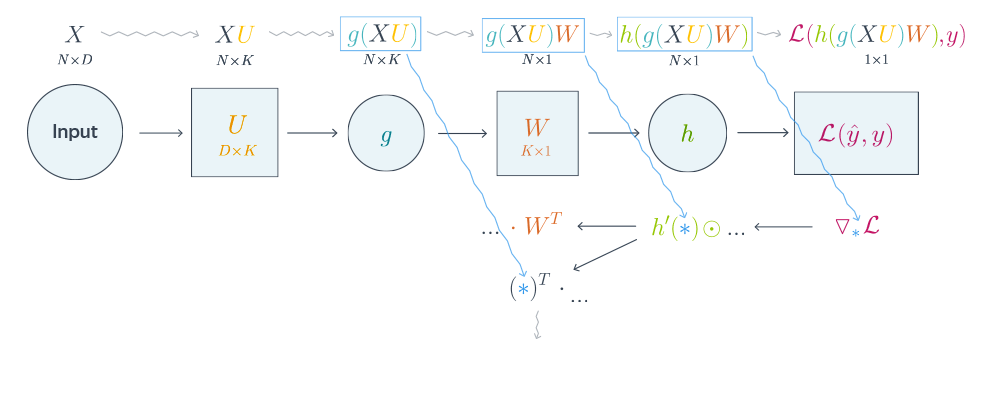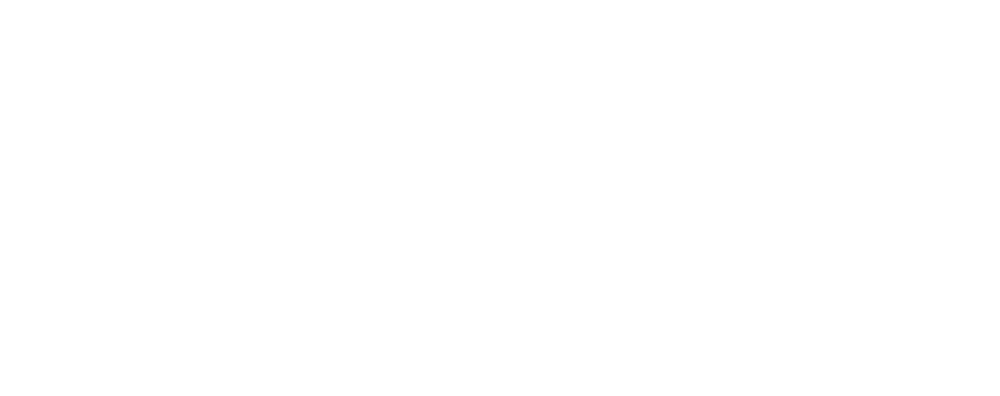
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
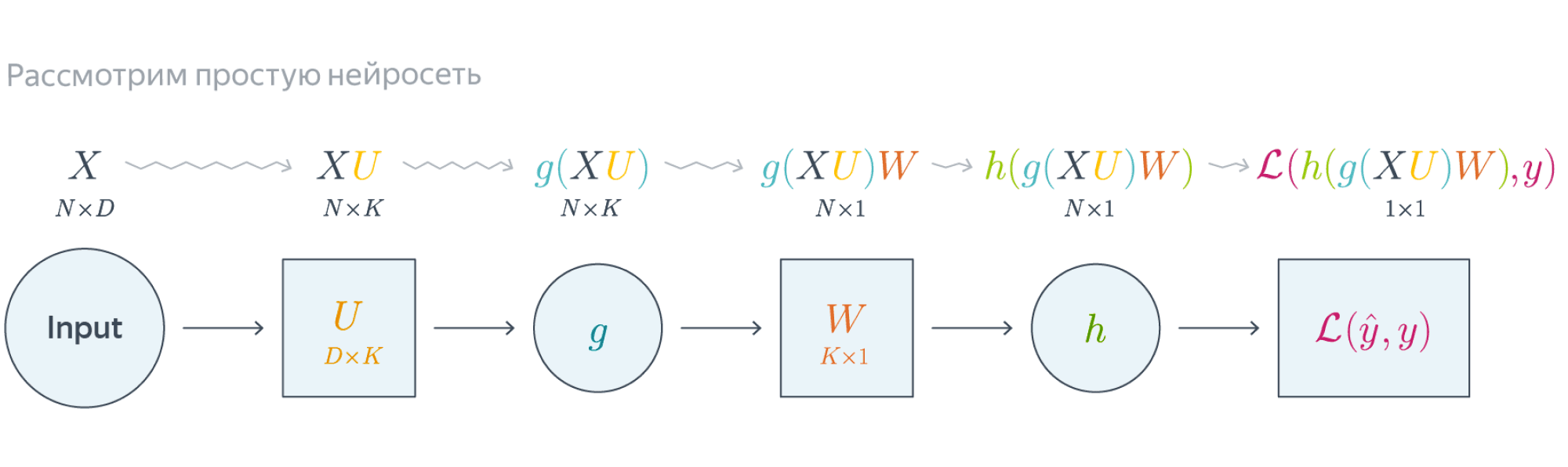
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Знакомимся с методом обратного распространения ошибки
Время прочтения
6 мин
Просмотры 36K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!
Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.
Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.
Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:
Для l = 3:
W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.
Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.
b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.
Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:
Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:
И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:
Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.
Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:
(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:
(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:
«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:
Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z2)3 и (a2)3:
Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».