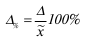Расхождения
между величиной какого-либо показателя,
найденного посредством статистического
наблюдения, и действительными его
размерами называются ошибками
наблюдения.В зависимости от
причин возникновения различают ошибки
регистрации и ошибки репрезентативности.
Ошибки
регистрациивозникают в результате
неправильного установления фактов или
ошибочной записи в процессе наблюдения
или опроса. Они бывают случайными или
систематическими. Случайные ошибки
регистрации могут быть допущены как
опрашиваемыми в их ответах, так и
регистраторами. Систематические ошибки
могут быть и преднамеренными, и
непреднамеренными. Преднамеренные –
сознательные, тенденциозные искажения
действительного положения дела.
Непреднамеренные вызываются различными
случайными причинами (небрежность,
невнимательность).
Ошибки
репрезентативности(представительности)
возникают в результате неполного
обследования и в случае, если обследуемая
совокупность недостаточно полно
воспроизводит генеральную совокупность.
Они могут быть случайными и систематическими.
Случайные ошибки репрезентативности
– это отклонения, возникающие при
несплошном наблюдении из-за того, что
совокупность отобранных единиц наблюдения
(выборка) неполно воспроизводит всю
совокупность в целом. Систематические
ошибки репрезентативности – это
отклонения, возникающие вследствие
нарушения принципов случайного отбора
единиц. Ошибки репрезентативности
органически присущи выборочному
наблюдению и возникают в силу того, что
выборочная совокупность не полностью
воспроизводит генеральную. Избежать
ошибок репрезентативности нельзя,
однако, пользуясь методами теории
вероятностей, основанными на использовании
предельных теорем закона больших чисел,
эти ошибки можно свести к минимальным
значениям, границы которых устанавливаются
с достаточно большой точностью.
Ошибки
выборки –разность между
характеристиками выборочной и генеральной
совокупности. Для среднего значения
ошибка будет определяться по формуле
(7.1)
где
Величина
называетсяпредельной ошибкойвыборки.
Предельная
ошибка выборки – величина случайная.
Исследованию закономерностей случайных
ошибок выборки посвящены предельные
теоремы закона больших чисел. Наиболее
полно эти закономерности раскрыты в
теоремах П. Л. Чебышева и А. М. Ляпунова.
Теорему П.
Л. Чебышева применительно к
рассматриваемому методу можно
сформулировать следующим образом: при
достаточно большом числе независимых
наблюдений можно с вероятностью, близкой
к единице (т. е. почти с достоверностью),
утверждать, что отклонение выборочной
средней от генеральной будет сколько
угодно малым. В теореме П. Л. Чебышева
доказано, что величина ошибки не должна
превышать.
В свою очередь величина,
выражающая среднее квадратическое
отклонение выборочной средней от
генеральной средней, зависит от
колеблемости признака в генеральной
совокупностии числа отобранных единицn. Эта
зависимость выражается формулой
,
(7.2)
где
зависит также от способа производства
выборки.
Величину
=
называютсредней ошибкой выборки. В
этом выражении– генеральная дисперсия,n– объем
выборочной совокупности.
Рассмотрим, как
влияет на величину средней ошибки число
отбираемых единиц n. Логически
нетрудно убедиться, что при отборе
большого числа единиц расхождения между
средними будут меньше, т. е. существует
обратная связь между средней ошибкой
выборки и числом отобранных единиц. При
этом здесь образуется не просто обратная
математическая зависимость, а такая
зависимость, которая показывает, что
квадрат расхождения между средними
обратно пропорционален числу отобранных
единиц.
Увеличение
колеблемости признака влечет за собой
увеличение среднего квадратического
отклонения, а следовательно, и ошибки.
Если предположить, что все единицы будут
иметь одинаковую величину признака, то
среднее квадратическое отклонение
станет равно нулю и ошибка выборки
также исчезнет. Тогда нет необходимости
применять выборку. Однако следует иметь
в виду, что величина колеблемости
признака в генеральной совокупности
неизвестна, поскольку неизвестны размеры
единиц в ней. Можно рассчитать лишь
колеблемость признака в выборочной
совокупности. Соотношение между
дисперсиями генеральной и выборочной
совокупности выражается формулой
Поскольку
величина
при достаточно большихnблизка к
единице, можно приближенно считать, что
выборочная дисперсия равна генеральной
дисперсии, т. е.
Следовательно,
средняя ошибка выборки показывает,
какие возможны отклонения характеристик
выборочной совокупности от соответствующих
характеристик генеральной совокупности.
Однако о величине этой ошибки можно
судить с определенной вероятностью. На
величину вероятности указывает множитель
Теорема А.
М. Ляпунова. А. М. Ляпунов доказал,
что распределение выборочных средних
(следовательно, и их отклонений от
генеральной средней) при достаточно
большом числе независимых наблюдений
приближенно нормально при условии, что
генеральная совокупность обладает
конечной средней и ограниченной
дисперсией.
Математически
теорему Ляпуноваможно записать
так:

где
,
(7.4)
где – математическая постоянная;
–предельная ошибка выборки,которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.
Значения этого
интеграла для различных значений
коэффициента доверия tвычислены и
приводятся в специальных математических
таблицах. В частности, при:
Поскольку tуказывает на вероятность расхождения,
т. е. на вероятность того, на какую
величину генеральная средняя будет
отличаться от выборочной средней, то
это может быть прочитано так: с вероятностью
0,683 можно утверждать, что разность между
выборочной и генеральной средними не
превышает одной величины средней ошибки
выборки. Другими словами, в 68,3 % случаев
ошибка репрезентативности не выйдет
за пределыС вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает(т. е. в 95 % случаев). С вероятностью
0,997, т. е. довольно близкой к единице,
можно ожидать, что разность между
выборочной и генеральной средней не
превзойдет трехкратной средней ошибки
выборки и т. д.
Логически связь
здесь выглядит довольно ясно: чем больше
пределы, в которых допускается
возможная ошибка, тем с большей
вероятностью судят о ее величине.
Зная выборочную
среднюю величину признака
и предельную ошибку выборки
,
можно определить границы (пределы),
в которых заключена генеральная
средняя
(7.5)
1.
Собственно-случайная выборка–
этот способ ориентирован на выборку
единиц из генеральной совокупности без
всякого расчленения на части или группы.
При этом для соблюдения основного
принципа выборки – равной возможности
всем единицам генеральной совокупности
быть отобранным – используются схема
случайного извлечения единиц путем
жеребьевки (лотереи) или таблицы случайных
чисел. Возможен повторный и бесповторный
отбор единиц
Средняя ошибка
собственно-случайной выборки
представляет собой среднеквадратическое
отклонение возможных значений выборочной
средней от генеральной средней. Средние
ошибки выборки при собственно-случайном
методе отбора представлены в табл. 7.2.
Таблица 7.2
|
Средняя ошибка |
При отборе |
|
|
повторном |
бесповторном |
|
|
Для средней |
|
|
|
Для доли |
|
|
В таблице
использованы следующие обозначения:
– дисперсия выборочной совокупности;
– численность выборки;
– численность генеральной совокупности;
– выборочная доля единиц, обладающих
изучаемым признаком;
– число единиц, обладающих изучаемым
признаком;
– численность выборки.
Для увеличения
точности вместо множителя
следует
брать множитель
,
но при большой численностиNразличие
между этими выражениями практического
значения не имеет.
Предельная
ошибка собственно-случайной выборки
рассчитывается по формуле
,
(7.6)
где t
– коэффициент доверия зависит от
значения вероятности.
Пример.При
обследовании ста образцов изделий,
отобранных из партии в случайном порядке,
20 оказалось нестандартными. С вероятностью
0,954 определите пределы, в которых
находится доля нестандартной продукции
в партии.
Решение.
Вычислим генеральную долю (Р):
.
Доля нестандартной
продукции:

Предельная
ошибка выборочной доли с вероятностью
0,954 рассчитывается по формуле (7.6) с
применением формулы табл. 7.2 для доли:
С вероятностью
0,954 можно утверждать, что доля нестандартной
продукции в партии товара находится в
пределах 12 % ≤ P≤ 28 %.
В практике
проектирования выборочного наблюдения
возникает потребность определения
численности выборки, которая необходима
для обеспечения определенной точности
расчета генеральных средних. Предельная
ошибка выборки и ее вероятность при
этом являются заданными. Из формулы
и формул средних ошибок выборки
устанавливается необходимая численность
выборки. Формулы для определения
численности выборки (n) зависят от
способа отбора. Расчет численности
выборки для собственно-случайной выборки
приведен в табл. 7.3.
Таблица 7.3
|
Предполагаемый |
Формулы |
|
|
для средней |
для доли |
|
|
Повторный |
|
|
|
Бесповторный |
|
|
2.
Механическая выборка– при этом
методе исходят из учета некоторых
особенностей расположения объектов в
генеральной совокупности, их упорядоченности
(по списку, номеру, алфавиту). Механическая
выборка осуществляется путем отбора
отдельных объектов генеральной
совокупности через определенный интервал
(каждый 10-й или 20-й). Интервал рассчитывается
по отношению,
гдеn– численность выборки,N–
численность генеральной совокупности.
Так, если из совокупности в 500 000 единиц
предполагается получить 2 %-ную выборку,
т. е. отобрать 10 000
единиц, то пропорция отбора составитОтбор
единиц осуществляется в соответствии
с установленной пропорцией через равные
интервалы. Если расположение объектов
в генеральной совокупности носит
случайный характер, то механическая
выборка по содержанию аналогична
случайному отбору. При механическом
отборе применяется только бесповторная
выборка [1, 5–10].
Средняя ошибка
и численность выборки при механическом
отборе подсчитывается по формулам
собственно-случайной выборки (см.
табл. 7.2 и 7.3).
3.
Типическая выборка, при котрой
генеральная совокупность делится по
некоторым существенным признакам на
типические группы; отбор единиц
производится из типических групп. При
этом способе отбора генеральная
совокупность расчленяется на однородные
в некотором отношении группы, которые
имеют свои характеристики, и вопрос
сводится к определению объема выборок
из каждой группы. Может бытьравномерная
выборка– при этом способе из каждой
типической группы отбирается одинаковое
число единицТакой подход оправдан лишь при равенстве
численностей исходных типических групп.
При типическом отборе, непропорциональном
объему групп, общее число отбираемых
единиц делится на число типических
групп, полученная величина дает
численность отбора из каждой типической
группы.
Более совершенной
формой отбора является пропорциональная
выборка. Пропорциональной называется
такая схема формирования выборочной
совокупности, когда численность выборок,
взятых из каждой типической группы в
генеральной совокупности, пропорциональна
численностям, дисперсиям (или комбинированно
и численностям, и дисперсиям). Условно
определяем численность выборки в 100
единиц и отбираем единицы из групп:
– пропорционально
численности их генеральной совокупности
(табл. 7.4). В таблице
обозначено:
Ni– численность типической группы;
dj
– доля (Ni/N);
N– численность
генеральной совокупности;
ni– численность выборки из типической
группы вычисляется:
, (7.7)
n – численность выборки из генеральной
совокупности.
Таблица
7.4
-
Группы
Ni
dj
ni
1
300
0,3
30
2
500
0,5
50
3
200
0,2
20
1000
1,0
100
–
пропорционально среднему квадратическому
отклонению(табл. 7.5).
здесь
i– среднее
квадратическое отклонение типических
групп;
ni
– численность выборки из типической
группы вычисляется по формуле
(7.8)
Таблица
7.5
-
Ni
i
ni
300
5
0,25
25
500
7
0,35
35
200
8
0,40
40
1000
20
1,0
100
–
комбинированно (табл. 7.6).
Численность
выборки вычисляется по формуле
. (7.9)
Таблица 7.6
-
i
iNi
300
5
1500
0,23
23
500
7
2100
0,53
53
200
8
1600
0.24
24
1000
20
6600
1,0
100
При проведении
типической выборки непосредственный
отбор из каждой группы проводится
методом случайного отбора.
Средние ошибки
выборки рассчитываются по формулам
табл. 7.7 в зависимости от способа отбора
из типических групп.
Таблица 7.7
|
Способ |
Повторный |
Бесповторный |
||
|
для |
для |
для |
для |
|
|
Непропорциональный |
|
|
|
|
|
Пропорциональный объему групп |
|
|
|
|
|
Пропорциональный |
|
|
|
|
здесь
– средняя из внутригрупповых дисперсий
типических групп;
– доля единиц, обладающих изучаемым
признаком;
– средняя из внутригрупповых дисперсий
для доли;
– среднее квадратическое отклонение
в выборке изi-й типической группы;
– объем выборки из типической группы;
– общий объем выборки;
–
объем типической группы;
– объем генеральной совокупности.
Численность
выборки из каждой типической группы
должна быть пропорциональна среднему
квадратическому отклонению в этой
группе
.Расчет численности
производится по формулам, приведенным
в табл. 7.8.
Таблица 7.8
|
Повторный |
Бесповторный |
|
|
Для определения |
|
|
|
Для определения |
|
|
4. Серийная
выборка– удобена в тех случаях,
когда единицы совокупности объединены
в небольшие группы или серии. При серийной
выборке генеральную совокупность делят
на одинаковые по объему группы – серии.
В выборочную совокупность отбираются
серии. Сущность серийной выборки
заключается в случайном или механическом
отборе серий, внутри которых производится
сплошное обследование единиц. Средняя
ошибка серийной выборки с равновеликими
сериями зависит от величины только
межгрупповой дисперсии. Средние ошибки
сведены в табл. 7.9.
Таблица 7.9
|
Способ |
Формулы |
|
|
для |
для |
|
|
Повторный |
|
|
|
Бесповторный |
|
|
Здесь
R– число серий в генеральной
совокупности;
r – число
отобранных серий;
– межсерийная (межгрупповая) дисперсия
средних;
– межсерийная (межгрупповая) дисперсия
доли.
При серийном
отборе необходимую численность отбираемых
серий определяют так же, как и при
собственно-случайном методе отбора.
Расчет численности
серийной выборки производится по
формулам, приведенным в табл. 7.10.
Таблица 7.10
|
Повторный |
Бесповторный |
|
|
Для |
|
|
|
Для |
|
|
Пример.В
механическом цехе завода в десяти
бригадах работает 100 рабочих. В целях
изучения квалификации рабочих была
произведена 20 %-ная серийная бесповторная
выборка, в которую вошли две бригады.
Получено следующее распределение
обследованных рабочих по разрядам:
|
Рабочие |
Разряды рабочих |
Разряды рабочих |
Рабочие |
Разряды |
Разряды |
|
1 2 3 4 5 |
2 4 5 2 5 |
3 6 1 5 3 |
6 7 8 9 10 |
6 5 8 4 5 |
4 2 1 3 2 |
Необходимо
определить с вероятностью 0,997 пределы,
в которых находится средний разряд
рабочих механического цеха.
Решение.
Определим выборочные средние по
бригадам и общую среднюю как среднюю
взвешенную из групповых средних:
Определим
межсерийную дисперсию по формулам
(5.25):
Рассчитаем
среднюю ошибку выборки по формуле табл.
7.9:
Вычислим
предельную ошибку выборки с вероятностью
0,997:
С вероятностью
0,997 можно утверждать, что средний разряд
рабочих механического цеха находится
в пределах
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Выборка. Типы выборок. Расчет ошибки выборки
Калькуляторы
Калькулятор расчета ошибки и размера выборки
Калькулятор расчета статистической значимости различий
Генеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих
определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и
времени. Примеры генеральных совокупностей
- Все жители Москвы (10,6 млн. человек по данным переписи 2002 года)
- Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года)
- Юридические лица России (2,2 млн. на начало 2005 года)
- Розничные торговые точки, осуществляющие продажу продуктов питания (20 тысяч на начало 2008 года) и
т.д.
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей
генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на
всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и
нерепрезентативной для разных генеральных совокупностей.
Пример:
- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население
Москвы. - Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать
москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках
соответственно.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от
ошибки никак не зависит от размера выборки.
Пример:
Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой
всех москвичей.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера
выборки. Чем больше размер выборки, тем она ниже.
Пример:
Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной
вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об
ошибке выборки, подразумевают именно статистическую ошибку.
Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих
результаты исследования в определенную сторону.
Пример:
- Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни.
Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например,
дома). - Проблема респондентов, отказывающихся отвечать на вопросы
анкеты (доля «отказников» в Москве, для разных опросов,
колеблется от 50% до 80%)
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот
или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные
1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов,
наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата
рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер
генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы
(страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются
случайным образом. Объекты внутри групп обследуются сплошняком.
2.Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности,
типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60
лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для
каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны
попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной
совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки
используются в маркетинговых исследованиях достаточно
часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег,
знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за
исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда
необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход,
респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения
и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство
интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром –
активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает
проблема выбора признака и определения его типичного значения.
Курс лекций по теории статистики
Более подробную информацию по выборочным наблюдениям можно получить просмотрев видеокурс по теории статистики:
Выборочное наблюдение Способы формирование выборки
Специальные виды отбора
Калькулятор расчета ошибки и размера выборки (для простой случайной выборки)
Пояснения к полям:
Доверительная вероятность
Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по
выборочным данным. В практике исследований чаще всего используют 95%-ую доверительную вероятность
Ошибка выборки (доверительный интервал)
Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное
истинное значение оцениваемого параметра распределения.
Доля признака
Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют,
необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Калькулятор расчета статистической значимости различий
Калькулятор позволяет проверить есть ли статистически значимая разница между долями признака, полученными из
независимых выборок.
Например, если до начала рекламной кампании марку знали 55% респондентов, а по окончании – 60% — есть ли между этими
долями статистически значимая разница, или же эта разница укладывается в ошибку выборки?
Примечание. Эта процедура может законно использоваться, только если обе выборки удовлетворяют следующему условию:
произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, должны быть не меньше 5.
Оставить свои комментарии по затронутой теме Вы можете на наших страницах в Facebook и Вконтакте.
При перепечатке материалов ссылка на маркетинговое агентство обязательна
FDF Group © 2023
Разработка сайта — Монохром
В каждой профессии есть свой набор любимых вопросов. Для исследователей рынка этот список возглавляет, безусловно, вопрос о размере выборки. Обычно его формулируют так:
- Мы хотели бы заказать исследование по посетителям московских торговых центров. Какая нам нужна выборка?
- Наша целевая аудитория – примерно 300 000 человек. Сколько людей нам нужно опросить, чтобы было репрезентативно? А если целевая аудитория будет 3 млн?
- Нам нужно оценить потенциал продаж квартир в Санкт-Петербурге жителям северных городов России. Какую сделать выборку?
Размер выборки действительно важен, потому что определяет стоимость будущего исследования, не говоря уже о качестве итоговых результатов и выводов. В этой статье мы расскажем о том, как рассчитать оптимальный размер выборки массового опроса. Наш материал будет полезен всем, кто так или иначе сталкивается с необходимостью проведения маркетинговых исследований своими силами или заказывает их у специализированного агентства.
Главное заблуждение о размере выборки
Многие уверены, что чем больше размер целевой группы, тем больше должен быть размер выборки. Поэтому, якобы, чтобы узнать мнение жителей маленького города, достаточно опросить человек 200-300, ну а для выяснения мнения по России в целом и 5000 будет мало.
Между тем, этот стереотип не имеет ничего общего с реальностью. Размер выборки не зависит от численности целевой группы (на языке статистики она называется «генеральной совокупностью») и определяется двумя совершенно другими факторами. Единственное исключение из этого правила – случаи, когда генеральная совокупность очень маленькая, например, 1-2 тысячи человек, но такие ситуации в реальной практике маркетинговых исследований встречаются редко.
Два фактора, от которых зависит размер выборки
Размер выборки массового опроса зависит от двух факторов:
- Точности данных, которые нужно получить на выходе – это та самая «статистическая погрешность». Для выборки в 100 респондентов она будет в пределах плюс-минус 10%, а для выборки в 1000 респондентов – в пределах плюс-минус 3,1%. Более подробно об этом – ниже.
- Количества и размера подгрупп, на которые нужно разбивать выборку при анализе. Например, если проводится электоральное исследование, то в основном нас будет интересовать ядро активных избирателей. Как правило, доля «ядра» редко превышает 20-25% от всего населения. Поэтому размер выборки нужно рассчитывать так, чтобы одна четверть от ее общего объема позволяла проводить полноценный статистический анализ.
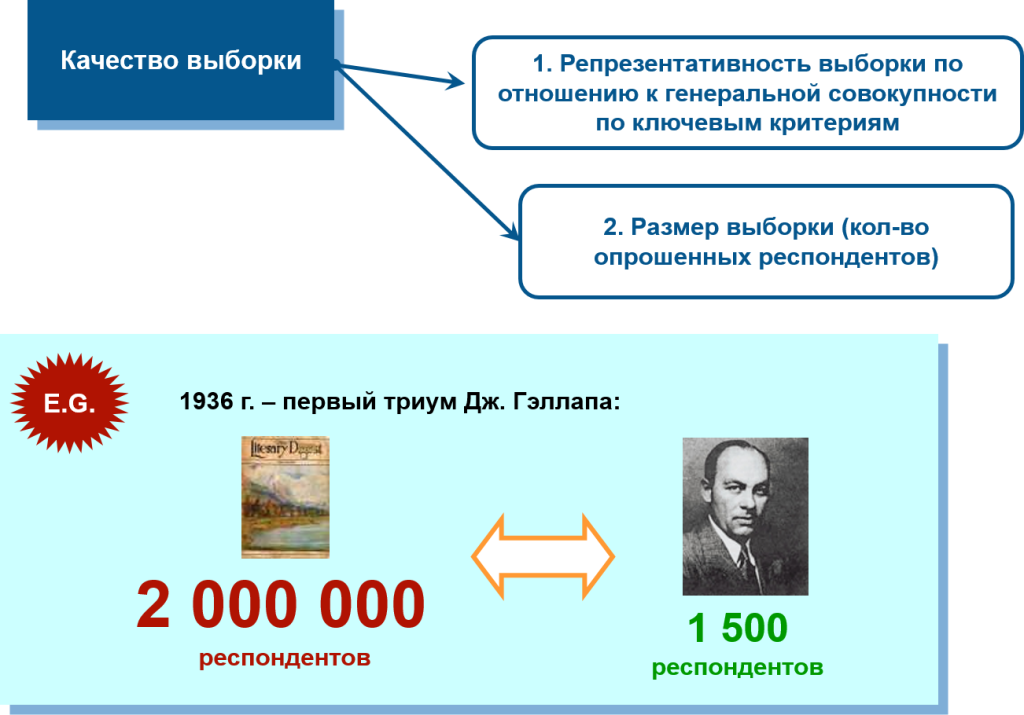
Вопреки расхожему мнению, качество выборки определяется не ее размером, а репрезентативностью. Репрезентативность – это соответствие между выборкой и генеральной совокупности по ключевым параметрам. Чаще всего, в качестве таких «реперных точек» используют легко измеряемые социально-демографические показатели: пол, возраст, образование, род занятий и место жительства.
Две разновидности ошибки выборки
Любое выборочное наблюдение (то есть когда мы опрашиваем не всех подряд, а делаем случайный отбор из генеральной совокупности) сопряжено с погрешностью данных. Эту погрешность обычно называют «ошибкой выборки». Она может быть двух видов:
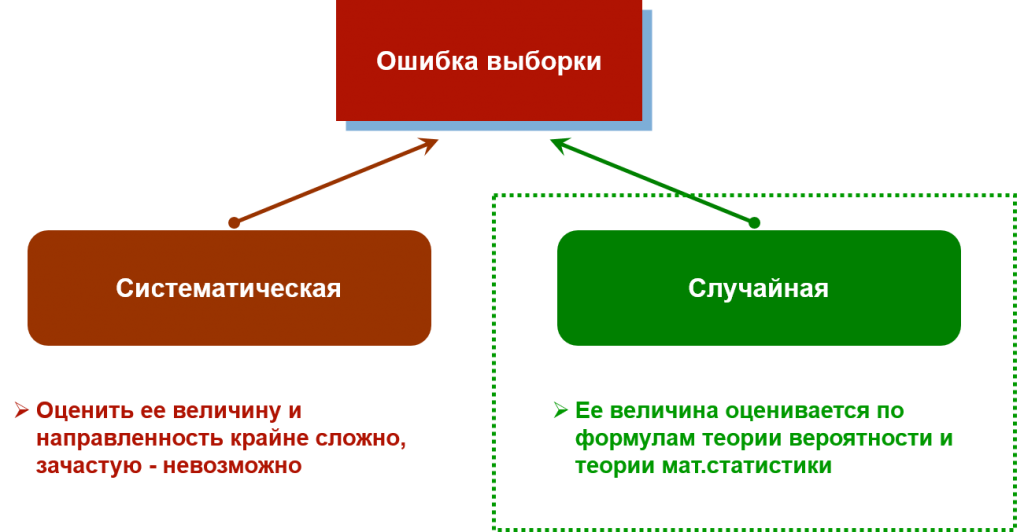
- Систематическая – связана с ошибками проектирования выборки. Оценить ее размер, направление и степень смещения очень сложно, чаще всего – невозможно. Например, если вопросы респондентам будут задавать представители маргинальных социальных слоев, это повлияет на готовность участвовать в исследовании со стороны представителей более обеспеченных групп населения. В итоге это приведет к крайне трудно оцениваемой систематической ошибке и искажению данных.
- Случайная – связана с действием законов статистики. Ее размер легко рассчитывается по формулам математической статистики и теории вероятности. Они позволяют делать обоснованные выводы о доверительном интервале признака. Например, если статистическая погрешность составляет плюс-минус 10%, а полученное значение показателя оказалось равно 25%, то доверительный интервал равен от 15% до 35%.
Задача исследователя – собрать данные так, чтобы минимизировать систематическую ошибку выборки. Тогда можно будет свести статпогрешность лишь к случайной ошибке, которую можно рассчитать по формулам.
Как рассчитать размер случайной ошибки выборки
Случайная ошибка выборки зависит не только от объема выборки, но и от дисперсии, то есть степени однородности данных. Чем однороднее данные (т.е. чем меньше разброс полученных значений, или дисперсия), тем меньше ошибка выборки.
Существует формула расчета случайной ошибки выборки, однако для удобства рекомендуем пользоваться онлайн-калькуляторами, например, вот этим. Он позволяет легко провести два вида расчета:
- рассчитать величину статистической погрешности на основе размера выборки и предполагаемой дисперсии;
- определить размер выборки, требуемый для получения оценки нужной степени точности.
Вот так выглядит его рабочее окно:
В качестве параметра доверительной надежности (одно из полей в калькуляторе) обычно используется значение в 95%. Это означает, что в 95% случаев распределение признака в генеральной совокупности попадет в рассчитанный доверительный интервал (т.е. само значение признака в выборке плюс-минус размер статистической погрешности). Реже используется значение надежности в 97% или 99% – оно, соответственно, означает, что подобное попадание произойдет в 97% или 99% случаев. В данном случае надежность выборки повышается, но увеличивается размер выборки.
Самое сложное при определении размера выборки – поиск компромисса между требуемой точностью и стоимостью сбора данных. Этот процесс усложняется тем, что увеличение размера выборки в четыре раза приводит к увеличению точности лишь в два раза (соответствует квадратному корню от величины прироста выборки).
Кейс: определение размера выборки для оценки потенциала рынка продаж столичной недвижимости покупателям из регионов
В ноябре-декабре 2016 года мы провели исследование спроса на квартиры в новостройках Москвы и Санкт-Петербурга со стороны жителей разных городов России. Исследование включало в себя три метода сбора данных: массовый репрезентативный опрос населения в возрасте от 20 до 60 лет (проводился с использованием технологии CATI), а также серию экспертных интервью с риэлторами и глубинных интервью с потенциальными покупателями квартир.
Исследование охватывало 33 города, отличающихся повышенным спросом на петербургскую и московскую недвижимость. Плановая выборка исследования, рассчитанная по формулам, составила 21 500 респондентов. Этот объем значительно больше «стандартного» объема выборки, используемого в маркетинговых исследованиях. С чем же связан такой большой размер выборки?
Все дело в том, что клиенту были нужны оценки отдельно по каждому городу, а не просто «в целом по стране». Фактически мы работаем не с 1 выборкой, а с 33 отдельными выборками по каждому городу. Доля людей, заинтересованных в покупке квартиры в Санкт-Петербурге или Москве, была экспертно определена в рамках 5% от числа жителей опрашиваемых городов.
В зависимости от важности города для заказчика, руководитель проекта со стороны Агентства определил допустимую статистическую погрешность, в которую должны укладываться итоговые результаты. Для этого мы использовали специальный макрос в MS Excel, но эти расчеты можно также выполнить с помощью калькулятора выборки. В результате размер выборки варьировал от 500 до 1000 респондентов по каждому из городов исследования, что в сумме и дало заявленные 21 500 человек.
Резюме
Чтобы рассчитать выборку маркетингового исследования, используйте следующий алгоритм:
- Определите структуру целевой группы. Планируете ли вы анализировать отдельные подгруппы или достаточно будет анализа по выборке в целом?
- Определите желаемую точность данных. Например, если нужно оценить динамику рыночной доли за год, подставьте в специальный калькулятор примерное значение доли и «поиграйте» с разными объемами выборки.
- Найдите баланс между стоимостью сбора данных (прямо пропорциональна объему выборки) и требуемой точностью.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.
Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.
Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.
Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.
Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.
Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.
В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:
где µx– стандартная ошибка.
Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µx зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).
Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:
В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.
Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:
Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.
Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности x и величину предельной ошибки этой средней ?x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна
Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.
Данный текст является ознакомительным фрагментом.
Читайте также
Наблюдения за объемом
Наблюдения за объемом
Имеет значение не сам объем, а его соотношения в различные периоды рыночного движения. Соотношения объемов – очень важный, но и наименее объективный из технических инструментов, так как здесь нет никаких непреложных правил. Вместо этого есть набор
Закономерности и наблюдения
Закономерности и наблюдения
Я верю в существование закономерностей на рынке и считаю, что отношусь к числу людей, которые способны их улавливать. Но я также хорошо помню и о том, что все закономерности нечеткие. Нечеткие они потому, что в них присутствует фактор
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
8. Способы статистического наблюдения
8. Способы статистического наблюдения
Способами получения статистической информа–ции являются документальный способ наблюдения; способ непосредственного наблюдения: опрос.Документальное наблюдение основано на исполь–зовании в качестве источника информации данных
9. Формы статистического наблюдения
9. Формы статистического наблюдения
В теории статистики рассматриваются и формы статистического наблюдения: отчетность; специально организованное статистическое наблюдение; реги–стры.Статистическая отчетность – основная форма статистического наблюдения, которая
2. Ошибки выборочного наблюдения
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но
19. Наблюдения
19. Наблюдения
Наблюдение представляет собой сбор первичной информации об объекте наблюдения для построения гипотез, проверки исходных данных и т. д.К способам проведения наблюдения относят:1) прямой, который предполагает непосредственное наблюдение за объектом
6. Организация статистического наблюдения
6. Организация статистического наблюдения
Начальным этапом статистического исследования является статистическое наблюдение.В процессе статистического наблюдения формируется оснавная информация, которая является основной для статистического
11. Ошибки статистического наблюдения и контроль материалов наблюдения
11. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Любое статистическое наблюдение предполагает получение данных, которые будут
34. Определение выборочного наблюдения
34. Определение выборочного наблюдения
Так как сплошное наблюдение дорого и трудоемко, то его заменили выборочным.Выборочное наблюдение – это способ несплошного наблюдения, при котором лишь часть совокупности, отобранная по определенным правилам выборки и
Часть 5 Наблюдения
Часть 5
Наблюдения
За свою тридцатипятилетнюю карьеру в бизнесе я смотрел на мир с разных точек зрения. Я был свидетелем взлетов и падений в экономике и отрасли, появления на рынке новых продуктов и их исчезновения. Я представлял новые товары, возрождал старые, закрывал
Введение процедуры наблюдения
Введение процедуры наблюдения
Наблюдение вводится с целью сохранения активов должника, проведения оценки его финансового состояния, изучения объективной возможности восстановления платежеспособности и продолжения функционирования организации.С момента введения
1. Организация статистического наблюдения
1. Организация статистического наблюдения
Статистическое наблюдение – это организованная работа по сбору первичных сведений об изучаемых массовых явлениях и процессах общественной жизни. Статистическое наблюдение проводится организованно и по заранее разработанным
5. Ошибки статистического наблюдения и контроль материалов наблюдения
5. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Точность – это уровень соответствия значения какого–либо признака или
1. Определение выборочного наблюдения
1. Определение выборочного наблюдения
Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности
Общие наблюдения и впечатления
Общие наблюдения и впечатления
Члены команды систематически выполняли требования восьми этапов цикла кайдзен и обнаружили, что с их помощью смогли построить процесс решения проблем в правильной последовательности. Использование таких инструментов, как «рыбий скелет»













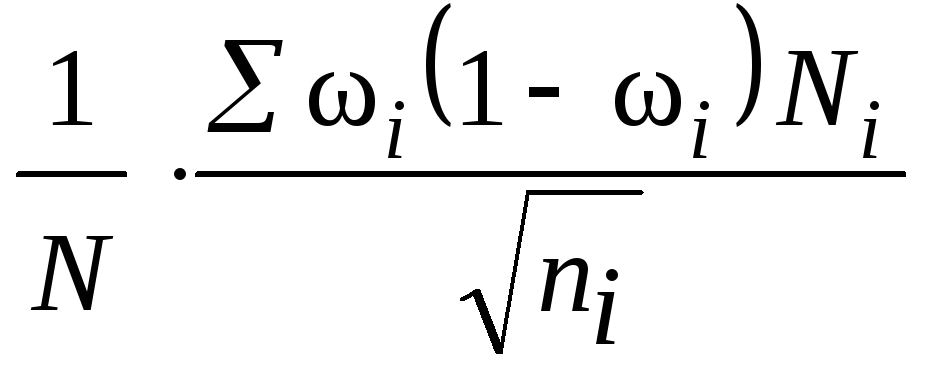


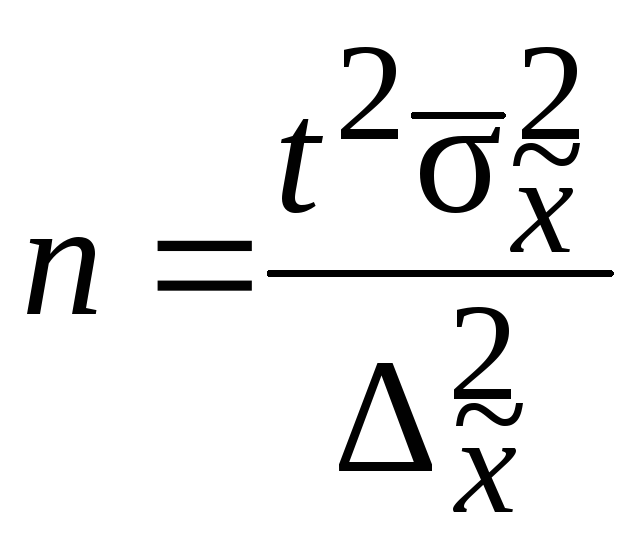

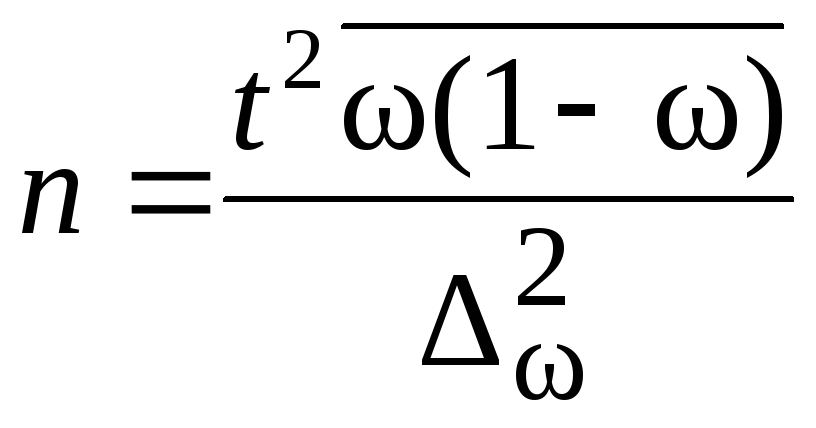



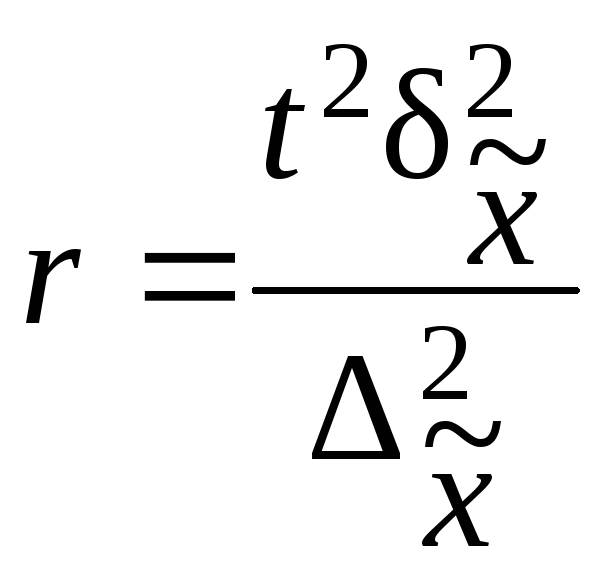

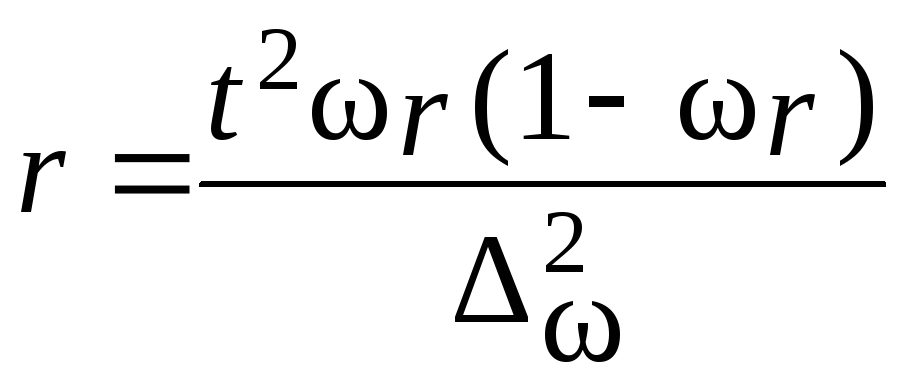
















 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп