Проблемы
При использовании функции ЛИНЕЙН на листе в Microsoft Excel результаты статистического вывода могут возвращать неверные значения. Средство регрессия в окне «пакет анализа» может также возвращать неверные значения.
Причина
Результат, возвращаемый функцией ЛИНЕЙН, может быть неправильным, если выполняется одно или несколько из указанных ниже условий.
-
Диапазон значений x перекрывает диапазон значений y.
-
Количество строк в диапазоне входных данных меньше числа столбцов в общем диапазоне (x-value + y-Value).
-
Вы задаете нулевую константу (для третьего аргумента функции ЛИНЕЙН установите значение истина).
Обходное решение
Случай 1: диапазоны x-value и y перекрываются
Если диапазоны x-value и y перекрываются, функция ЛИНЕЙН возвращает неверные значения во всех ячейках результата. Нормальная статистическая вероятность запрещает значения в диапазонах x и y для перекрытия (повторяющиеся друг друга). Не перекрывают диапазоны x и y при ссылке на ячейки в формуле.Примечание. Средство регрессия предупреждает об этой проблеме и не продолжает работу. Вы можете использовать средство регрессия вместо функции ЛИНЕЙН. В Microsoft Office Excel 2007 вы можете найти инструмент регрессия, щелкнув анализ данных в группе анализ на вкладке данные . В Microsoft Office Excel 2003 и более ранних версиях Excel можно найти инструмент регрессия, выбрав пункт анализ данных в меню Сервис .
Случай 2: количество строк меньше числа столбцов x-Columns.
Статистические функции не действительны, так как количество строк должно быть меньше числа столбцов x (переменных). Количество строк данных должно быть больше количества столбцов данных (столбцов x и y).
Случай 3: указывается нулевая константа
Не указывайте нулевые константы (b = 0) в функции.
Дополнительная информация
Средство регрессия входит в пакет анализа. Пакет анализа — это программа надстройки Excel. Оно доступно при установке Microsoft Office или Excel. Прежде чем использовать средство регрессия в Excel, вы должны загрузить анализ ToolPak.To в Excel 2007, выполнив указанные ниже действия.
-
Нажмите кнопку Microsoft Office, затем нажмите кнопку Параметры Excel.
-
Выберите пункт надстройки, а затем в поле Управление выберите пункт надстройки Excel .
-
Нажмите кнопку Перейти.
-
В окне Доступные надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК.Примечание. Если в списке Доступные надстройки не указан Пакет анализа , нажмите кнопку Обзор , чтобы найти его.
Чтобы сделать это в Excel 2003 и более ранних версиях Excel, выполните указанные ниже действия.
-
В меню Сервисвыберите пунктнадстройки.
-
В диалоговом окне надстройки выберите Пакет анализаи нажмите кнопку ОК,Обратите внимание на то, что Пакет анализа не указан в поле Доступные надстройки, нажмите кнопку Обзор , чтобы найти его.
Ссылки
Статистические вычисления на цифровом компьютере. Уильям J. Hemmerle. Blaisdell компания публикации: 1967. Глава 3, «вычисления с несколькими регрессиями» и раздел 3.2.1, «теория для предварительной регрессии».
Нужна дополнительная помощь?
|
Ошибки в регрессии |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Функция
ЛИНЕЙН()
специально создана для оценки параметров линейной регрессии, а также для вывода регрессионной статистики (коэффициента детерминации, стандартных ошибок,
F
-статистики
и др.).
Функция
ЛИНЕЙН()
может использоваться для
простой регрессии
(в этом случае прогнозируемая переменная Y зависит от одной контролируемой переменной Х) и для
множественной регрессии
(Y зависит от нескольких Х).
Рассмотрим функцию на примере
простой регрессии
(оценивается
наклон
и
сдвиг
линии регрессии). Использование функции в случае
множественной регрессии
рассмотрено в соответствующей статье про
множественную регрессию
.
Функция
ЛИНЕЙН()
возвращает несколько значений, поэтому для вывода результатов потребуется несколько ячеек. Часто функцию вводят как
формулу массива
: нажатием клавиш
CTRL
+
SHIFT
+
ENTER
,
но, как будет показано ниже, для вывода результатов вычислений это не обязательно.
Функция работает в 2-х режимах. В простейшем случае, когда 4-й аргумент функции опущен или установлен ЛОЖЬ, функция возвращает только 2 значения — это оценки параметров модели: наклона a и сдвига b.
Для того, чтобы вычислить оценки:
- выделите 2 ячейки в одной строке,
- в
Строке формул
введите, например, =
ЛИНЕЙН(C23:C83;B23:B83)
- нажмите
CTRL
+
SHIFT
+
ENTER
.
В левой ячейке будет рассчитано значение
наклона
, в правой –
сдвига
.
Примечание
: В справке MS EXCEL результат функции
ЛИНЕЙН()
соответствующий
наклону
обозначается буквой m, а
сдвиг
– буквой b.
Примечание
: Без
формул массива
можно обойтись. Для этого нужно использовать функцию
ИНДЕКС()
, которая выведет нужное значение. Например, чтобы вывести величину
сдвига
линии регрессии введите формулу =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;2)
. Если 4-й аргумент функции опущен или установлен ЛОЖЬ, то функция
ЛИНЕЙН()
в возвращает массив значений вида 1х2 (т.е. 2 ячейки, расположенные в одной строке). Поэтому, для вывода величины
сдвига
прямой линии регрессии, первый аргумент функции
ИНДЕКС()
, который является номером строки, должен быть равен 1, а второй аргумент, номер столбца, должен быть равен 2. Чтобы вывести значение
наклона
линии регрессии формулу
=ЛИНЕЙН(C23:C83;B23:B83)
достаточно ввести просто как обычную формулу и нажать
ENTER
. Конечно, можно использовать и формулу
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;1)
.
Теперь о втором, более сложном режиме функции. Этот режим нужно использовать, если требуется вывести дополнительную статистику (4-й аргумент функции должен быть установлен ИСТИНА). В этом случае функция
ЛИНЕЙН()
возвращает 10 значений в диапазоне 5х2 ячеек (5 строк и 2 столбца). Как и в более простом режиме, в первой строке возвращаются оценки параметров модели:
наклона
и
сдвига
.
Чтобы ввести функцию как
формулу массива
выполните следующие действия:
- выделите диапазон 5х2 ячеек (2 столбца и 5 строк),
- в
Строке формул
введите формулу
ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА)
- чтобы ввести формулу нажмите одновременно комбинацию клавиш
CTRL
+
SHIFT
+
ENTER
Примечание
: Чтобы обойтись без
формул массива
нужно использовать функцию
ИНДЕКС()
, которая выведет нужное значение. Например, чтобы вывести
коэффициент детерминации
R
2
введите формулу =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;1)
. 3 – это номер строки диапазона 5х2, а 1 – это номер столбца. В
файле примера на листе Линейный
в диапазоне
Q
26:
R
30
показано как вывести все значения, возвращаемые функцией
ЛИНЕЙН()
без
формул массива
.
Итак, установив 4-й аргумент равным ИСТИНА и введя функцию тем или иным способом, функция выведет:
- в строке 1:
оценки параметров модели
(наклон и сдвиг).
- в строке 2:
Стандартные ошибки для наклона и сдвига
. Ошибки обозначаются se и seb;
- в строке 3:
коэффициент детерминации
и
стандартную ошибку регрессии
. Обозначаются R
2
и SEy; - в строке 4:
значение F-статистики и число степеней свободы
. Обозначаются F и df;
- в строке 5: Суммы квадратов SSR, SSE определяющие
изменчивость объясненную и необъясненную моделью
(см. в статьеПростая линейная регрессия
разделы про коэффициент детерминации и
статью про F-тест
). В справке MS EXCEL SSR, SSE обозначаются как
ssreg
(Regression Sum of Squares) и
ssresid
(Residuals Sum of Squares) соответственно.
Примечание
: Разобраться в значениях, возвращаемых функцией
ЛИНЕЙН()
, можно лишь разобравшись в теории линейной регрессии.
В
файле примера
также приведены формулы, позволяющие сделать расчеты без функции
ЛИНЕЙН()
– см. диапазон
Q
34:
R
38
. Альтернативные формулы помогают разобраться в алгоритме расчета вышеуказанных статистических показателей.
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды.
Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y
по значениям независимой переменной X
. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y
по значениям нескольких зависимых переменных (Х 1 , Х 2 , …, X k
).
Скачать заметку в формате или , примеры в формате
Виды регрессионных моделей
где ρ
1
– коэффициент автокорреляции; если ρ
1
= 0 (нет автокорреляции), D
≈ 2; если ρ
1
≈ 1 (положительная автокорреляции), D
≈ 0; если ρ
1
= -1 (отрицательная автокорреляции), D
≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D
с критическими теоретическими значениями d L
и d U
для заданного числа наблюдений n
, числа независимых переменных модели k
(для простой линейной регрессии k
= 1) и уровня значимости α. Если D < d L
, гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > d U
, гипотеза не отвергается (то есть автокорреляция отсутствует); если d L < D < d U
, нет достаточных оснований для принятия решения. Когда расчётное значение D
превышает 2, то с d L
и d U
сравнивается не сам коэффициент D
, а выражение (4 – D
).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка
. Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).
Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D
= 0,883. Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (d L
и d U
), зависящими от числа наблюдений n
и уровня значимости α (рис. 17).
Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k
= 1), 15 наблюдений (n
= 15) и уровень значимости α = 0,05. Следовательно, d L
= 1,08 и d
U
= 1,36. Поскольку D
= 0,883 < d L
= 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y
при заданной величине переменной X
использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение
t
-критерия для наклона.
Проверяя, равен ли наклон генеральной совокупности β 1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X
и Y
. Если эта гипотеза отклоняется, можно утверждать, что между переменными X
и Y
существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0: β 1 = 0 (нет линейной зависимости), Н1: β 1 ≠ 0 (есть линейная зависимость). По определению t
-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11)
t
= (b
1
–
β
1
) /
S b
1
где b
1
– наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t
имеет t
-распределение с n – 2
степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t
-критерий выводится наряду с другими параметрами при использовании Пакета анализа
(опция Регрессия
). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t
Поскольку число магазинов n
= 14 (см. рис.3), критическое значение t
-статистики при уровне значимости α = 0,05 можно найти по формуле: t L
=СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n
– 2; t U
=СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t
-статистика = 10,64 > t U
= 2,1788 (рис. 19), нулевая гипотеза Н 0
отклоняется. С другой стороны, р
-значение для Х
= 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н 0
снова отклоняется. Тот факт, что р
-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение
F
-критерия для наклона.
Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F
-критерия. Напомним, что F
-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F
-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR
, деленной на количество независимых переменных k
), к дисперсии ошибок (MSE = S Y
X
2
).
По определению F
-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F
=
MSR
/
MSE
, где MSR =
SSR
/
k
, MSE =
SSE
/(n
– k – 1), k
– количество независимых переменных в регрессионной модели. Тестовая статистика F
имеет F
-распределение с k
и n
– k – 1
степенями свободы.
При заданном уровне значимости α решающее правило формулируется так: если F > F
U
, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.
Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t
-критерию F
-критерий выводится в таблицу при использовании Пакета анализа
(опция Регрессия
). Полностью результаты работы Пакета анализа
приведены на рис. 4, фрагмент, относящийся к F
-статистике – на рис. 21.
Рис. 21. Результаты применения F
-критерия, полученные с помощью Пакета анализа Excel
F-статистика равна 113,23, а р
-значение близко к нулю (ячейка Значимость
F
). Если уровень значимости α равен 0,05, определить критическое значение F
-распределения с одной и 12 степенями свободы можно по формуле F U
=F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F
= 113,23 > F U
= 4,7472, причем р
-значение близко к 0 < 0,05, нулевая гипотеза Н 0
отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.
Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β 1 .
Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β 1 и убедиться, что гипотетическое значение β 1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β 1 , является выборочный наклон b
1
, а его границами — величины b 1 ±
t n
–2
S b
1
Как показано на рис. 18, b
1
= +1,670, n
= 14, S b
1
= 0,157. t
12
=СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b 1 ±
t n
–2
S b
1
= +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β 1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование
t
-критерия для коэффициента корреляции.
был введен коэффициент корреляции r
, представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0
: ρ = 0 (нет корреляции), Н 1
: ρ ≠ 0 (есть корреляция). Проверка существования корреляции:
где r
= +
, если b
1
> 0, r
= –
, если b
1
< 0. Тестовая статистика t
имеет t
-распределение с n – 2
степенями свободы.
В задаче о сети магазинов Sunflowers r 2
= 0,904, а b 1
— +1,670 (см. рис. 4). Поскольку b 1
> 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r
= +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t
-статистику:
При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t
= 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r
зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y
и предсказания индивидуальных значений Y
при заданных значениях переменной X
.
Построение доверительного интервала.
В примере 2 (см. выше раздел Метод наименьших квадратов
) регрессионное уравнение позволило предсказать значение переменной Y
X
. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика
при заданном значении переменной X
:
где 
b
0
+
b
1
X i
– предсказанное значение переменное Y
при X
= X i
, S YX
– среднеквадратичная ошибка, n
– объем выборки, X
i
— заданное значение переменной X
, µ
Y
| X
=
X
i
– математическое ожидание переменной Y
при Х
= Х i
, SSX =
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений X
i
. Если значение переменной Y
предсказывается для величин X
, близких к среднему значению
, доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения.
Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X
, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Y
X
=
Xi
при конкретном значении переменной X
i
определяется по формуле:
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).
Рис. 23. Четыре набора искусственных данных
Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа
(кликните на рисунке, чтобы увеличить изображение)
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.
Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х 8
= 19, Y
8
= 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X
и Y
всегда начинайте с построения диаграммы разброса. - Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
Резюме.
Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t
-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.
Рис. 27. Структурная схема заметки
Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
· линейной (у = а + bx);
· параболической (y = a + bx + cx 2);
· экспоненциальной (y = a * exp(bx));
· степенной (y = a*x^b);
· гиперболической (y = b/x + a);
· логарифмической (y = b * 1n(x) + a);
· показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.
Основные задачи и виды регрессии
Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных.
К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.
Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.
Основные задачи построения регрессионной модели заключаются в следующем:
- Отбор значимых независимых переменных (Х1, Х2, …, Xk).
- Выбор вида функции.
- Построение оценок для коэффициентов.
- Построение доверительных интервалов и функции регрессии.
- Проверка значимости вычисленных оценок и построенного уравнения регрессии.
Регрессионный анализ бывает нескольких видов:
- парный (1 зависимая и 1 независимая переменные);
- множественный (несколько независимых переменных).
Уравнения регрессии бывает двух видов:
- Линейные, иллюстрирующие строгую линейную связь между переменными.
- Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.
Инструкция построения модели
Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:
Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача:
Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
Теперь стали видны и данные регрессионного анализа.
Статистическая обработка данных может также проводиться с помощью надстройки ПАКЕТ АНАЛИЗА
(рис. 62).
Из предложенных пунктов выбирает пункт «РЕГРЕССИЯ
» и щелкаем на нем левой кнопкой мыши. Далее нажимаем ОК.
Появится окно, показанное на рис. 63.
Инструмент анализа «РЕГРЕССИЯ
» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
Инструмент «Регрессия» использует функцию ЛИНЕЙН
.
Диалоговое окно «РЕГРЕССИЯ»
Метки Установите флажок, если первая строка или первый столбец входного диапазона содержит заголовки. Снимите этот флажок, если заголовки отсутствуют. В этом случае подходящие заголовки для данных выходной таблицы будут созданы автоматически.
Уровень надежности Установите флажок, чтобы включить в выходную таблицу итогов дополнительный уровень. В соответствующее поле введите уровень надежности, который следует применить, дополнительно к уровню 95%, применяемому по умолчанию.
Константа — ноль Установите флажок, чтобы линия регрессии прошла через начало координат.
Выходной интервал Введите ссылку на левую верхнюю ячейку выходного диапазона. Отведите как минимум семь столбцов для выходной таблицы итогов, которая будет включать в себя: результаты дисперсионного анализа, коэффициенты, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.
Новый рабочий лист Установите переключатель в это положение, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. При необходимости введите имя для нового листа в поле, расположенном напротив соответствующего положения переключателя.
Новая рабочая книга Установите переключатель в это положение для создания новой книги, в которой результаты будут добавлены в новый лист.
Остатки Установите флажок для включения остатков в выходную таблицу.
Стандартизированные остатки Установите флажок для включения стандартизированных остатков в выходную таблицу.
График остатков Установите флажок для построения графика остатков для каждой независимой переменной.
График подбора Установите флажок для построения графика зависимости предсказанных значений от наблюдаемых.
График нормальной вероятности
Установите флажок, для построения графика нормальной вероятности.
Функция ЛИНЕЙН
Для проведения расчетов выделяем курсором ячейку, в которой хотим отобразить среднее значение и нажимаем на клавиатуре клавишу =. Далее в поле Имя указываем нужную функцию, например СРЗНАЧ
(рис. 22).
Функция ЛИНЕЙН
рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Можно также объединять функцию ЛИНЕЙН
с другими функциями для вычисления других видов моделей, являющихся линейными в неизвестных параметрах (неизвестные параметры которых являются линейными), включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Уравнение для прямой линии имеет следующий вид:
y=m 1 x 1 +m 2 x 2 +…+b (в случае нескольких диапазонов значений x),
где зависимое значение y — функция независимого значения x, значения m — коэффициенты, соответствующие каждой независимой переменной x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН
возвращает массив{mn;mn-1;…;m 1 ;b}. ЛИНЕЙН
может также возвращать дополнительную регрессионную статистику.
ЛИНЕЙН
(известные_значения_y; известные_значения_x; конст; статистика)
Известные_значения_y — множество значений y, которые уже известны для соотношения y=mx+b.
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Известные_значения_x — необязательное множество значений x, которые уже известны для соотношения y=mx+b.
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы_известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если массив_известные_значения_x опущен, то предполагается, что этот массив {1;2;3;…} имеет такой же размер, как и массив_известные_значения_y.
Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если аргумент «конст» имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
Если аргумент «конст» имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y=mx.
Статистика — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.
Если аргумент «статистика» имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив будет иметь следующий вид: {mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid}.
Если аргумент «статистика» имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.(табл.17)
| Величина | Описание |
| se1,se2,…,sen | Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
| seb | Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент «конст» имеет значение ЛОЖЬ). |
| r2 | Коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т. е. различия между фактическим и оценочным значениями y не существует. В противоположном случае, если коэффициент детерминированности равен 0, использовать уравнение регрессии для предсказания значений y не имеет смысла. Для получения дополнительных сведений о способах вычисления r2, см. «Замечания» в конце данного раздела. |
| sey | Стандартная ошибка для оценки y. |
| F | F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
| df | Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Для получения дополнительных сведений о вычислении величины df см. «Замечания» в конце данного раздела. Далее в примере 4 показано использование величин F и df. |
| ssreg | Регрессионная сумма квадратов. |
| ssresid | Остаточная сумма квадратов. Для получения дополнительных сведений о расчете величин ssreg и ssresid см. «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика (рис. 64).
Замечания:
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m): чтобы определить наклон прямой, обычно обозначаемый через m, нужно взять две точки прямой (x 1 ,y 1) и(x 2 ,y 2); наклон будет равен (y 2 -y 1)/(x 2 -x 1).
Y-пересечение (b): Y-пересечением прямой, обычно обозначаемым через b, является значение y для точки, в которой прямая пересекает ось y.
Уравнение прямой имеет вид y=mx+b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон: ИНДЕКС (ЛИНЕЙН(известные_значения_y; известные_значения_x); 1)
Y-пересечение: ИНДЕКС (ЛИНЕЙН (известные_значения_y; известные_значения_x); 2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. Когда имеется только одна независимая переменная x, m и b вычисляются по следующим формулам:
где x и y – выборочные средние значения, например x = СРЗНАЧ (известные_значения_x), а y = СРЗНАЧ (известные_значения_y).
Функции аппроксимации ЛИНЕЙН и ЛГРФПРИБЛ могут вычислить прямую или экспоненциальную кривую, наилучшим образом описывающую данные. Однако они не дают ответа на вопрос, какой из двух результатов больше подходит для решения поставленной задачи. Можно также вычислить функцию ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x) для прямой или функцию РОСТ(известные_значения_y; известные_значения_x) для экспоненциальной кривой. Эти функции, если не задавать аргумент новые_значения_x, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. После этого можно сравнить вычисленные значения с фактическими значениями. Можно также построить диаграммы для визуального сравнения.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Коэффициент r2 равен ssreg/sstotal.
В некоторых случаях один или более столбцов X (пусть значения Y и X находятся в столбцах) не имеет дополнительного предикативного значения в других столбцах X. Другими словами, удаление одного или более столбцов X может привести к значениям Y, вычисленным с одинаковой точностью. В этом случае избыточные столбцы X будут исключены из модели регрессии. Этот феномен называется «коллинеарностью», поскольку избыточные столбцы X могут быть представлены в виде суммы нескольких неизбыточных столбцов. Функция ЛИНЕЙН проверяет на коллинеарность и удаляет из модели регрессии все избыточные столбцы X, если обнаруживает их. Удаленные столбцы X можно определить в выходных данных ЛИНЕЙН по коэффициенту, равному 0, и по значению se, равному 0. Удаление одного или более столбцов как избыточных изменяет величину df, поскольку она зависит от количества столбцов X, в действительности используемых для предикативных целей. Подробнее о вычислении величины df см. ниже в примере 4. При изменении df вследствие удаления избыточных столбцов значения sey и F также изменяются. Часто использовать коллинеарность не рекомендуется. Однако ее следует применять, если некоторые столбцы X содержат 0 или 1 в качестве индикатора указывающего, входит ли предмет эксперимента в отдельную группу. Если конст = ИСТИНА или значение этого аргумента не указано, функция ЛИНЕЙН вставляет дополнительный столбец X для моделирования точки пересечения. Если имеется столбец со значениями 1 для указания мужчин и 0 — для женщин, а также имеется столбец со значениями 1 для указания женщин и 0 — для мужчин, то последний столбец удаляется, поскольку его значения можно получить из столбца с «индикатором мужского пола».
Вычисление df для случаев, когда столбцы X не удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
Формулы, которые возвращают массивы, должны быть введены как формулы массива.
При вводе массива констант в качестве, например, аргумента известные_значения_x следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть различными в зависимости от параметров, заданных в окне «Язык и стандарты» на панели управления.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН
, отличается от основного алгоритма функций НАКЛОН
и ОТРЕЗОК
. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
Функция ЛИНЕЙН
возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН
используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
Функции НАКЛОН и ОТРЕЗОК возвращают ошибку #ДЕЛ/0!. Алгоритм функций НАКЛОН и ОТРЕЗОК используется для поиска только одного ответа, а в данном случае их может быть несколько.
Помимо вычисления статистики для других типов регрессии функцию ЛИНЕЙН можно использовать при вычислении диапазонов для других типов регрессии, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y=m 1 x+m 2 x 2 +m 3 x 3 +b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
Лабораторная
работа №5
«Введение в
множественную регрессию»
Часто приходится
использовать несколько независимых
переменных ()
для предсказания значения зависимой
переменной. В этих случаях для оценки
интересующей нас зависимости можно
применять либо вариант множественной
регрессии в Пакете
анализа,
либо функцию ЛИНЕЙН().
Множественная
регрессия предполагает, что зависимость
между y
и
описывается уравнением вида
Программа Excel
вычисляет значения Константы
и
для расчёта с помощью данного уравнения
как можно более точных (с точки зрения
минимизации суммы квадратов ошибок)
прогнозируемых значений.
Наша фабрика
производит три вида изделий. Как можно
предсказать производственные расходы
фабрики на основе количества выпускаемых
изделий?
На рабочем листе
Данные
содержатся текущие производственные
расходы за 19 месяцев, а также количество
штук изделия А, изделия В и изделия С,
выпускаемых каждый месяц (рис. 1).
Найдем наиболее
точный прогноз месячных производственных
расходов вида:
Месячные
производственные расходы = Константа+
+(Произведенные
изделия А)+ (1)
+(Произведенные
изделия В)+
+(Произведенные
изделия С).
Для этого щелкните
кнопкой мыши команду Анализ
данных в
меню Сервис
и в появившемся окне выберите вариант
Регрессия.
Заполните диалоговое окно Регрессия,
как показано на рис. 2.
Поле Входной
интервал Y,
B3:B22,
содержит зависимую переменную или
данные (включая заголовок Расходы),
значения которых мы хотим предсказать.
Рис. 1. Данные для
прогнозирования месячных текущих
производственных расходов
Рис. 2. Диалоговое
окно Регрессия
-
Поле Входной
интервал X,
C3:E22,
содержит данные или независимые
переменные (включая заголовки
ПроизведенныеА,
ПроизведенныеВ,
ПроизведенныеС),
которые мы хотим использовать в прогнозе. -
Поскольку и входной
диапазон x,
и входной диапазон y
включают заголовки, установлен флажок
Метки.
-
Результаты
размещаются на отдельном листе Регрессия. -
Установка флажка
Остатки
позволяет выводить для каждого наблюдения
предсказанное значение, рассчитанное
уравнением (1), и остаток, равный разности
наблюдаемого расхода и предсказанного
значения.
После нажатия
кнопки ОК
мы получим результат, показанный на
рис. 3 и 4.
Рис. 3. Результат
расчёта исходной множественной регрессии
Рис. 4. Список
остатков исходной множественной
регрессии
Какое уравнение
прогнозирования можно считать лучшим.
Лучшим уравнением,
применяемым для прогнозирования месячных
расходов (столбец Коэффициенты),
считается следующее:
Прогнозируемые
месячные расходы = 35102.90+
+(Произведенные
изделия А)+
+(Произведенные
изделия В)+
+(Произведённые
изделия С).
Какие из независимых
переменных полезны для предсказания
месячных производственных расходов
Когда мы считаем
показатели регрессии для каждой
независимой переменной, выводится
показатель р-значение,
лежащее между 0 и 1. Любая независимая
переменная с р-значением
(столбец Е), меньшим или равным 0.15,
считается полезной для предсказания
значений зависимой переменной.
Следовательно, чем меньше р-значение,
тем сильнее влияние независимой
переменной на прогноз. У трёх независимых
переменных следующие р-значения:
0.23 (для Произведенные А), 0.025 (для
Произведенные В) и 0.017 (для Произведенные
С). Эти значения можно трактовать
следующим образом:
-
Когда для
предсказания месячных производственных
расходов используются переменные
Произведенные В и Произведенные С,
вероятность того, что переменная
Произведенные А повысит точность
прогноза, равна 77% (1-0.23). -
Когда для
предсказания месячных производственных
расходов используются переменные
Произведенные А и Произведенные С,
вероятность того, что переменная
Произведенные В повысит точность
прогноза, равна 97.5% (1-0.025). -
Когда для
предсказания месячных производственных
расходов используются переменные
Произведенные А и Произведенные В,
вероятность того, что переменная
Произведенные С повысит точность
прогноза, равна 98.3% (1-0.017).
Величины наших
р-значений
показывают, что переменная Произведенные
А не слишком усиливает прогнозирующую
способность переменных Произведенные
В и Произведенные С, т.е. если у нас есть
Произведенные В и Произведенные С, мы
можем предсказать месячные производственные
расходы примерно так же хорошо, как если
бы мы включили в прогноз ещё и переменную
Произведенные А в качестве независимой
переменной. Следовательно, мы можем
попробовать удалить из прогноза
независимую переменную Произведенные
А.
Скопируйте данные
на рабочий лист А
удалены и
удалите столбец Произведенные
А (столбец
С). Затем исправьте входной диапазон x
на C3:D22.
Результат представлен на листе Без
А (рис. 5 и
6).
У обеих переменных
Произведенные В и Произведенные С очень
низкие р-значения
(0.002 и 0.007). Они указывают на наличие у
обеих переменных значительной
прогнозирующей способности. С помощью
новых коэффициентов можно предсказать:
Прогнозируемые
месячные расходы = 35475+
+(Произведенные
В)+
+(Произведенные
С).
Рис. 5. Параметры
множественной регрессии без данных
независимой переменной Произведенные
А
Рис. 6. Перечень
остатков, вычисленных после удаления
данных независимой переменной
Произведенные А
Насколько точны
прогнозы месячных производственных
расходов, основанные на объёме выпускаемой
продукции.
На рабочем листе
Без А
с параметрами регрессии в ячейке В5
приведен показатель достоверности
аппроксимации R2=0.61.
Подобное значение R2
указывает,
что переменные Произведенные В и
Произведенные С вместе обуславливают
61% колебаний месячных производственных
расходов. В параметрах первоначальной
регрессии, включающей независимую
переменную Произведенные А, R2=0.65.
Это означает, что включение независимой
переменной Произведенные А объясняет
только дополнительные 4% колебаний
текущих производственных расходов.
Столь малая разница согласуется с
решением удалить из анализа независимую
переменную Произведенные А.
В выходных параметрах
регрессии на листе Без
А, в ячейке
В7, стандартная ошибка регрессии с
независимыми переменными Произведенные
В и Произведенные С равна 1274. Мы
рассчитываем, что 68% наших прогнозов с
помощью нашей регрессии будут точны в
пределах одной стандартной ошибки, и
95% прогнозов с помощью множественной
регрессии будут определены с точностью
в пределах двух стандартных ошибок.
Любой прогноз, отличающийся от
действительного значения более чем на
2 стандартные ошибки, рассматривается
как выброс. Следовательно, если у
прогнозируемого значения текущих
производственных расходов ошибка 2548
(21274),
руб., считаем это наблюдение выбросом.
В разделе остатков
регрессионного анализа даётся для
каждого наблюдения прогнозируемое
значение расходов и остаток, равный
реальным расходам, уменьшенным на
величину прогнозируемого значения
расходов. Например, для первого наблюдения
мы предсказали расходы, равные 43 381,10
руб. Остаток 1057,95 руб. означает, что
прогноз меньше реального значения на
1057,95 руб.
Расчёт показателей
множественной регрессии с помощью
функции ЛИНЕЙН().
У функции ЛИНЕЙН()
следующая синтаксическая запись
ЛИНЕЙН
(известные_значения_y;
известные_значения_x;ИСТИНА;ИСТИНА)
Если третий аргумент
равен ЛОЖЬ, в уравнении отсутствует
константа. Изменение четвёртого аргумента
на ЛОЖЬ приведет к пропуску расчёта
большого числа параметров регрессии,
и функция ЛИНЕЙН() вернёт только уравнение
множественной регрессии.
Для применения
функции ЛИНЕЙН() к m
независимым переменным на рабочем листе
А удалены
выделите диапазон F5:H9.
Введите формулу
=ЛИНЕЙН(B4:B22;
C4:D22;
ИСТИНА; ИСТИНА). Затем нажмите
<Ctrl>+<Shift>+<Enter>.
Результат представлен на рис. 7.
В строке 5 находится
описание уравнения прогнозирования
(коэффициенты приводятся справа налево,
начиная с константы):
Прогнозируемые
месячные расходы = 35475.3+
+(Произведенные
В)+(Произведенные
изделия С).
В строке 6 содержатся
стандартные ошибки приближенного
расчёта всех коэффициентов, но они не
слишком важны. В ячейке F7
приведено значение R2=0.61,
а в ячейке G7
– стандартная ошибка регрессии, равная
1274. В строках 8 и 9 содержится информация
(F-статистика,
степени свободы, регрессионная сумма
квадратов и остаточная сумма квадратов),
которая тоже не имеет большого значения.
Рис. 7. Применение
функции ЛИНЕЙН() для вычисления параметров
множественной регрессии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача отыскания функциональной зависимости очень важна, поэтому для ее решения в MS Excel введен набор функций, основанных на методе наименьших квадратов. В качестве результата выдаются не только коэффициенты функции, приближающей данные, но и статистические характеристики полученных результатов.
Смысл выходной статистической информации функции ЛИНЕЙН
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, вычисляя прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую.
Общий синтаксис вызова функции ЛИНЕЙН имеет следующий вид:
ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)
Для работы с функцией необходимо заполнить как минимум 1 обязательный и при необходимости 3 необязательных аргумента:
- Известные_значения_y − это множество значений y, которые уже известны для соотношения y=mx+b.
- Известные_значения_x − это множество известных значений x. Если этот аргумент опущен, то предполагается, что это массив {1; 2; 3; …} такого же размера, как и известные_значения_y.
- Конст − это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если в функции ЛИНЕЙН аргумент константа имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx.
- Статистика − это логическое значение, которое указывает, требуется ли выдать дополнительную статистику по регрессии.
Примеры использования функции ЛИНЕЙН в Excel
Для решения первой задачи – о соотношении часов подготовки студентов к тесту и результатов теста, как х и у соответственно, – необходимо применить следующий порядок действий (в связи с тем, что ЛИНЕЙН является функцией, которая возвращает массив):
- Выделите диапазон D2:Е2, так как функция ЛИНЕЙН возвращает массив из двух значений, расположенных по горизонтали, но не по вертикали.
- Введите известные значения y – баллы, которые студенты заработали на последнем тестировании (диапазон ячеек В2:В12).
- Затем введите известные значения х – количество часов, которые студенты потратили на подготовку к тестам (диапазон А2:А12).
- Опустите аргумент [конст].
- Опустите аргумент [статистика].
- Введите формулу с помощью Ctrl+Shift+Enter.
Результатом применения функции становится:
Теперь, на примере решения второй задачи, разберем необходимость в отображении не только наклона и отрезка, но и дополнительной статистики. Для примера, на диапазоне А1:В6 выстроим таблицу с соотношением у и х соответствующих сумме заработка студентом денежных средств за период в 5 месяцев. Так как мы имеем лишь одну переменную х, то необходимо выделить диапазон состоящий из двух столбцов и пяти строк. Важно отметить, что в том случае, если переменных х будет больше, то количество столбцов может изменяться соответственно их количеству, однако строк будет всегда 5.
Применительно к решаемой нами задаче, выделим диапазон Е2:F6, затем введем формулу аналогично предыдущей задаче, но в данном случае третьему и четвертому аргументу присвоим значение 1 соответствующее ИСТИНЕ. Для вывода параметров статистики функции ЛИНЕЙН необходимо нажат Ctrl+Shift+Enter, результат должен соответствовать следующему рисунку, на котором представлено обозначение дополнительных статистик:
Вернемся к примеру № 1, касающемуся зависимости между часами подготовки студентов к тесту и баллов за тест. Добавим к условию задачи данные о баллах за домашнее задание — представляющие дополнительную переменную х, что свидетельствует о необходимости применения множественной регрессии.
В случае множественной регрессии, когда значения «y» зависят от двух переменных «х», функция ЛИНЕЙН возвращает 12 статистик. На рисунке с модифицированной таблицей от 1 примера, представленном ниже используются следующие обозначения:
- y = зависимая переменная;
- x1 = независимая переменная 1 = баллы за домашнее задание;
- x2 = независимая переменная 2 = часы подготовки к тесту.
Чтобы выполнить множественную регрессию:
- Выделите диапазон В3:D7 (число столбцов = число переменных +1; число строк всегда равно 5).
- Наберите формулу =ЛИНЕЙН(D14:D24;B14:C24;1;1). Для аргумента известные_значения_х, выделите оба столбца значений x из диапазона В14:С24.
- Введите функцию с помощью клавиш Ctrl+Shift+Enter.
- Обратите внимание, что несмотря на то, что значения х1 указаны в диапазоне В14:С24 до значений х2, наклон сначала указан для х2.
Диапазон D5:D7 содержит ошибку #Н/Д – значащую, что формула не может обнаружить значения для данных ячеек. Визуально наличие ошибки отвлекает от сути решения, поэтому далее предложим вариант избавления от нее. Так, если дополнить формулу содержащую функцию ЛИНЕЙН функцией ЕСЛИОШИБКА, то можно значительно улучшить вид таблицы, результат которой представлен ниже:
Распределение статистик в таблице их значение представлено на следующем рисунке:
Скачать примеры функции ЛИНЕЙН в Excel
В результате мы получили всю необходимую выходную статистическую информацию, которая нас интересует.
Функция
ЛИНЕЙН()
специально создана для оценки параметров линейной регрессии, а также для вывода регрессионной статистики (коэффициента детерминации, стандартных ошибок,
F
-статистики
и др.).
Функция
ЛИНЕЙН()
может использоваться для
простой регрессии
(в этом случае прогнозируемая переменная Y зависит от одной контролируемой переменной Х) и для
множественной регрессии
(Y зависит от нескольких Х).
Рассмотрим функцию на примере
простой регрессии
(оценивается
наклон
и
сдвиг
линии регрессии). Использование функции в случае
множественной регрессии
рассмотрено в соответствующей статье про
множественную регрессию
.
Функция
ЛИНЕЙН()
возвращает несколько значений, поэтому для вывода результатов потребуется несколько ячеек. Часто функцию вводят как
формулу массива
: нажатием клавиш
CTRL
+
SHIFT
+
ENTER
,
но, как будет показано ниже, для вывода результатов вычислений это не обязательно.
Функция работает в 2-х режимах. В простейшем случае, когда 4-й аргумент функции опущен или установлен ЛОЖЬ, функция возвращает только 2 значения — это оценки параметров модели: наклона a и сдвига b.
Для того, чтобы вычислить оценки:
- выделите 2 ячейки в одной строке,
-
в
Строке формул
введите, например, =
ЛИНЕЙН(C23:C83;B23:B83)
-
нажмите
CTRL
+
SHIFT
+
ENTER
.
В левой ячейке будет рассчитано значение
наклона
, в правой –
сдвига
.
Примечание
: В справке MS EXCEL результат функции
ЛИНЕЙН()
соответствующий
наклону
обозначается буквой m, а
сдвиг
– буквой b.
Примечание
: Без
формул массива
можно обойтись. Для этого нужно использовать функцию
ИНДЕКС()
, которая выведет нужное значение. Например, чтобы вывести величину
сдвига
линии регрессии введите формулу =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;2)
. Если 4-й аргумент функции опущен или установлен ЛОЖЬ, то функция
ЛИНЕЙН()
в возвращает массив значений вида 1х2 (т.е. 2 ячейки, расположенные в одной строке). Поэтому, для вывода величины
сдвига
прямой линии регрессии, первый аргумент функции
ИНДЕКС()
, который является номером строки, должен быть равен 1, а второй аргумент, номер столбца, должен быть равен 2. Чтобы вывести значение
наклона
линии регрессии формулу
=ЛИНЕЙН(C23:C83;B23:B83)
достаточно ввести просто как обычную формулу и нажать
ENTER
. Конечно, можно использовать и формулу
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;1)
.
Теперь о втором, более сложном режиме функции. Этот режим нужно использовать, если требуется вывести дополнительную статистику (4-й аргумент функции должен быть установлен ИСТИНА). В этом случае функция
ЛИНЕЙН()
возвращает 10 значений в диапазоне 5х2 ячеек (5 строк и 2 столбца). Как и в более простом режиме, в первой строке возвращаются оценки параметров модели:
наклона
и
сдвига
.
Чтобы ввести функцию как
формулу массива
выполните следующие действия:
- выделите диапазон 5х2 ячеек (2 столбца и 5 строк),
-
в
Строке формул
введите формулу
ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА)
-
чтобы ввести формулу нажмите одновременно комбинацию клавиш
CTRL
+
SHIFT
+
ENTER
Примечание
: Чтобы обойтись без
формул массива
нужно использовать функцию
ИНДЕКС()
, которая выведет нужное значение. Например, чтобы вывести
коэффициент детерминации
R
2
введите формулу =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;1)
. 3 – это номер строки диапазона 5х2, а 1 – это номер столбца. В
файле примера на листе Линейный
в диапазоне
Q
26:
R
30
показано как вывести все значения, возвращаемые функцией
ЛИНЕЙН()
без
формул массива
.
Итак, установив 4-й аргумент равным ИСТИНА и введя функцию тем или иным способом, функция выведет:
-
в строке 1:
оценки параметров модели
(наклон и сдвиг).
-
в строке 2:
Стандартные ошибки для наклона и сдвига
. Ошибки обозначаются se и seb;
-
в строке 3:
коэффициент детерминации
и
стандартную ошибку регрессии
. Обозначаются R
2
и SEy; -
в строке 4:
значение F-статистики и число степеней свободы
. Обозначаются F и df;
-
в строке 5: Суммы квадратов SSR, SSE определяющие
изменчивость объясненную и необъясненную моделью
(см. в статьеПростая линейная регрессия
разделы про коэффициент детерминации и
статью про F-тест
). В справке MS EXCEL SSR, SSE обозначаются как
ssreg
(Regression Sum of Squares) и
ssresid
(Residuals Sum of Squares) соответственно.
Примечание
: Разобраться в значениях, возвращаемых функцией
ЛИНЕЙН()
, можно лишь разобравшись в теории линейной регрессии.
В
файле примера
также приведены формулы, позволяющие сделать расчеты без функции
ЛИНЕЙН()
– см. диапазон
Q
34:
R
38
. Альтернативные формулы помогают разобраться в алгоритме расчета вышеуказанных статистических показателей.
Практическая
работа №1
Тема:
Парная
линейная регрессия
Цель
работы
Построение
парной линейной регрессии и проверка
значимости
(
— показатель,
—
объясняющая переменная).
Парную
линейную регрессию строят при изучении
связи между исследуемым показателем и
объясняющей переменной.
При
наличии статистически значимой линейной
связи ПЛР можно применять для
прогнозирования показателя и для оценки
влияния возможных изменений фактора
на показатель.
Оборудование
и средства
Персональный
компьютер, электронные таблицы MS
Excel.
Содержание
отчета
и представление работы
-
Отчет
по работе оформляется в виде файла
Excel
и должен содержать полученные результаты
с необходимыми пояснениями.
Задание
к работе
Исходные
данные смоделированы на основе линейной
эконометрической модели:
,
где
случайные величины
взаимно независимы и нормально
распределены с нулевым математическим
ожиданием и дисперсией
.
Исходные
данные представляют
собой двумерную выборку
По
выборке необходимо построить парную
линейную регрессию и проверить ее
статистическую значимость.
1.
Для заданных
исходных данных
постройте
поле корреляции — диаграмму зависимости
показателя
от первого
фактора
.
При
построении выберите тип диаграммы
«Точечная»
(без отрезков, соединяющих точки).
2*.
Вычислите выборочные характеристики:
— выборочные
средние
и
(функция СРЗНАЧ);
— выборочные
дисперсии
и
(функция
ДИСПР);
— выборочное
среднее квадратические отклонения
и
(функция СТАНДОТКЛОНП);
— выборочный
коэффициент корреляции
(функция ПИРСОН
или КОРРЕЛ).
3.
Вычислите
коэффициенты выборочной линейной
регрессии.
Для
вычисления коэффициентов регрессии
воспользуйтесь встроенной функцией
ЛИНЕЙН (функция находится в категории
«Статистические»),
обратите внимание, что эта функция
является функцией
массива,
поэтому ее использование подразумевает
выполнение следующих шагов:
1)
В свободном месте рабочего листа выделите
область ячеек размером 5 строк и 2 столбца
для вывода результатов;
2)
В Мастере функций (категория
«Статистические») выберите функцию
ЛИНЕЙН.
3)
Заполните поля аргументов функции:
Известные_значения_y
— адреса
ячеек, содержащих значения признака
;
Известные_значения_x
— адреса
ячеек, содержащих значения фактора
;
Константа
— значение
(логическое), указывающее на наличие
свободного члена в уравнении регрессии:
укажите в поле Константа
значение 1,
тогда свободный член рассчитывается
обычным образом (если значение поля
Константа
равно 0, то
свободный член полагается равным 0);
Статистика
— значение
(логическое), которое указывает на то,
следует ли выводить дополнительную
информацию по регрессионному анализу
или нет: укажите в поле Статистика
значение
равное 1, тогда будет выводиться
дополнительная регрессионная информация
(если Статистика=0,
то выводятся только оценки коэфициентов
уравнения регрессии);
4)
После того, как будут заполнены все
аргументы функции, нажмите комбинацию
клавиш <CTRL>+<SHIFT>+<ENTER>.
Результаты
расчета параметров регрессионной модели
будут выведены в виде следующей таблицы:
|
Значение |
Значение |
|
Стандартная |
Стандартная |
|
Коэффициент |
Стандартное |
|
Значение |
Число |
|
Регрессионная |
Остаточная |
4*.
Проверьте полученные значения
коэффициентов
,
непосредственным вычислением по
формулам.
5.
Запишите найденной уравнение эмпирической
регрессии. Дайте интерпретацию
коэффициенту
.
Вычислите по уравнению эмпирической
регрессии значения
.
6.
Постройте на корреляционном поле прямую
выборочной линейной регрессии по точкам
.
7.
Вычислите остатки
.
8.
Постройте график остатков (тип диаграммы
— «Точечная»).
9.
Найдите величину средней ошибки
аппроксимации

10*.
Вычислите коэффициент детерминации
непосредственно по формуле. Дайте
интерпретацию. Сравните полученное
значение коэффициента детерминации с
вычисленным ранее с помощью функции
КОРЕЛЛ выборочным коэффициентом
корреляции.
11*.
Рассчитайте значение
,
стандартные ошибки параметров линейной
регрессии и коэффициента корреляции
непосредственно по формулам.
12.
Вычислите значения
—статистик
коэффициентов выборочной регрессии.
Проверьте статистическую значимость
полученных значений коэффициентов
регрессии и коэффициента корреляции.
Табличные значения определите с помощью
функции СТЬЮДРАСПОБР. Аргументы этой
функции:
Вероятность
— уровень
значимости
(можно принять равным 0,05, т.е. 5%);
Степени_свободы
— число
степеней свободы, для парной линейной
регрессии равно
,
где
— число наблюдений.
13.
Проверьте значимость в целом полученного
уравнения регрессии по критерию Фишера.
Значение
определите с помощью функции FРАСПОБР.
Аргументы этой функции:
Вероятность
— уровень
значимости
(можно принять равным 0,05, т.е. 5%);
Степени_свободы1
— число
степеней свободы числителя, для парной
регрессии равно 1 (т.к. один фактор);
Степени_свободы2
— число
степеней свободы знаменателя, для парной
регрессии равно
,
где
— число наблюдений.
14.
Вычислите доверительные интервалы
параметров линейной регрессии. Дайте
им интерпретацию.
15.
Постройте прогноз среднего значения
показателя и точечный прогноз значения
при значении
в 3 раза
больше, чем среднее значение
.
16.
Вычислите стандартные ошибки прогноза
функции регрессии и индивидуального
значения и доверительные интервалы
полученных прогнозов.
17.
Получите результаты регрессионного
анализа с помощью Пакета Анализа
(Сервис/Анализ
данных … Регрессия |Tools/Data Analysis
…Regression).
Пакет анализа, при необходимости, может
быть активирован в пункте Надстройки
меню Сервис.
В
бланке запроса этой процедуры поля
Входной
интервал y,
Входной
интервал x,
Константа
имеют тот
же смысл, что и для функции LINEST/ЛИНЕЙН.
В
поле Метки
поставьте
флажок, если первая строка в указанном
диапазоне данных содержит названия
столбцов.
Поставьте
флажок в полях Остатки,
График остатков, График подбора
для того, чтобы получить соответствующую
дополнительную информацию.
18.
Проведите расчеты для второго фактора.
Проанализируйте результаты и сделайте
вывод о том, какой фактор лучше использовать
для описания показателя и построения
прогнозов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Линейная парная регрессия на точечной диаграмме в MS Excel
Рассмотрим один из самых простых и быстрых способов получения статистической модели взаимосвязи между двумя случайными переменными в виде уравнения парной линейной регрессии. Для этого будем использовать точечную диаграмму и линию тренда в среде электронных таблиц MS Excel.
Уравнение линейной парной регрессии имеет вид:
где 
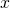

Стандартной задачей является нахождение параметров 

Пример. Изучается зависимость себестоимости единицы изделия (
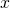

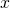 |
2 | 3 | 4 | 5 | 6 |
 |
1,9 | 1,7 | 1,8 | 1,6 | 1,4 |
Найти уравнение линейной парной регрессии 
Источник: Просветов Г.И. Эконометрика: задачи и решения: учебно-методическое пособие. — М.: Издательство «Альфа-пресс», 2008. — 192 с. (Пример 18, с.32)
Решение. Введем исходные данные в таблице MS Excel:
Выделим диапазон исходных данных:
В меню Вставка выбираем инструмент Точечная диаграмма (именно эта диаграмма позволяет строить точки по двум координатам):
Появляется диаграмма (в статистике этот график называют корреляционным полем):
Выполняем правый щелчок мыши по любой точке на диаграмме, появляется контекстное меню, в котором выбираем команду Добавить линию тренда :
Появляется окно диалога:
В окне диалога Формат линии тренда выбираем вид Линейная (обычно выбрано по умолчанию) и ставим флажок Показывать уравнение на диаграмме , нажимаем кнопку Закрыть . На точечной диаграмме появляется сглаживающая линия и ее уравнение, это и есть искомое уравнение регрессии:
Таким образом, уравнение регрессии имеет вид:
Сделаем вывод: коэффициент регрессии 
Задание на СР: Найти уравнение линейной парной регрессии, если 
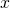
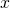 |
5 | 8 | 6 | 5 | 3 | 9 | 12 | 4 | 3 | 10 |
 |
72 | 76 | 78 | 70 | 68 | 80 | 82 | 65 | 62 | 90 |
Источник: Просветов Г.И. Эконометрика: задачи и решения: учебно-методическое пособие. — М.: Издательство «Альфа-пресс», 2008. — 192 с. (Задача 18, с.32)
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12765 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
источники:
http://lumpics.ru/regression-analysis-in-excel/
http://excel2.ru/articles/prostaya-lineynaya-regressiya-v-ms-excel
|
0 / 0 / 0 Регистрация: 08.05.2018 Сообщений: 25 |
|
|
1 |
|
Функция «ЛИНЕЙН» не считает полином03.03.2020, 06:05. Показов 5395. Ответов 10
Здравствуйте.
__________________
0 |
|
5906 / 3128 / 688 Регистрация: 23.11.2010 Сообщений: 10,450 |
|
|
03.03.2020, 06:51 |
2 |
|
РешениеПопробуйте такой вариант формулой массива Код =ЛИНЕЙН(ТРАНСП(DataY_Column);ТРАНСП(DataX_Column)^{1:2:3:4:5:6};1;0)
0 |
|
0 / 0 / 0 Регистрация: 08.05.2018 Сообщений: 25 |
|
|
03.03.2020, 07:16 [ТС] |
3 |
|
«=ЛИНЕЙН(ТРАНСП(DataY_Column);ТРАНСП(DataX_Column) ^{1:2:3:4:5:6};1;0)» — выдает «0». Добавлено через 2 минуты Добавлено через 1 минуту
0 |
|
5906 / 3128 / 688 Регистрация: 23.11.2010 Сообщений: 10,450 |
|
|
03.03.2020, 07:18 |
4 |
|
РешениеDed60, формула массива — ввод Ctrl+Shift+Enter
1 |
|
0 / 0 / 0 Регистрация: 08.05.2018 Сообщений: 25 |
|
|
03.03.2020, 08:36 [ТС] |
5 |
|
Прошу прощения, затупил. Все получилось! Добавлено через 1 час 11 минут
0 |
|
5906 / 3128 / 688 Регистрация: 23.11.2010 Сообщений: 10,450 |
|
|
03.03.2020, 08:40 |
6 |
|
ТРАНСП() стандартная функция, Вы сейчас о чем?
0 |
|
0 / 0 / 0 Регистрация: 08.05.2018 Сообщений: 25 |
|
|
03.03.2020, 09:06 [ТС] |
7 |
|
Формула «=ЛИНЕЙН(ТРАНСП(nm_DataChart);ТРАНСП(nm_DataChartX )^{1:2:3:4:5:6};1;0)» не работает на листе, отличном от расположения данных. Но это не очень принципиально — просто для общего развития. Добавлено через 2 минуты
0 |
|
5906 / 3128 / 688 Регистрация: 23.11.2010 Сообщений: 10,450 |
|
|
03.03.2020, 09:06 |
8 |
|
Ded60, если записать значения через точку с запятой {1;2;3;4;5;6}, у Вас было через двоеточие, то считает норм и без транспонирования Код =ЛИНЕЙН(DataY_Column;DataX_Column^{1;2;3;4;5;6};1;0)
1 |
|
Ded60 0 / 0 / 0 Регистрация: 08.05.2018 Сообщений: 25 |
||||
|
03.03.2020, 09:39 [ТС] |
9 |
|||
|
Fairuza, кажется, нашел причину моей проблемы.
В итоге, в ячейки вводится «{=ЛИНЕЙН(nm_DataChart;nm_DataChartX^{1:2:3:4:5:6};1;0)}».
0 |
|
5906 / 3128 / 688 Регистрация: 23.11.2010 Сообщений: 10,450 |
|
|
03.03.2020, 09:44 |
10 |
|
Из справки: Если элементы списка разделяются точками с запятой, будет создан горизонтальный массив (строка). Если элементы разделяются двоеточиями, будет создан вертикальный массив (столбец). Для создания двумерного массива следует разделять элементы в каждой строке запятыми и разделять каждую строку точкой с запятой. Надо попробовать проделать….
1 |
|
0 / 0 / 0 Регистрация: 08.05.2018 Сообщений: 25 |
|
|
03.03.2020, 09:58 [ТС] |
11 |
|
Теперь понятно, что надо больше читать справки — было бы время.
0 |
В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды.
Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y
по значениям независимой переменной X
. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y
по значениям нескольких зависимых переменных (Х 1 , Х 2 , …, X k
).
Скачать заметку в формате или , примеры в формате
Виды регрессионных моделей
где ρ
1
– коэффициент автокорреляции; если ρ
1
= 0 (нет автокорреляции), D
≈ 2; если ρ
1
≈ 1 (положительная автокорреляции), D
≈ 0; если ρ
1
= -1 (отрицательная автокорреляции), D
≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D
с критическими теоретическими значениями d L
и d U
для заданного числа наблюдений n
, числа независимых переменных модели k
(для простой линейной регрессии k
= 1) и уровня значимости α. Если D < d L
, гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > d U
, гипотеза не отвергается (то есть автокорреляция отсутствует); если d L < D < d U
, нет достаточных оснований для принятия решения. Когда расчётное значение D
превышает 2, то с d L
и d U
сравнивается не сам коэффициент D
, а выражение (4 – D
).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка
. Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).
Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D
= 0,883. Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (d L
и d U
), зависящими от числа наблюдений n
и уровня значимости α (рис. 17).
Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k
= 1), 15 наблюдений (n
= 15) и уровень значимости α = 0,05. Следовательно, d L
= 1,08 и d
U
= 1,36. Поскольку D
= 0,883 < d L
= 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y
при заданной величине переменной X
использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение
t
-критерия для наклона.
Проверяя, равен ли наклон генеральной совокупности β 1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X
и Y
. Если эта гипотеза отклоняется, можно утверждать, что между переменными X
и Y
существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0: β 1 = 0 (нет линейной зависимости), Н1: β 1 ≠ 0 (есть линейная зависимость). По определению t
-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11)
t
= (b
1
–
β
1
) /
S b
1
где b
1
– наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t
имеет t
-распределение с n – 2
степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t
-критерий выводится наряду с другими параметрами при использовании Пакета анализа
(опция Регрессия
). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t
Поскольку число магазинов n
= 14 (см. рис.3), критическое значение t
-статистики при уровне значимости α = 0,05 можно найти по формуле: t L
=СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n
– 2; t U
=СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t
-статистика = 10,64 > t U
= 2,1788 (рис. 19), нулевая гипотеза Н 0
отклоняется. С другой стороны, р
-значение для Х
= 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н 0
снова отклоняется. Тот факт, что р
-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение
F
-критерия для наклона.
Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F
-критерия. Напомним, что F
-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F
-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR
, деленной на количество независимых переменных k
), к дисперсии ошибок (MSE = S Y
X
2
).
По определению F
-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F
=
MSR
/
MSE
, где MSR =
SSR
/
k
, MSE =
SSE
/(n
– k – 1), k
– количество независимых переменных в регрессионной модели. Тестовая статистика F
имеет F
-распределение с k
и n
– k – 1
степенями свободы.
При заданном уровне значимости α решающее правило формулируется так: если F > F
U
, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.
Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t
-критерию F
-критерий выводится в таблицу при использовании Пакета анализа
(опция Регрессия
). Полностью результаты работы Пакета анализа
приведены на рис. 4, фрагмент, относящийся к F
-статистике – на рис. 21.
Рис. 21. Результаты применения F
-критерия, полученные с помощью Пакета анализа Excel
F-статистика равна 113,23, а р
-значение близко к нулю (ячейка Значимость
F
). Если уровень значимости α равен 0,05, определить критическое значение F
-распределения с одной и 12 степенями свободы можно по формуле F U
=F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F
= 113,23 > F U
= 4,7472, причем р
-значение близко к 0 < 0,05, нулевая гипотеза Н 0
отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.
Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β 1 .
Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β 1 и убедиться, что гипотетическое значение β 1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β 1 , является выборочный наклон b
1
, а его границами — величины b 1 ±
t n
–2
S b
1
Как показано на рис. 18, b
1
= +1,670, n
= 14, S b
1
= 0,157. t
12
=СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b 1 ±
t n
–2
S b
1
= +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β 1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование
t
-критерия для коэффициента корреляции.
был введен коэффициент корреляции r
, представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0
: ρ = 0 (нет корреляции), Н 1
: ρ ≠ 0 (есть корреляция). Проверка существования корреляции:
где r
= +
, если b
1
> 0, r
= –
, если b
1
< 0. Тестовая статистика t
имеет t
-распределение с n – 2
степенями свободы.
В задаче о сети магазинов Sunflowers r 2
= 0,904, а b 1
— +1,670 (см. рис. 4). Поскольку b 1
> 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r
= +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t
-статистику:
При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t
= 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r
зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y
и предсказания индивидуальных значений Y
при заданных значениях переменной X
.
Построение доверительного интервала.
В примере 2 (см. выше раздел Метод наименьших квадратов
) регрессионное уравнение позволило предсказать значение переменной Y
X
. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика
при заданном значении переменной X
:
где 
b
0
+
b
1
X i
– предсказанное значение переменное Y
при X
= X i
, S YX
– среднеквадратичная ошибка, n
– объем выборки, X
i
— заданное значение переменной X
, µ
Y
| X
=
X
i
– математическое ожидание переменной Y
при Х
= Х i
, SSX =
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений X
i
. Если значение переменной Y
предсказывается для величин X
, близких к среднему значению
, доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения.
Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X
, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Y
X
=
Xi
при конкретном значении переменной X
i
определяется по формуле:
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).
Рис. 23. Четыре набора искусственных данных
Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа
(кликните на рисунке, чтобы увеличить изображение)
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.
Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х 8
= 19, Y
8
= 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X
и Y
всегда начинайте с построения диаграммы разброса. - Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
Резюме.
Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t
-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.
Рис. 27. Структурная схема заметки
Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
· линейной (у = а + bx);
· параболической (y = a + bx + cx 2);
· экспоненциальной (y = a * exp(bx));
· степенной (y = a*x^b);
· гиперболической (y = b/x + a);
· логарифмической (y = b * 1n(x) + a);
· показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.
Основные задачи и виды регрессии
Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных.
К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.
Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.
Основные задачи построения регрессионной модели заключаются в следующем:
- Отбор значимых независимых переменных (Х1, Х2, …, Xk).
- Выбор вида функции.
- Построение оценок для коэффициентов.
- Построение доверительных интервалов и функции регрессии.
- Проверка значимости вычисленных оценок и построенного уравнения регрессии.
Регрессионный анализ бывает нескольких видов:
- парный (1 зависимая и 1 независимая переменные);
- множественный (несколько независимых переменных).
Уравнения регрессии бывает двух видов:
- Линейные, иллюстрирующие строгую линейную связь между переменными.
- Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.
Инструкция построения модели
Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:
Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача:
Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
Теперь стали видны и данные регрессионного анализа.
Статистическая обработка данных может также проводиться с помощью надстройки ПАКЕТ АНАЛИЗА
(рис. 62).
Из предложенных пунктов выбирает пункт «РЕГРЕССИЯ
» и щелкаем на нем левой кнопкой мыши. Далее нажимаем ОК.
Появится окно, показанное на рис. 63.
Инструмент анализа «РЕГРЕССИЯ
» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
Инструмент «Регрессия» использует функцию ЛИНЕЙН
.
Диалоговое окно «РЕГРЕССИЯ»
Метки Установите флажок, если первая строка или первый столбец входного диапазона содержит заголовки. Снимите этот флажок, если заголовки отсутствуют. В этом случае подходящие заголовки для данных выходной таблицы будут созданы автоматически.
Уровень надежности Установите флажок, чтобы включить в выходную таблицу итогов дополнительный уровень. В соответствующее поле введите уровень надежности, который следует применить, дополнительно к уровню 95%, применяемому по умолчанию.
Константа — ноль Установите флажок, чтобы линия регрессии прошла через начало координат.
Выходной интервал Введите ссылку на левую верхнюю ячейку выходного диапазона. Отведите как минимум семь столбцов для выходной таблицы итогов, которая будет включать в себя: результаты дисперсионного анализа, коэффициенты, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.
Новый рабочий лист Установите переключатель в это положение, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. При необходимости введите имя для нового листа в поле, расположенном напротив соответствующего положения переключателя.
Новая рабочая книга Установите переключатель в это положение для создания новой книги, в которой результаты будут добавлены в новый лист.
Остатки Установите флажок для включения остатков в выходную таблицу.
Стандартизированные остатки Установите флажок для включения стандартизированных остатков в выходную таблицу.
График остатков Установите флажок для построения графика остатков для каждой независимой переменной.
График подбора Установите флажок для построения графика зависимости предсказанных значений от наблюдаемых.
График нормальной вероятности
Установите флажок, для построения графика нормальной вероятности.
Функция ЛИНЕЙН
Для проведения расчетов выделяем курсором ячейку, в которой хотим отобразить среднее значение и нажимаем на клавиатуре клавишу =. Далее в поле Имя указываем нужную функцию, например СРЗНАЧ
(рис. 22).
Функция ЛИНЕЙН
рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Можно также объединять функцию ЛИНЕЙН
с другими функциями для вычисления других видов моделей, являющихся линейными в неизвестных параметрах (неизвестные параметры которых являются линейными), включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Уравнение для прямой линии имеет следующий вид:
y=m 1 x 1 +m 2 x 2 +…+b (в случае нескольких диапазонов значений x),
где зависимое значение y — функция независимого значения x, значения m — коэффициенты, соответствующие каждой независимой переменной x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН
возвращает массив{mn;mn-1;…;m 1 ;b}. ЛИНЕЙН
может также возвращать дополнительную регрессионную статистику.
ЛИНЕЙН
(известные_значения_y; известные_значения_x; конст; статистика)
Известные_значения_y — множество значений y, которые уже известны для соотношения y=mx+b.
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Известные_значения_x — необязательное множество значений x, которые уже известны для соотношения y=mx+b.
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы_известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если массив_известные_значения_x опущен, то предполагается, что этот массив {1;2;3;…} имеет такой же размер, как и массив_известные_значения_y.
Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если аргумент «конст» имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
Если аргумент «конст» имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y=mx.
Статистика — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.
Если аргумент «статистика» имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив будет иметь следующий вид: {mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid}.
Если аргумент «статистика» имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.(табл.17)
| Величина | Описание |
| se1,se2,…,sen | Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
| seb | Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент «конст» имеет значение ЛОЖЬ). |
| r2 | Коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т. е. различия между фактическим и оценочным значениями y не существует. В противоположном случае, если коэффициент детерминированности равен 0, использовать уравнение регрессии для предсказания значений y не имеет смысла. Для получения дополнительных сведений о способах вычисления r2, см. «Замечания» в конце данного раздела. |
| sey | Стандартная ошибка для оценки y. |
| F | F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
| df | Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Для получения дополнительных сведений о вычислении величины df см. «Замечания» в конце данного раздела. Далее в примере 4 показано использование величин F и df. |
| ssreg | Регрессионная сумма квадратов. |
| ssresid | Остаточная сумма квадратов. Для получения дополнительных сведений о расчете величин ssreg и ssresid см. «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика (рис. 64).
Замечания:
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m): чтобы определить наклон прямой, обычно обозначаемый через m, нужно взять две точки прямой (x 1 ,y 1) и(x 2 ,y 2); наклон будет равен (y 2 -y 1)/(x 2 -x 1).
Y-пересечение (b): Y-пересечением прямой, обычно обозначаемым через b, является значение y для точки, в которой прямая пересекает ось y.
Уравнение прямой имеет вид y=mx+b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон: ИНДЕКС (ЛИНЕЙН(известные_значения_y; известные_значения_x); 1)
Y-пересечение: ИНДЕКС (ЛИНЕЙН (известные_значения_y; известные_значения_x); 2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. Когда имеется только одна независимая переменная x, m и b вычисляются по следующим формулам:
где x и y – выборочные средние значения, например x = СРЗНАЧ (известные_значения_x), а y = СРЗНАЧ (известные_значения_y).
Функции аппроксимации ЛИНЕЙН и ЛГРФПРИБЛ могут вычислить прямую или экспоненциальную кривую, наилучшим образом описывающую данные. Однако они не дают ответа на вопрос, какой из двух результатов больше подходит для решения поставленной задачи. Можно также вычислить функцию ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x) для прямой или функцию РОСТ(известные_значения_y; известные_значения_x) для экспоненциальной кривой. Эти функции, если не задавать аргумент новые_значения_x, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. После этого можно сравнить вычисленные значения с фактическими значениями. Можно также построить диаграммы для визуального сравнения.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Коэффициент r2 равен ssreg/sstotal.
В некоторых случаях один или более столбцов X (пусть значения Y и X находятся в столбцах) не имеет дополнительного предикативного значения в других столбцах X. Другими словами, удаление одного или более столбцов X может привести к значениям Y, вычисленным с одинаковой точностью. В этом случае избыточные столбцы X будут исключены из модели регрессии. Этот феномен называется «коллинеарностью», поскольку избыточные столбцы X могут быть представлены в виде суммы нескольких неизбыточных столбцов. Функция ЛИНЕЙН проверяет на коллинеарность и удаляет из модели регрессии все избыточные столбцы X, если обнаруживает их. Удаленные столбцы X можно определить в выходных данных ЛИНЕЙН по коэффициенту, равному 0, и по значению se, равному 0. Удаление одного или более столбцов как избыточных изменяет величину df, поскольку она зависит от количества столбцов X, в действительности используемых для предикативных целей. Подробнее о вычислении величины df см. ниже в примере 4. При изменении df вследствие удаления избыточных столбцов значения sey и F также изменяются. Часто использовать коллинеарность не рекомендуется. Однако ее следует применять, если некоторые столбцы X содержат 0 или 1 в качестве индикатора указывающего, входит ли предмет эксперимента в отдельную группу. Если конст = ИСТИНА или значение этого аргумента не указано, функция ЛИНЕЙН вставляет дополнительный столбец X для моделирования точки пересечения. Если имеется столбец со значениями 1 для указания мужчин и 0 — для женщин, а также имеется столбец со значениями 1 для указания женщин и 0 — для мужчин, то последний столбец удаляется, поскольку его значения можно получить из столбца с «индикатором мужского пола».
Вычисление df для случаев, когда столбцы X не удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
Формулы, которые возвращают массивы, должны быть введены как формулы массива.
При вводе массива констант в качестве, например, аргумента известные_значения_x следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть различными в зависимости от параметров, заданных в окне «Язык и стандарты» на панели управления.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН
, отличается от основного алгоритма функций НАКЛОН
и ОТРЕЗОК
. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
Функция ЛИНЕЙН
возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН
используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
Функции НАКЛОН и ОТРЕЗОК возвращают ошибку #ДЕЛ/0!. Алгоритм функций НАКЛОН и ОТРЕЗОК используется для поиска только одного ответа, а в данном случае их может быть несколько.
Помимо вычисления статистики для других типов регрессии функцию ЛИНЕЙН можно использовать при вычислении диапазонов для других типов регрессии, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y=m 1 x+m 2 x 2 +m 3 x 3 +b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.




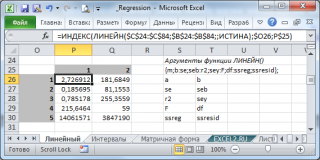




















































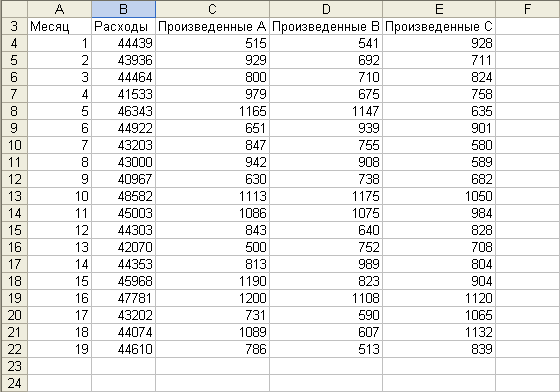
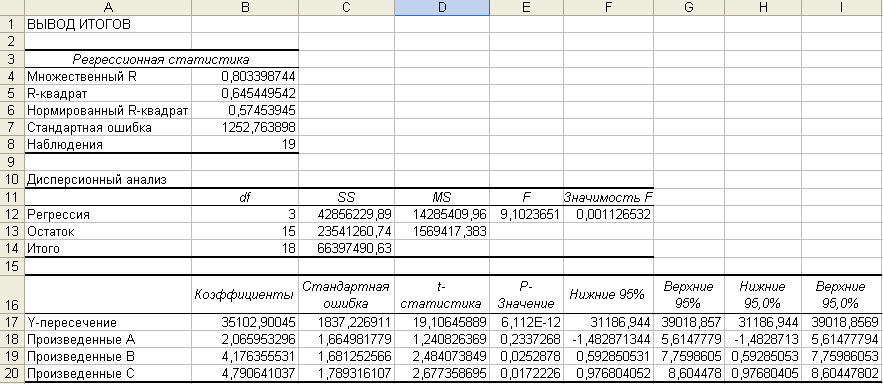


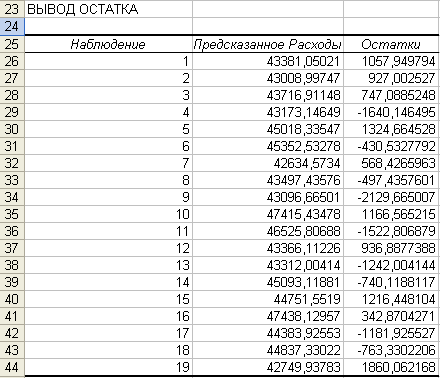

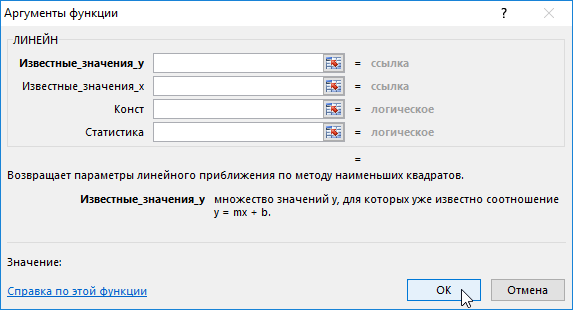
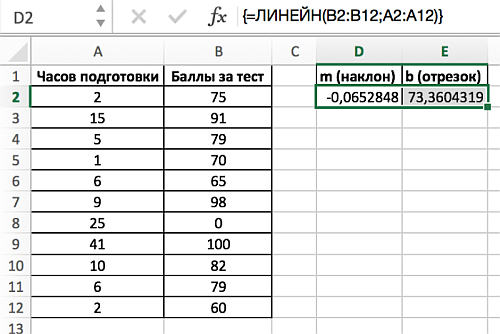
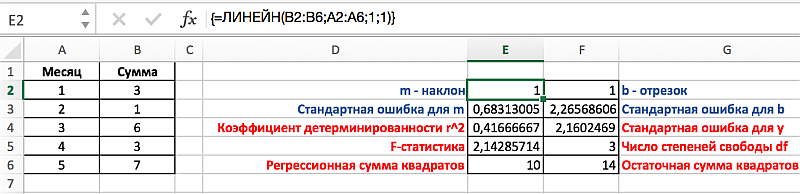
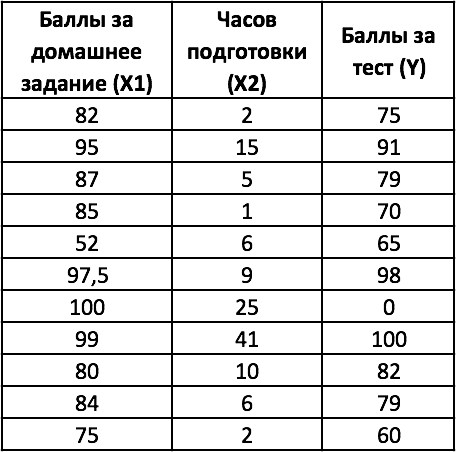
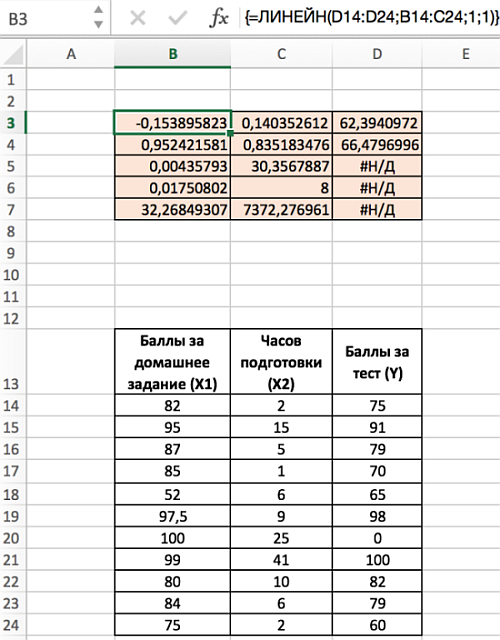
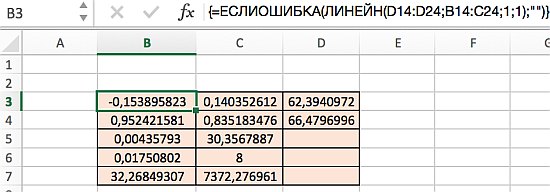
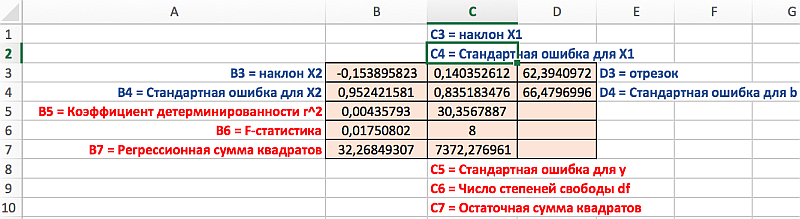










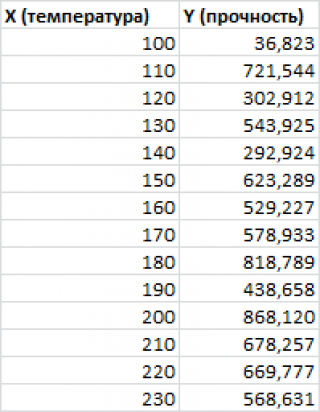
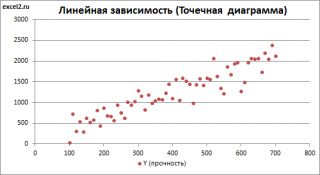
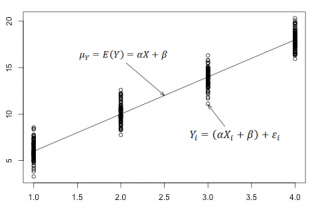
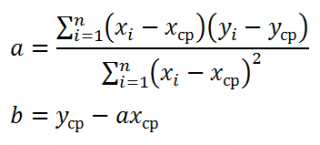
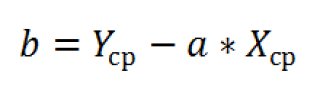
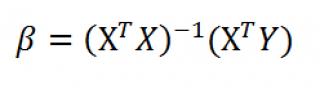
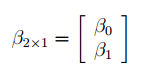
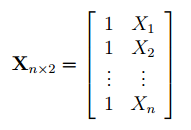
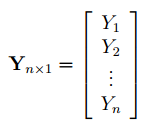
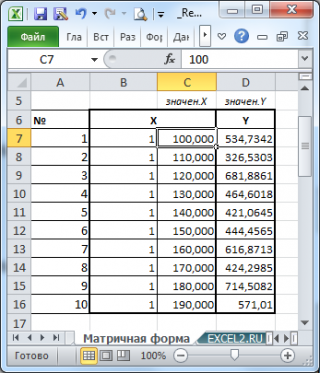
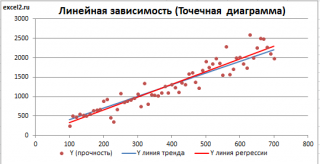
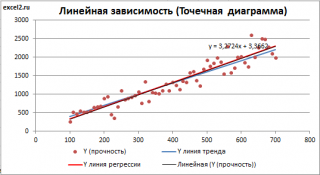
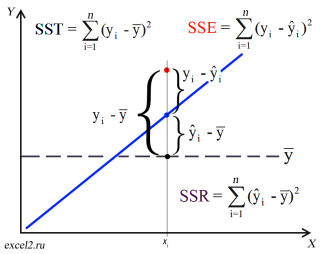
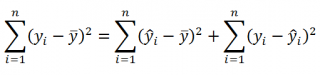
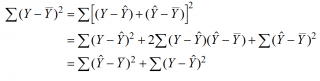
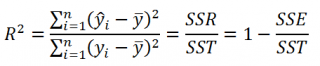
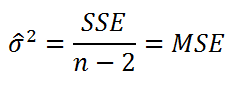
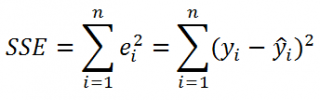
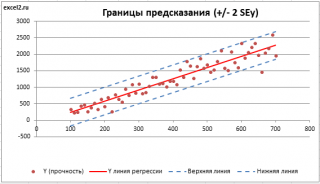
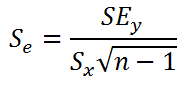
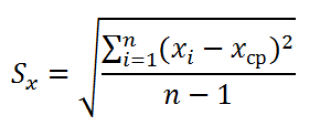
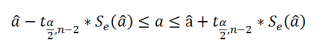
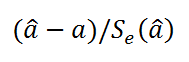
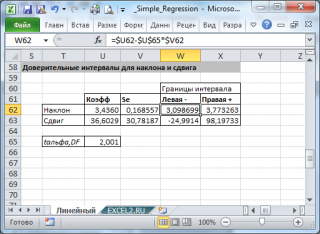
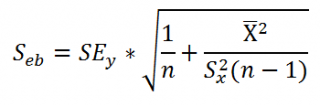
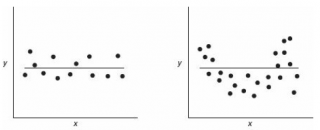
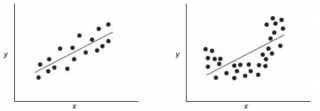
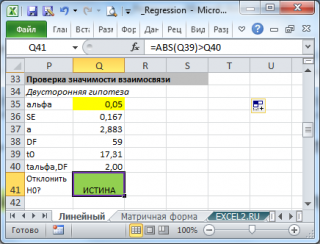
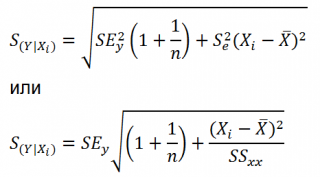
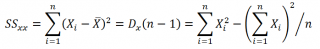
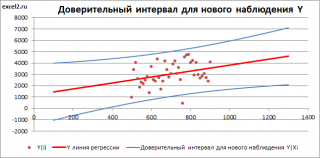
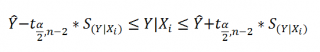
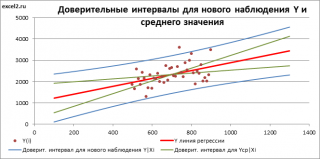
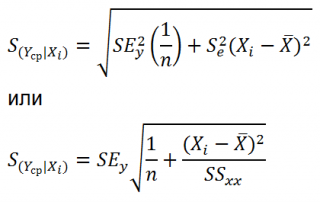
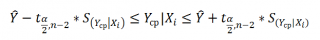
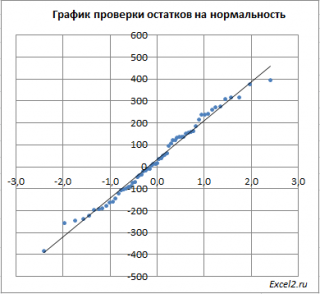
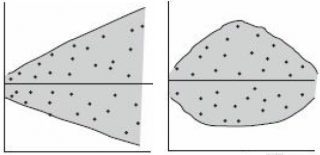
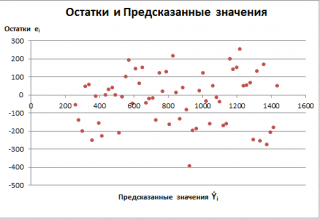
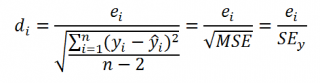
 Сообщение было отмечено Ded60 как решение
Сообщение было отмечено Ded60 как решение
 ataX_Column^{1:2:3:4 :5:6};1;0))» — выдает «#ЗНАЧ!».
ataX_Column^{1:2:3:4 :5:6};1;0))» — выдает «#ЗНАЧ!».