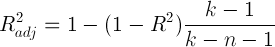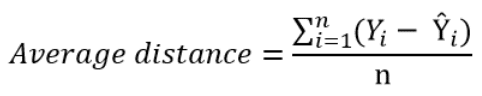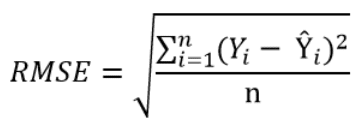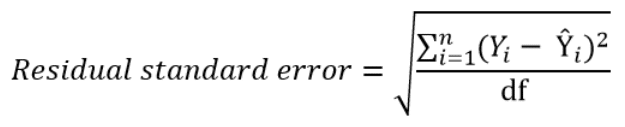Residual standard error что это - Исправление ошибок и поиск оптимальных решений проблем

The residual standard error is used to measure how well a regression model fits a dataset.

In simple terms, it measures the standard deviation of the residuals in a regression model.

It is calculated as:

Residual standard error = √Σ(y – ŷ)²/df

where:

y: The observed value
ŷ: The predicted value
df: The degrees of freedom, calculated as the total number of observations – total number of model parameters.

The smaller the residual standard error, the better a regression model fits a dataset. Conversely, the higher the residual standard error, the worse a regression model fits a dataset.

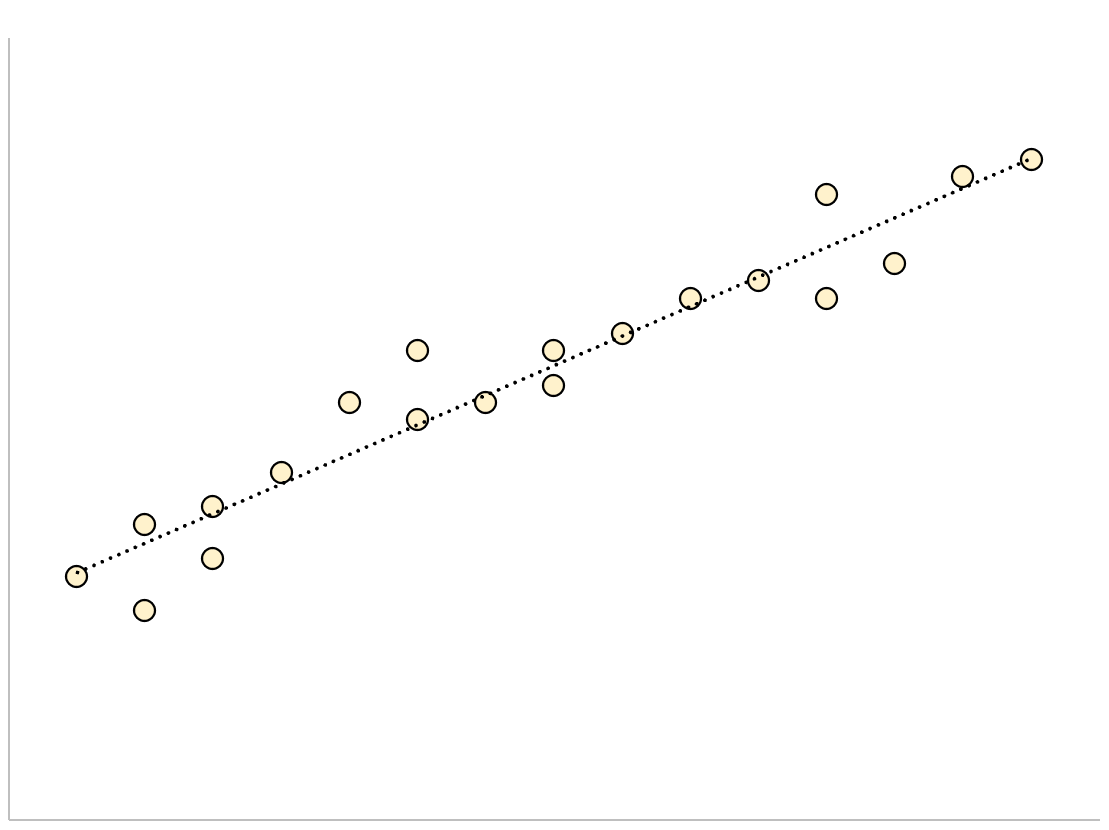
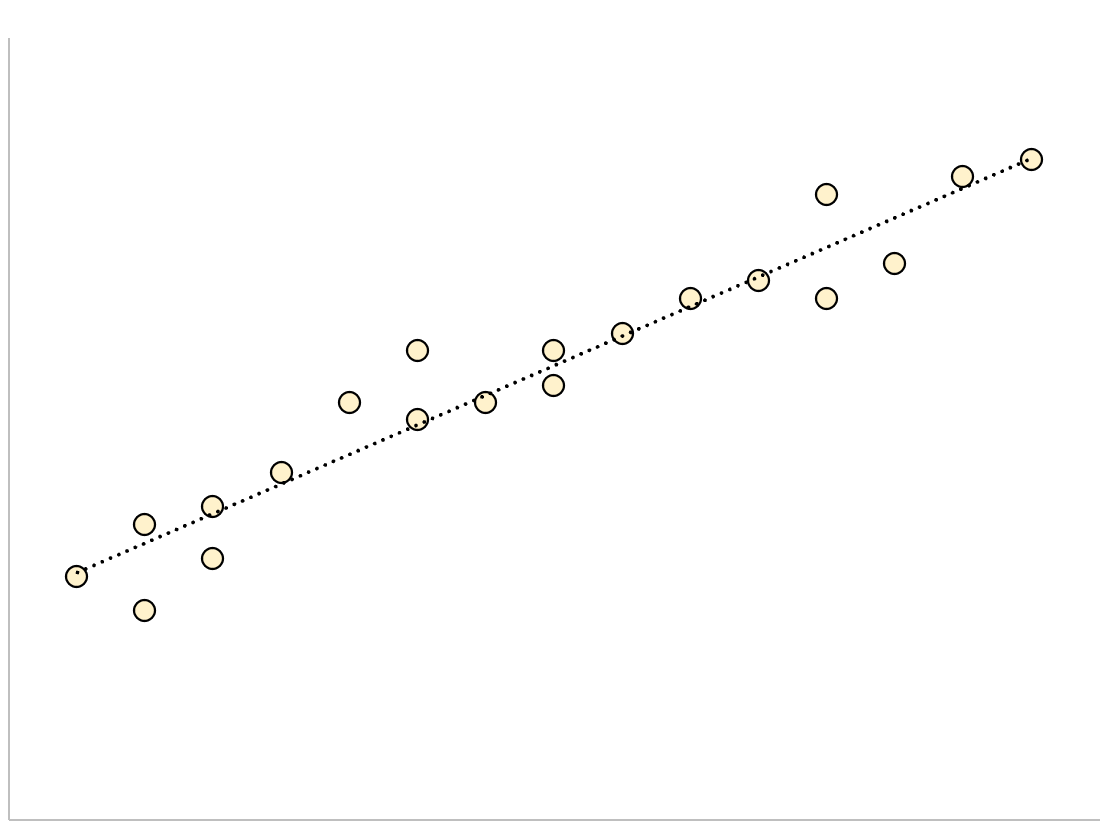
A regression model that has a small residual standard error will have data points that are closely packed around the fitted regression line:

The residuals of this model (the difference between the observed values and the predicted values) will be small, which means the residual standard error will also be small.

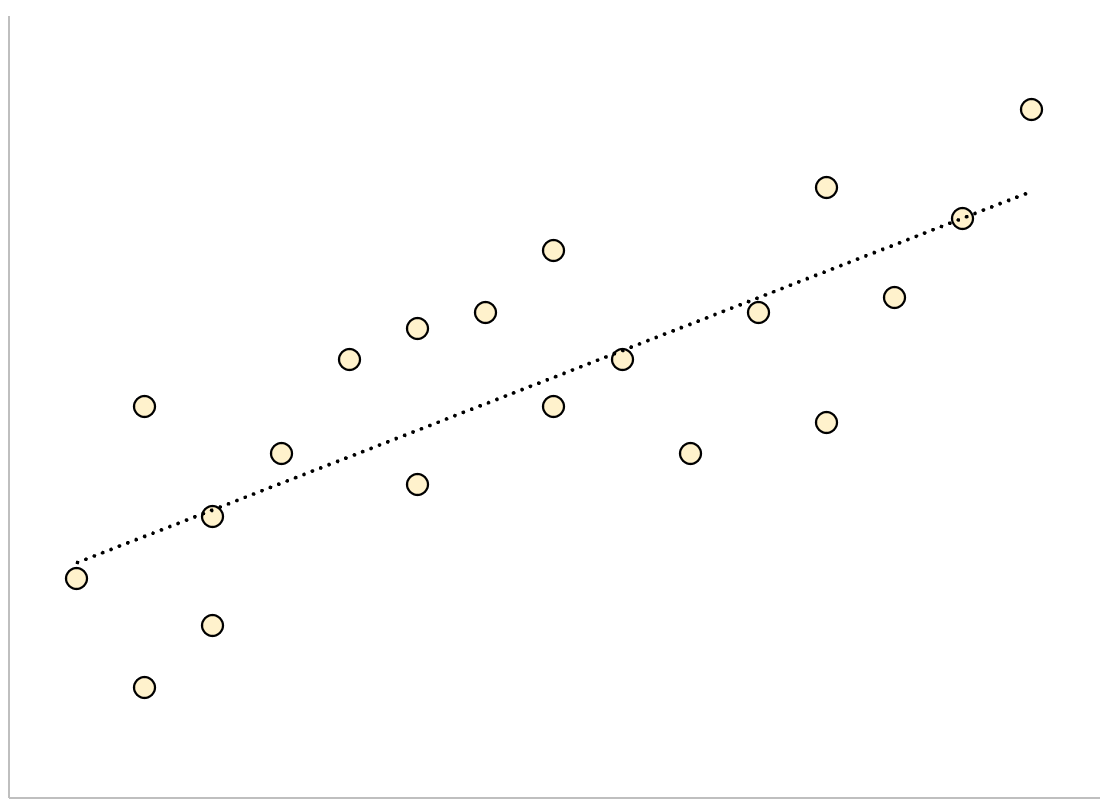
Conversely, a regression model that has a large residual standard error will have data points that are more loosely scattered around the fitted regression line:

The residuals of this model will be larger, which means the residual standard error will also be larger.

The following example shows how to calculate and interpret the residual standard error of a regression model in R.

Example: Interpreting Residual Standard Error

Suppose we would like to fit the following multiple linear regression model:

mpg = β₀ + β₁(displacement) + β₂(horsepower)

This model uses the predictor variables “displacement” and “horsepower” to predict the miles per gallon that a given car gets.

The following code shows how to fit this regression model in R:

#load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7945 -2.3036 -0.8246  1.8582  6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904   1.331566  23.083  < 2e-16 ***
disp        -0.030346   0.007405  -4.098 0.000306 ***
hp          -0.024840   0.013385  -1.856 0.073679 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared:  0.7482,	Adjusted R-squared:  0.7309 
F-statistic: 43.09 on 2 and 29 DF,  p-value: 2.062e-09

Near the bottom of the output we can see that the residual standard error of this model is 3.127.

This tells us that the regression model predicts the mpg of cars with an average error of about 3.127.

Using Residual Standard Error to Compare Models

The residual standard error is particularly useful for comparing the fit of different regression models.

For example, suppose we fit two different regression models to predict the mpg of cars. The residual standard error of each model is as follows:

Residual standard error of model 1: 3.127
Residual standard error of model 2: 5.657

Since model 1 has a lower residual standard error, it fits the data better than model 2. Thus, we would prefer to use model 1 to predict the mpg of cars because the predictions it makes are closer to the observed mpg values of the cars.

Additional Resources

How to Perform Simple Linear Regression in R
How to Perform Multiple Linear Regression in R
How to Create a Residual Plot in R

Источник

Как интерпретировать остаточную стандартную ошибку

17 авг. 2022 г.
читать 2 мин

Остаточная стандартная ошибка используется для измерения того, насколько хорошо модель регрессии соответствует набору данных.

Проще говоря, он измеряет стандартное отклонение остатков в регрессионной модели.

Он рассчитывается как:

Остаточная стандартная ошибка = √ Σ(y – ŷ) 2 /df

куда:

y: наблюдаемое значение
ŷ: Прогнозируемое значение
df: Степени свободы, рассчитанные как общее количество наблюдений – общее количество параметров модели.

Чем меньше остаточная стандартная ошибка, тем лучше регрессионная модель соответствует набору данных. И наоборот, чем выше остаточная стандартная ошибка, тем хуже регрессионная модель соответствует набору данных.

Модель регрессии с небольшой остаточной стандартной ошибкой будет иметь точки данных, которые плотно упакованы вокруг подобранной линии регрессии:

Остатки этой модели (разница между наблюдаемыми значениями и прогнозируемыми значениями) будут малы, что означает, что остаточная стандартная ошибка также будет небольшой.

И наоборот, регрессионная модель с большой остаточной стандартной ошибкой будет иметь точки данных, которые более свободно разбросаны по подобранной линии регрессии:

Остатки этой модели будут больше, что означает, что стандартная ошибка невязки также будет больше.

В следующем примере показано, как рассчитать и интерпретировать остаточную стандартную ошибку регрессионной модели в R.

Пример: интерпретация остаточной стандартной ошибки

Предположим, мы хотели бы подогнать следующую модель множественной линейной регрессии:

миль на галлон = β 0 + β 1 (смещение) + β 2 (лошадиные силы)

Эта модель использует переменные-предикторы «объем двигателя» и «лошадиная сила» для прогнозирования количества миль на галлон, которое получает данный автомобиль.

В следующем коде показано, как подогнать эту модель регрессии в R:

#load built-in *mtcars* dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
 Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
 Estimate Std. Error t value Pr(>|t|) 
(Intercept) 30.735904 1.331566 23.083 < 2e-16 ***
disp -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679.
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

В нижней части вывода мы видим, что остаточная стандартная ошибка этой модели составляет 3,127 .

Это говорит нам о том, что регрессионная модель предсказывает расход автомобилей на галлон со средней ошибкой около 3,127.

Использование остаточной стандартной ошибки для сравнения моделей

Остаточная стандартная ошибка особенно полезна для сравнения соответствия различных моделей регрессии.

Например, предположим, что мы подогнали две разные регрессионные модели для прогнозирования расхода автомобилей на галлон. Остаточная стандартная ошибка каждой модели выглядит следующим образом:

Остаточная стандартная ошибка модели 1: 3,127
Остаточная стандартная ошибка модели 2: 5,657

Поскольку модель 1 имеет меньшую остаточную стандартную ошибку, она лучше соответствует данным, чем модель 2. Таким образом, мы предпочли бы использовать модель 1 для прогнозирования расхода автомобилей на галлон, потому что прогнозы, которые она делает, ближе к наблюдаемым значениям расхода автомобилей на галлон.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как создать остаточный график в R

Источник

Содержание

Оценка результатов линейной регрессии
Введение
Модель линейной регрессии
Функция summary.lm() и оценка получившихся результатов
Заключение
Как интерпретировать остаточную стандартную ошибку
Пример: интерпретация остаточной стандартной ошибки
Использование остаточной стандартной ошибки для сравнения моделей
Residual Standard Deviation/Error: Guide for Beginners
Residual standard deviation vs residual standard error vs RMSE
How to interpret the residual standard deviation/error
Further reading
About Me

Оценка результатов линейной регрессии

Введение

Модель линейной регрессии

Итак, пусть есть несколько независимых случайных величин X1, X2, . Xn (предикторов) и зависящая от них величина Y (предполагается, что все необходимые преобразования предикторов уже сделаны). Более того, мы предполагаем, что зависимость линейная, а ошибки рапределены нормально, то есть

где I — единичная квадратная матрица размера n x n.

Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так: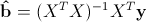

где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.

Функция summary.lm() и оценка получившихся результатов

Теперь рассмотрим пример построения модели линейной регрессии в языке R:

Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.

Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат:

при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0: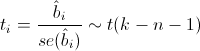

где
— стандартная ошибка оценки коэффициента, а t(k-n-1) — распределение Стьюдента с k-n-1 степенями свободы.

Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.

В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.

Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.

А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared:

где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.

Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.

Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.

Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:

Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.

Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы:

Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().

Заключение

В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.

Источник

Как интерпретировать остаточную стандартную ошибку

Проще говоря, он измеряет стандартное отклонение остатков в регрессионной модели.

Он рассчитывается как:

Остаточная стандартная ошибка = √ Σ(y – ŷ) 2 /df

y: наблюдаемое значение
ŷ: Прогнозируемое значение
df: Степени свободы, рассчитанные как общее количество наблюдений – общее количество параметров модели.

Остатки этой модели будут больше, что означает, что стандартная ошибка невязки также будет больше.

Пример: интерпретация остаточной стандартной ошибки

Предположим, мы хотели бы подогнать следующую модель множественной линейной регрессии:

миль на галлон = β 0 + β 1 (смещение) + β 2 (лошадиные силы)

В следующем коде показано, как подогнать эту модель регрессии в R:

В нижней части вывода мы видим, что остаточная стандартная ошибка этой модели составляет 3,127 .

Использование остаточной стандартной ошибки для сравнения моделей

Остаточная стандартная ошибка особенно полезна для сравнения соответствия различных моделей регрессии.

Остаточная стандартная ошибка модели 1: 3,127
Остаточная стандартная ошибка модели 2: 5,657

Источник

Residual Standard Deviation/Error: Guide for Beginners

The residual standard deviation (or residual standard error) is a measure used to assess how well a linear regression model fits the data. (The other measure to assess this goodness of fit is R 2 ).

But before we discuss the residual standard deviation, let’s try to assess the goodness of fit graphically.

Consider the following linear regression model:

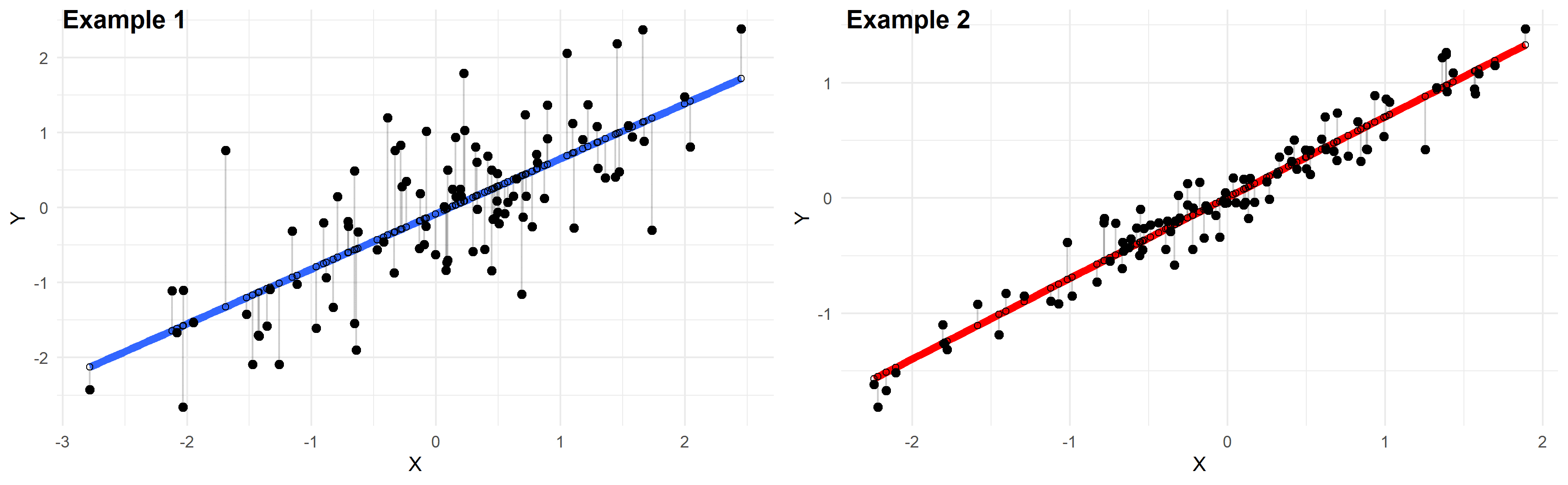
Plotted below are examples of 2 of these regression lines modeling 2 different datasets:

Just by looking at these plots we can say that the linear regression model in “example 2” fits the data better than that of “example 1”.

This is because in “example 2” the points are closer to the regression line. Therefore, using a linear regression model to approximate the true values of these points will yield smaller errors than “example 1”.

In the plots above, the gray vertical lines represent the error terms — the difference between the model and the true value of Y.

Mathematically, the error of the i th point on the x-axis is given by the equation: (Y_i – Ŷ_i), which is the difference between the true value of Y (Y_i) and the value predicted by the linear model (Ŷ_i) — this difference determines the length of the gray vertical lines in the plots above.

Now that we developed a basic intuition, next we will try to come up with a statistic that quantifies this goodness of fit.

Residual standard deviation vs residual standard error vs RMSE

The simplest way to quantify how far the data points are from the regression line, is to calculate the average distance from this line:

Where n is the sample size.

But, because some of the distances are positive and some are negative (certain points are above the regression line and others are below it), these distances will cancel each other out — meaning that the average distance will be biased low.

In order to remedy this situation, one solution is to take the square of this distance (which will always be a positive number), then calculate the sum of these squared distances for all data points and finally take the square root of this sum to obtain the Root Mean Square Error (RMSE):

We can take this equation one step further:

Instead of dividing by the sample size n, we can divide by the degrees of freedom df to obtain an unbiased estimation of the standard deviation of the error term ε. (If you’re having trouble with this idea, I recommend these 4 videos from Khan Academy which provide a simple explanation mainly through simulations instead of math equations).

The quantity obtained is sometimes called the residual standard deviation (as referred to it in the textbook Data Analysis Using Regression and Multilevel Hierarchical Models by Andrew Gelman and Jennifer Hill). Other textbooks refer to it as the residual standard error (for example An Introduction to Statistical Learning by Gareth James, Daniela Witten, Trevor Hastie and Robert Tibshirani).

In the statistical programming language R, calling the function summary on the linear model will calculate it automatically.

The degrees of freedom df are the sample size minus the number of parameters we’re trying to estimate.

For example, if we’re estimating 2 parameters β and β₁ as in:

If we’re estimating 3 parameters, as in:

Now that we have a statistic that measures the goodness of fit of a linear model, next we will discuss how to interpret it in practice.

How to interpret the residual standard deviation/error

Simply put, the residual standard deviation is the average amount that the real values of Y differ from the predictions provided by the regression line.

We can divide this quantity by the mean of Y to obtain the average deviation in percent (which is useful because it will be independent of the units of measure of Y).

Here’s an example:

Suppose we regressed systolic blood pressure (SBP) onto body mass index (BMI) — which is a fancy way of saying that we ran the following linear regression model:

After running the model we found that:

β = 100
β1 = 1
And the residual standard error is 12 mmHg

So we can say that the BMI accurately predicts systolic blood pressure with about 12 mmHg error on average.

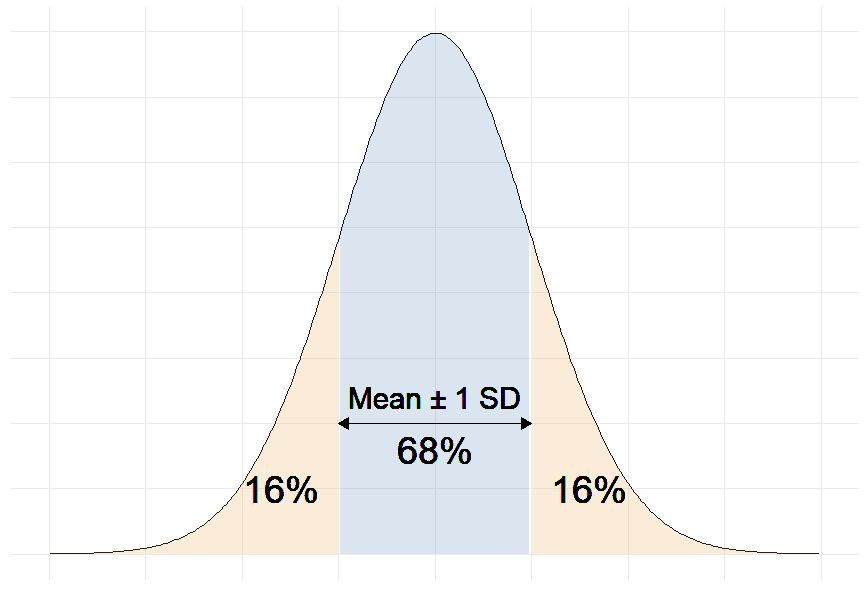
More precisely, we can say that 68% of the predicted SBP values will be within ∓ 12 mmHg of the real values.

Remember that in linear regression, the error terms are Normally distributed.

And one of the properties of the Normal distribution is that 68% of the data sits around 1 standard deviation from the average (See figure below).

Therefore, 68% of the errors will be between ∓ 1 × residual standard deviation.

For example, our linear regression equation predicts that a person with a BMI of 20 will have an SBP of:

SBP = β + β₁×BMI = 100 + 1 × 20 = 120 mmHg.

With a residual error of 12 mmHg, this person has a 68% chance of having his true SBP between 108 and 132 mmHg.

Moreover, if the mean of SBP in our sample is 130 mmHg for example, then:

12 mmHg ÷ 130 mmHg = 9.2%

So we can also say that the BMI accurately predicts systolic blood pressure with a percentage error of 9.2%.

The question remains: Is 9.2% a good percent error value? More generally, what is a good value for the residual standard deviation?

The answer is that there is no universally acceptable threshold for the residual standard deviation. This should be decided based on your experience in the domain.

In general, the smaller the residual standard deviation/error, the better the model fits the data. And if the value is deemed unacceptably large, consider using a model other than linear regression.

About Me

I am George Choueiry, PharmD, MPH, my objective is to help you conduct studies, from concept to publication.

Источник

But before we discuss the residual standard deviation, let’s try to assess the goodness of fit graphically.

Consider the following linear regression model:

Y = β₀ + β₁X + ε

Plotted below are examples of 2 of these regression lines modeling 2 different datasets:

Just by looking at these plots we can say that the linear regression model in “example 2” fits the data better than that of “example 1”.

In the plots above, the gray vertical lines represent the error terms — the difference between the model and the true value of Y.

Mathematically, the error of the i^th point on the x-axis is given by the equation: (Y_i – Ŷ_i), which is the difference between the true value of Y (Y_i) and the value predicted by the linear model (Ŷ_i) — this difference determines the length of the gray vertical lines in the plots above.

Now that we developed a basic intuition, next we will try to come up with a statistic that quantifies this goodness of fit.

Residual standard deviation vs residual standard error vs RMSE

The simplest way to quantify how far the data points are from the regression line, is to calculate the average distance from this line:

Where n is the sample size.

We can take this equation one step further:

In the statistical programming language R, calling the function summary on the linear model will calculate it automatically.

The degrees of freedom df are the sample size minus the number of parameters we’re trying to estimate.

For example, if we’re estimating 2 parameters β₀ and β₁ as in:

Y = β₀ + β₁X + ε

Then, df = n – 2

If we’re estimating 3 parameters, as in:

Y = β₀ + β₁X₁ + β₂X₂ + ε

Then, df = n – 3

And so on…

Now that we have a statistic that measures the goodness of fit of a linear model, next we will discuss how to interpret it in practice.

How to interpret the residual standard deviation/error

Simply put, the residual standard deviation is the average amount that the real values of Y differ from the predictions provided by the regression line.

We can divide this quantity by the mean of Y to obtain the average deviation in percent (which is useful because it will be independent of the units of measure of Y).

Here’s an example:

Suppose we regressed systolic blood pressure (SBP) onto body mass index (BMI) — which is a fancy way of saying that we ran the following linear regression model:

SBP = β₀ + β₁×BMI + ε

After running the model we found that:

β₀ = 100
β1 = 1
And the residual standard error is 12 mmHg

So we can say that the BMI accurately predicts systolic blood pressure with about 12 mmHg error on average.

More precisely, we can say that 68% of the predicted SBP values will be within ∓ 12 mmHg of the real values.

Why 68%?

Remember that in linear regression, the error terms are Normally distributed.

And one of the properties of the Normal distribution is that 68% of the data sits around 1 standard deviation from the average (See figure below).

Therefore, 68% of the errors will be between ∓ 1 × residual standard deviation.

For example, our linear regression equation predicts that a person with a BMI of 20 will have an SBP of:

SBP = β₀ + β₁×BMI = 100 + 1 × 20 = 120 mmHg.

With a residual error of 12 mmHg, this person has a 68% chance of having his true SBP between 108 and 132 mmHg.

Moreover, if the mean of SBP in our sample is 130 mmHg for example, then:

12 mmHg ÷ 130 mmHg = 9.2%

So we can also say that the BMI accurately predicts systolic blood pressure with a percentage error of 9.2%.

The question remains: Is 9.2% a good percent error value? More generally, what is a good value for the residual standard deviation?

The answer is that there is no universally acceptable threshold for the residual standard deviation. This should be decided based on your experience in the domain.

In general, the smaller the residual standard deviation/error, the better the model fits the data. And if the value is deemed unacceptably large, consider using a model other than linear regression.

На прошлой посиделке мы узнали, что можно обучить линейную регрессию с помощью функции lm. Наши данные находятся в датасете data. Мы хотим предсказать заработную плату человека (income). Нашим единственныи признаком является количество лет, которые человек отучился (education).

##                                               
## 1 function (x, df1, df2, ncp, log = FALSE)    
## 2 {                                           
## 3     if (missing(ncp))                       
## 4         .Call(C_df, x, df1, df2, log)       
## 5     else .Call(C_dnf, x, df1, df2, ncp, log)
## 6 }

Нарисуем график рассеяния этих двух переменных. На этом графике мы видим линейную зависимость переменных.

Обучим линейную регрессию.

В переменной model находится наша модель. Она имеет тип list. Из него можно получить значение коэффициентов или ошибки, совершенные моделью.

Также можно получить более подробную информацию с помощью функции summary.

## 
## Call:
## lm(formula = income ~ education, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -15538.4  -2544.3    581.5   2725.4   7689.2 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  13964.3     2232.9   6.254 1.03e-07 ***
## education     4742.3      159.2  29.783  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4550 on 48 degrees of freedom
## Multiple R-squared:  0.9487, Adjusted R-squared:  0.9476 
## F-statistic:   887 on 1 and 48 DF,  p-value: < 2.2e-16

Интерпретация полученных коэффициентов

Из модели мы видим:

Cвободный коэффициент равен 8683. Это означает, что в среднем человек, который проучился 0 лет будет зарабатывать 8683 рубля.
Коэффициент перед переменной education равен 5091. Это означает, что если человек учится на один год больше, то в среднем он начинает зарабывать на 5091 рубль больше.

Эти оценки могут быть неточными. Чтобы получить доверительный интервалы, можно использовать функцию confint.

##                2.5 %    97.5 %
## (Intercept) 9474.648 18453.873
## education   4422.140  5062.432

Выбросы

Выбросы очень сильно влияют на линейную регрессию.

set.seed(42)
n <- 50
data <- tibble(education = seq(7, 20, length.out = n) + rnorm(n, sd = 2),
               income = 10000 + 5000 * education + rnorm(n, sd = 5000))
data <- add_row(data, education=c(19, 20, 21), income=c(1000, 1400, 2000))

На графике видно, что видимо кто-то указал зарплату не в рублях, а в долларах. Попробуем оценить линейную регрессию и нарисовать ее.

## 
## Call:
## lm(formula = income ~ education, data = data)
## 
## Coefficients:
## (Intercept)    education  
##       37295         2611

Видно, что линия регрессии проходит не через основное облако точек.

Использование большего количества признаков

Вы можете использовать несколько признаков для построения вашей модели.

Для этого в формуле вам нужно просто перечислить те, которые вы хотите использовать.

## 
## Call:
## lm(formula = y ~ x1 + x2 + x3, data = df)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -4.255e-14 -1.313e-15 -3.270e-16  1.294e-15  3.416e-14 
## 
## Coefficients:
##               Estimate Std. Error    t value Pr(>|t|)    
## (Intercept)  5.000e+00  9.760e-15  5.123e+14   <2e-16 ***
## x1           2.000e+00  6.254e-16  3.198e+15   <2e-16 ***
## x2          -3.000e+00  3.402e-16 -8.819e+15   <2e-16 ***
## x3          -7.312e-17  6.935e-16 -1.050e-01    0.916    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.196e-15 on 96 degrees of freedom
## Multiple R-squared:      1,  Adjusted R-squared:      1 
## F-statistic: 1.286e+32 on 3 and 96 DF,  p-value: < 2.2e-16

Категориальные переменные

Давайте рассмотрим следующий набор данных.

n <- 50
data <- tibble(education = seq(7, 20, length.out = n) + rnorm(n, sd = 2),
               type = rep(c('college', 'university'), times = n/2),
               income = ifelse(type=='college', 
                               10000 + 5000 * education + rnorm(n, sd = 5000),
                               40000 + 5000 * education + rnorm(n, sd = 5000)))

Изначально кажется, что тут имеется линейная зависимость и можно провести одну линию регрессии.

Но если попробовать покрасить точки, используя переменную type, то можно понять, что доход зависит от типа образования, которое получил человек.

Бинарная переменная

Чтобы отобразить это в моделе можно закодировать нашу переменную type в 0, если образование college, и в 1, если образование university. Это можно сделать с помощью функции ifelse.

## # A tibble: 6 x 4
##   education type       income type_encode
##       <dbl> <chr>       <dbl>       <dbl>
## 1      9.67 college    51830.           0
## 2      5.53 university 72208.           1
## 3      7.64 college    49063.           0
## 4      7.89 university 80150.           1
## 5      6.90 college    45046.           0
## 6      6.33 university 70655.           1

Попробуем обучить эту модель используя бинарную переменную.

## 
## Call:
## lm(formula = income ~ education + type_encode, data = data)
## 
## Coefficients:
## (Intercept)    education  type_encode  
##       12024         4885        29895

Коэффициент перед type_encode показывает на сколько в среднем человек с высшим образованием зарабатывает больше чем человек со средним образованием.

Label Encoding

Что делать, если переменная принимает больше двух значений?

n <- 60
data <- tibble(education = seq(7, 20, length.out = n) + rnorm(n, sd = 2),
               type = rep(c('college', 'university', 'PhD'), times = n/3),
               income = ifelse(type=='college', 
                               10000 + 5000 * education + rnorm(n, sd = 5000),
                               ifelse(type=='university',
                                      40000 + 5000 * education + rnorm(n, sd = 5000),
                                      60000 + 5000 * education + rnorm(n, sd = 5000))))

head(data)

## # A tibble: 6 x 3
##   education type        income
##       <dbl> <chr>        <dbl>
## 1      3.88 college     20058.
## 2      7.87 university  81797.
## 3      7.13 PhD         97475.
## 4      9.42 college     58450.
## 5      9.38 university  90140.
## 6      8.70 PhD        107226.

Визуализируем данные.

Давайте просто закодируем переменную как в прошлый раз.

## # A tibble: 6 x 4
##   education type        income type_encode
##       <dbl> <chr>        <dbl>       <dbl>
## 1      3.88 college     20058.           1
## 2      7.87 university  81797.           2
## 3      7.13 PhD         97475.           3
## 4      9.42 college     58450.           1
## 5      9.38 university  90140.           2
## 6      8.70 PhD        107226.           3

Обучим модель.

## 
## Call:
## lm(formula = income ~ education + type_encode, data = data)
## 
## Coefficients:
## (Intercept)    education  type_encode  
##      -13907         5015        25022

Смотрим на результат.

Такой подход не очень хорош. Попробуем закодировать наши переменные по-другому.

## # A tibble: 6 x 4
##   education type        income type_encode
##       <dbl> <chr>        <dbl>       <dbl>
## 1      3.88 college     20058.           1
## 2      7.87 university  81797.           3
## 3      7.13 PhD         97475.           2
## 4      9.42 college     58450.           1
## 5      9.38 university  90140.           3
## 6      8.70 PhD        107226.           2

Обучим модель.

## 
## Call:
## lm(formula = income ~ education + type_encode, data = data)
## 
## Coefficients:
## (Intercept)    education  type_encode  
##        7221         4945        14922

Смотрим на результат.

В данном случае кодировка очень важна, потому что 1 и 2 ближе чем 1 и 3.

One Hot Encoding

Чтобы избежать проблем с Label Encoding можно использовать One Hot Encoding (OHE).

Можно использовать готовую функцию. В качестве аргумента вы подаете ваш датасет, в котором все переменные, которые вы хотите закодировать являются факторными.

n <- 60
data <- tibble(education = seq(7, 20, length.out = n) + rnorm(n, sd = 2),
               type = rep(c('college', 'university', 'PhD'), times = n/3),
               income = ifelse(type=='college', 
                               10000 + 5000 * education + rnorm(n, sd = 5000),
                               ifelse(type=='university',
                                      40000 + 5000 * education + rnorm(n, sd = 5000),
                                      60000 + 5000 * education + rnorm(n, sd = 5000))))

head(data)

## # A tibble: 6 x 3
##   education type        income
##       <dbl> <chr>        <dbl>
## 1      7.52 college     42433.
## 2      7.54 university  78656.
## 3      9.30 PhD        109513.
## 4      7.54 college     42139.
## 5      7.98 university  85471.
## 6      5.96 PhD         92444.

Попробуем на нашем датасете.

## # A tibble: 6 x 5
##   education `type=college` `type=PhD` `type=university`  income
##       <dbl>          <dbl>      <dbl>             <dbl>   <dbl>
## 1      7.52              1          0                 0  42433.
## 2      7.54              0          0                 1  78656.
## 3      9.30              0          1                 0 109513.
## 4      7.54              1          0                 0  42139.
## 5      7.98              0          0                 1  85471.
## 6      5.96              0          1                 0  92444.

Переменных уже много и писать их вручную не очень. Вместо этого можно поставить точку. Тогда все переменные, которые есть в вашем наборе данных будут использованы. В данном случае мы хотим оценить нашу модель без свободного коэффициента, поэтому поставим -1.

## 
## Call:
## lm(formula = income ~ . - 1, data = data)
## 
## Coefficients:
##      education     typecollege         typePhD  typeuniversity  
##           5091            9329           59416           38955

Смотрим на результат.

Источник

Example: Interpreting Residual Standard Error

Using Residual Standard Error to Compare Models

Additional Resources

Как интерпретировать остаточную стандартную ошибку

Пример: интерпретация остаточной стандартной ошибки

Использование остаточной стандартной ошибки для сравнения моделей

Дополнительные ресурсы

Оценка результатов линейной регрессии

Введение

Модель линейной регрессии

Функция summary.lm() и оценка получившихся результатов

Заключение

Как интерпретировать остаточную стандартную ошибку

Пример: интерпретация остаточной стандартной ошибки

Использование остаточной стандартной ошибки для сравнения моделей

Residual Standard Deviation/Error: Guide for Beginners

Residual standard deviation vs residual standard error vs RMSE

How to interpret the residual standard deviation/error

Further reading

About Me

Residual standard deviation vs residual standard error vs RMSE

How to interpret the residual standard deviation/error

Further reading

Функция lm

Интерпретация полученных коэффициентов

Выбросы

Использование большего количества признаков

Категориальные переменные

Бинарная переменная

Label Encoding

One Hot Encoding