What Is a Serial Correlation?
Serial correlation occurs in a time series when a variable and a lagged version of itself (for instance a variable at times T and at T-1) are observed to be correlated with one another over periods of time. Repeating patterns often show serial correlation when the level of a variable affects its future level. In finance, this correlation is used by technical analysts to determine how well the past price of a security predicts the future price.
Serial correlation is similar to the statistical concepts of autocorrelation or lagged correlation.
Key Takeaways
- Serial correlation is the relationship between a given variable and a lagged version of itself over various time intervals.
- It measures the relationship between a variable’s current value given its past values.
- A variable that is serially correlated indicates that it may not be random.
- Technical analysts validate the profitable patterns of a security or group of securities and determine the risk associated with investment opportunities.
Serial Correlation Explained
Serial correlation is used in statistics to describe the relationship between observations of the same variable over specific periods. If a variable’s serial correlation is measured as zero, there is no correlation, and each of the observations is independent of one another. Conversely, if a variable’s serial correlation skews toward one, the observations are serially correlated, and future observations are affected by past values. Essentially, a variable that is serially correlated has a pattern and is not random.
Error terms occur when a model is not completely accurate and results in differing results during real-world applications. When error terms from different (usually adjacent) periods (or cross-section observations) are correlated, the error term is serially correlated. Serial correlation occurs in time-series studies when the errors associated with a given period carry over into future periods. For example, when predicting the growth of stock dividends, an overestimate in one year will lead to overestimates in succeeding years.
Serial correlation can make simulated trading models more accurate, which helps the investor develop a less risky investment strategy.
Technical analysis uses measures of serial correlation when analyzing a security’s pattern. The analysis is based entirely on a stock’s price movement and associated volume rather than a company’s fundamentals. Practitioners of technical analysis, if they use serial correlation correctly, identify and validate the profitable patterns or a security or group of securities and spot investment opportunities.
The Concept of Serial Correlation
Serial correlation was originally used in engineering to determine how a signal, such as a computer signal or radio wave, varies compared to itself over time. The concept grew in popularity in economic circles as economists and practitioners of econometrics used the measure to analyze economic data over time.
Almost all large financial institutions now have quantitative analysts, known as quants, on staff. These financial trading analysts use technical analysis and other statistical inferences to analyze and predict the stock market. These modelers attempt to identify the structure of the correlations to improve forecasts and the potential profitability of a strategy. In addition, identifying the correlation structure improves the realism of any simulated time series based on the model. Accurate simulations reduce the risk of investment strategies.
Quants are integral to the success of many of these financial institutions since they provide market models that the institution then uses as the basis for its investment strategy.
Serial correlation was originally used in signal processing and systems engineering to determine how a signal varies with itself over time. In the 1980s, economists and mathematicians rushed to Wall Street to apply the concept to predict stock prices.
Serial correlation among these quants is determined using the Durbin-Watson (DW) test. The correlation can be either positive or negative. A stock price displaying positive serial correlation has a positive pattern. A security that has a negative serial correlation has a negative influence on itself over time.
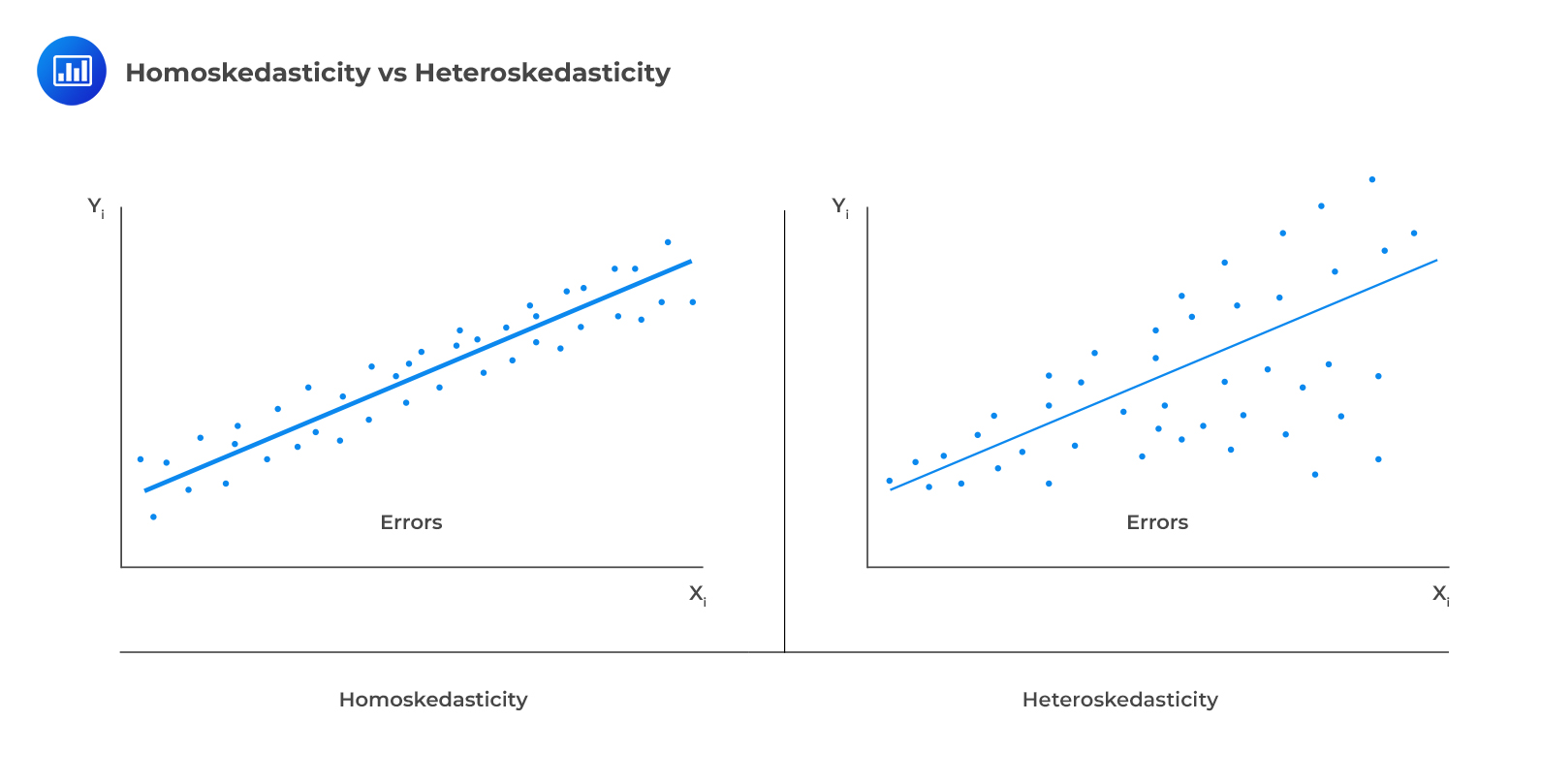
One of the assumptions underpinning multiple regression is that regression errors are homoscedastic. In other words, the variance of the error terms is equal for all observations:
$$E(epsilon_{i}^{2})=sigma_{epsilon}^{2}, i=1,2,…,n$$
In reality, the variance of errors differs across observations. This is known as heteroskedasticity.
The following figure illustrates homoscedasticity and heteroskedasticity.
 Types of Heteroskedasticity
Types of Heteroskedasticity
Unconditional Heteroskedasticity
Unconditional heteroskedasticity occurs when the heteroskedasticity is uncorrelated with the values of the independent variables. Although this is a violation of the homoscedasticity assumption, it does not present major problems to statistical inference.
Conditional Heteroskedasticity
Conditional heteroskedasticity occurs when the error variance is related/conditional on the values of the independent variables. It poses significant problems for statistical inference. Fortunately, many statistical software packages can diagnose and correct this error.
Effects of Heteroskedasticity
i. It does not affect the consistency of the regression parameter estimators.
ii. Heteroskedastic errors make the F-test overall significance of the regression unreliable.
iii. Heteroskedasticity introduces bias into estimators of the standard error of regression coefficients making the t-tests for the significance of individual regression coefficients unreliable.
iv. More specifically, it results in inflated t-statistics and underestimated standard errors.
Testing Heteroskedasticity
Breusch-Pagan chi-square test
The Breusch-Pagan chi-square test looks at the regression of the squared residuals from the estimated regression equation on the independent variables. The presence of conditional heteroskedasticity in the original regression equation substantially explains the variation in the squared residuals.
The test statistic is given by:
$$text{BP chi}-text{square test statistic}=ntimes{R^{2}}$$
Where:
- (n) = number of observations.
- (R^{2}) = the (R^{2}) in the regression of the squared residuals.
This test statistic is a chi-square random variable with k degrees of freedom.
The null hypothesis is that there is no conditional heteroskedasticity, i.e., the squared error term is uncorrelated with the independent variables. The Breusch-pagan test is a one-tailed test as we should be mainly concerned with heteroskedasticity for large values of the test statistic.
Example: Breusch-Pagan chi-square test
Consider the multiple regression of the price of the USDX on the inflation rates and the real interest rates. The investor regresses the squared residuals from the original regression on the independent variables. The new (R^{2}) is 0.1874. Test for the presence of heteroskedasticity at the 5% significance level.
Solution
The test statistic is:
$$text{BP chi}- text{square test statistic}=ntimes{R^{2}}$$
$$text{Test statistic}= 10times0.1874=1.874$$
The one-tailed critical value for a chi-square distribution with two degrees of freedom at the 5% significance level is 5.991.
Therefore, we cannot reject the null hypothesis of no conditional heteroskedasticity. As a result, we conclude that the error term is NOT conditionally heteroskedastic.
Correcting Heteroskedasticity
In the investment world, it is crucial to correct heteroskedasticity as it may change inferences about a particular hypothesis test, thus impacting an investment decision. There are two methods that can be applied to correct heteroskedasticity:
- Calculating robust standard errors: This approach corrects the standard errors of the model’s estimated coefficients to account for the conditional heteroskedasticity. These are also known as white-corrected standard errors. These standard errors are then used to calculate the t-statistics again using the original regression coefficients.
- Generalized least squares: The original regression equation is modified to eliminate heteroskedasticity. The modified equation is then estimated, assuming that heteroskedasticity is no longer a problem.
Serial Correlation (Autocorrelation)
Autocorrelation occurs when the assumption that regression errors are uncorrelated across all observations is violated. In other words, autocorrelation is evident when errors in one period are correlated with errors in other periods. This is common with time-series data (which we will see in the next reading).
Types of Serial Correlation
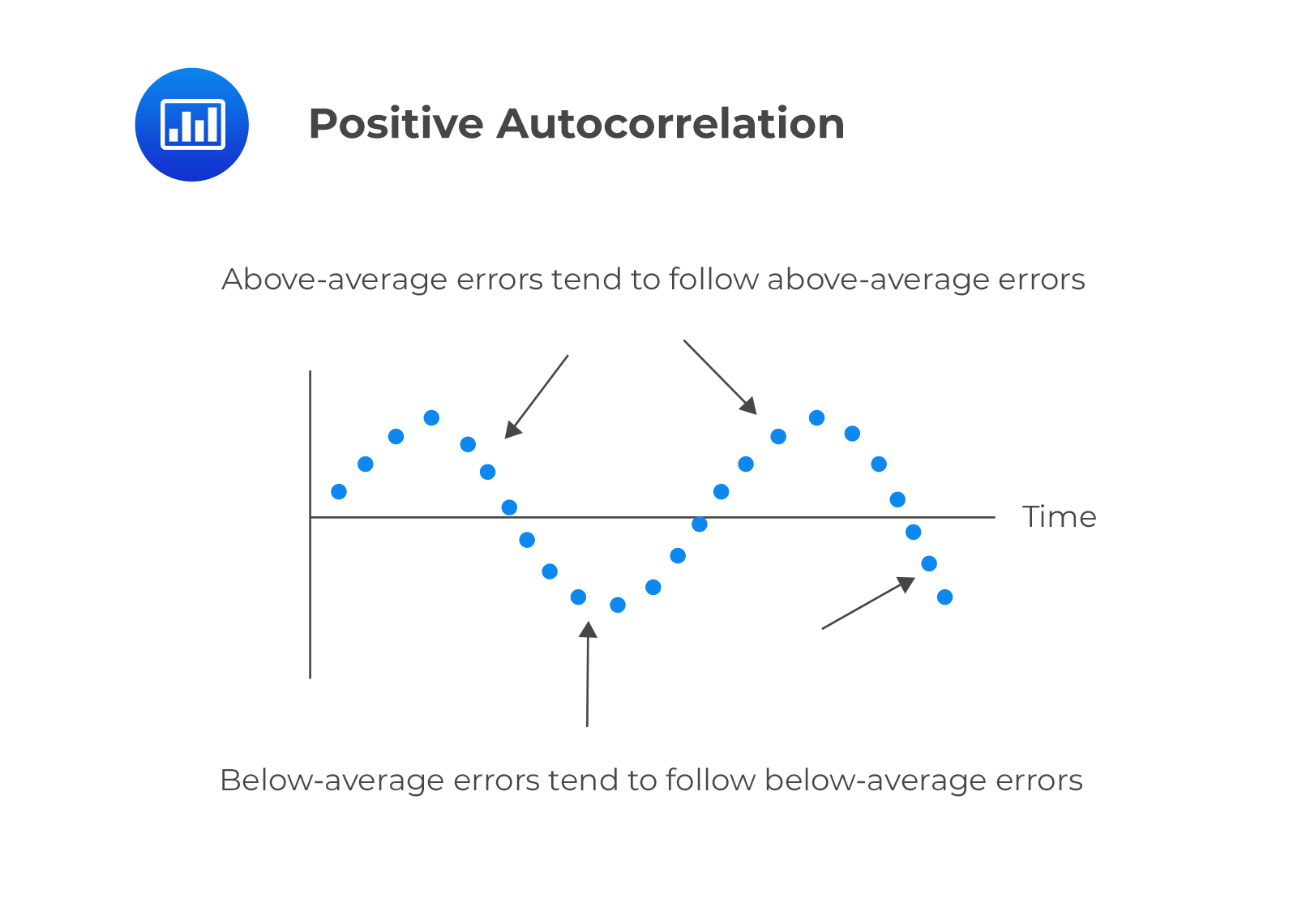
Positive serial correlation
This is a serial correlation in which positive regression errors for one observation increases the possibility of observing a positive regression error for another observation.
 Negative serial correlation
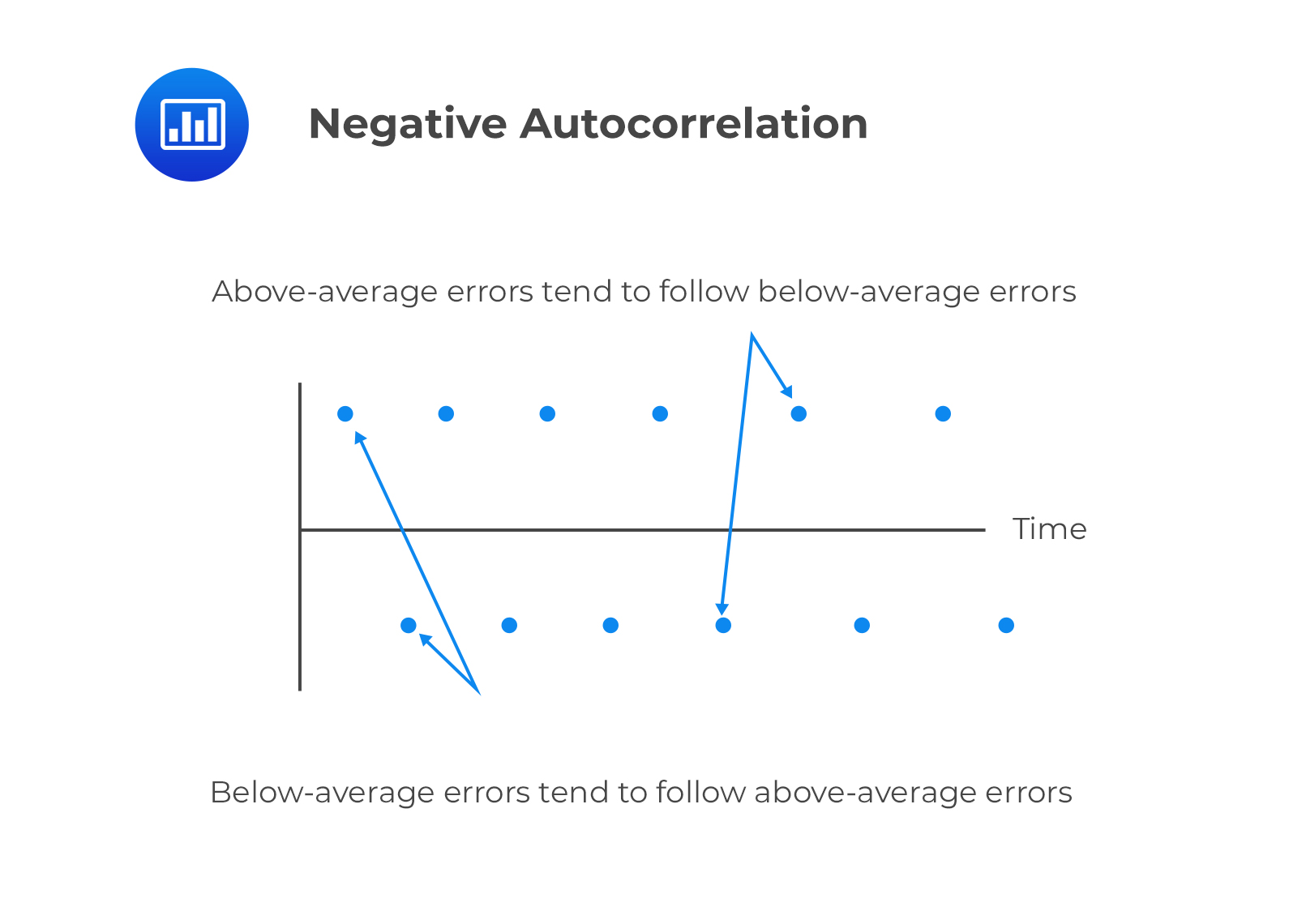
Negative serial correlation
This is serial correlation in which a positive regression error for one observation increases the likelihood of observing a negative regression error for another observation.
Effects of Serial Correlation
Autocorrelation does not cause bias in the coefficient estimates of the regression. However, a positive serial correlation inflates the F-statistic to test for the overall significance of the regression as the mean squared error (MSE) will tend to underestimate the population error variance. This increases Type I errors (the rejection of the null hypothesis when it is actually true).
The positive serial correlation makes the ordinary least squares standard errors for the regression coefficients underestimate the true standard errors. Moreover, it leads to small standard errors of the regression coefficient, making the estimated t-statistics seem to be statistically significant relative to their actual significance.
On the other hand, negative serial correlation overestimates standard errors and understates the F-statistics. This increases Type II errors (The acceptance of the null hypothesis when it is actually false).
Testing for Serial Correlation
The first step of testing for serial correlation is by plotting the residuals against time. The other most common formal test is the Durbin-Watson test.
Durbin-Watson Test
The Durbin Watson tests the null hypothesis of no serial correlation against the alternative hypothesis of positive or negative serial correlation.
The Durbin-Watson Statistic (DW) is approximated by:
$$DW=2(1-r)$$
Where:
- (r) = Sample correlation between regression residuals from one period and the previous period.
The Durbin Watson statistic can take on values ranging from 0 to 4. i.e., (0<DW<4).
i. If there is no autocorrelation, the regression errors will be uncorrelated, and thus DW = 2.
$$DW=2(1-r)=2(1-0)=2$$
ii. For positive serial autocorrelation, (DW<2).
For example, if serial correlation of the regression residuals (=1,DW=2(1-1)=0)
iii. For negative autocorrelation, (DW>2).
For example, if serial correlation of the regression regression residual (=-1, DW=2(1-(-1))=4).
The null hypothesis of no positive autocorrelation is rejected if the Durbin–Watson statistic is below a critical value, (d^{*}), where (d^{*}) lies between an upper value (d_{u}) and a lower value (d_{l}) or outside of these values.
This is illustrated below.
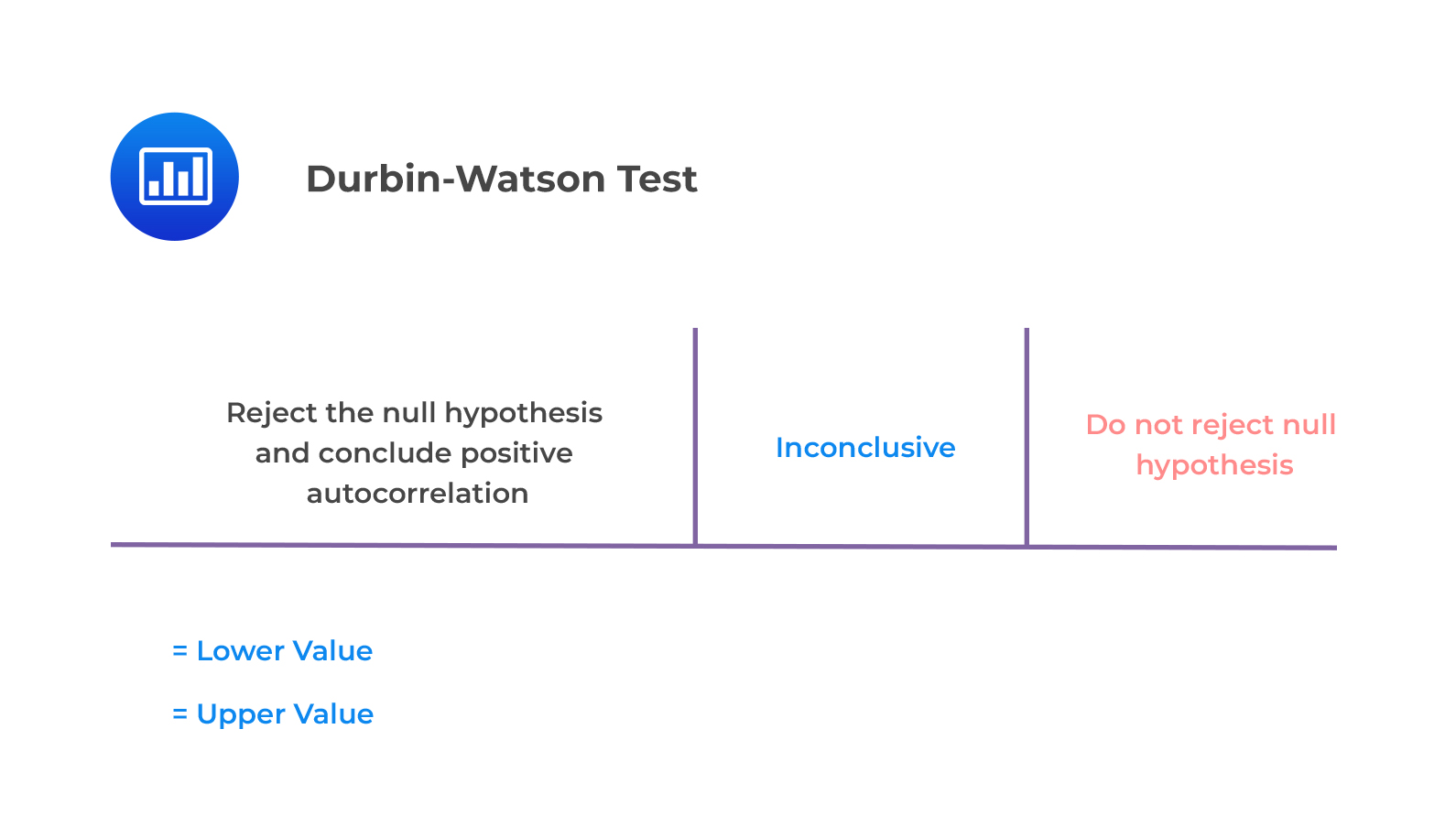
- If (d<d_{l}), reject (H_{0}: ρ =0) (and so accept (H_{1}:ρ >0)).
- If (d>d_{u}), do not reject (H_{0}:ρ =0).
- If (d_{l}< d<d_{u}), the test is inconclusive.
Example: The Durbin Watson Test for Serial Correlation
Consider a regression output that includes two independent variables that generate a DW statistic of 0.654. Assume that the sample size is 15. Test for serial correlation of the error terms at the 5% significance level.
Solution
From the Durbin Watson table with (n=15) and (k=2), we see that (d_{l}=0.95) and (d_{u}=1.54). Since (d=0.654<0.95=d_{l}), we reject the null hypothesis and conclude that there is significant positive autocorrelation.
Correcting Autocorrelation
We can correct serial correlation by:
i. Adjusting the coefficient standard errors for the regression estimates to take into account serial correlation. This is done using the Hansen method. This method can also be used to correct conditional heteroskedasticity. Hansen white standard errors are then used for hypothesis testing of the regression coefficient.
ii. Modifying the regression equation to eliminate the serial correlation.
Question
Consider a regression model with 80 observations and two independent variables. Suppose that the correlation between the error term and a first lagged value of the error term is 0.15. The most appropriate decision is:
A. Reject the null hypothesis of positive serial correlation.
B. Fail to reject the null hypothesis of positive serial correlation.
C. Declare that the test results are inconclusive.
Solution
The correct answer is B.
The test statistic is:
$$DW≈2(1-r)=2(1-0.18)=1.64$$
The critical values from the Durbin Watson table with (n=80) and (k=2) is (d_{l}=1.59) and (d_{u}=1.69)
Because (1.64>1.59), we fail to reject the null hypothesis of positive serial correlation.
Reading 2: Multiple Regression
LOS 2 (k) Explain the types of heteroskedasticity and how heteroskedasticity and serial correlation affect statistical inference.
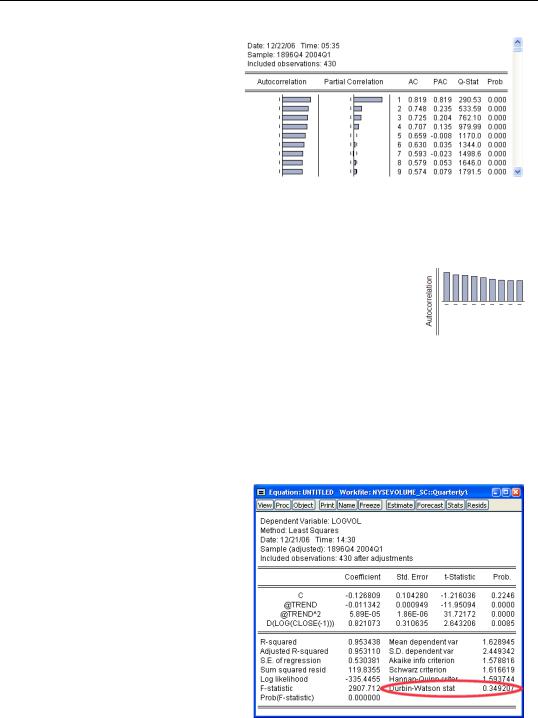
Testing for Serial Correlation—319
To plot the autocorrelations of the residuals, click the 
Diagnostics/Correlogram — Q-Sta- tistics…. Choose the number of autocorrelations you want to see—the default, 36, is fine—and EViews pops up with a combined graphical and numeric look at the autocorrelations. The unlabeled
column in the middle of the display, gives the lag number (1, 2, 3, and so on). The column marked AC gives estimated autocorrelations at the corresponding lag. This correlogram shows substantial and persistent autocorrelation.
The left-most column gives the autocorrelations as a bar graph. The graph is a little easier to read if you rotate your head 90 degrees to put the autocorrelations on the vertical axis and the lags on the horizontal, giving a picture something like the one to the right showing slowing declining autocorrelations.
Visual checks provide a great deal of information, but you’ll probably want to follow up with one or more formal statistical tests for serial correlation. EViews provides three test statistics: the Durbin-Watson, the Breusch-Godfrey, and the Ljung-Box Q-statistic.
Durbin-Watson Statistic
The Durbin-Watson, or DW, statistic is the traditional test for serial correlation. For reasons discussed below, the DW is no longer the test statistic preferred by most econometricians. Nonetheless, it is widely used in practice and performs excellently in most situations. The Durbin-Watson tradition is so strong that EViews routinely reports it in the lower panel of regression output.
The Durbin-Watson statistic is unusual in that under the null hypothesis (no serial correlation)

320—Chapter 13. Serial Correlation—Friend or Foe?
the Durbin-Watson centers around 2.0 rather than 0. You can roughly translate between the Durbin-Watson and the serial correlation coefficient using the formulas:
DW = 2 – 2r
r = 1 – (DW ⁄ 2)
If the serial correlation coefficient is zero, the Durbin-Watson is about 2. As the serial correlation coefficient heads toward 1.0, the Durbin-Watson heads toward 0.
To test the hypothesis of no serial correlation, compare the reported Durbin-Watson to a table of critical values. In this example, the Durbin-Watson of 0.349 clearly rejects the absence of serial correlation.
Hint: EViews doesn’t compute p-values for the Durbin-Watson.
The Durbin-Watson has a number of shortcomings, one of which is that the standard tables include intervals for which the test statistic is inconclusive. Econometric Theory and Methods, by Davidson and MacKinnon, says:
…the Durbin-Watson statistic, despite its popularity, is not very satisfactory.… the DW statistic is not valid when the regressors include lagged dependent variables, and it cannot be easily generalized to test for higher-order processes.
While we recommend the more modern Breusch-Godfrey in place of the Durbin-Watson, the truth is that the tests usually agree.
Econometric warning: But never use the Durbin-Watson when there’s a lagged dependent variable on the right-hand side of the equation.
Breusch-Godfrey Statistic
The preferred test statistic for checking for serial correlation is the Breusch-Godfrey. From the 
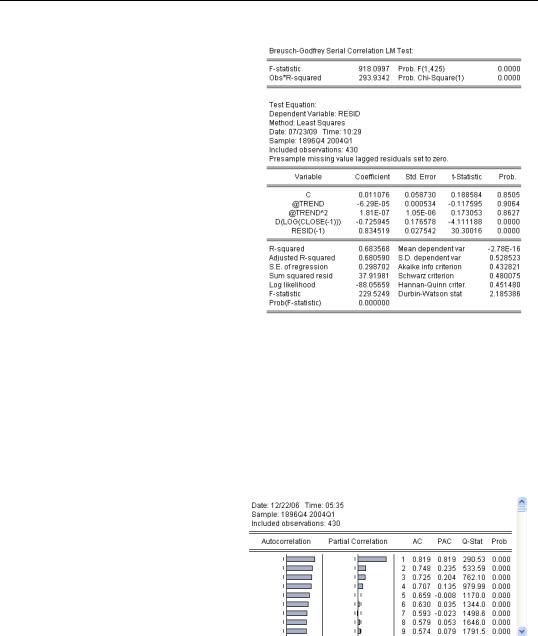
Testing for Serial Correlation—321
The view to the right shows the results of testing for first-order serial correlation. The top part of the output gives the test results in two versions: an F— statistic and a x2 statistic. (There’s no great reason to prefer one over the other.) Associated p-values are shown next to each statistic. For our stock market volume data, the hypothesis of no serial correlation is easily rejected.
The bottom part of the view provides extra information showing the auxiliary regression used to create the test statistics reported at the top. This extra regression is sometimes interesting, but you don’t need it for conducting the test.
Ljung-Box Q-statistic
A different approach to checking for serial correlation is to plot the correlation of the residual with the residual lagged once, the residual with the residual lagged twice, and so on. As we saw above in The Correlogram, this plot is called the correlogram of the residuals. If there is no serial correlation then correlations should all be zero, except for random fluctuation.
To see the correlogram, choose Residual Diagnostics/Correlogram — Q-statistics… from the 
show.
The correlogram for the residuals from our volume equation is repeated to the right. The column headed “Q-Stat” gives the LjungBox Q-statistic, which tests for a particular row the hypothesis that all the correlations up to and including that row equal zero. The column marked “Prob” gives the corresponding p-value. Continuing
along with the example, the Q-statistic against the hypothesis that both the first and second correlation equal zero is 553.59. The probability of getting this statistic by chance is zero to three decimal places. So for this equation, the Ljung-Box Q-statistic agrees with the evi-

322—Chapter 13. Serial Correlation—Friend or Foe?
dence in favor of serial correlation that we got from the Durbin-Watson and the BreuschGodfrey.
Hint: The number of correlations used in the Q-statistic does not correspond to the order of serial correlation. If there is first-order serial correlation, then the residual correlations at all lags differ from zero, although the correlation diminishes as the lag increases.
More General Patterns of Serial Correlation
The idea of first-order serial correlation can be extended to allow for more than one lag. The correlogram for first-order serial correlation always follows geometric decay, while higher order serial correlation can produce more complex patterns in the correlogram, which also decay gradually. In contrast, moving average processes, below, produce a correlogram which falls abruptly to zero after a finite number of periods.
Higher-Order Serial Correlation
First-order serial correlation is the simplest pattern by which errors in a regression equation may be correlated over time. This pattern is also called an autoregression of order one, or AR(1), because we can think of the equation for the error terms as being a regression on one lagged value of itself. Analogously, second-order serial correlation, or AR(2), is written
ut = r1ut – 1 + r2ut – 2 + et . More generally, serial correlation of order p, AR(p), is written ut = r1ut – 1 + r2ut – 2 + … + rput – p + et .
When you specify the number of lags for the Breusch-Godfrey test, you’re really specifying the order of the autoregression to be tested.
Moving Average Errors
A different specification of the pattern of serial correlation in the error term is the moving average, or MA, error. For example, a moving average of order one, or MA(1), would be written ut = et + vet – 1 and a moving average of order q, or MA(q), looks like
ut = et + v1et – 1 + … + vqet – q . Note that the moving average error is a weighted average of the current innovation and past innovations, where the autoregressive error is a weighted average of the current innovation and past errors.
Convention Hint: There are two sign conventions for writing out moving average errors. EViews uses the convention that lagged innovations are added to the current innovation. This is the usual convention in regression analysis. Some texts, mostly in time series analysis, use the convention that lagged innovations are subtracted instead. There’s no consequence to the choice of one convention over the other.
Соседние файлы в папке EViews Guides BITCH
- #
- #
- #

You can learn more about serial correlation and other quant based stock trading theories in this course on mastering charting reading and technical analysis.
Serial Correlation for Laymen
First, let’s try to arrive at a definition of serial correlation in plainspeak: serial correlation is the relationship of a quantity with itself over time.
For example, we know that stock prices are time dependent, i.e. they vary with time. Now suppose we were tasked with estimating the dividend from a stock within a specific time frame, say, a quarter. If we were to somehow overestimate the dividend from the stock (called ‘error term’ in econometrics) in one quarter, serial correlation would dictate that the overestimation would carry over to subsequent quarters.
In the simplest possible terms, serial correlation defines how past values affect present values.
Serial correlation was originally a concept used in signal processing and systems engineering to determine how a signal varies with itself over time. It was later adopted by fields like econometrics to make sense data that varies with time. In the 1980s, as economists and mathematicians invaded Wall Street, they brought over the idea of serial correlation to predict stock prices.
Today, serial correlation is extensively used by trading analysts to see how past prices of a stock vary over a time interval. Since trading analysts (often called ‘quants’ in the business) essentially predict future prices based on data, not company fundamentals, serial correlation gives them an indicator of future price movements based on past prices. Therefore, understanding this correlation is important for anyone who wants to trade on the ‘quant’ model.
New to trading? Understand how option spreads and credit spreads work in this course!
Understanding the Theory Behind Serial Correlation
Now that we know what serial correlation is, let’s try to arrive at a more theoretically sound definition for it.
Let us suppose that we have two error terms, εi and εj , where εi is the magnitude of error at some time interval i and εj is the magnitude of the error at some time interval j, such that i ≠ j. When εi does not have a relation with εj, i.e. the magnitude of one error does not influence the magnitude of another error, the two error terms are said to be independent or unrelated.
However, more often than not, there is some distinct relationship between two error terms separated by a time interval. The most common of these relationships is serial correlation where one error term, εi has a positive/negative correlation with another error term, εj. When this happens, the assumptions in the original model are violated and thus, we have to account for the relationship between error terms. Practically, if there is something causing an error term in one time period, i, it only follows that it would cause an error in another time period, j.
Mathematically speaking, a serial correlation in a linear regression model can be denoted as:
corr(εj – εi) ≠ 0
That is, the correlation between the two terms is not equal to zero.
A popular test for verifying serial correlation is the Durbin-Watson test which can be calculated as:
Going deeper into regression models and the Durbin-Watson tests is beyond the scope of this tutorial. What we will look at, however, is the different types of serial correlation and how it applies to stock trading.
Types of Serial Correlation
Serial correlation can be either positive or negative. A brief definition of both is given below:
1. Positive Serial Correlation: Sometimes also called positive first-order serial correlation, this is the most common type of correlation where an error term has a positive bias on subsequent error terms. The correlation is mostly serial, that is, an error term in one time period has a positive bias on error terms in a subsequent time periods (say, like two successive quarters). It can also be non-linear – for example, an error term in the third quarter manifesting a positive bias in the third quarter of the subsequent year.
Mathematically, this can be represented as:
corr(εj – εi) > 0
2. Negative Serial Correlation: Also called negative first-order serial correlation, here, a positive error is followed by a negative error, or a negative error followed by a positive one. That is, the error term has a negative influence on subsequent error terms. This type of serial correlation is far less common. Mathematically, it can be represented as:
corr(εj – εi) < 0
Trading options? This course on essential strategies for mastering the stock market will help you make the most of your investment.
Serial correlation defines how a specific quantity relates to itself over time. As mentioned before, it is a statistical term with applications in multiple fields, including mathematics, signal processing, trading analysis, and of course, statistics. The most useful application of serial correlation, thus, is in determining not just how a quantity relates to itself, but also to predict future correlations.
For example, in stock trading there is a widely held belief that today’s price changes in a stock relates valuable information about tomorrow’s price changes (εj affects εi). As per this assumption, an increase in prices today may cause prices tomorrow to:
-
Go up, as momentum from the positive change carries onwards.
-
Go down, as investors cash out their profits.
-
Remain the same, i.e. there is no correlation between prices on subsequent days and each day begins anew.
Scenario #1 is clearly a case of positive correlation. If the correlation is statistically significant, a trader can predict the positive future movement of the stock price.
Scenario #2 is an example of negative correlation. Again, if correlation is apparent statistically, a trader may move money out of the stock in anticipation for the predicted drop.
Scenario #3 assumes that there is either no correlation between day-to-day prices, or that the correlation is not statistically significant enough to be considered valuable.
Keep in mind that correlation is highly dependent on time periods. While one may observe a correlation in day to day or even hour to hour prices, the correlation may be absent or statistically insignificant if the time period is larger, i.e. year to year or even quarter to quarter.
As a trader, you can use serial correlation to make decisions about buying or selling a stocks, provided the data is statistically significant enough. You can learn more about trading in this course technical analysis of stock charts.
What are your favorite stock trading tips and tricks? Share them with us in the comments below!

 Types of Heteroskedasticity
Types of Heteroskedasticity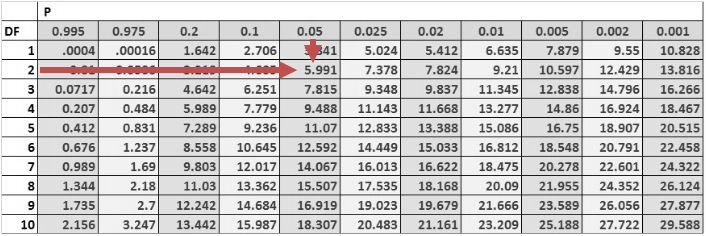
 Negative serial correlation
Negative serial correlation