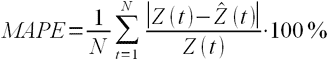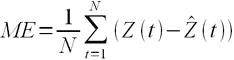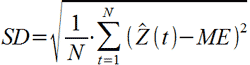МАТЕМАТИЧЕСКИЕ И ИНСТРУМЕНТАЛЬНЫЕ МЕТОДЫ
Д-р экон. наук Н. П. Тихомиров Д. А. Максимов А. В. Щербаков
ВЕРИФИКАЦИЯ ПРОГНОЗОВ НА ОСНОВЕ АНАЛИЗА РИСКОВ ИХ ОШИБОК1
Рассмотрены подходы верификации социально-экономических прогнозов на основе оценок рисков их ошибок. Представлены методы оценки рисков случайной и систематической ошибки с использованием операции свертки их законов распределений.
Ключевые слова и словосочетания: прогноз, ошибка прогноза, распределение ошибки.
Верификация прогноза социально-экономического процесса является завершающим этапом прогнозного исследования. Его цель состоит в определении степени обоснованности, качества полученного результата и возможности использования его в управлении. Эти понятия можно увязать с оценкой ошибки прогноза, которая разделяется на случайную и систематическую составляющие. Систематическая ошибка характеризуется односторонним отклонением прогноза от основной тенденции развития процесса. Ее появление обусловлено ошибочными решениями на различных этапах разработки прогноза: при выявлении основных закономерностей развития процесса, оценке влияния на них различных факторов, формировании исходной информации, выборе адекватной закономерностям развития процесса прогнозной модели и т. п.
Случайная ошибка характеризуется нулевым математическим ожиданием и симметрическим распределением. Она проявляется как результат влияния некоторой совокупности случайных, независимых между собой причин (идеализация модели, округление исходных данных и т. п.). Вместе с тем большая дисперсия такой ошибки также является признаком невысокого качества прогноза, поскольку она предопределяет возможность значительного отклонения прогноза от фактического результата.
Применяемые на практике подходы и процедуры верификации прогнозов, как правило, не учитывают свойства прогнозных ошибок, они не основываются на каких-либо объективных их количественных оценках. В связи с этим решения в этой сфере часто характеризуются значительной долей субъективизма и принимаются на основе достаточно общих рассуждений о возможностях расхождений прогнозных результатов с действительностью и причинах, их обусловливающих, анализа чувствительности прогнозных решений к возможным изменениям прогнозного фона и т. п.
1 Статья написана при поддержке Российского фонда фундаментальных исследований, проект № 10-06 00175.
Попытки разработки более объективных показателей качества прогнозных оценок базируются на формировании плотности распределения расчетного значения прогноза как свертки плотностей его случайной и возможных систематических ошибок с использованием следующего выражения:
где ф(х) — безусловная плотность распределения фактического значения рассматриваемого процесса х относительно его прогнозного значения х0;
Яо = 1 — 21 Яг ;
5(х0) — дельта-функция в точке х0;
® — операция свертки плотностей распределений;
Яг — вероятность проявления г-го фактора;
/( А г) — безусловная плотность распределения г-й систематической ошибки прогноза Аг под воздействием г-го неучтенного в прогнозе случайного фактора;
/о(в) — безусловная плотность распределения случайной ошибки прогноза в с нулевым математическим ожиданием и известной дисперсией.
Для двух случайных величин V и и с функциями распределения /1(у) и /2(и) она определяется следующим выражением:
При конкретизации выражения (1) обычно используются следующие предположения:
1. Случайная ошибка в распределена по нормальному закону. Его дисперсия в общем случае может быть оценена на основе ковариационной матрицы параметров прогнозной модели и дисперсий и ковариаций прогнозного фона.
2. Возможность проявления г-го фактора, г = 1, п , обусловливающего существование г-й систематической ошибки Аг, характеризуется вероятностью яг, относительно малой по величине. В противном случае это событие целесообразно было учесть в прогнозной модели.
3. Плотности /(А г) имеют специфическую форму для каждого из событий .
4. События г = 1, 2, …, п независимы между собой.
При условии, что х находится на положительной полуоси, принятие решения о верифицируемости прогноза базируется в этом случае на оценке выполнимости одного или обоих неравенств следующего вида:
ф(х) = (Яо 5(Хо) + ® Яг/¡(Ьх/)) ®/о(в),
(1)
(2)
P1 > p(x < xi )= J ф(х)dx
о
да
P2 > p(x < x*2 )= J ф(х~)dx
(3)
где Р* — заданное (нормативное) значение вероятности того, что реальное значение процесса х не превысит нижний предел допустимой для системы
управления области его существования х^;
Р*2 — аналогичное значение вероятности для верхнего предела этой об-
2
ласти х* .
Выражение (3) означает, что если вероятности невыхода реального зна-
1 2
чения процесса х за устраивающие систему управления пределы х* и х* области существования прогноза не превышают некоторых нормативов (например, 0,05; 0,01 и т. п.), то прогноз х0 может быть верифицирован и использован в управлении.
Представление общей ошибки прогноза е в виде суммы случайной (е) и систематической (А) ошибок (е = е + А) и разработка подходов к оценке ее дисперсии и закона распределения обусловливают необходимость формирования некоторых базовых предположений в отношении возможного характера распределения систематических составляющих общей ошибки. При этом могут быть выдвинуты различные предположения. Например, при негативном воздействии /-го фактора на прогнозный результат, но с неизвестной силой и временем воздействия, можно использовать предположение, что вызванная им систематическая ошибка будет также подчинена нормальному закону с положительным математическим ожиданием. Такая ситуация характерна для прогнозов временных показателей инвестиционных проектов, когда случайные, хотя и редкие, события ведут в основном к увеличению периода времени завершения работ (срывы сроков поставок, задержки в выполнении отдельных работ и т. п.), а более раннее завершение отдельных работ не ведет к уменьшению сроков выполнения проекта из-за того, что их результаты не могут быть использованы до завершения смежных (параллельных) этапов проекта. Это связано с тем, что в большинстве случаев работы заранее запланированы, существуют определенные договоренности по срокам с поставщиками комплектующих и оборудования и исполнителями работ, и каждый новый этап не представляется возможным начать раньше, чем намечалось изначально.
При прогнозировании стоимостных показателей возможность проявления систематической ошибки с левым сдвигом вследствие влияния неучтенной случайной причины представляется более реальной. Примером такой причины является значительное удешевление комплектующих изделий, обусловливающих снижение себестоимости и цены продукции, выпускаемой по проекту.
Несмотря на то, что нормальное распределение, или распределение Гаусса, является наиболее универсальным, удобным и широко применяемым, зачастую его использование ведет к искажению результатов при попытке учесть влияние на прогнозы рисков, обусловленных воздействием неблагоприятных факторов. Систематические ошибки зачастую характеризуются распределением с «толстыми хвостами», так как в условиях реальной экономики сильные отклонения процесса от его сложившейся тенденции под влиянием какого-либо фактора гораздо более вероятны, чем это описывает нормальный закон распределения. Например, кризисные явления, дефолты соисполнителей проекта часто влекут за собой даже не увеличение сроков его реализации, а его остановку, характеризующуюся гораздо большими потерями.
Для учета подобных экстремальных отклонений часто используют так называемые распределения с «тяжелыми хвостами». Формально их можно определить следующим выражением:
Ит еКхР[х > X] = да, V X > 0. (4)
Вероятность больших отклонений фактического значения процесса от прогнозного для распределений прогнозных ошибок с «тяжелым хвостом» существенно выше, что, естественно, сказывается на выполнимости неравенства (3). Обычно явления кризисного типа, включая техногенные и природные катастрофы, характеризуются еще и тем, что распределения систематических ошибок параметров проекта являются асимметричными с «тяжелым правым хвостом», как, например, у распределения Вейбулла. Закон Вейбулла характеризуется следующими функциями плотности и закона распределения:
/(А) = йЛйАй-1е-(М)», А > о, (5)
^(А) = 1 -е-(АА)», А > о, Л > о, й > о, (6)
где X — параметр масштаба;
й — параметр формы.
Частным случаем закона распределения Вейбулла является экспоненциальный закон распределения:
Экспон (X) = Вейб (й = 1, X).
С учетом выражений (5) и (6) плотность и функция распределения экспоненциального закона имеет вид:
/(А) = Ле-(М), А > о; (7)
ДА) = 1 — е-(М), А > о. (8)
Для экспоненциального закона распределения часто вводят параметр сдвига с, который показывает минимально возможное значение исследуемой случайной величины. Тогда
^(А) = 1 — е-(Д(А-С)), А > с. (9)
Рассмотрим примеры использования некоторых из рассмотренных распределений при построении закона распределения общей ошибки прогноза с использованием выражения (1).
С учетом того, что распределение суммарной ошибки е = е + А определяется формулой свертки типа (2), то вероятность события х > х*? может быть оценена на основе следующего выражения:
р(х0 + е > х*?) = р(е > Ах* = х*? — х0) = J УА (у) J У (г)dtdy =
—те Ах* — у
+те Ах* +те +те
= / УА (у) / У (г)dtdy + / Уа (у) / У (г)dtdy =
—те Ах* —у —те Ах*
+те
= (1 — ^(Ах*)) + /УА(у)((Ах*) — ^(Ах* — у)^у , (I0)
—те
х
где Fz (х) = J /е (г )Л — функция нормального закона распределения случай-
—те
ной ошибки.
Дальнейшие преобразования выражения (10) с учетом вида функций УА (х) ведут к следующему результату:
p(e > Ах* = х2 — х0) = (1 -Fe (Ах*)) + q0 Jö(y)(F(Ах*) -Fe (Ax* — y)dy +
-ад
+ад
+ S qi J f (y)(Fe (Ax*) — F (Ax* — y))dy =
-ад
+ад
х*)) +
i=1 -ад
n ^
(1 — Fe (Ax*)) + S qt J f (y)(Fe (Ax*) — Fe (Ax* — y))dy . (11)
Поскольку случайная ошибка распределена по нормальному закону, то имеем
1 — Ft (Ах*) = А0(Ах*), (12)
где А0 (Ax*) = Ф
r Ax.^
V G о J
где Ф (z) — табличное значение стандартного нор-
мального распределения переменной г, 2 ~ N(0,1).
Обозначим вклад условной систематической ошибки 1-го фактора в оценку риска ошибки прогноза через
+те
аг- (Ах*) = / У (у)(^Е (Ах*) — ^ (Ах* — y))dy. (13)
—те
Тогда оценку вероятности превышения ошибки прогноза норматив Ах* можно определить с использованием следующего выражения:
р(е > Ах* = х*2 — х0) = Д,(Ах*) + ^ ца(Ах*). (14)
+ад
Значение qi аi (Ах*) можно интерпретировать как прирост вероятности
ошибки прогноза, обусловленный влиянием /-го фактора, / = 1, п . Рассмотрим частные случаи полученных результатов. 1. Предположим, что условная плотность распределения систематической ошибки А является нормальной с параметрами т и оД. Тогда с учетом выражений (13) и (14) имеем
р(е > Ах. = х*2 -х0) = 1 — (1 — ^1)Ф
V ао
— ^Ф
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
( Ах* — т
л/°2 + аА у
(15)
2. Предположим, что условная плотность распределения систематической ошибки Д является экспоненциальной с параметром X. Математическое
1 1 „ ожидание такого распределения равно —, а дисперсия — —. Т огда согласно
Л X2
выражению (13) получим:
а(Ах.) = |/ (0(1 — е-А(Лх*-г))А = |/ (г)Жг — |/е
-Л(Ах*-г)
А =
= Ф
Ах* СТП
—
¿лх
I
о0422П
—2+р-Л( Ах*-г)
2 о2 Жг =
= Ф
А А Л
Ах*
о
Ах*
— е
—Л Ах*
V °о у
1 /»о
/1 -+2Ла2 ■/—== е 2а2 2а2 2а2 =
1~Г — /’
= Ф
Г Ах, ^
V ао у
_ ао42П
Л2а2 Ах*
— е~КАх* е~
(/-Ла2) е~ 2а0 Жг =
=Ф
Г Ах ^
V ао у
— е -КАх* е 2 Ф
-ш ^о
^ ГАх* -Хо2 ^
а,
(16)
о у
С учетом этого результата оценка вероятности превышения верхнего предела для прогнозного показателя определяется выражением
р(е > х*2 -хо) = 1 — (1 — д)Ф
Г Ах, ^
V о о у
де~ХАх’ е
X 2а2
(
2
о Ф
Ах* — Хо ап
2
(17)
На практике с целью избежания сложных выкладок можно использовать упрощенный подход, согласно которому оценке подлежит только дисперсия плотности ф(х) по известным дисперсиям ао = а и а2ы — случайной и систематических ошибок, а функциональная зависимость ф(х), выражающая конкретный закон распределения ошибки е, постулируется или определяется экспертными или какими-либо другими доступными методами.
Выражение, определяющее дисперсию общей ошибки прогноза е = е + Д, имеет достаточно сложный вид даже в случае известных значений дисперсий ошибок а2ы = а2 условных распределений / (А 1 //). На практике его
2
1
1
о
можно получить, воспользовавшись известными взаимосвязями между первым и вторым (центральным и начальным) моментами ошибок.
Очевидно, что математические ожидания общей и систематической ошибок прогноза равны между собой и определяются следующим выражением:
М[е] = М[д] = Х дг Дг . (18)
I=1
С учетом независимости ошибок е и Д7 дисперсию ошибки прогноза е можно оценить с использованием следующего выражения:
+ад ад
ст2 = (е — М [е])2 ф(е)ёе = ов2 + Х (Д, — Я, Д) 5(0) + Я / (Д, / ШД, =
— ад 7 —ад
= о2 + Х [ЯМ (Д,)—2я2м 2(Д,) + Я3М 2(Д,) + Я0 яМ 2(д ,)], (19)
I
+ад
где М(Д7) = | Д/• (Дi /7)йД7- условное математическое ожидание 7-й систе-
-ад
матической ошибки;
+ад
М 2(Д7) = | (Д7 )2 /7 (Д7 / 7)йД — условное математическое ожидание квад-
—ад
рата 7-й систематической ошибки. Поскольку
М (Д 7) = о 2 + М 2(Д 7), (20)
то выражение (19) можно привести к следующему виду:
о 2 = о2 + X я о2 + яМ2 (Д 7) — 2я2 м 2 (д 7) + ЯЗМ 2(Д 7) +
г
+ Яо ЯМ2 (Д7) = о 2 + X я7 о 2 + X (Я ([1 — Я7 )2 + Яо]М2 (Д7)). (21)
I /
С учетом (21) в предположении, что суммарная ошибка прогноза распределена по нормальному закону с математическим ожиданием
М [е]=Х Я 7 Д7, оценку вероятности превышения верхнего предела прогноза
можно определить согласно следующему выражению:
р(х > х*2 ) = 1 — Ф
‘Дх >
(22)
V 0 е У
где Дх* = х*2 — х0 — X Яi Д7 .
Рассмотрим случай, когда систематическая ошибка распределена по экспоненциальному закону
/ (Д /1) = Хе-ХД (23)
1 2 1 2 с параметрами М (Д) = —, о 2(Д) = —, М (Д) = —.
XX X
Тогда на основании выражения (21) общая дисперсия прогноза ошибки будет определяться следующим выражением:
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
о2 — с2 + Ч + 2^1((1 -?1)2 +(1 — А)) _ о2 + Ч + 2Ч д0 + 2дд20 (24) 0 _Сс +12 + X2 _ 0 + X2 ‘ ( )
где Ч _1 — ?1-
Заметим, что в выражении (24) второе слагаемое 41 + 2Ч1Ч|° + 2ч1^2 определяет поправку к дисперсии случайной ошибки прогноза. Поправка к математическому ожиданию х2 сделанного прогноза определяется как —, т. е.
X
1 _
Х2 _ Х2 + х ‘
Рассмотрим пример верификации прогноза цены сложного технического изделия, полученного на основе линейной эконометрической модели, учитывающей влияние на цену некоторых факторов (себестоимости, рыночной конъюнктуры и т. п.):
3
х = ^ а^ • (25)
I _1
Количественные характеристики а, и значений прогнозного фона 2, представлены в табл. 1.
Т а б л и ц а 1
Количественные значения переменных, используемых для разработки прогноза
Характеристика (/) 1 2 3
а. 2,4 2,2 2,1
2 ¡, тыс. руб. 12 12 15
Оценка дисперсии случайной ошибки прогноза х2 может быть получена при условии независимости параметров а., 2, / = 1, 2, 3, на основе следующего выражения:
о2 _ ^ (соу(а,., а,)^ + ар, соу(2,. , 2,) + соу(2,. , 2,) • соу(а,., а,)), (26)
с
где соу — ковариация соответствующих параметров модели (25).
Предположим, что ковариационная матрица параметров а. имеет следующий вид (табл. 2).
Т а б л и ц а 2
Ковариационная матрица параметров а1
1 2 3
1 2,216 -2,2224 2,2222
2 -2,2224 2,2224 -2,2221
3 2,2222 -2,2221 2,2221
Значения элементов ковариационной матрицы параметров представлены в табл. 3.
Ковариационная матрица параметров zi
Т а б л и ц а 3
i 1 2 3
1 1,0 0,36 0,4
2 0,36 0,44 0,9
3 0,4 0,9 2,25
Подставляя значения характеристик, содержащихся в табл. 3, в выражение (26), получим следующее значение прогноза цены:
у0 = 0,4 -10 + 0,2 -12 + 0,1-15 = 7,9 тыс. руб.
Для оценки дисперсии случайной ошибки прогноза используем выражение (26), соответствующее случаю наличия ковариационных взаимосвязей между однотипными параметрами а1 и гг-:
ое2(х) = 0,42 -10 + 0,22 -12 + 0,12 -15 +1,02 — 0,016 +1,22 — 0,0004 +1,52 — 0,0001 + + 2[1,0 -1,2 — (-0,0004) +1,0 -1,5 — (0,0002) +1,2 -1,5 — (-0,0001)] = 2,2.
Рассмотрим примеры оценки риска ошибки прогноза цены сложного технического изделия на основе предложенных выше подходов.
Предположим, что распределение цены под воздействием случайной ошибки принадлежит нормальному закону со следующими характеристиками: т = 7,9 тыс. рублей, о2 = 2,2 тыс. рублей, о = 1,48 тыс. рублей:
f (x) =
1
(x-7,9)2 4,4
(27)
1,483л/2л ‘
Пусть на цену накладываются следующие ограничения:
— цена не должна быть ниже хкрит = 5,6 тыс. рублей, так как в противном случае проект не окупится;
— цена не должна превысить значение хкрит = 10,0, так как в этом случае изделие не будет реализовано.
Таким образом, цена изделия должна находиться в интервале (5,6; 10,0). Предположим, что допустимый уровень риска ошибки прогноза равен 0,1, т. е. вероятность выхода цены за границы этого интервала не должна превысить 0,1. Найдем вероятность того, что прогнозное значение цены принадлежит данному интервалу (см. выражение (3)):
скрит -т)._
x — m x P(x < X ) + P(x > xкрит) = Ф(-^-) +1 — Ф(-
L)=
56 — 79 100 — 79
= фр° +1 — Ф( ‘ ‘) = 0,06 +1 — 0,982 = 0,078 .
1,48
1,48
о
о
Этот результат свидетельствует, что с вероятностью ~ 0,078 цена сложного технического изделия выйдет за границы интервала (5,6; 10,0), причем она может опуститься ниже порогового значения 5,6 тыс. рублей с вероятностью 0,06, а превысит критическое значение 10,0 с вероятностью 0,018. Таким образом, в отсутствие систематической ошибки прогноз цены в 7,9 может быть верифицирован.
Предположим, что общая ошибка прогноза представляет собой сумму случайной и систематической ошибок. При этом условная плотность распределения систематической ошибки А является нормальной с параметрами m = 2 тыс. рублей и оА = 2,24 тыс. рублей. Вероятность наступления события, обусловливающего появление этой ошибки, равна 0,05. Рассмотрим оценку вероятности превышения прогноза цены верхней границы критического значения в 10,0 тыс. рублей (см. выражение (15)):
Р* _ Р(е > Ах _ х — х*2) _ 1 — (1 — ч)Ф(—) — дФ( — т ) _
V
_ 1 — 2,95 • 2,919 — 2,25 • 2,28 « 2,12.
22 о 2 + о А
Поскольку 0,125 > 0,1, то прогноз не может быть верифицирован. Предположим, что условная плотность распределения систематической ошибки А является экспоненциальной с параметром X _ 2,4. Тогда согласно
1
характеристикам экспоненциального закона математическое ожидание m _ —
X
2 1
равно 2,5, а дисперсия о _ —- _ 6,25 . Вероятность наступления данного со-
X2
бытия ч = 0,01. В этом случае значение вероятности превышения верхнего предела цены определяется выражением (17):
1 Лг ^2°2 Ах — ^о2
Р* _ Р(е > Ах _ х*2 — _ 1 — (1 — ч)Ф(—) — дв-}лв 2 Ф(Ах 2Ло2) =
02 02
_ 1 — 2,95 • 2,918 — 2,25 • 2,6 • 2,71 _ 2,146.
Это значение также свидетельствует, что прогноз цены не может быть верифицирован.
Рассмотрим упрощенный подход к оценке риска ошибки прогноза, согласно которому эта характеристика предполагается распределенной по нормальному закону вне зависимости от того, по какому закону была распределена систематическая ошибка. Пусть вероятность появления фактора риска равна 0,01, математическое ожидание обусловленной им систематической ошибки равно 2,0 тыс. рублей, а ее дисперсия — 2,25.
С учетом этого получим, что М [А] = 4 + 2,25 = 6,25. В предположении, что общая ошибка цены распределена по нормальному закону, скорректируем математическое ожидание цены и ее дисперсию (см. выражение (22)):
т1 _ х2 + ч • т _ 7,92;
о2 _ 2,2 + 2,21 • 2,25 + 2,21[(1 — 2,21)2 + 2,99] • 6,25 « 2,35 .
Среднее квадратическое отклонение в этом случае равно 1,58 тыс. рублей. Найдем оценку риска превышения верхнего предела цены для этого случая:
Р(х > х*2) _ 1 — Ф(х2 -т’ ) _ 1 — фГ12,2 — 7,9251 _ 1 — 2,9147 = 2,2853.
ое I. 1,51 )
Вероятность превышения цены критической оценки в 10,0 с учетом поправки составляет ~0,09, что не превышает установленное для нее ограничение в 0,1.
Рассмотренные подходы к верификации прогнозов в качестве исходной информации используют предполагаемые известными законы распределения их ошибок. Такая ситуация соответствует неопределенности прогноза третьей степени, характеризующейся достаточной статистикой для формирования законов распределения ошибок. В ее отсутствие, т. е. при неопределенности прогноза более высокой степени, вместо функции плотностей можно исследовать функции принадлежности ошибок, характеризующих их распределение на нечетких множествах. В этом случае при верификации прогноза можно использовать а-срез функции принадлежности прогноза. Напомним, что нижняя и верхняя границы а-среза по своему содержанию эквивалентны пределам х1 и х*2 , а значение а эквивалентно величине вероятности 1 — Р*1 — Р*2 нахождения прогноза в интервале ( х*1 , х*2 ).
Список литературы
1. Ахмедов Н. А. Методологические основы анализа, методов оценки и прогнозирования инвестиционной деятельности в экономических системах // Вестник Российской экономической академии имени Г. В. Плеханова. — 2212. — № 3 (33).
2. Давыдов Д. В. Методология принятия экономических решений с позиции субъективной неопределенности // Вестник Российской экономической академии имени Г. В. Плеханова. — 2229. — № 2 (26).
3. Справочник по теории вероятностей и математической статистике. -М. : Наука, 1985.
4. Тихомиров Н. П. Бюджетное планирование в условиях риска // Финансы и кредит. — 2229. — № 22 (358).
5. Тихомиров Н. П., Дорохина Е. Ю. Эконометрика. — М. : Экзамен,
2223.
6. Тихомиров Н. П., Тихомирова Т. М. Риск-анализ в экономике. — М. : Экономика, 2010.
Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.
В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
Статистические методы
Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.
В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.
К ним относятся:
MAPE – средняя абсолютная ошибка в процентах
где Z(t) – фактическое значение временного ряда, а 
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
ME – средняя ошибка
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

.
SD – стандартное отклонение
где ME – есть средняя ошибка, определенная по формуле выше.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>
Связь точности и ошибки прогнозирования
В начале этого обсуждения разберемся с определениями.
Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:
- Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
- Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.
Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)
Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:
где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
300% |
|
№3 |
1 |
4 |
75% |
Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:
В таком случае для тех же примеров ошибка рассчитается иначе:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
75% |
|
№3 |
1 |
4 |
75% |
Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.
Визуальный метод – графический
Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.
По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.


Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.
Использование формул ошибки прогнозирования на практике
Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.
Пример расчета такой оценки Вы сможете увидеть в файле Excel.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.
Для чего используется ошибка прогнозирования
В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.
Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.
В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.
Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».
Источник: сайт http://uppravuk.net/
В прогнозировании есть одна простая истина, к которой прогнозисты пришли достаточно давно: высокая точность аппроксимации данных не гарантирует высокую точность прогнозов. Это означает, что модель, дающая наименьшие ошибки по обучающей выборке, не обязательно даст такие же наименьшие ошибки по тестовой выборке. Противоположное («чем лучше аппроксимация, тем точнее прогноз») вообще возможно лишь для обратимых процессов, в которых никаких качественных изменений не происходит. Но, как мы знаем, в мире нет ничего более постоянного, чем перемены.
Впрочем, помимо этой простой истины есть ещё и другая: модель, заведомо плохо аппроксимирующая ряд данных, навряд ли даст точный прогноз. Это в свою очередь означает, что для получения более точных прогнозов, модель должна точно описывать ряд по внутренней выборке, быть адекватной поставленной задаче и включать все существенные переменные. Потому что, если модель представляет собой очень грубое и условное описание объекта, то по ней нельзя сделать адекватных выводов о самом объекте исследования.
Как видим, перед нами противоречие: модель должна хорошо описывать данные, но хорошее описание не гарантирует получения точных прогнозов. Противоречие решается достаточно легко, если следовать одному из базовых буддистский принципов — придерживаться срединного пути. Но как же найти эту середину? Для этого надо просто научиться оценивать качество построенной модели. А в этом нам помогут различные графики и ряд коэффициентов.
Графический анализ моделей
С графическим анализом всё просто. Все те инструменты, которые мы рассмотрели ранее в параграфе «Графический анализ данных«, сейчас нам пригодятся для того, чтобы понять, какая из моделей лучше и почему. Как всё это сделать в R мы так же уже рассматривали ранее, так что не будем тратить в этот раз время на примеры.
Самый простой метод оценки полученной модели — линейный график. На него достаточно нанести фактические значения, расчётные и прогнозные. Так мы сможем увидеть, как модель описала данные и насколько полученный прогноз соответствует сложившейся динамике. Более того, так можно понять (на основе знаний о прогнозируемом процессе), насколько полученные прогноз правдоподобен.
Очень простой пример с линейным графиком показан наследующем рисунке.
Линейный график по несезонной модели ETS(M,N,N)
На нём показан ряд фактических значений (чёрная сплошная линия «Series»), ряд расчётных (фиолетовая пунктирная линия «Fitted values»), точечный прогноз (синяя сплошная линия «Point forecast») и 95% прогнозный интервал («95% prediction interval»). Уже глядя на этот график можно сделать несколько выводов:
- Ряд фактических значений был описан моделью неплохо, хотя основные характеристики ряда выявлены не были — это видно потому что расчётные значения всё время как будто отстают от фактических на один шаг. К тому же, ряд расчётных значений не такой гладкий, как хотелось бы и в ряде наметились элементы сезонности (это особенно чётко видно с 1986 года) — каждый четвёртый квартал виден пик показателя. Это не криминал, но может говорить о том, что стоило бы обратиться к другой модели либо другому методу оценивания.
- Прогноз по нашей модели представляет собой прямую линию, параллельную оси абсцисс. Это хороший прогноз в случае, если ряд данных не имеет явной тенденции к росту либо снижению. Однако в нашем случае ряд данных явно демонстрирует увеличение показателя во времени. Поэтому такая тенденция в будущем хоть и возможна, но, скорее всего, не соответствует ожиданиям. Для того, чтобы здесь сделать какой-то однозначный вывод, нужно, конечно, понимать, с каким показателем мы имеем дело, и насколько реалистичен такой сценарий на практике.
- Прогнозные интервалы значительно расширяются и к последнему наблюдению составляют 5800 — 6500. Опять же, такие широкие интервалы — это не страшно, но одна из потенциальных причин этой ширины — неправильно выбранная (или специфицированная) модель. Так же на возможно неправильно выбранную модель указывает неровность прогнозного интервала при таком ровном прогнозе. Возможно, всё-таки надо было использовать другую модель (с трендом и сезонностью), а, может быть, мы не учли какие-то важные факторы.
На основе этих пунктов уже можно заключить, что стоит попробовать ещё какую-нибудь модель для прогнозирования этого ряда данных.
Если мы используем для выбора модели процедуру ретропрогноза, то на тот же самый график стоит нанести значения из проверочной выборки. Другая модель, построенная по тому же ряду данных, показана на рисунке ниже.
Линейный график по сезонной модели ETS(M,A,M)
По этому рисунку тоже можно сделать ряд выводов:
- Фактические значения описаны этой моделью лучше, чем предыдущей, но всё ещё есть ряд промежутков, аппроксимированных моделью не очень хорошо (как, например, наблюдение в начале 1984 года). Возможно, это говорит о том, что в это время происходили какие-то события, которые наша экстраполяционная модель не может уловить, а, может быть, нужно просто изменить метод оценки модели. При прогнозировании на практике стоит выяснить, что происходило в эти моменты, чтобы понять, носят ли эти события чисто случайный характер.
- Прогноз по модели получился с учётом сезонности, и, как видно по тестовой выборке, это сыграло модели на руку — она дала прогноз точнее, чем это сделала бы предыдущая модель ETS(M,N,N).
- Прогнозный интервал оказался уже, чем в предыдущем случае и по своей динамике соответствует поведению точечного прогноза (что говорит о том, что мы смогли уловить важные элементы ряда).
В общем, всё в этом графике указывает на то, что стоит обратиться к модели с трендом и сезонностью.
В ряде случаев по одному лишь линейному графику бывает сложно сделать выводы о качестве модели. Например, те же самые выбросы оценить по нему на глаз непросто. В этом случае нужно обратиться к графикам по остаткам модели. Даже простой линейный график по остаткам может дать много полезной информации.
Однако прежде чем приступать к непосредственному анализу, надо понять, что нам нужно. В идеальной модели остатки ни от чего не зависят, выглядят распределёнными случайно и желательно даже нормально. Графически это должно выражаться отсутствием какой-либо предсказуемости в остатках и ровными гистограммами и ящичковыми диаграммами.
На следующих рисунках приведены четыре графика по остаткам модели ETS(M,N,N) (той, которая соответствует первому графику в этой статье).
Линейный график по остаткам модели ETS(M,N,N)
Гистограмма по остаткам модели ETS(M,N,N)
Ящичковая диаграмма по остаткам модели ETS(M,N,N)
Точечная диаграмма по остаткам модели ETS(M,N,N)
Взглянем критически на эти графики и попробуем вынести какую-нибудь полезную информацию.
- Линейный график по остаткам демонстрирует периодические колебания (которые особенно заметны примерно с 1986 года) — это всё из-за того, что мы не учли в модели сезонность. По остаткам она видна более явно, чем по графику по исходному ряду.
- Гистограмма по остаткам демонстрирует явную асимметрию: очень много ошибок лежит выше нуля (справа). Это так же указывает на неправильную спецификацию модели. Обычно исследователи при построении разных моделей стараются добиваться нормально распределённых остатков, но это требование на практике очень сложно удовлетворить. Именно поэтому нам нужно, чтобы они были хотя бы симметрично распределены относительно нуля. Это будет указывать на то, что модель построена без систематических ошибок.
- Ящичковая диаграмма показывает то же, что и гистограмма: мы имеем дело с асимметричным распределением. Помимо этого она ещё показала, что практически все отрицательные остатки можно статистически считать выбросами — то есть они настолько редко случаются, что играют небольшую роль в описательной способности модели. На себя так же обращает внимание завышенное среднее значение ошибки (красная точка по середине ящичка) — это так же сигнализирует о неправильной спецификации.
- Точечная диаграмма, построенная по расчётным значениям (Fitted) и абсолютным остаткам модели была построена для дополнительной информации. Она нам может показать, есть ли в модели гетероскедастичность. Другими словами, постоянна ли дисперсия остатков модели. Видно, что при меньших расчётных значениях остатки лежат в пределах от нуля до 0.015, в то время как при достижении 6000 по оси абсцисс разброс увеличивается. Это указывает на непостоянность дисперсии, что в свою очередь опять говорит о возможных проблемах модели.
Теперь рассмотрим точно такие же графики, но уже по модели с трендом и сезонностью.
Линейный график по остаткам модели ETS(M,A,M)
Гистограмма по остаткам модели ETS(M,A,M)
Точечная диаграмма по остаткам модели ETS(M,A,M)
Ящичковая диаграмма по остаткам модели ETS(M,A,M)
По ним можно заключить следующее:
- Линейный график демонстрирует более случайный характер распределения остатков, чем в предыдущем примере. Та самая пресловутая сезонность уже менее заметна. Но на себя обращают внимание три отрицательные ошибки, соответствующие 1984, 1989 и 1990 годам. Возможно, у таких ошибок есть какое-то объяснение. На практике стоило бы выяснить, что происходило в эти кварталы для того, чтобы улучшить описательные и прогнозные свойства модели.
- Гистограмма имеет более симметричный вид. Если бы не те несколько отрицательных ошибок, она бы выглядела вообще прекрасно.
- Ящичковая диаграмма так же демонстрирует большую симметрию относительно нуля (по сравнению с предыдущей моделью), а так же указывает на наличие нескольких выбросов. Это те самые отрицательные ошибки, которые мы отметили ранее. Всё-таки что-то с ними надо сделать!
- Последний график всё так же, как и в предыдущем примере указывает на наличие гетероскедастичности. Это значит, что при построении прогнозных интервалов сей неприятный эффект надо учесть, иначе интервалы могут оказаться либо слишком узкими, либо излишне широкими.
Как видим, на основе такого небольшого анализа можно получить много полезной информации об аппроксимационных свойствах модели и принять решение о том, что делать с моделью либо к какой модели обратиться.
Но помимо приведённых графиков есть ещё один, специализированный, который позволяет сравнивать распределение случайной величины с некоторым заданным. Называется он «квантиль-квантиль» потому что позволяет проводить поквантильное сравнение фактических и теоретических значений. Пример такого графика представлен на этом рисунке:
График квантиль-квантиль по остаткам
По нему видно, что наблюдения, находящиеся в хвостах распределения выбиваются и из-за них распределение остатков оказывается непохожим на нормальное. В идеале мы хотели бы, чтобы все точки на графике находились если не непосредственно на прямой линии, то хотя бы близко к ней, вокруг неё.
Как это сделать в R
В R такой график можно построить с помощью функций qqplot() и qqline(). Если нас интересует сравнение с нормальным распределением, то можно так же использовать функцию qqnorm(). Например:
x <- rnorm(100,0,1) qqnorm(x) qqline(x)
Попробуйте и посмотрите, какой получится график.
Коэффициенты для оценки качества моделей
Но, конечно же, одним графическим анализом ограничиваться не стоит. Очевидно, что глаз не всегда может увидеть то, что легко показал бы какой-нибудь коэффициент.
Первая группа коэффициентов, которые могут использоваться для оценки качества, обычно используется на остатках модели. Это все те статистические показатели, которые мы рассмотрели раньше в параграфе «Статистический анализ данных». Ничего нового и интересного относительно них сказать нельзя, поэтому здесь на них мы останавливаться не будем.
Добавим в нашу коллекцию два коэффициента, которые могут помочь при оценке описательной способности модели. Первый — это коэффициент корреляции, рассчитанный по фактическим и расчётным значениям. Чем ближе коэффициент к единице, тем в среднем ближе связь между этими значениями к линейной, то есть тем точнее описаны данные нашей моделью. Этот коэффициент мы уже обсуждали в параграфе «Выявление связей между переменными».
Второй полезный коэффициент — коэффициент детерминации. Он показывает процент объяснённой моделью дисперсии и рассчитывается по формуле:
begin{equation} label{eq:mq_Rsquared}
R^2 = 1 -frac{SSE}{TSS} ,
end{equation}
где ( SSE = sum_{t=1}^T e_t^2 ) — это сумма квадратов ошибок модели (иногда обозначается ещё как RSS, SSR), (TSS = sum_{t=1}^T (y_t -bar{y})^2) — сумма квадратов отклонений фактических значений от средней величины. Здесь SSE соответствует «Sum of Squared Errors», RSS — «Residuals Sum of Squares», SSR — «Sum of Squared Ressiduals», TSS — «Total Sum of Squares». Все эти суммы квадратов на самом деле близки по смыслу к дисперсии остатков и дисперсии по исходному ряду данных. Просто в формуле eqref{eq:mq_Rsquared} не происходит деление на число наблюдений.
Коэффициент детерминации более популярен в регрессионном анализе, нежели в других разделах прогнозирования, но может спокойно использоваться и при оценке экстраполяционных моделей. В случае, если модель идеально описывает ряд данных, SSE становится равной нулю, в результате чего (R^2) становится равен единице. Если же модель ряд совсем не описывает, а представляет собой просто прямую линию, то коэффициент детерминации становится равным нулю. В случаях с нелинейными моделями коэффициент может так же становиться отрицательным, но при этом неинтерпретируемым.
Несмотря на то, что коэффициент детерминации показывает этот самый процент той самой объяснённой дисперсии, сильно полагаться на него не стоит. Во-первых, он считается по обучающей части выборки, а значит просто показывает, насколько хорошо мы описали данные. При этом точность описания не гарантирует точность прогнозов. В некоторых случаях даже наоборот: излишне точное описание приводит к ухудшению прогнозных свойств модели (так как та начинает слишком сильно реагировать на шум). Простой пример — полиномы: чем выше степень полинома, тем выше (R^2), но тем обычно хуже точность прогнозов. Во-вторых, коэффициент детерминации будет всегда тем выше, чем выше число параметров в модели. То есть (R^2) у модели (y = a_0 + a_1 x_1 + e) будет всегда ниже, чем у модели (y = a_0 + a_1 x_1 + a_2 x_2 + e), даже если (x_2) в принципе ненужен. Именно поэтому иногда в эконометрике обращаются к так называемому скорректированному коэффициенту детерминации — (R^2)-adjusted. Но о нём мы поговорим в следующем параграфе.
В заключение по коэффициенту детерминации хотелось бы лишь добавить, что при построении моделей он не должен являться самоцелью: «Посмотрите, какая у меня хорошая модель получилась: (R^2=0,936)!» — типичная ошибка начинающих аналитиков. (R^2) может выступать лишь индикатором того, насколько модель адекватна. Низкие значения коэффциента детерминации могут указывать на то, что модель особого смысла не имеет, но при этом высокие значения не говорят о том, что перед нами хорошая модель.
По коэффициентам аппроксимации у меня всё. Но, если бы мы ограничивались лишь анализом аппроксимационных свойств моделей, то не было бы смысла вообще писать этот параграф. Нас, ведь, на самом деле больше интересует оценка точности прогнозов. Оценить её можно при использовании процедуры ретропрогноза. В этом случае наш интерес сдвигается с того, как модель себя повела на обучающей выборке на то, как она себя повела на тестовой. И здесь уже есть, куда развернуться.
Конечно, анализ этот можно проводить по аналогии с анализом обычной случайной величины, а значит и использовать весь стандартный набор коэффициентов, но в некоторых случаях стандартные методы просто неприменимы, а в других случаях не дадут полной информации о прогнозных свойствах моделей.
Например, коэффициент MAE, к которому мы обращались в параграфе «Простые методы оценки параметров моделей», будет в этом случае рассчитываться так:
begin{equation} label{eq:mq_MAE}
text{MAE} = frac{1}{h} sum_{j=1}^h | e_{T+j} |,
end{equation}
где (e_{T+j}) — ошибка на прогнозном шаге j, h — срок прогнозирования, T — номер последнего наблюдения в обучающей выборке.
У этого коэффициента есть два недостатка, которые проявляются только в случае анализа прогнозной точности моделей:
- Его значение сложно интерпретировать. Вот, допустим, получилось, что (MAE = 1547.13). О чём это говорит? Это много или мало? Если сравнить с другой моделью, то станет, конечно, ясно. Но какова будет реакция начальника, когда на вопрос прогнозисту: «Штурман, приборы?» — он услышит: «1547.13»?
- С помощью этого коэффициента можно проводить сравнение только между моделями по одному ряду данных. Но на практике часто стоит задача понять, как себя ведёт модель по нескольким рядам данных по сравнению с другими моделями. И тут уже полученные по разным рядам MAE складывать друг с другом нельзя, так как при сложении яблок с гвоздями получается абсурд.
Для того, чтобы так или иначе справиться с одной из или обеими этими проблемами, было разработано несколько коэффициентов.
MAPE — «Mean Absolute Percentage Error» — Средняя абсолютная процентная ошибка:
begin{equation} label{eq:mq_MAPE}
text{MAPE} = frac{1}{h} sum_{j=1}^h frac{| e_{T+j} |}{y_{T+j}},
end{equation}
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что (MAPE = 11.4%), то это говорит о том, что ошибка составила 11,4% от фактических значений. Этот коэффициент можно легко складывать по разным рядам. Можно даже рассчитать MAPE и изучить его распределение, используя инструменты статистического анализа. С другой стороны, можно отбросить в eqref{eq:mq_MAPE} часть, отвечающую за «Mean»:
begin{equation} label{eq:mq_APE}
text{APE} = frac{| e_{T+j} |}{y_{T+j}},
end{equation}
и изучить распределение прогнозных ошибок на некоторый шаг j, используя всё те же статистические методы. Можно вместо «M», средней, посчитать «Md», медиану. Можно обратиться к квантилям… В общем, ни в чём себе не отказывайте, чувствуйте себя как дома!
Но, конечно же, без проблем быть не может. Из-за деления на фактические значения этот коэффициент оказался чувствительным к масштабу. Так, в случае, если (y_{T+j}) близко к нулю, то значение eqref{eq:mq_APE} из-за деления на очень маленькое число взлетит. А уж если (y_{T+j}=0), то нас вообще ждёт бедствие вселенского масштаба.
Но на этом ещё не всё. Коэффициент по разному относится к положительным и отрицательным ошибкам. Допустим, что наш точечный прогноз на 137-м наблюдении составил (hat{y}_{137} = 20), а фактическое значение при этом было (y_{137}=10). Какой будет ошибка APE в этом случае? Подставим эти значения в формулу eqref{eq:mq_APE}, чтобы получить (frac{|10-20|}{10}=1=100%). А какой была бы ошибка, если бы фактическое значение было равно 30? Очевидно, что (frac{|30-20|}{30}=0,33(3)=33.(3)%). Вроде бы ошибка та же, но, по объективным причинам, она во втором случае составляет 33.3% от фактического значения, а не 100%. Получается, что этот коэффициент жестче относится к случаям завышенных прогнозов, чем заниженных. В случае с агрегированием прогнозов по разным значениям, это приводит к искажениям — прогнозист не получает достоверной информации о том, насколько его прогноз точен. Такая асимметрия не могла не привести к появлению других коэффициентов.
Один из вариантов решения проблемы предложили Spyros Makridakis и Michele Hibon, назвав коэффициент SMAPE — «Symmetric MAPE» — симметричная MAPE:
begin{equation} label{eq:mq_SMAPE}
text{SMAPE} = frac{1}{h} sum_{j=1}^h frac{2 | e_{T+j} |}{|y_{T+j}| + |hat{y}_{T+j}|} .
end{equation}
Число «2» в этой формуле не случайно. Дело в том, что в соответствии с первоначальной задумкой в знаменателе должно быть среднее между фактическим и расчётным значениями: (bar{y_t} = frac{y_t + hat{y}_t}{2} ). При подстановке этого значения в знаменатель, двойка переносится в числитель, поэтому мы и получаем то, что получаем.
Трактовка у коэффициента примерно такая же, как и у MAPE: какой процент составляет ошибка от этой самой величины (bar{y_t}).
Идея, надо сказать, хорошая, но, конечно же, всё так же не лишена проблем. Коэффициент должен бы быть симметричным, но таковым до конца не является. Рассмотрим это на примере. Пусть наш прогноз на всё том же 137-м наблюдении составил (hat{y}_{137} = 110), а фактическое значение было (y_{137} = 100). SMAPE в этом случае составит (frac{2 cdot |100 — 110|}{100+110} = 9.52%). Если же прогноз оказался заниженным и составил (hat{y}_{137} = 90), то SMAPE получится равным (frac{2 cdot |100 — 90|}{100+90} = 10.53%). То есть, опять же, коэффициент демонстрирует смещение, только в этот раз в сторону завышенных прогнозов: завышенные прогнозы приводят к меньшей ошибке, чем заниженные. Сейчас уже в среде прогнозистов сложилось более-менее устойчивое понимание, что SMAPE на является хорошей ошибкой. Тут дело не только в завышении прогнозов, но ещё и в том, что наличие прогноза в знаменателе позволяет манипулировать результатами оценки. Кроме того, неясно, что именно минимизирует SMAPE. Поэтому я бы лично рекомендовал эту ошибку не использовать при оценки прогнозов (да, мы её активно использовали в нашем учебнике по прогнозированию, но сейчас я бы этого не стал делать).
Это, конечно же, не могло не привести к появлению ещё нескольких коэффициентов.
MASE расшифровывается как «Mean Absolute Scaled Error» и переводится как «Средняя абсолютная масштабированная ошибка». Предложена была Робом Хайндманом и Анной Коелер и рассчитывается так:
begin{equation} label{eq:mq_MASE}
text{MASE} = frac{T-1}{h} frac{sum_{j=1}^h | e_{T+j} |}{sum_{t=2}^T |y_{t} — y_{t-1}|} .
end{equation}
Обратите внимание, что в eqref{eq:mq_MASE} мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза по методу Naive. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тендецию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Но, конечно же, без минусов нельзя. Проблема MASE в том, что её тяжело интерпретировать. Например, (MASE = 1.21) ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более. Показывать шефу эти цифры опасно для жизни аналитика.
Можно, конечно, знаменатель eqref{eq:mq_MASE} заменить на простую среднюю по всему ряду, чтобы получить другую среднюю абсолютную масштабированную (относительно среднего уровня ряда) ошибку (sMAE — scaled MAE, иногда обозначается как MAE/mean). Для пущей безопасности в знаменателе можно взять среднее абсолютное значение ряда:
begin{equation} label{eq:mq_MASALE}
text{sMAE} = frac{T}{h} frac{sum_{j=1}^h | e_{T+j} |}{sum_{t=1}^T |y_{t}|} .
end{equation}
Модуль в знаменателе нужен для ситуаций, когда мы имеем дело как с положительными, так и отрицательными величинами, средняя величина по которым может быть близка к нулю. Если в такой ситуации брать просто среднюю, мы столкнёмся со всё той же проблемой масштаба. В общем случае значение eqref{eq:mq_MASALE} будет показывать, какой процент от средней составляют ошибки прогноза. Эта величина всё так же будет несмещённой (по сравнению с MAPE и SMAPE), и может легко складываться с другими такими же величинами. Единственная проблема — тренд в ряде данных может влиять на итоговое значение eqref{eq:mq_MASALE}. Но зато такой коэффициент легче интерпретировать, чем eqref{eq:mq_MASE} — эта ошибка может легко измеряться в процентах.
Заметим, знаменатель sMAE может быть равен нулю только в одном случае — если все фактические значения в обучающей выборке оказались равны нулю. Такое возможно лишь в ситуациях с целочисленным спросом, если в распоряжении исследователя ещё не было ни одного ненулевого значения. В общем, очень экзотическая ситуация, в которой надо обращаться к нестатистическим методам прогнозирования. А так ошибка может использоваться как при прогнозировании положительных, так и отрицательных значений.
sMAE — практически идеальный показатель. У него есть лишь один небольшой недостаток — он никак не ограничен сверху. То есть теоретически возможны ситуации, когда (sMAE = 1000%) (например, когда в проверочной выборке продажи неожиданно взлетели в разы, а в обучающей до этого составляли единицы), и с этим ничего не поделать. Такие ситуации, впрочем, тоже необычны, нечасто встречаются и будут приводить к похожим результатам во всех рассмотренных выше ошибках.
Ну, и не забываем о том, что вместо средней «M» в eqref{eq:mq_MASE} и eqref{eq:mq_MASALE} можно использовать и что-нибудь другое…
Но и даже на этом ещё не всё. Роберт Файлдс в 1992 году предложил нечто под названием «GMRAE» — «Geometric Mean Relative Absolute Error»:
begin{equation} label{eq:mq_GMRAE}
text{GMRAE} = prod_{j=1}^h left( frac{| e_{a,T+j} |}{| e_{b,T+j} |} right)^{frac{1}{h}} ,
end{equation}
где (e_{b,T+j}) — ошибка по некоторой второй модели.
GMRAE показывает, во сколько раз наша модель оказалась хуже (или лучше), чем выбранная для сравнения (модель-бенчмарк). Если (GMRAE>1), то наша модель оказалась менее точной, в противоположной ситуации — более точной. В качестве той самой второй модели для простоты можно выбрать Naive. Однако, можно и не ограничиваться Naive. Что именно выбрать обычно остаётся на совести прогнозиста, и в свою очередь может вызывать некоторые сложности. Действительно, почему именно Naive? Почему бы не модель экспоненциального сглаживания с демпфированным трендом или какая-нибудь ARIMA(2,1,3)?! Вопрос открытый. Но важно, чтобы по разным рядам происходило сравнение с одной и той же моделью.
Как видно, GMRAE легче интерпретировать, чем MASE, но сложнее, чем MAPE, SMAPE или sMAE. Впрочем, она всё так же не ограничена сверху и может теоретически достигать заоблачных величин.
Но без ложки дёгтя не обошлось. Из-за того, что эта ошибка представляет собой среднюю геометрическую, она не может использоваться в ситуациях, когда хотя бы одна из ошибок одной из моделей оказалась равной нулю — в этом случае GMRAE становится равной либо нулю, либо бесконечности.
Одна из модификаций этой ошибки — rMAE — Relative MAE (относительная MAE):
begin{equation} label{eq:mq_rMAE}
text{rMAE} = frac{text{MAE}_a}{text{MAE}_b} .
end{equation}
Здесь мы фактически просто рассчитываем MAE двух моделей, и дальше делим одну величину на другую. Интерпретация получается похожей на интерпретацию GMRAE, но сама ошибка при этом оказывается более робастной (так как ситуация, когда MAE=0 оказывается значительно менее вероятной, чем ситуация, когда одна какая-то ошибка оказалась нулевой).
Последний коэффициент, который мы рассмотрим, призван оценивать не точность прогноза, а его смещение. Называется он «Mean Percentage Error» — средняя процентная ошибка:
begin{equation} label{eq:mq_MPE}
text{MPE} = frac{1}{h} sum_{j=1}^h frac{ e_{T+j} }{y_{T+j}}
end{equation}
Можно заметить, что он похож на eqref{eq:mq_MAPE}, но отличается лишь отсутствием модулей в числителе. Он показывает процент смещения прогноза. Положительные значения MPE указывают на систематическое занижение прогноза (то есть, мы недооценили спрос), а отрицательные — на завышения. Его значение так же, как и MAPE eqref{eq:mq_MAPE} может измеряться в процентах. Он обладает теми же преимуществами и недостатками, что и MAPE.
На основе этой идеи со средними ошибками можно предложить и симметричную MPE, и среднюю масштабированную ошибку sME. Подробней на этом мы останавливаться не будем.
Ну, и совсем уж напоследок. Иногда в литературе встречается сравнение моделей на основе RMSE («Root Mean Squared Error» — «Корня из средней квадратичной ошибки»):
begin{equation} label{eq:mq_RMSE}
text{RMSE} = sqrt{ frac{1}{h} sum_{j=1}^h { e_{T+j} }^2}
end{equation}
Раньше бытовало мнение, что такое сравнение некорректно (см. Armstrong and Colopy, 1992), так как обычно приводит к выбору неправильной модели (то есть не самой точной). Всё из-за того, что эта ошибка сильно подвержена влиянию выбросов (из-за квадрата в формуле). Однако сейчас уже есть понимание, что проблема тут не в корректности и правильности, а в том, с чем именно мы имеем дело. Дело в том, что ошибки на основе MSE минимизируются с помощью средней величины, в то время как ошибки на основе MAE минимизируются медианами. Так что всё сводится к тому, что именно вы хотите увидеть.
Один из примеров эффективного использования ошибок на основе MSE — это прогнозирование прерывистого спроса. В этом случае число нулей в выборке может быть настолько большим (может легко перевалить за 50%), что все ошибки, основанные на модулях будут отдавать предпочтение нулевому прогнозу (мы ничего не продадим, поэтому нечего запасать — депрессивный прогноз). Это всё из-за того самого эффекта со средними и медианами (см. параграф методы оценки моделей).
На основе eqref{eq:mq_RMSE} можно, например, предложить rRMSE:
begin{equation} label{eq:mq_rRMSE}
text{rRMSE} = frac{text{RMSE}_a}{text{RMSE}_b} ,
end{equation}
которая может интерпретироваться аналогично rMAE.
На этом все самые популярные и полезные коэффициенты заканчиваются. В жизни встречаются, конечно же, и другие, но они обычно либо обладают большим количеством недостатков, либо значительно менее популярны среди прогнозистов.
Пример в R
В пакете smooth рассмотренные выше коэффициенты уже реализованы. Подключим пакет:
library("smooth")
И посмотрим, как они работают на примере следующих двух моделей:
x <- es(M3$N1234$x,model="MNN",h=8)$forecast y <- es(M3$N1234$x,model="MAN",h=8)$forecast
Переменные x и y теперь содержат прогнозы на 8 наблюдений вперёд по моделям ETS(M,N,N) и ETS(M,A,N) по ряду N1234 базы M3-Competition.
Ряд N1234 и модель ETS(M,A,N)
График исходного ряда (см. выше) демонстрирует рост, и, откровенно говоря, модель ETS(M,A,N) выглядит на обучающей выборке неплохо. Она улавливает тенденцию к росту. Если не прибегать ни к какому фундаментальному анализу, то можно заключить, что возрастающий тренд — это то, что нас ждёт в ближайшем будущем. Но будущее таки не предопределено, именно об этом нам в очередной раз говорит следующий график, на котором показана модель ETS(M,N,N) и значения из проверочной выборки.
Ряд N1234 и модель ETS(M,N,N)
И именно поэтому прогнозирование всегда должно осуществляться параллельно с фундаментальным анализом.
Тем не менее, посмотрим, насколько точными оказались прогнозы по этим двум моделям. Для начала рассчитаем MPE:
MPE(M3$N1234$xx,x) [1] -0.009 MPE(M3$N1234$xx,y) [1] -0.037
Как видим, прогноз по второй модели оказался более смещённым — он составил -3,7%, по сравнению с -0,9% первой модели. Не удивительно — ситуация в проверочной выборке изменилась кардинально по сравнению с тем, что мы видели в обучающей!
Что же там с точностью прогнозов?
MAPE(M3$N1234$xx,x) [1] 0.009 MAPE(M3$N1234$xx,y) [1] 0.037
Из-за того, что прогнозы по обеим моделям оказались завышенными, значение MPE оказывается равным по модулю значению MAPE. Вторая модель ошиблась сильнее, чем первая.
Симметричная MAPE даст нам примерно то же самое:
SMAPE(M3$N1234$xx,x) [1] 0.009 SMAPE(M3$N1234$xx,y) [1] 0.036
Для MASE нам понадобится значение, по которому мы будем масштабировать ошибки. Рассмотрим классические вариант со средней абсолютной ошибкой в знаменателе:
MASE(M3$N1234$xx,x,mean(abs(diff(M3$N1234$x)))) [1] 1.218 MASE(M3$N1234$xx,y,mean(abs(diff(M3$N1234$x)))) [1] 4.820
Очевидно, что вторая модель ошиблась по сравнению с первой в четыре раза. Но, к сожалению, по MASE особо больше нечего сказать.
А теперь масштабируем её относительно среднего абсолютного уровня (sMAE):
MASE(M3$N1234$xx,x,mean(abs(M3$N1234$x))) [1] 0.011 MASE(M3$N1234$xx,y,mean(abs(M3$N1234$x))) [1] 0.043
Получили примерно ту же картину, только эти значения можно измерять в процентах и они несут чуть больше смысла.
Ну, и напоследок рассчитаем GMRAE. Для этого для сначала дадим прогноз по модели Naive, чтобы было, с чем сравнивать:
es(M3$N1234$x,model="ANN",persistence=1,h=8)$forecast->z
А теперь посчитаем GMRAE:
GMRAE(M3$N1234$xx,x,z) [1] 1 GMRAE(M3$N1234$xx,y,z) [1] 4.877
Первая модель, как видим, дала точно такой же прогноз, как и Naive — GMRAE оказалась равной единице. Вторая же модель спрогнозировала ряд в несколько раз хуже, чем это сделала Naive.
В этом нашем примере все ошибки дали примерно один и тот же результат. Однако на других рядах данных результаты могут различаться. Попробуйте, например, используя всё те же модели, сравнить прогнозы на следующем условном ряде данных:
example <- rnorm(100,2,1)
-
Формирование ожиданий. Концепция адаптивных ожиданий. Модель «обучения на ошибках».
Формирование и
концепция
Ожидания – это
прогноз будущего со стороны экономических
субъектов.
Поскольку д/х и фирмы
стали принимать решения, ориентируясь
на долгосрочный период времени, то в
условиях стабильной и предсказуемой
экономики стал успешно использоваться
прошлый опыт. В отличие от кейнсианской
модели, в монетаристской модели экономики
фирмы и д/х являются активными
экономическими объектами. Они способны
не только адаптироваться к экономической
конъюнктуре и мероприятиям экономической
политики государства, но и своими
действиями активно влиять на результаты
этой политики. Действия самих экономических
агентов основаны на их ожиданиях. Так,
например, если экономика находится в
фазе спада, то политика правительства
будет оценена позитивно, что вызовет
рост потребления и инвестиций (т.е.
гос-во оказывает воздействие на ожидание
предпринимателей и населения) и наоборот.
Адаптивные ожидания
– ретроспективные ожидания, означающие,
что экономические субъекты прогнозируют
будущие значения экономических
показателей, основываясь исключительно
на их прошлых значениях.
Свойства адаптивных
ожиданий
-
Для составления
прогноза используется только информация
о прошлых значениях экономических
переменных.
-
Текущая информация
и информация о будущих событиях
игнорируется.
-
Происходит частичное
приспособление ожиданий к происходящим
переменам.
-
Систематическая
ошибка прогноза увеличивается, если
экономические переменные будут
изменяться не эпизодически, или случайно,
а постоянно. -
Адаптивные ожидания
пригодны в условиях стабильной экономики,
они обладают «индукционной способностью»
– если правительство поддерживает
неизменный темп роста экономических
переменных, то ожидаемые значения
приближаются к фактическим.
Модель обучения на
ошибках
Предполагается, что
адаптивные ожидания хозяйствующих
субъектов формируются с учетом прошлых
ошибок прогнозирования, т.е. включают
в себя корректировку прошлых прогнозов.
Если фактическое
значение параметра больше чем
прогнозировалось, то величина ожидаемого
значения корректируется в сторону
увеличения, если меньше – в сторону
уменьшения.
Пусть Pt
– фактическое значение параметра в
текущем периоде t, а Pet
– ожидаемое значение параметра в текущем
периоде t, которое было
спрогнозировано в предыдущем периоде
(t-1)
Величина (Pt-Pet)
является ошибкой прогноза, сделанного
в предыдущем периоде (t-1)
Для корректировки
ожиданий экономические субъекты
сравнивают в каждый период времени
ожидаемую величину параметра в прошлом
с фактическим его значением сейчас.
Величина корректировки пропорциональна
размеру ошибки прогноза, т.е. представляет
от него некую долю ʎ от этой ошибки, т.е:
∆Pe
=
Pet+1
—
Pet
=
ʎ(Pt
—
Pet),
где
0<=ʎ<=1
λ –
коэффициент адаптации
если λ
= 0, то прогноз никогда не меняется,
если λ
= 1, то статические ожидания
если 0<λ<1,
происходит постепенная корректировка
прогноза
Прогнозируемый
экономическим субъектом уровень цен
формируется на следующей основе:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
[c.57]
Другое дело систематические ошибки — они являются неслучайными и имеют определенную направленность. Такие ошибки очень опасны, так как приводят к искажению результатов статистического исследования. Эти ошибки, как правило, являются преднамеренными. Известно, например, что люди предпочитают преуменьшать свои доходы, округлять возраст, стараются показать большую осведомленность в области культуры, науки, чем это есть на самом деле. Предприятия также могут внести элементы недостоверности в свою информацию, особенно в те характеристики, от которых зависят величина налоговых платежей, расчеты с кредиторами и т. п. Все ошибки такого рода необходимо выявить и исправить. Поэтому после проверки полноты данных проводится их контроль — счетный и логический.
[c.39]
Ошибки регистрации — это отклонения между значением показателя, полученного в ходе статистического наблюдения, и фактическим, действительным его значением. Такой вид ошибок имеет место и при сплошном, и при несплошном наблюдениях. Ошибки регистрации бывают случайными и систематическими. Случайные ошибки — это результат действия различных случайных факторов (например, цифры переставлены местами, перепутаны соседние строки или графы при заполнении статистического формуляра). Систематические ошибки регистрации всегда имеют одинаковую тенденцию либо к увеличению, либо к уменьшению значения показателей по каждой единице наблюдения, и поэтому величина показателя по совокупности в целом будет включать в себя накопленную ошибку. Примером статистической ошибки регистрации при проведении социологических опросов может служить округление возраста населения, как правило, на цифрах, оканчивающихся на 5 и 0. Многие
[c.21]
Систематические ошибки репрезентативности появляются вследствие нарушения принципов отбора единиц из исходной совокупности, которые должны быть подвергнуты наблюдению. Для устранения ошибок наблюдения необходимо осуществить контроль полученной информации.
[c.22]
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (когда из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому отбор целесообразно начинать с середины первого интервала, например при 5%-ной выборке отобрать 10, 30, 50, 70-ю и с таким же интервалом последующие единицы.
[c.136]
Однако может оказаться, что данные о доходе, полученные в результате опроса, на самом деле являются искаженными, — например, в среднем заниженными, т.е. объясняющие переменные измеряются с систематическими ошибками. В этом случае люди, действительно обладающие доходом X, будут на самом деле тратить на исследуемый товар в среднем величину, меньшую, чем ДА), т.е. в рассмотренном примере объ-
[c.12]
Систематические ошибки измерения объясняющих переменных — одна из возможных причин того, что эконометрическая модель не является регрессионной. В экономических исследованиях подобная ситуация встречается достаточно часто. Одним из возможных путей устранения этого, как правило, довольно неприятного обстоятельства, является выбор других объясняющих переменных (эти вопросы рассматриваются в гл. 8 настоящего учебника).
[c.13]
Определение стандартных затрат имеет ряд недостатков, например, возможны систематические ошибки в определении нормативов и деструктивный результат от задания неадекватных норм и стандартов.
[c.101]
Если систематические ошибки (износ режущего инструмента, температурные деформации и т. д.) приводят к смещению средних значений, то применяются контрольные диаграммы для среднего значения или для медиан. Если же систематические ошибки приводят к увеличению разброса параметров,
[c.90]
Это означает, что отсутствует систематическая ошибка в определении линии регрессии, следовательно оценки параметров регрессии являются несмещенными, то есть математическое ожидание оценки каждого параметра равно его истинному значению.
[c.107]
В противном случае мы принимаем гипотезу HI. Это означает, что при заданном уровне значимости в уравнении регрессии присутствует систематическая ошибка, и это уравнение должно быть уточнено.
[c.125]
Текущие процедуры матричной оценки вторичных ценных бумаг, выпущенных на базе пула ипотек, подвергались критике за неадекватный учет возможностей, предоставляемых этими ценными бумагами (таких, как предоставляемая домовладельцам возможность производить авансовые выплаты по закладным в рассрочку). Эта возможность имеет свою внутреннюю стоимость, и то, что модель не в состоянии адекватно включить ее в цену вторичной ценной бумаги, порождает систематические ошибки.
[c.441]
В принципе надо учитывать только случайные потери, не поддающиеся прямому расчету, непосредственному прогнозированию и потому не учтенные в предпринимательском проекте. Если потери можно заранее предвидеть, то они должны рассматриваться не как потери, а как неизбежные расходы и входить в расчетную калькуляцию. Так, предвидимое движение цен, налогов, их изменение в ходе осуществления хозяйственной деятельности предприниматель обязан учесть в бизнес-плане. Только в силу несовершенства используемых методов расчета предпринимательской деятельности или недостаточно глубокой проработки бизнес-плана систематические ошибки могут рассматриваться как потери в том смысле что они способны изменить ожидаемый результат в худшую сторону. Следовательно, прежде, чем оценивать риск, обусловленный действием сугубо случайных факторов, крайне желательно отделить систематическую составляющую потери от случайных.
[c.117]
В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений п. Если число параметров при х — равно от и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.
[c.119]
Экспериментальные торговые районы были выбраны случайным образом из числа разрешенных, и таким же образом были сформированы 27 комбинаций условий. Очевидно, что использование заданного перечня районов могло внести систематическую ошибку в наши результаты, но мы надеялись, что и на этот раз
[c.175]
Общий объем выборки при этом остался равным 64. Во избежание систематической ошибки, связанной с различным количеством листвы в ярусах, ветви в каждом из них брались с таким расчетом, чтобы количество листьев на них было пропорционально общей массе листьев в этом ярусе.
[c.150]
При изучении правильности устанавливается общая приемлемость данного способа измерения (шкалы или системы шкал). Непосредственно понятие правильности связано с возможностью учета в результате измерения различного рода систематических ошибок. Систематические ошибки имеют некоторую стабильную природу возникновения либо они являются постоянными, либо меняются по определенному закону. Возможно, что последующие этапы окажутся излишними, если в самом начале выяснится полная неспособность данного инструмента на требуемом уровне дифференцировать изучаемую совокупность, иначе говоря, если окажется, что систематически не используется какая-то часть шкалы либо та или иная градация шкалы или вопроса. И, наконец, возможно, что исходный признак не обладает дифференцирующей способностью в отношении объекта измерения. Прежде всего нужно ликвидировать или уменьшить такого рода недостатки шкалы и только затем использовать ее в исследовании.
[c.155]
Визуализация объектов и процессов управления. При внедрении системы визуализации необходимо согласовывать характеристики электронных карт и образов управляемых объектов, используемых разными менеджерами. Это особенно важно из-за больших объемов данных. Пользователи-менеджеры, не имеющие опыта работы с ВИС-приложениями, пытаются создать план-карты образов в малом масштабе. В то же время для решения задач информационного менеджмента, например наладки тепловой сети, и для визуализации других управляемых сетей необходимо для исключения систематической ошибки иметь образы большого масштаба.
[c.199]
Надежность. При изучении различных аспектов разработки и использования тестов важную роль играет анализ ошибок измерения, ибо при составлении тестов, как и в любой работе, возможны ошибки. Обычно выделяют три класса ошибок промахи, систематические ошибки и случайные ошибки.
[c.78]
Систематические ошибки остаются постоянными или закономерно меняются от измерения к измерению и в силу этих особенностей могут быть предсказаны заранее, а в некоторых случаях и устранены. К этой группе относятся ошибки, возникающие в связи с использованием различных методов сбора данных.
[c.78]
Систематическую ошибку можно устранить, изменив процедуру формирования выборки. Случайная же ошибка будет присутствовать всегда, при любом выборочном опросе для общего результата значительно опаснее систематическая, так как по выборке ее невозможно выявить и оценить. Случайная ошибка подчиняется определенным законам и, используя статистические методы, ее можно оценить.
[c.150]
В-третьих, метод статистических испытаний дает систематическую ошибку, возникающую вследствие подмены подлинных вероятностей относительными частотами, и для получения выводов с необходимой точностью иногда требуется огромное количество испытаний, находящееся на пределе возможностей вычислительной техники (чтобы получить в ответе еще один верный десятичный знак, нужно увеличить число имитаций в 100 раз).
[c.24]
Правильность анализа определяется близостью к нулю его систематической ошибки (отклонением математического ожидания серии измерений от истинного значения).
[c.63]
Правильность анализа характеризуется близостью к нулю его систематической ошибки, оцениваемой по результатам внешнего геологического контроля. При внешнем контроле повторный (контрольный) анализ проб выполняется в другой, более квалифицированной лаборатории. Критерием правильности анализов служит при этом величина t [c.88]
Средние содержания ценных компонентов обычно рассчитывают способом взвешивания по мощности. Однако при подсчете часто приходится иметь дело со столовыми (видимыми) значениями мощности, причем пересчет их в истинные значения не всегда может быть осуществлен достаточно надежно. Расчет средних при этом обычно ведут со взвешиванием по значениям стволовых мощностей. Такое взвешивание может приводить к систематическим ошибкам, если между углами встречи тела полезного ископаемого выработками и качеством сырья в отдельных его частях возникает некоторая связь. Так, на полиметаллическом месторождении Степное (Казахстан) вертикальные скважины закономерно пересекали среднюю часть седловидной залежи под углами, близкими к прямому, а фланговые части — под более острыми углами, что определяло повышенные значения стволовых мощностей на флангах и пониженные в центре (рис. 3.8). Однако фланговые части залежи на крыльях антиклинали как раз характеризовались пониженным качеством руд. Взвешивание по стволовым мощностям приводило в данном случае к занижению среднего качества руд по залежи в целом. Аналогичные погрешности могут возникать при разведке неоднородных по качеству сырья линейных тел веерными скважинами.
[c.90]
Особенно необходимо учитывать случайные потери, не поддающиеся прямому расчету, непосредственному прогнозированию и потому неучтенные в предпринимательском проекте. Если потери можно заранее предвидеть, то они должны рассматриваться не как потери, а как неизбежные расходы и включаться в расчетную калькуляцию. Так, предвидимое движение цен, налогов, их изменение в ходе осуществления хозяйственной деятельности необходимо учесть в бизнес-плане. Только в силу несовершенства используемых методов расчета производственной деятельности систематические ошибки могут рассматриваться как потери в том смысле, что они способны изменить в худшую сторону ожидаемый результат.
[c.35]
Задача может быть модифицирована и обобщена в различных направлениях. Жесткое ограничение — несмещенность оценки (равенство нулю систематической ошибки) обычно можно ослабить и заменить ограничениями сверху и снизу величины первого момента ошибок про-
[c.41]
В общем случае при постановке задачи о сглаживании и прогнозе случайных процессов исключение систематических ошибок экстраполяции (равенство нулю первого момента ошибок упреждения) не является обязательным и тем более единственным требованием рациональной фильтрации или рационального прогнозирования. Больше того, в ряде случаев целесообразно расширить область определения задачи и заменить требование о нулевых систематических ошибках ограничениями на их величину. Могут быть указаны и другие неравенства и логические соотношения, которым в тех или иных содержательных задачах фильтрации и прогноза должны удовлетворять, сглаженные или упрежденные точки. Например, может быть ограничена дисперсия или корреляционные моменты случайных величин, зависящих от г (/о + п) и (М- Можно указать содержательные постановки, в которых область определения задачи естественно задавать вероятностными или жесткими ограничениями. Таким образом, в общем случае ограничения задачи сглаживания и экстраполяции высекают в Я не линейное подпространство и не линейное многообразие, а некоторую выпуклую или невыпуклую область G.
[c.309]
Свяжем с задачей А задачу А» прогнозирования по минимуму дисперсии при [нулевых систематических ошибках прогноза. Задача А формулируется следующим образом.
[c.329]
Увольнение в связи с обнаружившимся несоответствием рабочего или служащего занимаемой должности или выполняемой работе вследствие недостаточной квалификации либо состояния здоровья, препятствующих продолжению данной работы (п. 2 ст. 33 КЗоТ). Признаками несоответствия вследствие недостаточной квалификации могут быть систематические ошибки при выполнении порученной работнику работы, невыполнение нормы выработки, брак и т. п. Расторжение трудового договора в случаях, предусмотренных в п. 2 ст. 33 КЗоТ, недопустимо с работниками, не имеющими необходимого опыта работы в связи с непродолжительностью трудового стажа, а также по мотиву отсутствия специального образования, если оно, согласно закону, не является обязательным условием при заключении трудового договора (79, п. И).
[c.545]
Оба вида ошибок могут иметь случайный и систематический характер. Случайные ошибки возникают по разным случайным причинам (описка, пропуск, неточный подсчет и т. д.) и воздействуют на точность данных как в сторону их увеличения, так и уменьшения. При достаточно большом количестве наблюдений согласно закону больших чисел эти ошибки взаимно погашаются и не оказывают существенного влияния на точность наблюдений. Систематические ошибки возникают по какой-либо определенной причине и вызывают одностороннее изменение данных (ошибки программы наблюдений, нарушение принципов отбора объектов наблюдения и т. п.), искажая их. Мерами предупреждения этих ошибок является правильное определение количества наблюдений, обоснованный выбор объектов наблюдения и др.
[c.91]
Такая же опасность возникает при замене по какой-либо причине единиц, попавших в выборку, другими единицами (например, вместо отобранного домохозяйства, где в момент прихода интервьюера никто не открыл дверь, был проведен опрос в соседней квартире или интервьюер встретил решительный отказ участвовать в опросе и был вынужден пойти на замену домохозяйства). Как отмечает социолог В. И. Паниотто, систематические ошибки представляют собой некоторое постоянное смещение, которое не уменьшается с увеличением числа опрошенных и вызвано недостатками и просчетами в системе отбора респондентов. Если, например, для изучения общественного мнения жителей города в архитектурном управлении получить сведения о жилом фонде и из всех имеющихся в городе квартир отобрать случайным образом 400 квартир, а затем предложить интервьюерам опросить всех, кого они застанут в момент посещения в этих квартирах, то полученные данные не будут репрезентативны. Допущена систематическая ошибка более подвижная часть населения попадает в выборку в меньшей пропорции, а менее подвижная — в большей пропорции, чем в генеральной совокупности. Пенсионеров, например, можно чаще застать дома, чем студентов-вечерников. При увеличении выборки эта ошибка не устраняется если мы проведем опрос в 800 квартирах или даже во всех квартирах города (сплошной опрос), то полученные данные будут репрезентативны для населения, находящегося дома в момент прихода интервьюера, а не для всех жителей города.
[c.164]
Чтобы минимизировать систематическую ошибку, возникающую при оптимизации, мы ограничились простым перекрестным правилом скользящих средних (СМА = rossing-Moving-Averages) — это правило торговли пропагандируют Брок и др. [56]. Правило очень простое в том отношении, что в вычислении индикатора не участвуют числа Фибоначчи. Здесь важно, что технический анализ стремится предсказать, главным образом, направление изменения цены (вниз, вверх, на том же уровне), а не величину этого изменения.
[c.215]
Можно еще дальше усовершенствовать эксперимент, связанный с определением урожайности культуры и зависимый от качества обработки почвы. Если каждого рабочего закрепить за определенным полем, то вследствие различности почв может появиться систематическая ошибка. Обозначим поля буквами W, X, У, ZH определим условия эксперимента рабочих между полями таким образом, чтобы каждый из них обслуживал поле только один день. В этом случае получим план, называемый греко-латинским квадратом, который позволяет усреднить влияние таких факторов, как день, поле, рабочий (табл. 4.6).
[c.160]
НЕСМЕЩЕННАЯ ОЦЕНКА [unbiased estimator] — статистическая точечная оценка, математическое ожидание которой совпадает с оцениваемой величиной (у нее нет систематической ошибки).
[c.226]
СИСТЕМАТИЧЕСКАЯ ОШИБКА [systemati error] — понятие математической статистики — ошибка, которая постоянно либо преувеличивает, либо преуменьшает результаты измерений оценок наблюдаемых величин) в результате воздействия определенных факторов, систематически влияющих на эти измерения и изменяющих их в одном направлении (в отличие от случайных ошибок). Оценки, лишенные систематических ошибок, называются несмещенными оценками.
[c.327]
Расчетное значение критерия t сравнивается с табличным значением статистического критерия Стьюдента для данного числа пар и выбранного уровня значимости. Систематическая ошибка считается отсутствующей, если tpa 4 < табл.
[c.88]
Однострелочные секундомеры простого действия используют для измерения элементов операций по отдельным отсчетам затрат времени при выборочном и цикловом методах хронометража. Они имеют одну основную центральную стрелку, движущуюся по круговому циферблату, шкала которого может иметь секундную или деся- тичную градуировку. Пределы измерения шкалы 30 или 60 с. Секундомер может иметь один или два дополнительных счетчика для отсчета целого числа минут, прошедших с момента начала наблюдения. Их недостаток — малая точность при хронометрировании по текущему времени вследствие накопления систематической ошибки, вызываемой накапливанием запаздываний в пуске стрелки после считывания показаний. Этого недостатка лишен однострелочный секундомер суммирующего действия. Но он более сложен по конструкции и менее надежен в работе.
[c.139]
Минимизация систематической ошибки. Практическое использование излагаемых выше предложений по повышению устойчивости оценок коэффициентов регрессии наталкивается на следующие неопределенности. Какую минимизируемую функцию риска выбрать Все предлагаемые оценки содержат параметры v — в п. 7.2.1, k — в п. 7.2.2 и К — в п. 7.2.3 и 7.2.4. Какими брать значения этих параметров Если полезно уменьшать веса больших отклонений прогнозируемой переменной, то, может быть, полезно взвешивать и предикторные переменные [c.221]
Для анализа результатов расчета прогноза, в продолжение ряда вы можете рассчитать следующие ошибки:
- MAPE – средняя абсолютная ошибка в % . Ошибка оценивает на сколько велики ошибки в сравнении со значением ряда и с ошибками в соседних рядах.
Подробнее читайте в статье на нашем сайте: http://4analytics.ru/metodi-analiza/mape-%E2%80%93-srednyaya-absolyutnaya-oshibka-praktika-primeneniya.html - MRPE – средняя относительная ошибка в %, оценивает на сколько велика дельта между фактом и прогнозом. Чем ближе к 100%, тем больше ошибка, чем ближе к нулю, тем ошибка меньше.
- MSE – средняя квадратическая ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mse-%E2%80%93-srednekvadraticheskaya-oshibka-v-excel.html - MPE – средняя процентная ошибка – показывает завышен или занижен прогноз относительно факта. Если ошибка меньше нулю, то прогноз последовательно завышен, если ошибка больше нуля, то прогноз последовательно занижен.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mpe-%E2%80%93-srednyaya-procentnaya-oshibka-v-excel.html - MAD – среднее абсолютное отклонение. Используется, когда важно измерить ошибку в тех же единицах, что и исходный ряд.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/planirovanie-i-prognozirovanie-praktika/dopolnitelnie-oborotnie-sredstva-za-schet-povisheniya-tochnosti-prognoza.html - A MAPE – ошибка, которая показывает отклонение средних значений ряда к средним значениям модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
- S MAPE – ошибка, которая показывает отклонение суммы значения ряда к сумме значений модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
А также 2 показателя «Точность прогноза»:
- Точность прогноза = 1 – МАРЕ
- Точность прогноза 2 = 1 – MRPE
Для расчета ошибок одновременно с прогнозом, нажимаем кнопку «Расчет ошибок» в меню «FORECAST»
В открывшемся окне выбираем нужные для расчета ошибки:
Теперь при расчете прогноза, в продолжение ряда, программа автоматически сделает расчет отмеченных Вами ошибок: