В прогнозировании есть одна простая истина, к которой прогнозисты пришли достаточно давно: высокая точность аппроксимации данных не гарантирует высокую точность прогнозов. Это означает, что модель, дающая наименьшие ошибки по обучающей выборке, не обязательно даст такие же наименьшие ошибки по тестовой выборке. Противоположное («чем лучше аппроксимация, тем точнее прогноз») вообще возможно лишь для обратимых процессов, в которых никаких качественных изменений не происходит. Но, как мы знаем, в мире нет ничего более постоянного, чем перемены.
Впрочем, помимо этой простой истины есть ещё и другая: модель, заведомо плохо аппроксимирующая ряд данных, навряд ли даст точный прогноз. Это в свою очередь означает, что для получения более точных прогнозов, модель должна точно описывать ряд по внутренней выборке, быть адекватной поставленной задаче и включать все существенные переменные. Потому что, если модель представляет собой очень грубое и условное описание объекта, то по ней нельзя сделать адекватных выводов о самом объекте исследования.
Как видим, перед нами противоречие: модель должна хорошо описывать данные, но хорошее описание не гарантирует получения точных прогнозов. Противоречие решается достаточно легко, если следовать одному из базовых буддистский принципов — придерживаться срединного пути. Но как же найти эту середину? Для этого надо просто научиться оценивать качество построенной модели. А в этом нам помогут различные графики и ряд коэффициентов.
Графический анализ моделей
С графическим анализом всё просто. Все те инструменты, которые мы рассмотрели ранее в параграфе «Графический анализ данных«, сейчас нам пригодятся для того, чтобы понять, какая из моделей лучше и почему. Как всё это сделать в R мы так же уже рассматривали ранее, так что не будем тратить в этот раз время на примеры.
Самый простой метод оценки полученной модели — линейный график. На него достаточно нанести фактические значения, расчётные и прогнозные. Так мы сможем увидеть, как модель описала данные и насколько полученный прогноз соответствует сложившейся динамике. Более того, так можно понять (на основе знаний о прогнозируемом процессе), насколько полученные прогноз правдоподобен.
Очень простой пример с линейным графиком показан наследующем рисунке.
Линейный график по несезонной модели ETS(M,N,N)
На нём показан ряд фактических значений (чёрная сплошная линия «Series»), ряд расчётных (фиолетовая пунктирная линия «Fitted values»), точечный прогноз (синяя сплошная линия «Point forecast») и 95% прогнозный интервал («95% prediction interval»). Уже глядя на этот график можно сделать несколько выводов:
- Ряд фактических значений был описан моделью неплохо, хотя основные характеристики ряда выявлены не были — это видно потому что расчётные значения всё время как будто отстают от фактических на один шаг. К тому же, ряд расчётных значений не такой гладкий, как хотелось бы и в ряде наметились элементы сезонности (это особенно чётко видно с 1986 года) — каждый четвёртый квартал виден пик показателя. Это не криминал, но может говорить о том, что стоило бы обратиться к другой модели либо другому методу оценивания.
- Прогноз по нашей модели представляет собой прямую линию, параллельную оси абсцисс. Это хороший прогноз в случае, если ряд данных не имеет явной тенденции к росту либо снижению. Однако в нашем случае ряд данных явно демонстрирует увеличение показателя во времени. Поэтому такая тенденция в будущем хоть и возможна, но, скорее всего, не соответствует ожиданиям. Для того, чтобы здесь сделать какой-то однозначный вывод, нужно, конечно, понимать, с каким показателем мы имеем дело, и насколько реалистичен такой сценарий на практике.
- Прогнозные интервалы значительно расширяются и к последнему наблюдению составляют 5800 — 6500. Опять же, такие широкие интервалы — это не страшно, но одна из потенциальных причин этой ширины — неправильно выбранная (или специфицированная) модель. Так же на возможно неправильно выбранную модель указывает неровность прогнозного интервала при таком ровном прогнозе. Возможно, всё-таки надо было использовать другую модель (с трендом и сезонностью), а, может быть, мы не учли какие-то важные факторы.
На основе этих пунктов уже можно заключить, что стоит попробовать ещё какую-нибудь модель для прогнозирования этого ряда данных.
Если мы используем для выбора модели процедуру ретропрогноза, то на тот же самый график стоит нанести значения из проверочной выборки. Другая модель, построенная по тому же ряду данных, показана на рисунке ниже.
Линейный график по сезонной модели ETS(M,A,M)
По этому рисунку тоже можно сделать ряд выводов:
- Фактические значения описаны этой моделью лучше, чем предыдущей, но всё ещё есть ряд промежутков, аппроксимированных моделью не очень хорошо (как, например, наблюдение в начале 1984 года). Возможно, это говорит о том, что в это время происходили какие-то события, которые наша экстраполяционная модель не может уловить, а, может быть, нужно просто изменить метод оценки модели. При прогнозировании на практике стоит выяснить, что происходило в эти моменты, чтобы понять, носят ли эти события чисто случайный характер.
- Прогноз по модели получился с учётом сезонности, и, как видно по тестовой выборке, это сыграло модели на руку — она дала прогноз точнее, чем это сделала бы предыдущая модель ETS(M,N,N).
- Прогнозный интервал оказался уже, чем в предыдущем случае и по своей динамике соответствует поведению точечного прогноза (что говорит о том, что мы смогли уловить важные элементы ряда).
В общем, всё в этом графике указывает на то, что стоит обратиться к модели с трендом и сезонностью.
В ряде случаев по одному лишь линейному графику бывает сложно сделать выводы о качестве модели. Например, те же самые выбросы оценить по нему на глаз непросто. В этом случае нужно обратиться к графикам по остаткам модели. Даже простой линейный график по остаткам может дать много полезной информации.
Однако прежде чем приступать к непосредственному анализу, надо понять, что нам нужно. В идеальной модели остатки ни от чего не зависят, выглядят распределёнными случайно и желательно даже нормально. Графически это должно выражаться отсутствием какой-либо предсказуемости в остатках и ровными гистограммами и ящичковыми диаграммами.
На следующих рисунках приведены четыре графика по остаткам модели ETS(M,N,N) (той, которая соответствует первому графику в этой статье).
Линейный график по остаткам модели ETS(M,N,N)
Гистограмма по остаткам модели ETS(M,N,N)
Ящичковая диаграмма по остаткам модели ETS(M,N,N)
Точечная диаграмма по остаткам модели ETS(M,N,N)
Взглянем критически на эти графики и попробуем вынести какую-нибудь полезную информацию.
- Линейный график по остаткам демонстрирует периодические колебания (которые особенно заметны примерно с 1986 года) — это всё из-за того, что мы не учли в модели сезонность. По остаткам она видна более явно, чем по графику по исходному ряду.
- Гистограмма по остаткам демонстрирует явную асимметрию: очень много ошибок лежит выше нуля (справа). Это так же указывает на неправильную спецификацию модели. Обычно исследователи при построении разных моделей стараются добиваться нормально распределённых остатков, но это требование на практике очень сложно удовлетворить. Именно поэтому нам нужно, чтобы они были хотя бы симметрично распределены относительно нуля. Это будет указывать на то, что модель построена без систематических ошибок.
- Ящичковая диаграмма показывает то же, что и гистограмма: мы имеем дело с асимметричным распределением. Помимо этого она ещё показала, что практически все отрицательные остатки можно статистически считать выбросами — то есть они настолько редко случаются, что играют небольшую роль в описательной способности модели. На себя так же обращает внимание завышенное среднее значение ошибки (красная точка по середине ящичка) — это так же сигнализирует о неправильной спецификации.
- Точечная диаграмма, построенная по расчётным значениям (Fitted) и абсолютным остаткам модели была построена для дополнительной информации. Она нам может показать, есть ли в модели гетероскедастичность. Другими словами, постоянна ли дисперсия остатков модели. Видно, что при меньших расчётных значениях остатки лежат в пределах от нуля до 0.015, в то время как при достижении 6000 по оси абсцисс разброс увеличивается. Это указывает на непостоянность дисперсии, что в свою очередь опять говорит о возможных проблемах модели.
Теперь рассмотрим точно такие же графики, но уже по модели с трендом и сезонностью.
Линейный график по остаткам модели ETS(M,A,M)
Гистограмма по остаткам модели ETS(M,A,M)
Точечная диаграмма по остаткам модели ETS(M,A,M)
Ящичковая диаграмма по остаткам модели ETS(M,A,M)
По ним можно заключить следующее:
- Линейный график демонстрирует более случайный характер распределения остатков, чем в предыдущем примере. Та самая пресловутая сезонность уже менее заметна. Но на себя обращают внимание три отрицательные ошибки, соответствующие 1984, 1989 и 1990 годам. Возможно, у таких ошибок есть какое-то объяснение. На практике стоило бы выяснить, что происходило в эти кварталы для того, чтобы улучшить описательные и прогнозные свойства модели.
- Гистограмма имеет более симметричный вид. Если бы не те несколько отрицательных ошибок, она бы выглядела вообще прекрасно.
- Ящичковая диаграмма так же демонстрирует большую симметрию относительно нуля (по сравнению с предыдущей моделью), а так же указывает на наличие нескольких выбросов. Это те самые отрицательные ошибки, которые мы отметили ранее. Всё-таки что-то с ними надо сделать!
- Последний график всё так же, как и в предыдущем примере указывает на наличие гетероскедастичности. Это значит, что при построении прогнозных интервалов сей неприятный эффект надо учесть, иначе интервалы могут оказаться либо слишком узкими, либо излишне широкими.
Как видим, на основе такого небольшого анализа можно получить много полезной информации об аппроксимационных свойствах модели и принять решение о том, что делать с моделью либо к какой модели обратиться.
Но помимо приведённых графиков есть ещё один, специализированный, который позволяет сравнивать распределение случайной величины с некоторым заданным. Называется он «квантиль-квантиль» потому что позволяет проводить поквантильное сравнение фактических и теоретических значений. Пример такого графика представлен на этом рисунке:
График квантиль-квантиль по остаткам
По нему видно, что наблюдения, находящиеся в хвостах распределения выбиваются и из-за них распределение остатков оказывается непохожим на нормальное. В идеале мы хотели бы, чтобы все точки на графике находились если не непосредственно на прямой линии, то хотя бы близко к ней, вокруг неё.
Как это сделать в R
В R такой график можно построить с помощью функций qqplot() и qqline(). Если нас интересует сравнение с нормальным распределением, то можно так же использовать функцию qqnorm(). Например:
x <- rnorm(100,0,1) qqnorm(x) qqline(x)
Попробуйте и посмотрите, какой получится график.
Коэффициенты для оценки качества моделей
Но, конечно же, одним графическим анализом ограничиваться не стоит. Очевидно, что глаз не всегда может увидеть то, что легко показал бы какой-нибудь коэффициент.
Первая группа коэффициентов, которые могут использоваться для оценки качества, обычно используется на остатках модели. Это все те статистические показатели, которые мы рассмотрели раньше в параграфе «Статистический анализ данных». Ничего нового и интересного относительно них сказать нельзя, поэтому здесь на них мы останавливаться не будем.
Добавим в нашу коллекцию два коэффициента, которые могут помочь при оценке описательной способности модели. Первый — это коэффициент корреляции, рассчитанный по фактическим и расчётным значениям. Чем ближе коэффициент к единице, тем в среднем ближе связь между этими значениями к линейной, то есть тем точнее описаны данные нашей моделью. Этот коэффициент мы уже обсуждали в параграфе «Выявление связей между переменными».
Второй полезный коэффициент — коэффициент детерминации. Он показывает процент объяснённой моделью дисперсии и рассчитывается по формуле:
begin{equation} label{eq:mq_Rsquared}
R^2 = 1 -frac{SSE}{TSS} ,
end{equation}
где ( SSE = sum_{t=1}^T e_t^2 ) — это сумма квадратов ошибок модели (иногда обозначается ещё как RSS, SSR), (TSS = sum_{t=1}^T (y_t -bar{y})^2) — сумма квадратов отклонений фактических значений от средней величины. Здесь SSE соответствует «Sum of Squared Errors», RSS — «Residuals Sum of Squares», SSR — «Sum of Squared Ressiduals», TSS — «Total Sum of Squares». Все эти суммы квадратов на самом деле близки по смыслу к дисперсии остатков и дисперсии по исходному ряду данных. Просто в формуле eqref{eq:mq_Rsquared} не происходит деление на число наблюдений.
Коэффициент детерминации более популярен в регрессионном анализе, нежели в других разделах прогнозирования, но может спокойно использоваться и при оценке экстраполяционных моделей. В случае, если модель идеально описывает ряд данных, SSE становится равной нулю, в результате чего (R^2) становится равен единице. Если же модель ряд совсем не описывает, а представляет собой просто прямую линию, то коэффициент детерминации становится равным нулю. В случаях с нелинейными моделями коэффициент может так же становиться отрицательным, но при этом неинтерпретируемым.
Несмотря на то, что коэффициент детерминации показывает этот самый процент той самой объяснённой дисперсии, сильно полагаться на него не стоит. Во-первых, он считается по обучающей части выборки, а значит просто показывает, насколько хорошо мы описали данные. При этом точность описания не гарантирует точность прогнозов. В некоторых случаях даже наоборот: излишне точное описание приводит к ухудшению прогнозных свойств модели (так как та начинает слишком сильно реагировать на шум). Простой пример — полиномы: чем выше степень полинома, тем выше (R^2), но тем обычно хуже точность прогнозов. Во-вторых, коэффициент детерминации будет всегда тем выше, чем выше число параметров в модели. То есть (R^2) у модели (y = a_0 + a_1 x_1 + e) будет всегда ниже, чем у модели (y = a_0 + a_1 x_1 + a_2 x_2 + e), даже если (x_2) в принципе ненужен. Именно поэтому иногда в эконометрике обращаются к так называемому скорректированному коэффициенту детерминации — (R^2)-adjusted. Но о нём мы поговорим в следующем параграфе.
В заключение по коэффициенту детерминации хотелось бы лишь добавить, что при построении моделей он не должен являться самоцелью: «Посмотрите, какая у меня хорошая модель получилась: (R^2=0,936)!» — типичная ошибка начинающих аналитиков. (R^2) может выступать лишь индикатором того, насколько модель адекватна. Низкие значения коэффциента детерминации могут указывать на то, что модель особого смысла не имеет, но при этом высокие значения не говорят о том, что перед нами хорошая модель.
По коэффициентам аппроксимации у меня всё. Но, если бы мы ограничивались лишь анализом аппроксимационных свойств моделей, то не было бы смысла вообще писать этот параграф. Нас, ведь, на самом деле больше интересует оценка точности прогнозов. Оценить её можно при использовании процедуры ретропрогноза. В этом случае наш интерес сдвигается с того, как модель себя повела на обучающей выборке на то, как она себя повела на тестовой. И здесь уже есть, куда развернуться.
Конечно, анализ этот можно проводить по аналогии с анализом обычной случайной величины, а значит и использовать весь стандартный набор коэффициентов, но в некоторых случаях стандартные методы просто неприменимы, а в других случаях не дадут полной информации о прогнозных свойствах моделей.
Например, коэффициент MAE, к которому мы обращались в параграфе «Простые методы оценки параметров моделей», будет в этом случае рассчитываться так:
begin{equation} label{eq:mq_MAE}
text{MAE} = frac{1}{h} sum_{j=1}^h | e_{T+j} |,
end{equation}
где (e_{T+j}) — ошибка на прогнозном шаге j, h — срок прогнозирования, T — номер последнего наблюдения в обучающей выборке.
У этого коэффициента есть два недостатка, которые проявляются только в случае анализа прогнозной точности моделей:
- Его значение сложно интерпретировать. Вот, допустим, получилось, что (MAE = 1547.13). О чём это говорит? Это много или мало? Если сравнить с другой моделью, то станет, конечно, ясно. Но какова будет реакция начальника, когда на вопрос прогнозисту: «Штурман, приборы?» — он услышит: «1547.13»?
- С помощью этого коэффициента можно проводить сравнение только между моделями по одному ряду данных. Но на практике часто стоит задача понять, как себя ведёт модель по нескольким рядам данных по сравнению с другими моделями. И тут уже полученные по разным рядам MAE складывать друг с другом нельзя, так как при сложении яблок с гвоздями получается абсурд.
Для того, чтобы так или иначе справиться с одной из или обеими этими проблемами, было разработано несколько коэффициентов.
MAPE — «Mean Absolute Percentage Error» — Средняя абсолютная процентная ошибка:
begin{equation} label{eq:mq_MAPE}
text{MAPE} = frac{1}{h} sum_{j=1}^h frac{| e_{T+j} |}{y_{T+j}},
end{equation}
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что (MAPE = 11.4%), то это говорит о том, что ошибка составила 11,4% от фактических значений. Этот коэффициент можно легко складывать по разным рядам. Можно даже рассчитать MAPE и изучить его распределение, используя инструменты статистического анализа. С другой стороны, можно отбросить в eqref{eq:mq_MAPE} часть, отвечающую за «Mean»:
begin{equation} label{eq:mq_APE}
text{APE} = frac{| e_{T+j} |}{y_{T+j}},
end{equation}
и изучить распределение прогнозных ошибок на некоторый шаг j, используя всё те же статистические методы. Можно вместо «M», средней, посчитать «Md», медиану. Можно обратиться к квантилям… В общем, ни в чём себе не отказывайте, чувствуйте себя как дома!
Но, конечно же, без проблем быть не может. Из-за деления на фактические значения этот коэффициент оказался чувствительным к масштабу. Так, в случае, если (y_{T+j}) близко к нулю, то значение eqref{eq:mq_APE} из-за деления на очень маленькое число взлетит. А уж если (y_{T+j}=0), то нас вообще ждёт бедствие вселенского масштаба.
Но на этом ещё не всё. Коэффициент по разному относится к положительным и отрицательным ошибкам. Допустим, что наш точечный прогноз на 137-м наблюдении составил (hat{y}_{137} = 20), а фактическое значение при этом было (y_{137}=10). Какой будет ошибка APE в этом случае? Подставим эти значения в формулу eqref{eq:mq_APE}, чтобы получить (frac{|10-20|}{10}=1=100%). А какой была бы ошибка, если бы фактическое значение было равно 30? Очевидно, что (frac{|30-20|}{30}=0,33(3)=33.(3)%). Вроде бы ошибка та же, но, по объективным причинам, она во втором случае составляет 33.3% от фактического значения, а не 100%. Получается, что этот коэффициент жестче относится к случаям завышенных прогнозов, чем заниженных. В случае с агрегированием прогнозов по разным значениям, это приводит к искажениям — прогнозист не получает достоверной информации о том, насколько его прогноз точен. Такая асимметрия не могла не привести к появлению других коэффициентов.
Один из вариантов решения проблемы предложили Spyros Makridakis и Michele Hibon, назвав коэффициент SMAPE — «Symmetric MAPE» — симметричная MAPE:
begin{equation} label{eq:mq_SMAPE}
text{SMAPE} = frac{1}{h} sum_{j=1}^h frac{2 | e_{T+j} |}{|y_{T+j}| + |hat{y}_{T+j}|} .
end{equation}
Число «2» в этой формуле не случайно. Дело в том, что в соответствии с первоначальной задумкой в знаменателе должно быть среднее между фактическим и расчётным значениями: (bar{y_t} = frac{y_t + hat{y}_t}{2} ). При подстановке этого значения в знаменатель, двойка переносится в числитель, поэтому мы и получаем то, что получаем.
Трактовка у коэффициента примерно такая же, как и у MAPE: какой процент составляет ошибка от этой самой величины (bar{y_t}).
Идея, надо сказать, хорошая, но, конечно же, всё так же не лишена проблем. Коэффициент должен бы быть симметричным, но таковым до конца не является. Рассмотрим это на примере. Пусть наш прогноз на всё том же 137-м наблюдении составил (hat{y}_{137} = 110), а фактическое значение было (y_{137} = 100). SMAPE в этом случае составит (frac{2 cdot |100 — 110|}{100+110} = 9.52%). Если же прогноз оказался заниженным и составил (hat{y}_{137} = 90), то SMAPE получится равным (frac{2 cdot |100 — 90|}{100+90} = 10.53%). То есть, опять же, коэффициент демонстрирует смещение, только в этот раз в сторону завышенных прогнозов: завышенные прогнозы приводят к меньшей ошибке, чем заниженные. Сейчас уже в среде прогнозистов сложилось более-менее устойчивое понимание, что SMAPE на является хорошей ошибкой. Тут дело не только в завышении прогнозов, но ещё и в том, что наличие прогноза в знаменателе позволяет манипулировать результатами оценки. Кроме того, неясно, что именно минимизирует SMAPE. Поэтому я бы лично рекомендовал эту ошибку не использовать при оценки прогнозов (да, мы её активно использовали в нашем учебнике по прогнозированию, но сейчас я бы этого не стал делать).
Это, конечно же, не могло не привести к появлению ещё нескольких коэффициентов.
MASE расшифровывается как «Mean Absolute Scaled Error» и переводится как «Средняя абсолютная масштабированная ошибка». Предложена была Робом Хайндманом и Анной Коелер и рассчитывается так:
begin{equation} label{eq:mq_MASE}
text{MASE} = frac{T-1}{h} frac{sum_{j=1}^h | e_{T+j} |}{sum_{t=2}^T |y_{t} — y_{t-1}|} .
end{equation}
Обратите внимание, что в eqref{eq:mq_MASE} мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза по методу Naive. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тендецию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Но, конечно же, без минусов нельзя. Проблема MASE в том, что её тяжело интерпретировать. Например, (MASE = 1.21) ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более. Показывать шефу эти цифры опасно для жизни аналитика.
Можно, конечно, знаменатель eqref{eq:mq_MASE} заменить на простую среднюю по всему ряду, чтобы получить другую среднюю абсолютную масштабированную (относительно среднего уровня ряда) ошибку (sMAE — scaled MAE, иногда обозначается как MAE/mean). Для пущей безопасности в знаменателе можно взять среднее абсолютное значение ряда:
begin{equation} label{eq:mq_MASALE}
text{sMAE} = frac{T}{h} frac{sum_{j=1}^h | e_{T+j} |}{sum_{t=1}^T |y_{t}|} .
end{equation}
Модуль в знаменателе нужен для ситуаций, когда мы имеем дело как с положительными, так и отрицательными величинами, средняя величина по которым может быть близка к нулю. Если в такой ситуации брать просто среднюю, мы столкнёмся со всё той же проблемой масштаба. В общем случае значение eqref{eq:mq_MASALE} будет показывать, какой процент от средней составляют ошибки прогноза. Эта величина всё так же будет несмещённой (по сравнению с MAPE и SMAPE), и может легко складываться с другими такими же величинами. Единственная проблема — тренд в ряде данных может влиять на итоговое значение eqref{eq:mq_MASALE}. Но зато такой коэффициент легче интерпретировать, чем eqref{eq:mq_MASE} — эта ошибка может легко измеряться в процентах.
Заметим, знаменатель sMAE может быть равен нулю только в одном случае — если все фактические значения в обучающей выборке оказались равны нулю. Такое возможно лишь в ситуациях с целочисленным спросом, если в распоряжении исследователя ещё не было ни одного ненулевого значения. В общем, очень экзотическая ситуация, в которой надо обращаться к нестатистическим методам прогнозирования. А так ошибка может использоваться как при прогнозировании положительных, так и отрицательных значений.
sMAE — практически идеальный показатель. У него есть лишь один небольшой недостаток — он никак не ограничен сверху. То есть теоретически возможны ситуации, когда (sMAE = 1000%) (например, когда в проверочной выборке продажи неожиданно взлетели в разы, а в обучающей до этого составляли единицы), и с этим ничего не поделать. Такие ситуации, впрочем, тоже необычны, нечасто встречаются и будут приводить к похожим результатам во всех рассмотренных выше ошибках.
Ну, и не забываем о том, что вместо средней «M» в eqref{eq:mq_MASE} и eqref{eq:mq_MASALE} можно использовать и что-нибудь другое…
Но и даже на этом ещё не всё. Роберт Файлдс в 1992 году предложил нечто под названием «GMRAE» — «Geometric Mean Relative Absolute Error»:
begin{equation} label{eq:mq_GMRAE}
text{GMRAE} = prod_{j=1}^h left( frac{| e_{a,T+j} |}{| e_{b,T+j} |} right)^{frac{1}{h}} ,
end{equation}
где (e_{b,T+j}) — ошибка по некоторой второй модели.
GMRAE показывает, во сколько раз наша модель оказалась хуже (или лучше), чем выбранная для сравнения (модель-бенчмарк). Если (GMRAE>1), то наша модель оказалась менее точной, в противоположной ситуации — более точной. В качестве той самой второй модели для простоты можно выбрать Naive. Однако, можно и не ограничиваться Naive. Что именно выбрать обычно остаётся на совести прогнозиста, и в свою очередь может вызывать некоторые сложности. Действительно, почему именно Naive? Почему бы не модель экспоненциального сглаживания с демпфированным трендом или какая-нибудь ARIMA(2,1,3)?! Вопрос открытый. Но важно, чтобы по разным рядам происходило сравнение с одной и той же моделью.
Как видно, GMRAE легче интерпретировать, чем MASE, но сложнее, чем MAPE, SMAPE или sMAE. Впрочем, она всё так же не ограничена сверху и может теоретически достигать заоблачных величин.
Но без ложки дёгтя не обошлось. Из-за того, что эта ошибка представляет собой среднюю геометрическую, она не может использоваться в ситуациях, когда хотя бы одна из ошибок одной из моделей оказалась равной нулю — в этом случае GMRAE становится равной либо нулю, либо бесконечности.
Одна из модификаций этой ошибки — rMAE — Relative MAE (относительная MAE):
begin{equation} label{eq:mq_rMAE}
text{rMAE} = frac{text{MAE}_a}{text{MAE}_b} .
end{equation}
Здесь мы фактически просто рассчитываем MAE двух моделей, и дальше делим одну величину на другую. Интерпретация получается похожей на интерпретацию GMRAE, но сама ошибка при этом оказывается более робастной (так как ситуация, когда MAE=0 оказывается значительно менее вероятной, чем ситуация, когда одна какая-то ошибка оказалась нулевой).
Последний коэффициент, который мы рассмотрим, призван оценивать не точность прогноза, а его смещение. Называется он «Mean Percentage Error» — средняя процентная ошибка:
begin{equation} label{eq:mq_MPE}
text{MPE} = frac{1}{h} sum_{j=1}^h frac{ e_{T+j} }{y_{T+j}}
end{equation}
Можно заметить, что он похож на eqref{eq:mq_MAPE}, но отличается лишь отсутствием модулей в числителе. Он показывает процент смещения прогноза. Положительные значения MPE указывают на систематическое занижение прогноза (то есть, мы недооценили спрос), а отрицательные — на завышения. Его значение так же, как и MAPE eqref{eq:mq_MAPE} может измеряться в процентах. Он обладает теми же преимуществами и недостатками, что и MAPE.
На основе этой идеи со средними ошибками можно предложить и симметричную MPE, и среднюю масштабированную ошибку sME. Подробней на этом мы останавливаться не будем.
Ну, и совсем уж напоследок. Иногда в литературе встречается сравнение моделей на основе RMSE («Root Mean Squared Error» — «Корня из средней квадратичной ошибки»):
begin{equation} label{eq:mq_RMSE}
text{RMSE} = sqrt{ frac{1}{h} sum_{j=1}^h { e_{T+j} }^2}
end{equation}
Раньше бытовало мнение, что такое сравнение некорректно (см. Armstrong and Colopy, 1992), так как обычно приводит к выбору неправильной модели (то есть не самой точной). Всё из-за того, что эта ошибка сильно подвержена влиянию выбросов (из-за квадрата в формуле). Однако сейчас уже есть понимание, что проблема тут не в корректности и правильности, а в том, с чем именно мы имеем дело. Дело в том, что ошибки на основе MSE минимизируются с помощью средней величины, в то время как ошибки на основе MAE минимизируются медианами. Так что всё сводится к тому, что именно вы хотите увидеть.
Один из примеров эффективного использования ошибок на основе MSE — это прогнозирование прерывистого спроса. В этом случае число нулей в выборке может быть настолько большим (может легко перевалить за 50%), что все ошибки, основанные на модулях будут отдавать предпочтение нулевому прогнозу (мы ничего не продадим, поэтому нечего запасать — депрессивный прогноз). Это всё из-за того самого эффекта со средними и медианами (см. параграф методы оценки моделей).
На основе eqref{eq:mq_RMSE} можно, например, предложить rRMSE:
begin{equation} label{eq:mq_rRMSE}
text{rRMSE} = frac{text{RMSE}_a}{text{RMSE}_b} ,
end{equation}
которая может интерпретироваться аналогично rMAE.
На этом все самые популярные и полезные коэффициенты заканчиваются. В жизни встречаются, конечно же, и другие, но они обычно либо обладают большим количеством недостатков, либо значительно менее популярны среди прогнозистов.
Пример в R
В пакете smooth рассмотренные выше коэффициенты уже реализованы. Подключим пакет:
library("smooth")
И посмотрим, как они работают на примере следующих двух моделей:
x <- es(M3$N1234$x,model="MNN",h=8)$forecast y <- es(M3$N1234$x,model="MAN",h=8)$forecast
Переменные x и y теперь содержат прогнозы на 8 наблюдений вперёд по моделям ETS(M,N,N) и ETS(M,A,N) по ряду N1234 базы M3-Competition.
Ряд N1234 и модель ETS(M,A,N)
График исходного ряда (см. выше) демонстрирует рост, и, откровенно говоря, модель ETS(M,A,N) выглядит на обучающей выборке неплохо. Она улавливает тенденцию к росту. Если не прибегать ни к какому фундаментальному анализу, то можно заключить, что возрастающий тренд — это то, что нас ждёт в ближайшем будущем. Но будущее таки не предопределено, именно об этом нам в очередной раз говорит следующий график, на котором показана модель ETS(M,N,N) и значения из проверочной выборки.
Ряд N1234 и модель ETS(M,N,N)
И именно поэтому прогнозирование всегда должно осуществляться параллельно с фундаментальным анализом.
Тем не менее, посмотрим, насколько точными оказались прогнозы по этим двум моделям. Для начала рассчитаем MPE:
MPE(M3$N1234$xx,x) [1] -0.009 MPE(M3$N1234$xx,y) [1] -0.037
Как видим, прогноз по второй модели оказался более смещённым — он составил -3,7%, по сравнению с -0,9% первой модели. Не удивительно — ситуация в проверочной выборке изменилась кардинально по сравнению с тем, что мы видели в обучающей!
Что же там с точностью прогнозов?
MAPE(M3$N1234$xx,x) [1] 0.009 MAPE(M3$N1234$xx,y) [1] 0.037
Из-за того, что прогнозы по обеим моделям оказались завышенными, значение MPE оказывается равным по модулю значению MAPE. Вторая модель ошиблась сильнее, чем первая.
Симметричная MAPE даст нам примерно то же самое:
SMAPE(M3$N1234$xx,x) [1] 0.009 SMAPE(M3$N1234$xx,y) [1] 0.036
Для MASE нам понадобится значение, по которому мы будем масштабировать ошибки. Рассмотрим классические вариант со средней абсолютной ошибкой в знаменателе:
MASE(M3$N1234$xx,x,mean(abs(diff(M3$N1234$x)))) [1] 1.218 MASE(M3$N1234$xx,y,mean(abs(diff(M3$N1234$x)))) [1] 4.820
Очевидно, что вторая модель ошиблась по сравнению с первой в четыре раза. Но, к сожалению, по MASE особо больше нечего сказать.
А теперь масштабируем её относительно среднего абсолютного уровня (sMAE):
MASE(M3$N1234$xx,x,mean(abs(M3$N1234$x))) [1] 0.011 MASE(M3$N1234$xx,y,mean(abs(M3$N1234$x))) [1] 0.043
Получили примерно ту же картину, только эти значения можно измерять в процентах и они несут чуть больше смысла.
Ну, и напоследок рассчитаем GMRAE. Для этого для сначала дадим прогноз по модели Naive, чтобы было, с чем сравнивать:
es(M3$N1234$x,model="ANN",persistence=1,h=8)$forecast->z
А теперь посчитаем GMRAE:
GMRAE(M3$N1234$xx,x,z) [1] 1 GMRAE(M3$N1234$xx,y,z) [1] 4.877
Первая модель, как видим, дала точно такой же прогноз, как и Naive — GMRAE оказалась равной единице. Вторая же модель спрогнозировала ряд в несколько раз хуже, чем это сделала Naive.
В этом нашем примере все ошибки дали примерно один и тот же результат. Однако на других рядах данных результаты могут различаться. Попробуйте, например, используя всё те же модели, сравнить прогнозы на следующем условном ряде данных:
example <- rnorm(100,2,1)
Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.
В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
Статистические методы
Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.
В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.
К ним относятся:
MAPE – средняя абсолютная ошибка в процентах
где Z(t) – фактическое значение временного ряда, а 
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
ME – средняя ошибка
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

.
SD – стандартное отклонение
где ME – есть средняя ошибка, определенная по формуле выше.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>
Связь точности и ошибки прогнозирования
В начале этого обсуждения разберемся с определениями.
Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:
- Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
- Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.
Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)
Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:
где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
300% |
|
№3 |
1 |
4 |
75% |
Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:
В таком случае для тех же примеров ошибка рассчитается иначе:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
75% |
|
№3 |
1 |
4 |
75% |
Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.
Визуальный метод – графический
Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.
По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.


Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.
Использование формул ошибки прогнозирования на практике
Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.
Пример расчета такой оценки Вы сможете увидеть в файле Excel.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.
Для чего используется ошибка прогнозирования
В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.
Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.
В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.
Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».
Источник: сайт http://uppravuk.net/
Важным этапом прогнозирования
социально-экономических явлений
является оценка точности и надежности
прогнозов.
Эмпирической мерой точности прогноза,
служит величина его ошибки, которая
определяется как разность между
прогнозными ()
и фактическими (уt)
значениями исследуемого показателя.
Данный подход возможен только в двух
случаях:
а) период упреждения известен, уже
закончился и исследователь располагает
необходимыми фактическими значениями
прогнозируемого показателя;
б) строится ретроспективный прогноз,
то есть рассчитываются прогнозные
значения показателя для периода времени
за который уже имеются фактические
значения. Это делается с целью проверки
разработанной методики прогнозирования.
В данном случае вся имеющаяся информация
делится на две части в соотношении 2/3
к 1/3. Одна часть информации (первые 2/3
от исходного временного ряда) служит
для оценивания параметров модели
прогноза. Вторая часть информации
(последняя 1/3 части исходного ряда)
служит для реализации оценок прогноза.
Полученные, таким образом, ретроспективно
ошибки прогноза в некоторой степени
характеризуют точность предлагаемой
и реализуемой методики прогнозирования.
Однако величина ошибки ретроспективного
прогноза не может в полной мере и
окончательно характеризовать используемый
метод прогнозирования, так как она
рассчитана только для 2/3 имеющихся
данных, а не по всему временному ряду.
В случае если, ретроспективное
прогнозирование осуществлять по связным
и многомерным динамическим рядам, то
точность прогноза, соответственно,
будет зависеть от точности определения
значений факторных признаков, включенных
в многофакторную динамическую модель,
на всем периоде упреждения. При этом,
возможны следующие подходы к
прогнозированию по связным временным
рядам: можно использовать как фактические,
так и прогнозные значения признаков.
Все показатели оценки точности
статистических прогнозов условно можно
разделить на три группы:
-
аналитические;
-
сравнительные;
-
качественные.
Аналитические показатели точности
прогноза позволяют количественно
определить величину ошибки прогноза.
К ним относятся следующие показатели
точности прогноза:
Абсолютная ошибка прогноза (D*)
определяется как разность между
эмпирическим и прогнозным значениями
признака и вычисляется по формуле:
, (16.1)
где уt– фактическое
значение признака;
—
прогнозное значение признака.
Относительная ошибка прогноза (d*отн)
может быть определена как отношение
абсолютной ошибки прогноза (D*):
-
к
фактическому значению признака (уt):
(16.2)
— к прогнозному
значению признака ()
(16.3)
Абсолютная и относительная ошибки
прогноза являются оценкой проверки
точности единичного прогноза, что
снижает их значимость в оценке точности
всей прогнозной модели, так как на
изучаемое социально-экономическое
явление подвержено влиянию различных
факторов внешнего и внутреннего
свойства. Единично удовлетворительный
прогноз может быть получен и на базе
реализации слабо обусловленной и
недостаточно адекватной прогнозной
модели и наоборот – можно получить
большую ошибку прогноза по достаточно
хорошо аппроксимирующей модели.
Поэтому на практике иногда определяют
не ошибку прогноза, а некоторый
коэффициент качества прогноза (Кк),
который показывает соотношение между
числом совпавших (с) и общим числом
совпавших (с) и несовпавших (н) прогнозов
и определяется по формуле:
(16.4)
Значение Кк= 1 означает, что имеет
место полное совпадение значений
прогнозных и фактических значений и
модель на 100% описывает изучаемое
явление. Данный показатель оценивает
удовлетворительный вес совпавших
прогнозных значений в целом по временному
ряду и изменяющегося в пределах от 0 до
1.
Следовательно, оценку точности получаемых
прогнозных моделей целесообразно
проводить по совокупности сопоставлений
прогнозных и фактических значений
изучаемых признаков.
Средним показателем точности прогноза
является средняя абсолютная ошибка
прогноза (),
которая определяется как средняя
арифметическая простая из абсолютных
ошибок прогноза по формуле вида:

де n– длина временного
ряда.
Средняя абсолютная ошибка прогноза
показывает обобщенную характеристику
степени отклонения фактических и
прогнозных значений признака и имеет
ту же размерность, что и размерность
изучаемого признака.
Для оценки точности прогноза используется
средняя квадратическая ошибка прогноза,
определяемая по формуле:

Размерность средней квадратической
ошибки прогноза также соответствует
размерности изучаемого признака. Между
средней абсолютной и средней квадратической
ошибками прогноза существует следующее
примерное соотношение:
(16.7)
Недостатками средней абсолютной и
средней квадратической ошибками
прогноза является их существенная
зависимость от масштаба измерения
уровней изучаемых социально-экономических
явлений.
Поэтому на практике в качестве
характеристики точности прогноза
определяют среднюю ошибку аппроксимации,
которая выражается в процентах
относительно фактических значений
признака, и определяется по формуле
вида:
(16.8)
Данный показатель является относительным
показателем точности прогноза и не
отражает размерность изучаемых
признаков, выражается в процентах и на
практике используется для сравнения
точности прогнозов полученных как по
различным моделям, так и по различным
объектам. Интерпретация оценки точности
прогноза на основе данного показателя
представлена в следующей таблице:
-
,%
Интерпретация
точности< 10
10 – 20
20 – 50
> 50
Высокая
Хорошая
Удовлетворительная
Не удовлетворительная
В качестве сравнительного показателя
точности прогноза используется
коэффициент корреляции между прогнозными
и фактическими значениями признака,
который определяется по формуле:

где
—
средний уровень ряда динамики прогнозных
оценок.
Используя данный коэффициент в оценке
точности прогноза следует помнить, что
коэффициент парной корреляции в силу
своей сущности отражает линейное
соотношение коррелируемых величин и
характеризует лишь взаимосвязь между
временным рядом фактических значений
и рядом прогнозных значений признаков.
И даже если коэффициент корреляции R= 1, то это еще не предполагает полного
совпадения фактических и прогнозных
оценок, а свидетельствует лишь о наличии
линейной зависимости между временными
рядами прогнозных и фактических значений
признака.
Одним из показателей оценки точности
статистических прогнозов является
коэффициент несоответствия (КН), который
был предложен Г. Тейлом и может
рассчитываться в различных модификациях:
-
Коэффициент несоответствия (КН1),
определяемый как отношение средней
квадратической ошибки к квадрату
фактических значений признака:

КН = о, если

то есть полное совпадение фактических
и прогнозных значений признака.
КН = 1, если при прогнозировании получают
среднюю квадратическую ошибку адекватную
по величине ошибке, полученной одним
из простейших методов экстраполяции
неизменности абсолютных цепных
приростов.
КН > 1, когда прогноз дает худшие
результаты, чем предположение о
неизменности исследуемого явления.
Верхней границы коэффициент несоответствия
не имеет.
2.Коэффициент несоответствия КН2определяется как отношение средней
квадратической ошибки прогноза к сумме
квадратов
отклонений
фактических значений признака от
среднего уровня исходного временного
ряда за весь рассматриваемый период:

где — средний уровень исходного ряда
динамики.
Если КН > 1, то прогноз на уровне среднего
значения признака дал бы лучший
результат, чем имеющийся прогноз.
3.Коэффициент несоответствия (КН3),
определяемый как отношение средней
квадратической ошибке прогноза к сумме
квадратов отклонений фактических
значений признака от теоретических,
выравненных по уравнению тренда:

где — теоретические уровни временного ряда,
полученные по
модели тренда.
Если КН > 1, то прогноз методом
экстраполяции тренда дает хороший
результат.
Оценка ошибки прогнозирования временного ряда
Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
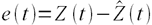
где Z(t) – фактическое значение временного ряда, а 
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.
MAPE – средняя абсолютная ошибка в процентах
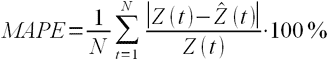
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка
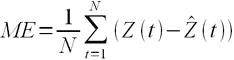
SD – стандартное отклонение
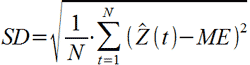
Связь точности и ошибки прогнозирования
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE
Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.
При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.















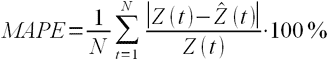
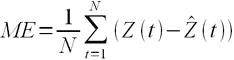
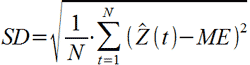








![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)
