Государственное
бюджетное профессиональное образовательное учреждение
Иркутской области
«Братский педагогический колледж»
Учебно-методический
комплекс для специальности: 44.02.02 Преподавание в начальных классах
Практическое занятие по теме:
Математические понятия
Тема: Определение родовых отношений между
понятиями. Решение задач на распознавание понятий
Цель: На основе
систематизации теоретических знаний о видах и структуре определений понятий
раскрыть логико-математическую структуру типичных для школьного курса
математики определений понятий; освоить основные учебные действия, необходимые
для усвоения понятий.
План:
1. Теоретическое обобщение знаний о понятиях
2. Решение упражнений
3. Самостоятельная работа
Вопросы:
— Группы понятий, изучаемых в начальной школе.
— Понятие как форма мышления.
— Существенное и несущественное свойства для объекта.
—
Объем и содержание понятия.
—
Понятие рода и вида.
— Определение понятия.
— Структура явного определения.
— Условные определения.
— Требования к определениям понятий.
— Процесс составления задачи на распознавание понятия.
Решение упражнений
Указания: Вспомните, что
такое объем, существенные и несущественные свойства понятия, отношение рода и
вида между понятиями, какие требования к определениям должны выполняться и
выполните задания.
1. Начертите три геометрические фигуры, принадлежащие
объему понятия:
а)
параллелограмм; б) трапеция; в) равнобедренный треугольник.
2.
Назовите пять существенных свойств понятия:
а)
параллелограмм; б) трапеция; в) равнобедренный треугольник.
3.
Каков объем понятия:
а)
однозначное число; б) натуральное число?
4.
Какое из следующих утверждений верное? Ответ объясните.
а)
Всякое свойство квадрата присуще прямоугольнику.
б)
Всякое свойство прямоугольника присуще квадрату.
5.
Находятся ли в отношении рода и вида следующие пары понятий:
а)
многоугольник и четырехугольник;
б)
угол и острый угол;
в)
луч и прямая;
г)
круг и окружность?
6. Среди понятий, изучаемых в начальном курсе математики,
есть такие, как «четное число», «треугольник», «многоугольник», «число»,
«трехзначное число», «прямой угол», «сумма», «слагаемое», «выражение». Есть ли
среди них понятия, находящиеся в отношении рода и вида?
7. Есть ли логические ошибки в следующих определениях?
Если можете, то исправьте их.
а) Прямоугольником называется четырехугольник, у
которого противоположные стороны равны.
б) Биссектрисой угла называется прямая, делящая угол
пополам.
в) Сложением называется действие, при котором числа складываются.
г) Квадратом называется прямоугольник с равными
сторонами.
Самостоятельная работа
Задание 1. В каких из
приведенных ниже определений математических понятий имеются ошибки?
Указание: Если в
определении есть ошибка, то укажите ее причину, исправьте ее, если это
возможно. Для верного определения сформулируйте эквивалентное ему определение.
Результаты оформите в таблицу.
I. Вариант
II. Вариант
|
1 |
Биссектрисой |
1 |
Прямоугольником |
|
2 |
Сложением |
2 |
Диаметром |
|
3 |
Прямоугольником |
3 |
Касательной |
|
4 |
Остроугольным |
4 |
Параллелограммом |
|
5 |
Смежными |
5 |
Решением |
|
6 |
Равнобедренным |
6 |
Тупоугольным |
Оформление
выполненного задания
|
№ п/п |
Ошибка понятия |
Правильное понятия |
Эквивалентное |
|
1. |
|||
|
2. |
|||
|
3. |
|||
|
4. |
|||
|
5 |
|||
|
6. |
Задание
2. Выполните логический анализ определений, приведенных
ниже понятий:
|
1. |
Квадрат |
1. |
Числовое |
|
2. |
Угол |
2. |
Прямоугольник |
|
3. |
Умножение |
3. |
Окружность |
|
4. |
Прямоугольный |
4. |
Многоугольник |
|
5. |
Неравенство |
5. |
Уравнение |
|
6. |
Двузначное |
6. |
Цифра |
Указание:
Вспомните определение понятия (или прочитайте его в учебнике), определите его
вид, род, видовые отличия и результат оформите в таблицу.
|
№ п/п |
Определение понятия |
Термин |
Род |
Видовые отличия |
Вид понятия |
|
1. |
|||||
|
2. |
|||||
|
3. |
|||||
|
4. |
|||||
|
5. |
|||||
|
6. |
Задание 3. Выполните действие
подведения под определение объекта. Результат оформите таблицей, записав
сначала 1) определение понятия; 2) его свойства; 3) логическую связь между
свойствами. Примеры объектов, подлежащих распознаванию, привести самим.
ФГБОУ ВПО САХАЛИНСКИЙ ГОСУДВРСТВЕННЫЙ УНИВЕРСИТЕТ
ЮЖНО-САХАЛИНСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ
ДОКЛАД
ПО МАТЕМАТИКЕ
НА ТЕМУ:ТРЕБОВАНИЯ К ОПРЕДЕЛЕНИЮ ПОНЯТИЙ.
Выполнила:
Шемякина Т.Е.
Южно-Сахалинск
Основные правила составления определений.
Одно и то же математическое понятие может быть определено различными способами. Например, такое простейшее понятие, как «треугольник», в разных учебниках по математике определяется по-разному:
-
Треугольник — это замкнутая ломаная линия, состоящая из трех звеньев»;
-
Многоугольник, имеющий три стороны, называется треугольником;
-
Если А, В и С — любые три точки, не лежащие на одной прямой, то объединение трех отрезков АВ, ВС и АС называется треугольником.
Все эти определения, как и ранее приведенное, правильные. Однако иногда, воспроизводя определения, имеющиеся в учебнике, или строя определения самостоятельно, ученики и, не только они, допускают разные ошибки. Чтобы строить и воспроизводить определения математических понятий правильно, нужно знать основные требования к логическому определению понятий.
Рассмотрим эти требования, попутно указывая наиболее часто встречающиеся ошибки в определении математических понятий.
Определения должны быть научно правильными.
Это означает, что, определяя то или иное понятие, надо это сделать так, чтобы не исказить научный смысл этого понятия. Так, например, смысл понятия «отношение» (в математике) состоит в том, что оно есть какое-то число. Между тем иногда это понятие определяют так: «Отношение есть сравнение двух чисел или величин посредством деления». Но сравнение есть некоторый процесс, а не число. В данном случае неверно выбрано родовое понятие и тем самым искажен научный смысл определяемого понятия. Другой пример. Иногда приходится слышать от ученика такое определение: «Абсолютной величиной, или модулем числа, называется это число без знака». Получается, что существуют какие-то числа без знака, но таких чисел (кроме нуля) математика не знает: в математике рассматриваются лишь положительные, отрицательные числа и нуль, других чисел нет. Если число написано без знака, то это положительное число, а не какое-то «беззначное». Поэтому приведенное определение неверное.
Определения не должны содержать «порочного круга».
Один ученик на вопрос, что такое умножение, например, ответил: «Умножением называется действие отыскания произведения». Когда же его спросили, а что такое произведение, он с уверенностью заявил, что это результат умножения. Следовательно, у этого ученика получается, что умножение определяется через понятие произведения, а произведение через понятие умножения. Получается «порочный круг» в определении. Ясно, что такой способ определения является грубо ошибочным. Еще пример ошибки «порочного круга» в определении: «Угол называется прямым, если его стороны перпендикулярны» и «Прямые называются перпендикулярными, если при пересечении они образуют прямые углы». Схему этих двух определений можно изобразить так.
Как видим, эти определения действительно образуют «порочный круг». Следовательно, строя определения математических понятий, надо следить за тем, чтобы они не образовали друг с другом «порочного круга».
Определение должно содержать указание на ближайшее родовое понятие.
Как бы ни было построено определение математического понятия, в нем должно быть указано ближайшее родовое понятие к определяемому понятию. Нарушение этого требования приводит к различным ошибкам. Так, например, иногда учащиеся, формулируя определения, вовсе не указывают родовое понятие. На вопрос, какие фигуры называется равновеликими, они отвечают: «Это если две фигуры имеют равные площади». Что означает «это», можно лишь догадываться. Или: на предложение сформулировать определение равнобедренных треугольников, иногда можно услышать такой ответ: «Это такие, у которых две стороны равны». Такая небрежность в формулировке определений недопустима. Другой тип ошибок связан с тем, что в определении указывается не ближайшее родовое понятие, а более широкое. Вот пример такого определения: «Параллелограмм есть фигура, у которой противоположные стороны параллельны». В этом определении указано не ближайшее для параллелограмма родовое понятие — «четырехугольник», а более далекое, более широкое — «фигура». И тем самым это определение становится неверным, ибо фигурой, у которой противоположные стороны параллельны, может быть не только параллелограмм, но и, например, правильный шестиугольник. Или другой пример. Давая определение диаметра круга, ученик сформулировал его так: «Диаметр круга есть прямая, проходящая через центр круга». Ученик указал в качестве родового понятия прямую, а ведь диаметр — это не вся прямая, а лишь отрезок прямой.
Определение не должно быть тавтологией, т. е. повторяющей в иной словесной форме ранее сказанное.
Сущность такой ошибки заключается в том, что понятие определяется через само себя. Вот примеры тавтологии в некоторых определениях: «Сложением называется действие, при котором числа складываются»(здесь сложение определено через понятие «складывание», что одно и то же). «Фигура А называется симметричной фигуре В, если они расположены симметрично относительно оси симметрии» (здесь «симметричные фигуры» определены через понятие «фигуры, расположенные симметрично»). Ясно, что такие определения являются грубо ошибочными.
Определение должно быть достаточным.
Это означает, что в определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия. Если же это требование нарушается, то под определение можно подвести не только объекты определяемого понятия, но и другие объекты. Так, например, иногда ученики дают такое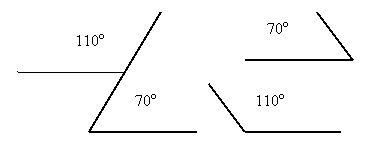 
определение смежных углов: «Смежными называются углы, которые в сумме составляют 180°». Недостаточность этого определения становится очевидной, если взглянуть на рисунок. На нем изображены две пары углов, сумма которых равна 180°, но они не смежные. Ошибка здесь в том, что указано лишь одно свойство смежных углов, оно недостаточно для их определения. Можно было бы, например, так определить их: «Смежными называются два угла, имеющие общую сторону, которые расположены в разных полуплоскостях от этой общей стороны и в сумме составляют 180°».
Например, медиану треугольника определили следующим образом: «Медианой треугольника называется отрезок, делящий его сторону пополам». Очевидно, что и в этом определении указано недостаточное число признаков медианы. Поэтому под это определение подходят не только медиана треугольника, но и средняя линия (ведь и она делит сторону треугольника пополам) и вообще любой отрезок, делящий сторону треугольника пополам. Для построения правильного определения медианы треугольника надо добавить еще и такой признак: «Медиана выходит из вершины треугольника». Тогда получаем такое правильное определение: «Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны».
Определение не должно быть избыточным.
Это означает, что в определении не должно быть указано лишних признаков, являющихся следствием других признаков определяемого понятия. Например, весьма часто встречается такое определение ромба: «Ромбом называется параллелограмм, все стороны которого равны между собой». Это определение явно избыточное, ибо достаточно равенства двух смежных сторон параллелограмма для того, чтобы были равны все его стороны. Следовательно, правильнее определять ромб следующим образом: «Ромбом называется параллелограмм, две смежные стороны которого равны». Вот другой пример: «Диаметром круга называется наибольшая хорда, проходящая через центр круга». Здесь первый признак «наибольшая» является следствием второго признака «проходящая через центр», а второй является следствием первого. Поэтому правильное определение такое: «Диаметром круга называется хорда, проходящая через центр круга» или: «Диаметром крута называется наибольшая хорда».
Мы указали лишь основные требования к определению математических понятий и привели примеры ошибок, возникающих при нарушении этих требований. Для того чтобы избежать таких ошибок, надо знать эти требования, учитывать их при формулировании тех или иных определений, учиться строить правильные определения.
Определяемое понятие — понятие существенные признаки которого отыскиваются. Определяющее понятие — понятие посредством которого определяется неизвестное понятие.
В определении понятия через ближайший род и видовые отличиня нужно следиить за тем, чтобы использовался ближайший род, но не образовывался порочный круг.
Тавтология в определении — логическая ошибка заключающаяся в том, что понятие определяется само через себя.
Слишком узкое определение понятия — логическая ошибка, состоящее в том, что нарушается принцип соразмерности, в результате чего объем определяемого понятия оказывается меньше объема определяющего понятия.
В определении понятия через ближайший род и видовые отличиня нужно следиить за тем, чтобы использовалось минимальное и в тоже время достаточное количество существенных признаков видовых отличий.
Подборка по базе: Лабораторная работа 2 Физика 1 Данилов.docx, Практическая работа 2 экономика.docx, Курсовая работа.Заварзина.docx, Белобородов Курсовая работа.docx, курсовая работа.docx, Лабораторная работа.docx, кр работа по психологии.docx, Разгоняева Практическая №5 (1).rtf, контрольная работа.docx, Практическая работа по МДК 04.docx
Практическая работа по математике
Выполнила студентка гр. ПНОз-181
Юненко А.С.
Стр. 45 п.13 №1-6.
№1
Начертите три геометрические фигуры, принадлежащие объёму понятий:
А) параллелограмм
Б) трапеция
В) окружность
№2
Назовите пять существенных свойств понятия:
А) Треугольник.
1) Против большей стороны лежит больший угол, и наоборот.
2) Против равных сторон лежат равные углы, и наоборот.
3)Сумма углов треугольника равно 180° (можно сказать, что каждый угол равностороннем треугольнике равна 60°).
4)Продолжая одну из сторон треугольника, получаем внешний угол.
5) Любая сторона треугольника меньше суммы двух других сторон и больше из разности.
Б) Круг
1) Круг является выпуклой фигурой.
2) При вращении плоскости относительно центра круг переходит сам в себя.
3) Круг является фигурой, имеющей наибольшую площадь при заданном периметре. Или что тоже самое, образующей наименьшим периметром при заданной S.
4) Площадь круга радиуса R, обозначаемая S, равна S=πR², где π=3,14.
5) Периметр круга (длина граничной окружности): L=2πR.
№3
Каков объём понятия:
А) однозначное число – всегда записано одной цифрой;
Б) натуральное число – начинается с 1 и по порядку до бесконечности;
В) луч – имеет начало, но не имеет конца.
№4
Назовите несколько свойств, общих для прямоугольника и квадрата. Какое из утверждений верное:
А) Всякое свойство квадрата присуще прямоугольнику. (Неверно)
Б) Всякое свойство прямоугольника присуще квадрату. (Верно)
Свойства:
- У прямоугольника и квадрата прямые углы;
- Противоположные стороны равны;
- Диагонали равны и точкой пересечения делятся пополам.
№5
Находятся ли в отношении рода и вида следующие пары понятий:
А) многоугольник и треугольник – отношение рода и вида.
Б) угол и острый угол – отношение рода и вида
В) луч и прямая – отношение «часть и целое»
Г) ромб и квадрат — – отношение рода и вида
Д) круг и окружность — – отношение «часть и целое»
№6
Изобрази при помощи кругов Эйлера отношения между объёмами понятий a, b, c, если:
А
А)
В
С
A – «четырёхугольник»,
B – «трапеция»,
c – «прямоугольник»
В
Б)
А
A – «натуральное число, кратное 3»,
B – «натуральное число, кратное 4»,
c – «натуральное число» С
В)
С
A – «треугольник», А В
B – «равнобедренный треугольник»,
c – «равносторонний треугольник»
Стр. 51 п.14 № 1,2,3,6
№1
Переформулируйте следующие определения, используя слова «тогда и только тогда, когда»:
А) Чётным называется число тогда и только тогда, когда оно делится на 2.
Б) Множество А называется подмножеством В тогда и только тогда, когда каждый элемент множества А принадлежит множеству В.
В) Множества А и В называется равными тогда и только тогда, когда А ⸦ В и В ⸦ А.
Г) Треугольником называется фигура тогда и только тогда, когда состоит из трех точек, не лежавших на одной прямой, и трех попарно соединяющих их отрезков.
№2
В следующих определениях выделите определяемое и определяющие понятие, родовое понятие (по отношению к определяемому) и видовое отличие:
А) Параллелограммом называют четырёхугольник, у которого противоположные стороны попарно параллельны.
Определяемое понятие – параллелограммом
Определяющие понятие – четырёхугольник, у которого противоположные стороны попарно параллельны
Родовое понятие (по отношению к определяемому) – четырёхугольник
Видовое отличие — у которого противоположные стороны попарно параллельны
Б) Отрезок, соединяющий середины двух сторон треугольника, называется средней линией.
Определяемое понятие – средней линией
Определяющие понятие – отрезок, соединяющий середины двух сторон треугольника
Родовое понятие (по отношению к определяемому) – отрезок
Видовое отличие — соединяющий середины двух сторон треугольника
№3
Назовите все свойства, которые содержатся в видовом отличие из следующих определений:
А) Биссектрисой угла называется луч, входящий из вершины угла делящий угол пополам.
Ответ: это геометрическое место точек, равноудалённых от сторон этого угла.
Б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Ответ: если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
№6
Есть ли логические ошибки в следующих определениях? Если можете, исправьте их.
А) Прямоугольником называется четырёхугольник, у которого противоположные стороны равны и все четыре угла равны.
Б) Биссектрисой угла называется прямая, делящая угол пополам.
В) Сложением называется действие, при котором числа складываются: если все числа положительные или отрицательные, либо вычитаются: если все числа положительные или отрицательные.
Г) Равносторонним треугольником называется треугольник, у которого равны все стороны или углы.
Д) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.
1)
Что нужно знать об объекте, чтобы иметь
представление о нем? Чтобы
иметь представление об объекте нужно
знать его существенные свойства.
2)
Какие свойства объекта различают?
Среди
свойств какого-либо объекта имеются
существенные и несущественные для его
определения.
3)
Что называют содержанием понятия?
Содержание
понятия
— это
совокупность существенных и отличительных
признаков предмета, качества или
множества однородных предметов,
отражённых в этом понятии
4)
Дать определения объема понятия.
Объем
понятия- это отображенное в нашем
сознании множество предметов, каждый
из которых имеет признаки, зафиксированные
в исследуемом понятии.
5)
Какова взаимосвязь между объемом и
содержанием понятия?
Они
взаимосвязаны: чем больше объем понятия,
тем меньше его содержание, и наоборот:
чем меньше объем, тем больше содержание
понятия.
Так,
например, объем понятия «равнобедренный
треугольник» меньше объема понятия
«треугольник», в объем первого понятия
входят не все треугольники, а лишь
равнобедренные. А содержание первого
понятия больше содержания второго, так
как равнобедренный треугольник обладает
не только всеми свойствами треугольника,
но и особыми свойствами, присущими
только равнобедренным треугольникам.
6)
Что называется определением понятия?
Определение
понятия — это логическая операция, в
процессе которой раскрывается содержание
понятия.
7)
Приведите примеры явных определений
(неявных определений).
Явные
определения раскрывают существенные
признаки предмета; к неявным относятся
определение через отношение предмета
к своей противоположности, контекстуальное,
остенсивное и некоторые другие виды
определений. Явное определение:
«Радиус-это отрезок, соединяющий центр
окружности с любой точкой окружности».,
«Уравнение- это равенство, содержащее
неизвестную величину». Неявные
определения: «Свобода
-есть познанная необходимость»;
«Возможность — потенциальная
действительность»; «Действительность
— реализованная возможность».
Какие определения называются
контекстуальными? Остенсивные?
В
контекстуальном определении содержание
понятия раскрывается в относительно
самостоятельном по смыслу отрывке
письменной или устной речи (контексте).
Определение остенсивное(от лат. ostentus —
показывание, выставление напоказ)
неявное определение, раскрывающее
содержание понятия путем непосредственного
показа, ознакомления обучаемого с
предметами, действиями и ситуациями,
обозначаемыми данным понятием. Можно,
напр., предъявить стол и сказать: «Это
— стол, и все вещи, похожие на него, тоже
столы»
9)
Как определить понятие через род и
видовое отличие? (приведите примеры).
Определение
через ближайший род и видовые отличие
— это логический прием определения
понятия, который заключается в том, что
отыскивается ближайший род и отличительные
признаки, имеющиеся только у данного
вида предметов. Например
: «четные числа- это натуральные числа
кратные 2», родовое понятие — натуральные
числа, видовые отличия — кратны числу
2. «Параллелограммом называется
четырехугольник, противоположные
стороны которого параллельны»
Четырехугольник – родовое понятие,
видовые отличия- противоположные стороны
параллельны»
10)
Какие требования предъявляются для
оценки правильности явных определений?
Определения
должны быть научно правильными.
Это означает, что, определяя то или иное
понятие, надо это сделать так, чтобы не
исказить научный смысл этого понятия.
Так, например, смысл понятия «отношение»
(в математике) состоит в том, что оно
есть какое-то число. Между тем иногда
это понятие определяют так: «Отношение
есть сравнение двух чисел или величин
посредством деления». Но сравнение есть
некоторый процесс, а не число. Определения
не должны содержать «порочного круга».
В
определении понятия через ближайший
род и видовые отличия нужно следить за
тем, чтобы использовался ближайший род,
но не образовывался порочный круг. «Угол
называется прямым, если его стороны
перпендикулярны». Определение
должно содержать указание на ближайшее
родовое понятие.
Как
бы ни было построено определение
математического понятия, в нем должно
быть указано ближайшее родовое понятие
к определяемому понятию. Нарушение
этого требования приводит к различным
ошибкам. «Параллелограмм есть фигура,
у которой противоположные стороны
параллельны». В этом определении указано
не ближайшее для параллелограмма родовое
понятие — «четырехугольник», а более
далекое, более широкое — «фигура». И
тем самым это определение становится
неверным, ибо фигурой, у которой
противоположные стороны параллельны,
может быть не только параллелограмм,
но и, например, правильный шестиугольник.
Определение не должно быть тавтологией,
т.
е. повторяющей в иной словесной форме
ранее сказанное. Сущность такой ошибки
заключается в том, что понятие определяется
через само себя. Вот примеры тавтологии
в некоторых определениях: «Сложением
называется действие, при котором числа
складываются»
Определение
должно быть достаточным.
Это
означает, что в определении должны быть
указаны все признаки, позволяющие
однозначно выделить объекты определяемого
понятия. Если же это требование нарушается,
то под определение можно подвести не
только объекты определяемого понятия,
но и другие объекты.
Например,
медиану треугольника определили
следующим образом: «Медианой треугольника
называется отрезок, делящий его сторону
пополам». Очевидно, что и в этом определении
указано недостаточное число признаков
медианы. Поэтому под это определение
подходят не только медиана треугольника,
но и средняя линия (ведь и она делит
сторону треугольника пополам) и вообще
любой отрезок, делящий сторону треугольника
пополам. Для построения правильного
определения медианы треугольника надо
добавить еще и такой признак: «Медиана
выходит из вершины треугольника». Тогда
получаем такое правильное определение:
«Медианой треугольника называется
отрезок, соединяющий вершину треугольника
с серединой противоположной стороны».
Определение
не должно быть избыточным.
Это
означает, что в определении не должно
быть указано лишних признаков, являющихся
следствием других признаков определяемого
понятия. Например, весьма часто встречается
такое определение ромба: «Ромбом
называется параллелограмм, все стороны
которого равны между собой». Это
определение явно избыточное, ибо
достаточно равенства двух смежных
сторон параллелограмма для того, чтобы
были равны все его стороны.
Темы:
№2, №3 Математические предложения.
Математические доказательства.
1)
Чем характеризуется математическое
предложение? Суждение
–
это такая форма мышления, в которой
отражается наличие или отсутствие
самого объекта, наличие или отсутствие
его свойств, связей. Математическое
суждение принято называть предложением.
2)
Что называют логическими связками?
Логические
связки представляют собой формальные
аналоги союзов нашего родного естественного
языка. Как сложные предложения строятся
из простых с помощью союзов «однако»,
«так как», «или» и т.п., так и сложные
суждения образуются из простых с помощью
логических связок. Логическая
связка — это любая логическая операция
над высказыванием. Например, употребляемые
в обычной речи слова и словосочетания
«не», «и», «или», «если… , то», «тогда и
только тогда» являются логическими
связками.
3)
Дайте определение высказывания.
Высказывание
—
термин математической логики, обозначающий
формализованную структурированную
запись мысли с помощью буквенных символов
и логических связок, рассматриваемую
с точки зрения истинностных значений.
4)
Когда высказывание «А и В» истинно?
«А
и В» истинно только тогда, когда они
одновременно истинны.
5)
Когда
истинно высказывание вида «А или В»?
Отрицание
высказывания А?
высказывание
вида «А или В»
истинное только тогда, когда хотя бы
одно из них истинно. Отрицание
высказывания А
логическое высказывание, принимающее
значение «истинно», если исходное
высказывание ложно, и наоборот.
6)
Какие слова называются кванторами?
КВАНТОР
[< лат. quantum сколько] — символ математической
логики; логическая операция, дающая
количественную характеристику области
предметов, к которым относится выражение,
получаемое в результате ее применения.
7)
Назовите кванторы общности и
существования.
—
квантор
общности (для любого, все и т. д.)
— квантор
существования (существует, для некоторых).
Как устанавливается истинность
высказываний с кванторами общности и
существования?
Для
доказательства утверждения с квантором
общности необходимо убедиться в том,
что при подстановке каждого из значений
х высказывание обращается в истинное
. Если множество Х конечно, то это можно
сделать путем перебора всех случаев;
если же множество Х бесконечно, то
необходимо провести рассуждения в общем
виде. Чтобы убедиться в истинности
высказывания с квантором существования,
достаточно привести пример и таким
образом доказать.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #