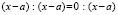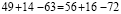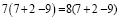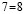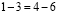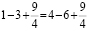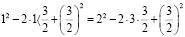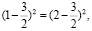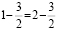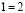Математические софизмы
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Атеев А.С. 1Самарина Е.А. 1
1МБОУ «ООШ № 12» Асбестовского городского округа
Самофалова В.В. 1
1МБОУ «ООШ № 12»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
1. Введение
Математика — один из наших любимых школьных предметов. Он нам нравится не только потому, что это основной школьный предмет, но и потому, что без математических знаний в жизни не обойтись. Занятие математикой развивает логическое мышление, сосредоточенность, находчивость, устойчивое внимание, хорошую память, смекалку.
Тема нашей работы «Софизмы в нашей жизни». Мы выбрали эту тему для своего проекта не случайно. Как-то вечером папа задал мне вопрос: «Саша, а ты знаешь, что 6 = 7? Мне стало интересно. Папа с легкостью доказал это равенство.
Вот как это было: 6=7.
Запишем верное равенство: 42 +12 — 54 = 49 +14 – 63.
Вынесем общий множитель за скобки: 6(7 + 2 – 9) = 7(7 + 2 – 9)
Разделим обе части на общий множитель (7 + 2 – 9).
Получим, что 6 = 7 , что и требовалось доказать. Где ошибка? Ведь этого быть не может. Папа сказал, что есть такое понятия, как софизм. Так я определился с темой проекта. Катя сама выбрала тему из списка, который был предложен учителем математики. Для нее понятие софизм тоже было неизвестно, поэтому она решила узнать, что означает это незнакомое и интересное слово.
В процессе работы мы выяснили, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой (например, 34 =7), так и то, что прямой угол равен тупому.
Эта тема сейчас актуальна, потому что софизм — это обман, а так как не каждый может его распознать, то с помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия назад.
Цель: узнать, что такое софизмы и научиться находить ошибку в софизмах.
Задачи:
1. Познакомиться с историей софизмов.
2. Узнать, какие бывают софизмы. Классификация софизмов.
3. Понять, как найти ошибку в софизмах?
4. Разбор софизмов.
5. Составить анкету для обучающихся, познакомить одноклассников с результатами работы.
6. Составить рекомендации для нахождения ошибок в софизмах.
Гипотеза: софизмы — тренировка для ума.
Объект и предмет исследования: софизмы
Методы исследования:
1. Анализ литературы и информации, полученной из Интернет источников
2. Обсуждение темы с учителем, родными и одноклассниками
3. Анкетирование одноклассников
4. Анализ и обобщение полученных данных.
2. Теоретическая часть
Что такое софизмы?
Софизм (от греч. — мастерство, умение, хитрая выдумка, уловка, мудрость) — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.
Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами.
2.2. История возникновения софизмов
Мы изучили историю возникновения софизмов. Софистика – это искусство ведения спора. Она вошла в моду в Греции в V веке до нашей эры. Имея в этом выгоду или просто интерес, многие умные и хитрые люди строго логически доказывали, что черное – это белое, истина – это ложь, добро – это зло и т.д. Так появились софизмы – формально кажущиеся правильными, но по существу ложными умозаключениями. Эти рассуждения могут быть истинны в каждой отдельной части, но неверные в целом.
Софизм – слово греческого происхождения, в переводе означающее хитроумную выдумку, ухищрение или головоломку. Речь идет о «доказательстве», направленном на формально – логическое установление абсурдного положения. В основном математические софизмы строятся на неверном словоупотреблении, на неточности формулировок, на скрытом выполнении невозможных действий, на незаконных обобщениях.
Систематический анализ софизмов был дан впервые Аристотелем (384-322 до н. э.) в особом трактате, в котором все ошибки разделяются на два класса: «неправильности речи» и ошибки «вне речи», т.е. в мышлении. Каков бы ни был софизм, он обязательно содержит замаскированные ошибки. Часто в математических софизмах скрыто выполняются запрещенные действия или не учитываются условия применения теорем, формул и правил.
Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы. К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно. Ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики.
Софист – это:
1. Человек, прибегающий к софизмам для доказательства заведомо неверных мыслей, положений.
2. В древней Греции первоначальный мудрец, знаток, потом платный учитель философии, красноречия, искусства спора, а также — философ, расходившийся с общепринятыми взглядами в вопросах религии и морали и обвинявшийся противниками в пользовании софизмами.
Наиболее серьезную роль сыграли математические софизмы, придуманные в V веке до нашей эры мудрецом Зеноном из южно-итальянского города Элеи. Например, одна из них: «В каждый момент времени летящая стрела неподвижна. Значит, она неподвижна во все моменты времени, и ее движение никогда не сможет начаться».
В истории развития математики софизмы способствовали повышению строгости в рассуждениях и более глубокому пониманию понятий и методов математики.
2.3. Классификация ошибок в софизмах
Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении.
Софисты в своих рассуждениях использовали разные ошибки, такие как:
Логические и ошибки в рассуждениях. Например: «Закон Моисеев запрещал воровство. Но закон Моисеев потерял свою силу, следовательно, воровство не запрещено», или «Все люди разумные существа, жители планет не люди, следовательно, они не разумные существа;
Терминологические ошибки – неправильное употребление слов или построение предложения. Например, «Все углы треугольника равны 180 градусам» в смысле «Сумма углов треугольника равна 180 градусам».
Ошибки в применении формул. Например : Чётное и нечётное. 5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные!
Практическая часть
3.1. Разбор математических софизмов
Рассмотрим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики. Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Математические софизмы делятся на 4 вида: арифметические, алгебраические, геометрические, логические. Мы рассмотрим некоторые из них.
Арифметические софизмы– это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Дважды два – пять (2 * 2 = 5)
Доказательство:
Пусть исходное соотношение — очевидное равенство:
4:4= 5:5 (1) .
Вынесем за скобки общий множитель каждой части (1) равенства, и мы получим:
4*(1:1)=5*(1:1) (2)
Разложим число 4 на произведение 2 *2
(2*2)* (1:1)=5*(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5.
Ошибка заключается в том, что нельзя было выносить множитель за скобки в в частном, множитель можно выносить либо из суммы, либо из разности.
Один рубль не равен ста копейкам
Доказательство:
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
Перемножая эти равенства почленно, получим 10 р.=100000 коп.
Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: необходимо переходить к единым единицам измерения.
Софизм «5 = 6»
Докажем, что 5 =6. С этой целью возьмем числовое равенство 35 + 10- 45 = 42 + 12 — 54. Вынесем общий множитель левой и правой части за скобки. Получим 5(7 + 2 — 9) = 6 (7 + 2 — 9). Разделим обе части этого равенства на общий множитель (7 + 2 — 9). Получаем 5=6. В чем ошибка?
Ошибка: нельзя делить на равенство (7 + 2 — 9), т. к. (7 + 2 — 9)= 0. Ма знаем еще из начальной школы, что на 0 делить нельзя.
Таки образом, можно доказать равенство любых разных двух чисел.
Софизм «Пропавший рубль»
Три подруги зашли в кафе выпить по чашке кофе7 Выпили. Официант принес им счет на 30 рублей. Подруги заплатили по 10 рублей и вышли. Однако хозяин кафе решил сделать скидку посетительницам, сказав что кофе стоит 25 рублей. Официант взял деньги и побежал доганять подруг, но пока он бежал, подумал, что им будет трудно делить 5 рублей, ведь их трое, поэтому решил отдать им по 1 рублю, а 2 рубля оставить себе. Так и сделал.
Что же получилось? Подруги заплатили по 9 рублей. 9 . 3 = 27 рублей, да 2 рубля осталось у официанта. А где же еще 1 рубль?
Ошибка. Задача сформулирована так, чтобы запутать читателя. Подруги заплатили 27 рублей, из этой суммы 25 рублей осталось у хозяина кафе, а 2 рубля у официанта. И никакого пропавшего рубля!
Логические софизмы
Софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными. Приведем некоторые примеры:
Полный стакан равен пустому
Рассмотрим стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану наполовину пустому.
Увеличивая обе части равенства вдвое, получим, что стакан полный равен
стакану пустому. Где ошибка?
Ясно, что приведенное рассуждение неверно, так как в нем применяется неправомерное действие: увеличение вдвое. В данной ситуации его применение бессмысленно, т.к. пустое увеличить вдвое не возможно.
Софизм учебы
Данным софизмом является песенка, сочиненная английскими студентами:
The more you study, the more you know
The more you know, the more you forget
The more you forget, the less you know
The less you know, the less you forget
The less you forget, the more you know
So why study?
Перевод:
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
Это стихотворение можно смело назвать логическим софизмом!
Геометрические софизмы
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
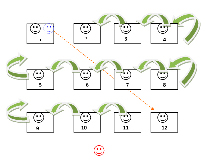
Софизм «Загадочное исчезновение» (Приложение 1). У нас есть произвольный прямоугольник на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. Куда исчезла 13-я линия?
Разбор софизма. 13-я линия удлинила каждую из оставшихся на 1/12 своей длины.
Примеры софизмов приведены в Приложении 2.
Работая над проектом, мы составили рекомендации по нахождению ошибок в софизмах (Приложение 3).
3.2. Анкетирование
Мы провели анкетирование среди обучающихся 7 классов на знание софизмов. В анкетировании приняло участие 40 человек. Были заданы следующие вопросы:
1. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы «Два равно трём»?
«Да» – 24 человека, 60 %
2. Знакомо ли вам понятие «софизм»?
«Да» — 10 человек, 25 %
3. Хотелось ли вам познакомиться с софизмами?
«Да» — 36 человек, 90 %.
Анкетирование показало, что немногим ребятам известно понятие «софизм». 90 % обучающихся хотели бы больше узнать о софизмах. Мы выступим перед ребятами с нашим проектом.
Заключение
Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы — это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.
Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.
Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться. К концу работы над проектом ошибки стали находиться быстрее. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свою речь.
Вообще, решение софизмов – интересное и познавательное занятие. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Работая над проектом, мы составили рекомендации по разбору софизмов (Приложение 3). Наш проект будет полезен людям, которые начинают работать с софизмами с целью развития свих интеллектуальных способностей.
Мы считаем, наш проект актуален и имеет практическое применение. Задачи выполнены, цель достигнута.
Решение софизмов тренируют наш мозг, то есть наша гипотеза верна.
Действительно, софизмы являются тренировкой для ума.
Информационные источники
«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003.
«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.
Т.Н. Михеева. Софизмы
«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971.
«Парадоксы науки». Автор: А.К.Сухотин. Издательство «Молодая гвардия», 1978 г.
Приложение 1
«Загадочное исчезновение»
Приложение 2
Лекарства
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
Девушка — не человек
Доказательство от противного. Допустим, девушка – человек. Девушка – молодая, значит девушка – молодой человек. Молодой человек – это парень. Противоречие. Значит девушка — не человек.
Вор
Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.
Разговор софиста и любителя спорить
Софист: “Может ли мёд быть сладким и несладким одновременно?”
Любитель: “нет”
Софист: “ А мёд сладкий?”
Любитель: “Да”
Софист: “А мёд желтый?”
Любитель: “Да”
Софист: “А жёлтый — значит сладкий?”
Любитель: “Нет”
Софист: “Значит мёд сладкий и несладкий одновременно!”
Не знаешь то, что знаешь
— Знаешь ли ты то, о чём я хочу тебя спросить?
— Нет.
— Знаешь ли ты, что добродетель есть добро?
— Знаю.
— Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь.
Примеры геометрических софизмов, которые можно услышать на уроке геометрии:
— Смежные углы равны 180 градусам;
— Накрест лежащие углы равны.
Приложение 3
Рекомендации по нахождению ошибок в софизмах
Внимательно прочитать условие предложенной вам задачи.
Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат получается из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки.
Установить темы, которые отражены в софизме. Обучающиеся, учителя привыкли, что задания, предлагаемые в учебнике, не содержат ошибок в условии, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
Воспроизвести вслух точные формулировки утверждений. Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие.
Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности. Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма.
Проверять преобразования. После каждого перехода проверить полученный результат обратным действием. Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».
Просмотров работы: 10770
Другой же софизм гласит, что «Единица равна двум»
Простым
вычитанием легко убедиться в справедливости
равенства
1-3
= 4-6.
Добавив
к обеим частям этого равенства число ,
получим новое равенство
1-3
+ =
4-6+,
в
котором, как нетрудно заметить, правая
и левая части представляют собой полные
квадраты, т. е.
(1-)
=(2-
)
Извлекая
из правой и левой частей предыдущего
равенства квадратный корень, получаем
равенство:
1-=2-
откуда
следует, что
1=2.
Где
ошибка?
Разбор
софизма:
По
определению представляет
собой некоторое неотрицательное число,
которое, будучи возведено в квадрат,
дастх. Ясно,
что этому определению удовлетворяют
два числа, а именно х и -х. Итак,
если число х неотрицательно (х>0), то=х; если
же число х отрицательно, то есть
число -х положительно, то=
— x. Отсюда заключаем, что(свойство
арифметического квадратного корня),
что не учитывается в содержании этих
софизмов и приводит к ложным выводам.
«Всякое число равно своей половине.»
Запишем
очевидное для любого числа a тождествоa2 —
a2 =
a2 —
a2,где
а-любое число.
Вынесем a в
левой части за скобку, а правую часть
разложим на множители по формуле разности
квадратов, получим a(a
– a) = (a + a)(a — a).
Разделив
обе части на a
— a,
получим a
= a + a,
или a=2a.
Разделим
на 2 и получим
а= а/2
Где
ошибка?
Мы
делим обе части на ноль, а деление на
ноль запрещено.
«Меньшее число больше,чем большее.»
Очевидно,что7>5
и что -8=-8
Тогда:7-8>5-8
или -1>-3
Это
не противоречит основному понятию об
отрицательных величина, на основании
которого мы считаем меньшей ту
отрицательную величину,численное
значение которой больше,и наоборот.
Умножим
обе части последнего неравенства на
(-4).
Получим
(-1)∙ (-4)>(-3)∙(-4) или 4>12
Где
ошибка?
Разбор
софизма:
При
умножении неравенства на отрицательное
число, знак неравенства изменяется на
противоположный.
«Через точку на прямую можно опустить два перпендикуляра»
Попытаемся
«доказать», что через точку, лежащую
вне прямой, к этой прямой можно провести
два перпендикуляра. С этой целью возьмем
треугольник АВС. На сторонах АВ и ВС
этого треугольника, как на диаметрах,
построим полуокружности. Пусть эти
полуокружности пересекаются со стороной
АС в точках Е и D.
Соединим точки Е и D
прямыми с точкой В. Угол АЕВ прямой, как
вписанный, опирающийся на диаметр; угол
ВДС также прямой. Следовательно, ВЕ
перпендикулярна АС и ВD
перпендикулярна АС. Через точку В
проходят два перпендикуляра к прямой
АС.
Где
ошибка?
Разбор
софизма:
Рассуждения,
о том, что из точки на прямой можно
опустить два перпендикуляра, опирались
на ошибочный чертеж. В действительности
полуокружности пересекаются со стороной
АС в одной точке, т.е. ВЕ совпадает с ВD.
Значит, из одной точки на прямой нельзя
опустить два перпендикуляра.
Всякое
положительное число является отрицательным.
Пусть
n-положительное число.
Очевидно,
2n-1<2n.
Возьмём
другое произвольное положительное
число a и умножим обе части неравенства
на (-а): -2an+a<-2an.
Вычитая
из обеих частей этого неравенства
величину (-2an), получим неравенство a<0,
доказывающее, что всякое положительное
число является отрицательным.
Где
ошибка?
Разбор
софизма:
При
умножении на отрицательное число знак
неравенства меняется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Администрация города Нижнего Новгорода
Департамент образования
Муниципальное бюджетное общеобразовательное учреждение
«Школа №181»
—————————————————————————————————
603124, город Нижний Новгород, улица Лесной городок, дом 6-а тел.
2218983
Исследовательская работа
Математические софизмы
Выполнил: Мокрушенко Георгий
ученик 6 «А» класса
МБОУ «Школа №181»
Научный руководитель: Грязева
Наталья Викторовна
учитель математики
Нижний Новгород
2017
СОДЕРЖАНИЕ.
1. Введение…. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . 3
2. Что такое софизмы . . . . . . …. . . . . . . . . . . . . . . . . .
. . . . 4
3. Экскурс в историю. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . 5
4. Арифметические софизмы. . . . . . . . . . . . . . . . . . . . . . .
. . 6
5. Алгебраические софизмы. . . . . . . . . . . . . . . . . . . . . . .
. . . 8
6. Геометрические софизмы . . . . . . . . . . . . . . . . . . . . . .
. . . 10
7. Прочие софизмы. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . 12
8. Исследовательская часть . . . . . . . . . . . . . . . . . . . . . .
. . . . 15
9. Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . 16
10. Список литературы. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . 17
11. Приложение 1. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 18
Введение
«История ошибок человеческого ума,
возможно, так же важна,
как история его движения вперед к истине».
П. Теннери
Наверняка, каждый человек хоть раз в жизни слышал
подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем». На самом
деле, таких примеров можно привести много, но что все они обозначают? Кто их
выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь
вымысел?
Именно эти вопросы я хочу рассмотреть в своей работе,
название которой – «Математические софизмы: обман или путь к открытию?». Речь в
ней пойдет о софизмах.
Неслучайно я выбрал именно софизмы. Во-первых, я очень
люблю решать задачи и разгадывать математические ребусы, а математические
софизмы — это «задачи-ловушки», которые помогают развивать логическое мышление.
Во-вторых, мне было интересно узнать, что некоторые заведомо ложные
утверждения, оказывается, можно доказать.
В процессе работы я выяснил, что существует великое
множество софизмов, и с их помощью можно доказать практически что угодно: как
равенство всех чисел между собой, так и то, что прямой угол равен тупому.
Теме софизмов посвящено много публикаций и книг, таких
как, книга для учащихся 7-11 классов Мадера А.Г и Мадера Д.А. «Математические
софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям»,
книга Литцмана В. «Где ошибка?» и множество других замечательных авторов, среди
которых не могу не упомянуть нашего земляка Михаила Андреевича Давыдова,
который в своей книге «Красота математики» посвятил одну из глав математическим
софизмам.
Эта тема сейчас актуальна, потому что софизм — это ложь, обряженная в одежды истины
(как остроумно заметил писатель Даниил Гранин), а так как не каждый может это распознать, то с
помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия
назад.
Цель моего исследования – понять, что такое
математические софизмы, научиться их разгадывать. Для достижения данной цели
передо мной стояли следующие задачи:
·
узнать, как и откуда появились
софизмы
·
привести примеры софизмов
·
разобрать несколько
примеров
·
понять, как найти ошибку в
них
- проведя разбор софизмов, сделать вывод
Что такое софизмы
Определение софизма в различных
толковых словарях и энциклопедиях подобны. Рассмотрим самые известные из них.
Софизм — логически порочное
умозаключение, в котором ложные посылки выдаются за истинные или делается вывод
с нарушением законов логики (Большая советская энциклопедия, том 40, стр.136).
Софизм — формально кажущееся
правильным, но по существу ложное умозаключение, основанное на преднамеренно
неправильном подборе исходных положений (Толковый словарь русского языка С. И.
Ожегова).
Софизм — мудрствованье, ложный
вывод, заключенье, сужденье, которому придан внешний вид истины. Софистическое
рассуждение — ложное, ошибочное, под видом истинного (Толковый словарь В. И.
Даля).
Софизм — формально правильное, но
ложное по существу умозаключение, основанное на натяжке, на преднамеренно
неправильном подборе исходных положений в цепи рассуждений (Толковый словарь
русского языка Д. Н. Ушакова).
Таким образом, анализируя
определения софизма из различных энциклопедий и толковых словарей, можно
выделить основные существенные признаки:
ü это утверждение (умозаключение)
ü формально — правильное
ü по существу — ложное
ü ошибка допущена и замаскирована намеренно.
Софизмы встречаются в различных
областях знаний, но выделенные критерии всегда присутствуют. Поэтому
определение математического софизма не будет существенно отличаться от всех
вышеперечисленных. В математическом софизме замаскированная ошибка, в процессе
вывода приводит к абсурдному результату, нарушающему все законы математики.
Каков бы ни был софизм, он
обязательно содержит одну или несколько замаскированных ошибок. Особенно часто
в математических софизмах скрыто выполняются запрещенные действия или не
учитываются условия применимости теорем, формул и правил. Иногда рассуждения
ведутся с использованием ошибочного чертежа или опираются на приводящие к
ошибочным заключениям, «очевидности». Встречаются софизмы, содержащие и другие
ошибки.
В истории развития математики
софизмы играли существенную роль. Они способствовали повышению строгости в
математических рассуждениях и содействовали более глубокому уяснению понятий и
методов математики. Роль софизмов в развитии математики сходна с той ролью,
какую играли непреднамеренные ошибки в математических доказательствах,
допускаемые даже выдающимися математиками. И.П. Павлов говорил, что «правильно
понятая ошибка — это путь к открытию». Действительно, уяснение ошибок, в математических
рассуждениях часто содействовало развитию математики.
Экскурс в историю
Софистика – направление философии, которое возникло в
V-IV вв. до н.э. в Греции и стало очень популярным а Афинах. Софистами называли
платных «учителей мудрости», которые учили граждан риторике, искусству слова,
приемам ведения спора, красноречию. Одним из представителей софистов был
философ Протагор, который говорил: «Я обучаю людей риторике, а это и есть
гражданское искусство».
Софисты считали, что истина субъективна, то есть у каждого
человека своя истина, человек сам создает себе истину и сам же её оценивает,
поэтому в суждениях об истине очень много личного. Справедливость, как и
истина, у каждого человека тоже своя, а значит, о каждой вещи можно судить
двояко, то есть о каждой вещи есть два противоположных мнения. Софисты учили
людей оценивать одно и то же событие, как положительное и как отрицательное
одновременно, таким образом, они приучали людей к широте взглядов.
Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей
эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то
есть в мышлении.
Софисты в своих рассуждениях использовали разные ошибки, такие как:
·
логические и ошибки в
рассуждениях. Например: «Закон Моисеев запрещал воровство, закон Моисеев
потерял свою силу, следовательно, воровство не запрещено», «Все люди разумные
существа, жители планет не люди, следовательно, они не разумные существа».
·
терминологические –
неправильное употребление слов или построение предложения. Например, «Все углы
треугольника = π» в смысле «Сумма углов треугольника = π», «Сколько будет:
пять плюс два умножить на два?» Здесь трудно решить имеется ли в виду 9 (т.е. 5
+ (2*2)) или 14 (т.е. (5 + 2) * 2).
- ошибки в применении
формул. Например, «Чётное и нечётное»: 5 есть 2 + 3 («два и три»). Два —
число чётное, три — нечётное, выходит, что пять — число и чётное и
нечётное. Пять не делится на два, так же, как и 2 + 3, значит, оба числа
нечётные.
Примеры софизмов
Разбор и решение любого рода
математических задач, а в особенности нестандартных, помогает развивать
смекалку и логику. Математические софизмы относятся именно к таким задачам. В
этом разделе работы я рассмотрю три типа математических софизмов:
арифметические, алгебраические и геометрические.
Арифметические
софизмы
Арифметика — (греч. arithmetika, от arithmys — число), наука о числах,
в первую очередь о натуральных (целых положительных) числах и (рациональных)
дробях, и действиях над ними.
Так что же такое
арифметические софизмы? Арифметические софизмы – это числовые выражения,
имеющие неточность или ошибку, незаметную с первого взгляда.
1. 4 руб. = 40000 коп
Возьмем
верное равенство 2руб. = 200 коп. и возведем его по частям в квадрат. Получится
4 руб. = 40000коп.
Вопрос: В чем ошибка?
Ответ: Возведение в квадрат величин не имеет смысла.
В квадрат возводятся только числа.
Точно
так же можно показать, к примеру, что1 руб. = 10 коп.
Так
как ¼ руб. = 25 коп., то √ ¼ руб. = √ 25 коп.,
следовательно: ½ руб. = 5 коп. или 1 руб. = 10 коп.
В
данных математических софизмах нарушены правила действий с именованными
величинами.
2. Два умножить на два будет пять
2 · 2 = 5
Имеем числовое
равенство (верное): 4 : 4 = 5 : 5.
Вынесем за скобки в
каждой части его общий множитель.
Получим: 4 ·
(1 : 1) = 5 · (1 : 1).
Числа в скобках
равны, поэтому 4 = 5, или 2 · 2 = 5.
Вопрос: Где здесь ошибка?
Ответ: Ошибка допущена в вынесении общего множителя
за скобки в левой и правой частях тождества 4 : 4 = 5 : 5.
3. Два равно трем
2 = 3
Возьмем
два верных равенства:
10 — 10 = 0
15 — 15 = 0
Так
как правые части равны, то приравняем левые: 10 — 10 = 15 — 15
2· (5 — 5) = 3· (5 — 5)
2 = 3
Вопрос: В чем ошибка?
Ответ: Ошибка в том, что на ноль (5 — 5)
делить нельзя.
4. Единица равна двум
1 = 2
Простым
вычитанием легко убедиться в справедливости равенства
1 — 3 = 4 — 6.
Добавив
к обеим частям этого равенства число , получим новое равенство
1 – 3 + = 4 – 6 +
,
в
котором, как нетрудно заметить, правая и левая части представляют собой полные
квадраты, т. е.
(1 — )
= (2 —
)
Извлекая
из правой и левой частей предыдущего равенства квадратный корень, получаем
равенство:
1 — = 2 —
откуда
следует, что 1 = 2.
5. Пять равно одному
5 = 1
Для
доказательства, что 5 = 1, будем рассуждать так. Из чисел 5 и 1 по
отдельности вычтем одно и то же число 3:
5 – 3 = 2 и 1 – 3 = — 2.
При
возведении в квадрат этих чисел получаются равные числа:
22 = 4 и (- 2)2 = 4.
Значит, должны быть равны и исходные числа 5 и 1.
Вопрос: Где ошибка?
Ответ: Из равенства квадратов двух чисел не следует,
что сами эти числа равны.
6. Четыре равно пяти
4 = 5
Рассмотрим верное
числовое равенство:
16 – 36 = 25 – 45
16 – 36 + 20,25 =
25 – 45 + 20,25
(4 – 4,5)2 = (5 –
4,5)2; 4 – 4,5 = 5 – 4,5;
4 = 5.
Вопрос: В чём ошибка?
Ответ: (4 – 4,5) · 2 = (5 – 4,5) · 2 , только тогда, когда |4 – 4,5| = |5 – 4,5|.
Алгебраические
софизмы
Алгебра — один из больших разделов математики, принадлежащий наряду с
арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также
методы алгебры, отличающие её от других отраслей математики, создавались
постепенно, начиная с древности. Алгебра возникла под влиянием нужд
общественной практики, в результате поисков общих приёмов для решения
однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и
решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в
уравнениях и числовых выражениях.
Все, мною рассмотренные до этого софизмы о
равенстве чисел, можно рассмотреть в общем случае:
1. Все числа равны между собой
Возьмем два
произвольных неравных между собой числа а и b и запишем для них очевидное
тождество:
а2— 2ab + b
= b
— 2ab + а2
Слева и справа стоят
полные квадраты, т. е. можем записать
(а — b)2
= (b — а)2
Извлекая из обеих
частей последнего равенства квадратный корень, получим:
а — b = b — a
или 2а = 2b,
или окончательно
a = b.
Или, 2. Неравные числа равны
Возьмем два неравных
между собой произвольных числа а и b. Пусть их разность равна с, т. е. а — b
= с. Умножив обе части этого равенства на а — b, получим
(а — b)2
= c(a — b),
a раскрыв скобки,
придем к равенству
a2 —
2ab + b2 = ca — cb,
из которого следует
равенство
а2 — аb
— ас = аb –b 2 — bc.
Вынося общий
множитель а слева, и общий множитель b справа за скобки, получим
а(а – b — с) = b(а
– b — с)
Разделив последнее
равенство на (а – b — с), получаем, что
а = b,
другими словами, два неравных между собой
произвольных числа а и b равны.
В данных софизмах рассмотрены наиболее популярные ошибки: неправильное
извлечение квадратного корня из квадрата выражения и деление на 0.
Приведу еще несколько примеров алгебраических
софизмов, решение которых мне пока сложно постичь до конца в силу малого багажа
знаний.
3. Всякое число равно своему удвоенному значению.
Запишем очевидное для любого числа а тождество
а2 — а2
= а2 — а2.
Вынесем
а в левой части за скобку, а правую часть разложим на множители по
формуле разности квадратов, получив
а(а
— а) = (а + а)(а — а).
Разделив
обе части на а — а, получим а = а + а, или
а =2а.
Итак, всякое число равно своему
удвоенному значению.
4. Из двух неравных чисел
первое всегда больше второго.
Пусть a и b – произвольные числа и a ≠ b.
Имеем:
(a – b)2 > 0,
т.е. a2 – 2ab – b2 > 0,
или a2 +
b2 > 2ab.
К обеим частям этого
неравенства прибавим – 2b2.
Получим:
а2 –
b2 > 2ab – 2b2, или (a + b) (a – b) > 2b (a – b).
После деления обеих
частей на (a – b) имеем:
a + b > 2b, откуда следует, что a > b.
Геометрические софизмы
Геометрические софизмы – это умозаключения или
рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или
парадоксальное утверждение, связанное с геометрическими фигурами и действиями
над ними.
1. Софизм об исчезающем квадрате.
Большой квадрат составлен из четырёх одинаковых
четырёхугольников и маленького квадрата (рис. 1).
Если четырёхугольники
развернуть (рис. 2), то они заполнят площадь, занимаемую маленьким квадратом,
хотя площадь большого квадрата визуально не изменится.
В чём же тут ошибка?
Посмотрим внимательно на ход действий.
Одинаковая ли площадь у обоих квадратов? Нет, так как
сторона и площадь нового квадрата меньше стороны и площади того, который был
вначале. При решении данного софизма я воспользовался разрезанием этого
квадрата, сложив части, и сравнив с исходным квадратом, получил, что он
действительно становится меньше.
2. Задача о треугольнике.
Дан прямоугольный треугольник 13×5 клеток, составленный из 4
частей (Рис.1)
После перестановки частей при визуальном сохранении
изначальных пропорций появляется дополнительная, не занятая ни одной частью,
клетка (Рис. 2).
Однако же, если посмотрим внимательно на чертежи, то заметим,
что гипотенузы больших треугольников не совпадают.
Ошибка станет хорошо видна, если провести точное построение.
На самом деле новая фигура не будет треугольником. Это будет ломаный
четырехугольник (Рис.3)
Прочие софизмы
Кроме математических софизмов, существует множество других, например:
логические, терминологические, психологические и т.д. Понять абсурдность таких
утверждений проще, но от этого они не становятся менее интересными. Очень
многие софизмы выглядят как лишенная смысла и цели игра с языком; игра,
опирающаяся на многозначность языковых выражений, их неполноту, недосказанность,
зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно
наивными и несерьезными.
Логические софизмы
Логические софизмы – это софизмы, ошибки которых заключаются в неправильных
рассуждениях.
1. Нет
правил без исключений
Это предложение, очевидно, само является
правилом, следовательно, и из этого утверждения имеются исключения. Тем самым
мы приходим к противоречию.
2. Не знаешь то, что знаешь
Знаешь ли ты, о чём я хочу
тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» —
«Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что
знаешь».
3. Может ли всемогущий маг создать камень,
который не сможет поднять?
Если не может — значит, он не всемогущий. Если
может — значит, всё равно не всемогущий, т.к. он не может поднять это камень.
4. Полупустое и полуполное
«Полупустое есть то же, что и полуполное. Если
равны половины, значит равны и целые. Следовательно, пустое есть то же, что и
полное».
5. Равен ли полный стакан пустому?
Пусть имеется стакан, наполненный водой до
половины. Тогда можно сказать, что стакан, наполовину полный равен стакану,
наполовину пустому. Увеличивая обе части равенства вдвое, получим, что стакан
полный равен стакану пустому.
6. Лекарства
«Лекарство, принимаемое больным, есть добро.
Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно
больше».
7. Некто
А говорит В: «Я солгал в своей жизни только три раза».
На это В отвечает: «Тогда ты лжешь теперь в четвертый раз».
Это заключение противоречиво: либо А действительно до сих пор солгал
только три раза и тогда он, сейчас говорит правду, либо он лгал больше, чем три
раза, и тогда в данный момент он солгал более, чем в четвертый раз.
8. Крокодил
У одной египтянки крокодил похитил ребенка. Египтянка просила вернуть
ребенка, и крокодил обещал ей это, если она правильно укажет, как поступит
крокодил.
Мать ребенка сказала: «Ты не возвратишь мне
моего ребенка»
На это крокодил ответил: «Если ты
действительно права, то ты, как сама говоришь, не получишь назад ребенка; если
же твое высказывание неверно, то, согласно нашему уговору, ты не получишь
ребенка. В любом случае ребенок должен остаться у меня»
«Наоборот, — возразила женщина,- если мое
высказывание, верно, то я получу ребенка в силу нашего условия; если же я
ошиблась, то это означает, что ты сам вернешь мне ребенка. В каждом из случаев
я должна получить ребенка назад»
Кто из них прав?
9. Кто виноват?
Некто купил шапку, которая оказалась для него негодной, она была
слишком мала.
Кто виноват, шапка или голова?
Шапка во всяком случае не виновата, так как если бы голова была меньше,
она бы подошла.
Следовательно, виновата голова!
Но это также неверно. Если бы шапка была больше, то она была бы годна.
Следовательно, ни шапка, ни голова не виноваты.
10. Хитрый хозяин
В приведенных ниже стишках, взятых из одного
английского журнала, выходившего в прошлом веке, рассказывается о хитром
хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что
каждому из них досталось по отдельной комнате.
МАТЕМАТИЧЕСКИЙ СОФИЗМ – удивительное
утверждение, в доказательстве которого кроются
незаметные, а подчас и довольно тонкие ошибки.Мартин ГАРДНЕР
Трудно, изучая математику, не заинтересоваться
математическими софизмами. В 2003 году в
издательстве “Просвещение” вышла книга А.Г.
Мадеры и Д.А.Мадеры “Математические софизмы”, в
которой более восьмидесяти математических
софизмов, по крупицам собранным из различных
источников. Цитата из книги: “Математический
софизм представляет собой, по существу,
правдоподобное рассуждение, приводящее к
неправдоподобному результату. Причем полученный
результат может противоречить всем нашим
представлениям, но найти ошибку в рассуждении
зачастую не так-то просто; иной раз она может быть
и довольно тонкой и глубокой. Поиск заключенных в
софизме ошибок, ясное понимание их причин ведут к
осмысленному постижению математики. Обнаружение
и анализ ошибки, заключенной в софизме, зачастую
оказываются более поучительными, чем просто
разбор решений “безошибочных” задач. Эффектная
демонстрация “доказательства” явно неверного
результата, в чем и состоит смысл софизма,
демонстрация того, к какой нелепице приводит
пренебрежение тем или иным математическим
правилом, и последующий поиск и разбор ошибки,
приведшей к нелепице, позволяют на эмоциональном
уровне понять и “закрепить” то или иное
математическое правило или утверждение. Такой
подход при обучении математике способствует
более глубокому ее пониманию и осмыслению.”
Для развития познавательной деятельности
математические софизмы можно применять при
изучении математики в школе:
- на уроках, чтобы сделать их более интересными,
для создания проблемных ситуаций; - в домашних задачах, для более осмысленного
понимания материала, пройденного на уроках
(найти ошибку в МС, придумать свои МС); - при проведении различных математических
соревнований, для разнообразия; - на занятиях факультативов, для более глубокого
изучения тем математики; - при написании реферативных и исследовательских
работ.
Математические софизмы в зависимости от
содержания и “прячущейся” в них ошибке можно
применять с различными целями на уроках
математики при изучении различных тем.
При разборе МС выделяются основные ошибки,
“прячущиеся” в МС:
- деление на 0;
- неправильные выводы из равенства дробей;
- неправильное извлечение квадратного корня из
квадрата выражения; - нарушения правил действия с именованными
величинами; - путаница с понятиями “равенства” и
“эквивалентность” в отношении множеств; - проведение преобразований над математическими
объектами, не имеющими смысла; - неравносильный переход от одного неравенства к
другому; - выводы и вычисления по неверно построенным
чертежам; - ошибки, возникающие при операциях с
бесконечными рядами и предельным переходом.
Самыми популярными являются 1-3.
Цели применения МС на уроках математики могут
быть самыми разнообразными:
- изучение исторического аспекта темы;
- создание проблемной ситуации при объяснении
нового материала; - проверка уровня усвоения изученного материала;
- для занимательного повторения и закрепления
изученного материала.
Часто применяя на уроках МС, я составила с
помощью учеников на факультативных занятиях
таблицу применения МС на уроках алгебры в7-8-[
классах (Приложение1). Это
была интересная и познавательная для ребят
работа, которая завершилась важным практическим
результатом, которым можно воспользоваться при
проведении урока.
В книге[1] представлена большая группа софизмов,
которые можно применять при изучении темы
“Свойства арифметического квадратного корня”,
повторяя при этом темы “Преобразование
многочленов”, “Формулы сокращённого
умножения”.
Например:
“Все числа равны между собой”
Возьмем два произвольных неравных между собой
числа а и b и запишем для них очевидное тождество:
а
-2ab+b
= b
-2ab+ а
Слева и справа стоят полные квадраты, т. е. можем
записать
(а-b)2 = (b-а)2. (1)
Извлекая из обеих частей последнего равенства
квадратный корень, получим:
a-b = b-a (2)
или 2а = 2b, или окончательно
a=b.
“Единица равна двум”
Простым вычитанием легко убедиться в
справедливости равенства
1-3 = 4-6.
Добавив к обеим частям этого равенства число ,
получим новое равенство
1-3 +
= 4-6+,
в котором, как нетрудно заметить, правая и левая
части представляют собой полные квадраты, т. е.
(1-
)
=(2-
)
Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство:
1-
=2-
откуда следует, что
1=2.
Комментарий.
По определению представляет собой некоторое
неотрицательное число, которое, будучи возведено
в квадрат, даст х2. Ясно, что этому
определению удовлетворяют два числа, а именно х
и -х. Итак, если число х неотрицательно (х>0),
то =х;
если же число х отрицательно, т. е. число -х
положительно, то = — x. Отсюда заключаем, что
(свойство
арифметического квадратного корня), что не
учитывается в содержании этих софизмов и
приводит к ложным выводам.
Но все же самой популярной ошибкой в софизмах
является “Деление на 0”. “Деление на нуль
является одним из наиболее распространенных
источников ошибок при проведении преобразований
различных выражений и при решении уравнений.
“Сокращение” уравнений на общий множитель
зачастую приводит либо к потере корней
уравнения, либо к приобретению посторонних
корней, либо вообще к бессмыслице.” [1]
Предупредить ошибки подобного рода поможет
рассмотрение софизмов. Например при изучении
темы “Преобразования многочленов” в 7кл.
“Неравные числа равны.”
Возьмем два неравных между собой произвольных
числа а и b. Пусть их разность равна с, т. е. а-b = с.
Умножив обе части этого равенства на а-b, получим
(а-b)2 = = c(a-b),
a раскрыв скобки, придем к равенству
a2-2ab + b2 = = ca-cb,
из которого следует равенство
а2— аb — ас = аb -b2 -bc.
Вынося общий множитель а слева, и общий
множитель b справа за скобки, получим
а(а-b-с) = b(а-b-с). (1)
Разделив последнее равенство на (а-b-с),
получаем, что
а=b,
другими словами, два неравных между собой
произвольных числа а и b равны.
Разбор софизма: Здесь ошибка совершена при
переходе от равенства (1) к равенству а = b. Действительно,
согласно условию разность двух произвольных
чисел а и b равна с, т. е. а-b = с, откуда
а-b-с = 0. Можно записать равенство (1) в виде а-0=
b-0. Переход от равенства (1) к равенству а = b осуществляется
путем деления обеих частей (1) на равное нулю
число а-b-с = 0. Следовательно, здесь мы имеем
деление нуля на нуль, которое не имеет смысла,
поскольку равенство а0 = b
0 выполняется при любых а и b. Поэтому
вывод, сделанный в софизме, что числа а и b равны,
неверен.
Неоценимую помощь оказывают МС для более
глубокого осмысления материала на уроках
геометрии. Например, софизм, который можно
использовать на уроке по теме “Окружность”,
повторяя при этом тему “Признаки равенства
треугольников”:
“В любой окружности хорда, не проходящая через
её центр, равна её диаметру”
В произвольной окружности проводим
диаметр АВ и хорду АС. Через середину D этой
хорды и точку В проводим хорду BE. Соединив
точки С и Е, получаем два треугольника ABD и
CDE. Углы ВАС и СЕВ равны как вписанные в
одну и ту же окружность, опирающиеся на одну и ту
же дугу; углы ADB и CDE равны как
вертикальные; стороны AD и CD равны по
построению.
Отсюда заключаем, что треугольники ABD и CDE равны
(по стороне и двум углам). Но стороны равных
треугольников, лежащие против равных углов, сами
равны, а потому
АВ=СЕ
т. е. диаметр окружности оказывается равным
некоторой (не проходящей через центр окружности)
хорде, что противоречит утверждению о том, что
диаметр больше всякой не проходящей через центр
окружности хорды.
Разбор софизма.
В софизме доказывается, что два треугольника ABD
и CDE равны, ссылаясь при этом на признак
равенства треугольников по стороне и двум углам.
Однако такого признака нет. Правильно
сформулированный признак равенства
треугольников гласит:
Если сторона и прилежащие к ней углы одного
треугольника равны соответственно стороне и
прилежащим к ней углам другого треугольника, то
такие треугольники равны.
Рассматривая МС на уроках геометрии можно в
ненавязчивой форме подчеркнуть важность
соответствия условия задачи и правильно
построенного к ней чертежа или схемы.
Например, один из самых интересных софизмов:
“Окружность имеет два центра”
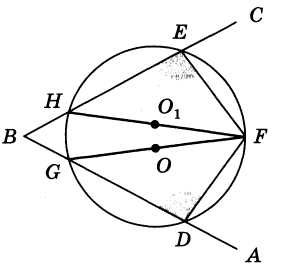
Построим произвольный угол ABC и, взяв на его
сторонах две произвольные точки D и Е,
восстановим из них перпендикуляры к сторонам
угла . Перпендикуляры эти должны пересечься (если
бы они были параллельны, параллельны были бы и
стороны АВ и СВ). Обозначим их точку
пересечения буквой F.
Через три точки D, E, F проводим окружность,
что всегда возможно, так как эти три точки не
лежат на одной прямой. Соединив точки Н и G (точки
пересечения сторон угла ABC с окружностью) с
точкой F, получим два вписанных в окружность
прямых угла GDF и HEF.
Итак, мы получили две хорды GF и HF, на
которые опираются вписанные в окружность прямые
углы GDF и HEF. Но в окружности вписанный
прямой угол всегда опирается на ее диаметр,
следовательно, хорды GF и HF представляют
собой два диаметра, имеющие общую точку F, лежащую
на окружности.
Поскольку эти две хорды, являющиеся, как мы
установили, диаметрами, не совпадают, то,
следовательно, точки О и О19 делящие
отрезки GF и HF пополам, представляют собой
не что иное, как два центра одной окружности.
Разбор софизма.
Ошибка здесь кроется в неправильно построенном
чертеже. На самом деле окружность, проведенная
через точки Е, F и, обязательно пройдет через
вершину В угла ABC, т. е. точки В, Е, F и D обязательно
должны лежать на одной окружности. Тогда,
конечно, никакого софизма не возникает.
Действительно, восстановив перпендикуляры в
точках Е и D к прямым ВС и ВА соответственно
и продолжив их до взаимного пересечения в точке F,
получаем четырехугольник BEFD. У этого
четырехугольника сумма двух его противоположных
углов BEF и BDF равна 180°. Но согласно
известному в геометрии утверждению вокруг
четырехугольника можно описать окружность тогда
и только тогда, когда сумма двух его
противоположных углов равна 180°.
Отсюда следует, что все вершины
четырехугольника BEFD должны принадлежать
одной окружности. Поэтому точки G и Н совпадут
с точкой В и у окружности окажется, как и должно
быть, один центр.
Очевидна и важность геометрических фактов,
повторяемых во время разбора этого МС.
С большим интересом воспринимают МС ребята 5-6-х
классов. Например МС, где нарушены правила
действий с именованными величинами.
Один рубль не равен 100 копеек.
1 р=100 коп
10 р=1000 коп
Умножим обе части этих верных равенств,
получим:10 р=100000 коп, откуда следует:
1 р=10000 коп.
Применение этого софизма является также
пропедевтикой использования именованных
величин при решении физических задач.
И, конечно, я всегда начинаю знакомить ребят с
математическими софизмами, утверждая, что:
“Два умножить на два будет пять”
2*2=4
4
4=5
5,
вынесем за скобки слева 4, справа5
4(1
1)=5(1
1),
разделим левую и правую часть на (11),
получим
4=5, откуда следует
2*2=5.
Начиная с этого урока, ребята с нетерпением
ждут новых МС.
Очень интересны МС древнегреческих
философов-математиков Зенона, Прокла, Перрона.
Они открывают обширное поле деятельности для
исследовательских работ учащихся. В книге [1]
представлены следующие “авторские” МС:
парадокс Зенона “Ахиллес никогда не догонит
черепаху”, софизм Прокла “Две непараллельные на
плоскости прямые не пересекаются”, софизм
Перрона “Единица есть наибольшее натуральное
число”.
Хотелось бы рекомендовать коллегам
использовать математические софизмы более
разнообразно в своей практике. Это сделает
изучение математики более увлекательным.
Огромную помощь окажет им замечательная книга
А.Г. Мадеры и Д.А.Мадеры “Математические
софизмы”.
(В Приложении 2
содержаться тексты математических софизмов из
таблицы Приложение1.)
Литература.
- А.Г. Мадера и Д.А.Мадера, “Математические
софизмы”, М., “Просвещение”, 2003г. - Обреимов В.И., , “Математические
софизмы”,СПб,1989г.
МОУ «Лесогорская СОШ»
СОЧИНЕНИЕ ПО МАТЕМАТИКЕ
на тему
«Математические софизмы»
|
Работу выполнил Воробьев Илья, 5 класс |
|
|
Руководитель Жилова Зоя Геннадьевна |
|
|
Адрес: 607710, Нижегородская обл., Шатковский р-н, п.Лесогорск, ул.Электриков, д.8 |
|
|
E-mail – les-mou@yandex.ru Тел. 8-831-90-4-60-80 |
«Математику уже затем учить надо,
что она ум в порядок приводит»
М.В.Ломоносов
Наверняка, каждый человек хоть раз в жизни слышал подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем». На самом деле, таких примеров можно привести очень много, но что все они обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь вымысел???
Именно эти вопросы я и хотел рассмотреть. Само понятие математических софизмов предполагает несколько видов софизмов, ведь в математические можно включить и алгебраические, и геометрические, и простейшие арифметические.
Поскольку я пока еще учусь в 5 классе, то рассмотрю простейшие арифметические софизмы доступные для моего понимания.
Софизм — (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок. Что же такое математический софизм?
Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Математический софизм представляет собой, по существу, правдоподобное рассуждение, приводящее к неправдоподобному результату. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям.
Основные создатели софизмов – древнегреческие ученые-философы. Они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения.
Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества (5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространения мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса.
Что касается самих софизмов, то, пожалуй, самым популярным на тот момент в Древней Греции был софизм Евбулида: «Что ты не терял, ты имеешь. Рога ты не терял. Значит у тебя рога». Единственная неточность, которую возможно было допустить, то это — двусмысленность высказывания. Данная постановка фразы является нелогичной, но логика возникла намного позже, благодаря Аристотелю, поэтому, если бы фраза строилась так: «Все, что ты не терял…», то вывод стал бы логически безупречным.
Наиболее серьезную роль сыграли математические софизмы, или апории, придуманные в V веке до нашей эры мудрецом Зеноном из южно-итальянского города Элей. Так, Зенон доказывал, что Ахиллес, один из самых сильных и храбрых героев, осаждавших древнюю Трою, никогда не догонит черепаху, которая, как известно, отличается крайне медленной скоростью передвижения.
Вот примерная схема рассуждений Зенона. Предположим, что Ахиллес и черепаха начинают свое движение одновременно, и Ахиллес стремится догнать черепаху. Примем для определенности, что Ахиллес движется в 10 раз быстрее
черепахи, и что их отделяют друг от друга 100 шагов. Когда Ахиллес пробежит расстояние в 100 шагов, отделяющее его от того места, откуда начала двигаться черепаха, то в этом месте он туже ее не застанет, так как она пройдет вперед
расстояние в 10 шагов. Когда Ахиллес минует и эти 10 шагов, то и там черепахи уже не будет, поскольку она успеет перейти на 1 шаг вперед. Достигнув и этого места, Ахиллес опять не найдет там черепахи, потому что она успеет пройти расстояние, равное 1/10 шага, и снова окажется несколько впереди его. Это рассуждение можно продолжать до бесконечности, и придется признать, что быстроногий Ахиллес никогда не догонит медленно ползающую черепаху.
А вот и некоторые современные математические софизмы, которые наиболее популярны и известны.
«Спичка вдвое длиннее телеграфного столба».
Пусть а дм- длина спички и b дм — длина столба. Разность между b
и a обозначим через c .
Имеем b — a = c, b = a + c. Перемножаем два эти равенства по
частям, находим: b2 — ab = ca + c2.
Вычтем из обеих частей bc.
Получим: b2- ab — bc = ca + c2- bc, или b(b -a — c) = — c(b — a -c),
откуда
b = — c, но c = b — a, поэтому b = a — b, или a = 2b.
В чем ошибка?
Разбирая софизм, выясняем, что:
Мы делили обе части равенства на выражение b-a-c,
Но b-a=с, значит b-a-c=0,
Мы разделили на 0!
«Два умножить на два будет пять»
Напишем 44=5
5,
вынесем за скобки слева 4, справа5
4(11)=5(1
1),
разделим левую и правую часть на (11), получим
4=5, откуда следует
2*2=5.
Ошибка скрылась в самом начале, при выносе за скобку выносится только числитель, знаменатель должен оставаться прежним.
«Один рубль не равен 100 копеек».
1 р=100 коп (1)
10 р=1000 коп (2)
Умножим обе части этих верных равенств, получим:
10 р=100000 коп (3), откуда следует:
1 р=10000 коп.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство
10 р.2 =100 000 к .2 ,
которое после деления на 10 дает
1 р. 2 = 10 000 коп. 2, (*)
а не равенство (3), как это записано в условии софизма. Извлекая квадратный корень из равенства (*), получаем верное равенство 1р.=100 коп.
«Единица равна двум»
Простым вычитанием легко убедиться в справедливости равенства
1-3 = 4-6.
Добавив к обеим частям этого равенства число , получим новое равенство
1-3 + = 4-6+
,
в котором, как нетрудно заметить, правая и левая части представляют собой полные квадраты, т. е.
(1-)
=(2-
)
Извлекая из правой и левой частей предыдущего равенства квадратный корень, получаем равенство:
1-=2-
откуда следует, что
1=2.
В преобразования, разумеется, закралась ошибка. А именно, совсем забыли, что равенство квадратов вовсе не означает равенство значений, возведенных в квадрат: они могут быть противоположны друг другу, как в нашем случае: 4-9/2 равно -1/2, а 5-9/2 равно 1/2. А квадраты этих значений одинаковы.
Что касается типичных ошибок в софизмах, то они таковы:
- Деление на 0;
- Неправильные выводы из равенства дробей;
- Неправильное извлечение квадратного корня из квадрата выражения;
- Нарушения правил действия с именованными величинами;
- Путаница с понятиями «равенства» и «эквивалентность» в отношении множеств;
- Проведение преобразований над математическими объектами, не имеющими смысла;
- Неравносильный переход от одного неравенства к другому;
- Выводы и вычисления по неверно построенным чертежам;
Математические софизмы:
- приучают внимательно и настороженно продвигаться вперед в изучении математики, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций;
- помогают развивать логику и навыки правильного мышления;
- развивают наблюдательность, вдумчивость, критическое отношение к тому, что изучается;
- это увлекательно!
Часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.
В нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений. Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.
Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
Использованная литература:
1. А.Г. Мадера, Д.А. Мадера «Математические софизмы», Москва, «Просвещение», 2003г.
2. Ф.Ф. Нагибин, Е.С. Канин «Математическая шкатулка» Москва, «Просвещение», 1988г.
3. «Большая энциклопедия Кирилла и Мефодия», 2004г.
Интернет ресурсы:
www.gadaika.ru
Софизмы в математике
Секция: Математические науки.
Автор: Шеметова Анастасия, Глазунова Екатерина, 8 класс
МБОУ «СОШ №18».
Научный руководитель: Лукьянова Ольга Георгиевна, учитель
математики МБОУ «СОШ №18».
Г. Миасс
Челябинская
область
Оглавление
Введение
I.
Софизм и история его возникновения
1.1. Софизм и софистика
1.2. Экскурс в историю
II.
Математические софизмы и их классификация
2.1. Софизмы и типичные ошибки в
них
2.2. Математические софизмы
2.3. Разбор математических
софизмов
2.4. Логические софизмы
2.5. Источники софизмов
III. «Софизмы из наших школьных тетрадей»
Заключение
Список литературы
Приложение 1.
Приложение 2. Арифметические софизмы
Приложение 3. Алгебраические софизмы
Приложение 4. Геометрические софизмы
В
математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.
И. Ньютон
Введение
У ученых есть такое свойство — поставят в
тупик все человечество, а потом целое поколение или даже несколько поколений с
трудом из него выбираются, проявляя чудеса изобретательности и изворотливости.
И одним из средств не только учёных, но и любознательных остроумных людей,
любящих ставить окружающих в тупик, является «софизм». Нас заинтересовал факт
глубокой древности зарождения софизмов и популярности их у ученых.
Актуальность: Наверное,
каждый человек хоть раз в жизни слышал фразу: «Дважды два равно пяти» или «Два
равно трем». Что они обозначают? Кто их выдумал? Имеют ли они какое-нибудь
логическое объяснение или же это лишь вымысел? Чтобы ответить на эти и подобные
им вопросы, мы в своей работе рассматриваем математические софизмы. Математический софизм – удивительное утверждение, в
доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
Поэтому нам представляется актуальным изучение ошибок в софизмах, потому что их
понимание ведёт к пониманию математике в целом, помогает развивать логику и
навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее
осознал, а осознание ошибки предупреждает от ее повторения в дальнейших
математических рассуждениях.
Цель: изучение типичных ошибок, которые возникают у учащихся
в процессе изучения математики, их причин и способов предупреждения на примере
математических софизмов.
Задачи:
1.
изучить понятие софизма и историю его возникновения;
2.
рассмотреть виды софизмов и дать классификацию их ошибок;
3.
составить сборник разбора задач на софизмы по различным разделам
математики для 6 — 9 классов.
Гипотеза исследования: если в процессе обучения математике целенаправленно
и систематически организовывать работу учащихся над типичными ошибками, на
примере софизмов, то это будет способствовать повышению качества математической
подготовки учащихся.
I. Софизм и история его возникновения
1.1. Софизм и софистика
Софизм в
переводе с греческого означает дословно: уловка, выдумка или мастерство. Этим
термином называют утверждение, являющееся ложным, но не лишенным элемента
логики, за счет чего при поверхностном взгляде на него кажется верным.
Софизмы основаны на сознательном и преднамеренном обмане, нарушении логики.
Софизм — преднамеренная ошибка, совершаемая с целью запутать
противника и выдать ложное суждение за истинное.
Софистика –
направление философии, которое возникло в V — IV вв. до н.э. в Греции и
стало очень популярным в Афинах.
1.2. Экскурс в историю
Во
второй половине V века до н.э. в Греции появились софисты. Софистами называли
группу древнегреческих философов достигших большого искусства в логике. Они
появились во время становления демократии в Афинах и на подвластных Афинам
территориях. Софисты — это мудрецы, но мудрецы особого рода. Этих мудрецов
истина не интересовала. Они были, как правило, платными «учителями мудрости».
Их нанимали политики для того, чтобы организовать свою предвыборную компанию, в
частности, переспорить оппонентов на собрании, а также для того, чтобы выиграть
судебное дело. В Греции софистами называли и простых ораторов —
философов-учителей, задачей которых было научить своих учеников «мыслить,
говорить и делать». Одним из представителей
софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а
это и есть гражданское искусство» (приложение 1, рис. 1).
Чтобы выйти победителем в словесном
поединке, софисты часто пользовались тем, что противник недостаточно глубоко
знает предмет, о котором идет речь, недостаточно внимателен и наблюдателен, и
поэтому не в состоянии отличить ложь от истины. В результате словесного
поединка противник должен был согласиться с доводами софиста и признать себя
побежденным, хотя истина, казалось, была на его стороне. Софизмы существуют и
обсуждаются более двух тысячелетий, причем острота их обсуждения не снижается с
годами. Если софизмы — всего лишь хитрости и словесные уловки, выведенные на
чистую воду еще Аристотелем, то долгая их история и устойчивый интерес к ним
непонятны. Однако софизмы существовали задолго до философов-софистов, а
наиболее известные и интересные были сформулированы позднее в сложившихся под
влиянием Сократа философских школах.(Приложение 1,рис.2)
Термин «софизм» впервые ввел Аристотель
(приложение 1, рис.3), охарактеризовавший софистику как мнимую, а не
действительную мудрость. К софизмам им были отнесены и «апории Зенона» (внешне парадоксальные рассуждения
на тему о движении и множестве), направленные
против движения и множественности вещей, и рассуждения собственно софистов, и
все те софизмы, которые открывались в других философских школах. Это говорит о
том, что софизмы не были изобретением одних софистов, а являлись скорее чем-то
обычным для многих школ античной философии. Аристотель называл софизмом «мнимые
доказательства», в которых обоснованность заключения кажущаяся и обязана чисто
субъективному впечатлению, вызванному недостаточностью логического анализа.
Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана
с хорошо замаскированной ошибкой, с использованием, например, «неразрешённых»
или даже «запрещённых» правил или действий.
Современный софизм, основной задачей
которого является манипуляция общественным сознанием, существует в
многочисленных формах. Современные софисты, прежде всего, — специалисты по
пиару. Работа, которых заключается в навязывании обществу тех или иных
политических деятелей.
В обычном и распространенном понимании
софизм — это умышленный обман, основанный на нарушении правил. Но обман тонкий
и завуалированный. Цель софизма – выдать ложь за истину.
В нашей работе мы рассматриваем
математические софизмы.
II. Математические софизмы и их классификация
2.1. Софизмы и типичные ошибки в
них
Математический софизм — удивительное утверждение, в
доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
История математики полна неожиданных и
интересных софизмов, разрешение которых порой служило толчком к новым
открытиям. Математические софизмы приучают внимательно и настороженно
продвигаться вперед, тщательно следить за точностью формулировок, правильностью
записи чертежей, за законностью математических операций. Поиск и нахождение
ошибок в софизме способствует пониманию математики в целом и развивает
логическое мышление.
К типичным ошибкам
в софизмах относятся:
· запрещенные
действия;
· пренебрежение условиями
теорем, формул и правил;
· ошибочный чертеж;
· опора на ошибочные
умозаключения.
Нередко, ошибки,
допущенные в софизме, настолько умело скрыты, что даже опытный математик не
сразу их выявит. Именно в этом и проявляется связь математики и философии в
софизмах.
2.2. Математические софизмы
Математические
софизмы делятся на:
1. Арифметические софизмы — это числовые
выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Пример: « Дважды два — пять!».
Возьмем в качестве исходного соотношения
следующее очевидное равенство: 4:4= 5:5. После вынесения за скобки общего
множителя из каждой части равенства будем иметь: 4∙(1:1)=5∙(1:1)
или (2∙2)(1:1)=5(1:1) Наконец, зная, что 1:1=1, из соотношения 4(1:1)=5(1:1)
устанавливаем: 4=5, 2∙2=5.
Ошибка.
Распределительный закон умножения применяется
только для сложения и вычитания: ав + ас = а(в + с).
2. Алгебраические
софизмы —
намеренно скрытые ошибки в уравнениях и числовых выражениях.
Алгебра — один из больших разделов
математики, принадлежащий наряду с арифметикой и геометрией к числу старейших
ветвей этой науки. Задачи, а также методы алгебры отличаются от других отраслей
математики.
Приёмы
эти заключаются обычно в составлении и решении уравнений.
Пример: «Любое отрицательное число больше
положительного, имеющего то же абсолютное значение».
Этот софизм основан на очевидной истине:
«Если в равенстве числитель левой дроби больше знаменателя в n раз, то и в
правой части равенства соотношение внутри дроби будет таким же».
Напишем следующие равенства:
и
; т.е.
.
Другими словами, если в левой части
равенства + a > — a, то и в правой части равенства должно соблюдаться то же
соотношение.
Т.е. – a > + a.
Ошибка.
Чтобы получить из равенства +a > -a
равенство –a>+a, нужно первое равенство умножить на -1, но при это нужно сменить
знак неравенства (–a<+a).
3.Геометрические софизмы – это
умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость,
абсурд или противоречивое утверждение, связанное с геометрическими фигурами и
действиями над ними.
Пример: «Из точки на прямую можно
опустить два перпендикуляра.»
Рассмотрим
треугольник АВС.
Разделим стороны АВ и ВС пополам точками M
и N. На этих сторонах, как на диаметрах, опишем окружности с центрами в точках
M и N. Окружности пересекут сторону АС в точках D и E.
Углы
AEB и BDC опираются на диаметры АВ и ВС соответственно, значит они прямые.
Следовательно, отрезки BD и BE, исходящие
из точки В, будут перпендикулярны, стороне АС, следовательно, из точки В можно
опустить два перпендикуляра на сторону АС.
Ошибка.
Действительно, опустив из B перпендикуляр
на AC , получим два прямоугольных треугольника, гипотенузами которых будут
стороны BC и AB, и если вокруг этих треугольников описать окружности, их
гипотенузы будут диаметрами. Неправильный чертеж. Известно,
что окружности, построенные на двух сторонах треугольника как на диаметрах,
пересекаются в одной точке, лежащей на третьей стороне.
2.3. Разбор математических софизмов
В математических софизмов выделяются 6 основных
ошибок:
1. Деление на 0.
Софизм №1 «Пять равно шести».
Возьмем тождество 35+10-45=42+12-54.
В каждой части вынесем за скобки общий
множитель:
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Ошибка.
При делении верного равенства
5(7+2-9)=6(7+2-9) на число 7+2-9, равное 0. Этого нельзя делать. Любое
равенство можно делить только на число, отличное от 0.
Софизм №2 «Уравнение x-a=0 не имеет
корней».
Дано уравнение x –a = 0. Разделив обе
части этого уравнения на x-a, получим, что 1 = 0. Поскольку это равенство
неверное, то это означает, что исходное уравнение не имеет корней.
Ошибка.
Поскольку x = a – корень уравнения, то,
разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому
получили неверное равенство 1=0.(x—a=0 -на ноль делить нельзя).
2. Неправильные выводы из равенства дробей;
Софизм №3 «Отклонение от алгоритма может
привести к приобретению посторонних корней данного уравнения».
3. Неправильное извлечение квадратного корня из
квадрата выражения.
Софизм №4 =
=
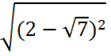
Ошибка.
При
вычислении квадратного корня 2- < 0
=
=
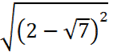
ç=
— 2
4. Нарушения правил действия с величинами.
Софизм №5 «Один метр не равен ста
сантиметрам».
Известно, что любые два равенства можно
перемножить почленно, не нарушая при этом равенства, т. е. если а = b и c = d,
то ac = bd. Применим это положение к двум очевидным равенствам: 1 метр =
100сантиметрам и 10 метров = 1000 сантиметрам. Перемножая эти равенства почленно,
получим 10 метров = 100000 сантиметров и, разделив последнее равенство на 10,
получим, что 1 метр = 10000 сантиметров .
Ошибка.
Она состоит в нарушении правила действий
с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.
«Один рубль не равен ста копейкам».
Возьмем верное равенство: 2р. = 200к. и
возведем его по частям в квадрат. Мы получим: 4 р. = 40 000 к.
Ошибка.
Здесь надо вспомнить, что
возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не
величины.
5. Проведение преобразований над математическими
объектами, не имеющими смысла.
Софизм №6 «Два
неодинаковых натуральных числа равны между собой».
Решим систему двух уравнений:
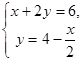
Сделаем это
подстановкой у из 2-го уравнения в 1-е, получаем х+8-х=6, откуда
8=6.
Ошибка
Уравнение (2)
можно записать как х+2у=8, так, что исходная система запишется в виде: .
В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.
Графически это
означает, что прямые у=3- и у=4-
параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
6. Неравносильный переход от одного неравенства к
другому.
Софизм №7 «Если А
больше В, то А всегда больше, чем 2В».
Возьмем два произвольных
положительных числа А и В, такие, что А>В. Умножив это неравенство на В,
получим новое неравенство АВ>В*В, а отняв от обеих его частей А*А, получим
неравенство АВ-А*А>В*В-А*А, которое равносильно следующему: А(В-А)>(В+А)(В-А).
(1)
После деления обеих частей
неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому
неравенству почленно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к
примеру, что из неравенства 6>5 следует, что 6>10.
Ошибка.
Здесь совершен неравносильный
переход от неравенства (1) к неравенству (2). Действительно, согласно условию А
> В, поэтому В – А < 0.Это означает, что обе части неравенства (1)
делятся на отрицательное число. Но согласно правилу преобразования неравенств
при делении или умножении неравенства на одно и то же отрицательное число знак
неравенства необходимо изменить на противоположный. С учетом сказанного из
неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к
которому почленно исходное неравенство В<А, получим просто исходное
неравенство А+В<В+2А.
7. Выводы и вычисления по неверно построенным чертежам;
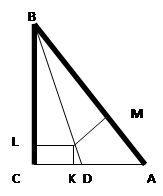
№8 ∟С=90, ВД — биссектриса угла СВА, СК=КА, ОК перпендикулярна СА, О —
точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС.
∟С=90, ВД — биссектриса ∟ СВА,
СК=КА, ОК ^ СА, О —
точка пересечения прямых ОК и ВД, ОМ ^ АВ, ОL ^
ВС.
Имеем: D
LВО=D МВО, ВL = ВМ, ОМ = ОL = СК = КА,
D КОА=D ОМА (ОA- общая сторона, КА = ОМ, ∟ ОКА и
∟ ОМА — прямые), ∟ ОАК =
∟ МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и
потому ВА = ВС
Ошибка.
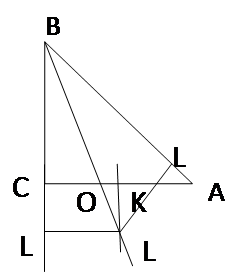 |
Рассуждения о
том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка
пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к
катету АС, находится вне треугольника АВС.
2.4. Логические софизмы
Один из видов
математических софизмов является логический софизм.
Пример № 1: «Полупустое или полуполное».
Полупустое есть то же, что и полуполное.
Если равны половины, значит, равны и целые. Следовательно, пустое есть то же,
что и полное
Ошибка.
Полупустое не является половиной чего либо
пустого, а является чем либо наполовину наполненным.
Пример
№2: «Когда
же учиться?»
1. По ночам занятий нет, половина суток свободна.
Остаётся: 365-182=183 дня. 2.
2. В школе ученики занимаются половину дня, значит, вторая
половина (или четвёртая часть суток) может быть свободна.
Остаётся:183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы
приходится 15 дней, таким образом, выходных в учебном году52-15=37 дней.
Итого остаётся 137-37=100 дней.
4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние
(7 дней), летние (78 дней). Всего 5+10+7+78=100 дней.
5. Итак, школьники заняты в году 100-100=0 дней. Когда же
учиться?!
2.5. Источники софизмов
Источниками
софизмов может выступать терминология, которая используется во время спора.
Многие слова имеют несколько смыслов (доктор может быть врачом или же научным
сотрудником, имеющим ученую степень), за счет чего и происходит нарушение
логики. Софизмы в математике, например, основаны на изменении чисел путем
перемножения их и последующего сравнения исходных и полученных данных.
Неправильное ударение тоже может быть оружием софиста, ведь множество слов при
изменении ударения меняют и смысл. Построение фразы иногда очень запутанно,
как, например, «два умножить на два плюс пять». В данном случае непонятно
имеется ли в виду сумма двойки и пятерки, умноженная на два, или же сумма
произведения двоек и пятерки.
Разбор и
решение любого рода математических задач, а в особенности нестандартных,
помогает развивать смекалку и логику. Математические софизмы относятся именно к
таким задачам.
III.
«Софизмы из наших школьных тетрадей»
Цель практической работы: проанализировать наши тетради для
контрольных работ по математике, выявить софизмы и найти ошибки, заключенные
в них.
Известная истина гласит «Умные люди учатся
на чужих ошибках». В математике приходится учиться, в основном, на собственных
ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и
полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.
С помощью задач,
содержащих противоречие в условии, можно предупредить ошибки учащихся,
связанные с работой над математическими объектами, которые не существуют при
заданных условиях. Если учащиеся решают задачу, работая с несуществующими
объектами, то происходит выход за границы применяемости теоремы, свойства и
т.д. Эти ошибки возникают по той причине, что большинство учебных задач
содержит информацию непротиворечивую и приводящую к единственному решению.
|
Софизм |
Ошибка |
|
№1 |
Неправильный
|
|
№2
|
Нарушение
|
|
|
|
|
№4
ОДЗ:
Умножим обе 2 Разложили 2 = (x — 2) (2x + 1) (x — 2) (2x + 1) = x2 (x — 2) Разделим х — X2 -2x -1 =0 Д=4+4=8 X1= X2=1- Корни Ответ: |
Ошибка: (x-2)(2x+1)=x2 (x-2) , на x-2произошла Верное x2 (x-2) – (x-2) (2x+1)=0 (x-2) (x2-2x-1)=0 х — x = 2 или x1=1 + Уравнение 1 + Но Ответ: |
|
№5
|
Верное Ошибка: Правило: |
|
№6 Периметр треугольника равен 6, его стороны относятся как |
Задача провоцирует учащихся на то, чтобы дать ответ 2. При |
|
|
Известные элементы (радиус окружности и угол, образуемый |
Заключение
Исторические
сведения о софистике и софистах помогли нам разобраться, откуда же все-таки
началась история софизмов. Вначале мы думали, что софизмы бывают исключительно
математические. Причем в виде конкретных задач, но, начав исследование в этой
области, мы поняли, что софистика — это целая наука, а именно математические
софизмы — это лишь часть большого течения.
Разбор софизмов
развивает логическое мышление, помогает сознательному усвоению изучаемого
материала, воспитывая вдумчивость, наблюдательность, критическое отношение к
тому, что изучается. Кроме того, разбор софизмов увлекателен. Мы с большим
интересом воспринимали софизмы, чем труднее софизм, тем большее удовлетворение
доставляет его разбор. Порой сам попадаешься на уловки софиста.
Гипотеза, которую
мы ставили в начале работы «Если в процессе обучения математике целенаправленно и
систематически организовывать работу учащихся над типичными ошибками, на примере
софизмов, то это будет способствовать повышению качества математической подготовки
учащихся», подтвердилась.
Благодаря знанию
софизмов можно научиться искать ошибки в рассуждениях других, научится
грамотно строить свои рассуждения и логические объяснения. Когда ребенок раз
притронется к горячему предмету, то впоследствии он постарается этого не
делать. Он будет много осторожнее. Так, изучающий математику, впоследствии
проявит больше осторожности, чтобы не повторить осознанную ошибку. Значит, математические софизмы заставляют внимательно
и настороженно продвигаться вперед, тщательно следить за точностью
формулировок, правильностью записей и чертежей, за допустимостью обобщений, за
законностью выполняемых операций. Все это нужно и полезно. Только очень сухого
человека не может увлечь интересный софизм. Как приятно бывает обнаружить
ошибку в математическом софизме и тем как бы восстановить истину в ее правах.
Математические софизмы показали нам, как важно строго соблюдать правила и
формулировки теорем при логических умозаключениях.
Нам
было очень интересно работать над данной темой. Мы создали сборник «Софизмы из
наших школьных тетрадей».
Задания,
предложенные нами в работе, можно использовать как на уроках алгебры и
геометрии, так и на внеклассных мероприятиях.
Список
литературы
1. «Софисты»
под редакцией Б.С. Чернышева
2. «Софизмы. Алгебра.
Геометрия. Тригонометрия» под редакцией Т.Н. Михеевой
3. http://gamzatovasm.ru/node/88 — Алгебраические
софизмы
4. http://reshit.ru/sofizm — Геометрические
софизмы
5. http://sophisms.ucoz.ru/index/arifmeticheskie_sofizmy/0-6 — Арифметические софизмы
6. http://referatwork.ru/category/logika/view/131832_sofizmy — Логические софизмы
7. https://ru.wikipedia.org/wiki/Апории_Зенона — Апории Зенона
Приложения
Приложение 1.


2 Сократ

Приложение 2.
Арифметические софизмы
1.
Верно ли равенство 7 = 8?
35 +
14 – 49 = 40 + 16 — 56
7(5 +
2 — 7)=8(5 + 2 — 7)
Следовательно,
7 = 8
Ошибка.
Обе части равенства разделили на (5 + 2 — 7),
но нарушено правило, что на «0» делить нельзя (5 + 2 – 7 = 0)
2.
Некто
утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы
последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же
чисел, но взятых в обратном порядке (от 1 до 9):
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2
Будем
последовательно вычитать числа второй строки из чисел первой. Например, так как
9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь
нетрудно установить,
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2 = 45.
Итак,
45 – 45 = 45.
Ошибка состоит в том,
что занимаемую единицу возводили в ранг десятка.
3.Меньшее число больше, чем большее».
Очевидно,что7 > 5 и что – 8 = — 8
Тогда:7 – 8 > 5 — 8 или – 1 > — 3
Это не противоречит основному понятию об
отрицательных величина, на основании которого мы считаем меньшей ту
отрицательную величину, численное значение которой больше, и наоборот.
Умножим обе части последнего неравенства на (- 4).
Получим (-1)*(-4)>(-3)*(-4) или 4 > 12
Ошибка.
При умножении неравенства на отрицательное
число, знак неравенства изменяется на противоположный.
Приложение 3. Алгебраические софизмы
1.«Отрицательное число больше положительного».
Возьмем два положительных
числа а и с. Сравним два отношения: и
Они равны, так как каждое из них равно –(а/с). Можно составить
пропорцию:
Но если в пропорции предыдущий член первого отношения больше последующего,
то предыдущий член второго отношения также больше своего последующего. В нашем
случае а > — с, следовательно, должно быть –а > с, т.е. отрицательное
число больше положительного.
Ошибка.
Данное свойство пропорции может оказаться неверным, если некоторые
члены пропорции отрицательны.
2. « Если
одно число больше другого, то эти числа равны»
Возьмем два
произвольных числа т и п, такие, что m > n , и другие три произвольных числа а, b и с, сумма которых
равна d, т.е. а + b + c = d. Умножив обе части этого равенства на n, а затем на
m, получим:
ma + mb + mc
= md, na + nb + nc = nd.
Сложив почленно равенства:
ma + mb + mc
= md и nd = na
+ nb + nc
получим: ma + mb + mc + nd = na + nc + nb + md.
Перенося здесь nd вправо, а md влево, имеем
ma + mb + mc
– md = na + nb + nc — nd.
Вынося слева число m, а справа число n за скобки,
придем к соотношению m (a + b + c — d) = n (a + b + c — d).
Разделив обе части последнего равенства на
(a + b + c — d), находим, что m = n.
Ошибка.
a + b + c – d =0, на ноль делить нельзя.
4.
«Любое число равно нулю»
Возьмем произвольное положительное число а и
рассмотрим сумму х бесконечного числа слагаемых, равных а: х = а + а + а + а +…
Очевидно, что мы можем представить эту сумму как х = а + (а + а + а +….) в
которой сумма, стоящая в скобках, также равна х как сумма бесконечного числа слагаемых,
равных а. Так что можем записать, что х = а + х, откуда заключаем, что а=0.
Ошибка допущена в равенстве (1) , в котором бесконечная сумма чисел
а обозначена конечным числом х.
4.
Решим систему двух
уравнений:
Сделаем это подстановкой у из 2го
уравнения в 1, получаем х + 8 — х = 6, откуда
8 = 6
Ошибка.
Уравнение (2) можно записать как х + 2у = 8,
так что исходная система запишется в виде:
В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.
Графически это
означает, что прямые у=3 — и у = 4
— параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
5. «Если “a” больше “b”, то “a” всегда больше,
чем “2b”»
Возьмем два
произвольных положительных числа a и b, такие, что a > b. Умножив это
неравенство на b, получим новое неравенство:
ab > bb, а отняв от обеих
его частей a·a, получим
неравенство:
ab—aa > bb — aa, которое
равносильно следующему: a(b—a) > (b+a)(b—a).(1)
После деления обеих частей неравенства (1)
на b—a получим, что a > b+a (2),
Прибавив к этому неравенству почленно
исходное неравенство a> b, имеем
2a >
2b + a,
откуда a > 2b.
Итак, если a > b, то a > 2b.
Ошибка совершена при
переходе от равенства (1) к (2).
Т.к. a > b, то b — a<0,
следовательно, при делении неравенства (1) на b – a, мы должны
поменять знак неравенства на противоположный.
6.«Единица равна двум»
Простым вычитанием легко убедиться в
справедливости равенства
1 — 3 = 4-6.
Добавив к обеим частям этого равенства
число 9/4, получим новое равенство
1 — 3 + 9/4 = 4 — 6
+ 9/4,
в котором, как нетрудно заметить, правая и
левая части представляют собой полные квадраты, т. е. (1 — 3/2)=(2 — 3/2)
Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство: 1 — 3/2
=2 — 3/2
откуда следует, что 1=2.
Ошибка.
По определению представляет собой некоторое
неотрицательное число, которое, будучи возведено в квадрат, даст х. Ясно, что
этому определению удовлетворяют два числа, а именно х и -х. Итак, если число х
неотрицательно (х ≥ 0), то= х; если же число х отрицательно (х<0), то есть число –х положительно, то
= — x. Отсюда заключаем, что
(свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.
7.
«Всякое
число равно своей половине.»
Запишем очевидное для любого числа a
тождество a2— a2= a2— a2,где
а — любое число.
Вынесем a в левой части за скобку,
а правую часть разложим на множители по формуле разности квадратов, получим
a(a – a) = (a + a)(a — a).
Разделив обе части на a — a, получим a = a + a, или a=2a.
Разделим на 2 и получим а
= а/2
Ошибка.
Мы делим обе части на ноль, а деление на
ноль запрещено
Приложение 4. Геометрические софизмы
1. , а длина всякой окружности равна ее
диаметру.
Построим
на отрезке МN как на диаметре окружность. Радиус окружности обозначим через . Тогда длина окружности будет
равна:
Поделим
MO и NO пополам точками и
и построим новые окружности с центрами в
этих точках радиусами .
Найдем
длины новых окружностей:
Сумма
их длин будет равна
т.е.
равна длине большой окружности C.
Таким
же образом будем строить окружности и далее и находить сумму их длин.
Так,
сумма длин окружностей и
. и будет равна
Продолжая
деление далее, мы будем делить диаметр NM на все меньшие части, а радиусы новых
окружностей будут равны и т.д. При этом сумма длин всех этих
окружностей всегда будет равна .
Так
как число делений большого диаметра будет бесконечно большим, окружности станут
настолько малыми, что сольются с диаметром, и сумма их длин в пределе будет
равна длине диаметра, так что она будет равна.
С
другой стороны, сумма длин этих окружностей постоянна и равна , следовательно,
Из
этого равенства получаем или, деля на
:
Ошибка: Так как сумма
длин бесконечно малых окружностей постоянна, то она и в пределе равна . Пусть
— длина малой
окружности,
— ее радиус. Как бы такая окружности ни была мала, всегда имеем или
Отсюда
видим, что эта бесконечно-малая окружность никогда не будет равна своему
диаметру ,
что следовало бы из результата софизма.
2.« Отрезки параллельных прямых, заключенные между сторонами
угла, равны»
Рассмотрим произвольный угол с
вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки
которых АВ и CD заключены между сторонами этого угла.
Как известно параллельные
прямые отсекают от сторон угла пропорциональные отрезки, следовательно, АЕ :
CE = BE : DE,
Откуда АЕ·DE = BE·CE
Умножив обе части последнего
равенства на отличную от нуля разность (АВ –CD), запишем
AE·DE·AB — AE·DE·CD = AE·DE·CD
— BE·CE·CD,
или
AB(AE·DE — BE·CE) = CD(AE·DE —
BE·CE)
Разделив обе части последнего равенства на (AE·DE — BE·CE), получим
равенство АВ=CD.
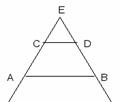
Ошибка.
AE·DE — BE·CE=0
3.Все треугольники равнобедренные.
Рассмотрим
произвольный ∆АВС (рис.2).
Проведем
в нем биссектрису угла B и серединный перпендикуляр к стороне АС. Точку их
пересечения обозначим через О.
Из
точки O опустим перпендикуляр OD на сторону АВ и перпендикуляр ОЕ на сторону
ВС. Очевидно, что ОА = ОС и OD = ОЕ. Но тогда ∆AOD = ∆СОЕ по катету и
гипотенузе. Поэтому ∟DAO = ∟ЕСО. В то же время ∟ОАС = ∟ОСА,
так как ∆АОС -равнобедренный.
Получаем:
∟ВАС = ∟DAO + ∟ОАС = ∟ЕСО + ∟ОСА = ∟ВСА
Итак, угол ВАС равен углу ВСА, поэтому ∆АВС — равнобедренный:
АВ=ВС.
Ошибка. При построения чертежа. Серединный перпендикуляр к
стороне и биссектриса противоположного ей угла для не равнобедренного
треугольника, пересекаются вне этого треугольника.
Приложение 4.
Логические софизмы.
1.
Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше.
Значит, лекарств нужно принимать как можно больше».
2. Одна
песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n+1
песчинка – тоже не куча. Следовательно, никакое число песчинок не образует кучу
песка. К этому парадоксу можно сделать следующий комментарий: метод полной
математической индукции нельзя применять, как показывает парадокс, к объёмно
неопределённым понятиям, каковым является понятие «куча песка».
3.
Что появилось раньше: яйцо или курица. Для того чтобы появилось яйцо, должна
существовать курица, но ведь курица может вылупиться только из яйца, а значит,
первичным является именно оно.
4.«Может ли
всемогущий маг создать камень, который не сможет поднять?»
Если не может – значит, он не всемогущий.
Если может – значит, всё равно не всемогущий, т.к. он не может поднять это
камень.
6.В мире нет ни одного человека,
говорящего на моем языке; или короче: ни одного человека, говорящего; или еще
короче: ни одного человека.
Скачано с www.znanio.ru
- Авторы
- Научный руководитель
- Файлы
- Литература
Апатикова М.Г.
1
1 7 = 8 или тренировка для ума – парадоксы и софизмы в математике
Чернышева В.С. (Наро-Фоминск, МАОУ СОШ №3 СУИОП)
1. Мадера А.Г., Мадера Д.А. Математические софизмы. – М.: Просвещение, 2003.
2. Обреимов В.И. Математические софизмы. – СПб., 1989.
3. Михеева Т.Н. Софизмы (Софизмы. Алгебра. Геометрия. Тригонометрия). – М.: Грамотей, 2007.
4. Ивлев Ю.В. Логика. – М.: Проспект, 2006.
5. Шамина В.В., Матешин В.Е., Ефремова А.А., Шмелева О.В. Математические парадоксы и софизмы // Юный ученый. – 2016. – №6.1. – С. 47–50.
6. Маслов А.Н. Логика для детей и взрослых.
7. Гусев Д.А. Удивительная логика (о чем умолчали учебники). – М., 2010.
8. Генри Дьюдени Средневековые головоломки.
10.https://infourok.ru/materialy_k_uroku_matematiki_na_temu_sofizmy_i_paradoksy-137969.htm
11.http://nsportal.ru/ap/library/drugoe/2013/10/31/matematicheskie-sofizmy-i-paradoksy
12.https://ru.wikipedia.org/wiki/ %D0 %A1 %D0 %BE %D1 %84 %D0 %B8 %D0 %B7 %D0 %BC
Математика – один из моих любимых школьных предметов. Она мне нравится не только потому, что это основной школьный предмет, но и потому, что без математических знаний в жизни не обойтись. Математика одна из древнейших наук. Она сопровождает нас везде: в науке, медицине, строительстве, сельском хозяйстве, торговле и юриспруденции. Занятие математикой развивает логическое мышление, сосредоточенность, находчивость, устойчивое внимание, хорошую память, смекалку.
В повседневной жизни мы сталкиваемся с интересными и очень забавными вещами, при виде которых хочется удивляться, любоваться и изумляться красоте и изяществу.
Вот, например:
(1+2–3–4)(5–6–7–8–9)=100
2•9=2592.
Я люблю решать задачи, докапываться до истины, разгадывать вместе с бабушкой математические ребусы, головоломки, шарады, кроссворды и играть в интеллектуальные игры. В ноябре этого года мы с классным руководителем посетили музей «Экспериментаниум», и там я в подарок бабушке купила несколько книг: «Логика для детей и взрослых» А.Н. Маслова, «Удивительная логика» Д.А. Гусева и «Средневековые головоломки» Генри Дьюдени. Как-то вечером, после просмотра очередного детектива, бабушка мне говорит: «Маша, а ты знаешь, что 7=8!»
Я заинтересовалась….
Бабушка с легкостью доказала это равенство…
Вот как это было: 7=8.
Запишем верное равенство:
49+14–63=56+16–72,
вынесем общий множитель за скобки
7(7+2–9)=8(7+2–9),
разделим обе части на (7+2–9).
Получим, что 7=8, что и требовалось доказать….
Где ошибка? Я попыталась решить (Приложение 6).
Работая над проектом, я узнала, что в математике есть такие понятия, как софизмы и парадоксы. И это не одно и то же. Парадоксы и софизмы очень поучительны и интересны, а история математики полна неожиданных софизмов и парадоксов, а их разрешение, порой, служило толчком к новым открытиям, из которых, в свою очередь, вырастали новые софизмы и парадоксы.
Процесс нахождения ошибок в софизмах и парадоксах ведет к осмысленному постижению математики. Такой подход при изучении математики способствует более глубокому ее пониманию и осмыслению и, кроме того, показывает, что математика – это живая наука, а не собрание закостенелых догм, выдуманных по чьей-то злой воле. Как сказал выдающийся ученый Блез Паскаль: «Предмет математики настолько серьёзен, что полезно не упускать случая, делать его немного занимательным».
Актуальность темы: В жизни, к сожалению, часто можно столкнуться с обманом, мошенничеством. Я считаю, что очень важно научиться отличать ложь от истины и уметь противостоять манипуляциям со стороны других. Благодаря математическим софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, грамотно строить свои рассуждения и логические объяснения.
Гипотеза: Парадоксы и софизмы – тренировка для ума.
Цель: изучить данную тему, а именно, узнать, что такое софизмы и парадоксы. Найти применение полученных знаний на практике, в жизни.
Задачи:
1. Познакомиться с парадоксами и софизмами.
2. Узнать, в чем их отличие.
3. Понять, как найти ошибку в парадоксах и софизмах?
4. Узнать, как проклассифицировать парадоксы и софизмы, по каким критериям?
5. Составить свой софизм или парадокс.
6. Познакомить одноклассников с результатами работы.
Объект и предмет исследования: софизмы и парадоксы.
Методы исследования:
1. Анализ литературы и информации, полученной из Интернет-источников
2. Обсуждение темы с учителем, родными и одноклассниками
3. Анкетирование одноклассников
4. Анализ и обобщение полученных данных.
Этапы исследования:
1. Сбор информации в книгах и интернете
2. Беседы с учителем, родными и одноклассниками
3. Анализ собранного материала
4. Анкетирование одноклассников
5. Обработка анкет
6. Поиск практического применения полученных знаний
7. Создание презентации
8. Оформление буклета.
Узнала я от бабушки, что 7=8,
А 2+2=5,
Три тоже, что и Два.
И числа все равны…
Что вор – не вор,
И спичка великан.
Часы идут, когда лежат,
Стоят, когда висят.
Софизм и парадокс – красивые слова….
Где правда, а где ложь,
Ведь сразу не поймешь.
Но если знания имеешь ты
И с логикой знаком,
То распознать обман
Легко сумеешь ты,
И доказать, что 7=7,
А 2+2=4.
Что вор – есть вор,
И что лекарства не всегда добро.
Все в меру и с умом.
Желание и труд,
Усилие и терпение.
Твой мозг в работу приведут,
Ведь главное – учение!
Теоретическая часть
В данном разделе мы собрали информацию, полученную из прочитанных книг, научных статей и со страниц Интернета. Я познакомилась с понятиями софизма и парадокса, с помощью учителя установила их связь с математикой, мы доказали, что умение решать софизмы способствует развитию логики, математические софизмы и парадоксы могут использоваться на уроках математики, быть основой игры КВН.
Что такое софизм – понятия и определения
Из словаря Ожегова С.И. мы узнали:
Софизм, -а, м. (книжн.). Формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положении.
В Википедии мы нашли:
Софизм (от греч. σ?φισμα, «мастерство, умение, хитрая выдумка, уловка, мудрость») – (1) сложное рассуждение, иногда намеренно запутанное с целью показать умственное превосходство или ввести в заблуждение; (2) нестандартная задача, как правило, имеющая несколько решений; (3) приём обучения и метод исследования, введённый древнегреческими софистами; широко практиковался в средневековых университетах (sophismata), послужил прообразом современных сборников задач и упражнений; (4) ошибочное рассуждение, неправильный аргумент. Софизм основан на преднамеренном, сознательном нарушении правил логики. Это отличает его от паралогизма и апории, которые могут содержать непреднамеренную ошибку либо вообще не иметь логических ошибок, но приводить к явно неверному выводу.
Из литературы мы собрали информацию:
Слово софизм – красивое и весьма необычное, к тому же его мы не употребляем в повседневной жизни, поэтому некоторые люди не знают, что оно означает, а порой, и впервые слышат. Софизмы были замечены еще в древности[1]. Термин софизм впервые ввел Аристотель, который охарактеризовал софистику как мнимую, а не действительную мудрость. Возникновение софизмов можно отнести к V—IV вв. до нашей эры. Наиболее известные и интересные софизмы были сформулированы в сложившихся под влиянием Сократа философских школах.Позднее в древней Греции софистами стали называть философов – учителей, которые учили своих учеников «мыслить, говорить и делать» [5]. Софисты были глубоко образованными людьми, они стремились научить учеников владеть искусством словесных состязаний. Чтобы выйти победителем в словесном поединке, софисты часто пользовались тем, что противник недостаточно глубоко знает предмет, о котором идет речь, недостаточно внимателен и наблюдателен, и поэтому не в состоянии отличить ложь от истины. В результате словесного поединка противник должен был согласиться с доводами софиста и признать себя побежденным, хотя истина, казалось, была на его стороне. Наиболее известна деятельность старших софистов, к которым относят Зенона, Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса (Приложение 7). Суть деятельности софистов много больше, чем простое обучение искусству красноречия.
Софизм – это то же надувательство, только выполненное намного изящнее и незаметнее [1].
В юриспруденции, которой я собираюсь заниматься в будущем, софизм считается помехой в споре. Использование софизмов уводит рассуждение в сторону: вместо выбранной темы приходится говорить о правилах и принципах логики. Вот пример древнего софизма: «Вор не желает приобрести ничего дурного; приобретение хорошего – есть дело хорошее; следовательно, вор желает хорошего».
Софизмы делятся на математические и логические.
В математических софизмах выполняются «запрещенные» действия, идущие не по правилам и законам математики. Решение (разбор) софизмов – очень увлекательное занятие [3].
Различают три типа математических софизмов: алгебраические, арифметические и геометрические (Приложение 5).
Роль софизмов в математике
Способствуют повышению строгости математических рассуждений. Содействуют более глубокому уяснению понятий и методов математики. Софизмы развивают логическое мышление. Обнаружить ошибку в софизме – это значит осознать её, а осознание ошибки предупреждает от повторения её в других математических рассуждениях. Разбор софизмов помогает сознательному усвоению изучаемого материала, развивает наблюдательность, вдумчивость. Разбор софизмов увлекателен. Софистика – это целая наука, а математические софизмы – это лишь часть одного большого течения. Поиск в софизме ошибок, ясное понимание их причин ведет к осмысленному, глубокому изучению математики.
Парадоксы – понятие и определения
«А разве сама жизнь не парадокс?» (Л. Кэррол, «Полуночные задачи»)
Из словаря Ожегова С.И.: Парадокс, -а, м. (книжн.). 1. Странное, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее (иногда только на первый взгляд) здравому смыслу. Говорить парадоксами. 2. Явление, кажущееся невероятным и неожиданным.
В Википедии мы нашли: Парадокс (от др.-греч. παρ?δοξος – неожиданный, странный от др.греч. παρα-δοκ?ω – кажусь) – ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения. В самом широком смысле под парадоксом понимают высказывание, которое расходится с общепринятым мнением и кажется нелогичным (зачастую лишь при поверхностном понимании). Парадокс, в отличие от афоризма, поражает неожиданностью. Например, уайльдовский «Разводы совершаются на небесах». Парадокс – это всегда полуправда и это, как говорил Оскард Уальд, «лучшее, чего мы можем достичь, потому что абсолютных правд не существует». Парадокс своей стилизованной формой напоминает афоризм. В парадоксе привычная истина рушится на глазах и даже высмеивается. Например, «Я слышал столько клеветы в Ваш адрес, что у меня нет сомнений: Вы – прекрасный человек!» (О. Уайльд), «Взаимное непонимание – самая подходящая основа для брака» (О. Уайльд).
Из литературы мы узнали: Парадоксы – это справедливые, хотя и неожиданные утверждения, в то время как софизмы – ложные результаты, полученные с помощью рассуждений, которые только кажутся правильными, но обязательно содержат ту или иную ошибку[2]. В широком смысле парадокс – высказывание, истинность которого неочевидна; в этом смысле парадоксальными принято называть любые неожиданные противоречивые высказывания, особенно, если неожиданность их смысла выражена в остроумной форме. Библер В.С. замечает: «Понятие парадокса существует сейчас в самых различных смыслах – от чисто словарного и повседневного (красиво звучащая бессмыслица, до строго формального (логического), наиболее осознанного в парадоксах теории множества».
Парадокс – это нечто необычное и удивительное, то, что расходится с привычными ожиданиями, здравым смыслом и жизненным опытом. Это высказывание, истинность которого не очевидна; справедливое, но неожиданное утверждение.
Математический парадокс – высказывание, которое в данной теории равным образом может быть доказано и как истинна, и как ложь. В математике парадокс – ситуация, когда в данной теории доказываются два взаимоисключающих суждения, причём каждое из них выведено убедительными с точки зрения данной теории средствами, то есть парадокс – высказывание, которое в данной теории равным образом может быть доказано и как истина, и как ложь. Парадокс в современном значении – это два противоположных утверждения, для каждого из которых имеются представляющиеся убедительными аргументы. Грань между софизмом и парадоксом не является сколько-нибудь определенной. В случае многих конкретных рассуждений невозможно решить на основе стандартных определений софизма и парадокса, к какому из этих двух классов следует отнести суждение. В разных источниках, мы встречали термин «апории» (греч. «затруднение») по отношению и к софизмам, и к парадоксам. Даже в отношении таких знаменитых «апорий», как «Покрытый», «Протагор и Еватл» не решено, относить их к софизмам или парадоксам. От этого тема парадоксов и софизмов стала для меня еще интереснее.
Выводы: Софизм и парадокс это не одно и тоже. Отличие между софизмом и парадоксом: отношение к истине. Несмотря на то, что и софизм и парадокс доказывают на первый взгляд абсурдные вещи, парадокс это верное утверждение, в то время как софизм изначально ложное. В отличие от парадокса, в софизме ошибка сделана специально, но скрыта, якобы, под правильным действием. Парадокс – это абсолютная истина, софизм – относительная истина. Разбор софизмов и анализ парадоксов очень увлекателен, узнав одно, хочется искать что-то новое. Работа с софизмами и парадоксами способствует развитию современных идей и методов. Этими вопросами занимается наука, называемая математической логикой.
Практическая часть
Мы поработали с книгами и учебниками по логике и основам математики, посмотрели статьи в интернете и работы сверстников по моей теме. Я побеседовала с родными и близкими, с одноклассниками.
С Викторией Сергеевной, моим учителем по математике и руководителем данной работы, мы определили цель и поставили перед собой задачи, выдвинули гипотезу, выбрали методы и продумали этапы исследования, составили вопросы анкеты.
В первую очередь мы решили собрать информацию о софистах, людях, которые зарождали эту науку. Сведения о них мы опубликовали в Приложении №7. Выяснили, что, благодаря софистам, в словесных упражнениях, какими были софистические рассуждения, неосознанно отрабатывались первые, еще не ловкие приемы логического анализа языка и мышления. А превращение языка в серьезный предмет особого анализа, в объект систематического исследования было первым шагом в направлении создания науки логика. Софизмы содействовали строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Уяснение ошибок в математическом рассуждении часто содействовало развитию математики.
Провели в школе первый этап анкетирования, в анкетировании принимало участие 40 человек, учащиеся 5 и 6 классов. Ребята ответили на первые четыре вопроса анкеты (результаты приведены в Приложении №4). 70 % ребят знакомы со словом парадокс и софизм, сталкивались в жизни с простейшими софизмами и парадоксами.
Бабушка помогла мне подобрать литературу и выбрать интересные примеры софизмов и парадоксов, с ней мы их вместе решали по вечерам. В итоге собрали интересные примеры софизмов и парадоксов, оформили буклет (Приложение 6).
Мама предложила мне встретиться и поговорить о проекте с очень интересным человеком, которая всю свою жизнь посвятила школе, любимому предмету – математике, с Нечаевой Ларисой Ивановной, что я и сделала. Лариса Ивановна очень много нового рассказала мне о софизмах и парадоксах и о науке под названием логика. Поставила передо мной вопрос: «зачем нам нужна логика, какую роль она играет в нашей жизни?».
Исчерпывающий ответ, с которым я полностью согласна, я нашла в литературе: логическая культура – это знание и соблюдение основных принципов и требований правильного построения и выражения мыслей как в устной, так и в письменной речи. Отсутствие такой культуры приводит к многочисленным и разнообразным логическим ошибкам, которые засоряют не только научное, но и повседневное мышление, мешают нам думать, общаться, понимать друг друга и самих себя. Неясность и неопределенность мышления, его непоследовательность и сумбурность, противоречивость и необоснованность являются прямым результатом отсутствия должного уровня логической культуры.
Каждый из нас хорошо знает, что по содержанию человеческое мышление бесконечно многообразно, ведь мыслить (думать) можно о чем угодно, например, об устройстве мира и происхождении жизни на Земле, о прошлом человечества и его будущем, о прочитанных книгах и просмотренных фильмах, о сегодняшних занятиях и завтрашнем отдыхе… Но самое главное заключается в том, что наши мысли возникают и строятся по одним и тем же законам, подчиняются одним и тем же принципам, укладываются в одни и те же схемы или формы. Причем если содержание нашего мышления чрезвычайно разнообразно, то форм, в которых выражается это разнообразие, совсем немного.
Приведем простой пример. Рассмотрим три высказывания: Все караси – это рыбы; Все треугольники – это геометрические фигуры; Все стулья – это предметы мебели. Несмотря на различное содержание, у этих высказываний есть нечто общее, что-то их объединяющее. Что же это? Их объединяет форма. Отличаясь по содержанию, они сходны по форме, ведь каждое из трех высказываний строится по форме Все А – это В, где А и В – какие-либо объекты. Понятно, что само высказывание Все А – это В лишено всякого содержания. Это высказывание представляет собой чистую форму, которую можно наполнить любым содержанием, например: Все сосны – это деревья; Все города – это населенные пункты; Все школы – это учебные заведения; Все тигры – это хищники и т. п.
Другой пример. Возьмем три различных по содержанию высказывания: Если наступает осень, то опадают листья; Если завтра пройдет дождь, то на улице будут лужи; Если вещество – металл, то оно электропроводно. Будучи непохожими друг на друга по содержанию, эти высказывания сходны между собой тем, что строятся по одной и той же форме: Если А, то В. Понятно, что и к этой форме можно подобрать множество содержательных высказываний, например: Если не подготовиться к контрольной работе, то можно получить двойку; Если взлетная полоса покрыта льдом, то самолеты не смогут взлететь; Если слово стоит в начале предложения, то его надо писать с большой буквы и т. п [7]. Если логическая культура не дается человеку от природы, то как же она формируется? Логической культурой мышления овладевают в ходе общения, учебы в школе и вузе, в процессе чтения литературы. Встречаясь неоднократно с теми или иными способами рассуждения, мы постепенно начинаем усваивать, какие из них правильные, а какие – нет. Затем начинаем сами рассуждать в соответствии с правильными способами рассуждения. Наша культура мышления повышается. Однако такой стихийный путь формирования логической культуры не является лучшим. Люди, не изучавшие логику, как правило, не владеют теми или иными логическими приемами. Кроме того, у таких людей разная логическая культура, что не способствует взаимопониманию. Логика систематизирует правильные способы рассуждения, а также типичные ошибки в рассуждениях. Она предоставляет логические средства для точного выражения мыслей, без чего оказывается малоэффективной любая мыслительная деятельность, начиная с обучения и кончая научно-исследовательской работой [4]. Итак, логика помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше понимать собеседника, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях.
Лариса Ивановна также подтвердила мои предположения, что сведения, собранные в данной работе, пригодятся в дальнейшей моей юридической практике (если я не изменю свое решение стать юристом). Еще мне очень понравилась цитата, которую в беседе со мной использовала Лариса Ивановна: «Математика – гимнастика ума» – так сказал А.В. Суворов, а продолжила она так, учиться надо играючи, чтобы было желание постигать изо дня в день что-нибудь новое. Поэтому в приложении к работе я собрала понравившиеся мне цитаты (Приложение 8).
Дальше я направилась к моей тете Климовой Татьяне Кузьминичне, она тоже учитель математики. Татьяна Кузьминична внимательно посмотрела собранный материал, и предложила на практике применить полученные мною знания, например, показать ребятам наглядно, что 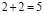
Следующим шагом нашей практической работы был второй этап анкетирования ребят, учеников 5 и 6 класса. В двух классах я рассказала о нашей работе, показала презентацию, наглядные опыты. Одноклассники и ребята 6 класса с вниманием выслушали мое выступление и заполнили вторую часть анкеты. Нам с Викторией Сергеевной было очень интересно узнать их мнение. Обработав анкеты, мы сделали вывод, что вопрос ребятам интересен, 77 % опрошенных считают полезным решение парадоксов и софизмов (Приложение 4).
Вместе с ребятами мы выбрали простой софизм и на его примере придумали свой, по которому написали сценарий сценки в двух вариантах (Приложение 1).
Разобрали несколько математических софизмов. При их разборе мы выделили ряд основных тщательно замаскированных ошибок в софизмах:
• деление на 0;
• неправильные выводы из равенства дробей;
• нарушения правил действия с именованными величинами;
• неравносильный переход от одного равенства (неравенства) к другому;
• неправильное извлечение квадратного корня из квадрата выражения;
• проведение преобразований над математическими объектами, не имеющими смысла;
• неверно построенные чертежи и сделанные по ним выводы.
Составили памятку по разбору софизмов и сравнительную таблицу (Приложение 5).
Выводы: В ходе практической части мы выяснили, что софизм – это рассуждение, содержащее замаскированные ошибки. Научились различать математические софизмы на арифметические, алгебраические, геометрические и логические.
Умение маскировать и маскироваться является основным в таких сферах, как международное право, банковское дело, оборона, внешняя и внутренняя разведка, защита информации. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики.
Я считаю, наш проект актуален и имеет практическое применение.
Результат работы. Выводы. Заключение
Разнообразных, простых и замысловатых софизмов и парадоксов в математике огромное множество. В своей работе мы рассмотрели небольшую их часть. Но уже сейчас мы можем с уверенностью сказать, что некоторые из них останутся в истории и на их основе будут рождаться все новые и новые софизмы и парадоксы. Работа по решению софизмов и парадоксов развивает логическое мышление. Не обладая логическим мышлением, человек может чувствовать, что или он сам, или кто-то другой рассуждает неправильно. Но в чем ошибка? Как найти ошибку в обосновании какого-либо положения? Более того, как доказать, что противоположная сторона ошибается? Ведь простое утверждение: «Вы ошибаетесь» – никого не убедит. Нужно указать, в чем человек ошибается. Изучение логики не только помогает убеждать людей в ошибочности их рассуждений, но и ускоряет нахождение ошибок в рассуждениях. Изучив типичные ошибки и приобретя навыки их обнаружения, их замечают мгновенно, почти автоматически [4]. Являясь теоретической наукой, логика объясняет, почему тот или иной способ рассуждения является правильным или неправильным, что дает возможность анализировать способы рассуждения, с которыми ранее человек даже не встречался.
Выводы: математические софизмы и парадоксы имеют будущее, они могут найти применение на уроках математики при изучении различных тем, а также их можно использовать для сценариев КВН, проведения различных математических соревнований, олимпиад, конкурсов, капустников.
Было бы здорово, если бы в школьном расписании были уроки логики. Логика развивает мышление. Решение парадоксов и софизмов тренируют наш мозг, то есть гипотеза доказана.
Парадоксы и софизмы являются тренировкой для ума.
Анкетирование одноклассников и ребят из 6 класса показало, что 77 % ребят хотят, чтобы изучение парадоксов входило в школьную программу. В.А. Сухомлинский писал: «Я стремился к тому… чтобы законы мышления дети осознавали, как стройное сооружение, архитектура которого подсказана еще более стройным сооружением – природой». Практический результат работы – небольшая юмористическая математическая сценка, на ближайшем утреннике в классе мы ее разыграем с одноклассниками, кроссворд, сводная информация о софистах и их трудах, сборник софизмов и парадоксов, памятка по разбору софизмов. Работа над софизмами и парадоксами – это тренировка ума, мышления и логики. Она способствует развитию мозговой деятельности. Изучить логику для практических целей вполне возможно каждому. Для подтверждения этого приведем высказывание Д.С. Милля: «Когда я принимаю в соображение, как проста теория умозаключения, какого небольшого времени достаточно для приобретения полного знания ее принципов и правил и даже значительной опытности в их применении, я не нахожу никакого извинения для тех, кто, желая заниматься с успехом каким-нибудь умственным трудом, упускает это изучение. Логика есть великий преследователь темного и запутанного мышления; она рассеивает туман, скрывающий от нас наше невежество и заставляющий нас думать, что мы понимаем предмет, в то время, когда мы его не понимаем» [4]. В наше динамическое время высока потребность в эрудированных, логически продвинутых, предприимчивых, деловых, компетентных специалистах в той или иной сфере общественной, политической, экономической, социальной и производственной деятельности. Уверена, полученные мною знания мне пригодятся. В дальнейшем я буду продолжать постигать мир логики.
Приложение 1
Сценка «3=2, а 4=5» Вариант 1
Встречаются два друга.
Вова: Дим, здорово!
Дима: Привет, Вова. Как дела, как день провел?
Вова: Пойдет. А что это ты такой весёлый?
Дима: Да, я сегодня тройку по математике получил!
Вова: Нашел, чему радоваться. Вот если бы четверку или пятёрку, а то тройку… А знаешь ли ты, что всякая тройка равна двойке?
Дима: Тройка равна двойке? Не может быть!
Вова: А я тебе сейчас это докажу.
Дима: Вот насмешил – докажу! Ты попробуй, докажи! А если не докажешь, сникерс подаришь.
Вова: А если докажу, то сникерс мой.
Итак……
Ты, конечно, не будешь отрицать, что
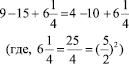
или можно записать так
Поэтому из
следует
или
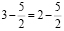
следовательно, 3=2. Вот и всё доказательство. Гони сникерс.
Дима: Вот это да! На, держи (передает другу сникерс).
Вова: Ну ладно, мне некогда. Пока.
Дима: Пока.
Прошло несколько дней, и опять встретились два друга Дима и Вова.
Дима: Привет, Вова.
Вова: Привет, ты всё веселишься?
Дима: Как же мне не веселиться, я сегодня пятёрку по математике получил. Хочешь, дневник покажу?
Вова: Покажи. (Смотрит дневник) Послушай, но ведь здесь стоит четвёрка, а не пятерка.
Дима: (Хихикает) а разве ты не знаешь, что всякая четвёрка равна пятёрке? Я тебе сейчас это докажу. Готовь сникерс.
Ты, конечно, не будешь отрицать, что
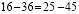
Вова: Нет, а что?
Дима: Прибавим к обеим частям равенства по 20 целых и 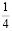
следует, что
по формуле сокращенного умножения
а из 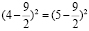
Отсюда имеем
или 4=5
Вова: Молодец! Держи, сникерс твой.
Конечно, производя вычисления, и Вова, и Дима допустили ошибки, но сценка удалась.
(Ошибка: из равенства квадратов следует равенство их оснований по модулю, а не просто оснований. В первой скобке под знаком квадрата стоит отрицательное число, а во второй – противоположное ему положительное. Их модули равны, а сами числа нет.)
Сценка «3=2, а 4=5» Вариант 2
Встречаются два друга.
Вова: Дим, здорово!
Дима: Привет, Вова. Как дела, как день провел?
Вова: Пойдет. А что это ты такой весёлый?
Дима: Да, я сегодня тройку по математике получил!
Вова: Нашел чему радоваться. Вот если бы четверку или пятёрку, а то тройку… А знаешь ли ты, что всякая тройка равна двойке?
Дима: Тройка равна двойке? Не может быть!
Вова: а я тебе сейчас это докажу.
Дима: Вот насмешил – докажу! Ты попробуй, докажи! А если не докажешь, сникерс подаришь.
Вова: А если докажу, то сникерс мой.
Ты, конечно, не будешь отрицать, что
заменяем на
значит 3=2 . . …
Вот и всё доказательство. Гони сникерс.
Дима: Вот это да! На, держи (передает другу сникерс).
Вова: Ну ладно, мне некогда. Пока.
Дима: Пока.
Прошло несколько дней, и опять встретились два друга Дима и Вова.
Дима: Привет, Вова.
Вова: Привет, ты всё веселишься?
Дима: Как же мне не веселиться, я сегодня пятёрку по математике получил. Хочешь, дневник покажу?
Вова: Покажи. (Смотрит дневник) Послушай, но ведь здесь стоит четвёрка, а не пятерка.
Дима: (Хихикает) а разве ты не знаешь, что всякая четвёрка равна пятёрке? Я тебе сейчас это докажу. Готовь сникерс.
Ты, конечно, не будешь отрицать, что 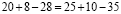
Вова: Нет, а что?
Дима: смотри, что я делаю, выношу общий множитель за скобку
Получаю
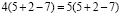
то есть 4=5, что и требовалось доказать
Вова: Молодец! Держи, сникерс твой.
Конечно, производя вычисления и Вова, и Дима допустили ошибки, но сценка удалась.
(Ошибка заключается в том, что общий множитель (3+2–5) и (5 + 2 – 7) равен 0, а делить на 0 нельзя).
Приложение 2
Опыт 1. «2+2=5»
Берем две отдельные веревки, на каждой из них вяжем по два узла. Связываем эти две веревки одним узлом. В итоге у нас получилась одна веревка с пятью узлами. Отсюда следует доказательство, что 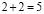
Опыт 2. «Загадочное исчезновение»
На прямоугольном куске картона начертим 13 одинаковых палочек на равном расстоянии друг от друга. Разрежем прямоугольник по прямой, проходящей через верхний конец первой палочки и через нижний конец последней. Теперь сдвинем одну из половин, при этом вторую оставив на месте. Проделав это, мы можем увидеть любопытное явление: вместо 13 палочек перед нами оказываются лишь 12! Одна палочка исчезла беседно. Давайте подумаем, куда она делась.
Итак, если сопоставить изначальные и получившееся длины палочек, то можно обнаружить, что вторые на 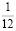
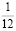
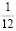
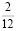
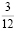
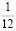
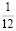
Приложение 3
Кроссворд «А разве сама жизнь не парадокс?»
По горизонтали:
1. Наука о правильном мышлении, исследующая общезначимые формы и средства мысли; является основой логического (дискурсивного) познания.
2. Какой Древнегреческий софист, родом из Абдер, объявил, что люди являются мерилом всего. Все, что мы говорим об истине – это всего лишь чье-то мнение.
3. Кто из древнегреческих мыслителей называл софизмом «мнимые доказательства», в которых обоснованность заключения кажется верной и обязана чисто субъективному впечатлению, вызванному недостаточностью логического или семантического анализа. Фраза которого была: «Людям, которые желают идти верной дорогой, важно также знать и об отклонениях.»
4. Наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
5. Автор строк: «А разве сама жизнь не парадокс?»
8. Каким термином называют утверждение, являющееся ложным, но не лишенным элемента логики, за счет чего при поверхностном взгляде на него кажется верным утверждение.
По вертикали:
3. Древнегреческий философ софист, по свидетельству Ксенофонта, оппонент Сократа.
6. Древнегреческий философ-софист, утверждающий, что «не существует ничего».
Истинного знания не существует, ведь даже то, что мы лично пережили, мы припоминаем и познаем с трудом; нам следует довольствоваться правдоподобным мнением
7. Вымышленная, логически верная ситуация (высказывание, утверждение, суждение или вывод), которая не может существовать в реальности
9. Автор строк: «Я слышал столько клеветы в Ваш адрес, что у меня нет сомнений: Вы – прекрасный человек!»
10. Ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения
11. Древнегреческий философ, ученик Парменида, представитель Элейской школы, автор многочисленных апорий, среди которых апория Ахиллес и черепаха.
2.
По горизонтали:
1. Автор строк: «А разве сама жизнь не парадокс?»
2. Кто из древнегреческих мыслителей называл софизмом «мнимые доказательства», в которых обоснованность заключения кажется верной и обязана чисто субъективному впечатлению, вызванному недостаточностью логического или семантического анализа. Фраза которого была: «Людям, которые желают идти верной дорогой, важно также знать и об отклонениях.»
3. Древнегреческий философ-софист, утверждающий, что «не существует ничего». Истинного знания не существует, ведь даже то, что мы лично пережили, мы припоминаем и познаем с трудом; нам следует довольствоваться правдоподобным мнением
4. Наука о правильном мышлении, исследующая общезначимые формы и средства мысли; является основой логического (дискурсивного) познания.
5. Какой Древнегреческий софист, родом из Абдер, объявил, что люди являются мерилом всего. Все, что мы говорим об истине – это всего лишь чье-то мнение.
6. Древнегреческий философ софист, по свидетельству Ксенофонта, оппонент Сократа. логического объяснения
7. Ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет
15. Крупнейший позднеантичный ритор, представитель младшей софистики, один из учителей Иоанна Златоуста, схоларх (руководитель риторической школы) в Антиохии.
16. Древнегреческий философ, ученик Парменида, представитель Элейской школы, автор многочисленных апорий, среди которых апория Ахиллес и черепаха
По вертикали:
8. Вымышленная, логически верная ситуация (высказывание, утверждение, суждение или вывод), которая не может существовать в реальности.
9. Каким термином называют утверждение, являющееся ложным, но не лишенным элемента логики, за счет чего при поверхностном взгляде на него кажется верным утверждение.
10. Наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
11. Древнегреческий философ, автор строк: «любое знание есть добро; любое зло, порок совершается от незнания».
12. Автор строк: «Я слышал столько клеветы в Ваш адрес, что у меня нет сомнений: Вы – прекрасный человек!»
13. Древнегреческий философ-идеалист, представитель мегарской школы, известен своими парадоксами или «апориями» («Лжец», «Куча», «Плешивый», «Рогатый» и др.
14. Древнегреческий софист -учитель спора, автор строк: «Удвоенное желание есть страсть, удвоенная страсть становится безумием. Из всех приправ самая лучшая – огонь. Человеческая жизнь неизбежно исполнена многих страданий».
17. Греческий философ-поэт, представитель второй софистики, автор сочинения «Биография софистов».
3.
По горизонтали:
1. Автор строк: «А разве сама жизнь не парадокс?»
2. наука о правильном мышлении, исследующая общезначимые формы и средства мысли; является основой логического (дискурсивного) познания.
3. Древнегреческий философ-софист, утверждающий, что «не существует ничего». Истинного знания не существует, ведь даже то, что мы лично пережили, мы припоминаем и познаем с трудом; нам следует довольствоваться правдоподобным мнением
4. Каким термином называют утверждение, являющееся ложным, но не лишенным элемента логики, за счет чего при поверхностном взгляде на него кажется верным утверждение.
5. Какой Древнегреческий софист, родом из Абдер, объявил, что люди являются мерилом всего. Все, что мы говорим об истине – это всего лишь чье-то мнение.
6. Кто из древнегреческих мыслителей называл софизмом «мнимые доказательства», в которых обоснованность заключения кажется верной и обязана чисто субъективному впечатлению, вызванному недостаточностью логического или семантического анализа. Фраза которого была: «Людям, которые желают идти верной дорогой, важно также знать и об отклонениях.»
7. Древнегреческий философ, ученик Парменида, представитель Элейской школы, автор многочисленных апорий, среди которых апория Ахиллес и черепаха
По вертикали:
1. Вымышленная, логически верная ситуация (высказывание, утверждение, суждение или вывод), которая не может существовать в реальности
2. Наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
3. Древнегреческий философ, автор строк: «любое знание есть добро; любое зло, порок совершается от незнания».
4. Автор строк: «Я слышал столько клеветы в Ваш адрес, что у меня нет сомнений: Вы – прекрасный человек!»
5. Ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения.
Приложение 4
Анкета
(Перед рассказом о софизмах и парадоксах)
1. Укажите в каком классе Вы учитесь_____
2. Укажите ваш пол М/Ж
3. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем»? Да/Нет
4. Знакомо ли вам понятия «Софизм», «Парадокс»? Да/Нет
(После рассказа о софизмах и парадоксах)
1. Заинтересовала ли Вас тема о софизмах и парадоксах Да/Нет
2. Надо ли знакомить учащихся на уроках с софизмами, парадоксами? Да/Нет
3. Как ты думаешь, для чего нужны софизмы, парадоксы? ________________________
4. Хотел бы ты больше узнать о софизмах, парадоксах? Да/Нет
5. Как ты считаешь, какую роль для тебя может сыграть более глубокое знакомство с софизмами, парадоксами? ______________
Результат обработки анкет:
Было обработано 40 анкет
Из них, учащихся 5 класса – 15; мальчиков – 7, девочек – 8
учащихся 6 класса – 25; мальчиков – 12, девочек – 13
3. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем»? Да 30 /Нет 10
4. Знакомо ли вам понятия «Софизм», «Парадокс»? Да 28 /Нет 12
(После рассказа о софизмах и парадоксах)
1. Заинтересовала ли Вас тема о софизмах и парадоксах Да 30 /Нет 10
2. Надо ли знакомить учащихся на уроках с софизмами, парадоксами? Да 31 /Нет 9
3. Как ты думаешь, для чего нужны софизмы, парадоксы? развитие логики, ума, улучшает память, чтобы запутать человека и выиграть спор, обмануть по закону, не знаю, для решения задач, для размышления, для красноречия, для розыгрыша, для логики, развитие интеллекта, чтобы доказать, что у всех правил есть исключения, развитие мышления, для успехов в учебе.
4. Хотел бы ты больше узнать о софизмах, парадоксах? Да 27 /Нет 13
5. Как ты считаешь, какую роль для тебя может сыграть более глубокое знакомство с софизмами, парадоксами?
Ответы. Они могут помочь в сложных ситуациях, помогут развить логику и мышление, добиться всего, не знаю, для хорошей работы мышления и мозга, разовьют мышления и высказывания, смогу решать математические задачи, запас лексикона, узнать больше нового, буду мыслить логично, не как все, умение отстоять свою позицию, не чего хорошего, никакую, для изучения будущей профессии, не знаю, поставить одноклассников на место, выиграть в спорах, узнаю что то важное.
Приложение 5
Памятка по работе с математическими софизмами в школе, разбор и поиск ошибок
Для развития логического мышления софизмы можно применять при изучении математики в школе на уроках, чтобы сделать их более интересными, для создания проблемных ситуаций; в домашних задачах, для более осмысленного понимания материала, пройденного на уроках; при проведении различных математических соревнований, для разнообразия; на занятиях факультативов, для более глубокого изучения тем математики;
После анализа литературы, мы смогли выделить следующие этапы работы с софизмами на уроках математики:
Знакомство с «бытовыми софизмами»
На данном этапе ведется анализ рассуждений, которые могут привести к ложным выводам. Работу по реализации данного этапа необходимо начинать со II класса. Примерами софизмов могут быть следующие цепочки рассуждений: «Сидящий встал; кто встал, тот стоит; следовательно, сидящий стоит» или: «Для того чтобы видеть, вовсе необязательно иметь глаза, ведь без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет; поэтому ясно, что глаза не являются необходимыми для зрения»
Развитие навыков по классификации софизмов
На этом этапе мы учимся классифицировать софизмы.
Алгебраические софизмы – это софизмы, алгебраические ошибки в которых скрыты, «завуалированы» в уравнениях и числовых выражениях. (Алгебра – один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы, отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений.
Например: «Все числа равны между собой».
Возьмём два разных числа, такие что:
Тогда существует такое 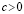
Умножим обе части на 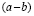
Раскрываем скобки, имеем:
cb переносим вправо, имеем:
Ошибка:
По определению:
Значит,
И выражение
Тождественно
Арифметические софизмы – это софизмы, в числовых выражениях которых, имеется неточность или ошибка, не заметная с первого взгляда. (Арифметика – (греч. arithmetika, от arithmys – число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними).
Например: 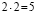
Решение:
Пусть исходное соотношение – очевидное равенство:
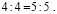
Вынесем за скобки общий множитель каждой чести (1) равенства, и мы получим:
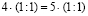
Разложим число 4 на произведение 2•2
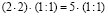
Наконец, зная, что 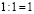
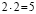
Ошибка:
Ошибка заключается в том, что нельзя было выносить множитель за скобки в уравнение (2). Такая ошибка разрешается достаточно легко – нужно лишь произвести вычитание одного из другого, что выявит неравенство двух этих числовых значений. Также опровержение возможно записью через дробь.
Также можно рассмотреть следующее доказательство софизма
Дважды два равно пять.
А именно, имеем равенство:
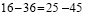
Прибавим к левой и правой части 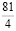
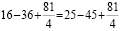
Преобразуем выражение:
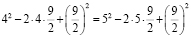
Теперь можно заметить, что в левой и правой части выражения (3) записаны произведения вида:
то есть, квадрат разности: 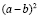
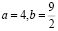
а справа 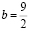
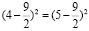
А следовательно,
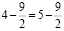
И наконец, получаем долгожданное равенство: 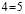
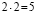
Ошибка. В преобразования, разумеется, закралась ошибка. А именно, при переходе из (4) в (5) совсем забыли, что равенство квадратов вовсе не означает равенство значений, возведенных в квадрат: они могут быть противоположны друг другу, как в нашем случае: 4–9/2 равно -1/2, а 5–9/2 равно 1/2. А квадраты этих значений одинаковы.
Геометрические софизмы – это софизмы, которые обосновывают какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
Например: «Через точку на прямую можно опустить два перпендикуляра».
Попытаемся «доказать», что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник АВС. На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е и D. Соединим точки Е и D прямыми с точкой В. Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВDС также прямой. Следовательно, ВЕ перпендикулярна АС и ВD перпендикулярна АС. Через точку В проходят два перпендикуляра к прямой АС.
Ошибка. Рассуждения, о том, что из точки на прямой можно опустить два перпендикуляра, опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ совпадает с ВD. Значит, из одной точки на прямой нельзя опустить два перпендикуляра.
Софизм «Cпичка длиннее, чем телеграфный столб, причем вдвое».
Разбор софизма: Длину спички будет обозначать a, длину столба – b. Разность между этими величинами – c. получается, что 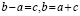
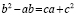
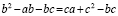
или
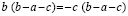
Откуда 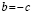
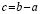
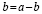
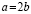
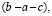
Логические софизмы – игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными. Например: «Арбуз – планета» (Земля, Марс и т.д. – круглые. Значит, все планеты круглые. Арбуз тоже круглый, значит арбуз – планета?).
Логические софизмы – софизмы, ошибки которых заключаются в неправильных рассуждениях.
Например: «Полупустое тоже, что и полуполное»
Доказательство: Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное
(Ошибка: полупустое не является половиной чего либо пустого, а является чем либо наполовину наполненным.) [1].
Софизмы иногда кажутся настолько случайными и несерьезными, что некоторые философы и ученые относили их к шуткам. Так, известный немецкий историк философии В. Виндельбанд, писал: “Тот большой успех, каким пользовались эти шутки в Греции, особенно в Афинах, обусловливается юношеской склонностью к остроумным выходкам, любовью южан к болтовне и пробуждением разумной критики повседневных привычек”.
Многие софизмы выглядят как лишенная цели и смысла игра с языком. Эти софизмы кажутся особенно наивными и несерьезными.
Вот, например, Платон описывает, как два софиста запутывают простодушного человека по имени Ктесипп.
– Скажи-ка, есть ли у тебя собака?
– И очень злая, – отвечал Ктесипп.
– А есть ли у нее щенята?
– Да, тоже злые.
– А их отец, конечно, собака же?
– Конечно.
– И этот отец тоже твой?
– Конечно.
– Значит, ты утверждаешь, что твой отец – собака и ты брат щенят![3]
Смешно, правда?!
Или софизм «глаза не нужны для зрения»
Доказательство: закрыв любой из глаз, мы продолжаем видеть.
Или такое рассуждение:
“Тот, кто лжет, говорит о деле, о котором идет речь, или не говорит о нем; если он говорит о деле, он не лжет; если он не говорит о деле, он говорит о чем-то несуществующем, а о нем невозможно ни мыслить, ни говорить”.
В софизмах часто обыгрывается тема недопустимости противоречий в мышлении.
Например:
– Скажи, – обращается софист к молодому любителю споров, – может одна и та же вещь иметь какое-то свойство и не иметь его?
– Очевидно, нет.
– Посмотрим. Мед сладкий?
– Да.
– И желтый тоже?
– Да, мед сладкий и желтый. Но что из этого?
– Значит, мед сладкий и желтый одновременно. Но желтый – это сладкий или нет?
– Конечно, нет. Желтый – это желтый, а не сладкий.
– Значит, желтый – это не сладкий?
– Конечно.
– О меде ты сказал, что он сладкий и желтый, а потом согласился, что желтый значит не сладкий, и потому как бы сказал, что мед является сладким и не сладким одновременно. А ведь вначале ты твердо говорил, что ни одна вещь не может и обладать и не обладать каким-то свойством.
Софисту, конечно, не удалось доказать, что мед имеет противоречащие друг другу свойства, являясь сладким и несладким вместе. Подобные утверждения невозможно доказать: они несовместимы с логическим законом противоречия, говорящим, что высказывание и его отрицание («мед сладкий» и «мед не является сладким») не могут быть истинными одновременно.[4]
Отличительной особенностью софизма является его двойственность, наличие, помимо внешнего, еще и определенного внутреннего содержания. В этом он подобен символу и притче.
Подобно притче, внешне софизм говорит о хорошо известных вещах. При этом рассказ обычно строится так, чтобы поверхность не привлекала самостоятельного внимания и тем или иным способом – чаще всего путем противоречия здравому смыслу – намекала на иное, лежащее в глубине содержание. Последнее, как правило, неясно и многозначно. Оно содержит в неразвернутом виде, как бы в зародыше, проблему, которая чувствуется, но не может быть сколь-нибудь ясно сформулирована до тех пор, пока софизм не помещен в достаточно широкий и глубокий контекст. Только в нем она обнаруживается в сравнительно отчетливой форме. С изменением контекста и рассмотрением софизма под углом зрения иного теоретического построения обычно оказывается, что в том же софизме скрыта совершенно иная проблема.
В русских сказках встречается мотив очень неопределенного задания. «Пойди туда, не знаю куда, принеси то, не знаю, что». Как это ни удивительно, однако герой, отправляясь «неизвестно куда», находит именно то, что нужно. Задача, которую ставит софизм, подобна этому заданию, хотя и является намного более определенной.[5]
Слово софизм имеет, кроме этого современного и хорошо устоявшегося смысла, еще и иной смысл. В этом другом смысле софизм представляет собой неизбежную на определенном этапе развития теоретического мышления форму постановки проблем. Сходным образом и само слово «софист» означает не только «интеллектуального мошенника», но и философа, впервые задумавшегося над проблемами языка и логики.
Все в истории повторяется, появляясь в первый раз как трагедия, а во второй – как фарс. Перефразируя этот афоризм, можно сказать, что софизм, впервые выдвигающий некоторую проблему, является, в сущности, трагедией недостаточно зрелого и недостаточно знающего ума, пытающегося как-то понять то, что он пока не способен выразить даже в форме вопроса. Софизм, вуалирующий известную и, возможно, уже решенную проблему, повторяющий тем самым то, что уже пройдено, является, конечно, фарсом.
Важно отметить, что существуют специальные правила математической логики, которые являются основными при построении логических выводов.
Например: «Если число делится на 2, то оно – четное. Число 16 делится на 2, значит, оно четное» (правило заключения), «Если число делится на 2, то оно – четное. Число 7 – нечетное, следовательно, оно не делится на 2» (правило отрицания). На этом этапе с помощью простых примеров проводится работа по закреплению данных правил».
Работа по выявлению ошибок в софизмах
На этом этапе строятся цепочки рассуждений, устраняются неточности высказываний, формулируются правильные выводы. Деятельность на данном этапе идет от простейших софизмов к сложным.
Работа по составлению учащимися собственных софизмов
На данном этапе грамотно составить софизм может не каждый ученик. Учителю необходимо поощрять учащихся к этому виду деятельности. Ученики могут предлагать софизмы, которые аналогичны ранее разобранным, но при постоянной работе круг их предложений постепенно расширяется. Приведем пример детского софизма: «Есть ли у тебя то, что ты не терял? Конечно есть. Ты копыта не терял, значит, они у тебя есть».
Для полноценной работы с софизмами на уроках математики мало знать этапы работы с ними, нужно еще и уметь методически верно преподнести их.
Мы можем предложить следующую методику работы по раскрытию софизмов:
1. Для того чтобы решить софизм, необходимо найти ошибку, она в свою очередь и будет являться решением.
Начинать поиск ошибки стоит с условия предложенного софизма. В некоторых софизмах ложный результат, получается, из-за неполных или противоречивых данных в условии, не верного первоначального предположения, а далее все рассуждения проводятся верно.
При разборе софизмов мы выделили ряд основных тщательно замаскированных ошибок в софизмах:
• деление на 0;
• неправильные выводы из равенства дробей;
• нарушения правил действия с именованными величинами;
• неравносильный переход от одного равенства (неравенства) к другому;
• неправильное извлечение квадратного корня из квадрата выражения;
• проведение преобразований над математическими объектами, не имеющими смысла;
• неверно построенные чертежи и сделанные по ним выводы.
Например, такая задача:
«Маме 32 года, сыну 5 лет. Через сколько лет мама будет в 10 раз старше сына?»
Решение: пусть х – лет искомый срок, тогда маме будет 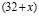
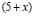
Таким образом, через –2 года мама будет в 10 раз старше сына. Так как по смыслу задачи x. лжно быть больше нуля, то полученный результат вызывает недоумение.
Уравнение само по себе составлено и решено верно, ошибка заключается в некорректной постановке вопроса. Это как раз тот самый случай, когда задача «думает» за нас.
2. Установить темы, которые отражены в софизме, предложенных преобразованиях.
3. Воспроизвести точные формулировки утверждений, используемых в софизме.
4. Выяснить, соблюдены ли все условия применимости теорем, правил, формул.
5. «Правило портного».
Вручную обычно иглой шов делается так: стежок вперёд и назад, ещё вперёд и сва назад и т.д.
оверять преобразования нужно также, как портной делает шов. После каждого перехода надо «оглянуться назад», проверить полученный результат обратным действием.
Рассмотрим софизм «2 • 2 = 5»:
Ошибку можно быстро обнаружить, если после вынесения «общего множителя за скобку» выполнить обратную операцию и внести 4 и 5 за скобки.
6. «Правило программиста».
Работа блоками. Невозможно отлаживать программу в целом. Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока. Предложенные рекомендации с одной стороны помогут ученикам при разборе софизмов, с другой стороны будут способствовать обогащению набора приёмов самопроверки и самоконтроля. Работа с софизмами требует тщательной дополнительной подготовки, умения «держать» и вести слушающих в нужном направлении, так как выстроить логическую цепочку рассуждений может не каждый. Как показывает опыт, занятия с использованием математических софизмов могут проходить очень интересно.
|
№ п/п |
Софизм |
Решение софизма |
Математический раздел по содержанию софизма |
Ошибка |
Элементы математики |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
Единица равна минус единице |
Пусть число х равно 1. Тогда можно записать, что х=1, или Разделив обе части этого равенства на х-1, имеем х + 1 = 0 и х = –1. (2) Поскольку по условию х = 1, то отсюда приходим к равенству 1 = –1. |
Равенство неравных величин |
Деление на 0 |
Деление на 0, разность квадратов двух выражений, равносильные преобразования |
|
2 |
Софизм: |
Зная, что 1 : 1 = 1, получаем: 4 · 4 = 25. |
Равенство неравных величин |
Неверно переносить распределительный закон умножения на деление. |
Разложение на множители |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
3 |
Софизм |
Рассмотрим очевидное равенство: (2–5/2)=(3–5/2) Тогда 2–5/2=3–5/2 Прибавив к обеим частям равенства по 5/2, получим 2=3 |
Равенство неравных величин |
Если (2–5/2)=(3–5/2) , то |2–5/2|=|3–5/2|, а не 2–5/2=3–5/2 |
Формулы сокращенного умножения, модуль |
|
4 |
Софизм: |
Возьмем тождество:
Разделим обе части на (7+2–9), получим 5=6 |
Равенство неравных величин |
Деление на 0
|
Тождества, разложение на множители |
|
5 |
Всякое число равно своему удвоенному значению |
Запишем очевидное для любого числа a тождество a – a = a – a, вынесем a в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим a(a – a)= = (a + a)(a – a).Разделив обе части на a – a, получим a = a + a, или a=2a. Итак, всякое число равно своему удвоенному значению. |
Равенство неравных величин |
Деление на 0 Здесь ошибочен переход к равенству a=2a. В самом деле, число a-a, на которое делится равенство a(a – a) = (a + a)(a – a) равно нулю. Поэтому его можно записать в виде , откуда, очевидно, следует, что число a слева и число a+a справа могут принима любые, отнюдь не равные друг другу значения. Деление же обеих частей этого равенства на неравное нулю число a–a приводит к бессмыслице |
Преобразование многочленов |
|
6 |
Любые два неравных числа равны |
Возьмем два неравных между собой произвольных числа а и b. Пусть их разность равна с, т. е. а–b = с. Умножив обе части этого равенства на а–b, получим (а–b) = c(a–b), раскрыв скобки, придем к равенству Разделив последнее равенство на |
Равенство неравных величин |
Извлечение квадратного корня из квадрата выражения |
Квадрат разности; арифметический квадратный корень; определение модуля выражения |
|
7 |
Один рубль не равен 100 копейкам |
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd. Применим это положение к двум очевидным равенствам 1 р.=100 коп., (1) 10р.=10•100 коп. (2) перемножая эти равенства почленно, получим |
Неравенство одинаковых величин |
Нарушения правил действия с именованными величинами. Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с инованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями. |
Равносильные преобразования равенств, действия с именованными числами |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
10 р.=100000 коп. (3) и, наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп. таким образом, один рубль не равен ста копейкам. |
Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство 10 р. =100 000 к., которое после деления на 10 дает 1 р. = 10 000 коп., (*) а не равенство 1р=10 000 к, как это записано в условии софизма. Извлекая квадратный корень из равенства (*), получаем верное равенство 1р.=100 коп. |
||||
|
8 |
Единица равна нулю |
Возьмем уравнение. Разделив обе его части на Откуда сразу же получаем требуемое равенство 1 = 0. |
Равенство неравных величин |
Деление на 0 |
Линейное уравнение, равносильные уравнения, рациональные выражения Деление на 0 |
Приложение 6
Примеры софизмов и парадоксов.
Софизм «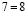
Возьмём числовое тождество:
Вынесем общие множители левой и правой частей за скобки.
Получим:
Разделим обе части этого равенства на общий множитель (заключённый в скобки).
Получаем
(Ошибка заключается в том, что общий множитель (7 + 2 – 9) равен 0, а делить на 0 нельзя).
Софизм «1=2»
Прибавим к обеим частям равенства по 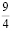
или
отсюда следует, что
или
(Ошибка в том, что квадраты противоположных чисел равны, но отсюда не следует, что равны сами числа, то есть положительное число не равно отрицательному).
Софизм учебы
Песенка – софизм, сочиненная английскими студентами:
The more you study, the more you know
The more you know, the more you forget
The more you forget, the less you know
The less you know, the less you forget
The less you forget, the more you know
So why study?
Перевод
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
Софизм «1 рубль не равен 100 копейкам»
Возьмем верное равенство:
1 р. = 100 к.,
Возведем его по частям в квадрат, получим:
1 р. = 10000 к.
Таким образом, один рубль не равен ста копейкам.
(Ошибка заключается в том, что возведение в квадрат величин не имеет смысла, в квадрат возводятся только числа).
Софизм «6 кг=6000000 г».
2 кг=2000 г и 3 кг=3000 г.
Перемножу почленные равенства, получу 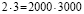
т.е 6 кг=6000000 г.
Ошибка заключается в том, что действия над величинами не имеют смысла).
Софизм «Когда же учиться?»
По ночам занятий нет, половина суток свободна. Остаётся:
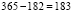
В школе ученики занимаются половину дня, значит, вторая половина (или четвёртая часть суток) может быть свободна. Остаётся:
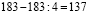
В году 52 воскресенья. Из них на каникулы приходится 15 дней, таким образом выходных в учебном году 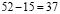
Итого остается 137–37=100 дней.
Но есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние (7 дней), летние (78 дней).
Всего 5+10+7+78=100 дней.
Итак, школьники заняты в году
100–100=0 дней.
Когда же учиться?
Софизм «2•2=5»
У нас есть верное числовое равенство: 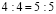
Вынесем за скобки в каждой части его общий множитель. Получим: 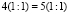
Числа в скобках равны, поэтому 4=5 или 2•2=5.
(Ошибка допущена в левой и правой частях тождества 4:4=5:5 при вынесении общего множителя за скобки).
Софизм «Рогатый»
Что ты не терял – то имеешь. Рога ты не терял; значит у тебя рога.
Этот софизм наивен и несерьезен, понятно, что он не убедит даже школьника. Но он оттачивает красноречие. Этот софизм заставляет искать аргументы для его опровержения.
Софизм Кратила
Диалектик Гераклит, провозгласив тезис «все течет», пояснял, что в одну и ту же реку (образ природы) нельзя войти дважды, ибо когда входящий будет входить в следующий раз, на него будет течь уже другая вода. Его ученик Кратил, сделал из утверждения учителя другие выводы: в одну и ту же реку нельзя войти даже один раз, ибо пока ты входишь, она уже изменится. Поэтому Кратил предлагал не называть вещи, а указывать на них: пока произносишь название, вещь уже станет иной.
Софизм Эватла
Эватл брал уроки софистики у философа Протагора на условии, что внесет плату за обучение тогда, когда после окончания школы выиграет свой первый процесс. Школу он окончил, время шло, но он и не думал браться за ведение процессов и, вместе с тем, считал себя свободным от уплаты за учебу. Тогда Протагор, разозлившись, пригрозил судом, заявив, что в любом случае Эватл ему заплатит, если судьи приговорят к оплате, то в силу решения суда, если не присудят, то по их договору. Однако, Эватл возразил, что не станет платить в любом случае: если присудят к уплате, то процесс будет проигран, и согласно их условию, платить не будет. А если не присудят, то уже из-за судейского вердикта.
Софизм «Ты не человек»
Я человек, ты не я, значит ты не человек.
Софизм «Гостиница»
В небольшую гостиницу, в которой было 12 свободных номеров, прибыли 13 постояльцев, каждый из которых хотел получить отдельный номер. Однако хозяин не смутился и обещал удовлетворить всех гостей. Для этого он попросил тринадцатого гостя временно посидеть в первом номере, – в итоге в первом номере оказалось два человека, затем он поселил третьего гостя во второй номер, четвертого – в третий, и так дошел до одиннадцатого номера, куда был поселен двенадцатый гость. После этого хозяин вернулся в первую комнату и проводил тринадцатого гостя в двенадцатую комнату – все постояльцы оказались поселены по одному. Как же это получилось?
Наше рассуждение: Нарисуем двенадцать прямоугольников, каждый из которых обозначает один номер, заселим в них людей, как написано в парадоксе. В условие сказано, что все гости расселились, но на самом деле второй гость оказался не заселенным.
Софизм «Вор»
«Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего».
Парадокс Лжеца – «король парадоксов»
Парадокс Лжеца был открыт в Древней Греции, но актуальность не потерял и в наши дни.
– Сказанное Платоном – ложно, – говорит Сократ.
– То, что сказал Сократ – истина, – говорит Платон.
Возникает вопрос, кто из них высказывает истину, а кто ложь? В простейшем варианте данного парадокса человек произносит всего одну фразу:
«Я лгу».
Действительно, истинно или ложно высказывание: «Я лгу»? Рассуждения по данному высказыванию идут по кругу. По другому, эти рассуждения называют «бесконечный спуск».
Парадокс лжеца произвел громадное впечатление на греков. Вопрос, который в нем ставится, с первого взгляда абсолютно прост: лжет ли тот, кто говорит о том, что он лжет? Но ответ «да» приводит к ответу «нет». И размышление ничуть не проясняет ситуацию. За простотой вопроса открывается неясная и неизмеримая пустота.
Парадокс о бегуне Ахилле и черепахе
Быстроногий Ахилл хочет поймать черепаху, которая находится на расстоянии 1 км от него. К тому времени, когда Ахилл добегает до того места, где первоначально находилась черепаха, та успевает уползти вперед на 10 м. За то время, которое требуется Ахиллу, чтобы пробежать эти 10 м, черепаха снова успевает уползти на какое-то расстояние. Черепаха: «Где тебе догнать меня, старина! Каждый раз, когда ты добежишь до того места, где я была, я успею уползти на какое-то расстояние вперед, хоть на толщину волоса!»
То есть какое бы расстояние ни оставалось между Ахиллом и черепахой, на преодоление этого расстояния, разумеется, потребуется некоторое время, а за это время черепаха продвинется еще вперед. В этой логике нет изъяна, но она самым очевидным образом противоречит нашему опыту.
Парадокс «Не знаешь то, что знаешь»
«Знаешь ли ты, о чём я хочу тебя спросить?» – «Нет». – «Знаешь ли ты, что добродетель есть добро?» – «Знаю». – «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».
Парадокс «Лекарства»
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
Парадокс «Мудрец на необитаемом острове»
Хорошо известна следующая легенда: один мудрец, оказавшийся на необитаемом острове, сказал, что все люди, находящиеся на острове, лжецы. Проанализируйте данную ситуацию и скажите, пожалуйста, можно ли её назвать парадоксальной и почему?
(Можно. Если все люди, находящиеся на острове, лжецы, а сам мудрец тоже находится на острове, то и он лжец. Другими словами, то, что он сказал, неправда. Следовательно, не все люди, находящиеся на острове, лжецы, но так как на острове всего один человек – мудрец, то он не лжец и сказал правду, что все люди, находящиеся на острове, лжецы. Но тогда мудрец тоже лжец, следовательно, он сказал неправду, поэтому он не лжец, т.е. то, что он сказал, правда и т.д. и т.д. Понятно, что так можно рассуждать бесконечно долго).
Парадокс «Два слова, спасшие жизнь»
Рассказывают, что во время франко-прусской войны произошёл следующий любопытный случай.
Один французский офицер имел несчастье попасться в плен к пруссакам, и его по подозрению в шпионаже было решено отдать под суд и судить по законам военного времени, которые, как известно, карают за шпионаж смертной казнью.
Когда подсудимому вынесли смертный приговор и несчастный, выслушав его, уже готов был покориться своей участи, судьям пришло в голову оказать осуждённому снисхождение, правда, несколько странного свойства.
– Вам, молодой человек, – сказали они офицеру, – предлагается в виде особой милости самому выбрать род казни: или смерть через повешение, или расстрел. Для этого мы предлагаем вам произнести какую-нибудь фразу, заключающую в себе или явную правду, или явную ложь. При этом заметьте, что за сказанную вами правду вы будете повешены, а за неправду вас расстреляют.
Всё это было, конечно, очень жестоко, немилосердно, но … странное дело! По мере того, как молодой человек слушал бесстрастную речь своих судей, его бледное умное лицо прояснялось всё более и более, и, наконец, после некоторого размышления он медленно произнёс ….
Судьи своим решением создали парадоксальную ситуацию.
Офицер понял это и произнёс два слова:
– Меня расстреляют!
– Ну и что же? Что вы хотите этим сказать? – спросили судьи с недоумением.
– Только то, что вы потребовали от меня! – ответил молодой человек. – Я сказал фразу, а что она в себе заключает – правду или неправду – я предоставляю судить вам! Но предупреждаю вас, господа судьи, что, какой бы род казни вы ни применили ко мне, теперь вы всё равно окажетесь глубоко неправыми и несправедливыми судьями, не умеющими держать своё слово.
Дерзкая речь француза задела за живое судей. Но офицер поспешил пояснить сказанное.
– Я сказал: “Меня расстреляют”. Следовательно, если вы меня повесите, то окажется, что я сказал неправду, а за неправду вы же сами обещали меня расстрелять. Если же вы решите меня подвергнуть расстрелу, то окажется, что я сказал правду, а за правду меня следовало, согласно вашему же условию, повесить. Ясно, что и в том, и в другом случае вы будете неправы, но … я к вашим услугам!
Судьи настолько были поражены простой, логичной и остроумной речью молодого французского офицера, что, из уважения к его уму, единогласно решили его помиловать.
Парадокс «Генерал и брадобрей»
Этот парадокс состоит в следующем: каждый солдат может сам себя брить или бриться у другого солдата. Генерал издал приказ о выделении одного специального солдата-брадобрея, у которого брились бы только те солдаты, которые себя не бреют. У кого должен бриться этот специально выделенный солдат-брадобрей?
Если он хочет сам себя брить, то он не может этого сделать, так как он может брить только тех солдат, которые себя не бреют. Если же он не будет себя брить, то, как и все солдаты, не бреющие себя, он должен бриться только у одного специального солдата-брадобрея, т. е. у себя. Итак, он не может ни брить себя, ни не брить себя.
Парадокс Эпименида
Критянин Эпименид сказал: «Все критяне лжецы».
Он сам критянин, соответственно лжец. Если он лжец, значит, он врет и все критяне не лжецы, т е правдивы. Но если он, как и его народ, правдив, то его утверждение верно. Следовательно, все критяне лжецы. Так можно продолжать еще очень долго, а правды так и не выяснить.
Парадокс «Сапожник и лишний талер»
Старый сапожник Карл сшил сапоги и послал своего сына Ганса на базар – продать их за 25 талеров. На базаре к мальчику подошли два инвалида (один без левой ноги, другой – без правой) и попросили продать им по сапогу. Ганс согласился и продал каждый сапог за 12,5 талера. Когда мальчик пришёл домой и рассказал всё отцу, Карл решил, что инвалидам надо было продать сапоги дешевле – каждому за 10 талеров. Он дал Гансу 5 талеров и велел вернуть каждому инвалиду по 2,5 талера. Пока мальчик искал на базаре инвалидов, он увидел, что продают сладости, не смог удержаться и истратил 3 талера на конфеты. После этого он нашёл инвалидов и отдал им оставшиеся деньги – каждому по одному талеру. Возвращаясь домой, Ганс понял, как нехорошо он поступил. Он рассказал всё отцу и попросил прощения. Сапожник сильно рассердился и наказал сына, посадив его в тёмный чулан. Сидя в чулане, Ганс задумался. Получалось, что раз он вернул по одному талеру, то инвалиды заплатили за каждый сапог по 11,5 талера: 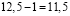
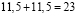
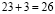
Разбор парадокса: Инвалиды заплатили за сапоги 23 талера, но Карл от них получил только 20, поскольку остальные 3 талера Ганс истратил на конфеты. Ганс, сидя в чулане, складывал доход (23 талера) с расходом (3 талера). Эта сумма не имеет никакого смысла. Другое дело, если бы он вычислил разность дохода и расхода – тогда остался бы «чтый» доход, т.е. те самые 20 талеров, которые в итоге получил Карл.
Парадокс «Завещание»
Эта старинная задача была известна ещё в Древнем Риме. Богатый сенатор, умирая, оставил жену в ожидании ребёнка. После смерти сенатора выяснилось, что на своё имущество, равное 210 талантам, он составил следующее завещание: «В случае рождения сына отдать мальчику две трети состояния (т.е. 140 талантов), а остальную треть (т.е. 70 талантов) – матери; в случае же рождения дочери отдать девочке одну треть состояния (т.е. 70 талантов), а остальные две трети (т.е. 140 талантов) – матери». У вдовы сенатора родились близнецы – мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между тремя наследниками с наилучшим приближением к условию завещания?
Разбор парадокса: Поскольку все требования завещателя выполнить невозможно, придётся выполнять только часть из них. В зависимости от того, какую именно часть мы выполним, получим тот или иной ответ. Вариантов много. Например: 1) из первого условия завещания следует, что сын должен получить 2 3 состояния, а из второго – что дочь должна получить в два раза меньше матери; 2) из первого условия завещания следует, что доля матери в 2 раза меньше доли сына, а из второго – что эта доля в 2 раза больше доли дочери; 3) в каждом из условий доля матери не меньше 1 3 , при этом доля сына в 4 раза больше доли дочери. Можно предложить и другие варианты. Эта задача возникла из практики. Такой случай действительно произошёл в Древнем Риме. Там суд разделил наследство так, как предложено во втором варианте: отдал сыну 4 7 состояния, матери – 2 7 , дочери – 1 7 , т.е. 120 талантов сыну, 60 – матери, 30 – дочери.
Парадокс «100 рублей»
Заходит в магазин покупатель, выбирает товар стоимостью 20 рублей, даёт продавцу сторублёвку. Смотрит продавец – нету сдачи. Пошёл в соседний отдел, разменял сотню. Отдал покупателю товар и сдачу. Ушёл покупатель. Вдруг прилетает продавец из соседнего отдела, приносит ту сотню. Фальшивка! Отдал наш продавец ему свою сотню. На сколько в итоге прогорел наш горе-продавец?
Разбор парадокса: Продавец дал покупателю товара и сдачи на сумму 100 руб., да ещё второму продавцу заплатил 100 руб., но и от второго продавца он предварительно получил 100 руб. Так что вся пропажа – 100 руб. Можно решить и по-другому. Покупатель, фактически, «недодал» продавцу 100 руб. На эти-то 100 руб. и погорел продавец.
Парадокс «Года»
Коля однажды сказал: «Позавчера мне было 10 лет, а в будущем году исполнится 13». Может ли так быть?
Разбор парадокса: Если в будущем году Коле исполнится 13 лет, значит, в нынешнем ему 12, а в прошлом году было 11 лет. Но поскольку позавчера Коле было 10, то единственный день, когда ему могло успеть исполниться 11 (в прошлом году) – это вчера, а именно 31 декабря. Значит, сегодня 1 января, и 31 декабря этого года Коле исполнится 12 лет, а в будущем году – 13.
Парадокс «Лесорубы»
Два лесоруба, Иван и Прохор, работали вместе в лесу и сели перекусить. У Ивана было 4 лепёшки, а у Прохора – 8. Тут к ним подошёл охотник. – Вот, братцы, заблудился в лесу, до деревни далеко, а есть очень хочется. Пожалуйста, поделитесь со мной хлебом-солью! – Ну что ж, садись, чем богаты, тем и рады, – сказали лесорубы. Двенадцать лепёшек были разделены поровну на троих. После еды охотник пошарил в карманах, нашёл гривенник и полтинник и сказал: – Не обессудьте, братцы, больше при себе ничего нет. Поделитесь, как знаете! Охотник ушёл, а лесорубы заспорили. Прохор говорит: – По-моему, деньги надо разделить поровну! А Иван ему возражает: – За 12 лепёшек – 60 коп., значит за каждую лепёшку по 5 коп. Раз у тебя было 8 лепёшек – тебе 40 коп., у меня 4 лепёшки – мне 20 коп.! А как бы вы разделили эти деньги между лесорубами?
Разбор парадокса: Ошибаются и Иван, и Прохор. На каждого едока пришлось по 4 лепёшки, следовательно, Иван съел все свои лепёшки сам, а Прохор половину своих лепёшек отдал охотнику. Это означает, что все 60 коп. должен получить Прохор[6].
Приложение 7
СОФИСТЫ
|
Софист |
Годы жизни |
Краткая биография |
Учения, труды |
|
1 |
2 |
3 |
4 |
|
ЗЕНОН |
около 490 до н.э. – около 430 до н.э. |
Древнегреческий философ, ученик Парменида, представитель Элейской школы. Сын Телевтагора, учился у Ксенофана и Парменида. Как сообщает Диоген Лаэртский, Зенон участвовал в заговоре против элейского тирана того времени, имя которого Диогену точно было неизвестно. Был арестован. На допросе, при требовании выдать сообщников, вёл себя стойко и даже, согласно Антисфену, откусил собственный язык и выплюнул его в лицо тирану. |
Знаменит своими апориями, которыми он пытался доказать противоречивость концепций движения, пространства и множестваhttps://ru.wikipedia.org/wiki/ %D0 %97 %D0 %B5 %D0 %BD %D0 %BE %D0 %BD_ %D0 %AD %D0 %BB %D0 %B5 %D0 %B9 %D1 %81 %D0 %BA %D0 %B8 %D0 %B9 – cite_note-.D0.91.D0.A1.D0.AD-4. Научные дискуссии, вызванные этими парадоксальными рассуждениями, существенно углубили понимание таких фундаментальных понятий, как роль дискретного и непрерывного в природе, адекватность физического движения и его математической модели и др. Эти дискуссии продолжаются и в настоящее время. |
|
1 |
2 |
3 |
4 |
|
Присутствовавшие граждане были настолько потрясены произошедшим, что побили тирана камнями. По сведениям же Гермиппа, Зенон был тираном казнён: его бросили в ступу и истолкли в ней |
Апория: Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху. Чтобы преодолеть путь, нужно сначала преодолеть половину пути, а чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности. Летящая стрела неподвижна, так как в каждый момент времени она занимает равное себе положение, то есть покоится; поскольку она покоится в каждый момент времени, то она покоится во все моменты времени, то есть не существует момента времени, в котором стрела совершает движение. Пусть по стадиону движутся по параллельным прямым равные массы с равной скоростью, но в противоположных направлениях. Пусть ряд А1, А2, А3, А4 обозначает неподвижные массы, ряд В1, В2, В3, В4 – массы, движущиеся вправо, а ряд Г1, Г2, Г3, Г4 – массы, движущиеся влево. Будем теперь рассматривать массы Аi, Вi, Гi как неделимые. В неделимый момент времени Вi и Гi проходят неделимую часть пространства. Действительно, если бы в неделимый момент времени некоторое тело проходило бы более одной неделимой части пространства, то неделимый момент времени был бы делим, если же меньше, то можно было бы разделить неделимую часть пространства. Рассмотрим теперь движение неделимых Вi и Гi друг относительно друга: за два неделимых момента времени Вi пройдёт две неделимые части Аi и одновременно отсчитает четыре неделимые части Гi, то есть неделимый момент времени окажется делимым. Апория направлена против представления о мере отрезка как о сумме мер неделимых. |
||
|
ПРОТАГОР |
около 480 – около 410 до н. э. |
Протагор происходил из Абдер (берег Фракии), как и Демокрит, и был его слушателем. Протагор приобрел известность благодаря преподавательской деятельности в нескольких греческих городах, в частности, в Сицилии и Италии. В Афинах, помимо других, он общался с Периклом и Еврипидом (ок. 480–410 до н.э.). человеком, и сам Протагор, как и Демокрит общался с персидскими магами во время похода Ксеркса в Элладу. В молодости Протагор промышлял ремеслом носильщика дров. Демокрит, случайно увидев Протагора с огромной связкой дров на спине, заинтересовался, как тому удалось охватить дрова одной короткой веревкой и держать их в равновесии. Демокрит увидел здесь геометрический расчет и пришел в восхищение от остроумия и ловкости этого необразованного человека. |
«Все есть таким, каким оно кажется нам» «Упражнение, друзья, даёт больше, чем хорошее природное дарование» «Как мы чувствуем, так оно и есть на самом деле» «О богах я не могу знать, есть ли они, нет ли их, потому что слишком многое препятствует такому знанию, – и вопрос тёмен, и людская жизнь коротка» «О всяком предмете можно сказать двояко и противоположным образом» «Упражнение дает больше, чем хорошее природное дарование» «Теория без практики (упражнения) и практика без теории есть ничто» Протагора рисует беспомощное состояние человека до образования государства, проводит идеи восходящего развития культуры и совершенствования общественной жизни по мере накопления знаний. Законы относятся к произведению искусства, справедливости в общественных делах можно научиться. |
|
1 |
2 |
3 |
4 |
|
Отец Протагора был богатым Он сказал: «Дорогой юноша, так как у тебя выдающиеся способности делать все хорошо, то ты можешь совершить вместе со мной более значительные и лучшие дела». Демокрит приблизил Протагора к себе и научил его философии. Такова легенда. Но из неё неясно, почему сын богача оказался необразованным носильщиком дров. Более ясно, однако, что Протагор и Демокрит – земляки. Дело происходило в городе Абдерах. Правда, некоторые считают местом рождения Протагора ионийский город Теос. Протагор был профессиональным преподавателем риторики и эристики – искусства речи и искусства спора. Он одним из первых стал брать деньги за обучение философии. Протагор объехал всю Элладу. Был он и в «Великой Греции» (области, колонизованной эллинами в Италии), где написал законы для города Фурии. В Афинах, где Протагор был дважды, он по поручению Перикла разработал проект новой конституции. Однако вскоре афиняне схватили его и приговорили к смертной казни. Причиной послужила его книга «О богах», которая была конфискована и публично сожжена. Протагора изгнали из Афин. Он утонул в Мессинском проливе на пути из Южной Италии в Сицилию. Протагору принадлежало более десятка сочинении. Среди них «О сущем», «О науках», «О государстве», «О богах», «Прения, или Искусство спорить», «Истина, или Ниспровергающие речи». Ни одно из них до нас не дошло за исключением небольших фрагментов. Важнейшими источниками наших знаний о Протагоре и его учении являются диалоги Платона «Протагор» и «Теэтет» и трактаты Секста Эмпирика «Против ученых» и «Три книги пирроновых положений». В этих трактатах проскальзывает краткая, но незаменимая характеристика важнейших моментов мировоззрения Протагора. |
В управлении государством должны участвовать все граждане. Носитель знания и справедливости – не только мудрец, но и каждый отдельный человек. Протагор утверждал, что законы являются той высшей справедливостью, на которую не может претендовать ни один человек, каким бы мудрым и добродетельным он ни был. Закон есть выражение согласованной, взаимной справедливости, нечто вроде суммы индивидуальных добродетелей. Протагор и другие старшие софисты подчеркивали изменчивый характер представлений человека. Об одном и том же предмете, учил Протагор, может быть высказано два противоположных мнения, и ни одно из них не будет более истинным, чем другое. Например, больному человеку еда покажется горькой, а здоровому – сладкой и вкусной. Они оба будут по-своему правы. Общепризнанной истины и единого блага просто не бывает. Носителем знаний и справедливости является не только мудрец, но и каждый отдельный человек. Эту мысль Протагор выразил в формуле, которая воспринималась современниками как своеобразный лозунг софистов: Мера всех вещей – человек, существующих, что они существуют, а несуществующих, что не существуют. Протагор объявил, что люди являются мерилом всего. Все, что мы говорим об истине – это всего лишь чье-то мнение. Протагор заключил договор со своим учеником о том, что этот ученик ему заплатит гонорар после того, как выиграет свой первый судебный процесс. Ученик учился у Протагора на адвоката. Однако ученик, видимо, был ленивый и идти работать не торопился. На что Протагор сказал, что он на него подаст в суд и суд заставит его выплатить деньги. Тот удивился и спросил: «Почему?» – «Как почему? Если я пойду и подам на тебя в суд и т ы выиграешь, то ты заплатишь деньги, потому что таковы условия нашего с тобой договора, а если выиграю я, то ты отдашь мне деньги по решению суда». На что ученик, который, видимо, был хорошим учеником, сказал: «Н-е-е-е-т, если ты подашь в суд и я выиграю, то, значит, я не должен платить тебе деньги. А если ты выиграешь, то, значит, по условиям договора я не должен платить тебе». Так что софизм имеет и обратное свойство. Но это уже не софизм, а парадокс. |
||
|
ГОРГИЙ |
480 до н.э. – 380 до н.э. |
Известный древнегреческий философ-софист Горгий происходил из «Великой Эллады», из сицилийского города Леонтины. Его непосредственный учитель – Эмпедокл. В 427 г. он прибыл в Афины в качестве главы посольства города |
Возглавляя Леонийское посольство в Афинах. Горгий был одним из первых ораторов нового типа – не только практиком, но и теоретиком красноречия. Горгий утверждал, что он учит не добродетели и мудрости, а только ораторскому искусству. Речь Горгия отличалась особой поэтической выразительностью. |
|
1 |
2 |
3 |
4 |
|
Леонтины, просившего у Афин защиты от Сиракуз (шла Пелопоннесская война). Затем большую часть своей жизни Горгий провел в Фессалии. Горгий прожил более ста лет, чему, как он сам думал, обязан был своей воздержанности от удовольствий. Его ученик, афинский оратор Исократ (IV в. до Р. Х.), объясняет долгожительство Горгия тем, что тот, не будучи гражданином какого-либо города, не платил налогов, не занимался общественными делами, а также, не имея семьи, был свободен и от этой обременительной общественной повинности. |
Он разработал и применял особые риторические приемы, прозванные горгианскими фигурами: аналогичные по форме и соответствующие по объему фразы, использование параллельных членов предложения и членов предложения, находящихся в антитезе. Если сущее вечно, оно не имеет начала, а следовательно, беспредельно, а если оно беспредельно, то его нигде нет, а если его нигде нет, то его вообще нет. Если же предположить, что сущее временно, то, значит, оно возникло. Но возникнуть оно могло или из сущего, или из несущего. Однако несущее ничего из себя породить не может. Происхождение же сущего из сущего не есть возникновение, при таком происхождении сущее вечно. Так же неразрешима проблема единого и многого. Из этого следует вывод, что нельзя сказать, что «сущее существует». Но тогда нельзя сказать, что существует сущее и несущее – ведь то, что не существует порознь, не существует и вместе. Продемонстрировав всё это, Горгий заключает: «не существует ничего». Истинного знания не существует, ведь даже то, что мы лично пережили, мы припоминаем и познаем с трудом; нам следует довольствоваться правдоподобным мнением. Сохранились также выдержки из сочинения под названием О небытии, или О природе (Peri tu me ontos e peri physeos). Горгий пытался в ней обосновать три парадоксальных тезиса: а) ничего не существует; б) если бы что-то и существовало, то человек не мог бы этого познать; в) если бы даже он мог познать, то не был бы в состоянии этого выразить в словах и доказать другим людям. Слова Горгия у Платона: «Риторика есть творец убеждения». Выделял добродетель для мужчины и женщины, свободного и раба, для каждого возраста и конкретного дела. Мораль относительна и условна. Справедливость поступков необходимо оценивать в зависимости от условий места и времени, состояния человека и т.д. |
||
|
СОКРАТ |
470/469 г. до н. э.— 399 г. до н. э. |
Сократ был сыном скульптора Софрониска и повитухи Фенареты, у него был старший брат по матери Патрокл, наследовавший имущество отца. Родившись 6–го фаргелиона в нечистый день афинского календаря, Сократ стал «фармаком», то есть пожизненным жрецом здравия афинского государства без содержания, и в архаическое время мог быть принесен в жертву по приговору народного собрания в случае наличия общественных проблем. В молодости учился искусствам у Дамона и Конона, слушал Анаксагора и Архелая, умел читать и писать, однако, никаких сочинений после себя не оставил. |
«Познай самого себя» Древнегреческий философ, учение которого знаменует поворот в философии – от рассмотрения природы и мира к рассмотрению человека. Его деятельность – поворотный момент античной философии. Своим методом анализа понятий (майевтика, диалектика) и отождествлением положительных качеств человека с его знаниями он направил внимание философов на важное значение человеческой личности. Сократа называют первым философом в собственном смысле этого слова. В лице Сократа философствующее мышление впервые обращается к себе самому, исследуя собственные принципы и приёмы. Сократ использовал в стремлении достижения истины те же логические приемы, что и софисты. Он ставил все вещи под сомнение и принимал их за истину только после тщательного рассмотрения, благодаря чему этот мыслитель считается первым представителем критической философии. |
|
1 |
2 |
3 |
4 |
|
Был женат вторым браком на женщине по имени Ксантиппа и имел от неё нескольких сыновей, младшему из которых на момент смерти философа исполнилось семь лет. Отличился в ряде сражений и был примером личной храбрости как афинский ополченец-гоплит. Вел образ жизни афинского парасита и нищего мудреца и никогда не покидал Аттику. Славился как непобедимый спорщик и бессеребренник, отказывавшийся от дорогих подарков и всегда ходивший в старой одежде и босиком. Был высмеян как софист и платный учитель красноречия в комедии Аристофана «Облака» (около 423 г. до н. э.), на представлении которой встал, предлагая собравшимся сравнить себя с актером. Сократ считал, что благородные люди смогут управлять государством без участия философов, но, защищая истину, часто вынужден был принимать активное участие в общественной жизни Афин. Участвовал в Пелопоннесской войне – сражался под Потидеей, при Делии, при Амфиполе. Защищал от несправедливого суда демоса осуждённых на смерть стратегов, в том числе, сына своих друзей Перикла и Аспазии. Был наставником афинского политика и полководца Алкивиада, спас его жизнь в бою. |
Сократ как мыслитель был хорошо известен в свое время благодаря ораторскому мастерству и общественной деятельности. Сам он ничего не написал, так что при его изучении мы полагаемся лишь на записи, оставленные его учениками (в частности, Ксенофонтом и Платоном. Сократ официально не принадлежал к указанным группам, но разделял многие идеи софистов и использовал софистику в практической деятельности. Философ был сторонником этического реализма, согласно которому: любое знание есть добро; любое зло, порок совершается от незнания. Сократ не был понят официальными властями и воспринимался ими как обычный софист, подрывающий устои общества, сбивающий с толку молодежь и не чтящий богов. За это он был в 399 г. до н.э. приговорен к смерти и принял чашу с ядом – цикутой. Историческое значение деятельности Сократа в том, что он: способствовал распространению знаний, просвещению граждан; искал ответы на извечные проблемы человечества – добра и зла, любви, чести и т.д.; открыл метод майевтики, широко применяемый в современном образовании; ввел диалогический метод нахождения истины – путем ее доказательства в свободном споре, а не декларированная, как это делал ряд прежних философов; воспитал много учеников, продолжателей своего дела (например, Платона), стоял у истоков целого ряда так называемых «сократических школ». Спор нужен не ради спора, а ради достижения истины, и понятие, являющееся главным компонентами знания не должны быть противоречивыми. |
||
|
ПРОДИК |
ок. 465–ок. 390 гг. до н. э. |
древнегреческий софист. Возможно, был учеником Протагора. В 431 или в 421 г. до н. э. прибыл с посольством в Афины, где получил громкое признание. Учениками Продика, по преданию, были Еврипид, Фукидид, Терамен и др. Продик занимался синонимикой, подчеркивая различия между словами с похожим значением. Он развивал учение Протагора о правильной речи, оказал влияние на Антисфена. Платон полагал, что синонимика Продика была подготовительным этапом к учению Сократа о дефинициях. Единственным произведением Продика, о котором известно достоверно, являются Времена года (Horai), в которых автор доказывал, что возникновение земледелия привело к развитию человеческой культуры; он представил также теорию происхождения религии. |
Удвоенное желание есть страсть, удвоенная страсть становится безумием. Из всех приправ самая лучшая – огонь. Человеческая жизнь неизбежно исполнена многих страданий. Продик был учителем спора. (Сократ шутливо называл его «мой маэстро»). Предлагаемая им техника основывалась на синонимии, т.е. различении синонимов и точном определении оттенков смысловых значений. Такая техника немало повлияла на методологию Сократа по части исследования того, «что есть это?», т.е. сущности различных вещей. В этике он стал известен своей интерпретацией софистической доктрины на примере знакомого мифа о Геракле, который на распутье делает выбор между добродетелью и пороком, где добродетель интерпретировалась как подходящее средство достижения истинной выгоды и настоящей пользы. Оригинально его понимание богов. По Продику, боги суть ничто иное как «гипостазирование полезного и выгодного». «Древние придумали богов в силу превосходства, избыточности, которые от них проистекали: солнце, луна, источники всех сил, которые влияют на нашу жизнь, как, например, Нил на жизнь египтян». |
|
1 |
2 |
3 |
4 |
|
Продик был создателем теории, провозглашавшей, что люди стали воздавать божественные почести полезным для них вещам (род фетишизма), а затем их изобретателям (теория, позднее названная эвфемеризмом; см. Эвфемер); он первый объяснил происхождение религии психологическими причинами (чувство благодарности) и обозначил два этапа ее развития. Название произведения он связывал с богинями времен года, почитаемыми на Кеосе. Из этого произведения взят рассказ о Геракле на распутье, который в конце концов выбирает тяжкий путь добродетели; он свидетельствует, что Продик не был гедонистом и не признавал этического релятивизма. |
В качестве отличительной черты Продика древние отмечали исключительный интерес к языку, к номинативной функции слов. |
||
|
ГИППИЙ |
460 до н.э.- 400 до н.э. |
Древнегреческий философ-софист и математик, современник Сократа. |
Он прославился умением произносить речь на любую тему без предварительной подготовки. В своих сочинениях о политике он различал правовые отношения по природе и по человеческому закону. Закон – то, что граждане по общему соглашению написали, установив, что нужно делать и от чего надо воздерживаться. Гиппий отличал общечеловеческие, естественные законы, например почитание родителей. Гиппий видел цель жизни в достижении состояния автаркии – самоудовлетворенности. В этом этический идеал Гиппия. |
|
КРИТИЙ |
460 до н.э.—403 до н. э. |
Критий происходил из знатного царского рода Кодридов. Знатное происхождение Крития обусловило соответствующее его воспитание и образование, и его лаконофильство, преклонение перед олигархической Спартой. Критий был в той или иной степени близок как к софистам, так и к Сократу. С Сократом он позже порвал, и стал видным представителем софистического движения. Начав с общей неприязни к демократии илаконофильства, Критий в молодости стал членом антидемократической олигархической гетерии. Участие в перевороте 411 года до н. э. было для Крития первым серьёзным шагом в политике. Тогда он, вероятно, принадлежал к умеренному направлению олигархического движения. В 407 г. до н. э. Критий, как сторонник олигархии, был изгнан из Афин. Годы изгнания он провёл в Фессалии. После возвращения в Афины в 404 г. до н. э. он стал одним из членов коллегии Тридцати тиранов. Критий, который уже был крайним олигархом, и его сторонники со временем укрепили свои позиции. Начались репрессии против нелояльных к режиму. |
О Критии говорили, что он «учился у философов и считался невеждой среди философов и философом среди невежд». Родственник Крития Платон вывел его в диалогах «Тимей» и «Критий». В отличие от других софистов, над которыми Платон обычно иронизировал, Критий изображен им с уважением. Критий был автором ряда произведений, не дошедших до нас. Его можно считать атеистом, поскольку он отрицал реальное существование богов. Секст Эмпирик сообщает: «Многие говорят, что боги существуют; другие, как последователи Диагора Мелийского, Феодора и Крития Афинского, говорят, что они не существуют». Но, с другой стороны, как политик Критий считал религию социально полезной выдумкой. Секст Эмпирик пишет об этом так: «Еще Критий… принадлежал к числу безбожников, поскольку он говорил, что древние законодатели сочинили бога в качестве некоего надсмотрщика за хорошими поступками и за прегрешениями людей, чтобы никто тайно не обижал ближнего, остерегаясь наказания от богов». Критий видел главное орудие улучшения людей в воспитании, утверждая, что большинство хороших людей обязаны этим своим качеством не природе, а воспитанию. Он рассматривал государство и религию как средства, делающие плохих от природы людей хорошими, а террор – как средство управления, без которого не может обойтись ни одно правительство. |
|
1 |
2 |
3 |
4 |
|
Критий устранил вождя умеренных Ферамена и стал проводить собственную политику без какого-либо противодействия. Демократы-изгнанники, которыми командовал Фрасибул, перешли к активным действиям и вторглись в Аттику. Успешному наступлению демократов способствовала утрата популярности режима Тридцати в народе. В 403 году до н.э. Он был главным из тридцати тиранов. После поражения Афин в Пелопоннесской войне спартанцы потребовали отмены демократии в Афинах. Была создана комиссия из тридцати человек для составления новой антидемократической конституции. Во главе ее и оказался Критий – ученик старших софистов Протагора и Горгия, а также в какой-то мере и Сократа. Эта комиссия узурпировала власть и вошла в историю как правление «тридцати тиранов». Недолгое правление этой олигархии стоило жизни нескольким тысячам афинских граждан. Но афиняне, наконец, восстали – и тираны были разбиты в битве при Мунихии. |
В одной из своих «Элегий» Критий выступал против пьянства. Оно развязывает язык для мерзких речей, ослабляет тело, размягчает ум, застилает глаза мутным туманом и отшибает память. Расточительство разрушает дом. Итак, надо «есть и пить соответственно требованиям разума так, чтобы быть в состоянии работать. Пусть ни один день не будет отдан неумеренному пьянству». «Если до нашего сведения доходит, что кто-либо враждебно относится к олигархическому правлению, мы принимаем все возможные меры для устранения таких лиц». |
||
|
АНТИФОНТ |
V в. до н. э |
Древнегреческий философ софист, по свидетельству Ксенофонта, оппонент Сократа. В основном сочинении «Истина» условности социальных установлений и моральных норм противопоставлял естественные склонности и инстинкты человека |
Как и Гиппий, Антифонт занимался науками (астрономией, метеорологией, математикой). В области математики Антифонт пытался решить задачу на квадратуру круга, однако он допустил здесь столько ошибок, что в древности даже сложилось особое выражение – «ошибка Антифонта». Антифонт думал, что все возникло из вихря, что все едино, что в действительности нет ни вещей, ни времени, что «время – [наша] мысль или мера, а не сущность» [ДК 87(80) В 9]. Сочинения Антифонта «Истина», «О согласии» – не сохранились. Больше нам известно об этических взглядах Антифонта. Они оригинальны. Для Антифонта, как и для Гиппия, веления природы и требования закона антагонистичны. Источник всех бед в том, что законы заставляют людей поступать вопреки своей природе. «[В поступках, противоречащих природе], заключается [причина] того, что люди страдают больше, когда можно было бы меньше страдать, и испытывают меньше удовольствий, когда можно было бы больше наслаждаться, и чувствуют себя несчастными, когда можно не быть таковыми». А это все оттого, что «многие [предписания, признаваемые] справедливыми по закону, враждебны природе [человека]». Здесь под справедливостью Антифонт понимает стремление не нарушать законы государства, в котором состоишь гражданином. Из антагонизма закона и природы и из бедственности следования закону. Антифонт делает вывод, что человек должен быть двуличным и, делая вид, что он следует законам общества и государства, следовать природе, которую, в отличие от людей, обмануть нельзя: «Человек будет извлекать для себя наибольше пользы, если он в присутствии свидетелей станет соблюдать законы, высоко чтя их, оставаясь же наедине, без свидетелей, [будет следовать] законам природы. |
|
1 |
2 |
3 |
4 |
|
Антифонт – родоначальник договорной теории происхождения государства. Этику Антифонт определял как искусство быть беспечальным. Антифонт, рассуждая с Сократом, сказал: «Сократ, я могу назвать тебя человеком справедливым, но умным ни в коем случае. Кажется, ты и сам это сознаешь. Ты, например, ни с кого не берешь денег за собеседование, между тем ты же, не говорю, не отдал бы никому даром своего платья, дома или другой вещи, которую считаешь стоящей денег, но даже не взял бы меньше стоимости. Очевидно, если бы ты считал свое собеседование чем-нибудь стоящим, ты брал бы за него деньги не менее стоимости. Ты, может быть справедлив, потому что никого не обманываешь из-за любостяжания, но ты не можешь быть умным, потому что знаешь то, что ничего не стоит». На это Сократ отвечал: «Антифонт, у нас существует мнение, что как красоту, так и знание можно направить в хорошую сторону и в дурную. Если кто продает свою красоту за деньги, того называют известным именем, но если кто, познакомившись с любителем прекрасного, делает его для себя другом, того мы считаем благоразумным. Можно также и тех людей, которые продают за деньги свою мудрость желающему, назвать софистами, тогда как относительно того, кто, познакомившись с человеком даровитым, учит его, по возможности, прекрасному, мы говорим, что он занимается делом, приличным вполне образованному гражданину. Я сам, Антифонт, гораздо более рад добрым друзьям, чем иной раз хорошей лошади, собаке, птице; даже представляю их другим людям, которые, по моему соображению, могут помочь им в добродетели. С такими друзьями я просматриваю сокровища древних мудрых мужей, которые оставили нам последние в своих сочинениях; и если мы встретим что-нибудь хорошее, заимствуем и считаем великой для себя прибылью, если бываем полезны друг другу. Когда я слышал подобные слова, мне этот человек казался счастливцем, ведущим своих слушателей к истинному добру и красоте». Противопоставление того, что существует по природе, тому, что установлено людьми, позволило Антифонту поставить вопрос о происхождении рабства. Для Антифонта рабство – общественное установление, противоречащее природе. До нас дошли слова Антифонта о том, что «по природе мы все во всех отношениях равны, притом [одинаково] и варвары, и эллины». «Тех, которые происходят от знатных родителей, мы уважаем и чтим, тех же, которые не из знатного дома, мы не уважаем и не почитаем. В этом мы поступаем по отношению друг к другу как варвары, потому что по природе мы все во всех отношениях равны, притом [одинаково] и варвары, и эллины. [Здесь] уместно обратить внимание на то, что у всех людей нужды от природы одинаковы… И в самом деле, мы все [одинаково] дышим воздухом – через рот и нос и едим мы все [одинаково] – при помощи рук». |
|||
|
1 |
2 |
3 |
4 |
|
Учение Антифонта о природном равенстве людей шло вразрез с господствующей в Древней Греции идеологией – идеологией рабовладельческой формации. Рассказывают, что когда Антифонт отпустил своих рабов на волю, а сам вступил в брак со своей бывшей рабыней, то он был объявлен сумасшедшим и лишен гражданских прав. Приравнивал справедливость к исполнению закона. Справедливость заключается в том, чтобы не нарушать законы государства, в котором состоишь гражданином. Предписания законов – результат соглашения. Законы искусственны и произвольны, тогда как в природе все происходит само собой. |
|||
|
ФРАСИМАХ |
459 до н.э. – 400 до н.э. |
древнегреческий софист. Фрасимах был гражданином города Халкидон, расположенного у пролива Босфор. Предположительно он работал софистом в Афинах. |
Имя «Фрасимах» означает «агрессивный воин», что, возможно, оказало влияние на его роль в диалоге. Своей значимостью Фрасимах обязан главным образом Платону, сделавшему его персонажем своего диалога «Государство». Как человек мыслящий, Фрасимах имеет достаточно много общего с философами, чтобы иметь возможность защитить философию в городе. Политика по Фрасимаху – прежде всего сфера человеческого, а не божественного действия, а посему и область проявления человеческих сил, возможностей, и интересов. Властвует и побеждает, согласно его теории, сильнейший. «Справедливость, утверждаю я, это то, что пригодно сильнейшему» – говорил он. А обладание властью, в свою очередь – это преимущество. Так же, говорил он про то, что «Справедливость и справедливое – в сущности, это чужое благо, это нечто, устраивающее сильнейшего, правителя, а для подневольного исполнителя это чистый вред, тогда как несправедливость – наоборот: она правит, честно говоря, простоватыми, а потому и справедливыми людьми». «Так слушай же. Справедливость, утверждаю я, это то, что пригодно и сильнейшему» |
|
АРИСТОТЕЛЬ |
384 до н.э.– 322 до н.э. |
Родители будущего ученого, которого часто именовали Стагиритом, имели благородное происхождение. Никомах, отец будущего ученого, потомственный лекарь, служил придворным врачом и обучал своего наследника азам врачебного искусства и философии, на то время нераздельной с медициной. Аристотель с детских лет был тесно связан с македонским двором и прекрасно знал своего ровесника, сына царя Аминты III, Филиппа. Еще ребенком Аристотель осиротел и находился на воспитании родственника Проксена. Последний возложил на свои плечи заботы о юноше: помогал в получении образования, всячески поощрял любознательность подростка, тратил деньги на приобретение книг, являвшихся по тем временам очень дорогим удовольствием, практически роскошью. Благоприятствовало таким расходам состояние, оставшееся после смерти родителей. |
Как и большинство мыслителей древних времен, Аристотель помимо философии усердно занимался различными науками и стал основателем некоторых разделов: логики, научной риторики, грамматики. Также великий мыслитель установил большое количество важных фактов в анатомии и зоологии, первым создал философию искусства и теорию поэзии. Наиболее важными и известными трудами Аристотеля считаются «Политика», «Метафизика», «Поэтика», «Физика». Философская система греческого просветителя затрагивала различные стороны человечества и глобально повлияла на последующее развитие научного мышления. В географии Аристотель высказал мысль о цельности и беспредельности Мирового океана. В биологии ученый описал около полутысячи видов животных и основал зоологическую систематику, первую в научной истории. Изучая животных, разделил их на 2 группы: бескровные и животные с кровью (во главе поставил человека), что практически соответствует сегодняшнему понятию: позвоночные и беспозвоночные. Великий философ считается отцом метеорологии (впервые этот термин был упомянут в трактате о небесных явлениях). |
|
1 |
2 |
3 |
4 |
|
Биография Аристотеля, краткое содержание которой вызывает неподдельный интерес у современной молодежи, поистине внушает глубокое уважение к этому человеку, возложившему на свои плечи ответственность за просвещение остальных людей, заинтересованных в благоприятном будущем своей страны. Реклама Платон мне друг Биография Аристотеля кратко повествует о том, как с целью изучения философии в 367 году до н. э. Аристотель перебрался в Афины, где остался на два десятка лет. В прославленном греческом городе молодой человек поступил учеником в Академию, открытую великим философом Платоном. Наставник, обратив внимание на блестящие умственные достоинства ученика, стал выделять его среди остальных слушателей. Аристотель же постепенно начал отступать от взглядов и идей своего учителя и опираться на собственное мировоззрение. Это не очень понравилось Платону, однако на личных отношениях двух гениев различие во взглядах никак не отразилось. Больше всего мнения двух великих умов расходились в учении об идеях, которыми, как полагал Платон, образован бестелесный мир. Для его ученика Аристотеля идеи являлись всего лишь сущностью происходящих материальных явлений, облаченных в эти самые идеи. По поводу данного спора Аристотелем была озвучена известная фраза, звучащая в сокращенном варианте как: «Платон мне друг, но истина дороже». |
Аристотель называл софизмом «мнимые доказательства», в которых обоснованность заключения кажется верной и обязана чисто субъективному впечатлению, вызванному недостаточностью логического или семантического анализа. «Людям, которые желают идти верной дорогой, важно также знать и об отклонениях.» |
||
|
ЕВБУЛИД |
IV век до н. э. |
древнегреческий философ-идеалист, представитель мегарской школы, известен своими парадоксами или «апориями» («Лжец», «Куча», «Плешивый», «Рогатый» и др.). |
«Говорит ли правду или неправду человек, заявляющий «Я лгу»?» или, если сформулировать по-другому: Человек произносит: «Я лгу», или «То, что я сейчас говорю, является ложью», или же «Это высказывание ложно». Если высказывание ложно, то говорящий сказал правду и, сказанное им, не является ложью. Если же высказывание не является ложным, а говорящий утверждает, что оно ложно, то это его высказывание ложно. Таким образом, если говорящий лжет, он говорит правду, и наоборот. Парадокс «Лжец» произвел громадное впечатление на современников Евбулида. Существует даже легенда, что некий Филит Косский, отчаявшись разрешить этот парадокс, покончил с собой, а известный древнегреческий логик Диодор Кронос, дав обет не принимать пищу до тех пор, пока не найдет решение «Лжеца», умер, так и не разрешив проблему. |
|
1 |
2 |
3 |
4 |
|
«Если прибавлять по одному зерну, с какого момента появится куча, и значит ли это, что куча возникает в результате прибавления одного зерна?» или, если сформулировать по-другому: Одно зерно кучи не составляет. Если прибавить ещё одно зерно – это тоже не куча. Так с какого же зерна начинается куча? «Потеряв один волос, еще не становишься лысым; потеряв второй волос – тоже; когда же начинается лысина?» или, если сформулировать по-другому: «Если волосы с головы выпадают по одному, с какого момента человек становится лысым?» «Что ты не потерял, ты имеешь. Рогов ты не терял. Стало быть, ты рогат.» Это последнее высказывание основано на логической ошибке и относится уже к категории софизмов. |
|||
|
ЛИКОФРОН |
IV в. до н. э. |
древнегреческий философ-софист, ученик Горгия. |
Известен по утверждению, процитированному в «Политике» Аристотеля, что «законы являются соглашением и гарантом справедливости в отношениях друг с другом». Это означает, что он рассматривал законы не более, как средство, в контексте (возможно ещё примитивной) теории общественного договора, не придавая им особое значение, в противовес, например, Платону, но схоже с Фрасимахом и Калликлом, хотя их теории (как можно установить из доступных источников) имели более специфический характер. Трудности в учении о бытии, на которые указывали элеаты, Ликофрон пытался преодолеть, изъяв из философских рассуждений глагол «быть» . Считал, что законы и государство должны лишь защищать граждан от посягательств сограждан на их права, явившись предшественником современных либеральных теорий государства. Привилегии знатного происхождения отвергал. Стиль сочинений Ликофрона, которые не дошли до нас, Аристотель характеризовал как напыщенный. «государство… должно заботиться о добродетели. В противном случае сообщество граждан превратится в военный союз… а закон сделается соглашением и, гарантом справедливости в отношениях друг с другом, но не будет способен делать граждан добродетельными и справедливыми» |
|
АЛКИДАМАНТ |
IV в. до н. э. |
древнегреческий философ-софист, ученик Горгия, был он из Элаи в Мисии. Также он известен как ритор. После кончины Горгия стал во главе школы, которую основал Горгий. |
«О софистах» содержала в себе критику школы Исократа, эта речь была направлена против письменной речи, бывшей тогда весьма популярной, являлась речь Алкидаманта своеобразной пропагандой риторики, речей устных. «Одисей» же представляла собой речь-обвинение, направлена была против Паламеда. Кстати, позже Аристотель в своих выступления пользовался цитатами из речей Алкидаманта, брал он их в качестве примеров «холодного» стиля, так называли речи, с помощью которых невозможно добиться нужного эффекта воздейтвия на слушаетелей. |
|
1 |
2 |
3 |
4 |
|
В списке работ Алкидаманта найдено и сочинение «Мусейон» – это была антология, направление ее литертурно-историческое, возможно, что написано это сочинение было для последующего составления речей. В составе этого сочинения обаботана народный вариант легенды «Состязание Гесиода и Гомера». Для него эти люди были отличными импровизаторами, при выступлении и составлении речей. Что касается истории философии, то для этой науки важным стала классификаия утверждений и отрицаний, а также вопросов и обращений, составленная Алкидамантом. Классификация эта была доработкой существовавших ранее высказываний Прошагора. Ценными представляются ныне и некоторые высказывания «Мессенской речи». Здесь содерится критика и отрицание рабства. По мнению философа все мы свободны. Так что смело можно говорить о том, что в естественном праве и истории философии этот человек занимает далеко не последнее место. Его авторству приписывается трактат «Состязания Гомера с Гесиодом». Был известен своей техникой импровизации, которой обучился у Горгия, а также демократическими взглядами на устройство общества и равноправие всех граждан. Говорил, что бог сделал всех свободными, а природа никого не сделала рабом. Выступал против аристократических теорий, в которых рабство обосновывалось ссылками на природу. |
|||
|
АЛКИДАМ |
1 пол. 4 в.до.н.э |
древнегреческий философ-софист. Один из учеников Горгия. |
Алкидам развил далее учение Антифонта о равенстве людей и противоестественности рабства. Если Антифонт говорил о равенстве эллинов и варваров от природы, то Алкидам – о том, что рабов вообще нет. При этом Алкидам ссылается не только на природу, но и на авторитет бога: «Бог создал всех свободными, природа никого не создала рабом». Эти замечательные слова Алкидама содержатся в схолии (комментарии) к «Риторике» Аристотеля. |
|
ЕВКЛИД |
330 г. до н.э.-260 г. до н.э. |
Евклид родился в 330 году до н.э. в небольшом городе Тире, недалеко от Афин. История не оставила подробного описания жизни одного из самых знаменитых математиков всех времен и народов. Однажды царь Птолемей спросил Евклида, существует ли другой, не такой трудный путь познания геометрии, чем тот, который изложил ученый в своих «Началах». Евклид ответил: «О царь, в геометрии нет царских дорог». Долгое время ученые считали, что не было конкретного исторического лица, что под именем Евклида скрывалась группа математиков, что-то вроде нашего современника Бурбаки, кстати, великого педагога. |
ся Начала. Книги с таким же названием, в которых последовательно излагались основные факты геометрии и теоретической арифметики, создавались и ранее другими античными авторами, однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Предшественники Евклида – Фалес, Пифагор, Аристотель и другие много сделали для развития геометрии. Но все это были отдельные фрагменты, а не единая логическая схема. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино. Из других сочинений Евклида до нашего времени сохранились: Данные – о том, что необходимо, чтобы задать фигуру; Основное сочинение Евклида называетО делении фигур – это сочинение сохранилось частично и только в арабском переводе; оно рассказывает о делении геометрических фигур на части, равные или состоящие между собой в заданном отношении; |
|
1 |
2 |
3 |
4 |
|
Однако в рукописи XII века на арабском языке читаем: «Евклид, сын Наукрата, сын Зенарха, известный под именем Геометра, ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира».Евклид, ученик Платона, по приглашению царя Птолемея переехал в Александрию, где находился знаменитый научный центр с Александрийской библиотекой. Знаменитое произведение «Начала» (Stoicheia) сделало имя Евклида бессмертным. «Начала» состоят из тринадцати книг. Другие труды Евклида меньше известны и меньше по объему. Это прежде всего «Данные» (Data), «Оптика», «О делении фигур», «Ложные заключения» (утеряна), «Сечение канона», «Явления». Евклид – великий педагог-энциклопедист, преподававший в Александрии, в Мусейоне. Это настоящий дворец науки с библиотекой, астрономической обсерваторией, ботаническим садом, зоопарком. В Мусейон приглашались известные ученые, они вели здесь научную работу, причем получали хорошее вознаграждение Труд ученого стал профессией. Евклид преподает в Мусейоне геометрию, арифметику и астрономию. |
Явления – приложения сферической геометрии к астрономии; Оптика – о прямолинейном распространении света. По кратким описаниям известны также: Поризмы – об условиях, определяющих кривые; Конические сечения; Поверхностные места – о свойствах конических сечений; Псевдария – об ошибках в геометрических доказательствах. Таким образом, Эвклид был автором первого из известных сборников математических софизмов и парадоксов. |
||
|
ЛУКИАН САМОСАТСКИЙ |
120/125–ок.190 гг. |
Лукиан (по месту рождения, сирийскому городу, Самосаты его называют Самосатским) – известнейший греческий писатель-сатирик, оратор. Даты его рождения в разных источниках разнятся, называются приблизительно 120 и 125 гг. Известно, что отцом его был небогатый мелкий ремесленник, а сам Лукиан сначала хотел быть скульптором, но быстро бросил обучение этому ремеслу, стал изучать риторику и философию, получил не только общее, но и риторическое образование. Греческий язык Лукиан благодаря огромному старанию изучил в совершенстве. |
Он был софистом. Много времени проводил в путешествиях, был во многих местностях Малой Азии, побывал в таких странах, как Греция, Галлия, Италия, Македония. Во всех главных центрах риторики – Риме, Афинах, Эфесе, Смирне, Антиохии – по торжественным поводам он произносил речи, которые считались образцовыми. Больше всего времени этот странствующий ритор провел в Массилии. Он стал прославленным оратором и достаточно обеспеченным человеком. Первые литературные сочинения проникнуты риторическим духом, но уже в софистических декламациях того периода («Похвала мухе»: «Какой позор! Бесстрашно муха на людей Стремит полет отважный, жаждет смерти их, И воины робеют пред копьем врага… Мертвая муха, посыпанная пеплом, воскресает и начинает жизнь снова», «Тираноубийца», «Сон» и др.) проявляются задатки Лукиана-сатирика. Проведя немного времени на Востоке, Лукиан с 165 г. селится в Афинах, где изучает право и более глубоко – философию. Он видит противоречивость различных философских учений, и следствием этого становится отсутствие пристрастий к какой-либо одной из школ и дух критицизма, скепсис, отрицание догматизма в любом его виде. |
|
1 |
2 |
3 |
4 |
|
В то же время более других его интересовала философия киников, позднее – Эпикура. Риторика и грамматика его разочаровывают и более того – становятся объектом сатирических выпадов. Период жизни с 165 по 180 гг. стал для Лукиана творческим расцветом, появлением лучших произведений. До наших дней сохранилось (не в оригинальном виде) около 80 сочинений, приписываемых этому автору, но ученые отказывают в подлинности около 30 из них. Лукиан писал разножанровые произведения: рассказы, пародии, биографии, памфлеты, эпиграммы; его даже нередко считают предтечей научной фантастики (в романах «Икароменипп» и «Икароменипп, или Заоблачный полет» герои попадают на Луну). Однако его излюбленным жанром был сатирический диалог, в котором Лукиан предстает не только остроумным и бесстрашным обличителем, но и автором, умеющим талантливо, метко, тонко использовать богатство языка для выражения идей. Мощь социальной сатиры и антирелигиозный ее пафос были причиной того, что как литератора Лукиана не слишком жаловали его современники. Однако в творчестве поздних авторов, например, Томаса Мора, Ф. Рабле, Э. Роттердамского, Дж. Свифт и др., отчетливо слышны влияние и отголоски его сатиры. Последний период жизненного пути Лукиана связан с Египтом: в этой стране по приглашению император Комодда он работал начальником канцелярии, был прокуратором. |
|||
|
ФЛАВИЙ ФИЛОСТРАТ |
170–247 г. |
писатель из рода Филостратов, представитель второй софистики. Учился и долго жил в Афинах (некоторые позднейшие авторы называют его «Афинским»), но впоследствии был включен в кружок приближенных императрицы Юлии Домны, стал её придворным ритором и переселился в Рим, где ему было дано поручение написать исчерпывающий труд об Аполлонии. Он посвятил ему много лет и закончил его, вероятно, уже после трагической смерти императрицы в 217 году. |
Автор дошедших до нас прозаических произведений: «Жизнь Аполлония Тианского», «Биографии софистов», «О гимнастике» и сборника «Писем». Религиозно-философский роман «Жизнь Аполлония Тианского» в 8 книгах написан по желанию жены императора Септимия Севера Юлии Домны (ум. в 217 г.); цель произведения – доказать, что знаменитый чудотворец язычества, неопифагореец Аполлоний, живший в 1 в. по Р. Х., был не магом и волшебником, а выдающимся подвижником, проповедником, одаренным свыше провидцем, чудотворцем и истинным мудрецом. По рассказу Филострата, Аполлоний ознакомился в Вавилоне с мудростью халдейских волхвов, в Индии – с мудростью браминов. Описание Индии представляет собой образчик утопий, которыми столь богата греческая литература. По возвращении в Ионию Аполлоний начинает деятельность проповедника и учителя; к нему являются для исцеления больные, города обращаются к нему за советами в делах гражданской и религиозной жизни. С таким же восторгом принимают его как в Элладе, так и в Риме. Позже Аполлоний предпринимает путешествие к Геркулесовым столбам и в Испании вступает в сношения с противниками Нерона; оттуда он отправляется в Египет, и в Александрии он встречается и беседует с дружественно расположенным к нему Веспасианом. Из Александрии Аполлоний отправляется к гимнософистам в Эфиопию, затем посещает Финикию и Киликию, повсюду совершая чудеса, учась и поучая. Своими советами он оказывает поддержку Титу. |
|
1 |
2 |
3 |
4 |
|
При Домициане Аполлоний вооружается против тирании императора и по требованию его бесстрашно прибывает в Рим. Заключенный в темницу, он подвергается истязаниям, но на суде в убедительной речи доказывает свою невиновность, после чего чудесно исчезает из судилища и поселяется в храме Зевса Олимпийского. Теперь слава Аполлония достигает апогея; около него образуется значительный круг последователей, особенно когда он вынес из Трофониевой пещеры в Лебадии книгу пифагорейской философии, которая должна была служить ответом на предложенный им Трофонию вопрос о лучшей и совершеннейшей философии. После двухлетнего пребывания в Греции Аполлоний переселяется в Ионию. В Ефесе он возвещает об убийстве Домициана, которое чудесно прозревает. Когда вступил на престол Нерва, Аполлоний посылает к нему друга своего Дамиса, а сам, предчувствуя близкую кончину, остается в Ионии, где вскоре и умирает чудесной смертью. В Аполлонии Филострат изобразил мудреца, стремящегося не только к религиозному, но и к философскому знанию; это философ в самом широком значении слова, софист императорского периода, обнимающий всю ширь современной ему науки, компетентный судья во всех вопросах жизни и знания и вместе с тем аскет, мистик-неопифагореец. Идеализация Аполлония сделала из него живой образ, которым язычество воспользовалось в борьбе с христианством: так, в конце III в. по Р. Х. вифинский наместник Перокл в своем сочинении «Филалет» противопоставил Аполлония Христу, возвышая первого над вторым и упрекая христиан в легкомыслии за то, что они признали богом Иисуса, совершившего немногие чудеса, тогда как язычника Аполлония, сделавшего несравненно более, признают не богом, а только богоугодным мужем. В сочинении «Биографии софистов» в 2 книгах Филострат дает очерк развития софистики с V в. до Р. Х. до своего времени. В первой книге он характеризует прежде всего софистов, если не по названию, то по духу – Евдокса Книдского, Леонта Византийского, Карнеада, Диона Прузского, Аполлония, Евфрата, Фаворина; затем он переходит к обзору собственно древней софистики в лице ее главных представителей – Горгия, Протагора, Гиппия, Продика, Пола, Фрасимаха, Антифонта, Крития и Исократа – и, наконец, выводит ряд представителей второй софистики – Эсхина, Никета, Исея, Скопелиана, Дионисия Милетского, Лоллиана, Марка Византийского, Поламона, Секунда, за которыми во второй книге следует Герод Аттик с многочисленными современными Филострату софистами. Не отличаясь ни систематичностью изложения, ни стремлением дать какую-либо историческую перспективу, сочинение это представляет собой хаотическую массу материала о софистах, который нельзя назвать ни биографическим, ни критическим. |
|||
|
1 |
2 |
3 |
4 |
|
Это скорее ряд портретов, которые Филострат набрасывал, пользуясь сборниками писем, преданиями школы, речами и личными воспоминаниями; в этом смысле материал «Биографий» представляется весьма ценным, хотя портреты софистов расплывчаты, характеристики страдают гиперболичностью, стиль отличается напыщенностью и в общем произведение представляется поверхностным и малосодержательным |
|||
|
ЛИБАНИЙ |
314–393 гг. |
Крупнейший позднеантичный ритор, представитель младшей софистики, один из учителей Иоанна Златоуста, схоларх (руководитель риторической школы) в Антиохии. Либаний происходил из семьи среднего достатка; его отец был либо средней руки купцом, либо служащим городского управления. Родившись в Антиохии в 314 г., Либаний изучал риторику сначала на родине у Зенобия, затем в Афинах у Диофанта в 336–340 гг., преподавал с интервалами в Константинополе (в столице имел успех, но из-за интриг и зависти коллег уехал); с 344 г. работал в Никомедии. Вернулся в Антиохию в первый раз в 353 г., и, наконец, поселился в своем родном городе, где он стал официальным софистом города на общественном жаловании, и состоял в этой должности около 40 лет, с 354 до 393 гг. Император Юлиан Отступник высоко ценил Либания и дал ему сан квестора. Когда он был убит, Либаний в страстной монодии выразил свою скорбь по поводу гибели надежд, которые он возлагал на безвременно погибшего императора. Ему удалось, однако, добиться влияния и у императоров Валента и Феодосия. Либаний рано потерял отца, воспитывался матерью и впоследствии никогда не женился, предпочтя семье труд ритора и схоларха. От служанки, сопровождавшей его всю жизнь, он имел сына Кимона и возлагал большие надежды на его карьеру, но сын рано умер. Либаний никогда не упоминал спутницу жизни в своих сочинениях, пока она была жива. В 334 г. Либаний пострадал от удара молнии, после чего всю жизнь мучился периодическими внезапными тяжелыми головными болями и обмороками. Этот эпизод, несомненно, можно было расматривать как избранничество богов, если бы не боль, которую причиняли его последствия. |
Либаний обладал прекрасной памятью и великолепным голосом; читаемые им речи были настоящим зрелищем и искусством. Вместе с тем, Либаний производит впечатление очень образованного, но не очень умного человека – он не выстраивал карьеры, а полагал, что его талант и искусство автоматически обеспечат ему успех. На этом он и ошибся в Афинах, где не смог утвердиться в ведущей школе риторики, проиграв Проэресию. Однако, потерпев это поражение, он создал мир вокруг себя таким, какой он хотел, в Антиохии. Характер Либания ярко отражен во многих письмах: немало людей, желая использовать его близость к Юлиану, обращалось к нему с просьбами о рекомендации и помощи, и он, по своему природному добродушию, охотно уступал их просьбам (таких писем особенно много в первый период его переписки). Напротив, в письмах к своим коллегам-риторам нередко отражается свойственная Либанию склонность к самовосхвалению и самоутверждению; ему часто не хватало похвал и публичного признания своего лидерства в риторике империи. Знаменитый учитель красноречия, среди учеников которого были между прочим «отцы церкви» Иоанн Златоуст, Василий Великий, Григорий Назианзин. Сохранившаяся подробная автобиография Либания, его обширная переписка и речи, а также биография его, написанная Евнапием, современником Либания, дают достаточно материала для характеристики его личности и деятельности. Родившись в Антиохии в богатой семье, Либаний получил хорошее образование; в 336 г. он отправился в Афины, чтобы закончить свое образование, выдвинулся там, и в 25 лет он уже был назначен в коллегию, ведавшую преподаванием в Афинах. Бессодержательный формализм – основная черта второй софистики, и самые талантливые ее представители давали лишь безупречные с точки зрения языка, но ничтожные по содержанию риторические упражнения. Либаний – типичный представитель новой софистики. Его изощренное красноречие, стяжавшее ему великую славу при жизни и считавшееся в течение многих веков образцовым, поражает своей пустотой, отсутствием каких бы то ни было широких общественных интересов, неумением не только разрешить, но и поставить какие бы то ни было общие философские, политические, экономические проблемы. А между тем Либаний находился в гуще политической и умственной жизни господствующего класса и общался с наиболее выдающимися людьми своего времени. |
|
1 |
2 |
3 |
4 |
|
В 383/384 г. Либаний был удостоен титула почетного префекта претория, что уравнивало его с высшей знатью империи и давало право на участие в императорском консистории. Однако, в Антиохии высшие круги муниципальной знати его недолюбливали, и ритор часто конфликтовал с ее представителями. Либаний умер на пике интенсивности своего творчества и профессиональной деятельности, устав от борьбы с врагами и болезней, во многом разочарованный жизнью и ее итогами. |
Поэтому ни речи Либания, которых дошло до нас 64, ни его обширная переписка (сохранилось 1605 его писем) не дают нам даже того исторического материала, которого можно было бы ожидать, и за исключением нескольких речей и писем произведения Либания представляют для современного историка относительно незначительный интерес. Как и все софисты того времени, Либаний цеплялся за древнюю эллинскую религию и горячо приветствовал реформу Юлиана, восстановившего на время культ древних богов. |
||
|
ЮЛИАН ОСТУПНИК |
331–363 гг. |
Юлиан Отступник, Флавий Клавдий (Flavius Claudius Julianus Apostata), римский император в 361– 363. Племянник Константина Великого, воспитывался епископом Евсевием. Большое влияние на его духовное развитие оказал страстный поклонник эллинской культуры евнух Мардоний, поэтому Юлиан Отступник уже с юных лет был тайным приверженцем языч. религии. В 355 он был возведён имп. Констанцием в цезари и назначен наместником Галлии. В 360 восставшие против Констанция галльские легионы провозгласили Юлиан Отступник императором-августом; после смерти Констанция (361) Юлиан Отступник стал единодержавным правителем Римской империи. Он расширил права муниципальных курий, уменьшил налоги, сократил дворцовый штат, отказался от роскошного, дорогостоящего двора. Став императором, Юлиан Отступник, поддержанный частью интеллигенции, открыто объявил себя сторонником языч. религии, реформировав её на базе неоплатонизма; он издал два эдикта против христиан, восстановил языч. храмы. Юлиан Отступник является автором ряда соч. (трактатов, речей, писем), направленных против христиан. Деятельность Юлиан Отступник вызывала ненависть со стороны христ. духовенства, давшего ему прозвище Отступник (Apostata). После смерти Юлиана (умер от ран в войне против персов на р. Тигр) антихристианские эдикты были отменены имп. Иовианом, прекратившим гонения на христиан. |
Юлиан оставил после себя ряд сочинений, которые позволяют ближе познакомиться с этой интересной личностью. Центром религиозного мировоззрения Юлиана является культ Солнца, создавшийся под непосредственным влиянием культа персидского светлого бога Митры и идей выродившегося к тому времени платонизма. Уже с самых юных лет Юлиан любил природу, особенно же небо. В своём рассуждении «О Царе-Солнце», главном источнике религии Юлиана, он писал, что с юных лет был охвачен страстной любовью к лучам божественного светила; он не только днем желал устремлять на него свои взоры, но и в ясные ночи он оставлял все, чтобы идти восхищаться небесными красотами; погруженный в это созерцание, он не слышал тех, кто с ним говорил, и даже терял сознание. Довольно темно изложенная Юлианом его религиозная теория сводится к существованию трёх миров в виде трех солнц. Первое солнце есть высшее Солнце, идея всего существующего, духовное, мыслимое целое; это – мир абсолютной истины, царство первичных принципов и первопричин. Видимый нами мир и видимое солнце, мир чувственный, является лишь отражением первого мира, но отражением не непосредственным. Между этими двумя мирами, мыслимым и чувственным, лежит мир мыслящий со своим солнцем. Получается, таким образом, троица (триада) солнц, мыслимого, или духовного, мыслящего и чувственного, или материального. Мыслящий мир является отражением мыслимого, или духовного мира, но сам, в свою очередь, служит образцом для мира чувственного, который является, таким образцом, отражением отражения, воспроизведением во второй ступени абсолютного образца. Высшее Солнце слишком недоступно для человека; солнце чувственного мира слишком материально для обоготворения. Поэтому Юлиан сосредоточивает все своё внимание на центральном мыслящем Солнце, его называет «Царем-Солнцем» и ему поклоняется. Юлиан оставил после себя ряд сочинений, которые позволяют ближе познакомиться с этой интересной личностью. Центром религиозного мировоззрения Юлиана является культ Солнца, создавшийся под непосредственным влиянием культа персидского светлого бога Митры и идей выродившегося к тому времени платонизма. Уже с самых юных лет Юлиан любил природу, особенно же небо. |
|
1 |
2 |
4 |
5 |
|
В своём рассуждении «О Царе-Солнце», главном источнике религии Юлиана, он писал, что с юных лет был охвачен страстной любовью к лучам божественного светила; он не только днем желал устремлять на него свои взоры, но и в ясные ночи он оставлял все, чтобы идти восхищаться небесными красотами; погруженный в это созерцание, он не слышал тех, кто с ним говорил, и даже терял сознание. Довольно темно изложенная Юлианом его религиозная теория сводится к существованию трёх миров в виде трех солнц. Первое солнце есть высшее Солнце, идея всего существующего, духовное, мыслимое целое; это – мир абсолютной истины, царство первичных принципов и первопричин. Видимый нами мир и видимое солнце, мир чувственный, является лишь отражением первого мира, но отражением не непосредственным. Между этими двумя мирами, мыслимым и чувственным, лежит мир мыслящий со своим солнцем. Получается, таким образом, троица (триада) солнц, мыслимого, или духовного, мыслящего и чувственного, или материального. Мыслящий мир является отражением мыслимого, или духовного мира, но сам, в свою очередь, служит образцом для мира чувственного, который является, таким образцом, отражением отражения, воспроизведением во второй ступени абсолютного образца. Высшее Солнце слишком недоступно для человека; солнце чувственного мира слишком материально для обоготворения. Поэтому Юлиан сосредоточивает все своё внимание на центральном мыслящем Солнце, его называет «Царем-Солнцем» и ему поклоняется. Самое значительное сочинение Юлиана – «Против христиан» – было уничтожено и известно только по полемике христианских писателей против него. Утрачены стихотворные речи, панегирики, эпиграммы, труд о военных механизмах, трактат о происхождении зла и сочинение о войне с германцами (описание собственных действий в Галлии до 357 г.). Юлиан был аттицистом, в его речах мы встречаем множество классических реминисценций (от Гомера и Гесиода до Платона и Демосфена), а также софистических (от Диона Прусского до Фемистия и Либания). Однако он пишет туманным, трудным для понимания, порой хаотичным языком. Сочинения Юлиана представляют больше ценности в качестве документа эпохи, чем как литературные произведения. |
Для софистов характерно:
• критическое отношение к окружающей действительности;
• стремление все проверить на практике, логически доказать правильность или неправильность той или иной мысли; неприятие основ старой, традиционной цивилизации;
• отрицание старых традиций, привычек, правил, основанных на недоказанном знании;
• стремление доказать условность государства и права, их несовершенство;
• восприятие норм морали не как абсолютной данности, а как предмет критики;
• субъективизм в оценках и суждениях, отрицание объективного бытия и попытки доказать то, что действительность существует только в мыслях человека.
Приложение 8
Цитаты и высказывания великих людей
«Правильно понятая ошибка – это путь к открытию». (И.П. Павлов).
«Математику уже затем надо учить, что она ум в порядок приводит» (М.В. Ломоносов).
«Математика представляет искуснейшие изобретения, способные удовлетворить любознательность, облегчить ремёсла и уменьшить труд людей». (Р. Декарт)
«Науки математические с самой глубокой древности обращали на себя особенное внимание, в настоящее время они получили еще больше интереса по влиянию своему на искусство и промышленность». (П.Л. Чебышев)
«…Нельзя быть математиком, не будучи в тоже время поэтом в душе» (С.В Ковалевская).
«Тот, кто не знает математики, не может узнать никакой другой науки и даже не может обнаружить своего невежества». (Роджер Бэкон)
«Полет – это математика» (В.П. Чкалов).
«Умственный труд на уроках математики – пробный камень мышления». (В.А. Сухомлинский)
«Задача заключается не в том, чтобы учить математике, а в том, чтобы при посредстве математике дисциплинировать ум». (В. Шрадер)
«Людям, которые желают идти верной дорогой, важно также знать и об отклонениях». (Аристотель)
«Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе». (М.И. Калинин)
Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива». (Р. Петер)
«Предмет математики настолько серьезен, что полезно не упускать случая сделать его немного занимательным» (Б. Паскаль)
«Чистая математика – это такой предмет, где мы не знаем, о чем мы говорим, и не знаем, истинно ли то, что мы говорим». (Бертран Рассел)
«Часто говорят, что цифры управляют миром; по крайней мере нет сомнения в том, что цифры показывают, как он управляется». (И. Гете)
«Математика уступает свои крепости лишь сильным и смелым». (А.П. Конфорович)
«В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками». (И. Ньютон)
«Метод решения хорош, если с самого начала мы можем предвидеть и далее подтвердить это, что, следуя этому методу, мы достигнем цели». (Г. Лейбниц)
«Решайте задачи и не бойтесь трудностей. Преодоление их вам доставит не только глубокое удовлетворение, но и большую радость, так как «в математике есть своя красота, как в поэзии и музыке» (Н.Е. Жуковский).
«Пусть не читает меня в основаниях моих тот, кто не математик» (Леонардо да Винчи)
«Приобретай в юности то, что с годами возместит тебе ущерб, причиненный старостью. И, поняв, что пищей старости является мудрость, действуй в юности так, чтобы старость не осталась без пищи» (Леонардо да Винчи).
«Спокойной скромности утверждений обыкновенно сопутствует истинно научное, а там, где хлестко и с судейскими приемами стараются зажать рот всякому противоречию, – истинной науки нет». (Д.И. Менделеев).
«Нет без явно усиленного трудолюбия ни талантов, ни гениев». (Д.И. Менделеев).
[1]Ивин А.А. Логика: Учебное пособие. 2-е изд. – М.: Знание, 1998.
[2]Сидоренко Е.А. Логика. Парадоксы. Возможные миры. (Размышления о мышлении в девяти очерках). УРСС. – М., 2002.
[3]Ивин А.А. Логика: Учебное пособие. 2-е изд. – М.: Знание, 1998.
[4]Там же..
[5]Ивин А.А. По законам логики. – Эврика, 1983.
[6]Козлова Е.Г. Сказки и подсказки задачи для математического кружка. 2-е изд., исправ. и доп. – М.: МЦНМО, 2004.
Библиографическая ссылка
Апатикова М.Г. 7 = 8 ИЛИ ТРЕНИРОВКА ДЛЯ УМА – ПАРАДОКСЫ И СОФИЗМЫ В МАТЕМАТИКЕ // Старт в науке. – 2017. – № 6-1.
;
URL: https://science-start.ru/ru/article/view?id=907 (дата обращения: 13.02.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

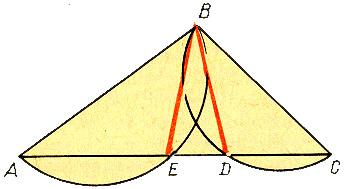





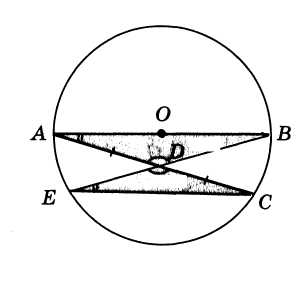
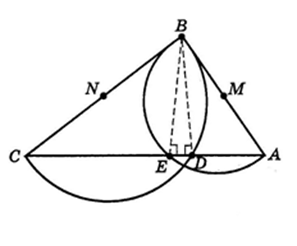

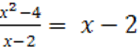
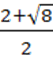
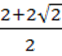
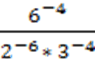
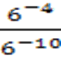
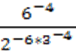
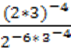
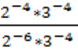
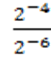
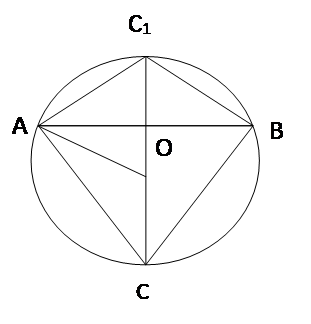
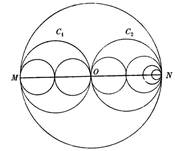
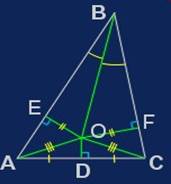





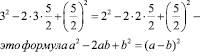
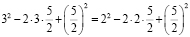
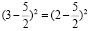
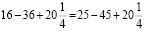
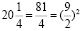
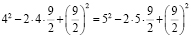
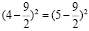
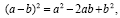
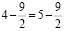
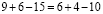
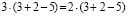
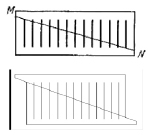
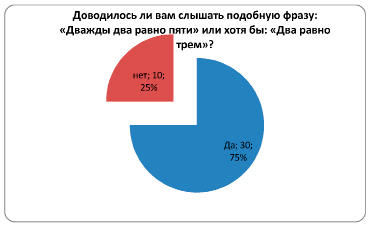
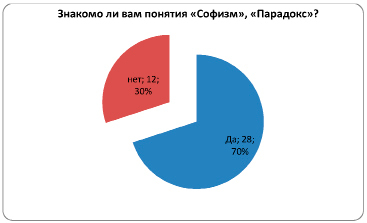
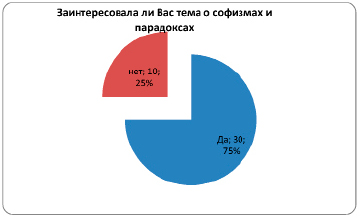
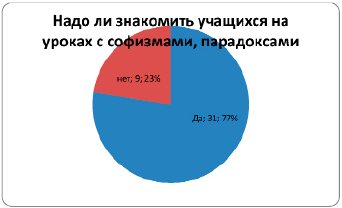
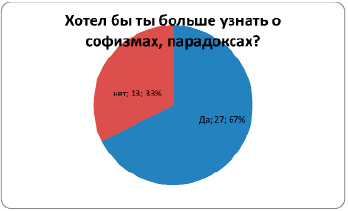
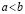
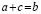
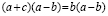
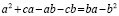
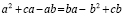
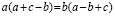
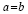
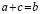
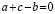
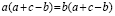
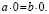
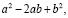
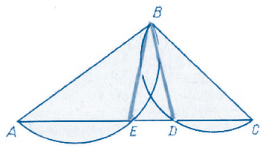
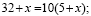
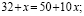
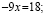
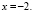
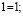
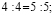
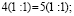
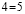
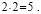
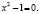 Раскладывая
Раскладывая 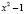 по формуле разности квадратов, получим
по формуле разности квадратов, получим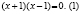
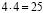
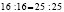 . Это очевидное равенство. Вынесем за скобки общий множитель:
. Это очевидное равенство. Вынесем за скобки общий множитель: 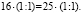
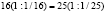
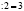
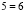
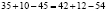 Вынесем за скобки общий множитель:
Вынесем за скобки общий множитель: 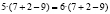 .
.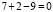 , а на 0 делить нельзя.
, а на 0 делить нельзя.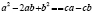 , из которого следует равенство
, из которого следует равенство 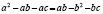 . Вынося общий множитель а, слева и общий множитель b справа за скобки, получим
. Вынося общий множитель а, слева и общий множитель b справа за скобки, получим 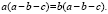 (1)
(1)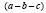 , получаем, что
, получаем, что 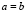 , значит, два неравных между собой произвольных числа равны.
, значит, два неравных между собой произвольных числа равны.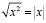
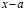 , получим
, получим